第28届印度数学奥林匹克竞赛试题及解答
第28届俄罗斯数学奥林匹克

2
九年级
9. 1 能否将自然数 1 至 2 002 填写到一个 2 002
分别 取 点 M 和 N , 使 得 2 ∠MON = ∠AOC. 证 明 : △MBN 的周长不小于边 AC 之长 . 9. 8 在区间 (22 n ,23 n ) 中任取 22 n - 1 + 1 个奇数 . 证明 : 在所取出的数中必有两个数 , 其中每一个数的 平方都不能被另一个数整除 .
9. 6 有一个红色卡片盒和 k 个 ( k > 1) 蓝色卡片 盒 ,还有一副卡片 ,共有 2 n 张 , 它们被分别编为 1 至 2 n 号 . 开始时 ,这副卡片被按任意顺序叠置在红色卡
片盒中 . 从任何一个卡片盒中都可以取出最上面的一 张卡片 ,或者把它放到空盒中 , 或者把它放到比它号 码大 1 的卡片的上方 . 对于怎样的最大的 n , 可以通
10. 6 同 9. 6. 10. 7 设 △ABC 的一个旁切圆与边 BC 相切于点
2002 年第 5 期
A′ ,过点 A′ 作 ∠A 平分线的平行直线 a , 再分别类似
2
31 2 002 ,从而对于位于该行与该列相交处的方格 ,题中
地作出直线 b 和 c . 证明 : 直线 a 、 b、 c 相交于同一点 .
第 28 届俄罗斯数学奥林匹克于 2002 年 4 月 21 日至 29 日在俄罗斯阿迪格共和国首府迈科普市举行 ,来自 俄罗斯全国各地的 199 名选手参加了比赛 . 考试分为两天 ,各个年级都是 8 道试题 ,每天 4 道题 ,5 个小时 ,每道 题满分都是 7 分 . 我国派出了东北育才学校的 6 名选手参加了此次竞赛 . 竞赛设一二三等奖 . 其中一等奖仅有 6 名选手获得 ,约占参赛人数的 3 % ,我国选手李晓东以总分第二名的优秀成绩荣列其中 ; 此外 ,还颁发了 45 个二 等奖和 57 个三等奖 ,我国选手获得 1 个二等奖和 4 个三等奖 . 以下各个年级的前 4 题为第一天的试题 ,后 4 题为第二天的试题 . 过这种操作把所有卡片移到其中一个蓝色卡片盒中 ?
2017年28届亚太杯四年级竞赛初赛试题解析

2 x 3 y 74 (1) 2 y 3x 66 (2)
(1)+(2)可得, x y ,将(3)带入(2)可得,x=10。 (74 66) 5=28 (3)
所以,双胞胎的年龄为 10 岁。
关键词:数论(质数、合数) 答案:12 解析: 10 以内的质数: 2/3/5/7, 共 4 个, x=4; 偶数: 2、 4、 6、 8、 10, 共有 5 个, y=5;完全平方数:1=12、 4=22、9=32 共有 3 个,z=3;所以,x+y+z=4+5+3=12。
6、现有一个正方形和一个长方形,长方形的周长比正方形的周长多 6 厘米,宽比正方形的边 长少 1 厘米,那么长方形的长比正方形的边长多多少厘米?
关键词:行程问题(流水行船) 答案:6 小时 解析: 逆水速度=V 静-V 水=144÷8=18 千米/小时, V 水=21-18=3 千米/小时, 所以顺水速度=V 静+V 水=21+3=24 千米/小时,则返回甲港需要时间=144÷24=6 小时。
20、有一列数,前面四个数是 2016,从第五个数开始,每个数是前面四个数的和除以 4 所得 的余数,那么这一列数中第 1203 个数是多少?
关键词:数列问题 周期问题 答案:1 解析:根据题意可写出 2016 后面的数字分别为:2016100303201210030320120 ……,发现周期为: 0030320121,共 10 个数字, (1203-5)÷10=119…8。余数为 8,则第 8 个数为 1。所以,第 1203 个数 数 1。
26、如图正方形中有两个小正方形,面积分别为 20 平方厘米和 5 平方厘米,则正方形 ABCD 的面积是多少平方厘米?
数学家吴宝珠的成长启示实实在在解决一个问题

数学家吴宝珠的成长启示:实实在在解决一个问题以慢节奏滴水穿石的研究成为第一位获得菲尔茨奖的越南人吴宝珠并没有通常人们所认为的那种天才的光芒,但他的思考很深入,是水滴石穿的类型。
吴宝珠(左二)同1989年德国第30届国际数学奥林匹克参赛生合影。
在长达十年的时间里,吴宝珠能够以他特有的慢节奏滴水穿石地做研究,而不需要考虑发表论文的问题。
他对写低质量的论文没有兴趣,而只想写几篇好论文。
令人望而生畏的猜想在日本推理小说家东野圭吾的小说《嫌疑人X的献身》中,侦查命案的物理学家问了痴迷数学的嫌疑人一个问题:“拟一个无法解答的问题,和解答那个问题,何者比较困难?”嫌疑人没有正面回答,他只是说:“的确是耐人寻味的题目。
我会好好想想。
”“这名嫌疑人是个非常聪明的人。
”美国普林斯顿高等研究院数学教授罗伯特·朗兰兹(RobertLanglands)说,“我认为这个问题没有答案。
”1967年,朗兰兹给数论专家安德雷·韦依写了封信。
在这封著名的信中,朗兰兹说:“如果您能把(我的信)当作纯粹的猜测来读,我会很感激;如果不行——我相信您的手边就有废纸篓。
”接着,朗兰兹就写下了一系列宏大的数学猜想。
这一系列猜想组成了“朗兰兹纲领”。
2010年,越南数学家吴宝珠因证明了朗兰兹纲领中的基本引理而获得国际数学界的最高奖——菲尔茨奖。
他成为了第一位获得菲尔茨奖的越南人。
加拿大多伦多大学数学教授詹姆斯·阿瑟(JamesArthur)评价吴宝珠的工作时说:“它是一个深刻又优美的论证,建立在数学家们三十多年时间里所贡献的洞见之上。
”朗兰兹纲领是一个宏伟得令人望而生畏的猜想,横跨当代数学中的数论、群论、表示论和代数几何等几大领域。
一旦得到完整的证明,这些领域中的诸多中心问题将迎刃而解。
尽管直到今天,纲领中的绝大部分猜想仍然没有得到证明,但阿瑟称基本引理的证明“将会成为该课题的一块奠基石”。
纲领的完整证明也许仍需要几代数学家的努力。
多项式学生版

w ww .q bx t.cn多项式0.1基本知识和性质多项式是代数学的一个基本概念,是中学代数的重要内容之一,也是各类数学考试以及数学竞赛内容的重要部分.本节我们先介绍一些多项式的基本概念和性质.定义1.设n 是一个非负整数,称形式表达式a n x n +a n −1x n −1+···+a 1x +a 0(1)为一元多项式.其中,a 0,a 1,···,a n 为实数(或复数).在多项式(1)中,a 0称为常数项,a i x i 称为i 次项,a i 称为i 次项系数.一元多项式常用符号f (x ),g (x ),···或者f,g,···等来表示.定义2.如果在多项式f (x )与g (x )中,同次项系数都相等,则称f (x )与g (x )相等.记为f (x )=g (x ).系数全部为0的多项式称为零多项式,记作0.在多项式(1)中,若a n =0,则称a n x n 为多项式(1)的最高次项或首项,称a n 为最高次项系数或首项系数.此时,n 称为多项式(1)的次数,零多项式是唯一不定义次数的多项式.多项式f (x )的次数记作deg(f (x ))或者∂(f (x )).给定一个数c 以及多项式f (x )=a n x n +a n −1x n −1+···+a 1x +a 0,在f (x )的表达式中用c 代替x 所得的数a n c n +a n −1c n −1+···+a 1c +a 0称作当x =c 时f (x )的值,并用f (c )来表示.这样一来f (x )就定义了一个函数,称为多项式函数.两个多项式相等当且仅当它们定义的多项式函数相等.和数的运算一样,多项式的运算满足加法交换律,加法结合律,乘法交换律,乘法结合律以及乘法对加法的分配律.性质1.f (x )g (x )的首项系数等于f (x )和g (x )的首项系数的乘积,并且∂(f (x )±g (x ))≤max(∂(f (x )),∂(g (x ))),∂(f (x )g (x ))=∂(f (x ))+∂(g (x )).性质2.若f (x )g (x )=0,则或者f (x )=0,或者g (x )=0.1w ww .q bx t.cn2性质3.若f (x )g (x )=f (x )h (x ),并且f (x )=0,则g (x )=h (x ).二.例题例1.设多项式f (x ),g (x )和h (x )的系数全部为实数.证明:若f 2(x )=xg 2(x )+xh 2(x ),(2)则f (x )=g (x )=h (x )=0.例2.设n 为自然数,证明:(1+x )(1+x 2)(1+x 4)···(1+x 2n −1)=1+x +x 2+x 3+···+x 2n −1.(3)例3.试求所有实数p ,使得三次方程5x 3−5(p +1)x 2+(71p −1)x +1=66p.(4)的三个根全部为自然数.例4.给定自然数n 以及二次多项式f (x )=ax 2+bx +c,a =0.试证:最多存在一个n 次多项式g (x ),使得f (g (x ))=g (f (x )).例5.设多项式f (x )=a 0+a 1x +a 2x 2+···+a 2n x 2n =(x +2x 2+···+nx n )2.求证:2n Pk =n +1a k =1n (n +1)(5n 2+5n +2).例6.设多项式f (x )满足条件(1)f (0)=0;(2)f (x )=12(f (x +1)+f (x −1)).求f (x )的表达式.例7.设多项式f (x )=ax 2+bx +c 的系数满足:a,b,c >0,a +b +c =1.证明:若正数x 1,x 2,···,x n 满足x 1x 2···x n =1,则f (x 1)f (x 2)···f (x n )≥1.例8.设a,b,c,d 为实数,多项式函数p (x )=ax 3+bx 2+cx +d 满足:对任何|x |<1,有|p (x )|≤1.求证:|a |+|b |+|c |+|d |≤7.例9.(第28届国际数学奥林匹克预选题)给定自然数n ,试求出所有低于n 次的多项式p (x ),使之满足如下条件:n X k =0p (k )(−1)k C kn =0.(5)三.习题习题1.将多项式f (x )=1−x +x 2−x 3+···+x 16−x 17写成g (y )=a 0+a 1y +a 2y 2+···+a 17y 17的形式,其中y =x +1,每个a i 为常数.试确定a 2的值.w ww .q bx t.cn0.2实系数和复系数多项式3习题2.解方程:x 4−x 2+8x −16=0.习题3.求所有满足f (x 2)=f 2(x )的非零多项式f (x ).习题4.试证明:多项式f (x )=1x 9−1x 7+13x 5−82x 3+32x 对所以整数x 都取整数值.习题5.分解因式:S n (x )=1−x +12!x (x −1)−13!x (x −1)(x −2)+···+(−1)nn !x (x −1)···(x −n +1).习题6.已知非常数实数列a 0,a 1,a 2,···,满足a i −1+a i +1=2a i ,i =1,2,3,···.求证:对于任意自然数n ,p n (x )=a 0C 0n (1−x )n +a 1C 1n x (1−x )n −1+a 2C 2n x 2(1−x )n −2+···+a n −1C n −1nx n −1(1−x )+a n C n n x n 是x 的一次多项式.习题7.设多项式f (x )=ax 3+bx 2+cx +d 当x =−1,x =0,x =1,x =2时取值为整数.试证明:对于任意整数n ,f (n )为整数.习题8.求满足f (x 2−2x )=f 2(x −2)的所有非零多项式f (x ).0.2实系数和复系数多项式一.基本知识和性质在以下两节我们针对复数,实数,有理数和整数的特点,分别讨论复系数,实系数,有理系数和整系数多项式的根和因式分解以及其他相关问题.定理1.(代数基本定理)设f (x )为n (n >0)次复系数多项式,则f (x )至少有一个复根.定理2.任何n (n >0)次复系数多项式恰好有n 个复根(重根按重数计算).定理3.任何n (n >0)次复系数多项式都可以分解为n 个1次复系数因式的乘积.由定理2和定理3,设x 1,x 2,···,x k 为n (n >0)次复系数多项式f (x )的所有复根,重数分别为n 1,n 2,···,n k ,则n 1+n 2+···+n k =n 并且f (x )=a (x −x 1)n 1(x −x 2)n 2···(x −x k )n k .若不讨论复系数多项式的根的相重,即将m 重根看做m 个根,则可以得到多项式的根与系数的关系.事实上,记n (n >0)次复系数多项式f (x )=a 0+a 1x +···+a n −1x n −1+a n x n的n 个根为x 1,x 2,···,x n ,则有f (x )=a n (x −x 1)(x −x 2)···(x −x n ).(6)w ww .q bx t.cn4将(6)展开再比较系数可得根与系数的关系:8>>>>>>>><>>>>>>>>:x 1+x 2+···+x n =−a n −1a n ,X 1≤i<j ≤nx i x j =a n −2a n,······,x 1x 2···x n =(−1)na 1a n.其中常用的是第一个和最后一个等式.反之,当上式成立时x 1,x 2,···,x n 为多项式f (x )=a 0+a 1x +···+a n −1x n −1+a n x n的n 个根.推论1.任何n (n >0)次实系数多项式的非实数的复根两两成对出现.推论2.每一个实系数多项式都可以分解成实系数的一次因式和二次因式的乘积.我们指出,n 次单位根在实际解题过程(尤其是分解因式,多项式的整除等)中具有特殊的作用.在前面几节的某些例题和习题中我们实际已经用到了单位根的部分性质.设1,ω,ω2,···,ωn −1为全部n 次单位根,ω=cos 2πn +i sin 2πn ,则有x n −1=(x −1)(x −ω)(x −ω2)···(x −ωn −1),从而有x n −1+x n −2+···+1=(x −ω)(x −ω2)···(x −ωn −1),这个恒等式经常用到.并且由这个恒等式可知ω,ω2,···,ωn −1为多项式p (x )=x n −1+x n −2+···+1的全部n −1个根.二.例题例1.已知关于x 的方程x 4−(3m +2)x 2+m 2=0的四个实根成等差数列,求m .例2.设n 为自然数,f (x )=x 2+x +1,g (x )=(x +1)2n +1+x n +2.试证明:f (x )|g (x ).例3.设a,b,c 为实数,且多项式f (x )=x 3+ax 2+bx +c 的三个实根成等差数列.试指出a,b,c 应满足的充分必要条件.例4.设多项式f (x ),g (x ),h (x )和p (x )满足f (x 5)+xg (x 5)+x 2h (x 5)=(x 4+x 3+x 2+x +1)p (x 5),(7)试证:(x −1)|f (x ).例5.设复系数n 次多项式f (x )=x n +c n −1x n −1+···+c 1x +c 0满足|f (i )|<1(其中i =√−1).求证:存在实数a,b 使得f (a +bi )=0,且(a 2+b 2+1)2<4b 2+1.w ww .q bx t.cn0.2实系数和复系数多项式5例6.设实系数多项式f (x )=1+a 1x +···+a n −1x n −1+x n 的各项系数非负.证明:如果f (x )有n 个不同的实根,则f (2)≥3n .例7.设f (x )=x n +a 1x n −1+···+a n −1x +a n 与g (x )=x n +b 1x n −1+···+b n −1x +b n 为两个复系数多项式,g (x )的根为f (x )的根的平方.证明:若a 1+a 3+a 5+···和a 2+a 4+a 6+···为实数,则b 1+b 2+···+b n 为实数.例8.设n 次多项式f (x )=x n +a n −1x n −1+···+a 1x +a 0的系数全部为实数,且满足条件0<a 0≤a 1≤a 2≤···≤a n −1≤1.证明:若λ为f (x )的复根,且|λ|≥1则λn +1=1.例9.给定多项式序列如下:P 1(x )=x 2−2,P k (x )=P (P k −1(x )),k =2,3,···.求证:对任意自然数n ,方程P n (x )=x 的解为互不相同的实数.例10.设f (x )和g (x )都是不低于1次的多项式.对于复数a ,f (a )=0当且仅当g (a )=0;f (a )=1当且仅当g (a )=1.求证:f (x )=g (x ).三.习题习题1.设n 为自然数,证明:如果(x −1)|f (x n ),那么(x n −1)|f (x n ).习题2.为使实系数多项式f (x )=x 3+ax 2+bx +c 有三个成等比数列的不同实根,a,b,c 应满足什么条件?习题3.试通过考虑单位根确定所有自然数对(m,n ),使得多项式f (x )=1+x n +x 2n +···+x mn 能被g (x )=1+x +x 2+···+x m 整除.习题4.设n 为自然数,求证:多项式f (x )=x n +1−x n −1有一个模为1的复根的充分必要条件是6|n +2.习题5.设多项式f (x ),g (x )满足条件(x 2+x +1)|f (x 3)+xg (x 3),求证:(x −1)|f (x ),(x −1)|g (x ).(8)习题6.给定复系数n 次多项式f (x )=c 0+c 1x +···+c n x n .求证:存在复数z 0满足|z 0|≤1,且|f (z 0)|≥|c 0|+|c n |.习题7.设l,m,n 为自然数,证明:多项式f (x )=x 3l +x 3m +1+x 3n +2能被g (x )=x 2+x +1整除.习题8.设l,m,n 为自然数,试确定多项式f (x )=x 3l −x 3m +1+x 3n +2能被g (x )=x 2−x +1整除的条件.习题9.设l,m,n 为自然数,试确定多项式f (x )=x 3l +x 3m +1+x 3n +2能被g (x )=x 4+x 2+1整除的条件.。
高中数学竞赛-历届IMO试题(1-46届)及答案

1.求证(21n+4)/(14n+3) 对每个自然数 n都是最简分数。
2.设√(x+√(2x-1))+√(x-√(2x-1))=A,试在以下3种情况下分别求出x的实数解:(a) A=√2;(b)A=1;(c)A=2。
3.a、b、c都是实数,已知 cos x的二次方程a cos2x +b cos x +c = 0,试用a,b,c作出一个关于 cos 2x的二次方程,使它的根与原来的方程一样。
当a=4,b=2,c=-1时比较 cos x和cos 2x的方程式。
4.试作一直角三角形使其斜边为已知的 c,斜边上的中线是两直角边的几何平均值。
5.在线段AB上任意选取一点M,在AB的同一侧分别以AM、MB为底作正方形AMCD、MBEF,这两个正方形的外接圆的圆心分别是P、Q,设这两个外接圆又交于M、N,(a.) 求证 AF、BC相交于N点;(b.) 求证不论点M如何选取直线MN 都通过一定点 S;(c.) 当M在A与B之间变动时,求线断 PQ的中点的轨迹。
6.两个平面P、Q交于一线p,A为p上给定一点,C为Q上给定一点,并且这两点都不在直线p上。
试作一等腰梯形ABCD(AB平行于CD),使得它有一个内切圆,并且顶点B、D分别落在平面P和Q上。
1.找出所有具有下列性质的三位数 N:N能被11整除且 N/11等于N的各位数字的平方和。
2.寻找使下式成立的实数x:4x2/(1 - √(1 + 2x))2< 2x + 93.直角三角形ABC的斜边BC的长为a,将它分成 n 等份(n为奇数),令α为从A点向中间的那一小段线段所张的锐角,从A到BC边的高长为h,求证:tan α = 4nh/(an2 - a).4.已知从A、B引出的高线长度以及从A引出的中线长,求作三角形ABC。
5.正方体ABCDA'B'C'D'(上底面ABCD,下底面A'B'C'D')。
初中数学奥林匹克竞赛题及答案

初中数学奥林匹克竞赛题及答案奥数题一一、选择题(每题1分,共10分)1.如果a,b都代表有理数,并且a+b=0,那么 ( )A.a,b都是0B.a,b之一是0C.a,b互为相反数D.a,b互为倒数答案:C解析:令a=2,b=-2,满足2+(-2)=0,由此a、b互为相反数。
2.下面的说法中正确的是 ( )A.单项式与单项式的和是单项式B.单项式与单项式的和是多项式C.多项式与多项式的和是多项式D.整式与整式的和是整式答案:D解析:x²,x3都是单项式.两个单项式x3,x²之和为x3+x²是多项式,排除A。
两个单项式x²,2x2之和为3x2是单项式,排除B。
两个多项式x3+x2与x3-x2之和为2x3是个单项式,排除C,因此选D。
3.下面说法中不正确的是 ( )A. 有最小的自然数B.没有最小的正有理数C.没有最大的负整数D.没有最大的非负数答案:C解析:最大的负整数是-1,故C错误。
4.如果a,b代表有理数,并且a+b的值大于a-b的值,那么 ( )A.a,b同号B.a,b异号C.a>0D.b>0答案:D5.大于-π并且不是自然数的整数有 ( )A.2个B.3个C.4个D.无数个答案:C解析:在数轴上容易看出:在-π右边0的左边(包括0在内)的整数只有-3,-2,-1,0共4个.选C。
6.有四种说法:甲.正数的平方不一定大于它本身;乙.正数的立方不一定大于它本身;丙.负数的平方不一定大于它本身;丁.负数的立方不一定大于它本身。
这四种说法中,不正确的说法的个数是 ( )A.0个B.1个C.2个D.3个答案:B解析:负数的平方是正数,所以一定大于它本身,故C错误。
7.a代表有理数,那么,a和-a的大小关系是 ( )A.a大于-aB.a小于-aC.a大于-a或a小于-aD.a不一定大于-a答案:D解析:令a=0,马上可以排除A、B、C,应选D。
8.在解方程的过程中,为了使得到的方程和原方程同解,可以在原方程的两边( ) A.乘以同一个数B.乘以同一个整式C.加上同一个代数式D.都加上1答案:D解析:对方程同解变形,要求方程两边同乘不等于0的数,所以排除A。
第28届中国数学奥林匹克决赛成绩

第28届中国数学奥林匹克决赛成绩揭晓,超清晰名单和感想中国数学会主办的第28届中国数学奥林匹克(CMO)2013年1月10-14日在沈阳举行,由东北育才中学承办。
来自各省、市、自治区,香港、澳门特别行政区和俄罗斯的300多名中学生参加了这次赛事。
比赛设有一至三等奖。
成绩优异的学生进入国家集训队,最后将在其中选拔6名同学组成国家队参加今年的国际数学奥林匹克。
今天下午,中国数学会在其官方网站公布了2013中国数学奥林匹克获奖名单、第54届国际数学奥林匹克中国国家集训队名单及2013中国数学奥林匹克成绩,都是PDF版本的,我把获奖名单和集训队名单转成了超清晰图片发表于本博客,也把文本文档贴上。
我是第一次想出这样的办法,用了1个多小时才想到的。
本届CMO共有317人参赛,产生了一等奖(金牌)61枚、二等奖(银牌)133枚、三等奖(铜牌)107枚,获奖人数共301人。
没有获奖的其他16人的成绩分别是6分、3分和0分,我不列出他们的名单了,但他们都能代表自己省份参加全国决赛,也是很优秀的。
北京参赛学生中,人大附中学生7人参赛,4金3银,成绩挺好,但比上海中学的6金2银还是有些差距。
人大附中另有数学竞赛高手在全国高中数学联赛意外失手,未能取得参加全国决赛资格,这种情况几乎每年都在发生。
而2012年IMO金牌得主陈景文没有参加全国决赛,则是意料之中的事。
人大附中这次4名男生、3名女生参赛,应该是中国数学奥林匹克决赛历史上一个学校女生参赛人数最多的一次,她们都获得银牌,且排名靠前,陈然和李双平以78分并列第93名,何婧铱以66分并列第124名。
北京四中时隔多年,重新有人夺得CMO金牌,值得祝贺。
往年的各级数学竞赛,主办方都不敢公布最终成绩,可能是被“素质教育大佬们”批怕了吧。
今年中国数学会带了个好头,鼓掌!祝贺这些数学竞赛获奖和参赛选手!虽然他们当中绝大部分人不会把纯数学研究作为终生职业,还是希望他们一直喜爱数学之纯,传递数学之美之美!2013中国数学奥林匹克决赛金牌榜:2013中国数学奥林匹克获奖名单一等奖名次姓名性别学校总分1张灵夫男四川绵阳中学 1262宋杰傲男上海中学 1263刘宇韬男上海中学 1264肖非依男华中师范大学一附中 1265夏剑桥男郑州外国语学校 1266陈嘉杰男华南师范大学附属中学 1267高奕博男人大附中 1268胥晓宇男人大附中 1269柳何园男上海中学 12310杨赛超男石家庄二中南校 12311孟涛男北京四中 12312刘驰洲男乐清市乐成公立寄宿学校 120 13李大为男复旦大学附属中学 12014郝晨杰男江苏省启东中学 12015马玉聪男武汉二中 12016余张逸航男华中师范大学一附中 120 17王翔男深圳中学 12018刘潇男乐清市乐成公立寄宿学校 11719宋一凡男石家庄二中 11720饶家鼎男深圳市第三高级中学 11721段柏延男人大附中 11722陈凯文男鄞州中学 11423顾超男格致中学 11424沈澈男人大附中 11425金辉男镇海中学 11126涂瀚宇男四川南充高中 10827李辰星男郑州一中 10828周韫坤男深圳中学 10829陈成男镇海中学 10530朱晶泽男华东师范大学第二附属中学 105 31邓杨肯迪男湖南师大附中 10532廖宇轩男郑州外国语学校 10533任卓涵男郑州一中 10534李爽男育才中学 10535高继杨男上海华育中学 10236李笑男湖南师大附中 10237颜公望男武汉六中 10238黄开男华中师范大学一附中 10239田方泽男中山纪念中学 10240占玮男合肥一中 10241黄迪男四川自贡蜀光中学 9942杨卓熠男成都七中 99名次姓名性别学校总分43杨承业男成都七中 9944丁允梓男上海中学 9945涂绪山男湖南师大附中 9946王柏然女衡水中学 9947张益深男清华附中 9948韩松奇男耀华中学 9649张谦男成都市实验外国语学校 96 50董方宏男复旦大学附属中学 9651杨羽轩男东北育才学校 9652刘飚男湖南师大附中 9653张文瀚男石家庄二中 9654李艺轩男耀华中学 9355陈希睿男成都七中 9356尤润琪男复旦大学附属中学 9357张耿宇男上海中学 9358刘畅男上海中学 9359姚金江男西安铁一中 9360唐彦涛男长沙市长郡中学 9361苏肇祺男厦门双十中学 93二等奖62于科屹男耀华中学 9063浦鸿铭男东北师大附中 9064孙胜扬男衡水中学 9065顾潇屹男重庆一中 9066康宇衡男重庆第八中学 9067沈剑豪男镇海中学 8768徐则驰男乐清市乐成公立寄宿学校 87 69严正奇男江苏省靖江高级中学 8770李志远男江苏省天一中学 8771樊申祺男武钢三中 8772王梓仲男华南师范大学附属中学 8773邵春霖男耀华中学 8474牟文龙男省实验中学 8475周忠鹏男江苏省新海高级中学 8476杨昊霖男吉林一中 8477谌澜天男湖南师大附中 8478汪伟男男武钢三中 8479梁桢枭男重庆一中 8480薛钟行男北师大实验中学 8481苏启舟男北京市十一学校 8482张子函男宿城一中 8483张赛特男乐清市乐成公立寄宿学校 81 84刘畅男华东师范大学第二附属中学 81 85黄若谷男湖南师大附中 8186何育泽男大庆一中 81名次姓名性别学校总分87何乐男深圳中学 8188赖泽华男泉州五中 8189黄熹之男福州一中 8190黄义鸣男重庆南开中学 8191高子珺女北京四中 8192李兴远男北师大实验中学 8193陈湛江男乐清市乐成公立寄宿学校 78 94张书茂男成都七中 7895王琦男吉大附中 7896吴晨玮男东北师大附中 7897潘圣其男黄冈中学 7898陈然女人大附中 7899李双平女人大附中 78100辛未男耀华中学 75101徐炜杰男复旦大学附属中学 75102朱逸庭男复旦大学附属中学 75103薛宋恺男复旦大学附属中学 75104张翔宇男西安铁一中 75105李昕洋男东北育才学校 75106严靖凯男南京市外国语学校 75107余道骅女武汉二中 75108于鹏飞男哈师大附中 75109陆禹男南宁二中 75110刘祝崧男北京四中 75111牛泽昊男合肥一中 75112张骏男大连育明高中 72113徐博通男辽宁省实验中学 72114周鑫男东北育才学校 72115鞠昊天男哈师大附中 72116张志鹏男石家庄二中 72117周智泽男铜陵市一中 72118薛越天男东北师大附中 69119王乾男衡水中学 69120杨策男石家庄二中南校 69121郭瀚民男华南师范大学附属中学 69 122吴秉杰男福建师大附中 69123刘春晨男重庆南开中学 69124吴铮男耀华中学 66125胡浩男江西师大附中 66126车希明男南昌大学附中 66127刘思佳女吉林一中 66128周东若男长沙市雅礼中学 66129王奕凡男长沙市雅礼中学 66130黄晃男长沙市雅礼中学 66131谢淳宇男武汉二中 66132孙霏女华中师范大学一附中 66名次姓名性别学校总分133李冠男男衡水中学 66134林植茂男广东实验中学 66135何婧铱女人大附中 66136袁晓璠女实验中学 63137戴昕悦女上海中学 63138曹洪玮男辽宁省实验中学 63139安圣美女吉大附中 63140范博宇男东北师大附中 63141郑钥方男东北师大附中 63142徐超意男武钢三中 63143陆石男深圳中学 63144陈昺弘男华南师范大学附属中学 63 145高峻男铜陵市一中 63152杨卓科男江苏省南菁高级中学 63 146李心雨女上海中学 60147王高明男平遥中学 60148齐仁睿男历城二中 60149刘子博男大连市第二十四中学 60 150周心涵男江西师大附中 60151汪昱东男南昌大学附中 60153郑迪文男东北师大附中 60154陈景林男福州一中 60155赵田杰男江苏省兴化中学 57156郝天泽男吉大附中 57157李忠羿男武汉二中 57158马成男北师大实验中学 57159古瀚林男铜陵市一中 57160郑亦如女乐清市乐成公立寄宿学校 54 161陈高翔男温州中学 54162刘倬瑞男西工大附中 54163张开来男长沙市长郡中学 54164商亮男哈师大附中 54165张宏博男郑州一中 54166贾浩男石家庄二中 54167王琰女海南中学 54168蓝启骏男皇仁书院 51169李健辉男中华传道会安柱中学 51170许百楠男喇沙书院 51171童晗爽男乐清市乐成公立寄宿学校 51 172李林骏男四川绵阳中学 51173袁正男西安高新第一中学 51174李越女山西大学附中 51175乐慧女南昌大学附中 51176王俞涵男吉大附中 51177李崇文男邯郸一中 51178陈天聪男华南师范大学附属中学 51名次姓名性别学校总分179计宇亮男芜湖一中 51180文肇亨男中华基督教会铭贤书院 48 181张悦眉女复旦大学附属中学 48182程鹏宇男西安铁一中 48183杨博文男江西师大附中 48184薛廉广男吉大附中 48185谢天男东北师大附中 48186唐铭亮男长沙市长郡中学 48187冯标健男海南中学 48188李娇阳女甘肃省兰州第一中学 48 189李君诚男龙岩一中 48190杨依灵女重庆一中 48191刘芷宁男重庆第八中学 48192彭泽昀男北京景山学校 48193孙元男合肥一中 48194李渊男西北师范大学附中 48三等奖195王浩旭男南开中学 45196欧宇哲男成都外国语学校 45 197赵欣怡女成都七中 45198刘季青男四川绵阳中学 45199刘新阳男太原五中 45200白志豪男临沂第一中学 45201汤小涛男鹰潭一中 45202汪裕洲男景德镇二中 45203周围男南京市外国语学校 45 204邱天蓝男长沙市一中 45205欧阳王剑男长沙市雅礼中学 45 206赵昱男哈师大附中 45207李菁华男哈师大附中 45208张雨潇男邯郸一中 45209谷健男马鞍山二中 45210张力男鄂尔多斯一中 42211房桢女大连市第二十四中学 42 212钱鑫男华中师范大学一附中 42 213陈景发男泉州七中 42214陈洁锋男南安一中 42215秦翊宸男重庆第八中学 42216杨宇琛男北师大实验中学 42217牟卓群男台州中学 39218姜伊昇男复旦大学附属中学 39219王雨桐男西安铁一中 39220杨航远男南昌二中 39221陈章鑫男江西省抚州市临川一中 39 222周开宇男海南中学 39名次姓名性别学校总分223任訸男贵阳市第一中学 39224韦中炜男南宁二中 39225王凡非男北京四中 39226薛雅菲女北大附中 39227牛启鑫男西工大附中 36228龚昊男省实验中学 36229张伟楠男东营胜利一中 36230孙占睿男内蒙古师大附中 36231赵国豪男东北育才学校 36232仝睿男徐州市第一中学 36233伍培全男濠江中学 33234蔡期男诸暨中学 33235欧阳惠雨男实验中学 33236高炜男陕西师大附中 33237都汐滢女西工大附中 33238马蓉女山西大学附中 33239潘豪男深圳中学 33240何兰青男安庆一中 33241王诗雅女拔萃女书院 30242萧浩梁男教业中学 30243姜越鑫男曲靖一中 30244孟庆轩男新疆生产建设兵团第二中学 30 245潘长在男耀华中学 30246杨帅泓男成都七中 30247房炜杰男寿光现代中学 30248王书泽男包头九中 30249傅瑞得男南京师范大学附属中学 30250王子路男哈尔滨第三中学 30251赵浩然男贵阳市第一中学 30252姚华东男贵阳市第一中学 30253张桢佩男西北师范大学附中 30254高晖胜男重庆第八中学 30255王季康男合肥八中 30256区智杰男培正中学 27257周昊天男培正中学 27258陈诚男杭州二中 27259薛嘉炜男乐清市乐成公立寄宿学校 27 260王宇晨男西工大附中 27261赵艺轩男西工大附中 27262崔震男甘肃省兰州第一中学 27263王何叶女云南师大附中 24264杨亦君女华东师范大学第二附属中学 24 265冯俊博男东北育才学校 24266王南男吉大附中 24267赵浩天男郑州一中 24268吴侃男柳州高级中学 24名次姓名性别学校总分269马明智男重庆巴蜀中学 24270李佳颖女复旦大学附属中学 21271刘浩男宁夏平罗中学 21272张浩林男大连市第二十四中学 21273秦臻男郑州一中 21274陈朗天男拔萃男书院 18275陈彦匡男圣保罗男女中学 18276刘冰露女新疆乌鲁木齐市第一中学 18277赵洛晨男新疆乌鲁木齐八一中学 18 278陈冠溥男山西大学附中 18279林治荐男吉大附中 18280孙焱男郑州一中 18281方伟权男镜平学校(中学部) 15 282林歆喆男青岛二中 15283高乾男呼市三中 15284刘洛甫男重庆南开中学 15285杨润男四川遂宁射洪中学 12286张翔男西工大附中 12287李步选男长治二中 12288江相华男鹰潭一中 12289何润生男湖南师大附中 12290朱旭男湖南师大附中海口中学 12 291肖翰珅男重庆南开中学 12292曹喜萌男新疆乌鲁木齐市第一中学 9 293赵浩男民院附中 9294赵正泽男西工大附中 9295李正浩男西安交大附中 9296温凯男莘县实验高中 9297杨真男青海油田一中 9298陈诺男宁夏银川二中 9299林祖迪男贵阳市第一中学 9300任志杰男甘肃省兰州第一中学 9301余春雨男重庆南开中学 9第54届国际数学奥林匹克中国国家集训队名单姓名性别学校张灵夫男四川绵阳中学宋杰傲男上海中学刘宇韬男上海中学肖非依男华中师范大学一附中夏剑桥男郑州外国语学校陈嘉杰男华南师范大学附属中学高奕博男人大附中胥晓宇男人大附中柳何园男上海中学杨赛超男石家庄二中南校孟涛男北京四中刘驰洲男乐清市乐成公立寄宿学校李大为男复旦大学附属中学郝晨杰男江苏省启东中学马玉聪男武汉二中余张逸航男华中师范大学一附中王翔男深圳中学刘潇男乐清市乐成公立寄宿学校宋一凡男石家庄二中饶家鼎男深圳市第三高级中学段柏延男人大附中陈凯文男鄞州中学顾超男格致中学沈澈男人大附中金辉男镇海中学涂瀚宇男四川南充高中李辰星男郑州一中周韫坤男深圳中学陈成男镇海中学朱晶泽男华东师范大学第二附属中学邓杨肯迪男湖南师大附中廖宇轩男郑州外国语学校任卓涵男郑州一中李爽男育才中学高继杨男上海华育中学李笑男湖南师大附中颜公望男武汉六中黄开男华中师范大学一附中田方泽男中山纪念中学占玮男合肥一中黄迪男四川自贡蜀光中学杨卓熠男成都七中杨承业男成都七中丁允梓男上海中学涂绪山男湖南师大附中王柏然女衡水中学张益深男清华附中韩松奇男耀华中学张谦男成都市实验外国语学校董方宏男复旦大学附属中学杨羽轩男东北育才学校刘飚男湖南师大附中张文瀚男石家庄二中李艺轩男耀华中学陈希睿男成都七中尤润琪男复旦大学附属中学张耿宇男上海中学刘畅男上海中学姚金江男西安铁一中唐彦涛男长沙市长郡中学苏肇祺男厦门双十中学于科屹男耀华中学浦鸿铭男东北师大附中康宇衡男重庆第八中学。
初二数学奥林匹克竞赛题及答案

初二数学奥林匹克竞赛题及答案1、如图,梯形ABCD 中,AD ∥BC ,DE =EC ,EF ∥AB 交BC 于点F ,EF =EC ,连结DF 。
(1)试说明梯形ABCD 是等腰梯形;(2)若AD =1,BC =3,DC DCF 的形状;(3)在条件(2)下,射线BC 上是否存在一点P ,使△PCD 是等腰三角形,若存在,请直接写出PB 的长;若不存在,请说明理由.2、在边长为6的菱形ABCD 中,动点M 从点A 出发,沿A →B →C 向终点C 运动,连接DM 交AC 于点N 。
(1)如图25-1,当点M 在AB 边上时,连接BN .①求证:△ABN ≌△ADN ; ②若∠ABC = 60°,AM = 4,求点M 到AD 的距离; (2)如图25-2,若∠ABC = 90°,记点M 运动所经过的路程为x (6≤x ≤12)试问:x 为何值时,△ADN 为等腰三角形.3、对于点O 、M ,点M 沿MO 的方向运动到O 左转弯继续运动到N ,使OM =ON ,且OM ⊥ON ,这一过程称为M 点关于O 点完成一次“左转弯运动".正方形ABCD 和点P ,P 点关于A 左转弯运动到P 1,P 1关于B 左转弯运动到P 2,P 2关于C 左转弯运动到P 3,P 3关于D 左转弯运动到P 4,P 4关于A 左转弯运动到P 5,……. (1)请你在图中用直尺和圆规在图中确定点P 1的位置;(2)连接P 1A 、P 1B ,判断 △ABP 1与△ADP 之间有怎样的关系?并说明理由。
(3)以D 为原点、直线AD 为y 轴建立直角坐标系,并且已知点B 在第二象限,A 、P 两点的坐标为(0,4)、(1,1),请你推断:P 4、P 2009、P 2010三点的坐标.BA4、如图1和2,在20×20的等距网格(每格的宽和高均是1个单位长)中,Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速度先向下平移,当BC边与网的底部重合时,继续同样的速度向右平移,当点C与点P重合时,Rt△ABC停止移动.设运动时间为x秒,△QAC的面积为y.(1)如图1,当Rt△ABC向下平移到Rt△A1B1C1的位置时,请你在网格中画出Rt △A1B1C1关于直线QN成轴对称的图形;(2)如图2,在Rt△ABC向下平移的过程中,请你求出y与x的函数关系式,并说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?(3)在Rt△ABC向右平移的过程中,请你说明当x取何值时,y取得最大值和最小值?最大值和最值分别是多少?为什么?5、如图①,△ABC中,AB=AC,∠B、∠C的平分线交于O点,过O点作EF∥BC 交AB、AC于E、F.(1)图中有几个等腰三角形?猜想: EF与BE、CF之间有怎样的关系,并说明理由.(2)如图②,若AB≠AC,其他条件不变,图中还有等腰三角形吗?如果有,分别指出它们.在第(1)问中EF与BE、CF间的关系还存在吗?(3)如图③,若△ABC中∠B的平分线BO与三角形外角平分线CO交于O,过O点作OE∥BC交AB于E,交AC于F.这时图中还有等腰三角形吗?EF与BE、CF关系又如何?说明你的理由。
国际数学奥林匹克(IMO)竞赛试题(第28届)

1.设pn(k)是集合{1,2,3,...,n}上具有k个固定点的排列的个数,求证k从0到n对(k pn(k) )的求和是n!.
[一个集合S的一个排列是从S到它自身的一一映射.元素i称为是f形ABC的内角A的角平分线交BC于L,交ABC的外接圆于N,从L点向AB,AC做垂线,垂足分别是K、M,求证四边形AKNM的面积与三角形ABC的面积相等.
5.n是大于或等于3的整数,求证存在一个由平面上n个点构成的集合满足任何两点的距离都是无理数并且任何三点构成一个面积为有理数的非退化的三角形.
6.n是大于或等于2的整数,如果对所有0≤k≤√n/3都有k2+ k + n是素数,则
当0≤k≤n-2时,k2+ k + n都是素数.
3.x1,x2,...,xn是实数并且满足x12+ x22+ ... + xn2= 1,求证对每个正整数k≥2存在不全为0的整数a1,a2,...,an,使得对每个i有|ai|≤k - 1及
|a1x1+ a2x2+ ... + anxn|≤(k - 1)√n/(kn-1).
4.求证不存在从非负整数到非负整数的函数f满足对所有n有f(f(n)) = n + 1987成立.
八年级数学竞赛培优专题及答案 28 整体与完形
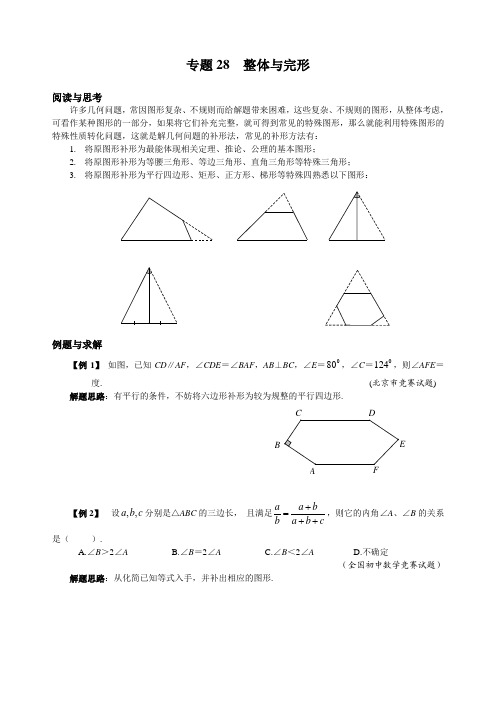
专题28 整体与完形阅读与思考许多几何问题,常因图形复杂、不规则而给解题带来困难,这些复杂、不规则的图形,从整体考虑,可看作某种图形的一部分,如果将它们补充完整,就可得到常见的特殊图形,那么就能利用特殊图形的特殊性质转化问题,这就是解几何问题的补形法,常见的补形方法有:1.将原图形补形为最能体现相关定理、推论、公理的基本图形;2.将原图形补形为等腰三角形、等边三角形、直角三角形等特殊三角形;3.将原图形补形为平行四边形、矩形、正方形、梯形等特殊四熟悉以下图形:例题与求解【例1】如图,已知CD∥AF,∠CDE=∠BAF,AB⊥BC,∠E=080,∠C=0124,则∠AFE=_________度. (北京市竞赛试题) 解题思路:有平行的条件,不妨将六边形补形为较为规整的平行四边形.B【例2】设,,a b c分别是△ABC的三边长,且满足a a bb a b c+=++,则它的内角∠A、∠B的关系是().A.∠B>2∠AB.∠B=2∠AC.∠B<2∠AD.不确定(全国初中数学竞赛试题)解题思路:从化简已知等式入手,并补出相应的图形.【例3】 如图1,BD ,CE 分别是△ABC 的外角平分线,过点A 作AF ⊥BD ,AG ⊥CE ,垂足分别为F ,G ,连结FG ,延长AF ,AG ,与直线BC 相交,易证()12FG AB BC AC =++. 若(1)BD ,CE 分别是△ABC 的内角平分线(如图2);(2)BD 为∠ABC 的内角平分线;(3)CE 为△ABC 的外角平分线(如图3),则在图2、图3两种情况下,线段FG 与△ABC 三边又有怎样的数量关系?请写出你的猜想,并对其中的一种情况给予证明.(黑龙江省中考试题)解题思路:既有平分线又有垂线,联想到等腰三角形性质,考虑将图形补成等腰三角形.图3图2图1【例4】 如图,四边形ABCD 中,∠ABC =0135,∠BCD =0120,AB ,BC =5 CD =6,求AD 的长.(全国初中数学竞赛试题)解题思路:由于四边形ABCD 是一般四边形,所以直接求AD 比较困难,应设法将AD 转化为特殊三角形的边.A23A 54例4题图 例5题图 【例5】 如图,凸八边形1238...A A A A 中,∠1A =∠5A ,∠2A =∠6A ,∠3A =∠7A ,∠4A =∠8A ,试证明:该凸八边形内任意一点到8条边的距离之和是一个定值.(山东省竞赛试题)解题思路:本例是一个几何定值证明问题,关键是将八边形问题转化为三角形或四边形问题来解决,若连结对角线,则会破坏一些已知条件,应当考虑向外补形.【例6】 如图,在△ABC 中,∠ABC =045,点D 在边BC 上,∠ADC =060,且12BD CD =.将△ACD 以直线AD 为轴作轴对称变换,得到△AC D ',连结BC '. (1) 证明:BC '⊥BC ; (2) 求∠C 的大小.(全国初中数学竞赛天津赛区初赛试题)解题思路:本题分别考查了等边三角形的性质与判定、全等三角形的性质与判定及轴对称的性质,解题的关键是利用角平分线的性质与判定构造全等三角形,然后利用全等三角形的性质即可解决问题.D能力训练1.如图,在四边形ABCD 中,∠A =∠C =090,AB =AD ,若这个四边形的面积为12,则BC +CD =_____________. (山东省竞赛试题) 2. 如图,凸五边形ABCDE 中,∠A =∠B =0120,EA =AB =BC =2,CD =DE =4,则这个五边形的面积为_______________.(美国AHSME 试题)3. 如图,一个凸六边形六个内角都是0120,其中连续四条边的长依次为1,9,9,5,则该六边形的周长为______________.第1题图第2题图第3题图B4. 如图,ABCDEF 是正六边形,M ,N 分别是边CD ,DE 的中点,线段AM 与BN 相交于P ,则BPPN=_________. (浙江省竞赛试题)5. 如图,长为2的三条线段,,AA BB CC '''交于O 点,并且∠B OA '=∠C OB '=∠A OC '=060,则三个三角形的面积和123S S S ++,“=”,或“>”).(“希望杯”邀请赛试题)6. 如图,在四边形ABCD 中,∠A =060,∠B =∠D =090,BC =2,CD =3,则AB = ( ). A. 4 B. 5C.D.(广西壮族自治区中考试题)第6题图第5题图第4题图DB7. 如图,在△ABC 中,M 为BC 中点,AN 平分∠A ,AN ⊥BN 于N ,且AB =10,AC =16,则MN 等于( ).A. 2B. 2.5C. 3D. 3.58. 如图,在四边形ABCD 中,AB =BC ,∠ABC =∠CDA =090,BE ⊥AD 于E ,8ABCD S =四边形,则BE 的长为( )A. 2B. 3C.D.第7题图第8题图第9题图AA9. 如图,在四边形ABCD 中,AB =4-BC =1,CD =3,∠B =0135,∠C =090,则∠D 等于( )A. 060 B. 067.5 C. 075 D.条件不够,无法求出(重庆市竞赛试题)10. 如图,在△ABC 中,E 是AC 中点,D 是BC 边上一点,若BC =1,∠ABC =060,∠BAC =0100,∠CED =080,求2ABC CDE S S ∆∆+的值.CB11. 如图,设c 是Rt ABC ∆的斜边长,,a b是直角边,求证:a b +≤.(加拿大中学生竞赛试题)a CA12. 如图,已知八边形ABCDEFGH 所有的内角都相等,而且边长都是整数.求证:这个八边形的对边相等.FB C13. 如图,设P 为△ABC 的中位线DE 上的一点,BP 交AC 于N ,CP 交AB 于M ,求证:1AN AMNC MB+=. (齐齐哈尔市竞赛试题)B14. 一个圆内接八边形相邻的四条边长是1,另四条边长是2,求八边形的面积.专题28 整体与完形——补形法例1 134 例2 B 提示:由已知得b a ca b+=例 3 (1)()12FG AB AC BC =+-,分别延长AG 、AF 交BC 于H ,K ,则AF=KF ,AB=KB,AG=HG,AC=HC.()()111222FG HK BK BH AB AC BC ==-=+-.(2)()12FG BC AC AB =+-例4 提示:作DG ⊥BC 交BC 延长线于Q ,AM ⊥CB 交CB 延长线于M ,DN ⊥MA 于N ,则MNDQ 为矩形,19AD =例5 延长A 8A 1,A 3A 2相交于M ,延长A 2A 3,A 5A 4相交于N ,延长A 4A 5、A 7A 6相交于P ,延长A 6A 7、A 1A 8相交于Q.∵∠A 1=∠A 5, ∠A 2=∠A 6,∴∠MA 1A 2=∠PA 5A 6, ∠MA 2A 1=∠PA 6A 5, ∴∠M=∠P ,同理可证:∠N=∠Q 。
2019年印度高中数学国家奥林匹克竞赛试题

2019印度国家奥林匹克
1.△ABC中,∠BAC>90°.线段BC上一点D满足AB与△ACD外接圆相切于点A,线段AD上一点E满足BE⊥AD.已知CA=CD,AE=CE,求∠BCA.
2.设A1B1C1D1E1为正五边形.对2≤n≤11,设A n B n C n D n E n的五个顶点为五边形A n-1B n-1C n-1D n-1E n-1的五条边的五个中点.所有这11个五边形的5个顶点都被任意地染成红色或者蓝色.求证:这55个点中一点存在4个共圆的同色点.
3.设m,n为互异的正实数.证明
gcd(m,n)+gcd(m+1,n+1)+gcd(m+2,n+2)≤2|m-n|+1.
并求出取等号的条件.
4.设正实数M,n满足M>n n-1.证明:存在n个互异的实数p1,p2,...,p n使得p j|M+j对所有的1≤j≤n 成立.
5.设AB为圆Γ的直径,设C为Γ上异于A或B的一个点.过C作CD⊥AB于D.线段CD上一点K 满足AC等于△ADK的半周长.
证明:△ADK中,A所对的旁接圆与Γ相切.
6.对实数(x,y):x,y∈R,xy≠0,f(x,y)定义为满足以下条件的正实数的集合:
(i)对所有x,y≠0,f(xy,z)=f(x,z)∙f(y,z)
(ii)对所有x,y≠0,f(x,yz)=f(x,y)∙f(x,z)
(iii)对所有x≠0,1,f(x,1-x)=1
求证:
(1)对所有x≠0,f(x,x)=f(x,-x)=1
(2)对所有x,y≠0,f(x,y)∙f(y,x)=1。
印度数学竞赛题目及答题

印度数学竞赛题目及答题
印度数学竞赛是世界著名的数学比赛之一,其题目难度极高,涉及多个数学领域,包括代数、几何、数论等。
以下是一道典型的印度数学竞赛题目及其解答:
题目:有一个圆,其周长为 20。
假设从圆心出发,画出一个四边形 ABCD,使得其四个角均为直角,且 AB = 6,BC = 8。
求此四边形的面积。
解答:由于圆的周长等于 2πr,其中 r 为圆的半径,因此可得r = 10/π。
由于 ABCD 为一个矩形,且直角位于 B 和 C 处,因此 BD = AC = r√2。
于是可以得到 BD = AC = 10√2/π。
另一方面,根据勾股定理可得 AD + BD = AB,即 AD + (10√2/π) = 6。
解方程可得 AD = 2√10/π。
因此,矩形 ABCD 的面积为 AB × AD = 12√10/π。
约等于1.206。
- 1 -。
印度数学竞赛题

印度数学竞赛题
以下是一道印度数学竞赛题的示例:
题目:证明对于所有正整数n,存在一个正整数x,使得x(x + 1)能够被n整除。
解答:我们首先观察到,如果n是一个质数,那么取x=n-1即可满足题目要求,因为此时n和n-1互质,所以x(x+1)能够被n整除。
接下来考虑n为一个合数的情况。
我们知道,如果一个数a能够整除一个数b,那么a也能够整除b的倍数。
所以,我们可以递推地构造满足题目要求的x和n的关系。
设n的质因数分解为p1^a1 * p2^a2 * ... * pk^ak。
我们可以取x = (p1-1)(p2-1)...(pk-1) * b,其中b为任意正整数。
这样,由于每个pk-1与pk互质,所以x(x+1)能够被pk整除。
而对于除pk之外的质因数pi,其必然被pi-1整除,所以也能够整除x(x+1)。
因此,这样构造的x满足题目要求。
综上所述,无论n是质数还是合数,都存在一个正整数x,使得x(x + 1)能够被n整除。
跃峰奥数W代数组合之一道印度数学奥林匹克中的染色问题

代数组合之一道印度数学奥林匹克中的染色问题冯跃峰【题目】给定正整数n 、p ,其中3<p≤2n ,将正n 边形的p 个顶点染红色,其余顶点染蓝色,证明:存在2个全等的至少有[2p ]+1个顶点的多边形,其中一个的顶点全为红色,另一个的顶点全为蓝色。
(1998年印度数学奥林匹克试题)【题感】题目条件非常简洁(正n 边形的p 个顶点染红色),看不出对解题的任何启示,宜从目标入手。
【逐步逼近】从目标看,找一个红色与蓝色“大”多边形(顶点不少于r=[2p ]+1,称为子图形)全等,可退一步,先找一个红色子图形,进而找全等的蓝色子图形。
找红色子图形就是一个很简单的问题了,题给了p 个红点,红色子图形有s=C p r +C p r+1+…+C p p 个,从中任取一个即可。
【整体思考】现在的问题是,如何适当地选取其中一个红色子图形,它能与一个蓝色子图形全等。
这自然想到整体思考,考察所有s 个红色子图形,每个都找与自己全等的子图形(发动群众),然后证明必有一个找到的为蓝色。
【充分条件】现在需要考虑的是,每个子图形如何去寻找与自己全等的子图形形呢?注意其顶点都是“正n 边形的顶点”,一个充分条件是将所有红色子图形的顶点在圆周上旋转找全等子图形(除此之外,对称法也能找全等子图形)。
显然,每个红色子图形的顶点在圆周上旋转找全等,等价于将整个红色p 边形的顶点在圆周上旋转找全等。
实际上,记图中红色顶点构成的p 边形为W 1,假定W 1旋转到W i (2≤i≤n ),则W i 的每个子多边形与与W 1对应的子多边形全等。
于是,我们只需在W i 中找到一个蓝色的子图形即可。
【整体估计】因为有n-p 个蓝点,且旋转中每个蓝点共出现在p 个W i 中(对任一蓝点A ,它与p 边形W 的各顶点重合一次,从而出现在p 个W i 中),n-p 个蓝点共旋转得(n-p )p 个蓝点。
将其归入n-1个位置(最初位置无蓝点),由平均数抽屉原理,必有一个位7置蓝点数不少于1p --n p n )(12n --≥n p n )(12n -⋅=n p 21n p n ⋅-=.2p >于是,必有一个位置W i 存在蓝色子图形,它与W 1中对应的红色子图形全等,命题获证。
2020年印度国家数学奥林匹克选拔赛(无答案)

2020印度国家奥林匹克选拔赛第一天1.已知,圆T1,T2圆心分别为O1,O2,两圆相交于点A,B。
已知两个圆心均在另一个圆外.过B作T1切线与圆T2再次相交于点C。
过B作T2切线与圆T1再次相交于点D。
∠DAB平分线与圆T1再次相交于X。
∠CAB平分线与圆T2,再次相交于Y。
若P,Q分别为△ACD,△AYX 外心。
求证:PQ⊥O1O2。
2.实系数多项式P(x)满足P(cosθ+sinθ)=P( cosθ-sinθ)任意实数θ成立。
证明P(x)可以表示为P(x)=a0+a1(1-x2)+a2(1-x2)2+…+a n(1-x2)n的形式。
其中a0,a1…a n 为实数,n为非负整数。
3设S为集合{0,1,2,…,9}的子集。
若存在正整数N,使得对任意整数n>N,总能找到正实数a,b,满足a+b=n,且a,b在十进制表示下的所有数字(不包括开头的0)都属于集合S.求S的最小值。
第二天4.整数n≥2.实数1≤a1≤a2≤……≤a n,满足a1+a2+……+a n=2n。
求证:a1a2……a n-1+a1a2……a n-2+……+a1a2+a1+2≤a1a2……a n。
5.平面上有无数条互相平行且等距的直线。
若可以作一个正n边形,使得它的所有顶点都在这些直线上,且任意一条直线上的顶点都不超过1个,就称n是“可转换的”。
(1)证明:3、4、6是“可转换的”。
(2)证明:n≥7时,n不可“可转换的”。
(3)判定边数为5时,是否“可转换的”,说明理由。
6.我们将3×1的矩形称为”长牌”现在有一个5×5的正方形,由25个1×1的小正方形组成。
请证明:无法用16张长牌将其盖住,使得每个小正方形都被1个或2个长牌覆盖。
