(完整word版)高中数学符号意义

(完整word版)高数符号大全

高等数学常用符号大全及符号的含义acsc xy，余割函数反函数在x处的值，即 x = csc y θ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a•ba、b向量的点积(a•b)a、b向量的点积|v|向量v的模|x|数x的绝对值表示求和，通常是某项指数。

下边界值写在其下部，上边界值写在Σ其上部。

如j从1到100 的和可以表示成：。

这表示 1+ 2 + … + nM表示一个矩阵或数列或其它|v>列向量，即元素被写成列或可被看成k×1阶矩阵的向量<v|被写成行或可被看成从1×k阶矩阵的向量dx变量x的一个无穷小变化，dy, dz, dr等类似ds长度的微小变化ρ变量 (x2+ y2+ z2)1/2或球面坐标系中到原点的距离r 变量 (x2+ y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式，其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值，为一个面积、体积或超体积d2f/dx2f关于x的二阶导数f(2)(x)同样也是f关于x的二阶导数f(k)(x)f关于x的第k阶导数，f(k-1)(x)的导数T 曲线切线方向上的单位向量，如果曲线可以描述成 r(t), 则T =(dr/dt)/|dr/dt|ds沿曲线方向距离的导数κ曲线的曲率，单位切线向量相对曲线距离的导数的值：|dT/ds|NdT/ds投影方向单位向量，垂直于TB平面T和N的单位法向量，即曲率的平面τ曲线的扭率： |dB/ds|g重力常数F力学中力的标准符号k弹簧的弹簧常数pi第i个物体的动量H物理系统的哈密尔敦函数，即位置和动量表示的能量{Q, H}Q, H的泊松括号以一个关于x的函数的形式表达的f(x)的积分函数f 从a到b的定积分。

(完整word版)高中数学公式及知识点总结大全(精华版)

高中文科数学公式及知识点速记一、函数、导数1、函数的单调性(1)设2121],,[x x b a x x <∈、那么],[)(0)()(21b a x f x f x f 在⇔<-上是增函数； ],[)(0)()(21b a x f x f x f 在⇔>-上是减函数.(2)设函数)(x f y =在某个区间内可导，若0)(>'x f ，则)(x f 为增函数；若0)(<'x f ，则)(x f 为减函数.2、函数的奇偶性对于定义域内任意的x ，都有)()(x f x f =-，则)(x f 是偶函数；对于定义域内任意的x ，都有)()(x f x f -=-，则)(x f 是奇函数。

奇函数的图象关于原点对称，偶函数的图象关于y 轴对称。

3、函数)(x f y =在点0x 处的导数的几何意义函数)(x f y =在点0x 处的导数是曲线)(x f y =在))(,(00x f x P 处的切线的斜率)(0x f '，相应的切线方程是))((000x x x f y y -'=-.*二次函数：（1）顶点坐标为24(,)24b ac b a a --；（2）焦点的坐标为241(,)24b ac b a a-+- 4、几种常见函数的导数①'C 0=；②1')(-=n n nxx ； ③x x cos )(sin '=；④x x sin )(cos '-=；⑤a a a xx ln )('=；⑥xx e e =')(； ⑦a x x a ln 1)(log '=；⑧xx 1)(ln '= 5、导数的运算法则（1）'''()u v u v ±=±. （2）'''()uv u v uv =+. （3）'''2()(0)u u v uv v v v -=≠. 6、会用导数求单调区间、极值、最值7、求函数()y f x =的极值的方法是：解方程()0f x '=．当()00f x '=时： (1) 如果在0x 附近的左侧()0f x '>，右侧()0f x '<，那么()0f x 是极大值； (2) 如果在0x 附近的左侧()0f x '<，右侧()0f x '>，那么()0f x 是极小值．指数函数、对数函数分数指数幂(1)m na =0,,a m n N *>∈，且1n >）.(2)1m nm naa-==（0,,a m n N *>∈，且1n >）.根式的性质（1）当na =；当n,0||,0a a a a a ≥⎧==⎨-<⎩.有理指数幂的运算性质(1) r sa a⋅=(2) ()r s rsa a=(3)()r rab a b=注：若a＞0，指数幂都适用..(0,1,0)a a N>≠>..1a≠,0m>,且1m≠,0N>).对数恒等式：).推论logmnab).常见的函数图象822sin cosθθ+9απ±kα看成锐角时该函数的符号；αππ±+2kα看成锐角时该函数的符号。

(完整word版)高中数学公式及知识点总结大全(精华版)

高中文科数学公式及知识点速记一、函数、导数1、函数的单调性(1)设2121],,[x x b a x x <∈、那么],[)(0)()(21b a x f x f x f 在⇔<-上是增函数； ],[)(0)()(21b a x f x f x f 在⇔>-上是减函数.(2)设函数)(x f y =在某个区间内可导，若0)(>'x f ，则)(x f 为增函数；若0)(<'x f ，则)(x f 为减函数.2、函数的奇偶性对于定义域内任意的x ，都有)()(x f x f =-，则)(x f 是偶函数；对于定义域内任意的x ，都有)()(x f x f -=-，则)(x f 是奇函数。

奇函数的图象关于原点对称，偶函数的图象关于y 轴对称。

3、函数)(x f y =在点0x 处的导数的几何意义函数)(x f y =在点0x 处的导数是曲线)(x f y =在))(,(00x f x P 处的切线的斜率)(0x f '，相应的切线方程是))((000x x x f y y -'=-.*二次函数：（1）顶点坐标为24(,)24b ac b a a --；（2）焦点的坐标为241(,)24b ac b a a-+- 4、几种常见函数的导数①'C 0=；②1')(-=n n nxx ； ③x x cos )(sin '=；④x x sin )(cos '-=；⑤a a a xx ln )('=；⑥xx e e =')(； ⑦a x x a ln 1)(log '=；⑧xx 1)(ln '= 5、导数的运算法则（1）'''()u v u v ±=±. （2）'''()uv u v uv =+. （3）'''2()(0)u u v uv v v v -=≠. 6、会用导数求单调区间、极值、最值7、求函数()y f x =的极值的方法是：解方程()0f x '=．当()00f x '=时： (1) 如果在0x 附近的左侧()0f x '>，右侧()0f x '<，那么()0f x 是极大值； (2) 如果在0x 附近的左侧()0f x '<，右侧()0f x '>，那么()0f x 是极小值．指数函数、对数函数分数指数幂(1)m na =0,,a m n N *>∈，且1n >）.(2)1m nm naa-==（0,,a m n N *>∈，且1n >）.根式的性质（1）当na =；当n,0||,0a a a a a ≥⎧==⎨-<⎩.有理指数幂的运算性质(1) r sa a⋅=(2) ()r s rsa a=(3)()r rab a b=注：若a＞0，指数幂都适用..(0,1,0)a a N>≠>..1a≠,0m>,且1m≠,0N>).对数恒等式：).推论logmnab).常见的函数图象822sin cosθθ+9απ±kα看成锐角时该函数的符号；αππ±+2kα看成锐角时该函数的符号。

(完整word版)物理公式和符号汇总(word文档良心出品)

数学物理里面的公式符号读法：A :阿尔法AlphaB :贝塔Betar :丫伽玛Gamma△ 3德尔塔DelteE飞艾普西龙Epsilonz z捷塔ZetaE n依塔Eta0刃西塔ThetaI:艾欧塔IotaK K喀帕KappaA入：拉姆达LambdaM 口缪MuN v拗NuS辽克西XiO o欧麦克轮Omicronn n 派PiP p 柔Rho 刀:（r西格玛SigmaT T套TauY u宇普西龙Upsilon① © fai PhiX x器ChiW书普赛PsiQ ①欧米伽Omega 符号大全（1）数量符号：女口:i, 2 + i, a, x，自然对数底e,圆周率n（2）运算符号：如加号（+），减号（-）,乘号（X或•，除号（^或/），两个集合的并集（U）,交集（0），根号（），对数（log, lg，ln），比（：），微分（d）,积分（力等。

（3）关系符号：如“堤等号，“或“是近似符号，“是不等号，'”是大于符号，是小于符号，“表示变量变化的趋势，为'是相似符号，奎”是全等号, 是平行符号，1 ”是垂直符号，& ”是正比例符号，& '是属于符号等。

4）结合符号：如圆括号“（）”方括号“［，］”花括号“｛括｝”线“—”(5)性质符号：如正号“ +,负号-“”绝对值符号11(6)省略符号：如三角形(△)，正弦(sin) , X的函数(f(x)),极限(lim), 因为(•.•)，所以(•••)，总和(刀)，连乘(n,从N个元素中每次取出R 个元素所有不同的组合数(C ),幕(aM)，阶乘(！)等。

符号意义g无穷大PI 圆周率|x| 函数的绝对值U集合并n集合交>大于等于<小于等于三恒等于或同余In(x)以e为底的对数lg(x) 以10 为底的对数floor(x) 上取整函数ceil(x) 下取整函数x mod y 求余数小数部分x - floor(x)/ f(x)不定积分/ [a:b]f(x) 到X^a的定积分P 为真等于1 否则等于0刀[1 < k < n]f对n进行求和,可以拓广至很多情况如：刀[n is prime][n < 10]f(n)刀刀[1 < i奇〃2c n] lim f(x) (x->?) 求极限f(z) f 关于z 的m 阶导函数C(n:m)组合数,n 中取m P(n:m) 排列数m|n m 整除n m丄n m与n互质a € Aa属于集合A #A 集合A 中的元素个数初中物理公式：物理量(单位) 公式备注公式的变形速度V (m/S) v= S :路程/t :时间重力G (N) G=mg m ：质量g：9.8N/kg 或者10N/kg密度P(kg/m3 ) p =m/V m：质量V :体积合力F合(N) 方向相同：F合=F1+F2 方向相反：F合=F1 —F2方向相反时，F1>F2 浮力F 浮(N) F浮=G物一G视G视：物体在液体的重力浮力 F 浮(N) F浮=G物此公式只适用物体漂浮或悬浮浮力F 浮(N) F浮=G排=m排g= p液gV排G 排:排开液体的重力m 排：排开液体的质量p液：液体的密度V 排：排开液体的体积(即浸入液体中的体积)杠杆的平衡条件F1L1= F2L2 F1 :动力L1 :动力臂F2 :阻力L2 :阻力臂定滑轮F=G 物S=h F :绳子自由端受到的拉力G 物:物体的重力S :绳子自由端移动的距离h :物体升高的距离动滑轮F= (G物+G轮)S=2 h G 物:物体的重力G 轮:动滑轮的重力滑轮组F= (G物+G轮) S=n h n :通过动滑轮绳子的段数机械功W(J) W=Fs F :力s :在力的方向上移动的距离有用功W有总功W总W有=G物hW总=Fs适用滑轮组竖直放置时机械效率n = x 100%功率P（w）P=W :功t :时间压强p （Pa）P=F :压力S:受力面积液体压强p（Pa）P=p gh p液体的密度h :深度（从液面到所求点的竖直距离）热量Q（J）Q=cm △ t c:物质的比热容m :质量△ t:温度的变化值燃料燃烧放出的热量Q（J）Q=mq m ：质量q：热值常用的物理公式与重要知识点一．物理公式单位）公式备注公式的变形串联电路电流I(A) 1=11=12= ..... 电流处处相等串联电路电压U(V) U=U1+U2+……串联电路起分压作用串联电路电阻R ( Q)R=R1+R2•+…• •并联电路电流I(A) 1=11+12+……干路电流等于各支路电流之和（分流）并联电路电压U(V) U=U仁U2……并联电路电阻R ( Q)= + + ……欧姆定律I= 电路中的电流与电压成正比，与电阻成反比电流定义式I=Q：电荷量（库仑）t:时间（S）电功W（J）W=Ult=Pt U :电压I:电流t:时间P:电功率电功率P=UI=I2R=U2/R U:电压I :电流R:电阻电磁波波速与波长、频率的关系C=Xv C物理量单位公式名称符号名称符号质量m 千克kg m=pv 温度t 摄氏度°C 速度v 米／秒m/s v=s/t 密度p 千克／米3 kg/m3 p=m/v 力（重力）F 牛顿（牛）N G=mg 压强P 帕斯卡（帕）Pa P=F/S功W 焦耳（焦）J W=Fs功率P 瓦特（瓦）w P=W/t电流I 安培（安） A I=U/R电压U 伏特（伏）V U=IR电阻R 欧姆（欧）R=U/I电功W 焦耳（焦）J W=UIt电功率P 瓦特（瓦）w P=W/t=UI热量Q 焦耳（焦）J Q=cm(t-t °)比热 c 焦／（千克°C) J/(kg °C)真空中光速3X108米／秒g 9.8 牛顿／千克15°C 空气中声速340 米／秒初中物理公式汇编【力学部分】1、速度: V=S/t2、重力：G=mg3、密度：p =m/V4 、压强：p=F/S5、液体压强：p=p gh6、浮力：(1)、F浮二F' —F (压力差)(2)、F浮二G —F (视重力)(3)、F浮二G (漂浮、悬浮)(4)、阿基米德原理：F浮=G排二p液gV排7、杠杆平衡条件：F1 L1 = F2 L28、理想斜面：F/G = h/L9、理想滑轮：F=G/n10、实际滑轮：F= (G + G动” n (竖直方向)11、功：W = FS = Gh (把物体举高)12、功率：P =W/t = FV13、功的原理：W手=W机14、实际机械：W总=W有+ W额外15、机械效率：n= W 有/W总16 、滑轮组效率：(1)、n= G/ nF(竖直方向)(2)、n= G/(G + G动)(竖直方向不计摩擦)(3)、n= f / nF (水平方向)【热学部分】1、吸热：Q 吸=Cm(t —tO) = Cm^t2、放热：Q 放=Cm(tO —t) = Cm^t3、热值：q = Q/m4、炉子和热机的效率：n= Q有效利用/Q燃料5、热平衡方程：Q放=Q吸6、热力学温度：T = t + 273K【电学部分】1、电流强度：1= Q电量/t2、电阻：R=p L/S3、欧姆定律：I= U/R4、焦耳定律：(1)、Q = I2Rt普适公式)(2)、Q=UIt=Pt=UQ 电量= U2t/R (纯电阻公式) 5、串联电路：(1)、I=I1=I2(2)、U = U1 + U2(3)、R = R1 + R2(4)、U1/U2 = R1/R2 (分压公式)(5)、P1/P2 = R1/R26 、并联电路：(1)、1= 11 + I2(2)、U = U1 = U2(3)、1/R=1/R1＋1/R2 [ R=R1R2/(R1 ＋R2)](4)、I1/I2 = R2/R1 (分流公式)(5)、P1/P2=R2/R17 定值电阻：(1)、I1/I2=U1/U2(2)、P1/P2=I12/I22(3)、P1/P2=U12/U228 电功：(1)、W=UIt=Pt=UQ (普适公式)(2)、W=I2Rt=U2t/R (纯电阻公式)9 电功率：(1)、P=W/t=UI (普适公式)(2)、P=I2R=U2/R (纯电阻公式)【常用物理量】1、光速：C = 3x108m/s (真空中)2、声速：V = 340m/s (15 C)3、人耳区分回声：>0 1s4、重力加速度：g = 9. 8N/kg〜10N/kg5、标准大气压值：760毫米水银柱高=1 . 01 X105Pa6、水的密度：p= 1 . 0X03kg/m37、水的凝固点：0C8、水的沸点：100C9、水的比热容：C= 4．2X103J/(kg? C )10 、元电荷：e= 1 ．6X10-19C11 、一节干电池电压：1．5V12 、一节铅蓄电池电压：2V13、对于人体的安全电压： < 36V(不高于36V)14、动力电路的电压：380V15 、家庭电路电压：220V16、单位换算：(1 )、1m/s = 3. 6km/h(2)、1g/cm3 = 103kg/m3(3)、1kw?h = 3. 6X106J 初中物理公式汇编【力学部分】1 、速度：V=S/t2、重力：G=mg3、密度：p =m/V4 、压强：p=F/S5、液体压强：p=p gh6、浮力：(1)、F浮二F' —F (压力差)(2)、F浮二G —F (视重力)(3)、F浮二G (漂浮、悬浮)(4)、阿基米德原理：F浮=G排二p液gV排7、杠杆平衡条件：F1 L1 = F2 L28、理想斜面：F/G = h/L9、理想滑轮：F=G/n10、实际滑轮：F= (G + G动” n (竖直方向)11、功：W = FS = Gh (把物体举高)12、功率：P =W/t = FV13、功的原理：W手=W机14、实际机械：W总=W有+ W额外15、机械效率：n= W 有/W总16 、滑轮组效率：(1)、n= G/ nF(竖直方向)(2)、n= G/(G + G动)(竖直方向不计摩擦)(3)、n= f / nF (水平方向)【热学部分】1、吸热：Q 吸=Cm(t —10) = Cm^t2、放热：Q 放=Cm(t0 —t) = Cm^t3、热值：q = Q/m4、炉子和热机的效率：n= Q有效利用/Q燃料5、热平衡方程：Q放=Q吸6、热力学温度：T = t + 273K 【电学部分】1、电流强度：1= Q电量/t2、电阻：R=p L/S3、欧姆定律：1= U/R4、焦耳定律：(1)、Q=I2Rt 普适公式)(2)、Q = Ult = Pt = UQ 电量=U2t/R (纯电阻公式) 5、串联电路：( 1)、l= l1= l2(2)、U=U1＋U2( 3)、R= R1＋R2(4)、U1/U2 = R1/R2 (分压公式)(5)、P1/P2 = R1/R26 、并联电路：( 1)、l= l1＋l2(2)、U=U1=U2(3)、1/R=1/R1＋1/R2 [ R = R1R2/(R1＋R2)](4)、I1/I2 = R2/R1(分流公式)(5)、P1/P2=R2/R17 定值电阻：(1)、I1/I2=U1/U2(2)、P1/P2=I12/I22(3)、P1/P2=U12/U228 电功：(1)、W=UIt=Pt=UQ (普适公式)(2)、W=I2Rt=U2t/R (纯电阻公式)9 电功率：(1)、P=W/t=UI (普适公式)(2)、P=I2R=U2/R (纯电阻公式) 【常用物理量】1、光速：C = 3x108m/s (真空中)2、声速：V = 340m/s (15 C)3、人耳区分回声：＞0 1s4、重力加速度：g = 9. 8N/kg〜10N/kg5、标准大气压值：760毫米水银柱高=1 . 01 X105Pa6、水的密度：p= 1 . 0X103kg/m37、水的凝固点：0 C8、水的沸点：100 C9、水的比热容：C= 4. 2X103J/（kg? C）10、元电荷：e = 1 . 6X10-19C11、一节干电池电压：1．5V12 、一节铅蓄电池电压：2V13、对于人体的安全电压： < 36V（不高于36V）14 、动力电路的电压：380V15 、家庭电路电压：220V16 、单位换算：（1 ）、1m/s = 3. 6km/h（2）、1g/cm3 = 10A3kg/m A3物理量单位公式名称符号名称符号质量m千克kg m=p v温度t 摄氏度°C速度v 米／秒m/s v=s/t密度p 千克/米 3 kg/m3p =m/v力（重力）F 牛顿（牛) N G=mg压强P Pa 帕斯卡（帕）P=F/S功W J 焦耳（焦）W=Fs功率：P 瓦特（瓦）w P=W/t电流：I 安培（安）A I=U/R电压：U 伏特（伏）V U=IR电阻：R 欧姆（欧）R=U/I电功：W 焦耳（焦）J W=UIt电功率：P 瓦特（瓦）w P=W/t=UI热量：Q 焦耳（焦）J Q=cm(t-t°)比热： c 焦/（千克°C) J/(kg °C)真空中光速3X108米/秒g ：9.8 牛顿／千克15°C 空气中声速340 米/秒初中物理公式汇编【力学部分】1 、速度：V=S/t2、重力：G=mg3、密度：p =m/V4、压强：p=F/S5、液体压强：p=p gh6、浮力：(1)、F浮二F' —F (压力差)(2)、F浮二G —F (视重力)(3)、F浮二G (漂浮、悬浮)(4)、阿基米德原理：F浮=G排二p液gV排7、杠杆平衡条件：F1 L1 = F2 L28、理想斜面：F/G = h/L9、理想滑轮：F=G/n10、实际滑轮：F= (G + G动” n (竖直方向)11、功：W = FS = Gh (把物体举高)12、功率：P =W/t = FV13、功的原理：W手=W机14、实际机械：W总=W有+ W额外15、机械效率：n= W 有/W总16 、滑轮组效率：(1)、n= G/ nF(竖直方向)(2)、n= G/(G + G动)(竖直方向不计摩擦)(3)、n= f / nF (水平方向)【热学部分】1、吸热：Q 吸=Cm(t —tO) = CmX t2、放热：Q 放=Cm(t0 —t) = Cm^ t3、热值：q = Q/m4、炉子和热机的效率：n= Q有效利用/Q燃料5、热平衡方程：Q放=Q吸6、热力学温度：T = t + 273K【电学部分】1、电流强度：1= Q电量/t2、电阻：R=p L/S3、欧姆定律：I= U/R4、焦耳定律：(1)、Q = I2Rt普适公式)(2)、Q=UIt=Pt=UQ 电量= U2t/R (纯电阻公式) 5、串联电路：(1)、I=I1=I2( 2)、U= U1 + U2(3)、R=R1+R2 (1)、W=UIt=Pt=UQ (普适公式) (2)、W=I2Rt=U2t/R (纯电阻公式)6、并联电路：(1)、1= 11 + 12(2)、U = U1 = U2(3)、1/R=1/R1＋1/R2 [ R=R1R2/(R1 ＋R2)](4)、11/12 = R2/R1(分流公式)(5)、P1/P2=R2/R17 定值电阻：(1)、I1/I2=U1/U2(2)、P1/P2=I12/I22(3)、P1/P2=U12/U228 电功：(1)、W=UIt=Pt=UQ (普适公式)(2)、W=I2Rt=U2t/R (纯电阻公式)9 电功率：(1)、P=W/t=UI (普适公式)(2)、P=I2R=U2/R (纯电阻公式)【常用物理量】1、光速：C = 3x108m/s (真空中)2、声速：V = 340m/s (15 C)3、人耳区分回声：> 0.1s4、重力加速度：g = 9.8N/kg〜10N/kg5、标准大气压值：760毫米水银柱高=1.01 X05Pa6、水的密度：p= 1.0 X103kg/m37、水的凝固点：0C8、水的沸点：100C9、水的比热容：C = 4.2 X103J/(kg? C)10、元电荷：e = 1.6 X10-19C11、一节干电池电压：1.5V12、一节铅蓄电池电压：2V13、对于人体的安全电压：< 36V(不高于36V)14、动力电路的电压：380V15、家庭电路电压：220V16、单位换算：(1)、1m/s=3.6km/h(2)、1g/cm3 =103kg/m3(3)、1kw?h = 3.6 X106J重力G (N) G=mg m ：质量g：9.8N/kg 密度P(kg/m3 ) p =m/V m：质量V :体积合力F合（N）F合=F1+F2方向相同F合=F1-F2方向相反时，F1>F2方向相反：浮力F浮（N） F浮=G物-G视G视：物体在液体的重力浮力F浮（N） F浮=G物此公式只适用浮力F浮（N） F浮=G排=m排g= p液gV排杠杆的平衡条件F1L1= F2L2动滑轮F= G物+G轮压强p（Pa）P= F/S热量Q（J）Q=cm △ t 机械功W（J）W=Fs 功率P（w）P=W/t机械效率n = x 100%液体压强p（Pa ）P=p gh燃料燃烧放出的热量Q （J）Q=mq m :质量q：热值物体漂浮或悬浮G 排:排开液体的重力m排：排开液体的质量p液：液体的密度V排：排开液体的体积（即浸入液体中的体积）:动力L1 :动力臂F2 :阻力L2:阻力臂定滑轮F=G 物S=h F :绳子自由端受到的拉力G物：物体的重力S :绳子自由端移动的距离h :物体升高的距离S=2 h G 物：物体的重力G 轮:动滑轮的重力滑轮组F= （G物+G轮）S=n h n：通过动滑轮绳子的段数F:力s:在力的方向上移动的距离有用功W有总功W总W有=G物hW总=Fs适用滑轮组竖直放置时W :功t :时间F :压力S :受力面积P：液体的密度h :深度（从液面到所求点的竖直距离）:物质的比热容m :质量t :温度的变化值物理量(单位) 公式备注公式的变形重力 G (N ) G=mg m :质量 g : 9.8N/kg 或者 10N/kg密度P (kg/m3 ) p =m/V m :质量 V :体积合力F 合(N ) 方向相同：F 合=F1+F2方向相反：F 合=F1-F2方向相反时，F1>F2 浮力F 浮(N)F 浮=G 物-G 视 G 视：物体在液体的重力浮力F 浮(N)F 浮=G 物此公式只适用物体漂浮或悬浮浮力F 浮(N)F 浮=G 排=m 排g= p 液gV 排 G 排:排开液体的重力 m 排：排开液体的质量 p 液：液体的密度 V 排:排开液体的体积(即浸入液体中的体积 )杠杆的平衡条件 F1L 仁F2L2F1:动力L1 :动力臂 F2 :阻力 L2 :阻力臂定滑轮 F=G 物S=h F :绳子自由端受到的拉力G 物：物体的重力 S :绳子自由端移动的距离 h :物体升高的距离动滑轮F= (G 物+G 轮)S=2 h G 物:物体的重力 G 轮:动滑轮的重力滑轮组F= (G 物+G 轮)S=n h n ：通过动滑轮绳子的段数机械功W (J ) W=Fs F :力 s :在力的方向上移动的距离有用功W 有总功W 总 W 有=G 物hW 总=Fs 适用滑轮组竖直放置时机械效率n = x 100%功率P (w ) P=W/t W :功 t :时间压强p (Pa ) P= F/S F :压力 S :受力面积液体压强p (Pa ) P=p gh p ：液体的密度 h :深度(从液面到所求点的竖直距离) 热量Q (J ) Q=cm △ t c :物质的比热容 m :质量 △ t :温度的变化值燃料燃烧放出的热量Q (J ) Q=mq m :质量 q ：热值1=11=12= .... 电流处处相等 U=U1+U2+… 串联电路起分压作用 R=R1+R2+ ……I=I1+I2+ …… 干路电流等于各支路电流之和(分流)U=U 仁U2…… 串联电路：电流 I (A ) 串联电路：电压 U (V ) 串联电路：电阻R (Q) 并联电路:电流 I (A ) 并联电路：电压U (V ) 并联电路电阻R ( Q)R= 1/R1+ 1/R2+ ……电路中的电流与电压成正比，与电阻成反比 Q :电荷量（库仑）t :时间（S ） U :电压I :电流 t :时间P :电功率 U:电压I :电流R :电阻电磁波波速与波长、频率的关系 C=Xv C :真空中的光速速度 V （m/S ） v=S/tS :路程 t :时间重力 G （N ）G=mgm :质量g ：重力加速度，常数，9.8N/kg 或者10N/kg密度 P （kg/m3） p =m/vm :质量V :体积合力F 合（N ）方向相同：F 合=F1+F2方向相反：F 合=F1-F2方向相反时，F1>F2浮力F 浮（N ）F 浮=G 物-G 视G 视：物体在液体的重力浮力F 浮（N ）F 浮=G 物此公式只适用物体漂浮或悬浮浮力F 浮（N ）F 浮=G 排=m 排g=p 液gV 排G 排:排开液体的重力 m 排:排开液体的质量 p 液：液体的密度 V 排：排开液体的体积（即浸入液体中的体积）杠杆的平衡条件F1L 仁F2L2F1 :动力L1 :动力臂 F2 :阻力L2:阻力臂定滑轮 F=G 物S=hF :绳子自由端受到的拉力G 物:物体的重力S :绳子自由端移动的距离h :物体升高的距离动滑轮 F=（G 物 +G 轮）/2S=2hG 物：物体的重力G 轮：动滑轮的重力滑轮组 F=（G 物 +G 轮）欧姆定律 I= U/R 电流定义式 I=Q/t 电功 W （J ）W=UIt=Pt 电功率P=UI=I2R=U2/RS=nhn ：通过动滑轮绳子的段数机械功W（J）W=FsF :力s :在力的方向上移动的距离有用功W有=G物h总功W总W总=Fs适用滑轮组竖直放置时机械效率n =W W/W总X100%功率P（w）P=w/tW :功t:时间压强p（Pa ）P=F/sF :压力S:受力面积液体压强p （Pa）P=p ghp:液体的密度h :深度（从液面到所求点的竖直距离）热量Q（J）Q=cm △tc:物质的比热容m ：质量△ t:温度的变化值燃料燃烧放出的热量Q（J）Q=mqm :质量q：热值常用的物理公式与重要知识点．物理公式(单位)公式备注公式的变形串联电路电流I (A) 1=11=12=……电流处处相等串联电路电压U (V) U=U1+U2+•… 串联电路起分压作用串联电路电阻R ( Q) R=R1+R2……并联电路电流I (A) I=I1+I2+ ••…干路电流等于各支路电流之和(分流)并联电路电压U(V) U=U1=U2=……并联电路电阻R ( Q) 1/R=1/R1+1/R2+……欧姆定律I=U/I电路中的电流与电压成正比，与电阻成反比电流定义式I=Q/tQ:电荷量(库仑)t:时间(S)电功W(J) W=UIt=PtU:电压I:电流t:时间P:电功率电功率P=UI=I2R=U2/RU:电压I :电流R :电阻电磁波波速与波长、频率的关系C=Xv C波速(电磁波的波速是不变的，等于3X108m/s ) 入：波长V频率需要记住的几个数值a •声音在空气中的传播速度：340m/sb光在真空或空气中的传播速度:3x108m/sc.水的密度：1.0 %03kg/m3d •水的比热容：4.2 X103J/ (kgo C)e .一节干电池的电压：1.5Vf .家庭电路的电压：220Vg.安全电压：不高于36V。

高中数学第二章数与符号 2.3 数学符号课件北师大版

-8-
§3 数学符号
Y预习导引 U XI DAO YIN
H 互动课堂 U DONG KE TANG
重难点拨
思悟升华
例1
例2
这段话的意思用表格表示计算过程就是: 把每人所出的钱数写出来(表第 1 行:所出率),多余、不足的钱数分别写在
它们的下面(表第 2 行:盈不足).将它们分别与所出的钱数交错相乘(“维乘”即
§3 数学符号
-1-
§3 数学符号
激趣诱思
新知预习
Y预习导引 U XIDAO YIN
H 互动课堂 U DONG KE TANG
数学除了记数以外,还需要一套数学符号来表示数和数、数和形的相互关系.数学符号的发明和使用比数字晚,但是数量多得多.现在常用的数学符号有 200 多个,初中数学书里就不下 20 多种.你了解它们的经历吗?学完本节,你就会有答案了.
平方根号曾经用拉丁文“Radix”(根)的首尾两个字母合并起来表示,17 世纪初,法国数学家笛卡儿在他的《几何学》中,第一次用“ ” 表示根号.
-5-
§3 数学符号
重难点拨
思悟升华
Y预习导引 U XI DAO YIN
H 互动课堂 U DONG KE TANG
例1
例2
16 世纪法国数学家维叶特用“=”表示两个量的差别.可是英国牛津大学数学、修辞学教授雷科德觉得:用两条平行而又相等的直线来表示两数相等是最合适不过的了,于是等于符号“=”就从 1540 年开始使用起来.
-4-
§3 数学符号
Y预习导引 U XI DAO YIN
H 互动课堂 U DONG KE TANG
重难点拨
思悟升华
例1
例2
乘号曾经用过十几种,现在通用两种.一个是“×”,一个是“·”,最早是由英国数学家奥特雷德 1631 年提出的.德国数学家莱布尼茨认为:“×”号像拉丁字母“X”,加以反对,而赞成用“·”号.他自己还提出用“n”表示相乘.可是这个符号现在应用到集合论中去了.

(word版)人教版高中数学知识点汇总,文档

人教版高中数学高中数学主要知识点必修1数学知识第一章、集合与函数概念、集合1、把研究的对象统称为元素，把一些元素组成的总体叫做集合。

集合三要素：确定性、互异性、无序性。

2、只要构成两个集合的元素是一样的，就称这两个集合相等。

3、常见集合：正整数集合：N*或N，整数集合：Z，有理数集合：Q，实数集合：R.4、集合的表示方法：列举法、描述法.§、集合间的根本关系1、一般地，对于两个集合A、B，如果集合A中任意一个元素都是集合B中的元素，那么称集合A是集合B的子集。

记作A B.2、如果集合A B，但存在元素xB，且x A，那么称集合A是集合B的真子集.记作：A B.3、把不含任何元素的集合叫做空集.记作：.并规定：空集合是任何集合的子集.4、如果集合A中含有n个元素，那么集合A有2n个子集.§、集合间的根本运算1、一般地，由所有属于集合A或集合B的元素组成的集合，称为集合A与B的并集.记作：A B.2、一般地，由属于集合A且属于集合B的所有元素组成的集合，称为A与B的交集.记作：A B.3、全集、补集？C U A{x|x U,且x U}运算交集并集类型定由所有属于A且属由所有属于集合A或义于B的元素所组成属于集合B的元素所的集合,叫做A,B的组成的集合，叫做A,B交集．记作AB〔读的并集．记作：AB作‘A交B’〕，即〔读作‘A并B’〕，即补集设S是一个集合，A是S的一个子集，由S中所有不属于A的元素组成的集合，叫做S中子集A的补集〔或余集〕记作C S A，即A B=｛x|x A，且 A B={x|x A，或xB｝．xB})．{x|xS,且xA}C S A=-1-人教版高中数学韦恩A B A B SA图示图1图2性A A=A A A=A(C u A)(C u B)AΦ=ΦAΦ=A=C u(A B)A B=BA A B=B A(C u A)(C u B)A BA A BＡ质ABB ABB=C u(AB)A(C u A)=UA(C u A)=Φ．§、函数的概念1、设A、B是非空的数集，如果按照某种确定的对应关系f，使对于集合A中的任意一个数x，在集合B中都有惟一确定的数fx和它对应，那么就称f:A B为集合A到集合B的一个函数，记作：y fx,x A.2、一个函数的构成要素为：定义域、对应关系、值域.如果两个函数的定义域相同，并且对应关系完全一致，那么称这两个函数相等.§、函数的表示法1、函数的三种表示方法：解析法、图象法、列表法.、单调性与最大〔小〕值单调性的定义：见书P281、注意函数单调性证明的一般格式：解：设x1,x2a,b且x1x2，那么：fx1fx2=、奇偶性1、一般地，如果对于函数fx的定义域内任意一个x，都有f x fx，那么就称函数fx为偶函数.偶函数图象关于y轴对称.2、一般地，如果对于函数fx的定义域内任意一个x，都有f x fx，那么就称函数fx为奇函数.奇函数图象关于原点对称.第二章、根本初等函数〔Ⅰ〕§、指数与指数幂的运算1、一般地，如果x n a，那么x叫做a的n次方根。

(完整word)高等数学符号

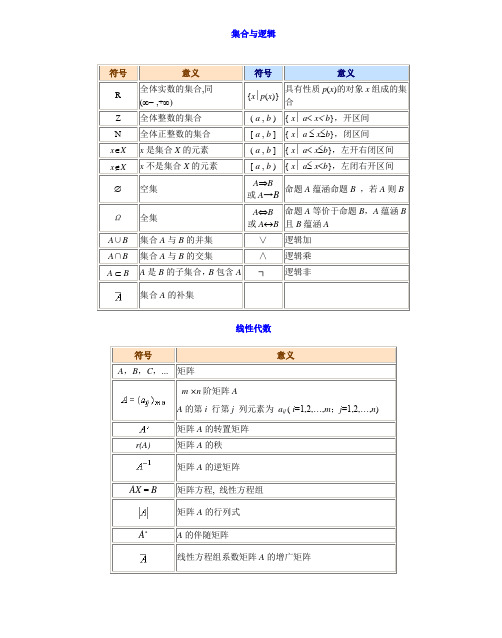
集合与逻辑符号意义符号意义R 全体实数的集合,同(∞- ,+∞){x∣p(x)}具有性质p(x)的对象x组成的集合Z 全体整数的集合( a , b ) { x∣a<x< b}，开区间N 全体正整数的集合[ a , b ] { x∣a≤x≤b}，闭区间x∈X x是集合X的元素( a , b ] { x∣a< x≤b}，左开右闭区间x∉X x不是集合X的元素[ a , b ) { x∣ a≤ x<b}，左闭右开区间∅空集A⇒B或A→B命题A蕴涵命题B ，若A则BΩ全集A⇔B或A↔B命题A等价于命题B，A蕴涵B且B蕴涵AA∪B集合A与B的并集∨逻辑加A∩B集合A与B的交集∧逻辑乘A⊂B A是B的子集合，B包含A┐逻辑非集合A的补集线性代数符号意义A，B，C，... 矩阵m×n阶矩阵AA的第i 行第j列元素为a ij (i=1,2,…,m；j=1,2,…,n)矩阵A的转置矩阵r(A)矩阵A的秩矩阵A的逆矩阵AX= B 矩阵方程, 线性方程组矩阵A的行列式A*A的伴随矩阵线性方程组系数矩阵A的增广矩阵数列、函数与极限符号意义符号意义u1,u2,…,u n,…或{u n} 以u n为通项的数列n趋于无穷大时数列{y n} 的极限以u n为通项的无穷级数和x 趋于无穷大时函数f(x)的极限有限项u1+u2+…+u n的和x趋于正无穷大时函数f(x)的极限x在对应规律f下对应到yx趋于负无穷大时函数f(x)的极限函数f ：X为定义域，f为对应规律，x为自变量，y为因变量x趋于a时函数f(x)的极限D f函数f的定义域x>a且x趋于a时函数f(x)的右极限R f函数f的值域x<a且x趋于a时函数f(x)的左极限Γf函数f 的图像x→✉，f(x) ~ g(x) 在x→✉的变化过程中，无穷小（大）量f(x)与g(x)的等价函数 f :X→Y 与g : Y →Z的复合函数函数y=y(x)在自变量x0处的值f-1函数f的反函数函数f(x)在[a,b]上的平均值f( x , y ) 以x , y为自变量的二元函数符号意义符号意义函数y关于x的导(函)数函数f(x , y)在（x0 , y0）处关于x的偏导数函数f(x)关于x的导(函)数函数f(x , y)在（x0 , y0）处关于y的偏导数函数y在x0的导数函数f(x)的不定积分函数f(x)在x0的导数函数f(x)的黎曼和函数f(x)在x0的右导数函数f(x)在[a, b]上的定积分函数f(x)在x0的左导数差数F(b) F(a)变量u的改变量f(x)在无穷区间[a, +∞)上的无穷（广义）积分du 变量u的微分f(x)在无穷区间（-∞, b]上的无穷（广义）积分函数y关于x的n 阶导数，n∈N f(x)在无穷区间（-∞, +∞）上的无穷（广义）积分二元函数z=f(x,y)关于x或y 的偏导数概率论与数理统计∅不可能事件ω基本事件Ω={ω1,ω2,…,ωn} 样本空间，基本事件组A⊂ B或B⊃ A事件B包含事件AA + B事件A与B的和AB事件A与事件B的积事件A1，A2，…，A n的积A– B事件A与事件B的差事件A的对立事件, 或称为事件A的互补事件P(A) 事件A的概率ξ、η、ζ或X、Y、Z 随机变量χ2(n) 自由度为n的χ2分布t(n) 自由度为n的t分布F( n1, n2) 第一自由度为n1和第二自由度为n2的F分布χ2分布的临界值tα(n) t分布的临界值Fα(n1，n2) F分布的临界值其它符号意义[x] 不超过x的最大整数a ( mod n )用n除a所得的余数（n∈N，a∈N）e极限，自然对数的底经济学函数y= f(x)的弹性⊥直线或线段的垂直∥直线或线段的平行。

(完整word版)向量的点乘和叉乘,以及几何意义

所谓点乘（也常称作内积），数学定义如下：点乘只是表达这个结果的一种方式，符号不重要，叫法也不重要，我可以叫点乘，内积，也可以叫"相乘"，定义"#"字符代替“·” 符号都可以，只是人们约束习惯这么这么写，那我们就也都这么写。

而且，也不要纠结为什么是这么定义，没有为什么，人们就是这么“龟腚”这个公式的，我们要研究的是这个规定到底能干嘛？有啥具体意义？a.点乘的具体几何意义：根据公式，我们可以得出a·b=|a| |b|cosθ我试着证明为什么会是这样（为了能让大家看的方便，我将向量标为蓝色，具体长度标为红色）：定义向量c=a - b这样就形成了一个封闭的三角形，c向量为他的第三边由于余弦定理我们可以知道c² =a² +b² - 2ab cos(θ) (这里的a,b,c全部都是每一边的具体长度)根据定义我们可以推导出c·c=c²(有兴趣的朋友可以去试着推导一下)所以：c·c=a·a+b·b- 2ab cos(θ)因为向量的点乘满足分配率：a·(b+c)=a·b+a·cc=a - bc·c=(a -b)·(a - b)c·c=(a·a-2a·b+b·b)(a·a - 2a·b + b·b)=a²+b²- 2ab cos(q)约掉a·a=a²,b·b=b²;-2a·b= -2ab cos(θ)a·b=ab cos(θ)因为a=|a|所以a·b=|a| |b|cosθ跟据这个公式，我们能拿到两个向量之间的夹角，这对于判断两个向量是否同一方向，是否正交(也就是垂直)，很有用处。

(完整word版)高中数学必修三知识点总结

高中数学必修 3 知识点第一章算法初步算法的观点1、算法观点：在数学上，现代意义上的“算法” 往常是指能够用计算机来解决的某一类问题是程序或步骤，这些程序或步骤一定是明确和有效的，并且能够在有限步以内达成.2.算法的特色 :(1) 有限性：一个算法的步骤序列是有限的，一定在有限操作以后停止，不可以是无穷的.(2)确立性：算法中的每一步应当是确立的并且能有效地履行且获得确立的结果，而不该当是含糊其词 .(3)次序性与正确性：算法从初始步骤开始，分为若干明确的步骤，每一个步骤只好有一个确立的后继步骤，前一步是后一步的前提，只有履行完前一步才能进行下一步，并且每一步都正确无误，才能达成问题 .(4) 不独一性：求解某一个问题的解法不必定是独一的，关于一个问题能够有不一样的算法.(5)广泛性：好多详细的问题，都能够设计合理的算法去解决，如默算、计算器计算都要经过有限、预先设计好的步骤加以解决.程序框图1、程序框图基本观点：（一）程序构图的观点：程序框图又称流程图，是一种用规定的图形、指向线及文字说明来正确、直观地表示算法的图形。

一个程序框图包含以下几部分：表示相应操作的程序框；带箭头的流程线；程序框外必需文字说明。

（二）构成程序框的图形符号及其作用程序框名称功能表示一个算法的开端和结束，是任何流程图起止框不行少的。

表示一个算法输入和输出的信息，可用在算输入、输出框法中任何需要输入、输出的地点。

赋值、计算，算法中办理数据需要的算式、办理框公式平分别写在不一样的用以办理数据的处理框内。

判断某一条件能否建立，建即刻在出口处标判断框明“是”或“Y ”；不建即刻注明“否”或“N ”。

学习这部分知识的时候，要掌握各个图形的形状、作用及使用规则，画程序框图的规则以下：1 、使用标准的图形符号。

2 、框图一般按从上到下、从左到右的方向画。

3 、除判断框外，大部分流程图符号只有一个进入点和一个退出点。

判断框拥有超出一个退出点的独一符号。

完整word版高数符号大全

高等数学常用符号大全及符号的含义acsc x y，余割函数反函数在x处的值，即 x = csc y角度的一个标准符号，不注明均指弧度，尤其用于表示θ atan x/y，当x、y 、z用于表示空间中的点时i, j, k 分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b) 以a、b为元素的向量(a, b) a、b向量的点积a?ba、b向量的点积(a?b)a、b向量的点积|v| 向量v的模|x| 数x的绝对值表示求和，通常是某项指数。

下边界值写在其下部，上边界值写在Σ其上部。

如j从1到100 的和可以表示成： 1。

这表示 + 2 + … + nM 表示一个矩阵或数列或其它|v> 阶矩阵的向量列向量，即元素被写成列或可被看成k×1<v| 1×k被写成行或可被看成从阶矩阵的向量dx 的一个无穷小变化，dy, dz, dr等类似变量xds 长度的微小变化1/2222 )或球面坐标系中到原点的距离 (x变量ρ + y + z1/222轴的距离) 或三维空间或极坐标中到z (x变量r + y的行列式，其值是矩阵的行和列决定的平行区域的面积或体矩阵|M| M 积的行列式的值，为一个面积、体积或超体积M 矩阵||M||22 df/dxf关于x的二阶导数(2)(x) f同样也是f关于x的二阶导数(k)(x) f(k-1) (x)f的导数 f关于x的第k阶导数，曲线切线方向上的单位向量，如果曲线可以描述成 r(t), 则T =T (dr/dt)/|dr/dt|ds 沿曲线方向距离的导数κ曲线的曲率，单位切线向量相对曲线距离的导数的值：|dT/ds|N dT/ds投影方向单位向量，垂直于TB 平面T和N的单位法向量，即曲率的平面τ曲线的扭率： |dB/ds|g 重力常数F 力学中力的标准符号k 弹簧的弹簧常数p i第i个物体的动量H 物理系统的哈密尔敦函数，即位置和动量表示的能量{Q, H} Q, H的泊松括号以一个关于x的函数的形式表达的f(x)的积分函数f 从a到b的定积分。

(完整word版)高数符号大全

高等数学常用符号大全及符号的含义acsc xy，余割函数反函数在x处的值，即 x = csc y θ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a•ba、b向量的点积(a•b)a、b向量的点积|v|向量v的模|x|数x的绝对值表示求和，通常是某项指数。

下边界值写在其下部，上边界值写在Σ其上部。

如j从1到100 的和可以表示成：。

这表示 1+ 2 + … + nM表示一个矩阵或数列或其它|v>列向量，即元素被写成列或可被看成k×1阶矩阵的向量<v|被写成行或可被看成从1×k阶矩阵的向量dx变量x的一个无穷小变化，dy, dz, dr等类似ds长度的微小变化ρ变量 (x2+ y2+ z2)1/2或球面坐标系中到原点的距离r 变量 (x2+ y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式，其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值，为一个面积、体积或超体积d2f/dx2f关于x的二阶导数f(2)(x)同样也是f关于x的二阶导数f(k)(x)f关于x的第k阶导数，f(k-1)(x)的导数T 曲线切线方向上的单位向量，如果曲线可以描述成 r(t), 则T =(dr/dt)/|dr/dt|ds沿曲线方向距离的导数κ曲线的曲率，单位切线向量相对曲线距离的导数的值：|dT/ds|NdT/ds投影方向单位向量，垂直于TB平面T和N的单位法向量，即曲率的平面τ曲线的扭率： |dB/ds|g重力常数F力学中力的标准符号k弹簧的弹簧常数pi第i个物体的动量H物理系统的哈密尔敦函数，即位置和动量表示的能量{Q, H}Q, H的泊松括号以一个关于x的函数的形式表达的f(x)的积分函数f 从a到b的定积分。

(完整word版)数学符号及读法大全

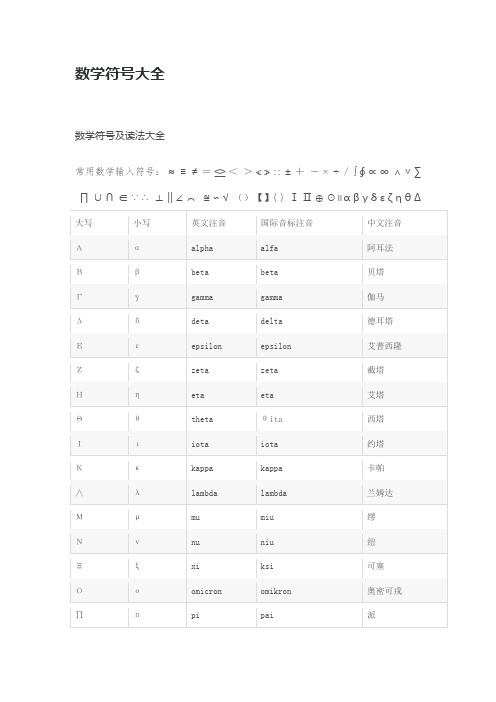
数学符号大全数学符号及读法大全常用数学输入符号：≈≡≠＝≤≥＜＞≮≯∷±＋－×÷／∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒≌∽√（）【】｛｝ⅠⅡ⊕⊙∥αβγδεζηθΔ公式输入符号≈≡≠＝≤≥＜＞≮≯∷±＋－×÷／∫∮∝∞∧∨∑∏∪∩∈∵∴⊥‖∠⌒⊙≌∽√+:plus(positive正的)-：minus（negative负的）*：multiplied by÷：divided by=:be equal to≈:be approximately equal to():round brackets(parenthess)[]:square brackets{}:braces∵:because∴:therefore≤:less than or equal to≥：greater than or equal to∞：infinityLOGnX:logx to the base nxn:the nth power of xf(x):the function of xdx:diffrencial of xx+y:x plus y(a+b):bracket a plus b bracket closeda=b: a equals ba≠b： a isn't equal to ba>b : a is greater than ba>>b: a is much greater than ba≥b: a is greater than or equal to bx→∞：approches infinityx2:x squarex3:x cube√￣x:the square root of x3√￣x:the cube root of x3‰：three peimilln∑i=1xi:the summation of x where x goes from 1to nn∏i=1xi:the product of x sub i where igoes from 1to n ∫ab:integral betweens a and b数学符号（理科符号）——运算符号1.基本符号：＋－ × ÷（／）2.分数号：／3.正负号：±4.相似全等：∽≌5.因为所以：∵∴6.判断类：＝≠＜≮（不小于）＞≯（不大于）7.集合类：∈（属于）∪（并集）∩（交集）8.求和符号：∑9.n次方符号：¹（一次方） ²（平方） ³（立方）⁴（4次方）ⁿ（n次方）10.下角标:₁₂₃₄(如:A₁B₂C₃D₄效果如何?)11.或与非的"非":￢12.导数符号(备注符号):′〃13.度:°℃14.任意:∀15.推出号:⇒16.等价号:⇔17.包含被包含:⊆⊇⊂⊃18.导数:∫∬19.箭头类:↗↙↖↘↑↓↔↕↑↓→←20.绝对值:｜21.弧:⌒22.圆:⊙11.或与非的"非":￢12.导数符号(备注符号):′〃13.度:°℃14.任意:∀15.推出号:⇒16.等价号:⇔17.包含被包含:⊆⊇⊂⊃18.导数:∫∬19.箭头类:↗↙↖↘↑↓↔↕↑↓→←20.绝对值:｜21.弧:⌒22.圆:⊙αβγδεζηθικλμνξοπρστυφχψωΑΒΓΔΕΖΗΘΙΚ∧ΜΝΞΟ∏Ρ∑ΤΥΦΧΨΩабвгдеёжзийклмнопрстуфхцчшщъыьэюяАБВГДЕЁЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯΔ。

高中数学公式符号归纳(含无法打出的) (1)

高中数学公式符号大全sA= N+N+╮＋－×÷±＜＞•∶∴∵∷⊙∫∮∝∞∧∨º¹²³ ½ ¾ ¼≠≤≥≈≡‖＝≌∽≮≯∑∏∪∩∈⊿⌒√∟㏒㏑￠∠⊥％‰℅°℃℉′〒¤○µ㎎㎏㎜㎝㎞㎡㏄㏎㏒＄￡￥㏕♂♀ X¹ X² X³1°1′1〃↑ ↓ ← → ↖↗↙↘㊣◎⊕⊙○ ● △▲☆★◇◆□■▽▼§￥￡※♀♂∵∴φω ░ ▒☻☺☼♠◈♤♦◊♨♣♧♥♡▦▩▣▧▨▤▥▪ ▫ ◘ ◙ ☏☎☜☞◑◐◦ ° ☑₪╮，、～％＃＊‧；∶… ¨ ，• ˙ ‘ ’〃′ εїз ™ ✿｡◕‿◕｡◎☺☻►◄▧▨◐◑↔ ↕ ㊊㊋㊌㊍㊎㊏㊐▀▄ █ ▌▬ (ε.メ)▣▤▥▦▩♭☀ஐ☈➽〠〄㍿㊚㊛㊙℗♯♩♫♬¤큐≡:,⊆⊂⊇⊃试比较cos1°与tan44°的大小。

1、几何符号⊥‖∠⌒⊙≡≌△° |a| ⊥∽∠∟‖|2、代数符号∝∧∨～∫ ≤ ≥ ≈ ∞ :〔〕〈〉《》「」『』】【〖3、运算符号{× ÷ √ ± ≠ ≡≮≯4、集合符号∪∩∈Φ ? ￠sA= N+N+{ } [ ] （）5、特殊符号∑ π（圆周率）＠＃☆★○●◎◇◆□■▓⊿※￥Γ Δ Θ ∧Ξ Ο ∏ ∑ Φ Χ Ψ Ω ∏6、推理符号←↑→↓↖↗↘↙∴∵∶∷T ? ü7、标点符号` ˉ ˇ ¨ 、· ‘’8、其他& ; § ℃№ ＄￡￥‰ ℉♂♀①②③④⑤⑥⑦⑧⑨⑩Γ Δ Θ ∧Ξ Ο ∏ ∑ Φ Χ Ψ Ω希腊字母α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ σ τ υ φ χ ψ ωⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹ∈∏ ∑ ∕ √ ∝∞ ∟∠∣‖∧∨∩∪∫ ∮∴∵∶∷∽≈ ≌≈ ≠ ≡≤ ≥ ≤ ≥ ≮≯⊕⊙⊥⊿⌒指数0123：o123 〃? ? ?符号意义∞ 无穷大PI 圆周率|x| 函数的绝对值∪集合并∩集合交≥ 大于等于≤ 小于等于≡恒等于或同余ln(x) 以e为底的对数lg(x) 以10为底的对数floor(x) 上取整函数ceil(x) 下取整函数x mod y 求余数{x} 小数部分x - floor(x)∫f(x)δx 不定积分∫[a:b]f(x)δx a到b的定积分∑[1≤k≤n]f(k) 对n进行求和,可以拓广至很多情况，如：∑[n is prime][n < 10]f(n)∑∑[1≤i≤j≤n]n^2lim f(x) (x->?) 求极限C(n:m) 组合数,n中取mP(n:m) 排列数m|n m整除n(m,n)=1 m与n互质a ∈A a属于集合ACard(A) 集合A中的元素个数|a| ⊥∽△∠∩∪≠ ∵∴≡± ≥ ≤ ∈←↑→↓↖↗↘↙‖∧∨¼ ½ ¾§①②③④⑤⑥⑦⑧⑨⑩α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ σ τ υ φ χ ψ ωⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹ∈∏∑∕√∝∞∟∠∣‖∧∨∩∪∫∮∴∵∶∷∽≈≌≈≠≡≤≥≤≥≮≯⊕⊙⊥⊿⌒为了方便，也做些约定！x的平方，可以打成x^2 （其它的以此类推）x+1的开方，可以打成√(x+1)，记住加括号；x分之一，可以输入1/x;如果是x+1分之一，请输入1/(x+1)，分子、分母请加括号<> 或>< 表示不等于例：a<>b 即a不等于b；<= 表示小于等于（不大于）例：a<=b 即a不大于b；>= 表示大于等于（不小于）例：a>=b 即a不小于b；^ 表示乘方例：a^b 即a的b次方, 也可用于开根号，例：a^(1/2) 表示a的平方根* 表示乘……/ 表示浮点除例：3/2=1.5\ 表示整除例：3\2=1……1（）广义括号，允许多重嵌套，无大、中、小之分，优先级最高1 几何符号⊥‖∠⌒⊙≡ ≌△2 代数符号∝∧∨～∫ ≠ ≤ ≥ ≈ ∞ ∶3运算符号× ÷ √ ±4集合符号∪∩ ∈5特殊符号∑ π（圆周率）6推理符号|a| ⊥∽△∠∩ ∪≠ ≡ ± ≥ ≤ ∈←↑ → ↓ ↖↗↘↙‖∧∨&; §①②③④⑤⑥⑦⑧⑨⑩Γ Δ Θ ∧Ξ Ο ∏ ∑ Φ Χ Ψ Ωα β γ δ ε ζ η θ ι κ λ μ νξ ο π ρ σ τ υ φ χ ψ ωⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹ∈∏ ∑ ∕ √ ∝∞ ∟ ∠∣‖∧∨∩ ∪∫ ∮∴∵∶∷∽≈ ≌≈ ≠ ≡ ≤ ≥ ≤ ≥ ≮≯⊕⊙⊥⊿⌒℃指数0123：º¹²³符号意义∞ 无穷大PI 圆周率|x| 函数的绝对值∪集合并∩ 集合交≥ 大于等于≤ 小于等于≡ 恒等于或同余ln(x) 自然对数lg(x) 以2为底的对数log(x) 常用对数floor(x) 上取整函数ceil(x) 下取整函数x mod y 求余数{x} 小数部分x - floor(x)∫f(x)δx 不定积分∫[a:b]f(x)δx a到b的定积分[P] P为真等于1否则等于0∑[1≤k≤n]f(k) 对n进行求和,可以拓广至很多情况如：∑[n is prime][n < 10]f(n)∑∑[1≤i≤j≤n]n^2lim f(x) (x->?) 求极限f(z) f关于z的m阶导函数C(n:m) 组合数,n中取mP(n:m) 排列数m|n m整除nm⊥n m与n互质a ∈A a属于集合A#A 集合A中的元素个数∑(n=p,q)f(n) 表示f(n)的n从p到q逐步变化对f(n)的连加和，如果f(n)是有结构式，f(n)应外引括号；∑(n=p,q ; r=s,t)f(n,r) 表示∑(r=s,t)[∑(n=p,q)f(n,r)],如果f(n，r)是有结构式，f(n，r)应外引括号；∏(n=p,q)f(n) 表示f(n)的n从p到q逐步变化对f(n)的连乘积, 如果f(n)是有结构式，f(n)应外引括号；∏(n=p,q ; r=s,t)f(n,r) 表示∏(r=s,t)[∏(n=p,q)f(n,r)],如果f(n，r)是有结构式，f(n，r)应外引括号；lim(x→u)f(x) 表示f(x) 的x 趋向u 时的极限,如果f(x)是有结构式，f(x)应外引括号；lim(y→v ; x→u)f(x,y) 表示lim(y→v)[lim(x→u)f(x,y)],如果f(x，y)是有结构式，f(x，y)应外引括号；∫(a,b)f(x)dx 表示对f(x) 从x=a 至x=b 的积分,如果f(x)是有结构式，f(x)应外引括号；∫(c,d ; a,b)f(x,y)dxdy 表示∫(c,d)[∫(a,b)f(x,y)dx]dy,如果f(x，y)是有结构式，f(x，y)应外引括号；∫(L)f(x,y)ds 表示f(x,y) 在曲线L 上的积分,如果f(x，y)是有结构式，f(x，y)应外引括号；∫∫(D)f(x,y,z)dσ 表示f(x,y,z) 在曲面D 上的积分,如果f(x，y，z)是有结构式，f(x，y，z)应外引括号；∮(L)f(x,y)ds 表示f(x,y) 在闭曲线L 上的积分,如果f(x，y)是有结构式，f(x，y)应外引括号；∮∮(D)f(x,y,z)dσ 表示f(x,y,z) 在闭曲面 D 上的积分, 如果f(x，y)是有结构式，f(x，y)应外引括号；∪(n=p,q)A(n) 表示n从p到q之A(n)的并集，如果A(n)是有结构式，A(n)应外引括号；∪(n=p,q ; r=s,t)A(n,r) 表示∪(r=s,t)[∪(n=p,q)A(n,r)], 如果A(n，r)是有结构式，A(n，r)应外引括号；∩(n=p,q)A(n) 表示n从p到q逐步变化对A(n)的交集, 如果A(n)是有结构式，A(n)应外引括号；∩(n=p,q ; r=s,t)A(n,r) 表示∩(r=s,t)[∩(n=p,q)A(n,r)],如果A(n，r)是有结构式，A(n，r)应外引括号；。

(完整word版)高数符号大全,推荐文档

高等数学常用符号大全及符号的含义acsc xy，余割函数反函数在x处的值，即 x = csc y θ角度的一个标准符号，不注明均指弧度，尤其用于表示atan x/y，当x、y、z用于表示空间中的点时i, j, k分别表示x、y、z方向上的单位向量(a, b, c)以a、b、c为元素的向量(a, b)以a、b为元素的向量(a, b)a、b向量的点积a•ba、b向量的点积(a•b)a、b向量的点积|v|向量v的模|x|数x的绝对值表示求和，通常是某项指数。

下边界值写在其下部，上边界值写在Σ其上部。

如j从1到100 的和可以表示成：。

这表示 1+ 2 + … + nM表示一个矩阵或数列或其它|v>列向量，即元素被写成列或可被看成k×1阶矩阵的向量<v|被写成行或可被看成从1×k阶矩阵的向量dx变量x的一个无穷小变化，dy, dz, dr等类似ds长度的微小变化ρ变量 (x2+ y2+ z2)1/2或球面坐标系中到原点的距离r 变量 (x2+ y2)1/2或三维空间或极坐标中到z轴的距离|M| 矩阵M的行列式，其值是矩阵的行和列决定的平行区域的面积或体积||M|| 矩阵M的行列式的值，为一个面积、体积或超体积d2f/dx2f关于x的二阶导数f(2)(x)同样也是f关于x的二阶导数f(k)(x)f关于x的第k阶导数，f(k-1)(x)的导数T 曲线切线方向上的单位向量，如果曲线可以描述成 r(t), 则T =(dr/dt)/|dr/dt|ds沿曲线方向距离的导数κ曲线的曲率，单位切线向量相对曲线距离的导数的值：|dT/ds|NdT/ds投影方向单位向量，垂直于TB平面T和N的单位法向量，即曲率的平面τ曲线的扭率： |dB/ds|g重力常数F力学中力的标准符号k弹簧的弹簧常数pi第i个物体的动量H物理系统的哈密尔敦函数，即位置和动量表示的能量{Q, H}Q, H的泊松括号以一个关于x的函数的形式表达的f(x)的积分函数f 从a到b的定积分。

【高中数学】数学中的符号

【高中数学】数学中的符号由于研究的需要，人类创造了大量的数学符号，来代替和表示某些数学概念和规律，简化了数学研究工作，促进了数学的发展。

在中学数学中，常见的数学符号有以下六种：一、数量符号如3／4，圆周率π；a,x等。

二、运算符号如加号（+），减号（-），乘号（×或），除号（÷或-），比号（：）等。

三、关系符号例如“=”就是“等号”，读成“等同于”；“≈”或“=”就是“约等号”读成“相当于”；“≠”就是“不等号”。

读成“不等同于”；“＞”就是“大于符号”，读成“大于”；“＜”就是“大干活符号”，读成“大于”；“∥”就是“平行符号”，读成“平行于”；“⊥”就是“横向符号”，读成“旋转轴”等。

四、结合符号如小括号（），中括号[]，大括号{}。

五、性质符号例如正号（+）、负号（-），绝对值符号（||）。

六、简写符号如三角形（△），圆（⊙），幂（）等。

这些符号的产生，一就是源于象形，实际上就是增大的图形。

例如平行符号“∥”就是两条平行的直线；横向符号“⊥”就是互相横向的两条直线；三角形符号“△”就是一个增大了的三角形；符号“⊙”则表示一个圆，中间的一点则表示圆心，以免与数0及英文字母o混为一谈。

二就是源于会意，即为由图形就可以窥见某种特定的意义。

例如用两条长度成正比的线段“=”同列在一起，则表示等号；提一条斜线“≠”，则表示不等号；用符号“＞”则表示大于（左侧小，右边大），“＜”则表示大于（左侧大，右边小），意思不难理解；用括号“（）”、“[］”、“｛｝”把若干个量融合在一起，也就是不言而喻的。

三就是源于文字的简写。

例如我们以后将要教给的平方根号“”中的“√”，从拉丁字母radix（根值）的第一个字母r演进而去。

相近符号“∽”就是把拉丁字母s横过来写下，而s就是sindlar（相近）的第一个字母。

除了大量的符号就是人们经过规定延用下来的。

当然这些符号并不是一已经开始就都就是这种形状，而是存有一个演进过程的，这里就不多谈了。

【高中数学】常用数学符号大全及意义

【高中数学】常用数学符号大全及意义数学符号的发明及使用比数字要晚，但其数量却超过了数字。

现在常用的数学符号已超过了200个，其中，每一个符号都有一段有趣的经历。

常用数学符号有哪些?下面是常用数学符号大全及意义，供参考。

1常用数学符号大全数学符号大全及意义之运算符号如加号(+)，减号(-)，乘号(×或・)，除号(÷或/)，两个集合的并集(∪)，交集(∩)，根号(√￣)，对数(log，lg，ln，lb)，比(:)，绝对值符号| |，微分(d)，积分(∫)，闭合曲面(曲线)积分(∮)等。

数学符号大全及意义之关系符号如“=”是等号，“≈”是近似符号(即约等于)，“≠”是不等号，“>”是大于符号，“数学符号大全及意义之结合符号如小括号“()”，中括号“[]”，大括号“{}”，横线“―”=。

数学符号大全及意义之性质符号如正号“+”，负号“-”，正负号“ ”(以及与之对应使用的负正号“”)数学符号大全及意义之省略符号如三角形(△)，直角三角形(Rt△)，正弦(sin)(见三角函数)，双曲正弦函数(sinh)，x的函数(f(x))，极限(lim)，角(∠)，∵ 因为(一个脚站着的，站不住)∴ 所以(两个脚站着的，能站住)(口诀：因为站不住，所以两个点;因为上面两个点，所以下面两个点)总和，连加：∑，求积，连乘：∏，从n个元素中取出r个元素所有不同的组合数(n元素的总个数;r参与选择的元素个数)，幂等。

数学符号大全及意义之排列组合符号C 组合数A (或P) 排列数n 元素的总个数r 参与选择的元素个数! 阶乘，如5!=5×4×3×2×1=120，规定0!=1!! 半阶乘(又称双阶乘)，例如7!!=7×5×3×1=105,10!!=10×8×6×4×2=3840数学符号大全及意义之离散数学符号? 全称量词?存在量词├ 断定符(公式在L中可证)? 满足符(公式在E上有效，公式在E上可满足)? 命题的“非”运算，如命题的否定为?p∧ 命题的“合取”(“与”)运算∨ 命题的“析取”(“或”，“可兼或”)运算→ 命题的“条件”运算? 命题的“双条件”运算的p<=>q 命题p与q的等价关系p=>q 命题p与q的蕴涵关系(p是q的充分条件，q是p的必要条件)A* 公式A的对偶公式，或表示A的数论倒数(此时亦可写为 )wff 合式公式iff 当且仅当↑ 命题的“与非” 运算(“与非门”)↓ 命题的“或非”运算(“或非门”)□ 模态词“必然”◇ 模态词“可能”?空集∈ 属于(如"A∈B"，即“A属于B”) ? 不属于P(A) 集合A的幂集|A| 集合A的点数R2=R○R [R=R○R] 关系R的“复合”? Aleph,阿列夫? 包含?(或?) 真包含另外,还有相应的?,?,?等∪ 集合的并运算U(P)表示P的领域∩ 集合的交运算-或\ 集合的差运算? 限制集合关于关系R的等价类A/R 集合A上关于R的商集[a] 元素a产生的循环群I环，理想Z/(n) 模n的同余类集合r(R) 关系 R的自反闭包s(R) 关系 R的对称闭包CP 命题演绎的定理(CP 规则)EG 存在推广规则(存在量词引入规则)ES 存在量词特指规则(存在量词消去规则)UG 全称推广规则(全称量词引入规则)US 全称特指规则(全称量词消去规则)R 关系r 相容关系R○S 关系与关系的复合domf 函数的定义域(前域)ranf 函数的值域f:x→y f是x到y的函数(x,y) x与y的最大公约数，有时为避免混淆，使用gcd(x,y) [x,y] x与y的最小公倍数，有时为避免混淆，使用lcm(x,y) aH(Ha) H关于a的左(右)陪集Ker(f) 同态映射f的核(或称f同态核)[1，n] 1到n的整数集合d(A,B),|AB|,或AB 点A与点B间的距离d(V) 点V的度数G=(V,E) 点集为V，边集为E的图GW(G) 图G的连通分支数k(G) 图G的点连通度Δ(G) 图G的最大点度A(G) 图G的邻接矩阵P(G) 图G的可达矩阵M(G) 图G的关联矩阵C 复数集I 虚数集N 自然数集，非负整数集(包含元素"0")N*(N+) 正自然数集，正整数集(其中*表示从集合中去掉元素“0”，如R*表示非零实数)P 素数(质数)集Q 有理数集R 实数集Z 整数集Set 集范畴Top 拓扑空间范畴Ab 交换群范畴Grp 群范畴Mon 单元半群范畴Ring 有单位元的(结合)环范畴Rng 环范畴CRng 交换环范畴R-mod 环R的左模范畴mod-R 环R的右模范畴Field 域范畴Poset 偏序集范畴1常用数学符号意义汇总= 等于≠ 不等于≈ 约等于< 小于> 大于// 平行平行且相等⊥垂直≥ 大于或等于≤ 小于或等于≡ 恒等于或同余π 圆周率约为3.1415926536e 自然常数约为 2.7182818285|x| 绝对值或(复数的)模∽ 相似≌ 全等远大于<< 远小于∪ 并集∩ 交集? 包含于∈ 属于⊙ 圆\ 除，求商值，部分编程语言中理解为整除α，β，γ，φ… 角度;系数∞无穷大(包括正无穷大+∞与负无穷大-∞) lnx 以e为底的对数(自然对数)lgx 以10为底的对数(常用对数)lbx 以2为底的对数lim 求极限floor(x) 或[x],亦可写为下取整函数(直译为“地板函数”)，又称高斯函数 ceil(x) 亦可写为上取整函数(直译为“天花板函数”)x mod y模，求余数x-floor(x) 或{x} 表示x的小数部分dy，df(x) 函数y=f(x)的微分(或线性主部)∫f(x)dx 不定积分，函数f的全体原函数感谢您的阅读，祝您生活愉快。

（完整word版）高等数学符号

（完整word版）⾼等数学符号集合与逻辑符号意义符号意义R 全体实数的集合,同(∞- ,+∞){x∣p(x)}具有性质p(x)的对象x组成的集合Z 全体整数的集合( a , b ) { x∣aN 全体正整数的集合[ a , b ] { x∣a≤x≤b}，闭区间x∈X x是集合X的元素( a , b ] { x∣a< x≤b}，左开右闭区间x?X x不是集合X的元素[ a , b ) { x∣ a≤ x 空集A?B或A→B命题A蕴涵命题B ，若A则BΩ全集A?B或A?B命题A等价于命题B，A蕴涵B且B蕴涵AA∪B集合A与B的并集∨逻辑加A∩B集合A与B的交集∧逻辑乘A?B A是B的⼦集合，B包含A┐逻辑⾮集合A的补集线性代数符号意义A，B，C，... 矩阵m×n阶矩阵AA的第i ⾏第j列元素为a ij (i=1,2,…,m；j=1,2,…,n)矩阵A的转置矩阵r(A)矩阵A的秩矩阵A的逆矩阵AX= B 矩阵⽅程, 线性⽅程组矩阵A的⾏列式A*A的伴随矩阵线性⽅程组系数矩阵A的增⼴矩阵数列、函数与极限符号意义符号意义u1,u2,…,u n,…或{u n} 以u n为通项的数列n趋于⽆穷⼤时数列{y n} 的极限以u n为通项的⽆穷级数和x 趋于⽆穷⼤时函数f(x)的极限有限项u1+u2+…+u n的和x趋于正⽆穷⼤时函数f(x)的极限x在对应规律f下对应到yx趋于负⽆穷⼤时函数f(x)的极限函数f ：X为定义域，f为对应规律，x为⾃变量，y为因变量x趋于a时函数f(x)的极限D f函数f的定义域x>a且x趋于a时函数f(x)的右极限R f函数f的值域xf(x)的左极限Γf函数f 的图像x→?，f(x) ~ g(x) 在x→?的变化过程中，⽆穷⼩（⼤）量f(x)与g(x)的等价函数 f :X→Y 与g : Y →Z的复合函数函数y=y(x)在⾃变量x0处的值f-1函数f的反函数函数f(x)在[a,b]上的平均值f( x , y ) 以x , y为⾃变量的⼆元函数符号意义符号意义函数y关于x的导(函)数函数f(x , y)在（x0 , y0）处关于x的偏导数函数f(x)关于x的导(函)数函数f(x , y)在（x0 , y0）处关于y的偏导数函数y在x0的导数函数f(x)的不定积分函数f(x)在x0的导数函数f(x)的黎曼和函数f(x)在x0的右导数函数f(x)在[a, b]上的定积分函数f(x)在x0的左导数差数F(b) F(a)变量u的改变量f(x)在⽆穷区间[a, +∞)上的⽆穷（⼴义）积分du 变量u的微分f(x)在⽆穷区间（-∞, b]上的⽆穷（⼴义）积分函数y关于x的n 阶导数，n∈N f(x)在⽆穷区间（-∞, +∞）上的⽆穷（⼴义）积分⼆元函数z=f(x,y)关于x或y 的偏导数概率论与数理统计不可能事件ω基本事件Ω={ω1,ω2,…,ωn} 样本空间，基本事件组A? B或B? A事件B包含事件AA + B事件A与B的和AB事件A与事件B的积事件A1，A2，…，A n的积A– B事件A与事件B的差事件A的对⽴事件, 或称为事件A的互补事件P(A) 事件A的概率ξ、η、ζ或X、Y、Z 随机变量χ2(n) ⾃由度为n的χ2分布t(n) ⾃由度为n的t分布F( n1, n2) 第⼀⾃由度为n1和第⼆⾃由度为n2的F分布χ2分布的临界值tα(n) t分布的临界值Fα(n1，n2) F分布的临界值其它符号意义[x] 不超过x的最⼤整数a ( mod n )⽤n除a所得的余数（n∈N，a∈N）e极限，⾃然对数的底经济学函数y= f(x)的弹性⊥直线或线段的垂直∥直线或线段的平⾏。

(完整word版)梯度,散度,旋度以及其混合运算的简单应用与物理含义

梯度、散度和旋度是矢量分析里的重要概念。

之所以是“分析”，因为三者是三种偏导数计算形式.这里假设读者已经了解了三者的定义。

它们的符号分别记作如下:从符号中可以获得这样的信息：①求梯度是针对一个标量函数，求梯度的结果是得到一个矢量函数。

这里φ称为势函数；②求散度则是针对一个矢量函数，得到的结果是一个标量函数，跟求梯度是反一下的；③求旋度是针对一个矢量函数,得到的还是一个矢量函数.这三种关系可以从定义式很直观地看出，因此可以求“梯度的散度"、“散度的梯度"、“梯度的旋度"、“旋度的散度"和“旋度的旋度”，只有旋度可以连续作用两次,而一维波动方程具有如下的形式（1）其中a为一实数,于是可以设想，对于一个矢量函数来说,要求得它的波动方程,只有求它的“旋度的旋度”才能得到。

下面先给出梯度、散度和旋度的计算式：（2)(3）（4)旋度公式略显复杂.这里结合麦克斯韦电磁场理论，来讨论前面几个“X度的X度”。

I。

梯度的散度：根据麦克斯韦方程有：而（5)则电势的梯度的散度为这是一个三维空间上的标量函数，常记作(6）称为泊松方程，而算符▽2称为拉普拉斯算符.事实上因为定义所以有当然，这只是一种记忆方式。

当空间内无电荷分布时,即ρ=0,则称为拉普拉斯方程当我们仅需要考虑一维情况时,比如电荷均匀分布的无限大平行板电容器之间（不包含极板）的电场，我们知道该电场只有一个指向,场强处处相等,于是该电场满足一维拉普拉斯方程，即这就是说如果那边平行板电容器的负极板接地,则板间一点处的电压与该点距负极板的距离呈线性关系。

II.散度的梯度：散度的梯度，从上面的公式中可以看到结果会比较复杂，但是它的物理意义却是很明确的，因为从麦克斯韦方程可以看出空间某点处电场的散度是该点处的电荷密度，那么再求梯度就是空间中电荷密度的梯度.这就好比说清水中滴入一滴红墨水,起初水面红色浓度最高，杯底浓度最低，这样水面与杯底形成一个浓度梯度，红墨水由水面向杯底扩散，最后均匀。

小学,初中,高中数学符号

小学，初中，高中数学符号运算符：± × ÷∶∫ ∮≡ ≌≈ ∸∝≈ ≠ ≡ ≤ ≥ ≤ ≥ ≮≯／√ ‰ ∑ ∏ ＆关系运算符：∧∨集合符号：∪∩ ∈∣⊆序号：≳≴≵≶≷≸≹≺≻≼ⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹ≈ 一二三四五六七八九十其它：～± × ‚ ∑ ∪∩ ∈√ ‖∠≰≡ ≌≈∸≠ ≮≯≤≥ ∞ ∵∴♂ ♀ ℃｟‰ ☆★○ ● ◎◇◆□ ■ △▲→ ⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫ＊∏ α β γ δ ε δε ζ η θ ι κ μ ν π ξ ζ ηυ θ χ ψ ωΑ Β Γ Γ Δ Ε Ζ Θ Η Κ ∧Μ Ν Ξ Ο ∏ Ρ ∑ Τ Υ Φ Φ Χ Ψ α β γ δ ε δ ε ζ η θ ι κ λ μ ν π ξ ζ η υ θ χ ψ ω← ↑ → ↓ ↖↗↘↙∞ ∴∵∶∷° ′ 〃℃⊕⊿△≰∠≲≱‖〓〔〈〉《》「」『』〕〖【】（）〓〔｛｝ⅼ§ № ※＃＆＠☆★○ ● ◎△▲ ◇◆□ ■ 〒◣◥◤◢♀ ♂←↑→↓↖↗↘↙∈∏∑≱⊿∕√∝∞∟∠∣‖∧∨∩∪∫∮∴∵∶∷∸≈≌≈≠≡≤≥≤≥≮≯＃＆＊＋－＜＞＝﹨＄％＠！？！”＃＄％＆’＊＼＾＿‘｜～｟｠ⅺ｡ⅻ｢⊕≰≲▔▕■□▲△▼▽◆◇○◎●◢◣◤◥★☆≰♀♂、。

〃〆〇〒〒”〃＊╳×±·＋，－．／（）｛｝〓〔【】《》＾〉「」『』﹍（）（）｛｝＜＞〓〔〓〔〓〔｛｝〈〉《》「」『』【】〕〖ΑΒΓΓΔΕΖΘΗΚ∧ΜΝΞΟ∏Ρ∑ΤΥΦΦΧΨαβγδεδεζηθικλμνπξζηυθχψωАБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЪЫЬЭЮЯЁабвгдежзийклмнопрстуфхцчшщъыьэюяѐa（≤ A 表示a为A的子集；A ≥）a 表示A包含a；a（＜A 表示a为A的真子集；A ＞）a 表示a为A的真子集；∑(n=p,q)f(n) 表示f(n)的n从p到q逐步变化对f(n)的连加和，如果f(n)是有结构式，f(n)应外引括号；∑(n=p,q ; r=s,t)f(n,r) 表示∑(r=s,t)[∑(n=p,q)f(n,r)],如果f(n，r)是有结构式，f(n，r)应外引括号；∏(n=p,q)f(n) 表示f(n)的n从p到q逐步变化对f(n)的连乘积, 如果f(n)是有结构式，f(n)应外引括号；∏(n=p,q ; r=s,t)f(n,r) 表示∏(r=s,t)[∏(n=p,q)f(n,r)],如果f(n，r)是有结构式，f(n，r)应外引括号；lim(x→u)f(x) 表示f(x) 的x 趋向u 时的极限,如果f(x)是有结构式，f(x)应外引括号；lim(y→v ; x→u)f(x,y) 表示lim(y→v)[lim(x→u)f(x,y)],如果f(x，y)是有结构式，f(x，y)应外引括号；∫(a,b)f(x)dx 表示对f(x) 从x=a 至x=b 的积分,如果f(x)是有结构式，f(x)应外引括号；∫(c,d ; a,b)f(x,y)dxdy 表示∫(c,d)[∫(a,b)f(x,y)dx]dy,如果f(x，y)是有结构式，f(x，y)应外引括号；∫(L)f(x,y)ds 表示f(x,y) 在曲线L 上的积分,如果f(x，y)是有结构式，f(x，y)应外引括号；∫∫(D)f(x,y,z)dζ 表示f(x,y,z) 在曲面D 上的积分,如果f(x，y，z)是有结构式，f(x，y，z)应外引括号；∮(L)f(x,y)ds 表示f(x,y) 在闭曲线L 上的积分,如果f(x，y)是有结构式，f(x，y)应外引括号；∮∮(D)f(x,y,z)dζ 表示f(x,y,z) 在闭曲面D 上的积分,如果f(x，y)是有结构式，f(x，y)应外引括号；∪(n=p,q)A(n) 表示n从p到q之A(n)的并集，如果A(n)是有结构式，A(n)应外引括号；∪(n=p,q ; r=s,t)A(n,r) 表示∪(r=s,t)[∪(n=p,q)A(n,r)],如果A(n，r)是有结构式，A(n，r)应外引括号；∩(n=p,q)A(n) 表示n从p到q逐步变化对A(n)的交集,如果A(n)是有结构式，A(n)应外引括号；∩(n=p,q ; r=s,t)A(n,r) 表示∩(r=s,t)[∩(n=p,q)A(n,r)],如果A(n，r)是有结构式，A(n，r)应外引括号；回答者：蓝伞- 大魔法师八级2009-9-7 12:00符号意义∞ 无穷大π 圆周率|x| 绝对值∪并集∩ 交集≥ 大于等于≤ 小于等于≡ 恒等于或同余ln(x) 以e为底的对数lg(x) 以10为底的对数floor(x) 上取整函数ceil(x) 下取整函数x mod y 求余数x - floor(x) 小数部分∫f(x)dx 不定积分∫[a:b]f(x)dx a到b的定积分>>远远大于号<<远远小于号⊆包括≰圆θ 直径β 贝塔回答者：_masquerade - 魔法师五级2009-9-7 12:00运算符：± × ÷∶∫ ∮≡ ≌≈ ∸∝≈ ≠ ≡ ≤ ≥ ≤ ≥ ≮≯／√ ‰ ∑ ∏ ＆关系运算符：∧∨集合符号：∪∩ ∈∣⊆序号：≳≴≵≶≷≸≹≺≻≼ⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹ≈ 一二三四五六七八九十参考资料：如果您的回答是从其他地方引用，请表明出处回答者：xiongxyt2 - 助理二级2009-9-7 12:01运算符：± × ÷∶∫ ∮≡ ≌≈ ∸∝≈ ≠ ≡ ≤ ≥ ≤ ≥ ≮≯／√ ‰ ∑ ∏ ＆关系运算符：∧∨集合符号：∪∩ ∈∣⊆序号：≳≴≵≶≷≸≹≺≻≼ⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫⅰⅱⅲⅳⅴⅵⅶⅷⅸⅹ≈ 一二三四五六七八九十其它：～± × ‚ ∑ ∪∩ ∈√ ‖∠≰≡ ≌≈ ∸≠ ≮≯≤≥ ∞ ∵∴♂ ♀ ℃｟‰ ☆★○ ● ◎◇◆□ ■ △▲→ ⅠⅡⅢⅣⅤⅥⅦⅧⅨⅩⅪⅫ＊∏ α β γ δ ε δε ζ η θ ι κ μ ν π ξ ζ ηυ θ χ ψ ωΑ Β Γ Γ Δ Ε Ζ Θ Η Κ ∧Μ Ν Ξ Ο ∏ Ρ ∑ Τ Υ Φ Φ Χ Ψ α β γ δ ε δ ε ζ η θ ι κ λ μ ν π ξ ζ η υ θ χ ψ ω← ↑ → ↓ ↖↗↘↙∞ ∴∵∶∷° ′ 〃℃⊕⊿△≰∠≲≱‖〓〔〈〉《》「」『』〕〖【】（）〓〔｛｝ⅼ§ № ※＃＆＠☆★○ ● ◎△▲ ◇◆□ ■ 〒◣◥◤◢♀ ♂←↑→↓↖↗↘↙∈∏∑≱⊿∕√∝∞∟∠∣‖∧∨∩∪∫∮∴∵∶∷∸≈≌≈≠≡≤≥≤≥≮≯＃＆＊＋－＜＞＝﹨＄％＠！？！”＃＄％＆’＊＼＾＿‘｜～｟｠ⅺ｡ⅻ｢⊕≰≲▔▕■□▲△▼▽◆◇○◎●◢◣◤◥★☆≰♀♂、。

(完整word版)高中数学符号意义

(完整word版)高数符号大全

(完整word版)高中数学公式及知识点总结大全(精华版)

(完整word版)高中数学公式及知识点总结大全(精华版)

(完整word版)物理公式和符号汇总(word文档良心出品)

高中数学 第二章 数与符号 2.3 数学符号课件 北师大版

(word版)人教版高中数学知识点汇总,文档

(完整word)高等数学符号

(完整word版)向量的点乘和叉乘,以及几何意义

(完整word版)高中数学必修三知识点总结

完整word版高数符号大全

(完整word版)高数符号大全

(完整word版)数学符号及读法大全

高中数学公式符号归纳(含无法打出的) (1)

(完整word版)高数符号大全,推荐文档

【高中数学】数学中的符号

【高中数学】常用数学符号大全及意义

（完整word版）高等数学符号

(完整word版)梯度,散度,旋度以及其混合运算的简单应用与物理含义

小学,初中,高中数学符号

高中数学第二章数与符号 2.3 数学符号课件北师大版