深圳十年中考数学压轴题汇总
深圳市近10年中考数学试题及答案
6.一件标价为 元的商品,若该商品按八折销售,则该商品的实际售价是( )
A. 元B. 元C. 元D. 元
7.一组数据 , , , , 的方差是( )
A. B. C. D.
8.若 ,则 的值是( )
A. B. C. D.
9.如图2,直线 ,则 的度数是( )
A. B. C. D.
A.百亿位B.亿位C.百万位D.百分位
4.下列图形中,是轴对称图形的为
ABCD
5.下列不等式组的解集,在数轴上表示为如图2所示的是
A. B.
C. D. 图2
6.班主任为了解学生星期六、日在家的学习情况,家访了班内的六位学生,了解到他们
在家的学习时间如下表所示.那么这六位学生学习时间的众数与中位数分别是
∴OC=2 (-2 舍去)
∴线段OC的长为2 ……3分
(2)解:∵△OCA∽△OBC
∴
设AC=k,则BC= k
由AC +BC =AB 得
k +( k) =(6-2)
解得k=2(-2舍去)
∴AC=2,BC=2 =OC……1分
过点C作CD⊥AB于点D
∴OD= OB=3
∴CD=
∴C的坐标为(3, )……2分
A.至多6人B.至少6人C.至多5人D.至少5人
9.如图4,王华晚上由路灯A下的B处走到C处时,测得
影子CD的长为1米,继续往前走3米到达E处时,测
得影子EF的长为2米,已知王华的身高是1.5米,那么
路灯A的高度AB等于
A.4.5米B.6米
C.7.2米D.8米
图4
10.如图5,在□ABCD中,AB:AD = 3:2,∠ADB=60系式.
解:
深圳历年中考数学压轴题(选择题)(1)(1)

深圳历年中考数学压轴题(选择题20)1.二次函数2(0)y ax bx c a =++≠的图像如图1所示,则下列结论正确的是( )A .0abc >B .20a b +<C .30a c +<D .方程230ax bx c ++-=有两个不相等的实数根2.如图2,A 、B 是反比例函数12y x=图像上的两点,过点A 作x 轴的平行线,过点B 作y 轴的平行线,交于点P ,连接OA 、OB 、AB ,则下列说法正确的是( ) ①AOP BOP ∆≅∆;②AOP BOP S S ∆∆=;③若OA OB =,则OP 平分AOB ∠;④若4BOP S ∆=,则16PAB S ∆= A .①③ B .②③ C .②④ D .③④3.如图3,在扇形AOB 中∠AOB=90°,正方形CDEF 的顶点C 是的中点,点D 在OB 上, 点E 在OB 的延长线上,当正方形CDEF 的边长为2时,则阴影部分的面积为( )A .2π﹣4B .4π﹣8C .2π﹣8D .4π﹣4图3 图44.如图4,CB=CA ,∠ACB=90°,点D 在边BC 上(与B 、C 不重合),四边形ADEF 为正方形,过点F 作FG ⊥CA ,交CA 的延长线于点G ,连接FB ,交DE 于点Q ,给出以下结论:①AC=FG ;②S △FAB :S 四边形CBFG =1:2;③∠ABC=∠ABF ;④AD 2=FQ •AC , 其中正确的结论的个数是( )A .1B .2C .3D .45.如图5,已知正方形ABCD的边长为12,BE=EC,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①△ADG≌△FDG;②GB=2AG;③△GDE∽△BEF;④S△BEF=.在以上4个结论中,正确的有()(图5)A.1 B.2 C.3 D.46.二次函数y=ax2+bx+c图象如图6,下列正确的个数为()①bc>0;②2a﹣3c<0;③2a+b>0;④ax2+bx+c=0有两个解x1,x2,当x1>x2时,x1>0,x2<0;⑤a+b+c>0;⑥当x>1时,y随x增大而减小.(图6)A.2 B.3 C.4 D.57.如图7,已知四边形ABCD为等腰梯形,AD∥BC,AB=CD,AD=,E为CD中点,连接AE,且AE=2,∠DAE=30°,作AE⊥AF交BC于F,则BF=()(图7)(图8)A.1 B.3﹣C.﹣1 D.4﹣28.如图8,已知l1∥l2∥l3,相邻两条平行直线间的距离相等,若等腰直角△ABC的三个顶点分别在这三条平行直线上,则sinα的值是()A.B.C.D.9.如图9,⊙C过原点,且与两坐标轴分别交于点A、点B,点A的坐标为(0,3),M是第三象限内上一点,∠BMO=120°,则⊙C的半径长为()A.6 B.5 C.3 D.3(图9)(图10)10.如图10,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A6B6A7的边长为()A.6 B.12 C.32 D.6411.如图11,△ABC与△DEF均为等边三角形,O为BC、EF的中点,则AD:BE的值为()(图11)(图12)A.:1 B.:1 C.5:3 D.不确定12.如图12,点P(3a,a)是反比例函数y=(k>0)与⊙O的一个交点,图中阴影部分的面积为10π,则反比例函数的解析式为()A.y=B.y=C.y=D.y=13.如图13,已知点A,B,C,D均在已知圆上,AD∥BC,AC平分∠BCD,∠ADC=120°,四边形ABCD的周长为10cm.图中阴影部分的面积为()(图13)(图14)A.cm2B.(π﹣)cm2C.cm2D.cm214.如图14,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的弧EF上时,弧BC的长度等于()A.B.C.D.15.如图15,在▱ABCD中,AB:AD=3:2,∠ADB=60°,那么cos∠A的值等于()A.B.C.D.(图15)(图16)16.如图16,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是()A.π﹣B.πC.π﹣D.π17.如图17,⊙O的两弦AB、CD相交于点M,AB=8cm,M是AB的中点,CM:MD=1:4,则CD=()A.12cm B.10cm C.8cm D.5cm(图17)(图18)18.如图18,圆内接四边形ABCD中,AC平分∠BAD,EF切圆于C,若∠BCD=120°,则∠BCE=()A.30°B.40°C.45°D.60°19.如图19,抛物线过点A(2,0)、B(6,0)、C(1,),平行于x轴的直线CD交抛物线于点C、D,以AB为直径的圆交直线CD于点E、F,则CE+FD的值是()A.2 B.4 C.5 D.6(如图19)(如图20)20.如图20,直线l1∥l2,AF:FB=2:3,BC:CD=2:1,则AE:EC是()A.5:2 B.4:1 C.2:1 D.3:2。
深圳深圳市教苑中学中考数学期末几何综合压轴题易错汇编

深圳深圳市教苑中学中考数学期末几何综合压轴题易错汇编一、中考数学几何综合压轴题1.(探究函数y=x+的图象与性质)(1)函数y=x+的自变量x的取值范围是;(2)下列四个函数图象中函数y=x+的图象大致是;(3)对于函数y=x+,求当x>0时,y的取值范围.请将下列的求解过程补充完整.解:∵x>0∴y=x+=()2+()2=(﹣)2+∵(﹣)2≥0∴y≥.[拓展运用](4)若函数y=,则y的取值范围.解析:(1)x≠0;(2)C(3)4;4;(4)y≥13【解析】试题分析:根据反比例函数的性质,一次函数的性质;二次函数的性质解答即可.试题解析:(1)函数y=x+的自变量x的取值范围是x≠0;(2)函数y=x+的图象大致是C;(3)解:∵x>0∴y=x+=()2+()2=(﹣)2+4∵(﹣)2≥0∴y≥4. (4)y==x+﹣5═()2+()2﹣5=(+)2+13∵(﹣)2≥0,∴y≥13.考点:1.反比例函数的性质;一次函数的性质;二次函数的性质. 2.问题背景 如图1,点E 在BC 上,AB ⊥BC ,AE ⊥ED ,DC ⊥DC ,求证:=AE BEDE DC.尝试应用 如图2,在▱ABCD 中,点F 在DC 边上,将△ADF 沿AF 折叠得到△AEF ,且点E 恰好为BC 边的中点,求FCFD的值. 拓展创新 如图3,在菱形ABCD 中,点E ,F 分别在BC ,DC 边上,∠AFE =∠D ,AE ⊥FE ,FC =2.EC =6.请直接写出cos ∠AFE 的值. 解析:(1)见解析;(2)12FC FD =;(3)cos ∠AFE =25.【分析】(1) 根据相似三角形的判定定理证△ABE ∽△ECD 即可;(2) 在AB 边取点G ,使GE =BE ,则∠B =∠BGE ,证△AGE ∽△ECF ,列比例式即可; (3) 作FM =FD ,FN ⊥AD ,同(2)构造△AMF ∽△FCE ,证△AEF ∽△FHD ,求出AM 长即可. 【详解】解:(1)∵ AB ⊥BC ,AE ⊥ED ,DC ⊥DC∴∠B =∠C =90° ,∠BAE +∠AEB =90°,∠CED +∠AEB =90°, ∴∠BAE =∠CED , ∴△ABE ∽△ECD ∴AE BEDE DC=. (2)在AB 边取点G ,使GE =BE ,则∠B =∠BGE又∵∠B +∠C =180° ,∠BGE +∠AGE =180° ∴∠AGE =∠C ∵∠B =∠D =∠AEF又∵∠B +∠BAE =∠AEF +∠FEC ∴∠BAE =∠FEC , ∴△AGE ∽△ECF ∴FC EF EG AE =,即FC EGEF AE=∵EF =FD , ∴FC EGFD AE= ∵GE =BE ,AE =BC =2BE , ∴12FC BE FD BC == (3)cos ∠AFE =25如图:作FM =FD ,FN ⊥AD ,由(2)同理可证△AMF ∽△FCE , ∴3FM ECAM FC== 设AM =x ,FM =FD =3x ,则AD =CD =32x +,MD =22x +,ND =1x + ∵∠AEF =∠FND =90°,∠AFE =∠D , ∴△AEF ∽△FND , ∴EF AF ND FD =,即EF NDAF FD =, ∵FC EF AM AF=,FC NDAM FD∴= ∴213x x x+=,解得,5x =,经检验,是原方程的解; ∴ cos ∠AFE =25EF FC AF AM ==. 【点睛】本题考查了相似三角形的判定与性质和解直角三角形,解题关键是依据已知条件构造相似三角形,列比例式解决问题.3.定义:有一组对角互补的四边形叫做“对补四边形”,例如,四边形ABCD 中,若180A C ∠+∠=︒或180B D ∠+∠=︒,则四边形ABCD 是“对补四边形”.(概念理解)(1)如图1,四边形ABCD 是“对补四边形”. ①若::3:2:1A B C ∠∠∠=,则D ∠=________;②若90B ∠=︒.且3,2AB AD ==时.则22CD CB -=_______; (拓展提升)(2)如图,四边形ABCD 是“对补四边形”,当AB CB =,且12EBF ABC ∠=∠时,图中,,AB CF EF 之间的数量关系是 ,并证明这种关系;(类比应用)(3)如图3,在四边形ABCD 中,,AB CB BD =平分ADC ∠; ①求证:四边形ABCD 是“对补四边形”; ②如图4,连接AC ,当90ABC ∠=︒,且12ACD ABCS S=时,求tan ACD ∠的值. 解析:(1)①90︒,②5;(2)AE CF EF +=,理由见解析;(3)①见解析,②23 【分析】(1)①根据“对补四边形”的定义,结合::3:2:1A B C ∠∠∠=,即可求得答案; ②根据“对补四边形”的定义,由90B ∠=︒,得D ∠90=︒,再利用勾股定理即可求得答案;(2)延长EA 至点K ,使得AK CF =,连接BK ,根据“对补四边形”的定义,可证明ABK CBF △≌△,继而证明BEK BEF △≌△,从而可得结论;(3)①过点B 作BM AD ⊥于点M ,BN AC ⊥于点N ,则90BMA BNC ∠=∠=︒,可证Rt ABM Rt CBN △≌△,进而可证四边形ABCD 是“对补四边形”;②设,AD a DC b ==,则tan aACD b∠=根据222AC a b =+,再运用12ACD ABCS S=建立方程,解方程即可求得tan ACD ∠. 【详解】 (1)::3:2:1A B C ∠∠∠=,设3,2,A x B x C x ∠=∠=∠=, 根据“对补四边形”的定义, 180A C ∠+∠=︒,即3180x x +=︒, 解得45x =︒,290B x ∴∠==︒,180B D ∠+∠=︒,90D ∴∠=︒.故答案为:90︒. ②如图1,连接AC ,90B ∠=︒,180B D ∠+∠=︒,90D ∴∠=︒,在Rt ABC 中22BC AC AB =-, 在Rt ADC 中222CD AC AD =-,22222222()CD CB AC AD AC AB AB AD ∴-=---=-, 3,2AB AD ==,2222325CD CB ∴-=-=,故答案为:5.(2)AE CF EF +=,理由如下:如图2,延长EA 至点K ,使得AK CF =,连接BK ,四边形ABCD 是“对补四边形”,∴180BAD C ∠+∠=︒,180BAK BAD ∠+∠=︒,∴BAK C ∠=∠,,AK CF AB CB ==,∴()ABK CBF SAS △≌△,∴,ABK CBF BK BF ∠=∠=, ∴ABK ABF CBF ABF ∠+∠=∠+∠,即KBF ABC ∠=∠,12EBF ABC ∠=∠,∴12EBF KBF ∠=∠, ∴EBK EBF ∠=∠,,BK BF BE BE ==,∴()BEK BEF SAS △≌△, ∴EK EF =,∴AE CF AE AK EK EF +=+==,即AE CF EF +=, 故答案为:AE CF EF +=.(3)①证明:如图3,过点B 作BM AD ⊥于点M ,BN AC ⊥于点N ,则90BMA BNC ∠=∠=︒,BD 平分ADC ∠,BM BN ∴=,AB CB =,()Rt ABM Rt CBN HL ∴△≌△,BAM C ∴∠=∠, 180BAM BAD ∠+∠=︒,180C BAD ∴∠+∠=︒,BAD ∴∠与C ∠互补,∴四边形ABCD 是“对补四边形”;②由①可知四边形ABCD 是“对补四边形”, 180ABC ADC ∴∠+∠=︒,90ABC ∠=︒,90ADC ∴∠=︒,设AD a DC b ==,,则22222AC AD CD a b =+=+, AB BC =,2222211()22AB BC AC a b ∴===+, 1122ACD S AD CD ab ∴=⋅=△, 222111()224ABC S AB BC AB a b =⋅==+△,12ACD ABCS S=, 22112=12()4ab a b ∴+,整理得:2()410a ab b-⨯+=,解得:2ab= 在Rt ABC 中,tan a ACD b∠=,∴tan ACD∠=2.【点睛】本题考查了勾股定理,四边形内角和定理,全等三角形的性质与判定,解一元二次方程,三角函数的定义等知识,熟练掌握勾股定理和全等三角形的判定和性质,准确理解新定义是解题的关键.4.(问题情境)如图1,点E 是平行四边形ABCD 的边AD 上一点,连接BE 、CE .求证:BCE1S2=S 平行四边形ABCD .(说明:S 表示面积) 请以“问题情境”为基础,继续下面的探究(探究应用1)如图2,以平行四边形ABCD 的边AD 为直径作⊙O ,⊙O 与BC 边相切于点H ,与BD 相交于点M .若AD =6,BD =y ,AM =x ,试求y 与x 之间的函数关系式. (探究应用2)如图3,在图1的基础上,点F 在CD 上,连接AF 、BF ,AF 与CE 相交于点G ,若AF =CE ,求证:BG 平分∠AGC .(迁移拓展)如图4,平行四边形ABCD 中,AB :BC =4:3,∠ABC =120°,E 是AB 的中点,F 在BC 上,且BF :FC =2:1,过D 分别作DG ⊥AF 于G ,DH ⊥CE 于H ,请直接写出DG :DH 的值.解析:【问题情境】见解析;【探究应用1】18y x=;【探究应用2】见解析;【迁移拓1927 【分析】(1)作EF ⊥BC 于F ,则S △BCE =12BC×EF ,S 平行四边形ABCD =BC×EF ,即可得出结论; (2)连接OH ,由切线的性质得出OH ⊥BC ,OH =12AD =3,求出平行四边形ABCD 的面积=AD×OH =18,由圆周角定理得出AM ⊥BD ,得出△ABD 的面积=12BD×AM =12平行四边形的面积=9,即可得出结果;(3)作BM ⊥AF 于M ,BN ⊥CE 于N ,同图1得:△ABF 的面积=△BCE 的面积=12平行四边形ABCD 的面积,得出12AF×BM =12CE×BN ,证出BM =BN ,即可得出BG 平分∠AGC .(4)作AP ⊥BC 于P ,EQ ⊥BC 于Q ,由平行四边形的性质得出∠ABP =60°,得出∠BAP =30°,设AB =4x ,则BC =3x ,由直角三角形的性质得出BP =12AB =2x ,BQ =12BE ,AP =3=3,由已知得出BE =2x ,BF =2x ,得出BQ =x ,EQ 3,PF =4x ,QF =3x ,QC =4x ,由勾股定理求出AF 22AP PF +=7,CE 22EQ QC +19,连接DF 、DE ,由三角形的面积关系得出AF×DG =CE×DH ,即可得出结果. 【详解】(1)证明:作EF ⊥BC 于F ,如图1所示: 则S △BCE =12BC×EF ,S 平行四边形ABCD =BC×EF ,∴12BCEABCDSS =.(2)解:连接OH ,如图2所示: ∵⊙O 与BC 边相切于点H , ∴OH ⊥BC ,OH =12AD =3,∴平行四边形ABCD 的面积=AD×OH =6×3=18, ∵AD 是⊙O 的直径, ∴∠AMD =90°, ∴AM ⊥BD ,∴△ABD 的面积=12BD×AM =12平行四边形的面积=9, 即12xy =9,∴y 与x 之间的函数关系式y =18x; (3)证明:作BM ⊥AF 于M ,BN ⊥CE 于N ,如图3所示:同图1得:△ABF 的面积=△BCE 的面积=12平行四边形ABCD 的面积, ∴12AF×BM =12CE×BN ,∵AF =CE , ∴BM =BN , ∴BG 平分∠AGC .(4)解:作AP ⊥BC 于P ,EQ ⊥BC 于Q ,如图4所示: ∵平行四边形ABCD 中,AB :BC =4:3,∠ABC =120°, ∴∠ABP =60°,∴∠BAP =30°,设AB =4x ,则BC =3x ,∴BP =12AB =2x ,BQ =12BE ,AP =, ∵E 是AB 的中点,F 在BC 上,且BF :FC =2:1, ∴BE =2x ,BF =2x , ∴BQ =x ,∴EQ ,PF =4x ,QF =3x ,QC =4x ,由勾股定理得:AF =,CE , 连接DF 、DE ,则△CDE 的面积=△ADF 的面积=12平行四边形ABCD 的面积, ∴AF×DG =CE×DH ,∴DG :DH =CE :AF :=【点睛】本题是圆的综合题目,考查了圆周角定理、平行四边形的性质、三角形面积公式、含30°角的直角三角形的性质、勾股定理、角平分线的判定等知识;本题综合性强,需要添加辅助线,熟练掌握平行四边形的性质和勾股定理是解题的关键.5.(感知)如图1,在平面直角坐标系中,点C 的坐标为(0,0.5),点A 的坐标为(1,0),将线段CA 绕着点C 按逆时针方向旋转90︒至线段CB ,过点B 作BM y ⊥轴,垂足为点M ,易知AOC CMB ∆∆≌,得到点B 的坐标为(0.5,1.5).(探究)如图2,在平面直角坐标系中,点A 的坐标为(1,0),点C 的坐标为(0,)(0)m m >,将线段CA 绕着点C 按逆时针方向旋转90︒至线段CB . (1)求点B 的坐标.(用含m 的代数式表示) (2)求出BC 所在直线的函数表达式.(拓展)如图3,在平面直角坐标系中,点A 的坐标为(1,0),点C 在y 轴上,将线段CA 绕着点C 按逆时针方向旋转90︒至线段CB ,连结BO 、BA ,则BO BA +的最小值为_______.解析:【探究】(1)点B 坐标为(,1)m m +;(2)1y x m m=+5 【分析】探究:(1)证明△AOC ≌△CMB (AAS ),即可求解;(2)根据点B 的坐标为(m ,m+1),点C 坐标()0,m ,即可求解;拓展:BO+BA=2222(1)(1)(1)m m m m +++-++,BO+BA 的值,相当于求点P (m ,m )到点M (1,-1)和点N (0,-1)的最小值,即可求解.【详解】解:探究:(1)过点B 作BM y ⊥轴,垂足为点M .BMC 90∠∴=︒,MCB B 90∠∠∴+=︒.线段CA 绕着点C 按逆时针方向旋转90︒至线段CB ,BCA 90CB CA ∠∴=︒=,.MCB ACO 90∠∠∴+=︒.B ACO ∠∠∴=.ACO 90∠=︒,ΔAOC ΔCMB ∴≌,MC OA,MB OC ∴==.点C 坐标()0,m ,点A 坐标()1,0,∴点B 坐标为()m,m 1+(2)∵点B 的坐标为(m ,m+1),点C 为(0,m ),设直线BC 为:y=kx+b ,1b m km b m =⎧⎨+=+⎩,解得:1k m b m⎧=⎪⎨⎪=⎩, ∴1y x m m=+; 则BC 所在的直线为:1y x m m =+; 拓展:如图作BH ⊥OH 于H .设点C 的坐标为(0,m ),由(1)知:OC=HB=m ,OA=HC=1,则点B (m ,1+m ),则:BO+BA=2222(1)(1)(1)m m m m +++-++,BO+BA 的值,相当于求点P (m ,m )到点M (1,-1)和点N (0,-1)的最小值,相当于在直线y=x 上寻找一点P (m ,m ),使得点P 到M (0,-1),到N (1,-1)的距离和最小,作M 关于直线y=x 的对称点M′(-1,0),易知PM+PN=PM′+PN≥NM′,22(11)(01)5--++故:BO+BA 55【点睛】本题为一次函数综合题,主要考查的是三角形全等的思维拓展,其中拓展,将BO+BA 的值转化点P (m ,m )到点M (1,-1)和点N (0,-1)的最小值,是本题的新颖点 6.综合与实践(1)(探索发现)在ABC ∆中. AC BC =,ACB α∠=,点D 为直线BC 上一动点(点D 不与点B ,C 重合),过点D 作//DF AC 交直线AB 于点F ,将AD 绕点D 顺时针旋转α得到ED ,连接BE .如图(1),当点D 在线段BC 上,且90α=︒时,试猜想:①AF 与BE 之间的数量关系:______;②ABE ∠=______.(2)(拓展探究)如图(2),当点D 在线段BC 上,且090α︒<<︒时,判断AF 与BE 之间的数量关系及ABE ∠的度数,请说明理由.(3)(解决问题)如图(3),在ABC ∆中,AC BC =,4AB =,ACB α∠=,点D 在射线BC 上,将AD 绕点D 顺时针旋转α得到ED ,连接BE .当3BD CD =时,直接写出BE 的长.解析:(1)①AF BE =;②90︒;(2)AF BE =,ABE α∠=.理由见解析;(3)BE 的长为1或2.【分析】(1)由“SAS”△ADF ≌△EDB ,可得AF=BE ,再利用“8字型”字母∠OBE=∠ADO=90°即可解决问题;(2)结论:AF=BF ,∠ABE=a .由“SAS”△ADF ≌△EDB ,即可解决问题;(3)分当点D 在线段BC 上和当点D 在BC 的延长线上两种情形讨论,利用平行线分线段成比例可求解.【详解】解:(1)如图1中,设AB 交DE 于O .∵∠ACB=90°,AC=BC ,∴∠ABC=45°,∵DF ∥AC ,∴∠FDB=∠C=90°,∴∠DFB=∠DBF=45°,∴DF=DB ,∵∠ADE=∠FDB=90°,∴∠ADF=∠EDB ,且DA=DE ,DF=DB∴△ADF ≌△EDB (SAS ),∴AF=BE ,∠DAF=∠E ,∵∠AOD=∠EOB ,∴∠ABE=∠ADO=90°故答案为AF=BE ,90°.(2)AF BE =,ABE α∠=.理由:∵//DF AC ,∴FDB ACB α∠=∠=,CAB DFB ∠=∠.∵AC BC =,∴ABC CAB ∠=∠.∴ABC DFB ∠=∠.∴DB DF =∵ADE FDB α∠==∠,ADF ADE FDE ∠=∠-∠,EDB FDB FDE ∠=∠-∠,∴ADF EDB ∠=∠.又∵AD DE =,∴ADF EDB ∆≅∆.∴AF BE =,AFD EBD ∠=∠.∴AFD ABC FDB ∠=∠+∠,DBE ABD ABE ∠=∠+∠,∴ABE FDB α∠=∠=.(3)1或2.解:当点D 在线段BC 上时,过点D 作//DF AC 交直线AB 于点F ,如图(1).∵//DF AC ,∴3BF BD AF CD==. ∵4AB BF AF =+=,∴1AF =.∵//DF AC ,∴BDF C ADE α∠=∠=∠=,DFB CAB ∠=∠.∵ADF ADE FDE ∠=∠-∠,EDB FDB FDE ∠=∠-∠,∴ADF EDB ∠=∠.∵AC BC =,∴CAB CBA ∠=∠.∴DFB DBF ∠=∠.∴DF DB =.又AD DE =,∴ADF EDB ∆≅∆,1BE AF ==.当点D 在线段BC 的延长线上时,过点D 作//DF AC '交BA 的延长线于点F ',如图(2). ∵//DF AC ', ∴2AB BC AF CD=='. ∴24AB AF '==.∴2AF '=.同理可得2BE AF '==.综上可得,BE 的长为1或2.【点睛】本题考查几何变换综合题、等腰三角形的性质、全等三角形的判定和性质、平行线分线段成比例定理等知识,解题的关键是正确寻找全等三角形解决问题,属于中考压轴题.7.(1)探究发现:下面是一道例题及解答过程,请补充完整:如图①在等边△ABC内部,有一点P,若∠APB=150°,求证:AP2+BP2=CP2证明:将△APC绕A点逆时针旋转60°,得到△AP’B,连接PP’,则△APP’为等边三角形∴∠APP’=60° ,PA=PP’ ,PC=∵∠APB=150°,∴∠BPP’=90°∴P’P2+BP2= ,即PA2+PB2=PC2(2)类比延伸:如图②在等腰△ABC中,∠BAC=90°,内部有一点P,若∠APB=135°,试判断线段PA,PB,PC之间的数量关系,并证明.(3)联想拓展:如图③在△ABC中,∠BAC=120°,AB=AC,点P在直线AB上方,且∠APB=60°,满足(kPA)2+PB2=PC2(其中k>0),请直接写出k的值.解析:(1)P’B,P’B2;(2)2PA2+PB2=PC2,见解析;(3)3【分析】(1)根据旋转的性质和勾股定理直接写出即可.(2)将△APC绕A点逆时针旋转90°,得到△AP′B,连接PP′,论证PP′=2PA,再根据勾股定理代换即可.(3)将△APC 绕A点顺时针旋转120°得到△AP′B,连接PP′,过点A作AH⊥PP′,论证3,再根据勾股定理代换即可.【详解】(1)PC=P’B,P’P2+BP2=P’B2(2)关系式为:2PA2+PB2=PC2证明:将△APC 绕A 点逆时针旋转90°,得到△AP’B ,连接PP’,则△APP’为等腰直角三角形,∴∠APP’=45°,PP’=2PA ,PC=P’B ,∵∠APB=135°,∴∠BPP’=90°,∴P’P 2+BP 2=P’B 2,∴2PA 2+PB 2=PC 2.(3)k=3将△APC 绕点A 顺时针旋转120°得到△AP’B ,连接PP’,过点A 作AH ⊥PP’,可得303,APP PP PA PC P B '︒''∠===60APB ︒∠=90BPP '︒∴∠=222P P BP P B ''∴+=222(3)PA PB PC ∴+=222()kPA PB PC +=3k ∴=【点睛】本题考查了旋转三角形的问题,掌握旋转的性质、勾股定理是解题的关键.8.问题提出(1)如图①,在△ABC 中,BC =6,D 为BC 上一点,AD =4,则△ABC 面积的最大值是 .问题探究(2)如图②,已知矩形ABCD 的周长为12,求矩形ABCD 面积的最大值. 问题解决(3)如图③,△ABC 是葛叔叔家的菜地示意图,其中AB =30米,BC =40米,AC=50米,现在他想利用周边地的情况,把原来的三角形地拓展成符合条件的面积尽可能大、周长尽可能长的四边形地,用来建鱼塘.已知葛叔叔欲建的鱼塘是四边形ABCD,且满足∠ADC=60°.你认为葛叔叔的想法能否实现?若能,求出这个四边形鱼塘周长的最大值;若不能,请说明理由.解析:(1)12;(2)9;(3)能实现;170(米).【分析】(1)当AD⊥BC时,△ABC的面积最大.(2)由题意矩形邻边之和为6,设矩形的一边为m,另一边为6﹣m,可得S=m(6﹣m)=﹣(m﹣3)2+9,利用二次函数的性质解决问题即可.(3)由题意,AC=100,∠ADC=60°,即点D在优弧ADC上运动,当点D运动到优弧ADC的中点时,四边形鱼塘面积和周长达到最大值,此时△ACD为等边三角形,计算出△ADC的面积和AD的长即可得出这个四边形鱼塘面积和周长的最大值.【详解】(1)如图①中,∵BC=6,AD=4,∴当AD⊥BC时,△ABC的面积最大,最大值=1×6×4=12.2故答案为12.(2)∵矩形的周长为12,∴邻边之和为6,设矩形的一边为m,另一边为6﹣m,∴S=m(6﹣m)=﹣(m﹣3)2+9,∵﹣1<0,∴m=3时,S有最大值,最大值为9.(3)如图③中,∵AC =50米,AB =40米,BC =30米,∴AC 2=AB 2+BC 2∴∠ABC =90°,作△AOC ,使得∠AOC =120°,OA =OC ,以O 为圆心,OA 长为半径画⊙O ,∵∠ADC =60°,∴点D 在优弧ADC 上运动,当点D 是优弧ADC 的中点时,四边形ABCD 面积取得最大值,设D ′是优弧ADC 上任意一点,连接AD ′,CD ′,延长CD ′到F ,使得D ′F =D ′A ,连接AF ,则∠AFC =30°=12∠ADC ,∴点F 在D 为圆心DA 为半径的圆上,∴DF =DA ,∵DF +DC ≥CF ,∴DA +DC ≥D ′A +D ′C ,∴DA +DC +AC ≥D ′A +D ′C +AC ,∴此时四边形ADCB 的周长最大,最大值=40+30+50+50=170(米).答:这个四边形鱼塘周长的最大值为170(米).【点睛】本题主要是最大值的考查,求最大值,常用方法为:(1)利用平方为非负的性质求解;(2)利用三角形两边之和大于第三边求解,在求解过程中,关键在与将要求解的线段集中到一个三角形中9.如图1,在正方形ABCD 中,点,E F 分别在边,AB AD 上,且AE AF =,延长FD 到点G ,使得DG DF =,连接,,EF GE CE .(特例感知)(1)图1中GE 与CE 的数量关系是______________.(结论探索)(2)图2,将图1中的AEF 绕着点A 逆时针旋转()090αα︒<<︒,连接FD 并延长到点G ,使得DC DF =,连接,,GE CE BE ,此时GE 与CE 还存在(1)中的数量关系吗?判断并说明理由.(拓展应用)(3)在(2)的条件下,若5,AB AE ==EFG 是以EF 为直角边的直角三角形时,请直接写出GE 的长.解析:(1) GE ,(2)存在,证明见解析,(3)16或4.【分析】(1)连接GC ,证△CDG ≌△CBE ,得出△GCE 为等腰直角三角形即可;(2)类似(1)的方法,先证△AFD ≌△AEB ,再证△CDG ≌△CBE ,得出△GCE 为等腰直角三角形即可;(3)根据E 、F 是直角顶点分类讨论,结合(2)中结论,利用勾股定理求解即可.【详解】解:(1)连接GC ,∵AE =AF ,AD =AB ,∴DF =BE ,∵DG DF =,∴DG = BE ,∵∠GDC =∠B =90°,DC =BC ,∴△CDG ≌△CBE ,∴CE =CG ,∠GCD =∠ECB ,∵∠ECB +∠DCE =90°,∴∠GCE =∠GCD +∠DCE =90°,∴GE;故答案为:GE ;(2) 存在,连接GC,∵AE=AF,AD=AB,∠FAE=∠DAB=90°,∴∠FAD=∠EAB,∴△FAD≌△EAB,∴FD=EB=GD,∠FDA=∠EBA,∵∠GDC+∠FDA=90°,∠EBC+∠EBA=90°,∴∠GDC=∠EBC,∵DC=BD,∴△CDG≌△CBE,与(1)同理,GE=2CE;(3)当∠FEG=90°时,如图1,因为∠FEA=∠GEC=45°,所以,A、E、C在一条直线上,∵AB=5,∴AC=52,CE=52-32=22,GE=2EC=4;如图2,E在CA延长线上,同理可得,EC=82,GE=2EC=16;当∠EFG=90°时,如图3,∠AFD=∠EFG+∠AFE=135°,由(2)得,∠AFD=∠AEB=135°,DF=BE,所以,B、E、F在一条直线上,作AM⊥EF,垂足为M,∵5,32==AB AE∴EF=6,AM=ME=MF=3,224=-,BM AB AMBE=DF=1,FG=2,22210GE FG EF =+=;如图4,同图3,BE =DF =7,FG =14,EF =6,22258GE FG EF =+=,综上,GE 的长为2581016或4.【点睛】本题考查了旋转的性质、全等三角形的判定与性质、勾股定理和等腰直角三角形的性质,解题关键是恰当的连接辅助线,构造全等三角形;会分类讨论,结合题目前后联系,解决问题.10.如图1,边长为4的正方形与边长为()14a a <<的正方形CFEG 的顶点C 重合,点E 在对角线AC 上.问题发现(1)如图1,AE 与BF 的数量关系为______.类比探究(2)如图2,将正方形CFEG 绕点C 旋转m 度(030m ︒<<︒).请问(1)中的结论还成立吗?若不成立,请说明理由.拓展延伸(3)若F 为BC 的中点,在正方形CFEG 的旋转过程中,当点A ,F ,G 在一条直线上时,线段AG 的长度为______.解析:(1)2AE BF =;(2)成立,见解析;(3)302+或302-【分析】问题发现:证出AB ∥EF ,由平行线分线段成比例定理得出2AE CE BF CF ==,即可得出结论;类比探究:证明△ACE ∽△BCF ,得出2AE AC BF CB==,即可的结论; 拓展延伸:分两种情况,连接CE 交GF 于H ,由正方形的性质得出AB=BC=4,242AC AB ==,2GF CE CF ==,GH=HF=HE=HC ,得出122CF BC ==,22GF CE ==,2HF HE HC ===,由勾股定理求出2230AH AC HC =-=,即可得出答案.【详解】[问题发现]解:2AE BF =,理由如下:∵四边形ABCD 和四边形CFEG 是正方形,∴∠B=∠CFE=90°,∠FCE=∠BCA=45°,CE=2CF ,CE ⊥GF ,∴AB ∥EF ,∴2AE CE BF CF∴==, 2AE BF ∴=;故答案为:2AE BF ∴=;[类比探究]解:上述结论还成立,理由如下:连接CE ,如图2所示:∵∠FCE=∠BCA=45°,∴∠BCF=∠ACE=45°-∠ACF ,在Rt △CEG 和Rt △CBA 中, 2,2CE CF CA CB ==, 2CE CA CF CB∴==, ∴△ACE ∽△BCF , 2AE AC BF CB ∴==, 2AE BF ∴=;[拓展延伸]解:分两种情况:①如图3所示:连接CE 交GF 于H ,∵四边形ABCD 和四边形CFEG 是正方形,∴AB=BC=4,AC=2AB=42,GF=CE=2CF ,HF=HE=HC ,∵点F 为BC 的中点,∴CF=12BC=2,GF=CE=22,GH=HF=HE=HC=2,∴2222(42)(2)30AH AC HC =-=-=,∴302AG AH HG =+=+;②如图4所示:连接CE 交GF 于H ,同①得:2∴2222(42)(2)30AH AC HC --,∴302AG AH HG =-=302302【点睛】本题是四边形综合题目,考查了正方形的性质、旋转的性质、平行线分线段成比例定理、相似三角形的判定与性质、勾股定理等知识;熟练掌握正方形的性质,证明三角形相似是解题的关键.11.问题背景:如图1,在矩形ABCD 中,23AB =,30ABD ∠=︒,点E 是边AB 的中点,过点E 作EF AB ⊥交BD 于点F .实验探究:(1)在一次数学活动中,小王同学将图1中的BEF 绕点B 按逆时针方向旋转90︒,如图2所示,得到结论:①AE DF=_____;②直线AE 与DF 所夹锐角的度数为______. (2)小王同学继续将BEF 绕点B 按逆时针方向旋转,旋转至如图3所示位置.请问探究(1)中的结论是否仍然成立?并说明理由.拓展延伸:在以上探究中,当BEF 旋转至D 、E 、F 三点共线时,则ADE 的面积为______. 解析:(1)32,30°;(2)成立,理由见解析;拓展延伸:133398+或133398- 【分析】(1)通过证明FBD EBA ∆∆∽,可得32AE BE DF BF ==,BDF BAE ∠=∠,即可求解; (2)通过证明ABE DBF ∆∆∽,可得32AE BE DF BF ==,BDF BAE ∠=∠,即可求解; 拓展延伸:分两种情况讨论,先求出AE ,DG 的长,即可求解.【详解】解:(1)如图1,30ABD ∠=︒,90DAB ∠=︒,EF BA ⊥,3cos 2BE AB ABD BF DB ∴∠===, 如图2,设AB 与DF 交于点O ,AE 与DF 交于点H ,BEF ∆绕点B 按逆时针方向旋转90︒,90DBF ABE ∴∠=∠=︒,FBD EBA ∴∆∆∽, ∴32AE BE DF BF ==,BDF BAE ∠=∠, 又DOB AOF ∠=∠,30DBA AHD ∴∠=∠=︒,∴直线AE 与DF 所夹锐角的度数为30,故答案为:32,30; (2)结论仍然成立, 理由如下:如图3,设AE 与BD 交于点O ,AE 与DF 交于点H ,将BEF ∆绕点B 按逆时针方向旋转,ABE DBF ∴∠=∠, 又32BE AB BF DB ==, ABE DBF ∴∆∆∽,∴32AE BE DF BF ==,BDF BAE ∠=∠, 又DOH AOB ∠=∠,30ABD AHD ∴∠=∠=︒,∴直线AE 与DF 所夹锐角的度数为30.拓展延伸:如图4,当点E 在AB 的上方时,过点D 作DG AE ⊥于G ,23AB =30ABD ∠=︒,点E 是边AB 的中点,90DAB ∠=︒,3BE ∴=2AD =,4DB =,30EBF ∠=︒,EF BE ⊥,1EF ∴=,D 、E 、F 三点共线,90DEB BEF ∴∠=∠=︒,2216313DE BD BE ∴-=-30DEA ∠=︒, 11322DG DE ∴==, 由(2)可得:32AE BE DF BF ==, ∴32131AE=+, 3932AE +∴=, ADE ∴∆的面积11393131333922228AE DG ++=⨯⨯=⨯⨯=; 如图5,当点E 在AB 的下方时,过点D 作DG AE ⊥,交EA 的延长线于G ,同理可求:ADE ∆的面积11393131333922228AE DG --=⨯⨯=⨯⨯=; 故答案为:133398+或133398-. 【点睛】 本题是几何变换综合题,考查了矩形的性质,相似三角形的判定和性质,直角三角形的性质,旋转的性质等知识,利用分类讨论思想解决问题是解题的关键.12.如图1,将两个完全相同的三角形纸片ABC 和DEC 重合放置,其中∠C=90°,∠B=∠E=30°.(1)操作发现如图2,固定△ABC ,使△DEC 绕点C 旋转.当点D 恰好落在BC 边上时,填空:线段DE 与AC 的位置关系是 ;②设△BDC 的面积为S 1,△AEC 的面积为S 2.则S 1与S 2的数量关系是 .(2)猜想论证当△DEC 绕点C 旋转到图3所示的位置时,小明猜想(1)中S 1与S 2的数量关系仍然成立,并尝试分别作出了△BDC 和△AEC 中BC ,CE 边上的高,请你证明小明的猜想. (3)拓展探究已知∠ABC=60°,点D 是其角平分线上一点,BD=CD=4,OE ∥AB 交BC 于点E (如图4),若在射线BA 上存在点F ,使S △DCF =S △BDC ,请直接写出相应的BF 的长解析:解:(1)①DE ∥AC .②12S S =.(2)12S S =仍然成立,证明见解析;(3)433或833. 【详解】(1)①由旋转可知:AC=DC ,∵∠C=90°,∠B=∠DCE=30°,∴∠DAC=∠CDE=60°.∴△ADC 是等边三角形.∴∠DCA=60°.∴∠DCA=∠CDE=60°.∴DE ∥AC .②过D 作DN ⊥AC 交AC 于点N ,过E 作EM ⊥AC 交AC 延长线于M ,过C 作CF ⊥AB 交AB 于点F .由①可知:△ADC 是等边三角形, DE ∥AC ,∴DN=CF,DN=EM .∴CF=EM .∵∠C=90°,∠B =30°∴AB=2AC .又∵AD=AC∴BD=AC .∵1211S CF BD S AC EM 22=⋅=⋅, ∴12S S =.(2)如图,过点D 作DM ⊥BC 于M ,过点A 作AN ⊥CE 交EC 的延长线于N ,∵△DEC 是由△ABC 绕点C 旋转得到,∴BC=CE ,AC=CD ,∵∠ACN+∠BCN=90°,∠DCM+∠BCN=180°-90°=90°,∴∠ACN=∠DCM ,∵在△ACN 和△DCM 中,ACN DCM CMD N AC CD ∠∠⎧⎪∠∠⎨⎪⎩=== , ∴△ACN ≌△DCM (AAS ),∴AN=DM ,∴△BDC 的面积和△AEC 的面积相等(等底等高的三角形的面积相等),即S 1=S 2;(3)如图,过点D 作DF 1∥BE ,易求四边形BEDF 1是菱形,所以BE=DF 1,且BE 、DF 1上的高相等,此时S △DCF1=S △BDE ;过点D 作DF 2⊥BD ,∵∠ABC=60°,F 1D ∥BE ,∴∠F 2F 1D=∠ABC=60°,∵BF 1=DF 1,∠F 1BD=12∠ABC=30°,∠F 2DB=90°,∴∠F 1DF 2=∠ABC=60°,∴△DF 1F 2是等边三角形,∴DF 1=DF 2,过点D 作DG ⊥BC 于G ,∵BD=CD ,∠ABC=60°,点D 是角平分线上一点,∴∠DBC=∠DCB=12×60°=30°,∴∠CDF 1=180°-∠BCD=180°-30°=150°,∠CDF 2=360°-150°-60°=150°,∴∠CDF 1=∠CDF 2,∵在△CDF 1和△CDF 2中, 1212DF DF CDF CDF CD CD ⎧⎪∠⎨⎪⎩===, ∴△CDF 1≌△CDF 2(SAS ),∴点F 2也是所求的点,∵∠ABC=60°,点D 是角平分线上一点,DE ∥AB ,∴∠DBC=∠BDE=∠ABD=12×60°=30°,又∵BD=4,∴BE=12×4÷cos30°, ∴BF 1BF 2=BF 1+F 1F 2, 故BF.13.(1)问题发现如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.填空:线段AD,BE之间的关系为 .(2)拓展探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.(3)解决问题如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.解析:(1) AD=BE,AD⊥BE.(2) AD=BE,AD⊥BE.(3) 5-32≤PC≤5+32.【分析】(1)根据等腰三角形性质证△ACD≌△BCE(SAS),得AD=BE,∠EBC=∠CAD,延长BE 交AD于点F,由垂直定义得AD⊥BE.(2)根据等腰三角形性质证△ACD≌△BCE(SAS),AD=BE,∠CAD=∠CBE,由垂直定义得∠OHB=90°,AD⊥BE;(3)作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,PC=BE,当P、E、B共线时,BE最小,最小值=PB-PE;当P、E、B共线时,BE最大,最大值=PB+PE,故5-32≤BE≤5+32.【详解】(1)结论:AD=BE,AD⊥BE.理由:如图1中,∵△ACB与△DCE均为等腰直角三角形,∴AC=BC,CE=CD,∠ACB=∠ACD=90°,在Rt △ACD 和Rt △BCE 中AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩=== ∴△ACD ≌△BCE (SAS ),∴AD=BE ,∠EBC=∠CAD延长BE 交AD 于点F ,∵BC ⊥AD ,∴∠EBC+∠CEB=90°,∵∠CEB=AEF ,∴∠EAD+∠AEF=90°,∴∠AFE=90°,即AD ⊥BE .∴AD=BE ,AD ⊥BE .故答案为AD=BE ,AD ⊥BE .(2)结论:AD=BE ,AD ⊥BE .理由:如图2中,设AD 交BE 于H ,AD 交BC 于O .∵△ACB 与△DCE 均为等腰直角三角形,∴AC=BC ,CE=CD ,∠ACB=∠ECD=90°,∴ACD=∠BCE ,在Rt △ACD 和Rt △BCE 中AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===, ∴△ACD ≌△BCE (SAS ),∴AD=BE ,∠CAD=∠CBE ,∵∠CAO+∠AOC=90°,∠AOC=∠BOH ,∴∠BOH+∠OBH=90°,∴∠OHB=90°,∴AD⊥BE,∴AD=BE,AD⊥BE.(3)如图3中,作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,∴PC=BE,图3-1中,当P、E、B共线时,BE最小,最小值=PB-PE=5-32,图3-2中,当P、E、B共线时,BE最大,最大值=PB+PE=5+32,∴5-32≤BE≤5+32,即5-32≤PC≤5+32.【点睛】本题是几何变换综合题,考查了旋转的性质、等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找三角形全等的条件,学会添加辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考压轴题.14.性质探究如图①,在等腰三角形ABC 中,0120ACB ∠=,则底边AB 与腰AC 的长度之比为________.理解运用⑴若顶角为120°的等腰三角形的周长为83+________;⑵如图②,在四边形EFGH 中,EF EG EH ==.①求证:EFG EHG FGH ∠+∠=∠;②在边,FG GH 上分别取中点,M N ,连接MN .若0120FGH ∠=,10EF =,直接写出线段MN 的长.类比拓展顶角为2σ的等腰三角形的底边与一腰的长度之比为________(用含σ的式子表示). 解析:31)432)①见解析;②532sin α.【分析】性质探究:作CD ⊥AB 于D ,则∠ADC=∠BDC=90°,由等腰三角形的性质得出AD=BD ,∠A=∠B=30°,由直角三角形的性质得出AC=2CD ,3,得出3,即可得出结果;理解运用:(1)同上得出则AC=2CD ,3,由等腰三角形的周长得出33CD=2,得出3(2)①由等腰三角形的性质得出∠EFG=∠EGF ,∠EGH=∠EHG ,得出∠EFG+∠EHG=∠EGF+∠EGH=∠FGH 即可;②连接FH ,作EP ⊥FH 于P ,由等腰三角形的性质得出PF=PH ,由①得:∠EFG+∠EHG=∠FGH=120°,由四边形内角和定理求出∠FEH=120°,由等腰三角形的性质得出∠EFH=30°,由直角三角形的性质得出PE=12EF=5,PF=3PE=53,得出FH=2PF=103,证明MN 是△FGH 的中位线,由三角形中位线定理即可得出结果; 类比拓展:作AD ⊥BC 于D ,由等腰三角形的性质得出BD=CD ,∠BAD=12∠BAC=α,由三角函数得出BD=AB×sinα,得出BC=2BD=2AB×sinα,即可得出结果.【详解】性质探究 解:作CD ⊥AB 于D ,如图①所示:则∠ADC=∠BDC=90°,∵AC=BC ,∠ACB=120°,∴AD=BD ,∠A=∠B=30°,∴AC=2CD ,3,∴3, ∴23AB CD AC 3 3 理解运用(1)解:如图①所示: 同上得:AC=2CD ,3,∵3∴33解得:CD=2,∴3∴△ABC 的面积=12AB×CD=1233故答案为3(2)①证明:∵EF=EG=EH ,∴∠EFG=∠EGF ,∠EGH=∠EHG ,∴∠EFG+∠EHG=∠EGF+∠EGH=∠FGH ;②解:连接FH ,作EP ⊥FH 于P ,如图②所示:则PF=PH ,由①得:∠EFG+∠EHG=∠FGH=120°,∴∠FEH=360°-120°-120°=120°,∵EF=EH ,∴∠EFH=30°,∴PE=12EF=5, ∴PF=3PE=53,∴FH=2PF=103,∵点M 、N 分别是FG 、GH 的中点,∴MN 是△FGH 的中位线,∴MN=12FH=53;类比拓展解:如图③所示:作AD ⊥BC 于D ,∵AB=AC ,∴BD=CD ,∠BAD=12∠BAC=α,∵sinα=BD AB , ∴BD=AB×sinα,∴BC=2BD=2AB×sinα,∴2sin BC AB AB ABα⋅==2sinα; 故答案为2sinα.【点睛】本题是四边形综合题目,考查了等腰三角形的性质、直角三角形的性质、三角形中位线定理、四边形内角和定理、就直角三角形等知识;本题综合性强,熟练掌握等腰三角形的性质和含30°角的直角三角形的性质是解题的关键.15.(1)证明推断:如图(1),在正方形ABCD 中,点E ,Q 分别在边BC ,AB 上,DQ AE ⊥于点O ,点G ,F 分别在边CD ,AB 上,GF AE ⊥.①求证:DQ AE =;②推断:GF AE 的值为 ; (2)类比探究:如图(2),在矩形ABCD 中,BC k AB =(k 为常数).将矩形ABCD 沿GF 折叠,使点A 落在BC 边上的点E 处,得到四边形FEPG ,EP 交CD 于点H ,连接AE 交GF 于点O .试探究GF 与AE CP 之间的数量关系,并说明理由;(3)拓展应用:在(2)的条件下,连接CP ,当23k =时,若3tan 4CGP ∠=,210GF =,求CP 的长.解析:(1)①证明见解析;②解:结论:1GF AE=.理由见解析;(2)结论:FG k AE =.理由见解析;(3)955PC =. 【解析】【分析】(1)①由正方形的性质得AB=DA ,∠ABE=90°=∠DAH .所以∠HAO+∠OAD=90°,又知∠ADO+∠OAD=90°,所以∠HAO=∠ADO ,于是△ABE ≌△DAH ,可得AE=DQ .②证明四边形DQFG 是平行四边形即可解决问题.(2)结论:FG k AE=如图2中,作GM ⊥AB 于M .证明:△ABE ∽△GMF 即可解决问题. (3)如图2-1中,作PM ⊥BC 交BC 的延长线于M .利用相似三角形的性质求出PM ,CM 即可解决问题.【详解】(1)①证明:∵四边形ABCD 是正方形,∴AB DA =,90ABE DAQ ∠==∠.∴90QAO OAD ∠+∠=.∵AE DH ⊥,∴90ADO OAD ∠+∠=.∴QAO ADO ∠=∠.∴ABE ∆≌DAQ ∆()ASA ,∴AE DQ =.②解:结论:1GF AE=. 理由:∵DQ AE ⊥,FG AE ⊥,∴//DQ FG ,∵//FQ DG ,∴四边形DQFG 是平行四边形,∴FG DQ =,∵AE DQ =,∴FG AE =,∴1GF AE=. 故答案为1. (2)解:结论:FG k AE =. 理由:如图2中,作GM AB ⊥于M .∵AE GF ⊥, ∴90AOF GMF ABE ∠=∠=∠=,∴90BAE AFO ∠+∠=,90AFO FGM ∠+∠=,∴BAE FGM ∠=∠,∴ABE ∆∽GMF ∆,∴GF GM AE AB=, ∵90AMG D DAM ∠=∠=∠=,∴四边形AMGD 是矩形,∴GM AD =,∴GF AD BC k AE AB AB===. (3)解:如图2﹣1中,作PM BC ⊥交BC 的延长线于M .∵//FB GC ,//FE GP ,∴CGP BFE ∠=∠, ∴3tan tan 4BE CGP BFE BF∠=∠==, ∴可以假设3BE k =,4BF k =,5EF AF k ==, ∵23FG AE =,210FG = ∴310AE = ∴222(3)(9)(310)k k +=,∴1k =或﹣1(舍弃),∴3BE =,9AB =,∵:2:3BC AB =,∴6BC =,∴3BE CE ==,6AD PE BC ===,∵90BEF FEP PME ∠=∠=∠=,∴90FEB PEM ∠+∠=,90PEM EPM ∠+∠=,∴FEB EPM ∠=∠,∴FBE ∆∽EMP ∆, ∴EF BF BE PE EM PM ==, ∴5436EM PM==, ∴245EM =,185PM =, ∴249355CM EM EC ===-=, ∴22955PC CM PM =+=【点睛】本题属于相似形综合题,考查了正方形的性质,矩形的性质,全等三角形的判定和性质,相似三角形的判定和性质,解直角三角形等知识,解题的关键是正确寻找全等三角形或相似三角形解决问题,学会利用参数构建方程解决问题,属于中考压轴题.16.如图1,△ABC 和△DCE 都是等边三角形.探究发现(1)△BCD 与△ACE 是否全等?若全等,加以证明;若不全等,请说明理由. 拓展运用(2)若B 、C 、E 三点不在一条直线上,∠ADC =30°,AD =3,CD =2,求BD 的长. (3)若B 、C 、E 三点在一条直线上(如图2),且△ABC 和△DCE 的边长分别为1和2,求△ACD 的面积及AD 的长.解析:(1)全等,理由见解析;(2)BD 133)△ACD 3AD 3 【分析】 (1)依据等式的性质可证明∠BCD =∠ACE ,然后依据SAS 可证明△ACE ≌△BCD ; (2)由(1)知:BD =AE ,利用勾股定理计算AE 的长,可得BD 的长;(3)过点A 作AF ⊥CD 于F ,先根据平角的定义得∠ACD =60°,利用特殊角的三角函数可得AF 的长,由三角形面积公式可得△ACD 的面积,最后根据勾股定理可得AD 的长.【详解】解:(1)全等,理由是:∵△ABC 和△DCE 都是等边三角形,∴AC =BC ,DC =EC ,∠ACB =∠DCE =60°,∴∠ACB +∠ACD =∠DCE +∠ACD ,即∠BCD =∠ACE ,在△BCD 和△ACE 中,CD CE BCD ACE BC AC =⎧⎪∠=∠⎨⎪=⎩, ∴△ACE ≌△BCD (SAS );(2)如图3,由(1)得:△BCD ≌△ACE ,∴BD =AE ,∵△DCE 都是等边三角形,∴∠CDE =60°,CD =DE =2,∵∠ADC =30°,∴∠ADE =∠ADC +∠CDE =30°+60°=90°,在Rt △ADE 中,AD =3,DE =2, ∴229413AE AD DE ++=。
2004-2012深圳中考压轴题

21、直线y= -x+m 与直线y=33x+2相交于y 轴上的点C ,与x 轴分别交于点A 、B 。
(1)求A 、B 、C 三点的坐标;(3分)(2)经过上述A 、B 、C 三点作⊙E ,求∠ABC 的度数,点E 的坐标和⊙E 的半径;(4分)(3)若点P 是第一象限内的一动点,且点P 与圆心E 在直线AC 的同一侧,直线PA 、PC 分别交⊙E 于点M 、N ,设∠APC=θ,试求点M 、N 的距离(可用含θ的三角函数式表示)。
(5分)21、已知△ABC 是边长为4的等边三角形,BC 在x 轴上,点D 为BC 的中点,点A 在第一象限内,AB 与y 轴的正半轴相交于点E ,点B (-1,0),P 是AC 上的一个动点(P 与点A 、C 不重合) (1)(2分)求点A 、E 的坐标; (2)(2分)若y=c bx x 7362++-过点A 、E ,求抛物线的解析式。
(3)(5分)连结PB 、PD ,设L 为△PBD 的周长,当L 取最小值时,求点P 的坐标及L 的最小值,并判断此时点P 是否在(2)中所求的抛物线上,请充分说明你的判断理由。
22、(9分)AB 是⊙O 的直径,点E 是半圆上一动点(点E 与点A 、B 都不重合),点C 是BE 延长线上的一点,且CD ⊥AB ,垂足为D ,CD 与AE 交于点H ,点H 与点A 不重合。
(1)(5分)求证:△AHD ∽△CBD (2)(4分)连HB ,若CD=AB=2,求HD+HO 的值。
xAO D BH EC2006年深圳中考压轴题:(动点,一次函数,圆,二次函数)21.(10分)如图9,抛物线2812(0)y ax ax a a =-+<与x 轴交于A 、B 两点(点A 在点B 的左侧),抛物线上另有一点C 在第一象限,满足∠AC B 为直角,且恰使△O C A ∽△OBC . (1)(3分)求线段O C 的长. 解:(2)(3分)求该抛物线的函数关系式. 解:(3)(4分)在x 轴上是否存在点P ,使△B C P 为等腰三角形?若存在,求出所有符合条件的P 点的坐标;若不存在,请说明理由.解:图10-122.(10分)如图10-1,在平面直角坐标系xo y 中,点M 在x 轴的正半轴上, ⊙M 交x 轴于 A B 、两点,交y 轴于C D 、两点,且C 为 AE 的中点,A E 交y 轴于G 点,若点A 的坐标为(-2,0),A E 8(1)(3分)求点C 的坐标.解:(2)(3分)连结M G BC 、,求证:M G ∥B C 证明:(3)(4分) 如图10-2,过点D 作⊙M 的切线,交x 轴于点P .动点F 在⊙M 的圆周上运动时,PFOF 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律.解:2007年深圳中考压轴题:(动点,一次函数,圆,二次函数)22.如图6,在平面直角坐标系中,正方形A O C B的边长为1,点D在x轴的正半轴上,且O D O B=,B D交O C于点E.(1)求B E C∠的度数.(2)求点E的坐标.(3)求过B O D,,三点的抛物线的解析式.(计算结果要求分母有理化.参考资料:把分5==②1==2==等运算都是分母有理化)图623.如图7,在平面直角坐标系中,抛物线2164y x =-与直线12y x =相交于A B ,两点.(1)求线段A B 的长.(2)若一个扇形的周长等于(1)中线段A B 的长,当扇形的半径取何值时,扇形的面积最大,最大面积是多少? (3)如图8,线段A B 的垂直平分线分别交x 轴、y 轴于C D ,两点,垂足为点M ,分别求出O M O C O D ,,的长,并验证等式222111O CO DO M+=是否成立.(4)如图9,在R t ABC △中,90ACB =∠,C D AB ⊥,垂足为D ,设B C a =,A C b =,A B c =.C D b =,试说明:222111abh+=.图7图8图9D2008年深圳中考压轴题:(动点,一次函数,圆,二次函数)20.如图8,点D 是⊙O 的直径CA 延长线上一点,点B 在⊙O 上,且AB =AD =AO . (1)求证:BD 是⊙O 的切线. (2)若点E 是劣弧BC 上一点,AE 与BC 相交于点F , 且△BEF 的面积为8,cos ∠BFA =32,求△ACF 的面积.图 8C22.如图9,在平面直角坐标系中,二次函数)0(2>++=a c bx ax y 的图象的顶点为D 点,与y 轴交于C 点,与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0), OB =OC ,tan ∠ACO =31.(1)求这个二次函数的表达式.(2)经过C 、D 两点的直线,与x 轴交于点E ,在该抛物线上是否存在这样的点F ,使以点A 、C 、E 、F 为顶点的四边形为平行四边形?若存在,请求出点F 的坐标;若不存在,请说明理由.(3)若平行于x 轴的直线与该抛物线交于M 、N 两点,且以MN 为直径的圆与x 轴相切,求该圆半径的长度.(4)如图10,若点G (2,y )是该抛物线上一点,点P 是直线AG 下方的抛物线上一动点,当点P 运动到什么位置时,△APG 的面积最大?求出此时P 点的坐标和△APG 的最大面积.22.(9分)如图,在直角坐标系中,点A的坐标为(-2,0),连结OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)求点B的坐标;(2)求经过A、O、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C的坐标;若不存在,请说明理由.(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由。
中考数学压轴题十大题型(含详细答案)

一、中考数学压轴题1.如图,在平面直角坐标系中,点O 为坐标原点,直线y =-x + m 交 y 轴的正半轴于点A ,交x 轴的正半轴于点B ,过点A 的直线AF 交x 轴的负半轴于点F ,∠AFO=45°. (1)求∠FAB 的度数;(2)点 P 是线段OB 上一点,过点P 作 PQ ⊥OB 交直线 FA 于点Q ,连接 BQ ,取 BQ 的中点C ,连接AP 、AC 、CP ,过点C 作 CR ⊥AP 于点R ,设 BQ 的长为d ,CR 的长为h ,求d 与 h 的函数关系式(不要求写出自变量h 的取值范围);(3)在(2)的条件下,过点 C 作 CE ⊥OB 于点E ,CE 交 AB 于点D ,连接 AE ,∠AEC=2∠DAP ,EP=2,作线段 CD 关于直线AB 的对称线段DS ,求直线PS 与直线 AF 的交点K 的坐标.2.已知:如图,在平面直角坐标系中,点O 为坐标原点,()2,0C .直线26y x =+与x 轴交于点A ,交y 轴于点B .过C 点作直线AB 的垂线,垂足为E ,交y 轴于点D . (1)求直线CD 的解析式;(2)点G 为y 轴负半轴上一点,连接EG ,过点E 作EH EG ⊥交x 轴于点H .设点G 的坐标为()0,t ,线段AH 的长为d .求d 与t 之间的函数关系式(不要求写出自变量的取值范围)(3)过点C 作x 轴的垂线,过点G 作y 轴的垂线,两线交于点M ,过点H 作HN GM ⊥于点N ,交直线CD 于点K ,连接MK ,若MK 平分NMB ∠,求t 的值.3.如图1,抛物线2(0)y ax bx c a =++≠的顶点为C (1,4),交x 轴于A 、B 两点,交y 轴于点D ,其中点B 的坐标为(3,0).(1)求抛物线的解析式;(2)如图2,点E 是BD 上方抛物线上的一点,连接AE 交DB 于点F ,若AF=2EF ,求出点E 的坐标.(3)如图3,点M 的坐标为(32,0),点P 是对称轴左侧抛物线上的一点,连接MP ,将MP 沿MD 折叠,若点P 恰好落在抛物线的对称轴CE 上,请求出点P 的横坐标.4.如图,在梯形ABCD 中,AD//BC ,AB=CD=AD=5,cos 45B =,点O 是边BC 上的动点,以OB 为半径的O 与射线BA 和边BC 分别交于点E 和点M ,联结AM ,作∠CMN=∠BAM ,射线MN 与边AD 、射线CD 分别交于点F 、N .(1)当点E 为边AB 的中点时,求DF 的长;(2)分别联结AN 、MD ,当AN//MD 时,求MN 的长;(3)将O 绕着点M 旋转180°得到'O ,如果以点N 为圆心的N 与'O 都内切,求O 的半径长.5.如图,在平面直角坐标系中,直线6y x =+与x 轴交于点A ,与y 轴交于点B ,点C 在x 轴正半轴上,2ABC ACB ∠=∠.(1)求直线BC 的解析式;(2)点D 是射线BC 上一点,连接AD ,设点D 的横坐标为t ,ACD ∆的面积为S ()0S ≠,求S 与t 的函数解析式,并直接写出自变量t 的取值范围;(3)在(2)的条件下,AD 与y 轴交于点E ,连接CE ,过点B 作AD 的垂线,垂足为点H ,直线BH 交x 轴于点F ,交线段CE 于点M ,直线DM 交x 轴于点N ,当:7:12NF FC =时,求直线DM 的解析式.6.在梯形ABCD 中,//AD BC ,90B ∠=︒,45C ∠=︒,8AB =,14BC =,点E 、F 分别在边AB 、CD 上,//EF AD ,点P 与AD 在直线EF 的两侧,90EPF ∠=︒,PE PF =,射线EP 、FP 与边BC 分别相交于点M 、N ,设AE x =,MN y =.(1)求边AD 的长;(2)如图,当点P 在梯形ABCD 内部时,求关于x 的函数解析式,并写出定义域; (3)如果MN 的长为2,求梯形AEFD 的面积.7.如图,已知正方形ABCD 中,4,BC AC BD =、相交于点O ,过点A 作射线AM AC ⊥,点E 是射线AM 上一动点,连接OE 交AB 于点F ,以OE 为一边,作正方形OEGH ,且点A 在正方形OEGH 的内部,连接DH .(1)求证:EDO EAO ∆≅∆;(2)设BF x =,正方形OEGH 的边长为y ,求y 关于x 的函数关系式,并写出定义域;(3)连接AG ,当AEG ∆是等腰三角形时,求BF 的长.8.问题提出(1)如图①,在ABC 中,42,6,135AB AC BAC ==∠=,求ABC 的面积.问题探究(2)如图②,半圆O 的直径10AB =,C 是半圆AB 的中点,点D 在BC 上,且2CD BD =,点P 是AB 上的动点,试求PC PD +的最小值.问题解决(3)如图③,扇形AOB 的半径为20,45AOB ∠=在AB 选点P ,在边OA 上选点E ,在边OB 上选点F ,求PE EF FP ++的长度的最小值.9.如图,在ABC ∆中,14AB =,45B ∠=︒,4tan 3A =,点D 为AB 中点.动点P 从点D 出发,沿DA 方向以每秒1个单位长度的速度向终点A 运动,点P 关于点D 对称点为点Q ,以PQ 为边向上作正方形PQMN .设点P 的运动时间为t 秒.(1)当t =_______秒时,点N 落在AC 边上.(2)设正方形PQMN 与ABC ∆重叠部分面积为S ,当点N 在ABC ∆内部时,求S 关于t 的函数关系式.(3)当正方形PQMN 的对角线所在直线将ABC ∆的分为面积相等的两部分时,直接写出t 的值.10.对于平面直角坐标系xOy 中的任意点()P x y ,,如果满足x y a += (x ≥0,a 为常数),那么我们称这样的点叫做“特征点”.(1)当2≤a ≤3时,①在点(1,2),(1,3),(2.5,0)A B C 中,满足此条件的特征点为__________________;②⊙W 的圆心为(,0)W m ,半径为1,如果⊙W 上始终存在满足条件的特征点,请画出示意图,并直接写出m 的取值范围;(2)已知函数()10Z x x x=+>,请利用特征点求出该函数的最小值.11.如图,在平面直角坐标系中,点(1,2)A ,(5,0)B ,抛物线22(0)y ax ax a =->交x 轴正半轴于点C ,连结AO ,AB .(1)求点C 的坐标;(2)求直线AB 的表达式; (3)设抛物线22(0)y ax ax a =->分别交边BA ,BA 延长线于点D ,E .①若2AE AO =,求抛物线表达式;②若CDB △与BOA △相似,则a 的值为 .(直接写出答案)12.如图1,在平面直角坐标系中,抛物线239334y x x =--x 轴交于A B 、两点(点A 在点B 的左侧),与y 轴交于点C . (1)过点C 的直线5334y x =-x 轴于点H ,若点P 是第四象限内抛物线上的一个动点,且在对称轴的右侧,过点P 作//PQ y 轴交直线CH 于点Q ,作//PN x 轴交对称轴于点N ,以PQ PN 、为邻边作矩形PQMN ,当矩形PQMN 的周长最大时,在y 轴上有一动点K ,x 轴上有一动点T ,一动点G 从线段CP 的中点R 出发以每秒1个单位的速度沿R K T →→的路径运动到点T ,再沿线段TB 以每秒2个单位的速度运动到B 点处停止运动,求动点G 运动时间的最小值:(2)如图2, 将ABC ∆绕点B 顺时针旋转至A BC ''∆的位置, 点A C 、的对应点分别为A C ''、,且点C '恰好落在抛物线的对称轴上,连接AC '.点E 是y 轴上的一个动点,连接AE C E '、, 将AC E ∆'沿直线C E '翻折为A C E ∆'', 是否存在点E , 使得BAA ∆'为等腰三角形?若存在,请求出点E 的坐标;若不存在,请说明理由.13.(1)如图1,A 是⊙O 上一动点,P 是⊙O 外一点,在图中作出PA 最小时的点A . (2)如图2,Rt △ABC 中,∠C =90°,AC =8,BC =6,以点C 为圆心的⊙C 的半径是3.6,Q 是⊙C 上一动点,在线段AB 上确定点P 的位置,使PQ 的长最小,并求出其最小值. (3)如图3,矩形ABCD 中,AB =6,BC =9,以D 为圆心,3为半径作⊙D ,E 为⊙D 上一动点,连接AE ,以AE 为直角边作Rt △AEF ,∠EAF =90°,tan ∠AEF =13,试探究四边形ADCF 的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.14.(问题探究)课堂上老师提出了这样的问题:“如图①,在ABC 中,108BAC ∠=︒,点D 是BC 边上的一点,7224BAD BD CD AD ∠=︒==,,,求AC 的长”.某同学做了如下的思考:如图②,过点C 作CE AB ∥,交AD 的延长线于点E ,进而求解,请回答下列问题:(1)ACE ∠=___________度;(2)求AC 的长.(拓展应用)如图③,在四边形ABCD 中,12075BAD ADC ∠=︒∠=︒,,对角线AC BD 、相交于点E ,且AC AB ⊥,22EB ED AE ==,,则BC 的长为_____________.15. 在平面直角坐标系中,点O 为坐标原点,直线y =﹣x+4与x 轴交于点A ,过点A 的抛物线y =ax 2+bx 与直线y =﹣x+4交于另一点B ,且点B 的横坐标为1.(1)该抛物线的解析式为;(2)如图1,Q 为抛物线上位于直线AB 上方的一动点(不与B 、A 重合),过Q 作QP ⊥x 轴,交x 轴于P ,连接AQ ,M 为AQ 中点,连接PM ,过M 作MN ⊥PM 交直线AB 于N ,若点P 的横坐标为t ,点N 的横坐标为n ,求n 与t 的函数关系式;在此条件下,如图2,连接QN 并延长,交y 轴于E ,连接AE ,求t 为何值时,MN ∥AE .(3)如图3,将直线AB 绕点A 顺时针旋转15度交抛物线对称轴于点C ,点T 为线段OA 上的一动点(不与O 、A 重合),以点O 为圆心、以OT 为半径的圆弧与线段OC 交于点D ,以点A 为圆心、以AT 为半径的圆弧与线段AC 交于点F ,连接DF .在点T 运动的过程中,四边形ODFA 的面积有最大值还是有最小值?请求出该值.16.如图,抛物线25y ax bx =+-交x 轴于点A 、B (A 在B 的左侧),交y 轴于点C ,且OB OC =,()2,0A -.(1)求抛物线的解析式;(2)点P 为第四象限抛物线上一点,过点P 作y 轴的平行线交BC 于点D ,设P 点横坐标为t ,线段PD 的长度为d ,求d 与t 的函数关系式.(不要求写出t 的取值范围) (3)在(2)的条件下,F 为BP 延长线上一点,且45PFC ∠=︒,连接OF 、CP 、PB ,FOB ∆的面积为3600169,求PBC ∆的面积.17.如图①,△ABC是等腰直角三角形,在两腰AB、AC外侧作两个等边三角形ABD和ACE,AM和AN分别是等边三角形ABD和ACE的角平分线,连接CM、BN,CM与AB交于点P.(1)求证:CM=BN;(2)如图②,点F为角平分线AN上一点,且∠CPF=30°,求证:△APF∽△AMC;(3)在(2)的条件下,求PFBN的值.18.如图,在⊙O中,直径AB=10,tanA=3.(1)求弦AC的长;(2)D是AB延长线上一点,且AB=kBD,连接CD,若CD与⊙O相切,求k的值;(3)若动点P以3cm/s的速度从A点出发,沿AB方向运动,同时动点Q以32cm/s的速度从B点出发沿BC方向运动,设运动时间为t (0<t<103),连结PQ.当t为何值时,△BPQ为Rt△?19.如图,在矩形ABCD中,点E为BC的中点,连接AE,过点D作DF AE⊥于点F,过点C作CN DF⊥于点N,延长CN交AD于点M.(1)求证:AM MD=(2)连接CF,并延长CF交AB于G①若2AB=,求CF的长度;②探究当ABAD为何值时,点G恰好为AB的中点.20.在一次数学课上,李老师让同学们独立完成课本第23页第七题选择题(2)如图 1,如果 AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=()A.180° B.270° C.360° D.540°(1)请写出这道题的正确选项;(2)在同学们都正确解答这道题后,李老师对这道题进行了改编:如图2,AB∥EF,请直接写出∠BAD,∠ADE,∠DEF之间的数量关系.(3)善于思考的龙洋同学想:将图1平移至与图2重合(如图3所示),当AD,ED分别平分∠BAC,∠CEF时,∠ACE与∠ADE之间有怎样的数量关系?请你直接写出结果,不需要证明.(4)彭敏同学又提出来了,如果像图4这样,AB∥EF,当∠ACD=90°时,∠BAC、∠CDE 和∠DEF之间又有怎样的数量关系?请你直接写出结果,不需要证明.21.如图1,以AB为直径作⊙O,点C是直径AB上方半圆上的一点,连结AC,BC,过点C作∠ACB的平分线交⊙O于点D,过点D作AB的平行线交CB的延长线于点E.(1)如图1,连结AD,求证:∠ADC=∠DEC.(2)若⊙O的半径为5,求CA•CE的最大值.(3)如图2,连结AE,设tan∠ABC=x,tan∠AEC=y,①求y关于x的函数解析式;②若CBBE=45,求y的值.22.发现来源于探究.小亮进行数学探究活动,作边长为a的正方形ABCD和边长为b的正方形AEFG(a>b),开始时,点E在AB上,如图1.将正方形AEFG绕点A逆时针方向旋转.(1)如图2,小亮将正方形AEFG 绕点A 逆时针方向旋转,连接BE 、DG ,当点G 恰好落在线段BE 上时,小亮发现DG ⊥BE ,请你帮他说明理由.当a=3,b=2时,请你帮他求此时DG 的长.(2)如图3,小亮旋转正方形AEFG ,点E 在DA 的延长线上,连接BF 、DF .当FG 平分∠BFD 时,请你帮他求a :b 及∠FBG 的度数.(3)如图4,BE 的延长线与直线DG 相交于点P ,a=2b .当正方形AEFG 绕点A 从图1开始,逆时针方向旋转一周时,请你帮小亮求点P 运动的路线长(用含b 的代数式表示).23.问题探究(1)如图1.在ABC 中,8BC =,D 为BC 上一点,6AD =.则ABC 面积的最大值是_______.(2)如图2,在ABC 中,60BAC ∠=︒,AG 为BC 边上的高,O 为ABC 的外接圆,若3AG =,试判断BC 是否存在最小值?若存在,请求出最小值:若不存在,请说明理由.问题解决:如图3,王老先生有一块矩形地ABCD ,6212AB =,626BC =+,现在他想利用这块地建一个四边形鱼塘AMFN ,且满足点E 在CD 上,AD DE =,点F 在BC 上,且6CF =,点M 在AE 上,点N 在AB 上,90MFN ∠=︒,这个四边形AMFN 的面积是否存在最大值?若存在,求出面积的最大值;若不存在,请说明理由.24.问题一:如图①,已知AC =160km ,甲,乙两人分别从相距30km 的A ,B 两地同时出发到C 地.若甲的速度为80km /h ,乙的速度为60km /h ,设乙行驶时间为x (h ),两车之间距离为y (km ).(1)当甲追上乙时,x = .(2)请用x 的代数式表示y .问题二:如图②,若将上述线段AC 弯曲后视作钟表外围的一部分,线段AB 正好对应钟表上的弧AB (1小时的间隔),易知∠AOB =30°.(3)分针OD 指向圆周上的点的速度为每分钟转动 km ,时针OE 指向圆周上的点的速度为每分钟转动 °;(4)若从2:00起计时,求几分钟后分针与时针第一次重合?25.在平面直角坐标系中,点O 为坐标原点,抛物线(2)()y a x x m =++与x 轴交于点A C 、(点A 在点C 的左侧),与y 轴正半轴交于点B ,24OC OB ==.(1)如图1,求a m 、的值;(2)如图2,抛物线的顶点坐标是M ,点D 是第一象限抛物线上的一点,连接AD 交抛物线的对称轴于点N ,设点D 的横坐标是t ,线段MN 的长为d ,求d 与t 的函数关系式;(3)如图3,在(2)的条件下,当154d =时,过点D 作DE x 轴交抛物线于点E ,点P 是x 轴下方抛物线上的一个动点,连接PE 交x 轴于点F ,直线211y x b =+经过点D 交EF 于点G ,连接CG ,过点E 作EH CG 交DG 于点H ,若3CFG EGH S S =△△,求点P 的坐标.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题1.F解析:(1)∠FAB=90°;(2)22d h =;(3)直线PS 与直线AF 的交点K(-2,6).【解析】【分析】(1)通过直线AB 的解析式可求出点A 、B 的坐标,可知AOB 是等腰直角三角形,再结合已知条件即可确定90FAB ∠=︒;(2)根据已知条件证明CP=AC=QC=BC 从而得出△ACP 是等腰直角三角形,在Rt △CRP 中,利用sin ∠CPR 22CR CP ==,推出2CP CR =,继而得出22BQ CR =,得出答案; (3)过点 A 作AH ⊥CE 交 EC 的延长线于点 H ,延长 CH 到点 G ,使 HG=CH ,连接AG ,证明△AHC ≌△CEP ,设AH CE n ==,得出EG=CE+CH+GH=n+2+2=n+4,再通过角的等量代换,得出∠EAG=∠G ,从而有EG=EA=n+4,在Rt △AHE 中,通过勾股定理AE²=HE²+AH²可求出n 的值为6,从而得出直线AF 的解析式y = x + 8 ,再求出直线PS 的解析式为 y=-x+4,求交点即可.【详解】解:(1)如下图,y = -x + m ,当x=0时,y=m∴A (0,m ),OA=m当y=0时,0=-x+m ,x=m ,∴B (m ,0),OB=m∴OA=OB∴∠OAB=∠OBA=45°∵∠AFO=45°,∠FAB+∠FBA+∠AFB=180°∴∠FAB=90°(2)如下图 ,∵CP 、AC 分别是 Rt △QPB 和 Rt △QAB 的斜边上的中线∴CP= 12QB ,12AC QB =, ∴CP=AC=QC=BC∴∠CAB=∠CBA设∠CAB=∠CBA=α,∴∠CBP=45°+α∴∠CPB=∠CBP=45°+α∴∠PCB=180°-(∠CPB+∠CBP )=90°-2α∵∠ACB=180°-∠CAB-∠CBA=180°-2α∴∠ACP=∠ACB-∠PCB=180°-2α-(90°-2α)=90°∵AC=CP∴△ACP 是等腰直角三角形∴∠CPA=∠CAP=45°∵CR ⊥AP ,∴∠CRP=90°,在Rt △CRP 中sin ∠CPR 22CR CP == ∴2CP CR =∵12CP BQ =, ∴22BQ CR =即22d h =(3)过点 A 作AH ⊥CE 交 EC 的延长线于点 H ,延长 CH 到点 G ,使 HG=CH ,连接AG ∴∠AHC=∠CEP=90°∴∠HAC+∠HCA=∠PCE+∠HCA∴∠HAC=∠PCE ,∵AC=CP∴△AHC ≌△CEP∴CH=PE=2,AH=CE ,∴GH=CH=2,AH CE n ==∴EG=CE+CH+GH=n+2+2=n+4设∠DAP=β,则∠AEG=2β∴α+β=45°∵∠EBD=∠EDB=∠HDA=∠HAD=45°∴∠CAH=∠HAD-α=45°-α=β∵AH 垂直平分 GC∴AG=AC∴∠GAH=∠CAH=β∴∠G=90°-β 在△EAG 中∠EAG=180°-∠G-∠AEG=180°-(90°-β)-2β =90°-β∴∠EAG=∠G∴EG=EA=n+4在 Rt △AHE 中,AE²=HE²+AH²222(4)(2)n n n +=++126,2n n ==-(舍)∴AH=OE=6,EP=EB=2∴OB=OE+BE=8∴m=8,∴A (0,8)∴OA=OF=8 , ∴F (-8,0)∴直线 AF 的解析式为 y = x + 8∵CD=CE-DE=CE-BE=6-2=4∵线段 CD 关于直线 AB 的对称线段 DS∴SD=CD=4,∠CDA=∠SDA=45°∴∠CDS=90°,∴SD ∥x 轴过点 S 分别作 SM ⊥x 轴于点 M ,SN ⊥y 轴于点 N∴四边形 OMSN 、SMED 都是矩形∴OM=SN=OE-ME=2,ON=SM=DE=BE=2∴S(2,2)∵OP=OE-EP=6-2=4,∴P(4,0)设直线 PS 的解析式为 y=ax+b∴4022a b a b +=⎧⎨+=⎩,解得:14a b =-⎧⎨=⎩∴直线 PS 的解析式为 y=-x+4设直线PS 与直线AF 的交点K(x ,y)∴48y x y x =-+⎧⎨=+⎩解得26x y =-⎧⎨=⎩∴直线PS 与直线AF 的交点K(-2,6).【点睛】本题考查的知识点是一次函数与几何图形,将一次函数的图象与几何图形综合在一起的问题,是考查学生综合素质和能力的热点题型,它充分体现了数学解题中的数形结合思想和整体转化思想.本题考查的知识点有一次函数图象与坐标轴的交点问题、等腰直角三角形的判定及性质、三角形内角和定理、全等三角形的判定及性质、矩形的性质、待定系数法求一次函数解析式、线段垂直平分线等.2.C解析:(1)112y x =-+;(2)1d t =-+;(3)6215t -= 【解析】【分析】(1)根据互相垂直两直线斜率积为-1,设出直线CE 的解析式,再将点C 坐标代入即可求解;(2)过点E 作EM ⊥y 轴于点M ,过点E 作EN x ⊥轴于点N ,通过解直角三角形可证EDM ≌EAN ,ENH ≌EMG ,得到AN =DM ,HN =GM ,进而得到AH DG =,再根据CE 解析式求出D 点坐标,即可找出d 与t 之间的函数关系式;(3)过点B 作BT CM ⊥于点T ,在直线BT 上截取TL NK =,证四边形BGMT 与四边形HNMC 均为矩形,得MN MT =,再进一步证明ENH ≌EMG ,利用全等三角形的性质通过角度计算,得出△BML 为等腰三角形且BM BL =,再用含有t 的代数式表示BM ,最后在Rt △BMG 中利用勾股定理建立等式,求出t 的值.【详解】解:(1)∵CE ⊥AB ,∴设直线CE 的解析式为:12y x c =-+, 把点C (2,0)代入上述解析式,得1c =,∴直线CD 的解析式为:112y x =-+; (2)过点E 作EM ⊥y 轴于点M ,过点E 作EN x ⊥轴于点N ,令26 112y xy x=+⎧⎪⎨=-+⎪⎩,解得22xy=-⎧⎨=⎩,∴()2,2E-,易证EDM≌EAN,ENH≌EMG,∴AN=DM ,HN=GM,∴AH DG=,由直线CE的解析式112y x=-+,可求点D(0,1)∴DG=1—t,∴1d t=-+;(3)过点B作BT CM⊥于点T,在直线BT上截取TL NK=,易证四边形BGMT与四边形HNMC均为矩形,由(2)问可知1tAH GD==-,则6tHC=-∴6tBG MT==-,∴MN MT=,∵90KNM LTM∠=∠=︒,∴ENH≌EMG,∴LNKM∠=∠,设KMNα∠=,则KMB KMNα∠=∠=,∴90NKM α∠=︒-,∴90NKM L α∠=∠=︒-,∵//BL MN ,∴2MBL BMN α∠=∠=,∴18090BML MBL L α∠=︒-∠-∠=︒-,∴BM BL =, ∵1tan 2KCH ∠=, ∴11322KH CH t ==-, ∴133322KN KH HN t t t TL =+=--=-=, ∴352BL BT TL t BM =+=-=, 在Rt BMG △中, 222BM BG GM =+,解得t =(不合题意舍去)或t =故,65t -=. 【点睛】本题一次函数综合题,考查了待定系数法求解析式,一次函数的性质,全等三角形的判定与性质,角平分线的性质,勾股定理等,利用已知条件求相等交,相等线段是解决本题的关键.3.E解析:(1)2y x 2x 3=-++;(2)E (2,3)或(1,4);(3)P 点横坐标为118【解析】【分析】(1) 抛物线2(0)y ax bx c a =++≠的顶点为C (1,4),设抛物线的解析式为2(1)4y a x =-+,由抛物线过点B,(3,0),即可求出a 的值,即可求得解析式; (2)过点E 、F 分别作x 轴的垂线,交x 轴于点M 、N ,设点E 的坐标为()2,23x xx -++,求出A 、D 点的坐标,得到OM=x ,则AM=x+1,由AF=2EF 得到22(1)33x AN AM +==,从而推出点F 的坐标21210(,)3333x x --+,由23FN EM =,列出关于x 的方程求解即可;(3)先根据待定系数法求出直线DM 的解析式为y=-2x+3,过点P 作PT ∥y 轴交直线DM 于点T ,过点F 作直线GH ⊥y 轴交PT 于点G ,交直线CE 于点H.证明△FGP ≌△FHQ ,得到FG=FH ,PT=45GH.设点P (m ,-m²+2m+3),则T (m ,-2m+3),则PT=m²-4m ,GH=1-m , 可得m²-4m=45(1-m ),解方程即可. 【详解】(1)∵抛物线的顶点为C (1,4),∴设抛物线的解析式为2(1)4y a x =-+,∵抛物线过点B,(3,0),∴20(31)4a =-+,解得a=-1,∴设抛物线的解析式为2(1)4y x =--+,即2y x 2x 3=-++;(2)如图,过点E 、F 分别作x 轴的垂线,交x 轴于点M 、N ,设点E 的坐标为()2,23x x x -++,∵抛物线的解析式为2y x 2x 3=-++,当y=0时,2023x x =-++,解得x=-1或x=3,∴A (-1.0),∴点D (0,3),∴过点BD 的直线解析式为3y x =-+,点F 在直线BD 上,则OM=x ,AM=x+1,∴22(1)33x AN AM +==, ∴2(1)2111333x x ON AN +=-=-=-, ∴21210(,)3333x x F --+,∴2210332233FN EM x x x +--++==, 解得x=1或x=2, ∴点E 的坐标为(2,3)或(1,4);(3)设直线DM 的解析式为y=kx+b ,过点D (0,3),M (32,0), 可得,3023k b b ⎧+=⎪⎨⎪=⎩,解得k=-2,b=3,∴直线DM 的解析式为y=-2x+3,∴32OM =,3OD =, ∴tan ∠DMO=2, 如图,过点P 作PT ∥y 轴交直线DM 于点T ,过点F 作直线GH ⊥y 轴交PT 于点G ,交直线CE 于点H.∵PQ ⊥MT ,∴∠TFG=∠TPF ,∴TG=2GF ,GF=2PG ,∴PT=25GF , ∵PF=QF ,∴△FGP ≌△FHQ ,∴FG=FH ,∴PT=45GH. 设点P (m ,-m²+2m+3),则T (m ,-2m+3),∴PT=m²-4m ,GH=1-m ,∴m²-4m=45(1-m ), 解得:1112018m -=,或2112018m +=(不合题意,舍去), ∴点P 的横坐标为11201-. 【点睛】 本题考查二次函数综合题、平行线分线段成比例定理、轴对称性质等知识,解题的关键是学会用转化的思想思考问题,学会用数形结合的思想解决问题,有一定难度.4.D解析:(1)DF 的长为158;(2)MN 的长为5;(3)O 的半径长为258. 【解析】【分析】(1)作EH BM ⊥于H ,根据中位线定理得出四边形BMFA 是平行四边形,从而利用cos 45B =解直角三角形即可求算半径,再根据平行四边形的性质求FD 即可; (2)先证AMB CNM ∠=∠,再证MAD CNM ∠=∠,从而证明AFM NFD ∆~∆,得到AF MF AF DF NF MF NF DF=⇒=,再通过平行证明AFN DFM ∆~∆,从而得到AF NF AF MF NF DF DF MF=⇒=,通过两式相乘得出AF NF =再根据平行得出NF DF =, 从而得出答案.(3)通过图形得出MN 垂直平分'OO ,从而得出90BAM CMN ∠=∠=︒,再利用cos 45B =解三角函数即可得出答案. 【详解】(1)如图,作EH BM ⊥于H :∵E 为AB 中点,45,cos 5AB AD DC B ====∴52AE BE ==∴cos 45BH B BE == ∴2BH = ∴2253222EH ⎛⎫=-= ⎪⎝⎭设半径为r ,在Rt OEH ∆中:()222322r r ⎛⎫=-+ ⎪⎝⎭ 解得:2516r =∵,E O 分别为,BA BM 中点 ∴BAM BEO OBE ∠=∠=∠又∵CMN BAM ∠=∠∴CMN OBE ∠=∠∴//MF AB∴四边形BMFA 是平行四边形∴2528AF BM r ===∴2515588FD AD AF =-=-= (2)如图:连接MD AN ,∵,B C BAM CMN ∠=∠∠=∠∴AMB CNM ∠=∠又∵AMB MAD ∠=∠∴MAD CNM ∠=∠又∵AFM NFD ∠=∠∴AFM NFD ∆~∆∴AF MF AF DF NF MF NF DF=⇒=① 又∵//MD AN ∴AFN DFM ∆~∆∴AF NF AF MF NF DF DF MF=⇒=② 由①⨯②得; 22AF NF AF NF =⇒=∴NF DF =∴5MN AD ==故MN 的长为5;(3)作如图:∵圆O 与圆'O 外切且均与圆N 内切设圆N 半径为R ,圆O 半径为r∴'=NO R r NO -=∴N 在'OO 的中垂线上 ∴MN 垂直平分'OO∴90NMC ∠=︒∵90BAM CMN ∠=∠=︒∴A 点在圆上∴54cos 5AB B BM BM === 解得:254BM = O 的半径长为258【点睛】 本题是一道圆的综合题目,难度较大,掌握相似之间的关系转化以及相关线段角度的关系转化是解题关键.5.A解析:(1)6y x =-+;(2)636S t =-,()6t >;(3)5599y x =+ 【解析】【分析】(1)求出点A 、B 的坐标,从而得出△ABO 是等腰直角三角形,再根据2ABC ACB ∠=∠可得△OCB 也是等腰直角三角形,从而可求得点C 的坐标,将点B 、C 代入可求得解析式;(2)存在2种情况,一种是点D 在线段BC 上,另一种是点D 在线段BC 的延长线上,分别利用三角形的面积公式可求得;(3)如下图,先证ACR CAD ∆≅∆,从而推导出//RD AC ,进而得到CF RG =,同理还可得NF DG =,RD CN =,然后利用:7:12NF FC =可得到N 、D 的坐标,代入即可求得.【详解】解:(1)直线6y x =+与x 轴交于点A ,与y 轴交于点B ,(6,0)A ∴-,(0,6)B .6OA OB ∴==.45BAO ∴∠=︒,180BAO ABC BCO ∠+∠+∠=︒,2ABC ACB ∠=∠,45BCO ∴∠=︒6OC OB ∴==,()6,0C ∴.设直线BC 的解析式为y kx b =+,将B 、C 两点坐标代得606k b b +=⎧⎨=⎩ 解得16k b =-⎧⎨=⎩∴直线BC 的解析式为6y x =-+.(2)点D 是射线BC 上一点,点D 的横坐标为t ,(,6)D t t ∴-+,6(6)12AC =--=.如下图,过点D 作DK AC ⊥于点K ,当点D 在线段BC 上时,6DK t =-+,16362S AC DK t ∴=⋅=-+()06t ≤<; 如下图,当点D 在线段BC 的延长线上时,6DK t =-,636S t ∴=-()6t >.(3)如图,延长CE 交AB 于点R ,连接DR 交BF 于点G ,交y 轴于点P .45BAO BCO ∠=∠=︒,BA BC ∴=.AO CO =,BO AC ⊥EA EC ∴=,EAC ECA ∴∠=∠.ACR CAD ∴∆≅∆.BAD BCR ∴∠=∠.AR CD ∴=.BR BD ∴=.//RD AC ∴.BH AD ⊥,HBD BAD BCR ∴∠=∠=∠.MB MC ∴=,∠MRB MRB MBR ∠=∠MR MB ∴=.CM MR ∴=.//RD AC ,::1:1CF RG CM RM ∴==.CF RG ∴=.同理NF DG =.RD CN =.∵:7:12NF FC =.:7:12DG RG ∴=.RP PD BP ==,5tan 19PG OF OBF BP OB∴==∠= 6OB ∴=,3019OF ∴=,6OC =,8419CF ∴=. 7RD GN ∴==.1ON ∴=,72PD =.52OP OB BP ∴=-=. (1,0)N ∴-,75,22D ⎛⎫ ⎪⎝⎭. 设直线 DN 的解析式为y ax c =+,将N 、D 两点代入,07522a c a c -+=⎧⎪⎨+=⎪⎩解得5959 ac⎧=⎪⎪⎨⎪=⎪⎩∴直线DM的解析式为5599y x=+.【点睛】本题考查了一次函数与图形的综合,需要用到全等、三角函数和平面直角坐标系的知识,解题关键是想办法确定函数图像上点的坐标.6.D解析:(1)6;(2)y=-3x+10(1≤x<103);(2)1769或32【解析】【分析】(1)如下图,利用等腰直角三角形DHC可得到HC的长度,从而得出HB的长,进而得出AD的长;(2)如下图,利用等腰直角三角形的性质,可得PQ、PR的长,然后利用EB=PQ+PR得去x、y的函数关系,最后根据图形特点得出取值范围;(3)存在2种情况,一种是点P在梯形内,一种是在梯形外,分别根y的值求出x的值,然后根据梯形面积求解即可.【详解】(1)如下图,过点D作BC的垂线,交BC于点H∵∠C=45°,DH⊥BC∴△DHC是等腰直角三角形∵四边形ABCD是梯形,∠B=90°∴四边形ABHD是矩形,∴DH=AB=8∴HC=8∴BH=BC-HC=6∴AD=6(2)如下图,过点P作EF的垂线,交EF于点Q,反向延长交BC于点R,DH与EF交于点G∵EF ∥AD,∴EF ∥BC∴∠EFP=∠C=45°∵EP ⊥PF∴△EPF 是等腰直角三角形同理,还可得△NPM 和△DGF 也是等腰直角三角形∵AE=x∴DG=x=GF,∴EF=AD+GF=6+x∵PQ ⊥EF,∴PQ=QE=QF∴PQ=()162x + 同理,PR=12y ∵AB=8,∴EB=8-x∵EB=QR∴8-x=()11622x y ++ 化简得:y=-3x+10 ∵y >0,∴x <103 当点N 与点B 重合时,x 可取得最小值则BC=NM+MC=NM+EF=-3x+10+614x +=,解得x=1∴1≤x <103(3)情况一:点P 在梯形ABCD 内,即(2)中的图形 ∵MN=2,即y=2,代入(2)中的关系式可得:x=83=AE ∴188176662339ABCD S ⎛⎫=⨯++⨯= ⎪⎝⎭梯形 情况二:点P 在梯形ABCD 外,图形如下:与(2)相同,可得y=3x -10则当y=2时,x=4,即AE=4 ∴()16644322ABCD S =⨯++⨯=梯形 【点睛】本题考查了等腰直角三角形、矩形的性质,难点在于第(2)问中确定x 的取值范围,需要一定的空间想象能力. 7.A解析:(1)详见解析;(2)2448x x y -+=(04x <<);(3)当AEG ∆是等腰三角形时,2BF =或43【解析】【分析】 (1)根据正方形的性质得到∠AOD=90°,AO=OD ,∠EOH=90°,OE=OH ,由全等三角形的性质即可得到结论;(2)如图1,过O 作ON ⊥AB 于N ,根据等腰直角三角形的性质得到122AN BN ON AB ====, 根据勾股定理得到()222222248OF FN ON x x x =+=-+=-+线段成比例定理即可得到结论;(3)①当AE=EG 时,△AEG 是等腰三角形,②当AE=AG 时,△AEG 是等腰三角形,如图2,过A 作AP ⊥EG 于P ③当GE=AG 时,△AEG 是等腰三角形,如图3,过G 作GQ ⊥AE 于Q ,根据相似三角形的性质或全等三角形的性质健即可得到结论.【详解】(1)∵四边形ABCD 是正方形,,OA OD AC BD ∴=⊥,90AOD ∴∠=︒,∵四边形OEGH 是正方形,,90OE OH EOH ∴=∠=︒,AOD EOH ∴∠=∠,AOD AOH EOH AOH ∴∠-∠=∠-∠,即HOD EOA ∠=∠,HDO EAO ∴∆≅∆.(2)如图1,过O 作ON⊥AB 于N ,则122AN BN ON AB ====, ∵BF=x,∴AF=4-x ,∴FN=2-x , ∴()222222248OF FN ON x x x =+=-+=-+∴248EF y x x =-+ ∵AM⊥AC,∴AE∥OB,∴BF OF AF EF=, ∴2248448x x x x y x x -+=---+, ∴)24804x x y x x-+≤=<; (3)①当AE=EG 时,△AEG 是等腰三角形,则AE=OE ,∵∠EAO=90°,∴这种情况不存在;②当AE=AG 时,△AEG 是等腰三角形,如图2,过A 作AP⊥EG 于P ,则AP∥OE,∴∠PAE=∠AEO,∴△APE∽△EAO,∴PE AE OA OE=,∵AE=AG,∴2421482x xxPE y-+==,()22248xAE yx-=-=,∴()22222224448448xx xxx xx---+=+,解得:x=2,②当GE=AG时,△AEG是等腰三角形,如图3,过G作GQ⊥AE于Q,∴∠GQE=∠EAO=90°,∴∠GEQ+∠EGQ=∠GEQ+∠AEO=90°,∴∠EGQ=∠AEO,∵GE=OE,∴△EGQ≌△OEA(AAS),∴22EQ AO==∴224242()xAE E Q-===∴43x =, ∴BF=2或43. 【点睛】本题考查了四边形的综合题,正方形的性质,全等三角形的判定和性质,相似三角形的判定和性质,等腰三角形的性质,勾股定理,正确的作出辅助线构造全等三角形是解题的关键.8.B解析:(1)12;(2)3)【解析】【分析】(1)如图1中,过点B 作BD CA ⊥,交CA 延长线于点D ,通过构造直角三角形,求出BD 利用三角形面积公式求解即可.(2)如图示,作点D 关于AB 的对称点Q ,交AB 于点H ,连接CQ ,交AB 于点P ,连接PD 、OD 、OC ,过点Q 作QM CO ⊥,交CO 延长线于点M ,确定点P 的位置,利用勾股定理与矩形的性质求出CQ 的长度即为答案.(3)解图3所示,在AB 上这一点作点P 关于OA 的对称点S ,作点P 关于OB 的对称点N ,连接SN ,交OA 于点E ,交OB 于点F ,连接OS ON OP EP FP 、、、、,通过轴对称性质的转化,最终确定最小值转化为SN 的长.【详解】(1)如解图1所示,过点B 作BD CA ⊥,交CA 延长线于点D ,135BAC ∠=,180********BAD BAC ∴∠=-∠=-=,BD CA ⊥,交CA 延长线于点D ,BAD ∴为等腰直角三角形,且90BDA ∠=,BD AD ∴=,在BAD 中,,90BD AD BDA =∠=,222BD AD AB ∴+=,即222BD AB =,4AB =222232BD AB ∴===,解得:4BD =,6AC =,11641222ABC S AC BD ∴=⋅=⨯⨯=.(2)如解图2所示,作点D 关于AB 的对称点Q ,交AB 于点H ,连接CQ ,交AB 于点P ,连接PD 、OD 、OC ,过点Q 作QM CO ⊥,交CO 延长线于点M , D 关于AB 的对称点Q ,CQ 交AB 于点P ,PD PQ ∴=,PC PD PC PQ CQ ∴+=+=,点P 为AB 上的动点,PC PD CQ ∴+≥,∴当点P 处于解图2中的位置,PC PD +取最小值,且最小值为CQ 的长度, 点C 为半圆AB 的中点,90COB ∴∠=,90BOD COD COB ∠+∠=∠=,11903033BOD COB ∴∠=∠=⨯=, 10AB =,1110522OD AB ∴==⨯=, 在Rt ODH △中,由作图知,90OHD ∠=,且30HOD BOD ∠=∠=, 155,222DH OD QH DH ∴==∴==, 222255352OH OD DH ⎛⎫∴=-=-= ⎪⎝⎭, 由作图知,四边形OMQH 为矩形,553,2OM QH MQ OH ∴==== 515522CM OM OC ∴=+=+=, 222215535322CQ CM MQ ⎛⎫⎛⎫∴=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭,PC PD ∴+的最小值为53.(3)如解图3所示,在AB 上这一点作点P 关于OA 的对称点S ,作点P 关于OB 的对称点N ,连接SN ,交OA 于点E ,交OB 于点F ,连接OS ON OP EP FP 、、、、, 点P 关于OA 的对称点S ,点P 关于OB 的对称点N ,连接SN ,交OA 于点E ,交OB 于点F ,PE SE ∴=,FP FN =,SOA POA ∠=∠,,NOB POB OS OP ON ∠=∠==,.PE EF FP SE EF FN SN ∴++=++=,SOA NOB POA POB ∠+∠=∠+∠,E 为OA 上的点,F 为OB 上的点PE EF FP SN ∴++≥,∴当点E F 、处于解图3的位置时,PE EF FP ++的长度取最小值,最小值为SN 的长度,45POA POB AOB ∠+∠=∠=,45SOA NOB ∴∠+∠=,454590SON SOA AOB NOB ∴∠=∠+∠+∠=+=.扇形AOB 的半径为20,20OS ON OP ∴===,在Rt SON 中,90SON ∠=,20,90OS ON SON ==∠=PE EF FP ∴++的长度的最小值为202【点睛】本题主要考察了轴对称、勾股定理、圆、四边形等相关内容,理解题意,作出辅助线是做题的关键.9.A解析:(1)145;(2)2274,0314971421,2235t tSt t t⎧⎛⎫<≤⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+-<<⎪⎪⎝⎭⎩;(3)t的值为477或727.【解析】【分析】(1)如下图,根据4tan3A=,可得出PN与AP的关系,从而求出t的值;(2)如下图,存在2种情况,一种是点M在△ABC内,另一种是点M在△ABC外部,分别根据正方形和三角形求面积的公式可求解;(3)如下图,存在2种情况,一种是PM所在的直线将△ABC的面积平分,另一种是QN 所在的直线将△ABC的面积平分.【详解】(1)如图1,点N在AC上图1由题意可知:PD=DQ=t ,AP=7-t∴PN=PQ=2t ∵4tan 3A = ∴43NP AP =,即2473t t =- 解得:t=145 (2)①如图2,图2四边形PQMN 是正方形,90BQM ∴∠=︒,45B ∠=︒,BQ MQ ∴=,即72t t -=解得73t =, 故当0t <≤73时,22(2)4S t t ==; ②如图3, 图390BQF ∠=︒,45B ∠=︒,7BQ FQ t ∴==-,45BFQ MFE ∠=∠=︒,则37MF MQ QF t =-=-,90M ∠=︒,37ME MF t ∴==-, 则2221149(2)(37)21222S t t t t =--=-+-71435t ⎛⎫<< ⎪⎝⎭; 综上,2274,0314971421,2235t t S t t t ⎧⎛⎫<≤ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+-<< ⎪⎪⎝⎭⎩. (3)如下图,过点C 作AB 的垂线,交AB 于点G图4∵4tan 3A = ∴设CG=4x ,则AG=3x∵∠B=45°∴△CBG 是等腰直角三角形∴GB=GC=4x∵AB=14∴3x+4x=14,解得:x=2∴1148562ABC S== ∴1282ABCS = 情况一:PM 所在的直线平分△ABC 的面积,如下图,PM 与BC 交于点E图5则28PBES=∵四边形PQMN是正方形,∴∠EPB=45°∵∠B=45°∴△PBE是等腰直角三角形∵1282PBES PE PB==∴PE=PB=214∴PB=47∵PB=AB-PA=14-(7-t)=7+t∴7+t=47t=477-情况二:如下图,QN所在线段平分△ABC的面积,QF交AC于点F,过点F作AB的垂线,交AB于点H图6同理,28AFQS=∵四边形PQMN是正方形,∴∠EQH=45°∴△FHQ是等腰直角三角形∵4 tan3A=∴设FH=4y,则AH=3y,HQ=FH=4y,∴AQ=7y∴174282AFQS y y==,解得:2∵AQ=AB-QB=14-(7-t)=7+t∴2解得:27∴综上得:t的值为477或727.【点睛】本题考查动点问题,解题关键是根据动点的变化情况,适当划分为几种不同的形式分别分析求解.10.A。
(完整word版)深圳市近十年中考数学试题分类汇编10圆(含解析),推荐文档

2002年-2012年广东省深圳市中考数学试题分类解析汇编专题10:圆一、选择题1.(深圳2003年5分)如图,已知四边形ABCD 是⊙O 的内接四边形,且AB =CD =5,AC =7,BE =3,下列命题错误的是【 】A 、△AED ∽△BECB 、∠AEB =90ºC 、∠BDA =45ºD 、图中全等的三角形共有2对 【答案】 D 。
【考点】圆周角定理,相似三角形的判定,等腰三角形的判定和性质,勾股定理逆定理,全等的三角形的判定。
【分析】A 、根据圆周角定理的推论,可得到:∠ADE =∠BCE ,∠DAE =∠CBE ∴△AED ∽BED ,正确;B 、由四边形ABCD 是⊙O 的内接四边形,且AB =CD ,有»»ABCD ,从而根据等弧所对圆周角相等的性质,得∠EBC =∠ECB ,由等腰三角形等角对等边的性质,得BE =CE ,∴BE =CE =3,AB =5,AE =AC -CE =4,根据勾股定理的逆定理,△ABE 为直角三角形,即∠AEB =90°,正确;C 、AE =DE ,∴∠EAD =∠EDA =45°,正确;D 、从已知条件不难得到△ABE ≌△DCE 、△ABC ≌△DCB 、△ABD ≌DCA 共3对,错误。
故选D 。
2.(深圳2004年3分)已知⊙O 1的半径是3,⊙O 2的半径是4,O 1O 2=8,则这两圆的位置关系是【 】A 、相交B 、相切C 、内含D 、外离 【答案】D 。
【考点】两圆的位置关系。
【分析】根据两圆的位置关系的判定:外切(两圆圆心距离等于两圆半径之和),内切(两圆圆心距离等于两圆半径之差),相离(两圆圆心距离大于两圆半径之和),相交(两圆圆心距离小于两圆半径之和大于两圆半径之差),内含(两圆圆心距离小于两圆半径之差)。
∵⊙O 1的半径是3,⊙O 2的半径是4,O 1O 2=8,则3+4=7<8,∴两圆外离。
深圳深圳实验学校中考数学期末几何综合压轴题易错汇编

深圳深圳实验学校中考数学期末几何综合压轴题易错汇编一、中考数学几何综合压轴题1.(操作)如图①,在矩形ABCD 中,E 为对角线AC 上一点(不与点A 重合),将ADE ∆沿射线AB 方向平移到BCF ∆的位置,E 的对应点为F .已知ADE BCF ∆∆≌(不需要证明).(探究)过图①中的点E 作//EG BC 交FB 延长线于点G ,连接AG ,其它条件不变,如图②.求证:EGA BCF ∆∆≌.(拓展)将图②中的BCF ∆沿BC 翻折得到BCF '∆,连接GF ',其它条件不变,如图③.当GF '最短时,若4AB =,2BC =,直接写出FF '的长和此时四边形BFCF '的周长.解析:探究:见解析;拓展:'4,FF = 四边形'BFCF 的周长为4 5. 【分析】探究:证明四边形EGBC 是平行四边形,推出EG=BC ,利用SAS 证明三角形全等即可. 拓展:如图3中,连接BD 交AC 于点O ,作BK ⊥AC 于K ,F′H ⊥BC 于H .由题意四边形AGFC 是平行四边形,推出GF=AC=25,由BF=BF′,可以假设BF=x ,则BG=25,x -利用相似三角形的性质,求出BH ,HF′,利用勾股定理求出GF′,再利用二次函数的性质,求出GF′的值最小时BF′的值,推出BF′=5 此时点F′与O 重合,由此即可解决问题.【详解】解:探究:由平移AE BF =,//AE BF∴//AC GF ,即//CE BG又∵//EG BC ,∴四边形BCEG 为平行四边形∴EG BC =∵//AC FG ,∴∠CBF=∠ACB ,∵//EG BC∴∠AEG=∠ACB ,∴∠AEG=∠CBF∴EGA BCF ∆∆≌.拓展:如图3中,连接BD 交AC 于点O ,作BK ⊥AC 于K ,F′H ⊥BC 于H .∵四边形ABCD 是矩形, ∴∠ABC=90°,AB=4,BC=2, ∴22224225,AC AB BC +=+∵11,22AB CB AC BK •=• ∴45BK = ∴22224535(5)()5OK OB BK -=- 由题意四边形AGFC 是平行四边形, ∴GF=AC=5∵BF=BF′,可以假设BF=x ,则BG=25,x∵AC ∥GF , ∴∠BOK=∠HBF′,∵∠BKO=∠F′HB=90°,∴△F′HB ∽△BKO ,∴ '',F H BH BF BK OK OB== ∴'45355== ∴'4338,,2525,5555F H x BH x GH BG BH x x x ===-=-= ∴''222224816325()(25)20,5555GF F H GH x x x x =++--+ ∵ 165>0, ∴当32555,1625x -=-=⨯ 时,GF′的值最小, 此时点F′与O 重合,由对折得:'',,CF CF BF BF ==由矩形的性质得:'',BF CF ='',BF CF BF CF ∴===∴ 四边形BFCF′是菱形,∴ 四边形BFCF′的周长为45, ',FF BC ∴⊥ 且'FF 与BC 互相平分, 由勾股定理得:'222(5)1 4.FF =-=【点睛】本题属于四边形综合题,考查了矩形的性质,翻折变换,平行四边形的判定和性质,相似三角形的判定和性质,二次函数的性质等知识,解题的关键是学会添加常用辅助线,构造相似三角形解决问题,学会构建二次函数解决最值问题,属于中考压轴题.2.如图,在菱形ABCD 中,120BAD ∠=,将边AB 绕点A 逆时针旋转至'AB ,记旋转角为α.过点D 作DF BC ⊥于点F ,过点B 作BE ⊥直线'B D 于点E ,连接EF . (探索发现)(1)填空:当60α=时,'EBB ∠ = .'EF DB 的值是 (验证猜想)(2)当0360α<<时,(1)中的结论是否仍然成立?若成立,请仅就图2的情形进行证明;若不成立,请说明理由;(拓展应用)(3)在(2)的条件下,若22AB =,当BDE ∆是等腰直角三角形时,请直接写出线段EF 的长.解析:(1)3032)当0360α<<时,(1)中的结论仍然成立,理由见解析;(3)线段EF 的长为33【分析】(1)当60α=时,点B ′与点C 重合,BE ⊥ CD ,由四边形ABCD 为菱形,可求∠ABE =90°,由120BAD ∠=,可求∠ABC =60°,'EBB ∠=30°,由DF ⊥BC ,DC ∥AB ,∠FDC =∠EBC =30°,由sin ∠FDC =sin ∠EBC =CF CE DC BC=,可得CF =CE ,可求∠CEF =∠FDC =30°即可; (2)当0360α<<时, (1)中的结论仍然成立.先求'60EB B ∠=︒,再证'EBB CBD ∠=∠.最后证'DBB FBE ∆∆∽即可;(3) 连接AC ,BD 交于点O .先求OB =DE ='2EB =.分两种情况:①如图先求'2B D =,再证△B′BD ∽△EBF ,可得EF B D ′②如图先求'2B D =.再证△B′BD ∽△EBF ,EF B D ′ 【详解】(1)当60α=时,点B ′与点C 重合,∵BE ⊥ CD ,四边形ABCD 为菱形,CD ∥AB ,∴BE ⊥AB ,∴∠ABE =90°,∵120BAD ∠=,AD ∥BC ,∴∠ABC =180°-∠BAD =180°-120°=60°,∴'EBB ∠=∠ABE -∠ABC =90°-60°=30°,∵DF ⊥BC ,DC ∥AB ,∴DF ⊥AD ,∠CDA =180°-∠BAD =60°,∴∠FDC =90°-∠CDA =30°,∠FCD =90°-∠FDC =60°,∴∠FDC =∠EBC =30°,∴sin ∠FDC =sin ∠EBC =CF CE DC BC =, ∵DC =BC ,∴CF =CE ,∴∠CFE =∠CEF =12∠FCD =30°,∴∠CEF =∠FDC =30°,∴DF =FE ,∵cos ∠FDC =DF DC =,∴'EF DB =DF DC =故答案为30(2)当0360α<<时, (1)中的结论仍然成立.证明:如图1,连接BD .'AB AD AB ==, 1'(180)9022AB B αα∴∠=︒-=︒-,1'[180(120)]3022AB D αα∠=︒-︒-=︒+. '180''180(90)(30)6022EB B AB D AB B αα∴∠=︒-∠-∠=︒-︒--︒+=︒, '30EBB ∴∠=︒. 11(180)3022CBD ABC BAD ∠=∠=︒-∠=︒. 'EBB CBD ∴∠=∠.'''EBB FBB CBD FBB ∴∠+∠=∠+∠,即'DBB EBF ∠=∠.3cos 2BF DBF BD ∠==,3cos ''2BE EBB BB ∠==, 'BF BE BD BB ∴=. 'DBB FBE ∆∆∽.3''2EF BE DB BB ∴==,(3)线段EF 的长为3333连接AC ,BD 交于点O .AC DB ⊥,1602BAO BAD ∠=∠=︒,sin 6OB AB BAO ∴=⋅∠=226BD OB ∴== ∵DE =BE ,∠DEB =90°,∴∠EDB =∠EBD =45°,2sin 26232DE BE BD DBE ∴==⋅∠=⨯=. 'AB AD AB ==,∠B′EB =90°,1'(180)9022AB B αα∴∠=︒-=︒-,1'[180(120)]3022AB D αα∠=︒-︒-=︒+. '180''180(90)(30)6022EB B AB D AB B αα∴∠=︒-∠-∠=︒-︒--︒+=︒, '30EBB ∴∠=︒. 3'tan '2322EB BE EBB ∴=⋅∠=⨯=. 分两种情况:①如图,''232B D DE B E =+=+,∵∠B′BE =∠DBF =30°,∴cos ∠B ′BE =cos ∠DBF =3=2EB FB B B DB =', 又∵∠B′BE +∠EBD =∠EBD +∠DBF ,∴∠B′BD =∠EBF ,∴△B′BD ∽△EBF ,∴3==2EB FB EF B B DB B D ='', 33(232)3322EF B D '∴==⨯+=+ .②如图,''232B D DE B E =-=.∵∠B′BE =∠DBF =30°,∴cos ∠B′BE =cos ∠DBF =3EB FB B B DB =' 又∵∠B′BE -∠FBB′=∠DBF-∠FBB ′,∴∠B′BD =∠EBF ,∴△B′BD ∽△EBF , ∴3==2EB FB EF B B DB B D ='', 33(232)3322EF B D '∴=⨯=⨯-=-.综上所述,线段EF 的长为33+或33-.【点睛】本题考查图形旋转变换,菱形性质,锐角三角函数值,等腰直角三角形性质,三角形相似判定与性质,掌握图形旋转变换,菱形性质,锐角三角函数值,等腰直角三角形性质,三角形相似判定与性质是解题关键.3.(问题原型)如图,在矩形ABCD 中,对角线AC 、BD 交于点O ,以AC 为直径作O .求证:点B 、D 在O 上.请完成上面问题的证明,写出完整的证明过程.(发现结论)矩形的四个顶点都在以该矩形对角线的交点为圆心,对角线的长为直径的圆上.(结论应用)如图,已知线段2AB =,以线段AB 为对角线构造矩形ACBD .求矩形ACBD 面积的最大值.(拓展延伸)如图,在正方形ABCD 中,2AB =,点E 、F 分别为边AB 、CD 的中点,以线段EF 为对角线构造矩形EGFH ,矩形EGFH 的边与正方形ABCD 的对角线AC 交于M 、N 两点,当MN 的长最大时,矩形EGFH 的面积为_____________________解析:问题原型:见解析;结论应用:见解析;发现结论:2;拓展延伸:2【分析】问题原型:运用矩形对角线互相平分且相等,即可求证四点共圆;结论应用:根据结论矩形面积最大时为正方形,利用对角线的长求得正方形的面积; 拓展延伸:由上一问的结论,可知四边形EGFH 为正方形, 证明四边形AEOH 是正方形,继而求得面积【详解】解:【问题原型】∵AC 为O 直径,∴OA 为O 半径.令OA r =.∵四边形ABCE 为矩形,∴AC BD =,12OA OC AC ==,.12OB OD BD == ∴OB OD OA r ===.∴点B 、D 在O 上.【结论应用】连续CD 交AB 于点O ,过点D 作DE AB ⊥于点E .∴DE OD ≤.由【发现结论】可知,点D 在以AB 为直径的圆上,即112OD OA AB ===, ∴当1DE OD ==即AB CD ⊥时,矩形ACBD 的面积最大.2AB CD ==∴矩形ACBD 的面积最大值为22112222AB =⨯=. 【拓展延伸】 如图,连接GH ,设AC 与EF 的交点为O四边形ABCD 是正方形2AB ∴=,90BAD ADC ∠=∠=︒,//AE DF点E 、F 分别为边AB 、CD 的中点1AE EB CF FD ∴====,2EF =∴四边形AEFD 是矩形//EF AD ∴EF AB ⊥,由【结论应用】可知,2EF =时,矩形EGFH 的面积最大为2122EF = 此时四边形EGFH 为正方形,此时MN 最大,EF GH ∴⊥,112EO OF OH OG EF ===== ∴四边形AEOH 是正方形∴112AE AH AB === ∴2222112EH AE AH =+=+=∴正方形EGFH 的面积为:22(2)2EH ==【点睛】本题考查了矩形的性质,正方形的性质与判定,灵活运用矩形,正方形的性质和判定是解题的关键.4.在ABC 中,点D ,E 分别是AB AC ,边上的点,//DE BC .基础理解:(1)如图1,若43AD BD ==,,求AE AC 的值; 证明与拓展:(2)如图2,将ADE 绕点A 逆时针旋转a 度,得到11AD E △,连接11,BD CE ; ①求证:11BD AD CE AE=; ②如图3,若90,6,BAC AB AC AD ADE ∠=︒<=,在旋转的过程中,点1D 恰好落在DE 上时,连接1113,4BD EE CE =,则11E D E 的面积为________. 解析:(1)47;(2)①见详解;②13.44 【分析】(1)利用平行线分线段定理,直接求解即可;、 (2)①先推出11AD AB AE AC=,从而得11ABD ACE ∽,进而即可得到结论;②先推出AE =AE 1 =8,DE =D 1E 1=10,过点A 作AM ⊥DE 于点M ,则DM = 3.6,D 1E =2.8,再证明∠D 1EE 1=90°,进而即可求解.【详解】解:(1)∵//DE BC ,43AD BD ==,, ∴AE AC =44437AD AB ==+; (2)①∵将ADE 绕点A 逆时针旋转a 度,得到11AD E △, ∴1AD =AD ,1AE =AE ,∠BAD 1=∠CAE 1,∵//DE BC , ∴AD AE AB AC =,即AD AB AE AC=, ∴11AD AB AE AC=, ∴11ABD ACE ∽, ∴1111BD AD AD CE AE AE ==;②由①可知11ABD ACE ∽, ∴111134BD AD CE AE ==, ∵将ADE 绕点A 逆时针旋转,得到11AD E △,点1D 恰好落在DE 上, ∴AD 1=AD =6,∠D 1AE 1=∠DAE =90°,∴AE =AE 1=43AD 1=8,DE =D 1E 1=226810+=,过点A 作AM ⊥DE 于点M ,则DM =D 1M =AD ×cos ∠ADE = AD ×ADDE =6×610=3.6,∴D 1E =10-3.6 ×2=2.8, ∵∠D 1AE 1=∠DAE =90°, ∴∠DAD 1=∠EAE 1, 又∵AD 1=AD ,AE =AE 1, ∴∠ADE =11118018022DAD EAE AEE ︒-∠︒-∠==∠,∴∠AED +1AEE ∠=∠AED +∠ADE =90°,即:∠D 1EE 1=90°, ∴22110 2.89.6EE -, ∴11E D E 的面积=12D 1E ∙EE 1=12×2.8×9.6=13.44. 故答案是:13.44. 【点睛】本题主要考查相似三角形的判定和性质,解直角三角形,勾股定理,平行线分线段成比例定理,旋转的性质,熟练掌握相似三角形的判定和性质,是解题的关键. 5.[探究函数4y x x=+的图象与性质] (1)函数4y x x=+的自变量x 的取值范围是 ; (2)下列四个函数图象中函数4y x x=+的图象大致是 ;(3)对于函数4y x x=+,求当x 0>时,y 的取值范围. 请将下列的求解过程补充完整. 解:∵x 0> ∴()2224y x x x xx x =+=+=+∵20x x ≥∴ y ≥ .[拓展运用](4)若函数259x x y x -+=,则y 的取值范围 .解析:(1)0x ≠;(2)C ;(3)4,4;(4)1y ≥ 【详解】试题分析:本题的⑴问抓住函数是由分式给定的,所以抓住是分母不为0,即可确定自变量的取值范围.本题的⑵问结合第⑴问中的0x ≠,即0x >或0x <进行分类讨论函数值y 的大致取值范围,即可得到函数的大致图象.本题的第⑶问根据函数的配方逆向展开即推出“( )”应填写“常数”部分,再根据配方情况可以得到当当0x >时,y 的取值范围.本题的⑷问现将函数改写为95y x x=+-的形式,再按⑶的形式进行配方变形即可求y 的取值范围. 试题解析:(1)由于函数4y x x=+是分式给定的,所要满足分母不为0,所以0x ≠. 故填:0x ≠.(2)0x ≠即0x >或0x <;当0x >时,y 的值是正数,此时画出的图象只能在第一象限;当0x <时,y 的值是负数,此时画出的图象只能在第三象限;所以函数4y x x=+的图象只在直角坐标系的一、三象限.故其大致图象应选C.(3)∵244x x x x =-+,∴(()22244y x x x xx x =+=+=+.故分别填:44,; (4) ∵0x >(这里隐含有y 首先是正数)∴()222259933551x x y x x x x xx x -+⎛⎫⎛⎫==-+=+-=-+ ⎪ ⎪⎝⎭⎝⎭∵230x x ⎛⎫-≥ ⎪⎝⎭∴ 1y ≥.6.(问题情境)如图1,点E 是平行四边形ABCD 的边AD 上一点,连接BE 、CE .求证:BCE1S2=S 平行四边形ABCD .(说明:S 表示面积) 请以“问题情境”为基础,继续下面的探究(探究应用1)如图2,以平行四边形ABCD 的边AD 为直径作⊙O ,⊙O 与BC 边相切于点H ,与BD 相交于点M .若AD =6,BD =y ,AM =x ,试求y 与x 之间的函数关系式. (探究应用2)如图3,在图1的基础上,点F 在CD 上,连接AF 、BF ,AF 与CE 相交于点G ,若AF =CE ,求证:BG 平分∠AGC .(迁移拓展)如图4,平行四边形ABCD 中,AB :BC =4:3,∠ABC =120°,E 是AB 的中点,F 在BC 上,且BF :FC =2:1,过D 分别作DG ⊥AF 于G ,DH ⊥CE 于H ,请直接写出DG :DH 的值.解析:【问题情境】见解析;【探究应用1】18y x=;【探究应用2】见解析;【迁移拓1927 【分析】(1)作EF ⊥BC 于F ,则S △BCE =12BC×EF ,S 平行四边形ABCD =BC×EF ,即可得出结论; (2)连接OH ,由切线的性质得出OH ⊥BC ,OH =12AD =3,求出平行四边形ABCD 的面积=AD×OH =18,由圆周角定理得出AM ⊥BD ,得出△ABD 的面积=12BD×AM =12平行四边形的面积=9,即可得出结果;(3)作BM ⊥AF 于M ,BN ⊥CE 于N ,同图1得:△ABF 的面积=△BCE 的面积=12平行四边形ABCD 的面积,得出12AF×BM =12CE×BN ,证出BM =BN ,即可得出BG 平分∠AGC .(4)作AP ⊥BC 于P ,EQ ⊥BC 于Q ,由平行四边形的性质得出∠ABP =60°,得出∠BAP =30°,设AB =4x ,则BC =3x ,由直角三角形的性质得出BP =12AB =2x ,BQ =12BE ,AP ==,由已知得出BE =2x ,BF =2x ,得出BQ =x ,EQ ,PF =4x ,QF =3x ,QC =4x ,由勾股定理求出AF =,CE ,连接DF 、DE ,由三角形的面积关系得出AF×DG =CE×DH ,即可得出结果. 【详解】(1)证明:作EF ⊥BC 于F ,如图1所示: 则S △BCE =12BC×EF ,S 平行四边形ABCD =BC×EF , ∴12BCEABCDSS =.(2)解:连接OH ,如图2所示: ∵⊙O 与BC 边相切于点H , ∴OH ⊥BC ,OH =12AD =3,∴平行四边形ABCD 的面积=AD×OH =6×3=18, ∵AD 是⊙O 的直径, ∴∠AMD =90°, ∴AM ⊥BD ,∴△ABD 的面积=12BD×AM =12平行四边形的面积=9, 即12xy =9,∴y 与x 之间的函数关系式y =18x; (3)证明:作BM ⊥AF 于M ,BN ⊥CE 于N ,如图3所示:同图1得:△ABF 的面积=△BCE 的面积=12平行四边形ABCD 的面积, ∴12AF×BM =12CE×BN ,∵AF =CE , ∴BM =BN , ∴BG 平分∠AGC .(4)解:作AP ⊥BC 于P ,EQ ⊥BC 于Q ,如图4所示: ∵平行四边形ABCD 中,AB :BC =4:3,∠ABC =120°, ∴∠ABP =60°,∴∠BAP =30°,设AB =4x ,则BC =3x ,∴BP =12AB =2x ,BQ =12BE ,AP =, ∵E 是AB 的中点,F 在BC 上,且BF :FC =2:1, ∴BE =2x ,BF =2x , ∴BQ =x ,∴EQ =3x ,PF =4x ,QF =3x ,QC =4x ,由勾股定理得:AF =22AP PF +=27x ,CE =22EQ QC +=19x , 连接DF 、DE ,则△CDE 的面积=△ADF 的面积=12平行四边形ABCD 的面积, ∴AF×DG =CE×DH ,∴DG :DH =CE :AF =19x :27x 19:27=.【点睛】本题是圆的综合题目,考查了圆周角定理、平行四边形的性质、三角形面积公式、含30°角的直角三角形的性质、勾股定理、角平分线的判定等知识;本题综合性强,需要添加辅助线,熟练掌握平行四边形的性质和勾股定理是解题的关键. 7.()1问题发现如图①,正方形,ABCD DEFG 、将正方形DEFG 绕点D 旋转,直线AE CG 、交于点,P 请直接写出线段AE 与CG 的数量关系是 ,位置关系是 _;()2拓展探究如图②,矩形,2,2,ABCD DEFG AD DE AB DG ==、将矩形DEFG 绕点D 旋转,直线,AE CG 交于点,P ()1中线段关系还成立吗/若成立,请写出理由;若不成立,请写出线段AE CG 、的数量关系和位置关系,并说明理由;()3解决问题在()2的条件下,24,28,AD DE AB DG ====矩形DEFG 绕D 点旋转过程中,请直接写出当点P 与点G 重合时,线段AE 的长,解析:()1,AE CG AE CG =⊥;()()21中数量关系不成立,位置关系成立.1,2AE AE CG CG =⊥,理由见解析;()32565【分析】(1)证明△ADE ≌△CDG (SAS ),可得AE =CG ,∠DAG =∠DCG ,再由直角三角形两个锐角互余即可证得AE ⊥CG ;(2)先证明△ADE ∽△CDG ,利用相似三角形的性质证明即可.(3)先通过作图找到符合题意的两种情况,第一种情况利用勾股定理求解即可;第二种情况借助相似三角形及勾股定理计算即可. 【详解】(1),AE CG AE CG =⊥;理由如下:由题意知在正方形ABCD DEFG 、中,90EDG ADC ∠=∠=︒,,AD DC DE DG ==,EDG GDA ADC GDA ∴∠+∠=∠+∠ EDA GDC ∴∠=∠在△ADE 与△CDG 中,AD DC ADE CDG DE DG =⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△CDG (SAS ) ∴AE CG =,DEA DGC ∠=∠ ∵对顶角相等,∴,DEA EDG DGC GPE ∠+∠=∠+∠ 90.GPE ∴∠=AE CG ∴⊥.(2)(1)中数量关系不成立,位置关系成立.即:1,2AE AE CG CG =⊥ 理由如下:由题意知在矩形ABCD DEFG 、中,90EDG ADC ∠=∠=︒,EDG GDA ADC GDA ∴∠+∠=∠+∠EDA GDC ∴∠=∠2,2AD DE AB DG ==,12ED DG AD DC ∴== .EDAGDC ∴12AE CG ∴=,DEA DGC ∠=∠ ∵对顶角相等∴,DEA EDG DGC GPE ∠+∠=∠+∠ 90.GPE ∴∠=AE CG ∴⊥.综上所述:1,2AE AE CG CG =⊥ (3)如图1,当点G 、P 在点A 处重合时,连接AE , 则此时∠ADE =∠GDE =90°∴在Rt △ADE 中,AE 22224225AD DE +=+,如图1,当点G 、P 重合时, 则点A 、E 、G 在同一直线上, ∵AD =DG =4, ∴∠DAG =∠DGA ,∵∠ADC =∠AGP =90°,∠AOD =∠COG , ∴∠DAG =∠COG , ∴∠DGA =∠COG , 又∵∠GDO =∠CDG , ∴△GDO ∽△CDG , ∴DO DG OGDG DC CG == ∴448DO OGCG== ∴DO =2,CG =2OG , ∴OC =DC -DO =8-2=6, ∵在Rt △COG 中,OG 2+GC 2=OC 2, ∴OG 2+(2OG )2=62, ∴OG 655∴CG 1255由(2)得:12AE CG =∴AE 655综上所述,AE 的长为25655【点睛】本题综合考查了全等三角形及相似三角形的判定及性质,以及勾股定理的应用,根据题意画出符合题意的图形是解决本题的关键. 8.问题探究(1)如图1,△ABC 和△DEC 均为等腰直角三角形,∠ACB =∠DCE =90°,点B ,D ,E 在同一直线上,连接AD ,BD .①请探究AD与BD之间的位置关系:________;②若AC=BC=10,DC=CE=2,则线段AD的长为________;拓展延伸(2)如图2,△ABC和△DEC均为直角三角形,∠ACB=∠DCE=90°,AC=21,BC=7,CD=3,CE=1.将△DCE绕点C在平面内顺时针旋转,设旋转角∠BCD为α(0°≤α<360°),作直线BD,连接AD,当点B,D,E在同一直线上时,画出图形,并求线段AD 的长.解析:(1)①垂直,②4;(2)作图见解析,33或23【分析】(1)①由“SAS”可证△ACD≌△BCE,可得∠ADC=∠BEC=45°,可得AD⊥BD;②过点C作CF⊥AD于点F,由勾股定理可求DF,CF,AF的长,即可求AD的长;(2)分点D在BC左侧和BC右侧两种情况讨论,根据勾股定理和相似三角形的性质可求解.【详解】解:(1)∵△ABC和△DEC均为等腰直角三角形,∴AC=BC,CE=CD,∠ABC=∠DEC=45°=∠CDE∵∠ACB=∠DCE=90°,∴∠ACD=∠BCE,且AC=BC,CE=CD∴△ACD≌△BCE(SAS)∴∠ADC=∠BEC=45°∴∠ADE=∠ADC+∠CDE=90°∴AD⊥BD故答案为:垂直②如图,过点C作CF⊥AD于点F,∵∠ADC=45°,CF ⊥AD ,CD=2 ∴DF=CF=1∴22AF AC CF 3=-= ∴AD=AF+DF=4 故答案为:4. (2)①如图:∵∠ACB =∠DCE =90°,AC =21,BC =7,CD =3,CE =1, ∴AB=27,DE=2,∠ACD =∠BCE, 7AC BCDC CE==. ∴△ACD ∽△BCE . ∴∠ADC =∠E ,3AD ACBE BC==. 又∵∠CDE+∠E=90°,∴∠ADC+∠CDE =90°,即∠ADE=90°. ∴AD ⊥BE .设BE=x ,则AD=3x .在Rt △ABD 中,222AD BD AB +=,即2223)(2)(27)x x +-=(. 解得123,2x x ==-(负值舍去). ∴AD=33. ②如图,同①设BE=x ,则3.在Rt △ABD 中,222AD BD AB +=,即2223)(+2)(27)x x +=(. 解得122,3x x ==-(负值舍去). ∴AD=3综上可得,线段AD 的长为332 3.或 【点睛】本题是几何变换综合题,考查了全等三角形的判定和性质,相似三角形的判定和性质,勾股定理,等腰三角形的性质等知识点,关键是添加恰当辅助线. 9.(基础巩固)(1)如图①,ABC ACD CED α∠=∠=∠=,求证:ABC CED ∽△△. (尝试应用)(2)如图②,在菱形ABCD 中,60A ∠=︒,点E ,F 分别为边,AD AB 上两点,将菱形ABCD 沿EF 翻折,点A 恰好落在对角线DB 上的点P 处,若2PD PB =,求AEAF的值. (拓展提高)(3)如图③,在矩形ABCD 中,点P 是AD 边上一点,连接,PB PC ,若2,4,120PA PD BPC ==∠=︒,求AB 的长.解析:(1)见解析;(2)54;(3)113AB = 【分析】(1)由,ABC ACD ACE A ABC α∠=∠=∠=∠+∠证明A DCE ∠=∠,再根据相似三角形的判定方法解题即可;(2)由菱形的性质,得到AB AD =,60A ∠=︒,继而证明ABD △是等边三角形,结合(1)中相似三角形对应边成比例的性质,设,2,,BP a DP a AE PE x AF PF y ======,则3,3DE a x BF a y =-=-可整理得到54x y =,据此解题; (3)在AD 边上取点E ,F ,使得30ABE DCF ∠=∠=︒,由矩形的性质,得到120BEP BPC PFC ∠=∠=∠=︒,结合(1)中相似三角形对应边成比例的性质解题即可.【详解】解:(1)证明:∵,ABC ACD ACE A ABC α∠=∠=∠=∠+∠, ∴DCE A αα∠+=∠+,即A DCE ∠=∠, ∵ABC CED α∠=∠=, ∴ABC CED ∽△△; (2)∵四边形ABCD 是菱形, ∴AB AD =, ∴60A ∠=︒,∴ABD △是等边三角形,∴60EPF A ADB ABD ∠=∠=∠=∠=︒,由(1)得,EPD PFB ∽, ∴DE PD PEPB BF PF==, 设,2,,BP a DP a AE PE x AF PF y ======,则3,3DE a x BF a y =-=- ∴323a x a xa a y y-==-, 可得3ay xy ax -=①,32ax xy ay -=②, ①-②,得332ay ax ax ay -=-, ∴54x y =, ∴AE AF 的值为54; (3)如图,在AD 边上取点E ,F ,使得30ABE DCF ∠=∠=︒,设AB =CD =m ,∵四边形ABCD 是矩形, ∴90A D ∠=∠=︒,∴120BEP BPC PFC ∠=∠=∠=︒, 60BPE DFC ︒∠=∠=1,sin 60233AB BE CF AE BE ∴====︒= DF , 223PE AE ∴=-= 443PF DF ∴=-= 由(1)可得,BEP PFC ∽, ∴BE EPPF FC=, ∴2332433m m -=-22380m m +-=, 解得113m =311m = ∴113AB =. 【点睛】本题考查相似三角形的综合题、等边三角形的性质、菱形的性质、矩形的性质等知识,是重要考点,难度一般,掌握相关知识是解题关键.10.在Rt ABC ∆中,90,7,2ACB AB AC ︒∠===,过点B 作直线//m AC ,将ABC ∆绕点C 顺时针旋转得到A B C ''∆(点,A B 的对应点分别是,A B ''),射线,CA CB ''分别交直线m 于点,P Q .(1)问题发现:如图1所示,若P 与A '重合,则ACA '∠的度数为_________________ (2)类比探究:如图2,所示,设A B ''与BC 的交点为M ,当M 为A B ''中点时,求线段PQ 的长;(3)拓展延伸:在旋转过程中,当点,P Q 分别在,CA CB ''的延长线上时,试探究四边形PA B Q ''的面积是否存在最小值,若存在,直接写出四边形PA B Q ''的最小面积;若不存在,请说明理由解析:(1)60°;(2)72;(3)存在,33【分析】(1)由旋转可得:AC=A'C=2,进而得到3∠A'BC=90°,可得cos ∠A'CB=3BC A C '=,即可得到∠A'CB=30°,∠ACA'=60°; (2)根据M 为A'B'的中点,即可得出∠A=∠A'CM ,进而得到PB= 3BC A C '=tan ∠BQC=tan ∠33,进而得出PQ=PB+BQ=72; (3)依据S 四边形PA'B′Q =S △PCQ -S △A'CB '=S △PCQ 3S 四边形PA'B′Q 最小,即S △PCQ 最小,而S △PCQ =123,利用几何法或代数法即可得到S △PCQ 的最小值=3,S 四边形PA'B′Q =3-3【详解】解(1)由旋转得:2AC A C '==, 90,7,2,3ACB AB AC BC ︒∠===∴=90,//ACB m AC ︒∠=, 90A BC ︒'∴∠=,3cos BC A CB A C '∴∠==' 30A CB ︒'∴∠=, 60A CA ︒'∴∠=;(2)因为M 是AA '中点,所以A CM MA C ''∠=∠,A MA C '∠=∠,A A CM '∴∠=∠,3tan tan 2PCB A ∠=∠=∴, 3322PB BC ∴==. ∵∠PCQ=∠PBC=90°,∴∠BQC+∠BPC=∠BCP+∠BPC=90°, ∴∠BQC=∠BCP=∠A , 3tan tan 2BQC A ∴∠=∠=, 223BQ BC ∴=⨯=, 72PQ PB BQ ∴=+=; (3) 3PA B Q PCQ A CB PCQ S S S S ''''∆=-=-, PA B Q S ''∴最小,即PCQ S 最小,1322PCQ S PQ BC PQ ∴=⨯=, 取PQ 的中点G ,190,2PCQ CG PQ ︒∠=∴=,即PQ=2CG , 当CG 最小时, PQ 最小,CG PQ ∴⊥, CG 与CB 重合,CG 最小,∵CG 3PA B Q S ''∴33= 【点睛】本题属于四边形综合题,主要考查了旋转的性质,解直角三角形以及直角三角形的性质的综合运用,解题时注意:旋转变换中,对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.11.数学课外活动小组的同学在学习了完全平方公式之后,针对两个正数之和与这两个正数之积的算术平方根的两倍之间的关系进行了探究,请阅读以下探究过程并解决问题. 猜想发现:由5525510+=⨯;11112233333+=⨯=;0.40.420.40.40.8+=⨯=;1155255+>⨯=;0.2 3.220.2 3.2 1.6+>⨯;1111128282+>⨯ 猜想:如果0a >,0b >,那么存在2a b ab +≥(当且仅当a b =时等号成立).猜想证明:∵()20a b-≥∴①当且仅当0a b -=,即a b =时,20a ab b -+=,∴2a b ab +=; ②当0a b -≠,即ab 时,20a ab b -+>,∴2a b ab +>.综合上述可得:若0a >,0b >,则2a b ab +≥成立(当日仅当a b =时等号成立). 猜想运用:(1)对于函数()10y x x x=+>,当x 取何值时,函数y 的值最小?最小值是多少?变式探究:(2)对于函数()133y x x x =+>-,当x 取何值时,函数y 的值最小?最小值是多少?拓展应用:(3)疫情期间、为了解决疑似人员的临隔离问题.高速公路榆测站入口处,检测人员利用检测站的一面墙(墙的长度不限),用63米长的钢丝网围成了9间相同的长方形隔离房,如图.设每间离房的面积为S (米2).问:每间隔离房的长、宽各为多少时,可使每间隔离房的面积S 最大?最大面积是多少?解析:(1)1x =,函数y 的最小值为2;(2)4x =,函数y 的最小值为5;(3)每间隔离房长为72米,宽为218米时,S 的最大值为214716米 【分析】猜想运用:根据材料以及所学完全平方公式证明求解即可;变式探究:将原式转换为1333y x x =+-+-,再根据材料中方法计算即可; 拓展应用:设每间隔离房与墙平行的边为x 米,与墙垂直的边为y 米,依题意列出方程,然后根据两个正数之和与这两个正数之积的算术平方根的两倍之间的关系探究最大值即可. 【详解】 猜想运用: ∵0x >, ∴10x>, ∴1122y x x x x=+≥⋅,∴当1x x=时,min 2y =, 此时21x =, 只取1x =,即1x =时,函数y 的最小值为2. 变式探究: ∵3x >, ∴30x ->,103x ,∴133353y x x =+-+≥=-, ∴当133x x =--时,min 5y =, 此时()231x -=, ∴14x =,22x =(舍去),即4x =时,函数y 的最小值为5.拓展应用:设每间隔离房与墙平行的边为x 米,与墙垂直的边为y 米,依题意得:91263x y +=,即3421x y +=, ∵30x >,40y >, ∴34x y +≥,即21≥ 整理得:14716xy ≤, 即14716S ≤, ∴当34x y =时max 14716S =, 此时72x =,218y =, 即每间隔离房长为72米,宽为218米时,S 的最大值为214716米. 【点睛】本题主要考查根据完全平方公式探究两个正数之和与这两个正数之积的算术平方根的两倍之间的关系,熟练运用完全平方公式并参照材料中步骤进行计算是解题关键,属于创新探究题.12.如图1,在Rt ABC △中,90B ∠=︒,30C ∠=︒,4BC =,点D ,E 分别是边BC ,AC 的中点,连接DE .将EDC △绕点C 按逆时针方向旋转,记旋转角为α.(1)问题发现 ①当0α=︒时,BD AE =;②当180α=︒时,BDAE=; (2)拓展探究试判断:当0360α︒≤<︒时,BDAE的大小有无变化?请仅就图2的情形给出证明; (3)问题解决当EDC △旋转至//DE AC 时,请直接写出BD 的长. 解析:(1)332)不变,证明见解析;(3)37【分析】(1)①当α=0°时,在Rt △ABC 中,由勾股定理,求出AC 的值是多少;然后根据点D 、E 分别是边BC 、AC 的中点,分别求出AE 、BD 的大小,即可求出BD 、AE 的比值; ②中,图形如下,与①有所变化,但求解方法完全相同; (2)证明△ECA ∽△DCB ,从而根据边长成比例得出比值;(3)存在2种情况,一种是当0180α︒<<︒时,//DE AC ;另一种是当180360α︒<<︒时,//DE AC ,分别利用勾股定理可求得.【详解】(1)①∵在Rt ABC △中,90B ∠=︒,30C ∠=︒,4BC =,点D ,E 分别是边BC ,AC 的中点∴CD=BD=2,在Rt △ABC 中,4383∴43∴343BD AE =;②图形如下:同理可知:BC=4,AC=833,DC=2,DE=233,CE=433∴BD=DC+CB=2+4=6,AE=EC+AC=438333+=1233∴6321233BD AE ==;(2)不变,理由如下 ∵∠ECD=∠ACB , ∴∠ECA=∠DCB , 又∵32DC CB EC CA ==, ∴△ECA ∽△DCB , ∴32BD DC AE EC ==; (3)情况一:当0180α︒<<︒时,//DE AC ,图形如下,过点D 作BC 的垂线,交BC 延长线于点F∵ED ∥AC ,∴∠ACD=∠EDC=90° ∵∠ACB=∠ECD=30° ∴∠ECF=30°,∴∠FCD=60° ∵CD=2∴在Rt △DCF 中,CF=1,3∴FB=FC=CB=1+4=5∴在Rt △FDB 中,DB=22DF FB +=27;情况二:当180360α︒<<︒时,//DE AC ,图形如下,过点D 作BC 的垂线,交BC 于点F∵DE ∥AC ,∴∠ACD=90° ∵∠ACB=30°,∴∠DCF=60°∵CD=2,∴在Rt △CDF 中,CF=1,DF=3 ∴FB=CB -CF=4-1=3∴在Rt △FDB 中,DB=22DF FB +=23 综上得:DB 的长为23或27. 【点睛】此题属于旋转的综合题.考查了旋转的性质、相似三角形的判定与性质以及勾股定理等知识.注意掌握分类讨论思想的应用是解此题的关键. 13.问题背景:已知的顶点在的边所在直线上(不与,重合).交所在直线于点,交所在直线于点.记的面积为,的面积为.(1)初步尝试:如图①,当是等边三角形,,,且,时,则;(2)类比探究:在(1)的条件下,先将点沿平移,使,再将绕点旋转至如图②所示位置,求的值;(3)延伸拓展:当是等腰三角形时,设.(I )如图③,当点在线段上运动时,设,,求的表达式(结果用,和的三角函数表示). (II )如图④,当点在的延长线上运动时,设,,直接写出的表达式,不必写出解答过程.解析:(1)12;(2)12;(3)(ab)2sin2α.(ab)2sin2α.【解析】试题分析:(1)首先证明△ADM,△BDN都是等边三角形,可得S1=•22=,S2=•(4)2=4,由此即可解决问题;(2)如图2中,设AM=x,BN=y.首先证明△AMD∽△BDN,可得,推出,推出xy=8,由S1=•AD•AM•sin60°=x,S2=DB•sin60°=y,可得S1•S2=x•y=xy=12;(3)Ⅰ如图3中,设AM=x,BN=y,同法可证△AMD∽△BDN,可得xy=ab,由S1=•AD•AM•sinα=axsinα,S2=DB•BN•sinα=bysinα,可得S1•S2=(ab)2sin2α.(Ⅱ)结论不变,证明方法类似;试题解析:(1)如图1中,∵△ABC是等边三角形,∴AB=CB=AC=6,∠A=∠B=60°,∵DE∥BC,∠EDF=60°,∴∠BND=∠EDF=60°,∴∠BDN=∠ADM=60°,∴△ADM,△BDN都是等边三角形,∴S1=•22=,S2=•(4)2=4,∴S1•S2=12,(2)如图2中,设AM=x,BN=y.∵∠MDB=∠MDN+∠NDB=∠A+∠AMD,∠MDN=∠A,∴∠AMD=∠NDB,∵∠A=∠B,∴△AMD∽△BDN,∴,∴,∴xy=8,∵S1=•AD•AM•sin60°=x,S2=DB•sin60°=y,∴S1•S2=x•y=xy=12.(3)Ⅰ如图3中,设AM=x,BN=y,同法可证△AMD∽△BDN,可得xy=ab,∵S1=•AD•AM•sinα=axsinα,S2=DB•BN•sinα=bysinα,∴S1•S2=(ab)2sin2α.Ⅱ如图4中,设AM=x,BN=y,同法可证△AMD∽△BDN,可得xy=ab,∵S1=•AD•AM•sinα=axsinα,S2=DB•BN•sinα=bysinα,∴S1•S2=(ab)2sin2α.考点:几何变换综合题.14.如图1,在Rt△ABC中,∠B=90°,BC=2AB=8,点D,E分别是边BC,AC的中点,连接DE,将△EDC绕点C按顺时针方向旋转,记旋转角为α.(1)问题发现① 当0α︒=时,AEBD=;② 当时,AEBD=(2)拓展探究试判断:当0°≤α<360°时,AEDB的大小有无变化?请仅就图2的情况给出证明.(3)问题解决当△EDC旋转至A、D、E三点共线时,直接写出线段BD的长.解析:(1)55.(2)无变化;理由参见解析.(3)5125.【分析】(1)①当α=0°时,在Rt△ABC中,由勾股定理,求出AC的值是多少;然后根据点D、E分别是边BC、AC的中点,分别求出AE、BD的大小,即可求出AEBD的值是多少.②α=180°时,可得AB∥DE,然后根据AC BCAE BD=,求出AEBD的值是多少即可.(2)首先判断出∠ECA=∠DCB,再根据5EC ACDC BC==△ECA∽△DCB,即可求出AE BD 的值是多少,进而判断出AEBD的大小没有变化即可.(3)根据题意,分两种情况:①点A,D,E所在的直线和BC平行时;②点A,D,E所在的直线和BC相交时;然后分类讨论,求出线段BD的长各是多少即可.【详解】(1)①当α=0°时,∵Rt△ABC中,∠B=90°,∴2222(82)845AB BC+÷+=∵点D、E分别是边BC、AC的中点,∴45252AE ==,BD=8÷2=4, ∴25542AE BD ==. ②如图1,,当α=180°时, 可得AB ∥DE ,∵AC BC AE BD =, ∴45582AE AC BD BC === (2)如图2,,当0°≤α<360°时,AE BD 的大小没有变化, ∵∠ECD=∠ACB ,∴∠ECA=∠DCB ,又∵52EC AC DC BC ==, ∴△ECA ∽△DCB ,∴52AE EC BD DC ==. (3)①如图3,,∵5CD=4,CD ⊥AD ,∴2222(45)480168AC CD ---∵AD=BC ,AB=DC ,∠B=90°,∴四边形ABCD 是矩形,∴BD=AC=45. ②如图4,连接BD ,过点D 作AC 的垂线交AC 于点Q ,过点B 作AC 的垂线交AC 于点P ,,∵AC=45,CD=4,CD ⊥AD ,∴AD=2222(45)480168AC CD -=-=-=,∵点D 、E 分别是边BC 、AC 的中点,∴DE=111(82)4222AB =⨯÷=⨯=2, ∴AE=AD-DE=8-2=6,由(2),可得52AE BD =, ∴BD=6125552=.综上所述,BD 的长为45或1255. 15.(问题)如图1,在Rt ABC 中,90,ACB AC BC ∠=︒=,过点C 作直线l 平行于AB .90EDF ∠=︒,点D 在直线l 上移动,角的一边DE 始终经过点B ,另一边DF 与AC 交于点P ,研究DP 和DB 的数量关系.(探究发现)(1)如图2,某数学兴趣小组运用“从特殊到一般”的数学思想,发现当点D 移动到使点P 与点C 重合时,通过推理就可以得到DP DB =,请写出证明过程;(数学思考)(2)如图3,若点P 是AC 上的任意一点(不含端点A C 、),受(1)的启发,这个小组过点D 作DG CD ⊥交BC 于点G ,就可以证明DP DB =,请完成证明过程;(拓展引申)(3)如图4,在(1)的条件下,M 是AB 边上任意一点(不含端点AB 、),N 是射线BD 上一点,且AM BN =,连接MN 与BC 交于点Q ,这个数学兴趣小组经过多次取M 点反复进行实验,发现点M 在某一位置时BQ 的值最大.若4AC BC ==,请你直接写出BQ 的最大值.解析:【探究发现】(1)见解析;【数学思考】(2)见解析;【拓展引申】(3)22AM =BQ 有最大值为2.【分析】根据等腰三角形的性质及平行的定义即可解得根据证明()CDP GDB ASA ≌即可推出DP DB =过点M 作MH MN ⊥交AC 于点H ,连接,CM HQ ,可证明()AMH BNQ ASA ≌,再推出ACM BMQ ∽即可得AC AM BM BQ =42AM BQAM =-,则22AM = 【详解】证明:【探究发现】 (1)∵90,ACB AC BC ∠=︒=∵CD AB∴45CBA DCB ∠=∠=︒,且BD CD ⊥∴45DCB DBC ∠=∠=︒∴DB DC =即DB DP =【数学思考】(2)∵,45DG CD DCB ⊥∠=︒∴45DCG DGC ∠=∠=︒∴,135DC DG DCP DGB =∠=∠=︒,∵90BDP CDG ∠=∠=︒∴CDP BDG ∠=∠,且,135DC DG DCP DGB =∠=∠=︒,∴()CDP GDB ASA ≌∴BD DP =【拓展引申】(3)如图4,过点M 作MH MN ⊥交AC 于点H ,连接,CM HQ ,∵MH MN ⊥,∴90AMH NMB ∠+∠=︒∵,90CD AB CDB ∠=︒∥∴90DBM ∠=︒∴90NMB MNB ∠+∠=︒∴HMA MNB ∠=∠,且,45AM BN CAB CBN =∠=∠=︒∴()AMH BNQ ASA ≌∴AH BQ =∵90,4ACB AC BC ∠=︒==, ∴42,AB AC AH BC BQ =-=-∴CH CQ =∴45CHQ CQH CAB ∠=∠=︒=∠∴HQ AB ∥∴HQM QMB ∠=∠∵90ACB HMQ ∠=∠=︒∴点H ,点M ,点Q ,点C 四点共圆,∴HCM QMB ∠=∠,且45A CBA ∠=∠=︒∴ACM BMQ ∽ ∴AC AM BM BQ = ∴442AM BQ AM=- ∴2(22)24AM BQ --=+ ∴22AM =时,BQ 有最大值为2.【点睛】本题考查等腰三角形,解题关键在于熟练掌握等腰三角形的性质.16.如图,四边形ABCD 是正方形,点O 为对角线AC 的中点.(1)问题解决:如图①,连接BO ,分别取CB ,BO 的中点P ,Q ,连接PQ ,则PQ 与BO 的数量关系是_____,位置关系是____;(2)问题探究:如图②,AO E ∆'是将图①中的AOB ∆绕点A 按顺时针方向旋转45︒得到的三角形,连接CE ,点P ,Q 分别为CE ,BO '的中点,连接PQ ,PB .判断PQB ∆的形状,并证明你的结论;(3)拓展延伸:如图③,AO E ∆'是将图①中的AOB ∆绕点A 按逆时针方向旋转45︒得到的三角形,连接BO ',点P ,Q 分别为CE ,BO '的中点,连接PQ ,PB .若正方形ABCD 的边长为1,求PQB ∆的面积.解析:(1)12PQ BO =,PQ BO ⊥;(2)PQB ∆的形状是等腰直角三角形,理由见解析;(3)316【分析】(1)根据题意可得PQ 为△BOC 的中位线,再根据中位线的性质即可求解;(2)连接O P '并延长交BC 于点F ,根据题意证出 O PE FPC ∆'∆≌,'O BF ∆为等腰直角三角形,BPO ∆'也为等腰直角三角形,由'PQ O B ⊥且PQ BQ =可得PQB ∆是等腰直角三。
深圳历年中考数学压轴题(综合题)(1)

深圳历年中考数学压轴题(综合题30)1.如图,⊙O 是ABC ∆的外接圆,AB AC =,2BC =,cos ABC ∠,点D 为»AC 上的动点,连接AD 并延长,交BC 的延长线于点E 。
(1)试求AB 的长;(2)试判断AD AE g 的值是否为定值?若为定值,请求出这个定值,若不为定值,请说明理由。
(3)如图2,连接BD ,过点A 作AH ⊥BD 于点H ,连接CD ,求证:BH CD DH =+。
2.如图,顶点为A 的抛物线21()22y a x =--经过3,22B ⎛⎫- ⎪⎝⎭,5,22C ⎛⎫⎪⎝⎭两点。
(1)试求抛物线的解析式;(2)如图2,连接AB ,交x 轴于点M ,交y 轴于点E ,抛物线与y 轴交于点F 。
若在直线AB 上有一点P ,使得OPM MAF ∠=∠,试求POE ∆的面积;(3)如图3,若点Q 是折线A B C --上一点,过点Q 作QN ∥y 轴,过点E 作EN ∥x 轴,直线QN 与直线EN 交于点N ,连接QE ,将QEN ∆沿QE 翻折得到1QEN ∆。
若点1N 落在x 轴上,请直接写出Q 点的坐标。
图2图1图1 图2 图33.如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC(1)求CD的长;(2)求证:PC是⊙O的切线;(3)点G为的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交于点F(F与B、C不重合).问GE•GF是否为定值?如果是,求出该定值;如果不是,请说明理由.4.如图,抛物线y=ax2+2x﹣3与x轴交于A、B两点,且B(1,0)(1)求抛物线的解析式和点A的坐标;(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;(3)如图2,已知直线y=x﹣分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.5.如图1,水平放置一个三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,AB=BC=6cm,OD=3cm,开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动.(1)当B与O重合的时候,求三角板运动的时间;(2)如图2,当AC与半圆相切时,求AD;(3)如图3,当AB和DE重合时,求证:CF2=CG•CE.6.如图1,关于x的二次函数y=﹣x2+bx+c经过点A(﹣3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上.(1)求抛物线的解析式;(2)DE上是否存在点P到AD的距离与到x轴的距离相等?若存在求出点P,若不存在请说明理由;(3)如图2,DE的左侧抛物线上是否存在点F,使2S△FBC=3S△EBC?若存在求出点F的坐标,若不存在请说明理由.7.如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD.(1)求⊙M的半径;(2)证明:BD为⊙M的切线;(3)在直线MC上找一点P,使|DP﹣AP|最大.8.如图,直线AB的解析式为y=2x+4,交x轴于点A,交y轴于点B,以A为顶点的抛物线交直线AB于点D,交y轴负半轴于点C(0,﹣4).(1)求抛物线的解析式;(2)将抛物线顶点沿着直线AB平移,此时顶点记为E,与y轴的交点记为F,①求当△BEF与△BAO相似时,E点坐标;②记平移后抛物线与AB另一个交点为G,则S△EFG与S△ACD是否存在8倍的关系?若有请直接写出F点的坐标.9.如图1,过点A(0,4)的圆的圆心坐标为C(2,0),B是第一象限圆弧上的一点,且BC⊥AC,抛物线y=x2+bx+c经过C、B两点,与x轴的另一交点为D.(1)点B的坐标为(,),抛物线的表达式为;(2)如图2,求证:BD∥AC;(3)如图3,点Q为线段BC上一点,且AQ=5,直线AQ交⊙C于点P,求AP的长.10.如图1,直线AB过点A(m,0),B(0,n),且m+n=20(其中m>0,n>0).(1)m为何值时,△OAB面积最大?最大值是多少?(2)如图2,在(1)的条件下,函数的图象与直线AB相交于C、D两点,若,求k的值.(3)在(2)的条件下,将△OCD以每秒1个单位的速度沿x轴的正方向平移,如图3,设它与△OAB的重叠部分面积为S,请求出S与运动时间t(秒)的函数关系式(0<t<10).11.如图,已知△ABC的三个顶点坐标分别为A(﹣4,0)、B(1,0)、C(﹣2,6).(1)求经过A、B、C三点的抛物线解析式;(2)设直线BC交y轴于点E,连接AE,求证:AE=CE;(3)设抛物线与y轴交于点D,连接AD交BC于点F,试问以A、B、F为顶点的三角形与△ABC相似吗?12.如图,在平面直角坐标系中,直线l:y=﹣2x+b(b≥0)的位置随b的不同取值而变化.(1)已知⊙M的圆心坐标为(4,2),半径为2.当b=时,直线l:y=﹣2x+b(b≥0)经过圆心M;当b=时,直线l:y=﹣2x+b(b≥0)与⊙M相切;(2)若把⊙M换成矩形ABCD,其三个顶点坐标分别为:A(2,0)、B(6,0)、C(6,2).设直线l扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式.13.如图1,一张矩形纸片ABCD,其中AD=8cm,AB=6cm,先沿对角线BD对折,点C 落在点C′的位置,BC′交AD于点G.(1)求证:AG=C′G;(2)如图2,再折叠一次,使点D与点A重合,得折痕EN,EN交AD于点M,求EM的长.14.如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0).(1)求抛物线的解析式;(2)如图2,过点A的直线与抛物线交于点E,交y轴于点F,其中点E的横坐标为2,若直线PQ为抛物线的对称轴,点G为直线PQ上的一动点,则x轴上是否存在一点H,使D、G,H、F四点所围成的四边形周长最小?若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由;(3)如图3,在抛物线上是否存在一点T,过点T作x轴的垂线,垂足为点M,过点M作MN∥BD,交线段AD于点N,连接MD,使△DNM∽△BMD?若存在,求出点T的坐标;若不存在,请说明理由.15.如图所示,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(﹣2,0),B(﹣1,﹣3).(1)求抛物线的解析式;(2)点M为y轴上任意一点,当点M到A,B两点的距离之和为最小时,求此时点M的坐标;(3)在第(2)问的结论下,抛物线上的点P使S△PAD=4S△ABM成立,求点P的坐标.16.如图1所示,以点M(﹣1,0)为圆心的圆与y轴,x轴分别交于点A,B,C,D,直线y=﹣x﹣与⊙M相切于点H,交x轴于点E,交y轴于点F.(1)请直接写出OE,⊙M的半径r,CH的长;(2)如图2所示,弦HQ交x轴于点P,且DP:PH=3:2,求cos∠QHC的值;(3)如图3所示,点K为线段EC上一动点(不与E,C重合),连接BK交⊙M于点T,弦AT交x轴于点N.是否存在一个常数a,始终满足MN•MK=a,如果存在,请求出a的值;如果不存在,请说明理由.17.如图,在直角坐标系中,点A的坐标为(﹣2,0),连接OA,将线段OA绕原点O顺时针旋转120°,得到线段OB.(1)求点B的坐标;(2)求经过A、O、B三点的抛物线的解析式;(3)在(2)中抛物线的对称轴上是否存在点C,使△BOC的周长最小?若存在,求出点C 的坐标;若不存在,请说明理由;(4)如果点P是(2)中的抛物线上的动点,且在x轴的下方,那么△PAB是否有最大面积?若有,求出此时P点的坐标及△PAB的最大面积;若没有,请说明理由.(注意:本题中的结果均保留根号).18.如图,在平面直角坐标系中,直线l:y=﹣2x﹣8分别与x轴,y轴相交于A,B两点,点P(0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作⊙P.(1)连接PA,若PA=PB,试判断⊙P与x轴的位置关系,并说明理由;(2)当k为何值时,以⊙P与直线l的两个交点和圆心P为顶点的三角形是正三角形.19.如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.(1)求证:BD是⊙O的切线;(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为8,cos∠BFA=,求△ACF的面积.20.如左图,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象的顶点为D点,与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3,0),OB=OC,tan∠ACO=.(1)求这个二次函数的表达式.(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形?若存在,请求出点F的坐标;若不存在,请说明理由.(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.(4)如图,若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△APG的面积最大?求出此时P点的坐标和△APG的最大面积.21.如图,抛物线y=ax2﹣8ax+12a(a<0)与x轴交于A、B两点(点A在点B的左侧),抛物线上另有一点C在第一象限,满足∠ACB为直角,且恰使△OCA∽△OBC.(1)求线段OC的长;(2)求该抛物线的函数关系式;(3)在x轴上是否存在点P,使△BCP为等腰三角形?若存在,求出所有符合条件的P点的坐标;若不存在,请说明理由.22.如图1,在平面直角坐标系xOy中,点M在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C、D两点,且C为的中点,AE交y轴于G点,若点A的坐标为(﹣2,0),AE=8.(1)求点C的坐标;(2)连接MG、BC,求证:MG∥BC;(3)如图2,过点D作⊙M的切线,交x轴于点P.动点F在⊙M的圆周上运动时,的比值是否发生变化?若不变,求出比值;若变化,说明变化规律.23.已知△ABC是边长为4的等边三角形,BC在x轴上,点D为BC的中点,点A在第一象限内,AB与y轴的正半轴相交于点E,点B(﹣1,0),P是AC上的一个动点(P与点A、C不重合)(1)求点A、E的坐标;(2)若y=x2+bx+c过点A、E,求抛物线的解析式;(3)连接PB、PD,设L为△PBD的周长,当L取最小值时,求点P的坐标及L的最小值,并判断此时点P是否在(2)中所求的抛物线上,请充分说明你的判断理由.24.AB是⊙O的直径,点E是半圆上一动点(点E与点A、B都不重合),点C是BE延长线上的一点,且CD⊥AB,垂足为D,CD与AE交于点H,点H与点A不重合.(1)求证:△AHD∽△CBD;(2)连HO,若CD=AB=2,求HD+HO的值.25.等腰梯形ABCD中,如图1,AB∥CD,AD=BC,延长AB到E,使BE=CD,连接CE.(1)求证:CE=CA;(2)上述条件下,如图2,若AF⊥CE于点F,且AF平分∠DAE,,求sin∠CAF 的值.26.直线y=﹣x+m与直线y=x+2相交于y轴上的点C,与x轴分别交于点A、B.(1)求A、B、C三点的坐标;(2)经过上述A、B、C三点作⊙E,求∠ABC的度数,点E的坐标和⊙E的半径;(3)若点P是第一象限内的一动点,且点P与圆心E在直线AC的同一侧,直线PA、PC 分别交⊙E于点M、N,设∠APC=θ,试求点M、N的距离.(可用含θ的三角函数式表示)27.如图,已知△ABC,∠ACB=90°,AC=BC,点E、F在AB上,∠ECF=45°.(1)求证:△ACF∽△BEC;(2)设△ABC的面积为S,求证:AF•BE=2S;(3)试判断以线段AE、EF、FB为边的三角形的形状并给出证明.28.如图,已知A(5,﹣4),⊙A与x轴分别相交于点B、C,⊙A与y轴相且于点D,(1)求证过D、B、C三点的抛物线的解析式;(2)连接BD,求tan∠BDC的值;(3)点P是抛物线顶点,线段DE是直径,直线PC与直线DE相交于点F,∠PFD的平分线FG交DC于G,求sin∠CGF的值.29.已知:如图,直线y=﹣x+3与x轴、y轴分别交于B、C,抛物线y=﹣x2+bx+c经过点B、C,点A是抛物线与x轴的另一个交点.(1)求B、C两点的坐标和抛物线的解析式;(2)若点P在线段BC上,且,求点P的坐标.30.如图,等腰梯形ABCD中,AD∥BC,AB=DC,以HF为直径的圆与AB、BC、CD、DA相切,切点分别是E、F、G、H.其中H为AD的中点,F为BC的中点.连接HG、GF.(1)若HG和GF的长是关于x的方程x2﹣6x+k=0的两个实数根,求⊙O的直径HF(用含k的代数式表示),并求出k的取值范围.(2)如图,连接EG,DF.EG与HF交于点M,与DF交于点N,求的值.。
近五年深圳中考压轴题集锦
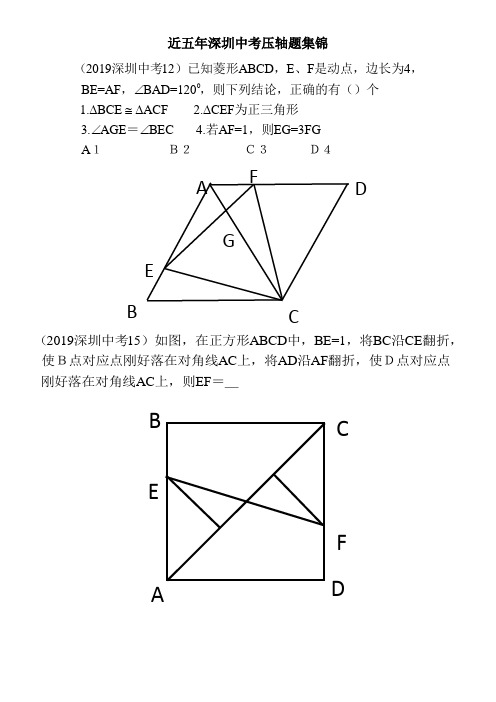
近五年深圳中考压轴题集锦0201912ABCD E F 4BE=AF BAD=1201.BCE ACF 2.CEF 3.AGE BEC 4.AF=1EG=3FGA ∠∆≅∆∆∠∠(深圳中考)已知菱形,、是动点,边长为,,,则下列结论,正确的有()个为正三角形=若,则1 B2 C3 D4201915ABCD BE=1BC CE AC AD AF AC EF (深圳中考)如图,在正方形中,,将沿翻折,使B点对应点刚好落在对角线上,将沿翻折,使D点对应点刚好落在对角线上,则=_ GD B C EF AB A CDEF0201916A 0-3ABC=90BAC AD=3CD y _k y k x∠∠=(深圳中考)如图,在平面直角坐标系中,(,),,轴平分,,点C在反例函数=上,则2201922(1,0),(0,3),OB=OCD E 1DE=1D ACDE y ax bx c A C x =++-=(深圳中考)如图:抛物线过且1.求抛物线的解析式及其对称轴2.点、是直线上的两个动点,且,点在点E的上方求四边的周长的最小值CP APBC P 3.点P为抛物线上一点,连接CP直线将四边形面积分为3:5的两个部分,求点的坐标.A DCB x yO B A Cxy23(3,0),(3,0),(3,8),BC E AC E OD OD E A B C --(2019深圳中考)已知在平面直角坐标系中,点以线段为直径作圆,圆心为直线交于点D,连接,1.求证:直线是的切线F CF EG BG tan x FCA ∠2.为轴上任意一点,连接交于点,连接1当=,求所有的F点的坐标___;72018深圳中考12题如图,A 、B 是函数y= 12x 上两点,P 为一动点,作PB ∥y 轴,PA ∥x 轴,下列说法正确的是 ( )①△AOP ≌△BOP ;②S △AOP=S △BOP ;③若OA=OB ,则OP 平分∠AOB ;④若S △BOP=4,则S △ABP=16A .①③B .②③C .②④D .③④2018深圳中考16题在Rt △ABC 中,∠C=90°,AD 平分∠CAB ,BE 平分∠ABC ,AD 、BE 相交于点F ,且AF=4, ,则AC=________2018深圳中考22题如图,△ABC 内接于⊙O ,BC=2,AB=AC ,点D 为上的动点,且cosB=10. (1)求AB 的长度;(2)在点D 的运动过程中,弦AD 的延长线交BC 延长线于点E ,问AD •AE 的值是否变化?若不变,请求出AD •AE 的值;若变化,请说明理由;(3)在点D 的运动过程中,过A 点作AH ⊥BD ,求证:BH=CD+DH.2018深圳中考23题已知顶点为A 抛物线21()22y a x =-- 经过点 32B (-,2). (1)求抛物线的解析式;(2)如图1,直线AB 与x 轴相交于点M ,y 轴相交于点E ,抛物线与y 轴相交于点F ,在直线AB 上有一点P ,若∠OPM=∠MAF ,求△POE 的面积;(3)如图2,点Q 是折线A ﹣B ﹣C 上一点,过点Q 作QN ∥y 轴,过点E 作EN ∥x 轴,直线QN 与直线EN 相交于点N ,连接QE ,将△QEN 沿QE 翻折得到△QEN1,若点N1落在x 轴上,请直接写出Q 点的坐标.2017深圳中考12如图,正方形ABCD的边长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD,BC交于点F,E,连接AE,下列结论:①AQ⊥DP;②OA2=OE•OP;③S△AOD=S四边形OECF;④当BP=1时,tan∠OAE= 13 16,其中正确结论的个数是()A.1B.2C.3D.42017深圳中考16如图,在Rt△ABC中,∠ABC=90°,AB=3,BC=4,Rt△MPN,∠MPN=90°,点P 在AC上,PM交AB于点E,PN交BC于点F,当PE=2PF时,AP=.2017深圳中考22如图,线段AB是⊙O的直径,弦CD⊥AB于点H,点M是上任意一点,AH=2,CH=4.(1)求⊙O的半径r的长度;(2)求sin∠CMD;(3)直线BM交直线CD于点E,直线MH交⊙O于点N,连接BN交CE于点F,求HE•HF的值.2017深圳中考23如图,抛物线y=ax2+bx+2经过点A(﹣1,0),B(4,0),交y轴于点C;(1)求抛物线的解析式(用一般式表示);(2)点D为y轴右侧抛物线上一点,是否存在点D使S△ABC=2/3S△ABD?若存在请直接给出点D坐标;若不存在请说明理由;(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.2016深圳中考12如图,CB=CA,∠ACB=90°,点D在边BC上(与B、C不重合),四边形ADEF为正方形,过点F 作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB:S四边形CBFG=1:2;③∠ABC=∠ABF;④AD2=FQ•AC,其中正确的结论的个数是()A.1 B.2 C.3 D.42016深圳中考16如图,四边形ABCO是平行四边形,OA=2,AB=6,点C在x轴的负半轴上,将▱ABCO 绕点A逆时针旋转得到▱ADEF,AD经过点O,点F恰好落在x轴的正半轴上,若点D在反比例函数y=kx(x<0)的图象上,则k的值为.2016深圳中考22如图,已知⊙O的半径为2,AB为直径,CD为弦.AB与CD交于点M,将沿CD翻折后,点A与圆心O重合,延长OA至P,使AP=OA,连接PC(1)求CD的长;(2)求证:PC是⊙O的切线;(3)点G为的中点,在PC延长线上有一动点Q,连接QG交AB于点E.交于点F(F与B、C不重合).问GE•GF 是否为定值?如果是,求出该定值;如果不是,请说明理由.2016深圳中考23如图,抛物线y=ax2+2x﹣3与x轴交于A、B两点,且B(1,0)(1)求抛物线的解析式和点A的坐标;(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;(3)如图2,已知直线y=2/3x﹣4/9分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE 的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.2015深圳中考12如图,已知正方形ABCD 的边长为12,BE=EC ,将正方形边CD 沿DE 折叠到DF ,延长EF 交AB 于G ,连接DG ,现在有如下4个结论:BEF 721.ADG FDG2.GB 2AG3.GDE BEF4.S =5∆∆≅∆∆∆ = 正确的有()个2015深圳中考16如图,已知点A 在反比例函数上,作RT ⊿ABC ,点D 为斜边AC 的中点,连DB 并延长交y 轴于点E ,若⊿BCE 的面积为8,则k=2015深圳中考22如图1,水平放置一个三角板和一个量角器,三角板的边AB 和量角器的直径DE 在一条直线上,,3,6cm OD cm BC AB === 开始的时候BD=1cm,现在三角板以2cm/s 的速度向右移动。
中考初三数学整合压轴题100题附答案

中考初三数学整合压轴题100题附答案一、中考压轴题1.用两种方法解答:已知m、n是关于x的方程x2+(p﹣2)x+1=0两个实数根,求代数式(m2+mp+1)(n2+np+1)的值.【分析】本题主要是利用韦达定理来计算.已知m、n是关于x的方程x2+(p﹣2)x+1=0两个实数根,有四个等式可供使用:m+n=2﹣p①,mn=1②,m2+(p﹣2)m+1=0③,n2+(p﹣2)n+1=0④.通过变形方法,合理地选择解题方法.【解答】解:∵m、n是x2+(p﹣2)x+1=0的根,∴m+n=2﹣p,mn=1.方法一:m2+(p﹣2)m+1=0,n2+(p﹣2)n+1=0.即m2+pm+1=2m,n2+pn+1=2n.原式=2m×2n=4mn=4.方法二:(m2+mp+1)(n2+np+1)=(m2+mp)(n2+np)+m2+mp+n2+np+1=m2n2+m2np+mpn2+mnp2+m2+mp+n2+np+1=1+mp+np+p2+m2+n2+mp+np+1=2+p2+m2+n2+2(m+n)p=2+p2+m2+n2+2(2﹣p)p=2+p2+m2+n2+4p﹣2p2=2+(m+n)2﹣2mn+4p﹣2p2+p2=2+(2﹣p)2﹣2+4p﹣2p2+p2=4﹣4p+p2+4p﹣p2=4.【点评】本题主要是通过根与系数的关系来求值.注意把所求的代数式转化成m+n=2﹣p,mn=1的形式,正确对所求式子进行变形是解题的关键.2.已知:y关于x的函数y=(k﹣1)x2﹣2kx+k+2的图象与x轴有交点.(1)求k的取值范围;(2)若x1,x2是函数图象与x轴两个交点的横坐标,且满足(k﹣1)x12+2kx2+k+2=4x1x2.①求k的值;②当k≤x≤k+2时,请结合函数图象确定y的最大值和最小值.【分析】(1)分两种情况讨论,当k=1时,可求出函数为一次函数,必与x轴有一交点;当k≠1时,函数为二次函数,若与x轴有交点,则△≥0.(2)①根据(k﹣1)x12+2kx2+k+2=4x1x2及根与系数的关系,建立关于k的方程,求出k 的值;②充分利用图象,直接得出y的最大值和最小值.【解答】解:(1)当k=1时,函数为一次函数y=﹣2x+3,其图象与x轴有一个交点.当k≠1时,函数为二次函数,其图象与x轴有一个或两个交点,令y=0得(k﹣1)x2﹣2kx+k+2=0.△=(﹣2k)2﹣4(k﹣1)(k+2)≥0,解得k≤2.即k≤2且k≠1.综上所述,k的取值范围是k≤2.(2)①∵x1≠x2,由(1)知k<2且k≠1,函数图象与x轴两个交点,∴k<2,且k≠1.由题意得(k﹣1)x12+(k+2)=2kx1①,将①代入(k﹣1)x12+2kx2+k+2=4x1x2中得:2k(x1+x2)=4x1x2.又∵x1+x2=,x1x2=,∴2k•=4•.解得:k1=﹣1,k2=2(不合题意,舍去).∴所求k值为﹣1.②如图,∵k1=﹣1,y=﹣2x2+2x+1=﹣2(x﹣)2+.且﹣1≤x≤1.由图象知:当x=﹣1时,y最小=﹣3;当x=时,y最大=.∴y的最大值为,最小值为﹣3.【点评】本题考查了抛物线与x轴的交点、一次函数的定义、二次函数的最值,充分利用图象是解题的关键.3.如图①,有四张编号为1、2、3、4的卡片,卡片的背面完全相同.现将它们搅匀并正面朝下放置在桌面上.(1)从中随机抽取一张,抽到的卡片是眼睛的概率是多少?(2)从四张卡片中随机抽取一张贴在如图②所示的大头娃娃的左眼处,然后再随机抽取一张贴在大头娃娃的右眼处,用树状图或列表法求贴法正确的概率.【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.【解答】解:(1)所求概率为;(2)方法①(树状图法)共有12种可能的结果:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)∵其中有两种结果(1,2),(2,1)是符合条件的,∴贴法正确的概率为,方法②(列表法)1 2 3 4第一次抽取第二次抽取1(2,1)(3,1)(4,1)2(1,2)(3,2)(4,2)3(1,3)(2,3)(4,3)4(1,4)(2,4)(3,4)共有12种可能的结果:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),∵其中有两种结果(1,2),(2,1)是符合条件的,∴贴法正确的概率为.【点评】此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.4.如图,反比例函数的图象经过点A(4,b),过点A作AB⊥x轴于点B,△AOB 的面积为2.(1)求k和b的值;(2)若一次函数y=ax﹣3的图象经过点A,求这个一次函数的解析式.【分析】(1)由△AOB的面积为2,根据反比例函数的比例系数k的几何意义,可知k的值,得出反比例函数的解析式,然后把x=4代入,即可求出b的值;(2)把点A的坐标代入y=ax﹣3,即可求出这个一次函数的解析式.【解答】解:(1)∵反比例函数的图象经过点A,AB⊥x轴于点B,△AOB的面积为2,A(4,b),∴OB×AB=2,×4×b=2,∴AB=b=1,∴A(4,1),∴k=xy=4,∴反比例函数的解析式为y=,即k=4,b=1.(2)∵A(4,1)在一次函数y=ax﹣3的图象上,∴1=4a﹣3,∴a=1.∴这个一次函数的解析式为y=x﹣3.【点评】本题主要考查了待定系数法求一次函数的解析式和反比例函数中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.5.我国年人均用纸量约为28公斤,每个初中毕业生离校时大约有10公斤废纸;用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大树.(1)若我市2005年4万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使多少亩森林免遭砍伐?(2)我市从2000年初开始实施天然林保护工程,大力倡导废纸回收再生,如今成效显著,森林面积大约由2003年初的50万亩增加到2005年初的60.5万亩.假设我市年用纸量的20%可以作为废纸回收、森林面积年均增长率保持不变,请你按全市总人口约为1000万计算:在从2005年初到2006年初这一年度内,我市因回收废纸所能保护的最大森林面积相当于新增加的森林面积的百分之几?(精确到1%)【分析】(1)因为每个初中毕业生离校时大约有10公斤废纸,用1吨废纸造出的再生好纸,所能节约的造纸木材相当于18棵大树,而平均每亩森林只有50至80棵这样的大树,所以有40000×10÷1000×18÷80,计算出即可求出答案;(2)森林面积大约由2003年初的50万亩增加到2005年初的60.5万亩,可先求出森林面积年均增长率,进而求出2005到2006年新增加的森林面积,而因回收废纸所能保护的最大森林面积=1000×10000×28×20%÷1000×18÷50,然后进行简单的计算即可求出答案.【解答】解:(1)4×104×10÷1000×18÷80=90(亩).答:若我市2005年4万名初中毕业生能把自己离校时的全部废纸送到回收站使之制造为再生好纸,那么最少可使90亩森林免遭砍伐.(2)设我市森林面积年平均增长率为x,依题意列方程得50(1+x)2=60.5,解得x1=10%,x2=﹣2.1(不合题意,舍去),1000×104×28×20%÷1000×18÷50=20160,20160÷(605000×10%)≈33%.答:在从2005年初到2006年初这一年度内,我市因回收废纸所能保护的最大森林面积相当于新增加的森林面积的33%.【点评】本题以保护环境为主题,考查了增长率问题,阅读理解题意,并从题目中提炼出平均增长率的数学模型并解答的能力;解答时需仔细分析题意,利用方程即可解决问题.6.广安市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.(1)求平均每次下调的百分率.(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?【分析】(1)根据题意设平均每次下调的百分率为x,列出一元二次方程,解方程即可得出答案;(2)分别计算两种方案的优惠价格,比较后发现方案①更优惠.【解答】解:(1)设平均每次下调的百分率为x,则6000(1﹣x)2=4860,解得:x1=0.1=10%,x2=1.9(舍去),故平均每次下调的百分率为10%;(2)方案①购房优惠:4860×100×(1﹣0.98)=9720(元);方案②可优惠:80×100=8000(元).故选择方案①更优惠.【点评】本题主要考查一元二次方程的实际应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解,属于中档题.7.如图,一次函数y=﹣x﹣2的图象分别交x轴、y轴于A、B两点,P为AB的中点,PC⊥x轴于点C,延长PC交反比例函数y=(x<0)的图象于点Q,且tan∠AOQ=.(1)求k的值;(2)连接OP、AQ,求证:四边形APOQ是菱形.【分析】(1)由一次函数解析式确定A点坐标,进而确定C,Q的坐标,将Q的坐标代入反比例函数关系式可求出k的值.(2)由(1)可分别确定QC=CP,AC=OC,且QP垂直平分AO,故可证明四边形APOQ是菱形.【解答】(1)解:∵y=﹣x﹣2令y=0,得x=﹣4,即A(﹣4,0)由P为AB的中点,PC⊥x轴可知C点坐标为(﹣2,0)又∵tan∠AOQ=可知QC=1∴Q点坐标为(﹣2,1)将Q点坐标代入反比例函数得:1=,∴可得k=﹣2;(2)证明:由(1)可知QC=PC=1,AC=CO=2,且A0⊥PQ∴四边形APOQ是菱形.【点评】本题考查了待定系数法求函数解析式,又结合了几何图形进行考查,属于综合性比较强的题目,有一定难度.8.某公司经营杨梅业务,以3万元/吨的价格向农户收购杨梅后,分拣成A、B两类,A类杨梅包装后直接销售;B类杨梅深加工后再销售.A类杨梅的包装成本为1万元/吨,根据市场调查,它的平均销售价格y(单位:万元/吨)与销售数量x(x≥2)之间的函数关系如图;B类杨梅深加工总费用s(单位:万元)与加工数量t(单位:吨)之间的函数关系是s=12+3t,平均销售价格为9万元/吨.(1)直接写出A类杨梅平均销售价格y与销售量x之间的函数关系式;(2)第一次,该公司收购了20吨杨梅,其中A类杨梅有x吨,经营这批杨梅所获得的毛利润为w万元(毛利润=销售总收入﹣经营总成本).①求w关于x的函数关系式;②若该公司获得了30万元毛利润,问:用于直销的A类杨梅有多少吨?(3)第二次,该公司准备投入132万元资金,请设计一种经营方案,使公司获得最大毛利润,并求出最大毛利润.【分析】(1)这是一个分段函数,分别求出其函数关系式;(2)①当2≤x<8时及当x≥8时,分别求出w关于x的表达式.注意w=销售总收入﹣经营总成本=w A+w B﹣3×20;②若该公司获得了30万元毛利润,将30万元代入①中求得的表达式,求出A类杨梅的数量;(3)本问是方案设计问题,总投入为132万元,这笔132万元包括购买杨梅的费用+A类杨梅加工成本+B类杨梅加工成本.共购买了m吨杨梅,其中A类杨梅为x吨,B类杨梅为(m﹣x)吨,分别求出当2≤x<8时及当x≥8时w关于x的表达式,并分别求出其最大值.【解答】解:(1)①当2≤x<8时,如图,设直线AB解析式为:y=kx+b,将A(2,12)、B(8,6)代入得:,解得,∴y=﹣x+14;②当x≥8时,y=6.所以A类杨梅平均销售价格y与销售量x之间的函数关系式为:y=;(2)设销售A类杨梅x吨,则销售B类杨梅(20﹣x)吨.①当2≤x<8时,w A=x(﹣x+14)﹣x=﹣x2+13x;w B=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x∴w=w A+w B﹣3×20=(﹣x2+13x)+(108﹣6x)﹣60=﹣x2+7x+48;当x≥8时,w A=6x﹣x=5x;w B=9(20﹣x)﹣[12+3(20﹣x)]=108﹣6x∴w=w A+w B﹣3×20=(5x)+(108﹣6x)﹣60=﹣x+48.∴w关于x的函数关系式为:w=.②当2≤x<8时,﹣x2+7x+48=30,解得x1=9,x2=﹣2,均不合题意;当x≥8时,﹣x+48=30,解得x=18.∴当毛利润达到30万元时,直接销售的A类杨梅有18吨.(3)设该公司用132万元共购买了m吨杨梅,其中A类杨梅为x吨,B类杨梅为(m﹣x)吨,则购买费用为3m万元,A类杨梅加工成本为x万元,B类杨梅加工成本为[12+3(m﹣x)]万元,∴3m+x+[12+3(m﹣x)]=132,化简得:x=3m﹣60.①当2≤x<8时,w A=x(﹣x+14)﹣x=﹣x2+13x;w B=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12∴w=w A+w B﹣3×m=(﹣x2+13x)+(6m﹣6x﹣12)﹣3m=﹣x2+7x+3m﹣12.将3m=x+60代入得:w=﹣x2+8x+48=﹣(x﹣4)2+64∴当x=4时,有最大毛利润64万元,此时m=,m﹣x=;②当x≥8时,w A=6x﹣x=5x;w B=9(m﹣x)﹣[12+3(m﹣x)]=6m﹣6x﹣12∴w=w A+w B﹣3×m=(5x)+(6m﹣6x﹣12)﹣3m=﹣x+3m﹣12.将3m=x+60代入得:w=48∴当x>8时,有最大毛利润48万元.综上所述,购买杨梅共吨,其中A类杨梅4吨,B类吨,公司能够获得最大毛利润,最大毛利润为64万元.【点评】本题是二次函数、一次函数的综合应用题,难度较大.解题关键是理清售价、成本、利润三者之间的关系.涉及到分段函数时,注意要分类讨论.9.经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/小时,研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.(1)求大桥上车流密度为100辆/千米时的车流速度;(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/小时,应控制大桥上的车流密度在什么范围内?(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.【分析】(1)当20≤x≤220时,设车流速度v与车流密度x的函数关系式为v=kx+b,根据题意的数量关系建立方程组求出其解即可;(2)由(1)的解析式建立不等式组求出其解即可;(3)设车流量y与x之间的关系式为y=vx,当x<20和20≤x≤220时分别表示出函数关系由函数的性质就可以求出结论.【解答】解:(1)设车流速度v与车流密度x的函数关系式为v=kx+b,由题意,得,解得:,∴当20≤x≤220时,v=﹣x+88,当x=100时,v=﹣×100+88=48(千米/小时);(2)由题意,得,解得:70<x<120.∴应控制大桥上的车流密度在70<x<120范围内;(3)设车流量y与x之间的关系式为y=vx,当0≤x≤20时y=80x,∴k=80>0,∴y随x的增大而增大,∴x=20时,y最大=1600;当20≤x≤220时y=(﹣x+88)x=﹣(x﹣110)2+4840,∴当x=110时,y最大=4840.∵4840>1600,∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆.【点评】本题考查了车流量=车流速度×车流密度的运用,一次函数的解析式的运用,一元一次不等式组的运用,二次函数的性质的运用,解答时求出函数的解析式是关键.10.⊙O1与⊙O2相交于A、B两点,如图(1),连接O2O1并延长交⊙O1于P点,连接P A、PB并分别延长交⊙O2于C、D两点,连接CO2并延长交⊙O2于E点.已知⊙O2的半径为R,设∠CAD=α.(1)求CD的长(用含R、α的式子表示);(2)试判断CD与PO1的位置关系,并说明理由;(3)设点P’为⊙O1上(⊙O2外)的动点,连接P’A、P’B并分别延长交⊙O2于C’、D’,请你探究∠C’AD’是否等于α?C’D’与P’O1的位置关系如何?并说明理由.(注:图(2)与图(3)中⊙O1和⊙O2的大小及位置关系与图(1)完全相同,若你感到继续在图(1)中探究问题(3),图形太复杂,不便于观察,可以选择图(2)或图(3)中的一图说明理由).【分析】(1)作⊙O2的直径CE,连接DE.根据圆周角定理的推论,得∠E=∠CAD=α,再利用解直角三角形的知识求解;(2)连接AB,延长PO1与⊙O1相交于点E,连接AE.根据圆内接四边形的性质,得∠ABP′=∠C′,根据圆周角定理的推论,得∠ABP′=∠E,∠EAP′=90°,从而证明∠AP′E+∠C′=90°,则CD与PO1的位置关系是互相垂直;(3)根据同弧所对的圆周角相等,则说明∠C’AD’等于α;根据(2)中的证明过程,则可以证明C’D’与P’O1的位置关系是互相垂直.【解答】解:(1)连接DE.根据圆周角定理的推论,得∠E=∠CAD=α.∵CE是直径,∴∠CDE=90°.∴CD=CE•sin E=2R sinα;(2)CD与PO1的位置关系是互相垂直.理由如下:连接AB,延长PO1与⊙O1相交于点E,连接AE.∵四边形BAC′D′是圆内接四边形,∴∠ABP′=∠C′.∵P′E是直径,∴∠EAP′=90°,∴∠AP′E+∠E=90°.又∠ABP′=∠E,∴∠AP′E+∠C′=90°,即CD与PO1的位置关系是互相垂直;(3)根据同弧所对的圆周角相等,则说明∠C’AD’等于α;根据(2)中的证明过程,则可以证明C’D’与P’O1的位置关系是互相垂直.【点评】此题综合运用了圆周角定理及其推论、直角三角形的性质、圆内接四边形的性质.注意:连接两圆的公共弦、构造直径所对的圆周角都是圆中常见的辅助线.11.如图,已知直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,连接PC 并延长PC交y轴于点D(0,3).(1)求证:△POD≌△ABO;(2)若直线l:y=kx+b经过圆心P和D,求直线l的解析式.【分析】(1)首先连接PB,由直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,可求得∠APB=∠DPO=60°,∠ABO=∠POD=90°,即可得△P AB是等边三角形,可得AB=OP,然后由ASA,即可判定:△POD≌△ABO;(2)易求得∠PDO=30°,由OP=OD•tan30°,即可求得点P的坐标,然后利用待定系数法,即可求得直线l的解析式.【解答】(1)证明:连接PB,∵直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,∴∠APB=∠DPO=×180°=60°,∠ABO=∠POD=90°,∵P A=PB,∴△P AB是等边三角形,∴AB=P A,∠BAO=60°,∴AB=OP,∠BAO=∠OPD,在△POD和△ABO中,∴△POD≌△ABO(ASA);(2)解:由(1)得△POD≌△ABO,∴∠PDO=∠AOB,∵∠AOB=∠APB=×60°=30°,∴∠PDO=30°,∴OP=OD•tan30°=3×=,∴点P的坐标为:(﹣,0)∴,解得:,∴直线l的解析式为:y=x+3.【点评】此题考查了圆周角定理、全等三角形的判定与性质、直角三角形的性质、等边三角形的判定与性质以及待定系数法求一次函数的解析式.此题综合性较强,难度适中,注意准确作出辅助线,注意数形结合思想的应用.12.如图,△ABC内接于⊙O,AB=6,AC=4,D是AB边上一点,P是优弧BAC的中点,连接P A、PB、PC、PD.(1)当BD的长度为多少时,△P AD是以AD为底边的等腰三角形?并证明;(2)在(1)的条件下,若cos∠PCB=,求P A的长.【分析】(1)根据等弧对等弦以及全等三角形的判定和性质进行求解;(2)过点P作PE⊥AD于E.根据锐角三角函数的知识和垂径定理进行求解.【解答】解:(1)当BD=AC=4时,△P AD是以AD为底边的等腰三角形.∵P是优弧BAC的中点,∴=.∴PB=PC.又∵∠PBD=∠PCA(圆周角定理),∴当BD=AC=4,△PBD≌△PCA.∴P A=PD,即△P AD是以AD为底边的等腰三角形.(2)过点P作PE⊥AD于E,由(1)可知,当BD=4时,PD=P A,AD=AB﹣BD=6﹣4=2,则AE=AD=1.∵∠PCB=∠P AD(在同圆或等圆中,同弧所对的圆周角相等),∴cos∠P AD=cos∠PCB=,∴P A=.【点评】综合运用了等弧对等弦的性质、全等三角形的判定和性质、锐角三角函数的知识以及垂径定理.13.已知⊙O1与⊙O2相交于A、B两点,点O1在⊙O2上,C为⊙O2上一点(不与A,B,O1重合),直线CB与⊙O1交于另一点D.(1)如图(1),若AD是⊙O1的直径,AC是⊙O2的直径,求证:AC=CD;(2)如图(2),若C是⊙O1外一点,求证:O1C丄AD;(3)如图(3),若C是⊙O1内的一点,判断(2)中的结论是否成立?【分析】(1)连接C01,利用直径所对圆周角等于90度,以及垂直平分线的性质得出即可;(2)根据已知得出四边形AEDB内接于⊙O1,得出∠ABC=∠E,再利用=,得出∠E=∠AO1C,进而得出CO1∥ED即可求出;(3)根据已知得出∠B=∠EO1C,又∠E=∠B,即可得出∠EO1C=∠E,得出CO1∥ED,即可求出.【解答】(1)证明:连接C01∵AC为⊙O2直径∴∠AO1C=90°即CO1⊥AD,∵AO1=DO1∴DC=AC(垂直平分线的性质);(2)证明:连接AO1,连接AB,延长AO1交⊙O1于点E,连接ED,∵四边形AEDB内接于⊙O1,∴∠E+∠ABD=180°,∵∠ABC+∠ABD=180°,∴∠ABC=∠E,又∵=,∴∠ABC=∠AO1C,∴∠E=∠AO1C,∴CO1∥ED,又AE为⊙O1的直径,∴ED⊥AD,∴O1C⊥AD,(3)(2)中的结论仍然成立.证明:连接AO1,连接AB,延长AO1交⊙O1于点E,连接ED,∵∠B+∠AO1C=180°,∠EO1C+∠AO1C═180°,∴∠B=∠EO1C,又∵∠E=∠B,∴∠EO1C=∠E,∴CO1∥ED,又ED⊥AD,∴CO1⊥AD.【点评】此题主要考查了圆周角定理以及相交两圆的性质和圆内接四边形的性质,根据圆内接四边形的性质得出对应角之间的关系是解决问题的关键.14.如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且=,弦AD的延长线交切线PC于点E,连接BC.(1)判断OB和BP的数量关系,并说明理由;(2)若⊙O的半径为2,求AE的长.【分析】(1)首先连接OC,由PC切⊙O于点C,可得∠OCP=90°,又由∠BAC=30°,即可求得∠COP=60°,∠P=30°,然后根据直角三角形中30°角所对的直角边等于斜边的一半,证得OB=BP;(2)由(1)可得OB=OP,即可求得AP的长,又由=,即可得∠CAD=∠BAC=30°,继而求得∠E=90°,继而在Rt△AEP中求得答案.【解答】解:(1)OB=BP.理由:连接OC,∵PC切⊙O于点C,∴∠OCP=90°,∵OA=OC,∠OAC=30°,∴∠OAC=∠OCA=30°,∴∠COP=60°,∴∠P=30°,在Rt△OCP中,OC=OP=OB=BP;(2)由(1)得OB=OP,∵⊙O的半径是2,∴AP=3OB=3×2=6,∵=,∴∠CAD=∠BAC=30°,∴∠BAD=60°,∵∠P=30°,∴∠E=90°,在Rt△AEP中,AE=AP=×6=3.【点评】此题考查了切线的性质、直角三角形的性质以及圆周角定理.此题难度适中,注意掌握数形结合思想的应用,注意掌握辅助线的作法.15.如图,菱形、矩形与正方形的形状有差异,我们将菱形、矩形与正方形的接近程度称为“接近度”.在研究“接近度”时,应保证相似图形的“接近度”相等.(1)设菱形相邻两个内角的度数分别为m°和n°,将菱形的“接近度”定义为|m﹣n|,于是|m﹣n|越小,菱形越接近于正方形.①若菱形的一个内角为70°,则该菱形的“接近度”等于40;②当菱形的“接近度”等于0时,菱形是正方形.(2)设矩形相邻两条边长分别是a和b(a≤b),将矩形的“接近度”定义为|a﹣b|,于是|a﹣b|越小,矩形越接近于正方形.你认为这种说法是否合理?若不合理,给出矩形的“接近度”一个合理定义.【分析】(1)根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,相似图形的“接近度”相等.所以若菱形的一个内角为70°,则该菱形的“接近度”等于|m﹣n|;当菱形的“接近度”等于0时,菱形是正方形;(2)不合理,举例进行说明.【解答】解:(1)①∵内角为70°,∴与它相邻内角的度数为110°.∴菱形的“接近度”=|m﹣n|=|110﹣70|=40.②当菱形的“接近度”等于0时,菱形是正方形.(2)不合理.例如,对两个相似而不全等的矩形来说,它们接近正方形的程度是相同的,但|a﹣b|却不相等.合理定义方法不唯一.如定义为,越接近1,矩形越接近于正方形;越大,矩形与正方形的形状差异越大;当时,矩形就变成了正方形,即只有矩形的越接近1,矩形才越接近正方形.【点评】正确理解“接近度”的意思,矩形的“接近度”|a﹣b|越小,矩形越接近于正方形.这是解决问题的关键.16.如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)①画出△ABC关于x轴对称的△A1B1C1;②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2;③△A1B1C1与△A2B2C2成轴对称图形吗?若成轴对称图形,画出所有的对称轴;④△A1B1C1与△A2B2C2成中心对称图形吗?若成中心对称图形,写出所有的对称中心的坐标.【分析】(1)将三角形的各顶点,向x轴作垂线并延长相同长度得到三点的对应点,顺次连接;(2)将三角形的各顶点,绕原点O按逆时针旋转90°得到三点的对应点.顺次连接各对应点得△A2B2C2;(3)从图中可发现成轴对称图形,根据轴对称图形的性质画出对称轴即连接两对应点的线段,做它的垂直平分线;(4)成中心对称图形,画出两条对应点的连线,交点就是对称中心.【解答】解:如下图所示:(3)成轴对称图形,根据轴对称图形的性质画出对称轴即连接两对应点的线段,作它的垂直平分线,或连接A1C1,A2C2的中点的连线为对称轴.(4)成中心对称,对称中心为线段BB2的中点P,坐标是(,).【点评】本题综合考查了图形的变换,在图形的变换中,关键是找到图形的对应点.17.图(1)是一个10×10格点正方形组成的网格.△ABC是格点三角形(顶点在网格交点处),请你完成下面的两个问题:(1)在图(1)中画出与△ABC相似的格点△A1B1C1和△A2B2C2,且△A1B1C1与△ABC的相似比是2,△A2B2C2与△ABC的相似比是;(2)在图(2)中用与△ABC,△A1B1C1,△A2B2C2全等的格点三角形(每个三角形至少使用一次),拼出一个你熟悉的图案,并为你设计的图案配一句贴切的解说词.【分析】(1)△A1B1C1与△ABC的相似比是2,则让△ABC的各边都扩大2倍就可.△A2B2C2与△ABC的相似比是;△ABC的直角边是2,所以△A2B2C2与的直角边是即一个对角线的长度.斜边为2.依此画图即可;(2)拼图有审美意义即可,答案不唯一.【解答】解:【点评】本题主要考查了相似图形的画法,做这类题时根据的是相似图形的性质,即相似比相等.对应角相等.18.如图,矩形ABCD的边AD、AB分别与⊙O相切于点E、F,(1)求的长;(2)若,直线MN分别交射线DA、DC于点M、N,∠DMN=60°,将直线MN沿射线DA方向平移,设点D到直线的距离为d,当时1≤d≤4,请判断直线MN与⊙O的位置关系,并说明理由.【分析】(1)连接OE、OF,利用相切证明四边形AFOE是正方形,再根据弧长公式求弧长;(2)先求出直线M1N1与圆相切时d的值,结合1≤d≤4,划分d的范围,分类讨论.【解答】解:(1)连接OE、OF,∵矩形ABCD的边AD、AB分别与⊙O相切于点E、F,∴∠A=90°,∠OEA=∠OF A=90°∴四边形AFOE是正方形∴∠EOF=90°,OE=AE=∴的长==π.(2)如图,将直线MN沿射线DA方向平移,当其与⊙O相切时,记为M1N1,切点为R,交AD于M1,交BC于N1,连接OM1、OR,∵M1N1∥MN∴∠DM1N1=∠DMN=60°∴∠EM1N1=120°∵MA、M1N1切⊙O于点E、R∴∠EM1O=∠EM1N1=60°在Rt△EM1O中,EM1===1∴DM1=AD﹣AE﹣EM1=+5﹣﹣1=4.过点D作DK⊥M1N1于K在Rt△DM1K中DK=DM1×sin∠DM1K=4×sin∠60°=2即d=2,∴当d=2时,直线MN与⊙O相切,当1≤d<2时,直线MN与⊙O相离,当直线MN平移到过圆心O时,记为M2N2,点D到M2N2的距离d=DK+OR=2+=3>4,∴当2<d≤4时,MN直线与⊙O相交.【点评】本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d 与圆半径大小关系完成判定.19.如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.(1)试判断DE与BD是否相等,并说明理由;(2)如果BC=6,AB=5,求BE的长.【分析】(1)可通过连接AD,AD就是等腰三角形ABC底边上的高,根据等腰三角形三线合一的特点,可得出∠CAD=∠BAD,根据圆周角定理即可得出∠DEB=∠DBE,便可证得DE=DB.(2)本题中由于BE⊥AC,那么BE就是三角形ABC中AC边上的高,可用面积的不同表示方法得出AC•BE=CB•AD.进而求出BE的长.【解答】解:(1)DE=BD证明:连接AD,则AD⊥BC,在等腰三角形ABC中,AD⊥BC,∴∠CAD=∠BAD(等腰三角形三线合一),∴=,∴DE=BD;(2)∵AB=5,BD=BC=3,∴AD=4,∵AB=AC=5,∴S△ABC=•AC•BE=•CB•AD,∴BE=4.8.【点评】本题主要考查了等腰三角形的性质,圆周角定理等知识点的运用,用等腰三角形三线合一的特点得出圆周角相等是解题的关键.20.下框中是小明对一道题目的解答以及老师的批改.题目:某村计划建造如图所示的矩形蔬菜温室,要求长与宽的比为2:1,在温室内,沿前侧内墙保留3m的空地,其他三侧内墙各保留1m的通道,当温室的长与宽各为多少时,矩形蔬菜种植区域的面积是288m2?解:设矩形蔬菜种植区域的宽为xm,则长为2xm,根据题意,得x•2x=288.解这个方程,得x1=﹣12(不合题意,舍去),x2=12所以温室的长为2×12+3+1=28(m),宽为12+1+1=14(m)答:当温室的长为28m,宽为14m时,矩形蔬菜种植区域的面积是288m2.我的结果也正确!小明发现他解答的结果是正确的,但是老师却在他的解答中画了一条横线,并打了一个?.结果为何正确呢?(1)请指出小明解答中存在的问题,并补充缺少的过程:变化一下会怎样…(2)如图,矩形A′B′C′D′在矩形ABCD的内部,AB∥A′B′,AD∥A′D′,且AD:AB=2:1,设AB与A′B′、BC与B′C′、CD与C′D′、DA与D′A′之间的距离分别为a、b、c、d,要使矩形A′B′C′D′∽矩形ABCD,a、b、c、d应满足什么条件?请说明理由.【分析】(1)根据题意可得小明没有说明矩形蔬菜种植区域的长与宽之比为2:1的理由,所以应设矩形蔬菜种植区域的宽为xm,则长为2xm,然后由题意得,矩形蔬菜种植区域的长与宽之比为2:1,再利用小明的解法求解即可;(2)由使矩形A′B′C′D′∽矩形ABCD,利用相似多边形的性质,可得,即,然后利用比例的性质,即可求得答案.【解答】解:(1)小明没有说明矩形蔬菜种植区域的长与宽之比为2:1的理由.在“设矩形蔬菜种植区域的宽为xm,则长为2xm.”前补充以下过程:设温室的宽为xm,则长为2xm.则矩形蔬菜种植区域的宽为(x﹣1﹣1)m,长为(2x﹣3﹣1)m.∵,∴矩形蔬菜种植区域的长与宽之比为2:1;(2)要使矩形A′B′C′D′∽矩形ABCD,就要,即,即,即2AB﹣2(b+d)=2AB﹣(a+c),∴a+c=2(b+d),即.【点评】此题考查了相似多边形的性质.此题属于阅读性题目,注意理解题意,读懂题目是解此题的关键.21.二次函数y=ax2+bx+c图象的一部分如图所示,则a的取值范围是﹣1<a<0.。
深圳深圳市福田区岗厦中学中考数学期末几何综合压轴题易错汇编

深圳深圳市福田区岗厦中学中考数学期末几何综合压轴题易错汇编一、中考数学几何综合压轴题1.(1)问题发现如图1,△ACB和△DCE均为等腰直角三角形,∠ACB=90°,B,C,D在一条直线上.填空:线段AD,BE之间的关系为 .(2)拓展探究如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,请判断AD,BE的关系,并说明理由.(3)解决问题如图3,线段PA=3,点B是线段PA外一点,PB=5,连接AB,将AB绕点A逆时针旋转90°得到线段AC,随着点B的位置的变化,直接写出PC的范围.解析:(1) AD=BE,AD⊥BE.(2) AD=BE,AD⊥BE.(3) 5-32≤PC≤5+32.【分析】(1)根据等腰三角形性质证△ACD≌△BCE(SAS),得AD=BE,∠EBC=∠CAD,延长BE 交AD于点F,由垂直定义得AD⊥BE.(2)根据等腰三角形性质证△ACD≌△BCE(SAS),AD=BE,∠CAD=∠CBE,由垂直定义得∠OHB=90°,AD⊥BE;(3)作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,PC=BE,当P、E、B共线时,BE最小,最小值=PB-PE;当P、E、B共线时,BE最大,最大值=PB+PE,故5-32≤BE≤5+32.【详解】(1)结论:AD=BE,AD⊥BE.理由:如图1中,∵△ACB与△DCE均为等腰直角三角形,∴AC=BC,CE=CD,∠ACB=∠ACD=90°,在Rt△ACD和Rt△BCE中AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩=== ∴△ACD ≌△BCE (SAS ),∴AD=BE ,∠EBC=∠CAD延长BE 交AD 于点F ,∵BC ⊥AD ,∴∠EBC+∠CEB=90°,∵∠CEB=AEF ,∴∠EAD+∠AEF=90°,∴∠AFE=90°,即AD ⊥BE .∴AD=BE ,AD ⊥BE .故答案为AD=BE ,AD ⊥BE .(2)结论:AD=BE ,AD ⊥BE .理由:如图2中,设AD 交BE 于H ,AD 交BC 于O .∵△ACB 与△DCE 均为等腰直角三角形,∴AC=BC ,CE=CD ,∠ACB=∠ECD=90°,∴ACD=∠BCE ,在Rt △ACD 和Rt △BCE 中AC BC ACD BCE CD CE ⎧⎪∠∠⎨⎪⎩===, ∴△ACD ≌△BCE (SAS ),∴AD=BE ,∠CAD=∠CBE ,∵∠CAO+∠AOC=90°,∠AOC=∠BOH ,∴∠BOH+∠OBH=90°,∴∠OHB=90°,∴AD⊥BE,∴AD=BE,AD⊥BE.(3)如图3中,作AE⊥AP,使得AE=PA,则易证△APE≌△ACP,∴PC=BE,图3-1中,当P、E、B共线时,BE最小,最小值=PB-PE=5-32,图3-2中,当P、E、B共线时,BE最大,最大值=PB+PE=5+32,∴5-32≤BE≤5+32,即5-32≤PC≤5+32.【点睛】本题是几何变换综合题,考查了旋转的性质、等腰直角三角形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找三角形全等的条件,学会添加辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考压轴题.2.综合与实践数学问题:(1)如图1,ABC是等腰直角三角形,过斜边的中点D作正方形DECF,分别交BC,AC于点E,F,则AB,BE,AF之间的数量关系为______.问题解决:(2)如图2,在任意Rt ABC内,找一点D,过点D作正方形DECF,分别交BC,AC 于点E,F,若AB BE AF∠的度数;=+,求ADB图2拓展提升:(3)如图3,在(2)的条件下,分别延长ED,FD,交AB于点M,N,则MN,AM ,BN 的数量关系为______.图3(4)在(3)的条件下,若3AC =,4BC =,则MN =______.解析:(1))2AB AF BE +;(2)135°;(3)222MN AM BN =+;(4)2512【分析】(1)根据等腰直角三角形的斜边与直角边的关系及正方形的性质即可得出数量关系; (2) 延长AC 至点P ,使FP BE =,连接DP ,根据正方形的性质易证DFP DEB △△≌,从而可得DP =DB ,进而可证ADP ADB △△≌,从而可得12DAC DAB CAB ∠=∠=∠,12ABD CBD ABC ∠=∠=∠,由三角形内角和定理即可求得∠ADB 的度数; (3)由正方形的对边平行的性质易得AM =DM ,BN =DN ,从而在Rt △MDN 中,由勾股定理即可得MN 、AM 、BN 的数量关系;(4)由(2)知FP =BE ,即可求得DE =DF =1,根据相似三角形的性质可分别求得EM 、FN 的长,从而可得DM 、DN 的长,在Rt △MDN 中,由勾股定理即可求得MN 的长.【详解】(1)∵ABC 是等腰直角三角形,且AB =AC , ∴2AB =,∠A =∠B =45°,∵四边形DECF 是正方形,且D 是AB 的中点,∴DF =FC =CE =DE ,∠DFA =∠DEB =90°,DF ∥BC ,DE ∥AC ,∴∠ADF =∠B =45°,∠BDE =∠A =45°,∴AF =DF ,BE =DE ,∴F 、E 分别是AC 、BC 的中点,∴CF =BE ,∴AC =AF +CF =AF +BE , ∴)2AB AF BE +;(2)延长AC 至点P ,使FP BE =,连接DP .∵四边形DECF 是正方形,∴DF DE =,90DFC DEC ∠=∠=︒.∵FP BE =,90DFC DEB ∠=∠=︒,DF DE =,∴()SAS DFP DEB ≌△△.∴DP DB =.∵AB AF BE =+,AP AF FP =+,FP BE =,∴AP AB =.又∵DP DB =,AD AD =,∴()SSS ADP ADB ≌△△. ∴12DAC DAB CAB ∠=∠=∠. 同理可得:12ABD CBD ABC ∠=∠=∠. ∵90ACB ∠=︒,∴90CAB CBA ∠+∠=︒. ∴()1452DAB ABD CAB CBA ∠+∠=∠+∠=︒. ∴()180135ADB DAB ABD ∠=︒-∠+∠=︒.(3)∵DF ∥BC ,DE ∥AC ,∴∠CBD =∠NDB , ∠DAC =∠ADM ,∵ABD CBD ∠=∠,DAC DAB ∠=∠,∴∠ABD =∠NDB ,∠ADM =∠DAB ,∴BN =DN ,AM =DM .在Rt △MDN 中,由勾股定理得:22222MD DN MN AM BN ==++故答案为:222MN AM BN =+,(4)∵△ABC 是直角三角形,AC =3,BC =4,∴由勾股定理得:AB =5,设正方形DECF 的边长为x ,由(2)知,AP =AB =5,BE =FP ,CP =AP -AC =2,∵FP =CP +CF ,BE =BC -CE ,即4-x =2+x ,解得x =1,∴BE =BC -CE =3,AF =AC -CF =2,∵EM ∥AC ,FN ∥BC ,∴△BME ∽△BAC ,△AFN ∽△ACB ∴34ME BE AC BC ==,23FN AF BC AC ==, ∴94ME =,83FN =. ∵DM =ME -DE =54,DN =FN -DF =53, 222255254312MN DM DN ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭. 故答案为:2512MN =. 【点睛】 本题考查了正方形的性质,等腰三角形的性质,全等三角形的判定与性质,相似三角形的判定与性质,勾股定理等知识,截长补短法作辅助线是本题的关键.3.(了解概念)在凸四边形中,若一边与它的两条邻边组成的两个内角相等,则称该四边形为邻等四边形,这条边叫做这个四边形的邻等边.(理解运用)(1)在邻等四边形ABCD 中,40A ∠=︒,60B ∠=︒,若CD 是这个邻等四边形的邻等边,则C ∠的度数为__________;(2)如图,凸四边形ABCD 中,P 为AB 边的中点,ADP PDC ∽,判断四边形ABCD 是否为邻等四边形,并证明你的结论;(拓展提升)(3)在平面直角坐标系中,AB 为邻等四边形ABCD 的邻等边,且AB 边与x 轴重合,已知(2,0)A -,(,3)C m ,(2,4)D ,若在边AB 上使DPC BAD ∠=∠的点P 有且仅有1个,则m 的值是__________.解析:(1)130°;(2)四边形ABCD 是邻等四边形,理由见解析;(3)﹣6【分析】(1)根据邻等四边形的定义即可求解;(2)由△ADP ∽△PDC ,可得AP AD PC PD =,∠DAP =∠DPC ,∠APD =∠PCD ,由P 为AB 的中点,可得AP =BP ,则PB AD PC PD=,可证△BPC ∽△ADP ,由相似三角形的性质得出∠A =∠B 即可;(3)①若点B 在点A 右侧,如图,由AB 为邻等边,则有∠DAB =∠ABC =∠DPC ,可证△ADP ∽△BPC ,可得AP BC =AD BP ,设点P (n ,0),由等腰直角三角形可求∠BAD =45°,可求B 、C 横坐标之差为3,B (m +3,0),将AP ,BP ,AD ,BC ,代入得:n 2+(m +1)n +2m ﹣18=0,由题意可知n 只有一个解,可求得m =﹣;②若点B 在点A 左侧,可求得∠BAD =135°,可证△ADP ∽△BPC ,可得APBC =AD BP ,可求得B 、C 横坐标之差为3=m =﹣5﹣. 【详解】解:(1)∵CD 为邻等边,∴∠C =∠D ,又∵40A ∠=︒,60B ∠=︒,∴∠C =∠D =(360°﹣∠A ﹣∠B )÷2=130°,∴∠C =130°.故答案为:130°;(2)四边形ABCD 是邻等四边形,理由如下:∵△ADP ∽△PDC , ∴AP AD PC PD=,∠DAP =∠DPC ,∠APD =∠PCD ,∠ADP =∠PDC , 又∵P 为AB 的中点,∴AP =BP , ∴PB AD PC PD =, ∴PB PC AD PD=, ∵∠APD +∠BPC =180°﹣∠DPC ,∠PCD +∠PDC =180°﹣∠DPC ,且∠APD =∠PCD ,∴∠BPC =∠PDC ,∵∠ADP =∠PDC ,∴∠ADP =∠BPC ,∴△BPC ∽△ADP ,∴∠B =∠A ,∴四边形ABCD 为邻等四边形;(3)若点B在点A右侧,如图,∵AB为邻等边,则有∠DAB=∠ABC=∠DPC,又∵∠ADP+∠DPA=180°﹣∠DAB,∠BPC+∠DPA=180°﹣∠DPC,∴∠DAB=∠DPC,∠ADP=∠BPC,∴△ADP∽△BPC,∴APBC =ADBP,设点P(n,0),∵A(﹣2,0),D(2,4),∴∠BAD=45°,∴∠ABC=45°,过点C作CE⊥x轴于点E,则∠CEB=90°,∠BCE=∠ABC=45°,∴CE=BE,∵点C(m,3),∴CE=3,∴BE=3,∴B(m+3,0),∴AP=n+2,BP=m+3﹣n,∴AD22(22)4++2BC2233+32代入APBC=ADBP得:4232整理可得:﹣n2+(m+1)n+2m﹣18=0,由题意可知n只有一个解,∴△=(m+1)2+4(2m﹣18)=0,解得:m=﹣6又∵点C 在点D 右侧,∴m =﹣5+46;②若点B 在点A 左侧,如图,此时,∵A (﹣2,0),D (2,4),∴∠OAD =45°,∴∠BAD =∠ABC =∠DPC =135°,∵∠ADP +∠DPA =180°﹣∠DAB ,∠BPC +∠DPA =180°﹣∠DPC ,∴ADP =∠BPC ,∴△ADP ∽△BPC ,∴AP BC =AD BP, 由①得:B (m +3,0),C (m ,3),P (n ,0),AP =﹣2﹣n ,BP =n ﹣m ﹣3,AD =42BC =32 ∴42332n m =--, 解得:m =﹣6又∵点C 在点D 左侧,∴m =﹣5﹣6;综上所述:m =﹣6.【点睛】本题是相似综合题,考查新定义图形,仔细阅读题目,抓住定义中的性质,会验证新定义图形,相似三角形的判定与性质,一元二次方程根的判别式,利用相似三角形的性质构造关于n 的一元二次方程是解题关键.4.平面上,矩形ABCD 与直径为QP 的半圆K 如图摆放,分别延长DA 和QP 交于点O ,且∠BOQ =60°,OQ =OD =3,OP =2,OA =AB =1.让线段OD 及矩形ABCD 位置固定,将线段OQ 连带着半圆K 一起绕着点O 按逆时针方向形如旋转,设旋转角为α(0°≤α≤60°).发现(1)当α=0°,即初始位置时,点P____直线AB上.(填“在”或“不在”)求当α是多少时,OQ经过点B?(2)在OQ旋转过程中.简要说明α是多少时,点P,A间的距离最小?并指出这个最小值:(3)如图,当点P恰好落在BC边上时.求α及S阴影.拓展如图.当线段OQ与CB边交于点M,与BA边交于点N时,设BM=x(x>0),用含x的代数式表示BN的长,并求x的取值范围.探究当半圆K与矩形ABCD的边相切时,求sin α的值.解析:发现:(1)在,15°;(2)当α=60°时,最小距离为1;(3)30°,3=+1624S π阴影.拓展:x 的范围是0221x <≤-; 探究:sinα的值为43310-或62110-或32. 【详解】 解:发现(1)在;当OQ 过点B 时,在Rt △OAB 中,AO =AB , 得∠DOQ =∠ABO =45°, ∴α=60°-45°=15°. (2)如图3.连AP ,有OA +AP≥OP ,当OP 过点A ,即α=60°时等号成立. ∴AP≥OP -OA =2-1=1.∴当α=60°时.P ,A 间的距离最小. ∴PA 的最小值为1. (3)如图3,设半圆K 与PC 交点为R ,连接RK ,过点P 作PH ⊥AD 于点H ,过点R 作RE ⊥KQ 于点E . 在Rt △OPH 中,PH =AB =1,OP =2,∴∠POH =30°, ∴α=60°-30°=30°.由AD//BC 知,∠RPQ =∠POH =30°. ∴∠RKQ =2×30°=60°.2160236024KRQS ππ⎛⎫⋅ ⎪⎝⎭∴==扇形, 在Rt △RKE 中,3sin 604RE RK =⋅︒=, 13·216PRK S PK RE ∆∴==, 32416S π∴=+阴影; 拓展如图5,∠OAN =∠MBN =90°,∠ANO =∠BNM ,所以△AON ∽△BMN . ∴AN AO BN BM =,即11BN BN x-=, ∴1xBN x =+. 如图4,当点Q 落在BC 上时,x 取最大值,作QF ⊥AD 于点F . 2222311221BQ AF OQ QF AO ==--=--=-.∴x 的范围是0221x <≤-.【注:如果考生答“221x ≤-或221x <-”均不扣分】探究半圆与矩形相切,分三种情况:①如图5,半圆K 与BC 切于点T ,设直线KT 与AD 和OQ 的初始位置所在直线分别交于S ,O′,则∠KSO =∠KTB =90°,作KG ⊥OO′于点G . Rt △OSK 中,222253222OS OK SK ⎛⎫⎛⎫=-=-= ⎪ ⎪⎝⎭⎝⎭.Rt △OSO′中,tan 6023SO OO ︒''==,3232KO '=-. Rt △KGO′中,∠O′=30°,KG=13=3-.24KO 'Rt △OGK 中,334334sin 5102KGOKα--===②半圆K 与AD 切于点T ,如图6,同理可得 11()22sin 5522O K O T KT KG OKα''-=== 225113222621510⎛⎫⎛⎫-⨯-⎪ ⎪-⎝⎭⎝⎭==.③当半圆K 与CD 相切时,成Q 与点D 重合,且为切点. ∴α=60°,∴3sin sin 60α=︒= 综上述,sinα433-621-3考点:圆,直线与圆的位置关系,锐角三角函数,相似,三角形法则求最值5.综合与实践如图①,在中Rt ABC △中,90ACB ∠=︒,4AC =,3BC =,过点C 作CD AB ⊥于D ,将CDB △绕点D 逆时针方向旋转,得到C DB ''△,连接B C ',C A ',记旋转角为α. (1)问题发现 如图②,当90α=︒时,B CAC '='__________;如图③,当180α=︒时,B CAC '='__________. (2)拓展探究试判断:当0360α︒≤≤︒时,B CAC ''的大小有无变化?请仅就图④的情形给出证明. (3)问题解决如图⑤,当CDB △绕点D 逆时针旋转至点C '落在边AC 上时,求线段B C '的长.解析:(1)34,34;(2)无变化,理由详见解析;(3)2125B C '=.【分析】(1)首先利用勾股定理可求出AB 的值,再根据三角形面积求出CD 的值,再次利用勾股定理求出AD 、BD 的值,再分情况进一步得出,AC B C ''的值即可;(2)根据旋转的性质可得出95B D BD '==,125C D CD '==,再证明CDB ADC ''△∽△即可得出结论;(3)过点D 作DE AC ⊥于E ,证DEC ADC ∽△△,推出3625CE =,得出72225CC CE '==,继而得到2825AC AC CC ''=-=,再根据34B C AC '=',即可得出答案. 【详解】解:(1)∵90ACB ∠=︒,4AC =,3BC = ∴5AB = ∵1122ABCSAC BC AB CD =⋅=⋅ ∴125CD =∴2216169,5555AD AC CD BD AB AD =-==-=-= 当90α=︒时,34,55B C CD B D CD BD AC AD C D AD CD ''''=-=-==-=-=∴34B C AC '=' 当180α=︒时,3,4B C BC AC AC ''=====∴34B C AC '=' 故答案为:34;34;(2)无变化.证明:∵在Rt ABC △中,4AC =,3BC =,90ACB ∠=︒,∴5AB ==. ∵CD AB ⊥, ∴90BDC ∠=︒.∵90BDC ACB ∠=∠=︒,B B ∠=∠, ∴BDC BCA ∽△△. ∴BD CD BC BC AC AB ==,即33445BD CD CD ===. ∴95BD =,125CD =. ∴165AD AB BD =-=. 由旋转可知95B D BD '==,125C D CD '==,90B DC BDC ''∠=∠=︒.∴34B D CDCD AD '=='. ∵90B DC ADC ''∠=∠=︒, ∴CDB ADC ''∠=∠. ∴CDB ADC ''△∽△. ∴34B C CD AC AD '=='. (3)如图,过点D 作DE AC ⊥于E . ∵DC DC '=, ∴12CE CC '=.∵90DEC ADC ∠=∠=︒,DCE ACD ∠=∠, ∴DEC ADC ∽△△. ∴CE CDCD AC=,即1251244CE =.∴3625CE =. ∴72225CC CE '==. ∴2825AC AC CC ''=-=. ∵34B C AC '=', ∴321425B C AC ''==.【点睛】本题考查了勾股定理、三角形的面积公式、旋转的性质、相似三角形的判定及性质等多个知识点,综合性较强,要会利用数形结合的思想把代数和几何图形结合起来,会利用相似三角形的性质解题,此题结构精巧,考查范围广.6.如图1,已知点G 在正方形ABCD 的对角线AC 上,GE ⊥BC ,垂足为点E ,GF ⊥CD ,垂足为点F .(1)证明:四边形CEGF 是正方形; (2)探究与证明:将正方形CEGF 绕点C 顺时针方向旋转α角(0°<α<45°),如图2所示,试探究线段AG 与BE 之间的数量关系,并说明理由; (3)拓展与运用:正方形CEGF 绕点C 顺时针方向旋转α角(0°<α<45°),如图3所示,当B ,E ,F 三点在一条直线上时,延长CG 交AD 于点H ,若AG =6,GH =22,求BC 的长.解析:(1)证明见解析;(2)AG 2BE ,理由见解析;(3)5 【分析】(1)先说明GE ⊥BC 、GF ⊥CD ,再结合∠BCD=90°可证四边形CEGF 是矩形,再由∠ECG=45°即可证明;(2)连接CG ,证明△ACG ∽△BCE ,再应用相似三角形的性质解答即可;(3)先证△AHG ∽△CHA 可得AG GH AHAC AH CH==,设BC =CD =AD =a ,则AC =2a ,求出AH=23a ,DH=13a ,CH=103a ,最后代入AG AH AC CH =即可求得a 的值. 【详解】(1)∵四边形ABCD 是正方形, ∴∠BCD =90°,∠BCA =45°, ∵GE ⊥BC 、GF ⊥CD ,∴∠CEG =∠CFG =∠ECF =90°,∴四边形CEGF 是矩形,∠CGE =∠ECG =45°, ∴EG =EC ,∴四边形CEGF 是正方形. (2)结论:AG =2BE ; 理由:连接CG ,由旋转性质知∠BCE =∠ACG =α, 在Rt △CEG 和Rt △CBA 中,CE CG =cos45°2,2cos 45CB CA ︒==, ∴2CE CA CG CB =, ∴△ACG ∽△BCE , ∴2AG CABE CB== ∴线段AG 与BE 之间的数量关系为AG 2; (3)∵∠CEF =45°,点B 、E 、F 三点共线, ∴∠BEC =135°, ∵△ACG ∽△BCE , ∴∠AGC =∠BEC =135°, ∴∠AGH =∠CAH =45°, ∵∠CHA =∠AHG , ∴△AHG ∽△CHA , ∴AG GH AHAC AH CH==, 设BC =CD =AD =a ,则AC 2a ,则由AG GH AC AH =,得6222AHa =, ∴AH =23a ,则DH =AD ﹣AH =13a ,2210CH CD DH 3a =+=,∴AG AH AC CH=,得2632103aa = , 解得:a =35,即BC =35. 【点睛】本题属于四边形综合题,主要考查相似形的判定和性质、正方形的性质等知识点,解题的关键是正确寻找相似三角形解决问题并利用参数构建方程解决问题. 7.如图1,在中,,,点,分别在边,上,,连接,点,,分别为,,的中点.(1)观察猜想 图1中,线段与的数量关系是 ,位置关系是 ;(2)探究证明 把绕点逆时针方向旋转到图2的位置,连接,,,判断的形状,并说明理由; (3)拓展延伸 把绕点在平面内自由旋转,若,,请直接写出面积的最大值.解析:(1)PM=PN ,;(2)等腰直角三角形,理由详见解析;(3).【详解】试题分析:(1)已知 点,,分别为,,的中点,根据三角形的中位线定理可得,,,根据平行线的性质可得∠DPM=∠DCE ,∠NPD=∠ADC ,在中,,,,可得BD=EC ,∠DCE+∠ADC=90°,即可得PM=PN ,∠DPM+∠NPD=90°,即;(2)是等腰直角三角形,根据旋转的性质易证△BAD ≌△CAE ,即可得BD=CE ,∠ABD=∠ACE ,根据三角形的中位线定理及平行线的性质(方法可类比(1)的方法)可得PM="PN," ∠MPD=∠ECD,∠PNC=∠DBC,所以∠MPD=∠ECD=∠ACD+∠ACE=∠ACD+∠ABD,∠DPN=∠PNC+∠PCN =∠DBC+∠PCN,即可得∠MPN=∠MPD+∠DPN=∠ACD+∠ABD+∠DBC+∠PCN=∠ABC+∠ACB=90°,即△PMN为等腰直角三角形;(3)把绕点旋转到如图的位置,此时PN=(AD+AB)="7,"PM=(AE+AC)=7,且PN、PM的值最长,由(2)可知PM=PN,,所以面积的最大值为 .试题解析:(1)PM=PN,;(2)等腰直角三角形,理由如下:由旋转可得∠BAD=∠CAE,又AB=AC,AD=AE∴△BAD≌△CAE∴BD=CE,∠ABD=∠ACE,∵点,分别为,的中点∴PM是△DCE的中位线∴PM=CE,且,同理可证PN=BD,且∴PM="PN," ∠MPD=∠ECD,∠PNC=∠DBC,∴∠MPD=∠ECD=∠ACD+∠ACE=∠ACD+∠ABD,∠DPN=∠PNC+∠PCN =∠DBC+∠PCN,∴∠MPN=∠MPD+∠DPN=∠ACD+∠ABD+∠DBC+∠PCN=∠ABC+∠ACB=90°,即△PMN为等腰直角三角形.(3).考点:旋转和三角形的综合题.8.探究:小明在求同一坐标轴上两点间的距离时发现,对于平面直角坐标系内任意两点P1(x1,y1),P2(x2,y2),可通过构造直角三角形利用图1得到结论:他还利用图2证明了线段P1P2的中点P(x,y)P的坐标公式:,.(1)请你帮小明写出中点坐标公式的证明过程;运用:(2)①已知点M(2,﹣1),N(﹣3,5),则线段MN长度为;②直接写出以点A(2,2),B(﹣2,0),C(3,﹣1),D为顶点的平行四边形顶点D 的坐标:;拓展:(3)如图3,点P(2,n)在函数(x≥0)的图象OL与x轴正半轴夹角的平分线上,请在OL、x轴上分别找出点E、F,使△PEF的周长最小,简要叙述作图方法,并求出周长的最小值.解析:(1)答案见解析;(2)①;②(﹣3,3)或(7,1)或(﹣1,﹣3);(3).【详解】试题分析:(1)用P1、P2的坐标分别表示出OQ和PQ的长即可证得结论;(2)①直接利用两点间距离公式可求得MN的长;②分AB、AC、BC为对角线,可求得其中心的坐标,再利用中点坐标公式可求得D点坐标;(3)设P关于直线OL的对称点为M,关于x轴的对称点为N,连接PM交直线OL于点R,连接PN交x轴于点S,则可知OR=OS=2,利用两点间距离公式可求得R的坐标,再由PR=PS=n,可求得n的值,可求得P点坐标,利用中点坐标公式可求得M点坐标,由对称性可求得N点坐标,连接MN交直线OL于点E,交x轴于点S,此时EP=EM,FP=FN,此时满足△PEF的周长最小,利用两点间距离公式可求得其周长的最小值.试题解析:(1)∵P1(x1,y1),P2(x2,y2),∴Q1Q2=OQ2﹣OQ1=x2﹣x1,∴Q1Q=,∴OQ=OQ1+Q1Q=x1+=,∵PQ为梯形P1Q1Q2P2的中位线,∴PQ= =,即线段P1P2的中点P(x,y)P的坐标公式为x=,y=;(2)①∵M (2,﹣1),N (﹣3,5),∴MN==,故答案为;②∵A (2,2),B (﹣2,0),C (3,﹣1),∴当AB 为平行四边形的对角线时,其对称中心坐标为(0,1),设D (x ,y ),则x+3=0,y+(﹣1)=2,解得x=﹣3,y=3,∴此时D 点坐标为(﹣3,3),当AC 为对角线时,同理可求得D 点坐标为(7,1),当BC 为对角线时,同理可求得D 点坐标为(﹣1,﹣3),综上可知D 点坐标为(﹣3,3)或(7,1)或(﹣1,﹣3),故答案为(﹣3,3)或(7,1)或(﹣1,﹣3);(3)如图,设P 关于直线OL 的对称点为M ,关于x 轴的对称点为N ,连接PM 交直线OL 于点R ,连接PN 交x 轴于点S ,连接MN 交直线OL 于点E ,交x 轴于点F ,又对称性可知EP=EM ,FP=FN ,∴PE+PF+EF=ME+EF+NF=MN ,∴此时△PEF 的周长即为MN 的长,为最小,设R (x ,),由题意可知OR=OS=2,PR=PS=n ,∴=2,解得x=﹣(舍去)或x=,∴R (,),∴,解得n=1,∴P (2,1),∴N (2,﹣1),设M (x ,y ),则=,=,解得x=,y=,∴M(,),∴MN==,即△PEF 的周长的最小值为.考点:一次函数综合题;阅读型;分类讨论;最值问题;探究型;压轴题. 9.(基础巩固)(1)如图①,ABC ACD CED α∠=∠=∠=,求证:ABC CED ∽△△. (尝试应用)(2)如图②,在菱形ABCD 中,60A ∠=︒,点E ,F 分别为边,AD AB 上两点,将菱形ABCD 沿EF 翻折,点A 恰好落在对角线DB 上的点P 处,若2PD PB =,求AEAF的值. (拓展提高)(3)如图③,在矩形ABCD 中,点P 是AD 边上一点,连接,PB PC ,若2,4,120PA PD BPC ==∠=︒,求AB 的长.解析:(1)见解析;(2)54;(3)113AB = 【分析】(1)由,ABC ACD ACE A ABC α∠=∠=∠=∠+∠证明A DCE ∠=∠,再根据相似三角形的判定方法解题即可;(2)由菱形的性质,得到AB AD =,60A ∠=︒,继而证明ABD △是等边三角形,结合(1)中相似三角形对应边成比例的性质,设,2,,BP a DP a AE PE x AF PF y ======,则3,3DE a x BF a y =-=-可整理得到54x y =,据此解题; (3)在AD 边上取点E ,F ,使得30ABE DCF ∠=∠=︒,由矩形的性质,得到120BEP BPC PFC ∠=∠=∠=︒,结合(1)中相似三角形对应边成比例的性质解题即可.【详解】解:(1)证明:∵,ABC ACD ACE A ABC α∠=∠=∠=∠+∠, ∴DCE A αα∠+=∠+,即A DCE ∠=∠, ∵ABC CED α∠=∠=, ∴ABC CED ∽△△; (2)∵四边形ABCD 是菱形, ∴AB AD =, ∴60A ∠=︒,∴ABD △是等边三角形,∴60EPF A ADB ABD ∠=∠=∠=∠=︒, 由(1)得,EPD PFB ∽, ∴DE PD PEPB BF PF==, 设,2,,BP a DP a AE PE x AF PF y ======,则3,3DE a x BF a y =-=- ∴323a x a xa a y y-==-, 可得3ay xy ax -=①,32ax xy ay -=②, ①-②,得332ay ax ax ay -=-,∴54x y =, ∴AE AF 的值为54; (3)如图,在AD 边上取点E ,F ,使得30ABE DCF ∠=∠=︒,设AB =CD =m ,∵四边形ABCD 是矩形, ∴90A D ∠=∠=︒,∴120BEP BPC PFC ∠=∠=∠=︒, 60BPE DFC ︒∠=∠=21,sin 60233AB m mBE CF AE BE ∴=====︒= DF , 223mPE AE ∴=-=-443m PF DF ∴=-=-, 由(1)可得,BEP PFC ∽, ∴BE EPPF FC=, ∴22332433m mm m -=-,整理,得22380m m +-=, 解得113m =-或311m =--(舍去), ∴113AB =-. 【点睛】本题考查相似三角形的综合题、等边三角形的性质、菱形的性质、矩形的性质等知识,是重要考点,难度一般,掌握相关知识是解题关键.10.问题背景:我们学习等边三角形时得到直角三角形的一个性质:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半.即:如图1,在Rt △ABC 中,∠ACB=90°,∠ABC=30°,则:AC=12AB .探究结论:小明同学对以上结论作了进一步研究.(1)如图1,连接AB 边上中线CE ,由于CE=12AB ,易得结论:①△ACE 为等边三角形;②BE 与CE 之间的数量关系为 .(2)如图2,点D 是边CB 上任意一点,连接AD ,作等边△ADE ,且点E 在∠ACB 的内部,连接BE.试探究线段BE与DE之间的数量关系,写出你的猜想并加以证明.(3)当点D为边CB延长线上任意一点时,在(2)条件的基础上,线段BE与DE之间存在怎样的数量关系?请直接写出你的结论.拓展应用:如图3,在平面直角坐标系xOy中,点A的坐标为(﹣3,1),点B是x轴正半轴上的一动点,以AB为边作等边△ABC,当C点在第一象限内,且B(2,0)时,求C点的坐标.解析:(1)EC=EB;(2)ED=EB,理由见解析;(3)ED=EB;拓展应用:C(1,2+3).【分析】探究结论:(1)只要证明△ACE是等边三角形即可解决问题;(2)如图2中,结论:ED=EB.想办法证明EP垂直平分线段AB即可解决问题;(3)结论不变,证明方法类似;拓展应用:利用(2)中结论,可得CO=CB,设C(1,n),根据OC=CB=AB,构建方程即可解决问题.【详解】探究结论(1),如图1中,∵∠ACB=90°,∠B=30°,∴∠A=60°,∵AC=1AB=AE=EB,2∴△ACE是等边三角形,∴EC=AE=EB,故答案为:EC=EB;(2)如图2中,结论:ED=EB.理由:连接PE,∵△ACP,△ADE都是等边三角形,∴AC=AD=DE,AD=AE,∠CAP=∠DAE=60°,∴∠CAD=∠PAE,∴△CAD ≌△PAE , ∴∠ACD=∠APE=90°, ∴EP ⊥AB ,∵PA=PB , ∴EA=EB ,∵DE=AE , ∴ED=EB ;(3)当点D 为边CB 延长线上任意一点时,同法可证:ED=EB , 故答案为:ED=EB ;拓展应用:如图3中,作AH ⊥x 轴于H ,CF ⊥OB 于F ,连接OA ,∵A 31), ∴∠AOH=30°, 由(2)可知,CO=CB , ∵CF ⊥OB , ∴OF=FB=1,∴可以假设C (1,n ), ∵OC=BC=AB , ∴1+n 2=1+3)2, ∴3 ∴C (1,3 【点睛】本题考查三角形综合题、等边三角形的判定和性质、全等三角形的判定和性质、勾股定理、线段的垂直平分线的性质等知识,正确添加常用辅助线,构造全等三角形是解决问题的关键.11.(1)阅读理解:我国是最早了解勾股定理的国家之一,它被记载于我国古代的数学著作《周髀算经》中.汉代数学家赵爽为了证明勾股定理,创制了一幅如图①所示的“弦图”,后人称之为“赵爽弦图”.根据“赵爽弦图”写出勾股定理和推理过程;(2)问题解决:勾股定理的证明方法有很多,如图②是古代的一种证明方法:过正方形ACDE 的中心O ,作FG HP ⊥,将它分成4份.所分成的四部分和以BC 为边的正方形恰好能拼成以AB 为边的正方形.若12,5AC BC ==,求EF 的值;(3)拓展探究:如图③,以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到“勾股树”的部分图形.设大正方形N 的边长为定值n ,小正方形,,,A B C D 的边长分别为a b c d ,,,.已知123α∠=∠=∠=,当角9(0)0αα︒<<︒变化时,探究b 与c 的关系式,并写出该关系式及解答过程(b 与c 的关系式用含n的式子表示).解析:(1)见详解;(2)EF=172或72;(3)c+b=n,理由见详解【分析】(1)根据大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和,即可得到结论;(2)设EF=a,FD=b,由图形的特征可知:a+b=12,a-b=±5,进而即可求解;(3)设正方形E的边长为e,正方形F的边长为f,由相似三角形的性质可知:22e cnf bn==,,结合勾股定理,可得222e f n+=,进而即可求解.【详解】(1)证明:∵在图①中,大正方形的面积等于四个全等的直角三角形的面积与中间小正方形面积的和.∴c2=12ab×4+(b−a)2,化简得:a2+b2=c2;(2)由题意得:正方形ACDE被分成4个全等的四边形,设EF =a ,FD =b , ∴a +b =12,∵正方形ABIJ 是由正方形ACDE 被分成的4个全等的四边形和正方形CBLM 拼成, ∴E F EF ''=,KF FD '=,5E K BC '==, 当EF >DF 时, ∵E F KF E K ''''-=, ∴a -b =5,∴125a b a b +=⎧⎨-=⎩,解得:a =172,∴EF =172; 同理,当EF <DF 时,EF =72故EF =172或72(3)设正方形E 的边长为e ,正方形F 的边长为f , ∵123α∠=∠=∠=,∴图中①与②与③,三个直角三角形相似, ∴c e b fe nf n==,,即:22e cn f bn ==,, ∵图形③是直角三角形, ∴222e f n +=,∴2cn bn n +=,即:c +b =n ,【点睛】本题主要考查勾股定理及其证明过程,相似三角形的判定和性质,找准图形中线段长和面积的数量关系,是解题的关键. 12.(问题)如图1,在Rt ABC 中,90,ACB AC BC ∠=︒=,过点C 作直线l 平行于AB .90EDF ∠=︒,点D 在直线l 上移动,角的一边DE 始终经过点B ,另一边DF 与AC交于点P ,研究DP 和DB 的数量关系.(探究发现)(1)如图2,某数学兴趣小组运用“从特殊到一般”的数学思想,发现当点D 移动到使点P 与点C 重合时,通过推理就可以得到DP DB =,请写出证明过程;(数学思考)(2)如图3,若点P 是AC 上的任意一点(不含端点A C 、),受(1)的启发,这个小组过点D 作DG CD ⊥交BC 于点G ,就可以证明DP DB =,请完成证明过程;(拓展引申)(3)如图4,在(1)的条件下,M 是AB 边上任意一点(不含端点AB 、),N 是射线BD 上一点,且AM BN =,连接MN 与BC 交于点Q ,这个数学兴趣小组经过多次取M 点反复进行实验,发现点M 在某一位置时BQ 的值最大.若4AC BC ==,请你直接写出BQ 的最大值.解析:【探究发现】(1)见解析;【数学思考】(2)见解析;【拓展引申】(3)22AM =BQ 有最大值为2.【分析】根据等腰三角形的性质及平行的定义即可解得 根据证明()CDP GDB ASA ≌即可推出DP DB =过点M 作MH MN ⊥交AC 于点H ,连接,CM HQ ,可证明()AMH BNQ ASA ≌,再推出ACM BMQ ∽即可得AC AM BM BQ =42AMBQAM =-,则22AM = 【详解】证明:【探究发现】(1)∵90,ACB AC BC ∠=︒= ∴45CAB CBA ∠=∠=︒ ∵CDAB∴45CBA DCB ∠=∠=︒,且BD CD ⊥ ∴45DCB DBC ∠=∠=︒ ∴DB DC = 即DB DP = 【数学思考】(2)∵,45DG CD DCB ⊥∠=︒ ∴45DCG DGC ∠=∠=︒∴,135DC DG DCP DGB =∠=∠=︒,∵90BDP CDG ∠=∠=︒∴CDP BDG ∠=∠,且,135DC DG DCP DGB =∠=∠=︒,∴()CDP GDB ASA ≌∴BD DP =【拓展引申】(3)如图4,过点M 作MH MN ⊥交AC 于点H ,连接,CM HQ ,∵MH MN ⊥,∴90AMH NMB ∠+∠=︒∵,90CD AB CDB ∠=︒∥∴90DBM ∠=︒∴90NMB MNB ∠+∠=︒∴HMA MNB ∠=∠,且,45AM BN CAB CBN =∠=∠=︒∴()AMH BNQ ASA ≌∴AH BQ =∵90,4ACB AC BC ∠=︒==, ∴42,AB AC AH BC BQ =-=-∴CH CQ =∴45CHQ CQH CAB ∠=∠=︒=∠∴HQ AB ∥∴HQM QMB ∠=∠∵90ACB HMQ ∠=∠=︒∴点H ,点M ,点Q ,点C 四点共圆,∴HCM HQM ∠=∠∴HCM QMB ∠=∠,且45A CBA ∠=∠=︒∴ACM BMQ ∽ ∴AC AM BM BQ = ∴42AM BQ AM=- ∴2(22)2AM BQ --=∴22AM =时,BQ 有最大值为2.【点睛】本题考查等腰三角形,解题关键在于熟练掌握等腰三角形的性质.13.性质探究如图①,在等腰三角形ABC 中,0120ACB ∠=,则底边AB 与腰AC 的长度之比为________.理解运用⑴若顶角为120°的等腰三角形的周长为83+________;⑵如图②,在四边形EFGH 中,EF EG EH ==.①求证:EFG EHG FGH ∠+∠=∠;②在边,FG GH 上分别取中点,M N ,连接MN .若0120FGH ∠=,10EF =,直接写出线段MN 的长.类比拓展 顶角为2σ的等腰三角形的底边与一腰的长度之比为________(用含σ的式子表示). 解析:31)432)①见解析;②532sin α. 【分析】性质探究:作CD ⊥AB 于D ,则∠ADC=∠BDC=90°,由等腰三角形的性质得出AD=BD ,∠A=∠B=30°,由直角三角形的性质得出AC=2CD ,3,得出3,即可得出结果;理解运用:(1)同上得出则AC=2CD ,3,由等腰三角形的周长得出33CD=2,得出3 (2)①由等腰三角形的性质得出∠EFG=∠EGF ,∠EGH=∠EHG ,得出∠EFG+∠EHG=∠EGF+∠EGH=∠FGH 即可;②连接FH ,作EP ⊥FH 于P ,由等腰三角形的性质得出PF=PH ,由①得:∠EFG+∠EHG=∠FGH=120°,由四边形内角和定理求出∠FEH=120°,由等腰三角形的性质得出∠EFH=30°,由直角三角形的性质得出PE=12EF=5,333MN 是△FGH 的中位线,由三角形中位线定理即可得出结果; 类比拓展:作AD ⊥BC 于D ,由等腰三角形的性质得出BD=CD ,∠BAD=12∠BAC=α,由三角函数得出BD=AB×sinα,得出BC=2BD=2AB×sinα,即可得出结果.【详解】性质探究解:作CD ⊥AB 于D ,如图①所示:则∠ADC=∠BDC=90°,∵AC=BC ,∠ACB=120°,∴AD=BD ,∠A=∠B=30°,∴AC=2CD ,AD=3CD , ∴AB=2AD=23CD , ∴232AB CD AC CD=3; 故答案为3; 理解运用(1)解:如图①所示:同上得:AC=2CD ,AD=3CD ,∵AC+BC+AB=8+43,∴4CD+23CD=8+43,解得:CD=2,∴AB=43,∴△ABC 的面积=12AB×CD=12×43×2=43;故答案为43(2)①证明:∵EF=EG=EH ,∴∠EFG=∠EGF ,∠EGH=∠EHG ,∴∠EFG+∠EHG=∠EGF+∠EGH=∠FGH ;②解:连接FH ,作EP ⊥FH 于P ,如图②所示:则PF=PH ,由①得:∠EFG+∠EHG=∠FGH=120°,∴∠FEH=360°-120°-120°=120°,∵EF=EH ,∴∠EFH=30°,∴PE=12EF=5,∴33∴FH=2PF=103, ∵点M 、N 分别是FG 、GH 的中点,∴MN 是△FGH 的中位线,∴MN=12FH=53;类比拓展解:如图③所示:作AD ⊥BC 于D ,∵AB=AC ,∴BD=CD ,∠BAD=12∠BAC=α,∵sinα=BD AB , ∴BD=AB×sinα,∴BC=2BD=2AB×sinα,∴2sin BC AB AB ABα⋅==2sinα; 故答案为2sinα.【点睛】本题是四边形综合题目,考查了等腰三角形的性质、直角三角形的性质、三角形中位线定理、四边形内角和定理、就直角三角形等知识;本题综合性强,熟练掌握等腰三角形的性质和含30°角的直角三角形的性质是解题的关键.14.如图1,在等腰三角形ABC 中,120,,A AB AC ∠==点D E 、分别在边AB AC 、上,,AD AE =连接,BE 点M N P 、、分别为DE BE BC 、、的中点.(1)观察猜想图1中,线段NM NP 、的数量关系是____,MNP ∠的大小为_____;(2)探究证明把ADE 绕点A 顺时针方向旋转到如图2所示的位置,连接,MP BD CE 、、判断MNP △的形状,并说明理由;(3)拓展延伸把ADE 绕点A 在平面内自由旋转,若1,3AD AB ==,请求出MNP △面积的最大值. 解析:(1)相等,60;(2)MNP △是等边三角形,理由见解析;(3)MNP △面积的【分析】(1)根据"120,,A AB AC ∠==,AD AE =点M N P 、、分别为DE BE BC 、、的中点",可得MN //BD ,NP //CE ,根据三角形外角和定理,等量代换求出MNP ∠.(2)先求出ABD ACE △≌△,得出ABD ACE ∠=∠,根据MN //BD ,NP //CE ,和三角形外角和定理,可知MN=PN ,再等量代换求出MNP ∠,即可求解.(3)根据BD AB AD ≤+,可知BD 最大值,继而求出MNP △面积的最大值.【详解】()1由题意知:AB=AC ,AD=AE ,且点M N P 、、分别为DE BE BC 、、的中点,∴BD=CE ,MN //BD ,NP //CE ,MN=12BD ,NP=12EC∴MN=NP又∵MN //BD ,NP //CE ,∠A=120︒,AB=AC ,∴∠MNE=∠DBE ,∠NPB=∠C ,∠ABC=∠C=30根据三角形外角和定理,得∠ENP=∠NBP+∠NPB∵∠MNP=∠MNE+∠ENP ,∠ENP=∠NBP+∠NPB ,∠NPB=∠C ,∠MNE=∠DBE ,∴∠MNP=∠DBE+∠NBP+∠C=∠ABC+∠C =60. ()2MNP 是等边三角形.理由如下:如图,由旋转可得BAD CAE ∠=∠ 在ABD 和ACE 中AB AC BAD CAE AD AE =⎧⎪∠=∠⎨⎪=⎩()ABD ACE SAS ∴≌BD CE ABD ACE ,=∠=∠∴.点M N 、分别为DE BE 、的中点,MN ∴是EBD △的中位线,12MN BD ∴=且//MN BD 同理可证12PN CE =且//PN CE ,MN PN MNE DBE NPB ECB ,∴=∠=∠∠=∠MNE DBE ABD ABE ACE ABE ∠=∠=∠+∠=∠+∠。
2002-2019深圳中考数学试题分类汇编 24选择题压轴题--函数+几何多选题 教师版

近十五年深圳数学中考题分类汇编函数+几何多选题1.(2014)(3分)二次函数2y ax bx c =++图象如图,下列正确的个数为( ) ①0bc >; ②230a c -<; ③20a b +>;④20ax bx c ++=有两个解1x ,2x ,当12x x >时,10x >,20x <; ⑤0a b c ++>;⑥当1x >时,y 随x 增大而减小.A .2B .3C .4D .5【思路点拨】主要考查图象与二次函数系数之间的关系,二次函数的性质,会利用对称轴的范围求2a 与b 的关系,以及二次函数与方程之间的转换.根据抛物线开口向上可得0a >,结合对称轴在y 轴右侧得出0b <,根据抛物线与y 轴的交点在负半轴可得0c <,再根据有理数乘法法则判断①;再由不等式的性质判断②;根据对称轴为直线1x =判断③;根据图象与x 轴的两个交点分别在原点的左右两侧判断④;由1x =时,0y <判断⑤;根据二次函数的增减性判断⑥.【详细解答】解:①抛物线开口向上,0a ∴>,对称轴在y 轴右侧,a ∴,b 异号即0b <,抛物线与y 轴的交点在负半轴,0c ∴<,0bc ∴>,故①正确;②0a >,0c <,230a c ∴->,故②错误;③对称轴12bx a=-<,0a >, 2b a ∴-<,20a b ∴+>,故③正确;④由图形可知二次函数2y ax bx c =++与x 轴的两个交点分别在原点的左右两侧, 即方程20ax bx c ++=有两个解1x ,2x ,当12x x >时,10x >,20x <,故④正确; ⑤由图形可知1x =时,0y a b c =++<,故⑤错误; ⑥0a >,对称轴1x =,∴当1x >时,y 随x 增大而增大,故⑥错误.综上所述,正确的结论是①③④,共3个. 故选:B .2.(2015)(3分)二次函数2(0)y ax bx c a =++≠的图象如图所示,下列说法正确的个数是( )①0a >;②0b >;③0c <;④240b ac ->.A .1B .2C .3D .4【思路点拨】本题考查了二次函数图象与系数的关系:对于二次函数2(0)y ax bx c a =++≠,二次项系数a 决定抛物线的开口方向和大小,当0a >时,抛物线向上开口;当0a <时,抛物线向下开口;一次项系数b 和二次项系数a 共同决定对称轴的位置:当a 与b 同号时(即0)ab >,对称轴在y 轴左; 当a 与b 异号时(即0)ab <,对称轴在y 轴右.(简称:左同右异);常数项c 决定抛物线与y 轴交点:抛物线与y 轴交于(0,)c .抛物线与x 轴交点个数由△决定:△240b ac =->时,抛物线与x 轴有2个交点;△240b ac =-=时,抛物线与x 轴有1个交点;△240b ac =-<时,抛物线与x 轴没有交点.根据抛物线开口方向对①进行判断;根据抛物线的对称轴位置对②进行判断;根据抛物线与y 轴的交点位置对③进行判断;根据抛物线与x 轴的交点个数对④进行判断. 【详细解答】解:抛物线开口向下,0a ∴<,所以①错误;抛物线的对称轴在y 轴右侧,02ba∴->, 0b ∴>,所以②正确;抛物线与y 轴的交点在x 轴上方,0c ∴>,所以③错误;抛物线与x 轴有2个交点,∴△240b ac =->,所以④正确.故选:B .3.(2015)(3分)如图,已知正方形ABCD 的边长为12,BE EC =,将正方形边CD 沿DE 折叠到DF ,延长EF 交AB 于G ,连接DG ,现在有如下4个结论:①ADG FDG ∆≅∆;②2GB AG =;③GDE BEF ∆∆∽;④725BEF S ∆=.在以上4个结论中,正确的有( )A .1B .2C .3D .4【思路点拨】本题综合性较强,考查了翻折变换的性质和正方形的性质,全等三角形的判定与性质,勾股定理,平行线的判定,三角形的面积计算,有一定的难度.根据正方形的性质和折叠的性质可得AD DF =,90A GFD ∠=∠=︒,于是根据“HL ”判定ADG FDG ∆≅∆,再由12GF GB GA GB +=+=,EB EF =,BGE ∆为直角三角形,可通过勾股定理列方程求出4AG =,8BG =,进而求出BEF ∆的面积,再抓住BEF ∆是等腰三角形,而GED ∆显然不是等腰三角形,判断③是错误的. 【详细解答】解:由折叠可知,DF DC DA ==,90DFE C ∠=∠=︒,90DFG A ∴∠=∠=︒, ADG FDG ∴∆≅∆,①正确;正方形边长是12,6BE EC EF ∴===,设AG FG x ==,则6EG x =+,12BG x =-, 由勾股定理得:222EG BE BG =+, 即:222(6)6(12)x x +=+-, 解得:4x =4AG GF ∴==,8BG =,2BG AG =,②正确;6BE EF ==,BEF ∆是等腰三角形,易知GED ∆不是等腰三角形,③错误;168242S GBE ∆=⨯⨯=,67224105EF S BEF S GBE EG ∆=∆==,④正确. 故选:C .4.(2016)如图,CB CA =,90ACB ∠=︒,点D 在边BC 上(与B 、C 不重合),四边形ADEF 为正方形,过点F 作FG CA ⊥,交CA 的延长线于点G ,连接FB ,交DE 于点Q ,给出以下结论:①AC FG =;②:1:2FAB CBFG S S ∆=四边形;③ABC ABF ∠=∠;④2AD FQ AC =, 其中正确的结论的个数是( )A .1B .2C .3D .4【思路点拨】本题考查了相似三角形的判定与性质、全等三角形的判定与性质、正方形的性质、矩形的判定与性质、等腰直角三角形的性质;熟练掌握正方形的性质,证明三角形全等和三角形相似是解决问题的关键.由正方形的性质得出90FAD ∠=︒,AD AF EF ==,证出CAD AFG ∠=∠,由AAS 证明FGA ACD ∆≅∆,得出AC FG =,①正确;证明四边形CBFG 是矩形,得出1122FAB CBFG S FB FG S ∆=⋅=四边形,②正确; 由等腰直角三角形的性质和矩形的性质得出45ABC ABF ∠=∠=︒,③正确; 证出ACD FEQ ∆∆∽,得出对应边成比例,得出2AD FE AD FQ AC ==,④正确. 【详细解答】解:四边形ADEF 为正方形,90FAD ∴∠=︒,AD AF EF ==,90CAD FAG∴∠+∠=︒,FG CA⊥,90GAF AFG∴∠+∠=︒,CAD AFG∴∠=∠,在FGA∆和ACD∆中,G CAFG CADAF AD∠=∠⎧⎪∠=∠⎨⎪=⎩,()FGA ACD AAS∴∆≅∆,AC FG∴=,①正确;BC AC=,FG BC∴=,90ACB∠=︒,FG CA⊥,//FG BC∴,∴四边形CBFG是矩形,90CBF∴∠=︒,1122FAB CBFGS FB FG S∆=⋅=四边形,②正确;CA CB=,90C CBF∠=∠=︒,45ABC ABF∴∠=∠=︒,③正确;FQE DQB ADC∠=∠=∠,90E C∠=∠=︒,ACD FEQ∴∆∆∽,::AC AD FE FQ∴=,2AD FE AD FQ AC∴==,④正确;或:2AD表示正方形的面积;连接AQ,FQ AC FQ AB FQ GF AFQ⨯=⨯=⨯=∆面积的2倍(FQ为底,GF为高)AFQ=∆面积的2倍(AF为底,AD为高)=正方形的面积,所以结论4是对的故选:D.5.(2017)(3分)如图,正方形ABCD 的边长是3,BP CQ =,连接AQ ,DP 交于点O ,并分别与边CD ,BC 交于点F ,E ,连接AE ,下列结论:①AQ DP ⊥;②2OA OE OP =;③AOD OECF S S ∆=四边形;④当1BP =时,13tan 16OAE ∠=,其中正确结论的个数是( )A .1B .2C .3D .4【思路点拨】本题考查了相似三角形的判定和性质,全等三角形的判定和性质,正方形的性质,三角函数的定义,熟练掌握全等三角形的判定和性质是解题的关键.由四边形ABCD 是正方形,得到AD BC =,90DAB ABC ∠=∠=︒,根据全等三角形的性质得到P Q ∠=∠,根据余角的性质得到AQ DP ⊥;故①正确;根据相似三角形的性质得到2AO OD OP =,由OD OE ≠,得到2OA OE OP ≠;故②错误;根据全等三角形的性质得到CF BE =,DF CE =,于是得到ADF DFO DCE DOF S S S S ∆∆∆∆-=-,即AOD OECF S S ∆=四边形;故③正确;根据相似三角形的性质得到34BE =,求得134QE =,135QO =,3920OE =,由三角函数的定义即可得到结论. 【详细解答】解:四边形ABCD 是正方形,AD BC ∴=,90DAB ABC ∠=∠=︒,BP CQ =, AP BQ ∴=,在DAP ∆与ABQ ∆中,AD AB DAP ABQ AP BQ =⎧⎪∠=∠⎨⎪=⎩,DAP ABQ ∴∆≅∆,P Q ∴∠=∠, 90Q QAB ∠+∠=︒, 90P QAB ∴∠+∠=︒, 90AOP ∴∠=︒,AQ DP ∴⊥;故①正确;90DOA AOP ∠=∠=︒,90ADO P ADO DAO ∠+∠=∠+∠=︒, DAO P ∴∠=∠, DAO APO ∴∆∆∽,∴AO OPOD OA=, 2AO OD OP ∴=,AE AB >, AE AD ∴>,OD OE ∴≠,2OA OE OP ∴≠;故②错误; 在CQF ∆与BPE ∆中FCQ EBP Q P CQ BP ∠=∠⎧⎪∠=∠⎨⎪=⎩,CQF BPE ∴∆≅∆, CF BE ∴=, DF CE ∴=,在ADF ∆与DCE ∆中,AD CD ADC DCE DF CE =⎧⎪∠=∠⎨⎪=⎩,ADF DCE ∴∆≅∆,ADF DFO DCE DOF S S S S ∆∆∆∆∴-=-,即AOD OECF S S ∆=四边形;故③正确;1BP =,3AB =, 4AP ∴=, PBE PAD ∆∆∽,∴43PB PA EB DA ==, 34BE ∴=,134QE ∴=,QOE PAD ∆∆∽, ∴1345QO OE QE PA AD PD ===, 135QO ∴=,3920OE =, 1255AO QO ∴=-=, 13tan 16OE OAE OA ∴∠==,故④正确, 故选:C .6(2018)(3分)如图,A 、B 是函数12y x=上两点,P 为一动点,作//PB y 轴,//PA x 轴,下列说法正确的是( )①AOP BOP ∆≅∆;②AOP BOP S S ∆∆=;③若OA OB =,则OP 平分AOB ∠;④若4BOP S ∆=,则16ABP S ∆=A .①③B .②③C .②④D .③④【思路点拨】此题是反比例函数综合题,主要考查了反比例函数的性质,三角形面积公式,角平分线定理逆定理,矩形的判定和性质,正确作出辅助线是解本题的关键.由点P 是动点,进而判断出①错误,设出点P 的坐标,进而得出AP ,BP ,利用三角形面积公式计算即可判断出②正确,利用角平分线定理的逆定理判断出③正确,先求出矩形4OMPN =,进而得出4mn =,最后用三角形的面积公式即可得出结论. 【详细解答】解:点P 是动点,BP ∴与AP 不一定相等,BOP ∴∆与AOP ∆不一定全等,故①不正确;设(,)P m n ,//BP y ∴轴, 12(,)B m m∴, 12||BP n m∴=-, 1121|||12|22BOP S n m mn m ∆∴=-⨯=- //PA x 轴,12(A n ∴,)n ,12||AP m n∴=-, 1121|||12|22AOP S m n mn n ∆∴=-⨯=-, AOP BOP S S ∆∆∴=,故②正确;如图,过点P 作PF OA ⊥于F ,PE OB ⊥于E ,12AOP S OA PF ∆∴=⨯,12BOP S OB PE ∆=⨯,AOP BOP S S ∆∆=,OB PE OA PF ∴⨯=⨯, OA OB =,PE PF ∴=,PE OB ⊥,PF OA ⊥,OP ∴是AOB ∠的平分线,故③正确;如图1,延长BP 交x 轴于N ,延长AP 交y 轴于M ,AM y ∴⊥轴,BN x ⊥轴,∴四边形OMPN 是矩形,点A ,B 在双曲线12y x=上, 6AMO BNO S S ∆∆∴==,4BOP S ∆=,2PMO PNO S S ∆∆∴==, 4OMPN S ∴=矩形,4mn ∴=,4m n∴=, 12|||3|2||BP n n n n m∴=-=-=,128||||AP m n n =-=, 1182||822||APB S AP BP n n ∆∴=⨯=⨯⨯=,故④错误; ∴正确的有②③,故选:B .7.(2019•深圳)已知菱形ABCD ,E 、F 是动点,边长为4,BE =AF ,∠BAD =120°,则下列结论正确的有几个( )①△BEC ≌△AFC ;②△ECF 为等边三角形;③∠AGE =∠AFC ;④若AF =1,则=.A .1B .2C .3D .4【思路点拨】本题考查了菱形的性质,熟练运用菱形的性质、等边三角形性质以及全等三角形的判定与性质是解题的关键.①△REC≌△AFC(SAS),正确;②由△BEC≌△AFC,得CE=CF,∠BCE=∠ACF,由∠BCE+∠ECA=∠BCA =60°,得∠ACF+∠ECA=60,所以△CEF是等边三角形,正确;③因为∠AGE =∠CAF+∠AFG=60°+∠AFG,∠AFC=∠CFG+∠AFG=60°+∠AFG,所以∠AGE =∠AFC,故③正确;④过点E作EM∥BC交AC下点M点,易证△AEM是等边三角形,则EM=AE=3,由AF∥EM,则==.故④正确,【详细解答】解:①△REC≌△AFC(SAS),正确;②∵△BEC≌△AFC,∴CE=CF,∠BCE=∠ACF,∵∠BCE+∠ECA=∠BCA=60°,∴∠ACF+∠ECA=60,∴△CEF是等边三角形,故②正确;③∵∠AGE=∠CAF+∠AFG=60°+∠AFG;∠AFC=∠CFG+∠AFG=60°+∠AFG,∴∠AGE=∠AFC,故③正确正确;④过点E作EM∥BC交AC下点M点,易证△AEM是等边三角形,则EM=AE=3,∵AF∥EM,∴则==.故④正确,故①②③④都正确.故选:D.。
2002-2019深圳中考数学试题分类汇编 24选择题压轴题--函数+几何多选题 学生版
近十五年深圳数学中考题分类汇编函数+几何多选题1.(2014)(3分)二次函数2y ax bx c =++图象如图,下列正确的个数为( ) ①0bc >;②230a c -<;③20a b +>;④20ax bx c ++=有两个解1x ,2x ,当12x x >时,10x >,20x <; ⑤0a b c ++>;⑥当1x >时,y 随x 增大而减小.A .2B .3C .4D .52.(2015)(3分)二次函数2(0)y ax bx c a =++≠的图象如图所示,下列说法正确的个数是( )①0a >;②0b >;③0c <;④240b ac ->.A .1B .2C .3D .43.(2015)(3分)如图,已知正方形ABCD的边长为12,BE EC=,将正方形边CD沿DE折叠到DF,延长EF交AB于G,连接DG,现在有如下4个结论:①ADG FDG∆≅∆;②2GB AG=;③GDE BEF∆∆∽;④725BEFS∆=.在以上4个结论中,正确的有()A.1 B.2 C.3 D.44.(2016)如图,CB CA =,90ACB ∠=︒,点D 在边BC 上(与B 、C 不重合),四边形ADEF 为正方形,过点F 作FG CA ⊥,交CA 的延长线于点G ,连接FB ,交DE 于点Q ,给出以下结论:①AC FG =;②:1:2FAB CBFG S S ∆=四边形;③ABC ABF ∠=∠;④2AD FQ AC =, 其中正确的结论的个数是( )A .1B .2C .3D .45.(2017)(3分)如图,正方形ABCD 的边长是3,BP CQ =,连接AQ ,DP 交于点O ,并分别与边CD ,BC 交于点F ,E ,连接AE ,下列结论:①AQ DP ⊥;②2OA OE OP =;③AOD OECF S S ∆=四边形;④当1BP =时,13tan 16OAE ∠=,其中正确结论的个数是( )A .1B .2C .3D .46(2018)(3分)如图,A 、B 是函数12y x=上两点,P 为一动点,作//PB y 轴,//PA x 轴,下列说法正确的是( ) ①AOP BOP ∆≅∆;②AOP BOP S S ∆∆=;③若OA OB =,则OP 平分AOB ∠;④若4BOP S ∆=,则16ABP S ∆=A .①③B .②③C .②④D .③④7.(2019•深圳)已知菱形ABCD,E、F是动点,边长为4,BE=AF,∠BAD=120°,则下列结论正确的有几个()①△BEC≌△AFC;②△ECF为等边三角形;③∠AGE=∠AFC;④若AF=1,则=.A.1 B.2 C.3 D.4。
中考数学复习压轴题常规单动点问题解析

例1:.(广东省深圳市)已知二次函数y =ax 2+bx +3的图象分别与x 轴交于点A (3,0),C (-1,0),与y 轴交于点B .点D 为二次函数图象的顶点.(1)如图①所示,求此二次函数的关系式:(2)如图②所示,在x 轴上取一动点P (m ,0),且1<m <3,过点P 作x 轴的垂线分别交二次函数图象、线段AD ,AB 于点Q 、F ,E ,求证:EF =EP ;(3)在图①中,若R 为y 轴上的一个动点,连接AR ,则√1010BR +AR 的最小值______(直接写出结果).【答案】(1)y=-x 2+2x+3;(2)见解析;(3)6√105 【解析】解:(1)将A (3,0),C (-1,0)代入y=ax2+bx+3,得:{9a +3b +3=0a −b +3=0,解得:{a =−1b =2 , ∴此二次函数的关系式为y=-x 2+2x+3.(2)证明:∵y=-x 2+2x+3=-(x-1)2+4,∴点D 的坐标为(1,4). 设线段AB 所在直线的函数关系式为y=kx+c (k≠0),将A (3,0),C (0,3)代入y=kx+c ,得:{3k +c =0c =3 ,解得:{k =−1c =3, ∴线段AB 所在直线的函数关系式为y=-x+3.同理,可得出:线段AD 所在直线的函数关系式为y=-2x+6.∵点P 的坐标为(m ,0), ∴点E 的坐标为(m ,-m+3),点F 的坐标为(m ,-2m+6), ∴EP=-m+3,EF=-m+3,∴EF=EP .(3)如图③,连接BC ,过点R 作RQ ⊥BC ,垂足为Q .∵OC=1,OB=3,∴BC=√10.(勾股定理)∵∠CBO=∠CBO ,∠BOC=∠BQR=90°,∴△BQR ∽△AOB ,∴BR BC =QR OC ,即√10=QR 1, ∴RQ=√1010BR ,∴AR+√1010BR=AR+RQ , ∴当A ,R ,Q 共线且垂直AB 时,即AR+√1010BR=AQ 时,其值最小.∵∠ACQ=∠BCO ,∠BOC=∠AQC ,∴△CQA ∽△COB ,∴AQ BO =AC BC ,即AQ 3=√10 ∴AQ=6√105, ∴√1010BR+CR 的最小值为6√105. 故答案为:6√105. 例2:(2019年广西)如图,抛物线y =x 2-2x -3与x 轴交于A ,B 两点,与y 轴交于点C ,其对称轴与抛物线相交于点M ,与x 轴相交于点N ,点P 是线段MN 上的一个动点,连接CP ,过点P 作PE ⊥CP 交x 轴于点E .(1)求抛物线的顶点M 的坐标;(2)当点E 与原点O 的重合时,求点P 的坐标;(3)求动点E 到抛物线对称轴的最大距离是多少?【答案】(1)(1,-4).(2)当点E与原点O的重合时,点P的坐标为(1,−3−√52)或(1,√5−32).(3)点E到抛物线对称轴的最大距离是4.【解析】解:(1)∵y=x2-2x-3=(x-1)2-4,∴抛物线的顶点M的坐标为(1,-4).(2)当x=0时,y=x2-2x-3=-3,∴点C的坐标为(0,-3).过点C作CF⊥直线MN,垂足为点F,如图1所示.∵∠PON+∠OPN=90°,∠OPN+∠CPF=180°-∠CPO=90°,∴∠PON=∠CPF.又∵∠PNO=∠CFP=90°,∴△PON∽△CPF,∴CFPN =PFON,即1PN=3−PN1,∴PN=3±√52, ∴当点E 与原点O 的重合时,点P 的坐标为(1,−3−√52)或(1,√5−32). (3)过点C 作CF ⊥直线MN ,垂足为点F ,设PN=m ,分三种情况考虑,如图2所示.①当0<m <3时,由(2)可知:△PEN ∽△CPF ,∴EN PF =PN CF ,即EN 3−m =m ,∴EN=-m2+3m=-(m-32)2+94.∵-1<0,∴当m=32时,EN 取得最大值,最大值为94; ②当m=0或3时,点E 和点N 重合,此时EN=0;③当3<m≤4时,∵∠PCF+∠CPF=90°,∠CPF+∠EPN=90°,∴∠PCF=∠EPN .又∵∠CFP=∠PNE=90°,∴△PCF ∽△EPN ,∴EN PF =PN CF ,即EN m−3=m 1, ∴EN=m2-3m .∵1>0,∴当3<m≤4时,EN 的值随m 值的增大而增大,∴当m=4时,EN 取得最大值,最大值为4.综上所述:点E 到抛物线对称轴的最大距离是4.。
2010年中考数学压轴题100题精选(71-80题)含答案

合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网2010年中考数学压轴题100题精选(71-80题)【071】已知:抛物线()20y ax bx c a =++≠的对称轴为1x =-,与x 轴交于A B ,两点,与y 轴交于点C ,其中()30A -,、()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得PBC △的周长最小.请求出点P 的坐标. (3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE PC ∥交x 轴于点E .连接PD 、PE .设CD 的长为m ,PDE △的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.(第24题图)合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网【072】如图1所示,直角梯形OABC 的顶点A 、C 分别在y 轴正半轴与x 轴负半轴上.过点B 、C 作直线l .将直线l 平移,平移后的直线l 与x 轴交于点D ,与y 轴交于点E .(1)将直线l 向右平移,设平移距离CD 为t (t ≥0),直角梯形OABC 被直线l 扫过的面积(图中阴影部份)为s ,s 关于t 的函数图象如图2所示, OM 为线段,MN 为抛物线的一部分,NQ 为射线,N 点横坐标为4.①求梯形上底AB 的长及直角梯形OABC 的面积; ②当42<<t 时,求S 关于t 的函数解析式;(2)在第(1)题的条件下,当直线l 向左或向右平移时(包括l 与直线BC 重合),在直线..AB ..上是否存在点P ,使PD E ∆为等腰直角三角形?若存在,请直接写出所有满足条件的点P 的坐标;若不存在,请说明理由.【073】)如图,半径为O 内有互相垂直的两条弦AB 、CD 相交于P 点.合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网(1)求证:PA ·PB =PC ·PD ;(2)设BC 的中点为F ,连结FP 并延长交AD 于E ,求证:EF ⊥AD : (3)若AB =8,CD =6,求OP 的长.【074】如图,在平面直角坐标系中,点1O 的坐标为(40) ,,以点1O 为圆心,8为半径的圆与x 轴交于A B ,两点,过A 作直线l 与x 轴负方向相交成60°的角,且交y 轴于C 点,以点2(135)O ,为第23题图合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网圆心的圆与x 轴相切于点D . (1)求直线l 的解析式;(2)将2O ⊙以每秒1个单位的速度沿x 轴向左平移,当2O ⊙第一次与1O ⊙外切时,求2O ⊙平移的时间.【075】如图11,已知抛物线b ax ax y --=22(0>a )与x 轴的一个交点为(10)B -,,与y 轴的负半轴交于点C ,顶点为D .(1)直接写出抛物线的对称轴,及抛物线与x 轴的另一个交点A 的坐标; (2)以AD 为直径的圆经过点C . ①求抛物线的解析式;合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网②点E 在抛物线的对称轴上,点F 在抛物线上,且以E F A B ,,,四点为顶点的四边形为平行四边形,求点F 的坐标.【076】如图,抛物线n mx x y ++=221与x 轴交于A 、B 两点,与y 轴交于C 点,四边形OBHC 为矩形,CH 的延长线交抛物线于点D (5,2),连结BC 、AD . (1)求C 点的坐标及抛物线的解析式;(2)将△BCH 绕点B 按顺时针旋转90°后 再沿x 轴对折得到△BEF (点C 与点E 对应),判断点E 是否落在抛物线上,并说明理由;(3)设过点E 的直线交AB 边于点P ,交CD 边于点Q . 问是否存在点P ,使直线PQ 分梯形ABCD的面积为1∶3两部分?若存在,求出P 点坐标;若不存在,请说明理由.图11合并自: (奥数)、 (中考)、 (高考)、 (作文)、 (英语)、 (幼教)、 、 等站 E 度教育网【077】已知直线m x y +-=43与x 轴y 轴分别交于点A 和点B ,点B 的坐标为(0,6) (1)求的m 值和点A 的坐标;(2)在矩形OACB 中,点P 是线段BC 上的一动点,直线PD ⊥AB 于点D ,与x 轴交于点E ,设BP=a ,梯形PEAC 的面积为s 。
初中数学中考压轴题及答案详解(广东篇)

专题训练122. 如图,抛物线923212--=x x y 与x 轴交于A 、B 两点,与y 轴交于点C ,连接BC 、AC 。
(1)求AB 和OC 的长;(2)点E 从点A 出发,沿x 轴向点B 运动(点E 与点A 、B 不重合)。
过点E 作直线l 平行BC ,交AC 于点D 。
设AE 的长为m ,△ADE 的面积为s ,求s 关于m 的函数关系式,并写出自变量m 的取值范围; (3)在(2)的条件下,连接CE ,求△CDE 面积的最大值;此时,求出以点E 为圆心,与BC 相切的圆的面积(结果保留π)。
参考答案: 解:(1)令y=0,即0923212=--x x , 整理得 01832=--x x , 解得:31-=x ,62=x , ∴ A (—3,0),B (6,0) 令x = 0,得y = —9, ∴ 点C (0,—9)∴ 9)3(6=--=AB ,99=-=OC , (2)281992121=⨯⨯=⋅=∆OC AB S ABC, ∵ l ∥BC ,∴ △ADE ∽△ACB , ∴22ABAE S S ABC=∆,即229281m S = ∴ 221m S =,其中90<<m 。
(3)88129212192122+⎪⎭⎫ ⎝⎛--=-⨯⨯=-=∆∆∆m m m S S S ADEACE CDE , ∵ 021<-∴ 当29=m 时,S △CDE 取得最大值,且最大值是881。
这时点E (23,0),yA OB xElCD题22图∴29236=-=-=OE OB BE ,133962222=+=+=OC OB BC , 作EF ⊥BC ,垂足为F ,∵∠EBF=∠CBO ,∠EFB=∠COB , ∴△EFB ∽△COB ,∴CB BEOC EF =,即133299=EF ∴132627=EF , ∴ ⊙E 的面积为:πππ5272913262722=⎪⎭⎫⎝⎛⨯=⋅=EF S 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
代数几何综合201222/201123201022/200922/200822200722/200621/(压轴)2323232322
解析
压轴、
200621.如图9,抛物线y ax2 8ax 12a(a 0)与x轴交于A、B两点(点A在点B的左侧),
抛物线上另有一点C在第一象限,满足/
(1)(3分)求线段OC的长• 解:
(2)(3分)求该抛物线的函数关系式. 解:
(3)(4分)在x轴上是否存在点P,使△ BCP为等腰三角形若存在,求出所有符合条件的P点的坐标;若不存在,请说明理由•
解:
200622. (10分)如图10-1,在平面直角坐标系xoy中,点M在x轴的正半轴上,O M交x轴于A、B两点,交y轴于C、D两点,且C为A E的中点,AE交y轴于G点,若点A的坐标为(—2,0),AE 8
(1)(3分)求点C的坐标. 解:
(2)(3 分)连结MG、BC,求证:MG // BC 证明:
(3)(4分)如图10-2,过点D作O M的切线,交x轴于点P.动点F在O M的圆周上运动时, 的比值是否发生变化,若不变,求出比值;若变化,说明变化规律
解:
OF
PF
E
C
G
P O M
宾
图10 —
2
x
② J _
_ 2 1 (迈 1)(.2
1)
1
(辽
1)
辽1 ;®
V3 V5
5 、. 3
节等运算都是分
200722.如图6,在平面直角坐标系中,正方形 AOCB 的边长为1,点D 在x 轴的正半轴上, 且OD OB ,BD 交OC 于点E . (1) 求/ BEC 的度数. (2) 求点E 的坐标.
(3) 求过B , O , D 三点的抛物线的解析式.(计算结果要求分母有理化.参考资料:把分 母中的根号化去,叫分母有理化.例如:①-4=
75 2 5 2.5 ; 、5g.5 ~5- ?
(.■5 .3)(一
)
1 21
200723.如图7,在平面直角坐标系中,抛物线y x 6与直线y x相交于A, B两点.
4 2
(1)求线段AB的长.
(2)若一个扇形的周长等于(1)中线段AB的长,当扇形的半径取何值时,扇形的面积最大,最大面积是多少
(3)如图8,线段AB的垂直平分线分别交x轴、y轴于C,D两点,垂足为点M,分别求
111
出OM , OC, OD的长,并验证等式一2飞是否成立.
OC OD OM
(4) 如图9,在Rt A ABC 中, Z ACB 90o,CD AB,垂足为D,设BC a , AC b , Array
图8图9
200822.如图9,在平面直角坐标系中,二次函数y ax2bx c(a 0)的图象的顶点为D点,
与y轴交于C点,与x轴交于A、B两点,A点在原点的左侧,B点的坐标为(3, 0),
1
0B= OC , tan / ACO 丄•
3
(1)求这个二次函数的表达式.
(2)经过C、D两点的直线,与x轴交于点E,在该抛物线上是否存在这样的点F,使以点A、C、E、F为顶点的四边形为平行四边形若存在,请求出点F的坐标;若不存在,请说明理由.
(3)若平行于x轴的直线与该抛物线交于M、N两点,且以MN为直径的圆与x轴相切,求该圆半径的长度.
(4)如图10,若点G (2, y)是该抛物线上一点,点P是直线AG下方的抛物线上一动点,当点P运动到什么位置时,△ APG的面积最大求出此时P点的坐标和△ APG的最大面积.
200922.如图,在直角坐标系中,点A的坐标为(一2, 0),连结0A,将线段0A绕原点0 顺时针旋转120°,得到线段0B
(1)求点B的坐标;
(2)求经过A、0、B三点的抛物线的解析式;
(3)在(2)中抛物线的对称轴上是否存在点。
,使厶BOC的周长最小若存在,求出点C的坐标;若不存在,请说明理由•
200923.如图,在平面直角坐标系中,直线I: y= —2x—8分别与x轴,y轴相交于A, B两点, 点P (0,k)是y轴的负半轴上的一个动点,以P为圆心,3为半径作。
P.
(1)连结PA,若PA=PB,试判断O P与x轴的位置关系,并说明理由;
(2)当k为何值时,以。
P与直线I的两个交点和圆心P为顶点的三角形是正三角形
Ar
201022.(本题9分)如图9,抛物线y = ax2+ c (a>0)经过梯形ABCD的四个顶点,梯形的底AD 在x轴上,其中A (-2,0), B (- 1, —3).
(1)求抛物线的解析式;( 3 分)
(2)点M为y轴上任意一点,当点M到A、B两点的距离之和为最小时,求此时点M的坐
标;( 2 分)
(3)在第(2)问的结论下,抛物线上的点P使&PAD=4S M BM成立,求点P的坐标.(4分)
201023.(本题9分)如图10,以点M (—1,0)为圆心的圆与y轴、x轴分别交于点A、
^{35\/3
C、D,直线y=—亍x—寸与。
M相切于点H,交x轴于点E,交y轴于点F.
(1) 请直接写出OE、。
M的半径r、CH的长;(3分)
(2) 如图11,弦HQ交x轴于点P,且DRPH= 3:2, 求cos/ QHC的值;(3分)
(3) 如图12,点K为线段EC上一动点(不与E、C重合),连接BK交。
M于点T,弦AT
交x 轴于点N •是否存在一个常数a ,始终满足MN • MK = a ,如果存在,请求出a 的值;如 果不
存在,请说明理由•( 3分)
201123.如图13,抛物线 尸ax 2 + bx + c (a ^0)的顶点为C (1, 4),交x 轴于A 、B 两点, 交y 轴
于点D ,其中点B 的坐标为(3, 0)。
(1) 求抛物线的解析式;
(2) 如图14,过点A 的直线与抛物线交于点E ,交y 轴于点F ,其中点E 的横坐标为2,若 直线PQ
为抛物线的对称轴,点 G 为直线PQ 上的一动点,则x 轴上师范存在一点H ,使D 、 G 、H 、F 四
点所围成的四边形周长最小。
若存在,求出这个最小值及点 G 、H 的坐标;若不 存在,请说明理
由。
(3) 如图15,在抛物线上是否存在一点 T ,过点T 作x 轴的垂线,垂足为点M ,过点M 作 B
C M E A
H F O ;Dx
B C O E A H
F P M
图10
MN // BD,交线段AD 于点N ,连接MD ,使△ DNM s^ BMD 。
若存在,求出点 T 的坐标;若 不存在,请说明理由。
201222.如图8,已知△ ABC 的三个顶点坐标分别为 A( 4, 0),B(1, 0), C( 2, 6)
(1) 求经过A 、B 、C 三点抛物线的解析式
(2) 设直线BC 交y 轴于点E,连接AE,求证:AE=CE
(3) 设抛物线与y 轴交于点D ,连接AD 交BC 于点F ,试问以A 、B 、F 为顶点的三角形与△ ABC 相似吗请说明理由。
y f
图14
201223.如图9—①,平在面直角从标系中,直线l : y 2x b(b > 0)的位置随b的不同取值而变化。
(1)已知。
M的圆心坐标为(4, 2),半径为2
当b ________________ 时,直线l : y 2x b(b > 0)经过圆心M ;
当b ________________ 时,直线l : y 2x b(b > 0)与O M相切;
(2)若把O M换成矩形ABCD,如图9—②,其三个顶点的坐标分别为:A(2,0),B(6,0),C(6,2) <
设直线丨扫过矩形ABCD的面积为S,当b由小到大变化时,请求出S与b的函数关系式。
