正方体的十一种平面展开图
正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种(那些经旋转或翻转后方向不同但实质相同的图形不重复计算),具体来讲分以下4类。
口诀:需背诵
正方体:中间四个面,上下各一面(6种摆法-141)
中间三个面,一二隔河见(3种摆法-132/231)
中间二个面,楼梯天天见(1种摆法-222)
中间没有面,三三连一线(1种摆法-33)
“田”“凹”应弃之
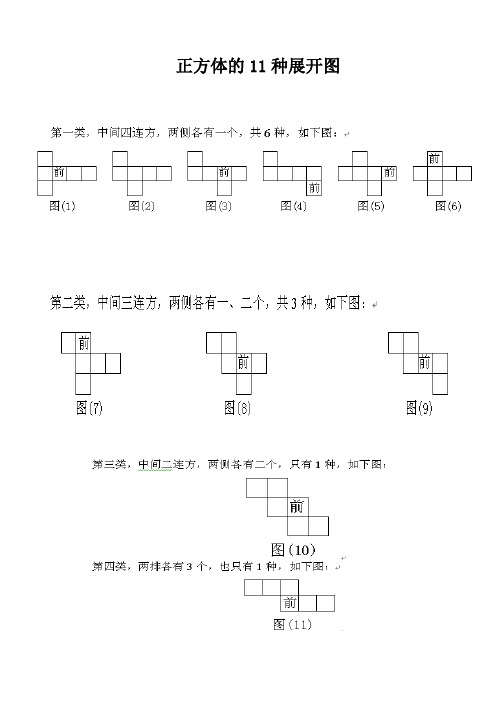
第一类:“1—4—1”型,其特点是有4个连成一排的正方形,两侧又各有1个正方形,共有6种。
口诀:中间四个面,上下各一面(上下面随便放)
第二类:“1—3—2”型,其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形,另一侧有2个正方形(其中只有1个与中间那一排相连),共有3种。
口诀:中间三个面,一二隔河见(二三位置是固定的)
第三类:“2—2—2”型,其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方形,只有1种。
口诀:中间二个面,楼梯天天见
第四类:“3—3”型,其特点是有3个连成一排的正方形,其一侧还有3个连成一排的正方形,只有1种。
中间没有面,三三连一线(1种摆法-33)。
正方体11种展开图

图9
第三类 (1种):中间二连方,两侧各有二个。
图 10
“二二二”型
第四类
(1种):两排各有三个。
“三三”型
图 11
展开1 第一类(6种):中间四连方,两侧各有一个。
展开2 第一类(6种):中间四连方,两侧各有一个。
展开3 第一类(6种):中间四连方,两侧各有一个。
展开4 第一类(6种):中间四连方,两侧各有一个。
展开5 第一类(6种):中间四连方,两侧各有一个。
展开6 第一类(6种):中间四连方,两侧各有一个。
展开7
第二类(3种):中间三连方,两侧各有一、二个。
展开8
第二类(3种):中间三连方,两侧各有一、二个。
展开9
第二类(3种):中间三连方,两侧各有一、二个。
展开10
第三类(1种):中间二连方,两侧各有二个。
正方体11种展开图
• 1、在正方体的相对的面上标上 相同的数字
• 2、在展开的过程中注意你剪开 了几条棱?
正方体展开图 共有11种,分为四类: 第一类 (6种):中间四连方,两侧各有一个。 “一四一”型
图1
图2
图3
图4
图5
图6
第二类 (3种):中间三连方,两侧各有二、一个。 “二三一”型
图7
图8
展开11
第四类(1种):两排各有三个。
判断下列图形能不能折成正方体?
(1)
(2)
(3)
(4)Leabharlann (5)(6)(7)
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
(16)
(17)
(18)
正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种(那些经旋转或翻转后方向不同但实质相同的图形不重复计算),具体来讲分以下4类。
口诀:需背诵
正方体:中间四个面,上下各一面(6种摆法-141)
中间三个面,一二隔河见(3种摆法-132/231)
中间二个面,楼梯天天见(1种摆法-222)
中间没有面,三三连一线(1种摆法-33)
“田”“凹”应弃之
第一类:“1—4—1”型,其特点是有4个连成一排的正方形,两侧又各有1个正方形,共有6种。
口诀:中间四个面,上下各一面(上下面随便放)
第二类:“1—3—2”型,其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形,另一侧有2个正方形(其中只有1个与中间那一排相连),共有3种。
口诀:中间三个面,一二隔河见(二三位置是固定的)
第三类:“2—2—2”型,其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方形,只有1种。
口诀:中间二个面,楼梯天天见
第四类:“3—3”型,其特点是有3个连成一排的正方形,其一侧还有3个连成一排的正方形,只有1种。
中间没有面,三三连一线(1种摆法-33)。
(完整版)正方体的11种展开图
正方体的11种展开图
判断技巧
我们知道,同一个立方体图形,按不同的方式展开得到的平面展开图形一般是不一样的。
常见的正方体平面展开图究竟有几种不同的形状呢?
同学们一定熟悉这样一种操作:把一个正方形纸片平均分成9个小正方形,剪去角上四个小正方形,可以拼成一个无盖的正方体纸盒,其中五个面按习惯不妨记为下、左、右、前、后,如图一。
好啦!现在只要把刚才剪去的一个小正方形作为“上”面,就可拼成一个正方体。
作为正方体平面展开图,这个“上”应该和图1(1)中哪个面拼接在一起呢?观察图1(2),知“上”和前、后、左、右任一个面拼接都行(这四种拼接看作同一种情形),不妨和“后”拼接在一起,如图2。
根据上和下、左和右、前和后相间隔这一规律,现在我们把图2中的“左”或“右”平移,可得图3~图7五种情形。
平移图2中的“前”,可得图8;再平移图8中的“左”,可得图9、图10;把图10中的“上”向左平移,得图11;若移动图8(或图9、图10)中的“左”,又可得图12。
同学们,当你和我一样,把图2~图12这11个图剪下来,动手折一折,得到11个漂亮的小正方体时,你一定为我们的收获感到欢欣鼓舞吧!
对正方体表面展开图的11种情况,为加深记忆,可编成如下口诀:一四一呈6种,一三二有3种,二二二与三三各1种,展开图共有11种。
“动手实践,自主探索和合作交流”是新课程标准倡导学习数学的三种重要方法,而实践活动是培养我们进行主动探索与合作交流的重要途径。
只要通过自己主动观察、实验、猜想、验证等数学活动,就能使我们“建立空间观念,发展几何直觉”,提高思维能力。
正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种(那些经旋转或翻转后方向不同但实质相同的图形不重复计算),具体来讲分以下4类。
口诀:需背诵
正方体:中间四个面,上下各一面(6种摆法-141)
中间三个面,一二隔河见(3种摆法-132/231)
中间二个面,楼梯天天见(1种摆法-222)
中间没有面,三三连一线(1种摆法-33)
“田”“凹”应弃之
第一类:“1—4—1”型,其特点是有4个连成一排的正方形,两侧又各有1个正方形,共有6种。
口诀:中间四个面,上下各一面(上下面随便放)
第二类:“1—3—2”型,其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形,另一侧有2个正方形(其中只有1个与中间那一排相连),共有3种。
口诀:中间三个面,一二隔河见(二三位置是固定的)
第三类:“2—2—2”型,其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方形,只有1种。
口诀:中间二个面,楼梯天天见
第四类:“3—3”型,其特点是有3个连成一排的正方形,其一侧还有3个连成一排的正方形,只有1种。
中间没有面,三三连一线(1种摆法-33)。
正方体11种平面展开图(精心整理)

正方体的11种平面展开图
正方体的平面展开图共有11种(经旋转或翻转后方向不同但实质相同的图形不重复计算),具体来讲分以下4类:
口诀:需背诵
正方体:中间四个面,上下各一面(6种摆法-141)
中间三个面,一二隔河见(3种摆法-132/231)
中间二个面,楼梯天天见(1种摆法-222)
中间没有面,三三连一线(1种摆法-33)
“田”“凹”应弃之
第一类:“1—4—1”型,其特点是有4个连成一排的正方形,两侧又各有1个正方形,共有6种。
口诀:中间四个面,上下各一面(上下面随便放)
第二类:“1—3—2”型,其特点是有3个连成一排的正方形,这一排正方形的一侧有1个正方形,另一侧有2个正方形(其中只有1个与中间那一排相连),共有3种。
口诀:中间三个面,一二隔河见(二三位置是固定的)
第三类:“2—2—2”型,其特点是有2个连成一排的正方形,其两侧又各有2个连成一排的正方
形,只有1种。
口诀:中间二个面,楼梯天天见
第四类:“3—3”型,其特点是有3个连成一排的正方形,其一侧还有3个连成一排的正方形,只有1种。
中间没有面,三三连一线(1种摆法-33)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正方体的十一种平面展开图可记忆成下面口诀:
一三二,一四一,一在同层可任意,两个三,日状连,三个二,成阶梯,相邻必有日,整体没有田。
相对的两个面之间总隔着一个面
正方体:中间四个面,上下各一面(6种摆法-141)
中间三个面,一二隔河见(3种摆法-132/231)
中间二个面,楼梯天天见(1种摆法-222)
中间没有面,三三连一线(1种摆法-33)
例1 在图13中(每个小四边形皆为全等的正方形),可以是一个正方体表面展开图的是( ).
例2图14是一个正方体包装盒的表面展开图,若在其中的三个正方形A、B、C 内分别填上适当的数,使得这个表面展开图沿虚线折成正方体后,相对面上的两个数互为相反数,则填在A、B、C内的三个数依次是( ).
A.0,-2,1
B.0,1,-2
C.1,0,-2
D.-2,0,1
例3图15所示的是一个正方体包装盒的表面展开图,各个面上标注的数字分别为1,2,3,4,5,6。
现将表面展开图复原为正方体包装盒,则标注数字1和3的两个面是互相平行的,请你写出另一组相互平行的面上所对应的数字:
_______。
注:例1、例2、例3的答案分别为:C;A;2与5或4与6。
是不是有点多此一举?
例4 一个无盖的正方体纸盒,将它展开成平面图形,可能情况总共有()。
A.12种 B.11种 C.9种 D.8种
千万注意,你可不要选B呦!选D才对。
我又在炫耀了,不过你能很快画出这8个平面展开图吗?
下面是示意图,黑方块表示展开图,白方块表示空缺。
(一)
□■□
■■■
□■□
(二)
■■■■
■□□□
(三)
■■■■
□■□□
(四)
■■■■
□□■□
(五)
■■■■
□□□■
(六)
□■□
■■■
□□■
(七)
□□■
■■■□□■(八)■□□■■■□□■。
