实验三 用EXCEL进行指数分析
EXCEL实验报告

EXCEL实验报告实验一利用 Excel对数据进行描述统计分析 (2)实验二 Excel图表制作及编辑 (13)实验三 Excel区间估计 (24)实验四一元线性性回归模型 (26)实验五长期趋势分析 (29)实验六 Excel综合指数计算实验 (36)实验七方差分析 (39)实验一利用 Excel对数据进行描述统计分析一、实验目的1、掌握Excel的基本知识2、学会应用Excel创建表格,输入和编辑信息3、熟练运用excel的公式和函数求各种统计指标4、利用Excel的分析工具对数据进行描述性统计5、掌握组距式变量数列的编制原理6、用EXCEL进行数据抽样二、实验要求1、掌握Excel的基本操作方法2、通过练习,能够独立运用Excel进行数据整理和数据分析3、掌握利用Excel对数据进行分组编制的基本操作方法;4、掌握利用EXCEL对数据进行抽样的方法。
三、实验内容1、分别用函数和数据分析工具计算这31 个地区人口的总和、平均值、中位数、众数、标准差。
表1-1 2008年全国各地区人口统计地 区 总人口(万人) 地区 总人口(万人)北京1695 山东 9417天津1176 河南 9429河北6989 湖北 5711山西 3411 湖南 6380内蒙 2414 广东 9544辽宁 4315 广西 4816吉林 2734 海南 854黑龙江 3825 重庆 2839上海 1888 四川 8138江苏 7677 贵州 3793浙江 5120 云南 4543安徽 6135 西藏 287福建 3604 陕西 3762青海 554 宁夏 618新疆 2131 甘肃 2628江西 44002、根据抽样调查,某月X市50户居民购买消费品支出资料如下(单位:元):表1-2 某月X市50户居民购买消费品支出830 880 1230 1100 1180 1580 1210 1460 1170 10801050 1100 1070 1370 1200 1630 1250 1360 1270 14201180 1030 870 1150 1410 1170 1230 1260 1380 15101010 860 810 1130 1140 1190 1260 1350 930 14201080 1010 1050 1250 1160 1320 1380 1310 1270 1250 根据以上数据,以 900、1000、1100、1200、1300、1400、1500、1600为组限,对居民户月消费支出额编制组距式变量数列,并计算居民户月消费支出额的累计频数和频率。
excel指数计算公式

excel指数计算公式excel指数计算公式是计算数学中最常见的指数计算公式,也是excel中最常用的公式之一。
excel指数计算公式的使用方法比较灵活,可以用在许多不同类型的数据计算上。
下面,我们将介绍excel指数计算公式的基本概念,以及如何在excel中应用它的相关知识。
一、excel指数计算公式的基本概念excel指数计算公式是一种数学计算,它可以将一组数据中的指定列转换为指数形式。
所谓指数,即在一定变动范围内存在“指数定律”,也就是说,某一段时间内,响应的数字越大,其增长越快。
二、excel指数计算公式的使用在excel中,我们可以使用excel指数计算公式来表示和计算一组数据。
这种数据可以是月份下单数量,销售额,收入等等数据。
用这种计算公式,我们可以得出一组数据的指数形态,从而更容易观察、分析数据变化趋势。
三、使用excel指数计算公式的注意事项1.动范围太宽,可能不能正确反映变动趋势:当一组数据的变动范围过宽,比如数据的最大值比最小值大太多,则使用excel指数计算公式可能不能很好地反映出变动趋势。
2.据量不足,可能导致不准确:当一组数据的总量不够大,比如少于10个数据,则使用excel指数计算公式可能得到的结果不够准确。
3.议使用样本试验:当使用excel指数计算公式时,要记得先用一小部分数据做样本试验,以确保得到的计算结果是否准确无误。
四、总结excel指数计算公式是excel中最常用的一种数学计算公式,它可以将一组数据中的指定列转换为指数形式,并被广泛用于各种不同类型的数据计算中。
在使用excel指数计算公式时,要注意变动范围不能太宽,且要保证数据量足够大,最好还是要做样本试验,以确保计算结果的准确性。
统计学学习读书笔记_作文3000字_读书笔记_

统计学学习读书笔记学了统计学后,有何呢?下面是小编精心为您整理的统计学学习,希望您喜欢!统计学学习读书笔记一本学期我们学了统计学这门课程,通过一学期的学习我们对统计学应用领域及其类型和基本概念有了一个基本的了解,掌握了数据的收集、展示、分析的技术。
同时学校也安排了我们学期末统计分析实习,是希望通过这次实习提高我们动手操作的能力和把理论应用到实践中去的思想,也通过实习加深我们对课本上理论的认识和掌握。
这次实习中我们不仅复习巩固了统计学的理论知识,我们也收获了很多新知识,同时通过分组实习也锻炼了我们团结协作的能力,给我们的感触良多。
统计是处理数据的一门科学,统计学是收集、处理、分析、解释数据并从数据中得出结论的科学,统计方法是适用于所有学科领域的通用数据分析方法,只要有数据的地方就会用到统计方法。
随着社会经济和现代科学的发展,统计理论、方法和应用进入了一个全面发展阶段。
一方面,统计学受计算机科学、信息论、混沌理论、人工智能等现代科学技术的影响,新的研究领域层出不穷,如多元统计分析、现代时间序列分析、贝叶斯统计、非参数统计、线性统计模型、探索性数据分析、数据挖掘等。
另一方面,统计方法的应用领域不断扩展,几乎所有的科学研究都离不开统计方法。
应为不论是自然科学、工程技术、农学、医学、军事科学,还是社会科学都离不开数据,要对数据进行研究和分析就必然用到统计方法,现在连纯文科领域的法律、历史、语言、新闻等都越来越重视对统计数据的分析。
这次统计分析实习,我们组选择的公司是七匹狼。
在实习中我们运用数据的搜集、数据的图表展示等理论以及运用EXCEL软件对数据进行处理、分析、解释完成了本次实习的任务。
我们搜集七匹狼有关股票的数据信息有每股收益、每股净资产、净资产收益率、主营业务收入、净利润、利润率、每股公积金、每股未分配利润、每股现金流量等。
通过对这些数据的整理、分析和总结,我们可以了解七匹狼公司的业绩、经营状况、财务状况和预测未来的发扎趋势等相关信息。
实验三 电子表格软件Excel应用实验

实验三 电子表格软件Excel应用实验
土木工程10级13班20105959周述燚
一、实验目的
(1) 掌握Excel工作表和工作薄之间的区别;
(2) 掌握使用Excel制作数据表格的方法;
(3) 掌握Excel数据表格的计算、数据排序、数据筛选、分类汇总方法;
(4) 掌握Excel工作表中数据图表化的方法。
二、实验内容
实验内容:学生成绩电子表格处理
三、实验过程(结果见各工作表)
其实验过程及结果记录如下各工作表中内容:
四、实验分析总结
通过本次实验,我学到了:
1. 使用Office Excel创建各类数据表的方法;
2. Excel中数据的处理(公式计算、排序、筛选、汇总)的使用; 实验中得到的试验体会:
1. Excel比Word难;
2. Excel若学好了,很有用;
3. Excel功能有很多;
4. 老师的指导很有帮助,同学之间的相互学习也十分的重要;
法;;。
统计学四篇实验报告

《统计学》四篇实验报告实验一:用Excel构建指数分布、绘制指数分布图图1-2:指数分布在日常生活中极为常见,一般的电子产品寿命均服从指数分布。
在一些可靠性研究中指数分布显得尤为重要。
所以我们应该学会利用计算机分析指数分布、掌握EXPONDIST函数的应用技巧。
指数函数还有一个重要特征是无记忆性。
在此次实验中我们还学会了产生“填充数组原理”。
这对我们今后的工作学习中快捷地生成一组有规律的数组有很大的帮助。
实验二:用Excel计算置信区间一、实验目的及要求1、掌握总体均值的区间估计2、学习CONFIDENCE函数的应用技巧二、实验设备(环境)及要求1、实验软件:Excel 20072、实验数据:自选某市卫生监督部门对当地企业进行检查,随机抽取当地100家企业,平均得分95,已知当地卫生情况的标准差是30,置信水平0.5,试求当地企业得分的置信区间及置信上下限。
三、实验内容与步骤某市卫生监督部门对当地企业进行检查,随机抽取当地100家企业,平均得分95,已知当地卫生情况的标准差是30,置信水平0.5,试求当地企业得分的置信区间及置信上下限。
第1步:打开Excel2007新建一张新的Excel表;第2步:分别在A1、A2、A3、A4、A6、A7、A8输入“样本均值”“总体标准差”“样本容量”“显著性水平”“置信区间”“置信上限”“置信下限”;在B1、B2、B3、B4输入“90”“30”“100”“0.5”第3步:在B6单元格中输入“=CONFIDENCE(B4,B2,B3)”,然后按Enter键;第4步:在B7单元格中输入“=B1+B6”,然后按Enter键;第5步:同样在B8单元格中输入“=B1-B6”,然后按Enter键;计算结果如图2-1四、实验结果或数据处理图2-1:实验二:用Excel产生随机数见图3-1实验二:正态分布第1步:同均匀分布的第1步;第2步:在弹出“随机数发生器”对话框,首先在“分布”下拉列表框中选择“正态”选项,并设置“变量个数”数值为1,设置“随机数个数”数值为20,在“参数”选区中平均值、标准差分别设置数值为30和20,在“输出选项”选区中单击“输出区域”单选按钮,并设置为D2 单元格,单击“确定”按钮完成设置。
实验三 用EXCEL进行指数分析

实验三用EXCEL进行指数分析实验目的:用EXCEL进行指数分析实验步骤:指数分析法是研究社会经济现象数量变动情况的一种统计分析法。
指数有总指数与平均指数之分,在这一节我们介绍如何用Excel进行指数分析与因素分析。
一、用Excel计算总指数【例1】:图中是某企业甲、乙、丙三种产品的生产情况,以基期价格p作为同度量因素,计算生产量指数。
如图1图1用EXCEL计算总指数资料及结果计算步骤:第一步:计算各个p0q0:在G2中输入“=C2*D2”,并用鼠标拖曳将公式复制到G2:G4区域。
第二步:计算各个p0*q1:有H2中输入“=C2*F2”,并用鼠标拖曳将公式复制到H2:H4区域。
第三步:计算Σp0q0和Σp0q1:选定G2:G4区域,单击工具栏上的“Σ”按钮,在G5出现该列的求和值。
选定H2:H4区域,单击工具栏上的“Σ”按钮,在H5出现该列的求和值。
第四步:计算生产量综合指数Iq=Σp0q1/Σp0q0:在C6中输入“=H5/G5”便可得到生产量综合指数注意:在输入公式的时候,不要忘记等号,否则就不会出现数值。
二、用Excel计算平均指数现以生产量平均指数为例,说明加权算术平均法的计算方法。
【例2】:图中的A1:A4区域内是某企业生产情况的统计资料,我们要以基期总成本为同度量因素,计算生产量平均指数。
如图2图2用EXCEL计算平均指数资料及结果计算步骤:第一步:计算个体指数k=q1/q0:在F2中输入“=D2/C2”。
并用鼠标拖曳将公式复制到F2:F4区域。
第二步:计算k*p0q0并求和。
在G2中输入“=F2*E2”并用鼠标拖曳将公式复制到G2:G4区域。
选定G2:G4区域,单击工具栏上的:“Σ”按钮,在G5列出现该列的求和值。
第三步:计算生产量平均指数:在C7中输入“=G5/E5”即得到所求的值。
三、用Excel进行因素分析【例3】:我们还用上面的例子,有关资料如图3图3用EXCEL进行因素分析资料及结果进行因素分析的计算步骤如下:第一步:计算各个p0*q0和∑p0q0:在G2中输入“C2*D2”,并用鼠标拖曳将公式复制到G2:G4区域。
利用excel图表功能处理物理实验数据

利用excel 图表功能处理高中物理实验数据佛山市顺德区北滘中学 吴启程物理学科是一门以实验为基础的基础学科,在高中物理课程中,很多结论是在实验的基础上建立起来的。
而在实际的课堂教学过程中,由于受到学生能力和课堂上时间的限制,要让高中学生在课堂、课后通过手工计算和画图来从实验数据中归纳出实验结论是比较困难的,所以老师往往会直接给出最终的实验结论,甚至连实验探究的环节也被免掉了。
这也是很多学生素质并不是很高的镇一级学校在实际的教学过程中实验开出率较低的原因之一。
当然,在一些学生素质较高和设备条件较好的学校中,可以借助先进的传感器、数据采集器以及通过软件来实现物理测量和对实验数据进行处理,但是以上两个条件都具备的学校毕竟还是不多。
本文阐述在“研究自由落体运动”教学过程中,借助office 2007的excel 的强大的表格计算功能和插入图表的功能,在课堂上处理实验数据并得出图像,引导学生根据实验数据和图像得出实验结论,同时得出各物理量之间的定量关系。
这种方法也可以用在其它实验教学中。
一. 问题的提出在高中物理必修一模块中,“通过实验来探究自由落体运动的规律”这一教学环节是可以说是一个经典的教学内容。
在实际教学过程中,教材的处理方法是:先假设自由落体运动是一匀加速直线运动,然后通过推导得出位移公式和速度公式如下:221at s = at v =通过对自由落体运动的纸带上位移和对应的时间关系的测量和分析,算出物体的加速度,从而证明自由落体运动是匀加速直线运动。
这一方法对学生来说是非常抽象的,在实际教学过程中往往很多学生还是被动的记住了最后的结论,而对其中的过程和方法并没有得到很好的体验和认识,没有体会到实验探究的乐趣。
那么能不能有更好而且又较为简单的方法来使得学生能根据自己的实验数据,非常直观的得出自由落体运动的本质,同时得出位移公式、速度公式,并得出重力加速度的大小呢?于是,在教学过程中,我想到了最原始的方法,干脆让学生根据实验数据画出 h- t 图像,观察其变化规律,然后再画出h- t 2图像、v-t 图像,从而得出根据v-t 图像是一条直线得出结论:自由落体运动是匀加速直线运动。
利用Excel进行综合指数分析

利用Excel进行综合指数分析某企业3种商品销售情况有关资料如下表所示:产品名称计量单位产品销售量单位价格(元)基期q0报告期q1基期p0报告期p1A 套1000 1400 10 8B 件3000 2800 16 16C 个4000 4500 15 20要求:利用Excel计算综合指数。
具体操作步骤如下:(1)打开Excel表格,将3种产品的销售情况录入到新建的sheet1中。
如图8.1所示:图8.1 A、B、C3种产品销售情况表(2)计算每种产品销售额基期“p0q0”。
a.在单元格H3内先输入“=”,然后用鼠标选中单元格C3,紧接着输入“*”,再用鼠标选中单元格E3,之后单击“enter”键即得到A产品基期销售额结果。
如图8.2、图8.3所示:图8.2 A产品基期销售额计算过程表图8.3 A产品基期销售额计算结果表b.选中H3使用自动填充功能按住鼠标左键向下拖至单元格H5,松开鼠标,即可得到单元格H4和H5的数据。
如图8.4所示:图8.4 B产品和C产品基期销售额计算结果表c.单击单元格H6,菜单栏上选择“公式”选项,找到自动求和里的第一个选项“求和”并单击,再单击“enter”键即可得出所有产品基期的销售额合计数。
如图8.5、图8.6所示:图8.5 3种产品基期销售额求和计算过程表图8.6 3种产品基期销售额求和计算结果表(3)计算每种产品销售额报告期“p1q1”。
a.在单元格I3内先输入“=”,然后用鼠标选中单元格D3,紧接着输入“*”,再用鼠标选中单元格F3,之后单击“enter”键即得到A产品报告期销售额结果。
如图8.7、图8.8所示:图8.7 A产品报告期销售额计算过程表图8.8 A产品报告期销售额计算结果表b.选中I3使用自动填充功能按住鼠标左键向下拖至单元格I5,松开鼠标,即可得到单元格I4和I5的数据。
如图8.9所示:图8.9 B产品和C产品报告期销售额计算结果表c.单击单元格I6,菜单栏上选择“公式”选项,找到自动求和里的第一个选项“求和”并单击,再单击“enter”键即可得出所有产品报告期的销售额合计数。
Excel统计实验03:用EXCEL平均数、众数和中位数的计算及应用

---------------------------------------------------------------最新资料推荐------------------------------------------------------Excel统计实验03:用EXCEL平均数、众数和中位数的计算及应用Excel 统计实验 03 :平均数、众数、中位数的计算及应用【知识点】众数:一组数据中出现次数最多的数据就是这组数据的众数。
众数也常作为一组数据的代表,用来描述数据的集中趋势。
当一组数据有较多的重复数据时,众数往往是人们所关心的一个量。
中位数:将一组数据按照由小到大(或由大到小)的顺序排列,如果数据的个数是奇数,则处于中间位置的一个数是这组数据的中位数;如果数据的个数是偶数,则处于中间位置的两个数椐的平均数就是这组数据的中位数;中位数也是用来描述数据的集中趋势的,它是一个位置代表值。
如果知道一组数据的中位数,那么可以知道,小于或大于这个中位数的数据约各占一半。
⑴计算平均数的时候,所有的数据都参加运算,它能充分利用数据所提供的信息,在现实生活中较为常用;但它容易受到极端值的影响。
⑵中位数不受个别偏大或偏小数据的影响,当一组数据中的个别数据与平均数偏差较大时,一般用他来描述集中趋势。
1 / 7但不能充分利用所有数据的信息。
⑶一组数据中某些数据多次重复出现时,众数往往是人们尤为关心的一个量,但各个数据的重复次数大致相等时,众数往往没有特别意义。
一、平均数实例 1 :某市三个郊县的人数及人均耕地面积如下表: 郊县人数/ 万人均耕地面积/ 公顷 A 15 0.15 B 7 0.21 C 10 0.18 对该数据进行图表绘制,并统计这个市郊县的人均耕地面积是多少?(精确到 0.01 公顷) 统计步骤:1.打开一个 excel 工作薄,输入数据。
绘制柱状图,如下图 1.1 2.用平均数进行统计,结果如下图1.2:结果如下图 1.3 ,并以实例 1 1 命名保存到课堂文件夹中。
Excel在统计学中的应用

Excel在统计学中的应用《统计学》实验指导书前言1.实验目的《统计学》是关于数据的科学,它是论述在社会经济范围内搜集数据、整理数据、分析数据与解释数据的基本理论、基本知识、基本方法的科学,这就决定了本课程的地位——经济与管理类各专业的必修核心课,是最重要的专业基础课之一。
通过本课程的教学,能够使学生系统地掌握统计学的基本理论、基本知识与基本方法,为加强定量分析,更好地解决经济管理各专业实际问题打下良好的基础。
在上机实验的设计上,力争使每个学生都能较系统的掌握EXCEL在统计的应用,但避免枯燥的操作介绍,而是有针对性的要求学生结合问卷调查的数据与有关案例数据,运用EXCEL完成数据整理、数据分析及其结果的指标解释。
上机按照分班分期集中的形式完成相应内容的教学任务,由实验教师指导学生进行数据整理与数据分析。
⒉适用专业统计学实验适用的专业是经济与管理类各专业。
⒊先修课程概率与数理统计、统计学⒋⒌数量要求)本实验按自然班分组,每次实验指导教师指导一个实验小组,为此统计上机实验需设35个座位,实验台上配备Excel统计数据的实际案例,如教科书,教师搜集到的最新的经济管理类有关的统计数据、统计图、统计表并复印给每位学生,教授学生Excel统计功能的幻灯片及实际操作的随堂作业;××统计调查报告的范本等等。
要紧统计调查报告的制作流程图要悬挂在实验室墙壁上,便于学生参阅及按步骤有的放矢的完成调查报告,同时营造良好的实验环境。
⒍实验总体要求(1)通过统计学上机实验,进一步巩固课堂所学的理论知识。
在实验中,要将理论课所讲的内容与实际操作进行参照,弄清模拟实验资料中全部经济数据的统计处理。
(2)进行操作,提高实际工作能力。
在实验中,为学生配备了有关的经济管理类数据分析内容,比如:近几年的居民消费价格指数与分析预测内容,学生要按要求进行图表绘制并根据结果进行适当的定性分析,提高实际分析能力。
(3)通过实验,掌握统计学的基本常识,为进一步处理复杂经济现象形成的数据分析打下良好的基础。
统计学心得

试验总结与心得经过了为期两天的统计学实验,主要通过EXCEL这个软件来完成这次的实验。
首先掌握用EXCEL进行数据的搜集整理和显示,要求熟练运用EXCEL搜集数据,统计分组,制作统计图。
这是最基础的操作,让我们首先对EXCEL有一个初步的了解和认识。
实验二是用EXCEL计算描述统计量,可以运用函数描述统计量。
要求我们掌握基础的常用的函数对数据进行初步归纳,了解统计学中最常用的函数组成。
实验三用EXCEL进行时间序列分析。
首先是测定增长量和平均增长量,然后计算出长期趋势。
得出我们所要统计的结果的一个预计变动趋势。
让调研人员有一个机动的应变对策。
这个实验特别主义对时间序列的把握,常常会搞错要除去的年数。
这在实验中常常出错。
实验四用EXCEL进行指数分析,指数分析是统计学中最主要的一个数据分析。
先计算出总指数,再得出平均指数,最后进行因素分析。
其中平均数是通过加权算数平均法得来的。
实验五是用EXCEL进行相关与回归分析。
用EXCEL进行相关分析有两种方法,一是利用相关系数函数,在EXCEL中,提供了两个计算两个变量之间相关系数的方法,CORREL函数和PERSON函数,这两个函数是等价的,实验中我运用了用CORREL函数计算相关系数来进行对数据的分析。
另一种是利用相关分析宏。
EXCEL进行回归分析同样分函数和回归分析宏两种形式,其提供了9个函数用于建立回归模型和预测。
这9个函数分别是:INTERCEPT 返回线性回归模型的截距、SLOPE 返回线性回归模型的斜率、RSQ 返回线性回归模型的判定系数、FORECAST 返回一元线性回归模型的预测值、STEYX 计算估计的标准误、TREND 计算线性回归线的趋势值、GROWTH 返回指数曲线的趋势值、LINEST 返回线性回归模型的参数、LOGEST 返回指数曲线模型的参数。
在实验过程中我使用的是回归分析宏进行回归分析。
实验六是用EXCEL进行预测。
主要有移动平均法、指数平滑法、趋势预测法。
excel解指数方程

excel解指数方程摘要:一、引言二、指数方程的基本概念三、使用Excel 解指数方程的方法1.手动输入数据2.使用公式直接求解四、结论正文:一、引言在日常生活和工作中,我们可能会遇到需要解决指数方程的问题。
Excel 作为一款功能强大的数据处理软件,可以很方便地帮助我们解决这一问题。
本文将介绍如何使用Excel 解指数方程。
二、指数方程的基本概念指数方程是一种含有指数的方程,形式通常为:a^x = b,其中a 和b 是已知数,x 是未知数。
解指数方程就是求解x 的值。
三、使用Excel 解指数方程的方法1.手动输入数据在Excel 中,我们可以通过手动输入数据来解指数方程。
首先,在Excel 单元格中分别输入已知数a、b 和待求解的指数x,然后在旁边单元格中输入公式=a^x,最后按Enter 键,即可得到结果。
例如,若我们需要解方程3^x = 27,可以在Excel 中输入如下数据:| a | b | x | a^x ||-------|---------|-----|--------|| 3 | 27 | x | =3^x |按Enter 键后,可以看到单元格中显示的结果为27,即x=3。
2.使用公式直接求解除了手动输入数据外,我们还可以直接使用Excel 公式求解指数方程。
在Excel 中,可以使用内置函数`SOLVER` 求解指数方程。
例如,我们需要解方程3^x = 27,可以在Excel 中输入如下公式:`=SOLVER(3^x=27, x)`按Enter 键后,可以看到单元格中显示的结果为3,即x=3。
四、结论通过本文的介绍,我们可以知道,使用Excel 解指数方程有手动输入数据和使用公式直接求解两种方法。
实验三 用EXCEL进行参数估计和假设检验
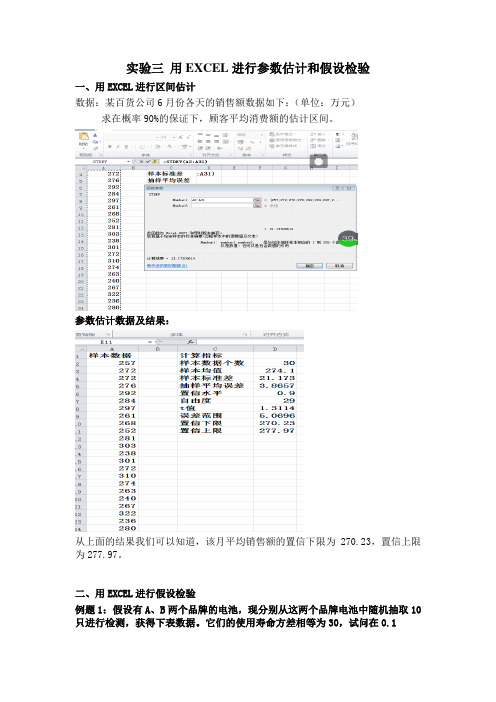
实验三用EXCEL进行参数估计和假设检验一、用EXCEL进行区间估计数据:某百货公司6月份各天的销售额数据如下:(单位:万元)求在概率90%的保证下,顾客平均消费额的估计区间。
参数估计数据及结果:从上面的结果我们可以知道,该月平均销售额的置信下限为270.23,置信上限为277.97。
二、用EXCEL进行假设检验例题1:假设有A、B两个品牌的电池,现分别从这两个品牌电池中随机抽取10只进行检测,获得下表数据。
它们的使用寿命方差相等为30,试问在0.1的显著性水平下,可否认为两个品牌的平均使用寿命存在显著差异?据上,提出原假设:A、B两个品牌的电池使用寿命不存在显著差异,备择假设:A、B两个品牌的电池使用寿命存在显著差异。
进行Z检验-双样本平均差检验:得如下所示结果:此次检验属于双尾检验,P=01101282872 > 显著性水平0.1,所以在0.1的显著性水平下不能拒绝原假设,即可以认为两个品牌的平均使用寿命不存在显著性差异。
例题2:用某种药物治疗9例再生障碍性贫血患者,治疗前后患者血红蛋白变化的数据如下表所示。
问在0.05的显著性水平下,能否认为这种药物至少可以使血红蛋白数量增加15个单位?提出原假设:这种药物不能使患者血红蛋白至少增加15个单位;备择假设:这种药物可以使患者的血红蛋白至少增加15个单位。
由于总体平均差已知,选用t-检验:平均值的成对二样本分析:得结果如下:由于显著性水平为0.05大于P值0.00037558,因此要拒绝原假设,即可以认为这种药物至少能使血红蛋白数量增加15个单位。
例题3:某研究所试验出一批新品种,想知道新品种产量是否比老品种产量有显著提高,随机抽取新老品种产量各9个,数据如下(单位:千克)。
试问,在0.05的显著性水平下,可否认为新品种比老品种的产量有显著提高?据条件,提出原假设:新品种比老品种产量没有显著提高;备择假设:新品种比老品种产量显著提高。
得出t检验:双样本异方差分析结果如下:在显著性水平为0.05的单侧检验下,P值为0.097038594,大于显著性水平,应拒绝原假设,即可以认为在0.05的显著性水平下,新品种比老品种的产量有显著提高。
excel三指数平滑模型

excel三指数平滑模型
在Excel中实现三次指数平滑模型的具体步骤如下:
1. 确定初始值:对于一次指数平滑,初始值以前8期的均值来确定。
对于二次指数平滑和三次指数平滑,可以使用Excel的内置函数来计算。
2. 建立模型:在Excel中,可以使用指数平滑预测工具来建立模型。
选择“数据”选项卡中的“数据分析”工具,选择“指数平滑”,并选择适当的预测模型(例如,三次指数平滑)。
3. 输入数据:在Excel工作表中输入原始数据,并设置输出区域。
4. 运行模型:单击“确定”按钮,Excel将自动运行所选的指数平滑模型,并生成预测结果。
5. 分析结果:分析预测结果,并根据需要进行调整。
需要注意的是,Excel中的指数平滑模型可能无法处理季节性数据,或者可能需要额外的设置来处理季节性数据。
此外,Excel中的指数平滑模型也可能无法处理异常值或缺失值。
在处理这些情况时,可能需要使用更复杂的统计软件包或编程语言来实现三次指数平滑模型。
统计学原理实习报告

统计学原理实习报告实习日期:1月4日——1月9日班级:** 姓名:** 学号:**指导老师:**实验一用Excel搜集与整理数据 (3)实验二用EXCEL计算描述统计量 (4)实验三用EXCEL进行时间序列分析 (6)实验四用EXCEL进行指数分析 (8)实验五用EXCEL进行相关与回归分析 (9)六统计学实习心得 (11)实验一用Excel搜集与整理数据实验目的:掌握用EXCEL进行数据的搜集整理和显示实验步骤:一、用Excel搜集数据假定有100个总体单位,每个总体单位给一个编号,共有从1到100个编号,输入工作表。
进行抽样分析,即可得图-1。
图-1二、用Excel进行统计分组用直方图工具来进行,输入数据。
(数据来源:http://219.235.129.58/reportView.do?Url=/xmlFiles/cef27b97a3424dfcb7e4e7224bc97 196.xml&id=54e87e18a6024ef99769f74ea8d7d7fb&bgqDm=20030010&i18nLang=zh_CN)得到结果,见图-2。
图-2三、用Excel作统计图把数据输入到工作表。
(数据来源:浙江省计算机二级AOA考试指导用书P45)得出结果,见图-3。
图-3实验结果:均见上图结果分析:一、用来进行随机抽样,体现抽样的公平性。
二、可以用于对大量数据进行统计分组,大大减少工作量。
三、用于了解各个数据所占的比重,用于分析产品销售状况,直观且方便。
实验二用EXCEL计算描述统计量实验目的:用EXCEL计算描述统计量实验步骤:EXCEL中用于计算描述统计量的方法有两种,函数方法和描述统计工具的方法。
一、用函数计算描述统计量,计算众数,中位数,平均误差等。
为了解某门考试整个专业学生的分数情况,随机抽取50人,分数如下:97 88 98 78 60 94 95 96 92 54 89 100 92 84 58 90 86 96 81 76 81 86 92 78 61 78 100 67 85 75 88 82 45 96 65 97 95 56 74 78 71 89 66 79 68 91 90 60 86 53(数据来源:百度文库/view/921baf69011ca300a6c3902e.html)得出结果,见图-4。
统计学实验指导书

目录实验一用Excel搜集与整理数据 (1)实验二用Excel进行时间序列分析 (3)实验三用Excel进行指数分析 (6)实验四用Excel进行相关与回归分析 (8)实验五用Excel进行预测 (12)主要参考文献 (17)实验一用Excel整理数据一、实验目的和任务掌握用EXCEL进行数据的搜集整理和显示二、实验仪器、设备及材料计算机三、实验原理及步骤小麦的单位面积产量与降雨量和温度有一定关系。
为了解它们之间的关系形态,收集数据如下表;要求:绘制小麦产量与降雨量和温度的气泡图,并分析它们之间的关系。
第一步:把数据输入到工作表中,如图1所示:图1第二步:选中某一单元格,单击插入菜单,选择图表选项,弹出图表向导对话框,再选择气泡图。
如图2:图2第三步:单击下一步,再在子图表类型中选择一种类型,这里我们选用系统默认的方式。
然后单击下一步按钮,打开源数据对话框。
再选择系列按钮,在对话框中填入数据X、Y以及其对应值,如图3所示:图3第四步:单击完成按钮,即可得如图4所示的气泡图:图4四、实验结论从气泡图上可以看出,随着气温的增高,降雨量也在增加;随着气温好降雨量的增加,小麦的产量也在提高(气泡变大)。
实验二用Excel进行时间序列分析一、实验目的和任务用EXCEL进行时间序列分析二、实验仪器、设备及材料计算机三、实验原理及步骤1、我国1990年至2004年人均GDP的情况如下:年份1991991199219931994199519961997199819992002001200220032004人均GDP(元)1634187922872939392348545576605463086551708676518214911110561(2)计算长期趋势2季度/年销售额(万元)2003年2004年2005年1 3890 3840 41252 2500 2190 31463 1989 1765 24344 4365 4213 4531(一)测定发展速度和平均发展速度图5第一步:在A列输入年份,在B列输入人均GDP。
使用Excel的EXP函数计算指数

使用Excel的EXP函数计算指数Excel是一款功能强大的电子表格软件,广泛应用于各个领域的数据处理和分析工作中。
其中的EXP函数是Excel提供的一个数学函数,用于计算指数。
本文将介绍如何使用Excel的EXP函数来进行指数计算,并给出一些实际应用的例子。
一、Excel的EXP函数概述EXP函数是Excel提供的数学函数之一,用于计算自然指数。
它的语法格式如下:EXP(number)其中,number表示一个数值,可以是常数、单元格引用或其他数学表达式。
EXP函数将返回数值e(自然对数的底数)的number次方。
二、使用EXP函数进行指数计算在Excel中,使用EXP函数进行指数计算非常简单。
以下是一个使用EXP函数计算指数的示例:假设我们要计算e的平方,可以在一个单元格中输入如下的公式:=EXP(2)在按下回车键后,Excel会立即返回计算结果,结果为7.389056。
同样地,我们也可以利用单元格引用来进行指数计算。
例如,我们可以在A1单元格输入2,然后在B1单元格中输入如下公式:=EXP(A1)按下回车键后,B1单元格将显示计算结果,即e的平方,结果为7.389056。
需要注意的是,EXP函数计算的是自然指数,即使用常数e作为底数的指数计算。
如果需要计算以其他底数为底的指数,可以使用POWER函数。
三、EXP函数的实际应用EXP函数在实际工作中有许多应用,以下是一些常见的例子:1. 财务分析在财务分析中,经常需要进行指数增长率的计算。
例如,某公司过去几年的销售额数据是按照指数增长的趋势增长的,我们可以利用EXP函数来预测未来几年的销售额。
假设过去三年的销售额分别为100万、150万和225万,我们可以使用如下公式来计算未来第四年的销售额:=225万*EXP(0.5)计算结果为338.687,即预测未来第四年的销售额为338.687万元。
2. 自然科学研究在自然科学研究中,经常需要进行指数增长或衰减的计算。
应用Excel进行定量分析实验.

1
主要内容
1、用Excel进行回归分析
一元线性回归:工具实现和函数实现
非线性回归:对数函数和指数函数
2、用Excel进行时间序列分析 移动平均及线性趋势预测 指数平滑及线性趋势预测 时间序列综合分解 3、用Excel进行层次分析
2
1、用Excel进行回归分析
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
44
(1)建立趋势T:用消除季节后的销量进行回归分析
趋势线 8 7 6 5 4 3 2 1 0 0 5 10
y = 0.1471x + 5.0996 R 2 = 0.9208
15
20
Tt 5.100 0.147t
用趋势得到1到16期估计值
移动平均及线性趋势预测
1.打开EXCEL建立工作表; 2.生成散点,分析和判断时间序列有无趋势T; 3.由图可知:商场的年销售额有明显的线性增长趋势T。
23
2. 用EXCEL进行时间序列分析
4.利用Excel 进行一次和二次移动平均:工具-数据分析-
移动平均。
5.建立移动平均线Байду номын сангаас预测模型。
利用公式求at和bt的值,得出线性模型。
2
3
4
5.475 5.738 5.975 6.188 6.325 6.400 6.538 6.675 6.763 6.838 6.938 7.075
1.096 1.133 0.971 0.840 1.075 1.156 0.918 0.839 1.109 1.141 0.908 0.834
42
0.971 0.918 0.908 第一季度季节指数 0.93 3 0.840 0.839 0.834 第二季度季节指数 0.84 3 1.096 1.075 1.109 第三季度季节指数 1.09 3 1.133 1.156 1.141 第四季度季节指数 1.14 3
exell-用指数回归方程

exell 用指数回归方程
在Excel中,可以使用“指数回归”功能来求解指数回归方程。
以下是如何在Excel中进行指数回归分析的步骤:
1. 打开Excel,将所需数据输入工作表中。
通常,我们将自变量(如技改投入x)放在一列,因变量(如销售额y)放在另一列。
2. 选择“数据”选项卡,然后点击“数据分析”。
3. 在“数据分析”对话框中,选择“回归”选项,然后点击“确定”。
4. 在“回归”对话框中,分别设置因变量区域和自变量区域。
在本例中,选择包含y值和x值的工作表区域。
5. 在“输出区域”设置框中,选择一个空白区域存放回归结果。
例如,可以选择C1作为输出区域。
6. 在“选项”区域,勾选“标签”以显示列名,并确保“残差”选项为“线性”。
7. 点击“确定”,Excel将生成回归结果,包括系数、R²值等。
8. 根据输出结果,我们可以得到指数回归方程。
例如,如果输出结果中的系数为0.8619,常数项为3.1579,那么指数回归方程为:y = 3.1579 * (x)^0.8619。
需要注意的是,在实际应用中,Excel可能无法直接得到完美的指数回归方程,因此有时需要对数据进行进一步处理,如对数变换等。
此外,根据实际需求,我们还可以使用其他统计软件(如SPSS、R语言等)进行指数回归分析。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三用EXCEL进行指数分析
实验目的:用EXCEL进行指数分析
实验步骤:
指数分析法是研究社会经济现象数量变动情况的一种统计分析法。
指数有总指数与平均指数之分,在这一节我们介绍如何用Excel进行指数分析与因素分析。
一、用Excel计算总指数
【例1】:图中是某企业甲、乙、丙三种产品的生产情况,以基期价格p作为同度量因素,计算生产量指数。
如图1
图1用EXCEL计算总指数资料及结果
计算步骤:
第一步:计算各个p0q0:在G2中输入“=C2*D2”,并用鼠标拖曳将公式复制到G2:G4区域。
第二步:计算各个p0*q1:有H2中输入“=C2*F2”,并用鼠标拖曳将公式复制到H2:H4区域。
第三步:计算Σp0q0和Σp0q1:选定G2:G4区域,单击工具栏上的“Σ”按钮,在G5出现该列的求和值。
选定H2:H4区域,单击工具栏上的“Σ”按钮,在H5出现该列的求和值。
第四步:计算生产量综合指数Iq=Σp0q1/Σp0q0:在C6中输入“=H5/G5”便可得到生产量综合指数
注意:在输入公式的时候,不要忘记等号,否则就不会出现数值。
二、用Excel计算平均指数
现以生产量平均指数为例,说明加权算术平均法的计算方法。
【例2】:图中的A1:A4区域内是某企业生产情况的统计资料,我们要以基期总成本为同度量因素,计算生产量平均指数。
如图2
图2用EXCEL计算平均指数资料及结果
计算步骤:
第一步:计算个体指数k=q1/q0:在F2中输入“=D2/C2”。
并用鼠标拖曳将公式复制到F2:F4区域。
第二步:计算k*p0q0并求和。
在G2中输入“=F2*E2”并用鼠标拖曳将公式复制到G2:G4区域。
选定G2:G4区域,单击工具栏上的:“Σ”按钮,在G5列出现该列的求和值。
第三步:计算生产量平均指数:在C7中输入“=G5/E5”即得到所求的值。
三、用Excel进行因素分析
【例3】:我们还用上面的例子,有关资料如图3
图3用EXCEL进行因素分析资料及结果
进行因素分析的计算步骤如下:
第一步:计算各个p0*q0和∑p0q0:在G2中输入“C2*D2”,并用鼠标拖曳将公式复制到G2:G4区域。
选定G2:G4区域,单击工具栏上的“∑”按钮,在G5出现该列的求和值。
第二步:计算各个p0*q1和∑p0*q1:在H2中输入“=C2*F2”,并用鼠标拖曳将公式复制到H2:H4区域。
选定H2:H6区域,单击工具栏上的“∑”按钮,在H5出现该列的求和值。
第三步:计算各个p1*q1和∑p1*q1:在I2中输入“=E2*F2”,并用鼠标拖曳将公式复制到I2:I4区域。
选定I2:I4区域,单击工具栏上的“∑”按钮,在I5出现该列的求和值。
第四步:计算总成本指数:在C6中输入“=I5/G5”,即求得总成本指数。
第五步:计算产量指数:在C7中输入“=H5/G5”,即得产量指数
第六步:计算单位成本指数:在C8中输入“=I5/H5”即求得单位成本指数用Excel进行加权指数计算和指数体系分析
[例4]一个家庭2004年和2005年春节期间的肉类消费情况如表1。
表中还列出了同期肉类的市场平均价格。
试根据表中的数据分析:这个家庭用于肉类消费的支出2005年比2004年增加多少?其中多少是由于消费数量的变化引起的?多少是由于价格变动引起的?
计算过程参见图9-22。
在F3单元格中输入公式“=B3*D3”,并把公式复制到F4:F6,在单元格F7中输入公式“=SUM(F3:F6)”,可以计算出2004年的总支出。
用类似的方法在单元格G7中计算p0q1的合计值,在单元格H7中计算2005年的总支出。
在F8单元格中输入公式“=H7/F7*100”,在F9单元格中输入公式“=H7-F7”,可以得到2004-2005年消费支出变动的相对数和绝对数;在G8单元格中输入公式“=G7/F7*100”可以得到消费数量的加权指数(拉氏指数),在F9单元格中输入公式“=G7-F7”可以得到消费数量变化引起的消费额变动绝对数;在H8单元格中输入公式“=H7/G7*100”可以得到加权价格指数(帕氏指数),在F9单元格中输入公式“=H7-G7”,可以得到价格变化引起的消费额变动绝对数。
图4 加权指数的计算过程
相应的计算结果为:136.64%=126.10%×108.36;91.05 =64.85 +26.20。
总支出增加了36.64%,91.05元,其中由于消费数量增加了26.1% 增加支出64.85元,由于价格上涨8.36%增加支出26.20元。
用Excel进行时间序列的价格调整
指数理论在经济学领域的最重要的应用之一就是根据现价(当年价格)数据计算可比价数据。
在很多情况下我们直接得到的宏观经济总量数据,如GDP、总消费、总投资等等都是以当年价格计算的,而我们在经济分析中需要首先剔除价格因素的影响,这时就需要用相应的价格指数来“缩减”(deflate)现价指标。
在宏观经济分析中的一个重要误区就是直接把总值指标中作为物量指标来分析,而忽略了其中包含的价格因素的影响。
[例5] 1990-2003年我国的总消费(当年价格)和居民消费价格指数如表2。
根据数据计算以2000年价格衡量的总消费。
表2 1990-2003年我国的总消费(当年价格)和居民消费价格指数年份最终消费消费价格指数年份最终消费消费价格指数
亿元,当年价格(上年=100)亿元,当年价格(上年=100) 199011365.2103.1199743579.4102.8
199113145.9103.4199846405.999.2
199215952.1106.4199949722.798.6
199320182.1114.7200054600.9100.4
199426796124.1200158927.4100.7
199533635117.1200262798.599.2
199640003.9108.3200367442.5101.2
要完成要求的任务需要计算以2000年价格为100的定基价格指数。
为了计算方便,我们先计算以序列的第一年(即1990年)为100的定基价格指数,然后再把基期调整为2000年。
具体的计算过程参见图5。
先在单元格D2中输入数值100,然后再单元格D3中输入公式“=C3*D2/100”,再通过拖动填充柄把公式复制到区域D3:D15。
这样得到的序列是以1990年为基期的不变价序列。
在E2中输入公式“=D2/$D$12*100”,再把公式复制到区域E3:E15,就得到了以2000年为基期的不变价序列。
最后,在F2中输入公式“=B2/E2*100”,再把公式复制到区域F3:F15,就得到了以2000年价格计算的各年的总消费。
计算结果如图9-24。
从图中可以看出,由于1997年以前各年的通货膨胀率较高,现价总消费与不变价总消费的差异较大。
1997年及以后各年的现价与可比价总消费的差别不大。
图5 不变价总消费的计算过程
top↑
图6 不变价与现价总消费的比较
[例7] GDP缩减指数是衡量一个国家通货膨胀程度的指标之一,等于现价GDP除以用上一年价格计值的当年的GDP。
根据《中国统计年鉴2004》我国1991-2003年的现价GDP 和GDP指数(上年=100,可比价)的资料如表9-9。
表3我国1991-2003年的现价GDP和GDP指数(上年=100,可比价)年份GDP(亿元)GDP环比指数年份GDP(亿元)GDP环比指数
199121617.8109.2199878345.2107.8
199226638.1114.2199982067.5107.1
199334634.4113.5200089468.1108
199446759.4112.6200197314.8107.5
199558478.1110.52002105172.3108.3
199667884.6109.62003117251.9109.3
199774462.6108.8
top↑计算过程可参见图7。
在单元格D3中输入公式“=B3/B2*100”并把公式复制到区域D4:D14,可以得到GDP的总值指数。
根据统计指数之间的关系,在E列中用GDP总值指数除以环比指数(实物量指数)得到的指数就是GDP缩减指数。
计算结果与消费价格指数的比较见图8。
图7 GDP缩减指数的计算过程
图8 GDP缩减指数与消费价格指数的比较。
