第一章 第三节
第一章 第三节 生物反应器的生物学基础-理化条件对微生物生长的影响

µ是流体的动力粘度系数,ρ是流体密度,g是重
力加速度,������������ 为反应器界面气体速率。
生物反应过程剪切力的控制
选择反应器类型
机械搅拌反应器>气升反应器
选择搅拌器类型
涡轮状叶轮>平叶轮>螺旋状叶轮
控制搅拌强度和通气强度
不同微生物对pH要求不同
微生物的生长pH值范围极广,从pH2-8之间都有
微生物能生长。但是绝大多数种类都生活在 pH5.0-9.0之间。
微生物生长的pH值三基点: 各种微生物都有其生长的最低、最适和最高pH值。低于 最低、或超过最高生长pH值时,微生物生长受抑制或导 致死亡。
一些微生物生长的pH值范围
阿伦尼乌斯方程 ������������ = ������ ������������ −������������ /(������������) − ������′ ������ −������������/(������������) ������������
其中������和 ������′ 是经验常数, ������������ 是细胞合成代 谢活化能,������������ 是死亡的活化能,������ 是理想气 体常数,������是凯氏温度。
物理化学因素对微生物生长的影响
温度影响微生物生长速率的阿伦尼乌斯方程 ������������ = ������ µ − ������������ ������������ ������������ = ������ ������������ −������������ /(������������) − ������′ ������ −������������ /(������������) ������������
第一章第三节化学键

正确。若含离子键,应属离子化合物。
判断:
• 含有共价键的化合物一定是共价化合物
错,如:NaOH Na2SO4
• 全部由非金属元素组成的化合物一定是共价 化合物
错,如 NH4Cl 等铵盐
• 在气态单质分子里一定有共价键
错,He、Ne等稀有气体
七、分子间作用力和氢键
··
五、共价键---非极性键和极性键
氢分子的形成: H ·+ ·H → H H H﹣H(结构式)
非极性共价键: (同种非金属原子)
共用电子对不偏移,成键原子不显电性
氯化氢分子的形成: 极性H共·价+键·:C····l:(→不同H种非C··金··l属原H子﹣)Cl(结构式)
共用电子对偏向偏向吸引电子能力强的原子一边(氯 原子),氯原子带部份负电荷,氢原子带部份正电荷。
··
··
·· ﹕ ﹕ : :
::
★判要断得下多列少物电质子的就键得的拿极出性多,少并个写出出来电共子享式
氯气 :Cl :Cl:
非极性键
溴化氢 氮气
·· ……
H ﹕Br ﹕ ★书写时极共性价键键时应
注意各原子均不用加
NN
上“[ ]非”和极电性荷键符号
甲烷
H H﹕C﹕H
H
水 H ··O ··H
极性键 极性键
先画出钠和氯的原子结构示意图
氯化钠的形成 2Na+Cl2 =△= 2NaCl
不稳定
电子转移
稳定
更稳定
Na+
Cl-
由阴、阳离子的静电作用形成
一、离子键
定义: 使阴、阳离子结合成化合物的静电 作用,叫做离子键。
成键微粒: 阴、阳离子
第一章 第三节 交易性金融资产

借:交易性金融资产——成本(公允价值) 应收股利/应收利息(价款包含的股利或利息)
ቤተ መጻሕፍቲ ባይዱ
投资收益(交易费用)(影响当期损益)
贷:银行存款 【解释】针对购买的债券核算时使用“应收利息”科目核算,针对购
买的股票核算时使用“应收股利”科目核算。
【解释1】交易性金融资产的入账价值(交易费用另外支付)=实际支 付的价款-其中包含股利或利息。 【解释2】交易性金融资产的入账价值(交易费用在支付的价款里)= 实际支付的价款-其中包含的股利或利息-交易费用的部分。 【解释3】取得交易性金融资产的方式不同,贷方登记的科目也不同, 如果是直接购入某公司的股票,则贷方登记“银行存款”科目;如 果是委托证劵公司购买,则贷方登记“其他货币资金——存出投资 款”科目。
(1)2×14年1月1日,购入B公司的公司债券时: 借:交易性金融资产——成本 应收利息 投资收益 贷:其他货币资金 取的债券利息时: 借:其他货币资金 贷:应收利息 500 000 500 000 25 500 000 500 000 300 000 26 300 000
(2)2×14年1月8日,收到购买价款中包含的已到付息期但尚未领
借:银行存款等(价款扣除手续费) 贷:交易性金融资产 投资收益(差额,也可能在借方)
同时: 借:公允价值变动损益(原计入该金融资产的公允价值变动) 贷:投资收益 或: 借:投资收益 贷:公允价值变动损益 【解释】公允价值变动损益和投资收益均属于损益类的科目,这两个 科目之间的变动不影响当期损益的总额。
第三节 交易性金融资产
【重难点提示】 1、掌握交易性金融资产的初始计量(入账价值) 2、掌握交易性金融资产持有期间获得现金股利或债券利息的核算( 投资收益) 3、掌握交易性金融资产期末计量(公允价值变动损益) 4、掌握交易性金融资产处置的核算(投资收益)
第一章第三节果实和种子的形成

4、在种子的受精过程中,受精卵发育 成( B )
A.种皮 B.胚 C.胚乳 D.果皮
5、夏季到来,西瓜甘甜可口,是清 凉解渴的佳品。下列结构能发育成 西瓜果实的是(C) A受精卵 B胚珠 C子房 D花托 6、人们通常食用桃的哪一部分?(B) A 种皮 B果皮 C子房 D种子
7、绿色开花植物在完成受精作用后,所形成
胚乳
种 子
胚
总结:果实和种子的形成
子房壁
子 房
珠被
胚珠 卵细胞
极核
受精后 受精后
果皮
种皮 胚 种子
果 实
胚乳
在从花到果实的发育过程中,花的各部分 结构产生什么变化?用连线的方法表示出 来。
花瓣
雄蕊 花柱 子房 子房壁 胚珠 受精卵
胚 果实 果皮 种子 凋落
练习:
1.有一个描述花生的谜语说: 麻屋子,红帐子,里头住着白胖子。
第三节 果实和种子的形成
一、果实和种子的发育
思考:受精以后花的各部分发生 怎样的变化?
发育初期:花萼、花冠、雄蕊 及雌蕊的柱头和花柱都凋落只 有子房继续发育。
思考:果皮和种子分别由子房的哪部分发育而 来?
子
子房壁
果皮
果
房
胚珠
种子
实
胚珠怎么发育成种子的?
珠被
种皮
胚 珠
极核 受精后 受精极核 卵细胞 受精后 受精卵
单子叶植物:种子的胚具有一片子叶的植物
练习:.在图中指出菜豆种子和玉米 种子的结构?
胚轴 3
4 胚芽
胚根 2 种皮 1
(二片,肥厚) 5 子叶
菜豆种子
胚芽
胚
胚轴 胚根
子叶
1 果皮和种皮
高中物理第一章 第3节带电粒子在匀强磁场中的运动

第3节 带电粒子在匀强磁场中的运动核心素养导学一、带电粒子在匀强磁场中的运动1.带电粒子沿着与磁场垂直的方向射入匀强磁场,由于带电粒子初速度的方向和洛伦兹力的方向都在与磁场方向 的平面内。
所以,粒子只能在该平面内运动。
2.洛伦兹力总是与粒子运动方向垂直,只改变粒子速度的方向,不改变粒子速度的大小。
3.粒子速度大小不变,粒子在匀强磁场中所受洛伦兹力大小也不改变,洛伦兹力提供粒子做圆周运动的向心力,粒子做 运动。
带电粒子在匀强磁场中做匀速圆周运动,带电粒子的重力忽略不计,洛伦兹力提供向心力。
二、带电粒子在磁场中做圆周运动的半径和周期1.半径公式由洛伦兹力提供向心力q v B =m v 2r ,可得圆周运动的半径r = 。
2.周期公式匀速圆周运动的周期T =2πr v ,将r =m v qB 代入,可得T = 。
1.电子以某一速度进入洛伦兹力演示仪中。
(1)励磁线圈通电前后电子的运动情况相同吗?提示:①通电前,电子做匀速直线运动。
②通电后,电子做匀速圆周运动。
(2)电子在洛伦兹力演示仪中做匀速圆周运动时,什么力提供向心力?提示:洛伦兹力提供向心力。
2.如图,带电粒子在匀强磁场中做匀速圆周运动。
判断下列说法的正误。
(1)运动电荷在匀强磁场中做匀速圆周运动的周期与速度有关。
( )(2)带电粒子做匀速圆周运动的半径与带电粒子进入匀强磁场时速度的大小有关。
( )(3)带电粒子若垂直进入非匀强磁场后做半径不断变化的运动。
( )新知学习(一)⎪⎪⎪带电粒子做圆周运动的半径和周期[任务驱动]美丽的极光是由来自太阳的高能带电粒子流进入地球高空大气层出现的现象。
科学家发现并证实,向地球两极做螺旋运动的这些高能粒子的旋转半径是不断减小的,这主要与哪些因素有关?提示:一方面磁场在不断增强,另一方面由于大气阻力粒子速度不断减小,根据r =m v qB,半径r 是不断减小的。
[重点释解]1.由公式r =m v qB 可知,带电粒子在匀强磁场中做圆周运动的半径r 与比荷q m 成反比,与速度v 成正比,与磁感应强度B 成反比。
马克思主义基本原理第一章第三节
•
(二)客观规律性和主观能动性的辩 证关系
1、尊重客观规律性是发挥主观能动性的关 键 ; 2、充分发挥人的主观能动性是认识和利用 客观规律的必要条件; 3、方法论意义:坚持二者的辩证统一,必 须尊重客观规律,从现实条件出发,把高 度的革命热情同踏实的科学态度结合起来。
尊重客观 规律性
关键 实 践 条件
荀子
“天行有常,不为 尧存,不为桀亡”
规律的客观性总结
我们既要反对藐视规律的主观 随意性和经验主义,又要反对在规 律面前无所作为的思想。在这里, 理论思维是十分重要的,正确的理 论思维能使人们增强驾驭规律的能 力,错误的思维会走向真理的反面。
(二)自然规律与社会规律的联系与区别
自然规律是自然现象固有的、本质 的、必然的、稳定的联系。 社会规律是通过人们的活动表现出 来的社会生活过程诸现象间的本质的、 必然的、稳定的联系。
孙 中 山
典型实践: 辛亥革命
三民主义: 驱除鞑虏,恢复中华 创立民国,平均地权
社会历史趋向与主体选择的关系
建国以后,在社会主 义改造和社会主义建设问 题上 ,同样面临着不同 的选择。经过反复实践和 探索,我们走上了建设中 国特色社会主义的成功之 路。所以,主体选择在社 会发展中的作用是不容忽 视的,关键在于主体选择 不能与历别
主要表现在:自然规律是作为一种 盲目的无意识的力量起作用,社会规律 则是通过抱有一定目的和意图的人的有 意识的活动实现的。 自然规律只要具备了同样的客观物质 条件就可以以完全相同的形式反复出现。 社会规律则是历史的,在不同的社会、 国家、民族以及不同的历史阶段都有不 同的表现形式。
二、意识的能动作用
(一)意识的作用
第一章第三节开集、闭集和博雷尔集

第三节 nR 中的开集、闭集和Borel 集一、nR 的几个基本概念度量空间:设X ≠∅,(,)d x y 是定义在X X ⨯(:d X X R ⨯→)上的一个二元实函数,若(,)d x y 满足:(1)非负性:对任意,x y X ∈,(,)0d x y ≥,且(,)0d x y x y =⇔=; (2)对称性:对任意,x y X ∈,(,)(,)d x y d y x =;(3)三角不等式:对任意,,x y z X ∈,(,)(,)(,)d x y d x z d y z ≤+, 则称(,)d x y 为,x y 之间的距离或度量,(),X d 称为距离(度量)空间.特别,取n X R =,(,)d x y =()()1212,,,,,,,n n x x x x y y y y ==,则(),X d 称为n 维欧式空间,仍记为nR .注:实变函数涉及的函数主要是nR 的点集上的实函数.集合的直径与有界集:设nE R ⊂,(){}diam sup ,,E d x y x y E =∈称为E 的直径;E 有界⇔0diam E ≤<+∞.E 有界的其他描述方法:如球覆盖和方覆盖.开球(球邻域)、闭球和球面:设0n x R ∈,0δ>,()(){}00,,n B x x R d x x δδ=∈<称为以0x 为心的开球(球邻域),简记为()0B x ; ()(){}00,,n B x x R d x x δδ=∈≤称为以0x 为心的闭球,简记为()0B x ; ()(){}00,,n S x x R d x x δδ=∈=称为以0x 为心的球面,简记为()0S x .n R 中的区间及区间的体积:设i I (1,2,,i n =)为R 上的n 个区间,则121ni n i I I I I =∏=⨯⨯⨯称为n R 上的区间;若iI (1,2,,i n =)都是开区间,则称1n i i I =∏为开区间;若i I (1,2,,i n =)都是闭区间,则称1ni i I =∏为闭区间;若i I (1,2,,i n =)都是同类的半开半闭区间,则称1ni i I =∏为半开半闭区间;设121ni n i I I I I =∏=⨯⨯⨯是nR 上的区间,则121nin i I I I I =∏称为1ni i I =∏的体积.二、开集、闭集的定义及基本性质1、开集的定义与性质:定义:设nG R ⊂,G 是开集是指对任意x G ∈,存在()B x G ⊂;易见,,n R ∅均为开集;()0B x 是开集;nR 上的开区间等都是开集.开集的性质:τ表示nR 中的开集全体,则 (1),n R τ∅∈;(2)对任意12,G G τ∈,总有12G G τ⋂∈,即τ对集合的有限交运算封闭; (3)对任意G ατ∈,α∈Λ,总有G αατ∈Λ∈,即τ对集合的任意并运算封闭.注:τ是nR 上的一个拓扑--------称为欧式拓扑. 2、闭集的定义与性质:定义:设nF R ⊂,F 是闭集是cF 是开集; 易见,开集和闭集在集合的余运算下是对偶的;,n R ∅均为闭集;()(){}00,cB x x d x x δ=>是闭集;()()(){}{}000,cS x B x x d x x δ=⋃>是闭集指对任意x G ∈,存在()B x G ⊂;闭集的性质:μ表示nR 中的闭集全体,则 (1),nR μ∅∈;(2)对任意12,F F μ∈,总有12F F μ⋃∈,即μ对集合的有限并运算封闭; (3)对任意F αμ∈,α∈Λ,总有F ααμ∈Λ∈,即μ对集合的任意交运算封闭.注意:一列开集的交不一定是开集;一列闭集的并不一定是闭集;τμ.三、开集、闭集的等价条件1、开集的等价条件1)点关于点集的一种分类关系(点集的内点、外点和边界点) 邻域的推广:设nx R ∈,若G 是开集,且x G ∈,则称G 为x 的一个邻域,\{}G x 为x 的一个去心邻域; 显然,()B x 就是x 的一个邻域,()\{}B x x 是x 的一个去心邻域. 点集的内点、外点和边界点: 设n x R ∈,nE R ⊂,(1)若存在x 的一个邻域G ,使得G E ⊂,则称x 为E 的内点,记0E 为E 的内点全体-------称为E 的内部(或内核或开核),显然0E E ⊂;(2)若存在x 的一个邻域G ,使得G E ⋂=∅,即cG E ⊂,则称x 为E 的外点,显然E 的外点一定不属于E ,其全体就是()c E;(3)若对x 的任意邻域G ,总有G E ⋂≠∅,cG E ⋂≠∅,则称x 为E 的边界点,记E ∂表示E 的边界点全体-----称为E 的边界.点关于点集的内点,外点和边界点关系是一个分类关系注:设nE R ⊂,则()n c R E E E=⋃∂⋃;记0E E E E E =⋃∂=⋃∂-----称为E 的闭包,则()()0c c E E =是闭集.()()0c c E E E∂=⋃是闭集.2)开集的等价条件 定理:设nE R ⊂,则 (1)0E 是开集;(2)E 是开集⇔0E E =.2、闭集的等价条件1)点列收敛设n k x R ∈,1,2,k =,0n x R ∈,若()0lim ,0k k d x x →∞=,则称{}k x 当k →∞时收敛于0x ,记为:0lim k k x x →∞=或0k x x →(k →∞).注:1)如何用邻域来反映点列收敛?2)点列收敛与坐标收敛有何关系?即,记()()00012012,,,,,,,k kk k n n x x x x x x x x ==,则0k x x →(k →∞)与0k i i x x →(k →∞)1,2,,i n =有何关系?2)点关于点集的另一种分类关系(点集的聚点、孤立点和外点) 设n x R ∈,nE R ⊂,(1)若对x 的任一个邻域G ,总有\{}G x E ⋂≠∅,则称x 为E 的聚点,记E '为E 的聚点全体-------称为E 的导集;(2)若存在x 的一个邻域G ,使得\{}G x E ⋂=∅,若x E ∈,即{}G E x ⋂=,则称x 为E 的孤立点,E 的孤立点全体所成的集称为E 的孤立点集,显然E 的孤立点集⊂E ;若x E ∉,即G E ⋂=∅,即cG E ⊂,则称x 为E 的外点,其全体就是()c E .点关于点集的聚点,孤立点和外点的关系也是一个分类关系 注:设nE R ⊂,则{}()0nc R E E E '=⋃⋃的孤立点全体,{}E E E E E ''=⋃=⋃的孤立点全体---------闭包的另一种表示.注:10孤立点集是至多可数集20聚点的等价条件:设nx R ∈,nE R ⊂,则下面的说法等价: (1)x 为E 的聚点;(2)对x 的任一球邻域(,)B x δ,总有(,)\{}B x x E δ⋂≠∅; (3)存在E 中一列彼此互异的点列{}k x ,使得k x x →(k →∞); (4)对x 的任一个邻域G ,总有G E ⋂为无限集. 证明:(1)⇒(2)显然;(2)⇒(3)只要δ取一列适当的趋于0的数列即可把满足要求的彼此互异的点列{}k x 取出来;(3)⇒(4)由极限定义的邻域形式即可; (4)⇒(1)显然. 注意:由等价形式立即可得,x 不是E 的聚点,即x E '∉⇔存在x 的一个邻域G ,使得G E ⋂为有限集. 30导集和闭包保持集合的有限并运算,但保持可数并运算;事实上,设有一列点集{}n E ,则()1212n n E E E E E E ''''⋃⋃⋃=⋃⋃⋃, ()1212n n E E E E E E ⋃⋃⋃=⋃⋃⋃,但11n n n n E E ∞∞=='⎛⎫'⊃ ⎪⎝⎭,11n n n n E E ∞∞==⊃. 证明?3)闭集的等价条件定理:设nE R ⊂,则下面的说法等价: (1)E 为闭集; (2)E E '⊂; (3)E E =;(4)对E 中的任意一列点{}k x ,若k x x →,则x E ∈. 证明 (1)⇒(2)对任意x E '∈,倘若x E ∉,即cx E ∈.因c E 为开集,存在()c B x E ⊂,从而()B x E ⋂=∅,这与x E '∈(x 为E 的聚点矛盾),故x E ∈.(2)⇒(3)显然,事实上,E EE E E E '⊂'=⋃=. (3)⇒(4)事实上,对E 中的点列{}k x ,k x x →,由聚点的等价条件,或者x E ∈或者x E E E '∈⊂=,即必有x E ∈.(4)⇒(1)反证法:倘若E 不是闭集,即cE 不是开集,则存在cx E ∈,使得对x 的任意球邻域(,)B x δ,都有(,)B x E δ⋂≠∅,于是,通过取δ为一列适当的趋于0的数列即可在E 中选取点列{}k x ,使得k x x →,从而x E ∈,这与cx E ∈矛盾,故E 必为闭集.注:利用上述等价条件可更为方便地判断一些集是闭集,例如,E '是闭集(因为易得()E E '''⊂);E 为有限点集,则E 为闭集(因为易得E E '=∅⊂);同理nE R ⊂整点集,则E 为闭集.四、聚点原理、Borel 有限覆盖定理和林德洛夫(Lindelof )至多可数覆盖定理聚点原理和有限覆盖定理是nR 中的两个基本定理,是nR 完备性的两种表现形式: 聚点原理:若nE R ⊂是有界无限点集,则E 至少有一个聚点(即E '≠∅); 致密性定理:若{}k x 是nR 中的有界无限点列,则{}k x 至少有一个收敛子列{}i k x ;Borel 有限覆盖定理:若nE R ⊂是有界闭集,ℑ为E 的一个开覆盖,则存在ℑ中的有限个开集,记为12,,,m G G G ,使得12m E G G G ⊂⋃⋃⋃.问题:若nE R ⊂不是有界闭集,则是否存在ℑ中的一列开集,记为12,,,,k G G G ,使得1k k E G ∞=⊂?林德洛夫(Lindelof )至多可数覆盖定理:若nE R ⊂,ℑ为E 的一个开覆盖,则存在ℑ中的一列开集,记为12,,,,k G G G ,使得1k k E G ∞=⊂.证明 对任意x E ∈,由ℑ为E 的一个开覆盖可得,存在开集x G ∈ℑ,使得x x G ∈.由有理点的稠密性,存在有理点x x q G ∈和有理正数x r ,使得(,)x x x x B q r G ∈⊂,显然{}(,)x x B q r x E ∈是至多可数集,且仍覆盖E ,记{}{}11(,)(,),,(,),k k xx x x x x B q r x E B q r B q r ∈=,则相应的开集12,,,,k x x x G G G 也覆盖E .注:试用林德洛夫至多可数覆盖定理证明:nR 任一个非空开集G 总可表示成至多可数个开区间的并集.五、几类与开集、闭集相关的集1、自密集和完全集 设nE R ⊂,自密集:若E E '⊂,则称E 是自密集(特点:E 没有孤立点). 例如,∅,n Q ,()cn Q(无理点集),nR ,开区间,闭区间,半开半闭区间,非空开集都是自密集.完全集:若E E '⊂且E E '⊂,即E E '=,则称E 是自密集(特点:E 没有孤立点的闭集). 例如,∅,nR ,闭区间都是完全集.思考:(1)非空有限点集一定不是自密集,更不是完全集; (2)有限个完全集的并仍是完全集; (3)一列完全集的并不一定是完全集; (4)完全集的交集不一定是完全集.记住一个结论:设E ≠∅是完全集,则E c =. 2、稠密集和疏朗集 设nE R ⊂,稠密集:若n E R =(即对任意n x R ∈以及x 的任意邻域G ,总有G E ⋂≠∅),则称E 在nR 中稠密,或E 是nR 中的稠密集.显然,E 是稠密集⇔对任意非空开集G ,G E ⋂≠∅(今后判断稠密集的常用方法).易见,nQ ,()cnQ (无理点集)均为n R 中的稠密集.疏朗集:若对任意的非空开集G ,总存在G 的非空开子集V G ⊂,使得V E ⋂=∅(即c V E ⊂),则称E 为疏朗集.易见,∅,有限点集,整点集都是疏朗集;疏朗集一定没有内点,但无内点的集并不一定是疏朗集.稠密集与疏朗集: 设nE R ⊂,(1)若E 为疏朗集,则cE 为稠密集,但反之不成立;证明 对任意非空开集G ,由E 为疏朗集可得,存在非空开子集V G ⊂,使得cV E ⊂,从而c V E G ⊂⋂,故c E G ⋂≠∅,即cE 为稠密集.反之,取n E Q =即可. (2)若E 为稠密开集,则cE 为疏朗闭集; 证明 显然,cE 为闭集,下证c E 为疏朗集.事实上,对任意非空开集G ,取V G E =⋂≠∅,显然V 为开集,cV E ⋂=∅,故c E 为疏朗集.综合(1)(2)得,(3)E 为稠密开集⇔cE 为疏朗闭集.3、三分Cantor 集三分Cantor 集构造图如图示,我们将[]01,中永远去不掉的点所成的集称为三分Cantor 集,记为P . 注:10P 的两种表示方法:[]12n=111P 0,1\(())n n n k n k F I -∞∞====;20 P 是闭集,完全集; 30 P 是疏朗集; 40 P c =; 50 mP 0=; 60nk=1P ∏称为nR中的Cantor 集,nk=1P c =∏.思考:(1)如何解释疏朗集不一定是至多可数集?(2)如何解释在[]01,去掉一个不可数集,不一定改变其长度?4、F σ型集、G δ型集和Borel 集1)F σ型集:若nE R ⊂能表示成可数个闭集的并,则称E 是F σ型集;G δ型集:若n E R ⊂能表示成可数个开集的交,则称E 是G δ型集.注:10 开集是G δ型集,闭集是F σ型集;20 问题:开集是F σ型集,闭集是G δ型集?可见,F σ型集和G δ型集都是比开集、闭集更广的两类集;30 至多可数个F σ型集的并仍为F σ型集,至多可数个G δ型集的交仍为G δ型集;40 F σ型集与G δ型集在余运算下相互转化;从而,nR 中至多可数集一定F σ型集,至多可数集的余集一定是G δ型集;50 问题:有理数集Q 是否G δ型集?无理数集c W Q =是否F σ型集?2)Borel 集记τ表示开集全体,则由τ生成的σ代数()στℜ称为Borel 体,其中的元素称为Borel 集. Borel 集一定是从开集出发经过至多可数次并、交、差、余运算得到的(Borel 集的结构). 易见,开集,闭集,F σ型集和G δ型集都是Borel 集.六、开集的结构开集的结构定理:(1)R 上的任一个非空开集总可表示称至多可数个互不相交的开区间的并;(2)nR (2n ≥)上的任一个非空开集总可表示成至多可数个互不相交的半开半闭区间的并.注:10(1)中构成R 中非空开集G 的互不相交的每个开区间(),αβ满足:(),G αβ⊂,且,G G αβ∉∉,它们都称为G 的构成区间.20 开集的结构定理的更一般的说法:(1)R 上的任一个开集或为∅,或总可表示称至多可数个互不相交的开区间的并;(2)nR (2n ≥)上的任一个开集或为∅,总可表示成至多可数个互不相交的半开半闭区间的并.七、点与集合间的距离,集合与集合间的距离1、点与集合间的距离,集合与集合间的距离的定义设nx R ∈,nE R ⊂,记(){},inf (,)inf (,)y Ed x E d x y y E d x y ∈∈=称为x 与E 间的距离;设12,n E E R ⊂,记(){}121212,,inf (,),inf(,)x E y E d E E d x y x E y E d x y ∈∈∈∈=称为1E 和2E 间的距离.注:由定义可得10 (){}{}122112,i n f (,)i n f(,)d E E d x E x E d y E y E=∈=∈; 事实上,对任意1x E ∈,2y E ∈,由定义,()()12,,d E E d x y ≤,()()2,,d x E d x y ≤对第一个不等式两边先对2y E ∈取下确界得,()()122,,d E E d x E ≤;再对1x E ∈取下确界得,(){}1221,inf (,)d E E d x E x E ≤∈.对第二个不等式两边同时对1x E ∈,2y E ∈取下确界得,{}()2112inf (,),d x E x E d E E ∈≤.综上所述,即得结论.20 若x E ∈,则(),0d x E =,反之不一定成立,如取0x =,(0,1)E =即可; 30 x E ∈⇔(),0d x E =;事实上,x E ∈⇔存在E 中的一列点{}k x ,使得k x x →,即(),0k d x x →⇔(),0d x E =.40 特别,若E 为闭集,则x E ∈⇔(),0d x E =;50 若12E E ⋂≠∅,则()12,0d E E =,反之不一定成立,如取1(0,1)E =,2(1,2)E =即可.引理((),d x E 在nR 上的连续性):设nE R ⊂,记()(),f x d x E =(nx R ∈),则()f x 在n R 上一致连续.事实上,对任意,nx y R ∈,z E ∈,由()()(),,,d x z d x y d y z ≤+,()()(),,,d y z d x y d x z ≤+对z E ∈取下确界可得()()(),f x f y d x y -≤,()()(),f y f x d x y -≤,即()()(),f x f y d x y -≤.2、距离可达到的条件(1)点到集合间的距离可达到的条件:设0n x R ∈,nE R ⊂为非空闭集,则存在0y E ∈,使得()()000,,d x y d x E =. (2)集合间的距离可达到的条件:设,nE F R ⊂均为非空闭集,且至少有一个有界,则存在0x E ∈,0y F ∈,使得 ()(),,d x y d E F =.思考:如何利用(1)和连续函数的最值性来证明?注:(2)中,n E F R ⊂都无界,结论不一定成立.3、闭集的分离性分离性定理:设,n E F R ⊂均为非空闭集,若E F ⋂=∅,则存在两个开集12,G G ,使得,1E G ⊂,2F G ⊂,且12G G ⋂=∅.4、闭集一定是G δ型集,开集一定是F σ型集先证一个结论:设n E R ⊂,0δ>,则{}()(,),n x R d x E U E δδ∈<为开集,且(),E U E δ⊂.再证结论:设n E R ⊂为闭集,取1n δ=(1,2,n =),则1,U E n ⎛⎫ ⎪⎝⎭为一列包含E 的开集,下证:11,n E U E n ∞=⎛⎫= ⎪⎝⎭.易见,11,n E U E n ∞=⎛⎫⊂ ⎪⎝⎭,反之,对任意11,n x U E n ∞=⎛⎫∈ ⎪⎝⎭有,1,x U E n ⎛⎫∈ ⎪⎝⎭,从而()1,0d x E n <→,所以(),0d x E =,注意到E 是闭集得,x E ∈,所以,11,n E U E n ∞=⎛⎫⊃ ⎪⎝⎭,故11,n E U E n ∞=⎛⎫= ⎪⎝⎭.。
第一章第三节 自由落体运动和竖直上抛运动

变式练习2
原地起跳,先屈腿下蹲,然后突然蹬地。从开始 蹬地到离地是加速过程(视为匀加速)加速过程 中重心上升的距离称为“加速距离”。离地后重 心继续上升,在此过程中重心上升的最大距离称 为“竖直高度” 。现有下列数据:人原地上跳的 “加速距离” d1=0.5m ,“竖直高度”h2=1.0m; 跳蚤原地上跳的“加速距离” d1=0.00080m ,“竖 直高度” h2=0.1m 。假想人具有与跳蚤相等的起 跳加速度,而“加速距离”仍为0.50m,则人上跳 的“竖直高度”是多少?
能为5m/s,方向向下; C.小球在这段时间内的平均速度大小可 能为5m/s,方向向上;
D.小球的位移大小一定是15m
ACD
作业 同步训练第一章第三节 (P181-182)
要点回顾
1.自由落体运动 只受重力;从静止开始下落
2.重力加速度g g与高度和纬度有关; 2 通常取g=9.8m/s
3.自由落体运公式 (1)速度公式 (2)位移公式 (3)速度和位移的关系
4.竖直上抛运动 以某一初速度竖直上抛; 只受重力 (1)速度公式 (2)位移公式 (3)速度和位移的关系
例题1 将小球A以10m/s的速度是竖直上 抛,同时,在小球A的正上方20m 处小球B同时自由下落,试求AB 两球相遇的碰撞的时间。(g取 2 10m/s ,空间足够大且不计空气 阻力)
变式练习1
水滴从屋檐自由落下,经过高 为1.8m的窗户历时0.2s,若不 2 计空气阻力,g取10m/s ,求 屋檐离窗顶的距离。
5.竖直上抛运动的对称性
(1)空间对称:在抛出点上方运动 时,将两次经过空间的同一位置。
(2)速率对称:上升和下落经过同 一位置时速度大小相等,方向相反。 (3)时间对称:经过同一段高度, 上升和下落的时间相同
第一章第三节 新闻价值要素

以下摘录上网的《新闻联播》新闻第二则旁白 文稿《未来,让我们共同开创——闭幕会侧记》 的描写部份:
“日出千山秀,花开万里春。气势雄伟的人民大会堂, 在旭日映照下更加庄严肃穆。....沐浴着晨辉,近 3000名全国人大代表...目光果敢坚定,他们的步履 自信从容。.....红日已近中天,阳光普洒大地。..... 代表们豪情满怀。勉励的话语,共同的承诺,与一 双双紧握的手,汇成激情的海洋。.... 才送春风吹绿 柳,又见桃花映红墙。‘十五’开局之年盛事不断, 喜事连连。....‘二月二,龙抬头’。今天恰逢农历二 月初二,东方巨龙将再一次昂首腾飞。”
回眸:主旋律响亮,主动仗漂亮,主基调明亮 “大事喜事临门,热点难点纷纭。”人大代表、政 协委员们这样描述刚刚走过的新世纪第一年。的确, 这一年神州大地大事喜事连连:庆祝建党80周年、 “七一”重要讲话、申奥成功、加入世贸、APEC 会议……桩桩振奋精神;国际形势错综复杂,党和 政府沉着应对。 在纷繁复杂的形势面前,我们宣传思想战线的广大 干部群众是怎样凝聚民心、鼓舞干劲的呢?代表、 委员们普遍认为,去年的宣传思想战线,逢喜事而 不躁,处大变而不惊,主题突出,基调鲜明,导向 正确,把握平稳。
新闻价值要素的具体含义
1.重要性
指新闻所提供的信息,对诸多受众具有 重要意义,是受众应该或必须知晓的。 这种重要性是一种客观存在,它往往不 以受众的个人兴趣为转移。有时要经过 新闻本身对受众启发与影响,受众方能 明白其是必不可少的。
2.新鲜性 指一则新闻给性回答的问题: 你为什么现在报道这个事件?
扶风气之正 聚民心之齐(两会特稿) ———全国人大代表、政协委员对宣传思想工 作回眸与展望
(《人民日报》 2002年3月8日第一版)
第一章 第三节 测量的三项基本工作

第一章:绪论 第三节:测量的三项基本工作
第三节 测量的三项基本工作
第一章:绪论 第三节:测量的三项基本工作
测量工作的实质是确定地面点的点位。点位 有点的平面位置x、y与高程位置H所决定的,而坐 标值x、y与高程值H并不能直接测量得出。测量工 作就是先测出决定点位的三个要素,即点位之间 的高差、水平角和水平距离,再经过一定的计算 程序推算得点的三个坐标量x、y、H。
一、高差 要确定点的位置须测量高差这个要素, 由高差经过计算得到点的高程,这一工作就 是高程测量。 高差是地面两点的高程差。
h 第一章:绪论 AB H B H A h AB H B H A 第三节:测量的三项基本工作
B
hAB
A
HB H A′ HA H B′ 假定高程起算面
大地水准面 黄海平均海水面 铅垂线 铅垂线
h AB hBA
第一章:绪论 第三节:测量的三项基本工作
二、水平角与水平距离
点的平面位置的确定须测量两个要素,即水平角和水平 距离。测量水平角的工作称为角度测量,测量水平距离 的工作称为距离测量。
P B β A DAP
测定地面点平面直角坐标的主要测量工作是测量水 平角和水平距离。 测量的基本工作是:高程测量、角度测量、距离测量。
第一章:绪论 第三节:测量的三项基本工作
第一章:绪论 第三节:测量的三项基本工作
第一章:绪论 第三节:测量的三项基本工作
第一章:绪论 第三节:测量的三项基本工作
第一章:绪论 第三节:测量的三项基本工作
第一章:绪论 第三节:测量的三项基本工作
第一章:绪论 第三节测量的三项基本工作
第一章:绪论 第三节:测量的三项基本工作
高程和高差
地面点A、B的高程分别为HA、HB 用h表示。高差有方向和正负。B点对A点的高差为:
第一章第三节化学键

第⼀章第三节化学键第⼀章第三节同位素、化学键知识点⼀元素、核素、同位素、同素异形体的⽐较例1:下列互为同位素的是( )A.H2D2B.14N 14C C.16O 17O D.⾦刚⽯⽯墨例2:下列8种化学符号:11H2、21H2、14 6C、63Li、2311Na、14 7N、73Li、2412Mg(1)表⽰核素的符号共________种。
(2)互为同位素的是________和________。
(3)质量数相等,但不能互称同位素的是________和________。
(4)中⼦数相等,但质⼦数不相等的核素是________和________。
练习1.下列说法中,错误的是( )A.13C和14C属于同⼀种元素,它们互为同位素B.1H和2H是不同的核素,它们的质⼦数相同C.14C和14N的质量数相同,它们的中⼦数不同D.6Li和7Li的电⼦数相同,中⼦数也相同2.有关H、D、T、HD、H2、D+、H-这七种粒⼦的说法正确的是( )A.互为同位素 B.是七种氢元素C.HD和H2均是单质 D.电⼦数相同3.由21H和18 8O组成的11 g⽔中,含有的中⼦的物质的量为( )A.4.5 mol B.5 mol C.5.5 mol D.6 mol4.⾦属钛对⼈体体液⽆毒且能与肌⾁和⾻骼⽣长在⼀起,有“⽣物⾦属”之称。
下列有关48Ti和50Ti的说法正确的是( )A.48Ti和50Ti的质⼦数相同,互称同位素B.48Ti和50Ti的质量数不同,属于两种元素C.48Ti和50Ti的质⼦数相同,是同⼀种核素D.48Ti和50Ti的质⼦数相同,中⼦数不同,互称同素异形体知识点⼆化学键⼀、电⼦式1.概念:在元素符号周围⽤“·”或“×”来表⽰原⼦的最外层电⼦(价电⼦)的式⼦。
2.电⼦式的书写(1)原⼦的电⼦式书写原⼦的电⼦式时,⼀般将原⼦的最外层电⼦写在元素符号的上、下、左、右四个位置上。
例如Si P Na Mg(2)简单阳离⼦的电⼦式简单阳离⼦是原⼦失去最外层电⼦后形成的,其电⼦式就是简单阳离⼦的离⼦符号,例如Na+、Mg2+等。
第一章 第三节 民族 基础知识讲解 人教版地理八年级上册

第一章 从世界看中国第三节民族知识点1:中华民族大家庭中华民族悠久的历史和灿烂的文明,是我国各民族共同创造的。
在中华民族大家庭中,各民族文化既相互交融,又多元发展。
(1)语言和文字:大多数民族有民族语言,有些民族有民族文字。
【注】繁体中文,现主要通用于港、澳、台地区。
(2)各民族在建筑、饮食、服饰,风俗、节庆、艺术、体育、宗教等方面的文化精粹,共同组成了中华优秀传统文化,受到世界各国人民的尊重和关注。
乐器举例重大节日或传统活动举例)其他区少数民族的乐器(5)部分民族的特色建筑知识点2:民族分布特点1.民族分布①大杂居:大杂居指汉族和各少数民族分散在全国各地,汇合居住。
②小聚居:小聚居指少数民族主要聚居在边疆地区,且同一民族主要聚居在同一地区。
③交错居住:交错居住指在汉族集中的地区居住着许多少数民族,在某一少数民族聚居区,也有汉族和其他少数民族居住。
我国在少数民族聚居地区实行民族区域自治制度,设置了自治区、自治州、自治县、民族乡等行政区域。
各少数民族在自治区域内行使自治权。
我国的民族政策包括:(1)坚持民族平等和民族团结。
(2)实行民族区域自治制度。
(3)尊重少数民族的风俗习惯和宗教信仰自由。
(4)积极发展少数民族地区的政治,经济、文化事业。
(5)尊重和发展少数民族的语言文字。
3.少数民族地区的发展现状中华人民共和国成立以来,我国民族区域自治地方贯彻国家的民族政策,在政治、经济、社会、文化等方面都取得了长足的进步。
各个民族对国家统一以及国家的经济建设、社会发展、边疆安定都作出了重要贡献。
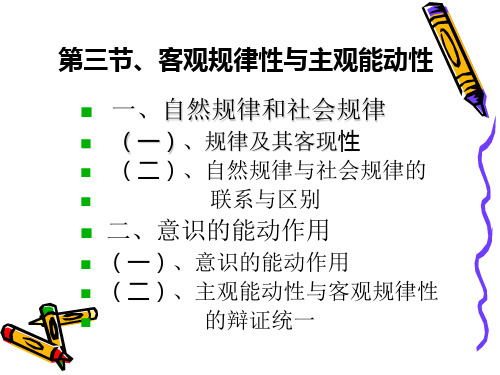
马克思基本原理第一章第三节客观规律性与主观能动性

客观规律性与主观能动性
一、自然规律和社会规律
二、意识的能动作用
1
一、 自然规律和 社会规律
2
讲授内容
(一)规律及其客观性
(二)自然规律与社会规律的联系 与区别
3
(一)规律及其客观性
1、规律的含义 规律是事物本身所固有的本质的、 必然的、稳定的联系。 规律是事物的本质联系 “规律就是关系”, 就是“本质的关系或本质 之间的关系。” 列宁
————中国式的历史唯心主义
21
讨论: 心有多大,舞台就有多大
22
4
规律是事物的必然联系
电流变化引起磁 场变化,磁场变化引 起电流变化。
5
规律是事物的稳定联系
6
2、规律的客观性
规律的客观性是指, 规律是客观事物本身所固 有的,它不以人的主观意 志为转移。
7
2、规律的客观性
罗马教皇可以烧死布鲁 诺,但它永远烧不死“日心 说”。
8
3、规律的层次性
客观规律因其起作用 的范围和层次不同而具有 不同的层次。 个别规律
特殊规律
一般规律
9
(二)自然规律与社会规律的联系与区别
1、自然规律与社会规律的含义 自然规律是自然现象固有的、本质 的、必然的、稳定的联系。 社会规律是通过人们的活动表现出 来的社会生活过程诸现象间的本质的、 必然的、稳定的联系。
10
2、自然规律与社会规律的联系与区别
联系主要表现:自然规律和社会规 律都具有不以人的意志为转移的客观性。 人不能任意改变、创造或消灭自然规律。 区别主要表现:自然规律是作为一 种盲目的无意识的力量起作用,社会规 律则是通过抱有一定目的和意图的人的 有意识的活动实现的。
11
马克思主义基本原理概论 第一章 第三节

第一,要从实际出发,努力认识和把握 事物的发展规律。 第二,实践是发挥人的主观能动性的基 本途径。 第三,主观能动性的发挥,要依赖于一 定的物质条件和物质手段。
2、社会历史趋向与主体选择的关系
社会历史趋向属于历史决定论的内容,讲的是社会历 史规律的决定作用。主体选择讲的是历史主体在社会 历史发展中的能动性和选择性。历史发展的必然性, 规定了人们的活动要受规律性的制约,但不否认人在 可能的空间内的选择。 主体选择是在既定历史条件下对社会生活未来发展的 多种可能的方向、目标、方式的选择。在这当中,社 会生活未来发展存在着多种可能性是主体选择的客观 前提,主体利益和需要是选择的内在根据。马克思主 义历史决定论之所以强调社会历史规律的客观性,是 为了实现主体的正确选择,从而推动社会历史的前进。
第三,规律是事物的稳定联系。规律是变动 不居的现象中相对稳定和巩固的联系。规律 的稳定性突出地表现为它的重复性。就是说, 无论在什么地方、什么时候,只要具备了一 定的客观条件,就必然会表现出某种特定的 自然过程和规律,某种合乎规律的现象就必 定会重复出现。 第四,规律是客观的。客观性是规律的根本 特点,它不依赖于人的意识而存在。唯心主 义否认规律的客观性。人们在实践中可以发 现、认识和利用规律,但不能创造和消灭规 律。
自然规律可以完全相同的形式反复出现而社会规律则是历史的在不同社会国家民族以及不同的历史阶段具有不同的表现形二意识的能动作用辩证唯物主义认为
化工原理课件 第一章第三节

如图所示,设有上、下两块面积很大且相距 很近的平行平板,板间充满某种静止液体。 若将下板固定,而对上板施加一个恒定的外 力,上板就以恒定速度u沿x方向运动。 若u较小,则两板间的液体就会分成无数平行 的薄层而运动,粘附在上板底面下的一薄层流体 以速度u随上板运动, 其下各层液体的速度 依次降低,紧贴在下 板表面的一层液体, 因粘附在静止的下板 上, 其速度为零,两平 板间流速呈线性变化。
随着流体的向前流动,流速受影响的区域逐 渐扩大,即在垂直于流体流动方向上产生了速度 梯度。 流动边界层:存在着较大速度梯度的流体层区 域,即流速降为主体流速的99% 以内的区域。
边界层厚度:边界层外缘与壁面间的垂直距离。
流体在平板上流动时的边界层: 如图1-26所示, 由于边界层的形成,把沿壁面 的流动分为两个区域:边界层区和主流区。
二、流体的粘度 (动力粘度)
1.粘度的物理意义
流体流动时在与流动方向垂直的方向上产 生单位速度梯度所需的剪应力。 粘度总是与速度梯度相联系,流体只有在运 动时才显现出来。分析静止流体的规律时就不用 考虑粘度这个因素。 粘度的物理本质:分子间的引力和分子的运动与 碰撞。
讨论 :
μ=f(p,T) T位时间通过单位截面积流体的质量;
μu/d 与流体内的黏滞力成正比。
u /( u / d )
2
du
Re
Re 数实际上反映了流体流动中惯性力与
黏滞力的比。标志着流体流动的湍动程度。 当惯性力较大时, Re 数较大;
当黏滞力较大时, Re 数较小;
一、层流时的速度分布 实验和理论分析都已证明,层流时的速度分 布为抛物线形状,如图1- 23所示。以下进行理论 推导。
物理单位制:
第一章 第三节 电气控制原理图

KM SB
不能点动! 不能点动!
30
4、多电动机的连锁控制线路 1) 两台电动 机的互锁 (a) 工 作 互 锁 , 可同时停车
其关键在于:IKM的常开触点串接在2KM的控制回路中。 其关键在于:IKM的常开触点串接在2KM的控制回路中。 的常开触点串接在2KM的控制回路中
7
A QC FU KM
B C 停车 按钮 SB1 C' B' KM 自保持 起动 按钮 SB2 KM
自保( 自保(锁)的作用
按下按钮(SB),线圈(KM)通电, 按下按钮(SB),线圈(KM)通电, ),线圈 M 3~ 电机起动;同时,辅助触头(KM)闭合, 电机起动;同时,辅助触头(KM)闭合, 即使按钮松开,线圈保持通电状态, 即使按钮松开,线圈保持通电状态,电机 连续运转。 连续运转。
机械互锁
SB1
A B C QC FU KMF KMR
FR KMR KMF
SBF
SBR
KMF KMR KMF KMR
电器互锁
FR
M 3~
双保险
机械互锁(复合按钮) 机械互锁(复合按钮) 电器互锁(互锁触头) 电器互锁(互锁触头)
26
继电器—接触器自动控制的基本线路 接触器自动控制的基本线路2 二、继电器 接触器自动控制的基本线路2 3.点动控制线路 还有一种调整工作状态,要求是一点一动, 还有一种调整工作状态,要求是一点一动, 即按一次按钮动一下,连续按则连续动, 即按一次按钮动一下,连续按则连续动,不按 则不动,这种动作常称为“点动” 点车” 则不动,这种动作常称为“点动”或“点车”。
11
自动空气断路器(自动开关) 自动空气断路器(自动开关)
第一章 第三节 中国的世界遗产

应用体验不可少 我国“三江并流”由三条河流并肩流过云南省西北部,因 其气势磅礴形成独特的地理景观,被列为世界遗产地。读图, 完成1~2题。
1.图中的河流,其上游属于“三江并流”自然遗产地的是 ( )
A.甲、乙
B.乙、丁
C.甲、乙、丙
D.乙、丙、戊
2.下列选项中,属于“三江并流”自然遗产地核心景观的是( )
①高山湖泊 ②火山锥 ③峡谷 ④冰川 ⑤地堑
A.①②③
B.②③④
C.①③④
D.③④⑤
解析:第1题,图中甲河为红河,其上游为元江;乙河是湄公河, 在我国境内称澜沧江;丙河为湄南河;丁河为萨尔温江,其上游 段为怒江;戊河为伊洛瓦底江。“三江并流”中的“三江”是指 金沙江、澜沧江和怒江。第2题,三江的源地位于青藏高原区,有 高山湖泊和山地冰川分布;三江流经横断山区,山高谷深。 答案:1.B 2.C
—————— 重点难点掌握好 ——————— 一、中国世界遗产的价值体现(以泰山为例) 泰山具有作为文化遗产的历史文化价值,作为自然遗产的 美学、科学价值,作为旅游资源还具有经济价值。 泰山把富有美学、科学与历史文化价值的自然景观与人文 景观融为一体,成为我国乃至全人类珍贵的遗产,于 1987 年被 联合国教科文组织作为文化和自然遗产列入《世界遗产名录》。 泰山的突出价值如下表所示:
三清山
所在省级 行政单位
四川 云南、贵 州、广西
江西
简要说明
包括卧龙、四姑娘山、夹金山脉, 面积9245km2 包括云南石林、贵州荔波、重庆 武隆,有着多样的喀斯特地貌 国家重点风景名胜区。景区内千 峰竞秀、万壑奔流、古木茂盛、 珍禽栖息。同时又是一座具有 1 600余年历史的道教名山
项目
所在省级 行政单位
第一章第三节昼夜交替和时差

思考: 中国的领土共跨越了五个时区, 那中国是不是有五个不同的时间 表呢?
特别的计时方法: 在实际生活中,在分区计时 • 12 的基础上,世界各国根据本国 的具体情况,采用了一些特别 的计时方法: ① 有的国家根据领土跨越 经度广泛的实际,不同的时区 分别采用不同的区时作为标准 时间;
② 有的国家为了国内各地联系 方便,统一采用首都所在地的区 时; ③ 还有的国家为了充分利用太 阳照明,将本国东部时区的中央 经线的地方时作为全国统一使用 的时间标准;
晨昏线由晨线(半圆)和昏线 (半圆)两部分组成;顺着地球自 转方向,由夜半球过渡到昼半球的 分界线为晨线,由昼半球过渡到夜 半球的分界线为昏线;晨昏线的太 阳高度为0,晨线上的所有地点正 值日出,昏线上的所有地点正值日 落。
昼夜弧:晨昏线把所经过的纬线 分割成昼弧和夜弧;
二、昼夜交替现象 (1)产生原因:①地球是一个既 不发光也不透明的球体;②地球不 停地自转; (2)昼夜交替的周期:一个太阳 日,24h,因此,太阳日被作为基 本的时间单位;
172.5 °E
180 °
172.5 °W
加一天 东12区
西12区 减一天
例题6: 北京时间早晨六点钟,一位老太太 手中拿着一张过期(兑奖日期在昨天 )的国际中奖彩票,捶胸顿足,非常 难过,聪明的你能让这张彩票“死而 复生”吗?
(2)0时经线(自然日界线) 含义:地球上的日期最多存在 两天,分界线一条是人为规定的 日界线(理论上为180°经线) ;另一条是自然日界线,即地方 时为0时或24时所在的经线。
(4)日界线的实际应用 ①判定日期 顺着地球的自转方向,从180°经 线 至0时所在经线的范围为旧的一天 的区域;逆着地球的自转方向,从 180°到0时所在经线的范围为新的 一天的区域;
第一章第三节影响幼儿社会性发展的因素

第三节影响幼儿社会性发展的因素一、幼儿自身的气质气质是一个人所特有的心理活动的动力特征,是人的个性和社会性发展的生物基础,它是高级神经活动类型的外在表现。
(一)气质概述1.气质类型的生理基础:高级神经活动类型2.气质的类型:胆汁质、多血质、粘液质、抑郁质(二)气质对幼儿社会性发展的影响1.气质对社会认知的影响:林崇德研究发现,多血质和胆汁质的幼儿解题速度和灵活性都明显超过粘液质和抑郁质的幼儿。
多血质和胆汁质的情绪和情感表现都比较强烈,而他们的抑制力又较差,因此比较难以从事需要细致和持久的智力活动;(开拓创新类工作)而粘液质和抑郁质的人其情绪情感表现都比较弱,但体验深刻,能经常分析自己,因此他们比较适合从事那些需要细致和持久的智力活动。
(科研活动)2.气质对幼儿性别角色的影响所谓性别角色,是指特定社会对男性和女性社会成员所期待的适当行为的总和。
性别社会化是指在特定的文化中,幼儿获得适合于某一性别的价值观、动机和行为的过程。
幼儿在2岁左右就初步形成了一些性别角色意识。
男孩的性别角色知识发展的速度高于女孩,也比女孩更丰富和详细。
在社会行为方面,女孩对年幼男童的抚养性行为显著多于男孩,而男孩的支配和攻击性行为多于女孩。
与父母交往方面,男孩对父母的管教较多表现出抗议、不依从的行为,女孩则较容易与父母形成积极的互动关系。
3.气质对亲子关系的影响(1)影响父母的反应性和敏感性。
易抚养型幼儿的气质特点会对亲子关系产生积极的影响,难抚养型幼儿的气质特点会对亲子关系产生消极影响。
(2)影响学前幼儿的依恋模式。
4.气质对道德品质的影响近年来的研究表明,气质是良心发展的生物基础,特别是唤醒水平对良心有重要作用。
二、认知发展水平幼儿的认知能力和思维方式影响着他们对人对事的理解。
研究表明幼儿不能协调自己和客体之间的关系,缺乏社会经验和知识,对事物的认识和理解存在很大的受暗示性,还不能理解道德概念的实质,认识易受具体形象和情景的感染,模仿性很强,对自己感兴趣的事才会主动去做,对自己喜欢和尊敬的人尤其是老师所提出的要求回坚决遵从。
第一章 第三节 合伙企业法

与第三人的关系
合伙企业对合伙人执行合伙事务及对外代 表合伙企业权利的限制,不得对抗善意第 三人。
入伙、退伙
入伙
协议—须经全体合伙人一致同意+书面入伙协议; 新入伙人对入伙前合伙企业债务无限连带。
退伙 自愿退伙 协议退 -约定合伙期限 通知退(提前30日) 当然退 除名退(其他合伙人一致同意)
法定退伙
出资
• 货币 • 实物、知识产权、土地使用权或者其他财 产权利 • 劳务出资——全体合伙人协商确定
(二)普通合伙企业的财产
1、财产性质 共有财产 合伙人的出资 企业收益 依法取得的其他财产
2、财产转让 对外转让 其他合伙人一致同意,优先购买权 对内转让 通知其他合伙人 3、出质 其他合伙人一致同意。否则行为人承担赔偿责任。
清算程序
全体合伙人担任清算人或指定 清算人职责 清偿顺序: 清算费用 工资和社保 税款 债务 出资 注销后债务承担:原普通合伙共同管理和使用。 对合伙财产的占有、使用、收益、处分, 均应依据全体合伙人的共同意志进行;
归合伙人共同所有 2)合伙人在合伙企业解散前,不得请求
分割合伙企业的财产。
• 出质,也就是质押,分动产质押和权利质 押,就是把自己所有的物品或权利交付出 去作为抵押。出质在质押行为中,是指债 务人或第三人(出质人)将其动产或权利移 交给债权人的民事法律行为。
(五)有人与普人的转化
普人和有人的互变,全体合伙人一致同意。 有人变普人,对有人期间债务无限连带; 普人变有人,对普人期间债务无限连带。
四、合伙企业解散和清算
解散情形
七种
清算费用,是指清算过程中 所发生的各项费用支出,包 括清算组人员工资、办公费、 公告费、差旅费、诉讼费、 审计费、公证费、财产估价 费和变卖费等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三节 化学反应热的计算[学习目标定位] 1.知道盖斯定律的内容,能用盖斯定律进行有关反应热的简单计算。
2.学会有关反应热计算的方法技巧,进一步提高化学计算的能力。
一 盖斯定律1.在化学科学研究中,常常需要通过实验测定物质在发生化学反应的反应热。
但是某些反应的反应热,由于种种原因不能直接测得,只能通过化学计算的方式间接地获得。
通过大量实验证明,不管化学反应是一步完成或分几步完成,其反应热是相同的。
换句话说,化学反应的反应热只与反应体系的始态和终态有关,而与反应的途径无关,这就是盖斯定律。
2.从能量守恒定律理解盖斯定律从S →L ,ΔH 1<0,体系放出热量; 从L →S ,ΔH 2>0,体系吸收热量。
根据能量守恒,ΔH 1+ΔH 2=0。
3.根据以下两个反应:C(s)+O 2(g)===CO 2(g) ΔH 1=-393.5kJ·mol -1CO(g)+12O 2(g)===CO 2(g) ΔH 2=-283.0kJ·mol -1根据盖斯定律,设计合理的途径,计算出C(s)+12O 2(g)===CO(g)的反应热ΔH 。
答案 根据所给的两个方程式,反应C(s)+O 2(g)===CO 2(g)可设计为如下途径:ΔH 1=ΔH +ΔH 2 ΔH =ΔH 1-ΔH 2=-393.5kJ·mol -1-(-283.0kJ·mol -1)=-110.5kJ·mol -1。
4.盖斯定律的应用除了“虚拟路径”法外,还有热化学方程式“加合”法,该方法简单易行,便于掌握。
试根据上题中的两个热化学方程式,利用“加合”法求C(s)+12O 2(g)===CO(g)的ΔH 。
答案 C(s)+O 2(g)===CO 2(g) ΔH 1=-393.5kJ·mol -1CO 2(g)===CO(g)+12O 2(g) ΔH 2′=+283.0kJ·mol -1上述两式相加得:C(s)+12O 2(g)===CO(g) ΔH =-110.5kJ·mol -1。
盖斯定律的应用方法(1)“虚拟路径”法若反应物A 变为生成物D ,可以有两个途径 ①由A 直接变成D ,反应热为ΔH ;②由A 经过B 变成C ,再由C 变成D ,每步的反应热分别为ΔH 1、ΔH 2、ΔH 3。
如图所示:则有ΔH =ΔH 1+ΔH 2+ΔH 3。
(2)“加合”法运用所给热化学方程式通过加减乘除的方法得到所求的热化学方程式。
先确定待求的反应方程式⇒找出待求方程式中各物质在已知方程式中的位置⇒根据待求方程式中各物质的计量数和位置对已知方程式进行处理,得到变形后的新方程式⇒将新得到的方程式进行加减(反应热也需要相应加减)⇒写出待求的热化学方程式 关键提醒 运用盖斯定律计算反应热的3个关键 (1)热化学方程式的化学计量数加倍,ΔH 也相应加倍。
(2)热化学方程式相加减,同种物质之间可加减,反应热也相应加减。
(3)将热化学方程式颠倒时,ΔH 的正负必须随之改变。
1.已知下列反应:SO 2(g)+2OH -(aq)===SO 2-3(aq)+H 2O(l) ΔH 1ClO -(aq)+SO 2-3(aq)===SO 2-4(aq)+Cl -(aq) ΔH 2CaSO 4(s)===Ca 2+(aq)+SO 2-4(aq) ΔH 3则反应SO 2(g)+Ca 2+(aq)+ClO -(aq)+2OH -(aq)===CaSO 4(s) +H 2O(l) +Cl -(aq)的ΔH =________。
答案 ΔH 1+ΔH 2-ΔH 3解析 将已知反应依次编号:①SO 2(g)+2OH -(aq)===SO 2-3(aq)+H 2O(l) ΔH 1②ClO -(aq)+SO 2-3(aq)===SO 2-4(aq)+Cl -(aq) ΔH 2③CaSO 4(s)===Ca 2+(aq)+SO 2-4(aq) ΔH 3,则根据盖斯定律可知①+②-③即得到反应:SO 2(g)+Ca 2+(aq)+ClO -(aq) +2OH -(aq)===CaSO 4(s) +H 2O(l) +Cl -(aq)的ΔH ,则ΔH =ΔH 1+ΔH 2-ΔH 3。
技法点拨 盖斯定律的解题模板(加合法)写出目标反应——根据题目要求写出所要求的反应,并注明状态将已知反应变形—根据目标反应中的物质在已知反应中的位置将已知反应变形将变形后的反应相加——将变形后的反应相加得总反应,ΔH 也要相加 2.已知P 4(白磷,s)+5O 2(g)===P 4O 10(s) ΔH 1=-2983.2kJ·mol-1①P(红磷,s)+54O 2(g)===14P 4O 10(s)ΔH 2=-738.5kJ·mol-1②试用两种方法求白磷转化为红磷的热化学方程式。
答案 (1)“虚拟路径”法 根据已知条件可以虚拟如下过程:根据盖斯定律ΔH =ΔH 1+(-ΔH 2)×4=-2983.2kJ·mol -1+738.5kJ·mol -1×4=-29.2kJ·mol -1热化学方程式为P 4(白磷,s)===4P(红磷,s) ΔH =-29.2kJ·mol -1(2)“加合”法P 4(白磷,s)+5O 2(g)===P 4O 10(s) ΔH 1=-2983.2kJ·mol -1P 4O 10(s)===5O 2(g)+4P(红磷,s) ΔH 2′=+2954kJ·mol -1上述两式相加得:P 4(白磷,s)===4P(红磷,s) ΔH =-29.2kJ·mol -1。
二 反应热的计算与比较1.已知:①Zn(s)+12O 2(g)===ZnO(s)ΔH =-348.3kJ·mol -1②2Ag(s)+12O 2(g)===Ag 2O(s)ΔH =-31.0kJ·mol -1则Zn(s)+Ag 2O(s)===ZnO(s)+2Ag(s)的ΔH 等于________________。
答案 -317.3kJ·mol -1解析 根据盖斯定律,将方程式①-②得目标方程式,所以ΔH =-348.3kJ·mol -1-(-31.0kJ·mol -1)=-317.3kJ·mol -1。
2.试比较下列三组ΔH 的大小(填“>”“<”或“=”) (1)同一反应,生成物状态不同时 A(g)+B(g)===C(g) ΔH 1<0 A(g)+B(g)===C(l) ΔH 2<0 则ΔH 1____ΔH 2。
答案 >解析 因为C(g)===C(l) ΔH 3<0 则ΔH 3=ΔH 2-ΔH 1,ΔH 2<ΔH 1。
(2)同一反应,反应物状态不同时 S(g)+O 2(g)===SO 2(g) ΔH 1<0 S(s)+O 2(g)===SO 2(g) ΔH 2<0 则ΔH 1____ΔH 2。
答案 <解析 S(g)――→ΔH 3S(s)――→ΔH 2SΔH 1O 2(g)ΔH 2+ΔH 3=ΔH 1,则ΔH 3=ΔH 1-ΔH 2,又ΔH 3<0,所以ΔH 1<ΔH 2。
(3)两个有联系的不同反应相比 C(s)+O 2(g)===CO 2(g) ΔH 1<0 C(s)+12O 2(g)===CO(g) ΔH 2<0则ΔH 1____ΔH 2。
答案 <解析 根据常识可知CO(g)+12O 2(g)===CO 2(g) ΔH 3<0,又因为ΔH 2+ΔH 3=ΔH 1,所以ΔH 2>ΔH 1。
1.有关反应热计算的依据 (1)根据热化学方程式计算反应热与反应物各物质的物质的量成正比。
(2)根据盖斯定律计算根据盖斯定律,可以将两个或两个以上的热化学方程式包括其ΔH 相加或相减,得到一个新的热化学方程式。
(3)根据物质燃烧放热数值(或燃烧热)计算可燃物完全燃烧产生的热量=可燃物的物质的量×其燃烧热。
(4)根据反应物和生成物的键能计算。
ΔH =反应物的键能和-生成物的键能和。
2.利用状态,迅速比较反应热的大小 若反应为放热反应(1)当反应物状态相同,生成物状态不同时,生成固体放热最多,生成气体放热最少。
(2)当反应物状态不同,生成物状态相同时,固体反应放热最少,气体反应放热最多。
(3)在比较反应热(ΔH )的大小时,应带符号比较。
对于放热反应,放出的热量越多,ΔH 反而越小。
3.室温下,将1mol 的CuSO 4·5H 2O(s)溶于水会使溶液温度降低,热效应为ΔH 1,将1mol 的CuSO 4(s)溶于水会使溶液温度升高,热效应为ΔH 2;CuSO 4(s)·5H 2O(s)受热分解的化学方程式为CuSO 4·5H 2O(s)=====△CuSO 4(s)+5H 2O(l),热效应为ΔH 3。
则下列判断正确的是( ) A .ΔH 2>ΔH 3 B .ΔH 1<ΔH 3 C .ΔH 1+ΔH 3=ΔH 2 D .ΔH 1+ΔH 2>ΔH 3答案 B解析 方法一:“虚拟”路径法。
根据盖斯定律:ΔH 1=ΔH 3+ΔH 2由于ΔH 1>0,ΔH 3>0,ΔH 2<0 所以ΔH 1<ΔH 3。
方法二:方程式叠加法。
CuSO 4·5H 2O(s)===Cu 2+(aq)+SO 2-4(aq)+5H 2O(l)ΔH 1>0①CuSO 4(s)===Cu 2+(aq)+SO 2-4(aq) ΔH 2<0②CuSO 4·5H 2O(s)=====△CuSO 4(s)+5H 2O(l) ΔH 3>0③ ②+③:CuSO 4·5H 2O(s)===Cu 2+(aq)+SO 2-4(aq)+5H 2O(l)ΔH 1=ΔH 2+ΔH 3由于ΔH 1>0,ΔH 2<0,ΔH 3>0,所以ΔH 1<ΔH 3。
4.已知葡萄糖(C 6H 12O 6)的燃烧热是2804kJ·mol -1,当它氧化生成1g 水时放出的热量是( )A .26.0kJB .51.9kJC .155.8kJD .467.3kJ 答案 A解析 1molC 6H 12O 6完全燃烧生成H 2O 为6mol(即6×18g)时放出热量2804kJ ,所以当C 6H 12O 6氧化生成1g 水时放出的热量为2804kJ 6×18g≈26.0kJ 。
