智能小车pid算法
智能车PID的算法推荐
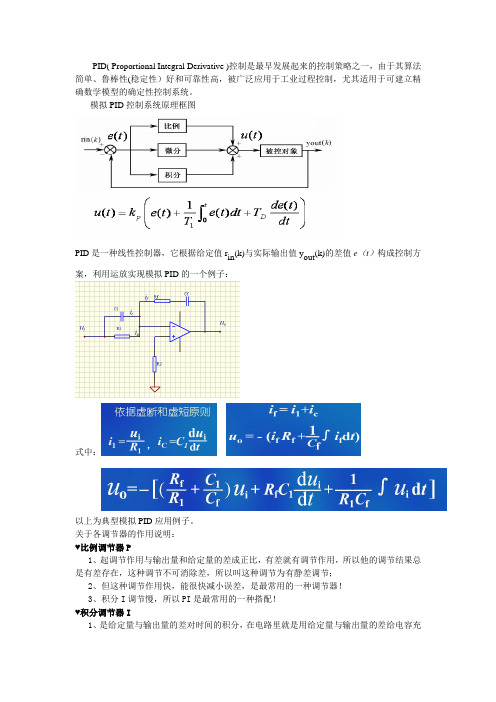
PID( Proportional Integral Derivative )控制是最早发展起来的控制策略之一,由于其算法简单、鲁棒性(稳定性)好和可靠性高,被广泛应用于工业过程控制,尤其适用于可建立精确数学模型的确定性控制系统。
模拟PID控制系统原理框图PID是一种线性控制器,它根据给定值r in(k)与实际输出值y out(k)的差值e(t)构成控制方案,利用运放实现模拟PID的一个例子:式中:以上为典型模拟PID应用例子。
关于各调节器的作用说明:♥比例调节器P1、起调节作用与输出量和给定量的差成正比,有差就有调节作用,所以他的调节结果总是有差存在,这种调节不可消除差,所以叫这种调节为有静差调节;2、但这种调节作用快,能很快减小误差,是最常用的一种调节器!3、积分I调节慢,所以PI是最常用的一种搭配!♥积分调节器I1、是给定量与输出量的差对时间的积分,在电路里就是用给定量与输出量的差给电容充电,只要时间足够长,电容器的电压总会到达给定量,使输出量与给定量的差为零;2、积分调节器是一种无静差调节器,意思是说可调节到给定值,做到精确、准确输出;♥微分控制调节器D1、,这种控制总是以输出量与给定量的差的变化率成正比,差变化越剧烈,调节作用越大,差变化越平稳,调节作用越弱;2、这种微分调节作用,使得输出量平稳而很少波动;3、这种微分调节作用,对输出量的变化、波动产生强烈的阻尼、抑制的作用,就像摩擦力的作用;数字式PID应用:增量式PID的算式为:如果换换成智能车里的方向控制就变为:Pwm_offset=PWMMiddle+PID_P*(error-last_error)+PID_I*(error)+PID_D*(error+pre_error-2*la st_error);其中:error=middle-offset,注意这个公式里的offset应该有正负之分,左右偏移的值互为相反。
这样自然就确定了最后的方向。
智能车PID的算法推荐

PID( Proportional Integral Derivative )控制是最早发展起来的控制策略之一,由于其算法简单、鲁棒性(稳定性)好和可靠性高,被广泛应用于工业过程控制,尤其适用于可建立精确数学模型的确定性控制系统。
模拟PID控制系统原理框图PID是一种线性控制器,它根据给定值r in(k)与实际输出值y out(k)的差值e(t)构成控制方案,利用运放实现模拟PID的一个例子:式中:以上为典型模拟PID应用例子。
关于各调节器的作用说明:♥比例调节器P1、起调节作用与输出量和给定量的差成正比,有差就有调节作用,所以他的调节结果总是有差存在,这种调节不可消除差,所以叫这种调节为有静差调节;2、但这种调节作用快,能很快减小误差,是最常用的一种调节器!3、积分I调节慢,所以PI是最常用的一种搭配!♥积分调节器I1、是给定量与输出量的差对时间的积分,在电路里就是用给定量与输出量的差给电容充电,只要时间足够长,电容器的电压总会到达给定量,使输出量与给定量的差为零;2、积分调节器是一种无静差调节器,意思是说可调节到给定值,做到精确、准确输出;♥微分控制调节器D1、,这种控制总是以输出量与给定量的差的变化率成正比,差变化越剧烈,调节作用越大,差变化越平稳,调节作用越弱;2、这种微分调节作用,使得输出量平稳而很少波动;3、这种微分调节作用,对输出量的变化、波动产生强烈的阻尼、抑制的作用,就像摩擦力的作用;数字式PID应用:增量式PID的算式为:如果换换成智能车里的方向控制就变为:Pwm_offset=PWMMiddle+PID_P*(error-last_error)+PID_I*(error)+PID_D*(error+pre_error-2*la st_error);其中:error=middle-offset,注意这个公式里的offset应该有正负之分,左右偏移的值互为相反。
这样自然就确定了最后的方向。
PID算法在智能车方向控制中的应用

PID算法在智能车方向控制中的应用智能车是指能够感知、分析、决策和执行动作的汽车。
它可以通过集成传感器、图像识别、机器学习和控制算法来实现自主导航和安全驾驶。
在智能车的控制系统中,方向控制是一个重要的组成部分。
PID算法是智能车方向控制中常用的一种算法,它能够通过实时调整车辆转向角度来实现车辆的精确控制。
PID算法是一种反馈控制算法,它通过不断地对系统输出与期望输出的差异进行检测和调整,以实现控制系统的稳定。
PID算法由比例控制、积分控制和微分控制三个部分组成。
比例控制部分根据系统输出与期望输出的差异进行比例调整,积分控制部分根据系统输出与期望输出的累积差异进行积分调整,微分控制部分根据系统输出与期望输出的变化速率进行微分调整。
这三个部分共同作用,通过实时调整控制信号来达到期望输出。
在智能车的方向控制中,PID算法可以通过以下步骤应用:1.传感器数据获取:智能车通常配备了多种传感器,如惯性传感器、陀螺仪和激光雷达等,用于感知车辆的运动状态和周围环境。
PID算法需要读取传感器数据作为反馈信号。
2.设置期望输出:根据预定的路线或目标,可以设置一个期望的转向角度作为系统的期望输出。
3.计算误差:将传感器数据中获取的实际转向角度与期望转向角度进行比较,计算得出误差。
误差可以表示为实际转向角度减去期望转向角度的差异。
4.比例控制:根据误差的大小,比例控制部分会调整控制信号的大小,从而影响车辆的转向角度。
比例系数越大,车辆的响应速度越快,但可能会引起过冲或震荡现象。
5.积分控制:积分控制部分会通过累积误差来调整控制信号,从而消除系统的稳态误差。
积分系数越大,车辆的稳定性越好,但可能会引起过冲现象。
6.微分控制:微分控制部分会通过测量误差的变化率来调整控制信号,从而降低车辆的震荡现象。
微分系数越大,车辆的稳定性越好,但可能会引起过度补偿。
7.发送控制信号:根据比例控制、积分控制和微分控制的结果,生成控制信号并发送给车辆的转向系统,从而实现转向角度的调整。
PID算法

1.Arduino 智能小车寻迹原理寻迹采用的主要原理就是红外探测法,即利用红外线在不同颜色的物体表面具有不同的反射性质的特点Arduino 单片机就是以是否收到反射回来的红外光为依据来确定黑线的位置和小车的行走路线。
红外探测器探测距离有限,一般最大不应超过15cm。
对于发射和接收红外线的红外探头,可以自己制作或直接采用集成式红外探头2.Arduino 寻迹模块简介3.Arduino pwm 调速4.PID算法5.PID 算法与寻迹6.代码:.#include "pid.h"....#ifdef ARDUINO_DEBUG..int debugLeftSpeed;..int debugRightSpeed;..uint8_t debugIrs = 0;..#endif....const float motorSpeed = 140; //小车输出速度..const int IR_PIN[] = {A0, A1, A2, A3, A4}; //寻迹板引脚定义..const int IN_A1 = 7; //..const int IN_A2 = 6; //..const int IN_B1 = 5; //..const int IN_B2 = 4; //..const int _pwmLeftPin = 10;//左边 pwm 引脚..const int _pwmRightPin = 11;//右边 pwm 引脚..pid_t pid;..float pidValue = 0; //pid 值..bool turnFlag = false;....void setup(void)..{..int i;....//设置引脚功能..pinMode(IN_A1, OUTPUT); ..pinMode(IN_A2, OUTPUT); ..pinMode(IN_B1, OUTPUT); ..pinMode(IN_B2, OUTPUT); ....//设置寻迹板引脚为 INPUT..for (i = 0; i < 5; i++) { .pinMode(IR_PIN[i], INPUT);..}......pid.sampleTime = SAMPLE_TIME;//初始化采样时间..pid.Kp = KP_VALUE;..pid.Ki = KI_VALUE;..pid.Kd = KD_VALUE;..pid.error = 0;..pid.previous_error = 0;....Serial.begin(115200);//设置波特率..delay(5000);//延时 5s....analogWrite(_pwmLeftPin, motorSpeed );.analogWrite(_pwmRightPin, motorSpeed ); ....goForward();//小车向前行驶....return;..}........../**..获取寻迹板红外数据..*/..uint8_t getIrData(void)..{..int i, j;..uint8_t level;..uint8_t temp;..uint8_t irs[9] = {0};....//获取10组数据..for (j = 0; j < 9; j ++) {....for (i = 0; i < 5; i++) {..level = digitalRead(IR_PIN[i]); ..if (level) {..bitSet(irs[j], i);//设置对应位为1 ..} else {..bitClear(irs[j], i);//设置对应为0 .}..}..}....//对所有的数据进行排序..for (i = 0; i < 9 - 1; i ++) {..for (j = 0; j < 9 - i - 1; j ++) { ..if (irs[j] > irs[j + 1]) {..temp = irs[j];..irs[j] = irs[j + 1];..irs[j + 1] = temp;..}..}..}...#ifdef ARDUINO_DEBUG..debugIrs = irs[4];..#endif....//返回中间值..return irs[4];..}..../**..计算误差值..@param irs :获取的寻迹传感器的值..*/..int calcErrorByIrsValue(uint8_t irs) ..{..int curError = pid.error;....switch (irs) {..case B11110: curError = -8; break; ....case B10000:..case B11000: curError = -7; break; ....case B11100: curError = -6; break; ..case B11101: curError = -4; break; ..case B11001: curError = -2; break; ....case B00000:..case B11011: curError = 0; break; ...case B10011: curError = 2; break;..case B10111: curError = 4; break;..case B00111: curError = 6; break;....case B00011:..case B00001: curError = 7; break;....case B01111: curError = 8; break;..case B11111: curError = pid.error > 0 ? 9 : - 9; break; ..}....return curError;..}...../**..排序函数..*/..void _sortData(int *p, int n)..{..int temp;..int i, j;....for (i = 0; i < n - 1; i ++) {..for (j = 0; j < n - i - 1; j ++) { ..if (p[j] > p[j + 1]) {..temp = p[j];..p[j] = p[j + 1];..p[j + 1] = temp;..}..}..}....return;..}....../**..计算误差值..*/..void calcCurrentError(void) ..{..int i;..uint8_t irs;.float sum = 0;..int errorData[10];....//获取 10组数据..for (i = 0; i < 10; i ++) {..irs = getIrData();..errorData[i] = calcErrorByIrsValue(irs); ..}...._sortData(errorData, 10);....for (i = 1; i < 10 - 1; i ++) {..sum += errorData[i];..}...pid.error = sum / 8;....return;..}....void turnRight(void)..{..digitalWrite(IN_A1, LOW); ..digitalWrite(IN_A2, HIGH); ..digitalWrite(IN_B1, HIGH); ..digitalWrite(IN_B2, LOW); ..}....void turnLeft(void)..{..digitalWrite(IN_A1, HIGH); ..digitalWrite(IN_A2, LOW); ..digitalWrite(IN_B1, LOW); ..digitalWrite(IN_B2, HIGH); ..}....void goForward(void)..{..digitalWrite(IN_A1, HIGH); ..digitalWrite(IN_A2, LOW); ..digitalWrite(IN_B1, HIGH); ..digitalWrite(IN_B2, LOW); ..}.../**..小车控制函数..@param pidValue : 计算出来的 pid 值..@param turnFlag : 方向标志..*/..void motorControl(float pidValue, bool turnFlag)..{....int leftMotorSpeed = 0;..int rightMotorSpeed = 0;....//根据 pid 的值调整小车左右电机的速度..leftMotorSpeed = constrain((motorSpeed + pidValue), -255, 255); ..rightMotorSpeed = constrain((motorSpeed - pidValue), -255, 255); ...//当转弯标志被设置时,则需要使用左边与右边的轮子正转与反转来调整,提高调整速度..if (turnFlag) {..//按照较大的 pwm 值进行调整,速度最快,左边速度与右边速度一致..if (abs(leftMotorSpeed) > abs(rightMotorSpeed)) {..leftMotorSpeed = abs(leftMotorSpeed);..rightMotorSpeed = leftMotorSpeed;..} else {..rightMotorSpeed = abs(rightMotorSpeed);..leftMotorSpeed = rightMotorSpeed;..}..} else {..//当速度为正时,则取原值,当速度为负时,则取相反数,保持 pwm 的值为正值..leftMotorSpeed = leftMotorSpeed > 0 ? leftMotorSpeed : -leftMotorSpeed; ..rightMotorSpeed = rightMotorSpeed > 0 ? rightMotorSpeed : -rightMotorSpeed; ..}....analogWrite(_pwmLeftPin, leftMotorSpeed ); ..analogWrite(_pwmRightPin, rightMotorSpeed); ....#ifdef ARDUINO_DEBUG..debugLeftSpeed = leftMotorSpeed ;..debugRightSpeed = rightMotorSpeed;..#endif....return;..}..../***..计算 pid 的值.*/..bool calculatePid(float *pValue)..{..float P = 0;..static float I = 0 ;..float D = 0 ;..static unsigned long lastTime = 0; ..unsigned long now = millis();..int timeChange = now - lastTime; ....//没有到达采样时间..if (timeChange < pid.sampleTime) { ..return false;..}...P = pid.error;//错误值..I = I + pid.error;//积累误差..D = pid.error - pid.previous_error;//计算错误的变化率....*pValue = (pid.Kp * P) + (pid.Ki * I) + (pid.Kd * D) + 1; ..*pValue = constrain(*pValue, -motorSpeed,motorSpeed);....pid.previous_error = pid.error;..lastTime = now;....return true;..}....#if ARDUINO_DEBUG..void print_debug()..{..int i;..String irs2bin = String(debugIrs, 2); ..int len = irs2bin.length();..if (len < 5) {..for (i = 0; i < 5 - len; i++) {..irs2bin = "0" + irs2bin;..}..}....Serial.print("IRS : ");..Serial.print(irs2bin);..Serial.print(" ML:");..Serial.print(debugLeftSpeed);..Serial.print(" MR:");..Serial.print(debugRightSpeed);..Serial.print(" ERROR:");..Serial.print(pid.error, OCT);..Serial.println();..}..#endif..../**..计算运动方向..*/..void calcDirection(void)..{....if (pid.error >= 7 && pid.error <= 9) {..turnLeft();..turnFlag = true;..} else if (pid.error >= -9 && pid.error <= -7) { ..turnRight();..turnFlag = true;..} else {..goForward();..turnFlag = false;..}....return;..}....void loop(void)..{..bool ok;..float pidValue;....//计算错误值..calcCurrentError();..//计算 pid 的值..ok = calculatePid(&pidValue);..if (ok) {..calcDirection();//计算小车运动方向..motorControl(pidValue, turnFlag);//控制电机..}....//delay(500);....#if ARDUINO_DEBUG ..print_debug(); ..delay(1000); ..#endif....return;..}.。
模糊PID控制算法在智能小车中的研究与应用

模糊PID控制算法在智能小车中的研究与应用一、本文概述随着科技的快速发展和智能化水平的提高,智能小车在各个领域的应用越来越广泛,如无人驾驶、物流运输、环境监测等。
然而,智能小车的运动控制是一个复杂的问题,需要解决路径规划、避障、速度控制等多个方面的问题。
其中,速度控制是智能小车运动控制的核心问题之一。
传统的PID控制算法在速度控制方面有着广泛的应用,但由于其对于系统参数变化的敏感性,使得其在实际应用中往往难以达到理想的控制效果。
因此,本文提出了一种基于模糊PID控制算法的智能小车速度控制方法,旨在提高智能小车的运动控制精度和稳定性。
本文首先对模糊PID控制算法的基本原理和特点进行了介绍,然后详细阐述了模糊PID控制算法在智能小车速度控制中的应用方法。
在此基础上,通过实验验证了模糊PID控制算法在智能小车速度控制中的有效性和优越性。
本文的研究工作不仅为智能小车的运动控制提供了一种新的方法,同时也为模糊PID控制算法在其他领域的应用提供了有益的参考。
接下来,本文将从模糊PID控制算法的基本原理、智能小车的运动控制模型、模糊PID控制算法在智能小车速度控制中的应用方法、实验结果与分析等方面展开详细的阐述。
二、模糊PID控制算法的基本原理模糊PID控制算法是一种结合了模糊逻辑和传统PID控制算法的控制策略。
该算法利用模糊逻辑处理PID控制中的非线性、不确定性和复杂性问题,从而提高了系统的鲁棒性和控制精度。
模糊逻辑是一种基于模糊集合和模糊推理的控制系统设计方法。
在模糊逻辑中,变量不再局限于具体的数值,而是可以在一定的范围内取任意值,这种变量被称为模糊变量。
模糊逻辑通过模糊集合和模糊运算,能够处理不确定性、非线性和不精确性等问题,使系统更加适应复杂环境。
PID控制算法是一种经典的闭环控制算法,由比例(P)、积分(I)和微分(D)三个部分组成。
PID控制器通过比较实际输出与期望输出的偏差,根据偏差的大小和方向,调整控制量以实现系统的稳定控制。
PID算法原理及调整规律

PID算法原理及调整规律一、PID算法简介在智能车竞赛中,要想让智能车根据赛道的不断变化灵活的行进,PID算法的采用很有意义。
首先必须明确PID算法是基于反馈的。
一般情况下,这个反馈就是速度传感器返回给单片机当前电机的转速。
简单的说,就是用这个反馈跟预设值进行比较,如果转速偏大,就减小电机两端的电压;相反,则增加电机两端的电压。
顾名思义,P指是比例(Proportion),I指是积分(Integral),D指微分(Differential)。
在电机调速系统中,输入信号为正,要求电机正转时,反馈信号也为正(PID算法时,误差=输入-反馈),同时电机转速越高,反馈信号越大。
要想搞懂PID算法的原理,首先必须先明白P,I,D各自的含义及控制规律:比例P:比例项部分其实就是对预设值和反馈值差值的发大倍数。
举个例子,假如原来电机两端的电压为U0,比例P为0.2,输入值是800,而反馈值是1000,那么输出到电机两端的电压应变为U0+0.2*(800-1000)。
从而达到了调节速度的目的。
显然比例P越大时,电机转速回归到输入值的速度将更快,及调节灵敏度就越高。
从而,加大P值,可以减少从非稳态到稳态的时间。
但是同时也可能造成电机转速在预设值附近振荡的情形,所以又引入积分I解决此问题。
积分I:顾名思义,积分项部分其实就是对预设值和反馈值之间的差值在时间上进行累加。
当差值不是很大时,为了不引起振荡。
可以先让电机按原转速继续运行。
当时要将这个差值用积分项累加。
当这个和累加到一定值时,再一次性进行处理。
从而避免了振荡现象的发生。
可见,积分项的调节存在明显的滞后。
而且I值越大,滞后效果越明显。
微分D:微分项部分其实就是求电机转速的变化率。
也就是前后两次差值的差而已。
也就是说,微分项是根据差值变化的速率,提前给出一个相应的调节动作。
可见微分项的调节是超前的。
并且D值越大,超前作用越明显。
可以在一定程度上缓冲振荡。
比例项的作用仅是放大误差的幅值,而目前需要增加的是“微分项”,它能预测误差变化的趋势,这样,具有比例+微分的控制器,就能够提前使抑制误差的控制作用等于零,甚至为负值,从而避免了被控量的严重超调。
小车循迹的pid算法

小车循迹的pid算法小车循迹的PID算法引言:小车循迹是指通过感知地面上的黑线或者白线,使小车能够沿着线路行驶。
为了实现精确的循迹,PID算法被广泛应用于小车循迹控制中。
本文将介绍PID算法的原理和应用于小车循迹的具体实现。
一、PID算法原理PID算法是一种基于反馈控制的算法,其全称为比例-积分-微分控制算法。
其基本原理是通过不断调整输出信号,使系统的输出值尽量接近给定的目标值。
1. 比例控制(Proportional Control):比例控制是根据当前误差的大小来调整输出信号。
当误差较大时,输出信号也会相应增大;当误差较小时,输出信号也会相应减小。
这样可以实现系统的快速响应。
2. 积分控制(Integral Control):积分控制是根据误差的累积值来调整输出信号。
当误差持续存在时,积分项会逐渐增大,从而加大输出信号,以消除积累误差。
积分控制可以解决系统静差的问题。
3. 微分控制(Derivative Control):微分控制是根据误差的变化率来调整输出信号。
当误差的变化率较大时,输出信号也会相应增大;当误差的变化率较小时,输出信号也会相应减小。
微分控制可以提高系统的稳定性和抑制振荡。
二、PID算法在小车循迹中的应用小车循迹是指通过感知地面上的黑线或者白线,使小车能够沿着线路行驶。
PID算法可以根据当前的线路位置误差来调整小车的转向角度,从而实现循迹控制。
1. 感知线路:小车循迹需要通过感知地面上的黑线或者白线来判断当前的位置误差。
通常使用光敏电阻或红外传感器来感知地面的亮度,并将其转换为电信号。
2. 计算误差:根据感知到的线路信息,可以计算出当前的位置误差。
位置误差可以定义为小车当前位置与目标位置之间的距离差。
3. 调整转向角度:根据计算得到的位置误差,可以使用PID算法来调整小车的转向角度。
比例控制项可以根据位置误差的大小来调整转向角度;积分控制项可以消除积累误差,使小车能够更好地沿着线路行驶;微分控制项可以提高系统的稳定性,防止小车出现过大的震荡。
智能车PID的算法推荐

智能车PID的算法推荐智能车PID控制算法是一种常用的控制算法,它通过不断地调整车辆的控制量来实现目标状态与当前状态之间的误差最小化。
PID算法的名称源于它的三个部分:比例(P)、积分(I)和微分(D),而车辆的控制量则是根据这三个部分的权重参数进行计算。
比例项(P)是通过比较目标状态和当前状态的误差得到的,其控制效果是与误差成比例的。
当误差较大时,比例项会产生较大的输出,有助于加快系统响应速度;而当误差较小时,比例项的输出将减小,以减小振荡。
积分项(I)可以追踪已经发生的误差,得到误差的累积项。
它在误差持续存在时提供控制输出,可以在误差较小或者趋于零时,对系统进行微调以消除持久性误差。
微分项(D)是根据误差的变化率来调整系统的输出。
它可以提供一个反馈信号,预测误差的变化趋势,并制定适当的控制输出来减小误差的变化速度,以克服过冲或振荡的问题。
在实际应用中,选择合适的PID权重参数是非常重要的。
通常的做法是先设置P和D的值,然后逐渐增加I的值直到系统稳定。
这个过程可能需要多次试验和微调,以获得最佳的参数组合。
除了基本的PID算法,还有一些改进的PID算法可供选择,其中一些常用的包括:1.增量PID算法:在每个控制周期中,通过计算误差的变化量来更新控制量,以提高控制系统对于误差变化的敏感性。
2.自适应PID算法:根据系统当前状态和性能,动态调整PID参数,以适应不同的工况和外部扰动。
3.模糊PID算法:结合模糊逻辑和PID算法,通过定义模糊规则来调整PID参数,以更好地适应非线性和不确定性系统。
4.基于模型的PID算法:通过对系统动态建模,根据建模结果自动调整PID参数,以提高系统的控制精度和稳定性。
5.改进的积分项算法:针对积分项可能导致的问题(如积分饱和),进行改进和优化,以避免控制系统出现过度响应或不稳定的情况。
6.鲁棒PID算法:通过考虑外部扰动和模型不确定性,设计具有鲁棒性的PID控制器,以提高系统的抗干扰能力和稳定性。
智能车PID算法实现原理讲解

智能车PID算法实现原理讲解引言智能车是一种能够通过传感器收集环境信息,然后分析、决策、控制并实现自主导航的车辆。
PID(Proportional-Integral-Differential)控制算法是智能车中常用的一种控制方法,可以实现对车辆的位置、速度等参数进行精确调节。
本文将对PID算法的实现原理进行详细讲解。
一、PID控制算法原理PID控制算法是一种经典的反馈控制算法,通过对系统的误差进行连续检测和调整,使得系统能够自动调整到期望值附近并保持稳定。
PID算法由三个部分组成:比例控制(P),积分控制(I)和微分控制(D)。
1.比例控制(P)比例控制是基于误差的当前值来进行控制调整的,它通过将误差乘以一个比例系数来调整控制量的变化。
这意味着当误差增大时,控制量的变化也会增大。
2.积分控制(I)积分控制是基于误差的历史累积值来进行控制调整的,它通过将误差的累积值乘以一个积分系数来调整控制量的变化。
这意味着当误差持续存在时,控制量的变化会逐渐增大,从而更好地调整系统。
3.微分控制(D)微分控制是基于误差的变化率来进行控制调整的,它通过将误差的变化率乘以一个微分系数来调整控制量的变化。
这意味着当误差快速变化时,控制量的变化也会被加大。
二、PID算法实现步骤基于PID算法的智能车控制实现需要按照以下步骤进行:1.设定目标值(设定值)和实际值(反馈值)。
目标值为期望的位置或速度,实际值通过传感器获取。
2.计算误差。
误差可以通过将设定值减去实际值得到。
3.计算比例控制量。
比例控制量可以通过将误差乘以比例系数得到。
4.计算积分控制量。
积分控制量可以通过将误差的累积值乘以积分系数得到。
5.计算微分控制量。
微分控制量可以通过将误差的变化率乘以微分系数得到。
6.将比例控制量、积分控制量和微分控制量相加得到最终的控制量。
7.根据最终的控制量来调整车辆的状态,例如调整轮速、转向角度等。
8.循环执行上述步骤,使得车辆能够持续地调整控制量,使得实际值逐渐接近设定值,从而实现稳定的控制。
模糊PID控制算法在智能小车中的研究与应用

模糊PID控制算法在智能小车中的研究与应用模糊PID控制算法在智能小车中的研究与应用摘要:智能小车是一种通过感知、决策和执行等功能实现自主导航的机器人系统。
在智能小车的控制系统中,PID控制算法通常被广泛应用于姿态控制和路径跟踪等方面。
然而,由于PID控制算法依赖于人工设定的参数,对于复杂的非线性系统来说,往往难以取得良好的控制效果。
模糊PID控制算法则结合了模糊逻辑控制和PID控制的特点,具有适应性强、鲁棒性好等优势,因此在智能小车中的研究与应用十分重要。
一、引言智能小车是人工智能领域的一个重要应用方向。
其核心任务是通过传感器收集环境信息,实现自主导航和路径规划,同时在运动过程中保持稳定姿态。
PID控制算法是一种经典的控制算法,在实际应用中具有高效简单的特点。
然而在某些情况下,传统PID控制的控制效果不理想。
因此,研究模糊PID控制算法在智能小车中的应用价值具有重要意义。
二、模糊PID控制算法原理模糊PID控制算法是将模糊逻辑控制与PID控制相结合的一种控制策略。
通过模糊化处理将传感器获取到的环境信息转化为模糊语言变量,然后根据模糊规则和模糊推理机制求取模糊输出,并通过去模糊化处理得到PID控制器的输出信号。
模糊PID控制算法利用了模糊规则的简单性和PID控制算法的高效性,提高了系统的自适应性和鲁棒性。
三、智能小车中的模糊PID控制算法应用在智能小车的控制系统中,模糊PID控制算法可以应用于姿态控制和路径跟踪等方面。
在姿态控制方面,智能小车需要通过控制电机或舵机等执行器,保持平稳的行驶姿态。
传统PID控制算法的参数设定较为困难,容易受到扰动的影响而失去稳定性。
而模糊PID控制算法通过根据模糊规则对车辆姿态进行调整,可以更好地适应不同工况下的姿态调节。
在路径跟踪方面,智能小车需要根据预先规划的路径,在实际行驶中进行修正。
传统PID控制算法容易受到路面不平和弯道等因素的干扰,导致车辆跟踪误差增大。
模糊PID控制算法在智能小车中的研究与应用

模糊PID控制算法在智能小车中的研究与应用智能小车是近年来智能化技术的一项重要应用,模糊PID控制算法作为一种自适应控制算法,被广泛应用于智能小车领域。
本文将从智能小车的研究背景入手,介绍模糊PID控制算法的原理和特点,以及在智能小车中的研究和应用,最后总结并展望未来研究的方向。
一、研究背景智能小车是一种能够自主运动、感知环境并做出决策的机器人,其运动控制是实现智能小车基本功能的核心。
传统的PID控制算法在许多自动控制系统中得到广泛应用,它通过不断地调整比例、积分和微分三个参数来实现系统的稳定控制。
然而,传统PID控制算法的主要问题是在非线性、时变或不确定性的系统中效果不佳。
为了解决这一问题,模糊PID控制算法被引入到智能小车的控制中。
模糊PID控制算法是基于模糊逻辑理论和PID控制理论的结合,通过对系统内外环境进行模糊化表示,将模糊规则集与PID控制算法相结合,从而提高了系统的稳定性和鲁棒性。
二、模糊PID控制算法原理和特点1.模糊化:将系统的输入和输出进行模糊化处理,将连续值转化为模糊变量。
2.模糊规则库构建:根据系统的特性和经验知识,构建一组模糊规则。
3.模糊推理:根据当前的系统输入和模糊规则库,进行模糊推理,得到模糊输出。
4.解模糊化:将模糊输出转化为真实的控制量。
5.输出:将解模糊化得到的控制量输出给被控对象,实现控制。
1.对系统非线性和时变性具有较好的适应性,能够应对实际环境中的各种变化和干扰。
2.理论基础扎实,可以通过专家知识和经验知识来构建模糊规则库,适用于复杂系统。
3.可以处理模糊和不确定性信息,提高了控制系统的稳定性和鲁棒性。
智能小车作为一种自主决策和行动能力的机器人,其控制系统对稳定性要求较高。
模糊PID控制算法在智能小车中得到了广泛的研究和应用。
首先,模糊PID控制算法可以用于智能小车的路径规划和避障。
通过感知环境中的障碍物和目标点,将其模糊化处理,构建模糊规则库,实现智能小车的自主导航和避障功能。
循迹小车pid算法原理

循迹小车pid算法原理循迹小车是一种能够自主行驶并且能够按照指定路径行驶的智能小车。
在实现循迹功能时,PID算法被广泛应用。
PID算法是一种闭环控制算法,通过对系统的误差进行监测和调节,使系统能够快速、准确地响应外部指令,达到期望的控制效果。
PID算法的原理可以简要概括为:比例控制、积分控制和微分控制的结合。
在循迹小车中,PID算法通过不断调整电机的转速来实现循迹的功能。
循迹小车通过传感器获取当前车辆与指定路径的偏差值,也就是当前误差。
这个误差值可以通过两个循迹传感器(通常为红外线传感器)来测量得到。
当车辆偏离路径时,两个传感器所接收到的红外线强度会发生变化,进而产生不同的电压信号。
比例控制是PID算法的第一步,通过测量到的误差值和比例系数Kp的乘积来得到比例修正量。
比例系数Kp用于控制比例修正量的大小,当误差越大时,比例修正量也就越大。
比例修正量的作用是根据误差的大小来调整电机的转速,使车辆尽快回到指定路径。
然而,仅仅使用比例控制会导致循迹小车在靠近指定路径时产生超调现象,也就是车辆会来回摆动,难以稳定在路径上。
为了解决这个问题,需要引入积分控制。
积分控制是PID算法的第二步,通过将误差累加并与积分系数Ki的乘积得到积分修正量。
积分修正量的作用是消除稳态误差,即使车辆偏离路径一段时间后,积分修正量也会逐渐增大,使车辆更容易回到指定路径。
积分系数Ki用于控制积分修正量的增长速度,当误差较大或持续时间较长时,积分修正量也增大。
然而,仅仅使用积分控制会导致循迹小车在接近指定路径时产生振荡现象,也就是车辆会来回摆动,难以稳定在路径上。
为了解决这个问题,需要引入微分控制。
微分控制是PID算法的第三步,通过测量误差的变化率和微分系数Kd的乘积来得到微分修正量。
微分修正量的作用是根据误差的变化率来调整电机的转速,使车辆平稳地接近指定路径。
微分系数Kd 用于控制微分修正量的大小,当误差变化率较大时,微分修正量也就较大。
模糊pid控制算法在智能小车中的研究与应用

模糊pid控制算法在智能小车中的研究与应用
模糊PID控制算法是将模糊逻辑与PID控制相结合的一种控
制方法。
它通过模糊逻辑的模糊化、规则库的设计和模糊推理来根据系统的误差和误差变化率计算出控制器的输出值,从而实现对系统的控制。
在智能小车中,模糊PID控制算法可以应用于车辆的导航和
轨迹跟踪。
智能小车通常需要根据环境中的实时信息进行路径规划和避障,模糊PID控制算法可以根据车辆与目标点之间
的距离、偏离角度以及偏离角度的变化率等信息,计算出车辆的理想速度和转向角度,使其能够精确地跟随目标路径,避免碰撞和偏离轨道。
模糊PID控制算法的研究主要包括模糊化方法、规则库设计
和模糊推理算法等方面。
模糊化方法主要是将系统输入和输出的连续信号转化为模糊集合,常用的方法包括三角隶属函数、高斯隶属函数等。
规则库的设计是模糊PID控制算法的核心,需要根据系统的特点和需求,定义一系列的模糊规则来实现控制目标。
模糊推理算法是根据当前的系统状态和规则库中的模糊规则,通过模糊推理机制计算出控制器的输出值。
模糊PID控制算法在智能小车中的应用可以有效地提高车辆
的自主导航和轨迹跟踪能力,使其能够适应不同的环境和复杂的路况。
同时,模糊PID控制算法具有较好的鲁棒性和适应性,能够处理系统的非线性和不确定性,对于复杂的控制问题有很好的应用前景。
小车循迹的pid算法

小车循迹的pid算法小车循迹的PID算法引言:小车循迹是一种常见的机器人应用场景,它能够通过感知地面上的黑线或其他标记物,实现自动导航。
PID控制算法是循迹小车中常用的控制算法之一,它通过对误差进行反馈调节,使小车能够准确地跟随黑线运动。
本文将介绍PID算法的基本原理及其在循迹小车中的应用。
一、PID控制算法的基本原理PID控制算法是一种经典的反馈控制算法,它由比例(P)、积分(I)和微分(D)三个部分组成。
PID控制器根据当前误差的大小和变化率,计算出一个控制量,用于调节系统的输出,使得误差尽可能接近零。
具体来说,PID控制器的计算公式如下:输出 = Kp * 偏差 + Ki * 积分项 + Kd * 微分项其中,Kp、Ki和Kd分别是比例、积分和微分系数,偏差是当前误差,积分项是历史误差的累加,微分项是误差的变化率。
通过调节这三个系数,可以得到合适的控制效果。
二、PID算法在循迹小车中的应用在循迹小车中,PID算法可以用于控制小车的转向角度,以实现沿着黑线行驶。
具体来说,循迹小车通过感知地面上的黑线,将其转化为电信号输入到PID控制器中。
PID控制器根据当前偏差和偏差的变化率,计算出相应的控制量,用于调节小车的转向角度。
1. 比例控制(P):比例控制是PID控制算法的基础部分,它根据当前偏差的大小,产生一个与偏差成正比的控制量。
在循迹小车中,比例控制可以使小车快速响应偏差,但容易产生震荡。
2. 积分控制(I):积分控制是为了解决比例控制产生的静差问题而引入的,它根据历史偏差的累加,产生一个与偏差累加值成正比的控制量。
在循迹小车中,积分控制可以消除偏差,使得小车能够更加稳定地行驶。
3. 微分控制(D):微分控制是为了解决比例控制产生的震荡问题而引入的,它根据偏差的变化率,产生一个与偏差变化率成正比的控制量。
在循迹小车中,微分控制可以使小车对偏差的变化更加敏感,从而减少震荡。
综合应用:在循迹小车中,PID控制算法通常会综合应用比例、积分和微分控制,以实现更好的控制效果。
智能车速度控制pid(电机闭环控制算法)

智能车速度控制pid(电机闭环控制算法)智能车速度控制pid(电机闭环控制算法)对于智能车的电机闭环控制算法,我之所以标题没有写上智能车电机PID闭环控制算法是因为PID 算法根本就不是特别好的适用于智能车这种变化很快的系统,对于智能车,电机的调速可以说是时时刻刻再进行调速控制的,我上面说描述的经典PID 算法,都是针对一些惰性系统,也就是说是变化比较慢的系统的,所以对于智能车的电机调速采用完完整整的PID 算法,是根本不可取的,及时采用了,你必须要经过一些变换和改进才能使用。
以上的简述只是鄙人自己的看法,如有错误,请各位高手指正。
现在估计您会疑问,PID 不适用于智能车的电机控制,那什么才适用呢?鄙人原来做过智能车,从鄙人本身的理解,P 算法控制电机,也就是比例控制是最好的,反应速度快,控制精度高,不存在积分和微分效应,非常适用于适用于控制周期短的系统,当然,对于一些特殊的逻辑控制算法,可能要采用PD算法,用微分来做补偿,防止震荡和超调。
下面来说下电机控制算法从开始的加入到最终的确定的方法:当然这一切的前提就是安装了编码器,车速有反馈,只有加上编码器,有了反馈,才能组成一个闭环系统。
当然您也可以加上码盘,或者霍尔开关等一切可以返回车速的东西都可以。
(1)首先建议在车速比较慢的时候,采用PID 算法来控制电机,为什么开始要建议您采用PID 呢?主要是为了让您更加深刻理解PID 算法的精髓和调试步骤方法等,有助于以后对控制算法更加深入的研究和书写。
调试PID 三个参数的方法,很多地方都提供了,我在这里简单的说下:首先将ID 参数都变为0,先调整P 比例参数,调整到速度基本上跟您给定的速度差不多,也就是说基本稳定在您给定的脉冲数,当然这个时候会非常的震荡,不要担心,接下来调整I,调整I 的结果就是震荡会消除很多,但是车速会变化缓慢,也就是说会有一些延迟,然后再调整D,调整D 的结果就是增强调节的灵活性和预见性,在给定速度变化的过程中,能够以一个平稳过渡来变换,而且速度可以长时间稳定在给定速度附近,然后PID 三个参数的基本范围就确定了,然后再根据实际的跑车来微调这些参数,当然在您调试PID之前,请仔细阅读PID 理论知识,这样有助于您的调试和理解,。
计算机控制设计PID智能小车

计算机控制设计PID智能小车引言:在现代社会中,智能小车有着广泛的应用,例如自动驾驶汽车、无人机等。
其中,PID(Proportional-Integral-Derivative)控制是一种常见且有效的控制方法,可以使智能小车实现精确的轨迹跟踪和运动控制。
本文将介绍计算机控制设计PID智能小车的原理和实现方法。
一、PID控制原理PID控制是一种反馈控制方法,其基本原理是通过不断调整控制器的输出,使系统的实际输出与期望输出之间的误差不断减小,直到误差趋近于零为止。
PID控制器的输出是根据误差的大小和变化率来计算的,包括比例项、积分项和微分项。
1. 比例项(Proportional term):比例项与误差成正比,用来消除静态误差。
比例项越大,控制器的响应速度越快,但容易产生震荡。
2. 积分项(Integral term):积分项与误差的累积量成正比,用来消除积分误差。
积分项主要解决系统的静态稳态误差问题。
3. 微分项(Derivative term):微分项与误差的变化率成正比,用来消除误差的瞬时变化。
微分项主要解决系统的动态稳定性问题。
通过合理地调整比例、积分和微分的权重,可以得到一个稳定且响应速度较快的PID控制器。
二、实现PID控制的步骤1.确定系统模型:首先需要建立智能小车的数学模型,例如小车的动力学方程和传感器的响应特性。
系统模型的准确性对PID控制的性能有重要影响。
2.参数调整:选择合适的PID参数对系统进行调整。
一种常用的调整方法是试错法,通过不断调整参数,观察系统的响应,并根据实际需求进行优化。
3.实时控制:通过传感器获取实时数据,计算出误差,并根据PID控制算法调整输出。
通过实时调整控制器的输出,智能小车可以实现轨迹跟踪和运动控制。
4.系统稳定性:判断系统的稳定性,保证误差在可容忍的范围内,避免系统产生震荡或不稳定的情况。
三、具体实现步骤1.搭建硬件平台:搭建智能小车的硬件平台,包括电机、传感器、控制器等。
PID算法优化(以平衡小车代码为例)

PID算法优化(以平衡小车代码为例)PID控制是一种常用的反馈控制方法,广泛应用于自动控制系统中。
在平衡小车的代码中,PID算法被用于控制小车的平衡。
本文将以平衡小车代码为例,探讨如何优化PID算法。
优化PID算法的第一步是确定合适的初始参数。
可以使用经验法确定初始参数,然后再进行调整。
例如,可以将初始参数都设置为1,然后观察系统的响应情况,根据实际效果逐步调整。
其次,可以使用自适应或自校正的方法来优化PID算法。
自适应PID算法可以根据系统的实时状态动态调整PID参数,从而提高系统的控制效果。
自校正PID算法可以通过系统的实时反馈信息来判断是否需要调整PID参数,从而提高系统的稳定性和鲁棒性。
此外,可以考虑在PID算法中引入限制项,以避免超出系统能够承受的范围。
例如,在平衡小车代码中,可以限制小车的加速度和角度的变化范围,以防止系统过载或翻倒。
在优化PID算法过程中,还需要考虑系统的实时响应速度和稳定性。
必要时,可以进行系统参数的调整,以提高系统的响应速度和稳定性。
例如,可以调整调节参数的时间常数,改变PID算法的响应速度。
另外,可以考虑使用非线性控制方法来优化PID算法。
非线性控制方法可以更好地适应复杂的控制系统,提高系统的性能。
在平衡小车代码中,可以尝试使用基于神经网络的非线性控制方法,从而提高平衡小车系统的控制精度和稳定性。
最后,需要进行系统的实时监测和调试。
通过对系统的实时监测和调试,可以及时发现和解决问题,进一步提高系统的控制效果。
例如,可以使用PID调试工具对系统的实时响应进行监测和调试,从而找到问题的根源,进行相应的调整和优化。
综上所述,通过确定合适的初始参数、使用自适应或自校正的方法、引入限制项、调整系统参数、使用非线性控制方法和进行实时监测和调试,可以对PID算法进行优化,提高系统的控制效果和稳定性。
在平衡小车代码中,这些优化方法可以帮助实现更精确和稳定的平衡控制。
智能车PID算法实现原理讲解

智能车PID算法实现原理讲解智能车P I D算法实现原理讲解为了实现PID控制所需要的等间隔采样,我们使用了一个定时中断,每2ms进行一次数据采样和PID计算。
与此并行,系统中还设计了一个转速脉冲检测中断,从而实现了转速检测。
为了调试的需要,程序中还在main{}函数中加入了相关的调试代码,这部分代码有最低的优先级,可以在保证不影响控制策略的情况下实现发送调试数据等功能。
检测环节对整个控制系统的质量起到至关重要的作用4.3.2 PID控制调整速度本系统采用的是增量式数字PID控制,通过每一控制周期(10ms)读入脉冲数间接测得小车当前转速vi_FeedBack,将vi_FeedBack与模糊推理得到的小车期望速度vi_Ref比较,由以下公式求得速度偏差error1与速度偏差率d_error。
error1 = vi_Ref– vi_FeedBack; (公式3) d_error = error1 –vi_PreError; (公式4)公式4中, vi_PreError为上次的速度偏差。
考虑到控制周期较长,假设按2.5m/s的平均速度计算,则一个控制周期小车大概可以跑过2.5cm,如果按这种周期用上述PID调节速度,则会导致加速减速均过长的后果,严重的影响小车的快速性和稳定性。
为了解决这个问题,可以在PID调速控制中加入BANG-BANG控制思想:根据error1的大小,如果正大,则正转给全额占空比;如果负大,则自由停车或给一个反转占空比;否则就采用PID计算的占空比。
PID控制算法为了使赛车平滑得保持在黑线中央,即使赛车的偏移量平滑地保持在0,实用了PID控制算法。
P为比例参数,D为微分参数。
基准值为0,PID输入为水平偏移量X0,PID输出为转角,转角方向:向左转为正,向右转为负。
P参数在智能车控制器中表示水平偏差量的权,D参数在智能车控制器中表示水平偏差速度的权。
水平偏差量直接反映了赛车偏离黑线的程度,例如赛车偏向黑线的左边越厉害,则赛车的右转角度将越大。
智能平衡小车与PID控制算法

2020.091概述控制无处不在,无论是控制水杯的水量,还是调节航天飞机飞行的速度等都存在了一个控制的过程。
这篇文章将以智能平衡小车为例,在实现项目的同时,帮助大家了解一种非常经典的控制算法,学习控制算法在系统结构中的作用以及如何使用PID 算法。
从物理原理、系统硬件、软件原理3个角度讲解智能平衡小车系统的设计实现方法,并在软件设计中介绍PID 算法。
2物理原理小车平衡的规律与单摆模型的控制规律很相似,所以可以通过分析单摆模型来类推小车模型的平衡原理。
受力原理图如图1所示。
分析了图1的模型的受力情况可以得知:当摆钟不在垂直平衡位置之时,它便会受一个合力,让模型向平衡位置移动,这个力也就是平衡力,它的大小是F=_mg*sinθ,回复力驱使单摆进行周期运动。
而在现实情况下,单摆会收到空气的阻力,导致单摆会停止在垂直平衡位置,阻力越大单摆达到平衡位置的时间就越短。
而车模就像是一个倒立的钟摆,当物体偏移了一定角度之后,在重力的作用下很快就会倒下。
了解了原理之后就要设计平衡思路了。
如果想要小车平衡,通常的思路有如下两种:(1)使重力的方向改变。
(2)给予系统一个作用力,力的方向要与趋势模型倒塌的力相反。
很显然改变重力方向是不可能的。
因此只能用第二种方法,通过控制小车加减速前后运动自行产生“回复力”最终通过系统控制回复力的大小与方向使得小车保持在平衡状态。
通俗地讲就是:小车往前倒系统就往前加速,小车往后倒时系统就让小车往后加速,进行这两个操作给予系统“平衡力”来使得系统平衡。
3智能平衡小车所需最简硬件3.1STM32f103ARM 微型控制器STM32系列属于其中低端产品,该系列芯片是意法半导体(ST)公司出品,其内核是Cortex-M3。
该系列芯片按片内Flash 的大小可分为3大类:小容量(16K 和32K)、中容量(64K 和128K)、大容量(256K、384K 和512K)。
芯片集成定时器Timer,CAN,ADC,SPI,I2C,USB,UART 等多种外设功能。
智能小车pid算法

通过红外 LED 的电流为 5mA 左右。
采用了 TA0 来发生红外线,不干扰 CPU 的运行:
void TimerAInit()
{ //设置数组,对应频率分别为 38,41,44,48,54,60,67
TACTL |= TASSEL_2 + TACLR + MC_1 ; //TIMER_A 时钟源选为 SMCLK,清 TAR
if(IRE5_IN==0) // 如果接收到的信号为低电平,表明右前方有障碍物 {flag_4 = 1;BarrierData[4]=5-i;} else BarrierData[4]=0; PIRE5_L; // 关闭 5 号传感器 }
if(flag_0||flag_1||flag_2||flag_3||flag_4) {flag=1;} else flag=0;
光的强弱,小车都能稳定地、以大概相同的速度寻光进入车库。
这个问题要是深究下去还有很多值得研究的地方:比如同时有若干个强光
源,小车现在的算法是朝着这些光源合成的几何中心进行,如果要实现朝着光最
强的那个光源行进该采用什么样的算法。
避障算法采用了检测发射红外 LED,读一体化接收头的数据判断障碍物的
位置。这里采用 38Khz 敏感的接收头。为了使小车的检测距离适中,还需调整
}
3.3 串口通信
由于小车采用双核结构,所以就涉及到了两个单片机的通信问题。在整个进
行的过程中,由于两个单片机分工明确,需要通信的地方大概有如下几个地方:
1. 启动时,149 给 425 发送信号,开始计时;
2. 检测到金属时,425 发给 149 计数;
3. 检测到 C 点停车;
4. 车身入库后 149 发给 425 停车,停止计时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Temp_PID=Temp_PID*1/5;
//-1000~+1000 是左右满舵的输出,因此需要除以
0.5
/*单片机浮点运算非常慢,所以用乘 2 除 5 两次定点
运算来替代定点数要先乘后除,才能保证精度,同时要防止溢出,用起来比较麻烦,但 CPU
和内存开销小。*/
return (Temp_PID);
//开启串口 0 收发模块
U0TCTL |= SSEL0;
//选择 ACLK 作为串口波特率时钟源
U0BR1 = 0;
//
U0BR0 = 13;
//分频系数整数部分=13
U0MCTL = 0X6B;
//分频系数小数部分调制=5/8.(2400bps)
P3SEL |= BIT4 + BIT5;
U0CTL &=~ SWRST;
光的强弱,小车都能稳定地、以大概相同的速度寻光进入车库。
这个问题要是深究下去还有很多值得研究的地方:比如同时有若干个强光
源,小车现在的算法是朝着这些光源合成的几何中心进行,如果要实现朝着光最
强的那个光源行进该采用什么样的算法。
避障算法采用了检测发射红外 LED,读一体化接收头的数据判断障碍物的
位置。这里采用 38Khz 敏感的接收头。为了使小车的检测距离适中,还需调整
{flag_2 = 1;BarrierData[2]=5-i;} else BarrierData[2]=0; PIRE3_L; // 关闭 3 号传感器 } // 4 if(flag_3==0) { PIRE4_H ; // 打开 4 号传感器 Delay(34); // 延迟,等待数据稳定
if(IRE4_IN==0) // 如果接收到的信号为低电平,表明右前方有障碍物 {flag_3 = 1;BarrierData[3]=5-i;} else BarrierData[3]=0; PIRE4_L; // 关闭 4 号传感器 } // 5 if(flag_4==0) { Delay(34); PIRE5_H ; // 打开 5 号传感器 Delay(34); // 延迟,等待数据稳定
Last_Position[4]=Last_Position[3];
Last_Position[3]=Last_Position[2];
Last_Position[2]=Last_Position[1];
Last_Position[1]=Last_Position[0];
Last_Position[0]=Position;
//计算比例分量(P)=比例系数*本次位置差
Temp_D=D_coefficient*(Position-Last_Position[5]); //计算微分分量(D)=微分系数
*(本次位置差-前 3 次的位置差)
//注意由于采样比较快,用本次位置-前 3 次位置
才有足够大的控制量
Last_Position[6]=Last_Position[5];
//启动串口
IE1 |= URXIE0;
}
从串口读一个字节数据 char UART0_GetChar(unsigned char *Chr) {
if(UART_InpLen == 0) return (0); _DINT(); UART_InpLen--; *Chr = RX_BUFF[RX_IndexR]; if (++RX_IndexR >= RXBUF_SIZE) { RX_IndexR = 0; } _EINT(); return (1);
影响时设计的一个难点,引导小车的光源时 200W 的灯泡,在实际测试时,由于
白天和晚上环境光的不同,小车的实际 AD 采样值也有差异,会造成小车运行的
不稳定。
不过即使环境光再强烈,在题目要求的场地里也不及灯泡的亮度,该问题
解决方法是先大概感知周围环境的光强,再根据预设的值调整光强系数,自适应
调整电机转速,这样就能保证只要是 200W 的灯泡作为引导光源,无论周围环境
冲过黑线,黑线又偏右。然后控制过程反复,车身是在左右摇摆中向前行走的。
这种摇摆叫做“超调”,超调越大,控制越不稳定,容易出轨。
为了克服惯性,我们除了位置信息之外,还需要知道轨迹的变化趋势。我们
可以用黑线位置的微分值来提前得到变化趋势。用本次位置减去前次位置求出差
值,就大致知道偏移量的变化趋势。将该差值和比例相加后一起作为控制量,即
} }
3.2 寻光,避障算法
题目要求小车到达 C 点之后,在光源引导下避开障碍物进入车库,这就要 求小车同时完成寻光和避障的功能。如果只进行寻光,小车会撞上障碍物,如果 只进行避障,小车也许会离光源越来越远。理论上避障的优先级是要高于寻光的, 因为一旦接触上障碍便宣告失败。所以一旦检测到障碍物,小车会立刻执行避障 动作,一旦传感器环路没有检测到障碍小车就向光源靠拢,这样能够保证小车在 成功避障的条件下逐渐逼近光源,直到走出障碍区之后就能直奔光源而去。这种 算法小车执行寻光避障整体采用了状态机的切换,
if(IRE5_IN==0) // 如果接收到的信号为低电平,表明右前方有障碍物 {flag_4 = 1;BarrierData[4]=5-i;} else BarrierData[4]=0; PIRE5_L; // 关闭 5 号传感器 }
if(flag_0||flag_1||flag_2||flag_3||flag_4) {flag=1;} else flag=0;
}
3.3 串口通信
由于小车采用双核结构,所以就涉及到了两个单片机的通信问题。在整个进
行的过程中,由于两个单片机分工明确,需要通信的地方大概有如下几个地方:
1. 启动时,149 给 425 发送信号,开始计时;
2. 检测到金属时,425 发给 149 计数;
3. 检测到 C 点停车;
4. 车身入库后 149 发给 425 停车,停止计时。
if(Position==-128) return (No_black);
//错误处理(值得改进的地方)
else
{
Temp_I=Position;
for(k=0;k<5;k++)Temp_I+=Last_Position[k];
Temp_I*=I_coefficient;
Tห้องสมุดไป่ตู้mp_P=P_coefficient*Position;
由此可见,通信量并不是很大,而且通信距离不过十几个厘米,所以采用两
个单片机的串口直接相连的方式。全部收发均放在中断中执行,以下是串口
通信的部分程序:
149 串口初始化
UART_Init149()
{
U0CTL |= CHAR;
//异步通讯模式,8 位数据,无校验,1 位停止位
ME1 |= UTXE0 + URXE0;
//2 if(flag_1==0) { Delay(34);
PIRE2_H; // 打开 2 号传感器 Delay(34); // 延迟,等待数据稳定
if(IRE1_IN==0) // 如果接收到的信号为低电平,表明前方有障碍物 {flag_1 = 1;BarrierData[1]=5-i;}
else BarrierData[1]=0; PIRE2_L; } // 3 if(flag_2==0) { PIRE3_H ; // 打开 3 号传感器 Delay(34); // 延迟,等待数据稳定 if(IRE3_IN==0) // 如果接收到的信号为低电平,表明右前方有障碍物
3.1 寻迹算法
采用 PID(PD)控制算法,如果某时刻检测到黑线偏左,就要向左转弯;如果
检测到黑线偏右,就要向右转。偏得越多,就要向黑线方向打越大的转角。这就
是比例控制(P)。
遗憾的是,因为小车有惯性。假设黑线偏左,说明小车偏右了,需要左传舵,
等到小车回到中心的时候,停止转舵,可是小车的惯性会使车身继续左转,直到
通过红外 LED 的电流为 5mA 左右。
采用了 TA0 来发生红外线,不干扰 CPU 的运行:
void TimerAInit()
{ //设置数组,对应频率分别为 38,41,44,48,54,60,67
TACTL |= TASSEL_2 + TACLR + MC_1 ; //TIMER_A 时钟源选为 SMCLK,清 TAR
/*保存前 5 次的位置,以备用。
Temp_PID=Temp_P+Temp_D+Temp_I; //P 分量和 D 分量相加,得到控制量。
if(Temp_PID>5000) Temp_PID=5000; //防止控制量溢出
if(Temp_PID<-5000) Temp_PID=-5000; //控制量-5000~5000 作为左右满舵
可实现提前控制。这就叫做比例微分控制(PD 控制)
