实验报告模板一-自相关性
自相关实验报告

自相关实验报告摘要本实验旨在探究自相关的概念及其在信号处理和时间序列分析中的应用。
通过使用不同的信号样本进行自相关分析,我们可以了解信号之间的相关性以及信号的周期性特征。
本实验使用了Python编程语言进行实现,并使用Markdown文本格式进行输出。
引言自相关是信号处理和时间序列分析中常用的一种方法,用于描述信号的相关性和周期性。
自相关分析可以帮助我们了解信号在不同时间点之间的相关程度,以及寻找信号的周期性特征。
在信号处理领域,自相关常常用于信号的匹配和识别。
在时间序列分析中,自相关可以帮助我们了解时间序列数据的趋势和周期性变化。
因此,掌握自相关分析方法对于理解和应用信号处理和时间序列分析领域的研究具有重要意义。
实验步骤1. 生成信号样本首先,我们需要生成用于自相关分析的信号样本。
在本实验中,我们使用Python的NumPy库生成包含不同频率和振幅的信号样本。
import numpy as np# 生成信号样本def generate_signal(frequency, amplitude, duration, sampling_rate):time = np.arange(0, duration, 1 / sampling_rate) signal = amplitude * np.sin(2 * np.pi * frequency * time)return signal# 设置信号参数frequency = 10 # 频率为10Hzamplitude = 1 # 振幅为1duration = 5 # 信号时长为5秒sampling_rate = 1000 # 采样频率为1000Hz# 生成信号样本signal = generate_signal(frequency, amplitude, duratio n, sampling_rate)2. 计算自相关计算信号样本的自相关函数可以帮助我们分析信号的周期性,并找到信号中的重复模式。
《应用回归分析》自相关性的诊断及处理实验报告

《应用回归分析》自相关性的诊断及处理实验报告
二、实验步骤:(只需关键步骤)
1、分析→回归→线性→保存→残差
2、转换→计算变量;分析→回归→线性。
3、转换→计算变量;分析→回归→线性
三、实验结果分析:(提供关键结果截图和分析)
1.用普通最小二乘法建立y与x1和x2的回归方程,用残差图和DW检验诊断序列的自相关性;
由图可知y与x1和x2的回归方程为:
Y=574062+191.098x1+2.045x2
从输出结果中可以看到DW=0.283,查DW表,n=23,k=2,显著性水平由DW<1.26,也说明残差序列存在正的自相关。
自相关系数,也说明误差存在高度的自相关。
分析:从输出结果中可以看到DW=0.745,查DW表,n=52,k=3,显著性水平 =0.05,dL=1.47,dU=1.64.由DW<1.47,也说明残差序列存在正的自相关。
α
625.0745.02
1121-1ˆ=⨯-=≈DW ρ 也说明误差项存在较高度的自相关。
2.用迭代法处理序列相关,并建立回归方程;
回归方程为:y=-178.775+211.110x1+1.436x2
从结果中看到新回归残差的DW=1.716,
查DW 表,n=52,k=3,显著性水平0.5 由此可知DW 落入无自相关性区
域,说明残差序列无自相关
3.用一阶差分法处理序列相关,并建立回归方程;
从结果中看到回归残差的DW=2.042,根据P 104表4-4的DW 的取值范围来诊断 ,误差项。
实验报告(自相关性)

实验6.美国股票价格指数与经济增长的关系——自相关性的判定和修正一、实验内容:研究美国股票价格指数与经济增长的关系。
1、实验目的:练习并熟练线性回归方程的建立和基本的经济检验和统计检验;学会判别自相关的存在,并能够熟练使用学过的方法对模型进行修正。
2、实验要求:(1)分析数据,建立适当的计量经济学模型(2)对所建立的模型进行自相关分析(3)对存在自相关性的模型进行调整与修正二、实验报告1、问题提出通过对全球经济形势的观察,我们发现在经济发达的国家,其证券市场通常也发展的较好,因此我们会自然地产生以下问题,即股票价格指数与经济增长是否具有相关关系?GDP是一国经济成就的根本反映。
从长期看,在上市公司的行业结构与国家产业结构基本一致的情况下,股票平均价格的变动跟GDP的变化趋势是吻合的,但不能简单地认为GDP增长,股票价格就随之上涨,实际走势有时恰恰相反。
必须将GDP与经济形势结合起来考虑。
在持续、稳定、高速的GDP增长下,社会总需求与总供给协调增长,上市公司利润持续上升,股息不断增加,老百姓收入增加,投资需求膨胀,闲散资金得到充分利用,股票的内在含金量增加,促使股票价格上涨,股市走牛。
本次试验研究的1970-1987年的美国正处在经济持续高速发展的状态下,据此笔者利用这一时期美国SPI与GDP的数据建立计量经济学模型,并对其进行分析。
2、指标选择:指标数据为美国1970—1987年美国股票价格指数与美国GDP数据。
3、数据来源:实验数据来自《总统经济报告》(1989年),如表1所示:表14、数据处理将两组数据利用Eviews绘图,如图1、2所示:图1 GDP数据简图图2 SPI数据简图经过直观的图形检验,在1970-1987年间,美国的GDP 保持持续平稳上升,SPI 虽然有些波动,但波动程度不大,和现实经济相符,从图形上我们并没有发现有异常数据的存在。
所以可以保证数据的质量是可以满足此次实验的要求。
计量经济学自相关性检验实验报告

计量经济学自相关性检验实验报告计量经济学自相关性检验实验报告实验内容:自相关性检验商品进口主要由GDP决定。
为了考察GDP对商品进口的影响,可使用如下模型:;其中,X表示GDP,Y表示商品进口。
下表列出了中国1981--2000商品进口和国内生产总值的统计数据。
资料来源:《中国统计年鉴》一、估计回归方程OLS法的估计结果如下:Y=-8352.304+50.28935X (-2.838588)(17.36553)R2=0.943673,R2=0.940544,SE=7263.295,D.W.=0.870122。
二、进行序列相关性检验(1)图示检验法通过残差与残差滞后一期的散点图可以判断,随机干扰项存在不存在序列相关性。
(2)回归检验法一阶回归检验et=0.583346et-1+εt二阶回归检验et=1.444793et-1-1.172908et-2+εt可见:该模型存在二阶序列相关。
(3)杜宾-瓦森(D.W)检验法由OLS法的估计结果知:D.W.=0.870122。
本例中,在5%的显著性水平下,解释变量个数为2,样本容量为20,查表得dl=1.284,du=1.567,而D.W.=0.870122,小于下限dl=1.284,所以存在自相关性。
(4)拉格朗日乘数(LM)检验法由上表可知:含二阶滞后残差项的辅助回归为:et=668.0079-1.592283X+1.502666et-1-1.145731et-2(0.357417)(-0.822879) (5.825633) (-4.289558)R2=0.679813于是,LM=18×0.679813=12.236634,该值大于显著性水平为5%,自由度为2的χ序列相关性。
2的临界值Χ20.05,由此判断原模型存在2阶三、序列相关的补救(1)广义差分法估计模型由D.W.=0.870122,得到一阶自相关系数的估计值ρ=1-DW/2=0.564939则DY=Y-0.564939*Y(-1), DX=X-0.564939*X(-1);以DY为因变量,DX为解释变量,用OLS法做回归模型,这样就生成了经过广义差分后的模型。
计量经济学实验自相关性

计量经济学实验⾃相关性个⼈收集整理勿做商业⽤途⽬录 (1)⼀、回归模型地筛选 (3)⒈相关图分析 (3)⒉估计模型,利⽤LS命令分别建⽴以下模型 (3)⑴线性模型:LS Y C X (3)⑵双对数模型:GENR LNY=LOG(Y) (4)⑶对数模型:LS Y C LNX (5)⑷指数模型:LS LNY C X (5)⑸⼆次多项式模型:GENR X2=X^2 (6)⒊选择模型 (6)⼆、⾃相关性检验 (7)⒈DW检验; (7)⑴双对数模型 (7)⑵⼆次多项式模型 (7)⒉偏相关系数检验 (8)⒊BG检验 (8)三、⾃相关性地调整:加⼊AR项 (10)⒈对双对数模型进⾏调整; (10)⒉对⼆次多项式模型进⾏调整; (12)⒊从双对数模型和⼆次多项式模型中选择调整结果较好地模型.12四、重新设定双对数模型中地解释变量: (12)⒈检验⾃相关性; (12)⑴模型1 (12)⑵模型2 (13)⒉解释模型地经济含义. (14)⑴模型1 (14)⑵模型2 (15)实验五⾃相关性【实验⽬地】掌握⾃相关性地检验与处理⽅法.【实验内容】利⽤表5-1资料,试建⽴我国城乡居民储蓄存款模型,并检验模型地⾃相关性.【实验步骤】⼀、回归模型地筛选⒈相关图分析SCAT X Y相关图表明,GDP指数与居民储蓄存款⼆者地曲线相关关系较为明显.现将函数初步设定为线性、双对数、对数、指数、⼆次多项式等不同形式,进⽽加以⽐较分析.⒉估计模型,利⽤LS命令分别建⽴以下模型⑴线性模型:LS Y C XDependent Variable: YMethod: Least SquaresDate: 11/26/13 Time: 10:11Sample: 1978 1998Included observations: 21Variable Coefficient Std. Error t-Statistic Prob.C -14984.84 2234.690 -6.705557 0.0000X 92.50748 6.673634 13.86164 0.0000R-squared 0.910014 Mean dependent var 11996.07Adjusted R-squared 0.905278 S.D. dependent var 16346.06S.E. of regression 5030.809 Akaike info criterion 19.97494Sum squared resid 4.81E+08 Schwarz criterion 20.07442Log likelihood -207.7369 F-statistic 192.1450Durbin-Watson stat 0.161491 Prob(F-statistic) 0.000000(-6.706) (13.862)=0.9100 F=192.145 S.E=5030.809⑵双对数模型:GENR LNY=LOG(Y)GENR LNX=LOG(X)LS LNY C LNXDependent Variable: LNYMethod: Least SquaresDate: 11/26/13 Time: 10:15Sample: 1978 1998Included observations: 21Variable Coefficient Std. Error t-Statistic Prob.C -8.075343 0.255516 -31.60412 0.0000LNX 2.958841 0.046096 64.18896 0.0000R-squared 0.995410 Mean dependent var 8.236497Adjusted R-squared 0.995168 S.D. dependent var 1.756767 S.E. of regression 0.122115 Akaike info criterion -1.277311 Sum squared resid 0.283330 Schwarz criterion -1.177832 Log likelihood 15.41176 F-statistic 4120.223Durbin-Watson stat 0.706200 Prob(F-statistic) 0.000000 (-31.604) (64.189)=0.9954 F=4120.223 S.E=0.1221⑶对数模型:LS Y C LNXDependent Variable: YMethod: Least SquaresDate: 11/26/13 Time: 10:16Sample: 1978 1998Included observations: 21Variable Coefficient Std. Error t-Statistic Prob.C -118140.8 18172.70 -6.501005 0.0000LNX 23605.82 3278.412 7.200384 0.0000R-squared 0.731811 Mean dependent var 11996.07 Adjusted R-squared 0.717696 S.D. dependent var 16346.06 S.E. of regression 8685.043 Akaike info criterion 21.06698 Sum squared resid 1.43E+09 Schwarz criterion 21.16646 Log likelihood -219.2033 F-statistic 51.84553Durbin-Watson stat 0.137170 Prob(F-statistic) 0.000001 (-6.501) (7.200)=0.7318 F=51.8455 S.E=8685.043⑷指数模型:LS LNY C XDependent Variable: LNYMethod: Least SquaresDate: 11/26/13 Time: 10:17Sample: 1978 1998Included observations: 21Variable Coefficient Std. Error t-Statistic Prob.C 5.318459 0.224260 23.71558 0.0000X 0.010005 0.000670 14.93874 0.0000R-squared 0.921541 Mean dependent var 8.236497 Adjusted R-squared 0.917412 S.D. dependent var 1.756767S.E. of regression 0.504862 Akaike info criterion 1.561329Sum squared resid 4.842825 Schwarz criterion 1.660807Log likelihood -14.39396 F-statistic 223.1660Durbin-Watson stat 0.142738 Prob(F-statistic) 0.000000(23.716) (14.939)=0.9215 F=223.166 S.E=0.5049⑸⼆次多项式模型:GENR X2=X^2LS Y C X X2Dependent Variable: YMethod: Least SquaresDate: 11/26/13 Time: 10:18Sample: 1978 1998Included observations: 21Variable Coefficient Std. Error t-Statistic Prob.C 2944.560 785.8976 3.746747 0.0015X -44.54846 5.409513 -8.235208 0.0000X2 0.196604 0.007595 25.88588 0.0000R-squared 0.997646 Mean dependent var 11996.07Adjusted R-squared 0.997384 S.D. dependent var 16346.06S.E. of regression 835.9792 Akaike info criterion 16.42665Sum squared resid 12579501 Schwarz criterion 16.57587Log likelihood -169.4798 F-statistic 3814.274Durbin-Watson stat 1.247903 Prob(F-statistic) 0.000000(3.747) (-8.235) (25.886)=0.9976 F=3814.274 S.E=835.979⒊选择模型常数项都通过了检验,模型都较为显著.反,残差先呈连续递增趋势⽽后⼜转为连续递减趋势,因此,可以初步判断这两种函数形式设置是不当地.⽽且,这两个模型地拟合优度也较双对数模型和⼆次多项式模型低,所以⼜可舍弃线性模型和指数模型.双对数模型和⼆次多项式模型都具有很⾼地拟合优度,因⽽初步选定回归模型为这两个模型.⼆、⾃相关性检验⒈DW检验;⑴双对数模型Variable Coefficient Std. Error t-Statistic Prob.C -8.075343 0.255516 -31.60412 0.0000LNX 2.958841 0.046096 64.18896 0.0000 Durbin-Watson stat 0.706200 Prob(F-statistic) 0.000000因为n=21,k=1(平时地k只包含x个数,查表地时候k是x+c地个数,所以查表要查k=2),取显著性⽔平=0.05时,查表(P361)得=1.22,=1.42,⽽0<0.7062=DW<(P125),所以存在(正)⾃相关.⑵⼆次多项式模型Durbin-Watson stat 1.247903 Prob(F-statistic) 0.000000=1.22,=1.42,⽽<1.2479=DW<,所以通过DW检验并不能判断是否存在⾃相关.⒉偏相关系数检验在⽅程窗⼝中点击View/Residual Test/Correlogram-Q-statistics,并输⼊滞后期为10(表⽰显⽰⼏项),则会得到残差与地各期相关系数和偏相关系数,如图5-11、5-12所⽰.图5-1 双对数模型地偏相关系数检验图5-2 ⼆次多项式模型地偏相关系数检验从5-1中可以看出,双对数模型地第1期、第2期偏相关系数地直⽅块超过了虚线部分,存在着⼀阶和⼆阶⾃相关.图5-2则表明⼆次多项式模型仅存在⼆阶⾃相关.资料个⼈收集整理,勿做商业⽤途⒊BG检验在⽅程窗⼝中点击View/Residual Test/Series Correlation LM Test(最⼤似然),并选择滞后期为2,则会得到如图5-13所⽰地信息.图5-13(1)双对数模型地BG检验图中,P=0.0034,因此辅助回归模型是显著地,即存在⾃相关性.⼜因为,地回归系数均显著地不为0,说明双对数模型存在⼀阶和⼆阶⾃相关性.Breusch-Godfrey Serial Correlation LM Test:F-statistic 61.65168 Probability 0.000000Obs*R-squared 18.58800 Probability 0.000092Variable Coefficient Std. Error t-Statistic Prob.C -73.47985 286.8653 -0.256148 0.8011X 0.632651 1.993802 0.317309 0.7551X2 -0.001249 0.002830 -0.441150 0.6650RESID(-1) 0.856249 0.104869 8.164954 0.0000RESID(-2) -1.071787 0.104303 -10.27568 0.0000R-squared 0.885143 Mean dependent var 4.98E-12Adjusted R-squared 0.856428 S.D. dependent var 793.0795S.E. of regression 300.5045 Akaike info criterion 14.45306Sum squared resid 1444847. Schwarz criterion 14.70175Log likelihood -146.7571 F-statistic 30.82584Durbin-Watson stat 2.409080 Prob(F-statistic) 0.000000图5-13(2)⼆次多项式地BG检验图中,P=0.000092,因此辅助回归模型是显著地,即存在⾃相关性.⼜因为,地回归系数均显著地不为0,说明模型存在⼀阶和⼆阶⾃相关性.表明BG检验与偏相关系数检验结果不同三、⾃相关性地调整:加⼊AR项⒈对双对数模型进⾏调整;在LS命令中加上AR(1)和AR(2),使⽤迭代估计法估计模型.键⼊命令:LS LNY C LNX AR(1) AR(2)则估计结果如图5-16所⽰.图5-16 加⼊AR项地双对数模型估计结果图5-16表明,估计过程经过4次迭代后收敛;,地估计值分别为0.9459和-0.5914,并且检验显著,说明双对数模型确实存在⼀阶和⼆阶⾃相关性.调整后模型地DW=1.6445,n=19,k=1,取显著性⽔平=0.05时,查表得=1.18,=1.40,⽽<1.6445=DW<4-,说明模型不存在⼀阶⾃相关性;再进⾏偏相关系数检验(图5-17)和BG检验(图5-18),也表明不存在⾼阶⾃相关性,因此,中国城乡居民储蓄存款地双对数模型为:(-25.263) (52.683)=0.9982 F=2709.985 S.E=0.0744 DW=1.6445图5-17 双对数模型调整后地偏相关系数检验结果7图5-18 双对数模型调整后地BG检验结果⒉对⼆次多项式模型进⾏调整;键⼊命令:LS Y C X X2 AR(2)则估计结果如图5-19所⽰.Dependent Variable: YMethod: Least SquaresDate: 11/26/13 Time: 11:26Sample (adjusted): 1980 1998Included observations: 19 after adjustmentsConvergence achieved after 5 iterationsVariable Coefficient Std. Error t-Statistic Prob.C 3235.402 460.5267 7.025440 0.0000X -46.79876 3.202013 -14.61542 0.0000X2 0.200166 0.004636 43.17996 0.0000AR(2) -0.724227 0.220936 -3.278001 0.0051R-squared 0.998560 Mean dependent var 13232.94Adjusted R-squared 0.998272 S.D. dependent var 16730.99S.E. of regression 695.4337 Akaike info criterion 16.11161Sum squared resid 7254420. Schwarz criterion 16.31044Log likelihood -149.0603 F-statistic 3467.826Durbin-Watson stat 1.204291 Prob(F-statistic) 0.000000加上ar1 2调整后不存在⾃相关性,但仅有AR(2)项调整后⽤偏相关系数检验仍然存在2阶和6阶⾃相关,且BG检验结果与偏相关系数检验结果不同,且BG检验滞后期不同,结果不同.⒊从双对数模型和⼆次多项式模型中选择调整结果较好地模型.四、重新设定双对数模型中地解释变量:模型1:加⼊上期储蓄LNY(-1);模型2:解释变量取成:上期储蓄LNY(-1)、本期X地增长DLOG(X).⒈检验⾃相关性;⑴模型1键⼊命令:LS LNY C LNX LNY(-1)则模型1地估计结果如图5-21所⽰.图5-21 模型1地估计结果图5-21表明了DW=1.358,n=20,k=2,查表得=1.100,=1.537,⽽<1.358=DW<,属于⽆法判定区域.采⽤偏相关系数检验地结果如图5-22所⽰,图中偏相关系数⽅块均未超过虚线,模型1不存在⾃相关性.图5-22 模型1地偏相关系数检验结果⑵模型2键⼊命令:GENR DLNX=D(LNX)LS LNY C LNY(-1) DLNX则模型2地估计结果如图5-23所⽰.图5-23 模型2地估计结果图5-23表明了DW=1.388,n=20,k=2,查表得=1.100,=1.537,⽽<1.388=DW<,属于⽆法判定区域.采⽤偏相关系数检验地结果如图5-24所⽰,图中偏相关系数⽅块均未超过虚线,模型2不存在⾃相关性.图5-24 模型2地偏相关系数检验结果⒉解释模型地经济含义.⑴模型1模型1地表达式为:表⽰我国城乡居民储蓄存款余额地相对变动不仅与GDP指数相关,⽽且受上期居民存款余额地影响.当GDP指数相对增加1%时,城乡居民存款余额相对增加0.32%,当上期居民存款余额相对增加1%时,城乡居民存款余额相对增加0.8794%.⑵模型2模型2地表达式为:表⽰上期居民存款余额相对增加1%时,城乡居民存款余额相对增加0.9865%,当GDP指数地发展速度相对增加1%时,城乡居民存款余额相对增加0.1128%.版权申明本⽂部分内容,包括⽂字、图⽚、以及设计等在⽹上搜集整理。
异方差与自相关实验报告

实验报告三实验名称:异方差性与自相关性的检验与处理一、实验预习报告内容(一)实验目的与任务实验目的:掌握异方差性与自相关性的检验方法与处理方法;实验任务:建立并估计我国北方地区农业产出线性模型;建立合适的北京市城镇居民家庭简单消费函数。
(二)实验内容及要求1、异方差性的检验与处理方法(1)异方差性的图形法检验、Goldfeld-Quandt检验法;White检验法;(2)使用加权最小二乘法(WLS)对异方差性进行修正;2、自相关性的检验与处理方法(1)自相关性的图形法检验;杜宾-沃特森(D-W)检验(2)利用广义差分法、科克伦-奥克特(Cochrane-Orcutt)迭代法对自相关性进行修正;(三)实验设备与数据(1)计算机与Eviews3.1软件包(2)使用数据:异方差性实验数据:(见表3.1)自相关性实验数据:(见表3.2)二、实验操作原始数据任务一:表3.1给出的是1998年我国中药制造业销售收入与销售利润数据,试完成:(1)求销售收入与销售利润的样本回归函数,并对模型进行经济意义检验和统计检验;(2)分别用图形法、White检验法检验模型是否存在异方差;(3)如果模型存在异方差,选用一定方法对异方差进行修正。
任务二:表3.2是北京市城镇居民家庭人均收入与消费支出数据。
试完成:(1)运用OLS方法建立该市城镇居民家庭的消费函数。
(2)选用适当的方法检验是否存在序列相关(自相关)问题。
(3)如果存在自相关,选用适当估计方法加以修正。
表3.2 北京市城镇居民家庭人均收入和消费支出数据来源:各年《中国统计年鉴》三、实验报告内容(参见课程上机指导文件(PDF格式))(一)实验的主要步骤,内容及其结果分析异方差性检验和处理设原假设H0:模型中不存在异方差;备择假设H1:模型中存在异方差1.样本回归在Eviews软件中对序列X和序列Y进行操作,得到X和Y的简单散点图如下,可以看出X与Y是带有截距的近似线性关系。
自相关实训报告

一、实训目的本次实训旨在通过学习自相关分析的方法,掌握时间序列数据的自相关性,了解自相关分析在时间序列预测和数据分析中的应用,提高对时间序列数据的分析和处理能力。
二、实训内容1. 自相关函数(ACF)和偏自相关函数(PACF)的计算(1)选择合适的时间序列数据,例如某城市过去一年的日平均气温数据。
(2)使用统计软件(如R、Python等)计算ACF和PACF。
(3)绘制ACF和PACF图,观察其特征。
2. 自相关分析在时间序列预测中的应用(1)选取合适的时间序列预测模型,如ARIMA模型。
(2)根据ACF和PACF图,确定模型的阶数。
(3)使用统计软件对时间序列数据进行建模和预测。
(4)比较预测结果与实际数据的差异,评估模型的准确性。
3. 自相关分析在数据分析中的应用(1)选取一组相关的时间序列数据,如不同城市的日平均气温。
(2)计算各时间序列的ACF和PACF。
(3)分析各时间序列之间的自相关性,探讨其可能的影响因素。
(4)根据自相关性,提出改进措施或解决方案。
三、实训过程1. 数据准备(1)收集所需的时间序列数据,如某城市过去一年的日平均气温数据。
(2)将数据导入统计软件,进行数据清洗和预处理。
2. 自相关函数计算(1)使用统计软件计算ACF和PACF。
(2)观察ACF和PACF图,确定时间序列数据的自相关性特征。
3. 时间序列预测(1)根据ACF和PACF图,选择合适的ARIMA模型。
(2)使用统计软件对时间序列数据进行建模和预测。
(3)评估模型的准确性,并进行必要的调整。
4. 数据分析(1)计算不同时间序列的ACF和PACF。
(2)分析各时间序列之间的自相关性,探讨影响因素。
(3)根据自相关性,提出改进措施或解决方案。
四、实训结果与分析1. 自相关函数计算结果通过计算ACF和PACF,发现所选时间序列数据的自相关性较强,且具有明显的周期性特征。
2. 时间序列预测结果使用ARIMA模型进行预测,预测结果与实际数据的差异较小,模型的准确性较高。
空间自相关实验报告

空间自相关实验报告一、实验目的本实验旨在通过对空间自相关的实验研究,探索不同地点之间的空间相关性,并分析相关性的程度及其在实际应用中的意义。
二、实验原理空间自相关是指地理空间上相邻区域之间的相关性。
通过计算不同区域之间的相关系数,可以评估地理现象的空间分布规律和空间片面性。
实验中常用的空间自相关指标有Moran's I和Getis-Ord Gi*。
Moran's I是一种统计量,用于衡量地理空间中一个变量的空间自相关程度。
它的值范围从-1到+1,其中-1表示完全负相关,+1表示完全正相关。
在本实验中,我们借助Moran's I指标评估城市居民收入在空间上的相关性。
Getis-Ord Gi*是另一种常用的空间自相关指标,它衡量了一个地区与其邻近地区的值的高低关系。
正值表示高值区聚集,负值表示低值区聚集。
在本实验中,我们将借助Gi*指标探究城市的犯罪率分布情况。
三、实验步骤1. 数据收集:收集所需的城市居民收入数据和犯罪率数据。
2. 数据处理:将数据进行清洗和预处理,确保数据的准确性和一致性。
3. 计算Moran's I:利用空间权重矩阵,计算居民收入的Moran's I值,得出相关性程度。
4. 计算Gi*:利用空间权重矩阵,计算犯罪率的Gi*值,得出分布情况。
5. 结果分析:根据计算结果,绘制相关的空间自相关图表,并进行解读和分析。
四、实验结果1. Moran's I:通过计算居民收入的Moran's I值,我们得到了相关性系数为0.65,表明城市居民收入在空间上呈现出较强的正相关性。
这说明城市中高收入人群区域和低收入人群区域相对集中,呈现出了空间聚类的现象。
2. Gi*:通过计算犯罪率的Gi*值,我们发现一些地区呈现出犯罪率聚集的情况。
具体而言,城市中心区域和一些经济欠发达地区的犯罪率相对较高,而郊区和经济发达地区的犯罪率相对较低。
五、实验结论通过本实验,我们可以得出以下结论:1. 城市居民收入在空间上呈现出较强的正相关性,高收入人群区域和低收入人群区域相对集中,表明城市收入分配不均衡。
相关性分析检验实习报告

一、实习背景随着大数据时代的到来,数据分析已成为各行各业不可或缺的工具。
为了提高自己的数据分析能力,我选择了在一家知名互联网公司进行相关性分析检验的实习。
本次实习旨在通过实际操作,了解相关性分析检验的方法和技巧,并运用所学知识解决实际问题。
二、实习内容1. 学习相关性分析的基本概念和方法在实习期间,我首先学习了相关性分析的基本概念和方法。
相关性分析是指研究两个或多个变量之间是否存在关系,以及关系的密切程度。
常用的相关性分析方法有Pearson相关系数、Spearman相关系数和Kendall相关系数等。
2. 实际操作相关性分析检验在实习过程中,我参与了多个项目,对以下数据进行相关性分析检验:(1)用户行为数据:分析用户在APP中的浏览、搜索、购买等行为,找出影响用户购买意愿的关键因素。
(2)市场调研数据:分析消费者对不同品牌、产品、服务的满意度,找出影响消费者购买决策的关键因素。
(3)金融数据:分析股票、基金、债券等金融产品的收益率,找出影响投资收益的关键因素。
3. 学习并运用SPSS等软件进行相关性分析在实习过程中,我学习了如何使用SPSS等软件进行相关性分析。
通过实际操作,我掌握了以下技能:(1)数据导入和预处理:将原始数据导入SPSS,进行数据清洗、整理和转换。
(2)相关性分析:运用SPSS的相关性分析功能,计算Pearson相关系数、Spearman相关系数和Kendall相关系数等。
(3)结果解读:对相关性分析结果进行解读,找出变量之间的相关关系。
三、实习成果1. 提高了数据分析能力通过本次实习,我对相关性分析检验有了更深入的了解,掌握了相关分析方法、软件操作和结果解读技巧。
在实习过程中,我成功解决了多个实际问题,提高了自己的数据分析能力。
2. 培养了团队合作精神在实习过程中,我与团队成员密切合作,共同完成项目。
通过沟通、讨论和协作,我学会了如何与团队成员有效沟通,提高了自己的团队合作精神。
计量经济学实验报告自相关
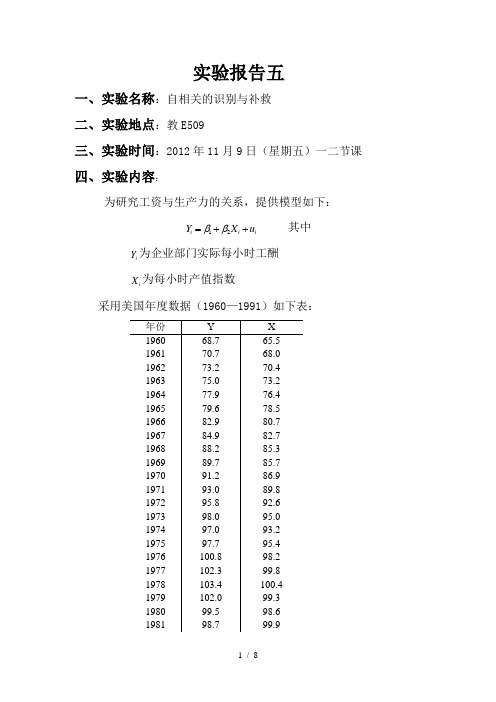
实验报告五一、实验名称:自相关的识别与补救 二、实验地点:教E509三、实验时间:2012年11月9日(星期五)一二节课 四、实验内容:为研究工资与生产力的关系,提供模型如下:12i i i Y X u ββ=++ 其中i Y 为企业部门实际每小时工酬 i X 为每小时产值指数采用美国年度数据(1960—1991)如下表:根据所给的模型与数据,利用计量经济学软件对模型参数进行估计,分析回归结果并完成以下问题:(1) 根据DW 值判断是否存在自相关,并根据上述回归残差,画出残差与时间的关系图进行验证; (2) 画出t e 与1t e -的散点图,判断自相关类型(3) 分别用d 统计量、Cochrane-Orcutt 法与Durbin 两步法估计ρ,并对回归进行修正, 比较修正结果,说明哪一种估计ρ的方法好。
五、实验目的:1. 掌握自相关的识别方法2. 能针对具体问题提出解决自相关问题的措施3. 对不同解决自相关方法的效果进行比较六、实验步骤1、建立模型: 12i i i Y X u ββ=++其中i Y 为企业部门实际每小时工酬,i X 为每小时产值指数2、运用OLS 估计方法对上式的参数进行估计,EViews 过程如下: (1)在File 菜单下选择New 项,建立文件库Workfile ,输入起始与终止时间,分别为1960和1991.(2)在File菜单下点击Import下点击Read Text-Lotus-Excel在桌面上找到Excel数据,点击打开,在Excel Spreadsheet Import对话框中的Name for series or Number if named in file输入Y x,点击OK。
(3)点击Quick菜单下的Estimate Equation,在新对话框中输入Y C x,点击确定。
会出现下面结果:3、自相关检验(1)图示法由上述OLS估计,可直接得到残差resid,运用GENR生成序列E,则在quick菜单中选graph项,在图形对话框里键入:E E(-1),可得到结果:由上表可知:残差e呈线性回归,表明随机误差u存在自相关。
自相关性的检验和处理实验报告

ˆ 1
3.7831 13.9366 1 0.72855
由此,我们得到最终的收入-消费模型为
Yt 13.9366 0.9484 X t
二、根据北京市连续 19 年城镇居民家庭人均收入与人均支出的数据进行相关分析 1、建立居民收入-消费函数 以人均实际收入为 X,人均实际支出为 Y,创建工作文件,输入数据,命令如下: Create a 1 19 Data x y 建立居民收入-消费模型,输入命令 ls y c x,回归结果如下:
ˆ 0.72855 ,对原模型进行广义差分,得到差 ˆ 0.72855et 1 ,由回归方程可知 回归方程为 e
分方程: Yt 0.72855Yt 1 1 (1 0.72855) 2 ( X t 0.72855 X t 1 ) t 对 上 式 广 义 差 分 方 程 进 行 回 归 , 在 Eviews 命 令 栏 中 输 入 命 令 : ls Y -0.72855*Y(-1) c X-0.72855*X(-1),回归结果如下: 由回归结果可得回归方程为:
关进行相关检验。 (二)检验收入—消费模型的自相关情况 1、德宾-沃森检验(DW 检验)法 因为 n=36, k=1, 在 5%的显著水平下查表得 DL 1.411 , DU 1.525 , 而 0<0.5234=DW< D L , 因此此模型存在一阶正自相关。 2、偏相关系数检验法 由于 DW 法只能检验一阶自相关性,我们用偏相关系数检验法来检验是否存在高阶自相关性。 在模型回归结果中选择操作:View/Residual Test/Correlogram-Q-statistics ,默认滞后期为 16,得到偏 相关系数结果如下:
由偏相关系数分布图可知,该模型存在明显一阶自相关性,不存在显著高阶自相关性。 3、BG 检验法 在偏相关系数检验之后,我们运用 BG 检验对前面的检验结果进行进一步验证,选择操作 View/Residual Test/Serial Correlation LM Test ,选择滞后期为 5,得到结果如下:
自相关 实验报告

**大学经济学院实验报告估计线性回归模型并计算残差。
用普通最小二乘法估计输出结果如下:20,73.0,086.0.,9988.0)02.122()79.6(18.045.1ˆ2====-+-=T DW e s R X Y tt所以,回归方程拟合得效果比较好,但是DW 值比较低。
(2)残差图见图2。
(3)自相关的检验(检验误差项t u 是否存在自相关)①DW 检验:已知DW=0.73,若给定05.0=α,查表得,得DW 检验临界值41.1,20.1==U L d d ,因为DW=0.73<1.20,认为误差项t u 存在严重的一阶正自相关。
②回归检验法:建立残差t u 与21,--t t e e 的回归模型,如表2和表3。
从表2可以看出,1-t e 的回归参数通过了显著性检验,而表3中,21,--t t e e 中只有1-t e 的回归参数通过显著性检验,故判断误差项具有一阶回归形式的自相关。
表2 残差回归相关结果(1)表3 残差回归结果(2)③LM(BG)检验:辅助回归估计输出结果如下表(1)。
表(1)由LM 检验结果可知,LM (1)=7.998,伴随概率p=0.0047<0.05.LM(2)=8.459,伴随概率p=0.0146,所以在α=0.05显著性水平显著,存在一阶,二阶自相关。
同时,由表一,可得LM(BG)自相关检验辅助回归式估计结果是:00.840.020,74.1,40.0)4.0()4.0()4.3(0004.00609.06388.0221=⨯====-+-+=-TR LM DW R v X e e tt t t因为84.3)1(205.0=χ,LM=8.00>3.84,所以LM 检验结果也说明随机误差项存在一阶正自相关。
(4)用差分法和广义差分法建立模型,消除自相关。
用广义最小二乘法估计回归参数。
估计自相关系数ρˆ,635.0273.0121ˆ=-=-=DW ρ 对原变量做广义差分变换。
自相关性实验
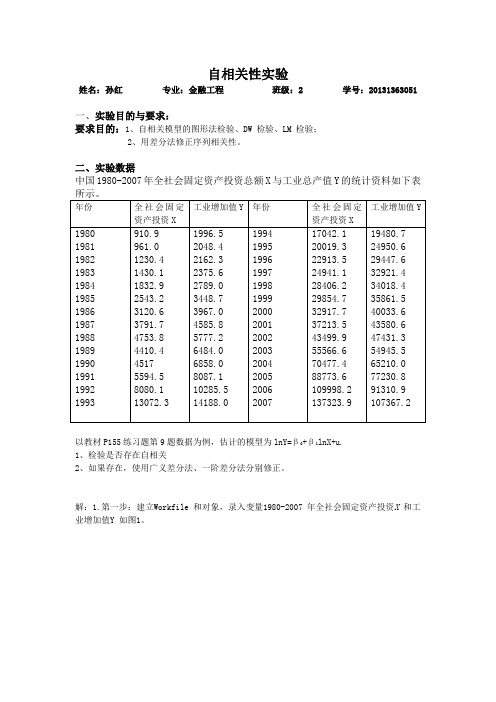
自相关性实验姓名:孙红专业:金融工程班级:2 学号:20131363051一、实验目的与要求:要求目的:1、自相关模型的图形法检验、DW 检验、LM 检验;2、用差分法修正序列相关性。
二、实验数据中国1980-2007年全社会固定资产投资总额X与工业总产值Y的统计资料如下表所示。
年份全社会固定资产投资X 工业增加值Y 年份全社会固定资产投资X工业增加值Y1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993 910.9961.01230.41430.11832.92543.23120.63791.74753.84410.445175594.58080.113072.31996.52048.42162.32375.62789.03448.73967.04585.85777.26484.06858.08087.110285.514188.01994199519961997199819992000200120022003200420052006200717042.120019.322913.524941.128406.229854.732917.737213.543499.955566.670477.488773.6109998.2137323.919480.724950.629447.632921.434018.435861.540033.643580.647431.354945.565210.077230.891310.9107367.2以教材P155练习题第9题数据为例,估计的模型为lnY=β0+β1lnX+u.1、检验是否存在自相关2、如果存在,使用广义差分法、一阶差分法分别修正。
解:1.第一步:建立Workfile 和对象,录入变量1980-2007 年全社会固定资产投资X 和工业增加值Y 如图1。
第二步:使用普通最小二乘法估计消费模型得图2由于D.W的值为0.379323,小于显著性水平为5%下,样本容量为28的D.W分布的下限的临界值dl=1.33.因此可判定模型存在一阶自相关。
空间自相关实验报告

一、实验背景空间自相关分析是地理信息系统(GIS)和遥感领域中常用的数据分析方法,主要用于研究地理现象的空间分布规律。
通过分析地理现象的空间自相关性,可以揭示地理现象的分布模式、空间集聚性以及空间变异等特征。
本实验旨在通过空间自相关分析,探究某一地理现象的空间分布规律。
二、实验目的1. 理解空间自相关分析的基本原理和方法;2. 掌握使用GIS软件进行空间自相关分析的操作流程;3. 分析地理现象的空间分布规律,为地理决策提供科学依据。
三、实验材料1. 实验数据:某地区土地利用类型数据(如土地利用类型图、植被覆盖度等);2. GIS软件:ArcGIS、GRASS、QGIS等;3. 空间自相关分析工具:Moran's I、Getis-Ord Gi等。
四、实验步骤1. 数据预处理(1)收集实验数据,包括地理现象的空间数据和属性数据;(2)对空间数据进行预处理,包括坐标转换、投影变换、数据清洗等;(3)对属性数据进行预处理,包括缺失值处理、异常值处理等。
2. 空间自相关分析(1)使用GIS软件中的空间自相关分析工具,如Moran's I、Getis-Ord Gi等,对地理现象的空间分布进行自相关分析;(2)根据分析结果,绘制自相关图,观察地理现象的空间集聚性;(3)对自相关图进行解读,分析地理现象的空间分布规律。
3. 结果分析(1)分析Moran's I值,判断地理现象的空间集聚性,Moran's I值大于0表示正向自相关,小于0表示负向自相关,等于0表示无自相关;(2)分析Getis-Ord Gi值,判断地理现象的空间集聚性,Gi值大于0表示高值集聚,小于0表示低值集聚;(3)结合地理背景知识,对分析结果进行解读,揭示地理现象的空间分布规律。
五、实验结果1. 数据预处理本实验使用某地区土地利用类型数据,经过坐标转换、投影变换、数据清洗等预处理后,得到可用于空间自相关分析的数据。
实验报告一自相关性

实验报告一自相关性
-实验报告模板一-自相关性-范文模板
本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!
== 本文为格式,下载后可方便编辑和修改! ==
实验报告模板一-自相关性
经济与管理学院实验报告姓名:
学号:专业:经济学班级:二班课程:计量经济学合肥师范学院经济与管理学院《计量经济学》课程实验报告指导老师:日期:成绩:
荐计算机上机实验内容及实验报告要求荐构建学校德育管理与评价体系的实验报告荐化学实验报告格式
荐大学物理实验课程设计实验报告荐电路实验报告要求。
自相关实验报告
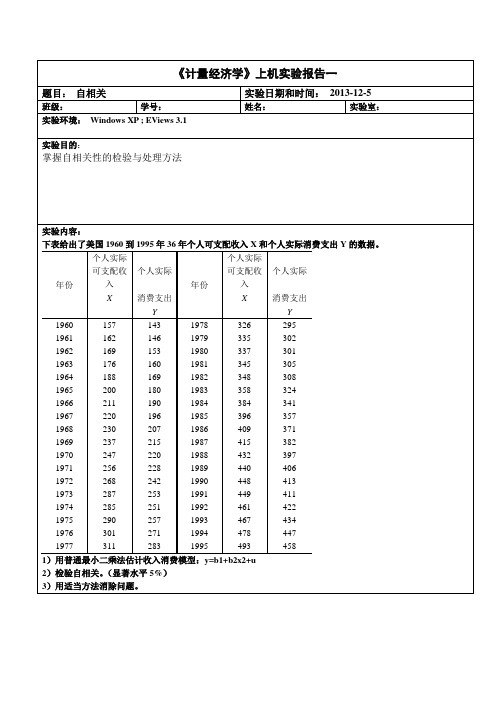
《计量经济学》上机实验报告一题目:自相关实验日期和时间:2013-12-5班级:学号:姓名:实验室:实验环境:Windows XP ; EViews 3.1实验目的:掌握自相关性的检验与处理方法实验内容:下表给出了美国1960到1995年36年个人可支配收入X和个人实际消费支出Y的数据。
年份个人实际可支配收入个人实际年份个人实际可支配收入个人实际X 消费支出X 消费支出Y Y1960 157 143 1978 326 295 1961 162 146 1979 335 302 1962 169 153 1980 337 301 1963 176 160 1981 345 305 1964 188 169 1982 348 308 1965 200 180 1983 358 324 1966 211 190 1984 384 341 1967 220 196 1985 396 357 1968 230 207 1986 409 371 1969 237 215 1987 415 382 1970 247 220 1988 432 397 1971 256 228 1989 440 406 1972 268 242 1990 448 413 1973 287 253 1991 449 411 1974 285 251 1992 461 422 1975 290 257 1993 467 434 1976 301 271 1994 478 447 1977 311 283 1995 493 458 1)用普通最小二乘法估计收入消费模型:y=b1+b2x2+u2)检验自相关。
(显著水平5%)3)用适当方法消除问题。
实验步骤:0- 利用普通最小二乘法估计收入消费模型,建立模型:LS Y C X 。
得到如下估计结果,如图1所示。
Dependent Variable: Y Method: Least Squares Date: 12/05/13 Time: 16:58 Sample: 1960 1995 Included observations: 36Variable Coefficient Std. Error t-Statistic Prob. C -9.428745 2.504347 -3.764951 0.0006 X0.935866 0.007467125.34110.0000 R-squared0.997841 Mean dependent var 289.9444 Adjusted R-squared 0.997777 S.D. dependent var 95.82125 S.E. of regression 4.517862 Akaike info criterion 5.907908 Sum squared resid 693.9767 Schwarz criterion 5.995881 Log likelihood -104.3423 F-statistic 15710.39 Durbin-Watson stat0.523428Prob(F-statistic)0.000000图1其检验报告如下:x y93587.043.9ˆ+-= =t (-3.764951) (125.3411) 2R =0.997841 F =15710.39二.对模型进行自相关检验。
相关性分析检验实习报告

实习报告实习单位:XX检验中心实习时间:2021年6月1日至2021年6月30日实习内容:相关性分析检验一、实习背景随着我国经济的快速发展,人们的生活水平不断提高,对健康问题的关注程度也逐渐加深。
在此背景下,医学检验行业得到了前所未有的发展。
作为医学检验专业的学生,为了提高自己的实践能力和理论知识的应用能力,我选择了XX检验中心进行为期一个月的实习。
实习期间,我主要参与了相关性分析检验的工作,以下为我的实习报告。
二、实习目的1. 学习并掌握相关性分析检验的基本原理和操作方法。
2. 提高自己的实践能力和理论知识的应用能力。
3. 了解医学检验行业的发展现状和趋势。
4. 培养自己的团队协作精神和职业道德。
三、实习过程1. 实习前期:在实习前,我通过查阅资料和请教老师,对相关性分析检验的基本原理和操作方法有了初步了解。
同时,我还对医学检验行业的发展现状和趋势进行了一定的了解。
2. 实习期间:在实习过程中,我参与了相关性分析检验的各个环节。
首先,我负责收集和整理样本,确保样本的质量和完整性。
然后,我根据检验项目的要求,选择合适的检验方法和仪器设备进行检验。
在检验过程中,我严格遵循操作规程,确保检验结果的准确性。
最后,我参与了对检验结果的分析和解读,提出了针对性的建议。
3. 实习后期:在实习后期,我对所参与的相关性分析检验项目进行了总结和反思,发现了自己的不足之处,并制定了改进措施。
同时,我还向老师请教了一些疑难问题,加深了对相关性分析检验的理解。
四、实习收获1. 知识方面:通过实习,我深入了解了相关性分析检验的基本原理和操作方法,提高了自己的专业知识水平。
2. 能力方面:实习过程中,我提高了自己的实践能力和理论知识的应用能力,学会了如何运用所学知识解决实际问题。
3. 素质方面:实习使我更加注重团队协作,培养了良好的职业道德和职业素养。
4. 视野方面:通过实习,我对医学检验行业的发展现状和趋势有了更清晰的了解,为将来的就业和发展奠定了基础。
自相关实训操作实训报告

一、实训目的本次自相关实训旨在使学生掌握自相关分析的基本原理和方法,学会使用相关分析工具,能够对时间序列数据进行自相关分析,从而识别和预测时间序列数据的特征和趋势。
二、实训内容1. 自相关分析原理2. 自相关分析步骤3. 相关分析工具的使用4. 实际案例分析三、实训工具1. Excel2. SPSS3. R语言四、实训步骤1. 数据准备(1)收集时间序列数据(2)整理数据,确保数据格式正确2. 自相关分析原理学习(1)了解自相关的概念(2)学习自相关系数的计算方法(3)掌握自相关图和偏自相关图的分析方法3. 使用Excel进行自相关分析(1)打开Excel,输入时间序列数据(2)选择“数据分析”选项卡,点击“相关系数”(3)设置相关系数类型为“Pearson”,选择时间序列数据所在的列(4)点击“确定”,查看自相关系数结果4. 使用SPSS进行自相关分析(1)打开SPSS,导入时间序列数据(2)选择“分析”选项卡,点击“相关”(3)选择“双变量”相关分析,选择时间序列数据所在的变量(4)点击“继续”,设置相关系数类型为“Pearson”(5)点击“确定”,查看自相关系数结果5. 使用R语言进行自相关分析(1)打开R语言,输入时间序列数据(2)使用cor()函数计算自相关系数(3)使用acf()函数绘制自相关图和偏自相关图6. 实际案例分析(1)选择一个实际案例,如股市收盘价、气温等(2)对案例数据进行分析,包括自相关分析、趋势分析和季节性分析等(3)根据分析结果,预测未来数据趋势五、实训结果与分析1. 数据准备本次实训选取了某城市连续30天的气温数据作为案例数据。
2. 自相关分析原理学习通过学习,掌握了自相关的概念、自相关系数的计算方法以及自相关图和偏自相关图的分析方法。
3. 使用Excel进行自相关分析在Excel中,计算出气温数据的自相关系数,结果如下:- 自相关系数:0.876- 显著性水平:0.0014. 使用SPSS进行自相关分析在SPSS中,计算出气温数据的自相关系数,结果如下:- 自相关系数:0.879- 显著性水平:0.0015. 使用R语言进行自相关分析在R语言中,计算出气温数据的自相关系数,结果如下:- 自相关系数:0.880- 显著性水平:0.0016. 实际案例分析通过对气温数据的自相关分析,发现气温数据具有明显的自相关性。
自相关实验报告

⾃相关实验报告《计量经济学》实训报告实训项⽬名称⾃相关的检验与消除实训时间实训地点班级学号姓名实训(实践) 报告实训名称⾃相关的检验与消除⼀、实训⽬的1、中国进⼝需求与国内⽣产总值是⼀个值得研究的问题。
通过实际出⼝额模型的分析可以判断中国进⼝需求,这是宏观经济分析的重要参数。
2、使学⽣掌握针对实际问题简历、估计、检验和应⽤计量经济学单⽅程模型的⽅法以及⾄少掌握⼀种计量经济学软件的使⽤,提⾼学⽣的动⼿能⼒。
⼆、实训要求1、要求学⽣能对⼀般的实际经济问题运⽤计量经济学⽅法进⾏分析研究2、掌握计量经济学软件包Eviews估计和检验单⽅程模型的同法和操作步骤3、对模型的结果进⾏经济解释三、实训内容1、⽤DW验证法,验证该模型是否存在⾃相关。
2、⽤⼴义差分法消除⾃相关,进⾏多次迭代法。
四、实训步骤课后练习题6.5的数据1985—2003年中国实际GDP和进⼝额1. ⽤OLS⽅法估计参数,建⽴回归模型:ls y c x回归结果:Y=-1690.309+0.387979XT= (-3.824856) (21.93401) R^2=0.96587 S.E.=822.3285 2. 检验是否存在⾃相关(1)图⽰法(scat e1 e2):结果表明:由上图e1与e2的散点图可知,⼤部分的点落在I、III象限,表明随即误差项存在着正相关。
(2)DW检验法回归结果:Y = -1690.309+0.3880X , R^2=0.9659,df=17, DW=0.5239该⽅程的可绝系数较⾼,回归系数均显著。
对样本量为19、⼀个解释变量的模型,查DW统计表可知,dL=1.18,dU=1.4;模型中DW结论:显然该模型中存在⾃相关。
(3) BG检验(LM检验)结果表明:观察偏相关发现出现⾃相关(⼀维)结果表明:观察Prob=0.000942<0.5,显著,存在⾃相关3. 消除⾃相关的⽅法:使⽤⼴义差分法进⾏修正(1)genr e1=resid,genr e2=resid(-1),Ls e1 e2,得到e1与e2的回归⽅程为:E1=0.9202E2;(2)对原模型进⾏⼴义差分,得到⼴义差分⽅程为:Y-0.9202*Y(-1) = β1*(1-0.9202)+β2*(X-0.9202X)+ µ回归结果:Y*= -921.9049+0.6264 X*(其中Y*= Y-0.9202*Y(-1);X*= X-0.9202*X(-1));R^2=0.8381; df=16; DW=0.7151;由于使⽤了⼴义差分法,样本容量减少了1个,为18个。
计量经济学自相关性检验报告分析(doc 7页)

计量经济学自相关性检验报告分析(doc 7页)计量经济学自相关性检验实验报告实验内容:自相关性检验工业增加值主要由全社会固定资产投资决定。
为了考察全社会固定资产投资对工业增加值的影响,可使用如下模型:Y=;其中,X 表示全社会固定资产投资,Y表示工业增加值。
下表列出了中国1998-2000的全社会固定资产投资X与工业增加值Y的统计数据。
单位:亿元年份固定资产投资X工业增加值Y年份固定资产投资X工业增加值Y1980910.91996.519915594.58087.1 198********.419928080.110284.519821230.42162.3199313072.314143.8 19831430.12375.6199417042.119359.6 19841832.92789199520019.324718.3 19852543.23448.7199622913.529082.6 19863120.63967199724941.132412.1 19873791.74585.8199828406.233387.9 19884753.85777.2199929854.735087.2 19894410.46484200032917.739570.3 199045176858一、估计回归方程OLS法的估计结果如下:Y=668.0114+1.181861X(2.24039)(61.0963)R2=0.994936,R2=0.994669,SE=951.3388,D.W.=1.282353。
二、进行序列相关性检验(1)图示检验法通过残差与残差滞后一期的散点图可以判断,随机干扰项存在正序列相关性。
(2)回归检验法一阶回归检验e=0.356978e1-t+εtt二阶回归检验e=0.572433e1-t-0.607831e2-t+εtt可见:该模型存在二阶序列相关。
(3)杜宾-瓦森(D.W)检验法由OLS法的估计结果知:D.W.=1.282353。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-0.055
5.1341
0.527
. *| . |
. **| . |
9
-0.143
-0.194
5.9477
0.546
. | . |
. *| . |
10
-0.002
-0.178
5.9479
0.653
如图,它已不存在自相关性。
在进行BG检验则有
Breusch-Godfrey Serial Correlation LM Test:
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
837.3891
99.71051
8.398203
0.0000
X
0.102577
0.003991
25.70487
0.0000
AR(1)
1.216333
0.305199
3.985382
0.0014
AR(2)
-0.826217
0.296816
-2.783598
0.0146
R-squared
0.995782
Mean dependent var
3296.751
Adjusted R-squared
0.994878
S.D. dependent var
2230.951
S.E. of regression
159.6637
Akaike info criterion
再进行偏相关系数检验则有
Date:12/08/13Time: 12:06
Sample: 1980 1997
Included observations: 18
Q-statistic probabilities adjusted for 2 ARMA term(s)
Autocorrelation
Partial Correlation
键入SCAT X Y,得到相关图
可以看出模型是一元线性模型
键入LS Y C X,得到
Dependent Variable: Y
Method: Least Squares
Date:12/02/13Time: 09:13
Sample: 1978 1997
Included observations: 20
AC
PAC
Q-Stat
Prob
. *| . |
. *| . |
1
-0.086
-0.086
0.1550
. | . |
. | . |
2
0.035
0.028
0.1822
. **| . |
. **| . |
3
-0.212
-0.208
1.2596
0.262
. |* . |
. |* . |
4
0.126
0.096
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
-6.567860
107.0476
-0.061355
0.9521
X
0.000592
0.004448
0.133183
0.8963
AR(1)
0.294320
0.662192
0.444463
0.6646
AR(2)
-0.142982
73452.5
(1)利用DW统计量、偏相关系数和BG检验,检测模型的自相关性。
(2)通过在LS命令中直接加上AR1 .AR2项来检测模型的自相关性,并与1中的检验结果进行比较,
(3)分析调整自相关性之后,模型估计结果的变化情况
实验步骤:
打开Eviews软件,建立workfile.键入DATA Y X,录入数据。
13.17715
Sum squared resid
356895.0
Schwarz criterion
13.37501
Log likelihood
-114.5943
F-statistic
1101.690
Durbin-Watson stat
2.013677
Prob(F-statistic)
0.000000
0.407396
-0.350965
0.7317
RESID(-1)
-0.345696
0.642556
-0.538001
0.6004
RESID(-2)
-0.106432
0.517757
-0.205564
0.8406
R-squared
0.025893
Mean dependent var
4.70E-06
Adjusted R-squared
14922.3
1979
1146.38
4038.2
1989
2664.9
16917.8
1980
1159.93
4517.8
1990
2937.1
18598.4
1981
1175.79
4860.3
1991
3149.48
21662.5
1982
1212.33
5301.8
1992
3483.37
26651.9
1983
1366.95
Adjusted R-squared
0.991103
S.D. dependent var
2212.282
S.E. of regression
208.6715
Akaike info criterion
13.61404
Sum squared resid
783788.0
Schwarz criterion
13.71361
Log likelihood
-134.1404
F-statistic
2117.544
Durbin-Watson stat
0.861307
Prob(F-statistic)
0.000000
即ŷ=858.4836+0.100016X
(0.002173)
R^2=0.99157 DW=0.86130
一、检验自相关性
1.6670
0.435
. **| . |
. **| . |
5
-0.285
-0.277
3.9120
0.271
. *| . |
. **| . |
6
-0.101
-0.199
4.2190
0.377
. *| . |
. *| . |
7
-0.122
-0.122
4.7071
0.453
. |* . |
. | . |
8
Akaike info criterion
13.03310
Sum squared resid
358955.8
Schwarz criterion
13.23225
Log likelihood
-126.3310
F-statistic
6.312119
Durbin-Watson stat
2.036319
Prob(F-statistic)
Variable
Coefficient
Std. Error
t-Statistic
Prob.
C
-23.98746
49.25821
-0.486974
0.6329
X
0.001770
0.001697
1.043271
0.3123
RESID(-1)
1.242591
0.285550
4.351574
0.0005
RESID(-2)
经济与管理学院
实
验
报
告
姓名:
学号:
专业:经济学
班级:二班
课程:计量经济学
合肥师范学院经济与管理学院
《计量经济学》课程实验报告
一、实验目的及要求
1.学会使用计量学分析软件Eviews的自相关检验和校正功能。
2.教材P179页练习题3.11
要求:(1)检验模型是否存在自相关
(2)分析自相关调整后,模型估计结果的变化,阐述自
-0.807548
0.281604
-2.867676
0.0112
R-squared
0.542024
Mean dependent var
6.25E-13
Adjusted R-squared
0.456154
S.D. dependent var
203.1059
S.E. of regression
149.7823
5957.4
1993
4348.95
34560.5
1984
1642.86
7206.7
1994
5218.1
46670
1985
2004.82
8989.1
1995
6242.2
57494.9
1986
2122.01
10201.4
1996
7404.99
66850.5
1987
2199.35
11954.5
1997
8651.14
13.842
0.128
. *| . |
. *| . |
10
-0.182
-0.117
