浙江大学 计算机 考博试题 计算理论及答案
计算机博士试题及答案

计算机博士试题及答案第一部分:计算机基础知识问题1:请解释什么是计算机网络,并列举几个常见的网络协议。
答案:计算机网络是指连接在一起的计算机系统,通过共享资源和信息传输来实现数据交换和通信的网络系统。
常见的网络协议包括TCP/IP协议、HTTP协议、FTP协议和SMTP协议等。
问题2:请解释什么是操作系统,并列举几个常见的操作系统。
答案:操作系统是指管理和控制计算机硬件与软件资源,为用户提供各种服务和程序运行环境的系统软件。
常见的操作系统包括Windows、macOS、Linux和Android等。
问题3:请解释什么是数据库,并列举几个常见的数据库管理系统。
答案:数据库是指按照特定数据模型组织、存储和管理数据的系统。
常见的数据库管理系统包括Oracle、MySQL、SQL Server和PostgreSQL等。
第二部分:计算机网络与通信问题4:请解释什么是IP地址,并说明IPv4和IPv6的区别。
答案:IP地址是指用于在计算机网络中唯一标识一个主机或网络接口的数字标识。
IPv4是目前广泛使用的IP地址版本,采用32位地址,约有42亿个可用地址。
IPv6是新一代IP地址版本,采用128位地址,具有更大的地址空间,可提供更多的地址。
问题5:请解释什么是HTTP协议,并说明与HTTPS的区别。
答案:HTTP协议是指超文本传输协议,用于在计算机网络中传输超文本及其相关中的客户端和服务器之间的通信。
HTTPS是在HTTP 协议基础上加入了SSL/TLS加密传输机制,提供了更安全的通信。
区别在于HTTPS使用了加密技术,可以保护数据传输的安全性。
问题6:请解释什么是TCP/IP协议,并说明它的工作原理。
答案:TCP/IP协议是指传输控制协议/因特网协议,是计算机网络中广泛使用的一套协议。
它将数据分割成一系列的数据包,在网络中进行传输,并利用IP地址对数据包进行寻址和路由。
TCP/IP协议基于客户端-服务器模式,通过三次握手的方式确保可靠的数据传输。
浙大计算机面试题库及答案

浙大计算机面试题库及答案一、算法与数据结构1. 请简述什么是最短路径算法,并列举几种常见的最短路径算法。
最短路径算法是用来寻找两个节点之间最短路径的一种算法。
常见的最短路径算法包括迪杰斯特拉算法(Dijkstra)、弗洛伊德算法(Floyd-Warshall)、贝尔曼-福特算法(Bellman-Ford)等。
2. 请解释什么是动态规划,并简要介绍动态规划的实现步骤。
动态规划是将一个大问题分解为若干个子问题,并通过保存子问题的解来降低求解复杂度的一种算法思想。
实现步骤包括定义状态、确定状态转移方程、确定初始条件和计算顺序。
二、操作系统1. 什么是进程和线程,它们之间有什么区别?进程是操作系统中资源分配的最小单位,是运行程序的载体,拥有独立的内存空间和执行环境;而线程是进程中的一个执行单元,与其他线程共享进程的资源,拥有独立的执行流程。
区别:- 进程间资源相互独立,线程间资源共享;- 进程拥有独立的地址空间,线程共享进程的地址空间;- 进程间切换开销比较大,线程间切换开销较小。
2. 请解释什么是死锁,并列举避免死锁的方法。
死锁是指系统中的进程或线程因为互相等待对方所持有的资源而无法继续执行的一种状态。
避免死锁的方法包括:资源分级法、资源有序性法、银行家算法、避免环路法等。
三、网络1. 简述HTTP和HTTPS的区别。
HTTP(Hypertext Transfer Protocol)是一种用于传输超文本的应用层协议,明文传输,安全性较低;而HTTPS(Hypertext Transfer Protocol Secure)是基于HTTP协议的一种安全的传输协议,通过SSL/TLS加密数据传输,保证数据的安全性。
2. 请解释什么是TCP/IP协议栈,并介绍TCP和UDP的区别。
TCP/IP协议栈是一组用于互联网中数据通信的网络协议的集合。
它由多层协议构成,包括物理层、数据链路层、网络层、传输层和应用层。
TCP(Transmission Control Protocol)是一种面向连接、可靠传输的协议,提供错误检测和重传机制,适用于对数据可靠性要求较高的场景;而UDP(User Datagram Protocol)是一种无连接、不可靠传输的协议,不提供错误检测和重传机制,适用于对实时性要求较高的场景。
计算机博士面试试题及答案

计算机博士面试试题及答案一、数据结构与算法1. 请解释什么是时间复杂度和空间复杂度,并给出一个例子。
时间复杂度是对算法运行时间的度量,表示随着输入规模的增长,算法运行所需时间的增长速度。
通常用大O表示法来表示时间复杂度。
空间复杂度是对算法所需存储空间的度量,表示随着输入规模的增长,算法所需的额外存储空间的增长量。
也通常用大O表示法来表示空间复杂度。
例如,对于一个数组的线性查找算法,最坏情况下需要遍历整个数组,时间复杂度是O(n),其中n是数组的大小。
而空间复杂度为O(1),因为只需要额外一个变量来存储查找结果。
2. 解释以下数据结构:栈、队列和链表。
栈是一种后进先出(LIFO)的数据结构,只允许在栈的顶部进行操作。
可以使用数组或链表来实现栈。
队列是一种先进先出(FIFO)的数据结构,只允许在队列的一端插入元素,在另一端删除元素。
同样,可以使用数组或链表来实现队列。
链表是一种由多个节点组成的数据结构,每个节点包含数据和指向下一个节点的指针。
链表可以分为单向链表和双向链表,分别只有一个指针和两个指针。
3. 请解释深度优先搜索(DFS)和广度优先搜索(BFS)算法,并比较它们的应用场景。
深度优先搜索是一种用于遍历或搜索树或图的算法,从根节点开始,递归地访问节点的所有子节点,直到到达叶子节点。
然后回溯到上一层节点,继续访问其他的子节点。
广度优先搜索是一种用于遍历或搜索树或图的算法,从根节点开始,依次访问根节点的所有相邻节点,然后再依次访问这些相邻节点的相邻节点,直到访问完所有节点。
深度优先搜索通常适用于解决路径问题,例如迷宫求解、拓扑排序等。
广度优先搜索通常适用于解决最短路径问题,例如寻找最短路径、社交网络中的人际关系等。
二、操作系统和网络1. 解释进程和线程的区别。
进程是一个正在执行的程序的实例,具有独立的内存空间和系统资源,是程序的执行单位。
每个进程都有自己的地址空间和指令执行序列。
线程是进程中的一条执行路径,是轻量级的执行单位。
浙江大学计算机考博考题操作系统 系统结构

浙江大学计算机考博考题操作系统系统结构一、判断题(选择一个最佳的答案, 每题3分,共18分)1. 测量计算机对事务处理的性能,所用的测试基准程序(Benchmark)应该是:(a) Whetstone; (b) SPECint; (c)TPC-C; (d) SPECfp2.从汇编语言程序员的角度看, 下列哪个是不透明的:(a)cache; (b) 数据通路的宽度;(c) 虚拟存储器;(d)流水线3.某个应用程序运行所需要的最少存储空间为320页,每页32KBytes。
某计算机实际物理内存为256MBytes, 但250Mbytes的内存已被其它程序占用,硬盘的容量为40GBytes, 操作系统为该程序分配的虚拟内存地址空间应该是:(a) 6MBytes; (b) 10MBytes; (c) 256MBytes; (d)40GBytes4.某个由多处理器构成的服务器中, 每个处理器都有自己的存储器, 但所有存储器都统一编址, 这种结构属于:(a) UMA (b)NUMA (c)SMP (d)CLUSTER5. 某计算机采用了超标量流水线技术, 其指令级并行度为8(即平均每个时钟周期完成8条指令的执行), 若已知该机采用了两条流水线, 其机器超流水线周期为:(a) 2个时钟周期; (b) 1个时钟周期; (c) 1/2个时钟周期; (d) 1/4个时钟周期;6.一台由8个磁盘构成的磁盘阵列,其冗余校验信息在某个磁盘中,所属的RAID级别是:(a) RAID0;(b) RAID1; (c)RAID3; (d) RAID5.二、问答题:(10分)1.RISC机和CISC机相比,提高性能的基本原理是什么? 在指令条数,CPI和时钟频率等方面,它提高性能的关键点在什么地方?(4分)....(3)(10分)某种机器具有层次型存储结构,包含cache,内存和磁盘系统。
内存的平均存取时间50个时钟周期,磁盘的平均存取时间1,000,000个时钟周期。
浙江大学经济学院博士生博弈论课程习题及答案

纳什均衡1.在下表所示的战略式博弈中,找出重复删除劣战略的占优均衡表1.1首先,找出S2的劣战略。
对于S2,M策略严格劣于R策略,所以M为严格劣策略。
删除后M再找出S1的劣战略,显然对于S1而言,M策略和D策略严格劣于U策略,所以M和D为严格劣策略。
删除M与D后找占优均衡为(U,L)即,(4,3)。
2.求解下表所示的战略博弈式的所有的纯战略纳什均衡表1.2首先看S1选择X策略。
如果S2同样选择X策略,那么S3一定选择Y策略;同样,如果S3选择Y策略,S2也一定会选择X策略,因此(X,X,Y)是一个纳什均衡;如果S2选择Y策略,那么S3一定选择X策略;同样,如果S3选择X策略,S2也一定会选择Y策略,因此,(X,Y,X)是一个纳什均衡。
其次看S1选择Y策略。
如果S2选择X策略,S3一定选择X策略;同样,如果S3选择X策略,S2也一定会选择X策略,因此(Y,X,X)是一个纳什么均衡。
如果S2选择Y策略,S3选择Y策略是理性的,如果S3选择X,S2将选择X,这样(Y,Y,X)将不是一个纳什均衡;同样,如果S3选择Y策略,S2也一定会选择Y策略,因此(Y,Y,Y)是一个纳什均衡。
所以该博弈式的纯战略纳什均衡有4个:(X,X,Y)(X,Y,X)(Y,X,X)(Y,Y,Y)。
3.(投票博弈)假定有三个参与人(1、2和3)要在三个项目(A、B和C)中选中一个。
三人同时投票,不允许弃权,因此,每个参与人的战略空间Si={A,B,C}。
得票最多的项目被选中,如果没有任何项目得到多数票,项目A被选中。
参与人的支付函数如下:U1(A)=U2(B)=U3(C)=2U1(B)=U2(C)=U3(A)=1U1(C)=U2(A)=U3(B)=0求解以上博弈的所有纯战略纳什均衡。
由上,ABC策略是无差异的,但均衡策略只能是参与人3选择A 策略,因此(A ,A ,A )是一个纳什均衡。
如果参与人2选择B 策略,参与人3选择AB 策略是差异的,但均衡策略只能是其选择A ,因此(A ,B ,A )是一个纳什均衡。
计算机考博试题及答案

计算机考博试题及答案一、选择题(每题2分,共20分)1. 在计算机科学中,冯·诺依曼体系结构的主要特点是______。
A. 程序存储B. 程序控制C. 程序执行D. 程序设计答案:A2. 以下哪项不是操作系统的主要功能?A. 进程管理B. 存储管理C. 文件管理D. 网络通信答案:D3. 在关系数据库中,用于从数据库表中检索数据的SQL语句是______。
A. CREATEB. UPDATEC. SELECTD. DELETE答案:C4. 下列哪个选项不是计算机网络的拓扑结构?A. 星型B. 环型C. 总线型D. 树型答案:D5. 在计算机组成原理中,CPU的主要组成部分不包括______。
A. 控制单元B. 算术逻辑单元C. 存储器D. 输入输出设备答案:D6. 以下哪个算法不是排序算法?A. 快速排序B. 归并排序C. 深度优先搜索D. 堆排序答案:C7. 在计算机安全领域,以下哪项措施不是防止病毒的?A. 安装防病毒软件B. 定期更新操作系统C. 使用防火墙D. 定期格式化硬盘答案:D8. 以下哪种编程语言不是面向对象的?A. JavaB. C++C. PythonD. C答案:D9. 在数据结构中,栈(Stack)是一种______的数据结构。
A. 线性B. 非线性C. 顺序D. 链式答案:A10. 以下哪个选项不是云计算服务的类型?A. IaaSB. PaaSC. SaaSD. DaaS答案:D二、填空题(每题2分,共20分)1. 在计算机组成原理中,______是计算机硬件与软件之间的接口。
答案:指令集2. 操作系统的______功能允许多个用户或多个程序共享计算机资源。
答案:多任务3. 在数据库设计中,______是用来表示实体间联系的。
答案:关系4. 计算机网络中的______协议是用于数据传输的协议。
答案:TCP/IP5. 在操作系统中,______是一种用于分配CPU时间的技术。
计算机考博试题及答案

计算机考博试题及答案1. 数据结构与算法1.1 平衡二叉树平衡二叉树,也称为AVL树,是一种特殊的二叉搜索树,它的左右子树的高度差不超过1。
请说明如何插入和删除节点以保持平衡。
答案:当向平衡二叉树中插入一个节点时,需要按照二叉搜索树的规则找到对应的位置。
插入节点后,如果破坏了平衡二叉树的平衡性,则需要进行相应的调整。
插入节点后,从插入节点到根节点的路径上的所有节点的平衡因子需要更新,并沿着路径向上检查,如果某个节点的平衡因子超过了1或小于-1,则需要进行旋转操作来恢复平衡。
当删除一个节点时,同样需要按照二叉搜索树的规则找到对应的位置,并将该节点删除。
删除节点后,同样需要从删除节点到根节点的路径上的所有节点的平衡因子进行更新,并进行相应的旋转操作来恢复平衡。
1.2 Dijkstra算法Dijkstra算法是一种用于求解加权有向图中单源最短路径问题的算法。
请简要介绍Dijkstra算法的原理及步骤。
答案:Dijkstra算法的原理是,通过不断找出当前距离源点最近的顶点,并更新其他顶点的距离和路径,最终得到源点到其他所有顶点的最短路径。
步骤如下:1) 初始化:将源点设置为当前顶点,将源点到其他顶点的距离初始化为无穷大,将源点到自身的距离初始化为0。
2) 循环:在未遍历的顶点中,选择当前距离源点最近的顶点作为当前顶点。
3) 更新:计算当前顶点的邻居顶点经过当前顶点到达源点的距离,若经过当前顶点到达邻居顶点的距离比已知的距离更短,则更新邻居顶点的距离和路径。
4) 标记:将当前顶点标记为已遍历。
5) 终止条件:当所有顶点都被标记为已遍历时,算法终止。
2. 操作系统2.1 进程和线程的区别进程和线程是操作系统中的两个重要概念,请简要说明它们的区别。
答案:进程是操作系统资源分配的基本单位,每个进程都拥有独立的内存空间和系统资源,进程之间通过进程间通信(IPC)来进行数据交换。
而线程是进程中的执行单元,每个进程可以包含多个线程,线程共享进程的内存空间和系统资源,线程之间可以直接访问共享的内存数据。
计算机博士试题及答案

计算机博士试题及答案一、选择题(每题2分,共20分)1. 在计算机科学中,用于表示数据的最小单位是:A. 字节B. 位C. 字D. 段答案:B2. 下列哪个不是操作系统的功能?A. 进程管理B. 文件管理C. 网络通信D. 数据加密答案:D3. 在数据库管理系统中,用于存储数据的逻辑结构是:A. 表B. 索引C. 视图D. 存储过程答案:A4. 以下哪种网络拓扑结构不是星型结构?A. 总线型B. 环形C. 树型D. 网状型答案:A5. 在软件开发过程中,需求分析阶段的主要任务是:A. 编写代码B. 设计数据库C. 确定软件功能D. 测试软件答案:C6. 以下哪个不是计算机硬件的组成部分?A. 中央处理器B. 存储器C. 操作系统D. 输入设备答案:C7. 在计算机系统中,用于表示二进制数的单位是:A. 位B. 字节C. 字D. 段答案:A8. 下列哪种编程语言不是面向对象的?A. JavaB. C++C. PythonD. C答案:D9. 在计算机网络中,用于在不同网络之间转发数据包的设备是:A. 路由器B. 交换机C. 集线器D. 网关答案:A10. 在计算机科学中,用于表示文件大小的单位是:A. 字节B. 位C. 千字节D. 兆字节答案:A二、填空题(每空1分,共20分)1. 在计算机系统中,CPU是______的缩写,它负责解释和执行存储在内存中的指令。
答案:中央处理器2. 计算机病毒是一种______,它能够自我复制并传播到其他计算机系统。
答案:恶意软件3. 在HTML中,用于定义网页标题的标签是______。
答案:<title>4. 在关系数据库中,用于创建表的SQL语句是______。
答案:CREATE TABLE5. 计算机的存储设备分为______存储和______存储。
答案:随机访问存储;顺序访问存储6. 在编程中,______是一种用于存储数据和程序的永久性存储设备。
计算机博士考核试题及答案

计算机博士考核试题及答案考核试题:1. 请解释什么是计算机网络,并列举其主要组成部分。
2. 请阐述数据库管理系统的基本原理和功能。
3. 解释什么是多线程和并发,并提供适用的例子。
4. 请解释什么是数据挖掘,并列举常用的数据挖掘算法。
5. 请解释什么是人工智能,并提供应用场景。
答案:1. 计算机网络是指在不同地理位置上的计算机和设备通过通信线路连接在一起,以实现数据和资源的共享。
主要组成部分包括计算机、通信链路、网络协议、网络设备和应用软件等。
2. 数据库管理系统(DBMS)是一种用于管理和组织数据的软件系统。
其基本原理是使用结构化方式存储数据,并提供了数据的查询、插入、更新和删除等功能。
DBMS还负责控制数据的一致性和安全性,以及提供数据备份和恢复等功能。
3. 多线程是指在一个程序中同时运行多个线程,每个线程执行相对独立的任务。
并发指的是在同一时间段内,系统能够处理多个任务。
例如,一个下载器程序可以使用多线程实现同时下载多个文件,这样可以提高下载效率。
4. 数据挖掘是从大量的数据中提取有用的信息和模式的过程。
常用的数据挖掘算法包括聚类分析、分类分析、关联规则挖掘和异常检测等。
聚类分析用于将数据划分为不同的簇群;分类分析用于将数据分为不同的类别;关联规则挖掘用于发现数据之间的关联关系;异常检测用于检测和识别异常数据。
5. 人工智能是模拟人类智能的一种技术与方法,其目标是使计算机具备理解、学习和决策等能力。
人工智能在各个领域都有广泛的应用,例如自动驾驶、语音识别和机器翻译等。
浙大计算机理论考博

浙江大学2009-2010学年秋冬学期研究生《计算理论》课程期终考试试卷考试形式:闭卷,考试时间:2010年1月21日,所需时间:120分钟学号:姓名:专业:任课教师:题序123456总分得分评卷人Zhejiang UniversityTheory of Computation,Fall-Winter2009Final Exam1.Choose the correct answer and justify you answer.(1)(6%)Let A={0n1n2n|n∈N}and(a)A⊆B,then B is decidable.(b)B⊆A,then B is decidable.(c)B≤τA,where recursive functionτis a reduction from A to B,then B isdecidable.The correct answer is().(2)(6%)Let A and B be any languages such that A≤τB.Under what conditionsis it the case that A≤B?(a)Only when both A and B are decidable.(b)Only when both A and B are recursively enumerable.(c)Always.The correct answer is().(3)(6%)Just as we encoded Turing Machines as strings,we can also encode DFAsas strings.Let“M”be the encoding string of DFA M.Consider the followinglanguage L dDF A ={“M”|“M”∈L(M)}.What can we say about L dDF A?(a)L dDF Ais regular.(b)L dDF Ais not regular but it is decidable.(c)L dDF Ais not recursively enumerable. The correct answer is().(4)(6%)Just as we encoded Turing Machines as strings,we can also encode PDAsas strings.Let“M”be the string encoding of PDA M.Consider the followinglanguage L dP DA ={“M”|“M”∈L(M)}.What can we say about L dP DA?(a)L dP DAis decidable.(b)L dP DAis not decidable but it is recursively enumerable.(c)L dP DAis not recursively enumerable.The correct answer is().(5)(6%)Let A and B be disjoint,recursively enumerable languages.Further letA∪B also be recursively enumerable.What can you say about A and B?(a)It is possible that neither A nor B is decidable.(b)At least one among A and B is decidable.(c)Both A and B are decidable.The correct answer is().2.(12%)Using the pumping theorem to show thatL1={w∈{a,b}∗|w has an equal number of a s and b s} is not regular.3.(16%)(a)Construct a context-free grammar that generates languageL2={a m b n c k|m,n,k∈N,and m+n≤k}.(b)Construct a pushdown automata that accepts language L2.4.(12%)Construct a Turing machine that computes the funcion f:{a,b}∗→{a,b}∗given byf(w)=w,if the length of w is even wa,if the length of w is odd.When describing the Turing machines above,you can use the elementary Turing machines described in textbook.Always assume that the Turing machines start computation from the configuration w where w∈{a,b}∗is the input string.5.(15%)Classify whether each of the following languages are recursive,recursivelyenumerable-but-not-recursive,or non-recursively enumerable.Prove your answers.(a)L4={“M”|Turing machine M halts on“M”};(b)L5={“M”|Turing machine M does not halt on“M”}.6.(15%)(a)Give the definition of N P-Complete problem.(b)Describe carefully what the ingredients of an N P-completeness proof are.(c)Consider the following problem,called the MAX-SAT problem:Given a setF of clauses,and an integer k,is there a truth assignment that satisfies at leastk clauses?Show that MAX SAT problem is N P-complete.。
浙江大学-计算理论-期末考试-考博复习-提纲和练习

Ars Digita University Theory of ComputationTopicsLanguagesAll computational problems can be reframed as questions of membership in a language (set). Drawing Deterministic Finite Automata (DFAs).Drawing Nondeterministic Finite Automata (NFAs).Converting NFAs to DFAsRegular Languages, Closure properties of Regular languages.Problems to work onWhat is a language?Draw a DFA that accepts the strings ending in 01.Draw a DFA that accepts the strings that have an even number of zeros.Draw a DFA that accepts the strings that have an even number of zeros or end in 01.Draw a DFA that accepts the strings that have an even number of zeros and end in 01.Draw a DFA that accepts the strings that have an even number of zeros but don't end in 01.Draw an NFA that accepts the strings that end in 01. Try to make it as simple as possible.Draw an NFA that accepts the strings that have an even number of zeros or end in 01 using six states.Draw an NFA that accepts any string that is a concatenation of a string that has an even number of zeros with a string that ends in 01.Draw an NFA that accepts the strings that have an even number of zeros and end in 01.Draw an NFA that accepts the language 0, using only two states.Convert the previous NFA into a DFA using the method described in class.Draw an NFA with two states that corresponds to the language 0?2*.Convert the previous NFA to a DFA.What is a regular language?Draw the DFA that corresponds to the language 10*10*.What is the Prefix of the language corresponding to the language 10*10*.Draw the DFA for the prefix of the language corresponding to the regular expression 10*10*. What is the MIN of the language 10*10*?Draw the DFA corresponding to the MIN of the language 10*10*.Main TopicsMore practice with NFAs, Converting to DFAs, getting rid of epsilons.Formal defintion of AutomataThe math mumbo-jumbo formulation is: Some five-tuple (Q, Sigma, delta, q, F)....But that's not as bad as it seems. This is just some object that contains four other objects and a method. Which one is the method?Operations on Languages: Our friends PREFIX and MINAn example Proof. Just so you have a reference, we'll show you how to "prove" that Regular languages are closed under difference, ie. L1-L2 is regular if L1 and L2 are.• Let M1 = (Q1, Sigma, delta1, q1, F1) accept L1, and let• Let M2 = (Q2, Sigma, delta2, q2, F2) accept L2• Then• M = (Q1xQ2, Sigma, delta, (q1,q2), F1 x(Q2-F2)) accepts L1-L2• where delta(r1,r2,a) = (delta1(r1,a), delta2(r2,a))At this point you should give a few words of justification about why you think this new machine would accept L1-L2. If the mathematical notation is just way to much for you, just try to explain things in intuitively.Regular expressionsIf we run out of things to talk about :-)Generalized NFAsNFA + reg. ex. transitions = GNFAConverting NFAs to Regular expressionsConverting Regular expressions to NFAsProblems to work onWrite out the NFA corresponding to the language and convert to a DFA: All strings that end in 0. Same for all strings whose penultimate character is 0.If you like this sort of thing: same things for all strings that that have 0 as the third to the last character.One more if you'd like the practice: All strings ending in {0,1}Write regular expressions for all strings that end in aaba. Where Sigma is just the usual alphabet. Do the same for all strings that do not contain a.Write a regular expression for the strings that contain the substring 0101, where Sigma = {0,1}.Do the same for all strings that alternate between 0 and 1 and end in 0.Do the same for strings that alternate between 0 and 1.Hard problem: Write a regular expression for the strings over {0,1} that are divisible by 3.Hard Problem: Build an automaton that recognizes the strings that have the same number of zeros and ones.TopicsThe Java Computability Toolkit.More on Regular Expressions.GNFAs and converting an NFA to a regular expression.Converting a Regular Expression to an NFA.Diagonalization.The Pumping Lemma.Problems to work on(Warm up) Give one string that is in the language and one that is not:a*b*a(ba)*ba* + b*(b + aaa)*aba+babWrite a regular expressionThat accepts the set of all strings.That accepts the set of all strings not containing 00 as a substring.Convert to regular expressions:Convert to an NFA:(001)*(1+e)(01*0 + e + 00)(001)*(1+e)(01*0 + e + 00)How long does a string in the following language have to be before we are guaranteed to have a loop?Is the set of all strings that are palindromes regular? Why or why not?Show that the set of all strings of zeros that have length that is a perfect cube can not be described by a regular expression.TopicsHow to minimize DFA's and why one would.Turning a DFA into a GrammarDecision Problems.Some applications of Regular expressionsEverything is a string / number.Problems to work onWhy do we care about minimizing DFA's ?Minimize the following DFA. What Language does it generate?Minimize the following DFA. What Language does it generate?Minimize the following DFA. What Language does it generate?Give a regular grammar that generates the same language as the DFA in problem 2.Give a regular grammars that generates the same language as the following regular expressions: 010*a(ab + bc)*Is the following a valid argument? Why or why not? The language L = {0m1m 2n | m, n >= 0 } is not regular, since we already know that M = { 0m 1m | m >= 0} is not regular by the pumping lemma, and since L contains M it cannot therefore be regular.Prove that the language { x2n | n >= 0 } is not regular.Give a decision algorithm which takes as input a regular language L and decides whether L contains the string 1000101.Give a decision algorithm which takes as input a regular language L and decides whether L equals the language {1000101}Give a decision algorithm which takes as input a regular language L and decides whether L contains the language given by the regular expression 10*10*1Miscellaneous problem: Eliminate the espilon transitons of this NFA, without converting it to a DFA (ie, figure out an easier way)Mildy Challenging and Surprising Problem: Let L be any language over the alphabet {0}, not necessarily regular. Show that L* is regular.Wicked hard challenging problem: Describe a grammar that generates the language { 0p| p is a prime }TopicsDecision ProblemsContext free grammars.Problems to work onDecision ProblemsFinish the decision problems form the last recitation handout.CFG warmupGive a context free grammar that generates the language of palindromes {w(0+1+epsilon)w R | w is in (0 + 1)*}Give a context free grammar that generates every possible string over {0,1}Give a context free grammar that generates the language 0n1 0n 111 0m 1r where n, m, r >= 0 Give a context free grammar that generates the language of all strings that contain 101.Give a context free grammar that generates the language of all strings with an equal number of zeros and ones.And/OrGive a context free grammar that generates the language that has equal numbers of 0's and 1's or contains 101.Give a context free grammar that generates the language that has equal numbers of 0's and 1's and contains 101.ComplementsGive a context free grammar that generates the language of all strings of the form 0m1n where n >= m >= 0.Give a context free grammar that generates the language of all strings of the form 0m1n where n > m >= 0.Give a context free grammar that generates the complement of the language 0*1*.Give a context free grammar that generates the language { w | w is not equal to 0n1n for any choice of n}Challenging problem: Give a context free grammar that generates the language { w | w is not apalindrome}TopicsRigorous proofs using the pumping lemma.More constructions with context free grammars.Chomsky Normal Form.Problems to work onFinish working on the CFG problems from the lst handout.(Warmup). Generate the grammar for 0*1(0+1)*.Using the grammar above, What are the leftmost and rightmost derivation for the strings 1001, 0011? What are the parse trees?(Text 2.13) Consider the following grammar.1.2.S --> TT | U3.T --> 0T | T0 | 14.U --> 0U00 | 15.Describe the language it generates.Chomsky Normal FormPut the following grammar in Chomsky Normal form. (Text 2.14)5.6. A --> BAB | B | epsilon7. B --> 00 | espilon8.Put the following grammar in Chomsky Normal form.9.10.A --> BAB | B | BC11.B --> 00 | epsilon12.C --> AA13.Rigorous pumping lemma proofsProblems from previous handouts kindly reproduced here. Rigorously prove using the pumping lemma.Prove that the language { x2n | n >= 0 } is not regular.Show that the set of all strings of zeros that have length that is a perfect cube can not be described by a regular expression.TopicsUsing regular expressions and context free grammars with Lex and Yacc to build complex programs quickly. A calculator example.Chomsky Normal Form (Finish problems on Chomsky Normal Form that we didn't get to last time, i.e. all of them ;-)Push Down Automata.Problems to work onGive a grammar for the language {a i b j | i <= j <= 2i}.Consider the grammar1.S --> z A s2. A --> xb B yz3. B --> cd A q | epsilonPlay around with this grammar and try to guess what a pumping lemma for CFG's might look like. Construct a PDA for {0n1n | n >= 0} without looking at your notes.Construct a PDA for {0n1m0m1n | n,m >= 0}TopicsToday we'll mainly catch up on all the problems from previous handouts we haven't done yet. Aisde: Languages as infinitely long streams of bits, complexity and compressionLeftmost and Rightmost derivations.Parse Trees.Chomsky Normal Form. What it is useful for.Converting a grammar to Chomsky normal form.Intro to the pumping lemma for context free languages.Languages and streams o' bitsHere is a list (well, the beginning of a list) of all possible strings that can be made from the characters a and b. They are ordered so that all strings of length 1 come first, then strings of length 2 then strings of length 3, ... etc.e a b aa ab ba bb aaa aab aba abb baa bab bba bbb aaaa aaab aaba aabb abaa abab abba abbb baaa baab baba babb bbaa bbab bbba bbbb aaaaa aaaab aaaba aaabb aabaa aabab aabba aabbb abaaa abaab ababa ababb abbaa abbab abbba abbbb baaaa baaab baaba baabb babaa babab babba babbb bbaaa bbaab bbaba bbabb bbbaa bbbab bbbba bbbbb aaaaaa aaaaab aaaaba aaaabb aaabaa aaabab aaabba aaabbb aabaaa aabaab aababa aababb aabbaa aabbab aabbba aabbbb abaaaa abaaab abaaba abaabb ababaa ababab ababba ababbb abbaaa abbaab abbaba abbabb abbbaa abbbab abbbba abbbbb baaaaa baaaab baaaba baaabb baabaa baabab baabba baabbb babaaa babaab bababa bababb babbaa babbab babbba babbbb bbaaaa bbaaab bbaaba bbaabb bbabaa bbabab bbabba bbabbb bbbaaa bbbaab bbbaba bbbabb bbbbaa bbbbab bbbbba bbbbbbA language is an infinite stream of bits. Example a(a+b)*0 1 0 1 1 0 0 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1 00 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 11 1 1 1 1 1 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 1 1 1 1 1 1 1 1 11 1 1 1 1 1 1 1 1 1 1 1 1 11 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 Example (ab)*1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 00 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Problems to work onWork on the problems from previous handoutsTopicsHow many languages are there?Nondeterministic Pushdown Automata.Deterministic Pushdown Automata.Converting Context Free Grammars to Pushdown Automata.Problems to work onLanguagesCould I ever write a computer program that enumerated (listed) all the possible languages? What about one that enumerated all the regular languages? What about one that enumerated all the context-free languages?Pushdown Automata WarmupWhat is the difference between a Nondeterministic Pushdown Automaton and a Deterministic Pushdown Automaton. Do you think they generate the same languages?(Warm up) Construct a PDA that accepts the language {0,1}*.(Warm up from last time:) Construct a PDA that accepts the language {0n1n| n >= 0}. Is your answer deterministic or not?Construct a PDA that accepts the language {0n1n | n >= 2}.More Pushdown AutomataConstruct a PDA that accepts the language { 0m1n | n > m >= 0}(From last time:) Construct a PDA that accepts the language {0n1m0m1n | n,m >= 0}.Construct a PDA that accepts the language { w | w is not a palindrome}And/OrConstruct a PDA that accepts the language { w | w is not a palindrome and w ends with a zero} Give a PDA that accepts the language {a i b j | i <= j <= 2i}Deterministic vs Nondeterministic PDA'sConstruct a NPDA that accepts the language of strings with the same number of zeros and ones. Construct a DPDA that accepts the language of strings with the same number of zeros and ones. Converting Grammars to PDA'sConvert the following Grammar to a PDA.1.S --> AB2. A --> 03. B --> 1Convert the following Grammar to a PDA.4.5. A --> BAB | B | epsilon6. B --> 00 | espilon7.Dimitri Kountourogiannis,。
计算理论考试题库及答案

计算理论考试题库及答案一、选择题1. 计算理论中的“图灵机”是由谁提出的?A. 阿兰·图灵B. 约翰·冯·诺伊曼C. 克劳德·香农D. 艾伦·纽曼答案:A2. 下列哪项不是图灵机的基本组成部分?A. 带子B. 读写头C. 状态寄存器D. 随机数生成器答案:D3. 形式语言理论中的“递归可枚举”是指什么?A. 可以通过图灵机在有限步内确定一个字符串是否属于该语言B. 可以通过图灵机枚举出该语言的所有字符串C. 可以通过图灵机在有限步内生成该语言的所有字符串D. 可以通过图灵机在有限步内枚举出该语言的所有字符串答案:B4. 确定性图灵机与非确定性图灵机的区别在于:A. 确定性图灵机有确定的输入输出B. 非确定性图灵机在每一步有多个可能的转移C. 确定性图灵机没有状态寄存器D. 非确定性图灵机有多个读写头答案:B5. 形式语言理论中的“可判定性问题”是指:A. 该问题有一个确定的答案B. 该问题有一个算法可以解决C. 该问题可以通过图灵机在有限步内判断D. 该问题可以通过图灵机枚举出所有可能的解答案:C二、简答题1. 请简述图灵机的工作原理。
答:图灵机由一个无限长的带子、一个读写头、一组状态寄存器和一个转移函数组成。
带子上的每个单元格可以存储一个符号,读写头可以读取、写入或擦除带子上的符号,并在带子上左右移动。
状态寄存器记录当前的状态,转移函数根据当前的状态和带子上的符号来决定读写头的下一步操作和状态寄存器的下一个状态。
图灵机通过这样的方式模拟计算过程。
2. 什么是“图灵完备性”?答:图灵完备性是指一个系统能够模拟任何图灵机的计算过程,也就是说,如果一个问题可以用图灵机解决,那么这个问题也可以在这个系统中解决。
具有图灵完备性的系统能够执行任何可以形式化的算法。
3. 请解释“不可解问题”与“难解问题”的区别。
答:不可解问题是指不存在任何算法能够在有限步内解决的问题,即这些问题是图灵不可判定的。
浙江大学-计算机-考博试题-计算理论及答案

浙江大学-计算机-考博试题-计算理论及答案work Information Technology Company.2020YEAR计算理论字母表:一个有穷的符号集合。
字母表上的字符串是该字母表中的符号的有穷序列。
一个字符串的长度是它作为序列的长度。
连接反转 Kleene星号 L* ,连接L中0个或多个字符串得到的所有字符串的集合。
有穷自动机:描述能力和资源极其有限的计算机模型。
有穷自动机是一个5元组M=(K,∑,δ,s,F),其中1)K是一个有穷的集合,称为状态集2)∑是一个有穷的集合,称为字母表3)δ是从KX∑→K的函数,称为转移函数4)s∈K是初始状态5)F⊆K是接收状态集M接收的语言是M接收的所有字符串的集合,记作L(M).对于每一台非确定型有穷自动机,有一台等价的确定型有穷自动机有穷自动机接受的语言在并、连接、Kleene星号、补、交运算下是封闭的。
每一台非确定型有穷自动机都等价于某一台确定型有穷自动机。
一个语言是正则的当且仅当它被有穷自动机接受。
正则表达式:称R是一个正则表达式,如果R是1)a,这里a是字母表∑中的一个元素。
2)ε,只包含一个字符串空串的语言3)∅,不包含任何字符串的语言4)(R1∪R2),这里R1和R2是正则表达式5)(R10R2),这里R1和R2是正则表达式6)(R1*),这里R1*是正则表达式一个语言是正则的当且仅当可以用正则表达式描述。
2000年4月1、根据图灵机理论,说明现代计算机系统的理论基础。
1936年,图灵向伦敦权威的数学杂志投了一篇论文,题为《论数字计算在决断难题中的应用》。
在这篇开创性的论文中,图灵给“可计算性”下了一个严格的数学定义,并提出著名的“图灵机”(Turing Machine)的设想。
“图灵机”不是一种具体的机器,而是一种思想模型,可制造一种十分简单但运算能力极强的计算机装置,用来计算所有能想像得到的可计算函数。
这个装置由下面几个部分组成:一个无限长的纸带,一个读写头。
浙江大学 计算机 考博试题 面向对象及答案

一、名词解释对象类封装多态、继承聚合关联多继承消息可见属性操作对象:系统中用来描述客观事物的一个实体,它是构成系统的一个基本单位,由一组属性和施加于这组属性的一组操作构成。
对象之间存在四种关系:一般-特殊;整体-部分;关联;消息类:具有相同属性和操作的一组对象的集合,它为属于该类的全部对象提供了统一的抽象描述,由一个类名,一组属性和一组操作构成。
类的命名应遵循的几条规则:类的名字应恰好符合这个类所包含的每一个对象;应该反映每个对象个体,而不是整个群体;采用名词或带有定语的名词;使用便于交流的语言文字。
封装:就是把对象的属性和操作结合为一个独立的系统单位,并尽可能隐蔽对象的内部细节。
多态性:在一般类中定义的属性或操作被特殊类继承之后,可以具有不同的数据类型或表现出不同的行为。
继承:特殊类的对象拥有的其一般类的全部属性与操作,称作特殊类对一般类的继承。
聚合:一个复杂的对象以若干比较简单的对象作为其组成部分成为聚合。
整体对象和部分对象之间的关系便是聚合关系。
关联:两个或多个类的对象实例集合之间的关系。
多继承:如果允许一个特殊类同时继承多个一般类的属性与操作,则这种继承叫做多继承。
消息:消息是向对象发出的服务请求。
对象之间在一次交互中所传送的信息。
包括接收消息的对象,该对象提供的服务操作,输入信息和回答信息。
同步消息:仅当发送者要发送一个消息而且接受者已做好接收这个消息的准备时才能传送的消息成为同步消息。
异步消息:发送者不管接受者是否做好接收准备都可以发送的消息成为异步消息。
可见:属性:用来描述对象静态特征的一个动作序列。
操作:用来描述对象动态特征的一个动作序列。
问题域系统责任永久对象主动对象系统边界参与者用况问题域:被开发的应用系统所考虑的整个业务范围。
系统责任:所开发的系统应该具备的职能。
永久对象:生存期可以超过程序的执行时间而长期存在的对象。
主动对象:至少有一个操作不需要接收消息就能主动执行的对象。
浙大计算机机试历年真题
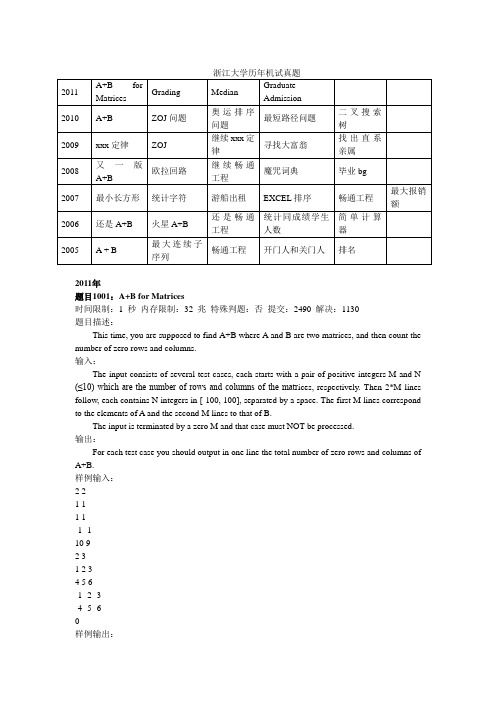
浙江大学历年机试真题2011 A+B forMatricesGrading MedianGraduateAdmission2010 A+B ZOJ问题奥运排序问题最短路径问题二叉搜索树2009 xxx定律ZOJ 继续xxx定律寻找大富翁找出直系亲属2008 又一版A+B欧拉回路继续畅通工程魔咒词典毕业bg2007 最小长方形统计字符游船出租EXCEL排序畅通工程最大报销额2006 还是A+B 火星A+B 还是畅通工程统计同成绩学生人数简单计算器2005 A + B 最大连续子序列畅通工程开门人和关门人排名2011年题目1001:A+B for Matrices时间限制:1 秒内存限制:32 兆特殊判题:否提交:2490 解决:1130题目描述:This time, you are supposed to find A+B where A and B are two matrices, and then count the number of zero rows and columns.输入:The input consists of several test cases, each starts with a pair of positive integers M and N (≤10) which are the number of rows and columns of the matr ices, respectively. Then 2*M lines follow, each contains N integers in [-100, 100], separated by a space. The first M lines correspond to the elements of A and the second M lines to that of B.The input is terminated by a zero M and that case must NOT be processed.输出:For each test case you should output in one line the total number of zero rows and columns of A+B.样例输入:2 21 11 1-1 -110 92 31 2 34 5 6-1 -2 -3-4 -5 -6样例输出:15题目1002:Grading题目描述:Grading hundreds of thousands of Graduate Entrance Exams is a hard work. It is even harder to design a process to make the results as fair as possible. One way is to assign each exam problem to 3 independent experts. If they do not agree to each other, a judge is invited to make the final decision. Now you are asked to write a program to help this process.For each problem, there is a full-mark P and a tolerance T(<P) given. The grading rules are: • A problem will first be assigned to 2 experts, to obtain G1 and G2. If the differenc e is within the tolerance, that is, if |G1 - G2| ≤ T, this problem's grade will be the average of G1 and G2.• If the difference exceeds T, the 3rd expert will give G3.• If G3 is within the tolerance with either G1 or G2, but NOT both, then this p roblem's grade will be the average of G3 and the closest grade.• If G3 is within the tolerance with both G1 and G2, then this problem's grade will be the maximum of the three grades.• If G3 is within the tolerance with neither G1 nor G2, a judge will give the final grade GJ.输入:Each input file may contain more than one test case.Each case occupies a line containing six positive integers: P, T, G1, G2, G3, and GJ, as described in the problem. It is guaranteed that all the grades are valid, that is, in the interval [0, P]. 输出:For each test case you should output the final grade of the problem in a line. The answer must be accurate to 1 decimal place.样例输入:20 2 15 13 10 18样例输出:14.0题目1004:Median题目描述:Given an increasing sequence S of N integers, the median is the number at the middle position. For example, the median of S1={11, 12, 13, 14} is 12, and the median of S2={9, 10, 15, 16, 17} is 15. The median of two sequences is defined to be the median of the non-decreasing sequence which contains all the elements of both sequences. For example, the median of S1 and S2 is 13.Given two increasing sequences of integers, you are asked to find their median.输入:Each input file may contain more than one test case.Each case occupies 2 lines, each gives the information of a sequence. For each sequence, the first positive integer N (≤1000000) is the size of that sequence. Then N integers follow, separated by a space.It is guaranteed that all the integers are in the range of long int.输出:For each test case you should output the median of the two given sequences in a line.样例输入:4 11 12 13 145 9 10 15 16 17样例输出:13题目1005:Graduate Admission题目描述:It is said that in 2011, there are about 100 graduate schools ready to proceed over 40,000 applications in Zhejiang Province. It would help a lot if you could write a program to automate the admission procedure.Each applicant will have to provide two grades: the national entrance exam grade GE, and the interview grade GI. The final grade of an applicant is (GE + GI) / 2. The admission rules are: • The applicants are ranked according to their final grades, and will be admitted one by one from the top of the rank list.• If there is a tied final grade, the applica nts will be ranked according to their national entrance exam grade GE. If still tied, their ranks must be the same.• Each applicant may have K choices and the admission will be done according to his/her choices: if according to the rank list, it is one's turn to be admitted; and if the quota of one's most preferred shcool is not exceeded, then one will be admitted to this school, or one's other choices will be considered one by one in order. If one gets rejected by all of preferred schools, then this unfortunate applicant will be rejected.• If there is a tied rank, and if the corresponding applicants are applying to the same school, then that school must admit all the applicants with the same rank, even if its quota will be exceeded.输入:Each input file may contain more than one test case.Each case starts with a line containing three positive integers: N (≤40,000), the total number of applicants; M (≤100), the total number of graduate schools; and K (≤5), the number of choices an applicant may have.In the next line, separated by a space, there are M positive integers. The i-th integer is the quota of the i-th graduate school respectively.Then N lines follow, each contains 2+K integers separated by a space. The first 2 integers are the applicant's GE and GI, respectively. The next K integers represent the preferred schools. For the sake of simplicity, we assume that the schools are numbered from 0 to M-1, and the applicants are numbered from 0 to N-1.输出:For each test case you should output the admission results for all the graduate schools. The results of each school must occupy a line, which contains the applicants' numbers that school admits. The numbers must be in increasing order and be separated by a space. There must be no extra space at the end of each line. If no applicant is admitted by a school, you must output anempty line correspondingly.样例输入:11 6 32 1 2 2 2 3100 100 0 1 260 60 2 3 5100 90 0 3 490 100 1 2 090 90 5 1 380 90 1 0 280 80 0 1 280 80 0 1 280 70 1 3 270 80 1 2 3100 100 0 2 4样例输出:0 1035 6 72 81 42010题目1003:A+B题目描述:给定两个整数A和B,其表示形式是:从个位开始,每三位数用逗号","隔开。
浙江大学 考博 考研 期末考试 计算机体系结构知识点复习

流水线竞争解决方法
数据、结构、 数据、结构、控制 Double Bump、Split、Forwarding、Stall Bump、Split、Forwarding、 四个BYPASSING ALU+ALU、Load+ALU、Load+Store(两种情况) ALU+ALU、Load+ALU、Load+Store(两种情况) 控制条件、 控制条件、目标计算
系统结构实验室
流水的软件方法
循环展开
展开 展开调度 精通例子
软件流水技术
象征性展开的含义 例子
路径调度
路径选择 路径压缩 路径补偿
系统结构实验室
多处理器概念
分类标准 典型结构
存储器组织标准 特性 框图 通信模型和存储模型的关系
系统结构实验室
Cache一致性 Caຫໍສະໝຸດ he一致性侦听协议写无效 写广播 cache数据块状态转换图 cache数据块状态转换图 精通例子
精通例子
系统结构实验室
基于Tomasulo的硬件投机 基于Tomasulo的硬件投机
四个节拍: 四个节拍:
Issue、EX、WB、 Issue、EX、WB、Commit
一些特性: 一些特性:
按序发射、乱序执行、按序完成 按序发射、乱序执行、按序完成 ROB 精确中断
看懂例子 记分牌、 记分牌、Tomasulo、硬件投机三者的综合比较 、
测试集
Real App -> Modify App -> Kernels -> Toy BenchmarksBenchmarks->Synthetic Benchmarks
定量设计原理
5个quantitative principles
浙江大学博士入学考试线性系统控制理论真题03-09

9. (12 分) 已知线性定常系统
⎡ ⎢ ⎣
x&1 x&2
⎤ ⎥ ⎦
=
⎡ ⎢ ⎣
A11 A21
A12 A22
⎤ ⎥ ⎦
⎡ x1
⎢ ⎣
x2
⎤ ⎥ ⎦
+
⎡ B1
⎢ ⎣
B2
⎤ ⎥u ⎦
=
Ax
+
Bu
,
y
=
⎡⎣ I q
0⎤⎦ x = Cx
其中 x1 ∈ Rq , x2 ∈ Rn−q ,试证明 {A,C} 完全能观测当且仅当 {A22 , A12 } 完全能观,设 {A,C}
−2⎥⎦
x
,
y
=
⎡a ⎢⎣1
2 4
b⎤ 1⎥⎦ x
试确定使系统完全能观时待定参数的取值范围。 4. (10 分) 给定连续时间的定常系统
⎧⎪ ⎨
x&1
⎪⎩
=
−x1x22 − (1+ x&2 = x12 x2
x1 )2
x1
判断其原点平衡状态是否为大范围渐进稳定。 5. (10 范围内) 已知某系统矩阵 A 满足
4
⎡-1 0 0 ⎤ ⎡1 0 ⎤
4.
x&
=
⎢ ⎢
0
⎢⎣ 1
-2 0
-3⎥⎥ x + ⎢⎢0 1 ⎥⎦ ⎢⎣0
1
⎥ ⎥
-1⎥⎦
u
,
y
=
⎡1
⎢ ⎣
0
2 1
0⎤ 1⎥⎦
x
,输出变换和状态反馈使闭环动态解耦,极
点 -1 , -1+j , -1-j ,求控制律。
浙江计算机理论试题及答案

浙江计算机理论试题及答案计算机理论试题1.描述什么是计算机体系结构,并列举两个不同类型的计算机体系结构。
2.解释计算机的指令周期并说明其中包含的阶段。
3.描述冯·诺依曼体系结构并解释其主要组成部分。
4.解释什么是操作系统的作用,并列举三个常见的操作系统。
5.描述存储器的层次结构,并解释每个层次在计算机系统中的作用。
6.解释什么是并行计算,并列举两种常见的并行计算模型。
7.描述计算机网络的基本组成部分,并解释每个组成部分的作用。
8.解释什么是算法的复杂性,并分别描述时间复杂性和空间复杂性。
9.描述计算机图形学的基本概念,并解释其在现实生活中的应用。
10.解释什么是人工智能,并列举两个常见的人工智能应用领域。
计算机理论答案1.计算机体系结构是指计算机系统中各个组成部分以及它们之间的连接和通信方式。
两个不同类型的计算机体系结构包括冯·诺依曼体系结构和哈佛体系结构。
2.计算机的指令周期是指执行一条计算机指令所需要的时间。
它包含取指令、译码、执行、访存和写回这五个阶段。
3.冯·诺依曼体系结构包括中央处理器(CPU)、存储器、输入设备和输出设备。
其中,CPU负责执行指令和进行数据处理,存储器用于存储指令和数据,输入设备用于接收外部输入,输出设备用于向外部输出结果。
4.操作系统是管理计算机硬件和软件资源的系统软件。
常见的操作系统包括Windows、Mac OS和Linux。
5.存储器的层次结构包括寄存器、缓存、内存和外存。
寄存器位于CPU内部,是最快的存储器;缓存位于CPU和内存之间,用于提高数据访问速度;内存用于存储被CPU访问的指令和数据;外存用于长期存储数据。
6.并行计算是指同一时间执行多个计算任务的计算方式。
常见的并行计算模型包括共享内存模型和消息传递模型。
7.计算机网络的基本组成部分包括服务器、客户端、路由器、交换机和网络线缆。
服务器用于提供服务,客户端用于访问服务,路由器和交换机用于转发数据,网络线缆用于连接各个网络设备。
大学计算机基础(浙江大学)题库

大学计算机基础(浙江大学)题库测试试卷:计科教材练习【01】--------------------------------------------------------------------------------一、判断题,共10题,总分:10分。
请直接点击选择TrueorFale.1.计算机文化是指能够理解计算机是什么以及它是如何作为资源被使用的。
(T)TrueFale2.计算思维的本质是对求解问题的抽象和实现问题处理的自动化。
如果说,数学思维是“抽象和关系”,那么计算思维则是“状态和过程”。
(T)TrueFale3.我们可以定义计算机系统是指计算机的所有资源。
它包括了计算机硬件和软件。
(T)TrueFale4.计算机系统结构是研究计算机的硬件互联使得计算机更有效、更高速和更可靠。
(T)TrueFale5.应用软件是管理计算机所需要的那些软件。
(F)TrueFale6.程序设计主要有面向文本设计技术和面向对象设计技术。
(F)TrueFale7.程序是算法的具体实现。
(T)TrueFale8.计算机被加电后进入工作状态,就开始执行程序,直到关机为止。
(T)TrueFale9.因特网的开放结构,主要表现在进入网络的机器,属于企业、机构、政府甚至个人的,它们之间的关系是平等地位,没有权限的定义。
(T)TrueFale10.因特网是一个庞大的计算机互联形成的网络,构建因特网的主要目的是实现各种通信。
(F)TrueFale--------------------------------------------------------------------------------二、单选题,共11题,总分:11分。
请四个中选择一个是正确的答案。
1.半导体技术是按一个较高的指数规律发展的。
根据摩尔定律,当价格不变时,集成电路上可容纳的晶体管数目,约每隔(D)个月便会增加一倍,性能也将提升一倍。
A.6B.12C.15D.182.以微处理器为核心的微型计算机属于第(D)代计算机。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算理论字母表:一个有穷的符号集合。
字母表上的字符串是该字母表中的符号的有穷序列。
一个字符串的长度是它作为序列的长度。
连接反转Kleene星号L* ,连接L中0个或多个字符串得到的所有字符串的集合。
有穷自动机:描述能力和资源极其有限的计算机模型。
有穷自动机是一个5元组M=(K,∑,δ,s,F),其中1)K是一个有穷的集合,称为状态集2)∑是一个有穷的集合,称为字母表3)δ是从KX∑→K的函数,称为转移函数4)s∈K是初始状态5)F⊆K是接收状态集M接收的语言是M接收的所有字符串的集合,记作L(M).对于每一台非确定型有穷自动机,有一台等价的确定型有穷自动机有穷自动机接受的语言在并、连接、Kleene星号、补、交运算下是封闭的。
每一台非确定型有穷自动机都等价于某一台确定型有穷自动机。
一个语言是正则的当且仅当它被有穷自动机接受。
正则表达式:称R是一个正则表达式,如果R是1)a,这里a是字母表∑中的一个元素。
2)ε,只包含一个字符串空串的语言3) ,不包含任何字符串的语言4)(R1∪R2),这里R1和R2是正则表达式5)(R10R2),这里R1和R2是正则表达式6)(R1*),这里R1*是正则表达式一个语言是正则的当且仅当可以用正则表达式描述。
2000年4月1、根据图灵机理论,说明现代计算机系统的理论基础。
1936年,图灵向伦敦权威的数学杂志投了一篇论文,题为《论数字计算在决断难题中的应用》。
在这篇开创性的论文中,图灵给“可计算性”下了一个严格的数学定义,并提出著名的“图灵机”(Turing Machine)的设想。
“图灵机”不是一种具体的机器,而是一种思想模型,可制造一种十分简单但运算能力极强的计算机装置,用来计算所有能想像得到的可计算函数。
这个装置由下面几个部分组成:一个无限长的纸带,一个读写头。
(中间那个大盒子),内部状态(盒子上的方块,比如A,B,E,H),另外,还有一个程序对这个盒子进行控制。
这个装置就是根据程序的命令以及它的内部状态进行磁带的读写、移动。
工作带被划分为大小相同的方格,每一格上可书写一个给定字母表上的符号。
控制器可以在带上左右移动,它带有一个读写出一个你期待的结果。
这一理论奠定了整个现代计算机的理论基础。
“图灵机”更在电脑史上与“冯·诺依曼机”齐名,被永远载入计算机的发展史中。
图灵机在理论上能模拟现代数字计算机的一切运算,可视为现代数字计算机的数学模型。
实际上,一切"可计算"函数都等价于图灵机可计算函数,而图灵机可计算函数类又等价于一般递归函数类。
2、说明按乔姆斯基分类,语言、文法、自动机的关系乔姆斯基将语言定义为,按一定规律构成的句子或符号串string 的有限的或无限的集合,记为L 。
数目有限的规则叫文法,记为G 。
刻画某类语言的有效手段是文法和自动机。
文法与自动机的关系:形式文法是从生成的角度来描述语言的,而自动机是从识别的角度来描述语言的.文法和自动机是形式语言理论的基本内容。
对某种语言来说,如果存在一个该语言的生成过程,就一定存在一个对于它的识别过程.就描述语言来讲,形式语言和自动机是统一的.文法在形式上定义为四元组:G =(VN,VT,S,P ),VN 是非终极符号,VT 是终极符号,S是VN 中的初始符号,P 是重写规则。
⏹ 文法是定义语言的一个数学模型,而自动机可看作是语言的识别系统。
⏹ 对于一个文法产生的语言,可以构造相应自动机接受该语言:一个自动机接受的语言,可以构造对应的文法产生该语言。
一定类型的自动机和某种类型的文法具有等价性。
2、乔姆斯基根据转换规则将文法分作4类。
每类文法的生成能力与相应的语言自动机最常见文法的分类系统是 诺姆·乔姆斯基 于 1956年 发展的 乔姆斯基谱系 ,这个分类谱系把所有的文法分成四类型: 无限制文法 、 上下文相关文法 、 上下文无关文法 和正规文法 。
四类文法对应的语言类分别是 递归可枚举语言 、 上下文相关语言 、 上下文无关语言 和 正规语言 。
这四种文法类型依次拥有越来越严的产生式规则,同时文法所能表达的言也越来越少。
尽管表达能力比无限文法和上下文相关文法要弱,但由于高效率的实现,四类文法中最重要的上下文无关文法和正规文法。
例如对下文无关语言存在算法可以生成高效的LL 分析器和LR 分析器。
3、证明HALT(X R,X)不是可计算的。
4、(1)、证明递归集都是递归可枚举集。
(2)、举例属于递归可枚举集但不是递归集的集合,并证明之。
5、(1)、证明L={(a,b)*|a,b的个数相同}为上下文无关语言。
(2)、并证明其不是正则的。
P56假设L是正则的,则根据在交下的封闭性,L∩a*b*也是封闭的,而后者正好是L1={ a i b i:i ≧0},假设L1是正则的,则存在满足泵引理的整数n。
考虑字符串w= a n b n∈L。
根据定理可以写成w=xyz使得|xy|≦n,且y≠e,即y=a i,其中i>0.但是xz= a n-i b n L,与定理矛盾。
2000年10月1、(1)给出图灵机的格局、计算及图灵机μ计算函数f的精确定义。
(2 ) 对图灵机模型而言,church论题是什么?(3)当x是完全平方时值为3x,否则为3x+1证明其是原始递归函数。
2、证明φ(X,X)是不可计算的。
3、证明L={ambn|m,n>0,m≠n}是上下文无关的,但不是正则的。
利用上下文无关语言在并、连接、Kleene星号下是封闭的。
正则语言在交运算下封闭。
4、A为有穷字母表,L是A*的无穷子集,(1)证明存在无穷序列ω0,ω1,ω2…,它由L的所有字组成,每个字恰好在其中只出现一次。
(2)是否存在从L构造序列ω0,ω1,ω2…,的算法(即i由计算ωi),为什么?2001年4月1、(1)当x是完全平方时值为2x,否则为2x+1证明其是原始递归函数。
(2)对图灵机模型而言,church论题是什么?(3)通用图灵机的描述。
2、(1)用有穷自动机构造正则语言,以a2b结尾的字符串组成的正则语言L(2)L={a3n bn |n>0}为上下文无关,但不是正则。
3、A为字母表,L为A*上任意的语言。
阐述其乔姆斯基层次及用可计算性表述它们的关系。
4、证明不存在可计算函数h(x),使φ(x,x)↓时h(x,x)= φ(x,x)+a,a∈N,φ(x,y)是编号为y输入为x时的程序。
2001年10月1、{a,b}上递归枚举语言是否可数?证明2、L={a,b,c数目相同的语言}是否CFL(上下文无关)?证明p95证:不是上下文无关的。
假设L是上下文无关的,则它与正则语言a* b*c*的交也是上下文无关的。
令L1={a n b n c n:n≧0}假设L1是上下文无关语言。
取常数p,ω=a p b p c p ,∣ω∣=3p≥p将ω写成ω=uvxyz使得v或y不是空串且uv i xy i z∈L1 I=0,1,2……其中∣xy∣≥1 且∣xuy∣≤p.有两种可能他们都导致矛盾。
如果vy中a、b、c三个符号都出现,则v和y中必有一个至少含有abc中的两个符号。
于是uv2xy2z中abc的排列顺序不对,有的b在a前或c在a或b前。
如果vy中只出现a、b、c中的一个或两个符号,则uv2xy2z 中a、b、c的个数不相等。
∴与L1是上下文无关语言假设矛盾。
综上,L不是2型语言。
3、被2,3整除的非负整数的十进制表示的集合是否正则。
∑={1,2,……9},L ∑*,令L1是非负整数十进制表示的集合,容易看到L1=0∪{1,2,……9}∑*,由于L1是用正则表达式表示的,故它是一个正则语言。
令L2是可以被2整除的非负整数的十进制表示的集合。
L2正好是以0,2,4,6,8结尾的L1的成员组成的集合,即L2=L1∩∑*{0,2,4,6,8},根据正则语言在交运算下封闭原则,故L2也是一个正则语言。
令是可以被3整除的非负整数的十进制表示的集合.一个数可以被3整除当且仅当它的数字之和可以被3整除。
构造一台有穷自动机,用它的有穷控制器保存输入数字的模3和。
L3是这台有穷自动机接受的语言与L1的交。
最后L=L2∪L3,它一定是个正则语言。
4、NonSelfAccepting是否递归集合2002年4月1.能被5整除的字符串是正则集吗2.用图灵机表示下列字符串。
Φ,e,{a},{a}*3. s->ss, s->asb, s->abs, 证明由s推得的字符串不可能以abb开头。
(可能记忆有误,具体形式就是这样)。
4 证明不是所有的递归可枚举集都是递归的。
定理:语言不是递归的;所以,递归语言类是递归可枚举语言类的真子集。
2002年10月1、什么是计算?计算理论研究的内容和意义是什么?为什么要使用计算的抽象模型?2、请写出一个正则表达式,描述下面的语言:在字母表{0,1}上,不包含00子串且以1结尾。
4、语言L={a n:n是素数}是不是正则语言,是不是上下文无关的?5、一个succ(n+1)的组合Turing机描述,说出它的作用。
P1276、什么是Turing机的停机问题?它是可判定的么?为什么?H={“M”“w”:Turing机M在输入w上停机},ATM ={<M, ω>|M是一个TM,且M接受ω}证明:假设ATM是可判定的,下面将由之导出矛盾。
设H是ATM的判定器。
令M是一个TM,ω是一个串。
在输入<M, ω>上,如果M接受ω,则H就停机且接受ω;如果M不接受ω,则H也会停机,但拒绝ω。
换句话说,H是一个TM使得:接受如果M接受ωH(<M, ω>)=拒绝如果M不接受ω现在来构造一个新的图灵机D,它以H作为子程序。
当M被输入它自己的描述<M>是,TM D就调用H,以了解M将做什么。
一旦得到这个信息,D就反着做,即:如果M接受,它就拒绝;如果M不接受,它就接受。
下面是D的描述。
D=”对于输入<M>,其中M是一个TM:1) 在输入<M,<M>>上运行H。
2) 输出H输出的相反结论,即,如果H接受,就拒绝;如果H拒绝,就接受。
”总而言之,接受如果M不接受<M>D(<M>)=拒绝如果M接受<M>当以D的描述<D>作为输入来运行D自身时,结果会怎样呢?我们得到:接受如果D不接受<M>D(<D>)=拒绝如果D接受<M>不论D做什么,它都被迫相反地做,这显然是一个矛盾。
所以,TM D和TM H都不存在。
它是不可判定的。
假设H是递归的,那么H1={“M”:Turing机M在输入字符串“M”上停机}也是递归的。
H1表示对角化程序的halts(X,X)部分。
