折叠问题与勾股定理例题总结

合集下载

折叠问题题型梳理

折叠问题题型梳理题型1 折痕为对角线1．如图，将▱ABCD 沿对角线AC 折叠，使点B 落在B ′处，若∠1=∠2=44°，则∠B 为A ．66°B ．104°C ．114°D ．124°【解析】∵四边形ABCD 是平行四边形，∴AB ∥CD ，∴∠ACD =∠BAC ，由折叠的性质得：∠BAC =∠B′AC ，∴∠BAC =∠ACD =∠B′AC =12∠1=22°∴∠B =180°–∠2–∠BAC =180°–44°–22°=114°；选C ． 2.如图，将▱ABCD 沿对角线BD 折叠，使点A 落在点E 处，交BC 于点F ，若ABD 48∠=，CFD 40∠=，则E ∠为( )A . 102B . 112C . 122D . 92 【解析】AD //BC ，ADB DBC ∠∠∴=，由折叠可得ADB BDF ∠∠=，DBC BDF ∠∠∴=，又DFC 40∠=，DBC BDF ADB 20∠∠∠∴===，又ABD 48∠=， A 1802048112∠=--=，E A 112∠∠∴==，选B3.如图，在矩形ABCD 中，BC =6，CD =3，将△BCD 沿对角线BD 翻折，点C 落在点C 1处，BC 1交AD 于点E ，则线段DE 的长为（）A . 3B . 154C . 5D . 152【解析】根据题意易证BE =DE ，设ED =x ，则AE =8﹣x ，在△ABE 中根据勾股定理得到关于线段AB 、AE 、BE 的方程x 2=42+（8﹣x ）2，解方程得x =5，即ED =5，故选C ．题型2 折痕过一顶点4.如图，在矩形ABCD 中，AB ＝4，BC ＝6，点E 为BC 的中点，将△ABE 沿AE 折叠，使点B 落在矩形内点F 处，连接CF ，则CF 的长为．【解析】连接BF ，∵BC ＝6，点E 为BC 的中点，∴BE ＝3又∵AB ＝4，∴AE ＝＝5，∴BH ＝，则BF ＝∵FE ＝BE ＝EC ，∴∠BFC ＝90°根据勾股定理得，CF ＝＝＝5.如图，矩形纸片ABCD ，对角线为BD ，沿过点D 的直线折叠，使点A 落在对角线BD 上的点E 处，折痕DG ，若4,3AB BC ==，则AG 的长是（）A . 43B . 32C . 125D . 23【解析】根据题意可得：∠GDA =∠GDB ，AD =ED ，∵四边形ABCD 是矩形，∴∠A =90°，AD =BC =3，∴AG =EG ，ED =3，∵AB =4，BC =3，∠A =90°，∴BD =5，设AG =x ，则GE =x ，BE ==2，BG =4-x ，在Rt △BEG 中，EG 2+BE 2=BG 2，即：x 2+4=（4-x ）2，解得：x =32，∴AG =32，选B ． 6.如图，在平行四边形ABCD 中，E 为边CD 上一点，将ADE 沿AE 折叠至AD E '处，AD '与CE 交于点F ．若54B ∠=︒，20DAE ∠=︒，则FED '∠的大小为（）A . 27°B . 32°C . 36°D . 40°【解析】∵四边形ABCD 是平行四边形，54B ∠=︒，∴54D B =∠=︒∠又∠DAE =20°，∴∠AED =180°-∠D -∠DAE =106°，根据折叠可得：106AED AED ∠=∠='︒ 又∠AEF =180°-∠AED =74°，∴32FED AED AEF ∠∠'=∠-='︒，选B7.如图，把正方形ABCD 沿对边中点所在的直线对折后展开，折痕为,MN 再过点B 折叠纸片，使点A 格在MN 上的点F 处，折痕为,BE 若AB 长为2,则EN 的长为(（）A . 3B . 3-C . 2D . 3【解析】∵四边形ABCD 为正方形，AB =2，过点B 折叠纸片，使点A 落在MN 上的点F 处，∴FB =AB =2，BM =12BC =1，BF =BA =2，∠BMF =90°，则在Rt △BMF 中，FM =∴2FN MN FM =-=设AE =FE =x ，则EN =1x -，∵Rt △EFN 中，222NE NF EF +=，∴()(22212x x -+=，解得：4x =-EN =13x -=，选A 8.如图，在正方形ABCD 中，E 为BC 上一点，将△ABE 沿AE 折叠至AB E '∆处，B E '与AC 交于点F ，若∠EFC =67°，则∠CAE 的度数为____．【解析】由正方形性质知：∠ACE =45°，∵∠EFC =67°，∴在△FEC 中，由外角定理有：∠BEF =∠EFC +∠ACE =67°+45°=112°，由折叠的性质可知：∠BEA =12∠BEF =56°，∴∠BAE =90°-∠BEA =90°-56°=34°， ∴∠EAC =45°-34°=11°．故答案为：11°．9.已知，如图：一张矩形纸片ABCD ，6AB =，8AD =，E 为AD 边上一动点，将矩形沿BE 折叠，要使点A 落在BC 上，则折痕BE 的长度是________；若点A 落在AC 上，则折痕BE 与AC 的位置关系是__________.若翻折后A 点的对应点是A '点，连接DA '，则在点E 运动的过程中，DA '的最小值是______.【解析】如图，由折叠的性质可知，,AB A B EAB BA E ''=∠=∠ ，∵四边形ABCD 是矩形，∴90ABA '∠=︒ ，∴四边形ABA E '是正方形，6AE AB ∴==，BE ∴==若点A 落在AC 上，根据折叠的性质可知，BE 垂直平分，所以折痕BE 与AC 的位置关系是垂直；如图，当A '在BD 上时，DA '的长度最小，6,8AB AD ==，10BD ∴== ．6BA BA '== ，4DA BD BA ''∴=-= ，∴DA '的最小值是4．10..如图，在矩形ABCD 中，2,AB AD m ==，动点P 从点D 出发，沿射线DA 以每秒1个单位的速度向点A 方向运动，连接CP ，把PDC △沿PC 翻折，得到PEC ．设点P 的运动时间为()t s ．（1）若3m =，当P E B 、、三点在同一直线上时，求t 的值；（2）若点E 到直线BC 的距离等于1，求t 的值；（3）若AE 的最小值为1，直接写出m 的值．【解析】（1）如图1中，设PD =t ．则P A =3-t∵P 、B 、E 共线，∴∠BPC =∠DP C ，∵AD ∥BC ，∴∠DPC =∠PCB ，∴∠BPC =∠PCB ，∴BP =BC =3，在Rt △ABP 中，∵AB 2+AP 2=BP 2，∴22+（3-t ）2=32，∴t =3 +5（舍去）或3-5∴当t =3 P E B 、、三点在同一直线上．，2，过点E 作MN ⊥BC ，交AD 于点M∵四边形ABCD 是矩形，MN ⊥BC ，∴MN ⊥AD∵点E 到直线BC 的距离等于1，∴EN =1，∵MN =AB =2, EC =CD =2,∴EN =MN -EN =2-1=1∴在Rt △ENC 中，NC MD = NC∵由题意得：MP =MD -PD -t ,ME =MN -EN =2-1=1,EP =PD =t∴在Rt △MPE 中，222=ME MP PE +，即：)2221=t +，解得：t ，3，如图，当点A ,点E ，点C 在同一条直线上时，AE 最短．由题意得：AE =1，EC =CD =AB =2，∴在Rt △ABC 中，BC∴m =AD =BC 题型3 不过顶点，折痕在内11.如图，将一个边长为4和8的长方形纸片ABCD 折叠，使C 点与A 点重合，则折痕EF 的长是（）A .B .C .D . 【解析】根据折叠的性质知，四边形AFEB 与四边形FDCE 全等，有EC =AF =AE ，由勾股定理得，AB 2+BE 2=AE 2即42+（8﹣AE ）2=AE 2，解得，AE =AF =5，BE =3，作EG ，AF 于点G ，则四边形AGEB 是矩形，有AG =3，GF =2，GE =AB =4，由勾股定理得EF =D12.如图，在矩形ABCD 中，9,3,AD cm AB cm ==将其折叠，使点D 与点B 重合，则重叠部分()BEF ∆的面积为（）2cmA . 15B . 152C . 6D . 5【解析】设DE ＝x ．由翻折的性质可知D E ＝EB ＝x ，∠DEF ＝∠BEF ，则AE ＝（9﹣x ）cm ．由勾股定理得；BE 2＝EA 2＋AB 2，即x 2＝（9﹣x ）2＋32，解得：x ＝5 ，DE ＝5cm ，，四边形ABCD 为矩形，，BC ∥AD ．，∠BF E ＝∠DEF ．，∠BFE ＝∠FEB ，，FB ＝BE ＝5cm ．，，BEF 的面积＝12BF •AB ＝12×3×5＝152（cm 2），选B 13.如图，将矩形ABCD 沿EF 折叠，使点C 恰好落在AB 边的中点C '上，点D 落在D '处，C 'D '交AE 于点M ．若AB =6，BC =9，求线段ED ．【解析】如图，连接C 'E设DE ＝D'E ＝x ，∵在矩形ABCD 中，AB ＝6，BC ＝9∴CD ＝AB ＝6，AD ＝BC ＝9，∠A ＝∠D ＝90°，，AE ＝AD －DE ＝9－x∵折叠，∴∠D'＝∠D ＝90°，C 'D '＝CD ＝6，∵点C '为AB 边的中点∴AC '＝12AB ＝3，在Rt ，AEC'中，C 'E 2＝AE 2＋AC '2＝32＋(9－x )2 在Rt △C'D'E 中，C 'E 2＝C 'D '2＋D 'E 2＝62＋x 2，∴32＋(9－x )2＝62＋x 2，解得x ＝3 ∴线段ED 的长为3。

勾股定理的应用解有关折叠问题

x2=42+(8−x)2. 解得x=5. ∴S△DBE=12×5×4=10；
这节课，你学习到了什么？
解决折叠问题的方法： 1. 找到等量关系，相等线段（折叠，垂直平分线，边
角关系，三角形全等……）， 2.运用勾股定理列方程（方程思想） 3.解方程并求出所求量作业： 1.完成学案 2.补充练习 3.思考题（选做）
动手操作
• 2.如图，折叠长方形纸片ABCD，使点D落在BC上一点F处，折痕的两端点分别在AD，CD上(含端点)，且AB＝6，BC＝10.设CF＝x，
• ①x的取值范围是______________；
• ②当CF取最小值时，折痕与线段CD的交点E与F的
距离为_____________
A
D
B
CБайду номын сангаас
解：由折叠可知
1．如图，在Rt△ABC中，∠B＝90°，AB=8,BC=6
⑴如图1将△ABC折叠，使得A、C重合，折痕MN，
求AM；
(2)如图2将△ABC折叠，使A点与BC的中点D重合，折痕为MN，求BN；
(3)如图3将△ABC折叠，使直角边AB折叠使它落在斜边AC上，折痕为AD，求BD。
图2
图3
用勾股定理列方程是解题的关键
• 思考1.如图，在边长为6的正方形ABCD中，E是边CD的中点，将△ADE沿AE对折至△AFE，延长交BC于点G，连接AG.
• (1)求证：△ABG≌△AFG；
• (2)求BG的长。
思考2：如图，将长方形ABCD沿直线EF折叠
(1) 使点C与点A重合，折痕交AD于点E，交BC于点F，
连接CE.
①求证：AE=AF=EC=CF； ②设AE=a，ED=b，DC=c，请写出一个a，b， c三者之间的数量关系式。 (2)如图2，当C的对应点C′在线段AD里运动时，C′E、

勾股定理中的折叠问题(分类整理版)

勾股定理中的折叠问题
1、如图，在Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，求
线段BN的长．
2、在一张直角三角形纸片中,两条直角边BC等于6,AC等于8,将三角形ABC按如图所示的方式折叠,使点A 和点B重合,折痕为DE,求CD的长
3、如图所示，在△ABC中，AB=20，AC=12，BC=16，把△ABC折叠，使AB落在直线AC上，求重叠部分（阴影部分）
的面积．
变式：如图，有一块直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使AC恰好落在
斜边AB上，且点C与点E重合，求CD的长。

4、如图所示,折叠长方形的一边AD,使点D落在BC边上的点F处,已知AB=8cm,BC=10CM,求DE的长
5、在长方形ABCD中,AB=6,BC=8,将长方形ABCD沿CE折叠后,点D恰好在对角线AC上的点F处、求EF的长。

6、如图，矩形纸片ABCD的边AB=10cm，BC=6cm，E为BC上一点，将矩形纸片沿AE折叠，点B恰好落
在CD边上的点G处，求BE的长.
7、如图，在长方形ABCD中，将△ABC沿AC对折至△AEC位置，CE与AD交于点F．
（1）试说明：AF=FC；
（2）如果AB=3，BC=4，求AF的长．。

折叠问题与勾股定理例题总结

CD E折叠问题与勾股定理例题总结1．如图，在矩形ABCD 中，AB ＝6，BC ＝8。

将矩形ABCD 沿CE 折叠后，使点D 恰好落在对角线AC 上的点F 处。

(1)求EF 的长；(2)求梯形ABCE 的面积。

2．如图所示，在?ABC 中，AB=20，AC=12，BC=16，把?ABC 折叠，使AB 落在直线AC 上，求重叠部分(阴影部分)的面积．3．如图，矩形纸片ABCD 的长AD=9cm ，宽AB=3cm ，将其折叠，使点D 与点B 重合，那么折叠后DE 的长是多少?4如图所示，有一块直角三角形纸片，两直角边AB=6，BC=8，将三角形ABC 折叠,使AB 落在斜边AC 上得到线段AB ’,折痕为AD ，求BD 的长为．5.如图，折叠长方形（四个角都是直角，对边相等）的一边AD 处，已知AB=8cm ，BC=10cm ．求EC 的长．6.如图，将边长为8cm 的正方形纸片ABCD 折叠，使点D 落在BC 点F 处，折痕为MN ，求线段CN 的长．(MN 的长)7．如题，在长方形ABCD 中，将?ABC 沿AC 对折至?AEC 位置，CE (1)试说明：AF=FC(2)如果AB=3，BC=4，求AF 的长。

8.把一张矩形纸片（矩形ABCD ）按如图方式折叠，使顶点B 和点D 重合，折痕为EF ．若AB=3cm ，BC=5cm ，（1）重叠部分△DEF 的面积是多少cm 2? （2）求EF 的长。

9.如图，在Rt △ABC 中，∠C=90°，M 为AB 边上中点，将Rt 使点C 与点A 重合得到△DEA ，设AE 交CB 于点N ． (1) 若∠B=25°,求∠BAE 的度数； (2) 若AC=2，BC=3，求CN 的长．10.如图，将矩形纸片ABCD 沿对角线AC 折叠，使点B 落到点于点E ．(1)求证：△AED ≌△CEB'；(2)AB ＝8，DE ＝3，点P 为线段AC 上任一点，PG ⊥AE 于G ，PH ⊥EC 于H ．求PG＋PH 的值，并说明理由．11.有一边长为2的正方形纸片ABCD ，先将正方形ABCD 对折，设折痕为EF ；再沿过点D的折痕将角A翻折，使得点A落在EF的H上，折痕交AE于点G,求EG的长。

《勾股定理》典型例题折叠问题

《勾股定理》典型例题折叠问题1、如图，有一张直角三角形纸片，两直角边AC=4 BC=8将△ABCW叠，使点B与点A重合, 折痕为DE则CD等于（）A. 25B. 22C. 7D. 54 3 4 32、如图所示，已知△ ABC中，/C=90° , AB的垂直平分线交BC?于M交AB于N,若AC=4MB=2MC求AB的长.3、折叠矩形ABCD勺一边AD,点D落在BC边上的点F处，已知AB=8CM,BC=10CM CF和EC4、如图，在长方形ABCLfr, DC=5在DC边上存在一点E,沿直线AE把△ABCff叠，使点D 恰好在BC边上，设此点为F,若4ABF的面积为30,求折叠的^ AED勺面积5、如图，矩形纸片ABCD勺长AD=9cm,宽AB=3cm,将其折叠，使点D与点B重合，那么折叠后DE 的长是多少？6、如图，在长方形ABCDK 将ABCS AC对折至AEC位置, CE与AD交于点F。

(1)试说明：AF=FC (2)如果AB=3, BC=4求AF的长7、如图2所示，将长方形ABCDS直线AE折叠，顶点D正好落在BC边上F点处，已知CE=3cm AB=8cm则图中阴影部分面积为8、如图2-3,把矩形ABCDS直线BD向上折叠，使点C落在C'的位置上，已知AB=?3, BC=7重合部分△ EBD勺面积为.9、如图5,将正方形ABCDT 叠，使顶点A 与CD4上白t 点M 重合，折痕交AD 于E,交BC 于 F,边AB 折叠后与BC 边交于点 G 如果M 为CD 边的中点，求证：DE DM EM=3 4: 5。

2-5,长方形ABCDfr, AB=3, BC=4若将该矩形折叠，使C 点与A 点重合，？则折2-51-3-11 ,有一块塑料矩形模板ABCD 长为10cm,宽为4cm,将你手中足够大的直角三角板PHF 的直角顶点P 落在AD 边上（不与A 、D 重合）,在AD 上适当移动三角板顶点P:①能否使你的三角板两直角边分别通过点 B 与点C?若能，请你求出这时AP 的长；若不能，请说明理由.②再次移动三角板位置，使三角板顶点 P 在AD 上移动，直角边PH 始终通过点B,另一直角边PF 与DC 的延长线交于点Q,与BC 交于点E,能否使CE=2cm 若能，请你求出这时AP 的长；若不能，请你说明理由.10、如图叠后痕迹 EF 的长为（）11、如图 C12、如图所示，△ ABC是等腰直角三角形，AB=AC D是斜边BC的中点，E、F分别是AB AC边上的点，且DEL DF,若BE=12 CF=5.求线段EF的长13、如图，公路MNF口公路PQ&点P处交汇，且/QPN= 30°，点A处有一所中学，AP= 160ml 假设拖拉机行驶时，周围100m以内会受到噪音的影响，那么拖拉机在公路MN±?吉PN方向行驶时，学校是否会受到噪声影响？请说明理由，如果受影响，已知拖拉机的速度为18km/h, 那么学校受影响的时间为多少秒?《勾股定理》典型复习题一、知识要点：1、勾股定理2、勾股定理的逆定理3、勾股数满足a2+ b2= c2的三个正整数，称为勾股数。

勾股定理中的折叠问题

勾股定理中的折叠问题姓名：例1：如图，有一个直角三角形纸片，两直角边AC =6cm ,BC =8cm ,现将直角边AC 沿∠CAB 的角平分线AD 折叠，使它落在斜边AB 上，且与AE 重合，你能求出CD 的长吗？E BCA D 对应练习：1、如图,已知矩形ABCD 沿着直线BD 折叠,使点C 落在C ／处,BC ／交AD 于E,AD=8,求BC ＇的长2、如图，有一块直角三角形纸片，两直角边AC ＝6cm ，BC ＝8cm ，现将直角边AC 沿直线AD 折叠，使它恰好落在斜边AB 上，且与AE 重合，求CD 的长． AB C DE C ／3、如图，将矩形纸片ABCD 折叠，使点D 与点B 重合，点C 落在C ′处，折痕为EF ，若AB=1，BC=2，（1）请找出图中的等腰三角形（2）求△ABE 和△BC ′F 的周长之和BAC D E4、如图①是一个直角三角形纸片，∠A=30°，BC=4cm，将其折叠，使点C落在斜边上的点C′处，折痕为BD，如图②，再将②沿DE折叠，使点A落在DC′的延长线上的点A′处，如图③，则折痕DE的长为（）5、如图，四边形ABCD是矩形，把矩形沿对角线AC折叠，点B落在点E处，CE与AD相交于点O．（1）求证：△AOE≌△COD；（2）若∠OCD=30°，AB=，求△AOC的面积．（3）请找出图中的等腰三角形6、如图，将矩形纸片ABCD沿其对角线AC折叠，使点B落在点B′的位置，AB′与CD 交于点E．（1）求证：△AED≌△CEB′；（2）求证：点E在线段AC的垂直平分线上；（3）若AB=8，AD=3，求图中阴影部分的周长．7、如图，在矩形ABCD中，AB=3，BC=4，点M、N、分别在BC、AB上，将矩形ABCD沿MN折叠，设点B的对应点是点E．（1）若点E在AD边上，BM=，求AE的长；（2）若点E在对角线AC上，请直接写出AE的取值范围：。

新人教版八下-折叠问题与勾股定理

例1．如图，在矩形ABCD 中，AB ＝6，BC ＝8。

将矩形ABCD 沿CE 折叠后，使点D 恰好落在对角线AC 上的点F 处。

(1)求EF 的长；(2)求梯形ABCE 的面积。

例2．如图，在∆ABC 中，AB=20，AC=12，BC=16，把∆ABC 折叠，使AB 落在直线AC 上，求重叠部分(阴影部分)的面积．例3．如图，矩形纸片ABCD 的长AD=9 cm ，宽AB=3 cm ，将其折叠，使点D 与点B 重合，那么折叠后DE 的长是多少?例4如图，有一块直角三角形纸片，两直角边AB=6，BC=8，将三角形ABC 折叠,使AB 落在斜边AC 上得到线段AB’,折痕为AD ，求BD 的长为．例5.如图，折叠长方形（四个角都是直角，对边相等）的一边AD ，点D 落在 BC 边的点F 处，已知AB=8cm ，BC=10cm ．求EC 的长．例6.如图，将边长为8 cm 正方形纸片ABCD 折叠，使点D 落在BC 中点E 处，点A 落在点F 处，折痕为MN ，求线段CN 的长．例7．如题，在长方形ABCD 中，将∆ABC 沿AC 对折至∆AEC 位置， CE 与AD 交于点F. (1)试说明：AF=FC (2)如果AB=3，BC=4，求AF 的长。

例8.把一张矩形纸片（矩形ABCD ）按如图方式折叠，使顶点B 和点D 重合，折痕为EF ．若AB = 3 cm ，BC = 5 cm ，（1）重叠部分△DEF 的面积是多少cm 2?（2）求EF 的长。

例9.如图，在Rt △ABC 中，∠C=90°，M 为AB 边上中点，将Rt △ABC 绕点M 旋转，使点C 与点A 重合得到△DEA ，设AE 交CB 于点N ． (1) 若∠B=25°,求∠BAE 的度数；(2) 若AC=2，BC=3，求CN 的长．B'D C B A FCDBAEABCMDNE F D AB C AB C D E FFE DA例10.如图，将矩形纸片ABCD 沿对角线AC 折叠，使点B 落到点B'位置，AB'与CD 交于点E ． (1)求证：△AED ≌△CEB'；(2) AB ＝8，DE ＝3，点P 为线段AC 上任一点，PG ⊥AE 于G ，PH ⊥EC 于H ．求PG ＋PH 的值，并说明理由．例11.有一边长为2的正方形纸片ABCD ，先将正方形ABCD 对折，设折痕为EF ；再沿过点D 的折痕将角A 翻折，使得点A 落在EF 的H 上，折痕交AE 于点G,求EG 的长。

专题05 勾股定理与几何图形折叠问题(解析版)

专题05 勾股定理与几何图形折叠问题一、单选题1．如图，在△ABC 中，AB =10，AC =6，BC =8，将△ABC 折叠，使点C 落在AB 边上的点E 处，AD 是折痕，则△BDE 的周长为( )A ．6B ．8C ．12D ．14【答案】C【分析】利用勾股定理求出AB=10，利用翻折不变性可得AE=AC=6，推出BE=4即可解决问题．【解析】在Rt△ABC 中，△AC =6，BC =8，△C =90°，△AB ==10，由翻折的性质可知：AE =AC =6，CD =DE ，△BE =4，△△BDE 的周长=DE +BD +BE =CD +BD +E =BC +BE =8+4=12．故选：C ．【小结】本题考查翻折变换，勾股定理等知识，解题的关键是熟练掌握基本知识，属于中考常考题型． 2．如图，有一张直角三角形纸片，90ACB ∠=︒，5cm AB =，3cm AC =，现将ABC ∆折叠，使边AC 与AB 重合，折痕为AE ，则CE 的长为（）A ．1cmB ．2cmC ．3cm 2D ．5cm 2【答案】C【分析】先根据勾股定理求出BC 的长度，再由折叠的性质可得CE=DE ，设CE x =，然后在Rt BDE 中利用勾股定理即可求出x 的值.【解析】△90ACB ∠=︒，5cm AB =，3cm AC =△4BC ===由折叠可知CE=DE,AC=AD ，90ADE ACE ∠=∠=︒设CE x =，则4,2,BE x BD AB AD =-=-=在Rt BDE 中△222DE BD BE +=△2222(4)x x +=- 解得32x =故选C【小结】本题主要考查勾股定理，掌握勾股定理的内容及方程的思想是解题的关键.3．如图，将等腰直角三角形ABC （90ABC ∠=︒）沿EF 折叠，使点A 落在BC 边的中点1A 处，6BC =，那么线段AE 的长度为A．5B．4C．4. 25D．154【答案】D【分析】由折叠的性质可求得AE=A1E，可设AE=A1E=x，则BE=6-x，且A1B=3，在Rt△A1BE中，利用勾股定理可列方程，则可求得答案．【解析】由折叠的性质可得AE=A1E，△△ABC为等腰直角三角形，BC=6，△AB=6，△A1为BC的中点，△A1B=3，设AE=A1E=x，则BE=6-x，在Rt△A1BE中，由勾股定理可得32+（6-x）2=x2，解得x=154，故选：D．【小结】本题考查折叠的性质，利用折叠的性质得到AE=A1E是解题的关键，注意勾股定理的应用．4．如图，矩形ABCD，AB=3，BC=4，点E是AD上一点，连接BE，将△ABE沿BE折叠，点A恰好落在BD上的点G处，则AE的长为（）A．2B．52C．32D．3【答案】C【分析】先用勾股定理求出BD，再由折叠得出BG=AB=3，从而求出DG=2，最后再用勾股定理求解即可．【解析】在Rt△ABD中，AB=3，AD=BC=4，△BD=5由折叠得，△BGE=△A=90°，BG=AB=3，EG=AE，△DG=BD-BG=2，DE=AD-AE=4-AE，在Rt△DEG中，EG2+DG2=DE2，△AE2+4=（4-AE）2，△AE=32．故选：C．【小结】本题考查翻折变换的性质，勾股定理，熟记性质并利用勾股定理列出方程是解题的关键．5．如图所示，在矩形纸片ABCD中，AB=4，AD=3，折叠纸片使边AD与对角线BD重合，点A落在点A′处，折痕为DG，则AG的长为( )A．2B．1C．43D．32【答案】D【解析】【分析】由题得BD=√AB2+AD2=5，根据折叠的性质得出△ADG△△A′DG，继而得A′G=AG，A′D=AD，A′B=BD-A′G，再Rt△A′BG根据勾股定理构建等式求解即可.【解析】由题得BD=√AB2+AD2=5，根据折叠的性质得出：△ADG△△A′DG ，△A′G=AG ，A′D=AD=3，A′B=BD -A′G=5-3=2，BG=4-A′G在Rt△A′BG 中，BG 2=A′G 2+A′B 2可得：（4−A′G)2=A′G 2+22，解得A′G=32，则AG=32，故选：D ．【小结】本题主要考查折叠的性质，由已知能够注意到△ADG△△A′DG 是解决的关键．6．如图，在四边形ABCD 中，△A ＝△B ＝90°，△C ＝60°，BC ＝CD ＝8，将四边形ABCD 折叠，使点C 与点A 重合，折痕为EF ，则BE 的长为（）A ．1B ．2CD 【答案】A【分析】作DG△BC ，连接AE ，先根据Rt△CDG ，△DCG=60°，得出CG=4，利用勾股定理求出AB=BE=x ，则CE=8-x ，根据折叠得AE= CE=8-x ，再根据勾股定理在Rt△ABE 列出方程进行求解.【解析】作DG△BC ，连接AE ，在Rt△CDG ，△DCG=60°，得出CG=4，设BE=x ，则CE=8-x ，根据折叠得AE= CE=8-x ，在Rt△ABE 中，AE 2=AB 2+BE 2，即(8-x)22+x 2故选A.【小结】此题主要考查勾股定理的应用，解题的关键是熟知勾股定理的应用.7．已知：如图，折叠矩形ABCD，使点B落在对角线AC上的点F处，若BC＝8，AB＝6，则线段CE的长度是（）A．3B．4C．5D．6【答案】C【分析】在Rt△ABC中利用勾股定理可求出AC＝10，设BE＝a，则CE＝8﹣a，根据折叠的性质可得出BE＝FE＝a，AF＝AB＝6，△AFE＝△B＝90°，进而可得出FC＝4，在Rt△CEF中，利用勾股定理可得出关于a的一元二次方程，解之即可得出a值，将其代入8﹣a中即可得出线段CE的长度．【解析】在Rt△ABC中，AB＝6，BC＝8，△AC＝10．设BE＝a，则CE＝8﹣a，根据翻折的性质可知，BE＝FE＝a，AF＝AB＝6，△AFE＝△B＝90°，△FC＝4．在Rt△CEF中，EF＝a，CE＝8﹣a，CF＝4，△CE2＝EF2+CF2，即（8﹣a）2＝a2+42，解得：a＝3，故选C．【小结】本题考查了翻折变换、矩形的性质、勾股定理以及解一元二次方程，在Rt△CEF中，利用勾股定理找出关于a的一元二次方程是解题的关键．8．如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的B'处，点AB C'=，则AM的长是（）的对应点为A'，且3A．1B．1.5C．2D．2.5【答案】C【分析】连接BM，MB′，由于CB′=3，则DB′=6，在Rt△ABM和Rt△MDB′中由勾股定理求得AM的值．【解析】连接BM，MB′，设AM=x，在Rt△ABM中，AB2+AM2=BM2，在Rt△MDB′中，B′M2=MD2+DB′2，△MB=MB′，△AB2+AM2=BM2=B′M2=MD2+DB′2，即92+x2=(9-x)2+(9-3)2，解得x=2，即AM=2，【小结】本题考查了翻折的性质，对应边相等，利用了勾股定理建立方程求解．9．如图，矩形纸片ABCD 中，4AB =，3AD =，折叠纸片使AD 边与对角线BD 重合，则折痕为DG 的长为（）A B C ．2 D 【答案】D【分析】首先设AG ＝x ，由矩形纸片ABCD 中，AB ＝4，AD ＝3，可求得BD 的长，又由折叠的性质，可求得A′B 的长，然后由勾股定理可得方程：x 2+22＝（4-x ）2，解此方程即可求得AG 的长，继而求得答案．【解析】设AG ＝x ，△四边形ABCD 是矩形，△△A ＝90°，△AB ＝4，AD ＝3，△BD 5，由折叠的性质可得：A′D ＝AD ＝3，A′G ＝AG ＝x ，△DA′G ＝△A ＝90°，△△BA′G ＝90°，BG ＝AB -AG ＝4-x ，A′B ＝BD -A′D ＝5-3＝2，△在Rt△A′BG 中，A′G 2+A′B 2＝BG 2，△x 2+22＝（4-x ）2，解得：x ＝32， △AG ＝32，△在Rt△ADG 中，DG =【小结】此题考查了折叠的性质、矩形的性质以及勾股定理．此题难度适中，注意掌握折叠前后图形的对应关系，注意掌握数形结合思想与方程思想的应用．10．如图，正方形ABCD 的边长为8，将正方形折叠，使顶点D 落在BC 边上的点E 处，折痕为GH ．若BE ＝EC ，则线段CH 的长是（）A ．3B ．4C ．5D ．6【答案】A【分析】根据折叠可得DH ＝EH ，在直角△CEH 中，设CH ＝x ，则DH ＝EH ＝8﹣x ，根据BE ＝EC ，可得CE ＝4，可以根据勾股定理列出方程，从而解出CH 的长．【解析】设CH ＝x ，则DH ＝EH ＝8﹣x ，△BC ＝8，△BE ＝EC ＝4，在Rt△ECH 中，EH 2＝EC 2+CH 2，△（8﹣x ）2＝42+x 2，解得：x ＝3，即CH ＝3．故选：A ．【小结】本题考查以正方形为背景的折叠问题，掌握正方形的性质，和折叠的轴对称性质，会利用中点求线段的长，会找问题所在的直角三角形，会利用勾股定理解决问题是关键．11．如图，把直角△ABC 沿AD 折叠后，使点B 落在AC 边上点E 处，若AB=6，AC=10，则CDE S =（）A ．15B ．12C ．9D ．6【答案】D【分析】由勾股定理求出BC 的长，再由折叠性质求出EC 的长、证明△DEC 是直角三角形、CD+DE=BC=8，由勾股定理列出关于DE 的方程，求出DE 后，由面积公式求出CDE S ∆【解析】△△ABC 是直角三角形，AB=6，AC=10由勾股定理得：BC= 8，由折叠可知：AE=AB=6，DE=BD ，△AED=△B=90°，△EC=AC -AE=10-6=4，设BD=x ，则DE=x ，，CD=8-x ，在Rt△CDE 中，222EC DE CD +=，即2224(8)x x +=-，解得x=3，即DE=3，所以△CDE 的面积为：3422DE EC ⋅⨯==6．故选：D△【小结】本题考查用勾股定理计算直角三角形边长．本题中Rt△CDE△△△△△△△△△△△△EC=4，和其它两边△△△△△△△△△DE+CD=8，此时列方程就很关键了．12．如图，将直角△ABC 沿AD 对折，使点C 落在AB 上的E 处，若AC=6，AB=10，则DB 的长度是（）A ．3B ．4C ．8D ．5【答案】D【分析】根据折叠对应边相等，找出对应边，再根据小直角三角形的三边关系即可求出．【解析】△直角△ABC 沿AD 对折，AC=6，AB=10△AE=AC=6，BE=4，DE=DC ，，△BED=△C=900在直角△DEB 中DE 2+BE 2=BD 2△42+（8-BD ）2=BD 2 解得BD=5故选D ．【小结】本题主要考察了勾股定理等知识点，准确找出对应边和找出新的直角三角形是解题关键．13．如图，在平行四边形ABCD 中，点E 为边BC 上一点，连接AE ，将ABE △沿AE 翻折，点B 的对应点是点B '，当点B '落在边AD 上时，8AE =，6BB '=，则边AB 的长是（）A ．5B ．6C ．7D ．9【答案】A【分析】由翻折可知，AE BB BF B F ''⊥=，，再根据平行四边形对边平行的性质，解得AB B B BE ''∠=∠，进而证明()BFE B FA ASA '≅，根据全等三角形对应边相等的性质，可解得AF EF =，结合已知条件及勾股定理，可解题．【解析】根据翻折的性质，可知AE BB BF B F ''⊥=，在平行四边形ABCD 中，//AB BE 'AB B B BE ''∴∠=∠AFB BFE '∠=∠()BFE B FA ASA '∴≅AF EF ∴=8AE =，6BB '=，43AF BF ∴==，，由勾股定理得5AB ==，故选：A ．【小结】本题考查翻折、平行四边形的性质、全等三角形的判定与性质、勾股定理等知识，是重要考点，难度较易，掌握相关知识是解题关键．14．如图，平行四边形纸片ABCD 的对角线AC 与BD 相交于点O ，将平行四边形纸片沿对角线BD 拆叠，使点C 落在平面上的点C '处，若45AOB ∠=︒，1AC =，则点A ，C '之间的距离是（）A ．1B C ．D 【答案】D【分析】连接A C '，由折叠的性质，解得O C '的长，45AOB CO D D C O ∠=∠='=∠︒，根据三角形内角和180°，解得90AOC ∠'=︒，最后根据勾股定理解题即可．【解析】连接A C '，根据折叠的性质可知1122OC OC AO AC '==== 45AOB CO D D C O ∠=∠='=∠︒ 18090AOC AOB C OD ∴∠'=︒-∠-∠'=︒在t AO R C '中AC '= 故选：D ．【小结】本题考查折叠的性质、三角形内角和定理、勾股定理等知识，是重要考点，难度较易，掌握相关知识是解题关键．15．如图，长方形纸片ABCD 中，6AB cm =，8BC cm =，现将其沿EF 对折，使得点C 与点A 重合，则AF 的长为（）A ．254B ．6C ．74D ．234【答案】A【分析】设AF=xcm ，则DF=（8-x ）cm ，利用矩形纸片ABCD 中，现将其沿EF 对折，使得点C 与点A 重合，由勾股定理求AF 即可．【解析】设AF=xcm ，则DF=（8-x ）cm ，△矩形纸片ABCD 中，AB=6cm ，BC=8cm ，现将其沿EF 对折，使得点C 与点A 重合，△DF=D′F ，在Rt△AD′F 中，△AF 2=AD′2+D′F 2，△x 2=62+（8-x ）2，解得：x=254，故选：A ．【小结】本题考查了图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变是解题关键．16．如图，有一块直角三角形纸片，两直角边6AC cm =，8BC cm =，现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上且与AE 重合，则CD 等于（）A ．2cmB ．3cmC ．4cmD ．5cm【答案】B【分析】根据翻折的性质可知：AC ＝AE ＝6，CD ＝DE ，设CD ＝DE ＝x ，在RT△DEB 中利用勾股定理解决．【解析】在RT△ABC 中，△AC ＝6，BC ＝8，△AB =10，△ADE 是由△ACD 翻折，△AC ＝AE ＝6，EB ＝AB−AE ＝10−6＝4，设CD ＝DE ＝x ，在RT△DEB 中，△DE 2＋EB 2＝DB 2，△x 2＋42＝（8−x ）2△x ＝3，△CD＝3．故选：B．【小结】本题考查翻折的性质、勾股定理，利用翻折不变性是解决问题的关键，学会转化的思想去思考问题．17．已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（）A．4cm2B．5cm2C．6cm2D．7cm2【答案】C【分析】根据折叠的条件可得：BE=DE，在直角△ABE中，利用勾股定理就可以求解．【解析】将此长方形折叠，使点B与点D重合，△BE=ED．△AD=9cm=AE+DE=AE+BE．△BE=9-AE，根据勾股定理可知AB2+AE2=BE2．解得AE=4．△△ABE的面积为3×4÷2=6．故选C．【小结】本题考查了利用勾股定理解直角三角形的能力即：直角三角形两直角边的平方和等于斜边的平方．18．直角三角形纸片的两直角边长分别为6，8，现将ABC如图折叠，使点A和点B重合，则折痕DE 的长是（）A ．3B ．3.5C ．3.75D ．4【答案】C【分析】由勾股定理求解AB ，由对折可得,5,AE BE BD AD ===设,BE x = 则,8,AE x CE x ==- 利用勾股定理求解x ，再利用勾股定理可得答案．【解析】90,6,8,C BC AC ∠=︒==10,AB ∴===由折叠可得：,5,AE BE BD AD ===设,BE x = 则,8,AE x CE x ==-()22286,x x ∴-+= 25,4x ∴=15 3.75,4DE ∴==== 故选C ．【小结】本题考查的是求一个数的算术平方根，轴对称的性质，勾股定理的应用，掌握以上知识是解题的关键． 19．如图，在矩形ABCD 中，8BC =，6CD =，将ABE △沿BE 折叠，使点A 恰好落在对角线BD 上的F 处，则折痕BE 的长是（）A ．3B ．5C ．D ．【答案】D【分析】由折叠性质，可知BEF BAE ≅，根据勾股定理，计算BD 的长，进而计算FD 的长，设EF AE x ==，再用勾股定理解得AE 的长，最终求BE 的长．【解析】在矩形ABCD 中，90BAD ∠=︒，由折叠可得BEF BAE ≅，EF BD AE EF AB BF ∴⊥==，，，在t R ABD 中，AB=CD=6,BC=AD=8，根据勾股定理得：BD=10，即FD=10-6=4，设EF AE x ==，则8ED x =-，根据勾股定理得：2224(8)x x +=-，解得：3x ，=BE ∴=故选：D ．【小结】本题考查折叠的性质、勾股定理等知识，是重要考点，难度较易，掌握相关知识是解题关键．20．如图，点F 是长方形ABCD 中BC 边上一点将△ABF 沿AF 折叠为△AEF ，点E 落在边CD 上，若AB ＝5，BC ＝4，则BF 的长为（）A ．73B ．52C ．136D ．56【答案】B【分析】根据矩形的性质可得CD=AB=5，AD=BC=4，△C=△D=90°，由折叠的性质可得AE=AB=5，BF=EF，利用勾股定理即可求出DE，从而求出CE，设BF=EF=x，利用勾股定理列出方程即可求出结论．【解析】△四边形ABCD为矩形，AB＝5，BC＝4，△CD=AB=5，AD=BC=4，△C=△D=90°由折叠的性质可得AE=AB=5，BF=EF在Rt ADE中，3=△CE=CD－DE=2设BF=EF=x，则CF=4－x在Rt CEF中，CF2＋CE2=EF2即（4－x）2＋22=x2解得x=5 2即BF=5 2故选B．【小结】此题考查的是矩形与折叠问题，掌握矩形的性质、折叠的性质和勾股定理是解决此题的关键．21．如图，ABC 中，△C=90°，AC=3，AB = 5，点D 是边BC 上一点，若沿将ACD翻折，点C刚好落在边上点E处，则BD等于（）A．2B．52C．3D．103【答案】B 【分析】根据勾股定理，求出BC 的长度，设 BD=x ，则DC= 4-x ，由折叠可知：DE= 4-x ，BE=2，在 Rt BDE 中，222BD =BE DE +，根据勾股定理即可求出x 的值，即BD 的长度．【解析】△△C= 90°，AC=3，AB=5∴BC= ，设BD=x ，则DC= 4-x ，由折叠可知：DE=DC=4-x ，AE=AC=3，△AED= △C=90°，△ BE= AB -AE = 2．在 Rt BDE 中，222BD =BE DE +，即：222x =2(4-x)+，解得：x=52，即BD=52，故选：B ．【小结】本题主要考查了折叠的性质、勾股定理，解题的关键在于写出直角三角形BDE 三边的关系式，即可求出答案．22．如图，把一张长方形纸片ABCD 沿EF 折叠，若△1＝40°，则△AEF 的度数为（）A ．130°B ．120°C ．110°D ．100°【答案】C【分析】如图，设B 的对应点为K ．由AD△BC ，推出△AEF+△BFE=180°，求出△BFE 即可解决问题．【解析】如图设B 的对应点为K ．△△BFE ＝△EFK ，△1＝40°，△△BFK ＝180°﹣40°＝140°，△△BFE ＝70°，△AD △BC ，△△AEF +△BFE ＝180°，△△AEF ＝110°，故选：C ．【小结】本题考查了矩形折叠的问题，掌握折叠的性质、矩形的性质、平行线的性质是解题的关键．23．在矩形纸片ABCD 中，6,10AB AD ==．如图所示，折叠纸片，使点A 落在BC 边上的A '处，折痕为PQ ，当点A '在BC 边上移动时，折痕的端点P 、Q 也随之移动，若限定点P 、Q 分别在线段AB 、AD 边上移动，则点A '在BC 边上可移动的最大距离为（）A ．3B ．4C ．5D ．6【答案】B【分析】根据翻折的性质，△当P 与B 重合时，可得BA′与AP 的关系，根据线段的和差，可得A′C ，△当Q 与D 重合时，根据勾股定理，可得A′C ，根据线段的和差，可得答案．【解析】△当P 与B 重合时，BA′＝BA ＝6，CA′＝BC−BA′＝10−6＝4，△当Q 与D 重合时，由勾股定理，得CA′8，CA′最大是8，CA′最小是4，点A′在BC 边上可移动的最大距离为8−4＝4，故选：B ．【小结】本题考查了翻折变换，利用了翻折的性质，勾股定理，分类讨论是解题关键．24．如图，Rt ABC 中，90ACB ∠=︒，3AC =，4BC =，将边AC 沿CE 翻折，使点A 落在AB 上的点D 处；再将边BC 沿CF 翻折，使点B 落在CD 的延长线上的点B '处，两条折痕与斜边AB 分别交于点E 、F ，则线段B F '的长为（）A ．45B ．35C ．23D ．34【答案】A【分析】根据折叠的性质可知AC=CD ，△A=△CDE ，CE△AB ，Rt△ABC 中根据勾股定理求得AB=5，再根据三角形的面积可求得B′F 的长．【解析】△Rt△ABC 中，△ACB ＝90°，AC ＝3，BC ＝4，△AB ＝5，根据折叠的性质可知AC ＝CD ，△A ＝△CDE ，CE △AB ，△B ′D ＝BC ﹣CD ＝4﹣3＝1，△DCE +△B ′CF ＝△ACE +△BCF ，△△ACB ＝90°，△△ECF ＝45°，△△ECF 是等腰直角三角形，△EF ＝CE ，△EFC ＝45°，△△BFC ＝△B ′FC ＝135°，△△B ′FD ＝90°，△S △ABC ＝12AC •BC ＝12AB •CE ， △AC •BC ＝AB •CE ，△CE ＝125，△EF ＝125，ED ＝AE 95=， △DF ＝EF ﹣ED ＝35△B ′F 45=．选：A ．【小结】此题主要考查了翻折变换，勾股定理的应用等，根据折叠的性质求得相等的角是本题的关键．25．如图，在ABCD 中，点E ，F 分别在边AB ，AD 上．将AEF 沿EF 折叠，点A 恰好落在BC 边上的点G 处．若45A ∠=︒，AB =5BE AE =，则AF 长度为（）A．152 B ．7 C ．6 D ．【答案】A【分析】过B 作BM△AD 于M ，作FH△BC 于H ，作EN△BC 于N ，交CB 延长线于N ，分别求出BN 、EN 、AM 、BM ，继而在Rt△GEN 中求出GN 的值，设FM=BH =x ，在Rt△GFH 中，由勾股定理列方程解出x ，即可得出结果．【解析】过B 作BM△AD 于M ，作FH△BC 于H ，作EN△BC 于N ，交CB 延长线于N ，如图1所示：则BM△BC ，BM=FH ，FM=BH ，由折叠的性质得：AE=GE= GF=AF ，△四边形ABCD 是平行四边形，△AD△BC ，△△EBN=△A=45°，△△ABM 和△BEN 是等腰直角三角形，△BN=EN=，AM=BM= ， △FH=6，在Rt△GEN 中，由勾股定理得：12+GN 2= 2，解得：GN=±7（负值舍去），△GN=7，设FM=BH =x ，则GH=7-1-x=6-x ，GF=AF=x+6，在Rt△GFH 中，由勾股定理得：62+（6-x ）2=（x+6）2，解得：x=32， △AF=32+6=152；故选：A ．【小结】本题考查了翻折变换的性质、平行四边形的性质．等腰直角三角形的判定与性质、勾股定理等知识；熟练掌握翻折变换的性质，由勾股定理得出方程是解题的关键．26．如图，已知 Rt ABC 中，90,6,8C AC BC ∠︒＝＝＝，将它的锐角A 翻折，使得点A 落在边 BC 的中点D 处，折痕交 AC 边于点E ，交AB 边于点F ，则 DE 的值为（）A ．5B ．4C ．133D ．143【答案】C【分析】由折叠可得△AEF△△DEF ，可知AE=DE ，由点 D 为边 BC 的中点，可求CD=118422CB =⨯=，设DE=x ，CE=6-x ，在Rt△CDE 中由勾股定理()22246x x +-=解方程即可．【解析】 △将它的锐角A 翻折，使得点A 落在边 BC 的中点 D 处，折痕交 AC 边于点E ，交AB 边于点F ， △△AEF△△DEF ，△AE=DE ，△点 D 为边 BC 的中点， △CD=118422CB =⨯=，设DE=x ，CE=6-x ，在Rt△CDE 中由勾股定理，222CD CE DE +=即()22246x x +-=，解得133x =．故选择：C ．【小结】本题考查折叠性质，中点定义，勾股定理，掌握折叠性质，中点定义，勾股定理，关键是利用勾股定理构造方程．27．如图，矩形纸片ABCD ，3AB =，5AD =，折叠纸片，使点A 落在BC 边上的E 处，折痕为PQ ，当点E 在BC 边上移动时，折痕的端点P 、Q 也随之移动，若限定点P 、Q 分别在AB 、AD 边上移动，则点E 在BC 边上可移动的最大距离为（）A．1B．2C．4D．5【答案】B【分析】根据翻折变换，当点Q与点D重合时，点E到达最左边，当点P与点B重合时，点E到达最右边，所以点E就在这两个点之间移动，分别求出这两个位置时EB的长度，然后两数相减就是最大距离．【解析】如图1，当点D与点Q重合时，根据翻折对称性可得ED=AD=5，在Rt△ECD中，ED2=EC2+CD2，即52=（5-EB）2+32，解得EB=1，如图2，当点P与点B重合时，根据翻折对称性可得EB=AB=3，△3-1=2，△点E在BC边上可移动的最大距离为2．故选：B．【小结】本题考查的是翻折变换及勾股定理，熟知图形翻折不变性的性质是解答此题的关键．28．如图，已知ABCD 是长方形纸片，3CD =，在CD 上存在一点E ，沿直线AE 将AED 折叠，D 恰好落在BC 边上的点F 处，且6AFB S =△，则AED 的面积是（）．A ．253B ．256 C ．43 D ．23 【答案】B 【分析】根据面积求出BF 、AF 、CF ，设DE 为x ，列方程求出即可．【解析】ABCD 是长方形纸片，△AB=CD=3，12AFB S AB BF =⋅△， △1632BF =⨯⋅， △BF=4，△AF=5=，△AF=AD=BC=5，CF=1，设DE 为x ，EF=DE=x ，EC=3-x ，x 2=(3-x)2+1，解得，x=53， △1152552236AED S AD ED ∆=⋅=⨯⨯=，故选：B ．【小结】本题考查了勾股定理与翻折，解题关键是恰当的设未知数，根据勾股定理列方程．29．如图，点A是y正半轴上一点，点B是x负半轴上一点，3BC=，AB=，点C（在B的右边）在x轴上，且5点D是x轴上一动点，将三角形ABD沿直线AD翻折，点B落在点E处，已知CE的最小值为1，则点A的坐标是（）A．（0，2）B．（0，2.4）C．（0，2.5）D．（0，1.8）【答案】B【分析】由折叠的性质可求AC的长，由勾股定理可求OA的长．【解析】△将三角形ABD沿直线AD翻折，点B落在点E处，△AB＝AE=3，△EC≥AC-AE，△当点A，点E，点C共线时，EC有最小值，如图，△CE的最小值为1，△AC＝4，△AO2+OC2＝16，AO2+（5﹣OC）2＝9，△OC=3.2,OA＝2.4，△点A坐标为（0，2.4），故选：B．【小结】本题考查了折叠的性质，勾股定理，利用勾股定理列出方程组是解决问题的关键．30．如图，在Rt△ABC中，△BAC＝90°，以Rt△ABC各边为斜边分别向外作等腰Rt△ADB、等腰Rt△AFC、等腰Rt△BEC，然后将等腰Rt△ADB和等腰Rt△AFC按如图方式叠放到等腰Rt△BEC中，其中BH＝BA，CI ＝CA，已知，S四边形GKJE＝1，S四边形KHCJ＝8，则AC的长为（）A．2B．52C．4D．6【答案】D【分析】设AD＝DB＝a，AF＝CF＝b，BE＝CE＝c，由勾股定理可求a2+b2＝c2，由S四边形GHCE＝S四边形GKJE+S四边形KHCJ＝9，可求b＝【解析】设AD＝DB＝a，AF＝CF＝b，BE＝CE＝c，△AB=，AC=，BC=，△△BAC＝90°，△AB2+AC2＝BC2，△2a2+2b2＝2c2，△a2+b2＝c2，△将等腰Rt△ADB 和等腰Rt△AFC 按如图方式叠放到等腰Rt△BEC ，△BG ＝GH ＝a ，△S 四边形GHCE ＝S 四边形GKJE +S 四边形KHCJ ＝9， △12（a +c ）（c ﹣a ）＝9， △c 2﹣a 2＝18，△b 2＝18，△b ＝△AC =＝6，故选：D ．【小结】本题考查了勾股定理，折叠的性质，利用整体思想解决问题是本题的关键．31．如图，矩形ABCD 中，6,8AB BC ==．点E 、F 分别为边BC 、AD 上一点，连接EF ，将矩形ABCD 沿着EF 折叠，使得点A 落到边CD 上的点A '处，且2DA A C '='，则折痕EF 的长度为（）A ．B ．C D【答案】A【分析】由2DA A C '='，6DC =，可求出DA '，A C '的长，再根据折叠和勾股定理可求出DF 和FA '，依据三角形相似可求出NC 、NA '，进而求出MF ，最后根据勾股定理求出EF ．【解析】如图，过点E 作EM AD ⊥，垂足为M ，2DA A C ''=，6DC =， 243DA DC '==，123A C DC '==，由折叠得，AF FA ='，6AB A B =''=，设DF x =，则8FA FA x ='=-，在Rt DFA ∆'中，由勾股定理得， 2224(8)x x +=-，解得3x =，即3DF =，835FA FA ∴='=-=，1809090NA C DA F ∠'+∠'=︒-︒=︒，90NA C A NC ∠'+∠'=︒， DA F A NC ∴∠'=∠'，90C D ∴∠=∠=︒，∴△A NC '∽△FA D '， ∴A C NC A N FD A D FA ''==''，即2345NC A N '==，解得83NC =，103A N '=， 108633B N A B A N NC ∴'=''-'=-==， ∴△()A CN ENB AAS '≅∆'，103EN A N ∴='=， 108633EC EN NC MD ∴=+=+==， 633MF ∴=-=，在Rt EFM ∆中，EF == 故选：A ．【小结】本题考查矩形的性质、折叠轴对称、相似三角形、全等三角形以及勾股定理等知识，掌握折叠的性质和直角三角形的边角关系是得出答案的前提，建立图形中线段之间的关系是解决问题的关键．32．如图，在△ABC 中，D 是BC 边上的中点，连结AD ，把△ACD 沿AD 翻折，得到△AD C '，D C '与AB 交于点E ，连结B C '，若BD ＝B C '＝2，AD ＝3，则点D 到A C '的距离( )AB C D 【答案】B【分析】连接CC '，交AD 于点M ，过点D 作DH AC '⊥于点H ，由翻折知，ADC ADC '∆≅∆，AD 垂直平分CC '，证BDC '∆为等边三角形，利用解直角三角形求出1DM =，C M '=2AM =，在Rt 'AC M ∆中，利用勾股定理求出AC '的长，在ADC '∆中利用面积法求出DH 的长．【解析】如图，连接CC '，交AD 于点M ，过点D 作DH AC '⊥于点H ，2BD BC ='=，D 是AC 边上的中点，2BD DC ==，由翻折知，ADC ADC '∆≅∆，AD 垂直平分CC '，2DC DC '∴==，AC AC '=，CM C M '=，2BD BC DC '∴='==，BDC '∴∆为等边三角形，60BDC BC D C BC '''∴∠=∠=∠=︒，DC DC '=，160302DCC DC C ''∴∠=∠=⨯︒=︒，在Rt △C DM '中，30DC C '∠=︒，2DC '=，1DM ∴=，C M '=312AM AD DM ∴=-=-=，在Rt 'AC M ∆中，AC ==' 1122ADC S AC DH AD CM ∆''==， ∴3=DH =，故选：B ．【小结】本题考查了轴对称的性质，解直角三角形，勾股定理等，解题关键是会通过面积法求线段的长度．二、填空题33．如图，AD 是ABC 的中线，45ADC ∠=︒，10BC =，把ABC 沿直线AD 折叠，点C 落在点C '处，那么BC '的长为________．【答案】【分析】由题意可得BD=CD=5，根据折叠的性质可得CD=C'D=5，△ADC=△ADC'=45°，根据勾股定理可求BC'的长．【解析】△AD 是ABC 的中线，10BC =，△BD=CD=5，△把ABC 沿直线AD 折叠，△CD=C'D ，△ADC=△ADC'=45°，△BD=C'D=5，△BDC'=90°，=故答案为：【小结】本题考查了翻折变换，勾股定理，熟练掌握折叠的性质是解题的关键．34．如图，在三角形纸片ABC 中，90,30,6C A AC ︒︒∠=∠==,折叠纸片，使点C 落在AB 边上的点D 处，折痕BE 与AC 交于点E ，则折痕BE 的长为_____________；【答案】4【分析】根据勾股定理求得BC =AB =△CBE=△ABE=12△ABC=30°，继而证得BE=AE ，在Rt△BCE 中，利用勾股定理列方程即可求得答案．【解析】在Rt△ABC 中，90,30,6C A AC ︒︒∠=∠==，设BC x =，则2AB x =，△222BC AC AB +=，即()22262x x +=，解得：x =△BC =AB =△折叠△ABC 纸片使点C 落在AB 边上的D 点处，△△CBE=△ABE ，在Rt△ABC 中，△A=30°，△△ABC=60°， △△CBE=△ABE=12△ABC=30°，△△ABE=△A=30°，△BE=AE ，在Rt△BCE 中，△C=90°，BC =6CE AC AE BE =-=-，△222BC CE BE +=，即(()2226BE BE +-=，解得：4BE =．【小结】本题主要考查了勾股定理的应用，含30度的直角三角形的性质以及折叠的性质，利用勾股定理构建方程求线段的长是解题的关键．领会数形结合的思想的应用．35．如图，在长方形ABCD 中，AB =3cm ，AD =9cm ，将此长方形折叠，使点D 与点B 重合，折痕为EF ，则ΔABE 的面积为________cm 2.【答案】6【解析】【分析】由折叠的性质可知AE 与BE 间的关系，根据勾股定理求出AE 长可得面积.【解析】由题意可知BE =ED .因为AD =AE +DE =AE +BE =9cm ，所以BE =(9−AE )cm.在RtΔABE 中，根据勾股定理可知，AB 2+AE 2=BE 2，所以32+AE 2=(9−AE )2，所以AE =4cm ，所以RtΔABE 的面积为12×AB ×AE =12×3×4=6（cm 2）. 故答案为：6【小结】本题考查了勾股定理，由折叠性质得出直角边与斜边的关系是解题的关键.36．如图，在Rt ABC ∆中，B 90∠=︒，AB 30=，BC 40=，将ABC ∆折叠，使点B 恰好落在边AC 上，与点B'重合，AE 为折痕，则EB'=_________.【答案】15【分析】根据折叠的性质可设BE=EB′=x，EC=40﹣x，然后再利用勾股定理在Rt△ABC中求得AC，进而在Rt△B′EC 中求解x即可.【解析】根据折叠的性质可得BE=EB′，AB′=AB=30，设BE=EB′=x，则EC=40﹣x，△△B=90°，AB=30，BC=40，△在Rt△ABC中，由勾股定理得，AC=50，△B′C=50﹣30=20，在Rt△B′EC中，由勾股定理得，x2+202=（40﹣x）2，解得x=15．故答案是15．【小结】勾股定理和翻折变换是本题的考点，熟练掌握勾股定理和折叠的性质是解题的关键.37．如图，长方形ABCD中，AB=8，BC=4，将其沿AC折叠，点D落在E处，CE与AB交于点F，且EF=FB，则重叠部分△ACF的面积是____________【答案】10【分析】因为BF=EF，所以可设EF=x，则在Rt△AFE中，根据勾股定理求x，进而求出即可．【解析】△EF=BF，△设EF =x ，则AF =8-x ，在Rt △AFE 中，（8-x ）2=x 2+42，解之得：x =3，△AF =AB -FB =8-3=5，1102AFC S AF BC ∴==△．故答案为：10．【小结】此题主要考查了翻折变换的性质以及勾股定理的应用，利用已知设EF =x ，根据直角三角形AFE 中运用勾股定理求x 是解题的关键．38．如图，在三角形纸片ABC 中，△C ＝90°，AC ＝18，将△A 沿DE 折叠，使点A 与点B 重合，折痕和AC 交于点E ，BC ＝12，则EC 的长为__________．【答案】5【分析】由翻折的性质可知BE =EA =18-EC ，最后在Rt △BCE 中由勾股定理求得EC 的长即可．【解析】△AC =18，△BE =AE =18-EC ，△可得()2221218EC EC +=-，解得：EC =5，故答案为：5．【小结】本题主要考查的是翻折的性质、勾股定理的应用，利用翻折的性质求得BE =EA =18-EC 是解题的关键． 39．如图，在菱形纸片ABCD 中，4AB =，60A ∠=︒，将菱形纸片翻折，使点A 落在CD 边的中点E 处，折痕为FG ，点F 、G 分别在边AB 、AD 上，则GE =_______．【答案】2.8【分析】过点E 作EH AD ⊥于H ，根据菱形的性质，得到//AB CD ，4AD BC CD AB ====，继而可证60A HDE ∠=∠=︒，再利用含30°角的直角三角形性质，解得12DH DE =，结合勾股定理解得HE 的长，根据折叠的性质，得到,AG GE AF EF ==，最后在Rt HGE 中利用勾股定理得222GE GH HE =+，据此整理解题即可．【解析】过点E 作EH AD ⊥于H ，ABCD 是菱形//AB CD ∴，4AD BC CD AB ====60A HDE ∴∠=∠=︒ E 是CD 中点2DE ∴=在Rt DHE △中，2DE =HE DH ⊥60HDE ∠=︒30HED ∴∠=︒1,DH HE ∴===折叠,AG GE AF EF ∴==在Rt HGE 中222GE GH HE =+22(41)3GE GE ∴=-++2.8GE ∴=故答案为：2.8．【小结】本题考查翻折变换、菱形的性质、含30°角的直角三角形等知识，是重要考点，难度较易，掌握相关知识是解题关键．40．如图，在Rt ABC △中，90ACB ∠=︒，6AC =，8BC =，点E 、F 分别在AC 、BC 上，将CEF △沿EF 翻折，使C 与AB 的中点M 重合，则CF 的长为______．【答案】258【分析】过点M 作MN BC ⊥于N ，则//MN AC ，可得MN 是Rt ABC △的中位线，利用三角形中位线定理可得MN=12AC=3，BN=CN=12BC=4，设CF=x ，则NF=4-x ，由折叠的性质可得MF=CF ，在Rt MNF △中，利用勾股定理即可求解．【解析】过点M 作MN BC ⊥于N ，△90ACB ∠=︒，MN BC ⊥，△//MN AC ，△M 是AB 的中点，△MN 是Rt ABC △的中位线， △MN=12AC=3，BN=CN=12BC=4，设CF=x ，则NF=4-x ，△将CEF △沿EF 翻折，使C 与AB 的中点M 重合，△MF=CF=x ，在Rt MNF △中，222MN NF MF +=，△()22234x x +-=，解得258x =， △CF=258．故答案为：258．【小结】本题考查折叠的性质，三角形的中位线定理，勾股定理等知识，熟练掌握三角形的中位线定理，利用勾股定理建立方程求解是解题的关键．41．如图，在直角三角形ABC 中，90C ∠=︒，6BC =，8AC =，点D 是AC 边上一点，将BCD △沿BD 折叠，使点C 落在AB 边的E 点，那么DE 的长度是________．【答案】3【分析】先根据勾股定理得到AB=10，再根据折叠的性质得到DC=DE ，BC=BE=6，则AE=4，设DE=x ，在Rt△ADE 中利用勾股定理得（8-x ）2=x 2+42，解得方程即可．【解析】△△C=90°，BC=6，AC=8，△10AB ==△将△BCD 沿BD 折叠，使点C 落在AB 边的E 点，△△BCD△△BED ，△△C=△BED=△AED=90°，DC=DE ，BC=BE=6，△AE=AB -BE=4，设DC=x ，则AD=8-x ，在Rt△ADE 中，AD 2=AE 2+ED 2，即（8-x ）2=x 2+42，解得x=3，△DE=3【小结】本题考查了折叠的性质以及勾股定理等知识，利用折叠性质折叠前后两图形全等，即对应角相等，对应线段相等，对应点的连线段被折痕垂直平分是解题关键．42．如图，在Rt ABC △中，90C ∠=︒，8AC =，6BC =，按图中所示方法将BCD △沿BD 折叠，使点C 落在边AB 上的点C '处，则点D 到AB 的距离=________．【答案】3【分析】首先根据勾股定理求出AB 的长，然后利用折叠的性质求出AC ′的长，在△AC ′D 中，设DC ′=x ，则AD =8-x ，根据勾股定理求出x 的值即可．【解析】△△C =90°，AC =8，BC =6，△AB =10．根据折叠的性质，BC =BC ′，CD =DC ′，△C =△AC ′D =90°．△AC ′=10-6=4．在△AC ′D 中，设DC ′=x ，则AD =8-x ，根据勾股定理得（8-x ）2=x 2+42．解得x =3．△DC ′=CD =3，故答案为3．【小结】本题考查图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后对应边、角相等．43．如图，在矩形ABCD 中，AB =6，BC =8，对角线AC 、BD 相交于点O ，点P 为边AD 上一动点，连接OP ，以OP 为折痕，将AOP 折叠，点A 的对应点为点E ，线段PE 与OD 相交于点F ．若PDF 为直角三角形，则DP 的长__________．【答案】52或1 【分析】先根据矩形的性质、折叠的性质可得90DAB ∠=︒,8AD =,10BD =,5OA OD OE ===，,EP AP E ADB =∠∠=∠，设DP x =，从而可得8EP x =-，再根据直角三角形的定义分90DFP ︒∠=和90DPF ︒∠=两种情况，然后分别利用相似三角形的判定与性质、勾股定理求解即可得．【解析】四边形ABCD 是矩形，6AB =，8BC =，90DAB ︒∴∠=，8AD BC ==，10BD =，152OA OD BD ===，。

专题05 勾股定理在折叠问题中的应用(解析版)

专题05 勾股定理在折叠问题中的应用折叠问题是中考的热点也是难点问题，通常与动点问题结合起来，这类问题的题设通常是将某个图形按一定的条件折叠，通过分析折叠前后图形的变换，借助轴对称性质、勾股定理等知识进行解答。

此类问题立意新颖，充满着变化，要解决此类问题，除了能根据轴对称图形的性质作出要求的图形外，还要能综合利用相关数学模型及方法来解答。

下面就从以下的题目中逐一进行论述.题1. 如图1-1，在Rt△ABC中，∠A=90°，AB=3，AC=4，现将△ABC沿BD进行翻折，使点A刚好落在BC上，则CD=__________．图1-1【答案】5 2 .【解析】∵∠A=90°，AB=3，AC=4∴在Rt△ABC中，由勾股定理得：BC=5. 由折叠的性质知：AB=AB’=3，AD=A’D∴A’C=2设CD=x，则AD=A’D=4－x在Rt△A’DC中，由勾股定理得：CD2=A’C2+A’D2x2=4+(4－x)2解得：52 x .故答案为5 2 .题2. 如图2-1，△ABC是一张纸片，∠C=90°，AC=6，BC=8，现将其折叠．使点B与点A重合，折痕为DE，则DE的长为（）A．1.75 B．3 C．3.75 D．4图2-1【答案】C.【解析】∵∠C=90°，AC=6，BC=8，∴在Rt△ABC中，由勾股定理得：AB=10.由折叠的性质知：AD=BD=3，AE=BE=5.设CD=x，则BD=AD=8－x，在Rt△ADC中，由勾股定理得：AD2=AC2+CD2(8－x)2=36+x2解得：x=1.75 .∴BD=6.25.在Rt△BDE中，由勾股定理得：DE=3.75.故答案为C.题3. 如图3-1，长方形ABCD中，AB=3，BC=4，点E是BC边上一点，连接AE，把∠B沿AE折叠，使点B 落在点B′处．当△CEB′为直角三角形时，BE的长为．【答案】3或1.5.【解析】分两种情况讨论：ABCDEB'图3-2①当∠CEB ′=90°时，如图3-2所示.由折叠性质得：AB =AB ′，四边形ABE B ′是矩形. 所以四边形ABE B ′是正方形. 此时，BE =AB =3.ABC DEB'图3-3②当∠CB ′E =90°时，如图3-3所示.由折叠性质知，∠AB ′C =90°，所以∠AB ′C+∠CB ′E =180°. ∴点A 、B ′、C 共线在Rt △ABC 中，由勾股定理得AC =5 由折叠得：AB = AB ′=3 所以B ′C =2设BE =x ，则B ′E =x ，EC =4－x在Rt △ABC 中，由勾股定理得：EC 2=B ′E 2+B ′C 2 即：（4-x ）2=x 2+22 解得：x =1.5.综上所述，BE 的值为3或1.5.【点睛】本题解题关键在准确对问题进行分类讨论，并作出相应图形利用折叠的性质及勾股定理解题. 题4. 如图4-1，四边形ABCD 中，AD ∥BC ，∠B =90°， E 为AB 上一点，分别以ED ，EC 为折痕将两个角（∠A ,∠B ）向内折起,点A ,B 恰好落在CD 边的点F 处.若AD =3，BC =5，则EF 的值是（）图4-1A.15B.215C.17D.217【答案】A.【解析】由折叠性质知：AE=EF，AD=DF，BE=EF，BC=CF∴CD=CF+FD=8，AE=BE=EF.∵∠AED=∠DEF，∠BEC=∠CEF∠AED+∠DEF+∠BEC+∠CEF=180°∴∠DEC=90°在Rt△BCE中，由勾股定理得：CE2=BE2+BC2同理得：DE2=AD2+AE2CD2=CE2+DE2∴CD2= BE2+BC2 +AD2+AE2即64=2EF2+9+25解得：EF=15.故答案为A.题5. 如图5-1，在长方形ABCD中，将∆DBC沿BD对折至∆DBC’位置，BC’与AD交于点E. （1）试说明：BE=DE；（2）如果AB=6，BC=8，求△EBD的面积.图5-1【答案】见解析.【解析】（1）证明：由折叠性质知：∠EBD =∠DBC ， ∵ABCD 是长方形， ∴AD ∥BC ∴∠EDB =∠DBC ∴∠EBD =∠EDB ∴BE =DE .（2）解：设DE =BE =x ，则AE =8-x ，在Rt △ABE 中，由勾股定理得：222BE AB AE =+即()22268x x =+- 解得：x =254. ∴△EBD 的面积为17524DE AB ⨯⨯=. 题6. 如图6-1所示，把长方形纸片ABCD 折叠，使点B 恰好落在CD 边的中点E 处，折痕为AF . 若CD =6，求AF 的长度.F图6-1【答案】见解析.【解析】由折叠性质知：∠BAF =∠F AE ，AB =AE ∵E 是长方形ABCD 的边CD 的中点， ∴AE =CD =2DE ∴∠DAE =30° ∴∠BAF =∠F AE =30° 设BF =x ，则AF =2x在Rt △ABF 中，由勾股定理得：222AF AB BF =+即()22226x x =+ 解得：x=∴AF =2x=题7. 如图7-1，在矩形OABC 中，OA =5，AB =4，点D 为边AB 上一点,将△BCD 沿直线CD 折叠,使点B 恰好落在OA 边上的点E 处，分别以OC ，OA 所在的直线为x 轴，y 轴建立平面直角坐标系. 求点D 的坐标.【答案】见解析.【解析】由折叠性质可知：BD =DE , BC =CE =5 ∵OC =AB =4∴在Rt △OCE 中，由勾股定理得：3OE ==.∴AE =OA -OE =2.设AD =x ，则BD =DE =4-x , 在Rt △ADE 中，由勾股定理得：222AD AE DE +=()22224x x +=-解得：x =32. 因为D 点在第三象限，所以D 点坐标为352⎛⎫-- ⎪⎝⎭，.题8. 如图8-1，在Rt ABC ∆中，90A ∠=︒，AB AC =，21BC =+，点M ，N 分别是边BC ，AB上的动点，沿MN 所在的直线折叠B ∠，使点B 的对应点'B 始终落在边AC 上.若'MBC ∆为直角三角形，则BM 的长为．21+ 1. 【解析】通过观察及分析可知，C 点不可能为直角顶点，分两种情况讨论.A (B')BCN图8-2①当∠CM B ′=90°时，如图8-2所示.由折叠知：∠BMN =∠B ′MB =45°，又因为∠B =45°，所以∠BNM =90°，∠MNB ′=90° 即∠BNM +∠MN B ′=180°，所以B 、N 、B ′三点共线，此时B ′与点A 重合. 所以，1212BM BC +==A BCN B'图8-3②当∠CB ′M =90°时，如图8-3所示.由折叠知∠B =∠B ′=45°，因为∠C =45°，可得∠B ′MC =45°，所以△B ′MC 是等腰直角三角形设BM = B ′M =x ，B ′C =x ，则MC = 2x因为BC 2+1所以x +2x=2+1 解得：x =1，即BM =1.故答案为：212或1. 题9. 如图9-1，AD 是△ABC 的中线，把△ADC 沿直线AD 翻折，点C 落在点C ’的位置，若∠ADC =45°，BC =4. 求BC ’的长.图9-1【答案】见解析. 【解析】由折叠性质得： ∠ADC =∠ADC ’=45°，CD =C ’D ∴∠C ’DC =∠BDC ’=90° 如图9-2所示.CAA (C')BD图9-2△BDC ’为等腰直角三角形，BD =C ’D =2，根据勾股定理，得BC ’ =22故BC ’的长为22题10. 已知，如图10-1长方形ABCD 中，AB =3cm ，AD =9cm ，将此长方形折叠，使点B 与点D 重合，折痕为EF ，则△ABE 的面积为AB CDEF图10-1【答案】6.【解析】由折叠性质得：DE=BE设AE=x，则BE=DE=9-x,在Rt△ABE中，由勾股定理得：222AB AE BE+=()22239x x+=-解得：x=4.所以三角形ABE的面积为：11346 22AB AE⨯⨯=⨯⨯=.故答案为6.题11. 动手操作：在矩形纸片ABCD中，AB=3，AD=5. 如图11-1所示，折叠纸片，使点A落在BC边上的A’处，折痕为PQ，当点A’在BC边上移动时，折痕的端点P、Q也随之移动. 若限定点P、Q分别在AB、AD边上移动，则点A’在BC边上可移动的最大距离为.图11-1【答案】2.【解析】此题根据题目要求准确判断出点A'的最左端和最右端位置.当点Q与点D重合时，A'的位置处于最左端，当点P与点B重合时，点A'的位置处于最右端. 根据分析结果，作出图形，利用折叠性质分别求出两种情况下的BA'或CA'的长度，二者之差即为所求.①当点Q与点D重合时，A'的位置处于最左端，如图11-2所示.确定点A'的位置方法：因为在折叠过程中，A'Q=AQ，所以以点Q为圆心，以AQ长为半径画弧，与BC的交点即为点A'. 再作出∠A'QA的角平分线，与AB的交点即为点P.AD (Q )C B P A'5534图11-2由折叠性质可知，AD = A 'D =5，在Rt △A 'CD 中，由勾股定理得，2222''534A C A D CD =-=-=②当点P 与点B 重合时，点A '的位置处于最右端，如图11-3所示.AD CB (P )A'Q332图11-3确定点A '的位置方法：因为在折叠过程中，A 'P =AP ，所以以点P 为圆心，以AP 长为半径画弧，与BC 的交点即为点A '. 再作出∠A 'P A 的角平分线，与A D 的交点即为点Q . 由折叠性质可知，AB = A 'B =3，所以四边形AB A 'Q 为正方形. 所以A 'C =BC －A 'B =5－3=2.综上所述，点A 移动的最大距离为4－2=2. 故答案为：2.【点睛】此题难度较大，主要考察学生的分析能力，作图能力。

勾股定理在折叠问题中的应用(习题及答案).

勾股定理在折叠问题中的应用（习题）例题示范例1：如图，在Rt △ABC 中，∠B =90°，AB =3，BC =4，将△ABC 沿过点A 的直线折叠，使点B 恰好落在AC 边上的点B ′处，若折痕交BC 于点E ，则B′E 的长为_________．思路分析:在Rt △ABC 中，∠B =90°，AB =3，BC =4由勾股定理，得AC =5找折痕，转移，表达设B′E =x ，由折叠，得BE =B′E =x ，AB′=AB =3∴CE =4-x ，B′C =2利用勾股定理列方程在Rt △EB′C 中，由勾股定理，得x 2+22=(4-x )2解得x =32巩固练习1.如图，直角三角形纸片OAB，∠AOB=90°，OA=1，OB=2，折叠该纸片，使点B与点A重合，若折痕交OB于点C，交AB于点D，则OC的长为_________．2.如图，折叠长方形ABCD的一边AD，使点D落在BC边上的点F处，若AB=4cm，BC=5cm，则EF的长为________．3.如图，在长方形纸片ABCD中，AD=8，折叠纸片使点B落在线段AC上的点F处，折痕交BC于点E，若EF=3，则AB 的长为_________．4.如图是一张直角三角形纸片，两直角边AC=6cm，BC=8cm，现将△ABC折叠，使点B与点A重合，若折痕交BC于点D，交AB于点E，则CD=________，DE=_________．5.如图，将正方形纸片ABCD沿MN折叠，使点D落在边AB上，对应点为D′，点C落在C′处．若AB=6，AD′=2，则DM=________，CN=_________．6.如图，长方形ABCD中，AB=8，BC=4，将长方形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为_________．7.如图，把长方形纸片ABCD折叠，使点C与点A重合，折痕为EF．若BC=8，AB=4，则AE=________，EF=_________．8.如图，将长方形ABCD折叠，使点A与点C重合，折痕分别交AD，BC于点E，F，若AB=3，AD=4，则DE的长为______．9.如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，若点D在线段BC上，将△ABC沿AD折叠，使点C的对应点C′恰好落在AB边上，则BD的长为_________．10.如图，长方形ABCD中，AB=12，AD=5，点E是CD边上一点，连接AE，把∠D沿AE折叠，使点D落在点D′处．当△CD′E为直角三角形时，DE的长为____________．思考小结1.请回顾轴对称（折叠）的思考层次（1）全等变换：对应边_______、对应角_______．（2）对称轴性质：①对应点所连线段_____________________；②对称轴上的点_______________________．（3）组合搭配：长方形背景下的折叠常出现______三角形．（4）作图：关注_______和________，有时需要依据不变特征分析转化，补全图形．①当对称轴已知时，直接作_____________找对应点；②当对应点已知时，作__________________________，找对称轴（折痕）；③当对称轴过定点时，常作_____找对应点．【参考答案】例题示范1.32巩固练习1.342.5cm23.64.7cm4，15cm 45.103，4 36.107.5，258.789.5310.103或5思考小结1.（1）相等，相等.（2）①被对称轴垂直平分；②到对应点的距离相等.（3）等腰（4）对称轴、对应点①点的对称点②对应点所连线段的垂直平分线③弧。

勾股定理应用中的翻折问题

D
E B
P
M
A
N Q
如图，公路MN和小路PQ在P处交汇,∠QPN=30°,点 A处有一所学校,AP=160m,假设拖拉机行使时,周围 100m内受噪音影响,那么拖拉机在公路MN上以 18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
N
D E 60 B 60 80 100
x=6 BC=2x=12
16-x 8
S
ABC
1
12 8
B
48
2
x
Dx
C
如图，∠B=∠C=∠D=∠E=90°，且AB=CD=3， BC=4，DE=EF=2，则求AF的长。
A
3
B
C
3
4
3 10
E
D
2
2
2
F
4
2
如图，一条河同一侧的两村庄A、B，其中A、B 到河岸最短距离分别为AC=1km，BD=2km， CD=4cm，现欲在河岸上建一个水泵站向A、B 两村送水，当建在河岸上何处时，使到A、B两村铺设水管总长度最短，并求出最短距离。
度是多少？
25 E 5
10 3
20
C6
10 B
D
8
A
如图，公路MN和小路PQ在P处交汇,∠QPN=30°, 点A处有一所学校,AP=160m,假设拖拉机行使时, 周围100m内受噪音影响,那么拖拉机在公路MN上以18km/h的速度沿PN方向行驶时,学校是否受到噪音的影响?如果学校受到影响,那么受影响将持续多长时间?
勾股定理之折
叠问题
SC SA+SB=SC SA a c
b
a2+b2=c2 SB

第11讲勾股定理折叠问题

第十一讲勾股定理折叠问题一、知识梳理初中数学中，有关折叠的问题也是相对比较难的问题，主要涉及求角的度数、求线段的长度、求周长、面积等，其中求线段的长度的问题必然用到勾股定理.图形折叠问题核心实质是轴对称性质，即先找出对称轴，再观察元素不变量与变量，然后运用所学知识合理、有序、全面解决问题。

图形折叠对象主要是三角形、矩形、梯形等，考查问题涉及点坐标、角度、线段、周长、面积、图形规律、最值、三角函数、比例、解析式等等，折叠问题中，“折”是过程，“叠”是结果，此题型灵活多变，能考查学生的自主探索能力与空间想象能力以及推理能力，解决折叠问题，首先要对图形折叠有一定准确定位，把握折叠实质，从点、线、面三个方面发现图形中的位置关系和数量关系，抓住图形的变量和不变量，其次探索折叠变化规律，充分挖掘图形隐含的几何性质，运用所学知识合理、有序、全面解决问题。

折叠性质：①对应线段相等（能够重合的线段）②对应角相等（能够重合的角）性质记忆：折叠必有角相等、边相等。

处理策略：求什么设什么，找直角三角形，用勾股定理二、典型例题（1）折叠与角度问题例1、如图，在Rt△ABC中，∠ACB=90°，点D在AB边上，将△CBD沿CD折叠，使点B恰好落在AC边上的点E处．若∠A=25°，则∠CDE=__________.解：∵将△CBD沿CD折叠，使点B恰好落在AC边上的点E处，∠ACB=90°，∴∠BCD=∠ECD=45°，∠B=∠CED，∵∠A=25°，∴∠B=90°-25°=65°，∴∠CED=65°，∴∠CDE=180°-45°-65°=70°，故答案为：70°．例2、如图，在△ABC 中，∠ACB=90°，将∠A 折叠，使点A 落在边CB 上的点A′处，折痕为CD ；若∠A′DC=84°，则∠B=________°．解：∵△CDA′与△CDA 关于CD 成轴对称，∴∠ADC=∠A′DC=84°，∵∠ACB=90°，∴∠DCA=∠DCB=45°，∵∠CDA=∠B+∠DCB ，∴∠B=84°-45°=39°故答案为：39．（2）折叠与线段长度例3、如图，有一张直角三角形纸片，90ACB ∠=︒，5cm AB =，3cm AC =，现将ABC ∆折叠，使边AC 与AB 重合，折痕为AE ，则CE 的长为（）A ．1cmB ．2cmC ．3cm2D ．5cm 2【解析】∵90ACB ∠=︒，5cm AB =，3cm AC =∴4BC ===由折叠可知CE=DE,AC=AD ，90ADE ACE ∠=∠=︒设CE x =，则4,2,BE x BD AB AD =-=-=在Rt BDE 中∵222DE BD BE +=∴2222(4)x x +=-解得32x =故选C例4、如图，在矩形ABCD 中，6,8AB AD ==，点E 是边A D 上一动点，将ABE △沿直线BE 对折，点A 的落点为A '，当A DE ' 为直角三角形时，线段AE 的长为（）A ．3B ．4C ．6或3D ．3或4【答案】C 【分析】当A DE ' 为直角三角形时，有两种情况：①当点A '在矩形内部时，如图1所示，先利用勾股定理求出BD =10，根据折叠的性质得90BA E DA E ''∠=∠=︒，设AE =x ，则A E x '=，DE =8-x ，然后在Rt A DE ' 中运用勾股定理计算出x 的值即可；②当点A '落在边BC 上时，如图2所示，此时四边形ABA E '是正方形，得出AE =AB =6．【详解】解：∵四边形ABCD 是矩形∴∠A =∠C =90°，AB =6，AD =8∴10BD ===当A DE ' 为直角三角形时，有两种情况：①当点A '在矩形内部时，如图1所示，由折叠的性质得，AE A E '=，6A B AB '==设AE x =，则A E x '=，8DE x =-∴1064DA BD A B ''=-=-=在Rt A DE ' 中，222A E DA DE ''+=∴2224(8)x x +=-解得，x =3∴AE =3；②当点A '落在边BC 上时，如图2所示，此时四边形ABA E '是正方形，∴AE =AB =6故选：C ．例5、如图，在Rt ABC 的纸片中，90C ∠=︒，5AC =，13AB =．点D 在边BC 上，以A D 为折痕将ADB △折叠得到AD B ' ，A B '与边BC 交于点E ．若D EB ' 为直角三角形，则BD 的长是_______．【答案】7或263【分析】由勾股定理可以求出BC 的长，由折叠可知对应边相等，对应角相等，当△DEB′为直角三角形时，可以分为两种情况进行考虑，分别利用勾股定理可求出BD 的长．【详解】解：在Rt ABC 中，12BC ===，（1）当90ED B ∠'=︒时，如图1，过点B ′作B F AC '⊥，交AC 的延长线于点F ，由折叠得：13AB AB ='=，BD B D C F ='=，设BD x =，则B D CF x '==，12B F CD x '==-，在Rt AFB' 中，由勾股定理得：222(5)(12)13x x ++-=，即：270x x -=，解得：10x =（舍去），27x =，因此，7BD =．（2）当90D EB ∠'=︒时，如图2，此时点E 与点C 重合，由折叠得：13AB AB ='=，则1358B C '=-=，设BD x =，则B D x '=，12CD x =-，在Rt △B CD ¢中，由勾股定理得：222(12)8x x -+=，解得：263x =，因此263BD =．故答案为：7或263．例6、如图，在Rt △ABC 中，∠ACB=90°，AC=6，BC=8，将边AC A 沿CE 翻折，使点A 落在AB 上的点D 处；再将边BC 沿CF 翻折，使点B 落在CD 的延长线上的点B'处，两条折痕与斜边AB 分别交于点E 、F ，则△B'FC 的面积为______________．【答案】9625【分析】由题意可得AB=10，根据面积可得CE=4.8，根据勾股定理可求BE=6.4，由折叠可求∠ECF=45°，可得EC=EF=4.8，即可求BF 的长，可求面积．【详解】解：∵Rt △ABC 中，∠ACB=90°，AC=6，BC=8，∴BA==10，∵将边AC 沿CE 翻折，使点A 落在AB 上的点D 处，∴∠AEC=∠CED ，∠ACE=∠DCE ，∵∠AED=180°，∴∠CED=90°，即CE ⊥AB ，∵S △ABC =12AB×EC=12AC×BC ，∴EC=4.8，在Rt △BCE 中，=6.4，∵将边BC 沿CF 翻折，使点B 落在CD 的延长线上的点B′处，∴BF=B'F ，∠BCF=∠B'CF ，∵∠BCF+∠B'CF+∠ACE+∠DCE=∠ACB=90°，∴ECF=45°，又CE ⊥AB ，∴∠EFC=∠ECF=45°，∴CE=EF=4.8，∵BF=BE-EF=6.4-4.8=1.6，∴△BFC 的面积为:12FB×EC=18249625525⨯⨯=，由翻折可知，△B'FC 的面积=△BFC 的面积=9625故答案为9625．【点睛】本题考查了折叠问题，勾股定理，根据折叠的性质求∠ECF=45°是本题的关键．（2）折叠与最值问题例7、如图，在ABC 中，,904C AC ︒∠==cm ，3BC =cm ，点D 、E 分别在AC 、BC上，现将DCE 沿DE 翻折，使点C 落在点'C 处，连接AC '，则AC '长度的最小值（）A ．不存在B ．等于1cmC ．等于2cmD ．等于2.5cm【解析】当C′落在AB 上，点B 与E 重合时，AC'长度的值最小，∵∠C=90°，AC=4cm ，BC=3cm ，∴AB=5cm ，由折叠的性质知，BC′=BC=3cm ，∴AC′=AB-BC′=2cm ．故选：C ．例8、如图，矩形纸片ABCD，3AD=，折叠纸片，使点A落在BC边上的E处，AB=，5折痕为PQ，当点E在BC边上移动时，折痕的端点P、Q也随之移动，若限定点P、Q分别在AB、A D边上移动，则点E在BC边上可移动的最大距离为（）A．1B．2C．4D．5【答案】B【分析】根据翻折变换，当点Q与点D重合时，点E到达最左边，当点P与点B重合时，点E到达最右边，所以点E就在这两个点之间移动，分别求出这两个位置时EB的长度，然后两数相减就是最大距离．【详解】解：如图1，当点D与点Q重合时，根据翻折对称性可得ED=AD=5，在Rt△ECD中，ED2=EC2+CD2，即52=（5-EB）2+32，解得EB=1，例9、如图2，当点P与点B重合时，根据翻折对称性可得EB=AB=3，∵3-1=2，∴点E在BC边上可移动的最大距离为2．故选：B ．例10、如图，在矩形ABCD 中，10AB =，12AD =，点E 是AB 的中点，点F 是A D 边上的动点，将AEF ∆沿EF 翻折，得到A EF '∆，则A C '的最小值是（）A ．6B ．7C ．8D ．9【答案】C 【分析】求A C '的最小值，先求出EC 的大小，再根据EA A C EC ''+≥，求出A C '的范围即可．【详解】解析：连接E C 在△A CE '中，可得EA A C EC ''+≥．在Rt EBC ∆中，由勾股定理，得13EC ==．由折叠可知，5EA EA '==，∴8A C '≥故选C ．【点睛】本题主要考查了三角形三边的大小关系及勾股定理，正确掌握三角形三边的大小关系及勾股定理是解题的关键．例11、如图在三角形纸片ABC 中，已知∠ABC =90º，AC =5，BC=4，过点A 作直线l 平行于BC ，折叠三角形纸片ABC ，使直角顶点B 落在直线l 上的点P 处，折痕为MN ，当点P 在直线l 上移动时，折痕的端点M 、N 也随之移动，若限定端点M 、N 分别在AB 、BC 边上（包括端点）移动，则线段AP 长度的最大值与最小值的差为________________．【答案】1【分析】分别找到两个极端,当M 与A 重合时，AP 取最大值，当点N 与C 重合时，AP 取最小，即可求出线段AP 长度的最大值与最小值之差【详解】如图所示，当M 与A 重合时，AP 取最大值，此时标记为P 1，由折叠的性质易得四边形AP 1NB是正方形，在Rt △ABC 中，，∴AP 的最大值为A P 1=AB=3如图所示，当点N 与C 重合时，AP 取最小，过C 点作CD ⊥直线l 于点D ，可得矩形ABCD ，∴CD=AB=3，AD=BC=4，由折叠的性质有PC=BC=4，在Rt △PCD 中，∴AP 的最小值为AD PD=4-线段AP 长度的最大值与最小值之差为(1AP AP=341----故答案为1例12、如图，在△ABC 中，∠C =90°，∠ABC =45°，D 是BC 边上的一点，BD =2，将△ACD 沿直线AD 翻折，点C 刚好落在AB 边上的点E 处.若P 是直线AD 上的动点，则△PEB 的周长的最小值是________．【答案】2【分析】连接CE，交AD于M，根据折叠和等腰三角形性质得出当P和D重合时，PE+BP的值最小，此时△BPE的周长最小，最小值是BE+PE+PB=BE+CD+DB=BC+BE，先求出BC和BE 长，代入求出即可．【详解】如图，连接CE，交AD于M，∵沿AD折叠C和E重合，∴∠ACD=∠AED=90°，AC=AE，∠CAD=∠EAD，∴AD垂直平分CE，即C和E关于AD对称，BD=2，∴，∴当P和D重合时，PE+BP的值最小，即此时△BPE的周长最小，最小值是BE+PE+PB=BE+CD+DB=BC+BE，∵∠DEA=90°，∴∠DEB=90°，∵∠ABC=45°，∴∠B=45°，∵，∴，即，∴△PEB 的周长的最小值是．故答案为．【点睛】本题考查了折叠性质，等腰三角形性质，轴对称-最短路线问题，勾股定理，含30度角的直角三角形性质的应用，关键是求出P 点的位置．三、课堂练习1.如图所示，将长方形ABCD 沿DE 折叠，使点C 恰好落在BA 边上，得到点C′，若∠C′EB=40°，求∠EDC′的度数．2.在Rt △ACB 中，∠ACB ＝90°，点D 在边AB 上，连接CD ，将△ADC 沿直线CD 翻折，点A 恰好落在BC 边上的点E 处，若AC ＝3，BE ＝1，则DE 的长是_____．【答案】157【分析】过点D 作DHAC ⊥于H ，DF BC ⊥于F ，由折叠的性质可得3AC CE ==，45ACD BCD ∠=∠=︒，由勾股定理可求5AB =，由面积法可求D F 的长，由勾股定理可求D E 的长．【详解】解：如图，过点D 作DHAC ⊥于H ，DF BC ⊥于F ，将ADC ∆沿直线CD 翻折，3AC CE ∴==，45ACD BCD ∠=∠=︒，4BC ∴=，D H AC ⊥ ，DF BC ⊥，45ACD BCD ∠=∠=︒，DF DH ∴=，45DCF FDC ∠=∠=︒，DF CF ∴=，22291625AB AC BC =+=+= ，5AB ∴=，111222ABC S AC BC AC DH BC DF ∆=⨯⨯=⨯⨯+⨯⨯ ，127DF ∴=，127DF ∴=，127DF CF ∴==，97EF =，157DE ∴===，故答案为：157．3.如图，矩形ABCD 中，AB=8，BC=4，把矩形ABCD 沿过点A 的直线AE 折叠，点D 落在矩形ABCD 内部的点D′处，则CD′的最小值是（）A ．4B ．C ．4-D ．4+【答案】C 【解析】【分析】根据翻折的性质和当点D'在对角线AC 上时CD′最小解答即可．【详解】解：当点D'在对角线AC 上时CD′最小，∵矩形ABCD中，AB=4，BC=2，把矩形ABCD沿过点A的直线AE折叠点D落在矩形ABCD内部的点D处，∴AD=AD'=BC=2，在Rt△ABC中，＝4∴，故选：C．4.如图，在长方形ABCD的边CD上适当选定一点E，沿直线AE把△ADE折叠，使点D恰好落在边BC上的点F处．已知AB＝6cm，△ABF的面积是24cm2．（1）求BF的长；（2）求AD的长；（3）求点E与点C的距离．【答案】（1）8cm；（2）10cm；（3）83 cm【分析】（1）由在长方形ABCD中，AB＝6cm，△ABF的面积是24cm2，即可求得BF的长；（2）由（1），易得AD＝AF，DE＝EF，即可求得AF的长，然后得出AD的长；（3）首先设EC＝xcm，则EF＝DE＝（6﹣x）cm．由勾股定理得：CE2+CF2＝EF2求出x 的值即可得出答案．【详解】（1）∵ABCD是长方形，∴△ABF是直角三角形，∵△ABF面积是24cm2，∴12AB•BF＝24．∵AB＝6cm，∴BF＝8cm；（2）由题意知，△ADE和△AFE重合，则△ADE≌△AFE，则AD＝AF，DE＝EF．在Rt△ABF中，由勾股定理得10AF===（cm）．则AD＝10cm；（3）∵BC＝AD＝10cm，∴CF＝BC﹣BF＝2cm.设EC ＝xcm ，则EF ＝DE ＝（6﹣x ）cm ．由勾股定理得：CE 2+CF 2＝EF 2，∴x 2+22＝（6﹣x ）2，解得：83x =，∴点E 与点C 间的距离是83cm.【点睛】此题考查长方形的性质、勾股定理、折叠的性质，（3）是此题的难点，根据（2）求出CF ，由折叠得到EF ＝DE ，设EC ＝xcm ，因此利用勾股定理列得关于x 的关系式解出x 的值，由此解答此题.5.在矩形纸片ABCD 中，3AB =，5AD =.如图所示，折叠纸片，使点A 落在BC 边上的'A 处，折痕为PQ ，当点'A 在BC 边上移动时，折痕的端点P ，Q 也随之移动，若限定点P 、Q 分别在线段AB 、A D 边上移动，则点'A 在BC 边上可移动的最大距离为（）A ．1B ．2C ．3D ．4【答案】B 【分析】根据翻折变换，当点Q 与点D 重合时，点A′到达最左边，当点P 与点B 重合时，点A′到达最右边，所以点A′就在这两个点之间移动，分别求出这两个位置时A′B 的长度，然后两数相减就是最大距离．【详解】解：如图1，当点D 与点Q 重合时，根据翻折对称性可得A’D=AD=5，在Rt △A’CD 中，A’D 2=A’C 2+CD 2，即52=(5-A’B)2+32，解得A’B=1；如图2，当点P与点B重合时，根据翻折对称性可得A’B=AB=3，∵3-1=2，∴点A’在BC边上可移动的最大距离为2．故选B．6.矩形ABCD中，AB=4，BC=6，点E是AB的中点，点F是BC上任意一点，把△EBF沿直线EF翻折，点B落在点P处，则PC的最小值是_______________．【答案】2【详解】连接CE，当点P在CE上时，CP的值最小．CE===∴=-=．CP CE EP2故答案为：2．7.如图，在长方形纸片ABCD 中，3AB =，9AD =，折叠纸片ABCD ，使顶点C 落在边A D 的点G 处，折痕分别交边A D 、BC 于点E 、F ．（1）求证：GEF △是等腰三角形（2）求GEF △面积的最大值．【答案】（1）见解析；（2）152【分析】（1）根据翻折的性质得到EFC EFG ∠=∠，根据//AD BC 得到EFC GEF ∠=∠，从而得到EFG GEF ∠=∠，问题得证；（2）根据GEF △高为AB=3，得到当点G 与点A 重合时，GEF △的面积最大．根据勾股定理求出AF=5，进而得到GE=5，即可求出GEF △的面积．【详解】（1）由翻折得：EFC EFG ∠=∠．∵//AD BC ，∴EFC GEF ∠=∠，∴EFG GEF ∠=∠，∴GE=GF ，∴GEF △是等腰三角形．（2）如图，∵GEF △高为AB=3，∴当GE 最大时GEF △的面积最大，∴当点G 与点A 重合时，GEF △的面积最大．在Rt ABF 中，222AF AB BF =+，∴()22239AF AF =+-，解得：5AF =，∴5GE AF ==，∴GEF △的面积最大值＝1155322=⨯⨯=．四、举一反三1.如图，EF 是正方形两对边中点的连线段，将∠A 沿DK 折叠，使它的顶点A落在EF 上的G 点，求∠DKG 的度数．2.如图，在Rt ABC 中，90,A AB AC ∠=︒==，点,E F 分别是边,AB BC 上的动点，沿EF 所在直线折叠B Ð，使点B 的对应点B ′始终落在边AC 上，若FB C ' 为直角三角形，则BF 的长为__________．【解析】90,A AB AC ∠=︒==，∴∠C=45°，2BC ==，折叠后，要使FB C ' 为直角三角形，则有：FB C ' 也为等腰直角三角形，①当90B FC '∠=︒时，∴45C FB C '∠=∠=︒，此时点B '与点C 重合，∴E 、F 分别是AB 、BC 的中点，∴112BF BC ==，②当90FB C'∠=︒时，∴45C B FC '∠=∠=︒，∴BF FB B C ''==，在Rt B FC '△中，FC F '=，BC=BF+FC ，∴)12BC BF BF =+=+=，解得：2BF =-；故答案为2-或1．3.如图，Rt △ABC 中，AB ＝18，BC ＝12，∠B ＝90°，将△ABC 折叠，使点A 与BC 的中点D 重合，折痕为MN ，则线段BN 的长为（）A ．8B ．6C ．4D ．104.如图，长方形纸片ABCD ，10AB =，8BC =，点P 在BC 边上，将CDP 沿DP 折叠，点C 落在E 处，PE ，D E 分别交AB 于点O ，F ，且OP OF =，则A F 长为______．【答案】103【分析】根据折叠的性质可得出DC=DE 、CP=EP ，由“AAS”可证△OEF ≌△OBP ，可得出OE=OB 、EF=BP ，设EF=x ，则BP=x 、DF=10-x 、BF=PC=8-x ，进而可得出AF=2+x ，在Rt △DAF 中，利用勾股定理可求出x 的值，即可得AF 的长．【详解】解：∵将△CDP 沿DP 折叠，点C 落在点E 处，∴DC=DE=10，CP=EP ．在△OEF 和△OBP 中，90EOF BOP E B OF OP ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△OEF ≌△OBP （AAS ），∴OE=OB ，EF=BP ．设EF=x ，则BP=x ，DF=DE -EF=10-x ，又∵BF=OB+OF=OE+OP=PE=PC ，PC=BC-BP=8-x ，∴AF=AB -BF=2+x ．在Rt △DAF 中，AF 2+AD 2=DF 2，∴（2+x ）2+82=（10-x ）2，∴43x =；∴410233AF =+=．故答案为：103．5.如图，在矩形ABCD 中，AB=3，AD=4，点E 是AD 边上一动点，将△ABE 沿BE 折叠，使点A 的对应点A′恰好落在矩形ABCD 的对角线上，则AE 的长为_______.答案：3924or 6.如图，已知等腰△ABC 中，AB =AC =5，BC =8，E 是BC 上的一个动点，将△ABE 沿着AE 折叠到△ADE 处，再将边AC 折叠到与AD 重合，折痕为AF ，当△DEF 是等腰三角形时，BE 的长是___________．【答案】52或258或74．【分析】分三种情况讨论：DE=DF ，DE=EF ，EF=DF ．利用等腰三角形的性质和全等三角形解题．【详解】解：由折叠可知，BE=DE ，DF=CF ，AD=AB=AC=5，当DE=DF 时，如图1，此时DE=DF=BE=CF ，∵AB=AC ，∴∠B=∠C ，在△ABE 和△ACF 中，AB AC B C BE CF =⎧⎪=⎨⎪=⎩∠∠∴△ABE ≌△ACF ，∴AE=AF ，∴AD 垂直平分EF ，∴EH=FH ，142BH CH BC ===，∴3AH ===，∴532HD =-=，设BE DE x ==，则4EH x =-，则在直角△DHE 中，()22242x x -+=，解得52x =，当DE=EF 时，如图2，作AH ⊥BC 于H ，连接BD ，延长AE 交BD 于N ，可知BE=DE=EF ，∵AH ⊥BC ，AB=AC ，BC=8∴BH=CH=4，∴3AH ===，设EH m =，则4BE EF m ==-，∴()8242CF m m =--=，即2DF m=∵AB=AD ，∠BAN=∠DAN ，∴AN ⊥BD ，BN=DN ，∴12EN DF m ==，∴EN EH=在△AHE 和△BNE 中，90AHE BNE EH ENAEH BEN ==︒⎧⎪=⎨⎪=⎩∠∠∠∠∴△AHE ≌△BNE ，∴AE=BE ，设BE AE x ==，则4EH x =-，在直角△AEH 中，()22243x x -+=，解得258x =，当DF=EF 时，如图3，过A 作AH ⊥BC 于H ，延长AF 交DC 于M，同理258 EF CF==∴252578884 BE=--=故答案为：52或258或74．【点睛】本题考查了折叠问题，全等三角形的判定和性质，等腰三角形的性质，注意分类讨论是解题的关键．7.如图，等腰△ABC中，AB=AC=10，BC=12，AD平分B A C∠，且AD=8，P，Q分别是AB、AD上的动点，连接BP，PQ，则BP+PQ的最小值为___．【答案】9.6【分析】过C作CQ⊥AB于Q，交AD于P，得到CQ=BP+PQ的最小值，由勾股定理不求得AD=8，再利用等面积法即可求得其值．【详解】∵AB=AC，AD是角平分线，∴AD⊥BC，BD=CD，∴B点，C点关于AD对称，如图，过C作CQ⊥AB于Q，交AD于P，则CQ=BP+PQ的最小值，根据勾股定理得，AD=8，利用等面积法得：AB•CQ=BC•AD，∴CQ=12310BC ADAB⨯==9.6故答案为：9.6．8.如图，在△ABC中，∠BAC＝90°，AB＝3，AC＝4，点D是BC的中点，将△ABD沿AD翻折得到△AED，联结CE．（1）求证：AD∥CE；（2）求CE的长．【答案】（1）见解析；（2）75【分析】（1）由折叠的性质可得DE=BD ，AE=AB ，可证EF=BF ，AD ⊥BE ，由等腰三角形的性质可求∠DBE ＝∠DEB ，∠DEC ＝∠DCE ，由三角形的内角和定理可求CE ⊥BE ，可得结论；（2）由三角形的面积公式可求BF 的长，由勾股定理可求CE 的长．【详解】证明：（1）∵∠BAC ＝90°，AB ＝3，AC ＝4，∴BC 5==，∵点D 是BC 的中点，∴AD ＝BD ＝DE ＝52，∵将△ABD 沿AD 翻折得到△AED ，∴DE ＝BD ，AE ＝AB ，∴AD 垂直平分BE ，∴EF ＝BF ，AD ⊥BE ，∵DE ＝DB ＝CD ，∴∠DBE ＝∠DEB ，∠DEC ＝∠DCE ，∵∠DBE +∠DEB +∠DEC +∠DCE ＝180°，∴∠DEB +∠DEC ＝90°，∴∠BEC ＝90°，∴CE ⊥BE ，∴AD ∥CE ；（2）∵S △ABC ＝12×AC ×AB ＝12×3×4＝6，且CD ＝BD ，∴S △ADB ＝12S △ABC ＝3，∴12AD ×FB ＝3，∴FB ＝125，∴BE ＝245，∴CE 75==．【点睛】本题考查了翻折变换，直角三角形的性质，平行线的判定，三角形的面积公式，勾股定理等知识，灵活运用这些性质解决问题是本题的关键．五、课后练习一、选择题1.如图，在△ABC 中，AB =10，AC =6，BC =8，将△ABC 折叠，使点C 落在AB 边上的点E 处，AD 是折痕，则△BDE 的周长为()A ．6B ．8C ．12D ．14【解析】在Rt △ABC 中，∵AC =6，BC =8，∠C =90°，∴AB ==10，由翻折的性质可知：AE =AC =6，CD =DE ，∴BE =4，∴△BDE 的周长=DE +BD +BE =CD +BD +E =BC +BE =8+4=12．故选：C ．2.如图，将等腰直角三角形ABC （90ABC ∠=︒）沿EF 折叠，使点A 落在BC 边的中点1A 处，6BC =，那么线段AE 的长度为（）A ．5B ．4C ．4.25D ．154【解析】由折叠的性质可得AE=A 1E ，∵△ABC 为等腰直角三角形，BC=6，∴AB=6，∵A 1为BC 的中点，∴A 1B=3，设AE=A 1E=x ，则BE=6-x ，在Rt △A 1BE 中，由勾股定理可得32+（6-x ）2=x 2，解得x=154，故选：D ．3.如图，矩形ABCD ，AB =3，BC =4，点E 是AD 上一点，连接BE ，将△ABE 沿BE 折叠，点A 恰好落在BD 上的点G 处，则AE 的长为（）A ．2B ．52C ．32D ．3【解析】在Rt △ABD 中，AB=3，AD=BC=4，∴BD=5由折叠得，∠BGE=∠A=90°，BG=AB=3，EG=AE ，∴DG=BD-BG=2，DE=AD-AE=4-AE ，在Rt △DEG 中，EG 2+DG 2=DE 2，∴AE 2+4=（4-AE ）2，∴AE=32．故选：C ．4.如图，在四边形ABCD 中，∠A ＝∠B ＝90°，∠C ＝60°，BC ＝CD ＝8，将四边形ABCD 折叠，使点C 与点A 重合，折痕为EF ，则BE 的长为（）A ．1B ．2CD ．2【解析】作DG ⊥BC ，连接AE ，在Rt △CDG ，∠DCG=60°，得出CG=4，∴DG=4AB=，设BE=x ，则CE=8-x ，根据折叠得AE=CE=8-x ，在Rt △ABE 中，AE 2=AB 2+BE 2，即(8-x)2)2+x 2解得x=1，故选A.5.如图，有一块直角三角形纸片，两直角边6AC cm =，8BC cm =，现将直角边AC 沿直线AD折叠，使它落在斜边AB上且与AE重合，则CD等于（）A．2cm B．3cm C．4cm D．5cm【解析】在RT△ABC中，∵AC＝6，BC＝8，∴AB=10，△ADE是由△ACD翻折，∴AC＝AE＝6，EB＝AB−AE＝10−6＝4，设CD＝DE＝x，在RT△DEB中，∵DE2＋EB2＝DB2，∴x2＋42＝（8−x）2∴x＝3，∴CD＝3．故选：B．6.如图，将矩形ABCD沿EF折叠，使顶点C恰好落在AB边的中点C′上．若AB＝6，BC ＝9，则BF的长为（）A．4B．C．4.5D．5【解析】∵点C′是AB边的中点，AB＝6，∴BC′＝3，由图形折叠特性知，C′F＝CF＝BC﹣BF＝9﹣BF，在Rt△C′BF中，BF2+BC′2＝C′F2，∴BF2+9＝（9﹣BF）2，解得，BF＝4，故选：A．二、填空题7.如图，在矩形ABCD 中，AB ＝5，BC ＝6，P 为AD 上一动点，把△ABP 沿BP 翻折，使点A 落在点F 处，连接CF ，若BF ＝CF ，则AP 的长为_____．【答案】53【分析】过点F 作EN ∥DC 交BC 于点N ，交AD 于点E ，设AP ＝x ，则PF ＝x ，得出（3﹣x ）2+12＝x 2，解方程即可得解．【详解】解：过点F 作EN ∥DC 交BC 于点N ，交AD 于点E ，∵四边形ABCD 是矩形，∴∠A ＝∠D ＝∠DCB ＝90°，∴FN ⊥BC ，FE ⊥AD ，∵BF ＝CF ，BC ＝6，∴CN ＝BN ＝3，由折叠的性质可知，AB ＝BF ＝5，AP ＝PF ，∴4FN ==，∴EF ＝EN ﹣FN ＝5﹣4＝1，设AP ＝x ，则PF ＝x ，∵PE 2+EF 2＝PF 2，∴（3﹣x ）2+12＝x 2，解得，53x =，故答案为：53．【点睛】本题主要考查了折叠变换的性质、等腰三角形的性质、矩形的性质、勾股定理的综合运用；熟练掌握折叠变换的性质、勾股定理是关键．8.如图，三角形纸片ABC 中，∠ACB =90 ，BC =6，AB =10．在AC 边上取一点E ，以BE 为折痕，使AB 的一部分与BC 重合，A 与BC 延长线上的点D 重合，则CE 的长为________．【答案】3【分析】根据折叠得，BD＝AB＝10，EA＝ED，求出CD＝4，在直角三角形CDE中，设未知数，利用勾股定理列方程求解即可．【详解】∵∠ACB=90 ，BC=6，AB=10∴8=由折叠得，BD＝AB＝10，EA＝ED，设CE＝x，则EA＝ED＝8−x，在Rt△DCE中，CD＝10−6＝4，由勾股定理得，x2＋42＝（8−x）2，解得，x＝3故填：3．9.如图，在四边形ABCD中，AD∥BC，AB⊥BC，点E在射线BC上运动，AD=AB=1，则△ADE的周长最小值为______.【答案】1+【分析】作D点关于BC的对称点D’,连接AD’与BC的交点即为E点，此时△ADE的周长为AD+AE+DE=AD+AD’,故可求解.【详解】作D点关于BC的对称点D’,连接AD’与BC的交点即为E点，此时△ADE的周长最小，即△ADE的周长AD+AE+DE=AD+AD’,∵在四边形ABCD中，AD∥BC，AB⊥BC，AD=AB=1∴四边形ABFD为正方形，∴AD+AD’=1+1+1+.10.如图，矩形ABCD中，AB=1，BC=2，点E是BC边上一点，连接AE，把∠B沿AE 折叠，使点B落在点B′处．当△CEB′为直角三角形时，BE的长为___________．【答案】12-或1．【分析】当△CEB′为直角三角形时，有两种情况：①当点B′落在矩形内部时，如答图1所示．连结AC，先利用勾股定理计算出据折叠的性质得∠AB′E=∠B=90°，而当△CEB′为直角三角形时，只能得到∠EB′C=90°，所以点A、B′、C共线，即∠B沿AE折叠，使点B落在对角线AC上的点B′处，则EB=EB′，AB=AB′=1，可计算出-1，设BE=x，则EB′=x，CE=2-x，然后在Rt△CEB′中运用勾股定理可计算出x．②当点B′落在AD边上时，如答图2所示．此时ABEB′为正方形．【详解】解：当△CEB′为直角三角形时，有两种情况：①当点B′落在矩形内部时，如图1所示．连结AC，在Rt△ABC中，AB=1，BC=2，∴=∵∠B沿AE折叠，使点B落在点B′处，∴∠AB′E=∠B=90°，当△CEB′为直角三角形时，只能得到∠EB′C=90°，∴点A、B′、C共线，即∠B沿AE折叠，使点B落在对角线AC上的点B′处，∴EB=EB′，AB=AB′=1，∴CB′=1-，设BE=x，则EB′=x，CE=2-x，在Rt△CEB′中，∵EB′2+CB′2=CE2，∴x2+1-）2=（2-x）2，解得x=51 2-，∴BE=1 2；②当点B′落在AD边上时，如图2所示．此时ABEB′为正方形，∴BE=AB=1．故答案为：12-或1．11.如图，在Rt△ABC中，∠C=90°，∠BAC=30°，点D是BC边上的点，AB=18，将△ABC沿直线AD翻折，使点C落在AB边上的点E处，若点P是直线AD上的动点，则BP+EP的最小值是____．【答案】9【分析】根据翻折变换的性质可得点C、E关于AD对称，再根据轴对称确定最短路线问题，BC与AD的交点D即为使PB+PE的最小值的点P的位置，然后根据直角三角形两锐角互余求出∠BAC=60°，再求出∠CAD=30°，然后解直角三角形求解即可．【详解】∵将△ACD沿直线AD翻折，点C落在AB边上的点E处，∴点C、E关于AD对称，∴点D即为使PB+PE的最小值的点P的位置，PB+PE=BC，∵∠C=90°，∠BAC=30°，∴BC=12AB，∴BC=9．∴PB+PE的最小值为9.故答案为9．12.如图，在Rt△ABC中，∠C=90°，AC=6，∠A=60°，点F在边AC上，并且CF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是_________．【答案】．【分析】延长FP交AB于M，当FP⊥AB时，点P到AB的距离最小．运用勾股定理求解.【详解】解:如图，延长FP交AB于M，当FP⊥AB时，点P到AB的距离最小．∵AC=6，CF=2，∴AF=AC-CF=4，∵∠A=60°，∠AMF=90°，∴∠AFM=30°，∴AM=12AF=2，∴，∵FP=FC=2，∴-2，∴点P到边AB距离的最小值是-2．故答案为:．【点睛】本题考查了翻折变换，涉及到的知识点有直角三角形两锐角互余、勾股定理等，解题的关键是确定出点P 的位置.12．如图，折叠矩形纸片ABCD ，使B 点落在A D 上一点E 处，折痕FG 的两端点分别在AB BC 、上(含端点)，且6,10AB BC ==．则AE 的最大值是_____，最小值是_______．【答案】6；2．【分析】点G 在AB 边上，点F 在BC 边上．分别利用当点F 与点C 重合时，以及当点G 与点A 重合时，求出AE 的极值进而得出答案：【详解】解：如图，设AE 的长度为,x 当点F 与点C 重合时，根据翻折对称性可得10,EC BC ==在Rt CDE ∆中，222,CE CD ED =+即()22210106AE =-+，解得2,AE =即2,x =如图，当点G 与点A 重合时，根据翻折对称性可得6,AE AB ==即6x =；所以AE 的最大值是6,最小值为2.故答案是：6,2．三、解答题13.如图，在矩形ABCD 中，AB=8，BC=10，E 为CD 边上一点，将△ADE 沿AE 折叠，使点D 落在BC 边上的点F 处．（1）求BF 的长；（2）求CE的长．【答案】（1）BF长为6；（2）CE长为3，详细过程见解析．【分析】（1）由矩形的性质及翻折可知，∠B=90°，AF=AD=10，且AB=8，在Rt△ABF中，可由勾股定理求出BF的长；（2）设CE=x，根据翻折可知，EF=DE=8-x，由（1）可知BF=6，则CF=4，在Rt△CEF中，可由勾股定理求出CE的长．【详解】解：（1）∵四边形ABCD为矩形，∴∠B=90°，且AD=BC=10，又∵ AFE是由 ADE沿AE翻折得到的，∴AF=AD=10，又∵AB=8，在Rt△ABF中，由勾股定理得：，故BF的长为6．（2）设CE=x，∵四边形ABCD为矩形，∴CD=AB=8，∠C=90°，DE=CD-CE=8-x，又∵△AFE是由△ADE沿AE翻折得到的，∴FE=DE=8-x，由（1）知：BF=6，故CF=BC-BF=10-6=4，CF+CE=EF，在Rt△CEF中，由勾股定理得：2224+x=(8-x)，解得：x=3，∴222故CE的长为3．14.如图，在△ABC中，∠C＝90°，把△ABC沿直线DE折叠，使△ADE与△BDE重合．(1)若∠A＝35°，则∠CBD的度数为________；(2)若AC＝8，BC＝6，求AD的长；(3)当AB＝m(m>0)，△ABC的面积为m＋1时，求△BCD的周长．(用含m的代数式表示)【答案】（1）∠CBD=20°；（2）AD=164；(3)△BCD 的周长为m+2【分析】（1）根据折叠可得∠1=∠A=35°，根据三角形内角和定理可以计算出∠ABC=55°，进而得到∠CBD=20°；（2）根据折叠可得AD=DB ，设CD=x ，则AD=BD=8-x ，再在Rt △CDB 中利用勾股定理可得x 2+62=（8-x ）2，再解方程可得x 的值，进而得到AD 的长；（3）根据三角形ACB 的面积可得112AC CB m =+ ，进而得到AC•BC=2m+2，再在Rt △CAB 中，CA 2+CB 2=BA 2，再把左边配成完全平方可得CA+CB 的长，进而得到△BCD 的周长．【详解】（1）∵把△ABC 沿直线DE 折叠，使△ADE 与△BDE 重合，∴∠1=∠A=35°，∵∠C=90°，∴∠ABC=180°-90°-35°=55°，∴∠2=55°-35°=20°，即∠CBD=20°；（2）∵把△ABC 沿直线DE 折叠，使△ADE 与△BDE 重合，∴AD=DB ，设CD=x ，则AD=BD=8-x ，在Rt △CDB 中，CD 2+CB 2=BD 2，x 2+62=（8-x ）2，解得：x=74，AD=8-74=164；（3）∵△ABC的面积为m+1，∴12AC•BC=m+1，∴AC•BC=2m+2，∵在Rt△CAB中，CA2+CB2=BA2，∴CA2+CB2+2AC•BC=BA2+2AC•BC，∴（CA+BC）2=m2+4m+4=（m+2）2，∴CA+CB=m+2，∵AD=DB，∴CD+DB+BC=m+2．即△BCD的周长为m+2．15.如图，长方形ABCD中，AB＝8，BC＝10，在边CD上取一点E，将△ADE折叠后点D恰好落在BC边上的点F处（1）求CE的长；（2）在（1）的条件下，BC边上是否存在一点P，使得PA+PE值最小？若存在，请求出最小值：若不存在，请说明理由．【答案】（1）3；（2．【分析】（1）先判断出AF=AD=8，进而利用勾股定理求出BF=6，最后在Rt△ECF，利用勾股定理，即可得出结论；（2）先作出点E关于BC的对称点E，进而求出DE'，再利用勾股定理即可得出结论．【详解】解：（1）长方形ABCD中，AB＝8，BC＝10，∴∠B＝∠BCD＝90°，CD＝AB＝8，AD＝BC＝10，由折叠知，EF＝DE，AF＝AD＝8，在Rt△ABF中，根据勾股定理得，BF6，∴CF＝BC﹣BF＝4，设CE＝x，则EF＝DE＝CD﹣CE＝8﹣x，在Rt△ECF中，根据勾股定理得，CF2+CE2＝EF2，∴16+x2＝（8﹣x）2，∴x＝3，∴CE＝3；（2）如图，延长EC 至E '使CE '＝CE ＝3，连接AE '交BC 于P ，此时，PA +PE 最小，最小值为AE '，∵CD ＝8，∴DE '＝CD +CE '＝8+3＝11，在Rt △ADE '中，根据勾股定理得，AE '．16.如图，在矩形ABCD 中，2,AB AD m ==，动点P 从点D 出发，沿射线DA 以每秒1个单位的速度向点A 方向运动，连接CP ，把PDC △沿PC 翻折，得到PEC V ．设点P 的运动时间为()t s ．（1）若3m =，当P E B 、、三点在同一直线上时，求t 的值；（2）若点E 到直线BC 的距离等于1，求t 的值；（3）若AE 的最小值为1，直接写出m 的值．【答案】（1）t=3（2）t=；（3）m=【分析】（1）如图1中，设PD=t ．则PA=3-t ．首先证明BP=BC=6，在Rt △ABP 中利用勾股定理即可解决问题；（2）通过添加辅助线，构造直角三角形再解决问题；（3）当点A,点E ，点C 在同一条直线上时，AE 最短，利用勾股定理求值即可．【详解】解：（1）如图1中，设PD=t ．则PA=3-t∵P 、B 、E 共线，∴∠BPC=∠DPC ，∵AD ∥BC ，∴∠DPC=∠PCB ，∴∠BPC=∠PCB ，∴BP=BC=3，在Rt △ABP 中，∵AB 2+AP 2=BP 2，∴22+（3-t ）2=32，∴t=3（舍去）或∴当t=3P E B 、、三点在同一直线上．（2）过点E 作MN ⊥BC ，交AD 于点M∵四边形ABCD 是矩形，MN ⊥BC∴MN ⊥AD∵点E 到直线BC 的距离等于1∴EN=1∵MN=AB=2,EC=CD=2,∴EN=MN-EN=2-1=1∴在Rt △ENC 中，∴MD=∵由题意得：-t,ME=MN-EN=2-1=1,EP=PD=t∴在Rt △MPE 中，222=ME MP PE +即：)2221=t +，解得：（3）如图，当点A,点E ，点C 在同一条直线上时，AE 最短．由题意得：AE=1，EC=CD=AB=2∴在Rt△ABC中，BC=∴．【点睛】本题考查四边形综合题、矩形的性质、勾股定理，学会构造图形思考问题是解答此题的关键，属于中考压轴题．。

(完整版)勾股定理中的折叠问题

C E勾股定理中的折叠问题例1：如图，小红用一张长方形纸片ABCD 进行折纸，已知该纸片宽AB 为8cm ，•长BC•为10cm ．当小红折叠时，顶点D 落在BC 边上的点F:处（折痕为AE ）(1)求BF 的长； (2)求EC 的长。

BC ，使点B 落在AD 边的F 处，已知：AB=3，BC=5，例2：已知，如图长方形ABCD 中，AB=3cm ，AD=9cm ，将此长方形折叠，使点B 与点D 重合，折痕为EF ，则△ABE 的面积为（）A 、6cm 2B 、8cm 2C 、10cm 2D 、12cm 2对应练习：1、如图2-2，把一张长方形纸片ABCD 折叠起来，使其对角顶点A 、C 重合，•若其长BC 为a ，宽AB 为b ，则折叠后不重合部分的面积是多少？第11题图AE BCDF2、如图2-3，把矩形ABCD 沿直线BD 向上折叠，使点C 落在C ′的位置上，已知AB=•3，BC=7，求重合部分△EBD 的面积例3：有一个直角三角形纸片，两直角边AC=6cm,BC=8cm,现将直角边AC 沿∠CAB 的角平分线AD 折叠，使它落在斜边AB 上，且与AE 重合，你能求出CD 的长吗？对应练习：1、如图，在△ABC 中，∠B= 90，AB=BC=6，把△ABC 进行折叠，使点A 与点D 重合，BD:DC=1:2，折痕为EF ，点E 在AB 上，点F 在AC 上，求EC 的长。

AECDB ADBCE F例4：如图，一块直角三角形的纸片，两直角边AC=6㎝，BC=8㎝。

现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，恰与AE 重合，求CD对应练习：1、如图，四边形ABCD 是矩形，AB =3，BC =4，把矩形沿直线AC 折叠，点B 落在点F 处，连接DF ，CF 与AD 相交于点E ，求DE 的长和△ACE 的面积.2、如图，折叠矩形纸片ABCD ，先折出折痕（对角线）BD ，再折叠，使AD 落在对角线BD 上，得折痕DG ，若AB = 2，BC = 1，求AG .ACD BEG A BC'EDCB A 总结：一、三角形中的折叠基本图形二、矩形FEDCBA EA(B)图1ACBDC ´ABCD E FA ′B ′。

(完整版)利用勾股定理解决折叠问题及答案

小专题(二) 利用勾股定理解决折叠与展开问题类型1 利用勾股定理解决平面图形的折叠问题 1．如图，有一张直角三角形纸片，两直角边AC ＝5 cm ，BC ＝10 cm ，将△ABC 折叠，使点B 与点A 重合，折痕为DE ，则CD 的长为( )A.252 cmB.152 cmC.254 cm D.154cm2．如图所示，有一块直角三角形纸片，∠C ＝90°，AC ＝4 cm ，BC ＝3 cm ，将斜边AB 翻折，使点B 落在直角边AC 的延长线上的点E 处，折痕为AD ，则CE 的长为( )A ．1 cmB ．1.5 cmC ．2 cmD ．3 cm3．(青岛中考)如图，将长方形ABCD 沿EF 折叠，使顶点C 恰好落在AB 边的中点C ′上，若AB ＝6，BC ＝9，则BF 的长为( )A ．4B ．3 2C ．4.5D ．54．如图，长方形纸片ABCD 中，已知AD ＝8，折叠纸片使AB 边与对角线AC 重合，点B 落在点F 处，折痕为AE ，且EF ＝3，则AB 的长为( )A ．3B ．4C ．5D ．65．(铜仁中考)如图，在长方形ABCD 中，BC ＝6，CD ＝3，将△BCD 沿对角线BD 翻折，点C 落在点C ′处，BC ′交AD 于点E ，则线段DE 的长为( )A ．3 B.154 C ．5 D.1526．如图，在长方形ABCD中，AB＝4，AD＝6，E是AB边的中点，F是线段BC上的动点，将△EBF沿EF所在直线折叠得到△EB′F，连接B′D，则B′D的最小值是( )A．210－2B．6C．213－2D．47．如图所示，在△ABC中，∠B＝90°，AB＝3，AC＝5，将△ABC折叠，使点C与点A重合，折痕为DE，则△ABE 的周长为________．8．如图，在Rt△ABC中，∠C＝90°，BC＝6 cm，AC＝8 cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB 边的C′点，那么△ADC′的面积是________．9．如图，已知Rt△ABC中，∠C＝90°，AC＝6，BC＝8，将它的锐角A翻折，使得点A落在BC边的中点D处，折痕交AC边于点E，交AB边于点F，则DE的值为________．10．如图，在Rt△ABC中，∠B＝90°，AB＝3，BC＝4，将△ABC折叠，使点B恰好落在边AC上，与点B′重合，AE为折痕，则EB′＝________．11．为了向建国六十六周年献礼，某校各班都在开展丰富多彩的庆祝活动，八年级(1)班开展了手工制作竞赛，每个同学都在规定时间内完成一件手工作品．陈莉同学在制作手工作品的第一、二个步骤是：①先裁下了一张长BC＝20 cm，宽AB＝16 cm的长方形纸片ABCD，②将纸片沿着直线AE折叠，点D恰好落在BC边上的F处，请你根据①②步骤解答下列问题：计算EC，FC的长．类型2 利用勾股定理解决立体图形的展开问题1．如图，一圆柱体的底面周长为24 cm，高AB为5 cm，BC是直径，一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是( )A．6 cm B．12 cmC．13 cm D．16 cm2．如图，圆柱形玻璃杯，高为12 cm，底面周长为18 cm，在杯内离杯底4 cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4 cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为________cm.3．如图，在一个长为2 m，宽为1 m的长方形草地上，放着一根长方体的木块，它的棱和场地宽AD平行且棱长大于AD，木块从正面看是边长为0.2 m的正方形，一只蚂蚁从点A处到达C处需要走的最短路程是________m(精确到0.01 m)．4．一位同学要用彩带装饰一个长方体礼盒．长方体高6 cm，底面是边长为4 cm的正方形，从顶点A到顶点C′如何贴彩带用的彩带最短？最短长度是多少？5．如图，一个长方体形状的木柜放在墙角处(与墙面和地面均没有缝隙)，有一只蚂蚁从柜角A处沿着木柜表面爬(1)请你画出蚂蚁能够最快到达目的地的可能路径；(2)当AB＝4，BC＝4，CC1＝5时，求蚂蚁爬过的最短路径的长．参考答案类型11．D 2.A 3.A 4.D 5.B 6.A 7.7 8.6 cm29.13310．1.511.因为△ADE与△AFE关于AE对称，所以△ADE≌△AFE.所以DE＝FE，AD＝AF.因为BC＝20 cm，AB＝16 cm，所以CD＝16 cm，AD＝AF＝20 cm.在Rt△ABF中，由勾股定理，得BF＝12 cm.所以CF＝20－12＝8(cm)．因为四边形ABCD是长方形，所以∠C＝90°.设CE＝x，则DE＝EF＝16－x，在Rt△CEF中，由勾股定理，得(16－x)2＝64＋x2.解得：x＝6.所以EC＝6 cm.答：EC＝6 cm，CF＝8 cm.类型21．C 2.15 3.2.604．把长方体的面DCC′D′沿棱C′D′展开至面ABCD上，如图．构成矩形ABC′D′，则A到C′的最短距离为AC′的长度，连接AC′交DC于O，易证△AOD≌△C′OC.∴OD＝OC.即O为DC的中点，由勾股定理，得AC′2＝AD′2＋D′C′2＝82＋62＝100，∴AC′＝10 cm.即从顶点A沿直线到DC中点O，再沿直线到顶点C′，贴的彩带最短，最短长度为10 cm.5．(1)如图，木柜的表面展开图是两个矩形ABC′1D1和ACC1A1.蚂蚁能够最快到达目的地的可能路径有如图所示的AC′1和AC1两种．(2)蚂蚁沿着木柜表面经线段A1B1到C′1，爬过的路径的长l1＝42＋（4＋5）2＝97.蚂蚁沿着木柜表面经线段BB1到C1，爬过的路径的长l2＝（4＋4）2＋52＝89.∵l1>l2，∴最短路径的长是89.。

勾股定理与折叠问题实例解析

勾股定理与折叠问题实例解析1.如图，在△ABC 中，∠B=90°,AB=3,BC=4, 将△ABD 沿 AD 折叠，使点B 落在边AC 上的点E 处，则CD 的长是解：根据题意得：将△ABD 沿AD 折叠，使点B 落在边AC 上的点E 处∴BD=DE,AB=AE,∠B=∠DEA=DEC=90°设DE=BD=x, ∵AB=3,BC=4,∠B=90°∴AC=5CE=AC-AE=AC-AB=5-3=2在Rt △CDE 中，由勾股定理得：DE ²+CE ²=CD ²即x ²+2²=(4-x)²,解得:x=32∴CD=BC-BD=BC-DE=4-32 =522.如图，长方形纸片ABCD 中，已知BC=8,折叠纸片使AB 边与对角线AC 重合，点B 落在点F 处，折痕为AE,且EF=3,求AB 的长.解：由折叠可知，△ABE ≌△AFE,∴AB=AF,BE=EF=3,∴CE=BC-BE=8-3=5.在Rt △CEF 中，由勾股定理得，CF= √CE 2−EF 2=4设AB=AF=a,则AC=AF+CF=a+4.在Rt △ABC 中，∵AB ²+BC ²=AC ²,∴a ²+8²=(a+4)²解得a=6,∴AB 的长是6。

3.如图，在矩形ABCD 中，AB=8,BC=4, 将矩形沿AC 折叠，点B 落在点B 处，则重叠部分△AFC 的面积为解：由旋转的性质及长方形可得：∠D=∠B ′=90°,AD=CB ′,在△AFD 和△CFB ′中，{∠D =∠B ′=90°∠AFD =∠B′FC AD=CB ′ △AFD ≌△CF B ′∴DF=B ′F设 DF=x,则AF=8-x,在Rt △AFD 中，(8-x)²=x ²+4²解得：x=3,∴AF=AB-FB ′=8-3=5,∴S △AFC=12×AF ×B ′C=12×5×4=104. 如图，把长方形纸片ABCD沿EF折叠，使得点D与点B重合，点C落在点C′的位置上.(1)试说明△ABE≌△C′BF;(2)若AB=4,AD=8,求△BEF的面积；解：(1)∵四边形ABCD 是长方形，∴AB=CD,∠A=∠D=90°∴BC′=AB,∠A=∠C′=90°∵把长方形纸片ABCD沿EF折叠∴BC′=CD,∠D=∠C′,∠DEF=∠BEF∵AD//BC∴∠DEF=∠EFB∴∠BEF=∠BFE∴BE=BF在Rt△ABE与Rt△C′BF中{AB=B C′BE=BF∴△ABE≌△C′BF5. 如图，把长方形纸片ABCD 沿EF 折叠，使得点D 与点B 重合，点C 落在点C ′的位置上.(1)试说明△ABE ≌△C ′BF;(2)若AB=4,AD=8,求△BEF 的面积；( 2 ) 设AE=x,根据翻折不变性，BE=DE=AD-AE=8-x在Rt △ABE 中，x ²+4²=(8-x)²解得：x =3, 即AE=3,则 D E = 5∵BE=BF=5,∴CF=3, 则S △BEF=S 长方形ABCD-S △ABE-S 梯形CDEF=4×8-12×3×4-12×(5+3)×4=106.如图，在长方形纸片ABCD 中，E 为BC 的中点，连接AE,将△ABE 沿AE 折叠得到△AFE, 连接CF.若AB=4,BC=6,则CF 的长为解：连接BF, 交AE 于点G, 如下图,由折叠的性质可得，AE 垂直平分BF即AE ⊥BF,BG=FG,∵AB=4,BC=6,E 为BC 的中点，∴BE=CE=BC=3,∴在Rt △ABE 中，AE=√AB 2+BE 2+=√42+32 =5∵AE 垂直平分BF,∴S △ABE=12 AB ×BE=12 AE ×BG 即12×4×3=12×5×BG 解得BG=2.4∴BF=2BG∵AE 垂直平分BF∴BE=FE∴BE=CE=FE∴∠EBF=∠EFB,∠EFC=∠ECF,∠BFC=∠EFB+∠EFC=12180°= 90°∴在Rt △BFC 中，CF=√BC 2−BF 2=√62−4.82=3.67.如图，在长方形ABCD中，AD=13,AB=24,点E为射线DC上一个动点，把△ADE沿直线AE折叠，当点D的对应点F刚好落在线段AB的垂直平分线上时，则DE的长为解：分两种情况：①如图1,当点F在长方形内部时，∵点F在AB的垂直平分线MN上，∴AN =12;∵AF=AD=13,由勾股定理得FN=5,∴FM=8,设DE为y,则EM=12-y,FE=y,在△EMF 中，由勾股定理得：y2 =(12-y)2+82∴y=263。

《勾股定理》典型例题折叠问题

《勾股定理》典型例题折叠问题1、如图，有一张直角三角形纸片，两直角边A Ｃ＝６,ＢＣ＝8，将△AB Ｃ折叠，使点B 与点A 重合,折痕为DE,则CD 等于( ）A. 425B. 322C. 47D ． 352、如图所示,已知△A ＢＣ中,∠C=9０°,ＡB 的垂直平分线交ＢC •于Ｍ,交AB 于N,若AC ＝4，MB=2M Ｃ,求ＡB 的长．3、折叠矩形AB ＣD 的一边ＡＤ,点D 落在BC 边上的点F 处,已知A Ｂ=8ＣＭ,BC=1０C Ｍ,求C Ｆ和EC 。

4、如图，在长方形ＡBCD 中，DC=5,在DC 边上存在一点E,沿直线A Ｅ把△ＡBC 折叠，使点D 恰好在BC 边上，设此点为F ，若△ABF 的面积为30,求折叠的△AE Ｄ的面积B CEDDCBAF E5、如图,矩形纸片ABCD 的长AD ＝9㎝，宽ＡＢ＝3㎝,将其折叠，使点Ｄ与点Ｂ重合，那么折叠后DE 的长是多少?6、如图,在长方形ＡB ＣＤ中,将∆ABC 沿AC 对折至∆ＡEC 位置，C Ｅ与AD 交于点F 。

（1）试说明：AF=FC ；（2)如果ＡＢ=3,B Ｃ=４,求A Ｆ的长7、如图2所示,将长方形ABCD 沿直线A Ｅ折叠,顶点Ｄ正好落在B Ｃ边上Ｆ点处,已知CE=3cm ，AB ＝8ｃｍ,则图中阴影部分面积为_______．8、如图２-3，把矩形ABＣD沿直线BD向上折叠,使点Ｃ落在C′的位置上,已知ＡB=•3,BC=7,重合部分△EＢＤ的面积为___＿＿_＿_.9、如图５,将正方形AＢCD折叠,使顶点A与ＣD边上的点M重合，折痕交ＡD于Ｅ,交BC于Ｆ，边AＢ折叠后与BC边交于点Ｇ。

如果Ｍ为CD边的中点,求证:DE：DM：EM=3:４:５。

１0、如图2-5,长方形ＡBＣＤ中，ＡB=3,BC＝4,若将该矩形折叠，使C点与A点重合，•则折叠后痕迹ＥＦ的长为（ )A．3．74 B．３.75 C．3.7６ D．３.7７2-511、如图1-３-11，有一块塑料矩形模板ABCＤ，长为10cｍ,宽为4cｍ，将你手中足够大的直角三角板ＰHＦ的直角顶点Ｐ落在AD边上(不与A、D重合）,在AD上适当移动三角板顶点P：①能否使你的三角板两直角边分别通过点B与点Ｃ？若能，请你求出这时ＡP 的长；若不能，请说明理由.②再次移动三角板位置,使三角板顶点P在AＤ上移动,直角边ＰH 始终通过点B,另一直角边PＦ与DC的延长线交于点Q,与BC交于点E，能否使CE＝２cm?若能，请你求出这时AP 的长;若不能,请你说明理由．１2、如图所示，△ABC是等腰直角三角形,AB＝AC，D是斜边ＢC的中点，E、Ｆ分别是AB、AC边上的点,且DE⊥DF，若BE=12，CF=５．求线段ＥＦ的长。

方法归纳利用勾股定理解决折叠问题

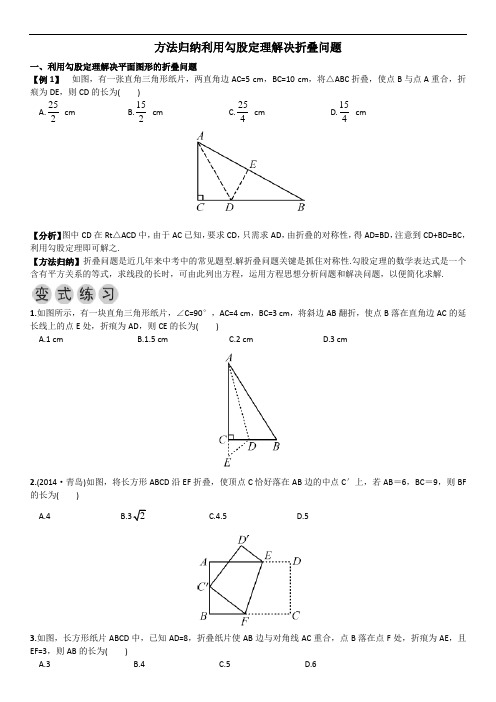
方法归纳利用勾股定理解决折叠问题一、利用勾股定理解决平面图形的折叠问题【例1】如图，有一张直角三角形纸片，两直角边AC=5 cm，BC=10 cm，将△ABC折叠，使点B与点A重合，折痕为DE，则CD的长为( )A.252cm B.152cm C.254cm D.154cm【分析】图中CD在Rt△ACD中，由于AC已知，要求CD，只需求AD，由折叠的对称性，得AD=BD，注意到CD+BD=BC，利用勾股定理即可解之.【方法归纳】折叠问题是近几年来中考中的常见题型.解折叠问题关键是抓住对称性.勾股定理的数学表达式是一个含有平方关系的等式，求线段的长时，可由此列出方程，运用方程思想分析问题和解决问题，以便简化求解.1.如图所示，有一块直角三角形纸片，∠C=90°，AC=4 cm，BC=3 cm，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CE的长为( )A.1 cmB.1.5 cmC.2 cmD.3 cm2.(2014·青岛)如图，将长方形ABCD沿EF折叠，使顶点C恰好落在AB边的中点C′上，若AB＝6，BC＝9，则BF 的长为( )A.4 C.4.5 D.53.如图，长方形纸片ABCD中，已知AD=8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，且EF=3，则AB的长为( )A.3B.4C.5D.64.如图，长方形ABCD的边AD沿折痕AE折叠，使点D落在BC上的F处，已知AB=6，△ABF的面积是24，则FC 等于( )A.1B.2C.3D.45.如图，四边形ABCD是边长为9的正方形纸片，将其沿MN折叠，使点B落在CD边上的B′处，点A对应点为A′，且B′C=3，则AM的长为( )A.1.5B.2C.2.25D.2.56.如图所示，在△ABC中，∠B=90°，AB=3，AC=5，将△ABC折叠，使点C与点A重合，折痕为DE，则△ABE的周长为__________.7.如图，在Rt△ABC中，∠C=90°，BC=6 cm，AC=8 cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB边的C′点，那么△ADC′的面积是__________.8.如图，已知Rt△ABC中，∠C=90°，AC=6，BC=8，将它的锐角A翻折，使得点A落在BC边的中点D处，折痕交AC边于点E，交AB边于点F，则DE的值为__________.二、利用勾股定理解决立体图形的展开问题【例2】如图，圆柱形玻璃杯，高为12 cm，底面周长为18 cm，在杯内离杯底4 cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4 cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为__________cm.【分析】将圆柱形平面展开，将A、C两点放在同一平面内,然后利用勾股定理进行计算.【方法归纳】在曲面上求两点之间的最短距离，根据“两点之间线段最短”和“化曲面为平面”两种思想，利用勾股定理解决.解决本题时要注意展开后有一直角边长是9 cm而不是18 cm.9.如图，一圆柱体的底面周长为24 cm，高AB为5 cm，BC是直径，一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是( )A.6 cmB.12 cmC.13 cmD.16 cm10.如图，在一个长为2 m，宽为1 m的长方形草地上，放着一根长方体的木块，它的棱和场地宽AD平行且棱长大于AD，木块从正面看是边长为0.2 m的正方形，一只蚂蚁从点A处到达C处需要走的最短路程是__________m（精确到0.01 m）.11.一位同学要用彩带装饰一个长方体礼盒.长方体高6 cm，底面是边长为4 cm的正方形，从顶点A到顶点C′如何贴彩带用的彩带最短？最短长度是多少？12.如图，一个长方体形状的木柜放在墙角处(与墙面和地面均没有缝隙)，有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C1处.(1)请你画出蚂蚁能够最快到达目的地的可能路径；(2)当AB=4，BC=4，CC1=5时，求蚂蚁爬过的最短路径的长.参考答案例1要使A，B两点重合，则折痕DE必为AB的垂直平分线.设CD=x，则AD=BD=10-x.在Rt△ACD中，由勾股定理，得x2+52=(10-x)2.解得x=15 4.故应选D. 变式练习1.A2.A3.D4.B5.B6.77.6 cm28.13 3例2如图，圆柱形玻璃杯展开（沿点A竖直剖开）后，侧面是一个长18 cm，宽12 cm的长方形，作点A关于杯上沿MN的对称点B，连接BC交MN于点P，连接BM，过点C作AB的垂线交剖开线MA于点D.由轴对称的性质和三角形三边关系知AP+PC为蚂蚁到达蜂蜜的最短距离，且AP=BP.由已知和长方形的性质，得DC=9,BD=12.在Rt△BCD中，由勾股定理得∴AP+PC=BP+PC=BC=15.即蚂蚁到达蜂蜜的最短距离为15 cm.变式练习9.C 10.2.6011.把长方体的面DCC′D′沿棱C′D′展开至面ABCD上，如图.构成矩形ABC′D′，则A到C′的最短距离为AC′的长度，连接AC′交DC于O，易证△AOD≌△C′OC.∴OD=OC.即O为DC的中点，由勾股定理得AC′2=AD′2+D′C′2=82+62=100,∴AC′=10 cm.即从顶点A沿直线到DC中点O，再沿直线到顶点C′，贴的彩带最短，最短长度为10 cm.12.(1)如图，木柜的表面展开图是两个矩形ABC1′D1和ACC1A1.蚂蚁能够最快到达目的地的可能路径有如图所示的AC1′和AC1两种.(2)蚂蚁沿着木柜表面经线段A1B1到C1′，爬过的路径的长l1.蚂蚁沿着木柜表面经线段BB1到C1，爬过的路径的长l2∵l1>l2，鱼儿，在水中串上串下，吐着顽皮的泡泡；鸟儿从荷叶上空飞过，想亲吻荷花姑娘的芳泽。

折叠问题与勾股定理例题总结

折叠问题题型梳理

勾股定理的应用解有关折叠问题

勾股定理中的折叠问题(分类整理版)

折叠问题与勾股定理例题总结

《勾股定理》典型例题折叠问题

勾股定理中的折叠问题

新人教版八下-折叠问题与勾股定理

专题05 勾股定理与几何图形折叠问题(解析版)

专题05 勾股定理在折叠问题中的应用(解析版)

勾股定理在折叠问题中的应用(习题及答案).

勾股定理应用中的翻折问题

第11讲勾股定理折叠问题

(完整版)勾股定理中的折叠问题

(完整版)利用勾股定理解决折叠问题及答案

勾股定理与折叠问题实例解析

《勾股定理》典型例题折叠问题

方法归纳 利用勾股定理解决折叠问题

方法归纳利用勾股定理解决折叠问题