多项式插值的震荡现象
多项式插值的振荡现象

数值分析实验报告多项式插值的振荡现象姓名:学院:数理与信息工程学院班级:学号:数值分析实验报告实验名称多项式插值的振荡现象实验时间2013年10月 23日姓名班级学号成绩一、 实验目的1.理解多项式插值,懂得它的振荡现象。
2. 研究样条插值,并分析它的收敛性。
3. 学会在实际生活中使用二维插值。
二、 实验内容1. 设区间[-1,1]上函数22511)(x x f +=考虑区间[-1,1]的一个等距划分,分点为n i nix i ,,2,1,0,21L =+-=则拉格朗日插值多项式为∑=+=ni ijn x l x x L 02)(2511)(其中的是n 次拉格朗日插值基函数。
n i x l i ,,2,1,0),(L =2. 请按一定的规则分别选择等距或者非等距的插值节点,并不断增加插值节点的个数。
考虑实验1中的函数或选择其他你有兴趣的函数,可以用MATLAB 的函数“spline”作此函数的三次样条插值。
3. 在一丘陵地带测量高程,x 和y 方向每隔100米测一个点,得高程数据如下。
试用MATLAB 的二维插值函数“interp2”进行插值,并由此找出最高点和该点的高程。
三、算法描述(1)编写好拉格朗日插值函数,保存在M 文件中;(2)考虑到:1、一幅图中太多的曲线会相互覆盖;2、n 取奇偶数可能结果不同;3、不同的节点选取方法可能导致不同的结果。
故而n 的选择分为n=2:2:8、n=3:2:9或者n=2:4:10、n=3:4:11与n=40三种情况;(3)节点的选取分为均匀节点、切比雪夫节点两种四、程序流程图由于实验方案明显、简单,实现步骤及流程图省略。
五、实验结果具体结果在实验分析里:整理的结果如下1>实验一的结果:1.22511)(x x f +=当节点为均匀节点时:插值点数目为奇数、偶数、40时,图像对称,但是不收敛,但是节点数越多,0附近的拟合效果越好,但是两端误差较大。
当节点为切比雪夫点时:插值点数目为奇数、偶数、40时,图像对称,但是可以收敛,节点数越多,拟合效果越好。
数值分析实验报告--实验2--插值法

1 / 21数值分析实验二:插值法1 多项式插值的震荡现象1.1 问题描述考虑一个固定的区间上用插值逼近一个函数。
显然拉格朗日插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式的次数增加时, 是否也更加靠近被逼近的函数。
龙格(Runge )给出一个例子是极著名并富有启发性的。
设区间[-1,1]上函数21()125f x x=+ (1)考虑区间[-1,1]的一个等距划分,分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为201()()125nn ii iL x l x x ==+∑(2)其中的(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。
实验要求:(1) 选择不断增大的分点数目n=2, 3 …. ,画出原函数f(x)及插值多项式函数()n L x 在[-1,1]上的图像,比较并分析实验结果。
(2) 选择其他的函数,例如定义在区间[-5,5]上的函数x x g xxx h arctan )(,1)(4=+=重复上述的实验看其结果如何。
(3) 区间[a,b]上切比雪夫点的定义为 (21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭(3)以121,,n x x x +为插值节点构造上述各函数的拉格朗日插值多项式,比较其结果,试分析2 / 21原因。
1.2 算法设计使用Matlab 函数进行实验, 在理解了插值法的基础上,根据拉格朗日插值多项式编写Matlab 脚本,其中把拉格朗日插值部分单独编写为f_lagrange.m 函数,方便调用。
1.3 实验结果1.3.1 f(x)在[-1,1]上的拉格朗日插值函数依次取n=2、3、4、5、6、7、10、15、20,画出原函数和拉格朗日插值函数的图像,如图1所示。
Matlab 脚本文件为Experiment2_1_1fx.m 。
可以看出,当n 较小时,拉格朗日多项式插值的函数图像随着次数n 的增加而更加接近于f(x),即插值效果越来越好。
应用多项式插值的流水线ADC后台数字校正方法

应用多项式插值的流水线ADC后台数字校正方法I. 绪论1.1 研究背景和意义1.2 研究目的与意义1.3 本文结构概述II. 基础知识介绍2.1 多项式插值基本原理2.2 流水线ADC工作原理2.3 数字校正原理III. 多项式插值在流水线ADC数字校正中的应用3.1 多项式插值法的优点3.2 多项式插值在流水线ADC数字校正中的应用IV. 实验方法与结果分析4.1 实验环境介绍4.2 实验步骤详述4.3 实验结果分析与总结V. 结论与展望5.1 结论5.2 不足与展望VI. 参考文献附录:插值算法代码I. 绪论1.1 研究背景和意义随着科学技术的迅速发展,数字信号处理技术在各种领域的应用越来越广泛。
其中,ADC(模数转换器)是将模拟信号转换为数字信号的重要设备,在各种领域的应用越来越广泛。
随着工艺的不断升级和电路的不断复杂,ADC在数字校正过程中所需要的准确度和精度也不断提高。
在ADC中,最常用的校准方法是数字校准法。
该方法使用校正电路的输出数字值来校正ADC的数字输出。
该方法可提高ADC的精度和准确度。
然而,在实践中,数字校准法也存在一些问题:数字校准电路对系统的时序有严格要求;ADC与数字校准电路之间存在时滞,这些特点使得数字校准误差较大。
因此,如何提高数字校准的精度和准确度一直是研究的热点问题。
为了解决数字校准法的缺陷,研究者们提出了许多方法来提高数字校准的精度和准确度。
其中,多项式插值法是一种常用的校准方法,可用于任何基于ADC的校准器。
而流水线ADC是现代高速转换器的重要形式之一,具有高速、分辨率高等优点。
本文将研究应用多项式插值法优化流水线ADC数字校准的方法。
1.2 研究目的与意义本文旨在提出一种基于多项式插值的流水线ADC数字校正方法,通过算法优化实现数字校正的自动化,提高数字校正的精度和准确度,减小误差。
同时,本文研究的方法可适用于各类流水线ADC,并具有工程应用意义。
此外,在理论研究和实践应用方面的探索,也将为后续相关领域的研究和应用提供理论与实践指导。
计算方法大作业1 克服Runge现象

x3
x2
x
1
S1 ( x)
-0.34685
0.2086
0.073964
0.038462
S2 (x)
S (xi 0 ) S x(i 0 )
S
'
(xi
0) S
xi' (
0 )i
S
'
'
x(i
0)S
xi' ' (
0)
1 ,n2, . . . , 1
(1)
这里共有了 3n-3 个条件,再加上条件(2)中的 n+1 个插值条件,共有 4n-2 个条件,
因此还需要 2 个方程才能确定 S (x) .通常可在区间[a, b]的端点 a x0,b xn 上各加一个边
dn1
1
2
Mn
dn
(6)
2 1
2
2
2
1 M1 d1
M2
d2
n 1
2
n
1
M
n
1
dn1
n
n 2 M n dn
由式(1)内点拼接条件,可得
i M i1 2M i i M i1 d j i 1, 2,..., n 1
(3) (4)
其中
i
hi 1 hi1
, hi
i
hi hi 1
实验2.1多项式插值的振荡现象

向宏志 20120047(2012-10-13)实验2.1(多项式插值的振荡现象)问题提出:考虑一个固定的区间上用插值逼近一个函数。
显然拉格朗日插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式的次数增加时,)(x L n 是否也更加靠近被逼近的函数。
龙格(Runge )给出一个例子是极著名并富有启发性的。
设区间[-1,1]上函数22511)(xx f += 实验内容:考虑区间[-1,1]的一个等距划分,分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为∑=+=ni ijn x l x x L 02)(2511)( 其中的n i x l i ,,2,1,0),( =是n 次拉格朗日插值基函数。
实验要求:(1) 选择不断增大的分点数目n=2,3….,画出原函数f(x)及插值多项式函数)(x L n 在[-1,1]上的图像,比较并分析实验结果。
(2)选择其他的函数,例如定义在区间[-5,5]上的函数x x g xxx h arctan )(,1)(4=+= 重复上述的实验看其结果如何。
(3)区间[a,b]上切比雪夫点的定义为 1,,2,1,)1(2)12(cos 22+=⎪⎪⎭⎫⎝⎛+--++=n k n k a b a b x k π 以121,,+n x x x 为插值节点构造上述各函数的拉格朗日插值多项式,比较其结果,试分析原因。
实验方法:考虑到:1、一幅图中太多的曲线会相互覆盖;2、n 取奇偶数可能结果不同;3、不同的节点选取方式可能导致不同的结果。
故而n 的选择分为n=2:2:8、n=3:2:9或者n=2:4:10、n=3:4:11与n=40三种情况;而节点的选取分为均匀节点、不均匀节点和切比雪肤节点三种。
说明:以下所有图中,蓝色曲线为原函数,绿色曲线为插值函数,插值节点数与两者交点数目相等。
实验数据及其分析:(1)22511)(x x f +=1. 节点为均匀节点时n i nix i ,,2,1,0,21 =+-=节点是对称的a)当节点数取为奇数个时,即n=2:2:8时。
数值分析实验报告模板

数值分析实验报告模板篇一:数值分析实验报告(一)(完整)数值分析实验报告12345篇二:数值分析实验报告实验报告一题目:非线性方程求解摘要:非线性方程的解析解通常很难给出,因此线性方程的数值解法就尤为重要。
本实验采用两种常见的求解方法二分法和Newton法及改进的Newton法。
利用二分法求解给定非线性方程的根,在给定的范围内,假设f(x,y)在[a,b]上连续,f(a)xf(b) 直接影响迭代的次数甚至迭代的收敛与发散。
即若x0 偏离所求根较远,Newton法可能发散的结论。
并且本实验中还利用利用改进的Newton法求解同样的方程,且将结果与Newton法的结果比较分析。
前言:(目的和意义)掌握二分法与Newton法的基本原理和应用。
掌握二分法的原理,验证二分法,在选对有根区间的前提下,必是收敛,但精度不够。
熟悉Matlab语言编程,学习编程要点。
体会Newton使用时的优点,和局部收敛性,而在初值选取不当时,会发散。
数学原理:对于一个非线性方程的数值解法很多。
在此介绍两种最常见的方法:二分法和Newton法。
对于二分法,其数学实质就是说对于给定的待求解的方程f(x),其在[a,b]上连续,f(a)f(b) Newton法通常预先要给出一个猜测初值x0,然后根据其迭代公式xk?1?xk?f(xk) f'(xk)产生逼近解x*的迭代数列{xk},这就是Newton法的思想。
当x0接近x*时收敛很快,但是当x0选择不好时,可能会发散,因此初值的选取很重要。
另外,若将该迭代公式改进为xk?1?xk?rf(xk) 'f(xk)其中r为要求的方程的根的重数,这就是改进的Newton 法,当求解已知重数的方程的根时,在同种条件下其收敛速度要比Newton法快的多。
程序设计:本实验采用Matlab的M文件编写。
其中待求解的方程写成function的方式,如下function y=f(x);y=-x*x-sin(x);写成如上形式即可,下面给出主程序。
数值计算中的插值方法与误差分析

数值计算中的插值方法与误差分析数值计算是一门应用数学学科,广泛应用于科学与工程领域。
在实际问题中,我们常常需要通过已知的离散数据点来估计未知的数值。
插值方法就是为了解决这个问题而设计的。
插值方法是一种基于已知数据点,推断出未知数据点的数值计算方法。
常见的插值方法有拉格朗日插值、牛顿插值等。
下面我们将重点介绍这两种方法。
1. 拉格朗日插值法拉格朗日插值法是插值方法中最常见的一种。
它是基于拉格朗日多项式的思想。
假设我们有一组已知的数据点(x1, y1), (x2, y2), ..., (xn, yn),我们想要估计一个未知点x的函数值y。
拉格朗日插值法的基本思想是通过插值多项式来逼近原函数。
具体步骤如下:(1)根据已知数据点构造Lagrange插值多项式:L(x) = Σ(yi * Li(x)), i = 0, 1, ..., n其中,Li(x) = Π((x-xj)/(xi-xj)), j ≠ i(2)计算未知点x对应的函数值y:y = L(x)拉格朗日插值法的优点是简单易懂,计算方便。
然而,它也存在着一些问题,比如插值多项式的次数较高时,多项式在插值区间外的振荡现象明显,容易引起插值误差。
2. 牛顿插值法牛顿插值法是另一种常见的插值方法。
它是基于差商的思想。
假设我们有一组已知的数据点(x1, y1), (x2, y2), ..., (xn, yn),我们想要估计一个未知点x的函数值y。
牛顿插值法的基本思想是通过插值多项式来逼近原函数。
具体步骤如下:(1)计算差商:f[xi, xi+1, ..., xi+k] = (f[xi+1, ..., xi+k] - f[xi, ..., xi+k-1]) / (xi+k - xi)(2)根据已知数据点构造Newton插值多项式:N(x) = f[x0] + Σ(f[x0, x1, ..., xi] * Π(x - xj)), i = 0, 1, ..., n-1(3)计算未知点x对应的函数值y:y = N(x)牛顿插值法的优点是适用范围广,可以方便地添加新的数据点进行插值。
数值分析实验报告2——Runge现象
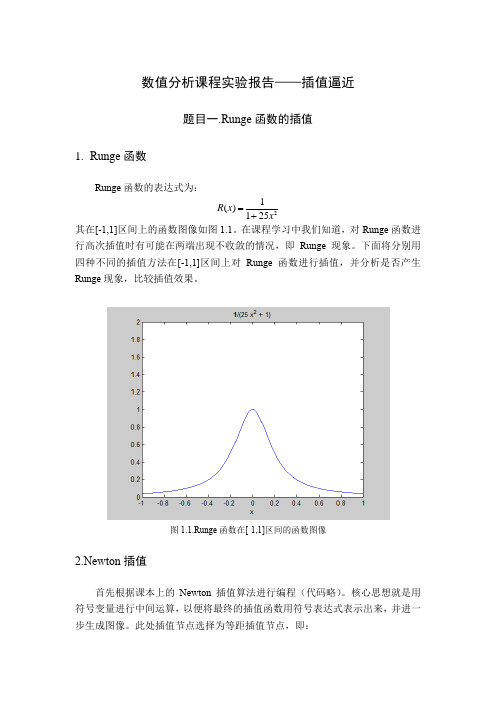
数值分析课程实验报告——插值逼近题目一.Runge 函数的插值1. Runge 函数Runge 函数的表达式为:21()125R x x =+ 其在[-1,1]区间上的函数图像如图1.1。
在课程学习中我们知道,对Runge 函数进行高次插值时有可能在两端出现不收敛的情况,即Runge 现象。
下面将分别用四种不同的插值方法在[-1,1]区间上对Runge 函数进行插值,并分析是否产生Runge 现象,比较插值效果。
图1.1.Runge 函数在[-1,1]区间的函数图像2.Newton 插值首先根据课本上的Newton 插值算法进行编程(代码略)。
核心思想就是用符号变量进行中间运算,以便将最终的插值函数用符号表达式表示出来,并进一步生成图像。
此处插值节点选择为等距插值节点,即:0.1(0,1,2,,)i x ih i =-+= (20)其中h=0.1。
插值曲线与原曲线的对比如图1.2(蓝色为原曲线,红色为插值曲线)。
从图中看出,在区间中部,二者吻合较好;但在区间两端二者则产生了明显偏差,甚至可以达到一个非常大的数值(e20量级)。
因此,在等距节点的20次Newton 插值下,产生了明显的Runge 现象。
图1.2.Newton 插值曲线与原曲线对比3. Lagrange 插值此处同样是根据Lagrange 插值的具体算法进行编程。
但插值节点不再是等距分布,而是如下形式:21cos()(0,1,2,,)42i i x i π+==…20 插值曲线与原曲线的对比如图1.3(蓝色为原曲线,红色为插值曲线)。
从图中看出,插值曲线与原曲线吻合的很好,没有产生明显的Runge 现象。
对比产生了明显Runge 现象的20次Newton 插值,Lagrange 插值的最高次数虽然也是20,但由于此处的插值节点不是等距分布的(事实上,此处采用的插值节点正是Chebyshev 多项式的零点),而是中间疏两边密,因此两侧较密的节点很好地抑制了Runge 现象。
数值分析课程设计-多项式插值的振荡现象matlab

数值分析课程设计多项式插值的振荡现象(姓名)(学号)指导教师学院名称专 业 名 称提交日期2012年6月一、 问题的提出考虑在一个固定区间上用插值逼近一个函数。
显然,Lagrange 插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式增加时,L n (x)是否也更加靠近被逼近的函数。
龙格(Runge)给出的一个例子是极著名并富有启发性的。
设区间[-1,1]上的函数21()125f x x=+ 考虑区间[-1,1]的一个等距划分,节点为21,0,1,2,,i i x i n n =-+=则拉格朗日插值多项式为201()()125nn i i i L x a x x ==+∑ 其中的a i (x),i=0,1,2,…,n 是n 次Lagrange 插值基函数。
二、 实验内容研究以下三个函数在各自区间上运用不同的划分1、21(),[1,1]125f x x x =∈-+ 2、4(),[5,5]1x h x x x=∈-+ 3、()arctan ,[5,5]g x x x =∈-运用在区间[-p,p]上等距划分(p>0),节点为2,0,1,2,,i i x p i n n =-+=以x 0,x 1,…,x n 为插值节点构造上述各函数的Lagrange 插值多项式。
运用区间[a,b]上切比雪夫(Chebychev)点的定义为(21)cos ,1,2,,1222(1)k b a b a k x k n n π⎛⎫+--=+=+ ⎪+⎝⎭以x 1,x 2,…,x n+1为插值节点构造上述各函数的Lagrange 插值多项式,比较其结果。
并分别比较两种划分方法,增加节点数,最大误差的变化。
三、 实验结果及分析(一) 等距划分 对于函数21(),[1,1]125f x x x =∈-+来说,使用等距划分其中绿色点线代表误差,红色划线代表Lagrange插值多项式,蓝色实线代表原函数。
可见对于等距划分来说节点数越多,最大误差越大,可是越靠近中间的误差越少。
数值分析课程设计---多项式插值的振荡现象

数值分析课程设计课程设计的目的和意义:⏹ 《课程设计》是数值分析的同步课程,是《数值分析》的上机实习课。
⏹ 《数值分析》课程中构造了各种有效的算法和有效公式,同学们通过上机作课程设计,学习揣摩这些算法的思想和构造,评价算法的优劣性。
⏹ 通过上机,可以提高我们运用数学软件编程解决问题的能力,为今后从事科学计算和软件开发打下良好的基础。
课程设计的题目:多项式插值的振荡现象设计目的:通过对多项式插值现象的观察,了解多项式的次数与逼近效 的关系,提高同学们分析实验结果的能力。
问题提出:考虑在一个固定区间上用插值逼近一个函数。
显然,Lagrange 插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式增加时,Ln(x)是否也更加靠近被逼近的函数。
龙格(Runge)给出的一个例子是极著名并富有启发性的。
设区间[-1,1]上的函数21()125f x x =+区间[-考虑设计1,1]的一个等距划分,节点为21,0,1,2,,i ix i nn=-+=则拉个朗日插值多项式为201()()125nn ii i L x l x x ==+∑其中的l i(x),i=0,1,2,…,n 是n 次Lagrange 插值基函数。
设计要求:1.选择不断增大的分点数n=2,3,…*画出原函数f(x)及插值多项式函数Ln(x)在[-1,1]上的图像; *给出每一次逼近的最大误差; *比较并分析实验结果。
2.选择其它函数,例如定义在区间[-5,5]上的函数。
4(),()arctan 1xh x g x x x ==+重复上述实验看其结果如何。
3.区间[a,b]上切比雪夫(Chebychev)点的定义为(21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+⎪+⎝⎭以x1,x2,…,xn+1为插值节点构造上述各函数的Lagrange 插值多项式,比较其结果。
设计过程:已知函数f (x )在n +1个点x 0,x 1,…,xn 处的函数值为 y 0,y 1,…,yn 。
第6章 实验五插值多项式的误差

第6章 实验五插值多项式的误差实验目的:明确插值多项式逼近函数是有误差的,了解误差的分布,哪些地方误差大些,哪些地方误差小些。
我们应该如何控制这些误差。
6.1 插值误差余项多项式举例说明多项式插值误差情况,用ππ≤≤-x 上的5个等距点对函数)cos(x y =进行插值估计,插值多项式是通过以下给定的数据点的四次多项式:⎥⎦⎤⎢⎣⎡--=ππππ,2,0,2,x[])sin(),2/sin(),0sin(),2/sin(),sin(ππππ--=y误差定义为:)()cos()(4x L x x e -=),())(cos(!5))(2/)(0)(2/)(()5(ππξξππππ-∈---++=x x x x x其中)(x e 是插值余项,)(4x L 是5个数据点的拉格朗日插值多项式。
图6.1是函数和误差的图形,可以观察到误差曲线是震荡的,它的值在接近端点的区间上最大,这种误差特性在等距多项式插值中十分典型,误差分布形状上的变化还取决于被插函数的性质及插值区间的大小a b -。
-0.8-0.6-0.4-0.20.20.40.60.8xc o s (x ) e (x )图6.1 函数和误差曲线的图形清单6.1 (是作图6.1的程序)clear clcx=[-pi,-pi/2,0,pi/2,pi]; % 插值节点横坐标 y=[cos(-pi),cos(pi/2),cos(0),cos(pi/2),cos(pi)]; % 插值节点纵坐标 x1=-pi:0.001:pi; % 绘图点的横坐标 y1=Lagran_(x,y,x1); % 绘图点的纵坐标 e=cos(x1)-y1; % 插值误差 y2=e;plot(x,cos(x),'.',x1,cos(x1),'b',x1,y2,'r') % 绘出两个函数曲线图形 xlabel('x');ylabel('cos(x) e(x)') text(1.2,0.6,'cos(x)','fontsize',18) text(-1.1,-0.1,'e(x)=cos(x)-y','fontsize',18)一般分析插值的误差:),()()!1()())(()(11)1(121+++∈+---=n n n x x f n x x x x x x x R ξξ)(m a x )!1()())(()()1(),(12111ξξ+∈+++---≤n x x n f n x x x x x x x R n 如果当被插值)(x f 是一个n 阶或更低阶多项式,则)(x R =0,即误差为零。
拉格朗日多项式插值

拉格朗日多项式插值法浅析摘要拉格朗日插值多项式是一种最常见的多项式插值法,也是一种最常用的逼近工具。
“学以致用 ”是每一门学科都致力追求的境界,数学自然也不例外。
下面,探讨拉格朗日插值法的基本原理、如何构造拉格朗日多项式、拉格朗日多项式的误差界,并用 MATLAB 程序来实现这一数学算法的自动化,为复杂的分析研究提供了一条数学算法的捷径。
【关键词】:拉格朗日多项式 算法实现 MATLAB在科学研究和实际的工程设计中,几乎所有的问题都可以用)(x f y =来表示其某种内在规律的数量关系。
但理想化的函数关系在实际工程应用中是很难寻找 的,对于那些没有明显解析式的函数关系表达式则只能通过实验观察的数据,利用多项式对某一函数的进行逼近,使得这个逼近函数能够反映)(x f 的特性,而且利用多项式就可以简便的计算相应的函数值。
例如我们不知道气温随日期变化的具体函数关系,但是我们可以测量一些孤立的日期的气温值,并假定此气温随日期变化的函数满足某一多项式。
这样,利用已经测的数据,应用待定系数法便可以求得一个多项式函数f (x )。
应用此函数就可以计算或者说预测其他日期的气温值。
一般情况下,多项式的次数越多,需要的数据就越多,而预测也就越 准确。
当然,构造组合多项式方法比较多,如线性方程求解、拉格朗日系数多项式以及构造牛顿多项式的分段差分和系数表等等,这里只对拉格朗日多项式插值法进行深入探讨。
一、拉格朗日多项式插值算法基本原理函数)(x f y =在区间[a,b]上有定义,在是[ a,b]上取定的 N + 1个互异节点, 且在这些点处的函数值)(0x f , )(1x f ,…,)(n x f 为已知, 即 yi =f (xi ) , (N i ...1,0=),若存在一个和)(x f 近似的函数)(x P N ,满足)()(i i N x f x P = (N i ...1,0=) (1)则称 φ(x) 为 f (x) 的一个插值函数, 点i x 为插值节点,(1)称为插值条件, 区间[a,b]称为插值区间, 而误差函数)()(x P x f E N N -=称为插值余项。
数值实验报告实验三

数值实验报告实验题三实验3.1 多项式插值的振荡现象3.1.1 问题提出考虑一个固定区间上用插值逼近一个函数。
显然拉格朗日插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式的次数增加时,是否也更加靠近被逼近的函数。
龙格(Runge )给出的一个例子是极著名并富有启发性的。
设区间[-1,1]上函数21()125f x x=+ 考虑[]1,1-的一个等距划分,分点为21,0,1,2,,i ix i n n=-+=则拉格朗日插值多项式为 201()()1+25nn ii L x l x x ==∑其中(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。
3.1.2 实验内容 3.1.2.1 第一小题选择不断增大的分点数目2,3,n =,画出原函数()f x 及插值多项式函数()n L x 在[1,1]-上的图像,比较并分析实验结果。
(1)MATLAB 代码程序3.1.1:拉格朗日插值公式函数lag_interp.mfunction f_n=lag_interp(xn,yn,x0) %Lagrange Interpolation %%Type 1: y=lag_interp(xn,yn,x0)%If x is input, then the function returns a numerical value Ln(x0), which%is equal to vpa(subs(lag_interp(xn,yn),x,x0)). %%Type 2: y=lag_interp(xn,yn)%If x is not input, the the function returns an symbolic function Ln(x).%Safeguards for input arguments[dim1,dim]=size(xn);if dim1~=1error('xn must be a line vector.')endif dim<=1error('There must be at least 2 points.')end[dim1,dim2]=size(yn);if dim1~=1error('yn must be a line vector.')endif dim2~=dimerror('The dimention of xn and yn must agree.') end%Langrange interpolationsyms x;f_result=0;for i=1:diml=1;for j=1:dimif i~=jl=l*(x-xn(j))/(xn(i)-xn(j));endendf_result=f_result+yn(i)*l;endif nargin==2%If x is not input, the the function returns an symbolic function Ln(x).f_n=f_result;elseif nargin==3%If x is input, then the function returns a numerical value Ln(x0).f_n=vpa(subs(f_result,x,x0));end程序3.1.2:产生n个分点的函数gen_eqpts.mfunction xn=gen_eqpts(left,right,n)%Returns an n-dimentional line vector of equidistant points on interval [left, right]%%Type: xn=gen_eqpts(left,right,n)%%'left' is the lower boundary of the interval.%'right' is the lower boundary of the interval.%'n' is the number of equidistant points. n must be an integer greater or equal to 2.%This m file is coded by Steve Zhao. For reference only.%%The author will not be responsible for any potential consequences that may%caused by this file.%%(c)2016 3g Studio. All rights reserved%Safeguards for input argumentsif left>=righterror('The upper bound must be greater than the lower bound.')endif mod(n,1)~=0error('n must be an integer.')endif n<2error('n must be at least 2.')end%Start generatingxn=zeros(1,n);xn(1)=left;for i=2:nxn(i)=left+(i-1)/(n-1)*(right-left);end程序3.1.3:第一小题主程序ex311.m%Experiment 3.1 (1)%Comparison of Lagrange Interpolation and originalfunction%%This m file is coded by Steve Zhao. For reference only.%%The author will not be responsible for any potential consequences that may%caused by this file.%%(c)2016 3g Studio. All rights reservedn=input('Please input the number of equidistant points. n=£º');hold onsyms x;f=@(x)1./(1+25*x.^2);x0=linspace(-1,1);y0=f(x0);plot(x0,y0,'-k');xn=gen_eqpts(-1,1,n);yn=f(xn);plot(x0,lag_interp(xn,yn,x0),'--b');(2)问题的探索n=2时,原函数图像(黑色实线)和插值函数图像(蓝色虚线)如图所示n=3时,图像如图所示n=4、5,图像如图所示:n=6、7时,图像如图所示n=8、9时,图像如图所示(3)结论我们可以发现,n 为6时,插值函数的走势与实际函数较为接近。
牛顿差值多项式

牛顿差值多项式牛顿差值多项式是一种用于插值的数学方法,它是由英国数学家艾萨克·牛顿在17世纪发明的。
牛顿差值多项式的主要作用是通过已知的数据点来推导出未知的数据点,从而实现数据的插值。
在本文中,我们将详细介绍牛顿差值多项式的原理、应用和优缺点。
牛顿差值多项式的原理基于牛顿插值法,它是一种基于多项式的插值方法。
牛顿插值法的基本思想是通过已知的数据点来构造一个多项式函数,然后利用这个多项式函数来估算未知的数据点。
牛顿插值法的优点是可以通过已知的数据点来构造一个高次多项式函数,从而实现更高精度的插值。
牛顿差值多项式的具体实现方法是通过差商来构造多项式函数。
差商是指在插值点上的函数值之间的差异,它可以用来计算多项式函数的系数。
具体来说,差商可以通过以下公式计算:f[x0,x1] = (f(x1) - f(x0)) / (x1 - x0)f[x0,x1,x2] = (f[x1,x2] - f[x0,x1]) / (x2 - x0)f[x0,x1,x2,x3] = (f[x1,x2,x3] - f[x0,x1,x2]) / (x3 - x0)其中,f[x0,x1]表示在x0和x1之间的差商,f[x0,x1,x2]表示在x0、x1和x2之间的差商,以此类推。
通过差商的计算,我们可以得到一个多项式函数,它可以用来估算未知的数据点。
二、牛顿差值多项式的应用牛顿差值多项式的应用非常广泛,它可以用于各种数据插值的场景。
以下是一些常见的应用场景:1. 数据平滑在数据分析中,我们经常需要对数据进行平滑处理,以便更好地理解数据的趋势和规律。
牛顿差值多项式可以用来平滑数据,从而实现更好的数据分析。
2. 图像处理在图像处理中,我们经常需要对图像进行插值处理,以便更好地显示图像的细节和特征。
牛顿差值多项式可以用来插值图像,从而实现更好的图像处理效果。
3. 信号处理在信号处理中,我们经常需要对信号进行插值处理,以便更好地分析信号的特征和趋势。
数值分析仿真报告--多项式插值中的振荡现象

2.1:多项式插值的振荡现象一、 实验问题:考虑在一个固定的区间上用插值逼近一个函数,显然Lagrange 插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式的次数增加时,L n (x)是否也更加靠近被逼近的函数。
Runge 给出的一个例子是极著名并富有启发性的。
设区间[-1, 1]上函数:21()125f x x =+二、 实验内容:考虑区间[-1, 1]的一个等距划分,分点为:21,0,1,2,,i ix i n n=-+=则拉格朗日插值多项式为:201()()125nn ii iL x l x x ==+∑其中,(),0,1,2,,i l x i n =是n 次Lagrange 插值基函数。
三、 实验要求:(1)选择不断增大的分点数目2,3,n =,画出原函数()f x 及插值多项式函数L n (x)在[-1, 1]上的图像,比较并分析实验结果。
(2)选择其他的函数,例如定义在区间[-5, 5]上的函数4(),()arctan 1xh x g x x x ==+ 重复上述的实验看其结果如何。
四、 仿真结果及分析1. 21()125f x x =+由上面12种不同分点数目n 下的插值函数与原函数的拟合图像可以分析得出以下几点结论:✓ 随着n 的增大,插值多项式在区间中部的拟合情况逐渐趋优,尤其当n 大于10时,区间中部的插值曲线与原曲线几乎重合;✓ 随着n 的增大,插值多项式在两端点附近的拟合情况既不是逐渐趋劣,也不是逐渐趋优,而是呈现不断振荡的特性,且振荡幅度呈现越来越大的趋势; ✓ 并不是n 越大,插值多项式的拟合效果越好。
比如n=20时,插值式与原曲线几乎完美拟合,但当n=25时,两端附近相对误差可大于100%,因此再在实际应用时,应准确把握n 的大小。
2. 4()1xf x x =+ 与21()125f x x =+,对4()1xf x x=+进行拉格朗日多项式插值时,随着n 的增大,插值多项式函数在区间中部的拟合情况愈来愈好,但是在端点附近的拟合情况会出现振荡的情况,且误差逐渐增大。
关节空间轨迹的插值计算

关节空间轨迹的插值计算关节空间轨迹的插值计算是指在给定初末状态和运动时间的情况下,通过插值算法计算出一系列连续的关节位置,使得机器人能够平滑地运动到目标位置。
这种插值计算是机器人运动规划中的重要问题,对于确保机器人运动的流畅性和运动速度的控制具有重要意义。
首先介绍线性插值法。
线性插值法是指在给定的两个关节位置之间进行线性插值,即将关节运动分为若干个小段,每一小段按照匀速直线运动进行插值。
具体计算步骤如下:1.通过给定的初末状态和时间计算出每个关节的速度,即关节位置随时间的导数。
2.将给定时间分割成若干小段,每一小段的时间长度相等。
3.根据关节速度和小段的时间长度,计算出每一小段的关节位置变化量。
4.累加每一小段的关节位置变化量,得到整个运动过程的关节位置轨迹。
线性插值法的优点是计算简单,但是其生成的插值轨迹存在速度突变的问题,可能造成机器人运动时的抖动,因此在实际应用中往往配合速度平滑的控制方法使用。
除了线性插值法,多项式插值法也是常用的关节空间轨迹插值算法。
多项式插值法通过构建一个多项式函数,使得关节位置随时间的函数具有一定的光滑性。
具体计算步骤如下:1.根据给定的初末状态和时间,构建一个关节位置的多项式函数。
2.求解多项式函数的系数,使得多项式函数满足给定的初末状态。
3.对多项式函数求导,得到关节速度随时间的函数。
4.根据给定的时间段和间隔,计算出每个时间点的关节位置。
多项式插值法的优点是生成的插值轨迹光滑性较好,能够避免速度突变的问题,但是其计算较为复杂,且在高阶多项式的情况下容易出现震荡现象。
此外,还有一种常用的关节空间轨迹插值算法是样条插值法。
样条插值法是通过构建一系列子段的插值曲线,使得整个关节运动过程具有较高的光滑性。
具体计算步骤如下:1.将给定的初末状态和时间分割成多个小段。
2.在每个小段内,构建插值曲线,并满足相邻小段之间的平滑条件。
3.根据插值曲线的参数方程,计算出每个时间点的关节位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
fplot('-abs(h(x)-Lh(x,20))',[-5 5],color(4))
legend('5次','10次','15次','20次')
title('逼近函数与原函数在区间上的误差')
grid on
(程序代码2.1.3)【计算误差】运行窗口主程序:
三、实验结果及分析
1.I.画出函数f(x)及其插值多项式函数Ln(x)在[-1,1]上的图像,如下图,
(程序代码1.1.1)
II.由于fminbnd函数的不可靠性,先通过编程绘出每次逼近在定义区间上的误差如下图,(程序代码1.1.2)
观察图像可知每次逼近的最大误差在哪个区间,再通过编程缩小区间,得到其每次逼近最大误差为(截图如下,程序代码1.1.3),
数值分析课程设计
多项式插值的震荡现象
指导教师
学院名称
专业名称
提交日期
一、问题的提出
在一个固定区间上用插值逼近一个函数。显然,拉格朗日插值中使用的节点越多,插值多项式的次数就越高。而插值多项式增加时,Ln(x)是否也更加靠近被逼近的函数。下面就这个问题展开实验。
二、实验内容
1.设区间[-1,1]上的函数 ,对其等距划分,写出其拉格朗日插值多项式为 。通过不断增加分点数n=2,3,…。
title('逼近函数与原函数在区间上的误差')%表明图像名称
grid on%图像中显示网格,易于观察
axis([-1,1,-2.2,0])%缩小观察范围
(程序代码1.1.3)【计算误差】运行窗口主程序:
[xmin(1),ymin(1)]=fminbnd('-abs(f(x)-Lf(x,5))',-0.2,0.2)
fplot('Lh(x,10)',[-5 5],color(2)) %插值的图像
fplot('Lh(x,15)',[-55],color(3))
fplot('Lh(x,20)',[-55],color(4))
legend('原函数','5次','10次','15次','20次')
title('多项式插值的震荡现象') %表明图像名称
axis([-5,5,-1,1]) %缩小观察范围
grid on %图像中显示网格,易于观察
(程序代码2.1.2)【绘图表示误差】运行窗口主程序:
hold on
color=['g','b','m','k']
fplot('-abs(h(x)-Lh(x,5))',[-5 5],color(1))
fplot('-abs(h(x)-Lh(x,10))',[-5 5],color(2))
Lh.m:function Ln=Lh(x,n)
Ln=0%初始化Ln
for i=1:n+1%平均划分节点,并存储在X矩阵内
X(i)=-5+10*(i-1)/n;
end
for i=1:n+1%该循环得出各项ai(x)f(xi)想加之和
q=h(X(i))
for j=1:n+1%该循环得出每一项的
if i~=j
%计算5次插值多项式与原函数之间差的最大值,下面同理
[xmin(2),ymin(2)]=fminbnd('-abs(f(x)-Lf(x,7))',-0.2,0.2)
[xmin(3),ymin(3)]=fminbnd('-abs(f(x)-Lf(x,9))',-1,-0.8)
[xmin(4),ymin(4)]=fminbnd('-abs(f(x)-Lf(x,11))',-1,-0.8)
[2]史万明 吴裕树,数值分析[M],北京,北京理工大学出版社,2010-4
六、附录
I.运行环境(计算机型号DELL N4030):
II.运行时间:2012年5月30日星期三20:00
III.程序代码:
1.定义两个m函数:
f.m:function z=f(x)
z=1/(1+25*(x^2))
Lf.m:function Ln=Lf(x,n)
color=['g','b','m','k','c','y'] %定义颜色字符组
fplot('-abs(f(x)-Lf(x,5))',[-1 1],color(1))%分别画出每次插值
fplot('-abs(f(x)-Lf(x,7))',[-1 1],color(2))%在定义区间上的误差
fplot('-abs(f(x)-Lf(x,9))',[-1 1],color(3))
并:I.画出原函数f(x)及插值多项式函数Ln(x)在[-1,1]上的图像;
II.给出每一次逼近的最大误差;
III.比较并分析实验结果。
2.选择其他函数,如定义在区间[-5,5]上的函数 和 ,重复上述I、II、III三个步骤看其结果如何。
3.区间[a,b]上切比雪夫点的定义为 ,k=1,2,…,n+1。以 , ,…, 为插值节点构造上述各函数的Lagrange插值多项式,比较其结果。
四、关于本设计的体会
做了两个星期的课程设计,首先的感触就是很烦,然后感觉收获了很多,包括对Matlab的熟悉程度有很大的提升、对Matlab一些内置函数也有了很好的理解和运用、锻炼了自己自习找资料的能力。而做这个课程设计的主要的困难就是做出第一个函数的绘图、误差分析等等,因为后面无论是其它两个函数或者用切比雪夫点构造的三个函数的插值函数,都是万变不离其宗。
2.h(x):
I.画出函数h(x)及其插值多项式函数Ln(x)在[-1,1]上的图像,如下图(程序代码2.1.1):
II.同理先通过编程绘出每次逼近在定义区间上的误差如下图(程序代码2.1.2),
再通过缩小区间,编程计算每次逼近最大误差如下(截图如下,程序代码2.1.3):
III.比较并分析实验结果:
Ln=0%初始化Ln
for i=1:n+1
X(i)=-1+2*(i-1)/n;%平均划分节点,并存储在X矩阵内
end
for i=1:n+1%该循环得出各项ai(x)f(xi)想加之和
q=f(X(i))
for j=1:n+1%该循环得出每一项的ai(x)f(xi)
if i~=j
q=q*(x-X(j))/(X(i)-X(j))
(2)就每次逼近的最大误差分析。其结果与上两个函数大致一样,就不做详细说明了。
3.以切比雪夫点为插值点构造上述3个函数的拉格朗日插值公式,并画图,
f(x)(程序代码3.1.1):
h(x)(程序代码3.2.1):
g(x)(程序代码3.3.1):
先通过画图并观察,缩小区间得到每次逼近的最大误差:
f(x)(程序代码3.1.2):
q=q*(x-X(j))/(X(i)-X(j))
end
end
Ln=Ln+q
end
(程序代码2.1.1)【绘图】运行窗口主程序:
fplot('h(x)',[-55],'r') %画出原函数图像
hold on %保留图像
color=['g','பைடு நூலகம்','m','k'] %定义颜色字符组
fplot('Lh(x,5)',[-5 5],color(1)) %分别画出5,7,9,11,13,15次
而这次设计的过程和结果,也存在较多不足之处。对Matlab一些函数的不了解,导致花大量的时间走了弯路,并得到不太理想的结果,例如:无法通过一个循环语句;还有就是在分析结果时,不能很透彻的分析到位,尚且有待提高。
五、参考文献
[1]任玉杰,数值分析及其MATLAB实现[M],北京,高等教育出版社,2007
fplot('-abs(f(x)-Lf(x,11))',[-1 1],color(4))
fplot('-abs(f(x)-Lf(x,13))',[-1 1],color(5))
fplot('-abs(f(x)-Lf(x,15))',[-1 1],color(6))
legend('5次','7次','9次','11次','13次','15次')
legend('原函数','5次','7次','9次','11次','13次','15次')
title('多项式插值的震荡现象') %表明图像名称
axis([-1,1,-1,1])%缩小观察范围
grid on%图像中显示网格,易于观察
(程序代码1.1.2)【绘图表示误差】运行窗口主程序:
hold on %保留图像
再通过缩小区间,编程计算每次逼近最大误差如下(截图如下,程序代码2.2.3):
III.比较并分析实验结果:
(1)在同一个坐标系中绘制g(x)及5次、10次等多次插值后的图像。从图中可以看出:与第1、2个函数不同,这里的10次插值函数整体拟合程度最好,在两端并没有发生较剧烈的震荡现象;而插值次数到了15或20次时,震荡非常强烈。
