高一年级数学幂函数知识点

合集下载

高中幂函数知识点总结

引言：高中幂函数是高中数学中的重要部分，它在数学研究和实际问题中有着广泛的应用。

本文将对高中幂函数的知识点进行总结和整理，帮助学生完善对幂函数的理解和掌握。

概述：幂函数是指形如y=x^n的函数，其中n是常数。

幂函数的特点是具有单调性和奇偶性，其图象通常为一条曲线。

在研究幂函数时，需要掌握其定义、性质和应用。

正文：一、幂函数的定义1.1 幂函数的基本形式幂函数的基本形式是y=x^n，其中n是常数。

幂函数的定义域为所有实数，且n可以是正整数、负整数、零和有理数。

1.2 幂函数的图象当n为正奇数时，幂函数的图象在第一象限和第三象限上单调递增；当n为正偶数时，幂函数的图象在第一象限上单调递增，且具有对称轴y=0；当n为负数时，幂函数的图象在第一、三象限上单调递减。

1.3 幂函数的特殊情况当n=1时，幂函数变为一次函数；当n=0时，幂函数变为常数函数；当n为正无穷大时，幂函数趋向于正无穷大；当n为负无穷大时，幂函数趋向于零。

二、幂函数的性质2.1 幂函数的单调性幂函数在定义域上的单调性与n的值有关。

当n为正奇数时，幂函数是增函数；当n为正偶数时，在非负区间上是增函数，在负区间上是减函数；当n为负数时，在非负区间上是减函数，在负区间上是增函数。

2.2 幂函数的奇偶性幂函数的奇偶性与n的奇偶性有关。

当n为奇数时，幂函数是奇函数；当n为偶数时，幂函数是偶函数。

2.3 幂函数的零点当n为正奇数时，幂函数的零点为x=0；当n为正偶数时，幂函数的零点为x=0；当n为负奇数时，幂函数没有零点；当n为负偶数时，幂函数的零点为x=0。

三、幂函数的图象变换3.1 幂函数的平移幂函数的平移是指将幂函数的图象沿横轴或纵轴方向移动。

平移的方向和距离与平移的规律有关，具体可利用平移的公式进行计算。

3.2 幂函数的伸缩幂函数的伸缩是指将幂函数的图象进行纵向或横向的拉伸或压缩。

伸缩的方式和伸缩的规律有关，可利用伸缩的公式进行计算。

3.3 幂函数的翻折幂函数的翻折是指将幂函数的图象进行关于横轴或纵轴的翻折。

高中数学-必修一4.1幂函数-知识点

高中数学-必修一4.1幂函数-知识点1、幂函数：y=x a（a是定值）.特征：①系数为1 ，且
只有1 项，②指数为常数，底数为自变量。

2、幂函数的图像，掌握两步法作图。

第一步：画出幂函数在第一象限的图像,如右图所示；
第二步：根据函数的奇偶性来确定剩余部分图像，需分类讨论：（1）当a是整数时
①若a是奇数②若a是偶数
y是奇函数，图像关于原点对称，另一半在第三象限。

y是偶函数，图像关于y轴对称，另一半在第二象限。

（2）当a是分数时，假定a=n/m（n/m是最简分数）
①n和m都是奇数②n是偶数，m是奇数③n是奇数，m是偶数
y是奇函数,图像关于原点对称,另一半在第三象限. y是偶函数,图像关于y轴
对称,另一半在第二象限.
x＜0时函数无意义,y是非奇
非偶函数,y轴左侧无图像.
3、幂函数的性质
（1）必过点必过点（1,1）；若a＞0，还必过（0,0）。

（2）单调性
①a＞0时，在第一象限严格增。

②a＜0时，在第一象限严格减。

（3）平移的规律左加右减，上加下减。

（4）定义域a＜0时,x不能取0，a为分数且分母是偶数时,x不能取负。

（5）值域(0，+∞)必取，0和(-∞，0)是否能取可结合图像来判断。

4、不同幂函数的指数大小的判断：在（0,1）上，指大图低（指数越大，图像越靠近x轴）；在（1，+∞）时，指大图高（指数越大，图像越远离x轴）。

5、比较幂函数值大小的方法：指数相同，底数不同，根据增减性去比较。

小初高个性化辅导，助你提升学习力！ 1。

高一数学复习考点知识与题型专题讲解12--- 幂函数

高一数学复习考点知识与题型专题讲解3．3 幂函数【考点梳理】知识点一幂函数的概念一般地，函数y＝xα叫做幂函数，其中x是自变量，α是常数．知识点二五个幂函数的图象与性质1．在同一平面直角坐标系内函数(1)y＝x；(2)y＝12x；(3)y＝x2；(4)y＝x－1；(5)y＝x3的图象如图．2．五个幂函数的性质y＝x y＝x2y＝x312y xy＝x－1定义域R R R[0，＋∞){x|x≠0}值域R[0，＋∞)R[0，＋∞){y|y≠0}奇偶性奇偶奇非奇非偶奇单调性增在[0，＋∞) 上增，增增在(0，＋∞)上减，在(－∞，0] 上减在(－∞，0)上减知识点三一般幂函数的图象特征1．所有的幂函数在(0，＋∞)上都有定义，并且图象都过点(1,1)．2．当α>0时，幂函数的图象通过原点，并且在区间[0，＋∞)上是增函数．特别地，当α>1时，幂函数的图象下凸；当0<α<1时，幂函数的图象上凸． 3．当α<0时，幂函数的图象在区间(0，＋∞)上是减函数．4．幂指数互为倒数的幂函数在第一象限内的图象关于直线y ＝x 对称．5．在第一象限，作直线x ＝a (a >1)，它同各幂函数图象相交，按交点从下到上的顺序，幂指数按从小到大的顺序排列．【题型归纳】题型一：幂函数的定义1．（2020·江苏省平潮高级中学高一月考）如果幂函数()22233m m y m m x --=-+的图象不过原点，则实数m 的取值为（） A ．1B ．2C ．1或2D ．无解2．（2021·云南省玉溪第一中学高一月考）已知幂函数()y f x =的图象过点()33，，则该函数的解析式为（）A ．2y x =B ．2y x =C ．3y x =D ．y x =3．（2020·江苏镇江市·）已知幂函数()2()33m f x m m x =--在区间()0,∞+上是单调递增函数，则实数m 的值是（）A ．-1或4B ．4C ．-1D ．1或4题型二：幂函数的值域问题4．（2021·全国高一课时练习）已知幂函数()f x x α=的图像过点(8,4)，则()f x x α= 的值域是（）A ．(),0-∞B ．()(),00,-∞⋃+∞C ．()0,∞+D ．[)0,+∞5．（2020·湖南衡阳市·高一月考）函数2y x -=在区间1,22⎡⎤⎢⎥⎣⎦上的最小值是（）A ．14B ．14-C ．4D ．4-6．（2018·南京市第三高级中学高一期中）以下函数12y x =，2y x =，23y x =，1y x -=中，值域为[0,)+∞的函数共（）个 A ．1B ．2C ．3D ．4题型三：幂函数的定点和图像问题7．（2021·高邮市临泽中学高一月考）已知幂函数1()(21)a g x a x +=-的图象过函数1()(0,1)2x b f x m m m -=->≠的图象所经过的定点，则b 的值等于（）A ．12±B ．22±C ．2D ．2± 8．（2020·南宁市银海三美学校高一月考）函数23y x =的图象是（）A ．B ．C ．D ．9．（2019·宁都县宁师中学高一月考）已知函数y ＝x a ，y ＝x b ，y ＝x c 的图象如图所示，则a ，b ，c 的大小关系为( )A ．c <b <aB ．a <b <cC ．b <c <aD ．c <a <b题型四：幂函数的单调性问题（比较大小、解不等式、参数）10．（2021·江西宜春市·高安中学高一月考）已知 1.13a =， 1.14b =，0.93c =，则a ，b ，c 的大小关系为（）A ．c a b <<B ．c b a <<C ．b a c <<D ．b c a <<11．（2020·江苏省平潮高级中学高一月考）幂函数223a a y x --=是奇函数，且在()0+∞，是减函数，则整数a 的值是（） A ．0B ．0或2C ．2D ．0或1或212．（2020·江西鹰潭一中）已知幂函数12()f x x =，若()()132f a f a +<-，则实数a 的取值范围是（）A ．[)1,3-B ．21,3⎡⎫-⎪⎢⎣⎭C ．[)1,0-D ．21,3⎛⎤- ⎥⎝⎦题型五：幂函数的奇偶性问题13．（2020·江西南昌市·南昌十中高一月考）已知幂函数y ＝f (x )经过点(3，3)，则f (x )（）A ．是偶函数，且在(0，＋∞)上是增函数B ．是偶函数，且在(0，＋∞)上是减函数C ．是奇函数，且在(0，＋∞)上是减函数D ．是非奇非偶函数，且在(0，＋∞)上是增函数14．（2021·吴县中学）有四个幂函数：①()2f x x -=；②()1f x x -=；③()3f x x =；④()3f x x =，某向学研究了其中的一个函数，并给出这个函数的三个性质：（1）()f x 为偶函数；（2）()f x 的值域为()(),00,-∞⋃+∞；（3）()f x 在(),0-∞上是增函数.如果给出的三个性质中，有两个正确，一个错误，则他研究的函数是（） A ．①B ．②C ．③D ．④15．（2020·乌苏市第一中学高一月考）已知112,1,,,1,2,322α⎧⎫∈---⎨⎬⎩⎭，若幂函数()f x x α=为偶函数，且在(0,)+∞上递减，则a =（） A ．1-，12-B ．1，3C ．2-D ．12，2【双基达标】一、单选题16．（2021·镇远县文德民族中学校高一月考）已知幂函数()()21f x m x =-，则实数m 等于（）A ．2B ．1C ．0D ．任意实数17．（2020·南京市第十三中学高一月考）函数 85y x =的图象是（）A ．B ．C ．D ．18．（2021·全国高一课时练习）下列结论中，正确的是（） A ．幂函数的图象都经过点(0，0)，(1，1) B ．幂函数的图象可以出现在第四象限C ．当幂指数α取1，3，12时，幂函数y ＝x α是增函数 D ．当α＝－1时，幂函数y ＝x α在其整个定义域上是减函数19．（2021·全国高一单元测试）已知幂函数()f x 的图象过点1(2,)2，则f （4）的值是（） A ．64B ．42C ．24D ．1420．（2021·全国高一专题练习）函数()()()102121f x x x -=-+-的定义域是（） A ．(],1-∞B ．11,,122⎛⎫⎛⎫-∞⋃ ⎪ ⎪⎝⎭⎝⎭C ．(),1-∞-D ．1,12⎛⎫⎪⎝⎭21．（2021·全国高一课前预习）已知幂函数()3m f x x -=(m ∈N *)为奇函数，且在区间(0，＋∞)上是减函数，则m 等于（） A ．1B ．2C ．1或2D ．322．（2021·全国）幂函数()f x 满足：对任意12x x R ∈、，当且仅当12x x =时，有12()()f x f x =，则(1)(0)(1)f f f -++=（）. A ．1-B ．0C ．1D ．223．（2021·全国）下列比较大小中正确的是（）.A ．0.50.532()()23<B ．1123()()35---<-C ．3377( 2.1)( 2.2)--<-D ．443311()()23-<24．（2019·云南昭通市第一中学高一月考）已知函数()f x x =，若(1)(102)f a f a+<-，则a 的取值范围是（）A ．(0,5)B ．(5,)+∞C ．[1,3)-D ．(3,5)25．（2021·全国）幂函数1y x -=，及直线,1,1y x y x ===将直角坐标系第一象限分成八个“卦限： I, II, III,IV, V, VI, VII, VIII （如图所示），那么，而函数13y x -=的图象在第一象限中经过的“卦限”是（）A ．IV,VII B ． IV,VIII C ． III, VIII D ． III, VII 【高分突破】一：单选题26．（2021·全国高一课前预习）幂函数2266()(33)m m f x m m x -+=-+在(0,)+∞上单调递增，则m的值为（） A ．1B ．2C ．3D ．1或227．（2021·浙江）下列函数中，在其定义域内既是奇函数又是减函数的是（） A ．()y x x R =-∈B ．3()y x x x R =--∈ C ．1()()2x y x R =∈D ．1y x=-(x R ∈，且0)x ≠28．（2021·全国高一课时练习）点(,8)m 在幂函数()(1)n f x m x =-的图象上，则函数()g x n x x m =-+-的值域为（）A ．0,2⎡⎤⎣⎦B ．1,2⎡⎤⎣⎦C ．2,2⎡⎤⎣⎦D ．[]2,329．（2021·全国高一课时练习）如图，①②③④对应四个幂函数的图像，其中②对应的幂函数是（）A ．3y x =B ．2y x =C ．y x =D ．y x =30．（2021·全国高一课时练习）已知幂函数()()2133m f x m m x +=-+的图象关于原点对称，则满足()()132m ma a +>-成立的实数a 的取值范围为（）A ．22,33⎛⎫- ⎪⎝⎭B ．22,3⎛⎫-- ⎪⎝⎭C ．22,3⎛⎫- ⎪⎝⎭D ．2,43⎛⎫ ⎪⎝⎭31．（2021·全国高一课时练习）设11,,1,2,32α⎧⎫∈-⎨⎬⎩⎭则“()f x x α=的图象经过()1,1--”是“()f x x α=为奇函数”的（）A ．充分不必要件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件32．（2021·浙江高一期末）已知实数a ，b 满足等式35a b =，给出下列五个关系式：①1b a <<；②1a b <<-；③01b a <<<；④10a b -<<<；⑤a b =，其中，可能成立的关系式有（） A ．1个B ．2个C ．3个D ．5个33．（2021·全国高一单元测试）已知函数1a y ax b =-+-是幂函数，直线20(0,0)mx ny m n -+=>>过点(,)a b ，则11n m ++的取值范围是（） A ．11,,333⎫⎫⎛⎛-∞⋃ ⎪ ⎪⎝⎝⎭⎭B ．(1,3)C ．1,33⎡⎤⎢⎥⎣⎦D ．1,33⎛⎫ ⎪⎝⎭二、多选题34．（2021·全国高一课时练习）下列关于幂函数y x α=的性质，描述正确的有（） A ．当1α=-时函数在其定义域上是减函数B ．当0α=时函数图象是一条直线 C ．当2α=时函数是偶函数D ．当3α=时函数在其定义域上是增函数35．（2021·全国高一课时练习）已知函数()21m m y m x -=-为幂函数，则该函数为（） A ．奇函数B ．偶函数C ．区间()0,∞+上的增函数D ．区间()0,∞+上的减函数36．（2021·全国高一课时练习）已知幂函数223()(1)m m f x m m x +-=--，对任意12,(0,)x x ∈+∞，且12x x ≠，都满足1212()()0f x f x x x ->-，若,a b ∈R 且()()0f a f b +<，则下列结论可能成立的有（）A ．0a b +> 且0ab <B ．0a b +< 且0ab <C ．0a b +< 且0ab >D ．以上都可能37．（2021·全国高一专题练习）已知幂函数9()5m f x m x ⎛⎫=+ ⎪⎝⎭，则下列结论正确的有（）A ．()13216f -=B ．()f x 的定义域是RC ．()f x 是偶函数D ．不等式()()12f x f -≥的解集是[)(]1,11,3-38．（2020·江苏常州市·常州高级中学高一期中）若函数()f x 同时满足：①对于定义域上的任意x ，恒有()()0f x f x +-=；②对于定义城上的任意1x ，2x ，当12x x ≠时，恒有()()12120f x f x x x -<-，则称函数()f x 为“理想函数”．下列四个函数中，能被称为“理想函数”的有（） A ．()2121x f x x -=+B ．()3f x x =-C ．()f x x =-D ．()22,0,,0x x f x x x ⎧-≥=⎨<⎩三、填空题39．（2021·湖南邵阳市·高一期末）已知幂函数()y f x =的图象过点()2,2，则()5f =______.40．（2021·雄县第二高级中学高一期末）已知幂函数()f x 过定点18,2⎛⎫ ⎪⎝⎭，且满足()()2150f a f ++->，则a 的范围为________．41．（2021·全国高一课时练习）不等式()()1133312a a -<+的解集为______42．（2021·上海上外浦东附中高一期末）已知幂函数()223()m m f x x m Z --=∈的图像关于y 轴对称，与x 轴及y 轴均无交点，则由m 的值构成的集合是__________．43．（2021·全国高一单元测试）已知112,1,,1,,2,322k ⎧⎫∈---⎨⎬⎩⎭，若幂函数()kf x x =为奇函数，且在()0,∞+上单调递减，则k =______．四、解答题44．（2021·全国高一课时练习）已知函数()()21212223m f x m m xn -=+-+-是幂函数，求2m n -的值．45．（2021·全国高一课时练习）已知函数()()()()1221a a f x a a x -+=--是幂函数()a R ∈，且()()12f f <.（1）求函数()f x 的解析式；（2）试判断是否存在实数b ，使得函数()()32g x f x bx =-+在区间[]1,1-上的最大值为6，若存在，求出b 的值；若不存在，请说明理由.46．（2021·全国高一专题练习）已知幂函数()()1222mf x m m x =--在()0,∞+上单调递减．（1）求实数m 的值．（2）若实数a 满足条件()()132f a f a ->+，求a 的取值范围．47．（2021·江西省乐平中学高一开学考试）已知幂函数()()()22322k k f x m m x k -=-+∈Z 是偶函数，且在()0,∞+上单调递增. （1）求函数()f x 的解析式；（2）若()()212f x f x -<-，求x 的取值范围：（3）若实数()*,,a b a b ∈R 满足237a b m +=，求3211a b +++的最小值.【答案详解】1．C 【详解】由幂函数的定义得m 2-3m +3=1，解得m =1或m =2；当m =1时，m 2-m -2=-2，函数为y =x -2，其图象不过原点，满足条件；当m =2时，m 2-m -2=0，函数为y =x 0，其图象不过原点，满足条件. 综上所述，m =1或m =2. 故选：C. 2．D 【详解】设()f x x α=，依题意()13332f αα==⇒=，所以()f x x =. 故选：D 3．B 【详解】幂函数()2()33mf x m m x =--在(0,)+∞上是增函数则2331m m m ⎧--=⎨>⎩ ，解得4m = 故选：B 4．D【详解】幂函数()f x x α=的图像过点(8,4)，84α∴=，解得23α=，2332(0)f x x x ∴==≥，∴()f x 的值域是[)0,+∞. 故选：D. 5．A 【详解】∵函数2y x -=在区间1,22⎡⎤⎢⎥⎣⎦上是减函数，∴2min 124y -==，故选：A. 6．C 【详解】函数12y x x ==，其定义域为[0,)+∞，值域为[0,)+∞；函数2y x =的定义域为R ，值域为[0,)+∞；函数2323y x x ==，20x ≥Q ，∴函数值域为[0,)+∞；函数331y x x -==，值域为(,0)(0,)-∞+∞． ∴值域为[0,)+∞的函数共3个．故选：C. 7．B 【详解】由于1()(21)a g x a x +=-为幂函数，则211a -=，解得：1a =，则2()g x x =；函数1()(0,1)2x b f x m m m -=->≠，当x b = 时，11()22b b f b a -=-=，故()f x 的图像所经过的定点为1,2b ⎛⎫ ⎪⎝⎭，所以1()2g b =，即212b =，解得：22b =±, 故选：B. 8．C 【详解】首先由分数指数幂运算公式可知()21233x x ⎛⎫=⎪⎝⎭，则()()23y f x x ==，()()f x f x -=，且函数的定义域为R ，所以函数是偶函数，关于y 轴对称，故排除AD ，因为2013<<，所以23y x =在第一象限的增加比较缓慢，故排除B ，故选：C 9．A试题：由幂函数图像特征知，1a >，01b <<，0c <，所以选A ． 10．A 【详解】由题意，构造函数 1.13,x y y x ==，由指数函数和幂函数的性质，可知两个函数在(0,)+∞单调递增；由于0.9 1.10.9 1.133c a <∴<∴<；由于 1.1 1.13434a b <∴<∴<；综上：c a b << 故选：A 11．B由于幂函数223a a y x --=是奇函数，且在(0,)+∞是减函数，故2230a a --<，且223a a --是奇数，且a 是整数，13a -<<∴，a Z ∈，当0a =时，2233a a --=-，是奇数，；当1a =时，2234a a --=-，不是奇数；当2a =时，2233a a --=-，是奇数；故0a =或2．故答选：B 12．B 【详解】因为幂函数()12f x x =是增函数，且定义域为[)0,+∞，由()()132f a f a +<-得13210320a aa a +<-⎧⎪+≥⎨⎪-≥⎩，解得213a -≤<.所以实数a 的取值范围是21,3⎡⎫-⎪⎢⎣⎭故选：B 13．D 【详解】设幂函数的解析式为y x α=，将点()3,3的坐标代入解析式得33α=，解得12α=， ∴12y x =，函数的定义域为[)0,+∞,是非奇非偶函数，且在()0,+∞上是增函数，14．A 【详解】对于①，函数()2f x x -=为偶函数，且()2210f x x x -==>，该函数的值域为()0,∞+，函数()2f x x -=在()0,∞+上为减函数，该函数在(),0-∞上为增函数，①满足条件；对于②，函数()11x x f x -==为奇函数，且()10f x x=≠，该函数的值域为()(),00,-∞⋃+∞，函数()f x 在(),0-∞上为减函数，②不满足条件；对于③，函数()3f x x =的定义域为R ，且()()33f x x x f x -=-=-=-，该函数为奇函数，当0x ≥时，()30f x x =≥；当0x <时，()30f x x =<，则函数()f x 的值域为R ，函数()3f x x =在()0,∞+上为增函数，该函数在(),0-∞上也为增函数，③不满足条件；对于④，函数()3f x x =为奇函数，且函数()3f x x =的值域为R ，该函数在(),0-∞上为增函数，④不满足条件. 故选：A. 15．C 【详解】112,1,,,1,2,322α⎧⎫∈---⎨⎬⎩⎭若幂函数()f x x α=为偶函数，且在(0,)+∞上递减，则0α<且2,k k Z α=∈，所以2a =-. 故选：C 16．A因为函数()()21f x m x =-为幂函数，所以m -1=1，则m =2.故选：A. 17．A 【详解】由幂函数85y x =可知: 85y x =是定义域为R 的偶函数，在(0,+∞)上单调递增，且当x >1时,函数值增长的比较快. 故选：A 18．C 【详解】当幂指数α＝－1时，幂函数y ＝x －1的图象不经过原点，故A 错误；因为所有的幂函数在区间(0，＋∞)上都有定义，且y ＝x α(α∈R)>0，所以幂函数的图象不可能出现在第四象限，故B 错误；当α>0时，y ＝x α是增函数，故C 正确；当α＝－1时，y ＝x －1在区间(－∞，0)，(0，＋∞)上是减函数，但在整个定义域上不是减函数，故D 错误．故选：C. 19．D 【详解】幂函数()a f x x =的图象过点1(2,)2，122a ∴=，解得1a =-，1()f x x∴=， f ∴（4）14=，故选：D . 20．B 【详解】因为()()()()121121211f x x x x x-=-+-=+--，则有10210x x ->⎧⎨-≠⎩，解得1x <且12x ≠，因此()f x 的定义域是11,,122⎛⎫⎛⎫-∞⋃ ⎪ ⎪⎝⎭⎝⎭．故选：B. 21．B 【详解】因为()3m f x x -=在(0，＋∞)上是减函数，所以m －3<0,所以m <3. 又因为m ∈N *，所以1m =或2.又因为()3m f x x -=是奇函数，所以m －3是奇数，所以m ＝2. 故选：B. 22．B 【详解】设()a f x x =，由已知，函数()f x 的定义域为R ，∴0a >，又∵对任意12x x R ∈、，当且仅当12x x =时，有12()()f x f x =，即y 与x 一一对应，()f x 必定不是偶函数，∴必定为奇函数，∴答案为0，故选：B. 23．C 【详解】A 选项，0.5y x =在[0)+∞，上是递增函数，0.50.523()()32<，错， B 选项，1y x -=在()0-∞，上是递减函数，1123()()35--->-，错， C 选项，37y x =在()0-∞，上是递增函数， 337721( 2.1)()10-=-，33775( 2.2)()11--=-，3377( 2.1)( 2.2)--<-，对，D 选项，43y x =在[0)+∞，上是递增函数， 443311()()22-=，443311()()23>，443311()()23->，错，故选：C ． 24．C 【详解】()f x x =的定义域为[)0,+∞，且在[)0,+∞单调递增，所以(1)(102)f a f a +<-可化为：1010201102a a a a +≥⎧⎪-≥⎨⎪+<-⎩，解得：13x -≤<. 故a 的取值范围是[1,3)-. 故选：C 25．B【详解】对于幂函数13y x -=，因为103-< ，所以13y x -=在第一象限单调递减，根据幂函数的性质可知：在直线1x =的左侧，幂函数的指数越大越接近y 轴，因为113->-，所以13y x -=的图象比1y x -=的图象更接近y 轴，所以进过第IV 卦限，在直线1x =的右侧，幂函数的指数越小越接近x 轴，因为1103-<-<，所以13y x -=的图象位于1y x -=和1y =之间，所以经过VIII 卦限，所有函数13y x -=的图象在第一象限中经过的“卦限”是IV,VIII ，故选：B 26．A 【详解】解：幂函数2266()(33)m m f x m m x -+=-+在(0,)+∞上单调递增，2331m m ∴-+=，且2660m m -+>，解2331m m -+=得1m =或2m =，当1m =时26610m m -+=>符合题意；当2m =时26620m m -+=-<不符合题意；故选：A ． 27．B 【详解】解：对于A 选项，()()f x x x f x -=--=-=，为偶函数，故错误；对于B 选项，()()()()33f x x x x x f x -=----=+=-，为奇函数，且函数3,y x y x =-=-均为减函数，故3()y x x x R =--∈为减函数，故正确；对于C 选项，指数函数没有奇偶性，故错误；对于D 选项，函数为奇函数，在定义域上没有单调性，故错误.故选：B28．B【详解】解：因为点(,8)m 在幂函数()(1)n f x m x =-的图象上，所以11m -=，即2m =，()()228n f m f ===，所以3n =，故()32g x x x =-+-，[]2,3x ∈， ()()22()12321256g x x x x x =+--=+-+-，因为[]2,3x ∈，所以21560,4x x ⎡⎤-+-∈⎢⎥⎣⎦，所以[]2()1,2g x ∈，所以函数()g x n x x m =-+-的值域为1,2⎡⎤⎣⎦.故选：B.29．C【详解】解：由图知：①表示y x =，②表示y x =，③表示2y x =，④表示3y x =.故选：C.30．D【详解】由题意得：2331m m -+=，得1m =或2m =当1m =时，2()f x x =图象关于y 轴对称，不成立；当2m =时，3()f x x =是奇函数，成立；所以不等式转化为22(1)(32)a a +>-，即231480a a -+<，解得243a <<.故选：D31．C【详解】由11,,1,2,32α⎧⎫∈-⎨⎬⎩⎭，由()f x x α=的图像经过()1,1--，则α的值为11,3-，，此时()f x x α=为奇函数. 又当()f x x α=为奇函数时，则α的值为11,3-，，此时()f x x α=的图象经过()1,1--. 所以“()f x x α=的图象经过()1,1--”是“()f x x α=为奇函数”的充要条件故选：C32．C【详解】在同一坐标系中画出函数3y x =和5y x =的图像，如图所示：数形结合可知，在（1）处1a b <<-；在（2）处10b a -<<<；在（3）处01a b <<<；在（4）处1b a <<；在1a b ==或1a b ==-也满足，故①②⑤对故选：C.33．D【详解】由1a y ax b =-+-是幂函数，知：1,1a b =-=，又(,)a b 在20mx ny -+=上，∴2m n +=，即20n m =->，则1341111n m m m m +-==-+++且02m <<， ∴11(,3)13n m +∈+. 故选：D.34．CD【详解】对于A 选项，1y x =，在(,0)-∞和(0,)+∞上递减，不能说在定义域上递减，故A 选项错误．对于B 选项，0y x =，0x ≠，图像是：直线1y =并且除掉点(0,1)，故B 选项错误．对于C 选项，2y x =，定义域为R ，是偶函数，所以C 选项正确．对于D 选项，3y x =，函数在其定义域上是增函数，所以D 选项正确．故选：CD35．BC【详解】由()21m m y m x -=-为幂函数，得11m -=，即m =2，则该函数为2y x =，故该函数为偶函数，且在区间()0,∞+上是增函数，故选：BC .36．BC【详解】因为223()(1)m m f x m m x +-=--为幂函数，所以211m m --=，解得：m =2或m =-1.因为任意12,(0,)x x ∈+∞，且12x x ≠，都满足1212()()0f x f x x x ->-，不妨设12x x >，则有12())0(f x f x ->，所以()y f x =为增函数，所以m =2，此时3()f x x =因为()33()()f x x x f x -=-=-=-，所以3()f x x =为奇函数.因为,a b ∈R 且()()0f a f b +<，所以()()f a f b <-.因为()y f x =为增函数，所以a b <-，所以0a b +<.故BC 正确.故选：BC37．ACD【详解】因为函数是幂函数，所以915m +=，得45m =-，即()45f x x -=， ()()()45451322216f --⎡⎤-=-=-=⎣⎦，故A 正确；函数的定义域是{}0x x ≠，故B 不正确； ()()f x f x -=，所以函数是偶函数，故C 正确；函数()45f x x -=在()0,∞+是减函数，不等式()()12f x f -≥等价于12x -≤，解得：212x -≤-≤，且10x -≠，得13x -≤≤，且1x ≠，即不等式的解集是[)(]1,11,3-，故D 正确.故选：ACD38．BCD【详解】对于①对于定义域内的任意x ，恒有()()0f x f x +-=，即()()f x f x -=-，所以()f x 是奇函数；对于②对于定义域内的任意1x ，2x ，当12x x ≠时，恒有()()12120f x f x x x -<-， ()f x 在定义域内是减函数；对于A ：()2121x f x x -=+，()113f =，()13f -=，故不是奇函数，所以不是“理想函数”；对于 B ：()3f x x =-是奇函数，且是减函数，所以是“理想函数”；对于C ：()f x x =-是奇函数，并且在R 上是减函数，所以是“理想函数”；对于D ：()22,0,0x x f x x x x x ⎧-≥==-⎨<⎩，()||()f x x x f x -==-，所以()22,0,0x x f x x x ⎧-≥=⎨<⎩是奇函数；根据二次函数的单调性，()f x 在(,0)-∞，(0,)+∞都是减函数，且在0x =处连续，所以()22,0,0x x f x x x ⎧-≥=⎨<⎩在R 上是减函数，所以是“理想函数”.故选：BCD.39．5【详解】设()f x x α=，则()12222f αα==⇒=，所以()(),55f x x f ==. 故答案为：540．()22-，【详解】设幂函数()y f x x α==，其图象过点18,2⎛⎫ ⎪⎝⎭，所以182α=，即3122α-=，解得：13α=-，所以()13f x x -=，因为()()()13f x x f x --=-=-，所以()13f x x -=为奇函数，且在()0-∞，和()0+∞，上单调递减，所以()()2150f a f ++->可化为()()()2155f a f f +>--=，可得215a +<，解得：22a -<<，所以a 的范围为()22-，，故答案为：()22-，． 41．()4,-+∞【详解】解：因为幂函数13y x =在R 上为增函数，()()1133312a a -<+，所以312a a -<+，解得4a >-，所以不等式的解集为()4,-+∞，故答案为：()4,-+∞42．{}1,1,3-【详解】由幂函数()f x 与x 轴及y 轴均无交点，得2230m m -≤-，解得13m -≤≤，又m Z ∈，即{}1,0,1,2,3m ∈-，()223()m m f x x m Z --=∈的图像关于y 轴对称，即函数为偶函数，故223m m --为偶数，所以{}1,1,3m ∈-，故答案为：{}1,1,3-.43．1-【详解】由题意知，幂函数()k f x x =在(0)+∞，上单调递减，则k 为负数，则k =-2，-1，12-，又由函数()k f x x =为奇函数，则k =-1，故答案为：-144．-6【详解】因为()()21212223m f x m m x n -=+-+-是幂函数，所以22221,10,230,m m m n ⎧+-=⎪-≠⎨⎪-=⎩，解得3,3,2m n =-⎧⎪⎨=⎪⎩，所以323262m n -=--⨯=-．45．（1）()2f x x =；（2）存在，2b =±. 解：因为函数()()()()1221a a f x a a x -+=--是幂函数，所以211a a --=，解得2a =或1a =-，当2a =时，()4f x x -=，则()()12f f >，故不符题意，当1a =-时，()2f x x =，则()()12f f <，符合题意，所以()2f x x =；（2）由（1）得 ()()()22232233g x f x bx x bx x b b =-+=-++=--++，函数图像开口向下，对称轴为：x b =，当1b ≤-时，函数()g x 在区间[]1,1-上递减，则()()11236max g x g b =-=--+=，解得2b =-，符合题意；当1b ≥时，函数()g x 在区间[]1,1-上递增，则()()11236max g x g b ==-++=，解得2b =，符合题意；当11b -<<时，()()22236max g x g b b b ==-++=，解得3b =±，不符题意，综上所述，存在实数2b =±满足题意.46．（1）1m =-；（2）32,,123⎛⎫⎛⎫-∞-- ⎪ ⎪⎝⎭⎝⎭．【详解】解：（1）()f x 是幂函数，2221m m ∴--=，解得：3m =或1m =-， 3m =时，()13f x x =在(0,)+∞上单调递增，1m =-时，()1f x x=在(0,)+∞递减，故1m =-；（2）若实数a 满足条件()()132f a f a ->+，则10320a a ->⎧⎨+<⎩或10320132a a a a ->⎧⎪+>⎨⎪-<+⎩或10320132a a a a-<⎧⎪+<⎨⎪-<+⎩，解得：32a <-或213a -<<，故a 的取值范围是32,,123⎛⎫⎛⎫-∞-- ⎪ ⎪⎝⎭⎝⎭． 47．（1）2()f x x =；（2）(1,1)-；（3）2．【详解】（1）()f x 是幂函数，则2221m m -+=，1m =，又()f x 是偶函数，所以23(3)k k k k -=-是偶数，()f x 在(0,)+∞上单调递增，则230k k ->，03k <<，所以1k =或2．所以2()f x x =；（2）由（1）偶函数()f x 在[0,)+∞上递增， (21)(2)f x f x -<-22(21)(2)212f x f x x x ⇔-<-⇔-<-11x ⇔-<<．所以x 的范围是(1,1)-．（3）由（1）237a b +=，2(1)3(1)12a b +++=，0,0a b >>， []3213219(1)2(1)2(1)3(1)121112111211b a a b a b a b a b ++⎛⎫⎛⎫+=++++=++ ⎪ ⎪++++++⎝⎭⎝⎭ 19(1)4(1)12221211b a a b ⎛⎫++≥+⨯= ⎪ ⎪++⎝⎭，当且仅当9(1)4(1)11b a a b ++=++，即2,1a b ==时等号成立．所以3211a b +++的最小值是2．。

大一高数幂函数知识点归纳

大一高数幂函数知识点归纳幂函数是大一高数中重要的概念之一，它在数学和科学领域具有广泛的应用。

在本文中，将对大一高数幂函数的知识点进行归纳总结，以帮助读者更好地理解和掌握这一内容。

一、幂函数的定义幂函数是指形如f(x) = x^n的函数，其中x为自变量，n为常数指数。

幂函数的特点是自变量x的幂次，它决定了函数的增长趋势和性质。

幂函数可以分为正幂函数和负幂函数两种情况。

正幂函数：当指数n为正数时，幂函数随着x的增大而增大，随着x的减小而减小。

例如，f(x) = x^2是一个正幂函数，其图像为开口向上的抛物线。

负幂函数：当指数n为负数时，幂函数随着x的增大而减小，随着x的减小而增大。

例如，f(x) = x^(-2)是一个负幂函数，其图像为开口向下的抛物线。

二、幂函数的性质1. 定义域和值域：对于幂函数f(x) = x^n，当n为正数时，定义域是整个实数集；当n为负数时，定义域是正实数集。

值域在正幂函数和负幂函数的情况下有所不同。

2. 奇偶性：当指数n为偶数时，幂函数是关于y轴对称的偶函数；当指数n为奇数时，幂函数是关于原点对称的奇函数。

3. 单调性：正幂函数在定义域上是递增的，负幂函数在定义域上是递减的。

4. 零点：当幂函数中的指数n为正数时，零点为x=0；当指数n为负数时，零点不存在。

5. 渐近线：对于正幂函数和负幂函数，它们都有y轴作为渐近线。

当幂函数的指数n为正数时，还可能有x轴作为渐近线。

三、幂函数的图像1. 正幂函数的图像：正幂函数在定义域上为开口向上的抛物线，图像越接近x轴，增长速度越慢。

当指数n越大时，抛物线的开口越窄。

2. 负幂函数的图像：负幂函数在定义域上为开口向下的抛物线，图像越接近x轴，减小速度越慢。

当指数n越小时，抛物线的开口越窄。

四、幂函数的应用1. 物理学中的应用：幂函数在物理学中具有广泛的应用，例如在力学中描述物体的抛体运动、空气阻力、电子流强度与电位差的关系等。

通过研究幂函数的性质和图像，可以帮助我们更好地理解这些物理现象。

高一数学幂知识点

高一数学幂知识点幂作为数学中的一个重要概念，在高一数学中占据着重要地位。

掌握好幂的定义、运算规则以及一些常见的性质和应用，对于理解和解决数学问题是至关重要的。

本文将为大家详细介绍高一数学中的幂知识点。

一、幂数的定义在数学中，幂是指将一个数乘以自身多次的运算。

其中，被乘的数称为底数，用字母a表示；乘积中相同的因数的个数称为指数，用字母n表示。

幂的表示方式为aⁿ。

例如，当a=2，n=3时，2ⁿ = 2³ = 2 × 2 × 2 = 8。

二、幂数的运算规则1. 幂的乘法规则：当两个幂的底数相同时，它们的指数相加。

即，aⁿ × aᵐ= aⁿ⁺ᵐ。

例如，2² × 2³ = 2⁵ = 2 × 2 × 2 × 2 × 2 = 32。

2. 幂的除法规则：当两个幂的底数相同时，将它们的指数相减。

即，aⁿ ÷ aᵐ= aⁿ⁻ᵐ。

例如，3⁵ ÷ 3² = 3³ = 3 × 3 × 3 = 27。

3. 幂的乘方规则：幂的乘方指的是将一个幂再次乘以指数。

即，(aⁿ)ᵐ= aⁿᵐ。

例如，(4²)³ = 4⁶ = 4 × 4 × 4 × 4 × 4 × 4 = 4096。

三、幂的性质1. 任何数的零次幂等于1：即，a⁰ = 1（其中a不等于0）。

例如，2⁰ = 1。

2. 任何非零数的负整数次幂等于其倒数的正整数次幂：即，a⁻ⁿ = 1 / (aⁿ)（其中a不等于0）。

例如，3⁻² = 1 / (3²) = 1 / 9。

3. 指数为1的幂等于底数本身：即，a¹ = a。

例如，5¹ = 5。

四、幂的应用幂的概念在数学中有着广泛的应用，尤其在代数、几何和物理等领域中经常被使用。

高一上数学必修一第四章《4.4幂函数》知识点梳理

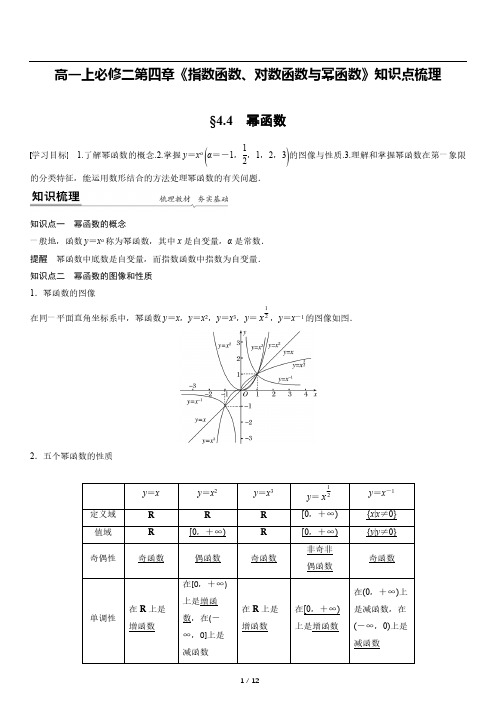
高一上必修二第四章《指数函数、对数函数与幂函数》知识点梳理§4.4　幂函数学习目标　1.了解幂函数的概念.2.掌握y ＝x α(α＝－1，12，1，2，3)的图像与性质.3.理解和掌握幂函数在第一象限的分类特征，能运用数形结合的方法处理幂函数的有关问题．知识点一　幂函数的概念一般地，函数y ＝x α称为幂函数，其中x 是自变量，α是常数．提醒　幂函数中底数是自变量，而指数函数中指数为自变量．知识点二　幂函数的图像和性质1．幂函数的图像在同一平面直角坐标系中，幂函数y ＝x ，y ＝x 2，y ＝x 3，y ＝，y ＝x －1的图像如图．2．五个幂函数的性质y ＝xy ＝x 2y ＝x 3y ＝y ＝x －1定义域R R R [0，＋∞){x |x ≠0}值域R [0，＋∞)R [0，＋∞){y |y ≠0}奇偶性奇函数偶函数奇函数非奇非偶函数奇函数单调性在R 上是增函数在[0，＋∞)上是增函数，在(－∞，0]上是减函数在R 上是增函数在[0，＋∞)上是增函数在(0，＋∞)上是减函数，在(－∞，0)上是减函数12x 12x公共点(1,1)1．y ＝－1x 是幂函数．(　×　)2．当x ∈(0,1)时，x 2>x 3.(　√　)3．y ＝与y ＝定义域相同．(　×　)4．若y ＝x α在(0，＋∞)上为增函数，则α>0.(　√　)一、幂函数的概念例1　(1)(多选)下列函数为幂函数的是( )A ．y ＝x 3 B ．y ＝(12)xC ．y ＝4x 2D ．y ＝x答案　AD解析　B 项为指数函数，C 中的函数的系数不为1，AD 为幂函数．(2)已知y ＝(m 2＋2m －2)＋2n －3是幂函数，求m ，n 的值．解　由题意得Error!解得Error!或Error!所以m ＝－3或1，n ＝32.反思感悟　判断一个函数是否为幂函数的方法判断一个函数是否为幂函数的依据是该函数是否为y ＝x α(α为常数)的形式，即函数的解析式为一个幂的形式，且需满足：(1)指数为常数；(2)底数为自变量；(3)系数为1.跟踪训练1　已知f (x )＝ax 2a ＋1－b ＋1是幂函数，则a ＋b 等于( )A ．2 B ．1 C.12 D ．0答案　A解析　因为f (x )＝ax 2a ＋1－b ＋1是幂函数，所以a ＝1，－b ＋1＝0，即a ＝1，b ＝1，则a ＋b ＝2.32x 64x 22m x二、幂函数的图像例2　如图所示，图中的曲线是幂函数y ＝x n 在第一象限的图像，已知n 取±2，±12四个值，则对应于c 1，c 2，c 3，c 4的n 依次为( )A ．－2，－12，12，2B ．2，12，－12，－2C ．－12，－2,2，12D ．2，12，－2，－12答案　B解析　根据幂函数y ＝x n 的性质，故c 1的n ＝2，c 2的n ＝12，当n <0时，|n |越大，曲线越陡峭，所以曲线c 3的n ＝－12，曲线c 4的n ＝－2.反思感悟　解决幂函数图像问题应把握的两个原则(1)依据图像高低判断幂指数大小，相关结论为：在(0,1)上，指数越大，幂函数图像越靠近x 轴(简记为指大图低)；在(1，＋∞)上，指数越大，幂函数图像越远离x 轴(简记为指大图高)．(2)依据图像确定幂指数α与0,1的大小关系，即根据幂函数在第一象限内的图像(类似于y ＝x －1 或y ＝或y ＝x 3)来判断．跟踪训练2　函数f (x )＝的大致图像是( )答案　A解析　因为－12<0，所以f (x )在(0，＋∞)上单调递减，排除选项B ，C ；又f (x )的定义域为(0，＋∞)，故排除选项D.三、比较幂值的大小12x 12x例3　比较下列各组数中两个数的大小：(1)(25)0.5与(13)0.5；(2)(－23)－1与(－35)－1；(3)与.解　(1)∵幂函数y ＝x 0.5在(0，＋∞)上是单调递增的，又25>13，∴(25)0.5>(13)0.5.(2)∵幂函数y ＝x －1在(－∞，0)上是单调递减的，又－23<－35，∴(－23)－1>(－35)－1.(3)∵函数y 1＝(23)x为R 上的减函数，又34>23，∴>.又∵函数y 2＝在(0，＋∞)上是增函数，且34>23，∴>，∴>.反思感悟　比较幂值大小的方法跟踪训练3　比较下列各组值的大小：(1)，；(2)，，1.42.解　(1)∵y ＝为R 上的偶函数，∴＝.又函数y ＝为[0，＋∞)上的增函数，且0.31<0.35，3423⎛⎫⎪⎝⎭2334⎛⎫⎪⎝⎭2323⎛⎫ ⎪⎝⎭3423⎛⎫ ⎪⎝⎭23x 2334⎛⎫⎪⎝⎭2323⎛⎫ ⎪⎝⎭2334⎛⎫ ⎪⎝⎭3423⎛⎫⎪⎝⎭()650.31-650.35121.2121.465x ()650.31-650.3165x∴<，即<.(2)∵y ＝在[0，＋∞)上是增函数，且1.2<1.4，∴<.又∵y ＝1.4x 为增函数，且12<2，∴<1.42，∴<<1.42.幂函数性质的应用典例　已知幂函数y ＝x 3m －9 (m ∈N ＋)的图像关于y 轴对称且在(0，＋∞)上单调递减，求满足的a 的取值范围．解　因为函数y ＝x 3m －9在(0，＋∞)上单调递减，所以3m －9<0，解得m <3.又因为m ∈N ＋，所以m ＝1,2.因为函数的图像关于y 轴对称，所以3m －9为偶数，故m ＝1.则原不等式可化为.因为y ＝在(－∞，0)，(0，＋∞)上单调递减，所以a ＋1>3－2a >0或3－2a <a ＋1<0或a ＋1<0<3－2a ，解得23<a <32或a <－1.故a 的取值范围是Error!.[素养提升]　(1)幂函数y ＝x α中只有一个参数α，幂函数的所有性质都与α的取值有关，故可由α确定幂函数的定义域、值域、单调性、奇偶性，也可由这些性质去限制α的取值．(2)通过具体实例抽象出幂函数的概念和性质，并应用单调性求解，体现了数学中数学运算与直观想象的核心素养．650.31650.35()650.31-650.3512x 121.2121.4121.4121.2121.433(1)(32)m m a a --+<-1133(1)(32)a a --+<-13x-1．下列函数是幂函数的是( )A ．y ＝5x B ．y ＝x 5C ．y ＝5x D ．y ＝(x ＋1)3答案　B解析　函数y ＝5x 是指数函数，不是幂函数；函数y ＝5x 是正比例函数，不是幂函数；函数y ＝(x ＋1)3的底数不是自变量x ，不是幂函数；函数y ＝x 5是幂函数．2．幂函数y ＝x α(α∈R )的图像一定不经过( )A ．第四象限 B ．第三象限C ．第二象限 D ．第一象限答案　A解析　由幂函数的图像可知，其图像一定不经过第四象限．3．设α∈{－1，1，12，3}，则使函数y ＝x α的定义域为R 且为奇函数的所有α值为( )A ．1,3B ．－1,1C ．－1,3D ．－1,1,3答案　A解析　可知当α＝－1,1,3时，y ＝x α为奇函数，又因为y ＝x α的定义域为R ，则α＝1,3.4．已知幂函数f (x )＝kx α(k ∈R ，α∈R )的图像过点(12，2)，则k ＋α等于( )A.12 B ．1 C.32 D ．2答案　A解析　∵幂函数f (x )＝kx α(k ∈R ，α∈R )的图像过点(12，2)，∴k ＝1，f(12)＝(12)α＝2，即α＝－12，∴k ＋α＝12.5．已知f (x )＝，若0<a <b <1，则下列各式中正确的是( )A ．f (a )<f (b )<f(1a )<f(1b)B ．f (1a )<f(1b )<f (b )<f (a )C ．f (a )<f (b )<f (1b )<f(1a )D ．f (1a )<f (a )<f(1b )<f (b )12x答案　C解析　因为函数f (x )＝在(0，＋∞)上是增函数，又0<a <b <1<1b <1a ，故f (a )<f (b )<f(1b )<f(1a).1．知识清单：(1)幂函数的概念．(2)幂函数的图像．(3)幂函数的性质及其应用．2．方法归纳：数形结合．3．常见误区：幂函数与指数函数的区别；幂函数的奇偶性．1．幂函数f (x )＝x α的图像经过点(2,4)，则f (－12)等于( )A.12B.14 C ．－14 D ．2答案　B解析　幂函数f (x )＝x α的图像经过点(2,4)，则2α＝4，解得α＝2；∴f (x )＝x 2，∴f (－12)＝(－12)2＝14.2．下列函数中，既是偶函数，又在区间(0，＋∞)上单调递减的函数是( )A ．y ＝x －2 B ．y ＝x －1C ．y ＝x 2 D ．y ＝答案　A解析　所给选项都是幂函数，其中y ＝x －2和y ＝x 2是偶函数，y ＝x －1和y ＝不是偶函数，故排除选项B ，D ，又y ＝x 2在区间(0，＋∞)上单调递增，不合题意，y ＝x －2在区间(0，＋∞)上单调递减，符合题意．3．设a ＝，b ＝，c ＝，则a ，b ，c 的大小关系是( )12x 13x13x 2535⎛⎫ ⎪⎝⎭3525⎛⎫⎪⎝⎭2525⎛⎫⎪⎝⎭A ．a >c >bB ．a >b >cC ．c >a >bD ．b >c >a答案　A解析　∵y ＝(x >0)为增函数，又35>25，∴a >c .∵y ＝(25)x (x ∈R )为减函数，又25<35，∴c >b .∴a >c >b .4．在同一坐标系内，函数y ＝x a (a ≠0)和y ＝ax －1a的图像可能是( )答案　C解析　选项A 中，幂函数的指数a <0，则y ＝ax －1a 应为减函数，A 错误；选项B 中，幂函数的指数a >1，则y ＝ax －1a 应为增函数，B 错误；选项D 中，幂函数的指数a <0，则－1a >0，直线y ＝ax －1a在y 轴上的截距为正，D 错误．5．若幂函数f (x )的图像过点(2，2)，则函数g (x )＝f (x )－3的零点是( )A.3 B ．9 C ．(3，0) D ．(9,0)答案　B解析　∵幂函数f (x )＝x α的图像过点(2，2)，∴f (2)＝2α＝2，解得α＝12，∴f (x )＝，∴函数g (x )＝f (x )－3＝－3，由－3＝0，得x ＝9.∴函数g (x )＝f (x )－3的零点是9.6．已知幂函数f (x )＝x α的部分对应值如表：x11225x 12x 12x 12xf (x )122则f (x )的单调递增区间是________．答案　[0，＋∞)解析　因为f(12)＝22，所以(12)α＝22，即α＝12，所以f (x )＝的单调递增区间是[0，＋∞)．7．已知幂函数f (x )＝x α(α∈R )的图像经过点(8,4)，则不等式f (6x ＋3)≤9的解集为________．答案　[－5,4]解析　由题意知8α＝4，故α＝log 84＝23，由于f (x )＝＝x 2为R 上的偶函数且在(0，＋∞)上递增，故f (6x ＋3)≤9即为f (6x ＋3)≤f (27)，所以|6x ＋3|≤27，解得－5≤x ≤4.8．设a ＝，b ＝，c ＝，则a ，b ，c 从小到大的顺序是________．答案　b <a <c解析　由a ＝，b ＝，可利用幂函数的性质，得a >b ，可由指数函数的单调性得c >a ，∴b <a <c .9．已知幂函数f (x )＝x α的图像过点P (2，14)，试画出f (x )的图像并指出该函数的定义域与单调区间．解　因为f (x )＝x α的图像过点P (2，14)，所以f (2)＝14，即2α＝14，得α＝－2，即f (x )＝x －2，f (x )的图像如图所示，定义域为(－∞，0)∪(0，＋∞)，单调递减区间为(0，＋∞)，单调递增区间为(－∞，0)．10．已知幂函数f (x )＝x 9－3m (m ∈N ＋)的图像关于原点对称，且在R 上单调递增．(1)求f (x )的解析式；(2)求满足f (a ＋1)＋f (3a －4)<0的a 的取值范围．解　(1)由幂函数f (x )＝x 9－3m (m ∈N ＋)的图像关于原点对称，且在R上单调递增，可得9－3m >0，解得m <3，m ∈N ＋，可得m ＝1,2，12x 23x 2312⎛⎫⎪⎝⎭2315⎛⎫ ⎪⎝⎭1312⎛⎫⎪⎝⎭2312⎛⎫ ⎪⎝⎭2315⎛⎫⎪⎝⎭若m ＝1，则f (x )＝x 6的图像不关于原点对称，舍去；若m ＝2，则f (x )＝x 3的图像关于原点对称，且在R 上单调递增，成立．则f (x )＝x 3.(2)由(1)可得f (x )是奇函数，且在R 上单调递增，由f (a ＋1)＋f (3a －4)<0，可得f (a ＋1)<－f (3a －4)＝f (4－3a )，即为a ＋1<4－3a ，解得a <34.11．若函数f (x )＝(m ＋2)x a 是幂函数，且其图像过点(2,4)，则函数g (x )＝ log a (x ＋m )的单调递增区间为( )A ．(－2，＋∞) B ．(1，＋∞)C ．(－1，＋∞) D ．(2，＋∞)答案　B解析　由题意得m ＋2＝1，解得m ＝－1，则f (x )＝x a ，将(2,4)代入函数的解析式得，2a ＝4，解得a ＝2，故g (x )＝log a (x ＋m )＝log 2(x －1)，令x －1>0，解得x >1，故g (x )在(1，＋∞)上单调递增．12．函数y ＝－1的图像关于x 轴对称的图像大致是( )答案　B解析　y ＝的图像位于第一象限且为增函数，所以函数图像是上升的，函数y ＝－1的图像可看作由y ＝的图像向下平移一个单位长度得到的(如选项A 中的图所示)，将y ＝－1的图像关于x 轴对称后即为选项B.13．为了保证信息的安全传输，有一种密钥密码系统，其加密、解密原理为：发送方由明文到密文(加密)，接收方由密文到明文(解密)．现在加密密钥为y ＝x α(α为常数)，如“4”通过加密后得到密文“2”．若接收方接到密文“3”，则解密后得到的明文是________．答案　9解析　由题意可知加密密钥y ＝x α(α为常数)是一个幂函数，所以要想求得解密后得到的明文，就必须先求出α的值．由题意，得2＝4α，解得α＝12，则y ＝.由＝3，得x ＝9，即明文是9.14．已知幂函数f (x )＝，若f (a ＋1)<f (10－2a )，则a 的取值范围是________．12x 12x 12x 12x 12x 12x 12x 12x答案　(3,5)解析　∵f (x )＝＝1x(x >0)，易知f (x )在(0，＋∞)上为减函数，又f (a ＋1)<f (10－2a )，∴Error!解得Error!∴3<a <5.15.幂函数y ＝x α，当α取不同的正数时，在区间[0,1]上它们的图像是一族美丽的曲线(如图)．设点A (1,0)，B (0,1)，连接AB ，线段AB 恰好被其中的两个幂函数y ＝x α，y ＝x β的图像三等分，即有BM ＝MN ＝NA ，那么，αβ等于________．答案　1解析　由条件，得M (13，23)，N (23，13)，可得13＝(23)α，23＝(13)β，即α＝13，β＝23.所以αβ＝13·23＝lg 13lg 23·lg 23lg 13＝1.16．已知幂函数g (x )过点(2，12)，且f (x )＝x 2＋ag (x )．(1)求g (x )的解析式；(2)讨论函数f (x )的奇偶性，并说明理由．解　(1)设幂函数的解析式g (x )＝x α(α为常数)．因为幂函数g (x )过点(2，12)，所以2α＝12，解得α＝－1，所以g (x )＝1x.(2)由(1)得f (x )＝x 2＋a x.①当a ＝0时，f (x )＝x 2.12x 23log 13log 23log 13log由于f(－x)＝(－x)2＝x2＝f(x)，可知f(x)为偶函数．②当a≠0时，由于f(－x)＝(－x)2＋a－x＝x2－ax≠x2＋ax＝f(x)，且f(－x)＝(－x)2＋a－x＝x2－ax≠－(x2＋a x)＝－f(x)，所以f(x)是非奇非偶函数．综上，①当a＝0时，f(x)为偶函数；②当a≠0时，f(x)为非奇非偶函数．。

【高中数学】高中数学知识点：幂函数

【高中数学】高中数学知识点：幂函数冥函数的定义：一般地，函数y=xα叫做幂函数，其中x是自变量，α是常数。

幂函数的解析公式：y=xα幂函数的图像：幂函数图像的性质：所有幂函数在(0，+∞)上都有定义．① α＞0，图像通过固定点（0,0）和（1,1）；在区间（0，+∞);②α＜0，图像都过定点（1，1）；在区间（0，+∞）上单调递减;③ 当o<a<L时，曲线是凸的，当a>L时，曲线是凸的④当a=l时，图象为过点(0，0)和(1，1)的直线．⑤ 当a=0时，表示过点(1，1)且平行于x轴的直线(除去点(0，1))。

幂函数图像的其他属性：(1)图象的对称性：幂函数的幂指数a（只讨论a是有理数的情况）表示成既约分数的形式（整数看作是分母1的分数），则不论a>0还是a<0，幂函数图像的对称性写在公式中：“奇数子和偶数母是单独的、单一的；奇数母和偶数子分为两个面；分子分母是奇数，原点是对称的，别忘了”，(2)图象的形状：① 如果a>0，则幂函数的图象为抛物线形，当a>l时，图象在[0，+∞）上是向下凸的（称为凸函数）；当o<a<l时，图象在[o，+∞）上是向上凸的（称为凹函数）．② 如果x轴是凸的，那么x轴是凸的∞).幂函数的单调性和奇偶性：幂函数（a∈r)．（1）单调性当a>0时，函数第一象限是一个递增函数；当a<0时，函数在第一象限内是减函数．（2）平价①当a为整数时，如果a是偶数，那么是偶函数；若a为奇数，则这是一个奇怪的函数。

②当n为分数，即（P，Q互质，P，Q）∈ z），如果分母q是奇数，那么当分子P是奇数，为奇函数；分子p为偶数时，是一个偶数函数。

如果分母q是偶数，那么为非奇非偶函数．。

高中数学,幂函数知识点及题型

第七节幂函数❖基础知识1．幂函数的概念一般地，形如y＝xα(α∈R)的函数称为幂函数，其中底数x是自变量，α为常数．幂函数的特征(1)自变量x处在幂底数的位置，幂指数α为常数；(2)xα的系数为1；(3)只有一项．2．五种常见幂函数的图象与性质函数特征性质y＝x y＝x2y＝x3y＝x12y＝x－1图象定义域R R R{x|x≥0}{x|x≠0} 值域R{y|y≥0}R{y|y≥0}{y|y≠0} 奇偶性奇偶奇非奇非偶奇单调性增(－∞，0)减，(0，＋∞)增增增(－∞，0)和(0，＋∞)减公共点(1,1) ❖常用结论对于形如f(x)＝x nm(其中m∈N*，n∈Z，m与n互质)的幂函数：(1)当n为偶数时，f(x)为偶函数，图象关于y轴对称；(2)当m，n都为奇数时，f(x)为奇函数，图象关于原点对称；(3)当m为偶数时，x>0(或x≥0)，f(x)是非奇非偶函数，图象只在第一象限(或第一象限及原点处)．考点一幂函数的图象与性质[典例](1)(2019·赣州阶段测试)幂函数y＝f(x)的图象经过点(3，33)，则f(x)是()A．偶函数，且在(0，＋∞)上是增函数B ．偶函数，且在(0，＋∞)上是减函数C ．奇函数，且在(0，＋∞)上是增函数D ．非奇非偶函数，且在(0，＋∞)上是减函数 (2)已知幂函数f (x )＝(n 2＋2n －2)x23－n n (n ∈Z)的图象关于y 轴对称，且在(0，＋∞)上是减函数，则n 的值为( )A ．－3B ．1C ．2D ．1或2[解析](1)设f (x )＝x α，将点(3，33)代入f (x )＝x α，解得α＝13，所以f (x )＝x 13，可知函数f (x )是奇函数，且在(0，＋∞)上是增函数，故选C. (2)∵幂函数f (x )＝(n 2＋2n －2)x23－n n在(0，＋∞)上是减函数，∴⎩⎪⎨⎪⎧n 2＋2n －2＝1，n 2－3n <0，∴n ＝1，又n ＝1时，f (x )＝x －2的图象关于y 轴对称，故n ＝1.[答案] (1)C (2)B[解题技法] 幂函数y ＝x α的主要性质及解题策略(1)幂函数在(0，＋∞)内都有定义，幂函数的图象都过定点(1,1)．(2)当α>0时，幂函数的图象经过点(1,1)和(0,0)，且在(0，＋∞)内单调递增；当α<0时，幂函数的图象经过点(1,1)，且在(0，＋∞)内单调递减．(3)当α为奇数时，幂函数为奇函数；当α为偶数时，幂函数为偶函数．(4)幂函数的性质因幂指数大于零、等于零或小于零而不同，解题中要善于根据幂指数的符号和其他性质确定幂函数的解析式、参数取值等．[题组训练]1.[口诀第3、4、5句]下列函数中，既是偶函数，又在区间(0，＋∞)上单调递减的为( )A ．y ＝x －4 B ．y ＝x －1 C ．y ＝x 2D ．y ＝x 13解析：选A 函数y ＝x －4为偶函数，且在区间(0，＋∞)上单调递减；函数y ＝x －1为奇函数，且在区间(0，＋∞)上单调递减；函数y ＝x 2为偶函数，且在区间(0，＋∞)上单调递增；函数y ＝x 13为奇函数，且在区间(0，＋∞)上单调递增．2.[口诀第2、3、4句]已知当x ∈(0,1)时，函数y ＝x p 的图象在直线y ＝x 的上方，则p 的取值范围是________．解析：当p >0时，根据题意知p <1，所以0<p <1；当p ＝0时，函数为y ＝1(x ≠0)，符合题意；当p <0时，函数y ＝x p 的图象过点(1,1)，在(0，＋∞)上为减函数，符合题意．综上所述，p 的取值范围是(－∞，1)．答案：(－∞，1)考点二比较幂值大小[典例] 若a ＝⎝⎛⎭⎫1223，b ＝⎝⎛⎭⎫1523，c ＝⎝⎛⎭⎫1213，则a ，b ，c 的大小关系是( ) A ．a <b <c B ．c <a <b C ．b <c <aD ．b <a <c[解析] 因为y ＝x 23在第一象限内是增函数，所以a ＝⎝⎛⎭⎫1223>b ＝⎝⎛⎭⎫1523，因为y ＝⎝⎛⎭⎫12x 是减函数，所以a ＝⎝⎛⎭⎫1223<c ＝⎝⎛⎭⎫1213，所以b <a <c . [答案] D[题组训练]1．若a ＝⎝⎛⎭⎫3525，b ＝⎝⎛⎭⎫2535，c ＝⎝⎛⎭⎫2525，则a ，b ，c 的大小关系是( ) A ．a >b >c B ．a >c >b C ．c >a >bD ．b >c >a解析：选B 因为y ＝x 25在第一象限内为增函数，所以a ＝⎝⎛⎭⎫3525>c ＝⎝⎛⎭⎫2525，因为y ＝⎝⎛⎭⎫25x 是减函数，所以c ＝⎝⎛⎭⎫2525>b ＝⎝⎛⎭⎫2535，所以a >c >b . 2．若(a ＋1)12<(3－2a )12，则实数a 的取值范围是________．解析：易知函数y ＝x 12的定义域为[0，＋∞)，在定义域内为增函数，所以⎩⎪⎨⎪⎧a ＋1≥0，3－2a ≥0，a ＋1<3－2a ，解得－1≤a <23.答案：⎣⎡⎭⎫－1，23 [课时跟踪检测]1．若幂函数y ＝f (x )的图象过点(4,2)，则f (8)的值为( )A ．4 B. 2 C ．2 2D ．1解析：选C 设f (x )＝x n ，由条件知f (4)＝2，所以2＝4n ，n ＝12，所以f (x )＝x 12，f (8)＝812＝2 2.2．若幂函数f (x )＝x k 在(0，＋∞)上是减函数，则k 可能是( )A ．1B ．2 C.12D ．－1解析：选D 由幂函数的性质得k <0，故选D. 3．已知幂函数f (x )＝(m 2－3m ＋3)x m＋1为偶函数，则m ＝( ) A ．1 B ．2 C ．1或2D ．3解析：选A ∵函数f (x )为幂函数，∴m 2－3m ＋3＝1，即m 2－3m ＋2＝0，解得m ＝1或m ＝2.当m ＝1时，幂函数f (x )＝x 2为偶函数，满足条件；当m ＝2时，幂函数f (x )＝x 3为奇函数，不满足条件．故选A.4．(2018·邢台期末)已知幂函数f (x )的图象过点⎝⎛⎭⎫2，14，则函数g (x )＝f (x )＋x24的最小值为( ) A ．1 B ．2 C ．4D ．6解析：选A 设幂函数f (x )＝x α.∵f (x )的图象过点⎝⎛⎭⎫2，14，∴2α＝14，解得α＝－2. ∴函数f (x )＝x －2，其中x ≠0. ∴函数g (x )＝f (x )＋x 24＝x －2＋x 24＝1x 2＋x 24≥21x 2·x 24＝1，当且仅当x ＝±2时，g (x )取得最小值1. 5．(2019·安徽名校联考)幂函数y ＝x |m －1|与y ＝x 23－m m (m ∈Z)在(0，＋∞)上都是增函数，则满足条件的整数m 的值为( )A ．0B ．1和2C ．2D ．0和3解析：选C 由题意可得⎩⎪⎨⎪⎧|m －1|>0，3m －m 2>0，m ∈Z ，解得m ＝2.6．已知a ＝345，b ＝425，c ＝1215，则a ，b ，c 的大小关系为( )A ．b <a <cB ．a <b <cC ．c <b <aD ．c <a <b解析：选C 因为a ＝8115，b ＝1615，c ＝1215，由幂函数y ＝x 15在(0，＋∞)上为增函数，知a >b >c ，故选C.7．设x ＝0.20.3，y ＝0.30.2，z ＝0.30.3，则x ，y ，z 的大小关系为( )A ．x <z <yB ．y <x <zC ．y <z <xD ．z <y <x解析：选A 由函数y ＝0.3x 在R 上单调递减，可得y >z .由函数y ＝x 0.3在(0，＋∞)上单调递增，可得x <z .所以x <z <y .8．已知幂函数f (x )＝(m －1)2x242－＋m m 在(0，＋∞)上单调递增，函数g (x )＝2x －k ，当x ∈[1,2)时，记f (x )，g (x )的值域分别为集合A ，B ，若A ∪B ＝A ，则实数k 的取值范围是( )A ．(0,1)B ．[0,1)C ．(0,1]D ．[0,1]解析：选D ∵f (x )是幂函数，∴(m －1)2＝1，解得m ＝2或m ＝0.若m ＝2，则f (x )＝x －2在(0，＋∞)上单调递减，不满足条件．若m ＝0，则f (x )＝x 2在(0，＋∞)上单调递增，满足条件，即f (x )＝x 2.当x ∈[1,2)时，f (x )∈[1,4)，即A ＝[1,4)；当x ∈[1,2)时，g (x )∈[2－k,4－k )，即B ＝[2－k,4－k )．∵A ∪B ＝A ，∴B ⊆A ，∴2－k ≥1且4－k ≤4，解得0≤k ≤1.9．若f (x )是幂函数，且满足f (9)f (3)＝2，则f ⎝⎛⎭⎫19＝________. 解析：设f (x )＝x α，∵f (9)f (3)＝9α3α＝3α＝2，∴f ⎝⎛⎭⎫19＝⎝⎛⎭⎫19α＝⎝⎛⎭⎫132α＝132α＝122＝14. 答案：1410．已知函数f (x )＝(m 2－m －5)x m 是幂函数，且在(0，＋∞)上为增函数，则实数m 的值是________．解析：由f (x )＝(m 2－m －5)x m 是幂函数⇒m 2－m －5＝1⇒m ＝－2或m ＝3.又f (x )在(0，＋∞)上是增函数，所以m ＝3. 答案：311．当0＜x ＜1时，f (x )＝x 2，g (x )＝x 12，h (x )＝x －2，则f (x )，g (x )，h (x )的大小关系是________________．解析：分别作出y ＝f (x )，y ＝g (x )，y ＝h (x )的图象如图所示，可知h (x )＞g (x )＞f (x )．答案：h (x )＞g (x )＞f (x )12．(2019·银川模拟)已知幂函数f (x )＝x12-，若f (a ＋1)<f (10－2a )，则a 的取值范围是________．解析：由题意得，幂函数f (x )＝x －12的定义域为(0，＋∞)，且函数f (x )在(0，＋∞)上单调递减，由f (a＋1)<f (10－2a )，得⎩⎪⎨⎪⎧a ＋1>10－2a ，a ＋1>0，10－2a >0，解得3<a <5.答案：(3,5)13．已知幂函数f (x )＝x()21－＋m m (m ∈N *)的图象经过点(2，2)．(1)试确定m 的值；(2)求满足条件f (2－a )>f (a －1)的实数a 的取值范围．解：(1)∵幂函数f (x )的图象经过点(2，2)，∴2＝2()21－＋m m ，即212＝2()21－＋m m .∴m 2＋m ＝2，解得m ＝1或m ＝－2. 又∵m ∈N *，∴m ＝1. (2)由(1)知f (x )＝x 12，则函数的定义域为[0，＋∞)，并且在定义域上为增函数．由f (2－a )>f (a －1)，得⎩⎪⎨⎪⎧2－a ≥0，a －1≥0，2－a >a －1，解得1≤a <32.∴a 的取值范围为⎣⎡⎭⎫1，32.。

高一数学幂函数知识点

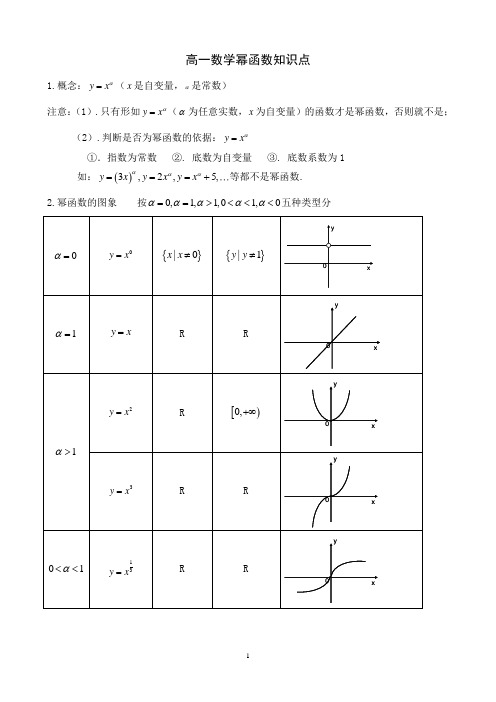
高一数学幂函数知识点1.概念：y x α=（x 是自变量，α是常数）注意：（1）.只有形如y x α=（α为任意实数，x 为自变量）的函数才是幂函数，否则就不是；（2）.判断是否为幂函数的依据：y x α=①．指数为常数 ②. 底数为自变量 ③. 底数系数为1 如：()3,2,5,y x y x y x ααα===+等都不是幂函数.2.幂函数的图象按0,1,1,01,0ααααα==><<<五种类型分3.幂函数y x α=在第一象限图象特征（1）.当1α>时，图象过（0,0），（1,1），下凸递增，如3y x = （2）.当01α<<时，图象过（0,0），（1,1），上凸递增，如12y x =（3）.当0α<时，图象过（1,1），下凸递减，且以两坐标轴为渐近线.如12y x -= 4.幂函数的性质（1）.所有的幂函数在()0,+∞上都有意义，图象都过（1,1）. （2）.如果0α>，则幂函数过原点，在()0,+∞上单调递增.（3）.如果0α<，图象在()0,+∞上单调递减，在第一象限内，当x 从右边趋向于原点时，图象在y 轴右方无限逼近y 轴；当x 趋向于+∞时，图象在x 轴上方无限逼近x 轴. （4）.①.当α为奇数时，幂函数为奇数 ②.当α为偶数时，幂函数为偶数 ③.当(),,pp q p q N qα+=∈为互质，时a. 若q 为奇数，则当p 为奇数时p q y x =为奇函数，当p 为偶数时p qy x =为偶函数 b. 若q 为偶数，则p 必为奇数，此时pqy x =为非奇非偶函数（5）.幂函数的定义域①.当N α+∈时，定义域为R ②.当0α=时，定义域为{}|,0x x R x ∈≠ ③.当α为负整数时，定义域为{}|,0x x R x ∈≠ ④.当(),,1,,pp q N q p q qα+=∈>且互质时 a. q 为偶数时，定义域为[)0,+∞ b. q 为奇数时，定义域为R ⑤.当()-,,1,,pp q N q p q qα+=∈>且互质时 a. q 为偶数，定义域为()0,+∞ b. q 为奇数，定义域为{}|,0x x R x ∈≠.。

高一数学知识点幂函数的总结

高一数学知识点幂函数的总结高一数学知识点关于幂函数的总结幂函数定义：形如y=x^a(a为常数)的函数，即以底数为自变量幂为因变量，指数为常量的函数称为幂函数。

定义域和值域：当a为不同的数值时，幂函数的定义域的不同情况如下：如果a为任意实数，则函数的定义域为大于0的所有实数;如果a为负数，则x肯定不能为0，不过这时函数的定义域还必须根[据q的奇偶性来确定，即如果同时q为偶数，则x不能小于0，这时函数的定义域为大于0的所有实数;如果同时q为奇数，则函数的定义域为不等于0的所有实数。

当x为不同的数值时，幂函数的值域的不同情况如下：在x大于0时，函数的值域总是大于0的实数。

在x小于0时，则只有同时q 为奇数，函数的值域为非零的实数。

而只有a为正数，0才进入函数的值域。

性质：对于a的取值为非零有理数，有必要分成几种情况来讨论各自的特性：首先我们知道如果a=p/q，q和p都是整数，则x^(p/q)=q次根号(x的p次方)，如果q是奇数，函数的定义域是R，如果q是偶数，函数的定义域是[0，+∞)。

当指数n是负整数时，设a=-k，则x=1/(x^k)，显然x≠0，函数的定义域是(-∞，0)∪(0，+∞).因此可以看到x所受到的限制来源于两点，一是有可能作为分母而不能是0，一是有可能在偶数次的根号下而不能为负数，那么我们就可以知道：排除了为0与负数两种可能，即对于x>0，则a可以是任意实数;排除了为0这种可能，即对于x<0和x>0的所有实数，q不能是偶数;排除了为负数这种可能，即对于x为大于且等于0的所有实数，a就不能是负数。

总结起来，就可以得到当a为不同的数值时，幂函数的定义域的不同情况如下：如果a为任意实数，则函数的定义域为大于0的所有实数;如果a为负数，则x肯定不能为0，不过这时函数的定义域还必须根据q的奇偶性来确定，即如果同时q为偶数，则x不能小于0，这时函数的定义域为大于0的所有实数;如果同时q为奇数，则函数的定义域为不等于0的所有实数。

(完整版)高一数学幂函数题型复习总结,推荐文档

第二课：幂函数 y xa
知识点一、幂的运算法则
初中知识点：（1） am an
（2） am n
指数幂与根式的互化： n am
1
练习： x3
例：计算
5 x2
am an
am bm
1 n am
x
2 3
an
1 4 x3
练习：
1
知识点二、幂函数图象
画图注意事项 1 定义域：偶次方根被开方数 0 ，奇次方根被开方数 R ，分母 0 . 2 奇偶性：判断 f (x) 与 f (x) 相等？相反数？ 3 闲着描描点！极限情况靠想象！快快慢慢！增增减减！秒悟！ 1、初级练场：常见幂函数图象：
1
（8） y x 4
3
（9） y x 2
总结：横看成岭侧成峰！
3
（1）（2）
4
5
3
3
2
练习：画函数图象 y x 3 ， y x 2 ， y x 5 ， y x 4 ， y x 5
知识点三、幂函数图象性质的应用
1、幂函数的定义
4
2、幂函数的图像
3、幂函数比较大小
1
1
例 1、（1）1.52
3、 4、比较大小 5、
7
“
”
“
”
At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!

高一数学幂函数知识点总结

高一数学幂函数知识点总结在高一数学的学习中，幂函数是一个重要的知识点。

它不仅在函数的学习中占据基础地位，对于后续数学知识的理解和应用也有着重要的影响。

下面就让我们一起来详细了解一下幂函数的相关知识。

一、幂函数的定义一般地，形如$y ＝ x^｛＼alpha}＄（＄＼alpha$为常数）的函数，即以底数为自变量，幂为因变量，指数为常数的函数称为幂函数。

其中，＄x$是自变量，＄＼alpha$是常数。

需要注意的是，在幂函数中，前面的系数必须为 1。

例如，＄y ＝ x^2$，＄y ＝ x^｛＼frac{1}｛2}｝＄，＄y ＝ x^｛－1}＄等都是幂函数，而$y ＝ 2x^2$，＄y ＝ 3x^｛＼frac{1}｛2}｝＄等就不是幂函数。

二、幂函数的图像和性质1、当$＼alpha ＞ 0$时（1）＄＼alpha ＝ 1$，函数$y ＝ x$的图像是一条经过原点和点$（1,1)＄的直线，在定义域$R$上单调递增。

（2）＄＼alpha ＝ 2$，函数$y ＝ x^2$的图像是一个开口向上的抛物线，对称轴为$y$轴，在$（＼infty, 0)＄上单调递减，在$（0, ＋＼infty)＄上单调递增。

（3）＄＼alpha ＝ 3$，函数$y ＝ x^3$的图像类似于一个“N”型，在定义域$R$上单调递增。

2、当$＼alpha ＜ 0$时（1）＄＼alpha ＝－1$，函数$y ＝ x^｛－1} ＝＼frac{1}｛x}＄的图像是位于第一、三象限的双曲线，在$（＼infty, 0)＄和$（0, ＋＼infty)＄上单调递减。

（2）＄＼alpha ＝＼frac{1}｛2}＄，函数$y ＝x^｛＼frac{1}｛2}｝＝＼frac{1}｛＼sqrt{x}｝＄的图像位于第一象限，在$（0, ＋＼infty)＄上单调递减。

3、当$＼alpha ＝ 0$时，函数$y ＝ x^0 ＝ 1$（＄x ＼neq 0$），其图像是一条去掉点$（0, 1)＄的直线。

高中数学幂函数知识点

⾼中数学幂函数知识点进⼊到⾼⼀阶段,⼤家的学习压⼒都是呈直线上升的,因此平时的积累也显得尤为重要,下⾯⼩编给⼤家分享⼀些⾼中数学幂函数知识，希望能够帮助⼤家，欢迎阅读!⾼中数学幂函数知识11.函数的单调性(局部性质)(1)增函数设函数y=f(x)的定义域为I，如果对于定义域I内的某个区间D内的任意两个⾃变量x1，x2，当x1如果对于区间D上的任意两个⾃变量的值x1，x2，当x1f(x2)，那么就说f(x)在这个区间上是减函数.区间D 称为y=f(x)的单调减区间.注意：函数的单调性是函数的局部性质;(2)图象的特点如果函数y=f(x)在某个区间是增函数或减函数，那么说函数y=f(x)在这⼀区间上具有(严格的)单调性，在单调区间上增函数的图象从左到右是上升的，减函数的图象从左到右是下降的.(3)函数单调区间与单调性的判定⽅法(A)定义法：a.任取x1，x2∈D，且x1b.作差f(x1)-f(x2);c.变形(通常是因式分解和配⽅);d.定号(即判断差f(x1)-f(x2)的正负);e.下结论(指出函数f(x)在给定的区间D上的单调性).(B)图象法(从图象上看升降)(C)复合函数的单调性复合函数f[g(x)]的单调性与构成它的函数u=g(x)，y=f(u)的单调性密切相关，其规律：“同增异减”注意：函数的单调区间只能是其定义域的⼦区间,不能把单调性相同的区间和在⼀起写成其并集.8.函数的奇偶性(整体性质)(1)偶函数⼀般地，对于函数f(x)的定义域内的任意⼀个x，都有f(-x)=f(x)，那么f(x)就叫做偶函数.(2)奇函数⼀般地，对于函数f(x)的定义域内的任意⼀个x，都有f(-x)=—f(x)，那么f(x)就叫做奇函数.(3)具有奇偶性的函数的图象的特征偶函数的图象关于y轴对称;奇函数的图象关于原点对称.利⽤定义判断函数奇偶性的步骤：a.⾸先确定函数的定义域，并判断其是否关于原点对称;b.确定f(-x)与f(x)的关系;c.作出相应结论：若f(-x)=f(x)或f(-x)-f(x)=0，则f(x)是偶函数;若f(-x)=-f(x)或f(-x)+f(x)=0，则f(x)是奇函数.注意：函数定义域关于原点对称是函数具有奇偶性的必要条件.⾸先看函数的定义域是否关于原点对称，若不对称则函数是⾮奇⾮偶函数.若对称，(1)再根据定义判定;(2)由f(-x)±f(x)=0或f(x)/f(-x)=±1来判定;(3)利⽤定理，或借助函数的图象判定.9、函数的解析表达式(1).函数的解析式是函数的⼀种表⽰⽅法，要求两个变量之间的函数关系时，⼀是要求出它们之间的对应法则，⼆是要求出函数的定义域.(2)求函数的解析式的主要⽅法有：1)凑配法2)待定系数法3)换元法4)消参法10.函数最⼤(⼩)值(定义见课本p36页)a.利⽤⼆次函数的性质(配⽅法)求函数的最⼤(⼩)值b.利⽤图象求函数的最⼤(⼩)值c.利⽤函数单调性的判断函数的最⼤(⼩)值：如果函数y=f(x)在区间[a，b]上单调递增，在区间[b，c]上单调递减则函数y=f(x)在x=b处有最⼤值f(b);如果函数y=f(x)在区间[a，b]上单调递减，在区间[b，c]上单调递增则函数y=f(x)在x=b处有最⼩值f(b);.⾼中数学幂函数知识2⼀、⼀次函数定义与定义式：⾃变量x和因变量y有如下关系：y=kx+b则此时称y是x的⼀次函数。

高中数学幂函数知识点

高中数学幂函数知识点高中数学幂函数学问11.函数的单调性(局部性质)(1)增函数设函数y=f(x)的定义域为I，假如对于定义域I内的某个区间D内的任意两个自变量x1，x2，当x1假如对于区间D上的任意两个自变量的值x1，x2，当x1f(x2)，那么就说f(x)在这个区间上是减函数.区间D称为y=f(x)的单调减区间.留意：函数的单调性是函数的局部性质;(2)图象的特点假如函数y=f(x)在某个区间是增函数或减函数，那么说函数y=f(x)在这一区间上具有(严格的)单调性，在单调区间上增函数的图象从左到右是上升的，减函数的图象从左到右是下降的.(3)函数单调区间与单调性的判定〔方法〕(A)定义法：a.任取x1，x2∈D，且x1b.作差f(x1)-f(x2);c.变形(通常是因式分解和配方);d.定号(即推断差f(x1)-f(x2)的正负);e.下结论(指出函数f(x)在给定的区间D上的单调性).(B)图象法(从图象上看升降)(C)复合函数的单调性复合函数f[g(x)]的单调性与构成它的函数u=g(x)，y=f(u)的单调性亲密相关，其规律：“同增异减”留意：函数的单调区间只能是其定义域的子区间,不能把单调性相同的区间和在一起写成其并集.8.函数的奇偶性(整体性质)(1)偶函数一般地，对于函数f(x)的定义域内的任意一个x，都有f(-x)=f(x)，那么f(x)就叫做偶函数.(2)奇函数一般地，对于函数f(x)的定义域内的任意一个x，都有f(-x)=—f(x)，那么f(x)就叫做奇函数.(3)具有奇偶性的函数的图象的特征偶函数的图象关于y轴对称;奇函数的图象关于原点对称.利用定义推断函数奇偶性的步骤：a.首先确定函数的定义域，并推断其是否关于原点对称;b.确定f(-x)与f(x)的关系;c.作出相应结论：若f(-x)=f(x)或f(-x)-f(x)=0，则f(x)是偶函数;若f(-x)=-f(x)或f(-x)+f(x)=0，则f(x)是奇函数.留意：函数定义域关于原点对称是函数具有奇偶性的必要条件.首先看函数的定义域是否关于原点对称，若不对称则函数是非奇非偶函数.若对称，(1)再依据定义判定;(2)由f(-x)±f(x)=0或f(x)/f(-x)=±1来判定;(3)利用定理，或借助函数的图象判定.9、函数的解析表达式(1).函数的解析式是函数的一种表示方法，要求两个变量之间的函数关系时，一是要求出它们之间的对应法则，二是要求出函数的定义域.(2)求函数的解析式的主要方法有：1)凑配法2)待定系数法3)换元法4)消参法10.函数最大(小)值(定义见课本p36页)a.利用二次函数的性质(配方法)求函数的最大(小)值b.利用图象求函数的最大(小)值c.利用函数单调性的推断函数的最大(小)值：假如函数y=f(x)在区间[a，b]上单调递增，在区间[b，c]上单调递减则函数y=f(x)在x=b处有最大值f(b);假如函数y=f(x)在区间[a，b]上单调递减，在区间[b，c]上单调递增则函数y=f(x)在x=b处有最小值f(b);.高中数学幂函数学问2一、一次函数定义与定义式：自变量x和因变量y有如下关系：y=kx+b则此时称y是x的一次函数。

幂函数知识点总结

幂函数知识点总结幂函数是高中数学中的一个重要概念，它在数学的各个领域中都有着广泛的应用。

从初中开始，我们就接触到了简单的幂函数，随着学习的深入，我们逐渐掌握了更多关于幂函数的知识。

在本文中，我们将对幂函数的相关概念、性质和应用进行总结和探讨。

1. 幂函数的定义和表示方式幂函数是指以一个常数为底数，自变量为指数的函数。

一般表示为：f(x) = a^x，其中a为常数，x为自变量，f(x)为函数值。

2. 幂函数的基本性质2.1 幂函数的奇偶性与增减性：当底数a为正数且不等于1时，幂函数f(x) = a^x在定义域内是奇函数；当底数a为负数时，幂函数f(x) = a^x是偶函数。

当底数a大于1时，幂函数是增函数，当底数a在(0,1)之间时，幂函数是减函数。

2.2 幂函数的单调性：当底数大于1时，幂函数是递增的；当底数小于1时，幂函数是递减的。

2.3 幂函数的相关性质：a^0=1，a^1=a，a^m * a^n = a^(m+n)，(a^m)^n = a^(m*n)，(a^m)/(a^n)=a^(m-n)，(a/b)^n=a^n/b^n。

3. 幂函数图像和特征幂函数的图像具有一些独特的特征，这在解析题或者问题求解时具有重要意义。

3.1 幂函数的渐近线：当底数大于1时，幂函数的图像在y轴上有一个水平渐近线；当底数小于1时，幂函数的图像在x轴上有一个水平渐近线。

3.2 幂函数的特殊点：当底数大于1时，幂函数的图像经过点(0,1)；当底数小于1时，幂函数的图像经过点(0,1)和点(1,a)。

3.3 幂函数的拐点：当幂函数的底数a大于1时，图像经过点(1,a)并且有一个拐点；当底数a小于1时，图像经过点(1,a)但没有拐点。

4. 幂函数的应用幂函数在实际问题的解决中有着广泛的应用，以下是一些典型的应用场景：4.1 音乐和声音强度的计算：声音的强度与音源与听者距离的幂函数关系密切，通过对幂函数的建模和计算，可以获得声音强度的变化规律。

高一数学知识点：幂函数知识点知识点总结

高一数学知识点：幂函数知识点知识点总结高一数学知识点：幂函数知识点总结在高一数学的学习中，幂函数是一个重要的知识点。

幂函数的形式简单，但其中蕴含的性质和规律却丰富多样。

下面我们就来详细总结一下幂函数的相关知识。

一、幂函数的定义一般地，形如$y ＝ x^｛＼alpha}＄（＄＼alpha$为常数）的函数，叫做幂函数。

其中，＄x$是自变量，＄＼alpha$是常数。

需要注意的是，幂函数的底数是自变量$x$，指数是常数$＼alpha$。

二、幂函数的图像幂函数的图像因指数$＼alpha$的不同而具有不同的特征。

当$＼alpha ＞ 0$时：若$＼alpha$为正整数，幂函数的图像在第一象限内单调递增。

例如，＄y ＝ x^2$的图像是一个开口向上的抛物线，对称轴为$y$轴。

若$＼alpha$为正分数，且分母为奇数，分子为偶数，幂函数的图像在第一象限内单调递增，且关于原点对称。

例如，＄y ＝x^｛＼frac{2}｛3}｝＄的图像在第一象限内类似于一个上凸的曲线。

若$＼alpha$为正分数，且分母为偶数，分子为奇数，幂函数的图像在第一象限内单调递增，且关于$y$轴对称。

例如，＄y ＝ x^｛＼frac{1}｛2}｝＄的图像是一个在第一象限内的半支抛物线。

当$＼alpha ＜ 0$时：幂函数的图像在第一象限内单调递减，且以坐标轴为渐近线。

例如，＄y ＝ x^｛－1}＄的图像是位于第一、三象限的双曲线。

三、幂函数的性质1、定义域当$＼alpha$为正整数时，定义域为$R$。

当$＼alpha$为正分数时，若分母为奇数，定义域为$R$；若分母为偶数，定义域为$0, ＋＼infty)＄。

当$＼alpha$为负整数时，定义域为$＼｛x|x ＼neq 0\｝＄。

当$＼alpha$为负分数时，定义域为$＼｛x|x ＞ 0\｝＄。

2、值域当$＼alpha ＞ 0$时，值域为$0, ＋＼infty)＄。

当$＼alpha ＜ 0$时，值域为$＼｛y|y ＼neq 0\｝＄。