图的邻接表创建方法
邻接矩阵转换成邻接表算法

邻接矩阵转换成邻接表算法邻接矩阵是一种常用的图的表示方法,它通过一个二维数组来表示图中各个节点之间的连接关系。
而邻接表则是另一种常见的图的表示方法,它通过链表的形式来表示图中各个节点之间的连接关系。
本文将介绍如何将邻接矩阵转换成邻接表的算法。
邻接矩阵是一个n*n的二维数组,其中n表示图中节点的个数。
邻接矩阵中的元素a[i][j]表示节点i和节点j之间是否存在连接,如果存在连接则为1,否则为0。
邻接表则是一个长度为n的链表数组,每个链表表示一个节点的邻接节点。
邻接矩阵转换成邻接表的算法可以分为以下几个步骤:1. 创建一个长度为n的链表数组,用于存储邻接表。
2. 遍历邻接矩阵的每个元素a[i][j],如果a[i][j]为1,则表示节点i 和节点j之间存在连接。
3. 在链表数组中的第i个链表中插入节点j,表示节点i和节点j之间存在连接。
4. 重复步骤2和步骤3,直到遍历完整个邻接矩阵。
下面是一个具体的示例,以便更好地理解邻接矩阵转换成邻接表的算法。
假设有一个邻接矩阵如下所示:```1 0 0 11 0 0 10 1 1 0```首先,创建一个长度为4的链表数组,用于存储邻接表。
```[][][][]```然后,遍历邻接矩阵的每个元素,如果元素为1,则将对应的节点插入到链表数组中。
遍历第一行,第一个元素为0,不需要插入节点;第二个元素为1,需要插入节点1;第三个元素为1,需要插入节点2;第四个元素为0,不需要插入节点。
此时链表数组的状态如下:```[][][]```接着,遍历第二行,第一个元素为1,需要插入节点0;第二个元素为0,不需要插入节点;第三个元素为0,不需要插入节点;第四个元素为1,需要插入节点3。
此时链表数组的状态如下:```[0][1, 2][3][]```继续遍历第三行和第四行,最终得到的邻接表如下所示:```[0][1, 2][3][1, 2]```通过以上步骤,我们成功地将邻接矩阵转换成了邻接表。
实现图的邻接矩阵和邻接表存储

实现图的邻接矩阵和邻接表存储1.需求分析对于下图所示的有向图G,编写一个程序完成如下功能:1.建立G的邻接矩阵并输出之2.由G的邻接矩阵产生邻接表并输出之3.再由2的邻接表产生对应的邻接矩阵并输出之2.系统设计1.图的抽象数据类型定义:ADT Graph{数据对象V:V是具有相同特性的数据元素的集合,称为顶点集数据关系R:R={VR}VR={<v,w>|v,w∈V且P(v,w),<v,w>表示从v到w的弧,谓词P(v,w)定义了弧<v,w>的意义或信息}基本操作P:CreatGraph(&G,V,VR)初始条件:V是图的顶点集,VR是图中弧的集合操作结果:按V和VR的定义构造图GDestroyGraph(&G)初始条件:图G存在操作结果:销毁图GInsertVex(&G,v)初始条件:图G存在,v和图中顶点有相同特征操作结果:在图G中增添新顶点v……InsertArc(&G,v,w)初始条件:图G存在,v和w是G中两个顶点操作结果:在G中增添弧<v,w>,若G是无向的则还增添对称弧<w,v>……DFSTraverse(G,Visit())初始条件:图G存在,Visit是顶点的应用函数操作结果:对图进行深度优先遍历,在遍历过程中对每个顶点调用函数Visit一次且仅一次。
一旦Visit()失败,则操作失败BFSTraverse(G,Visit())初始条件:图G存在,Visit是顶点的应用函数操作结果:对图进行广度优先遍历,在遍历过程中对每个顶点调用函数Visit一次且仅一次。
一旦Visit()失败,则操作失败}ADT Graph2.主程序的流程:调用CreateMG函数创建邻接矩阵M;调用PrintMatrix函数输出邻接矩阵M调用CreateMGtoDN函数,由邻接矩阵M创建邻接表G调用PrintDN函数输出邻接表G调用CreateDNtoMG函数,由邻接表M创建邻接矩阵N调用PrintMatrix函数输出邻接矩阵N3.函数关系调用图:3.调试分析(1)在MGraph的定义中有枚举类型typedef enum{DG,DN,UDG,UDN}GraphKind;//{有向图,有向网,无向图,无向网}赋值语句G.kind(int)=M.kind(GraphKind);是正确的,而反过来M.kind=G.kind则是错误的,要加上那个强制转换M.kind=GraphKind(G.kind);枚举类型enum{DG,DN,UDG,UDN}会自动赋值DG=0;DN=1,UDG=2,UDN=3;可以自动从GraphKind类型转换到int型,但不会自动从int型转换到GraphKind类型(2)算法的时间复杂度分析:CreateMG、CreateMGtoDN、CreateDNtoMG、PrintMatrix、PrintDN的时间复杂度均为O(n2) n为图的顶点数,所以main:T(n)= O(n2)4.测试结果用需求分析中的测试数据输入:输出:5、用户手册(1)输入顶点数和弧数;(2)输入顶点内容;(3)按行序输入邻接矩阵,输入各弧相应权值(4)回车输出邻接矩阵M、邻接表G和邻接矩阵N6、附录源程序:#include <stdio.h>#include <stdlib.h>#define MAX_VERTEX_NUM 20typedef int VRType;typedef int InfoType;typedef int VertexType;typedef enum{DG,DN,UDG,UDN}GraphKind;//{有向图,有向网,无向图,无向网} typedef struct ArcCell{VRType adj;//VRType是顶点关系类型,对无权图用1或0表示是否相邻;//对带权图则为权值类型InfoType *info;//该弧相关信息的指针}ArcCell,AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; typedef struct{VertexType vexs[MAX_VERTEX_NUM];//顶点向量AdjMatrix arcs;//邻接矩阵int vexnum,arcnum;//图的当前顶点数和弧数GraphKind kind;//图的种类标志}MGraph;void CreateMG(MGraph &M){int i,j;M.kind=DN;printf("输入顶点数:");scanf("%d",&M.vexnum);printf("输入弧数:");scanf("%d",&M.arcnum);printf("输入顶点:\n");for(i=0;i<M.vexnum;i++)scanf("%d",&M.vexs[i]);printf("建立邻接矩阵:\n");for(i=0;i<M.vexnum;i++)for(j=0;j<M.vexnum;j++)scanf("%d",&M.arcs[i][j].adj);printf("输入相应权值:\n");for(i=0;i<M.vexnum;i++)for(j=0;j<M.vexnum;j++)if(M.arcs[i][j].adj){scanf("%d",&M.arcs[i][j].info);}}typedef struct ArcNode{int adjvex;//该弧所指向的顶点在数组中的下标struct ArcNode *nextarc;InfoType *info;//该弧相关信息的指针}ArcNode;typedef struct VNode{VertexType data;//顶点信息ArcNode *firstarc;//指向第一条依附该顶点的弧的指针}VNode,AdjList[MAX_VERTEX_NUM];typedef struct{AdjList vertices;int vexnum,arcnum;//图的当前顶点数和弧数int kind;//图的种类标志}ALGraph;void PrintDN(ALGraph G){int i;ArcNode *p;printf("顶点:\n");for(i=0;i<G.vexnum;++i)printf("%2d",G.vertices[i].data);printf("\n弧:\n");for(i=0;i<G.vexnum;++i){p=G.vertices[i].firstarc;while(p){printf("%d→%d(%d)\t",i,p->adjvex,p->info);p=p->nextarc;}printf("\n");}//for}void CreateMGtoDN(ALGraph &G,MGraph M){//采用邻接表存储表示,构造有向图G(G.kind=DN)int i,j;ArcNode *p;G.kind=M.kind;G.vexnum=M.vexnum;G.arcnum=M.arcnum;for(i=0;i<G.vexnum;++i){//构造表头向量G.vertices[i].data=M.vexs[i];G.vertices[i].firstarc=NULL;//初始化指针}for(i=0;i<G.vexnum;++i)for(j=0;j<G.vexnum;++j)if(M.arcs[i][j].adj==1){p=(ArcNode*)malloc(sizeof(ArcNode));p->adjvex=j;p->nextarc=G.vertices[i].firstarc;p->info=M.arcs[i][j].info;G.vertices[i].firstarc=p;}}void CreateDNtoMG(MGraph &M,ALGraph G){int i,j;ArcNode *p;M.kind=GraphKind(G.kind);M.vexnum=G.vexnum;M.arcnum=G.arcnum;for(i=0;i<M.vexnum;++i)M.vexs[i]=G.vertices[i].data;for(i=0;i<M.vexnum;++i){p=G.vertices[i].firstarc;while(p){M.arcs[i][p->adjvex].adj=1;p=p->nextarc;}//whilefor(j=0;j<M.vexnum;++j)if(M.arcs[i][j].adj!=1)M.arcs[i][j].adj=0;}//for}void PrintMatrix(MGraph M){ int i,j;for(i=0;i<M.vexnum;++i){for(j=0;j<M.vexnum;++j) printf("%2d",M.arcs[i][j].adj); printf("\n");}}void main(){MGraph M,N;ALGraph G; CreateMG(M);PrintMatrix(M); CreateMGtoDN(G,M); PrintDN(G); CreateDNtoMG(N,G); PrintMatrix(N);}。
图的邻接表表示法

图的邻接表表示法图的邻接表表示法类似于树的孩子链表表示法。
对于图G中的每个顶点v i,该方法把所有邻接于v i的顶点v j链成一个带头结点的单链表,这个单链表就称为顶点v i的邻接表(Adjacency List)。
1.邻接表的结点结构(1:① 邻接点域adjvex存放与vi相邻接的顶点v j的序号j。
② 链域next将邻接表的所有表结点链在一起。
注意:若要表示边上的信息(如权值),则在表结点中还应增加一个数据域。
顶点v i邻接表的头结点包含两个域:① 顶点域vertex存放顶点v i的信息② 指针域firstedgev i的邻接表的头指针。
注意:① 为了便于随机访问任一顶点的邻接表,将所有头结点顺序存储在一个向量中就构成了图的邻接表表示。
② 有时希望增加对图的顶点数及边数等属性的描述,可将邻接表和这些属性放在一起来描述图的存储结构。
2.无向图的邻接表对于无向图,v i的邻接表中每个表结点都对应于与v i相关联的一条边。
因此,将邻接表的表头向量称为顶点表。
将无向图的邻接表称为边表。
【例】对于无向图G5,其邻接表表示如下面所示,其中顶点v0的边表上三个表结点中的顶点序号分别为1、2和3,它们分别表示关联于v0的三条边(v0,v1),(v0,v2)和(v0,v3)。
注意:n个顶点e条边的无向图的邻接表表示中有n个顶点表结点和2e个边表结点。
3.有向图的邻接表对于有向图,v i的邻接表中每个表结点都对应于以v i为始点射出的一条边。
因此,将有向图的邻接表称为出边表。
【例】有向图G6的邻接表表示如下面(a)图所示,其中顶点v1的邻接表上两个表结点中的顶点序号分别为0和4,它们分别表示从v1射出的两条边(简称为v1的出边):<v1,v0>和<v1,v4>。
注意:n个顶点e条边的有向图,它的邻接表表示中有n个顶点表结点和e个边表结点。
4.有向图的逆邻接表在有向图中,为图中每个顶点v i建立一个入边表的方法称逆邻接表表示法。
数据结构-邻接表

delete [ ] visited; }
8.4 图的遍历(续)
图的生成树
定义:G的所有顶点加上遍历过程中经过的边 所构成的子图称作图G的生成树G’
visited[v]=1;
/*标记第v个顶点已访问*/
/*访问第v个顶点邻接的未被访问过的顶点w,并从w出发递归地按照深度 优先的方式进行遍历*/
w= GetFirstNeighbor (v); /*得到第v个顶点的第一个邻接顶点w*/
while(w!= -1)
{ if(!visited[w]) DepthFirstSearch(w,visited,Visit); //递归调用
void BroadFirstSearch(const int v, int visited[ ], void visit(VT Vertex));
public:
AdjTWGraph(void);
~AdjTWGraph(void);
int NumOfVertices(void)const;
int NumOfEdges(void)const;
(2) 无向图:第i个链表中的表结点数为TD(vi); 能逆求邻有I接向D表(图vi。):。第为i个便链于表求中ID的(v表i) 可结另点外数建为立OD有(v向i),图不的
(3) 容易寻找顶点的邻接 点,但判断两顶点间是 否有边或弧,需搜索两 结点对应的单链表。
(4) 邻接表多用于稀疏 图的存储(e<<n2)
void Visit(VT item))
练习题(第6章)

第六章的练习题一、选择题1.设无向图的顶点个数为n ,则该图最多有( )条边。
A .n-1B .n(n-1)/2C . n(n+1)/2D .0E .n2 2.一个n 个顶点的连通无向图,其边的个数至少为( )。
A .n-1B .nC .n+1D .nlogn ; 3.要连通具有n 个顶点的有向图,至少需要( )条边。
A .n-lB .nC .n+lD .2n 4.n 个结点的完全有向图含有边的数目( )。
A .n*nB .n (n +1)C .n /2D .n*(n -l ) 5.一个有n 个结点的图,最少有( )个连通分量,最多有( )个连通分量。
A .0 B .1 C .n-1 D .n6.在一个无向图中,所有顶点的度数之和等于所有边数( )倍,在一个有向图中,所有顶点的入度之和等于所有顶点出度之和的( )倍。
A .1/2B .2C .1D .47.一个图中包含K 个连通分量,若按深度优先搜索方法访问所有结点,则必须调用( )次深度优先搜索遍历算法。
A .1B .K-1C .KD .K+1 8.下列哪一种图的邻接矩阵是对称矩阵?( )A .有向图B .无向图C .AOV 网D .AOE 网9. 从邻接阵矩可以看出,该图共有(①)个顶点;如果是有向图该图共有(②) 条弧;如果是无向图,则共有(③)条边。
①.A .9 B .3 C .6 D .1 E .以上答案均不正确 ②.A .5 B .4 C .3 D .2 E .以上答案均不正确 ③.A .5 B .4 C .3 D .2 E .以上答案均不正确 10.对某个无向图的邻接矩阵来讲,( )。
A .第i 行上的非零元素个数和第i 列的非零元素的个数一定相等B .矩阵中的非零元素个数等于图中的边数C .第i 行上,第i 列上非零元素总数等于顶点vi 的度数D .矩阵中非全零行的行数等于图中的顶点数11.无向图G=(V,E),其中:V={a,b,c,d,e,f},E={(a,b),(a,e),(a,c),(b,e),(c,f),(f,d),(e,d)},对该图进行深度优先遍历,得到的顶点序列正确的是( )。
图基本算法图的表示方法邻接矩阵邻接表

图基本算法图的表⽰⽅法邻接矩阵邻接表 要表⽰⼀个图G=(V,E),有两种标准的表⽰⽅法,即邻接表和邻接矩阵。
这两种表⽰法既可⽤于有向图,也可⽤于⽆向图。
通常采⽤邻接表表⽰法,因为⽤这种⽅法表⽰稀疏图(图中边数远⼩于点个数)⽐较紧凑。
但当遇到稠密图(|E|接近于|V|^2)或必须很快判别两个给定顶点⼿否存在连接边时,通常采⽤邻接矩阵表⽰法,例如求最短路径算法中,就采⽤邻接矩阵表⽰。
图G=<V,E>的邻接表表⽰是由⼀个包含|V|个列表的数组Adj所组成,其中每个列表对应于V中的⼀个顶点。
对于每⼀个u∈V,邻接表Adj[u]包含所有满⾜条件(u,v)∈E的顶点v。
亦即,Adj[u]包含图G中所有和顶点u相邻的顶点。
每个邻接表中的顶点⼀般以任意顺序存储。
如果G是⼀个有向图,则所有邻接表的长度之和为|E|,这是因为⼀条形如(u,v)的边是通过让v出现在Adj[u]中来表⽰的。
如果G是⼀个⽆向图,则所有邻接表的长度之和为2|E|,因为如果(u,v)是⼀条⽆向边,那么u会出现在v的邻接表中,反之亦然。
邻接表需要的存储空间为O(V+E)。
邻接表稍作变动,即可⽤来表⽰加权图,即每条边都有着相应权值的图,权值通常由加权函数w:E→R给出。
例如,设G=<V,E>是⼀个加权函数为w的加权图。
对每⼀条边(u,v)∈E,权值w(u,v)和顶点v⼀起存储在u的邻接表中。
邻接表C++实现:1 #include <iostream>2 #include <cstdio>3using namespace std;45#define maxn 100 //最⼤顶点个数6int n, m; //顶点数,边数78struct arcnode //边结点9 {10int vertex; //与表头结点相邻的顶点编号11int weight = 0; //连接两顶点的边的权值12 arcnode * next; //指向下⼀相邻接点13 arcnode() {}14 arcnode(int v,int w):vertex(v),weight(w),next(NULL) {}15 arcnode(int v):vertex(v),next(NULL) {}16 };1718struct vernode //顶点结点,为每⼀条邻接表的表头结点19 {20int vex; //当前定点编号21 arcnode * firarc; //与该顶点相连的第⼀个顶点组成的边22 }Ver[maxn];2324void Init() //建⽴图的邻接表需要先初始化,建⽴顶点结点25 {26for(int i = 1; i <= n; i++)27 {28 Ver[i].vex = i;29 Ver[i].firarc = NULL;30 }31 }3233void Insert(int a, int b, int w) //尾插法,插⼊以a为起点,b为终点,权为w的边,效率不如头插,但是可以去重边34 {35 arcnode * q = new arcnode(b, w);36if(Ver[a].firarc == NULL)37 Ver[a].firarc = q;38else39 {40 arcnode * p = Ver[a].firarc;41if(p->vertex == b) //如果不要去重边,去掉这⼀段42 {43if(p->weight < w)44 p->weight = w;45return ;46 }47while(p->next != NULL)48 {49if(p->next->vertex == b) //如果不要去重边,去掉这⼀段50 {51if(p->next->weight < w);52 p->next->weight = w;53return ;54 }55 p = p->next;56 }57 p->next = q;58 }59 }60void Insert2(int a, int b, int w) //头插法,效率更⾼,但不能去重边61 {62 arcnode * q = new arcnode(b, w);63if(Ver[a].firarc == NULL)64 Ver[a].firarc = q;65else66 {67 arcnode * p = Ver[a].firarc;68 q->next = p;69 Ver[a].firarc = q;70 }71 }7273void Insert(int a, int b) //尾插法,插⼊以a为起点,b为终点,⽆权的边,效率不如头插,但是可以去重边74 {75 arcnode * q = new arcnode(b);76if(Ver[a].firarc == NULL)77 Ver[a].firarc = q;78else79 {80 arcnode * p = Ver[a].firarc;81if(p->vertex == b) return; //去重边,如果不要去重边,去掉这⼀句82while(p->next != NULL)83 {84if(p->next->vertex == b) //去重边,如果不要去重边,去掉这⼀句85return;86 p = p->next;87 }88 p->next = q;89 }90 }91void Insert2(int a, int b) //头插法,效率跟⾼,但不能去重边92 {93 arcnode * q = new arcnode(b);94if(Ver[a].firarc == NULL)95 Ver[a].firarc = q;96else97 {98 arcnode * p = Ver[a].firarc;99 q->next = p;100 Ver[a].firarc = q;101 }102 }103void Delete(int a, int b) //删除以a为起点,b为终点的边104 {105 arcnode * p = Ver[a].firarc;106if(p->vertex == b)107 {108 Ver[a].firarc = p->next;109 delete p;110return ;111 }112while(p->next != NULL)113if(p->next->vertex == b)114 {115 p->next = p->next->next;116 delete p->next;117return ;118 }119 }120121void Show() //打印图的邻接表(有权值)122 {123for(int i = 1; i <= n; i++)124 {125 cout << Ver[i].vex;126 arcnode * p = Ver[i].firarc;127while(p != NULL)128 {129 cout << "->(" << p->vertex << "," << p->weight << ")";130 p = p->next;131 }132 cout << "->NULL" << endl;133 }134 }135136void Show2() //打印图的邻接表(⽆权值)137 {138for(int i = 1; i <= n; i++)140 cout << Ver[i].vex;141 arcnode * p = Ver[i].firarc;142while(p != NULL)143 {144 cout << "->" << p->vertex;145 p = p->next;146 }147 cout << "->NULL" << endl;148 }149 }150int main()151 {152int a, b, w;153 cout << "Enter n and m:";154 cin >> n >> m;155 Init();156while(m--)157 {158 cin >> a >> b >> w; //输⼊起点、终点159 Insert(a, b, w); //插⼊操作160 Insert(b, a, w); //如果是⽆向图还需要反向插⼊161 }162 Show();163return0;164 }View Code 邻接表表⽰法也有潜在的不⾜之处,即如果要确定图中边(u,v)是否存在,只能在顶点u邻接表Adj[u]中搜索v,除此之外没有其他更快的办法。
第七章∶图练习题

第七章:图练习题一、选择题1、一个有n个顶点的无向图最多有()条边。
A、nB、n(n-1)C、n(n-1)/2D、2n2、具有6个顶点的无向图至少有()条边才能保证是一个连通图。
A、5B、6C、7D、83、具有n个顶点且每一对不同的顶点之间都有一条边的图被称为()。
A、线性图B、无向完全图C、无向图D、简单图4、具有4个顶点的无向完全图有()条边。
A、6B、12C、16D、205、G是一个非连通无向图,共有28条边,则该图至少有()个顶点A、6B、7C、8D、96、存储稀疏图的数据结构常用的是()。
A、邻接矩阵B、三元组C、邻接表D、十字链表7、对一个具有n个顶点的图,采用邻接矩阵表示则该矩阵的大小为()。
A、nB、(n-1)2C、(n+1)2D、n28、设连通图G的顶点数为n,则G的生成树的边数为()。
A、n-1B、nC、2nD、2n-19、n个顶点的无向图的邻接表中结点总数最多有()个。
A、2nB、nC、n/2D、n(n-1)10、对于一个具有n个顶点和e条边的无向图,若采用邻接表表示,则表向量的大小为(),所有顶点邻接表的结点总数为()。
A、nB、n+1C、n-1D、2nE、e/2F、eG、2eH、n+e11、在有向图的邻接表存储结构中,顶点v在表结点中出现的次数是()。
A、顶点v的度B、顶点v的出度C、顶点v 的入度D、依附于顶点v的边数12、已知一个图,若从顶点a出发进行深度和广度优先搜索遍历,则可能得到的顶点序列分别为()和()(1)A、abecdf B、acfebd C、acebfd D、acfdeb(2)A、abcedf B、abcefd C、abedfc D、acfdeb13、采用邻接表存储的图的深度和广度优先搜索遍历算法类似于二叉树的()和()。
A、中序遍历B、先序遍历C、后序遍历D、层次遍历14、已知一有向图的邻接表存储结构如下图所示,分别根据图的深度和广度优先搜索遍历算法,从顶点v1出发,得到的顶点序列分别为()和()。
有向图的邻接表表示法

有向图的邻接表表⽰法图的邻接表表⽰法类似于树的孩⼦链表表⽰法。
对于图G中的每个顶点vi,该⽅法把所有邻接于vi的顶点vj链成⼀个带头结点的单链表,这个单链表就称为顶点vi的邻接表(Adjacency List)。
1.邻接表的结点结构(1)表结点结构┌────┬───┐│adjvex │next │└────┴───┘ 邻接表中每个表结点均有两个域: ①邻接点域adjvex 存放与vi相邻接的顶点vj的序号j。
②链域next 将邻接表的所有表结点链在⼀起。
注意: 若要表⽰边上的信息(如权值),则在表结点中还应增加⼀个数据域。
(2)头结点结构┌────┬─────┐│vertex │firstedge │└────┴─────┘ 顶点vi邻接表的头结点包含两个域: ①顶点域vertex 存放顶点vi的信息 ②指针域firstedge vi的邻接表的头指针。
注意: ①为了便于随机访问任⼀顶点的邻接表,将所有头结点顺序存储在⼀个向量中就构成了图的邻接表表⽰。
②有时希望增加对图的顶点数及边数等属性的描述,可将邻接表和这些属性放在⼀起来描述图的存储结构。
代码实例2.{输出结果为:int VexNum,ArcNum;//定义图的顶点数和边数VertexNode vertex[MAX_VERTEX_NUM];//定义头结点数组。
}AdjList;void CreateGraph(AdjList *adj,int *n){int e,s,d;cout<<"输⼊顶点数和边数"<<endl;cin>>*n>>e;//输⼊顶点数和边数。
adj->VexNum=*n;adj->ArcNum=e;EdgeNode *q=NULL;//初始化表头结点int i;for(i=1;i<=*n;i++){输⼊第2条边的起点和终点2 4输⼊第3条边的起点和终点2 1输⼊第4条边的起点和终点4 3输⼊第5条边的起点和终点3 6输⼊第6条边的起点和终点3 53.代码实例2(ps:补充于2011-6-14) 总体⽽⾔,邻接表表⽰法中主要含有两种结点,分别是头结点和表结点(也叫做边结点),在头结点(s)到表结点(d)之间存在着⼀条边。
数据结构邻接表实例

数据结构邻接表实例邻接表是一种常用于表示图的数据结构,特别适用于稀疏图(图中的边相对较少的情况)。
下面是一个简单的无向图的邻接表实例,使用Python 语言表示:```pythonclass Graph:def __init__(self):self.adjacency_list = {}def add_vertex(self, vertex):if vertex not in self.adjacency_list:self.adjacency_list[vertex] = []def add_edge(self, vertex1, vertex2):# 无向图,所以边需要同时在两个顶点的邻接表中添加if vertex1 in self.adjacency_list and vertex2 in self.adjacency_list:self.adjacency_list[vertex1].append(vertex2)self.adjacency_list[vertex2].append(vertex1)def display(self):for vertex in self.adjacency_list:print(f"{vertex}: {self.adjacency_list[vertex]}")# 创建一个无向图graph = Graph()# 添加顶点graph.add_vertex("A")graph.add_vertex("B")graph.add_vertex("C")graph.add_vertex("D")# 添加边graph.add_edge("A", "B")graph.add_edge("B", "C")graph.add_edge("C", "D")graph.add_edge("D", "A")# 显示邻接表graph.display()```在上述代码中,`Graph` 类包含了三个方法:- `add_vertex`: 用于添加顶点到图中。
图的邻接表表示法及顶点入度、出度的计算方法
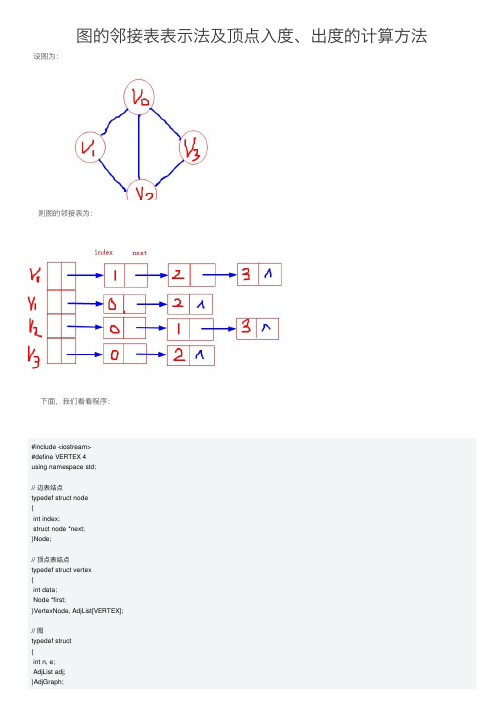
图的邻接表表⽰法及顶点⼊度、出度的计算⽅法 设图为:则图的邻接表为:下⾯,我们看看程序:#include <iostream>#define VERTEX 4using namespace std;// 边表结点typedef struct node{int index;struct node *next;}Node;// 顶点表结点typedef struct vertex{int data;Node *first;}VertexNode, AdjList[VERTEX];// 图typedef struct{int n, e;AdjList adj;}AdjGraph;// 创建图void createAdjGraph(AdjGraph &g){g.n = VERTEX;g.e = VERTEX + 1;// 下⾯创建AdjGraph的代码很丑陋,仅供⽰意Node *p1, *p2, *p3;p1 = new Node;p2 = new Node;p3 = new Node;p1->index = 1;p2->index = 2;p3->index = 3;g.adj[0].first = p1;p1->next = p2;p2->next = p3;p3->next = NULL;Node *q0, *q2;q0 = new Node;q2 = new Node;q0->index = 0;q2->index = 2;g.adj[1].first = q0;q0->next = q2;q2->next = NULL;Node *r0, *r1, *r3;r0 = new Node;r1 = new Node;r3 = new Node;r0->index = 0;r1->index = 1;r3->index = 3;g.adj[2].first = r0;r0->next = r1;r1->next = r3;r3->next = NULL;Node *s0, *s2;s0 = new Node;s2 = new Node;s0->index = 0;s2->index = 2;g.adj[3].first = s0;s0->next = s2;s2->next = NULL;}// 求图中顶点的⼊度void inDegree(AdjGraph g){Node *p;int i, inD;for(i = 0; i < g.n; i++){inD = 0;p = g.adj[i].first;while(NULL != p){inD++;p = p->next;}cout << "顶点" << i << "的⼊度为:" << inD << endl;cout << "顶点" << i << "的⼊度为:" << inD << endl;}}// 求图中顶点的出度void outDegree(AdjGraph g){Node *p;int i, outD;for(i = 0; i < g.n; i++){outD = 0;p = g.adj[i].first;while(NULL != p){outD++;p = p->next;}cout << "顶点" << i << "的出度为:" << outD << endl;}}int main(){AdjGraph g;createAdjGraph(g);inDegree(g); // 打印⼊度cout << endl;outDegree(g); // 打印出度return 0;}结果为:顶点0的⼊度为:3顶点1的⼊度为:2顶点2的⼊度为:3顶点3的⼊度为:2顶点0的出度为:3顶点1的出度为:2顶点2的出度为:3顶点3的出度为:2值得⼀提的是,对于有向图⽽⾔,我们⼀般采⽤的邻接表是正邻接表,在这种情况下,求图的各顶点的出度相对较易,⽽⼊度则不好直接求。
邻接表和逆邻接表

邻接表和逆邻接表邻接表和逆邻接表是图论中常用的两种数据结构,它们分别用于存储有向图和无向图的邻居关系,是算法设计和优化中最常用的数据结构之一。
下面,我们将分别介绍邻接表和逆邻接表的定义、构建和应用。
一、邻接表邻接表是一种用于表示有向图和无向图的数据结构,实际上就是将图中的每个结点与其相邻结点关联起来,并存储在一个链表中。
因此,邻接表的基本结构是一个链表数组,其中每个链表代表一个结点和其邻居结点的关系。
邻接表一般可以通过以下步骤进行构建:1. 定义一个链表数组,数组的长度等于图中结点的个数;2. 遍历图中每个结点,将每个结点与其直接相连的结点添加到该结点对应的链表中;3. 添加完毕后,邻接表即构建完成。
邻接表的应用非常广泛,例如:1. 求解最短路径:通过遍历邻接表中的每个结点,可以找到从起点到终点的最短路径;2. 求解连通分量:通过遍历邻接表,可以找到有多少个连通分量,并输出每个连通分量的结点集合;3. 拓扑排序:通过邻接表和入度数组即可实现拓扑排序算法等等。
二、逆邻接表逆邻接表是指有向图中每个结点的入度集合,即表示指向某个节点的所有其他节点的集合。
逆邻接表的构建比较简单,只需要将邻接表反向,即将有向图的每个结点的所有入边指向相应的出边即可。
逆邻接表同样有着广泛的应用,例如:1. 求解强连通分量:通过遍历逆邻接表,可以求解图中的所有强连通分量;2. 拓扑排序:通过逆邻接表和入度数组,即可实现基于反向边的拓扑排序算法;3. 最短路径算法优化:当搜索从终点到起点时,通过使用逆邻接表,可以加速搜索过程。
总的来说,邻接表和逆邻接表是在图论中应用非常广泛的两种数据结构。
我们可以运用它们构建和优化各种算法,从而提高程序效率。
因此,熟练掌握邻接表和逆邻接表的概念、构建方法和应用场景是每一个程序员必备的技能。
洛谷邻接矩阵、邻接表的例题c++

洛谷邻接矩阵、邻接表的例题c++一、概述在学习和理解图的基本概念时,邻接矩阵和邻接表是两种常用的表示方法。
它们可以帮助我们更加直观地理解和分析图的结构和特性。
本文将以洛谷上的一个例题为例,介绍如何使用C++语言结合邻接矩阵和邻接表来解决图相关问题。
二、洛谷例题描述题目描述:给定一个有向图,图中包含n个节点和m条边,每条边连接两个节点。
现在需要求解图中每个节点的入度和出度。
输入格式:第一行包含两个整数n和m,分别表示节点数和边数。
接下来m行,每行包含两个整数a和b,表示图中存在一条边从a指向b。
输出格式:按照节点编号从小到大的顺序,输出每个节点的入度和出度。
三、解题思路1. 使用邻接矩阵表示图的结构;2. 使用邻接表统计每个节点的入度和出度。
四、基于邻接矩阵和邻接表的C++程序实现```cpp#include <iostream>#include <vector>using namespace std;const int MAXN = 1005;int n, m;int g[MAXN][MAXN]; // 邻接矩阵vector<int> inDegree(MAXN, 0); // 入度vector<int> outDegree(MAXN, 0); // 出度int m本人n() {cin >> n >> m;// 初始化邻接矩阵for (int i = 0; i < m; i++) {int a, b;cin >> a >> b;g[a][b] = 1;}// 统计入度和出度for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (g[i][j] == 1) { // 有一条边从i指向joutDegree[i]++;inDegree[j]++;}}}// 输出结果for (int i = 1; i <= n; i++) {cout << "节点" << i << "的入度为:" << inDegree[i] << ",出度为:" << outDegree[i] << endl;}return 0;}```五、测试样例输入样例:```5 61 21 32 32 43 44 5```输出样例:```节点1的入度为:0,出度为:2节点2的入度为:1,出度为:2节点3的入度为:2,出度为:2节点4的入度为:2,出度为:1节点5的入度为:1,出度为:0```六、总结通过本文的讲解,我们了解了如何使用C++语言结合邻接矩阵和邻接表来解决有关图的问题。
图的邻接表建立C语言代码

#include <stdio.h>#include <stdlib.h>/*定义边节点*/struct arcnode{int adjvex; /*另一个顶点的下标*/int weight;/*边的权值*/struct arcnode *next;/*指向下一条边的指针*/ char *info; //is option};/*定义顶点节点的类型*/struct vnode{char data;/*顶点字符名称*/struct arcnode *first;/*指向边链表的头结点*/ };/*定义图的结构*/struct graph{struct vnode vex[20];/*顶点集,用数组存储*/ int vexnum,arcnum;int kind;};/*功能:创建一个边节点参数:k,边另一个节点的下标w,边的权值返回值:指向新创建的边节点的指针*/struct arcnode *newarc(int k,int w){struct arcnode *p;/*在堆上给边节点分配一块空间*/p=(arcnode *)malloc(sizeof(struct arcnode));/*把边的数据放入边节点*/p->adjvex = k;p->weight = w;p->next=NULL;return(p);}/*返回某个顶点在顶点数组中的下标*/int locate(struct graph gr,char c){int s;for(s=0;s<gr.vexnum;s++){if(gr.vex[s].data==c)return s;}}main(){int i,j,k,l,w;char v1,v2,c;struct arcnode *t,*q,*p;struct graph g;printf("\n请输入顶点数:");scanf("%d",&g.vexnum);printf("\n请输入边数:");scanf("%d",&g.arcnum);getchar();printf("\n请依次输入顶点字符,不用分隔:");for(i=0;i<g.vexnum;i++){scanf("%c",&(g.vex[i].data));g.vex[i].first=NULL;}printf("\n你输入的顶点数据是: ");for(i=0;i<g.vexnum;i++){printf("%c ",g.vex[i].data);}printf("\n请以:a,b,3;的形式依次输入各边,各边之间用回车分隔\n"); getchar();/*接收用户输入的各条边*/for(k=0;k<g.arcnum;k++){scanf("%c,%c,%d;",&v1,&v2,&w);/*查找两个顶点在数组中的下标*/i=locate(g,v1);j=locate(g,v2);/*分配两个边节点无向图的一条边对应两个边节点如果是有向图,只分配一个就可了*/t=newarc(i,w);q=newarc(j,w);/*分别把两个边节点插入到边节点链表中插入的时候都是往链表头上插入*/q->next=g.vex[i].first;g.vex[i].first=q;t->next=g.vex[j].first;g.vex[j].first=t;}for(k=0;k<g.vexnum;k++){printf("\n%c-> ",g.vex[k].data);for(p=g.vex[k].first;p!=NULL;p=p->next)printf("%d->",p->adjvex);printf("N"); } printf("\n");}。
图的两种存储方式---邻接矩阵和邻接表

图的两种存储⽅式---邻接矩阵和邻接表图:图是⼀种数据结构,由顶点的有穷⾮空集合和顶点之间边的集合组成,表⽰为G(V,E),V表⽰为顶点的集合,E表⽰为边的集合。
⾸先肯定是要对图进⾏存储,然后进⾏⼀系列的操作,下⾯对图的两种存储⽅式邻接矩阵和邻接表尽⾏介绍。
(⼀)、邻接矩阵存储:⽤两个数组分别进⾏存储数据元素(顶点)的信息和数据元素之间的关系(边或弧)的信息。
存储顶点:⽤⼀个连续的空间存储n个顶点。
存储顶点之间的边:将由n个顶点组成的边⽤⼀个n*n的矩阵来存储,如果两个顶点之间有边,则表⽰为1,否则表⽰为0。
下⾯⽤代码来实现邻接矩阵的存储:#define SIZE 10class Graph{public:Graph(){MaxVertices = SIZE;NumVertices = NumEdges = 0;VerticesList = new char[sizeof(char)*MaxVertices];Edge = new int*[sizeof(int*)*MaxVertices];int i,j;for(i = 0;i<MaxVertices;i++)Edge[i] = new int[sizeof(int)*MaxVertices];for(i = 0;i<MaxVertices;i++){for(j = 0;j<MaxVertices;++j)Edge[i][j] = 0;}}void ShowGraph(){int i,j;cout<<"";for(i = 0;i<NumVertices;i++)cout<<VerticesList[i]<<"";cout<<endl;for(i = 0;i<NumVertices;i++){cout<<VerticesList[i]<<"";for(j = 0;j<NumVertices;j++)cout<<Edge[i][j] <<"";cout<<endl;}cout<<endl;}int GetVertexPos(char v){int i;for(i = 0;i<NumVertices;i++){if(VerticesList[i] == v)return i;}return -1;}~Graph(){Destroy();}void Insert(char v){if(NumVertices < MaxVertices){VerticesList[NumVertices] = v;NumVertices++;}}void InsertEdge(char v1,char v2){int i,j;int p1 = GetVertexPos(v1);int p2 = GetVertexPos(v2);if(p1 == -1 || p2 == -1)return ;Edge[p1][p2] = Edge[p2][p1] = 1;NumEdges++;}void RemoveEdge(char v1,char v2){int p1 = GetVertexPos(v1);int p2 = GetVertexPos(v2);if(p1 == -1 || p2== -1)return;if(Edge[p1][p2] == 0)return;Edge[p1][p2] = Edge[p2][p1] = 0;NumEdges--;}void Destroy(){delete[] VerticesList;VerticesList = NULL;for(int i = 0;i<NumVertices;i++){delete Edge[i];Edge[i] = NULL;}delete[] Edge;Edge = NULL;MaxVertices = NumVertices = 0;}void RemoveVertex(char v){int i,j;int p = GetVertexPos(v);int reNum = 0;if(p == -1)return;for(i = p;i<NumVertices-1;i++){VerticesList[i] = VerticesList[i+1];}for(i = 0;i<NumVertices;i++){if(Edge[p][i] != 0)reNum++;}for(i = p;i<NumVertices-1;i++){for(j = 0;j<NumVertices;j++){Edge[i][j] = Edge[i+1][j];}}for(i = p;i<NumVertices;i++){for(j = 0;j<NumVertices;j++)Edge[j][i] = Edge[j][i+1];}NumVertices--;NumEdges = NumEdges - reNum;}private:int MaxVertices;int NumVertices;int NumEdges;char *VerticesList;int **Edge;};上⾯的类中的数据有定义最⼤的顶点的个数(MaxVertices),当前顶点的个数(NumVertices),当前边的个数(NumEdges),保存顶点的数组,保存边的数组。
数据结构实验 图的邻接表和邻接矩阵操作

p->weight=weight; p->nextarc=G.vertices[vv].firstarc; G.vertices[vv].firstarc=p; strcmp(G.vertices[vv].data,v);
q=(ArcNode *)malloc(sizeof(ArcNode)); q->adjvex=vv; q->weight=weight; q->nextarc=G.vertices[ww].firstarc; G.vertices[ww].firstarc=q; strcmp(G.vertices[ww].data,w);
实验报告 6
课程 数据结构 实验名称 图的建立及遍历
第页
专业
班级_ __ 学号_ ___ 姓名
实验日期: 2010 年 11 月 23 日
评分
一 、实验目的
1.学会用邻接矩阵和邻接表实现图结构和对图的基本操作。 2.掌握对图操作的具体实现; 3. 掌握图的两种遍历算法(深度优先、广度优先); 4、掌握求图的最小生成树和顶点间最短路径的算法;
int adjvex;//该弧指向的顶点的位置 ArcType weight; struct ArcNode *nextarc;//指向下一条弧指针 //InfoType *info;该弧相关信息的指针 }ArcNode; typedef struct VNode { VertexType data;//顶点信息 ArcNode *firstarc;//指向第一条依附该顶点的弧的指针 }VNode,AdjList[MAX_VEX_NUM]; typedef struct { AdjList vertices; int vexnum,arcnum; GraphKind kind; }ALGraph; ALGraph G; struct MiniSpanTree_Flag { VertexType adjvex; ArcType lowcost; }closedge[MAX_VEX_NUM]; typedef bool PathMatrix[MAX_VEX_NUM][MAX_VEX_NUM];
邻接表
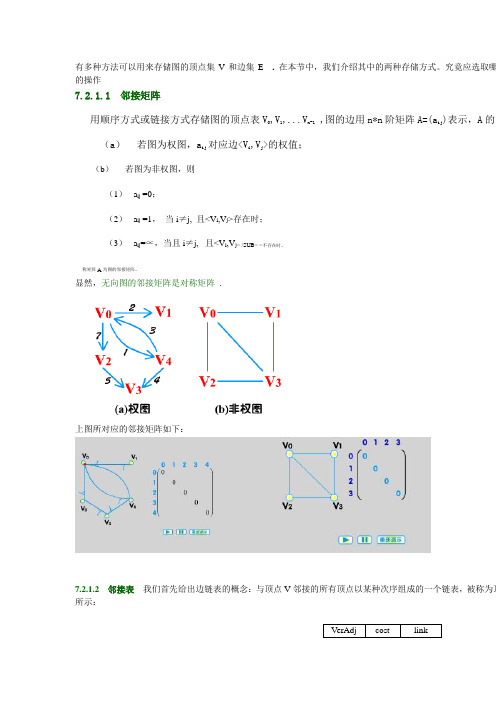
VerAdj cost
link
图 7.4 边结点 其中,VerAdj 域存放 V 的某个邻接顶点在顶点表中的序号;cost 域存放边<V,VerAdj>的权值;link 域存放指向 点显示的是边<V,VerAdj>的信息,因此称之为边结点。
对于无权图,边没有权值,边结点也就不需要包含 cost 域,所以边结点由两个域 VerAdj 和 l
(b) 若图为非权图,则 (1) aij =0; (2) aij =1, 当 i≠j, 且<Vi,Vj>存在时; (3) aij=∝,当且 i≠j, 且<Vi,Vj< /SUB> >不存在时。
称矩阵 A 为图的邻接矩阵。
显然,无向图的邻接矩阵是对称矩阵 .
上图所对应的邻接矩阵如下:
7.2.1.2 邻接表 我们首先给出边链表的概念:与顶点 V 邻接的所有顶点以某种次序组成的一个链表,被称为顶 所示:
对于无权图,边没有权值,边结点也就不需要包含 cost 域,所以边结点由两个域 VerAdj 和 l 用顺序存储方式存储图的顶点表 n-1,每个顶点的结构如图 7.5 所示
7.5 顶点结点
VerName adjacent
其中,VerName 域存放该顶点的名称,adjacent 域是指针域,存放指向 VerName 的边链表的头 adjacent 域存放的是顶点 VerName 的边链表的头指针。
info
头结点
data
firstarc
二、无向图的邻接表
ห้องสมุดไป่ตู้
图 7-5
三、有向图的邻接表和逆邻接表 (一)在有向图的邻接表中,第 i 个单链表链接的边都是顶点 i
发出的边。 (二)为了求第 i 个顶点的入度,需要遍历整个邻接表。因此可
建立邻接矩阵的方法和原理

建立邻接矩阵的方法和原理
邻接矩阵是图论中常用的一种数据结构,用于表示图中各个节点之间的关系。
它是一个二维数组,其中每个元素表示两个节点之间是否存在边。
在建立邻接矩阵时,需要考虑图的类型、节点数和边数等因素。
邻接矩阵的建立方法主要有两种:一种是基于有向图的邻接矩阵,另一种是基于无向图的邻接矩阵。
对于有向图,邻接矩阵中的元素表示从一个节点到另一个节点的有向边;而对于无向图,邻接矩阵中的元素表示两个节点之间是否存在无向边。
在建立邻接矩阵时,需要先确定图的节点数和边数。
假设有n个节点和m条边,那么邻接矩阵的大小为n×n。
对于有向图,如果从节点i到节点j存在一条有向边,则邻接矩阵中第i行第j列的元素为1;否则为0。
对于无向图,如果节点i和节点j之间存在一条无向边,则邻接矩阵中第i行第j列和第j行第i列的元素都为1;否则都为0。
邻接矩阵的优点是可以快速地判断两个节点之间是否存在边,时间复杂度为O(1);同时也可以方便地进行图的遍历和搜索。
但是邻接矩阵的缺点是空间复杂度较高,当节点数和边数较大时,会占用大量的内存空间。
此外,邻接矩阵只适用于稠密图,对于稀疏图来说,使用邻接表等数据结构更为合适。
邻接矩阵是一种常用的图数据结构,可以方便地表示图中各个节点之间的关系。
在建立邻接矩阵时,需要考虑图的类型、节点数和边数等因素,同时也需要注意空间复杂度的问题。
名词解释邻接表

邻接表邻接表(Adjacency List)是一种用于表示图的数据结构。
图是由节点(顶点)和边组成的数据结构,它们之间的关系可以用邻接表来表示和存储。
1. 图的基本概念在介绍邻接表之前,我们先简单了解一下图的基本概念。
•顶点(Vertex):也称为节点,是图中的一个元素。
顶点可以有一个或多个相关联的边。
•边(Edge):连接两个顶点的线段,表示两个顶点之间的关系。
•有向图(Directed Graph):每条边都有一个方向,从一个顶点指向另一个顶点。
•无向图(Undirected Graph):边没有方向,可以从任意一个顶点到达另一个顶点。
2. 邻接表的定义邻接表是一种用于表示图的数据结构,它使用链表来存储每个顶点及其相邻顶点之间的关系。
具体来说,对于每个顶点,我们使用一个链表来存储与该顶点相邻的其他顶点。
3. 邻接表的实现3.1 数据结构定义为了表示邻接表,我们需要定义两个数据结构:•节点(VertexNode):表示图中的一个顶点,包含一个指向第一个相邻顶点的指针。
•边(EdgeNode):表示图中的一条边,包含一个指向与之相邻的顶点的指针。
// 节点结构struct VertexNode {int vertex; // 顶点数据EdgeNode* firstEdge; // 指向第一条边的指针};// 边结构struct EdgeNode {int adjVertex; // 相邻顶点数据EdgeNode* nextEdge; // 指向下一条边的指针};3.2 邻接表的创建创建邻接表需要遍历图中每个顶点,并为每个顶点创建一个节点。
对于每个节点,我们需要遍历其相邻顶点,并为每个相邻顶点创建一条边。
// 创建邻接表void createAdjList(VertexNode*& adjList, int numOfVertices) {adjList = new VertexNode[numOfVertices]; // 创建节点数组for (int i = 0; i < numOfVertices; i++) {adjList[i].vertex = i + 1; // 给每个节点赋值cout << "请输入与" << adjList[i].vertex << "相邻的顶点(以0结束):" << endl;EdgeNode* pre = nullptr;EdgeNode* cur;int adjVertex;cin >> adjVertex;while (adjVertex != 0) {cur = new EdgeNode;cur->adjVertex = adjVertex;if (pre == nullptr) {adjList[i].firstEdge = cur;} else {pre->nextEdge = cur;}pre = cur;cin >> adjVertex;}}}3.3 邻接表的遍历遍历邻接表可以获取图中所有顶点及其相邻顶点的信息。
邻接表 java实现

邻接表 java实现一、什么是邻接表?邻接表是图的一种常见的表示方式,它将每个顶点与其相邻的顶点列表联系起来。
在邻接表中,每个顶点都有一个链表,链表中存储了该顶点与其他顶点相连的边。
二、邻接表的优缺点1. 优点:(1)空间复杂度低:对于稀疏图而言,使用邻接矩阵会浪费大量空间,而使用邻接表可以节省大量空间。
(2)查询效率高:对于稠密图而言,使用邻接矩阵查询效率高;对于稀疏图而言,使用邻接表查询效率高。
2. 缺点:(1)增加和删除边的操作比较麻烦。
(2)无法快速判断两个顶点之间是否存在一条边。
三、如何用 Java 实现邻接表?在 Java 中,我们可以通过链式存储结构来实现邻接表。
具体实现方式如下:1. 定义一个节点类 Node,表示一个链表节点。
该类包含两个属性:vertex 表示顶点编号;next 表示下一个节点。
```class Node {int vertex;Node next;public Node(int vertex) {this.vertex = vertex;this.next = null;}}```2. 定义一个邻接表类 AdjacencyList,表示整个邻接表。
该类包含两个属性:size 表示顶点数;adjList 表示邻接表数组。
```class AdjacencyList {int size;Node[] adjList;public AdjacencyList(int size) {this.size = size;adjList = new Node[size];for (int i = 0; i < size; i++) {adjList[i] = new Node(i);}}}```3. 实现添加边的方法 addEdge(int u, int v),其中 u 和 v 分别表示边的两个端点。
```public void addEdge(int u, int v) {Node node = new Node(v);node.next = adjList[u].next;adjList[u].next = node;```4. 实现打印邻接表的方法 printAdjacencyList()。
JAVA实现图的邻接表以及DFS

JAVA实现图的邻接表以及DFS ⼀:定义邻接表结构储存图package 图的遍历;//邻接表实现图的建⽴//储存边class EdgeNode {int index; // 习惯了⽤index,其实标准写法是(adjVertex)int value; // 权值EdgeNode nextArc; // 指向下⼀条弧}// 邻接表节点的类型class VertexNode {String name;EdgeNode firstArc = new EdgeNode(); // 指向第⼀条弧}public class Graph {VertexNode[] adjList; // 保存邻接表的头节点int e; // 图的边数int v; // 图的顶点数boolean[] visit;public Graph(int v, int e) {this.v = v;this.e = e;adjList = new VertexNode[e + 1]; // 学习Java养成的好习惯,动态分配空间,创建顶点表数组visit = new boolean[e + 1]; //标记for (int i = 0; i < e; i++) {visit[i] = false;}}} ⼆:DFS过程package 图的遍历;public class DFSGraph {public static void DFS(Graph G, int k) {System.out.println(G.adjList[k].name);G.visit[k] = true;EdgeNode p = new EdgeNode();p = G.adjList[k].firstArc;while(p!=null){if(G.visit[p.index]!=true){DFS(G,p.index);}p=p.nextArc;}}} 三:建⽴图package 图的遍历;import java.util.Scanner;public class CreateGraph {private static Graph G;public static Graph getGraph(){return G;}public static void createGraph() {Scanner sc = new Scanner(System.in);System.out.println("请输⼊顶点数v和边数e:");int v = sc.nextInt();int e = sc.nextInt();G = new Graph(v, e);System.out.println("请输⼊各顶点信息:");for (int i = 0; i < G.v; i++) {G.adjList[i] = new VertexNode();G.adjList[i].name = sc.next();G.adjList[i].firstArc = null; // 不可或缺}System.out.println("请输⼊各边信息(⽤空格隔开):");for (int i = 0; i < G.e; i++) {EdgeNode en1 = new EdgeNode();// 保证e1,e2都是合法输⼊String e1 = sc.next();String e2 = sc.next();int v1 = Index(e1);int v2 = Index(e2);en1.index = v1; // en1的下标是v1en1.nextArc = G.adjList[v2].firstArc;G.adjList[v2].firstArc = en1;EdgeNode en2 = new EdgeNode();en2.index = v2; // en2的下标是v2en2.nextArc = G.adjList[v1].firstArc;G.adjList[v1].firstArc = en2;}}public static void outputGraph() { //不知道为何空指针异常 try {System.out.println("输出邻接表存储情况:");EdgeNode en = new EdgeNode();for (int i = 0; i < G.e; i++) {System.out.print(G.adjList[i].name);en = G.adjList[i].firstArc;while (en != null) {System.out.print("->" + G.adjList[en.index].name);en = en.nextArc;}System.out.println();}} catch (NullPointerException e) {}}private static int Index(String e1) {for (int i = 0; i < G.v; i++) {if (G.adjList[i].name.equals(e1)){return i;}}return -1;}} 四:测试package 图的遍历;public class GraphDemo {public static void main(String[] args) {CreateGraph.createGraph();CreateGraph.outputGraph();System.out.println("DFS图的过程如下:");DFSGraph.DFS(CreateGraph.getGraph() , 0);}}/** 请输⼊顶点数v和边数e: 4 5* 请输⼊各顶点信息: a b c d* 请输⼊各边信息(⽤空格隔开):* a b* a c* a d* b c* b d*/ 五,测试结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
#include <stdio.h>
#include <conio.h>
int main()
{
ListGraph G;
cout<<"Is the graph have direction?(0/1)"<<endl;
cin>>G.Graphtype;
}EdgeNode;
//图的邻接链表定义
typedef struct
{
EdgeNode* Adjlist[MAXNUM];
int vertex_num;
int edge_num;
int Graphtype;
}ListGraph;
//生成图的邻接表
void Creatgraph(ListGraph *G)
s=G->Adjlist[i];
while(s)
{
cout<<"->"<<s->Vertex<<"("<<s->weight<<")";
s=s->next;
}
cout<<endl;
}
}
主函数调用测试:
#include "stdafx.h"
{
int i,weight,start,end;
EdgeNode *s;
for(i=0;i<G->vertex_num;i++) //clear the node pointer
G->Adjlist[i]=NULL;
for(i=0;i<G->edge_num;i++) //input the 2 node of each edge and weight
完整代码如下:
//下面介绍图的邻接表创建方法
typedef struct edgenode
{
int Ve //quan
struct edgenode *next; //the next edgenode
Creatgraph(&G);
cout<<"now the new matrix is follow:"<<endl;
OutList(&G);
getch();
return 0;
}
G->Adjlist[start]=s;
if(G->Graphtype == 0)
{
s=(EdgeNode *)malloc(sizeof(EdgeNode));
s->next=G->Adjlist[end];
s->Vertex=start;
s->weight=weight;
{
cout<<"the "<<i+1<<" edge:";
cin>>start>>end>>weight;
s=(EdgeNode *)malloc(sizeof(EdgeNode));
s->next=G->Adjlist[start];
s->Vertex=end;
s->weight=weight;
G->Adjlist[end]=s;
}
}
}
//输出邻接表
void OutList(ListGraph *G)
{
int i;
EdgeNode *s;
for(i=0;i<G->vertex_num;i++)
{
cout<<"Vertex:"<<i<<" ";
cout<<"please input the vertex_number and edge number:"<<endl;
cin>>G.vertex_num>>G.edge_num;
cout<<"input the two nodes of each edge and weight:"<<endl;
