结构力学习题与答案武汉大学
结构力学习题及答案武汉大学
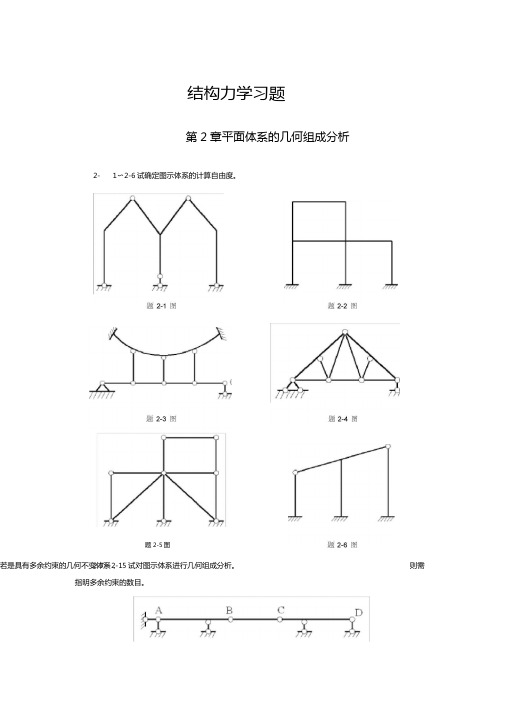
2-7〜2-15试对图示体系进行几何组成分析。
若是具有多余约束的几何不变体系, 则需结构力学习题第2章平面体系的几何组成分析2-1〜2-6试确定图示体系的计算自由度。
指明多余约束的数目。
题2-5图题2-7图题2-9图■/ ED FB Z77 7T1D 题2-14图题2-11图题2-15图题2-17图题2-20图2-1 W 12-1 W 92-3 W 32-4 W 22-5 W 12-6 W 42-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为(a)2-18、2-19瞬变体系 2-20、2-21具有三个多余约束的几何不变体系第3章 静定梁和静定平面刚架的内力分析3-1试作图示静定梁的内力图。
ZOAA' FFF20Jt.¥AJ H H i h i H i HI11 i Hrr誌*毗7cIttkA' tftc AA y BY " D 叮啣-m柿(C) (d)习题3-1图3-2试作图示多跨静定梁的内力图。
I" bi __皿 ■(b)2in20kX 15fc\(C)XV屮........................................................J习题3-2图3-3〜3-9试作图示静定刚架的内力图。
40kV u>L T L Hr.习题3-4图习题3-6图习题3-7图AR GA-A'm--------------------5C习题3-8图习题3-9图3-10试判断图示静定结构的弯矩图是否正确。
EHHUniDn~订H i 卄T 1 nL J\ /I(b)(a)(c) (d)部分习题答案3-1 ( a)M B 80kN m (上侧受拉),F Q R 60kN,F Q B60kN(b)M A 20kN m (上侧受拉),M B40kN m (上侧受拉),F QA 32.5kN,F QA 20kN,F QB47.5kN,F Q B 20kN(c)M e口(下侧受拉),F Q C匸COS4 23-2 (a) M E0,M F40kN m (上侧受拉),M B120kN m (上侧受拉)(b) RM H 15kN m(上侧受拉),M E11.25kN m (下侧受拉)(c) M G29kN m (下侧受拉),M D8.5kN m(上侧受拉),M H 15kN m(下侧受拉)3-3 M CB 10kN m (左侧受拉),M DF 8kN m (上侧受拉),M DE 20kN m (右侧受拉)3- 4 M BA 120kN m (左侧受拉)3-5 M F40kN m (左侧受拉),M DC160kN m (上侧受拉),M EB80kNm(右侧受拉)3- 6 M BA60kN m(右侧受拉),M BD45kN m (上侧受拉),F QBD28.46kN3-7 M 下70kN m (左侧受拉),M DE150kN m (上侧受拉),M EB70kN m(右侧受拉)3-8 M CB 0.36kN m (上侧受拉),M BA 0.36kN m (右侧受拉)3-9 M AB10kN m (左侧受拉),M BC10kN m (上侧受拉)3-10 (a)错误(b)错误(c)错误(d)正确第4章静定平面桁架和组合结构的内力分析4-1试判别习题4-1图所示桁架中的零杆。
结构力学考试题及答案
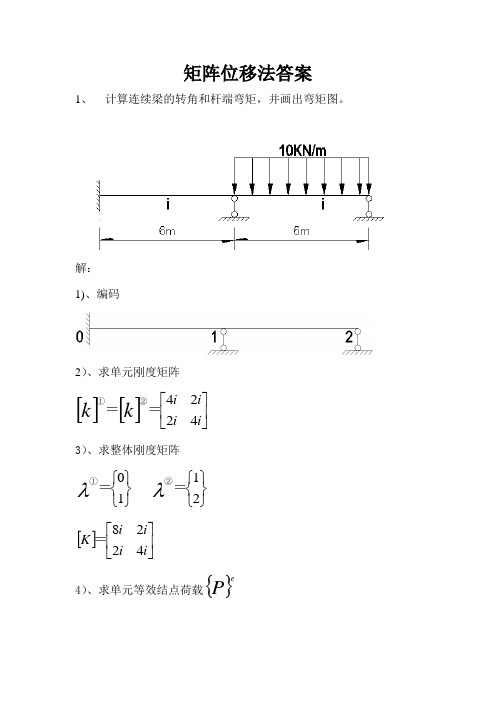
矩阵位移法答案1、 计算连续梁的转角和杆端弯矩,并画出弯矩图。
解: 1)、编码2)、求单元刚度矩阵[][]⎥⎦⎤⎢⎣⎡i i i i k k 4224==②①3)、求整体刚度矩阵⎭⎬⎫⎩⎨⎧⎭⎬⎫⎩⎨⎧2110==②①λλ[]⎥⎦⎤⎢⎣⎡i i i i K 4228=4)、求单元等效结点荷载{}P e{}{}m KN q q P P l l F F ⋅⎭⎬⎫⎩⎨⎧-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧-=⎭⎬⎫⎩⎨⎧=30301211210022②①{}{}{}F P P P eee-=={}{}m KN P P ⋅⎭⎬⎫⎩⎨⎧-⎭⎬⎫⎩⎨⎧303000==②①5)、集成结构等效结点荷载向量{}P{}m KN P ⋅⎭⎬⎫⎩⎨⎧-=30306)、解方程[]{}{}P K =∆ii i i i 717545303042282121⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧∆∆⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧∆∆⎥⎦⎤⎢⎣⎡ 7)、求各杆的杆端内力{}F e{}[]{}{}F k F P e e e e +∆=单元① {}m KN i i i i i F ⋅⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡=71.2586.120074504224①单元② {}m KN i i i i i i F ⋅⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧-+⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎥⎦⎤⎢⎣⎡=071.2530307757454224-②8)、做M 图2、 求图示刚架的M 、Q 、N 图。
解:1)、整理原始数据及编码2)、求局部坐标系中的单元刚度矩阵{}K e2442101.2,300,20,100cm KN E cm I cm A cm L ⨯====mKN LEI m KN L EI KN L EI m KN LEI m KN L EA ⋅⨯=⨯=⨯=⋅⨯=⨯=2232222106.122106.7512108.376102.2541042003)、计算整体坐标系中的单元刚度矩阵{}k e单元①和单元③单元②{}{}{}2102.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200⨯===⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------k k k ③②①[][]I T =,= 0α[][][][]②②①①=,=kk k k90=α[]⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--=100000001000010000000100000001000010T [][][][]2102.2508.376.1208.370420000420008.3716.758.3706.756.1208.372.2508.370420*********.3706.758.3706.75⨯==⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------T k T k T ②②4)、用单元集成法形成整体刚度矩阵{}K⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧000321000321321000===③②①λλλ {}2106.7508.3702.435108.3706.8475⨯⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=K5)、求单元等效结点荷载{}P e{}{}[]833.050833.050-=-=TF P P①①{}{}[]833.050833.050-=TP P ①①=6)、用单元集成法形成整体结构的等效结点荷载{}P{}[]TP 833.050-=7)、形成整体结构的综合结点荷载{}[]TF 402000={}{}[]TP F 167.392500=+8)、解方程[]{}{}{}0F P K +=∆[][]I T =,= 0α⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∆∆∆⨯⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--167.39250106.7508.3702.435108.3706.84753212 432110924.51575.0232.0-⨯⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧∆∆∆ 9)、求各杆的杆端内力{}F e{}[][]{}{}F T k F P e e e e +∆=单元①{}[][]{}{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧----+⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⨯⨯-⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------+∆=700.13193.24744.9492.5193.14744.9833.050833.05010924.51575.0232.000010422.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200=①①①①F T k F P{}[][]{}{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧-=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⨯⨯-⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------+∆=455.6452.19150.24997.12452.19150.2400000010000924.51575.0232.010421000010000100000001000000010000102.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200=②②②②F T kF P{}[][]{}{}⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧--=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧+⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⨯⨯-⎪⎪⎪⎭⎪⎪⎪⎬⎫⎪⎪⎪⎩⎪⎪⎪⎨⎧--------+∆=760.6062.20744.9302.13062.20744.900000010000924.51575.0232.010422.258.3706.128.3708.376.7508.376.7500042000042006.128.3702.258.3708.376.7508.376.750004200004200=③③③③F T k F P结构动力学作业答案1、求图示结构的自振频率。
结构力学考试题及答案

结构力学考试题及答案一、选择题1. 结构力学中,下列哪项不是结构的基本概念?A. 结构的刚度B. 结构的稳定性C. 结构的强度D. 结构的美观性答案:D2. 简支梁受均布荷载作用时,最大弯矩出现在:A. 跨中B. 支点处C. 任意截面D. 四分之三跨长处答案:A3. 在结构力学中,剪力和弯矩的方向约定为:A. 剪力向上为正,弯矩顺时针为正B. 剪力向下为正,弯矩逆时针为正C. 剪力向上为正,弯矩逆时针为正D. 剪力向下为正,弯矩顺时针为正答案:B4. 确定结构的内力分布情况通常采用的方法是:A. 能量法B. 虚功原理C. 弯矩分配法D. 刚度法答案:D5. 连续梁与简支梁相比,其特点是:A. 刚度更高B. 跨越能力更强C. 造价更低D. 所有上述选项答案:D二、填空题1. 结构力学中的__________是指结构在荷载作用下不发生位移的能力。
答案:刚度2. 结构的__________是指结构在荷载作用下不发生翻转的能力。
答案:稳定性3. 在进行结构分析时,通常首先需要确定结构的__________和反力。
答案:内力4. 结构力学中,__________是指构件截面上所有外力的集合效果。
答案:截面剪力5. 对于简支梁,当荷载作用在离支点一定距离处时,该点处的弯矩可以通过__________计算得出。
答案:剪力乘以距离三、简答题1. 请简述结构力学中的虚功原理及其应用。
答:虚功原理是指在一个平衡系统中,任何微小的位移或变形所对应的虚功等于该系统内力对该变形所做的功。
这个原理在结构力学中用于分析静不定结构,通过假设结构的位移或变形,计算出相应的虚功,然后根据虚功原理建立平衡方程,求解未知的反力或内力。
2. 描述简支梁受集中荷载作用时的弯矩图和剪力图。
答:简支梁受集中荷载作用时,弯矩图在荷载作用点会出现一个突变,即弯矩值突然增大到最大值,然后随着距离的增加逐渐减小回到零。
剪力图则显示在荷载作用点两侧的剪力值相反,一边为正值,另一边为负值,且随着距离的增加,剪力值逐渐减小到零。
结构力学习题及答案(武汉大学)

结构⼒学习题及答案(武汉⼤学)结构⼒学习题第2章平⾯体系的⼏何组成分析2-1~2-6 试确定图⽰体系的计算⾃由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图⽰体系进⾏⼏何组成分析。
若是具有多余约束的⼏何不变体系,则需指明多余约束的数⽬。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-1 1 W=2-1 9W-=2-3 3W-=2-4 2W=-2-5 1=W-2-6 4=W-2-7、2-8、2-12、2-16、2-17⽆多余约束的⼏何不变体系2-9、2-10、2-15具有⼀个多余约束的⼏何不变体系2-11具有六个多余约束的⼏何不变体系2-13、2-14⼏何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的⼏何不变体系第3章静定梁和静定平⾯刚架的内⼒分析3-1 试作图⽰静定梁的内⼒图。
(a)(b)(c) (d)习题3-1图3-2 试作图⽰多跨静定梁的内⼒图。
(a)(b)(c)习题3-2图3-3~3-9 试作图⽰静定刚架的内⼒图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图⽰静定结构的弯矩图是否正确。
(a)(b)(c)(d)部分习题答案3-1 (a )m kN M B ?=80(上侧受拉),kN F RQB 60=,kN F L QB 60-=(b )m kN M A ?=20(上侧受拉),m kN M B ?=40(上侧受拉),kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c) 4Fl M C =(下侧受拉),θcos 2F F L QC =3-2 (a) 0=E M ,m kN M F ?-=40(上侧受拉),m kN M B ?-=120(上侧受拉)(b )m kN M RH ?-=15(上侧受拉),m kN M E ?=25.11(下侧受拉)(c )m kN M G ?=29(下侧受拉),m kN M D ?-=5.8(上侧受拉),m kN M H ?=15(下侧受拉) 3-3 m kN M CB ?=10(左侧受拉),m kN M DF ?=8(上侧受拉),m kN M DE ?=20(右侧受拉) 3-4 m kN M BA ?=120(左侧受拉)3-5 m kN M F ?=40(左侧受拉),m kN M DC ?=160(上侧受拉),m kN M EB ?=80(右侧受拉)3-6 m kN M BA ?=60(右侧受拉),m kN M BD ?=45(上侧受拉),kN F QBD 46.28=3-7 m kN M C ?=70下(左侧受拉),m kN M DE ?=150(上侧受拉),m kN M EB ?=70(右侧受拉) 3-8 m kN M CB ?=36.0(上侧受拉),m kN M BA ?=36.0(右侧受拉) 3-9 m kN M AB ?=10(左侧受拉),m kN M BC ?=10(上侧受拉) 3-10 (a )错误(b )错误(c )错误(d )正确第4章静定平⾯桁架和组合结构的内⼒分析4-1 试判别习题4-1图所⽰桁架中的零杆。
结构力学的考试题型及答案

结构力学的考试题型及答案一、选择题1. 以下哪个选项是结构力学中的基本假设?A. 结构是连续的B. 结构是刚性的C. 结构是弹性的D. 结构是塑性的答案:C2. 梁在受到弯矩作用时,其截面上的应力分布规律是什么?A. 线性分布B. 抛物线分布C. 正弦分布D. 均匀分布答案:B二、填空题3. 在结构力学中,_______是指结构在受到外力作用时,其内部各点的位移和内力满足平衡条件和变形条件。
答案:结构分析4. 悬臂梁自由端受到集中荷载作用时,其最大弯矩为_______。
答案:P*L/2三、简答题5. 简述结构力学中虚功原理的基本思想。
答案:虚功原理的基本思想是,当一个结构处于平衡状态时,任何虚位移所做的虚功都等于零。
这意味着结构在受到任何虚位移时,外力所做的虚功等于内力所做的虚功。
6. 描述梁的剪力和弯矩之间的关系。
答案:梁的剪力是弯矩随梁长度变化的导数,即剪力等于弯矩对梁长度的一阶导数。
具体来说,弯矩是剪力的积分,而剪力是弯矩的微分。
四、计算题7. 已知一简支梁,跨中集中荷载为P,求梁的跨中挠度。
答案:跨中挠度可以通过弯矩方程和挠度方程计算得出,对于简支梁跨中集中荷载的情况,跨中挠度公式为δ_max = (PL^3) / (48EI),其中L为梁长,E为材料的弹性模量,I为截面惯性矩。
8. 计算一端固定一端简支梁在固定端集中荷载作用下的固定端弯矩。
答案:固定端弯矩可以通过弯矩分配法或弯矩方程计算得出。
对于一端固定一端简支梁在固定端集中荷载作用的情况,固定端弯矩公式为M_fixed = (P*L) / 2,其中P为集中荷载,L为梁长。
结构力学练习题及答案
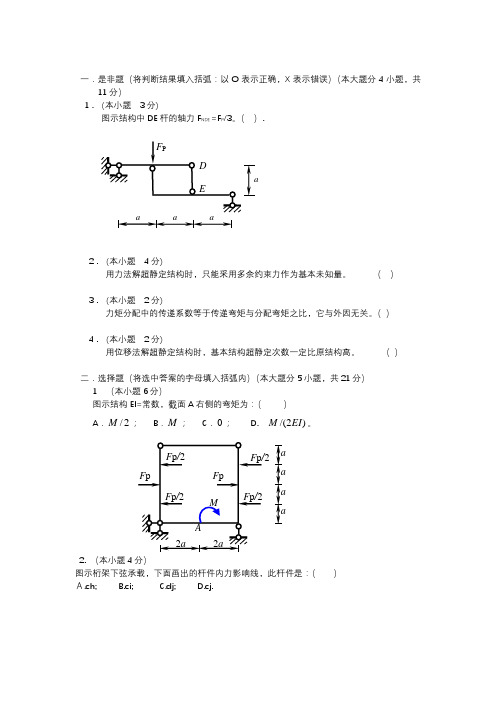
一.是非题(将判断结果填入括弧:以O 表示正确,X 表示错误)(本大题分4小题,共11分)1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。
( ).2 . (本小题 4分)用力法解超静定结构时,只能采用多余约束力作为基本未知量。
( )3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比,它与外因无关。
( )4 . (本小题 2分)用位移法解超静定结构时,基本结构超静定次数一定比原结构高。
( )二.选择题(将选中答案的字母填入括弧内)(本大题分5小题,共21分) 1 (本小题6分)图示结构EI=常数,截面A 右侧的弯矩为:( )A .2/M ;B .M ;C .0; D. )2/(EI M 。
2. (本小题4分)图示桁架下弦承载,下面画出的杆件内力影响线,此杆件是:( ) A.ch; B.ci; C.dj; D.cj.F p /2M2a2a a aa aA F p /2F p /2 F p /2F p F pa a aa F PED3. (本小题 4分)图a 结构的最后弯矩图为:A. 图b;B. 图c;C. 图d;D.都不对。
( )( a) (b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是: A.单位荷载下的弯矩图为一直线; B.结构可分为等截面直杆段; C.所有杆件EI 为常数且相同; D.结构必须是静定的。
( ) 5. (本小题3分)图示梁A 点的竖向位移为(向下为正):( ) A.F P l 3/(24EI); B. F P l 3/(!6EI); C. 5F P l 3/(96EI); D. 5F P l 3/(48EI).三(本大题 5分)对图示体系进行几何组成分析。
A l /2l /2EI 2EIF Pa d c eb fgh iklF P =11j llM /4 3M /4M /43M /43M /4M /4M /8 M /2EIEIM四(本大题 9分)图示结构B 支座下沉4 mm ,各杆EI=2.0×105 kN ·m 2,用力法计算并作M 图。
结构力学大题及答案
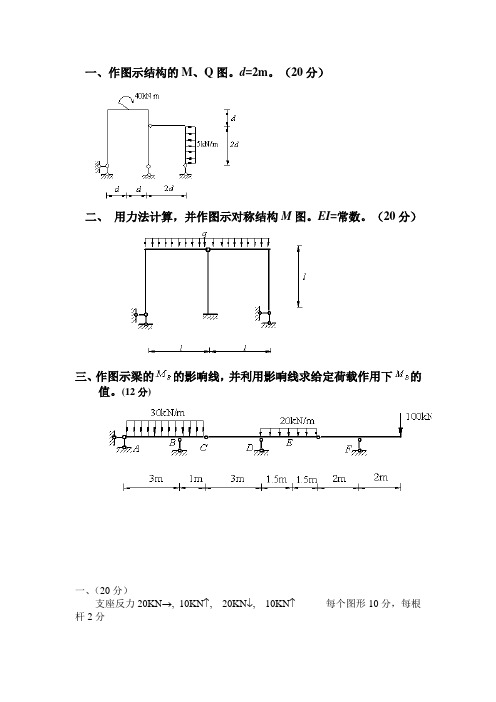
用力法计算,并作图示结构由于支座移动引起的M图。EI=常数,不考虑链杆的轴向变形。
十一、(本大题18分)
试用力矩分配法作图示刚架的弯矩图。EI=常数。(计算二轮)
四、(本大题4分)
几何不变,有一个多余约束。(4分)
十、(本大题10分)
, (10分)
十一、(本大题18分)
(12分)
三根链杆连接两刚片,为无多余约束的几何不变体系。
分析(3分)
结论(3分)
三、(本大题14分)
用力矩分配法计算图示结构(可利用对称性),并作弯矩图。已知各杆EI=常数。
解:半结构
(3分)
,
, (分配系数3分)
(3分)
三分析计算题(4小题,共计50分)
1分析图示体系的几何组成,说明分析过程并作出结论。(5分)
ADDA
DBBD
DCCD
分配系数
3/8
1/4
3/8
固端力
0 0
120 -120
0 0
分配、传递
0 -45
-30 -15
-45 0
杆端力
0 -45
90 -135
-45 0
一、(本大题14分)
用力矩分配法计算图示结构(可利用对称性),并作弯矩图。已知各杆EI=常数。
二、(本大题5分)
试分析图示体系的几何组成。
2、解:
分配系数
固端弯矩
分配弯矩
A B
C
分配系数
2/3
1/3
固端弯矩
48
-58
分配弯矩
220/3
110/3
杆端弯矩
121.33
-21.33
弯矩图为:
结构力学考试题及答案

结构力学考试题及答案一、选择题(每题2分,共20分)1. 下列哪项是结构力学中静定结构的特点?A. 有多余约束B. 无多余约束C. 可以承受任何外力D. 只能承受垂直荷载答案:B2. 梁的弯矩图是通过什么方法绘制的?A. 静力平衡B. 能量守恒C. 动量守恒D. 材料力学答案:A3. 简支梁在集中荷载作用下的挠曲线形状是:A. 直线B. 抛物线C. 正弦曲线D. 双曲线答案:B4. 连续梁与简支梁相比,其内力分布的特点是:A. 更均匀B. 更集中C. 更复杂D. 更简单答案:A5. 梁的剪力图在集中荷载作用点处的变化是:A. 突变B. 渐变C. 保持不变D. 先增后减答案:A6. 梁的弯矩图在集中荷载作用点处的变化是:A. 突变B. 渐变C. 保持不变D. 先增后减答案:A7. 梁的剪力图在集中力偶作用点处的变化是:A. 突变B. 渐变C. 保持不变D. 先增后减答案:C8. 梁的弯矩图在集中力偶作用点处的变化是:A. 突变B. 渐变C. 保持不变D. 先增后减答案:A9. 对于静定梁,下列哪项说法是正确的?A. 弯矩图的形状取决于梁的边界条件B. 弯矩图的形状取决于荷载的分布C. 弯矩图的形状取决于材料的性质D. 弯矩图的形状取决于梁的形状答案:A10. 梁的剪力和弯矩之间的关系是:A. 无关B. 成正比C. 成反比D. 线性关系答案:A二、填空题(每题2分,共20分)1. 静定结构在外力作用下,其内力和位移与外力之间存在______关系。
答案:单值2. 梁的挠度计算通常采用______法。
答案:积分3. 梁的弯矩与剪力之间的关系可以用______方程表示。
答案:微分4. 在结构力学中,梁的弯矩图通常用______表示。
答案:M5. 连续梁的内力分布比简支梁更______。
答案:均匀6. 梁的剪力图在支座处的值为______。
答案:零7. 梁的弯矩图在支座处的值为______。
答案:零8. 梁的剪力图在集中荷载作用点处的变化是______。
结构力学试题及答案

结构力学试题及答案一、选择题(每题2分,共20分)1. 下列选项中,哪一个是结构力学中常用的分析方法?A. 能量法B. 静力平衡法C. 动力学分析法D. 热力学分析法答案:A、B2. 梁的弯矩图通常表示的是:A. 剪力B. 弯矩C. 轴力D. 扭矩答案:B3. 悬臂梁在自由端受到垂直向下的集中力作用时,其弯矩图的形状是:A. 直线B. 抛物线C. 正弦曲线D. 余弦曲线答案:B4. 简支梁在跨中受到垂直向下的集中力作用时,其弯矩图的形状是:A. 直线B. 抛物线C. 正弦曲线D. 余弦曲线答案:B5. 梁的剪力图通常表示的是:A. 弯矩B. 剪力C. 轴力D. 扭矩答案:B6. 连续梁的内力分布特点是:A. 线性变化B. 非线性变化C. 恒定不变D. 周期性变化答案:B7. 在结构力学中,二阶效应通常指的是:A. 材料的非线性效应B. 几何非线性效应C. 动力效应D. 热效应答案:B8. 桁架结构中,节点的平衡条件是:A. 节点处的力矩平衡B. 节点处的力平衡C. 节点处的力和力矩都平衡D. 节点处的力不平衡答案:C9. 根据结构力学的基本原理,下列说法错误的是:A. 结构的内力与外力有关B. 结构的变形与内力有关C. 结构的稳定性与材料性质有关D. 结构的刚度与外力无关答案:D10. 梁的剪力和弯矩之间的关系是:A. 线性关系B. 非线性关系C. 没有关系D. 互为导数关系答案:D二、填空题(每题2分,共20分)1. 结构力学中,______是结构在荷载作用下产生的位移。
答案:变形2. 梁的剪力和弯矩之间存在______关系。
答案:互为导数3. 在结构力学中,______是结构在荷载作用下产生的内力。
答案:内力4. 悬臂梁在自由端受到垂直向下的集中力作用时,其弯矩图的形状是______。
答案:抛物线5. 简支梁在跨中受到垂直向下的集中力作用时,其弯矩图的形状是______。
答案:抛物线6. 连续梁的内力分布特点是______。
结构力学考试题及答案

结构力学考试题及答案一、单项选择题(每题2分,共20分)1. 结构力学中,以下哪一项不是结构分析的基本任务?A. 确定结构的内力B. 确定结构的位移C. 确定结构的稳定性D. 确定结构的美观性答案:D2. 在结构力学中,以下哪一项是静定结构的特点?A. 有多余约束B. 无多余约束C. 有多余支座D. 无多余支座答案:B3. 梁在弯曲时,以下哪一项是正确的弯矩图形状?A. 直线B. 抛物线C. 正弦曲线D. 余弦曲线答案:B4. 以下哪一项不是影响结构稳定性的因素?A. 材料性质B. 几何尺寸C. 载荷大小D. 环境温度答案:D5. 在结构力学中,以下哪一项是超静定结构的特点?A. 内力可以通过平衡方程确定B. 内力不能通过平衡方程确定C. 位移可以通过平衡方程确定D. 位移不能通过平衡方程确定答案:B6. 以下哪一项是结构力学中的动力分析?A. 确定结构在静载荷作用下的内力和位移B. 确定结构在动载荷作用下的内力和位移C. 确定结构在热载荷作用下的内力和位移D. 确定结构在风载荷作用下的内力和位移答案:B7. 以下哪一项是结构力学中的塑性分析?A. 确定结构在弹性范围内的内力和位移B. 确定结构在塑性变形范围内的内力和位移C. 确定结构在断裂时的内力和位移D. 确定结构在疲劳破坏时的内力和位移答案:B8. 在结构力学中,以下哪一项是结构的几何不变性?A. 结构在任何外力作用下形状不变B. 结构在任何外力作用下形状可以改变C. 结构在任何外力作用下形状保持不变D. 结构在任何外力作用下形状可以保持不变答案:C9. 以下哪一项是结构力学中的虚功原理?A. 通过平衡方程确定结构的内力B. 通过虚设位移确定结构的内力C. 通过虚设载荷确定结构的内力D. 通过虚设速度确定结构的内力答案:B10. 在结构力学中,以下哪一项是结构的自由度?A. 结构在空间中的运动方向数B. 结构在平面中的运动方向数C. 结构在空间中的约束数D. 结构在平面中的约束数答案:B二、多项选择题(每题3分,共15分)11. 结构力学中,以下哪些因素会影响结构的内力分布?A. 材料性质B. 几何尺寸C. 载荷分布D. 支撑条件答案:ABCD12. 在结构力学中,以下哪些是静定结构?A. 单跨梁B. 双跨连续梁C. 三铰拱D. 悬索桥答案:AC13. 以下哪些是结构力学中常用的分析方法?A. 弯矩分配法B. 力矩分配法C. 虚功原理D. 能量法答案:ABCD14. 以下哪些是结构力学中的动力分析类型?A. 自由振动B. 强迫振动C. 随机振动D. 瞬态振动答案:ABCD15. 在结构力学中,以下哪些是结构的稳定性问题?A. 屈曲B. 失稳C. 振动D. 疲劳答案:AB三、填空题(每题2分,共20分)16. 结构力学中,结构的内力包括______、______和______。
结构力学练习题及答案1doc资料

结构力学练习题及答案1结构力学习题及答案一. 是非题(将判断结果填入括弧:以O 表示正确,X 表示错误)(本大题分4小题,共11分) 1 . (本小题 3分)图示结构中DE 杆的轴力F NDE =F P /3。
( ).2 . (本小题 4分)用力法解超静定结构时,只能采用多余约束力作为基本未知量。
( )3 . (本小题 2分)力矩分配中的传递系数等于传递弯矩与分配弯矩之比,它与外因无关。
( )4 . (本小题 2分)用位移法解超静定结构时,基本结构超静定次数一定比原结构高。
( )二. 选择题(将选中答案的字母填入括弧内)(本大题分5小题,共21分) 1 (本小题6分)图示结构EI=常数,截面A 右侧的弯矩为:( ) A .2/M ; B .M ; C .0; D. )2/(EI M 。
2. (本小题4分)图示桁架下弦承载,下面画出的杆件内力影响线,此杆件是:( ) A.ch; B.ci; C.dj; D.cj.3. (本小题 4分)图a 结构的最后弯矩图为:2=1A. 图b;B. 图c;C. 图d;D.都不对。
( ) ( a) (b) (c) (d)4. (本小题 4分)用图乘法求位移的必要条件之一是: A.单位荷载下的弯矩图为一直线; B.结构可分为等截面直杆段; C.所有杆件EI 为常数且相同; D.结构必须是静定的。
( ) 5. (本小题3分)图示梁A 点的竖向位移为(向下为正):( )A.F P l 3/(24EI); B. F P l 3/(!6EI); C. 5F P l 3/(96EI); D. 5F P l 3/(48EI).三(本大题 5分)对图示体系进行几何组成分析。
F P四(本大题 9分)图示结构B 支座下沉4 mm ,各杆EI=2.0×105 kN·m 2,用力法计算并作M 图。
五(本大题 11分) 用力矩分配法计算图示结构,并作M 图。
EI=常数。
结构力学第1章习题及参考答案
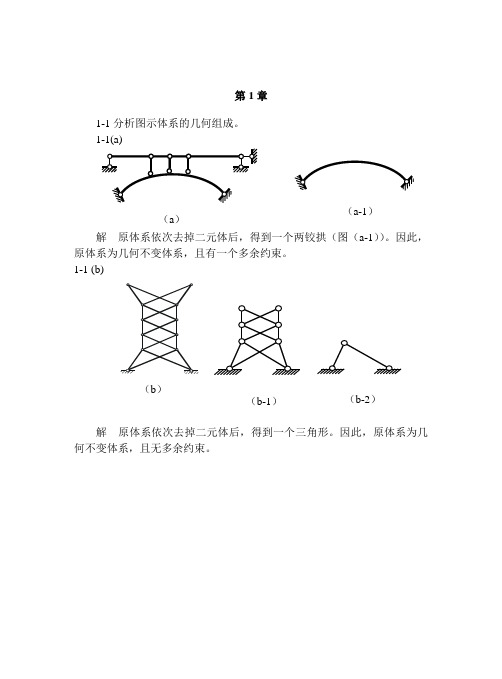
第1章1-1分析图示体系的几何组成。
解 原体系依次去掉二元体后,得到一个两铰拱(图(a-1))。
因此,原体系为几何不变体系,且有一个多余约束。
1-1 (b)解 原体系依次去掉二元体后,得到一个三角形。
因此,原体系为几何不变体系,且无多余约束。
(a )(a-1)(b )(b-1)(b-2)1-1 (c)(c-2) (c-3)解 原体系依次去掉二元体后,得到一个三角形。
因此,原体系为几何不变体系,且无多余约束。
1-1 (d)(d-1) (d-2) (d-3)解 原体系依次去掉二元体后,得到一个悬臂杆,如图(d-1)-(d-3)所示。
因此,原体系为几何不变体系,且无多余约束。
注意:这个题的二元体中有的是变了形的,分析要注意确认。
(d )(c-1)1-1 (e)解 原体系去掉最右边一个二元体后,得到(e-1)所示体系。
在该体系中,阴影所示的刚片与支链杆C 组成了一个以C 为顶点的二元体,也可以去掉,得到(e-2)所示体系。
在图(e-2)中阴影所示的刚片与地基只用两个链杆连接,很明显,这是一个几何可变体系,缺少一个必要约束。
因此,原体系为几何可变体系,缺少一个必要约束。
1-1 (f)解 原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相连,符合几何不变体系的组成规律。
因此,可以将该刚片和相应的约束去掉只分析其余部分。
很明显,余下的部分(图(f-1))是一个几何不变体系,且无多余约束。
因此,原体系为几何不变体系,且无多余约束。
1-1 (g)解 原体系中阴影所示的刚片与体系的其它部分用三个链杆相连,符合几何不变体系的组成规律。
因此,可以将该刚片和相应的约束去掉,只分析其余部分。
余下的部分(图(g-1))在去掉一个二元体后,只剩下一个悬臂杆(图(g-2))。
因此,原体系为几何不变体系,且无多余约束。
(e )(e-1)ABCAB (e-2)(f )(f-1) (g ) (g-1) (g-2)1-1 (h)解 原体系与基础用一个铰和一个支链杆相连,符合几何不变体系的组成规律。
《结构力学习题》(含答案解析)

第三章 静定结构的位移计算一、判断题:1、虚位移原理等价于变形谐调条件,可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下,静定结构不产生内力,但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时,其虚拟状态应取:A.;; B.D.C.=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图,用图乘法求位移的结果为:()/()ωω1122y y EI +。
M k M p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中,粱的转角ϕ与竖向位移δ间的关系为:δ=ϕ 。
8、图示桁架各杆E A 相同,结点A 和结点B 的竖向位移均为零。
a a9、图示桁架各杆EA =常数,由于荷载P 是反对称性质的,故结点B 的竖向位移等于零。
二、计算题:10、求图示结构铰A 两侧截面的相对转角ϕA ,EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ,a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l /3 2 /3/3q13、图示结构,EI=常数 ,M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
ql15、求图示刚架结点C 的转角和水平位移,EI = 常数 。
q16、求图示刚架中D点的竖向位移。
EI =常数。
l/217、求图示刚架横梁中D点的竖向位移。
EI=常数。
18、求图示刚架中D点的竖向位移。
E I = 常数。
qll l/219、求图示结构A、B两截面的相对转角,EI=常数。
l/23l/320、求图示结构A、B两点的相对水平位移,E I = 常数。
ll21、求图示结构B点的竖向位移,EI = 常数。
结构力学课后习题答案

结构力学课后习题答案(总23页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1~2-14试对图示体系进行几何组成分析,如果是具有多余联系的几何不变体系,则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)/20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图,试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图,并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=,试求D 截面的内力。
题5-1图5-2 带拉杆拱,拱轴线方程x x l lf y )(42-=,求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
结构力学章节习题与参考答案

第1章绪论(无习题)第2章平面体系的机动分析习题解答习题2.1是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W=0,则该体系一定为无多余约束的几何不变体系。
( )(3) 若平面体系的计算自由度W<0,则该体系为有多余约束的几何不变体系。
( )(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题2.1(5) 图所示体系去掉二元体CEF后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )习题2.1(5)图(6) 习题2.1(6)(a)图所示体系去掉二元体ABC后,成为习题2.1(6) (b)图,故原体系是几何可变体系。
( )(7) 习题2.1(6)(a)图所示体系去掉二元体EDF后,成为习题2.1(6) (c)图,故原体系是几何可变体系。
()(a)(b)(c)习题2.1(6)图习题2.2填空(1) 习题2.2(1)图所示体系为_________体系。
习题2.2(1)图(2) 习题2.2(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题2.2(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题2.2(3)图(4) 习题2.2(4)图所示体系的多余约束个数为___________。
习题 2.2(4)图(5) 习题2.2(5)图所示体系的多余约束个数为___________。
习题 2.2(5)图(6) 习题2.2(6)图所示体系为_________体系,有_________个多余约束。
习题 2.2(6)图(7) 习题2.2(7)图所示体系为_________体系,有_________个多余约束。
习题 2.2(7)图习题2.3 对习题2.3图所示各体系进行几何组成分析。
(a)(b)(c)(d)(e)(f)(h)(g)(i)(j)(k)(l)习题2.3图第3章 静定梁与静定刚架习题解答习题3.1 是非判断题(1) 在使用力图特征绘制某受弯杆段的弯矩图时,必须先求出该杆段两端的端弯矩。
结构力学第四版习题及答案

结构力学第四版习题及答案习题1:一个弹簧的刚度系数为k,长度为L,在其两端分别施加力F1和
F2,求弹簧的形变量。
答案:根据胡克定律,弹簧的形变量与施加的力成正比,即x = (F1 - F2) / k。
习题2:一个悬臂梁的长度为L,截面为矩形,宽度为b,高度为h,材料的弹性模量为E,梁上的集中力为P,求梁的最大弯矩。
答案:悬臂梁的最大弯矩发生在集中力作用点,即Mmax = P * L。
习题3:一根悬臂梁的长度为L,截面为矩形,宽度为b,高度为h,材料的弹性模量为E,梁上均匀分布的荷载为q,求梁的最大挠度。
答案:悬臂梁的最大挠度发生在梁的自由端,即δmax = (5qL^4) /
(384Ebh^3)。
习题4:一根梁上有两个集中力,分别为P1和P2,作用点距离为a,梁的长度为L,求梁的反力。
答案:根据力的平衡条件,可以得到反力F1和F2的表达式: F1 = (P1 * a + P2 * L) / L F2 = (P1 * (L - a) + P2 * L) / L
习题5:一根悬臂梁的长度为L,截面为矩形,宽度为b,高度为h,材料的弹性模量为E,梁上均匀分布的荷载为q,求梁的最大剪力。
答案:悬臂梁的最大剪力发生在梁的支点处,即Vmax = qL / 2。
《结构力学》习题解答(内含解答图)

习题2-13试对图示体系进行几何组成分析。
习题2-13图习题2-13解答图
解:将原图结点进行编号,并将支座6换为单铰,如图(b)。取基础为刚片Ⅰ,△134为刚片Ⅱ,△235为刚片Ⅲ,由规则一知,三刚片用三个不共线的铰联结组成几何不变体。在此基础上增加二元体674、785,而杆38看作多余约束。杆910由铰联结着链杆10,可看作二元体,则整个体系为有一个多余约束的几何不变体系。
习题2-7试对图示体系进行几何组成分析。
习题2-7图习题2-7解答图
解:将题中的折杆用直杆代替,如图(b)所示。杆CD和链杆1由铰D联结构成二元体可以去掉;同理,去掉二元体杆CE和链杆2,去掉二元体ACB,则只剩下基础,故整个体系为几何不变体系,且无多余约束。
另外也可用基础与杆AC、杆BC是由不共线的三个铰联结,组成几何不变体,在此几何不变体上增加二元体杆CD和链杆1、杆CE和链杆2的方法分析。,
习题2-8试对图示体系进行几何组成分析。
习题2-8图习题2-8解答图
解:为了便于分析,对图中的链杆和刚片进行编号,分析过程见图2-21(b)。首先去掉二元体NMI、JNI,然后分析剩余部分。杆AD由固定支撑与基础联结形成一体,构成几何不变体,在此基础上增加二元体DEB、EFC、EHF形成刚片Ⅰ(注意固定铰支座与铰相同);铰结△GIJ为刚片Ⅱ;刚片I与刚片Ⅱ之间用不交于一点的杆DI、杆GI、杆HJ相连,组成几何不变体。
习题2-18试对图示体系进行几何组成分析。
解:将原图结点进行编号,并将固定铰支座换为单铰,如图(b)。折杆AD上联结杆EF,从几何组成来说是多余约束;同理,折杆CD上联结杆EF也是多余约束。取基础为刚片Ⅰ,折杆AD为刚片Ⅱ,折杆CD为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由链杆A和杆BD相连,刚片Ⅰ与刚片Ⅲ是由链杆C相连,注意,杆BD只能使用一次。由规则二知,体系为几何可变体系。
《结构力学》试题及答案
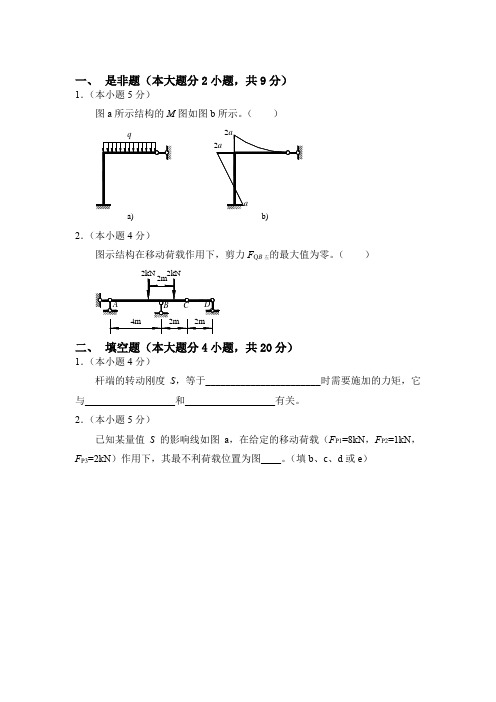
一、 是非题(本大题分2小题,共9分)1.(本小题5分)图a 所示结构的M 图如图b 所示。
( )2.(本小题4分)图示结构在移动荷载作用下,剪力F Q B 左的最大值为零。
( )二、 填空题(本大题分4小题,共20分)1.(本小题4分)杆端的转动刚度S ,等于_______________________时需要施加的力矩,它与__________________和__________________有关。
2.(本小题5分)已知某量值S 的影响线如图a ,在给定的移动荷载(F P1=8kN ,F P2=1kN ,F P3=2kN )作用下,其最不利荷载位置为图____。
(填b 、c 、d 或e )qa)b)3.(本小题6分)图示结构A 截面的剪力为________。
4.(本小题5分)图示桁架c 杆的轴力F N c =____。
P1F P2F P3F F P3P2F F P1F FFF F F F F F P2P3P1b)c)d)e)a)三、 (本大题6分)试选择图示对称结构在图示荷载作用下,用力法计算时的最优基本体系。
四、 (本大题5分)试分析图示体系的几何组成。
五、 (本大题6分)试确定图示结构位移法基本未知量数目和基本结构,两根链杆a 和b 需考虑轴向变形。
六、 (本大题10分)图示结构左支座B 向左移动1cm ,右支座D 向下移动2cm ,试求铰A 的竖向位移。
七、 (本大题14分)用位移法作图示结构M 图,横梁刚度EA →∞,两柱线刚度i 相同。
八、 (本大题16分)试写出用力法计算图示结构的典型方程(采用右图所示基本体系),并求出方程中的全部系数和自由项(不求解方程)。
已知各杆EI =常数。
24九、 (本大题14分)用力矩分配法计算图示结构(可利用对称性),并作弯矩图。
已知各杆EI =常数。
十、 是非题(本大题分2小题,共9分)1.(本小题5分)图a 所示结构的M 图如图b 所示。
(√)2.(本小题4分)图示结构在移动荷载作用下,剪力F Q B 左的最大值为零。
《结构力学》典型习题与解答-知识归纳整理

《结构力学》经典习题及详解一、判断题(将判断结果填入括弧内,以 √表示正确 ,以 × 表示错误。
)1.图示桁架结构中有3个杆件轴力为0 。
(×)2.图示悬臂梁截面A 的弯矩值是ql 2。
(×)l lqA3.静定多跨梁中基本部分、附属部分的划分与所承受的荷载无关。
(√ ) 4.普通来说静定多跨梁的计算是先计算基本部分后计算附属部分。
(× ) 5.用平衡条件能求出全部内力的结构是静定结构。
( √ )6.求桁架内力时截面法所截取的隔离体包含两个或两个以上的结点。
(√ ) 7.超静定结构的力法基本结构不是唯一的。
(√)8.在桁架结构中,杆件内力不是惟独轴力。
(×) 9.超静定结构由于支座位移可以产生内力。
(√ ) 10.超静定结构的内力与材料的性质无关。
(× ) 11.力法典型方程的等号右端项不一定为0。
(√ )12.计算超静定结构的位移时,虚设力状态可以在力法的基本结构上设。
(√)13.用力矩分配法计算结构时,汇交于每一结点各杆端分配系数总和为1,则表明分配系数的计算无错误。
(× )14.力矩分配法适用于所有超静定结构的计算。
(×) 15.当AB 杆件刚度系数i S AB3 时,杆件的B 端为定向支座。
(×)F P知识归纳整理二、单项挑选题(在每小题的四个备选答案中选出一具正确答案,并将其代号填在题干后面的括号内。
不选、错选或多选者,该题无分。
) 1.图示简支梁中间截面的弯矩为( A )qlA . 82qlB . 42ql C . 22ql D . 2ql2.超静定结构在荷载作用下产生的内力与刚度(B )A . 无关B . 相对值有关C . 绝对值有关D . 相对值绝对值都有关 3.超静定结构的超静定次数等于结构中(B )A .约束的数目B .多余约束的数目C .结点数D .杆件数4.力法典型方程是根据以下哪个条件得到的(C )。
(完整版)结构力学-习题集(含答案)
A.绝对不可; B.可以,但不必; C.一定条件下可以; D.必须。
33. 计算刚架时,位移法的基本结构是( C )。
A.单跨静定梁的集合体;
B.静定刚架;
C.单跨超静定梁的集合体; D.超静定铰结体。
34. 在位移法基本方程中,kij 代表( A )。
A.只有⊿j=1 时,由于⊿j=1 在附加约束 i 处产生的约束力;
54. 下图所示结构的超静定次数是 n=8。( X )
55. 超静定结构在荷载作用下的内力计算与各杆刚度相对值有关。( √ ) 56. 超静定结构在支座移动、温度变化影响下会产生内力。( √ ) 57. 超静定结构中的杆端力矩只取决于杆端位移。( X ) 58. 位移法的基本结构有多种选择。( X ) 59. 位移法是计算超静定结构的基本方法,不能求解静定结构。( X ) 60. 位移法方程的物理意义是结点位移的变形协调方程。( X )
由
Fy
0
, FRB
FRA
FP 2
( )(1
分)
取 BE 部分为隔离体
ME
0 , 6FyB
6FRB
即 FyB
FP 2
( )(2 分)
由
Fx
0
得
FyA
FP 2
(
)(1
分)
三、计算题 1 61. 解:
第 14 页 共 26 页
2qa2/3
q
D 2qa2/3 C
2qa2/3
B q(2a)2/8 = qa2/2
FxB
FxA A
FyB
FyA
取整体为研究对象,由 M A 0,得
2aFyB aFxB 2qa2 0 (1)(2 分)
取 BC 部分为研究对象,由 MC 0 ,得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结构力学习题第2章平面体系的几何组成分析2-1~2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7~2-15 试对图示体系进行几何组成分析。
若是具有多余约束的几何不变体系,则需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-1 1=W2-1 9-W=2-3 3-W=2-4 2-=W2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
(a)(b)(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
(a)(b)(c)习题3-2图3-3~3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定结构的弯矩图是否正确。
(a)(b)(c)(d)部分习题答案3-1 (a )m kN M B ⋅=80(上侧受拉),kN F RQB 60=,kN F L QB 60-=(b )m kN M A ⋅=20(上侧受拉),m kN M B ⋅=40(上侧受拉),kN F RQA 5.32=,kN F L QA 20-=,kN F LQB 5.47-=,kN F R QB 20=(c) 4Fl M C =(下侧受拉),θcos 2F F L QC =3-2 (a) 0=E M ,m kN M F ⋅-=40(上侧受拉),m kN M B ⋅-=120(上侧受拉)(b )m kN M RH ⋅-=15(上侧受拉),m kN M E ⋅=25.11(下侧受拉)(c )m kN M G ⋅=29(下侧受拉),m kN M D ⋅-=5.8(上侧受拉),m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10(左侧受拉),m kN M DF ⋅=8(上侧受拉),m kN M DE ⋅=20(右侧受拉) 3-4 m kN M BA ⋅=120(左侧受拉)3-5 m kN M F ⋅=40(左侧受拉),m kN M DC ⋅=160(上侧受拉),m kN M EB ⋅=80(右侧受拉)3-6 m kN M BA ⋅=60(右侧受拉),m kN M BD ⋅=45(上侧受拉),kN F QBD 46.28=3-7 m kN M C ⋅=70下(左侧受拉),m kN M DE ⋅=150(上侧受拉),m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0(上侧受拉),m kN M BA ⋅=36.0(右侧受拉) 3-9 m kN M AB ⋅=10(左侧受拉),m kN M BC ⋅=10(上侧受拉) 3-10 (a )错误 (b )错误 (c )错误 (d )正确第4章 静定平面桁架和组合结构的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
(a )习题4-1图4-2 试用结点法求习题4-2图所示桁架各杆的内力。
(a)(b)F=30kNy120kN20kN20kN6×3m=18m4m3246577F=0x1F=30kNy1(c)习题4-2图4-3 试用截面法计算习题4-3图所示桁架中指GJ、GH和EH杆件的内力。
习题4-3图4-4 试用比较简便的方法计算习题4-4图所示桁架中指定杆件的内力。
(a)(b)(c )习题4-4图4-5 试作习题4-5图所示组合结构中梁式杆件的弯矩图,并求桁架杆的轴力。
(a )(b )习题4-5图部分习题答案4-1 (a )杆JK 、JE 、FE 、HE 、HG 、EG 、GB 为零杆 4-2 (a )KN F N 451= (b)KNF NAB 45-=KN F NAC 120-=KN F NBC 75=KN F NBD 60=KN F NCE 50-= KN F NCD 0=KN F NCF 20-= KN F NDE 60= KN F NEF 15=KN F NEG 25= KN F NFG 20-=(c)KNF N 5.3712-=KN F N 5.2213=KN F N 5.1223=KN F N 3024-=KN F N 5.1234-= KN F N 5.3735= 由于结构和荷载的对称性右半部分中桁架杆的轴力与左半部分一样。
4-3 KN F NGJ 30-= KN F NGH 5.22-= KN F EH 30= 4-4 (a )KN F Na 62.45-= KN F Nb 53.19-= KN F Nc 60=(b )KN F N 451= KN F N 36.352-= KN F N 28.283= (c )KN F Na 40= KN F Na 20= KN F Na 89.17-=4-5 (a )KN F N 21.2121-= KN F C N 21.212-= KN F N 023= KN F C N 5.73= 由于结构和荷载的对称性右半部分中桁架杆的轴力与左半部分一样。
第五章 三铰拱的内力分析5-1 图示三铰拱的轴线方程为)(42x l x l fy -= (1)试求支座反力(2)试求集中荷载作用处截面D 的内力习题5-1图5-2 利用三铰拱的内力和反力计算公式,试计算如下图所示三铰刚架的支座反力及截面E 的内力。
习题5-2图5-3试求图示圆弧三铰拱,求支座反力及截面D 的内力。
习题5-3图5-4 已知图示三铰拱的拱轴线方程为()x l x lfy -=24 (1)求水平推力(2)求C 铰处的剪力和轴力(3)求集中力作用处轴线切线与水平轴的夹角。
习题5-4图5-5试求习题5-5图所示三铰拱的合理拱轴线方程,并绘出合理拱轴线图形。
习题5-5图答案5-1 KNFVA5.9=KNFVB5.8=mKNMD.11=KNFQD47.4=左KNFQD47.4=右KNFND29.12=左KNFND82.7=右5-2 KNFVA21=KNFVB29=mKNMD.6=KNFQD1=左KNFQD88.0-=右KNFND20-=左KNFND22.35-=右5-3 KNFFVBVA100==mKNMD.29-=KNFQD3.18=KNFND3.68-=5-4 (1)KNFH6=(2)KN F QC 1-= KN F NC 6-= (3) -26.34º5-5 250441648413224881282x x m y x m x m x x m x m ⎧≤≤⎪⎪⎪=-+≤≤⎨⎪⎪⎛⎫-+-≤≤ ⎪⎪⎝⎭⎩第6章 静定结构的位移计算6-1~6-6 试用位移计算公式计算图示结构中指定截面的位移。
设EI 、EA 为常数。
习题 6-1求图 A CV θ∆、习题 6-2图求A CV θ∆、习题 6.3图 求CV ∆F P习题 6.4图 求A CV θ∆、l/2R1.5RRFP习题 6-5图 求A CV θ∆、习题 6-6图 求CV ∆6-7~6-10 试用图乘法计算图示结构中指定截面的位移。
习题 6-7图-求C CH DH θ∆∆、、q3m3m3m习题 6-8图求B DH θ∆、习题 6-10图 求CV ∆习题 6-9图 求BH EV ∆∆、6-11 试用图乘法计算图示梁C 截面的竖向位移ΔCV 。
已知 。
习题 6-11图6-12 试求图示结构C 截面的竖向位移和铰D 两侧截面的相对角位移。
设EI 为常数。
qll/3l/32l/3习题 6-12图6-13 试求图示结构C 截面的竖向位移。
,,22412/101.2cm A cm kN E =⨯=。
43600cm I =25105.1m kN EI ⋅⨯=10kN/m习题 6-13图6-14 梁AB 下面加热t ℃,其它部分温度不变,试求C 、D 两点的水平相对位移。
设梁截面为矩形,高为h ,材料的线膨胀系数为α。
习题 6-14图6-15 图示刚架各杆截面为矩形,截面高度为h 。
设其内部温度增加20℃,外部增加10℃,材料的线膨胀系数为α。
试求B 点的水平位移。
习题 6-15图6-16 图示桁架其支座B 有竖向沉降c ,试求杆BC 的转角。
习题 6-16图6.17 图示梁,支座B 下沉c ,试求E 端的竖向线位移EV ∆和角位移E θ。
l l/2l/2l/4习题6-17图部分习题答案6-1 6-2 6-3 6-4 6-5 6-6 6-7 6-8 6-9 6-10 6-11)(48)(1632↓=∆=EIlFEIlFPCVPAθ)(16)(32↓=∆=EIMlEIMlCVAθ)(384174↓=∆EIqlCV)(8)(1232↓=∆=EIlFEIlFPCVPAθ))(234()(2532↓+=∆=πθEIRFEIRFPCVPA)()246(↓+=∆PCVFEA)(6)(3)(622→=∆→=∆=EIMaEIMaEIMaDHCHAθ)(123)(8153→=∆=EIqEIqBHBθ)(4860)(11340↓=∆←=∆EIEI EVBH)(61985↓=∆EIBV0.0013()CVm∆=↓6-126-136-146-156-166-17第7章 力法7-1 试确定下列结构的超静定次数。
)(4327)(48543'↑=∆=EIql EIql CVDDθ)(0247.0↓=∆mCV 1)()2H C D l tl h α-∆=-→←)(360→=∆hBH α)(2a cBC =θ33()()4E EV c c lθ=∆=↑(a)(b)(c)(d)(e)(f)7-2 试用力法计算图示超静定梁,并绘出M、F Q图。
(a)qAl l l(b)习题7-2图7-3 试用力法计算图示刚架结构,并绘M图。
Bl l(a)(b)q10m2.5mCl2.5m(c)EI=常数(d)EI=常数(e)EI=常数习题7-3图7-4 试用力法计算图(a)桁架的轴力以及图(b)指定杆件1、2杆的轴力,各杆EA=常数。
(a )(b )习题 7-4图7-5 试用力法计算图示排架,并作M 图。
12m6m习题 7-5图7-6 试计算图示组合结构各链杆的轴力,并绘横梁AB 的弯矩图。
设各链杆的EA 均相同,16IA。
习题 7-6图7-7 试利用对称性计算图示结构,并作弯矩图。
