例题解答与作业

第三章 PLC例题作业解答

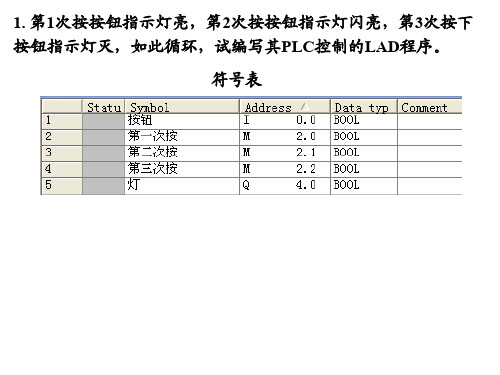
1. 第1次按按钮指示灯亮，第2次按按钮指示灯闪亮，第3次按下按钮指示灯灭，如此循环，试编写其PLC控制的LAD程序。符号表
2. 用一个按钮控制2盏灯，第1次按下时第1盏灯亮，第2盏灯灭；第2次按下时第1盏灯灭，第2盏灯亮；第3次按下时2盏灯都灭。
3. 编写PLC控制程序，使Q4.0输出周期为5s，。鼓风机系统一般有引风机和鼓风机两级构成。要求：（1).按下起动按钮后首先起动引风机，引风机指示灯亮， 10s后鼓风机自动起动，鼓风机指示灯亮；按下停止按钮后首先关断鼓风机，鼓风机指示灯灭，经20s后自动关断引风机和引风机指示灯。 (2).起动按钮接I0.0，停止按钮接I0.1。鼓风机及其指示由 Q4.1和Q4.2驱动，引风机及其指示由Q4.3和Q4.4驱动。
符号表
5. 某设备有3台风机，当设备处于运行状态时，如果有2台或2 台以上风机工作，则指示灯常亮，指示“正常”；如果仅有1台风机工作，则该指示灯以0.5Hz的频率闪烁，指示“一级报警”；如果没有风机工作了，则指示灯以2Hz的频率闪烁，指示“严重警报”。当设备不运转时，指示灯不亮。试用STL及LAD编写符合要求的控制程序。提示：本题要点是如何实现“一灯多用”功能。指示灯指示了4种状态：“正常、一级报警、严重警报、设备停止”。

建筑结构作业解答

1.已知某矩形截面梁b ×h ＝250 mm ×500mm ，由荷载产生的弯矩设计值M ＝88.13kN·m，混凝土强度等级为C20，钢筋采用HRB335级, 试求所需纵向受拉钢筋截面面积A s 。

解：查表得：f c =9.6N/mm2，f t =1.1N/mm2,； f y =300N/mm2；ξb =0.55；截面有效高度h 。

＝500-40＝460mm1.直接公式求解X 根据基本公式可推导出求解X 的公式如下：2.计算受拉钢筋面积将x 代入下式，受拉钢筋的截面面积为：3.验算条件最小配筋率经过计算比较取ρ min ＝0.2%A S=704mm2 由以上验算，截面符合适要求。

4.选配钢筋选用2Φ18+1Φ16（A s=710mm2）一排钢筋所需要的最小宽度为： b min =4×25+2×18+1×16=152mm ＜250mmmm 25346055.0mm 882506.90.188130000246046020b 2c 1200=⨯=<=⨯⨯⨯--=--=h bf Mh h x ξα2yc 1s mm 704300882506.90.1=⨯⨯⨯==f bxf A α<=⨯⨯=ρ2minmm 250500250002.0bh2.某钢筋混凝土矩形截面简支梁，跨中弯矩设计值M=80kN·m，梁的截面尺寸b×h=200×450mm，采用C25级混凝土，HRB400级钢筋。

试确定跨中截面纵向受力钢筋的数量。

【解】查表得f c=11.9 N/mm2，f t=1.27 N/mm2，f y=360 N/mm2，α1=1.0，ξb=0.5181.确定截面有效高度h0假设纵向受力钢筋为单层，则h0=h-35=450-35=415mm2.计算x，并判断是否为超筋梁==91.0mm＜=0.518×415=215.0mm不属超筋梁。

材料科学基础第1-2章例题、作业题及其解答

第2章例题（A ）1. 在面心立方晶胞中画出[012]和[123]晶向。

2. 在面心立方晶胞中画出（012）和（123）晶面。

3. 右图中所画晶面的晶面指数是多少？4. 设晶面（152）和（034）属六方晶系的正交坐标表述，试给出其四轴坐标的表示。

反之，求（3121）及（2112）的正交坐标的表示。

5. （练习），上题中均改为相应晶向指数，求相互转换后结果。

答案：2. (2110) 4. （1562），（0334） 5. [1322] [1214] （123）（212）[033] [302]第2章例题答案(A)4. （152） )2615(6)51()(⇒-=+-=+-=v u t（034） )4303(3)30()(⇒-=+-=+-=v u t（1213） ⇒ （123）（2112） ⇒ （212）5. [152] ]2231[22)51(31)(313)152(31)2(311)512(31)2(31⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==-=+-=+-==-⨯=-=-=-⨯=-=W w V U t U V v V U u [034] ]4121[41)30(31)(312)032(31)2(311)302(31)2(31⇒⎪⎪⎪⎭⎪⎪⎪⎬⎫==-=+-=+-==-⨯=-=-=-⨯=-=W w V U t U V v V U u]3121[]033[33)1(20)1(1⇒⎪⎭⎪⎬⎫===--=-==---=-=w W t v V t u U [2112]]302[20)1(13)1(2⇒⎪⎭⎪⎬⎫===---=-==--=-=w W t v V t u U第2章例题（B ）1. 已知Cu 的原子直径为2.56A ，求Cu 的晶格常数，并计算1mm 3Cu 的原子数。

2. 已知Al 相对原子质量Ar （Al ）=26.97，原子半径γ=0.143nm ，求Al 晶体的密度。

3. bcc 铁的单位晶胞体积，在912℃时是0.02464nm 3；fcc 铁在相同温度时其单位晶胞体积是0.0486nm 3。

平移典型例题及练习含答案

平移一、知识点复习知识点1：平移的定义：在平面内，一个图形沿某个方向移动一定的距离，这种图形的变换叫做平移。

知识点2：平移的要素1.平移的方向：原图上的点指向它的对应点的射线方向；2.平移的距离：连接原图与平移后图形上的一对对应点的线段的长度。

知识点3：平移的性质1.性质（1）平移只改变图形的位置，不改变图形的形状和大小。

（2）平移后的图形与原图形上对应点连成的线段，①数量关系是相等 .②位置关系是平行或在同一条直线上。

2.判断一组图形能不能通过平移得到的方法（1）看对应点连线是否平行或在同一条直线上；（2）看它的形状、大小是否发生变化，位置的变化是否由平移产生。

★★★特别注意：平移是由平移的方向和距离决定的，平移必须指明平移的方向和距离；平移是在平面内，整个图形沿着某一直线平行移动的过程，原图上的每个点都沿同一方向移动相同的距离；平移的距离不能为0；平移的方向是任意的，但就一次平移而言，只能有一个方向，一次平移完成后可以改变方向进行下一次平移。

二、典型例题题型1：生活中平移现象【例题1】（2017春•乌海期末）下列运动属于平移的是（）A．荡秋千 B．推开教室的门 C．风筝在空中随风飘动 D．急刹车时，汽车在地面上的滑动【例题2】：（2016春•淮安期中）下列现象：①电梯的升降运动，②飞机在地面上沿直线滑行，③风车的转动，④冷水加热过程中气泡的上升．其中属于平移的是（）A．①② B．①③ C．②③ D．③④题型2：平移的性质【例题4】：（2016春•沧州期末）在下列说法中：①△ABC在平移过程中，对应线段一定相等；②△ABC 在平移过程中，对应线段一定平行；③△ABC在平移过程中，周长保持不变；④△ABC在平移过程中，对应边中点所连线段的长等于平移的距离；⑤△ABC在平移过程中，面积不变，其中正确的有（）A．①②③④ B．①②③④⑤ C．①②③⑤ D．①③④⑤题型3：与平移有关的计算【例题5】：（2015春•石家庄期末）如图，将△ABC沿射线BC方向移动，使点B移动到点C，得到△DCE，连接AE，若△ABC的面积为2，则△ACE的面积为（）A．2 B．4 C．8 D．16【例题6】：（2017秋•兴化市期末）如图，将△ABE向右平移2cm得到△DCF，AE、DC交于点G．如果△ABE 的周长是16cm，那么△ADG与△CEG的周长之和是 cm。

小学数学环形跑道问题教案例题+练习+作业带答案

环形跑到问题1、知识点总结（1）环形跑道问题同一地点出发，如果是相向而行，则每合走一圈相遇一次（2）环形跑道问题同一地点出发，如果是同向而行，则每追上一圈相遇一次2、遇见多人多次相遇、追及能够借助线段图进行分析3、用比例解、数论等知识解环形跑道问题【例题1】一个圆形操场跑道的周长是500米，两个学生同时同地背向而行．黄莺每分钟走66米，麻雀每分钟走59米．经过几分钟才能相遇?黄莺和麻雀每分钟共行66+59=125（千米），那么周长跑道里有几个125米，就需要几分钟，即500÷（66+59）=4（分钟）．【巩固】小张和小王各以一定速度，在周长为500米的环形跑道上跑步．小王的速度是200米/分．⑴小张和小王同时从同一地点出发，反向跑步，1分钟后两人第一次相遇，小张的速度是多少米/分？⑵小张和小王同时从同一点出发，同一方向跑步，小张跑多少圈后才能第一次追上小王？⑴两人相遇，也就是合起来跑了一个周长的行程．小张的速度是500÷1-200=300（米/分）．⑵在环形的跑道上，小张要追上小王，就是小张比小王多跑一圈（一个周长），因此需要的时间是：500÷（300-200）=5（分）．300×5÷500=3（圈）．【例题2】上海小学有一长300米长的环形跑道，小亚和小胖同时从起跑线起跑，小亚每秒钟跑6米，小胖每秒钟跑4米，（1）小亚第一次追上小胖时两人各跑了多少米？（2）小亚第二次追上小胖两人各跑了多少圈？第一次追上时，小亚多跑了一圈，所以需要300÷（6-4）=150秒，小亚跑了6×150=900（米）。

小胖跑了4×150=600（米）；第一次追上时，小胖跑了2圈，小亚跑了3圈，所以第二次追上时，小胖跑4圈，小亚跑6圈。

【巩固】一条环形跑道长400米，甲骑自行车每分钟骑450米，乙跑步每分钟250米，两人同时从同地同向出发，经过多少分钟两人相遇？400÷（450-250）=2(分钟)．【例题3】在300米的环形跑道上，田奇和王强同学同时同地起跑，如果同向而跑2分30秒相遇，如果背向而跑则半分钟相遇，求两人的速度各是多少？同向而跑，这实质是快追慢．起跑后，由于两人速度的差异，造成两人路程上的差异，随着时间的增长，两人间的距离不断拉大，到两人相距环形跑道的半圈时，相距最大．接着，两人的距离又逐渐缩小，直到快的追上慢的，此时快的比慢的多跑了一圈．背向而跑即所谓的相遇问题，数量关系为：路程和÷速度和=相遇时间．同向而行2分30秒相遇，2分30秒＝150秒，两个人的速度和为：300÷150=2（米/秒），背向而跑则半分钟即30秒相遇，所以两个人的速度差为：300÷30=10（米/秒）.两人的速度分别为：（10-2）÷2=4(米/秒)， 10-4=6(米/秒)【巩固】在400米的环形跑道上，甲、乙两人同时同地起跑，如果同向而行3分20秒相遇，如果背向而行40秒相遇，已知甲比乙快，求甲、乙的速度各是多少？甲乙的速度和为：400÷40=10(米/秒)，甲乙的速度差为：400÷200=2(米/秒)，甲的速度为：（10+2）÷2=6(米/秒)，乙的速度为：（10-2）÷2=4(米/秒)．【例题4】两人在环形跑道上跑步，两人从同一地点出发，小明每秒跑3米，小雅每秒跑4米，反向而行，45秒后两人相遇。

趋势预测法例题参考及作业

例题1：某公司近五年的销售额数据如下：年份 | 销售额（万元）|2018 | 5002019 | 5502020 | 6002021 | 6502022 | 700解答思路：1. 计算销售额的平均增长率：计算每年的销售额增长量，然后求出这五年销售额增长量的平均值，即为平均增长率。

2. 预测2023年的销售额：根据平均增长率，计算2023年的销售额。

作业1：某学校近五年的学生人数数据如下：年份 | 学生人数|2018 | 10002019 | 10502020 | 11002021 | 11502022 | 1200例题2：某城市近五年的房价数据如下：年份 | 房价（元/平方米）|2018 | 100002019 | 110002020 | 120002021 | 130002022 | 14000解答思路：1. 计算房价的平均增长率：计算每年的房价增长量，然后求出这五年房价增长量的平均值，即为平均增长率。

2. 预测2023年的房价：根据平均增长率，计算2023年的房价。

作业2：某地区的居民收入数据如下：年份 | 居民收入（元/人）|2018 | 200002019 | 210002020 | 220002021 | 230002022 | 24000例题3：某电商平台的月销售额数据如下：月份 | 销售额（万元）|1月 | 3002月 | 3203月 | 3404月 | 3605月 | 380解答思路：1. 计算销售额的平均增长率：计算每个月的销售额增长量，然后求出这五个月销售额增长量的平均值，即为平均增长率。

2. 预测6月的销售额：根据平均增长率，计算6月的销售额。

作业3：某超市的月销售量数据如下：月份 | 销售量（件）|1月 | 10002月 | 11003月 | 12004月 | 13005月 | 1400。

平面直角坐标系典型例题含答案及解析

平面直角坐标系一、知识点复习1.有序数对：有顺序的两个数a 与b 组成的数对，记作),(b a 。

注意a 与b 的先后顺序对位置的影响。

2.平面直角坐标系（1）定义：在同一平面内画两条相互垂直并且原点重合的数轴，组成平面直角坐标系。

这个平面叫做坐标平面。

（2）平面直角坐标系中点的坐标：通常若平面直角坐标系中有一点A ，过点A 作横轴的垂线，垂足在横轴上的坐标为a ，过点A 作纵轴的垂线，垂足在纵轴上的坐标为b ，有序实数对),(b a 叫做点A 的坐标，其中a 叫横坐标，b 叫做纵坐标。

3.各象限内的点与坐标轴上的点的坐标特征：4. 特殊位置点的特殊坐标5.对称点的坐标特征：6.点到坐标轴的距离：点)P到X轴距离为y，到y轴的距离为x。

x,(y7.点的平移坐标变化规律：简单记为“左减右加，上加下减”二、典型例题讲解考点1：点的坐标与象限的关系1．在平面直角坐标系中，点P （-2，3）在第（）象限． A ．一 B ．二 C ．三 D ．四2.若点)2,(-a a P 在第四象限，则a 的取值范围是（）A. 02<<-aB.20<<aC.2>aD.0<a 3.在平面直角坐标系中，点P （-2，12+x ）所在的象限是（） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限考点2：点在坐标轴上的特点1.点)1,3(++m m P 在x 轴上，则P 点坐标为（） A ．)2,0(- B.)0,2( C.)0,4( D.)4,0(-2.已知点)12,(-m m P 在y 轴上，则P 点的坐标是。

3.若点P （x ，y ）的坐标满足xy=0（x ≠y ），则点P 必在（） A ．原点上 B ．x 轴上 C ．y 轴上 D ．x 轴上或y 轴上（除原点）考点3：对称点的坐标1.平面直角坐标系中，与点)3,2(-关于原点中心对称的点是（） A.)2,3(- B.)2,3(- C.)3,2(- D.（2,3）2.已知点A 的坐标为（-2，3），点B 与点A 关于x 轴对称，点C 与点B 关于y 轴对称，则点C 关于x 轴对称的点的坐标为（）A ．（2，-3）B ．（-2，3）C ．（2，3）D ．（-2，-3） 3.若坐标平面上点P （a ，1）与点Q （-4，b ）关于x 轴对称，则（） A ．a=4，b=-1 B ．a=-4，b=1 C ．a=-4，b=-1 D ．a=4，b=1 考点4：点的平移1.已知点A （-2，4），将点A 往上平移2个单位长度，再往左平移3个单位长度得到点A ′，则点A ′的坐标是（）A ．（-5，6）B ．（1，2）C ．（1，6）D ．（-5，2）2．已知A （2，3），其关于x 轴的对称点是B ，B 关于y 轴对称点是C ，那么相当于将A 经过（）的平移到了C ．A ．向左平移4个单位，再向上平移6个单位B ．向左平移4个单位，再向下平移6个单位C ．向右平移4个单位，再向上平移6个单位D ．向下平移6个单位，再向右平移4个单位3．如图，A，B的坐标为（2，0），（0，1），若将线段AB平移至A1B1，则a+b的值为（）A．2 B．3 C．4 D．5考点5：点到坐标轴的距离考点6：平行于x轴或y轴的直线的特点1.如图，AD∥BC∥x轴，下列说法正确的是（）A．A与D的横坐标相同 B．C与D的横坐标相同C．B与C的纵坐标相同 D．B与D的纵坐标相同2.已知点A（m+1，-2）和点B（3，m-1），若直线AB∥x轴，则m的值为（）A．2 B．-4 C．-1 D．33.已知点M（-2，3），线段MN=3，且MN∥y轴，则点N的坐标是（）A.（-2，0） B．（1，3）C．（1，3）或（-5，3） D．（-2，0）或（-2，6）考点7：角平分线的理解1．已知点A（3a+5，a-3）在二、四象限的角平分线上，则a= .考点8：特定条件下点的坐标1．如图，已知棋子“车”的坐标为（﹣2，3），棋子“马”的坐标为（1，3），则棋子“炮”的坐标为（）A．（3，2）B．（3，1）C．（2，2）D．（﹣2，2）考点9：面积的求法（割补法）1.（1）在平面直角坐标系中，描出下列3个点：A（-1，0），B（3，-1），C（4，3）；（ 2）顺次连接A，B，C，组成△ABC，求△ABC的面积．参考答案：（1）略（2）8.52.如图，在四边形ABCD中，A、B、C、D的四个点的坐标分别为（0，2）（1，0）（6，2）（2，4），求四边形ABCD的面积．3.在图中A（2，-4）、B（4，-3）、C（5，0），求四边形ABCO的面积．考点10：根据坐标或面积的特点求未知点的坐标1.已知A （a ，0）和B 点（0，10）两点，且AB 与坐标轴围成的三角形的面积等于20，则a 的值为（）A ．2B ．4C ．0或4D ．4或-4 2.如图，已知：)4,5(-A 、)2,2(--B 、)2,0(C 。

五上数学小数除法应用题训练例题+课后作业

五年级上学期小数除法应用题题型训练知识点总结：1、进一法：将结果中小数部分舍去，向各位进一2、去尾法：将结果中小数部分舍去3、注意：根据实际情况会用“进一法”或“去尾法”取商的近似数例题讲解：例1、平均数问题（1）张爷爷跑2.5千米用20分钟，他平均跑1千米需要（）分钟，平均每分钟跑（）千米。

（2）幼儿园把 1.25 千克的糖果平均分给 5 个小朋友，每小朋友分得（）千克。

（3）一辆汽车 2.4 小时行驶 60 千米，1 小时行驶（）千米，行驶 1 千米需要（）小时。

（4）一台拖拉机 0.75 小时耕地 60 公顷，1 小时耕地（）公顷，耕 1 公顷地需要（）小时。

演练1、练一练（1）5吨菜籽可以榨油 4 吨，榨 1 吨油需要（）吨菜籽，每吨菜籽可以榨（）吨油。

（2）一群小朋友去游乐场玩，他们玩激流勇进一共花了52.5元，玩碰碰车一共花了79.5元。

激流勇进每人3.5元，碰碰车每人多少钱？例2、货币兑换问题2018年2月27日，中国银行外汇牌价如下图，在这一天里：（1）100元人民币可以兑换多少港币？（保留两位小数）（2）一个书包标价3.9美元，100元人民币可以买几个？演练2、货币兑换问题下面是2018年2月5日的中国银行外汇牌价。

（单位：元）在这一天里：（1）200元人民币可以兑换多少美元?（结果保留两位小数)（2）同一款苹果手机在英国标价510英镑，在香港标价5288港元。

哪儿的标价低？（3）一个文具盒标价3.4美元，用100元人民币可以买几个?例3、分段计费问题王阿姨给在外省读大学的女儿寄衣服，衣服重26kg，需要付多少元快递费？演练3、分段计费问题为了鼓励市民节约用电，某市电力公司规定了以下的电费计算办法。

李阿姨家十一月份缴电费61.6元，她家十一月份用电多少千瓦时?例4、比一比打电话时，国内长途每分钟0.7元，国际长途每小时7.2元，小明打国际长途用了27.36元，小丽打国内长途用了6.86元，算一算，他们谁打电话的时间长一些。

三年级下学期数学位置与方向例题+课后作业带答案

三年级下学期位置与方向知识点总结：1.(东与西)相对，(南与北)相对，(东南与西北)相对，(西南与东北)相对。

面南左为东，面北左为西，面东左为北，面西左为南2.地图通常是按(上北、下南、左西、右东)来绘制的。

通常所说的八个方向：东、西、南、北、东南、西北、西南、东北。

3.会看简单的路线图，会描述行走路线。

(做题时先标出东南西北。

)注意：指南针是用来指示方向的，它的一个指针永远指向(南方)，另一端永远指向(北方)。

例题讲解：例1、1、（1）观察方向。

邮局在公园的（）面，学校在公园的（）面。

小娟家在学校的（）面，小娟家在晓峰家的（）面。

体育馆在博物馆的（）面，体育馆在学校的（）面。

答案：东北南东北西2、（2）完成下面的方位示意图。

答案：演练1、（1）在图上标出小猴、小兔、小马、小羊的房子：1. 小猴家在小牛家的南面；2. 小兔家在小牛家的西面；3. 小马家在小牛家的东南面；4. 小羊家在小牛家的西北面．答案：（2）如图是一所学校附近的地图．1.说一说建行、邮局、二中分别在学校的什么位置？2.一中在在学校的东北方向，电信局在学校的西北方向．请填在图中．3.建行在车站的面，公安局在邮政局的面．答案：1. 建行在学校的西面、邮局在学校的北面、二中在学校的东南位置；2.电信局一中3. 北，南．例2、（1）下图是某小区的平面图，请根据平面图填空。

（1）1号楼在中心花园的（）方向；3号楼在中心花园的（）方向。

4号楼在中心花园的（）方向。

（2）4号楼在2号楼的（）方向；1号楼在2号楼的（）方向。

（3）中心花园在（）的北面，（）的西北面，2号楼的（）方向。

（4）（）在（）的北面。

（5）5号楼的西面有（）号楼和（）号楼。

（1）西北西南南（2）西南西（3）四号楼二号楼西南（4）一号楼三号楼（5）3 4（2）我国的五座名山合称“五岳”，它们分别是中岳（），东岳（），北岳（），南岳（），西岳（），请在下面画出他们的示意图。

正比例反比例的拓展应用例题与课堂练习作业

课堂例题与练习1、一辆汽车从甲地开往乙地，每小时行驶40千米，返回时每小时行50千米，结果返回的时间比去的时间少48分钟，求甲乙两地之间的路程。

练习：从A城步行到B城办事，每小时走5千米，回来时骑自行车，每小时行15千米，往返共用6小时，求AB两地之间的距离。

2、甲乙两车分别从A、B两地同时出发，相向而行。

甲车每小时行驶48千米。

乙车每小时行驶42千米，当乙车行驶至全程的7/20时，甲车距中点还有24千米。

A、B两地相距多少千米？练习：甲乙两车分别从A、B两地同时出发，相向而行，甲每小时行56千米，乙每小时行40千米。

当乙行至全程的2/5时，甲车已超过中点12千米，求两地路程。

3、甲乙两车同时从A地开往B地，当甲车行至全程的1/3处时，乙车行了全程的1/2，当乙车到达B地时，甲车距B地还有20千米。

求A、B两地相距多少千米？练习：甲乙两车同时从A地开往B地，当甲车行至中点时，乙车行驶了全程的3/5。

当甲车到达B地时，乙车超过B地24千米。

求AB两地路程。

4、小王、小李和小张同时各做120个零件，小王做完时，小李做了100个。

小张做了60个。

找这样的速度。

小李做完十，小张还差多少个没做完？练习：甲、乙、丙三人进行百米赛跑，当甲到达终点时，乙距离终点还有20米，丙距离终点还有25米。

按这样的速度计算，当乙到达终点时，丙距离终点还有多少米？5、客货两车分别从A、B两地同时相对开出，已知客货两车的速度比是4:5。

两车在途中相遇后继续行驶，货车把速度提高20%。

客车速度不变，再行4小时后，货车到达A地，客车离B地还有112千米。

AB两地相距多少千米？练习：客车和货车分别从甲乙两地同时相对开出，经过若干小时在途中相遇。

相遇后又行驶5小时，货车到达甲地。

这时客车到乙地后又调头行了甲乙两地距离的25%。

客车和货车从出发到相遇用了几个小时？课后作业1、一辆汽车从甲地去乙地每小时行45千米，返回时每小时多行20%，往返共用11小时。

小学数学差倍问题完整版例题+作业(带详细答案)

差倍问题差倍问题就是已知大小两数的差，以及大小两数的倍数关系，求大小两数的问题．差倍问题的特点与和倍问题类似。

解答差倍问题的关键是要确定两个数量的差及相对应的倍数差，一般情况下，在题目中不直接给出，需要经过调整和计算才能得到。

解题思路：首先要在题目中找到1倍量，然后画图确定解题方法.被除数的数量和除数的倍数关系要相对应，相除后得到的结果是一倍量差倍问题的基本关系式：差÷(倍数－1)=1倍数(较小数)1倍数×几倍=几倍数(较大数)或较小数+差=较大数板块一、和差问题例题1、李爷爷家养的鸭比鹅多18只，鸭的只数是鹅的3倍，你知道李爷爷家养的鸭和鹅各有多少只吗？解答：鸭与鹅只数的倍数差是3-1=2（倍），鹅有18÷2=9 (只)，鸭有 9×3=27(只).举一反三：（1）两个书架，甲书架存书相当于乙书架存书量的5倍，甲书架比乙书架存书多120本，则乙书架存书多少本？解答：多的120本相当于乙书架的4倍，则乙书架的书为：120÷4=30（本）．（2）师、徒两人共加工105个零件，师父加工的个数比徒弟的3倍还多5个，师父和徒弟各加工零件多少个？知识梳理例题讲解：解答：把徒弟加工的个数看作1份数，师父加工的个数就比3份数还多5个，如果师父少加工5个，两人加工的总数就少5个，总数变为（105-5）个，徒弟做了：100÷（3+1）=25(个)，师父做了：25×3+5=80(个)．例题2、有两根铁丝，第一根长18米，第二根长10米，两根铁丝用去同样长的一段后，第一根剩下的长度是第二根剩下长度的3倍，两根铁丝各剩下多少米？解答：用去同样长的一段后，两段长度差为：18-10=8（米），且第一根比第二根多：3-1=2（倍），则第二根剩下：8÷2=4（米），第一根剩下：4×3=12（米）．举一反三：有两条纸带，一条长21厘米，一条长13厘米，两条纸带都剪下同样的一段后，长纸带剩下的长度是短纸带剩下的3倍，问剪下的一段有多长？解答：长纸带剩下长度比短纸带剩下的长度长：21-13=8（厘米），短纸带剩下：8÷（3-1）=4（厘米），剪下：13-4=9（厘米）．例题3、有两根同样长的绳子，第一根截去12米，第二根接上14米，这时第二根长度是第一根长的3倍，两根绳子原来各长多少米？解答：两根绳子原来的长度一样长，但是从第一根截去12米，第二根绳子又接上14米后，第二根的长度是第一根的3倍.应该把变化后的第一根长度看作1倍，而12+14=26（米），正好相当于第一根绳子剩下的长度的2倍.所以，当从第一根截去12米后剩下的长度可以求出来了，那么第一根、第二根原有长度也就可以求出来了。

牛吃草问题专题变式题(例题+练习+家庭作业)

牛吃草变式题牛吃草变式题根据牛吃草做的消长问题的扩充，涉及类型多样，包含“检票口问”“排水管问题”“扶梯问题”等︰解题步骤例用牛吃草进行类比:1) 设定一头牛一天吃草量为“1”2）草的生长速度＝草量差÷时间差；3）原有草量＝牛头数×吃的天数－草的生长速度×吃的天数；`4）吃的天数＝原有草量÷（牛头数－草的生长速度）；5)牛头数＝原有草量÷吃的天数＋草的生长速度。

这五个步骤公式是解决牛吃草问题的基础。

首先一般假设每头牛每天吃草量不变，设为"1"，解题关键是弄清楚已知条件，进行对比分析，从而求出每日新长草的数量，再求出草地里原有草的数量，进而解答题总所求的问题。

检票口问题例：旅客在车站候车室等车,并且排队的乘客按一定速度增加,检查速度也一定,当车站放一个检票口,需用半小时把所有乘客解决完毕,当开放2个检票口时,只要10分钟就把所有乘客OK了求增加人数的速度还有原来的人数？练习：一游乐场在开门前有100人排队等候，开门后每分钟来的游客是相同的，一个入口处每分钟可以放入10名游客，如果开放2个入口处20分钟就没人排队，现开放4个入口处，那么开门后多少分钟后没人排队？物美超市的收银台平均每小时有60名顾客前来排队付款，每一个收银台每小时能应付80名顾客付款。

某天某时刻，超市如果只开设一个收银台，付款开始4小时就没有顾客排队了，问如果当时开设两个收银台，则付款开始几小时就没有顾客排队了？电梯问题例、自动扶梯以均匀速度由下往上行驶着，两位性急的孩子要从扶梯上楼。

已知男孩每分钟走20级梯级，女孩每分钟走15级梯级，结果男孩用了5分钟到达楼上，女孩用了6分钟到达楼上。

问：该扶梯共有多少级？练习：两个顽皮孩子逆着自动扶梯行驶的方向行走，男孩每秒可走3级阶梯，女孩每秒可走2级阶梯，结果从扶梯的一端到达另一端男孩走了100秒，女孩走了300秒。

问该扶梯共有多少级？商场的自动滚梯以均匀的速度由下往上行驶着,两个孩子嫌滚梯走的太慢，于是在行驶的滚梯上,男孩每秒钟向上走1级台阶，女孩每3秒向上走2级台阶，结果男孩用50秒到达搂上，女孩用了60秒到达搂上。

2-2 典型例题解析(1)

2-2 典型例题解析1．________是作业存在的唯一标志。

A．作业名B．进程控制块C．作业控制块D．程序名【分析】当一个作业开始由输入设备输入时，系统为其建立一个作业控制块JCB，并对其进行初始化。

初始化所需要的大部分信息取自作业控制说明书，如作业标识、用户名称、调度参数和资源需求等；其他一些信息由资源管理程序给出，如作业进入时间等。

作业控制块是批处理作业存在的标志，其中保存了系统对于作业进行管理所需要的全部信息，它们被保存在磁盘区域中。

【答案】C2．当作业进入完成状态________。

A．将删除该作业并收回其所占资源，同时输出结果B．将该作业的控制块从当前作业队列中删除，收回其所占资源，并输出结果C．将收回该作业所占资源并输出结果D．将输出结果并删除内存中的作业【分析】当作业运行结束或异常终止时，作业进入完成状态。

这时作业调度程序收回它占用的所有资源，做必要的善后处理。

具体包括：回收发给该进程的资源，包括外设、内存空间，进程运行时打开的文件等；释放该作业的JCB（作业控制块），将此作业注销，输出结果。

【答案】B3．当中央处理机处于管态时，它可以执行的指令是________。

A．计算机系统中的全部指令B．仅限于非特权指令C．仅限于访管指令D．仅限于特权指令【分析】为了防止用户使用特权指令，保证系统的正确操作，将中央处理机的工作状态划分成：管态和目态。

当中央处理机处于管态时可以执行包括特权指令在内的一切机器指令，当中央处理机处于目态时不允许执行特权指令。

【答案】A4．作业调度又称________，其主要功能是按照某种原则从后备队列中选取作业，并为作业做好运行前的准备工作和作业完成后的善后处理工作。

【分析】在操作系统中的调度分为三种：高级调度、中级调度和低级调度。

高级调度又称作业调度，作用是从后备队列中按照某种原则选取作业调入内存；低级调度又称进程调度，作用是从就绪队列中按照某种原则选取进程使之占用处理机来运行；中级调度是为了解决内存紧张的问题，把一些暂不运行的进程从内存移到外存，待有条件运行时再把它们调回内存运行，中级调度相当于存储管理中的对换功能。

《分式的乘除法》经典例题及作业

《分式的乘除法》典型例题解析例1 下列分式a bc 1215，a b b a --2)(3，)(222b a b a ++，b a b a +-22中最简分式的个数是( ).A.1B.2C.3D.4例2 约分)6)(()23)(3(2222-+-+-+x x x x x x x x 例3 计算 (1)3x 2y ·2125xy ·(-x y 54) (2)6x 3y 2÷(-x y )·2yx ÷x 2(3)(22611cx b a -)÷(-222218121x c y a )·(-32592xb ay )例4 若432z y x ==,求222zy x zxyz xy ++++的值.例5 如果32=b a ，且a ≠2，那么51-++-b a b a =( ).例6 已知x 2+4y 2-4x+4y+5=0，求22442yxy x y x -+-·22y xy yx --÷(y y x 22+)2的值.例7 计算2223b a a ab -+÷b a ba -+3 例8 计算)22(2222a b ab b a a b ab ab a -÷-÷+--例9 计算(2334ba )2·(223ab -)3·(a b 3-)2 例10 计算(22932x x x --+)3·（-x x --13）2例11 先化简，再求值：(b a ab 22+)3÷2223)b a ab (-·[)(21b a -]2，其中a=-21,b=32【同步达纲练习】一、填空题(5分×6=30分)1.把一个分式的分子与分母的约去，叫做分式的约分.2.在分式xyxy y x 222+中，分子与分母的公因式是 .3.将下列分式约分：(1)258x x = (2)22357mn n m -= (3)22)()(a b b a --=4.计算2223362cab b c b a ÷= .5.计算42222ab a aab ab a b a --÷+-= . 6.计算(-y x )2·(-32yx )3÷(-y x )4= .二、解答题7.计算下列各题(10分×4=40分)(1)316412446222+⋅-+-÷+--x x x x x x x (2)yx y xy x -+-24422÷(4x 2-y 2)(3)4344516652222+-÷-++⋅-+-a a a a a a a a (4)22222x a bxx ax a ax -÷+-(5)（3-∏）0+[-22007×22009-]×(-21)2-8.当x=-3时，求xx x xx x 43342323-++-的值.(15分)9、若532zy x ==，且1423=-+z y x ，求x 、y 、z 的值。

约翰逊法则例题及解答

例题：假设有4个作业A、B、C和D，它们分别在两台设备上进行加工，加工时间如下：
作业A：在第一台设备上加工时间为3分钟，在第二台设备上加工时间为5分钟。

作业B：在第一台设备上加工时间为6分钟，在第二台设备上加工时间为2分钟。

作业C：在第一台设备上加工时间为2分钟，在第二台设备上加工时间为4分钟。

作业D：在第一台设备上加工时间为5分钟，在第二台设备上加工时间为3分钟。

请问如何按照约翰逊法则对这4个作业进行排序？
解答：根据约翰逊法则，我们首先需要找出在每个设备上加工时间最短的作业，然后按照以下步骤进行排序：
在第一台设备上，作业C的加工时间最短，为2分钟。

因此，将作业C放在第一台设备上加工。

在第二台设备上，作业B的加工时间最短，为2分钟。

因此，将作业B放在第二台设备上加工。

接下来，我们需要比较剩下的作业在第一台设备上的加工时间和在第二台设备上的加工时间。

对于作业A和D，它们在第一台设备上的加工时间分别为3分钟和5分钟，而在第二台设备上的加工时间分别为5分钟和3分钟。

因此，按照约翰逊法则，我们应该将作业A放在第一台设备上加工，然后将作业D放在第二台设备上加工。

最后，我们得到的排序结果为：C-B-A-D。

因此，按照约翰逊法则，应该先加工C，然后加工B，接着加工A，最后加工D。

牛吃草问题专题(例题+练习+作业)

牛吃草问题专题(例题+练习+作业)牛吃草问题，又称为消长问题或XXX牧场。

该问题最初由17世纪英国伟大的科学家XXX（1642-1727）提出。

典型牛吃草问题的条件是假设草的生长速度固定不变，不同头数的牛吃光同一片草地所需的天数各不相同，求若干头牛吃这片草地可以吃多少天。

解决牛吃草问题常用到五个基本公式：1.设定一头牛一天吃草量为“1”；2.草的生长速度=草量差/时间差；3.原有草量=牛头数×吃的天数-草的生长速度×吃的天数；4.吃的天数=原有草量/(牛头数-草的生长速度)；5.牛头数=原有草量/吃的天数+草的生长速度。

这五个公式是解决牛吃草问题的基础。

首先一般假设每头牛每天吃草量不变，设为“1”，解题关键是弄清楚已知条件，进行对比分析，从而求出每日新长草的数量，再求出草地里原有草的数量，进而解答题总所求的问题。

例1：一块牧场长满了草，每天均匀生长。

这块牧场的草可供10头牛吃40天，供15头牛吃20天。

问：这片牧草可供25头牛吃多少天？练：1.一块牧场长满了青草，每天还在匀速生长。

这块牧场的草可供10头牛吃40天，供15头牛吃20天。

可供25头牛吃多少天？2.一个牧场长满青草，牛在吃草而草又在不断生长。

已知牛27头，6天把草吃尽，同样一片牧场，23头牛9天把草吃尽。

如果有牛21头，几天能把草吃尽？3.牧场上长满了青草，而且每天还在匀速生长。

这片牧场上的草可供9头牛吃20天，可供15头牛吃10天。

如果要供18头牛吃，可吃几天？例2：由于天气逐渐寒冷，牧场上的牧草每天以均匀的速度减少，经测算，牧场上的草可供30头牛吃8天，可供25头牛吃9天。

那么可供21头牛吃几天？练：1.由于天气逐渐冷起来，牧场上的草不仅不长，反而以固定的速度在减少。

如果某块草地上的草可供25头牛吃4天，或可供16头牛吃6天，那么可供10头牛吃多少天？2.一片牧草，每天生长的速度相同。

现在这片牧草可供20头牛吃12天，或可供60只羊吃24天。

同济大学大学物理13相对论答案

解：（1）火箭飞船测得为原时
t空间站 t火箭 1 v2 c2 30 1 0.62 37.5min
空间站上时钟为午后12点37.5分
（2）宇航员测得距离 = v t火箭
0.63108 m/s 30 min 60s / min 3.241011m
例题13：一位宇航员乘一艘火箭飞船以 0.6c 的速度飞过地球，同时校准他的时钟与地球时钟均指正午12点。按照宇航员的测定，火箭飞船在午后12点30分通过一个相对地球静止不动的空间站，并用无线电向地球报告。（3）地球上观测者测定地球到空间站距离是多少？（4）地球上收到无线电讯号，地球上是什么时间？
m s1
8.89108s
例2：
A
例3：某宇宙飞船以 0.8c 的速度离开地球，若地球上接收到它发出的两个信号之间的时间间隔为 10 s ，则宇航员测出的相应的时间间隔为：
（A） 6 s
（B） 8 s
（C） 10 s
（D） 16.7 s
10s t0 1 0.82
t0 6s
例4：一火箭的固有长度为 L ，相对于地面匀速直线
运动的速率为 v1 ，火箭上的人从火箭后端向位于前端的靶发射子弹，子弹相对于火箭的速率为 v2 ，在火箭上测得子弹从射出到击中靶的时间间隔是：
L (A)
v1 v2 L
(C) v2 v1
L (B)
v2
(D)
L
v1 1 v12 c2
例5：宇宙飞船相对地球以 0.8c 飞行，一光脉冲从船尾传到船头，飞船上的观察者测得飞船长 90 m，地球上的观察者测得光脉冲从船尾传到船头两事件的空间间隔是：
（B） 4.0 MeV （D） 2.5 MeV
C
Ek mc2 m0c2

小学奥数几何模型之沙漏模型例题+作业带答案

小学几何模型之沙漏模型课前引入：相似三角形例题1如图：在平行四边形ABCD中，AB＝16厘米，AD＝10厘米，BE＝4厘米，求FC的长。

BC=AD=10厘米CD=AB=16厘米CF:BF=CD:BE=4:1FC的长：10÷（4+1）×4=8（厘米）练习1如图：在平行四边形ABCD中，CD＝14厘米，BE＝2厘米，AE和DE的长度相同，求DF 的长。

AB=CD=14厘米DE=AE=14+2=16（厘米）DF:FE=CD:BE=7:1DF的长：16÷（7+1）×7=14（厘米）例题2如图：在正方形ABCD中，CE＝2DE。

已知正方形ABCD的面积是96平方厘米，求阴影部分的面积。

△ABD的面积为96÷2=48（cm2）假设S△DEF为1份，那么S△ABF为9份，S△ADF为3份阴影部分面积：48÷（9+3）×1=4（cm2）练习2如图：在长方形ABCD中，点E是边DC的三等分点。

已知三角形DQE的面积是1平方厘米，求长方形ABCD的面积。

DE:AB=1:3△ABQ的面积为9cm2△ADQ的面积为3cm2△ABD的面积为9＋3=12 （cm2）长方形ABCD的面积为12×2=24 （cm2）例题3如图：在三角形ABC中，DE、FG、BC互相平行，并且AD＝DF＝FB，求三角形ADE、四边形DEGF和四边形FGCB之间的面积比。

AD:AF:AB=1:2:3S△ADE:S△AFG:S△ABC=1:4:9假设△ADE的面积为1份，那么△AFG的面积为4份，△ABC的面积为9份四边形DEGF的面积为4－1=3（份）四边形FGCB的面积为9－4=5（份）S△ADE:S四边形DEGF:S四边形FGCB=1:3:5练习3如图：在三角形ABC中，DE、FG、BC互相平行。

已知AD＝3厘米，DF＝2厘米，FB＝1厘米，求三角形ADE、三角形AFG和三角形ABC之间的面积比。

无人机喷洒例题

无人机喷洒例题
"无人机喷洒例题"可能指的是一个与无人机在农业领域应用相关的问题，比如计算无人机喷洒农药或者肥料的效率、所需时间、覆盖面积等。

以下是一个简化的示例题目及其解答：
例题：
假设一个农场需要对其100公顷的农田进行农药喷洒作业。

现有一款农用无人机，其喷洒宽度为5米，飞行速度为10公里/小时。

如果每次装满农药可以连续作业1小时，计算完成整个农场喷洒所需的时间。

解答：
首先，我们需要计算出无人机每小时可以喷洒的面积：
喷洒宽度= 5米
飞行速度= 10公里/小时= 10,000米/小时
每小时喷洒面积= 喷洒宽度×飞行速度
= 5米×10,000米/小时
= 50,000平方米/小时
= 5公顷/小时（因为1公顷= 10,000平方米）
接着，我们计算完成100公顷农田所需的总时间：
总需要喷洒面积= 100公顷
总时间= 总需要喷洒面积/ 每小时喷洒面积
= 100公顷/ 5公顷/小时
= 20小时
因此，无人机完成整个农场的农药喷洒作业需要20小时。

注意，这个计算没有考虑换装农药的时间以及无人机转移至起始位置和返回的时间。

在实际操作中，这些因素可能会影响总的作业时间。

此外，实际作业中可能会有重叠喷洒或是遗漏区域，需要通过实地测试来调整理论计算结果。