高等数学 习题册解答_11.线面积分(青岛理工大学).
高数线面积分

10 沿D内任何一闭路L上的积分为零,即 Pdx Qdy 0 ;
L
20 曲线积分 Pdx Qdy与路径无关,只与起点 A与终点B有关;
L( AB )
30 P Q 在D内恒成立; y x
40 在D内存在二元函数 u( x, y),使du Pdx Qdy .
.
等价的意义是: 若其中一个成立,另外三个也成立。
I a 2 x 2 y 2 dxdy a 2 x 2 y 2 (dxdy)
.
.
Dxy
Dxy
.
2
a 2 x 2 y 2 dxdy 2
2π
d
a
a 2 r 2 rdr
4π a3
.
Dxy
0
0
3
二4 :球面 x 2 y 2 z 2 a 2的外侧表面,Dxy为xOy平面上的圆域:
一型:对面积
二型:对坐标
三重积分
高斯公式
1. 第Ⅰ型、第Ⅱ型曲线积分的比较
曲线积分 标准形式 物理意义
计算方法
相似处
不同处
第一型 (对弧长)
第二型 (对坐标)
f ( x, y)ds
L
f ( x, y, z)ds
L
L指曲线
⌒
AB
当 f ( x, y) 0,
f ( x, y)ds表示
L
线密度为 f ( x,
y)的曲线型构
件的质量 M .
设曲线
L: x y
φ(t) (t)
t
1.都是化曲线积分为 定积分计算。
Pdx Qdy W Pdx Qdy 2.都要把曲线表示式 L
L
Pdx Qdy Rdz
表示力F P,Q
高等数学B(上)(山东联盟)知到章节答案智慧树2023年青岛理工大学

高等数学B(上)(山东联盟)知到章节测试答案智慧树2023年最新青岛理工大学
第一章测试
1.
参考答案:
周期函数
2.
参考答案:
3.
参考答案:
对
4.
参考答案:
5.
参考答案:
-4
第二章测试1.
参考答案:
2.
参考答案:
不一定可导
3.
参考答案:
4.
参考答案:
5.
参考答案:
充分必要条件第三章测试
1.
参考答案:
2
2.
参考答案:
3.
参考答案:
4.
参考答案:
5.
参考答案:
既非充分也非必要条件
第四章测试
1.
参考答案:
2.
参考答案:
错
3.
参考答案:
对
4.
参考答案:
对
5.
参考答案:
错
第五章测试
1.
参考答案:
恒为零
2.
参考答案:
3.
参考答案:
对
4.
参考答案:
错
5.
参考答案: 错。
第11章 曲线积分与曲面积分习题解答(开放课程)

d
L
02
2
1 a2
cos
d
2
cos
d
2 0 2
2
1 2
a
2
2
sin
2
0
2sin 2
2
2a 2
3.计算 x2 y 2 ds ,其中 L 为曲线 x acos t t sin t ,y asin t t cos t, L
解:
xydx
1
y2 y
y2
dy
2
1 y 4dy 21 y 5 1
4.
L
1
1
5 1 5
8. 计算 x3dx 3zy 2dy x 2 ydz ,其中 L 是从点 A3,2,1 到点 B0,0,0的直线 L
段 AB 。
解:直线段 AB 的方程为 x y z ,化成参数方程为 x 3t , y 2t , z t , 321
1x 0
1
x
2dx
2。
2.计算 x 2 y 2 ds ,其中 L 为圆周 x 2 y 2 ax 。 L
解:
L
的参数方程为
x
y
1 2 1 2
a cos a sin
1 2
a
, 0
2
则 x 2 y 2 1 a cos 1 a2 1 a sin 1 | a | 21 cos
0
ex
|0a
e
青岛理工大学线性代数练习册答案

第一章n 阶行列式1.求下列各排列的逆序数:(1) 134785692 (2) 139782645 (3) 13…(2n-1)24…(2n) (4) 13…(2n-1)(2n)(2n-2)…2 (11;17;2)1(-n n ;)1(-n n ) 2. 已知排列9561274j i 为偶排列,则=),(j i (8,3) .3.计算下列各阶行列式:(1) 600300301395200199204100103 (2)0d 0c 0b0a 0 (3)efcf bf de cd bdaeac ab --- [2000; 0; 4abcdef]4. 设xx x x x D 111123111212-=,则D 的展开式中3x 的系数为 -1 .5 求二次多项式()x f ,使得()61=-f ,()21=f ,()32=f解 设()c bx ax x f ++=2,于是由()61=-f ,()21=f ,()32=f 得⎪⎩⎪⎨⎧=++=++=+-32426c b a c b a c b a 求c b a ,,如下: 06124111111≠-=-=D ,61231121161-=-=D ,121341211612==D ,183242116113-=-=D 所以 11==D D a ,22-==D D b ,33==DD c故()322+-=x x x f 为所求。
行列式的性质;克拉默法则1.n 阶行列式ij a D =,则展开式中项11342312n n n a a a a a - 的符号为( D ). (A )- (B )+ (C )n)1(- (D )1)1(--n2.如果1a a a a a a a a a D 333231232221131211==,求333231312322212113121111a a 3a 2a 4a a 3a 2a 4a a 3a 2a 4--- [-12] 3. 已知4521011130112101--=D ,计算44434241A A A A +++ [-1] 4. 计算行列式383326229432231---- [-50] 5.计算下列各行列式(D k 为k 阶行列式)(1)a11a,其中对角线上元素都是a ,未写出的元素都是0; [2--n naa ](2) aa a a x a a a x ; [1)(--n a x a ](3)n1n 321a xxxxx a x x x x xa xxx x x a xx x x x a- [利用递推公式来求]递推公式为1121)()())((---+---=n n n n D x a x a x a x a x Dn D =)1)(())((2121xa xx a x x a x x a x a x a n n -++-+-+--- (4) n2222232222222221[)!2(-n ](5)β+ααββ+αβ+ααββ+ααββ+ααββ+α1000000100001000010000[n n n n βαββαα++++--11 ] 6.问λ,μ取何值时,齐次方程组⎪⎩⎪⎨⎧=+μ+=+μ+=++λ0x x 2x 0x x x 0x x x 321321321有非零解? [0;1==μλ]求每类商品的销售利润率。
青岛理工大学2011级高等数学(上)B试题及答案

一、选择题:每题2分,共10分 注意:请将答案填入下表,否则不给分。
1.“当0x x →时,A x f -)(是无穷小”是A x f x x =→)(lim 0的( )。
A.充分条件B.必要条件C.充分必要条件D.既非充分又非必要条件2.若)(0x f '存在,则xx f x x f x ∆-∆-→∆)()(lim000=( )。
A. )(0x f '-B.)(0x f 'C. )(20x f 'D.)(20x f '- 3.若)(x f 在],[b a 上连续,在),(b a 内可导,且),(b a x ∈时,0)(<'x f ,又0)(<a f ,则( )。
A.)(x f 在],[b a 上单增且)(b f >0B.)(x f 在],[b a 上单增且)(b f <0C.)(x f 在],[b a 上单减且)(b f <0D.)(x f 在],[b a 上单增,但)(b f 的符号无法确定 4.下列反常积分发散的是( )。
A.⎰1xdx B.⎰-112x dx C.⎰+∞-0dx xe xD.⎰+∞∞-+21x dx 5.如函数y=(C 1+C 2x)e 2x,满足初始条件: y|x=0=0, y '|x=0=1,则C 1,C 2的值为( )。
A. C 1=0,C 2=1 B. C 1=1,C 2=0 C. C 1=π,C 2=0 D. C 1=0,C 2=π 二、填空题:每题2分,共10分 注意:请将答案填入下表,否则不给分。
1.极限⎪⎭⎫ ⎝⎛+∞→x x x x x 7sin 3sinlim =_______________。
2.设x x f arctan )(=,则)0(f ''=_____________。
3.反常积分⎰+∞∞-++222x x dx=___________________。
高等数学 习题册解答_7.微分方程(青岛理工大学)

1 (u 1) u 1
2
2u 1
4
班级
姓名
学号
成绩:
2u 1 du 4dx u
2u-lnu=4x+C 2(x+2y)-ln(2+2y)=4x+C
§4 一阶线性微分方程 1、微分方程(y2+1)dx=y(y-2x)dy 的通解是( )
A.
y
1 1
y2
1
3
y3
C
B.
x
1 1
y2
1
3
y3
du dx 1 u2 x
ln u 1 u2 ln x ln C
u 1 u2 Cx
y
1
y
2
Cx
x
x
y x2 y2 Cx2
将 y|x=1=0 代入的特解为 y x2 y2 x2 或 y 1 x2 1 22
7、求曲线,使其上任一点到原点的距离等于该点的切线在 x 轴上的截距 解:设曲线上任一点 P(x,y),曲线:y=y(x),则由题意知:Y-y=y(X-x)
又 x2 y2 x y y
2
得
x y
1 x dx , y dy
令u x y
整理得: y du 1 u2 dy
解得: ln u 1 u2 ln y C
得通解 x x2 y2 C
六、求 y x 2y 1 的解。 2x 4y 1
解:令 u=x+2y,则 u=1+2y'
§5 全微分方程
1.下面方程中不是全微分方程的是( ) A. (3x2+6xy2)+(6x2y+4y2)dy=0 B. eydx+(xey-2y)dy=0
高等数学基础习题集(含答案)

【详解】①原式= lim
x 0
x2 x2 1 =2 ;②原式= lim 2 = ; x 0 2x 1 2 2 x 2 x sin x = lim x 0 x3 x (x 1 3 x + (x 3 )) 1 3! = 3 x 6
③原式= lim
x 0
6、求下列极限
2 x x 1 ) ① lim( x 1 x 1
x a
子也以 0 为极限,故 lim f ( x) f (a) 0 ,所以 lim f ( x) 存在,为 f (a) .
1 2 ex sin x 8、极限 lim 2 x 0 1 e x ln(1 x)
.
4
高等数学基础练习题
【解题思路】因为中间变量出现了
2019 考研 高等数学基础习题集 答案详解
目
第一章 第二章 第三章 第四章 第五章 第六章 第七章 第八章 第九章 第十章
录
函数、极限、连续............................................................................................................ 3 导数与微分........................................................................................................................ 9 中值定理及导数应用...................................................................................................... 14 不定积分.......................................................................................................................... 24 定积分及其应用.............................................................................................................. 29 常微分方程...................................................................................................................... 37 向量代数和空间解析几何(数一)..............................................................................47 多元函数微分学.............................................................................................................. 52 多元函数积分学.............................................................................................................. 60 无穷级数(数一、三).................................................................................................. 71
第十一章线面积分(何涛一)

一 基本要求1. 理解两类线面积分的概念,掌握两类线面积分的性质。
2. 掌握两类线积分以及两类面积分之间的联系和区别,会计算两类线面积分。
3. 熟练掌握格林(Green)公式,会用平面曲线积分与路径无关的条件。
4. 熟练掌握高斯(Gauss)公式,斯托克斯(Stokes)公式,会计算空间曲线积分5. 会用两类线面积分求一些几何量与物理量(如曲面面积,弧长,质量,重心,转动惯量,功等)。
6. 了解散度,旋度以及场论的概念及其计算方法.二 学习指导【11-1】第一型曲线积分的要点是什么? 答 第一型曲线积分是关于曲线弧长的积分(22)()(dy dx ds +=),计算时应根据不同的曲线方程变换相应的,转换成定积分. ds 【11-2】关于第一型曲线积分的对称性.1.设L 为光滑曲线,且关于轴对称,为曲线y 1L L 位于轴右侧的弧段, 在y (,)f x y L 上的连续,则10(,)2(,)LL f x f x y ds f x y ds f x ⎧⎪=⎨⎪⎩∫∫为的奇函数为的偶函数2. 设L 为光滑曲线,L 的方程关于y x ,具有轮换性,为(,)f x y L 上的连续函数,则(,)(,)LLf x y ds f y x ds =∫∫,3. 设为光滑的空间曲线,ΓΓ的方程关于z y x ,,具有轮换性,为上的连续函数,则(f Γ∫∫∫ΓΓΓ==ds z f ds y f ds x f )()()(222)()()(dz dy dx ds ++=)4.当被积函数1),(=y x f 时,(弧长计算公式)∫=LLds ds y x f ),(∫……………………………………………………………………………… 【11-3】第二型曲线积分的主要计算方法.(1) 将曲线方程(直角坐标,参数方程,极坐标方程)代入后化定积分计算. (2) 用格林(Green)公式化二重积分计算. (3) 用平面曲线积分与路径无关的条件计算.………………………………………………………………………………………… 【11-4】第一型曲面积分的要点是什么?计算应注意什么?答 第一型曲面积分是关于曲面面积的积分。
高等数学基础习题集(含答案)

sin x
,则 f ( x ) 是(
) (C)周期函数 (D)单调函数
(B)无界函数
【解题思路】把函数看成三个分函数,该指数函数无奇偶性, x 为非周期函数, tan x 无严 格单调性. 【详解】 f ( x ) x tan x e
sin x
中, tan x 无界,另负无穷到正无穷都能取到,故整体无界.
n
7、已知极限 lim
x a
f ( x) f (a) 存在,则 lim f ( x) 是否存在?若存在,为多少? x a xa f ( x) f (a) 0 中,分母趋向于 0,而此极限存在,故只能为 型,因此分 xa 0
x a x a
【解题思路】考虑极限的类型. 2、设 f ( x) 0, 1,
x 1, x 1, g ( x ) e x ,求 f [ g ( x)] 和 g[ f ( x)] ,并作出这两个函数的图形. x 1,
x
x x 【解题思路】求 f [ g ( x)] 时,中间变量为 g ( x ) e ,利用函数 y e 的单调性质,考虑 e
【解题思路】利用数列的单调有界准则. 先求出 a2 , a3 ,易猜测数列是单调递减的,故只需 证有下界即可. 【详解】由已知条件易得 an 0 ,利用基本不等式可得, an+1 = (an + 有下界;又因为 an +1 an = 限 lim an 存在. 证毕.
x a
子也以 0 为极限,故 lim f ( x) f (a) 0 ,所以 lim f ( x) 存在,为 f (a) .
1 2 ex sin x 8、极限 lim 2 x 0 1 e x ln(1 x)
高等数学课件--D11_习题课

y O
r
t
ax
d s x2 y2 d t
2013-8-9 同济版高等数学课件
目录 上页 下页 返回 结束
P244 3(3). 计算
其中L为摆线
上对应 t 从 0 到 2 的一段弧.
提示:
原式 a
2
0 t sin t d t
2π 0
2π
a t cos t sin t
D
上页
O
y
结束
x
下页 返回
2 I (4 x 2 y 3z )dS 3
y
2 ( x y 6) dxd y
D
O
1 D
1x
12 dxd y
D
24
D 的形心
x y0
2013-8-9
同济版高等数学课件
目录 上页 下页 返回 结束
二、曲面积分的计算法
2 2 2
目录 上页 下页
2
结束
同济版高等数学课件
返回
例8. 计算曲面积分
中 是球面 x 2 y 2 z 2 2 x 2 z .
解:
I
( x 2 y 2 z 2 ) 2x y 2 y z dS
(2 x 2 z ) d S 2 ( x z ) y dS
(2) 确定积分上下限
练习题: P244
2013-8-9
题 3 (1), (3), (6)
同济版高等数学课件
目录 上页 下页 返回 结束
解答提示: P244 3 (1)
计算 提示: 利用极坐标 , 其中L为圆周
ds
原式 =
第十一章青岛理工大学高数练习册答案

第十一章 无穷级数§ 1 常数项级数的概念和性质 1C,2D,3C 4、若+∞=∞→nn b lim ,0≠n b ,求 )11(11+∞=-∑n n n b b 的值 解: (=nS 11143322111)11......()11()11()11(++-=-+-+-+-n n n b b b b b b b b b b 所以11lim b S n n =∞→ 5、若级数∑∞=1n na收敛,问数列{n a }是否有界解:由于0lim =∞→nn a ,故收敛数列必有界。
6、若a a nn =∞→lim ,求级数)(11∑∞=+-n n n a a 的值解:=n S 1113221)......())(()(++-=-+-+-n n n a a a a a a a a故a a a a a a n n n n n-=-=-+∞→∞=+∑11111)(lim )(7、求)(12121-+∞=-∑n n n a a 的值解:=nS +-)(3a a a a a a a a n n n -=-+-+-+12121235)......()(故)(12121-+∞=-∑n n n a a =a a a n n -=-=+∞→1)(lim 128、求∑∞=++1)2)(1(1n n n n 的和 ()41§ 2 常数项级数的审敛法一、用比较审敛法或极限形式的比较审敛法判别下列级数的收敛性1、 判定级数∑∞=+-1)13)(23(1n n n 的敛散性解:由于)13)(23(1+-n n <21n,而∑∞=121n n收敛,故∑∞=+-1)13)(23(1n n n 收敛2、 判定敛散性∑∞=11n nnn解:nn = 2121).1(1.....1.1.<-=-+<nn n n n n n故n n n 1>n 21,而级数∑∞=121n n 发散,故∑∞=11n n nn 发散3、 判定敛散性∑∞=+111n na)0(>a,1>a 收敛; ≤<a 01, 发散4、 判定敛散性 ∑∞=-++13221n n nne n en ne (收敛);二、用比值或根值审敛法判别下列级数的收敛性5、 判定级数∑∞=1!.3n nn nn 的敛散性解:e a a nn n 3lim 1=+∞→>1,所以∑∞=1!.3n nn n n 发散6、 判定级数∑∞=-1354n nn n的敛散性解:154lim 1<=+∞→nn n a a ,所以∑∞=-1354n n nn收敛7、∑∞=+112tan.n n n π收敛8、 nn n an∑∞=+1)1( ,1>a 收敛三、判别下列级数是否收敛。
青岛理工大学2010级高等数学(上)B试题及解答

2010高等数学(上)B一、填空题:(每题3分,共18分)1、极限⎪⎭⎫ ⎝⎛-∞→x 2sin x xx sin lim x = 。
2、函数3x 3x 2x )x (f 2---=的间断点为 。
3、设函数2x sin y =,则y4、设函数3ax x 2y 23++=在x=1处取得极值,则5、设2x e 是函数f(x)的一个原函数,则不定积分⎰'(f6、定积分()⎰ππ-+22xdx cos x x =——二、选择题:(每题3分,共15分)1、设函数⎪⎩⎪⎨⎧≤+>=0x ,)x a ln(0x ,x1sin x )x (f 2在(-∞,+∞)上连续,则a= 。
A.1 B.e C.2 D.e1 2、设函数f(x)可导,y=f(x 2),则微分dy= 。
A.dx )x (f 2'B.dx )x (f 2C.d x )x (f x 22'D.dx ))x (f (x 22'3、设函数f(x)=x(x-1)(x-2)(x-3),则方程0)x (f ='的实根个数是 。
A.4B.3C.2D.14、不定积分⎰-dx xe x = 。
A.C e )1x (x +--B.C e )1x (x ++--C.C e )x 1(x +--D.C xe x +-5、在下列反常积分中收敛的是A.⎰∞+0dx xx ln B.⎰∞+e 2dx )x (ln x 1 C.⎰∞+e dx x ln x 1 D.⎰∞+e 21dx )x (ln x 1三、(6分)求极限)x 1ln()x cos 1(x 1cos x x sin 3lim 20x +++→。
四、(6分)设函数y=y(x)由参数方程⎪⎩⎪⎨⎧==⎰2t 02tcos y du u sin x 确定,求二阶导数22dx y d五、计算下列不定积分:(每题5分,共计10分)1、⎰++dx x2cos 1x cos 12 2、⎰xdx tan x 2六、(12分)求函数x xe x f -=2)(的单调区间、函数曲线的凹凸区间、极值及拐点。
高等数学习题课-线面积分的计算

y
C
L
I AB (x2 y) d x ( y2 x)dy B o A x
a
a
x
2
d
x
20
例4. 计算 其中L 是沿逆时针方向以原点为中心, a 为半径的上半圆周.
思考:
y
C
L
B o Ax
(利用格林公式)
(1) 若L 改为顺时针方向,如何计算下述积分:
I1 L (x2 3 y) d x ( y2 x) d y
o1
取辅助曲面 1 : y 3 取右侧 x
y
3 1
且有 I
1
1
26
求
2
I (8y 1)xdydz 2(1 y )dzdx 4yzdxdy
P Q R
1
(
x
y
z
)dxdydz
z
2
(8y 1 4y 4y)dxdydz
3
dv 1 dy dxdz
Dxz
3
( y 1)dy
2 ,
(沿L的正向) 格林公式
10
3.三重积分与曲面积分的联系
(P x
Q y
R)dv z
Pdydz
Qdzdx
Rdxdy
高斯公式
4.曲面积分与曲线积分的联系
R Q
P R
Q P
(
y
z
)dydz
( z
)dzdx (
x
x
)dxdy y
Pdx Qdy Rdz
斯托克斯公式
11
(三)场论初步
梯度
gradu
利用对称性
2(x z) d S 0
25
例2
第八章青岛理工大学高数练习册答案

第八章 多元函数的微分法及其应用§ 1 多元函数概念一二、求下列函数的定义域: 1、 };1|),{(22≠+x y y x 2、 };0,|),{(≠≤x x y y x三、求下列极限:1、0; 2 、 (6e ) 四、证明:当沿着x 轴趋于(0,0)时,极限为零,当沿着2x y =趋于(0,0)时,极限为21,二者不相等,所以极限不存在五 证明:当)0,0(),(≠y x 时,为初等函数,连续),(y x f 。
当)0,0(),(=y x 时,)0,0(01sin lim22)0,0(),(f yx xy y x ==+→,所以函数在(0,0)也连续。
所以函数 在整个xoy 面上连续。
六、设)(2y x f y x z+++=且当y=0时2x z =,求f(x)及z 的表达式.解:f(x)=x x-2,z y xy y x -++=2222§ 2 偏导数1证明:x yx yx ye x ,e x y e y +=∂∂-+=∂∂y z x z ,∴z xy xe xy xy x y+=++=∂∂+∂∂yzy x z x2、求空间曲线⎪⎩⎪⎨⎧=+=Γ21:22y y x z 在点(1,21,23)处切线与y 轴正向夹角(4π) 3、设yx y xy y x f arcsin )1(),(2-+=, 求)1,(x f x ( 1)4解:1-=∂∂y zx y z x u ,x x yz y u y zln 2-=∂∂ x x y z u y zln 1=∂∂ 5、设222z y x u ++=,证明 : u zu y u x u 2222222=∂∂+∂∂+∂∂ 6、)0,0(0),(lim 0f y x f y x ==→→ 连续; 201sinlim )0,0(xf x x →= 不存在, 000lim )0,0(0=--=→y f y y 7、设函数 f(x,y)在点(a,b )处的偏导数存在,求 xb x a f b x a f x ),(),(lim 0--+→(2f x (a,b))§ 3 全微分1、单选题(1)D 2B2、求下列函数的全微分:42244222222)()),,((y y x x y y x y y x f +-=+-=ϕ答案:1)xy ez= )1(2dy x dx x y edz xy +-=2))sin(2xy z = 解:)2()cos(22xydy dx y xy dz +=3)zy x u = 解:xdz x zyxdy x z dx x z y du z yz y z yln ln 121-+=- 3、设)2cos(y x y z-=, 求)4,0(πdz解:dy y x y y x dx y x y dz ))2sin(2)2(cos()2sin(-+-+--=∴)4,0(|πdz =dy dx 24ππ-4、设22),,(y x z z y x f +=求:)1,2,1(df)542(251dz dy dx +--5、讨论函数⎪⎩⎪⎨⎧=≠++=)0,0(),(,0)0,0(),(,1sin)(),(2222y x y x yx y x y x f 在(0,0)点处的连续性 、偏导数、 可微性 解:)0,0(01sin)(lim2222)0,0(),(f yx y x y x ==++→ 所以),(y x f 在(0,0)点处连续。
青岛理工大学《大物习题册》下第9和10章答案
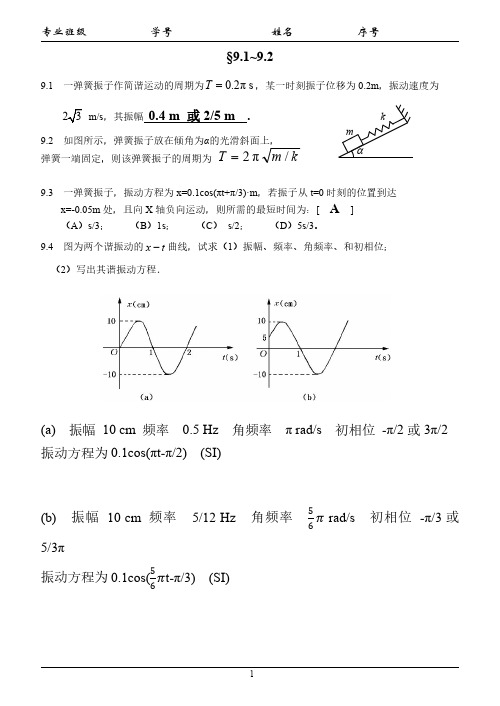
= t 时原点: t = ,
O -0.10
10.0m
x/m
t t 所以 =−
t = th th tt − SI 波函数 = th th tt − ttt −
SI
(2) y7.5 m=0.1cos(500πt-7.5*π/10-π/3)= 0.1cos(500πt-13π/12) SI
(3) t=0 时,v7.5 m=-ωAsin(ωt-φ)=-50πsin(-13π/12)=-40.6 m/s2
t+ t
= 6.0×10-2 m;
2 = /2 [图(b)]. 则运动方程为 x2 = 6.0×10-2 cos (10t+0.5) (m)
‘
2
专业班级
学号
姓名
序号
§9.3~9.7
9.7 一物体质量为 0.25 kg,在弹性力作用下作简谐运动,弹簧的劲度系数 k=25N/m,如果起
始振动时具有势能 0.01 J 和动能 0.01 J,则其振幅为:【 D 】
S2
的相位落后
1 2
π
,在
S1
、S2
的
连线上, S1 外侧各点(例如 P 点)两波引起的两简谐振动的相位差
/4
是[ A ]
(A) 0
(B) 1 π 2
(C) π
(D) 3 π2
P
S1 S2
10.9 一平面简谐波在弹性介质中传播时,某一时刻介质中某质元在负的最大位移处,则它的能量
是[ B ]
(A) 动能为零,势能最大 (C) 动能最大,势能最大
x1 x2
0.4 cos(2t )m 6
0.3cos(2t 5 )m 6
(1)画出 x1 和 x2 的振动曲线;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⎰⎰⎰
--+=-+
+=R
R
H
D dy y
R dz z
R R dydz y
R y z
R I yz
2
2
2
2
2
2
22
2
1. 1212
=2R
H
R y R z R R
H arctan 2].[arcsin][arctan0π=-
3、求曲面积分⎰⎰∑
++ds zx yz xy ( ,其中∑是锥面22y x z +=
=dydz z y x P , , (
(⎰⎰∑1
, , 2dydz z y x P C. (⎰⎰∑-1
, , 2dydz z y x P D.ABC都不对
2.设(0:2222≥=
++∑z a z y x取上侧,则下述积分不等于零的是( A ⎰⎰∑
dydz x 2∑
xdydz C ⎰⎰∑
ydxdy D ⎰⎰∑
0, πA的积分(
(dy y x dx y L
+++⎰213的值最小
解:(([]
30333
44cos sin 2sin 1a a dx x a x a x x a a I +
-=+++=⎰ππ
((
(0811, 014' ' 2
' >=⇒=⇒=-=I a a a I。, 1=a (a I最小,此时x y sin =
第十一章曲线积分与曲面积分§ 1对弧长的曲线积分
1设L关于x轴对称, 1L表示L在x轴上侧的部分,当(y x f ,关于y是偶函数时,
(=⎰L
ds y x f ,
(⎰1
, L ds y x f C. (⎰-1
, 2L ds y x f D.ABC都不对
2、设L是以点((((1, 0, 0, 1, 1, 0, 0, 1--D C B A为顶点的正方形边界,
y x dxdy d r r dr ππ
θθ∑
∑
∑
+≤==⎡⎤=--+-=
+-⎣⎦=--=-
⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰解:由对称性原式
三、用两类曲面积分之间的关系计算
1.求⎰⎰∑
++dS z y x cos cos cos (333γβα其中∑是柱面222a y x =+在h z ≤≤0部分,
γ
βαcos , cos , cos是∑的外法线的方向余弦
(00=ϕ,计算
((
(
⎰+1, 10
, 02dy x y dx xy ϕ的值解:取路径:沿0=x从(0, 0到(1, 0;再沿1=y从(1, 0到(1, 1则
(2
1
01
1
=
+=
⎰
⎰
xdx dy y I ϕ或
(((2' 00, 2x x x y
P
x Q ===⇒∂∂=∂∂ϕϕϕ得又
§4对面积的曲面积分1、计算曲面积分⎰⎰∑
解:由奇偶对称性
022=+L
dx y x , L :ππ→-==:, sin , cos t t a y t a x
=
I ((=
++⎰-
dt t a t t a dt t t a
cos 1ln cos sin cos sin 3
2
2
4
π
πππ
π
4
cos sin 4
2
2
4
a dt t t a =⎰-
3. (⎰Γ
y x ydy
xdx
3. L为222a y x =+的正向, =+--+L
y x dy
y x dx y x 2
2 ( ( A.2π
π C.0 D.π
二、计算
1. ((
dy y x dx y x L
⎰-++2222,其中L由曲线(2011≤≤--=x x y从
(0, 2A到(0, 0O方向
解:(1, 1B 01:, :; 12:, 2:___
((112
2
20
1
1112
14
xy
x
D z dxdy x y dxdy dx x y dy -∑
=--=--
=
=⎰⎰⎰⎰⎰⎰解:由轮换对称性原式
2. (x y dydz ∑
+⎰⎰其中∑为锥面22y x z +=被平面1=z所截部分的外侧
(2221
22
2
cos 3
x x y ydydz xdydz x z dxdy d r
x xdy ydx l
L
4、验证((
dy e xy dx ye y
x x +++22
在xoy面上是某函数(y x u ,的全微分,求出(y x u ,
解:
x e y y
P
x Q +=∂∂=∂∂2, (x ye xy y x u +=2, , 5、设曲线积分(⎰+dy x y dx xy ϕ2与路径无关,其中(x ϕ具有连续的导数,且
y x
原积分=222
2cos 2a adt t a ==⎰π
7. , 2⎰L
ds x其中L为球面2222a z y x =++与平面0=-y x的交线
解:将y x =代入方程2222a z y x =++得2222a z x =+于是L的参数方程:t
a z t a y t a x sin , sin 2
四、空间每一点处(z y x P , ,有力(z y x F , , →
,其大小与(z y x P , ,到z轴的距离成反比,方向垂直指向z轴,试求当质点沿圆周t z y t x sin , 1, cos ===从点(0, 1, 1M到
(1, 1, 0N时,力(z y x F , , →
所作的功
解:由已知(}0, ,
zdxdz
3.设∑为球面122=++z y x取外侧, 1∑为其上半球面,则有(
A.⎰⎰⎰⎰∑∑
=1
2zds zds ⎰⎰∑∑
=1
2zdxdy zdxdy C.⎰⎰⎰⎰∑∑
=1
222dxdy z dxdy z D. 0
二、计算
1. ∑
++dxdy z dzdx y dydz x 222其中∑由1=++z y x及三个坐标面所围成闭曲面的外侧
x t t , 2
1, 5100=-=z y
§2对坐标的曲线积分一、选择题
1.设L关于x轴对称, 1L表示L在x轴上侧的部分,当(y x P ,关于y是偶函数时, (=⎰L
dx y x P , A.0 B. (⎰1, 2L dx y x P C.(⎰-
, 2L dx y x P都不对
2.设L为1=+y x的正向,则=++L
____
→=→-=x x y BO x x y AB
=
I =
+
⎰
⎰____
___
BO
AB (((
(
((
3
41220
1
22
1
2
2
2
2
-
=++---+-+⎰⎰dx x x
dx x x dx x x
2. []
d y y x x xy y dx y x L
ln((2222+++++其中L是正向圆周曲线
222a y x =+
解:(
2
2
155121241
1
1
+
-=
+
+⎰
⎰
xdx dy y
y 5. , ds y L
⎰其中L为双纽线0(( (222222>-=+a y x a y x
解:原积分=((
22sin 4sin 4420
2
2' 21
-==+=⎰
⎰⎰a d a
d r r r ds y L χπ
π
θθθθθ
6. ⎰+L
ds y x , 22其中L为(022>=+a ax
=++++L
y x
y x dy
e dx y x 2ln 22222
解:将方程代入被积函数在由格林公式得
(=-=+-L
D
y dxdy dy e dx x 0 00(21ln 2
2. ((⎰+-+-L
dy y x x y dx x y xy , 3sin 21cos 23233其中L为点(0, 0O到⎪⎭
{
, , 2
2
2
2
y
x ky y
x kx z y x F +-+-=
2ln 2
cos 1
cos
cos 2
2
2
22
2
k
t d t t
k dy y x ky dx y x
kx
W L
=
+-=
+-+
+-=
⎰⎰π
五、将积分y y x Q x y x P L d , (d , (⎰+化为对弧长的积分,其中L沿上半圆周
+
+ds y x z 3
