齿轮范成程序MATLAB代码
MATLAB锥齿轮设计

MATLAB弧齿锥齿轮设计弧齿锥齿轮设计程序如下:clear all; clc;%%输入参数PI=3.1415926;M=12; %模数Z=40; %齿轮齿数Z_ASM=9; %相配合齿轮齿数ALPHA=22.5; %法向压力角ALPHA=ALPHA*PI/180; %转化成弧度制B=80; %齿宽系数HAX=0.85; %齿顶高系数,X代表*CX=0.188; %顶隙系数X=0; %变位修正系数BETA=35; %齿宽中点螺旋角BETA=BETA*PI/180; %转化成弧度制RD=533.4/2; %铣刀盘名义半径,查表得知%%%%各部分计算公式HA=(HAX+X)*M; %齿顶高HF=(HAX+CX-X)*M; %齿根高H=HA+HF; %全齿高DELTA=atan(Z/Z_ASM); %分锥角,节锥角D=M*Z; %分度圆直径RX=D/(2*sin(DELTA)); %锥距RM=RX-B/2; %中点锥距DB=D*cos(ALPHA); %基圆直径DA=D+2*HA*cos(DELTA); %齿顶圆直径DF=D-2*HF*cos(DELTA); %齿根圆直径HB=(D-DB)/(2*cos(DELTA)); %齿基高THETA_A=atan(HA/RX); %齿顶角THETA_B=atan(HB/RX); %齿基角THETA_F=atan(HF/RX); %齿根角DELTA_A=DELTA+THETA_A; %顶锥角DELTA_B=DELTA-THETA_B; %基锥角DELTA_F=DELTA-THETA_F; %根锥角UNFOLD_F=2*PI*sin(DELTA_F); %根锥展角UNFOLD_A=2*PI*sin(DELTA_A); %顶锥展角BA=B/cos(THETA_A); %齿顶宽BB=B/cos(THETA_B); %齿基宽Dzf=DF/cos(DELTA); %大端齿根圆直径Dzb=DB/cos(DELTA); %大端基圆直径Dz=D/cos(DELTA); %大端分度圆直径Dza=DA/cos(DELTA); %大端齿顶圆直径BF=B/cos(THETA_F); %齿根宽dzf=(DF-2*BF*sin(DELTA_F))/cos(DELTA); %小端齿根圆直径dzb=(DB-2*BB*sin(DELTA_B))/cos(DELTA); %小端基圆直径dza=(DA-2*BA*sin(DELTA_A))/cos(DELTA); %小端齿顶圆直径dz=(D-2*B*sin(DELTA))/cos(DELTA); %小端分度圆直径RX_AB=RX/cos(DELTA_A-DELTA); %大端球半径RX_AS=(RX-B)/cos(DELTA_A-DELTA); %小端球半径%《PRO/E环境下的弧齿锥齿轮三维参数化造型》% t=0:0.02:1; %参数方程的参数%%% R=RX_AB; %大端齿顶渐开线% % R=RX_AS; %小端齿轮渐开线%% if (DELTA_B<DELTA_F)% theta=DELTA_F+t.*(DELTA_A-DELTA_F); %球坐标下的两个角度% else% theta=DELTA_B+t.*(DELTA_A-DELTA_B);% end%%% phi=theta; %建立phi坐标数组% x=theta;% y=theta;% z=theta;%%% for I=1:length(theta)%phi(I)=acos(cos(theta(I))/cos(DELTA_B))/sin(DELTA_B)-acos(tan(DELTA_B)/tan(theta(I) )); %论文中符号有误% x(I)=R*cos(phi(I)).*sin(theta(I)); %球面渐开线极坐标向直角坐标转换% y(I)=R*sin(phi(I))*sin(theta(I));% z(I)=R*cos(theta(I));% end%计算齿顶锥和齿根锥上的四条齿形曲线L1=(RM^2+RD^2-2*RM*RD*sin(BETA))^0.5;R=RX_AS:0.5:RX_AB;R(length(R)+1)=RX_AB;zj=acos((R.^2+L1^2-RD^2)./(2*R.*L1));Q1=zj(1)/sin(DELTA);Q2=zj(length(R))/sin(DELTA); %Q2>Q1%theta值选其一,得到一条锥面上的齿形扫掠线% theta=DELTA_A; %计算面锥面上齿形扫掠线theta=DELTA_F; %计算根锥面上齿形扫掠线phi=zj/sin(DELTA)-Q1;x=R.*cos(phi).*sin(theta); %球面渐开线极坐标向直角坐标转换sinphi=sin(phi);y=R.*sinphi.*sin(theta);z=R.*cos(theta);x=x'; %转化成列向量y=y';z=z';save('xx.txt','x','-ASCII')save('yy.txt','y','-ASCII')save('zz.txt','z','-ASCII')。
利用matlab实现齿轮滚刀快速设计

利用matlab实现齿轮滚刀齿形快速设计随着齿轮行业发展近几十年,人们对齿轮的研究越来越深入,其中涉及到很多高等数学的运算,在早期,工程师们用纸笔的方式,进行大量的计算,计算过程非常复杂,工作量非常大,所以也很辛苦。
目前很多公司研发出专门针对高等数学运算的软件,非常好用,也节省了大量的计算工作量,不得不佩服当今科学发展的飞跃性速度。
现在我们借助matlab设计一款标准齿轮滚刀齿形:齿轮1:m=2,z=37,α=20°,d a1=φ78,r1=37,r b1=34.77齿轮2:z=41,d a2=φ86这里我们借用公式dnf=√[d−2(h∗an−x n−x f)m n]2+4[(h∗an−x n−x f)m n /tanαt]2 (因为标准齿轮,此处x n=0,x f=0,m n=m,αt=α)计算渐开线起始圆d nf=φ70.86,r nf=35.43起始圆压力角α0=arccos(r b1/r nf)=11.076°,转换成弧度为0.1933起始圆展角(及该点渐开线函数)θ0=tanα0-α0=0.0024;同样利用d a1=φ78, r b1=34.77计算出终止圆展角θa=0.038我们先看齿廓部分渐开线方程组:x=R b cosθ+R bθsinθy=R b sinθ-R bθcosθ该方程组在齿轮手册中的图形解释如下:可以看出,当l0=0时,渐开线起点在x轴上,起点在基圆,而我们一般研究时以y轴为纵坐标,且渐开线偏离y轴半个基圆弧齿厚。
所以,我们先旋转90°,即将x轴和y轴切换:x=R b sinθ-R bθcosθy=R b cosθ+R bθsinθ基圆弧齿厚计算公式:S b=[s+mzinv(α)]cosα此处s为分度圆齿厚s=πm/2,由以上两公式计算出s b=3.99基圆半弧齿厚s b/2=1.995基圆周长l=πd b=218.47故我们可以计算出齿形实际渐开线起点在基圆上偏离y轴的角度为s b/2/l×360°=3.29°于是,我们将渐开线方程组绕齿轮中心作旋转,旋转变换如下:Aφ1=[cos3.29°,sin3.29°,0][-sin3.29°,cos3.29°,0][0 , 0 , 1]渐开线方程组写成矩阵形式:A=[ R b sinθ-R bθcosθ][R b cosθ+R bθsinθ ][ 0 ]经过变换的齿廓曲线方程组如下:B= Aφ1*A,我们将这两个矩阵及变换输入matlab中,计算结果如下:B =[rb*sin(θ) - (57*rb*cos(θ))/10000 - (57*a*rb*sin(θ))/10000 -θ*rb*cos(θ)][ rb*cos(θ) + (57*rb*sin(θ))/10000 +θ*rb*sin(θ) - (57*θ*rb*cos(θ))/10000 ] [ 0 ]即x= rb*sin(θ) - (57*rb*cos(θ))/10000 - (57*a*rb*sin(θ))/10000 -θ*rb*cos(θ)Y= rb*cos(θ) + (57*rb*sin(θ))/10000 +θ*rb*sin(θ) - (57*θ*rb*cos(θ))/10000 当然该式中数字显示和我们平时习惯有点不一样,可以不理会它,这就是我们齿轮1齿廓曲线的实际方程组。
二级圆柱齿轮减速器优化设计及其MATLAB实现

36
注意 x6 的单位为度, 代入计算时应转为弧度。
( 2) 齿面接触与齿根弯曲强度要求
据 !H ! ""H #; #F! "$F $代 入 相 应 的 数 据 得 强 度 约 束
式:
33
g1(3 X) =cos3x6-3.079g10-6x1 x3 x5 !0
33
g1(4 X) =x5cos3x6-1.017g10-4x2 x4 !0
二级圆柱齿轮减速器优化设计及其 M A T L A B 实现
俞鸿斌 ( 金华职业技术学院 机电工程学院, 浙江 金华 321000)
摘要: 通过设计变量的选取、目标函数和约束条件的确定, 建立了二级斜齿圆柱齿轮减速器的优化设计数学模型, 最后借
助 M A T LA B 的优化工具箱进行了寻优计算。结果显示, 采用此方法不仅算法可靠有效, 而且编写程序简单, 设计效率得
以提高。
关键词: 二级斜齿圆柱齿轮减速器; M A T LA B 优化工具箱; 优化设计
中图分类号: T H 132.46
文献标识码: A
文章编号: 1672-545X (2007)05-0036-02
传统设计由于专业理论和计算工具的限制, 设计者只能根 据经验和判断先制定设计方案, 随后再对给定的方案进行系统 分析和校核, 往往要经几代人的不断研制、实践和改进, 才能使 某 类 产 品 达 到 较 满 意 的 程 度 。由 于 产 品 设 计 质 量 要 求 日 益 提 高 和设计周期要求日益缩短, 传统设计已越来越显得不能适应工 业发展的需要。优化设计作为一门新兴的学科, 被广泛应用于 生产管理 、军 事 指 挥 和 科 学 实 验 等 领 域 , 如 工 程 设 计 中 的 最 优 化设计等。但是, 为了达到优化设计的目的, 设计人员除了需具 有该学科的基本理论、专业知识和熟悉设计对象的构造原理 外, 还需 具 有 一 定 的 数 学 知 识( 对 各 种 优 化 算 法 如 函 数 法 等 都 很熟悉) 和编程能力, 才能顺利完成优化设计的任务。这就给设 计人员提出了很高的要求。笔者提出采用 M A TLA B 语言中的 优化工具箱, 对二级斜齿圆柱齿轮减速器进行了优化设计, 这 对齿轮传动减速器的设计具有一定的现实意义。
减速器matlab程序

disp('总传动效率')
n=n1*n2*n3*n4
disp('电机功率Pd ')
Pd = Pw/n
disp('总传动比应小于40,输出转速为')
Vo=(800/150)/(2*pi)*60
disp('最大传动比为40,因此电机输入最大转速为')
Nimax=Vo*40
disp('应力循环次数N,1表示齿轮转一圈同一齿面的齿合次数为1')
disp('假设1、3轮尺寸小于100,2、4大于200.---------------------------------------------------------------------------')
sgmas1=[373 373]
hrc1=[50 50]
sgmas2=[314 314]
SF=2
disp('实验齿轮的齿根弯曲疲劳极限sgmaFlim:应力特性为脉动循环')
disp('-------------------------------------------只和材料硬度有关146-----------------------------------------------查表')
fprintf(' %d %f %f %f\n',4,v4,p4,T4);
disp('确定传动件参数')
disp('齿轮材料:')
disp('硬齿面:采用锻件齿胚,材料为45,调质处理后切齿,再经表面硬化处理(达到中等要求),最后磨齿达到精度8级:')
基于MATLAB编程软的齿轮设计

摘要齿轮机构是现代机械中最重要的传动机构,应用十分广泛。
它是依靠轮齿齿廓直接接触来传递运动和动力的,具有传动比恒定,传动效率高,使用寿命长,适用范围广及承载能力高等特点,但也存在对制造和安装精度要求较高以及成本较高等缺点。
使用MATLAB编程软件可以简化齿轮设计中的计算过程,只需将参数输入就可以计算出正确的结果。
此设计编写了三个程序,分别为绘制标准直齿圆柱齿轮渐开线曲面,直齿轮几何尺寸设计,以及两齿轮相对滑动系数相等时的变位系数的选择。
在编写程序的过程中需用到一些特殊曲线公式,例如绘制渐开线曲面轮廓时就用到了此曲线在直角坐标系中的表达式。
另外,程序在运行中可能需要在程序代码中设置初始值,以便计算出正确的结果,所选初始值的大小应尽量接近正确的结果,在计算中有可能会出现输入值相同而计算结果不同,这可能是软件本身的问题,还需要弥补。
本次设计一对齿轮,根据给定的参数,使用Matlab计算出齿轮的其他参数及几何尺寸。
关键词:齿轮机构,Matlab计算,初始值,几何尺寸ABTRACTGears of modern machinery are the most important transmission mechanism, a wide range of applications. It is to rely on direct contact with gear tooth profile and the power to transfer the exercise. MATLAB programming software used to simplify the calculation of gear design process, simply enter the parameters you can calculate the correct results. The preparation of this design, three procedures, respectively, rendering the standard spur gear involute surfaces, the design of spur gear geometry, as well as the coefficient of relative sliding between gear changes when the same selection coefficient. In the preparation of the procedures required to process some special curve formula, such as drawing involute surface contours on the use of this curve in the Cartesian coordinate system of expression. In addition, the procedures in the operation code may need to set the initial value for the purpose of calculating the correct result, the size of the initial value selected should be as close as possible to correct the results of the calculation in the input value may be calculated the same the result is different, this may be the software itself, but also need to be filled. The design of a pair of gears, according to the given parameters, the use of Matlab to calculate the other parameters and gear geometry.This is the design of a pair of gear. In accordance with the given parameters, the use of Matlab to calculate the other parameters and gear geometry.KEY WORDS:gears,Matlab programming,Initial value,gear geometry dimension目录目录 (3)第一章前言 (5)1.1 MATLAB简介 (5)1.2 变量、函数与表达式 (6)1.2.1 MATLAB变量名的定义规则 (6)1.2.2 数学运算符号以及标点符号 (7)1.2.3 数学函数 (7)1.2.4 数组与矩阵 (7)1.2.5 MATLAB有两种常用的工作方式 (7)第二章渐开线齿轮机构 (8)2.1 渐开线齿轮的简介 (8)2.1.1 渐开线齿廓曲线 (8)2.1.2 渐开线的极坐标方程式 (9)2.1.3 渐开线齿廓曲线的计算 (10)2.2 渐开线直齿轮变位系数的选择 (10)2.2.1 关于渐开线直齿轮变位系数 (10)2.2.2 最小变位系数的求法 (11)2.2.3 齿轮干涉对变位系数的限制 (11)2.2.4 变位齿轮的啮合传动及几何尺寸 (11)2.3 按两齿轮相对滑动系数相等时的变位系数选择 (13)第三章使用MATLAB编写简单程序 (15)3.1Matlab编程绘制标准直齿圆柱齿轮渐开线曲面 (15)3.1.1 制作MATLAB界面 (15)3.2Matlab编程计算直齿轮的几何尺寸 (18)3.2.1 设计MATLAB界面的过程 (18)3.3 按等滑动系数原则选择变位系数 (20)结论 (21)致谢 (22)参考文献 (23)附录一 (24)附录二 (27)附录三 (37)第一章前言本次设计的目的是使用Matlab编一个程序,实现齿轮参数及几何尺寸的计算。
基于Matlab的渐开线齿轮的范成法仿真 (2)

基于Matlab的渐开线齿轮的范成法仿真摘要:本文介绍了应用编Matlab进行编程实现齿轮和齿圈的范成仿真,实现参数化设计.通过此程序可以得到齿轮的范成动态模拟图,从而更形象了表达了齿轮的加工过程,也能帮助设计人员提前发现齿轮传动过程中可能发生的干涉,提高了设计效率。
关键词:Matlab;齿轮;范成仿真;参数化设计K inematical simulation of gears based on MatlabTIAN Donglong WU Baolin(1.School of Mechanical Engineering Tianjin Polytechnic University TianJin 300387;2.Tianjin Polytechnic University Academic Affairs Office TianJin 300387)Abstract:The paper introduces themethod of Matlab simulation ofmaking involute gears and gear ring, and provides away of parametric design bymeans of Matlab language. We can get exact profile of gear teeththrough themethod. It can help the designer check the interference beforemanufacture, and enhance the design efficiency.Key words:Matlab; gear; kinematical simulation; parametric design0前言渐开线齿轮的范成是利用一对齿轮在相互啮合是,其共轭齿廓互为包络线的原理来加工齿轮的一种方法。
机械原理总复习题及解答第十章
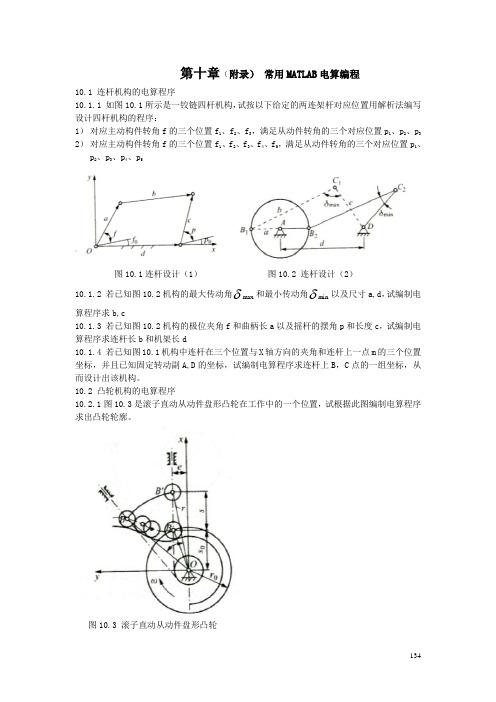
第十章(附录)常用MATLAB电算编程10.1 连杆机构的电算程序10.1.1 如图10.1所示是一铰链四杆机构,试按以下给定的两连架杆对应位置用解析法编写设计四杆机构的程序:1)对应主动构件转角f的三个位置f1、f2、f3,满足从动件转角的三个对应位置p1、p2、p3 2)对应主动构件转角f的三个位置f1、f2、f3、f4、f5,满足从动件转角的三个对应位置p1、p2、p3、p4、p5图10.1连杆设计(1)图10.2 连杆设计(2)10.1.2 若已知图10.2机构的最大传动角δmax和最小传动角δmin以及尺寸a,d,试编制电算程序求b,c10.1.3 若已知图10.2机构的极位夹角f和曲柄长a以及摇杆的摆角p和长度c,试编制电算程序求连杆长b和机架长d10.1.4 若已知图10.1机构中连杆在三个位置与X轴方向的夹角和连杆上一点m的三个位置坐标,并且已知固定转动副A,D的坐标,试编制电算程序求连杆上B,C点的一组坐标,从而设计出该机构。
10.2 凸轮机构的电算程序10.2.1图10.3是滚子直动从动件盘形凸轮在工作中的一个位置,试根据此图编制电算程序求出凸轮轮廓。
图10.3 滚子直动从动件盘形凸轮13413510.2.2 试编制求凸轮最大压力角的程序 10.3齿轮范成实验演示程序10.3.1编制一个加工齿轮的范成实验演示程序第10章 常用MATLAB 电算编程题解答与分析 10.1 连杆机构的电算程序 10.1.1 解:1)根据教材中的推导,令 ac b d c a R 222221-++=c d R =2 a d R =3 得:)]()cos[()cos()cos(0003021p f p f p p R f f R R -+-=+++- (10-1) 把对应位置的已知条件代入以上算式解方程组即可。
为方便起见取f 0=p 0=0以方便编程。
function linkage3(d,f1,p1,f2,p2,f3,p3) f1=f1*pi/180; f2=f2*pi/180; f3=f3*pi/180; p1=p1*pi/180; p2=p2*pi/180; p3=p3*pi/180;fc='r1-r2*cos(f)+r3*cos(p)=cos(f-p)'; s1=subs(fc,'f',f1); s1=subs(s1,'p',p1); s1=vpa(s1);s2=subs(fc,'f',f2); s2=subs(s2,'p',p2); s2=vpa(s2);s3=subs(fc,'f',f3); s3=subs(s3,'p',p3); s3=vpa(s3);[r1,r2,r3]=solve(s1,s2,s3,'r1','r2','r3'); a=d/(r3) c=d/(r2)b=sqrt(a^2+c^2+d^2-2*a*c*r1)例如:若已知图10.1中d=50,a 杆转角f 为45o 、90o 、135o 对应c 杆转角p 为52o 、82o 、112o可调用:>> linkage3(50,45,52,90,82,135,112) a =27.629285658965426760636076548711 c =41.110355468665232376141549605063 b =57.2362894665213494750616056630382)对于5个位置要求的情况,在程序中我们设定:对应图10.1,已知d ,对应主动件a 的转角f1、f2、f3、f4、f5,从动件有转角p1、p2、p3、p4、p5。
matlab面向齿轮的计算机辅助设计、制造及检测_毕业论文

毕业一、题目面向齿轮的计算机辅助设计、制造及检测二、研究主要内容本题选自正在建设的实验项目CAD/CAM一体化实验。
该项目的研究内容是以齿轮为实验对象,进行计算机辅助设计,在此基础上,利用数控线切割机进行计算机辅助加工,形成计算机辅助设计和数控加工的一体化实验,最后,对加工出来的齿轮进行公差组项目检测。
通过毕业设计,培养在工程设计、编程、调试的能力,提高查阅资料、外文翻译的能力,以及和综合应用基础理论和专业知识的能力,进一步增强分析问题和解决问题的能力。
三、主要技术指标•编制一渐开线标准直齿圆柱齿轮设计程序;•设计加工的齿轮精度等级为7级;•确定并检测齿轮三个公差组的检查组;四、进度和要求进行毕业设计开题2周2周(第1~2 周) 外文科技资料翻译1周1周(第 3 周) 了解齿轮啮合原理,掌握直齿圆柱齿轮的廓线形成方法1周(第 4 周) 掌握MATLAB编程语言2周(第5~6 周) 齿轮的计算机编程与设计2周(第7~8 周) 掌握线切割机床数据数据转换格式1周(第9 周)将计算数据导入线切割机1周(第10 周) 利用电火花数控线切割机加工所设计的齿轮1周(第11 周)针对所加工的齿轮进行齿轮公差组检测1周(第12 周) 绘制工作图1周(第13 周) 撰写论文1周(第14 周) 修改论文1周(第15 周) 制作答辩电子稿,准备答辩1周(第16 周) 毕业答辩1周(第17 周)五、主要参考书及参考资料[1] 孙桓,陈作模,葛文杰.机械原理.北京:高等教育出版社,2006,5[2] 王玉荣,张应昌,公差与测量技术.西安:陕西科学技术出版社,1990,8[3] DK7720电火花数控线切割机使用说明书[4] 张志勇主编.matlab教程.北京:北京航空航天大学出版社出版,2013[5] <齿轮便查手册>编委会编.齿轮便查手册.北京:机械工业出版社,2013,3摘要齿轮机构是现代机械中最重要的传动机构,应用十分广泛。
齿轮传动设计和MATLAB实现

齿轮传动设计和MATLAB实现郭仁生【摘要】摘要:描述齿轮传动设计的简化方法,并且说明基于MATLAB实现的基本流程和主要处理方法。
【期刊名称】机械【年(卷),期】2005(032)007【总页数】3【关键词】齿轮强度;数据处理;参数协调;MATLAB圆柱齿轮承载能力计算涉及齿轮的设计、制造工艺、材料和检验等各方面的因素,齿轮强度理论由经典的刚体啮合理论发展到弹塑性体的啮合理论,并不断引入齿形、速度、制造与安装精度、弹性和热变形、润滑、表面粗糙度和材质等因素的影响系数,是一个十分复杂的问题。
对于一般机械中的闭式齿轮传动,以齿面接触强度和轮齿弯曲强度作为其承载能力的计算依据。
按照GB10063“通用机械渐开线圆柱齿轮承载能力简化计算方法”,对齿轮承载能力计算的作了简化处理。
1 齿轮传动设计计算的简化方法齿轮传动设计是已知小齿轮传递功率、转速、载荷性质和传动比等条件下,选择齿轮材料和热处理方式,通过强度计算和参数协调,确定齿轮传动的基本参数和主要几何尺寸。
根据齿面接触强度估算齿轮传动尺寸(中心距或分度圆直径)的计算公式是根据齿根弯曲强度估算齿轮模数的计算公式是式中:“+”用于外啮合;“-”用于内啮合;、和是与齿轮螺旋角有关的常系数值;是载荷系数,根据载荷性质、齿宽大小、轴承布置、轴的刚性、齿轮精度和齿轮螺旋角大小等因素选取;是小齿轮传递的转矩,Nm;是齿数比;和是齿宽系数,分别表示齿轮宽度b与齿轮副中心距的比值;或是齿轮宽度与小齿轮分度圆直径的比值;它们的关系是;是复合齿形系数,用以考虑齿形与齿根的应力集中、以及压应力和剪应力等对齿根弯曲应力的影响;和分别是试验齿轮的许用接触应力和许用弯曲应力,。
2 M文件基本流程和主要处理方法除了已知数据的输入和计算结果的输出外,M程序文件主要包括3个部分内容:选择齿轮的材料和确定许用应力;按照设计准则计算和校核齿轮传动主要参数和几何尺寸;协调主要参数和几何尺寸。
在CAD环境下利用VB实现范成法加工齿轮的仿真

第7卷第3期2008年6月无锡职业技术学院学报Jour na l of W ux i I n s ti t u t e of T ec hnol o gyV01.7N o.3Jun.2008在C A D环境下利用V B实现范成法加工齿轮的仿真蔡小华,薛小雯(江南大学机械工程学院,江苏无锡214122)摘要:介绍了用V B对A utoC A D二次开发技术实现范成法加工齿轮的运动仿真。
文中阐明了三维模型的建立和实现三维运动仿真的详细步骤,生成的齿廓准确并能精确显示出齿轮加工的实际过程。
在产品设计、开发、科研及教学方面有很强的实用性。
关键词:范成法;齿轮;二次开发;运动仿真中图分类号:TH l l2文献标识码:A文章编号:1671—7880(2008)03—0029—03R ea l i ze K i nem at i c Si m ul at i on of M a ki ng G ear s w i nlG ener at i ng B as e d on A ut oC A D B y V B6.OC ai X i aohua.X ue X i ao w en(Ji angnan U ni ver si t y,形hi214122,C hi na)A b st r ac t:T he pa per i nt r oduces t hem et hod of ki ne m at i cal s i m ul at i on of m aki ng gear s w i t h gener at i ng by m ea l'l fl of A ut oC A D r e dev el opm ent t echno l ogy us edV B6.0.W e hav e bu i l t t he3D m odel i ng a nd f i m s hed t he pr og r am f or ki ne m at i cal dynam i c si m ul a-t i on of m aki ng gear s i n det ai l.W e get t he t oot h prof il e exact l y a nd it c an s how U S t he w h ol e m a nuf a ct u r i ng pr oces s i n t rut h.I t i s ver y us ef ul i n t he pr oduc t i on des i gn,deve l opm e nt,r esea r chi ng a nd t ea chi ng.K e y W or ds:ge ner at i ng;gear;,r edevel opm ent;ki n em at i cal s i m ul at i on齿轮机构是工业生产中最常用的机构之一,考虑加工制造和强度等因素,在生产中多用范成法来加工齿轮。
第三章 四连杆之MATLAB程式讲解
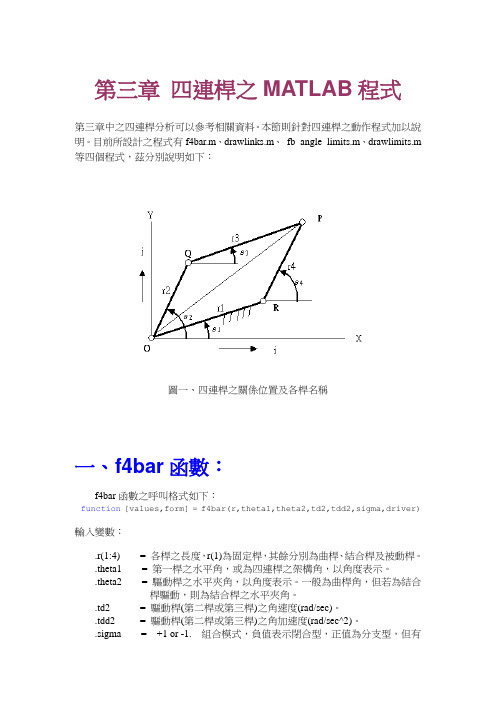
第三章四連桿之MATLAB程式第三章中之四連桿分析可以參考相關資料。
本節則針對四連桿之動作程式加以說明。
目前所設計之程式有f4bar.m、drawlinks.m、fb_angle_limits.m、drawlimits.m 等四個程式,茲分別說明如下:圖一、四連桿之關係位置及各桿名稱一、f4bar函數:f4bar函數之呼叫格式如下:function [values,form] = f4bar(r,theta1,theta2,td2,tdd2,sigma,driver)輸入變數:.r(1:4) = 各桿之長度,r(1)為固定桿,其餘分別為曲桿、結合桿及被動桿。
.theta1 = 第一桿之水平角,或為四連桿之架構角,以角度表示。
.theta2 = 驅動桿之水平夾角,以角度表示。
一般為曲桿角,但若為結合桿驅動,則為結合桿之水平夾角。
.td2 = 驅動桿(第二桿或第三桿)之角速度(rad/sec)。
.tdd2 = 驅動桿(第二桿或第三桿)之角加速度(rad/sec^2)。
.sigma = +1 or -1. 組合模式,負值表示閉合型,正值為分支型,但有時需視實際情況而定。
.driver = 0 (驅動桿為第二桿); 1 (驅動桿為第三桿)輸出變數:.form = 組合狀態,0 :表示無法組合;1:可以正確組合.values = 輸出矩陣,其大小為 4 X 7,各行之資料分配如下:其中第一行之連桿位置向量,屬於單桿的位置向量。
第二行為各桿之水平夾角,第三及第四行為各桿之角度速度及角加速度。
第五至七行則為P點與Q點之速度與加速度量,第五行為向量,第六行為絕對量,第七行為夾角。
值得一提的是第一行、三行、四行及五行之向量表示法屬於複數之型式。
故若要得到其絕對值僅需在MATLAB指令檔中,以abs()這一個函數指令即可求得,而以函數angle()則可求得其夾角,雖然第二行與第七行之輸出亦有相對應之夾角。
例一:為第二桿為驅動桿[val,form]=f4bar([3 2 4 2],0,60,10,0,-1,0)val = Columns 1 through 33 0 01 + 1.7321i 60 103.8682 - 1.0182i -14.7465.40781.8682 + 0.71389i 20.913 16.549 Columns 4 through 60 1 + 1.7321i 20 1.8682 + 0.71389i 2-127.58 173.21 - 100i 200-236.27 364.19 - 953.09i 1020.3 Column 76020.913-30-69.087form = 1 (表示可以組合)本例中,有框線者表示其為輸入值。
matlab直齿轮时变刚度代码

一、概述随着机械传动系统的日益复杂和精密化,对于直齿轮系统的时变刚度建模和分析需求日益增加。
直齿轮的时变刚度是指在工作过程中由于齿轮齿向变化、载荷变化等因素引起的齿轮传动系统的刚度随时间变化的现象。
本文将介绍如何使用MATLAB软件编写直齿轮时变刚度的代码,以方便工程师和研究人员进行系统分析和设计。
二、直齿轮时变刚度的原理直齿轮传动系统的刚度不仅取决于齿轮及其支撑系统的刚度,还与齿隙、齿向、压力角等因素有关。
在传统方法中,通常将直齿轮传动系统的刚度视为常数,然而在实际工作中,这种假设是不合理的。
需要采用时变刚度模型更为准确地描述直齿轮传动系统的动态特性。
三、MATLAB编程实现1. 数据准备在编写MATLAB代码之前,首先需要准备直齿轮传动系统的相关数据,包括齿轮的齿向变化、载荷变化等参数。
这些参数将作为输入,用于计算时变刚度。
2. 刚度计算利用MATLAB软件,可以编写函数来计算直齿轮传动系统的时变刚度。
这个函数将输入直齿轮系统的参数,进行计算得出对应的时变刚度值。
3. 结果分析利用MATLAB的数据可视化工具,对计算结果进行分析和展示,帮助工程师和研究人员更好地理解直齿轮传动系统的时变刚度特性。
四、示例代码下面是一个简单的MATLAB代码示例,用于计算直齿轮传动系统的时变刚度:```matlabfunction time_varying_stiffness =calculate_time_varying_stiffness(gear_data, load_data) 根据输入的齿轮数据和载荷数据,计算直齿轮传动系统的时变刚度这里假设输入的齿轮数据和载荷数据已经准备好,并且符合一定的格式要求进行时变刚度的计算这里可以根据具体的时变刚度计算方法进行实现返回计算得到的时变刚度结果time_varying_stiffness = calculated_time_varying_stiffness; end```以上代码中,函数calculate_time_varying_stiffness接受齿轮数据和载荷数据作为输入,进行时变刚度的计算,并返回计算结果。
用MATLAB解决齿轮计算中两类超越三角函数方程的求解问题

角 "#’ , 在使用双面啮合综合检查仪检测齿轮径向 综合误差时需知道调整度量中心距时的无侧隙啮 合角 " #$ , 在计算齿轮跨棒 ( 球)距时先要知道量 棒中心 ( 球心)的压力角 " % , 而这些角度值均要 ! !
收稿日期: "##$ % #& % ’( 作者简介: 佘明亮 ( ’)*( % ) , 男, 湖南长沙人, 南华大学机械工程学院工程师+ 主要研究方向: 机械计量和电子测试 技术+ 万方数据 万方数据
第 "# 卷第 " 期 "##$ 年 $ 月
南华大学学报 ( 自然科学版) 0-1234. -5 /43614 7389:2;8<= ( >?8:3?: 43@ A:?63-.-B=)
,-.+ "# /-+ " 013+ "##$
文章编号: ’$C& % ##$" ( "##$ ) #" % ##(( % #&
第 ’& 卷第 ’ 期) ) ) ) ) ) 佘明亮等: 用 123425 解决齿轮计算中两类超越三角函数方程的求解问题
+S
汽车里程表齿轮的设计计算中, 会遇到求解下面 !!"#! " $%#! " 超越三角函数方程中 ! 角的问题:ห้องสมุดไป่ตู้! " # & $ 式中: ! " 里程表从动齿轮分圆螺旋角; # ’ % & ’ ( )’ ; % " 两齿轮中心距; ’( " 齿 " # )( & )’ ; )( " 里程表主动轮齿数; )’ " 里程表 轮法向模数; 从动轮齿数$
基于MATLAB的齿轮传动系统设计

基于MATLAB的齿轮传动系统优化设计摘要:某高速重载齿轮进行了优化设计,在分析齿轮在各工况下的弯曲强度后,根据齿轮的优化设计原则,选择齿轮体积最小为优化设计原则,对传动齿轮中的小齿轮进行了优化设计,设计模数、齿数、齿宽系数、螺旋角为变量,根据各参数的设计要求来确定约束条件,同时根据齿根弯曲疲劳强度和齿面接触疲劳强度进行条件约束,最后用MATLAB进行编程计算,最后得出优化后的结果,该结果满足要求。
本文的研究对机械系统的优化设计具有指导意义和工程应用价值。
关键词:齿轮;优化设计;MATLAB;0引言优化设计是近年发展起来的一门新的学科,也是一项新技术,在工程设计的各个领域都已经得到了更为广泛的应用。
通过实际的应用过程表明:工程设计中采用优化设计这种新的科学设计方法,不仅使得在解决复杂问题时,能够从众多纷繁复杂的设计方案中找到尽可能完善的或者最适合的设计方案,而且,采用这种方法还能够提高设计效率和设计质量,使其的经济和社会效益都非常明显。
优化设计的理论基础是数学规划,采用的工具是计算机。
优化设计具有一般的设计方法所不具备的一些特点。
优化设计能够使各种设计参数自动向更优的方向进行调整,直到找到一个尽可能完善的或最适合的设计方案。
一般的设计方法只是依靠设计人员的经验来找到最佳方案,这样不足以保证设计参数一定能够向更优方向调整,也不能够保证一定能找到最适合的设计方案。
优化设计的手段是采用计算机,在很短的时间内就可以分析一个设计方案,并判断方案的优劣、是否可行,因此就能够从大量的方案中选出更加适合的设计方案,这是常规设计所不能比的。
1 机械系统优化设计方法概述许多机械工程设计都需要进行优化。
优化过程可以分为三个部分:综合与分析、评价、改变参数三部分组成。
其中,综合与分析部分的主要功能是建立产品设计参数与设计性能、设计要求之间的关系,这也就是一个建立数学模型的过程。
评价部分就是对该产品的性能和设计要求进行分析,这就相当于是评价目标函数是否得到改善或者达到最优,也就是检验数学模型中的约束条件是否全部得到满足。
matlab端面齿轮齿面方程

在MATLAB中,可以使用以下方程来描述端面齿轮的齿面形状: 1. 齿廓方程:
x = (R + h) * cos(theta) y = (R + h) * sin(theta) 其中,(x, y)为齿廓上的点坐标,R为齿轮的基圆半径,h为齿高,theta为参数角度。
2. 齿根方程: x = (R - h) * cos(theta) y = (R - h) * sin(theta) 其中,(x, y)为齿根上的点坐标,R为齿轮的基圆半径,h为齿高,theta为参数角度。
matlab端面齿轮齿面方程
这两个方程描述了齿轮齿面的几何形状,可以通过调整参数R和h来控制齿轮的大小和形状 。在实际应用中,还需要考虑齿轮的齿数、齿廓修形等因素,以满足特定的制造中可能会存在一 定的误差和修形需求。因此,在具体应用中,可能需要根据实际情况进行适当的调整和修正。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本人经过一个月的努力,写出了以下齿轮展成程序,是matlab格式的。
只要按照附图的标注定义出滚刀刀齿的形状,指定程序模拟的精度,就可以模拟出滚刀滚切齿轮的图形.下图为程序中定义刀具的尺寸示意图以下为源程序%shape of hob%input areacls;alpha=deg2rad(21); %压力角alphaf=deg2rad(31); %齿顶倒角压力角W0=1.85; %节圆半齿宽H=6; %全齿高ha0=3; %齿顶高hf0=1.44; %齿根倒角起点高度H1=0.064; %触角厚度hc=1.3; %触角高度ht=0.65; %触角凸部的高度rc=0.6; %齿顶圆角半径R=30; %工件分度圆半径P=7.54; %刀具齿距N=2; %刀齿数amount=10; %每段线上取点的个数step=100; %计算步数range=[-pi*0.15,pi*0.15];%计算范围%location of key-pointyr=ha0-rc; %齿顶圆角圆心xr=W0+(H1-rc)/cos(alpha)-yr*tan(alpha);point=zeros(6,2);point(1,2)=ha0;point(1,1)=xr;point(2,2)=ha0-rc*(1-sin(alpha));point(2,1)=xr+rc*cos(alpha);point(3,2)=ha0-ht;point(3,1)=(W0+H1/cos(alpha))-(ha0-ht)./cot(alpha);point(4,2)=ha0-hc;point(4,1)=W0-point(4,2)*tan(alpha);point(5,2)=-hf0;point(5,1)=W0-tan(alpha)*point(5,2);point(6,2)=ha0-H;point(6,1)=point(5,1)-tan(alphaf)*(point(6,2)-point(5,2));%-------------直线部分-------------theta=linspace(range(1),range(2),step);w11=linspace(point(4,1),point(5,1),amount)';h11=linspace(point(4,2),point(5,2),amount)';w12=repmat(w11,1,step);h12=repmat(h11,1,step);theta2=repmat(theta,amount,1);x12=(h12-R).*sin(theta2)+(R.*theta2-w12).*cos(theta2);y12=(R.*theta2-w12).*sin(theta2)+(R-h12).*cos(theta2);theta13=(w11-h11/tan(alpha))/R;x13=sin(theta13).*(h11-R)+cos(theta13).*(R.*theta13-w11);y13=sin(theta13).*(R*theta13-w11)+cos(theta13).*(R-h11);%-----------圆角部分--------gama=linspace(pi/2,alpha,amount);w21=(xr+rc.*cos(gama))';h21=(yr+rc.*sin(gama))';w22=repmat(w21,1,step);h22=repmat(h21,1,step);x22=(h22-R).*sin(theta2)+(R.*theta2-w22).*cos(theta2);y22=(R.*theta2-w22).*sin(theta2)+(R-h22).*cos(theta2);theta23=((xr-yr.*cot(gama))/R)';x23=sin(theta23).*(h21-R)+cos(theta23).*(R.*theta23-w21);y23=sin(theta23).*(R*theta23-w21)+cos(theta23).*(R-h21);rmin=R;for i=1:(length(x23)-2)[XX,YY,RR]=threepointcircle(x23(i),y23(i),x23(i+1),y23(i+1),x23(i+2),y2 3(i+2));if RR<rminrmin=RR;endend%---------凸角部分------------------w31=linspace(point(2,1),point(3,1),amount)';h31=linspace(point(2,2),point(3,2),amount)';w32=repmat(w31,1,step);h32=repmat(h31,1,step);theta2=repmat(theta,amount,1);x32=(h32-R).*sin(theta2)+(R.*theta2-w32).*cos(theta2);y32=(R.*theta2-w32).*sin(theta2)+(R-h32).*cos(theta2);theta33=(w31-h31/tan(alpha))/R;x33=sin(theta33).*(h31-R)+cos(theta33).*(R.*theta33-w31);y33=sin(theta33).*(R*theta33-w31)+cos(theta33).*(R-h31);%-------连接部分---------------alpha2=atan(point(4,1)-point(3,1))/(point(3,2)-point(4,2)); w41=linspace(point(3,1),point(4,1),amount)';h41=linspace(point(3,2),point(4,2),amount)';w42=repmat(w41,1,step);h42=repmat(h41,1,step);theta2=repmat(theta,amount,1);x42=(h42-R).*sin(theta2)+(R.*theta2-w42).*cos(theta2);y42=(R.*theta2-w42).*sin(theta2)+(R-h42).*cos(theta2);theta43=(w41-h41/tan(alpha2))/R;x43=sin(theta43).*(h41-R)+cos(theta43).*(R.*theta43-w41);y43=sin(theta43).*(R*theta43-w41)+cos(theta43).*(R-h41);%-------倒角部分---------------alpha3=atan(point(6,1)-point(5,1))/(point(5,2)-point(6,2)); w51=linspace(point(5,1),point(6,1),amount)';h51=linspace(point(5,2),point(6,2),amount)';w52=repmat(w51,1,step);h52=repmat(h51,1,step);theta2=repmat(theta,amount,1);x52=(h52-R).*sin(theta2)+(R.*theta2-w52).*cos(theta2);y52=(R.*theta2-w52).*sin(theta2)+(R-h52).*cos(theta2);theta53=(w51-h51/tan(alpha3))/R;x53=sin(theta53).*(h51-R)+cos(theta53).*(R.*theta53-w51);y53=sin(theta53).*(R*theta53-w51)+cos(theta53).*(R-h51);%----------全刀齿-----------w6=[w21;w31;w41;w11;w51];h6=[h21;h31;h41;h11;h51];w6=flipud(w6);h6=flipud(h6);w6=[w6;-flipud(w6)];h6=[h6;flipud(h6)];w62=w6;h62=h6;for i=2:Nw62=[w6+(i-1)*P;w62];h62=[h6;h62];endtheta6=repmat(theta,5*amount*2*N,1);w62=repmat(w62,1,step);h62=repmat(h62,1,step);x62=(h62-R).*sin(theta6)+(R.*theta6-w62).*cos(theta6);y62=(R.*theta6-w62).*sin(theta6)+(R-h62).*cos(theta6);%---------------------figure;plot(x12,y12);hold on;grid on;axis equal;plot(x22,y22);plot(x32,y32);plot(x42,y42);plot(x52,y52);figure;plot(x12',y12');hold on;grid on;axis equal;plot(x22',y22');plot(x32',y32');plot(x42',y42');plot(x52',y52');figure;plot(x13,y13);hold on;grid on;axis equal;plot(x23,y23,'o');plot(x33,y33,'*');plot(x43,y43,'.');plot(x53,y53,'+');figureplot(x12',y12');hold on;grid on;axis equal;plot(x22',y22');plot(x32',y32');plot(x42',y42');plot(x52',y52');plot(x13,y13,'*');plot(x23,y23,'*');plot(x33,y33,'*');plot(x43,y43,'*');plot(x53,y53,'*');figureplot(w62,h62);hold on;grid on;axis equal;figureplot(x62,y62);hold on;grid on;axis equal;以下为角度转化为弧度的子程序function rad=deg2rad(deg)rad=deg./180.*pi;以下为计算最小圆弧半径的子程序function [x,y,r]=threepointcircle(x1,y1,x2,y2,x3,y3)k12=(x2-x1)/(y1-y2);k23=(x3-x2)/(y2-y3);x=((y2+y3-y1-y2)/2+k12*(x1+x2)/2-k23*(x2+x3)/2)/(k12-k23); y=k12*(x-(x1+x2)/2)+(y1+y2)/2;r=((x-x1)^2+(y-y1)^2)^0.5;以下为程序运行输出的图形1,一个刀刃的展成过程2,一个刀刃上各个点的运动轨迹3,刀刃上各段切削刃分别所展成的齿形段4,两图合二为一5,刀齿的形状6,多个刀齿展成的情形7,将6图放大观察,也许是渐开线起始点的位置吧以上就是程序代码及输出的结果欢迎批评指正分享经验,交流心得,共同进步有意交流的+Q 252320995并说明来意李某人2013/6/30于重庆璧山。
