主成分分析matlab源程序代码
主成分分析 MATLAB代码

%特征向量图(效果等价于主成分载荷图)
figure(4); %创造第二个图形窗口
e1=-E(:,1);e2=-E(:,2); %提取特征向量并转换符号
Co2=Co1+A(:,2).^2; %提取2个主成分的公因子方差
Co3=Co2+A(:,3).^2; %提取3个主成分的公因子方差
Co4=Co3+A(:,4).^2; %提取4个主成分的公因子方差
Rz=cov(F); %计算协方差矩阵
Rz=corrcoef(F); %计算相关系数矩阵
Rz=corrcoef(Z); %计算相关系数矩阵
%计算非标准化数据协方差矩阵的三种方法
Covz=Z'*Z/(n-1); %计算协方差矩阵
Covz=cov(Z); %计算协方差矩阵
%计算主成分得分相关系数的四种方法
Rz=F'*F/(n-1); %计算相关系数矩阵
grid on %添加网格
%几个用于检验的语句
%计算再生相关系数矩阵
Rp=H*H'; %计算再生相关矩阵
Re=R-Rp; %计算相关矩阵的残差矩阵
%综合得分
S=Z(:,1)+Z(:,2)+Z(:,3)+Z(:,4) %非标准化得分四列加和
S1=F(:,1)*eigv(1)^0.5+F(:,2)*eigv(2)^0.5+F(:,3)*eigv(3)^0.5+F(:,4)*eigv(4)^0.5
%计算T平方统计量(2)
eigv=diag(G); %提取角矩阵的对角线元素
最新主成分分析及matlab实现

1.将原始数据标准化。这里不妨设上边矩阵已 标准化了。
2.建立变量的相关系数阵:
rij
n
(xki xi )(xkj xj )
k1
n
n
(xki xi )2 (xkj xj )2
k1
k1
3.求R的特征根 及相应的单位特征向量:
主成分分析及matlab实现
问题的提出:
在实际问题研究中,多变量问题是经常 会遇到的。变量太多,无疑会增加分析问题 的难度与复杂性,而且在许多实际问题中, 多个变量之间是具有一定的相关关系的。
因此,人们会很自然地想到,能否在相 关分析的基础上,用较少的新变量代替原来 较多的旧变量,而且使这些较少的新变量尽 可能多地保留原来变量所反映的信息?
1 1 .9 9 9 ,2 0 .9 9 8 ,3 0 .0 0 3
前2个主成分的累计贡献率在99%以上,故取2个主成分( x
* i
表示xi的标准化变量):
Z10.7063x* 10.0435x2 *0.7065x3 *,
Z20.0357x* 10.9990x2 *0.0258x3 *
由主成分回归得到的标准化回归方程为
第一步 将原始数据标准化。 第二步 建立指标之间的相关系数阵R如下
第三步 求R的特征值和特征向量。
从上表看,前3个特征值累计贡献率已达89.564%, 说明前3个主成分基本包含了全部指标具有的信息,我们 取前3个特征值,并计算出相应的特征向量:
因而前三个主成分为: 第一主成分:
第二主成分:
x1
149.3 161.2 171.5 175.5 180.8 190.7 202.1 212.4 226.1 231.9 239.0
主成分分析源代码)

1.function y = pca(mixedsig)2.3.%程序说明:y = pca(mixedsig),程序中mixedsig为 n*T 阶混合数据矩阵,n为信号个数,T为采样点数4.% y为 m*T 阶主分量矩阵。
5.% n是维数,T是样本数。
6.7.if nargin == 08. error('You must supply the mixed data as input argument.');9.end10.if length(size(mixedsig))>211. error('Input data can not have more than two dimensions. ');12.end13.if any(any(isnan(mixedsig)))14. error('Input data contains NaN''s.');15.end16.17.%——————————————去均值————————————18.meanValue = mean(mixedsig')';19.[m,n] = size(mixedsig);20.%mixedsig = mixedsig - meanValue*ones(1,size(meanValue)); %当数据本身维数很大时容易出现Out of memory21.for s = 1:m22. for t = 1:n23.mixedsig(s,t) = mixedsig(s,t) - meanValue(s);24. end25.end26.[Dim,NumofSampl] = size(mixedsig);27.oldDimension = Dim;28.fprintf('Number of signals: %d\n',Dim);29.fprintf('Number of samples: %d\n',NumofSampl);30.fprintf('Calculate PCA...');31.firstEig = 1;stEig = Dim;33.covarianceMatrix = corrcoef(mixedsig'); %计算协方差矩阵34.[E,D] = eig(covarianceMatrix); %计算协方差矩阵的特征值和特征向量35.36.%———计算协方差矩阵的特征值大于阈值的个数lastEig———37.%rankTolerance = 1;38.%maxLastEig = sum(diag(D) >= rankTolerance);39.%lastEig = maxLastEig;stEig = 10;41.43.eigenvalues = flipud(sort(diag(D)));44.45.%—————————去掉较小的特征值——————————46.if lastEig < oldDimension47. lowerLimitValue = (eigenvalues(lastEig) + eigenvalues(lastEig+ 1))/2;48.else49. lowerLimitValue = eigenvalues(oldDimension) - 1;50.end51.lowerColumns = diag(D) > lowerLimitValue;52.53.%—————去掉较大的特征值(一般没有这一步)——————54.if firstEig > 155. higherLimitValue = (eigenvalues(firstEig - 1) + eigenvalues(firstEig))/2;56.else57. higherLimitValue = eigenvalues(1) + 1;58.end59.higherColumns = diag(D) < higherLimitValue;60.61.%—————————合并选择的特征值——————————62.selectedColumns =lowerColumns & higherColumns;63.64.%—————————输出处理的结果信息—————————65.fprintf('Selected [%d] dimensions.\n',sum(selectedColumns));66.fprintf('Smallest remaining (non-zero) eigenvalue[ %g ]\n',eigenvalues(lastEig));67.fprintf('Largest remaining (non-zero) eigenvalue[ %g ]\n',eigenvalues(firstEig));68.fprintf('Sum of removed eigenvalue[ %g ]\n',sum(diag(D) .* (~selectedColumns)));69.70.%———————选择相应的特征值和特征向量———————71.E = selcol(E,selectedColumns);72.D = selcol(selcol(D,selectedColumns)',selectedColumns);73.74.%——————————计算白化矩阵———————————75.whiteningMatrix = inv(sqrt(D)) * E';76.dewhiteningMatrix = E * sqrt(D);77.78.%——————————提取主分量————————————79.y = whiteningMatrix * mixedsig;80.82.function newMatrix = selcol(oldMatrix,maskVector)83.if size(maskVector,1)~= size(oldMatrix,2)84. error('The mask vector and matrix are of uncompatible size.');85.end86.numTaken = 0;87.for i = 1:size(maskVector,1)88. if maskVector(i,1) == 189.takingMask(1,numTaken + 1) = i;90.numTaken = numTaken + 1;91. end92.end93.newMatrix = oldMatrix(:,takingMask);。
主成分分析及MATLAB应用 代码

主成分分析类型:一种处理高维数据的方法。
降维思想:在实际问题的研究中,往往会涉及众多有关的变量。
但是,变量太多不但会增加计算的复杂性,而且也会给合理地分析问题和解释问题带来困难。
一般说来,虽然每个变量都提供了一定的信息,但其重要性有所不同,而在很多情况下,变量间有一定的相关性,从而使得这些变量所提供的信息在一定程度上有所重叠。
因而人们希望对这些变量加以“改造”,用为数极少的互补相关的新变量来反映原变量所提供的绝大部分信息,通过对新变量的分析达到解决问题的目的。
一、总体主成分1.1 定义设 X 1,X 2,…,X p 为某实际问题所涉及的 p 个随机变量。
记 X=(X 1,X 2,…,Xp)T ,其协方差矩阵为()[(())(())],T ij p p E X E X X E X σ⨯∑==--它是一个 p 阶非负定矩阵。
设1111112212221122221122Tp p Tp pT pp p p pp p Y l X l X l X l X Y l X l X l X l X Y l X l X l X l X⎧==+++⎪==+++⎪⎨⎪⎪==+++⎩ (1) 则有()(),1,2,...,,(,)(,),1,2,...,.T T i i i i TT T i j ijij Var Y Var l X l l i p Cov Y Y Cov l X l X l l j p ==∑===∑= (2)第 i 个主成分: 一般地,在约束条件1T i i l l =及(,)0,1,2,..., 1.T i k i k Cov Y Y l l k i =∑==-下,求 l i 使 Var(Y i )达到最大,由此 l i 所确定的T i i Y l X =称为 X 1,X 2,…,X p 的第 i 个主成分。
1.2 总体主成分的计算设 ∑是12(,,...,)T p X X X X =的协方差矩阵,∑的特征值及相应的正交单位化特征向量分别为120p λλλ≥≥≥≥及12,,...,,p e e e则 X 的第 i 个主成分为1122,1,2,...,,T i i i i ip p Y e X e X e X e X i p ==+++= (3)此时(),1,2,...,,(,)0,.Ti i i i Ti k i k Var Y e e i p Cov Y Y e e i k λ⎧=∑==⎪⎨=∑=≠⎪⎩ 1.3 总体主成分的性质1.3.1 主成分的协方差矩阵及总方差记 12(,,...,)T p Y Y Y Y = 为主成分向量,则 Y=P T X ,其中12(,,...,)p P e e e =,且12()()(,,...,),T T p Cov Y Cov P X P P Diag λλλ==∑=Λ=由此得主成分的总方差为111()()()()(),p ppTTiii i i i Var Y tr P P tr PP tr Var X λ=====∑=∑=∑=∑∑∑即主成分分析是把 p 个原始变量 X 1,X 2,…,X p 的总方差1()pii Var X =∑分解成 p 个互不相关变量 Y 1,Y 2,…,Y p 的方差之和,即1()pii Var Y =∑而 ()k k Var Y λ=。
主成分分析(PCA)算法介绍及matlab实现案例

主成分分析(PCA)算法介绍及matlab实现案例主成分分析经常被⽤做模型分类时特征的降维,本篇⾸先介绍PCA的步骤,并根据步骤撰写对应的MATLAB代码,最后指明使⽤PCA的步骤。
我们在做分类时,希望提取的特征能够最⼤化将数据分开,如果数据很紧密,模型就⽐较难将其分开,如果数据⽐较离散,那么就⽐较容易分开,换句话说,数据越离散,越容易分开。
那怎么让数据离散呢?离散⼜⽤什么指标衡量呢?统计学的知识告诉我们,数据越离散,⽅差越⼤。
因此,PCA的问题就变为:寻找⼀个坐标轴,使得数据在该坐标轴上⾯离散度最⾼。
也就是寻找⼀个基使得所有数据在这个基上⾯的投影值的⽅差最⼤。
那具体怎么做呢?科学家们已经帮我们做好了,如下步骤:设有m个样本,每个样本有n个特征,组成m⾏n列的矩阵1)将每⼀列特征进⾏均值化处理,特征归⼀化,也称为数据中⼼平移到坐标原点2)求取协⽅差矩阵3)求取协⽅差矩阵的特征值和特征向量4)将特征向量按对应特征值⼤⼩从上到下按⾏排列成矩阵,取前K列组成系数矩阵matlab代码function [coffMatrix,lowData,eigValSort,explained,meanValue] = myPCA(data)%data为row⾏col列矩阵,row为样本数量,col为特征列,每⼀列代表⼀个特征[row , col] = size(data);% 求出每⼀列的均值meanValue = mean(data);% 将每⼀列进⾏均值化处理,特征归⼀化,数据中⼼平移到坐标原点normData = data - repmat(meanValue,[row,1]);%求取协⽅差矩阵covMat = cov(normData);%求取特征值和特征向量[eigVect,eigVal] = eig(covMat);% 将特征向量按对应特征值⼤⼩从上到下按⾏排列成矩阵[sortMat, sortIX] = sort(eigVal,'descend');[B,IX] = sort(sortMat(1,:),'descend');coffMatrix = eigVect(:,IX);% 排序后的特征向量就是新的坐标系lowData = normData * coffMatrix;% 分量得分explained = 100*B/sum(B);%特征值eigValSort = B;%%% [U,S,V] = svd(data);end我们在实际应⽤PCA的时候需要注意保留以下⼏个值。
主成分分析及matlab程序

举例:
某人要做一件上衣要测量很多尺寸,如身长、 袖长、胸围、腰围、肩宽、肩厚等十几项指标, 但某服装厂要生产一批新型服装绝不可能把尺寸 的型号分得过多 ,而是从多种指标中综合成几 个少数的综合指标,做为分类的型号,利用主成 分分析将十几项指标综合成3项指标,一项是反 映长度的指标,一项是反映胖瘦的指标,一项是 反映特体的指标。
2195.7 1408 422.61 4797 1011.8 119.0
5381.72 2699 1639.8 8250 656.5 114.0
1606.15 1314 382.59 5105 556.0 118.4
364.17 1814 198.35 5340 232.1 113.5
3534.00 1261 822.54 4645 902.3 118.5
111.6 1396.35
116.4 554.97
111.3 64.33
117.0 1431.81
117.2 324.72
118.1 716.65
114.9
5.57
117.0 600.98
116.5 468.79
116.3 105.80
115.3 114.40
116.7 428.76
1.将原始数据标准化。 2.建立指标之间的相关系数阵R如下:
正交化特征向量(通常用Jacobi法求特征向量):
a11
a12
1
=
a21
,
2
=
a22
,
a
p1
a
p
2
a1p
,
p
=
a2
p
,
a
主成分分析Matlab源码分析

主成分分析源程序代码分析function[pc, score, latent, tsquare] = princomp(x);% PRINCOMP Principal Component Analysis (centered and scaled data).% [PC, SCORE, LATENT, TSQUARE] = PRINCOMP(X) takes a data matri x X and% returns the principal components in PC, the so-called Z-scores in SCORE S,% the eigenvalues of the covariance matrix of X in LATENT, and Hotelling 's% T-squared statistic for each data point in TSQUARE.% Reference: J. Edward Jackson, A User's Guide to Principal Components % John Wiley & Sons, Inc. 1991 pp. 1-25.% B. Jones 3-17-94% Copyright 1993-2002 The MathWorks, Inc.% $Revision: 2.9 $ $Date: 2002/01/17 21:31:45 $[m,n] = size(x); % 得到矩阵的规模,m行,n列r = min(m-1,n); % max possible rank of x% 该矩阵最大的秩不能超过列数,% 也不能超过行数减1avg = mean(x); % 求每一列的均值,付给一个n维行向量centerx = (x - avg(ones(m,1),:));% x的每个元素减去该列的均值,% 使样本点集合重心与坐标原点重合[U,latent,pc] = svd(centerx./sqrt(m-1),0);% “经济型”的奇异值分解score = centerx*pc; % 得分矩阵即为原始矩阵乘主成分矩阵if nargout < 3, return; endlatent = diag(latent).^2; % 将奇异值矩阵转化为一个向量if (r<N)latent = [latent(1:r); zeros(n-r,1)];score(:,r+1:end) = 0;endif nargout < 4, return; endtmp = sqrt(diag(1./latent(1:r)))*score(:,1:r)';tsquare = sum(tmp.*tmp)';主成分分析[Matlab版]function main()%*************主成份分析************%读入文件数据X=load('data.txt');%==========方法1:求标准化后的协差矩阵,再求特征根和特征向量=================%标准化处理[p,n]=size(X);for j=1:nmju(j)=mean(X(:,j));sigma(j)=sqrt(cov(X(:,j)));endfor i=1:pfor j=1:nY(i,j)=(X(i,j)-mju(j))/sigma(j);endendsigmaY=cov(Y);%求X标准化的协差矩阵的特征根和特征向量[T,lambda]=eig(sigmaY);disp('特征根(由小到大):');disp(lambda);disp('特征向量:');disp(T);%方差贡献率;累计方差贡献率Xsum=sum(sum(lambda,2),1);for i=1:nfai(i)=lambda(i,i)/Xsum;endfor i=1:npsai(i)= sum(sum(lambda(1:i,1:i),2),1)/Xsum;enddisp('方差贡献率:');disp(fai);disp('累计方差贡献率:');disp(psai);%综合评价....略%+============方法2:求X的相关系数矩阵,再求特征根和特征向量================%X的标准化的协方差矩阵就是X的相关系数矩阵R=corrcoef(X);%求X相关系数矩阵的特征根和特征向量[TR,lambdaR]=eig(R);disp('特征根(由小到大):');disp(lambdaR);disp('特征向量:');disp(TR);。
主成分分析matlab代码

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%一如既往的x:m*n,n是样本个数,m是维度%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%错误之处望指正,虽然结果与pca函数一样吧function y=myPca(x)%%%%%%%%%%%%%%%%%%%%%求取x的协方差sigma=myCov(x)[V,D]=eig(sigma);%%%%%%%%%%%%%%%%%%%%%特征值排序和找出特征值向量duiJiao=diag(D);[xuLie,pos]=sort(duiJiao,'descend');cumsum(xuLie)/sum(xuLie);temp=cumsum(xuLie)/sum(xuLie);for i=1:length(xuLie)if temp(i)>0.85 %%%%%%%%近似一下,嘿嘿!index=i;ts=temp(i);break;endendnewXuLie=xuLie(1:index)newTezheng=V(:,pos(1:index))%%%%%%%%%%%%%%%%%%%%%求方差%%%%%%%%%%%%%%%%%%%%%下面我要开始对主成分得分了score=[];[m,n]=size(V);for i=1:nfor j=1:length(newXuLie)for k=1:mtemp(k)=newTezheng(k,j)*x(k,i);endtemp2(j)=sum(temp);endscore(:,i)=temp2;endcentered=centerMean(score); %%%%%%%%%%%%%%%%%%%%%%没有近似的temp3=V(:,pos(1:length(duiJiao))); score2=[];for i=1:nfor j=1:length(xuLie)for k=1:mtemp(k)=temp3(k,j)*x(k,i);endtemp2(j)=sum(temp);endscore2(:,i)=temp2;endcentered2=centerMean(score2);mda=newXuLie;y.score=score';y.scoreMean=centered';y.coeff=newTezheng;y.ts=ts;mdaO=xuLie;y.scoreO=score2';y.scoreOM=centered2';y.coeffO=V(:,pos(1:length(duiJiao)));%%%%%%%%%%%%%%%%%%%%%%子函数,求协方差function s=myCov(x)[p,n]=size(x);s=zeros(p,p);for i=1:pfor j=1:pfor k=1:nmeanij=mean(x,2);meani=meanij(i);meanj=meanij(j);xki=x(i,k);xkj=x(j,k);temp(k)=(xki-meani)*(xkj-meanj); ends(i,j)=sum(temp)/(n-1);endend %%%%%%%%%%%%%%%%%%%%%%%子函数,均值化function y=centerMean(x)[m,n]=size(x);A=ones(1,n);B=mean(x,2);y=x-kron(A,B);。
主元分析Matlab源程序

end
%%对数据进行标准化
m = mean(x);
s = std(x);
n = size(x,1);
x = (x - repmat(m,n,1))./repmat(s,n,1);
%%建立主元模型
n = 1000;
x1 = 8 + 0.1*randn(n,1);
x2 = 11 + 0.2*randn(n,1);
x3 = 17 + 0.3*randn(n,1);
x4 = -1.3*x1 + 0.2*x2 + 0.8*x3;
x5 = -0.8*x1 + 0.8*x2 + 0.9*x3;
Q(i) = x(i,:)*(eye(8) - p(:,1:a)*p(:,1:a)')*x(i,:)';
end
%%绘图
figure,
subplot(2,1,1),
plot(1:n,T2,'k -'),
xlabel('采样数'),
ylabel('T^2'),
hold on,
legend('统计量','阈值'),
%%贡献图
%1.确定造成失控状态的得分
T = x(170,:)*p(:,1:a);
r = [];
for i=1:a
if T(i)^2/latent(i) > T2c/a
r = cat(2,r,i);
end
%3.计算每个变量的总贡献
主成分分析报告matlab程序

主成分分析报告matlab程序主成分分析报告 Matlab 程序在数据分析和处理的领域中,主成分分析(Principal Component Analysis,PCA)是一种常用且强大的工具。
它能够将多个相关变量转换为一组较少的不相关变量,即主成分,同时尽可能多地保留原始数据的信息。
在 Matlab 中,我们可以通过编写程序来实现主成分分析,这为我们的数据处理和理解提供了极大的便利。
主成分分析的基本思想是找到数据中的主要方向或模式。
这些主要方向是通过对数据的协方差矩阵进行特征值分解得到的。
最大的特征值对应的特征向量就是第一主成分的方向,第二大的特征值对应的特征向量就是第二主成分的方向,以此类推。
在 Matlab 中,我们首先需要导入数据。
假设我们的数据存储在一个名为`data` 的矩阵中,每一行代表一个观测值,每一列代表一个变量。
```matlabdata = load('your_data_filetxt');%替换为您的数据文件路径```接下来,我们需要对数据进行中心化处理,即每个变量减去其均值。
```matlabcentered_data = data repmat(mean(data), size(data, 1), 1);```然后,计算协方差矩阵。
```matlabcov_matrix = cov(centered_data);```接下来进行特征值分解。
```matlabV, D = eig(cov_matrix);````V` 是特征向量矩阵,`D` 是对角矩阵,其对角元素是特征值。
我们对特征值进行从大到小的排序,并相应地对特征向量进行重新排列。
```matlablambda, index = sort(diag(D),'descend');sorted_V = V(:, index);```此时,`sorted_V` 的每一列就是一个主成分的方向。
为了计算每个观测值在主成分上的得分,我们可以使用以下代码:```matlabprincipal_components = centered_data sorted_V;```我们还可以计算每个主成分解释的方差比例。
主成分分析matlab程序

%数据主成分分析%------------------------------------------------------------------------------------%%数据预处理,便于调用%X=xlsread('d:\fubiao.xlsx',1,'B2:G34');将EXCEL附表中sheet1中的数据读取到matlab中%Y=X';将矩阵X生成转置矩阵Y%xlswrite('d:\fubiao.xlsx',Y,2,'B2:AH7');将矩阵Y的数据存储到EXCEL中sheet2中clcclear allB=xlsread('d:\fubiao.xlsx',2,'B2:AH7');%调用所需数据%%数据标准化处理A=log10(B);%由于数据的数量级相差较大,采用对数归一化a=size(A,1);%得到矩阵A的行数b=size(A,2);%得到矩阵A的列数name=[123456];%将省份按序编号放进矩阵:'山西为1','安徽为2'%'江西为3','河南为4','湖北为5','湖南为6'%%计算相关系数矩阵的特征值和特征向量CM=corrcoef(A);%计算相关系数矩阵[pc,la,tent]=princomp(CM);%主成分分析,pc为特征向量矩阵、la为得分矩阵%tent为特征值矩阵并且所有特征值已按降序排列for j=1:bTS(j,1)=tent(j);%将特征值赋给矩阵DS的第一列endfor i=1:bTS(i,2)=TS(i,1)/sum(TS(:,1));%各个主成分的贡献率TS(i,3)=sum(TS(1:i,1))/sum(TS(:,1));%累计贡献率end%%选择主成分及对应的特征向量T=1;%主成分信息保留率for k=1:bif TS(k,3)>=Tnumber=k;%保留主成分数目break;endendfor j=1:number%提取相对应的特征向量PC(:,j)=pc(:,j);end%%计算各个省份的主成分得分score=A*PC;for k=1:5P(k)=TS(k,2);S=P';endfor i=1:atotalscore(i,1)=sum(score(i,:)*S);totalscore(i,2)=name(i);endresult=[score,totalscore];%将主成分得分与总分放在同一矩阵中result=sortrows(result,-6);%按各省份的总分降序排列%%输出结果disp('特征值及其贡献率、累计贡献率:')TSdisp('信息保留率T对应的主成分数与特征向量')numberPCdisp('主成分得分及排序(按各省份所得总分降序排序,前五列为各主成分得分,第六列为各省份总得分,第七列为各省份编号)')result。
主成分分析matlab程序
Matlab编程实现主成分分析.程序结构及函数作用在软件Matlab中实现主成分分析可以采取两种方式实现:一是通过编程来实现;二是直接调用Matlab种自带程序实现。
下面主要主要介绍利用Matlab 的矩阵计算功能编程实现主成分分析。
1程序结构主函数子函数2函数作用——用总和标准化法标准化矩阵——计算相关系数矩阵;计算特征值和特征向量;对主成分进行排序;计算各特征值贡献率;挑选主成分(累计贡献率大于85%),输出主成分个数;计算主成分载荷——计算各主成分得分、综合得分并排序——读入数据文件;调用以上三个函数并输出结果3.源程序总和标准化法标准化矩阵%,用总和标准化法标准化矩阵function std=cwstd(vector)cwsum=sum(vector,1); %对列求和[a,b]=size(vector); %矩阵大小,a为行数,b为列数for i=1:afor j=1:bstd(i,j)= vector(i,j)/cwsum(j);endend计算相关系数矩阵%function result=cwfac(vector);fprintf('相关系数矩阵:\n')std=CORRCOEF(vector) %计算相关系数矩阵fprintf('特征向量(vec)及特征值(val):\n')[vec,val]=eig(std) %求特征值(val)及特征向量(vec)newval=diag(val) ;[y,i]=sort(newval) ; %对特征根进行排序,y为排序结果,i为索引fprintf('特征根排序:\n')for z=1:length(y)newy(z)=y(length(y)+1-z);endfprintf('%g\n',newy)rate=y/sum(y);fprintf('\n贡献率:\n')newrate=newy/sum(newy)sumrate=0;newi=[];for k=length(y):-1:1sumrate=sumrate+rate(k);newi(length(y)+1-k)=i(k);if sumrate> break;endend %记下累积贡献率大85%的特征值的序号放入newi中fprintf('主成分数:%g\n\n',length(newi));fprintf('主成分载荷:\n')for p=1:length(newi)for q=1:length(y)result(q,p)=sqrt(newval(newi(p)))*vec(q,newi(p));endend %计算载荷disp(result)%,计算得分function score=cwscore(vector1,vector2);sco=vector1*vector2;csum=sum(sco,2);[newcsum,i]=sort(-1*csum);[newi,j]=sort(i);fprintf('计算得分:\n')score=[sco,csum,j]%得分矩阵:sco为各主成分得分;csum为综合得分;j为排序结果%function print=cwprint(filename,a,b);%filename为文本文件文件名,a为矩阵行数(样本数),b为矩阵列数(变量指标数)fid=fopen(filename,'r')vector=fscanf(fid,'%g',[a b]);fprintf('标准化结果如下:\n')v1=cwstd(vector)result=cwfac(v1);cwscore(v1,result);4.程序测试例题原始数据中国大陆35个大城市某年的10项社会经济统计指标数据见下表。
主成分分析matlab程序
Matlab编程实现主成分分析.程序结构及函数作用在软件Matlab中实现主成分分析可以采取两种方式实现:一是通过编程来实现;二是直接调用Matlab种自带程序实现。
下面主要主要介绍利用Matlab 的矩阵计算功能编程实现主成分分析。
1程序结构2函数作用——用总和标准化法标准化矩阵——计算相关系数矩阵;计算特征值和特征向量;对主成分进行排序;计算各特征值贡献率;挑选主成分(累计贡献率大于85%),输出主成分个数;计算主成分载荷——计算各主成分得分、综合得分并排序——读入数据文件;调用以上三个函数并输出结果3.源程序总和标准化法标准化矩阵%,用总和标准化法标准化矩阵function std=cwstd(vector)cwsum=sum(vector,1); %对列求和[a,b]=size(vector); %矩阵大小,a为行数,b为列数for i=1:afor j=1:bstd(i,j)= vector(i,j)/cwsum(j);endend计算相关系数矩阵%function result=cwfac(vector);fprintf('相关系数矩阵:\n')std=CORRCOEF(vector) %计算相关系数矩阵fprintf('特征向量(vec)及特征值(val):\n')[vec,val]=eig(std) %求特征值(val)及特征向量(vec)newval=diag(val) ;[y,i]=sort(newval) ; %对特征根进行排序,y为排序结果,i为索引fprintf('特征根排序:\n')for z=1:length(y)newy(z)=y(length(y)+1-z);endfprintf('%g\n',newy)rate=y/sum(y);fprintf('\n贡献率:\n')newrate=newy/sum(newy)sumrate=0;newi=[];for k=length(y):-1:1sumrate=sumrate+rate(k);newi(length(y)+1-k)=i(k);if sumrate> break;endend %记下累积贡献率大85%的特征值的序号放入newi中fprintf('主成分数:%g\n\n',length(newi));fprintf('主成分载荷:\n')for p=1:length(newi)for q=1:length(y)result(q,p)=sqrt(newval(newi(p)))*vec(q,newi(p));endend %计算载荷disp(result)%,计算得分function score=cwscore(vector1,vector2);sco=vector1*vector2;csum=sum(sco,2);[newcsum,i]=sort(-1*csum);[newi,j]=sort(i);fprintf('计算得分:\n')score=[sco,csum,j]%得分矩阵:sco为各主成分得分;csum为综合得分;j为排序结果%function print=cwprint(filename,a,b);%filename为文本文件文件名,a为矩阵行数(样本数),b为矩阵列数(变量指标数)fid=fopen(filename,'r')vector=fscanf(fid,'%g',[a b]);fprintf('标准化结果如下:\n')v1=cwstd(vector)result=cwfac(v1);cwscore(v1,result);4.程序测试例题原始数据中国大陆35个大城市某年的10项社会经济统计指标数据见下表。
(完整版)主成分分析matlab源程序代码

(完整版)主成分分析m a t l a b源程序代码-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN263.862 1.61144 2.75468 0.266575268.764 2.07218 2.61756 0.182597261.196 1.59769 2.35037 0.182114248.708 2.09609 2.85279 0.257724253.365 1.69457 2.9492 0.189702268.434 1.56819 2.78113 0.13252258.741 2.14653 2.69111 0.136469244.192 2.02156 2.22607 0.298066219.738 1.61224 1.88599 0.166298244.702 1.91477 2.25945 0.187569245.286 2.12499 2.35282 0.161602251.96 1.83714 2.53519 0.240271251.164 1.74167 2.62961 0.211887251.824 2.00133 2.62665 0.211991257.68 2.14878 2.65686 0.203846]stdr=std(dataset); %求个变量的标准差[n,m]=size(dataset); %定义矩阵行列数sddata=dataset./stdr(ones(n,1),:); %将原始数据采集标准化sddata %输出标准化数据[p,princ,eigenvalue,t2]=princomp(sddata);%调用前三个主成分系数p3=p(:,1:3); %提取前三个主成分得分系数,通过看行可以看出对应的原始数据的列,每个列在每个主成分的得分p3 %输出前三个主成分得分系数sc=princ(:,1:3); %提取前三个主成分得分值sc %输出前三个主成分得分值e=eigenvalue(1:3)'; %提取前三个特征根并转置M=e(ones(m,1),:).^0.5; %输出前三个特征根并转置compmat=p3.*M; %利用特征根构造变换矩阵per=100*eigenvalue/sum(eigenvalue); %求出成分载荷矩阵的前三列per%求出各主成分的贡献率cumsum(per); %列出各主成分的累积贡献率figure(1)pareto(per); %将贡献率绘成直方图t2figure(2)%输出各省与平局距离plot(eigenvalue,'r+'); %绘制方差贡献散点图hold on%保持图形plot(eigenvalue,'g-'); %绘制方差贡献山麓图%关闭图形plot(princ(:,1),princ(:,2),'+'); %绘制2维成份散点图%gname%,(rowname) %标示个别散点代表的省data市[st2,index]=sort(t2);%st2=flipud(st2);%index=flipud(index);%extreme=index(1);。
主成分分析matlab程序
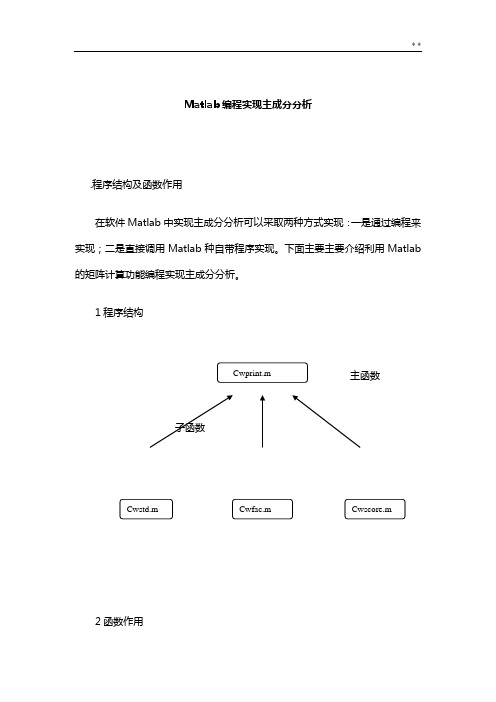
Matlab 编程实现主成分分析.程序结构及函数作用在软件Matlab 中实现主成分分析可以采取两种方式实现:一是通过编程来实现;二是直接调用Matlab 种自带程序实现。
下面主要主要介绍利用Matlab 的矩阵计算功能编程实现主成分分析。
1程序结构主函数子函数2函数作用Cwstd.m——用总和标准化法标准化矩阵Cwfac.m——计算相关系数矩阵;计算特征值和特征向量;对主成分进行排序;计算各特征值贡献率;挑选主成分(累计贡献率大于85%),输出主成分个数;计算主成分载荷Cwscore.m——计算各主成分得分、综合得分并排序Cwprint.m——读入数据文件;调用以上三个函数并输出结果3.源程序3.1 cwstd.m总和标准化法标准化矩阵%cwstd.m,用总和标准化法标准化矩阵function std=cwstd(vector)cwsum=sum(vector,1); %对列求和[a,b]=size(vector); %矩阵大小,a为行数,b为列数for i=1:afor j=1:bstd(i,j)= vector(i,j)/cwsum(j);endend3.2 cwfac.m计算相关系数矩阵%cwfac.mfunction result=cwfac(vector);fprintf('相关系数矩阵:\n')std=CORRCOEF(vector) %计算相关系数矩阵fprintf('特征向量(vec)及特征值(val):\n')[vec,val]=eig(std) %求特征值(val)及特征向量(vec)newval=diag(val) ;[y,i]=sort(newval) ; %对特征根进行排序,y为排序结果,i为索引fprintf('特征根排序:\n')for z=1:length(y)newy(z)=y(length(y)+1-z);endfprintf('%g\n',newy)rate=y/sum(y);fprintf('\n贡献率:\n')newrate=newy/sum(newy)sumrate=0;newi=[];for k=length(y):-1:1sumrate=sumrate+rate(k);newi(length(y)+1-k)=i(k);if sumrate>0.85 break;endend %记下累积贡献率大85%的特征值的序号放入newi中fprintf('主成分数:%g\n\n',length(newi));fprintf('主成分载荷:\n')for p=1:length(newi)for q=1:length(y)result(q,p)=sqrt(newval(newi(p)))*vec(q,newi(p));endend %计算载荷disp(result)3.3 cwscore.m%cwscore.m,计算得分function score=cwscore(vector1,vector2);sco=vector1*vector2;csum=sum(sco,2);[newcsum,i]=sort(-1*csum);[newi,j]=sort(i);fprintf('计算得分:\n')score=[sco,csum,j]%得分矩阵:sco为各主成分得分;csum为综合得分;j为排序结果3.4 cwprint.m%cwprint.mfunction print=cwprint(filename,a,b);%filename为文本文件文件名,a为矩阵行数(样本数),b为矩阵列数(变量指标数)fid=fopen(filename,'r')vector=fscanf(fid,'%g',[a b]);fprintf('标准化结果如下:\n')v1=cwstd(vector)result=cwfac(v1);cwscore(v1,result);4.程序测试例题4.1原始数据中国大陆35个大城市某年的10项社会经济统计指标数据见下表。
主成分分析法MATLAB的实现

主成分分析法MATLAB的实现在MATLAB中,主成分分析是通过`pca`函数实现的。
`pca`函数的语法如下:```[coeff,score,latent,tsquared,explained,mu] = pca(X)```- `latent`是一个长度为$p$的向量,表示每个主成分的方差。
- `tsquared`是一个长度为$n$的向量,表示每个样本在主成分上的投影平方和。
- `explained`是一个长度为$p$的向量,表示每个主成分的方差贡献率。
- `mu`是一个长度为$p$的向量,表示每个特征的平均值。
下面我们将用一个简单的例子演示如何使用MATLAB进行主成分分析。
假设我们有一个包含4个样本和3个特征的数据集:```matlabX=[1,2,3;2,4,6;3,6,9;4,8,12];```首先,我们需要对数据进行归一化处理,以保证不同特征之间的量纲一致。
```matlabX_norm = zscore(X);```然后,我们可以使用`pca`函数进行主成分分析:```matlab[coeff, score, latent, ~, explained, ~] = pca(X_norm);```在这个示例中,我们只关心`coeff`、`score`、`latent`和`explained`这四个输出。
`coeff`给出了主成分的系数,可以用于计算每个样本在每个主成分上的投影:```matlabproj = score * coeff';````latent`表示每个主成分的方差,我们可以通过对`latent`中的元素求和来得到总方差的百分比贡献:```matlabvar_contrib = cumsum(latent) / sum(latent);````explained`向量可以直接给出每个主成分的方差贡献率。
最后,我们可以绘制一个累积方差贡献率的曲线:```matlabplot(1:length(var_contrib), var_contrib, 'ro-');ylabel('Cumulative Variance Contribution');```这样,我们就完成了主成分分析的实现。
matlab主成分投影代码

matlab主成分投影代码
以下是一个简单的 MATLAB 代码示例,用于执行主成分分析(PCA)并对数据进行投影:
matlab.
% 生成示例数据。
data = [1 2 3; 4 5 6; 7 8 9; 10 11 12];
% 对数据进行中心化处理。
meanData = mean(data, 1);
centeredData = data meanData;
% 计算协方差矩阵。
covarianceMatrix = cov(centeredData);
% 计算特征值和特征向量。
[eigenvectors, eigenvalues] = eig(covarianceMatrix);
% 将数据投影到主成分上。
projectedData = centeredData eigenvectors;
% 显示投影后的数据。
disp('投影后的数据,');
disp(projectedData);
这段代码首先生成了一个简单的示例数据矩阵。
然后对数据进行中心化处理,计算协方差矩阵,接着计算协方差矩阵的特征值和特征向量。
最后,将数据投影到主成分上并显示投影后的数据。
需要注意的是,这只是一个简单的示例代码,实际应用中可能需要根据具体情况进行调整和扩展。
希望这段代码能够帮助到你理解如何在 MATLAB 中进行主成分分析和数据投影。
图像编程主成分分析的图像压缩和重建【matlab源码】

毕业论文(设计)题目学院学院专业学生姓名学号年级级指导教师教务处制表matlabͼÏñ±à³ÌÖ÷³É·Ö·ÖÎöµÄͼÏñѹËõºÍÖؽ¨一、程序说明本团队长期从事matlab编程与仿真工作,擅长各类毕业设计、数据处理、图表绘制、理论分析等,程序代做、数据分析具体信息联系二、程序示例clc; clear all; close all;I=imread('liftingbody.png');k=1;figure('Units', 'Normalized', 'Position', [0 0 1 1]);for p=1:5:20[Ipca,ratio,contribution]=pcaimage(I,p,[24 24]);subplot(2,2,k);imshow(Ipca)title(['Ö÷³É·Ö¸öÊý=',num2str(p),...',ѹËõ±È=',num2str(ratio),...',¹±Ï×ÂÊ=',num2str(contribution)],'fontsize',14);k=k+1;endfunction [Ipca,ratio,contribution]=pcaimage(I,pset,block)if nargin<1I=imread('football.jpg');endif nargin<2pset=3;endif nargin<3block=[16 16];endif ndims(I)==3I=rgb2gray(I);endX=im2col(double(I),block,'distinct')';[n,p]=size(X);m=min(pset,p);[coeff,score,contribution]=pcasample(X,m);X=score*coeff';Ipca=cast(col2im(X',block,size(I),'distinct'),class(I)); ratio=n*p/(n*m+p*m);function [coeff,score,rate]=pcasample(X,p)[V,D]=eig(X'*X);for i=1:size(V,2)[~,idx]=max(abs(V(:,i)));V(:,i)=V(:,i)*sign(V(idx,i));end[lambda,locs]=sort(diag(D),'descend');V=V(:,locs);coeff=V(:,1:p);score=X*V(:,1:p);rate=sum(lambda(1:p))/sum(lambda);。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
263.862 1.61144 2.754680.266575
268.764 2.07218 2.617560.182597
261.196 1.59769 2.350370.182114
248.708 2.09609 2.852790.257724
253.365 1.69457 2.94920.189702
268.434 1.56819 2.781130.13252
258.741 2.14653 2.691110.136469
244.192 2.02156 2.226070.298066
219.738 1.61224 1.885990.166298
244.702 1.91477 2.259450.187569
245.286 2.12499 2.352820.161602
251.96 1.83714 2.535190.240271
251.164 1.74167 2.629610.211887
251.824 2.00133 2.626650.211991
257.68 2.14878 2.656860.203846]
stdr=std(dataset);%求个变量的标准差
[n,m]=size(dataset);%定义矩阵行列数
sddata=dataset./stdr(ones(n,1),:);%将原始数据采集标准化
sddata%输出标准化数据
[p,princ,eigenvalue,t2]=princomp(sddata);%调用前三个主成分系数
p3=p(:,1:3);%提取前三个主成分得分系数,通过看行可以看出对应的原始数据的列,每个列在每个主成分的得分
p3%输出前三个主成分得分系数
sc=princ(:,1:3);%提取前三个主成分得分值
sc%输出前三个主成分得分值
e=eigenvalue(1:3)';%提取前三个特征根并转置
M=e(ones(m,1),:).^0.5;%输出前三个特征根并转置
compmat=p3.*M;%利用特征根构造变换矩阵
per=100*eigenvalue/sum(eigenvalue);%求出成分载荷矩阵的前三列
per
%求出各主成分的贡献率
cumsum(per);%列出各主成分的累积贡献率
figure(1)
pareto(per);%将贡献率绘成直方图
t2
figure(2)
%输出各省与平局距离
plot(eigenvalue,'r+');%绘制方差贡献散点图
hold on
%保持图形
plot(eigenvalue,'g-');%绘制方差贡献山麓图
%关闭图形
plot(princ(:,1),princ(:,2),'+');%绘制2维成份散点图
%gname
%,(rowname)%标示个别散点代表的省data市[st2,index]=sort(t2);
%st2=flipud(st2);
%index=flipud(index);
%extreme=index(1);。
