人教版九年级数学上册 23.1图形的旋转课时作业

合集下载

(含答案)九年级数学人教版上册课时练第23章《23.1 图形的旋转》

答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的小朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！课时练第23章旋转23.1图形的旋转一、选择题1．如图，在△ABC 中，AB ＝AC ，∠BAC ＝50°，将△ABC 绕着点A 顺时针方向旋转得△ADE ，AB ，CE 相交于点F ，若AD ∥CE 时，则∠BAE 的大小是（）A ．20°B ．25°C ．30°D ．35°2．如图，在等边△ABC 中，AC ＝9，点O 在AC 上，且AO ＝3，P 是AB 上一动点，连接OP ，将线段OP 绕点O 逆时针旋转60°得到线段OD ，若使点D 恰好落在BC 上，则线段AP 的长是()A ．4B ．5C ．6D ．83．如图，以正方形ABCD 的顶点A 为坐标原点，直线AB 为x 轴建立直角坐标系，对角线AC 与BD 相交于点E ，P 为BC 上一点，点P 坐标为(,)a b ，则点P 绕点E 顺时针旋转90°得到的对应点P 的坐标是()A ．(,)a b a -B ．(,)b aC ．(,0)a b -D ．(,0)b 4．如图，在△ABC 中，∠CAB ＝70°，将△ABC 在平面内绕点A 旋转到△AB ′C ′的位置，使CC ′∥AB ，则旋转角的度数为（）A．35°B．40°C．50°D．70°5．如图，在△ABC中，∠CAB＝∠ACB=25°，将△ABC绕点A顺时针进行旋转，得到△AED．点C恰好在DE的延长线上，则∠EAC的度数为（）A．75°B．90°C．105°D．120°6．已知直角梯形ABCD中，AB⊥BC，AD∥BC，AD＝2，BC＝3，将其中腰CD绕点D逆时针旋转90°至DE，连接AE，那么△ADE的面积为（）A．1B．2C．3D．67．如图，△ABC为等边三角形，AB=4，AD⊥BC，点E为线段AD上的动点，连接CE，以CE为边在下方作等边△CEF，连接DF，则线段DF的最小值为（）A．2B C．32D．18．如图，已知△AB C与△ADE都是以A为直角顶点的等腰直角三角形，△ADE绕顶点A旋转，连接BD，CE．以下四个结论：①BD=CE；②∠AEC+∠DBC=45°；③BD⊥CE；④∠BAE+∠DAC=180°．其中结论正确的个数是（）A．1B．2C．3D．49．如图，在△ABC中，∠CAB=65°，在同一平面内，将△ABC绕点A逆时针旋转到△AB'C'的位置，使得C'C∥AB，则∠B'AC等于()A ．30°B ．20°C ．10°D ．15°10．如图，将Rt △ABC 绕其直角顶点C 按顺时针方向旋转90°后得到Rt △DEC ，连接AD ，若∠B ＝55°，则∠ADE 等于()A ．5°B ．10°C ．15°D ．20°二、填空题11．如图，ABC 是等腰直角三角形，BC 是斜边，P 为ABC 内一点，将ABP △绕点A 逆时针旋转后与'ACP 重合，如果3AP =，那么线段'PP 的长等于________．12．如图，在Rt △ABC 中，∠ACB ＝90°，将△ABC 绕顶点C 逆时针旋转得到△A ′B ′C ，M 是BC 的中点，N 是A ′B ′的中点，连接MN ，若BC ＝4，∠ABC ＝60°，则线段MN 的最大值为___.13．如图，在Rt ABC △中，90ACB Ð=°，2AC BC ==，点P 是AB 上一动点，以点C 为旋转中心，将ACP △顺时针旋转到BCQ △的位置，则PQ 的最小值为________．14．如图，△ABC 中，AB ＝AC ，∠A ＝80°，将△ABC 绕着点B 旋转，使点A 落在直线BC 上的点A '处，点C 落在点C '处，那么∠BCC '＝___度．15．如图，ABC 中，90ACB Ð=°，AC BC a ==，点D 为AB 边上一点（不与点A ，B 重合），连接CD ，将线段CD 绕点C 逆时针旋转90°得到CE ，连接AE ．下列结论：①BDC D ≌AEC D ；②四边形AECD 的面积是2a ；③若105BDC Ð=°，则AD =；④2222AD BD CD +=．其中正确的结论是_____．（填写所有正确结论的序号）三、解答题16．如图，已知正方形ABCD 的边长为5，点E ，F 分别在BC 和CD 边上，分别连接AE ，AF ，EF ，若45EAF Ð=°，求CEF △的周长．17．如图，P 是等边三角形ABC 内的一点，且PA =6，PB =8，PC =10．若将△PAC 绕点A 逆时针旋转后，得到△P AB¢（1）点P 与点P ’之间的距离；（2）∠APB 的度数．18．如图，在△ABC 中，AB ＝AC ，∠BAC ＝100°，D 是BC 的中点．在射线AD 上任意取一点P ，连接PB ．将线段PB 绕点P 逆时针方向旋转80°，点B 的对应点是点E ，连接BE 、CE ．（1）如图1，当点E 落在射线AD 上时，①∠BEP ＝°；②直线CE 与直线AB 的位置关系是．（2）如图2，当点E落在射线AD的左侧时，试判断直线CE与直线AB的位置关系，并证明你的结论．19．把两个等腰直角△ABC和△ADE按如图1所示的位置摆放，将△ADE绕点A按逆时针方向旋转，如图2，连接BD，EC，设旋转角α（0°＜α＜360°）．（Ⅰ）当DE⊥AC时，旋转角α＝度，AD与BC的位置关系是，AE与BC的位置关系是；（Ⅱ）当点D在线段BE上时，求∠BEC的度数；（Ⅲ）当旋转角α＝时，△ABD的面积最大．20．如图1，将三角板ABC与三角板ADE摆放在一起，其中∠ACB＝30°，∠DAE＝45°，∠BAC ＝∠D＝90°．固定三角板ABC，将三角板ADE绕点A按顺时针方向旋转（如图2），记旋转角∠CAE＝α（0°＜α＜180°）．（1）当α为度时，AD∥BC；（2）当旋转角0°＜α＜45°时，试探究∠CAD与∠BAE之间的关系，并说明理由；（3）若△ADE旋转速度为5°/秒时，设旋转的时间为t，当DE边与△ABC的某一边平行（不共线）时，直接写出时间t的所有值．21．（1）发现：如图1，点A为线段BC外一动点，且BC＝a，AB＝b．填空：当点A 位于时，线段AC 的长取得最大值，且最大值为（用含a ，b 的式子表示）；（2）应用：点A 为线段BC 外一动点，且BC ＝3，AB ＝1，如图2所示，分别以AB ，AC 为边，作等边三角形ABD 和等边三角形ACE ，连接CD ，BE ；找出图中与BE 相等的线段，并说明理由；求线段BE 长的最大值．（3）拓展：如图3，在平面直角坐标系中，点A 的坐标为（2，0），点B 的坐标为（5，0），点P 为线段AB 外一动点，且PA ＝2，PM ＝PB ，∠BPM ＝90°，求线段AM 长的最大值及此时点P 的坐标．22．如图，直线122y x =-+交y 轴于点A ，交x 轴于点C ，抛物线214y x bx c =-++经过点A 与点C ，且交x 轴于另一点B ．（1）求此抛物线的解析式及点B 的坐标；（2）在直线AC 上方的抛物线上有一点M ，求ACM △面积的最大值及此时点M 的坐标；（3）将线段OA 绕x 轴上的动点(),0P m 顺时针旋转90°得到线段''O A ，若线段''O A 与抛物线只有一个公共点，请结合函数图象，直接写出m 的取值范围．23．在平面直角坐标系中，O 为原点，点(3,0)A ，点(0,4)B ，把ABO D 绕点A 顺时针旋转，得AB O ¢¢D ，点B ，O 旋转后的对应点为B ¢，O ．（1）如图①，当旋转角为90°时，求BB ¢的长；（2）如图②，当旋转角为120°时，求点O ¢的坐标；（3）在（2）的条件下，边OB 上的一点P 旋转后的对应点为P ¢，当O P AP ¢¢+取得最小值时，求点P ¢的坐标_______．（直接写出结果即可）参考答案1．C 2．C 3．D 4．B 5．C 6．A 7．D 8．C 9．D 10．B11．12．613．214．65°或15．①③④16．CEF △的周长为10．17．（1）6；（2）150°18．（1）①50；②CE ∥AB ；（2）CE ∥AB ．19．（Ⅰ）45；垂直；平行；（Ⅱ）90BEC Ð=°；（Ⅲ）90°或270°20．（1）15；（2）∠BAE -∠CAD =45°；（3）t =3或9或21或27或30．21．（1）CB 的延长线上，a +b ；（2）CD BE =，线段BE 长的最大值为4；（3），AM 长的最大值为，此时点P 的坐标是(2或(222．（1）211242y x x =-++，（-2，0）；（2）2，（2，2）；（3）34m -££-或32m -+££23．（1）BB ¢=；（2）9(,22O'；（3）27(,)55。

数学人教版九年级上册23.1图形的旋转第一课时作业设计

课后习题
[1] 课堂练习
1、下列现象中属于旋转的有( )个
①地下水位逐年下降；②传送带的移动；③方向盘的转动；④水龙头开关的转动；⑤钟摆的运动；⑥荡秋千运动.
A.2
B.3
C.4
D.5
2、钟表的分针匀速旋转一周需要60分.
（１）指出它的旋转中心；旋转中心是钟表的轴心
（２）经过20分，分针旋转了多少度？360
20=120 60
︒
⨯︒
︒
3、时钟的时针在不停地转动，从上午6时到上午9时，时针旋转的旋转角是多少度？从上午9时到上午10时呢？90度、30度
4、下列说法正确的是( B )
A.旋转改变图形的形状和大小
B.平移改变图形的位置
C. 图形可以向某方向旋转一定距离
D.由平移得到的图形也一定可由旋转得到
4、本图案可以看做是由一个菱形通过几次旋转得到的？每次旋转了多少度？
可以看作是由一个棱形通过5次旋转得到的，每次旋转60度
5、思考题：香港区徽可以看作是什么“基本图案”通过怎样的旋转而得到的？
可以看作是一个花瓣连续4次旋转所形成的，每次旋转分别等于720 ， 1440 ， 2160 ， 2880 [2] [2] 作业布置
1、完成配套课后练习题
2、预习提纲：
画旋转图形。

人教版九年级上册数学23.1图形的旋转同步作业

2019年秋人教版九年级上册数学23.1图形的旋转同步作业一、单选题1．如图，将直角三角形ABC 绕斜边AB 所在的直线旋转一周得到的几何体是( )A ．B ．C ．D ．2．下列这些美丽的图案都是在“几何画板”软件中利用旋转的知识在一个图案的基础上加工而成的，每一个图案都可以看作是它的“基本图案”绕着它的旋转中心旋转得来的，旋转的角度正确的为（）A ．30oB ．60oC ．120oD ．180o3．如图，△ABC 以点C 为旋转中心，旋转后得到△EDC ，已知AB ＝1.5，BC ＝4，AC ＝5，则DE ＝( )A ．1.5B ．3C ．4D ．54．在如图4×4的正方形网格中，△MNP 绕某点旋转一定的角度，得到△M 1N 1P 1，则其旋转中心可能是（）A ．点AB ．点BC ．点CD ．点D5．已知点()2,1A ，把点A 绕点O 逆时针旋转90o 后得到的点的坐标为（）A.(-2, 1)B.(-1, 2)C.(2, -1)D.(1, -2)6．如图，△ODC 是由△OAB 统点O 顺时针旋转30°后得到的图形，若点D 恰好落在AB 上，则△A 的度数为（）A ．70°B ．75°C ．60°D ．65°7．将图中所示的图案以圆心为中心，旋转180°后得到的图案是（）A ．B ．C ．D ．8．如图，在ABC ∆中，90ACB ∠=︒，2BC AC ==，M 为AB 中点，D 是射线BC 上一动点，连接AD ，将线段AD 绕点A 逆时针旋转90︒得到线段AE ，连接ED 、ME ，点D 在运动过程中ME 的最小值为（）A．1 B C 1- D 19．如图，△ABC 中，AB ＝AC ，点P 为△ABC 内一点，△APB ＝△BAC ＝120°．若AP ＋BP ＝4，则PC 的最小值为（）A ．2B ．CD ．3二、填空题10．如图，P 是正三角形ABC 内的一点，且6PA =，8PB =，10PC =.若将PAC ∆绕点A 逆时针旋转60°后，得到P AB '∆，则APB ∠=________.11．如图，正方形OABC 的两边OA 、OC 分别在x 轴、y 轴上，点()4,3D 在边AB 上，以C 为中心，把CDB ∆旋转90︒，则旋转后点D 的对应点D ¢的坐标是________.12．如图,点P 是等边三角形ABC 内一点,且PA=3,PB=4, PC=5,若将△APB 绕着点B 逆时针旋转后得到△CQB,则△APB 的度数______．13．已知矩形ABCD ，AB ＝6，AD ＝8，将矩形ABCD 绕点A 顺时针旋转θ（0°＜θ＜360°）得到矩形AEFG ，当θ＝_____°时，GC ＝GB ．14．如图,△ABC 的顶点A 和C 分别在x 轴、y 轴的正半轴上,且AB △y 轴,点B (1,3),将△ABC 以点B 为旋转中心顺时针方向旋转90°得到△DBE ，恰好有一反比例函数图象恰好过点D ,则k 的值为_________.15．在平面直角坐标系中，先将函数y=2x+3的图象向下平移3个单位长度，再沿y 轴翻折，所得函数对应的解析式为_____．16．如图，在直角坐标系中，已知点()30A -,，()0,4B ，对OAB ∆连续作旋转变换，依次得到1∆，2∆，3∆，4∆，…，则2020∆的直角顶点的坐标为______.三、解答题17．在平面直角坐标系中，△ABC 的三个顶点坐标分别是A （﹣1，1），B （﹣4，1），C （﹣3，3）.（1）将△ABC 向下平移5个单位长度后得到△A 1B 1C 1，请画出△A 1B 1C 1；并判断以O ，A 1，B 为顶点的三角形的形状（直接写出结果）；（2）将△ABC 绕原点O 顺时针旋转90°后得到△A 2B 2C 2，请画出△A 2B 2C 2，并求出点C 旋转到C 2所经过的路径长．18．如图，点O 是等边△ABC 内一点，△AOB ＝110°，△BOC ＝a ．将△BOC 绕点C 按顺时针方向旋转60°得△ADC ，连接OD ．（1）试说明△COD是等边三角形；（2）当a＝150°时，OB＝3，OC＝4，试求OA的长．19．如图，已知正方形ABCD的边长为3，E、F分别是AB、BC边上的点，且△EDF=45°，将△DAE 绕点D逆时针旋转90°，得到△DCM．若AE=1，求EF的长．20．四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如图所示，如果AF=4，AB=7，求：（1）指出旋转中心和旋转角度（2）求DE的长度（3）BE与DF的位置关系如何？并说明理由.21．(1)（操作发现）如图△，将△ABC绕点A顺时针旋转60°，得到△ADE,连接BD，则△ABD=____度；(2)（类比探究）如图△，在等边三角形ABC内任取一点P，连接PA，PB，PC，求证：以PA，PB，PC的长为三边必能组成三角形：(3)（解决问题）如图△的等边三角形ABC内有一点P，△APC=90°，△BPC=120°，求△APC的面积;(4)（拓展应用）图△是A，B，C三个村子位置的平面图，经测量AC=4，BC=5，△ACB=30°，P为△ABC内的一个动点，连接PA，PB，PC，求PA+PB+PC的最小值．答案1．D 2．D 3．A 4．B 5．B 6．B 7．C 8．A 9．B10．150° 11．()1,0-或()1,812．150° 13．60或30014．-6. 15．y=-2x ．16．()8076,017．解（1）如图，△A 1B 1C 1为所作，△OB =，1OA =1BA =△22211OB OA BA +＝，△以O ，A 1，B 为顶点的三角形为等腰直角三角形；（2）如图，△A 2B 2C 2为所作，点C 旋转到C 2所经过的路径长==． 18．解：证明：（1）△将△BOC 绕点C 按顺时针方向旋转60°得△ADC ， △CO ＝CD ，△OCD ＝60°，△△COD 是等边三角形．（2）△将△BOC 绕点C 按顺时针方向旋转60°得△ADC ，△△BOC△△ADC ，△△ADC ＝△BOC ＝150°，AD ＝OB ＝3，又△△COD 是等边三角形，△△ODC ＝60°，OD ＝OC ＝4△△ADO ＝△ADC ﹣△ODC ＝90°，△OA＝519．解：△△DAE 逆时针旋转90°得到△DCM ，△△FCM ＝△FCD ＋△DCM ＝180°，△F ，C ，M 三点共线，△DE ＝DM ，△EDM ＝90°，△△EDF ＋△FDM ＝90°，△△EDF ＝45°，△△FDM ＝△EDF ＝45°，在△DEF 和△DMF 中，DE DM EDF MDF DF DF =⎧⎪∠=∠⎨⎪=⎩△△DEF △△DMF (SAS )，△EF ＝MF ，设EF ＝MF ＝x ，△AE ＝CM ＝1，且BC ＝3，△EB ＝AB －AE ＝3－1＝2，BM ＝BC ＋CM ＝3＋1＝4，△BF ＝BM －MF ＝4－x ，在Rt△EBF 中，由勾股定理得：EB 2＋BF 2＝EF 2，即22＋(4－x )2＝x 2，解得x ＝52，即EF ＝52.20．解(1) 根据旋转的性质可知：△AFD△△AEB，所以,AE=AF=4,△EAF=90°，△EBA=△FDA，可得旋转中心为点A,旋转角度为90°或270°；(2)△△ADF按顺时针方向旋转一定角度后得到△ABE，△AE=AF=4，AD=AB=7，△DE=AD−AE=7−4=3；(3)BE、DF的关系为：BE△DF.理由如下：△△ADF按顺时针方向旋转一定角度后得到△ABE，△△ABE△△ADF，△BE=DF，△ABE=△ADF，△△ADF+△F=180°−90°=90°，△△ABE+△F=90°，△BE△DF，△BE、DF的关系为：BE△DF.21．解（1）【操作发现】60.理由：△△ABC绕点A顺时针旋转60°，得到△ADE,△AD=AB，△DAB=60°，△△DAB是等边三角形，△△ABD=60°.(2)【类比探究】证明：如图，以PA为边长作等边△PAD，使P，D分别在，AC的两侧，连接CD.△△BAC=△PAD=60°△△BAP=△CAD.△AB=AC ，AP=AD,△△PAB△△DAC(SAS)，△BP=CD.在△PCD 中，△PD+CD ＞PC.又△AP=PD ，△AP+BP ＞PC.△以PA ，PB ，PC 的长为三边必能组成三角形．(3)【解决问题】如图，将△APB 绕点A 按逆时针方向旋转60°，得到△AP′C ， △△AP′C=△APB=360°-90°-120°=150°，AP=AP′，△PAP′= 60º△△APP′是等边三角形，△PP′=AP,△AP′P=△APP′=60°,△△PP′C=150°-60°=90°, △P′PC=△APC-△APP′=30°，PC ,即．，△AP² +PC² =AC²，即222PC ⎫+=⎪⎪⎭，△PC=2（舍负），△APC 11S AP.PC 222∆===(4)【拓展应用】如图，将△APC 绕点C 顺时针旋转60°，得到△EDC,连接PD,BE. △将△APC 绕点C 顺时针旋转60°得到△EDC,△△APC△△EDC,△PCD=60°△△ACP=△ECD,AC=EC=4,△△ACB=△ACP+△PCB=△ECD+△PCB=30°，△△BCE=△ECD+△PCB+△PCD=30°+60°=90°.在Rt△BCE中，△BC=5,CE=4，△BE===，当P,D在BE上时,PA+PB+PC=BE，此时PA+PB+PC.。

九年级数学上册23-1《图形的旋转》基础课时练习题(含答案)

九年级数学上册23-1《图形的旋转》基础课时练习题（含答案）1、下面生活中的实例，不是旋转的是（）．A. 传送带传送货物B. 螺旋桨的运动C. 风车风轮的运动D. 自行车车轮的运动2、等边三角形至少旋转度才能与自身重合．3、如图，点A、B、C、D、O都在方格纸的格点上，若△COD是由△AOB绕点O逆时针方向旋转而得，则旋转的角度为（）．A. 30°B. 45°C. 90°D. 135°4、如图，在平面直角坐标系xOy中，点A的坐标为(–2,0)，B的坐标为(2,0)，等边三角形AOC经过平移或轴对称或旋转都可以得到△OBD．△AOC沿x轴向右平移得到△OBD，则平移的距离是个单位长度；△AOC与△BOD关于直线对称，则对称轴是；△AOC绕原点O顺时针旋转得到△DOB，则旋转角度可以是度．5、如图，将△ABC绕点A逆时针旋转100°，得到△ADE．若点D在线段BC的延长线上，则∠B的大小为（）．A. 30°B. 40°C. 50°D. 60°6、将△ABC绕点C顺时针旋转得到△A′B′C，已知∠ACA′=90°，BC=5，连接BB′，则BB′的长为．·7、如图，将△OAB绕点O逆时针旋转到△OA′B′，点B恰好落在边A′B′上已知AB=5cm，BB′=2cm，则A′B的长是（）．A. 1cmB. 2cmC. 3cmD. 4cm8、如图，在4×4的正方形网格中，△MNP绕某点旋转一定的角度，得到△M1N1P1，则其旋转中心可能是（）．A. 点AB. 点BC. 点CD. 点D9、如图，方格纸中每个小正方形的边长都是1个单位长度．Rt△ABC的三个顶点A(−2,2)，B(0,5)，C(0,2)．(1) 将△ABC以点O为旋转中心旋转180°，得到△A1B1C1，请画出△A1B1C1的图形．(2) 将△ABC以O为旋转中心，逆时针旋转90°，得到△A2B2C2，请画出△A2B2C2的图形．(3) 线段BB2的长度为．10、如图，四边形ABCD是正方形，E是CD上的一点，△ABF是△ADE的旋转图形．(1) 写出由△ADE顺时针旋转到△ABF的旋转中心、旋转角的度数．(2) 连接EF，判断并说明△AEF的形状．11、下列运动形式属于旋转的是（）．A. 在空中上升的氢气球B. 飞驰的火车C. 时钟上钟摆的摆动D. 运动员掷出的标枪12、正六边形绕其中心旋转一定的角度与原图形重合，则这个旋转角至少为．13、如图，把菱形ABOC绕点O顺时针旋转得到菱形DFOE，则下列角中不是旋转角的为（）．A. ∠BOFB. ∠AODC. ∠COED. ∠COF14、如图，将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，旋转角为α，若∠DAB′= 5α，则旋转角α的度数为（）．A. 25∘B. 22.5∘C. 20∘D. 30∘15、如图，将△ABC绕顶点A顺时针旋转一个角度后，恰好AB′//BC．若∠B=30°，则△ABC 旋转了（）．A. 10°B. 20°C. 30°D. 35°16、如图，△ABC是等腰直角三角形，BC是斜边，将△ABP绕点A逆时针旋转后，能与△ACP′重合，如果AP=3，那么PP′的长等于（）．A. 3√2B. 2√3C. 4√2D. 3√317、如图，已知正方形ABCD的边长为3，E为CD边上一点，DE=1．以点A为中心，把△ADE顺时针旋转90°，得△ABE′，连接EE′，则EE′的长等于．18、如图，在正方形网格中，△MPN绕某一点旋转某一角度得到△M′P′N′，则旋转中心可能是（）．A. 点AB. 点BC. 点CD. 点D19、如图，在平面直角坐标系中，△ABC的三个顶点坐标分别为A(3,2)，B(3,5)，C(1,2)．(1) 把三角形ABC绕点A顺时针旋转一定的角度，得到图中的△AB2C2，点C2在AB上．①旋转角的度数为．②B2的坐标为．(2) 如果点P在直线AB上，△PCB2的面积为10，则点P的坐标为．20、如图，点O是等边三角形ABC内的一点，∠BOC=150°，将△BOC绕点C按顺时针旋转得到△ADC，连接OD，OA．(1) 求∠ODC的度数．(2) 若OB=2，OC=3，求AO的长．1 、【答案】 A;【解析】传送带传送货物的过程中没有发生旋转．故选：A．2 、【答案】120;【解析】∵等边三角形的中心到三个顶点的距离相等，相邻顶点与中心连线的夹角相等，∴旋转角为360°÷3=120°，故至少旋转120°才能与自身重合．3 、【答案】 C;【解析】方法一 : ∵连接对应点与旋转中心可知旋转角为∠COA或者∠DOB，∴由格点可判断旋转角∠DOB=∠COA=90°.方法二 : 设小方格的边长为1，得，OC=√22+22=2√2，AO=√22+22=2√2，AC=4，∵OC2+AO2=(2√2)2+(2√2)2=16，AC2=42=16，∴△AOC是直角三角形，∴∠AOC=90°．4 、【答案】2;y轴;120;【解析】∵点A的坐标为(−2,0)，B的坐标为(2,0)，∴OA=OB=2，∴△AOC，△BOD都是等边三角形且全等，∴△AOC沿x轴向右平移得到△OBD，则平移的距离是2个单位长度；△AOC与△BOD关于直线对称，则对称轴是y轴，△AOC绕原点O 顺时针旋转得到△DOB，则旋转角度可以是120度．故答案为：2，y轴，120．5 、【答案】 B;【解析】∵将△ABC绕点A逆时针旋转100°，得到△ADE，∴AB=AD，∴△ABD为等腰三角形，又∵∠BAD=100°，∴∠B=40°．6 、【答案】5√2;【解析】∵将△ABC绕点C顺时针旋转得到△A′B′C，∴∠ACA′=∠BCB′=90°，BC=CB′=5，∴BB′=√BC2+B′C2=√25+25=5√2．故答案为5√2．7 、【答案】 C;【解析】由图形旋转的特征可得，A′B′=AB=5cm，所以A′B=5−2=3（cm）．8 、【答案】 B;【解析】方法一 : ∵旋转中心到对应点的距离相等，∴旋转中心在对应点连线线段的中垂线上.∴连接PP1，则在PP1的中垂线上的点有D、B、C，连接NN1，则在NN1的中垂线上的点有A、B，∴旋转中心为点B.方法二 : ∵△MNP绕某点旋转一定的角度，得到△M1N1P1，∴连接PP1、NN1、MM1，作PP1的垂直平分线过点B、D、C，作NN1的垂直平分线过点B、A，作MM1的垂直平分线过点B，∴三条线段的垂直平分线正好都过点B，即旋转中心是点B．故选B．9 、【答案】 (1) 画图见解析．;(2) 画图见解析．;(3) 5√2;【解析】 (1) △A1B1C1的图形如图所示．(2) △A2B2C2的图形如图所示．(3)在Rt△BOB2中，BB2=√OB2+B2O2=√52+52=5√2．故答案为：5√2．10 、【答案】 (1) A；90°．;(2) △AEF是等腰直角三角形，证明见解析．;【解析】 (1) 旋转中心为点A，旋转角是90°．(2) △AEF是等腰直角三角形．∵△ADE旋转得到△ABF，∴△ADE≌△ABF．∴AE=AF，∠DAE=∠BAF．∵四边形ABCD是正方形，∴∠DAB=90°．∴∠FAB+∠BAE=90°．∴△AEF是等腰直角三角形．11 、【答案】 C;【解析】 A选项 : 在空中上升的氢气球是平移，故A错误；B选项 : 飞驰的火车是平移，故B错误；C选项 : 时钟上钟摆的摆动，属于旋转，故C正确；D选项 : 运动员掷出的标枪是平移，故D错误，12 、【答案】60°;【解析】正六边形是中心对称图形，每个边都相等，每个边的两个端点与旋转中心所成夹角为360°÷6=60°，正六边形绕其中心旋转一定的角度与原图形重合，则这个旋转角至少为60°，故答案为：60°．13 、【答案】 D;【解析】∵对应点与旋转中心的连线构成的角叫旋转角，∵旋转中心为点O，点C旋转后的对应点为点E，∴选项D不是旋转角.14 、【答案】 B;【解析】∵矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置，∴∠D′AB′=∠D=90∘，∠DAD′=α，∵∠DAB′=5α，∴5α=90∘+α，解得：α=22.5∘，故选B．15 、【答案】 C;【解析】∵AB′//BC，∴∠B=∠B′AB=30°，而∠B′AB刚好为△ABC的旋转角，∴△ABC旋转了30°．故选C．16 、【答案】 A;【解析】∵△ACP′是由△ABP绕点A逆时针旋转后得到的，∴△ACP′≌△ABP，∴AP=AP′，∠BAP=∠CAP′，∵∠BAC=90°，∴∠PAP′=90°，故可得出△APP′是等腰直角三角形，又∵AP=3，∴PP′=3√2．17 、【答案】2√5;【解析】∵正方形ABCD，DE=1，AD=3，∴AE=√10，∵△ADE≌△ABE′，∴AE′=AE，∠DAE=∠BAE′，∴∠BAE′+∠BAE=90°，∴EE′=2√5．18 、【答案】 B;【解析】连接PP′，NN′，作PP′的垂直平分线，NN′的垂直平分线，两直线交于点B．∴旋转中心是点B．故选B．19 、【答案】 (1)①90°②(6,2);(2) (3,6)或(3,−2);【解析】 (1)①∵A(3,2)、B(3,5)、C(1,2)，∴AB=3，AC=2，∵AB//y轴，AC//x轴，∴∠CAB=90°，∵AC与AC2的夹角为∠CAC2，∴旋转角为90°．②∵AB=AB2=3，∴CB2=AC+AB2=5，∴B2的坐标为(6,2)．(2) ∵点P在直线AB上，∴设P点坐标为(3,n)，∵S△PCB2=12CB2⋅|n−2|=10，CB2=5，∴|n−2|=4，∴n=6或n=−2，∴P点坐标为(3,6)或(3,−2)．20 、【答案】 (1) ∠ODC=60°．;(2) AO=√13．;【解析】 (1) 由旋转的性质得，CD=CO，∠ACD=∠BCO，∵∠ACB=60°，∴∠DCO=60°，∴△OCD为等边三角形，∴∠ODC=60°．(2) 由旋转的性质得，AD=OB=2，∵△OCD为等边三角形，∴OD=OC=3，∵∠BOC=150°，∠ODC=60°，∴∠ADO=90°，在Rt△AOD中，由勾股定理得：AO=√AD2+OD2=√13．。

人教版九年级数学上册23.1.1《图形的旋转》试题及答案

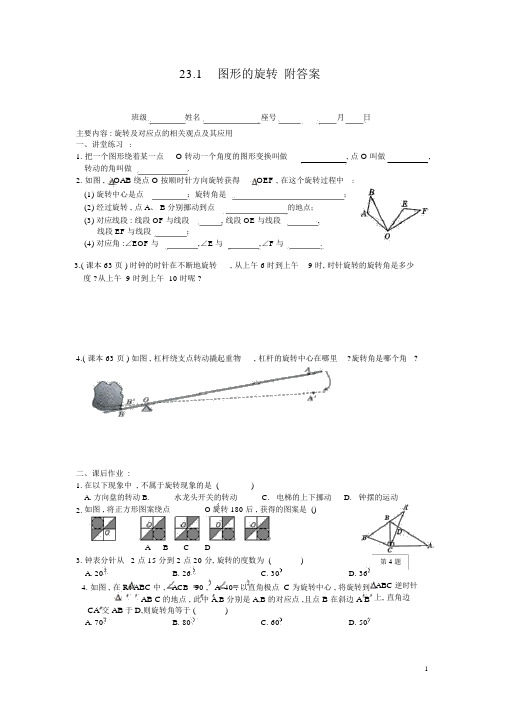
23.1图形的旋转附答案班级姓名座号月日主要内容 : 旋转及对应点的相关观点及其应用一、讲堂练习:1. 把一个图形绕着某一点O 转动一个角度的图形变换叫做, 点O叫做,转动的角叫做.2. 如图 ,OAB 绕点 O 按顺时针方向旋转获得OEF ,在这个旋转过程中:(1) 旋转中心是点；旋转角是；(2) 经过旋转 , 点 A、 B 分别挪动到点的地点；(3) 对应线段 : 线段 OF 与线段, 线段 OE 与线段,线段 EF 与线段；(4) 对应角 :∠EOF 与,∠E与,∠F与.3.( 课本 63 页 ) 时钟的时针在不断地旋转, 从上午 6 时到上午9 时, 时针旋转的旋转角是多少度 ?从上午 9 时到上午 10 时呢 ?4.( 课本 63 页 ) 如图 , 杠杆绕支点转动撬起重物, 杠杆的旋转中心在哪里?旋转角是哪个角?二、课后作业 :1.在以下现象中 , 不属于旋转现象的是 ()A. 方向盘的转动B.水龙头开关的转动C. 电梯的上下挪动D. 钟摆的运动2.如图 , 将正方形图案绕点O旋转 180 后 , 获得的图案是 ()A B C D3. 钟表分针从 2 点 15 分到 2 点 20 分, 旋转的度数为 ()A. 20B. 26C. 30D. 364. 如图 , 在Rt ABC中 , ACB 90 , A 40 , 以直角极点C为旋转中心 , 将旋转到AB C的地点,此中A,B分别是A,B的对应点,且点 B 在斜边 A B CA 交 AB于D,则旋转角等于()A. 70B. 80C. 60D. 50第 4 题ABC 逆时针上, 直角边15. 如图 ,ABC 与ADE 都是等腰直角三角形, C 和AED 都是直角,点 E 在 AB 上,假如ABC 经逆时针旋转后能与ADE 重合,那么旋转中心是点；旋转的度数是.6. 如图 ,ABC 为等边三角形, D 为ABC 内一点,ABD 经过旋转后抵达ACP 的地点,则(1) 旋转中心是点；(2)旋转角度是；(3)ADP 是三角形.第5题第6题7.( 课本 66 页 ) 如图 , 说出压水机压水时的旋转中心和旋转角.8.( 课本 66 页 ) 如图 , 吃米的小鸡是站立的小鸡经过旋转获得的, 旋转中心是O .从图上量一量旋转角是多少度.三、新课预习 :1.对应点到旋转中心的距离；对应点与旋转中心所连线段的夹角等于；旋转前、后的图形.2.如图 , OAB绕O点按顺时针方向旋转获得OEF ,在这个旋转过程中,找出图中相等的角和相等的线段 .3. 如图 , E 是正方形ABCD 中, CD 边上随意一点,以点 B 为中心,把 EBC 逆时针旋转90 ,画出旋转后的图形 .2参照答案一、讲堂练习:1. 把一个图形绕着某一点O 转动一个角度的图形变换叫做旋转, 点O叫做旋转中心,转动的角叫做旋转角.2. 如图 ,OAB 绕点 O 按顺时针方向旋转获得OEF ,在这个旋转过程中:(1) 旋转中心是点O；旋转角是∠ AOE、∠ BOF；(2) 经过旋转 , 点 A、 B 分别挪动到点E、F的地点；(3) 对应线段 : 线段 OF 与线段OB, 线段 OE 与线段OA,线段 EF 与线段AB；(4) 对应角 :∠EOF 与∠AOB,∠E与∠A,∠F 与∠B.3.( 课本 63 页 ) 时钟的时针在不断地旋转, 从上午 6 时到上午9 时, 时针旋转的旋转角是多少度 ?从上午 9 时到上午 10 时呢 ?解:时针1小时转30 ,从上午6时到9时,时针要旋转30 3 90 ；从 9时到 10时,时针要旋转 30 .4.( 课本 63 页 ) 如图 , 杠杆绕支点转动撬起重物, 杠杆的旋转中心在哪里?旋转角是哪个角?解 : 杠杆的旋转中心在点O,旋转角是∠ AOA .二、课后作业:1.在以下现象中 , 不属于旋转现象的是 ( C )A. 方向盘的转动B.水龙头开关的转动C.电梯的上下挪动D.钟摆的运动2. 如图 , 将正方形图案绕点O旋转 180 后, 获得的图案是( D )A B C D3.钟表分针从 2 点 15分到 2点 20分, 旋转的度数为 ( C )第 4 题A. 20B. 26C. 30D. 364. 如图 , 在Rt ABC中 ,ACB90, A 40, 以直角极点C为旋转中心 , 将ABC逆时针旋转到ABC的地点,此中A,B分别是 A,B 的对应点 , 且点B在斜边A B上, 直角边CA 交 AB于D ,则旋转角等于( B )A. 70B. 80C. 60D. 505.如图,ABC 与ADE 都是等腰直角三角形, C和AED都是直角 ,点E在 AB上,假如ABC 经逆时针旋转后能与ADE 重合,那么旋转中心是点A；旋转的度数是45°.6. 如图,ABC 为等边三角形, D 为ABC 内一点, ABD 经过旋转后抵达ACP 的地点,则(1) 旋转中心是点A； (2)旋转角度是60°；(3)ADP是等边三角形 .第5题第6题37.( 课本 66 页 ) 如图 , 说出压水机压水时的旋转中心和旋转角.解 : 压水机的旋转中心为把手柄与机体的连结点, 旋转角为把手柄旋转的角度 .8.( 课本 66 页 ) 如图 , 吃米的小鸡是站立的小鸡经过旋转获得的, 旋转中心是O .从图上量一量旋转角是多少度.解 : 经丈量旋转角AOA 约等于85.三、新课预习 :1.对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等 .2.如图 , OAB绕O点按顺时针方向旋转获得OEF ,在这个旋转过程中, 找出图中相等的角和相等的线段 .答 : 相等的角是 :A E , B F ,AOBEOF ,AOE BOF .相等的线段是 : AB EF ,OA OE,OB OF .3.如图 , E 是正方形ABCD中 , CD边上随意一点 , 以点B为中心 , 把 EBC 逆时针旋转 90 , 画出旋转后的图形 .答 : E BA是由EBC逆时针旋转90后获得的 .4。

人教版九年级数学上册第23章：旋转(课时作业1).docx

初中数学试卷
桑水出品
No.28 课题：中心对称图形预计完成时间： 15分
钟
班级组号学生姓名
设计人：王晶备课组长签名级部主任审批家长签名
（A）一、基础夯实
纠错区1.把一个图形绕着，如果它能够与，完
善区
那么就说这两个图形成中心对称.
2.中心对称的性质：
（1）中心对称的两个图形，对称点所连线段都，而且被 .
（2）中心对称的两个图形是．
3.把一个图形绕着，如果旋转后的图形与，
那么这个图形叫做中心对称图形，这个点就是它的 .
（B）二、巩固提高
4．下列图形中，既是轴对称图形，又是中心对称图形的是（） .
A．等边三角形 B．等腰梯形 C．平行四边形 D．正六边形
5．下列图形中，是中心对称图形，但不是轴对称图形的是（）.
A．正方形 B．矩形 C．菱形 D．平行四边形
6.如图，既是中心对称又是轴对称的图案是（）.
A．北京现代标志B．奥运五连环C．中国结 D．太极图
7．将矩形ABCD沿AE折叠，得到如图所示的图形，已知∠CED′=60°，
则∠AED的大小是（）
A．60° B．50° C．75° D．55°
8.如图，△ABC和△A’B’C’关于点O中心对称.求作对称中心点O.
第7题第8题
（C）三、拓展创新
9.下图是正六边形ABCDEF，请找出它的对称中心。

10.如图，已知直线AB和点P，求作平行四边形ABCD，使点P是它的对称中
心.
11.一生产车间现有一块如图所示的钢板，你能否用一条直线将他分成面积相
等的两部分？请说明理由。

等级：整洁正确日期：月日师生交流：。

人教版九年级数学上23.1图形的旋转第2课时旋转作图同步练习含答案

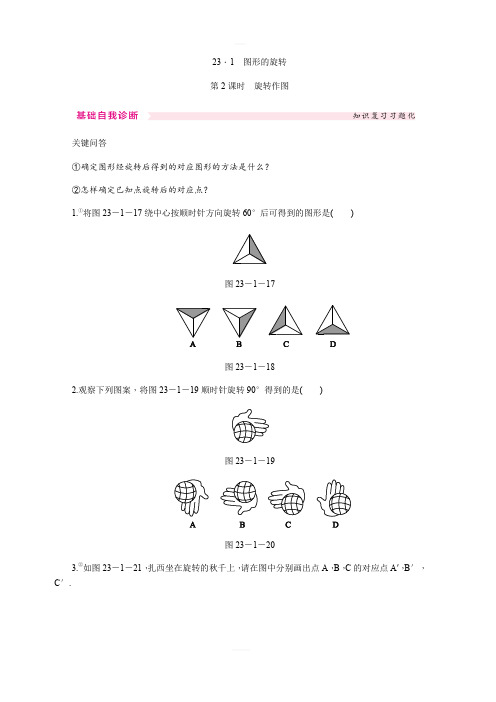
23．1图形的旋转第2课时旋转作图关键问答①确定图形经旋转后得到的对应图形的方法是什么？②怎样确定已知点旋转后的对应点？1.①将图23－1－17绕中心按顺时针方向旋转60°后可得到的图形是()图23－1－17图23－1－182.观察下列图案，将图23－1－19顺时针旋转90°得到的是()图23－1－19图23－1－203.②如图23－1－21，扎西坐在旋转的秋千上，请在图中分别画出点A，B，C的对应点A′，B′，C′.图23－1－21命题点1利用旋转性质作图[热度：90%]4．③将△AOB绕点O旋转180°得到△DOE，则下列作图正确的是()图23－1－22 方法点拨③旋转180°前后的两个图形，旋转中心和一组对应点在一条直线上．5.④图23－1－24中将图23－1－23在平面上旋转可以得到的是________．(填序号)图23－1－23图23－1－24解题突破④可根据图上方的顶点旋转后的位置来判断下方两分支的位置．6.⑤如图23－1－25，画出等边三角形ABC绕点B顺时针旋转90°后的图形(△A′BC′)，并连接AC′，CA′.直接写出∠ABC′，∠CAC′，∠A′CB，∠CA′B的度数．图23－1－25方法点拨⑤将作旋转图形转化成先作图形上的关键点旋转后的对应点再顺次连接对应点.命题点2在网格中利用旋转性质作图[热度：86%]7．⑥如图23－1－26，将方格纸中的图形绕点O逆时针旋转90°后得到的图形是()图23－1－26图23－1－27方法点拨⑥掌握在网格中作互相垂直且相等的两条线段的方法，是在网格中利用旋转性质作图的基础．8.⑦在如图23－1－28所示的方格纸中，每个小方格都是边长为1个单位长度的正方形，△ABC 的三个顶点都在格点上(每个小方格的顶点叫格点)．画出△ABC绕点O顺时针旋转90°后的△A′B′C′.图23－1－28易错警示⑦旋转作图时，一定要避免出现旋转方向的错误．9．⑧2017·宁夏如图23－1－29，在平面直角坐标系中，△ABC三个顶点的坐标分别为A(2，3)，B(1，1)，C(5，1)．(1)把△ABC平移后，其中点A移到点A1(4，5)，画出平移后得到的△A1B1C1；(2)把△A1B1C1绕点A1按逆时针方向旋转90°，画出旋转后的△A2B2C2.图23－1－29方法点拨⑧利用图形变换作图时，将图形的变换转化成图形的顶点的变换．点进行旋转变换时，要先把点与旋转中心连接，把长度记作a，再按要求的方向作旋转角，并在旋转角的另一边上找到与旋转中心的距离等于a的点，即对应点．命题点3旋转作图的综合应用[热度：90%]10．⑨2017·宁波如图23－1－30，在4×4的方格纸中，△ABC的三个顶点都在格点上．(1)在图23－1－30①中画出与△ABC成轴对称且与△ABC有公共边的格点三角形(画出一个即可)；(2)将图②中的△ABC绕点C按顺时针方向旋转90°，画出经旋转后的三角形．图23－1－30方法点拨⑨作已知图形的轴对称图形的对应点的方法是先过点作对称轴的垂线段，再在垂线段的延长线上截取等于垂线段长度的线段．11.○10⑪在Rt△ABC中，∠ACB＝90°，AC＝1，∠ABC＝30°，点O为Rt△ABC内一点，连接AO，BO，CO，且∠AOC＝∠COB＝∠BOA＝120°.(1)按要求画图：以点B为旋转中心，将△AOB绕点B按顺时针方向旋转60°，得到△A′O′B(点A，O的对应点分别为点A′，O′)．(2)求：①∠A′BC的度数；②OA＋OB＋OC的值．图23－1－31解题突破○10通过旋转，把OA＋OB＋OC转化成求A′，C两点间的距离．模型建立⑪实际上，若点O为Rt△ABC内任一点，则点O到三个顶点的距离和的最小值是斜边与长直角边平方和的算术平方根．12．⑫在俄罗斯方块游戏中，所有出现的方格体会自动下落，如果一行中九个方格齐全，那么这一行会自动消失．已拼好的图案如图23－1－32所示，现又出现一个小方格体，必须对其进行以下哪项操作，才能拼成一个完整图案，图23－1－33使其全部自动消失()A．顺时针旋转90°，向下平移至边界B．逆时针旋转90°，向下平移至边界C．顺时针旋转90°，向右平移至边界D．逆时针旋转90°，向右平移至边界易错警示⑫注意题目条件：所有出现的方格体会自动下落，因此不要误选向下平移．13．⑬你知道风靡全球的魔方吗？它是匈牙利建筑学教授鲁比克为帮助学生增强空间思维能力而发明的教学工具，魔方的任何一面都可水平转动而不影响其他方块．如图23－1－33是一个三阶魔方，如果将任何一面顺时针或逆时针旋转90°视作一次操作，那么由甲图到乙图至少需要进行这样的操作()图23－1－33.1次B．2次C．3次D．4次解题突破⑬可以进行具体操作来达到解题目的.典题讲评与答案详析1．B 2.A3．解：如图所示．4．D[解析] 将△AOB绕点O旋转180°得到△DOE后，点A，O，D在一条直线上，点B，O，E在一条直线上．5．③[解析] 已知题图上方的顶点旋转到左侧时，下方的两个分支中，粗分支在上，细分支在下，故③符合题意．6．[导学号：04402152] 解：△A ′BC ′如图所示． ∵△ABC 是等边三角形， ∴∠ABC ＝60°，∴∠ABC ′＝∠ABC ＋∠CBC ′＝60°＋90°＝150°. 在△ABC ′中，AB ＝BC ′，∴∠BAC ′＝12×(180°－150°)＝15°，∴∠CAC ′＝∠BAC －∠BAC ′＝60°－15°＝45°.在△A ′BC 中，BC ＝BA ′，∠A ′BC ＝∠CBC ′－∠C ′BA ′＝90°－60°＝30°，∴∠A ′CB ＝∠CA ′B ＝12×(180°－30°)＝75°.7．C8．解：△A ′B ′C ′如图所示．9．解：(1)如图，△A 1B 1C 1即为所求． (2)如图，△A 2B 2C 2即为所求．10．解：(1)(答案不唯一)如图所示．(2)如图，△A′B′C即为所求．11．解：(1)如图所示．(2)连接AA′，OO′如图所示．∵△A′O′B是由△AOB按顺时针方向旋转60°得到的，∴△OBO′，△ABA′是等边三角形，O′A′＝OA，∴∠BOO′＝∠BO′O＝60°，OB＝OO′，∠ABA′＝60°.∵∠BOC＝∠AOB＝∠A′O′B＝120°，∴∠BOC＋∠BOO′＝180°，∠BO′O＋∠A′O′B＝180°，∴C，O，O′，A′四点共线，∴OA＋OB＋OC＝OC＋OO′＋O′A′＝CA′.在Rt△ABC中，∵∠ABC＝30°，AC＝1，∴AB＝BA′＝2，BC＝3，∴∠A′BC＝∠ABC＋∠ABA′＝90°，∴CA′＝BC2＋A′B2＝7，∴OA＋OB＋OC＝7.12．[导学号：04402154]C[解析] 观察图形可知，出现的小方格体需顺时针旋转90°，向右平移至边界．13．[导学号：04402155]C【关键问答】①找图形上几个关键点(通常是顶点)，作关键点旋转后的对应点，顺次连接对应点可以得到图形旋转后对应的图形．②连接点与旋转中心，然后以旋转中心为顶点，顺时针(或逆时针)作旋转角，在旋转角的另一条边上，截取与已知点到旋转中心的距离等长的线段，便可以得到已知点的对应点．。

人教版九年级数学上册第二十三章旋转课时作业含答案

课时作业23.1图形的旋转一、选择题(每小题4分，共12分)1．如图，在△ABC中，AB＝4，BC＝6，∠B＝60°，将△ABC沿射线BC的方向平移，得到△A′B′C′，再将△A′B′C′绕点A′逆时针旋转一定角度，点B′恰好与点C重合，则平移的距离和旋转角的度数分别为(B) A．4,30°B．2,60°C．1,30°D．3,60°解析：由旋转得A′B′＝A′C，由平移可得∠A′B′C＝∠B＝60°，AB＝A′B′＝4，∴△A′B′C是等边三角形，∴∠B′A′C＝60°，B′C＝4，∴BB′＝6－4＝2.2．如图，在△ABC中，AC＝BC，点D，E分别是边AB，AC的中点，将△ADE绕点E旋转180°得△CFE，则四边形ADCF一定是(A)A．矩形B．菱形C．正方形D．梯形解析：∵△ADE绕点E旋转180°得△CFE，∴AE＝CE，DE＝EF，∴四边形ADCF是平行四边形．∵AC＝BC，点D是边AB的中点，∴∠ADC＝90°，∴四边形ADCF是矩形．3．如图，边长为1的两个正方形互相重合，按住其中一个不动，将另一个绕顶点A顺时针旋转45°，则这两个正方形重叠部分的面积是(D)A.12B．33C．1－33D．2－1解析：∵绕顶点A顺时针旋转45°，∴∠D′CE＝45°，∴CD′＝D′E. ∴延长AD′正好经过点C，∵AC＝2，∴CD ′＝2－1，∴正方形重叠部分的面积是＝12×1×1－12(2－1)(2－1)＝2－1.二、填空题(每小题4分，共12分)4．已知A 点的坐标为(－1,3)，将A 点绕坐标原点O 顺时针旋转90°，则点A 的对应点的坐标为(3,1)．5．如图，在等边△ABC 中，AB ＝6，点D 是BC 的中点．将△ABD 绕点A 旋转后得到△ACE ，那么线段DE 的长度为3 3.解析：∵△ABD 绕点A 旋转后得到△ACE ，∴AD ＝AE ，∠BAD ＝∠CAE ，又∵∠BAD ＋∠DAC ＝60°，∴∠CAE ＋∠DAC ＝60°，∴△ADE 是等边三角形．∴DE ＝AD .∵在等边△ABC 中，AB ＝AC ＝6，BD ＝CD ＝12BC ＝3，∴AD ⊥BC ，∴AD ＝62－32＝33，即DE ＝3 3.6．如图，在△AOB 中，∠AOB ＝90°，AO ＝3，BO ＝6，△AOB 绕顶点O 逆时针旋转到△A ′OB ′处，此时线段A ′B ′与BO 的交点E 为BO 的中点，则线段B ′E 的长度为95 5.解析：∵∠AOB ＝90°，AO ＝3，BO ＝6，∴AB ＝AO 2＋BO 2＝32＋62＝3 5.∵△AOB 绕顶点O 逆时针旋转到△A ′OB ′处，∴AO ＝A ′O ＝3，A ′B ′＝AB ＝3 5.∵点E 为BO 的中点，∴OE ＝12BO ＝12×6＝3，∴OE ＝A ′O .过点O作OF ⊥A ′B ′于点F ，如图，S △A ′OB ′＝12×35·OF ＝12×3×6，解得OF ＝655.在Rt △EOF 中，EF ＝OE 2－OF 2＝32－(655)2＝355，∵OE ＝A ′O ，OF ⊥A ′B ′，∴A ′E ＝2EF ＝2×355＝655(等腰三角形三线合一)，∴B ′E ＝A ′B ′－A ′E ＝35－655＝955.三、解答题(共26分)7．(满分10分)如图，在方格纸中，△ABC 的三个顶点和点P 都在小方格的顶点上．按要求画一个三角形，使它的顶点在方格的顶点上．(1)将△ABC 平移，使点P 落在平移后的三角形内部，在图甲中画出示意图；(2)以点C 为旋转中心，将△ABC 旋转，使点P 落在旋转后的三角形内部，在图乙中画出示意图．图甲图乙解：(1)如图所示：(2)如图所示：8．(满分16分)(1)如图1，在正方形ABCD 中，点E ，F 分别在边BC ，CD上，∠EAF＝45°，延长CD到点G，使DG＝BE，连接EF，AG.求证：EF＝FG；(2)如图2，等腰直角三角形ABC中，∠BAC＝90°，AB＝AC，点M，N在边BC上，且∠MAN＝45°.若BM＝1，CN＝3，求MN的长．图1图2(1)证明：∵四边形ABCD是正方形，∴AB＝AD，∠B＝∠ADF＝∠ADG＝∠BAD＝90°.又∵DG＝BE，∴△ABE≌△ADG.∴AE＝AG，∠BAE＝∠DAG.∵∠BAD＝90°，∠EAF＝45°，∴∠BAE＋∠F AD＝45°.∴∠DAG＋∠F AD＝45°，即∠F AG＝∠F AE＝45°.又∵AF＝AF，∴△AFE≌△AFG.∴EF＝FG.(2)解：如图，将△ABM绕点A逆时针旋转90°，得到△ACD，则CD＝BM ＝1，AM＝AD，∠B＝∠ACB＝∠ACD＝45°，连接ND，则∠NCD＝90°.∵∠BAC＝90°，∠MAN＝45°，∴∠BAM＋∠CAN＝45°.∴∠DAC＋∠CAN＝45°，即∠NAM＝∠NAD＝45°.又∵AN＝AN，∴△ANM≌△AND.∴MN＝ND.在Rt△CDN中，由勾股定理，得ND＝12＋32＝10，∴MN＝10.课时作业23.2.1中心对称一、选择题(每小题6分，共12分)1．如图，将一张矩形纸片沿对角线剪开得到两个直角三角形纸片，将这两个直角三角形纸片通过图形变换构成以下四个图形，这四个图形中两个三角形成中心对称的是(C)A B C D2．如图，△ABC以点O为旋转中心，旋转180°后得到△A′B′C′.ED是△ABC的中位线，经旋转后为线段E′D′.已知BC＝4，则E′D′等于(A)A．2B．3C．4D．15二、填空题(每小题4分，共12分)3．小明、小辉两家所在位置关于学校中心对称．如果小明家距学校2 km，那么他们两家相距__4__km.4．如图所示，在△ABC中，点D，E分别是AB，AC边的中点，若把△ADE 绕着点E按顺时针方向旋转180°得到△CFE，则CF与BD的数量与位置关系是CF＝BD，CF∥BD.5．如图，AB⊥BC，AB＝BC＝2 cm，关于点O中心对称，则AB，BC，所围成的面积是__2__cm2.解析：如图，连接AC.∵关于点O中心对称，∴点O为AC的中点，∴AB，BC，所围成的面积＝△BAC的面积＝12×2×2＝2(cm2)．三、解答题(共26分)6．(满分12分)如图，已知△ABC和点O，画出△DEF，使△DEF和△ABC关于点O成中心对称．解：①连接AO并延长AO到D，使OD＝OA，于是得到点A的对称点D；②同样画出点B和点C的对称点E和F；顺次连接DE，EF，FD.如图所示△DEF即为所求的三角形．7．(满分14分)如图，在△ABC中，∠A＝90°，D为BC的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，试探索线段BE，EF，FC之间的数量关系．解：FC2＋BE2＝EF2.理由如下：∵D为BC的中点，∴BD＝CD.作△BDE关于点D成中心对称的△CDG，如图．由中心对称的性质可得△BDE≌△CDG，∴CG＝BE，∠DCG＝∠B.又∵∠B＋∠ACB＝90°，∴∠DCG＋∠ACB＝90°，即∠FCG＝90°，∴FC2＋GC2＝FG2.又∵FD为EG的中垂线，∴FG＝EF，∴FC2＋BE2＝EF2.课时作业23.2.2中心对称图形一、选择题(每小题4分，共12分)1．下列图形是中心对称图形的是(C)A B C D2．下列图形中，既是轴对称图形，又是中心对称图形的是(A)A B C D3．若一个图案绕一个定点旋转一个角α(0°＜α≤180°)后能够与原来的图形重合，那么这个图形叫做旋转对称图形．例如等边三角形绕它的中心旋转120°，能够与原来的等边三角形重合，因而等边三角形是旋转对称图形．显然，中心对称图形都是旋转对称图形，但旋转对称图形不一定是中心对称图形．如图所示的图形中，是旋转对称图形但不是中心对称图形的有(B)A .1个B．2个C．3个D．4个解析：⑤是轴对称图形，不是中心对称图形也不是旋转对称图形，其他都是旋转对称图形，②④⑥是中心对称图形，所以是旋转对称图形但不是中心对称图形的只有①③两个．二、填空题(每小题4分，共12分)4．在艺术字中，有些字母是中心对称图形，下面的5个字母中，是中心对称图形的有__3__个．5．下面中心对称图形中，点A的对应点是点__E__，线段CD的对应线段是__HN__.6．如图，在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形，涂黑的小正方形的序号是②.解析：根据题意，可作出四种图形如下，其中旋转180°与自身重合的只有第2个图形，∴将②涂黑能构成中心对称图形．三、解答题(共26分)7．(满分12分)如图，方格纸中有三个点A，B，C，要求作一个四边形使这三个点在这个四边形的边(包括顶点)上，且四边形的顶点在方格的顶点上．甲图乙图丙图(1)在图甲中作出的四边形是中心对称图形但不是轴对称图形；(2)在图乙中作出的四边形是轴对称图形但不是中心对称图形；(3)在图丙中作出的四边形既是轴对称图形又是中心对称图形．解：答案不唯一，如图所示：甲图乙图丙图8. (满分14分)如图，AC＝BD，∠A＝∠B，点E，F在AB上，且DE∥CF，试说明该图是中心对称图形．解：连接CD 交AB 于点O ，∵AC ＝BD ，∠A ＝∠B ，又∵∠AOC ＝∠BOD ， ∴△ACO ≌△BDO (AAS)．∴OA ＝OB ，OC ＝OD ，∴A ，B 和C ，D 分别关于点O 对称．∵DE ∥CF ，∴∠ODE ＝∠OCF ，又∵∠DOE ＝∠COF ，OC ＝OD ，∴△ODE ≌△OCF (ASA)．∴OE ＝OF ，∴点E ，F 也关于点O 对称，∴此图形是中心对称图形，对称中心是点O .课时作业 23.2.3 关于原点对称的点的坐标一、选择题(每小题6分，共18分)1．已知点A (a,1)与点A ′(5，b )关于原点对称，则实数a ，b 的值为 (D)A ．a ＝5，b ＝1B ．a ＝－5，b ＝1C ．a ＝5，b ＝－1D ．a ＝－5，b ＝－12．点P (ac 2，b a )在第二象限，点Q (a ，b )关于原点对称的点在(A)A ．第一象限B ．第二象限C ．第三象限D ．第四象限解析：∵点P (ac 2，b a )在第二象限，∴ac 2＜0，b a >0，∴a ＜0，b ＜0.∴点Q (a ，b )在第三象限．∴点Q (a ，b )关于原点对称的点(－a ，－b )在第一象限．3．如图，点A，点B的坐标分别是(0,1)，(a，b)，将线段AB点A旋转180°后得到线段AC，则点C的坐标为(C)A．(－a，b＋1) B．(－a，－b－1)C．(－a，－b＋2) D．(－a，－b－2)解析：把线段BC向下平移1个单位，使点A与点O重合，则B点坐标为(a，b－1)，与其关于原点对称的点C的坐标为(－a，－b＋1)，将其向上平移1个单位，即得原点C的坐标(－a，－b＋2)．二、填空题(每小题6分，共18分)4．已知点P(3，－1)关于y轴的对称点Q的坐标是(a＋b,1－b)，则a b的值为__25__.解析：∵点P(3，－1)关于y轴的对称点Q的坐标是(a＋b,1－b)，∴a＋b＝－3,1－b＝－1，解得b＝2，a＝－5，∴a b＝25.5．如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称或中心对称变换，若原来点A坐标是(a，b)，则经过第2 017次变换后所得的A点坐标是(a，－b)．关于x 轴对称关于原点对称关于y轴对称关于x轴对称解析：∵2 017÷3＝672……1，第一次变换是各对应点关于x轴对称，点A 坐标是(a，b)，∴经过第2 017次变换后所得的A点坐标是(a，－b)．6．若将等腰直角三角形AOB按如图所示放置，OB＝2，则点A关于原点对称的点的坐标为(－1，－1)．解析：过点A作AD⊥OB于点D.∵△AOB是等腰直角三角形，OB＝2，∴OD＝AD＝1，∴点A的坐标为(1,1)，∴点A关于原点对称的点的坐标为(－1，－1)．三、解答题(共14分)7．如图的方格纸中，△ABC的顶点坐标分别为A(－2,5)，B(－4,1)和C(－1,3)．(1)作出△ABC关于y轴对称的△A1B1C1并写出A，B，C的对称点A1，B1，C1的坐标；(2)作出△ABC绕原点O逆时针旋转90°后的△A2B2C2，并写出A，B，C的对称点A2，B2，C2的坐标；(3)试判断：△A1B1C1与△A2B2C2是否关于原点O对称．(只需写出判断结果)解：(1)A1(2,5)，B1(4,1)，C1(1,3)；(2)A2(－5，－2)，B2(－1，－4)，C2(－3，－1)；(3)△A1B1C1与△A2B2C2关于原点O不对称．。

北大绿卡九年级数学上册 23.1 图形的旋转课时测试(含解析)(新版)新人教版-(新版)新人教版初中

图形的旋转时间40分钟满分100分班级____某某_________得分_______一、选择题(每题5分)1.如图,将△ABC绕点A按顺时针方向旋转60°得到△AEF,则下列结论错误的是()A.∠BAE=60°B.AC=AFC.EF=BCD.∠BAF=60°【答案】：D【解析】试题分析：根据旋转的定义进行判断.解：根据旋转的定义可得：A选项：∠BAE是旋转角，所以可得：∠BAE=60°，故A选项正确；B选项：AC、AF是对应边，所以AC=AF，故B选项正确；C选项：EF、BC是对应边，故C选项正确；D选项：∠BAF不是旋转角，所以∠BAF≠60°，故D选项错误..故选D.考点：旋转的定义2.在图形旋转中，下列说法中错误的是（）A. 图形上的每一点到旋转中心的距离相等B. 图形上的每一点移动的角度相同C. 图形上可能存在不动点D. 图形上任意两点的连线与其对应两点的连线相等【答案】：A【解析】试题分析：根据在平面内，一个图形旋转后得到的图形与原来的图形之间对应线段相等；对应角相等；对应点到旋转中心的距离相等；每对对应点与旋转中心连线所成的角都是相等的角，它们都等于旋转角进行判断.解：A选项：图形上对应点到旋转中心的距离相等，故A选项错误；B选项：图形上每一点移动的角度都等于旋转角，所以每一点移动的角度相同，故B选项正确；C选项：如果旋转中心在图形上，则这个点是不动点，故C选项正确；D选项：图形上任意两点的连线与其对应两点的连线是对应线段，所以相等，故D选项正确.故应选A考点：旋转的性质3.下列现象中属于旋转的有( )个①地下水位逐年下降；②传送带的移动；③方向盘的转动；④水龙头开关的转动；⑤钟摆的运动；⑥荡秋千运动.【答案】：C【解析】试题分析：根据旋转的定义进行判断解：旋转是指物体绕着某点的旋转运动，由旋转中心、旋转角、旋转方向三要素所决定。

经过判断可得：①地下水位逐年下降是平移；②传送带的移动是平移运动，③方向盘的转动是旋转；④水龙头开关的转动是旋转；⑤钟摆的运动是旋转；⑥荡秋千运动都旋转运动.所以属于旋转的有4个.故应选C.考点：旋转的定义.4. 如图，把菱形ABOC绕点O顺时针旋转得到菱形DFOE，则下列角中不是旋转角的为A．∠BOF B．∠AOD C．∠COE D．∠AOF【答案】：C【解析】试题分析：对应点与旋转中心连线的夹角是旋转角.解：A选项：因为点B与点F是对应点，所以∠BOF是旋转角；B选项：因为点A与点D是对应点，所以∠AOD是旋转角；C选项：因为点C与点E是对应点，所以∠COE是旋转角；D选项：因为点A与点F不是对应点，所以∠AOF不是旋转角.故应选D.考点：旋转角5.如图，该图形围绕自己的旋转中心，按下列角度旋转后不能与自身重合的是( )A. 72°B. 108°C. 144°°【答案】：B【解析】试题分析：图形被平均分成了5等份，所以图形最少旋转72°才能与自身重合，所以图形旋转后要与自身重合，则旋转角应是72°的整数倍.解：因为360°÷5=72°，所以旋转角应72°的整数倍，所以旋转72°、144°、216°都能与自身重合，旋转108°不能与自身重合.故应选B.考点：旋转角.6.如图，D是等腰Rt△ABC内一点，BC是斜边，如果将△ABD绕点A按逆时针方向旋转到△ACD′的位置，则∠ADD′的度数是( )°°°°【答案】：D【解析】试题分析：根据旋转的性质可以得到：AD＝AD′，∠DAD′=∠BAC=90°，所以△ADD′是等腰直角三角形，根据等腰直角三角形的性质可以求出∠ADD′的度数.解：根据旋转的性质可得：AD＝AD′，∠DAD′=∠BAC=90°，∴△ADD′是等腰直角三角形，∴∠ADD′=45°.故应选D.考点：旋转角7.如图，可以看作是一个等腰直角三角形旋转若干次而生成的则每次旋转的度数不可能是( )°°°°【答案】：B【解析】试题分析：因为图形被分成了8等份，所以图形最少旋转45°才能与自身重合，所以图形要与自身重合，则旋转角的度数应是45°的整数倍.解：因为360°÷8=45°，所以旋转角应45°的整数倍，所以旋转的度数应是45°、90°、135°，旋转的度数不可能是30°.故应选B.考点：旋转角.8．如图所示的图案需绕其中心旋转n°时与原图案重合，那么n的最小值是( )°°°°【答案】：C【解析】试题分析：根据图形被平均分成三份，可以求出每个中心角的度数，中心角的度数就是图形旋转的最小度数.解：图形被平均分成三份，所以旋转的最小度数是360°÷3=120°，故应选C.考点：旋转角9.如图，把边长为3的正三角形绕着它的中心旋转180°后，重叠部分的面积为( )93 433233432【答案】：B【解析】试题分析：根据旋转的定义可以求出空白部分的小三角形也是等边三角形，且边长为1，所以每个空白三角形的面积是△ABC的面积的19，用△ABC的面积减去三个空白小三角形的面积求出阴影部分的面积.解：如下图所示，∵△ABC是等边三角形，∴∠A=∠B=∠C=60°，∵旋转角是180°，∴∠ADE=∠AED=60°，∴△ADE是等边三角形，且AD=AE=DE=1，∴△ADE的面积是△ABC的面积的19，∵934ABCS=，∴阴影部分的面积是91933333 4942-⨯⨯=.故应选B.考点：旋转的性质二、填空题(每题6分)10.把一个平行四边形绕对角线交点旋转___________度后第一次与自身重合.【答案】：180°【解析】试题分析：平行四边形绕对角线交点旋转后与自身重合，则平行四边形的对角线也与自身重合，线段线段的中点至少旋转180°后与自身重合，故答案是180°.考点：旋转角11.如图，△ABC是等边三角形，D为BC边上的点，∠BAD=15°，△ABD经旋转后到达△ACE的位置，那么旋转角的度数是________.【答案】：60°【解析】试题分析：根据等边三角形的性质可以求出∠BAC=60°，因为旋转后点B与点C是对应点，所以旋转角是∠BAC，所以旋转角是60°.解：∵△ABC是等边三角形，∴∠BAC=60°，∵点B与点C是对应点，∴旋转角是∠BAC，∴旋转角是60°.考点：旋转角12.等边三角形至少旋转______度才能与自身重合。

人教版九年级数学上册第23章第1节《图形的旋转》课后练习题(附答案)

人教版九年级数学上册第23章第1节《图形的旋转》课后练习题（附答案）第1课时1.填空：如图，钟表的时针在不停地旋转，从3时到5时，时针的旋转中心是点，旋转角等于 °，点B的对应点是点 .2.填空：如图，杠杆绕支点转动撬起重物，杠杆的旋转中心是点，旋转角是∠ ，点A 的对应点是点 .3.如图，扎西坐在旋转的秋千上，请在图中画出点A ，B ，C 的对应点A ′，B ′，C ′.第2课时（一）基本训练，巩固旧知1.填空：把一个平面图形绕着平面内某一点O 转动一个角度，就叫做图形的旋转，点O 叫做旋转，转动的角叫做旋转 .如果图形上的点P 经过旋转变为点P ′，那么这两个点叫做旋转的 .2.填空： EDA C B(1)如图，△ABC 绕点A 旋转得到△ADE ，旋转中心是点，点B 的对应点是点，点C的对应点是点，∠ 等于于旋转角；(2)如图，△ABC 绕点O 旋转得到△DEF ，旋转中心是点，点A 的对应点是点，点B 的对应点是点，点C 的对应点是点，∠ 等于于旋转角.3.利用“对应点与旋转中心所连线段的夹角等于旋转角”，画出下图中的旋转角，并用量角器量出旋转角的度数.4.如图，四边形ABCD 是正方形，以点A 为中心，把△ADE 顺时针旋转90°，利用图形旋转的性质，画出旋转后的图形.（先让生做4题，然后师出示旋转后的图形，并利用性质解释点D 转到了点B ，点E 转到了点F ）第3课时（一）基本训练，巩固旧知 O .F E D A B C E D CB A1.填空：图形旋转的性质是：(1)旋转前后的图形； (2)对应点到旋转中心的距离；(3)对应点与旋转中心所连线段的夹角等于 .2.如图，以点O 为中心，把点P 顺时针旋转45°.3.如图，以点O 为中心，把线段AB 逆时针旋转90°.4.如图，以点O 为中心，把△ABC 顺时针旋转120°.5.如图，以点B 为中心，把△ABC 旋转180°.B AC B AC .O A B O ..O P .。

人教版九年级数学上册作业设计 23.1 第1课时认识图形的旋转

解：(1)∵△ABC 是等腰三角形，∴AB＝BC，∠A＝∠C，
∵将等腰△ABC 绕顶点 B 逆时针方向旋转 α 度到△A1BC1 的位置，∴A1B＝AB＝BC，∠A＝∠A1＝∠C，∠A1BD＝
∠C＝∠A1，
∠CBF，在△BCF 与△BA1D 中，BC＝A1B，
∴△
∠CBF＝∠A1BD，
BCF≌△BA1D
6．如图，以点O为旋转中心，将∠1按顺时针方向旋转 110°得到∠2.若∠1＝40°，则∠2＝___4_0_°_____．
7．如图，在Rt△OAB中，∠AOB＝30°，将△OAB绕点O逆时针旋转100°得到△OA1B1，则∠A1OB＝__7_0_°____．
8．如图，△ABC是等边三角形，点D是BC上一点，△ABD 经过旋转后到达△ACE的位置． (1)旋转中心是哪个点？ (2)旋转了多少度？ (3)若M是AB的中点，那么经过上述旋转后，点M转到了什么位置？
知识点1：认识旋转现象 1．将左图按顺时针方向旋转90°后得到的是( A )
2．(2016·株洲)如图，在三角形ABC中，∠ACB＝90°，
∠B＝50°，将此三角形绕点C沿顺时针方向旋转后得到三
角形A′B′C，若点B′恰好落在线段AB上，AC，A′B′交于点O，
则∠COA′的度数是( )
B
A．50° B．60° C．70° D．80°
10．如图，在等边△ABC中，D是边AC上一点，连接BD，将 △BCD绕点B逆时针旋转60°，得到△BAE，连接ED，若BC ＝5，BD＝4，则下列结论错误的是( B ) A．AE∥BC B．∠ADE＝∠BDC C．△BDE是等边三角形 D．△ADE的周长是9
11．如图，将等边△ABC绕顶点A顺时针方向旋转，使边AB与 AC重合得到△ACD，BC的中点E的对应点为F，则∠EAF的度数是__6_0_°___．

人教版九年级数学上册《23-1 第1课时图形的旋转》作业同步练习题及参考答案

23.1 图形的旋转第 1 课时图形的旋转1.将数字“6”旋转180°,得到数字“9”;将数字“9”旋转180°,得到数字“6”.现将数字“69”旋转180°,得到的数字是( )A.96B.69C.66D.992.如图,已知△OAB 是正三角形,OC⊥OB,OC=OB,将△OAB 绕点O 按逆时针方向旋转,使得OA 与OC 重合,得到△OCD,则旋转的角度是( )A.150°B.120°C.90°D.60°3.如图,在△ABC 中,∠C=90°,AC=4,BC=3,将△ABC 绕点A 逆时针旋转,使点C 落在线段AB 上的点E 处,点B 落在点D 处,则B,D 两点间的距离为( )A. 10B.2 2C.3D.2 54.如图,将△ABC 绕点C 顺时针旋转,使点B 落在AB 边上点B'处,此时,点A 的对应点A'恰好落在BC 边的延长线上,下列结论错误的是( )A.∠BCB'=∠ACA'B.∠ACB=2∠BC.∠B'CA=∠B'ACD.B'C 平分∠BB'A'5.如图所示,在△ABC 中,∠BAC=33°,将△ABC 绕点A 按顺时针方向旋转50°,对应得到△AB'C',则∠B'AC 的度数为.6.如图,有五个图形,其中四个是相同图形的不同摆法,另一个与众不同,与众不同的是.7.如图,把矩形OABC 放在平面直角坐标系中,OC 在x 轴上,OA 在y 轴上,且OC=2,OA=4,把矩形OABC 绕着原点顺时针旋转90°得到矩形OA'B'C',则点B'的坐标为.8.已知点P 的坐标为(1,1),若将点P 绕原点顺时针旋转45°,得到点P',则点P'的坐标为.9.如图,B,C,E 是同一直线上的三个点,四边形ABCD 与四边形CEFG 都是正方形.连接BG,DE.图中是否存在通过旋转能够互相重合的两个三角形?若存在,请说明理由,并指出旋转过程.10.观察图①和图②,回答下列问题:(1)请简述由图①变换为图②的形成过程;(2)若AD=3,DB=4,求△ADE 与△BDF 的面积和.11.如图,将△ABC 绕点B 顺时针旋转60°得到△DBE,点C 的对应点E 恰好落在AB 的延长线上,连接AD.下列结论一定正确的是( )A.∠ABD=∠EB.∠CBE=∠CC.AD∥BCD.AD=BC12.如图,网格纸上正方形小格的边长为1,图中线段AB 和点P 绕着同一个点做相同的旋转,分别得到线段A'B'和点P',则点P'所在的单位正方形区域是( )区 B.2 区 C.3 区 D.4 区13.如图,在Rt△ABC 中,∠ACB=90°,∠BAC=60°,AB=6.Rt△AB'C'可以看成是由Rt△ABC 绕点A 按逆时针方向旋转60°得到的,则线段B'C 的长为.14.如图,△ABC≌△DEF.△DEF 能否由△ABC 通过一次旋转得到?若能,请用直尺和圆规画出旋转中心; 若不能,试简要说明理由.★15.如图.(1)△ABC 按照逆时针方向转动一个角度后成为△AB'C',∠CAC'=90°,图中哪一点是旋转中心?旋转了多少度?(2)以点C'为旋转中心,顺时针旋转(1)问中相同的角度,那么线段AC 与A″C',BC 与B″C',AB 与A″B″有怎样的关系?B'C'与B″C'的位置关系呢?★16.如图,方格中每个小正方形的边长都是单位1,△ABC 在平面直角坐标系中的位置如图.(1)画出将△ABC 向右平移2 个单位得到的△A1B1C1;(2)画出将△ABC 绕点O 顺时针方向旋转90°得到的△A2B2C2.参考答案夯基达标1.B2.A3.A 由题意可知在△ABC 中AB 为斜边,易得AB=5,由图形的旋转可知△ABC≌△ADE,所以AC=AE=4,DE=BC=3.而AB=5,所以EB=AB-AE=5-4=1.连接DB,易得△DEB 为直角三角形,所以BD= ��2 + ��2 = 12 + 32 = 10. 故选A.4.C 根据旋转的性质得,∠BCB'和∠ACA'都是旋转角,则∠BCB'=∠ACA',故A 正确;∵CB=CB',∴∠B=∠BB'C.又∠A'CB'=∠B+∠BB'C,∴∠A'CB'=2∠B.又∠ACB=∠A'CB',∴∠ACB=2∠B,故 B 正确;∵∠A'B'C=∠B,∴∠A'B'C=∠BB'C ,∴B'C 平分∠BB'A',故 D 正确;故选 C .5.17° 由题意易知∠B'AB 为旋转角,∠B'AB=50°,∵∠BAC=33°,∴∠B'AC=50°-33°=17°.故答案为 17°.6.② 将图②③④⑤均绕各自对角线的交点旋转,使其含有黑点的三角形向上,此时图③④⑤与图① 完全相同,只有图②的阴影在含黑点的三角形的右侧.7.(4,2)8.( 2,0)9. 解存在,△BCG 和△DCE.理由:因为四边形 ABCD 和四边形 CEFG 都是正方形,所以 GC=CE ,BC=CD ,∠BCG=∠DCE=90°.所以△BCG ≌△DCE.所以△BCG 绕点 C 顺时针方向旋转 90°后能与△DCE 重合.10. 解 (1)把△ADE 绕点 D 逆时针旋转 90°得到△DA 1F ,即由图①变换为图②.(2)由题意,得∠A 1DB=90°,A 1D=AD=3,DB=4,所以�△+ �△= �△� ��= 1×3×4=6. ��12培优促能11.C ∵△ABC 绕点 B 顺时针旋转 60°得△DBE ,∴∠ABD=∠CBE=60°,AB=BD ,∴△ABD 是等边三角形,∴∠DAB=60°,∴∠DAB=∠CBE ,∴AD ∥BC ,故选 C .12.D 如图,连接 AA',BB',分别作 AA',BB'的中垂线,两直线的交点即为旋转中心,2由图可知,线段 AB 和点 P 绕着同一个点逆时针旋转 90°,点 P 逆时针旋转 90°后所得对应点 P'落在 4区,故选 D .13.3 7 如图,连接 BB'.在 Rt △ABC 中,∠ABC=90°-60°=30°,所以 AC=1AB=3.根据勾股定理,得BC= ��2-��2=3 3.根据旋转的性质知,B'C'=BC=3 3,AC'=AC=3,∠B'C'B=90°.所以 BC'=AB-AC'=3.在 Rt △B'C'B 中,BB'= �'�'2 + ��'2=6.由题易知∠B'BC 是直角,所以在 Rt △B'BC 中,B'C= ��'2 + ��2=3 7.14. 解能.如图,点 O 就是所求作的旋转中心.15. 解 (1)点 A 是旋转中心,旋转了 90°.(2)AC ∥A″C',且 AC=A″C';BC ∥B″C',且 BC=B″C';AB ∥A″B″,且 AB=A″B″.B'C'⊥B″C'.创新应用16.解(1)如图所示.(2)如图所示.。

人教版九年级上册数学第二十三章旋转23.1图形的旋转课后练习(含答案)

九年级上册数学《第二十三章23.1 图形的旋转》课后练习一、单项选择题1．如图，在平面直角坐标系中，将点P(2,3) 绕原点O顺时针旋转90°获得点P，则P的坐标为（）A．(3,2)B． (3, 1)C．(2,3)D．(3, 2)2．如图，在同一平面内，将△ ABC 绕点 A 逆时针旋转50°到△AB′ C的′地点，使得 C′C∥ AB ，则∠ CAB 等于（）A ．50°B． 60°C． 65°D． 70°3．如图，四边形ABCD 是边长为 5 的正方形， E 是DC 上一点，DE1，将ADE绕着点 A 顺时针旋转到与ABF重合，则EF（）A．41B．42C．52D．2134．如图，△ A′ B′是C由′△ ABC 经过平移获得的，△ A′ B′还C可′以看作是△ ABC经过如何的图形变化获得？以下结论：① 1 次旋转；② 1 次旋转和 1 次轴对称；③ 2 次旋转；④ 2 次轴对称．此中全部正确结论的序号是（）A ．①④B ． ②③C ． ②④D ． ③④5．在平面直角坐标系中，以原点为对称中心，把点A （ 3， 4）逆时针旋转90°，获得点 B ，则点B 的坐标为（）A ．（4， -3）B ．（ -4， 3）C ．（ -3， 4）D ．（ -3， -4）二、填空题6．在以下图的方格纸 (1 格长为 1 个单位长度 )中， △ABC 的极点都在格点上，将△ ABC绕点O 按顺时针方向旋转获得△ A'B'C' ，使各极点仍在格点上，则其旋转角的度数是____________ ．．7．如图，已知ABC 是等腰三角形， AB AC , BAC45 ,点 D 在 AC 边上，将 ABD绕点 A 逆时针旋转 45°获得 ACD ' ，且点 D ′、D 、B 三点在同一条直线上，则ABD 的度数是 _____．8．如图将 △ ABC 绕点 C 逆时针旋转获得△AB C ，此中点 A 与 A 是对应点，点 B ′与 B 是对应点，点B ′AC上，连结 A B ，若ACB 45 ， AC 3 ， BC 2 ，则 A B的落在边长为 __________．9．如图，在菱形ABCD 中，AB 2 , BAD 60，将菱形 ABCD 绕点 A 逆时针方向旋转，对应获得菱形AEFG ，点E在AC上，EF与CD交于点 P ，则DP的长是 _____．10．如图，将Rt ABC的斜边 AB 绕点 A 顺时针旋转090获得 AE，直角边AC绕点 A 逆时针旋转090 获得AF，连结EF．若AB=3，，且 B ，AC=2则 EF = _____．11．如图，等边三角形ABC 内有一点 P，分別连结 AP 、 BP、 CP，若AP6， BP8 ，CP 10 ．则 S ABP S BPC＝_______．12．如图，在平面直角坐标系中，点A1的坐标为 (10)，，以OA1为直角边作Rt OA1 A2，并使AOA ＝60 12，再以OA 为直角边作2Rt OA A ，并使23A OA＝6023，再以OA 为直角3边作 Rt OA3 A4，并使A3OA4＝60按此规律进行下去，则点A2019的坐标为_______．13．如图，将绕直角极点 C 顺时针旋转，获得，连结AD ，若，则______．三、解答题14． (1)问题发现如图1,△ACB和△DCE均为等腰直角三角形,∠ ACB=90° ,B,C,D在一条直线上.填空 :线段AD,BE之间的关系为.(2) 拓展研究如图2,△ACB和△DCE均为等腰直角三角形,∠ ACB= ∠ DCE=90° ,请判断AD,BE的关系 ,并说明原因.(3) 解决问题如图 3,线段 PA=3,点 B 是线段 PA 外一点 ,PB=5, 连结 AB, 将 AB 绕点 A 逆时针旋转 90°获得线段AC, 跟着点 B 的地点的变化 ,直接写出 PC 的范围 .15．如图 1，ABC 中，CA CB,ACB, D 为ABC内一点，将CAD 绕点 C 按逆时针方向旋转角获得CBE ，点A, D的对应点分别为点B, E ，且 A, D, E 三点在同向来线上．（ 1）填空：CDE（用含的代数式表示）；（ 2）如图 2，若60，请补全图形，再过点C作CF AE 于点F，而后研究线段CF , AE, BE 之间的数目关系，并证明你的结论；（3）若90 , AC 5 2 ，且点G知足AGB 90 , BG 6，直接写出点 C 到 AG 的距离．16．如图，在△ ABC 和△ADE 中，点 E 在 BC 边上，∠ BAC ＝∠ DAE ，∠ B＝∠ D， AB ＝AD ．（1）试说明△ ABC ≌△ ADE ；（2）假如∠ AEC ＝ 75°，将△ ADE 绕点 A 旋转一个锐角后与△ ABC 重合，求这个旋转角的大小．17．如图，在Rt △ABC 中，∠ C=90°， AB=10 ，AC=8 ．线段 AD 由线段 AB 绕点 A 按逆时针方向旋转90°获得，△ EFG 由△ ABC 沿 CB 方向平移获得，且直线EF 过点 D．（1）求∠BDF 的大小；（2）求 CG 的长．18．请仔细阅读下边的数学小研究系列，达成所提出的问题：研究1：如图1，在等腰直角三角形ABC中，，，将边AB绕点B 顺时针旋转获得线段BD，连结求证：的面积为提示：过点 D 作BC 边上的高 DE，可证≌研究2：如图2，在一般的中，，，将边AB 绕点B 顺时针旋转获得线段BD ，连结请用含 a 的式子表示的面积，并说明原因．研究 3：如图 3，在等腰三角形ABC 中，获得线段BD ，连结尝试究用含 a 的式子表示，，将边AB绕点B顺时针旋转的面积，要有研究过程．19．如图 1，矩形 ABCD 中， E 是 AD 的中点，以点 E 直角极点的直角三角形EFG 的两边EF，EG 分别过点 B ， C，∠ F＝ 30°.（ 1）求证： BE＝CE（ 2）将△ EFG 绕点 E 按顺时针方向旋转，当旋转到EF与 AD重合时停止转动.若EF，EG分别与AB，BC订交于点M，N.（如图2）①求证：△ BEM ≌△ CEN ；②若 AB ＝ 2，求△ BMN 面积的最大值；③当旋转停止时，点 B 恰幸亏 FG 上（如图3），求 sin∠ EBG 的值 .答案1． D2．C 3．D 4．D 5．B6． 90°7． 22.5 °8．139．31 10．|13|11．2416 322017 ,22017 313．12．14．解（ 1）结论： AD=BE ，AD ⊥BE．原因：如图 1 中，∵△ ACB 与△ DCE 均为等腰直角三角形，∴AC=BC ，CE=CD ，∠ ACB= ∠ ACD=90°，在 Rt△ ACD 和 Rt△BCE 中AC＝BCACD＝BCECD＝CE∴△ ACD ≌△ BCE （ SAS），∴AD=BE ，∠ EBC=∠ CAD延伸 BE交AD于点 F，∵BC⊥AD ，∴∠ EBC+∠ CEB=90°，∵∠ CEB=AEF ，∴∠ EAD+ ∠ AEF=90°，∴∠ AFE=90°，即 AD ⊥BE ．∴AD=BE ， AD ⊥ BE ．故答案为 AD=BE ， AD ⊥BE ．（ 2）结论： AD=BE ， AD ⊥ BE ．原因：如图 2 中，设 AD 交 BE 于 H，AD 交 BC 于 O．∵△ ACB 与△ DCE 均为等腰直角三角形，∴AC=BC ， CE=CD ，∠ ACB= ∠ECD=90°，∴ACD= ∠ BCE ，在 Rt△ ACD 和 Rt△BCE 中AC＝BCACD＝BCE ，CD＝CE∴△ ACD ≌△ BCE （ SAS），∴AD=BE ，∠CAD= ∠CBE ，∵∠ CAO+ ∠ AOC=90°，∠ AOC= ∠BOH ，∴∠ BOH+ ∠ OBH=90°，∴∠ OHB=90°，∴AD ⊥BE，∴AD=BE ，AD ⊥BE．（3）如图 3 中，作 AE ⊥ AP，使得 AE=PA ，则易证△ APE ≌△ ACP ，∴ PC=BE ，，图 3-1 中，当 P、 E、 B 共线时， BE 最小，最小值 =PB-PE=5-3 2，图 3-2 中，当 P、 E、 B 共线时， BE 最大，最大值 =PB+PE=5+3 2∴5-3 2 ≤BE≤5+32，即 5-3 2 ≤PC≤5+32．15．解：（1）将CAD 绕点 C 按逆时针方向旋转角获得 CBE ACD BCE ， DCE aCD CECDE 1802故答案为：1802（2）AE BE23CF 3原因以下：如图，将CAD 绕点 C 按逆时针方向旋转角60 获得CBE ACD BCEAD BE,CD CE,DCE60CDE是等边三角形，且CF DEDF EF3 CF3AE AD DF EF2 3AE BE CF3（ 3）如图，当点G 在AB上方时，过点C作CE AG 于点 E ，ACB90, AC BC52CAB ABC45,AB10ACB90AGB点C，点G ，点 B ，点 A 四点共圆AGC ABC45 ,且CE AGAGC ECG 45CE GEAB10,GB6, AGB 90AG AB2GB28AC2 AE2 CE2 ，(52) 2(8CE) 2CE 2CE 7 （不合题意舍去），CE1若点 G在AB的下方，过点C作CF AG，同理可得： CF7点C到 AG的距离为1或7．16.解：（ 1）、∵∠ BAC= ∠DAE ， AB=AD ，∠ B=∠ D，∴△ ABD ≌△ ADE.（ 2）、∵△ ABC ≌△ ADE ，∴ AC 与 AE 是一组对应边，∴∠ CAE的旋转角，∵ AE=AC ，∠AEC=75°，∴∠ ACE= ∠ AEC=75°，∴∠ CAE=180° —75°—75°=30°17．解（ 1）∵线段 AD 是由线段AB 绕点 A 按逆时针方向旋转90°获得，∴∠ DAB=90°， AD=AB=10 ，∴∠ ABD=45°，∵△ EFG 是△ ABC 沿 CB 方向平移获得，∴AB ∥ EF，∴∠ BDF= ∠ ABD=45°；（2）由平移的性质得， AE ∥ CG， AB ∥ EF，∴∠ DEA= ∠ DFC= ∠ABC ，∠ ADE+ ∠ DAB=180°，∵∠ DAB=90°，∴∠ ADE=90°，∵∠ ACB=90°，∴∠ ADE= ∠ ACB ，∴△ ADE ∽△ ACB ，∴，∵AB=8 ， AB=AD=10 ，∴ AE=12.5 ，由平移的性质得， CG=AE=12.5 ．18．解如图1，过点D作交CB的延伸线于E，，由旋转知，，，，，，在和中，，≌，，；的面积为，原因：如图2，过点 D 作 BC 的垂线，与BC 的延伸线交于点E，，线段AB绕点，B 顺时针旋转，获得线段BE ，，，，在和中，，≌，，，如图；3，过点 A 作与 F，过点 D 作的延伸线于点E，，，，，，，线段 BD 是由线段 AB 旋转获得的，，在和中，，≌，，，的面积为．19．解（ 1）证明：如图 1 中，∵四边形 ABCD 是矩形，∴AB=DC ，∠A= ∠D=90°，∵E 是 AD 中点，∴AE=DE ，∴△ BAE ≌△ CDE ，∴BE=CE ．（2）①解：如图 2 中，由（ 1）可知，△ EBC 是等腰直角三角形，∴∠ EBC=∠ ECB=45°，∵∠ ABC= ∠ BCD=90°，∴∠ EBM= ∠ ECN=45°，∵∠ MEN= ∠ BEC=90°，∴∠ BEM= ∠ CEN，∵EB=EC ，∴△ BEM ≌△ CEN ；②∵△ BEM ≌△ CEN ，∴BM=CN ，设 BM=CN=x ，则 BN=4-x ，2∴S△BMN =?x（ 4-x ） =-（x-2）+2，∵—＜ 0，∴ x=2 时，△ BMN 的面积最大，最大值为2．③解：如图 3 中，作 EH⊥ BG 于 H ．设 NG=m ，则 BG=2m ， BN=EN=m，EB= m．∴ EG=m+ m= （ 1+）m，∵S△BEG= ?EG?BN= ?BG?EH，∴ EH==m，在 Rt△ EBH 中， sin∠ EBH=．。

人教版九年级上《23.1图形的旋转》课时练含答案

第1页共6页九年级上第二十三章 23.1 图形的旋转课时练学校：姓名：班级：考号：一、选择题A 按顺时针方向旋转60°得到△AEF ,则下列结论错误的是 ( )A. ∠BAE =60°B. AC =AFC. EF =BCD. ∠BAF =60°2. 由图甲中的三角形仅经过一次平移,旋转或轴对称变换,不能得到的图形是 ( )甲 A. B. C. D.3. 如图,菱形OABC 的顶点O 在坐标原点,顶点A 在x 轴上,∠ABC =120°,OA =2,将菱形OABC 绕原点按顺时针旋转105°至菱形OA'B'C'的位置,则点B'的坐标为 ( )A. ( ,- )B. (-C. (2,-2)D. ( ,- )4. 如图所示的图形,可以看作是由一个等腰直角三角形旋转若干次形成的,则每次旋转的角度是 ( )A. 90°B. 60°C. 45°D. 30°5. 从5点15分到5点20分,分针旋转的度数为 ( )A. 20°B. 26°C.30° D. 36°6. 在下列现象中,属于旋转现象的是 ( )①方向盘的旋转;②水龙头开关的转动;③电梯的上下移动;④钟表分针的运动.A. ①②③B. ②③C. ②③④D. ①②④7.如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°后得到△AB'C'(点B的对应点是点B',点C的对应点是点C'),连接CC',若∠CC'B'=32°,则∠B的大小是()A. 32°B. 64°C. 77°D. 87°8.下列四个圆形图案中,分别以它们所在圆的圆心为旋转中心,顺时针旋转120°后,能与原图形完全重合的是( )A. B. C. D.9. 如图，将△ABC绕点P顺时针旋转90°得到△A′B′C′，则点P的坐标是( )A. (1，1)B. (1，2)C. (1，3)D. (1，4)10. 如图，△AOB为等腰三角形，顶点A的坐标为(2，)，底边OB在x轴上，将△AOB绕点B按顺时针方向旋转一定角度后得△A′O′B，点A的对应点A′在x轴上，则点O′的坐标为( )A. (，)B. (，)C. (，)D. (，4)二、填空题11. 把一个平行四边形绕对角线交点旋转度后第一次与自身重合.12. 如图所示,在矩形ABCD中,AB=3,BC=4,EF过AC,BD的交点O,则图中阴影部分的面积为.13.如图所示,在方格纸中,格点三角形甲经过旋转后得到格点三角形乙,则其旋转中心是.14. 如图,在△ABC中,∠C=30°.将△ABC绕点A顺时针旋转60°得△ADE,AE与BC交于点F,则∠AFB=°.15. 如图,在平面直角坐标系中,将点P(-4,2)绕原点O顺时针旋转90°,则其对应点Q的坐标为.16. 将点A(-3,5)绕坐标原点按逆时针方向旋转90°得到点B,则点B的坐标为______.17. 如图,平面直角坐标系的原点O是正方形ABCD的中心,顶点A,B的坐标分别为(1,1),(-1,1),把正方形ABCD绕点O逆时针方向旋转45°得正方形A'B'C'D',则正方形ABCD与正方形A'B'C'D'重叠部分所形成的正八边形的边长为.18. 如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为.第3页共6页19. 如图，已知正方形ABCD 的边长为3，E 为CD 边上一点，DE ＝1，以点A 为中心，把△ADE 顺时针旋转90°，得△ABE ′，连接EE ′，则EE ′的长等于__________.三、解答题 ,每个小方格都是边长为1个单位的正方形,△ABC 的三个顶点都在格点上(每个小方格的顶点叫做格点).(1)画出△ABC 向下平移3个单位后的△A 1B 1C 1;(2)画出△ABC 绕点O 顺时针旋转90°后的△A 2B 2C 2,并求出点A 旋转到A 2所经过的路线长.(结果保留π)21. 如图①,在△ABC 和△EDC 中,AC =CE =CB =CD ,∠ACB =∠ECD =90°,AB 与CE 交于F ,ED 与AB ,BC 分别交于M ,H .(1)试说明CF =CH ; (2)如图②,△ABC 不动,△EDC 绕点C 旋转到∠BCE =45°时,试判断四边形ACDM 是什么四边形,请证明你的结论.参考答案第5页共6页1. 【答案】D 【解析】注意找准对应边.2. 【答案】B 【解析】选项A 是由原图形平移得到的;选项C 是由原图形经过轴对称变换得到的;选项D 是由原图形旋转得到的,而选项B 不能由原图形经过一次平移,旋转或轴对称变换得到,故选B.注：选项B 需经过一次镜面反射变换才能得到.3. 【答案】A 【解析】如图,连接OB ,OB',过B'作B'E ⊥x 轴于E ,根据题意得∠BOB'=105°.∵四边形OABC 是菱形,∠ABC =120°,∴OA =AB ,∠AOB =60°.△OAB 是等边三角形,∠AOB'=∠BOB'-∠AOB =105°-60°=45°,∴OB =OA =2,∴OB'=OB =2,在Rt △OEB'中,根据勾股定理,得OE =B'E =.4. 【答案】C 【解析】这是纸风车的图案,共有8瓣,则每次旋转的角度是360°÷8=45°.5. 【答案】C 【解析】从5点15分到5点20分,分针旋转的度数为=30°. 6. 【答案】D 【解析】电梯的上下移动属于平移现象.7. 【答案】C 【解析】本题考查旋转变换的性质,有一定难度.∵旋转后对应线段相等,∴AC=AC',又∵∠BAC=∠B'AC'=90°,∴∠AC'C=45°,∴∠BCA=∠AC'B'=13°,∴∠B=77°.8. 【答案】A 【解析】A.此图顺时针旋转120°能与原图完全重合；B.此图顺时针旋转90°,180°,270°均能与原图完全重合；C.此图顺时针旋转180°能与原图完全重合；D.此图顺时针旋转72°,144°,216°,288°,360°均能与原图完全重合.故选A.9. 【答案】B 【解析】根据“对应点到旋转中心的距离相等”，分别连接AA ′、BB ′，分别作AA ′、BB ′的垂直平分线，它们的交点为(1，2)，∴旋转中心P 的坐标为(1，2).故选B.10. 【答案】C 【解析】由已知条件和勾股定理可得AO ＝AB ＝＝3，sin ∠OBA= ，cos ∠OBA ＝，OB ＝4，经过旋转后，∠O ′BA ′＝∠OBA ，BO ′＝BO ＝4，设点O ′的坐标为(x ，y )，则x ＝BO ＋×BO ′＝4＋ ×4＝，y ＝ ×BO ′＝ ×4＝，故选C.11. 【答案】18012. 【答案】313. 【答案】N14. 【答案】9015. 【答案】(2,4)16. 【答案】(-5,-3)17. 【答案】2-218. 【答案】1.619. 【答案】220.(1) 【答案】画出△A1B1C12分(2) 【答案】画出△A2B2C25分连接OA,OA2,由勾股定理得:OA==6分又∵∠AOA2=90°∴点A旋转到A2所经过的路线长为:l==8分21.(1) 【答案】因为∠ACB=∠ECD=90°,所以∠ACF+∠ECB=∠DCH+∠ECB,所以∠ACF=∠DCH.又因为AC=CF=CB=CD,所以∠A=∠D=45°,所以△ACF≌△DCH,所以CF=CH.(2) 【答案】菱形.证明如下:因为∠ACB=∠ECD=90°,∠BCF=45°,所以∠ACE=45°,∠DCB=45°.又因为∠E=∠B=45°,所以∠ACE=∠E,∠DCB=∠B,所以AC∥MD,CD∥AM.所以四边形ACDM是平行四边形,又因为AC=CD,所以四边形ACDM是菱形.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

23.1图形的旋转
一、选择题
1.图1可以看作是一个等腰直角三角形旋转若干次而生成的则每次旋转的度数可以是（）
A．900 B．600 C．450 D．300
2.如图2，图形旋转一定角度后能与自身重合,则旋转的角度可能是( )
A、300
B、600
C、900
D、1200
图1 图2 图3 图4
3．在26个英文大写字母中，通过旋转180°后能与原字母重合的有（）．
A．6个 B．7个 C．8个 D．9个
4．从5点15分到5点20分，分针旋转的度数为（）．
A．20° B．26° C．30° D．36°
5．如图1，在Rt△ABC中，∠ACB=90°，∠A=40°，以直角顶点C为旋转中心，•将△ABC 旋转到△A′B′C的位置，其中A′、B′分别是A、B的对应点，且点B在斜边A′B′上，直角边CA′交AB于D，则旋转角等于（）．
A．70° B．80° C．60° D．50°
(1) (2) (3)
二、填空题．
6．在平面内，将一个图形绕一个定点沿着某个方向转动一个角度，这样的图形运动称为________，这个定点称为________，转动的角为________．
7．如图2，△ABC与△ADE都是等腰直角三角形，∠C和∠AED都是直角，•点E•在AB上，如果△ABC经旋转后能与△ADE重合，那么旋转中心是点_________；旋转的度数是
__________．
8．如图3，△ABC为等边三角形，D为△ABC•内一点，•△ABD•经过旋转后到达△ACP的位置，则，（1）旋转中心是________；（2）•旋转角度是________；•（•3）•△ADP•是________三角形．
9.如图3，把△ABC绕着点C顺时针旋转350，得到△A＇B＇C，若∠BCA＇=1000，则∠B/CA 的度数是__________。

10.如图4，P是等边△ABC内一点，△BMC是由△BPA旋转所得，则∠PBM＝______°．
11.如图，O是等边△ABC内一点，将△AOB绕A点逆时针旋转，使得B、O两点的对应点分
别为C、D，则旋转角为________°，图中除△ABC外，还有等边三形
是__________．
12.如图所示，△ABP是由△ACE绕A点旋转得到的，那么△ABP与△ACE是什么关系？
若∠BAP＝40°，∠B＝30°，∠PAC＝20°，求旋转角及∠CAE=____°∠E=____°
∠BAE=____°
A E
P
13、△ABC 是等腰直角三角形，BC 是斜边，P 是△ABC 内一点，将△ABC 绕点A 逆时针旋转后于△ACQ 重合，，如果AP=3，则PQ=__________
三、综合提高题．
14．阅读下面材料：
如图4，把△ABC 沿直线BC 平行移动线段BC 的长度，可以变到△ECD 的位置．
如图5，以BC 为轴把△ABC 翻折180°，可以变到△DBC 的位置．
(4) (5) (6) (7)
如图6，以A 点为中心，把△ABC 旋转90°，可以变到△AED 的位置，像这样，•其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的，这种只改变位置，不改变形状和大小的图形变换，叫做三角形的全等变换．
回答下列问题
如图7，在正方形ABCD 中，E 是AD 的中点，F 是BA 延长线上一点，AF=AB ． 12
（1）在如图7所示，可以通过平行移动、翻折、旋转中的哪一种方法，•使△ABE移到△ADF的位置？
（2）指出如图7所示中的线段BE与DF之间的关系．
15．一块等边三角形木块，边长为1，如图，•现将木块沿水平线翻滚五个三角形，那么B 点从开始至结束所走过的路径长是多少？
16、在Rt△ABO中，∠OAB=90°，OA=AB=6，将△ABO绕点O逆时针方向旋转90°得到△OA1B1, （1）则线段OA1的长是__________，∠AOB1=_______°
（2）连接AA1，求证四边形OAA1B1是平行四边形；
(3)求四边形OAA1B1的面积？
答案:
一、1,C 2,C 3．B 4．C 5．B
二、6．旋转旋转中心旋转角 7．A 45° 8．点A 60°等边
9.如图3，把△ABC绕着点C顺时针旋转350，得到△A＇B＇C，若∠BCA＇=1000，则∠B/CA 的度数是30°。

10.如图4，P是等边△ABC内一点，△BMC是由△BPA旋转所得，则∠PBM＝60°．
11.如图，O是等边△ABC内一点，将△AOB绕A点逆时针旋转，使得B、O两点的对应点分别为C、D，则旋转角为60°，图中除△ABC外，还有等边三形是△AOD
12.如图所示，△ABP是由△ACE绕A点旋转得到的，那么△ABP与△ACE是全等关系？
若∠BAP＝40°，∠B＝30°，∠PAC＝20°，求旋转角及∠CAE=60°∠E=110°
∠BAE=100°
13、△ABC是等腰直角三角形，BC是斜边，P是△ABC内一点，将△ABC绕点A逆时针旋转后于△ACQ重合，，如果AP=3，则PQ=3√2
三、14．（1）通过旋转，即以点A为旋转中心，将△ABE逆时针旋转90°．
（2）BE=•DF，BE⊥DF
15．翻滚一次滚120°翻滚五个三角形，正好翻滚一个圆，所以所走路径是2．
16、在Rt△ABO中，∠OAB=90°，OA=AB=6，将△ABO绕点O逆时针方向旋转90°得到△OA1B1, （1）则线段OA1的长是6，∠AOB1=135°
（2）A1B1与OA平行且相等，四边形OAA1B1是平行四边形
(3)四边形OAA1B1的面积18。