第1章课后习题
配送管理第一章 习题

第一章课后习题一、概念题1、配送2、运输3、仓储4、共同配送5、供应配送二、单项选择题1、2001年4月发布的中国国家标准《物流术语》中,“物品从供应地向接收地的实体流动过程”是对()的定义。
A.物流B.运输C.配送D.送货2、下列不属于同一种关于配送分类的是()。
A.企业内部配送B.企业之间的配送C.企业共同配送D.企业对消费者的配送3、在物流系统中,起着缓冲、调节和平衡作用的物流活动是()。
A.运输B.配送C.装卸D.存储4、下列关于配送的说法,错误的是()。
A.配送处于“二次运输”的地位,与运输相比,它更直接面向并靠近用户。
B.长距离大批量快速运输的送货方式叫配送。
C.配送实际是一个货物的集散过程,它包括集中、分类和散发三个步骤。
D.对于配送而言,应当在时间、速度、服务水平、成本、数量等多方面寻求系统最优,而非某方面最优。
5、下列哪项是按配送品种和数量分类的配送类型()。
A.仓库配送B.专业配送C.多品种小批量配送D.共同配送6、下列哪项是按服务对象分类的配送类型()。
A.仓库配送B.专业配送C.企业对消费者配送D.共同配送7、下列哪项是按配送组织者分类的配送类型()。
A.仓库配送B.以零售商为主体的配送C.定时定量配送D.共同配送8、配货时,大多是按照入库日期的()原则进行。
A.先进先出B.先进后出C.后进先出D.任其自然9、以商品收发为主的库房是()。
A.配送型库房B.储存型库房C.流通型库房D.移动型库房10、下列()项是配送中心体积重量最大的拣货单位。
A.托盘B.箱C.单件D.散装三、多项选择题1、运输原理包括()。
A.规模原理B.效益原理C.距离原理D.动态原理E.速度原理2、运输系统的构成要素有()。
A.运输线路B.运输工具C.运输方式D.运输参与者E.运输结构3、下列()几项常被用作车辆路线安排问题的约束条件。
A.货物需求量B.交发货时间C.车辆行驶里程D.车辆容量E.货物供给量4、配送的基本功能要素主要包括()。
数据结构第一章课后习题与答案

第 1 章 绪 论(2005-07-14) -第 1 章 绪 论课后习题讲解1. 填空⑴( )是数据的基本单位,在计算机程序中通常作为一个整体进行考虑和处理。
【解答】数据元素⑵( )是数据的最小单位,( )是讨论数据结构时涉及的最小数据单位。
【解答】数据项,数据元素【分析】数据结构指的是数据元素以及数据元素之间的关系。
⑶ 从逻辑关系上讲,数据结构主要分为( )、( )、( )和( )。
【解答】集合,线性结构,树结构,图结构⑷ 数据的存储结构主要有( )和( )两种基本方法,不论哪种存储结构,都要存储两方面的内容:( )和()。
【解答】顺序存储结构,链接存储结构,数据元素,数据元素之间的关系⑸ 算法具有五个特性,分别是( )、( )、( )、( )、( )。
【解答】有零个或多个输入,有一个或多个输出,有穷性,确定性,可行性⑹ 算法的描述方法通常有( )、( )、( )和( )四种,其中,( )被称为算法语言。
【解答】自然语言,程序设计语言,流程图,伪代码,伪代码⑺ 在一般情况下,一个算法的时间复杂度是( )的函数。
【解答】问题规模⑻ 设待处理问题的规模为n,若一个算法的时间复杂度为一个常数,则表示成数量级的形式为( ),若为n*log25n,则表示成数量级的形式为( )。
【解答】Ο(1),Ο(nlog2n)【分析】用大O记号表示算法的时间复杂度,需要将低次幂去掉,将最高次幂的系数去掉。
2. 选择题⑴ 顺序存储结构中数据元素之间的逻辑关系是由( )表示的,链接存储结构中的数据元素之间的逻辑关系是由( )表示的。
A 线性结构B 非线性结构C 存储位置D 指针【解答】C,D【分析】顺序存储结构就是用一维数组存储数据结构中的数据元素,其逻辑关系由存储位置(即元素在数组中的下标)表示;链接存储结构中一个数据元素对应链表中的一个结点,元素之间的逻辑关系由结点中的指针表示。
⑵ 假设有如下遗产继承规则:丈夫和妻子可以相互继承遗产;子女可以继承父亲或母亲的遗产;子女间不能相互继承。
C语言程序设计 – 第 01 章课后习题

一、二、三、、选择1.2.3.4.5.、填空1.2.3.4.5.、算法1.2.1. 以下2. 在一3. 以下4. 结构5. 在程1. 一个2. 3. 算法4. 结构5. 结构算法设1. 求三2. 选择题以下叙A. B. C.D.(句在一个A. B. C.D.(程序以下叙A. B. C.D.(结构化A. B. C.D.(在程序A. B. C.D.填空题一个简一个算法的结构化结构化算法设计求三个求1+2择题 以下叙述 C 语言C. D. (解释句,另外 必须 可以C. 必须D. 必须(解释程序也就以下叙述 C 语言C. D. 同一(解释结构化程 程序 程序C. 程序D. 程序(解释在程序设 不限 减少C. 程序D. 程序空题 一个简单C 算法的特结构化程结构化程法设计题求三个数1+2+3下叙述不正一个语言程在一个解释:一个必须在程可以在任必须在程必须在系解释:序也就执下叙述中正在语言程构成同一个解释:构化程序设程序的规程序的易程序的执程序的可解释:程序设计时不限制减少或取程序越短程序结构个简单的语言法的特性是构化程序由构化程序设计题三个数中的+2+3+述不正确个C 语言语言程序C 语言程个C 语言:另外被C 须在程序以在任意须在程序须在系统:一个也就执行述中正确C 语言程语言程序成C 语言一个:程序设计序的规模序的易读序的执行序的可移:结构设计时限制got 少或取消序越短越序结构应单的语言程序特性是程序由程序设计 数中的最+3+不正确的语言程言程序的语言程序语言程C 语言程外被“程序中在程序的在任意地在程序的在系统调一个就执行完了中正确的语言程序言程序中语言程C 语言main 序设计主的规模的易读性的执行效的可移植结构化程计时,或取消注越短越好结构应有C 语言言程序是性是 有穷序由 顺序序设计方中的最大…正确的是语言程序程序的基本言程序中语言程序语言程序/*”序中,程序的最任意地方程序的最系统调用个C 程序行完了正确的是言程序中程序中有输语言程序语言程ain 函数设计主要强规模易读性执行效率可移植性构化程序,应采纳goto 语句取消注释短越好构应有助语言程程序是从顺序结设计方法的的最大者+100的是(言程序可的基本组程序中言程序必言程序中”和“,序的最后面意地方序的最前面统调用的库程序总完了)的是(程序中,中有输入言程序的语言程序函数在一主要强调读性行效率移植性化程序设应采纳的语句的消注释行越好应有助于读语言程序至序是从有穷性顺序结构方法的主大者。
《金融风险管理》课后习题答案

《金融风险管理》课后习题答案第一章课后习题答案一、重要名词答案略二、单项选择1-5 C B D A A 6-10 C A C C C 11-15 D A B D A 16-20 B C D D D 21-25 B B B B三、多项选择1. BCD2. ACDE3. ADE4. ABCDE5. ABDE6. BCDE7. AD8. ABCE9. ABCDE 10. ACDE11. ACE 12. ABCDE 13. ACDE 14. AB 15.ABC16. ACE 17. ABC 18.ABCDE四、判断题1-5 ××××√ 6-10 ×√×××11-15 √√××× 16-20 ×√√×√五、简答题答案略第二章课后习题答案一、重要名词答案略二、单项选择1-5 A C C AD 6-10 C B D D B 11-15 A A C C D 16-18 A D A三、多项选择1. A B C D2. A B C DE3. ABCDE4. ABCD5. ABCDE6. ABCDE7. ABCD8. ADE9. ACDE 10. ACE四、判断题1-5 ×√××× 6-8 ×√×五、简答题答案略第三章课后习题答案一、重要名词答案略二、单项选择1-5 ACBBB 6-10 ADBCD 11-15 DBBAC 16-21 DDABAB三、多项选择1. ABCE2. AD3. BCDE4. BDE5. BE6. CD7. BCDE8. ABCDE9. BDE 10. ABDE11. BCE 12. ABCE 13. ABCDE 14. ACE四、判断题1-5 √××√√ 6-10 ×√××× 11-15 ××××× 16-17 √×五、简答题答案略第四章课后习题答案二、单选1-5DCCAD 6-10AAABA 11-15DDCCB 15-20A ABBD三、多选1-5BCDE/CD / ABDE /ABCE /ABCDE 6-10ABCD/ ABCDE/ ABDE/CD/AC11-15ABCDE /ABCE/ACD/ABC/ABCD16-20ABCE/ABE/ABCDE/ABCDE/BCDE四、判断题1-5 错错错错错 6-10对对错对对 11-15对对对错对 16-18错错对第五章课后习题答案一、重要名词答案略二、单项选择1-5 ACCBB 6-10 ADDCD 11-15 CCBCD 16-20 ACDCC 21-25 CDBAC 26-30 DABBD 31-35 ABCAB 36-40 DACAB 41-45 CDAAC 46-48 AAD三、多项选择1. ABC2. ABD3. BCE4. AC5. BC6. BCE7. DE8. ADE9. ABCD 10. ABCD11. ABD 12. ABCD 13. ABC 14. ABCD 15. BC16. AB 17. ABCD 18. AC 19. AD 20. BCD21. CD 22. CD 23. AB四、判断题1-5 √×××√ 6-10 ××√×× 11-15 ××××√ 16-20 √××××21-25 √×√×× 26-30 ×√××× 31-35 ×√××× 36-40 √×√√√ 41-45 ××√√√ 46-47 ×√五、简答题答案略第六章课后习题答案二、单选1-5DCCAD 6-10AAABA 11-15DDCCB 15-20A ABBD四、多选1-5BCDE/CD / ABDE /ABCE /ABCDE 6-10ABCD/ ABCDE/ ABDE/CD/AC11-15ABCDE /ABCE/ACD/ABC/ABCD16-20ABCE/ABE/ABCDE/ABCDE/BCDE五、判断题1-5 错错错错错 6-10对对错对对 11-15对对对错对 16-18错错对第七章课后习题答案一、重要名词答案略二、单项选择1-5 BCDCA 6-10 BBDDD 11-15 CADCC三、多项选择1. ABCDE2. CDE3. ABCDE4. ABCDE5. BCE6. BDE7. ABCE8. BCE9. ABC 10. ABDE11. ABCDE 12. ABD 13. ABCD四、判断题1-10√××√××√×√五、案例分析题案例1:内部欺诈(未经授权交易导致资金损失)案例2:失职违规案例3:核心雇员流失案例4:违反用工发六、简答题答案略第八章课后习题答案一、重要名词答案略二、单项选择1-5 CDCCB 6-10 DCDAB 11-15 CADAA 16-20 DACCC三、多项选择1. ACE2. ABE3. ABCE4. ADE5. ABE6. ABCD7. ABCDE8.ABCD9. ABCD 10. ABC四、判断题1-11××√××√××√√五、简答题答案略第九章课后习题答案一、重要名词答案略二、单项选择1-5 ABDDD 6-10 AABBD 11-16 CCDDAB三、多项选择1. ABCD2. ABCD3. AC4. BCD5. ABCD6. ABCDE7. ACD8. ABCDE9. ABCDE 10. ABCDE四、判断题1-5 ×√××√ 6-10 √×√×× 11-14 √√√√五、简答题答案略第十章课后习题答案一、重要名词答案略二、单项选择1-5 ABBCB 6-10 CCBDA三、多项选择1. CD2. ADE3. AC4. BCDE5. CDE6.ABC7. ACE8. ABC9. ACDE 10.ABC四、判断题1-5 ×××√×五、简答题答案略第十一章课后习题答案二、单选题1-5DABCB 6-10DABDC 11-15DBAAB 16-20DCCAA三、多选题1-5ABD/ACD/AC/ABC/ACD 6-10 ABCD/ABD/ABCDE/ABCDE/ABCDE11-15ABCDE/ABCDE/ABCD/ABCDE/ABCDE16-20ACD/ ABCDE/ABCDE/ ACE/ADE四、1-5对错错对对 6-10对错对对错 11-15对对对对错 16-20对错对错对。
第一章 原生动物部分课后练习题

第一章原生动物部分课后练习题选择题:1.原生动物伸缩泡的主要功能是()A.排除代谢废物B.排除多余水分C.气体交换D.吸收营养2.衣滴虫的有性生殖为()A.配子生殖B.接合生殖C.复裂生殖D.出芽生殖3.大草履虫生活的环境为()A.洁净、缓流的淡水中B.有机质丰富、缓流的淡水中C.有机质丰富、水流急的淡水中D.洁净、水流急的淡水中4.痢疾内变形虫侵入人体的形态为()A.小滋养体B.大滋养体C.四核包囊D.鞭毛体5.间日疟原虫侵入人体的形态为()A.动合子B.裂殖子C. 子孢子D.大滋养体6.多核大球型有孔虫的生殖为()A.孢子生殖B.二裂生殖C.配子生殖D.复裂生殖7.原生动物完成呼吸作用的细胞器为()A.纤毛与鞭毛B.表膜C.伸缩泡D.溶酶体8.下列原生动物中无性生殖为出芽生殖的是()A.大草履虫B.足管虫C.疟原虫D.绿眼虫9 .下列哪一项是原生动物的共有特征( )A.身体微小,全部营寄生生活的单细胞动物B.身体微小,全部水生的单细胞动物,营养方式多样化C.身体微小,分布广泛的单细胞动物,营养方式多样化D.身体微小,全部自由生活的单细胞动物,营养方式多样化填空题10.原生动物的身体是由_______构成的。
它们靠_____进行呼吸和排泄,以_____和______来完成消化功能,由于这些细胞器具有多细胞动物_____的类似作用,故称这些细胞器为____。
11.绿眼虫、变形虫和草履虫的运动细胞器分别为____、____和____。
12.草履虫的大核又称___核,它控制细胞的_____。
小核又称___核,它控制细胞的_______。
13.原生动物的营养方式多样,包括______、________和________营养。
大变形虫属于_______营养。
14 .间日疟原虫有两个宿主,在人体内进行_____和____生殖前期,在按蚊体内进行____和____生殖,一般认为,____是疟原虫的终末宿主。
人教版 八年级物理第1章第3节:运动的快慢课后习题(包含答案)

人教版 八年级物理第1章第3节:运动的快慢课后习题(含答案)1.某物体做匀速直线运动,由速度公式可知,物体的A A .速度大小恒定不变 B .速度与路程成正比C .速度与时间成反比D .以上说法都对2.下列图像中,能正确表示物体做匀速直线运动的是C3.P 、Q 是同一直线上相距12米的两点,甲从P 点、乙从Q 点同时沿直线相向而行,它们运动的s-t 图像如图4所示,分析图像可知 CA .甲的速度小于乙的速度B .经过3秒,甲、乙相距4米C .乙到达P 点时,甲离Q 点6米D .甲到达Q 点时,乙离P 点2米4.().在学校运动会上,小明参加的项目是百米赛跑。
起跑后,小明越跑越快,最终以12.5 s 的优异成绩获得冠军。
关于上述小明的百米赛跑过程,下列说法正确的是A .小明在前50 m-定用了6.25 sB .小明每秒钟通过的路程都是8m CC .小明的平均速度是8 m/sD .小明的平均速度是8 km/h5.运动会上,100m 决赛,中间过程张明落后于王亮,冲刺阶段张明加速追赶,结果他们同时到达终点。
关于全过程中的平均速度,下列说法中正确的是CA.张明的平均速度比王亮的平均速度大B.张明的平均速度比王亮的平均速度小C.二者的平均速度相等D.不是匀速直线运动,无法比较6.可以用图像来表示物体的运动状态,如图所示,则表示物体运动速度相同的是: Bts vA.甲乙B.甲丁C.乙丙D.丙丁7. 汽车在平直公路上匀速行驶,在下图所示的四个图象中,能正确表示汽车速度与时间关系的图象是A8.(多选题).甲乙两同学沿平直路面步行,他们运动的路程随时间变化的规律如图所示,下面说法中正确的是A B CA.甲同学比乙同学晚出发4sB.4s~8s内,甲乙同学都匀速直线运动C.0s~8s内,甲乙两同学通过的路程相等D.8s末甲乙两同学速度相等9.下列各图中,表示物体处于匀速运动状态的是CA. B. C. D.10.下列物理量的单位,属于速度单位的是AA. m/sB.mC.sD.kg11.下列四个成语中描述物体运动的快慢最明确的是BA.离弦之箭B.一日千里C.姗姗来迟D.风驰电掣12.甲、乙两人同时从同一起跑线出发,同向做匀速直线运动,某时刻他们的位置如图3所示,图4中能正确反映两人运动距离与时间关系的是 D13..为宣传“绿色出行,低碳生活”理念,三个好朋友在某景点进行了一场有趣的运动比赛。
机械制造技术基础(第2版)第一章课后习题标准答案

《机械制造技术基础》部分习题参考解答第一章绪论1-1 什么是生产过程、工艺过程和工艺规程?答:生产过程——从原材料(或半成品)进厂,一直到把成品制造出来的各有关劳动过程的总称为该工厂的过程。
工艺过程——在生产过程中,凡属直接改变生产对象的尺寸、形状、物理化学性能以及相对位置关系的过程。
工艺规程——记录在给定条件下最合理的工艺过程的相关内容、并用来指导生产的文件。
1-2 什么是工序、工位、工步和走刀?试举例说明。
答:工序——一个工人或一组工人,在一个工作地对同一工件或同时对几个工件所连续完成的那一部分工艺过程。
工位——在工件的一次安装中,工件相对于机床(或刀具)每占据一个确切位置中所完成的那一部分工艺过程。
工步——在加工表面、切削刀具和切削用量(仅指机床主轴转速和进给量)都不变的情况下所完成的那一部分工艺过程。
走刀——在一个工步中,如果要切掉的金属层很厚,可分几次切,每切削一次,就称为一次走刀。
比如车削一阶梯轴,在车床上完成的车外圆、端面等为一个工序,其中,n, f, a p不变的为一工步,切削小直径外圆表面因余量较大要分为几次走刀。
1-3 什么是安装?什么是装夹?它们有什么区别?答:安装——工件经一次装夹后所完成的那一部分工艺过程。
装夹——特指工件在机床夹具上的定位和夹紧的过程。
安装包括一次装夹和装夹之后所完成的切削加工的工艺过程;装夹仅指定位和夹紧。
1-4 单件生产、成批生产、大量生产各有哪些工艺特征?答:单件生产零件互换性较差、毛坯制造精度低、加工余量大;采用通用机床、通用夹具和刀具,找正装夹,对工人技术水平要求较高;生产效率低。
大量生产零件互换性好、毛坯精度高、加工余量小;采用高效专用机床、专用夹具和刀具,夹具定位装夹,操作工人技术水平要求不高,生产效率高。
成批生产的毛坯精度、互换性、所以夹具和刀具等介于上述两者之间,机床采用通用机床或者数控机床,生产效率介于两者之间。
1-5 试为某车床厂丝杠生产线确定生产类型,生产条件如下:加工零件:卧式车床丝杠(长为1617mm ,直径为40mm ,丝杠精度等级为8级,材料为Y40Mn );年产量:5000台车床;备品率:5%;废品率:0.5%。
第一章课后习题答案

第一章课后习题答案1、5个女生,7个男生进行排列,(a) 若女生在一起有多少种不同的排列?(b) 女生两两不相邻有多少种不同的排列?(c) 两男生A和B之间正好有3个女生的排列是多少?解:(a) 若女生在一起,可将5个女生看作一个整体参与排列,有8!种方式,然后5个女生再进行排列,有5!种方式,根据乘法法则,共有8!5!种方式。
(b) 若女生两两不相邻,可将7个男生进行排列,有7!种方式,考虑到两个男生之间的6个位置和两头的2个位置,每个位置安排一个女生均符合题意,故从中选出5个位置,然后5个女生再进行排列,按顺序安排到这5个位置,有C(8, 5)5!种方式,根据乘法法则,共有7!C(8, 5)5!=7!P(8, 5)种方式。
(c) 若两男生A和B之间正好有3个女生,可以按照顺序操作如下:首先将女生分为两组,一组3人,一组2人,有C(5, 3)种方式;将男生A和B看作一个整体,加上其他5个男生,2人一组的女生进行排列,有8!种方式;将3人一组的女生安排到男生A和B之间进行排列,有3!种方式;男生A和B进行排列,有2!种方式。
根据乘法法则,所求的排列方式为8!C(5, 3)3!2!=8!P(5, 3)2!2、求3000到8000之间的奇整数的数目,而且没有相同的数字。
解:设介于3000到8000之间的奇整数表示为abcd,则a∈{3, 4, 5, 6, 7}, d∈{1, 3, 5, 7, 9},对a进行分类如下:(1) 若a∈{3, 5, 7},则d有4种选取方式,bc有P(8, 2)种方式,根据乘法法则,此类数字有3⨯4⨯P(8, 2)=672个(2) 若a∈{4, 6},则d有5种选取方式,bc仍有P(8, 2)种方式,根据乘法法则,此类数字有2⨯5⨯P(8, 2)=560个根据加法法则,3000到8000之间数字不同的奇整数的数目为672+560=1232个3、证明nC(n-1, r)=(r+1)C(n, r+1),并给出组合解释。
统计学课后第一章习题答案

第1章导论1、某森林公园的一项研究试图确定哪些因素有利于成年松树长到60英尺以上的高度.经估计,森林公园生长着25000颗成年松树,该研究需要从中随机抽取250颗成年松树并丈量它们的高度后进行分析。
该研究的总体是()A、250颗成年松树 B、公园中25000颗成年松树C、所有高于60英尺的成年松树D、森林公园中所有年龄的松树2、某森林公园的一项研究试图确定成年松树的高度。
该研究需要从中随机抽取250颗成年松树并丈量它们的高度后进行分析。
该研究所感兴趣的变量是()A、森林公园中松树的年龄B、森林公园中松树的数量C、森林公园中松树的高度D、森林公园中数目的种类3、推断统计的主要功能是()A、应用总体的信息描述样本B、描述样本中包含的信息C、描述总体中包含的信息D、应用样本信息描述总体4、对高中生的一项抽样调查表明,85%的高中生愿意接受大学教育.这一叙述是()的结果A、定性变量B、试验 C、描述统计 D、推断统计5、一名统计学专业的学生为了完成其统计学作业,在图书馆找到一本参考书中包含美国50个州的家庭收入中位数。
在该生的作业中,他应该将此数据报告来源于()A、试验B、实际观察 C、随机抽样D、已发表的资料6、某大公司的人力资源部主任需要研究公司雇员的饮食习惯。
他注意到,雇员的午饭要么从家里带来,要么在公司餐厅就餐,要么在外面的餐馆就餐。
该研究的目的是为了改善公司餐厅的现状。
这种数据的收集方式可以认为是()A、观察研究B、设计的试验C、随机抽样D、全面调查7、下列不属于描述统计问题的是()A、根据样本信息对总体进行的推断B、感兴趣的总体或样本C、图、表或其他数据汇总工具D、了解数据分布特征8、某大学的一位研究人员希望估计该大学一年级新生在教科书上的花费,为此,他观察了200名新生在教科书上的花费,发现他们每个学期平均在教科书上的花费是250元。
该研究人员感兴趣的总体是()A、该大学的所有学生B、所有的大学生C、该大学所有的一年级新生D、样本中的200名新生9、某大学的一位研究人员希望估计该大学一年级新生在教科书上的花费,为此,他观察了200名新生在教科书上的花费,发现他们每个学期平均在教科书上的花费是250元。
结构化学第一章课后习题答案

6.626 ×10−34 = = 8.95 × 10−10 m p 7.40 × 10−25
13. 在电视机显像管中运动的电子,假定加速电压为 1000 V,电子运动速度的不确定量Δυ为υ的 10%,
判断电子的波动性对荧光屏上成像有无影响? 解:根据不确定关系: Δx Δpx ≥ h Δx • m • Δυ x ≥ h ∴Δx = h h = m Δυ x m υ x 10%
l
px = ∫
0
2 nπ x ˆx sin p l l
2 nπ x dx sin l l 2 nπ x sin dx = 0 l l
=∫
0
l
2 nπ x ih d sin (− ) 2π dx l l h2 d 2 4π 2 dx 2
ˆ x2 = − pˆ x源自2ψ n ( x) = − ph2 d 2 h2 d 2 = − ψ ( ) x n 4π 2 dx 2 4π 2 dx 2
n πy n πx nπz 8 sin x sin y sin z 3 a a a a
8 2π x πy πz sin sin sin 3 a a a a πy 2 πz 2 8 2π x 2 * ∫ψ 211 ( x, y, z )ψ 211 ( x, y, z)dτ = a3 ∫ (sin a ) ∫ (sin a ) ∫ (sin a ) 2π z ⎤ 8 ⎡ Δx a 4π ( x + Δx) a 4π x ⎤ ⎡ Δy a 2π ( y + Δy ) a 2π y ⎤ ⎡ Δz a 2π ( z + Δz ) a = 3⎢ − + − + − + sin sin sin sin sin sin ⎢ ⎥ ⎢ ⎥ a ⎥ 8π 4π 4π a ⎣ 2 8π a a ⎦ ⎣ 2 4π a a ⎦ ⎣ 2 4π a ⎦ 8 πx πy 2π z ψ 112 ( x, y, z ) = 3 sin sin sin a a a a πx 2 πy 2 8 2π z 2 * ∫ψ 112 ( x, y, z)ψ 112 ( x, y, z )dτ = a3 ∫ (sin a ) ∫ (sin a ) ∫ (sin a ) 4π z ⎤ 8 ⎡ Δx a 2π ( x + Δx) a 2π x ⎤ ⎡ Δy a 2π ( y + Δy ) a 2π y ⎤ ⎡ Δz a 4π ( z + Δz ) a = 3⎢ − + − + − + sin sin sin sin sin sin ⎢ ⎢ ⎥ a ⎥ π π π π 4π 2 4 4 2 8 8 a ⎣ 2 4π a a ⎥ a a a ⎦ ⎦⎣ ⎦⎣
化工原理第四版第一章课后习题答案

第一章 流体的压力【1-1】容器A 中的气体表压为60kPa ,容器B 中的气体真空度为.⨯41210Pa 。
试分别求出A 、B 二容器中气体的绝对压力为若干帕,该处环境的大气压力等于标准大气压力。
解 标准大气压力为101.325kPa容器A 的绝对压力 ..p kPa ==A 101325+60161325 容器B 的绝对压力 ..B p kPa =-=1013251289325【1-2】某设备进、出口的表压分别为-12kPa 和157kPa ,当地大气压力为101.3kPa 。
试求此设备的进、出口的绝对压力及进、出的压力差各为多少帕。
解 进口绝对压力 ..进101312893 =-=p kPa出口绝对压力 ..出101 31572583 =+=p kPa 进、出口的压力差..p kPa p kPa ∆=--=+=∆=-=157(12)15712169 或 258 389 3169流体的密度【1-3】正庚烷和正辛烷混合液中,正庚烷的摩尔分数为0.4,试求该混合液在20℃下的密度。
解 正庚烷的摩尔质量为/kg kmol 100,正辛烷的摩尔质量为/kg kmol 114。
将摩尔分数换算为质量分数 正庚烷的质量分数 (104100)03690410006114ω⨯==⨯+⨯正辛烷的质量分数 ..2103690631ω=-=从附录四查得20℃下正庚烷的密度/kg m ρ=31684,正辛烷的密度为/kg m ρ=32703 混合液的密度 /..3169603690631684703ρ==+m kg m【1-4】温度20℃,苯与甲苯按4:6的体积比进行混合,求其混合液的密度。
解 20℃时,苯的密度为/3879kg m ,甲苯的密度为/3867kg m 。
混合液密度 ../3879048670.68718 ρ=⨯+⨯=m kg m 【1-5】有一气柜,满装时可装36000m 混合气体,已知混合气体各组分的体积分数为2224H N COCO CH .04 0.2 0.32 0.07 0.01操作压力的表压为5.5kPa ,温度为40℃。
统计学第一章课后习题及答案

第一章练习题一、单项选择题1.统计的含义有三种,其中的基础是()A.统计学B .统计方法 C.统计工作D .统计资料2. 对30名职工的工资收入进行调查,则总体单位是()A. 30名职工 C. 每一名职工 3. 下列属于品质标志的是()A. 某人的年龄 C. 某人的体重 4. 商业企业的职工人数,商品销售额是( A. 连续变量 C .前者是连续变量,后者是离散变量B. 30名职工的工资总额D. 每一名职工的工资B. 某人的性别D. 某人的收入)B •离散变量D .前者是离散变量,后者是连续变量5. 了解某地区工业企业职工的情况,下列哪个是统计指标( A .该地区每名职工的工资额C. 该地区职工的工资总额二、多项选择题 1. 社会经济统计的特点,可概括为( A .数量性 C.总体性 E. 社会性2. 统计学的研究方法是( A .大量观察法 C .统计模型法 E. 直接观察法3. 下列标志哪些属于品质标志( A.学生年龄B 教师职称4. 下列哪些属于离散型变量A 年龄B 机器台数C 人口数D 学生成绩5. 总体,总体单位,标志,指标这几个概念间的相互关系表现为(A. 没有总体单位就没有总体,总体单位也离不开总体而独立存在B. 总体单位是标志的承担者C. 统计指标的数值来源于标志D. 指标是说明统计总体特征的,标志是说明总体单位特征的E. 指标和标志都能用数值表现6. 指标和标志之间存在着变换关系,是指()A. 在同一研究目的下,指标和标志可以对调)B .该地区职工的文化程度D .该地区职工从事的工种 )B .同质性D .具体性 B .归纳推断法D .综合分析法)C 企业规模D 企业产值B.在研究目的发生变化时,指标有可能成为标志C.在研究目的发生变化时,标志有可能成为指标D.在不同研究目的下,指标和标志可以相互转化7.在说明和表现问题方面,正确的定义是()A.标志是说明总体单位特征的B.标志是说明统计总体特征的C.变异是可变的数量标志的差异D.变量是可变的数量标志E.标志值是变量的数量表现三、填空题1._____________________ 统计工作过程包括、、、四个阶段。
应用光学习题(第一章部分课后习题)
编号
出处
1_008
P125_13
答:(接上一页)
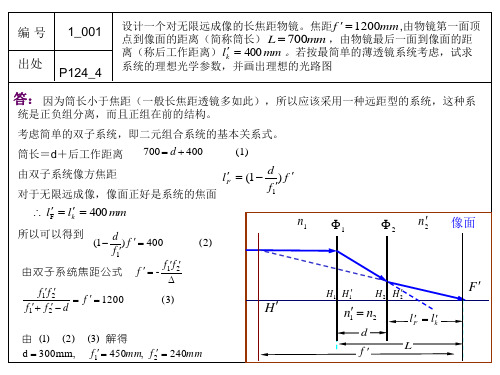
h1 d1 h1 d1 h2 h1 d1tgu1 n 1 h1 1 n 1 1 1
h1 d1 d2 d 2 h2 1 h3 h1 d1 d h h h 1 2 2 1 1 1 2 n 1 2 n 1 1 n2 n2 h1 2 1 n1 d1 d2 d 2 2 d1 h1 1 1 1 h1 1 1 n n n h n 1 2 2 1 1 d1 d2 d2 d1 d 2 h1 1 1 2 1 2 n 1 n n2 n1n1 1 2
答:由组合系统光焦度公式 1 h h h 1 1 2 2 3 3 h1 如果考虑平行光入射到 这个薄透镜系统, 即 tgu1 0,薄透镜系统处于空气中
n1 1 n n n 2 1 令 1 n3 n2 n 2 1 n3 光线在第二个子系统主 面上的高度 光线在第三个子系统主 面上的高度 而 由角度公式得, tgu1
f1 f 2
r1 n1 1.5 20 60m m n1 1.5 1 n1
n2 r2 1.5 ( 15 ) 132.35m m n2 n2 1.33 1.5
r2 n2 1.33 ( 15 ) 117.35m m n2 n2 1.33 1.5
答: 透镜的结构参数为: r1 20mm, r2 15mm
d 15mm
该透镜为双凸透镜
n1 1 n 2 n 1 .5 n1 n 1.33 2
(完整版)自动控制原理_第一章课后习题解答

第一章1.1 图1.18是液位自动控制系统原理示意图。
在任意情况下,希望液面高度c维持不变,试说明系统工作原理并画出系统方块图。
c+-SM___ 1Q浮浮浮浮浮浮2Q浮浮浮浮浮浮浮浮浮浮浮浮fi-+解:系统的控制任务是保持液面高度不变。
水箱是被控对象,水箱液位是被控变量。
电位器用来设置期望液位高度*c(通常点位器的上下位移来实现) 。
当电位器电刷位于中点位置时,电动机不动,控制阀门有一定的开度,使水箱的流入水量与流出水量相等,从而使液面保持在希望高度*c上。
一旦流出水量发生变化(相当于扰动),例如当流出水量减小时,液面升高,浮子位置也相应升高,通过杠杆作用使电位器电刷从中点位置下移,从而给电动机提供一定的控制电压,驱动电动机通过减速器减小阀门开度,使进入水箱的液体流量减少。
这时,水箱液位下降.浮子位置相应下降,直到电位器电刷回到中点位置为止,系统重新处于平衡状态,液位恢复给定高度。
反之,当流出水量在平衡状态基础上增大时,水箱液位下降,系统会自动增大阀门开度,加大流入水量,使液位升到给定高度*c。
系统方框图如图解1. 4.1所示。
1.2恒温箱的温度自动控制系统如图1.19所示。
(1) 画出系统的方框图;(2) 简述保持恒温箱温度恒定的工作原理;(3) 指出该控制系统的被控对象和被控变量分别是什么。
M放大器电机减速器调压器 220~热电偶电阻丝- +- +图1.19 恒温箱的温度自动控制系统解:恒温箱采用电加热的方式运行,电阻丝产生的热量与调压器电压平方成正比,电压增高,炉温就上升。
调压器电压由其滑动触点位置所控制,滑臂则由伺服电动机驱动.炉子的实际温度用热电偶测量,输出电压作为反馈电压与给定电压进行比较,得出的偏差电压经放大器放大后,驱动电动机经减速器调节调压器的电压。
在正常情况下,炉温等于期望温度T ,热电偶的输出电压等于给定电压。
此时偏差为零,电动机不动,调压器的滑动触点停留在某个合适的位置上。
贾月梅主编《流体力学》第一章课后习题答案

《流体力学》习题与答案周立强中南大学机电工程学院液压研究所第1章流体力学的基本概念1-1.是非题(正确的打“√”,错误的打“”)1. 理想流体就是不考虑粘滞性的、实际不存在的,理想化的流体。
(√)2. 在连续介质假设的条件下,液体中各种物理量的变化是连续的。
(√ )3. 粘滞性是引起流体运动能量损失的根本原因。
(√ )4. 牛顿内摩擦定律适用于所有的流体。
()5. 牛顿内摩擦定律只适用于管道中的层流。
()6. 有旋运动就是流体作圆周运动。
()7. 温度升高时,空气的粘度减小。
()8. 流体力学中用欧拉法研究每个质点的轨迹。
()9. 平衡流体不能抵抗剪切力。
(√ )10. 静止流体不显示粘性。
(√ )11. 速度梯度实质上是流体的粘性。
(√ )12. 流体运动的速度梯度是剪切变形角速度。
(√ )13. 恒定流一定是均匀流,层流也一定是均匀流。
()14. 牛顿内摩擦定律中,粘度系数m和v均与压力和温度有关。
()15. 迹线与流线分别是Lagrange和Euler几何描述;它们是对同一事物的不同说法;因此迹线就是流线,流线就是迹线。
()16. 如果流体的线变形速度θ=θx+θy+θz=0,则流体为不可压缩流体。
(√ )17. 如果流体的角变形速度ω=ωx+ωy+ωz=0,则流体为无旋流动。
(√ )18. 流体的表面力不仅与作用的表面积的外力有关,而且还与作用面积的大小、体积和密度有关。
()19. 对于平衡流体,其表面力就是压强。
(√ )20. 边界层就是流体的自由表明和容器壁的接触面。
()1-2已知作用在单位质量物体上的体积力分布为:,物体的密度,坐标量度单位为m;其中,,,;,,。
试求:如图1-2所示区域的体积力、、各为多少?题1-2图解:答:各体积力为:、、1-3作用在物体上的单位质量力分布为:,物体的密度为,如图1-3所示,其中,,,;。
试求:作用在图示区域内的质量总力?解:题图1-3答:各质量力为:、、,总质量力。
高中数学必修1课后习题答案完整版

高中数学必修1课后习题答案 第一章 集合与函数概念1.1集合1.1.1集合的含义与表示练习(第5页)1.用符号“∈”或“∉”填空:(1)设A 为所有亚洲国家组成的集合,则:中国_______A ,美国_______A ,印度_______A ,英国_______A ;(2)若2{|}A x x x ==,则1-_______A ; (3)若2{|60}B x x x =+-=,则3_______B ;(4)若{|110}C x N x =∈≤≤,则8_______C ,9.1_______C . 1.(1)中国∈A ,美国∉A ,印度∈A ,英国∉A ;中国和印度是属于亚洲的国家,美国在北美洲,英国在欧洲.(2)1-∉A 2{|}{0,1}A x x x ===.(3)3∉B 2{|60}{3,2}B x x x =+-==-. (4)8∈C ,9.1∉C 9.1N ∉. 2.试选择适当的方法表示下列集合:(1)由方程290x -=的所有实数根组成的集合; (2)由小于8的所有素数组成的集合;(3)一次函数3y x =+与26y x =-+的图象的交点组成的集合; (4)不等式453x -<的解集.2.解:(1)因为方程290x -=的实数根为123,3x x =-=,所以由方程290x -=的所有实数根组成的集合为{3,3}-; (2)因为小于8的素数为2,3,5,7,所以由小于8的所有素数组成的集合为{2,3,5,7};(3)由326y x y x =+⎧⎨=-+⎩,得14x y =⎧⎨=⎩,即一次函数3y x =+与26y x =-+的图象的交点为(1,4),所以一次函数3y x =+与26y x =-+的图象的交点组成的集合为{(1,4)};(4)由453x -<,得2x <,所以不等式453x -<的解集为{|2}x x <.1.1.2集合间的基本关系练习(第7页)1.写出集合{,,}a b c 的所有子集.1.解:按子集元素个数来分类,不取任何元素,得∅;取一个元素,得{},{},{}a b c ; 取两个元素,得{,},{,},{,}a b a c b c ; 取三个元素,得{,,}a b c ,即集合{,,}a b c 的所有子集为,{},{},{},{,},{,},{,},{,,}a b c a b a c b c a b c ∅.2.用适当的符号填空:(1)a ______{,,}a b c ; (2)0______2{|0}x x =; (3)∅______2{|10}x R x ∈+=; (4){0,1}______N ;(5){0}______2{|}x x x =; (6){2,1}______2{|320}x x x -+=.2.(1){,,}a a b c ∈ a 是集合{,,}a b c 中的一个元素;(2)20{|0}x x ∈= 2{|0}{0}x x ==;(3)2{|10}x R x ∅=∈+= 方程210x +=无实数根,2{|10}x R x ∈+==∅;(4){0,1}N (或{0,1}N ⊆) {0,1}是自然数集合N 的子集,也是真子集;(5){0}2{|}x x x = (或2{0}{|}x x x ⊆=) 2{|}{0,1}x x x ==;(6)2{2,1}{|320}x x x =-+= 方程2320x x -+=两根为121,2x x ==.3.判断下列两个集合之间的关系:(1){1,2,4}A =,{|8}B x x =是的约数;(2){|3,}A x x k k N ==∈,{|6,}B x x z z N ==∈;(3){|410}A x x x N +=∈是与的公倍数,,{|20,}B x x m m N +==∈.3.解:(1)因为{|8}{1,2,4,8}B x x ==是的约数,所以AB ;(2)当2k z =时,36k z =;当21k z =+时,363k z =+,即B 是A 的真子集,BA ;(3)因为4与10的最小公倍数是20,所以A B =.1.1.3集合的基本运算练习(第11页)1.设{3,5,6,8},{4,5,7,8}A B ==,求,A B A B .1.解:{3,5,6,8}{4,5,7,8}{5,8}A B ==, {3,5,6,8}{4,5,7,8}{3,4,5,6,7,8}AB ==.2.设22{|450},{|1}A x x x B x x =--===,求,AB A B .2.解:方程2450x x --=的两根为121,5x x =-=, 方程210x -=的两根为121,1x x =-=,得{1,5},{1,1}A B =-=-, 即{1},{1,1,5}AB A B =-=-.3.已知{|}A x x =是等腰三角形,{|}B x x =是直角三角形,求,A B A B .3.解:{|}A B x x =是等腰直角三角形,{|}AB x x =是等腰三角形或直角三角形.4.已知全集{1,2,3,4,5,6,7}U =,{2,4,5},{1,3,5,7}A B ==, 求(),()()U U U AB A B 痧?.4.解:显然{2,4,6}U B =ð,{1,3,6,7}U A =ð, 则(){2,4}U AB =ð,()(){6}U U A B =痧. 1.1集合习题1.1 (第11页) A 组1.用符号“∈”或“∉”填空:(1)237_______Q ; (2)23______N ; (3)π_______Q ;(4_______R ; (5Z ; (6)2_______N .1.(1)237Q ∈ 237是有理数; (2)23N ∈ 239=是个自然数;(3)Q π∉ π是个无理数,不是有理数; (4R(5Z3=是个整数; (6)2N ∈ 2)5=是个自然数.2.已知{|31,}A x x k k Z ==-∈,用 “∈”或“∉” 符号填空: (1)5_______A ; (2)7_______A ; (3)10-_______A . 2.(1)5A ∈; (2)7A ∉; (3)10A -∈. 当2k =时,315k -=;当3k =-时,3110k -=-; 3.用列举法表示下列给定的集合: (1)大于1且小于6的整数; (2){|(1)(2)0}A x x x =-+=; (3){|3213}B x Z x =∈-<-≤.3.解:(1)大于1且小于6的整数为2,3,4,5,即{2,3,4,5}为所求;(2)方程(1)(2)0x x -+=的两个实根为122,1x x =-=,即{2,1}-为所求; (3)由不等式3213x -<-≤,得12x -<≤,且x Z ∈,即{0,1,2}为所求. 4.试选择适当的方法表示下列集合:(1)二次函数24y x =-的函数值组成的集合; (2)反比例函数2y x=的自变量的值组成的集合;(3)不等式342x x ≥-的解集.4.解:(1)显然有20x ≥,得244x -≥-,即4y ≥-,得二次函数24y x =-的函数值组成的集合为{|4}y y ≥-;(2)显然有0x ≠,得反比例函数2y x =的自变量的值组成的集合为{|0}x x ≠; (3)由不等式342x x ≥-,得45x ≥,即不等式342x x ≥-的解集为4{|}5x x ≥.5.选用适当的符号填空:(1)已知集合{|233},{|2}A x x x B x x =-<=≥,则有:4-_______B ; 3-_______A ; {2}_______B ; B _______A ; (2)已知集合2{|10}A x x =-=,则有:1_______A ; {1}-_______A ; ∅_______A ; {1,1}-_______A ; (3){|}x x 是菱形_______{|}x x 是平行四边形; {|}x x 是等腰三角形_______{|}x x 是等边三角形.5.(1)4B -∉; 3A -∉; {2}B ; BA ;2333x x x -<⇒>-,即{|3},{|2}A x x B x x =>-=≥;(2)1A ∈; {1}-A ; ∅A ; {1,1}-=A ; 2{|10}{1,1}A x x =-==-;(3){|}x x 是菱形{|}x x 是平行四边形;菱形一定是平行四边形,是特殊的平行四边形,但是平行四边形不一定是菱形;{|}x x 是等边三角形{|}x x 是等腰三角形.等边三角形一定是等腰三角形,但是等腰三角形不一定是等边三角形.6.设集合{|24},{|3782}A x x B x x x =≤<=-≥-,求,AB A B .6.解:3782x x -≥-,即3x ≥,得{|24},{|3}A x x B x x =≤<=≥, 则{|2}AB x x =≥,{|34}A B x x =≤<.7.设集合{|9}A x x =是小于的正整数,{1,2,3},{3,4,5,6}B C ==,求A B ,AC ,()A B C ,()A B C .7.解:{|9}{1,2,3,4,5,6,7,8}A x x ==是小于的正整数, 则{1,2,3}AB =,{3,4,5,6}AC =, 而{1,2,3,4,5,6}B C =,{3}B C =, 则(){1,2,3,4,5,6}AB C =,(){1,2,3,4,5,6,7,8}A B C =.8.学校里开运动会,设{|}A x x =是参加一百米跑的同学,{|}B x x =是参加二百米跑的同学,{|}C x x =是参加四百米跑的同学,学校规定,每个参加上述的同学最多只能参加两项,请你用集合的语言说明这项规定, 并解释以下集合运算的含义:(1)AB ;(2)A C . 8.解:用集合的语言说明这项规定:每个参加上述的同学最多只能参加两项, 即为()A B C =∅.(1){|}A B x x =是参加一百米跑或参加二百米跑的同学; (2){|}AC x x =是既参加一百米跑又参加四百米跑的同学.9.设{|}S x x =是平行四边形或梯形,{|}A x x =是平行四边形,{|}B x x =是菱形,{|}C x x =是矩形,求BC ,A B ð,S A ð.9.解:同时满足菱形和矩形特征的是正方形,即{|}BC x x =是正方形,平行四边形按照邻边是否相等可以分为两类,而邻边相等的平行四边形就是菱形, 即{|}A B x x =是邻边不相等的平行四边形ð, {|}S A x x =是梯形ð.10.已知集合{|37},{|210}A x x B x x =≤<=<<,求()R AB ð,()R A B ð,()R A B ð,()R A B ð.10.解:{|210}A B x x =<<,{|37}A B x x =≤<,{|3,7}R A x x x =<≥或ð,{|2,10}R B x x x =≤≥或ð, 得(){|2,10}R A B x x x =≤≥或ð, (){|3,7}R A B x x x =<≥或ð, (){|23,710}R A B x x x =<<≤<或ð,(){|2,3710}R AB x x x x =≤≤<≥或或ð.B 组1.已知集合{1,2}A =,集合B 满足{1,2}A B =,则集合B 有 个.1.4 集合B 满足AB A =,则B A ⊆,即集合B 是集合A 的子集,得4个子集.2.在平面直角坐标系中,集合{(,)|}C x y y x ==表示直线y x =,从这个角度看,集合21(,)|45x y D x y x y ⎧-=⎫⎧=⎨⎨⎬+=⎩⎩⎭表示什么?集合,C D 之间有什么关系?2.解:集合21(,)|45x y D x y x y ⎧-=⎫⎧=⎨⎨⎬+=⎩⎩⎭表示两条直线21,45x y x y -=+=的交点的集合,即21(,)|{(1,1)}45x y D x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭,点(1,1)D 显然在直线y x =上,得D C .3.设集合{|(3)()0,}A x x x a a R =--=∈,{|(4)(1)0}B x x x =--=,求,A B A B .3.解:显然有集合{|(4)(1)0}{1,4}B x x x =--==, 当3a =时,集合{3}A =,则{1,3,4},A B A B ==∅; 当1a =时,集合{1,3}A =,则{1,3,4},{1}A B A B ==; 当4a =时,集合{3,4}A =,则{1,3,4},{4}AB A B ==;当1a ≠,且3a ≠,且4a ≠时,集合{3,}A a =,则{1,3,4,},AB a A B ==∅.4.已知全集{|010}U AB x N x ==∈≤≤,(){1,3,5,7}U A B =ð,试求集合B .4.解:显然{0,1,2,3,4,5,6,7,8,9,10}U =,由U AB =,得U B A ⊆ð,即()U UAB B =痧,而(){1,3,5,7}U A B =ð,得{1,3,5,7}U B =ð,而()U UB B =痧,即{0,2,4,6,8.9,10}B =.第一章 集合与函数概念1.2函数及其表示1.2.1函数的概念练习(第19页)1.求下列函数的定义域:(1)1()47f x x =+; (2)()1f x =.1.解:(1)要使原式有意义,则470x +≠,即74x ≠-,得该函数的定义域为7{|}4x x ≠-;(2)要使原式有意义,则1030x x -≥⎧⎨+≥⎩,即31x -≤≤,得该函数的定义域为{|31}x x -≤≤. 2.已知函数2()32f x x x =+,(1)求(2),(2),(2)(2)f f f f -+-的值; (2)求(),(),()()f a f a f a f a -+-的值.2.解:(1)由2()32f x x x =+,得2(2)322218f =⨯+⨯=,同理得2(2)3(2)2(2)8f -=⨯-+⨯-=,则(2)(2)18826f f +-=+=,即(2)18,(2)8,(2)(2)26f f f f =-=+-=;(2)由2()32f x x x =+,得22()3232f a a a a a =⨯+⨯=+,同理得22()3()2()32f a a a a a -=⨯-+⨯-=-, 则222()()(32)(32)6f a f a a a a a a +-=++-=,即222()32,()32,()()6f a a a f a a a f a f a a =+-=-+-=.3.判断下列各组中的函数是否相等,并说明理由:(1)表示炮弹飞行高度h 与时间t 关系的函数21305h t t =-和二次函数21305y x x =-; (2)()1f x =和0()g x x =.3.解:(1)不相等,因为定义域不同,时间0t >; (2)不相等,因为定义域不同,0()(0)g x x x =≠.1.2.2函数的表示法练习(第23页)1.如图,把截面半径为25cm 的圆形木头锯成矩形木料,如果矩形的一边长为xcm , 面积为2ycm ,把y 表示为x 的函数. 1,y ==,且050x <<,即(050)y x =<<.2.下图中哪几个图象与下述三件事分别吻合得最好?请你为剩下的那个图象写出一件事.(1)我离开家不久,发现自己把作业本忘在家里了,于是返回家里找到了作业本再上学;(2)我骑着车一路匀速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间; (3)我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速.2.解:图象(A )对应事件(2),在途中遇到一次交通堵塞表示离开家的距离不发生变化;(A )(B )(C )(D )图象(B )对应事件(3),刚刚开始缓缓行进,后来为了赶时间开始加速; 图象(D )对应事件(1),返回家里的时刻,离开家的距离又为零;图象(C )我出发后,以为要迟到,赶时间开始加速,后来心情轻松,缓缓行进. 3.画出函数|2|y x =-的图象.3.解:2,2|2|2,2x x y x x x -≥⎧=-=⎨-+<⎩,图象如下所示.{|},{0,1}A x x B ==是锐角,从A 到B 的映射是“求正弦”,4.设与A 中元素60相对应的B 中的元素是什么?与B 中的元素2相对应的A 中元素是什么?4.解:因为3sin 60=,所以与A 中元素60相对应的B ;因为2sin 452=,所以与B 中的元素2相对应的A 中元素是45. 1.2函数及其表示 习题1.2(第23页)1.求下列函数的定义域:(1)3()4xf x x =-; (2)()f x =(3)26()32f x x x =-+; (4)()1f x x =-.1.解:(1)要使原式有意义,则40x -≠,即4x ≠, 得该函数的定义域为{|4}x x ≠;(2)x R ∈,()f x =即该函数的定义域为R ;(3)要使原式有意义,则2320x x -+≠,即1x ≠且2x ≠,得该函数的定义域为{|12}x x x ≠≠且; (4)要使原式有意义,则4010x x -≥⎧⎨-≠⎩,即4x ≤且1x ≠, 得该函数的定义域为{|41}x x x ≤≠且.2.下列哪一组中的函数()f x 与()g x 相等?(1)2()1,()1x f x x g x x=-=-; (2)24(),()f x x g x ==;(3)2(),()f x x g x ==2.解:(1)()1f x x =-的定义域为R ,而2()1x g x x=-的定义域为{|0}x x ≠, 即两函数的定义域不同,得函数()f x 与()g x 不相等;(2)2()f x x =的定义域为R ,而4()g x =的定义域为{|0}x x ≥,即两函数的定义域不同,得函数()f x 与()g x 不相等;(32x =,即这两函数的定义域相同,切对应法则相同,得函数()f x 与()g x 相等.3.画出下列函数的图象,并说出函数的定义域和值域.(1)3y x =; (2)8y x=; (3)45y x =-+; (4)267y x x =-+. 3.解:(1)定义域是(,)-∞+∞,值域是(,)-∞+∞;(2)定义域是(,0)(0,)-∞+∞,值域是(,0)(0,)-∞+∞;(3)定义域是(,)-∞+∞,值域是(,)-∞+∞;(4)定义域是(,)-∞+∞,值域是[2,)-+∞.4.已知函数2()352f x x x =-+,求(f ,()f a -,(3)f a +,()(3)f a f +.4.解:因为2()352f x x x =-+,所以2(3(5(28f =⨯-⨯+=+即(8f =+同理,22()3()5()2352f a a a a a -=⨯--⨯-+=++,即2()352f a a a -=++;22(3)3(3)5(3)231314f a a a a a +=⨯+-⨯++=++,即2(3)31314f a a a +=++;22()(3)352(3)3516f a f a a f a a +=-++=-+,即2()(3)3516f a f a a +=-+.5.已知函数2()6x f x x +=-, (1)点(3,14)在()f x 的图象上吗?(2)当4x =时,求()f x 的值;(3)当()2f x =时,求x 的值.5.解:(1)当3x =时,325(3)14363f +==-≠-, 即点(3,14)不在()f x 的图象上;(2)当4x =时,42(4)346f +==--, 即当4x =时,求()f x 的值为3-;(3)2()26x f x x +==-,得22(6)x x +=-, 即14x =.6.若2()f x x bx c =++,且(1)0,(3)0f f ==,求(1)f -的值.6.解:由(1)0,(3)0f f ==,得1,3是方程20x bx c ++=的两个实数根,即13,13b c +=-⨯=,得4,3b c =-=,即2()43f x x x =-+,得2(1)(1)4(1)38f -=--⨯-+=, 即(1)f -的值为8.7.画出下列函数的图象:(1)0,0()1,0x F x x ≤⎧=⎨>⎩; (2)()31,{1,2,3}G n n n =+∈.7.图象如下:8.如图,矩形的面积为10,如果矩形的长为x ,宽为y ,对角线为d ,周长为l ,那么你能获得关于这些量的哪些函数?8.解:由矩形的面积为10,即10xy =,得10(0)y x x=>,10(0)x y y =>,由对角线为d ,即d =,得(0)d x =>, 由周长为l ,即22l x y =+,得202(0)l x x x =+>, 另外2()l x y =+,而22210,xy d x y ==+,得(0)l d ===>,即(0)l d =>.9.一个圆柱形容器的底部直径是dcm ,高是hcm ,现在以3/vcm s 的速度向容器内注入某种溶液.求溶液内溶液的高度xcm 关于注入溶液的时间ts 的函数解析式,并写出函数的定义域和值域.9.解:依题意,有2()2dx vt π=,即24v x t d π=,显然0x h ≤≤,即240v t h dπ≤≤,得204h d t v π≤≤, 得函数的定义域为2[0,]4h d vπ和值域为[0,]h . 10.设集合{,,},{0,1}A a b c B ==,试问:从A 到B 的映射共有几个?并将它们分别表示出来.10.解:从A 到B 的映射共有8个.分别是()0()0()0f a f b f c =⎧⎪=⎨⎪=⎩,()0()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()0()1()0f a f b f c =⎧⎪=⎨⎪=⎩,()0()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()0f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()1f a f b f c =⎧⎪=⎨⎪=⎩,()1()1()0f a f b f c =⎧⎪=⎨⎪=⎩,()1()0()1f a f b f c =⎧⎪=⎨⎪=⎩.B组1.函数()r f p =的图象如图所示.(1)函数()r f p =的定义域是什么?(2)函数()r f p =的值域是什么?(3)r 取何值时,只有唯一的p 值与之对应?1.解:(1)函数()r f p =的定义域是[5,0][2,6)-;(2)函数()r f p =的值域是[0,)+∞;(3)当5r >,或02r ≤<时,只有唯一的p 值与之对应.2.画出定义域为{|38,5}x x x -≤≤≠且,值域为{|12,0}y y y -≤≤≠的一个函数的图象.(1)如果平面直角坐标系中点(,)P x y 的坐标满足38x -≤≤,12y -≤≤,那么其中哪些点不能在图象上?(2)将你的图象和其他同学的相比较,有什么差别吗?2.解:图象如下,(1)点(,0)x 和点(5,)y 不能在图象上;(2)省略.3.函数()[]f x x =的函数值表示不超过x 的最大整数,例如,[ 3.5]4-=-,[2.1]2=.当( 2.5,3]x ∈-时,写出函数()f x 的解析式,并作出函数的图象.3.解:3, 2.522,211,10()[]0,011,122,233,3x x x f x x x x x x --<<-⎧⎪--≤<-⎪⎪--≤<⎪==≤<⎨⎪≤<⎪≤<⎪⎪=⎩图象如下4.如图所示,一座小岛距离海岸线上最近的点P的距离是2km,从点P沿海岸正东12km处有一个城镇.(1)假设一个人驾驶的小船的平均速度为3/km h ,步行的速度是5/km h ,t (单位:h )表示他从小岛到城镇的时间,x (单位:km )表示此人将船停在海岸处距P 点的距离.请将t 表示为x 的函数.(2)如果将船停在距点P 4km 处,那么从小岛到城镇要多长时间(精确到1h )?4.解:(112x -,得1235x t -=+,(012)x ≤≤,即1235x t -=+,(012)x ≤≤.(2)当4x =时,12483()355t h -=+=≈.第一章 集合与函数概念1.3函数的基本性质1.3.1单调性与最大(小)值练习(第32页)1.请根据下图描述某装配线的生产效率与生产线上工人数量间的关系.1.答:在一定的范围内,生产效率随着工人数量的增加而提高,当工人数量达到某个数量时,生产效率达到最大值,而超过这个数量时,生产效率随着工人数量的增加而降低.由此可见,并非是工人越多,生产效率就越高.2.整个上午(8:0012:00)天气越来越暖,中午时分(12:0013:00)一场暴风雨使天气骤然凉爽了许多.暴风雨过后,天气转暖,直到太阳落山(18:00)才又开始转凉.画出这一天8:0020:00期间气温作为时间函数的一个可能的图象,并说出所画函数的单调区间.2.解:图象如下[8,12]是递增区间,[12,13]是递减区间,[13,18]是递增区间,[18,20]是递减区间.3.根据下图说出函数的单调区间,以及在每一单调区间上,函数是增函数还是减函数.3.解:该函数在[1,0]-上是减函数,在[0,2]上是增函数,在[2,4]上是减函数,在[4,5]上是增函数.4.证明函数()21f x x =-+在R 上是减函数.4.证明:设12,x x R ∈,且12x x <,因为121221()()2()2()0f x f x x x x x -=--=->,即12()()f x f x >,所以函数()21f x x =-+在R 上是减函数.5.设()f x 是定义在区间[6,11]-上的函数.如果()f x 在区间[6,2]--上递减,在区间[2,11]-上递增,画出()f x 的一个大致的图象,从图象上可以发现(2)f -是函数()f x 的一个 .5.最小值.1.3.2单调性与最大(小)值练习(第36页)1.判断下列函数的奇偶性:(1)42()23f x x x =+; (2)3()2f x x x =- (3)21()x f x x+=; (4)2()1f x x =+. 1.解:(1)对于函数42()23f x x x =+,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有4242()2()3()23()f x x x x x f x -=-+-=+=,所以函数42()23f x x x =+为偶函数;(2)对于函数3()2f x x x =-,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有33()()2()(2)()f x x x x x f x -=---=--=-,所以函数3()2f x x x =-为奇函数;(3)对于函数21()x f x x+=,其定义域为(,0)(0,)-∞+∞,因为对定义域内 每一个x 都有22()11()()x x f x f x x x-++-==-=--, 所以函数21()x f x x+=为奇函数; (4)对于函数2()1f x x =+,其定义域为(,)-∞+∞,因为对定义域内每一个x 都有22()()11()f x x x f x -=-+=+=,所以函数2()1f x x =+为偶函数.2.已知()f x 是偶函数,()g x 是奇函数,试将下图补充完整.2.解:()f x 是偶函数,其图象是关于y 轴对称的;()g x 是奇函数,其图象是关于原点对称的.习题1.3A 组1.画出下列函数的图象,并根据图象说出函数()y f x =的单调区间,以及在各单调区间上函数()y f x =是增函数还是减函数.(1)256y x x =--; (2)29y x =-. 1.解:(1)函数在5(,)2-∞上递减;函数在5[,)2+∞上递增;(2)函数在(,0)-∞上递增;函数在[0,)+∞上递减.2.证明:(1)函数2()1f x x =+在(,0)-∞上是减函数;(2)函数1()1f x x=-在(,0)-∞上是增函数. 2.证明:(1)设120x x <<,而2212121212()()()()f x f x x x x x x x -=-=+-,由12120,0x x x x +<-<,得12()()0f x f x ->,即12()()f x f x >,所以函数2()1f x x =+在(,0)-∞上是减函数;(2)设120x x <<,而1212211211()()x x f x f x x x x x --=-=, 由12120,0x x x x >-<,得12()()0f x f x -<,即12()()f x f x <,所以函数1()1f x x=-在(,0)-∞上是增函数. 3.探究一次函数()y mx b x R =+∈的单调性,并证明你的结论.3.解:当0m >时,一次函数y mx b =+在(,)-∞+∞上是增函数;当0m <时,一次函数y mx b =+在(,)-∞+∞上是减函数,令()f x mx b =+,设12x x <,而1212()()()f x f x m x x -=-,当0m >时,12()0m x x -<,即12()()f x f x <,得一次函数y mx b =+在(,)-∞+∞上是增函数;当0m <时,12()0m x x ->,即12()()f x f x >,得一次函数y mx b =+在(,)-∞+∞上是减函数.4.一名心率过速患者服用某种药物后心率立刻明显减慢,之后随着药力的减退,心率再次慢慢升高.画出自服药那一刻起,心率关于时间的一个可能的图象(示意图).4.解:自服药那一刻起,心率关于时间的一个可能的图象为5.某汽车租赁公司的月收益y 元与每辆车的月租金x 元间的关系为21622100050x y x =-+-,那么,每辆车的月租金多少元时,租赁公司的月收益最大?最大月收益是多少?5.解:对于函数21622100050x y x =-+-, 当162405012()50x =-=⨯-时,max 307050y =(元), 即每辆车的月租金为4050元时,租赁公司最大月收益为307050元.6.已知函数()f x 是定义在R 上的奇函数,当0x ≥时,()(1)f x x x =+.画出函数()f x的图象,并求出函数的解析式.6.解:当0x <时,0x ->,而当0x ≥时,()(1)f x x x =+,即()(1)f x x x -=--,而由已知函数是奇函数,得()()f x f x -=-,得()(1)f x x x -=--,即()(1)f x x x =-,所以函数的解析式为(1),0()(1),0x x x f x x x x +≥⎧=⎨-<⎩.B 组1.已知函数2()2f x x x =-,2()2([2,4])g x x x x =-∈.(1)求()f x ,()g x 的单调区间; (2)求()f x ,()g x 的最小值.1.解:(1)二次函数2()2f x x x =-的对称轴为1x =,则函数()f x 的单调区间为(,1),[1,)-∞+∞,且函数()f x 在(,1)-∞上为减函数,在[1,)+∞上为增函数,函数()g x 的单调区间为[2,4],且函数()g x 在[2,4]上为增函数;(2)当1x =时,min ()1f x =-,因为函数()g x 在[2,4]上为增函数,所以2min ()(2)2220g x g ==-⨯=.2.如图所示,动物园要建造一面靠墙的2间面积相同的矩形熊猫居室,如果可供建造围墙的材料总长是30m ,那么宽x (单位:m )为多少才能使建造的每间熊猫居室面积最大?每间熊猫居室的最大面积是多少?2.解:由矩形的宽为x m ,得矩形的长为3032x m -,设矩形的面积为S , 则23033(10)22x x x S x --==-, 当5x =时,2max 37.5S m =,即宽5x =m 才能使建造的每间熊猫居室面积最大,且每间熊猫居室的最大面积是18.75m^2.3.已知函数()f x 是偶函数,而且在(0,)+∞上是减函数,判断()f x 在(,0)-∞上是增函数还是减函数,并证明你的判断.3.判断()f x 在(,0)-∞上是增函数,证明如下:设120x x <<,则120x x ->->,因为函数()f x 在(0,)+∞上是减函数,得12()()f x f x -<-,又因为函数()f x 是偶函数,得12()()f x f x <,所以()f x 在(,0)-∞上是增函数.复习参考题A 组1.用列举法表示下列集合:(1)2{|9}A x x ==;(2){|12}B x N x =∈≤≤;(3)2{|320}C x x x =-+=.1.解:(1)方程29x =的解为123,3x x =-=,即集合{3,3}A =-; (2)12x ≤≤,且x N ∈,则1,2x =,即集合{1,2}B =;(3)方程2320x x -+=的解为121,2x x ==,即集合{1,2}C =.2.设P 表示平面内的动点,属于下列集合的点组成什么图形?(1){|}P PA PB =(,)A B 是两个定点;(2){|3}P PO cm =()O 是定点.2.解:(1)由PA PB =,得点P 到线段AB 的两个端点的距离相等,即{|}P PA PB =表示的点组成线段AB 的垂直平分线;(2){|3}P PO cm =表示的点组成以定点O 为圆心,半径为3cm 的圆.3.设平面内有ABC ∆,且P 表示这个平面内的动点,指出属于集合{|}{|}P PA PB P PA PC ==的点是什么.3.解:集合{|}P PA PB =表示的点组成线段AB 的垂直平分线,集合{|}P PA PC =表示的点组成线段AC 的垂直平分线,得{|}{|}P PA PB P PA PC ==的点是线段AB 的垂直平分线与线段AC 的垂直平分线的交点,即ABC ∆的外心.4.已知集合2{|1}A x x ==,{|1}B x ax ==.若B A ⊆,求实数a 的值.4.解:显然集合{1,1}A =-,对于集合{|1}B x ax ==,当0a =时,集合B =∅,满足B A ⊆,即0a =;当0a ≠时,集合1{}B a =,而B A ⊆,则11a =-,或11a =, 得1a =-,或1a =,综上得:实数a 的值为1,0-,或1.5.已知集合{(,)|20}A x y x y =-=,{(,)|30}B x y x y =+=,{(,)|23}C x y x y =-=,求A B ,A C ,()()A B B C .5.解:集合20(,)|{(0,0)}30x y A B x y x y ⎧-=⎫⎧==⎨⎨⎬+=⎩⎩⎭,即{(0,0)}A B =;集合20(,)|23x y AC x y x y ⎧-=⎫⎧==∅⎨⎨⎬-=⎩⎩⎭,即A C =∅; 集合3039(,)|{(,)}2355x y B C x y x y ⎧+=⎫⎧==-⎨⎨⎬-=⎩⎩⎭; 则39()(){(0,0),(,)}55A B B C =-. 6.求下列函数的定义域:(1)y =(2)||5y x =-. 6.解:(1)要使原式有意义,则2050x x -≥⎧⎨+≥⎩,即2x ≥, 得函数的定义域为[2,)+∞;(2)要使原式有意义,则40||50x x -≥⎧⎨-≠⎩,即4x ≥,且5x ≠,得函数的定义域为[4,5)(5,)+∞. 7.已知函数1()1x f x x-=+,求:(1)()1(1)f a a +≠-; (2)(1)(2)f a a +≠-.7.解:(1)因为1()1x f x x-=+, 所以1()1a f a a -=+,得12()1111a f a a a-+=+=++, 即2()11f a a+=+; (2)因为1()1x f x x-=+, 所以1(1)(1)112a a f a a a -++==-+++, 即(1)2a f a a +=-+. 8.设221()1x f x x+=-,求证:50 (1)()()f x f x -=; (2)1()()f f x x=-. 8.证明:(1)因为221()1x f x x+=-, 所以22221()1()()1()1x x f x f x x x+-+-===---, 即()()f x f x -=;(2)因为221()1x f x x+=-, 所以222211()11()()111()x x f f x x x x++===---, 即1()()f f x x=-. 9.已知函数2()48f x x kx =--在[5,20]上具有单调性,求实数k 的取值范围.9.解:该二次函数的对称轴为8k x =, 函数2()48f x x kx =--在[5,20]上具有单调性, 则208k ≥,或58k ≤,得160k ≥,或40k ≤, 即实数k 的取值范围为160k ≥,或40k ≤.10.已知函数2y x -=,(1)它是奇函数还是偶函数?(2)它的图象具有怎样的对称性?(3)它在(0,)+∞上是增函数还是减函数?(4)它在(,0)-∞上是增函数还是减函数?10.解:(1)令2()f x x -=,而22()()()f x x x f x ---=-==,即函数2y x -=是偶函数;(2)函数2y x -=的图象关于y 轴对称;(3)函数2y x -=在(0,)+∞上是减函数;(4)函数2y x -=在(,0)-∞上是增函数.B 组1.学校举办运动会时,高一(1)班共有28名同学参加比赛,有15人参加游泳比赛,有8人参加田径比赛,有14人参加球类比赛,同时参加游泳比赛和田径比赛的有3人,同时参加游泳比赛和球类比赛的有3人,没有人同时参加三项比赛.问同时参加田径和球类比赛的有多少人?只参加游泳一项比赛的有多少人?1.解:设同时参加田径和球类比赛的有x 人,则158143328x ++---=,得3x =,只参加游泳一项比赛的有15339--=(人),即同时参加田径和球类比赛的有3人,只参加游泳一项比赛的有9人.2.已知非空集合2{|}A x R x a =∈=,试求实数a 的取值范围.2.解:因为集合A ≠∅,且20x ≥,所以0a ≥.3.设全集{1,2,3,4,5,6,7,8,9}U =,(){1,3}U AB =ð,(){2,4}U A B =ð,求集合B . 3.解:由(){1,3}U AB =ð,得{2,4,5,6,7,8,9}A B =, 集合A B 里除去()U A B ð,得集合B ,所以集合{5,6,7,8,9}B =.4.已知函数(4),0()(4),0x x x f x x x x +≥⎧=⎨-<⎩.求(1)f ,(3)f -,(1)f a +的值. 4.解:当0x ≥时,()(4)f x x x =+,得(1)1(14)5f =⨯+=;当0x <时,()(4)f x x x =-,得(3)3(34)21f -=-⨯--=;(1)(5),1(1)(1)(3),1a a a f a a a a ++≥-⎧+=⎨+-<-⎩. 5.证明:(1)若()f x ax b =+,则1212()()()22x x f x f x f ++=; (2)若2()g x x ax b =++,则1212()()()22x x g x g x g ++≤. 5.证明:(1)因为()f x ax b =+,得121212()()222x x x x a f a b x x b ++=+=++, 121212()()()222f x f x ax b ax b a x x b ++++==++, 所以1212()()()22x x f x f x f ++=; (2)因为2()g x x ax b =++, 得22121212121()(2)()242x x x x g x x x x a b ++=++++, 22121122()()1[()()]22g x g x x ax b x ax b +=+++++ 2212121()()22x x x x a b +=+++, 因为2222212121212111(2)()()0424x x x x x x x x ++-+=--≤, 即222212121211(2)()42x x x x x x ++≤+, 所以1212()()()22x x g x g x g ++≤. 6.(1)已知奇函数()f x 在[,]a b 上是减函数,试问:它在[,]b a --上是增函数还是减函数?(2)已知偶函数()g x 在[,]a b 上是增函数,试问:它在[,]b a --上是增函数还是减函数?6.解:(1)函数()f x 在[,]b a --上也是减函数,证明如下:设12b x x a -<<<-,则21a x x b <-<-<,因为函数()f x 在[,]a b 上是减函数,则21()()f x f x ->-,又因为函数()f x 是奇函数,则21()()f x f x ->-,即12()()f x f x >,所以函数()f x 在[,]b a --上也是减函数;(2)函数()g x 在[,]b a --上是减函数,证明如下:设12b x x a -<<<-,则21a x x b <-<-<,因为函数()g x 在[,]a b 上是增函数,则21()()g x g x -<-,又因为函数()g x 是偶函数,则21()()g x g x <,即12()()g x g x >,所以函数()g x 在[,]b a --上是减函数. 7.《中华人民共和国个人所得税》规定,公民全月工资、薪金所得不超过2000元的部分不必纳税,超过2000元的部分为全月应纳税所得额.此项税款按下表分段累计计算:某人一月份应交纳此项税款为26.78元,那么他当月的工资、薪金所得是多少?7.解:设某人的全月工资、薪金所得为x 元,应纳此项税款为y 元,则0,02000(2000)5%,2000250025(2500)10%,25004000175(4000)15%,40005000x x x y x x x x ≤≤⎧⎪-⨯<≤⎪=⎨+-⨯<≤⎪⎪+-⨯<≤⎩由该人一月份应交纳此项税款为26.78元,得25004000x <≤,25(2500)10%26.78x +-⨯=,得2517.8x =,所以该人当月的工资、薪金所得是2517.8元.第三章函数的应用3.1函数与方程练习(P88)1.(1)令f(x)=-x2+3x+5,作出函数f(x)的图象(图3-1-2-7(1)),它与x轴有两个交点,所以方程-x2+3x+5=0有两个不相等的实数根.(2)2x(x-2)=-3可化为2x2-4x+3=0,令f(x)=2x2-4x+3,作出函数f(x)的图象(图3-1-2-7(2)),它与x轴没有交点,所以方程2x(x-2)=-3无实数根.(3)x2=4x-4可化为x2-4x+4=0,令f(x)=x2-4x+4,作出函数f(x)的图象(图3-1-2-7(3)),它与x轴只有一个交点(相切),所以方程x2=4x-4有两个相等的实数根.(4)5x2+2x=3x2+5可化为2x2+2x-5=0,令f(x)=2x2+2x-5,作出函数f(x)的图象(图3-1-2-7(4)),它与x轴有两个交点,所以方程5x2+2x=3x2+5有两个不相等的实数根.图3-1-2-72.(1)作出函数图象(图3-1-2-8(1)),因为f(1)=1>0,f(1.5)=-2.875<0,所以f(x)=-x3-3x+5在区间(1,1.5)上有一个零点.又因为f(x)是(-∞,+∞)上的减函数,所以f(x)=-x3-3x+5在区间(1,1.5)上有且只有一个零点.(2)作出函数图象(图3-1-2-8(2)),因为f(3)<0,f(4)>0,所以f(x)=2x·ln(x-2)-3在区间(3,4)上有一个零点.又因为f(x)=2x·ln(x-2)-3在(2,+∞)上是增函数,所以f(x)在(3,4)上有且仅有一个零点.(3)作出函数图象(图3-1-2-8(3)),因为f(0)<0,f(1)>0,所以f(x)=e x-1+4x-4在区间(0,1)上有一个零点.又因为f(x)=e x-1+4x-4在(-∞,+∞)上是增函数,所以f(x)在(0,1)上有且仅有一个零点.(4)作出函数图象(图3-1-2-8(4)),因为f(-4)<0,f(-3)>0,f(-2)<0,f(2)<0,f(3)>0,所以f(x)=3(x+2)(x-3)(x+4)+x在(-4,-3),(-3,-2),(2,3)上各有一个零点.图3-1-2-8练习(P91)1.由题设可知f(0)=-1.4<0,f(1)=1.6>0,于是f(0)·f(1)<0,所以函数f(x)在区间(0,1)内有一个零点x0.下面用二分法求函数f(x)=x3+1.1x2+0.9x-1.4在区间(0,1)内的零点.取区间(0,1)的中点x1=0.5,用计算器可算得f(0.5)=-0.55.因为f(0.5)·f(1)<0,所以x0∈(0.5,1).再取区间(0.5,1)的中点x2=0.75,用计算器可算得f(0.75)≈0.32.因为f(0.5)·f(0.75)<0,所以x0∈(0.5,0.75).同理,可得x0∈(0.625,0.75),x0∈(0.625,0.687 5),x0∈(0.656 25,0.687 5).由于|0.687 5-0.656 25|=0.031 25<0.1,所以原方程的近似解可取为0.656 25.2.原方程可化为x+lgx-3=0,令f(x)=x+lgx-3,用计算器可算得f(2)≈-0.70,f(3)≈0.48.于是f(2)·f(3)<0,所以这个方程在区间(2,3)内有一个解x0.下面用二分法求方程x=3-lgx在区间(2,3)的近似解.取区间(2,3)的中点x1=2.5,用计算器可算得f(2.5)≈-0.10.因为f(2.5)·f(3)<0,所以x0∈(2.5,3).再取区间(2.5,3)的中点x2=2.75,用计算器可算得f(2.75)≈0.19.因为f(2.5)·f(2.75)<0,所以x0∈(2.5,2.75).同理,可得x0∈(2.5,2.625),x0∈(2.562 5,2.625),x0∈(2.562 5,2.593 75),x0∈(2.578 125,2.593 75),x0∈(2.585 937 5,2.59 375).由于|2.585 937 5-2.593 75|=0.007 812 5<0.01,所以原方程的近似解可取为2.593 75.习题3.1 A组(P92)1.A,C 点评:需了解二分法求函数的近似零点的条件.2.由x,f(x)的对应值表可得f(2)·f(3)<0,f(3)·f(4)<0,f(4)·f(5)<0,又根据“如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点.”可知函数f(x)分别在区间(2,3),(3,4),(4,5)内有零点.3.原方程即(x+1)(x-2)(x-3)-1=0,令f(x)=(x+1)(x-2)(x-3)-1,可算得f(-1)=-1,f(0)=5.于是f(-1)·f(0)<0,所以这个方程在区间(-1,0)内有一个解. 下面用二分法求方程(x+1)(x-2)(x-3)=1在区间(-1,0)内的近似解.取区间(-1,0)的中点x1=-0.5,用计算器可算得f(-0.5)=3.375.因为f(-1)·f(-0.5)<0,所以x0∈(-1,-0.5).再取(-1,-0.5)的中点x2=-0.75,用计算器可算得f(-0.75)≈1.58.因为f(-1)·f(-0.75)<0,所以x0∈(-1,-0.75).同理,可得x0∈(-1,-0.875),x0∈(-0.937 5,-0.875).由于|(-0.875)-(-0.937 5)|=0.062 5<0.1,所以原方程的近似解可取为-0.937 5.4.原方程即0.8x-1-lnx=0,令f(x)=0.8x-1-lnx,f(0)没有意义,用计算器算得f(0.5)≈0.59,f(1)=-0.2.于是f(0.5)·f(1)<0,所以这个方程在区间(0.5,1)内有一个解.下面用二分法求方程0.8x-1=lnx在区间(0,1)内的近似解.取区间(0.5,1)的中点x1=0.75,用计算器可算得f(0.75)≈0.13.因为f (0.75)·f (1)<0,所以x 0∈(0.75,1).再取(0.75,1)的中点x 2=0.875,用计算器可算得f (0.875)≈-0.04.因为f (0.875)·f (0.75)<0,所以x 0∈(0.75,0.875).同理,可得x 0∈(0.812 5,0.875),x 0∈(0.812 5,0.843 75).由于|0.812 5-0.843 75|=0.031 25<0.1,所以原方程的近似解可取为0.843 75.5.由题设有f (2)≈-0.31<0,f (3)≈0.43>0,于是f (2)·f (3)<0,所以函数f (x )在区间(2,3)内有一个零点.下面用二分法求函数f (x )=lnx x2-在区间(2,3)内的近似解. 取区间(2,3)的中点x 1=2.5,用计算器可算得f (2.5)≈0.12.因为f (2)·f (2.5)<0,所以x 0∈(2,2.5).再取(2,2.5)的中点x 2=2.25,用计算器可算得f (2.25)≈-0.08.因为f (2.25)·f (2.5)<0,所以x 0∈(2.25,2.5).同理,可得x 0∈(2.25,2.375),x 0∈(2.312 5,2.375),x 0∈(2.343 75,2.375),x 0∈(2.343 75,2.359 375),x 0∈(2.343 75,2.351 562 5),x 0∈(2.343 75,2.347 656 25).由于|2.343 75-2.347 656 25|=0.003 906 25<0.01,所以原方程的近似解可取为2.347 656 25.B 组1.将系数代入求根公式x 得x =223(3)42(1)22±--⨯⨯-⨯=4173+, 所以方程的两个解分别为x 1=4173+,x 2=4173-.下面用二分法求方程的近似解.取区间(1.775,1.8)和(-0.3,-0.275),令f (x )=2x 2-3x -1.在区间(1.775,1.8)内用计算器可算得f (1.775)=-0.023 75,f (1.8)=0.08.于是f (1.775)·f (1.8)<0.所以这个方程在区间(1.775,1.8)内有一个解.由于|1.8-1.775|=0.025<0.1,所以原方程在区间(1.775,1.8)内的近似解可取为1.8.同理,可得方程在区间(-0.3,-0.275)内的近似解可取为-0.275.所以方程精确到0.1的近似解分别是1.8和-0.3.2.原方程即x3-6x2-3x+5=0,令f(x)=x3-6x2-3x+5,函数图象如下图所示.图3-1-2-9所以这个方程在区间(-2,0),(0,1),(6,7)内各有一个解.取区间(-2,0)的中点x1=-1,用计算器可算得f(-1)=1.因为f(-2)·f(-1)<0,所以x0∈(-2,-1).再取(-2,-1)的中点x2=-1.5,用计算器可算得f(-1.5)=-7.375.因为f(-1.5)·f(-1)<0,所以x0∈(-1.5,-1).同理,可得x0∈(-1.25,-1),x0∈(-1.125,-1),x0∈(-1.125,-1.062 5).由于|(-1.062 5)-(-1.125)|=0.062 5<0.1,所以原方程在区间(-2,0)内的近似解可取为-1.062 5.同理,可得原方程在区间(0,1)内的近似解可取为0.7,在区间(6,7)内的近似解可取为6.3.3.(1)由题设有g(x)=2-[f(x)]2=2-(x2+3x+2)2=-x4-6x3-13x2-12x-2.(2)函数图象如下图所示.图3-1-2-10(3)由图象可知,函数g(x)分别在区间(-3,-2)和区间(-1,0)内各有一个零点.取区间(-3,-2)的中点x1=-2.5,用计算器可算得g(-2.5)=0.187 5.因为g(-3)·g(-2.5)<0,所以x0∈(-3,-2.5).再取(-3,-2.5)的中点x2=-2.75,用计算器可算得g(-2.75)≈0.28.因为g(-3)·g(-2.75)<0,所以x0∈(-3,-2.75).同理,可得x0∈(-2.875,-2.75),x0∈(-2.812 5,-2.75).由于|-2.75-(-2.812 5)|=0.062 5<0.1,所以原方程在区间(-3,-2)内的近似解可取为-2.812 5.同样可求得函数在区间(-1,0)内的零点约为-0.2.所以函数g(x)精确到0.1的零点约为-2.8或-0.2.点评:第2、3题采用信息技术画出函数图象,并据此明确函数零点所在的区间.在教学中,如果没有信息技术条件,建议教师直接给出函数图象或零点所在区间.第三章复习参考题A组(P112)1.C2.C3.设经过时间t后列车离C地的距离为y,则y=200100,02,100200,2 5.t tt t-≤≤⎧⎨-<≤⎩图3-24.(1)圆柱形; (2)上底小、下底大的圆台形;(3)上底大、下底小的圆台形; (4)呈下大上小的两节圆柱形. 图略.图3-35.令f(x)=2x3-4x2-3x+1,函数图象如图3-3所示:函数分别在区间(-1,0)、(0,1)和区间(2,3)内各有一个零点,所以方程2x3-4x2-3x+1=0的最大的根应在区间(2,3)内.取区间(2,3)的中点x1=2.5,用计算器可算得f(2.5)=-0.25.因为f(2.5)·f(3)<0,所以x0∈(2.5,3). 再取(2.5,3)的中点x2=2.75,用计算器可算得f(2.75)≈4.09.因为f(2.5)·f(2.75)<0,所以x0∈(2.5,2.75).同理,可得x0∈(2.5,2.625),x0∈(2.5,2.5625),x0∈(2.5,2.53125),x0∈(2.515625,2.53125),x0∈(2.515625,2.5234375).由于|2.523 437 5-2.515 625|=0.007 812 5<0.01,所以原方程的最大根约为2.523 437 5.6.令lgx =x 1,即得方程lgx x 1-=0,再令g (x )=lgx x1-,用二分法求得交点的横坐标约为2.5.图3-47.如图,作DE ⊥AB,垂足为E.由已知可得∠ADB=90°.因为AD=x ,AB=4,于是AD 2=AE×AB,即AE=AB AD 2=42x . 所以CD=AB-2AE=4-2×42x =422x -. 于是y =AB+BC+CD+AD=4+x +422x -+x =22x -+2x +8. 由于AD>0,AE>0,CD>0,所以x >0,42x >0,422x ->0,解得0<x <22. 所以所求的函数为y =22x -+2x +8,0<x <22. 8.(1)由已知可得N=N 0(λe 1)t .因为λ是正常数,e >1,所以e λ>1,即0<λe1<1. 又N 0是正常数,所以N=N 0(λe1)t 是在于t 的减函数. (2)N=N 0e -λt ,因为e -λt =0N N ,所以-λt =ln 0N N ,即t =λ1-ln 0N N . (3)当N=20N 时,t =λ1-002N N =λ1-ln 2. 9.因为f (1)=-3+12+8=17>0,f (2)=-3×8+12×2+8=8>0,f (3)<0,所以,下次生产应在两个月后开始.B 组1.厂商希望的是甲曲线;客户希望的是乙曲线.2.函数的解析式为y=f(t)=22,01, 2(2)12,22.tt tt<≤⎪⎪⎪⎪--+<≤⎨>⎪⎩函数的图象为图3-5备课资料[备选例题]【例】对于函数f(x)=ax2+(b+1)x+b-2(a≠0),若存在实数x0,使f(x0)=x0成立,则称x0为f(x)的不动点.(1)当a=2,b=-2时,求f(x)的不动点;(2)若对于任何实数b,函数f(x)恒有两个相异的不动点,求实数a的取值范围.解:(1)f(x)=ax2+(b+1)x+b-2(a≠0),当a=2,b=-2时,f(x)=2x2-x-4,设x为其不动点,即2x2-x-4=x,则2x2-2x-4=0,解得x1=-1,x2=2,即f(x)的不动点为-1,2.(2)由f(x)=x,得ax2+bx+b-2=0.关于x的方程有相异实根,则b2-4a(b-2)>0,即b2-4ab+8a>0.又对所有的b∈R,b2-4ab+8a>0恒成立,故有(4a)2-4·8a<0,得0<a<2.。
电工基础 第1章 课后习题

A: 220/n
B: 220/nR
C: 220/R
D: 220R/n 答案: C 9 已知A、B两点的电位分别为5伏和-5伏,则两点间的电压UAB为 伏。
A: 0
B: 10
C: -10
D: 15 答案: B 10 已知电路中A点的电位为5伏,AB两点的电压UAB ---10V,则B点电位为____.伏
A: 20
B: 10
C: 5
D: 40 答案:
C 7 n个相同阻值的电阻R,串联后接入电压为220V的电路中,则电阻R上的电压为 伏。
A: 220/n
B: 220/R
C: 2.20,/nR
D: 220R/n 答案: A 8 n个相同阻值的电阻R,并联接到电压为220V的电源上,则流过电阻R的电流为一一一安。 A, 220/n B、220/nR C, 220/R D, 220R/n
答案: 正确 19 在并联电路中,电阻的阻值越小,消耗的功率越小。
答案: 错误 20 在串联电路中,电阻的阻值越小,消耗的功率越小。
答案: 正确 21 电灯泡的灯丝断后,再搭上使用,灯泡反而更亮,其原因是灯丝电阻变小而功率增大了。
答案: 正确
22 扩大直流电流表量程的方法是在表头上串联电阻分流。 答案: 错误
A: 负电荷定向 B: 电子定向 C: 正电荷定向 D:
答案: C 25 Rl=lQ,R2 =3Q的两只电阻,并联接在相同电压下,则电流的比值为———。
A: 1:1 B: 3:1 C: 1:3 D: 4:1
答案: 26 R1 =2Q,R2 =3Q的两只电阻,串联接在20V的电压下,则R1上电压为 V。
A: 电源 B: 负载
C: 连接导线
D: 开关
《无极及分析化学》(第三版)第一章 课后习题答案详解

第1章思考题与习题参考答案一、选择题1.等压下加热5%的下列水溶液,最先沸腾的是()A. 蔗糖(C12H22O11)溶液B. 葡萄糖(C6H12O6)溶液C. 丙三醇(C 3H8O3)溶液D. 尿素((NH2)2 CO)溶液解:选D。
在等压下,最先沸腾就是指溶液的蒸气压最低。
根据难挥发非电解质稀溶液的依数性变化规律,溶液质量摩尔浓度增大,溶液的蒸气压下降。
这里,相同质量分数下,溶质的摩尔质量越小,质量摩尔浓度越大。
选项D中非电解质尿素的摩尔质量最小,尿素溶液的质量摩尔浓度最大,蒸气压最低,在等压下最先沸腾。
2.0.1mol·kg-1下列水溶液中凝固点最低的是()A. NaCl溶液B. C12H22O11溶液C. HAc溶液D. H2SO4溶液解:选D。
电解质溶液的依数性虽然不能用拉乌尔定律进行统一的定量计算,但仍然可以参照难挥发非电解质稀溶液的依数性进行定性描述。
即溶质的粒子数目增大,会引起溶液的蒸气压降低,沸点升高,凝固点下降和溶液的渗透压增大。
此题中,在相同质量摩尔浓度下,溶液中的粒子数目估算出来是H2SO4溶液最多,所以其凝固点最低。
3.胶体溶液中,决定溶胶电性的物质是()A. 胶团B. 电位离子C. 反离子D. 胶粒解:选D。
根据胶团结构,胶核和吸附层的整体称为胶粒,胶粒中反离子数比电位离子数少,故胶粒所带电荷与电位离子符号相同。
即胶粒带电,溶胶电性由胶粒决定。
4.溶胶具有聚结不稳定性,但经纯化后的Fe(OH)3溶胶可以存放数年而不聚沉,其原因是()A. 胶体的布朗运动B. 胶体的丁铎尔效应C. 胶团有溶剂化膜D. 胶粒带电和胶团有溶剂化膜解:选D。
溶胶具有动力学稳定性和聚结稳定性,而聚结稳定性是溶胶稳定的根本原因,它包含两个方面,胶粒带有相同电性的电荷,当靠近时会产生静电排斥,阻止胶粒聚结合并;而电位离子和反离子形成的溶剂化膜,也会阻隔胶粒的聚结合并。
由于纯化的Fe(OH)3溶胶具有这种聚结稳定性,从而可以存放数年而不聚沉。
第一章高分子链运动课后习题

第一章 高分子的链运动一.思考题1.高分子结构包含哪两个部分?各包括那些结构?2.单个高分子链的形态有哪几种?3.何谓高分子链的构型、构象?它们有何区别?4.什么是均方末端距和均方旋转半径?它们之间有何关系?5.何谓自由结合链、自由旋转链、受阻内旋链、等效自由连接链?计算这些链的均方末端距的公式有何区别?6.什么是高分子链的柔顺性?影响链柔顺性的内在、外在因素有哪些?7.为什么大多数的聚合物没有旋光性?8.与低分子相比较,高聚物结构较复杂的原因?9.哪些参数可以表征高分子链的柔顺性?如何表征?10.为什么等规立构聚苯乙烯在晶体中呈31螺旋构象,而间同立构聚氯乙烯分子链在晶体中呈平面锯齿构象?11.二、选择题1、下列哪种聚合物不存在旋光异构体?( )①聚乙烯 ②聚丙烯 ③聚异戊二烯2、异戊二烯1,4键接聚合形成顺式和反式两种构型的聚异戊二烯,它们称为( )①旋光异构体 ②几何异构体 ③间同异构体3、高分子链内旋转受阻程度越大,其均方末端距()①越大 ②越小 ③趋于恒定值4、高分子链柔性越好,其等效自由结合链的链段数目()①越多 ②越少 ③不变5、高分子链柔性越大,其等效自由结合链的链段长度()①越长 ②越短 ③不变6、自由结合链的均方末端距的公式是()①22Nl h = ②θθcos 1cos 1N h 22+-=l ③ϕϕθθcos 1cos 1cos 1cos 1h 22-+•+-=Nl (其中,θ为键角,ϕcos 为单键内旋转的余弦函数平均值)7、同一件聚合物样品,下列计算值哪个较大?()①自由结合链均方末端距②自由旋转链均方末端距③受阻内旋转均方末端距8、高聚物大分子自由旋转链的均方末端距的公式可以表示为()①22Nl h = ②2e e 2L N h = ③θθcos 1cos 1N h 22+-=l (其中,N 为键的数目,l 为键长,N e 为链段数目,L e 为链段长度,θ为键角)9、结晶性高聚物的晶区中存在的分子构象可以是()①无规线团 ②螺旋形 ③锯齿形10、柔性高聚物在溶液中存在的分子链构象是()①无规线团 ②螺旋形 ③锯齿形三、判断题(正确的划“√”,错误的划“×”)1.主链由饱和单键构成的高聚物,因分子链可以围绕单键进行内旋转,故链的柔性大,若主链中引用了一些非共轭双键,因双键不能内旋转,故导致链的柔性下降。
第一章X射线物理课后习题答案

第一章 X 射线物理习题一解答1-1 产生X 射线需要哪些条件?答:这个题目实际上把高速电子轰击靶产生X 射线这一事实在条件上予以明确。
首先要有产生电子的阴极和被轰击的阳极靶,电子加速的环境条件即在阴极和阳极间建立电位差,为防止阴极和阳极氧化以及电子与中性分子碰撞的数量损失,要制造压强小于4-Pa 的真空环境,为此要有一个耐压、密封的管壳。
1-2 影响X 射线管有效焦点大小的因素有哪些?答:影响有效焦点大小的因素有:灯丝大小、管电压和管电流、靶倾角。
1-3 在X 射线管中,若电子到达阳极靶面的速度为1.5⨯810ms -1,求连续X 射线谱的最短波长和相应的最大光子能量。
答:此题的思路是由动能公式221v m 求出电子的最大动能,此能量也是最大的光子能量,从而求出最短波长。
但当速度可与光速c=3⨯810ms -1相比较时,必须考虑相对论效应,我们可以用下面公式求出运动中电子的质量kg 3023122010052.1)2/1(11011.9/1--⨯=-⨯=-=c m m e vkeV 8.731018.1)105.1(10052.121211428302max =⨯=⨯⨯⨯⨯==--J m h e v ν nm 0169.0max min ==νλh hc此题的结果告诉我们,管电压为73.8KV 。
反过来,如果知道管电压,求电子到达阳极靶表面的电子速度时,同样需要考虑相对论效应。
1-4 下面有关连续X 射线的解释,哪些是正确的?A .连续X 射线是高速电子与靶物质轨道电子相互作用的结果;B .连续X 射线是高速电子与靶物质的原子核电场相互作用的结果;C .连续X 射线的最大能量决定于管电压;D .连续X 射线的最大能量决定于靶物质的原子序数;E .连续X 射线的质与管电流无关。
正确答案:B 、C 、E1-5 下面有关标识X 射线的解释,哪些是正确的?A .标识X 射线是高速电子与靶物质轨道电子相互作用的结果;B .标识X 射线的质与高速电子的能量有关;C .标识X 射线的波长由跃迁电子的能级差决定;D .滤过使标识X 射线变硬;E .靶物质原子序数越高,标识X 射线的能量就越大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1-3
(3) 27Co 3d 8、(1) 在下列各组中填入合适的量子数: 4s
n= ? l=2 n=2 n=3 n=4
m=2
ms = + ms = -
1 2 1 2 1 2Fra bibliotekl= ? m=1 l=1 l=0
m = ? ms = + m=0
ms = ?
(2) 指出电子所处的能级; (3) 指出电子所处的原子轨道。 解: (1) ① n≥3 (2) ①3d or 4d or 5d… 更具体按角度分布 3dx2−y2 or 4dx2−y2 等 (3) ①ψ322 orψ422 … ② ψ211 ③ ψ311,ψ310,ψ31−1 ④ ψ400 ② l=1 ② 2p or 2 px ③ m = +1or 0 or −1 ③ 3p or 3px,3pz,3py ④ms = + 2 or ④ 4s 仍是 4s
2+ 4 24Cr 电子结构[Ar]3d 27Co 48Cd 57La 3+ 2+
电子结构[Ar]3d6 电子结构[Kr]4d10
3+
电子结构[Xe]4f 0
20、 讨论图 1-4-3 中从 Na 到 Ar 第一电离能曲线为什么呈锯齿形变化?并写出曲线上各点对 应的元素名称。
Ar
Na
1-7
解:从图可见第一电离能 Mg>Al,P>S,它们的外电子层结构分别为: Mg 3s2, 电子成对 稳定结构 Al 3s23p1, P 3s23p3, 呈半充满 稳定结构 S 3s23p4
并指出它们各属于第几周期?第几族? 解:(1) 18Ar (2) 26Fe (3) 53I (4) 47Ag 1S2 2S22p63S23P6 1S2 2S22P63S23P63d64S2 第三周期 ⅧA 族 第四周期 ⅧB 族
1S2 2S22P63S23P63d104S24p64d10 5S25P5 第五周期 ⅦA 族 1S2 2S22P63S23P63d104S24P64d10 5S1 第五周期 ⅠB 族
1-5
14、第五周期某元素,其原子失去 2 个电子,在 l = 2 的轨道内电子刚好全充满,试推断该 元素的原子序数、电子结构,并指出位于周期表中哪一族?是什么元素? 解:该元素失去 2 个电子为 M2+,则电子结构[Kr] 4d105S0 该元素 M 其电子结构为[Kr] 4d105S2 原子序数 = 36 + 10 + 2 = 48 位于ⅡB 族,是 48Cd。
12、已知四种元素的原子的价电子层结构分别为: (1) 4s2 (2) 3s23p5 (3) 3d24s2 (4)5d106s2
试指出: (1) 它们在周期系中各处于哪一区?哪一周期?哪一族? (2) 它们的最高正氧化值各为多少? (3) 电负性的相对大小。 解: 外电子层结构 ① ② ③ ④ 4S2 3S23P5 3 d2 4 S 2 5d10 6S2 区 周期 四 三 四 六 族 ⅡA ⅦA ⅣB ⅡB 最高正氧化值 +2 +7 +4 +2
(3) n = 4 l = 2 m = 0 ms = + (4) n = 2 l = 1 m = 1 ms = + 解:(1) 不存在。 因为 l = n (2) 不存在。因为 m > l
1-1
(3) (4) 存在。 4、写出 Ni 原子最外两个电子层中每个电子的四个量子数。 解:28Ni 1s2 2s22p63s2 3p63d8 4s2 最外层两个电子层
1
− 1 2
9、写出 48Cd 的电子排布式,并画出 Cd 原子最外两层电子的原子轨道角度分布图。 解:48Cd 在亚层中的电子排布:1s2 2s2 2p6 3s2 3p6 4s2 4p6 4d10 5s2 最外两层是 4s2 4p6 4d10 和 5s2 对于 4s、5s 角度分布图只有一种取向:(图略) 对于 4p 角度分布图有三种取向: 对于 4d 角度分布图有五种取向:
m
1 2 0 0 0 1
ms
+ + + +
1 2 1 2 1 2 1 2 1 2 1 2
解:(1) 3d,(2) 4f,(3) 2s,(4) 3d,(5) 1s,(6) 3p 各电子按能量由低高到排序:(5) < (3) < (6) < (1) = ( 4) < (2) 6、对下列各组轨道,填充合适的量子数。 (1) n = ? l = 3 (2) n = 2 (3) n = 4 (4) n = 1 解:(1) n = 4
n
3s2 3 3 3 3 3 p6 3 3 3 3 3 3
8
l
0 0 1 1 1 1 1 1 2 2 2 2 2 2 2 2 0 0
m
0 0 +1 +1 0 0
ms
+
−
1 2
1 2
+
−
1 2
1 2
+
−
1 2
1 2
−1 −1
+2 +1 0
+
−
1 2
1 2
+ + + + +
− − −
1 2 1 2 1 2 1 2 1 2
所以 Mg 和 P 都是较稳定结构,较难失去电子,电离能较大,而呈现锯齿形变化。
21、(1) 确定下列化合物中铋、铬、钼、锇的氧化值: NaBiO3、K2Cr2O7、H2MoO4、(NH4)2OsCl6 (2) 指出上述 4 个元素在周期表中的位置(周期、族)和最高氧化值。 (3) 写出它们的外电子构型。 解: Bi (1) (2) +5 六周期ⅤA 族 +5 (3) Cr +6 四周期ⅥB 族 +6 (n-1)d5ns1 Mo +6 五周期ⅥB 族 +6 (n-1)d4ns2 Os +4 六周期ⅧB 族 +8 (n-1)d6~8ns2
16、指出相应于下列各特征元素的名称: (1) 具有 1s22s22p63s23p5 电子层结构的元素; (2) 碱金属族中原子半径最大的元素; (3) IIA 族中第一电离能最大的元素; (4) VIIA 族中具有最大电子亲和能的元素; (5) +2 离子具有[Ar]3d5 结构的元素。 解:(1) Cl;(2) Fr;(3) Be;(4) Cl;(5) Mn2+
c
λ
已知阿伏加德罗常数 N = 6.022 × 1023 mol −1 ,普朗克常数 h = 6.626 × 10 −34 J⋅ s 光速 c = 3 × 108 m⋅ s
−1
−1
I=
6.022 × 10 mol
23
× 6.626 × 10
−34
× 10 kJ ⋅ s × 3 × 10 m ⋅ s m
17、试解释下列事实: (1) 从混合物中,分离 V 与 Nb 容易,而分离 Nb 和 Ta 难。 (2) K 的第一电离能小于 Ca,而第二电离能则大于 Ca。 (3) Be 的第一电子亲和能为正值而 B 为负值;Cl 的第一电子亲和能负值大于 F。
1-6
解:(1) V、Nb 半径相差较大,性质差异大,易分离;Nb、Ta 由于镧系收缩而使半径 几乎相等,性质相似,不易分离。 (2) K:[Ar]4s1,外层一个电子,易失去; Ca:[Ar]4s2,外层二个电子,全充满,稳定,不易失去; 所以 I1(K) < I1(Ca )。 K 失去一个电子后成为 K+,电子结构为[Ar],具有稀有气体稳定结构,不易再失去电子, 所以第二电离能大于 Ca 的第二电离能。 (3) Be: [He]2s2 , 不易结合电子,B: [He]2s22p1 , 能获得电子。F 为第二周期元素, 半径小,对外来电子排斥力大,因此 Cl 的第一电子亲和能大于 F。 18、波长为 242nm 的辐射能恰好足够使钠原子最外层的 1 个电子完全移出。试计算钠 的电离能(kJ⋅mol-1)。 解:I = N⋅ΔE = N⋅h ⋅ N ⋅h ⋅
−3
8
−1
2420 × 10
−10
= 494.7 kJ⋅mol −1 19、写出下列离子的电子结构,并确定它们基态时未成对的电子数:
22Ti 3+
、24Cr2+、27Co3+、48Cd2+、57La3+ 未成对电子数 1 未成对电子数 4 未成对电子数 4 未成对电子数 0 未成对电子数 0
解:22Ti3+电子结构[Ar]3d1
24Cr 29Cu
1S2 2S22P63S23P64S1 1S2 2S22P63S23P63d54S1 1S2 2S22P63S23P63d104S1
处于 s 区,第四周期 ⅠA 族; 处于 d 区,第四周期 ⅥB 族; 处于 ds 区,第四周期ⅠB 族。
11、试用 s,p,d,f 符号来表示下列各元素的电子结构: (1) 18Ar (2) 26Fe (3) 53I (4) 47Ag
∆E =
=
hc λ
−34
6.626 × 10
J ⋅ s × 3 × 10 m ⋅ s
−7
8
−1
1.54 × 10 m
= 1.29×10 −18 J 3、下列的电子运动状态是否存在?为什么? (1) n = 2 l = 2 m = 0 ms = + (2) n = 3 l = 1 m = 2
1 2 1 ms = 2 1 2 1 2
1
1
2
5
又 ∆E = h£h ∴
ν =
ch ∆E
∆E h
λ=
c
ν
=
3 ×108 ms-1 × 6.626×10-34 J ⋅ s = = 4.34×10 −7 m = 434 nm 4.58×10-19 J
