立体几何判定平行垂直的20个判定定理
立体几何所有定理和判定

立体几何所有定理和判定立体几何是数学中的一个重要分支,研究的是三维空间中的图形和物体的性质。
在立体几何中,有许多重要的定理和判定,它们帮助我们理解和解决与立体图形相关的问题。
本文将介绍一些主要的定理和判定。
一、平行线与平面的关系1. 平行线定理:如果两条线与第三条线平行,则这两条线也互相平行。
2. 平行线截割定理:如果一对平行线被一组截线截割,则所得的对应线段成比例。
3. 平行线的垂直定理:如果两条平行线被一条截线垂直截断,则所得的对应线段也相互垂直。
二、线段与角的关系1. 点到直线的距离定理:一个点到一条直线的距离等于这条直线上任意一点到该点的距离。
2. 线段相等定理:如果两个线段的长度相等,则它们是相等的。
3. 角的平分线定理:如果一条直线将一个角分成两个相等的角,则这条直线是该角的平分线。
三、平面图形的性质1. 三角形内角和定理:三角形的三个内角的和等于180度。
2. 直角三角形定理:如果一个三角形的一个角是直角,则它是直角三角形。
3. 等腰三角形定理:如果一个三角形的两边相等,则它是等腰三角形。
4. 等边三角形定理:如果一个三角形的三边都相等,则它是等边三角形。
四、立体图形的性质1. 正方体的性质:正方体是一种六个面都是正方形的立体图形。
2. 立方体的性质:立方体是一种六个面都是正方形且相互平行的立体图形。
3. 正四面体的性质:正四面体是一种四个面都是等边三角形的立体图形。
五、空间图形的判定1. 平行四边形的判定:如果四边形的对边平行,则它是平行四边形。
2. 正多面体的判定:如果一个多面体的每个面都是正多边形且每个顶点的相邻边相等,则它是正多面体。
3. 立体图形的对称性判定:如果一个立体图形可以通过某种变换与自身完全重合,则它具有对称性。
以上只是立体几何中的一部分定理和判定,它们是我们理解和解决立体图形问题的基础。
通过运用这些定理和判定,我们可以更好地分析和推导立体图形的性质,从而解决各种与立体图形相关的问题。
立体几何的八大定理
l ⊥b ab
=
O
a
b
⇒l⊥α
ab⊥ ⊥αα⇒a∥b
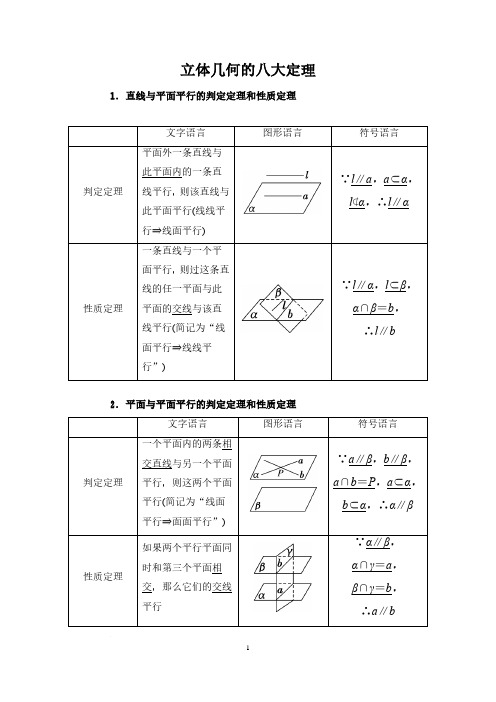
4. 平面与平面垂直的判定定理与性质定理
文字语言 一个平面过另 一个平面的垂 判定定理 线,则这两个平 面垂直
两个平面垂直, 则一个平面内 性质定理 垂直于交线的 直线与另一个 平面垂直
图形语言
符号语言
ll⊂ ⊥βα⇒α⊥β
αlαl⊂ ⊥⊥ ∩aβββ=a⇒
l⊥α
2
符号语言
∵a∥β,b∥β, a∩b=P,a⊂α,
b⊂α,∴α∥β
∵α∥β, α∩γ=a, β∩γ=b,
∴a∥b
1
3.直线与平面垂直的判定定理与性质定理
文字语言
图形语言
一条直线与一个 平面内的两条相 判定定理 交直线都垂直,则 该直线与此平面 垂直
垂直于同一个平 性质定理 面的两条符号语言
∵l∥a,a⊂α, l⊄α,∴l∥α
∵l∥α,l⊂β, α∩β=b, ∴l∥b
2. 平面与平面平行的判定定理和性质定理
文字语言
图形语言
一个平面内的两条相
交直线与另一个平面
判定定理 平行,则这两个平面
平行(简记为“线面
平行⇒面面平行”)
性质定理
如果两个平行平面同 时和第三个平面相 交,那么它们的交线 平行
立体几何的八大定理
1. 直线与平面平行的判定定理和性质定理
判定定理 性质定理
文字语言 平面外一条直线与 此平面内的一条直 线平行,则该直线与 此平面平行(线线平 行⇒线面平行) 一条直线与一个平 面平行,则过这条直 线的任一平面与此 平面的交线与该直 线平行(简记为“线 面平行⇒线线平 行”)
图形语言
立体几何基础平行与垂直的性质与判定

立体几何基础平行与垂直的性质与判定立体几何基础——平行与垂直的性质与判定立体几何是数学中的一个重要分支,它研究的对象是在三维空间内的图形和物体。
在立体几何中,平行和垂直是两个基本概念,它们在判断和解决几何问题时起着重要的作用。
本文将介绍平行与垂直的性质和判定方法,帮助读者更好地理解立体几何的基础知识。
一、平行的性质与判定平行是指在同一平面内,两条直线永不相交的性质。
在立体几何中,我们常用平行性质来推导和证明定理。
以下是一些与平行相关的性质和判定方法。
1. 平行线性质:(1)平行线上的对应角相等:如果两条平行线被一条横截线所交,那么对应的角都是相等的。
(2)平行线上的内错角互补:如果两条平行线被一条横截线所交,那么内错角互补,即相互补充的角和为180度。
(3)平行线上的同旁内角相等:如果两条平行线被一条横截线所交,那么同旁内角相等,即相邻的内角相等。
2. 判定平行线的方法:(1)两条线段平行的充要条件是斜率相等:如果两条线段的斜率相等,那么它们是平行的。
(2)两个向量平行的充要条件是比值相等:如果两个向量的坐标分量比值相等,那么它们是平行的。
(3)两条直线互相垂直的充要条件是斜率乘积为-1:如果两条直线的斜率乘积为-1,那么它们互相垂直。
二、垂直的性质与判定垂直是指两条直线或线段在交点处互相成直角的性质。
垂直的性质在几何证明中经常被用到,下面是关于垂直的一些性质和判定方法。
1. 垂直线性质:(1)垂直线上的对应角互补:如果两条垂直线被一条横截线所交,那么对应的角互补,即相互补充的角和为90度。
(2)垂直线上的内角相等:如果两条垂直线被一条横截线所交,那么内角相等,即相邻的内角相等。
2. 判定垂直线的方法:(1)两条线段垂直的充要条件是斜率乘积为-1:如果两条线段的斜率乘积为-1,那么它们是垂直的。
(2)两个向量垂直的充要条件是内积为0:如果两个向量的内积为0,那么它们是垂直的。
三、平行和垂直在实际中的应用平行和垂直的性质在日常生活和工程实践中有广泛的应用。
立体几何中的平行与垂直

立体几何中的平行与垂直1线面平行(1)定义直线与平面无交点.(2)判定定理如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.(3)性质定理一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行.2 面面平行(1)定义α∩β=∅⟹α|| β.(2)判定定理如果一个平面内的两条相交直线都平行于另一个平面,那么两个平面互相平行.(3)面面平行的性质(1) a⊂αα||β}⇒a||β (面面平行⇒线面平行)(2)α || βα∩γ=aβ∩ γ=b}⇒ a || b (面面平行⇒线线平行)(3) 夹在两个平行平面间的平行线段相等.3 线面垂直(1)定义若一条直线垂直于平面内的任意一条直线,则这条直线垂直于平面.符号表述:若任意a⊂α都有l⊥a,则 l⊥α.(2)判定定理如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.(3)性质定理垂直同一平面的两直线平行4 面面垂直(1) 定义若二面角α−l−β的平面角为90∘,则 α⊥β;(2) 判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.(3) 性质定理两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直.【例1】如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是()A.CC1与B1E是异面直线 B.AC⊥平面ABB1A1C.AE,B1C1为异面直线,且AE⊥B1C1 D.A1C1∥平面AB1E练习.1.如图是一几何体的平面展开图,其中四边形ABCD为正方形,△PDC,△PBC,△PAB,△PDA为全等的等边三角形,E、F分别为PA、PD的中点,在此几何体中,下列结论中错误的为()A.直线BE与直线CF共面 B.直线BE与直线AF是异面直线C.平面BCE⊥平面PAD D.面PAD与面PBC的交线与BC平行【例2】如图1,在△ABC中,∠ABC=90°,D为AC中点,AE⊥BD于E,延长AE交BC于F.将△ABD沿BD折起,得到三棱锥A1﹣BCD,如图2所示.(Ⅰ)若M是A1C的中点,求证:DM∥平面A1EF;(Ⅱ)若平面A1BD⊥平面BCD,试判断直线A1B与直线CD能否垂直?并说明理由.练习 2.如图,四边形ABCD为矩形,AD⊥平面ABE,F为CE上的点,且BF⊥平面ACE (Ⅰ)求证:AE⊥BE(Ⅱ)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.【例3】.如图,已知菱形AECD的对角线AC,DE交于点F,点E为的AB中点.将三角形ADE 沿线段DE折起到PDE的位置,如图2所示.(Ⅰ)求证:DE⊥平面PCF;(Ⅱ)证明:平面PBC⊥平面PCF;(Ⅲ)在线段PD,BC上是否分别存在点M,N,使得平面CFM∥平面PEN?若存在,请指出点M,N的位置,并证明;若不存在,请说明理由.练习3 .如图,直角三角形ABC中,A=60°,沿斜边AC上的高BD,将△ABD折起到△PBD的位置,点E在线段CD上.(1)求证:PE⊥BD;(2)过点D作DM⊥BC交BC于点M,点N为PB中点,若PE∥平面DMN,的值.求DEDC立体几何中的平行与垂直1线面平行(1)定义直线与平面无交点.(2)判定定理如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.(3)性质定理一条直线与一个平面平行,如果过该直线的平面与此平面相交,那么该直线与交线平行.2 面面平行(1)定义α∩β=∅⟹α|| β.(2)判定定理如果一个平面内的两条相交直线都平行于另一个平面,那么两个平面互相平行.(3)面面平行的性质(1) a⊂αα||β}⇒a||β (面面平行⇒线面平行)(2)α || βα∩γ=aβ∩ γ=b}⇒ a || b (面面平行⇒线线平行)(3) 夹在两个平行平面间的平行线段相等.3 线面垂直(1)定义若一条直线垂直于平面内的任意一条直线,则这条直线垂直于平面.符号表述:若任意a⊂α都有l⊥a,则 l⊥α.(2)判定定理如果一条直线与一个平面内的两条相交直线垂直,那么该直线与此平面垂直.(3)性质定理垂直同一平面的两直线平行4 面面垂直(1) 定义若二面角α−l−β的平面角为90∘,则 α⊥β;(2) 判定定理如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.(3) 性质定理两个平面垂直,如果一个平面内有一直线垂直于这两个平面的交线,那么这条直线与另一个平面垂直.【例1】如图,三棱柱ABC﹣A1B1C1中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是()A.CC1与B1E是异面直线 B.AC⊥平面ABB1A1C.AE,B1C1为异面直线,且AE⊥B1C1 D.A1C1∥平面AB1E解析 A不正确,因为CC1与B1E在同一个侧面中,故不是异面直线;B不正确,由题意知,上底面ABC是一个正三角形,故不可能存在AC⊥平面ABB1A1;C正确,因为AE,B1C1为在两个平行平面中且不平行的两条直线,故它们是异面直线;D不正确,因为A1C1所在的平面与平面AB1E相交,且A1C1与交线有公共点,故A1C1∥平面AB1E 不正确;故选:C.练习.1.如图是一几何体的平面展开图,其中四边形ABCD为正方形,△PDC,△PBC,△PAB,△PDA为全等的等边三角形,E、F分别为PA、PD的中点,在此几何体中,下列结论中错误的为()A.直线BE与直线CF共面 B.直线BE与直线AF是异面直线C.平面BCE⊥平面PAD D.面PAD与面PBC的交线与BC平行答案 C解析画出几何体的图形,如图,由题意可知,A,直线BE与直线CF共面,正确,因为E,F是PA与PD的中点,可知EF∥AD,所以EF∥BC,直线BE与直线CF是共面直线;B,直线BE与直线AF异面;满足异面直线的定义,正确.C,因为△PAB是等腰三角形,BE与PA的关系不能确定,所以平面BCE⊥平面PAD,不正确.D,∵AD∥BC,∴AD∥平面PBC,∴面PAD与面PBC的交线与BC平行,正确.故选:C.【例2】如图1,在△ABC中,∠ABC=90°,D为AC中点,AE⊥BD于E,延长AE交BC于F.将△ABD沿BD折起,得到三棱锥A1﹣BCD,如图2所示.(Ⅰ)若M是A1C的中点,求证:DM∥平面A1EF;(Ⅱ)若平面A1BD⊥平面BCD,试判断直线A1B与直线CD能否垂直?并说明理由.证明:(Ⅰ)取FC中点N.在图1中,由D,N分别为AC,FC中点,所以DN∥EF.在图2中,由M,N分别为A1C,FC中点,所以MN∥A1F,所以平面DMN∥平面A1EF,(5分)所以DM∥平面A1EF.解:(Ⅱ)直线A1B与直线CD不可能垂直.因为平面A1BD⊥平面BCD,EF⊂平面BCD,EF⊥BD,所以EF⊥平面A1BD,(8分)所以A1B⊥EF.假设有A1B⊥CD,注意到CD与EF是平面BCD内的两条相交直线,则有A1B⊥平面BCD.(1)(10分)又因为平面A1BD⊥平面BCD,A1E⊂平面A1BD,A1E⊥BD,所以A1E⊥平面BCD.(2)而(1),(2)同时成立,这显然与“过一点和已知平面垂直的直线只有一条”相矛盾,所以直线A1B与直线CD不可能垂直.练习 2.如图,四边形ABCD为矩形,AD⊥平面ABE,F为CE上的点,且BF⊥平面ACE (Ⅰ)求证:AE⊥BE(Ⅱ)设M在线段AB上,且满足AM=2MB,试在线段CE上确定一点N,使得MN∥平面DAE.证明:(Ⅰ)∵AD⊥平面ABE,AD∥BC,∴BC⊥平面ABE,∵AE⊂平面ABE,∴AE⊥BC,又∵BF⊥平面ACE,AE⊂平面ACE,∴AE⊥BF,∵BC∩BF=B,∴AE⊥平面BCE,又BE⊂平面BCE,∴AE⊥BE.(6分)解:(Ⅱ)在三角形ABE中过M点作MG∥AE交BE于G点,CE,在三角形BEC中过G点作GN∥BC交EC于N点,连MN,则由比例关系得CN=13∵MG∥AE MG⊄平面ADE,AE⊂平面ADE,∴MG∥平面ADE,同理,GN∥平面ADE,∴平面MGN∥平面ADE,又MN⊂平面MGN,∴MN∥平面ADE,∴N点为线段CE上靠近C点的一个三等分点.(12分)【例3】.如图,已知菱形AECD的对角线AC,DE交于点F,点E为的AB中点.将三角形ADE 沿线段DE折起到PDE的位置,如图2所示.(Ⅰ)求证:DE ⊥平面PCF ;(Ⅱ)证明:平面PBC ⊥平面PCF ;(Ⅲ)在线段PD ,BC 上是否分别存在点M ,N ,使得平面CFM ∥平面PEN ?若存在,请指出点M ,N 的位置,并证明;若不存在,请说明理由.【解答】证明:(Ⅰ)折叠前,因为四边形AECD 为菱形,所以AC ⊥DE ;所以折叠后,DE ⊥PF ,DE ⊥CF ,又PF∩CF=F,PF ,CF ⊂平面PCF ,所以DE ⊥平面PCF(Ⅱ)因为四边形AECD 为菱形,所以DC ∥AE ,DC=AE .又点E 为AB 的中点,所以DC ∥EB ,DC=EB .所以四边形DEBC 为平行四边形.所以CB ∥DE .又由(Ⅰ)得,DE ⊥平面PCF ,所以CB ⊥平面PCF .因为CB ⊂平面PBC ,所以平面PBC ⊥平面PCF .解:(Ⅲ)存在满足条件的点M ,N ,且M ,N 分别是PD 和BC 的中点.如图,分别取PD 和BC 的中点M ,N .连接EN ,PN ,MF ,CM .因为四边形DEBC 为平行四边形,所以EF ∥CN ,EF =12BC =CN .所以四边形ENCF 为平行四边形.所以FC ∥EN .在△PDE 中,M ,F 分别为PD ,DE 中点,所以MF ∥PE .又EN ,PE ⊂平面PEN ,PE∩EN=E,MF ,CF ⊂平面CFM ,所以平面CFM ∥平面PEN .练习3 .如图,直角三角形ABC 中,A=60°,沿斜边AC 上的高BD ,将△ABD 折起到△PBD 的位置,点E 在线段CD 上.(1)求证:PE ⊥BD ;(2)过点D 作DM ⊥BC 交BC 于点M ,点N 为PB 中点,若PE ∥平面DMN ,求DE DC 的值.解析 (1)∵BD 是AC 边上的高,∴BD ⊥CD ,BD ⊥PD ,又PD∩CD=D,∴BD ⊥平面PCD ,又PE ⊂平面PCD 中,∴BD ⊥PE ,即PE ⊥BD ;(2)如图所示,连接BE ,交DM 与点F ,∵PE ∥平面DMN ,∴PE ∥NF ,又点N 为PB 中点,∴点F 为BE 的中点;∴DF=12BE=EF ;又∠BCD=90°﹣60°=30°,∴△DEF 是等边三角形,设DE=a ,则BD=√3a ,DC=√3BD=3a ;∴DE DC =a 3a =13.。
3.1立体几何平行垂直有关定理总结
立体几何有关平行垂直定理总结 BHS
.
2.等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
3.推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等。
4.异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
5.两异面直线所成的角:过空间任意一点引两条直线分别平行(或重合)于两条异面直线,它们所成的锐角(或直角)。
范围为 ( 0°,90°]
6.斜线线与平面所成的角:平面的一条斜线和它在这个平面内的射影所成的锐角。
直线和平面所成角的取值范围为 [0°,90°]
7.二面角的平面角:以二面角的棱上任意一点为端点,在两个面内
分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角。
8.几何体的表面积和体积。
数学立体几何判定定理

一、判定两线平行的方法1.平行于同一直线的两条直线互相平行2.垂直于同一平面的两条直线互相平行3.如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和交线平行4.如果两个平行平面同时和第三个平面相交,那么它们的交线平行5.在同一平面内的两条直线,可依据平面几何的定理证明二、判定线面平行的方法1.据定义:如果一条直线和一个平面没有公共点2.如果平面外的一条直线和这个平面内的一条直线平行,则这条直线和这个平面平行3.两面平行,则其中一个平面内的直线必平行于另一个平面4.平面外的两条平行直线中的一条平行于平面,则另一条也平行于该平面5.平面外的一条直线和两个平行平面中的一个平面平行,则也平行于另一个平面三、判定面面平行的方法1.定义:没有公共点2.如果一个平面内有两条相交直线都平行于另一个平面,则两面平行3 垂直于同一直线的两个平面平行4.平行于同一平面的两个平面平行四、面面平行的性质1.两平行平面没有公共点2.两平面平行,则一个平面上的任一直线平行于另一平面3.两平行平面被第三个平面所截,则两交线平行4.垂直于两平行平面中一个平面的直线,必垂直于另一个平面五、判定线面垂直的方法1.定义:如果一条直线和平面内的任何一条直线都垂直,则线面垂直2.如果一条直线和一个平面内的两条相交线垂直,则线面垂直3.如果两条平行直线中的一条垂直于一个平面,则另一条也垂直于该平面4.一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面5.如果两个平面垂直,那么在一个平面内垂直它们交线的直线垂直于另一个平面6.如果两个相交平面都垂直于另一个平面,那么它们的交线垂直于另一个平面六、判定两线垂直的方法1.定义:成角2. 直线和平面垂直,则该线与平面内任一直线垂直3. 在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直4. 在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直5. 一条直线如果和两条平行直线中的一条垂直,它也和另一条垂直七、判定面面垂直的方法1. 定义:两面成直二面角,则两面垂直2. 一个平面经过另一个平面的一条垂线,则这个平面垂直于另一平面八、面面垂直的性质1. 二面角的平面角为2. 在一个平面内垂直于交线的直线必垂直于另一个平面3. 相交平面同垂直于第三个平面,则交线垂直于第三个平面。
立体几何平行与垂直所有概念、公理、定理汇总

立体几何的概念、公理、定理(一)立体几何三公理公理1:如果一条直线上的两点在一个平面内,那么这条直线上的所有的点都在这个平面内。
公理2:如果两个平面有一个公共点,那么它们有且只有一条通过这个点的公共直线.,A a A a公理3:经过不在同一直线上的三点,有且只有一个平面。
A、B、C不在同一直线上有且只有一个平面α,使A∈α,B∈α,C∈α推论1:经过一条直线和这条直线外的一点,有且只有一个平面。
A a 有且只有一个平面,使推论2:经过两条相交直线,有且只有一个平面。
a∩b=A有且只有一个平面,使推论3:经过两条平行直线,有且只有一个平面。
a∥b=A有且只有一个平面,使(二)空间直线公理4 :平行于同一条直线的两条直线互相平行。
a∥bb∥c等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等。
推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成的锐角(或直角)相等。
异面直线判定定理:用平面内一点与平面外一点的直线,与平面内不经过该点的直线是异面直线。
cbaaA∈a,B∈aA∈,B∈aA∈aababcba//a c////////AB A BAC A C///BAC B A CA∈PP(三)直线和平面直线和平面平行的判定定理:如果平面外一条直线和 这个平面内的一条直线平行,那么这条直线和这个平面平行。
直线和平面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。
定理 :如果两条平行直线中的一条直线垂直于一个平面,那么另一条直线也垂直这个平面。
定理:一条直线垂直于两个平行平面中的一个平面, 它也垂直于另一个平面。
直线与平面垂直的性质定理:如果两条直线同垂直于一个平面, 那么这两条直线平行。
射影定理:从平面外一点向这个平面所引的垂线段和斜线段中, (1)射影相等的两条斜线段相等,射影较长的斜线段也较长; (2)相等的斜线段的射影相等,较长的斜线段的射影也较长; (3)垂线段比任何一条斜线段都短。
立体几何平行与垂直的判定与性质

• 平行与垂直的基本概念 • 平行线的判定 • 垂直线的判定 • 平行与垂直的性质 • 立体几何平行与垂直的应用
目录
01
平行与垂直的基本概念
平行的定义
总结词
在立体几何中,如果两条直线在同一平面内,且永远不会相交,则这两条直线 被称为平行的。
详细描述
在平面几何中,两条平行线被定义为在同一平面内,且永远不会相交的两条直 线。这个定义在立体几何中同样适用。在三维空间中,两条平行线可能位于不 同的平面,但它们永远不会在任何平面上相交。
在三维建模软件中,平行和垂直关系 也是构建复杂几何体的基础。通过设 定平行或垂直的约束条件,可以确保 模型的准确性和一致性。
实际生活中的平行与垂直应用
在城市规划和建筑设计中,平行和垂直的应用同样广泛。例如,确定道路、建筑 物的位置和方向时,需要利用平行和垂直关系来确保规划的科学性和合理性。
在机械设计和制造中,平行和垂直关系也是非常重要的。例如,在制造精密仪器 或机械设备时,需要确保各个部件之间的平行和垂直关系,以保证设备的准确性 和稳定性。
总结词
平行和垂直是两种互为对立的几何关系,它 们在三维空间中共同构成了直线之间的基本 关系。
详细描述
平行和垂直是直线之间最重要的两种关系。 在三维空间中,除了平行和垂直之外,直线 之间还可以是斜交的。平行和垂直的对立关 系使得它们在解决几何问题时具有重要的作 用。例如,在建筑设计和工程实践中,垂直 关系常常用于确定物体的位置和方向,而平 行关系则常常用于确定物体的尺寸和比例。
详细描述
在立体几何中,如果两条直线被第三条直线所截,并且内错角相等,则这两条直 线平行。这是因为内错角相等说明两条直线在同一平面内,并且没有交点,因此 它们是平行的。
立体几何平面垂直的判定定理

立体几何平面垂直的判定定理一、定义在立体几何中,平面垂直的判定定理是指:如果两个平面的法线向量互相垂直,则这两个平面是垂直的。
二、判定方法根据平面的法线向量的定义,我们知道平面的法线向量是与该平面垂直的向量。
因此,要判断两个平面是否垂直,只需判断它们的法线向量是否互相垂直即可。
具体而言,设平面P1的法线向量为n1,平面P2的法线向量为n2,如果n1·n2 = 0,其中"·"表示向量的点积运算,那么平面P1与平面P2垂直;反之,如果n1·n2 ≠ 0,则两个平面不垂直。
三、相关应用平面垂直的判定定理在实际问题中有着广泛的应用。
以下是一些常见的应用场景:1. 建筑工程中的搭建在建筑工程中,平面垂直的判定定理被广泛应用于搭建建筑物的过程中。
例如,当建筑物的墙壁需要与地面垂直时,可以利用该定理判断墙壁的法线向量与地面的法线向量是否垂直,从而保证墙壁的竖直性。
2. 三维模型的设计在三维模型的设计过程中,平面垂直的判定定理常用于判断不同部位的平面是否垂直。
例如,当设计一个立方体时,可以利用该定理判断立方体的各个面是否相互垂直,从而确保模型的准确性。
3. 几何证明中的推理在几何证明中,平面垂直的判定定理是一种常用的推理方法。
通过运用该定理,可以推导出两个平面垂直的结论,然后应用于其他几何证明中。
四、总结立体几何平面垂直的判定定理是立体几何中的重要概念,能够帮助我们判断平面是否垂直。
通过判断两个平面的法线向量是否互相垂直,可以准确地判定平面的垂直性。
该定理在建筑工程、三维模型设计以及几何证明等领域都有着广泛的应用。
因此,掌握平面垂直的判定定理对于学习和应用立体几何都具有重要意义。
立体几何中平行与垂直证明方法归纳

a ∥
a∥
α
a a
β
3) 利用定义:直线在平面外,且直线与平面没有公共点
(三)平面与平面平行的证明
常见证明方法:
1) 利用平面与平面平行的判定定理: 一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
3
a ⊂ b ⊂
a ∩b P
a // b //
⇒ /性:如正方体的上下底面互相平行等
一条直线与一个平面内的两条相交直线都垂直,则该直线垂直于此平面。
a
b
ab
A
l
l a l b
l
b
Aa
4) 利用平面与平面垂直的性质定理: 两个平面垂直,则一个平面内垂直于交线的直线与另一个平面垂直。
5
l
a
a
a l
l
5) 利用常用结论:
① 一条直线平行于一个平面的一条垂线,则该直线也垂直于此平面。
在同一个平面内,垂直于同一条直线的两条直线互相平行。
8) 利用定义:在同一个平面内且两条直线没有公共点
(二)直线与平面平行的证明
1) 利用直线与平面平行的判定定理:
平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行。
a
a
b a∥
a∥b
b
2) 利用平面与平面平行的性质推论:
两个平面互相平行,则其中一个平面内的任一直线平行于另一个平面。
a b ba
b a
α
4) 利用平面与平面垂直的性质推论:
如果两个平面互相垂直,在这两个平面内分别作垂直于交线的直线,则这
两条直线互相垂直。
4
l a b al
bl
ab
β b
立体几何垂直判定定理

立体几何垂直判定定理立体几何垂直判定定理一、前言在立体几何中,垂直是一个非常重要的概念。
垂直关系不仅存在于平面内,也存在于空间中。
本文将介绍立体几何中的垂直判定定理。
二、定义在三维空间中,两条直线或两个平面互相垂直,当且仅当它们的方向向量互相垂直。
三、证明1. 两条直线的垂直判定对于两条不共面的直线l1和l2,它们互相垂直当且仅当它们的方向向量l1和l2满足以下条件:l1·l2=0(点乘为0)其中,“·”表示向量点乘运算。
证明如下:设l1的方向向量为a=(x1,y1,z1),l2的方向向量为b=(x2,y2,z2)。
则有:a·b=x1x2+y1y2+z1z2若a·b=0,则有x1x2+y1y2+z1z2=0。
这说明a与b互相垂直。
反之,若a与b互相垂直,则有a·b=0。
因此,两条不共面的直线互相垂直当且仅当它们的方向向量满足上述条件。
对于两条共面的直线,它们互相垂直当且仅当它们的方向向量l1和l2满足以下条件:l1·l2=0(点乘为0),且l1和l2不共线其中,“·”表示向量点乘运算。
证明如下:设l1的方向向量为a=(x1,y1,z1),l2的方向向量为b=(x2,y2,z2)。
则有:a·b=x1x2+y1y2+z1z2若a·b=0,则有x1x2+y1y2+z1z2=0。
这说明a与b互相垂直。
但是,如果a和b共线,则它们不可能互相垂直。
因此,我们需要加上一个限制条件:l1和l2不共线。
反之,若a与b互相垂直,且l1和l2不共线,则有a·b=0。
因此,两条共面的直线互相垂直当且仅当它们的方向向量满足上述条件。
综上所述,两条直线互相垂直当且仅当它们的方向向量满足上述条件。
2. 两个平面的垂直判定对于两个平面P1和P2,它们互相垂直当且仅当它们的法向量n1和n2满足以下条件:n1·n2=0(点乘为0)其中,“·”表示向量点乘运算。
高中数学知识点总结及公式大全立体几何中的平行与垂直问题

高中数学知识点总结及公式大全立体几何中的平行与垂直问题高中数学知识点总结及公式大全:立体几何中的平行与垂直问题在高中数学中,几何是一个重要的分支,而立体几何更是其中的重要内容之一。
在立体几何中,平行和垂直是我们经常遇到的问题。
本文将对高中数学中的立体几何知识点进行总结,并提供一些常用的公式。
一、平行与垂直的概念在几何中,平行和垂直是两个基本的关系。
平行指的是两条直线永远不会相交的情况,可以想象成两条铁轨永远平行。
垂直则指的是两条直线相互成直角,可以想象成两根彼此垂直的木棍。
二、平行与垂直的判定方法1. 平行关系的判定方法:(1) 同位角相等定理:如果两条直线被一组相交线段所切割,且这些相交线段的对应角相等,则这两条直线是平行的。
(2) 平行线的性质定理:如果一条直线上的两个点分别与另一条直线上的两个点相连,且相连的线段互相平行,则这两条直线是平行的。
(3) 平行线的判定定理:如果两条直线的斜率相等且不相交,则这两条直线是平行的。
2. 垂直关系的判定方法:(1) 两条直线相交且相交角为90度,则这两条直线是垂直的。
(2) 垂直线的性质定理:如果一条直线与另一条直线相互垂直,且这两条直线各自还与第三条直线相交,则第三条直线与这两条直线也是垂直的。
(3) 垂直线的判定定理:如果两条直线的斜率互为负倒数,则这两条直线是垂直的。
三、常用公式在立体几何中,我们经常使用一些公式来求解问题。
下面是一些常用的公式:1. 立方体的表面积公式:立方体的表面积等于6倍的边长平方。
2. 立方体的体积公式:立方体的体积等于边长的立方。
3. 正方体的表面积公式:正方体的表面积等于6倍的边长平方。
4. 正方体的体积公式:正方体的体积等于边长的立方。
5. 圆柱体的表面积公式:圆柱体的表面积等于2πr² + 2πrh,其中r为底面半径,h为高。
6. 圆柱体的体积公式:圆柱体的体积等于πr²h,其中r为底面半径,h为高。
立体几何线面垂直的证明

立体几何证明【知识梳理】1.直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行⇒线面平行”)相交,那么这条直线和交线平行.(“线面平行⇒线线平行”)2..直线与平面垂直判定定理一如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直⇒线面垂直”)判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.性质1.如果一条直线垂直于一个平面,那么这条直线垂直于这个平面内的所有直线。
(线面垂直⇒线线垂直)性质2:如果两条直线同垂直于一个平面,那么这两条直线平行.三。
平面与平面空间两个平面的位置关系:相交、平行.1.平面与平面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(“线面平行⇒面面平行”)2. 两个平面垂直判定定理:如果一条直线与一个平面垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直⇒面面垂直”)性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.(面面垂直⇒线面垂直)知识点一 【例题精讲】1.在棱长为2的正方体1111D C B A ABCD -中,E 、F 分别为1DD 、DB 的中点。
(1)求证:EF//平面11D ABC ;(2)求证: 平面B 11D C C B 1⊥ EF C B 1⊥; (3)求三棱锥EFC B -1的体积V.2.如图所示, 四棱锥P -ABCD 底面是直角梯形,,,2,BA AD CD AD CD AB PA ⊥⊥=⊥底面ABCD , E 为PC 的中点, PA =AD =AB =1. (1)证明: //EB PAD 平面; (2)证明: BE PDC ⊥平面; (3)求三棱锥B -PDC 的体积V .3、如图所示,在四棱锥P﹣ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点,证明:(1)AE⊥CD(2)PD⊥平面ABE.4、.如图,三棱柱ABC﹣A1B1C1中,CA=CB,AB=AA1,∠BAA1=60°(Ⅰ)证明:AB⊥A1C;练习1、如图,菱形ABCD与等边△PAD所在的平面相互垂直,AD=2,∠DAB=60°.(Ⅰ)证明:AD⊥PB;(Ⅱ)求三棱锥C﹣PAB的高.2.如图14所示,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F,G分别为AC,DC,AD的中点.求证:EF⊥平面BCG;3.如图11所示,三棱柱ABCA1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.(1)证明:AC1⊥A1B;4、如图,在三棱台ABC﹣DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.(Ⅰ)求证:BF⊥平面ACFD;(Ⅱ)求直线BD与平面ACFD所成角的余弦值.5、三棱锥P﹣ABC中,∠BAC=90°,PA=PB=PC=BC=2AB=2,(1)求证:面PBC⊥面ABC6.已知四棱锥P-ABCD中,底面四边形为正方形,侧面PDC为正三角形,且平面PDC⊥底面ABCD,E为PC的中点.(1)求证:PA∥平面EDB;(2)求证:平面EDB⊥平面PBC;7、如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAB⊥平面ABCD,PA⊥PB,BP=BC,E为PC的中点.(1)求证:AP∥平面BDE;2.求证BE 垂直平面PAC8、将如图一的矩形ABMD沿CD翻折后构成一四棱锥M﹣ABCD(如图二),若在四棱锥M﹣ABCD中有MA=.(1)求证:AC⊥MD;(2)求四棱锥M﹣ABCD的体积.作业1、如图1,菱形ABCD的边长为12,∠BAD=60°,AC交BD于点O.将菱形ABCD沿对角线AC折起,得到三棱锥B﹣ACD,点M,N分别是棱BC,AD 的中点,且DM=6.(Ⅰ)求证:OD⊥平面ABC;2、如图,在斜三棱柱ABC﹣A1B1C1中,O是AC的中点,A1O⊥平面ABC,∠BCA=90°,AA1=AC=BC.(Ⅰ)求证:A1B⊥AC1;3、如图所示,四棱锥P﹣ABCD的侧面PAD是边长为2的正三角形,底面ABCD 是∠ABC=60°的菱形,M为PC的中点,PC=.(Ⅰ)求证:PC⊥AD;AD,E,4、如图,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=12F分别为线段AD,PC的中点.(Ⅰ)求证:AP∥平面BEF;(Ⅱ)求证:BE⊥平面PAC.5、如图,四棱锥S﹣ABCD中,AB∥CD,BC⊥CD,侧面SAB为等边三角形.AB=BC=2,CD=1,SD=.(1)证明:CD⊥SD;6.如图,四棱锥S ﹣ABCD 中,△ABD 是正三角形,CB=CD ,SC ⊥BD .(Ⅰ)求证:SB=SD ;(Ⅱ)若∠BCD=120°,M 为棱SA 的中点,求证:DM ∥平面SBC .7、如图,在矩形ABCD 中,点E 为边AD 上的点,点F 为边CD 的中点,234A E D B A A ===,现将ABE ∆沿BE 边折至PBE ∆位置,且平面PBE ⊥平面BCDE .(1)求证:平面PBE ⊥平面PEF ;8、如图5.在椎体P-ABCD 中,ABCD 是边长为1的棱形, 且∠DAB=60︒,2PA PD ==,PB=2,E,F 分别是BC,PC 的中点.(1) 证明:AD ⊥平面DEF;AB CDEBCDEFP9、在如图所示的多面体ABCDEF 中,ABCD 为直角梯形,//AB CD ,90DAB ∠=︒,四边形ADEF 为等腰梯形,//EF AD ,已知AE EC ⊥,2AB AF EF ===,4AD CD ==.(Ⅰ)求证:平面ABCD ⊥平面ADEF10.如图,在底面为平行四边形的四棱锥P ABCD -中,AB AC ⊥,PA ⊥平面ABCD ,且PA AB =,点E 是PD 的中点. (Ⅱ)求证://PB 平面AEC ;11.棱长为2的正方体ABCD﹣A1B1C1D1中,M是棱AA1的中点,过C、M、D1作正方体的截面,则截面的面积是。
高中数学 -空间立体几何中的平行、垂直证明定理总结 (1)

l n
☺ 简称:线线垂直,线面垂直.
复习定理
空间中的垂直
2.直线与平面垂直性质
判定:如果一条直线和一个平面垂直,则称这条直线和这 个平面内任意一条直线都垂直.
l m
l
m
☺ 简称:线面垂直,线线垂直.
复习定理
空间中的垂直
3.平面与平面垂直判定
判定:如果一个平面经过另一个平面的一条垂线,则这两个 平面互相垂直.
(1)求证:BC1∥平面 CA1D; (2)求证:平面 CA1D⊥平面 AA1B1B. 证明:(1)连结AC1交A1C于E,连结DE.
∵AA1C1C为矩形,则E为AC1的中点. 又D是AB的中点,
∴在△ABC1中,DE∥BC1.
E
又DE⊂平面CA1D,
BC1⊄平面CA1D,
∴BC1∥平面CA1D.
证明:(2)∵AC=BC, D为AB的中点, ∴在△ABC中,AB⊥CD.
空间中的平行与垂直 定理总结
复习定理
空间中的平行
1.直线与平面平行的判定
平面外一条直线与此平面内的一条直线平行,则 该直线与此平面平行.
a
b
a
//
b
a // b
☺ 简称:线线平行,线面平行.
复习定理
空间中的平行
2.直线与平面平行的性质
一条直线与一个平面平行,则过这条直线的任一 平面与此平面的交线与该直线平行.
①若m⊥α,n∥α,则m⊥n;②若α⊥γ,β⊥γ,
则α∥β;
③若m∥α,n∥α,则m∥n;④若α∥β,β∥γ,
m⊥α,则m⊥γ.
正确的命题是( C)
A.①③
B.②③
C.①④
D.②④
解析 ②中平面α与β可能相交,③中m与n可以
立体几何判定平行垂直的20个判定定理
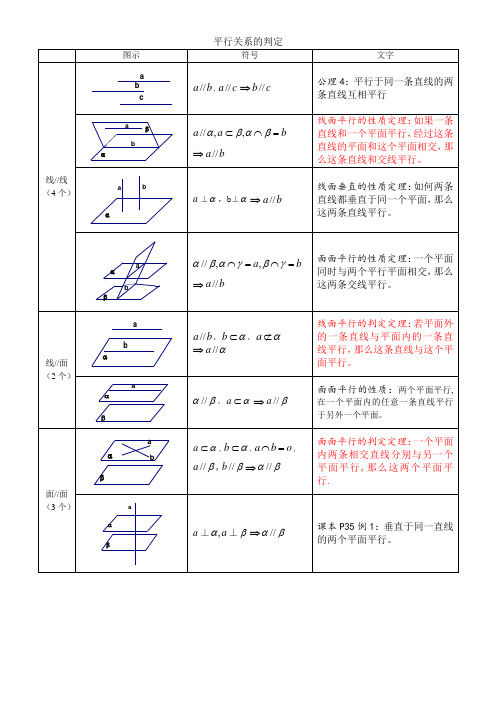
平行直线和平面的距离
平行平面间距离
X
⊥ , b⊥
线面垂直的性质:由线Hale Waihona Puke 平行得线面垂直。⊥ , ⊥
面面平行的性质:由面面平行得线面垂直。
面⊥面
(2个)
,
面面垂直的判定定理:一个平面经过另外一个平面的垂线,则这两个平面互相垂直。
, ⊥
补充:如果一个平面与另一个平面的垂线平行,那么这两个平面互相垂直。
平面的基本性质
基本性质
图示
作用
公理1:如果一条直线上的两个点在一个平面内,那么这条直线上所有点都在这个平面内.
线面垂直的性质定理:一条直线若垂直于一平面,则直线垂直于这个平面内任意一条直线。
c
⊥ , ⊥
两条平行直线,一条垂直第三条直线,则另一条也垂直于第三条直线。
补充:三个两两垂直的平面的交线垂直
线⊥面
(4个)
,
,
线面垂直的判定定理:一条直线与平面内两条相交直线都相交,那么这条直线与这个平面垂直。
, ,
⊥
面面垂直的性质定理:两个平面垂直,在第一个平面内垂直于交线的直线垂直于另一个平面。
线//面
(2个)
, ,
线面平行的判定定理:若平面外的一条直线与平面内的一条直线平行,那么这条直线与这个平面平行。
,
面面平行的性质:两个平面平行,在一个平面内的任意一条直线平行于另外一个平面。
面//面
(3个)
, , ,
,
面面平行的判定定理:一个平面内两条相交直线分别与另一个平面平行,那么这两个平面平行.
⊥ ⊥
课本P35例1:垂直于同一直线的两个平面平行。
,
补充:平行于同一平面的两个平面平行。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2个)
, ,
线面平行的判定定理:若平面外的一条直线与平面内的一条直线平行,那么这条直线与这个平面平行。
,
面面平行的性质:两个平面平行,在一个平面内的任意一条直线平行于另外一个平面。
面//面
(3个)
, , ,
,
面面平行的判定定理:一个平面内两条相交直线分别与另一个平面平行,那么这两个平面平行.
⊥ ⊥
课本P35例1:垂直于同一直线的两个平面平行。
,
补充:平行于同一平面的两个平面平行。
平行关系的判定
垂直关系的判定
图示
符号
文字
线⊥线
(5个)
⊥ , , ⊥
⊥
三垂线定理:平面内一直线若与斜线的射影垂直则它与斜线垂直。
⊥ , , ⊥
⊥
三垂线定理的逆定理:平面内一直线若与斜线垂直则与斜线的射影垂直。
⊥ ,
⊥ , b, ⊥
面面平行的性质:由面面平行得线面垂直。
面⊥面
(2个)
,
面面垂直的判定定理:一个平面经过另外一个平面的垂线,则这两个平面互相垂直。
, ⊥
补充:如果一个平面与另一个平面的垂线平行,那么这两个平面互相垂直。
平面的基本性质
基本性质
图示
作用
公理1:如果一条直线上的两个点在一个平面内,那么这条直线上所有点都在这个平面内.
平行直线和平面的距离
平行平面间距离
线面垂直的性质定理:一条直线若垂直于一平面,则直线垂直于这个平面内任意一条直线。
c
⊥ , ⊥
两条平行直线,一条垂直第三条直线,则另一条也垂直于第三条直线。
补充:三个两两垂直的平面的交线垂直
线⊥面
(4个)
,
,
线面垂直的判定定理:一条直线与平面内两条相交直线都相交,那么这条直线与这个平面垂直。
, ,
⊥
面面垂直的性质定理:两个平面垂直,在第一个平面内垂直于交线的直线垂直于另一个平面。
异面直线所成的角:作 , , 所成的角(锐角或直角)为异面直线所成的角
直线与平面所成的角:a’是a在平面上的射影,a与a’所成锐角为直线与平面所成的角。
二面角的平面角:O在棱上,OA在α内,OA⊥棱,OB在β内,OB⊥棱,∠AOB是二面角的平面角。
范围
空间距离
距离图示
定义
两平行直线间的距离
异面直线间的距离:两条异面直线的公垂线段的长度。
判断线在面内的依据
公理2:如果两个平面有一个公共点,那么它们有且仅有一条通过这个点的公共直线.
判断两个平面相交的依据;证明点在线上的依据;确定交线位置
公理3:经过不在同一直线上的三点有且仅有一个平面.
确定一个平面的依据
空间角
平面图形
空间图形
异面直线
直线和平面
两个平面
夹角图示
定义
由一点出发的两条射线组成的图形
平行关系的判定
图示
符号
文字
线//线
(4个)
,
公理4:平行于同一条直线的两条直线互相平行
线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
⊥ ,b⊥
线面垂直的性质定理:如何两条直线都垂直于同一个平面,那么这两条直线平行。
面面平行的性质定理:一个平面同时与两个平行平面相交,那么这两条交线平行。
