Maple常用函数

微分方程的maple求解

微分⽅程的maple求解1、常⽤函数1)求解常微分⽅程的命令dsolve.dsolve(常微分⽅程)dsolve(常微分⽅程，待解函数，选项)dsolve({常微分⽅程，初值}，待解函数，选项)dsolve({常微分⽅程组，初值}，{待解函数}，选项)其中选项设置解得求解⽅法和解的表⽰⽅式。

求解⽅法有type=formal_series(形式幂级数解)、type=formal_solution(形式解)、type=numeric(数值解)、type=series(级数解)、method=fourier(通过Fourier变换求解)、method=laplace(通过Laplace变换求解)等。

解的表⽰⽅式有explicit(显式)、implicit(隐式)、parametric(参数式)。

当⽅程⽐较复杂时，要想得到显式解通常⼗分困难，结果也会相当复杂。

这时，⽅程的隐式解更为有⽤，⼀般也要简单得多。

dsolve为标准库函数。

2)求解⼀阶线性常微分⽅程的命令linearsol.在Maple中求解⼀阶线性⽅程既可以⽤dsolve函数求解，也可以⽤Detools函数包中的linearsol函数求解。

linearsol是专门求解线性微分⽅程的命令，使⽤格式为: linearsol(线性⽅程，待解函数)linearsol的返回值为集合形式的解。

3)偏微分⽅程求解命令pdsolve.pdsolve(偏微分⽅程，待解变量，选项)pdsolve(偏微分⽅程，初值或边界条件，选项)pdsolve为标准库函数，可直接使⽤。

如果求解成功，将得到⼏种可能结果：⽅程的通解；拟通解(包含有任意函数，但不⾜以构造通解)；⼀些常微分⽅程的集合；2、⽅法1)⼀阶常微分⽅程的解法a 分离变量法 I 直接分离变量法。

如()()dyf xg y dx=，⽅程右端是两个分别只含x 或y 的函数因式乘积，其通解为()()dyf x dx Cg y =+?。

maple基本函数

第1章章数1.1 复数Re,Im - 返回复数型表达式的实部/虚部abs - 绝对值函数argument - 复数的幅角函数conjugate - 返回共轭复数csgn - 实数和复数表达式的符号函数signum - 实数和复数表达式的sign 函数51.2 MAPLE 常数已知的变量名称指数常数（以自然对数为底）I - x^2 = -1 的根infinity 无穷大1.3 整数函数! - 阶乘函数irem, iquo - 整数的余数/商isprime - 素数测试isqrfree - 无整数平方的因数分解max, min - 数的最大值/最小值mod, modp, mods - 计算对 m 的整数模rand - 随机数生成器randomize - 重置随机数生成器1.4 素数Randpoly, Randprime - 有限域的随机多项式/首一素数多项式ithprime - 确定第 i 个素数nextprime, prevprime - 确定下一个最大/最小素数1.5 数的进制转换convert/base - 基数之间的转换convert/binary - 转换为二进制形式convert/decimal - 转换为 10 进制convert/double - 将双精度浮点数由一种形式转换为另一种形式convert/float - 转换为浮点数convert/hex - 转换为十六进制形式convert/metric - 转换为公制单位convert/octal - 转换为八进制形式1.6 数的类型检查type - 数的类型检查函数第2章初等数学2.1 初等函数product - 确定乘积求和不确定乘积exp - 指数函数sum - 确定求和不确定求和sqrt - 计算平方根算术运算符+, -, *, /, ^add, mul - 值序列的加法/乘法2.2 三角函数arcsin, arcsinh, . - 反三角函数/反双曲函数sin, sinh, . - 三角函数/双曲函数2.3 LOGARITHMS 函数dilog - Dilogarithm 函数ln, log, log10 - 自然对数/一般对数，常用对数2.4 类型转换convert/`+`,convert/`*` - 转换为求和/乘积convert/hypergeom - 将求和转换为超越函数convert/degrees - 将弧度转换为度convert/expsincos - 将trig 函数转换为exp, sin, cosconvert/Ei - 转换为指数积分convert/exp - 将trig 函数转换为指数函数convert/ln - 将arctrig 转换为对数函数polar - 转换为极坐标形式convert/radians - 将度转换为弧度convert/sincos - 将trig 函数转换为sin, cos, sinh, cosh convert/tan - 将trig 函数转换为tanconvert/trig - 将指数函数转换为三角函数和双曲函数第3章求值3.1 假设功能3.2 求值Eval - 对一个表达式求值eval - 求值evala - 在代数数（或者函数）域求值evalb - 按照一个布尔表达式求值evalc - 在复数域上符号求值evalf - 使用浮点算法求值evalhf - 用硬件浮点数算法对表达式求值evalm - 对矩阵表达式求值evaln - 求值到一个名称evalr, shake - 用区间算法求表达式的值和计算范围evalrC - 用复数区间算法对表达式求值value - 求值的惰性函数第4章求根，解方程4.1 数值解fsolve - 利用浮点数算法求解solve/floats - 包含浮点数的表达式4.2 最优化extrema - 寻找一个表达式的相对极值minimize, maximize - 计算最小值/最大值maxnorm - 一个多项式无穷大范数4.3 求根allvalues -计算含有RootOfs的表达式的所有可能值isqrt, iroot - 整数的平方根/第n 次根realroot - 一个多项式的实数根的隔离区间root - 一个代数表达式的第n 阶根RootOf - 方程根的表示surd - 非主根函数roots - 一个多项式对一个变量的精确根turm, sturmseq - 多项式在区间上的实数根数和实根序列4.4 解方程eliminate - 消去一个方程组中的某些变量isolve - 求解方程的整数解solvefor - 求解一个方程组的一个或者多个变量isolate - 隔离一个方程左边的一个子表达式singular - 寻找一个表达式的极点solve/identity - 求解包含属性的表达式solve/ineqs - 求解不等式solve/linear - 求解线性方程组solve/radical - 求解含有未知量根式的方程solve/scalar - 标量情况（单变量和方程）solve/series - 求解含有一般级数的方程solve/system - 解方程组或不等式组第5章操作表达式5.1 处理表达式Norm - 代数数 (或者函数) 的标准型Power - 惰性幂函数Powmod -带余数的惰性幂函数Primfield - 代数域的原始元素Trace - 求一个代数数或者函数的迹charfcn - 表达式和集合的特征函数Indets - 找一个表达式的变元invfunc - 函数表的逆powmod - 带余数的幂函数Risidue - 计算一个表达式的代数余combine - 表达式合并(对tan,cot不好用)expand - 表达式展开Expand - 展开表达式的惰性形式expandoff/expandon - 抑制/不抑制函数展开5.2 因式分解Afactor - 绝对因式分解的惰性形式Afactors - 绝对因式分解分解项列表的惰性形式Berlekamp - 因式分解的Berlekamp 显式度factor - 多元的多项式的因式分解factors - 多元多项式的因式分解列表Factor - 函数factor 的惰性形式Factors - 函数factors 的惰性形式polytools[splits] - 多项式的完全因式分解第6章化简6.1 表达式化简118simplify - 给一个表达式实施化简规则simplify/@ - 利用运算符化简表达式simplify/Ei - 利用指数积分化简表达式simplify/GAMMA - 利用GAMMA 函数进行化简simplify/RootOf - 用RootOf 函数化简表达式simplify/wronskian - 化简含wronskian 标识符的表达式simplify/hypergeom - 化简超越函数表达式simplify/ln - 化简含有对数的表达式simplify/piecewise - 化简分段函数表达式simplify/polar - 化简含有极坐标形式的复数型表达式simplify/power - 化简含幂次的表达式simplify/radical - 化简含有根式的表达式simplify/rtable - 化简rtable 表达式simplify/siderels - 使用关系式进行化简simplify/sqrt - 根式化简simplify/trig - 化简trig 函数表达式simplify/zero - 化简含嵌入型实数和虚数的复数表达式6.2 其它化简操作Normal - normal 函数的惰性形式convert - 将一个表达式转换成不同形式radnormal - 标准化一个含有根号数的表达式rationalize - 分母有理化第7章操作多项式7.0 MAPLE 中的多项式简介7.1 提取coeff - 提取一个多项式的系数coeffs - 提取多元的多项式的所有系数coeftayl - 多元表达式的系数lcoeff, tcoeff - 返回多元多项式的首项和末项系数7.2 多项式约数和根gcd, lcm - 多项式的最大公约数/最小公倍数psqrt, proot - 多项式的平方根和第n次根rem,quo - 多项式的余数/商7.3 操纵多项式convert/horner - 将一个多项式转换成Horner形式collect - 象幂次一样合并系数compoly - 确定一个多项式的可能合并的项数convert/polynom - 将级数转换成多项式形式convert/mathorner - 将多项式转换成Horner矩阵形式convert/ratpoly - 将级数转换成有理多项式sort - 将值的列表或者多项式排序sqrfree - 不含平方项的因数分解函数7.4 多项式运算discrim - 多项式的判别式fixdiv - 计算多项式的固定除数norm - 多项式的标准型resultant - 计算两个多项式的终结式bernoulli - Bernoulli 数和多项式bernstein - 用Bernstein多项式近似一个函数content, primpart - 一个多元的多项式的内容和主部degree, ldegree - 一个多项式的最高次方/最低次方divide - 多项式的精确除法euler - Euler 数和多项式icontent - 多项式的整数部分interp - 多项式的插值prem, sprem - 多项式的pseudo 余数和稀疏pseudo 余数randpoly - 随机多项式生成器spline - 计算自然样条函数第8章有理表达式8.0 有理表达式简介8.1 操作有理多项式numer,denom - 返回一个表达式的分子/分母frontend - 将一般的表达式处理成一个有理表达式normal - 标准化一个有理表达式convert/parfrac - 转换为部分分数形式convert/rational - 将浮点数转换为接近的有理数ratrecon - 重建有理函数第9章微积分9.1 取极限Limit, limit - 计算极限limit[dir] - 计算方向极限limit[multi] - 多重方向极限limit[return] - 极限的返回值9.2 连续性测试discont - 寻找一个函数在实数域上的间断点fdiscont - 用数值法寻找函数在实数域上的间断点iscont - 测试在一个区间上的连续性9.3 微分计算D - 微分算子D, diff - 运算符D 和函数diffdiff, Diff - 微分或者偏微分convert/D - 将含导数表达式转换为D运算符表达式convert/diff - 将D(f)(x)表达式转换为diff(f(x),x)的形式implicitdiff - 由一个方程定义一个函数的微分9.4 积分计算Si, Ci …- 三角和双曲积分Dirac, Heaviside - Dirac 函数/Heaviside阶梯函数Ei - 指数积分Elliptic - 椭圆积分FresnelC, … - Fresnel 正弦,余弦积分和辅助函数int, Int - 定积分和不定积分LegendreP, …- Legendre 函数及其第一和第二类函数Li - 对数积分student[changevar] - 变量代换dawson - Dawson 积分ellipsoid - 椭球体的表面积evalf(int) - 数值积分intat, Intat - 在一个点上积分求值第10章微分方程10.1 微分方程分类odeadvisor - ODE-求解分析器DESol - 表示微分方程解的数据结构pdetest - 测试pdsolve 能找到的偏微分方程(PDEs)解10.2 常微分方程求解dsolve - 求解常微方程(ODE)dsolve - 用给定的初始条件求解ODE 问题dsolve/inttrans - 用积分变换方法求解常微分方程dsolve/numeric - 常微方程数值解dsolve/piecewise - 带分段系数的常微方程求解dsolve - 寻找ODE 问题的级数解dsolve - 求解ODEs 方程组odetest - 从ODE 求解器中测试结果是显式或者隐式类型10.3 偏微分方程求解pdsolve - 寻找偏微分方程 (PDEs) 的解析解第11章数值计算11.1 MAPLE 中的数值计算环境IEEE 标准和Maple数值计算数据类型特殊值环境变量11.2 算法标准算法复数算法含有0，无穷和未定义数的算法11.3 数据构造器254complex - 复数和复数构造器Float, …- 浮点数及其构造器Fraction - 分数及其的构造器integer - 整数和整数构造器11.4 MATLAB 软件包简介11.5 “”区间类型表达式第12章级数12.1 幂级数的阶数Order - 阶数项函数order - 确定级数的截断阶数12.2 常见级数展开series - 一般的级数展开taylor - Taylor 级数展开mtaylor - 多元Taylor级数展开poisson - Poisson级数展开.26812.3 其它级数eulermac - Euler-Maclaurin求和piecewise - 分段连续函数asympt - 渐进展开第13章特殊函数AiryAi, AiryBi - Airy 波动函数AiryAiZeros, AiryBiZeros - Airy函数的实数零点AngerJ, WeberE - Anger函数和Weber函数BesselI, HankelH1, …- Bessel函数和Hankel函数BesselJZeros, … - Bessel函数实数零点Beta - Beta函数EllipticModulus - 模数函数k(q)GAMMA, lnGAMMA - 完全和不完全Gamma函数GaussAGM - Gauss 算术的几何平均数JacobiAM, ., - Jacobi 振幅函数和椭圆函数JacobiTheta1, JacobiTheta4 - Jacobi theta函数JacobiZeta - Jacobi 的Zeta函数KelvinBer, KelvinBei - Kelvin函数KummerM, - Kummer M函数和U函数LambertW - LambertW函数LerchPhi - 一般的Lerch Phi函数LommelS1, LommelS2 - Lommel函数MeijerG - 一个修正的Meijer G函数Psi - Digamma 和Polygamma函数StruveH, StruveL - Struve函数WeierstrassP - Weierstrass P函数及其导数WhittakerM - Whittaker 函数Zeta - Zeta 函数erf, … - 误差函数，补充的误差函数和虚数误差函数harmonic - 调和函数hypergeom - 广义的超越函数pochhammer - 一般的pochhammer函数polylog - 一般的polylogarithm函数第14章线性代数14.1 ALGEBRA（代数）中矩阵，矢量和数组14.2 LINALG 软件包简介14.3 数据结构矩阵matrices（小写）矢量vectors（矢量）convert/matrix - 将数组，列表，Matrix 转换成matrixconvert/vector - 将列表，数组或Vector 转换成矢量vectorlinalg[matrix] - 生成矩阵matrix（小写）linalg[vector] - 生成矢量vector（小写）14.4 惰性函数Det - 惰性行列式运算符Eigenvals - 数值型矩阵的特征值和特征向量Hermite, Smith - 矩阵的Hermite 和Smith 标准型14.5 LinearAlgebra函数Matrix 定义矩阵Add 加/减矩阵Adjoint 伴随矩阵BackwardSubstitute 求解 A . X = B，其中 A 为上三角型行阶梯矩阵BandMatrix 带状矩阵Basis 返回向量空间的一组基SumBasis 返回向量空间直和的一组基IntersectionBasis 返回向量空间交的一组基BezoutMatrix 构造两个多项式的Bezout 矩阵BidiagonalForm 将矩阵约化为双对角型CharacteristicMatrix 构造特征矩阵CharacteristicPolynomial 构造矩阵的特征多项式CompanionMatrix 构造一个首一（或非首一）多项式或矩阵多项式的友矩阵（束）ConditionNumber 计算矩阵关于某范数的条件数ConstantMatrix 构造常数矩阵ConstantVector 构造常数向量Copy 构造矩阵或向量的一份复制CreatePermutation 将一个 NAG 主元向量转换为一个置换向量或矩阵CrossProduct 向量的叉积`&x` 向量的叉积DeleteRow 删除矩阵的行DeleteColumn 删除矩阵的列Determinant 行列式Diagonal 返回从矩阵中得到的向量序列DiagonalMatrix 构造（分块）对角矩阵Dimension 行数和列数DotProduct 点积BilinearForm 向量的双线性形式EigenConditionNumbers 计算数值特征值制约问题的特征值或特征向量的条件数Eigenvalues 计算矩阵的特征值Eigenvectors 计算矩阵的特征向量Equal 比较两个向量或矩阵是否相等ForwardSubstitute 求解 A . X = B，其中 A 为下三角型行阶梯矩阵FrobeniusForm 将一个方阵约化为 Frobenius 型（有理标准型）GaussianElimination 对矩阵作高斯消元ReducedRowEchelonForm 对矩阵作高斯－约当消元GetResultDataType 返回矩阵或向量运算的结果数据类型GetResultShape 返回矩阵或向量运算的结果形状GivensRotationMatrix 构造Givens 旋转的矩阵GramSchmidt 计算一个正交向量集HankelMatrix 构造一个Hankel 矩阵HermiteForm 计算一个矩阵的 Hermite 正规型HessenbergForm 将一个方阵约化为上Hessenberg 型HilbertMatrix 构造广义 Hilbert 矩阵HouseholderMatrix 构造 Householder 反射矩阵IdentityMatrix 构造一个单位矩阵IsDefinite 检验矩阵的正定性，负定性或不定性IsOrthogonal 检验矩阵是否正交IsUnitary 检验矩阵是否为酉矩阵IsSimilar 确定两个矩阵是否相似JordanBlockMatrix 构造约当块矩阵JordanForm 将矩阵约化为约当型KroneckerProduct 构造两个矩阵的Kronecker 张量积LeastSquares 方程的最小二乘解LinearSolve 求解线性方程组 A . x = bLUDecomposition 计算矩阵的 Cholesky，PLU 或 PLU1R 分解Map 将一个程序映射到一个表达式上，对矩阵和向量在原位置上进行处理MatrixAdd 计算两个矩阵的线性组合VectorAdd 计算两个向量的线性组合MatrixExponential 确定一个矩阵 A 的矩阵指数 exp(A)MatrixFunction 确定方阵 A 的函数F(A)MatrixInverse 计算方阵的逆或矩阵的Moore-Penrose 伪逆MatrixMatrixMultiply 计算两个矩阵的乘积MatrixVectorMultiply 计算一个矩阵和一个列向量的乘积VectorMatrixMultiply 计算一个行向量和一个矩阵的乘积MatrixPower 矩阵的幂MinimalPolynomial 构造矩阵的最小多项式Minor 计算矩阵的子式Multiply 矩阵相乘Norm 计算矩阵或向量的p-范数MatrixNorm 计算矩阵的p-范数VectorNorm 计算向量的p-范数Normalize 向量正规化NullSpace 计算矩阵的零度零空间OuterProductMatrix 两个向量的外积Permanent 方阵的不变量Pivot 矩阵元素的主元消去法PopovForm Popov 正规型QRDecomposition QR 分解RandomMatrix 构造随机矩阵RandomVector 构造随机向量Rank 计算矩阵的秩Row 返回矩阵的一个行向量序列Column 返回矩阵的一个列向量序列RowOperation 对矩阵作初等行变换ColumnOperation 对矩阵作出等列变换RowSpace 返回矩阵行空间的一组基ColumnSpace 返回矩阵列空间的一组基ScalarMatrix 构造一个单位矩阵的数量倍数ScalarVector 构造一个单位向量的数量倍数ScalarMultiply 矩阵与数的乘积MatrixScalarMultiply 计算矩阵与数的乘积VectorScalarMultiply 计算向量与数的乘积SchurForm 将方阵约化为 Schur 型SingularValues 计算矩阵的奇异值SmithForm 将矩阵约化为 Smith 正规型StronglyConnectedBlocks 计算方阵的强连通块SubMatrix 构造矩阵的子矩阵SubVector 构造向量的子向量SylvesterMatrix 构造两个多项式的 Sylvester 矩阵ToeplitzMatrix 构造Toeplitz 矩阵Trace 计算方阵的迹Transpose 转置矩阵HermitianTranspose 共轭转置矩阵TridiagonalForm 将方阵约化为三对角型UnitVector 构造单位向量VandermondeMatrix 构造一个 Vandermonde 矩阵VectorAngle 计算两个向量的夹角ZeroMatrix 构造一个零矩阵ZeroVector 构造一个零向量Zip 将一个具有两个参数的程序作用到一对矩阵或向量上LinearAlgebra[Generic] 子函数包[Generic] 子函数包提供作用在场，欧几里得域，积分域和环上的线性代数算法。

maple函数大全.doc

欧基里德几何
排列与有限群（群论相关函数）
积分变换李对称
基本线性代数包
图形化的网络计算函数数值逼近数论正交多项式 P 进制数转换包函数库内容绘图程序库
plottools polytools powseries process simplex stats student sumtools
tensor
Fresnelf/Frensnelg
GAMMA
GaussAGM
Gaussejord
Gausselim
Gcd
Gcdex
HankelH1
HankelH2
Heaviside
Im 函数名称
Interp
Inverse
Irreduc
JacobiAM
JacobiSN
JacobiCN
JacobiDN
JacobiNS
Matlab Link
Bacic calculations in algebras of
linear onerators
tools for solveing partial differential
eauations
Spreadsheets
Algebraic Curves
Code Generation
绝对因式分解
Afsctors
另一种返回形式的绝对因式分解
AiriAiZeros
返回 AiryAi 函数的实数根
AiriBiZeros
返回 AiryBi 函数的实数根
AiryAi
“爱里”A 型函数（The Aiy wave functions）
AiryBi
“爱里”B 型函数（The Aiy wave functions）

Maple常用计算命令

常用计算命令《Maple 指令》7.0版本第1xx xx数1.1 复数Re,Im - 返回复数型表达式的实部/虚部abs - 函数argument - 复数的幅角函数conjugate - 返回共轭复数csgn - 实数和复数表达式的符号函数signum - 实数和复数表达式的sign 函数5 1.2 MAPLE 常数已知的变量名称指数常数（以自然对数为底）I - x^2 = -1 的根infinity 无穷大1.3 整数函数! - 阶乘函数irem, iquo - 整数的余数/商isprime - 素数测试isqrfree - 无整数平方的因数分解max, min - 数的最大值/最小值mod, modp, mods - 计算对m 的整数模rand - 随机数生成器randomize - 重置随机数生成器1.4 素数Randpoly, Randprime - 有限域的随机多项式/首一素数多项式ithprime - 确定第i 个素数nextprime, prevprime - 确定下一个最大/最小素数1.5 数的进制转换convert/base - 基数之间的转换convert/binary - 转换为二进制形式convert/decimal - 转换为10 进制convert/double - 将双精度浮点数由一种形式转换为另一种形式convert/float - 转换为浮点数convert/hex - 转换为十六进制形式convert/metric - 转换为公制单位convert/octal - 转换为八进制形式1.6 数的类型检查type - 数的类型检查函数第2xx 初等数学2.1 初等函数product - 确定乘积求和不确定乘积exp - 指数函数sum - 确定求和不确定求和sqrt - 计算xx算术运算符+, -, *, /, ^add, mul - 值序列的加法/乘法2.2 三角函数arcsin, arcsinh, . - 反三角函数/反双曲函数sin, sinh, . - 三角函数/双曲函数2.3 LOGARITHMS 函数dilog - Dilogarithm 函数ln, log, log10 - 自然对数/一般对数，常用对数2.4 类型转换convert/`+`,convert/`*` - 转换为求和/乘积convert/hypergeom - 将求和转换为超越函数convert/degrees - 将弧度转换为度convert/expsincos - 将trig 函数转换为exp, sin, cos convert/Ei - 转换为指数积分convert/exp - 将trig 函数转换为指数函数convert/ln - 将arctrig 转换为对数函数polar - 转换为极坐标形式convert/radians - 将度转换为弧度convert/sincos - 将trig 函数转换为sin, cos, sinh, cosh convert/tan - 将trig 函数转换为tanconvert/trig - 将指数函数转换为三角函数和双曲函数第3xx 求值3.1 假设功能3.2 求值Eval - 对一个表达式求值eval - 求值evala - 在代数数（或者函数）域求值evalb - 按照一个求值evalc - 在复数域上符号求值evalf - 使用浮点算法求值evalhf - 用硬件浮点数算法对表达式求值evalm - 对矩阵表达式求值evaln - 求值到一个名称evalr, shake - 用区间算法求表达式的值和计算范围evalrC - 用复数区间算法对表达式求值value - 求值的惰性函数第4xx 求根，xx4.1 数值解fsolve - 利用浮点数算法求解solve/floats - 包含浮点数的表达式4.2 最优化extrema - 寻找一个表达式的相对极值minimize, maximize - 计算最小值/最大值maxnorm - 一个多项式无穷大范数4.3 求根allvalues -计算含有RootOfs的表达式的所有可能值isqrt, iroot - 整数的xx/第n 次根realroot - 一个多项式的实数根的隔离区间root - 一个代数表达式的第n 阶根RootOf - 方程根的表示surd - 非主根函数roots - 一个多项式对一个变量的精确根turm, sturmseq - 多项式在区间上的实数根数和实根序列4.4 xxeliminate - 消去一个方程组中的某些变量isolve - 求解方程的整数解solvefor - 求解一个方程组的一个或者多个变量isolate - 隔离一个方程左边的一个子表达式singular - 寻找一个表达式的极点solve/identity - 求解包含属性的表达式solve/ineqs - 求解不等式solve/linear - 求解线性方程组solve/radical - 求解含有未知量根式的方程solve/scalar - 标量情况（单变量和方程）solve/series - 求解含有一般级数的方程solve/system - 解方程组或不等式组第5xx 操作表达式5.1 处理表达式Norm - 代数数(或者函数) 的标准型Power - 惰性幂函数Powmod -带余数的惰性幂函数Primfield - 代数域的原始元素Trace - 求一个代数数或者函数的迹charfcn - 表达式和集合的特征函数Indets - 找一个表达式的变元invfunc - 函数表的逆powmod - 带余数的幂函数Risidue - 计算一个表达式的代数余expand - 表达式展开Expand - 展开表达式的惰性形式expandoff/expandon - 抑制/不抑制函数展开5.2 因式分解Afactor - 绝对因式分解的惰性形式Afactors - 绝对因式分解分解项列表的惰性形式Berlekamp - 因式分解的Berlekamp 显式度factor - 多元的多项式的因式分解factors - 多元多项式的因式分解列表Factor - 函数factor 的惰性形式Factors - 函数factors 的惰性形式polytools[splits] - 多项式的完全因式分解第6xx 化简6.1 表达式化简118simplify - 给一个表达式实施化简规则simplify/@ - 利用运算符化简表达式simplify/Ei - 利用指数积分化简表达式simplify/GAMMA - 利用GAMMA 函数进行化简simplify/RootOf - 用RootOf 函数化简表达式simplify/wronskian - 化简含wronskian 的表达式simplify/hypergeom - 化简超越函数表达式simplify/ln - 化简含有对数的表达式simplify/piecewise - 化简分段函数表达式simplify/polar - 化简含有极坐标形式的复数型表达式simplify/power - 化简含幂次的表达式simplify/radical - 化简含有根式的表达式simplify/rtable - 化简rtable 表达式simplify/siderels - 使用关系式进行化简simplify/sqrt - 根式化简simplify/trig - 化简trig 函数表达式simplify/zero - 化简含嵌入型实数和虚数的复数表达式6.2 其它化简操作Normal - normal 函数的惰性形式convert - 将一个表达式转换成不同形式radnormal - 标准化一个含有根号数的表达式rationalize - 分母有理化第7xx 操作多项式7.0 MAPLE 中的多项式简介7.1 提取coeff - 提取一个多项式的系数coeffs - 提取多元的多项式的所有系数coeftayl - 多元表达式的系数lcoeff, tcoeff - 返回多元多项式的首项和末项系数7.2 多项式约数和根gcd, lcm - 多项式的最大公约数/最小公倍数psqrt, proot - 多项式的xx和第n次根rem,quo - 多项式的余数/商7.3 操纵多项式convert/horner - 将一个多项式转换成Horner形式collect - 象幂次一样合并系数convert/polynom - 将级数转换成多项式形式convert/mathorner - 将多项式转换成Horner矩阵形式convert/ratpoly - 将级数转换成有理多项式sort - 将值的列表或者多项式排序sqrfree - 不含平方项的因数分解函数7.4 多项式运算discrim - 多项式的判别式fixdiv - 计算多项式的固定除数norm - 多项式的标准型resultant - 计算两个多项式的终结式bernoulli - Bernoulli 数和多项式bernstein - 用Bernstein多项式近似一个函数content, primpart - 一个多元的多项式的内容和主部degree, ldegree - 一个多项式的最高次方/最低次方divide - 多项式的精确除法euler - Euler 数和多项式icontent - 多项式的整数部分interp - 多项式的插值prem, sprem - 多项式的pseudo 余数和稀疏pseudo 余数randpoly - 随机多项式生成器spline - 计算自然样条函数第8xx 有理表达式8.0 有理表达式简介8.1 操作有理多项式numer,denom - 返回一个表达式的分子/分母frontend - 将一般的表达式处理成一个有理表达式normal - 标准化一个有理表达式convert/parfrac - 转换为部分分数形式convert/rational - 将浮点数转换为接近的有理数ratrecon - 重建有理函数第9xx 微积分9.1 取极限Limit, limit - 计算极限limit[dir] - 计算方向极限limit[multi] - 多重方向极限limit[return] - 极限的返回值9.2 连续性测试discont - 寻找一个函数在实数域上的间断点fdiscont - 用数值法寻找函数在实数域上的间断点iscont - 测试在一个区间上的连续性9.3 微分计算D - 微分算子D, diff - 运算符D 和函数diffdiff, Diff - 微分或者偏微分convert/D - 将含导数表达式转换为D运算符表达式convert/diff - 将D(f)(x)表达式转换为diff(f(x),x)的形式implicitdiff - 由一个方程定义一个函数的微分9.4 积分计算Si, Ci … - 三角和双曲积分Dirac, Heaviside - Dirac 函数/Heaviside阶梯函数Ei - 指数积分Elliptic -FresnelC, … - Fresnel 正弦,xx积分和辅助函数int, Int - 定积分和不定积分LegendreP, … - Legendre 函数及其第一和第二类函数Li - 对数积分student[changevar] - 变量代换dawson - Dawson 积分ellipsoid - 椭球体的表面积evalf(int) - 数值积分intat, Intat - 在一个点上积分求值第10xx 微分方程10.1 微分方程分类odeadvisor - ODE-求解分析器DESol - 表示微分方程解的pdetest - 测试pdsolve 能找到的偏微分方程(PDEs)解10.2 常微分方程求解dsolve - 求解常微方程(ODE)dsolve - 用给定的求解ODE 问题dsolve/inttrans - 用积分变换方法求解常微分方程dsolve/numeric - 常微方程数值解dsolve/piecewise - 带分段系数的常微方程求解dsolve - 寻找ODE 问题的级数解dsolve - 求解ODEs 方程组odetest - 从ODE 求解器中测试结果是显式或者隐式类型10.3 偏微分方程求解pdsolve - 寻找偏微分方程(PDEs) 的解析解第11xx 数值计算11.1 MAPLE 中的数值计算环境IEEE 标准和Maple数值计算数据类型特殊值环境变量11.2 算法标准算法复数算法含有0，无穷和未定义数的算法11.3 数据构造器254Float, … - 浮点数及其构造器Fraction - 分数及其的构造器integer - 整数和整数构造器11.4 MATLAB 简介11.5 “”区间类型表达式第12xx级数12.1 幂级数的阶数Order - 阶数项函数order - 确定级数的截断阶数12.2 常见级数展开series - 一般的级数展开taylor - Taylor 级数展开mtaylor - 多元Taylor级数展开poisson - Poisson级数展开.26812.3 其它级数eulermac - Euler-Maclaurin求和piecewise - 分段连续函数asympt - 渐进展开第13xx 特殊函数AiryAi, AiryBi - Airy 波动函数AiryAiZeros, AiryBiZeros - Airy函数的实数零点AngerJ, WeberE - Anger函数和Weber函数BesselI, HankelH1, … - Bessel函数和Hankel函数BesselJZeros, … - Bessel函数实数零点Beta - Beta函数EllipticModulus - 模数函数k(q)GAMMA, lnGAMMA - 完全和不完全Gamma函数GaussAGM - Gauss 算术的几何平均数JacobiAM, ., - Jacobi 振幅函数和JacobiTheta1, JacobiTheta4 - Jacobi theta函数JacobiZeta - Jacobi 的Zeta函数KelvinBer, KelvinBei - Kelvin函数KummerM, - Kummer M函数和U函数LambertW - LambertW函数LerchPhi - 一般的Lerch Phi函数LommelS1, LommelS2 - Lommel函数MeijerG - 一个xx的Meijer G函数Psi - Digamma 和Polygamma函数StruveH, StruveL - Struve函数WeierstrassP - Weierstrass P函数及其导数WhittakerM - Whittaker 函数Zeta - Zeta 函数erf, … - 误差函数，补充的误差函数和虚数误差函数harmonic - 调和函数hypergeom - xx的超越函数pochhammer - 一般的pochhammer函数polylog - 一般的polylogarithm函数第14xx 线性代数14.1 ALGEBRA（代数）中矩阵，矢量和14.2 LINALG 软件包简介14.3 数据结构矩阵matrices（小写）矢量vectors（矢量）convert/matrix - 将数组，列表，Matrix 转换成matrixconvert/vector - 将列表，数组或Vector 转换成矢量vectorlinalg[matrix] - 生成矩阵matrix（小写）linalg[vector] - 生成矢量vector（小写）14.4 惰性函数Det - 惰性行列式运算符Eigenvals - 数值型矩阵的特征值和特征向量Hermite, Smith - 矩阵的Hermite 和Smith 标准型14.5 LinearAlgebra函数Matrix 定义矩阵Add 加/减矩阵Adjoint 伴随矩阵BackwardSubstitute 求解A . X = B，其中A 为上三角型行阶梯矩阵BandMatrix 带状矩阵Basis 返回向量空间的一组基SumBasis 返回向量空间直和的一组基IntersectionBasis 返回向量空间交的一组基BezoutMatrix 构造两个多项式的Bezout 矩阵BidiagonalForm 将矩阵约化为双对角型CharacteristicMatrix 构造特征矩阵CharacteristicPolynomial 构造矩阵的特征多项式CompanionMatrix 构造一个首一（或非首一）多项式或矩阵多项式的xx （xx）ConditionNumber 计算矩阵关于某范数的条件数ConstantMatrix 构造常数矩阵ConstantVector 构造常数向量Copy 构造矩阵或向量的一份复制CreatePermutation 将一个NAG 主元向量转换为一个置换向量或矩阵CrossProduct 向量的叉积`&x` 向量的叉积DeleteRow 删除矩阵的行DeleteColumn 删除矩阵的列Determinant 行列式Diagonal 返回从矩阵中得到的向量序列DiagonalMatrix 构造（分块）Dimension 行数和列数DotProduct 点积BilinearForm 向量的双线性形式EigenConditionNumbers 计算数值特征值制约问题的特征值或特征向量的条件数Eigenvalues 计算矩阵的特征值Eigenvectors 计算矩阵的特征向量Equal 比较两个向量或矩阵是否相等ForwardSubstitute 求解A . X = B，其中A 为下三角型行阶梯矩阵FrobeniusForm 将一个方阵约化为Frobenius 型（有理标准型）GaussianElimination 对矩阵作消元ReducedRowEchelonForm 对矩阵作xx－约当消元GetResultDataType 返回矩阵或向量运算的结果数据类型GetResultShape 返回矩阵或向量运算的结果形状GivensRotationMatrix 构造Givens 旋转的矩阵GramSchmidt 计算一个正交向量集HankelMatrix 构造一个Hankel 矩阵HermiteForm 计算一个矩阵的Hermite 正规型HessenbergForm 将一个方阵约化为上Hessenberg 型HilbertMatrix 构造xx Hilbert 矩阵HouseholderMatrix 构造Householder 反射矩阵IdentityMatrix 构造一个单位矩阵IsDefinite 检验矩阵的正定性，负定性或不定性IsOrthogonal 检验矩阵是否正交IsUnitary 检验矩阵是否为酉矩阵IsSimilar 确定两个矩阵是否相似JordanBlockMatrix 构造约当块矩阵JordanForm 将矩阵约化为约当型KroneckerProduct 构造两个矩阵的Kronecker xxLeastSquares 方程的最小二乘解LinearSolve 求解线性方程组A . x = bMap 将一个程序映射到一个表达式上，对矩阵和向量在原位置上进行处理MatrixAdd 计算两个矩阵的线性组合VectorAdd 计算两个向量的线性组合MatrixExponential 确定一个矩阵A 的矩阵指数exp(A)MatrixFunction 确定方阵A 的函数F(A)MatrixInverse 计算方阵的逆或矩阵的Moore-Penrose 伪逆MatrixMatrixMultiply 计算两个矩阵的乘积MatrixVectorMultiply 计算一个矩阵和一个列向量的乘积VectorMatrixMultiply 计算一个行向量和一个矩阵的乘积MatrixPower 矩阵的幂MinimalPolynomial 构造矩阵的最小多项式Minor 计算矩阵的子式Multiply 矩阵相乘Norm 计算矩阵或向量的p-范数MatrixNorm 计算矩阵的p-范数VectorNorm 计算向量的p-范数Normalize 向量正规化NullSpace 计算矩阵的零度零空间OuterProductMatrix 两个向量的外积Permanent 方阵的不变量Pivot 矩阵元素的主元消去法PopovForm Popov 正规型RandomMatrix 构造RandomVector 构造随机向量Rank 计算Row 返回矩阵的一个行向量序列Column 返回矩阵的一个列向量序列RowOperation 对矩阵作初等行变换ColumnOperation 对矩阵作出等列变换RowSpace 返回矩阵行空间的一组基ColumnSpace 返回矩阵列空间的一组基ScalarMatrix 构造一个单位矩阵的数量倍数ScalarVector 构造一个单位向量的数量倍数ScalarMultiply 矩阵与数的乘积MatrixScalarMultiply 计算矩阵与数的乘积VectorScalarMultiply 计算向量与数的乘积SchurForm 将方阵约化为Schur 型SingularValues 计算矩阵的奇异值SmithForm 将矩阵约化为Smith 正规型StronglyConnectedBlocks 计算方阵的强连通块SubMatrix 构造矩阵的子矩阵SubVector 构造向量的子向量SylvesterMatrix 构造两个多项式的Sylvester 矩阵ToeplitzMatrix 构造Toeplitz 矩阵Trace 计算方阵的迹TransposeHermitianTranspose 共轭转置矩阵TridiagonalForm 将方阵约化为三对角型UnitVector 构造单位向量VandermondeMatrix 构造一个Vandermonde 矩阵VectorAngle 计算两个向量的夹角ZeroMatrix 构造一个零矩阵ZeroVector 构造一个零向量Zip 将一个具有两个参数的程序作用到一对矩阵或向量上LinearAlgebra[Generic] 子函数包[Generic] 子函数包提供作用在场，域，积分域和环上的线性代数算法。

maple函数大全.doc

Fresnelf/Frensnelg
GAMMA
GaussAGM
Gaussejord
Gausselim
Gcd
Gcdex
HankelH1
HankelH2
Heaviside
Im 函数名称
Interp
Inverse
Irreduc
JacobiAM
JacobiSN
JacobiCN
JacobiDN
JacobiNS
assigned assume asympt attribute bernstein branches bspline cat ceil charfcn chrem close coeff compiletable compoly conjugate content convergs clnvert copy cos cosh cot coth csc csch cdgn currentdir dawson 函数名称 define degree denom depends diff diffop dilog dinterp disassemble discont discrim dismantle divide
JacobiNC
JacobiND
JacobiSC
JacobiCS
JacobiSD
JacobiDS
JacobiCD
JacobiDC
JacobiTheta1 JacobiTheta2
JacobiTheta3 JacobiTheta4
JacobiZeta KelvinBei KelvinBer
第二类互余完全椭圆积分第一类互余完全椭圆积分第三类互余完全椭圆积分第二类完全或不完全椭圆积分第一类不完全椭圆积分第一类完全椭圆积分 q（k）=exp(-pi/*ElliptcCK(k)/EllipticK(k)) 第三类完全或不完全椭圆积分计算表达式简化 expand 函数快速傅立叶变换因式分解因式分解菲涅耳余弦积分菲涅耳正弦积分菲涅耳辅助函数 γ函数与不完全γ函数高斯算术、几何平均值高斯约当消元法高斯消元法最大公约数扩展多项式欧几里得代数函数第三类贝塞耳函数第三类贝塞耳函数亥维塞阶跃函数去复数的虚部基本功能多项式插值函数（interp 函数的简化形式）逆矩阵（inverse 函数的简化形式）即约性函数（irreduc 数的简化形式）雅可比幅值函数 am

Maple的常用内部数学函数要点

>display(c,scaling=CONSTRAINED,title=`UnitCircle` );
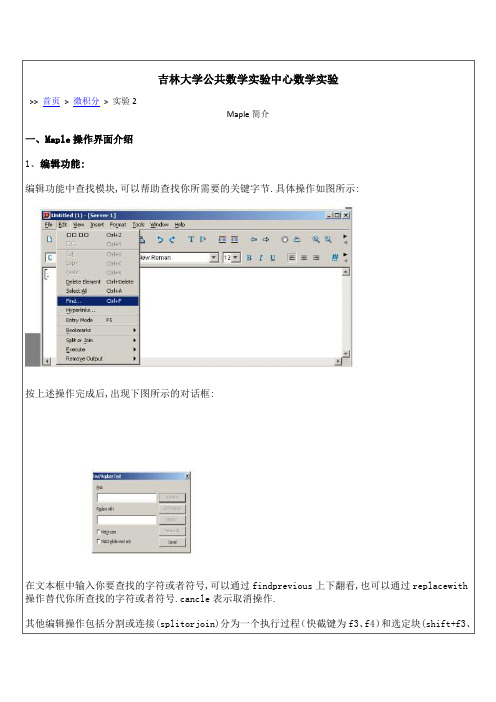
5、3D图象
Maple可以生成由显函数、参数型、微分方程的解给出的3D曲线和曲面。图像的外观如：字体、光照、着色等也可随便更改。
下例将生成二元函数：的图象。
>plot3d(x*exp(-x^2-y^2),x=-2..2,y=-2..2,axes=BOXED,
>eval(eqn,x=1/2*a);
4、解方程组
求解如下5元的方程组：
>eqn1:=a+2*b+3*c+4*d+5*e=41;
>eqn2:=5*a+5*b+4*c+3*d+2*e=20;
>eqn3:=3*b+4*c-8*d+2*e=125;
>eqn4:=a+b+c+d+e=9;
我们可以用变量e来表示其他未知数a，b，c，d得到一组解。如果5个未知数一起求，Maple将任选其一作为自由变量。
>expand(expr);
类似的你可以用factor命令对上面结果进行因式分解来验证。
>factor(%);
化简表达式
Maple可以使用包括三角恒等式在内的恒等关系对复杂的表达式进行化简。
考察 .
>simplify(cos(x)^5+sin(x)^4+2*cos(x)^2-2*sin(x)^2 -cos(2*x));
·Maple中乘号为星号“*”，两项相乘时乘号不能省略。
· 对变量赋值时用赋值运算符“：＝”，而不是通常的等号“；”。

Maple常用计算命令

常用计算命令《Maple 指令》7.0版本第1xx xx数1.1 复数Re,Im - 返回复数型表达式的实部/虚部abs - 函数argument - 复数的幅角函数conjugate - 返回共轭复数csgn - 实数和复数表达式的符号函数signum - 实数和复数表达式的sign 函数5 1.2 MAPLE 常数已知的变量名称指数常数（以自然对数为底）I - x^2 = -1 的根infinity 无穷大1.3 整数函数! - 阶乘函数irem, iquo - 整数的余数/商isprime - 素数测试isqrfree - 无整数平方的因数分解max, min - 数的最大值/最小值mod, modp, mods - 计算对 m 的整数模rand - 随机数生成器randomize - 重置随机数生成器1.4 素数Randpoly, Randprime - 有限域的随机多项式/首一素数多项式ithprime - 确定第 i 个素数nextprime, prevprime - 确定下一个最大/最小素数1.5 数的进制转换convert/base - 基数之间的转换convert/binary - 转换为二进制形式convert/decimal - 转换为 10 进制convert/double - 将双精度浮点数由一种形式转换为另一种形式convert/float - 转换为浮点数convert/hex - 转换为十六进制形式convert/metric - 转换为公制单位convert/octal - 转换为八进制形式1.6 数的类型检查type - 数的类型检查函数第2xx 初等数学2.1 初等函数product - 确定乘积求和不确定乘积exp - 指数函数sum - 确定求和不确定求和sqrt - 计算xx算术运算符+, -, *, /, ^add, mul - 值序列的加法/乘法2.2 三角函数arcsin, arcsinh, . - 反三角函数/反双曲函数sin, sinh, . - 三角函数/双曲函数2.3 LOGARITHMS 函数dilog - Dilogarithm 函数ln, log, log10 - 自然对数/一般对数，常用对数2.4 类型转换convert/`+`,convert/`*` - 转换为求和/乘积convert/hypergeom - 将求和转换为超越函数convert/degrees - 将弧度转换为度convert/expsincos - 将trig 函数转换为exp, sin, cos convert/Ei - 转换为指数积分convert/exp - 将trig 函数转换为指数函数convert/ln - 将arctrig 转换为对数函数polar - 转换为极坐标形式convert/radians - 将度转换为弧度convert/sincos - 将trig 函数转换为sin, cos, sinh, cosh convert/tan - 将trig 函数转换为tanconvert/trig - 将指数函数转换为三角函数和双曲函数第3xx 求值3.1 假设功能3.2 求值Eval - 对一个表达式求值eval - 求值evala - 在代数数（或者函数）域求值evalb - 按照一个求值evalc - 在复数域上符号求值evalf - 使用浮点算法求值evalhf - 用硬件浮点数算法对表达式求值evalm - 对矩阵表达式求值evaln - 求值到一个名称evalr, shake - 用区间算法求表达式的值和计算范围evalrC - 用复数区间算法对表达式求值value - 求值的惰性函数第4xx 求根，xx4.1 数值解fsolve - 利用浮点数算法求解solve/floats - 包含浮点数的表达式4.2 最优化extrema - 寻找一个表达式的相对极值minimize, maximize - 计算最小值/最大值maxnorm - 一个多项式无穷大范数4.3 求根allvalues -计算含有RootOfs的表达式的所有可能值isqrt, iroot - 整数的xx/第n 次根realroot - 一个多项式的实数根的隔离区间root - 一个代数表达式的第n 阶根RootOf - 方程根的表示surd - 非主根函数roots - 一个多项式对一个变量的精确根turm, sturmseq - 多项式在区间上的实数根数和实根序列4.4 xxeliminate - 消去一个方程组中的某些变量isolve - 求解方程的整数解solvefor - 求解一个方程组的一个或者多个变量isolate - 隔离一个方程左边的一个子表达式singular - 寻找一个表达式的极点solve/identity - 求解包含属性的表达式solve/ineqs - 求解不等式solve/linear - 求解线性方程组solve/radical - 求解含有未知量根式的方程solve/scalar - 标量情况（单变量和方程）solve/series - 求解含有一般级数的方程solve/system - 解方程组或不等式组第5xx 操作表达式5.1 处理表达式Norm - 代数数 (或者函数) 的标准型Power - 惰性幂函数Powmod -带余数的惰性幂函数Primfield - 代数域的原始元素Trace - 求一个代数数或者函数的迹charfcn - 表达式和集合的特征函数Indets - 找一个表达式的变元invfunc - 函数表的逆powmod - 带余数的幂函数Risidue - 计算一个表达式的代数余combine - 表达式合并(对tan,cot不好用) expand - 表达式展开Expand - 展开表达式的惰性形式expandoff/expandon - 抑制/不抑制函数展开5.2 因式分解Afactor - 绝对因式分解的惰性形式Afactors - 绝对因式分解分解项列表的惰性形式Berlekamp - 因式分解的Berlekamp 显式度factor - 多元的多项式的因式分解factors - 多元多项式的因式分解列表Factor - 函数factor 的惰性形式Factors - 函数factors 的惰性形式polytools[splits] - 多项式的完全因式分解第6xx 化简6.1 表达式化简118simplify - 给一个表达式实施化简规则simplify/@ - 利用运算符化简表达式simplify/Ei - 利用指数积分化简表达式simplify/GAMMA - 利用GAMMA 函数进行化简simplify/RootOf - 用RootOf 函数化简表达式simplify/wronskian - 化简含wronskian 的表达式simplify/hypergeom - 化简超越函数表达式simplify/ln - 化简含有对数的表达式simplify/piecewise - 化简分段函数表达式simplify/polar - 化简含有极坐标形式的复数型表达式simplify/power - 化简含幂次的表达式simplify/radical - 化简含有根式的表达式simplify/rtable - 化简rtable 表达式simplify/siderels - 使用关系式进行化简simplify/sqrt - 根式化简simplify/trig - 化简trig 函数表达式simplify/zero - 化简含嵌入型实数和虚数的复数表达式6.2 其它化简操作Normal - normal 函数的惰性形式convert - 将一个表达式转换成不同形式radnormal - 标准化一个含有根号数的表达式rationalize - 分母有理化第7xx 操作多项式7.0 MAPLE 中的多项式简介7.1 提取coeff - 提取一个多项式的系数coeffs - 提取多元的多项式的所有系数coeftayl - 多元表达式的系数lcoeff, tcoeff - 返回多元多项式的首项和末项系数7.2 多项式约数和根gcd, lcm - 多项式的最大公约数/最小公倍数psqrt, proot - 多项式的xx和第n次根rem,quo - 多项式的余数/商7.3 操纵多项式convert/horner - 将一个多项式转换成Horner形式collect - 象幂次一样合并系数compoly - 确定一个多项式的可能合并的项数convert/polynom - 将级数转换成多项式形式convert/mathorner - 将多项式转换成Horner矩阵形式convert/ratpoly - 将级数转换成有理多项式sort - 将值的列表或者多项式排序sqrfree - 不含平方项的因数分解函数7.4 多项式运算discrim - 多项式的判别式fixdiv - 计算多项式的固定除数norm - 多项式的标准型resultant - 计算两个多项式的终结式bernoulli - Bernoulli 数和多项式bernstein - 用Bernstein多项式近似一个函数content, primpart - 一个多元的多项式的内容和主部degree, ldegree - 一个多项式的最高次方/最低次方divide - 多项式的精确除法euler - Euler 数和多项式icontent - 多项式的整数部分interp - 多项式的插值prem, sprem - 多项式的pseudo 余数和稀疏pseudo 余数randpoly - 随机多项式生成器spline - 计算自然样条函数第8xx 有理表达式8.0 有理表达式简介8.1 操作有理多项式numer,denom - 返回一个表达式的分子/分母frontend - 将一般的表达式处理成一个有理表达式normal - 标准化一个有理表达式convert/parfrac - 转换为部分分数形式convert/rational - 将浮点数转换为接近的有理数ratrecon - 重建有理函数第9xx 微积分9.1 取极限Limit, limit - 计算极限limit[dir] - 计算方向极限limit[multi] - 多重方向极限limit[return] - 极限的返回值9.2 连续性测试discont - 寻找一个函数在实数域上的间断点fdiscont - 用数值法寻找函数在实数域上的间断点iscont - 测试在一个区间上的连续性9.3 微分计算D - 微分算子D, diff - 运算符D 和函数diffdiff, Diff - 微分或者偏微分convert/D - 将含导数表达式转换为D运算符表达式convert/diff - 将D(f)(x)表达式转换为diff(f(x),x)的形式implicitdiff - 由一个方程定义一个函数的微分9.4 积分计算Si, Ci … - 三角和双曲积分Dirac, Heaviside - Dirac 函数/Heaviside阶梯函数Ei - 指数积分Elliptic -FresnelC, … - Fresnel 正弦,xx积分和辅助函数int, Int - 定积分和不定积分LegendreP, … - Legendre 函数及其第一和第二类函数Li - 对数积分student[changevar] - 变量代换dawson - Dawson 积分ellipsoid - 椭球体的表面积evalf(int) - 数值积分intat, Intat - 在一个点上积分求值第10xx 微分方程10.1 微分方程分类odeadvisor - ODE-求解分析器DESol - 表示微分方程解的pdetest - 测试pdsolve 能找到的偏微分方程(PDEs)解10.2 常微分方程求解dsolve - 求解常微方程 (ODE)dsolve - 用给定的求解ODE 问题dsolve/inttrans - 用积分变换方法求解常微分方程dsolve/numeric - 常微方程数值解dsolve/piecewise - 带分段系数的常微方程求解dsolve - 寻找ODE 问题的级数解dsolve - 求解ODEs 方程组odetest - 从ODE 求解器中测试结果是显式或者隐式类型10.3 偏微分方程求解pdsolve - 寻找偏微分方程 (PDEs) 的解析解第11xx 数值计算11.1 MAPLE 中的数值计算环境IEEE 标准和Maple数值计算数据类型特殊值环境变量11.2 算法标准算法复数算法含有0，无穷和未定义数的算法11.3 数据构造器254complex - 复数和复数构造器Float, … - 浮点数及其构造器Fraction - 分数及其的构造器integer - 整数和整数构造器11.4 MATLAB 简介11.5 “”区间类型表达式第12xx级数12.1 幂级数的阶数Order - 阶数项函数order - 确定级数的截断阶数12.2 常见级数展开series - 一般的级数展开taylor - Taylor 级数展开mtaylor - 多元Taylor级数展开poisson - Poisson级数展开.26812.3 其它级数eulermac - Euler-Maclaurin求和piecewise - 分段连续函数asympt - 渐进展开第13xx 特殊函数AiryAi, AiryBi - Airy 波动函数AiryAiZeros, AiryBiZeros - Airy函数的实数零点AngerJ, WeberE - Anger函数和Weber函数BesselI, HankelH1, … - Bessel函数和Hankel函数BesselJZeros, … - Bessel函数实数零点Beta - Beta函数EllipticModulus - 模数函数k(q)GAMMA, lnGAMMA - 完全和不完全Gamma函数GaussAGM - Gauss 算术的几何平均数JacobiAM, ., - Jacobi 振幅函数和JacobiTheta1, JacobiTheta4 - Jacobi theta函数JacobiZeta - Jacobi 的Zeta函数KelvinBer, KelvinBei - Kelvin函数KummerM, - Kummer M函数和U函数LambertW - LambertW函数LerchPhi - 一般的Lerch Phi函数LommelS1, LommelS2 - Lommel函数MeijerG - 一个xx的Meijer G函数Psi - Digamma 和Polygamma函数StruveH, StruveL - Struve函数WeierstrassP - Weierstrass P函数及其导数WhittakerM - Whittaker 函数Zeta - Zeta 函数erf, … - 误差函数，补充的误差函数和虚数误差函数harmonic - 调和函数hypergeom - xx的超越函数pochhammer - 一般的pochhammer函数polylog - 一般的polylogarithm函数第14xx 线性代数14.1 ALGEBRA（代数）中矩阵，矢量和14.2 LINALG 软件包简介14.3 数据结构矩阵matrices（小写）矢量vectors（矢量）convert/matrix - 将数组，列表，Matrix 转换成matrix convert/vector - 将列表，数组或Vector 转换成矢量vectorlinalg[matrix] - 生成矩阵matrix（小写）linalg[vector] - 生成矢量vector（小写）14.4 惰性函数Det - 惰性行列式运算符Eigenvals - 数值型矩阵的特征值和特征向量Hermite, Smith - 矩阵的Hermite 和Smith 标准型14.5 LinearAlgebra函数Matrix 定义矩阵Add 加/减矩阵Adjoint 伴随矩阵BackwardSubstitute 求解 A . X = B，其中 A 为上三角型行阶梯矩阵BandMatrix 带状矩阵Basis 返回向量空间的一组基SumBasis 返回向量空间直和的一组基IntersectionBasis 返回向量空间交的一组基BezoutMatrix 构造两个多项式的 Bezout 矩阵BidiagonalForm 将矩阵约化为双对角型CharacteristicMatrix 构造特征矩阵CharacteristicPolynomial 构造矩阵的特征多项式CompanionMatrix 构造一个首一（或非首一）多项式或矩阵多项式的xx（xx）ConditionNumber 计算矩阵关于某范数的条件数ConstantMatrix 构造常数矩阵ConstantVector 构造常数向量Copy 构造矩阵或向量的一份复制CreatePermutation 将一个 NAG 主元向量转换为一个置换向量或矩阵CrossProduct 向量的叉积`&x` 向量的叉积DeleteRow 删除矩阵的行DeleteColumn 删除矩阵的列Determinant 行列式Diagonal 返回从矩阵中得到的向量序列DiagonalMatrix 构造（分块）Dimension 行数和列数DotProduct 点积BilinearForm 向量的双线性形式EigenConditionNumbers 计算数值特征值制约问题的特征值或特征向量的条件数Eigenvalues 计算矩阵的特征值Eigenvectors 计算矩阵的特征向量Equal 比较两个向量或矩阵是否相等ForwardSubstitute 求解 A . X = B，其中 A 为下三角型行阶梯矩阵FrobeniusForm 将一个方阵约化为 Frobenius 型（有理标准型）GaussianElimination 对矩阵作消元ReducedRowEchelonForm 对矩阵作xx－约当消元GetResultDataType 返回矩阵或向量运算的结果数据类型GetResultShape 返回矩阵或向量运算的结果形状GivensRotationMatrix 构造 Givens 旋转的矩阵GramSchmidt 计算一个正交向量集HankelMatrix 构造一个 Hankel 矩阵HermiteForm 计算一个矩阵的 Hermite 正规型HessenbergForm 将一个方阵约化为上 Hessenberg 型HilbertMatrix 构造xx Hilbert 矩阵HouseholderMatrix 构造 Householder 反射矩阵IdentityMatrix 构造一个单位矩阵IsDefinite 检验矩阵的正定性，负定性或不定性IsOrthogonal 检验矩阵是否正交IsUnitary 检验矩阵是否为酉矩阵IsSimilar 确定两个矩阵是否相似JordanBlockMatrix 构造约当块矩阵JordanForm 将矩阵约化为约当型KroneckerProduct 构造两个矩阵的 Kronecker xx LeastSquares 方程的最小二乘解LinearSolve 求解线性方程组 A . x = bLUDecomposition 计算矩阵的 Cholesky，PLU 或 PLU1R 分解Map 将一个程序映射到一个表达式上，对矩阵和向量在原位置上进行处理MatrixAdd 计算两个矩阵的线性组合VectorAdd 计算两个向量的线性组合MatrixExponential 确定一个矩阵 A 的矩阵指数 exp(A)MatrixFunction 确定方阵 A 的函数 F(A)MatrixInverse 计算方阵的逆或矩阵的 Moore-Penrose 伪逆MatrixMatrixMultiply 计算两个矩阵的乘积MatrixVectorMultiply 计算一个矩阵和一个列向量的乘积VectorMatrixMultiply 计算一个行向量和一个矩阵的乘积MatrixPower 矩阵的幂MinimalPolynomial 构造矩阵的最小多项式Minor 计算矩阵的子式Multiply 矩阵相乘Norm 计算矩阵或向量的p-范数MatrixNorm 计算矩阵的p-范数VectorNorm 计算向量的p-范数Normalize 向量正规化NullSpace 计算矩阵的零度零空间OuterProductMatrix 两个向量的外积Permanent 方阵的不变量Pivot 矩阵元素的主元消去法PopovForm Popov 正规型QRDecomposition QR 分解RandomMatrix 构造RandomVector 构造随机向量Rank 计算Row 返回矩阵的一个行向量序列Column 返回矩阵的一个列向量序列RowOperation 对矩阵作初等行变换ColumnOperation 对矩阵作出等列变换RowSpace 返回矩阵行空间的一组基ColumnSpace 返回矩阵列空间的一组基ScalarMatrix 构造一个单位矩阵的数量倍数ScalarVector 构造一个单位向量的数量倍数ScalarMultiply 矩阵与数的乘积MatrixScalarMultiply 计算矩阵与数的乘积VectorScalarMultiply 计算向量与数的乘积SchurForm 将方阵约化为 Schur 型SingularValues 计算矩阵的奇异值SmithForm 将矩阵约化为 Smith 正规型StronglyConnectedBlocks 计算方阵的强连通块SubMatrix 构造矩阵的子矩阵SubVector 构造向量的子向量SylvesterMatrix 构造两个多项式的 Sylvester 矩阵ToeplitzMatrix 构造 Toeplitz 矩阵Trace 计算方阵的迹TransposeHermitianTranspose 共轭转置矩阵TridiagonalForm 将方阵约化为三对角型UnitVector 构造单位向量VandermondeMatrix 构造一个 Vandermonde 矩阵VectorAngle 计算两个向量的夹角ZeroMatrix 构造一个零矩阵ZeroVector 构造一个零向量Zip 将一个具有两个参数的程序作用到一对矩阵或向量上LinearAlgebra[Generic] 子函数包 [Generic] 子函数包提供作用在场，域，积分域和环上的线性代数算法。

【免费下载】Maple常用函数

制表示形式[2;2;1]。注意要用 base 关键字。
指数函数对数函数
exp(x)
ln(x)或 log(x)
log[10](x) 或 log10(x)
log[a](x)
Maple 常用函数表
以 e 为底数
自然对数，即以 e 为底数的对数
常用对数，即以 10 为底数的对数以 a 为底数的 x 的对数
表示 x 的算术平方根
表示 x 的绝对值
正弦函数余弦函数正切函数余切函数正割函数余割函数反正弦函数反余弦函数反正切函数反余切函数反正割函数反余割函数双曲正弦函数双曲余弦函数双曲正切函数双曲余切函数双曲正割函数双曲余割函数反双曲正弦函数反双曲余弦函数
求角度函数
整数的最小公倍数函数
求 a 除以 b 的余数
求 a 除以 b 的正余数
以对称的方式求 a 除以 b 的余数
求 a 除以 b 的余数
求 a 除以 b 的余数,并将商存放在 q 中
求 a 除以 b 的商求 a 除以 b 的商,并将余数存放在 r 中
因数分解，即把整数 n 分解成质数的乘积
产生 12 位的随机整数
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，系电，力根通保据过护生管高产线中工敷资艺设料高技试中术卷资，配料不置试仅技卷可术要以是求解指，决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资，配料而置试且时卷可，调保需控障要试各在验类最；管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下，安与要全过加，度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高；试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中，核资或对料者定试对值卷某，弯些审扁异核度常与固高校定中对盒资图位料纸置试，.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置，弯高尤曲中其半资要径料避标试免高卷错等调误，试高要方中求案资技，料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高，术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术，管以术来架及避等系免多统不项启必方动要式方高，案中为；资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资，管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装，工置合作调理并试利且技用进术管行，线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确：指灵在导活分。。线对对盒于于处调差，试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷，术调应问试采题技用，术金作是属为指隔调发板试电进人机行员一隔，变开需压处要器理在组；事在同前发一掌生线握内槽图部内纸故，资障强料时电、，回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资，料料线试试缆卷卷敷试切设验除完报从毕告而，与采要相用进关高行技中检术资查资料和料试检，卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

maple函数大全

Gaoois Fieldc
Gaussian Integers
Groebner basis calculations in skew
algebras
Manipulate linear reurrence relation
Iinear aogebra package based on
rtable data structures
Groebner 基
线性递归相关函数基于 rtable 数据格式的线性代数相关程序包与 Matlab 的接口函数
线性算的基本代数运算
偏微分方程相关函数
扩展工作簿生成函数代数曲线程序代码生成器复合函数复合结构上下文敏感菜单偏微分代数微分形式金融数学有理数产生函数
欧基里德三维几何
基本图形绘制函数多项式相关函数幂级数 Unix 下的多线程计算函数线性优化统计函数学生综合函数库无限与有限求与
张量操作与广义相对论
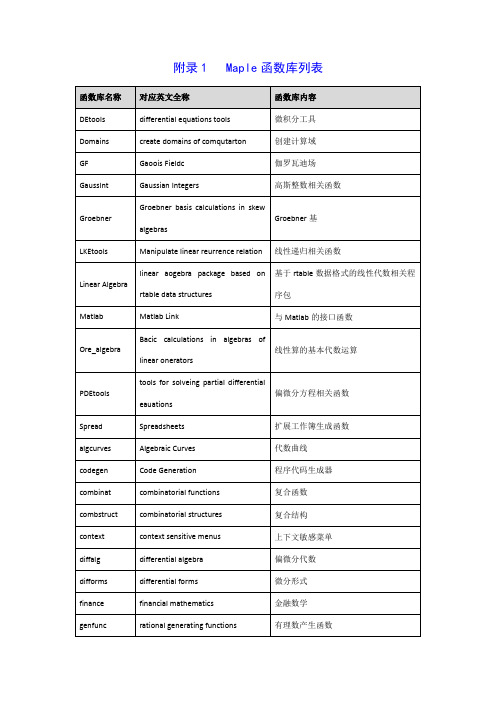
附录 2 Maple 基本函数库及其功能
此附录中收录的,就是几乎所有 Maple 系统的自带函数,即不须添加任何函数库可直接执行的函数。
函数名称
基本功能
Afsctor
geom3d
geometry
group
inttrans liesymm
linalg
networks numapprox numtheory orthopoly padic 函数库名称 plots
对应英文全称
differential equations tools
create domains of comqutarton
Matlab Link
Bacic calculations in algebras of

maple函数大全.doc

雅可比椭圆函数
雅可比椭圆函数雅
雅可比θ函数
雅可比ζ函数开尔文 Bei 函数开尔文 Her 函数
KelvinHei KelvinHer KelvinKei KelvinHer KummerM KummerU LanbertW Lcm LegendreP LegendreQ Lerchphi Li Linsolve Lommels1 Lommels2 MOLS Maple_floats MatlabMatrix MeijerG 函数名称 Normal Nullspace Power Powmod Prem Primitive Primpart 函数名称 ProbSplit Product Psi Quo RESol Randpoly Randprime Ratrecon Re Rem Resultant RootOf Roots Sprem Searchtext
双曲正弦函数正弦积分矩阵的 Smith 正交化非平方因式分解转移正弦积分 StruveH 函数 StruveL 函数 sum(求和）和函数的简化形式基本功能计算矩阵的奇异数/向量显示文本韦伯函数 Weierstrass P 函数 Weierstrass P 函数的导数 WeierstrassΣ函数 Weierstrassζ函数 Whittaker M 函数 Whittaker W 函数黎曼ζ函数绝对值加法添加坐标系得到所指表达式的内存地址对多项式子的替换定义缩写求出等式的全部可能解顺序显示已定义的变量名反对称参数应用运算规则反余弦函数反双曲余弦函数反余切函数反双曲余切函数反正割函数反双曲正割函数反正弦函数反双曲正弦函数反正切函数反双曲正切函数求复数坐标下的向量角度基本功能定义数组赋值

maple函数大全

rtable data structures
序包
Matlab
Matlab Link
与 Matlab 的接口函数
Ore_algebra
Bacic calculations in algebras of 线性算的基本代数运算
linear onerators
PDEtools
tools for solveing partial differential 偏微分方程相关函数
雅可比椭圆函数
雅可比椭圆函数雅
雅可比θ函数
JacobiZeta KelvinBei KelvinBer KelvinHei KelvinHer
雅可比ζ函数开尔文 Bei 函数开尔文 Her 函数开尔文 Hei 函数开尔文 Her 函数
KelvinKei KelvinHer KummerM KummerU LanbertW Lcm LegendreP LegendreQ Lerchphi Li Linsolve Lommels1 Lommels2 MOLS Maple_floats MatlabMatrix MeijerG 函数名称 Normal Nullspace Power Powmod Prem Primitive Primpart 函数名称
多项式可分解为同阶因式的可能性 Product（乘）函数的简化形式双γ函数与多γ函数 Quo（求多项式的商）函数的简化形式一种递归方程解的数据结构有限域的随机多项式有限域的随机 monic prime 多项式 Ratrecon（重组有理函数）的简化形式取复数的实部 rem（求多项式相除余项）函数的简化形式 Resultant（合成多项式）函数简化形式求方程的根多项式求模后的根 Sperm(异伪余式）函数的简化形式查找文本双曲正弦函数正弦积分矩阵的 Smith 正交化非平方因式分解转移正弦积分 StruveH 函数 StruveL 函数 sum(求和）和函数的简化形式基本功能计算矩阵的奇异数/向量显示文本

maple推导公式

maple推导公式
Maple是一款很强大的数学软件，它可以进行符号计算，求解方程、积分、微分等等。

在使用Maple进行数学推导时，我们可以用到一些常用的公式，这些公式可以帮助我们更快、更准确地进行推导。

下面是一些常用的Maple推导公式：
1. 求导公式：diff(f(x),x)，其中f(x)为函数，x为自变量。

2. 偏导公式：diff(f(x,y),x)，其中f(x,y)为函数，x为自变量，y为自变量。

3. 积分公式：int(f(x),x)，其中f(x)为函数，x为积分变量。

4. 二次方程公式：solve(a*x^2+b*x+c=0,x)，其中a、b、c为常数，x为未知数。

5. 三角函数公式：sin(x),cos(x),tan(x)，其中x为角度。

6. 对数函数公式：log(x)，其中x为底数。

7. 指数函数公式：exp(x)，其中x为指数。

通过应用这些公式，我们可以更加高效地进行Maple数学推导，提高我们的数学研究效率。

- 1 -。

Maple中基本函数指令

Maple用法Maple 函数用法一、基本命令重新开始：restart 命名：名字：= 引用前值：% 字符连接：|| 保护命名：protect 解除保护命名：unprotrct 变量类型：whattype 检验命名：assigned 别名：alias 宏：macro 帮助：？函数名map 把命令作用到每一个元素，seq 生成序列，add 生成与，mul 生成积二、基本运算1. 近似计算：evalf（表达式，小数位数），用 Digits 命令提前设定小数位数2. 取整运算：round 四舍五入，trunc 向 0 取整， ceil 向-∝取整， floor 向∝取整 3. 范围限定：assume（限定变量范围）frac 小数部分4. 绝对值（模）：abs（表达式），复数求其模5. 同余：mod（数 1，数 2），或者：数 1 mod 数 26. 平方根：sqrt（表达式），平方根最接近整数：isqrt（表达式）7. 阶乘：factorial（数），双阶乘：doublefactorial（数）8. 分解质因数：ifactor（数），分解质因数成组 ifactors （数）9. 商与余数：商 iquo（除数，被除数），余数 irem（除数，被除数）10.最大公约数：igcd（数 1，数 2），最小公倍数：ilcm（数 1，数 2）11.形如as+bt=（a，b）分解：igcdex（a，b，’s’,’t’）12.数组最大最小值：max（数1，数2，…），min（数1，数 2，…）13.实部、虚部与幅角：实部 Re（复数），虚部 Im（复数），幅角 argument14.共轭复数：conjugate（复数）15.形如 a+bi 整理：evalc（表达式）16.并集：集合 1 union 集合 2，交集：intersect，差集：minus17.元素个数：nops（集合），用 op 可把集合转化成表达式三、多项式1. 降幂排列：sort（多项式），字典排序plex（第三个参数）2. 次数：degree（多项式），系数：coeff（多项式，项），首项系数：lcoeff 尾项系数：tcoeff，所有系数：coeffs（多项式，变量，‘power‘）3. 合并同类项：collect（多项式，合并参数）4. 商式：quo（除式，被除式，变量），余式：rem，整除检验：divide5. 最大公因式：gcd（多项式 1，多项式 2），最小公倍式lcm6. 因式分解：factor（多项式），可用第二个参数限定数域缺省代表有理数域7. 分母有理化：rationalize（多项式），有理分式化简：normal 或者 factor8. 化简表达式：simplify，带假设化简：simplify（表达式，assume=范围）附加关系化简：simplify（表达式，{条件}）代换：subs（条件，表达式）9. 展开与合并：展开 expand（表达式），合并 combine （表达式）10.等价转换：convert（函数，转化成的函数）四、解方程1. 方程（组）：solve（{方程（组）}，{未知量（缺省对所有变量求解}）2. 数值解：fsolve（方程，变量范围（可缺省），数域（可缺省））3. 三角方程：添加＿EnvAllSolutions：=ture 以求得所有解4. 多项式方程解的区间：realroot（多项式）5. 不等式（组）：solve（{不等式（组）}，{变量}）6. 整数解：isolve（方程，变量）7. 模 m 的解：msolve（方程，模 m）8. 递推关系的通项：rsolve（{递推关系，初值}，{通项}）9. 函数方程：solve（函数方程，函数）10.系数匹配：match（式子 1=式子 2，变量，’s’）11.Grobner 基原理：先调用 with（grobner），此命令将方程的解等价化简 Gsolve（{式子 1，式子 2，…}，[变量 1，变量 2，…]12.微分方程：dsolve（{方程，初值（可缺）}，函数，’explicit’(可缺)）13.微分方程组：dsolve（{方程 1、2，…，初值}，{函数 1，函数 2，…}）14.拉普拉斯变换法：dsolve（{微分方程}，函数，method=laplace）15.微分方程级数解：dsolve（{微分方程}，函数，type=series）16.微分方程数值解：dsolve（{微分方程}，函数，type=numeric）17.微分方程图形解：DEplot 图形表示微分方程，dfielplot 箭头表示向量场， phaseportrait 向量场及积分曲线，DEplot3d 三维空间图形表示微分方程18.偏微分方程：pdsolve（偏微分方程，求解函数）19.分离变量解偏微分方程：pdsolve（方程，函数，HINT=’*’,’build’）20.偏微分方程图形解：PDEplot（方程，函数，ini 边界 s，s 范围）五、数据处理1. 统计软件包：先调用程序包 with(stats) ，有 7 个子包:anova 方差分析， describe 描述数据分析，fit 拟合回归分析，transform 数据形式变换， random 分布产生随机数，statevalf 分布的数值计算，statplots 统计绘图2. 基本命令：平均值 mean，方差 variance，标准差standarddeviation，中位数 median，众数 mode，数据求与 sumdata，协方差 covariance，相对标准差(标准差/平均值)coefficientofvariation，计数(非缺失)count，计缺失数countmissing，范围 range，几何平均值 geometricmean，线性相关数 linearcorrelation3. 统计图形：直方图 histogram，散点图 scatter2d、quantile2（先从小到大排序再作图），箱式图 boxplot4. 统计分布函数值：正态分布随机分布命令 normald[期望，方差] 先调用程序包 with（statevalf）用法 statevalf（分布函数，求解函数）连续分布:cdf 累积密度函数，icdf 逆累积密度函数，pdf 概率密度函数离散分布：dcdf 离散累积概率函数，idcdf 逆离散累积函数，pf 概率函数5. 插值插值：整体插值命令 f：=interp（数据 1，数据 2，变量）分段插值命令 f：=spline（数据 1，数据 2，变量，次数）6. 回归回归：leastsquare[[x,y],y=多项式，{多项式系数}]（[数据 1，数据 2]） f:=fit（数据 1，数据 2，拟合函数，变量）六、微积分1. 函数定义：函数名：=->表达式，复合函数：f（g（x）：=f@g ）2. 表达式转换成函数：unapply（表达式，函数变量）3. 极值：极大值 maximize（函数，变量，范围，location=true（极值点））极小值 minimize（函数，变量，范围，location=true（极值点））条件极值：extreme（函数，约束条件，{变量}，’s’(极值点)）4. 极限：limit（函数，x=趋值，方向（省缺，left，right，complex））5. 连续性：判断 iscont（函数，x=范围）第三个参数 closed 表示闭区间求解 discont（函数，变量）6. 微分：显函数 diff（函数，变量）对 x 多次求导用 x$n 微分算子 D 隐函数 implicitdiff（函数，依赖关系 y（x），对象y，变量 x）7. 切线作图：showtangent（函数，x=点，view=[x 范围，y 范围]）8. 不定积分：int（函数，积分变量），定积分：int（函数，x=下限..上限）9. 复函数积分：先求奇点 solve（denom（函数）），再用留数规则求解 2*Pi*I（residue（f，z=奇点 1）+ residue（f，z=奇点 2）+…）10.定积分矩形：下矩形：作图 leftbox（f，x=范围，块数）面积 leftsum （f，x=范围，块数）。

Maple的常用内部数学函数

吉林大学公共数学实验中心数学实验>> 首页> 微积分> 实验2Maple简介一、Maple操作界面介绍1、编辑功能:编辑功能中查找模块,可以帮助查找你所需要的关键字节.具体操作如图所示:按上述操作完成后,出现下图所示的对话框:在文本框中输入你要查找的字符或者符号,可以通过findprevious上下翻看,也可以通过replacewith 操作替代你所查找的字符或者符号.cancle表示取消操作.其他编辑操作包括分割或连接(splitorjoin)分为一个执行过程（快截键为f3、f4）和选定块(shift+f3、shift+f4)过程四个操作块运行操作(Execute)：运行选定或者当前的maple中的语句;删除运行结果操作（Removeoutput）：将选定或者当前的maple中运行结果从工作爷中删除或者不显示;2、示图操作（VIEW）文档在屏幕上的显示模式称为“示图”，maple示图菜单主要设置工作爷文档的一些视图属性，所包括菜单如上图所示。

工具条(toolbar)的功能和其他系统一样，主要包括打开文件、创建新文档、存盘、打印当前页面、复制、剪切、粘贴、撤消操作等。

内容工具条：“枫叶”表示设置工作页和标准公式和maple语言之间的转换“X”表示设置工作页和标准公式在活动和非活动方式之间的转换“（对号）”表示标准公式有效时自动检查输入表达式的正确性“！”表示运行当前表达式3、插入操作（INSERT）插入操作比较简单这里就不做详细介绍,主要功能分为:文本插入(textinput);标准maple数学表达式插入;运行单元executegroup插入其中包括在光标前插入和光标后插入图形插入plot,其中包括两维和三维图象的插入电子表格插入spreadsheet段落插入parigraph,其中包括光标前插入和光标后插入数学输入对象(image)插入插入超级连接hyperlink4、其他操作窗口的功能和其他软件基本相同，这里就不做详细介绍了。

Maple常用计算命令

minimize, maximize - 计算最小值/最大值
maxnorm - 一个多项式无穷大范数
4.3 求根
allvalues -计算含有RootOfs的表达式的所有可能值
isqrt, iroot - 整数的xx/第n 次根
realroot - 一个多项式的实数根的隔离区间
root - 一个代数表达式的第n 阶根
implicitdiff - 由一个方程定义一个函数的微分
9.4 积分计算
Si, Ci … - 三角和双曲积分
Dirac, Heaviside - Dirac 函数/Heaviside阶梯函数
Ei - 指数积分
Elliptic -
FresnelC, … - Fresnel 正弦,xx积分和辅助函数
int, Int - 定积分和不定积分
已知的变量名称
指数常数（以自然对数为底）
I - x^2 = -1 的根
infinity 无穷大
1.3 整数函数
! - 阶乘函数
irem, iquo - 整数的余数/商
isprime - 素数测试
isqrfree - 无整数平方的因数分解
max, min - 数的最大值/最小值
mod, modp, mods - 计算对 m 的整数模
polar - 转换为极坐标形式
convert/radians - 将度转换为弧度
convert/sincos - 将trig 函数转换为sin, cos, sinh, cosh
convert/tan - 将trig 函数转换为tan
convert/trig - 将指数函数转换为三角函数和双曲函数
第3xx 求值
convert/octal - 转换为八进制形式

(完整word版)maple函数大全

geom3d
geometry
group
inttrans liesymm
linalg
networks numapprox numtheory orthopoly padic 函数库名称 plots
对应英文全称
differential equations tools
create domains of comqutarton
Eigenvals
数值矩阵的特征值或特征向量
函数名称
基本功能
EllipticCE
EllipticCK
EllipticCPi
EllipticE
EllipticF
EllipticK
ElliptticNome
EllipticPi
Eval
Expand
FFT
FaeLC
FresnelS
Matlab Link
Bacic calculations in algebras of
linear onerators
tools for solveing partial differential
eauations
Spreadsheets
Algebraic Curves
Code Generation
Euclidean
three-dimensional
geometry
Euclidean geometry
Qermutagion and finitely-presented
group
integral transforms
Lie symmetries
Linear algebra package based on
Groebner 基

maple基本函数

第1章章数1.1 复数Re,Im - 返回复数型表达式的实部/虚部abs - 绝对值函数argument - 复数的幅角函数conjugate - 返回共轭复数csgn - 实数和复数表达式的符号函数signum - 实数和复数表达式的sign 函数51.2 MAPLE 常数已知的变量名称指数常数（以自然对数为底）I - x^2 = -1 的根infinity 无穷大1.3 整数函数! - 阶乘函数irem, iquo - 整数的余数/商isprime - 素数测试isqrfree - 无整数平方的因数分解max, min - 数的最大值/最小值mod, modp, mods - 计算对 m 的整数模rand - 随机数生成器randomize - 重置随机数生成器1.4 素数Randpoly, Randprime - 有限域的随机多项式/首一素数多项式ithprime - 确定第 i 个素数nextprime, prevprime - 确定下一个最大/最小素数1.5 数的进制转换convert/base - 基数之间的转换convert/binary - 转换为二进制形式convert/decimal - 转换为 10 进制convert/double - 将双精度浮点数由一种形式转换为另一种形式convert/float - 转换为浮点数convert/hex - 转换为十六进制形式convert/metric - 转换为公制单位convert/octal - 转换为八进制形式1.6 数的类型检查type - 数的类型检查函数第2章初等数学2.1 初等函数product - 确定乘积求和不确定乘积exp - 指数函数sum - 确定求和不确定求和sqrt - 计算平方根算术运算符+, -, *, /, ^add, mul - 值序列的加法/乘法2.2 三角函数arcsin, arcsinh, . - 反三角函数/反双曲函数sin, sinh, . - 三角函数/双曲函数2.3 LOGARITHMS 函数dilog - Dilogarithm 函数ln, log, log10 - 自然对数/一般对数，常用对数2.4 类型转换convert/`+`,convert/`*` - 转换为求和/乘积convert/hypergeom - 将求和转换为超越函数convert/degrees - 将弧度转换为度convert/expsincos - 将trig 函数转换为exp, sin, cosconvert/Ei - 转换为指数积分convert/exp - 将trig 函数转换为指数函数convert/ln - 将arctrig 转换为对数函数polar - 转换为极坐标形式convert/radians - 将度转换为弧度convert/sincos - 将trig 函数转换为sin, cos, sinh, cosh convert/tan - 将trig 函数转换为tanconvert/trig - 将指数函数转换为三角函数和双曲函数第3章求值3.1 假设功能3.2 求值Eval - 对一个表达式求值eval - 求值evala - 在代数数（或者函数）域求值evalb - 按照一个布尔表达式求值evalc - 在复数域上符号求值evalf - 使用浮点算法求值evalhf - 用硬件浮点数算法对表达式求值evalm - 对矩阵表达式求值evaln - 求值到一个名称evalr, shake - 用区间算法求表达式的值和计算范围evalrC - 用复数区间算法对表达式求值value - 求值的惰性函数第4章求根，解方程4.1 数值解fsolve - 利用浮点数算法求解solve/floats - 包含浮点数的表达式4.2 最优化extrema - 寻找一个表达式的相对极值minimize, maximize - 计算最小值/最大值maxnorm - 一个多项式无穷大范数4.3 求根allvalues -计算含有RootOfs的表达式的所有可能值isqrt, iroot - 整数的平方根/第n 次根realroot - 一个多项式的实数根的隔离区间root - 一个代数表达式的第n 阶根RootOf - 方程根的表示surd - 非主根函数roots - 一个多项式对一个变量的精确根turm, sturmseq - 多项式在区间上的实数根数和实根序列4.4 解方程eliminate - 消去一个方程组中的某些变量isolve - 求解方程的整数解solvefor - 求解一个方程组的一个或者多个变量isolate - 隔离一个方程左边的一个子表达式singular - 寻找一个表达式的极点solve/identity - 求解包含属性的表达式solve/ineqs - 求解不等式solve/linear - 求解线性方程组solve/radical - 求解含有未知量根式的方程solve/scalar - 标量情况（单变量和方程）solve/series - 求解含有一般级数的方程solve/system - 解方程组或不等式组第5章操作表达式5.1 处理表达式Norm - 代数数 (或者函数) 的标准型Power - 惰性幂函数Powmod -带余数的惰性幂函数Primfield - 代数域的原始元素Trace - 求一个代数数或者函数的迹charfcn - 表达式和集合的特征函数Indets - 找一个表达式的变元invfunc - 函数表的逆powmod - 带余数的幂函数Risidue - 计算一个表达式的代数余combine - 表达式合并(对tan,cot不好用)expand - 表达式展开Expand - 展开表达式的惰性形式expandoff/expandon - 抑制/不抑制函数展开5.2 因式分解Afactor - 绝对因式分解的惰性形式Afactors - 绝对因式分解分解项列表的惰性形式Berlekamp - 因式分解的Berlekamp 显式度factor - 多元的多项式的因式分解factors - 多元多项式的因式分解列表Factor - 函数factor 的惰性形式Factors - 函数factors 的惰性形式polytools[splits] - 多项式的完全因式分解第6章化简6.1 表达式化简118simplify - 给一个表达式实施化简规则simplify/@ - 利用运算符化简表达式simplify/Ei - 利用指数积分化简表达式simplify/GAMMA - 利用GAMMA 函数进行化简simplify/RootOf - 用RootOf 函数化简表达式simplify/wronskian - 化简含wronskian 标识符的表达式simplify/hypergeom - 化简超越函数表达式simplify/ln - 化简含有对数的表达式simplify/piecewise - 化简分段函数表达式simplify/polar - 化简含有极坐标形式的复数型表达式simplify/power - 化简含幂次的表达式simplify/radical - 化简含有根式的表达式simplify/rtable - 化简rtable 表达式simplify/siderels - 使用关系式进行化简simplify/sqrt - 根式化简simplify/trig - 化简trig 函数表达式simplify/zero - 化简含嵌入型实数和虚数的复数表达式6.2 其它化简操作Normal - normal 函数的惰性形式convert - 将一个表达式转换成不同形式radnormal - 标准化一个含有根号数的表达式rationalize - 分母有理化第7章操作多项式7.0 MAPLE 中的多项式简介7.1 提取coeff - 提取一个多项式的系数coeffs - 提取多元的多项式的所有系数coeftayl - 多元表达式的系数lcoeff, tcoeff - 返回多元多项式的首项和末项系数7.2 多项式约数和根gcd, lcm - 多项式的最大公约数/最小公倍数psqrt, proot - 多项式的平方根和第n次根rem,quo - 多项式的余数/商7.3 操纵多项式convert/horner - 将一个多项式转换成Horner形式collect - 象幂次一样合并系数compoly - 确定一个多项式的可能合并的项数convert/polynom - 将级数转换成多项式形式convert/mathorner - 将多项式转换成Horner矩阵形式convert/ratpoly - 将级数转换成有理多项式sort - 将值的列表或者多项式排序sqrfree - 不含平方项的因数分解函数7.4 多项式运算discrim - 多项式的判别式fixdiv - 计算多项式的固定除数norm - 多项式的标准型resultant - 计算两个多项式的终结式bernoulli - Bernoulli 数和多项式bernstein - 用Bernstein多项式近似一个函数content, primpart - 一个多元的多项式的内容和主部degree, ldegree - 一个多项式的最高次方/最低次方divide - 多项式的精确除法euler - Euler 数和多项式icontent - 多项式的整数部分interp - 多项式的插值prem, sprem - 多项式的pseudo 余数和稀疏pseudo 余数randpoly - 随机多项式生成器spline - 计算自然样条函数第8章有理表达式8.0 有理表达式简介8.1 操作有理多项式numer,denom - 返回一个表达式的分子/分母frontend - 将一般的表达式处理成一个有理表达式normal - 标准化一个有理表达式convert/parfrac - 转换为部分分数形式convert/rational - 将浮点数转换为接近的有理数ratrecon - 重建有理函数第9章微积分9.1 取极限Limit, limit - 计算极限limit[dir] - 计算方向极限limit[multi] - 多重方向极限limit[return] - 极限的返回值9.2 连续性测试discont - 寻找一个函数在实数域上的间断点fdiscont - 用数值法寻找函数在实数域上的间断点iscont - 测试在一个区间上的连续性9.3 微分计算D - 微分算子D, diff - 运算符D 和函数diffdiff, Diff - 微分或者偏微分convert/D - 将含导数表达式转换为D运算符表达式convert/diff - 将D(f)(x)表达式转换为diff(f(x),x)的形式implicitdiff - 由一个方程定义一个函数的微分9.4 积分计算Si, Ci …- 三角和双曲积分Dirac, Heaviside - Dirac 函数/Heaviside阶梯函数Ei - 指数积分Elliptic - 椭圆积分FresnelC, … - Fresnel 正弦,余弦积分和辅助函数int, Int - 定积分和不定积分LegendreP, …- Legendre 函数及其第一和第二类函数Li - 对数积分student[changevar] - 变量代换dawson - Dawson 积分ellipsoid - 椭球体的表面积evalf(int) - 数值积分intat, Intat - 在一个点上积分求值第10章微分方程10.1 微分方程分类odeadvisor - ODE-求解分析器DESol - 表示微分方程解的数据结构pdetest - 测试pdsolve 能找到的偏微分方程(PDEs)解10.2 常微分方程求解dsolve - 求解常微方程(ODE)dsolve - 用给定的初始条件求解ODE 问题dsolve/inttrans - 用积分变换方法求解常微分方程dsolve/numeric - 常微方程数值解dsolve/piecewise - 带分段系数的常微方程求解dsolve - 寻找ODE 问题的级数解dsolve - 求解ODEs 方程组odetest - 从ODE 求解器中测试结果是显式或者隐式类型10.3 偏微分方程求解pdsolve - 寻找偏微分方程 (PDEs) 的解析解第11章数值计算11.1 MAPLE 中的数值计算环境IEEE 标准和Maple数值计算数据类型特殊值环境变量11.2 算法标准算法复数算法含有0，无穷和未定义数的算法11.3 数据构造器254complex - 复数和复数构造器Float, …- 浮点数及其构造器Fraction - 分数及其的构造器integer - 整数和整数构造器11.4 MATLAB 软件包简介11.5 “”区间类型表达式第12章级数12.1 幂级数的阶数Order - 阶数项函数order - 确定级数的截断阶数12.2 常见级数展开series - 一般的级数展开taylor - Taylor 级数展开mtaylor - 多元Taylor级数展开poisson - Poisson级数展开.26812.3 其它级数eulermac - Euler-Maclaurin求和piecewise - 分段连续函数asympt - 渐进展开第13章特殊函数AiryAi, AiryBi - Airy 波动函数AiryAiZeros, AiryBiZeros - Airy函数的实数零点AngerJ, WeberE - Anger函数和Weber函数BesselI, HankelH1, …- Bessel函数和Hankel函数BesselJZeros, … - Bessel函数实数零点Beta - Beta函数EllipticModulus - 模数函数k(q)GAMMA, lnGAMMA - 完全和不完全Gamma函数GaussAGM - Gauss 算术的几何平均数JacobiAM, ., - Jacobi 振幅函数和椭圆函数JacobiTheta1, JacobiTheta4 - Jacobi theta函数JacobiZeta - Jacobi 的Zeta函数KelvinBer, KelvinBei - Kelvin函数KummerM, - Kummer M函数和U函数LambertW - LambertW函数LerchPhi - 一般的Lerch Phi函数LommelS1, LommelS2 - Lommel函数MeijerG - 一个修正的Meijer G函数Psi - Digamma 和Polygamma函数StruveH, StruveL - Struve函数WeierstrassP - Weierstrass P函数及其导数WhittakerM - Whittaker 函数Zeta - Zeta 函数erf, … - 误差函数，补充的误差函数和虚数误差函数harmonic - 调和函数hypergeom - 广义的超越函数pochhammer - 一般的pochhammer函数polylog - 一般的polylogarithm函数第14章线性代数14.1 ALGEBRA（代数）中矩阵，矢量和数组14.2 LINALG 软件包简介14.3 数据结构矩阵matrices（小写）矢量vectors（矢量）convert/matrix - 将数组，列表，Matrix 转换成matrixconvert/vector - 将列表，数组或Vector 转换成矢量vectorlinalg[matrix] - 生成矩阵matrix（小写）linalg[vector] - 生成矢量vector（小写）14.4 惰性函数Det - 惰性行列式运算符Eigenvals - 数值型矩阵的特征值和特征向量Hermite, Smith - 矩阵的Hermite 和Smith 标准型14.5 LinearAlgebra函数Matrix 定义矩阵Add 加/减矩阵Adjoint 伴随矩阵BackwardSubstitute 求解 A . X = B，其中 A 为上三角型行阶梯矩阵BandMatrix 带状矩阵Basis 返回向量空间的一组基SumBasis 返回向量空间直和的一组基IntersectionBasis 返回向量空间交的一组基BezoutMatrix 构造两个多项式的Bezout 矩阵BidiagonalForm 将矩阵约化为双对角型CharacteristicMatrix 构造特征矩阵CharacteristicPolynomial 构造矩阵的特征多项式CompanionMatrix 构造一个首一（或非首一）多项式或矩阵多项式的友矩阵（束）ConditionNumber 计算矩阵关于某范数的条件数ConstantMatrix 构造常数矩阵ConstantVector 构造常数向量Copy 构造矩阵或向量的一份复制CreatePermutation 将一个 NAG 主元向量转换为一个置换向量或矩阵CrossProduct 向量的叉积`&x` 向量的叉积DeleteRow 删除矩阵的行DeleteColumn 删除矩阵的列Determinant 行列式Diagonal 返回从矩阵中得到的向量序列DiagonalMatrix 构造（分块）对角矩阵Dimension 行数和列数DotProduct 点积BilinearForm 向量的双线性形式EigenConditionNumbers 计算数值特征值制约问题的特征值或特征向量的条件数Eigenvalues 计算矩阵的特征值Eigenvectors 计算矩阵的特征向量Equal 比较两个向量或矩阵是否相等ForwardSubstitute 求解 A . X = B，其中 A 为下三角型行阶梯矩阵FrobeniusForm 将一个方阵约化为 Frobenius 型（有理标准型）GaussianElimination 对矩阵作高斯消元ReducedRowEchelonForm 对矩阵作高斯－约当消元GetResultDataType 返回矩阵或向量运算的结果数据类型GetResultShape 返回矩阵或向量运算的结果形状GivensRotationMatrix 构造Givens 旋转的矩阵GramSchmidt 计算一个正交向量集HankelMatrix 构造一个Hankel 矩阵HermiteForm 计算一个矩阵的 Hermite 正规型HessenbergForm 将一个方阵约化为上Hessenberg 型HilbertMatrix 构造广义 Hilbert 矩阵HouseholderMatrix 构造 Householder 反射矩阵IdentityMatrix 构造一个单位矩阵IsDefinite 检验矩阵的正定性，负定性或不定性IsOrthogonal 检验矩阵是否正交IsUnitary 检验矩阵是否为酉矩阵IsSimilar 确定两个矩阵是否相似JordanBlockMatrix 构造约当块矩阵JordanForm 将矩阵约化为约当型KroneckerProduct 构造两个矩阵的Kronecker 张量积LeastSquares 方程的最小二乘解LinearSolve 求解线性方程组 A . x = bLUDecomposition 计算矩阵的 Cholesky，PLU 或 PLU1R 分解Map 将一个程序映射到一个表达式上，对矩阵和向量在原位置上进行处理MatrixAdd 计算两个矩阵的线性组合VectorAdd 计算两个向量的线性组合MatrixExponential 确定一个矩阵 A 的矩阵指数 exp(A)MatrixFunction 确定方阵 A 的函数F(A)MatrixInverse 计算方阵的逆或矩阵的Moore-Penrose 伪逆MatrixMatrixMultiply 计算两个矩阵的乘积MatrixVectorMultiply 计算一个矩阵和一个列向量的乘积VectorMatrixMultiply 计算一个行向量和一个矩阵的乘积MatrixPower 矩阵的幂MinimalPolynomial 构造矩阵的最小多项式Minor 计算矩阵的子式Multiply 矩阵相乘Norm 计算矩阵或向量的p-范数MatrixNorm 计算矩阵的p-范数VectorNorm 计算向量的p-范数Normalize 向量正规化NullSpace 计算矩阵的零度零空间OuterProductMatrix 两个向量的外积Permanent 方阵的不变量Pivot 矩阵元素的主元消去法PopovForm Popov 正规型QRDecomposition QR 分解RandomMatrix 构造随机矩阵RandomVector 构造随机向量Rank 计算矩阵的秩Row 返回矩阵的一个行向量序列Column 返回矩阵的一个列向量序列RowOperation 对矩阵作初等行变换ColumnOperation 对矩阵作出等列变换RowSpace 返回矩阵行空间的一组基ColumnSpace 返回矩阵列空间的一组基ScalarMatrix 构造一个单位矩阵的数量倍数ScalarVector 构造一个单位向量的数量倍数ScalarMultiply 矩阵与数的乘积MatrixScalarMultiply 计算矩阵与数的乘积VectorScalarMultiply 计算向量与数的乘积SchurForm 将方阵约化为 Schur 型SingularValues 计算矩阵的奇异值SmithForm 将矩阵约化为 Smith 正规型StronglyConnectedBlocks 计算方阵的强连通块SubMatrix 构造矩阵的子矩阵SubVector 构造向量的子向量SylvesterMatrix 构造两个多项式的 Sylvester 矩阵ToeplitzMatrix 构造Toeplitz 矩阵Trace 计算方阵的迹Transpose 转置矩阵HermitianTranspose 共轭转置矩阵TridiagonalForm 将方阵约化为三对角型UnitVector 构造单位向量VandermondeMatrix 构造一个 Vandermonde 矩阵VectorAngle 计算两个向量的夹角ZeroMatrix 构造一个零矩阵ZeroVector 构造一个零向量Zip 将一个具有两个参数的程序作用到一对矩阵或向量上LinearAlgebra[Generic] 子函数包[Generic] 子函数包提供作用在场，欧几里得域，积分域和环上的线性代数算法。

Maple常用计算命令

常用计算命令版本7.0指令》Maple 《章数章1第复数1.1 虚部/返回复数型表达式的实部Re,Im - 函数绝对值abs - 复数的幅角函数argument - 返回共轭复数conjugate - 实数和复数表达式的符号函数csgn - 5 函数sign 实数和复数表达式的signum - 常数1.2 MAPLE 已知的变量名称指数常数（以自然对数为底）的根I - x^2= -1 无穷大infinity 整数函数1.3 阶乘函数!- 商/整数的余数irem, iquo - 素数测试isprime - 无整数平方的因数分解isqrfree - 最小值/数的最大值max, min - 的整数模 m 计算对mod, modp, mods - 随机数生成器rand - 重置随机数生成器randomize - 素数1.4 首一素数多项式/有限域的随机多项式Randpoly, Randprime - 个素数 i 确定第ithprime - 最小素数/确定下一个最大nextprime, prevprime - 数的进制转换1.5 基数之间的转换convert/base - 转换为二进制形式convert/binary - convert/decimal - 进制 10 转换为将双精度浮点数由一种形式转换为另一种形式convert/double - 转换为浮点数convert/float - 转换为十六进制形式convert/hex - 转换为公制单位convert/metric - 转换为八进制形式convert/octal - 数的类型检查1.6 数的类型检查函数type - 初等数学章2第初等函数2.1 确定乘积求和不确定乘积product - 指数函数exp - 确定求和不确定求和sum - 计算平方根sqrt - +, -, *, /, ^ 算术运算符乘法/值序列的加法add, mul - 三角函数2.2 反双曲函数/反三角函数arcsin, arcsinh, . - 双曲函数/三角函数sin, sinh, . - 函数2.3 LOGARITHMS 函数dilog - Dilogarithm 一般对数，常用对数/自然对数ln, log, log10 - 类型转换2.4 乘积/转换为求和convert/`+`,convert/`*` - 将求和转换为超越函数convert/hypergeom - 将弧度转换为度convert/degrees - exp, sin, cos 函数转换为trig 将convert/expsincos - 转换为指数积分convert/Ei - 函数转换为指数函数trig 将convert/exp - 转换为对数函数arctrig 将convert/ln - 转换为极坐标形式polar - 将度转换为弧度convert/radians - sin, cos, sinh, cosh 函数转换为trig 将convert/sincos - tan 函数转换为trig 将convert/tan - 将指数函数转换为三角函数和双曲函数convert/trig - 章3第求值假设功能3.1 求值3.2 对一个表达式求值Eval - 求值eval -在代数数（或者函数）域求值evala - 求值布尔表达式按照一个evalb - 在复数域上符号求值evalc - 使用浮点算法求值evalf - 用硬件浮点数算法对表达式求值evalhf - 对矩阵表达式求值evalm - 求值到一个名称evaln - 用区间算法求表达式的值和计算范围evalr, shake - 用复数区间算法对表达式求值evalrC - 求值的惰性函数value - 求根，解方程章4第数值解4.1 利用浮点数算法求解fsolve - 包含浮点数的表达式solve/floats - 最优化4.2 寻找一个表达式的相对极值extrema - 最大值/计算最小值minimize, maximize - 一个多项式无穷大范数maxnorm - 求根4.3 的表达式的所有可能值RootOfs计算含有allvalues - 次根n 第/整数的平方根isqrt, iroot - 一个多项式的实数根的隔离区间realroot - 阶根n一个代数表达式的第root - 方程根的表示RootOf- 非主根函数surd - 一个多项式对一个变量的精确根roots - 多项式在区间上的实数根数和实根序列turm, sturmseq - 解方程4.4 消去一个方程组中的某些变量eliminate - 求解方程的整数解isolve - 求解一个方程组的一个或者多个变量solvefor - 隔离一个方程左边的一个子表达式isolate - 寻找一个表达式的极点singular - 求解包含属性的表达式solve/identity - 求解不等式solve/ineqs - 求解线性方程组solve/linear - 求解含有未知量根式的方程solve/radical -标量情况（单变量和方程）solve/scalar - 求解含有一般级数的方程solve/series - 解方程组或不等式组solve/system - 操作表达式章5第处理表达式5.1 的标准型) 或者函数 (代数数Norm - 惰性幂函数Power - 带余数的惰性幂函数Powmod - 代数域的原始元素 Primfield - 求一个代数数或者函数的迹Trace - 表达式和集合的特征函数charfcn - 找一个表达式的变元Indets - 函数表的逆invfunc - 带余数的幂函数powmod - 计算一个表达式的代数余Risidue - ) 不好用tan,cot对(表达式合并combine - 表达式展开expand - 展开表达式的惰性形式Expand - 不抑制函数展开/抑制expandoff/expandon - 因式分解5.2 绝对因式分解的惰性形式Afactor - 绝对因式分解分解项列表的惰性形式Afactors - 显式度Berlekamp 因式分解的Berlekamp - 多元的多项式的因式分解factor - 多元多项式的因式分解列表factors - 的惰性形式factor 函数Factor - 的惰性形式factors 函数Factors - 多项式的完全因式分解polytools[splits] - 化简章6第 118 表达式化简6.1 给一个表达式实施化简规则simplify - 利用运算符化简表达式simplify/@ - 利用指数积分化简表达式simplify/Ei - 函数进行化简GAMMA利用simplify/GAMMA - 函数化简表达式RootOf用simplify/RootOf -的表达式标识符wronskian 化简含simplify/wronskian - 化简超越函数表达式simplify/hypergeom - 化简含有对数的表达式simplify/ln - 化简分段函数表达式simplify/piecewise - 化简含有极坐标形式的复数型表达式simplify/polar - 化简含幂次的表达式simplify/power - 化简含有根式的表达式simplify/radical - 表达式rtable 化简simplify/rtable - 使用关系式进行化简simplify/siderels - 根式化简simplify/sqrt - 函数表达式trig 化简simplify/trig - 化简含嵌入型实数和虚数的复数表达式simplify/zero - 其它化简操作6.2 函数的惰性形式Normal - normal 将一个表达式转换成不同形式convert - 标准化一个含有根号数的表达式radnormal - 分母有理化rationalize - 操作多项式章7第中的多项式简介7.0 MAPLE 提取7.1 提取一个多项式的系数coeff - 提取多元的多项式的所有系数coeffs - 多元表达式的系数coeftayl - 返回多元多项式的首项和末项系数lcoeff, tcoeff - 多项式约数和根7.2 最小公倍数/多项式的最大公约数gcd, lcm - 次根n多项式的平方根和第psqrt, proot - 商/多项式的余数rem,quo - 操纵多项式7.3 形式Horner将一个多项式转换成convert/horner - collect - 象幂次一样合并系数确定一个多项式的可能合并的项数compoly - 将级数转换成多项式形式convert/polynom - 矩阵形式Horner将多项式转换成convert/mathorner - 将级数转换成有理多项式convert/ratpoly - 将值的列表或者多项式排序sort- 不含平方项的因数分解函数sqrfree -多项式运算7.4 多项式的判别式discrim - 计算多项式的固定除数fixdiv - 多项式的标准型norm - 计算两个多项式的终结式resultant - 数和多项式bernoulli - Bernoulli 多项式近似一个函数Bernstein用bernstein - 一个多元的多项式的内容和主部content, primpart - 最低次方/一个多项式的最高次方degree, ldegree - 多项式的精确除法divide - 数和多项式euler - Euler 多项式的整数部分icontent - 多项式的插值interp - 余数pseudo 余数和稀疏pseudo 多项式的prem, sprem - 随机多项式生成器randpoly - 计算自然样条函数spline - 有理表达式章8第有理表达式简介8.0 操作有理多项式8.1 分母/返回一个表达式的分子numer,denom - 将一般的表达式处理成一个有理表达式frontend - 标准化一个有理表达式normal - 转换为部分分数形式convert/parfrac - 将浮点数转换为接近的有理数convert/rational - 重建有理函数ratrecon - 微积分章9第取极限9.1 计算极限Limit, limit - 计算方向极限limit[dir] - 多重方向极限limit[multi] - 极限的返回值limit[return] - 连续性测试9.2 寻找一个函数在实数域上的间断点discont - 用数值法寻找函数在实数域上的间断点fdiscont - 测试在一个区间上的连续性iscont -微分计算9.3 微分算子D - diff 和函数D 运算符D, diff - 微分或者偏微分diff, Diff - 运算符表达式D将含导数表达式转换为convert/D - 的形式diff(f(x),x)表达式转换为D(f)(x)将convert/diff - 由一个方程定义一个函数的微分implicitdiff - 积分计算9.4 三角和双曲积分- Si, C i … 阶梯函数/Heaviside函数Dirac, Heaviside - Dirac 指数积分Ei - 椭圆积分Elliptic - 余弦积分和辅助函数,正弦- Fresnel FresnelC, … 定积分和不定积分int, Int - 函数及其第一和第二类函数- Legendre eP, … Legendr 对数积分Li - 变量代换student[changevar] - 积分dawson - Dawson 椭球体的表面积ellipsoid - 数值积分evalf(int) - 在一个点上积分求值intat, Intat - 微分方程章10第微分方程分类10.1 求解分析器odeadvisor - ODE- 数据结构表示微分方程解的DESol - 解(PDEs)能找到的偏微分方程pdsolve 测试pdetest - 常微分方程求解10.2 (ODE) 求解常微方程dsolve - 问题ODE 求解初始条件用给定的dsolve - 用积分变换方法求解常微分方程dsolve/inttrans - 常微方程数值解dsolve/numeric - 带分段系数的常微方程求解dsolve/piecewise - 问题的级数解ODE 寻找dsolve - 方程组ODEs 求解dsolve - 求解器中测试结果是显式或者隐式类型ODE 从odetest - 偏微分方程求解10.3 的解析解 (PDEs) 寻找偏微分方程pdsolve -数值计算章11第中的数值计算环境11.1 MAPLE 数值计算Maple标准和IEEE 数据类型特殊值环境变量算法11.2 标准算法复数算法，无穷和未定义数的算法0含有数据构造器11.3 254 复数和复数构造器complex - 浮点数及其构造器- Float, … 分数及其的构造器Fraction- 整数和整数构造器integer - 简介软件包11.4 MATLAB 11.5 “”区间类型表达式12第章级数幂级数的阶数12.1 阶数项函数Order - 确定级数的截断阶数order - 常见级数展开12.2 一般的级数展开series - 级数展开taylor - Taylor 级数展开Taylor多元mtaylor - .268 级数展开poisson- Poisson 其它级数12.3 求和eulermac - Euler-Maclaurin 分段连续函数piecewise - 渐进展开asympt - 13第特殊函数章波动函数AiryAi, AiryBi- Airy 函数的实数零点AiryAiZeros, AiryBiZeros - Airy 函数Weber函数和AngerJ, WeberE - Anger 函数Hankel函数和- BesselBesselI, HankelH1, … 函数实数零点- BesselBesselJZeros, … 函数Beta - Beta k(q) 模数函数EllipticModulus - 函数Gamma完全和不完全GAMMA, lnGAMMA - 算术的几何平均数GaussAGM - Gauss 椭圆函数振幅函数和JacobiAM, ., - Jacobi 函数JacobiTheta1, JacobiTheta4 - Jacobi theta 函数Zeta的JacobiZeta- Jacobi 函数KelvinBer, KelvinBei - Kelvin 函数U函数和KummerM, - Kummer M 函数LambertW - LambertW 函数Lerch Phi一般的LerchPhi - 函数LommelS1, LommelS2 - Lommel 函数Meijer G一个修正的MeijerG - 函数Polygamma和Psi - Digamma 函数StruveH, StruveL - Struve 函数及其导数WeierstrassP - Weierstrass P 函数WhittakerM - Whittaker 函数Zeta - Zeta 误差函数，补充的误差函数和虚数误差函数- erf, … 调和函数harmonic - 广义的超越函数hypergeom -一般的pochhammer - 函数pochhammer 函数polylogarithm一般的polylog - 线性代数章14第数组（代数）中矩阵，矢量和14.1 ALGEBRA 软件包简介14.2 LINALG 14.3 数据结构（小写）matrices矩阵（矢量）vectors矢量 matrix 转换成Matrix 将数组，列表，convert/matrix - vector转换成矢量Vector 将列表，数组或convert/vector - （小写）matrix生成矩阵linalg[matrix] - （小写）vector生成矢量linalg[vector] - 惰性函数14.4 惰性行列式运算符Det -数值型矩阵的特征值和特征向量Eigenvals - 标准型Smith 和Hermite 矩阵的Hermite, Smith - 函数14.5 LinearAlgebra 定义矩阵Matrix 减矩阵/加Add 伴随矩阵Adjoint 为上三角型行阶梯矩 A ，其中 A . X = B求解BackwardSubstitute 阵带状矩阵BandMatrix 返回向量空间的一组基Basis 返回向量空间直和的一组基SumBasis 返回向量空间交的一组基IntersectionBasis Bezout 构造两个多项式的BezoutMatrix 矩阵将矩阵约化为双对角型BidiagonalForm 构造特征矩阵CharacteristicMatrix 构造矩阵的特征多项式CharacteristicPolynomial 构造一个首一（或非首一）多项式或矩阵多项式的CompanionMatrix 友矩阵（束）计算矩阵关于某范数的条件数ConditionNumber 构造常数矩阵ConstantMatrix 构造常数向量ConstantVector 构造矩阵或向量的一份复制Copy NAG 将一个CreatePermutation 主元向量转换为一个置换向量或矩阵向量的叉积CrossProduct 向量的叉积`&x` 删除矩阵的行DeleteRow 删除矩阵的列DeleteColumn 行列式Determinant 返回从矩阵中得到的向量序列Diagonal 对角矩阵构造（分块）DiagonalMatrix 行数和列数Dimension 点积DotProduct 向量的双线性形式BilinearForm 计算数值特征值制约问题的特征值或特征向EigenConditionNumbers 量的条件数计算矩阵的特征值Eigenvalues 计算矩阵的特征向量Eigenvectors比较两个向量或矩阵是否相等Equal 为下三角型行阶梯矩阵 A ，其中 A . X = B求解ForwardSubstitute 型（有理标准型） Frobenius 将一个方阵约化为FrobeniusForm 消元高斯对矩阵作GaussianElimination 对矩阵作高斯－约当消元ReducedRowEchelonForm 返回矩阵或向量运算的结果数据类型GetResultDataType 返回矩阵或向量运算的结果形状GetResultShape 旋转的矩阵Givens 构造GivensRotationMatrix 计算一个正交向量集GramSchmidt 矩阵Hankel 构造一个HankelMatrix HermiteForm 正规型 Hermite 计算一个矩阵的型Hessenberg 将一个方阵约化为上HessenbergForm 矩阵Hilbert 构造广义HilbertMatrix 反射矩阵Householder 构造HouseholderMatrix 构造一个单位矩阵IdentityMatrix 检验矩阵的正定性，负定性或不定性IsDefinite 检验矩阵是否正交IsOrthogonal 检验矩阵是否为酉矩阵IsUnitary 确定两个矩阵是否相似IsSimilar 构造约当块矩阵JordanBlockMatrix 将矩阵约化为约当型JordanForm 张量积Kronecker 构造两个矩阵的KroneckerProduct 方程的最小二乘解LeastSquares A . x = b 求解线性方程组LinearSolve 分解PLU1R 或PLU ，Cholesky计算矩阵的LUDecomposition 将一个程序映射到一个表达式上，对矩阵和向量在原位置上进行Map 处理计算两个矩阵的线性组合MatrixAdd VectorAdd 计算两个向量的线性组合 exp(A) 的矩阵指数 A 确定一个矩阵MatrixExponential F(A) 的函数A 确定方阵MatrixFunction 伪逆Moore-Penrose 计算方阵的逆或矩阵的MatrixInverse 计算两个矩阵的乘积MatrixMatrixMultiply 计算一个矩阵和一个列向量的乘积MatrixVectorMultiply 计算一个行向量和一个矩阵的乘积VectorMatrixMultiply 矩阵的幂MatrixPower 构造矩阵的最小多项式MinimalPolynomial 计算矩阵的子式Minor矩阵相乘Multiply 范数p-计算矩阵或向量的Norm 范数p-计算矩阵的MatrixNorm 范数p-计算向量的VectorNorm 向量正规化Normalize 计算矩阵的零度零空间NullSpace 两个向量的外积OuterProductMatrix 方阵的不变量Permanent 矩阵元素的主元消去法Pivot 正规型PopovFormPopov 分解QRDecomposition QR 随机矩阵构造RandomMatrix 构造随机向量RandomVector 矩阵的秩计算Rank 返回矩阵的一个行向量序列Row 返回矩阵的一个列向量序列Column 对矩阵作初等行变换RowOperation 对矩阵作出等列变换ColumnOperation 返回矩阵行空间的一组基RowSpace 返回矩阵列空间的一组基ColumnSpace 构造一个单位矩阵的数量倍数ScalarMatrix 构造一个单位向量的数量倍数ScalarVector 矩阵与数的乘积ScalarMultiply 计算矩阵与数的乘积MatrixScalarMultiply VectorScalarMultiply 计算向量与数的乘积型Schur 将方阵约化为SchurForm 计算矩阵的奇异值SingularValues 正规型 Smith 将矩阵约化为SmithForm 计算方阵的强连通块StronglyConnectedBlocks 构造矩阵的子矩阵SubMatrix 构造向量的子向量SubVector 构造两个多项式的SylvesterMatrix 矩阵Sylvester 矩阵Toeplitz 构造ToeplitzMatrix 计算方阵的迹Trace 转置矩阵Transpose 共轭转置矩阵HermitianTranspose 将方阵约化为三对角型TridiagonalForm 构造单位向量UnitVector矩阵Vandermonde 构造一个VandermondeMatrix计算两个向量的夹角VectorAngle 构造一个零矩阵ZeroMatrix 构造一个零向量ZeroVector Zip 将一个具有两个参数的程序作用到一对矩阵或向量上子函数包提供作用在[Generic] 子函数包LinearAlgebra[Generic] 域，积分域和环上的线性代数算法。

Maple常用函数
在Maple中,想要查询某个函数具体的信息,比如你要查sin的信息,你可以在：
[>提示符后输入?sin来查询该函数.
另外，evalf()可以将一个精确的数值表达式转化为一个浮点数,通常以十位数字来表示这个浮点数,也可以指定包含的数目,例如evalf(pi,200)就可以以200个数字表示π，也可以通过指定digits变量来设定以后的表达式用多少位数字显示浮点数.
Maple可以对复数进行计算，以符号i表示－1的平方根。

convert函数可以将数字转换成其它进位制的表示形式,如convert(17, binary)将247转换成二进制10001；convert(1023, hex)将1023转化成十六进制数3FF；convert(17,base,3)将17转换成三进制表示形式[2;2;1]。

注意要用base关键字。

gamma 伽马函数
beta 贝特函数
plot({f1(x)，f2(x),…},x=a..b，选项)；。