离散数学答案(尹宝林版)第一章习题解答
(完整版)离散数学答案(尹宝林版)第一章习题解答

(完整版)离散数学答案(尹宝林版)第一章习题解答第一章命题逻辑习题与解答⒈ 判断下列语句是否为命题,并讨论命题的真值。
⑴ 2x - 3 = 0。
⑵ 前进!⑶ 如果8 + 7 > 20,则三角形有四条边。
⑷ 请勿吸烟!⑸ 你喜欢鲁迅的作品吗?⑹ 如果太阳从西方升起,你就可以长生不老。
⑺ 如果太阳从东方升起,你就可以长生不老。
解⑶,⑹,⑺表达命题,其中⑶,⑹表达真命题,⑺表达假命题。
⒉ 将下列命题符号化:⑴ 逻辑不是枯燥无味的。
⑵ 我看见的既不是小张也不是老李。
⑶ 他生于1963年或1964年。
⑷ 只有不怕困难,才能战胜困难。
⑸ 只要上街,我就去书店。
⑹ 如果晚上做完了作业并且没有其它事情,小杨就看电视或听音乐。
⑺ 如果林芳在家里,那么他不是在做作业就是在看电视。
⑻ 三角形三条边相等是三个角相等的充分条件。
⑼ 我进城的必要条件是我有时间。
⑽ 他唱歌的充分必要条件是心情愉快。
⑾ 小王总是在图书馆看书,除非他病了或者图书馆不开门。
解⑴ p :逻辑是枯燥无味的。
“逻辑不是枯燥无味的”符号化为 ?p 。
⑵ p :我看见的是小张。
q :我看见的是老李。
“我看见的既不是小张也不是老李”符号化为q p ?∧?。
⑶ p :他生于1963年。
q :他生于1964年。
“他生于1963年或1964年”符号化为p ⊕ q 。
⑷ p :害怕困难。
q :战胜困难。
“只有不怕困难,才能战胜困难”符号化为q → ? p 。
⑸ p :我上街。
q :我去书店。
“只要上街,我就去书店”符号化为p → q 。
⑹ p :小杨晚上做完了作业。
q :小杨晚上没有其它事情。
r :小杨晚上看电视。
s :小杨晚上听音乐。
“如果晚上做完了作业并且没有其它事情,小杨就看电视或听音乐”符号化为s r q p ∨→∧。
⑺ p :林芳在家里。
q :林芳做作业。
r :林芳看电视。
“如果林芳在家里,那么他不是在做作业就是在看电视”符号化为r q p ∨→。
⑻ p :三角形三条边相等。
离散数学第一章部分课后习题参考答案

第一章部分课后习题参考答案16 设p、q的真值为0;r、s的真值为1,求下列各命题公式的真值。
(1)p∨(q∧r)0∨(0∧1) 0(2)(p?r)∧(﹁q∨s) (0?1)∧(1∨1) 0∧10.(3)(p∧q∧r)?(p∧q∧﹁r) (1∧1∧1)? (0∧0∧0)0(4)(r∧s)→(p∧q) (0∧1)→(1∧0) 0→0 117.判断下面一段论述是否为真:“是无理数。
并且,如果3是无理数,则也是无理数。
另外6能被2整除,6才能被4整除。
”答:p: 是无理数 1q: 3是无理数0r: 是无理数 1s:6能被2整除 1t: 6能被4整除0命题符号化为:p∧(q→r)∧(t→s)的真值为1,所以这一段的论述为真。
19.用真值表判断下列公式的类型:(4)(p→q) →(q→p)(5)(p∧r) (p∧q)(6)((p→q) ∧(q→r)) →(p→r)答:(4)p q p→q q p q→p (p→q)→(q→p)0 0 1 1 1 1 10 1 1 0 1 1 11 0 0 1 0 0 11 1 1 0 0 1 1所以公式类型为永真式(5)公式类型为可满足式(方法如上例)(6)公式类型为永真式(方法如上例)第二章部分课后习题参考答案3.用等值演算法判断下列公式的类型,对不是重言式的可满足式,再用真值表法求出成真赋值.(1) (p∧q→q)(2)(p→(p∨q))∨(p→r)(3)(p∨q)→(p∧r)答:(2)(p→(p∨q))∨(p→r)(p∨(p∨q))∨(p∨r)p∨p∨q∨r1所以公式类型为永真式(3)P q r p∨q p∧r (p∨q)→(p∧r)0 0 0 0 0 10 0 1 0 0 10 1 0 1 0 00 1 1 1 0 01 0 0 1 0 01 0 1 1 1 11 1 0 1 0 01 1 1 1 1 1所以公式类型为可满足式4.用等值演算法证明下面等值式:(2)(p→q)∧(p→r)(p→(q∧r))(4)(p∧q)∨(p∧q)(p∨q) ∧(p∧q)证明(2)(p→q)∧(p→r)(p∨q)∧(p∨r)p∨(q∧r))p→(q∧r)(4)(p∧q)∨(p∧q)(p∨(p∧q)) ∧(q∨(p∧q)(p∨p)∧(p∨q)∧(q∨p) ∧(q∨q)1∧(p∨q)∧(p∧q)∧1(p∨q)∧(p∧q)5.求下列公式的主析取范式与主合取范式,并求成真赋值(1)(p→q)→(q∨p)(2)(p→q)∧q∧r(3)(p∨(q∧r))→(p∨q∨r)解:(1)主析取范式(p→q)→(q p)(p q)(q p)(p q)(q p)(p q)(q p)(q p)(p q)(p q)(p q)(p q)(p q)∑(0,2,3)主合取范式:(p→q)→(q p)(p q)(q p)(p q)(q p)(p(q p))(q(q p))1(p q)(p q) M1∏(1)(2) 主合取范式为:(p→q)q r(p q)q r(p q)q r0所以该式为矛盾式.主合取范式为∏(0,1,2,3,4,5,6,7)矛盾式的主析取范式为 0(3)主合取范式为:(p(q r))→(p q r)(p(q r))→(p q r)(p(q r))(p q r)(p(p q r))((q r))(p q r))1 11所以该式为永真式.永真式的主合取范式为 1主析取范式为∑(0,1,2,3,4,5,6,7)第三章部分课后习题参考答案14. 在自然推理系统P中构造下面推理的证明:(2)前提:p q,(q r),r结论:p(4)前提:q p,q s,s t,t r结论:p q证明:(2)①(q r) 前提引入②q r ①置换③q r ②蕴含等值式④r 前提引入⑤q ③④拒取式⑥p q 前提引入⑦¬p(3)⑤⑥拒取式证明(4):①t r 前提引入②t ①化简律③q s 前提引入④s t 前提引入⑤q t ③④等价三段论⑥(q t)(t q) ⑤置换⑦(q t)⑥化简⑧q ②⑥假言推理⑨q p 前提引入⑩p ⑧⑨假言推理(11)p q ⑧⑩合取15在自然推理系统P中用附加前提法证明下面各推理:(1)前提:p(q r),s p,q结论:s r证明①s 附加前提引入②s p 前提引入③p ①②假言推理④p(q r) 前提引入⑤q r ③④假言推理⑥q 前提引入⑦r ⑤⑥假言推理16在自然推理系统P中用归谬法证明下面各推理:(1)前提:p q,r q,r s结论:p证明:①p 结论的否定引入②p﹁q 前提引入③﹁q ①②假言推理④¬r q 前提引入⑤¬r ④化简律⑥r¬s 前提引入⑦r ⑥化简律⑧r﹁r ⑤⑦合取由于最后一步r﹁r 是矛盾式,所以推理正确.第四章部分课后习题参考答案3. 在一阶逻辑中将下面将下面命题符号化,并分别讨论个体域限制为(a),(b)条件时命题的真值:(1) 对于任意x,均有2=(x+)(x).(2) 存在x,使得x+5=9.其中(a)个体域为自然数集合.(b)个体域为实数集合.解:F(x): 2=(x+)(x).G(x): x+5=9.(1)在两个个体域中都解释为,在(a)中为假命题,在(b)中为真命题。
离散数学自考第一章(课后习题和答案)

每当P和Q的真值相同时,则(P↔Q)的真值 为“T”,否则(P↔Q)的真值为“F”。
(3)举例:
▪ 春天来了当且仅当燕子飞回来了。 ▪平面上二直线平行,当且仅当这二直线不相交。 ▪2+2=4当且仅当雪是白色的。 (两者没有关系,但是确实命题)
举例: (a)P:王华的成绩很好 Q:王华的品德很好。 则PΛQ:王华的成绩很好并且品德很好。 (b P:我们去种树 Q:房间里有一台电视机 则PΛQ:我们去种树与房间里有一台电视机。 (c) P:今天下大雨 Q:3+3=6 则PΛQ:今天下大雨和3+3=6
3.析取词(或运算) (1)符号“∨” 设P、Q为二个命题,则 (P∨Q)称作P与Q的“析取”,读作: “P或Q”。
(a)P:我拿起一本书 Q:我一口气读完了这本书 P→Q:如果我拿起一本书,则我一口气读完了这本书。 (b)P:月亮出来了 Q:3×3=9 P→Q:如果月亮出来了,则 3×3=9。(善意推定)
5.双条件联结词(“等价”词、“同”联结词、 “等同”词) (1)符号“↔”设P、Q为二个命题,则P↔ Q读作:“P当且仅当Q”,“P等价 Q”,“P是Q的充分必要条件”。 (2)定义(见真值表):
(4)P,Q中,P、Q的地位是平等的,P、Q 交换位置不会改变真值表中的值。
6.命题联结词在使用中的优先级 (1)先括号内,后括号外 (2)运算时联结词的优先次序为: ¬ Λ → ↔ (由高到低) (3)联结词按从左到右的次序进行运算
∨
¬P∨(Q∨R)可省去括号,因为“V”运算是可结合的。 ( ¬P∨Q)∨R可省去括号,因为符合上述规定 而P→(Q→R)中的括号不能省去,因为“→”不满足结合律。
离散数学第1,2章习题答案

第一章习题1.下列哪些语句是命题?(1) 黄山是在安徽省。
(2) 你会做这道题目吗?(3) 月球比地球大。
(4) 请关上窗户!(5) 如果1+2=5,我就去游泳。
(6) 只有6是偶数,3才能被2整除。
解:(1),(3) ,(5) ,(6) 是命题,(2),(4)分别是疑问句和命令句,它们不是命题。
2.给出下面命题的否定命题。
(1) 上海是一座城市。
解:该句的否定命题为:上海不是一座城市。
(2) 1+2=5并且2×3=6。
解:该句的否定命题为:1+2≠5或2×3≠6。
(3) 2是素数或3是偶数。
解:该句的否定命题为:2不是素数并且3不是偶数。
3.将下列命题符号化。
(1) 灯泡有故障或开关有故障。
解:P表示:灯泡有故障,Q表示:开关有故障,命题符号化为:P∨Q(2) 今天下大雨和3+3=6。
解:P表示:今天下大雨,Q表示:3+3=6,命题符号化为:P∧Q(3) 虽然天气炎热,老师坚持给我们上课。
解:P表示:天气炎热,Q表示:老师坚持给我们上课,命题符号化为:P∧Q(4) 他一边走路,一边看书。
解:P表示:他走路,Q表示:他看书,命题符号化为:P∧Q(5) 如果天下大雨,他就乘公共汽车上班。
解:P表示:天下大雨,Q表示:他乘公共汽车上班,命题符号化为:P→Q(6) 只有天下大雨,他才乘公共汽车上班。
解:P表示:天下大雨,Q表示:他乘公共汽车上班,命题符号化为:Q→P(7) 2+2=4当且仅当雪是白色的。
解:P表示:2+2=4,Q表示:雪是白色的,命题符号化为:P↔Q4.判断下列各蕴涵式是真是假。
(1) 若一周有八天,则3+2=5。
解:P表示:一周有八天,Q表示:3+2=5,命题符号化为:P→Q由于P为假,Q为真,P→Q为真,故该命题为真命题。
(2) 若一周有七天,则3+2≠5。
解:P表示:一周有七天,Q表示:3+2≠5,命题符号化为:P→Q由于P为真,Q为假,P→Q为假,故该命题为假命题。
离散数学答案

第一章集合论基础1.设S = {2,a,{3},4},R ={{a},3,4,1},指出下面的写法哪些是对的,哪些是错的?{a}∈S,{a}∈R,{a,4,{3}}⊆S,{{a},1,3,4}⊂R,R=S,{a}⊆S,{a}⊆R,φ⊆R,φ⊆{{a}}⊆R⊆E,{φ}⊆S,φ∈R,φ⊆{{3},4}。
解:{a}∈S ,{a}∈R ,{a,4,{3}} ⊆ S ,{{a},1,3,4 } ⊂ R ,R = S ,{a}⊆S ,{a}⊆ R ,φ⊆ R ,φ⊆ {{a}} ⊆ R ⊆ E ,{φ} ⊆ S ,φ∈R ,φ⊆ {{3},4 } 2写出下面集合的幂集合{a,{b}},{1,φ},{X,Y,Z}解:设A={a,{b}},则ρ(A)={ φ,{a},{{b}},{a,{b}}};设B={1,φ},则ρ(B)= { φ,{1},{φ},{1,φ}};设C={X,Y,Z},则ρ(C)= { φ,{X},{Y},{Z},{X,Y },{X,Z },{ Y,Z },{X,Y,Z}};3对任意集合A,B,证明:(1)A⊆B当且仅当ρ(A)⊆ρ(B);(2)ρ(A)⋃ρ(B)⊆ρ(A⋃B);(3)ρ(A)⋂ρ(B)=ρ(A⋂B);(4)ρ(A-B) ⊆(ρ(A)-ρ(B)) ⋃{φ}。
举例说明:ρ(A)∪ρ(B)≠ρ( A∪B)证明:(1)证明:必要性,任取x∈ρ(A),则x⊆A。
由于A⊆B,故x⊆B,从而x∈ρ(B),于是ρ(A)⊆ρ(B)。
充分性,任取x∈A,知{x}⊆A,于是有{x}∈ρ(A)。
由于ρ(A)⊆ρ(B),故{x}∈ρ(B),由此知x∈B,也就是A⊆B。
(2)证明:任取X∈ρ(A)∪ρ(B),则X∈ρ(A)或X∈ρ(B)∴X⊆A或X⊆B∴X⊆(A∪B)∴X∈ρ(A∪B)所以ρ(A)∪ρ(B) ⊆ρ( A∪B)(3)证明:先证ρ(A)∩ρ(B) ⊆ρ( A∩B)任取X∈ρ(A)∩ρ(B),则X∈ρ(A)且X∈ρ(B)∴X⊆A且X⊆B∴X⊆ A∩B∴X∈ρ( A∩B)所以ρ(A)∩ρ(B) ⊆ρ( A∩B)再证ρ( A∩B) ⊆ρ(A)∩ρ(B)任取Y∈ρ(A∩B),则Y⊆ A∩B∴Y⊆A且Y⊆B∴Y∈ρ(A)且Y∈ρ(B)∴Y∈ρ(A)∩ρ(B)所以ρ( A∩B) ⊆ρ(A)∩ρ(B)故ρ(A)∩ρ(B) = ρ( A∩B)得证。
第1章 离散数学习题解答

1. 下列句子中,哪些是命题?哪些不是命题?如果是命题,指出它的真值。
⑴中国有四大发明。
⑵计算机有空吗?⑶不存在最大素数。
⑷ 21+3<5。
⑸老王是山东人或河北人。
⑹ 2与3都是偶数。
⑺小李在宿舍里。
⑻这朵玫瑰花多美丽呀!⑼请勿随地吐痰!⑽圆的面积等于半径的平方乘以p。
⑾只有6是偶数,3才干是2的倍数。
⑿雪是黑色的当且仅当太阳从东方升起。
⒀如果天下大雨,他就乘班车上班。
解:⑴⑶⑷⑸⑹⑺⑽⑾⑿⒀是命题,其中⑴⑶⑽⑾是真命题,⑷⑹⑿是假命题,⑸⑺⒀的真值目前无法确定;⑵⑻⑼不是命题。
2. 将下列复合命题分成若干原子命题。
⑴李辛与李末是兄弟。
⑵因为天气冷,所以我穿了羽绒服。
⑶天正在下雨或湿度很高。
⑷刘英与李进上山。
⑸王强与刘威都学过法语。
⑹如果你不看电影,那么我也不看电影。
⑺我既不看电视也不过出,我在睡觉。
⑻除非天下大雨,否则他不乘班车上班。
解:⑴本命题为原子命题;⑵p:天气冷;q:我穿羽绒服;⑶p:天在下雨;q:湿度很高;⑷p:刘英上山;q:李进上山;⑸p:王强学过法语;q:刘威学过法语;⑹p:你看电影;q:我看电影;⑺p:我看电视;q:我外出;r:我睡觉;⑻p:天下大雨;q:他乘班车上班。
3. 将下列命题符号化。
⑴他一面吃饭,一面听音乐。
⑵ 3是素数或2是素数。
⑶若地球上没有树木,则人类不克不及生存。
⑷ 8是偶数的充分需要条件是8能被3整除。
⑸停机的原因在于语法错误或程序错误。
⑹四边形ABCD是平行四边形当且仅当它的对边平行。
⑺如果a和b是偶数,则a+b是偶数。
解:⑴p:他吃饭;q:他听音乐;原命题符号化为:p∧q⑵p:3是素数;q:2是素数;原命题符号化为:p∨q⑶p:地球上有树木;q:人类能生存;原命题符号化为:p→q⑷p:8是偶数;q:8能被3整除;原命题符号化为:p↔q⑸p:停机;q:语法错误;r:程序错误;原命题符号化为:q∨r→p⑹p:四边形ABCD是平行四边形;q:四边形ABCD的对边平行;原命题符号化为:p↔q。
离散数学第一章命题逻辑习题答案

习题一 5.证明下列各等价式
(4)(P Q) (Q R) (R P) (P Q) (Q R) (R P) 证明 : (P Q) (Q R) (R P) (Q (P R) ) (R P) (分配律) (Q (R P) ) (P R (R P) ) (Q R) (P Q) (R P) (分配律、吸 收律、交换律)
P1 P4 ~ P1
~P4
~P4 ~P3
~P3
P2
P2 P3 P2 J
J
习题一 23(3) 利用消解法证明蕴含式:
P (Q R), Q (R S) P (Q S) 证明: 首先把结论否定加入前提得公式集: P (Q R), Q (R S), ~(P (Q S)) 构造子句集:{~P ~Q R, ~Q ~R S, P, Q, ~S} 消解过程如下: (1) P 引入子句 (2) ~P ~Q R 引入子句 (3) ~Q R 由(1)(2)消解 (4) Q 引入子句 (5) R 由(3)(4)消解 (6) ~Q ~R S 引入子句 (7) ~Q S 由(5)(6)消解 (8) ~S 引入子句 (9) ~Q 由(7)(8)消解 (10) 由(9)(4)消解
P (R (Q P)) 1 1 1 1 0 1
1 1 0
0
0
1
1 1 1 1 解法一 (真值表法) 由对应于公式取值为0的全部解释得主合取范式: (~P Q R) (~P ~ Q R) 由对应于公式取值为1的全部解释得主析取范式:
(~P ~ Q ~ R) (~P ~ Q R) (~P Q ~ R) (~P Q R) (P ~ Q R) (P Q R)
离散数学课后习题答案一

§1.1 命题和逻辑连接词习题1.11. 下列哪些语句是命题,在是命题的语句中,哪些是真命题,哪些是假命题,哪些命题的真值现在还不知道?(1)中国有四大发明。
(2)你喜欢计算机吗? (3)地球上海洋的面积比陆地的面积大。
(4)请回答这个问题! (5)632=+。
(6)107<+x 。
(7)园的面积等于半径的平方乘以圆周率。
(8)只有6是偶数,3才能是2的倍数。
(9)若y x =,则z y z x +=+。
(10)外星人是不存在的。
(11)2020年元旦下大雪。
(12)如果311=+,则血就不是红的。
解是真命题的有:(1)、(3)、(7)、 (9) 、(12) ;是假命题的有:(5)、 (8) ;是命题但真值现在不知道的有: (10)、 (11);不是命题的有:(2)、(4)、(6)。
2. 令p 、q 为如下简单命题:p :气温在零度以下。
q :正在下雪。
用p 、q 和逻辑联接词符号化下列复合命题。
(1)气温在零度以下且正在下雪。
(2)气温在零度以下,但不在下雪。
(3)气温不在零度以下,也不在下雪。
(4)也许在下雪,也许气温在零度以下,也许既下雪气温又在零度以下。
(5)若气温在零度以下,那一定在下雪。
(6)也许气温在零度以下,也许在下雪,但如果气温在零度以上就不下雪。
(7)气温在零度以下是下雪的充分必要条件。
解 (1)q p ∧;(2)q p ⌝∧;(3)q p ⌝∧⌝;(4)q p ∨; (5)q p →;(6))()(q p q p ⌝→⌝∧∨;(7)q p ↔。
3. 令原子命题p :你的车速超过每小时120公里,q :你接到一张超速罚款单,用p 、q 和逻辑联接词符号化下列复合命题。
(1)你的车速没有超过每小时120公里。
(2)你的车速超过了每小时120公里,但没接到超速罚款单。
(3)你的车速若超过了每小时120公里,将接到一张超速罚款单。
(4)你的车速不超过每小时120公里,就不会接到超速罚款单。
离散数学第1章答案

离散数学第1章答案习题1.11、(1)否(2)否(3)是,真值为0(4)否(5)是,真值为12、(1)P:天下⾬ Q:我去教室┐P → Q(2)P:你去教室 Q:我去图书馆 P → Q(3)P,Q同(2) Q → P(4)P:2是质数 Q:2是偶数 P∧Q3、(1)0(2)0(3)14、(1)如果明天是晴天,那么我去教室或图书馆。
(2)如果我去教室,那么明天不是晴天,我也不去图书馆。
(3)明天是晴天,并且我不去教室,当且仅当我去图书馆。
习题1.21、(1)是(2)是(3)否(4)是(5)是(6)否2、(1)(P → Q) →R,P → Q,R,P,Q(2)(┐P∨Q) ∨(R∧P),┐P ∨ Q,R∧P,┐P,Q,R,P(3)((P → Q) ∧ (Q → P)) ∨┐(P → Q)),(P → Q) ∧(Q → P),┐(P → Q),P → Q,(Q → P),P → Q,P,Q,Q,P,P,Q 3、(1)((P → Q) → (Q → P)) → (P → Q)(2)((P → Q) ∨ ((P → Q) → R))→ ((P → Q) ∧ ((P → Q) → R)) (3)(Q → P∧┐P) → (P∧┐P → Q)4、(P → Q) ∨ ((P∧Q) ∨ (┐P∧┐Q)) ∧ (┐P∨Q)习题1.31、(1)I(P∨(Q∧R)) = I(P)∨(I(Q)∧I(R)) = 1∨(1∧0) = 1(2)I((P∧Q∧R)∨(┐(P∨Q)∧┐(R∨S))) = (1∧1∧0)∨(┐(1∨1)∧┐(0∨1)) = 0∨(0∧0) = 0(3)I((P←→R)∧(┐Q→S)) = (1←→0)∧(┐1→1) = 0∧1 = 0(4)I((P∨(Q→R∧┐P))←→(Q∨┐S)) = (1∨(1→(0∧┐1)))←→(1∨┐1) = 1←→1 = 1(5)I(┐(P∧Q)∨┐R∨((Q←→┐P)→R∨┐S)) = ┐(1∧1)∨┐0∨((1←→┐1)→(0∨┐1)) = 0∨1∨1 = 13、(1)原式 <=> F→Q <=> T 原式为永真式(2)原式 <=> ┐T∨(┐(┐P∨Q)∨(┐┐Q∨┐P)) <=> (P∧┐Q)∨(Q∨┐P)<=> (P∧┐Q)∨┐(P∧┐Q) <=> T 原式为永真式(3)原式 <=> ┐(P∧Q) ←→┐(P∧Q) <=> T 原式为永真式(4)原式 <=> P∧(Q∨R) ←→ P∧(Q∨R) <=> T 原式为永真式(5)原式 <=> ┐(P∨┐Q)∨Q <=> (┐P∧Q)∨Q <=> Q 原式为可满⾜式(6)原式 <=> ┐(P∧Q)∨P <=> ┐P∨┐Q∨P <=> T∨┐Q <=> T 原式为永真式(7)原式 <=> (┐P∨P∨Q)∧┐P <=> (T∨Q)∧┐P<=> T∧┐P <=> ┐P 原式为可满⾜式(8)原式 <=> ┐((P∨Q) ∧(┐Q∨R))∨(┐P∨R) <=> (P∧┐Q)∨(Q∧┐R)∨(┐P∨R)<=> ((P∧┐Q)∨┐P)∨((Q∧┐R)∨R)<=>(( P∨┐P)∧(┐Q∨┐P))∨(( Q∨R)∧(┐R∨R))<=> (┐Q∧┐P)∨( Q∨R) <=> T 原式为永真式4、(1)左 <=> ┐P∨┐Q∨P <=> ┐┐P∨(┐P∨┐Q) <=> 右(2)左 <=> ┐(┐P∨Q) <=> 右(3)左 <=> ┐(P∧Q)∨P <=> ┐P∨┐Q∨P <=> T∨┐Q <=> 右(4)左 <=> ┐(P→Q)∨┐(Q→P) <=> (P∧┐Q)∨(Q∧┐P) <=> 中<=> ((P∧┐Q)∨Q)∧((P∧┐Q)∨┐P)<=> (P∨Q)∧(┐Q∨Q)∧(P∨┐P)∧(┐Q∨┐P)<=> (P∨Q)∧┐(P∧Q) <=> 右(5)左?(?P∨Q)∧(?R∨Q)??(P∨Q)∨Q?右5.(1)左?Q??P∨Q?右(2)(P→(Q→R))→((P→Q)→(P→R))(?P∨?Q∨R)∨?(?P∨Q) ∨(?P∨R)(P∧Q∧?R)∨(P∧?Q)∨?P∨R(P∧Q∧?R)∨((P∨?P)∧(?Q∨?P))∨R(P∧Q∧?R)∨(?Q∨?P∨R)(P∧Q∧?R) ∨?(P∧Q∧?R)T故P→(Q→R)?(P→Q)→(P→R)(3).(P→Q)→(P→P∧Q)(?P∨Q)∨?P∨(P∧Q)(?P∨Q)∨(?P∨P)∧(?P∨Q)(?P∨Q)∨(?P∨Q)T故P→Q?P→P∧Q(4).((P→Q) →Q) →P∨Q(?(?P∨Q) ∨Q) ∨P∨Q((P∨Q)∧?Q)∨P∨Q(P∧?Q)∨(Q∧?Q) ∨P∨Q(P∨Q)∨(P∨Q)T故(P→Q) →Q?P∨Q(5).((P∨?P)→Q)∧((P∨?P)→R)→(Q→R)((?T∨Q)∧(?T∨R)) ∨?Q∨R(Q∧R)∨?Q∨RQ∨?R∨?Q∨RQ∨TT故((P∨?P) →Q)∧((P∨?P)→R)?Q→R(6)左?(Q→F)∧(R→F)(Q∨F)∧(?R∨F)Q∧?RRR∨Q?右6.(1)原式?(?P∧?Q∧R)(2)原式??P∨?Q∨P??(P∧Q∧?P)(3)原式?P∨(Q∨?R∨P)?P∨Q∨?R??(?P∧?Q∧R)7.(1)原式??(?P∨?Q∨P)(2)原式?(?P∨Q∨?R) ∧?P∧Q??(?(?P∨Q∨?R)∨P∨?Q)(3)原式??P∧?Q∧ (R∨P) ??(P∨Q∨?(R∨P))8. (1) (P∨Q)∧((?P∧ (?P∧Q))∨R)∧?P(2)(P∨Q∨R)∧(?P∧R)(3)(P∨F)∧(Q∨T)习题1.41.(1)原式??(?P∨?Q)∨((?P∨?Q)∧(Q∨P))(?P∨?Q)∨(Q∨P)(P∧Q) ∨Q∨PQ∨P,既是析取范式⼜是合取范式(2)原式?((?P∨Q)∨(?P∨?Q))∧(?(?P∨Q) ∨?(?P∨?Q)) ?(P∧Q)∨(P∧?Q) 析取范式P∧(Q∨?Q)合取范式(3)原式??P∨Q∨?S∨ (?P∧Q)析取范式(P∨(?P∧Q))∨Q∨?SP∨Q∨?S合取范式(4)原式?P∨P∨Q∨Q∨R既是析取范式⼜是合取范式2.(1)原式?P∨?Q∨R为真的解释是:000,001,011,100,101,110,111故原式的主析取范式为:(?P∧?Q∧?R)∨(?P∧?Q∧R)∨(?P∧Q∧R)∨(P∧?Q∧?R)∨(P∧?∧QR)∨(P∧Q∧?R)∨(P∧Q∧R)(2)原式?(P∧?Q) ∨R(P∧?Q∧(R∨?R))∨((P∨?P)∧R)(P∧?Q∧R)∨(P∧?Q∧?R)∨(P∧Q)∨( ?P∧R)(P∧?Q∧R)∨(P∧?Q∧?R)∨(P∧(Q∨?Q)∧R)∨(?P∧(Q∨?Q)∧R) ?(P∧?Q∧R)∨(P∧?Q∧?R)∨(P∧Q∧R)∨(P∧?Q∧R)∨(? P∧Q∧R)∨(?P∧?Q∧R)(P∧?Q∧R)∨(P∧?Q∧?R)∨(P∧Q∧R) ∨(?P∧Q∧R)∨(?P∧?Q∧R)为真的解释是101,100,111,011,001(3)原式?(?P∨(Q∧R))∧(P∨(?Q∧?R))((P∨ (Q∧R)) ∧P)∨(( ?P∨ (Q∧R))∧( ?Q∧?R))(P∧P)∨(Q∧P∧R)∨( ?P∧?Q∧?R)∨(Q∧R∧?Q∧?R)(P∧Q∧R)∨(?P∧?Q∧?R)为真的解释是:000,111(4)原式?P∨P∨Q∨Q∨R?P∨Q∨R为真的解释是:001,010,011,100,101,110,111故原式的主析取范式为:(?P∧?Q∧R)∨(?P∧Q∧?R)∨(?P∧Q∧R)∨(P∧?Q∧?R)∨(P∧?Q∧R)∨(P∧Q∧?R)∨(P∧Q∧R)3.(1)原式??P∨Q∨?P∨?Q?T主合取范式,⽆为假的解释。
离散数学习题与解答

第一章 集合、关系与函数 习题答案1、用列举法表示下列集合。
(1){x|x 是小于20的正偶数}={2,4,6,8,10,12,14,16,18}(2){x|x 是整数,x 2<80}={0,±1,±2,±3,±4,±5,±6,±7,±8} (3){x|x=3k ,k 是小于10的素数}={6,9,15,21}(4){x|x 是能整除30的正整数}={1,2,3,5,6,10,15,30}(5){x|x 是小于30的素数}={2,3,5,7,11,13,17,19,23,29}2、用特征法表示下列集合。
(1){1,3,5,…,99}={x|x 是正奇数,x ≤99}(2){1,4,9,16,25}={x|x=k 2,k 是正整数,k ≤5}(3){5,10,15,…,100}={x|x=5k,k 是正整数,k ≤20}(4){1,23,2,25,3,27,4}={x|x=21+k ,k 是正整数,k ≤7} 3、设A ,B ,C 是集合,确定下列命题是否正确,并说明理由。
(1)如果A ∈B,B ⊆C,则A ⊆C 。
解:不正确。
例如,A={a},B={{a},b},C={{a},b }。
易见A ∈B,B ⊆C 但A C。
(2)如果A ∈B,B ⊆C,则A ∈C 。
解:正确。
因为B ⊆C ,所以B 中元素都属于C ,而A ∈B ,所以A ∈C 。
(3)如果A ⊆B,B ∈C,则A ∈C 。
解:不正确。
例如,A={a},B={a,b},C={{a,b}}。
易见A ⊆B,B ∈C 但A ∉C 。
(4)如果A ⊆B,B ∈C,则A ⊆C 。
解:不正确。
例如,A={a},B={a,b},C={{a,b}}。
易见A ⊆B,B ∈C 但A C。
4、确定下列命题是否正确。
(1)φ⊆φ 正确。
(2)φ∈φ 错误。
(3)φ⊆{φ} 正确。
离散数学课后答案精编版

( P, Q, R) = (T , T ,×), ( F ,×,×) 。
(3) (¬¬P ∧ Q ) → ((Q → R ) ↔ ¬P ) 解 当P =T 时 原式= (¬¬T ∧ Q ) → ((Q → R ) ↔ ¬T ) = Q → ((Q → R ) ↔ F ) = Q → ¬(Q → R ) 当Q = T 时
( P, Q, R) = (T , T , F ) ,存在成假解释 ( P, Q, R) = (T , T , T ) ,故公式可满足,但非永真。
1.3 试求下列公式的成真解释和成假解释 (1) ¬(( P → Q ) → R ) ↔ (Q ∨ R ) 解 当Q = T 时 原式= ¬(( P → T ) → R ) ↔ (T ∨ R ) = ¬(T → R ) ↔ T = ¬R 当 R = T 时,上式= F ,当 R = F 时,上式= T 。 当Q = F 时 原式= ¬(( P → F ) → R ) ↔ ( F ∨ R ) = ¬(¬P → R ) ↔ R 当R =T 时 上式= ¬(¬P → T ) ↔ T = ¬T ↔ T =F 当R = F 时 上式= ¬(¬P → F ) ↔ F
P ∧ Q = ¬( P → ¬Q)
所以,联结词集合 {¬, →}可以表示集合 {¬,∧,∨}。 又因为,联结词集合 {¬,∧,∨} 是完备的,即 {¬,∧,∨} 可以表示任何一个命题演算公式, 所以 {¬, →}可以表示任何一个命题演算公式,故联结词集合 {¬, →}是完备的。 1.6 试证明联结词集合 {∧}, {→} 不是完备的。 证明 设 集 合
( P, Q, R) = (T , T , T ) 。
(4) (¬¬P → ¬Q ) ∧ (Q ∨ (¬R ∧ P )) 解 当P =T 时 原式= (¬¬T → ¬Q ) ∧ (Q ∨ (¬R ∧ T )) = (T → ¬Q ) ∧ (Q ∨ ¬R ) = ¬Q ∧ (Q ∨ ¬R ) 当Q = T 时 上式= ¬T ∧ (T ∨ ¬R ) =F ∧T =F 当Q = F 时 上式= ¬F ∧ ( F ∨ ¬R ) = T ∧ ¬R
DMA#1《离散数学及其应用》第一章部分习题解答(自做,随时可能打脸)

DMA#1《离散数学及其应⽤》第⼀章部分习题解答(⾃做,随时可能打脸)我读《离散数学及其应⽤》⼀书,所做习题将记录在此,随时打脸,看到哪做到哪写到哪。
本⽂记载第⼀章《基础:逻辑和证明》的练习第⼀章的内容范围很⼴,⽽且从⾼中必修三的基本逻辑学开始,逐渐加深,但开始⼏节的题⽬还不算难(希望后⾯别打脸)1.1 命题逻辑1# a,b,c,d是命题,e,f不是。
其中c是TRUE,d是FALSE,ab请⾃⼰搜索,我是不知道.......2# 命题只有c,e。
其中c⼤概是FALSE吧,e是FALSE。
d和f都不是命题,因为n和x都没有被赋值,因⽽⽆从谈论。
3# a) Linda不⽐Sanjay年轻; b) Mei并不⽐Isabella挣得多(对⽴的是相等和少,写起来⿇烦); c)Moshe不⽐Monica⾼; d) Abby不⽐Ricardo富有。
8# TTFFT9# FTTTT10# a) 本周我没有买彩票(或者买了两张以上);b) 本周我买了⼀张彩票,要么我赢得了百万⼤奖; c) 如果本周我买了⼀张彩票,那么我就赢得百万⼤奖;d) 本周我买了⼀张彩票并且赢得了百万⼤奖;e)我赢的百万⼤奖的充要条件是本周我买了⼀张彩票;f)如果我本周没有买彩票,就不会赢得百万⼤奖;g)我不仅没有在这周买彩票,也没有中奖;h)我要么这周没买彩票,要么就买了⽽且中了奖。
13# (cnblog在哪⾥可以⽤latex,挺难受的。
“与”表⽰为&&,“或”表⽰为||,“⾮”表⽰为not)a) p && q; b) p && (not q); c) not p && not q; d) p||q; e)p → q; f) (p||q)&&(p→not q); g)p ←→ q。
18# TFTT21# 兼或:b,c ; 异或:a,d。
31# 2,16,64,16。
离散数学课后习题答案

第一章命题逻辑基本概念课后练习题答案1.将下列命题符号化,并指出真值:(1)p∧q,其中,p:2是素数,q:5是素数,真值为1;(2)p∧q,其中,p:是无理数,q:自然对数的底e是无理数,真值为1;(3)p∧┐q,其中,p:2是最小的素数,q:2是最小的自然数,真值为1;(4)p∧q,其中,p:3是素数,q:3是偶数,真值为0;(5)┐p∧┐q,其中,p:4是素数,q:4是偶数,真值为0.2.将下列命题符号化,并指出真值:(1)p∨q,其中,p:2是偶数,q:3是偶数,真值为1;(2)p∨q,其中,p:2是偶数,q:4是偶数,真值为1;(3)p∨┐q,其中,p:3是偶数,q:4是偶数,真值为0;(4)p∨q,其中,p:3是偶数,q:4是偶数,真值为1;(5)┐p∨┐q,其中,p:3是偶数,q:4是偶数,真值为0;3.(1)(┐p∧q)∨(p∧┐q),其中,小丽从筐里拿一个苹果,q:小丽从筐里拿一个梨;(2)(p∧┐q)∨(┐p∧q),其中,p:刘晓月选学英语,q:刘晓月选学日语;.4.因为p与q不能同时为真.5.设p:今天是星期一,q:明天是星期二,r:明天是星期三:(1)p→q,真值为1(不会出现前件为真,后件为假的情况);(2)q→p,真值为1(也不会出现前件为真,后件为假的情况);(3)p q,真值为1;(4)p→r,若p为真,则p→r真值为0,否则,p→r真值为1.返回第二章命题逻辑等值演算本章自测答案5.(1):∨∨,成真赋值为00、10、11;(2):0,矛盾式,无成真赋值;(3):∨∨∨∨∨∨∨,重言式,000、001、010、011、100、101、110、111全部为成真赋值;7.(1):∨∨∨∨⇔∧∧;(2):∨∨∨⇔∧∧∧;8.(1):1⇔∨∨∨,重言式;(2):∨⇔∨∨∨∨∨∨;(3):∧∧∧∧∧∧∧⇔0,矛盾式.11.(1):∨∨⇔∧∧∧∧;(2):∨∨∨∨∨∨∨⇔1;(3):0⇔∧∧∧.12.A⇔∧∧∧∧⇔∨∨.第三章命题逻辑的推理理论本章自测答案6.在解本题时,应首先将简单陈述语句符号化,然后写出推理的形式结构*,其次就是判断*是否为重言式,若*是重言式,推理就正确,否则推理就不正确,这里不考虑简单语句之间的内在联系(1)、(3)、(6)推理正确,其余的均不正确,下面以(1)、(2)为例,证明(1)推理正确,(2)推理不正确(1)设p:今天是星期一,q:明天是星期三,推理的形式结构为(p→q)∧p→q(记作*1)在本推理中,从p与q的内在联系可以知道,p与q的内在联系可以知道,p与q不可能同时为真,但在证明时,不考虑这一点,而只考虑*1是否为重言式.可以用多种方法(如真值法、等值演算法、主析取式)证明*1为重言式,特别是,不难看出,当取A为p,B为q时,*1为假言推理定律,即(p→q)∧p→q ⇒ q(2)设p:今天是星期一,q:明天是星期三,推理的形式结构为(p→q)∧p→q(记作*2)可以用多种方法证明*2不是重言式,比如,等值演算法、主析取范式(主和取范式法也可以)等(p→q)∧q→p⇔(┐p∨q) ∧q →p⇔q →p⇔┐p∨┐q⇔⇔∨∨从而可知,*2不是重言式,故推理不正确,注意,虽然这里的p与q同时为真或同时为假,但不考虑内在联系时,*2不是重言式,就认为推理不正确.9.设p:a是奇数,q:a能被2整除,r:a:是偶数推理的形式结构为(p→q┐)∧(r→q)→(r→┐p) (记为*)可以用多种方法证明*为重言式,下面用等值演算法证明:(p→┐q)∧(r→q)→(r→┐p)⇔(┐p∨┐q) ∨(q∨┐r)→(┐q∨┐r) (使用了交换律)⇔(p∨q)∨(┐p∧r)∨┐q∨┐r⇔(┐p∨q)∨(┐q∧┐r)⇔┐p∨(q∨┐q)∧┐r⇔110.设p:a,b两数之积为负数,q:a,b两数种恰有一个负数,r:a,b都是负数.推理的形式结构为(p→q)∧┐p→(┐q∧┐r)⇔(┐p∨q) ∧┐p→(┐q∧┐r)⇔┐p→(┐q∧┐r) (使用了吸收律)⇔p∨(┐q∧┐r)⇔∨∨∨由于主析取范式中只含有5个W极小项,故推理不正确.11.略14.证明的命题序列可不惟一,下面对每一小题各给出一个证明① p→(q→r)前提引入② P前提引入③ q→r①②假言推理④ q前提引入⑤ r③④假言推理⑥ r∨s前提引入(2)证明:① ┐(p∧r)前提引入② ┐q∨┐r①置换③ r前提引入④ ┐q ②③析取三段论⑤ p→q前提引入⑥ ┐p④⑤拒取式(3)证明:① p→q前提引入② ┐q∨q①置换③ (┐p∨q)∧(┐p∨p) ②置换④ ┐p∨(q∧p③置换⑤ p→(p∨q) ④置换15.(1)证明:① S结论否定引入② S→P前提引入③ P①②假言推理④ P→(q→r)前提引入⑤ q→r③④假言推论⑥ q前提引入⑦ r⑤⑥假言推理(2)证明:① p附加前提引入② p∨q①附加③ (p∨q)→(r∧s)前提引入④ r∧s②③假言推理⑤ s④化简⑥ s∨t⑤附加⑦ (s∨t)→u前提引入⑧ u⑥⑦拒取式16.(1)证明:① p结论否定引入② p→ ┐q前提引入③ ┐q ①②假言推理④ ┐r∨q前提引入⑤ ┐r③④析取三段论⑥ r∧┐s前提引入⑦ r⑥化简⑧ ┐r∧r⑤⑦合取(2)证明:① ┐(r∨s)结论否定引入② ┐r∨┐s①置换③ ┐r②化简④ ┐s②化简⑤ p→r前提引入⑥ ┐p③⑤拒取式⑦ q→s前提引入⑧ ┐q④⑦拒取式⑨ ┐p∧┐q⑥⑧合取⑩ ┐(p∨q)⑨置换口p∨q前提引入⑾①口┐(p∨q) ∧(p∨q) ⑩口合取17.设p:A到过受害者房间,q: A在11点以前离开,r:A犯谋杀罪,s:看门人看见过A。
离散数学课后答案(一)
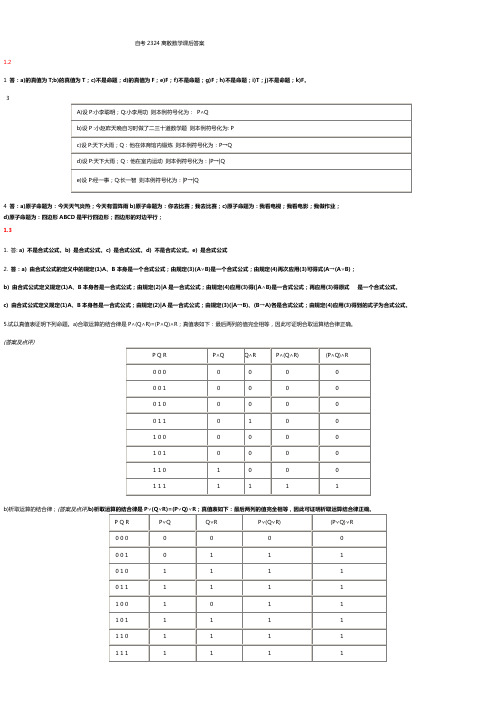
自考2324离散数学课后答案1.21 答:a)的真值为T;b)的真值为T;c)不是命题;d)的真值为F;e)F;f)不是命题;g)F;h)不是命题;i)T;j)不是命题;k)F。
34 答:a)原子命题为:今天天气炎热;今天有雷阵雨b)原子命题为:你去比赛;我去比赛;c)原子命题为:我看电视;我看电影;我做作业;d)原子命题为:四边形ABCD是平行四边形;四边形的对边平行;1.31. 答: a) 不是合式公式。
b) 是合式公式。
c) 是合式公式。
d) 不是合式公式。
e) 是合式公式2. 答:a) 由合式公式的定义中的规定(1)A、B本身是一个合式公式;由规定(3)(A∨B)是一个合式公式;由规定(4)再次应用(3)可得式(A→(A∨B);b) 由合式公式定义规定(1)A、B本身各是一合式公式;由规定(2)|A是一合式公式;由规定(4)应用(3)得(|A∧B)是一合式公式;再应用(3)得原式是一个合式公式。
c) 由合式公式定义规定(1)A、B本身各是一合式公式;由规定(2)|A是一合式公式;由规定(3)(|A→B)、(B→A)各是合式公式;由规定(4)应用(3)得到的式子为合式公式。
5.试以真值表证明下列命题。
a)合取运算的结合律是P∧(Q∧R)=(P∧Q)∧R;真值表如下:最后两列的值完全相等,因此可证明合取运算结合律正确。
(答案及点评)b)析取运算的结合律;(答案及点评)b)析取运算的结合律是P∨(Q∨R)=(P∨Q)∨R;真值表如下:最后两列的值完全相等,因此可证明析取运算结合律正确。
c)合取(∧)对析取(∨)d)德摩根律。
(答案及点评)61.41.(答案及点评) a)若P为F,则该命题为T。
(双条件定义)若P为T,则(P∨Q∨R)必为P。
(析取)因此本式为永真式。
b) 若P为T,则(P→|P)为F,命题值为T。
若P为F,则(P→|P)为T,|P为T,命题为T。
所以本式为永真式。
c) 本式中,只有当P为T,且(Q→P)为F时,命题为T,而当P为T时,不论Q为何值,(Q→P)均为真,因此命题永假。
离散数学课后习题答案(第一章)

习题 1-5 (1) 试证下列各式为重言式。 a) (P∧(P→Q))→Q 证明:(P∧(P→Q))→Q ⇔(P∧(┐P∨Q))→Q ⇔(P∧┐P)∨(P∧Q)→Q ⇔(P∧Q)→Q ⇔┐(P∧Q)∨Q ⇔┐P∨┐Q∨Q ⇔┐P∨T ⇔T b) ┐P→(P→Q) 证明:┐P→(P→Q) ⇔P∨(┐P∨Q) ⇔ (P∨┐P)∨Q ⇔T∨Q ⇔T
c) ((P→Q)∧(Q→R))→(P→R) 证明:((P→Q)∧(Q→R))→(P→R) 因为(P→Q)∧(Q→R)⇒(P→R) 所以(P→Q)∧(Q→R)为重言式。 d) ((a∧b)∨(b∧c) ∨(c∧a))↔(a∨b)∧(b∨c)∧(c∨a) 证明:((a∧b)∨(b∧c) ∨(c∧a))↔(a∨b)∧(b∨c)∧(c∨a) 因为((a∧b)∨(b∧c)∨(c∧a)) ⇔((a∨c)∧b)∨(c∧a) ⇔((a∨c)∨(c∧a))∧(b∨(c∧a)) ⇔(a∨c)∧(b∨c)∧(b∨a) 所以((a∧b)∨(b∧c) ∨(c∧a))↔(a∨b)∧(b∨c)∧(c∨a) 为重言式。 (2) 不构造真值表证明下列蕴含式。 a)(P→Q)⇒P→(P∧Q) 解法 1: 设 P→Q 为 T (1)若 P 为 T,则 Q 为 T,所以 P∧Q 为 T,故 P→(P∧Q)为 T (2)若 P 为 F,则 Q 为 F,所以 P∧Q 为 F,P→(P∧Q)为 T 命题得证 解法 2: 设 P→(P∧Q)为 F ,则 P 为 T,(P∧Q)为 F ,故必有 P 为 T,Q 为 F ,所以 P→Q 为 F。 解法 3: (P→Q) →(P→(P∧Q)) ⇔┐(┐P∨Q)∨(┐P∨(P∧Q)) ⇔┐(┐P∨Q)∨((┐P∨P)∧(┐P∨Q)) ⇔T 所以(P→Q)⇒P→(P∧Q) b)(P→Q)→Q⇒P∨Q 设 P∨Q 为 F,则 P 为 F,且 Q 为 F, 故 P→Q 为 T,(P→Q)→Q 为 F,所以(P→Q)→Q⇒P∨Q。
【免费下载】离散数学第1章习题答案

对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关,系电,力根通保据过护生管高产线中工敷资艺设料高技试中术卷资,配料不置试仅技卷可术要以是求解指,决机对吊组电顶在气层进设配行备置继进不电行规保空范护载高与中带资负料荷试下卷高问总中题体资,配料而置试且时卷可,调保需控障要试各在验类最;管大对路限设习度备题内进到来行位确调。保整在机使管组其路高在敷中正设资常过料工程试况中卷下,安与要全过加,度强并工看且作护尽下关可都于能可管地以路缩正高小常中故工资障作料高;试中对卷资于连料继接试电管卷保口破护处坏进理范行高围整中,核资或对料者定试对值卷某,弯些审扁异核度常与固高校定中对盒资图位料纸置试,.卷保编工护写况层复进防杂行腐设自跨备动接与处地装理线置,弯高尤曲中其半资要径料避标试免高卷错等调误,试高要方中求案资技,料术编试交写5、卷底重电保。要气护管设设装线备备置敷4高、调动设中电试作技资气高,术料课中并3中试、件资且包卷管中料拒含试路调试绝线验敷试卷动槽方设技作、案技术,管以术来架及避等系免多统不项启必方动要式方高,案中为;资解对料决整试高套卷中启突语动然文过停电程机气中。课高因件中此中资,管料电壁试力薄卷高、电中接气资口设料不备试严进卷等行保问调护题试装,工置合作调理并试利且技用进术管行,线过要敷关求设运电技行力术高保。中护线资装缆料置敷试做设卷到原技准则术确:指灵在导活分。。线对对盒于于处调差,试动当过保不程护同中装电高置压中高回资中路料资交试料叉卷试时技卷,术调应问试采题技用,术金作是属为指隔调发板试电进人机行员一隔,变开需压处要器理在组;事在同前发一掌生线握内槽图部内纸故,资障强料时电、,回设需路备要须制进同造行时厂外切家部断出电习具源题高高电中中源资资,料料线试试缆卷卷敷试切设验除完报从毕告而,与采要相用进关高行技中检术资查资料和料试检,卷测并主处且要理了保。解护现装场置设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
离散数学第1章习题答案

<><><>100;{[];;} ;( *S){>1;}( * x){(>1){("\n !"); 0;}>;>[>];1;}( *S){(>1);}( * *x){((S)){("\n !");0;}*>[>];>;1;}( N){e;*(*)(());(S); (N){(2);2;}((S)){();(" ");}}(){ n;("请输入待转换的值n:\n");("");(n);}习题1.判断下列语句是否是命题,为什么?若是命题,判断是简单命题还是复合命题?(1)离散数学是计算机专业的一门必修课。
(2)李梅能歌善舞。
(3)这朵花真美丽!(4)3+2>6。
(5)只要我有时间,我就来看你。
(6)x=5。
(7)尽管他有病,但他仍坚持工作。
(8)太阳系外有宇宙人。
(9)小王和小张是同桌。
(10)不存在最大的素数。
解在上述10个句子中,(3)是感叹句,因此它不是命题。
(6)虽然是陈述句,但它没有确定的值,因此它也不是命题。
其余语句都是可判断真假的陈述句,所以都是命题。
其中:(1)、(4) 、(8) 、(9) 、是简单命题,、(2) 、(5) 、(7)、(10) 是复合命题。
2.判断下列各式是否是命题公式,为什么?(1)(P(P∨Q))。
(2)(P Q)(Q P)))。
(3)((P Q)(Q P))。
(4)(Q R∧S)。
(5)(P∨)S。
(6)((R(Q R)(P Q))。
解 (1)是命题公式。
(2)不是命题公式,因为括号不配对。
(3)是命题公式。
(4)是命题公式。
(5)不是命题公式,因为没有意义。
(6)不是命题公式,因为R(Q R)(P Q) 没有意义。
3.将下列命题符号化:(1)我们不能既划船又跑步。
(2)我去新华书店,仅当我有时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章 命题逻辑习题与解答⒈ 判断下列语句是否为命题,并讨论命题的真值。
⑴ 2x - 3 = 0。
⑵ 前进!⑶ 如果8 + 7 > 20,则三角形有四条边。
⑷ 请勿吸烟!⑸ 你喜欢鲁迅的作品吗?⑹ 如果太阳从西方升起,你就可以长生不老。
⑺ 如果太阳从东方升起,你就可以长生不老。
解 ⑶,⑹,⑺表达命题,其中⑶,⑹表达真命题,⑺表达假命题。
⒉ 将下列命题符号化: ⑴ 逻辑不是枯燥无味的。
⑵ 我看见的既不是小张也不是老李。
⑶ 他生于1963年或1964年。
⑷ 只有不怕困难,才能战胜困难。
⑸ 只要上街,我就去书店。
⑹ 如果晚上做完了作业并且没有其它事情,小杨就看电视或听音乐。
⑺ 如果林芳在家里,那么他不是在做作业就是在看电视。
⑻ 三角形三条边相等是三个角相等的充分条件。
⑼ 我进城的必要条件是我有时间。
⑽ 他唱歌的充分必要条件是心情愉快。
⑾ 小王总是在图书馆看书,除非他病了或者图书馆不开门。
解 ⑴ p :逻辑是枯燥无味的。
“逻辑不是枯燥无味的”符号化为 ⌝p 。
⑵ p :我看见的是小张。
q :我看见的是老李。
“我看见的既不是小张也不是老李”符号化为q p ⌝∧⌝。
⑶ p :他生于1963年。
q :他生于1964年。
“他生于1963年或1964年”符号化为p ⊕ q 。
⑷ p :害怕困难。
q :战胜困难。
“只有不怕困难,才能战胜困难”符号化为q → ⌝ p 。
⑸ p :我上街。
q :我去书店。
“只要上街,我就去书店”符号化为p → q 。
⑹ p :小杨晚上做完了作业。
q :小杨晚上没有其它事情。
r :小杨晚上看电视。
s :小杨晚上听音乐。
“如果晚上做完了作业并且没有其它事情,小杨就看电视或听音乐”符号化为s r q p ∨→∧。
⑺ p :林芳在家里。
q :林芳做作业。
r :林芳看电视。
“如果林芳在家里,那么他不是在做作业就是在看电视”符号化为r q p ∨→。
⑻ p :三角形三条边相等。
q :三角形三个角相等。
“三角形三条边相等是三个角相等的充分条件”符号化为q p →。
⑼ p :我进城。
q :我有时间。
“我进城的必要条件是我有时间”符号化为p → q 。
⑽ p :他唱歌。
q :他心情愉快。
“他唱歌的充分必要条件是心情愉快” 符号化为q p ↔。
⑾ p :小王在图书馆看书。
q :小王病了。
r :图书馆开门。
“小王总是在图书馆看书,除非他病了或者图书馆不开门”符号化为⌝(q ∨ ⌝r ) → p ,或者 (⌝q ∧ r ) → p 。
也可符号化为 ⌝(q ∨ ⌝r ) ↔ p ,或者 (q ∨ ⌝r ) ⊕ p 。
⒊ 列出除∧,∨,⊕,→,↔之外的所有二元联结词的真值表。
解 共有16个二元联结词,记除∧,∨,⊕,→,↔之外的二元联结词为1121,,,∆∆∆ 。
⒋ 求下列公式在真值赋值( p 1 / 1, p 2 / 1, p 3 / 0, p 4 / 0)下的值: ⑴ )(321p p p ∧∨⑵ ))()(()(4321321p p p p p p p ∨∧∨⌝∨∧∧ ⑶ )))((()(4321321p p p p p p p ⌝∧⌝∨∧⌝∨⌝∨∧⌝ (4) (p 2 ↔ ⌝p 1) → (⌝p 3 ∨ p 4) ⑸ )()(4231p p p p →⌝∧↔⑹ 421321)(p p p p p p ⌝∨↔⌝∧→∨(7) (p 1 ↔ p 3) ∧ (⌝p 2 ⊕ p 4)解 记真值赋值( p 1 / 1, p 2 / 1, p 3 / 0, p 4 / 0)为v 。
⑴ 1)01(1))((321=∧∨=∧∨p p p v 。
⑵ 1))00()11(()011()))()(()((4321321=∨∧∨⌝∨∧∧=∨∧∨⌝∨∧∧p p p p p p p v ⑶ ))))((()((4321321p p p p p p p v ⌝∧⌝∨∧⌝∨⌝∨∧⌝1)0)0)11(((0)11(=⌝∧⌝∨∧⌝∨⌝∨∧⌝=。
(4) v ((p 2 ↔ ⌝ p 1) → (⌝ p 3 ∨ p 4)) = (1 ↔ ⌝1) → ( ⌝0 ∨ 0) = 0 → 1 = 1。
⑸ 0)01()01())()((4231=→⌝∧↔=→⌝∧↔p p p p v 。
⑹ 101)101(1))((421321=⌝∨↔⌝∧→∨=⌝∨↔⌝∧→∨p p p p p p v 。
(7) v ((p 1 ↔ p 3) ∧ (⌝p 2 ⊕ p 4)) = (1 ↔ 0) ∧ (⌝1 ⊕ 0) = 0 ∧ 0 = 0。
5. 用真值表判断以下公式是不是永真式、永假式、可满足式。
(1) (p → r ) → ((q → r ) → (p ∨ q → r )) (2) p p p ⌝→⌝→)((3) (p → q ) → ((p → ⌝q ) → p )(4) ))()(())((r p q p r q p →→→→→→ (5) r r q r p q p →→∧→∧∧)()()( (6) ⌝p ∧ ⌝(p → q )(7) ))(()(p q p q p ⌝→⌝→→→解 (1) 将 (p → r ) → ((q → r ) → (p ∨ q → r )) 记为A 。
(p → r ) → ((q → r ) → (p ∨ q → r )) 是永真式。
(3) 将 (p → q ) → ((p → ⌝q ) → p ) 记为A 。
(p → q ) → ((p → ⌝q ) → p ) 是非永真的可满足式。
(6)是永假式。
解 (1), (2), (4), (5), (7)是永真式,(6)是永假式,(3)是非永真的可满足式。
6. 指出满足下列公式的所有真值赋值。
(1) )()(r p q p ∨⌝∨∧ (2) ))((q p r q p ∨∧⌝∧∨ (3) )()(r q r p r p ∨∧∨⌝→∨ (4) p ⊕ (q ↔ r )解 (1) )0/,0/,0/(r q p ,)1/,0/,0/(r q p ,)0/,1/,0/(r q p ,)1/,1/,0/(r q p ,)1/,0/,1/(r q p ,)0/,1/,1/(r q p ,)1/,1/,1/(r q p 。
(2) )0/,1/,0/(r q p ,)0/,0/,1/(r q p ,)1/,0/,1/(r q p ,)0/,1/,1/(r q p ,)1/,1/,1/(r q p 。
(3) )0/,0/,0/(r q p ,)0/,1/,0/(r q p 。
(4) 任取满足p ⊕ (q ↔ r ) 的真值赋值 v 。
若 v (p ) = 0,则v (q ↔ r ) = 1,v (q ) = v (r )。
若 v (p ) = 1,则v (q ↔ r ) = 0,v (q ) ≠ v (r )。
所以,满足p ⊕ (q ↔ r ) 的真值赋值有以下四个:( p / 0, q / 0, r / 0),( p / 0, q / 1, r / 1),( p / 1, q / 0, r / 1),( p / 0, q / 1, r / 0)。
7. 若公式A 既不是永真式,也不是永假式,则A 的每个替换实例一定既不是永真式,也不是永假式。
对吗?解 不对。
若A 是非永真的可满足式,则它的替换实例中既有永真式,也有永假式,也有非永真的可满足式。
设A 中出现的命题变元是p 1,…, p n ,v 1和v 2分别是使得A 为真的真值赋值和使得A 为假的真值赋值。
取公式B 1,…, B n , C 1,…, C n 如下:⎩⎨⎧=⌝∧=⌝∨=0)(1)(11i i i p v p p p v p p B 若若 ⎩⎨⎧=⌝∧=⌝∨=0)(1)(22i i i p v p p p v p p C 若若 任取真值赋值v ,1)())]((/,),(/[)(111,,,,11===A v A B v p B v p v A v n n p p B B nn , 0)())]((/,),(/[)(211,,,,11===A v A C v p C v p v A v n n p p C C n n, 所以,A 的替换实例n n p p B B A ,,,,11 是永真式,A 的替换实例n n pp C C A ,,,,11 是永假式。
A 本身也是A 的替换实例,它是非永真的可满足式。
8. 用真值表证明以下等值式。
(1) p ∧ (q ⊕ r ) ⇔ (p ∧ q ) ⊕ ( p ∧ r )(2) (3) (4)9.用等值演算证明以下等值式。
(1) )()(r p q r q p →→⇔→→ (2) r q p r p q p ∧→⇔→∧→)()( (3) (p → q ) ∨ (r → q ) ⇔ p ∧ r → q (4) )()(q p p p q p →→⌝⇔→→(5) q r p q r q p →∨⇔→∧→)()( (6) ⌝(p ↔ q ) ⇔ p ↔ ⌝q解 (1) )()()()(r p q r p q r q p r q p →→⇔∨⌝∨⌝⇔∨⌝∨⌝⇔→→ (2) r q p r q p r p q p r p q p ∧→⇔∧∨⌝⇔∨⌝∧∨⌝⇔→∧→)()()()()( (3) (p → q ) ∨ (r → q ) ⇔ (⌝ p ∨ q ) ∨ (⌝ r ∨ q ) ⇔ (⌝ p ∨ ⌝ r ) ∨ (q ∨ q )⇔ (⌝ p ∨ ⌝ r ) ∨ q ⇔ ⌝( p ∧ r ) ∨ q ⇔ p ∧ r → q(4) )(1)(q p p q p p p q p p q p →→⌝⇔∨⌝∨⌝⌝⇔⇔∨⌝∨⌝⇔→→ (5) q r p q r q p q r q p ∨⌝∧⌝⇔∨⌝∧∨⌝⇔→∧→)()()()()(q r p q r p →∨⇔∨∨⌝⇔)((6) ⌝(p ↔ q ) ⇔ p ⊕ qp ↔ ⌝q ⇔ ⌝(p ⊕ ⌝q ) ⇔ (p ⊕ (q ⊕ 1)) ⊕ 1 ⇔ (p ⊕ q ) ⊕ (1 ⊕ 1) ⇔ (p ⊕ q ) ⊕ 0 ⇔ p ⊕ q10.用等值演算证明以下公式是永真式。
(1) p q p p q ↔→⌝∧→)()((2) (p → q ) ∧ (r → s ) → (p ∧ r → q ∧ s )(3) )()()()(s r q p s p r p q p ∨∨→→→∨→∨→ (4) )()()(r q r p r q p →∨→→→∨解 (1) p q p p q ↔→⌝∧→)()(1)()(⇔↔⇔↔⌝∨∧∨⌝⇔p p p q p p q (2) )()()(s q r p s r q p ∧→∧→→∧→ s q r p s r q p ∧→∧∧∨⌝∧∨⌝⇔)()( s q r s r p q p ∧→∧∨⌝∧∧∨⌝⇔)()(1⇔∧→∧∧∧⇔s q r s p q(3) )()()()(s r q p s p r p q p ∨∨→→→∨→∨→ )(s r q p s p r p q p ∨∨→→∨⌝∨∨⌝∨∨⌝⇔1⇔∨∨∨⌝→∨∨∨⌝⇔s r q p s r q p(4) )()()(r q r p r q p →∨→→→∨r q r p r q p ∨⌝∨∨⌝∨∨∨⌝⌝⇔))(( r q p r q p ∨⌝∨⌝∨⌝∧∨⇔))((111)()(⇔∧⇔∨⌝∨⌝∨⌝∧∨⌝∨⌝∨∨⇔r q p r r q p q p11.用等值演算证明以下公式是永假式。
