28自然数串趣题
最新人教版六年级数学上册自然数串趣题

自然数串趣题1.小明从1写到100,他共写了多少个数字“9”?2.把1到12这十二个数每两个数分为一组,要求每组的两个数之和都相等,怎么分?和是多少?3.用1、2、3、4、5、6、7、8、9这九个数编三个算式,一个加法、一个减法、一个乘法,每个数只许用一次。
4.用1、2、3、4、5、6、7、8、9这九个数字,写成三个三位数,使它们的和等于1953。
5.用1、2、3、4、5、6、7、8、9这九个数字,写成三个三位数,使它们的和等于1989。
6.一只老猫捉了12只老鼠,其中有一只小白鼠。
老猫自言自语地说:“我要分三批吃它们。
不过吃以前叫它们站好队,我从头一个开始吃,隔一个吃掉一个,也就是:我第一次吃掉站在第1,3,5,7,9,11号位置的小老鼠;剩下的叫它们不许动,第二次还是从头一个吃起,隔一个吃一个;第三次也是照这个办法吃。
但把最后剩下的一个放了。
”这话被聪明的小白鼠听见了,于是它站在了某个号的位置上,最后没有被吃掉。
小朋友,你知道小白鼠站的是第几号位置吗?习题解答1.解:小明共写了20个数字“9”。
因为从1到100的数中有18个数含有一个数字“9”,它们是:9、19、29、39、49、59、69、79、89、90、91、92、93、94、95、96、97、98。
另外自然数99含有两个数字9。
2.解:自然数串有一个特点,相邻的两个数中,后一个比前一个大1,因此可以进行如下的搭配分组:最小的数1和最大的数12成一组(1,12);次小的数2和次大的数11成一组(2,11);……中间的两个数6和7成一组(6,7);各组两个数相加之和都是13。
3.解:从受限制最强的乘法算式入手,在这九个数中两个数相乘的积等于另一个数而不发生重复数字出现的,只有2×3=6和2×4=8;经试验,可选用2×3=6,则剩下的六个数可组成两个等式1+7=8和4+5=9。
再经过适当的变换就可以列出满足题目要求的算式(答案不惟一)。
数学:第三讲《有趣的自然数串》讲义详解

二年级提高班第三讲有趣的自然数串【例1】下面的自然数串,共有多少个数?【分析】法一:1,2,3,4,……,31,32共有32个数;4,5,6,……,31,32比它少1,2,3,共少3个数,所以有32329−=(个)数;法二:4是第1个数,5是第2个数,6是第3个数,数字和第几个相差3.依此规律 32是第29个数;法三:尾-首+1,324129−+=.【例2】下面的自然数串,共有多少个数?【分析】法一:分组法.如果是1,2,3,4,5,6,7,8,……,55,56,57,58,我们很容易知道它有58个,我们可以将数列分组:(1,2),(3,4),(5,6),(7,8),……,(55,56),(57,58),分成58229÷=(组),每组的偶数就是我们题目的数列,所以有29个偶数.法二:找规律法.从第一个数2,加一个2,变成第二个数4,221=4+×;从第一个数2,加两个2,变成第三个数6,+×.我们很容易发现,后222=6面的数都是2加了若干个2变成的.那么58就是22=58+×?,可以计算出是2加了()(个)2变成58的.每−÷=582228加一个2,数串就多一个数,那一共加了28个2,也就是多了28个数,再加上原来就有的一个数2,这样就可以知道这个数串一共有281=29+(个)数.【例3】下面的自然数串,共有多少个数?第10个数是多少?【分析】找规律法.从第一个数4,加一个3,变成第二个数7,+×;从第一个数4,加两个431=73,变成第三个数10,432=10+×.我们很容易发现,后面的数都是4加了若干个3变成的.那么67就是43=67+×?,可以计算出是4加了674321()−÷=(个)3变成67的.每加一个3,数串就多一个数,那一共加了21个3,也就是多了21个数,再加上原来就有的一个数4,这样就可以知道这个数串一共有+(个)数.211=22由第一问可以知道,第十个数是4加了若干个3变成的.每加一个3,数串就多一个数,那第十个数,就是加了1019−=(个)3,也就是比第一个数多了39=27×,则第十个数是274=31+.【例4】把1,2,3,4,5,……,28,29,30这三十个数,从左往右依次写下来,成为一个数,这个数共写了多少个数字?【分析】法一:分段计算这个数共包含有多少个数字:1至9共有9个数字;10至19共有10个自然数,每个都由两个数字组成,这一段共有21020×=(个)数字.20至29这一段也有10个自然数,共有20个数字.30这个数由两个数字组成.所以这个数所包含的数字总数是:(个).法二:1至9共有9个数字;10至30共有3010121−+=(个)自然数,每个都由两个数字组成,这一段共有22142×=(个)数字.所以共有:94251+=(个)数字.法三:先把所有的数看成两位数,算出23060×=(个)数字,再去掉9个一位数,共有60951−=(个)数字【例5】一只猫捉了12只老鼠,其中有一只小白鼠.这只猫自言自语地说:“我要分三次吃掉它们,我先让它们站成一行编号,我从第一只开始吃,然后隔一只吃掉一只;吃完后我让它们不许动,第二次还是从剩下的第一只吃起,隔一只吃一只;第三次也是照这个办法吃,把最后一只放了.”猫的话被聪明的小白鼠听见了,于是它很快选好了一个位置,最后没有被吃掉.小朋友,小白鼠选的是第几号位置呢?【分析】因为每隔一只吃一只,我们可以分析出猫每次会吃哪些老鼠:第一次吃的老鼠是:1,3,5,7,9,11;还剩下:2,4,6,8,10,12;第二次吃的老鼠是:2,6,10;还剩下:4,8,12;第三次吃的老鼠是:4,12;还剩下:8.最后剩下的排在第8的老鼠会被放掉,所以小白鼠就站在了这排的第8个.。
第十讲 自然数串趣题

第十讲 自然数串趣题从1开始,1、2、3、4、5、6、7、8、9、10、11、12……连起来成一串,像一串糖葫芦,我们把这样的一串数叫作自然数串(也叫自然数列),其中的每一个数都叫作自然数。
自然数串的特点是:①从1开始,1是头;②在相邻的两个数中,后一个数比前一个数大1;③后面的数要多大有多大,也就是说,自然数串是有头无尾的。
在自然数串中,如果写到某一个数为止,就叫做有限自然数串,也简称自然数串。
这一讲的题目,都是与(有限)自然数串有关的。
例1 如下页图所示。
一份学习材料放在桌上,一阵风把材料吹落了一地。
小军拣起来一看,糟糕,少了两张。
根据下面拣到的材料的页码,你能说出少了哪几页吗?解:一张材料的正反两面用两个自然数作页码,这两个自然数是相邻的。
仔细观察找到的材料的页码,根据自然数串的特点,可知少了的两张纸的页码是(7、8)和(13、14)。
例2 从1连续地写到100,“0”出现了多少次?解:“0”出现了11次。
因为从1到100含有“0”的自然数是:10、20、30、40、50、60、70、80、90、100。
数一数,这些自然数中共有11个“0”。
例3 把1,2,3,4,5,……28,29,30这三十个数,从左往右依次排列起来,成为一个数,你知道这个数共有多少个数字吗?解:把这个数写出一部分来看看:123456789101112131415 (282930)下面,分段计算这个数共包含有多少个数字:1至9共有9个数字;10至19共有10个自然数,每个都由两个数字组成,这一段共有2×10=20个数字。
20至29这一段也有10个自然数,共有20个数字。
30这个数由两个数字组成。
所以这个数所包含的数字总数是:9+20+20+2=51(个)。
例4 小青每年都和家长一起参加植树节劳动。
七岁那年,他种了第一棵树,以后每年都比前一年多种一棵。
现在他已经长到15岁了,连续地种了九年树。
请你算一算,这九年中小青一共种了多少棵树?解:先把小青每年种几棵树写出来再把每年种树的棵树加起来1+2+3+4+5+6+7+8+9=45(棵)。
一年级自然数串趣题奥数习题

其实,任何一门学科都离,怎么会向高层次进军?尤其是语文学科涉猎的范围很广,要真正提高学生的写作水平,单靠分析文章的写作技巧是远远不够的,必须从基础知识抓起,每天挤一点时间让学生“死记”名篇佳句、名言警句,以及丰富的词语、新颖的材料等。这样,就会在有限的时间、空间里给学生的脑海里注入无限的内容。日积月累,积少成多,从而收到水滴石穿,绳锯木断的功效。
以上是查字典数学网为大家准备的自然数串趣题奥数习题,希望对大家有所帮助。
自然数串趣题—小学六年级数学专题二十五

自然数串趣题1.小明从1写到100,他共写了多少个数字“9”?2.把1到12这十二个数每两个数分为一组,要求每组的两个数之和都相等,怎么分?和是多少?3.用1、2、3、4、5、6、7、8、9这九个数编三个算式,一个加法、一个减法、一个乘法,每个数只许用一次。
4.用1、2、3、4、5、6、7、8、9这九个数字,写成三个三位数,使它们的和等于1953。
5.用1、2、3、4、5、6、7、8、9这九个数字,写成三个三位数,使它们的和等于1989。
6.一只老猫捉了12只老鼠,其中有一只小白鼠。
老猫自言自语地说:“我要分三批吃它们。
不过吃以前叫它们站好队,我从头一个开始吃,隔一个吃掉一个,也就是:我第一次吃掉站在第1,3,5,7,9,11号位置的小老鼠;剩下的叫它们不许动,第二次还是从头一个吃起,隔一个吃一个;第三次也是照这个办法吃。
但把最后剩下的一个放了。
”这话被聪明的小白鼠听见了,于是它站在了某个号的位置上,最后没有被吃掉。
小朋友,你知道小白鼠站的是第几号位置吗?习题解答1.解:小明共写了20个数字“9”。
因为从1到100的数中有18个数含有一个数字“9”,它们是:9、19、29、39、49、59、69、79、89、90、91、92、93、94、95、96、97、98。
另外自然数99含有两个数字9。
2.解:自然数串有一个特点,相邻的两个数中,后一个比前一个大1,因此可以进行如下的搭配分组:最小的数1和最大的数12成一组(1,12);次小的数2和次大的数11成一组(2,11);……中间的两个数6和7成一组(6,7);各组两个数相加之和都是13。
3.解:从受限制最强的乘法算式入手,在这九个数中两个数相乘的积等于另一个数而不发生重复数字出现的,只有2×3=6和2×4=8;经试验,可选用2×3=6,则剩下的六个数可组成两个等式1+7=8和4+5=9。
再经过适当的变换就可以列出满足题目要求的算式(答案不惟一)。
思维训练22-28
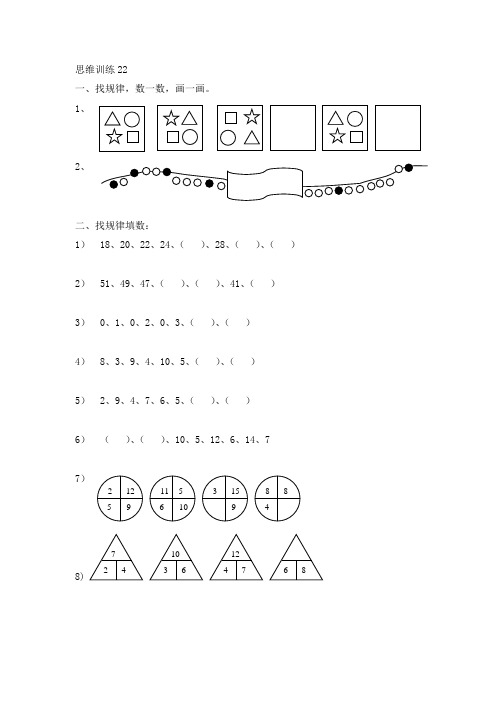
一、找规律,数一数,画一画。
1、2、二、找规律填数:1) 18、20、22、24、( )、28、( )、( )2) 51、49、47、( )、( )、41、( )3) 0、1、0、2、0、3、( )、( )4) 8、3、9、4、10、5、( )、( )5) 2、9、4、7、6、5、( )、( )6) ( )、( )、10、5、12、6、14、77)1、小红用同样的钱可以买5只蛋糕或者4只面包,蛋糕贵还是面包贵?()。
2、 3个男同学与4个女同学进行打球比赛,如果每个男同学都要与每个女同学比赛1次,一共需要比赛()次。
3、一根木头锯成6段,要锯()次。
4、二年级有50名运动员参加学校长跑比赛,号码排从1到50。
这些号码中共出现了()个“2”。
5、在括号里填数。
4+7=8+() 16-9=14-() 76-()〉72-2()+2=2+40 60-()=7+36、小李今年10岁,奶奶今年60岁,5年后,奶奶比小李大()岁。
7、小红有15本书,小冬有7本书,小红给小冬()本书,两个人就一样多了。
8、一个队伍有20人,小明从前数排在第7个,小红从后数排在第5个,你知道小明,小红中间有()个人。
9. 小猴与小兔去摘桃,小猴摘下15个桃,当小猴将自己的桃分2个给小兔子时,它俩的桃就一样多,你知道小兔子摘了()个桃。
1、填上数,使每条线上的三个数相加都等于15。
2、把3、4、5、6、7五个数填入右上图五个圆圈里,是横行、竖行圆圈里的数加起来的和都是15.3、方方和亮亮每人都有20本练习本。
亮亮送给方方7本后,方方比亮亮多 ( )本。
4、有8名队员参加乒乓球比赛。
小刚与每位参赛的队员都要打一场球,小刚共要打( )场。
5、三个小朋友比大小。
根据下面三句话,请你猜猜,谁最大?谁最小?亮亮比阳阳大3岁;丁丁比亮亮小1岁;( )最大,( )最小。
6、20块糖分成数量不同的4堆,要使其中一堆数量最多,那么数量最多的一堆有( )块糖。
六年级下册数学总复习试题-自然数串趣题-人教新课标含答案

1.小明从1 写到100,他共写了多少个数字“ 9”?2.把1到12这十二个数每两个数分为一组,要求每组的两个数之和都相等,怎么分?和是多少?3.用1、2、3、4、5、6、7、8、9 这九个数编三个算式,个加法、一个减法、一个乘法,每个数只许用一次。
4.用1、2、3、4、5、6、7、8、9这九个数字,写成三个三位数,使它们的和等于1953。
5.用1、2、3、4、5、6、7、8、9这九个数字,写成三个三位数,使它们的和等于1989。
6.一只老猫捉了12 只老鼠,其中有只小白鼠。
老猫自言自语地说:“我要分三批吃它们。
不过吃以前叫它们站好队,我从头一个开始吃,隔一个吃掉一个,也就是:我第一次吃掉站在第1,3,5,7,9,11 号位置的小老鼠;剩下的叫它们不许动,第二次还是从头一个吃起,隔一个吃一个;第三次也是照这个办法吃。
但把最后剩下的一个放了。
”这话被聪明的小白鼠听见了,于是它站在了某个号的位置上,最后没有被吃掉。
小朋友,你知道小白鼠站的是第几号位置吗?习题解答1.解:小明共写了20 个数字“ 9”。
因为从1 到100 的数中有18 个数含有一个数字“ 9”,它们是:9、19、29、39、49、59、69、79、89、90、91、92、93、94、95、96、97、98。
另外自然数99 含有两个数2.解:自然数串有一个特点,相邻的两个数中,后一个比前一个大1,因此可以进行如下的搭配分组:最小的数1 和最大的数12 成一组(1,12);次小的数2 和次大的数11 成一组(2,11);中间的两个数6 和7 成一组(6,7);各组两个数相加之和都是13。
3.解:从受限制最强的乘法算式入手,在这九个数中两个数相乘的积等于另一个数而不发生重复数字出现的,只有X 3=6和2X 4=8;经试验,可选用2X 3=6,则剩下的六个数可组成两个等式1+7=8和4+5=9。
再经过适当的变换就可以列出满足题目要求的算式(答案不惟一)1+7=8 9-4=5 2 X 3=6O4.解=分^(^1953=1800+140+13再分拆13=9+3+1作为三个数的个位上的数字;14-8+4+2作为三个数十位上的数字' 18=7+6+5作为三个数的百位上的数字,于罡,得到的三个数是789, 643, 521,检验;931 8427 65+注意,此题答案不惟一,同学们还可以试着写岀符合题g 要求的其他三个 数.5.解=思路与笫4题相同,分拆 1989二 1800+180+9 再分拆13=8+6+4作为三个数的百位上的数字,13=9+7+2作为三个数的十位上的数字; 9= 1+3+5作为三个数的个位上的数字; 于是,得到的三个数是別人673, 425, 检验’ 135 972 864+意题 合編上号:第一次吃掉: 第二次吃掉: 第三次吃^$: 最后剩下放掉: 888810 11 1210 11 1210 1212可见聪明的小白鼠如杲站在第8号位置上就可以不被吃掉。
第三讲 有趣的自然数串

第三讲有趣的自然数串① 请根据规律写出下面括号里的数字12,15,18,21,24,27( ),( ) 5,10,15,25,40,( ),105,( )256,128,64,32,( ),8,( ) 1,2,2,4,8,( ),256,81921,4,9,16,25,( ),( ),6450,10,45,20,40,40,35,80,( ),( )1,3,6,10,15,21,( ),( )1,2,4,5,7,8,10,( ),( ),14,16②请问用3,0,8这三个数字可以组成多少个数?(请分别列举)③请问在“6,7,8,9,10,……57”种,一共包含多少个数?多少个单数?多少个双数?多少个数字?④艾迪家养了一只小兔子,开始小兔子重2千克,艾迪每天喂她2千克的胡萝卜,第二天小兔子就能长2千克变成4千克,以此类推,请问小兔子到了第十一天,重多少千克?答案及详解------------------------------------------------------------①12,15,18,21,24,27,(30),(33)5,10,15,25,40,(65),105,(170)等差数列:+3 兔子数列:第三个数开始是前两个数相加的和256,128,64,32,(16),8,(4) 1,2,2,4,8,(32),256,8192等比数列:÷2 兔子数列变形:第三个数开始是前两个数相乘的积1,4,9,16,25,(36),(49),64 50,10,45,20,40,40,35,80,(30),(160)二次等差:正方形数1x1,2x2,3x3… 双重数列:相隔数——单数-5,双数x21,3,6,10,15,21,(28),(36) 1,2,4,5,7,8,10,(11),(13),14,16二次等差:三角形数1,1+2,1+2+3… 二次等差:+1,+2,+1,+2…②共11个数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自然数串趣题练习题
1.小明从1写到100,他共写了多少个数字“9”?
2.把1到12这十二个数每两个数分为一组,要求每组的两个数之和都相等,怎么分?和是多少?
3.用1、2、3、4、5、6、7、8、9这九个数编三个算式,一个加法、一个减法、一个乘法,每个数只许用一次。
4.用1、2、3、4、5、6、7、8、9这九个数字,写成三个三位数,使它们的和等于1953。
5.用1、2、3、4、5、6、7、8、9这九个数字,写成三个三位数,使它们的和等于1989。
6.一只老猫捉了12只老鼠,其中有一只小白鼠。
老猫自言自语地说:“我要分三批吃它们。
不过吃以前叫它们站好队,我从头一个开始吃,隔一个吃掉一个,也就是:我第一次吃掉站在第1,3,5,7,9,11号位置的小老鼠;剩下的叫它们不许动,第二次还是从头一个吃起,隔一个吃一个;第三次也是照这个办法吃。
但把最后剩下的一个放了。
”这话被聪明的小白鼠听见了,于是它站在了某个号的位置上,最后没有被吃掉。
小朋友,你知道小白鼠站的是第几号位置吗?
自然数串趣题练习题答案
1.解:小明共写了20个数字“9”。
因为从1到100的数中有18个数含有一个数字“9”,它们是:9、19、29、39、49、59、69、79、89、90、91、92、93、94、95、96、97、98。
另外自然数99含有两个数字9。
2.解:自然数串有一个特点,相邻的两个数中,后一个比前一个大1,因此可以进行如下的搭配分组:
最小的数1和最大的数12成一组(1,12);
次小的数2和次大的数11成一组(2,11);
……
中间的两个数6和7成一组(6,7);
各组两个数相加之和都是13。
3.解:从受限制最强的乘法算式入手,在这九个数中两个数相乘的积等于另一个数而不发生重复数字出现的,只有2×3=6和2×4=8;经试验,可选用2×3=6,则剩下的六个数可组成两个等式1+7=8和4+5=9。
再经过适当的变换就可以列出满足题目要求的算式(答案不惟一)。
1+7=8 9-4=5
2×3=6。
8.解:分段计算:
从1至9页,共9页,每页用一个铅字块共有1×9=9(块);
从10至19页,共10页,每页用两个铅字块共用2×10=20(块);从20至29页,共10页,每页用两个铅字块共用2×10=20(块);从30至39页,共10页,每页用两个铅字块共用2×10=20(块);从40至49页,共10页,每页用两个铅字块共用2×10=20(块);第50页,共1页(但为两位数)用两个铅字块,
所以:50页书共用9+20+20+20+20+2=91(块)(铅字)。
