连续时间信号和系统时域分析报告及MATLAB实现.docx
实验4连续信号与系统的频域分析及MATLAB实现.docx

实验4连续信号与系统的频域分析及MATLAB实现一、实验目的:1.用MATLAB实现非周期连续信号的傅里叶变换,并绘制出幅度谱和相位谱,利用仿真结果进一步加深对理论知识的理解。
2.掌握连续信号傅里叶变换的数值近似计算方法,并验证傅里叶变换的各项性质。
3.掌握求解连续时间系统的频响函数H(jw)的方法,并绘图分析频响函数的特性。
二、实验内容10.1(3):程序:syms t v w x phase im re;f=[sin(2*pi*t)/(2*pi*t)]^2;Fw=fourier(f)subplot(311);ezplot(f)axis([-pi pi -1 2]);title('原图');subplot(312);ezplot(abs(Fw))axis([-6 6 -1 1]);title('幅度谱');im=imag(Fw)re=real(Fw)phase=atan(im/re)subplot(313);ezplot(phase)axis([-6 6 -1 1]);title('相位谱');w =1/8/pi*(-(-w+4*pi)*heaviside(w-4*pi)-(-w-4*pi)*heaviside(w+4*pi)-2*w*heaviside(w))im =-1/2*i*(1/8/pi*(-(-w+4*pi)*heaviside(w-4*pi)-(-w-4*pi)*heaviside(w+4*pi)-2*w*heaviside(w))-1/ 8/pi*conj(-(-w+4*pi)*heaviside(w-4*pi)-(-w-4*pi)*heaviside(w+4*pi)-2*w*heaviside(w)))re =1/16/pi*(-(-w+4*pi)*heaviside(w-4*pi)-(-w-4*pi)*heaviside(w+4*pi)-2*w*heaviside(w))+1/16/pi *conj(-(-w+4*pi)*heaviside(w-4*pi)-(-w-4*pi)*heaviside(w+4*pi)-2*w*heaviside(w))phase =-i*atanh(1/2*(1/8/pi*(-(-w+4*pi)*heaviside(w-4*pi)-(-w-4*pi)*heaviside(w+4*pi)-2*w*heaviside (w))-1/8/pi*conj(-(-w+4*pi)*heaviside(w-4*pi)-(-w-4*pi)*heaviside(w+4*pi)-2*w*heaviside(w)))/ (1/16/pi*(-(-w+4*pi)*heaviside(w-4*pi)-(-w-4*pi)*heaviside(w+4*pi)-2*w*heaviside(w))+1/16/pi*conj(-(-w+4*pi)*heaviside(w-4*pi)-(-w-4*pi)*heaviside(w+4*pi)-2*w*heaviside(w))))10.2(1)程序:syms t w ;F=8*(sin(w/4))^2/(w)^2;f=ifourier(F,t)ezplot(f);axis([-1 1 -0.3 1]);title('时域波形')f =(2*t+1)*heaviside(t+1/2)+(2*t-1)*heaviside(t-1/2)-4*t*heaviside(t)10.4程序:dt=0.005;t=-2:dt:2;f1=Heaviside(t+1)-Heaviside(t-1); subplot(2,2,1)plot(t,f1)axis([-2 2 0 1.5]);title('f1(t)');f=dt*conv(f1,f1)n=-4:dt:4;subplot(2,2,2)plot(n,f)title('f(t)=f1(t)*f1(t)');axis([-4 4 0 2.5]);W1=2*pi*5;N=200;k=-N:N;W=k*W1/N;F1=f1*exp(-j*t'*W)*dt;F1=abs(F1)F=f*exp(-j*n'*W)*dt;F=abs(F)F=F.*Fsubplot(2,2,3)plot(W,F1)subplot(2,2,4)plot(W,F)axis([-10*pi 10*pi 0 10]); axis([-10*pi 10*pi 0 20]);10.5 程序:a=[0.04 0.4 2]; [h,w]=freqs(b,a,100); h1=abs(h);h2=angle(h); subplot(2,1,1)plot(w,h1)hold onaxis([0 60 0 1.6]); gridxlabel('角频率'); ylabel('幅度');title('幅频特性'); subplot(2,1,2)plot(w,h2*180/pi) axis([0 150 -250 0]); gridxlabel('角频率'); ylabel('幅度');title('相频特性');通过实验我对理论知识有了更深刻的理解,当周期信号的周期无限增大时,周期信号就转换为非周期信号。
实验四 连续时间信号与系统的频域分析的MATLAB实现

实验四连续时间信号与系统的频域分析的MATLAB实现[实验目的]1.掌握周期信号的频谱—— Fourier 级数的分析方法及其物理意义。
2.深入理解信号频谱的概念,掌握典型信号的频谱以及Fourier 变换的主要性质。
3 通过阅读、修改并调试本实验系统所给周期信号频谱分析的源程序,加强Matlab 编程能力实验原理:信号与系统的频谱分析就是将信号与系统的时域表征经过傅里叶变换转换到频域表征,从而获得信号与系统在频域的分布特性,使我们从频域的角度获得对信号与系统的性质更加深入与具体的了解。
频谱分析又称为傅里叶分析,他为我们提供了一种非常方便的信号与系统的表示法与分析方法,在信号与系统的分析与研究中有着特别重要的作用。
一. 周期信号振幅谱的MATLAB实现例1.试用MATLAB绘出如图1所示周期矩形脉冲信号的振幅频谱。
图1解:MATLAB程序如下:echo offa=-5;b=5;n=50;j=sqrt(-1);%积分精度tol=1e-6;%设置脉冲波形周期T0=b-a;%定义脉冲波波形xsqual=@(x)1/2.*(x==-1/2)+(x>-1&x<1/2)+1/2.*(x==-1/2);%计算直流分量out(1)=1/T0.*quad(xsqual,a,b,tol);%积分计算基波和各次谐波分量xfun=@(x,k,T)xsqual(x).*exp(-j*2*pi*x*k/T); for i=1:nout(i+1)=1/T0.*quad(xfun,a,b,tol,[],i,T0); endout1=out(n+1:-1:2);out1=[conj(out1),out];absout=abs(out1);n1=[-n:n];stem(n1(n+1:2*n+1),absout(n+1:2*n+1));titile(幅度谱);二. 非周期信号的傅立叶变换的MATLAB实现MATLAB的Symbolic Math Toolbox 提供了能直接求解傅立叶变换及与变换的函数fourier()与ifourier()。
连续时间系统的时域分析实验报告

实验二连续时间系统的时域分析一、实验目的通过使用MATLAB软件对连续时间线性非时变系统的时域特性进行仿真分析,熟悉IT 系统在典型激励下的响应及特征,熟悉相应MATLAB函数的调用格式和作用,熟悉井掌握用MATLAB函数求解冲激响应、阶跃响应、零输入响应、零状态响应及全响应的方法。
二、实验原理(一)连续时间系统的时域分析方法连续时间线性非时变系统(LTI)的输入/(/)与输出〉,(/)可以用线性常系数微分方程来描述:叨叫)+%产")(『)+…+引(0+ 3 (0訥,严⑺+…附⑺+仇他)如果已知系统的输入信号/'«)及系统的初始条件为y(O_),y(O_),y”(O_),…,〉,("⑷心),就可以利用解析方法求出系统的响应。
线性系统的全响应由零输入响应分量和零状态响应分量组成。
零输入响应是指当输入为零时仅由t=0的初始条件产生的系统响应,零状态响应是当初始条件(在t二0)假左为零时仅由t >0时的输入产生的系统响应分量。
零输入响应(单极点时)为:儿")=5小+c2e^ +•• • + *" =£fJI式中,C|、C2、…、q为任意待泄常数,由初始条件确立。
零状态响应为:y f(z)= J x/(r为(/一rMf此式是对任意输入/(/),用单位冲激响应〃(/)形式表示的零状态响应儿•(”的公式。
已知力(/)就可确定任意输入/(/)的零状态响应即系统对任意输入的响应都可以用单位冲激响应确定。
系统总响应为:y(»=儿(0+从)=土勺/+匸/的心-力“冃对于高阶系统,手工计算非常繁琐。
MATLAB的汁算功能能比较容易地确左系统的各种响应,如冲激响应、阶跃响应、零输入响应.零状态响应和全响应等。
三、实验内容4.1已知连续系统的微分方程为2/(r)+y(r)+8y(0=/W试用MATLAB:①给岀该系统在0~30秒范围内,并以时间间隔0. 01秒取样的冲激响应和阶跃响应的时域波形。
实验Matlab8_连续时间信号与系统的时域分析

虚指数信号(P132)
虚指数信号的一般形式为:
f (t ) Ae jwt A(cos wt j sin wt )
虚指数信号是时间t的复函数,因此,我们需要用两 个实信号来表示虚指数信号,即用模和相角或实部和 虚部来表示虚指数信号随时间变化的规律。 例5:画出信号 f ( t ) 2e 4 的波形。 实部、虚部、模、相角
连续信号的时域运算、时域变换
利用符号运算实现连续信号的时域变换(P147,P151)
f ( t ) f1 ( t ) f 2 ( t ) 相加 s=symadd(f1,f2),s=f1+f2, ezplot(s) f ( t ) f1 ( t ) f 2 ( t ) 相乘 s=symmul(f1,f2),s=f1*f2, ezplot(s) 移位 y=subs(f,t,t-t0):f(t-t0) y=subs(f,t,t+t0):f(t+t0) ezplot(y)
反折 y=subs(f,t,-t) ezplot(y) 尺度变换 y=subs(f,t,a*t) ezplot(y) 倒相 y=-f ezplot(y)
t 例7:设信号 f ( t ) ( 1 ) [ u( t 2 ) u( t 2 )] 2
求f(t+2),f(t-2),f(-t),f(2t),-f(t).
一些常用的信号的表示(P126)
单位阶跃信号
利用符号函数maple中的内核函数Heaviside
利用自编函sign( t ) 1 t 0
u(t)=1/2+(1/2)sign(t)
见shiyan1_2
(仅供参考)实验1 连续时间系统的时域分析及matlab实现

实验一连续时间系统的时域分析及matlab实现一.实验目的熟悉连续时间系统零状态响应的求解及matlab实现,用卷积方法求零状态响应,以及在系统分析中有重要意义的单位冲激响应和单位阶跃响应的求解。
二.实验内容1.连续系统的冲激响应、阶跃响应及MATLAB实现a1连续系统冲激响应及阶跃响应分别用matlab系统函数impulse()和step()实现,查看两个函数的帮助以确定如何应用。
习题1:0510152025-0.15-0.1-0.050.050.10.150.20.25Impulse ResponseTime (sec)A m p l i t u d e2.连续时间系统的零状态响应及MATLAB实现MATLAB的函数lsim()能对上述微分方程描述的LTI 连续系统的响应进行仿真。
lsim()函数能绘制连续系统在指定的任意时间范围内系统响应的时域波形图,还能求出连续系统在指定的任意时间范围内系统响应的数值解。
lsim()函数调用格式为lsim(b,a,x,t)习题2:已知描述某连续系统的微分方程为:ex00.050.10.150.20.250.30.350.400.10.20.30.40.50.60.70.80.91Linear Simulation ResultsTime (sec)A m p l i t u d e >>a=[121];>>b=[12];>>t=0:0.1:0.4;>>f=exp(-2*t);>>lsim(b,a,-2,t)3.用MATLAB 实现连续时间信号的卷积卷积积分在信号与线性系统分析中具有非常重要的意义,信号经过系统所产生的响应可以用二者的卷积求解。
卷积积分运算实际上可用信号的分段求和来实现,即:如果我们只求当t=n ∆ (n 为整数)时f(t)的值f(n ∆),则由上式可得:式中下面是利用MATLAB实现连续信号卷积的通用函数sconv(),function[f,k]=sconv(f1,f2,k1,k2,p)%计算连续信号卷积积分f(t)=f1(t)*f2(t)%f:卷积积分f(t)对应的非零样值向量%k:f(t)的对应时间向量%f1:f1(t)非零样值向量%f2:f2(t)的非零样值向量%k1:f1(t)的对应时间向量%k2:序列f2(t)的对应时间向量%p:取样时间间隔f=conv(f1,f2);%计算序列f1与f2的卷积和ff=f*p;k0=k1(1)+k2(1);%计算序列f非零样值的起点位置k3=length(f1)+length(f2)-2;%计算卷积和f的非零样值的宽度k=k0:p:k0+k3*p;%确定卷积和f非零样值的时间向量subplot(2,2,1)plot(k1,f1)%在子图1绘f1(t)时域波形图title('f1(t)')xlabel('t')ylabel('f1(t)')subplot(2,2,2)plot(k2,f2)%在子图2绘f2(t)时波形图title('f2(t)')xlabel('t')ylabel('f2(t)')subplot(2,2,3)plot(k,f);%画卷积f(t)的时域波形h=get(gca,'position');h(3)=2.5*h(3);set(gca,'position',h)%将第三个子图的横坐标范围扩为原来的2.5倍title('f(t)=f1(t)*f2(t)')xlabel('t')ylabel('f(t)')例3:已知两连续时间信号如下图所示,试用MATLAB 求)(*)()(21t f t f t f =,并绘出时域波形图。
Matlab讲义实验报告连续时间信号的分析.doc

连续时间信号的分析一、实验目的1.学习使用MATLAB 产生基本的连续信号、绘制信号波形。
2.实现信号的基本运算,为信号分析和系统设计奠定基础。
二、实验原理 1、基本信号的产生 时间间隔代替连续信号。
连续指数信号的产生连续矩形脉冲信号(门信号)的产生。
连续周期矩形波信号的产生。
2、信号的基本运算相加、相减、相乘、平移、反折、尺度变换。
三、实验内容1. 用MATLAB 编程产生正弦信号()sin(2),2,5Hz,3f t K ft K f ππθθ=+===,并画图。
代码如下: clc clear f0=5; w0=2*pi*f0; t=0:0.001:1; x=2*sin(w0*t+pi/3); plot(t,x) title('正弦信号')正弦信号2. 用MATLAB 编程产生信号122()0t f t -<<⎧=⎨⎩其它,画出波形。
代码如下:clc clear f0=2;t=0:0.0001:2.5; y=square(w0*t,50); plot(t,y);axis([0 2.5 -1.5 1.5]) title('周期方波');图形如下:单位阶跃信号3. 分别画出2中()f t 移位3个单位的信号(3)f t -、反折后的信号()f t -、尺度变换后的信号(3)f t 。
代码如下:clc cleart=-10:0.001:10; subplot(3,1,1) plot(t,f(t-3)) axis([-7 7 -2 2]) xlabel('t') ylabel('f(t-3)') title('移位') grid on subplot(3,1,2) plot(t,f(-t)) axis([-7 7 -2 2]) xlabel('t') ylabel('f(-t)') title('反折') grid on subplot(3,1,3) plot(t,f(3*t)) axis([-7 7 -2 2]) xlabel('t') ylabel('f(3t)') title('尺度变换') grid on 图形如下:xf (t )xf (t -3)xf (-t )xf (3*t )4. 用MATLAB编程画出下图描述的函数。
连续时间信号和系统时域分析及MATLAB实现之欧阳道创编

课程设计任务书学生姓名: 专业班级:指导教师:工作单位:题目:连续时间信号和系统时域分析及MATLAB 实现初始条件:MATLAB 6.5要求完成的主要任务:一、用MATLAB实现常用连续时间信号的时域波形(通过改变参数,分析其时域特性)。
1、单位阶跃信号,2、单位冲激信号,3、正弦信号,4、实指数信号,5、虚指数信号,6、复指数信号。
二、用MATLAB实现信号的时域运算1、相加,2、相乘,3、数乘,4、微分,5、积分三、用MATLAB实现信号的时域变换(参数变化,分析波形变化)1、反转,2、使移(超时,延时),3、展缩,4、倒相,5、综合变化四、用MATLAB实现信号简单的时域分解1、信号的交直流分解,2、信号的奇偶分解五、用MATLAB实现连续时间系统的卷积积分的仿真波形给出几个典型例子,对每个例子,要求画出对应波形。
六、用MATLAB实现连续时间系统的冲激响应、阶跃响应的仿真波形。
给出几个典型例子,四种调用格式。
七、利用MATLAB实现连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形。
给出几个典型例子,要求可以改变激励的参数,分析波形的变化。
时间安排:学习MATLAB语言的概况第1天学习MATLAB语言的基本知识第2、3天学习MATLAB语言的应用环境,调试命令,绘图能力第4、5天课程设计第6-9天答辩第10天指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要IABSTRACT II绪论11 MATLAB简介21.1MATLAB语言功能21.2MATLAB语言特点22常用连续时间信号的时域波形3 2.1单位阶跃信号32.2单位冲激信号42.3正弦信号42.4实指数信号52.5虚指数信号52.6复指数信号53 连续时间信号的时域运算63.1相加63.2相乘63.3数乘63.4微分73.5积分74 连续时间信号的时域变换74.1反转74.2时移84.3展缩84.4倒相84.5综合变化85连续时间信号简单的时域分解95.1信号的交直流分解95.2信号的奇偶分解96连续时间系统的卷积积分的仿真波形107连续时间系统的冲激响应、阶跃响应的仿真波形11 7.1IMPULSE()函数127.2STEP()函数138连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形148.1正弦信号的零状态响应158.2实指数信号的零状态响应169小结即心得体会17致谢18参考文献18附录19摘要MATLAB目前已发展成为由MATLAB 语言、MATLAB 工作环境、MATLAB 图形处理系统、MATLAB 数学函数库和MATLAB 应用程序接口五大部分组成的集数值计算、图形处理、程序开发为一体的功能强大的系统。
课程设计--连续时间信号和系统时域分析及MATLAB实现

课程设计任务书题目:连续时间信号和系统时域分析及MATLAB实现课题内容:一、用MATLAB实现常用连续时间信号的时域波形(通过改变参数,分析其时域特性)。
二、用MATLAB实现信号的时域运算三、用MATLAB实现信号的时域变换(参数变化,分析波形变化)1、反转,2、使移(超时,延时),3、展缩,4、倒相,5、综合变化四、用MATLAB实现信号简单的时域分解1、信号的交直流分解,2、信号的奇偶分解五、用MATLAB实现连续时间系统的卷积积分的仿真波形给出几个典型例子,对每个例子,要求画出对应波形。
六、用MATLAB实现连续时间系统的冲激响应、阶跃响应的仿真波形。
给出几个典型例子,四种调用格式。
七、利用MATLAB实现连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形。
给出几个典型例子,要求可以改变激励的参数,分析波形的变化。
时间安排:学习MATLAB语言的概况第1天学习MATLAB语言的基本知识第2、3天学习MATLAB语言的应用环境,调试命令,绘图能力第4、5天课程设计第6-9天答辩第10天指导教师签名:年月日目录摘要 (Ⅰ)1.绪论 (1)2.对课题内容的分析 (2)2.1连续时间信号概述 (2)2.2采样定理 (2)2.3总体思路 (2)3.设计内容 (2)3.1用MATLAB实现常用连续时间信号的时域波形 (2)3.1.1单位阶跃信号和单位冲击信号 (2)3.1.2正弦信号 (4)3.1.3指数信号 (5)3.1.4实指数信号和虚指数信号 (6)3.2用MATLAB实现信号的时域运算 (7)3.2.1相加 (7)3.2.2相乘 (8)3.2.3数乘 (9)3.2.4微分 (10)3.2.5积分 (12)3.3用MATLAB实现信号的时域变换 (13)3.4用MATLAB实现信号简单的时域分解 (15)3.4.1 交直流分解 (15)3.4.2 奇偶分解 (16)3.5用MATLAB实现连续时间系统的卷积积分的仿真波形 (18)3.6用MATLAB实现连续时间系统的冲激响应、阶跃响应的仿真波形 (19)3.7利用MATLAB实现连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形 (20)4.心得体会 (22)5.参考文献 (23)摘要本文介绍了基于MATLAB的连续时间信号与系统时域分析。
连续信号和系统时域分析的MATLAB实现

抽样函数 M 文件名:Sa.m
% 抽样函数(连续或离散) % 高度为 1, % 调用 y=Sa(t) 产生高度为 1,第一个过零点为 function f=Sa(t) f=sinc(t./pi); % sinc(t)=sin(t)/(t)是 Matlab 内部函数
符号函数 M 文件名:sign.m 是 Matlab 的内部函数
% 画正弦信号的程序 t0=-2*pi;t1=2*pi;dt=0.02; t=t0:dt:t1; f=sin(pi/2*t); max_f=max(f); min_f=min(f); plot(t,f,'linewidth',2); grid;line([t0 t1],[0 0]); axis([t0,t1,min_f-0.2,max_f+0.2]) xlabel('t(sec)'),title('正弦信号的波形') 图 1-1 正弦信号
调用格式 调用格式
Matlab 的内部函数
y=sawtooth(w0*t) 产生基频为 w0(周期 T=2/w0)的周期锯齿波。为正斜率。 y=sawtooth(w0*t,WIDTH) 参数 WIDTH=0.5,产生周期三角波;WIDTH=0,产生斜率为负的周期锯齿 波。
例 1 画出下列信号的波形图。 (a) 正弦信号 sin( 0.5 t ) ; (b) 门函数 G2 (t ) ; (c) 随机信号; (d) 离散信号 cos(0.1 k ) , k 0, 1, 2, (e) 周期 T=10s 的周期锯齿波信号。 (f) 指数衰减的余弦信号 2e t / 6 cos t 。 解:用Matlab计算的程序如下:
三角脉冲函数 M 文件名:tripuls.m, Matlab 的内部函数
《MATLAB》信号的时域表示与分析实验报告

《MATLAB》信号的时域表示与分析实验报告1、编写一个MATLAB程序,以Q2_1为文件名存盘,使之能够在同一个图形窗口中的两个子图中分别绘制信号x[n]=0.5|n| 和x(t)=cos(2πt)[u(t)-u(t-3)]。
要求选择的时间窗能够表现出信号的主要部分。
2、编写一个MATLAB程序,以Q2_2为文件名存盘,由给定信号x(t) = e-0.5t u(t) 求信号y(t) = x(1.5t+3),并绘制出x(t) 和y(t)的图形。
3、编写一个MATLAB程序,以Q2_3为文件名存盘。
给定两个连续时间序列:x(t)= 0.5t[u(t)-u(t-4)] h(t) = u(t)-u(t-4)计算它们的卷积,并分别绘制x(t)、h(t)和它们的卷积y(t)的图形。
2.4编写一个MA TLAB 程序,以Q2_4为文件名存盘。
给定两个离散时间序列: x[n] = 0.5n{u[n]-u[n-4]} h[n] = u[n]-u[n-4]计算它们的卷积,并分别绘制x[n]、h[n]和它们的卷积y[n]的图形。
2.5编写一个MATLAB 程序,以Q2_5为文件名存盘。
两个信号分别为:1()0.5[()(4)]f t t u t u t =--和 2()sin(4)f t t =π。
用MATLAB 绘制这两个信号,同时绘制两信号的和与积的波形。
2.6编写一个MATLAB 程序,以Q2_6为文件名存盘。
已知连续信号f(t)=u(t+1)-tu(t)+(t-1)u(t-1),用Matlab 绘制以下时域变换的时域波形:f 1(t)=2f(0.5t),f 2(t)=f(-2t+3),f 3(t)= ()df t dt ,4()()t f t f d ττ-∞=⎰。
《MATLAB》连续时间信号的频域分析和连续时间系统的时域分析实验报告
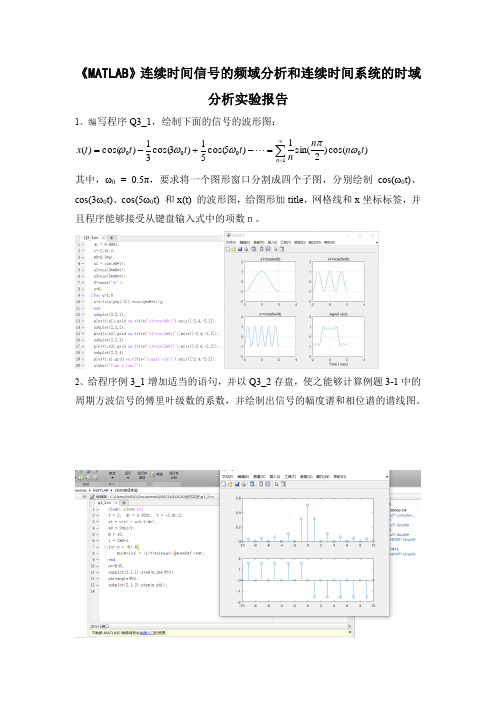
《MATLAB 》连续时间信号的频域分析和连续时间系统的时域分析实验报告1、编写程序Q3_1,绘制下面的信号的波形图:其中,ω0 = 0.5π,要求将一个图形窗口分割成四个子图,分别绘制cos(ω0t)、cos(3ω0t)、cos(5ω0t) 和x(t) 的波形图,给图形加title ,网格线和x 坐标标签,并且程序能够接受从键盘输入式中的项数n。
2、给程序例3_1增加适当的语句,并以Q3_2存盘,使之能够计算例题3-1中的周期方波信号的傅里叶级数的系数,并绘制出信号的幅度谱和相位谱的谱线图。
-+-=)5cos(51)3cos(31)cos()(000t t t t x ωωω∑∞==10)cos()2sin(1n t n n nωπ3.3反复执行程序例3_2,每次执行该程序时,输入不同的N值,并观察所合成的周期方波信号。
通过观察,你了解的吉布斯现象的特点是什么?3.4分别手工计算x1(t) 和x2(t) 的傅里叶级数的系数。
1.利用MATLAB 求齐次微分方程,,起始条件为,,时系统的零输入响应、零状态响应和全响应。
2. 已知某LTI 系统的方程为:其中,。
利用MATLAB 绘出范围内系统零状态响应的波形图。
3.已知系统的微分方程如下,利用MATLAB 求系统冲激响应和阶跃响应的数值解,并绘出其时域波形图。
(1)'''()2''()'()'()y t y t y t x t ++=()()t x t e u t -=(0)1y -='(0)1y -=''(0)2y -=''()5'()6()6()y t y t y t x t ++=()10sin(2)()x t t u t π=05t ≤≤''()3'()2()()y t y t y t x t ++=(2)''()2'()2()'()y t y t y t x t ++=。
连续时间信号的频域分析及Matlab实现

2. [Px,f] = psd(x,Nfft,Fs,window,noverlap,flag);
Fs = 1000;%被调信号x的采样频率 Fc = 400;%载波信号的载波频率 N = 1000;%FFT的长度
n = 0:N-2;
t = n/Fs; x = sin(2*pi*50*t);%被调信号 subplot(2,2,1);plot(t,x); window = hamming(512); [Pxx,f] = psd(x,1024,Fs,window,256,’none’);%求被调信号的功率谱 subplot(2,2,2);plot(f,Pxx);grid
t = 0:0.01:T; f = cell(1,Nf); f{1} = symA(1)/2 + symA(2)*cos(2*pi*t/5)+symB(2)*sin(2*pi*t/5);%基波 subplot(2,1,1) plot(t,f{1}) hold on axis([-5,5,-0.5,1.5]); e1 = sign(t+tao/2); e2 = sign(t-tao/2); y = h.*(e1-e2)/2;
2 0 -5
-4
-3
-2
-1
0
1
2
3
4
5
连续时间信号的傅里叶变换
傅里叶变换 绝对可积条件
F
j f t e j t d t
f t dt
j t
傅里叶逆变换 f
Matlab函数
1.Fourier变换
t F j e
function [A_sym,B_sym] = CTF2()
实验三连续时间LTI系统的时域分析报告

实验三 连续时间LTI 系统的时域分析一、实验目的1.学会用MATLAB 求解连续系统的零状态响应; 2. 学会用MATLAB 求解冲激响应及阶跃响应; 3.学会用MATLAB 实现连续信号卷积的方法;二、实验原理1.连续时间系统零状态响应的数值计算我们知道,LTI 连续系统可用如下所示的线性常系数微分方程来描述,()()0()()NMi j i j i j a yt b f t ===∑∑在MATLAB 中,控制系统工具箱提供了一个用于求解零初始条件微分方程数值解的函数lsim 。
其调用格式y=lsim(sys,f,t)式中,t 表示计算系统响应的抽样点向量,f 是系统输入信号向量,sys 是LTI 系统模型,用来表示微分方程,差分方程或状态方程。
其调用格式sys=tf(b,a)式中,b 和a 分别是微分方程的右端和左端系数向量。
例如,对于以下方程:''''''''''''32103210()()()()()()()()a y t a y t a y t a y t b f t b f t b f t b f t +++=+++可用32103210[,,,];[,,,];a a a a a b b b b b == (,)sys tf b a = 获得其LTI 模型。
注意,如果微分方程的左端或右端表达式中有缺项,则其向量a 或b 中的对应元素应为零,不能省略不写,否则出错。
例3-1 已知某LTI 系统的微分方程为 y’’(t)+ 2y’(t)+100y(t)=f(t)其中,'(0)(0)0,()10sin(2)y y f t t π===,求系统的输出y(t). 解:显然,这是一个求系统零状态响应的问题。
其MATLAB 计算程序如下: ts=0;te=5;dt=0.01; sys=tf([1],[1,2,100]); t=ts:dt:te; f=10*sin(2*pi*t); y=lsim(sys,f,t); plot(t,y);xlabel('Time(sec)'); ylabel('y(t)');2.连续时间系统冲激响应和阶跃响应的求解在MATLAB 中,对于连续LTI 系统的冲激响应和阶跃响应,可分别用控制系统工具箱提供的函数impluse 和step 来求解。
连续时间信号和系统时域分析及MATLAB实现(推荐文档)

课程设计任务书学生姓名:专业班级:指导教师:工作单位:题目:连续时间信号和系统时域分析及MATLAB实现初始条件:MATLAB 6.5要求完成的主要任务:一、用MATLAB实现常用连续时间信号的时域波形(通过改变参数,分析其时域特性)。
1、单位阶跃信号,2、单位冲激信号,3、正弦信号,4、实指数信号,5、虚指数信号,6、复指数信号。
二、用MATLAB实现信号的时域运算1、相加,2、相乘,3、数乘,4、微分,5、积分三、用MATLAB实现信号的时域变换(参数变化,分析波形变化)1、反转,2、使移(超时,延时),3、展缩,4、倒相,5、综合变化四、用MATLAB实现信号简单的时域分解1、信号的交直流分解,2、信号的奇偶分解五、用MATLAB实现连续时间系统的卷积积分的仿真波形给出几个典型例子,对每个例子,要求画出对应波形。
六、用MATLAB实现连续时间系统的冲激响应、阶跃响应的仿真波形。
给出几个典型例子,四种调用格式。
七、利用MATLAB实现连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形。
给出几个典型例子,要求可以改变激励的参数,分析波形的变化。
时间安排:学习MATLAB语言的概况第1天学习MATLAB语言的基本知识第2、3天学习MATLAB语言的应用环境,调试命令,绘图能力第4、5天课程设计第6-9天答辩第10天指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要 (I)ABSTRACT (II)绪论 (1)1 MATLAB简介 (2)1.1MATLAB语言功能 (2)1.2MATLAB语言特点 (2)2常用连续时间信号的时域波形 (3)2.1单位阶跃信号 (3)2.2单位冲激信号 (3)2.3正弦信号 (4)2.4实指数信号 (5)2.5虚指数信号 (5)2.6复指数信号 (6)3 连续时间信号的时域运算 (7)3.1相加 (7)3.2相乘 (7)3.3数乘 (8)3.4微分 (8)3.5积分 (9)4 连续时间信号的时域变换 (10)4.1反转 (10)4.2时移 (10)4.3展缩 (11)4.4倒相 (11)4.5综合变化 (12)5连续时间信号简单的时域分解 (13)5.1信号的交直流分解 (13)5.2信号的奇偶分解 (14)6连续时间系统的卷积积分的仿真波形 (15)7连续时间系统的冲激响应、阶跃响应的仿真波形 (16)7.1 IMPULSE()函数 (17)7.2 STEP()函数 (19)8连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形 (21)8.1正弦信号的零状态响应 (21)8.2实指数信号的零状态响应 (22)9小结即心得体会 (24)致谢 (25)参考文献 (26)附录 (27)摘要MATLAB目前已发展成为由MATLAB 语言、MATLAB 工作环境、MATLAB 图形处理系统、MATLAB 数学函数库和MATLAB 应用程序接口五大部分组成的集数值计算、图形处理、程序开发为一体的功能强大的系统。
信号与系统matlab实验3连续时间LTI分析报告

实验三连续时间LTI系统分析姓名学号班级通信一班一、实验目的(一)掌握使用Matlab进行连续系统时域分析的方法1、学会使用符号法求解连续系统的零输入响应和零状态响应2、学会使用数值法求解连续系统的零状态响应3、学会求解连续系统的冲激响应和阶跃响应(二)掌握使用Matlab进行连续时间LTI系统的频率特性及频域分析方法1、学会运用MATLAB分析连续系统地频率特性2、学会运用MATLAB进行连续系统的频域分析(三)掌握使用Matlab进行连续时间LTI系统s域分析的方法1、学会运用MATLAB求拉普拉斯变换(LT)2、学会运用MATLAB求拉普拉斯反变换(ILT)3、学会在MATLAB环境下进行连续时间LTI系统s域分析二、实验原理及实例分析(一)连续系统时域分析(详细请参见实验指导第二部分的第5章相关部分)(二)连续时间LTI系统的频率特性及频域分析(详细请参见实验指导第二部分的第8章相关部分)(三)拉普拉斯变换及连续时间系统的s域分析(详细请参见实验指导第二部分的第10、11章相关部分)三、实验过程(一)熟悉三部分相关内容原理(二)完成作业已知某系统的微分方程如下:)(3)()(2)(3)(t e t e t r t r t r +'=+'+''其中,)(t e 为激励,)(t r 为响应。
1、用MATLAB 命令求出并画出2)0(,1)0(),()(3='==---r r t u e t e t 时系统的零状态响应和零输入响应(零状态响应分别使用符号法和数值法求解,零输入响应只使用符号法求解);>> eq='D2y+3*Dy+2*y=0';>> cond='y(0)=1,Dy(0)=2';>> yzi = dsolve(eq,cond);yzi = simplify(yzi);>> eq1 = 'D2y+3*Dy+2*y=Dx+3*x';eq2 = 'x= exp(-3*t)*Heaviside(t)';cond = 'y(-0.01)=0,Dy(-0.001)=0';yzs = dsolve(eq1,eq2,cond);yzs = simplify(yzs.y)yzs =heaviside(t)*(-exp(-2*t)+exp(-t))>> yt = simplify(yzi+yzs)yt =-3*exp(-2*t)+4*exp(-t)-exp(-2*t)*heaviside(t)+exp(-t)*heaviside(t)>> subplot(3,1,1);>> ezplot(yzi,[0,8]);grid on;>> title ('rzi');>> subplot(3,1,2);>> ezplot(yzs,[0,8]);>> grid on;>> title('rzs');>> subplot(3,1,3);>> ezplot(yt,[0,8]);grid on;>> title('完全响应')sys = tf([1,3],[1,3,2]);t = ts:dt:te;f = exp(-3*t).*uCT(t);y = lsim(sys,f,t);plot(t,y),grid on;axis([0,8,-0.02,0.27]);xlable('Time(sec)'),ylable('y(t)'); title('零状态响应')2、)(3)()(2)(3)(t e t e t r t r t r +'=+'+''2)0(,1)0(),()(3='==---r r t u e t e t使用MATLAB 命令求出并画出系统的冲激响应和阶跃响应(数值法);用卷积积分法求系统的零状态响应并与(1)中结果进行比较;t = 0:0.001:4;sys = tf([1,3],[1,3,2]);h = impulse(sys,t);g = step(sys,t);subplot(2,1,1);plot(t,h),grid on;xlable('Time(sec)'),ylable('h(t)');title('冲激响应');subplot(2,1,2);plot(t,g),grid on;xlable('Time(sec)'),ylable('g(t)');title ('阶跃响应')_dt = 0.01;t1 = 0:dt:8;f1=exp(-3*t1);t2 = t1;sys = tf([1,3],[1,3,2]);f2 = impulse(sys,t2);[t,f]= ctsconv(f1,f2,t1,t2,dt)function[f,t] = ctsconv(f1,f2,t1,t2,dt)f = conv(f1,f2);f = f*dt;ts = min(t1)+min(t2);te = max(t1)+max(t2);t = ts:dt:te;subplot(1,1,1)plot(t,f);grid on;axis([min(t),max(t),min(f)-abs(min(f)*0.2),max(f)+abs(max(f)*0.2)]); title('卷积结果')3、)(3)()(2)(3)(t e t e t r t r t r +'=+'+''使用MATLAB 命令求出并画出此系统的幅频特性和相频特性;使用频域分析法求解系统的零状态响应并与(1)中结果进行比较;>> w = -3*pi:0.01:3*pi;b = [1,3];a = [1,3,2];H = freqs(b,a,w);subplot(2,1,1);plot(w,abs(H)),grid on;xlabel('\omega(rad/s)'),ylabel('|H(\omega)|');title ('H(w)的幅频特性');subplot(2,1,2);plot(w,angle(H)),grid on;xlabel('\omega(rad/s)'),ylabel('\phi(\omega)');title('H(w)的相频特性')H = sym('1/(i^2*w^2+3*i*w+2)'); H= simplify(ifourier(H)); subplot(3,1,1);ezplot(H,[0,8]),grid on;title('零状态响应')4、)(3)()(2)(3)(t e t e t r t r t r +'=+'+''使用MATLAB 命令求出并画出t t e 2cos )(=时系统的稳态响应;t = 0:0.1:20;w = 2;H = (j*w+3)/(j^2*w^2+3*j*w+2);f = cos(2*t);y = abs(H)*cos(w*t+angle(H));subplot(2,1,1);plot(t,f);grid on;ylabel('f(t)'),xlabel('Time(s)');title('输入信号的波形');subplot(2,1,2);plot(t,y);grid on;ylabel('y(t)'),xlabel('Time(sec)');title('稳态响应的波形')5、)(3)()(2)(3)(t e t e t r t r t r +'=+'+''若已知条件同(1),借助MATLAB 符号数学工具箱实现拉普拉斯正反变换的方法求出并画出2)0(,1)0(),()(3='==---r r t u e t e t 时系统的零状态响应和零输入响应,并与(1)的结果进行比较。
MATLAB信号的表示与时域分析,matlab与信号实验连续时间信号的时域分析

MATLAB信号的表⽰与时域分析,matlab与信号实验连续时间信号的时域分析matlab与信号实验连续时间信号的时域分析上机实验 1 连续时间信号的时域分析 ⼀、 实验⽬的 (1 ) 掌握连续时间信号的时域运算的基本⽅法; (2 ) 掌握相关函数的调⽤格式及作⽤; (3 ) 掌握连续信号的基本运算; (4 ) 掌握利⽤计算机进⾏卷积运算的原理和⽅法; (5 ) 熟悉连续信号卷积运算函数 conv 的应⽤。
⼆、 实验原理 信号的基本运算包括信号的相加(减)和相乘(除) 。
信号的时域变换包括信号的平移、翻 转、倒相、尺度变换等,由以下公式所描述。
(1 ) 加(减):f(t)=f 1 (t)±f 2 (t) (2 ) 乘:f(t)=f 1 (t)×f 2 (t) (3 ) 延时或平移:f(t) →f(t-t 0 ) t 0 >0 时右移;t 0 0 。
MATLAB 程序: clear all; t=0:0.0001:2; y=sin(2*pi*(t)); y1=sin(2*pi*(t-0.2)); plot(t, y, - ,t, y1, -- ); xlabel( t );ylabel( f(t) );title(信号的移位 ); 信号及其移位结果如下图所⽰。
4)翻转 信号的翻转就是将信号的波形以纵轴为对称轴翻转 180°。
将信号 f(t)中的⾃变量 t 替换成- t 即可得到其翻转信号。
MATLAB 程序: clear all; t=0:0.02:1; t1=-1:0.02:0; g1=3*t; g2=3*(-t1); grid on; plot(t, g1, -- ,t1, g2); xlabel( t );ylabel( g(t) );title( 信号的反折 ); 信号及其反折结果如下图所⽰。
2.程序设计实验 (1)已知信号 f1(t)=(-t+4)[U(t)-U(t-4)],f2(t)=sin(2πt),⽤ MATLAB 绘出下列信号的时域波形。
连续时间信号和系统时域分析及MATLAB实现之欧阳歌谷创编

课程设计任务书欧阳歌谷(2021.02.01)学生姓名: 专业班级:指导教师:工作单位:题目:连续时间信号和系统时域分析及MATLAB实现初始条件:MATLAB 6.5要求完成的主要任务:一、用MATLAB实现常用连续时间信号的时域波形(通过改变参数,分析其时域特性)。
1、单位阶跃信号,2、单位冲激信号,3、正弦信号,4、实指数信号,5、虚指数信号,6、复指数信号。
二、用MATLAB实现信号的时域运算1、相加,2、相乘,3、数乘,4、微分,5、积分三、用MATLAB实现信号的时域变换(参数变化,分析波形变化)1、反转,2、使移(超时,延时),3、展缩,4、倒相,5、综合变化四、用MATLAB实现信号简单的时域分解1、信号的交直流分解,2、信号的奇偶分解五、用MATLAB实现连续时间系统的卷积积分的仿真波形给出几个典型例子,对每个例子,要求画出对应波形。
六、用MATLAB实现连续时间系统的冲激响应、阶跃响应的仿真波形。
给出几个典型例子,四种调用格式。
七、利用MATLAB实现连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形。
给出几个典型例子,要求可以改变激励的参数,分析波形的变化。
时间安排:学习MATLAB语言的概况第1天学习MATLAB语言的基本知识第2、3天学习MATLAB语言的应用环境,调试命令,绘图能力第4、5天课程设计第6-9天答辩第10天指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要IABSTRACT II绪论11 MATLAB简介21.1MATLAB语言功能21.2MATLAB语言特点22常用连续时间信号的时域波形32.1单位阶跃信号32.2单位冲激信号32.3正弦信号42.4实指数信号42.5虚指数信号52.6复指数信号53 连续时间信号的时域运算53.1相加53.2相乘63.3数乘63.4微分63.5积分64 连续时间信号的时域变换74.1反转74.2时移74.3展缩74.4倒相74.5综合变化85连续时间信号简单的时域分解85.1信号的交直流分解85.2信号的奇偶分解86连续时间系统的卷积积分的仿真波形97连续时间系统的冲激响应、阶跃响应的仿真波形10 7.1IMPULSE()函数117.2STEP()函数128连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形138.1正弦信号的零状态响应138.2实指数信号的零状态响应149小结即心得体会15致谢16参考文献16附录17摘要MATLAB目前已发展成为由MATLAB 语言、MATLAB 工作环境、MATLAB 图形处理系统、MATLAB 数学函数库和MATLAB 应用程序接口五大部分组成的集数值计算、图形处理、程序开发为一体的功能强大的系统。
连续时间信号和系统时域分析及MATLAB实现之欧阳引擎创编

课程设计任务书欧阳引擎(2021.01.01)学生姓名: 专业班级:指导教师:工作单位:题目:连续时间信号和系统时域分析及MATLAB实现初始条件:MATLAB 6.5要求完成的主要任务:一、用MATLAB实现常用连续时间信号的时域波形(通过改变参数,分析其时域特性)。
1、单位阶跃信号,2、单位冲激信号,3、正弦信号,4、实指数信号,5、虚指数信号,6、复指数信号。
二、用MATLAB实现信号的时域运算1、相加,2、相乘,3、数乘,4、微分,5、积分三、用MATLAB实现信号的时域变换(参数变化,分析波形变化)1、反转,2、使移(超时,延时),3、展缩,4、倒相,5、综合变化四、用MATLAB实现信号简单的时域分解1、信号的交直流分解,2、信号的奇偶分解五、用MATLAB实现连续时间系统的卷积积分的仿真波形给出几个典型例子,对每个例子,要求画出对应波形。
六、用MATLAB实现连续时间系统的冲激响应、阶跃响应的仿真波形。
给出几个典型例子,四种调用格式。
七、利用MATLAB实现连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形。
给出几个典型例子,要求可以改变激励的参数,分析波形的变化。
时间安排:学习MATLAB语言的概况第1天学习MATLAB语言的基本知识第2、3天学习MATLAB语言的应用环境,调试命令,绘图能力第4、5天课程设计第6-9天答辩第10天指导教师签名:年月日系主任(或责任教师)签名:年月日目录摘要IABSTRACT II绪论11 MATLAB简介21.1MATLAB语言功能21.2MATLAB语言特点22常用连续时间信号的时域波形32.1单位阶跃信号32.2单位冲激信号32.3正弦信号42.4实指数信号42.5虚指数信号52.6复指数信号53 连续时间信号的时域运算53.1相加53.2相乘63.3数乘63.4微分63.5积分64 连续时间信号的时域变换74.1反转74.2时移74.3展缩74.4倒相74.5综合变化85连续时间信号简单的时域分解85.1信号的交直流分解85.2信号的奇偶分解86连续时间系统的卷积积分的仿真波形97连续时间系统的冲激响应、阶跃响应的仿真波形107.1IMPULSE()函数117.2STEP()函数128连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形138.1正弦信号的零状态响应138.2实指数信号的零状态响应149小结即心得体会15致谢16参考文献17附录17摘要MATLAB目前已发展成为由MATLAB 语言、MATLAB 工作环境、MATLAB 图形处理系统、MATLAB 数学函数库和MATLAB 应用程序接口五大部分组成的集数值计算、图形处理、程序开发为一体的功能强大的系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实用标准文案MATLAB课程设计任务书姓名:王 **学号:2010******010题目 :连续时间信号和系统时域分析及MATLAB实现初始条件:MATLAB 7.5.0 , Windows XP系统实验任务:一、用 MATLAB实现常用连续时间信号的时域波形(通过改变参数,分析其时域特性)。
1、单位阶跃信号,2、单位冲激信号,3、正弦信号,4、实指数信号,5、虚指数信号,6、复指数信号。
二、用 MATLAB实现信号的时域运算1、相加,2、相乘,3、数乘,4、微分,5、积分三、用 MATLAB实现信号的时域变换(参数变化,分析波形变化)1、反转,2、使移(超时,延时),3、展缩,4、倒相,5、综合变化四、用 MATLAB实现信号简单的时域分解1、信号的交直流分解,2、信号的奇偶分解五、用 MATLAB实现连续时间系统的卷积积分的仿真波形给出几个典型例子,对每个例子,要求画出对应波形。
六、用MATLAB实现连续时间系统的冲激响应、阶跃响应的仿真波形。
给出几个典型例子,四种调用格式。
七、利用 MATLAB实现连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形。
目录1 MATLAB简介 (1)1.1 MATLAB 设计目的 (1)1.2 MATLAB 语言特点 (1)2 常用连续时间信号的时域波形 (1)2.1单位阶跃信号 (1)2.2单位冲激信号 (2)2.3正弦信号 (3)2.4实指数信号 (4)2.5虚指数信号 (5)2.6复指数信号 (6)3 连续时间信号的时域运算 (7)3.1相加 (7)3.2相乘 (8)3.3数乘 (9)3.4微分 (10)3.5积分 (11)4.1反转 (12)4.2时移 (13)4.3展缩 (14)4.4倒相 (15)4.5综合变化 (16)5连续时间信号简单的时域分解 (17)5.1信号的交直流分解 (17)5.2信号的奇偶分解 (19)6连续时间系统的卷积积分的仿真波形 (20)7连续时间系统的冲激响应、阶跃响应的仿真波形 (23)7.1 IMPULSE()函数 (24)7.2STEP ()函数 (27)8连续时间系统对正弦信号、实指数信号的零状态响应的仿真波形 . (31)8.1正弦信号的零状态响应 (31)8.2实指数信号的零状态响应 (32)9 小结 (34)1 MATLAB简介1.1 MATLAB 设计目的深入研究连续时间信号和系统时域分析的理论知识。
利用MATLAB强大的图形处理功能、符号运算功能以及数值计算功能,实现连续时间信号和系统时域分析的仿真波形1.2 MATLAB 语言特点MATLAB和Mathematica 、 Maple并称为三大数学软件。
它在数学类科技应用软件中在数值计算方面首屈一指。
MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
MATLAB的最重要特征使他拥有解决特定应用问题的程序组,也就是TOOLBOX(工具箱 ) ,如信号处理工具箱,控制系统工具箱、神经网络工具箱、模糊逻辑工具箱、通信工具箱和数据采集工具箱等许多专用工具箱,对大多数用户来说,要想灵活、高效地运用这些工具箱,通常都需要学习相应的专业知识。
2常用连续时间信号的时域波形连续信号又称为模拟信号,其信号存在于整个时间范围内,包括单位阶跃信号,单位冲激信号,正弦信号,实指数信号,虚指数信号,复指数信号。
2.1 单位阶跃信号单位阶跃信号的定义如下:单位阶跃信号的 MATLAB程序 :>>t=-0.5:0.01:5;>>t0=1.0;>>q=stepfun(t,t0);>>plot(t,q);>>axis equal其信号图如下:2.2 单位冲激信号MATLAB实现程序如下 : >>t=-5:0.01:5;>>a=(t==0);>>plot(t,a);信号图如下:2.3 正弦信号正弦信号其 MATLAB实现程序如下:>>t=-1:0.0001:1;>>A=6;>>f=5;>>b=1;>>u=A*sin(2*pi*f*t+b);>>plot(t,u)>>axis([-1 1 -6.5 6.5])其信号图如下:2.4 实指数信号实指数信号可由下面的表达式来表示:MATLAB实现程序如下:>>t=0:0.002:3;>>A=3;>>a=0.5;>>b=A*exp(a*t);>>plot(t,b)>>axis([-0.2 3.1 -0.2 14])其信号图如下:2.5 虚指数信号虚指数信号可由下面的表达式来表示:A=2,的虚指数信号的MATLAB实现程序如下>>t=0:0.001:20;>>a=2;>>w=pi/4;>>b=a*exp(i*w*t);>>subplot(221),plot(t,real(b)),axis([0, 20,-4,4]),title('实部') >>subplot(222),plot(t,imag(b)),axis([0,20,-4,4]),title('虚部') >>subplot(223),plot(t,abs(b)),axis([0,20,1,4]),title('模 ')其信号图如下:2.6 复指数信号复指数信号可由下面的表达式来表示:MATLAB实现程序如下:>>t=0:0.01:4;>>a=-1;>>A=1;>>b=12;>>c=A*exp((a+i*b)*t);>>subplot(221),plot(t,real(c)),title('实部 ') >>subplot(222),plot(t,abs(c)),title('模')>>subplot(223),plot(t,imag(c)),title('虚部 ')>>subplot(224),plot(t,angle(c)),title('相角 ')其信号图如下:3连续时间信号的时域运算3.1 相加要实现两信号的相加,即 f ( t )=f 1(t )+f 2(t )f 1(t )为单位阶跃信号, f 2(t )为正弦信号,两信号相加的实现程序如下,>>t=-6:0.0001:10;>>t0=2;>>b=sin(2*pi*t);>>f=b+a;>>plot(t,f)>>axis([-6 10 -3 3])其信号图如下:3.2 相乘要实现两信号的相乘,即 f ( t )=f 1(t )* f 2(t )f 1(t )为单位阶跃信号, f 2(t )为正弦信号,两信号相乘的实现程序如下:>>t=0:0.0001:5;>>t0=0.5;>>a=stepfun(t,t0);>>b=sin(2*pi*t);>>f=a.*b;>>plot(t,f);>>axis([0 5 -2 2]);其信号图如下:3.3 数乘要实现信号的数乘,即 f (t )=A* f 1(t )A=3,f 1(t )为单位阶跃信号,信号数乘的实现程序如下:>>t=0:0.0001:5;>>a=3;>>t0=1;>>b=stepfun(t,t0);>>f=a*b;>>plot(t,f);>>axis([-2 5 0 5]);其信号图如下:3.4 微分微分即求信号的导数。
对函数 f (t )=t 2求一阶微分的实现程序如下:>>t=-40:0.002:40;>>a=t.*t;>>d=diff(a);>>subplot(211);>>plot(t,a,'-');>>subplot(212);>>plot(d,'-');其信号图如下:3.5 积分对 f (t )=t 2函数的一次积分的实现程序如下:>>t=-2:0.1:2;>>syms t;>>f=t*t;>>a=int(f);>>subplot(211);>>ezplot(f);>>subplot(212);>>ezplot(a);其信号图如下:4.1 反转信号的反转就是将信号的波形以某轴为对称轴翻转180?信号 f (t )=t 的反转 MATLAB程序如下:>>t=-10:1:10;>>f=t;>>a=fliplr(f);>>h=flipud(f);>>subplot(311);>>plot(t,f);>>axis([-2 2 -2 2]);>>title('原'); >>subplot(312); >>plot(t,a);>>axis([-5 5 -5 5]); >>title('上下 '); >>subplot(313); >>plot(t,h);>>axis([-5 5 -5 5]); >>title('左右’ ');其信号图如下:4.2 时移余弦信号的时移实现程序如下:>>t=0:0.0001:5;>>y=cos(2*pi*t);>>y1=cos(2*pi*(t-0.2));>>plot(t,y,'-',t,y1);>>axis([0 5 -1.5 1.5]);其信号图如下:4.3 展缩信号的展缩即将信号 f ( t )中的自变量 t 替换为 at ,a≠0。
正切信号的展缩实现程序如下:>>t=0:0.001:2;>>a=1;>>y=sin(2*pi*t);>>y1=subs(y,t,a*t);>>subplot(211);>>ezplot(y);>>subplot(212);>>ezplot(y1);其信号图如下:4.4 倒相连续信号的倒相是指将信号 f (t) 以横轴为对称轴对折得到- f (t) 。
