2010年云南省楚雄州市数学中考真题(word版含答案)
云南省楚雄彝族自治州中考数学试卷(b卷)

云南省楚雄彝族自治州中考数学试卷(b卷)姓名:________ 班级:________ 成绩:________一、选择题 (共12题;共24分)1. (2分)当|a|=﹣a时,则a是()A . a≤0B . a<0C . a≥0D . a>02. (2分)海关总署11月10日公布今年前10个月我国外贸进出口情况,据海关统计,1至10月,我国进出口总值为23934.1亿美元,将“23934.1”保留二个有效数字约()A . 2.3×104B . 0.23×105C . 2.4×104D . 2.4×1053. (2分)在平行四边形、菱形、矩形、正方形、圆中,既是中心对称图形又是轴对称图形的图形个数()A . 1B . 2C . 3D . 44. (2分) (2019九上·浙江期末) 如图,是从不同的方向看一个物体得到的平面图形,该物体的形状是()A . 圆锥B . 圆柱C . 三棱锥D . 三棱柱5. (2分) (2019八上·北京期中) 下列计算正确的是()A . a + a = aB . (ab ) = abC . a • a = aD . a ÷ a = a6. (2分)如图,△ABC中,D、E分别为AC、BC边上的点,AB∥DE,CF为AB边上的中线,若AD=5,CD=3,DE=4,则BF的长为()A .B .C .D .7. (2分)童装专卖店销售一种童装,若这种童装每天获利y(元)与销售单价x(元)满足关系y=-x2+50x-500,则要想获得最大利润每天必须卖出().A . 25件B . 20件C . 30件D . 40件8. (2分)(2017·浙江模拟) 若关于x的分式方程无解,则m的值为()A . -1.5B . 1C . -1.5或2D . -0.5或-1.59. (2分)已知m为﹣9,﹣6,﹣5,﹣3,﹣2,2,3,5,6,9中随机取的一个数,则m4>100的概率为()A .B .C .D .10. (2分)已知⊙O1与⊙O2的半径分别为3cm和5cm,若圆心距O1O2=8cm,则⊙O1与⊙O2的位置关系是()A . 外切B . 相交C . 内切D . 内含11. (2分)在半径为18的圆中,120°的圆心角所对的弧长是()A . 12πB . 10πC . 6πD . 3π12. (2分)如果圆的最大弦长是m,直线与圆心的距离为d,且直线与圆相离,那么()A . d>mB . d> mC . d≥ mD . d≤ m二、填空题 (共6题;共7分)13. (1分)因式分解4m2﹣n2= ________14. (1分)若m= ,则m5﹣2m4﹣2011m3的值是________.15. (1分) (2017九下·泰兴开学考) 函数y= 中自变量x的取值范围是________.16. (1分)如图,△ABC沿直线AB向下翻折得到△ABD,若∠ABC=25°,∠ADB=110°,则∠DAC的度数是________.17. (2分) (2017八下·顺义期末) 小东、小林两名射箭运动员在赛前的某次测试中各射箭10次,成绩及各统计量如下图、表所示:若让你选择其中一名参加比赛则你选择的运动员是:________理由是:________18. (1分) (2017九上·台江期中) 如图,在平面直角坐标系中,点A在抛物线y=x2﹣2x+2上运动.过点A 作AC⊥x轴于点C,以AC为对角线作矩形ABCD,连结BD,则对角线BD的最小值为________三、解答题. (共8题;共71分)19. (5分)(2017·河池) 计算:20110+()﹣1+4sin45°﹣|﹣ |20. (5分) (2016九下·杭州开学考) 先化简,再求值:÷(x+2﹣),其中x满足x(x2﹣4)=0.21. (6分)(2017·河源模拟) 已知△ABC,利用直尺和圆规,根据下列要求作图(保留作图痕迹,不要求写作法),并根据要求填空:(1)作∠ABC的平分线BD交AC于点D;(2)可得:线段EF与线段BD的关系为________.(2)作线段BD的垂直平分线交AB于点E,交BC于点F.由(1)、22. (3分)根据如图统计图,你获得哪些信息和结论?写出3条:(1) ________;(2) ________;(3) ________。
二次函数的图象和性质3(含答案)
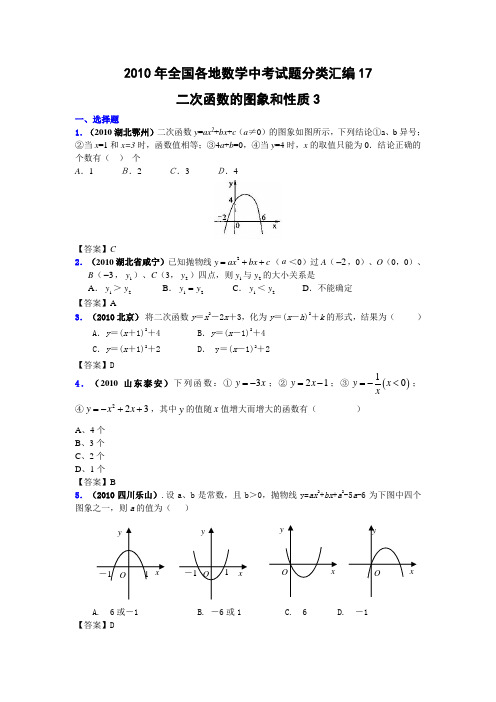
2010年全国各地数学中考试题分类汇编17二次函数的图象和性质3一、选择题 1.(2010湖北鄂州)二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,下列结论①a 、b 异号;②当x =1和x=3时,函数值相等;③4a +b =0,④当y =4时,x 的取值只能为0.结论正确的个数有( ) 个A .1 B.2 C.3 D.4【答案】C2.(2010湖北省咸宁)已知抛物线2y ax bx c =++(a <0)过A (2-,0)、O (0,0)、 B (3-,1y )、C (3,2y )四点,则1y 与2y 的大小关系是 A .1y >2y B .1y 2y = C .1y <2y D .不能确定【答案】A3.(2010北京) 将二次函数y =x 2-2x +3,化为y =(x -h )2+k 的形式,结果为( )A .y =(x +1)2+4 B .y =(x -1)2+4 C .y =(x +1)2+2D . y =(x -1)2+2【答案】D4.(2010山东泰安)下列函数:①3y x =-;②21y x =-;③()10y x x=-<;④223y x x =-++,其中y 的值随x 值增大而增大的函数有( )A 、4个B 、3个C 、2个D 、1个 【答案】B5.(2010四川乐山).设a 、b 是常数,且b >0,抛物线y=ax 2+bx +a 2-5a -6为下图中四个图象之一,则a 的值为( )A. 6或-1B. -6或1C. 6D. -1【答案】DyxO yx Oyx O1 -1 yxO1 -16.(2010黑龙江哈尔滨)在抛物线42-=x y 上的一个点是( )(A )(4,4) (B )(1,-4) (C )(2,0) (D ).(0,4) 【答案】C7.(2010江苏徐州)平面直角坐标系中,若平移二次函数y=(x-2009)(x-2010)+4的图象,使其与x 轴交于两点,且此两点的距离为1个单位,则平移方式为 A .向上平移4个单位 B .向下平移4个单位 C .向左平移4个单位 D .向右平移4个单位 【答案】B8.(2010陕西西安)已知抛物线103:2-==x x y C ,将抛物线C 平移得到抛物线C '若两条抛物线C 、C ' 关于直线1=x 对称,则下列平移方法中,正确的是A .将抛物线C 向右平移25个单位 B .将抛物线C 向右平移3个单位 C .将抛物线C 向右平移5个单位 D .将抛物线C 向右平移6个单位【答案】C9.(2010 福建三明)抛物线772--=x kx y 的图象和x 轴有交点,则k 的取值范围是( )A .47-≥k B .47-≥k 且0≠k C .47->k D .47->k 且0≠k 【答案】B10.(2010 山东东营) 二次函数2y ax bx c =++的图象如图所示,则一次函数ac bx y -=与反比例函数xcb a y +-=在同一坐标系内的图象大致为( )【答案】B二、填空题1.(2010江苏扬州)y =2x 2-bx +3的对称轴是直线x =1,则b 的值为__________.x(B)x(A)x(C)(D)【答案】42.(2010山东泰安)将y=2x 2-12x-12变为y=a (x-m )2+n 的形式,则m·n=. 【答案】-903.(2010湖北襄樊)将抛物线212y x =-向上平移2个单位,再向右平移1个单位后,得到的抛物线的解析式为____________..【答案】21(1)22x --+或21322x x -++ 4.(2010江苏 镇江)已知实数y x y x x y x +=-++则满足,033,2的最大值为 .【答案】45.6.7.8.9.10.11.12.13.14.15.16.17.18.19.20 三、解答题1.(2010湖北鄂州)如图,在直角坐标系中,A (-1,0),B (0,2),一动点P 沿过B 点且垂直于AB 的射线BM 运动,P 点的运动速度为每秒1个单位长度,射线BM 与x 轴交与点C .(1)求点C 的坐标.(2)求过点A 、B 、C 三点的抛物线的解析式.(3)若P 点开始运动时,Q 点也同时从C 出发,以P 点相同的速度沿x 轴负方向向点A 运动,t 秒后,以P 、Q 、C 为顶点的三角形为等腰三角形.(点P 到点C 时停止运动,点Q 也同时停止运动)求t 的值.(4)在(2)(3)的条件下,当CQ =CP 时,求直线OP 与抛物线的交点坐标.【答案】(1)点C 的坐标是(4,0);(2)设过点A 、B 、C 三点的抛物线的解析式为y =ax 2+bx +c (a ≠0),将点A 、B 、C 三点的坐标代入得:020164a b c c a b c =-+⎧⎪=⎨⎪=++⎩解得12322a b c ⎧=-⎪⎪⎪=⎨⎪=⎪⎪⎩,∴抛物线的解析式是:y = 12-x 2+32x +2. (3)设P 、Q 的运动时间为t 秒,则BP =t ,CQ =t .以P 、Q 、C 为顶点的三角形为等腰三角形,可分三种情况讨论.①若CQ =PC ,如图所示,则PC = CQ =BP =t .∴有2t =BC =5t 5②若PQ =QC ,如图所示,过点Q 作DQ ⊥BC 交CB 于点D ,则有CD =PD .由△ABC ∽△QDC ,可得出PD =CD =255t ,∴555t =,解得t =40511-. ③若PQ =PC ,如图所示,过点P 作PE ⊥AC 交AC 于点E ,则EC =QE =255PC ,∴12t =255(5t ),解得t 32540-(4)当CQ =PC 时,由(3)知t 5P 的坐标是(2,1),∴直线OP 的解析式是:y =12x ,因而有12x =12-x 2+32x +2,即x 2-2x -4=0,解得x =15OP 与抛物线的交点坐标为(5152)和(5,152). 2.(2010湖北省咸宁)已知二次函数2y x bx c =+-的图象与x 轴两交点的坐标分别为(m ,0),(3m -,0)(0m ≠).(1)证明243c b =;(2)若该函数图象的对称轴为直线1x =,试求二次函数的最小值.【答案】(1)证明:依题意,m ,3m -是一元二次方程20x bx c +-=的两根.根据一元二次方程根与系数的关系,得(3)m m b +-=-,(3)m m c ⨯-=-. ∴2b m =,23c m =. ∴224312c b m ==.(2)解:依题意,12b-=,∴2b =-.由(1)得2233(2)344c b ==⨯-=.∴2223(1)4y x x x =--=--. ∴二次函数的最小值为4-.3.(2010湖北恩施自治州) 如图,在平面直角坐标系中,二次函数c bx x y ++=2的图象与x 轴交于A 、B 两点, A 点在原点的左侧,B 点的坐标为(3,0),与y 轴交于C (0,-3)点,点P 是直线BC 下方的抛物线上一动点. (1)求这个二次函数的表达式.(2)连结PO 、PC ,并把△POC 沿CO 翻折,得到四边形POP /C , 那么是否存在点P ,使四边形POP /C 为菱形?若存在,请求出此时点P 的坐标;若不存在,请说明理由. (3)当点P 运动到什么位置时,四边形 ABPC 的面积最大并求出此时P 点的坐标和四边形ABPC 的最大面积.【答案】解:(1)将B 、C 两点的坐标代入得⎩⎨⎧-==+33c c b解得:⎩⎨⎧-=-=32c b所以二次函数的表达式为:322--=x x y(2)存在点P ,使四边形POP /C 为菱形.设P 点坐标为(x ,322--x x ), PP /交CO 于E若四边形POP /C 是菱形,则有PC =PO .连结PP / 则PE ⊥CO 于E ,∴OE=EC =23∴y =23-.∴322--x x =23-解得1x =2102+,2x =2102-(不合题意,舍去) ∴P 点的坐标为(2102+,23-)…………………………8分 (3)过点P 作y 轴的平行线与BC 交于点Q ,与OB 交于点F ,设P (x ,322--x x ),易得,直线BC 的解析式为3-=x y 则Q 点的坐标为(x ,x -3).EB QP OE QP OC AB S S S S CPQ BPQ ABC ABPC ⋅+⋅+⋅=++=∆∆∆212121四边形 3)3(2134212⨯+-+⨯⨯=x x =87523232+⎪⎭⎫ ⎝⎛--x当23=x 时,四边形ABPC 的面积最大 此时P 点的坐标为⎪⎭⎫⎝⎛-415,23,四边形ABPC 的 面积875的最大值为. 4.(2010北京)在平面直角坐标系xOy 中,抛物线23454122+-++--=m x x mx m y 与x 轴的交点分别为原点O 和点A ,点B (2,n )在这条抛物线上.(1)求B 点的坐标;(2)点P 在线段OA 上,从O 点出发向A 点运动,过P 点作x 轴的垂线,与直线OB 交与点E ,延长PE 到点D ,使得ED =PE ,以PD 为斜边,在PD 右侧做等等腰直角三角形PCD (当P 点运动时,C 点、D 点也随之运动).① 当等腰直角三角形PCD 的顶点C 落在此抛物线上时,求OP 的长;② 若P 点从O 点出发向A 点作匀速运动,速度为每秒1个单位,同时线段OA 上另一个点Q 从A 点出发向O 点作匀速运动,速度为每秒2个单位(当Q 点到达O 点时停止运动,P 点也同时停止运动).过Q 点做x 轴的垂线,与直线AB 交与点F ,延长QF 到点M ,使得FM =QF ,以QM 为斜边,在QM 的左侧作等腰直角三角形QMN (当Q点运动时,M 点、N 点也随之运动).若P 点运动到t分别有一条边恰好落在同一条直线上,求此刻t 的值.【答案】解:(1)∵抛物线23454122+-++--=m m x mx m y 经过原点, ∴m 2—3m +2=0. 解的m 1=1,m 2=2. 由题意知m ≠1. ∴m =2,∴抛物线的解析式为x x y 25412+-= ∵点B (2,n )在抛物线x x y 25412+-=,n=4.∴B 点的坐标为(2,4)(2)①设直线OB 的解析式为y =k 1x 求得直线OB 的解析式y =2x ∵A 点是抛物线与x 轴的一个交点, 可求得A 点的坐标为(10,0),设P 点的坐标为(a ,0),则E 点的坐标为(a ,2a ). 根据题意做等腰直角三角形PCD ,如图1.(第24题)可求得点C 的坐标为(3a ,2a ), 有C 点在抛物线上,得2a =-41x (3a )2+25x 3a . 即49a 2— 211a =0解得 a 1=922,a 2=0(舍去)∴OP =922②依题意作等腰直角三角形QMN . 设直线AB 的解析式y =k 2x +b由点A (10 ,0),点B (2,4),求得直线AB 的解析式为y =-21x +5 当P 点运动到t 秒时,两个等腰直角三角形分别有一条边恰好落在同一条直线上,有以下三种情况:第一种情况:CD 与NQ 在同一条直线上,如图2所示,可证△DPQ 为等腰直角三角形.此时QP 、OP 、AQ 的长可依次表示为t 、4t 、 2t 个单位. ∴PQ = DP = 4t ∴t +4t +2t =10 ∴t=710第二种情况:PC 与MN 在同一条直线上,如图3所示.可证△PQM 为等腰直角三角形.此时OP 、AQ 的长依次表示为t 、2t 个单位, ∴OQ = 10 - 2t ∵F 点在直线AB 上 ∴FQ =t ∵MQ =2t ∴PQ =MQ =CQ =2t ∴t +2t +2t =10 ∴t =2.第三种情况:点P 、Q 重合时,PD 、QM 在同一条直线上,如图4所示,此时OP 、AQ 的长依次表示为t 、2t 个单位.∴t +2t=10 ∴t =310 综上,符合题意的值分别为710,2,310. 5.(2010云南红河哈尼族彝族自治州)二次函数2x y =的图像如图8所示,请将此图像向右平移1个单位,再向下平移2个单位.(1)画出经过两次平移后所得到的图像,并写出函数的解析式.(2)求经过两次平移后的图像与x 轴的交点坐标,指出当x 满足什么条件时,函数值大于0?【答案】解:画图如图所示: 依题意得:2)1(2--=x y=2122-+-x x =122--x x∴平移后图像的解析式为:122--x x (2)当y=0时,122--x x =0 2)1(2=-x 21±=-x 212121+=-=x x ,∴平移后的图像与x 轴交与两点,坐标分别为(21-,0)和(21+,0) 由图可知,当x<21-或x>21+时,二次函数2)1(2--=x y 的函数值大于0. 6.(2010云南楚雄)已知:如图,抛物线2y ax bx c =++与x 轴相交于两点A (1,0),B (3,0).与y 轴相较于点C (0,3). (1)求抛物线的函数关系式; (2)若点D (7,2m )是抛物线2y ax bx c =++上一点,请求出m 的值,并求处此时△ABD 的面积.【答案】解:(1)由题意可知09303a b c a b c c ++=⎧⎪++=⎨⎪=⎩ 解得143a b c =⎧⎪=-⎨⎪=⎩所以抛物线的函数关系式为243y x x =-+. (2)把D (7,2m )代人函数解析式243y x x =-+中,得2775()43224m =-⨯+=.所以155(31)244ABD S ∆=⨯-⨯=. 7.(2010湖北随州)已知抛物线2(0)y ax bx c a =++≠顶点为C (1,1)且过原点O.过抛物线上一点P (x ,y )向直线54y =作垂线,垂足为M ,连FM (如图). (1)求字母a ,b ,c 的值;(2)在直线x =1上有一点3(1,)4F ,求以PM 为底边的等腰三角形PFM 的P 点的坐标,并证明此时△PFM 为正三角形;(3)对抛物线上任意一点P ,是否总存在一点N (1,t ),使PM =PN 恒成立,若存在请求出t 值,若不存在请说明理由.【答案】(1)a =-1,b =2,c =0(2)过P 作直线x=1的垂线,可求P 的纵坐标为14,横坐标为1132.此时,MP =MF =PF =1,故△MPF 为正三角形. (3)不存在.因为当t <54,x <1时,PM 与PN 不可能相等,同理,当t >54,x >1时,PM 与PN 不可能相等.8.(2010河南)在平面直角坐标系中,已知抛物线经过A(4,0),B(0,一4),C(2,0)三点.(1)求抛物线的解析式;(2)若点M 为第三象限内抛物线上一动点,点M 的横坐标为m ,△AMB 的面积为S.求S 关于m 的函数关系式,并求出S 的最大值;(3)若点P 是抛物线上的动点,点Q 是直线y=-x 上的动点,判断有几个位置能使以点P 、Q 、B 、0为顶点的四边形为平行四边形,直接写出相应的点Q 的坐标.【答案】(1)设抛物线的解析式为y =ax 2+bx +c (a ≠0),则有1640,4,420.a b c c a b c -+=⎧⎪=-⎨⎪++=⎩解得1,21,4.a b c ⎧=⎪⎪=⎨⎪=-⎪⎩∴抛物线的解析式y =12x 2+x ﹣4(2)过点M 作MD ⊥x 轴于点D .设M 点的坐标为(m ,n ). 则AD =m +4,MD =﹣n ,n =12m 2+m -4 . ∴S = S △AMD +S 梯形DMBO -S △ABO =12( m +4) (﹣n )+12(﹣n +4) (﹣m ) -12×4×4 = ﹣2n -2m -8 = ﹣2(12m 2+m -4) -2m -8 = ﹣m 2-4m (-4< m < 0)∴S 最大值 = 4(3)满足题意的Q 点的坐标有四个,分别是:(-4 ,4 ),(4 ,-4), (-2+52-25-2-52+59.(2010四川乐山)如图(13.1),抛物线y =x2+bx+c 与x 轴交于A ,B 两点,与y 轴交于点C(0,2),连接AC ,若tan ∠OAC =2. (1)求抛物线对应的二次函数的解析式;(2)在抛物线的对称轴l 上是否存在点P ,使∠APC =90°,若存在,求出点P 的坐标;若不存在,请说明理由;(3)如图(13.2)所示,连接BC ,M 是线段BC 上(不与B 、C 重合)的一个动点,过点M 作直线l ′∥l ,交抛物线于点N ,连接CN 、BN ,设点M 的横坐标为t .当t 为何值时,△BCN 的面积最大?最大面积为多少?【答案】解:(1)∵抛物线y=x2+bx+c过点C(0,2). ∴x=2又∵tan∠OAC=OCOA=2, ∴OA=1,即A(1,0).又∵点A在抛物线y=x2+bx+2上. ∴0=12+b×1+2,b=-3 ∴抛物线对应的二次函数的解析式为y=x2-3x+2(2)存在过点C作对称轴l的垂线,垂足为D,如图所示,∴x=-332212ba-=-=⨯.∴AE=OE-OA=32-1=12,∵∠APC=90°,∴tan∠PAE= tan∠CPD∴PE CDEA DP=,即12PE322PE=-,解得PE=12或PE=32,∴点P的坐标为(32,12)或(32,32)。
2010年云南省楚雄州中考数学试卷(含答案)

楚雄州2010年高中(中专)招生统一考试数学试题卷(全卷三个大题,共24小题,共8页;满分120分,考试用时120分钟)注意事项:1、本卷为试题卷,考生解题作答必须在答题卷上,答案书写在答题卷相应的位置上,在试题卷、草稿纸上作答无效2、考试结束后请将试题卷和答题卷一并交回。
一、选择题(本大题共8小题,每小题只有一个正确选项,每小题3分,共24分)1、下列计算正确的是A.B.C.D.考点:二次根式的乘除法;同底数幂的乘法;幂的乘方与积的乘方;负整数指数幂.分析:根据同底数幂的乘法、二次根式的除法、负整数指数幂、积的乘方等运算性质分别判断.解答:解:A、a2?a3=a5,故选项错误;B、正确;C、,故选项错误;D、(-a3)2=a6,故选项错误.故选B.点评:正确理解同底数幂的乘法、二次根式的除法、负整数指数幂、积的乘方等性质是解答问题的关键.2、如图是由四个相同的小正方体组成的立体图形,它的左视图为考点:简单组合体的三视图.分析:找到从左侧面看所得到的图形即可,注意所有的看到的棱都应表现在左视图中.解答:解:从左面看,这个立体图形有两层,且底层有两个小正方形,第二层的左边有一个小正方形.故选B.点评:本题考查了三视图的知识,左视图是从物体的左侧面看得到的视图.3、自去年入秋以来,楚雄州遭遇了百年不遇的严重旱灾,截止2010年4月19日,楚雄州共收到各级各类抗旱救灾资金108014500元,这个数据用科学记数法表示为A.B.C.D.考点:科学记数法—表示较大的数.专题:应用题.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于1时,n是正数;当原数的绝对值小于1时,n是负数.4、一元二次方程的解是A.B.C.D.考点:解一元二次方程-直接开平方法.分析:观察发现方程的两边同时加4后,左边是一个完全平方式,即x2=4,即原题转化为求4的平方根.解答:解:移项得:x2=4,∴x=±2,即x1=2,x2=-2.故选C.点评:(1)用直接开方法求一元二次方程的解的类型有:x2=a(a≥0);ax2=b(a,b同号且a≠0);(x+a)2=b(b≥0);a(x+b)2=c(a,c同号且a≠0).法则:要把方程化为“左平方,右常数,先把系数化为1,再开平方取正负,分开求得方程解”.5、已知⊙和⊙的半径分别为2cm和3cm,两圆的圆心距为5cm,则两圆的位置关系是A.外切B. 外离C. 相交D. 内切考点:圆与圆的位置关系.分析:两圆半径和等于圆心距时,两圆外切.设两圆的半径分别为R和r,且R≥r,圆心距为d:外离,则d>R+r;外切,则d=R+r;相交,则R-r<d<R+r;内切,则d=R-r;内含,则d<R-r.解答:解:∵2+3=5,由于两圆外切时圆心距等于两圆半径的和,∴两圆外切.故选A.点评:本题利用了两圆外切时圆心距等于两圆半径的和.6、已知等腰三角形的一个内角为70°,则另外两个内角的度数是A.55°,55°B. 70°,40°C. 55°,55°或70°,40°D.以上都不对考点:等腰三角形的性质.专题:分类讨论.分析:分别把70°看做等腰三角形的顶角和底角,分两种情况考虑,利用三角形内角和是180度计算即可.解答:解:当70°为顶角时,另外两个角是底角,它们的度数是相等的,为(180°-70°)÷2=55°,当70°为底角时,另外一个底角也是70°,顶角是180°-140°=40°.故选C.7、下列说法不正确的是A.在选举中,人们通常最关心的数据是众数B.掷一枚骰子,3点朝上是不确定事件C.数据3,5,4,1,-2的中位数是3D.有两边对应成比例且有一个角对应相等的两个三角形一定相似考点:推理与论证;相似三角形的判定;中位数;众数;随机事件.分析:此题涉及到中位数、众数,随机事件,相似三角形的判定等知识点,要针对各知识点分别进行判断.解答:解:A、众数表示的是一组数据中出现次数最多的数,在选举中,若某人的选票最多,则此人当选的可能性就越大,故A正确;B、在掷筛子的过程中,可能出现3点,也可能不是3点,所以3点朝上是不确定事件,故B正确;C、将这组数据从小到大排列,得:-2,1,3,4,5;中位数是3,故C正确;D、两对应边成比例,且夹角对应相等的两个三角形相似,故D错误;故选D.点评:此题需注意的是相似三角形的判定过程中,若已知了两组对应边成比例,一组角对应相等,那么这组角必须是两对应边的夹角.8、如图,四边形OABC是菱形,点B,C在以点O为圆心的弧EF上,且∠1=∠2,若扇形OEF的面积为,则菱形OABC的边长为A.B. 2C. 3D.4考点:扇形面积的计算;菱形的性质.分析:连接OB.根据菱形的各边相等和同圆的半径相等发现等边三角形OBC,再根据菱形的性质得到∠AOC=2∠BOC=120°,从而根据扇形的面积公式求得扇形所在圆的半径,即为菱形的边长.解答:解:连接OB.∵四边形OABC是菱形,∴OC=BC.又OC=OB,∴△OBC是等边三角形.∴∠COB=60°.∴∠AOC=2∠COB=120°.设扇形的半径是R.∴ 120πR2360=3π,R=3.故选C.点评:此题综合考查了菱形的性质和扇形的面积公式.二、填空题(本大题共7小题,每题3分,满分21分)9、的倒数是。
2010年云南省楚雄

楚雄2010高中招生统一考试物理试题卷注:计算时g取10N/Kg.一、选择题(每小题的四个选项中只有一个符合题意,请把符合题意的选项前的字母写在答题卷的指定位置。
每小题3分,8小题,共24分)1.(2010楚雄)下列接近实际情况的是A.书桌上的台灯正常工作时的电流约为1AB.人正常步行的速度约为10m/sC.人体正常的体温约为37℃D. 一本物理课本的的质量约为2Kg2. (2010楚雄)关于光现象的说法中正确的是A. 小孔成像是光沿直线传播形成的B. 平面镜成像是光的折射现象C. 照相机成虚像D. 凸透镜只能成实像3. (2010楚雄)如图1所示,当闭合开关S后看到灯L1发光,灯L2不发光,则可能的原因是断路 B. 灯L1短路A. 灯LC. 灯L2断路D. 灯L2短路4. (2010楚雄)关于温度、热量和内能的说法中不正确的是A. 0的冰块也有内能B. 温度高的物体,内能一定大C. 物体吸收热量,温度不一定升高D. 物体吸收热量,内能一定增大5. (2010楚雄)以下说法正确的是A. 以地球同步通讯卫星为参照物,地球是运动的B. 超导技术可应用于电饭锅和远距离输电线C. 色光的三原色是红、黄、蓝D. 发现有人触电时,应首先切断电源6. (2010楚雄)关于图2中四幅图的分析,正确的是A. 图2(a)表明磁场产生电流B. 图2(b)判断出电源的左端为正极C. 图2(c)是电动机的原理图D.图2(d)显示线圈匝数越多电磁铁的磁性越强7. (2010楚雄)关于图2中所示四幅图的分析,正确的是A. 图3(a)表示ρ甲>ρ乙B. 图3(b)表示晶体熔化的图像C. 图3(c)表示物体做匀速直线运动D. 图3)d)表示液体内部压强与深度的关系8. (2010楚雄)两个相同的容器中,分别盛有甲、乙两种液体,把完全相同的两个小球分别放入两个容器中,当两球静止时液面相平,球所处位置如图4所示。
甲、乙两种液体对容器底部的压强大小分别为P甲、P乙,两球在甲、乙两种液体中所受浮力大小分别为F甲、F乙,则它们的大小关系是A. P甲>P乙F甲=F乙B. P甲<P乙F甲=F乙C. P甲>P乙F甲>F乙D. P甲<P乙F甲<F乙二、填空题(每空1分,8小题,共20分)9. (2010楚雄)张丽同学发现妈妈在厨房炒菜时,在客厅里也能闻到香味,这是由于分子的原因;同时她听到的炒菜声是通过传播的;细心的她还发现吃饭时用的筷子是____ (填“省力”、“费力”或“等臂”)杠杆。
2010年云南省曲靖中考数学试卷(word版及答案)

曲靖市2010年高中(中专)招生统一考试数 学一、选择题(本大题共8个小题,每小题只有一个符合条件的选项,每小题3分,满分24分)1.从3时到6时,钟表的时针旋转角的度数是( ) A.30︒ B.60︒ C.90︒ D.120︒2.下列各式中,运算正确的是( )A.437()x x = B.842a a a ÷= C.325385+= D.315335÷=3.分式方程33122x x x-+=--的解是( ) A.2 B.1 C.-1 D.-24.下列事件属于必然事件的是( ) A.367人中至少有两人的生日相同 B.某种彩票的中奖率为1100,购买100张彩票一定中奖 C.掷一次骰子,向上的一面是6点 D.某射击运动员射击一次,命中靶心5.练习本比水性笔的单价少2元,小刚买了5本练习本和3支水性笔正好用去14元.如果设水性笔的单价为x 元,那么下列所列方程正确的是( ) A.5(2)314x x -+= B.5(2)314x x ++= C.53(2)14x x ++= D.53(2)14x x +-=6.不等式组322(4)1x xx +>⎧⎨--⎩≥的解集在数轴上表示正确的是( )7.如图摆放的正六棱柱的俯视图是( )8.函数y kx k =-与(0)ky k x=≠在同一坐标系中的大致图象是( )二、填空题(本大题共8个小题,每小题3分,满分24分) 9.12-的倒数是___________. 10.在你认识的图形中,写出一个既是轴对称又是中心对称的图形名称:________. 11.如图,AB CD ∥,AC BC ⊥,垂足为C .若40A ∠=︒,则BCD ∠=_______度.12.若2(1)2x -=,则代数式225x x -+的值为________.13.在Rt ABC △中,90C ∠=︒,若10BC AD =,平分BAC ∠交BC 于点D ,且32BD CD =∶∶,则点D 到线段AB 的距离为_______.14.如图,活动衣帽架由三个菱形组成,利用四边形的不稳定性,调整菱形的内角α,使衣帽架拉伸或收缩.当菱形的边长为18cm α=120︒,时,A B 、两点的距离为_______cm.15.在分别写有数字1012-,,,的四张卡片中,随机抽取一张后放回,再随机抽取一张.以第一次抽取的数字作为横坐标,第二次抽取的数字作为纵坐标的点落在第一象限的概率是_____. 16.把一个正三角形分成四个全等的三角形,第一次挖去中间一个小三角形,对剩下的三个A B C D 第11题图 第13题图 DC B A A B小正三角形再重复以上做法……一直到第n 次挖去后剩下的三角形有________个.三、解答题(本大题共8个小题,满分72分) 17.(6分)计算:119(2)(1)3-⎛⎫--+-- ⎪⎝⎭18.(7分)先化简,再求值.2216636x x x x x x x++-÷---,其中3x =19.(8分)如图,小明家所住楼房的高度10AB =米,到对面较高楼房的距离20BD =米,当阳光刚好从两楼房的顶部射入时,测得光线与水平线的夹角为40︒.据此,小明便知楼房CD 的高度.请你写出计算过程(结果精确到0.1米.参考数据:sin 400.6400.77tan 400.84︒≈︒≈︒≈,cos4,).第二次 第一次 第三次 第四次…BPAC D20.(9分)如图,E F 、是ABCD Y对角线AC 上的两点,且BE DF ∥. 求证:(1)ABE CDF △≌△; (2)12∠=∠.21.(10分)某校对中考前一次数学模拟考试进行抽样分析,把样本成绩按分数段分成A B C D E 、、、、五组(每组成绩含最低分,不含最高分)进行统计,并将结果绘制成下面两幅统计图.请根据图中信息,解答下列问题: (1)求A 组人数在扇形图中所占圆心角的度数; (2)求D 组人数;(3)判断考试成绩的中位数落在哪个组?(直接写出结果,不需要说明理由)22.(10分)如图,O ⊙的直径»12AB BC =,的长为2π,D 在OC 的延长线上,且CD OC =. (1)求A ∠的度数;(2)求证:DB 是O ⊙的切线; (参考公式:弧长公式π180n rl =,其中l 是弧长,r 是半径,n 是圆心角度数)ABC D EFB AAD E A 组 B 组 C 组 D 组 E 组 B DOAC23.(10分)如图,有一块等腰梯形的草坪,草坪上底长48米,下底长108米,上下底相距40米,现要在草坪中修建一条横、纵向的“H ”型甬道,甬道宽度相等,甬道面积是整个梯形面积的213.设甬道的宽为x 米. (1)求梯形ABCD 的周长;(2)用含x 的式子表示甬道的总长;(3)求甬道的宽是多少米?24.(12分)如图,在平面直角坐标系xoy 中,抛物线2y x =向左平移1个单位,再向下平移4个单位,得到抛物线2()y x h k =-+.所得抛物线与x 轴交于A B 、两点(点A 在点B 的左边),与y 轴交于点C ,顶点为D .(1)求h k 、的值;(2)判断ACD △的形状,并说明理由; (3)在线段AC 上是否存在点M ,使AOM △与ABC △相似.若存在,求出点M 的坐标;若不存在,说明理由.A DCFEBA y xBF D C O曲靖市2010年高中(中专)招生统一考试数学参考答案一、选择题1.C2.D3.B4.A5.A6.B7.D8.C 二、填空题9. 2 10.圆(答案不唯一) 11.50 12. 6 13. 4 14. 54 15.1416.3n三、解答题17.解:原式=3213++- ················································································· 4分3=. ····························································································· 6分 18.解:原式=1(6)(6)66(1)x x x x x x x x++--⨯--+ ·························································· 3分 66x x x x +-=-··············································································· 4分 12x =. ··························································································· 5分当x =原式==························································································· 7分 19.解:在Rt ABP △中,10tan 40AB BP BP︒==, 1011.90tan 40BP =︒≈ ···················································································· 4分 在Rt CDP △中,tan 4011.9020CD CDPD ︒==+, ·········································································· 6分 31.900.8426.8CD =⨯≈(米). 答:楼房CD 的高度为26.8米. ·········································································· 8分 20. 证明:(1)Q 四边形ABCD 是平行四边形,AB CD ∴∥. BAE DCF ∴∠=∠. ························································································ 2分 BE DF Q ∥,BEF DFE ∴∠=∠.AEB CFD ∴∠=∠. ························································································ 4分(AAS)ABE CDF ∴△≌△ ·············································································· 5分 (2)由ABE CDF △≌△得 BE DF =.BE DF Q ∥, ··············································································· 7分 ∴四边形BEDF 是平行四边形. ········································································ 8分 ∴12∠=∠. ·································································································· 9分 21.解:(1)A 组人数所占的百分比:1(26%30%22%12%)10%-+++=, ··············· 2分 A 组人数在扇形图中所占的圆心角的度数:36010%36︒⨯=; ······························· 4分 (2)样本人数:1530%50÷=(人), ······························································ 6分D 组人数=5022%11⨯=(人); ······································································ 8分 (3)考试成绩的中位数落在C 组. ···································································· 10分 22.(1)解:设BOC n ∠=︒, 据弧长公式,得π62π180n ⨯=, 60n =︒. ······································································································· 2分 据圆周角定理,得1302A BOC ∠=∠=︒. ···························································· 4分(2)证明:连接BC ,60OB OC BOC =∠=︒Q ,,BOC ∴△是等边三角形. ·················································································· 6分 60OBC OCB OC BC OB ∴∠=∠=︒==,. OC CD =Q , BC CD ∴=.1302CBD D OCB ∴∠=∠=∠=︒. ···································································· 8分 603090OBD OBC CBD ∴∠=∠+∠=︒+︒=︒. AB BD ∴⊥.DB ∴是O ⊙的切线. ····················································································· 10分 23.解:(1)在等腰梯形ABCD 中, 48AD EF ==,B DCOA()121(10848)23050AE BC DF BC BE CF BC EF AB CD ⊥⊥==-=-=∴===,,,,∴梯形ABCD 的周长=501085048256AB BC CD DA +++=+++=(米). ············· 2分(2)甬道的总长:402482(1282)x x ⨯+-=-米. ·············································· 4分 (3)根据题意,得21(1282)40(48108)132x x -=⨯⨯+. ·································································· 7分 整理,得2642400x x -+=,解之得12460x x ==,.因6048>,不符合题意,舍去.答:甬道的宽为4米. ····················································································· 10分 24.解:(1)2y x =Q 的顶点坐标为(0,0),2()y x h k ∴=-+的顶点坐标(14)D -,,1h k ∴=-,=-4. ··························································································· 3分 (2)由(1)得2(1)4y x =+-. 当0y =时,2(1)40x +-=. 1231x x =-=,.(30)10A B ∴-,,(,). ························································································ 4分当0x =时,22(1)4(01)43y x =+-=+-=-,C ∴点坐标为()03,-.又Q 顶点坐标()14D --,, ·············································································· 5分 作出抛物线的对称轴1x =-交x 轴于点E .作DF y ⊥轴于点F .在Rt AED △中,2222420AD =+=; 在Rt AOC △中,2223318AC =+=; 在Rt CFD △中,222112CD =+=;Q 222AC CD AD +=,ACD ∴△是直角三角形. ·················································································· 7分 (3)存在.由(2)知,AOC △为等腰直角三角形,45BAC ∠=︒, 连接OM ,过M 点作MG AB ⊥于点G ,AC ==①若AOM ABC △∽△,则AO AM AB AC =,即33444AM ⨯===. Q MG AB ⊥,222AG MG AM ∴+=.94AG MG ∴====,93344OG AO AG =-=-=.M Q 点在第三象限,3944M ⎛⎫∴-- ⎪⎝⎭,. ·························································································· 10分②若AOM ACB △∽△,则AO AMAC AB =4AM AM ===,2AG MG ∴====,321OG AO AG =-=-=. M Q 点在第三象限,()12M ∴--,.x综上①、②所述,存在点M 使AOM △与ABC △相似,且这样的点有两个,其坐标分别为()391244⎛⎫---- ⎪⎝⎭,,,. ················································································ 12分。
2010年云南省昆明市中考数学试卷

2010年云南省昆明市中考数学试卷一、选择题(共9小题,每小题3分,满分27分)1.(3分)3的倒数是()A.13B.﹣13C.3D.﹣32.(3分)若如图是某个几何体的三视图,则该几何体是()A.长方体B.三棱柱C.圆柱D.圆台3.(3分)某班六名同学在一次知识抢答赛中,他们答对的题数分别是:7,5,6,8,7,9.这组数据的平均数和众数分别是()A.7,7B.6,8C.6,7D.7,24.(3分)据2010年5月11日云南省委、省政府召开的通报会通报,全省各级各部门已筹集抗旱救灾救济资金32亿元,32亿元用科学记数法表示为()A.3.2×108元B.0.32×1010元C.3.2×109元D.32×108元5.(3分)一元二次方程x2+x﹣2=0的两根之积是()A.﹣1B.﹣2C.1D.26.(3分)如图,在△ABC中,CD是∠ACB的平分线,∠A=80°,∠ACB=60°,那么∠BDC=()A.80°B.90°C.100°D.110°7.(3分)下列各式运算中,正确的是()A.(a+b)2=a2+b2B.√(−3)2=3C.a3•a4=a12D.(3a)2=6a2(a≠0)8.(3分)如图,已知圆锥侧面展开图的扇形面积为65πcm2,扇形的弧长为10πcm,则圆锥母线长是()A.5cm B.10cm C.12cm D.13cm9.(3分)如图,在△ABC中,AB=AC,AB=8,BC=12,分别以AB、AC为直径作半圆,则图中阴影部分的面积是()A.64π−12√7B.16π﹣32C.16π−24√7D.16π−12√7二、填空题(共6小题,每小题3分,满分18分)10.(3分)﹣6的相反数是.11.(3分)如图,在△ABC中,点D、E、F分别是AB、AC、BC的中点,若△ABC的周长为12cm,则△DEF的周长是cm.12.(3分)化简:(1−1a+1)÷a=.13.(3分)计算:√8−√12=.14.(3分)半径为r的圆内接正三角形的边长为(结果可保留根号).15.(3分)如图,点A(x1,y1)、B(x2,y2)都在双曲线y=kx(x>0)上,且x2﹣x1=4,y1﹣y2=2;分别过点A、B向x轴、y轴作垂线段,垂足分别为C、D、E、F,AC与BF相交于G点,四边形FOCG的面积为2,五边形AEODB的面积为14,那么双曲线的解析式为.三、解答题(共10小题,满分75分)16.(5分)计算:(−14)−1−|−3|−20100+(√2)2.17.(6分)如图,点B、D、C、F在一条直线上,且BC=FD,AB=EF.(1)请你只添加一个条件(不再加辅助线),使△ABC≌△EFD,你添加的条件是;(2)添加了条件后,证明△ABC≌△EFD.18.(5分)解不等式组:{x−3≤0(1)x−12−2x−13>1(2).19.(7分)某校对九年级学生进行了一次数学学业水平测试,成绩评定分为A、B、C、D四个等级(注:等级A、B、C、D分别代表优秀、良好、合格、不合格),学校从九年级学生中随机抽取50名学生的数学成绩进行统计分析,并绘制成扇形统计图(如图所示).根据图中所给的信息答下列问题:(1)随机抽取的九年级学生数学学业水平测试中,D等级人数的百分率和D等级学生人数分别是多少?(2)这次随机抽样中,学生数学学业水平测试成绩的中位数落在哪个等级?(3)若该校九年级学生有800名,请你估计这次数学学业水平测试中,成绩达合格以上(含合格)的人数大约有多少人?20.(8分)在如图所示的直角坐标系中,解答下列问题:(1)分别写出A、B两点的坐标;(2)将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1;(3)求出线段B1A所在直线l的函数解析式,并写出在直线l上从B1到A的自变量x的取值范围.21.(8分)热气球的探测器显示,从热气球A处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,A处与高楼的水平距离为60m,这栋高楼有多高?(结果精确到0.1m,参考数据:√2≈1.414,√3≈1.732)22.(8分)如图,一个被等分成了3个相同扇形的圆形转盘,3个扇形分别标有数字1、3、6,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停止在指针所指的位置(指针指向两个扇形的交线时,重新转动转盘).(1)请用画树形图或列表的方法(只选其中一种),表示出分别转动转盘两次转盘自由停止后,指针所指扇形数字的所有结果;(2)求分别转动转盘两次转盘自由停止后,指针所指扇形的数字之和的算术平方根为无理数的概率.23.(7分)去年入秋以来,云南省发生了百年一遇的旱灾,连续8个多月无有效降水,为抗旱救灾,某部队计划为驻地村民新修水渠3600米,为了水渠能尽快投入使用,实际工作效率是原计划工作效率的1.8倍,结果提前20天完成修水渠任务.问原计划每天修水渠多少米?24.(9分)已知:如图,在梯形ABCD中,AD∥BC,∠DCB=90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.(1)当P点在BC边上运动时,求证:△BOP∽△DOE;(2)设(1)中的相似比为k,若AD:BC=2:3.请探究:当k为下列三种情况时,四边形ABPE是什么四边形?①当k=1时,是;②当k=2时,是;③当k=3时,是.并证明k=2时的结论.25.(12分)在平面直角坐标系中,抛物线经过O(0,0)、A(4,0)、E(3,−2√3 3)三点.(1)求此抛物线的解析式;(2)以OA的中点M为圆心,OM长为半径作⊙M,在(1)中的抛物线上是否存在这样的点P,过点P作⊙M的切线l,且l与x轴的夹角为30°?若存在,请求出此时点P的坐标;若不存在,请说明理由.(注意:本题中的结果可保留根号).2010年云南省昆明市中考数学试卷参考答案与试题解析一、选择题(共9小题,每小题3分,满分27分)1.(3分)3的倒数是()A.13B.﹣13C.3D.﹣3【解答】解:因为3×13=1,所以3的倒数为1 3.故选:A.2.(3分)若如图是某个几何体的三视图,则该几何体是()A.长方体B.三棱柱C.圆柱D.圆台【解答】解:根据主视图和左视图为矩形判断出是柱体,根据俯视图是正方形可判断出这个几何体应该是长方体,故选A.3.(3分)某班六名同学在一次知识抢答赛中,他们答对的题数分别是:7,5,6,8,7,9.这组数据的平均数和众数分别是()A.7,7B.6,8C.6,7D.7,2【解答】解:平均数=(7+5+6+8+7+9)÷6=7;数据7出现了2次,次数最多,所以众数是7.故选:A.4.(3分)据2010年5月11日云南省委、省政府召开的通报会通报,全省各级各部门已筹集抗旱救灾救济资金32亿元,32亿元用科学记数法表示为()A.3.2×108元B.0.32×1010元C.3.2×109元D.32×108元【解答】解:32亿元即3 200 000 000用科学记数法表示为3.2×109元.故选C.5.(3分)一元二次方程x2+x﹣2=0的两根之积是()A.﹣1B.﹣2C.1D.2【解答】解:根据题意有两根之积x1x2=ca=﹣2.故一元二次方程x2+x﹣2=0的两根之积是﹣2.故选:B.6.(3分)如图,在△ABC中,CD是∠ACB的平分线,∠A=80°,∠ACB=60°,那么∠BDC=()A.80°B.90°C.100°D.110°【解答】解:∵CD是∠ACB的平分线,∠ACB=60°,∴∠ACD=30°(平分线的定义),∵∠A=80°,∴∠BDC=110°(三角形的一个外角等于与它不相邻的两个内角的和).故选:D.7.(3分)下列各式运算中,正确的是()A.(a+b)2=a2+b2B.√(−3)2=3C.a3•a4=a12D.(3a)2=6a2(a≠0)【解答】解:A、(a+b)2=a2+2ab+b2,错误;B、√(−3)2=√9=3,正确;C、a3•a4=a12,错误;D、(3a)2=9a2,错误.故选:B.8.(3分)如图,已知圆锥侧面展开图的扇形面积为65πcm2,扇形的弧长为10πcm,则圆锥母线长是()A .5cmB .10cmC .12cmD .13cm 【解答】解:设母线长为R ,由题意得:65π=10π×R 2,解得R=13cm . 故选:D .9.(3分)如图,在△ABC 中,AB=AC ,AB=8,BC=12,分别以AB 、AC 为直径作半圆,则图中阴影部分的面积是( )A .64π−12√7B .16π﹣32C .16π−24√7D .16π−12√7【解答】解:设半圆与底边的交点是D ,连接AD .∵AB 是直径,∴AD ⊥BC .又∵AB=AC ,∴BD=CD=6.根据勾股定理,得AD=√AB 2−BD 2=2√7.∵阴影部分的面积的一半=以AB 为直径的半圆的面积﹣三角形ABD 的面积 =以AC 为直径的半圆的面积﹣三角形ACD 的面积,∴阴影部分的面积=以AB 为直径的圆的面积﹣三角形ABC 的面积=16π﹣12×12×2√7=16π﹣12√7.故选:D .二、填空题(共6小题,每小题3分,满分18分)10.(3分)﹣6的相反数是 6 .【解答】解:根据相反数的概念,得﹣6的相反数是﹣(﹣6)=6.11.(3分)如图,在△ABC 中,点D 、E 、F 分别是AB 、AC 、BC 的中点,若△ABC 的周长为12cm ,则△DEF 的周长是 6 cm .【解答】解:∵点D 、E 、F 分别是AB 、AC 、BC 的中点,∴DE=12BC ,EF=12AB ,DF=12AC , ∴△DEF 的周长=12(AB +BC +AC )=12×12=6cm . 故答案为:6.12.(3分)化简:(1−1a+1)÷a = 1a+1. 【解答】解:原式=a a+1×1a =1a+1. 13.(3分)计算:√8−√12= 32√2 . 【解答】解:原式=2√2﹣√22=3√22. 14.(3分)半径为r 的圆内接正三角形的边长为 √3r (结果可保留根号).【解答】解:如图所示,OB=OA=r ;∵△ABC 是正三角形,由于正三角形的中心就是圆的圆心,且正三角形三线合一,所以BO 是∠ABC 的平分线;∠OBD=60°×12=30°, BD=r•cos30°=r•√32;根据垂径定理,BC=2×√32r=√3r.15.(3分)如图,点A(x1,y1)、B(x2,y2)都在双曲线y=kx(x>0)上,且x2﹣x1=4,y1﹣y2=2;分别过点A、B向x轴、y轴作垂线段,垂足分别为C、D、E、F,AC与BF相交于G点,四边形FOCG的面积为2,五边形AEODB的面积为14,那么双曲线的解析式为y=6x.【解答】解:∵x2﹣x1=4,y1﹣y2=2∴BG=4,AG=2∴S△AGB=4∵S矩形AEOC =S矩形OFBD,四边形FOCG的面积为2∴S矩形AEOC =S矩形OFBD=12(S五边形AEODB﹣S△AGB﹣S四边形FOCG)+S四边形FOCG=12(14﹣4﹣2)+2=6即AE•AC=6∴y=6 x .故答案为:y=6 x .三、解答题(共10小题,满分75分)16.(5分)计算:(−14)−1−|−3|−20100+(√2)2.【解答】解:原式=﹣4﹣3﹣1+2=﹣6.17.(6分)如图,点B、D、C、F在一条直线上,且BC=FD,AB=EF.(1)请你只添加一个条件(不再加辅助线),使△ABC≌△EFD,你添加的条件是∠B=∠F或AB∥EF或AC=ED;(2)添加了条件后,证明△ABC≌△EFD.【解答】解:(1)∠B=∠F或AB∥EF或AC=ED;(2)证明:当∠B=∠F时在△ABC和△EFD中{AB=EF ∠B=∠F BC=FD∴△ABC≌△EFD(SAS).18.(5分)解不等式组:{x−3≤0(1)x−12−2x−13>1(2).【解答】解:解不等式①得:x≤3,(1分)由②得:3(x﹣1)﹣2(2x﹣1)>6,(2分)化简得:﹣x>7,(3分)解得:x<﹣7.(4分)∴原不等式组的解集为:x<﹣7.(5分)19.(7分)某校对九年级学生进行了一次数学学业水平测试,成绩评定分为A、B、C、D四个等级(注:等级A、B、C、D分别代表优秀、良好、合格、不合格),学校从九年级学生中随机抽取50名学生的数学成绩进行统计分析,并绘制成扇形统计图(如图所示).根据图中所给的信息答下列问题:(1)随机抽取的九年级学生数学学业水平测试中,D等级人数的百分率和D等级学生人数分别是多少?(2)这次随机抽样中,学生数学学业水平测试成绩的中位数落在哪个等级?(3)若该校九年级学生有800名,请你估计这次数学学业水平测试中,成绩达合格以上(含合格)的人数大约有多少人?【解答】解:(1)∵1﹣30%﹣48%﹣18%=4%,∴D等级人数的百分率为4%.∵4%×50=2,∴D等级学生人数为2人.(2)∵A等级学生人数30%×50=15人,B等级学生人数48%×50=24人,C等级学生人数18%×50=9人,D等级学生人数4%×50=2人.∴中位数落在B等级.(3)合格以上人数=800×(30%+48%+18%)=768.∴成绩达合格以上的人数大约有768人.20.(8分)在如图所示的直角坐标系中,解答下列问题:(1)分别写出A、B两点的坐标;(2)将△ABC绕点A顺时针旋转90°,画出旋转后的△AB1C1;(3)求出线段B1A所在直线l的函数解析式,并写出在直线l上从B1到A的自变量x的取值范围.【解答】解:(1)从图中可得出:A (2,0),B (﹣1,﹣4)(2分)(2)画图正确;(4分)(3)设线段B 1A 所在直线l 的解析式为:y=kx +b (k ≠0),∵B 1(﹣2,3),A (2,0),∴{−2k +b =32k +b =0,(5分) k =−34,b =32,(6分)∴线段B 1A 所在直线l 的解析式为:y =−34x +32,(7分)线段B 1A 的自变量x 的取值范围是:﹣2≤x ≤2.(8分)21.(8分)热气球的探测器显示,从热气球A 处看一栋高楼顶部的仰角为45°,看这栋高楼底部的俯角为60°,A 处与高楼的水平距离为60m ,这栋高楼有多高?(结果精确到0.1m ,参考数据:√2≈1.414,√3≈1.732)【解答】解:过点A作BC的垂线,垂足为D点.(1分)由题意知:∠CAD=45°,∠BAD=60°,AD=60.在Rt△ACD中,∠CAD=45°,AD⊥BC,∴CD=AD=60.(3分)在Rt△ABD中,∵tan∠BAD=BDAD,(4分)∴BD=AD•tan∠BAD=60√3.(5分)∴BC=CD+BD=60+60√3(6分)≈163.9(m).(7分)答:这栋高楼约有163.9m.(8分)(本题其它解法参照此标准给分)22.(8分)如图,一个被等分成了3个相同扇形的圆形转盘,3个扇形分别标有数字1、3、6,指针的位置固定,转动转盘后任其自由停止,其中的某个扇形会恰好停止在指针所指的位置(指针指向两个扇形的交线时,重新转动转盘).(1)请用画树形图或列表的方法(只选其中一种),表示出分别转动转盘两次转盘自由停止后,指针所指扇形数字的所有结果;(2)求分别转动转盘两次转盘自由停止后,指针所指扇形的数字之和的算术平方根为无理数的概率.【解答】解:(1)树形图如下:(2)数字之和分别为:2,4,7,4,6,9,7,9,12,算术平方根分别是:√2,2,√7,2,√6,3,√7,3,2√3,设两数字之和的算术平方根为无理数是事件A .∴P(A)=59.23.(7分)去年入秋以来,云南省发生了百年一遇的旱灾,连续8个多月无有效降水,为抗旱救灾,某部队计划为驻地村民新修水渠3600米,为了水渠能尽快投入使用,实际工作效率是原计划工作效率的1.8倍,结果提前20天完成修水渠任务.问原计划每天修水渠多少米?【解答】解:设原计划每天修水渠x 米.根据题意得:3600x −36001.8x=20, 解得:x=80.经检验:x=80是原分式方程的解.答:原计划每天修水渠80米.24.(9分)已知:如图,在梯形ABCD中,AD∥BC,∠DCB=90°,E是AD的中点,点P是BC边上的动点(不与点B重合),EP与BD相交于点O.(1)当P点在BC边上运动时,求证:△BOP∽△DOE;(2)设(1)中的相似比为k,若AD:BC=2:3.请探究:当k为下列三种情况时,四边形ABPE是什么四边形?①当k=1时,是平行四边形;②当k=2时,是直角梯形;③当k=3时,是等腰梯形.并证明k=2时的结论.【解答】(1)证明:∵AD∥BC∴∠OBP=∠ODE.又∠BOP=∠DOE,∴△BOP∽△DOE;(有两个角对应相等的两三角形相似);(2)解:①平行四边形;②直角梯形;③等腰梯形;证明:②当k=2时,BPDE=2,∴BP=2DE=AD又∵AD:BC=2:3,即BC=32 AD,∴PC=BC﹣BP=32AD﹣AD=12AD=ED,又ED∥PC,∴四边形PCDE是平行四边形,∵∠DCB=90°∴四边形PCDE是矩形∴∠EPB=90°又∵在直角梯形ABCD中AD∥BC,AB与DC不平行∴AE∥BP,AB与EP不平行四边形ABPE是直角梯形.25.(12分)在平面直角坐标系中,抛物线经过O(0,0)、A(4,0)、E(3,−2√3 3)三点.(1)求此抛物线的解析式;(2)以OA的中点M为圆心,OM长为半径作⊙M,在(1)中的抛物线上是否存在这样的点P,过点P作⊙M的切线l,且l与x轴的夹角为30°?若存在,请求出此时点P的坐标;若不存在,请说明理由.(注意:本题中的结果可保留根号).【解答】解:(1)设抛物线的解析式为:y=ax2+bx+c(a≠0)由题意得:{c=016a+4b+c=09a+3b+c=−2√33解得:a=2√39,b=−8√39,c=0∴抛物线的解析式为:y=2√39x2−8√39x(2)存在抛物线y=2√39x2−8√39x的顶点坐标是(2,−8√39),作抛物线和⊙M(如图),设满足条件的切线l与x轴交于点B,与⊙M相切于点C 连接MC,过C作CD⊥x轴于D∵MC=OM=2,∠CBM=30°,CM⊥BC∴∠BCM=90°,∠BMC=60°,BM=2CM=4,∴B(﹣2,0)在Rt△CDM中,∠DCM=∠CDM﹣∠CMD=30°∴DM=1,CD=√CM2−DM2=√3∴C(1,√3)设切线l的解析式为:y=kx+b(k≠0),点B、C在l上,可得:{k+b=√3−2k+b=0解得:k=√33,b=2√33∴切线BC的解析式为:y=√33x+2√33∵点P为抛物线与切线的交点,由{y=2√39x2−8√39xy=√33x+2√33,解得:{x1=−12y 1=√32,{x2=6y2=8√33,∴点P的坐标为:P1(−12,√32),P2(6,8√33);∵抛物线y=2√39x2−8√39x的对称轴是直线x=2此抛物线、⊙M都与直线x=2成轴对称图形于是作切线l关于直线x=2的对称直线l′(如图)得到B、C关于直线x=2的对称点B1、C1直线l′满足题中要求,由对称性,得到P1、P2关于直线x=2的对称点:P3(92,√32),P4(−2,8√33)即为所求的点;∴这样的点P共有4个:P1(−12,√32),P2(6,8√33),P3(92,√32),P4(−2,8√33).。
2010年云南省楚雄州中考数学真题(含答案解析)

楚雄州2010年高中(中专)招生统一考试数 学 试 题 卷一、选择题(本大题共8个小题,每小题只有一个正确选项,每小题3分,满分24分) 1.下列计算正确的是(B ) A .632·a a a=B .326=÷ C .2)21(1-=-D .623)(a a -=-2.如图是由四个相同的小正方体组成的立体图形,它的左视图为(B )3.自去年入秋以来,楚雄州遭遇了百年不遇的严重旱灾.截止2010年4月19日,楚雄州共收到各级各类抗旱救灾资金108014500元,这个数据用科学记数法表示为(D )A .71080145.10⨯ B .9101080145.0⨯ C .910080145.1⨯D .810080145.1⨯4.一元二次方程042=-x 的解是(A ) A .21=x , 22-=x B .2-=xC .2=xD .21=x , 02=x5.已知⊙O 1和⊙O 2的半径分别为2cm 和3cm ,两圆的圆心距为5cm ,则两圆的位置关系是(A ) A .外切 B .外离 C .相交 D .内切 6.已知等腰三角形的一个内角为70°,则另两个内角的度数是(C ) A .55°,55° B .70°,40° C .55°,55°或70°,40° D .以上都不对 7.下列说法不正确的是(D )A .在选举中,人们通常最关心的数据是众数B .掷一枚骰子,3点朝上是不确定事件C .数据3,5,4,1,-2的中位数是3D .有两边对应成比例且有一个角对应相等的两个三角形一定相似8.如图,四边形OABC 是菱形,点B ,C 在以点O 为圆心的弧EF 上,且∠1=∠2, 若扇形OEF 的面积为3π,则菱形OABC 的边长为(C ) A .23 B .2 C .3D .4A .B .C .D . 正面二、填空题(本大题共7个小题,每小题3分,满分21分) 9.21-的倒数是 -2 . 10.点(-2,3)在反比例函数)0(≠=k xky 的图象上,则这个反比例函数的表达式为xy 6-=.11.已知一个多边形的内角和是它的外角和的2倍,则这个多边形的边数为 6 . 12.在函数x y -=3中,自变量x 的取值范围是3≤x .13.如图,在□ABCD 中,对角线AC 与BD 相交于点O ,在不添加任何辅助线和字母的情况下,请添加一个条件,使□ABCD 变为矩形,需添加的条件是 任意写出一个正确答案即可(如AC=BD 或∠ABC=90°) .(写出一个即可)14.根据图中的程序,当输入x=2时,输出结果=y 2 .15.如图,用火柴棍摆出一列正方形图案,若按这种方式摆下去,摆出第n 个图案用 2n(n+1)或4(1+2+3+…n ) 根火柴棍(用含n 的代数式表示).三、解答题(本大题共9个小题,满分75分)16.(本小题6分)先化简,再求值:4212112--÷⎪⎭⎫ ⎝⎛-+m m m ,其中5-=m . 解:原式=)2(2)1)(1(2122--+÷⎪⎭⎫⎝⎛-+--m m m m m m =)1)(1()2(2·21-+---m m m m m 输 入 xy = -x + 4 ( x >1 )y = x + 4 ( x ≤1 )输 出 y① ② ③……=12+m …………………………………………………………………………5分 当5-=m 时,原式=2115212-=+-=+m ……………………………………6分17.(本小题7分)如图,点A E B D ,,,在同一直线上,DB AE =,AC DF =,AC DF ∥.请探索BC 与EF 有怎样的位置关系?并说明理由.解:BC ∥EF. 理由如下: ……………………………1分∵AE=DB(已知)∴AE+EB=DB+BE (等式的性质) 即AB=DE…………………………………………2分又∵AC ∥DF(已知)∴∠A=∠D(两直线平行,内错角相等) …………3分在△ABC 和△DEF 中⎪⎩⎪⎨⎧∠∠(已知)=(已证)=(已证)=DF AC D A DE AB ∴△ABC ≌△DEF (SAS )…………………………5分∴∠ABC=∠DEF(全等三角形的对应角相等) ………6分 ∴BC ∥EF(内错角相等,两直线平行) ………………7分18.(本小题7分)ABC △在平面直角坐标系中的位置如图所示. (1)作出ABC △关于x 轴对称的111A B C △,并写出点1A 的坐标; (2)作出将ABC △绕点O 顺时针方向旋转180°后的222A B C △. 解:(1)如图,画出111A B C △………(3分) )3,2(1--A ……………(4分) (2) 如图,画出222A B C △ ……(7分)ABEF19.(本小题8分)小明和小华为了获得一张2010年上海世博园门票,他们各自设计了一个方案:小明的方案是:转动如图所示的转盘,当转盘停止转动后,如果指针停在阴影区域,则小明获得门票;如果指针停在白色区域,则小华获得门票(转盘被等分成6个扇形,若指针停在边界处,则重新转动转盘).小华的方案是:有三张卡片,上面分别标有数字1,2,3,将它们背面朝上洗匀后,从中摸出一张,记录下卡片上的数字后放回,重新洗匀后再摸出一张.若摸出两张卡片上的数字之和为奇数,则小明获得门票;若摸出两张卡片上的数字之和为偶数,则小华获得门票.(1)在小明的方案中,计算小明获得门票的概率,并说明小明的方案是否公平? (2)用树状图或列表法列举小华设计方案中可能出现的所有结果,计算小华获得门票的概率,并说明小华的方案是否公平? 解:(1)小明获得门票的概率是2163 ,小明的方案是公平的,因为双方获得门票的可能性都是21…………………………………(3分) (2)或……………………………………………………………………5分小华获得门票的概率是95,小华的方案不公平,因为双方获得门票的可能性不相同. 小华获得门票的可能性是95 ,小明获得门票的可能性是94…………………8分1 2 3 1 2 3 4 2 3 4 5 3456开始12 3 1 2 3 1 2 3 1 2 3数字之和:2 3 4 3 4 5 4 5 6 第二次第一次和20.(本小题8分)如图,河流的两岸PQ、MN互相平行,河岸PQ上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN的A处测得∠DAN = 35°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CE(结果保留两个有效数字).(参考数据:sin35°≈ 0.57, cos35°≈ 0.82, tan35°≈ 0.70sin 70°≈ 0.94, cos70°≈ 0.34, tan70°≈ 2.75 )解:过点C作CF//DA交AB于点F.ΘMN//PQ,CF//DA∴四边形AFCD是平行四边形∴AF=CD=50米,∠CFB=35°∴FB=AB-AF=120-50=70 …3分F又Θ∠CBN=∠CFB+∠BCF∴∠BCF=70°-35°=35°=∠CFB∴BC=BF=70 ………………………………………………5分在Rt△BEC中,CESin70°=BCCE=BC·Sin70°≈70⨯0.94 = 65.8≈66 ………………7分答:河流的宽度CE约为66米.……………………………8分21.(本小题9分)在2009年楚雄州“火把节”房交会期间,某房地产公司对参加本次房交会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者年收入的情况整理后,制成表格如下:年收入(万元) 1.2 1.8 3.0 5.0 10.0被调查的消费者数(人)200 500 a70 30根据调查问卷,将消费者打算购买住房面积的情况整理后,作出部分频数分布直方图和扇形统计图.根据以上信息回答下列问题:(1)根据表格可得a =________,被调查的1000名消费者的平均年收入为万元.(2)补全频数分布直方图和扇形统计图.(3)若楚雄州现有购房打算的约有40000人,请估计购房面积在80至120平方米的大约有多少人?解:(1)根据表格可得 a = 200 ,被调查的1000名消费者的平均年收入为2.39万元.……………………………………………………………………………………(3分)(2)答案如图所示………………………………………………………………(6分)(3))(24000100024036040000人=+⨯答:估计购房面积在80至120平方米的大约有24000人.……………………(9分)22.(本小题8分)已知:如图,抛物线cbxaxy++=2与x轴相交于两点A(1,0),B(3,0),与y轴相交于点C(0,3).(1)求抛物线的函数关系式;(2)若点D(27,m)是抛物线cbxaxy++=2△ABD的面积.解:(1)由已知得⎪⎩⎪⎨⎧==++=++339ccbacba………………………………3分解之得⎪⎩⎪⎨⎧=-==341cba……………………………4分∴342+-=xxy……………………………………………………5分4321-1-2-2 -1 1 2 3 4ACO xyBD(2)∵),27(m D 是抛物线342+-=x x y 上的点 ∴45=m ……………………………………………………………6分∴4545221ABD =⨯⨯=△S …………………………………………8分23.(本小题9分)今年四月份,李大叔收获洋葱30吨,黄瓜13吨,现计划租用甲、乙两种货车共10辆将这两种蔬菜全部运往外地销售,已知一辆甲种货车可装洋葱4吨和黄瓜1吨;一辆乙种货车可装洋葱和黄瓜各2吨.(1)李大叔安排甲、乙两种货车时有几种方案?请你帮助设计出来;(2)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1300元,请帮李大叔算一算应选择哪种方案,才能使运费最少?最少运费是多少元?解:(1)设李大叔安排x 辆甲种货车,乙种货车有(10-x )辆,则有 ⎩⎨⎧≥-+≥-+13)10(230)10(24x x x x………………………………………………3分 解之得:5≤x ≤7………………………………………………4分因为x 应取正整数.所以x 取5,6,7………………………………5分方案如下:①安排5辆甲种货车,5辆乙种货车;②安排6辆甲种货车,4辆乙种货车;③安排7辆甲种货车,3辆乙种货车. …………………………6分(2)方案①:5×2000+5×1300=16500(元)方案②:6×2000+4×1300=17200(元) 方案③:7×2000+3×1300=17900(元)所以,李大叔应选择方案①才能使运费最少,最少运费是16500元.……………9分24.(本小题13分)已知:如图,⊙A 与y 轴交于C 、D 两点,圆心A 的坐标为(1,0),⊙A 的半径为5,过点C 作⊙A 的切线交x 轴于点B (-4,0). (1)求切线BC 的解析式;(2)若点P 是第一象限内⊙A 上的一点,过点P 作⊙A 的切线与直线BC 相交于点G ,且∠CGP=120°,求点G 的坐标;(3)向左移动⊙A (圆心A 始终保持在x 轴上),与直线BC 交于E 、F ,在移动过程中是否存在点A ,使△AEF 是直角三角形?若存在,求出点A 的坐标;若不存在,请说明理由.解:(1)如图1所示,连接AC ,则AC=5在Rt △AOC 中,AC=5 ,OA=1 ,则OC=2∴点C 的坐标为(0,2)设切线BC 的解析式为b kx y +=,它过点C (0,2),B (−4,0),则有⎩⎨⎧=+-=042b k b 解之得⎪⎩⎪⎨⎧==221b k∴221+=x y ………………………………………………4分(2)如图1所示,设点G 的坐标为(a ,c ),过点G 作GH ⊥x 轴,垂足为H 点,则OH=a , GH=c =21a + 2 ……………………………………………………5分连接AP, AG因为AC=AP , AG=AG , 所以Rt △ACG ≌Rt所以∠AGC=21×1200=600 在Rt △ACG 中,∠AGC= 600,AC=5 ∴Sin600=AGAC∴AG =3152在Rt △AGH 中, AH=OH -OA=a -1 ,GH=21a + 2 Θ2AH +2GH =2AG∴2)1(-a +2)221(+a =2)3152(解之得:1a =332 ,2a = −332(舍去) …………………………………………7分 点G 的坐标为(332,33+ 2 ) …………………………………………………8分(3) 如图2所示,在移动过程中,存在点A ,使△AEF 为直角三角形. ………………9分要使△AEF 为直角三角形ΘAE=AF∴∠AEF=∠AFE ≠ 900 ∴只能是∠EAF=900当圆心A 在点B 的右侧时,过点A 作 AM ⊥BC,垂足为点M.在Rt △AEF 中 ,AE=AF=5, 则EF=10, AM=21EF=2110在Rt △OBC 中,OC=2 , OB=4,则BC=25Θ∠BOC= ∠BMA=900 ,∠OBC= ∠OBM∴△BOC ∽△BMA∴AM OC =ABBC∴AB=225∴OA=OB -AB=4-225 ∴点A 的坐标为(-4+225,0) ………………………………………………11分当圆心A 在点B 的左侧时,设圆心为A ′,过点A ′作A ′M ′⊥BC 于点M ′,可得 △A ′M ′B ≌△AMB A ′B =AB =225 ∴O A ′=OB+ A ′B =4 +225 ∴点A ′的坐标为(-4-225,0) 综上所述,点A 的坐标为(-4+225,0)或(-4-225,0) ……………13分。
2010年昆明中考数学试题及答案

合并自:(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
2010年昆明中考数学试题及答案
E度教育网
合并自:(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自:(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自:(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自:(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自:(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自:(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自:(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自:(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
合并自:(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网
中国最大的教育门户网站
合并自:(奥数)、(中考)、(高考)、(作文)、(英语)、(幼教)、、等站
E度教育网。
2010年云南省曲靖市中考数学试卷(含解析)

2010年云南省曲靖市中考数学试卷一、选择题1、从3时到6时,钟表的时针旋转角的度数是()A.30B.60°C.90°D.120°2、下列各式中,运算正确的是()A.(x4)3=x7B.a8÷a4=a2C.D.3、分式方程的解是()A.2B.1C.-1D.-24、下列事件属于必然事件的是()A.367人中至少有两人的生日相同B.某种彩票的中奖率为,购买100张彩票一定中奖C.掷一次筛子,向上的一面是6点D.某射击运动员射击一次,命中靶心5、练习本比水性笔的单价少2元,小刚买了5本练习本和3支水性笔正好用去14元.如果设水性笔的单价为x元,那么下列所列方程正确的是()A.5(x-2)+3x=14B.5(x+2)+3x=14C.5x+3(x+2)=14D.5x+3(x-2)=146、不等式组的解集在数轴上表示正确的是()A .B .C .D .7、如图摆放的正六棱柱的俯视图是( )A .B .C .D .8、函数y=kx-k 与在同一坐标系中的大致图象是( ) A .B .C .D .二、填空题9、||的倒数是__________.10、在你认识的图形中,写出一个既是轴对称又是中心对称的图形名称:__________.11、如图,AB∥CD,AC⊥BC,垂足为C .若∠A=40°,则∠BCD=__________度.12、若(x-1)2=2,则代数式x2-2x+5的值为__________.13、在Rt△ABC中,∠C=90°,若BC=10,AD平分∠BAC交BC于点D,且BD:CD=3:2,则点D到线段AB的距离为__________.14、如图,活动衣帽架由三个菱形组成,利用四边形的不稳定性,调整菱形的内角α,使衣帽架拉伸或收缩.当菱形的边长为18cm,α=120°时,A、B两点的距离为__________cm.15、在分别写有数字-1,0,1,2的四张卡片中,随即抽取一张后放回,再随即抽取一张.以第一次抽取的数字作为横坐标,第二次抽取的数字作为纵坐标的点落在第一象限的概率是__________.16、把一个正三角形分成四个全等的三角形,第一次挖去中间的一个小三角形,对剩下的三个小正三角形再重复以上做法…一直到第n次挖去后剩下的三角形有__________个.三、解答题17、计算:18、先化简,再求值:,其中.19、如图,小明家所住楼房的高度AB=10米,到对面较高楼房的距离BD=20米,当阳光刚好从两楼房的顶部射入时,测得光线与水平线的夹角为40°.据此,小明便知楼房CD的高度.请你写出计算过程(结果精确到0.1米.参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)20、如图,E、F是▱ABCD对角线AC上的两点,且BE∥DF.求证:(1)△ABE≌△CDF;(2)∠1=∠2.21、某校对中考前一次数学模拟考试进行抽样分析,把样本成绩按分数段分成A、B、C、D、E五组(每组成绩含最低分,不含最高分)进行统计,并将结果绘制成下面两幅统计图.请根据图中信息,解答下列问题:(1)求A组人数在扇形图中所占圆心角的度数;(2)求D组人数;(3)判断考试成绩的中位数落在哪个组?(直接写出结果,不需要说明理由)22、如图,⊙O的直径AB=12,的长为2π,D在OC的延长线上,且CD=OC.(1)求∠A的度数;(2)求证:DB是⊙O的切线.(参考公式:弧长公式l=,其中l是弧长,r是半径,n是圆心角度数)23、如图,有一块等腰梯形的草坪,草坪上底长48米,下底长108米,上下底相距40米,现要在草坪中修建一条横、纵向的“H”型甬道,甬道宽度相等.甬道面积是整个梯形面积的.设甬道的宽为x米.(1)求梯形ABCD的周长;(2)用含x的式子表示甬道的总长;(3)求甬道的宽是多少米?24、如图,在平面直角坐标系xoy中,抛物线y=x2向左平移1个单位,再向下平移4个单位,得到抛物线y=(x-h)2+k,所得抛物线与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,顶点为D.(1)求h、k的值;(2)判断△ACD的形状,并说明理由;(3)在线段AC上是否存在点M,使△AOM与△ABC相似?若存在,求出点M的坐标;若不存在,说明理由.2010年云南省曲靖市中考数学试卷的答案和解析一、选择题1、答案:C试题分析:时针1小时走1大格,1大格为30°.试题解析:从3时到6时,钟表的时针旋转角的度数是(6-3)×30°=90°,故选C.2、答案:D试题分析:熟悉幂运算的性质:同底数的幂相除,底数不变,指数相减;幂的乘方,底数不变,指数相乘.二次根式的加减的实质是合并同类二次根式;二次根式相乘除,等于它们的被开方数相乘除.试题解析:A、(x4)3=x12,故此选项错误;B、a8÷a4=a4,故此选项错误;C、因为3和5不是同类二次根式,不能合并,故此选项错误;D、根据二次根式的除法法则,故此选项正确.故选D.3、答案:B试题分析:本题考查解分式方程的能力.本题因为2-x=-(x-2),可知最简公分母为(x-2).试题解析:(1)方程两边同乘(x-2),得:x-3+x-2=-3,整理解得x=1.经检验x=1是原方程的解.故选B.4、答案:A试题分析:根据必然事件的概念(必然事件指在一定条件下一定发生的事件)可判断正确答案.试题解析:A、一年最多有366天,367人中至少有两人的生日相同,是必然事件;B、某种彩票的中奖率为,购买100张彩票一定中奖,是随机事件;C、掷一次筛子,向上的一面是6点,是随机事件;D、某射击运动员射击一次,命中靶心,是随机事件.5、答案:A试题分析:等量关系为:5本练习本总价+3支水性笔总价钱=14.试题解析:水性笔的单价为x元,那么练习本的单价为(x-2)元.∴5(x-2)+3x=14,故选:A.6、答案:B试题分析:先求出各不等式的解集在数轴上表示出来,再求出其公共部分即可.试题解析:(1)移项、合并同类项得,x>-2,(2)去括号得,-x+4≥1,移项、合并得,-x≥-3,化系数为1得,x≤3,故原不等式组的解集为:-2<x≤3.在数轴上表示为:故选B.7、答案:D试题分析:找到从上面看所得到的图形即可,注意看见的棱用实线表示.试题解析:从上面看可得到左右三个长方形相邻,这三个长方形中所有的棱都能看到,所以都为实线,故选D.8、答案:C试题分析:比例系数相等,那么这两个函数图象必有交点,进而根据一次函数与y轴的交点判断正确选项即可.试题解析:当k>0时,一次函数过一三四象限,反比例函数过一三象限,符合选项C,故选C.二、填空题9、答案:试题分析:先计算绝对值,再计算倒数.试题解析:||=,的倒数是2.试题分析:根据轴对称图形与中心对称图形的概念,分析图形的特征求解.试题解析:在认识的图形中,既是轴对称又是中心对称的图形名称:圆(答案不唯一).11、答案:试题分析:先根据直角三角形两锐角互余求出∠B的度数,再根据两直线平行,内错角相等解答.试题解析:∵∠A=40°,AC⊥BC,∴∠B=90°-40°=50°,∵AB∥CD,∴∠BCD=∠B=50°.12、答案:试题分析:根据完全平方公式展开,先求出x2-2x的值,然后再加上5计算即可.试题解析:∵(x-1)2=2,∴x2-2x+1=2,∴x2-2x=1,两边都加上5,得x2-2x+5=1+5=6.故答案为:6.13、答案:试题分析:根据角平分线的性质“角的平分线上的点到角的两边的距离相等”,可得点D到AB的距离=点D到AC的距离=CD.试题解析:∵BC=10,且BD:CD=3:2,∴CD=4,∵AD平分∠BAC交BC于点D,∴点D到AB的距离=CD=4.14、答案:试题分析:根据α=120°得出菱形的锐角是60°,所以A、B两点的距离是边长的3倍,代入求解即可.试题解析:∵α=120°,∴菱形的锐角为60°,∴AB=3×18=54cm.故答案为,54.15、答案:试题分析:列举出所有情况,看所求的情况占总情况的多少即可.试题解析:列树状图得:共有16种情况,落在第一象限的有4种,所以概率是.16、答案:试题分析:本题可依次解出n=1,2,3,…,剩下的三角形的个数.再根据规律以此类推,可得出第n次挖去后剩下的三角形个数.试题解析:∵n=1时,有3个,即31个;n=2时,有9个,即32个;n=3时,有27个,即33个;…;∴n=n时,有3n个.三、解答题17、答案:试题分析:本题涉及零指数幂、负指数幂、二次根式化简3个考点.在计算时,需要针对每个考点分别进行计算,然后根据实数的运算法则求得计算结果.试题解析:原式=3+2+1-3=3.18、答案:试题分析:这道求代数式值的题目,不应考虑把x的值直接代入,通常做法是先把代数式化简,然后再代入求值.分式的四则运算是整式四则运算的进一步发展,是有理式恒等变形的重要内容之一.在计算时,首先要弄清楚运算顺序,先除再减.试题解析:原式=(3分)=(1分)=(1分)当x=时,原式=.(2分)19、答案:试题分析:在直角△ABP中,利用三角函数求得BP,即得到PD;再在直角△PCD中利用三角函数即可求解CD.试题解析:在△ABP中,tan40°=,BP=.(4分)在Rt△CDP中,tan40°=,(2分)CD=31.90×0.84≈26.8(米).答:楼房CD的高度为26.8米.(2分)20、答案:试题分析:(1)根据平行四边形的性质得到AB=CD,∠BAE=∠DCF,再根据BE∥DF得到∠BEF=∠DFE,所以它们的邻补角相等,三角形全等;(2)由三角形全等得到BE=DF,所以四边形BFDE是平行四边形,根据对角相等即可得证.证明:(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∴∠BAE=∠DCF,∵BE∥DF,∴∠BEF=∠DFE.∴∠AEB=∠CFD,∴△ABE≌△CDF(AAS).(2)由△ABE≌△CDF得,BE=DF∵BE∥DF,∴四边形BEDF是平行四边形∴∠1=∠2.21、答案:试题分析:(1)由A、B、C、D、E五组所占的百分比之和等于1进行计算,用该组所占的百分比乘以360°;(2)由直方图中的信息,先算出总人数,再乘以D组的百分比;(3)利用中位数的定义判断.试题解析:(1)A组人数所占的百分比:1-(26%+30%+22%+12%)=10%,A组人数在扇形图中所占的圆心角的度数:360°×10%=36°.(2)样本人数:15÷30%=50(人),D组人数=50×22%=11(人).(3)考试成绩的中位数落在C组.22、答案:试题分析:(1)根据弧长公式l=,得n=,求得∠BOC的度数,进一步根据圆周角定理进行求解;(2)要证明DB是⊙O的切线,只需证明∠OBD=90°,根据(1)发现等边三角形OBC,从而根据三角形一边上的中线等于这边的一半,证明即可.试题解析:(1)设∠BOC=n°.根据弧长公式,得,n=60°.根据圆周角定理,得∠A=∠BOC=30°.(2)证明:连接BC.∵OB=OC,∠BOC=60°,∴△BOC是等边三角形.∴∠OBC=∠OCB=60°,OC=BC=OB.∵OC=CD,∴BC=CD.∴∠CBD=∠D=∠OCB=30°.∴∠OBD=∠OBC+∠CBD=60°+30°=90°.∴AB⊥BD.∴DB是⊙O的切线.23、答案:试题分析:(1)欲求周长,只要再求出腰长就可以了,根据等腰梯形的性质BE=FC=(BC-AD),再利用勾股定理即可求出腰长AB;(2)根据图形,甬道的总长等于两个高长加上横向甬道,而横行甬道的长是上底的长减去两个甬道的宽度;(3)根据甬道的面积等于甬道的总长×宽,再根据甬道面积是整个梯形面积的列出方程求解即可.试题解析:(1)在等腰梯形ABCD中,AD=EF=48,AE⊥BC,DF⊥BC,BE=FC=(BC-AD)=(BC-EF),=(108-48),=30,∴AB=CD=,=50,∴梯形ABCD的周长=AB+BC+CD+DA=50+108+50+48=256.(米)(2分)(2)甬道的总长:40×2+48-2x=(128-2x)米.(2分)(3)根据题意,得(128-2x)x=×40(48+108),(3分)整理得x2-64x+240=0,解之得x1=4,x2=60,因60>48,不符合题意,舍去.答:甬道的宽为4米(3分)24、答案:试题分析:(1)根据“左加右减,上加下减”的平移规律即可得到h、k的值;(2)根据(1)题所得的抛物线的解析式,即可得到A、C、D的坐标,进而可求出AC、AD、CD的长,然后再判断△ACD的形状;(3)易求得B点的坐标,即可得到AB、AC、OA的长;△AOM和△ABC中,已知的相等角是∠OAM=∠BAC,若两三角形相似,可考虑两种情况:①∠AOM=∠ABC,此时OM∥BC,△AOM∽△ABC;②∠AOM=∠ACB,此时△AOM∽△ACB;根据上述两种情况所得到的不同比例线段即可求出AM的长,进而可根据∠BAC的度数求出M点的横、纵坐标,即可得到M点的坐标.(1)∵y=x2的顶点坐标为(0,0),∴y=(x-h)2+k的顶点坐标D(-1,-4),∴h=-1,k=-4 (3分)(2)由(1)得y=(x+1)2-4当y=0时,(x+1)2-4=0x 1=-3,x2=1∴A(-3,0),B(1,0)(1分)当x=0时,y=(x+1)2-4=(0+1)2-4=-3∴C点坐标为(0,-3)又∵顶点坐标D(-1,-4)(1分)作出抛物线的对称轴x=-1交x轴于点E作DF⊥y轴于点F在Rt△AED中,AD2=22+42=20在Rt△AOC中,AC2=32+32=18在Rt△CFD中,CD2=12+12=2∵AC2+CD2=AD2∴△ACD是直角三角形;(3)存在.由(2)知,OA=3,OC=3,则△AOC为等腰直角三角形,∠BAC=45°;连接OM,过M点作MG⊥AB于点G,AC=①若△AOM∽△ABC,则,即,AM=∵MG⊥AB∴AG2+MG2=AM2∴OG=AO-AG=3-∵M点在第三象限∴M();②若△AOM∽△ACB,则,即,∴AG=MG=OG=AO-AG=3-2=1∵M点在第三象限∴M(-1,-2).综上①、②所述,存在点M使△AOM与△ABC相似,且这样的点有两个,其坐标分别为(),(-1,-2).。
云南省2010年各地州数学中考试题

ABC DEF第11题图俯视图 主视图 左视图 第2题图第9题图D AB C第6题图云南省2010年各市(地、州)中考数学试题昆 明 市一、选择题(每小题3分,满分27分.在每小题给出的四个选项中,只有一项是正确的;每小题选出答案后,用2B 铅笔将答题卡上对应题目的答案标号的小框涂黑) 1.3的倒数是( )。
A .3B .3-C .13D .13-2.若右图是某个几何体的三视图,则该几何体是( )。
A .长方体 B .三棱柱C .圆柱D .圆台3.某班六名同学在一次知识抢答赛中,他们答对的题数分别是:7,5,6,8,7,9. 这组数据的平均数和众数分别是( ) 。
A .7,7 B .6,8 C .6,7 D .7, 24.据2010年5月11日云南省委、省政府召开的通报会通报,全省各级各部门已筹集抗旱救灾救济资金32亿元,32亿元用科学记数法表示为( )。
A .83.210⨯元B .100.3210⨯元C .93.210⨯元D .83210⨯元5.一元二次方程220x x +-=的两根之积是( 。
)A .-1B .-2C .1D .26.如图,在△ABC 中,CD 是∠ACB 的平分线,∠A = 80°,∠ACB=60°,那 么∠BDC=( )。
A .80° B .90° C .100° D .110°7.下列各式运算中,正确的是( ) 。
A .222()a b a b +=+ B 3C .3412a a a ⋅=D .2236()(0)a aa=≠ 8.如图,已知圆锥侧面展开图的扇形面积为65πcm 2,cm ,则圆锥母线长是( )。
A .5cm B .10cm C .12cm D .13cm9.如图,在△ABC 中,AB = AC ,AB = 8,BC = 12,分别以AB 、AC 为直径作半圆,则图中阴影部分的面积是( )。
2010年云南省曲靖市数学中考真题(word版含答案)

曲靖市2010年高中(中专)招生统一考试数 学一、选择题(本大题共8个小题,每小题只有一个符合条件的选项,每小题3分,满分24分)1.从3时到6时,钟表的时针旋转角的度数是( ) A.30︒ B.60︒ C.90︒ D.120︒2.下列各式中,运算正确的是( )A.437()x x = B.842a a a ÷= C.= D.=3.分式方程33122x x x-+=--的解是( ) A.2 B.1 C.-1 D.-24.下列事件属于必然事件的是( ) A.367人中至少有两人的生日相同 B.某种彩票的中奖率为1100,购买100张彩票一定中奖 C.掷一次骰子,向上的一面是6点 D.某射击运动员射击一次,命中靶心5.练习本比水性笔的单价少2元,小刚买了5本练习本和3支水性笔正好用去14元.如果设水性笔的单价为x 元,那么下列所列方程正确的是( ) A.5(2)314x x -+= B.5(2)314x x ++= C.53(2)14x x ++= D.53(2)14x x +-=6.不等式组322(4)1x xx +>⎧⎨--⎩≥的解集在数轴上表示正确的是( )7.如图摆放的正六棱柱的俯视图是( )8.函数y kx k =-与(0)ky k x=≠在同一坐标系中的大致图象是( )二、填空题(本大题共8个小题,每小题3分,满分24分) 9.12-的倒数是___________. 10.在你认识的图形中,写出一个既是轴对称又是中心对称的图形名称:________. 11.如图,AB CD ∥,AC BC ⊥,垂足为C .若40A ∠=︒,则BCD ∠=_______度. 12.若2(1)2x -=,则代数式225x x -+的值为________.13.在Rt ABC △中,90C ∠=︒,若10BC AD =,平分BAC ∠交BC 于点D ,且32BD CD =∶∶,则点D 到线段AB 的距离为_______.14.如图,活动衣帽架由三个菱形组成,利用四边形的不稳定性,调整菱形的内角α,使衣帽架拉伸或收缩.当菱形的边长为18cm α=120︒,时,A B 、两点的距离为_______cm.15.在分别写有数字1012-,,,的四张卡片中,随机抽取一张后放回,再随机抽取一张.以第一次抽取的数字作为横坐标,第二次抽取的数字作为纵坐标的点落在第一象限的概率是_____.A .xB . xC . xD .A B A B C D第11题图 第13题图 DB A C16.把一个正三角形分成四个全等的三角形,第一次挖去中间一个小三角形,对剩下的三个小正三角形再重复以上做法……一直到第n次挖去后剩下的三角形有________个.三、解答题(本大题共8个小题,满分72分)17.(6分)计算:11(2)(1)3-⎛⎫-+-- ⎪⎝⎭18.(7分)先化简,再求值.2216636x x x xx x x++-÷---,其中x=19.(8分)如图,小明家所住楼房的高度10AB=米,到对面较高楼房的距离20BD=米,当阳光刚好从两楼房的顶部射入时,测得光线与水平线的夹角为40︒.据此,小明便知楼房CD的高度.请你写出计算过程(结果精确到0.1米.参考数据:sin400.6400.77tan400.84︒≈︒≈︒≈,cos4,).第二次第一次第三次第四次…BPACD20.(9分)如图,E F 、是ABCD 对角线AC 上的两点,且BE DF ∥. 求证:(1)ABE CDF △≌△; (2)12∠=∠.21.(10分)某校对中考前一次数学模拟考试进行抽样分析,把样本成绩按分数段分成A B C D E 、、、、五组(每组成绩含最低分,不含最高分)进行统计,并将结果绘制成下面两幅统计图.请根据图中信息,解答下列问题: (1)求A 组人数在扇形图中所占圆心角的度数; (2)求D 组人数;(3)判断考试成绩的中位数落在哪个组?(直接写出结果,不需要说明理由)22.(10分)如图,O ⊙的直径12AB BC =,的长为2π,D 在OC 的延长线上,且CD OC =. (1)求A ∠的度数;(2)求证:DB 是O ⊙的切线; (参考公式:弧长公式π180n rl =,其中l 是弧长,r 是半径,n 是圆心角度数)ABC D EF 12分数段 B AD E12% 22% 30% 26%CD23.(10分)如图,有一块等腰梯形的草坪,草坪上底长48米,下底长108米,上下底相距40米,现要在草坪中修建一条横、纵向的“H ”型甬道,甬道宽度相等,甬道面积是整个梯形面积的213.设甬道的宽为x 米. (1)求梯形ABCD 的周长;(2)用含x 的式子表示甬道的总长; (3)求甬道的宽是多少米?24.(12分)如图,在平面直角坐标系xoy 中,抛物线2y x =向左平移1个单位,再向下平移4个单位,得到抛物线2()y x h k =-+.所得抛物线与x 轴交于A B 、两点(点A 在点B 的左边),与y 轴交于点C ,顶点为D .(1)求h k 、的值;(2)判断ACD △的形状,并说明理由; (3)在线段AC 上是否存在点M ,使AOM △与ABC △相似.若存在,求出点M 的坐标;若不存在,说明理由.A DCFEBx曲靖市2010年高中(中专)招生统一考试数学参考答案一、选择题1.C2.D3.B4.A5.A6.B7.D8.C 二、填空题9. 2 10.圆(答案不唯一) 11.50 12. 6 13. 4 14. 54 15.1416.3n三、解答题17.解:原式=3213++-······································································································· 4分3=. ····················································································································· 6分 18.解:原式=1(6)(6)66(1)x x x x x x x x++--⨯--+ ·········································································· 3分 66x x x x +-=- ··································································································· 4分 12x=.···················································································································· 5分当x =原式==·················································································································· 7分 19.解:在Rt ABP △中,10tan 40AB BP BP︒==, 1011.90tan 40BP =︒≈ ·········································································································· 4分在Rt CDP △中,tan 4011.9020CD CDPD ︒==+, ······························································································ 6分31.900.8426.8CD =⨯≈(米). 答:楼房CD 的高度为26.8米. ······························································································ 8分 20. 证明:(1)四边形ABCD 是平行四边形,AB CD ∴∥. BAE DCF ∴∠=∠. ··············································································································· 2分 BE DF ∥,BEF DFE ∴∠=∠. AEB CFD ∴∠=∠. ··············································································································· 4分(AAS)ABE CDF ∴△≌△ ··································································································· 5分(2)由ABE CDF △≌△得 BE DF =.BE DF ∥, ···································································································· 7分∴四边形BEDF 是平行四边形. ··························································································· 8分 ∴12∠=∠. ···························································································································· 9分 21.解:(1)A 组人数所占的百分比:1(26%30%22%12%)10%-+++=, ··················· 2分A 组人数在扇形图中所占的圆心角的度数:36010%36︒⨯=; ······································· 4分 (2)样本人数:1530%50÷=(人), ··············································································· 6分 D 组人数=5022%11⨯=(人); ························································································ 8分 (3)考试成绩的中位数落在C 组. ······················································································ 10分22.(1)解:设BOC n ∠=︒, 据弧长公式,得π62π180n ⨯=, 60n =︒. ·································································································································· 2分据圆周角定理,得1302A BOC ∠=∠=︒. ············································································ 4分(2)证明:连接BC , 60OB OC BOC =∠=︒,,BOC ∴△是等边三角形. ········································································································ 6分 60OBC OCB OC BC OB ∴∠=∠=︒==,. OC CD =, BC CD ∴=.1302CBD D OCB ∴∠=∠=∠=︒. ······················································································ 8分603090OBD OBC CBD ∴∠=∠+∠=︒+︒=︒. AB BD ∴⊥.DB ∴是O ⊙的切线. ············································································································ 10分23. 解:(1)在等腰梯形ABCD 中, 48AD EF ==,D()121(10848)23050AE BC DF BC BE CF BC EF AB CD ⊥⊥==-=-=∴===,,,,∴梯形ABCD 的周长=501085048256AB BC CD DA +++=+++=(米). ················· 2分 (2)甬道的总长:402482(1282)x x ⨯+-=-米. ··························································· 4分 (3)根据题意,得21(1282)40(48108)132x x -=⨯⨯+. ··················································································· 7分 整理,得2642400x x -+=,解之得12460x x ==,.因6048>,不符合题意,舍去.答:甬道的宽为4米. ············································································································ 10分 24. 解:(1)2y x =的顶点坐标为(0,0), 2()y x h k ∴=-+的顶点坐标(14)D -,, 1h k ∴=-,=-4. ··················································································································· 3分(2)由(1)得2(1)4y x =+-. 当0y =时,2(1)40x +-=. 1231x x =-=,.(30)10A B ∴-,,(,). ··············································································································· 4分当0x =时,22(1)4(01)43y x =+-=+-=-,C ∴点坐标为()03,-.又顶点坐标()14D --,, ·································································································· 5分 作出抛物线的对称轴1x =-交x 轴于点E .作DF y ⊥轴于点F .在Rt AED △中,2222420AD =+=; 在Rt AOC △中,2223318AC =+=; 在Rt CFD △中,222112CD =+=;222AC CD AD +=,ACD ∴△是直角三角形. ········································································································ 7分(3)存在.由(2)知,AOC △为等腰直角三角形,45BAC ∠=︒, 连接OM ,过M 点作MG AB ⊥于点G ,AC ==①若AOM ABC △∽△,则AO AM AB AC =,即34AM ===MG AB ⊥,222AG MG AM ∴+=.94AG MG ∴===,93344OG AO AG =-=-=.M 点在第三象限,3944M ⎛⎫∴-- ⎪⎝⎭,. ·················································································································· 10分 ②若AOM ACB △∽△,则AO AM AC AB =4AM AM ===,2AG MG ∴====,321OG AO AG =-=-=. M 点在第三象限,()12M ∴--,.x综上①、②所述,存在点M 使AOM △与ABC △相似,且这样的点有两个,其坐标分别为()391244⎛⎫---- ⎪⎝⎭,,,. ······································································································ 12分。
2010年全国各地中考数学选择题、填空题答案及参考答案

2010年全国各地中考数学选择题、填空题答案及参考解答第一部分 选择题1.C解:设抛物线的对称轴与x 轴交于点E如图1,当∠CAD =60°时,则DE =1,BE =3 ∴B (1+3,0),C (1,-1)将B (1+3,0),C (1,-1)代入y =a (x -1)2+k ,解得k =-1,a =31∴y =31(x -1)2-1如图2,当∠ACB =60°时,由菱形性质知A (0,0),C (1,3) 将A (0,0),C (1,3)代入y =a (x -1)2+k ,解得k =-3,a =3 ∴y =3(x -1)2-3同理可得:y =-31(x -1)2+1,y =-3(x -1)2+3所以符合条件的抛物线的解析式共4个3.D解:设DE =x ,则EC =x 2,BD =x 6,BC =x +x 8 由△AGF ∽△ABC 得:xx x 22+=xx x 8+,∴x4=16,x =2,∴正方形DEFG 的面积为4∴S △ABC =1+1+3+4=94.C解:如图,过A 作BC 的垂线交CB 的延长线于H ,则HD =AH ,HC =3AH∴HC -HD =(3-1)AH =3,∴AH =23(3+1),HB =23(3+1)-3=23(3-1) ∴AB =22HB AH+=235.B6.D∠ACD 、∠BAD 、∠ODA 、∠ODE 、∠OED7.D解:如图,则有⎩⎨⎧a2+1=r2(2-a )2+(21)2=r2解得:a =1613,r =161758.A解:如图,连结BD S 1=21π×32-S △ABD -S 弓形=2π,S 2=21AB ·BC -S △ABD -S 弓形 S 1-S 2=21π×32-21AB ·BC =2π,AB ·BC =8π,BC =34π9.B解:由已知得:AB +AC +BC =2CD +AC +BC =2+AC +BC =52+,∴AC +BC =5 ∴(AC +BC )2=AC 2+BC 2+2AC ·BC =5又AC 2+BC 2=AB 2=(2CD )2=4,∴2AC ·BC =1∴S △ABC =21AC ·BC =4110.C解:如图,延长AD 至E ,使DE =AD ,连结BE 、CE ,则四边形ABEC是平行四边形 ∴BE =AC =13,∴AB 2+AE 2=52+122=169=132=BE 2∴△ABD 是直角三角形∴BD =22AD AB+=2265+=61,∴BC =61211.A解:如图,延长MN 交BC 的延长线于点E∵∠AMB =∠NMB ,∠AMB =∠MBC ,∠NMB =∠MBC ,∴BE =ME 易知△NDM ≌△NCE ,∴CE =MD ,MN =NE ,∴ME =2MN 设正方形边长为2,MD =x ,则AM =2- x ,DN =1,BE =x +2在直角三角形DMN 中,由勾股定理得:MN =12+x ,∴ME =122+xB AD CAB CD EDBCAMNE∴x +2=122+x ,解得:x =0(不合题意,舍去),或x =34∴AM =2-34=32,AM :AB =3112.A解:设正方形DEFG 的边长为x ,△ABC 的BC 边上的高为h由△AGF ∽△ABC 得:a x =h x h -,∴x =h a ah +,∴S 2=2)(h a ah +又S 1=ah 21,∴212S S =222221)(h a ha ah+=ah h a 2)(+·41≥ah h a 22)(·41=1 ∴S 1≥2S 213.B解:由△BEM ∽△AED 得:边上的高边上的高AD BM =AD BM =21,∴BM 边上的高=31AB =31∴S 阴影=2(21-31)=3114.C 解:如图,连结OE 、OF 、OC 、OD 、OG∵AE 、BF 为半圆的切线,∴OE ⊥AE ,OF ⊥BF ,又AE =BF ,OE =OF ∴△AOE ≌△BOF ,∴∠AOE =∠BOF∵CD 切半圆于G ,∴CF =CG .仿上可得∠COF =∠COG ,同理∠DOE =DOG ∵∠AOE +∠DOE +∠DOG +∠COG +∠COF +∠BOF =180°,∴∠AOE +∠DOE +∠COF =90° ∴∠BCO =90°-∠COF =∠AOE +∠DOE =∠AOD同理∠BOC =∠ADO ,∴△BCO ∽△AOD ,∴BC/AO =BO/AD设AO =BO =a ,则y =xa 215.B解:用排除法:从函数图象可以看出:①的支出费用减少,反映了建议(1);③的支出费用没改变,提高了车票价格,反映了建议(2);②、④不符合题意。
2010年云南省西双版纳中考数学试题(含答案解析)

2010年云南省西双版纳初中毕业升学考试数学试题解析一、选择题(本大题共8小题,每小题3分,满分24分)1.下列计算正确的是( ),错误;2.据有关部门统计,2010年西双版纳州森林覆盖面积约为14877平方公里,这个数字用科学记数法可表示为( )43353.如图,是一个由若干个相同的小正方体组成的几何体的三视图,则组成这个几何体的小正方体的个数是( )A .9B .8C .7D .65.一次函数y=-x+3的图象不经过...()6.众志成城,抗旱救灾.某小组7名同学积极捐出自己的零花钱支援灾区,他们捐款的数额(单位:元)分别是:50、30、30、40、35、25、105.这组数据的中位数是()7.如图,C、D是线段AB上两点,若BC=5cm,BD=8cm,且D是AC的中点,则AC的长等于()B.6cm C.8cm D.11cmA.3cmC8.已知一个圆锥的底面直径是6cm 、母线长8cm ,求得它的表面积为( )222213.如图,CD是⊙O的直径,AB是⊙O的弦,AB⊥CD,垂足为M,根据以上条件,请写角:③∠ADC=∠BDC,④∠A=∠B,弧:④= ,⑤,…答案不唯一.14.已知△ABC ∽△C B A ''',且S ∶S =16∶9,若AB =2,则B A ''= 1.5 .三、解答题(本大题共9小题,满分75分)16.(6分)先化简,再求值:⎝⎛⎭⎫1- 1x +3 ÷ x 2-4 x 2+3x,其中x =6.=× = ,= .17.(8分)近来,校园安全问题引起了社会的极大关注,为了让学生了解安全知识,增强安全意识,某校举行了一次“安全知识竞赛”.为了了解这次竞赛的成绩情况,从中抽取了部分学生的成绩为样本,绘制了下列统计图(说明:A 级:90分—100分;B 级:75分—89分;C 级:60分—74分;D 级:60分以下). 请结合图中提供的信息,解答下列问题:(1)请把条形统计图补充完整;(2)样本中C 级的学生人数占抽样学生人数的百分比是 ;(3)扇形统计图中C 级所在的扇形的圆心角度数是 ;(4)若该校共有2000名学生,请你用此样本估计安全知识竞赛中A 级和B 级的学生共约有多少人?D(2)C级的学生百分比为10÷100=10%;息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.×= .19.(8分)第41届世界博览会“中国2010年上海世界博览会”5月1日召开了,小亮计划在暑假期间为他们全家5人预订世博会门票.根据图中的对话内容,请你求出甲、乙两种门票的价格.,.用二元一次方程组求解的应用题一般情况下题中要给出2个等量关系,准确地找到等量关系并用方程组表示出来是解题的关键.20.(8分)如图,四边形ABCD是菱形,BE⊥AD、BF⊥CD,垂足分别为E、F.=5=5BE= ×BE= .21.(7分)某地震救援队探测出某建筑物废墟下方点C处有生命迹象,已知废墟一侧地面上探测点A、B相距4m,探测线与地面的夹角分别是30º和60º,试确定生命所在点C的深度(结果精确到0.1m,参考数据:2≈1.414,:3≈1.732).=2 (22.(8分)小颖的爸爸只有一张《阿凡达》的电影票,她和哥哥两人都很想去观看.哥哥想了一个办法:拿了8张扑克牌,将数字为2、3、5、9的四张牌给小颖,将数字为4、6、7、10的四张牌给自己,并按如下游戏规则进行:小颖和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,如果和为偶数,则小颖去;如果和为奇数,则哥哥去.(1)请用画树状图或列表的方法求小颖去看电影的概率;(2)各个设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你修改规则使游((= = .=1- = ,因为<,所以哥哥设计的游戏规则不公平;,那么游戏规则就是公平的.,那么游戏规则也是公平的.23.(10分)已知A(1,5)和B(m,-2)是一次函数y=kx+b的图象与反比例函数y=nx的图象的两个交点.(1)求m的值和函数y=nx的解析式;(2)在同一直角坐标系中画出这两个函数的大致图象,并根据图象直接写出使一次函数的值大于反比例函数的值的x的取值范围.y= ,求出y= 的解析式,再把y= ,y= .-2= ;m=- .(2)把A(1,5)和B(- ,-2)代入y=kx+b,得 ,解得 .∴一次函数的解析式为y=2x+3.在同一直角坐标系中画出函数y= 与y=2x+3的图象,如右图所示,观察图象,可知当- <x <0或x >1时,一次函数的值大于反比例函数的值.24.(12分)如图,已知点A (-3,0)和B (1,0),直线y =kx -4经过点A 并且与y 轴交于点C .(1)求点C 的坐标;(2)求经过A 、B 、C 三点的抛物线的解析式和对称轴;(3)半径为1个单位长度的动圆⊙P 的圆心P 始终在抛物线的对称轴上.当点P 的纵坐标为5时,将⊙P 以每秒1个单位长度的速度在抛物线的对称轴上移动.那么,经过几秒,⊙P 与直线AC 开始有公共点?经过几则有:a a= ,y= (= x2+ x-4 x=- ,即CA= = =5,= ,= ;同理= ,把;y=- x-4y=- ;MN=|- |= ,= - =1=6+2×=9 ,=9 ÷1=9 (秒)9 秒后,⊙切线的性质等知识,综合性强,难度较大.试卷分析:。
中考数学真题分类汇编找规律

一、选择题 1.(2010安徽省中中考)下面两个多位数1248624……、6248624……,都是按照如下方法得到的:将第一位数字乘以2,若积为一位数,将其写在第2位上,若积为两位数,则将其个位数字写在第2位。
对第2位数字再进行如上操作得到第3位数字……,后面的每一位数字都是由前一位数字进行如上操作得到的。
当第1位数字是3时,仍按如上操作得到一个多位数,则这个多位数前100位的所有数字之和是…………………………………………( )A )495B )497C )501D )503 【答案】A 2.(2010江苏盐城)填在下面各正方形中的四个数之间都有相同的规律,根据此规律,m 的值是A .38B .52C .66D .74 【答案】D3.(2010山东日照)古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16,…,这样的数为正方形数.下列数中既是三角形数又是正方形数的是(A )15 (B )25 (C )55 (D )1225【答案】D 4.(2010山东烟台)如图,一串有趣的图案按一定的规律排列,请仔细观察,按此规律第2010个图案是0 2 8 4 2 4 6 22 4 6 844 m 6【答案】B 5.(2010江苏淮安)观察下列各式:()1121230123⨯=⨯⨯-⨯⨯ ()1232341233⨯=⨯⨯-⨯⨯()1343452343⨯=⨯⨯-⨯⨯……计算:3×(1×2+2×3+3×4+…+99×100)=A .97×98×99B .98×99×100C .99×100×101D .100×101×102【答案】C 6.(2010 四川绵阳)如图,在一个三角点阵中,从上向下数有无数多行,其中各行点数依次为2,4,6,…,2n ,…,请你探究出前n 行的点数和所满足的规律.若前n 行点数和为930,则n =( ).A .29B .30C .31D .32【答案】B7.(2010 山东淄博)如图所示的运算程序中,若开始输入的x 值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2010次输出的结果为(A )6 (B )3 (C )200623 (D )10033231003⨯+x 21输出输入xx +3x 为偶数x 为奇数(第11题)【答案】B 8.(2010广东茂名)用棋子摆出下列一组“口”字,按照这种方法摆下去,则摆第n 个“口”字需用棋子A .4n 枚B .(4n -4)枚C .(4n+4)枚D . n 2枚 【答案】A9.(2010广东深圳)观察下列算式,用你所发现的规律得出20102的末位数字是( ) 21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,… A .2 B .4 C .6 D .8 【答案】B 10.(2010广东湛江)观察下列算式:,65613,21873,7293,2433,813,273,93,1387654321========,通过观察,用你所发现的规律确定20023的个位数字是( )A.3B.9C.7D.1 【答案】B 11.当对应所得分数为132分时,则挪动的珠子数 颗。
全国各地数学中考试题分类汇编实数的运算含答案

实数的运算一、选择题1.2010江苏盐城20100的值是 A .2010 B .0 C .1 D .-1答案C2.2010山东威海计算()201020092211-⨯⎪⎭⎫⎝⎛-的结果是A .-2B .-1C .2D .3答案B3.2010台湾计算 | 135 || 61167 | 之值为何 A 37 B 31 C 34 D311; 答案A4.2010台湾计算1061023104之值为何A 108 B 109 C 1010 D 1012; 答案A5.2010台湾下列四个选项中的数列,A 5,5,5,5,5B 1,4,925C5,25,35,45,55 D 1,22,33,44,55 ;答案D6.2010台湾图五数在线的A 、B 、C 三点所表示的数分别为 a 、b 、c ;根据图中各点位置,判断下列各式何者 正确 A a 1b 1>0 B b 1c 1>0 C a 1b 1<0 D b 1c 1<0 ;答案D7.2010浙江杭州 计算 – 12 + – 13 =A.– 2B. – 1C. 0D. 2 答案C8.2010 浙江义乌28 cm 接近于 ▲ A .珠穆朗玛峰的高度 B .三层楼的高度 C .姚明的身高 D .一张纸的厚度答案C9.2010 福建德化2-的3倍是A 、 6-B 、1C 、6D 、5- 答案AA B C O a bc 0 1 1 图五10.2010 山东济南某市2009年元旦的最高气温为2℃,最低气温为-8℃,那么这天的最高气温比最低气温高 A .-10℃ B .-6℃ C .6℃ D .10℃ 答案D11.2010 东济南下列各式中,运算正确的是A=B.+=C .632a a a ÷=D .325()a a =答案A12.2010山东临沂计算()21-的值等于 A -1 B1 C -2 D2 答案B13.2010 河北计算3×-2 的结果是A .5B .-5C .6D .-6答案D14.2010 河北下列计算中,正确的是A .020=B .2a a a =+C3=±D .623)(a a =答案D15.2010 山东省德州下列计算正确的是 A020= B331-=-3==答案C16.2010江苏宿迁3)2(-等于A .-6B .6C .-8D .8 答案C17.2010 山东莱芜如图,数轴上A 、B 两点分别对应实数a 、b ,则下列结论正确的是A .0>abB .0>-b aC .0>+b aD .0||||>-b a答案D1 0 -1 a b B A 第5题图18.2010江西 计算 -2- 6的结果是A .-8B . 8C . -4D . 4 答案A19.2010年贵州毕节有一人患了流感,经过两轮传染后共有100人患了流感,那么每轮传染中,平均一个人传染的人数为 A .8人 B .9人 C .10人 D .11人答案B.20.2010湖北荆门()()2012321-+-+⎪⎭⎫⎝⎛--π的值为A .-1B .-3C . 1D . 0答案C21.2010 四川成都3x 表示A 3xB x x x ++C x x x ⋅⋅D 3x + 答案C22.2010湖北荆州温度从-2°C 上升3°C 后是A .1°CB . -1°C C .3°CD .5°C 答案A23.2010湖北荆州下面计算中正确的是 A .532=+ B .()111=--C . ()2010201055=- D . x 32x •=x 6答案C24.2010湖北荆州在电子显微镜下测得一个圆球体细胞的直径是5×105-cm.,3102⨯个这样的细胞排成的细胞链的长是A .cm 210- B .cm 110- C .cm 310- D .cm 410- 答案B25.2010湖北省咸宁下列运算正确的是 A .263-=- B .24±=C .532a a a =⋅D .3252a a a +=答案C26.2010江苏淮安观察下列各式:()1121230123⨯=⨯⨯-⨯⨯ ()1232341233⨯=⨯⨯-⨯⨯()1343452343⨯=⨯⨯-⨯⨯……计算:3×1×2+2×3+3×4+…+99×100=A .97×98×99B .98×99×100C .99×100×101D .100×101×102 答案C27.2010湖南怀化下列运算结果等于1的是 A .)3()3(-+- B .)3()3(--- C .)3(3-⨯-D .)3()3(-÷-答案D28.2010山东泰安如图,数轴上A 、B 两点对应的实数分别为,a b ,则下列结论不正确的是 A 、0a b +> B 、0ab < C 、0a b -< D 、0a b ->1-1答案D29.2010云南红河哈尼族彝族自治州下列计算正确的是A .-1-1=1 B.-32=-6 C.π0=1 D.-26÷-23=-22 答案C30.2010云南楚雄下列计算正确的是A .a 2·a 3=a 6B .6÷2=3C .21-2=-2 D . -a 32=-a 6 答案B31. 2010湖北随州下列运算正确的是A .1331-÷= B a = C .3.14 3.14ππ-=- D .326211()24a b a b =答案D32. 2010四川乐山计算-2×3的结果是A -6 B6 C -5 D5答案A33. 2010黑龙江哈尔滨某年哈尔滨市一月份的平均气温为-18℃,三月份的平均气温为2℃,则三月份的平均气温比一月份的平均气温高 A16℃ B20℃ C -16℃ D .-20℃ 答案B34. 2010 福建三明如果□,1)23(=-⨯则□内应填的实数是A .23-B .32-C .23 D .32 答案B35. 2010湖北襄樊某市2010年元旦这天的最高气温是8℃,最低气温是-2℃,则这天的最高气温比最低气温高A .10℃B .-10℃C .6℃D .-6℃答案A36. 2010 湖北孝感2010)1(-的值是A .1B .—1C .2010D .—2010答案A37.2010 山东淄博下列结论中不能由0=+b a 得到的是A ab a -=2B b a =C 0=a ,0=bD 22b a = 答案C38.2010 山东淄博如图所示的运算程序中,若开始输入的x 值为48,我们发现第一次输出的结果为24,第二次输出的结果为12,…,则第2010次输出的结果为A6 B3 C200623 D10033231003⨯+答案B39.2010云南玉溪 的结果是)(计算12010)21(1:.1--- A. 1 B. -1D. 2答案B40.2010 甘肃()=-21A .1B .-1C .2D .-2答案A41.2010 山东荷泽2010年元月19日,山东省气象局预报我市元月20日的最高气温是4℃,最低气温是-6℃,那么我市元月20日的最大温差是 A .10℃ B .6℃ C .4℃ D .2℃答案A42.2010青海西宁 计算)3(21-⨯--的结果等于A.5B.5-C.7D.7-第11题答案A43.2010广西梧州用0,1,2,3,4,5,6,7,8这9个数字组成若干个一位数或两位数每个数字都只用一次,然后把所得的数相加,它们的和不可能是 A .36 B .117 C .115 D .153 答案44.2010广东深圳观察下列算式,用你所发现的规律得出20102的末位数字是 21=2,22=4,23=8,24=16,25=32,26=64,27=128,28=256,…A .2B .4C .6D .8 答案B45.2010湖北宜昌冰箱冷冻室的温度为-6℃,此时房屋内的温度为20℃,则房屋内的温度比冰箱冷冻室的温度高 ;A.26℃B.14℃C.-26℃D.-14℃ 答案A46.2010湖北宜昌如图,数轴上A,B 两点分别对应实数a,b,则下列结论正确的是 ; A. |a|>|b| B. a+b>0 C. ab<0 D. |b|=bAB10-1-2b a答案C47.2010吉林如图,检测4个足球,其中超过标准质量的克数记为正数,不足标准质量的克数记为负数,从轻重的角度看,最接近标准的是答案C48.2010广东湛江观察下列算式:,65613,21873,7293,2433,813,273,93,1387654321========,通过观察,用你所发现的规律确定20023的个位数字是.9 C 答案B49.2010广东清远计算:0-12= A.12 B. -2 C.-12D. 2 答案C 二、填空题1.2010山东烟台计算-2sin60°+π-12=_____________________;答案+12.2010 福建晋江计算:.______32=-答案913.2010江苏无锡一种商品原来的销售利润率是47%.现在由于进价提高了5%,而售价没变,所以该商品的销售利润率变成了 ▲.注:销售利润率=售价—进价÷进价答案40%4.2010 山东莱已知:3212323=⨯⨯=C ,1032134535=⨯⨯⨯⨯=C ,154321345646=⨯⨯⨯⨯⨯⨯=C ,…, 观察上面的计算过程,寻找规律并计算=610C .答案2105. 10.2010江西按照下图所示的操作步骤,若输入x 的值为-2,则给出的值为 .答案76.2010湖北武汉计算:sin30︒= ,-3a 22= ,= .答案12,9a 4,5 7.2010四川 巴中符号“f ”表示一种运算,它对一些数的运算结果如下:1f 1=0,f 2 = 1,f 3=2,f 4= 3,…… 21111()()()()23452,3,4,5ff ff ====……利用以上规律计算:1(2010)()2010ff -=答案18.2010浙江湖州“五.一”期间,某服装商店举行促销活动,全部商品八折销售.一件标价为10°元的 运动服,打折后的售价应是 元. 答案80.9.2010江苏常州计算:12-+= ,2-= ,(2)--= ,34()a = ; 答案1,2,-2,a1210.2010湖南怀化计算102)7(-++π=_______.答案23 11.2010 山东滨州计算-22·-10-13-1= . 答案112.2010湖北荆门观察下列计算:211211-=⨯ 3121321-=⨯ 4131431-=⨯ 5141541-=⨯ … … 从计算结果中找规律,利用规律计算+⨯+⨯+⨯+⨯541431321211…=⨯+201020091 ; 答案2010200913.2010河南计算:21-+(-2)= . 答案514.2010黑龙江哈尔滨某种衬衫每件的标价为150元,如果每件以八折即按标价的80%出售,那么这种衬衫每件的实际售价应为元 ; 答案12015.2010 福建三明计算:2122|21|-+--= ; 答案-316.2010 江苏镇江计算:—3+2= ; —3×2= .答案—1,—617.2010 甘肃观察:1234111111113243546a a a a =-=-=-=-,,,,…,则n a = n=1,2,3,…. 答案211+-n n 18.2010 重庆江津先观察下列等式:111122=-⨯ 1112323=-⨯ 1113434=-⨯ …… 则计算111111223344556++++=⨯⨯⨯⨯⨯ .答案5619.2010 重庆江津我们定义a b c dad bc =-,例如2345=2×5-3×4=10-12=-2.若x 、y 均为整数,且满足1<14x y <3,则x y +的值是_________.答案3±20.2010 福建泉州南安计算:=-0)2010(.答案121.2010 山东荷泽刘谦的魔术表演风靡全国,小明也学起了刘谦发明了一个魔术盒,当任意实数对b ,a 进入其中时,会得到一个新的实数:a 2+b -1,例如把3,-2放入其中,就会得到32+-2-1=6.现将实数对-2,-3放入其中,得到实数是 . 答案022.2010 广西钦州市根据如图所示的计算程序,若输入的值x =-1,则输出的值 y = _ ▲_ .答案223.2010 广西钦州市计算 -2 +3的结果是_▲_; 答案124.2010青海西宁 2010的相反数是 ;4-1= . 答案-2010,125.2010鄂尔多斯“五一”期间,某服装商店举行促销活动,全部商品八折销售,小华购买一件为140元的运动服,打折后他比按原价购买节省了 元;答案28 26.2010广西南宁古希腊数学家把数 ,21,15,10,6,3,1叫做三角数,它有一定的规律性.若把一个三角形数记为1a ,第二个三角形数记为 ,2a ,第n 个三角形数记为n a ,计算12a a -,,,3423a a a a --,由此推算,=-99100a a ,=100a .答案100,505027.2010云南昭通计算:-30+1=_______________. 答案228.2010贵州遵义如图,在宽为30m,长为40m 的矩形地面上修建两条宽都是1m 的道路,余下部分种植花草,那么,种植花草的面积为 m 2.答案113129.2010贵州遵义小明玩一种挪动珠子的游戏,每次挪动珠子的颗数与对应所得的分数如下表:x 为负数第9题输入x输出yy=x -5 y=x 2 +1x 为正数当对应所得分数为132分时,则挪动的珠子数 颗; 答案1230.2010广东佛山在算式1-︱-2口3︱中的口里,填入运算符号 ,使得算式的值最小在符号+,-,×,÷中选择一个. 答案×31.2010辽宁沈阳计算:=-⨯0)3(218 ; 答案12-32.2010福建省南平计算:20=_______. 答案:133.2010贵州铜仁定义运算“”的运算法则为:xy =xy -1,则234=__ __. 答案1934.2010广东湛江计算:2010-π0 -1= . 答案:0 .35.2010湖南娄底计算:-20100 +|-1|=_________ 答案236.2010内蒙赤峰北京市从2010年7月1日起开始上调最低工资标准,由原来的每月800元上调至960元,则这次上 调的百分比是____________. 答案20%37.2010内蒙赤峰观察式子:),7151(21751),5131(21531),311(21311-=⨯-=⨯-=⨯……. 由此计算:+⨯+⨯+⨯751531311…=⨯+201120091_____________.答案20111005 三、解答题1.2010江苏苏州计算:01243⎛⎫-+- ⎪⎝⎭.答案2.2010江苏南通1203(4)(π3)2|5|-+---- 答案解:原式=16+1-8-5=4.3.2010江苏盐城1 30cos )31(31-+--答案1解:原式=3+3-错误! ……………………………………………………3分 =6-错误! ………………………………………………………………4分4.2010山东济宁计算:084sin 45(3)4-︒+-π+-答案解:原式2224142=-⨯++ ································································· 4分 5= ··························································································· 5分5.2010山东济宁观察下面的变形规律:211⨯=1-12; 321⨯=12-31;431⨯=31-41;…… 解答下面的问题: 1若n 为正整数,请你猜想)1(1+n n = ;2证明你猜想的结论; 3求和:211⨯+321⨯+431⨯+…+201020091⨯. 答案 1111n n -+ ···································································································· 1分 2证明:n 1-11+n =)1(1++n n n -)1(+n n n =1(1)n nn n +-+=)1(1+n n . ······················· 3分3原式=1-12+12-31+31-41+…+20091-20101=12009120102010-=. ····································································· 5分 6.2010四川凉山计算:1201002(60)(1)|28|(301)21cos tan -÷-+--⨯--; 答案7.2010四川眉山计算:1021()(52)18(2)23---答案解:原式=313242-+ ……………………4分 =22 ………………………………6分8.2010浙江嘉兴1计算:0)2(2+-;答案10)2(2+-12+=3=. …4分9.2010浙江绍兴1计算: |2-|o 2o 12sin30(3)(tan 45)-+--+; 答案解:1 原式= 2+1-3+1=1.10.2010 浙江省温州本题l0分1计算:()121320108-⎪⎭⎫⎝⎛--+.答案11.2010 浙江台州市1计算:)1()2010(40---+; 答案1解:原式=2+1+1 =412.2010 浙江义乌1计算:14tan 45⎪-° 答案解:1原式=1+2-1=213.2010 重庆计算:102010)51()5(97)1(-+-⨯+---π. 答案解:原式51371+⨯+-= 2=.14.2010重庆市潼南县 6分计算:π-0-|-3|+121-⎪⎭⎫⎝⎛--12010.答案解:原式=1-3+2-1 = -115.2010 福建德化15分计算: |-2|-2-错误!0+2)21(-- ;答案解:原式=412+-=516.2010 福建晋江8分计算:()0220103134-÷---. 答案 解:原式13194-÷-=1394-⨯-=24-=17.2010湖南长沙计算1023tan 30(2010)π-+--答案解:102tan 30(2010)π---1123=+- 1112=+- 12= 18.2010江苏宿迁本题满分8分计算:01)2(3)31(5---+--π.答案解:原式=5-3+3-1 =4 19.2010浙江金华本题6分计算:4cos30°.答案解:原式﹦1+33-32﹦1+3.20.2010 四川南充计算:()228cos303-+︒--.答案解:原式=42832+⨯⨯-=43+ =1.21.2010 山东济南计算:12-4cos30°-3+210答案原式=23-4×23-3+1 = -122.2010 浙江衢州计算:012sin 302+--︒. 答案解:原式=111222++- =3 23.2010江苏泰州计算:112)21(30tan 3)21(01+-+︒---;答案原式=3231233--⨯++=23123--++=13-+. 24.2010福建福州 计算:|-3|+-10-错误! 答案原式=3+1-3=125.2010江苏无锡111|1|()2---+2(-3) 答案原式= 9—1+2=1026.2010湖南邵阳计算:113-⎛⎫⎪⎝⎭-5×15+38答案113-⎛⎫⎪⎝⎭-5×15+38=3-1+2=4.27.2010年上海计算:12131427(31)()231-+--++ .答案解:12131427(31)()231-+--++.=342322(31)+--+-. =3.28.2010安徽芜湖1计算:12010× 错误!-3+sin58°- 错误!0+|错误!-4cos600| 答案29.2010甘肃兰州本小题满分4分60tan 2-—0)14.3(-π+2)21(--1221+答案本题满分10分1本小题满分4分 解:原式=34132++-- ……………………………………………2分=3332++- ………………………………………………………3分 =5 …………………………………………………………………………4分 30.2010重庆綦江县计算:()()1312222π-⎛⎫---++- ⎪⎝⎭. 答案原式=2-1+2-8=-5 31. 2010四川宜宾1计算:错误!+10+– 错误!–1 – 错误!–2sin45°答案错误!+10+– 错误!–1 – 错误!–2sin45°=1+-3+2-2-2=-4. 32. 2010 江苏连云港本题满分8分计算:1-22+3×-2 - 错误! -2;答案33. 2010 广东珠海计算:92|21|)3(12-+---- 答案解:原式=6321219=-+-34. 2010四川 巴中计算:01118(21)2sin 454----︒-()答案原式=4222123-⨯-- 35.2010浙江湖州计算:201004(1)tan 45+--..答案原式=4+1-1=4.36. 2010江苏常州计算120433--- 答案37. 2010江苏淮安11913---; 答案1原式=3+1-3=1.38. 2010 湖南株洲1计算:()22tan 452010-+︒+答案原式=411++6=40. 2010 四川成都计算:()121126.330tan 6-⎪⎭⎫⎝⎛+--+︒π.答案1解:原式=3612323⨯+-=3 41. 2010广东中山计算:001)2(60cos 2)21(4π-+-+-.答案解:原式=121222+⨯-+ =442.2010广东中山阅读下列材料:)210321(3121⨯⨯-⨯⨯=⨯,)321432(3132⨯⨯-⨯⨯=⨯,)432543(3143⨯⨯-⨯⨯=⨯,由以上三个等式相加,可得.2054331433221=⨯⨯⨯=⨯+⨯+⨯读完以上材料,请你计算下列各题:11110433221⨯++⨯+⨯+⨯ 写出过程; 2)1(433221+⨯++⨯+⨯+⨯n n = ; 3987543432321⨯⨯++⨯⨯+⨯⨯+⨯⨯ = . 答案解:11110433221⨯⨯+⨯+⨯=)210321(31⨯⨯-⨯⨯+)321432(31⨯⨯-⨯⨯+…+)11109121110(31⨯⨯-⨯⨯=12111031⨯⨯⨯ =440. 2)2)(1(31++n n n 3987543432321⨯⨯++⨯⨯+⨯⨯+⨯⨯ =)32104321(41⨯⨯⨯-⨯⨯⨯+)43215432(41⨯⨯⨯-⨯⨯⨯ +…+)987610987(41⨯⨯⨯-⨯⨯⨯=1098741⨯⨯⨯⨯ =126043. 2010湖南常德如图3,一个数表有7行7列,设ij a 表示第i 行第j 列上的数其中i=1,2,3,…,7,j=1,2,3,…,7. 例如:第5行第3列上的数537a =. 则123225253()()a a a a -+-= ; 2此数表中的四个数,,,np nk mp mk a a a a 满足()()np nk mk mp a a a a -+-= .答案10 2044. 2010湖南常德计算:03111()(2)()|2|23--+-++- 答案解:原式= 1-8+3+2= -245. 2010湖南郴州计算:118122sin 60tan 602.答案 解:原式=+12246. 2010湖北荆州计算:()21182010---+答案解:原式=()12122--+=12122+-+ =22+47. 2010江苏扬州1计算:-12+tan 60°-π+20100答案1原式=131-+ =348. 2010湖北恩施自治州计算:2+()()()121212010-++--313⨯-答案解:原式=2+1+1-1 =31 2 3 4 3 2 1 2 3 4 5 4 3 2 3 4 5 6 5 4 3 4 5 6 7 6 5 4 5 6 7 8 7 6 5 6 7 8 9 8 7 6 7 8 9 10 9 8 7 图349. 2010北京计算:+--012010)31|-43|-tan60° 答案解:原式=3-1+43-3=2+33 . 50. 2010江苏徐州192120101+--)(; 答案解原式=1-2+3=251. 2010云南昆明计算:1021()320104-----+ 答案解:原式 = 4312---+ = 6-52. 2010四川内江已知a =错误!-1,b =2cos45°+1,c =2010-π0,d =|1-错误!|.1请化简这四个数;2根据化简结果,列式表示这四个数中“有理数的和”与“无理数的积”的差,然后计算结果. 答案解:1a =错误!-1=3,b =2cos45°+1=2×错误!+1=错误!+1,c =2010-π0=1,d =|1-错误!|=错误!-12∵a ,c 为有理数,b ,d 为无理数,∴a +c -bd =3+1-错误!+1 错误!-1 =4-2-1 =3.53.2010四川内江已知非负数a ,b ,c 满足条件a +b =7,c -a =5,设S =a +b +c 的最大值为m ,最小值为n ,则m -n = . 答案754.2010广东东莞计算:01)2(60cos 2)21(4π-++︒--.答案原式=2+2-2×21+1=4-1+1=455.2010广东东莞阅读下列材料:1×2=311×2×3-0×1×2, 2×3=312×3×4-1×2×3,3×4=313×4×5-2×3×4,由以上三个等式相加,可得 1×2+2×3+3×4=31×3×4×5=20.读完以上材料,请你计算下各题:⑴1×2+2×3+3×4+…+10×11写出过程; ⑵1×2+2×3+3×4+…+n ×n +1= ;⑶1×2×3+2×3×4+3×4×5+…+7×8×9= .答案⑴1×2+2×3+3×4+…+10×11=31×1×2×3-0×1×2+2×3×4-1×2×3…+10×11×12-9×10×11 =31×10×11×12 =440⑵1×2+2×3+3×4+…+n ×n +1 =31×1×2×3-0×1×2+2×3×4-1×2×3+… +)1()1()2()1(+⨯⨯--+⨯+⨯n n n n n n =)2()1((31+⨯+⨯n n n ⑶1×2×3+2×3×4+3×4×5+…+7×8×9=41×1×2×3×4-0×1×2×3×4+2×3×4×5-1×2×3×4+…+7×8×9×10-6×7×8×9=41×7×8×9×10 =126056.2010 四川绵阳1计算:π-20100 +sin60︒-1-︱tan30︒-3︱+38. 答案1原式= 1 +|333|)23(1---+ 2 = 3 +33232-= 3 +332332-= 3. 57.2010 江苏镇江1|;4|)60(cos )5(02-+-答案原式415+-==858.2010 广东汕头计算:()01260cos 2)21(4π-+︒--+-.答案原式1212)2(2+⨯--+= 110+-= 0=.59.2010 广东汕头阅读下列材料:1×2 =311×2×3-0×1×2,2×3 =312×3×4-1×2×3, 3×4 = 313×4×5-2×3×4,由以上三个等式相加,可得 1×2+2×3+3×4=31×3×4×5 = 20. 读完以上材料,请你计算下列各题:(1) 1×2+2×3+3×4+···+10×11写出过程; (2) 1×2+2×3+3×4+···+n ×n +1 = _________;(3) 1×2×3+2×3×4+3×4×5+···+7×8×9 = _________. 答案解:1∵1×2 =311×2×3-0×1×2, 2×3 = 312×3×4-1×2×3,3×4 = 313×4×5-2×3×4,… 10×11 =3110×11×12-9×10×11, ∴1×2+2×3+3×4+···+10×11=31×10×11×12=440.2)2)(1(31++n n n . 31260.60.2010四川 泸州 计算:-12010+3--1答案-12010+3--1 =1+3-4+12-1=1+3-4+2=261.2010 湖南湘潭计算:2o(1)(3)2cos 60-+π-- 答案解:原式=21211⨯-+ =162.2010广西桂林计算:101()2)3---4cos30°+答案解:原式=314--=31--=26.2010湖北十堰计算:30(2)|5|2)2sin 30-+--+︒答案原式=-8 + 5-1+ 2×错误!=-3.63.2010 广西玉林、防城港计算:10122-⎛⎫⨯- ⎪⎝⎭答案原式=2=2 64.2010 重庆江津计算:120114520104-⎛⎫-+︒+ ⎪⎝⎭答案解:原式141=-++……………每个知识点1分4分 1411=-+++ 5=9.2010 福建泉州南安计算: 43)85(41)1(12+⨯--÷--. 答案解:原式=231)3(41+⨯--⨯………………5分 =214++…………… ……………7分=7……………………………… … 9分65.2010 四川自贡计算π-2°+31-1-27cos30° 答案-1266.2010 山东荷泽计算:12-4sin 60°+4-π0答案⑴原式=123432+⨯-=1 67.2010宁夏回族自治区计算:011( 3.14)()12π--+--. 答案解:原式=)12()2(231---++ =122231+--+=2268.2010 广西钦州市计算:42(1)3cos 45--+答案解:1原式 =1+19=1+19-1 =1969.2010青海西宁计算:4401425.0)14.3()21(⨯+---π 答案.解:原式=2-1+4)441(⨯ = 2-1+1 = 2 70.2010鄂尔多斯计算:0132)2()31(272-⨯--+--π 答案1计算:0132)2()31(272-⨯--+--π 解:原式=-4-3-3=-1071.2010广西南宁计算:1)2(60tan 3)2010()1(-+︒-︒-+--π 答案解:1)2(60tan 3)2010()1(-+︒-︒-+--π213311+⨯-+= 4分 2132+-= 5分 21-= 72.2010年山西计算:.)23(45sin 2)21(91 -+--+- 答案解:原式1222)2(3+⨯--+= .11123=+--= 73.2010广东茂名计算:1022)2010()2(4--+---.答案解:原式=21144-+-···················4分 =21.···························7分 ① ②74.2010贵州遵义计算:∣-22∣-8-2-1+3-20 答案解:原式=1222212--+………………………………………4分 =12…………………………………………………………6分 20.2010广东深圳计算:302)1(821)14.3(45sin 2)31(-++-+︒--π 答案原式=1922122192-++⨯-= 75.2010广西柳州计算:-23+2010-30-tan45答案解:原式=-8+1-1 =-876.2010辽宁本溪计算:20183()(2010)4sin 453π-+⨯----︒. 答案77.2010 福建莆田计算:23|32|23-+- 答案78.2010广西河池计算:(()2032212sin 60+--+ 答案解:原式=234123-++ =5 79.2010年福建省泉州计算:01|3|(3)8242π--+--+⨯.答案解:原式=2144813⨯+-+ ……………………………………………7分=224+- …………………………………………………………8分 =4 ……………………………………………………………… 9分80.2010贵州铜仁 -20100+│12sin60°答案解:原式=11-2=081.2010广东肇庆计算:10330tan ·3)8(--︒+- 答案解:原式=1+3133·3-=1+3131-=1 82.2010云南曲靖计算:10)31()1()2(9---+--答案解:原式=3+2+1-3 =383.2010四川广安计算:001||(4)sin 302π-+-+.答案001||(4)sin 302π-+-+ =12211321++-+- =12-84.2010四川达州计算:20100(1)1)--.答案解: 原式=1-1 =0.85.2010福建清远计算:∣-1∣-sin30°+12--10. 答案:原式=1-12+12-1=0.86.2010内蒙呼和浩特计算:101(2010)2cos6022π-⎛⎫--+︒ ⎪⎝⎭.答案解:原式=1-2+1-2 2 =287.2010内蒙赤峰计算:02)23(22)21(45sin 42--+----o答案解:原式=12242242-+-⨯- =-3 88.2010湖北黄石计算:2-32+3+()20101-()02π--121-⎪⎭⎫ ⎝⎛ 答案。
2010年云南省文山中考数学试题及答案

2010年文山州高中(中专)招生统一考试数 学(全卷三个大题,共23个小题,共6页;满分120分,考试用时120分钟) 注意事项:1. 本卷为试题卷,考生必须在答题卷上解题作答,答案书写在答题卷相应位置上,在试题卷、草稿纸上作答无效.2. 考试结束后,请将试题卷和答题卷一并交回.一、选择题(本大题共7小题,每小题只有一个正确先项,每小题3分,满分21分) 1.下列结论错误的是A2= B.方程240x -=的解为2x = C.22()()a b a b a b +-=- D.22x y xy += 2.下列图形是轴对称图形的是3.下列运算正确的是A .235x x x =· B.222()a b a b +=+ C.235()a a = D.235a a a +=4.下列事件中是必然事件的是A . 一个直角三角形的两个锐角分别是40°和60° B.抛掷一枚硬币,落地后正面朝上 C.当x 是实数时,20x ≥D.长为5cm 、5cm 、11cm 的三条线段能围成一个三角形 5.某物体的三视图如图1所示,那么该物体的形状是 A .圆柱 B.球 C.正方体 D.长方体6.如图2, AB CD ∥,EF AB ⊥于E ,EF 交CD 于F ,已知230∠=°,则1∠是A. B. C.D.图1图2A .20° B.60° C.30° D.45°7.二次函数2y ax bx c =++的图象如图3所示,则下列结论正确的是 A .200040a b c b ac <<>->,,, B.200040a b c b ac ><>-<,,, C.200040a b c b ac <><->,,, D.200040a b c b ac <>>->,,,二、填空题(本大题共8小题,每小题3分,满分24分) 8.3的相反数是__________. 9.计算:0(3)1-+=__________. 10.分解因式:234a b ab -=__________.11.如图4,上海世博会的中国馆建筑外观以“东方之冠,鼎盛中华,天下粮仓,富庶百姓”为构思主题,建筑面积4.6457万平方米,保留两个有效数字是__________万平方米. 12.不等式1302x -≤的解集为_________.13.如图5,O ⊙的弦8AB =,M 是AB 的中点,且OM 为3,则O ⊙的半径为_________. 14.如果两个相似三角形的一组对应边分别为3cm 和5cm ,且较小三角形的周长为15cm ,则较大三角形的周长为__________cm .15.某种火箭被竖直向上发射时,它的高度(m)h 与时间(s )t 的关系可以用公式2515010h t t =-++表示.经过________s ,火箭达到它的最高点.三、解答题(本大题共8小题,满分75分)16.(7分)先化简再求值:239242x x x x --÷--,其中5x =-.图3图4 图517.(8分)如图6,ABCD 的两条对角线AC 、BD 相交于点O . (1) 图中有哪些三角形是全等的?(2) 选出其中一对全等三角形进行证明.18.(8分)水是生命之源,水是希望之源,珍惜每一滴水,科学用水,有效节水,就能播种希望.某居民小区开展节约用水活动,3月份各户用水量均比2月份有所下降,其中的20(1) 节水量众数是多少立方米?(2) 该小区3月份比2月份共节约用水多少立方米? (3) 该小区3月份平均每户节约用水多少立方米? 19.(9分)全球变暖,气候开始恶化,中国政府为了对全球气候变暖负责任,积极推进节能减排,在全国范围内从2008年起,三年内每年推广5000万只节能灯.居民购买节能灯,国家补贴50%购灯费.某县今年推广财政补贴节能灯时,李阿姨买了4个8W 和3个24W 的节能灯,一共用了29元,王叔叔买了2个8W 和2个24W 的节能灯,一共用了17元. 求:(1)该县财政补贴50%后,8W 、24W 节能灯的价格各是多少元? (2)2009年我省已推广通过财政补贴节能灯850万只,预计我省一年可节约电费2.3亿元左右,减排二氧化碳43.5万吨左右,请你估算一下全国一年大约可节约电费多少亿元?大约减排二氧化碳多少万吨?(结果精确到0.1)图620.(8分)小颖为学校联欢会设计了一个“配紫色”的游戏;下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形,游戏者同时转动两个转盘,如果转盘A 转出了红色,转盘B 转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色. (1) 利用树状图或列表的方法表示出游戏所有可能出现的结果; (2) 游戏者获胜的概率是多少?21.(10分)云南2009年秋季以来遭遇百年一遇的全省性特大旱灾,部分坝塘干涸,小河、小溪断流,更为严重的情况是有的水库已经见底,全省库塘蓄水急剧减少,为确保城乡居民生活用水,有关部门需要对某水库的现存水量进行统计,以下是技术员在测量时的一些数据:水库大坝的横截面是梯形ABCD (如图7所示),AD BC ∥,EF 为水面,点E 在DC 上,测得背水坡AB 的长为18米,倾角30B ∠=°,迎水坡CD 上线段DE 的长为8米,120ADC ∠=°.(1) 请你帮技术员算出水的深度(精确到0.011.732);(2) 就水的深度而言,平均每天水位下降必须控制在多少米以内,才能保证现有水量至少能使用20天?(精确到0.01米)A 盘B 盘图722.(11分)在如图8所示的方格图中,每个小正方形的顶点称为“格点”,且每个小正方形的边长均为1个长度单位,以格点为顶点的图形叫做“格点图形”,根据图形解决下列问题:(1) 图中格点A B C '''△是由格点ABC △通过怎样变换得到的?(2) 如果建立直角坐标系后,点A 的坐标为(5-,2),点B 的坐标为(50)-,,请求出过A 点的正比例函数的解析式,并写出图中格点DEF △各顶点的坐标.23.(14分)如图9,已知直线l 的解析式为6y x =-+,它与x 轴、y 轴分别相交于A 、B 两点,平行于直线l 的直线n 从原点O 出发,沿x 轴正方向以每秒1个单位长度的速度运动,运动时间为t 秒,运动过程中始终保持n l ∥,直线n 与x 轴,y 轴分别相交于C 、D 两点,线段CD 的中点为P ,以P 为圆心,以CD 为直径在CD 上方作半圆,半圆面积为S ,当直线n 与直线l 重合时,运动结束. (1) 求A 、B 两点的坐标;(2) 求S 与t 的函数关系式及自变量t 的取值范围; (3) 直线n 在运动过程中,①当t 为何值时,半圆与直线l 相切? ②是否存在这样的t 值,使得半圆面积12ABCD S S =梯形?若存在,求出t 值,若不存在,说明理由.图8图9(1)图9(2)备用图2010年文山州中考数学答案一、选择题:1.D 2.B 3.A 4.C 5.D 6.B 7.D 二、填空题:8.3- 9.2 10.(34)ab a - 11.4.6 12.6x ≤ 13.5 14.25 15.15 三、解答题:16.解:239242x x x x --÷--=232249x x x x ----·322(2)(3)(3)x x x x x --=-+-·12(3)x =+ ···································································································· 5分当5x =-时,原式112(53)4==--+ ································································· 7分17.解:(1)AOB COD △≌△、AOD COB △≌△、 ABD CDB △≌△、ADC CBA △≌△ ························································································· 4分 (2)以AOB COD △≌△为例证明, 四边形ABCD 是平行四边形, OA OC OB OD ==,. 在AOB △和COD △中,OA OC AOB COD OB OD =⎧⎪∠=∠⎨⎪=⎩,,. AOB COD ∴△≌△.······················································································ 8分 18.解:(1)节水量的众数是2.5立方米. ························································· 2分 (2)该小区3月份比2月份共节约用水:220 2.5120360520⨯+⨯+⨯=(立方米). ······················································· 5分 (3)该小区3月份平均每户节约用水:220 2.51203602012060x ⨯+⨯+⨯=++ 2.6=(立方米). ·················································· 8分 19.解:(1)设8W 节能灯的价格为x 元,24W 节能灯的价格为y 元. ···················· 1分则43292217x y x y +=⎧⎨+=⎩, ①. ②·················································································· 2分解之 3.55x y =⎧⎨=⎩,.································································································ 4分答:该县财政补贴50%后,8W 节能灯的价格为3.5元,24W 节能灯的价格为5元. ··················································································································· 5分 (2)全国一年大约可节约电费:2.3500013.5850⨯≈(亿元) ································· 7分 大约减排二氧化碳:43.55000255.9850⨯≈(万吨) ·············································· 9分 20.解:(1)用树状图表示:··················································································································· 4分 所有可能结果:(红、黄),(红、绿),(红、蓝),(白、黄),(白、绿),(白、蓝)····· 6分(2)P (获胜)=6. ···················································································· 8分 21.解:分别过A 、D 作AM BC ⊥于M 、DN BC ⊥于N , ····························· 1分 在Rt ABM △中, 30B ∠=°,192AM AB ∴==.AD BC AM BC DN BC ⊥⊥∥,,,9AM DN ∴==. ························································································ 2分 DN BC ⊥, DN AD ∴⊥, 90ADN ∴∠=°.1209030CDN ADC ADN ∠=∠-∠=-=°°°. 延长FE 交DN 于H .在Rt DHE △中,cos HDEDH DE∠=,cos308DH=°,8DH ∴== ················································································· 6分994 1.732 2.07HN DN DH ∴=-=-=-⨯≈.(米) ································· 8分(2)2.070.10350.1020=≈(米). ·································································· 9分 答:平均每天水位下降必须控制在0.10米以内,才能保证现有水量至少能使用20天.················································································································· 10分 22.解:(1)格点A B C '''△是由格点ABC △先绕点B 逆时针旋转90°,然后向右平移13个长度单位(或格)得到的. ·············································································· 4分 (注:先平移后旋转也行)(2)设过A 点的正比例函数解析式为y kx =, 将(52)A -,代入上式得25k =-,25k =-.∴过A 点的正比例函数的解析式为25y x =-. ····················································· 8分DEF △各顶点的坐标为:(24)(08)(77)D E F ---,,,,,. ·································································· 11分 23.解:(1)6y x =-+,令0y =,得06x =-+,6x =,(60)A ∴,. 令0x =,得6y =,(06)B ∴,. ······································································· 2分(2)6OA OB ==,AOB ∴△是等腰直角三角形. n l ∥,45CDO BAO ∴∠=∠=°, COD ∴△为等腰直角三角形, OD OC t ∴==.CD ==.12PD CD ∴==,222111πππ224S PD t ⎫===⎪⎪⎝⎭·,21π(06)4S t t ∴=<≤. ················································································· 8分 (3)①分别过D 、P 作DE AB ⊥于E 、PF AB ⊥于F .6AD OA OD t =-=-,在Rt ADE △中,sin DEEAD AD∠=, (6)2DE t =-·,)PF DE t ∴==-. 当PF PD =时,半圆与l 相切.即)22t -=, .当3t =时,半圆与直线l 相切. ······································································ 11分②存在.21116618222AOB COD ABCD S S S t t t =-=⨯⨯-⨯=-△△梯形·.21π4S t =. 若12ABCD S S =梯形,则22111π18422t t ⎛⎫=- ⎪⎝⎭,2(π1)36t +=,2361t π=+,6t ==<.∴存在t =,使得12ABCD S S =梯形. ······················································· 14分。
2010年全国中考数学试题汇编《代数式》
2010年全国中考数学试题汇编《代数式》(05)填空题121.(2010•眉山)如图,将第一个图(图①)所示的正三角形连接各边中点进行分割,得到第二个图(图②);再将第二个图中最中间的小正三角形按同样的方式进行分割,得到第三个图(图③);再将第三个图中最中间的小正三角形按同样的方式进行分割,…,则得到的第五个图中,共有_________个正三角形.122.(2010•柳州)2010年广州亚运会吉祥物取名“乐羊羊”,图中各图是按照一定规律排列的羊的组图,图①有1只羊,图②有3只羊,…,则图⑩有_________只羊.123.(2010•连云港)如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为_________,再分别取A1C、B1C的中点A2、B2,A2C、B2C的中点A3、B3,依次取下去….利用这一图形,能直观地计算出+++…+=_________.124.(2010•荆州)用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数是_________.125.(2010•吉林)用正三角形、正四边形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案中正三角形的个数都比上一个图案中正三角形的个数多4个,则第n个图案中正三角形的个数为_________(用含n的代数式表示).127.(2010•衡阳)如图是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,…,第n(n是正整数)个图案中由_________个基础图形组成.128.(2010•哈尔滨)观察下列图形:它们是按一定规律排列的,依照此规律,第9个图形中共有_________个★.129.(2010•恩施州)如图,有一个形如六边形的点阵,它的中心是一个点,作为第一层,第二层每边有两个点,第三层每边有三个点,依此类推,如果n层六边形点阵的总点数为331,则n等于_________.130.(2010•鄂尔多斯)如图,用小棒摆下面的图形,图形(1)需要3根小棒,图形(2)需要7根小棒,…照这样的规律继续摆下去,第n个图形需要_________根小棒(用含n的代数式表示).131.(2010•东营)观察下表,回答问题,第_________个图形中“△”的个数是“○”的个数的5倍.132.(2010•德州)电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为P n(n为正整数),则点P2009与点P2010之间的距离为_________.133.(2010•楚雄州)如图,用火柴棍摆出一列正方形图案,若按这种方式摆下去,摆出第n个图案用_________根火柴棍(用含n的代数式表示).134.(2010•崇左)下列每个形如四边形的图案,都是由若干个圆点按照一定规律组成的.当每条边上有n(n≥2)个圆点时(包括顶点),图案的圆点数为S n,那么,按此规律S n与n的函数关系式为S n=_________.135.(2010•常州)如图,圆圈内分别标有:0,1,2,3,4,…,11这12个数字.电子跳蚤每跳一次,可以从一个圆圈跳到相邻的圆圈,现在,一只电子跳蚤从标有数字“0”的圆圈开始,按逆时针方向跳了2010次后,落在一个圆圈中,该圆圈所标的数字是_________.136.(2008•陕西)搭建如图①的单顶帐篷需要17根钢管,这样的帐篷按图②、图③的方式串起来搭建,则串7顶这样的帐篷需要_________根钢管.137.(2010•本溪)一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分(如图所示),则这串珠子被盒子遮住的部分有_________颗.解答题138.(2010•济宁)观察下面的变形规律:=1﹣;=﹣;=﹣;…解答下面的问题:(1)若n为正整数,请你猜想=_________;(2)证明你猜想的结论;(3)求和:+++…+.139.(2010•东莞)阅读下列材料:1×2=(1×2×3﹣0×1×2),2×3=(2×3×4﹣1×2×3),3×4=(3×4×5﹣2×3×4),由以上三个等式相加,可得:1×2+2×3+3×4=×3×4×5=20.读完以上材料,请你计算下列各题:(1)1×2+2×3+3×4+…+10×11(写出过程);(2)1×2+2×3+3×4+…+n×(n+1)=_________;(3)1×2×3+2×3×4+3×4×5+…+7×8×9=_________.140.(2010•杭州)已知直四棱柱的底面是边长为a的正方形,高为h,体积为V,表面积等于S.(1)当a=2,h=3时,分别求V和S;(2)当V=12,S=32时,求+的值.141.(2010•株洲)(1)计算:(﹣2)2+tan45°+20100(2)在2x2y,﹣2xy2,3x2y,﹣xy四个代数式中,找出两个同类项,并合并这两个同类项.2010年全国中考数学试题汇编《代数式》(05)参考答案与试题解析填空题121.(2010•眉山)如图,将第一个图(图①)所示的正三角形连接各边中点进行分割,得到第二个图(图②);再将第二个图中最中间的小正三角形按同样的方式进行分割,得到第三个图(图③);再将第三个图中最中间的小正三角形按同样的方式进行分割,…,则得到的第五个图中,共有17个正三角形.122.(2010•柳州)2010年广州亚运会吉祥物取名“乐羊羊”,图中各图是按照一定规律排列的羊的组图,图①有1只羊,图②有3只羊,…,则图⑩有55只羊.123.(2010•连云港)如图,△ABC的面积为1,分别取AC、BC两边的中点A1、B1,则四边形A1ABB1的面积为,再分别取A1C、B1C的中点A2、B2,A2C、B2C的中点A3、B3,依次取下去….利用这一图形,能直观地计算出+++…+=1﹣.×;﹣.=++=﹣(﹣)﹣故答案为:.124.(2010•荆州)用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数是3n+2.125.(2010•吉林)用正三角形、正四边形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案中正三角形的个数都比上一个图案中正三角形的个数多4个,则第n个图案中正三角形的个数为4n+2(用含n 的代数式表示).126.(2010•牡丹江)观察下表,请推测第5个图形有45根火柴棍.根.127.(2010•衡阳)如图是一组有规律的图案,第1个图案由4个基础图形组成,第2个图案由7个基础图形组成,…,第n(n是正整数)个图案中由(3n+1)个基础图形组成.128.(2010•哈尔滨)观察下列图形:它们是按一定规律排列的,依照此规律,第9个图形中共有28个★.129.(2010•恩施州)如图,有一个形如六边形的点阵,它的中心是一个点,作为第一层,第二层每边有两个点,第三层每边有三个点,依此类推,如果n层六边形点阵的总点数为331,则n等于11.×130.(2010•鄂尔多斯)如图,用小棒摆下面的图形,图形(1)需要3根小棒,图形(2)需要7根小棒,…照这样的规律继续摆下去,第n个图形需要4n﹣1根小棒(用含n的代数式表示).131.(2010•东营)观察下表,回答问题,第20个图形中“△”的个数是“○”的个数的5倍.132.(2010•德州)电子跳蚤游戏盘是如图所示的△ABC,AB=AC=BC=6.如果跳蚤开始时在BC边的P0处,BP0=2.跳蚤第一步从P0跳到AC边的P1(第1次落点)处,且CP1=CP0;第二步从P1跳到AB边的P2(第2次落点)处,且AP2=AP1;第三步从P2跳到BC边的P3(第3次落点)处,且BP3=BP2;…;跳蚤按照上述规则一直跳下去,第n次落点为P n(n为正整数),则点P2009与点P2010之间的距离为2.133.(2010•楚雄州)如图,用火柴棍摆出一列正方形图案,若按这种方式摆下去,摆出第n个图案用2n(n+1)或4(1+2+3+…n)根火柴棍(用含n的代数式表示).×=2n134.(2010•崇左)下列每个形如四边形的图案,都是由若干个圆点按照一定规律组成的.当每条边上有n(n≥2)个圆点时(包括顶点),图案的圆点数为S n,那么,按此规律S n与n的函数关系式为S n=4(n﹣1).135.(2010•常州)如图,圆圈内分别标有:0,1,2,3,4,…,11这12个数字.电子跳蚤每跳一次,可以从一个圆圈跳到相邻的圆圈,现在,一只电子跳蚤从标有数字“0”的圆圈开始,按逆时针方向跳了2010次后,落在一个圆圈中,该圆圈所标的数字是6.136.(2008•陕西)搭建如图①的单顶帐篷需要17根钢管,这样的帐篷按图②、图③的方式串起来搭建,则串7顶这样的帐篷需要83根钢管.137.(2010•本溪)一串有黑有白,其排列有一定规律的珠子,被盒子遮住一部分(如图所示),则这串珠子被盒子遮住的部分有27颗.解答题138.(2010•济宁)观察下面的变形规律:=1﹣;=﹣;=﹣;…解答下面的问题:(1)若n为正整数,请你猜想=;(2)证明你猜想的结论;(3)求和:+++…+.)解:=﹣﹣==+﹣+﹣+139.(2010•东莞)阅读下列材料:1×2=(1×2×3﹣0×1×2),2×3=(2×3×4﹣1×2×3),3×4=(3×4×5﹣2×3×4),由以上三个等式相加,可得:1×2+2×3+3×4=×3×4×5=20.读完以上材料,请你计算下列各题:(1)1×2+2×3+3×4+…+10×11(写出过程);(2)1×2+2×3+3×4+…+n×(n+1)=[n×(n+1)×(n+2)];(3)1×2×3+2×3×4+3×4×5+…+7×8×9=1260.[a2=((11=(+(++(+[n((((((+(+(140.(2010•杭州)已知直四棱柱的底面是边长为a的正方形,高为h,体积为V,表面积等于S.(1)当a=2,h=3时,分别求V和S;(2)当V=12,S=32时,求+的值.h==∴==.141.(2010•株洲)(1)计算:(﹣2)2+tan45°+20100(2)在2x2y,﹣2xy2,3x2y,﹣xy四个代数式中,找出两个同类项,并合并这两个同类项.。
初三数学升中考最后冲刺:应用题训练(含答案)

初三数学升中考最后冲刺:应用题训练(含答案)应用题训练1. (2009 山西省太原市) 某公司计划生产甲、乙两种产品共20件,其总产值w(万元)满足:1150<w<1200,相关数据如下表.为此,公司应怎样设计这两种产品的生产方案.产品名称每件产品的产值(万元)甲 45乙 752. (2009 新疆乌鲁木齐) 有一批图形计算器,原售价为每台800元,在甲、乙两家公司销售.甲公司用如下方法促销:买一台单价为780元,买两台每台都为760元.依此类推,即每多买一台则所买各台单价均再减20元,但最低不能低于每台440元;乙公司一律按原售价的75%促销.某单位需购买一批图形计算器:(1)若此单位需购买6台图形计算器,应去哪家公司购买花费较少?(2)若此单位恰好花费7 500元,在同一家公司购买了一定数量的图形计算器,请问是在哪家公司购买的,数量是多少?3. (2010 福建省福州市) 郑老师想为希望小学四年(3)班的同学购买学习用品,了解到某商店每个书包价格比每本词典多8元,用124元恰好可以买到3个书包和2本词典.(1)每个书包和每本词典的价格各是多少元?(2)郑老师计划用1000元为全班40位学生每人购买一件学习用品(一个书包或一本词典)后,余下不少于100元且不超过120元的钱购买体育用品.共有哪几种购买书包和词典的方案?4. (2010 云南省楚雄州市) 今年四月份,李大叔收获洋葱30吨,黄瓜13吨,现计划租用甲、乙两种货车共10辆将这两种蔬菜全部运往外地销售,已知一辆甲种货车可装洋葱4吨和黄瓜1吨;一辆乙种货车可装洋葱和黄瓜各2吨.(1)李大叔安排甲、乙两种货车时有几种方案?请你帮助设计出来;(2)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1300元,请帮李大叔算一算应选择哪种方案,才能使运费最少?最少运费是多少元?5. (2010 广东省茂名市) 已知一只纸箱中装有除颜色外完全相同的红色、黄色、蓝色乒乓球共100个.从纸箱中任意摸出一球,摸到红色球、黄色球的概率分别是0.2、0.3.(1)试求出纸箱中蓝色球的个数;(3分)(2)假设向纸箱中再放进红色球x个,这时从纸箱中任意取出一个球是红色球的概率为0.5,试求x的值.(4分)6. (2010 山东省济南市) 如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求该矩形草坪BC边的长. 16米A D草坪 B C7. (2010 河南省) 为鼓励学生参加体育锻炼,学校计划拿出不超过1 600元的资金再购买一批篮球和排球.已知篮球和∶2,单价和为80元.排球的单价比为3(1)篮球和排球的单价分别是多少元?(2)若要求购买的篮球和排球的总数量是36个,且购买的篮球数量多于25个,有哪几种购买方案?8. (2010 山东省莱芜市) 为打造“书香校园”,某学校计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.(1)问符合题意的组建方案有几种?请你帮学校设计出来;(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明在(1)中哪种方案费用最低?最低费用是多少元?9. (2010 江苏省南京市) 某批发商以每件50元的价格购进800件T恤.第一个月以单价80元销售,售出了200件;第二个月如果单价不变,预计仍可售出200件,批发商为增加销售量,决定降价销售,根据市场调查,单价每降低1元,可多售出10件,但最低单价应高于购进的价格;第二个月结束后,批发商将对剩余的T恤一次性清仓销售,清仓时单价为40元.设第二个月单价降低x元.(1)填表(不需化简):(2)如果批发商希望通过销售这批T恤获利9 000元,那时间第一个月第二个月清仓时么第二个月的单价应是多少元?单价(元) 80 40销售量(件) 20010. (2010 山东省临沂市) 为落实素质教育要求,促进学生全面发展,我市某中学2009年投资11万元新增一批电脑,计划以后每年以相同的增长率进行投资,2011年投资18.59万元. (1)求该学校为新增电脑投资的年平均增长率;(2)从2009年到2011年,该中学三年为新增电脑共投资多少万元?11. (2010 山东省青岛市) 某学校组织八年级学生参加社会实践活动,若单独租用35座客车若干辆,则刚好坐满;若单独租用55座客车,则可以少租一辆,且余45个空座位.(1)求该校八年级学生参加社会实践活动的人数;(2)已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.根据租车资金不超过1500元的预算,学校决定同时租用这两种客车共4辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金.12. (2010 山东省泰安市) 某商店经销一种泰山旅游纪念品,4月份的营业额为2000元,为扩大销售量,5月份该商店对这种纪念品打9折销售,结果销售量增加20件,营业额增加700元.(1)求该种纪念品4月份的销售价格;(2)若4月份销售这种纪念品获利800元,5月份销售这种纪念品获利多少元?13. (2010 山东省威海市) 某市从今年1月1日起调整居民用天燃气价格,每立方米天燃气价格上涨25%.小颖家去年12月份的燃气费是96元.今年小颖家将天燃气热水器换成了太阳能热水器,5月份的用气量比去年12月份少10m3,5月份的燃气费是90元.求该市今年居民用气的价格.14. (2010 广西贺州市) “玉树”地震后,某工厂一号车间接到紧急任务,急需为地震灾区生产15000顶帐篷,如果按照一号车间现有的人数和每个工人的生产速度(每个工人的生产速度一样),15天才能完成任务.生产两天后,由于情况紧急,厂领导决定从二号车间调来60名工人一起加入生产,调整后每个工人的生产工作效率都提高了40% .结果提前8天完成任务.求原来一号车间有多少名工人?15. (2010 江苏省宿迁市) 某花农培育甲种花木2株,乙种花木3株,共需成本1700元;培育甲种花木3株,乙种花木1株,共需成本1500元.(1)求甲、乙两和种花木每株成本分别为多少元;(2)据市场调研,1株甲种花木的售价为760元,1株乙种花木的售价为540元.该花农决定在成本不超过30000元的前提下培育甲乙两种花木,若培育乙种花木的株数是甲种花木的3倍还多10株,那么要使总利润不少于21600元,花农有哪几种具体的培育方案?16. (2010 广西梧州市) 2010年的世界杯足球赛在南非举行. 为了满足球迷的需要,某体育服装店老板计划到服装批发市场选购A、B两种品牌的服装. 据市场调查得知,销售一件A品牌服装可获利润25元,销售一件B品牌服装可获利润32元. 根据市场需要,该店老板购进A种品牌服装的数量比购进B种品牌服装的数量的2倍还多4件,且A种品牌服装最多可购进48件. 若服装全部售出后,老板可获得的利润不少于1740元. 请你分析这位老板可能有哪些选购方案?17. (2010 广西桂林市) 某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.(1)该校初三年级共有多少人参加春游?(2)请你帮该校设计一种最省钱的租车方案....18. (2010 浙江省绍兴市) 某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5 000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5 000元.(1)当每间商铺的年租金定为13万元时,能租出多少间?(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为275万元?19. (2010 湖北省咸宁市) 随着人们节能意识的增强,节能产品的销售量逐年增加.某商场高效节能灯的年销售量2008年为5万只,预计2010年将达到7.2万只.求该商场2008年到2010年高效节能灯年销售量的平均增长率.20. (2010 湖北省襄樊市) 如图,是上海世博园内一个矩形花园,花园的长为100米,宽为50米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.已知种植花草部分的面积为3 600米2,那么矩形花园各角处的正方形观光休息亭的边长为多少米?第1题答案.解:设计划生产甲产品x件,则生产乙产品?20?x?件,根据题意,得? 解得10?x???45x?75?20?x??1150,45x?7520?x?1200.????35. 3此时,20?x?9(件). x为整数,∴x?11.答:公司应安排生产甲产品11件,乙产品9件.第2题答案.解:(1)在甲公司购买6台图形计算器需要用6?(800?20?6)?4080(元);在乙公司购买需要用.应去乙公司购买; 75%?800?6?3600(元)?4080(元)(2)设该单位买x台,若在甲公司购买则需要花费x(800?20x)元;若在乙公司购买则需要花费75%?800x?600x元;①若该单位是在甲公司花费7 500元购买的图形计算器,则有x(800?20x)?7500,解之得x?15,x?25.当x?15时,每台单价为800?20?15?500?440,符合题意,当x?25时,每台单价为800?20?25?300?440,不符合题意,舍去.②若该单位是在乙公司花费7 500元购买的图形计算器,则有600x?7500,解之得x?12.5,不符合题意,舍去.故该单位是在甲公司购买的图形计算器,买了15台.第3题答案.(1)解:设每个书包的价格为x元,则每本词典的价格为(x?8)元. 根据题意得:3x?2(x?8)?124 解得:x?28 0 ∴ x?8?2.答:每个书包的价格为28元,每本词典的价格为20元.(2)解:设购买书包y个,则购买词典(40?y)本. 根据题意得:?1000??28y?20(40?y)?≥100,? ?1000?28y?20(40?y)≤120.????解得 10≤y ≤12.5 .因为y取整数,所以y的值为10或11或12.所以有三种购买方案分别是:①书包10个,词典30本;②书包11个,词典29本;③书包12个,词典28本.第4题答案.解:(1)设李大叔安排x辆甲种货车,乙种货车有(10-x)辆,则有??4x?2(10?x)?30?x?2(10?x)?13解之得:5≤x≤7因为x应取正整数.所以x取5,6,7方案如下:①安排5辆甲种货车,5辆乙种货车;②安排6辆甲种货车,4辆乙种货车;③安排7辆甲种货车,3辆乙种货车.(2)方案①:5×2000+5×1300=16500(元)方案②:6×2000+4×1300=17200(元)方案③:7×2000+3×1300=17900(元)所以,李大叔应选择方案①才能使运费最少,最少运费是16500元.第5题答案.解:(1)由已知得纸箱中蓝色球的个数为:100?(1?0.2?0.3)?50(个) (2) 方法一:根据题意得:20?x?0.5,100?x解得:x?60.检验x?60,100?x?0,∴x?60为原方程的解.答略.方法二:由已知得红色球20个、黄色球30个,蓝色球50个,为使任意取出一个球是红色球的概率为0.5,所以纸箱中红色球的个数等于黄色球与蓝色球个数之和,得:x+20=30+50,解得:x?60.答略.第6题答案.解:设BC边的长为x米,根据题意得 x32?x?120, 2解得:x1?12,x2?20,∵20>16,∴x2?20不合题意,舍去,答:该矩形草坪BC边的长为12米.第7题答案.(1)设篮球的单价为x元,则排球的单价为8分2x元.依题意得 3x?2x?80. 32x?32. 3解得x?48.?即篮球和排球的单价分别是48元、32元.(2)设购买的篮球数量为n个,则购买的排球数量为(36?n)个.?n?25, ??(36?n)≤1 600.?48n?32解得25?n≤28.9,8.所以共有三种购买方案.而n为整数,所以其取值为26,27,28,对应的36?n的值为10,方案一:购买篮球26个,排球10个;方案二:购买篮球27个,排球9个;方案三:购买篮球28个,排球8个.第8题答案. 解:(1)设组建中型图书角x个,则组建小型图书角为(30-x)个.由题意得?(30?x)?1900?80x?30(30?x)?1620?50x?60解这个不等式组得18≤x≤20.由于x只能取整数,∴x的取值是18,19,20.当x=18时,30-x=12;当x=19时,30-x=11;当x=20时,30-x=10.故有三种组建方案:方案一,组建中型图书角18个,小型图书角12个;方案二,组建中型图书角19个,小型图书角11个;方案三,组建中型图书角20个,小型图书角10个.(2)方法一:由于组建一个中型图书角的费用大于组建一个小型图书角的费用,因此组建中型图书角的数量越少,费用就越低,故方案一费用最低,最低费用是860×18+570×12=22320(元).方法二:①方案一的费用是:860×18+570×12=22320(元);②方案二的费用是:860×19+570×11=22610(元);③方案三的费用是:860×20+570×10=22900(元).故方案一费用最低,最低费用是22320元.第9题答案. 解:(1)80-x 200+10x 800-200-(200+10x) (2)根据题意,得80×200+(80-x)(200+10x)+40[800-200-(200+10x)]-50×800=9 000.整理,得 x2-20x+100=0.解这个方程,得 x1=x2=10.当x=10时,80-x=70>50.答:第二个月的单价应是70元.第10题答案.解:(1)设该校为新增电脑投资的年平均增长率为x 根据题意,得一元二次方程11?1?x??18.59.解这个方程,得x1?0.3,x2??2.3(不合题意,舍去). 答:该学校为新增电脑投资的年平均增长率为30%. (2)11?11??1?0.3??18.59?43.89(万元). 答:从2009年到2010年,该中学三年为新增电脑共投资43.89万元. 第11题答案.解:(1)设单独租用35座客车需x辆,由题意得:35x?55(x?1)?45,解得:x?5.∴35x?35?5?175(人).答:该校八年级参加社会实践活动的人数为175人.(2)设租35座客车y辆,则租55座客车(4?y)辆,由题意得:?35y?55(4?y)≥175, ?320y?400(4?y)≤1500?211解这个不等式组,得1≤y≤2.44∵y取正整数,∴y = 2.∴4-y = 4-2 = 2.∴320×2+400×2 = 1440(元).所以本次社会实践活动所需车辆的租金为1440元.第12题答案. 解:(1)设该种纪念品4月份的销售价格为x元,根据题意得20002000?700??20 x0.9x解之得x?50.经检验x?50是所得方程的解.∴该种纪念品4月份的销售价格是50元.(2)由(1)知4月份销售件数为∴4月份每件盈利2000?40件, 50800?20元. 405月份销售件数为40?20?60件,且每件售价为50?0.9?45,每件比4月份少盈利5元,为15元,所以5月份销售这种纪念品获利60?15?900元.第13题答案.解:设该市去年居民用气的价格为x元/ m3,则今年的价格为(1+25%)x元/ m3. 9690??10.根据题意,得x(1?25%)x解这个方程,得x=2.4.经检验,x=2.4是所列方程的根. 2.4×(1+25%)=3 (元).所以,该市今年居民用气的价格为3元/ m3.第14题答案.解:设原来一号车间有x名工人,依题意得:15000?21500015?(1?40%)? 15x(15?2?8)(x?60)15000?化简得15000?1.413000 ?15x5(x?60)解之得:x=70 经检验:x=70是原方程的根.答:原来一号车间有70名工人.(注:用其它方法解答正确的均给予相应的分值.)第15题答案. (1)解:(1)设甲、乙两种花木的成本价分别为x元和y元.由题意得:??2x?3y?1700?3x?y?1500?x?400解得:?y?300?(2)设种植甲种花木为a株,则种植乙种花木为(3a+10)株.则有:?解得:400a?300(3a?10)?30000??(760?400)a?(540?300)(3a?10)?21600160270?a? 913由于a为整数,∴a可取18或19或20,所以有三种具体方案:①种植甲种花木18株,种植乙种花木3a+10=64株;②种植甲种花木19株,种植乙种花木3a+10=67株;③种植甲种花木20株,种植乙种花木3a+10=70株. 第16题答案.解:设选购B种服装x件,则选购A种服装为(2x+4)件,由题意得 ??25(2x?4)?32x?1740?2x?4?48?x?22?x?20解之得?∴20≤x≤22∵x 为正整数∴x1=20,x2=21,x3=22. ∴当x1=20时,2x?4=2×20+4=44,当x2=21时,2x?4=2×21+4=46,当x3=22时,2x?4=2×22+4=48. ∴老板有三种选购方案:购进B种品牌服装20件,购进A种品牌服装44件;购进B种品牌服装21件,购进A种品牌服装46件;购进B种品牌服装22件,购进A种品牌服装48件…10分第17题答案.解:(1)设租36座的车x辆.据题意得:??36x?42(x?1)?36x?42(x?2)?30解得:??x?7?x?9由题意x应取8则春游人数为:36?8=288(人).(2) 方案①:租36座车8辆的费用:8?400=3200元,方案②:租42座车7辆的费用:7?440?3080元方案③:因为42?6?36?1?288,租42座车6辆和36座车1辆的总费用:6?440?1?400?3040元所以方案③:租42座车6辆和36座车1辆最省钱.(说明:只要给出方案③就可得满分2分)第18题答案.解:(1)∵ 30 000÷5 000=6, ∴能租出24间. (2)设每间商铺的年租金增加x万元,则(30-xxx)×(10+x)-(30-)×1-×0.5=275, 0.50.50.5 2 x 2-11x+5=0,∴ x=5或0.5,∴每间商铺的年租金定为10.5万元或15万元.第19题答案.解:设年销售量的平均增长率为x,依题意得:5(1?x)2?7.2.解这个方程,得x1?0.2,x2??2.2.因为x为正数,所以x?0.2?20%.答:该商场2008年到2010年高效节能灯年销售量的平均增长率为20%.第20题答案.解:设正方形观光休息亭的边长为x米.依题意,有(100?2x)(50?2x)?3 600. 整理,得x?75x?350?0. 解得x1?5,x2?70.2x?70?50,不合题意,舍去,?x?5.答:矩形花园各角处的正方形观点休息亭的边长为5米. 7分∴老板有三种选购方案:购进B种品牌服装20件,购进A种品牌服装44件;购进B种品牌服装21件,购进A种品牌服装46件;购进B种品牌服装22件,购进A种品牌服装48件…10分第17题答案.解:(1)设租36座的车x辆.据题意得:??36x?42(x?1)?36x?42(x?2)?30解得:??x?7?x?9由题意x应取8则春游人数为:36?8=288(人).(2) 方案①:租36座车8辆的费用:8?400=3200元,方案②:租42座车7辆的费用:7?440?3080元方案③:因为42?6?36?1?288,租42座车6辆和36座车1辆的总费用:6?440?1?400?3040元所以方案③:租42座车6辆和36座车1辆最省钱.(说明:只要给出方案③就可得满分2分)第18题答案.解:(1)∵ 30 000÷5 000=6, ∴能租出24间. (2)设每间商铺的年租金增加x万元,则(30-xxx)×(10+x)-(30-)×1-×0.5=275, 0.50.50.5 2 x 2-11x+5=0,∴ x=5或0.5,∴每间商铺的年租金定为10.5万元或15万元.第19题答案.解:设年销售量的平均增长率为x,依题意得:5(1?x)2?7.2.解这个方程,得x1?0.2,x2??2.2.因为x为正数,所以x?0.2?20%.答:该商场2008年到2010年高效节能灯年销售量的平均增长率为20%.第20题答案.解:设正方形观光休息亭的边长为x米.依题意,有(100?2x)(50?2x)?3 600. 整理,得x?75x?350?0. 解得x1?5,x2?70.2x?70?50,不合题意,舍去,?x?5.答:矩形花园各角处的正方形观点休息亭的边长为5米. 7分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
楚雄州2010年高中(中专)招生统一考试数 学 试 题 卷(全卷三个大题,共24个小题,共8页;满分120分,考试用时120分钟)注意事项:1.本卷为试题卷,考生解题作答必须在答题卷上,答案书写在答题卷相应位置上,在试题卷、草稿纸上作答无效. 2.考试结束后请将试题卷和答题卷一并交回.一、选择题(本大题共8个小题,每小题只有一个正确选项,每小题3分,满分24分) 1.下列计算正确的是 A .632·a a a=B .326=÷C .2)21(1-=-D .623)(a a -=-2.如图是由四个相同的小正方体组成的立体图形,它的左视图为3.自去年入秋以来,楚雄州遭遇了百年不遇的严重旱灾.截止2010年4月19日,楚雄州共收到各级各类抗旱救灾资金108014500元,这个数据用科学记数法表示为 A .10.80145×107 B .0.1080145×109C .1.080145×109D .1.080145×1084.一元二次方程042=-x 的解是 A .21=x , 22-=x B .2-=xC .2=xD .21=x , 02=x5.已知⊙O 1和⊙O 2的半径分别为2cm 和3cm ,两圆的圆心距为5cm ,则两圆的位置关系是 A .外切 B .外离 C .相交 D .内切 6.已知等腰三角形的一个内角为70°,则另两个内角的度数是 A .55°,55° B .70°,40° C .55°,55°或70°,40° D .以上都不对 7.下列说法不正确的是 A .在选举中,人们通常最关心的数据是众数 B .掷一枚骰子,3点朝上是不确定事件A .B .C .D . 正面C .数据3,5,4,1,-2的中位数是3D .有两边对应成比例且有一个角对应相等的两个三角形一定相似8.如图,四边形OABC 是菱形,点B ,C 在以点O 为圆心的弧EF 上,且∠1=∠2, 若扇形OEF 的面积为3π,则菱形OABC 的边长为 A .23 B .2 C .3D .4二、填空题(本大题共7个小题,每小题3分,满分21分) 9.21-的倒数是 . 10.点(-2,3)在反比例函数)0(≠=k xky 的图象上,则这个反比例函数的表达式为 .11.已知一个多边形的内角和是它的外角和的2倍,则这个多边形的边数为 . 12.在函数x y -=3中,自变量x 的取值范围是 . 13.如图,在□ABCD 中,对角线AC 与BD 相交于点O ,在不添加任何辅助线和字母的情况下,请添加一个条件,使□ABCD 变为矩形,需添加的条件是 .(写出一个即可) 14.根据图中的程序,当输入x=2时,输出结果=y .15.如图,用火柴棍摆出一列正方形图案,若按这种方式摆下去,摆出第n 个图案用 根火柴棍(用含n 的代数式表示).三、解答题(本大题共9个小题,满分75分)①②③……16.(本小题6分)先化简,再求值:4212112--÷⎪⎭⎫ ⎝⎛-+m m m ,其中5-=m .17.(本小题7分)如图,点A E B D ,,,在同一直线上,DB AE =,AC DF =,AC DF ∥.请探索BC 与EF 有怎样的位置关系?并说明理由.18.(本小题7分)ABC △在平面直角坐标系中的位置如图所示. (1)作出ABC △关于x 轴对称的111A B C △,并写出点1A 的坐标; (2)作出将ABC △绕点O 顺时针方向旋转180°后的222A B C △.19.(本小题8分)小明和小华为了获得一张2010年上海世博园门票,他们各自设计了一个方案: 小明的方案是:转动如图所示的转盘,当转盘停止转动后,如果指针停在阴影区域,则小明获得门票;如果指针停在白色区域,则小华获得门票(转盘被等分成6个扇形,若指针停在边界处,则重新转动转盘).小华的方案是:有三张卡片,上面分别标有数字1,2,3,将它们背面朝上洗匀后,从中摸出一张,记录下卡片上的数字后放回,重新洗匀后再摸出一张.若摸出两张卡片上的数字之和为奇数,则小明获得门票;若摸出两张卡片上的数字之和为偶数,则小华获得门票.(1)在小明的方案中,计算小明获得门票的概率,并说明小明的方案是否公平? (2)用树状图或列表法列举小华设计方案中可能出现的所有结果,计算小华获得门票的概率,并说明小华的方案是否公平? 20.(本小题8分)如图,河流的两岸PQ 、MN 互相平行,河岸PQ 上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN 的A 处测得∠DAN = 35°,然后沿河岸走了120米到达B 处,测得∠CBN=70°.求河流的宽度CE(结果保留两个有效数字). (参考数据: sin35°≈ 0.57, cos35°≈ 0.82, tan35°≈ 0.70sin 70°≈ 0.94, cos70°≈ 0.34, tan70°≈ 2.75 )21.(本小题9分)在2009年楚雄州“火把节”房交会期间,某房地产公司对参加本次房交会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者打算购买住房面积的情况整理后,作出部分频数分布直方图和扇形统计图.根据以上信息回答下列问题:(1)根据表格可得a =_______,被调查的1000名消费者的平均年收入为万元.(2)补全频数分布直方图和扇形统计图.(3)若楚雄州现有购房打算的约有40000人,请估计购房面积在80至120平方米的大约有多少人?22.(本小题8分)已知:如图,抛物线c bx ax y ++=2与x 轴相交于两点A(1,0),B(3,0),与y 轴相交于点C (0,3). (1)求抛物线的函数关系式; (2)若点D (27,m )是抛物线c bx ax y ++=2上的一点,请求出m 的值,并求出此时△ABD 的面积.23.(本小题9分)今年四月份,李大叔收获洋葱30吨,黄瓜13吨,现计划租用甲、乙两种货车共10辆将这两种蔬菜全部运往外地销售,已知一辆甲种货车可装洋葱4吨和黄瓜1吨;一辆乙种货车可装洋葱和黄瓜各2吨.(1)李大叔安排甲、乙两种货车时有几种方案?请你帮助设计出来;(2)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1300元,请帮李大叔算一算应选择哪种方案,才能使运费最少?最少运费是多少元?24.(本小题13分)已知:如图,⊙A与y轴交于C、D两点,圆心A的坐标为(1,0),⊙A的半径为5,过点C作⊙A的切线交x轴于点B(-4,0).(1)求切线BC的解析式;(2)若点P是第一象限内⊙A上的一点,过点P作⊙A的切线与直线BC相交于点G,且∠CGP=120°,求点G的坐标;(3)向左移动⊙A(圆心A始终保持在x轴上),与直线BC交于E、F,在移动过程中是否存在点A,使△AEF是直角三角形?若存在,求出点A的坐标;若不存在,请说明理由.数学一、选择题(本大题共8个小题,每小题只有一个正确选项,每小题3分,满分24分) 1.下列计算正确的是(B ) A .632·a a a=B .326=÷ C .2)21(1-=-D .623)(a a -=-2.如图是由四个相同的小正方体组成的立体图形,它的左视图为(B )3.自去年入秋以来,楚雄州遭遇了百年不遇的严重旱灾.截止2010年4月19日,楚雄州共收到各级各类抗旱救灾资金108014500元,这个数据用科学记数法表示为(D )A .71080145.10⨯ B .9101080145.0⨯ C .910080145.1⨯ D .810080145.1⨯ 4.一元二次方程042=-x 的解是(A ) A .21=x , 22-=x B .2-=xC .2=xD .21=x , 02=x5.已知⊙O 1和⊙O 2的半径分别为2cm 和3cm ,两圆的圆心距为5cm ,则两圆的位置关系是(A ) A .外切 B .外离 C .相交 D .内切 6.已知等腰三角形的一个内角为70°,则另两个内角的度数是(C ) A .55°,55° B .70°,40° C .55°,55°或70°,40° D .以上都不对 7.下列说法不正确的是(D )A .在选举中,人们通常最关心的数据是众数B .掷一枚骰子,3点朝上是不确定事件C .数据3,5,4,1,-2的中位数是3D .有两边对应成比例且有一个角对应相等的两个三角形一定相似8.如图,四边形OABC 是菱形,点B ,C 在以点O 为圆心的弧EF 上,且∠1=∠2, 若扇形OEF 的面积为3π,则菱形OABC 的边长为(C ) A .23 B .2 C .3D .4A .B .C .D .二、填空题(本大题共7个小题,每小题3分,满分21分) 9.21-的倒数是 -2 . 10.点(-2,3)在反比例函数)0(≠=k xky 的图象上,则这个反比例函数的表达式为xy 6-=.11.已知一个多边形的内角和是它的外角和的2倍,则这个多边形的边数为 6 . 12.在函数x y -=3中,自变量x 的取值范围是3≤x .13.如图,在□ABCD 中,对角线AC 与BD 相交于点O ,在不添加任何辅助线和字母的情况下,请添加一个条件,使□ABCD 变为矩形,需添加的条件是 任意写出一个正确答案即可(如AC=BD 或∠ABC=90°) .(写出一个即可)14.根据图中的程序,当输入x=2时,输出结果=y 2 .15.如图,用火柴棍摆出一列正方形图案,若按这种方式摆下去,摆出第n 个图案用 2n(n+1)或4(1+2+3+…n ) 根火柴棍(用含n 的代数式表示).三、解答题(本大题共9个小题,满分75分)16.(本小题6分)先化简,再求值:4212112--÷⎪⎭⎫ ⎝⎛-+m m m ,其中5-=m . 解:原式=)2(2)1)(1(2122--+÷⎪⎭⎫⎝⎛-+--m m m m m m =)1)(1()2(2·21-+---m m m m m① ② ③……=12+m …………………………………………………………………………5分 当5-=m 时,原式=2115212-=+-=+m ……………………………………6分17.(本小题7分)如图,点A E B D ,,,在同一直线上,DB AE =,AC DF =,AC DF ∥.请探索BC 与EF 有怎样的位置关系?并说明理由.解:BC ∥EF. 理由如下: (1)∵AE=DB(已知)∴AE+EB=DB+BE (等式的性质) 即AB=DE…………………………………………2分又∵AC ∥DF(已知)∴∠A=∠D(两直线平行,内错角相等) …………3分在△ABC 和△DEF 中⎪⎩⎪⎨⎧∠∠(已知)=(已证)=(已证)=DF AC D A DE AB ∴△ABC ≌△DEF (SAS )…………………………5分∴∠ABC=∠DEF(全等三角形的对应角相等) ………6分 ∴BC ∥EF(内错角相等,两直线平行) ………………7分18.(本小题7分)ABC △在平面直角坐标系中的位置如图所示. (1)作出ABC △关于x 轴对称的111A B C △,并写出点1A 的坐标; (2)作出将ABC △绕点O 顺时针方向旋转180°后的222A B C △. 解:(1)如图,画出111A B C △………(3分) )3,2(1--A ……………(4分) (2) 如图,画出222A B C △ ……(7分)A19.(本小题8分)小明和小华为了获得一张2010年上海世博园门票,他们各自设计了一个方案:小明的方案是:转动如图所示的转盘,当转盘停止转动后,如果指针停在阴影区域,则小明获得门票;如果指针停在白色区域,则小华获得门票(转盘被等分成6个扇形,若指针停在边界处,则重新转动转盘).小华的方案是:有三张卡片,上面分别标有数字1,2,3,将它们背面朝上洗匀后,从中摸出一张,记录下卡片上的数字后放回,重新洗匀后再摸出一张.若摸出两张卡片上的数字之和为奇数,则小明获得门票;若摸出两张卡片上的数字之和为偶数,则小华获得门票.(1)在小明的方案中,计算小明获得门票的概率,并说明小明的方案是否公平? (2)用树状图或列表法列举小华设计方案中可能出现的所有结果,计算小华获得门票的概率,并说明小华的方案是否公平? 解:(1)小明获得门票的概率是2163 ,小明的方案是公平的,因为双方获得门票的可能性都是21…………………………………(3分)(2)或……………………………………………………………………5分小华获得门票的概率是95,小华的方案不公平,因为双方获得门票的可能性不相同. 小华获得门票的可能性是95 ,小明获得门票的可能性是94…………………8分20.(本小题8分)如图,河流的两岸PQ 、MN 互相平行,河岸PQ 上有一排小树,已知相邻两树之间的距离CD=50米,某人在河岸MN 的A 处测得∠DAN = 35°,然后沿河岸走了120米到达B 处,测得∠CBN=70°.求河流的宽度CE(结果保留两个有效数字). (参考数据: sin35°≈ 0.57, cos35°≈ 0.82, tan35°≈ 0.70sin 70°≈ 0.94, cos70°≈ 0.34, tan70°≈ 2.75 )解:过点C 作CF//DA 交AB 于点F . MN//PQ ,CF//DA∴四边形AFCD 是平行四边形 ∴AF=CD=50米,∠CFB=35°∴ FB=AB -AF=120-50=70 …3分又 ∠CBN=∠CFB+∠BCF ∴∠BCF=70°-35°=35°=∠CFB ∴BC=BF=70 ………………………………………………5分在Rt △BEC 中,开始 12 3 1 2 3 1 2 3 1 2 3数字之和:2 3 4 3 4 5 4 5 6 FCESin70°=BCCE=BC·Sin70°≈70⨯0.94 = 65.8≈66 ………………7分答:河流的宽度CE约为66米.……………………………8分21.(本小题9分)在2009年楚雄州“火把节”房交会期间,某房地产公司对参加本次房交会的消费者进行了随机问卷调查,共发放1000份调查问卷,并全部收回.根据调查问卷,将消费者年收入的情况整理后,制成表格如下:根据调查问卷,将消费者打算购买住房面积的情况整理后,作出部分频数分布直方图和扇形统计图.根据以上信息回答下列问题:(1)根据表格可得a =________,被调查的1000名消费者的平均年收入为万元.(2)补全频数分布直方图和扇形统计图.(3)若楚雄州现有购房打算的约有40000人,请估计购房面积在80至120平方米的大约有多少人?解:(1)根据表格可得 a = 200 ,被调查的1000名消费者的平均年收入为 2.39万元.……………………………………………………………………………………(3分)(2)答案如图所示………………………………………………………………(6分)(3))(24000100024036040000人=+⨯答:估计购房面积在80至120平方米的大约有24000人.……………………(9分) 22.(本小题8分)已知:如图,抛物线c bx ax y ++=2与x 轴相交于两点A(1,0),B(3,0),与y 轴相交于点C (0,3). (1)求抛物线的函数关系式; (2)若点D (27,m )是抛物线c bx ax y ++=2上的一点,请求出m 的值,并求出此时△ABD 的面积.解:(1)由已知得⎪⎩⎪⎨⎧==++=++30390c c b a c b a ………………………………3分解之得 ⎪⎩⎪⎨⎧=-==341c b a ……………………………4分∴342+-=x x y ……………………………………………………5分(2)∵),27(m D 是抛物线342+-=x x y 上的点∴45=m ……………………………………………………………6分∴4545221ABD =⨯⨯=△S …………………………………………8分23.(本小题9分)今年四月份,李大叔收获洋葱30吨,黄瓜13吨,现计划租用甲、乙两种货车共10辆将这两种蔬菜全部运往外地销售,已知一辆甲种货车可装洋葱4吨和黄瓜1吨;一辆乙种货车可装洋葱和黄瓜各2吨.(1)李大叔安排甲、乙两种货车时有几种方案?请你帮助设计出来;(2)若甲种货车每辆要付运输费2000元,乙种货车每辆要付运输费1300元,请帮李大叔算一算应选择哪种方案,才能使运费最少?最少运费是多少元?解:(1)设李大叔安排x 辆甲种货车,乙种货车有(10-x )辆,则有 ⎩⎨⎧≥-+≥-+13)10(230)10(24x x x x………………………………………………3分 解之得:5≤x ≤7………………………………………………4分因为x 应取正整数.所以x 取5,6,7………………………………5分方案如下:①安排5辆甲种货车,5辆乙种货车;②安排6辆甲种货车,4辆乙种货车;③安排7辆甲种货车,3辆乙种货车. …………………………6分(2)方案①:5×2000+5×1300=16500(元)方案②:6×2000+4×1300=17200(元) 方案③:7×2000+3×1300=17900(元)所以,李大叔应选择方案①才能使运费最少,最少运费是16500元.……………9分24.(本小题13分)已知:如图,⊙A 与y 轴交于C 、D 两点,圆心A 的坐标为(1,0),⊙A 的半径为5,过点C 作⊙A 的切线交x 轴于点B (-4,0). (1)求切线BC 的解析式;(2)若点P 是第一象限内⊙A 上的一点,过点P 作⊙A 的切线与直线BC 相交于点G ,且∠CGP=120°,求点G 的坐标;(3)向左移动⊙A (圆心A 始终保持在x 轴上),与直线BC 交于E 、F ,在移动过程中是否存在点A ,使△AEF 是直角三角形?若存在,求出点A 的坐标;若不存在,请说明理由.解:(1)如图1所示,连接AC ,则AC=5在Rt △AOC 中,AC=5 ,OA=1 ,则OC=2∴点C 的坐标为(0,2)设切线BC 的解析式为b kx y +=,它过点C (0,2),B (−4,0),则有⎩⎨⎧=+-=042b k b 解之得⎪⎩⎪⎨⎧==221b k∴221+=x y ………………………………………………4分(2)如图1所示,设点G 的坐标为(a ,c ),过点G 作GH ⊥x 轴,垂足为H 点,则OH=a , GH=c =21a + 2 ……………………………………………………5分连接AP, AG因为AC=AP , AG=AG , 所以Rt △ACG ≌Rt所以∠AGC=21×1200=600 在Rt △ACG 中 ,∠AGC= 600,AC=5 ∴Sin600=AG AC ∴AG =3152在Rt △AGH 中, AH=OH -OA=a -1 ,GH=21a + 2 2AH +2GH =2AG∴2)1(-a +2)221(+a =2)3152(解之得:1a =332 ,2a = −332(舍去) …………………………………………7分 点G 的坐标为(332,33+ 2 ) …………………………………………………8分 (3) 如图2所示,在移动过程中,存在点A ,使△AEF 为直角三角形. ………………9分要使△AEF 为直角三角形AE=AF∴∠AEF=∠AFE 900 ∴只能是∠EAF=900当圆心A 在点B 的右侧时,过点A 作 AM ⊥BC,垂足为点M.在Rt △AEF 中 ,AE=AF=5, 则EF=10, AM=21EF=2110在Rt △OBC 中,OC=2 , OB=4,则BC=25∠BOC= ∠BMA=900 ,∠OBC= ∠OBM∴△BOC ∽△BMA∴AM OC =ABBC∴AB=225 ∴OA=OB -AB=4-225 ∴点A 的坐标为(-4+225,0) ………………………………………………11分 当圆心A 在点B 的左侧时,设圆心为A ′,过点A ′作A ′M ′⊥BC 于点M ′,可得 △A ′M ′B ≌△AMB A ′B =AB =225 ∴O A ′=OB+ A ′B =4 +225 ∴点A ′的坐标为(-4-225,0) 综上所述,点A 的坐标为(-4+225,0)或(-4-225,0) ……………13分。
