分式和分式方程知识点总结及练习(供参考)
2024中考数学复习核心知识点精讲及训练—分式(含解析)

2024中考数学复习核心知识点精讲及训练—分式(含解析)1.了解分式、分式方程的概念,进一步发展符号感;2.熟练掌握分式的基本性质,会进行分式的约分、通分和加减乘除四则运算,发展学生的合情推理能力与代数恒等变形能力;3.能解决一些与分式有关的实际问题,具有一定的分析问题、解决问题的能力和应用意识;4.通过学习能获得学习代数知识的常用方法,能感受学习代数的价值。
考点1:分式的概念1.定义:一般地,如果A、B表示两个整式,并且B中含有字母,那么式子AB叫做分式.其中A叫做分子,B叫做分母.2.最简分式:分子与分母没有公因式的分式;3.分式有意义的条件:B≠0;4.分式值为0的条件:分子=0且分母≠0考点2:分式的基本性质分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变,这个性质叫做分式的基本性质,用式子表示是:A A M A A MB B M B B M⨯÷==⨯÷,(其中M是不等于零的整式).考点3:分式的运算考点4:分式化简求值(1)有括号时先算括号内的;(2)分子/分母能因式分解的先进行因式分解;(3)进行乘除法运算(4)约分;(5)进行加减运算,如果是异分母分式,需线通分,变为同分母分式后,分母不变,分子合并同类项,最终化为最简分式;(6)带入相应的数或式子求代数式的值【题型1:分式的相关概念】【典例1】(2022•怀化)代数式x,,,x2﹣,,中,属于分式的有()A.2个B.3个C.4个D.5个【答案】B【解答】解:分式有:,,,整式有:x,,x2﹣,分式有3个,故选:B.【典例2】(2023•广西)若分式有意义,则x的取值范围是()A.x≠﹣1B.x≠0C.x≠1D.x≠2【答案】A【解答】解:∵分式有意义,∴x+1≠0,解得x≠﹣1.故选:A.1.(2022•凉山州)分式有意义的条件是()A.x=﹣3B.x≠﹣3C.x≠3D.x≠0【答案】B【解答】解:由题意得:3+x≠0,∴x≠﹣3,故选:B.2.(2023•凉山州)分式的值为0,则x的值是()A.0B.﹣1C.1D.0或1【答案】A【解答】解:∵分式的值为0,∴x2﹣x=0且x﹣1≠0,解得:x=0,故选:A.【题型2:分式的性质】【典例3】(2023•兰州)计算:=()A.a﹣5B.a+5C.5D.a 【答案】D【解答】解:==a,故选:D.1.(2020•河北)若a≠b,则下列分式化简正确的是()A.=B.=C.=D.=【答案】D【解答】解:∵a≠b,∴,故选项A错误;,故选项B错误;,故选项C错误;,故选项D正确;故选:D.2.(2023•自贡)化简:=x﹣1.【答案】x﹣1.【解答】解:原式==x﹣1.故答案为:x﹣1.【题型3:分式化简】【典例4】(2023•广东)计算的结果为()A.B.C.D.【答案】C【解答】解:==.故本题选:C.1.(2023•河南)化简的结果是()A.0B.1C.a D.a﹣2【答案】B【解答】解:原式==1.故选:B.2.(2023•赤峰)化简+x﹣2的结果是()A.1B.C.D.【答案】D【解答】解:原式=+==,故选:D.【题型4:分式的化简在求值】【典例5】(2023•深圳)先化简,再求值:(+1)÷,其中x=3.【答案】,.【解答】解:原式=•=•=,当x=3时,原式==.1.(2023•辽宁)先化简,再求值:(﹣1)÷,其中x=3.【答案】见试题解答内容【解答】解:原式=(﹣)•=•=x+2,当x=3时,原式=3+2=5.2.(2023•大庆)先化简,再求值:,其中x=1.【答案】见试题解答内容【解答】解:原式=﹣+====,当x=1时,原式==.3.(2023•西宁)先化简,再求值:,其中a,b是方程x2+x﹣6=0的两个根.【答案】,6.【解答】解:原式=[﹣]×a(a﹣b)=×a(a﹣b)﹣=﹣=;∵a,b是方程x2+x﹣6=0的两个根,∴a+b=﹣1ab=﹣6,∴原式=.1.(2023春•汝州市期末)下列分式中,是最简分式的是()A.B.C.D.【答案】C【解答】解:A、=,不是最简分式,不符合题意;B、==,不是最简分式,不符合题意;C、是最简分式,符合题意;D、==﹣1,不是最简分式,不符合题意;故选:C.2.(2023秋•岳阳楼区校级期中)如果把分式中的x和y都扩大2倍,那么分式的值()A.不变B.扩大2倍C.扩大4倍D.缩小2倍【答案】B【解答】解:∵==×2,∴如果把分式中的x和y都扩大2倍,那么分式的值扩大2倍,故选:B.3.(2023•河北)化简的结果是()A.xy6B.xy5C.x2y5D.x2y6【答案】A【解答】解:x3()2=x3•=xy6,故选:A.4.(2023秋•来宾期中)若分式的值为0,则x的值是()A.﹣2B.0C.2D.【答案】C【解答】解:由题意得:x﹣2=0且3x﹣1≠0,解得:x=2,故选:C.5.(2023秋•青龙县期中)分式的最简公分母是()A.3xy B.6x3y2C.6x6y6D.x3y3【答案】B【解答】解:分母分别是x2y、2x3、3xy2,故最简公分母是6x3y2;故选:B.6.(2023春•沙坪坝区期中)下列分式中是最简分式的是()A.B.C.D.【答案】A【解答】解;A、是最简二次根式,符合题意;B、=,不是最简二次根式,不符合题意;C、==,不是最简二次根式,不符合题意;D、=﹣1,不是最简二次根式,不符合题意;故选:A.7.(2023春•原阳县期中)化简(1+)÷的结果为()A.1+x B.C.D.1﹣x【答案】A【解答】解:原式=×=×=1+x.故选:A.8.(2023•门头沟区二模)如果代数式有意义,那么实数x的取值范围是()A.x≠2B.x>2C.x≥2D.x≤2【答案】A【解答】解:由题意得:x﹣2≠0,解得:x≠2,故选:A.9.(2023春•武清区校级期末)计算﹣的结果是()A.B.C.x﹣y D.1【答案】B【解答】解:﹣==.故答案为:B.10.(2023春•东海县期末)根据分式的基本性质,分式可变形为()A.B.C.D.【答案】C【解答】解:=﹣,故选:C.11.(2023秋•莱州市期中)计算的结果是﹣x.【答案】﹣x.【解答】解:÷=•(﹣)=﹣x,故答案为:﹣x.12.(2023秋•汉寿县期中)学校倡导全校师生开展“语文阅读”活动,小亮每天坚持读书.原计划用a天读完b页的书,如果要提前m天读完,那么平均每天比原计划要多读的页数为(用含a、b、m的最简分式表示).【答案】.【解答】解:由题意得:平均每天比原计划要多读的页数为:﹣=﹣=,故答案为:.13.(2023春•宿豫区期中)计算=1.【答案】1.【解答】解:===1,故答案为:1.14.(2023•广州)已知a>3,代数式:A=2a2﹣8,B=3a2+6a,C=a3﹣4a2+4a.(1)因式分解A;(2)在A,B,C中任选两个代数式,分别作为分子、分母,组成一个分式,并化简该分式.【答案】(1)2a2﹣8=2(a+2)(a﹣2);(2)..【解答】解:(1)2a2﹣8=2(a2﹣4)=2(a+2)(a﹣2);(2)选A,B两个代数式,分别作为分子、分母,组成一个分式(答案不唯一),==.15.(2023秋•思明区校级期中)先化简,再求值:(),其中.【答案】,.【解答】解:原式=÷(﹣)=÷=•=,当x=﹣1时,原式==.16.(2023秋•长沙期中)先化简,再求值:,其中x=5.【答案】,.【解答】解:原式=(﹣)•=•=,当x=5时,原式==.17.(2023•盐城一模)先化简,再求值:,其中x=4.【答案】见试题解答内容【解答】解:原式=(+)•=•=•=x﹣1,当x=4时,原式=4﹣1=3.18.(2022秋•廉江市期末)先化简(﹣x)÷,再从﹣1,0,1中选择合适的x值代入求值.【答案】﹣,0.【解答】解:原式=(﹣)•=﹣•=﹣,∵(x+1)(x﹣1)≠0,∴x≠±1,当x=0时,原式=﹣=0.1.(2023秋•西城区校级期中)假设每个人做某项工作的工作效率相同,m个人共同做该项工作,d天可以完成若增加r个人,则完成该项工作需要()天.A.d+y B.d﹣r C.D.【答案】C【解答】解:工作总量=md,增加r个人后完成该项工作需要的天数=,故选:C.2.(2023秋•长安区期中)若a=2b,在如图的数轴上标注了四段,则表示的点落在()A.段①B.段②C.段③D.段④【答案】C【解答】解:∵a=2b,∴=====,∴表示的点落在段③,故选:C.3.(2023秋•东城区校级期中)若x2﹣x﹣1=0,则的值是()A.3B.2C.1D.4【答案】A【解答】解:∵x2﹣x﹣1=0,∴x2﹣1=x,∴x﹣=1,∴(x﹣)2=1,∴x2﹣2+=1,∴x2+=3,故选:A.4.(2023秋•鼓楼区校级期中)对于正数x,规定,例如,,则=()A.198B.199C.200D.【答案】B【解答】解:∵f(1)==1,f(1)+f(1)=2,f(2)==,f()==,f(2)+f()=2,f(3)==,f()==,f(3)+f()=2,…f(100)==,f()==,f(100)+f()=2,∴=2×100﹣1=199.故选:B.5.(2023秋•延庆区期中)当x分别取﹣2023,﹣2022,﹣2021,…,﹣2,﹣1,0,1,,,…,,,时,计算分式的值,再将所得结果相加,其和等于()A.﹣1B.1C.0D.2023【答案】A【解答】解:当x=﹣a和时,==0,当x=0时,,则所求的和为0+0+0+⋯+0+(﹣1)=﹣1,故选:A.6.(2022秋•永川区期末)若分式,则分式的值等于()A.﹣B.C.﹣D.【答案】B【解答】解:整理已知条件得y﹣x=2xy;∴x﹣y=﹣2xy将x﹣y=﹣2xy整体代入分式得====.故选:B.7.(2023春•铁西区月考)某块稻田a公顷,甲收割完这块稻田需b小时,乙比甲多用0.3小时就能收割完这块稻田,两人一起收割完这块稻田需要的时间是()A.B.C.D.【答案】B【解答】解:乙收割完这块麦田需要的时间是(b+0.3)小时,甲的工作效率是公顷/时,乙的工作效率是公顷/时.故两人一起收割完这块麦田需要的工作时间为=(小时).故选:B.8.(2023春•临汾月考)相机成像的原理公式为,其中f表示照相机镜头的焦距,u表示物体到镜头的距离,v表示胶片(像)到镜头的距离.下列用f,u表示v正确的是()A.B.C.D.【答案】D【解答】解:∵,去分母得:uv=fv+fu,∴uv﹣fv=fu,∴(u﹣f)v=fu,∵u≠f,∴u﹣f≠0,∴.故选:D.9.(2023•内江)对于正数x,规定,例如:f(2)=,f()=,f(3)=,f()=,计算:f()+f()+f()+…+f()+f()+f(1)+f(2)+f(3)+…+f(99)+f(100)+f(101)=()A.199B.200C.201D.202【答案】C【解答】解:∵f(1)==1,f(2)=,f()=,f(3)=,f()=,f(4)==,f()==,…,f(101)==,f()==,∴f(2)+f()=+=2,f(3)+f()=+=2,f(4)+f()=+=2,…,f(101)+f()=+=2,f()+f()+f()+…+f()+f()+f(1)+f(2)+f(3)+…+f(99)+f(100)+f(101)=2×100+1=201.故选:C.10.(2023春•灵丘县期中)观察下列等式:=1﹣,=﹣,=﹣,…=﹣将以上等式相加得到+++…+=1﹣.用上述方法计算:+++…+其结果为()A.B.C.D.【答案】A【解答】解:由上式可知+++…+=(1﹣)=.故选A.11.(2023秋•顺德区校级月考)先阅读并填空,再解答问题.我们知道,(1)仿写:=,=,=.(2)直接写出结果:=.利用上述式子中的规律计算:(3);(4).【答案】(1),;;(2);(3);(4).【解答】解:(1),=;=,故答案为:,;;(2)原式=1﹣+++...++=1﹣=;故答案为:;(3)==1﹣+﹣+﹣+⋯⋯+=1﹣=;(2)原式=×()+×()+×()+...+×()=()==.12.(2023秋•株洲期中)阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”,而假分数都可化为带分数.如:.我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如,这样的分式就是假分式;,这样的分式就是真分式.类似地,假分式也可以化为带分式(即:整式与真分式的和的形式).如:,;解决下列问题:(1)分式是真分式(填“真”或“假”);(2)将假分式化为带分式;(3)如果x为整数,分式的值为整数,求所有符合条件的x的值.【答案】(1)真;(2)x﹣2+;(3)﹣1或﹣3或11或﹣15.【解答】解:(1)分式是真分式;故答案为:真;(2);(3)原式=,∵分式的值为整数,∴x+2=±1或±13,∴x=﹣1或﹣3或11或﹣15.13.(2023秋•涟源市月考)已知,求的值.解:由已知可得x≠0,则,即x+.∵=(x+)2﹣2=32﹣2=7,∴.上面材料中的解法叫做“倒数法”.请你利用“倒数法”解下面的题目:(1)求,求的值;(2)已知,求的值;(3)已知,,,求的值.【答案】(1);(2)24;(3).【解答】解:(1)由,知x≠0,∴.∴,x•=1.∵=x2+=(x﹣)2+2=42+2=18.∴=.(2)由=,知x≠0,则=2.∴x﹣3+=2.∴x+=5,x•=1.∵=x2+1+=(x+)2﹣2+1=52﹣1=24.∴=.(3)由,,,知x≠0,y≠0,z≠0.则=,=,y+zyz=1,∴+=,+=,+=1.∴2(++)=++1=.∴++=.∵=++=,∴=.14.(2022秋•兴隆县期末)设.(1)化简M;(2)当a=3时,记M的值为f(3),当a=4时,记M的值为f(4).①求证:;②利用①的结论,求f(3)+f(4)+…+f(11)的值;③解分式方程.【答案】(1);(2)①见解析,②,③x=15.【解答】解:(1)=====;(2)①证明:;②f(3)+f(4)+⋅⋅⋅+f(11)====;③由②可知该方程为,方程两边同时乘(x+1)(x﹣1),得:,整理,得:,解得:x=15,经检验x=15是原方程的解,∴原分式方程的解为x=15.15.(2023春•蜀山区校级月考)【阅读理解】对一个较为复杂的分式,若分子次数比分母大,则该分式可以拆分成整式与分式和的形式,例如将拆分成整式与分式:方法一:原式===x+1+2﹣=x+3﹣;方法二:设x+1=t,则x=t﹣1,则原式==.根据上述方法,解决下列问题:(1)将分式拆分成一个整式与一个分式和的形式,得=;(2)任选上述一种方法,将拆分成整式与分式和的形式;(3)已知分式与x的值都是整数,求x的值.【答案】(1);(2);(3)﹣35或43或﹣9或17或1或7或3或5.【解答】解:(1)由题知,,故答案为:.(2)选择方法一:原式==.选择方法二:设x﹣1=t,则x=t+1,则原式=====.(3)由题知,原式====.又此分式与x的值都是整数,即x﹣4是39的因数,当x﹣4=±1,即x=3或5时,原分式的值为整数;当x﹣4=±3,即x=1或7时,原分式的值为整数;当x﹣4=±13,即x=﹣9或17时,原分式的值为整数;当x﹣4=±39,即x=﹣35或43时,原分式的值为整数;综上所述:x的值为:﹣35或43或﹣9或17或1或7或3或5时,原分式的值为整数.16.(2023春•兰州期末)阅读下列材料:通过小学的学习我们知道,分数可分为“真分数”和“假分数”,而假分数都可以化为带分数,如:.我们定义:在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.如,这样的分式就是假分式;再如:这样的分式就是真分式.类似的,假分式也可以化为带分式(即:整式与真分式的和的形式),如:.解决下列问题:(1)分式是真分式(填“真分式”或“假分式”);(2)将假分式化为整式与真分式的和的形式:=2+.若假分式的值为正整数,则整数a的值为1,0,2,﹣1;(3)将假分式化为带分式(写出完整过程).【答案】(1)真分式;(2)2+;1,2,﹣1;(3)x﹣1﹣.【解答】解:(1)由题意得:分式是真分式,故答案为:真分式;(2)==2+,当2+的值为正整数时,2a﹣1=1或±3,∴a=1,2,﹣1;故答案为:2+;1,2,﹣1;(3)原式===x﹣1﹣.1.(2023•湖州)若分式的值为0,则x的值是()A.1B.0C.﹣1D.﹣3【答案】A【解答】解:∵分式的值为0,∴x﹣1=0,且3x+1≠0,解得:x=1,故选:A.2.(2023•天津)计算的结果等于()A.﹣1B.x﹣1C.D.【答案】C【解答】解:====,故选:C.3.(2023•镇江)使分式有意义的x的取值范围是x≠5.【答案】x≠5.【解答】解:当x﹣5≠0时,分式有意义,解得x≠5,故答案为:x≠5.4.(2023•上海)化简:﹣的结果为2.【答案】2.【解答】解:原式===2,故答案为:2.5.(2023•安徽)先化简,再求值:,其中x=.【答案】x+1,.【解答】解:原式==x+1,当x=﹣1时,原式=﹣1+1=.6.(2023•广安)先化简(﹣a+1)÷,再从不等式﹣2<a<3中选择一个适当的整数,代入求值.【答案】;﹣1.【解答】解:(﹣a+1)÷=•=.∵﹣2<a<3且a≠±1,∴a=0符合题意.当a=0时,原式==﹣1.7.(2023•淮安)先化简,再求值:÷(1+),其中a=+1.【答案】,.【解答】解:原式=÷(+)=÷=•=,当a=+1时,原式==.8.(2023•朝阳)先化简,再求值:(+)÷,其中x=3.【答案】,1.【解答】解:原式=[+]•=•=,当x=3时,原式==1.。
(完整版)初中数学分式章节知识点及典型例题解析

分式的知识点及典型例题分析1、分式的定义:例:下列式子中,y x +15、8a 2b 、-239a 、y x b a --25、4322b a -、2—a 2、m 1、65xy x 1、21、212+x 、πxy 3、y x +3、ma 1+中分式的个数为( ) (A ) 2 (B ) 3 (C ) 4 (D) 5 练习题:(1)下列式子中,是分式的有 .⑴275x x -+; ⑵ 123x -;⑶25a a -;⑷22x x π--;⑸22b b -;⑹222xy x y +。
(2)下列式子,哪些是分式?5a -; 234x +;3y y ; 78x π+;2x xy x y +-;145b-+。
2、分式有,无意义,总有意义:(1)使分式有意义:令分母≠0按解方程的方法去求解; (2)使分式无意义:令分母=0按解方程的方法去求解; 注意:(12+x ≠0)例1:当x 时,分式51-x 有意义; 例2:分式xx -+212中,当____=x 时,分式没有意义 例3:当x 时,分式112-x 有意义. 例4:当x 时,分式12+x x有意义例5:x ,y 满足关系 时,分式x yx y-+无意义; 例6:无论x 取什么数时,总是有意义的分式是( )A .122+x x B 。
12+x x C 。
133+x x D 。
25xx - 例7:使分式2+x x有意义的x 的取值范围为( )A .2≠x B .2-≠x C .2->x D .2<x例8:要是分式)3)(1(2-+-x x x 没有意义,则x 的值为( )A. 2 B 。
—1或—3 C 。
-1 D 。
3同步练习题:3、分式的值为零:使分式值为零:令分子=0且分母≠0,注意:当分子等于0使,看看是否使分母=0了,如果使分母=0了,那么要舍去.例1:当x 时,分式121+-a a的值为0 例2:当x 时,分式112+-x x 的值为0例3:如果分式22+-a a 的值为为零,则a 的值为( ) A. 2± B 。
分式及分式方程知识点总结

分式及分式方程 聚焦考点☆温习理解一、分式1、分式的概念一般地,用A 、B 表示两个整式,A ÷B 就可以表示成B A 的形式,如果B 中含有字母,式子B A 就叫做分式。
其中,A 叫做分式的分子,B 叫做分式的分母。
分式和整式通称为有理式。
2、分式的性质(1)分式的基本性质:分式的分子和分母都乘以(或除以)同一个不等于零的整式,分式的值不变。
(2)分式的变号法则:分式的分子、分母与分式本身的符号,改变其中任何两个,分式的值不变。
3、分式的运算法则;;bcad c d b a d c b a bd ac d c b a =⨯=÷=⨯ );()(为整数n ba b a n n n = ;cb ac b c a ±=± bdbc ad d c b a ±=± 二、分式方程1、分式方程分母里含有未知数的方程叫做分式方程。
2、分式方程的一般方法解分式方程的思想是将“分式方程”转化为“整式方程”。
它的一般解法是:(1)去分母,方程两边都乘以最简公分母(2)解所得的整式方程(3)验根:将所得的根代入最简公分母,若等于零,就是增根,应该舍去;若不等于零,就是原方程的根。
3、分式方程的特殊解法换元法:换元法是中学数学中的一个重要的数学思想,其应用非常广泛,当分式方程具有某种特殊形式,一般的去分母不易解决时,可考虑用换元法。
名师点睛☆典例分类考点典例一、分式的值【例1】(2015·黑龙江绥化)若代数式6265x 2-+-x x 的值等于0 ,则x=_________.【点睛】分式6265x 2-+-x x 的值为零则有x 2-5x+6为0分母2x-6不为0,从而即可求出x 的值. 【举一反三】1.要使分式x 1x 2+-有意义,则x 的取值应满足( ) A. x 2≠ B. x 1≠- C. x 2= D. x 1=-2.(2015·湖南常德)若分式211x x -+的值为0,则x = 考点典例二、分式的化简【例2】化简:2x x x 1x 1---=( ) A 、0 B 、1 C 、x D 、1x x -【点睛】观察所给式子,能够发现是同分母的分式减法。
分式与分式方程知识点总结

分式与分式方程知识点总结分式是一种特殊的代数表达式,有分子和分母组成,通常用斜杠“/”或者横线“-”表示分数线。
分式可以表示为a/b的形式,其中a为分子,b为分母。
分式的乘法和除法的法则:1.分式乘法法则:分式的乘法可以简化为分子相乘,分母相乘的运算。
即(a/b)*(c/d)=(a*c)/(b*d)。
2.分式除法法则:将除法转化为乘法后,取除数的倒数,然后按照分式乘法法则进行运算。
即(a/b)/(c/d)=(a*d)/(b*c)。
分式的加法和减法的法则:1.分式加法法则:要进行分式的加法,需要先找到两个分式的共同分母。
然后将分式的分子按照共同分母的比例进行加法运算。
即a/b+c/d=(a*d+b*c)/(b*d)。
2.分式减法法则:和分式加法法则类似,需要找到两个分式的共同分母。
然后将分式的分子按照共同分母的比例进行减法运算。
即a/b-c/d=(a*d-b*c)/(b*d)。
分式的化简:将分式化简为最简形式的步骤如下:1. 如果分子和分母有相同的公因子,可以约分掉。
即a/b =(a/gcd(a,b)) / (b/gcd(a,b))。
2.如果分数的分子和分母都是整数,并且分子能整除分母,可以化简为整数。
即a/b=a/b,其中a能整除b。
3.如果分式的分子和分母都是多项式,并且可以进行因式分解,可以使用因式分解后的形式来化简分式。
分式方程是包含一个或多个分式的方程。
求解分式方程的一般步骤如下:1.将方程两边的分式通过相乘分母的方法,化简为有理式。
2.对于有理式的方程,可以通过解方程的方法求出x的值。
3.检验所求得的x的值是否满足原方程,如果满足,即为解;如果不满足,则该方程无解。
在求解分式方程时,需要注意以下几个问题:1.分母不能为0,需要排除分母为0的解。
2.对于含有分式的方程,需要注意去除分式的分母后方程是否成立,避免出现无意义的解。
3.可能出现分母为0的情况,需要排除该解,以免引起除法运算错误。
分式知识点及典型例题

分式知识点及典型例题一、分式的定义如果 A、B 表示两个整式,并且 B 中含有字母,那么式子 A/B 就叫做分式。
其中 A 叫做分子,B 叫做分母。
需要注意的是:分式的分母不能为 0,因为分母为 0 时,分式无意义。
例如:1/x ,(x + 1)/(x 2)都是分式,而 1/2 就不是分式,因为它的分母 2 不含字母。
二、分式有意义的条件分式有意义的条件是分母不为 0。
即:对于分式 A/B,B ≠ 0 时,分式有意义。
例如:对于分式 1/(x 1) ,要使其有意义,则x 1 ≠ 0,即x ≠ 1。
三、分式的值为 0 的条件分式的值为 0 时,要同时满足两个条件:1、分子为 0 ,即 A = 0 。
2、分母不为 0 ,即B ≠ 0 。
例如:若分式(x 1)/(x + 2)的值为 0,则 x 1 = 0 且 x +2 ≠0 ,解得 x = 1 。
四、分式的基本性质分式的分子和分母同时乘以(或除以)同一个不为 0 的整式,分式的值不变。
即:A/B =(A×C)/(B×C), A/B =(A÷C)/(B÷C)(C ≠ 0 )例如:将分式 2x/3y 的分子分母同时乘以 2 ,得到 4x/6y ,分式的值不变。
五、约分把一个分式的分子和分母的公因式约去,叫做约分。
约分的关键是确定分子和分母的公因式。
确定公因式的方法:1、系数:取分子和分母系数的最大公因数。
2、字母:取相同字母的最低次幂。
例如:对分式(6xy)/(9x²y)进行约分,分子分母的系数 6 和 9 的最大公因数是 3 ,字母部分 x 的最低次幂是 1 ,y 的最低次幂是 1 ,所以公因式是 3xy ,约分后得到 2/(3x) 。
六、通分把几个异分母的分式分别化成与原来的分式相等的同分母的分式,叫做通分。
通分的关键是确定几个分式的最简公分母。
确定最简公分母的方法:1、取各分母系数的最小公倍数。
2、凡单独出现的字母连同它的指数作为最简公分母的一个因式。
分式和分式方程知识点总结及练习(供参考)

分式和分式方程知识点总结一、分式的基本概念 1、分式的定义 一般地,我们把形如BA的代数式叫做分式,其中 A ,B 都是整式,且B 含有字母。
A 叫做分式的分子,B 叫做分式的分母。
分式也可以看做两个整式相除(除式中含有字母)的商。
2.分式的基本性质分式的分子和分母同乘(或除以)一个不为0的整式,分式的值不变。
MB M A M B M A B A ÷÷=⨯⨯=。
其中,M 是不等于0的整式。
3.分式的约分把分式中分子和分母的公因式约去,叫做分式的约分。
4.最简分式分子和分母没有公因式的分式叫做最简分式。
利用分式的基本性质可以对分式进行化简 二、分式的运算 1、分式的乘除 分式的乘法法则分式与分式相乘,用分子的积作为积的分子,分母的积作为积的分母。
分式的除法法则分式除以分式,把除式的分子与分母颠倒位置后,与被除式相乘。
2、分式的加减同分母的分式加减法法则同分母的两个分式相加(减),分母不变,把分子相加(减)。
异分母的分式加减法法则异分母的两个分式相加(减),先通分,化为同分母的分式,再加(减)。
分式的通分把几个异分母分式分别化为与它们相等的同分母分式,叫做分式的通分,这个相同的分母叫做这几个分式的公分母。
几个分式的公分母不止一个,通分时一般选取最简公分母分式的混合运算分式的混合运算,与数的混合运算类似。
先算乘除,再算加减;如果有括号,要先算括号里面的。
三、分式方程1、分式方程的定义分母中含有未知数的方程叫做分式方程。
2、分式方程的解使得分式方程等号两端相等的未知数的值叫做分式方程的解(也叫做分式方程的根)。
3、解分式方程的步骤1.通过去分母将分式方程转化为整式方程,2.解整式方程3.将整式方程的根代入分式方程(或公分母)中检验。
4、分式方程的应用。
典型例题1.(2014•温州,第4题4分)要使分式有意义,则x 的取值应满足( ) A . x ≠2B . x ≠﹣1C . x =2D . x =﹣12.(2014•毕节地区,第10题3分)若分式的值为零,则x 的值为( ) A . 0B . 1C . ﹣1D . ±13. ( 2014•福建泉州,第10题4分)计算:+= .4. (2014•泰州,第14题,3分)已知a 2+3ab +b 2=0(a ≠0,b ≠0),则代数式+的值等于 . 5.(2014年山东泰安,第21题4分)化简(1+)÷的结果为 .6.(2014•襄阳,第13题3分)计算:÷= .7. ( 2014•广东,第18题6分)先化简,再求值:(+)•(x 2﹣1),其中x =.8. ( 2014•珠海,第13题6分)化简:(a 2+3a )÷.9. ( 2014•广西贺州,第19题(2)4分)(2)先化简,再求值:(a 2b +ab )÷,其中a =+1,b =﹣1.10 解方程: 730100-=x x. 11.解分式方程:+=1.12.解方程:=1.13. ( 2014•广东,第21题7分)某商场销售的一款空调机每台的标价是1635元,在一次促销活动中,按标价的八折销售,仍可盈利9%. (1)求这款空调每台的进价(利润率==).(2)在这次促销活动中,商场销售了这款空调机100台,问盈利多少元?14( 2014•广西贺州,第23题7分)马小虎的家距离学校1800米,一天马小虎从家去上学,出发10分钟后,爸爸发现他的数学课本忘记拿了,立即带上课本去追他,在距离学校200米的地方追上了他,已知爸爸的速度是马小虎速度的2倍,求马小虎的速度. 课后练习1.(2013湖北孝感,6,3分)化简xy x yy x x⎛⎫--÷⎪⎝⎭的结果是( ) A.1y B. x y y + C. x yy- D. y 2. (2013山东威海,8,3分)计算:211(1)1mm m+÷⋅--的结果是( ) A .221m m ---B .221m m -+-C .221m m --D .21m -3. (2013四川南充市,8,3分) 当8、分式21+-x x 的值为0时,x 的值是( ) (A )0 (B )1 (C )-1 (D )-2 4. (2013浙江丽水,7,3分)计算1a -1 – aa -1的结果为( ) A. 1+aa -1B. -a a -1C. -1D.1-a5. (2013江苏苏州,7,3分)已知2111=-b a ,则b a ab-的值是 A.21 B.-21C.2D.-2 6. ( 2013重庆江津, 2,4分)下列式子是分式的是( ) A.2x B.1+x x C. y x +2 D. 3x 7. (2013江苏南通,10,3分)设m >n >0,m 2+n 2=4mn ,则22m n mn-的值等于A. 336D. 38. (2013山东临沂,5,3分)化简(x -x 1-x 2)÷(1-x 1)的结果是( ) A .x1B .x -1C .x 1-xD .1-x x9. (2013广东湛江11,3分)化简22a b a b a b---的结果是 A a b + B a b - C 22a b - D1 10.(2013浙江金华,7,3分)计算1a -1 – aa -1的结果为( ) A.1+a a -1 B. -aa -1C. -1D.1-a 二、填空题1. (2013浙江省舟山,11,4分)当x 时,分式x-31有意义. 2. (2013福建福州,14,4分)化简1(1)(1)1m m -++的结果是 . 3. (2013山东泰安,22 ,3分)化简:(2x x+2-x x-2)÷xx 2-4的结果为 。
分式及分式方程知识点总结

分式及分式方程知识点总结分式(Fraction)是由两个整数构成的比值,其中一个是分子(Numerator),另一个是分母(Denominator)。
分式可以表示为 a/b,其中 a 是分子,b 是分母。
分式可以是一个整数、一个小数、或者是两个整数的比值。
分式可以用于表示实际问题中的比例、率、百分比等。
在数学中,分式经常被用于代替除法运算,因为分式的形式更加简洁。
在处理分式时,有几个关键概念和知识点需要了解。
一、分式的简化与等价分式2.等价分式:如果两个分式的值相等,那么它们是等价的。
可以通过将一个分式的分子乘以另一个分式的分母,分母乘以另一个分式的分子,化简两个分式,然后判断它们的值是否相等,确定它们是否等价。
二、分式的加减乘除2.分式的乘除:两个分式的乘积等于它们的分子乘积作为新分子,分母乘积作为新分母;两个分式的除法等于第一个分式的分子乘以第二个分式的倒数作为新分子,第一个分式的分母乘以第二个分式的分子作为新分母。
三、分式方程分式方程(Fractional Equation)是包含一个或多个分式的方程。
解分式方程的关键是找到合适的方法将方程转化为整式方程。
1.方法一:通分2.方法二:消去如果分式方程中有一个分式,可以通过消去(Cancellation)或者消去因子(Cancellation Factor)的方式将分母消去,得到一个整式方程。
3.方法三:代入如果分式方程比较复杂,无法通过通分或者消去的方法解得,可以通过代入(Substitution)的方法,将一个变量用另一个变量的表达式代入,然后去掉分式,得到一个整式方程进行求解。
需要注意的是,在解分式方程时,需要验证得到的解是否满足原方程,因为有时候方程中的一些值可能导致分母为零,从而使分式无解。
四、常见的分式及分式方程1.比例和比例方程:比例是两个分式的等价形式,比例方程是一个或多个比例的方程。
2.百分比和百分比方程:百分比是分数的一种特殊形式,百分比方程是包含百分比的方程。
(完整)第十五章--分式方程(知识点+题型分类练习),推荐文档

.
2x a
6.(2013•牡丹江)若关于 x 的分式方程 x 1 =1 的解为正数,那么字母 a 的取值范围是
.
x 3a
7.(2013•齐齐哈尔)若关于 x 的分式方程 x 1 2x 2 -2 有非负数解,则 a 的取值范围是
.
8.若分式方程 x 2 a 有增根,则 a 的值为
x4
x4
()
(m≠0)
3、 约分:根据
把一个分式分子和分母的
约去叫做分式的约分。
约分的关键是确保分式的分子和分母中的
,约分的结果必须是
分式。
4、通分:根据
把几个异分母的分式化为
分母分式的过程叫做分式的通分,通分的
关键是确定各分母的
提醒:①最简分式是指
② 约分时确定公因式的方法:当分子、分母是多项式时,公因式应取系数的
1
0
的根.
2.(2012•遵义)先化简
(
x
x 1
x
x2
) 1
x2
x2
x 2x
1
,并从-1≤x≤3
中选一个你认为合适的整数
x
代入求
值.
3.先化简,再求值:
2
4 x
x2 x
4
,其中
x=﹣4.
4 x2
x
x
22
4.先化简,再求值: x 1
,其中 x=
7.
第 5 页 共 10 页
5.先化简,再求值:
.
x 1 m
16.(2013•威海)若关于 x 的方程 x 5 10 2x 无解,则 m=
.
考点二、解分式方程
1.解下列分式方程
分式知识点总结及例题

分式知识点总结及例题一、分式的概念分式是指以分数的形式表示的数,通常由分子和分母两部分组成,分子表示分数的一部分,分母表示分数的总份额。
分式通常用来表示比例、部分和整体的关系。
二、分式的基本性质1. 分式的分子和分母可以分别约分。
2. 分式的值与分子和分母的乘除有关。
3. 分式的运算可以转化为通分和通分的计算问题。
三、分式的化简分式的化简是指将分式表示的数化为最简形式的操作,主要包括分子分母约分、常数和分式的转化等。
四、分式的加减法分式的加减法是指对分式的分子和分母进行通分后,进行加减运算的操作。
五、分式的乘法和除法分式的乘法是指对分式的分子和分母分别进行乘法运算后,化简为最简形式的操作。
分式的除法是指对分式进行倒数运算,然后化简为最简形式的操作。
六、分式的应用分式在实际问题中有着广泛的应用,如物体的比例尺、物体的比重、长方形的面积和周长等问题都可以用分式进行表示和计算。
七、例题1. 化简分式$\frac{6}{8}$解:分子和分母可以同时除以2,得到$\frac{6}{8}=\frac{3}{4}$,所以$\frac{6}{8}$的最简形式为$\frac{3}{4}$。
2. 计算$\frac{3}{5}+\frac{2}{3}$解:先将两个分式通分,得到$\frac{3}{5}+\frac{2}{3}=\frac{9}{15}+\frac{10}{15}=\frac{19}{15}$,再化简得$\frac{19}{15}=1 \frac{4}{15}$。
3. 计算$\frac{5}{6} \times \frac{2}{3}$解:将两个分式分别相乘得到$\frac{5}{6} \times \frac{2}{3}=\frac{10}{18}$,再将$\frac{10}{18}$化简为最简形式,得$\frac{10}{18}=\frac{5}{9}$。
4. 计算$\frac{4}{5} \div \frac{2}{3}$解:将两个分式进行倒数运算,得到$\frac{4}{5} \div \frac{2}{3}=\frac{4}{5} \times\frac{3}{2}=\frac{12}{10}=1 \frac{2}{10}=1 \frac{1}{5}$。
分式与分式方程辅导讲义
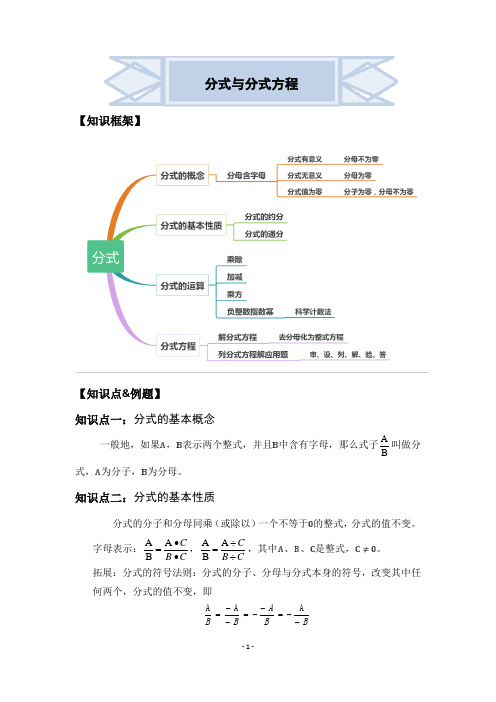
分式与分式方程【知识框架】【知识点&例题】知识点一:分式的基本概念一般地,如果,表示两个整式,并且中含有字母,那么式子B A 叫做分式,为分子,为分母。
知识点二:分式的基本性质 分式的分子和分母同乘(或除以)一个不等于的整式,分式的值不变。
字母表示:C B C••=A B A,C B C÷÷=A B A ,其中、、是整式,。
拓展:分式的符号法则:分式的分子、分母与分式本身的符号,改变其中任何两个,分式的值不变,即B B AB B --=--=--=AAA注意:在应用分式的基本性质时,要注意这个限制条件和隐含条件B ≠0。
知识点三:分式的乘除法法则分式乘分式:用分子的积作为积的分子,分母的积作为积的分母。
式子表示为:db c a d c b a ••=•分式除以分式:把除式的分子、分母颠倒位置后,与被除式相乘。
式子表示为cc ••=•=÷bd a d b a d c b a 分式的乘方:把分子、分母分别乘方。
式子n n nb a b a =⎪⎭⎫ ⎝⎛巩固练习:1.若分式的值为0,则x 的值为 .2.当= 时,分式的值为零.3.计算x xy y xy y xy y x xy y22222222++-÷+-+4.先化简,再求值:其中.242x x --x 26(1)(3)x x x x ----2291333x x x x x ⎛⎫-⋅ ⎪--+⎝⎭13x =5.先化简,再求值:,其中.6、先化简,再求值:,其中7、解下列方程:(1)(2)(3) (4)532224x x x x -⎛⎫--÷ ⎪++⎝⎭3x 22144(1)1a a a a a-+-÷--1a =-3522x x =-223444x x x x =--+22093x x x +=-+35012x x -=+9、在年春运期间,我国南方出现大范围冰雪灾害,导致某地电路断电.该地供电局组织电工进行抢修.供电局距离抢修工地千米.抢修车装载着所需材料先从供电局出发,分钟后,电工乘吉普车从同一地点出发,结果他们同时到达抢修工地.已知吉普车速度是抢修车速度的倍,求这两种车的速度。
分式与分式方程知识点

分式与分式方程知识点一、分式的定义1. 分式(Fraction):形如 A/B 的代数表达式,其中 A 是分子,B 是分母,B ≠ 0。
2. 有理表达式(Rational Expression):包含分式的代数表达式。
二、分式的基本性质1. 等值变换:分式可以通过乘以或除以相同的非零表达式进行等值变换。
例如:(2/3) * (4/5) = (2*4)/(3*5) = 8/152. 分式的加减法:只有当分母相同时,才能直接进行加减运算。
例如:(2/5) + (3/5) = (2+3)/5 = 5/5 = 13. 分式的乘除法:分子乘分子,分母乘分母。
例如:(2/3) * (4/5) = (2*4)/(3*5) = 8/154. 分式的化简:通过约分,将分子和分母中的公因数相除,得到最简分式。
例如:(12/16) -> (12÷4)/(16÷4) = 3/4三、分式方程1. 分式方程(Fractional Equation):含有分式的方程。
2. 解分式方程的基本原则:将分式方程转化为整式方程进行求解。
3. 去分母:通过将方程两边同时乘以所有分母的最简公分母,消除分母。
例如:(2/x) + (3/y) = 5 => 2y + 3x = 5xy (假设 x, y > 0) 4. 检验解:将求得的整式解代入最简公分母中,确保不会得到零。
四、特殊类型的分式方程1. 一元一次分式方程:只含有一个未知数,且未知数的最高次数为一的分式方程。
2. 二元一次分式方程:含有两个未知数,且每个未知数的最高次数为一的分式方程。
3. 高次分式方程:含有未知数的最高次数大于一的分式方程。
五、解分式方程的步骤1. 确定最简公分母。
2. 去分母,将分式方程转化为整式方程。
3. 解整式方程,求得未知数的值。
4. 检验解的有效性。
5. 写出最终解。
六、应用题1. 理解题意,找出等量关系。
2. 列出分式方程。
分式与分式方程知识点总结

分式与分式方程专题一、分式基本知识1、分式的定义:如果A 、B 表示两个整式,并且B 中含有字母,那么式子BA叫做分式。
(1)分式与整式最本质的区别:分式的分母必须含有字母,即未知数;分子可含字母可不含字母。
(2)分式有意义的条件:分母不为零,即分母中的代数式的值不能为零。
(3)分式的值为零的条件:分子为零且分母不为零。
2、分式的基本性质:分式的分子与分母同乘或除以一个不等于0的整式,分式的值不变。
用式子表示 其中A 、B 、C 为整式(0≠C ) (1)利用分式的基本性质进行分式变形是恒等变形,不改变分式值的大小,只改变形式。
(2)应用基本性质时,要注意C ≠0,以及隐含的B ≠0。
(3)注意“都”,分子分母要同时乘以或除以,避免只乘或只除以分子或分母的部分项,或避免出现分子、分母乘除的不是同一个整式的错误。
3、分式的通分和约分:关键先是分解因式(1)分式的约分定义:利用分式的基本性质,约去分式的分子与分母的公因式,不改变分式的值。
(2)最简分式:分子与分母没有公因式的分式(3)分式的通分的定义:利用分式的基本性质,使分子和分母同乘适当的整式,不改变分式的值,把几个异分母的分式化成分母相同的分式。
(4)最简公分母:取“各个分母”的“所有因式”的最高次幂的积做公分母,它叫做最简公分母。
4、分式的符号法则:分式的分子、分母与分式本身的符号,改变其中任何两个分式的值不变。
注:分子与分母变号时,是指整个分子或分母同时变号,而不是指改变分子或分C B C A B A ⋅⋅=CB CA B A ÷÷=鑫鹏学校母中的部分项的符号。
5、分式的运算:(1)分式乘法法则:分式乘分式,用分子的积作为积的分子,分母的积作为分母。
(2)分式除法法则:分式除以分式,把除式的分子、分母颠倒位置后,与被除式相乘。
(3)分式乘方法则:分式乘方要把分子、分母分别乘方。
(4)分式乘方、乘除混合运算:先算乘方,再算乘除,遇到括号,先算括号内的,不含括号的,按从左到右的顺序运算(5)分式的加减法则:同分母的分式相加减,分母不变,把分子相加减。
分式知识+分式方程专题练习50题,学会了就是送分题

分式知识+分式方程专题练习50题,学会了就是送分题分式知识点关键词:分式、分式的基本性质、分式的约分、分式的通分、分式的运算、整数指数幂、科学计数法、分式方程、最后结果一定时最简形式必须清晰知道的基本概念:分式:1,定义:一般地,如果A和B为两个整式,并且B中含有字母,那么式子A/B就叫做分式,A为分子,B为分母。
请联系前面讲的分数,基本是一样的2,与分式有关的一些知识点:1>分式有意义,要求分母不为0,隐含分母要有字母;2>分式无意义,分母为0;3>分式值为0,分子为0 ,且分母不为0;4>分式值为负或小于0,分子分母异号;5>分式值为正或大于0,分子分母同号;6>分式值为1,分子分母值相等;7>分式值为-1,分子分母值互为相反数;这些知识点看上去非常简单,甚至给人感觉都是废话。
那是因为没有放在具体的题目中,其实你那些没有拿到的分都是从这些很简单的知识里面来的。
比如,一个很复杂的分式,分子分母都很复杂,但是如果能够知道它的值为1,则表示分子和分母是相等的。
这些东西要有谦虚的心态在以后的学习中才能慢慢体会到的。
这里给大家强调三点!1.分母中一定要含有字母的式子才叫分式;也就是分式的分母要满足两个条件的,a>不为0,b>必须含有字母;2.分式与整式的和,也是分式。
3.判断分式有无意义时,一定要讨论原分式,而不能时化简后的分式!举例:问(x2-1)/x2-x-2何时有意义?答案是x≠2和x≠-1;而如果化简后只能得到x≠2这个答案了。
分式的基本知识:1.分式的基本性质,分式的分子分母同时乘以或除以一个不等于0的数,分式的值不变;2.分式的符号,分式的分子分母和分式本身的符号,改变其中任何两个,分式的值不变;3.分式的约分,就是把一个分式的分子和分母的公因式约去,约至它们再也没有公因式时就是最简分式了。
1.分子分母均为单项式时可以直接约分,即约去它们系数的最大公约数,然后约去分子分母的相同因式的最低次幂;分子分母为多项式时,要先将它们进行因式分解,再约分。
分式与分式方程知识总结

第五章分式与分式方程知识总结【知识网络】【要点梳理】要点一、分式的有关概念及性质1.分式一般地,如果A、B表示两个整式,并且B中含有字母,那么式子叫做分式.其中A叫做分子,B叫做分母.要点诠释:分式中的分母表示除数,由于除数不能为0,所以分式的分母不能为0,即当B≠0时,分式才有意义.2.分式的基本性质(M为不等于0的整式).3.最简分式分子与分母没有公因式的分式叫做最简分式.如果分子、分母中含有公因式,要进行约分化简.要点二、分式的运算1.约分利用分式的基本性质,把一个分式的分子和分母中的公因式约去,不改变分式的值,这样的分式变形叫做分式的约分.2.通分利用分式的基本性质,使分子和分母同乘以适当的整式,不改变分式的值,把异分母的分式化为同分母的分式,这样的分式变形叫做分式的通分.3.基本运算法则分式的运算法则与分数的运算法则类似,具体运算法则如下:(1)加减运算;同分母的分式相加减,分母不变,把分子相加减.;异分母的分式相加减,先通分,变为同分母的分式,再加减.(2)乘法运算,其中是整式,.两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母.(3)除法运算,其中是整式,.两个分式相除,把除式的分子和分母颠倒位置后,与被除式相乘.(4)乘方运算分式的乘方,把分子、分母分别乘方.4.分式的混合运算顺序先算乘方,再算乘除,最后加减,有括号先算括号里面的.要点三、分式方程1.分式方程的概念分母中含有未知数的方程叫做分式方程.2.分式方程的解法解分式方程的关键是去分母,即方程两边都乘以最简公分母将分式方程转化为整式方程.3.分式方程的增根问题增根的产生:分式方程本身隐含着分母不为0的条件,当把分式方程转化为整式方程后,方程中未知数允许取值的范围扩大了,如果转化后的整式方程的根恰好使原方程中分母的值为0,那么就会出现不适合原方程的根---增根.要点诠释:因为解分式方程可能出现增根,所以解分式方程必须验根.验根的方法是将所得的根带入到最简公分母中,看它是否为0,如果为0,即为增根,不为0,就是原方程的解.要点四、分式方程的应用列分式方程解应用题与列一元一次方程解应用题类似,但要稍复杂一些.解题时应抓住“找等量关系、恰当设未知数、确定主要等量关系、用含未知数的分式或整式表示未知量”等关键环节,从而正确列出方程,并进行求解.。
八年级数学下-第五章 分式与分式方程 知识点归纳与练习

八年级数学下-第五章 分式与分式方程 知识点归纳与练习1、分式:一般地,用,A B 表示两个整式,A B ÷可以表示成A B 的形式,如果B 中含有字母,那么称A B为分式,其中A 称为分式的分子,B 称为分式的分母,对于任意一个分式,分母都不能为零. 练习1、下列各式中哪些是整式?哪些是分式? 211(1);;(3);(4);2242b a b x xy x y a x ++-+- (2) 2、分式的基本性质:分式的分子与分母都乘(或除以)同一个不等于零的整式,分式的值保持不变.这一性质可以用式子表示为:,(0)b b m b b m m a a m a a m ⋅÷==≠⋅÷. 把一个分式的分子和分母的公因式约去,这种变形称为分式的约分.练习2、化简下列分式2225(1);;20xy a ab x y b ab++ (2)最简分式:在化简的结果中,如果分子和分母已没有公因式,这样的分式称为最简分式,化简分式时,通常要使结果成为最简分式或是整式.3、分式的乘除法:两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母;两个分式相除,把除式的分子和分母颠倒位置后在与被除式相乘.这一法则可以用式子 表示为:;b d bd b d b c bc a c ac a c a d ad⋅=÷=⋅= . 练习3、 计算2222244(1);(4);2x xy xy x xy y x y x y x y x y+-+÷÷---+ (2)4、分式的加减法:同分母的分式相加减,分母不变,把分子相加减. 这一法则可以用式子表示为:b c b c a a a±±=.练习4,计算222(1);(2);(3);22a b x y m n n n a b b a x y y x n m n m n m++++-------- 通分:根据分式的基本性质,异分母的分式可以化为同分母的分式,这一过程称为分式的通分,为了计算方便,异分母分式通分时,通常取最简单的公分母(最简公分母)作为它们的共同分母. 异分母分式的加减法法则是:异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.这一法则可以用式子表示为:;b d bc ad bc ad a c ac ac ac±±=±= 练习5,计算22111(1);(2);(3);423332a b a a a x x a b--+---+ 5、分式方程:分母中含有未知数的方程叫做分式方程.因为解分式方程可能产生增根,所以解分式方程必须检验.通常只需检验所得的根是否使原方程中分式的分母的值等于零就好了,如果使原方程中分式的分母的值等于零,则舍去此根. 练习6、解方程653121(1);(2)1;(3)2;1(1)4433x x y x x x x x y y+--=+==-++---- 巩固练习:。
八年级下册数学《分式》分式方程 知识点整理

15.3分式方程一、本节学习指导解分式方程和我们前面学习的解方程有很多相似之处,期间会运用到很多分式的计算方式,就这一节来说并不难。
做适当练习即能掌握。
二、知识要点1、分式方程:含分式,并且分母中含未知数的方程叫做分式方程。
(1)、分式方程的解法:解分式方程的基本思想方法是:分式方程转化去分母整式方程.解分式方程的一般方法和步骤:①去分母:即在方程的两边都同时乘以最简公分母,把分式方程化为整式方程,依据是等式的基本性质;②解这个整式方程;③检验:把整式方程的解代入最简公分母,使最简公分母不等于0的解是原方程的解,使最简公分母等于0的解不是原方程的解,即说明原分式方程无解。
注意:①去分母时,方程两边的每一项都乘以最简公分母,不要漏乘不含分母的项;②解分式方程必须要验根,千万不要忘了!(2)、解分式方程的步骤:(1)能化简的先化简;(2)方程两边同乘以最简公分母,化为整式方程;(3)解整式方程;(4)验根.(3)、分式方程检验方法:将整式方程的解带入最简公分母,如果最简公分母的值不为0,则整式方程的解是原分式方程的解;否则,这个解不是原分式方程的解。
(4)、含有字母的分式方程的解法:在数学式子的字母不仅可以表示未知数,也可以表示已知数,含有字母已知数的分式方程的解法,也是去分母,解整式方程,检验这三个步骤,需要注意的是要找准哪个字母表示未知数,哪个字母表示未知数,还要注意题目的限制条件。
计算结果是用已知数表示未知数,不要混淆。
2、列分式方程解应用题(1)列分式方程解应用题的步骤:①审:审清题意;②找: 找出相等关系;③设:设未知数;④列:列出分式方程;⑤解:解这个分式方程;⑥验:既要检验根是否是所列分式方程的解,又要检验根是否符合题意;⑦答:写出答案。
(2)应用题有几种类型;基本公式是什么?常见的有以下五种:①行程问题基本公式:路程=速度×时间而行程问题中又分相遇问题、追及问题.②数字问题:在数字问题中要掌握十进制数的表示法.③工程问题基本公式:工作量=工时×工效.④顺水逆水问题=+•=-v v v v v v顺水静水水逆水静水水3、科学记数法:把一个数表示成的形式10na⨯(其中≤a,n是整数)的记数方法叫做科学记数法.1<10(1)、用科学记数法表示绝对值大于1的数时,应当表示为10na⨯的形式,其中1≤︱a︱<10,n为原整数部分的位数减1;(2)、用科学记数法表示绝对值小于1的数时,则可表示为10n⨯的形式,其中n为原数第1个不为0的a-数字前面所有0的个数(包括小数点前面的那个0),1≤︱a︱<10.三、经验之谈:这一节考点比较多的应该是分式方程的应用题和科学计数法,但应用题基本不会单独命题,步骤虽繁琐,但是难度并不大。
分式知识点总结与分式方程的应用

知识点1、分式概念重点:掌握分式的概念和分式有意义的条件难点:分式有意义、分式值为0的条件 分式的概念:形如B A ,其中分母B 中含有字母,分数是整式而不是分式. (1)分式无意义时,分母中的字母的取值使分母为零,即当B=0时分式无意义.(2)求分式的值为零时,必须在分式有意义的前提下进行,分式的值为零要同时满足分母的值不为零及分子的值为零,这两个条件缺一不可.(3)分式有意义,就是分式里的分母的值不为零.易错易混点(1) 对分式的定义理解不准确;(2)不注意分式的值为零的条件;知识点2、分式的基本性质重点:正确理解分式的基本性质.难点:运用分式的基本性质,将分式约分、通分分式的基本性质:分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变,用式子表示是:AB=MB M A ⨯⨯,AB=M B M A ÷÷.(其中M 是不等于零的整式)分式中的A ,B ,M 三个字母都表示整式,其中B 必须含有字母,除A 可等于零外,B ,M 都不能等于零.因为若B=0,分式无意义;若M=0,那么不论乘或除以分式的分母,都将使分式无意义.分式的约分和通分(1)约分的概念:把一个分式的分子与分母的公因式约去,叫做分式的约分.(2)分式约分的依据:分式的基本性质.(3)分式约分的方法:把分式的分子与分母分解因式,然后约去分子与分母的公因式.(4)最简分式的概念:一个分式的分子与分母没有公因式时,叫做最简分式.求几个分式的最简公分母的步骤:1.取各分式的分母中系数最小公倍数;2.各分式的分母中所有字母或因式都要取到;3.相同字母(或因式)的幂取指数最大的;4.所得的系数的最小公倍数与各字母(或因式)的最高次幂的积(其中系数都取正数)即为最简公分母。
各个分式的分母都是多项式,并且可以分解因式。
这时,可先把各分式的分母中的多项式分解因式,再确定各分式的最简公分母,最后通分。
易错易混点分式的分子、分母都是几个因式的积的形式,所以约去分子、分母中相同因式的最低次幂,注意系数也要约分。
(人教版)八年级上册第十五章分式知识点总结及练习【精美版】

第十五章 分式一、知识概念: 1.分式:形如AB,A B 、是整式,B 中含有字母且B 不等于0的整式叫做分式.其中A 叫做分式的分子,B 叫做分式的分母. 2.分式有意义的条件:分母不等于0.3.分式的基本性质:分式的分子和分母同时乘以(或除以)同一个不为0的整式,分式的值不变.4.约分:把一个分式的分子和分母的公因式(不为1的数)约去,这种变形称为约分.5.通分:异分母的分式可以化成同分母的分式,这一过程叫做通分.6.最简分式:一个分式的分子和分母没有公因式时,这个分式称为最简分式,约分时,一般将一个分式化为最简分式.7.分式的四则运算:⑴同分母分式加减法则:同分母的分式相加减,分母不变,把分子相加减.用字母表示为:a b a bccc±±=⑵异分母分式加减法则:异分母的分式相加减,先通分,化为同分母的分式,然后再按同分母分式的加减法法则进行计算.用字母表示为: a c ad cbbdbd±±=⑶分式的乘法法则:两个分式相乘,把分子相乘的积作为积的分子,把分母相乘的积作为积的分母.用字母表示为:a cac b dbd⨯=⑷分式的除法法则:两个分式相除,把除式的分子和分母颠倒位置后再与被除式相乘.用字母表示为:a c a d ad bdb cbc÷=⨯=⑸分式的乘方法则:分子、分母分别乘方.用字母表示为:nn n a a b b ⎛⎫= ⎪⎝⎭8.整数指数幂:⑴m n m na a a +⨯=(m n 、是正整数)⑵()nm mn aa =(m n 、是正整数) ⑶()nn n ab a b =(n 是正整数)⑷mnm na a a-÷=(0a ≠,m n 、是正整数,m n >)⑸nn n a a b b ⎛⎫= ⎪⎝⎭(n 是正整数)⑹1nn a a-=(0a ≠,n 是正整数)9. 分式方程的意义:分母中含有未知数的方程叫做分式方程.10.分式方程的解法:①去分母(方程两边同时乘以最简公分母,将分式方程化为整式方程);②按解整式方程的步骤求出未知数的值;③验根(求出未知数的值后必须验根,因为在把分式方程化为整式方程的过程中,扩大了未知数的取值范围,可能产生增根).分式常考例题精选1.若分式2a+1有意义,则a 的取值范围是 ( ) A.a=0 B.a=1 C.a ≠-1D.a ≠02.把分式方程2x+4=1x 转化为一元一次方程时,方程两边需同乘以 ( ) A.xB.2xC.x+4D.x(x+4)3.分式方程12x −9-2x−3=1x+3的解为 ( ) A.3B.-3C.无解D.3或-34.今年我省荔枝喜获丰收,有甲、乙两块面积相同的荔枝园,分别收获荔枝8 600kg 和9 800kg ,甲荔枝园比乙荔枝园平均每亩少60kg ,问甲荔枝园平均每亩收获荔枝多少kg?设甲荔枝园平均每亩收获荔枝xkg ,根据题意,可得方程 ( )A.8 600x= 9 800x+60B.8 600x= 9 800x−60C.8 600x−60=9 800xD.8 600x+60=9 800x5.若分式 2x−1 有意义,则x 的取值范围是 .6.若代数式 2x−1 -1的值为零,则x= ________.7.若关于x 的分式方程xx−1=3a2x−2-2有非负数解,则a 的取值范围是 .8.化简:(a −1a)÷a 2−2a+1a.9.先化简,再求值:(1m −1n )÷m 2−2mn+n 2mn,其中m=-3,n=5.10.某车队要把4000t 货物运到雅安地震灾区(方案定后,每天的运量不变). (1)从运输开始,每天运输的货物吨数n(单位:t)与运输时间t(单位:天)之间有怎样的函数关系式?(2)因地震,到灾区的道路受阻,实际每天比原计划少运20%,则推迟1天完成任务,求原计划完成任务的天数.11.先化简,再求值:(x+2x−x−1x−2)÷x−4x −4x+4,其中x 是不等式3x+7>1的负整数解.12.某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球.回校后,王老师和李老师编写了一道题: 请求出篮球和排球的单价各是多少元?1.分式1x -1有意义,则x 的取值范围是( ) A .x>1 B .x ≠1 C .x<1 D .一切实数2.下列各分式与ba 相等的是( ) A .b 2a 2 B .b +2a +2 C .aba 2 D .a +b 2a3.下列分式的运算正确的是( ) A .1a +2b =3a +bB .(a +b c )2=a 2+b 2c 2C .a 2+b 2a +b =a +bD .3-a a 2-6a +9=13-a4.化简(a +3a -4a -3)(1-1a -2)的结果等于( ) A .a -2c B .a +2 C .a -2a -3 D .a -3a -25.若x =3是分式方程a -2x -1x -2=0的根,则a 的值是( )A .5B .-5C .3D .-36.已知关于x 的分式方程m x -1+31-x =1的解是非负数,则m 的取值范围是( )A .m>2B .m ≥2C .m ≥2且m ≠3D .m>2且m ≠37.小明上月在某文具店正好用20元钱买了几本笔记本,本月再去买时,恰遇此文具店搞优惠酬宾活动,同样的笔记本,每本比上月便宜1元,结果小明只比上次多用了4元钱,却比上次多买了2本.若设他上月买了x 本笔记本,则根据题意可列方程( )A .24x +2-20x =1B .20x -24x +2=1C .24x -20x +2=1D .20x +2-24x =18.当x =1时,分式x -b x +a 无意义;当x =2时,分式2x -b3x +a 的值为0,则a +b= .9.方程5x =7x -2的解是x = .10.若(x -y -2)2+|xy +3|=0,则(3x x -y -2x x -y )÷1y的值是 .11.关于x 的分式方程m x 2-4-1x +2=0无解,则m = .12.计算或化简:(1)38-2-1+|2-1|;(2)2xx2-4-1x-2;(3)3-a2a-4÷(a+2-5a-2).13.解分式方程:(1)1x-x-2x=1; (2)12x-1=12-34x-2.14.先化简(1+1x-2) ÷x-1x2-4x+4,再从1,2,3三个数中选一个合适的数作为x的值,代入求值;15.小明去离家2.4 km的体育馆看球赛,进场时,发现门票还放在家中,此时离比赛还有45 min,于是他立即步行(匀速)回家取票,在家取票用时2 min,取到票后,他马上骑自行车(匀速)赶往体育馆.已知小明骑自行车从家赶往体育馆比从体育馆步行回家所用时间少20 min,骑自行车的速度是步行速度的3倍.(1)小明步行的速度是多少?(2)小明能否在球赛开始前赶到体育馆?第1节探究电流与电压、电阻的关系实验(建议时间:20分钟)1. (2019铜仁)小李为了探究“电流与电压的关系”,请你与他合作并完成以下实验步骤.(1)请你在虚线框中设计出相应的电路图.第1题图(2)小李在探究电流与电压的关系时,要控制________不变.通过实验探究,得到以下数据,在进行数据分析时,小李发现表格中有一组错误的数据,请你找出第________组数据是错误的.序号 1 2 3 4 5电压U/V 0.8 1.2 1.6 2.0 2.4电流I/A 0.16 0.24 0.32 0.44 0.48(3)为了分析电流与电压的定量关系,请你利用正确的数据,在坐标中绘制出电流与电压关系的图像.2. (2019巴中)同学们想探究“导体中电流跟导体两端电压的关系”:(1)小明同学通过学习知道了________是形成电流的原因,因此做出了如下三种猜想:A. 电流跟电压成反比B. 电流跟电压成正比C. 电流跟电压无关(2)为了验证猜想,小明设计了如图甲所示的电路图,其中电源为三节新干电池,电阻R为10 Ω,滑动变阻器R标有“50 Ω 1 A”字样,电压表电流表均完好.第2题图实验次数 1 2 3电压U/V 2 2.6 3电流I/A 0.20 0.26 0.30第2题图丙①根据甲电路图将乙图实物电路连接完整;②闭合开关前,小明应将滑动变阻器滑片移到________阻值处(选填“最大”或“最小”);③他检查电路时发现电压表、电流表位置互换了,若闭合开关电流表________(选填“会”或“不会”)被烧坏;④排除故障后小明进行了实验,得到表格中的实验数据.分析数据,可得出的正确结论是:电阻一定时,________________________________.(3)小明还想用这个电路测量小灯泡的额定功率,于是他将电阻R换成一只额定电压是4 V 的小灯泡(阻值约为13 Ω),电阻一定时,并将电压表量程更换为15 V,闭合开关S后,调节滑片至电压表示数为4.0 V时,电流表示数如图丙所示为______A,小灯泡的额定功率为________W.3. (2019临沂)在“探究电流与电阻关系”的实验中,小明依次选用阻值为5 Ω、10 Ω、20 Ω的定值电阻进行实验.第3题图(1)图甲是实验的实物连线图,其中有一条导线连接错误,请在该导线上打“×”并画出正确连线.(2)改正错误后闭合开关,电流表有示数而电压表无示数,电路故障可能是________.(3)排除故障后闭合开关,移动滑动变阻器的滑片至某一位置,电流表的示数如图乙所示,此时电路中的电流为________A.(4)断开开关,将5 Ω的定值电阻换成10 Ω的并闭合开关,此时应将滑动变阻器的滑片向______(选填“左”或“右”)端移动,这一过程中眼睛要一直观察________表示数的变化.(5)下表是实验中记录的数据,分析数据可知:①10 Ω定值电阻的功率为________W.②当导体两端的电压一定时,通过导体的电流与导体的电阻成________比.参考答案第十五章欧姆定律第1节探究电流与电压、电阻的关系实验1. (1)如答图甲所示第1题答图甲(2)电阻 4 (3)如答图乙所示第1题答图乙2. (1)电压(2)①如答图所示②最大③不会④导体中的电流与它两端的电压成正比(3)0.3 1.2第2题答图3. (1)如答图所示(2)R短路 (3)0.4 (4)右电压(5)①0.4 ②反第3题答图第十五章电流和电路摩擦起电:摩擦过的物体具有吸引轻小物体的现象——带电体==本质:电荷的转移正电荷:被丝绸摩擦过的玻璃棒带的电荷种类电荷负电荷:被毛皮摩擦过的橡胶棒带的电荷性质:同种电荷互相排斥,异种电荷互相排斥检验:验电器——原理:同种电荷互相排斥电量:q 单位:库伦简称:库符号:CC元电荷:最小电荷:e=1.6×1019组成:电源、开关、导线、用电器电源:提供电能开关:控制电路通断作用用电器:消耗电能导线:传输电能的路径导体:金属、人体、食盐水两种材料绝缘体:橡胶、玻璃、塑料电流产生条件①电路闭合②保持通路定义:正电荷移动的方向电路电流的方向在电源中电源的正极→用电器→电源的负极1617单位:A −→−310mA −→−310A μ 工具:电流表 ○A测量 使用方法 ①电流表必须和被测的用电器串联 电流的大小(I ) ②看清量程、分度值,不准超过电流表的量程 ③必须正入负出④任何情况下都不能直接连到电源的两极 电路的连接:先串后并,就近连线,弄清首尾 通路:接通的电路 三种状态 断路:断开的电路短路:电流不经过用电器直接回到电源的负极 两种类型:一、电荷1、物体有了吸引轻小物体的性质,我们就说物体带了电荷;换句话说,带电体具有吸引轻小物体的性质。
分式和分式方程知识点总结大全

分式和分式方程知识点总结大全分式:分式是指含有变量的有理数表达式,通常以a/b的形式表示,其中a和b是整数,而b不等于0。
基本概念:1.分子和分母:分数中的a称为分子,b称为分母。
2.真分数和假分数:如果分子小于分母,则分式称为真分数;如果分子大于或等于分母,则分式称为假分数。
3.约分:对于一个分式a/b,如果a和b有公约数,则可以将a和b同时除以它们的最大公约数,得到分式的最简形式。
4.相等分式:两个分子和分母比值相等的分式称为相等分式。
例如,2/3和4/6是相等的分式。
分式的运算:1.加法和减法:对于两个分式a/b和c/d来说,只有当b和d相等时,才能进行加法和减法运算。
运算结果的分母保持不变,并将分子相加或相减。
2.乘法:两个分式a/b和c/d相乘,将分子相乘得到新的分子,分母相乘得到新的分母。
结果要简化。
3.除法:两个分式a/b和c/d相除,将第一个分式的分子乘以第二个分式的分母,第一个分式的分母乘以第二个分式的分子。
结果要简化。
分式方程:分式方程是指含有分式的方程。
解分式方程的步骤:1.清除分母:将分式方程的两边同乘以分母的最小公倍数,从而消除分母。
2.化简方程:将方程中的分式进行化简,得到方程的最简形式。
3.解方程:根据方程的形式,进行求解。
常见的方法包括合并同类项、配方、移项等等。
常见的分式方程类型:1.一次分式方程:方程中只含有一次分式的方程。
例如,(x+1)/2=32.二次分式方程:方程中含有二次分式的方程。
例如,(x^2+1)/(x+2)=43.多次分式方程:方程中含有多次分式的方程。
例如,(x^3+1)/(x^2+2)=5应用场景:分式和分式方程在数学中的应用非常广泛,尤其在代数、几何、经济学等领域中有着重要的应用。
例如,在解决实际问题中,经常会用到比例关系,而分式可以很好地描述比例关系。
在几何学中,分式用于解决一些面积、体积等问题。
在经济学中,分式用于解决利润、成本等相关问题。
分式 知识点及典型例题

分式知识点及典型例题正文:分式,又称有理数,是数学中的一个重要概念,它由分子和分母组成,表示两个数的比值关系。
在分式的运算中,我们需要了解一些基本知识点,并且通过典型的例题来加深理解。
一、分式的定义和基本性质分式可以用“a/b”的形式表示,其中a为分子,b为分母。
分子和分母都可以是整数、小数或者其他分式。
分式也可以是正数、负数或者零。
分式的基本性质有:1. 当分子为0时,分式的值为0,即0/b=0。
2. 当分母为1时,分式的值等于分子本身,即a/1=a。
3. 当分子和分母互为相反数时,分式的值为-1,即(-a)/a=-1。
二、分式的运算1. 分式的加减运算分式的加减运算遵循相同分母则分子相加减的原则。
具体步骤如下:(1)将两个分式的分母化为相同的分母;(2)将两个分式的分子按照相同分母相加减;(3)将结果化简为最简形式。
例如:计算1/3 + 1/4 - 1/6。
解:首先将三个分式的分母化为12,得到4/12 + 3/12 - 2/12,再将分子相加减,得到5/12。
2. 分式的乘除运算分式的乘除运算遵循分子相乘除,分母相乘除的原则。
具体步骤如下:(1)将两个分式的分子相乘或相除;(2)将两个分式的分母相乘或相除;(3)将结果化简为最简形式。
例如:计算2/3 × 5/8 ÷ 4/5。
解:根据乘除法的原则,分子相乘得到10,分母相乘得到24,再将结果化简为最简形式,得到5/12。
三、分式的简化分式的简化是将分子和分母的公因式约去,使其达到最简形式。
具体步骤如下:(1)求分子和分母的最大公因数;(2)将分子和分母分别除以最大公因数。
例如:将12/18简化为最简分式。
解:求12和18的最大公因数为6,将分子和分母都除以6,得到最简分式2/3。
四、分式的应用举例1. 问题:小明爸爸买了一块布长3米,要均分给他和他妹妹,他分到几分之几的布?解:设小明分到的布的长度为x米,他妹妹分到的布的长度为y米,则由题意可得分式x/y=3/2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
分式和分式方程知识点总结一、分式的基本概念 1、分式的定义 一般地,我们把形如BA的代数式叫做分式,其中 A ,B 都是整式,且B 含有字母。
A 叫做分式的分子,B 叫做分式的分母。
分式也可以看做两个整式相除(除式中含有字母)的商。
2.分式的基本性质分式的分子和分母同乘(或除以)一个不为0的整式,分式的值不变。
MB M A M B M A B A ÷÷=⨯⨯=。
其中,M 是不等于0的整式。
3.分式的约分把分式中分子和分母的公因式约去,叫做分式的约分。
4.最简分式分子和分母没有公因式的分式叫做最简分式。
利用分式的基本性质可以对分式进行化简 二、分式的运算 1、分式的乘除 分式的乘法法则分式与分式相乘,用分子的积作为积的分子,分母的积作为积的分母。
DB C A D C B A ••=• 分式的除法法则分式除以分式,把除式的分子与分母颠倒位置后,与被除式相乘。
C BD A C D B A D C B A ••=•=÷2、分式的加减同分母的分式加减法法则同分母的两个分式相加(减),分母不变,把分子相加(减)。
BCA B C B A ±=± 异分母的分式加减法法则异分母的两个分式相加(减),先通分,化为同分母的分式,再加(减)。
分式的通分把几个异分母分式分别化为与它们相等的同分母分式,叫做分式的通分,这个相同的分母叫做这几个分式的公分母。
几个分式的公分母不止一个,通分时一般选取最简公分母BDBCAD BD BC BD AD D C B A ±=±=± 分式的混合运算分式的混合运算,与数的混合运算类似。
先算乘除,再算加减;如果有括号,要先算括号里面的。
三、分式方程 1、分式方程的定义分母中含有未知数的方程叫做分式方程。
2、分式方程的解使得分式方程等号两端相等的未知数的值叫做分式方程的解(也叫做分式方程的根)。
3、解分式方程的步骤1.通过去分母将分式方程转化为整式方程,2.解整式方程3.将整式方程的根代入分式方程(或公分母)中检验。
4、分式方程的应用。
典型例题1.(2014•温州,第4题4分)要使分式有意义,则x的取值应满足()A.x≠2B.x≠﹣1 C.x=2 D.x=﹣12.(2014•毕节地区,第10题3分)若分式的值为零,则x的值为()A.0B.1C.﹣1 D.±13. (2014•福建泉州,第10题4分)计算:+=.4. (2014•泰州,第14题,3分)已知a2+3ab+b2=0(a≠0,b≠0),则代数式+的值等于.5.(2014年山东泰安,第21题4分)化简(1+)÷的结果为.6.(2014•襄阳,第13题3分)计算:÷=.7.(2014•广东,第18题6分)先化简,再求值:(+)•(x2﹣1),其中x=.8. ( 2014•珠海,第13题6分)化简:(a 2+3a )÷.9. ( 2014•广西贺州,第19题(2)4分)(2)先化简,再求值:(a 2b +ab )÷,其中a =+1,b =﹣1.10 解方程: 730100-=x x.11.解分式方程:+=1.12.解方程:=1.13. ( 2014•广东,第21题7分)某商场销售的一款空调机每台的标价是1635元,在一次促销活动中,按标价的八折销售,仍可盈利9%. (1)求这款空调每台的进价(利润率==).(2)在这次促销活动中,商场销售了这款空调机100台,问盈利多少元?14( 2014•广西贺州,第23题7分)马小虎的家距离学校1800米,一天马小虎从家去上学,出发10分钟后,爸爸发现他的数学课本忘记拿了,立即带上课本去追他,在距离学校200米的地方追上了他,已知爸爸的速度是马小虎速度的2倍,求马小虎的速度.课后练习1.(2013湖北孝感,6,3分)化简xy x yy x x⎛⎫--÷⎪⎝⎭的结果是( ) A.1y B. x y y + C. x yy- D. y 2. (2013山东威海,8,3分)计算:211(1)1mm m+÷⋅--的结果是( ) A .221m m ---B .221m m -+-C .221m m --D .21m -3. (2013四川南充市,8,3分) 当8、分式21+-x x 的值为0时,x 的值是( ) (A )0 (B )1 (C )-1 (D )-2 4. (2013浙江丽水,7,3分)计算1a -1 – aa -1的结果为( ) A. 1+aa -1B. -a a -1C. -1-a5. (2013江苏苏州,7,3分)已知2111=-b a ,则ba ab-的值是 A.21 B.-21D.-2 6. ( 2013重庆江津, 2,4分)下列式子是分式的是( ) A.2x B.1+x x C. y x +2 D. 3x 7. (2013江苏南通,10,3分)设m >n >0,m 2+n 2=4mn ,则22m n mn-的值等于A. 336D. 38. (2013山东临沂,5,3分)化简(x -x 1-x 2)÷(1-x 1)的结果是( ) A .x1B .x -1C .x 1-xD .1-x x9. (2013广东湛江11,3分)化简22a b a b a b---的结果是A a b +B a b -C 22a b - D1 10.(2013浙江金华,7,3分)计算1a -1 – aa -1的结果为( ) A.1+a a -1 B. -aa -1C. -1 -a二、填空题1. (2013浙江省舟山,11,4分)当x 时,分式x-31有意义. 2. (2013福建福州,14,4分)化简1(1)(1)1m m -++的结果是 . 3. (2013山东泰安,22 ,3分)化简:(2x x+2-x x-2)÷xx 2-4的结果为 。
4. (2013浙江杭州,15,4)已知分式235x x x a--+,当x =2时,分式无意义,则a = ,当a <6时,使分式无意义的x 的值共有 个. 5. (2013 浙江湖州,11,4)当x =2时,分式11x -的值是 6. (2013浙江省嘉兴,11,5分)当x 时,分式x-31有意义. 7. (2013福建泉州,14,4分)当x = 时,分式22+-x x 的值为零. 8. (2013山东聊城,15,3分)化简:2222222a b a ba ab b a b --÷+++=__________________.9. (2013四川内江,15,5分)如果分式23273x x --的值为0,则x 的值应为 .10.(2013四川乐山11,3分)当x= 时,112x =- 11. (2013四川乐山15,3分)若m 为正实数,且13m m-=,221m m -则=12. (2013湖南永州,5,3分)化简a a a -+-111=________. 13. (2013江苏盐城,13,3分)化简:x 2 - 9x - 3= .三、解答题1. (2013安徽,15,8分)先化简,再求值:12112---x x ,其中x =-2.2. (2013江苏扬州,19(2),4分)(2)xx x 1)11(2-÷+3. (2013四川南充市,15,6分)先化简,再求值:21x x -(xx 1--2),其中x =2.4. (2013浙江衢州,17(2),4分)化简:3a b a ba b a b-++--.5. (2013四川重庆,21,10分)先化简,再求值:(x -1x -x -2x +1)÷2x 2-xx 2+2x +1,其中x 满足x 2-x -1=0.6. (2013福建泉州,19,9分)先化简,再求值2221x xx x x +⋅-,其中2x =.7. (2013湖南常德,19,6分)先化简,再求值.221211, 2.111x x x x x x x ⎛⎫-+-+÷= ⎪+-+⎝⎭其中8. (2013湖南邵阳,18,8分)已知111x =-,求211x x +--的值。
9. (2013广东株洲,18,4分)当2x =-时,求22111x x x x ++++的值.10.(2013江苏泰州,19(2),4分)aba b a b b a +⋅+)2﹢﹣(11. ((2013山东济宁,16,5分)计算:22()a b ab b a a a--÷-12. ( 2013重庆江津, 21(3),6分)先化简,再求值: )121(212-+÷+-x x x ,其中31=x ·13. (2013江苏南京,18,6分)计算221()a ba b a b b a -÷-+-14. (2013广东肇庆,19,7分) 先化简,再求值:)211(342--⋅--a a a ,其中3-=a .15. (20011江苏镇江,18(1),4分) (2)化简:22142x x x ---16. (2013重庆市潼南,21,10分)先化简,再求值:2121(1)1a a a a++-⋅+,其中a 217. (2013山东枣庄,19,8分)先化简,再求值:⎝ ⎛⎭⎪⎫1+ 1 x -2÷ x 2-2x +1x 2-4,其中x =-5.。
