西工大研究生 信息论与编码部分答案
信息理论及编码参考答案

2.3 一副充分洗乱的牌〔含52〕,试问:〔1〕任一特定排列所给出的不确定性是多少?〔2〕随机抽取13牌,13牌的点数互不一样时的不确定性是多少? 解:〔1〕52扑克牌可以按不同的顺序排列,所有可能的不同排列数就是全排列种数,为 因为扑克牌充分洗乱,任一特定排列出现的概率相等,设事件A 为任一特定排列,则其发生概率为可得,该排列发生所给出的信息量为()()22log log 52225.58I A P A =-=!≈ bit 67.91≈ dit〔2〕设事件B 为从中抽取13牌,所给出的点数互不一样。
扑克牌52中抽取13,不考虑排列顺序,共有1352C 种可能的组合。
13牌点数互不一样意味着点数包括A ,2,…,K ,而每一种点数有4种不同的花色意味着每个点数可以取4中花色。
所以13牌中所有的点数都不一样的组合数为134。
因为每种组合都是等概率发生的,所以则发生事件B 所得到的信息量为()()13213524log log 13.208I B P B C =-=-≈ bit3.976≈ dit2.5 设在一只布袋中装有100只对人手的感觉完全一样的木球,每只上涂有1种颜色。
100只球的颜色有以下三种情况:(1) 红色球和白色球各50只; (2) 红色球99只,白色球1只; (3) 红,黄,蓝,白色各25只。
求从布袋中随意取出一只球时,猜想其颜色所需要的信息量。
解:猜想木球颜色所需要的信息量等于木球颜色的不确定性。
令R ——"取到的是红球〞,W ——"取到的是白球〞, Y ——"取到的是黄球〞,B ——"取到的是蓝球〞。
〔1〕假设布袋中有红色球和白色球各50只,即 则 ()()221log log 212I R I W ==-== bit 〔2〕假设布袋中红色球99只,白色球1只,即 则 ()()22log log 0.990.0145I R P R =-=-= bit()()22log log 0.01 6.644I W P W =-=-=bit〔3〕假设布袋中有红,黄,蓝,白色各25只,即 则 ()()()()21log 24I R I Y I B I W ====-= bit 2.7 设信源为 求()()62log iiiP x P x -∑,井解释为什么()()622log log6i i iP x P x ->∑,不满足信源熵的极值性。
《信息论与编码》习题解答-第二章

《信息论与编码》习题解答第二章 信源熵-习题答案2-1解:转移概率矩阵为:P(j/i)=,状态图为:⎪⎩⎪⎨⎧==∑∑j jj ij ii W W P W 1,⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=++=+=++=1323221313121321233123211W W W W W W W W W W W W 解方程组求得W=2-2求平稳概率符号条件概率状态转移概率解方程组得到 W=2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求: (1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
解: (1)bitx p x I x p i i i 170.4181log )(log )(18161616161)(=-=-==⨯+⨯=(2)bitx p x I x p i i i 170.5361log )(log )(3616161)(=-=-==⨯=(3)共有21种组合:其中11,22,33,44,55,66的概率是3616161=⨯ 其他15个组合的概率是18161612=⨯⨯symbol bit x p x p X H ii i / 337.4181log 18115361log 3616)(log )()(=⎪⎭⎫ ⎝⎛⨯+⨯-=-=∑(4)参考上面的两个点数的排列,可以得出两个点数求和的概率分布如下:symbolbit x p x p X H X P Xii i / 274.3 61log 61365log 365291log 912121log 1212181log 1812361log 3612 )(log )()(36112181111211091936586173656915121418133612)(=⎪⎭⎫ ⎝⎛+⨯+⨯+⨯+⨯+⨯-=-=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎥⎦⎤⎢⎣⎡∑(5)bit x p x I x p i i i 710.13611log)(log )(3611116161)(=-=-==⨯⨯=2-4(4)2.5 居住某地区的女孩子有25%是大学生,在女大学生中有75%是身高160厘米以上的,而女孩子中身高160厘米以上的占总数的一半。
信息论与编码习题参考答案(全)
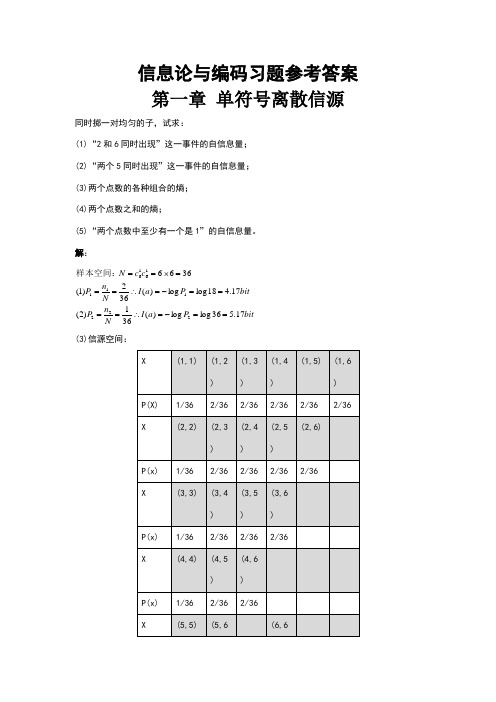
信息论与编码习题参考答案 第一章 单符号离散信源同时掷一对均匀的子,试求:(1)“2和6同时出现”这一事件的自信息量; (2)“两个5同时出现”这一事件的自信息量; (3)两个点数的各种组合的熵; (4)两个点数之和的熵;(5)“两个点数中至少有一个是1”的自信息量。
解:bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间:(3)信源空间:bit x H 32.436log 3616236log 36215)(=⨯⨯+⨯⨯=∴ (4)信源空间:bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴++ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==如有6行、8列的棋型方格,若有两个质点A 和B ,分别以等概落入任一方格内,且它们的坐标分别为(Xa ,Ya ), (Xb ,Yb ),但A ,B 不能同时落入同一方格内。
(1) 若仅有质点A ,求A 落入任一方格的平均信息量; (2) 若已知A 已落入,求B 落入的平均信息量; (3) 若A ,B 是可辨认的,求A ,B 落入的平均信息量。
解:bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率bitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知bitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为%.如果你问一位男士:“你是否是红绿色盲”他的回答可能是:“是”,也可能“不是”。
《信息论与编码》第三章部分习题参考答案

第三章习题参考答案第三章习题参考答案3-1解:(1)判断唯一可译码的方法:①先用克劳夫特不等式判定是否满足该不等式;②若满足再利用码树,看码字是否都位于叶子结点上。
如果在叶节点上则一定是唯一可译码,如果不在叶节点上则只能用唯一可译码的定义来判断是不是。
可译码的定义来判断是不是。
其中C1,C2,C3,C6都是唯一可译码。
都是唯一可译码。
对于码C2和C4都满足craft 不等式。
但是不满足码树的条件。
但是不满足码树的条件。
就只能就只能举例来判断。
举例来判断。
对C5:61319225218ki i ---==+´=>å,不满足该不等式。
所以C5不是唯一可译码。
译码。
(2)判断即时码方法:定义:即时码接收端收到一个完整的码字后,就能立即译码。
特点:码集任何一个码不能是其他码的前缀,即时码必定是唯一可译码, 唯一可译码不一定是即时码。
唯一可译码不一定是即时码。
其中C1,C3,C6都是即时码。
都是即时码。
对C2:“0”是“01”的前缀,……,所以C2不是即时码。
不是即时码。
(1) 由平均码长61()i i i K p x k ==å得1236 3 1111712(3456) 241681111712(3456) 2416811152334 24162K bitK bit K bitK bit==´+´+´+++==´+´+´+++==´+´+´´=62111223366()()log () 2 /()266.7%3()294.1%178()294.1%178()280.0%52i i i H U p u p u H U K H U K H U K H U K h h h h ==-=============å比特符号3-7解:(1)信源消息的概率分布呈等比级数,按香农编码方法,其码长集合为自然数数列1, 2, 3, ···, i, ·, i, ····;对应的编码分别为:0, 10, 110, ···, 111…110 ( i 110 ( i –– 1个1), ·1), ····。
信息论与编码考题标准答案

信 息 论 与 编 码 考题与标准答案第一题 选择题1.信息是( b )a. 是事物运动状态或存在方式的描述b.是事物运动状态或存在方式的不确定性的描述c.消息、文字、图象d.信号 2.下列表达式哪一个是正确的(e )a. H (X /Y )=H (Y /X )b. )();(0Y H Y X I <≤c.)/()(),(X Y H X H Y X I -=d. )()/(Y H Y X H ≤e. H (XY )=H (X )+H (Y /X )3.离散信源序列长度为L ,其序列熵可以表示为( b )a. )()(1X LH X H =b.c. ∑==Ll lXH X H 1)()(d. )()(X H X H L =4.若代表信源的N 维随机变量的取值被限制在一定的范围之内,则连续信源为( c ),具有最大熵。
a. 指数分布b. 正态分布c. 均匀分布d. 泊松分布 5.对于平均互信息);(Y X I ,下列说法正确的是( b )a. 当)(i x p 一定时,是信道传递概率)(i j x y p 的上凸函数,存在极大值b. 当)(i x p 一定时,是信道传递概率)(i j x y p 的下凸函数,存在极小值c.当)(i j x y p 一定时,是先验概率)(i x p 的上凸函数,存在极小值d.当)(i j x y p 一定时,是先验概率)(i x p 的下凸函数,存在极小值 6.当信道输入呈( c )分布时,强对称离散信道能够传输最大的平均信息量,即达到信道容量 a. 均匀分布 b. 固定分布 c. 等概率分布 d. 正态分布7.当信道为高斯加性连续信道时,可以通过以下哪些方法提高抗干扰性(b d ) a. 减小带宽 b. 增大发射功率 c. 减小发射功率 d.增加带宽第二题 设信源 ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡6.04.0)(21x x X p X 通过一干扰信道,接收符号为Y={y 1,y 2},信道传递矩阵为⎥⎦⎤⎢⎣⎡43416165 求:(1) 信源 X 中事件 x 1 和 x 2 分别含有的自信息量。
信息论与编码理论习题答案

第二章 信息量和熵2.2八元编码系统,码长为3,第一个符号用于同步,每秒1000个码字,求它的信息速率.解:同步信息均相同,不含信息,因此 每个码字的信息量为 2⨯8log =2⨯3=6 bit因此,信息速率为 6⨯1000=6000 bit/s2。
3 掷一对无偏骰子,告诉你得到的总的点数为:(a ) 7; (b) 12。
问各得到多少信息量.解:(1) 可能的组合为 {1,6},{2,5},{3,4},{4,3},{5,2},{6,1})(a p =366=61得到的信息量 =)(1loga p =6log =2。
585 bit (2) 可能的唯一,为 {6,6})(b p =361得到的信息量=)(1logb p =36log =5。
17 bit2.4 经过充分洗牌后的一副扑克(52张),问:(a) 任何一种特定的排列所给出的信息量是多少?(b) 若从中抽取13张牌,所给出的点数都不相同时得到多少信息量?解:(a ) )(a p =!521信息量=)(1loga p =!52log =225.58 bit (b) ⎩⎨⎧⋯⋯⋯⋯花色任选种点数任意排列13413!13)(b p =1352134!13A ⨯=1352134C 信息量=1313524log log -C =13。
208 bit2.9随机掷3颗骰子,X 表示第一颗骰子的结果,Y 表示第一和第二颗骰子的点数之和,Z 表示3颗骰子的点数之和,试求)|(Y Z H 、)|(Y X H 、),|(Y X Z H 、)|,(Y Z X H 、)|(X Z H 。
解:令第一第二第三颗骰子的结果分别为321,,x x x ,1x ,2x ,3x 相互独立,则1x X =,21x x Y +=,321x x x Z ++=)|(Y Z H =)(3x H =log 6=2.585 bit )|(X Z H =)(32x x H +=)(Y H=2⨯(361log 36+362log 18+363log 12+364log 9+365log 536)+366log 6 =3。
信息论与编码理论习题答案全解

第二章 信息量和熵2.2 八元编码系统,码长为3,第一个符号用于同步,每秒1000个码字,求它的信息速率。
解:同步信息均相同,不含信息,因此 每个码字的信息量为 2⨯8log =2⨯3=6 bit因此,信息速率为 6⨯1000=6000 bit/s2.3 掷一对无偏骰子,告诉你得到的总的点数为:(a) 7; (b) 12。
问各得到多少信息量。
解:(1) 可能的组合为 {1,6},{2,5},{3,4},{4,3},{5,2},{6,1})(a p =366=61得到的信息量 =)(1loga p =6log =2.585 bit (2) 可能的唯一,为 {6,6})(b p =361得到的信息量=)(1logb p =36log =5.17 bit2.4 经过充分洗牌后的一副扑克(52张),问:(a) 任何一种特定的排列所给出的信息量是多少?(b) 若从中抽取13张牌,所给出的点数都不相同时得到多少信息量?解:(a) )(a p =!521信息量=)(1loga p =!52log =225.58 bit (b) ⎩⎨⎧⋯⋯⋯⋯花色任选种点数任意排列13413!13)(b p =1352134!13A ⨯=1352134C 信息量=1313524log log -C =13.208 bit2.9 随机掷3颗骰子,X 表示第一颗骰子的结果,Y 表示第一和第二颗骰子的点数之和,Z 表示3颗骰子的点数之和,试求)|(Y Z H 、)|(Y X H 、),|(Y X Z H 、)|,(Y Z X H 、)|(X Z H 。
解:令第一第二第三颗骰子的结果分别为321,,x x x ,1x ,2x ,3x 相互独立,则1x X =,21x x Y +=,321x x x Z ++=)|(Y Z H =)(3x H =log 6=2.585 bit )|(X Z H =)(32x x H +=)(Y H=2⨯(361log 36+362log 18+363log 12+364log 9+365log 536)+366log 6=3.2744 bit)|(Y X H =)(X H -);(Y X I =)(X H -[)(Y H -)|(X Y H ]而)|(X Y H =)(X H ,所以)|(Y X H = 2)(X H -)(Y H =1.8955 bit或)|(Y X H =)(XY H -)(Y H =)(X H +)|(X Y H -)(Y H而)|(X Y H =)(X H ,所以)|(Y X H =2)(X H -)(Y H =1.8955 bit),|(Y X Z H =)|(Y Z H =)(X H =2.585 bit)|,(Y Z X H =)|(Y X H +)|(XY Z H =1.8955+2.585=4.4805 bit2.10 设一个系统传送10个数字,0,1,…,9。
《信息论与编码》部分课后习题参考答案

P ( y1 = 0 | M 1 ) P ( y1 = 0)
因为信道为无记忆信道,所以
P( y1 = 0 | M 1 ) = P( y1 = 0 | x11 x12 = 00) = P( y1 = 0 | x11 = 0) = P(0 | 0) = p
同理,得 I ( y1 = 0 | M i ) = P ( y1 = 0 | xi1 xi 2 ) = P ( y1 = 0 | xi1 ) 输出第一个符号是 y1=0 时, 有可能是四个消息中任意一个第一个数字传送来的。 所以
第二章
2.1 同时掷两个骰子,设每个骰子各个面向上的概率都是 1/6。试求: (1)事件“2 和 6 同时出现”的自信息量; (2)事件“两个 3 同时出现”的自信息量; (3)事件“两个点数中至少有一个是 5”的自信息量; (4)两个点数之和的熵。 答: (1)事件“2 和 6 同时出现”的概率为:
《信息论与编码》
部分课后习题参考答案
1.1 怎样理解消息、信号和信息三者之间的区别与联系。 答:信号是一种载体,是消息的物理体现,它使无形的消息具体化。通信系统中传输的是 信号。 消息是信息的载体, 信息是指消息中包含的有意义的内容, 是消息中的未知成分。 1.2 信息论的研究范畴可以分成哪几种,它们之间是如何区分的? 答:信息论的研究范畴可分为三种:狭义信息论、一般信息论、广义信息论。 1.3 有同学不同意“消息中未知的成分才算是信息”的说法。他举例说,他从三岁就开始背 诵李白诗句“床前明月光,疑是地上霜。举头望明月,低头思故乡。 ” ,随着年龄的增长, 离家求学、远赴重洋,每次读到、听到这首诗都会带给他新的不同的感受,怎么能说这 些已知的诗句没有带给他任何信息呢?请从广义信心论的角度对此现象作出解释。 答:从广义信息论的角度来分析,它涉及了信息的社会性、实用性等主观因素,同时受知识 水平、文化素质的影响。这位同学在欣赏京剧时也因为主观因素而获得了享受,因此属于广 义信息论的范畴。
《信息论与编码》课后习题答案

《信息论与编码》课后习题答案第二章2.1一个马尔可夫信源有3个符号{}1,23,u u u ,转移概率为:()11|1/2p u u =,()21|1/2p u u =,()31|0p u u =,()12|1/3p u u =,()22|0p u u =,()32|2/3p u u =,()13|1/3p u u =,()23|2/3p u u =,()33|0p u u =,画出状态图并求出各符号稳态概率。
解:状态图如下状态转移矩阵为:1/21/201/302/31/32/30p ⎛⎫ ⎪= ⎪ ⎪⎝⎭设状态u 1,u 2,u 3稳定后的概率分别为W 1,W 2、W 3由1231WP W W W W =⎧⎨++=⎩得1231132231231112331223231W W W W W W W W W W W W ⎧++=⎪⎪⎪+=⎪⎨⎪=⎪⎪⎪++=⎩计算可得1231025925625W W W ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩2.2 由符号集{0,1}组成的二阶马尔可夫链,其转移概率为:(0|00)p =0.8,(0|11)p =0.2,(1|00)p =0.2,(1|11)p =0.8,(0|01)p =0.5,(0|10)p =0.5,(1|01)p =0.5,(1|10)p =0.5。
画出状态图,并计算各状态的稳态概率。
解:(0|00)(00|00)0.8p p == (0|01)(10|01)0.5p p ==(0|11)(10|11)0.2p p == (0|10)(00|10)0.5p p == (1|00)(01|00)0.2p p == (1|01)(11|01)0.5p p == (1|11)(11|11)0.8p p == (1|10)(01|10)0.5p p ==于是可以列出转移概率矩阵:0.80.200000.50.50.50.500000.20.8p ⎛⎫ ⎪⎪= ⎪ ⎪⎝⎭ 状态图为:设各状态00,01,10,11的稳态分布概率为W 1,W 2,W 3,W 4 有411i i WP W W ==⎧⎪⎨=⎪⎩∑ 得 13113224324412340.80.50.20.50.50.20.50.81W W W W W W W W W W W W W W W W +=⎧⎪+=⎪⎪+=⎨⎪+=⎪+++=⎪⎩ 计算得到12345141717514W W W W ⎧=⎪⎪⎪=⎪⎨⎪=⎪⎪⎪=⎩2.3 同时掷出两个正常的骰子,也就是各面呈现的概率都为1/6,求:(1) “3和5同时出现”这事件的自信息; (2) “两个1同时出现”这事件的自信息;(3) 两个点数的各种组合(无序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的子集)的熵; (5) 两个点数中至少有一个是1的自信息量。
信息论与编码第二版答案 (3)

信息论与编码第二版答案第一章:信息论基础1.问题:信息论的基本概念是什么?答案:信息论是一种数学理论,研究的是信息的表示、传输和处理。
它的基本概念包括:信息、信息的熵和信息的编码。
2.问题:什么是信息熵?答案:信息熵是信息的度量单位,表示信息的不确定度。
它的计算公式为H(X) = -ΣP(x) * log2(P(x)),其中P(x)表示事件x发生的概率。
3.问题:信息熵有什么特性?答案:信息熵具有以下特性:•信息熵的值越大,表示信息的不确定度越高;•信息熵的值越小,表示信息的不确定度越低;•信息熵的最小值为0,表示信息是确定的。
4.问题:信息熵与概率分布有什么关系?答案:信息熵与概率分布之间存在着直接的关系。
当概率分布均匀时,信息熵达到最大值;而当概率分布不均匀时,信息熵会减小。
第二章:数据压缩1.问题:数据压缩的目的是什么?答案:数据压缩的目的是通过消除冗余和重复信息,使数据占用更少的存储空间或传输更快。
2.问题:数据压缩的两种基本方法是什么?答案:数据压缩可以通过无损压缩和有损压缩两种方法来实现。
无损压缩是指压缩后的数据可以完全还原为原始数据;而有损压缩则是指压缩后的数据不完全还原为原始数据。
3.问题:信息压缩的度量单位是什么?答案:信息压缩的度量单位是比特(bit),表示信息的数量。
4.问题:哪些方法可以用于数据压缩?答案:数据压缩可以通过以下方法来实现:•无结构压缩方法:如霍夫曼编码、算术编码等;•有结构压缩方法:如词典编码、RLE编码等;•字典方法:如LZW、LZ77等。
第三章:信道容量1.问题:什么是信道容量?答案:信道容量是指在给定信噪比的条件下,信道传输的最大数据速率。
2.问题:信道容量的计算公式是什么?答案:信道容量的计算公式为C = W * log2(1 + S/N),其中C表示信道容量,W表示信道带宽,S表示信号的平均功率,N表示噪声的平均功率。
3.问题:信道容量与信噪比有什么关系?答案:信道容量与信噪比成正比,信噪比越高,信道容量越大;反之,信噪比越低,信道容量越小。
信息论与编码课后习题答案

1. 有一个马尔可夫信源,已知p(x 1|x 1)=2/3,p(x 2|x 1)=1/3,p(x 1|x 2)=1,p(x 2|x 2)=0,试画出该信源的香农线图,并求出信源熵。
解:该信源的香农线图为:1/3○ ○2/3 (x 1) 1 (x 2)在计算信源熵之前,先用转移概率求稳定状态下二个状态x 1和 x 2 的概率)(1x p 和)(2x p 立方程:)()()(1111x p x x p x p =+)()(221x p x x p=)()(212x p x p + )()()(1122x p x x p x p =+)()(222x p x x p =)(0)(2131x p x p + )()(21x p x p +=1 得431)(=x p 412)(=x p 马尔可夫信源熵H = ∑∑-IJi j i jix x p x xp x p )(log )()( 得 H=0.689bit/符号2.设有一个无记忆信源发出符号A 和B ,已知4341)(.)(==B p A p 。
求: ①计算该信源熵;②设该信源改为发出二重符号序列消息的信源,采用费诺编码方法,求其平均信息传输速率; ③又设该信源改为发三重序列消息的信源,采用霍夫曼编码方法,求其平均信息传输速率。
解:①∑-=Xiix p x p X H )(log )()( =0.812 bit/符号②发出二重符号序列消息的信源,发出四种消息的概率分别为1614141)(=⨯=AA p 1634341)(=⨯=AB p 1634143)(=⨯=BA p 1694343)(=⨯=BB p用费诺编码方法 代码组 b iBB 0 1 BA 10 2 AB 110 3 AA 111 3无记忆信源 624.1)(2)(2==X H X H bit/双符号 平均代码组长度 2B =1.687 bit/双符号BX H R )(22==0.963 bit/码元时间③三重符号序列消息有8个,它们的概率分别为641)(=AAA p 643)(=AAB p 643)(=BAA p 643)(=ABA p 649)(=BBA p 649)(=BAB p 649)(=ABB p 6427)(=BBB p用霍夫曼编码方法 代码组 b i BBB 6427 0 0 1 BBA 649 0 )(6419 1 110 3 BAB 649 1 )(6418 )(644 1 101 3 ABB 649 0 0 100 3AAB 643 1 )(646 1 11111 5BAA 3 0 1 11110 5ABA643 1 )(6440 11101 5AAA641 0 11100 5)(3)(3X H X H ==2.436 bit/三重符号序列3B =2.469码元/三重符号序列3R =BX H )(3=0.987 bit/码元时间 3.已知符号集合{ 321,,x x x }为无限离散消息集合,它们的出现概率分别为 211)(=x p ,12)(=x p 13)(=x p ···i i x p 21)(=···求: ① 用香农编码方法写出各个符号消息的码字(代码组); ② 计算码字的平均信息传输速率; ③ 计算信源编码效率。
信息论与编码习题答案

信息论与编码习题答案信息论与编码习题答案信息论与编码是一门研究信息传输、存储和处理的学科,它的基本原理和方法被广泛应用于通信、数据压缩、密码学等领域。
在学习信息论与编码的过程中,习题是不可或缺的一部分。
下面将为大家提供一些信息论与编码习题的答案,希望能对大家的学习有所帮助。
习题一:请解释信息熵的概念。
答案:信息熵是信息论中的一个重要概念,用来衡量一个随机变量的不确定性。
对于一个离散型随机变量X,其信息熵H(X)定义为:H(X) = -Σ P(x)log2P(x)其中,P(x)表示随机变量X取值为x的概率。
信息熵的单位是比特(bit),表示信息的平均不确定性。
信息熵越大,表示随机变量的不确定性越高,反之亦然。
习题二:请计算以下离散型随机变量的信息熵。
1. 对于一个均匀分布的随机变量,其取值范围为{1, 2, 3, 4},请计算其信息熵。
答案:由于均匀分布,每个取值的概率相等,即P(1) = P(2) = P(3) = P(4) = 1/4。
代入信息熵的计算公式可得:H(X) = - (1/4)log2(1/4) - (1/4)log2(1/4) - (1/4)log2(1/4) - (1/4)log2(1/4)= - (1/4)(-2) - (1/4)(-2) - (1/4)(-2) - (1/4)(-2)= 22. 对于一个二值随机变量,其取值为{0, 1},且P(0) = 0.8,P(1) = 0.2,请计算其信息熵。
答案:代入信息熵的计算公式可得:H(X) = - 0.8log2(0.8) - 0.2log2(0.2)≈ 0.7219习题三:请解释信道容量的概念。
答案:信道容量是指在给定的信道条件下,能够传输的最大信息速率。
在信息论中,信道容量是衡量信道传输效率的重要指标。
对于一个离散无记忆信道,其信道容量C定义为:C = max{I(X;Y)}其中,X表示输入信号集合,Y表示输出信号集合,I(X;Y)表示输入信号X和输出信号Y之间的互信息。
信息论与编码(第3版)第3章部分习题答案

3.1设信源()12345670.20.190.180.170.150.10.01X a a a a a a a P X ⎛⎫⎧⎫=⎨⎬ ⎪⎩⎭⎝⎭ (1) 求信源熵()H X (2) 编二进制香农码(3) 计算平均码长及编码效率。
答:(1)根据信源熵公式()()()()21log 2.6087bit/symbol i i i H X p a p a ==−=∑(2)利用到3个关键公式:①根据()()()100,0i a i k k p a p a p a −===∑计算累加概率;②根据()()*22log 1log ,i i i i p a k p a k N −≤<−∈计算码长;③根据()a i p a 不断地乘m 取整(m 表示编码的进制),依次得到的i k 个整数就是i a 对应的码字根据①②③可得香农编码为(3)平均码长公式为()13.14i i i K p a k ===∑单符号信源L =1,以及二进制m =2, 根据信息率公式()2log bit/symbol m KR K L==编码效率()83.08%H X Rη==3.2对习题3.1的信源编二进制费诺码,计算其编码效率答:将概率从大到小排列,且进制m=2,因此,分成2组(每一组概率必须满足最接近相等)。
根据平均码长公式为()12.74i iiK p a k===∑单符号信源L=1,以及二进制m=2, 根据信息率公式()2log bit/symbolmKR KL==编码效率(信源熵看题3.1)()95.21%H XRη==3.3对习题3.1的信源编二进制赫夫曼码,计算平均码长和编码效率答:将n个信源符号的概率从大到小排列,且进制m=2。
从m个最小概率的“0”各自分配一个“0”和“1”,将其合成1个新的符号,与其余剩余的符号组成具有n-1个符号的新信源。
排列规则和继续分配码元的规则如上,直到分配完所有信源符号。
必须保证两点:(1)当合成后的信源符号与剩余的信源符号概率相等时,将合并后的新符号放在靠前的位置来分配码元【注:“0”位表示在前,“1”表示在后】,这样码长方差更小;(2)读取码字时是从后向前读取,确保码字是即时码。
信息论与编码课后习题答案

信息论与编码课后习题答案信息论与编码课后习题答案第⼆章2.3 同时掷出两个正常的骰⼦,也就是各⾯呈现的概率都为1/6,求:(1) “3和5同时出现”这事件的⾃信息; (2) “两个1同时出现”这事件的⾃信息;(3) 两个点数的各种组合(⽆序)对的熵和平均信息量; (4) 两个点数之和(即2, 3, … , 12构成的⼦集)的熵; (5) 两个点数中⾄少有⼀个是1的⾃信息量。
解:(1)bitx p x I x p i i i 170.4181log )(log )(18161616161)(=-=-==+=(2)bitx p x I x p i i i 170.5361log )(log )(3616161)(=-=-===(3)两个点数的排列如下: 11 12 13 14 15 16 21 22 23 24 25 26 31 32 33 34 35 36 41 42 43 44 45 46 51 52 53 54 55 56 61 62 63 64 65 66共有21种组合:其中11,22,33,44,55,66的概率是3616161=? 其他15个组合的概率是18161612=?symbol bit x p x p X H ii i / 337.4181log 18115361log 3616)(log )()(=??? ??+-=-=∑参考上⾯的两个点数的排列,可以得出两个点数求和的概率分布如下:bit x p x p X H X P X ii i / 274.3 61log 61365log 365291log 912121log 1212181log 1812361log 3612 )(log )()(36112181111211091936586173656915121418133612)(=?+?+?+?+?+?-=-==?∑(5)bit x p x I x p i i i 710.13611log)(log )(3611116161)(=-=-===2.42.12 两个实验X 和Y ,X={x 1 x 2 x 3},Y={y 1 y 2 y 3},l 联合概率(),i j ij r x y r =为1112132122233132337/241/2401/241/41/2401/247/24r r r r r r rr r=(1)如果有⼈告诉你X 和Y 的实验结果,你得到的平均信息量是多少?(2)如果有⼈告诉你Y 的实验结果,你得到的平均信息量是多少?(3)在已知Y 实验结果的情况下,告诉你X 的实验结果,你得到的平均信息量是多少?解:联合概率(,)i j p x y 为 22221(,)(,)log (,)724112log 4log 24log 4247244i j i j ijH X Y p x y p x y ==?=2.3bit/符号X 概率分布 21()3log 3 1.583H Y =?=bit/符号(|)(,)() 2.3 1.58H X Y H X Y H Y =-=- Y 概率分布是 =0.72bit/符号 Y y1 y2 y3 P8/248/248/242.15P(j/i)=2.16 ⿊⽩传真机的消息元只有⿊⾊和⽩⾊两种,即X={⿊,⽩},⼀般⽓象图上,⿊⾊的Y X y1y 2 y 3 x 1 7/24 1/24 0 x 2 1/24 1/4 1/24 x 31/247/24X x 1 x 2 x 3 P8/248/248/24出现概率p(⿊)=0.3,⽩⾊出现的概率p(⽩)=0.7。
西工大研究生 信息论与编码部分答案

1. 简述Shannon 的信源编码定理及信道编码定理。
[10分] 答:熵:H ,信道容量:C ,传信率:R 。
信源编码:当R>H 时,一定存在某种信源编码方式使信息能够完全传送;否则,当R<=H 时,是不可能的。
信道编码:当R<C 时,一定存在某种信道编码方式使信息能够可靠传送;否则,当R>=C 时,是不可能的。
2. 简述差错控制编码的基本原理。
为何软判决译码比硬判决译码可以得到较高的编码增益?[10分]差错控制编码的定理是发送方对准备传输的数据进行抗干扰编码,即按某种算法附加上一定的冗余位,构成一个码字后再发送。
接收方收到数据后进行校验,即检查信息为和附加冗余位之间的关系,以检查传输过程中是否有差错发生。
硬判决译码,即在译码前对接收量进行二电平量化后再进行判决译码。
种种量化方式比较粗糙,将丢失较多有用信息。
而软判决译码的量化电平数Q>2,(常取Q>8),量化越精细,损失也就越小,故将获得较硬判决译码更大的编码增益。
3. 一个数据传输信道,带宽为1MHz,信噪比为50dB,计算在这个信道上能实现的最大信息传输率。
为什么信息传输率是受限的?[10分] 16.7Mbps信息传输率受限是因为信道带宽限制,以及信道中的噪声干扰。
4. 设一个[7,4]码的生成阵为试求该码的全部码字、一致校验矩阵以及最小汉明距离。
[20分]信息位有四位,应有16种组合——信息组0000 0001 0010 00110100 0101 0110 01111000 1001 1010 10111100 1101 1110 1111C={C| c=mG}⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001110001001101001011000111G全部码字:0000000 0001110 0010011 00111010100101 0101011 0110110 01110001000111 1001001 1010100 10110101100010 1101100 1110001 11111111一致校验矩阵G=[I A]H=[AT I]最小汉明距离:第4,5,6列的和为0,所以最小汉明距离为:35.循环冗余校验(CRC)的生成多项式为CRC-16: x16+x15+x2+1,试画出其编译码电路。
《信息论、编码与密码学》部分课后习题答案

+∞
当 0 ≤ x ≤ a 时, p( x ) = a −1 ,则
H ( X ) = − ∫ a −1 log a −1dx =
0
a
1 log a a ⋅ log a ⋅ [x ]0 = ⋅ a = log a a a
当 x < 0 或 x > a 时, p( x ) = 0 ,则 H ( X ) → ∞ 根据得到的结果可以画出相应的平面图,由图可以看到随着 a 的增加,即 p( x ) 的 减小,微分熵 H ( X ) 相应的增加。
∞ 1 B ⋅ log ∑ ∞ ∞ ∞ ∞ 1 log( AB ) n=2 B =? 则熵为:H ( X ) = ∑ P ( X )I ( X ) = ∑ =∑ log( AB ) = ∑ ∞ 1 AB n=2 n = 2 AB n=2 n=2 B⋅∑ n=2 B
1.8 计算概率分布函数为
x1 x1 x1 x1 x1 x2 x1 x2 x1 x2 x1 x1 x1 x2 x2
1 0 1 1.0 0.5 0
0.5 0.4 0.1
图 1.11 霍夫曼编码
则霍夫曼码如下表:
符号 x1 x2 x3
概率 0.5 0.4 0.1
码字 1 00 01
该信源的熵为:
H ( X ) = −∑ pk log 2 pk
k =1
3
= −(0.5log 2 0.5 + 0.4 log 2 0.4 + 0.1log 2 0.1) = 0.5000 + 0.5288 + 0.3322 = 1.3610(bit )
= 1(bit )
时 , 信 源 熵
对 于 三 元 离 散 信 源 , 当 概 率
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 简述Shannon 的信源编码定理及信道编码定理。
[10分] 答:熵:H ,信道容量:C ,传信率:R 。
信源编码:当R>H 时,一定存在某种信源编码方式使信息能够完全传送;否则,当R<=H 时,是不可能的。
信道编码:当R<C 时,一定存在某种信道编码方式使信息能够可靠传送;否则,当R>=C 时,是不可能的。
2. 简述差错控制编码的基本原理。
为何软判决译码比硬判决译码可以得到较高的编码增益?[10分]差错控制编码的定理是发送方对准备传输的数据进行抗干扰编码,即按某种算法附加上一定的冗余位,构成一个码字后再发送。
接收方收到数据后进行校验,即检查信息为和附加冗余位之间的关系,以检查传输过程中是否有差错发生。
硬判决译码,即在译码前对接收量进行二电平量化后再进行判决译码。
种种量化方式比较粗糙,将丢失较多有用信息。
而软判决译码的量化电平数Q>2,(常取Q>8),量化越精细,损失也就越小,故将获得较硬判决译码更大的编码增益。
3. 一个数据传输信道,带宽为1MHz,信噪比为50dB,计算在这个信道上能实现的最大信息传输率。
为什么信息传输率是受限的?[10分] 16.7Mbps信息传输率受限是因为信道带宽限制,以及信道中的噪声干扰。
4. 设一个[7,4]码的生成阵为试求该码的全部码字、一致校验矩阵以及最小汉明距离。
[20分]信息位有四位,应有16种组合——信息组0000 0001 0010 00110100 0101 0110 01111000 1001 1010 10111100 1101 1110 1111C={C| c=mG}⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=0001110001001101001011000111G全部码字:0000000 0001110 0010011 00111010100101 0101011 0110110 01110001000111 1001001 1010100 10110101100010 1101100 1110001 11111111一致校验矩阵G=[I A]H=[AT I]最小汉明距离:第4,5,6列的和为0,所以最小汉明距离为:35.循环冗余校验(CRC)的生成多项式为CRC-16: x16+x15+x2+1,试画出其编译码电路。
若用MATLAB软件实现,信息序列为500bit的随机序列,给出其主要软件和编码结果。
(译码时仅考虑检错)[20分] dec2bin(2009201211)1110111110000011111101000111011编码电路:移位脉冲cp在前1-k个节拍内,k1,k2打向“1”,各信息元直接经k1输出,成为前k个码元;在k+1~n个节拍内,k1,k2打向“2”,使移位寄存器中各校验元依次输出,形成一个长为n的码字。
译码电路:当寄存器为全零时,表示无错,输出c的前k个码字,即为正确的信息吗。
%发送端对信息进行编码Ip=[1 1 1 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 1 0 1 0 0 0 1 1 1 0 1 1]msg=[ip,randint(1,469)]generator=[1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1];c=[1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0];multip=conv(c,msg);[divid,remainder]=deconv(multip,generator);remainder=mod(remainder(end-15:end),2);code=[msg,remainder];%接收端对信息进行校验[divid,remainder]=deconv(code,generator);remainder=mod(remainder(end-15:end),2);if isequal(remainder,[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]);msgbox(['crc[',num2str(code(end-16:end)),'] 校验正确!']);elsemsgbox(['crc[',num2str(remainder),'] 校验错误!']);endclcclearid=[1 1 1 0 1 1 1 1 1 0 0 0 0 0 1 1 1 1 1 1 0 1 0 0 0 1 1 1 1 0 0]msg=[id,randint(1,469)]poly=[1 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 1];[M N]=size(poly)mseg=[msg zeros(1,N-1)][q r]=deconv(mseg,poly)r=abs(r)for i=1:length(r)a=r(i);if ( mod(a,2)== 0 )r(i)=0;elser(i)=1;endendcrc=r(length(msg)+1:end)frame = bitor(mseg,r)[divid,remainder]=deconv(frame,poly);remainder=mod(remainder(end-15:end),2);if isequal(remainder,[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]);msgbox(['crc[',num2str(frame(end-16:end)),'] 校验正确!' ] );elsemsgbox(['crc[',num2str(remainder),'] 校验错误!']);end6.卷积码的码率为R=1/2,约束度为k=7,生成多项式为G1=133,G0=171,请画出该卷积码的编码器和部分格网图。
采用Viterbi软判决译码时要考虑哪些关键步骤,用软件(C或MATLAB 实现其主要部分。
[20分](2,1,7)有六个寄存器。
由网格图的输入支路特点分析可知,产生任意一个状态节点Si的输入条件mi是确定的,即mi=‘1’,i为偶数;mi=‘0’,i为奇数。
输入条件mi表示译码器最终需要输出的比特信息。
此外,译码器所要找的留选路径是不同状态的组合。
对于(2,1,6)卷积码而言,具有2m=26=64(m为编码存储)个不同状态,可以用6位比特向量来表示所有的状态。
将mi作为最高位加在状态向量上,用7位比特向量同时表示每一状态和对应的输入支路的译码信息,这样在译码器回溯时就可以直接输出存储向量的高位作为译码器的输出。
采用这种方法大大降低了回溯路径和译码器判决的难度,由此降低了译码器结构的复杂性。
G1=1011011,G0=1111001Viterbi软判决译码时,要首先对接受序列进行多比特量化,理想软判决情况下,信道接受值直接用于译码器。
另外,软判决算法在距离度量上采用的是欧几里德度量。
由于编码器有6级移位寄存器,故存在64个状态,分别为s0~s63.在这里只取s。
(000000),s1(000001),s2(000010),s3(000011)作部分网格图:在卷积码译码中,Viterbi译码算法是纠错能力很强的一种,已广泛应用于卫星通信系统。
Viterbi译码算法是一种最大似然译码算法[1]。
Viterbi译码算法的步骤:(1)根据接收码符号,计算出相应的分支量度值;(2)将进入某一状态的2条分支量度与其前面的状态量度累加求和;(3)比较到达同一状态的2条新的路径量度的大小,选择最小者作为新的状态量度存储起来,并记住与此路径(幸存路径)对应的信息码元;(4)对所有的2m个状态都实施上述相加/比较/选择(ACS)运算;路径量度最小的一条路径(约为以前码元长度的5倍)作为译码数据输出;(6)将译码时刻向前延伸一步,重复以上步骤,直至译码结束。
7.如果有一个BCH码(15,11),请说明其系统码的编译码过程,并画出原理电路。
[10分]gx=x4+x2+x+1可纠1位错误。
检验矩阵为H=111101*********011110101100100001111010110010111010110010001编码过程:首先将信息元多项式m(x)乘以x4,得到xn-k×m(x),即将信息码置为(c14,c13,c12,……,c4),设为c1。
然后找出校验码cr满足cr=c1(modg(x))=(c3,c2,c1,c0)这样使得到带发送码字c(x)=c1+cr=(c14,c13,……,c0).解码过程:1,计算接收到的码字向量R的2t伴随矩阵;2,计算错误定位多项式;3,解多项式,得到错误位置;4,如果不是二进制BCH码,就计算错误位置的误差值。
编码电路:前1~11节拍,k1置于1 ,第12~15节拍,k1置于2 。
译码电路:图按错误图样为(100000000000000)设计。
当m=1时,使D0~D3清零。
BCH码的译码方法可以有时域译码和频域译码两类。
频移译码是把每个码组看成一个数字信号,把接受到的信号进行离散傅氏变换(DFT),然后利用数字信号处理技术在“频域”内译码,最后进行傅氏反变换得到译码后的码组。
时域译码则是在时域直接利用码的代数结构进行译码。
BCH的时域译码方法有很多,而且纠多个错误的BCH码译码算法十分复杂。
常见的时域BCH译码方法有彼得森译码、迭代译码等。
BCH的彼得森译码基本过程为:1、用的各因式作为除式,对接收到的码多项式求余,得到t个余式,称为“部分校验式”。
2、用t个部分校验式构造一个特定的译码多项式,它以错误位置数为根。
3、求译码多项式的根,得到错误位置。
4、纠正错误。
