车架计算
车架计算

XXX车架强度计算报告现根据需要,对XXXX车架结构进行调整,对比调整前后的结构状态,进行车架强度计算。
根据协议要求,需保证更改后车架的强度满足安全使用要求,同时在支腿工作时,车架的变形量不大于6mm。
一、模型的建立鉴于UG软件不但具有很强的建模能力,而且还具有很强的数值运算能力和高效的求解技术,本车架利用UGNX8.0建立物理模型后,直接从UG建模模块切换至CAE模块进行有限元网格划分、边界条件加载、NASTRAN求解器求解等工作,从而避免了不同软件模型之间传递的失真问题。
1. 车架的物理模型整个车架由主纵梁、主横梁、支腿、座圈和支架等几部分组成。
保证各个零件之间的相对位置,并且保证它们的联结关系。
车架变更前后的物理模型见图1。
图1a 图1b图1 车架更改前后物理模型2. 车架的约束主要考虑上装工作时车架的实际工作情况,可以假定支腿的四个端面为固定面,因此将这四个面上的所有点的自由度全部进行约束,即约束所有点的六个自由度。
3. 车架的载荷加载根据车架各主要部件的位置,将驾驶室、发动机、变速箱、分动器、油箱等总成的载荷按实际重量加载在车架上,并将16吨的上装载荷加载在座圈三个垫块上,载荷安全系数取3,如图2所示。
图2 模型的边界条件及加载4. 车架的网格划分对车架进行网格划分,为提高计算精度,对座圈等关键位置网格细分,见图3.图3 座圈位置网格细分二、计算结果1. 更改前后车架强度图4(a) 更改前图4(b) 更改后图4更改前后车架等效应力云图局部位置应力强度对比见图5、6、7:图5(a) 更改前图5更改前后座圈等效应力云图图6(a) 更改前图6更改前后后纵梁等效应力云图图7(a) 更改前图7(b) 更改后图7更改前后前支腿支架等效应力云图2. 更改前后车架位移图8(a) 更改前图8(b) 更改后图8车架更改前后位移量云图3. 计算结果(1)通过计算对比了车架更改前后,车架、座圈、后纵梁及支腿支架等位置的应力状况,发现这些部位在后纵梁加长250mm后,应力极值变大,而极值出现的部位基本不变。
车架受力分析基础

车架受力分析基础一、对车架整车的受力要求二、车架的受力情况具体分析三、车架的结构分析1.车架的基本结构形式2.车架宽度的确定3.纵梁的形式、主参数的选择4.车架的横梁及结构形式5.车架的连接方式及特点6.载货车辆采用铆接车架的优点四、车架的计算1.简单强度计算分析2.简单刚度计算分析3.CAE综合分析五、附表2000年7月1日一、整车对车架的要求车架是整车各总成的安装基体,对它有以下要求:1.有足够的强度。
要求受复杂的各种载荷而不破坏。
要有足够的疲劳强度,在大修里程内不发生疲劳破坏。
2.要有足够的弯曲刚度。
保证整车在复杂的受力条件下,固定在车架上的各总成不会因车架的变形而早期损坏或失去正常工作能力。
3.要有足够的扭转刚度。
当汽车行使在不平的路面上时,为了保证汽车对路面不平度的适应性,提高汽车的平顺性和通过能力,要求车架具有合适的扭转刚度。
对载货汽车,具体要求如下:3.1车架前端到驾驶室后围这一段车架的扭转刚度较高,因为这一段装有前悬架和方向机,如刚度弱而使车架产生扭转变形,势必会影响转向几何特性而导致操纵稳定性变坏。
对独立悬架的车型这一点很重要。
3.2包括后悬架在内的车架后部一段的扭转刚度也应较高,防止由于车架产生变形而影响轴转向,侧倾稳定性等。
3.3驾驶室后围到驾驶室前吊耳以前部分车架的刚度应低一些,前后的刚度较高,而大部分的变形都集中在车架中部,还可防止因应力集中而造成局部损坏现象。
4.尽量减轻质量,按等强度要求设计。
二、车架的受力情况分析1.垂直静载荷:车身、车架的自重、装在车架上个总成的载重和有效载荷(乘员和货物),该载荷使车架产生弯曲变形。
2.对称垂直动载荷:车辆在水平道路上高速行使时产生,其值取决于垂直静载荷和加速度,使车架产生弯曲变形。
3.斜对称动载荷在不平道路上行使时产生的。
前后车轮不在同一平面上,车架和车身一起歪斜,使车架发生扭转变形。
其大小与道路情况,车身、车架及车架的刚度有关。
公路车山地车自行车车架与身高尺寸的计算图解
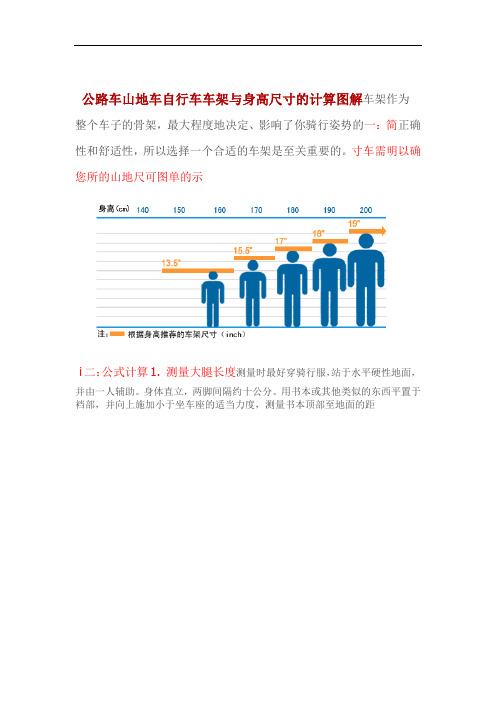
公路车山地车自行车车架与身高尺寸的计算图解车架作为整个车子的骨架,最大程度地决定、影响了你骑行姿势的一:简正确性和舒适性,所以选择一个合适的车架是至关重要的。
寸车需明以确您所的山地尺可图单的示
i二:公式计算1. 测量大腿长度测量时最好穿骑行服,站于水平硬性地面,
并由一人辅助。
身体直立,两脚间隔约十公分。
用书本或其他类似的东西平置于裆部,并向上施加小于坐车座的适当力度,测量书本顶部至地面的距
2. 测量身长t相同,测量锁1离:姿势与步骤i
t
骨之间V字槽底部至书本上端的距离:a测量臂长3. 水平站立,平伸手臂、掌心向前,测量从虎口到肋骨所在平面的距
s宽测量肩4. 离a度宽的处节关肩量测,臂两松放,立直
以上尺寸每个测量三次,取平s值均:车到你所需要的架尺寸以上根据以数据可得i*0.67-=((i X 0.67cm)山地车架尺寸公路车架尺寸=公路/2+x] - et(=[t+a)把立长度11.0)X 0.394(英寸)
(车架上lengthtop et=effective tube ;=山地;=车x4 x8你所适合的曲柄长度:)”o“的s管有效长度就是第一张图中。
(完整word版)车架计算

汽车车架是整个汽车的基体,是将汽车的主要总成和部件连接成汽车整体的金属构架,对于这种金属构架式车架,生产厂家在生产设计时应考虑结构合理,生产工艺规范,要采取一切切实可行的措施消除工艺缺陷,保证它在各种复杂的受力情况下不至于被破坏。
车架作为汽车的承载基体,为货车、中型及以下的客车、中高级和高级轿车所采用,支撑着发动机离合器、变速器、转向器、非承载式车身和货箱等所有簧上质量的有关机件,承受着传给它的各种力和力矩。
为此,车架应有足够的弯曲刚度,以使装在其上的有关机构之间的相对位置在汽车行驶过程中保持不变并使车身的变形最小;车架也应有足够的强度,以保证其有足够的可靠性与寿命,纵梁等主要零件在使用期内不应有严重变形和开裂。
车架刚度不足会引起振动和噪声,也使汽车的乘坐舒适性、操纵稳定性及某些机件的可靠性下降。
车架受力状态极为复杂.汽车静止时,它在悬架系统的支撑下,承受着汽车各部件及载荷的重力,引起纵梁的弯曲和偏心扭转(局部扭转)。
如汽车所处的路面不平,车架还将呈现整体扭转.汽车行驶时,载荷和汽车各部件的自身质量及其工作载荷(如驱动力、制动力和转向力等)将使车架各部件承受着不同方向、不同程度和随机变化的动载荷,车架的弯曲、偏心扭转和整体扭转将更严重,同时还会出现侧弯、菱形倾向,以及各种弯曲和扭转振动。
同时,有些装置件还可能使车架产生较大的装置载荷。
钢板经冷冲成形后,其疲劳强度要降低,静强度高、延伸率小的材料的降低幅度更大。
常用车架材料在冲压成形后的疲劳强度约为140~160Mpa。
轻型货车冲压纵梁的钢板厚度为5。
0~7.0mm,槽型断面纵梁上下翼缘的宽度尺寸约为其腹板高度尺寸的35%~40%.随着计算机技术的发展,在产品开发阶段,对车架静应力、刚度、振动模态以至动应力和碰撞安全等已可进行有限元分析,对其轻量化、使用寿命,以及振动和噪声特性也可以做出初步判断,为缩短产品开发周期创造了有利条件.当车架纵梁承受的是均匀分布的载荷时,车架强度的简化计算可按下述进行,但须做一定假设。
车架尺寸计算公式

车架尺寸计算公式(转自车友论坛)参加自行车运动,最重要的器材莫过于您的坐骑——自行车了。
车架作为整个车子的骨架,最大程度地决定、影响了你骑行姿势的正确性和舒适性,所以选择一个合适的车架是至关重要的。
在Airborne网站上看到了度量身体个部位长度和计算车架尺寸的公式,供大家参考使用。
1. 测量大腿长度i测量时最好穿骑行服,站于水平硬性地面,并由一人辅助。
身体直立,两脚间隔约十公分。
用书本或其他类似的东西平置于裆部,并向上施加小于坐车座的适当力度,测量书本顶部至地面的距离:i2. 测量身长t姿势与步骤1相同,测量锁骨之间V字槽底部至书本上端的距离:t 3. 测量臂长a水平站立,平伸手臂、掌心向前,测量从虎口到肋骨所在平面的距离4. 测量肩宽s直立,放松两臂,测量肩关节处的宽度s以上尺寸每个测量三次,取平均值根据以上数据可以得到你所需要的车架尺寸:公路车架尺寸=i*0.67(cm)山地车架尺寸=(i*0.67-11.0)*0.394(英寸)把立长度=[(t+a)/2+x]-et公路车x=4;山地x=8;et=effective top tube length(车架上管有效长度就是第一张图中的“o”)你所适合的曲柄长度:腿长范围(cm)曲柄长度65cm - 70cm 165mm71cm - 76cm 170mm79cm - 81cm 172.5mm82cm - 90cm 175mm弯把宽度:(弯把的宽度是指中心至中心的长度)肩宽范围s 把宽cm38cm 38 - 4039cm 4040cm 4041cm 40 – 4242cm 4243cm 42 – 4444cm 4445cm 4446cm 44 - 46。
车架计算资料讲解

车架计算汽车车架是整个汽车的基体,是将汽车的主要总成和部件连接成汽车整体的金属构架,对于这种金属构架式车架,生产厂家在生产设计时应考虑结构合理,生产工艺规范,要采取一切切实可行的措施消除工艺缺陷,保证它在各种复杂的受力情况下不至于被破坏。
车架作为汽车的承载基体,为货车、中型及以下的客车、中高级和高级轿车所采用,支撑着发动机离合器、变速器、转向器、非承载式车身和货箱等所有簧上质量的有关机件,承受着传给它的各种力和力矩。
为此,车架应有足够的弯曲刚度,以使装在其上的有关机构之间的相对位置在汽车行驶过程中保持不变并使车身的变形最小;车架也应有足够的强度,以保证其有足够的可靠性与寿命,纵梁等主要零件在使用期内不应有严重变形和开裂。
车架刚度不足会引起振动和噪声,也使汽车的乘坐舒适性、操纵稳定性及某些机件的可靠性下降。
车架受力状态极为复杂。
汽车静止时,它在悬架系统的支撑下,承受着汽车各部件及载荷的重力,引起纵梁的弯曲和偏心扭转(局部扭转)。
如汽车所处的路面不平,车架还将呈现整体扭转。
汽车行驶时,载荷和汽车各部件的自身质量及其工作载荷(如驱动力、制动力和转向力等)将使车架各部件承受着不同方向、不同程度和随机变化的动载荷,车架的弯曲、偏心扭转和整体扭转将更严重,同时还会出现侧弯、菱形倾向,以及各种弯曲和扭转振动。
同时,有些装置件还可能使车架产生较大的装置载荷。
钢板经冷冲成形后,其疲劳强度要降低,静强度高、延伸率小的材料的降低幅度更大。
常用车架材料在冲压成形后的疲劳强度约为140~160Mpa 。
轻型货车冲压纵梁的钢板厚度为5.0~7.0mm ,槽型断面纵梁上下翼缘的宽度尺寸约为其腹板高度尺寸的35%~40%.随着计算机技术的发展,在产品开发阶段,对车架静应力、刚度、振动模态以至动应力和碰撞安全等已可进行有限元分析,对其轻量化、使用寿命,以及振动和噪声特性也可以做出初步判断,为缩短产品开发周期创造了有利条件。
当车架纵梁承受的是均匀分布的载荷时,车架强度的简化计算可按下述进行,但须做一定假设。
无砟轨道混凝土浇筑机车架的设计与计算

线 采 用 双 块 式 无 砟 轨 道 技 术 , 用 工 具 轨 法 施 工 , 大 致 应 其
担 了 各 部 分 的调 整 功 能 , 因 此 浇 筑 机 车 架 结 构 的 合 理 设 计和 强 度 、 度 、 定 性 的精确 计 算 与分 析对 浇筑 机 的工 刚 稳 作性 能 和 浇筑质 量 的保证 都 是至 关 重要 的 。
【 摘
要 】 对客 运 专线 无砟 轨 道 混凝 土 浇筑 机 的工 作过 程 、 工 要 求和 各工 作 机构 布 置情 况进 行 分 析 的基础 上 , 在 施 完
成 了整 机 车 架 部 分 的 结 构 设 计 : 究 浇 筑 机 的 各 种 工 况 , 定 了 恶 劣 工 况 , 采 用 有 限 元 计 算 法 , 用 A YS 算 软 研 确 并 应 NS 计 件 对 车 架 进 行 了 强 度 、 度 的 精 确 计 算 和 稳 定 性 分 析 。 计 算 结 果 表 明 : 架 的 强 度 和 刚度 满 足 承 载 的 设 计 要 求 , 横 刚 车 但 向 和 纵 向 抗 倾 覆 稳 定 性 在 最 恶 劣 工 况 下 不 足 ; 取 车 架 和 螺 旋 输 送 器 后 端 分 别 加 配 重 块 的 措 施 后 , 限 元 计 算 结 果 采 有
基本型半挂车悬架高度的计算方法

通用型半挂车基本高度尺寸的计算方法1、13米直梁式半挂车首先确定牵引车的牵引座上平面的离地高度(基准参数);一般采用实测方法获得。
再确定半挂车纵梁截面高度(通过技术或用户要求选择)将以上参数确定后即可通过以下公式计算获得半挂车的悬挂高度。
首先这几个参数是不变的:车架前后高度1.(牵引中心至第二桥中心)差40mm(6×4牵引车)2.(牵引中心至第二桥中心)差90mm(6×2牵引车);钢板弹簧(普通型10片)作用长度内的弧高60mm。
牵引座上平面的离地高度(mm)+半挂车前鹅颈高度(mm)-半挂车纵梁截面高度(mm)-轮胎半径(mm)-车桥半径(mm)-桥上卡板厚度(mm)-钢板弹簧总厚度(mm)-钢板弹簧的弧高(60mm)-半挂车的前后倾斜高度(40mm)=悬挂高度(mm)2、13米鹅颈式半挂车前后平台高度的确定首先确定牵引车的牵引座上平面的离地高度(基准参数);一般采用实测方法获得。
再确定用户选择的轮胎型号将以上参数确定后即可通过以下步骤计算获得半挂车的货台高度。
首先这几个参数是不变的:吊耳(正装)高度130mm;车架前后高度1.(牵引中心至第二桥中心)差40mm(6×4牵引车)2.(牵引中心至第二桥中心)差60mm(6×2牵引车);钢板弹簧(普通型10片)作用长度内的弧高60mm。
1、前平台高度(mm)=牵引车的牵引座上平面离地高度(mm)+前鹅颈高度(mm)。
2、后平台高度(mm)=轮胎直径(mm)+150mm(边梁圆弧下平面顶部切点至轮胎圆周顶部切点)+边梁高度80mm~90mm(边梁圆弧顶部切点至边梁上平面)。
3、确定后平台纵梁高度(mm)=后平台高度(mm)-(轮胎半径(mm)+车桥半径75mm+桥上卡板厚度20mm+钢板弹簧总厚度130mm+钢板弹簧的弧高60mm+悬架吊耳高度130mm)。
4、鹅颈式半挂车前后高度差(6×4牵引车)=前平台高度-后平台高度-40mm。
车架的载荷计算公式为

车架的载荷计算公式为车架的载荷计算公式。
车架是汽车的骨架,承担着车身、发动机、底盘等部件的重量,同时还要承受来自路面的冲击力和扭矩。
因此,车架的设计和计算是汽车工程中非常重要的一部分。
在车架设计中,载荷计算是必不可少的一环,通过合理的载荷计算可以确保车架的强度和刚度满足使用要求,同时还可以减轻车架的重量,提高汽车的燃油经济性和行驶性能。
在进行车架的载荷计算时,需要考虑以下几个方面的载荷,静载荷、动载荷和振动载荷。
静载荷是指车辆在静止状态下受到的重力和惯性力,包括车身、发动机、底盘等部件的重量,以及车辆自身的重量。
静载荷的计算可以通过简单的重力加速度公式来进行,即静载荷 = 质量×重力加速度。
在实际计算中,静载荷还需要考虑车辆的载重量、乘客和货物的重量等因素,以确保车架在静态状态下不会发生变形或破坏。
动载荷是指车辆在行驶过程中受到的各种力,包括加速度、制动力、转向力等。
动载荷的计算需要考虑车辆的加速度、速度、质量分布、路面状况等因素,以确保车架在行驶过程中不会发生疲劳破坏或失稳。
振动载荷是指车辆在行驶过程中受到的振动力,包括路面的颠簸、车辆的颠簸、发动机的振动等。
振动载荷的计算需要考虑车辆的振动频率、振幅、路面状况等因素,以确保车架在振动过程中不会发生疲劳破坏或共振现象。
在进行车架的载荷计算时,需要使用一些专业的工程计算软件,如ANSYS、ABAQUS等,通过有限元分析等方法来进行载荷计算和强度分析。
同时,还需要考虑车架的材料、结构形式、焊接工艺等因素,以确保车架的强度和刚度满足设计要求。
在实际的工程中,车架的载荷计算是一个复杂而又重要的工作。
通过合理的载荷计算,可以确保车架的强度和刚度满足使用要求,同时还可以减轻车架的重量,提高汽车的燃油经济性和行驶性能。
因此,对于汽车工程师来说,掌握车架的载荷计算方法是非常重要的,可以为汽车的设计和制造提供重要的技术支持。
总之,车架的载荷计算是汽车工程中非常重要的一环,通过合理的载荷计算可以确保车架的强度和刚度满足使用要求,同时还可以减轻车架的重量,提高汽车的燃油经济性和行驶性能。
平车车架自重计算公式
品牌车架尺寸与身高对照

最简单的选择-----品牌车架尺寸与身高对照关系:捷安特GIANT15寸:152-170CM17寸:165-180CM19寸:173-185CM21寸:185CM以上美丽达Merida14寸:150-165CM16寸:160-175CM18寸:170-185CM20寸:185CM以上以下是专业的两种选择方法:教你怎样选择适合自己使用的车架,把立的长度,把横的宽度,以及曲柄的长度(贴图表示)参加自行车运动,最重要的器材莫过于您的坐骑——自行车了。
车架作为整个车子的骨架,最大程度地决定、影响了你骑行姿势的正确性和舒适性,所以选择一个合适的车架是至关重要的。
在Airborne网站上看到了度量身体个部位长度和计算车架尺寸的公式,供大家参考使用。
1. 测量大腿长度i测量时最好穿骑行服,站于水平硬性地面,并由一人辅助。
身体直立,两脚间隔约十公分。
用书本或其他类似的东西平置于裆部,并向上施加小于坐车座的适当力度,测量书本顶部至地面的距离:i2. 测量身长t姿势与步骤1相同,测量锁骨之间V字槽底部至书本上端的距离:t 3. 测量臂长a水平站立,平伸手臂、掌心向前,测量从虎口到肋骨所在平面的距离4. 测量肩宽s直立,放松两臂,测量肩关节处的宽度s以上尺寸每个测量三次,取平均值根据以上数据可以得到你所需要的车架尺寸:公路车架尺寸=iX0.67(cm)山地车架尺寸=(iX0.67-11.0)X0.394(英寸)把立长度=[(t+a)/2+x]=et公路车x=4;山地x=8;et=effective top tube length(车架上管有效长度)你所适合的曲柄长度:腿长范围(cm)曲柄长度65cm - 70cm 165mm71cm - 76cm 170mm79cm - 81cm 172.5mm82cm - 90cm 175mm弯把宽度:(弯把的宽度是指中心至中心的长度)肩宽范围s 把宽cm38cm 38 - 4039cm 4040cm 4041cm 40 – 4242cm 4243cm 42 – 4444cm 4445cm 4446cm 44 - 46-----------------------------------------------------------------------------------------------------------------另外一篇相关的贴子:车架尺寸的问题,对于我等业余爱好者,想把这个问题搞清楚还是很困难的,这是有位车友的相关探讨,很有实用性,如果有选车架尺寸的疑惑,可以借鉴一下!首先,我简单说下车架尺寸的重要性。
重型车车架的静动态计算分析

文献标识码 : A
文章 编 号 :0 0— 9 8 2 0 )7— 0 2—0 10 4 9 (0 7 0 0 3 4
车 架 是 汽 车 的 重 要 组 成 部 分 , 汽 车 整 车 设 计 中 在
板 、 角 支 撑 板 和 后 轴 等 部 分 。 虑 到 车 架 几 何 模 型 的 三 考 复杂性 , 在 三维 C 可 AD 软 件 UG 里 建 立 车 架 的 面 模 型 , 人 到 Hy emeh软 件 中 进 行 网 格 划 分 等 前 置 处 导 pr s 理 , 后 提 交 到 AN Y 然 S S解 算 。 架 各 层 之 间 的 铆 钉 联 车 接 , 以 用 Hy eme h—c n e tr 可 pr s o n co s中 的 b r单 元 来 模 a 拟 铆 钉 联 接 , 应 的 是 ANS 对 YS的 MP C单 元 , 车 架 各 因
架为研 究 对象 , 该 车架 结构 的动 、 态特 性进 行分 析 对 静
计算 , 化 、 收 欧洲 的先 进技 术 并在 此基 础上 进行 自 消 吸 主创 新 设 计 。 析 手 段 主要 是 通 过 建立 正 确 的有 限元 分 分析模 型 , 车架 进行 典 型工 况 的静 态分 析 、 态分 析 对 模
铆 钉联 接 , 种结 构 与具 有 连续横 截 面 的车架 不 同 , 这 其
力 的传递 是不 连续 的。
2 静 力 分 析
2 1 边 界 条 件 的 确 定 .
车 架 通 过 悬 架 系 统 、 轮 支 承 在 地 面 上 , 有 限元 车 当
模 型将 悬 架 系统 与车 架 组 合 成整 体 式 计 算模 型后 , 边
由 于 车 架 是 由一 系 列 薄 壁 件 组 成 , 限 元 模 型 采 用 壳 有
公路车车架尺寸

公路车车架尺寸怎么算啊 2010-03-03 23:51龙城影视公路车车架[ 标签:, 尺寸 ]我该怎么选一款适合自己的公166 需求一款公路车普通的本人嫌大本人身高尺寸应该要多大啊路车啊83%好评率:满意答案自行车运动参加,最重要的器材莫过于您的坐骑——自行车了。
车架作为整个车子的骨架,最大程度地决定、影响了你骑行姿势的正确性和舒适性,所以选择一个合适的车架是至关重要的。
在Airborne网站上看到了度量身体个部位长度和计算车架尺寸的公式,供大家参考使用。
1. 测量大腿长度i此主题相关图片如下:骑行服测量时最好穿,站于水平硬性地面,并由一人辅助。
身体直立,两脚间隔约十公分。
用书本或其他类似的东西平置于裆部,并向上施加小于坐车座的适当力度,测量书本顶部至地面的距离:i2. 测量身长t此主题相关图片如下:姿势与步骤1相同,测量锁骨之t字槽底部至书本上端的距离:V间.a测量臂长3.此主题相关图片如下:水平站立,平伸手臂、掌心向前,测量从所在平面的距离肋骨虎口到s测量肩宽4.此主题相关图片如下:s 肩关节宽度处的直立,放松两臂,测量以上尺寸每个测量三次,取平均值根据以上数据可以得到你所需要的车架尺寸:公路车架尺寸=i*0.67(cm)山地车架尺寸=(i*0.67-11.0)*0.394(英寸)把立长度=[(t+a)/2+x]-et公路车x=4;山地x=8;et=effective top tube length(车架上管有效长度就是第一张图中的“o”)你所适合的曲柄长度:腿长范围(cm)曲柄长度65cm - 70cm 165mm71cm - 76cm 170mm79cm - 81cm 172.5mm82cm - 90cm 175mm弯把宽度:(弯把的宽度是指中心至中心的长度)肩宽范围s 把宽cm38cm 38 - 4039cm 4040cm 4041cm 40 – 4242cm 4244 –43cm 4244cm 4445cm 4446cm 44 - 46我就想要知道准确的数值看不懂继续追问:这些对我来说没用 700*48 补充回答:继续追问:你这个尺寸和人家店家告诉我的尺寸不一样啊465mm 人家告诉我我应该选择你这个尺寸是什么意思啊 48CM是车架补充回答:700C是轮子继续追问:是什么意思啊那你告诉我人家告诉我的465mm就是车架尺寸46.5cm补充回答: 465有车友表示上一期对于座杆影响上管长度解释的不够清楚。
车架四种工况计算公式

车架四种工况计算公式车架作为汽车的支撑载体,承载着汽车百分之八十以上的重量,因此在轻量化评价及优化设计的研究中,对车架的轻量化设计是不可缺少的一部分。
LCK6105PHENV型系列电动公交车的基本配置参数,以该电动公交车为参考,设计出新的电动公交车车架。
该电动车公交车为纯电动车,搭载锂离子电池,能够持续续航200km,最高车速可达90km/h。
满足国家政策要求以及各大中城市的要求,并且能够实现零排放,能够达到节能减排的目的。
依据所研究的电动公交车车架的样本数据为基础,进行必要改动设计后,在Pro/E中对该电动公交车车架进行参数化建模,并以IGES格式保存。
在ANSYS中导入车架模型的IGES文件,并将有限元模型单元材料选择为Q235,材料设置属性为E=210GPa,σ=0.3,ρ=7.9E+03kg/m3,焊点为RBE2刚性单元,部分焊点使用节点合并。
根据电动公交车的工况与实际载荷,在保证车架整体性能的前提下,以60mm为基准,对车架使用板壳单元网格划分。
参数化设定后得的车架有限元模型及坐标在车架前左、右悬架装座处,对X、Y、Z三个方向的自由度进行约束,对车架后段区域左、右纵梁Y方向限定平动自由度。
当设定约束点后,根据电动公交车的实际运行工况,结合动态系数,对车架垂直Y方向施加53520N 的荷载。
对车架前左悬架装座处进行X、Y、Z方向的平动自由度进行约束,右悬架不限制自由度,对车架后段区域左、右纵梁添加Y方向的约束。
设定约束点后,根据电动公交车在实际运行中的情况,结合动态系数,对车架垂直Y方向施加38000N的荷载。
通过计算,并查看求解结果,得到弯曲、扭转工况下的车架变形云图以及等效应力云图,如图2所示。
由以上静应力分析可知,车架在弯曲工况下的等效应力最大值为107.48MPa,扭转工况下的等效应力极限为174.18MPa,均小于Q235的屈服极限,满足车架使用的强度条件,存在强度富裕,可进一步轻量化。
第六章车身的简化计算

第六章 车身的简化计算§6-1 概 述到目前为止,对待汽车尤其是车身计算载荷的方法,与对待其它交通工具的方法是不一样的。
至今未制订出计算载荷的基本准则。
飞机、船舶、铁道车辆等——以载荷的各种计算方法和标准规范为基础。
不平路面→汽车激起不同的振动→车身、车架承受随机载荷→汽车结构产生疲劳损坏。
——难以准确确定,随着科学技术的发展——如随机振动理论、结构分析技术、测试技术等的迅猛发展,为深入开展此项研究提供了基础。
汽车行驶中所受的载荷一—两大类:1.疲劳载荷——造成疲劳破坏的随机载荷。
只能用统计的方法描述。
获得方法: ① 道路试验法对汽车在典型路面上进行短距离实测,然后用数理统计的方法对所测得 的资料进行整理和推断,最后编制成载荷谱的方法来取得载荷资料。
② 数学分析法——根据积累的路面不平度的测量统计资料(路面功率谱密度)和反映 结构参数的系统频率响应函数→求得相应的输出功率谱和均方值→进而求出构件的载荷方差和均方值。
——可参考有关资料。
疲劳载荷——适用于计算零部件的疲劳强度,估算疲劳寿命。
均有设计标准规范车轮和路轨的撞击力。
—铁道车辆河、海水的浪高;—船舶行驶中受力;按不同飞机的起飞曲线—飞机的起飞载荷⎪⎭⎪⎬⎫有关,且相当复杂汽车结构参数等使用条件路面状况载荷大小及其特性⎪⎩⎪⎨⎧2.偶然的大载荷——偶然因路面冲击引起这种大载荷将使构件的工作应力超过材料的屈服极限或强度极限而破坏。
试验表明:若结构尺寸选择正确,能承受最大的偶然载荷的作用,则它的疲劳强度也足够。
学习本章的目的在于对计算所需外力进行系统分析并给予科学、合理的确定。
§6-2 车身的计算载荷一、动载荷和静载荷的关系静载荷——静止时,汽车悬挂着的自身载荷G r 和车身有效载荷(悬挂质量和额定装载质量)。
动载荷——汽车在不平路面上行驶时所承受的载荷。
汽车行驶时所受的载荷: ⎩⎨⎧最大动载(道路不平)—次数极少经常反复出现的动载—最多的经验表明:如结构的尺寸选择正确,该结构能承受最大的偶然载荷的作用,因此,疲劳强度亦足够。
某铁路车辆车架结构设计及静强度计算与试验

某铁路车辆车架结构设计及静强度计算与试验1. 引言1.1 研究背景铁路车辆是现代交通运输系统中不可或缺的重要组成部分。
车架作为铁路车辆的核心结构之一,直接影响着车辆的运行安全和稳定性。
随着铁路运输的快速发展,铁路车辆运行环境的复杂性和要求也在不断提高,因此车架结构的设计和静强度计算及试验显得尤为重要。
在过去的研究中,铁路车辆车架结构设计和强度计算一直是学术界和工程界关注的焦点。
通过对车架结构设计原理的探索和静强度计算方法的研究,可以为提高铁路车辆的安全性和稳定性提供重要的参考。
本研究旨在通过对某铁路车辆车架结构进行设计及静强度计算与试验,探讨车架结构设计的原理和方法,分析试验结果并提出设计优化建议,从而为铁路车辆的安全运行提供技术支持。
通过本研究的开展,将为铁路车辆车架结构设计及强度计算领域的进一步研究提供重要参考,也将推动铁路运输行业的发展和进步。
1.2 研究目的本研究的研究目的是通过对某铁路车辆车架结构设计及静强度计算与试验的研究,探讨提高车架结构设计的效率和安全性。
具体目的包括:1. 分析车架结构设计原理,了解车架各部件的功能和作用,为后续的设计和计算工作提供理论支撑;2. 探讨静强度计算方法,通过建立数学模型和进行有限元分析,对车架结构的强度进行评估;3. 制定合理的试验方案,进行静强度试验,验证计算结果的准确性和可靠性;4. 分析试验结果,发现车架结构存在的问题和不足,并提出设计优化建议,进一步提高车架结构的性能和安全性。
通过本研究,旨在为铁路车辆的设计和改进提供科学依据,提高车辆的运行效率和安全性。
1.3 研究意义铁路车辆作为重要的运输工具,在确保安全运行的基础上,对车架结构的设计和静强度计算至关重要。
具有合理的车架结构能够有效分担车辆荷载,提高车辆的稳定性和安全性,同时也能减少车辆的能耗和维护成本。
静强度计算是评估车架结构承受各种载荷情况下的强度和稳定性的重要手段,可以帮助工程师设计出更加安全可靠的车辆。
车架尺寸如何计算公式图片

车架尺寸如何计算公式图片车架尺寸是指自行车车架的尺寸大小,它直接影响到骑行者的舒适度和骑行的稳定性。
正确的车架尺寸能够让骑行者在骑行过程中更加舒适,减少受伤的可能性。
因此,选择合适的车架尺寸对于购买自行车来说是非常重要的。
车架尺寸的计算公式是一种较为复杂的计算方法,需要考虑到骑行者的身高、腿长、臂长等因素。
一般来说,车架尺寸的计算公式可以通过以下步骤进行:首先,测量骑行者的身高。
骑行者站立时,用尺子从地面到头顶的距离即为身高。
其次,测量骑行者的腿长。
骑行者站立时,用尺子从骨盆骨到地面的距离即为腿长。
然后,测量骑行者的臂长。
骑行者伸直手臂,用尺子从肩膀到手指尖的距离即为臂长。
最后,根据身高、腿长和臂长的测量结果,可以使用以下的车架尺寸计算公式来计算出合适的车架尺寸:合适的车架尺寸 = 身高 x 0.67 + 腿长 x 0.83。
这个计算公式是根据骑行者的身高和腿长来确定车架尺寸的,通过这个公式可以得到一个大致的车架尺寸范围。
然而,由于每个人的身体比例不同,所以这个计算公式只能作为参考,最终的车架尺寸还需要根据实际情况进行调整。
除了以上的计算公式外,还有一些其他的方法可以帮助确定合适的车架尺寸。
例如,可以通过试骑来感受不同尺寸的车架,从而确定哪种尺寸更适合自己。
此外,还可以向专业的自行车店或者骑行教练咨询,他们可以根据经验和专业知识来帮助确定合适的车架尺寸。
在选择车架尺寸时,除了考虑骑行者的身高、腿长和臂长外,还需要考虑到自行车的类型和用途。
不同类型的自行车(如山地车、公路车、城市车等)对车架尺寸的要求也不同。
因此,在确定车架尺寸时,还需要考虑到自行车的类型和用途,以确保选择到最适合自己的车架尺寸。
总之,车架尺寸的选择对于购买自行车来说是非常重要的。
合适的车架尺寸能够让骑行者在骑行过程中更加舒适,减少受伤的可能性。
因此,在选择车架尺寸时,需要考虑到骑行者的身高、腿长、臂长等因素,同时还需要考虑到自行车的类型和用途。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
汽车车架是整个汽车的基体,是将汽车的主要总成和部件连接成汽车整体的金属构架,对于这种金属构架式车架,生产厂家在生产设计时应考虑结构合理,生产工艺规范,要采取一切切实可行的措施消除工艺缺陷,保证它在各种复杂的受力情况下不至于被破坏。
车架作为汽车的承载基体,为货车、中型及以下的客车、中高级和高级轿车所采用,支撑着发动机离合器、变速器、转向器、非承载式车身和货箱等所有簧上质量的有关机件,承受着传给它的各种力和力矩。
为此,车架应有足够的弯曲刚度,以使装在其上的有关机构之间的相对位置在汽车行驶过程中保持不变并使车身的变形最小;车架也应有足够的强度,以保证其有足够的可靠性与寿命,纵梁等主要零件在使用期内不应有严重变形和开裂。
车架刚度不足会引起振动和噪声,也使汽车的乘坐舒适性、操纵稳定性及某些机件的可靠性下降。
车架受力状态极为复杂。
汽车静止时,它在悬架系统的支撑下,承受着汽车各部件及载荷的重力,引起纵梁的弯曲和偏心扭转(局部扭转)。
如汽车所处的路面不平,车架还将呈现整体扭转。
汽车行驶时,载荷和汽车各部件的自身质量及其工作载荷(如驱动力、制动力和转向力等)将使车架各部件承受着不同方向、不同程度和随机变化的动载荷,车架的弯曲、偏心扭转和整体扭转将更严重,同时还会出现侧弯、菱形倾向,以及各种弯曲和扭转振动。
同时,有些装置件还可能使车架产生较大的装置载荷。
钢板经冷冲成形后,其疲劳强度要降低,静强度高、延伸率小的材料的降低幅度更大。
常用车架材料在冲压成形后的疲劳强度约为
140~160Mpa 。
轻型货车冲压纵梁的钢板厚度为5.0~7.0mm ,槽型断面纵梁上下翼缘的宽度尺寸约为其腹板高度尺寸的35%~40%.
随着计算机技术的发展,在产品开发阶段,对车架静应力、刚度、振动模态以至动应力和碰撞安全等已可进行有限元分析,对其轻量化、使用寿命,以及振动和噪声特性也可以做出初步判断,为缩短产品开发周期创造了有利条件。
当车架纵梁承受的是均匀分布的载荷时,车架强度的简化计算可按下述进行,但须做一定假设。
即认为纵梁为支承在前后轴上的简支梁;空车时簧上负荷Gs 均布在左右纵梁的全长上,满载时有效载荷Ge 则均布在车箱长度范围内的纵梁上;忽略不计局部扭矩的影响。
R f 为一根纵梁的前支承反力,由该图可求得:
R f =)]2()2([412c c Ge b L Gs l
-+- (1) 在驾驶室的长度范围内这一段纵梁的弯矩为
Mx=R f x-2)(4a x L
Gs + (2) 驾驶室后端至后轴这一段纵梁的弯矩为:
Mx ˊ= R f x-2)(4a x L Gs +-21)]([4x l c c
Ge -- (3) 显然,最大弯矩就发生在这一段梁内。
可用对上式中的弯矩 Mx ˊ=f (x )求导数并令其为0的方法求出最大弯矩发生的位置x ,即 0)(2)(2'1=+--+-=c l x c
Ge a x L Gs R dx dMx f (4) 由此求得: )(])(2[1c Ge L Gs c c l Ge L a Gs R x f +-+•-
= (5)
将上式带入(3),即可求出纵梁承受的最大弯矩Mmax 。
如果再考虑到动载荷系数k d =2.5 ~4.0及疲劳安全系数n=1.15~1.40,并将
它们代入式 M dmax =nk d M max (动载荷下的最大弯矩) (6)
和σw=W
M d max (弯曲应力) (7) 式中W ——纵梁再计算断面处的弯曲截面系数,对于槽型断面的纵梁 W=6
)6(th b h + (8) 式中 h ——槽型断面的腹板高;
b ——翼缘宽;
t ——梁断面的厚度。
则可求出纵梁的最大弯曲应力。
按(7)求得的弯曲应力不应大于纵梁材料的疲劳极限σ-1。
对16Mn 钢板,σ-1=220~260MPa 。
当纵梁受力变形时,翼缘可能会受力破裂,为此可按薄板理论进行校核,由于临界弯曲应力为
σcr =0.4≤-22)(1b
t E μ350MPa (9) 式中 E ——材料的弹性模量,对低碳钢和16Mn 钢:E=2.06×105MPa ;
μ——泊松比,对低碳钢和16Mn 钢,取μ=0.290; t ——纵梁断面的厚度;
b ——纵梁槽型断面的翼缘宽度。
将E ,μ值代入式(9),得 b ≤16t (10)
为了保证整车及有关机件的正常工作,对纵梁的最大挠度应予以限制。
这就要求对纵梁的弯曲刚度进行校核。
如果把纵梁看成是支承跨度l 为轴距的简支梁,根据材料力学给出的截面惯性矩为J 的简支梁在其跨度l 的中间承受集中载荷P 时,挠度f 与刚度EJ 的关系式f=EJ
Pl 483可知Ef P J 483 。
根据德国对各种汽车车架的实验结果表明,当轴距l 的单位为m ,J 的单位为cm 4时,为使纵梁再满载时的挠度在容许值以内,则应使J/l 3≥12,或应使J ≥12l 3。
大多数汽车的J/l 3值在20~30间,日本的一些4t 平头载货汽车甚至达到58.3。
