MATLAB数学实验一百例题解.docx

合集下载

数学实验(MATLAB)课后习题答案

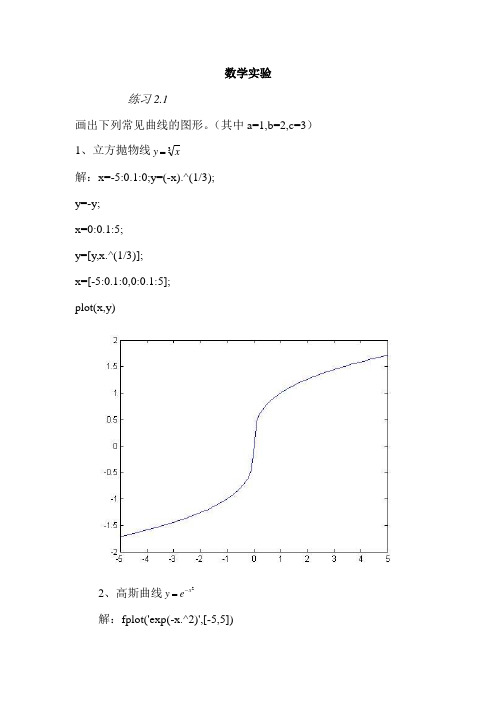
数学实验练习2.1画出下列常见曲线的图形。

（其中a=1,b=2,c=3）1、立方抛物线3xy=解：x=-5:0.1:0;y=(-x).^(1/3);y=-y;x=0:0.1:5;y=[y,x.^(1/3)];x=[-5:0.1:0,0:0.1:5];plot(x,y)2、高斯曲线2x e=y-解：fplot('exp(-x.^2)',[-5,5])3、笛卡儿曲线)3(13,1333222axy y x t at y t at x =++=+=解：ezplot('x.^3+y.^3-3*x*y',[-5,5])xyx.3+y.3-3 x y = 0或t=-5:0.1:5; x=3*t./(1+t.^2); y=3*t.^2./(1+t.^2); plot(x,y)4、蔓叶线)(1,1322322xa x y t at y t at x -=+=+=解：ezplot('y.^2-x.^3/(1-x)',[-5,5])xyy.2-x.3/(1-x) = 0或t=-5:0.1:5; x=t.^2./(1+t.^2); y=t.^3./(1+t.^2); plot(x,y)5、摆线)cos 1(),sin (t b y t t a x -=-= 解：t=0:0.1:2*pi;x=t-sin(t); y=2*(1-cos(t)); plot(x,y)6、星形线)(sin ,cos 32323233a y x t a y t a x =+== 解：t=0:0.1:2*pi; x=cos(t).^3; y=sin(t).^3;plot(x,y)或ezplot('x.^(2/3)+y.^(2/3)-1',[-1,1])xyx.2/3+y.2/3-1 = 07、螺旋线ct z t b y t a x ===,sin ,cos 解：t=0:0.1:2*pi; x=cos(t); y=2*sin(t); z=3*t; plot3(x,y,z) grid on8、阿基米德螺线θa r = 解：x =0:0.1:2*pi; r=x; polar(x,r)902701809、对数螺线θa e r = 解：x =0:0.1:2*pi; r=exp(x); polar(x,r)90270180010、双纽线))()((2cos 22222222y x a y x a r -=+=θ 解：x=0:0.1:2*pi; r=sqrt(cos(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-(x.^2-y.^2)',[-1,1]) grid onxy(x.2+y.2).2-(x.2-y.2) = 011、双纽线)2)((2sin 222222xy a y x a r =+=θ 解：x=0:0.1:2*pi; r=sqrt(sin(2*x)); polar(x,r)90270或ezplot('(x.^2+y.^2).^2-2*x*y',[-1,1]) grid onxy(x.2+y.2).2-2 x y = 012、心形线)cos 1(θ+=a r 解：x =0:0.1:2*pi; r=1+cos(x); polar(x,r)90270练习2.21、求出下列极限值。

MATLAB习题及参考答案经典.doc

习题：1，计算⎥⎦⎤⎢⎣⎡=572396a 与⎥⎦⎤⎢⎣⎡=864142b 的数组乘积。

2，对于B AX =，如果⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=753467294A ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=282637B ，求解X 。

3，已知：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=987654321a ，分别计算a 的数组平方和矩阵平方，并观察其结果。

4，角度[]604530=x ，求x 的正弦、余弦、正切和余切。

(应用sin,cos,tan.cot)5，将矩阵⎥⎦⎤⎢⎣⎡=7524a 、⎥⎦⎤⎢⎣⎡=3817b 和⎥⎦⎤⎢⎣⎡=2695c 组合成两个新矩阵：（1）组合成一个4⨯3的矩阵，第一列为按列顺序排列的a 矩阵元素，第二列为按列顺序排列的b 矩阵元素，第三列为按列顺序排列的c 矩阵元素，即 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡237912685574（2）按照a 、b 、c 的列顺序组合成一个行矢量，即 []2965318772546，将(x -6)(x -3)(x -8)展开为系数多项式的形式。

(应用poly,polyvalm)7，求解多项式x 3-7x 2+2x +40的根。

(应用roots)8，求解在x =8时多项式(x -1)(x -2) (x -3)(x -4)的值。

(应用poly,polyvalm)9，计算多项式9514124234++--x x x x 的微分和积分。

(应用polyder,polyint ，poly2sym)10，解方程组⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡66136221143092x 。

(应用x=a\b)11，求欠定方程组⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡5865394742x 的最小范数解。

(应用pinv) 12，矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=943457624a ，计算a 的行列式和逆矩阵。

(应用det,inv)13， y =sin(x )，x 从0到2π，∆x =0.02π，求y 的最大值、最小值、均值和标准差。

MATLAB实验及答案详解

《MATLAB原理及应用》实验报告实验一MATLAB环境熟悉及基本操作一、实验目的熟悉MATLAB软件的工作环境和练习MATLAB命令窗口的基本操作。

二、实验内容1.命令窗口（Command Window）运行如入门【实验1-1】求23)]47(212[÷-⨯+的算术运算结果。

用键盘在MATLAB命令窗口中命令提示符“>>”后输入一下内容：(12+2*(7-4))/(3^2)在上述表达式输入完成后，按【Enter】键，该命令被执行。

在命令执行后，MATLAB命令窗口中将显示结果。

ans =2【实验1-2】简单矩阵⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=15524974111415412869811105132316A的输入步骤。

(1)用键盘在MATLAB命令窗口中命令提示符“>>”后输入一下内容：A=[16 3 2 13 -1 -4;5 10 11 8 7 9;9 6 8 12 -4 2;4 15 14 1 -5 15](2)按【Enter】键，该命令被执行。

(3)在命令执行后，MATLAB命令窗口中将显示结果.(4)采用分行输入，在命令窗口输入：A=[16 3 2 13 -1 -45 10 11 8 7 99 6 8 12 -4 24 15 14 1 -5 15]【实验1-3】用简短命令计算并绘制在0≤x≤6范围内的sin(Ax)、sinAx2、sin2(Ax)。

( A代表你的学号）在命令窗口输入：x=0:0.01:6;y=[sin(1*x);sin(1*x.^2);sin(1*x).^2];plot(x,y)(2) 按【Enter】键，该命令执行结果如图1图1 函数曲线图(3)在命令窗口输入：x=0:0.01:6;y1=sin(1*x);y2=sin(1*x.^2);y3=sin(1*x).^2; subplot(2,2,1),plot(x,y1),title('sin(1*x)') subplot(2,2,2),plot(x,y2),title('sin(1*x.^2)') subplot(2,2,3),plot(x,y3),title('sin(1*x) .^2') (4) 按【Enter】键，该命令执行结果如图2图2子图形式函数曲线图2.命令窗口（Command Window）常用的基本操作【实验1-4】命令行操作过程示例。

MATLAB数学实验答案（全）

MATLAB数学实验答案（全）第⼀次练习教学要求：熟练掌握Matlab 软件的基本命令和操作，会作⼆维、三维⼏何图形，能够⽤Matlab 软件解决微积分、线性代数与解析⼏何中的计算问题。

补充命令vpa(x,n) 显⽰x 的n 位有效数字，教材102页fplot(‘f(x)’,[a,b]) 函数作图命令，画出f(x)在区间[a,b]上的图形在下⾯的题⽬中m 为你的学号的后3位（1-9班）或4位（10班以上） 1.1 计算30sin limx mx mx x →-与3sin lim x mx mxx →∞-syms xlimit((902*x-sin(902*x))/x^3) ans =366935404/3limit((902*x-sin(902*x))/x^3,inf)//inf 的意思 ans = 0 1.2 cos1000xmxy e =，求''y syms xdiff(exp(x)*cos(902*x/1000),2)//diff 及其后的2的意思 ans =(46599*cos((451*x)/500)*exp(x))/250000 - (451*sin((451*x)/500)*exp(x))/250 1.3 计算221100x y edxdy +??dblquad(@(x,y) exp(x.^2+y.^2),0,1,0,1)//双重积分 ans = 2.13941.4 计算4224x dx m x +? syms xint(x^4/(902^2+4*x^2))//不定积分 ans =(91733851*atan(x/451))/4 - (203401*x)/4 + x^3/12 1.5 (10)cos ,x y e mx y =求//⾼阶导数syms xdiff(exp(x)*cos(902*x),10) ans =-356485076957717053044344387763*cos(902*x)*exp(x)-3952323024277642494822005884*sin(902*x)*exp(x)1.6 0x =的泰勒展式(最⾼次幂为4).syms xtaylor(sqrt(902/1000+x),5,x)//泰勒展式 ans =-(9765625*451^(1/2)*500^(1/2)*x^4)/82743933602 +(15625*451^(1/2)*500^(1/2)*x^3)/91733851-(125*451^(1/2)*500^(1/2)*x^2)/406802 + (451^(1/2)*500^(1/2)*x)/902 +(451^(1/2)*500^(1/2))/500 1.7 Fibonacci 数列{}n x 的定义是121,1x x ==12,(3,4,)n n n x x x n --=+=⽤循环语句编程给出该数列的前20项（要求将结果⽤向量的形式给出）。

matlab编程实例100例之欧阳育创编

1-32是：图形应用篇33-66是：界面设计篇67-84是：图形处理篇85-100是：数值分析篇实例1：三角函数曲线（1）function shili01h0=figure('toolbar','none',...'position',[198 56 350 300],...'name','实例01');h1=axes('parent',h0,...'visible','off');x=-pi:0.05:pi;y=sin(x);plot(x,y);xlabel('自变量X');ylabel('函数值Y');title('SIN( )函数曲线');grid on实例2：三角函数曲线（2）function shili02h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例02');x=-pi:0.05:pi;y=sin(x)+cos(x);plot(x,y,'-*r','linewidth',1);grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例3：图形的叠加function shili03h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例03');x=-pi:0.05:pi;y1=sin(x);y2=cos(x);plot(x,y1,...'-*r',...x,y2,...'--og');grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例4：双y轴图形的绘制function shili04h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例04');x=0:900;a=1000;b=0.005;y1=2*x;y2=cos(b*x);[haxes,hline1,hline2]=plotyy(x,y1,x,y2,'semilogy','plot'); axes(haxes(1))ylabel('semilog plot');axes(haxes(2))ylabel('linear plot');实例5：单个轴窗口显示多个图形function shili05h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例05');t=0:pi/10:2*pi;[x,y]=meshgrid(t);subplot(2,2,1)plot(sin(t),cos(t))axis equalsubplot(2,2,2)z=sin(x)-cos(y);plot(t,z)axis([0 2*pi -2 2])subplot(2,2,3)h=sin(x)+cos(y);plot(t,h)axis([0 2*pi -2 2])subplot(2,2,4)g=(sin(x).^2)-(cos(y).^2);plot(t,g)axis([0 2*pi -1 1])实例6：图形标注function shili06h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例06');t=0:pi/10:2*pi;h=plot(t,sin(t));xlabel('t=0到2\pi','fontsize',16);ylabel('sin(t)','fontsize',16);title('\it{从 0to2\pi 的正弦曲线}','fontsize',16) x=get(h,'xdata');y=get(h,'ydata');imin=find(min(y)==y);imax=find(max(y)==y);text(x(imin),y(imin),...['\leftarrow最小值=',num2str(y(imin))],... 'fontsize',16)text(x(imax),y(imax),...['\leftarrow最大值=',num2str(y(imax))],...'fontsize',16)实例7：条形图形function shili07h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例07');tiao1=[562 548 224 545 41 445 745 512];tiao2=[47 48 57 58 54 52 65 48];t=0:7;bar(t,tiao1)xlabel('X轴');ylabel('TIAO1值');h1=gca;h2=axes('position',get(h1,'position'));plot(t,tiao2,'linewidth',3)set(h2,'yaxislocation','right','color','none','xticklabel',[])实例8：区域图形function shili08h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例08');x=91:95;profits1=[88 75 84 93 77];profits2=[51 64 54 56 68];profits3=[42 54 34 25 24];profits4=[26 38 18 15 4];area(x,profits1,'facecolor',[0.5 0.9 0.6],...'edgecolor','b',...'linewidth',3)hold onarea(x,profits2,'facecolor',[0.9 0.85 0.7],...'edgecolor','y',...'linewidth',3)hold onarea(x,profits3,'facecolor',[0.3 0.6 0.7],...'edgecolor','r',...'linewidth',3)hold onarea(x,profits4,'facecolor',[0.6 0.5 0.9],...'edgecolor','m',...'linewidth',3)hold offset(gca,'xtick',[91:95])set(gca,'layer','top')gtext('\leftarrow第一季度销量')gtext('\leftarrow第二季度销量')gtext('\leftarrow第三季度销量')gtext('\leftarrow第四季度销量')xlabel('年','fontsize',16);ylabel('销售量','fontsize',16);实例9：饼图的绘制function shili09h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例09');t=[54 21 35;68 54 35;45 25 12;48 68 45;68 54 69];x=sum(t);h=pie(x);textobjs=findobj(h,'type','text');str1=get(textobjs,{'string'});val1=get(textobjs,{'extent'});oldext=cat(1,val1{:});names={'商品一：';'商品二：';'商品三：'};str2=strcat(names,str1);set(textobjs,{'string'},str2)val2=get(textobjs,{'extent'});newext=cat(1,val2{:});offset=sign(oldext(:,1)).*(newext(:,3)-oldext(:,3))/2; pos=get(textobjs,{'position'});textpos=cat(1,pos{:});textpos(:,1)=textpos(:,1)+offset;set(textobjs,{'position'},num2cell(textpos,[3,2]))实例10：阶梯图function shili10h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例10');a=0.01;b=0.5;t=0:10;f=exp(-a*t).*sin(b*t);stairs(t,f)hold onplot(t,f,':*')hold offglabel='函数e^{-(\alpha*t)}sin\beta*t的阶梯图'; gtext(glabel,'fontsize',16)xlabel('t=0:10','fontsize',16)axis([0 10 -1.2 1.2])实例11：枝干图function shili11h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例11');x=0:pi/20:2*pi;y1=sin(x);y2=cos(x);h1=stem(x,y1+y2);hold onh2=plot(x,y1,'^r',x,y2,'*g');hold offh3=[h1(1);h2];legend(h3,'y1+y2','y1=sin(x)','y2=cos(x)') xlabel('自变量X');ylabel('函数值Y');title('正弦函数与余弦函数的线性组合');实例12：罗盘图function shili12h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例12');winddirection=[54 24 65 84256 12 235 62125 324 34 254];windpower=[2 5 5 36 8 12 76 14 10 8];rdirection=winddirection*pi/180;[x,y]=pol2cart(rdirection,windpower); compass(x,y);desc={'风向和风力','北京气象台','10月1日0：00到','10月1日12：00'};gtext(desc)实例13：轮廓图function shili13h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例13');[th,r]=meshgrid((0:10:360)*pi/180,0:0.05:1);[x,y]=pol2cart(th,r);z=x+i*y;f=(z.^4-1).^(0.25);contour(x,y,abs(f),20)axis equalxlabel('实部','fontsize',16);ylabel('虚部','fontsize',16);h=polar([0 2*pi],[0 1]);delete(h)hold oncontour(x,y,abs(f),20)实例14：交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点'); x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例14：交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点'); x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例15：变换的傅立叶函数曲线function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren')h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20)for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例16：劳伦兹非线形方程的无序活动function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren')h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20)for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例17：填充图function shili17h0=figure('toolbar','none',...'position',[200 150 450 250],... 'name','实例17');t=(1:2:15)*pi/8;x=sin(t);y=cos(t);fill(x,y,'r')axis square offtext(0,0,'STOP',...'color',[1 1 1],...'fontsize',50,...'horizontalalignment','center')例18：条形图和阶梯形图function shili18h0=figure('toolbar','none',...'position',[200 150 450 250],... 'name','实例18');subplot(2,2,1)x=-3:0.2:3;y=exp(-x.*x);bar(x,y)title('2-D Bar Chart')subplot(2,2,2)x=-3:0.2:3;y=exp(-x.*x);bar3(x,y,'r')title('3-D Bar Chart')subplot(2,2,3)x=-3:0.2:3;y=exp(-x.*x);stairs(x,y)title('Stair Chart')subplot(2,2,4)x=-3:0.2:3;y=exp(-x.*x);barh(x,y)title('Horizontal Bar Chart')实例19：三维曲线图function shili19h0=figure('toolbar','none',...'position',[200 150 450 400],... 'name','实例19');subplot(2,1,1)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,y1,z1,x,y2,z2,x,y3,z3) grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:3-D Plot')subplot(2,1,2)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,z1,y1,x,z2,y2,x,z3,y3) grid onxlabel('X轴');zlabel('Z轴');title('Figure2:3-D Plot')实例20：图形的隐藏属性function shili20h0=figure('toolbar','none',...'position',[200 150 450 300],... 'name','实例20');subplot(1,2,1)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure1:Opaque')hidden onsubplot(1,2,2)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure2:Transparent') hidden off实例21PEAKS函数曲线function shili21h0=figure('toolbar','none',...'position',[200 100 450 450],... 'name','实例21');[x,y,z]=peaks(30);subplot(2,1,1)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfc(x,y,z)xlabel('X轴');zlabel('Z轴');title('Figure1:surfc函数形成的曲面') subplot(2,1,2)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfl(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:surfl函数形成的曲面') 实例22：片状图function shili22h0=figure('toolbar','none',...'position',[200 150 550 350],...'name','实例22');subplot(1,2,1)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trimesh(t,x,y,z)hidden offtitle('Figure1:Triangular Surface Plot'); subplot(1,2,2)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trisurf(t,x,y,z)title('Figure1:Triangular Surface Plot');实例23：视角的调整function shili23h0=figure('toolbar','none',...'position',[200 150 450 350],... 'name','实例23');x=-5:0.5:5;[x,y]=meshgrid(x);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;subplot(2,2,1)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure1')view(-37.5,30)subplot(2,2,2)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure2')view(-37.5+90,30)subplot(2,2,3)surf(x,y,z)xlabel('X-axis')。

matlab编程实例100例(精编文档).doc

【最新整理，下载后即可编辑】1-32是：图形应用篇33-66是：界面设计篇67-84是：图形处理篇85-100是：数值分析篇实例1：三角函数曲线（1）function shili01h0=figure('toolbar','none',...'position',[198****0300],...'name','实例01');h1=axes('parent',h0,...'visible','off');x=-pi:0.05:pi;y=sin(x);plot(x,y);xlabel('自变量X');ylabel('函数值Y');title('SIN( )函数曲线');grid on实例2：三角函数曲线（2）function shili02h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例02');x=-pi:0.05:pi;y=sin(x)+cos(x);plot(x,y,'-*r','linewidth',1);grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例3：图形的叠加function shili03h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例03');x=-pi:0.05:pi;y1=sin(x);y2=cos(x);plot(x,y1,...'-*r',...x,y2,...'--og');grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例4：双y轴图形的绘制function shili04h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例04');x=0:900;a=1000;b=0.005;y1=2*x;y2=cos(b*x);[haxes,hline1,hline2]=plotyy(x,y1,x,y2,'semilogy','plot'); axes(haxes(1))ylabel('semilog plot');axes(haxes(2))ylabel('linear plot');实例5：单个轴窗口显示多个图形function shili05h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例05');t=0:pi/10:2*pi;[x,y]=meshgrid(t);subplot(2,2,1)plot(sin(t),cos(t))axis equalsubplot(2,2,2)z=sin(x)-cos(y);plot(t,z)axis([0 2*pi -2 2])subplot(2,2,3)h=sin(x)+cos(y);plot(t,h)axis([0 2*pi -2 2])subplot(2,2,4)g=(sin(x).^2)-(cos(y).^2);plot(t,g)axis([0 2*pi -1 1])实例6：图形标注function shili06h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例06');t=0:pi/10:2*pi;h=plot(t,sin(t));xlabel('t=0到2\pi','fontsize',16);ylabel('sin(t)','fontsize',16);title('\it{从0to2\pi 的正弦曲线}','fontsize',16) x=get(h,'xdata');y=get(h,'ydata');imin=find(min(y)==y);imax=find(max(y)==y);text(x(imin),y(imin),...['\leftarrow最小值=',num2str(y(imin))],...'fontsize',16)text(x(imax),y(imax),...['\leftarrow最大值=',num2str(y(imax))],...'fontsize',16)实例7：条形图形function shili07h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例07');tiao1=[562 548 224 545 41 445 745 512];tiao2=[47 48 57 58 54 52 65 48];t=0:7;bar(t,tiao1)xlabel('X轴');ylabel('TIAO1值');h1=gca;h2=axes('position',get(h1,'position'));plot(t,tiao2,'linewidth',3)set(h2,'yaxislocation','right','color','none','xticklabel',[]) 实例8：区域图形function shili08h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例08');x=91:95;profits1=[88 75 84 93 77];profits2=[51 64 54 56 68];profits3=[42 54 34 25 24];profits4=[26 38 18 15 4];area(x,profits1,'facecolor',[0.5 0.9 0.6],...'edgecolor','b',...'linewidth',3)hold onarea(x,profits2,'facecolor',[0.9 0.85 0.7],...'edgecolor','y',...'linewidth',3)hold onarea(x,profits3,'facecolor',[0.3 0.6 0.7],...'edgecolor','r',...'linewidth',3)hold onarea(x,profits4,'facecolor',[0.6 0.5 0.9],...'edgecolor','m',...'linewidth',3)hold offset(gca,'xtick',[91:95])set(gca,'layer','top')gtext('\leftarrow第一季度销量') gtext('\leftarrow第二季度销量') gtext('\leftarrow第三季度销量') gtext('\leftarrow第四季度销量') xlabel('年','fontsize',16);ylabel('销售量','fontsize',16);实例9：饼图的绘制function shili09h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例09');t=[54 21 35;68 54 35;45 25 12;48 68 45;68 54 69];x=sum(t);h=pie(x);textobjs=findobj(h,'type','text');str1=get(textobjs,{'string'});val1=get(textobjs,{'extent'});oldext=cat(1,val1{:});names={'商品一：';'商品二：';'商品三：'};str2=strcat(names,str1);set(textobjs,{'string'},str2)val2=get(textobjs,{'extent'});newext=cat(1,val2{:});offset=sign(oldext(:,1)).*(newext(:,3)-oldext(:,3))/2; pos=get(textobjs,{'position'});textpos=cat(1,pos{:});textpos(:,1)=textpos(:,1)+offset;set(textobjs,{'position'},num2cell(textpos,[3,2]))实例10：阶梯图function shili10h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例10');a=0.01;b=0.5;t=0:10;f=exp(-a*t).*sin(b*t);stairs(t,f)hold onplot(t,f,':*')hold offglabel='函数e^{-(\alpha*t)}sin\beta*t的阶梯图'; gtext(glabel,'fontsize',16)xlabel('t=0:10','fontsize',16)axis([0 10 -1.2 1.2])实例11：枝干图function shili11h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例11');x=0:pi/20:2*pi;y1=sin(x);y2=cos(x);h1=stem(x,y1+y2);hold onh2=plot(x,y1,'^r',x,y2,'*g');hold offh3=[h1(1);h2];legend(h3,'y1+y2','y1=sin(x)','y2=cos(x)') xlabel('自变量X');ylabel('函数值Y');title('正弦函数与余弦函数的线性组合'); 实例12：罗盘图function shili12h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例12');winddirection=[54 24 65 84256 12 235 62125 324 34 254];windpower=[2 5 5 36 8 12 76 14 10 8];rdirection=winddirection*pi/180;[x,y]=pol2cart(rdirection,windpower); compass(x,y);desc={'风向和风力','北京气象台','10月1日0：00到','10月1日12：00'};gtext(desc)实例13：轮廓图function shili13h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例13');[th,r]=meshgrid((0:10:360)*pi/180,0:0.05:1); [x,y]=pol2cart(th,r);z=x+i*y;f=(z.^4-1).^(0.25);contour(x,y,abs(f),20)axis equalxlabel('实部','fontsize',16);ylabel('虚部','fontsize',16);h=polar([0 2*pi],[0 1]);delete(h)hold oncontour(x,y,abs(f),20)实例14：交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点');x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例14：交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点');x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例15：变换的傅立叶函数曲线function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren')h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20)for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例16：劳伦兹非线形方程的无序活动function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren')h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20)for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例17：填充图function shili17h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例17');t=(1:2:15)*pi/8;x=sin(t);y=cos(t);fill(x,y,'r')axis square offtext(0,0,'STOP',...'color',[1 1 1],...'fontsize',50,...'horizontalalignment','center') 例18：条形图和阶梯形图function shili18h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例18');subplot(2,2,1)x=-3:0.2:3;y=exp(-x.*x);bar(x,y)title('2-D Bar Chart')subplot(2,2,2)x=-3:0.2:3;y=exp(-x.*x);bar3(x,y,'r')title('3-D Bar Chart')subplot(2,2,3)x=-3:0.2:3;y=exp(-x.*x);stairs(x,y)title('Stair Chart')subplot(2,2,4)x=-3:0.2:3;y=exp(-x.*x);barh(x,y)title('Horizontal Bar Chart')实例19：三维曲线图function shili19h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例19');subplot(2,1,1)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,y1,z1,x,y2,z2,x,y3,z3)grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:3-D Plot')subplot(2,1,2)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,z1,y1,x,z2,y2,x,z3,y3)grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:3-D Plot')实例20：图形的隐藏属性function shili20h0=figure('toolbar','none',...'position',[200 150 450 300],...'name','实例20');subplot(1,2,1)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure1:Opaque')hidden onsubplot(1,2,2)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure2:Transparent') hidden off实例21PEAKS函数曲线function shili21h0=figure('toolbar','none',...'position',[200 100 450 450],...'name','实例21');[x,y,z]=peaks(30);subplot(2,1,1)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfc(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:surfc函数形成的曲面') subplot(2,1,2)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfl(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:surfl函数形成的曲面') 实例22：片状图function shili22h0=figure('toolbar','none',...'position',[200 150 550 350],...'name','实例22');subplot(1,2,1)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trimesh(t,x,y,z)hidden offtitle('Figure1:Triangular Surface Plot'); subplot(1,2,2)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trisurf(t,x,y,z)title('Figure1:Triangular Surface Plot'); 实例23：视角的调整function shili23h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例23');x=-5:0.5:5;[x,y]=meshgrid(x);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;subplot(2,2,1)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure1')view(-37.5,30)subplot(2,2,2)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure2')view(-37.5+90,30) subplot(2,2,3)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure3')view(-37.5,60)subplot(2,2,4)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure4')view(180,0)实例24：向量场的绘制function shili24h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例24');subplot(2,2,1)z=peaks;ribbon(z)title('Figure1')subplot(2,2,2)[x,y,z]=peaks(15);[dx,dy]=gradient(z,0.5,0.5); contour(x,y,z,10)hold onquiver(x,y,dx,dy)hold offtitle('Figure2')subplot(2,2,3)[x,y,z]=peaks(15);[nx,ny,nz]=surfnorm(x,y,z);surf(x,y,z)hold onquiver3(x,y,z,nx,ny,nz)hold offtitle('Figure3')subplot(2,2,4)x=rand(3,5);y=rand(3,5);z=rand(3,5);c=rand(3,5);fill3(x,y,z,c)grid ontitle('Figure4')实例25：灯光定位function shili25h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例25');vert=[1 1 1;1 2 1;2 2 1;2 1 1;1 1 2;12 2;2 2 2;2 1 2];fac=[1 2 3 4;2 6 7 3;4 3 7 8;15 8 4;1 2 6 5;5 6 7 8];grid offsphere(36)h=findobj('type','surface');set(h,'facelighting','phong',...'facecolor',...'interp',...'edgecolor',[0.4 0.4 0.4],...'backfacelighting',...'lit')hold onpatch('faces',fac,'vertices',vert,...'facecolor','y');light('position',[1 3 2]);light('position',[-3 -1 3]);material shinyaxis vis3d offhold off实例26：柱状图function shili26h0=figure('toolbar','none',...'position',[200 50 450 450],...'name','实例26'); subplot(2,1,1)x=[5 2 18 7 39 8 65 5 54 3 2];bar(x)xlabel('X轴');ylabel('Y轴');title('第一子图');subplot(2,1,2)y=[5 2 18 7 39 8 65 5 54 3 2];barh(y)xlabel('X轴');ylabel('Y轴');title('第二子图');实例27：设置照明方式function shili27h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例27');subplot(2,2,1)sphereshading flatcamlight leftcamlight rightlighting flatcolorbaraxis offtitle('Figure1')subplot(2,2,2)sphereshading flatcamlight leftcamlight rightlighting gouraudcolorbaraxis offtitle('Figure2')subplot(2,2,3)sphereshading interpcamlight rightcamlight leftlighting phongaxis offtitle('Figure3')subplot(2,2,4)sphereshading flatcamlight leftcamlight rightlighting nonecolorbaraxis offtitle('Figure4')实例28：羽状图function shili28h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例28');subplot(2,1,1)alpha=90:-10:0;r=ones(size(alpha));m=alpha*pi/180;n=r*10;[u,v]=pol2cart(m,n);feather(u,v)title('羽状图')axis([0 20 0 10])subplot(2,1,2)t=0:0.5:10;y=exp(-x*t);feather(y)title('复数矩阵的羽状图')实例29：立体透视（1）function shili29h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例29');[x,y,z]=meshgrid(-2:0.1:2,...-2:0.1:2,...-2:0.1:2);v=x.*exp(-x.^2-y.^2-z.^2);grid onfor i=-2:0.5:2;h1=surf(linspace(-2,2,20),...linspace(-2,2,20),...zeros(20)+i);rotate(h1,[1 -1 1],30)dx=get(h1,'xdata');dy=get(h1,'ydata');dz=get(h1,'zdata');delete(h1)slice(x,y,z,v,[-2 2],2,-2)hold onslice(x,y,z,v,dx,dy,dz)hold offaxis tightview(-5,10)drawnowend实例30：立体透视（2）function shili30h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例30');[x,y,z]=meshgrid(-2:0.1:2,...-2:0.1:2,...-2:0.1:2);v=x.*exp(-x.^2-y.^2-z.^2); [dx,dy,dz]=cylinder;slice(x,y,z,v,[-2 2],2,-2)for i=-2:0.2:2h=surface(dx+i,dy,dz);rotate(h,[1 0 0],90)xp=get(h,'xdata');yp=get(h,'ydata');zp=get(h,'zdata');delete(h)hold onhs=slice(x,y,z,v,xp,yp,zp);axis tightxlim([-3 3])view(-10,35)drawnowdelete(hs)hold offend实例31：表面图形function shili31h0=figure('toolbar','none',...'position',[200 150 550 250],...'name','实例31');subplot(1,2,1)x=rand(100,1)*16-8;y=rand(100,1)*16-8;r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;xlin=linspace(min(x),max(x),33); ylin=linspace(min(y),max(y),33); [X,Y]=meshgrid(xlin,ylin);Z=griddata(x,y,z,X,Y,'cubic'); mesh(X,Y,Z)axis tighthold onplot3(x,y,z,'.','Markersize',20) subplot(1,2,2)k=5;n=2^k-1;theta=pi*(-n:2:n)/n;phi=(pi/2)*(-n:2:n)'/n;X=cos(phi)*cos(theta);Y=cos(phi)*sin(theta);Z=sin(phi)*ones(size(theta)); colormap([0 0 0;1 1 1])C=hadamard(2^k);surf(X,Y,Z,C)axis square实例32：沿曲线移动的小球h0=figure('toolbar','none',...'position',[198****8468],...'name','实例32');h1=axes('parent',h0,...'position',[0.15 0.45 0.7 0.5],...'visible','on');t=0:pi/24:4*pi;y=sin(t);plot(t,y,'b')n=length(t);h=line('color',[0 0.5 0.5],...'linestyle','.',...'markersize',25,...'erasemode','xor');k1=uicontrol('parent',h0,...'style','pushbutton',...'position',[80 100 50 30],...'string','开始',...'callback',[...'i=1;',...'k=1;,',...'m=0;,',...'while 1,',...'if k==0,',...'break,',...'end,',...'if k~=0,',...'set(h,''xdata'',t(i),''ydata'',y(i)),',...'drawnow;,',...'i=i+1;,',...'if i>n,',...'m=m+1;,',...'i=1;,',...'end,',...'end,',...'end']);k2=uicontrol('parent',h0,...'style','pushbutton',...'position',[180 100 50 30],...'string','停止',...'callback',[...'k=0;,',...'set(e1,''string'',m),',...'p=get(h,''xdata'');,',...'q=get(h,''ydata'');,',...'set(e2,''string'',p);,',...'set(e3,''string'',q)']); k3=uicontrol('parent',h0,...'style','pushbutton',...'position',[280 100 50 30],...'string','关闭',...'callback','close');e1=uicontrol('parent',h0,...'style','edit',...'position',[60 30 60 20]);t1=uicontrol('parent',h0,...'style','text',...'string','循环次数',...'position',[60 50 60 20]);e2=uicontrol('parent',h0,...'style','edit',...'position',[180 30 50 20]);t2=uicontrol('parent',h0,...'style','text',...'string','终点的X坐标值',...'position',[155 50 100 20]);e3=uicontrol('parent',h0,...'style','edit',...'position',[300 30 50 20]);t3=uicontrol('parent',h0,...'style','text',...'string','终点的Y坐标值',...'position',[275 50 100 20]);实例33：曲线转换按钮h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例33');x=0:0.5:2*pi;y=sin(x);h=plot(x,y);grid onhuidiao=[...'if i==1,',...'i=0;,',...'y=cos(x);,',...'delete(h),',...'set(hm,''string'',''正弦函数''),',...'h=plot(x,y);,',...'grid on,',...'else if i==0,',...'i=1;,',...'y=sin(x);,',...'set(hm,''string'',''余弦函数''),',...'delete(h),',...'h=plot(x,y);,',...'grid on,',...'end,',...'end'];hm=uicontrol(gcf,'style','pushbutton',...'string','余弦函数',...'callback',huidiao);i=1;set(hm,'position',[250 20 60 20]);set(gca,'position',[0.2 0.2 0.6 0.6])title('按钮的使用')hold on实例34：栅格控制按钮h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例34');x=0:0.5:2*pi;y=sin(x);plot(x,y)huidiao1=[...'set(h_toggle2,''value'',0),',...'grid on,',...];huidiao2=[...'set(h_toggle1,''value'',0),',...'grid off,',...];h_toggle1=uicontrol(gcf,'style','togglebutton',...'string','grid on',...'value',0,...'position',[20 45 50 20],...'callback',huidiao1);h_toggle2=uicontrol(gcf,'style','togglebutton',...'string','grid off',...'value',0,...'position',[20 20 50 20],...'callback',huidiao2);set(gca,'position',[0.2 0.2 0.6 0.6])title('开关按钮的使用')实例35：编辑框的使用h0=figure('toolbar','none',...'position',[200 150 350 250],...'name','实例35');f='Please input the letter';huidiao1=[...'g=upper(f);,',...'set(h2_edit,''string'',g),',...];huidiao2=[...'g=lower(f);,',...'set(h2_edit,''string'',g),',...];h1_edit=uicontrol(gcf,'style','edit',...'position',[100 200 100 50],...'HorizontalAlignment','left',...'string','Please input the letter',...'callback','f=get(h1_edit,''string'');',...'background','w',...'max',5,...'min',1);h2_edit=uicontrol(gcf,'style','edit',...'HorizontalAlignment','left',...'position',[100 100 100 50],...'background','w',...'max',5,...'min',1);h1_button=uicontrol(gcf,'style','pushbutton',...'string','小写变大写',...'position',[100 45 100 20],...'callback',huidiao1);h2_button=uicontrol(gcf,'style','pushbutton',...'string','大写变小写',...'position',[100 20 100 20],...'callback',huidiao2);实例36：弹出式菜单h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例36');x=0:0.5:2*pi;y=sin(x);h=plot(x,y);grid onhm=uicontrol(gcf,'style','popupmenu',...'string',...'sin(x)|cos(x)|sin(x)+cos(x)|exp(-sin(x))',...'position',[250 20 50 20]);set(hm,'value',1)huidiao=[...'v=get(hm,''value'');,',...'switch v,',...'case 1,',...'delete(h),',...'y=sin(x);,',...'h=plot(x,y);,',...'grid on,',...'case 2,',...'delete(h),',...'y=cos(x);,',...'h=plot(x,y);,',...'grid on,',...'case 3,',...'delete(h),',...'y=sin(x)+cos(x);,',...'h=plot(x,y);,',...'grid on,',...'case 4,',...'delete(h),',...'y=exp(-sin(x));,',...'h=plot(x,y);,',...'grid on,',...'end'];set(hm,'callback',huidiao)set(gca,'position',[0.2 0.2 0.6 0.6]) title('弹出式菜单的使用')实例37：滑标的使用h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例37');[x,y]=meshgrid(-8:0.5:8);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;h0=mesh(x,y,z);h1=axes('position',...[0.2 0.2 0.5 0.5],...'visible','off');htext=uicontrol(gcf,...'units','points',...'position',[20 30 45 15],...'string','brightness',...'style','text');hslider=uicontrol(gcf,...'units','points',...'position',[10 10 300 15],...'min',-1,...'max',1,...'style','slider',...'callback',...'brighten(get(hslider,''value''))'); 实例38：多选菜单h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例38');[x,y]=meshgrid(-8:0.5:8);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;h0=mesh(x,y,z);hlist=uicontrol(gcf,'style','listbox',...'string','default|spring|summer|autumn|winter',...'max',5,...'min',1,...'position',[20 20 80 100],...'callback',[...'k=get(hlist,''value'');,',...'switch k,',...'case 1,',...'colormap default,',...'case 2,',...'colormap spring,',...'case 3,',...'colormap summer,',...'case 4,',...'colormap autumn,',...'case 5,',...'colormap winter,',...'end']);实例39：菜单控制的使用h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例39');x=0:0.5:2*pi;y=cos(x);h=plot(x,y);grid onset(gcf,'toolbar','none')hm=uimenu('label','example');huidiao1=[...'set(hm_gridon,''checked'',''on''),',...'set(hm_gridoff,''checked'',''off''),',...'grid on'];huidiao2=[...'set(hm_gridoff,''checked'',''on''),',...'set(hm_gridon,''checked'',''off''),',...'grid off'];hm_gridon=uimenu(hm,'label','grid on',...'checked','on',...'callback',huidiao1);hm_gridoff=uimenu(hm,'label','grid off',...'checked','off',...'callback',huidiao2);实例40：UIMENU菜单的应用h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例40');h1=uimenu(gcf,'label','函数');h11=uimenu(h1,'label','轮廓图',...'callback',[...'set(h31,''checked'',''on''),',...'set(h32,''checked'',''off''),',...'[x,y,z]=peaks;,',...'contour3(x,y,z,30)']);h12=uimenu(h1,'label','高斯分布',...'callback',[...'set(h31,''checked'',''on''),',...'set(h32,''checked'',''off''),',...'mesh(peaks);,',...'axis tight']);。

MATLAB全部实验及答案

MATLAB全部实验及答案实验一、MATLAB基本操作实验内容及步骤1、命令窗口的简单使用（1）简单矩阵的输入（2）求[12+2×(7-4)]÷32的算术运算结果2、有关向量、矩阵或数组的一些运算（1）设A=15；B=20；求C=A+B与c=a+b？（2）设A=[1 2 3;4 5 6;7 8 9]，B=[9 8 7;6 5 4;3 2 1]；求A*B与A.*B？A*B就是线代里面的矩阵相乘 A.*B是对应位置的元素相乘（3）设a=10，b=20；求i=a/b=0.5与j=a\b=2？（4）设a=[1 -2 3;4 5 -4;5 -6 7]请设计出程序，分别找出小于0的矩阵元素及其位置（单下标、全下标的形式），并将其单下标转换成全下标。

clear,clca=[1 -2 3;4 5 -4;5 -6 7];[x,y]=find(a<0);c=[];for i=1:length(x)c(i,1)=a(x(i),y(i));c(i,2)=x(i);c(i,3)=y(i);c(i,4)=(y(i)-1)*size(a,2)+x(i);endc（5）在MATLAB命令行窗口运行A=[1,2;3,4]+i*[5,6;7,8]；看结果如何？如果改成运行A=[1,2;3,4]+i[5,6;7,8]，结果又如何？前面那个是虚数矩阵，后面那个出错（6）请写出完成下列计算的指令：a=[1 2 3;3 4 2;5 2 3]，求a^2=？,a.^2=？a^2= 22 16 1625 26 2326 24 28a.^2=1 4 99 16 425 4 9（7）有一段指令如下，请思考并说明运行结果及其原因clearX=[1 2;8 9;3 6];X( : ) 转化为列向量（8）使用三元组方法，创建下列稀疏矩阵2 0 8 00 0 0 10 4 0 06 0 0 0方法一：clear,clcdata=[2 8 1 4 6];ir=[1 1 2 3 4 ];jc=[1 3 4 2 1];s=sparse(ir,jc,data,4,4);full(s)方法二：不用三元组法clear,clca=zeros(4,4);a(1,[1,3])=[2,8];a(2,4)=1;a(3,2)=4;a(4,1)=6;a（9）写出下列指令的运行结果>> A = [ 1 2 3 ]; B = [ 4 5 6 ];>> C = 3.^A>> D = A.^B3、已知⎪⎭⎫ ⎝⎛+⋅=-334sin 234πt e y t 若需要计算t ∈[-1,1]，取间隔为0.01，试计算出相对应的y 值。

MATLAB数学实验100例题解

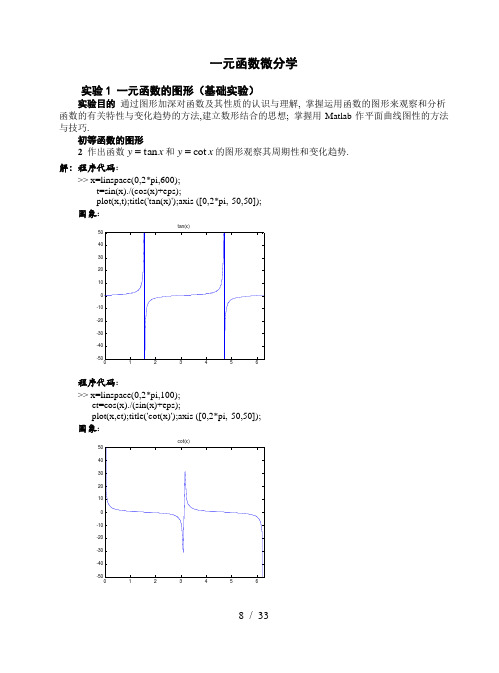
一元函数微分学实验1 一元函数的图形（基础实验）实验目的通过图形加深对函数及其性质的认识与理解, 掌握运用函数的图形来观察和分析函数的有关特性与变化趋势的方法,建立数形结合的思想; 掌握用Matlab 作平面曲线图性的方法与技巧.初等函数的图形2 作出函数x y tan =和x y cot =的图形观察其周期性和变化趋势. 解：程序代码：>> x=linspace(0,2*pi,600); t=sin(x)./(cos(x)+eps);plot(x,t);title('tan(x)');axis ([0,2*pi,-50,50]); 图象：程序代码：>> x=linspace(0,2*pi,100); ct=cos(x)./(sin(x)+eps);plot(x,ct);title('cot(x)');axis ([0,2*pi,-50,50]); 图象：4在区间]1,1[-画出函数xy 1sin =的图形. 解：程序代码：>> x=linspace(-1,1,10000);y=sin(1./x); plot(x,y);axis([-1,1,-2,2]) 图象：二维参数方程作图6画出参数方程⎩⎨⎧==t t t y tt t x 3cos sin )(5cos cos )(的图形：解：程序代码：>> t=linspace(0,2*pi,100);plot(cos(t).*cos(5*t),sin(t).*cos(3*t)); 图象：极坐标方程作图8 作出极坐标方程为10/t e r =的对数螺线的图形. 解：程序代码：>> t=0:0.01:2*pi; r=exp(t/10);polar(log(t+eps),log(r+eps)); 图象：90270分段函数作图10 作出符号函数x y sgn =的图形. 解：程序代码：>> x=linspace(-100,100,10000); y=sign(x); plot(x,y);axis([-100 100 -2 2]);函数性质的研究12研究函数)3(log 3)(35x e x x f x -++=在区间]2,2[-上图形的特征. 解：程序代码：>> x=linspace(-2,2,10000);y=x.^5+3*exp(x)+log(3-x)/log(3); plot(x,y); 图象：实验2 极限与连续（基础实验）实验目的通过计算与作图, 从直观上揭示极限的本质,加深对极限概念的理解. 掌握用 Matlab 画散点图, 以及计算极限的方法. 深入理解函数连续的概念,熟悉几种间断点的图形特征,理解闭区间上连续函数的几个重要性质.作散点图14分别画出坐标为)10,,2,1(),4,(),,(3222 =+i i i i i i 的散点图, 并画出折线图. 解：散点图程序代码： >> i=1:10; plot(i,i.^2,'.')或：>> x=1:10;y=x.^2;for i=1:10;plot(x(i),y(i),'r')hold onend折线图程序代码：>> i=1:10;plot(i,i.^2,'-x')程序代码：>> i=1:10;plot(i.^2,4*(i.^2)+i.^3,'.')>> i=1:10;plot(i.^2,4*(i.^2)+i.^3,'-x')数列极限的概念16通过动画观察当∞→n 时数列21n a n =的变化趋势.解：程序代码： >> n=1:100; an=(n.^2); n=1:100; an=1./(n.^2); n=1:100; an=1./(n.^2); for i=1:100plot(n(1:i),an(1:i)),axis([0,100,0,1]) pause(0.1) end 图象：函数的极限18在区间]4,4[-上作出函数xx xx x f --=339)(的图形, 并研究 )(lim x f x ∞→ 和 ).(lim 1x f x →解：作出函数x x xx x f --=339)(在区间]4,4[-上的图形 >> x=-4:0.01:4;y=(x.^3-9*x)./(x.^3-x+eps); plot(x,y)从图上看，()f x 在x →1与x →∞时极限为0两个重要极限 20计算极限⎪⎭⎫⎝⎛+→x x x x x sin 11sin lim )1(0 x x e x 2lim )2(+∞→30sin tan lim )3(xx x x -→ x x x 0lim )4(+→ x xx ln cot ln lim )5(0+→ x x x ln lim )6(20+→ xx xx x x sin cos sin lim)7(20-→ 125523lim )8(323+++-∞→x x x x x xx x e e x x x sin 2lim )9(0----→ xx x x cos 110sin lim )10(-→⎪⎭⎫ ⎝⎛ 解：（1）>> limit(x*sin(1/x)+1/x*sin(x))ans =1(2) >> limit(x^2/exp(x),inf) ans = 0(3) >> limit((tan(x)-sin(8))/x^3) ans =NaN(4) >> limit(x^x,x,0,'right') ans =1(5) >> limit(log(cot(x))/log(x),x,0,'right') ans =-1(6) >> limit(x^2*log(x),x,0,'right') ans =0(7) >> limit((sin(x)-x.*cos(x))./(x.^2.*sin(x)),x,0) ans =1/3(8) >> limit((3*x.^3-2*x.^2+5)/(5*x.^3+2*+1),x,inf) ans =3/5(9) >> limit((exp(x)-exp(-x)-2*x)./(x-sin(x))) ans =2(10) >> limit((sin(x)/x).^(1/(1-cos(x)))) ans =exp(-1/3)实验3 导数（基础实验）实验目的深入理解导数与微分的概念, 导数的几何意义. 掌握用Matlab 求导数与高阶导数的方法. 深入理解和掌握求隐函数的导数, 以及求由参数方程定义的函数的导数的方法. 导数概念与导数的几何意义22作函数71232)(23+-+=x x x x f 的图形和在1-=x 处的切线. 解：作函数71232)(23+-+=x x x x f 的图形程序代码： >> syms x;>> y=2*x^3+3*x^2-12*x+7; >> diff(y) ans =6*x^2+6*x-12 >> syms x;y=2*x^3+3*x^2-12*x+7; >> f=diff(y) f =6*x^2+6*x-12 >> x=-1;f1=6*x^2+6*x-12 f1 = -12>> f2=2*x^3+3*x^2-12*x+7 f2 = 20>> x=linspace(-10,10,1000);y1=2*x.^3+3*x.^2-12*x+7; y2=-12*(x+1)+20; plot(x,y1,'r',x,y2,'g')求函数的导数与微分24求函数bx ax x f cos sin )(=的一阶导数. 并求.1⎪⎭⎫⎝⎛+'b a f解：求函数bx ax x f cos sin )(=的一阶导数程序代码： >> syms a b x y;y= sin(a*x)*cos(b*x); D1=diff(y,x,1) 答案：D1 =cos(a*x)*a*cos(b*x)-sin(a*x)*sin(b*x)*b求.1⎪⎭⎫ ⎝⎛+'b a f程序代码： >> x=1/(a+b);>> cos(a*x)*a*cos(b*x)-sin(a*x)*sin(b*x)*b 答案：ans =cos(a/(a+b))*a*cos(b/(a+b))-sin(a/(a+b))*sin(b/(a+b))*b 拉格朗日中值定理26对函数),2)(1()(--=x x x x f 观察罗尔定理的几何意义. (1) 画出)(x f y =与)(x f '的图形, 并求出1x 与.2x 解：程序代码：>> syms x;f=x*(x-1)*(x-2); f1=diff(f) f1 =(x-1)*(x-2)+x*(x-2)+x*(x-1) >> solve(f1) ans =1+1/3*3^(1/2) 1-1/3*3^(1/2)>> x=linspace(-10,10,1000); y1=x.*(x-1).*(x-2);y2 =(x-1).*(x-2)+x.*(x-2)+x.*(x-1); plot(x,y1,x,y2)(2)画出)(x f y 及其在点))(,(11x f x 与))(,(22x f x 处的切线. 程序代码：>> syms x; >> f=x*(x-1)*(x-2); >> f1=diff(f) f1 =(x-1)*(x-2)+x*(x-2)+x*(x-1) >> solve(f1) ans =1+1/3*3^(1/2) 1-1/3*3^(1/2)>> x=linspace(-3,3,1000); >> y1=x.*(x-1).*(x-2);>> y2 =(x-1).*(x-2)+x.*(x-2)+x.*(x-1); >> plot(x,y1,x,y2) >> hold on>> x=1+1/3*3^(1/2); >> yx1=x*(x-1)*(x-2) yx1 =-0.3849>> x=1-1/3*3^(1/2); >> yx2=x*(x-1)*(x-2) yx2 =0.3849x=linspace(-3,3,1000); yx1 =-0.3849*x.^0; yx2 =0.3849*x.^0; plot(x,yx1,x,yx2)28求下列函数的导数:(1) 31+=x e y ; 解：程序代码：>> syms x y; y=exp((x+1)^3); D1=diff(y,1) 答案：D1 =3*(x+1)^2*exp((x+1)^3)(2) )]42ln[tan(π+=x y ;解：程序代码：>> syms x;y=log(tan(x/2+pi/4)); D1=diff(y,1) 答案：D1 =(1/2+1/2*tan(1/2*x+1/4*pi)^2)/tan(1/2*x+1/4*pi)(3) x x y sin ln cot 212+=;解：程序代码：>> syms x;y=1/2*(cot(x))^2+log(sin(x)); D1=diff(y,1) 答案：D1 =cot(x)*(-1-cot(x)^2)+cos(x)/sin(x) (4) xy 2arctan21=. 解：程序代码：>> syms x;>> y=sqrt(2)*atan(sqrt(2)/x); >> D1=diff(y,1) 答案：D1 =-2/x^2/(1+2/x^2)一元函数积分学与空间图形的画法实验4 一元函数积分学(基础实验)实验目的掌握用Matlab 计算不定积分与定积分的方法. 通过作图和观察, 深入理解定积分的概念和思想方法. 初步了解定积分的近似计算方法. 理解变上限积分的概念. 提高应用定积分解决各种问题的能力.不定积分计算30求.)1(532⎰-dx x x解：程序代码：>> syms x y;>> y=x^2*(1-x^3)^5; >> R=int(y,x) 答案：R =-1/18*x^18+1/3*x^15-5/6*x^12+10/9*x^9-5/6*x^6+1/3*x^332求.arctan 2⎰xdx x解：程序代码：>> syms x y;>> y=x^2*atan(x); >> R=int(y,x) 答案：R =1/3*x^3*atan(x)-1/6*x^2+1/6*log(x^2+1)定积分计算34 求.)(102⎰-dx x x解：程序代码：>> syms x y; >> y=x-x^2;>> R=int(y,x,0,1) 答案： R =1/6变上限积分 36 画出变上限函数⎰x dt t t 02sin 及其导函数的图形.解：程序代码：>> syms x y t; >> y=t*sin(t^2); >> R=int(y,x,0,x) 答案：R =t*sin(t^2)*x 再求导函数程序代码：>> DR=diff(R,x,1) 答案：DR =t*sin(t^2)实验5 空间图形的画法(基础实验)实验目的掌握用Matlab 绘制空间曲面和曲线的方法. 熟悉常用空间曲线和空间曲面的图形特征,通过作图和观察, 提高空间想像能力. 深入理解二次曲面方程及其图形.一般二元函数作图38作出函数2214y x z ++=的图形.解：程序代码：>> x=linspace(-5,5,500); [x,y]=meshgrid(x); z=4./(1+x.^2+y.^2); mesh(x,y,z);xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');title('function')40作出函数)94cos(22y x z +=的图形. 解：程序代码：>> x=-10:0.1:10;[x,y]=meshgrid(x);z=cos(4*x.^2+9*y.^2); mesh(x,y,z);xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');title('function')讨论：坐标轴选取范围不同时，图形差异很大，对本题尤为明显，如右图为坐标轴[-1，1]二次曲面42作出单叶双曲面1941222=-+z y x 的图形.(曲面的参数方程为 ,tan 3,cos sec 2,sin sec u z v u y v u x === (.20,2/2/πππ≤≤<<-v u ))解：程序代码：>> v=0:pi/100:2*pi; >> u=-pi/2:pi/100:pi/2; >> [U,V]=meshgrid(u,v); >> x=sec(U).*sin(V); >> y=2*sec(U).*cos(V); >> z=3*tan(U); >> surf(x,y,z)44 可以证明: 函数xy z =的图形是双曲抛物面. 在区域22,22≤≤-≤≤-y x 上作出它的图形.解：程序代码：>> x=-2:0.01:2;[x,y]=meshgrid(x); >> z=x.*y;>> mesh(x,y,z);46 画出参数曲面]2,001.0[],4,0[)5/2/ln(tan cos sin sin sin cos ∈∈⎪⎩⎪⎨⎧++===v u u v v z vu y v u x π 的图形.解：程序代码：>> v=0.001:0.001:2; >> u=0:pi/100:4*pi;>> [U,V]=meshgrid(u,v); >> x=cos(U).*sin(V); >> y=sin(U).*sin(V);>> z=cos(V)+log(tan(V/2)+U/5); >> mesh(x,y,z);空间曲线48 作出空间曲线)60(2,sin ,cos π≤≤===t t z t t y t t x 的图形. 解：程序代码：>> syms t;ezplot3(t*cos(t),t*sin(t),2*t,[0,6*pi])-1010-20-100100xx = t cos(t), y = t sin(t), z = 2 tz50绘制参数曲线 ⎪⎪⎩⎪⎪⎨⎧=+==t z t y t x arctan 211cos 2的图形.解：程序代码：>> t=-2*pi:pi/100:2*pi;x=cos(t).*cos(t);y=1./(1+2*t);z=atan(t); plot3(x,y,z);grid;xlabel('x'),ylabel('y'),zlabel('z')xyz多元函数微积分实验6 多元函数微分学（基础实验）实验目的掌握利用Matlab 计算多元函数偏导数和全微分的方法, 掌握计算二元函数极值和条件极值的方法. 理解和掌握曲面的切平面的作法. 通过作图和观察, 理解二元函数的性质、方向导数、梯度和等高线的概念.求多元函数的偏导数与全微分52设),(cos )sin(2xy xy z +=求.,,,222yx zx z y z x z ∂∂∂∂∂∂∂∂∂解：程序代码：>> syms x y;S=sin(x*y)+(cos(x*y))^2; D1=diff(S,'x',1); D2=diff(S,'y',1); D3=diff(S,'x',2); D4=diff(S,'y',2); D1,D2,D3,D4答案： D1 = cos(x*y)*y-2*cos(x*y)*sin(x*y)*yD2 = cos(x*y)*x-2*cos(x*y)*sin(x*y)*xD3 =-sin(x*y)*y^2+2*sin(x*y)^2*y^2-2*cos(x*y)^2*y^2 D4 = -sin(x*y)*x^2+2*sin(x*y)^2*x^2-2*cos(x*y)^2*x^2实验7 多元函数积分学（基础实验）实验目的掌握用Matlab 计算二重积分与三重积分的方法; 深入理解曲线积分、曲面积分的概念和计算方法. 提高应用重积分和曲线、曲面积分解决各种问题的能力.计算重积分54计算,2dxdy xyD⎰⎰ 其中D 为由,,2y x y x ==+ 2=y 所围成的有界区域.解：程序代码：>> syms x y;int(int(x*y^2,x,2-y,sqrt(y)),y,1,2) 答案：ans =193/120 重积分的应用56求旋转抛物面224y x z --=在Oxy 平面上部的面积.S 解：程序代码：>> int(2*pi*r,r,0,2) 答案： ans =4*pi无穷级数与微分方程实验8 无穷级数（基础实验）实验目的观察无穷级数部分和的变化趋势,进一步理解级数的审敛法以及幂级数部分和对函数的逼近. 掌握用Matlab 求无穷级数的和, 求幂级数的收敛域, 展开函数为幂级数以及展开周期函数为傅里叶级数的方法.数项级数58(1) 观察级数∑∞=121n n的部分和序列的变化趋势.解：程序代码：for i=1:100 s=0; for n=1:i s=s+1/n^2; endplot(i,s,'.');hold on; end(2) 观察级数∑∞=11n n 的部分和序列的变化趋势.>> for i=1:100 s=0; for n=1:i s=s+1/n; endplot(i,s,'.'); hold on; end60 求∑∞=++123841n n n的值.解：程序代码：>> syms n;score=symsum(1/(4*n^2+8*n+3),1,inf) 答案： score =1/6函数的幂级数展开62求x arctan 的5阶泰勒展开式. >> syms x;>> T5=taylor(atan(x),6)答案：T5 =x-1/3*x^3+1/5*x^5实验9 微分方程（基础实验）实验目的理解常微分方程解的概念以及积分曲线和方向场的概念,掌握利用 Matlab 求微分方程及方程组解的常用命令和方法.求解微分方程64求微分方程 22x xe xy y -=+'的通解. 解：程序代码：>> y=dsolve('Dy+2*x*y=x*exp(-x^2)','x') 答案：y =(1/2*x^2+C1)*exp(-x^2)66求微分方程x e y y y x 2cos 52=+'-''的通解. 解：程序代码：>> y=dsolve('D2y-2*Dy+5*y=exp(x)*cos(2*x)','x') 答案： y =exp(x)*sin(2*x)*C2+exp(x)*cos(2*x)*C1+1/4*exp(x)*sin(2*x)*x68求微分方程组⎪⎪⎩⎪⎪⎨⎧=--=++02y x dtdy e y x dt dxt 在初始条件0,100====t t y x 下的特解.解：程序代码：>> [x,y]=dsolve('Dx+x+2*y-exp(t)','Dy-x-y','x(0)=1','y(0)=0','t') 答案： x = cos(t)y = 1/2*sin(t)-1/2*cos(t)+1/2*exp(t)70求解微分方程,)1(122/5+=+-x x y dx dy 并作出积分曲线. 解：程序代码：>> syms x yy=dsolve('Dy-2*y/(x+1)-(x+1)^(5/2)','x') 答案：y =(2/3*(x+1)^(3/2)+C1)*(x+1)^2 做积分曲线由>> syms x yx=linspace(-5,5,100); C=input('请输入C 的值:'); y=(2/3*(x+1).^(3/2)+C).*(x+1).^2; plot(x,y)例如对应有：请输入C 的值:2 请输入C 的值:20矩阵运算与方程组求解实验10 行列式与矩阵实验目的掌握矩阵的输入方法. 掌握利用Matlab 对矩阵进行转置、加、减、数乘、相乘、乘方等运算, 并能求矩阵的逆矩阵和计算方阵的行列式.矩阵A 的转置函数Transpose[A]72 求矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛411365243271的转置. 解：程序代码：>> A=[1,7,2;3,4,2;5,6,3;1,1,4]; >> Sove=A' 答案：Sove =1 3 5 1 7 4 6 12 234 矩阵线性运算 73设,291724,624543⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛=B A 求.24,A B B A -+ 解：程序代码：>> A=[3,4,5;4,2,6]; B=[4,2,7;1,9,2];S1=A+BS2=4*B-2*A答案：S1 =7 6 125 11 8S2 =10 0 18-4 32 -474设,148530291724,36242543⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=mb ma 求矩阵ma 与mb 的乘积. 解：程序代码：>> ma=[3,4,5,2;4,2,6,3];>> mb=[4,2,7;1,9,2;0,3,5;8,4,1];>> Sove=ma*mb答案：Sove =32 65 5642 56 65矩阵的乘法运算 75设,101,530291724⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=B A 求AB 与,A B T 并求.3A解：程序代码：>> A=[4 2 7;1 9 2;0 3 5];B=[1;0;1];>> AB=A*BAB =1135>> BTA=B'*ABTA =4 5 12>> A3=A^3A3 =119 660 555141 932 44454 477 260求方阵的逆76 设,5123641033252312⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=A 求.1-A 解：程序代码：>> A=[2,1,3,2;5,2,3,3;0,1,4,6;3,2,1,5];Y=inv(A)答案：Y =-1.7500 1.3125 0.5000 -0.68755.5000 -3.6250 -2.0000 2.37500.5000 -0.1250 0.0000 -0.1250-1.2500 0.6875 0.5000 -0.312577 设,221331317230,5121435133124403⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=B A 求.1B A - 解：程序代码：>> A=[3 0 4 4 ;2 1 3 3 ;1 5 3 4;1 2 1 5];B=[0 3 2 ;7 1 3;1 3 3 ;1 2 2];Solve=A'*B答案：Solve =16 16 1714 20 2225 26 2830 37 3978 解方程组⎪⎩⎪⎨⎧-=-+=+-=++.2442,63,723z y x z y x z y x解：程序代码：>> A=[3 2 1;1 -1 3;2 4 -4];b=[7 6 -2];>> A\b'答案：ans =1.00001.00002.0000求方阵的行列式79 求行列式 .3351110243152113------=D 解：程序代码：>> A=[3,1,-1,2;-5,1,3,-4;2,0,1,-1;1,-5,3,-3];D=det(A)答案：D =4080求.11111111111122222222d d d d c c c c b b b b a a a a D ++++= 解：程序代码：>> syms a b c d;D=[a^2+1/a^2 a 1/a 1;b^2+1/b^2 b 1/b 1;c^2+1/c^2 c 1/c 1;d^2+1/d^2 d 1/d 1];det(D)答案：ans =-(-c*d^2*b^3+c^2*d*b^3-c^3*d^2*a+c^3*d*a^2*b^4+c*d^2*a^3-c^3*d^2*a*b^4-c^2*d*a^3-c*d^2*b^3*a^4+c^2*d*b^3*a^4+c^3*d^2*b*a^4-c^3*d*b^2*a^4-c^2*d^3*b*a^4+c*d^3*b^2*a^4+c*d ^2*a^3*b^4-c^2*d*a^3*b^4+c^3*d^2*b-c^3*d*b^2-c^2*d^3*b+c*d^3*b^2+c^3*d*a^2+c^2*d^3*a-c *d^3*a^2-b*d^2*a^3+b^2*d*a^3+b^3*d^2*a-b^3*d*a^2-b^2*d^3*a+b*d^3*a^2+b*c^2*a^3-b^2*c*a ^3-b^3*c^2*a+b^3*c*a^2+b^2*c^3*a-b*c^3*a^2+c^2*d^3*a*b^4-c*d^3*a^2*b^4-b*d^2*a^3*c^4+b ^2*d*a^3*c^4+b^3*d^2*a*c^4-b^3*d*a^2*c^4-b^2*d^3*a*c^4+b*d^3*a^2*c^4+b*c^2*a^3*d^4-b^2*c*a^3*d^4-b^3*c^2*a*d^4+b^3*c*a^2*d^4+b^2*c^3*a*d^4-b*c^3*a^2*d^4)/a^2/c^2/d^2/b^281 计算范德蒙行列式.1111145444342413534333231252423222154321x x x x x x x x x x x x x x x x x x x x 解：程序代码：>> syms x1 x2 x3 x4 x5; >> A=[1,1,1,1,1;x1,x2,x3,x4,x5;x1^2,x2^2,x3^2,x4^2,x5^2;x1^3,x2^3,x3^3,x4^3,x5^3;x1^4,x2^4,x3^4,x4^4,x5^4];>> DC=det(A);>> DS=simple(DC)答案：DS =(-x5+x4)*(x3-x5)*(x3-x4)*(-x5+x2)*(x2-x4)*(x2-x3)*(-x5+x1)*(x1-x4)*(x1-x3)*(x1-x2)82 设矩阵 ,60975738723965110249746273⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=A 求.),(|,|3A A tr A 解：程序代码：>> A=[3,7,2,6,-4;7,9,4,2,0;11,5,-6,9,3;2,7,-8,3,7;5,7,9,0,-6];>> D=det(A),T=trace(A),A3=A^3答案：D =11592T =3A3=726 2062 944 294 -3581848 3150 26 1516 2281713 2218 31 1006 4041743 984 -451 1222 384801 2666 477 745 -125向量的内积83 求向量}3,2,1{=u 与}0,1,1{-=v 的内积.解：程序代码：>> u=[1 2 3];v=[1 -1 0];solve=dot(u,v)答案：solve =-184设,001001⎪⎪⎪⎭⎫⎝⎛=λλλA 求.10A 一般地?=k A (k 是正整数).解：程序代码：>> syms r;>> A=[r,1,0;0,r,1;0,0,r];>> A^10答案：ans =[ r^10, 10*r^9, 45*r^8][ 0, r^10, 10*r^9][ 0, 0, r^10]85.求⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛+++++a a a a a 1111111111111111111111111的逆.解：程序代码：>> syms aA=[1+a,1,1,1,1;1,1+a,1,1,1;1,1,1+a,1,1;1,1,1,1+a,1;1,1,1,1,1+a];solve=inv(A)答案：solve =[ 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5), -1/a/(a+5),-1/a/(a+5)] [ -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5),-1/a/(a+5)][ -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5)][ -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5)][ -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5)] 实验11 矩阵的秩与向量组的极大无关组实验目的学习利用Matlab 求矩阵的秩,作矩阵的初等行变换; 求向量组的秩与极大无关组. 求矩阵的秩86 设,815073*********⎪⎪⎪⎭⎫ ⎝⎛-------=M 求矩阵M 的秩.解：程序代码：>> M=[3,2,-1,-3,-2;2,-1,3,1,-3;7,0,5,-1,-8];R=rank(M)答案：R=2向量组的秩87求向量组)0,3,0,2(),2,5,4,0(),1,1,2,1(231=--=-=ααα的秩.解：程序代码：>> A=[1,2,-1,1;0,-4,5,-2;2,0,3,0];R=rank(A)答案：R =288向量组)7,5,1,3(),5,4,3,1(),1,1,1,1(),3,2,1,1(4321==-==αααα是否线性相关?解：由>> A=[1 1 2 3;1 -1 1 1;1 3 4 5;3 1 5 7];rank(A)ans = 3即rank(A)=3 小于阶数489向量组)3,1,1(),2,1,3(),7,2,2(321=-==ααα是否线性相关?解：由>> A3=[2,2,7;3,-1,2;1,1,3];R=rank(A3)得 R = 3即rank(A3)=3 等于阶数3故向量组线性无关。

Matlab实验习题集答案.docx

1：用以上两种形式计算56+sin^ + e 3算术运算结果。

» 5A 6+sin(pi)+exp(3)ans =1.5645e+004» x=5A 6+sin(pi)+exp(3)»A=[1 2;1 2];» B=[l 1;2 2];» C=(A<B)&(A==B)C =0 0 03：对数d = 5 + sin7用五位定点、十五位定点以及有理数形式表示出来。

»a=5+sin(7); format short,a 5.6570» a=5+sin(7);» format long,aa =» A=[l 2 3;4 15 60;7 8 9]A =12 3 415 60 7 8 9 n i n i i i5：输入矩阵U 1 1丿。

％利用MATLAB 命令直接输入矩阵OneMatrix=ones(33J)OneMatrix =8 10 9 101 1 11 1 11 1 1‘0 0 0 0 0、c养」0 0 0 0 0,» OneMatrix=ones(2,5；l);ZeroMatrix=zeros(size(OneMatrix)) ZeroMatrix =0 0 0 0 00 0 0 0 07：生成3阶魔方矩阵。

» magic(3) ans =8 1 63 5 749 28：操作符冒号”：”的应用a）步长为1的等差数列b）步长为2的等差数列c）步长为-2的等差、递减数列» 0:1:10 ans =» 0:2:10 ans =» 10:(-2):0C）取矩阵A 的A （2）, A （3）, A （4）d）取矩阵A的第一行e）取矩阵A的第三列D把矩阵A的第一行第三列元素赋值给变吊: g）把矩阵A的第二行第列元素修改为100» A=[l 23 56;sin(3) 7 9;log(2) 6 1]» A(2,3)fl 3 100) c 二,利用A 与B 生成矩阵V 6 9 0 A ans = ans =23 » A ⑵,A ⑶,A(4)ans =0.141120008059867ans =0.693147180559945 ans =23»A(1,:)ans =1 23 56» A(:,3)ans =5691» x=A(l,3)56 » A(2,1)=100L0000 100.0000 0.6931 23.0000 7.0000 6.000056.00009.00001.00001 3 A =6 9 io ：己知矩阵 L° R _(A 0) D = (A B)曲=〔0 B 丿»A=[13;6 9];B=[1 5;0 8]; » C=[AB(:,1)];» C(l,3)=100c =1 3 1006 9 0» A=[l 3;6 9];B=[1 5;0 8];D=[A B]D =公比为10°" » A=[l 23 56;sin(3) 7 9;log(2) 6 1];»A(1,:)=[]A =0.1411 7.0000 9.00000.6931 6.0000 1.000012： 1 inspace(0, 1, 6) / %给出区间[0, 1]的6个等分点数据logspace(0, 1,6) / %给出区间的6个等比点数据,»linspace(0J,6) ans =» a=l:5 b=3:2:ll c=a>*a a = 1 2b = 3 5c = 1 4» a.*bans = 3 103 4 57 9 119 16 2521 36 55■兀 . sm(k ——),k = ±2, ±1,014：计算 2 的值。

MATLAB数学实验100例题解

matlab编程实例100例之欧阳道创编

1-32是：图形应用篇33-66是：界面设计篇67-84是：图形处理篇85-100是：数值分析篇实例1：三角函数曲线（1）function shili01h0=figure('toolbar','none',...'position',[198 56 350 300],...'name','实例01');h1=axes('parent',h0,...'visible','off');x=-pi:0.05:pi;y=sin(x);plot(x,y);xlabel('自变量X');ylabel('函数值Y');title('SIN( )函数曲线');grid on实例2：三角函数曲线（2）function shili02h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例02');x=-pi:0.05:pi;y=sin(x)+cos(x);plot(x,y,'-*r','linewidth',1);grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例3：图形的叠加function shili03h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例03');x=-pi:0.05:pi;y1=sin(x);y2=cos(x);plot(x,y1,...'-*r',...x,y2,...'--og');grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例4：双y轴图形的绘制function shili04h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例04');x=0:900;a=1000;b=0.005;y1=2*x;y2=cos(b*x);[haxes,hline1,hline2]=plotyy(x,y1,x,y2,'semilogy','plot'); axes(haxes(1))ylabel('semilog plot');axes(haxes(2))ylabel('linear plot');实例5：单个轴窗口显示多个图形function shili05h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例05');t=0:pi/10:2*pi;[x,y]=meshgrid(t);subplot(2,2,1)plot(sin(t),cos(t))axis equalsubplot(2,2,2)z=sin(x)-cos(y);plot(t,z)axis([0 2*pi -2 2])subplot(2,2,3)h=sin(x)+cos(y);plot(t,h)axis([0 2*pi -2 2])subplot(2,2,4)g=(sin(x).^2)-(cos(y).^2);plot(t,g)axis([0 2*pi -1 1])实例6：图形标注function shili06h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例06');t=0:pi/10:2*pi;h=plot(t,sin(t));xlabel('t=0到2\pi','fontsize',16);ylabel('sin(t)','fontsize',16);title('\it{从 0to2\pi 的正弦曲线}','fontsize',16) x=get(h,'xdata');y=get(h,'ydata');imin=find(min(y)==y);imax=find(max(y)==y);text(x(imin),y(imin),...['\leftarrow最小值=',num2str(y(imin))],... 'fontsize',16)text(x(imax),y(imax),...['\leftarrow最大值=',num2str(y(imax))],... 'fontsize',16)实例7：条形图形function shili07h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例07');tiao1=[562 548 224 545 41 445 745 512];tiao2=[47 48 57 58 54 52 65 48];t=0:7;bar(t,tiao1)xlabel('X轴');ylabel('TIAO1值');h1=gca;h2=axes('position',get(h1,'position'));plot(t,tiao2,'linewidth',3)set(h2,'yaxislocation','right','color','none','xticklabel',[])实例8：区域图形function shili08h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例08');x=91:95;profits1=[88 75 84 93 77];profits2=[51 64 54 56 68];profits3=[42 54 34 25 24];profits4=[26 38 18 15 4];area(x,profits1,'facecolor',[0.5 0.9 0.6],...'edgecolor','b',...'linewidth',3)hold onarea(x,profits2,'facecolor',[0.9 0.85 0.7],...'edgecolor','y',...'linewidth',3)hold onarea(x,profits3,'facecolor',[0.3 0.6 0.7],...'edgecolor','r',...'linewidth',3)hold onarea(x,profits4,'facecolor',[0.6 0.5 0.9],...'edgecolor','m',...'linewidth',3)hold offset(gca,'xtick',[91:95])set(gca,'layer','top')gtext('\leftarrow第一季度销量')gtext('\leftarrow第二季度销量')gtext('\leftarrow第三季度销量')gtext('\leftarrow第四季度销量')xlabel('年','fontsize',16);ylabel('销售量','fontsize',16);实例9：饼图的绘制function shili09h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例09');t=[54 21 35;68 54 35;45 25 12;48 68 45;68 54 69];x=sum(t);h=pie(x);textobjs=findobj(h,'type','text');str1=get(textobjs,{'string'});val1=get(textobjs,{'extent'});oldext=cat(1,val1{:});names={'商品一：';'商品二：';'商品三：'};str2=strcat(names,str1);set(textobjs,{'string'},str2)val2=get(textobjs,{'extent'});newext=cat(1,val2{:});offset=sign(oldext(:,1)).*(newext(:,3)-oldext(:,3))/2; pos=get(textobjs,{'position'});textpos=cat(1,pos{:});textpos(:,1)=textpos(:,1)+offset;set(textobjs,{'position'},num2cell(textpos,[3,2]))实例10：阶梯图function shili10h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例10');a=0.01;b=0.5;t=0:10;f=exp(-a*t).*sin(b*t);stairs(t,f)hold onplot(t,f,':*')hold offglabel='函数e^{-(\alpha*t)}sin\beta*t的阶梯图'; gtext(glabel,'fontsize',16)xlabel('t=0:10','fontsize',16)axis([0 10 -1.2 1.2])实例11：枝干图function shili11h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例11');x=0:pi/20:2*pi;y1=sin(x);y2=cos(x);h1=stem(x,y1+y2);hold onh2=plot(x,y1,'^r',x,y2,'*g');hold offh3=[h1(1);h2];legend(h3,'y1+y2','y1=sin(x)','y2=cos(x)')xlabel('自变量X');ylabel('函数值Y');title('正弦函数与余弦函数的线性组合');实例12：罗盘图function shili12h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例12');winddirection=[54 24 65 84256 12 235 62125 324 34 254];windpower=[2 5 5 36 8 12 76 14 10 8];rdirection=winddirection*pi/180;[x,y]=pol2cart(rdirection,windpower); compass(x,y);desc={'风向和风力','北京气象台','10月1日0：00到','10月1日12：00'};gtext(desc)实例13：轮廓图function shili13h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例13');[th,r]=meshgrid((0:10:360)*pi/180,0:0.05:1); [x,y]=pol2cart(th,r);z=x+i*y;f=(z.^4-1).^(0.25);contour(x,y,abs(f),20)axis equalxlabel('实部','fontsize',16);ylabel('虚部','fontsize',16);h=polar([0 2*pi],[0 1]);delete(h)hold oncontour(x,y,abs(f),20)实例14：交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点'); x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例14：交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点'); x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例15：变换的傅立叶函数曲线function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren')h=uicontrol('style','slider','position',... [100 10 500 20],'min',1,'max',20)for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例16：劳伦兹非线形方程的无序活动function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren')h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20)for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例17：填充图function shili17h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例17');t=(1:2:15)*pi/8;x=sin(t);y=cos(t);fill(x,y,'r')axis square offtext(0,0,'STOP',...'color',[1 1 1],...'fontsize',50,...'horizontalalignment','center')例18：条形图和阶梯形图function shili18h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例18');subplot(2,2,1)x=-3:0.2:3;y=exp(-x.*x);bar(x,y)title('2-D Bar Chart')subplot(2,2,2)x=-3:0.2:3;y=exp(-x.*x);bar3(x,y,'r')title('3-D Bar Chart')subplot(2,2,3)x=-3:0.2:3;y=exp(-x.*x);stairs(x,y)title('Stair Chart')subplot(2,2,4)x=-3:0.2:3;y=exp(-x.*x);barh(x,y)title('Horizontal Bar Chart')实例19：三维曲线图function shili19h0=figure('toolbar','none',...'position',[200 150 450 400],... 'name','实例19');subplot(2,1,1)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,y1,z1,x,y2,z2,x,y3,z3) grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:3-D Plot') subplot(2,1,2)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,z1,y1,x,z2,y2,x,z3,y3) grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:3-D Plot')实例20：图形的隐藏属性function shili20h0=figure('toolbar','none',...'position',[200 150 450 300],... 'name','实例20');subplot(1,2,1)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure1:Opaque')hidden onsubplot(1,2,2)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure2:Transparent') hidden off实例21PEAKS函数曲线function shili21h0=figure('toolbar','none',...'position',[200 100 450 450],...'name','实例21');[x,y,z]=peaks(30);subplot(2,1,1)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfc(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:surfc函数形成的曲面') subplot(2,1,2)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfl(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:surfl函数形成的曲面') 实例22：片状图function shili22h0=figure('toolbar','none',...'position',[200 150 550 350],...'name','实例22');subplot(1,2,1)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trimesh(t,x,y,z)hidden offtitle('Figure1:Triangular Surface Plot'); subplot(1,2,2)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trisurf(t,x,y,z)title('Figure1:Triangular Surface Plot');实例23：视角的调整function shili23h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例23');x=-5:0.5:5;[x,y]=meshgrid(x);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;subplot(2,2,1)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure1')view(-37.5,30)subplot(2,2,2)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure2')view(-37.5+90,30)subplot(2,2,3)surf(x,y,z)xlabel('X-axis')。

matlab实用教程100例

matlab实用程序百例1-32是：图形应用篇33-66是：界面设计篇67-84是：图形处理篇85-100是：数值分析篇实例1：三角函数曲线〔1〕function shili01h0=figure('toolbar','none',...'position',[198 56 350 300],...'name','实例01');h1=axes('parent',h0,...'visible','off');x=-pi:0.05:pi;y=sin(x);plot(x,y);xlabel('自变量X');ylabel('函数值Y');title('SIN( )函数曲线');grid on实例2：三角函数曲线〔2〕function shili02h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例02');x=-pi:0.05:pi;y=sin(x)+cos(x);plot(x,y,'-*r','linewidth',1);grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例3：图形的叠加function shili03h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例03');x=-pi:0.05:pi;y1=sin(x);y2=cos(x);plot(x,y1,...'-*r',...x,y2,...'--og');grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例4：双y轴图形的绘制function shili04h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例04');x=0:900;a=1000;b=0.005;y1=2*x;y2=cos(b*x);[haxes,hline1,hline2]=plotyy(x,y1,x,y2,'semilogy','plot'); axes(haxes(1))ylabel('semilog plot');axes(haxes(2))ylabel('linear plot');实例5：单个轴窗口显示多个图形function shili05h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例05');t=0:pi/10:2*pi;[x,y]=meshgrid(t);subplot(2,2,1)plot(sin(t),cos(t))axis equalsubplot(2,2,2)z=sin(x)-cos(y);plot(t,z)axis([0 2*pi -2 2])subplot(2,2,3)h=sin(x)+cos(y);plot(t,h)axis([0 2*pi -2 2])subplot(2,2,4)g=(sin(x).^2)-(cos(y).^2);plot(t,g)axis([0 2*pi -1 1])实例6：图形标注function shili06h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例06');t=0:pi/10:2*pi;h=plot(t,sin(t));xlabel('t=0到2\pi','fontsize',16);ylabel('sin(t)','fontsize',16);title('\it{从0to2\pi 的正弦曲线}','fontsize',16) x=get(h,'xdata');y=get(h,'ydata');imin=find(min(y)==y);imax=find(max(y)==y);text(x(imin),y(imin),...['\leftarrow最小值=',num2str(y(imin))],...'fontsize',16)text(x(imax),y(imax),...['\leftarrow最大值=',num2str(y(imax))],...'fontsize',16)实例7：条形图形function shili07h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例07');tiao1=[562 548 224 545 41 445 745 512];tiao2=[47 48 57 58 54 52 65 48];t=0:7;bar(t,tiao1)xlabel('X轴');ylabel('TIAO1值');h1=gca;h2=axes('position',get(h1,'position'));plot(t,tiao2,'linewidth',3)set(h2,'yaxislocation','right','color','none','xticklabel',[]) 实例8：区域图形function shili08h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例08');x=91:95;profits1=[88 75 84 93 77];profits2=[51 64 54 56 68];profits3=[42 54 34 25 24];profits4=[26 38 18 15 4];area(x,profits1,'facecolor',[0.5 0.9 0.6],...'edgecolor','b',...'linewidth',3)hold onarea(x,profits2,'facecolor',[0.9 0.85 0.7],...'edgecolor','y',...'linewidth',3)hold onarea(x,profits3,'facecolor',[0.3 0.6 0.7],...'edgecolor','r',...'linewidth',3)hold onarea(x,profits4,'facecolor',[0.6 0.5 0.9],...'edgecolor','m',...'linewidth',3)hold offset(gca,'xtick',[91:95])set(gca,'layer','top')gtext('\leftarrow第一季度销量')gtext('\leftarrow第二季度销量')gtext('\leftarrow第三季度销量')gtext('\leftarrow第四季度销量')xlabel('年','fontsize',16);ylabel('销售量','fontsize',16);实例9：饼图的绘制function shili09h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例09');t=[54 21 35;68 54 35;45 25 12;48 68 45;68 54 69];x=sum(t);h=pie(x);textobjs=findobj(h,'type','text');str1=get(textobjs,{'string'});val1=get(textobjs,{'extent'});oldext=cat(1,val1{:});names={'商品一：';'商品二：';'商品三：'};str2=strcat(names,str1);set(textobjs,{'string'},str2)val2=get(textobjs,{'extent'});newext=cat(1,val2{:});offset=sign(oldext(:,1)).*(newext(:,3)-oldext(:,3))/2; pos=get(textobjs,{'position'});textpos=cat(1,pos{:});textpos(:,1)=textpos(:,1)+offset;set(textobjs,{'position'},num2cell(textpos,[3,2]))实例10：阶梯图function shili10h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例10');a=0.01;b=0.5;t=0:10;f=exp(-a*t).*sin(b*t);stairs(t,f)hold onplot(t,f,':*')hold offglabel='函数e^{-(\alpha*t)}sin\beta*t的阶梯图'; gtext(glabel,'fontsize',16)xlabel('t=0:10','fontsize',16)axis([0 10 -1.2 1.2])实例11：枝干图function shili11h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例11');x=0:pi/20:2*pi;y1=sin(x);y2=cos(x);h1=stem(x,y1+y2);hold onh2=plot(x,y1,'^r',x,y2,'*g');hold offh3=[h1(1);h2];legend(h3,'y1+y2','y1=sin(x)','y2=cos(x)') xlabel('自变量X');ylabel('函数值Y');title('正弦函数与余弦函数的线性组合');实例12：罗盘图function shili12h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例12');winddirection=[54 24 65 84256 12 235 62125 324 34 254];windpower=[2 5 5 36 8 12 76 14 10 8];rdirection=winddirection*pi/180;[x,y]=pol2cart(rdirection,windpower); compass(x,y);desc={'风向和风力','北京气象台','10月1日0：00到','10月1日12：00'};gtext(desc)实例13：轮廓图function shili13h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例13');[th,r]=meshgrid((0:10:360)*pi/180,0:0.05:1); [x,y]=pol2cart(th,r);z=x+i*y;f=(z.^4-1).^(0.25);contour(x,y,abs(f),20)axis equalxlabel('实部','fontsize',16);ylabel('虚部','fontsize',16);h=polar([0 2*pi],[0 1]);delete(h)hold oncontour(x,y,abs(f),20)实例14：交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点');x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例14：交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点'); disp('单击鼠标右键点取最后一个点'); but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点');x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例15：变换的傅立叶函数曲线function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren')h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20)for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例16：劳伦兹非线形方程的无序活动function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren')h=uicontrol('style','slider','position',...[100 10 500 20],'min',1,'max',20) for j=1:20plot(fft(eye(j+16)))set(h,'value',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例17：填充图function shili17h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例17');t=(1:2:15)*pi/8;x=sin(t);y=cos(t);fill(x,y,'r')axis square offtext(0,0,'STOP',...'color',[1 1 1],...'fontsize',50,...'horizontalalignment','center')例18：条形图和阶梯形图function shili18h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例18');subplot(2,2,1)x=-3:0.2:3;y=exp(-x.*x);bar(x,y)title('2-D Bar Chart')subplot(2,2,2)x=-3:0.2:3;y=exp(-x.*x);bar3(x,y,'r')title('3-D Bar Chart')subplot(2,2,3)x=-3:0.2:3;y=exp(-x.*x);stairs(x,y)title('Stair Chart')subplot(2,2,4)x=-3:0.2:3;y=exp(-x.*x);barh(x,y)title('Horizontal Bar Chart')实例19：三维曲线图function shili19h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例19');subplot(2,1,1)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,y1,z1,x,y2,z2,x,y3,z3)grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:3-D Plot')subplot(2,1,2)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,z1,y1,x,z2,y2,x,z3,y3)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:3-D Plot')实例20：图形的隐藏属性function shili20h0=figure('toolbar','none',...'position',[200 150 450 300],...'name','实例20');subplot(1,2,1)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure1:Opaque')hidden onsubplot(1,2,2)[x,y,z]=sphere(10);mesh(x,y,z)axis offtitle('Figure2:Transparent')hidden off实例21PEAKS函数曲线function shili21h0=figure('toolbar','none',...'position',[200 100 450 450],...'name','实例21');[x,y,z]=peaks(30);subplot(2,1,1)x=x(1,:);y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfc(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:surfc函数形成的曲面') subplot(2,1,2)y=y(:,1);i=find(y>0.8&y<1.2);j=find(x>-0.6&x<0.5);z(i,j)=nan*z(i,j);surfl(x,y,z)xlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:surfl函数形成的曲面') 实例22：片状图function shili22h0=figure('toolbar','none',...'position',[200 150 550 350],...'name','实例22');subplot(1,2,1)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trimesh(t,x,y,z)hidden offtitle('Figure1:Triangular Surface Plot');subplot(1,2,2)x=rand(1,20);y=rand(1,20);z=peaks(x,y*pi);t=delaunay(x,y);trisurf(t,x,y,z)title('Figure1:Triangular Surface Plot'); 实例23：视角的调整function shili23h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例23');x=-5:0.5:5;[x,y]=meshgrid(x);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;subplot(2,2,1)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure1')view(-37.5,30)subplot(2,2,2)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure2')view(-37.5+90,30)subplot(2,2,3)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure3')view(-37.5,60)subplot(2,2,4)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure4')view(180,0)实例24：向量场的绘制function shili24h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例24');subplot(2,2,1)z=peaks;ribbon(z)title('Figure1')subplot(2,2,2)[x,y,z]=peaks(15);[dx,dy]=gradient(z,0.5,0.5); contour(x,y,z,10)quiver(x,y,dx,dy)hold offtitle('Figure2')subplot(2,2,3)[x,y,z]=peaks(15);[nx,ny,nz]=surfnorm(x,y,z);surf(x,y,z)hold onquiver3(x,y,z,nx,ny,nz)hold offtitle('Figure3')subplot(2,2,4)x=rand(3,5);y=rand(3,5);z=rand(3,5);c=rand(3,5);fill3(x,y,z,c)grid ontitle('Figure4')实例25：灯光定位function shili25h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例25');vert=[1 1 1;1 2 1;2 2 1;2 1 1;1 1 2;12 2;2 2 2;2 1 2];fac=[1 2 3 4;2 6 7 3;4 3 7 8;15 8 4;1 2 6 5;5 6 7 8];grid offsphere(36)h=findobj('type','surface');set(h,'facelighting','phong',...'facecolor',...'interp',...'edgecolor',[0.4 0.4 0.4],...'backfacelighting',...'lit')patch('faces',fac,'vertices',vert,...'facecolor','y');light('position',[1 3 2]);light('position',[-3 -1 3]); material shinyaxis vis3d offhold off实例26：柱状图function shili26h0=figure('toolbar','none',...'position',[200 50 450 450],...'name','实例26');subplot(2,1,1)x=[5 2 18 7 39 8 65 5 54 3 2];bar(x)xlabel('X轴');ylabel('Y轴');title('第一子图');subplot(2,1,2)y=[5 2 18 7 39 8 65 5 54 3 2];barh(y)xlabel('X轴');ylabel('Y轴');title('第二子图');实例27：设置照明方式function shili27h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例27');subplot(2,2,1)sphereshading flatcamlight leftcamlight rightlighting flatcolorbaraxis offtitle('Figure1')subplot(2,2,2)sphereshading flatcamlight leftcamlight rightlighting gouraudcolorbaraxis offtitle('Figure2')subplot(2,2,3)sphereshading interpcamlight rightcamlight leftlighting phongcolorbaraxis offtitle('Figure3')subplot(2,2,4)sphereshading flatcamlight leftcamlight rightlighting nonecolorbaraxis offtitle('Figure4')实例28：羽状图function shili28h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例28');subplot(2,1,1)alpha=90:-10:0;r=ones(size(alpha));m=alpha*pi/180;n=r*10;[u,v]=pol2cart(m,n);feather(u,v)title('羽状图')axis([0 20 0 10])subplot(2,1,2)t=0:0.5:10;x=0.05+i;y=exp(-x*t);feather(y)title('复数矩阵的羽状图')实例29：立体透视〔1〕function shili29h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例29');[x,y,z]=meshgrid(-2:0.1:2,...-2:0.1:2,...-2:0.1:2);v=x.*exp(-x.^2-y.^2-z.^2);grid onfor i=-2:0.5:2;h1=surf(linspace(-2,2,20),...linspace(-2,2,20),...zeros(20)+i);rotate(h1,[1 -1 1],30)dx=get(h1,'xdata');dy=get(h1,'ydata');dz=get(h1,'zdata');delete(h1)slice(x,y,z,v,[-2 2],2,-2)hold onslice(x,y,z,v,dx,dy,dz)hold offaxis tightview(-5,10)drawnowend实例30：立体透视〔2〕function shili30h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例30');[x,y,z]=meshgrid(-2:0.1:2,...-2:0.1:2,...-2:0.1:2);v=x.*exp(-x.^2-y.^2-z.^2); [dx,dy,dz]=cylinder;slice(x,y,z,v,[-2 2],2,-2)for i=-2:0.2:2h=surface(dx+i,dy,dz);rotate(h,[1 0 0],90)xp=get(h,'xdata');yp=get(h,'ydata');zp=get(h,'zdata');delete(h)hold onhs=slice(x,y,z,v,xp,yp,zp);axis tightxlim([-3 3])view(-10,35)drawnowdelete(hs)hold offend实例31：外表图形function shili31h0=figure('toolbar','none',...'position',[200 150 550 250],...'name','实例31');subplot(1,2,1)x=rand(100,1)*16-8;y=rand(100,1)*16-8;r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;xlin=linspace(min(x),max(x),33); ylin=linspace(min(y),max(y),33); [X,Y]=meshgrid(xlin,ylin);Z=griddata(x,y,z,X,Y,'cubic'); mesh(X,Y,Z)axis tighthold onplot3(x,y,z,'.','Markersize',20)subplot(1,2,2)k=5;n=2^k-1;theta=pi*(-n:2:n)/n;phi=(pi/2)*(-n:2:n)'/n;X=cos(phi)*cos(theta);Y=cos(phi)*sin(theta);Z=sin(phi)*ones(size(theta));colormap([0 0 0;1 1 1])C=hadamard(2^k);surf(X,Y,Z,C)axis square实例32：沿曲线移动的小球h0=figure('toolbar','none',...'position',[198 56 408 468],...'name','实例32');h1=axes('parent',h0,...'position',[0.15 0.45 0.7 0.5],...'visible','on');t=0:pi/24:4*pi;y=sin(t);plot(t,y,'b')n=length(t);h=line('color',[0 0.5 0.5],...'linestyle','.',...'markersize',25,...'erasemode','xor');k1=uicontrol('parent',h0,...'style','pushbutton',...'position',[80 100 50 30],...'string','开始',...'callback',[...'i=1;',...'k=1;,',...'m=0;,',...'while 1,',...'if k==0,',...'break,',...'end,',...'if k~=0,',...'set(h,''xdata'',t(i),''ydata'',y(i)),',...'drawnow;,',...'i=i+1;,',...'if i>n,',...'m=m+1;,',...'i=1;,',...'end,',...'end,',...'end']);k2=uicontrol('parent',h0,...'style','pushbutton',...'position',[180 100 50 30],...'string','停止',...'callback',[...'k=0;,',...'set(e1,''string'',m),',...'p=get(h,''xdata'');,',...'q=get(h,''ydata'');,',...'set(e2,''string'',p);,',...'set(e3,''string'',q)']);k3=uicontrol('parent',h0,...'style','pushbutton',...'position',[280 100 50 30],...'string','关闭',...'callback','close');e1=uicontrol('parent',h0,...'style','edit',...'position',[60 30 60 20]);t1=uicontrol('parent',h0,...'style','text',...'string','循环次数',...'position',[60 50 60 20]);e2=uicontrol('parent',h0,...'style','edit',...'position',[180 30 50 20]);t2=uicontrol('parent',h0,...'style','text',...'string','终点的X坐标值',...'position',[155 50 100 20]); e3=uicontrol('parent',h0,...'style','edit',...'position',[300 30 50 20]);t3=uicontrol('parent',h0,...'style','text',...'string','终点的Y坐标值',...'position',[275 50 100 20]);实例33：曲线转换按钮h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例33');x=0:0.5:2*pi;y=sin(x);h=plot(x,y);grid onhuidiao=[...'if i==1,',...'i=0;,',...'y=cos(x);,',...'delete(h),',...'set(hm,''string'',''正弦函数''),',...'h=plot(x,y);,',...'grid on,',...'else if i==0,',...'i=1;,',...'y=sin(x);,',...'set(hm,''string'',''余弦函数''),',...'delete(h),',...'h=plot(x,y);,',...'grid on,',...'end,',...'end'];hm=uicontrol(gcf,'style','pushbutton',...'string','余弦函数',...'callback',huidiao);i=1;set(hm,'position',[250 20 60 20]);set(gca,'position',[0.2 0.2 0.6 0.6]) title('按钮的使用')hold on实例34：栅格控制按钮h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例34');x=0:0.5:2*pi;y=sin(x);plot(x,y)huidiao1=[...'set(h_toggle2,''value'',0),',...'grid on,',...];huidiao2=[...'set(h_toggle1,''value'',0),',...'grid off,',...];h_toggle1=uicontrol(gcf,'style','togglebutton',...'string','grid on',...'value',0,...'position',[20 45 50 20],...'callback',huidiao1);h_toggle2=uicontrol(gcf,'style','togglebutton',...'string','grid off',...'value',0,...'position',[20 20 50 20],...'callback',huidiao2);set(gca,'position',[0.2 0.2 0.6 0.6])title('开关按钮的使用')实例35：编辑框的使用h0=figure('toolbar','none',...'position',[200 150 350 250],...'name','实例35');f='Please input the letter';huidiao1=[...'g=upper(f);,',...'set(h2_edit,''string'',g),',...];huidiao2=[...'g=lower(f);,',...'set(h2_edit,''string'',g),',...];h1_edit=uicontrol(gcf,'style','edit',...'position',[100 200 100 50],...'HorizontalAlignment','left',...'string','Please input the letter',...'callback','f=get(h1_edit,''string'');',...'background','w',...'max',5,...'min',1);h2_edit=uicontrol(gcf,'style','edit',...'HorizontalAlignment','left',...'position',[100 100 100 50],...'background','w',...'max',5,...'min',1);h1_button=uicontrol(gcf,'style','pushbutton',...'string','小写变大写',...'position',[100 45 100 20],...'callback',huidiao1);h2_button=uicontrol(gcf,'style','pushbutton',...'string','大写变小写',...'position',[100 20 100 20],...'callback',huidiao2);实例36：弹出式菜单h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例36');x=0:0.5:2*pi;y=sin(x);h=plot(x,y);grid onhm=uicontrol(gcf,'style','popupmenu',...'string',...'sin(x)|cos(x)|sin(x)+cos(x)|exp(-sin(x))',...'position',[250 20 50 20]);set(hm,'value',1)huidiao=[...'v=get(hm,''value'');,',...'switch v,',...'case 1,',...'delete(h),',...'y=sin(x);,',...'h=plot(x,y);,',...'grid on,',...'case 2,',...'delete(h),',...'y=cos(x);,',...'h=plot(x,y);,',...'grid on,',...'case 3,',...'delete(h),',...'y=sin(x)+cos(x);,',...'h=plot(x,y);,',...'grid on,',...'case 4,',...'delete(h),',...'y=exp(-sin(x));,',...'h=plot(x,y);,',...'grid on,',...'end'];set(hm,'callback',huidiao)set(gca,'position',[0.2 0.2 0.6 0.6]) title('弹出式菜单的使用')实例37：滑标的使用h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例37');[x,y]=meshgrid(-8:0.5:8);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;h0=mesh(x,y,z);h1=axes('position',...[0.2 0.2 0.5 0.5],...'visible','off');htext=uicontrol(gcf,...'units','points',...'position',[20 30 45 15],...'string','brightness',...'style','text');hslider=uicontrol(gcf,...'units','points',...'position',[10 10 300 15],...'min',-1,...'max',1,...'style','slider',...'callback',...'brighten(get(hslider,''value''))'); 实例38：多项选择菜单h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例38');[x,y]=meshgrid(-8:0.5:8);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;h0=mesh(x,y,z);hlist=uicontrol(gcf,'style','listbox',...'string','default|spring|summer|autumn|winter',...'max',5,...'min',1,...'position',[20 20 80 100],...'callback',[...'k=get(hlist,''value'');,',...'switch k,',...'case 1,',...'colormap default,',...'case 2,',...'colormap spring,',...'case 3,',...'colormap summer,',...'case 4,',...'colormap autumn,',...'case 5,',...'colormap winter,',...'end']);实例39：菜单控制的使用h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例39');x=0:0.5:2*pi;y=cos(x);h=plot(x,y);grid onset(gcf,'toolbar','none')hm=uimenu('label','example');huidiao1=[...'set(hm_gridon,''checked'',''on''),',...'set(hm_gridoff,''checked'',''off''),',...'grid on'];huidiao2=[...'set(hm_gridoff,''checked'',''on''),',...'set(hm_gridon,''checked'',''off''),',...'grid off'];hm_gridon=uimenu(hm,'label','grid on',...'checked','on',...'callback',huidiao1);hm_gridoff=uimenu(hm,'label','grid off',...'checked','off',...'callback',huidiao2);实例40：UIMENU菜单的应用。

数学实验(MATLAB)课后习题答案

数学实验练习2.1画出下列常见曲线的图形。

matlab仿真实例100题

matlab仿真实例100题Matlab是一种强大的数学软件，广泛应用于科学计算、数据分析和工程仿真等领域。

在学习和使用Matlab的过程中，通过实例的方式进行仿真练习是一种非常有效的学习方法。

下面将给出100个Matlab仿真实例题目，帮助读者更好地掌握Matlab的使用。

1. 编写一个程序，计算并输出1到100之间所有奇数的和。

2. 编写一个程序，计算并输出1到100之间所有偶数的乘积。

3. 编写一个程序，计算并输出1到100之间所有素数的个数。

4. 编写一个程序，计算并输出1到100之间所有整数的平方和。

5. 编写一个程序，计算并输出1到100之间所有整数的立方和。

6. 编写一个程序，计算并输出1到100之间所有整数的阶乘和。

7. 编写一个程序，计算并输出1到100之间所有整数的倒数和。

8. 编写一个程序，计算并输出1到100之间所有整数的平均值。

9. 编写一个程序，计算并输出1到100之间所有整数的中位数。

10. 编写一个程序，计算并输出1到100之间所有整数的标准差。

11. 编写一个程序，计算并输出1到100之间所有整数的方差。

12. 编写一个程序，计算并输出1到100之间所有整数的最大值。

13. 编写一个程序，计算并输出1到100之间所有整数的最小值。

15. 编写一个程序，计算并输出1到100之间所有整数的平方根和。

16. 编写一个程序，计算并输出1到100之间所有整数的立方根和。

17. 编写一个程序，计算并输出1到100之间所有整数的对数和。

18. 编写一个程序，计算并输出1到100之间所有整数的指数和。

19. 编写一个程序，计算并输出1到100之间所有整数的正弦和。

20. 编写一个程序，计算并输出1到100之间所有整数的余弦和。

21. 编写一个程序，计算并输出1到100之间所有整数的正切和。

22. 编写一个程序，计算并输出1到100之间所有整数的双曲正弦和。

23. 编写一个程序，计算并输出1到100之间所有整数的双曲余弦和。

高数之MATLAB例题解析【全】

①打开程序编辑器，编辑函数文件 function a=lx5(a1,a2,a3) if a1>a2
a=a2 elseif a1<a2
a=a1 elseif a>a3
a=a else
a=a3 end ②在保存文件为lx5,并且命名。 ③命令窗口得到结果： >> a=lx5(1,2,3) a=
1
2021/10/10
2021/10/10
8
工作空间浏览器简介
2021/10/10
9
Command History Command History历史指令窗简介
2021/10/10
10
历史指令行的再运行
• 【例4】再运行图1.5-2所示历史指令窗中的三行指令。
2021/10/10
11
2021/10/10
12
2021/10/10
x= 13579
2021/10/10
23
一维数组的访问
格式：x（n ）功能：访问数组x的第n个元素
【例6】访问向量x=(1 3 5 7 9)的第3，5个元素。 >> x=1:2:9 x=
13579 >> x(3) ans =
5 >> x(5) ans =
9
2021/10/10
24
练习作业
1.编写一个函数文件，求任意给定的3个数的最小值。
返回2021返/10回/10 目录
5
通用操作界面 Command Window运行入门 Command Window指令窗简介
2021/10/10
6
最简单的计算器使用法
【例1】求的算术运算结果。
（1）用键盘在MATLAB指令窗中输入以下内容

数学建模：MatLab实验(解答)

MatLab 实验一、编写函数文件，给出求解席位问题的Q 值方法对应的MatLab 方法，输入的参数为总席位数及各单位的人数. （程序：qf.m ）二、编写函数文件，计算矩阵正常意义下的乘积，在矩阵阶数不匹配的时候，返回错误信息. （用循环方式）（程序：lx2.m ）三、编写脚本文件，用数据模拟方法近似计算椭圆周22123x y +=所围成的面积，要求总共模拟一千次，每次抽取50万个随机点，最后以平均值作为相应的面积近似值. （程序：lx3.m ）四、利用二重积分计算椭球面2221946x y z ++=的面积. 曲面积分的参数积分形式：若曲面能表示成：()()(),,,,,x x u v y y u v z z u v ===确定，则相应的积分为()()()(),d ,,,,,d .uvD f x y S f x u v y u v z u v u v ∑=⎡⎣⎰⎰⎰⎰ 其中222222,,.u u u v v v u v u v u v E x y x G x y x F x x y y z z =++=++=++对该问题，做变换：()()3cos sin ,2sin sin ,sqrt 6cos ,02π,0πx u v y y v z v u v ===≤≤≤≤，代入上式后得积分值79.6432. （程序：lx4.m ）五、用两种方法求解微分方程1,0x xy x y y ='=-⎧⎪⎨=⎪⎩并作出函数在区间[]0.1,3内的图形.（程序：lx5.m ）注该微分方程的解析解为：11.22y x x=-六、用两种方法求解微分方程()0cos 2,1,00x y x y y y =''=-⎧⎪⎨'==⎪⎩并作出函数在区间[]2π,2π-内的图形.注该微分方程的解析解为：41cos cos2.33x x -七、用两种方法求解微分方程02/,1x y y x y y ='=-⎧⎪⎨=⎪⎩并作出函数在区间[]0,4内的图形，并对图形作比较.八、编写函数文件，输入参数为矩阵的阶数，要求生成一个元素介于1090的随机整数矩阵，找出其中既是3又是5的元素，将其行标和列标分别写人两个向量中，并求出这些元素的和，平均值及个数，存入到变量中，最后输出.，若没有这样的元素存在，显示“no such elements founded!” （程序Lx8.m ）九、追踪问题缉私雷达发现: 距离c 处有一走私船正一匀速a 沿直线行驶, 缉私船立即以最大速度（匀速v ）追赶, 若用雷达进行跟踪, 保持船的瞬时速度方向始终指向走私船, 则缉私船的运动轨迹如何? 是否能追上走私船? 如果能追上, 需要多长时间? （取20,40,15a v c ===）（程序Chasing.m ）问题的进一步探讨若走私船与x 轴的夹角为,θ则问题将如何十、用数据模拟的方法计算两球()2222221,11x y z x y z ++≤++-≤相交的体积。

(完整word版)matlab数值分析例题

1、在MATLAB 中用Jacobi 迭代法讨论线性方程组,1231231234748212515x x x x x x x x x -+=⎧⎪-+=-⎨⎪-++=⎩（1）给出Jacobi 迭代法的迭代方程，并判定Jacobi 迭代法求解此方程组是否收敛。

（2）若收敛，编程求解该线性方程组.解（1）：A=[4 -1 1;4 —8 1;-2 1 5］ %线性方程组系数矩阵A =4 -1 1 4 -8 1 —2 1 5>> D=diag(diag(A)）D =4 0 0 0 —8 0 0 0 5〉〉 L=—tril （A,-1) ％ A 的下三角矩阵L =0 0 0 —4 0 0 2 —1 0〉〉U=-triu(A，1）% A的上三角矩阵U =0 1 —10 0 —10 0 0B=inv（D）*（L+U）% B为雅可比迭代矩阵B =0 0.2500 —0。

25000.5000 0 0.12500。

4000 —0.2000 0〉〉r=eigs(B,1）%B的谱半径r =0。

3347 〈1Jacobi迭代法收敛。

(2）在matlab上编写程序如下:A=[4 —1 1;4 -8 1;—2 1 5]；〉〉b=［7 —21 15］'；>〉x0=［0 0 0]’;〉〉［x,k］=jacobi（A,b，x0，1e—7)x =2。

00004.00003。

0000k =17附jacobi迭代法的matlab程序如下：function [x,k］=jacobi（A,b，x0，eps)% 采用Jacobi迭代法求Ax=b的解％A为系数矩阵％b为常数向量％x0为迭代初始向量％eps为解的精度控制max1= 300; %默认最多迭代300，超过300次给出警告D=diag（diag（A）)；％求A的对角矩阵L=-tril(A，—1); %求A的下三角阵U=—triu（A,1); %求A的上三角阵B=D\(L+U);f=D\b;x=B＊x0+f；k=1；%迭代次数while norm（x-x0）>=epsx0=x;x=B＊x0+f；k=k+1;if（k〉=max1)disp(’迭代超过300次，方程组可能不收敛’）；return；endend2、设有某实验数据如下：（1)在MATLAB中作图观察离散点的结构,用多项式拟合的方法拟合一个合适的多项式函数；（2）在MATLAB中作出离散点和拟合曲线图。

MATLAB数学实验100例题解

一元函数微分学实验1 一元函数的图形（基础实验）实验目的通过图形加深对函数及其性质的认识与理解, 掌握运用函数的图形来观察和分析函数的有关特性与变化趋势的方法,建立数形结合的思想; 掌握用Matlab 作平面曲线图性的方法与技巧.初等函数的图形2 作出函数x y tan =和x y cot =的图形观察其周期性和变化趋势. 解：程序代码：>> x=linspace(0,2*pi,600); t=sin(x)./(cos(x)+eps);plot(x,t);title('tan(x)');axis ([0,2*pi,-50,50]); 图象：程序代码：>> x=linspace(0,2*pi,100); ct=cos(x)./(sin(x)+eps);plot(x,ct);title('cot(x)');axis ([0,2*pi,-50,50]); 图象：4在区间]1,1[-画出函数xy 1sin =的图形.解：程序代码：>> x=linspace(-1,1,10000);y=sin(1./x); plot(x,y);axis([-1,1,-2,2]) 图象：二维参数方程作图6画出参数方程⎩⎨⎧==t t t y tt t x 3cos sin )(5cos cos )(的图形：解：程序代码：>> t=linspace(0,2*pi,100);plot(cos(t).*cos(5*t),sin(t).*cos(3*t)); 图象：极坐标方程作图8 作出极坐标方程为10/t e r =的对数螺线的图形. 解：程序代码：>> t=0:0.01:2*pi; r=exp(t/10);polar(log(t+eps),log(r+eps)); 图象：90270分段函数作图10 作出符号函数x y sgn =的图形. 解：>> x=linspace(-100,100,10000); y=sign(x); plot(x,y);axis([-100 100 -2 2]);函数性质的研究12研究函数)3(log 3)(35x e x x f x -++=在区间]2,2[-上图形的特征.解：程序代码：>> x=linspace(-2,2,10000);y=x.^5+3*exp(x)+log(3-x)/log(3); plot(x,y); 图象：实验2 极限与连续（基础实验）实验目的通过计算与作图, 从直观上揭示极限的本质,加深对极限概念的理解. 掌握用 Matlab 画散点图, 以及计算极限的方法. 深入理解函数连续的概念,熟悉几种间断点的图形特征,理解闭区间上连续函数的几个重要性质.作散点图14分别画出坐标为)10,,2,1(),4,(),,(3222 =+i i i i i i 的散点图, 并画出折线图. 解：散点图程序代码：plot(i,i.^2,'.')或：>> x=1:10;y=x.^2;for i=1:10;plot(x(i),y(i),'r')hold onend折线图程序代码：>> i=1:10;plot(i,i.^2,'-x')程序代码： >> i=1:10;plot(i.^2,4*(i.^2)+i.^3,'.')>> i=1:10;plot(i.^2,4*(i.^2)+i.^3,'-x')数列极限的概念16通过动画观察当∞→n 时数列21n a n =的变化趋势.解：程序代码： >> n=1:100; an=(n.^2); n=1:100; an=1./(n.^2); n=1:100; an=1./(n.^2); for i=1:100plot(n(1:i),an(1:i)),axis([0,100,0,1]) pause(0.1) end 图象：函数的极限18在区间]4,4[-上作出函数xx xx x f --=339)(的图形, 并研究 )(lim x f x ∞→ 和 ).(lim 1x f x →解：作出函数x x xx x f --=339)(在区间]4,4[-上的图形>> x=-4:0.01:4;y=(x.^3-9*x)./(x.^3-x+eps); plot(x,y)16从图上看，()f x 在x →1与x →∞时极限为0两个重要极限 20计算极限⎪⎭⎫⎝⎛+→x x x x x sin 11sin lim )1(0 x x e x 2lim )2(+∞→30sin tan lim )3(xx x x -→ x x x 0lim )4(+→ x xx ln cot ln lim )5(0+→ x x x ln lim )6(20+→ x x xx x x sin cos sin lim )7(20-→ 125523lim )8(323+++-∞→x x x x x xx x e e x x x sin 2lim )9(0----→ xx x x cos 110sin lim )10(-→⎪⎭⎫ ⎝⎛ 解：（1）>> limit(x*sin(1/x)+1/x*sin(x))ans =1(2) >> limit(x^2/exp(x),inf) ans = 0(3) >> limit((tan(x)-sin(8))/x^3) ans =NaN(4) >> limit(x^x,x,0,'right') ans =1(5) >> limit(log(cot(x))/log(x),x,0,'right') ans =-1(6) >> limit(x^2*log(x),x,0,'right') ans =0(7) >> limit((sin(x)-x.*cos(x))./(x.^2.*sin(x)),x,0) ans =1/3(8) >> limit((3*x.^3-2*x.^2+5)/(5*x.^3+2*+1),x,inf) ans =3/5(9) >> limit((exp(x)-exp(-x)-2*x)./(x-sin(x))) ans =2(10) >> limit((sin(x)/x).^(1/(1-cos(x)))) ans =exp(-1/3)实验3 导数（基础实验）实验目的深入理解导数与微分的概念, 导数的几何意义. 掌握用Matlab 求导数与高阶导数的方法. 深入理解和掌握求隐函数的导数, 以及求由参数方程定义的函数的导数的方法. 导数概念与导数的几何意义22作函数71232)(23+-+=x x x x f 的图形和在1-=x 处的切线. 解：作函数71232)(23+-+=x x x x f 的图形程序代码： >> syms x;>> y=2*x^3+3*x^2-12*x+7; >> diff(y) ans =6*x^2+6*x-12 >> syms x;y=2*x^3+3*x^2-12*x+7; >> f=diff(y) f =6*x^2+6*x-12 >> x=-1;f1=6*x^2+6*x-12 f1 = -12>> f2=2*x^3+3*x^2-12*x+7 f2 = 20>> x=linspace(-10,10,1000);y1=2*x.^3+3*x.^2-12*x+7; y2=-12*(x+1)+20; plot(x,y1,'r',x,y2,'g')求函数的导数与微分24求函数bx ax x f cos sin )(=的一阶导数. 并求.1⎪⎭⎫⎝⎛+'b a f解：求函数bx ax x f cos sin )(=的一阶导数程序代码： >> syms a b x y;y= sin(a*x)*cos(b*x); D1=diff(y,x,1) 答案：D1 =cos(a*x)*a*cos(b*x)-sin(a*x)*sin(b*x)*b求.1⎪⎭⎫ ⎝⎛+'b a f程序代码： >> x=1/(a+b);>> cos(a*x)*a*cos(b*x)-sin(a*x)*sin(b*x)*b答案：ans =cos(a/(a+b))*a*cos(b/(a+b))-sin(a/(a+b))*sin(b/(a+b))*b 拉格朗日中值定理26对函数),2)(1()(--=x x x x f 观察罗尔定理的几何意义. (1) 画出)(x f y =与)(x f '的图形, 并求出1x 与.2x 解：程序代码：>> syms x;f=x*(x-1)*(x-2); f1=diff(f) f1 =(x-1)*(x-2)+x*(x-2)+x*(x-1) >> solve(f1) ans =1+1/3*3^(1/2) 1-1/3*3^(1/2)>> x=linspace(-10,10,1000); y1=x.*(x-1).*(x-2);y2 =(x-1).*(x-2)+x.*(x-2)+x.*(x-1); plot(x,y1,x,y2)(2)画出)(x f y =及其在点))(,(11x f x 与))(,(22x f x 处的切线. 程序代码：>> syms x; >> f=x*(x-1)*(x-2); >> f1=diff(f) f1 =(x-1)*(x-2)+x*(x-2)+x*(x-1) >> solve(f1) ans =1+1/3*3^(1/2) 1-1/3*3^(1/2)>> x=linspace(-3,3,1000); >> y1=x.*(x-1).*(x-2);>> y2 =(x-1).*(x-2)+x.*(x-2)+x.*(x-1); >> plot(x,y1,x,y2) >> hold on>> x=1+1/3*3^(1/2); >> yx1=x*(x-1)*(x-2) yx1 =-0.3849>> x=1-1/3*3^(1/2); >> yx2=x*(x-1)*(x-2) yx2 =0.3849x=linspace(-3,3,1000); yx1 =-0.3849*x.^0; yx2 =0.3849*x.^0; plot(x,yx1,x,yx2)28求下列函数的导数:(1) 31+=x e y ; 解：程序代码：>> syms x y; y=exp((x+1)^3); D1=diff(y,1) 答案：D1 =3*(x+1)^2*exp((x+1)^3)(2) )]42ln[tan(π+=x y ;解：程序代码：>> syms x;y=log(tan(x/2+pi/4)); D1=diff(y,1) 答案：D1 =(1/2+1/2*tan(1/2*x+1/4*pi)^2)/tan(1/2*x+1/4*pi)(3) x x y sin ln cot 212+=;解：程序代码：>> syms x;y=1/2*(cot(x))^2+log(sin(x)); D1=diff(y,1) 答案：D1 =cot(x)*(-1-cot(x)^2)+cos(x)/sin(x) (4) xy 2arctan21=. 解：程序代码：>> syms x;>> y=sqrt(2)*atan(sqrt(2)/x); >> D1=diff(y,1) 答案：D1 =-2/x^2/(1+2/x^2)一元函数积分学与空间图形的画法实验4 一元函数积分学(基础实验)实验目的掌握用Matlab 计算不定积分与定积分的方法. 通过作图和观察, 深入理解定积分的概念和思想方法. 初步了解定积分的近似计算方法. 理解变上限积分的概念. 提高应用定积分解决各种问题的能力.不定积分计算30求.)1(532⎰-dx x x解：程序代码：>> syms x y;>> y=x^2*(1-x^3)^5; >> R=int(y,x) 答案：R =-1/18*x^18+1/3*x^15-5/6*x^12+10/9*x^9-5/6*x^6+1/3*x^332求.arctan 2⎰xdx x解：程序代码：>> syms x y;>> y=x^2*atan(x); >> R=int(y,x) 答案：R =1/3*x^3*atan(x)-1/6*x^2+1/6*log(x^2+1)定积分计算34 求.)(102⎰-dx x x解：程序代码：>> syms x y; >> y=x-x^2;>> R=int(y,x,0,1) 答案： R =1/6变上限积分36 画出变上限函数⎰x dt t t 02sin 及其导函数的图形.解：程序代码：>> syms x y t; >> y=t*sin(t^2); >> R=int(y,x,0,x) 答案：R =t*sin(t^2)*x 再求导函数程序代码：>> DR=diff(R,x,1) 答案：DR =t*sin(t^2)实验5 空间图形的画法(基础实验)实验目的掌握用Matlab 绘制空间曲面和曲线的方法. 熟悉常用空间曲线和空间曲面的图形特征,通过作图和观察, 提高空间想像能力. 深入理解二次曲面方程及其图形.一般二元函数作图38作出函数2214y x z ++=的图形.解：程序代码：>> x=linspace(-5,5,500); [x,y]=meshgrid(x); z=4./(1+x.^2+y.^2); mesh(x,y,z);xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');title('function')40作出函数)94cos(22y x z +=的图形. 解：程序代码：>> x=-10:0.1:10;[x,y]=meshgrid(x);z=cos(4*x.^2+9*y.^2); mesh(x,y,z);xlabel('x-axis'),ylabel('y-axis'),zlabel('z-axis');title('function')讨论：坐标轴选取范围不同时，图形差异很大，对本题尤为明显，如右图为坐标轴[-1，1]二次曲面42作出单叶双曲面1941222=-+z y x 的图形.(曲面的参数方程为 ,tan 3,cos sec 2,sin sec u z v u y v u x === (.20,2/2/πππ≤≤<<-v u ))解：程序代码：>> v=0:pi/100:2*pi; >> u=-pi/2:pi/100:pi/2; >> [U,V]=meshgrid(u,v); >> x=sec(U).*sin(V); >> y=2*sec(U).*cos(V); >> z=3*tan(U); >> surf(x,y,z)44 可以证明: 函数xy z =的图形是双曲抛物面. 在区域22,22≤≤-≤≤-y x 上作出它的图形.解：程序代码：>> x=-2:0.01:2;[x,y]=meshgrid(x); >> z=x.*y;>> mesh(x,y,z);46 画出参数曲面]2,001.0[],4,0[)5/2/ln(tan cos sin sin sin cos ∈∈⎪⎩⎪⎨⎧++===v u u v v z vu y v u x π 的图形.解：程序代码：>> v=0.001:0.001:2; >> u=0:pi/100:4*pi;>> [U,V]=meshgrid(u,v); >> x=cos(U).*sin(V); >> y=sin(U).*sin(V);>> z=cos(V)+log(tan(V/2)+U/5); >> mesh(x,y,z);空间曲线48 作出空间曲线)60(2,sin ,cos π≤≤===t t z t t y t t x 的图形. 解：程序代码：>> syms t;ezplot3(t*cos(t),t*sin(t),2*t,[0,6*pi])xx = t cos(t), y = t sin(t), z = 2 tz50绘制参数曲线 ⎪⎪⎩⎪⎪⎨⎧=+==t z t y t x arctan 211cos 2的图形.解：程序代码：>> t=-2*pi:pi/100:2*pi;x=cos(t).*cos(t);y=1./(1+2*t);z=atan(t); plot3(x,y,z);grid;xlabel('x'),ylabel('y'),zlabel('z')xyz多元函数微积分实验6 多元函数微分学（基础实验）实验目的掌握利用Matlab 计算多元函数偏导数和全微分的方法, 掌握计算二元函数极值和条件极值的方法. 理解和掌握曲面的切平面的作法. 通过作图和观察, 理解二元函数的性质、方向导数、梯度和等高线的概念.求多元函数的偏导数与全微分 52设),(cos )sin(2xy xy z +=求.,,,222yx z x z y z x z ∂∂∂∂∂∂∂∂∂ 解：程序代码：>> syms x y;S=sin(x*y)+(cos(x*y))^2; D1=diff(S,'x',1); D2=diff(S,'y',1); D3=diff(S,'x',2); D4=diff(S,'y',2); D1,D2,D3,D4答案： D1 = cos(x*y)*y-2*cos(x*y)*sin(x*y)*yD2 = cos(x*y)*x-2*cos(x*y)*sin(x*y)*xD3 =-sin(x*y)*y^2+2*sin(x*y)^2*y^2-2*cos(x*y)^2*y^2 D4 = -sin(x*y)*x^2+2*sin(x*y)^2*x^2-2*cos(x*y)^2*x^2实验7 多元函数积分学（基础实验）实验目的掌握用Matlab 计算二重积分与三重积分的方法; 深入理解曲线积分、曲面积分的概念和计算方法. 提高应用重积分和曲线、曲面积分解决各种问题的能力.计算重积分54计算,2dxdy xy D⎰⎰其中D 为由,,2y x y x ==+ 2=y 所围成的有界区域.解：程序代码：>> syms x y;int(int(x*y^2,x,2-y,sqrt(y)),y,1,2) 答案：ans =193/120 重积分的应用56求旋转抛物面224y x z --=在Oxy 平面上部的面积.S 解：程序代码：>> int(2*pi*r,r,0,2) 答案： ans =4*pi无穷级数与微分方程实验8 无穷级数（基础实验）实验目的观察无穷级数部分和的变化趋势,进一步理解级数的审敛法以及幂级数部分和对函数的逼近. 掌握用Matlab 求无穷级数的和, 求幂级数的收敛域, 展开函数为幂级数以及展开周期函数为傅里叶级数的方法.数项级数58(1)观察级数∑∞=12 1n n的部分和序列的变化趋势.解：程序代码：for i=1:100 s=0;for n=1:i s=s+1/n^2;endplot(i,s,'.');hold on;end(2) 观察级数∑∞=11n n的部分和序列的变化趋势.>> for i=1:100 s=0; for n=1:i s=s+1/n; endplot(i,s,'.'); hold on; end60 求∑∞=++123841n n n 的值. 解：程序代码：>> syms n;score=symsum(1/(4*n^2+8*n+3),1,inf) 答案： score =1/6函数的幂级数展开62求x arctan 的5阶泰勒展开式. >> syms x;>> T5=taylor(atan(x),6) 答案：T5 =x-1/3*x^3+1/5*x^5实验9 微分方程（基础实验）实验目的理解常微分方程解的概念以及积分曲线和方向场的概念,掌握利用 Matlab 求微分方程及方程组解的常用命令和方法.求解微分方程64求微分方程 22x xe xy y -=+'的通解. 解：程序代码：>> y=dsolve('Dy+2*x*y=x*exp(-x^2)','x') 答案：y =(1/2*x^2+C1)*exp(-x^2)66求微分方程x e y y y x 2cos 52=+'-''的通解. 解：程序代码：>> y=dsolve('D2y-2*Dy+5*y=exp(x)*cos(2*x)','x') 答案： y =exp(x)*sin(2*x)*C2+exp(x)*cos(2*x)*C1+1/4*exp(x)*sin(2*x)*x68求微分方程组⎪⎪⎩⎪⎪⎨⎧=--=++02y x dtdy e y x dt dx t 在初始条件0,100====t t y x 下的特解.解：程序代码：>> [x,y]=dsolve('Dx+x+2*y-exp(t)','Dy-x-y','x(0)=1','y(0)=0','t') 答案： x = cos(t)y = 1/2*sin(t)-1/2*cos(t)+1/2*exp(t)70求解微分方程,)1(122/5+=+-x x y dx dy 并作出积分曲线. 解：程序代码：>> syms x yy=dsolve('Dy-2*y/(x+1)-(x+1)^(5/2)','x') 答案：y =(2/3*(x+1)^(3/2)+C1)*(x+1)^2 做积分曲线由>> syms x yx=linspace(-5,5,100); C=input('请输入C 的值:'); y=(2/3*(x+1).^(3/2)+C).*(x+1).^2; plot(x,y)例如对应有：请输入C 的值:2 请输入C 的值:20矩阵运算与方程组求解实验10 行列式与矩阵实验目的掌握矩阵的输入方法. 掌握利用Matlab 对矩阵进行转置、加、减、数乘、相乘、乘方等运算, 并能求矩阵的逆矩阵和计算方阵的行列式.矩阵A 的转置函数Transpose[A]72 求矩阵⎪⎪⎪⎪⎪⎭⎫⎝⎛411365243271的转置. 解：程序代码：>> A=[1,7,2;3,4,2;5,6,3;1,1,4]; >> Sove=A' 答案：Sove =1 3 5 1 7 4 6 12 234 矩阵线性运算 73设,291724,624543⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫⎝⎛=B A 求.24,A B B A -+ 解：程序代码：>> A=[3,4,5;4,2,6]; B=[4,2,7;1,9,2]; S1=A+B S2=4*B-2*A 答案：S1 =7 6 12 5 11 8 S2 =10 0 18 -4 32 -474设,148530291724,36242543⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛=mb ma 求矩阵ma 与mb 的乘积. 解：程序代码：>> ma=[3,4,5,2;4,2,6,3];>> mb=[4,2,7;1,9,2;0,3,5;8,4,1]; >> Sove=ma*mb 答案：Sove =32 65 56 42 56 65 矩阵的乘法运算75设,101,530291724⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛=B A 求AB 与,A B T 并求.3A解：程序代码：>> A=[4 2 7;1 9 2;0 3 5]; B=[1;0;1]; >> AB=A*B AB = 11 3 5 >> BTA=B'*A BTA =4 5 12 >> A3=A^3 A3 =119 660 555 141 932 444 54 477 260 求方阵的逆 76 设,5123641033252312⎪⎪⎪⎪⎪⎭⎫⎝⎛=A 求.1-A 解：程序代码：>> A=[2,1,3,2;5,2,3,3;0,1,4,6;3,2,1,5];Y=inv(A)答案：Y =-1.7500 1.3125 0.5000 -0.6875 5.5000 -3.6250 -2.0000 2.3750 0.5000 -0.1250 0.0000 -0.1250 -1.2500 0.6875 0.5000 -0.3125 77 设,221331317230,5121435133124403⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫⎝⎛=B A 求.1B A - 解：程序代码：>> A=[3 0 4 4 ;2 1 3 3 ;1 5 3 4;1 2 1 5]; B=[0 3 2 ;7 1 3;1 3 3 ;1 2 2]; Solve=A'*B 答案：Solve =16 16 17 14 20 22 25 26 28 30 37 3978 解方程组⎪⎩⎪⎨⎧-=-+=+-=++.2442,63,723z y x z y x z y x解：程序代码：>> A=[3 2 1;1 -1 3;2 4 -4]; b=[7 6 -2]; >> A\b' 答案：ans =1.0000 1.00002.0000 求方阵的行列式79 求行列式 .3351110243152113------=D解：程序代码：>> A=[3,1,-1,2;-5,1,3,-4;2,0,1,-1;1,-5,3,-3]; D=det(A) 答案：D =4080求.11111111111122222222ddd d c c c c b b b b a a a a D ++++=解：程序代码：>> syms a b c d;D=[a^2+1/a^2 a 1/a 1;b^2+1/b^2 b 1/b 1;c^2+1/c^2 c 1/c 1;d^2+1/d^2 d 1/d 1]; det(D) 答案：ans =-(-c*d^2*b^3+c^2*d*b^3-c^3*d^2*a+c^3*d*a^2*b^4+c*d^2*a^3-c^3*d^2*a*b^4-c^2*d*a^3-c*d^2*b^3*a^4+c^2*d*b^3*a^4+c^3*d^2*b*a^4-c^3*d*b^2*a^4-c^2*d^3*b*a^4+c*d^3*b^2*a^4+c*d ^2*a^3*b^4-c^2*d*a^3*b^4+c^3*d^2*b-c^3*d*b^2-c^2*d^3*b+c*d^3*b^2+c^3*d*a^2+c^2*d^3*a-c *d^3*a^2-b*d^2*a^3+b^2*d*a^3+b^3*d^2*a-b^3*d*a^2-b^2*d^3*a+b*d^3*a^2+b*c^2*a^3-b^2*c*a ^3-b^3*c^2*a+b^3*c*a^2+b^2*c^3*a-b*c^3*a^2+c^2*d^3*a*b^4-c*d^3*a^2*b^4-b*d^2*a^3*c^4+b ^2*d*a^3*c^4+b^3*d^2*a*c^4-b^3*d*a^2*c^4-b^2*d^3*a*c^4+b*d^3*a^2*c^4+b*c^2*a^3*d^4-b^2*c*a^3*d^4-b^3*c^2*a*d^4+b^3*c*a^2*d^4+b^2*c^3*a*d^4-b*c^3*a^2*d^4)/a^2/c^2/d^2/b^281 计算范德蒙行列式.1111145444342413534333231252423222154321x x x x x x x x x x x x x x x x x x x x 解：程序代码：>> syms x1 x2 x3 x4 x5;>> A=[1,1,1,1,1;x1,x2,x3,x4,x5;x1^2,x2^2,x3^2,x4^2,x5^2; x1^3,x2^3,x3^3,x4^3,x5^3;x1^4,x2^4,x3^4,x4^4,x5^4];>> DC=det(A);>> DS=simple(DC) 答案：DS =(-x5+x4)*(x3-x5)*(x3-x4)*(-x5+x2)*(x2-x4)*(x2-x3)*(-x5+x1)*(x1-x4)*(x1-x3)*(x1-x2) 82 设矩阵 ,60975738723965110249746273⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----=A 求.),(|,|3A A tr A 解：程序代码：>> A=[3,7,2,6,-4;7,9,4,2,0;11,5,-6,9,3;2,7,-8,3,7;5,7,9,0,-6]; >> D=det(A),T=trace(A),A3=A^3 答案：D =11592 T = 3 A3=726 2062 944 294 -358 1848 3150 26 1516 228 1713 2218 31 1006 404 1743 984 -451 1222 384 801 2666 477 745 -125 向量的内积83 求向量}3,2,1{=u 与}0,1,1{-=v 的内积. 解：程序代码：>> u=[1 2 3]; v=[1 -1 0]; solve=dot(u,v) 答案：solve =-184设,001001⎪⎪⎪⎭⎫ ⎝⎛=λλλA 求.10A 一般地?=k A (k 是正整数).解：程序代码：>> syms r;>> A=[r,1,0;0,r,1;0,0,r]; >> A^10 答案：ans =[ r^10, 10*r^9, 45*r^8] [ 0, r^10, 10*r^9] [ 0, 0, r^10]85.求⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+++++a a a aa1111111111111111111111111的逆.解：程序代码：>> syms aA=[1+a,1,1,1,1;1,1+a,1,1,1;1,1,1+a,1,1;1,1,1,1+a,1;1,1,1,1,1+a]; solve=inv(A) 答案：solve =[ 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), -1/a/(a+5)] [ -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5), -1/a/(a+5)] [ -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5), -1/a/(a+5)] [ -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5), -1/a/(a+5)] [ -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), -1/a/(a+5), 1/a*(a+4)/(a+5)]实验11 矩阵的秩与向量组的极大无关组实验目的学习利用Matlab 求矩阵的秩,作矩阵的初等行变换; 求向量组的秩与极大无关组. 求矩阵的秩86 设,815073*********⎪⎪⎪⎭⎫ ⎝⎛-------=M 求矩阵M 的秩.解：程序代码：>> M=[3,2,-1,-3,-2;2,-1,3,1,-3;7,0,5,-1,-8]; R=rank(M) 答案：R=2 向量组的秩87求向量组)0,3,0,2(),2,5,4,0(),1,1,2,1(231=--=-=ααα的秩. 解：程序代码：>> A=[1,2,-1,1;0,-4,5,-2;2,0,3,0]; R=rank(A) 答案：R =288向量组)7,5,1,3(),5,4,3,1(),1,1,1,1(),3,2,1,1(4321==-==αααα是否线性相关? 解：由>> A=[1 1 2 3;1 -1 1 1;1 3 4 5;3 1 5 7];rank(A) ans = 3即rank(A)=3 小于阶数489向量组)3,1,1(),2,1,3(),7,2,2(321=-==ααα是否线性相关? 解：由>> A3=[2,2,7;3,-1,2;1,1,3];R=rank(A3) 得 R = 3即rank(A3)=3 等于阶数3 故向量组线性无关。

南邮MATLAB数学实验精选

注意:在下面的题目中m 为你的学号的后4位第一次练习题1．求032=-x e x 的所有根。

（先画图后求解）2．求下列方程的根。

1)0155=++x x 2）至少三个根）(021sin =-x x3）所有根0cos sin 2=-x x x3．求解下列各题： 1）3sin lim x mx mx x->- 2） )10(,cos y x e y x求=3）21/20(17mxe dx⎰精确到位有效数字） 4）424x dx m x+⎰ 5） 081000mx x +=将在展开（最高次幂为）6） 1sin (3)()xy e y m =求( 精确到17位有效数字)4． 1)求矩阵21102041100A m ⎛⎫ ⎪- ⎪= ⎪ ⎪ ⎪-⎝⎭ 的逆矩阵1-A 及特征值和特征向量。

2)求点(1,1,4)到直线l: (x-3)/-1 =y/0=(z+1)/2的距离。

5．已知,21)(222)(σμσπ--=x ex f 分别在下列条件下画出)(x f 的图形：）；（在同一坐标系上作图，，＝时＝、）；（在同一坐标系上作图，－，＝时、421,0)2(110,1)1(σμμσ=、6．画下列函数的图形：（1）202004cos sin ≤≤≤≤⎪⎪⎩⎪⎪⎨⎧===u t t z tu y t u x(2) 30,30)sin(≤≤≤≤=y x xy z（3）sin (3cos )02cos (3cos )02sin x t u t y t u u z u ππ=+⎧≤≤⎪=+⎨≤≤⎪=⎩（第6题只要写出程序）. 第二次练习题1、设11()/23n nnm x x x x +⎧=+⎪⎨⎪=⎩，数列}{n x 是否收敛？若收敛，其值为多少？精确到6位有效数字。

2、设 ,131211p p p n nx ++++=Λ }{n x 是否收敛？若收敛，其值为多少？精确到17位有效数字（提示：当n x 与1n x +的前17位有效数字一致时终止计算）注：学号为单号的取7=p ，学号为双号的取.8=p 书上习题：(实验四)1，2，4，7（1），8，12（改为：对例2，取 120,55,25,5.4=a 观察图形有什么变化．），13，14 。