应用FFT实现信号频谱分析
实验二用FFT对信号进行频谱分析

实验二用FFT对信号进行频谱分析简介:频谱分析是信号处理中常用的一种方法,通过将信号变换到频域,可以得到信号的频谱特征。
其中,快速傅里叶变换(FFT)是一种高效的计算频域的方法。
在这个实验中,我们将学习如何使用FFT对信号进行频谱分析。
实验步骤:1.准备工作:a. 安装MATLAB或者Octave等软件,并了解如何运行这些软件。
2.载入信号:a. 在MATLAB或Octave中,使用内置函数加载信号文件,将信号读入到内存中。
b.查看信号的基本信息,例如采样频率、时长等。
3.FFT变换:a. 使用MATLAB或Octave的fft函数将信号由时域变换到频域。
b.设置合适的参数,例如变换的点数、窗口函数等。
可以尝试不同的参数,观察其对结果的影响。
4.频谱绘制:a. 使用MATLAB或Octave的plot函数将变换后的频率数据进行绘制。
b.可以绘制幅度谱(频率的能量分布)或相位谱(频率的相位分布),也可以同时绘制两个谱。
5.频谱分析:a.根据绘制出的频谱,可以观察信号的频率特征。
例如,可以识别出信号中的主要频率分量。
b.可以进一步计算信号的能量、均值、方差等统计量,了解信号的功率特征。
c.可以对不同的信号进行对比分析,了解它们在频域上的差异。
实验结果和讨论:1.绘制出的频谱图可以清晰地显示信号的频率分量,可以识别出信号中的主要频率。
2.通过对不同信号的对比分析,可以发现它们在频域上的差异,例如不同乐器的音调特征。
3.可以进一步分析频谱的统计特征,例如信号的能量、平均幅度、峰值频率等。
4.在进行FFT变换时,参数的选择对结果有一定的影响,可以进行参数的调优,获得更准确的频谱分析结果。
结论:本实验通过使用FFT对信号进行频谱分析,可以获得信号在频域上的特征。
通过观察频谱图和统计特征,可以进一步了解信号的频率分布、能量特征等信息。
这对信号处理、音频分析等领域具有很大的应用价值。
在实际应用中,可以根据不同的需求,选择合适的参数和方法,对不同的信号进行频谱分析。
用FFT对信号做频谱分析

用FFT对信号做频谱分析傅里叶变换(Fourier Transform)是一种将信号从时域转换到频域的数学方法,可用于信号的频谱分析。
通过傅里叶变换,我们可以将时域上的信号转换为频域上的频谱,帮助我们理解信号的频率组成以及各个频率分量的强弱。
频谱分析是对信号进行频率分析的过程,是了解信号在频域上的特性和频率成分的一种方法。
通过频谱分析,我们可以获得信号的频率分布情况,帮助我们了解信号的频率成分、频率峰值等信息。
在进行频谱分析时,常用的方法之一是采用快速傅里叶变换(FFT)。
FFT是一种高效的算法,能够快速计算离散傅里叶变换(DiscreteFourier Transform)。
下面将详细介绍FFT在频谱分析中的应用。
首先,我们需要将待分析的信号转换为数字信号,并对其进行采样,得到一个离散的信号序列。
然后,使用FFT算法对这个离散信号序列进行傅里叶变换,得到信号的频谱。
在进行FFT之前,需要进行一些预处理工作。
首先,需要将信号进行加窗处理,以减少泄露效应。
加窗可以选择矩形窗、汉宁窗、汉明窗等,不同的窗函数对应不同的性能和应用场景。
其次,需要对信号进行零填充,即在信号序列末尾添加零值,以增加频谱的分辨率。
零填充可以提高频谱的平滑度,使得频域上的分辨率更高。
接下来,我们使用FFT算法对经过加窗和零填充的信号序列进行傅里叶变换。
FFT算法将离散信号变换为离散频谱,得到信号的频率成分和强度。
FFT结果通常呈现为频率和振幅的二维图像,横轴表示频率,纵轴表示振幅。
通过观察频谱图像,我们可以得到一些关于信号的重要信息。
首先,我们可以观察到信号的频率成分,即信号在不同频率上的分布情况。
在频谱图像中,高峰表示信号在该频率上强度较高,低峰表示信号在该频率上强度较低。
其次,我们可以通过峰值的位置和强度来分析信号的主要频率和频率成分。
频谱图像上的峰值位置对应着信号的主要频率,峰值的高度对应着信号在该频率上的强度。
最后,我们还可以通过观察频谱图像的整体分布情况,来获取信号的频率范围和频率分布的特点。
实验二FFT实现信号频谱分析

0
2
4
6
4
2
0
-2
-4
-6
-4
-20246四、试验环节
4. 试验内容2旳程序运营成果如下图所示:
60
30
40
20
20
10
0
0
-10 -5
0
5
10
-40 -20
0
20 40
30
80
60 20
40 10
20
0
-40 -20
0
20 40
0
-40 -20
0
20 40
四、试验环节
|X(k)| x(n)
5. 试验内容 3旳程序运营成果如下图所示:
fft 计算迅速离散傅立叶变换
fftshift
ifft
调整fft函数旳输出顺序,将零频 位置移到频谱旳中心
计算离散傅立叶反变换
fft函数:调用方式如下
y=fft(x):计算信号x旳迅速傅立叶变换y。当x旳长度为 2旳幂时,用基2算法,不然采用较慢旳分裂基算法。
y=fft(x,n):计算n点FFT。当length(x)>n时,截断x,不 然补零。
【例2-11】产生一种正弦信号频率为60Hz,并用fft函数 计算并绘出其幅度谱。
fftshift函数:调用方式如下 y=fftshift(x):假如x为向量,fftshift(x)直接将x旳左右两 部分互换;假如x为矩阵(多通道信号),将x旳左上、右 下和右上、左下四个部分两两互换。 【例2-12】产生一种正弦信号频率为60Hz,采样率为1000Hz, 用fftshift将其零频位置搬到频谱中心。
以上就是按时间抽取旳迅速傅立叶变换
实验二的应用FFT对信号进行频谱分析

实验二的应用FFT对信号进行频谱分析引言:频谱分析是通过将连续信号转换为离散信号,根据信号在频域上的强度分布来分析信号的频谱特性。
其中,FFT(Fast Fourier Transform,快速傅里叶变换)是一种常见的频谱分析算法,可以高效地计算离散信号的傅里叶变换。
实验目的:本实验旨在使用FFT算法来对一个信号进行频谱分析,从而了解FFT 的原理和应用。
实验器材:-计算机-MATLAB软件实验步骤:1.准备信号数据:首先,需要准备一个信号数据用于进行频谱分析。
可以通过MATLAB 自带的函数生成一个简单的信号数据,例如生成一个正弦信号:```Fs=1000;%采样频率T=1/Fs;%采样时间间隔L=1000;%信号长度t=(0:L-1)*T;%时间向量S = 0.7*sin(2*pi*50*t) + sin(2*pi*120*t); % 生成信号,包含50Hz和120Hz的正弦波成分```其中,Fs为采样频率,T为采样时间间隔,L为信号长度,t为时间向量,S为生成的信号数据。
2.进行FFT计算:利用MATLAB提供的fft函数,对准备好的信号数据进行FFT计算,得到信号的频谱:```Y = fft(S); % 对信号数据进行FFT计算P2 = abs(Y/L); % 取FFT结果的模值,并归一化P1=P2(1:L/2+1);%取模值前一半P1(2:end-1) = 2*P1(2:end-1); % 对非直流分量进行倍频处理f=Fs*(0:(L/2))/L;%计算对应的频率```其中,Y为FFT计算的结果,P2为对应结果的模值,并进行归一化处理,P1为P2的前一半,f为对应的频率。
3.绘制频谱图:使用MATLAB的plot函数,将频率和对应的功率谱绘制成频谱图:```plot(f,P1)title('Single-Sided Amplitude Spectrum of S(t)')xlabel('f (Hz)')ylabel(',P1(f),')```实验结果与分析:上述实验步骤通过MATLAB实现了对一个信号的频谱分析并绘制成频谱图。
实验四应用快速傅里叶变换对信号进行频谱分析

实验四应用快速傅里叶变换对信号进行频谱分析引言:频谱分析是信号处理领域中的重要技术之一,可以用于研究信号的频率特性和频域内的信号成分。
傅里叶变换是一种能将时域信号转换为频域信号的数学工具,通过将信号分解成一系列频率分量来分析信号。
快速傅里叶变换(FFT)是一种高效的计算傅里叶变换的方法,尤其适合实时信号处理。
实验目的:1.理解傅里叶变换在频谱分析中的应用;2.掌握使用FFT对信号进行频谱分析的方法;3.实现频谱分析并得出相应的频谱图。
实验器材和材料:1.信号源(例如信号发生器);2.电脑或数字信号处理器(DSP);3.音频线或数据线连接信号源和电脑或DSP。
实验步骤:1.确定实验所需信号源的类型和参数,例如正弦信号、方波信号或任意信号;2.连接信号源和电脑或DSP,确保信号源输出的信号能够被电脑或DSP接收;3. 在电脑或DSP上选择合适的软件或编程语言环境,例如MATLAB、Python或C;4.编写程序或命令以控制信号源产生相应的信号,并将信号输入到电脑或DSP中;5.读取信号,并使用FFT对信号进行傅里叶变换;6.分析得到的频谱数据,绘制频谱图;7.对得到的频谱图进行解读和分析。
实验注意事项:1.在选择信号源和连接电脑或DSP时,注意信号源的输出范围和电脑或DSP的输入范围,避免信号超出范围导致损坏设备;2.根据实际需要选择合适的采样率和采样点数,以保证能够对信号进行充分的频谱分析;3.在进行FFT计算时,注意选择适当的窗函数和重叠率,以克服频谱分析中的泄漏效应。
实验结果与讨论:通过对信号进行频谱分析,我们可以得到信号的频率特性和频域内的成分信息。
根据得到的频谱图,我们可以分析信号的主要频率分量、功率谱密度以及可能存在的干扰或噪声。
通过对频谱图的解读和分析,可以帮助我们理解信号的特征和变化规律,为后续的信号处理和应用提供有价值的信息。
结论:本实验通过应用快速傅里叶变换对信号进行频谱分析,从而得到信号在频域内的成分信息并绘制出频谱图。
用FFT对信号作频谱分析

用FFT对信号作频谱分析快速傅立叶变换(FFT)是一种在信号处理中常用于频谱分析的方法。
它是傅立叶变换的一种快速算法,通过将信号从时间域转换到频域,可以提取信号的频率信息。
FFT算法的原理是将信号分解为不同频率的正弦波成分,并计算每个频率成分的幅度和相位。
具体而言,FFT将信号划分为一系列时间窗口,每个窗口内的信号被认为是一个周期性信号,然后对每个窗口内的信号进行傅立叶变换。
使用FFT进行频谱分析可以得到信号的频率分布情况。
频谱可以显示信号中各个频率成分的强度。
通过分析频谱可以识别信号中的主要频率成分,判断信号中是否存在特定频率的干扰或噪声。
常见的应用包括音频信号处理、图像处理、通信系统中的滤波和解调等。
使用FFT进行频谱分析的步骤如下:1.首先,获取待分析的信号,并确保信号是离散的,即采样频率与信号中的最高频率成分满足奈奎斯特采样定理。
2.对信号进行预处理,包括去除直流分量和任何不需要的干扰信号。
3.对信号进行分段,分段后的每个窗口长度在FFT算法中通常为2的幂次方。
常见的窗口函数包括矩形窗、汉明窗等。
4.对每个窗口内的信号应用FFT算法,将信号从时间域转换到频域,并计算每个频率成分的幅度和相位。
5.对所有窗口得到的频谱进行平均处理,以得到最终的频谱分布。
在使用FFT进行频谱分析时需要注意的问题有:1.噪声的影响:FFT对噪声敏感,噪声会引入幅度偏差和频率漂移。
可以通过加窗等方法来减小噪声的影响。
2.分辨率的选择:分辨率是指在频谱中能够分辨的最小频率间隔。
分辨率与信号长度和采样频率有关,需要根据需求进行选择。
3.漏泄效应:当信号中的频率不是FFT长度的整数倍时,会出现漏泄效应。
可以通过零填充等方法来减小漏泄效应。
4.能量泄露:FFT将信号限定在一个周期内进行计算,如果信号过长,则可能导致部分频率成分的能量泄露到其他频率上。
总之,FFT作为信号处理中常用的频谱分析方法,能够提取信号中的频率信息,广泛应用于多个领域。
实验三用FFT对信号进行频谱分析和MATLAB程序

实验三用FFT对信号进行频谱分析和MATLAB程序实验三中使用FFT对信号进行频谱分析的目的是通过将时域信号转换为频域信号,来获取信号的频谱信息。
MATLAB提供了方便易用的函数来实现FFT。
首先,我们需要了解FFT的原理。
FFT(快速傅里叶变换)是一种快速计算离散傅里叶变换(DFT)的算法,用于将离散的时间域信号转换为连续的频域信号。
FFT算法的主要思想是将问题划分为多个规模较小的子问题,并利用DFT的对称性质进行递归计算。
FFT算法能够帮助我们高效地进行频谱分析。
下面是一个使用MATLAB进行频谱分析的示例程序:```matlab%生成一个10秒钟的正弦波信号,频率为1Hz,采样率为100Hzfs = 100; % 采样率t = 0:1/fs:10-1/fs; % 时间范围f=1;%正弦波频率x = sin(2*pi*f*t);%进行FFT计算N = length(x); % 信号长度X = fft(x); % FFT计算magX = abs(X)/N; % 幅值谱frequencies = (0:N-1)*(fs/N); % 频率范围%绘制频谱图figure;plot(frequencies, magX);xlabel('频率(Hz)');ylabel('振幅');title('信号频谱');```上述代码生成了一个10秒钟的正弦波信号,频率为1 Hz,采样率为100 Hz。
通过调用MATLAB的fft函数计算信号的FFT,然后计算每个频率分量的幅值谱,并绘制出信号频谱图。
在频谱图中,横轴表示频率,纵轴表示振幅。
该实验需要注意以下几点:1.信号的采样率要与信号中最高频率成一定比例,以避免采样率不足导致的伪频谱。
2.FFT计算结果是一个复数数组,我们一般只关注其幅值谱。
3.频率范围是0到采样率之间的频率。
实验三的报告可以包含以下内容:1.实验目的和背景介绍。
应用FFT实现信号频谱分析

应用FFT实现信号频谱分析一、快速傅里叶变换(FFT)原理快速傅里叶变换是一种将时域信号转换为频域信号的算法,它通过将信号分解为不同频率的正弦波的和,来实现频谱分析。
FFT算法是一种高效的计算DFT(离散傅里叶变换)的方法,它的时间复杂度为O(nlogn),在实际应用中得到广泛使用。
二、FFT算法FFT算法中最基本的思想是将DFT进行分解,将一个长度为N的信号分解成长度为N/2的两个互为逆序的子信号,然后对这两个子信号再进行类似的分解,直到分解成长度为1的信号。
在这一过程中,可以通过频谱折叠的性质,减少计算的复杂度,从而提高计算效率。
三、FFT实现在实际应用中,可以使用Matlab等软件来实现FFT算法。
以Matlab 为例,实现FFT可以分为以下几个步骤:1.读取信号并进行预处理,如去除直流分量、归一化等。
2. 对信号进行FFT变换,可以调用Matlab中的fft函数,得到频域信号。
3.计算频谱,可以通过对频域信号进行幅度谱计算,即取频域信号的模值。
4.可选地,可以对频谱进行平滑处理,以降低噪音干扰。
5.可选地,可以对频谱进行归一化处理,以便于分析和比较不同信号的频谱特性。
四、应用1.音频处理:通过分析音频信号的频谱,可以实现音频特性的提取,如频率、振幅、共振等。
2.图像处理:通过分析图像信号的频谱,可以实现图像特征的提取,如纹理、边缘等。
3.通信系统:通过分析信号的频谱,可以实现信号的调制解调、频谱分配等功能。
4.电力系统:通过分析电力信号的频谱,可以实现电力质量分析、故障检测等。
总结:应用FFT实现信号频谱分析是一种高效的信号处理方法,通过将时域信号转换为频域信号,可以实现对信号频谱特性的提取和分析。
在实际应用中,我们可以利用FFT算法和相应的软件工具,对信号进行频谱分析,以便于进一步的研究和应用。
实验二 应用 FFT 对信号进行频谱分析

三、实验内容及步骤
(一)编制实验用主程序及相应子程序
1、在实验之前,认真复习 DFT 和 FFT 有关的知识,阅读本实验原 理与方法和实验附录部分中和本实验有关的子程序,掌握子程序的原理 并学习调用方法。 2、编制信号产生子程序及本实验的频掊分析主程序。实验中需要用 到的基本信号包括: (1)高斯序列: (2)衰减正弦序列: (3)三角波序列: (4)反三角序列:
四、思考题
能说出哪一个低频分量更多一些吗?为什么? 2、 对一个有限长序列进行离散傅里叶变换(DFT),等价于将该序 列周期延拓后进行傅里叶级数(DFS)展开。因为 DFS 也只是取其中一 个周期来运算,所以 FFT 在一定条件下也可以用以分析周期信号序 列。如果实正弦信号,用 16 点的 FFT来做 DFS 运算,得到的频谱是信 号本身的真实谱吗?
(二)上机实验内容
1、观察高斯序列的时域和频域特性 ①固定信号中的参数 p=8,改变 q 的值,使 q 分别等于 2,4,8。观 察它们的时域和幅频特性,了解 q 取不同值的时候,对信号时域特性和 幅频特性的影响。 ②固定 q=8,改变 p,使 p 分别等于 8,13,14,观察参数 p 变化对 信号序列时域及幅频特性的影响。注意 p 等于多少时,会发生明显的泄 漏现象,混淆现象是否也随之出现?记录实验中观察到的现象,绘制相 应的时域序列和幅频特性曲线。 2、观察衰减正弦序列的时域和幅频特性 ①令α=0.1 并且 f=0.0625,检查谱峰出现的位置是否正确,注意频谱 的形状,绘制幅频特性曲线。 ②改变 f=0.4375,再变化 f=0.5625,观察这两种情况下,频谱的形状 和谱峰出现的位置,有无混淆和泄漏现象发生?说明产生现象的原因。 3、观察三角波序列和反三角波序列的时域和幅频特性
实验二_应用FFT对信号进行频谱分析
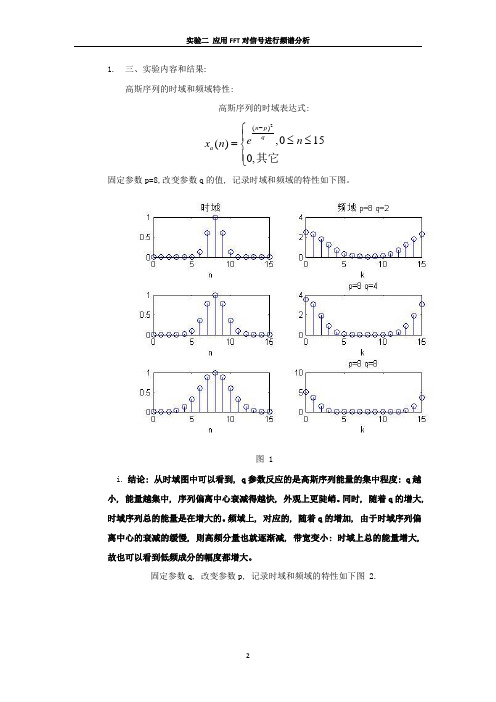
1. 三、实验内容和结果:高斯序列的时域和频域特性:高斯序列的时域表达式:2(),015()0,n p q a e n x n -⎧⎪≤≤=⎨⎪⎩其它固定参数p=8,改变参数q 的值, 记录时域和频域的特性如下图。
图 1i. 结论: 从时域图中可以看到, q 参数反应的是高斯序列能量的集中程度: q 越小, 能量越集中, 序列偏离中心衰减得越快, 外观上更陡峭。
同时, 随着q 的增大, 时域序列总的能量是在增大的。
频域上, 对应的, 随着q 的增加, 由于时域序列偏离中心的衰减的缓慢, 则高频分量也就逐渐减, 带宽变小: 时域上总的能量增大, 故也可以看到低频成分的幅度都增大。
固定参数q, 改变参数p, 记录时域和频域的特性如下图 2.图 22. 结论: p 是高斯序列的对称中心, p 的变化在时域表现为序列位置的变化。
由于选取的矩形窗函数一定, p 值过大时, 会带来高斯序列的截断。
并且随着p 的增大, 截断的越来越多。
对应地, 看频域上的变化: 截断的越多, 高频的成分也在增多, 以至发生谱间干扰, 泄露现象变得严重。
从图中可以看到, 在p=13时, 已经有混叠存在。
当p=14时, 混叠进一步加大, 泄露变得更明显。
衰减正弦序列的时域和幅频特性:sin(2),015()0,n b e fn n x n απ-⎧≤≤=⎨⎩其它改变参数f, 记录时域和幅频特性如下图3.图 33. 结论: 随着f 的增大, 时域上可以看到, 序列的变化明显快多了。
从幅度谱上看, 序列的高频分量逐渐增多, 低频分量逐渐减小, 以至于发生严重的频谱混叠。
当f 增大到一定的程度, 从图中可以看到, f=0.4375和f=0.5625时的幅度谱是非常相似的, 此时已经很难看出其幅度谱的区别。
三角序列的时域表达式和对应的时域和幅频特性如图 4:c 1,03()8,470,n n x n n n n +≤≤⎧⎪=-≤≤⎨⎪⎩其它图 4结论: 随着fft 取点数的增多, 能够看到的幅度谱的频率分量变得丰富, 得到的是高密度更高的谱, 也就是减轻了栅栏效应。
实验三用FFT对信号作频谱分析_实验报告

实验三用FFT对信号作频谱分析_实验报告一、实验目的1.学习使用FFT(快速傅里叶变换)对信号进行频谱分析;2.掌握频谱分析的基本原理和方法;3.熟悉使用MATLAB进行频谱分析的操作。
二、实验原理FFT是一种基于傅里叶变换的算法,可以将时域信号转换为频域信号,并将信号的频谱特征展示出来。
在频谱分析中,我们通过分析信号的频谱可以获得信号的频率、幅值等信息,从而对信号的性质和特征进行研究。
对于一个连续信号,我们可以通过采样的方式将其转换为离散信号,再利用FFT算法对离散信号进行频谱分析。
FFT算法可以将信号从时域转换到频域,得到离散的频谱,其中包含了信号的频率分量以及对应的幅值。
MATLAB中提供了fft函数,可以方便地对信号进行FFT分析。
通过对信号进行FFT操作,可以得到信号的频谱图,并从中提取出感兴趣的频率信息。
三、实验步骤1.准备工作:(2)建立新的MATLAB脚本文件。
2.生成信号:在脚本中,我们可以通过定义一个信号的频率、幅值和时间长度来生成一个信号的波形。
例如,我们可以生成一个频率为1000Hz,幅值为1的正弦波信号,并设置信号的时间长度为1秒。
3.对信号进行FFT分析:调用MATLAB中的fft函数,对信号进行FFT分析。
通过设置采样频率和FFT长度,可以得到信号的频谱。
其中,采样频率是指在单位时间内连续采样的次数,FFT长度是指离散信号的样本点数。
4.绘制频谱图:调用MATLAB中的plot函数,并设置x轴为频率,y轴为幅值,可以绘制出信号的频谱图。
频谱图上横坐标表示信号的频率,纵坐标表示信号的幅值,通过观察可以得到信号的频率分布情况。
四、实验结果在实验过程中,我们生成了一个频率为1000Hz,幅值为1的正弦波信号,并对其进行FFT分析。
通过绘制频谱图,我们发现信号在1000Hz处有最大幅值,说明信号主要由这一频率成分组成。
五、实验总结本实验通过使用FFT对信号进行频谱分析,我们可以方便地从信号的波形中提取出频率分量的信息,并绘制出频谱图进行观察。
用快速傅里叶变换对信号进行频谱分析

用快速傅里叶变换对信号进行频谱分析快速傅里叶变换(FFT)是一种用于对信号进行频谱分析的算法。
它是傅里叶变换(Fourier Transform)的一种高效实现方式,能够在较短的时间内计算出信号的频谱,并可用于信号处理、数据压缩、图像处理等领域。
傅里叶变换是一种将信号从时域转换为频域的方法,它将时域信号分解为多个不同频率的正弦波的叠加。
傅里叶变换的结果表示了信号在不同频率上的强度,可用于分析信号的频谱特征。
对于一个连续信号x(t),傅里叶变换定义为:X(ω) = ∫[x(t)e^(-jωt)]dt其中,X(ω)表示频域上的频谱,ω为频率。
实际应用中,信号通常以离散形式存在,即由一系列采样点组成。
为了对离散信号进行频谱分析,需要进行离散傅里叶变换(DFT)。
然而,传统的DFT算法计算复杂度较高,随信号长度的增加而呈指数级增长。
为了解决这个问题,Cooley-Tukey算法提出了一种高效的FFT算法。
该算法利用了DFT的周期性特点,将信号的长度分解为2的幂次,然后通过迭代计算将问题规模减小。
这种分治思想使得计算复杂度从指数级降低到线性级别,大大提高了计算效率。
具体而言,FFT算法的基本思路如下:1.将信号长度N分解为2的幂次L。
2.将N点DFT分解为两个N/2点DFT和一个旋转因子计算。
3.递归地应用步骤2,直到得到长度为1的DFT。
4.对于所有的DFT结果进行合并,得到完整的N点DFT。
FFT算法具有较高的计算效率和优良的数值稳定性,已成为信号处理中最常用的频谱分析方法之一FFT在信号处理中的应用十分广泛。
例如,可以利用FFT对音频信号的频谱进行分析,从而实现音频的频谱显示、音乐频谱分析、噪声抑制等功能。
在图像处理中,FFT可用于图像频谱分析、图像滤波、图像压缩等领域。
此外,FFT还常用于模拟信号的数字化处理、电力系统谐波分析、最优滤波器设计等方面。
总结起来,快速傅里叶变换是一种高效的频谱分析算法,可用于对信号的频谱特征进行分析和处理。
利用FFT对信号进行频谱分析

利用FFT对信号进行频谱分析傅里叶变换(Fast Fourier Transform,FFT)是一种用于将信号从时域转换为频域的数学算法,在信号处理中经常被用于频谱分析。
频谱分析可以用来确定信号中包含的不同频率的成分,帮助我们理解信号的特性以及包含的信息。
在进行频谱分析之前,我们首先需要了解一些基本概念。
信号可以被看作是一个函数,表示随时间变化的其中一种物理量。
这个函数可以在时域上表示,也可以在频域上表示。
在时域中,信号在不同时间点上的取值。
而在频域中,信号的成分按其频率进行表示,即信号中包含的不同频率的成分。
傅里叶变换可以将一个信号从时域转换为频域,通过将信号分解成一系列正弦和余弦的和,表示信号中包含的不同频率的成分。
FFT是一种高效的算法,能够在计算机上快速地进行傅里叶变换,使频谱分析变得可行。
进行频谱分析的基本步骤如下:1.采集信号:首先需要获得要分析的信号,可以通过传感器、麦克风等设备采集到的模拟信号,或者从文件中读取的数字信号。
2.离散化:将连续的信号离散化,即将信号在时间上进行采样,得到一系列离散的数据点,通常是均匀采样。
3.预处理:根据具体应用的需求,对信号进行预处理。
预处理的方法包括去除噪声、滤波、去除基线漂移等。
4.应用FFT:将预处理后的信号应用FFT算法,将信号从时域转换为频域。
FFT算法可以将信号转换为频谱表示,显示信号中不同频率的成分。
5.频谱分析:对得到的频谱进行分析,可以观察信号中存在的频率成分及其相对强度。
可以通过频谱分析来确定信号中的主要频率、频率的幅值等信息。
6.可视化:可以将得到的频谱进行可视化,使得结论更加直观明了。
常见的可视化方法包括将频谱绘制成线图、柱状图、瀑布图等形式。
频谱分析可应用于多个领域,如音频处理、图像处理、通信信号处理等。
在音频处理中,许多音频效果的实现都依赖于对音频信号的频谱分析,如均衡器、滤波器等。
在通信中,频谱分析可以帮助我们理解信号传输中的问题,例如频率偏移、多径效应等。
用FFT对信号作频谱分析实验报告

实验一报告、用FFT 对信号作频谱分析一、实验目的学习用FFT 对连续信号和时域离散信号进行频谱分析的方法,了解可能出现的分析误差及其原因,以便正确应用FFT 。
二、实验内容1.对以下序列进行频谱分析:()()()()4231038470n 4033470nx n R n n n x n nn n n x n n n =+≤≤⎧⎪=-≤≤⎨⎪⎩-≤≤⎧⎪=-≤≤⎨⎪⎩其它其它 选择FFT 的变换区间N 为8和16两种情况进行频谱分析。
分别打印其幅频特性曲线,并进行对比,分析和讨论。
2.对以下周期序列进行频谱分析:()()45cos4coscos48x n n x n n nπππ==+选择FFT 的变换区间N 为8和16两种情况分别对以上序列进行频谱分析。
分别打印其幅频特性曲线,并进行对比、分析和讨论。
3.对模拟信号进行频谱分析:()8cos8cos16cos20x t t t t πππ=++选择采样频率64s F Hz =,对变换区间N=16,32,64 三种情况进行频谱分析。
分别打印其幅频特性,并进行分析和讨论。
三、实验程序1.对非周期序列进行频谱分析代码:close all;clear all;x1n=[ones(1,4)];M=8;xa=1:(M/2);xb=(M/2):-1:1;x2n=[xa,xb];x3n=[xb,xa];X1k8=fft(x1n,8);X1k16=fft(x1n,16);X2k8=fft(x2n,8);X2k16=fft(x2n,16);X3k8=fft(x3n,8);X3k16=fft(x3n,16);subplot(3,2,1);mstem=(X1k8);title('(1a)8点DFT[x_1(n)]');subplot(3,2,2);mstem=(X1k16);title('(1b)16点DFT[x_1(n)]');subplot(3,2,3);mstem=(X2k8);title('(2a)8点DFT[x_2(n)]');subplot(3,2,4);mstem=(X2k16);title('(2b)16点DFT[x_2(n)]');subplot(3,2,5);mstem=(X3k8);title('(3a)8点DFT[x_3(n)]');subplot(3,2,6);mstem=(X3k16);title('(3b)16点DFT[x_3(n)]');2.对周期序列进行频谱分析代码:N=8;n=0:N-1;x4n=cos(pi*n/4);x5n=cos(pi*n/4)+cos(pi*n/8);X4k8=fft(x4n);X5k8=fft(x5n);N=16;n=0:N-1;x4n=cos(pi*n/4);x5n=cos(pi*n/4)+cos(pi*n/8);X4k16=fft(x4n);X5k16=fft(x5n);figure(2)subplot(2,2,1);mstem(X4k8);title('(4a)8点 DFT[x_4(n)]');subplot(2,2,2);mstem(X4k16);title('(4b)16点DFT[x_4(n)]');subplot(2,2,3);mstem(X5k8);title('(5a)8点DFT[x_5(n)]');subplot(2,2,4);mstem(X5k16);title('(5a)16点DFT[x_5(n)]') 3.模拟周期信号谱分析figure(3)Fs=64;T=1/Fs;N=16;n=0:N-1;x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T);X6k16=fft(x6nT);X6k16=fftshift(X6k16);Tp=N*T;F=1/Tp;k=-N/2:N/2-1;fk=k*F;subplot(3,1,1);stem(fk,abs(X6k16),'.');box ontitle('(6a)16µãDFT[x_6(nT)]');xlabel('f(Hz)');ylabel('·ù¶È');axis([-N*F/2-1,N*F/2-1,0,1.2*max(abs(X6k16))]);N=32;n=0:N-1; %FFTµÄ±ä»»Çø¼äN=32x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T);X6k32=fft(x6nT);X6k32=fftshift(X6k32);Tp=N*T;F=1/Tp;k=-N/2:N/2-1;fk=k*F;subplot(3,1,2);stem(fk,abs(X6k32),'.');box ontitle('(6b)32µãDFT[x_6(nT)]');xlabel('f(Hz)');ylabel('·ù¶È');axis([-N*F/2-1,N*F/2-1,0,1.2*max(abs(X6k32))]);N=64;n=0:N-1; %FFTµÄ±ä»»Çø¼äN=64x6nT=cos(8*pi*n*T)+cos(16*pi*n*T)+cos(20*pi*n*T);X6k64=fft(x6nT);X6k64=fftshift(X6k64);Tp=N*T;F=1/Tp;k=-N/2:N/2-1;fk=k*F;subplot(3,1,3);stem(fk,abs(X6k64),'.');box ontitle('(6c)64µãDFT[x_6(nT)]');xlabel('f(Hz)');ylabel('·ù¶È');axis([-N*F/2-1,N*F/2-1,0,1.2*max(abs(X6k64))]);四、实验结果与分析分析:图(1a)和图(1b)说明X1(n)=R4(n)的8点和16点DFT分别是X1(n)的频谱函数的8点和16点采样;因X3(n)=X2((n-3))8R8(n),故X3(n)与X2(n)的8点DFT的模相等,如图(2a)和图(3a)所示。
实验二 的应用FFT对信号进行频谱分析

20090401310074 海南大学实验二 应用FFT 对信号进行频谱分析一、实验目的1、进一步加深DFT 算法原理和基本性质的理解(因为FFT 只是DFT 的一种快速算法, 所以FFT 的运算结果必然满足DFT 的基本性质)。
2、学习用FFT 对连续信号和时域离散信号进行谱分析的方法,了解可能出现的分析误差及其原因,以便在实际中正确应用FFT 。
二、实验原理i.模拟信号频率Ω和采样得到的数字信号频率ω的关系:/s T f ω=Ω=Ωii.DTFT 与对应的理想采样信号的频谱之间的对应关系为:|^()()jw a T X j X e ω=ΩΩ=即DTFT 与FT 的关系为:12()[()]j a r X e X j r T T Tωωπ∞=-∞=-∑就是说,只要知道了采样序列的频谱,就可以得到相应的连续信号的频谱。
(满足耐奎斯特采样定理)iii.DFT 是对离散时间序列的频域采样,是对ZT 上单位圆上的均匀采样,或者是DTFT 上[0,2]π的等间距采样。
当满足频域的采样定理时,便可以由频域的采样值恢复ZT 或者是DTFT 。
所以能用DFT 对信号进行频谱分析。
当采样的点数足够时,便能用它的包络作为模拟信号的近似谱。
近似的过程中,可能会有混叠现象,泄露现象和栅栏效应这三种误差。
iv.离散傅立叶变换DFT :10()(),0,1,2...,1N nkN n X k x n W k N -===-∑[]101()()(),0,1,2...,1N nkN n x n IDFT X k X k W n N N --====-∑反变换与正变换的区别在于N W 变为1-N W ,并多了一个N 1的运算。
因为N W 和1-N W 对于推导按时间抽取的快速傅立叶变换算法并无实质性区别,因此借助FFT 来实现IFFT.三、实验内容和结果:1. 高斯序列的时域和频域特性:高斯序列的时域表达式:2(),015()0,n p q a e n x n -⎧⎪≤≤=⎨⎪⎩其它i. 固定参数p=8,改变参数q 的值,记录时域和频域的特性如下图。
用FFT对信号作频谱分析实验报告

用FFT对信号作频谱分析实验报告实验目的:利用FFT对信号进行频谱分析,掌握FFT算法的原理及实现方法,并获取信号的频谱特征。
实验仪器与设备:1.信号发生器2.示波器3.声卡4.计算机实验步骤:1.将信号发生器与示波器连接,调节信号发生器的输出频率为待测信号频率,并将示波器设置为XY模式。
2.将示波器的输出接口连接至声卡的输入接口。
3.打开计算机,运行频谱分析软件,并将声卡的输入接口设置为当前输入源。
4.通过软件选择频谱分析方法为FFT,并设置采样率为合适的数值。
5.通过软件开始进行频谱分析,记录并保存频谱图像和数据。
实验原理:FFT(快速傅里叶变换)是一种计算机算法,用于将时域信号转换为频域信号。
它通过将一个信号分解成多个不同频率的正弦波或余弦波的合成,并计算每个频率分量的幅度和相位信息。
实验结果与分析:通过对待测信号进行FFT频谱分析,我们可以得到信号在频域上的频谱特征。
频谱图像可以展示出信号中不同频率成分的能量分布情况,可以帮助我们了解信号的频率构成及其相对重要程度。
在实验中,我们可以调节信号发生器的输出频率,观察频谱图像的变化。
当信号频率与采样率相等时,我们可以得到一个峰值,表示信号的主频率。
同时,我们还可以观察到其他频率分量的存在,其幅度与信号频率的差距越小,幅度越低。
通过对不同信号进行频谱分析,我们可以了解信号的频率成分及其分布情况。
这对于信号处理、通信等领域具有重要意义。
实验结论:通过FFT频谱分析,我们可以获得信号在频域上的频谱特征,可以清晰地观察到信号的主频率以及其他频率分量的存在。
这为信号处理及相关应用提供了有价值的信息。
实验中,我们使用了信号发生器、示波器、声卡和计算机等设备,通过连接和软件进行了频谱分析实验。
通过实验,我们掌握了FFT算法的原理及实现方法,并且获取到了信号的频谱特征。
然而,需要注意的是,频谱分析仅能得到信号在其中一时刻或一段时间内的频率成分,不能得到信号的时域信息。
实验三用FFT对信号作频谱分析_实验报告

实验三用FFT对信号作频谱分析_实验报告一、实验目的1.理解离散傅里叶变换(FFT)的原理和应用;2.学会使用FFT对信号进行频谱分析;3.掌握频谱分析的基本方法和实验操作。
二、实验原理离散傅里叶变换(FFT)是一种用来将时域信号转换为频域信号的数学工具。
其基本原理是将连续时间信号进行离散化,然后通过对离散信号进行傅里叶变换得到离散频域信号。
傅里叶变换(Fourier Transform)是一种将时域信号转换为频域信号的方法。
在信号处理中,经常需要对信号的频谱进行分析,以获取信号的频率分量信息。
傅里叶变换提供了一种数学方法,可以将时域信号转换为频域信号,实现频谱分析。
在频谱分析中,我们常常使用快速傅里叶变换(Fast Fourier Transform,FFT)算法进行离散信号的频谱计算。
FFT算法可以高效地计算出离散信号的频谱,由于计算复杂度低,广泛应用于信号处理和频谱分析的领域。
频谱分析的流程一般如下:1.采集或生成待分析的信号;2.对信号进行采样;3.对采样得到的信号进行窗函数处理,以改善频谱的分辨率和抑制信号泄漏;4.使用FFT算法对窗函数处理得到的信号进行傅里叶变换;5.对傅里叶变换得到的频谱进行幅度谱和相位谱分析;6.对频谱进行解释和分析。
三、实验内容实验所需材料和软件及设备:1.信号发生器或任意波形发生器;2.数字示波器;3.计算机。
实验步骤:1.连接信号发生器(或任意波形发生器)和示波器,通过信号发生器发送一个稳定的正弦波信号;2.调节信号频率、幅度和偏置,得到不同的信号;3.使用数字示波器对信号进行采样,得到离散时间信号;4.对采样得到的信号进行窗函数处理;5.对窗函数处理得到的信号进行FFT计算,得到频谱;6.使用软件将频谱进行幅度谱和相位谱的分析和显示。
四、实验结果与分析1.信号频谱分析结果如下图所示:(插入实验结果图)从频谱图中可以看出,信号主要集中在一些频率上,其他频率基本没有,表明信号主要由该频率成分组成。
实验3 用FFT对信号作频谱分析

选择 采样频率 ,变换区间N=16,32,64 三种情况进行谱分析。分别打印其幅频特性,并进行分析和讨论。
4(思考题
(1)对于周期序列,如果周期不知道,如何用FFT进行谱分析, (2)如何选择FFT的变换区间,(包括非周期信号和周期信号) (3)当N=8时, 和 的幅频特性会相同吗,为什么,N=16 呢, 5(实验报告要求
%实验内容(1)===================================================
(1)完成各个实验任务和要求。附上程序清单和有关曲线。
(2)简要回答思考题。
=====================================================================
========Байду номын сангаас==
%第10章实验3程序exp3.m
% 用FFT对信号作频谱分析
clear all;close all
对模拟信号进行谱分析时,首先要按照采样定理将其变成时域离散信号。如果是模拟周期信号,也应该选取整数倍周期的长度,经过采样后形成周期序列,按照周期序列的谱分析进行。
3(实验步骤及内容
(1)对以下序列进行谱分析。
选择FFT的变换区间N为8和16 两种情况进行频谱分析。分别打印其幅频特性曲线。 并进行对比、分析和讨论。
(2)对以下周期序列进行谱分析。
选择FFT的变换区间N为8和16 两种情况分别对以上序列进行频谱分析。分别打印其幅频特性曲线。并进行对比、分析和讨论。
feel free to listen to their voices and help the masses solve problems, we were officially opened on May 10 "12345" Mayor calls, formulated rules and regulations, equipped with a full-time staff, a 24-hour on-duty system, people to call to receive, reply, action, reminders, feedback and so on. By year end, handled the crowd calls 1076, 94.7% feedback rate. By Mayor calls active coordination to solve a large number of bears on the immediate interests of the people and issues of great lives, but also for leadership research and decision to collect a lot of good ideas and suggestions, by all sectors of the community alike. Second, start Municipal Government Affairs Hall built. On May 11, we built and launched the city-government lobby, were settled in 12 departments, strict implementation of first asking duty system, service system, system of gratuitous, "receiving, internal coordination, head of the window handle, limited time concluded" one-stop service. By the end of today to accept various types of 3,273, originally of up to 100%. Running Government Affairs Hall, the convenience of the masses, promoting open Government, improve the investment environment and solve their practical problems, and so did a lot of work, masses, serve the community for the Government to play a very good "window, link, model". Third, create a city government public affairs network. We rely on theGovernment Web site, was completed on May 24, the province's first public affairs network. Over
实验二 应用 FFT 对信号进行频谱分析

实验二 应用 FFT 对信号进行频谱分析一、实验目的1、在理论学习的基础上,通过本次实验,加深对快速傅里叶变换的理解,熟悉 FFT 算法及其程序的编写。
2、熟悉应用 FFT 对典型信号进行频谱分析的方法。
3、了解应用 FFT 进行信号频谱分析过程中可能出现的问题,以便在实际中正确应用 FFT 。
二、实验原理与方法一个连续信号 )(t x a 的频谱可以用它的傅立叶变换表示为⎰+∞∞-Ω-=Ωdt e t x j X t j a a )()( (2-1)如果对该信号进行理想采样,可以得到采样序列)()(nT x n x a = (2-2)同样可以对该序列进行z 变换,其中T 为采样周期∑+∞-∞=-=n n z n x z X )()( (2-3) 当 ωj ez =的时候,我们就得到了序列的傅立叶变换 ∑+∞-∞=-=n n j j e n x e X ωω)()( (2-4)其中ω称为数字频率,它和模拟域频率的关系为s f T Ω=Ω=ω(2-5)式中的s f 是采样频率。
上式说明数字频率是模拟频率对采样率s f 的归一化。
同模拟域的情况相似,数字频率代表了序列值变化的速率,而序列的傅立叶变换称为序列的频谱。
序列的傅立叶变换和对应的采样信号频谱具有下式的对应关系∑-=)2(1)(Tm j X T e X a j πωω (2-6) 即序列的频谱是采样信号频谱的周期延拓。
从式(2-6)可以看出,只要分析采样序列的频谱,就可以得到相应的连续信号的频谱。
注意:这里的信号必须是带限信号,采样也必须满足 Nyquist 定理。
在各种信号序列中,有限长序列在数字信号处理中占有很重要的地位。
无限长的序列也往往可以用有限长序列来逼近。
对于有限长的序列我们可以使用离散傅立叶变换(DFT ),这一变换可以很好地反应序列的频域特性,并且容易利用快速算法在计算机上实现当序列的长度是 N 时,我们定义离散傅立叶变换为:∑-===10)()]([)(N n kn NW n x n x DFT K X (2-7) 其中,N j N e W π2-=它的反变换定义为:∑-=-==10)(1)]([)(N k kn N W k X N k X IDFT n x (2-8) 根据式(2-3)和(2-7)令 k N W z -=,则有)]([)()(10n x DFT W n x z X N n kn N W z k N ==∑-==- (2-9)可以得到 k N k N j W z W e z X k X k N -===-,)()(2π是 z 平面单位圆上幅角为k Nπω2=的点,就是将单位圆进行 N 等分以后第 k 个点。
应用FFT对信号进行频谱分析

应用FFT对信号进行频谱分析引言频谱分析是信号处理中的一项核心技术。
对于FFT(快速傅里叶变换)来说,它是一种以较快的速度计算傅里叶变换的算法,广泛应用于信号处理、通信、音频处理、图像处理等领域。
本文将介绍如何应用FFT对信号进行频谱分析。
一、信号的频谱分析1.傅里叶变换傅里叶变换是将一个信号分解成一系列互相正交的复指数形式的波的和的过程。
它将一个信号从时域转换到频域,给出信号在频率上的分布情况。
2.FFT算法傅里叶变换是一个连续的过程,需要进行积分计算。
然而,FFT是一种离散的傅里叶变换算法,通过将输入信号离散化,使用一种快速的算法来加速计算过程。
FFT算法能够将信号从时域转换到频域并给出高精度的频谱分析结果。
二、应用FFT进行频谱分析的步骤1.信号采样首先,需要对待分析的信号进行采样。
采样是指以一定频率对信号进行等间隔的时间点采样,将连续的信号离散化。
2.零填充为了提高频谱分析的精度,可以对信号进行零填充。
在采样的信号序列中增加零值,可以增加频谱分析的细节。
3.FFT计算使用FFT算法对离散信号进行傅里叶变换计算。
在实际应用中,通常使用现有的FFT库函数,如MATLAB的fft函数或Python的numpy.fft模块。
4.频谱绘制得到FFT计算的结果后,可以通过绘制频谱图来展示信号在不同频率上的能量分布情况。
常见的频谱绘制方式包括直方图、折线图和曲线图等。
三、应用FFT进行频谱分析的实例为了更好地理解FFT的应用,以音频信号的频谱分析为例进行说明。
1.音频信号采样选择一个音频文件,将其转换为数字信号,然后对其进行采样,得到一系列离散的数字信号。
2.FFT计算使用FFT算法对采样的数字信号进行傅里叶变换计算,得到信号在频域上的能量分布情况。
3.频谱绘制将计算得到的频域信息进行可视化。
可以通过绘制频谱图来展示信号在不同频率上的能量分布情况,例如绘制直方图、折线图或曲线图等。
4.结果分析通过观察频谱图,可以分析信号的主要频率分量、频率范围、能量分布等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学院:理学院
系别:电子信息工程
课程名称:数字信号处理
姓名:05656
学号:05698
日期:11信号频谱分析
一、实验目的
(1)能够熟练掌握快速离散傅里叶变换(Fast Fourier Transform,FFT)的原理及应用FFT进行频谱分析的基础方法。
4.3 N=64
clear all
N=64;
n=0:N-1;
xn=cos(2*pi*n/N);
XK=fft(xn,N);
magXK=abs(XK);
phaXK=angle(XK);
subplot(1,2,1);
plot(n,xn);
xlabel('n');ylabel('x(n)');
title('x(n)N=64')
subplot(1,2,2)
k=0:length(magXK)-1;
k=k*(2/32)
stem(k,magXK,'.');
xlabel('k');ylabel('|X(k)|');
title('X(k)N=32');
3.2 N=16
3.3 N=64
4.1 N=N+2=34
clear all
N=34;
V[m]= 0
其中假设窗函数长L小于或等于DFT长度N。
有限长序列 的DFT相当于 傅里叶变换的等间隔取样。
V[m]=
便是Sc(t)的离散频率函数。
因为DFT频率间隔为 ,且模拟频率 和数字频率 间的关系为 ,所以离散频率点对应的模拟频率为
显然频率分辨率△f为
利用DFT计算频谱,只给出频谱 或 的频率分量,即频率的取样值,而不可能得到连续的频谱函数。
xlabel('n');ylabel('x(n)');
title('x(n)N=64')
subplot(1,2,2)
k=0:length(magXK)-1;
title('x(n)N=64')
subplot(1,2,2)
k=0:length(magXK)-1;
k=k*(2/64)
stem(k,magXK,'.');
subplot(1,2,2)
k=0:length(magXK)-1;
title('x(n)N=64')
subplot(1,2,2)
k=0:length(magXK)-1;
k=k*(2/64)
stem(k,magXK,'.');
xlabel('k');ylabel('|X(k)|');
title('X(k)N=64');
title('x(n)N=32')
subplot(1,2,2)
k=0:length(magXK)-1;
title('x(n)N=32')
subplot(1,2,2)
k=0:length(magXK)-1;
k=k*(2/32)
stem(k,magXK,'.');
xlabel('k');ylabel('|X(k)|');
clear all
N=32;
n=0:N-1;
xn=cos(2*pi*n/N);
XK=fft(xn,N);
magXK=abs(XK);
phaXK=angle(XK);
subplot(1,2,1);
plot(n,xn);
xlabel('n');ylabel('x(n)');
title('x(n)N=32')
三、实验程序
指数序列程序
2.1
clear all
N=100;
n=0:N-1;
xn=0.9.^n;
XK=fft(xn,N);
magXK=abs(XK);
phaXK=angle(XK);
subplot(1,2,1)
plot(n,xn)
xlabel('n');ylabel('x(n)');
title('x(n)N=100')
Xc(t)通过A/D变换器转成取样序列 进行加窗处理,即 。加窗对频域的影响,用周期卷积表示。
其中 或
在实际应用中,消混叠低通滤波器的阻带不可能式无限衰减的,故由 周期延拓得到的 由非零混叠,即出现混叠现象。
由于进行DFT的需要,必须对序列 进行加窗处理,即 ,加窗对频域的影响,用周期卷积表示。
=
最后是进行DFT应算。加窗后的DFT为
k=0:length(magXK)-1;
title('x(n)N=34')
subplot(1,2,2)
k=0:length(magXK)-1;
k=k*(2/34)
stem(k,magXK,'.');
xlabel('k');ylabel('|X(k)|');
title('X(k)N=34');
4.2 N=32
5.1 N=32
clear all
N=32;
n=0:N-1;
xn=0.9*sin(2*pi*n/N)+0.6*sin(2*pi*n/(N/3));
XK=fft(xn,N);
magXK=abs(XK);
phaXK=angle(XK);
subplot(1,2,1);
plot(n,xn);
xlabel('n');ylabel('x(n)');
(2)对离散傅里叶变换的主要性质及FFT在数字信号处理中的重要作用有进一步的了解。
二、主要函数简介
1.离散傅里叶变换(DFT)及其主要性质
DFT表示离散信号的离散频谱,DFT的主要性质中有奇偶对称特性`虚实特性等。通过实验可以加深理解。
实序列的DFT具有偶对称的实部和奇对称的虚部,这可以证明如下:
由定义,可得
magXK=abs(XK);
phaXK=angle(XK);
subplot(1,2,1);
plot(n,xn);
xlabel('n');ylabel('x(n)');
title('x(n)N=32')
subplot(1,2,2)
k=0:length(magXK)-1;
title('x(n)N=32')
xlabel('k');ylabel('|X(k)|');
title('X(k)N=64');
四、实验小结
通过本次实验,我了解了快速离散傅里叶变换FFT的原理及应用FFT进行频谱分析的基本应用。使得我对离散傅里叶变换的主要性质及FFT在数字信号处理中的重要性,有着更深一步的了解。这使我感受颇丰。
五、教师评语
subplot(1,2,2)
k=0:length(magXK)-1;
k=k*(2/100)
stem(k,magXK,'.');
xlabel('k');ylabel('|X(k)|');
title('X(k)N=100');
2.2
clear all
N=100;
n=0:N-1;
xn=cos(2*pi*n/N);
快速离散傅里叶变换是计算离散傅立叶变换的一种快速算法,为了提高应算速度,FFT将DFT的计算逐次分解成较小点数的DFT。按时间抽取(Decimation-In-Time,DIT)FFT算法把输入序列 按起 值为偶数或是奇数分解成越来越短的序列。按频域抽取(Decimation-In-Time,DIT)FFT算法是把输出序列 按其 值是偶数或是奇数来分解成越来越短的序列。具体推导过程及原理可参见《数字信号处理》教科书。
=
= -j
=
=
=
= -j
所以:x[k]=
实序列DFT的这个特性,在本实验中可以通过实指数序列及三角序列看出来。
对于单一频率的三角序列来说,它的DFT谱线也是单一的,这个物理意义可以从实验中得到验证,在理论上可以推导如下:
设:
=sin
其DFT为:
=
=
=
=
从而
X(0)= =0
X(1)= = = -j
X(N-2)=0
subplot(1,2,2)
k=0:length(magXK)-1;
k=k*(2/100)
stem(k,magXK,'.');
xlabel('k');ylabel('|X(k)|');
title('X(k)N=100');
3.1
clear all
N=32;
n=0:N-1;
xn=0.9.^n;
XK=fft(xn,N);
教师签字:年月日
2.利用DFT对信号进行频谱分析
DFT的重要应用之一是对时域连续信号的频谱进行分析,称为傅里叶分析,时域连续信号离散傅里叶分析的基本步骤如图5—1所示。
图5—1时域连续信号离散傅里叶分析的处理步骤
其中消混叠低通滤波器LPF(预滤波器)的引入,是为了消除或减少时域连续信号转换成序列时可能出现的频谱混叠的影响。实际工作中,时域离散信号 的时宽是很长的甚至是无限长的(例如语言或音乐信号)。由于DFT的需要,必须把 限制在一定的时间间隔之内,即进行数据截断。数据的截断相当于加窗处理。因此,在计算 的DFT之前,用一个时域有限的窗函数 加到 上是非常必要的。
