概率论课后习题及例题(考试重点)
概率论(仅供参考)

前言由于汤老师不给力,下面由刘老师来为你们划重点 内部使用,仅供参考,不承当任何后果。
参考: 课本 课件第一章该章概型和公式比较多,每个都配上了一个例题便于理解第一节重点:德·摩根律公式交换律:A ∪B=B ∪A ,AB=BA 结合律(A ∪B)∪C=A ∪(B ∪C )(A∩B)∩C=A∩(B∩C )分配律:A∩(B ∪C) = (A∩B)∪( A∩C )A ∪(B∩C) = (A ∪B)∩(A ∪C ) 德·摩根律A B AB A B A B ==第二节频率性质1. 样本任意一事件概率不小于0(非负性)2. 样本事件概率和为1(规范性)3. 如果AB 互斥 ()()()n n n f A B f A f B =+4. 如果AB 不排斥 ()()()()n n n n f A B f A f B f A B =+-⋂5. ()1().P A P A =-第三节 古典概型性质1. 样本空间中样本点有限,既事件有限2. 样本点概率等可能发生3. ()==k A P A n 中所含的基本事件数基本事件总数例题排列组合问题(要是考应该不会太难)几何概型求法:1.求出状态方程2.根据定义域画图3.求概率=阴影面积/总面积第四节条件概型公式:()()()() (|).()()()()AB AB P AB P A BB B P BμμμΩμμμΩ===条件概率满足概率的一切性质既非法性,规范性,可加性例题11()()()()n ni i i i i P B P BA P A P B A ====∑∑例题 书 p251()(|)(|)()(|)i i i ni ii P A P B A P A B P A P B A ==∑第五节独立性如果AB事件独立P AB P A P B()()()若多事件相互独立,理论仍然成立贝努利概型既服从二项分布模型抽取n次的组合次数第二章重点章节,几大分布都是后几章的基础第二节 离散型随机变量及其分布律1. 两点分布、0﹣1分布既随机变量 X 只可能取0或1两个值,事件执行一次只有两种情况,例如抛硬币 记为 X~b (1,p ) p 表示事件的概率,样本点个数为1, 并且1-p 表示相反事件概率 2. 二项分布(应用于上章的贝努利概型)与0-1分布类似,事件执行n 次,记为 X~b (n ,p ) p 表示事件的概率 样本点个数为n 3. 泊松分布{}e ,0,1,2,,!kP X k k k λλ-===⋅⋅⋅记为 X~π(λ),如果出题,应该会标明是泊松分布,或者给出明确的λ二项分布X~b (n ,p )当n 充分大,p 充分小时,对于任意固定的非负整数k ,与泊松分布概率近视相等,并且λ=nb (数学期望相等) 4. 几何分布既抽取问题中可放回情况,该分布具有无记忆性-1{}(1),1,2,k P X k p p k ==-=5. 超几何分布既抽取问题不放回情况12{},0,1,2,k n k N N nNC C P X k k C-===第三节 随机变量及其分布随机变量分布(感觉这个知识点必考,虽然不知道会是什么题) 求事件概率公式,p511. 已知分布函数求分布律,并求事件概率(习题2第一题)根据公式000{}(0)(0)P X x F x F x ==+--求出各个点的概率,并画出分布表,求事件概率可以不会套公式,可以直接看表。
概率论习题及答案习题详解

222习题七( A )1、设总体X 服从参数为N 和p 的二项分布,n X X X ,,,21 为取自X 的一个样本,试求参数p 的矩估计量与极大似然估计量.解:由题意,X 的分布律为: ()(1),0k N kN P X k p p k N k -⎛⎫==-≤≤⎪⎝⎭. 总体X 的数学期望为(1)(1)011(1)(1)1NNk N k k N k k k N N EX k p p N p p p k k ----==-⎛⎫⎛⎫=-=- ⎪ ⎪-⎝⎭⎝⎭∑∑ 1((1))N N p p p N p -=+-=则E X p N=.用X 替换E X 即得未知参数p 的矩估计量为ˆX pN=.设12,,n x x x 是相应于样本12,,n X X X 的样本值,则似然函数为111211(,,;)()(1)nniii i n nx nN x n i i i i NL x x x p P Xx pp x ==-==∑∑⎛⎫===⋅- ⎪⎝⎭∏∏取对数111ln ln ln ()ln(1)nn ni i i i i iN L x p nN x p x ===⎛⎫=+⋅+-⋅- ⎪⎝⎭∑∑∑,11ln (1)nnii i i xnN x d L dpp p ==-=--∑∑.223令ln 0d L dp=,解得p 的极大似然估计值为11ˆnii x npN==∑.从而得p 的极大似然估计量为11ˆnii X X npNN===∑.2,、设n X X X ,,,21 为取自总体X 的一个样本,X 的概率密度为22,0(;)0,x x f x θθθ⎧<<⎪=⎨⎪⎩其它.其中参数0θ>,求θ的矩估计.解:取n X X X ,,,21 为母体X 的一个样本容量为n 的样本,则222()3xE X xf x dx x dx θθθ+∞-∞==⋅=⎰⎰32E X θ⇒=用X 替换E X 即得未知参数θ的矩估计量为3ˆ2X θ=.3、设12,,,n X X X 总体X 的一个样本, X 的概率密度为⎪⎩⎪⎨⎧≤>=--0,0,0,);(1x x ex x f xαλαλαλ其中0>λ是未知参数,0>α是已知常数,求λ的最大似然估计.解:设12,,,n x x x 为样本12,,,n X X X 的一组观测值,则似然函数为2241()1121(),0(,,,;)0,ni i n x n n i i n i x e x L x x x αλαλαλ=--=⎧∑⎪⋅≥=⎨⎪⎩∏ 其他 取对数 11ln ln ln (1)(ln )()n ni i i i L n n x x αλααλ===++--∑∑解极大似然方程1ln 0ni i d L nx d αλλ==-=∑得λ的极大似然估计值为1ˆnii nxαλ==∑从而得λ的极大似然估计量为1ˆnii nXαλ==∑.4、设总体X 服从几何分布,10,,2,1,)1()(1<<=-==-p k p p k X P k 试利用样本值n x x x ,,,21 ,求参数p 的矩估计和最大似然估计.解:因11111(1)(1)k k k k EX k p p p k p p∞∞--===⋅-=⋅-=∑∑,用X 替换E X 即得未知参数p 的矩估计量为1ˆpX=.在一次取样下,样本值12(,,,)n x x x 即事件1122{},{},,{}n n X x X x X x === 同时发生,由于12,,,n X X X 相互独立,得联合分布律为121122(,,,;)()(),,()n n n L x x x p P X x P X x P X x ====22512111(1)(1)(1)n x x x p p p p p p ---=-⋅-- ,即得极大似然函数为1()(1)ni i x nnL p p p =-∑=-取对数 1ln ()ln ()ln(1)ni i L p n p x n p ==+--∑解极大似然方程1ln ()01nii xnd L p n dppp=-=-=-∑得p 的极大似然估计值为11ˆ1nii pxn==∑从而得p 的极大似然估计量为111ˆ1nii pXXn===∑.5、设总体X 的概率密度为()1;exp ,2x f x σσσ⎧⎫=-⎨⎬⎩⎭0σ>为未知参数, n X X X ,,,21 为总体X 的一样本,求参数σ的最大似然估计.解:设12,,,n x x x 为样本12,,,n X X X 的一组观测值,则似然函数为121111(,,,;)(;)(;)exp{||}(2)nn n ini L x x x f x f x xσσσσσ====-∑取对数1211ln (,,,;)ln(2)||nn ii L x x x n xσσσ==--∑226解极大似然方程21ln 1||0nii d L nxd σσσ==-+=∑得σ的极大似然估计值11ˆ||nii x nσ==∑从而得σ的极大似然估计量为11ˆ||nii Xnσ==∑.6、证明第5题中σ的最大似然估计量为σ的无偏估计量.证明:由第5题知σ的最大似然估计量为11ˆ||nii X nσ==∑故 1111ˆ(||)||nniii i E E XE X nnσ====∑∑又1||||||exp{}2i x E X x dx σσ+∞-∞=⋅-⎰12exp{}exp{}()2x x x x dx x d σσσσ+∞+∞=⋅-=⋅-⎰⎰[exp{}|exp{}]xxx dx σσσ+∞+∞=-⋅---=⎰从而 ˆE σσ=,即ˆσ是σ的无偏估计. 7,、设总体X 的概率密度为()222220;0x x e x f x σσσ-⎧⎪>=⎨⎪⎩,,,其它.,20σ>为未知参数, n X X X ,,,21 为总体X 的一个样本,求参数2σ的的矩估计量和最大似然估计量.解:因22222(;)2xxE X x f x dx x e dx σσσ-+∞+∞-∞=⋅=⋅⎰⎰222222222002()[2|2]xxxxd exeedx σσσ---+∞+∞+∞=-=--⎰⎰22722222202xxedx edx σσ--+∞+∞===⎰⎰用X 替换E X 即得未知参数σ的矩估计量为ˆX σ=从而得未知参数2σ的估计量为22ˆ)X σ=设12,,,n x x x 为样本12,,,n X X X 的一组观测值,则似然函数为21211()222211212(,,,;)(;)(;)ni nix i n n nx L x x x f x f x eσσσσσ=-=∑==∏取对数222111ln ln ln 2nniii i L xn xσσ===--∑∑解极大似然方程22241ln 102nii d L nxd σσσ==-+=∑得2σ的极大似然估计值2211ˆ2nii x nσ==∑从而得未知参数2σ的估计量为2211ˆ2nii xnσ==∑.8、设总体),(~2σμN X ,μ已知,σ为未知参数, n X X X ,,,21 为X 的一个样本,∑=∧-=ni i X c 1||μσ, 求参数c ,使∧σ为σ的无偏估计.解:由无偏估计的定义,要使∧σ为σ的无偏估计,则ˆE σσ=228又11ˆ(||)||n ni i i i E E c X u c E X u σ===-=-∑∑由题意知总体),(~2σμN X ,从而22()2||||x u i E X u x u dx σ--+∞-∞-=-⎰2222()()2211[()]()x u x u u ux u dx x u dx σσ----+∞-∞=--+-⎰⎰且2222()220()x u yx u yux u dxydy σσ--=--+∞+∞-=⎰⎰22222()2yyed σσ-+∞=--=⎰由对称性有||i E X u -=从而有cnσ=,即2c n=.9、设θˆ是参数θ的无偏估计量,且有0)ˆ(>θD ,试证22)ˆ(ˆθθ=不是2θ的无偏估计量.证明:因为θˆ是参数θ的无偏估计量,故ˆE θθ=,且0)ˆ(>θD有22222ˆˆˆˆˆ()()()()E E D E D θθθθθθθ==+=+>即22)ˆ(ˆθθ=不是2θ的无偏估计量.10、设总体),(~2σμN X ,321,,X X X 是来自X 的样本,试证:估计量32112110351ˆX X X ++=μ;32121254131ˆX XX ++=μ;3213216131ˆX XX ++=μ229都是μ的无偏估计,并指出它们中哪一个最有效.证明:总体),(~2σμN X ,321,,X X X 是来自X 的样本,则1123123131131ˆ()51025102E E X X X E X E X E X u μ=++=++= 2123123115115ˆ()34123412E E X X X EX EX EX u μ=++=++=3123123111111ˆ()362362E E X X X EX EX EX u μ=++=++=即估计量123ˆˆˆ,,μμμ都是μ的无偏估计. 又211231231311911ˆ()510225100450D D X X X D X D X D X μσ=++=++=22123123115112525ˆ()341291614472D D X X X D X D X D X μσ=++=++=231231231111117ˆ()362936418D D X X X D X D X D X μσ=++=++=有 213ˆˆˆD D D μμμ<<,从而估计量2ˆμ最有效. 11,、设12,,,n X X X 是总体()20,X N σ 的一个样本,20σ>,证明:211ni i X n=∑是2σ的相合估计量.证明:由题意,总体()20,X N σ ,则220,EXEXσ==由样本的独立同分布性知2221111()nniii i E X EX nnσ====∑∑,即211ni i X n=∑是2σ的无偏估计.2221111()()nniii i D X D Xnn===∑∑又2422()()i i i D X E X E X =-,且23022222224432222|3]xxxi EX xdx x ex edx σσσ---+∞+∞+∞-∞-∞-∞==-⎰⎰2222423xx edx σσσ-+∞-∞==故2422444()()32i i i D X EX EX σσσ=-=-=,有42112()0()nii D X n nnσ==→→∞∑故211ni i X n=∑是2σ的相合估计量12、设总体X 的数学期望为μ,方差为2σ,分别抽取容量为1n 和2n 的两个独立样本,1X ,2X 分别为两样本均值,试证明:如果,a b 满足1a b +=,则12Y aX bX =+是μ的无偏估计量,并确定,a b ,使得()D Y最小.解:由题意,2,EX u D X σ==,且1X ,2X 分别为容量为1n 和2n 的两个独立样本得样本均值,故2111,E X u D X n σ==,2222,E X u D X n σ==.当1a b +=时,有12()EY aEX bEX a b u u=+=+=,即12Y aX bX =+是μ的无偏估计量.222221212()abD Y a D X b D X n n σ=+=+令2212(1)()aa g a n n -=+,由()0g a '=知函数()g a 的稳定点为231112n a n n =+,且1121211()2()0n g n n n n ''=+>+,故112n a n n =+为函数唯一极小值点,即当121212,n n a b n n n n ==++时,()D Y 最小.13、设12,,,n X X X 是总体X 的一个样本, X 的概率密度为();f x θ,0θ>,未知,已知()222nXn χθ,试求θ的置信水平为1α-的置信区间.解:由题意,统计量()222nXn χθ,则给定置信度为1α-时,有()()22122(22)1nXP n n ααχχαθ-≤≤=- ()()221222()122nXnXP n n ααθαχχ-⇔≤≤=-由置信区间的定义知,θ的置信水平为1α-的置信区间为()()221222,22nX nX n n ααχχ-⎛⎫⎪⎪ ⎪⎝⎭. 14、从大批彩色显像管中随机抽取100只,其平均寿命为10000小时,可以认为显像管的寿命X 服从正态分布.已知均方差40=σ小时,在置信水平0.95下求出这批显像管平均寿命的置信区间.解:设12,,,n X X X 是母体X 的样本容量为n 的子样,则显像管平均寿命(10000,16)X N构造统计量(0,1)X uU N -=,有232111222(||)1(1P U UP X UU X Uααααα---<=-⇔-<<+=-由题意10.950.05αα-=⇒=,查表可得0.975 1.96U =,故显像管平均寿命X 的置信度为95%的置信区间为:4040(10000 1.96 1.96(100007.84)-+=±.15、设随机地调查26年投资的年利润率(%),得样本标准差(%)15=S ,设投资的年利润率X 服从正态分布,求它的方差的区间估计(置信水平为0.95).解:由题意,构造统计量2222(1)(1)n Sn χχσ-=- ,则给定置信水平为1α-,有2222122(1)((1)(1))1n SP n n ααχχασ---<<-=-22222122(1)(1)()1(1)(1)n Sn SP n n αασαχχ---⇔<<=---取26,0.15,10.95n S α==-=,查表可得20.025(25)13.120χ=,20.975(25)40.616χ=,故方差的置信度为95%的置信区间为2222122(1)(1)(,)(0.014,0.043)(1)(1)n Sn Sn n ααχχ---=--.16,、从一批钉子中抽取16枚,测得其长度为(单位:厘米)2.14, 2.10, 2.13, 2.15, 2.13, 2.12, 2.13, 2.10, 2.15, 2.12, 2.14, 2.10, 2.13, 2.11, 2.14, 2.11.设钉子的长度X 服从正态分布,试求总体均值μ的置信水平为0.90的置信区间.233解:设1216,,,X X X 是母体X 的样本容量为16的子样,由题意知2.215X =,242.933310S -=⨯.构造统计量(1)X u t t n -=- ,有111222(||)1(1P t tP X tu X tααααα---<=-⇔-<<+=-由题意10.900.10αα-=⇒=,查表可得0.95(15) 1.7459t =,故显像管平均寿命X的置信度为90%的置信区间为:(2.1175,2.1325)=±. 17、生产一个零件所需时间(单位:秒)),(~2σμN X ,观察25个零件的生产时间得5.5=x ,73.1=s .试求μ和2σ的置信水平为0.95的置信区间.解:设1225,,,X X X 是母体X 的样本容量为25的子样,由题意知5.5X =, 1.73S =.构造统计量(1)X u t t n -=- ,有111222(||)1(1P t tP X tu X tααααα---<=-⇔-<<+=-由题意10.950.05αα-=⇒=,查表可得0.975(24) 2.0639t =,故参数μ的置信度为95%的置信区间为:(4.786,6.214)(5.50.714)=±.234构造统计量2222(1)(1)n Sn χχσ-=- ,则给定置信水平为1α-,有2222122(1)((1)(1))1n SP n n ααχχασ---<<-=-22222122(1)(1)()1(1)(1)n Sn SP n n αασαχχ---⇔<<=---取16, 1.73,0.05n S α===,查表可得20.025(15) 6.2621χ=,20.95(15)27.4884χ=,故方差的置信度为95%的置信区间为(1.825,5.. 18、产品的某一指标),(~2σμN X ,已知04.0=σ,μ未知.现从这批产品中抽取n 只对该指标进行测定,问n 需要多大,才能以95%的可靠性保证μ的置信区间长度不大于0.01?19、设A 和B 两批导线是用不同工艺生产的,今随机地从每批导线中抽取5根测量其电阻,算得721007.1-⨯=A s ,62103.5-⨯=B s ,若A 批导线的电阻服从),(211σμN ,B 批导线的电阻服从),(222σμN ,求2221σσ的置信水平为0.90的置信区间.20,、从甲乙两个蓄电池厂的产品中分别抽取6个产品,测得蓄电池的容量(A.h)如下:甲厂 140 , 138 , 143 , 141 , 144 , 137;乙厂135 , 140 , 142 , 136 , 138 , 140设蓄电池的容量服从正态分布,且方差相等,求两个工厂生产的蓄电池的容量均值差的95%置信区间.( B )1、设总体X 的概率分别为235其中102θθ⎛⎫<<⎪⎝⎭是未知参数,利用总体X 的如下样本值: 3, 1, 3, 0, 3, 1, 2, 3求θ的矩估计值和最大似然估计值.解:由题意可知总体X 为离散型随机变量,则总体X 的数学期望为()32()2123(12)34k EX kP Xk θθθθθ====-++-=-∑有34E X θ-=,由样本值可知2X =,用X 替换E X 即得未知参数θ的矩估计量为3ˆ4X θ-=,矩估计值1ˆ4θ=.设12340,1,2,3x x x x ====是相应于样本1234,,,X X X X 的样本值,则似然函数为12341234(,,,;)(0)(1)(2)(3)L x x x x P X P X P X P X θ=====462(12)4(1)θθθ=--取对数 ln 4ln(12)6ln 42ln(1)L θθθ=-++- 解极大似然方程ln 8620121d L d θθθθ-=+-=--有2121430θθ-+=,从而7ˆ12θ±=又当ˆ12θ=712106θ+-=-<矛盾,故舍去.所以θ的最大似然估计值ˆ12θ=2、设()111ˆˆ ,,n X X θθ= 和()221ˆˆ,,n X X θθ= 是参数θ的两个相236互独立的无偏估计量,且方差()()12ˆˆ2D D θθ=,试确定常数,a b ,使得12ˆˆa b θθ+是θ的无偏估计量,且在一切这样的线性估计类中方差最小.解:由题意,1ˆ θ和2ˆθ是参数θ的两个相互独立的无偏估计量,则 12ˆˆ,E E θθθθ==.要使得12ˆˆa b θθ+是θ的无偏估计量,有 1212ˆˆˆˆ()()E a b aE bE a b θθθθθθ+=+=+=恒成立,即1a b +=.又1ˆ θ,2ˆθ相互独立,且()()12ˆˆ2D D θθ=,则222212122ˆˆˆˆˆ()()()(2)()D a b a D b D a b D θθθθθ+=+=+令2222()22(1)g a a b a a =+=+-,由()0g a '=知函数()g a 的稳定 点为13a =,且1()03g ''>,故线性估计类中方差最小时13a =,23b =.3、在测量反应时间中,一心理学家估计的标准差为0.05秒,为了以0.95的置信水平使他对平均反应时间的估计误差不超过0.01秒,应取多大的样本容量.习题八1.在正常情况下,某炼钢厂的铁水含碳量(%)2(4.55,)X N σ .一日测得5炉铁水含碳量如下:4.48,4.40,4.42,4.45,4.47在显著性水平0.05α=下,试问该日铁水含碳量得均值是否有明显变化. 解:设铁水含碳量作为总体X ,则2(4.55,)X N σ ,从中选取容量为5的样本,测得24.444,0.0011X S ==.由题意,设原假设为0: 4.55H u =237构造检验统计量||(4)X u t t -=,则7.051t ==在显著性水平0.05α=下,查表可得0.97512(4)(4) 2.77647.051tt α-==<,拒绝原假设0H ,即认为有显著性变化.2.根据某地环境保护法规定,倾入河流的废物中某种有毒化学物质含量不得超过3ppm.该地区环保组织对某厂连日倾入河流的废物中该物质的含量的记录为:115,,x x .经计算得知15148ii x==∑, 1521156.26i i x ==∑.试判断该厂是否符合环保法的规定.(该有毒化学物质含量X 服从正态分布)解:设有毒化学物质含量作为总体X ,则2(,)X N u σ ,从中选取容量为15的样本,测得1511 3.215ii X x===∑,22221111()()0.1911nnii i i S x x x nx n n ===-=-=--∑∑.由题意,设原假设为0:3H u <,备择假设为1:3H u >.构造检验统计量||(14)X u t t -=,则|3.23| 1.777t -==,在显著性水平0.05α=下,查表可得10.95(14)(14) 1.7613 1.777t t α-==<,即拒绝原假设0H ,接受备择假设1H ,认为该厂不符合环保的规定.3.某厂生产需用玻璃纸作包装,按规定供应商供应的玻璃纸的横向延伸率238不应低于65.已知该指标服从正态分布2(,)N μσ,5.5σ=.从近期来货中抽查了100个样品,得样本均值55.06x =,试问在0.05α=水平上能否接受这批玻璃纸?解:设玻璃纸的横向延伸率为总体X ,则2(,5.5)X N u ,从中选取容量为100的样本,测得55.06x =.由题意,设原假设为0:65H u >,备择假设为1:65H u <.构造检验统计量||(0,1)X u U N -=,则|55.0665|18.07275.5U -==在显著性水平0.05α=下,查表可得10.95 1.644918.0727U U α-==<,即拒绝原假设0H ,接受备择假设1H ,不能接受该批玻璃纸..4.某纺织厂进行轻浆试验,根据长期正常生产的累积资料,知道该厂单台布机的经纱断头率(每小时平均断经根数)的数学期望为9.73根,标准差为1.60根.现在把经纱上浆率降低20%,抽取200台布机进行试验,结果平均每台布机的经纱断头率为9.89根,如果认为上浆率降低后均方差不变,问断头率是否受到显著影响(显著水平α=0.05)? 解:设经纱断头率为总体X ,则9.73u EX ==, 1.6σ==,从中选取容量为200的样本,测得9.89x =.由题意,设原假设为0:9.73H u =,备择假设为1:9.73H u ≠.构造检验统计量||(0,1)X u U N -=,则|9.899.73|1.4142U -==在显著性水平0.05α=下,查表可得0.975121.96 1.4142UU α-==>,即接受原假设0H ,认为断头率没有受到显著影响.2395. 某厂用自动包装机装箱,在正常情况下,每箱重量服从正态分布2(100,)N σ.某日开工后,随机抽查10箱,重量如下(单位:斤):99.3,98.9,100.5,100.1,99.9,99.7,100.0,100.2,99.5,100.9.问包装机工作是否正常,即该日每箱重量的数学期望与100是否有显著差异?(显著性水平α=0.05)解:设每箱重量为总体X ,则2(100,)X N σ ,从中选取容量为10的样本,测得99.9x =,20.34S =.由题意,设原假设为0:100H u =,备择假设为1:100H u ≠.构造检验统计量||(9)X u t t -=,则|99.9100|0.5423t -==,在显著性水平0.05α=下,查表可得0.97512(9)(9) 2.26220.5423tt α-==>,即接受原假设0H ,认为每箱重量无显著差异.6.某自动机床加工套筒的直径X 服从正态分布.现从加工的这批套筒中任取5个,测得直径分别为15,,x x (单位m μ:),经计算得到51124i i x ==∑, 5213139i i x ==∑.试问这批套筒直径的方差与规定的27σ=有无显著差别?(显著性水平0.01α=)解:设这批套筒直径为总体X ,则2(,)X N u σ ,从中选取容量为5的样本,测得151124.815ii X x===∑,22221111()()15.9511nnii i i S xx x nx n n ===-=-=--∑∑.由题意,设原假设为24020:7H σ=,备择假设为21:7H σ≠.构造检验统计量2222(1)(4)n Sχχσ-=,则2415.959.11437χ⨯==,在显著性水平0.01α=下,查表可得220.99512(4)(4)14.86αχχ-==,220.0052(4)(4)0.2070αχχ==,从而222122(4)(4)ααχχχ-<<,即接受原假设0H ,认为这批套筒直径的方差与规定的27σ=无显著差别.7.甲、乙两台机床同时独立地加工某种轴,轴的直径分别服从正态分布211(,)N μσ、222(,)N μσ(12,μμ未知).今从甲机床加工的轴中随机地任取6根,测量它们的直径为16,,x x ,从乙机床加工的轴中随机地任取9根,测量它们的直径为19,,y y ,经计算得知:61204.6ii x==∑, 6216978.9i i x ==∑91370.8i i y ==∑92115280.2i i y ==∑问在显著性水平0.05α=下,两台机床加工的轴的直径方差是否有显著差异?解:设两台机床加工的轴的直径分别为总体,X Y ,则211(,)X N μσ 、222(,)Y N μσ ,从总体X 中选取容量为6的样本,测得61134.16ii X x ===∑222211111()()0.40811nnii i i S x x x nx n n ===-=-=--∑∑241从总体Y 中选取容量为9的样本,测得91141.29i i Y y ===∑222221111()()0.40511nnii i i S y y y ny n n ===-=-=--∑∑ 由题意,设原假设为22012:H σσ=,备择假设为22112:H σσ≠.构造检验统计量2122(5,8)S F F S = ,则0.408 1.0070.405F ==,在显著性水平0.05α=下,查表可得0.97512(5,8)(5,8) 6.76FF α-==,0.0252(5,8)(5,8)0.1479F F α==,从而122(5,8)(5,8)F F Fαα-<<,即接受原假设0H ,认为两台机床加工的轴的直径方差无显著差异.8.某维尼龙厂根据长期正常生产积累的资料知道所生产的维尼龙纤度服从正态分布,它的标准差为0.048.某日随机抽取5根纤维,测得其纤度为1.32,1.55,1.36,1.40,1.44.问该日所生产得维尼龙纤度的均方差是否有显著变化(显著性水平α=0.1)?解:设维尼龙纤度为总体X ,则2(,0.048)X N u ,从中选取容量为5的样本,测得5111.4145ii X x ===∑,2211()0.00781nii S x x n ==-=-∑.由题意,设原假设为0:0.048H σ=,备择假设为1:0.048H σ≠.构造检验统计量2222(1)(4)n Sχχσ-=,则2240.007813.542(0.048)χ⨯==在显著性水平0.1α=下,查表可得220.9512(4)(4)9.487713.542αχχ-==<即拒绝原假设0H ,认为维尼龙纤度的均方差有显著变化.9.某项考试要求成绩的标准差为12,先从考试成绩单中任意抽出15份,计算样本标准差为16,设成绩服从正态分布,问此次考试的标准差是否符242合要求(显著性水平α=0.05)?解:设考试成绩为总体X ,则2(,12)X N u ,从中选取容量为15的样本,测得16S =.由题意,设原假设为0:12H σ=,备择假设为1:12H σ≠.构造检验统计量2222(1)(14)n Sχχσ-=,则222141619.055612χ⨯==.在显著性水平0.05α=下,查表可得220.97512(14)(14)26.1189αχχ-==,220.0252(14)(14) 5.6287αχχ==,从而222122(14)(14)ααχχχ-<<,即接受原假设0H ,认为此次考试的标准差符合要求.10.某卷烟厂生产甲、乙两种香烟,分别对他们的尼古丁含量(单位:毫克)作了六次测定,获得样本观察值为:甲:25,28,23,26,29,22;乙:28,23,30,25,21,27.假定这两种烟的尼古丁含量都服从正态分布,且方差相等,试问这两种香烟的尼古丁平均含量有无显著差异(显著性水平α=0.05,)?对这两种香烟的尼古丁含量,检验它们的方差有无显著差异(显著性水平α=0.1)?解:设这两种烟的尼古丁含量分别为总体,X Y ,则211(,)X N μσ 、222(,)Y N μσ ,从中均选取容量为6的样本,测得61125.56ii X x ===∑,22111()7.51nii S x x n ==-=-∑,61125.66676i i Y y ===∑,22211()11.06671nii S y y n ==-=-∑,由题意,在方差相等时,设原假设为012:H u u =,备择假设为112:H u u ≠.243构造检验统计量12(2)t t n n =+- ,其中222112212(1)(1)9.2834(2)wn S n S Sn n -+-==+-.则0.0948t ==,在显著性水平0.05α=下,查表可得120.97512(2)(10) 2.22810.0948tn n t α-+-==>,即接受原假设0H ,认为这两种香烟的尼古丁平均含量无显著差异.由题意,在方差待定时,设原假设为22012:H σσ=,备择假设为22112:H σσ≠.构造检验统计量2122(5,5)S F F S=,则7.50.677711.0667F ==,在显著性水平0.1α=下,查表可得0.9512(5,8)(5,5) 5.0503FF α-==,0.052(5,8)(5,5)0.1980F F α==,从而122(5,5)(5,5)F F Fαα-<<,即接受原假设0H ,认为它们的方差无显著差异.。
概率论课后习题

第一章 概率论的基本概念(一)1、多选题:⑴ 以下命题正确的是( )。
A B A AB a =)()(. ; A AB B A b =⊂则若,.;A B B A c ⊂⊂则若,.; B B A B A d =⊂ 则若,..⑵ 某学生做了三道题,i A 表示第i 题做对了的事件)3,2,1(=i ,则至少做对了两道题的事件可表示为( ). ;.;.133221321321321A A A A A A b A A A A A A A A A a ..;.321321321321133221A A A A A A A A A A A A d A A A A A A c2、A 、B 、C 为三个事件,说明下述运算关系的含义:.)6(.)5(.)4(.)3(.)2(.1ABC C B A C B A C B A C B A )(3、个工人生产了三个零件,i A 与i A )3,2,1(=i 分别表示他生产的第i 个零件为正、次品的事件。
试用i A 与i A )3,2,1(=i 表示以下事件:⑴ 全是正品;⑵ 至少有一个零件是次品;⑶ 恰有一个零件是次品;⑷ 至少有两个零件是次品。
4、下列命题中哪些成立,哪些不成立: ⑴B B A B A =;⑵ B A B A =;⑶ C B A C B A = ;⑷ ()∅=)(B A AB ;⑸ AB A B A =⊂则若;⑹ A B B A ⊂⊂则若。
(二)1、选择题:⑴ 若事件A 与B 相容,则有( ))()()(.B P A P B A P a += ; )()()()(.AB P B P A P B A P b -+= ; )()(1)(.B P A P B A P c --= ; )()(1)(.B P A P B A P d -=⑵ 事件A 与B 互相对立的充要条件是( ),1)(0)(.),()()(.===B A P AB P b B P A P AB P a 且∅=Ω=∅=AB d B A AB c .,.. 且2、袋中有12个球,其中红球5个,白球4个,黑球3个。
概率论·课后答案(绝对详解)

i习题一3 设,,B A 为二事件,化简下列事件:B B B A B BA B A B A B A =⋃=⋃⋃=⋃⋃)()())()(1(B B A B B A A A B A B A =⋃⋃⋃=⋃⋃)())()(2(4 电话号码由5个数字组成,每个数字可能是从0到9这10个数字中的任一个,求电话号码由5个不同数字组成的概率。
3024.010302410427210678910445==⋅=⋅⋅⋅⋅=p5 n 张奖券中有m 张有奖的,k 个人购买,每人一张,求其中至少有一人中奖的概率。
答案:.1k n k mn C C --6 从5双不同的鞋子中任取4只,这4只鞋子中“至少有两只配成一双”的概率是多少?解;将这五双靴子分别编号分组},,,,{};,,,,{5432154321b b b b b B a a a a a A ==,则C 表示:“至少有两只配成一双”;从5双不同的鞋子中任取4只,其可能选法有.45C不能配对只能是:一组中选i 只,另一组中选4-i 只,且编号不同,其可能选法为)0,1,2,3,4(;455=--i C C i i i41045341523251235451)(1)(C C C C C C C C C C P C P ++++-=-= 2113218177224161247720104060401011234789105453245224551=-=⋅⋅-=⋅++++-=⋅⋅⋅⋅⋅⋅⋅+⋅+⋅⋅+⋅⋅+-= 7在[—1,1]上任取一点,求该点到原点的距离不超过51的概率。
答案:518在长度为a 的线段内任取两点,将其分成三段,求它们可以构成三角形的概率。
,0,0a y a x <<<<且a y x <+<0,又41222,,=⎪⎪⎪⎩⎪⎪⎪⎨⎧<<>+⇒⎪⎩⎪⎨⎧--<---<--->+P ay a x a y x y x a x y y x a y x y x a y x 9在区间)1,0(内任取两个数,求这两个数的积小于41的概率。
概率论_习题集(含答案)

《概率论》课程习题集一、计算题1. 10只产品中有2只次品, 在其中取两次, 每次任取一只,作不放回抽样,求下列事件的概率:(1)两只都是正品;(2)一只是正品,一只是次品;(3)第二次取出的是次品。
2. 一个学生接连参加同一课程的两次考试。
第一次及格的概率为p ,若第一次及格则第二次及格的概率也为p ;若第一次不及格则第二次及格的概率为.2/p 求 (1)若至少有一次及格则他能取得某种资格,求他取得该资格的概率; (2)若已知他第二次已经及格,求他第一次及格的概率3. 用某种方法普查肝癌,设:A ={ 检验反映呈阳性 },C ={ 被检查者确实患有肝癌 },已知()()5.C A P ,.C A P 90950==()5.C P 000=且现有一人用此法检验呈阳性,求此人真正患有肝癌的概率.4. 两台机床加工同样的零件,第一台出现次品的概率是0.03, 第二台出现次品的概率是0.02,加工出来的零件放在一起,并且已知第一台加工的零件比第二台的多一倍。
(1)求随意取出的零件是合格品的概率(2)如果随意取出的零件经检验是次品,求它是由第二台机床加工的概率5. 某人有5把钥匙,但忘了开房门的是哪一把,现逐把试开,求∶(1) 恰好第三次打开房门锁的概率(2) 三次内打开房门锁的概率(3) 如5把钥匙内有2把是开房门的,三次内打开房门锁的概率6. 设X 是连续型随机变量,其密度函数为()()⎩⎨⎧<<-=其它020242x x x c x f求:(1);常数c (2){}.1>X P7. 设X ~⎩⎨⎧≤≤=其他,02,)(x o cx x f 求(1)常数c ;(2)分布函数)(x F ;8. 一工厂生产的某种元件的寿命X (以小时计)服从参数为σμ,160= 的正态分布。
若要求,80.0)200120(≥≤<X P 允许σ最大为多少?9. 证明:指数分布有无记忆性(或称无后效性),即证:如果)(~λE X ,则有)()|(t X P s X t s X P >=>+>,0,0≥≥t s10. 对球的直径作测量,设测量值均匀地分布在],[b a 内,求球的体积的概率密度.11. 设随机变量X 的概率密度为⎪⎩⎪⎨⎧≤≤-=其他,021),11(2)(2x xx f ,求X 的分布函数。
概率论习题答案及答题范例

P( A) 1
202 212 22
242
311 1152
5
P59,习题34
6
(N 1)! 1
P( Ai )
N!
N
P( Ai Aj )
(N 2)! N!
1 N(N
1)
,
i j
P( A1A2 A3...AN
P57,习题6
1Байду номын сангаас
P57,习题10
• 甲袋中有3只白球,7只红球,15只黑球,乙袋中有10只 白球,6只红球,9只黑球,现从两袋中各取一球,求两 球颜色相同的概率。
• 解:分别求出同取白、红、黑球的概率,再相加即可
P 3 10 7 6 15 9 207 25 25 25 25 25 25 625
15
P114,习题37
7
C7k 0.6k 0.47k 0.71
k 4
16
P115,习题41
P( A)
1
20 0!
e 2
5
0.484
P(B)
5 k3
C5k
1
20 0!
e 2
k
20 0!
e 2
5k
=0.98
17
P115,习题47
• 某车间宣称自己产品的合格率超过99%,检验人员从该 车间的10000件产品中抽查了100件,发现有两件次品, 能否据此断定该车间谎报合格率?
2
P58,习题13
• 从6双不同的手套中任取4只,问其中恰有一双配对的概 率是多少?
• 解:
P C61C52C21C21 16
概率论重点及课后题答案9
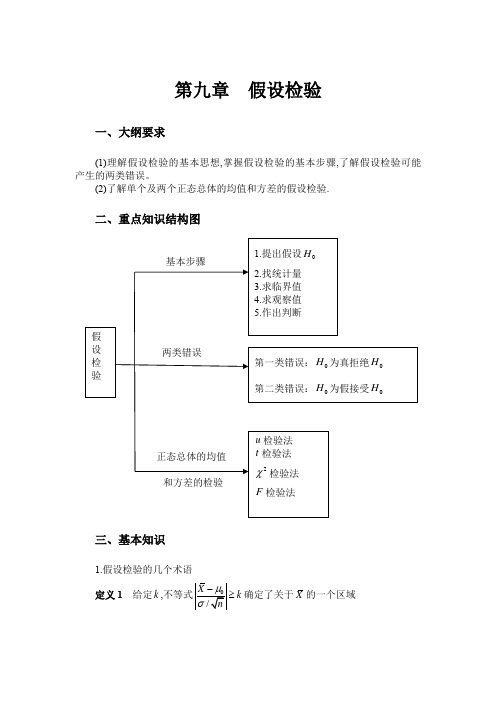
第九章假设检验一、大纲要求(1)理解假设检验的基本思想,掌握假设检验的基本步骤,了解假设检验可能产生的两类错误。
(2)了解单个及两个正态总体的均值和方差的假设检验.二、重点知识结构图三、基本知识1.假设检验的几个术语 定义1给定k ,k ≥确定了关于X 的一个区域00,k μμ⎛⎛⎫-∞-++∞ ⎪⎝⎝⎭当X 落入此区域内,就拒绝0H (接受1H ),称上式这类区域为0H 的拒绝域,记为Z .k <确定了关于X 的另外一个区域00k k μμ⎛-+ ⎝当X 落入此区域内,就接受0H (拒绝1H ),称上类区域为接受域,记为Z .不等式k <称为临界值形式的接受域,00k k μμ⎛-+ ⎝称为区间形式的接受域.定义2称0H 为原假设(或零假设),称1H 为备择假设(或备选假设、对立假设). 定义3称允许作判断有错误的概率α为显著性水平(或检验水平),它是用来衡量原假设与实际情况差异是否明显的标准.定义4称k 为临界值小概率原理:小概率事件在一次试验中是不大会发生的.2.假设检验的两类错误第一类错误:0H 正确,但拒绝了它,这类错误称为“弃真错误”. 第二类错误:0H 不正确,但接受了它,这类错误称为“存伪错误”.3.假设检验的基本步骤 (1)提出假设;(2)找统计量(这里要求该统计量含有待检验的参数); (3)求临界值(求接受域); (4)求观察值; (5)作出判断.4.u 检验法已知方差2σ,假设检验00:H μμ=. (1)提出假设00:H μμ=.(2)找统计量.确定样本函数:()~0,1X u N =,称其为u 的统计量,它含有待检验参数μ.(3)求临界值.给定显著性水平()01αα<<,查正态分布表求出临界值/2u α,使{}/2P u u αα≥=,即{}/21P u u αα<=-.(4)求观察值.根据给定的样本求出统计量u 的观察值1u . (5)作出判断.若1/2u u α<,则接受0H ;若1/2u u α≥,则拒绝0H .5.t 检验法未知方差2σ,假设检验00:H μμ=. (1)提出假设00:H μμ=.(2)找统计量.因为2σ未知,这时u 已不是统计量,所以不能用u 检验法,这里用2S 来代替2σ,找出统计量:X t =(3)求临界值.对给定显著性水平()01αα<<,由t 分布表查得临界值,使{}/2P t t αα≥=.(4)求观察值.根据给定的样本算出统计量t 的观察值1t . (5)作出判断.若1/2t t α<,则接受0H ;若1/2t t α≥,则拒绝0H .6.2χ检验法已知期望μ,假设检验220:H σσ=. (1)提出假设220:H σσ=.(2)找统计量.确定样本函数的统计量:()222211()~nii Xn χμχσ==-∑(3)求临界值.对给定显著性水平()01αα<<,由2χ分布表查得临界值()2/2n αχ与()21/2n αχ-,使(){}(){}2222/21/2, 22P n P n ααααχχχχ-≥=≤=即()(){}2221/2/21P n n ααχχχα-<<=-(4)求观察值.根据给定的样本算出统计量2χ的观察值21χ.(5)作出判断.若()()2221/2/2n n ααχχχ-<<,则接受0H ;若()221/2n αχχ≥或21χ≤()21/2n αχ-,则拒绝0H .7.F 检验法已知期望12,μμ,假设检验21022:H σσσ=(1)提出假设21022:H σσσ=.(2)找统计量()12212111122221221()~,1()n ii n i i Xn F F n n Y n μσμσ==-=-∑∑(3)求临界值.对给定显著性水平()01αα<<,查F 分布表,求得()/212,F n n α及()1/212,F n n α-,使(){}(){}/2121/212,, ,22P F F n n P F F n n αααα-≥=≤=即()(){}1/212/212,,1P F n n F F n n ααα-<<=-(4)求观察值.由所给定的样本算出统计量的值1F .(5)作出判断.若()()1/212/212,,F n n F F n n αα-<<,则接受0H ;若()1/212,F F n n α≥或()11/212,F F n n α-≤,则拒绝0H .四、典型例题例1有两批棉纱,为比较其断裂强度,从中各取一个样本,测试得到:第一批棉纱样本11200,0.523kg,0.218kg n X S ===; 第二批棉纱样本22100,0.576kg,0.176kg n X S ===.试验证两批棉纱断裂强度的均值有无显著差异(检验水平0.05α=)?如果0.1α=呢?解这是两个正态总体的均值检验问题,检验0:H EX EY =.()()~0,1,~0,1X Y N N因为是大样本(12,n n 均较大),所以DX 、DY 可用2212S S 、代入,近似有221212~,, ~,S S X N EX Y N EY n n ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭故221212~,S S X Y N EX EY n n ⎛⎫--+ ⎪⎝⎭由于X 与Y 相互独立,若0:H EX EY =成立,则221212~0,S S X Y N n n ⎛⎫-+ ⎪⎝⎭故()~0,1X Y u N =因此,只要是大样本(容量较大时),不管总体X 、Y 是否服从正态分布,是否DX DY =,都可以按u 检验法2σ已知的情况去做近似检验.由已知得2211200, 0.523, 0.218n X S ===2222100, 0.576, 0.176n X S ===故 1.88X Y u ===-当0.05α=时,查表得/2 1.96u α=.因/21.88 1.96u u α=<=,故0H 被接受,即在检验水平0.05α=下可以认为这两种棉纱的强力值无显著差异.当0.10α=时,查表得/2 1.65u α=.因/21.88 1.65u u α=>=,u 落入拒绝域,应否定0H ,即在检验水平0.10α=下可以认为这两种棉纱的强力值有显著差异.例2某农业试验站为了研究某种新化肥对农作物产量的效力,在若干小区进行试验.测得产量(单位:kg)如下:施肥 34 35 32 33 30 34 未施肥 29 27 32 28 31 32 31设农场的产量服从正态分布,检验该种化肥对提高产量的效力是否显著?()0.10α=解设X 为施肥后的产量,Y 为施肥前的产量.已知()211~,,~X N Y Nμσ()222,μσ.由于总体方差21σ和22σ均未知,应先对方差进行检验,即22012:H σσ=,22112:H σσ≠. 由题意可知67111133, 3067i i i i X X Y Y ======∑∑672222121111() 3.2, ()456i i i i S X X S Y Y ===-==-=∑∑2122 3.20.84S F S ===已知120.1,6,7n n α===,查表得()()/2120.051,15,6 4.95F n n F α--==.因为()0.055,6F F <,所以接受0H ,即认为2212σσ=. 提出检验问题,即11012112:,:H H μμμμ≤>2.828X Yt == 已知()0.10α=,查表得()()120.1211 1.3634t n n t α+-==.因为()0.12.82811t t =>,所以拒绝0H ,即认为该种化肥对提高产量的效力显著.例3某种配偶的后代按体格的属性分为三类,各类的数据是:10,53,46.按照某种遗传模型,其频率之比应为()()22:21:1p p p p --,问数据与模型是否相符?()0.05α=解令()()22123,21,1p p p p p p p ==-=-,欲检验的假设为0H :数据与模型相符.设观察到的三类数量分别为123,,n n n ,其中123n n n n ++=,则p 的似然函数为()()()()()31222123211 10,53,46n n n L p pp p p n n n ⎡⎤=--===⎡⎤⎣⎦⎣⎦由于()1222ln 212011L p n n n n p p p p p∂--=+++=∂--解得p 的极大似然估计为12220530.3352218n n p n ++=== 从而 2210.3350.112p p ===()22120.3350.6650.45p p p =-=⨯⨯= ()22310.6650.44p p=-==统计量观测值为()2321i ii in n p n p χ=-=∑()()()222101090.112531090.45461090.441090.1121090.451090.44-⨯-⨯-⨯=++⨯⨯⨯0.801=已知0.05α=,自由度11321n --=-=,查表得()20.051 3.84χ= 由于()220.801 3.841αχχ=<=,故接受0H ,即数据与模型相符.例4设某次考试考生成绩服从正态分布,从中随机抽取36位考生的成绩,算得平均成绩为66.5分,标准差为15分,问在0.05α=时是否可以认为这次考试全体考生的平均成绩为70分?解设该次考试考生的成绩为X ,则()2~,X N μσ.把从X 中抽取的容量为n 的样本均值记为X ,样本标准差记为S ,检验假设01:70,:70H H μμ=≠.则()1/21u t n α-=-已知()0.97536,66.5,15,361 2.0301n X S t ===-=,所以()0.97566.57035 2.030115u n t -=≥= 所以接受假设0:70H μ=,即0.05α=时,可以认为这次考试全体考生的平均成绩为70分.例5某一指标服从正态分布,今对该指标测量8次,所得数据为:68,43,70,65, 55,56,60,72.在以下两种条件下,检验()220:80.05H σα==.(1)总体均值μ未知;(2)总体均值60μ=.解 (1)检验假设220:8H σ=,用2χ检验,得()882211154.875, 1()652.88i i i i X X n S X X ====-=-=∑∑故()22221652.810.28n S χσ-==≈ 查表得()()220.0250.975817.535,8 2.180χχ==.因()()2220.0250.97588χχχ>>,故接受0H .(2)检验假设220:8H σ=,而60μ=,故()82211()663i i n SX μ=-=-=∑()2222166310.48n S χσ-=== 由于()()2220.0250.97588χχχ>>,故接受0H .例6从某锌矿的东西两支矿脉中,各抽取容量分别为9和8的样本分析后,计算其样本含锌量(%)的平均值与方差分别如下:东支2110.230, 0.1337, 9X S n ===西支2220.269, 0.1736, 8Y S n ===假定东西两支矿脉的含锌量都服从正态分布,对于0.05α=,能否认为两支矿脉的含锌量相同?解设东支矿脉的含锌量为X ,()211~,X N μσ;西支矿脉的含锌量为Y ,~Y ()222,N μσ;其中1μ、、、均为未知参数.(1)检验假设.则已知,计算得查表得 因,故接受假设,即认为. (2)检验假设,这属于检验,检验统计量为已知,计算得查表得.因,故接受假设,即认为两支矿脉的含锌量相同.例7在20世纪70年代后期人们发现,酿啤酒时,在麦芽糖干燥过程中会形成致癌物质亚硝基二甲胺(NDMA),于是80年代初期开发了一种新的麦芽糖干燥过程.下面给出分别在新老两种过程中所形成的(NDMA)含量(以10亿份中的份数计).老过程 6 4 5 5 6 5 5 6 4 6 7 4 新过程 2 1 2 2 1 0 3 2 1 0 1 3设两样本分布来自正态总体,两总体方差相等,两样本独立,分别以、记2μ21σ22σ222201121112:,:H H σσσσ=≠()211222~1,1S F F n n S =--2211229,0.1337,8,0.1736n S n S ====0.13370.77020.1736F ==()()()0.0250.9750.025118,7 4.90,8,77,8 4.53F F F ===1 4.904.53F <<01H 2212σσ=02121212:,:H H μμμμ=≠t ()12~2t t n n =+-2211229,0.1337,8,0.1736n S n S ====0.2180t ==-()0.02515 2.1315t = 2.1315t <02H 1μ2μ对应于新老两过程的总体均值,检验假设.解该检验的拒绝域为已知,查表得. 由已知数据计算得由于在拒绝域中,故应拒绝.例8某厂使用两种不同的原料A 、B 生产同一类产品,各在一周的产品中取样进行分析比较,取使用原料A 生产的样品220件,测得平均重量为2.46kg,样本标准差;取使用原料B 生产的样品205件,测得平均重量为2.55kg,样本标准差,设这两个样本独立,问在下能否认为使用原料B 的产品平均重量比使用原料A 大?解检验假设. 这个问题是大样本问题,故可近似认为统计量:于是检验的拒绝域为()012112:2,:20.05H H μμμμα-=->=()122X Y W t t n n α⎧⎫⎪⎪⎪⎪==≥+-⎨⎬⎪⎪⎪⎪⎩⎭1212,12,0.05n n α===()()120.05222 1.7171t n n t α+-==5.25, 1.5X Y ==()()2211222121110.25 6.50.7283123Wn S n S S n n -+-+===+-11.87 1.7171t ==>t 0H 0.57kg S =0.48kg S =0.05α=012112:0,:0H H μμμμ-=-<()~0,1X Y Z N =X Y W Z Z α⎧⎫⎪⎪⎪⎪==≤-⎨⎬⎪⎪⎪⎪⎩⎭已知,所以由于落在拒绝域中,故应拒绝,即认为使用原料B 的产品平均重量比使用原料A 的大.例9某种导线,要求其电阻的标准差不得超过0.005(单位:).今在生产的一批导线中取样本9根,测得,设总体为正态分布,问在下能否认为这批导线的标准差显著地偏大?解检验假设. 该检验的拒绝域为已知,所以由于落在拒绝域中,故应拒绝,即在下这批导线的标准差显著偏大.例10一自动车床加工零件的长度服从正态分布,车床正常时,加工零件长度为10.5,经过一段时间生产后,要检验这车床是否正常工作,为此抽取该车床加工的31个零件,测得数据如下:零件长度 10.1 10.3 10.6 11.2 11.5 11.8 12.0 频率 1 3 7 10 6 3 1若加工零件长度方差不变,问此车床工作是否正常?()解检验假设.则0.050.05, 1.65Z α== 1.76 1.65Z ==-<-Z 0H Ω0.007S =0.05α=01:0.005,:0.005H H σσ≤>()()2222011n S W n αχχσ⎧⎫-⎪⎪==≥-⎨⎬⎪⎪⎩⎭()20.05,9,115.507n n ααχ==-=22280.00715.6815.5070.005χ⨯==>2χ0H 0.05α=()2,N μσ0.05α=0010:10.5,:10.5H H μμμμ==≠=()~,1X t t n =于是检验的拒绝域为 已知,计算得.从而查表得.由于,故拒绝.即可以认为该车床工作不正常. 例11某车间的白糖包装机包装量,其中,未知.一天开工后为检验包装量是否正常,抽取了已经装好的糖9袋,算得样本均值,样本标准差为,试确定包装机工作是否正常?()解检验假设(可省略).样本均值,样本方差.于是已知,查表得. 由于,故接受.可认为包装机工作正常.例12某市居民上月平均伙食费为235.5元,随机抽取49个居民,他们本月的伙食费平均为236.5元,由这49个样本算出的标准差元.假设该市居民月伙食费方差正态分布,试分别在和时,检验“本月该市居民平均伙食费较之上个月无变化”的假设.解检验假设. 由于方差未知,故采用检验法,其拒绝域为已知,计算得()/21W t t n α⎧⎫⎪⎪==>-⎨⎬⎪⎪⎩⎭31n =11.08,0.516X S == 6.26t ===()()/20.025130 2.0423t n t α-==()0.0256.2630 2.0423t t =>=0H ()20~,X N μσ2500g,μσ=504g X =5g S =0.01α=01:500,:500H H μμ=≠504X =225S= 2.4X t ===0.01,18n α=-=()()/20.00518 3.3554t n t α-==()/21t t n α<-0H 3.5S =X 0.05α=0.01α=01:235.5,:235.5H H μμ=≠2σt()/21W t t n α⎧⎫⎪⎪==≥-⎨⎬⎪⎪⎩⎭49,236.5, 3.5n X S ===由于,故可用代替.当时,,故应拒绝.即本月该市居民平均伙食费较之上个月有显著升高.当时,,故接受.即本月该市居民平均伙食费较之上个月无显著变化.例13一位研究者声称至少有80%的观众对商业广告感到厌烦,现在随机询问了120位观众,其中70人同意此观点,在时,问是否可同意该研究者的观点?解把“观众对商业广告感到厌烦”(即)作为原假设.本问题的归结为在时,检验假设.设随机向量在为真时,为来自总体服从两点分布的一个样本,且.由于较大,由中心极限定理可知于是检验的拒绝域为 已知,计算得故拒绝,即在此数据的基础上,不能同意该研究者的观点.2t ===4914830-=>/2u α()/2491t α-0.05α=0.025 1.962u =<0H 0.01α=0.005 2.582u =>0H 0.05α=0.8p ≥0H 0.05α=0010:0.8,:0.8H p p H p p ≥=<=()11,2,,1200i i X i i ⎧==⎨⎩第个观众同意此观点第个观众不同意此观点0H 12120,,,X X X ()1,0.8B 0.8,0.16i i EX DX ==120n =()0~0,1niXnp u N -=∑00ni X np W u u ⎧⎫-⎪⎪⎪⎪==<-⎨⎬⎪⎪⎪⎪⎩⎭∑12000.051120,70,0.8, 1.65i i n X p u =====∑ 5.93 1.65u ==-<-0H五、课本习题全解9-1 ①提出假设.②找统计量..③求临界值.对给定的,查表得;对给定的,查表 得.④求观察值..⑤作出判断.当时,,所以拒绝;当时,,所以接受.9-2 ①提出假设.②找统计量..③求临界值.对给定的,查表得. ④求观察值..⑤作出判断.当时,,所以拒绝. 9-3 (1)①提出假设.②找统计量..③求临界值.对给定的,查表得. ④求观察值..⑤作出判断.当时,,所以拒绝. (2)①提出假设. ②找统计量.. 010:32.05H μμ==()~0,1X u N =0.05α=0.025 1.96u =0.01α=0.005 2.575u =31.13, 2.05X u ==-0.05α= 2.05 1.96u =>0H 0.01α=u 2.05 2.275=<0H 00:5H μμ==()~0,1X u N =0.01α=0.005 2.575u =5.32, 3.2X u ==0.01α= 3.2 2.275u =>0H 00:50H μμ==()~0,1X u N =0.05α=0.025 1.96u =2.25u =0.05α= 2.25 1.96u =>0H 00:50H μμ==()~1X t t n =-③求临界值.对给定的,查表得. ④求观察值..⑤作出判断.当时,,所以接受.9-4 ①提出假设.②找统计量.. ③求临界值.对给定的,查表得. ④求观察值.. ⑤作出判断.当时,,所以接受. 9-5 ①提出假设.②找统计量..③求临界值.对给定的,查表得. ④求观察值..⑤作出判断.当,,所以拒绝. 9-6 (1)①提出假设.②找统计量..③求临界值.对给定的,查表得. ④求观察值..⑤作出判断.当时,,所以接受.(2)①提出假设.②找统计量. .0.05α=()0.0258 2.31t =48.5, 2.5, 1.8X S t ===-0.05α= 1.8 2.31t =<0H 00: 2.7H μμ==()~1X t t n =-0.05α=()0.02529 2.04t =0.18,301 2.05/29n S S t n ==-⨯0.05α= 2.04t <0H 00:H μμ=()~0,1X u N =0.01α=0.005 2.575u =1.5u =0.01α= 1.5 2.575u =<0H 00:100H μμ==()~0,1X u N =0.05α=0.025 1.96u =99.9,0.25X u ==0.05α=0.25 1.96u =<0H 22200: 1.2H σσ==()9222211()~ii Xn χμχσ==-∑③求临界值.对给定的,查表得.④求观察值. .⑤作出判断.当时,,所以接受.9-7 ①提出假设.②找统计量..③求临界值.对给定的,查表得.④求观察值..⑤作出判断.当时,,所以拒绝,有显著差异. 9-8 ①提出假设.②找统计量.. ③求临界值.对给定的,查表得.④求观察值..⑤作出判断.当时,,所以接受,即可认为溶化时间 的标准差为9.9-9 (1)①提出假设.②找统计量..③求临界值.对给定的,查表得. ④求观察值..⑤作出判断.当时,,所以接受,即包装机工作 正常.(2)①提出假设.0.05α=()()220.0250.975919.0,9 2.7χχ==28.2χ=0.05α=22.719.0χ<<0H 2200:0.04H σσ==()222211()~1nii XX n χχσ==--∑0.05α=()()220.0250.9751426.1,14 5.63χχ==2 1.84χ=0.05α=2 5.63χ<0H 00:9H σσ==()222211()~1nii XX n χχσ==--∑0.05α=()()220.0250.975919.0,9χχ==2.72221162.9,(62.9)9nii X Xχ===-∑0.05α=22.719χ<<0H 00:500H μμ==()~0,1X u N =0.05α=0.025 1.96u =501.3,0.82X u ==0.05α=0.82 1.96u =<0H 00: 2.7H μμ==②找统计量.. ③求临界值.对给定的,查表得. ④求观察值.. ⑤作出判断.当时,,所以接受.9-10 (1)①提出假设.②找统计量..③求临界值.对给定的,查表得.④求观察值..⑤作出判断.当时,,所以接受. (2)①提出假设. ②找统计量..③求临界值.对给定的,查表得.④求观察值.. ⑤作出判断.当时,,所以接受.9-11 ①提出假设.②找统计量..③求临界值.对给定的,查表得. ④求观察值.⑤作出判断.当时,,所以拒绝.()~1t t n =-0.05α=()0.0259 2.26t =2501.3,31.57,0.73X S t ===0.05α= 2.26t <0H 2200:25H σσ==()2222101()~nii XX n χχσ==-∑0.05α=()()220.0250.9751020.5,10 3.25χχ==212χ=0.05α=23.2520.5χ<<0H 00:5H σσ==()2222101()~1nii XX n χχσ==--∑0.05α=()()220.0250.975919.0,9χχ==2.722501.3,31.57,11.37X S χ===0.05α=22.719χ<<0H 02:0H μμ-=()~0,1X Y u N μμ---=0.05α=0.025 1.96u =u =0.05α= 1.96u >0H9-12 (1)①提出假设.②找统计量..③求临界值.对给定的,查表得④求观察值..⑤作出判断.当时,,所以接受. (2)①提出假设. ②找统计量..③求临界值.对给定的,查表得. ④求观察值..⑤作出判断.当时,,所以接受.9-13 (1)①提出假设.②找统计量..③求临界值.对给定的,查表得. ④求观察值..1022:1H σ=()12211122121()1~1,11()1n i i n i i X X n F F n n Y Y n ==--=----∑∑0.05α=()()0.0250.9755,57.15,5,50.14F F ==222112221139.33,269,0.14655S S S F S =⨯=⨯==0.05α=0.147.15F <<0H 012:0H μμ-=()12~2X Y t t n n μμ---=+-0.05α=()0.02510 2.23t =0.14067,0.13883,0.57X Y t ===0.05α=0.57 2.23t =<0H 21022:1H σσ=()12211122121()1~1,11()1n i i n i i X X n F F n n Y Y n ==--=----∑∑0.01α=()()0.0050.9958,9 6.69,8,9F F ==17.342221122264,226,0.28S S S F S ====⑤作出判断.当时,,所以接受. (2)①提出假设. ②找统计量..③求临界值.对给定的,查表得. ④求观察值.⑤作出判断.当时,,所以拒绝.9-14 ①提出假设.②找统计量..③求临界值.对给定的,查表得. ④求观察值..⑤作出判断.当时,,所以接受.9-15 (1)①提出假设.②找统计量.. ③求临界值.对给定的,查表得.④求观察值..0.01α=16.697.34F <<0H 02:0H μμ-=()12~2X Y t t n nμμ---=+-0.01α=()0.00517 2.9t =533,562,X Y t ===0.01α= 2.9t >0H 012:0H μμ-=()12~2X Y t t n n μμ---=+-0.05α=()0.02511 2.20t =17.681,17.630,X Y t ===0.05α= 2.2t <0H 21022:1H σσ=()12211122121()1~1,11()1n i i n i i X X n F F n n Y Y n ==--=----∑∑0.10α=()()0.050.9518,5 4.82,8,5 3.69F F ==22211222113.69,19.2,0.1285S S S F S =⨯=⨯==⑤作出判断.当时,,所以拒绝. (2)①提出假设.②找统计量.. ③求临界值.对给定的,查表得 ④求观察值.. ⑤作出判断.当时,,所以拒绝. 9-16 ①提出假设.②找统计量..③求临界值.对给定的,查表得. ④求观察值..⑤作出判断.当时,,所以接受.9-17 ①提出假设.②找统计量.. ③求临界值.对给定的,查表得. ④求观察值..⑤作出判断.当时,,所以接受. 0.10α=13.69F <0H 21022:1H σσ=()1221111222121()~,1()n i i n i i X n F F n n Y n μμ==-=-∑∑0.10α=()()0.050.9519,6 4.06,9,6 3.37F F ==0.128F =0.10α=13.37F <0H 02:0H μμ-=()12~2X Y t t n n μμ---=+-0.05α=()0.02513 2.16t=t =0.05α= 2.16t <0H 21022:1H σσ=()12211122121()1~1,11()1n i i n i i X X n F F n n Y Y n ==--=----∑∑0.05α=()()0.0250.97516,751.2,6,7 5.7F F ==222112220.1048,0.0272, 3.85S S S F S ====0.10α=15.125.7F <<0H9-18 根据题目要求,考虑假设检验.其中 服从泊松分布,其分布律为的极大似然估计为样本均值,其观察值为则统计量为其中,是按的泊松分布律计算出的的取值为0,1,2,3,4 这五种情况的概率.查表得,故接受.9-19 根据题目要求,考虑假设检验,其中服从等概率分布,其 分布律为由观测数据得,则统计量为其中.查表得,故接受.六、自测题及答案1.设总体是来自的样本,记,当和未知时,则(1)检验假设所使用的统计量是.(2)检验假设所使用的统计量是.()()()()0010:,:H F x F x H F x F x =≠0F {}() 0,1,2,!kP X k e k k λλ-=== λX ()106544940.61200X =++++=()25210.7853i i i in np np χ=-==∑200n =i p 0.61λ=X ()220.0549.49χχ=>0H ()()00:H F x F x =0F {}()11,2,,66P X k e k λ-=== 120,20i n np ==()()26211936102525 4.820i i i in np np χ=-==+++++=∑120n =()220.05511.1χχ=>0H ()212~,,,,,n X N X X X μσ X 211,ni i i X X n σ===∑21()nii XX =-∑μ2σ00:H μμ=________2200:H σσ=________2.设总体服从正态分布,方差未知,对假设进行假设检验时,通常采取的统计量是,服从分布,自由度是.3.在检验时,用统计量,若时,用检验,它的拒绝域为.若时,用检验,它的拒绝域为.4.设总体,设假设检验的拒绝域为,则犯第一类错误的概率为;犯第二类错误的概率为.5.某加工厂生产一批轴承,质量检查规定,废品率不超过3%可以出厂,否则不能出厂.现从这批产品中抽查100件,发现有5件废品.为判断这批产品能否出厂,要求检验的假设为;在显著性水平下,选定的统计量为,其观测值为;该统计量近似服从分布,拒绝域为.6.设总体,和未知,假设检验.若采用检验法,则在显著性水平之下,其拒绝域为( ).(A) (B) (C) (D)7.设和是来自正态总体的样本均值和样本方差,样本容量为,为( ). (A)的拒绝域 (B)的接受域 (C)的一个置信区间 (D)的一个置信区间 8.设总体,其中未知,假设检验.若取得显X ()2,N μσ2σ0211:,:H H μμμ=≠2μ________________________2χ()2221n S χσ-=2200:H σσ=________________2200:H σσ≠________________()~,X B n p 0010:;:H p p H p p =≠W ={}{}()1212,X C X C C C ≤≥< ________________01:0.03;:0.03H p H p =>α________________________________()2~,X N μσμ2σ0010:,:H H μμμμ=≠t α()1/21t t n α-<-()1/21t t n α-≥-()11t t n α-≥-()11t t n α-<--X 2S ()2,N μσn (00.051X t n μ->-00:H μμ=00:H μμ=μ2σ()2~,X N μσ2σ01:1,:1H H μμ≤>著性水平,则其拒绝域为( ).(A) (B) (C) (D)9.对正态分布的数学期望进行假设检验,如果在显著性水平0.05下接受,那么在显著性水平0.01下,下列结论中正确的是( ).(A)必接受 (B)可能接受,也可能拒绝(C)必拒绝 (D)不接受,也不拒绝 10.自动包装机装出的每袋重量服从正态分布,规定每袋重量的方差不超过,为了检查自动包装机的工作是否正常,对它生产的产品进行抽样检查,假设检验,则下列命题正确的是( ).(A)如果生产正常,则检测结果也认为生产正常的概率为0.95 (B)如果生产不正常,则检测结果也认为生产不正常的概率为0.95 (C)如果检测结果认为生产正常,则生产确实正常的概率为0.95(D)如果检测结果认为生产不正常,则生产确实不正常的概率为0.95 11.设为正态总体中抽取的样本,在显著性水平下检验.取拒绝域为.试求当时,所烦的第二类错误的概率.12.甲、乙两台机床生产同一型号的滚球,现从这两台机床的产品中分别抽取8个和9个,测得滚球珠的直径(单位:mm)如下:甲机床 15.0 14.5 15.2 15.5 14.8 15.1 15.2 14.8 乙机床 15.2 15.0 14.8 15.2 15.0 14.8 15.1 14.8设滚珠直径服从正态分布,问乙机床的加工精度是否比甲机床高()? 13.一种元件,要求其使用寿命不得低于1000h,现在从一批这种元件中随机地抽取25件,测得其寿命平均值为950h,已知该元件寿命服从标准差的正态分布,试在下,确定该批元件是否合格?14.某台机器加工某种零件,规定零件长度为100cm,标准差不得超过2cm,每天定时检查机器运行情况,某日抽取10个零件,取到平均长度,样本标准差为,设加工的零件长度服从正态分布.问该日机器工作状况是否正常()?0.05α=0.051X u ->(0.0511X t n >+-0.051X t ->(0.0511X t n <--μ00:H μμ=0H 0H 0H 0H 0H 0H α2201:,:;0.05H a H a σσα≤>=12,,,n X X X (),1N μα()01:0:0H H μμ=≠(){}121/2,,,nW X X XX u α-=> 1μ=0.05α=100h σ=0.05α=101cm X =2cm S =0.05α=15.甲、乙相邻两地段各取了50块和52块岩心进行磁化率测定,算出样本标准差分别为,试问甲、乙两段的标准差是否有显著差异()?16.在集中教育开课前对学员进行测验,过了一段时间后,又对学员进行了与前一次同样程度的考查,目的是了解学员两次考试的分数是否有差别().从两次考卷中随机抽取12份考试成绩,如下表:考查次数考分总计平均第1次80.5 91.0 81.0 85.0 70.0 86.0 69.5 74.0 72.5 83.0 69.0 78.5 940 78.5 第2次76.0 90.0 91.5 73.0 64.5 77.5 81.0 83.5 86.0 78.5 85.0 73.5 960 80.0 [答案]1.(1)当未知时,检验假设,应选服从个自由度的分布统计量其中.于是.(2)检验假设,应选统计量.2.;分布;.3.双边;;左边;.4..5..6.的含义为.7.由可知.故A项正确.8.,故B项正确.9.检验水平越小,接受域的范围越大,也就是说,在下的接受域包含在下的接受域.如果在时,接受,即样本值落在接受域内,则此样本值也一定落在22120.0139,0.0053S S==0.05α=0.05α= 2σ00:Hμμ=1n-tXt=S=Xt=2200:Hσσ=()22222001n Sσχσσ-==()2211iS X Xn=--t1n-()()2222/21/21,1n nααχχχχ->-<-()2211nαχχ-<-()()()122110000111111;1C Cnn i m i n ii i i i i in n ni i C i CC p p C p p C p pαβ----===+=-+-=-∑∑∑()0,1;2XNμμα=>()11t nα--()(){}1111P t n t nαα--≤-=-(00.051X t nμ->-0.05t>()0.051Xt n>-α0.01α=0.05α=0.05α=H的接受域内,因此接受.即A 项正确.10.因为,从而,因而A 项正确.而B 、C 、D 三项分别反映的是条件概率、、,由假设检验中犯两类错误的概率之间的关系知,这些概率一般不能由唯一确定,故B 、C 、D 三项不正确.11.第二类错误的为.当时,来自,此时因此12.设甲、乙机床生产的滚珠直径分别为,检验乙机床的加工精度是否比甲机床高,即看是否比小.此问题归结为在下,检验假设. 容易想到用统计量,但是在为真时,不知其服从什么分布,只知随机变量而对于,有即事件是一个小概率事件,可惜乙机床计算不出来.但因0.01α=0H {}00P H H α=拒绝为真{}001P H H α-=接受为真{}00P H H 拒绝不真{}00P H H 为真接受{}00P H H 不真拒绝α()1P W μ=1μ=()12,,,n X X X ()1,1N )()1~1,,1~0,1X N X N n ⎛⎫- ⎪⎝⎭}111/2P P X U μμα==-=<)11/21/2111P X μαα=--⎫=-≤-≤-⎪⎭((1/21/2=ΦΦU U αα----))1/21/2=ΦΦU U αα---()()221122~,,~,X N Y N μσμσ22σ21σ0.05α=2222012112:,:H H σσσσ≤>2122S F S =0H ()2211122222/~1,1/S Z F n n S σσ=--α(){}121,1P Z F n n αα>--=(){}121,1Z F n n α>--F与有关,在为真时,有故事件 从而于是仍选用作为检验的统计量.的拒绝域为.已知,得,又查表得.由于,故拒绝.即认为乙机床的加工精度比甲机床的高.13.在下,检验假设. 由于已知,故拒绝域为已知,得故拒绝,即认为这批元件不合格.14.设加工的零件长度为,且,、均未知.(1)检验假设.这是检验问题,当成立时,统计量为于是拒绝域为已知,得Z 0H 22222112112222222122//S S S Z F S S S σσσσ==≥=(){}(){}12121,11,1F F n n Z F n n αα>--⊆>--(){}(){}12121,11,1P F F n n P Z F n n ααα>--⊆>--=2122S F S =0H 0H ()121,1F F n n α>--128,9n n ==221215.01,0.09554,14.99,0.02611X S Y S ====()()120.051,17,8 3.5F n n F α--==2212/0.09554/0.02611 3.695 3.5F S S ===>0H 0.05α=0010:1000,:1000H H μμμμ==<=2σ()120.050,,,:n X W x x x Z Z ⎧⎫==<-⎨⎬⎩⎭00.0525,950,100, 1.65n X Z σ====95010002.5 1.65100Z -==-<-0H X ()2~,X N μσμ2σ010110:100,:100H H μμμμ==≠=t 01H ()~1X T t n =-()(){}12/2,,,:1n W x x x t t n α=≥- 22101,10,2X n S ===已知,查表得,由于,故接受假设,即认为.(2)检验假设.这是检验问题,当成立时,统计量为于是拒绝域为计算得 已知,查表得,由于,故接受假设,即认为.综合(1)(2),可以认为该机器工作状态正常. 15.假设检验,则有由于统计量.查表得故. 因为,所以拒绝假设,即认为甲、乙段岩心磁化率,测定数据的标准差在时有显著差异.16.此为双正态总体方差的假设检验,两总体均值未知,要检验假设1.5811t ==0.05α=()0.0259 2.2622t = 1.5811 2.2622t =<01H 100μ=222222020120:2,:2H H σσσσ==>=2χ02H ()22212()~1nii n XX n χχσ=-=-∑()(){}2212,,,:1n n n W x x x n χχ=≥- ()22222019292nn S χσ-⨯===0.05α=()20.05916.9χ=2916.9n χ=<02H 222σ<012:H σσ=250211501500.0139()0.01425014949i i S X X =⨯⨯-===-∑(大)252221521520.053()0.00545215151i i S Y Y =⨯⨯-===-∑(小)2111222210.01422.630.00541n S n n S n -==-F=()()0.050.0149,51 1.59, 49,51 1.93F F ==()()/20.0250.050.01111.59 1.93 1.7622F F F F α==+=+=/22.63 1.76F F α=>=012:H σσ=0.05α=选取统计量于是拒绝域为 由题意可知因此查表得.由于,故在下,接受,即认为两次考试中学员的成绩无显著差异.2222012112: :H H σσσσ=≠()211222~1,1S F F n n S =--()()/2121/2121,1, 1,1F F n n F F n n αα->--<--221253.15, 60.23S S ==212253.150.882560.23S F S ===()()0.0250.97511,11 3.43,11,110.2915F F ==()()1/20.02511,110.882511,11 3.43F F F α-<=<=0.05α=0H。
概率论课后习题答案

习题1解答1. 写出下列随机试验的样本空间Ω:(1)记录一个班一次数学考试的平均分数(设以百分制记分); (2)生产产品直到有10件正品为止,记录生产产品的总件数;(3)对某工厂出厂的产品进行检查,合格的记为“正品”,不合格的记为“次品”,如连续查出了2件次品就停止检查,或检查了4件产品就停止检查,记录检查的结果; (4)在单位圆内任意取一点,记录它的坐标.解:(1)以n 表示该班的学生人数,总成绩的可能取值为0,1,2,…,100n ,所以该试验的样本空间为{|0,1,2,,100}ii n nΩ==.(2)设在生产第10件正品前共生产了k 件不合格品,样本空间为{10|0,1,2,}k k Ω=+=,或写成{10,11,12,}.Ω=(3)采用0表示检查到一个次品,以1表示检查到一个正品,例如0110表示第一次与第四次检查到次品,而第二次与第三次检查到的是正品,样本空间可表示为{00,100,0100,0101,0110,1100,1010,1011,0111,1101,1110,1111}Ω=.(3)取直角坐标系,则有22{(,)|1}x y x y Ω=+<,若取极坐标系,则有{(,)|01,02π}ρθρθΩ=≤<≤<.2.设A 、B 、C 为三事件,用A 、B 、C 及其运算关系表示下列事件. (1)A 发生而B 与C 不发生; (2)A 、B 、C 中恰好发生一个; (3)A 、B 、C 中至少有一个发生; (4)A 、B 、C 中恰好有两个发生; (5)A 、B 、C 中至少有两个发生; (6)A 、B 、C 中有不多于一个事件发生.解:(1)ABC 或A B C --或()A B C -;(2)ABC ABC ABC ;(3)AB C 或ABCABCABCABCABCABCABC ;(4)ABC ABCABC .(5)AB AC BC 或ABC ABC ABCABC ;(6)ABCABCABCABC .3.设样本空间{|02}x x Ω=≤≤,事件{|0.51}A x x =≤≤,{|0.8 1.6}B x x =<≤,具体写出下列事件:(1)AB ;(2)A B -;(3)A B -;(4)A B .解:(1){|0.81}AB x x =<≤; (2){|0.50.8}A B x x -=≤≤;(3){|00.50.82}A B x x x -=≤<<≤或; (4){|00.5 1.62}AB x x x =≤<<≤或.4. 一个样本空间有三个样本点, 其对应的概率分别为22,,41p p p -, 求p 的值. 解:由于样本空间所有的样本点构成一个必然事件,所以2241 1.p p p ++-=解之得1233p p =-=-,又因为一个事件的概率总是大于0,所以3p =- 5. 已知()P A =0.3,()P B =0.5,()P A B =0.8,求(1)()P AB ;(2)()P A B -;(3)()P AB .解:(1)由()()()()P AB P A P B P AB =+-得()()()()030.50.80P AB P A P B P A B =+-=+-=.(2) ()()()0.300.3P A B P A P AB -=-=-=. (3) ()1()1()10.80.2.P AB P AB P AB =-=-=-=6. 设()P AB =()P AB ,且()P A p =,求()P B . 解:由()P AB =()1()1()1()()()P AB P AB P AB P A P B P AB =-=-=--+得()()1P A P B +=,从而()1.P B p =-7. 设3个事件A 、B 、C ,()0.4P A =,()0.5P B =,()0.6P C =,()0.2P AC =,()P BC =0.4且AB =Φ,求()P A B C .解:()()()()()()()()0.40.50.600.20.400.9.P A B C P A P B P C P AB P AC P BC P ABC =++---+=++---+=8. 将3个球随机地放入4个杯子中去,求杯子中球的最大个数分别为1,2,3的概率. 解:依题意可知,基本事件总数为34个.以,1,2,3i A i =表示事件“杯子中球的最大个数为i ”,则1A 表示每个杯子最多放一个球,共有34A 种方法,故34136().416A P A ==2A 表示3个球中任取2个放入4个杯子中的任一个中,其余一个放入其余3个杯子中,放法总数为211343C C C 种,故211343239().416C C C P A == 3A 表示3个球放入同一个杯子中,共有14C 种放法,故14331().416C P A ==9. 在整数0至9中任取4个,能排成一个四位偶数的概率是多少?解:从0至9 中任取4个数进行排列共有10×9×8×7种排法.其中有(4×9×8×7-4×8×7+9×8×7)种能成4位偶数. 故所求概率为4987487987411098790P ⨯⨯⨯-⨯⨯+⨯⨯==⨯⨯⨯. 10. 一部五卷的文集,按任意次序放到书架上去,试求下列事件的概率:(1)第一卷出现在旁边;(2)第一卷及第五卷出现在旁边;(3)第一卷或第五卷出现在旁边;(4)第一卷及第五卷都不出现在旁边;(5)第三卷正好在正中.解:(1)第一卷出现在旁边,可能出现在左边或右边,剩下四卷可在剩下四个位置上任意排,所以5/2!5/!42=⨯=p .(2)可能有第一卷出现在左边而第五卷出现右边,或者第一卷出现在右边而第五卷出现在左边,剩下三卷可在中间三人上位置上任意排,所以 10/1!5/!32=⨯=p .(3)p P ={第一卷出现在旁边}+P{第五卷出现旁边}-P{第一卷及第五卷出现在旁边}2217551010=+-=. (4)这里事件是(3)中事件的对立事件,所以 10/310/71=-=P .(5)第三卷居中,其余四卷在剩下四个位置上可任意排,所以5/1!5/!41=⨯=P . 11. 把2,3,4,5诸数各写在一X 小纸片上,任取其三而排成自左向右的次序,求所得数是偶数的概率.解:末位数可能是2或4.当末位数是2(或4)时,前两位数字从剩下三个数字中选排,所以 23342/1/2P A A =⨯=.12. 一幢10层楼的楼房中的一架电梯,在底层登上7位乘客.电梯在每一层都停,乘客从第二层起离开电梯,假设每位乘客在哪一层离开电梯是等可能的,求没有两位及两位以上乘客在同一层离开的概率.解:每位乘客可在除底层外的9层中任意一层离开电梯,现有7位乘客,所以样本点总数为79.事件A “没有两位及两位以上乘客在同一层离开”相当于“从9层中任取7层,各有一位乘客离开电梯”.所以包含79A 个样本点,于是7799)(A A P =.13. 某人午觉醒来,发觉表停了, 他打开收音机,想听电台报时, 设电台每正点是报时一次,求他(她)等待时间短于10分钟的概率.解:以分钟为单位, 记上一次报时时刻为下一次报时时刻为60, 于是这个人打开收音机的时间必在),60,0(记 “等待时间短于10分钟”为事件,A 则有(0,60),Ω=)60,50(=A ,⊂Ω于是)(A P 6010=.61= 14. 甲乙两人相约812-点在预定地点会面。
《概率论与数理统计》习题及答案要点

概率论与数理统计第一部份 习题第一章 概率论基本概念一、填空题1、设A ,B ,C 为3事件,则这3事件中恰有2个事件发生可表示为 。
2、设3.0)(,1.0)(=⋃=B A P A P ,且A 与B 互不相容,则=)(B P 。
3、口袋中有4只白球,2只红球,从中随机抽取3只,则取得2只白球,1只红球的概率 为 。
4、某人射击的命中率为0.7,现独立地重复射击5次,则恰有2次命中的概率为 。
5、某市有50%的住户订晚报,有60%的住户订日报,有80%的住户订这两种报纸中的一种,则同时订这两种报纸的百分比为 。
6、设A ,B 为两事件,3.0)(,7.0)(==B A P A P ,则=)(B A P 。
7、同时抛掷3枚均匀硬币,恰有1个正面的概率为 。
8、设A ,B 为两事件,2.0)(,5.0)(=-=B A P A P ,则=)(AB P 。
9、10个球中只有1个为红球,不放回地取球,每次1个,则第5次才取得红球的概率 为 。
10、将一骰子独立地抛掷2次,以X 和Y 分别表示先后掷出的点数,{}10=+=Y X A {}Y X B >=,则=)|(A B P 。
11、设B A ,是两事件,则B A ,的差事件为 。
12、设C B A ,,构成一完备事件组,且,7.0)(,5.0)(==B P A P 则=)(C P ,=)(AB P 。
13、设A 与B 为互不相容的两事件,,0)(>B P 则=)|(B A P 。
14、设A 与B 为相互独立的两事件,且4.0)(,7.0)(==B P A P ,则=)(AB P 。
15、设B A ,是两事件,,36.0)(,9.0)(==AB P A P 则=)(B A P 。
16、设B A ,是两个相互独立的事件,,4.0)(,2.0)(==B P A P 则=)(B A P 。
17、设B A ,是两事件,如果B A ⊃,且2.0)(,7.0)(==B P A P ,则=)|(B A P 。
高等数学(概率论)习题及解答

高等数学(概率论)习题及解答高等数学(概率论)题及解答
1. 题一
1.1. 题目
已知事件A和B的概率分别为P(A) = 0.2,P(B) = 0.3,且P(A∪B) = 0.4,求P(A∩B)。
1.2. 解答
根据概率的加法定理,有:
P(A∪B) = P(A) + P(B) - P(A∩B)
代入已知数据得:
0.4 = 0.2 + 0.3 - P(A∩B)
P(A∩B) = 0.1
所以,P(A∩B)的概率为0.1。
2. 题二
2.1. 题目
已知某城市一天中的天气分为晴天、阴天和雨天三种情况,其中晴天的概率为0.4,阴天的概率为0.3。
现已知,当下为晴天时,随后一天也是晴天的概率为0.7;当下为阴天时,随后一天为晴天的概率为0.5。
求当下为晴天时,随后一天为阴天的概率。
2.2. 解答
设事件A为当下为晴天,事件B为随后一天为阴天。
根据条件概率的定义,有:
P(B|A) = P(A∩B) / P(A)
已知 P(A) = 0.4,P(B|A) = 0.5,代入并整理得:
0.5 = P(A∩B) / 0.4
P(A∩B) = 0.5 * 0.4
P(A∩B) = 0.2
所以,当下为晴天时,随后一天为阴天的概率为0.2。
以上是高等数学(概率论)习题及解答的部分内容,如有更多问题或需要补充,请随时告知。
概率论各章精选习题(PDF)

概率统计各章节习题§1.1 随机事件1、写出下列各试验的样本空间及指定事件所含的样本点; (i )将一枚硬币抛掷三次,{}A =第一次掷出正面、{}B =三次掷出同一面、{}C =有正面掷出; (ii )将一颗骰子掷两次,{}A =点数相同、{}B =其中一次点数是另一次的两倍、{}6C =点数之和是;2、从某图书馆里任取一本书,事件A 表示“取到数学类图书”,事件B 表示“取到中文版图书”,事件C 表示“取到精装图书”; ①试述ABC 的含义;②何种情况下,C B ⊂?;③何种情况下,A B =3、设1234,,,A A A A 为某一试验中的四个事件,试用事件的运算表达如下事件:①“四个事件中至少有一个发生”;②“恰好发生两个”;③“至少发生三个”;④“至多发生一个”;4、试述下列事件的对立事件:①A = “射击三次皆命中目标”;②B =“甲产品畅销乙产品滞销”;③C =“加工四个零件至少有一个是合格品”;5、在区间[]0,1中任取一点x ,记:203A x ⎧⎫=≤≤⎨⎬⎩⎭、1344B x ⎧⎫=<≤⎨⎬⎩⎭、 213C x ⎧⎫=≤<⎨⎬⎩⎭,试用相同的作法表示如下诸事件:①AB ;②AB ; ③()A B A C ; 6、试证明以下事件的运算公式:(i )A AB AB =;(ii )A B A AB =;§1.2 频率与概率1、任取两整数,求“两数之和为偶数”的概率;2、①袋中有7个白球3个黑球,现从中任取2个,试求“所取两球颜色相同”的概率;②甲袋中有球5白3黑,乙袋中有球4白6黑,现从两袋中各取一球,试求“所取两球颜色相同”的概率;3、①n 个人任意地坐成一排,求“甲、乙两人坐在一起”的概率;②n 个人随机地围一圆桌而坐,求“甲、乙相邻”的概率;③n 个男生、m 个女生(1m n ≤+)坐成一排,求“任意两个女生都不相邻”的概率;4、从()0,1中随机地取两个数,试求:①“两数之和小于65”的概率;②“两数之积小于14”的概率;5、①已知事件,A B 满足:AB AB =,若()P A a =,试求()P B ;②已知事件,A B 满足:()()P AB P AB =,若()P A a =,试求()P B ;6、设,A B 为两事件,且()0.4P A =,()0.7P B =,问:①在什么条件下,()P AB 取得最大值,最大值是多少?②在什么条件下,()P AB 取得最小值,最小值是多少?若()0.5P B =,结果又如何?7、某班n 名战士各有一支归自己保管使用的枪,这些枪外形完全一样;在一次夜间紧急集合中,每人随机地取一支枪,求“至少有一人拿到自己的枪”的概率;8、证明:①()()()1P AB P A P B ≥+-;②()()()()()12121n n P A A A P A P A P A n ≥+++--;9、试证明:若,A B 为两事件,则()()()14P AB P A P B -≤; §1.3 条件概率、全概率公式与贝叶斯(Bayes )公式1、已知()0.3P A =,()0.4P B =,()0.5P A B =;试求:()P AB 、 ()P A B 、()P B A 、()P B A B 、()P A B A B; 2、已知()12P A =,()13P B =,()16P A B =,试求()P A B ; 3、已知()0.8P A =,()0.7P B =,()0.2P A B -=,试求()P B A ; 4、已知()14P A =,()13P B A =,()12P A B =,试求()P AB ; 5、设一批产品中一、二、三等品各占60%、35%、5%,从中任取一件,结果不是三等品,求“取到的是一等品”的概率;6、设10件产品中有4件是不合格品,从中任取两件,已知其中一件是不合格品,求“另一件也是不合格品”的概率;7、袋中有4白1红5只球,现有5人依次从袋中各取一球,取后不放回,试求“第i (1,2,,5i =)人取到红球”的概率;8、两台车床加工同样的零件,“第一台出现不合格品”的概率是0.03,“第二台出现不合格品”的概率是0.06,加工出来的零件放在一起,并且已知第一台加工的零件比第二台加工的零件多一倍,①试求“任取一个零件是合格品”的概率;②如果取出的零件是不合格品,求“它是由第二台车床加工”的概率;9、某商店正在销售10台彩电,其中7台是一级品,3台是二级品;某人到商店时,彩电已售出2台,试求“此人能买到一级品”的概率;10、甲袋中有2只白球1只黑球,乙袋中有1只白球2只黑球,今从甲袋中任取一球放入乙袋,再从乙袋中任取一球,求“此球是白球”的概率;11、有两箱零件,第一箱装50件,其中20件是一等品;第二箱装30件,其中18件是一等品;现从两箱中随意挑出一箱,然后从该箱中先后任取两个零件,试求:①“第一次取出的零件是一等品”的概率;②“第二次取出的零件是一等品”的概率;③在第一次取出的是一等品的条件下,“第二次取出的零件仍然是一等品”的概率;④在第二次取出的是一等品的条件下,“第一次取出的零件仍然是一等品”的概率;12、玻璃杯成箱出售,每箱20只,假设各箱有0,1,2只次品的概率分别为0.8,0.1,0.1;一个顾客欲购一箱玻璃杯,在购买时售货员随机取一箱,顾客开箱随机地查看4只,若无次品,就买下这箱玻璃杯,否则退回;试求:①“顾客买下这箱玻璃杯”的概率;②“在顾客买下的一箱中,确实没有次品”的概率;13、证明:()()()()()P A B P A BC P C B P A BC P C B=+;14、设有N个袋子,每个袋子中都装有a个白球b个黑球,现从第一个袋中任取一球放入第二个袋中,然后从第二个袋中任取一球放入第三个袋中,如此下去,求“从最后一个袋中取出一白球”的概率;§1.4 事件的独立性1、假设()0.4P A=,()0.9P A B=,在以下情形下求()P B:①,A B互斥;②,A B独立;③A B⊂;2、甲乙两人独立地对同一目标射击一次,其命中率分别为0.8和0.7,现已知目标被击中,求“它是甲命中”的概率;3、若事件,A B独立,且两事件“仅A发生”与“仅B发生”的概率都是14,试求()P A与()P B;4、三人独立地破译一个密码,他们单独译出的概率分别为13、14、15,求“此密码被译出”的概率;5、一射手对同一目标独立地射击四次,若“至少命中一次”的概率为8081,试求该射手进行一次射击的命中率;6、三门高射炮独立地向一飞机射击,已知“飞机中一弹被击落”的概率为0.4,“飞机中两弹被击落”的概率为0.8,中三弹则必然被击落;假设每门高射炮的命中率为0.6,现三门高射炮各对飞机射击一次,求“飞机被击落”的概率;7、甲、乙二人轮流射击,首先命中目标者获胜;已知甲的命中率为a ,乙的命中率为b ,甲先射击,试求“甲(乙)获胜”的概率;8、甲、乙两选手进行乒乓球单打比赛,已知每局中“甲获胜”的概率为0.6,“乙获胜”的概率为0.4;比赛可采用三局两胜制或五局三胜制,问:何种赛制对甲更有利?§2.1 随机变量及其分布函数1、箱中装有次品12,a a 与正品123,,b b b ,现从中一次取出两件产品,①写出此试验的样本空间;②令ξ表示所取两件产品中的次品个数,标出ξ在每个样本点上的值;③写出{}{}0,1,ξξ=≤ {}2ξ≥所包含的样本点;2、设随机变量(..r v )X 的分布函数(..d f )为()0,0;1,03;41,36;31,6;x x F x x x <⎧⎪≤<⎪=⎨≤<⎪⎪≥⎩,试求()3P X <、()3P X ≤、()1P X >、()1P X ≥; 3、设..r v X 的..d f 为()0,1;ln ,1;1,;x F x x x e x e <⎧⎪=≤<⎨⎪≥⎩,试求:()2P X <、()03P X ≤≤、 ()2 2.5P X <<;4、已知..r v X 的分布函数为()0,0;2,01;23,12;1112,23;1,3;x x x F x x x x <⎧⎪≤<⎪⎪=≤<⎨⎪≤<⎪≥⎪⎩,试求:()3P X <、()13P X ≤<、12P X ⎛⎫> ⎪⎝⎭、()3P X =; 5、设随机变量ξ的分布函数为()F x ,试用()F x 表示下列事件的概率:{}{}{}{}{}231,23,215,4,8ξξξξξ<-<+>≤<;6、若()()121,1P X x P X x αβ≥=-≤=-,其中12x x <,试求()12P x X x ≤≤;7、①设..r v ξ的分布函数为:()0,1;arcsin ,11;1,1;x F x a b x x x <-⎧⎪=+-≤<⎨⎪≥⎩,试确定常数,a b ;②设..r v ξ的分布函数为()arctan ,F x A B x x R =+∈,试确定常数,A B ;8、①在半径为R 的圆内任取一点,求此点到圆心距离X 的分布函数及概率23P X R ⎛⎫> ⎪⎝⎭;②在ABC ∆内任取一点P ,记X 为点P 到底边BC 的距离,试求X 的分布函数;9、设()()12,F x F x 分别是两个随机变量的分布函数,,0a b >且 1a b +=,试证明:()()()12F x aF x bF x =+也是一个分布函数; §2.2 离散型随机变量及其分布律1、试判断下列分布列中所含的未知参数c :① (),1,2,,c P k k N N ξ===; ② (),0,1,2,3!k c P k k k ξ===⋅; 2、现有三只盒子,第一只盒中装有1只白球4只黑球,第二只盒中装有2只白球3只黑球,第三只盒中装有3只白球2只黑球;现任取一只盒子,从中任取3只球,以X 表示所取到的白球数,试求:①X 的分布列;②“取到白球数不少于2”的概率;3、袋中有5只球,编号为1,2,3,4,5;现从中任取3只,以X 表示3只球中的最大号码;①试求X 的分布列;②写出X 的分布函数并作图;4、已知..r v X 的..d f 为()0,0;0.5,01;0.7,13;1,3;x x F x x x <⎧⎪≤<⎪=⎨≤<⎪⎪≥⎩,试求X 的分布列; 5、已知...d r v X 的分布列为:1010.25a b -⎛⎫ ⎪⎝⎭,其分布函数为: (),1;,10;0.75,01;,1;c xd x F x xe x <-⎧⎪-≤<⎪=⎨≤<⎪⎪≥⎩,试求,,,,a b c d e ; 6、从1,2,3,4,5五个数中任取三个,按大小顺序排列记为: 123x x x <<,令2X x =,试求: X 的分布函数及()()2,4P X P X <>;7、连续“独立”地掷n 次骰子,记,X Y 分别为n 个点数的最小、最大值,试求,X Y 的分布列;8、设()X P λ~,试求X 的最大可能值,即:k 取何值时,概率()P X k =取最大值?§2.3 连续型随机变量及其概率密度1、设..r v X 的分布函数为:()20,0;,01;1,1;x F x Ax x x <⎧⎪=≤<⎨⎪≥⎩,试求:① A;②()()0.3,0.7P X ∈;③X 的概率密度函数(...p d f );2、设..r v X 的...p d f 为(),01;2,12;0,;x x f x x x ≤<⎧⎪=-≤<⎨⎪⎩其他,试求:①X 的分布函数;②32P X ⎛⎫≥ ⎪⎝⎭; 3、已知..r v X 的...p d f 为(),x f x ce x -=-∞<<+∞,试确定常数c 并求X 的..d f ;4、设..r v X 有()11;...29,36;0,;x p d f f x x ≤≤⎧⎪=≤≤⎨⎪⎩其他,若()23P X k ≥=,试确定k 的取值范围;5、设..,r v X Y 同分布(又记为:d X Y =),且X 有...p d f 为()23,02;80,;x x f x ⎧<<⎪=⎨⎪⎩其他;已知事件{}A X a =>与{}B Y a =>独立,且 ()34P A B =,试求常数a ; 6、设A 为曲线22y x x =-与x 轴所围成的区域,在A 中任取一点,求该点到y 轴的距离ξ的分布函数及密度函数;7、设[]..0,5r v U ξ~,试求“方程24420x x ξξ+++=有实根”的概率;8、设..r v ξ的...p d f 为()221,x x f x x -+-=-∞<<+∞,试求()02P ξ≤≤;9、设()2..3,2r v X N ~,试求:①()()25,2P X P X<≤>;②确定c ,使得()()P X c P X c >=<;③设d 满足()0.9P X d >≥,d 至多为多少?10、由学校到火车站有两条路线,所需时间随交通堵塞状况有所变化,若以分钟计算,第一条路线所需时间()2150,10N ξ~,第二条路线所需时间()2260,4N ξ~,如果要求:①在70分钟内赶到火车站;②在65分钟内赶到火车站;试问:各应选择哪条路线? 11、假设一机器的检修时间(单位:小时)服从12λ=的指数分布,试求:①“检修时间超过2小时”的概率;②若已经检修4小时,求“总共至少5小时检修好”的概率;12、①设()2,5X U ~,试求“对X 进行三次独立地观测中,至少有两次观测值大于3”的概率;②设顾客在某银行的窗口等待服务的时间X (以分钟记)服从参数为15的指数分布,某顾客在窗口等待服务若超过10分钟他就离开;他一个月要到银行五次,以Y 表示一个月内他未等到服务而离开窗口的次数,试求()1P Y ≥;13、对某地考生抽样调查的结果表明:考生的外语成绩(百分制)近似服从()272,N σ(0σ>未知);已知96分以上的考生占考生总数的2.3%,试求“考生成绩介于60分与84分之间”的概率;14、设()2..0,1r v N ξ~,ηξ=或ηξ=-视1ξ≤或1ξ>而定,试求η的分布;§2.4 随机变量的函数的分布1、①设...d r v X 有分布列:210131111115651530--⎛⎫ ⎪ ⎪ ⎪⎝⎭,试求2Y X =与Z X =的分布列;②设()...1,2c r v X U -~,记1,0;1,0;X Y X ≥⎧=⎨-<⎩,试求Y 的分布列; 2、设随机变量X 的概率分布为:()1,1,2,2k P X k k ===;试求sin 2Y X π⎛⎫= ⎪⎝⎭的分布律; 3、假设一设备开机后无故障工作的时间15X E ⎛⎫ ⎪⎝⎭~,设备定时开机,出现故障时自动关机;且在无故障的情况下工作2小时便关机,试求该设备每次开机无故障工作的时间Y 的分布函数()Y F y ,并指明Y 是否为连续型随机变量?4、设..r v X 的...p d f 为()[]1,8;0,;x f x ∈=⎩其他,()F x 为X的..d f ,试求随机变量()Y F X =的分布函数;5、①设()..0,1r v X U ~,试求1X -的分布;②设()..2r v X E ~,试证:21X Y e -=与221X Y e -=-均服从()0,1上的均匀分布;6、若()2..ln ,r v X N μσ~,则称X 服从对数正态分布;①试求X 的概率密度函数()X f x ;②若()2ln 1,4X N ~,求31P X e e ⎛⎫≤≤ ⎪⎝⎭; 7、设()..0,1r v X U ~,试求以下Y 的密度函数; ① 2ln Y X =- ;② 31Y X =+ ;③ X Y e = ;④ ln Y X = ;8、设()21,03;..90,;x x r v X f x ⎧<<⎪=⎨⎪⎩~其他,且2,1;,12;1,2;X Y X X X ≤⎧⎪=<<⎨⎪≥⎩,试求:①Y 的分布函数;②()P X Y ≤;§3.1 二维随机变量及其分布1、袋中有1红2黑3白共6个球,现有放回地从袋中取两次,每次取一球,以,,X Y Z 分别表示两次取到的红、黑、白球的个数,①求()10P X Z ==;②求(),X Y 的概率分布;2、袋中有10个大小相等的球,其中6个红球4个白球;现随机抽取2次,每次抽取1个,定义随机变量,X Y 如下:1,0X ⎧=⎨⎩第一次抽到红球;,第一次抽到白球;、1,0Y ⎧=⎨⎩第二次抽到红球;,第二次抽到白球;,试就以下两种情况,分别求出(),X Y 的联合分布:①第一次抽取后放回;②第一次抽取后不放回;3、将一枚硬币抛掷三次,以X 表示三次中掷出正面的次数,以Y 表示掷出正面与反面次数之差的绝对值,试求(),X Y 的联合分布;4、①假设,X Y 同分布,且101111424X -⎛⎫ ⎪ ⎪⎝⎭~,()01P XY ==,试求(),X Y 的联合分布及()P X Y =;②设,X Y 为离散型随机变量,且101111442X -⎛⎫ ⎪ ⎪⎝⎭~,1101513124Y -⎛⎫ ⎪ ⎪ ⎪⎝⎭~,已知()0P X Y <=,()14P X Y >=,试求(),X Y 的联合分布; 5、①设(),X Y 的联合概率密度为()22,1;,0,;cx y x y f x y ⎧≤≤=⎨⎩其他,(i )确定常数c ;(ii )求()(),P X Y D ∈,2:21D x y ≤≤; ②设(),X Y 具有联合密度()()6,02,24;,0,;k x y x y f x y ⎧--≤≤≤≤=⎨⎩其他,(i )确定常数k ;(ii )求()1,3P X Y ≤<、()1.5P X ≤、()4P X Y +≤;6、从()0,1中随机地取两个数,求“其积不小于316且其和不大于1”的概率; 7、设()0.5,10;..0.25,02;0,;x r v X f x x -<<⎧⎪=≤<⎨⎪⎩~其中,令2Y X =,(),F x y 为二维随机向量(),X Y 的联合分布函数,①求Y 的()...Y p d f f y ;②求1,42F ⎛⎫- ⎪⎝⎭; §3.3 条件分布1、①将2只球放入3只盒中,以,X Y 分别表示1号盒与2号盒中的球数,试求在0Y =的条件下X 的条件分布; ②从1,2,3,4,5中任取一个数,记为X ;再从1,,X 中任取一个数记为Y ,试求(),X Y 的联合分布及Y 的分布;2、设..,r v X Y 独立,且()1X P λ~,()1Y P λ~,试求给定X Y n +=时,X 的条件分布;3、①设()()3,01;,,0,;x y x X Y f x y <<<⎧=⎨⎩~其他,试求给定X x =(01x <<)时,Y 的条件密度函数()Y X f y x ;②设()()1,,0;,,0,;xy y e e x y X Y f x y y --⎧⋅>⎪=⎨⎪⎩~其他,0y ∀>,试求给定Y y =时,X 的条件密度函数()X Y f x y 及()1P X Y y >=;③设()()2221,1;,,40,;x y x y X Y f x y ⎧≤≤⎪=⎨⎪⎩~其他,试由此求条件概率 ()0.750.5P Y X ≥=;4、①设()0,1X U ~,已知X x =(01x <<),10,Y U x ⎛⎫ ⎪⎝⎭~,试求Y 的 ()...Y p d f f y ;②设ξ在区间[]0,1上随机地取值,当观察到x ξ=时,η在区间[],1x 上随机地取值,试求η的密度函数;③设()2,0;0,0;x xe x f x x λξλξ-⎧>=⎨≤⎩~,η在()0,ξ上均匀分布,试求η的密度函数;④设()45,01;0,;Y y y Y f y ⎧<<=⎨⎩~其他,给定Y y =(01y <<)时,X 的条件密度为()233,0;0,;X Y x x y f x y y ⎧<<⎪=⎨⎪⎩其他,试求()0.5P X >;5、设[]2,4Y U ~,且给定Y y =(24y ≤≤)时,()X E y ~,试求:①(),X Y 的....J p d f (联合密度函数);②试证:()1XY E ~; 6、①设,X Y 为两个随机变量,010.70.3Y ⎛⎫ ⎪⎝⎭~,且给定Y k =时, ()2,1X N k ~,0,1k =;试求X 的分布; ②设121122X ⎛⎫ ⎪ ⎪⎝⎭~,且给定X k =时,()0,Y U k ~,1,2k =;试求Y 的分布,并求EY ;7、设[]0,1X U ~,试求给定12X >时,X 的条件分布; §3.4 随机变量的独立性1、 设(),X Y 有如下联合分布:/01104114X Y b a ,且事件{}0X =与 {}1X Y +=相互独立,①确定常数,a b ;②问:,X Y 是否独立?2、设101111424X -⎛⎫ ⎪ ⎪⎝⎭~,011122Y ⎛⎫ ⎪ ⎪⎝⎭~,如果()221P X Y ==,①试求(),X Y 的联合分布;②,X Y 是否独立?3、设随机变量,X Y 独立同分布,且011X p p ⎛⎫ ⎪-⎝⎭~,令 1,0X Y Z X Y +⎧=⎨+⎩若为偶数;,若为奇数;,问:p 取何值时,,X Z 相互独立? 4、设随机向量(),X Y 具有如下的联合密度: ①(),4,0,1f x y xy x y =<<;②(),8,01f x y xy x y =<<<;试讨论以上两种情形下,,X Y 是否独立?5、①设()(),X Y U D ~,其中22:1D x y +≤,试讨论,X Y 的独立性;②设()(),X Y U G ~,其中[][]0,10,2G =⨯,试讨论,X Y 的独立性;6、设()()()2,,0;,,0,;x y ce x y X Y f x y -+⎧>⎪=⎨⎪⎩~其他,①确定常数c ;②试求X 的边缘密度及条件密度,讨论,X Y 是否独立?③求(),X Y 的联合分布函数;7、①设..,r v X Y 独立,且[]0,1X U ~,12Y E ⎛⎫⎪⎝⎭~,(i )试写出(),X Y 的联合密度函数;(ii )试求“方程220t Xt Y ++=有实根”的概率;②从长度为a 的线段的中点两边随机各选取一点,求“两点间距离小于3a ”的概率;8、试用概率方法证明:0a ∀>22x aa e dx --≤⎰9、设随机向量(),X Y 的联合密度为()1,1,1;,40,;xyx y f x y +⎧-<<⎪=⎨⎪⎩其他,试证:,X Y 不独立,但22,X Y 是独立地;§3.5 二维随机变量的函数的分布1、设,X Y 满足()30,07P X Y ≥≥=,且()()4007P X P Y ≥=≥=,试求{}()max ,0P X Y ≥;2、设..,r v X Y 具有分布:101111424X -⎛⎫ ⎪⎪⎝⎭~,011122Y ⎛⎫⎪⎪⎝⎭~;已知 ()01P XY ==,试求()max ,Z X Y X Y =∨=的分布;3、 设随机变量1234,,,X X X X 独立同分布,且 ()01i P X ==-()10.6,1,2,3,4i P X i ===,试求行列式1234X X X X X =的概率分布;4、 设,A B 为两个事件,且()14P A =,()13P B A =,()12P A B =,令1,0,;A X ⎧=⎨⎩若发生;否则,1,0,;B Y ⎧=⎨⎩若发生;否则,试求:①(),X Y 的概率分布;②22Z X Y =+的概率分布;5、设某一设备装有三个同类的电器元件,各元件工作相互独立,且工作时间服从参数为λ的指数分布;当三个元件都正常工作时,设备才正常工作;试求设备正常工作时间T 的概率分布;6、①设()(),X Y U D ~,(){},02,01D x y x y =≤≤≤≤,试求边长为,X Y 的矩形面积S 的概率分布;②设,X Y 独立同()20,1N分布,则Z =Rayleigh )分布,试求Z 的密度函数;7、设,X Y 独立,且()1X E λ~,()2Y E λ~,若{}()1min ,1P X Y e ->=,()13P X Y ≤=,试求12,λλ; 8、①设..,r v X Y 独立,且()13P Xi ==,1,0,1i =-;[)0,1Y U ~,记: Z X Y =+,试求: 102P Z X ⎛⎫≤= ⎪⎝⎭、Z 的()...Z p d f f z ;②设..,r v X Y 独立,且120.30.7X ⎛⎫ ⎪⎝⎭~,()Y Y f y ~,试求Z X Y =+的概率分布;9、①设,X Y 独立同()0,1U 分布,试求Z X Y =+的密度; ②设()()3,01;,,0,;x y x X Y f x y <<<⎧=⎨⎩~其他,试求Z X Y =-的密度;③设()()2,0,1;,,0,;x y x y X Y f x y --<<⎧=⎨⎩~其他,试求Z X Y =+的密度;④设,X Y 独立同()1E 分布,试求Z X Y =-的密度;10、(最大值与最小值分布)设12,,,n X X X 相互独立,若()12max ,,,n Y X X X =,()12min ,,,n Z X X X =,试在以下情况下求,Y Z 的分布;① i X 具有()..i d f F x ,1,2,,i n =;②诸i X 同分布,且有 ()..d f F x ,1,2,,i n =;③诸i X 为...c r v 且同分布,()i X f x ~,1,2,,i n =;④()i X E λ~,1,2,,i n =;11、设,X Y 独立同[]0,1U 分布,若(),01;1,12;X Y X Y Z X Y X Y +≤+≤⎧=⎨+-<+≤⎩,试问:Z 服从什么分布? §4.1 数学期望2、某新产品在未来市场的占有率X 是仅在()0,1上取值的随机变量,其密度函数为()()341,01;0,;x x f x ⎧-<<⎪=⎨⎪⎩其他,试求其平均占有率;3、设..r v X 的...p d f 为()2,01;0,;a bx x f x ⎧+≤≤=⎨⎩其他,若23EX =,试求,a b ;4、①设()X P λ~,试求2321Y X X =+-的数学期望;②设()1X E ~,试求()2X E X e -+; ③设()20,1X N ~,试求()2X E Xe ;5、①假设一部机器在一天内发生故障的概率为0.2,机器发生故障时全天停止工作,若一周五个工作日里无故障,可获利润10万元;发生一次故障仍可获利润5万元;发生两次故障获得利润0元;发生三次或三次以上故障要亏损2万元;试求机器一周内所获得的平均利润;②游客乘电梯从底层到电视塔顶层观光。
概率论课后习题解答

一、习题详解:1.1 写出下列随机试验的样本空间:(1) 某篮球运动员投篮时, 连续5 次都命中, 观察其投篮次数;解:连续5 次都命中,至少要投5次以上,故}{ ,7,6,51=Ω;(2) 掷一颗匀称的骰子两次, 观察前后两次出现的点数之和;解:}{12,11,4,3,22 =Ω;(3) 观察某医院一天内前来就诊的人数;解:医院一天内前来就诊的人数理论上可以从0到无穷,所以}{,2,1,03=Ω; (4) 从编号为1,2,3,4,5 的5 件产品中任意取出两件, 观察取出哪两件产品; 解:属于不放回抽样,故两件产品不会相同,编号必是一大一小,故:()}{;51,4≤≤=Ωj i j i(5) 检查两件产品是否合格;解:用0 表示合格, 1 表示不合格,则()()()()}{1,1,0,1,1,0,0,05=Ω;(6) 观察某地一天内的最高气温和最低气温(假设最低气温不低于T1, 最高气温不高于T2); 解:用x 表示最低气温, y 表示最高气温;考虑到这是一个二维的样本空间,故: ()}{216,T y x T y x ≤≤=Ω ;(7) 在单位圆内任取两点, 观察这两点的距离;解:}{207 x x =Ω;(8) 在长为l 的线段上任取一点, 该点将线段分成两段, 观察两线段的长度.解:()}{l y x y x y x =+=Ω,0,0,8 ;1.2 设A ,B ,C 为三事件, 用A;B;C 的运算关系表示下列各事件:(1) A 与B 都发生, 但C 不发生; C AB ;(2) A 发生, 且B 与C 至少有一个发生;)(C B A ⋃;(3) A,B,C 中至少有一个发生; C B A ⋃⋃;(4) A,B,C 中恰有一个发生;C B A C B A C B A ⋃⋃;(5) A,B,C 中至少有两个发生; BC AC AB ⋃⋃;(6) A,B,C 中至多有一个发生;C B C A B A ⋃⋃; (7) A;B;C 中至多有两个发生;ABC ;(8) A,B,C 中恰有两个发生.C AB C B A BC A ⋃⋃ ;注意:此类题目答案一般不唯一,有不同的表示方式。
1—7章概率论课后习题及答案

第一章 随机事件及其概率§1.1-2 随机试验、随机事件1. 多项选择题:⑴ 以下命题正确的是 ( ) A .()()AB AB A =; B .,A B AB A ⊂=若则;C .,A B B A ⊂⊂若则;D .,A B A B B ⊂=若则.⑵某学生做了三道题,以i A 表示“第i 题做对了的事件”)3,2,1(=i ,则该生至少做对了两道题的事件可表示为 ( ) A .123123123A A A A A A A A A ; B .122331A A A A A A ; C .122331A A A A A A ; D .123123123123A A A A A A A A A A A A .2. A 、B 、C 为三个事件,说明下述运算关系的含义:⑴ A ; ⑵ B C ; ⑶ AB C ; ⑷ A B C ; ⑸ AB C ; ⑹ABC .3. 一个工人生产了三个零件,以i A 与i A )3,2,1(=i 分别表示他生产的第i 个零件为正 品、次品的事件.试用i A 与i A )3,2,1(=i 表示以下事件:⑴ 全是正品;⑵ 至少有一个零件是次品;⑶ 恰有一个零件是次品;⑷ 至少有两个零件是次品.§1.3-4 事件的概率、古典概型1. 多项选择题:⑴ 下列命题中,正确的是 ( ) A .B B A B A =;B .B A B A =;C .C B A C B A = ;D .()∅=)(B A AB . ⑵ 若事件A 与B 相容,则有 ( ) A .()()()P AB P A P B =+; B .()()()()P A B P A P B P AB =+-;C .()1()()P A B P A P B =--;D .()1()()P A B P A P B =-.⑶ 事件A 与B 互相对立的充要条件是 ( ) A .()()()P AB P A P B = ; B .()0()1P AB P AB ==且;C .AB A B =∅=Ω且;D . AB =∅.2. 袋中有12只球,其中红球5只,白球4只,黑球3只. 从中任取9只,求其中恰好有4只红球,3只白球,2只黑球的概率.3. 求寝室里的六个同学中至少有两个同学的生日恰好同在一个月的概率.4. 10把钥匙中有三把能打开门,今任取两把,求能打开门的概率.5. 将三封信随机地放入标号为1、2、3、4的四个空邮筒中,求以下概率:(1) 恰有三个邮筒各有一封信;(2)第二个邮筒恰有两封信;(3)恰好有一个邮筒有三封信.6. 将20个足球球队随机地分成两组,每组10个队,进行比赛.求上一届分别为第一、二名的两个队被分在同一小组的概率.§1.5 条件概率1. 多项选择题:⑴ 已知0)(>B P 且∅=21A A ,则( )成立.A .1(|)0P AB ≥; B .1212(()|)(|)(|)P A A B P A B A B =+;C .12(|)0P A A B =;D . 12(|)1P A A B =.⑵ 若0)(,0(>>B P A P )且)(|(A P B A P =),则( )成立.A .(|)()PB A P B =;B .(|)()P A B P A =;C .,A B 相容;D .,A B 不相容.2. 已知61)|(.41)|(,31)(===B A P A B P A P ,求)(B A P3. 某种灯泡能用到3000小时的概率为0.8,能用到3500小时的概率为0.7.求一只已用到了3000小时还未坏的灯泡还可以再用500小时的概率.4.两个箱子中装有同类型的零件,第一箱装有60只,其中15只一等品;第二箱装有40只,其中15只一等品.求在以下两种取法下恰好取到一只一等品的概率:⑴将两个箱子都打开,取出所有的零件混放在一堆,从中任取一只零件;⑵从两个箱子中任意挑出一个箱子,然后从该箱中随机地取出一只零件.5.某市男性的色盲发病率为7 %,女性的色盲发病率为0.5 % .今有一人到医院求治色盲,求此人为女性的概率.(设该市性别结构为男:女=0.502:0.498)6.袋中有a只黑球,b只白球,甲、乙、丙三人依次从袋中取出一只球(取后不放回),分别求出他们各自取到白球的概率.§1.6 独立性1. 多项选择题 :⑴ 对于事件A 与B ,以下命题正确的是( ).A .若B A 、互不相容,则B A 、也互不相容;B .若B A 、相容,则B A 、也相容;C .若B A 、独立,则B A 、也独立;D .若B A 、对立,则B A 、也对立. ⑵ 若事件A 与B 独立,且0)(,0)(>>B P A P , 则( )成立.A .(|)()PB A P B =;B .(|)()P A B P A =;C .B A 、相容;D .B A 、不相容.2. 已知C B A 、、互相独立,证明C B A 、、也互相独立.3. 一射手对同一目标进行四次独立的射击,若至少射中一次的概率为8180,求此射手每次射击的命中率.*4. 设C B A 、、为互相独立的事件,求证B A AB B A -、、 都与C 独立.5. 甲、乙、丙三人同时各用一发子弹对目标进行射击,三人各自击中目标的概率分别是0.4、0.5、0.7.目标被击中一发而冒烟的概率为0.2,被击中两发而冒烟的概率为0.6,被击中三发则必定冒烟,求目标冒烟的概率.6. 甲、乙、丙三人抢答一道智力竞赛题,他们抢到答题权的概率分别为0.2、0.3、0.5 ;而他们能将题答对的概率则分别为0.9、0.4、0.4.现在这道题已经答对,问甲、乙、丙三人谁答对的可能性最大.7. 某学校五年级有两个班,一班50名学生,其中10名女生;二班30名学生,其中18名女生.在两班中任选一个班,然后从中先后挑选两名学生,求(1)先选出的是女生的概率;(2)在已知先选出的是女生的条件下,后选出的也是女生的概率.第二章 一维随机变量及其分布§2.1 离散型随机变量及其概率分布1.填空题:⑴ 当c = 时()/,(1,,)P X k c N k N ===是随机变量X 的概率分布,当c = 时()(1)/,(1,,)P Y k c N k N ==-=是随机变量Y 的概率分布; ⑵ 当a = 时)0,,1,0(!)(>===λλ k k a k Y P k是随机变量Y 的概率分布;⑶ 进行重复的独立试验,并设每次试验成功的概率都是0.6. 以X 表示直到试验获得成功时所需要的试验次数,则X 的分布律为; ⑷ 某射手对某一目标进行射击,每次射击的命中率都是,p 射中了就停止射击且至多只 射击10次. 以X 表示射击的次数,则X 的分布律为; ⑸ 将一枚质量均匀的硬币独立地抛掷n 次,以X 表示此n 次抛掷中落地后正面向上的次数,则X 的分布律为 .2.设在15只同类型的零件中有2只是次品,从中取3次,每次任取1只,以X 表示取出的3只中次品的只数. 分别求出在 ⑴ 每次取出后记录是否为次品,再放回去;⑵ 取后不放回,两种情形下X 的分布律.3.一只袋子中装有大小、质量相同的6只球,其中3只球上各标有1个点,2只球上各标有2个点,1只球上标有3个点.从袋子中任取3只球,以X 表示取出的3只球上点数的和. ⑴ 求X 的分布律;⑵ 求概率(46),(46),(46),(46)P X P X P X P X <≤≤<<<≤≤.4.某厂有7个顾问,假定每个顾问贡献正确意见的可能性都是6.0. 现在为某件事的可行与否个别地征求每个顾问的意见,并按多数顾问的意见作决策.求作出正确决策的概率.5.袋子中装有5只白球,3只黑球,从中任取1只,如果是黑球就不放回去,并从其它地方取来一只白球放入袋中,再从袋中取1只球. 如此继续下去,直到取到白球为止. 求直到取到白球为止时所需的取球次数X 的分布律.§2.2 连续型随机变量及其概率分布1.多项选择题:以下函数中能成为某随机变量的概率密度的是 ( )A .⎪⎩⎪⎨⎧<<=它其20,0,cos )(πx x x f ;B .⎪⎩⎪⎨⎧<<=它其πx x x f 0,0,2cos )( ; C .⎪⎩⎪⎨⎧<<-=它其22,0,cos )(ππx x x f ; D .⎩⎨⎧<<=它其10,0,)(x xe x f x . 2.设随机变量X 的概率分布律如右,求X 的分布函数及)32(),30(),2(≤≤<<≤X P X P X P .3.设一只袋中装有依次标有数字-1、2、2、2、3、3的六只球,从此袋中任取一只球,并以X 表示取得的球上所标有的数字.求X 的分布律与分布函数.4.设连续型随机变量X 的概率密度如右,试求:⑴ 系数A ;⑵ X 的分布函数;⑶ (0.10.7)P X <<5.设连续型随机变量X ⑴ 系数k ;⑵ X 的概率密度;⑶ (||0.5)P X <.6.设连续型随机变量X 的分布函数为()arctan ()F x A B x x R =+∈,试求:⑴ 系数A 与B ;⑵ X 的概率密度;⑶ X 在区间(,)a b 内取值的概率.(),011,1F x kx x x ⎧⎪=≤≤⎨⎪≥⎩,§2.31.设离散型随机变量X 的分布律如右,求12,22,12+=-=+=X W X V X U 的分布律.2.设随机变量X 的概率密度为,0,0,)(<≥⎩⎨⎧=-x x e x f x 求随机变量X e Y =的概率密度.3.设随机变量X 在区间(0,)π上服从均匀分布,求:⑴ 随机变量2ln Y X =-的概率密度;⑵ 随机变量sin Z X =的分布函数与概率密度.4.设连续型随机变量X 的概率密度为2/2()()x f x e x R -=∈,求||Y X =的密度.*5.设1()F x 与2()F x 分别为两个随机变量的分布函数,证明:当0,0a b ≥≥且1a b +=时,)()()(21x bF x aF x +=φ可以作为某个随机变量的分布函数.§2.4 一维随机变量的数字特征1.一批零件中有9件合格品与3件次品,往机器上安装时任取一件,若取到次品就弃置一边. 求在取到合格品之前已取到的次品数的期望、方差与均方差.2.设随机变量X 的概率密度为||()0.5,,x f x e x -=-∞<<+∞求,EX DX .3.设随机变量X 的概率密度为2(1),01(),0,x x f x -≤≤⎧=⎨⎩其它求EX 与DX .4.某路公汽起点站每5分钟发出一辆车,每个乘客到达起点站的时刻在发车间隔的5分钟内均匀分布.求每个乘客候车时间的期望(假定汽车到站时,所有候车的乘客都能上车).5.某工厂生产的设备的寿命X(以年计)的概率密度为/400.25,()0,x xef xx->⎧=⎨<⎩,工厂规定,出售的设备若在一年之内损坏可以调换.若出售一台设备可赢利100元,调换一台设备厂方需花费300元,试求厂方出售一台设备净赢利的数学期望.*6.某工厂计划开发一种新产品,预计这种产品出售一件将获利500元,而积压一件将损失2000元. 而且预测到这种产品的销售量Y(件)服从指数分布(0.0001)E. 问要获得利润的数学期望最大,应生产多少件产品?第三章 多维随机变量及其分布§3.1 二维随机变量1.设随机变量),(Y X 只取下列数组中的值:)0,0(、)1,1(-、)31,1(-、)0,2(且相应的概率依次为61、31、121、125.求随机变量),(Y X 的分布律与关于X 、Y 的边缘分布律.2.一只口袋中装有四只球,球上分别标有数字1、2、2、3. 从此袋中任取一只球,取后不放回,再从袋中任取一只球.分别以X 与Y 表示第一次、第二次取到的球上标有的数字,求X 与Y 的联合分布律与关于X 、Y 的边缘分布律.3.设随机变量),(Y X 的概率密度,其它+∞≤≤+∞≤≤⎩⎨⎧=+-y x ce y x f y x 0,0,0,),()(2 试求:⑴ 常数c ;⑵ ),(Y X 的分布函数),(y x F ;⑶ }1{≤+Y X P .4.设随机变量),(Y X 的概率密度为 4.8(2),01,0(,)0,y x x y xf x y -≤≤≤≤⎧=⎨⎩,其它求关于X 、Y 的边缘概率密度.5.设随机变量),(Y X 在G 上服从均匀分布,其中G 由x 轴、y 轴及直线12+=x y 所围成,试求:⑴ ),(Y X 的概率密度),(y x f ;⑵ 求关于X 、Y 的边缘概率密度.*6.设某班车起点站上车的人数X 服从参数为(0)λλ>的泊松分布,每位乘客在中途下车的概率为(01),p p <<乘客中途下车与否相互独立,并以Y 表示在中途下车的人数.求:⑴ 在发车时有n 个乘客的条件下,中途有m 人下车的概率;⑵ (,)X Y 的分布律.§1.设随机变量X 与Y 相互独立右表给出二维随机变量),(Y X 律及边缘分布律中的部分数值.试将 其余数值填入表中的空白处.2.设随机变量),(Y X 分布律如右:⑴ a 、b 、c 时X 与Y 相互独立?⑵写出),(Y X 的分布律与边缘分布律.3.设随机变量X 在1、2、3、4四个整数中等可能地取值,而随机变量Y 在X ~1中等可能地取一个整数.求:⑴=X 2时Y ,的条件分布律;⑵=Y 1时X ,的条件分布律.4.设随机变量),(Y X 的概率密度为其它0,0,0,),()(>>⎩⎨⎧=+-y x e y x f y x .⑴ 求)|(|x y f X Y ;⑵ 求)|(|y x f Y X ;⑶ 说明X 与Y 的独立性.*5. 箱子中装有12只开关(其中2只是次品),从中取两次,每次取一只,并定义随机变量如下:0,1,X ⎧=⎨⎩若第一次取出的是正品若第一次取出的是次品; 0,1,Y ⎧=⎨⎩若第二次取出的是正品若第二次取出的是次品 ,试在放回抽样与不放回抽样的两种试验中,求关于X 与Y 的条件分布律,并说明X 与Y 的独立性.* 6.设随机变量),(Y X 的概率密度为,||,10(,)0,cy x x f x y <--<<⎧=⎨⎩,其它求参数c 与条件概率密度)|(,)|(||y x f x y f Y X X Y .§3.31. 设),(Y X 的分布律如右,求 ⑴0|3{,}2|2{====X Y P Y X P ⑵ ),max(Y X V =的分布律;⑶ ),min(Y X U =的分布律;⑷ Y X W +=的分布律.2.设X 与Y 是相互独立的随机变量,它们分别服从参数为1λ、2λ的泊松分布. 证明Y X Z +=服从参数为21λλ+的泊松分布.3.设随机变量X 与Y 相互独立,且都服从参数为0.25p =的两点分布,记随机变量Z 为1,0,X Y Z X Y +⎧=⎨+⎩为奇数,非为奇数求X 与Z 的联合分布律与EZ .4.设随机变量X 与Y 相互独立,其概率密度分别为321100,,(),(),32000,0,yxX Y x y e e f x f y x y --⎧⎧≥≥⎪⎪==⎨⎨<<⎪⎪⎩⎩求随机变量U X Y =+的概率密度.5.某种商品一周的需求量X 是一个随机变量,其概率密度为⎩⎨⎧≤>=-0,0,)(x x xe x f x .设各周的需求量是相互独立的,试求:⑴ 两周;⑵ 三周的需求量的概率密度.6.设某种型号的电子管的寿命(以小时记)近似地服从(1160)E 分布. 随机地选取4只,将其串联在一条线路中,求此段线路的寿命超过180小时的概率。
概率论课后习题答案

概率论课后习题答案概率论与数理统计习题及答案习题⼀4.设A ,B 为随机事件,且P (A )=0.7,P (A -B )=0.3,求P (AB ). 【解】 P (AB )=1-P (AB )=1-[P (A )-P (A -B )] =1-[0.7-0.3]=0.66.设A ,B ,C 为三事件,且P (A )=P (B )=1/4,P (C )=1/3且P (AB )=P (BC )=0,P (AC )=1/12,求A ,B ,C ⾄少有⼀事件发⽣的概率.【解】 P (A ∪B ∪C )=P (A )+P (B )+P (C )-P (AB )-P (BC )-P (AC )+P (ABC )=14+14+13-112=3413. ⼀个袋内装有⼤⼩相同的7个球,其中4个是⽩球,3个是⿊球,从中⼀次抽取3个,计算⾄少有两个是⽩球的概率. 【解】设A i ={恰有i 个⽩球}(i =2,3),显然A 2与A 3互斥.213434233377C C C 184(),()C 35C 35P A P A ====故 232322()()()35P A A P A P A =+=23. 设P (A )=0.3,P (B )=0.4,P (A B )=0.5,求P (B |A ∪B )【解】 ()()()()()()()()P AB P A P AB P B A B P A B P A P B P AB -==+- 0.70.510.70.60.54-==+-33. 三⼈独⽴地破译⼀个密码,他们能破译的概率分别为15,13,14,求将此密码破译出的概率.【解】设A i ={第i ⼈能破译}(i =1,2,3),则310.6534=-= 34. 甲、⼄、丙三⼈独⽴地向同⼀飞机射击,设击中的概率分别是0.4,0.5,0.7,若只有⼀⼈击中,则飞机被击落的概率为0.2;若有两⼈击中,则飞机被击落的概率为0.6;若三⼈都击中,则飞机⼀定被击落,求:飞机被击落的概率. 【解】设A ={飞机被击落},B i ={恰有i ⼈击中飞机},i =0,1,2,3由全概率公式,得3()(|)()i i i P A P A B P B ==∑=(0.4×0.5×0.3+0.6×0.5×0.3+0.6×0.5×0.7)0.2+(0.4×0.5×0.3+0.4×0.5×0.7+0.6×0.5×0.7)0.6+0.4×0.5×0.7 =0.458习题⼆1.⼀袋中有5只乒乓球,编号为1,2,3,4,5,在其中同时取3只,以X 表⽰取出的3只球中的最⼤号码,写出随机变量X 的分布律. 【解】353524353,4,51(3)0.1C 3(4)0.3C C (5)0.6C X P X P X P X ========== 故所求分布律为4.(1)设随机变量X 的分布律为P {X =k }=!k akλ,其中k =0,1,2,…,λ>0为常数,试确定常数a . (2)设随机变量X 的分布律为P {X =k }=a/N , k =1,2,…,N ,试确定常数a . 【解】(1)由分布律的性质知1()e !ka λ-=(2) 由分布律的性质知111()N Nk k aP X k a N======∑∑即 1a =.8.已知在五重贝努⾥试验中成功的次数X 满⾜P {X =1}=P {X =2},求概率P {X =4}. 【解】设在每次试验中成功的概率为p ,则1422355C (1)C (1)p p p p -=-故 13p =所以 4451210(4)C ()33243P X ===. 21.设X ~N (3,22),(1)求P {222X P X P ---??<≤=<≤11(1)(1)1220.841310.69150.5328ΦΦΦΦ=--=-+ ? ?=-+=433103(410)222X P X P ----??(||2)(2)(2)P X P X P X >=>+<-323323222215151122220.691510.99380.6977X X P P ΦΦΦΦ-----=>+< ? ?=--+-=+- ? ? ? ?????????=+-=333(3)()1(0)0.522X P X P Φ->=>=-=- (2) c=322.由某机器⽣产的螺栓长度(cm )X ~N (10.05,0.062),规定长度在10.05±0.12内为合格品,求⼀螺栓为不合格品的概率.【解】10.050.12(|10.05|0.12)0.060.06X P X P ?-?->=>1(2)(2)2[1(2)]0.0456ΦΦΦ=-+-=-=24.设随机变量X 分布函数为F (x )=e ,0,(0),00.xt A B x ,x λ-?+≥>?(1)求常数A ,B ;(2)求P {X ≤2},P {X >3};(3)求分布密度f (x ).【解】(1)由00lim ()1lim ()lim ()x x x F x F x F x →+∞→+→-==??得11A B =??=-?(2) 2(2)(2)1e P X F λ-≤==-33(3)1(3)1(1e )e P X F λλ-->=-=--=(3) e ,0()()0,0x x f x F x x λλ-?≥'==?44.若随机变量X 在(1,6)上服从均匀分布,则⽅程y 2+Xy +1=0有实根的概率是多少?0,x f x ?<24(40)(2)(2)(2)5P X P X P X P X -≥=≥+≤-=≥=习题三(1)求关于X 和关于Y 的边缘分布;(2) X 与Y 是否相互独⽴?【解】(1)X 和Y 的边缘分布如下表(2) 因{2}{0.4}0.20.8P X P Y ===? 0.160.15(2,0.4),P X Y =≠=== 故X 与Y 不独⽴.习题四1.设随机变量X 的分布律为求【解】(1) 11111()(1)012;82842E X =-?+?+?+?= (2) 2222211115()(1)012;82844E X =-?+?+?+?=(3) 1(23)2()32342E X E X +=+=?+=5.设随机变量X 的概率密度为f (x )=??≤≤-<≤.,0,21,2,10,其他x x x x求E (X ),D (X ). 【解】12201()()d d (2)d E X xf x x x x x x x +∞-∞=332011 1.33x x x ??=+-=?122232017()()d d (2)d 6E X x f x x x x x x x +∞-∞==+-=故 221()()[()].6D XE X E X =-=7.设随机变量X ,Y 相互独⽴,且E (X )=E (Y )=3,D (X )=12,D (Y )=16,求E (3X -2Y ),D (2X -3Y ). 【解】(1) (32)3()2()3323 3.E X Y E X E Y -=-=?-?=(2) 22(23)2()(3)412916192.D X Y D X DY -=+-=?+?=习题七2.设总体X 的密度函数f (x ,θ)=22(),0,0,.x x θθθ?-<X 1,X 2,…,X n 为其样本,试求参数θ的矩法估计. 【解】23022()()d ,233x x E X x x x θθθθθθθ??=-=-=令E (X )=A 1=X ,因此3θ=X 所以θ的矩估计量为 ^3.X θ=3.设总体X 的密度函数为f (x ,θ),X 1,X 2,…,X n 为其样本,求θ的极⼤似然估计.(1) f (x ,θ)=,0,0,0.e x x x θθ-?≥?(2) f (x ,θ)=1,01,0,.x x θθ-?<【解】(1)似然函数111(,)ee eniii n nx x nn ii i L f x θθθθθθ=---==∑===∏∏1ln ln ni i g L n x θθ===-∑i i g L n x θθθ===-=∑知 1 nii nxθ==∑所以θ的极⼤似然估计量为1 Xθ=. (2) 似然函数11,01nni i i L x x θθ-==<<∏,i =1,2,…,n.1ln ln (1)ln ni i L n x θθ==+-∏由1d ln ln 0d ni i L n x θθ==+=∏知11?ln ln nniii i n nxx θ===-=-∑∏ii nxθ==-∑10.设某种砖头的抗压强度X ~N (µ,σ2),今随机抽取20块砖头,测得数据如下(kg ·cm -2):64 69 49 92 55 97 41 84 88 99 84 66 100 98 72 74 87 84 48 81 (1)求µ的置信概率为0.95的置信区间. (2)求σ2的置信概率为0.95的置信区间. 【解】76.6,18.14,10.950.05,20,x s n α===-==/20.025222/20.0250.975(1)(19)2.093,(1)(19)32.852,(19)8.907t n t n ααχχχ-==-===(1) µ的置信度为0.95的置信区间/2(1)76.6 2.093(68.11,85.089)a x n-== ? ?????(2)2σ的置信度为0.95的置信区间222222/21/2(1)(1)1919,18.14,18.14(190.33,702.01)(1)(1)32.8528.907n s n s n n ααχχ-??--??=??= ?--其中θ(0<θ<2)是未知参数,利⽤总体的如下样本值3,1,3,0,3,1,2,3,求θ的矩估计值和极⼤似然估计值. 【解】8i x E X E X x x x θθ=-=-====∑令得⼜所以θ的矩估计值31 .44x θ-== (2)似然函数86241(,)4(1)(12).ii L P x θθθθ===--∏2ln ln 46ln 2ln(1)4ln(1),d ln 628628240,d 112(1)(12)L L θθθθθθθθθθθθ=++-+--+=--==----解2628240θθ-+=得 1,2θ=.由于71,122+>所以θ的极⼤似然估计值为 7?2θ=。
概率论课后习题第3章答案

第三章 多维随机向量及其概率分布(一)基本题答案1、设X 和Y 的可能取值分别为.2,1,0;3,2,1,0,==j i j i 则与因盒子里有3种球,在这3种球中任取4个,其中黑球和红球的个数之和必不超过4.另一方面,因白球只有2个,任取的4个球中,黑球和红球个数之和最小为2个,故有j i 与ٛ且,42≤+≤j i ./),(474223C C C C j Y i X p j i j i −−===因而 或0),(===j Y i X P 2).2,1,0;3,2,1,0,4(<+j i ==>+j i j i于是 ,0)0,0(1111======y Y x X P P ,0)0,0(2112======y Y x X P p.35/1/)0,0(472212033113=======C C C C y Y x X P p即 2、X 和. ⎥⎦⎤⎢⎣⎡04.032.064.0210~X ⎥⎦⎤⎢⎣⎡25.05.025.0210~Y 由独立性知,X 和Y 的联合分布为3、Y 的分布函数为显知有四个可能值:).0(0)(),0(1)(≤=>−=−y y F y e y F y ),(21X X }{{}{}11−=e ,2,10,0).1,1(),0,1(),1,0(),0,0(121−≤=≤≤===Y P Y Y P X X P 易知{}{}{}{}{},221−−−=e e 12<=P ,10,1,02,11,02121≤≤>====>≤===Y Y Y P X X P Y Y P X X P{}{}{},212,10,12121−=≤<=≤>===e e Y P Y Y P X X P {}−− {}{}.22,11,1221−=>=>>===e Y P Y Y P X X P于是,可将X 1和X 24、∑=====nm m n P n X P 0),()(ηζ∑=−−−−=nm mn m n e m n m p p 0)!(!)1(λλ()[]).,2,1,0(!1!)1()!(!!!==−+=−−=−−−=−∑n n e p p n e p p m n m n n e n n n mn m nm n λλλλλλ即X 是服从参数为λ的泊松分布.∑∑∞=−−∞=−−−−−=−−==mn mn m n mn m m mn m n m n p m e p em n m p p m Y P )!()1(!)!(!)1()(λλλλλ).,2,1,0(,!)(!)()1( ==⋅=−−−−m m ep e e m ep pmp mλλλλλλ即Y 是服从参数为λp 的泊松分布.5、由定义F (y x ,)=P {}∫∫∞−∞−=≤≤x y dxdy y x y Y x X .),(,ϕ因为ϕ(y x ,)是分段函数,要正确计算出F (y x ,;1>y ),必须对积分区域进行适当分块:等5个部分.10,10,1;1,1;10,100≤≤≤≤>>>≤≤<x y x y x y y x 或;0<≤≤x (1)对于 有 F (,00<<y x 或y x ,)=P{X ≤,x Y ≤y}=0; (2)对于 有 ;,10,10≤≤≤≤y x 2204),(y x vdudv u y x F x y ==∫∫(3)对于, 有 10,1≤≤>y x {};,1),(2y y Y X P y x F =≤≤= (4)对于, 有 10,1≤≤>x y {}21,),(x Y x X P y x F =≤≤=; (5)对于 有 ,1,1>>y x 1),(=y x F .故X 和Y 的联合分布函数⎪⎪⎪⎩⎪⎪⎪⎨⎧<<≤≤<<≤≤≤≤≤≤<<=.1,1,.1,10,1,,1,10,,10,10,,00,0),(2222y x y x y y x x y x y x y x y x F 或6、(1) ,0,0;0),(,00>>=≤≤y x y x F y x 或),(y x F =∫∫+−x y t s dsdt ze)2())(())((200202yt x s y t x se e dt e ds e−−−−−−==∫∫=)1)(1(2y x e e −−−−即⎩⎨⎧>>−−=−−.,0,0,0),1)(1(),(2其它y x e e y x F y x (2)P ()()220(),22x x y x yxy xY X f x y dxdy dx e dy e e d +∞+∞−−−−<≤===−∫∫∫∫∫x∫∫∞+−−−∞+−−=−−=03220)(2)1(2dx e e dx e e x x x x .312131(2)2131(2023=−−=−=∞+−−x x e e7、(1)时,0>x ,0)(,0;)(=≤==∫∞+−−x f x e dy e x f X Xx y X 时 即 ⎩⎨⎧≤>=−.0,0,0,)(x x e x f x X (2){}2/111210121),(1−−≤+−−−+===≤+∫∫∫∫e e dy e dxdxdy y x f Y X P y x x xy8、(1)(i )时,,;),()(计算根据公式∫∞+∞−=dy y x f x f X 0≤x 当10;0)(<<=x x f X 当时()();24.224.2)2(8.4)(202x x x y dy x y x f xx X −=−=−=∫0)(,1=≥x f x X 时当即⎩⎨⎧<<−=.,0;10),2(4.2)(2其它x x x x f X (ii ) 利用公式计算. 当∫∞+∞−=dx y x f y f Y ),()(;0)(,0=≤y f y Y 时,10时当<<y112)22(8.4)2(8.4)(y y Y x x y dx x y y f ∫−=−=⎥⎥⎦⎤⎢⎢⎣⎡⎟⎟⎠⎞⎜⎜⎝⎛−−⎟⎠⎞⎜⎝⎛−=222128.42y y y );43(4.2)2223(8.422y y y y y y +−=+−=当时,1≥y .0)(=y f Y 即⎩⎨⎧<<+−=.0;10),43(4.2)(2其它y y y y y f Y 121111222211111(2)((1(,1(,)1.22222P X Y P X Y f x y dxdy dx dxdy +∞+∞⎧⎫<<=−≥≥=−=−=⎨⎬⎩⎭∫∫∫∫∪58、47809、本题先求出关于x 的边缘概率密度,再求出其在2=x 之值. 由于平面区域D 的面积为)2(X f ,2121=dx =∫x S e D 故(X,Y )的联合概率密度为⎪⎩⎪⎨⎧∈=.,0;),(,21),其它D y x y x (f易知,X 的概率密度为∫∞+∞−⎪⎩⎪⎨⎧<<==,,0,1,21),()(2其它e x xdy y x f x f X 故.41221)2(=×=X f 10、(1)有放回抽取:当第一次抽取到第个数字时,第二次可抽取到该数字仍有十种可能机会,即为 k {}).9, ,1,0(101====i k Y i X P (2)不放回抽取:(i )当第一次抽取第)90(≤≤k k 个数时,则第二次抽到此(第个)数是不可能的,故 k {}.)9,,1,0,; =k i k (0====i k Y i X P(ii )当第一次抽取第个数时,而第二次抽到其他数字(非k )的机会为,知)90(≤≤k k 9/1{}.)9,,1,0,; =k i k (9/1≠===i k Y i X P 11、(1)因∫−=−=12,)1(12)1(24)(yy y ydx x y f η.,0)(;10其它=≤≤y f y n 故在0≤y ≤1时,⎩⎨⎧≤≤−−=;1)1/()1(2)(2其它x y y x y x f ηξ因()∫−=−=x y x ydy x x f 022,)1(12124)(ξ.,0)(;10其它=≤≤x f x ξ故在0≤x ≤1时,⎩⎨⎧≤≤=.0,0/2)(2其它x y x y x y f ξη(2)因;1,121)(2/12∞≤≤==∫x x nxdy y x X f x x ξ;,0)(其它=x f ξ故在1≤x<时,∞⎪⎩⎪⎨⎧<<=.,1121)(其它x y xnxy x y f ξη因 ⎪⎪⎪⎩⎪⎪⎪⎨⎧∞<<=≤<==∫∫∞∞,002121102121)(22/12其它y y dx y x y dx y x y f y y η 故在10≤<y 时,⎪⎩⎪⎨⎧∞<<=;011)(2其它x y y x x y f ξη 而在,1时∞<<y ⎪⎩⎪⎨⎧∞<<=.0)(2其它x y x yx y f ξη(3)在x >0,.0,0)(;0,)(≤=>==∫∞−−x x f x e dy e x f x xy ξξ⎪⎩⎪⎨⎧>=−.0,)(其它x y e x y f y x ξη ;0,)(0>==∫−−y ye dx e y f y yy η .故在y>0时,0,0)(≤=y y f η⎪⎩⎪⎨⎧<<=.0,01)(其它y x y y x f ηξ12、1(1)(2)2(),0(1)(1)X n n n n n f x dy x x y x ∞−−−−==+++∫>,故12(1)(2)0,(/1)0.n nY X n y y f y −⎧−+>=⎨⎩其它 13、X 和Y 是否独立,可用分布函数或概率密度函数验证.方法一:X 的分布函数的分布函数分别为 Y x F X 和)()(y F Y ⎩⎨⎧<≥−=+∞=−,0001),()(5.0x x e x F x F x X ⎩⎨⎧<≥−=+∞=−.0001),()(5.0y y e y F y F yY 由于独立.Y X y F x F y x F Y X 和知),()(),(={}{}{}[][]1.005.005.0)1.0(1)1.0(11.01.01.0,1.0−−−=⋅=−⋅−=>⋅>=>>=e e e F F Y P X P Y X P Y X αY X Y X x f x f y x f Y X 和分别表示和),,()()(),,(方法二:以的概率密度,可知 ⎩⎨⎧≥≥=∂∂∂=+−.00,025.0),(),()(5.02其它y x e y x y x F y x f y x ∫∞+∞−−⎩⎨⎧<≥==,0005.0),()(5.0x x e dy y x f x f x X ∫∞+∞−−⎩⎨⎧<≥==.00,05.0),()(5.0y y e dx y x f y f yY ∫∫∞+∞+−+−==>>==1.01.01.0)(5.0.25.0}1.0,1.0{.),()(),(e dxdy e Y X P a Y X y f x f y x f y x Y X 独立和知由于)()(),(j i j i y Y P x x P y Y x X P =⋅====14、因知X 与Y 相互独立,即有 . )3,2,1,2,1(==j i 首先,根据边缘分布的定义知 .2418161),(11=−===y Y x X P 又根据独立性有),(61)()(},{2411111i x X p y Y p x X p y Y x X p ===⋅===== 解得41)(==i x X P ,从而有 1218124141),(31=−−===y Y x X P 又由 )()(),(2121y Y P x X P y Y x X P =⋅====, 可得 ),(41812y Y P == 即有21)(2==y Y P , 从而 838121),(22=−===y Y x X P .类似地,由),()(),(3131y Y P x X P y Y x X P ===== 有),(411213y Y P ==得31)(3==y Y P ,从而,.111),(31=−===y Y x X P 最后=)(2x X P =1+3+1=3. 将上述数值填入表中有1x1/24 1/8 1/12 1/4 2x1/8 3/8 1/4 3/4 {}j P y X P j ⋅==1/6 1/2 1/3115、本题的关键是由题设P{X 1X 2=0}=1,可推出P{X 1X 2≠0}=0;再利用边缘分布的定义即可列出概率分布表.(1)由P{X 1X 2=0}=1,可见易见,0}1,1{}1,1{2121=====−=X X P X X P 25.0}1{}0,1{121=−===−=X P X X P 5.0}1{}1,0{221=====X P X X P 25.0}1{}0,1{121=====X P X X P 0}0,0{21===X X P121212.16、(1) ⎩⎨⎧<<=,,0,10,1)(其他x x f X ⎪⎩⎪⎨⎧≤>=−.0,0,021)(2y y ey f yY 因为X ,Y 独立,对任何y x ,都有 ).,()()y x f y f x Y =⋅(f X ⎪⎩⎪⎨⎧><<=−.,0,0,10,21),(2其他所以有y x e y x f y(2)二次方程 有实根,△ t Y Xt t 中022=++,04)2(2≥−=Y X ,02≥−Y X 即,2X Y ≤ 故=)(有实根t P dydx e dydx y x f X Y P yx y x 2122221),(}{−≤∫∫∫∫==≤∫−−=1022)(dx ex y=dx edx edx x x x 2101010222221211)21(−−∫∫−=−=−πππ21−=[∫∫∞−∞−−−−1022222121dx edx exx ππ].1445.08555.01]5.08413.0[21)]0()1([21=−≈−−≈Φ−Φ−=ππ17、(1)因为X ,Y 独立,所以 .⎩⎨⎧>>==+−.,0,0,0,)()(),()(其他y x e y f x f y x f uy x Y X λλμ(2)根据Z 的定义,有 P{z=1}=P{Y ≥X}∫∫∫∫∞+∞−+−≥==)(),(xy x xy dydx e dydx y x f μλλμ∫∫∞+∞+−−=)(dx dy e e xy x μλμλ ),0u dx ee x x +=⋅=∫∞+−−λλλμλ{}{110=−==Z P Z P Z 的分布函数为⎪⎪⎩⎪⎪⎨⎧≥<≤+<=.1,1,10,,0,0)(z z z z F Z μλμ18、∵X 、Y 分别仅取0,1两个数值,∴Z 亦只取0,1两个数值. 又∵X 与Y 相互独立,∴{}{}{}{}==========00)0,0(0),max(0Y P X P Y X P Y X P Z P 1/2×1/2=1/4, 故{}{}.4/34/110111=−==−===Z P Z P 19、 X 由2×2阶行列式表示,仍是一随机变量,且X=X 1X 4--X 2X 3,根据X 1,X 2,X 3,X 4的地位是等价且相互独立的,X 1X 4与X 2X 3也是独立同分布的,因此可先求出X 1X 4和X 2X 3的分布律,再求X 的分布律. ,则X=Y 1--Y 2.随机变量Y 1和Y 2独立同分布:322411,X X Y X X Y ==记}{}{}{{}.84.016.01}0{0112121=−========Y P Y Y P Y P 16.01,132===P X X P 显见, 随机变量X=Y 1--Y 2有三个可能值--1,0,1.易见 P{X=--1}=P{Y 1=0,Y 2=1}=0.84×0.16= 0.1344, P{X=1}=P{Y 1=1,Y 2=0}=0.16×0.84=0.1344, P{X=0}=1--2×0.1344=0.7312. 于是,行列式的概率分布为 4321X X X X X =~ ⎥⎦⎤⎢⎣⎡−1344.07312.01344.010120、因为{Z=i }={X+Y=i }={X=0,Y=i }}.0,{}1,1{==−==Y i X i Y X ∪ ∪∪ 由于上述各事件互不相容,且注意到X 与Y 相与独立,则有 ∑∑==−===−====i k ik k i Y P k X P k i Y k X P i Z P 00}{}{},{}{∑=+−−−−−=−−=iik ki n ki k i nkn kk n P p pC P p c 022111()1()1∑=−−+ik k i n k n in n C Cp 02121)(,,1,0,)1(212121n n i p p C i n n i i n n+=−=−++).,(~21p n n B Y X Z ++=故注:在上述计算过程中,已约定:当r>n 时,用到了公式 并,0=rnC .12121∑=+−=ik i n n k i n k n C C C21、X 和Y 的概率分布密度为},2)(exp{21)(22σσπy x x f X −−=);(+∞<<−∞x ⎩⎨⎧≤≤−=.,0,),2/(1)(其它πππy y f Y 因X 和Y 独立,考虑到 )仅在[)(y f Y ππ,−]上才有非零值,故由卷积公式知Z 的概率密度为.221)()()(222)(dy edy y f y z f z f a y z Y X Z ∫∫−−−−∞+∞−=−=ππμσππ令σμ−−=y z t ,则上式右端等于.(2122122⎥⎦⎤⎢⎣⎡⎟⎠⎞⎜⎝⎛−−Φ−−+Φ=∫−+−−−σμπσμππππσμπσμπz z dt e z z t 22、(1)由题设知 {}y X X P y M P y F n M ≤=≤=),,max()()(1),,(1y X y X P n ≤≤= )()()()()(121y F y F y X P y X P y X P Xn X n =≤≤≤=.∵),1(],0[~:,,1n i U X X X i n ≤≤θ独立且同分布 ∴⎪⎩⎪⎨⎧><<≤=,0,1,0,,0,0)(x x x x x F i X θθ∴⎪⎪⎩⎪⎪⎨⎧≥<<≤=.,1,0,,0,0)(θθθy y y y y F n n M 故⎪⎩⎪⎨⎧<<=−.,0,0,)(1其它θθy ny y f n n M(2){}y X X P y N P y N P y F n N >−=>−=≤=),,min(1)(1)()(1()y X P y X P y X P y X y X y X P n n >>>−=>>>−= )()(1,,,12121()[])(11)(11y F y X P i X i ni −−=>Π−==故 ⎪⎩⎪⎨⎧<<−=⎪⎩⎪⎨⎧<<−−−=−−其它其它,0,00,)(,001(1()(11y y n y y n y f n n n N θθθθθ 23、由题设容易得出随机变量(X ,Y )的概率密度,本题相当于求随机变量X 、Y 的函数S=XY 的概率密度,可用分布函数微分法求之.依题设,知二维随机变量(X ,Y )的概率密度为()()()⎩⎨⎧∉∈=G y x Gy x y x f ,,0,2/1,若若 设为S 的分布函数,则 当{s S P s F ≤=)(}0≤s 时,()0=s F ; 当时, .2≥s ()1=s F 现设0<s<2. 曲线s xy =与矩形G 的上边交于点(s,1);位于曲线s xy =上方的点满足s xy >,位于下方的点满足s xy <. 故(){}{}{}).ln 2ln 1(2211211121s sdy dx dxdy S XY P s XY P s S P s F s x s sxy −+=−=−=>−=≤=≤=∫∫∫∫>于是,⎩⎨⎧≥≤<<−=.20,0,20,2/)ln 2(ln )(s s s s s f 或若若(二)、补充题答案1.由于即{},0)(),,min(,,max =<==Y X P Y X 故知ηξηξ{}{}{}03,23,12,1=========Y X P Y X P Y X P ;又易知{}{}{}{},9/1111,11,1==⋅=======ηξηξP P P Y X P{}{},9/12,22,2======ηξP Y X P {}{},9/13,33,3======ηξP Y X P {}{}{},9/29/19/11,22,11,2=+===+=====ηξηξP P Y X P{}{}{},9/22,33,22,3===+=====ηξηξP P Y X P {}.9/29/711,3=−===Y X P 所以2.(1)x{}.,2,1,0,0,)1( =≤≤−===n n m P P C n X m Y P m n {}(2){}{}n X P n X m Y P m Y n X P ======,.,2,1,0,0,!)1( =≤≤⋅⋅−=−−n n m e P P C n m n mm n λλ3.22)1()1()1()0()0()1(p p Y P X P Y P X P z P +−===+====)1(2)0()1()1()0()0(p p Y P X P Y P X P z P −===+====而,由2)1,1()1,1(p Y X P Z X P ======),1()1()1,1(=====Z P X P Z X P 得. 2/1=p 5.:设随机变量ξ和η相互独立,都服从分 )1,0(N 布.则⎭⎬⎫⎩⎨⎧+−⋅=)(21exp 21),(22y x y x p π.显然, ,),(),(∫∫∫∫<SGdxdy y x p dxdy y x p,其中 G 和S 分别是如图所示的矩形ABCD 和圆.22/)21(),(2∫∫∫−−=a ax Gdx e dxdy y x p π,令,sin ,cos ϕγϕγ==y x 则 ∫∫∫∫=ππ20221),(a aSdxdy y x p 所以221212/a aaxe dx e −−−−<∫π.6.设这类电子管的寿命为ξ,则(1)三个管子均不要替换的概率为;(2)三个管子均要替换的概率为 .∫∞+==>1502.3/2)/(100)150(dx x P ξ21(−27/8)3/2(3=27/1)3/3=7.假设总体X 的密度函数为,分布函数为,第次的观察值为,独立同分布,其联合密度函数)(x f ,(1x f )(x F )()2x f i (n x )1(n i X i ≤≤i X )(),1n f x f x =.依题意,所求的概率为{}∫∫∫∫∫∫∞+∞−∞−∞−∞−−−−=−==>>><n n n nx i x x x x n n nn nn n i n n n n dx x f dx x f dx x f dx x f dx dx xx f X X X X X X P 112211111,...,2,1121)(...)()()(),,(.,...,,∫∫∞+∞−∞+∞−−−==)()()()(11n n n n n n n x dF x F dx x f x F.1)(1n x F nn n=∞−∞+=8.)(),()(21211211n P n k P n k P =+=+===+=ξξξξξξξξ)()()(2121n P k n P k P =+−===ξξξξ.由普哇松分布的可加性,知服从参数为的普哇松分布,所以 21ξξ+21λλ+)(21212112121!)()!(!)(λλλλλλλλξξξ+−−−−+−⋅==+=e n e k n ek n k P n k n k.1211211kn kk n −⎟⎟⎠⎞⎜⎜⎝⎛+−⎟⎟⎠⎞⎜⎜⎝⎛+⎟⎟⎠⎞⎜⎜⎝⎛=λλλλλλ9.当,0≤z (),0)(=≤=z Z P z F z ,0>z 当()z Z P z F z ≤=)(∫∫−+−=20)2(02xz y x z dy e dx∫∫−−−−−−−==202012x z z z y z x ze e dy e dxe ,所以 Y X z 2+=的分布函数为 ⎩⎨⎧>+−≤=−.0,)1(1,0,0),(z e z z y x F z10.由条件知X 和Y 的联合密度为⎪⎩⎪⎨⎧≤≤≤≤=其他若,0,31,31,41),(y x y x p以表示随机{})()(∞<<−∞≤=u u U P u F 变量U 的分布函数.显然,当0≤u 时, 0)(=u F ;当时,; 2≥u 1)(=u F 当,则20<<u []∫∫∫∫≤−uy x y x p ||,(≤−−−=−−===uy x u u dxdy dxdy u F ||2)2(411)2(44141))(2u−于是,随机变量的密度为⎪⎩⎪⎨⎧<<−=其他,0;20),2(21)(u u u p .11.记为这3个元件无故障工作的时间,则的分布函数321,,X X X ),,min(321X X X T ={}[][].)(1),,min(1(31321t X P t X X X P t F T −=>−(11)13X P t ≤−−=>)()t T P =≤=⎩⎨⎧≤>−=∴⎩⎨⎧=≤>−=−−,0,0,0,1)()3,2,1(,0,0,0,1)(~3t t e t F i t t e t F X t T t i λλ∵ 故 ⎪⎩⎪⎨⎧≤>==−.0,0,0,3)(')(3t t e t F t f t T T λλ。
概率论课后题答案.

7. 人体血型的一个简化模型包括4种血型和2种抗体: A、B、AB与O型, 抗A与抗B. 抗体根据血型与人的血液以
不同的形式发生作用. 抗A只与A、AB型血发生作用, 不与
B、O型血作用, 抗B只与B、AB型血发生作用, 不与A、O
型血作用, 假设一个人的血型是O型血的概率为0.5, 是A
型血的概率为0.34, 是B型血的概率为0.12, 求: (1) 抗A, 抗B分别与任意一人的血型发生作用的概率;
求P(B).
解 由于 P(AB)=P(A)+P(B)-P(A+B)
=P(A)+P(B)-1+P(A+B) =P(A)+P(B)-1+P(A B) 所以, P(A)+P(B)-1=0 即, P(B)=1-P(A)=1-p
第一章习题1.3(第19页)
2. 在1500个产品中, 有400个次品, 1100个正品, 从
5. 进行一个试验: 先抛一枚均匀的硬币, 然后抛一个
均匀的骰子,
(1) 描述该试验的样本空间;
(2) 硬币是正面且骰子点数是奇数的概率是多少?
解 (1) 设试验是观察硬币正反面和骰子的点数, 则 ={ (正面, 1点), (正面, 2点), (正面, 3点), (正面, 4点), (正面, 5点), (正面, 6点), (反面, 1点), (反面, 2点), (反面, 3点), (反面, 4点), (反面, 5点), (反面, 6点), } (2) P=3/12=1/4=0.25
1. 某城市共发行三种报纸A, B, C, 已知城市居民订购
A的占45%, 订购B的占35%, 订购C的占30%, 同时订购A
与B的占10%, 同时订购A与C的占8%, 同时订购B与C的占 5%, 同时订购A, B, C的占3%, 求下列事件的概率: (5) 至少订购一种报纸; P{至少订购一种报纸}=P{只订购一种报纸} +P{正好订购两种报纸}+P{订购三种报纸}=0.9 或 P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC) +P(ABC)=0.9 (6) 不订购任何报纸; P{不订购任何报纸}=1-P{至少订购一种报纸} =1-0.9=0.1
概率论重点及课后题答案5
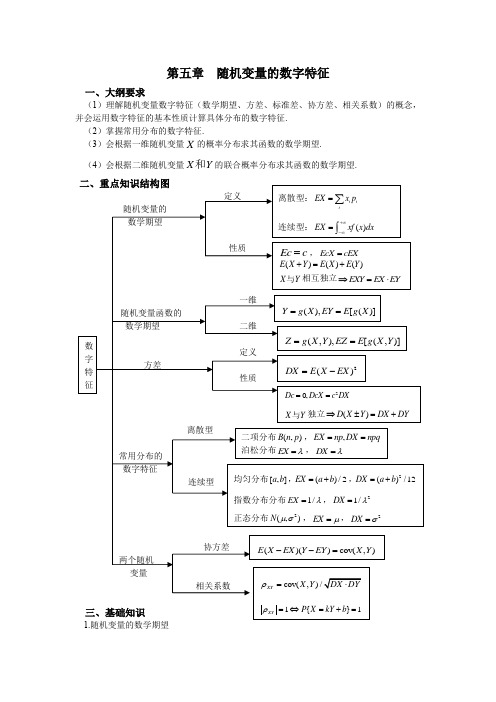
第五章随机变量的数字特征一、大纲要求(1)理解随机变量数字特征(数学期望、方差、标准差、协方差、相关系数)的概念,并会运用数字特征的基本性质计算具体分布的数字特征.(2)掌握常用分布的数字特征.(3)会根据一维随机变量X的概率分布求其函数的数学期望.和的联合概率分布求其函数的数学期望.(4)会根据二维随机变量X Y1.随机变量的数学期望(1)离散型随机变量的数学期望 定义若离散型随机变量X 的分布律是{}i i p P X x ==,(1,2,)i = ,且级数i i ix p ∑绝对收敛,则称此级数的和为X 的数学期望(或均值),记为EX .即i i iEX x p =∑简单地说,离散型随机变量的数学期望等于各个取值与对应概率的乘积之和. (2)连续型随机变量的数学期望 定义若随机变量X 有概率密度函数()f x ,并且积分()xf x dx +∞-∞⎰绝对收敛,则称此积分为X 的数学期望,记为EX ,即()EX xf x dx +∞-∞=⎰2.随机变量函数的数学期望(1)离散型随机变量函数的数学期望 设二维离散型随机变量(,)X Y 的分布律为{,}i j ij P X x Y y p ===(,1,2,)i j =如果,(,)ijiji jg x y p∑绝对收敛,则(,)g X Y 的数学期望存在,且有,(,)(,)i j ij i jEg X Y g x y p =∑(2)连续型随机变量函数的数学期望设二维连续型随机变量(,)X Y 的分布密度函数为(,)f x y ,如果(,)(,)g x y f x y dxdy +∞+∞-∞-∞⎰⎰绝对收敛,则(,)g X Y 的数学期望存在,且有(,)(,)(,)Eg X Y g x y f x y dxdy +∞+∞-∞-∞=⎰⎰特别有(,)(,)()X EXxf x y dxdy x f x y dy dx xf x dx +∞+∞+∞+∞+∞-∞-∞-∞-∞-∞⎡⎤===⎢⎥⎦⎣⎰⎰⎰⎰⎰ 式中,()X f x 为X 的分布密度函数.3.数学期望的性质性质1一个常数c 的数学期望等于这个常数,即Ec c =. 性质 2 设c 是常数,若随机变量X 的数学期望EX 存在,则EcX 也存在,并且有EcX cEX =.性质 3 若随机变量(,)X Y 的数学期望存在,则X Y +的数学期望也存在,并且有()E X Y EX EY +=+.性质4 若性质3的条件成立,且X Y 与相互独立,则EXY 存在,且有()E XY EX =EY .4.方差和标准差定义设X 是一个随机变量,若2()E X EX -存在,则称2()E X EX -为X 的方差,记作DX ,即2()DXE X EX =-.X 的标准差或均方差.对于离散型随机变量X ,若有分布律i p ,则2()i i iDX x EX p =-∑.对于连续型随机变量X ,若有密度函数()f x ,则2()()DX x EX f x dx +∞-∞=-⎰5. 方差的性质性质10Dc =(c 是常数). 性质22DcXc DX =(c 是任意常数).性质3当X Y 与相互独立时,()()()D X Y D X D Y ±=+.性质40DX =的充要条件是X 以概率1取常数c ,即{}1P X c ==(显然,应有EX c =).6.协方差与相关系数 对于随机变量X Y 与,若()()E X E X Y E Y --存在,则称其为随机变量X Y 与的协方差,记作c o v (,)[()(X Y E X E X Y E Y=--.若X Y 与的方差都不等于零.称cov(,)/XY X Y ρ=为随机变量X Y 与的相关系数.定理1对给定的二维随机变量(,)X Y , (1)若X Y 与独立,则cov(,)0X Y =; (2)[]2cov(,)()()X Y D X D Y ≤.定理2 对给定的二维随机变量(,)X Y ,XY ρ为X Y 与的相互系数, (1)若X Y 与独立,则0XY ρ=;(2)11XYρ-≤≤,当且仅当X Y 与有严格的线性关系时,等号成立.若(,)X Y 服从二维正态分布,则X Y 与独立的充要条件是X Y 与不相关,即0XY ρ=.定理3 若(,)X Y 是二维随机变量,则(1)()cov(,)E XY EX EY X Y =⋅+;(2)()()()2cov(,)D XY D X D Y X Y +=++.对不相关的随机变量X Y 与,必有()E XY EX EY =⋅,()()()D X Y D X D Y +=+若12,,,n X X X 是两两独立的随机变量,则必有11()n nk k k k D X DX ===∑∑7.矩定义设X 为随机变量,c 为常数,k 为正整数,则[()]kE x c -称为X 关于c 点的k 阶矩.(1)当0c =时,()k k a E X =称为X的k 阶原点矩;(2)当()c E X =时,[()]k k E X EX μ=-称为X 的k 阶中心矩.四、典型例题例1 设随机变量X 在区间[1,2]-上服从均匀分布,随机变量100010X Y X X >⎧⎪==⎨⎪-<⎩当当当则方差()D Y =_________. 解X 的密度函数为112()30x f x ⎧-≤≤⎪=⎨⎪⎩当其他2012{0}33P X dx >==⎰,0111{0}33P X dx -<==⎰,{0}0P X ==因此211100(1)333EY =⨯+⨯+-⨯=222221100(1)133EY =⨯+⨯+-⨯=2218()199DY EY EY =-=-= 例2设随机变量X Y 与的方差存在且不等于0,则()D X Y DX DY +=+是X Y 与(). (A )不相关的充分条件,但不是必要条件(B )独立的必要条件,但不是充分条件 (C )不相关的充分必要条件 (D )独立的充分必要条件 解若X Y 与独立,则一定有()D XY DX DY +=+.但若()D X Y DX DY +=+ ,则X Y 与不一定独立.因此()D XY DX DY +=+是X Y 与独立的充分条件,但不是必要条件.因此B 项不正确.从而D 项也不正确. 例3设随机变量X 的概率密度为2330(,)0x x f x θθθ⎧<<⎪=⎨⎪⎩当其他已知7{1}8P X>=,求θ和EX 的值解由7{1}8P X>=,得71{1}1{1}188P X P X ≤=->=-= 又因为211331{1}(,)8x P Xf x dx dx θθ-∞≤===⎰⎰所以2θ=,3233()82x EXxf x dx dx +∞-∞===⎰⎰例4 设A B 、是两个事件,则随机变量11A X A ⎧=⎨-⎩当出现当不出现,11B Y B ⎧=⎨-⎩当出现当不出现试证明随机变量X Y 与不相关的充分必要条件是A B 与相互独立. 证设1212(),(),()P A p P B p P AB p ===,由数学期望定义可得11()(1)()()()21EX P A P A P A P A p =⨯+-⨯=-=-同理221EYp =-由于XY 只取两个可能值1和-1,可见{1}()()()()P XY P AB P AB P AB P A B ==+=+()1()P AB P A B =+-()1()()()P AB P A P B P AB =+--+121221p p p =--+1212{1}1{1}2P XY P XY p p p =-=-==+-所以12121{1}(1){1}4221EXYP XY P XY p p p =⨯=+-⨯=-=--+从而1212cov(,)44X Y EXYEX EY p p p =-⋅=-又因为X Y 与不相关的充要条件为cov(,)0X Y =,即12121212440p p p p p p -=⇒=即A B 与相互独立.例5若连续型随机变量X 的密度函数为201()0ax bx c x f x ⎧++<<=⎨⎩当其他 已知12EX=,320DX =,求系数a b c 、、. 解由于()1f x dx +∞-∞=⎰,所以120()1ax bx c dx ++=⎰,即11132a b c ++=(1) 已知12EX =,所以有1201()2x ax bx c dx ++=⎰,即11114322a b c ++=(2) 由22()DX EX EX =-知225EX =,所以12202()5x ax bx c dx ++=⎰,即11125435a b c ++=(3) 联立式(1)(2)(3),解得12,12,3a b c ==-=.例6假设在国际市场上每年对我国某种出口商品的需求量是随机变量X (单位:t ),已知X 服从[2000,4000]上的均匀分布,设每售出这种商品1t ,可为国家挣得外汇3万元,但若销售不出而囤积于仓库,则每吨需浪费保养费1万元,问应组织多少货源,才能使国家的收益最大?解用y 表示预备某年出口的此种商品量(20004000y ≤≤),Y 表示获得的收益(单位:万元),则3()3()yx y Y H x x y x x y≥⎧==⎨--<⎩当当从而每年平均收益为4000200011()()(4)320002000y X y EY H x f x dx y dx ydx +∞-∞==-+⎰⎰⎰ 26211(7000410)[825000(3500)]10001000y y y =-+-⨯=-- 故当3500yt =时,可使平均收益达到最大.例7 设袋中有k 号的球k 个(1,2,,)k n = ,从中摸出一球,试求所得号码的数学期望.解以X 表示摸出一球的号码数,注意袋中球的总数为12n +++ ,即有2{}12(1)k kP X k n n n ===++++ (1,2,,)k n =从而,X 的数学期望为112{}(1)nni i kEX kP X k kn n =====+∑∑ 2(1)(21)21(1)63n n n n n n +++==+ 例8设X 为n 次独立试验中事件A 出现的次数,在第i 次试验中事件A 出现的概率为i p (1,2,,)i n = ,求DX ,并证明:在11ni i p p n ==∑(常数)的条件下,当且仅当12n p p p p ==== 时,DX 达到最大.[分析]在证明是,将DX 进行正确的合并时解答本题的关键. 解设10ii A X i A ⎧=⎨⎩第次试验中事件出现第次试验中事件不出现则i X 互相独立且具有相同的分布:i X 0 1P 1i p -i p于是i i EX p =,(1)i i i DX p p =-(1,2,,)i n =由于1ni i Xx ==∑,则11(1)n ni i i i i DX DX p p ====-∑∑当11ni i p p n ==∑时,有 22111()nnni i i i i i DX p p np p p p ====-=--+∑∑∑221[()2()]ni i i np p p p p p p ==--+-+∑21(1)2()ni i np p p p p ==---∑所以,当且仅当i p p =时,DX 最大.例9设随机变量X 服从均值为2、方差为2σ的正态分布,且{24}0.3P X <<=,求{0}P X<.[分析]求正态分布的概率时,先将其转化为标准正态分布,在查表,即可求得结果.所用定理为:若2~(,)XN μσ,则~(0,1)X N μσ-.这个定理一定要熟练掌握.解由于22242{24}X P X P σσσ---⎧⎫<<=<<⎨⎬⎩⎭()200.3φφσ⎛⎫=-= ⎪⎝⎭所以有()200.30.50.30.8φφσ⎛⎫=+=+=⎪⎝⎭因此2022{0}X P XP φσσσ---⎧⎫⎛⎫<=<=⎨⎬ ⎪⎩⎭⎝⎭2110.80.2φσ⎛⎫=-=-= ⎪⎝⎭例10设X 在11,22⎡⎤-⎢⎥⎣⎦上服从均匀分布,ln 0()00x x y g x x >⎧==⎨≤⎩当当,求随机变量()Y g X =的数学期望及方差.解X 的概率密度为111()220x f x ⎧-≤≤⎪=⎨⎪⎩当其他于是120[()]()()ln EY E g X g x f x dx xdx +∞-∞===⎰⎰11/22011[ln ](1ln 2)2x x x dx x =-=-+⎰112221/2220ln [ln ]2ln EY xdx x x xdx ==-⎰⎰21ln 2ln 212=++ 所以222211()ln 2ln 21(1ln 2)24DY EY EY =-=++-+2113ln 2ln 2424=++ 例11游客乘电梯从电视塔底层到顶层观光,电梯于每个整点的5分钟、15分钟和55分钟从底层起行,假设一游客在早上8点的第X 的分钟到达底层电梯处,且X 在[0,60]上服从均匀分布,求该游客等候时间的数学期望.解已知X 在[0,60]上服从均匀分布,则其密度函数为1060()60x f x ⎧≤≤⎪=⎨⎪⎩当其他 设Y 为游客等候电梯的时间(单位:分),则50525525()5525556055560x x x x Y g x x x x x -<≤⎧⎪-<≤⎪==⎨-<≤⎪⎪-+<≤⎩当当当当因此601[()]()()()60EY E g x g x f x dx g x dx +∞-∞===⎰⎰52555600525551(5)(25)(55)(605)60x dx x dx x dx x dx ⎡⎤=-+-+-+-+⎢⎥⎣⎦⎰⎰⎰⎰ 1(12.520045037.5)11.67()60=+++=分 例12 设ξ在(,)ππ-上服从均匀分布,sin Xξ=,cos Y ξ=,求X Y 与的相关系数XY ρ.解根据随机变量函数的数学期望的计算公式,有1sin 02EX d ππθθπ-==⎰,1cos 02EY d ππθθπ-==⎰ 所以2211sin 22DX EX d ππθθπ-===⎰ 2211cos 22DY EY d ππθθπ-===⎰又因为1sin cos 02EXYd ππθθθπ-==⎰从而得cov(,)0X Y EXY EX EY =-⋅=于是XYρ==五、课本习题全解5-1 (1)1111210(1)12666EX=⨯+⨯+⨯+-⨯=,222211117210(1)26663EX=⨯+⨯+⨯+-⨯=,11(21)(221)(211)(201)26E X-+=-⨯+⨯+-⨯+⨯+-⨯+⨯11(2(1)1)166+-⨯-+⨯=-;(2)224()3DX EX EX=-=,()Xσ==.5-2 (1)00;k kk kqEX kpq pq qp∞∞=='⎛⎫===⎪⎝⎭∑∑(2)22222210000k k k kk k k k EX k pq pq k q pq q pq kq∞∞∞∞--====''⎛⎫===+⎪⎝⎭∑∑∑∑200k kk kpq q pq q∞∞=='''⎛⎫⎛⎫=+⎪ ⎪⎝⎭⎝⎭∑∑222q qp p=+2222222q q q q qDXp p p p p=+-=+5-3 (1)1()02xEX xf x dx x e dx+∞+∞--∞-∞===⎰⎰;(2)2221()2(3)22xDX EX EX x e dx+∞-=-==Γ=⎰.5-4 (1)0(1)1EX p p p =⨯-+⨯=,0(1)1EY p p p =⨯-+⨯=;(2)由于20(1)1EXp p p =⨯-+⨯=,20(1)1EY p p p =⨯-+⨯=;22()(1)DX EX EX p p =-=-,22()(1)DY EY EY p p =-=-;(3)由于00(1)11EXYp p p =⨯⨯-+⨯⨯=,故2cov(,)(1)X Y EXY EX EY p p p p =-⋅=-=-.5-5222()()2g t E X t EX tEX t =-=-+, ()220dg t t EX dt=-=, 因此,t EX =,即t EX =时,()g t 达到最小值为DX .5-6 当2YX =时,022x EY xe dx +∞-==⎰;当3XYe-=时,3014x x EYe e dx +∞--==⎰. 5-7222()/2(ln 2)/2xx u a EY a dx a e μσσ+∞---∞==⎰22()DY EY EY =-222222()/2(ln 2)/222ln 2ln 2()()(1)xx u a u a a a dx a e a e e μσσσσ+∞---∞=-=-⎰5-8 由于12102()23EXx x dx x dx ϕ+∞-∞===⎰⎰,(5)20()y EY y y dy ye dy ϕ+∞+∞---∞==⎰⎰6=,且X Y 与相互独立,所以有2643EXY EX EY =⋅=⨯=,220(+)+633E X Y EX EY ==+=5-9 证明)0EYE EX EX==-= 22221()()1DY EY EY E E X EXDX =-==-=5-10证明0XYρ===()()0E X EX Y EY ⇒--=()0E XY Y EX X EY EX EY ⇒-⋅-⋅+⋅=0EXY EX EY ⇒-⋅=()2cov(,)D X Y DX DY X Y DX DY ⇒+=++=+5-15 (1)由于220(,)sin()x y dxdy A x y dxdy ππϕ+∞+∞-∞-∞=+⎰⎰⎰⎰20cos cos 2A x x dx ππ⎡⎤⎛⎫=-+- ⎪⎢⎥⎝⎭⎣⎦⎰21A ==,故12A =. (2)22200011sin()cos cos 2224EX x x y dxdy x x x x dx πππππ⎡⎤⎛⎫=+=++= ⎪⎢⎥⎝⎭⎣⎦⎰⎰⎰, 由于X Y 与相互对称,故有4EYEX π==;2222222200011sin()[sin cos ]22282EX x x y dxdy x x x x dx πππππ=+=+=+-⎰⎰⎰22222()22824162DX EX EX πππππ⎛⎫=-=+--=+- ⎪⎝⎭由于X Y 与相互对称,故有22162DYππ=+-.(3)222000112sin()sin cos 222EXY xy x y dxdy x x x dx ππππ-⎛⎫=+=+ ⎪⎝⎭⎰⎰⎰22π-=2cov(,)1162X Y EXY EX EY ππ=-⋅=-+-2211622162XYππρππ-+-==+-5-12 二维随机变量(,)X Y的联合分布函数为1(,)(,)x y Af x y∈⎧=⎨⎩当其他12(1)12(1)000012,33x xEX xdydx EY ydydx--====⎰⎰⎰⎰12(1)0016xEXY xydydx-==⎰⎰.5-13 设抽到次品所需要次数为X,则X服从下列分布:X 1 2 3 kP2n221nn n-⋅-23212n nn n n--⋅⋅--2(2)(3)()(1)(2)(1)n n n kn n n n k-------即2{}1n kP X kn n-==⋅-,因此11112{}1n nk kn kEX k P X k kn n--==-=⋅==⋅⋅-∑∑1121121(2)3n nk knkn kn n--==+⎛⎫=-=⎪-⎝⎭∑∑122121nkn kEX kn n-=-=⋅⋅-∑11231121(1)(2)6n nk kk n k n nn n--==⎛⎫=-=+⎪-⎝⎭∑∑221()(1)(2)18DX EX EX n n=-=+-5-15 (1)11005(2)12EX x x y dydx=--=⎰⎰,512EY EX==.1122001(2)4EX x x y dydx=--=⎰⎰,2214EY EX==2211()144DX DY EX EX ==-= 11001(2)6EXY xy x y dydx =--=⎰⎰2151cov(,)612144X Y EXY EX EY ⎛⎫=-⋅=-=- ⎪⎝⎭5()2cov(,)36D X Y DX DY X Y +=++=(2)103()(2)2X f x x y dy x =--=-⎰,103()(2)2Y f y x y dx y =--=-⎰可见,()()(,)X Y f x f y f x y ≠,所以两者不独立.111441111144XYρ-===-故两者相关. 5-16(5)5()22y X f x xedy x +∞--==⎰,1(5)(5)0()2y y Y f y xe dx e ----==⎰可见,()()(,)X Y f x f y f x y =,故两者独立.1(5)054y EXY xye dydx +∞--==⎰⎰5-17 两台仪器无故障时间的密度分布为1511150()0x e x f x -⎧>=⎨⎩当其他,2522250()0x e x f x -⎧>=⎨⎩当其他联合密度函数为125()121212250,0(,)()()0x x e x x f x x f x f x -+⎧>>==⎨⎩当其他 设无故障工作时间为12y x x =+,则联合分布函数为1125()5512210(,)()2551y y x x x y y F x x F y e dx dx ye e --+--===--+⎰⎰5()()25y df y F y e y dy-==所以密度函数为5250()0y e y y f y -⎧>=⎨⎩当其他 2502255y EY y e dy +∞-==⎰,235062525y EY y e dy +∞-==⎰ 262225525DY ⎛⎫=-= ⎪⎝⎭5-18 根据题意有()EXP A =,()EY P B =,()EXY P AB ={1}()P XY P AB ==,{0}1()P XY P AB ==-已知0XYρ=,所以cov(,)0X Y =,即cov(,)()()()0X Y EXY EX EY P AB P A P B =-⋅=-=故()()()P AB P A P B =.事件A B 与相互独立,由事件的独立性定理可得:A ,A ,B ,B 两两相互独立,即{11}{1}{1}P X Y P X P Y =====, {10}{1}{0}P X Y P X P Y =====, {01}{0}{1}P X Y P X P Y =====, {00}{0}{0}P X Y P X P Y =====,因此,X Y 和相互独立. 5-19 已知11~0,,~0,22XN Y N ⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,由正态分布的性质可知:()1D X Y DX DY -=+=,()0E X Y -=故()()~0,1XY N -,令Z X Y=-,则()~0,1ZN.22()z E Z z e dz +∞--∞==22222()()()()1D Z EZ E Z DZ EZ E Z π=-=+-=-⎡⎤⎡⎤⎣⎦⎣⎦六、自测题及答案1.设随机变量X 的密度函数为()()0ba x x a f x a x a ⎧-<⎪=⎨⎪≥⎩当当且已知1DX=,则常数a =____________,b =____________.2.设随机变量X 的方差为1DX =,(,)Y X αβαβ=+为非零常数,则DY =__________.3.设X 表示10次独立重复射中目标的次数,每次射中目标的概率为0.4,则2EX =__________.4.设随机变量123X X X 、、相互独立,其中2123~(0,6),~(0,2),~(3)X U X N X P,记12323YX X X =-+,则DY =_________.5.设随机变量X 服从于参数为λ的泊松分布,且已知[(1)(2)]1E X X --=,则λ=___________.6.设X 是一个随机变量,其概率密度为110()1010x x f x x x +-≤≤⎧⎪=-<<⎨⎪⎩当当其他则方差DX =_____________.7.设一次试验成功的概率为p ,进行100次独立重复试验,当p =_____________时,成功次数的标准差的值最大,其最大值为____________.8.设随机变量X 的分布函数为300()0111x F x x x x <⎧⎪=≤≤⎨⎪>⎩当当当则EX=().(A )40x dx +∞⎰(B )1401x dx xdx +∞+⎰⎰(C )1203x dx ⎰(D )1303x dx ⎰9.设随机变量X Y 与独立,且21ZX Y =-+,则DZ =().(A )4DX DY -(B )4DX DY + (C )21DX DY ++(D )21DX DY -+10.设随机变量X 的密度函数为2(1)/2()xf x--=则以下()成立.(A){1}{1}P X P X<=>(B){0}{2}P X P X≤<≥(C)1EX=(D)1DX=11.如果随机变量X Y与满足D X Y D X Y+-()=(),则必须有()成立.(A)X Y与独立(B)X Y与不相关(C)0DY=(D)0DX DY⋅=12.设随机变量X服从参数为2的指数分布,随机变量22xY x e-=+,则DY=().(A)32(B)5 (C)34(D)4313.设X Y与是两个相互独立的随机变量,其概率密度分别为201()x xf x≤≤⎧=⎨⎩当其他,(5)5()ye yf y--⎧>=⎨⎩当其他则EXY=().(A)2 (B)3 (C)4 (D)514.设随机变量X Y与独立,且21~(,)X Nμσ,22~(,)Y Nμσ,则()D X Y-=().(A)22122()1σσπ⎛⎫+-⎪⎝⎭(B)2212σσ+(C)2212σσ-(D)22122()1σσπ⎛⎫--⎪⎝⎭15.设X是一个随机变量,2,EX DXμσ==,(22,0μσ>是常数),则对任意常数C,有().(A)222()E X C EX C-=-(B)22()()E X C E Xμ-=-(C)22()()E X C E Xμ-<-(D)22()()E X C E Xμ-≥-16.设随机变量12X X、的概率密度分别为2120()00x e x f x x -⎧>=⎨≤⎩当当,4240()00x e x f x x -⎧>=⎨≤⎩当当 (1)求12()E X X +和212(23)E X X -;(2)假设12X X 、相互独立,求12EX X . 17.一工厂生产的某种设备的寿命X (以年计)服从指数分布,其概率密度为410()400xe xf x x -⎧>⎪=⎨⎪≤⎩当当工厂规定,出售的设备若在售出一年之内损坏可予以调换,若工厂售出一台设备盈利100元,调换一台设备厂方需花费300元,试求厂方出售一台设备净盈利的数学期望.18.流水作业线上生产出的每个产品为不合格的概率为p ,当生产出k 个不合格品时,即停工检修一次,求在两次检修之间产品总数的数学期望与方差.19.五家商店联营,它们每两周售出的某农产品的数量(单位:kg )分别为123X X X 、、、45X X 、,已知1~(200,225)X N ,2~(240,240)X N ,3~(180,225)X N ,4~X (260,265)N ,5~(320,270)X N ,且123X X X 、、、45X X 、相互独立.(1)求五家商店两周的总销售量的均值和方差;(2)商店每隔两周进货一次,为了使新的供货到达前商店不会脱销的概率大于0.99,问商店的仓库应至少储存多少千克该产品?20.某人有一串钥匙(钥匙数量为n )其中只有一把能打开自己的家门,若他在下列情况下随意地试用这串钥匙,试求打开门时已被使用过的钥匙数的数学期望与方差:(1)把每把试用过的钥匙分开;(2)把每次试用过的钥匙再混杂在这串钥匙中.21.设一口袋中装有n 个球,每个球上标有各不相同的数字,不放回地从袋中取球,每次一个球,第k 次取到的球上的数字定义为k X (1,2,,)k n = ,对任意的j k ≠,求j k X X 和的相关系数.【答案】1.因为x a <,说明0a >,所以0()()0a a a EX x a x dx x a x dx b -⎡⎤=++-=⎢⎥⎣⎦⎰⎰502220()()6a a a a EX x a x dx x a x dx b b -⎡⎤=++-=⎢⎥⎣⎦⎰⎰ 已知22()1DXEX EX =-=,可得516a b=①又因为00()()()1a a a a f x dx a x dx a x dx b b +∞-∞-⎡⎤=++-=⎢⎥⎣⎦⎰⎰⎰,可得31a b=②联立①②,得a b ==2.22()DY D X DX αβαα=+==3.18.44.由2123~(0,6),~(0,2),~(3)X U X N X P ,可得21(60)312DX -==,24DX =,33DX =所以123123(23)493449346D X X X DX DX DX -+=++=+⨯+⨯=5.已知X 服从参数为λ的泊松分布,即EX λ=,而22[(1)(2)](32)32E X X E X X EX EX --=-+=-+ 22()3232DX EX EX λλλ=+-+=+-+ 2221λλ=-+=解得1λ=. 6.167.若X 满足二项分布,则(1)DX np p =-,1(1)(12)02dDX n p np n p p dp =--=-=⇒= 221220p d DXn dp ==-<故12p =是方差的最大值点,也是标准差的最大点.方差最大值为 (1)25DX np p =-=从而标准差最大值为25.8.由X 的分布函数可得其密度函数为2301()0x x f x ⎧≤≤=⎨⎩当其他 故1123033EXx x dx x dx =⋅=⎰⎰.因此D 项正确.9.由于X Y 与相互独立,所以(21)(2)4DZ D X Y D X DY DX DY =-+=+=+.因此B 项正确. 10.因为22(1)21()x f x --⨯=,所以~(1,1)XN .其中21,1EX DX μσ====.由于()f x 的曲线关于1x μ==对称,故{1}{1}P X P X >=<.因此,A 、C 、D 三项均正确.11.因为()2cov(,)D XY DX DY X Y +=++()2cov(,)2cov(,)D X Y DX DY X Y DX DY X Y -=++-=+-又因为()()D XY D X Y -=+所以cov(,)0X Y =,即0XY ρ=,故X Y 与不相关.因此B 项正确.12.A 13.C 14.A 15.D 16.(1)2110()2x EX xf x dx xe dx +∞+∞--∞==⎰⎰2201[]2x x xee dx +∞-+∞-=-+=⎰ 4220()4x EX xf x dx xe dx +∞+∞--∞==⎰⎰4401[]4x x xee dx +∞-+∞-=-+=⎰ 2224220()4x EX x f x dx x e dx +∞+∞--∞==⎰⎰24400[]2x x x exe dx +∞-+∞-=-+⎰4400111228x x xe e dx +∞+∞--⎡⎤=-+=⎢⎥⎣⎦⎰所以1212113()244E X X EX EX +=+=+= 221212115(23)2323288E X X EX EX -=-=⨯-⨯=(2)若12X X 、相互独立,则有1212111248EX X EX EX =⋅=⨯=17.售出一台设备的盈利函数为20001()1001x g x x -<<⎧=⎨>⎩当当则[()]()()E g x g x f x dx +∞-∞=⎰1401(200)4xe dx -=-⨯⎰ 111444401200[]100[]200200100xxe e e e----+∞=-=-+14300200e -=-18.设第1i -个不合格品出现后到第i 个不合格品出现时的产品数为iX (1,2,i =,)n ,又设两次检修之间产品总数为X ,则1ki i X X ==∑,12,,,,k X X X 独立同分布,且1{}(1)j i P X j p p -==-(1,2,,;1,2,)i k j ==由此得111(1)j i j EX j p p p∞-==-=∑22222211()i i i p pDX EX EX p p p--=-=-= 所以1ki i k EX EX p ===∑,21(1)ki i k p DX DX p =-==∑ 19.(1)设X 表示五家商店的总销售量,则51i i XX ==∑.512002401802603201200i i EX EX ===++++=∑521225240225265270122535i i DX DX ===++++==∑(2)设商店的仓库至少应储存Y kg 该产品,求使得{0}0.99P Y X -≥≥的Y ,又因为2~(1200,35)XN ,故120012001200{}0.99353535X Y Y P X Y P φ---⎧⎫⎛⎫≤=≤=≥⎨⎬ ⎪⎩⎭⎝⎭查表得12002.3335Y -≥,即120035 2.331281.55Y ≥+⨯=故至少应储存1281.55kg 该产品. 20.设X 为试用过的钥匙数. (1)12111{}121n n n k P Xk n n n k n k n---+==⋅⋅=--+-- (1,2,,)k n = 又因为1112nk n EXk n =+=⋅=∑ 2211(1)(21)6nk n n EX k n =++=⋅=∑ 所以2221()12n DX EX EX -=-=(2)111{}k n P X k n n--⎛⎫==⋅⎪⎝⎭(1,2,)k = 又因为1111k nk n EX k n n n-=-⎛⎫=⋅⋅= ⎪⎝⎭∑ 12221112k nk n EX k n n n n-=-⎛⎫=⋅⋅=- ⎪⎝⎭∑ 所以22()(1)DXEX EX n n =-=-21.设这n 个各不相同的数为12,,,n a a a ,则有1{}j i P X a n==(1,2,,)i n = 故11nj i i EX a n ==∑22112()nni i i i j n a a DX n==⋅-=∑∑(1,2,,)j n =()k j X X j k ≠和的联合分布律为1{,}(1)j i k l P X a X a n n ===-(,1,2,,)i l n =故cov(,)k j k jk j X X EX X EX EX =-⋅21121(1)i jn i j ni i a a a n n n ≤<≤=⎛⎫=- ⎪-⎝⎭∑∑2221112()()(1)n nni ii i i i a a a n n n ===-=--∑∑∑22112()(1)nni i i i a n a n n ==-=-∑∑因此cov(,)11k jX X X X nρ==-。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课本P25 3、设A ,B ,C 是三事件,且0)()(,41)()()(=====BC P AB P C P B P A P ,81)(=AC P . 求A ,B ,C 至少有一个发生的概率。
解:P (A ,B ,C 至少有一个发生)=P (A +B +C )= P (A )+ P (B )+ P (C )-P (AB )-P (BC )-P (AC )+ P (ABC )= 8
508143=+- 7、某油漆公司发出17桶油漆,其中白漆10桶、黑漆4桶,红漆3桶。
在搬运中所标笺脱落,交货人随意将这些标笺重新贴,问一个定货4
桶白漆,3桶黑漆和
2桶红漆顾客,按所定的颜色如数得到定货的概率是多少? 记所求事件为A 。
在17桶中任取9桶的取法有917C 种,且每种取法等可能。
取得4白3黑2红的取法有2334
4
10C C C ⨯⨯ 故 2431252)(617
2334410=⨯⨯=C C C C A P 14、)(,2
1)|(,31)|(,41)(B A P B A P A B P A P ⋃===求。
解:由61)()(314121)()|()()()()|(=⇒⨯=−−−−→−=B P B P B P A B P A P B P AB P B A P 有定义由已知条件 得121)|()()(==A B P A P AB P P84 3、设随机变量(X ,Y )概率密度为⎪⎩⎪⎨⎧<<<<--=其它,042,20),6(),(y x y x k y x f (1)确定常数k 。
(2)求P {X <1, Y <3} (3)求P (X <1.5} (4)求P (X+Y ≤4}
分析:利用P {(X , Y)∈G}=⎰⎰
⎰⎰⋂=o D G G dy dx y x f dy dx y x f ),(),(再化为累次积分,其中⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧<<<<=42,20),(y x y x D o 解:(1)∵⎰⎰⎰⎰+∞∞-+∞∞---==
2012)6(),(1dydx y x k dy dx y x f ,∴81=k (2)8
3)6(81)3,1(3210⎰⎰=--=<<dy y x dx Y X P (3)3227)6(81),5.1()5.1(425.10=--=∞<≤=≤⎰⎰dy y x dx Y X P X P (4)
7、设二维随机变量(X ,Y )的概率密度为
⎪
⎩⎪⎨⎧≤≤≤≤-=其它求边缘概率密度0.0,10)2(8.4),(x y x x y y x f 解:⎪⎩⎪⎨⎧≤≤-=-==⎰⎰∞+∞-其它0
10)2(4.2)2(8.4),()(0
2x x x dy x y dy y x f x f x X ⎪⎩⎪⎨⎧≤≤+-=-==⎰
⎰∞+∞-其它0
10)43(4.2)2(8.4),()(12y y y y dx x y dx y x f y f y Y
P114 7、设随机变量X 的概率密度为
⎩⎨⎧≤>=-0
,00,)(x x e x f x 求(1)Y=2X (2)Y=e -2x 的数学期望。
解:(1)⎰⎰+∞-+∞∞
-==02)(2)(dx xe dx x xf y E x []2022=∞+--=--x x e xe (2)⎰
⎰+∞--+∞∞--==022)()(ex e e dx x f e Y E x x x 310313=∞-=-x e 15、将n 只球(1~n 号)随机地放进n 只盒子(1~n 号)中去,一只盒子装一只球。
将一只球装入与球同号的盒子中,称为一个配对,记X 为配对的个数,求E (X )
P35 例3、某人进行射击,设每次射击的命中率为0.02,独立射击400次, 试求至少击中2次的概率。
【解】将一次射击看成一次伯努利试验,设击中的次数为X ,则X~b(400, 0.02), X 的分布律为
于是所求的概率为:
例5、计算机硬件公司制造某种特殊型号的微型芯片,次品率达0.1%,各芯片成为次品相对独立,求在1000只产品中至少有2
只次品的概率. 解:以X 记产品中的次品数,X~b(1000,0.001)。
例2 一个靶子是半径为2cm 的圆盘。
设击中靶上任一同心圆【盘上的点的概率与该圆盘的面积呈正比,并设射击都能击中
靶,以X 表示弹着点与圆心的距离,试求随机变量
X 的分布函数。
例1设随机变量X 具有概率密度
,03,()2,34,20,.kx x x f x x ≤<⎧⎪⎪=-≤≤⎨⎪⎪⎩其他
(1)确定常数k ; (2)
求 X 的分布函数();F x (3)求
7{1}.2P X <≤
例3 设二维随机变量(,)X Y 的概率密度为 (2)2,0,0(,)0,x y e x y f x y -+⎧>>=⎨⎩其他
(1) 求分布函数 (,)F x y ; (2)求概率 {}P Y X ≤ 解:(1)(,)(,)y x F x y f x y dxdy -∞-∞=⎰⎰ (2)002,0,00,y x x y e dxdy x y -+⎧>>⎪=⎨⎪⎩⎰⎰其他
即有 2(1)(1),0,0(,)0,x y e e x y F x y --⎧-->>=⎨⎩其他 (2)将),(Y X 看作是平面上随机点的坐标,即有
{}{(
,)}Y X X Y G ≤=∈ 其中G 为xOy 平面上直线 y x =及其下方的部分,如
图4于是{}{(,)}(,)G P Y X P X Y G f x y dxdy ≤=∈=⎰⎰ (2)00123x y e dxdy +∞+∞-+==⎰⎰ 例2 一简单电路中,两电阻 串联,设 相互独立, 他们的概率密度均为
10,010()500,x x f x -⎧≤≤⎪=⎨⎪⎩其他 求总电阻 的概率密度
例2 设随机变量X 和Y 具有联合概率密度:
26,(,)0,x y x f x y ⎧≤≤=⎨⎩其他 求边缘概率密度()()X Y f x f y ,。
