SPSS第3次实验报告
spss实验报告,心得体会

spss实验报告,心得体会篇一:SPSS实验报告SPSS应用——实验报告班级:统计0801班学号:1304080116 姓名: 宋磊指导老师:胡朝明2010.9.8一、实验目的:1、熟悉SPSS操作系统,掌握数据管理界面的简单的操作;2、熟悉SPSS结果窗口的常用操作方法,掌握输出结果在文字处理软件中的使用方法。
掌握常用统计图(线图、条图、饼图、散点、直方图等)的绘制方法;3、熟悉描述性统计图的绘制方法;4、熟悉描述性统计图的一般编辑方法。
掌握相关分析的操作,对显著性水平的基本简单判断。
二、实验要求:1、数据的录入,保存,读取,转化,增加,删除;数据集的合并,拆分,排序。
2、了解描述性统计的作用,并1掌握其SPSS的实现(频数,均值,标准差,中位数,众数,极差)。
3、应用SPSS生成表格和图形,并对表格和图形进行简单的编辑和分析。
4、应用SPSS做一些探索性分析(如方差分析,相关分析)。
三、实验内容:1、使用SPSS进行数据的录入,并保存: 职工基本情况数据:操作步骤如下:打开SPSS软件,然后在数据编辑窗口(Data View)中录入数据,此时变量名默认为var00001,var00002,…,var00007,然后在Variable View窗口中将变量名称更改即可。
具体结果如下图所示:输入后的数据为:将上述的数据进行保存:单击保存即可。
2、读取上述保存文件:选择菜单File--Open—Data;选择数据文件的类型,并输入文件名进行读取,出现如下窗口:选定职工基本情况.sav文件单击打开即可读取数据。
3、对上述数据新增一个变量工龄,其操作步骤为将当前数据单元确定在某变量上,选择菜单Data—Insert Variable,SPSS自动在当前数据单元所在列的前一列插入一2个空列,该列的变量名默认为var00016,数据类型为标准数值型,变量值均是系统缺失值,然后将数据填入修改。
结果如下图所示:篇二:SPSS相关分析实验报告本科教学实验报告(实验)课程名称:数据分析技术系列实验实验报告学生姓名:一、实验室名称:二、实验项目名称:相关分析三、实验原理相关关系是不完全确定的随机关系。
SPSS实验报告

重庆邮电大学课程报告2016 - 2017 学年第2 学期课程名称:《数据分析方法与实训》姓名:XX学号:*******XXX班级:0104150X专业:信息工程指导教师:**2017年7 月2 日(1)基于前述操作,继续在myzy.sav中完成以下任务:①分别绘制语文、数学、外语成绩的箱体图,并对箱体图的输出结果进行解释。
②分别绘制语文、数学、外语成绩的茎叶图,并对茎叶图的输出结果进行解释。
③分别绘制语文、数学、外语成绩的Q-Q图,并对Q-Q图的输出结果进行解释。
箱体图操作方法:1)在SPSS中打开yyyy.sav,处于“数据视图”状态。
2)利用【分析】——【描述统计】——【探索】命令。
3)变量“数学”从左侧列表移到右侧的“因变量列表”中;4)变量“姓名”从左侧列表移到右侧“标注个案”中;5)在“探索”对话框中,单击右侧【绘制】;6)在“探索.图”对话框中,从左上角的“箱图”选中【不分组】,“描述性”选中【茎叶图】,单击【继续】,【确定】。
操作结果:图1.1关于语文的数据分析图1.2关于语文的箱体图输出结果分析:矩形中部的横线表明,语文的中位数为84.50。
箱体部分对应四分位间距,箱体外无数据说明分值较为集中,无异常值(异常值被定义为小于Q1-1.5IQR或大于Q3+1.5IQR的值)图1.3关于数学的数据分析图1.4关于数学的箱体图输出结果分析:矩形中部的横线表明,语文的中位数为82.00。
距离箱体很远的被标记“*”号的为极端值,“张一81”、“张一79”等为极端值。
图1.5关于外语的数据分析图1.6关于外语的箱体图输出结果分析:矩形中部的横线表明,语文的中位数为825.00。
距离箱体很远的被标记“*”号的为极端值,“张一75”、“张一73”等为极端值。
观测值位于触手之外但3倍箱体之内的个案位奇异值,标记为“o”,“张一71”、“张一17”为奇异值。
三个科目的茎叶图如下:图1.7语文图1.8数学图1.9外语输出结果分析:“Frequency”:频数,“Stem”:茎,“Leaf”:叶子。
spss实验报告

《统计分析与SPSS 的应用》学院 ( 系 )专业名称班级姓名学号实习地点起止时间2022 年 5 月至2022 年7 月数据文件的合并是把外部数据与当前数据合并成一个新的数据文件, SPSS提供两种形式的合并: 一是横向合并, 指从外部数据文件中增加变量到当前数据 文件中; 二是纵向合并, 指从外部数据文件增加观测数据到当前文件中。
横向合 并即增加变量,而增加变量有两种方式:一是从外部数据文件中获取变量数据, 加入当前数据文件中; 二是按关键变量合并, 要求两个数据文件有一个共同的关 键变量,而且两个数据文件的关键变量中还有一定数量相同值的观测值。
拆分并非要把数据文件分成几个, 而是根据实际情况, 根据变量对数据进 行分组,为以后的分组统计提供便利。
例 2-2 实验步骤:打开 data2-2.sav→点 击菜单栏的数据,拆分文件,弹出“分割文件”→按照产品类型拆分数据,选择 “比较组”,激活“分组方式”栏。
选中“产品”变量移入其中,单击“确定” 按钮结束。
点击菜单“分析→描述性统计→描述…”,弹出“描述性”对话框, 选择变量“金额”,“数量”进行分析,单击“选择”按钮设置要计算的统计量, 统计金额和数量的和,设置好后单击确定按钮,得到表 1 所示的统计量:从表 1 可以得出彩电、空调、热水器、微波炉、洗衣机的数量、金额的极大 值、极小值、和、均值标准差这四个描述性统计量是多少。
N 极小值 极大值 和 均值 标准差 4 12 50 144 36.00 16.5734 38400 160000 460800 115200.00 53033.826 41 3 3 3 3.00 . 1 9600 9600 9600 9600.00 . 12 11 24 35 17.50 9.1922 25300 55200 80500 40250.00 21142.493 22 1 24 25 12.50 16.2632 2100 50400 52500 26250.00 34153.258 22 5 48 53 26.50 30.4062 11000 105600 116600 58300.00 66892.302 2产品彩电 数量金额有效的 N (列表状态)空调 数量金额有效的 N (列表状态) 热水器 数量金额有效的 N (列表状态) 微波炉 数量金额有效的 N (列表状态) 洗衣机 数量金额有效的 N (列表状态)SPSS 的观察量加权功能是在数据文件中选择一个变量,这个变量力的值是 相应的观测量浮现的次数, 这个变量叫做权变量, 经过加权的数据文件叫做加权 文件。
市场营销研究spss个人实习报告

竭诚为您提供优质文档/双击可除市场营销研究spss个人实习报告篇一:spss实习报告spss统计分析软件实验报告石河子大学经济与管理学院经济与贸易系国际经济与贸易专业20XX级1班雍荣20XX165106实验一spss基本操作一、实验目的1.熟悉spss的菜单和窗口界面,熟悉spss各种参数的设置;2.掌握spss的数据管理功能。
二、实验内容及步骤(一)数据的输入和保存1.spss界面当打开spss后,展现在我们面前的界面如下:请注意窗口顶部显示为“spssforwindowsDataeditor”,表明现在所看到的是spss的数据管理窗口。
这是一个典型的windows软件界面,有菜单栏、工具栏。
该界面和exceL 极为相似,很多操作也与exceL类似,同学们可以自己试试。
2.定义变量选择菜单Data==>DefineVariable。
系统弹出定义变量对话框如下:对话框最上方为变量名,现在显示为“VAR00001”,这是系统的默认变量名;往下是变量情况描述,可以看到系统默认该变量为数值型,长度为8,有两位小数位,尚无缺失值,显示对齐方式为右对齐;第三部分为四个设置更改按钮,分别可以设定变量类型、标签、缺失值和列显示格式;第四部分实际上是用来定义变量属于数值变量、有序分类变量还是无序分类变量,现在系统默认新变量为数值变量;最下方则依次是确定、取消和帮助按钮。
假如有两组数据如下:gRoup1:0.841.051.201.201.391.531.671.801.872.072.11 gRoup2:0.540.640.640.750.760.811.161.201.341.351.48 1.561.87先来建立分组变量gRoup。
请将变量名改为gRoup,然后单击oK按钮。
现在spss的数据管理窗口如下所示:第一列的名称已经改为了“group”,这就是我们所定义的新变量“group”。
现在我们来建立变量x。
spss统计学软件实验报告

西安邮电大学统计软件实习报告书系部名称:经济与管理学院营销策划系学生姓名:陈志强专业名称:商务策划管理时间:2012年5月21日至2012年5月25日实习内容:熟悉和学习SPSS软件,包括1.基本统计实验(均值、中位数、众数、全距、方差与标准差、四分位数、十分位数、频数、峰度、偏度);2均值比较和T检验(均值比较、单一样本T检验、两独立样本T检验和两配对样本T检验);3.相关分析(二元定距变量的相关分析、二元定序变量的相关分析、偏相关分析、距离相关分析);4.回归分析(一元线形回归和多元线形回归)。
实习目的:掌握SPSS基本的统计描述方法,可以对要分析的数据的总体特征有比较准确的把握,从而为以后实验项目选择其他更为深入的统计分析方法打下基础。
实习过程:实验1:二元定距变量的相关分析★研究问题:某工厂生产多种产品,分别对其进行两标准评分,评分结果如下表,现在要研究这两个标准之间是否具有相关性。
★实现步骤『步骤1』在“Analyze”菜单“Correlate”中选择Bivariate命令,如图3-1所示。
图3-1 选择Bivariate Correlate 菜单『步骤2』在弹出的如图3-2所示Bivariate Correlate对话框中,从对话框左侧的变量列表中分别选择“标准1”和“标准2”变量,单击按钮使这两个变量进入Variables框。
在Correlation Coefficients框中选择相关系数,本例选用Pearson项。
在Test of significance框中选择相关系数的双侧(Two-tailed)检验,检验两个变量之间的相关取向,也就是从结果中来得到是正相关还是负相关。
图3-2 Bivariate Correlate对话框选中Flag significations correlations选项,则相关分析结果中将不显示统计检验的相伴概率,而以星号(*)显示。
一个星号表示当用户指定的显著性水平为0.05时,统计检验的相伴概率值小于等于0.05,即总体无显著性相关的可能性小于等于0.05;两个星号表示当用户指定的显著性水平为0.01时,统计检验的相伴概率值小于等于0.01,即总体无显著线形相关的可能性小于等于0.01。
spss实验报告

初始
提取
a1
1.000
.928
a2
1.000
.738
a3
1.000
.900
a4
1.000
.872
a5
1.000
.901
a6
1.000
.867
a7
1.000
.919
a8
1.000
.907
a9
1.000
.965
a10
1.000
.939
提取方法:主成份分析。
由表可知,从提取一列看,各个变量的共同度都比较大,说明变量空间转化为因子空间时,保留比较多的信息,因此,因子分析的效果显著。
70.9000
9.90454
3.13209
独立样本检验
方差方程的Levene检验
均值方程的t检验
差分的95%置信区间
F
Sig.
t
df
Sig.(双侧)
均值差值
标准误差值
下限
上限
成绩
假设方差相等
.071
.793
2.570
18
.019
11.10000
4.31908
2.02595
20.17405
假设方差不相等
图7-1
结果如下:
描述性统计量
均值
标准差
N
平时成绩
75.15
10.664
20
高考成绩
20.15
4.891
20
相关性
平时成绩
高考成绩
平时成绩
Pearson相关性
1
.824**
显著性(双侧)
.000
spss描述统计实验报告

spss描述统计实验报告SPSS描述统计实验报告引言SPSS(Statistical Package for the Social Sciences)是一种用于数据分析和统计建模的软件工具。
它可以帮助研究人员对数据进行描述统计分析,从而得出结论并做出预测。
本实验旨在利用SPSS软件对实验数据进行描述统计分析,以探究数据的特征和规律。
实验设计本实验选取了一组包括性别、年龄、身高和体重等信息的样本数据,共计100个样本。
通过SPSS软件对这组数据进行描述统计分析,包括均值、标准差、频数分布等指标,以便对样本数据进行全面的了解。
结果分析首先,我们对样本数据中的性别进行了频数分布分析。
结果显示,样本中有55%的男性和45%的女性,性别分布相对均衡。
接着,我们对年龄、身高和体重等连续变量进行了均值和标准差的分析。
结果显示,样本的平均年龄为30岁,标准差为5岁;平均身高为170厘米,标准差为8厘米;平均体重为65公斤,标准差为10公斤。
这些数据表明样本中的年龄、身高和体重分布较为集中,且具有一定的变异性。
结论通过对样本数据的描述统计分析,我们得出了对样本特征和规律的初步认识。
样本中男女比例相对均衡,年龄、身高和体重分布较为集中且具有一定的变异性。
这些结果为我们进一步的数据分析和研究提供了重要参考。
总结SPSS软件作为一种强大的数据分析工具,可以帮助研究人员对数据进行描述统计分析,从而深入了解数据的特征和规律。
本实验利用SPSS对样本数据进行了描述统计分析,得出了对样本特征和规律的初步认识,为后续的研究工作奠定了基础。
希望本实验能够对SPSS软件的应用和描述统计分析方法有所启发,为相关研究工作提供参考。
中南财大-SPSS-实验报告-3

5.点击确定按钮,等待输出结果。
结果分析:
1.从表中可以看出,样本总共有60个,全部参加分析,没有缺失值。
表1案例处理基本统计表
2.变量统计结果表:
表2变量统计结果表
3.从表可以看出,学生态度得分的均值为47.00,标准值为13.629。
第二问
操作步骤
1.回到数据视图,选择“分析”→“比较均值”→“单样本T检验”,弹出如下图对话框:
第二问:
操作步骤:
1.对数据进行分组。点击“数据”→“分割文件”,进入分割文件对话框。选择“method”,点击中间的向右箭头,使之成为分组方式。如图:
图14分割文件
2.点击确定完成分组设置。单击“分析”→“描述统计”→“频率”,弹出频率对话框。选中scoreadd变量,单击向右箭头使之进入变量列表框。如下图:
图10单样本T检验
点击选项,在置信区间百分比输入“95”,即设置显著性水平为5%。在“缺失值”选项组中选中“按分析顺序排除个案”,也就是说,只有分析计算涉及到该记录缺失的变量时,才删去该记录。如下图:
图11单样本T检验:选项
4.设置完毕,点击“继续”按钮返回“单样本T检验”对话框。单击“确定”按钮,等待结果输出。
表7统计量
第三问:
操作步骤:
1.点击“分析”→“比较均值”→“独立样本T检验”,选中“socreadd”并点击右侧第一个向右箭头,使之进入检验变量列表框;选中“method”,单击右侧第二个向右箭头,使之进入分组变量列表框。如图:
图16独立样本T检验
2.单击定义组,在组1(1)输入“1.00”,在组2(2)输入“2.00”。单击继续,如图:
图5单样本T检验对话框
2.将变量态度反应得分(x)移动到右侧的检测变量对话框中,并在“检测值”列表框中输入47.00,作为目标值。
SPSS实验报告(20200623015657)

统计分析软件课程期末案例分析作业性别及职称对工资的影响因素分析--- 基于有序选择模型的实证分析员兵帅学院商学院、专业:会计学、学号:20133150144、邮箱: yunbingshuai@一、研究背景亚当斯密《国富论》中说:“一国国民每年的劳动,本来就是供给他们每年消费的一切生活必需品和便利的源泉。
”一个劳动者的工资,要用来养家糊口,因此对于它的研究至关重要。
职工工资的增长逐渐成为一个热点话题,在百度中输入“职工工资”,你会得到非常多相关报道,工资协商制、工资拖欠、工资保障机制也成为学术界人士争相研究的焦点。
而也是随着职工工资的增长,其他的一些问题,诸如个税征收、社会保障机制改革等接踵而来。
因此,研究好职工工资的影响因素,对于预测工资走向,安排生产生活,体制改革等有积极意义。
影响工资的因素有很多,在此我们主要选性别和职称这两个因素来研究,从该研究中发现更深层次的原因,这就是本问研究的主要目的二、研究方法、数据来源和变量选择本文选取了不同员工的性别、职称、工资等数据,以分析性别、职称对职工员工工资的影响,三、实验描述及实验过程(一)实验描述一、针对数据职工数据•绘制统计图1•生成年龄和基本工资的统计图2•生成职称和基本工资的统计图3•生成文化程度和基本工资的统计图二、针对数据职工数据•求出描述性统计量(如均值,方差,标准差等)三、进行一元回归分析四、进行多元回归分析㈡实验过程(一)利用SPSS绘制统计图1、打开“职工数据.sav”,调用Graphs菜单的Bar功能,绘制直条图。
直条图用直条的长短来表示非连续性资料的数量大小。
弹出Bar Chart定义选项。
2、在定义选项框的下方有一数据类型栏,大多数情形下,统计图都是以组为单位的形式来体现数据的。
在定义选项框的上方有3种直条图可选:Simple为单一直条图、Clustered为复式直条图、Stacked为堆积式直条图,本实验选单一直条图。
3、点击 Define 钮,弹出 Define Clustered Bar: Summaries for groups of cases 对话框,在左侧的 变量列表中选基本工资点击按钮使之进入 Ba 申-Represan 栏的Othe 頑'summary fun ction4、点击Titles 钮,弹出Titles 对话框,在Title 栏内输入“不同性别的基本工资状况”/ “不同职称的基本工资状况”/ “不同文化程度的基本工资状况”,点击 Continue 钮返回DefineClustered Chart: Summaries for groups of cases 对话框,再点击 OK 钮即完成。
SPSS实验报告

《统计分析与SPSS的应用》实验报告班级:090911学号:09091141姓名:律江山评分:南昌航空大学经济管理学院南昌航空大学经济管理学院学生实验报告实验课程名称:统计分析与SPSS的应用专业经济学班级学号09091141 姓名律江山成绩实验地点G804 实验性质:演示性 验证性综合性设计性实验项目名称基本统计分析(交叉分组下的频数分析)指导教师周小刚一、实验目的掌握利用SPSS 软件进行基本统计量均值与均值标准误、中位数、众数、全距、方差和标准差、四分位数、十分位数和百分位数、频数、峰度、偏度的计算,进行标准化Z分数及其线形转换,统计表、统计图的显示。
二、实验内容及步骤(包括实验案例及基本操作步骤)(1)实验案例:居民储蓄存款。
(2)基本步骤:1、单击菜单选项analyze→descriptive statistics→crosstabs2、选择行变量到row(s)框中,选择列变量到column(s)框中3、选择dispiay clustered bar charts选项,指定绘制各变量交叉分组下的频数分布棒图。
三、实验结论(包括SPSS输出结果及分析解释)实验结论:较大部分储户认为在未来收入会基本不变,收入会增加的比例高于会减少的比例;城镇储户中认为收入会增加的比例高于会减少的比例,但农村储户恰恰相反;可见城镇和农村储户在对该问题的看法上存在分歧。
城镇户口较内存户口收入有明显的增加,但未来收入减少的比例差距不大。
其中二者未来收入大部分基本保持不变。
实验课程名称:统计分析与SPSS的应用专业经济学班级学号09091141 姓名律江山成绩实验地点G804 实验性质:演示性 验证性综合性设计性实验项目名称参数检验(两独立样本T检验)指导教师周小刚一、实验目的掌握利用 SPSS 进行单样本 T 检验、两独立样本 T 检验和两配对样本 T 检验的基本方法,并能够解释软件运行结果。
利用来自两个总体的独立样本,推断两个总体的均值是否存在显着差异。
spss统计学实验报告

竭诚为您提供优质文档/双击可除spss统计学实验报告篇一:统计学spss实验报告spss实验报告一.实验目的1.掌握spss的基本操作,能够熟练应用spss进行基本的统计分析。
2.在用spss对具体实例进行分析的基础上能对结果进行正确的解释。
3.在对spss基本操作熟练的情况下,进一步自学spss 更强大的分析能。
二.实验要求1.掌握如何通过spss进行数据的获取和管理,包括数据的录入,保存,读取,转化,增加,删除;数据集的合并,拆分,排序。
2.了解描述性统计的作用,并掌握其spss的实现(频数,均值,标准差,中位数,众数,极差)。
3.应用spss生成表格和图形,并对表格和图形进行简单的编辑和分析。
4.应用spss做一些探索性分析(如方差分析,相关分析)三.实验内容(一).问题的提出对不同广告方式和不同地区对某商品销售额影响进行分析。
在制定某商品的广告策略时,收集了该商品在不同地区采用不同广告形式促销后的销售额数据,分析广告形式和地区是否影响商品销售额。
自变量为广告方式(x1)和地区(x2),因变量为销售额(Y)。
涉及地区18个,每个地区抽取样本8个,共有案例144个。
具体数据如下:x11.002.004.003.001.002.004.003.001.002.004.003.001.002.004.003.001.002.004.003.00x21.001.001.001.002.002.002.002.003.003.003.003 .004.004.004.004.005.005.005.005.00Y75.0069.0063.00 52.0057.0051.0067.0061.0076.00100.0085.0061.0077.00 90.0080.0076.0075.0077.0087.0057.002.006.004.006.003.006.001.007.002.007.00 4.007.003.007.001.008.002.008.00 4.008.003.008.001.009.002.009.00 4.009.003.009.001.0010.002.0010.00 4.0010.003.0010.001.0011.002.0011.00 4.0011.001.0012.002.0012.00 4.0012.003.0012.001.0013.002.0013.004.0013.003.0011.003.0013.001.0014.002.0014.004.0014.003.0014.001.0015.002.0015.004.0015.003.0015.001.0016.002.0016.004.0016.003.0016.0060.0062.0052.0076.0033.0070.0033.0081.0079 .0075.0069.0063.0073.0040.0060.0094.00100.0064.0061 .0054.0061.0040.0070.0068.0067.0066.0087.0068.0051. 0041.0065.0065.0063.0061.0058.0065.0083.0075.0050.0079.0076.0064.0044.002.0017.004.0017.003.0017.001.0018.002.0018.004.0018.003.0018.001.001.002.001.004.001.003.001.001.002.002.002.004.002.003.002.001.003.002.003.004.003.003.003.001.004.002.004.004.004.00 3.004.001.005.002.005.00 4.005.003.005.001.006.002.006.00 4.006.003.006.001.007.002.007.00 4.007.003.007.001.008.002.008.00 4.008.003.008.001.009.002.009.00 4.009.003.009.0073.0050.0045.0075.0074.0062.0058.0068.0054. 0058.0041.0075.0078.0082.0044.0083.0079.0078.0086.0 066.0083.0087.0075.0066.0074.0070.0075.0076.0069.00 77.0063.0070.0068.0068.0052.0086.0075.0061.0061.006 2.0065.0055.0043.001.002.004.003.001.002.004.003.001.002.004.003.001.002.004.003.001.002.004.003.001.002.004.003.001.002.004.003.001.002.004.003.001.002.004.003.0010.0010.0010.0010.0011.0011.0011.0011.0012.0012.0012.0012.0013.0013.00 13.0013.0014.0014.0014.0014.0015.0015.0015.0015.001 6.0016.0016.0016.0017.0017.0017.0017.0018.0018.0018.0018.0088.0070.0076.0069.0056.0053.0070.0043.0086. 0073.0077.0051.0084.0079.0042.0060.0077.0066.0071.0 052.0078.0065.0065.0055.0080.0081.0078.0052.0062.00 57.0037.0045.0070.0065.0083.0060.00x1一列中,1表示报纸,2表示广播,3表示宣传品,4表示体验。
SPSS实验报告册

《SPSS统计软件应用》实验报告册20 - 20 学年第学期班级:学号:姓名:授课教师:实验教师:实验学时:实验组号:目录实验一SPSS的数据管理 (3)实验二描述性统计分析 (5)实验三均值检验 (6)实验四相关分析 (7)实验五因子分析 (8)实验六聚类分析 (11)实验七回归分析 (13)实验八判别分析 (14)实验一SPSS的数据管理一、实验目的1.熟悉SPSS的菜单和窗口界面,熟悉SPSS各种参数的设置;2.掌握SPSS的数据管理功能。
二、实验内容及步骤:1、定义spss数据结构。
下表是某大学的一个问卷调查,要求将问卷调查结果表示成spss可识别的数据文件,利用spss软件进行分析和处理。
练习:创建数据文件的结构,即数据文件的变量和定义变量的属性。
表1 大学教师基本情况调查表1.定义spss数据结构。
下表是某大学的一个问卷调查,要求将问卷调查结果表示成spss可识别的数据文件,利用spss软件进行分析和处理。
练习:创建数据文件的结构,即数据文件的变量和定义变量的属性。
实验步骤:(1)、打开定义变量的界面启动SPSS,进入主界面,单击图6-2所示的屏幕左下角的“Variable View”选项卡,打开定义变量的表格。
(2)、输入变量名,符合变量的命名规则在“Name”列的第一个单元格输入第一个变量名,如:“xm”。
(3)、确定变量类型,单击“Type”列的第一个单元格,如图6-3所示,SPSS的默认变量类型为数值型。
单击数值型变量后的“···”,弹出如图6-4所示的对话框,用户可以从该对话框中选择其他的变量类型。
(4)、设置字段值(5)、依次按要求输入完毕即可实验结果:实验分析:本实验,主要是按照要求一步一步来设置条件即可完满完成实验。
2 、高校提前录取名单的确定某高校今年对部分考生采取单独出题、提前录取的招生模式。
现有20名来自国内不同省市的考生报考该校,7个录取名额。
SPSS第3次实验报告
成绩
性别均值N标准差
男12
女12
总计24
二、T检验
(一)单样本T检验
1.原理:
单样本T检验的目的是利用来自某总体的样本数据,推断该总体的均值是否与指定检验值之间存在显著性差异。
这里前提是要求样本来自的总体服从正态分布。
2.步骤:
1)根据题意提出原假设H0和备择假设H1
2)选择检验统计量
当总体分布为正态分布时,样本均值的抽样分布仍为正态分布,该正态分布的均值为μ,方差为σ2/n,即
X——~N(μ,σ2/n)
式中,μ为总体均值,当原假设成立时,μ=μ0,σ2为总体方差。
n为样本数。
总体分布近似服从正态分布时,通常总体方差是未知的,此时可以用样本方差S2替代,得到的检验统计量为t统计量,。
SPSS实验报告

安徽建筑大学数据统计分析实验报告专业统计学班级二班学生姓名陈永帅学号 *********** 实验日期实验一描述性统计分析一、实验目的与要求统计分析的目的在于研究总体特征。
但是,由于各种各样的原因,我们能够得到的往往只能是从总体中随机抽取的一部分观察对象,他们构成了样本,只有通过对样本的研究,我们才能对总体的实际情况作出可能的推断。
因此描述性统计分析是统计分析的第一步,做好这一步是进行正确统计推断的先决条件。
通过描述性统计分析可以大致了解数据的分布类型和特点、数据分布的集中趋势和离散程度,或对数据进行初步的探索性分析(包括检查数据是否有错误,对数据分布特征和规律进行初步观察)。
本本实验旨在于:引到学生利用正确的统计方法对数据进行适当的整理和显示,描述并探索出数据内在的数量规律性,掌握统计思想,培养学生学习统计学的兴趣,为继续学习推断统计方法及应用各种统计方法解决实际问题打下必要而坚实的基础。
二、实验原理描述统计是统计分析的基础,它包括数据的收集、整理、显示,对数据中有用信息的提取和分析,通常用一些描述统计量来进行分析。
集中趋势的特征值:算术平均数、调和平均数、几何平均数、众数、中位数等。
其中均数适用于正态分布和对称分布资料,中位数适用于所有分布类型的资料。
离散趋势的特征值:全距、内距、平均差、方差、标准差、标准误、离散系数等。
其中标准差、方差适用于正态分布资料,标准误实际上反映了样本均数的波动程度。
分布特征值:偏态系数、峰度系数、他们反映了数据偏离正态分布的程度。
三、实验内容与步骤下面给出的一个例题是来自SPSS软件自带的数据文件“Employee.data”,该文件包含某公司员工的工资、工龄、职业等变量,我们将利用此例题给出相关的描述统计说明,本例中,我们将以员工的当前工资为例,计算该公司员工当前工资的一些描述统计量,如均值、频数、方差等描述统计量的计算。
频率附注创建的输出16-12月-2013 15时55分55秒注释输入数据C:\Users\YSC\Desktop\data12-01.sav 活动的数据集数据集1过滤器<none>权重<none>拆分文件<none>工作数据文件中的N 行12 缺失值处理对缺失的定义用户定义的丢失值作为丢失对待。
应用回归分析实验报告3
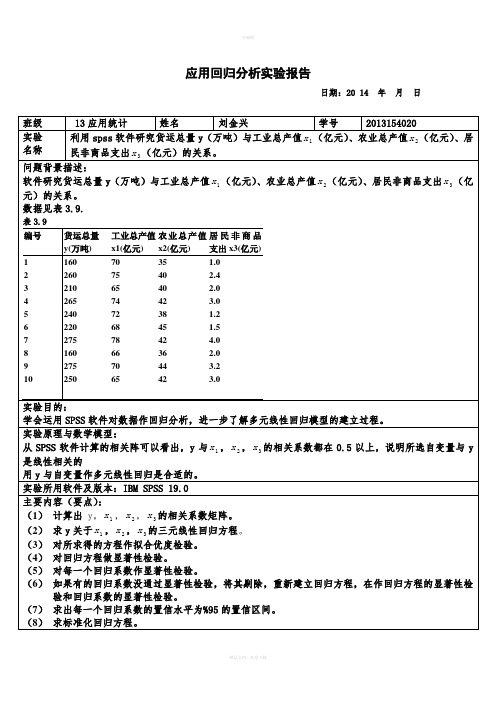
做t检验:设原假设为 ,
统计量服从自由度为n-p-1=6的t分布,给定显著性水平0.05,查得单侧检验临界值为1.943,X1的t值=1.942<1.943,处在否定域边缘。
X2的t值=2.465>1.943。拒绝原假设。
由上表可得,在显著性水平 时,只有 的P值<0.05,通过检验,即只有 的回归系数较为显著 ;其余自变量的P值均大于0.05,即x1,x2的系数均不显著。
用y与自变量作多元线性回归是合适的。
实验所用软件及版本:IBM SPSS 19.0
主要内容(要点):
(1)计算出y, , , 的相关系数矩阵。
(2)求y关于 , , 的三元线性回归方程。
(3)对所求得的方程作拟合优度检验。
(4)对回归方程做显著性检验。
(5)对每一个回归系数作显著性检验。
(6)如果有的回归系数没通过显著性检验,将其剔除,重新建立回归方程,在作回归方程的显著性检验和回归系数的显著性检验。
10.569
.277
1.178
.284
2
(常量)
-459.624
153.058
-3.003
.020
x1
4.676
1.816
.479
2.575
.037
x2
8.971
2.468
.676
3.634
.008
1
(常量)
-348.280
176.459
-1.974
.096
x1
3.754
1.933
.385
1.942
.053
14.149
x3
12.447
10.569
spss实验报告

试验3:统计推断一、试验目的与要求1.熟悉点估计概念与操作方法2.熟悉区间估计的概念与操作方法3.熟练掌握T检验的SPSS操作4.学会利用T检验方法解决身边的实际问题二、试验原理1.参数估计的基本原理2.假设检验的基本原理实验3-1实验数据实验结果/TESTVAL=65/MISSING=ANALYSIS/VARIABLES=英语成绩从表中可以得出,英语成绩区间估计(置信度为95%)为(.37,9.23)。
点估计是.035。
实验3-2T-TEST GROUPS=性别('男' '女')/MISSING=ANALYSIS/VARIABLES=成绩/CRITERIA=CI(.95).组统计量性别N 均值标准差均值的标准误成绩男18 81.28 10.369 2.444女14 76.29 11.432 3.055分别给出不同总体下的样本容量、均值、标准差和平均标准误。
从表中可以看出,平均成绩男为相等)下,F=0.647,因为其P-值大于显著性水平,即:Sig.=0.428>0.05,说明不能拒绝方差相等的原假设,接受两个总体方差是相等的假设。
因此男女生英语成绩之差95%的区间估计为[-2.898, 12.882]。
T-test for Equality of Means 为检验总体均值是否相等的t 检验,由于在本例中,其P-值大于显著性水平,即:Sig.=0.206>0.05,因此不应该拒绝原假设,也就是说男女生英语成绩没有显著差异。
试验4:方差分析一、试验目标与要求1.帮助学生深入了解方差及方差分析的基本概念,掌握方差分析的基本思想和原理2.掌握方差分析的过程。
3.增强学生的实践能力,使学生能够利用SPSS统计软件,熟练进行单因素方差分析、两因素方差分析等操作,激发学生的学习兴趣,增强自我学习和研究的能力。
二、试验原理方差分析也是一种假设检验,它是对全部样本观测值的变动进行分解,将某种控制因素下各组样本观测值之间可能存在的由该因素导致的系统性误差与随即误差加以比较,据以推断各组样本之间是否存在显著差异。
SPSS相关分析实验报告_实验报告_

SPSS相关分析实验报告篇一:spss对数据进行相关性分析实验报告实验一一.实验目的掌握用spss软件对数据进行相关性分析,熟悉其操作过程,并能分析其结果。
二.实验原理相关性分析是考察两个变量之间线性关系的一种统计分析方法。
更精确地说,当一个变量发生变化时,另一个变量如何变化,此时就需要通过计算相关系数来做深入的定量考察。
P值是针对原假设H0:假设两变量无线性相关而言的。
一般假设检验的显著性水平为0.05,你只需要拿p值和0.05进行比较:如果p值小于0.05,就拒绝原假设H0,说明两变量有线性相关的关系,他们无线性相关的可能性小于0.05;如果大于0.05,则一般认为无线性相关关系,至于相关的程度则要看相关系数R值,r越大,说明越相关。
越小,则相关程度越低。
而偏相关分析是指当两个变量同时与第三个变量相关时,将第三个变量的影响剔除,只分析另外两个变量之间相关程度的过程,其检验过程与相关分析相似。
三、实验内容掌握使用spss软件对数据进行相关性分析,从变量之间的相关关系,寻求与人均食品支出密切相关的因素。
(1)检验人均食品支出与粮价和人均收入之间的相关关系。
a.打开spss软件,输入“回归人均食品支出”数据。
b.在spssd的菜单栏中选择点击,弹出一个对话窗口。
C.在对话窗口中点击ok,系统输出结果,如下表。
从表中可以看出,人均食品支出与人均收入之间的相关系数为0.921,t检验的显著性概率为0.000<0.01,拒绝零假设,表明两个变量之间显著相关。
人均食品支出与粮食平均单价之间的相关系数为0.730,t检验的显著性概率为0.000<0.01,拒绝零假设,表明两个变量之间也显著相关。
(2)研究人均食品支出与人均收入之间的偏相关关系。
读入数据后:A.点击系统弹出一个对话窗口。
B.点击OK,系统输出结果,如下表。
从表中可以看出,人均食品支出与人均收入的偏相关系数为0.8665,显著性概率p=0.000<0.01,说明在剔除了粮食单价的影响后,人均食品支出与人均收入依然有显著性关系,并且0.8665<0.921,说明它们之间的显著性关系稍有减弱。
SPSS实验报告

描述性统计分析一、实验目的1.进一步了解掌握SPSS专业统计分析软件,能更好地使用其进行数据统计分析。
2.学习描述性统计分析及其在SPSS中的实现,内容具体包括基本描述性统计量的定义及计算﹑频率分析﹑描述性分析﹑探索性分析﹑交叉表分析等。
3.复习权重等前章的知识。
二﹑实验内容题目一打开数据文件“data4-5.sav”,完成以下统计分析:(1)计算各科成绩的描述统计量:平均成绩、中位数、众数、标准差、方差、极差、最大值和最小值;(2)使用“Recode”命令生成一个新变量“成绩段”,其值为各科成绩的分段:90~100为1,80~89为2,70~79为3,60~69为4,60分以下为5,其值标签设为:1-优,2-良,3-中,4-及格,5-不及格。
分段以后进行频数分析,统计各分数段的人数,最后生成条形图和饼图。
1.解决问题的原理因为问题涉及各科成绩,用描述性分析,第二问要先进行数据分段,其后利用频数分析描述统计量并可以生成条形图等。
2.实验步骤针对第一问第1步打开数据菜单选择:“文件→打开→数据”,将“data4-8.sav”导入。
第2步文件拆分菜单选择:“数据→拆分文件”,打开“分割文件”对话框,点击比较组按钮,将“科目”加入到“分组方式”列表框中,并确定。
第3步描述分析设置:(1)选择菜单:“分析→描述统计→描述”,打开“描述性”对话框,将“成绩””加入到“变量”列表框中。
打开“选项”对话框,选中如下图中的各项。
点击“继续”按钮。
(4)回到“描述性”对话框,点击确定。
针对第二问第1步频率分析设置:(1)选择菜单:“分析→描述统计→频率”,(2)打开“频率(F)”对话框,点击“合计”。
再点击“继续”按钮.(3)打开“图表”对话框,选中“条形”复选框,点击“继续”按钮。
(4)回到“频率(F)”对话框,点击确定。
(5)重复步骤(1)(2)把步骤(3)改成打开“图表”对话框,选中“饼图”复选框,点击“继续”按钮。
SPSS实验报告

通过计算诸如样本均值、中位数、样本方差等重要基本统计量,并辅助于SPSS 提供的图形功能,能够使分析者把握数据的基本特征和数据的整体分布形态,对进一步的统计判断和数据建模工作起到重要作用。
并且,通过例子学习描述性统计分析及其在 SPSS 中的实现,包括统计量的定义及计算、频率分析、描述性分析、探索性分析、交叉表分析和多重响应分析,能够使分析者更好的掌握基本的统计分析,即单变量频数分布的编制、基本统计量的计算以及数据的探索性分析等。
1.打开数据文件 data4-8.sav,完成以下统计分析。
(1)计算各科成绩的描述统计量:平均成绩、中位数、众数、标准差、方差、极差、最大值和最小值;①解决问题的原理:描述性分析②实验步骤:通过“分析-描述统计-描述”,打开“描述性”对话框,根据题目所需要的统计量进行设置。
③结果及分析:表中分析变量“成绩”的个案数、所有个案中的极大值、极小值、均值、标准差及方差。
(2)使用 Recode 命令生成一个新变量“成绩段”,其值为各科成绩的分段: 90~100 为 1,80~89 为 2,70~79 为 3,60~69 为4,60 分以下为 5,其值标签: 1—优, 2—良, 3—中, 4—及格, 5—不及格。
分段以后进行频数分析,统计各分数段的人数,最后生成条形图和饼图。
①解决问题的原理:频率分析。
②实验步骤:通过“分析-描述统计-频率”,打开“频率”对话框,根据题目所需要的统计量进行设置。
③结果及分析:有效1519242830323334363743495055频率11111211121111百分比2.22.22.22.22.24.42.22.22.24.42.22.22.22.2有效百分比2.22.22.22.22.24.42.22.22.24.42.22.22.2积累百分比2.24.46.78.911.115.617.820.022.226.728.931.133.3全距极小值83 15成绩有效的 N (列表状态) N4545标准差23.048极大值98方差531.210均值60.518.9 6.7 2.2 2.2 2.2 2.2 6.7 2.2 2.2 2.2 2.2 2.2 2.2 4.4 2.2 4.4 2.2 4.4 2.2 100.0表中显示了变量“成绩段”在各个取值上浮现的次数(频率)、其频率占所有个案中的百分比、有效百分比及积累百分比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
准误
间
下限
上限
df Sig.(双 侧)
11 .007
该生对待本次实验的态度 本次实验的过程情况 对实验结果的展示 文档书写符合规范程度
□认真 □良好 □一般 □比较差 □很好 □较好 □一般 □比较差 □很好 □良好 □一般 □比较差 □很好 □良好 □一般 □比较差
成绩
指导教师签名
刘静静
日期
结果显示统计量 t=,P 值=<,因此接受原假设,即可以认为干预前后该地区贫血儿 童血红蛋白(%)平均水平有变化,且变化方向为增长。
对1
干预前 干预后
表8 成对样本统计量
均值
N
标准差
12
12
均值的标准误
对 干预前 - 干预后
1
成绩评定:
表9 成对样本检验
成对差分
t
均值
标准差 均值的标 差分的 95% 置信区
当总体分布为正态分布时,样本均值的抽样分布仍为正态分布,该正态分布的 均值为μ,方差为σ2/n,即
—X—~N(μ,σ2/n) 式中,μ为总体均值,当原假设成立时,μ=μ0,σ2 为总体方差。n 为样本数。 总体分布近似服从正态分布时,通常总体方差是未知的,此时可以用样本方差 S2 替代,得到的检验统计量为 t 统计量,
如果概率 P 值小于显着性水平α,则应拒绝原假设;反之,则应接受原假设。 3. 实际操作
案例来源:《SPSS 统计分析大全:清华大学出版社》 某药物在某种溶剂中溶解后的标准浓度为 L。先采用某种方法,测量该药物溶解液 11 次。问:用该方法测量所得的结果是否与标准浓度值有所不同
分析:目的是利用来自某总体的样本数据,推断该总体的均值是否与指定检验值之 间存在显着性差异,假设样本来自的总体服从正态分布,用单样本 T 检验。
过程:
H0:用该方法测量所得的结果与标准浓度值相同 H1:用该方法测量所得的结果与标准浓度值不同 使用 SPSS 得出下表
表中显示 N=11,均值为,标准差为;在检验值为,置信水平为的数值下的 t 统计量为,不在
(,)之内;P 值=<
所以拒绝 H0,暂时接受 H1
表3 单个样本统计量
N
均值
标准差 均值的标准误
实际操作:案例来源:《SPSS 统计分析大全:清华大学出版社》
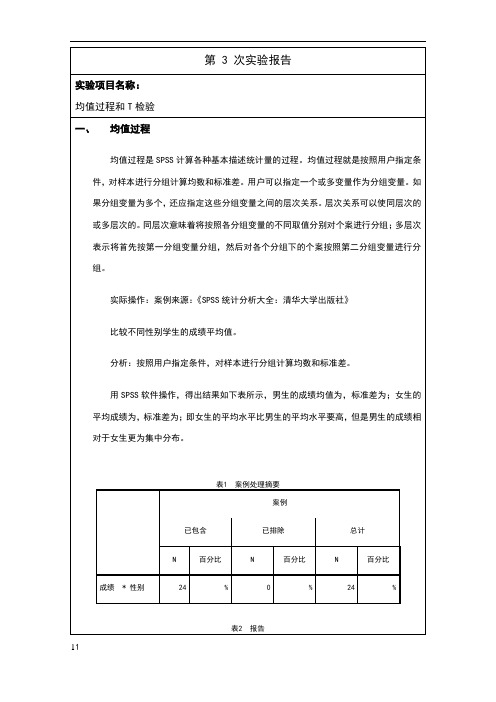
比较不同性别学生的成绩平均值。
分析:按照用户指定条件,对样本进行分组计算均数和标准差。
用 SPSS 软件操作,得出结果如下表所示,男生的成绩均值为,标准差为;女生的 平均成绩为,标准差为;即女生的平均水平比男生的平均水平要高,但是男生的成绩相 对于女生更为集中分布。
class
表5 组统计量
N
均值
标准差
均值的标准误
score 甲班
Байду номын сангаас20
乙班
20
方差方程的 Levene 检验
表6 独立样本检验 均值方程的 t 检验
F
Sig. t
df Sig.(双 均值差 标准误 差分的 95% 置信
侧)
值
差值
区间
下限 上限
假设方差 相等 score 假设方差 不相等
.733
.397
H0:考试后的成绩不存在差异
H1:考试后的成绩存在差异
甲班样本数为 20,均值为,标准差为;乙班样本数为 20,均值为,标准差为。说 明甲班成绩均值高于乙班且标准差小于乙班,波动较小。
95% 置信区间里,t 统计量在置信区间的上下限范围之内,因此,我们选择接受原 假设,即甲乙两班考试后的成绩不存在差异。
3) 计算检验统计量观测值和概率 P 值 4) 给定显着性水平α,并作出决策
3. 实际操作
案例来源:《SPSS 统计分析大全:清华大学出版社》
现希望评价两位老师的教学质量,是比较其分别任教的甲、乙两班(设甲、乙两班 原成绩相近,不存在差别)考试后的成绩是否存在差异
分析:有两个总体的独立样本,推断两个总体的均值是否存在显着差异。 过程:
成绩 * 性别
表1 案例处理摘要 案例
已包含
已排除
N
百分比
N
百分比
24
%
0
%
总计
N
百分比
24
%
成绩 性别 男 女 总计
表2 报告
均值
N
标准差
12 12 24
二、 T 检验
(一) 单样本 T 检验 1. 原理:
单样本 T 检验的目的是利用来自某总体的样本数据,推断该总体的均值是否与指定 检验值之间存在显着性差异。这里前提是要求样本来自的总体服从正态分布。 2. 步骤: 1) 根据题意提出原假设 H0 和备择假设 H1 2) 选择检验统计量
实验项目名称: 均值过程和 T 检验
第 3 次实验报告
一、 均值过程
均值过程是 SPSS 计算各种基本描述统计量的过程。均值过程就是按照用户指定条 件,对样本进行分组计算均数和标准差。用户可以指定一个或多变量作为分组变量。如 果分组变量为多个,还应指定这些分组变量之间的层次关系。层次关系可以使同层次的 或多层次的。同层次意味着将按照各分组变量的不同取值分别对个案进行分组;多层次 表示将首先按第一分组变量分组,然后对各个分组下的个案按照第二分组变量进行分 组。
A. 当量总体方差未知且相等,即σ1=σ2 时,采用合并的方差作为两个总体的 方差估计,数学定义为:(t 统计量服从个自由度的 t 分布)
B. 当量总体方差未知且不相等,即σ1≠σ2 时,分别采用各自的方差,此时 两样本均值差的抽样分布的方差σ212 为:(t 统计量服从修正自由度的 t 分布)
于是,两总体均值差的检验统计量为 t 统计量:
式中,t 统计量服从自由度为 n-1 的 t 分布。单样本 T 检验的统计量即为 t 统 计量。当认为原假设成立时用μ代替μ0。 3) 计算检验统计量的观测值和概率值
该步目的是计算检验统计量的观测值和相应的概率 P 值。SPSS 将自动将样本均 值、μ0 样本方差、样本数带入式中,计算出 t 统计量的观测值和对应的概率 P 值。 4) 给定显着性水平α,并作出决策
38
.004
.004
(三) 配对样本 T 检验
1. 原理:
利用来自两个不同总体的配对样本,推断两个总体的均值是否存在显着差异。在配 对设计得到的样本数据中,每对数据之间都有一定的相关,如果忽略这种关系就会浪费 大量的统计信息,因此配对样本 T 检验的前提要求为:(1)两样本必须是配对的。配对 可以从两个因素考虑,首先,两样本的观察值数目相等;其次,两样本的栓差值的书序 不能随意更改。(2)样本来自的两个总体应服从正态分布。
平有无变化
分析:干预前后的数据可以当成是来自两个不同总体的配对样本,推断两个总体的 均值是否存在显着差异。
过程:
H0:干预前后该地区贫血儿童血红蛋白(%)平均水平有变化
H1:干预前后该地区贫血儿童血红蛋白(%)平均水平没有变化
结果:表所示为配对样本 T 检验分析的结果,干预前的均值为,标准差为,干预后 的均值为,标准差为,说明干预后该地区贫血儿童血红蛋白(%)平均水平有增长,且 波动幅度不大。
浓度
11
.32186
t 浓度
表4 单个样本检验 检验值 =
df
Sig.(双侧) 均值差值 差分的 95% 置信区间
下限
上限
10
.012
.98364
.2665
(二) 独立样本 T 检验 1. 原理:
利用两个总体的独立样本,推断两个总体的均值是否存在显着差异。这个检验的前 提要求是:(1)独立。两组数据相互独立,互不相关;(2)正态,剂量组样本来自的总 体符合正态分布;(3)方差齐性。即两组方差相等。 2. 步骤: 1) 提出零假设 2) 选择检验统计量
2. 步骤
1) 提出原假设
2) 选择检验统计量
3) 计算检验统计量观测值和概率 P 值
4) 给定显着性水平α,并作出决策
3. 实际操作
案例来源:《SPSS 统计分析大全:清华大学出版社》
某地区随机抽取 12 名贫血儿童的家庭,实行健康教育干预三个月,干预前后儿童 的血红蛋白(%)测量结果如 sav,试问干预前后该地区贫血儿童血红蛋白(%)平均水
