期权历史数据
汇点期权使用说明书

汇点期权使用说明书V6.5.6.5汇点期权使用说明书1. 汇点期权简介2. 快速入门2.1 系统安装登录及退出2.2 系统界面3. 报价界面3.1 T型报价3.2 全部行情3.3 自选行情3.4 自定义页面3.5 波动率指数3.6 期权策略3.7 T报主力3.8 期权操盘3.9 指标条件单4. 分时图画面4.1 股票期权分时走势4.2 历史回忆4.3 叠加商品4.4 快捷调入指标4.5 持仓线5. K线图画面5.1 股票期权K线图5.2 变换指标5.3 调整指标参数5.4 叠加/删除均线5.5 主图类型5.6 主图坐标5.7 变换周期5.8 任意周期设置5.9 五彩K线5.10 除权状态5.11 改变画面组合5.12 保存多组指标参数5.13 区间统计5.14 画线工具5.15 变换画面5.16 持仓线5.17 PCR指标6. 信息窗口6.1 信息窗口说明6.2 状态及分笔信息6.3 特征值信息窗口6.4 快捷交易窗口6.5 快鼠交易窗口6.6 隐藏/显示信息窗口6.7 股票特殊信息窗口7. F10资料画面8. 弹窗工具8.1 弹出式下单面板8.2 批量下单面板8.3 债券参数设置8.4 期权筛选8.5 期权卖方分析8.6 期权定价计算8.7 期权统计8.8 培训视频8.9 预警设置8.10 预警列表8.11 选股工具9. 股票期权下单方式9.1 登录交易系统9.2 交易界面9.3 三键下单9.4 闪电下单9.5 买入下单9.6 卖出下单9.7 键盘下单9.8 闪电精灵下单9.9 点价下单9.10 快鼠下单9.11 快键下单9.12 弹出式下单9.13 批量下单9.14 下单条下单10. 股票期权交易10.1 委托栏10.2 可撤栏10.3 成交栏10.4 持仓10.5 委托汇总10.6 锁定解锁10.7 查询10.8 参数设置10.9 银衍转账10.10 修改密码10.11 汇点本地组合11. 条件单和止损止盈11.1 条件单11.2 止损止盈12. 策略保证金12.1 上海策略保证金12.2 深圳策略保证金12.3 普通备兑互转12.4 历史委托13. 行权13.1 普通行权13.2 上海合并行权13.3 深圳合并行权13.4 自动行权14. 普通证券交易14.1 登录交易系统14.2 交易界面14.3 撤单14.4 快鼠下单14.5 点价下单14.6 查询14.7 参数设置15. 其他功能15.1 公式管理器15.2 预警系统15.3 编辑表头15.4 系统设置15.5 数据下载15.6 特色选股15.7 行情切换服务器15.8 计算器16. 帮助和服务16.1 服务16.2 版本升级16.3 版本信息16.3 版本信息1. 汇点期权简介汇点期权基于专业的衍生品交易系统架构设计开发,不仅功能完备成熟稳定,而且在行情展示和交易方面做了丰富的设计,使整个交易过程更为顺畅、效率更高,轻松应对期权高速交易频率,受到众多终端用户的好评。
收益波动率计算

THANKS
感谢观看
市场走势分析
总结词
市场走势分析是收益波动率计算的一个重要应用,通过分析历史波动率,可以预测市场 的未来走势。
详细描述
在市场走势分析中,历史波动率是一个重要的参考指标。通过对历史波动率的分析,可 以了解市场的走势和未来可能的走势。同时,结合其他技术指标和市场信息,可以对市
场走势进行更加准确的预测。
06
收益波• 历史波动率计算 • 隐含波动率计算 • 预测波动率计算 • 实际应用与案例分析 • 总结与展望
01
CATALOGUE
收益波动率概述
定义与意义
定义
收益波动率是衡量资产收益率变 动幅度的指标,表示资产收益率 的不确定性或风险。
意义
收益波动率对于投资者来说具有 重要的参考价值,能够帮助他们 评估投资风险、制定投资策略和 进行资产配置。
01
利用历史数据计算收益率的标准差或方差,以此作为历史波动
率的度量。
计算隐含波动率
02
通过期权定价公式反解出隐含波动率,基于市场价格和无套利
原则。
计算预期波动率
03
基于预测模型对未来波动率进行预测,结合市场信息和历史数
据。
预测波动率的优缺点
优点
能够为投资者提供未来市场走势的参考,有助于制定投资策略和风险管理。
将得到的理论价格与市场价格进行比较,调整波动率参数,使得理论 价格与市场价格一致。
迭代计算
重复上述步骤,直到波动率参数收敛。
隐含波动率的优缺点
优点
能够反映市场参与者对未来波动率的预期,有助于评估期权的合理价格。
缺点
依赖于期权定价模型的准确性,对于非线性衍生品定价可能存在局限性;同时,隐含波动率受到市场供需关系的 影响,可能存在套利机会。
期权(课堂PPT原创)ppt文档全文预览

竞价机制
投资者通过竞价方式买卖期权合约, 交易所按照价格优先、时间优先的 原则进行撮合成交。
投资者适当性管理
投资者分类
根据投资者的风险承受能 力和投资经验,将投资者 分为专业投资者和普通投 资者。
适当性评估
对投资者进行适当性评估, 确保其了解期权市场的风 险并具备相应的风险承受 能力。
投资者教育
开展投资者教育活动,提 高投资者对期权市场的认 知和风险意识。
CHAPTER 03
期权定价模型与方法
Black-Scholes模型原理及应用
模型假设
股票价格服从对数正态 分布,无风险利率和波 动率恒定,无交易费用
和税收等。
定价公式
通过求解偏微分方程得 到期权价格公式,包括 欧式看涨期权、欧式看
期权(课堂PPT原 创)ppt文档全文预览
目录
• 期权基本概念与原理 • 期权市场与交易制度 • 期权定价模型与方法 • 期权策略类型与运用 • 期权风险管理技巧与实践 • 期权产品创新与发展趋势
CHAPTER 01
期权基本概念与原理
期权定义及分类
定义
期权是一种合约,赋予持有人在某一 特定日期或该日之前的任何时间以固 定价格购进或售出一种资产的权利。
CHAPTER 02
期权市场与交易制度
全球主要期权市场概述
1 2
芝加哥期权交易所(CBOE) 全球最大、最活跃的期权交易所,提供多元化的 期权产品。
欧洲期货交易所(Eurexห้องสมุดไป่ตู้ 欧洲领先的衍生品交易所,提供广泛的股票期权 和指数期权。
3
香港交易所(HKEX)
上证所 历史数据接口说明书

上海证券交易所历史数据接口说明书文档状态[]初稿[]评审通过[]修改[√]发布[]作废文档标识历史数据接口说明书当前版本 1.1.1(技术开发稿)作者市场数据部发布者上证所信息网络有限公司完成日期2022/11/02文档变动说明1.数据说明上交所行情历史数据提供与证券行情相关的历史数据服务。
从行情品种来看,包括Level-1行情、Level-2行情及股票期权历史数据。
从数据内容来看,包括快照类数据、逐笔类数据及K线数据,其中快照类数据包括开盘集合竞价数据、行情快照数据、盘后固定价格交易行情快照,逐笔类数据包括竞价逐笔成交数据、竞价逐笔委托数据、盘后固定价格交易逐笔成交数据和债券逐笔类数据,K线数据包括分钟K线和日K线数据。
2.文件格式文件采用CSV格式,每个字段间用“,”(英文半角)分割,使用UTF-8字符集,换行符使用“0x0A”。
3.数据内容不同行情品种提供的历史数据种类有所差异,具体见表3-1所示。
表3-1行情品种和数据种类对照表品种行情快照逐笔成交逐笔委托日K线分钟K线Level-1行情√√√Level-2行情√√√√√股票期权行情√√√3.1Level-1行情Level-1行情包括快照类数据和K线数据。
3.1.1快照类数据Level-1快照类数据包括行情快照和盘后固定价格交易行情快照。
3.1.1.1行情快照Level-1行情快照数据的快照间隔为3秒或5秒(其中,部分指数快照间隔为5秒,个股及部分指数快照间隔为3秒,相邻快照如果完全相同就保留第一幅),将全天所有证券的快照保存在同一个文件中。
需要注意的是,集合竞价数据包含在Level-1行情快照中。
Level-1行情快照数据的存储目录及文件名为sh1\yyyymmdd\Snapshot.csv,具体内容详见表3-2。
表3-2Level-1行情快照数据内容表NumTrades成交笔数NUMBERIOPV净值估值NUMBER(3)从20221104日开始为NUMBER(5)从20221104日开始,该值表示为5位精度NAV净资产价值NUMBER(3)PhaseCode交易时段STRING该字段为8位字符串,左起每位表示特定的含义,无定义则填空格。
布莱克舒尔斯期权定价模型

第二节 布莱克-舒尔斯期权定价模型
一、布莱克-舒尔斯微分方程 风险中性定价原理在远期合约定价中的应用: ❖ 边界条件:
布莱克舒尔斯期权定价模型
第二节 布莱克-舒尔斯期权定价模型
二、布莱克-舒尔斯期权定价公式
❖ 股票价格服从对数正态分布,风险中性条件下以r取代μ,即:
❖ 在风险中性的条件下,无收益资产欧式看涨期权到期时(T 时刻)的期望值为:
第一节 证券价格的变化过程
四、证券价格的变化过程 几何布朗运动
❖ :证券在单位时间内的连续复利的期望收益率 ❖ :证券收益率单位时间的方差 ❖ :证券价格的波动率(Volatility) ❖ :遵循标准布朗运动
几何布朗运动的离散形式
布莱克舒尔斯期权定价模型
第一节 证券价格的变化过程
四、证券价格的变化过程
几何布朗运动的基本特征: ❖ 在短时间 后,证券价格比率的变化值
为:
❖ 因此: 方差为
❖ 即:
也具有正态分布特征,其均值为 , ,标准差为
表示均值为m ,标准差为s的正态分布
布莱克舒尔斯期权定价模型
第一节 证券价格的变化过程
四、证券价格的变化过程
对几何布朗运动的理解:
❖ 但是,在一个较长的时间T后, 不再具有正态分 布的性质:这是百分比多期收益率的乘积问题。
三、BS定价公式的基本扩展 无收益资产美式看涨期权的定价公式 在标的资产无收益情况下,美式看涨期权提前执行 是不合理的,因此C=c 无收益资产美式看涨期权的定价公式是:
布莱克舒尔斯期权定价模型
第二节 布莱克-舒尔斯期权定价模型
三、BS定价公式的基本扩展
有收益资产欧式期权-1
在收益已知情况下,标的证券价格可以分解成两部分: 期权有效期内已知现金收益的现值部分 一个有风险部分
BS期权定价公式

Black-Scholes 期权定价模型一、Black-Scholes 期权定价模型的假设条件Black-Scholes 期权定价模型的七个假设条件如下:1. 风险资产(Black-Scholes 期权定价模型中为股票),当前时刻市场价格为S。
S 遵循几何布朗运动,即dS dt dz。
S其中,dz 为均值为零,方差为dt 的无穷小的随机变化值( dz dt ,称为标准布朗运动,代表从标准正态分布(即均值为0、标准差为1 的正态分布)中取的一个随机值),为股票价格在单位时间内的期望收益率,则是股票价格的波动率,即证券收益率在单位时间内的标准差。
和都是已知的。
简单地分析几何布朗运动,意味着股票价格在短时期内的变动(即收益)来源于两个方面:一是单位时间内已知的一个收益率变化,被称为漂移项,可以被看成一个总体的变化趋势;二是随机波动项,即dz ,可以看作随机波动使得股票价格变动偏离总体趋势的部分。
2.没有交易费用和税收,不考虑保证金问题,即不存在影响收益的任何外部因素。
3.资产价格的变动是连续而均匀的,不存在突然的跳跃。
4.该标的资产可以被自由地买卖,即允许卖空,且所有证券都是完全可分的。
5.在期权有效期内,无风险利率 r 保持不变,投资者可以此利率无限制地进行借贷。
6.在衍生品有效期间,股票不支付股利。
7.所有无风险套利机会均被消除。
1、 Black-Scholes 期权定价模型一) B-S 期权定价公式Black 和 Scholes 得到了如下适用于无收益资产欧式看涨期权的 Black-Schole 微分方程:其中 f 为期权价格,其他参数符号的意义同前。
通过这个微分方程, Black 和 Scholes 得到了如下适用于无收益资产欧式看 涨期权的定价公式: c SN(d 1) Xe r (T t) N(d 2)其中,Ttd ln(S/X) (r 2/2)(T t) dT td 2 d 1T t Tt c 为无收益资产欧式看涨期权价格; N ( x )为标准正态分布变量的累计概率 分布函数(即这个变量小于 x 的概率),根据标准正态分布函数特性,我们有 N( x) 1 N(x) 。
中国金融期权波动率指数特征与应用研究

三、中国期权波动率指数特征的实证 分析
(一) 研究思路与模型选择 Nhomakorabea升幅度。即当行情变差时,投资者往往产生一
1研究思路
系列恐慌情绪,通过大量抛售现货或增加执行
中国波动率指数 (iVIX) 是由上海证券交
价更低的认沽期权头寸来避险保值,波动率指 易所发布,基于期权交易数据按照方差互换原
数由此大幅上涨;然而市场上行阶段,投资者 理编制的波动率指数,用于预测上证 50指数未
二、国内外期权波动率指数的发展概况
波动率是一个统计概念,它是用于衡量资 产价格波动程度,用来衡量标的资产价格变动 幅度。目前,波动率指数的功能主要在于反映 市场恐慌情绪,预警市场行情,管理市场风险。
(一) 美国期权波动率指数发展概况
1993年,芝 加 哥 期 权 交 易 所 (CBOE) 提 出了 VIX指数 (VolatilityIndex) 概念,也是最 重要的波动率指数,2003年 CBOE更新了 VIX 算法,把标的指数从 S&P100指数改成 S&P500 指数,推出了基于 S&P500指数的期权的实时价 格的 VIX指数,来代表整个期权市场投资者对 未来 30天股价指数波动率的预期。
因此推升股指期权价格,进而使得其平均隐含 该指数由中证指数有限公司维护。
波动率上升,即波动率指数上升;反之当投资
中国波动率指数具有三个特点,其一使用
者预期股市平稳或上涨时,则会减少对冲头寸, 时下最为流行的无模型法编制;其二使用真实
压低股指期权价格,进而使得波动率指数下降。 的上证 50ETF期权交易数据,而不是虚拟的交
即波动率指数与标的指数在大部分时间都呈现 际情况,在期权价格确定时综合考虑成交价、买
出明显的负相关关系。
隐含波动率和历史波动率

历史波动率和隐含波动率1 历史波动率历史波动率反映了过去股价波动程度的大小,可根据股价的历史数据进行客观度量。
根据B-S 期权定价理论,股票价格运动为几何布朗运动,运动过程可用如下随机过程描述:dS Sdt Sdz μσ=+ (1)两边同除以S 可得:dz dt S dS σμ+= (2) 其中dz 为一标准布朗运动,该项为股价随机性的来源。
接下来考虑运动过程ln S ,由于S 为一随机过程,显然Ln S 也是一随机过程,并且根据伊藤引理可得:dz dt S d σσμ+-=)2(ln 2(3)在一段小的时间间隔t ∆ 中 ,由(2)式可得t t z t S S ∆+∆=∆+∆=∆σεμσμ (4) 可见,收益率S S ∆也具有正态分布特征,其均值为t ∆μ,标准差为t ∆σ,方差为t ∆2σ。
换句话说),(~t t S S ∆∆∆σμφ (5) 由(3)式可得t t z t S ∆+∆-=∆+∆-=∆σεσμσσμ)2()2(ln 22 (6)可见,S ln ∆具有正态分布特征,其均值为t ∆-)2(2σμ,标准差为t ∆σ,方差为t ∆2σ。
也即),)2((~ln 2t t S ∆∆-∆σσμφ (7) S ln ∆为连续复利收益率,考虑连续复利的情况tr t t t e S S ∆∆+⋅= (8)t r ∆为时间t ∆内的连续复利收益率,显然等于S ln ∆。
由收益率SS ∆和连续复利收益率S ln ∆的标准差为t ∆σ,便可求得波动率σ。
案例现已获得ETF50指数基金的历史交易数据,试求2015年3月2日这一天的年历史波动率。
解:首先选取2014年3月3日至2015年3月2日的历史成交数据,根据这些数据算出在这一年时间中每一天的收益率SS ∆和连续复利收益率S ln ∆,然后求出它们的标准差即为t ∆σ,最后再除以t ∆,便可得到波动率σ。
注意:这里t ∆表示一个交易日,需要将其年化,即为1/237年最终运算结果为,以收益率算得波动率为0.243121,而以连续复利收益率算得波动率为0.241397811,与同花顺结果0.247基本一致。
赫尔《期权、期货及其他衍生产品》(第7版)课后习题详解(估计波动率与相关系数)

21.2 课后习题详解一、问答题1.解释如何用指数加权移动平均(EWMA )模型和历史数据来估算波动率。
Explain the exponentially weighted moving average (EWMA) model for estimating volatility from historical data.答:定义:其中S i为在第i 天的市场变量价值。
在EWMA 模型中,市场变量的方差率(即波动率的平方)是的加权平均值。
对于某些常数λ而言(0<λ<1),给予的权重是给予的权重的λ倍。
在第n-1天末估计出的波动率σn 与在第n-2天末21--i n u 2i n u -估计出的波动率之间的关系为:。
这一公式说明EWMA 模型有一个十分有吸引力的特性。
为了计算出第n 天波动率的估计值,只需知道第n—l 天的波动率估计值以及就足够了。
具体可参见本章复习笔记。
2.采用EWMA 及CARCH (1,1)对波动率进行更新的不同之处是什么?What is the difference between the exponentially weighted moving average model and the GARCH (l. l) model for updating volatilities?答:EWMA 模型提供了第n 天的日方差率预测,它是以下两部分的加权平均值:第n-1天的日方差率预测值及第n-1天变化百分比的平方。
GARCH(1,1)模型提供的第n 天日方差率预测是以下三部分的加权平均值:第n-1天的日方差率预测值,第n-1天变化百分比的平方及长期平均方差率。
GARCH(1,1)模型在EWMA 模型的基础上,给予长期平均方差率一定的权重。
在EWMA 模型中不存在均值回归,而GARCH(1,1)模型与均值回复方差率模型一致。
3. 某一资产波动率的最新估计值为1.5%,资产在昨天交易结束时的价格为30美元。
金融工具实验报告(3篇)

第1篇一、实验目的本次实验旨在通过模拟操作,让学生深入了解金融工具的基本原理、特性及其在金融市场中的应用,提高学生对金融工具的分析和运用能力。
实验内容包括但不限于股票、债券、期货、期权等金融工具的定价、交易策略以及风险管理。
二、实验内容1. 股票市场实验- 实验目的:了解股票市场的运作机制,学习股票定价模型。
- 实验内容:- 收集某上市公司股票的历史交易数据。
- 利用技术分析软件,绘制股票价格走势图。
- 运用股票定价模型(如股息贴现模型、资本资产定价模型等)计算股票的理论价值。
- 分析股票市场波动与公司基本面、宏观经济等因素的关系。
2. 债券市场实验- 实验目的:掌握债券的基本特征,学习债券定价和利率风险管理。
- 实验内容:- 收集某债券的历史交易数据。
- 利用债券定价模型(如债券定价公式、利率期限结构模型等)计算债券的理论价格。
- 分析债券利率风险,并探讨利率风险管理的策略。
- 比较不同信用等级债券的利率差异。
3. 期货市场实验- 实验目的:了解期货市场的运作机制,学习期货交易策略和风险管理。
- 实验内容:- 收集某期货品种的历史交易数据。
- 利用技术分析软件,绘制期货价格走势图。
- 学习期货交易的基本策略,如套期保值、投机等。
- 分析期货市场波动与现货市场、宏观经济等因素的关系。
4. 期权市场实验- 实验目的:掌握期权的特性,学习期权定价和交易策略。
- 实验内容:- 收集某期权品种的历史交易数据。
- 利用期权定价模型(如布莱克-斯科尔斯模型等)计算期权的理论价格。
- 学习期权交易的基本策略,如看涨期权、看跌期权等。
- 分析期权市场波动与股票市场、宏观经济等因素的关系。
三、实验步骤1. 数据收集:通过网络、数据库等渠道收集相关金融工具的历史交易数据。
2. 数据处理:利用统计软件对数据进行处理和分析。
3. 模型应用:运用相关金融工具定价模型进行理论计算。
4. 策略分析:分析金融工具的交易策略和风险管理方法。
实物期权法模型分析

实物期权法模型分析实物期权模型介绍⼀、模型简介(⼀)期权及实物期权期权是⼀种未来的选择权,是指购买⽅向卖⽅⽀付⼀定的费⽤(期权费)后所获得的在将来某⼀特定到期⽇或某⼀时间内按协定的价格购买 (买权,看涨期权)或出售 (卖权,看跌期权)⼀定数量的某种标的资产的权利。
实物期权,⼀种期权,其底层证券是既⾮股票⼜⾮期货的实物商品。
这实物商品⾃⾝(货币,债券,货物)构成了该期权的底层实体。
实物期权(real options),把⾦融市场的规则引⼊企业内部战略投资决策,⽤于规划与管理战略投资。
在公司⾯临不确定性的市场环境下,实物期权的价值来源于公司战略决策的实物期权。
每⼀个公司都是通过不同的投资组合,确定⾃⼰的实物期权,并对其进⾏管理、运作,从⽽为股东创造价值。
实物期权法应⽤⾦融期权理论,给出动态管理的定量价值,从⽽将不确定性转变成企业的优势。
根据标的资产不同,期权分⾦融期权和实物期权。
实物期权是⼀种与⾦融期权相对应的⾮⾦融性选择权,实物期权模型在⾦融期权模型的基础上发展,以类⽐的思维将存在期权性质的项⽬或资产进⾏测算。
继 1973 年著名的 B-S 定价模型之后,美国学者 Stewart Myers 在 1977 年⾸次提出了实物期权的概念,即把具有期权特性的实物资产看做看涨期权,此期权的执⾏价格是投资的成本价格,期权的价值取决于投资项⽬的价值和是否对此投资的决策。
实物期权定价的理论模型是建⽴在⾮套利均衡的基础上,其核⼼思想是“在确定投资机会的价值和最优投资策略时,投资者不应简单地使⽤主观概率⽅法或效⽤函数,理性的投资者应寻求⼀种建⽴在市场基础上的使项⽬价值最⼤化的⽅法”。
(⼆)实物期权常⽤模型从建模的⾓度来看,实物期权分析建模思想有两⼤类,离散型模型主要是动态规划的⽅法,⽽连续型主要有偏微分法和模拟的⽅法。
(1) 动态规划法:其⽅法是推算出期权到期⽇标的资产的可能价值并推导出未来最优决策的价值。
它⾸先列出了基础资产在期权⽣命周期内可能出现的价格,在多种情况或路径下,最终形成了相关的价值,最后需要把这个价值折现后进⾏评价。
案例十六1998年长期资本管理公司事件

案例十六:1998年长期资本管理公司事件美国长期资本管理公司(Long-Term Capital Management,简称LTCM)成立于1994年2月,总部设在离纽约市不远的格林威治,是一家主要从事定息债务工具套利活动的对冲基金。
自创立以来,LTMC一直保持骄人的业绩,公司的交易策略是"市场中性套利"即买入被低估的有价证券,卖出被高估的有价证券。
LTMC将金融市场的历史资料、相关理论学术报告及研究资料和市场信息有机的结合在一起,通过计算机进行大量数据的处理,形成一套较为完整的电脑数学自动投资系统模型,建立起庞大的债券及衍生产品的投资组合,进行投资套利活动,LTMC凭借这个优势,在市场上一路高歌。
1996年,LTMC大量持有意大利、丹麦、希腊政府债券,而沽空德国债券,LTMC模型预测,随着欧元的启动上述国家的债券与德国债券的息差将缩减,市场表现与LTMC的预测惊人的一致,LTMC获得巨大收益。
LTMC的数学模型,由于建立在历史数据的基础上,在数据的统计过程中,一些概率很小的事件常常被忽略掉,因此埋下了隐患:一旦这个小概率事件发生,其投资系统将产生难以预料的后果。
所谓Black-Scholes-Merton公式仍以正态分布为基础(这是因为该公式涉及Wiener过程,而Wiener过程的定义涉及正态分布),故“长期资本”的风险投资策略仍以“线性”和“连续”的资产价格模型为出发点。
具体来说,该对冲基金的核心策略是“收敛交易”。
此策略并不关心某一股票或债券的价格是升还是降,而是赌在相关股票或债券的价格向“常态”收敛上。
“长期资本”的一项赌注下在美国30年国库卷和29年国库卷的价格收敛上(卖空前者,买入后者),本以为可以不论价格升降都稳操胜券。
不料,亚洲和俄国的金融危机使惊恐的投资者一窝蜂地涌向似更安全吉祥的30年国库卷,结果造成30年国库卷和29年国库卷的价格发散,而非收敛。
类似的其它几个"收敛交易"也都以发散而告终。
布莱克斯克尔斯期权定价模型

布莱克斯克尔斯期权定价模型汇报人:日期:目录CATALOGUE•引言•布莱克斯克尔斯模型原理•模型应用•模型优势与局限•布莱克斯克尔斯模型与其他模型的比较•未来展望与研究方向01 CATALOGUE引言1背景介绍23布莱克斯克尔斯模型起源于1973年,由费雪·布莱克斯克尔斯(Fischer Black)和迈伦·斯科尔斯(Myron Scholes)提出。
当时,该模型是为了解决金融衍生品,特别是期权定价的问题而建立的。
金融衍生品是一种金融合约,其价值取决于其他金融资产或指标。
模型发展历程布莱克斯克尔斯模型的发展得益于许多重要的突破,其中包括无套利原则:模型利用无套利原则,这意味着在市场上不能通过买卖资产来赚取无风险利润。
欧式期权定价:该模型适用于欧式期权,即只能在到期日行使的期权。
随机过程:模型运用随机过程来描述股票价格的变化。
模型应用领域布莱克斯克尔斯模型被广泛应用于金融衍生品市场,包括期权:该模型用于定价欧式和美式期权。
互换:该模型用于定价利率互换和其他类型的互换合约。
其他衍生品:该模型还可用于定价其他金融衍生品,如期货、认股权证等。
02CATALOGUE布莱克斯克尔斯模型原理基础概念布莱克斯克尔斯模型是一种用于定价欧式期权的数学模型,该模型基于随机过程,并使用偏微分方程来描述。
在该模型中,期权价格被表示为时间t和股票价格S的函数,用C(t,S)表示。
股票价格服从几何布朗运动,即dS = μSdt + σSdwt,其中μ是股票的预期收益率,σ是股票的波动率,wt是威纳过程。
布莱克斯克尔斯模型的期权定价公式为:C(t, S) = SN(d1) - Ke^(-r)(T-t)N(d2),其中N是正态分布函数,d1和d2是由模型参数确定的公式。
d2 = d1 - σ√(T - t)K 是期权的执行价格,r 是无风险利率,T 是到期时间,t 是当前时间,σ是股票的波动率。
d1 = (ln(S/K) + (r + 0.5σ^2)(T - t)) / (σ√(T - t))期权定价公式参数确定方法参数σ(波动率)通常由历史数据估计得出,也可以使用市场波动率作为其近似值。
期权定价理论与方法综述

期权定价理论与方法综述期权定价理论是现代金融学基础之一。
在对金融衍生品研究中,期权定价的模型与方法是最重要、应用最广泛、难度最大的一种。
1973年,被誉为“华尔街第二次革命”B-S-M期权定价模型正式提出,随之成为现代期权定价研究的基石。
这与现代期权在1973年的上市一起,标志着金融衍生品发展的关键转折。
现代期权定价的理论和方法在国外经过三十多年的发展已经日趋成熟。
随着沪深300股指期权的积极推进,国内金融市场或将迎来期权这一全新金融工具。
因此,国内期权定价的研究会更具发展前景和现实意义。
期权最重要的用途之一是管理风险,要对风险进行有效的管理,就必须对期权进行正确的估价。
期权定价理论和方法的产生和完善对于推动期权市场的发展起到了巨大的作用。
期权定价研究得出的基本原理和方法被广泛应用于宏观、微观的经济和管理问题的分析和决策,其中在财务方面的应用最为集中,以及在投资决策等方面都有广泛的应用。
本文主要是对期权定价的综述,内容包括两个方面:1期权定价理论模型1.1B-S-M模型之前的期权定价理论1.2B-S-M模型1.3B-S-M模型之后的期权定价理论2期权定价数值方法2.1树形方法2.2蒙特卡洛模拟2.3有限差分方法2.4新兴方法:神经网络2.5非完全市场下的期权定价方法1.期权定价理论模型的发展1.1.B-S-M模型之前的期权定价理论历史上的期权交易可以追溯到古希腊时期,并于17世纪荷兰“郁金香投机泡沫”和18世纪美国农产品交易中相继出现。
期权定价的理论模型的历史却比较短。
期权定价理论的研究始于1900年,由法国数学家巴舍利耶(L.Bachelier)在博士论文《投机理论》中提出。
他首次引入了对布朗运动的数学描述,并认为股票价格变化过程就是一个无漂移的标准算术布朗运动。
这一发现沉寂了五十年后才被金融界所接受,被称为“随机游走”或“酒鬼乱步”。
巴舍利耶在此基础上,通过高斯概率密度函数将布朗运动和热传导方程联系起来,得出到期日看涨期权的期望值公式:V S N K N n=-+g g其中S是股票价格,K是期权执行价格,σ是股票价格遵循的布朗运动的方差,T是期权期限,()N⋅与()n⋅是标准正态分布的分布函数和密度函数。
累计期权定价与风险估值研究——以中信泰富为例

累计期权定价与风险估值研究——以中信泰富为例1 研究背景从2007年起,中信泰富开始购买澳元的累计外汇期权合约进行对冲(Accumulator)。
2008年10月20日,中信泰富发布公告称,为对冲澳大利亚铁矿项目汇率风险,该公司自2007年底起签订了多份累计杠杆式外汇买卖合约,该澳元累计目标可赎回远期合约,因澳元大幅贬值,已经确认155亿港元亏损。
此项亏损将达其净资产600亿港元的近1/4。
公告一出,市场哗然,投资者纷纷抛售该股票。
到10月29日,由于澳元的进一步贬值,该合约亏损已接近200亿港元。
11月12日,中信泰富再次发布公告,与母公司中信集团达成初步重组协议,其一是中信集团以强制性可转债方式,向中信泰富注资15亿美元。
其二是以“外科手术”般的方式将部分衍生品交易合约从上市公司剔除,中信集团将协助中信泰富分两步重组现存的87亿澳元合约。
按照公告,中信集团希望在12月30日前完成重组。
此次衍生产品巨额亏损事件阶段性地告一段落。
2008年12月2日,中信泰富在港交所发布的股东通函首次披露公司与花旗银行、汇丰银行等13家银行签订的外汇累计期权合约细节。
通函显示,中信泰富2007年8月至2008年8月间,分别与汇丰银行、花旗银行、摩根士丹利资本、美国银行、巴克莱银行、瑞信国际、法国巴黎银行等13家银行签订24份外汇累计期权合约,合约币种涉及澳元、欧元及人民币。
股东通函还显示,由于澳元进一步走低,中信泰富外汇衍生合约变现亏损及公平价定值亏损总额已由11月12日公告中的168亿港元,扩大至186亿港元。
2 累计期权定价原理由于奇异期权本身结算方式的复杂性,目前很难、甚至不能给出它定价的理论表达式,不能用布莱克-斯科尔斯公式求出解析解。
此时利用计算机编程进行数值计算是目前为这样的奇异期权定价的最有效的方法,而蒙特卡罗方法(Monte Carlo method)是应用最广泛的方法。
此外还有离散化方法(Discretization method)以及马尔可夫链蒙特卡罗方法(Markov chain-Monte Carlo method)等也有重要应用。
期权定价理论的起源与发展

期权定价理论的起源与发展近年来,⾦融衍⽣品市场的发展已成为影响全球经济发展的重要因素。
⾦融衍⽣品市场的四种基本⾦融⼯具是:期货,期权,远期和互换。
期权因其具有良好的规避风险、风险投资和价值发现等功能,同时⼜表现出灵活性和多样性的特点,因此近20年来,特别是20世纪90年代以来,期权成为最有活⼒的⾦融衍⽣产品。
根据期权的定义,期权的持有者具有在某⼀特定时间或某⼀特定时间内按某⼀预先确定的价格购买或出售某项资产(如股票,商品,外汇等)的权利。
对于期权购买者来说,可以在期权有效期内⾏使这种权利,也可以放弃这种权利。
相反,对于期权出售者来说,他存在潜在的义务:如果期权持有者要执⾏期权的话,他必须履约。
因为期权给了其持有者⼀定的权利⽽不是义务,所以它有⼀定的价值,⽽这个价值就是期权费,⼜称权利⾦。
同时,期权出售者应该因承担义务⽽得到相应的补偿。
期权市场的快速发展不仅有其内在优势,同时也得益于期权理论的不断深化。
期权理论研究的重点在于两个⽅⾯:⼀⽅⾯是如何构造出新型的期权,以满⾜不断变化的市场投资的需要;另⼀⽅⾯是如何确定这些⽇趋复杂的期权的价值,以便对风险进⾏有效的管理。
期权的价格实质是⼀种风险价格,影响期权价格的因素众多,包括标的资产当前价格,标的资产的执⾏价格,标的资产的波动率和⽆风险利率等诸多因素。
如何对期权进⾏正确的定价,⼀直是困扰⼈们的难题。
期权定价理论的发展主要分为三个阶段:第⼀阶段:期权定价理论的起源期权的定价理论最初源于1900年法国数学家路易斯巴舍利耶(Louis Bachelier)的博⼠论⽂——《投机理论》,在此⽂中,路易斯巴舍利耶⾸次提出股票价格过程为绝对的布朗运动,单位时间⽅差为且没有漂移,那么看涨期权的价格为:式中,S是股票价格,X是执⾏价格,是距到期⽇的时间,C是买权的价格,和分别是标准正态分布累积函数和正态分布密度函数。
这个模型存在两个⽅⾯的缺陷:⼀是绝对布朗运动允许股票价格为负,这是⼀个与有限债务假设相悖的条件;另⼀个是平均预期价格变化为零的假设,它忽视了资⾦的时间价值为正。
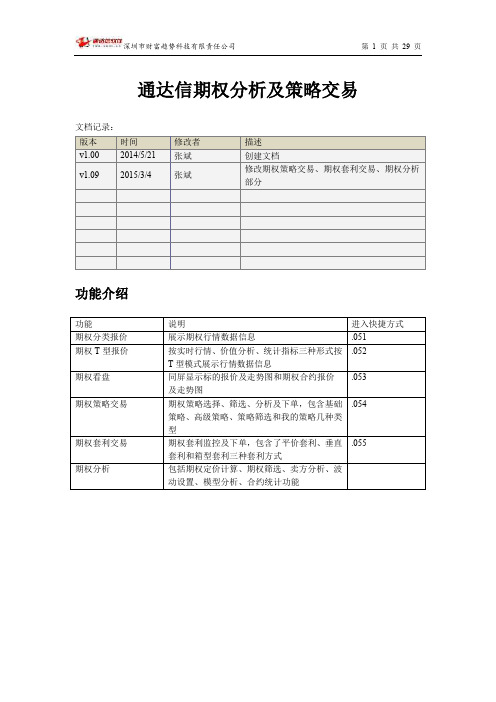
通达信期权分析及策略交易
交易方向 适用情况
标的证券有重大消息即将
出台,会引起价格波动加
买入看涨
期权+买入
剧,但方向不明确。价格 向上或向下大幅突破执行
看跌期权
价时最大收益无限,价格
(同月份) 在执行价附近浮动不大时
最大损失全部权利金
标的证券价格稳定,预计
卖出看涨 后市波动不大维持牛皮盘
期权+卖出 整。价格大幅上涨或下跌 看跌期权 时最大损失无限,价格在
期权套利交易 期权分析
说明 展示期权行情数据信息 按实时行情、价值分析、统计指标三种形式按 T 型模式展示行情数据信息 同屏显示标的报价及走势图和期权合约报价 及走势图 期权策略选择、筛选、分析及下单,包含基础 策略、高级策略、策略筛选和我的策略几种类 型 期权套利监控及下单,包含了平价套利、垂直 套利和箱型套利三种套利方式 包括期权定价计算、期权筛选、卖方分析、波 动设置、模型分析、合约统计功能
期权的 delta 值介于-1 到 1 之间。对于看涨期权,delta 的变动范围为 0 到 1,深实值看 涨期权的 delta 趋近于 1, 平值看涨期权 delta 为 0.5,深虚值看涨期权的 delta 则逼近于 0。 对于看跌期权,delta 变动范围为-1 到 0, 深实值看跌期权的 delta 趋近-1,平值看跌期权的
深圳市财富趋势科技有限责任公司
Байду номын сангаас
第 4 页 共 29 页
delta 为-0.5,深虚值看跌期权的 delta 趋近于 0。期货的 delta 为 1。delta 的取值范围在-1 到 +1 之间。 示例:
某投资者持有 10 手看跌期权,期权的 Delta 值为-0.2,部位总 delta 为-0.2*10=-2,投资 者可以采取以下任何一种交易,对冲部位风险:
期货期权交易行情接口

期货期权交易⾏情接⼝本⽂将先介绍期货交易所以及⾏情交易接⼝相关内容,然后简要介绍CTP接⼝。
期货交易所国内⽬前有三个商品期货交易所,分别是⼤连商品交易所、上海期货交易所、郑州商品交易所,还有⼀个中国⾦融期货交易所。
(Zhengzhou Commodity Exchange,CZCE)主要交易合约品种有:农产品(⽩糖、棉花、苹果等),⾮农产品(玻璃、甲醇)、期权(⽩糖)(Dalian Commodity Exchange,DCE)主要交易合约品种有农产品(⽟⽶、⼤⾖、⾖粕),⾮农产品(聚⼄烯、聚丙烯)、期权(⾖粕)(Shanghai Futures Exchange,SHFE)主要交易合约品种有⾦属(铜、铝)、能源化⼯(原油、沥青、纸浆)、期权(铜)主要交易合约品种有股指期货(沪深300、中证500、上证50)、国债期货(2年期、5年期、10年期)、期权(股指期权[仿真测试阶段])提供场内期权(上证50ETF、个股期权[仿真测试阶段]),以及期权业务平台(DTP)场外股票期权⽬前直接对接各个券商,以定制化⽅式提供。
国内⼤型证券、基⾦以及期货公司均是上述交易所的会员。
在期货市场的功能类似中登公司在证券市场的功能,主要负责期货账户管理、保证⾦监控、交易结算、市场监控等职责。
该公司提供的,可供期货投资者查询开户基本资料、交易结算账单、保证⾦账户等相关信息,相关账号和密码由开户期货公司负责提供。
⾏情交易接⼝概览各⼤期货交易所均有信息技术⼦公司对外提供⾏情交易接⼝服务,⼩结如下:郑商所下属⼦公司接⼝代表:启明星API⼤商所下属⼦公司接⼝代码:XSpeed上期所下属⼦公司,接⼝代表:CTP、CTPMini中⾦所下属⼦公司,接⼝代表:飞马以上四家公司在期权期货⾏情市场上算是⼀级批发商,提供各⾃期货期权合约⾏情资讯、交易接⼝以及为国内期货公司提供交易系统运维托管服务。
随着市场技术趋势发展,各个公司不仅仅提供⾃家数据,也可对接其他期货交易所和证券交易所。
