神经网络实验七.ppt
深度学习-神经网络PPT学习课件

激活函数的主要作用是提供网络的非线性建模能力。如果没有激活函数,那么该网络 仅能够表达线性映射,此时即便有再多的隐藏层,其整个网络跟单层神经网络也是等价 的。因此也可以认为,只有加入了激活函数之后,深度神经网络才具备了分层的非线性 映射学习能力。
线性可分视角:神经网络的学习就是学习如何利用矩阵的线性变换加激活函数的非 线性变换,将原始输入空间投向线性可分/稀疏的空间去分类/回归。
增加节点数:增加维度,即增加线性转换能力。 增加层数:增加激活函数的次数,即增加非线性转换次数。
2/29/2020
13
2.2.2、物理视角:“物质组成”
回想上文由碳氧原子通过不同组合形成若干分子的例子。从分子层面继续迭代这种 组合思想,可以形成DNA,细胞,组织,器官,最终可以形成一个完整的人。不同层级之 间都是以类似的几种规则再不断形成新物质。
2/29/2020
16
➢Sigmoid
sigmoid 是使用范围最广的一类激活函数,具 有指数函数形状,它在物理意义上最为接近生物神 经元。此外,(0, 1) 的输出还可以被表示作概率, 或用于输入的归一化,代表性的如Sigmoid交叉熵 损失函数。
然而,sigmoid也有其自身的缺陷,最明显的 就是饱和性。 软饱和激活函数:
2/29/2020
17
➢Tanh
➢ReLU
可以看到,当x<0时,ReLU硬饱和,
tanh也是一种非常常见的激活函数。 与sigmoid相比,它的输出均值是0, 使得其收敛速度要比sigmoid快,减少 迭代次数。然而,从途中可以看出, tanh一样具有软饱和性,从而造成梯 度消失。
7基于神经网络的模式识别实验要求

实验七基于神经网络的模式识别实验一、实验目的理解BP神经网络和离散Hopfield神经网络的结构和原理,掌握反向传播学习算法对神经元的训练过程,了解反向传播公式。
通过构建BP网络和离散Hopfield 网络模式识别实例,熟悉前馈网络和反馈网络的原理及结构。
二、实验原理BP学习算法是通过反向学习过程使误差最小,其算法过程从输出节点开始,反向地向第一隐含层(即最接近输入层的隐含层)传播由总误差引起的权值修正。
BP 网络不仅含有输入节点和输出节点,而且含有一层或多层隐(层)节点。
输入信号先向前传递到隐节点,经过作用后,再把隐节点的输出信息传递到输出节点,最后给出输出结果。
离散Hopfield神经网络的联想记忆过程分为学习和联想两个阶段。
在给定样本的条件下,按照Hebb学习规则调整连接权值,使得存储的样本成为网络的稳定状态,这就是学习阶段。
联想是指在连接权值不变的情况下,输入部分不全或者受了干扰的信息,最终网络输出某个稳定状态。
三、实验条件Matlab 7.X 的神经网络工具箱:在Matlab 7.X 的命令窗口输入nntool,然后在键盘上输入Enter键,即可打开神经网络工具箱。
四、实验内容1.针对教材P243例8.1,设计一个BP网络结构模型(63-6-9),并以教材图8.5 为训练样本数据,图8.6为测试数据。
(1)运行train_data.m和test_data.m文件,然后从Matlab工作空间导入(Import)训练样本数据(inputdata10,outputdata10)和测试数据(testinputdata,testoutputdata),其次新建一个神经网络(New Network),选择参数如下表1,给出BP神经网络结构图。
表1 BP网络结构模型的各项参数设置Network Name(神经网络名称)nn10_1Network Type(神经网络类型)Feed-forward backprop(前馈反向传播)Input ranges(输入信息范围)来自训练样本的输入数据(inputdata10)Training function(训练函数)TRAINGD(梯度下降BP算法)Performance function(性能函数)MSE(均方误差)Number of layers(神经网络层数)2Layer1(第1层)的Number ofneurons (神经元个数)6Layer1(第1层)的TransferFunction (传递函数)LOGSIG(S型函数)Layer2(第2层)的Number ofneurons (神经元个数)9Layer2(第2层)的TransferFunction (传递函数)LOGSIG(S型函数)(2)输入训练样本数据(inputdata10,outputdata10),随机初始化连接权(Initialize Weights),然后进行训练(Train),训练参数设置如表2所示,并观察训练目标值变化曲线图,最后把BP神经网络训练成功后(即误差不再变化后)的误差值填入表3。
实验七基于神经网络的模式识别实验

实验七基于神经网络的模式识别实验一、实验目的利用神经网络实现模式识别,并验证其性能。
掌握基于神经网络的模式识别方法。
二、实验原理1.神经网络神经网络是一种模仿生物神经系统的计算模型,它由大量的神经元节点相互连接而成。
在模式识别中,我们一般采用多层前向神经网络进行模式的训练和识别。
2.神经网络的训练过程神经网络的训练过程可以分为两步:前向传播和反向传播。
前向传播是指将输入样本通过网络的各个层传递到输出层,并计算输出结果。
反向传播是指根据输出结果和目标结果之间的误差,将误差反向传播到网络的各个层,并根据误差调整网络中的权值。
3.模式识别对于模式识别问题,我们首先需要将输入模式转化为特征向量,然后通过神经网络来训练这些特征向量,并将其与已知类别的模式进行比较,从而进行模式的识别。
三、实验步骤1.数据准备选择适当的模式识别数据集,例如手写数字识别的MNIST数据集,将其分为训练集和测试集。
2.特征提取对于每个输入模式,我们需要将其转化为一个特征向量。
可以使用各种特征提取方法,例如像素值,轮廓等。
3.神经网络设计设计合适的神经网络结构,包括输入层、隐藏层和输出层,并确定各层的神经元数目。
4.神经网络训练使用训练集对神经网络进行训练,包括前向传播和反向传播过程。
可以使用各种优化算法,例如梯度下降法。
5.模式识别使用测试集对训练好的神经网络进行测试和验证,计算识别的准确率和性能指标。
6.性能评估根据得到的结果,评估神经网络的性能,并分析可能的改进方法。
四、实验结果通过实验我们可以得到神经网络模式识别的准确率和性能指标,例如精确度、召回率和F1-score等。
五、实验总结在本次实验中,我们利用神经网络实现了模式识别,并验证了其性能。
通过实验,我们可以掌握基于神经网络的模式识别方法,了解神经网络的训练和识别过程,以及模式识别中的特征提取方法。
实验结果表明,神经网络在模式识别问题中具有较好的性能,并且可以根据需要进行改进和优化。
神经网络专题ppt课件

(4)Connections Science
(5)Neurocomputing
(6)Neural Computation
(7)International Journal of Neural Systems
7
3.2 神经元与网络结构
人脑大约由1012个神经元组成,而其中的每个神经元又与约102~ 104个其他神经元相连接,如此构成一个庞大而复杂的神经元网络。 神经元是大脑处理信息的基本单元,它的结构如图所示。它是以细胞 体为主体,由许多向周围延伸的不规则树枝状纤维构成的神经细胞, 其形状很像一棵枯树的枝干。它主要由细胞体、树突、轴突和突触 (Synapse,又称神经键)组成。
15
4.互连网络
互连网络有局部互连和全互连 两种。 全互连网络中的每个神经元都 与其他神经元相连。 局部互连是指互连只是局部的, 有些神经元之间没有连接关系。 Hopfield 网 络 和 Boltzmann 机 属于互连网络的类型。
16
人工神经网络的学习
学习方法就是网络连接权的调整方法。 人工神经网络连接权的确定通常有两种方法:
4
5. 20世纪70年代 代表人物有Amari, Anderson, Fukushima, Grossberg, Kohonen
经过一段时间的沉寂后,研究继续进行
▪ 1972年,芬兰的T.Kohonen提出了一个与感知机等神经 网络不同的自组织映射理论(SOM)。 ▪ 1975年,福岛提出了一个自组织识别神经网络模型。 ▪ 1976年C.V.Malsburg et al发表了“地形图”的自形成
6
关于神经网络的国际交流
第一届神经网络国际会议于1987年6月21至24日在美国加州圣地亚哥 召开,标志着神经网络研究在世界范围内已形成了新的热点。
实验七基于神经网络的模式识别实验

实验七基于神经网络的模式识别实验
一、实验背景
模式识别是机器学习领域中的一项重要研究领域,它可以被应用于多个领域,包括计算机视觉,图像处理,智能交通,自然语言处理和生物信息学等。
模式识别的目的是从观察到的数据中检测,理解和预测结果。
其中,神经网络(应用模式识别)是人工智能的关键部分,它模拟人类的神经元的工作方式,并且可以被用来识别,分类,计算和获取模式。
二、实验目标
本次实验的目的是,探讨神经网络在模式识别中的应用,并使用一个基于神经网络的模式识别系统来识别模式。
三、实验内容
(一)数据预处理
在进行本次实验之前,需要进行数据预处理,以便能够更好地使用神经网络。
数据预处理的目的是通过将原始数据处理成神经网络可以处理的格式,以便更好地提取特征。
(二)神经网络模型设计
(三)神经网络模型训练
在训练神经网络模型时,首先需要准备一组被识别的模式。
神经网络学习PPT课件

牛顿法
总结词
牛顿法是一种基于二阶泰勒级数的优化算法,通过迭 代更新参数,以找到损失函数的极小值点。在神经网 络训练中,牛顿法可以用于寻找最优解。
详细描述
牛顿法的基本思想是,利用二阶泰勒级数近似损失函数 ,并找到该函数的极小值点。在神经网络训练中,牛顿 法可以用于寻找最优解。具体来说,根据二阶导数矩阵 (海森矩阵)和当前点的梯度向量,计算出参数更新的 方向和步长,然后更新参数。通过不断迭代,参数逐渐 调整到最优解附近。与梯度下降法相比,牛顿法在迭代 过程中不仅考虑了梯度信息,还考虑了二阶导数信息, 因此具有更快的收敛速度和更好的全局搜索能力。
07
未来展望与挑战
深度学习的发展趋势
模型可解释性
随着深度学习在各领域的广泛应用,模型的可解释性成为研究热 点,旨在提高模型决策的透明度和可信度。
持续学习与终身学习
随着数据不断增长和模型持续更新,如何实现模型的持续学习和终 身学习成为未来的重要研究方向。
多模态学习
随着多媒体数据的普及,如何实现图像、语音、文本等多模态数据 的融合与交互,成为深度学习的另一发展趋势。
深度学习
通过构建深层的神经网络结构, 提高了对复杂数据的处理能力。
循环神经网络
适用于序列数据,如自然语言 处理和语音识别等领域。
02
神经网络的基本结构
感知机模型
感知机模型是神经网络的基本单 元,由一个输入层和一个输出层 组成,通过一个或多个权重和偏
置项来计算输出。
感知机模型只能实现线性分类, 对于非线性问题无法处理。
详细描述
反向传播算法的基本思想是,首先计算神经网络的输出层与实际值之间的误差,然后将误差逐层反向传播,并根 据梯度下降法更新每一层的权重。通过不断迭代,权重逐渐调整,使得神经网络的输出逐渐接近实际值,从而降 低误差。反向传播算法的核心是计算每一层的梯度,即权重的导数,以便更新权重。
神经网络方法-PPT课件精选全文完整版

信号和导师信号构成,分别对应网络的输入层和输出层。输
入层信号 INPi (i 1,根2,3据) 多传感器对标准试验火和各种环境条件
下的测试信号经预处理整合后确定,导师信号
Tk (k 1,2)
即上述已知条件下定义的明火和阴燃火判决结果,由此我们
确定了54个训练模式对,判决表1为其中的示例。
15
基于神经网络的融合算法
11
局部决策
局部决策采用单传感器探测的分析算法,如速率持续 法,即通过检测信号的变化速率是否持续超过一定数值来 判别火情。 设采样信号原始序列为
X(n) x1 (n), x2 (n), x3 (n)
式中,xi (n) (i 1,2,3) 分别为温度、烟雾和温度采样信号。
12
局部决策
定义一累加函数 ai (m为) 多次累加相邻采样值 的xi (差n) 值之和
样板和对应的应识别的结果输入人工神经网络,网络就会通过
自学习功能,慢慢学会识别类似的图像。
第二,具有联想存储功能。人的大脑是具有联想功能的。用人
工神经网络的反馈网络就可以实现这种联想。
第三,具有容错性。神经网络可以从不完善的数据图形进行学
习和作出决定。由于知识存在于整个系统而不是一个存储单元
中,一些结点不参与运算,对整个系统性能不会产生重大影响。
18
仿真结果
19
仿真结果
20
2
7.2 人工神经元模型—神经组织的基本特征
3
7.2 人工神经元模型—MP模型
从全局看,多个神经元构成一个网络,因此神经元模型的定义 要考虑整体,包含如下要素: (1)对单个人工神经元给出某种形式定义; (2)决定网络中神经元的数量及彼此间的联结方式; (3)元与元之间的联结强度(加权值)。
深度学习之神经网络(CNN-RNN-GAN)算法原理+实战课件PPT模板可编辑全文

8-5showandtell模型
8-2图像生成文本评测指标
8-4multi-modalrnn模型
8-6showattendandtell模型
8-10图像特征抽取(1)-文本描述文件解析
8-8图像生成文本模型对比与总结
8-9数据介绍,词表生成
8-7bottom-uptop-downattention模型
第6章图像风格转换
06
6-1卷积神经网络的应用
6-2卷积神经网络的能力
6-3图像风格转换v1算法
6-4vgg16预训练模型格式
6-5vgg16预训练模型读取函数封装
6-6vgg16模型搭建与载入类的封装
第6章图像风格转换
单击此处添加文本具体内容,简明扼要的阐述您的观点。根据需要可酌情增减文字,与类别封装
06
7-12数据集封装
第7章循环神经网络
7-13计算图输入定义
7-14计算图实现
7-15指标计算与梯度算子实现
7-18textcnn实现
7-17lstm单元内部结构实现
7-16训练流程实现
第7章循环神经网络
7-19循环神经网络总结
第8章图像生成文本
08
第8章图像生成文本
02
9-9文本生成图像text2img
03
9-10对抗生成网络总结
04
9-11dcgan实战引入
05
9-12数据生成器实现
06
第9章对抗神经网络
9-13dcgan生成器器实现
9-14dcgan判别器实现
9-15dcgan计算图构建实现与损失函数实现
9-16dcgan训练算子实现
9-17训练流程实现与效果展示9-14DCGAN判别器实现9-15DCGAN计算图构建实现与损失函数实现9-16DCGAN训练算子实现9-17训练流程实现与效果展示
《神经网络电子教案》课件

《神经网络电子教案》PPT课件第一章:神经网络简介1.1 神经网络的定义1.2 神经网络的发展历程1.3 神经网络的应用领域1.4 神经网络的基本组成第二章:人工神经元模型2.1 人工神经元的结构2.2 人工神经元的激活函数2.3 人工神经元的训练方法2.4 人工神经元的应用案例第三章:感知机3.1 感知机的原理3.2 感知机的训练算法3.3 感知机的局限性3.4 感知机的应用案例第四章:多层前馈神经网络4.1 多层前馈神经网络的结构4.2 反向传播算法4.3 多层前馈神经网络的训练过程4.4 多层前馈神经网络的应用案例第五章:卷积神经网络5.1 卷积神经网络的原理5.2 卷积神经网络的结构5.3 卷积神经网络的训练过程5.4 卷积神经网络的应用案例第六章:递归神经网络6.1 递归神经网络的原理6.2 递归神经网络的结构6.3 递归神经网络的训练过程6.4 递归神经网络的应用案例第七章:长短时记忆网络(LSTM)7.1 LSTM的原理7.2 LSTM的结构7.3 LSTM的训练过程7.4 LSTM的应用案例第八章:对抗网络(GAN)8.1 GAN的原理8.2 GAN的结构8.3 GAN的训练过程8.4 GAN的应用案例第九章:强化学习与神经网络9.1 强化学习的原理9.2 强化学习与神经网络的结合9.3 强化学习算法的训练过程9.4 强化学习与神经网络的应用案例第十章:神经网络的优化算法10.1 梯度下降算法10.2 动量梯度下降算法10.3 随机梯度下降算法10.4 批梯度下降算法10.5 其他优化算法简介第十一章:神经网络在自然语言处理中的应用11.1 词嵌入(Word Embedding)11.2 递归神经网络在文本分类中的应用11.3 长短时记忆网络(LSTM)在序列中的应用11.4 对抗网络(GAN)在自然语言中的应用第十二章:神经网络在计算机视觉中的应用12.1 卷积神经网络在图像分类中的应用12.2 递归神经网络在视频分析中的应用12.3 对抗网络(GAN)在图像合成中的应用12.4 强化学习在目标检测中的应用第十三章:神经网络在推荐系统中的应用13.1 基于内容的推荐系统13.2 协同过滤推荐系统13.3 基于神经网络的混合推荐系统13.4 对抗网络(GAN)在推荐系统中的应用第十四章:神经网络在语音识别中的应用14.1 自动语音识别的原理14.2 基于神经网络的语音识别模型14.3 深度学习在语音识别中的应用14.4 语音识别技术的应用案例第十五章:神经网络在生物医学信号处理中的应用15.1 生物医学信号的特点15.2 神经网络在医学影像分析中的应用15.3 神经网络在生理信号处理中的应用15.4 神经网络在其他生物医学信号处理中的应用重点和难点解析重点:1. 神经网络的基本概念、发展历程和应用领域。
神经网络基础PPT课件

AlexNet
VGGNet
ResNet
DenseNet
由Yann LeCun等人提出 ,是最早的卷积神经网 络之一,用于手写数字 识别。
由Alex Krizhevsky等人 提出,获得了2012年 ImageNet图像分类竞 赛的冠军,引入了ReLU 激活函数和数据增强等 技巧。
由牛津大学Visual Geometry Group提出 ,通过反复堆叠3x3的小 型卷积核和2x2的最大池 化层,构建了深度较深 的网络结构。
内部表示。
隐藏层
通过循环连接实现信息 的持久化,捕捉序列中
的动态信息。
输出层
将隐藏层的状态转化为 具体的输出。
循环连接
将隐藏层的状态反馈到 输入层或隐藏层自身, 实现信息的循环传递。
序列建模与长短时记忆网络(LSTM)
序列建模
01
RNN通过循环连接实现对序列数据的建模,能够处理任意长度
的序列输入。
久化。
Jordan网络
与Elman网络类似,但将输出 层的状态反馈到隐藏层。
LSTM网络
长短时记忆网络,通过引入门 控机制实现对长期依赖信息的
有效处理。
GRU网络
门控循环单元网络,一种简化 的LSTM结构,具有较少的参
数和较快的训练速度。
06 深度学习框架 TensorFlow使用指南
TensorFlow安装与配置教程
非线性可分问题
不存在一条直线(或超平面)能够将两类样本完全分开的 问题。对于这类问题,需要使用非线性分类器或者核方法 等技巧进行处理。
处理非线性可分问题的方法
包括使用多项式核、高斯核等核函数将数据映射到高维空 间使其线性可分;或者使用神经网络等非线性模型对数据 进行建模和分类。
神经网络实验七PPT课件
%在坐标系中画出样本点
>> axis([0 9 -1 4]); %调整坐标平面显示区域
>> title(‘待逼近函数’); %图像标题
>> xlabel(‘P’);
%给横轴标注>> ylab来自l('T');
第3页/%共23给页 纵轴标注
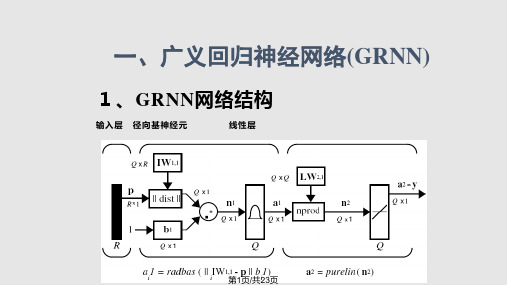
一、广义回归神经网络(GRNN)
第4页/共23页
一、广义回归神经网络(GRNN)
SPREAD—径向基层的散布常数,缺省值为
1.
第2页/共23页
一、广义回归神经网络(GRNN)
例1:已知8个样本点,用GRNN网络对该样本进
行函数逼近
>> P=[1 2 3 4 5 6 7 8]; %输入变量值
>> T=[0 1 2 3 2 1 2 1]; %期望输出
>> plot(P,T,'.','markersize',30);
第21页/共23页
二、概率神经网络(PNN)
第22页/共23页
感谢您的观看!
第23页/共23页
第13页/共23页
二、概率神经网络(PNN)
%绘制出输入向量及其类别 >> P=[1 2;2 2;1 1]'; >> Tc=[1 2 3]; >> plot(P(1,:),P(2,:),'.','markersize',30);
第14页/共23页
二、概率神经网络(PNN)
>> for i=1:3,text(P(1,i)+0.1,P(2,i),…
第7页/共23页
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、概率神经网络(PNN)
例2:已知三组二维向量 P=[1 2; 2 2; 1 1]
以及其相对应的三个类别 Tc=[1 2 3]
构建一个PNN网络实现对输入向量进 行正确分类。
二、概率神经网络(PNN)
%绘制出输入向量及其类别 >> P=[1 2;2 2;1 1]'; >> Tc=[1 2 3]; >> plot(P(1,:),P(2,:),'.','markersize',30); >> axis([0 3 0 3]);
P—Q个R维输入向量组成的R×Q矩阵. T—Q个S维期望输出向量组成的S×Q矩阵. SPREAD—径向基层的散布常数,缺省值为
1.
一、广义回归神经网络(GRNN)
例1:已知8个样本点,用GRNN网络对该样本进
行函数逼近
>> P=[1 2 3 4 5 6 7 8]; %输入变量值
>> T=[0 1 2 3 2 1 2 1]; %期望输出
一、广义回归神经网络(GRNN)
一、广义回归神经网络(GRNN)
>> P2=0:0.1:9; >> A2=sim(net,P2); >> plot(P2,A2,'linewidth',4,'color',[1 0 0]); %绘制拟合曲线 >> title('函数逼近'); >> xlabel('P和P2'); >> ylabel('T和A2');
二、概率神经网络(PNN)
>> for i=1:3,text(P(1,i)+0.1,P(2,i),… sprintf('class%g',Tc(i))),end
>> title('三个向量及类别'); >> xlabel('P(1,:)'); >> ylabel('P(2,:)');
二、概率神经网络(PNN)
二、概率神经网络(PNN)
%网络设计 >> T=ind2vec(Tc); %将类别指针转换为向量T >> spread=1; >> net=newpnn(P,T,spread); %测试网络 >> A=sim(net,P); >> Ac=vec2ind(A);
二、概率神经网络(PNN)
>> plot(P(1,:),P(2,:),'.','markersize',30); >> axis([0 3 0 3]); >> for i=1:3,text(P(1,i)+0.1,P(2,i),…
一、广义回归神经网络(GRNN)
二、概率神经网络(PNN)
1、PNN网络的结构
输入层 径向基神经元
竞争层
二、概率神经网络(PNN)
2、PNN网络的设计 调用格式:
net = newpnn(P,T,SPREAD) 功能描述:设计一个PNN网络 参数说明:
P—Q个R维输入向量组成的RxQ矩阵. T—Q个S维期望输出向量组成的SxQ矩阵. SPREAD—径向基层的散布常数,缺省值 为1.
10,'color',[1 0 0]);
二、概率神经网络(PNN)
>> text(p(1)+0.1,p(2),… sprintf('class%g',ac));
>> hold off; >> title('对新向量分类'); >> xlabel('P(1,:)与p(1,:)'); >> ylabel('P(2,:)与p(2,:)');
sprintf('class%g',Ac(i))),end; >> title('网络测试结果'); >> xlabel('P(1,:)'); >> ylabel('P(2,:)');
二、概率神经网络(PNN)
二、概率神经网络(PNN)
%对新的向量分类 >> p=[2;1.5]; >> a=sim(net,p); >> ac=vec2ind(a); >> hold on; >> plot(P(1,:),P(2,:),'.','markersize',…
%画出测试结果
>> title('检测网络');
>> xlabel('P');
>> ylabel('T和A');
一、广义回归神经网络(GRNN)
一、广义回归神经网络(GRNN)
>> p=3.5; >> a=sim(net,p); %对新的数据点进行仿真 >> plot(p,a,'+','markersize',10,'color',[1 0 0]); %画出测试点 >> xlabel('P和p'); >> ylabel('T和a');
神经网络实验课件
实验七 广义回归神经网络与概率神经网络的设计
一、广义回归神经网络(G向基神经元
线性层
一、广义回归神经网络(GRNN)
2、GRNN网络的设计 调用格式:
net = newgrnn(P,T,SPREAD) 功能描述:
设计一个GRNN网络 参数说明:
一、广义回归神经网络(GRNN)
>> spread=0.7;
%确定散布常数
>> net=newgrnn(P,T,spread); %设计网络
>> A=sim(net,P);
%网络仿真
>> hold on;
>> outputline=plot(P,A,'O','markersize',10, …
'color',[1 0 0]);
>> plot(P,T,'.','markersize',30);
%在坐标系中画出样本点
>> axis([0 9 -1 4]); %调整坐标平面显示区域
>> title(‘待逼近函数’); %图像标题
>> xlabel(‘P’);
%给横轴标注
>> ylabel('T');
%给纵轴标注
一、广义回归神经网络(GRNN)
二、概率神经网络(PNN)
9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。 2020/11/102020/11/10Tuesday, November 10, 2020
10、人的志向通常和他们的能力成正比例。2020/11/102020/11/102020/11/1011/10/2020 10:14:58 PM 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2020/11/102020/11/102020/11/10Nov-2010-Nov-20 12、越是无能的人,越喜欢挑剔别人的错儿。2020/11/102020/11/102020/11/10Tuesday, November 10, 2020 13、志不立,天下无可成之事。2020/11/102020/11/102020/11/102020/11/1011/10/2020
