第12章 MATLAB 数值模拟实例解析
MATLAB在模拟仿真中的应用案例分析

MATLAB在模拟仿真中的应用案例分析一、引言MATLAB是一种高级语言与交互式环境,主要用于数值计算、可视化和编程。
它的强大功能和易于学习的特点,使其成为科学计算、工程设计和模拟仿真中广泛应用的工具。
本文将从模拟仿真的应用角度分析MATLAB的相关案例。
二、MATLAB在信号处理中的应用信号处理是一种对信号进行分析、改善或提取信息的方法,应用广泛,如图像处理、音频处理等。
MATLAB中的信号处理工具箱,包括数字滤波器设计、频域分析、时频分析和窗口设计等功能,可以快速处理各种信号。
例如,使用MATLAB进行图像滤波处理,可以去噪、增强图像等,进而提高图像质量。
三、MATLAB在控制系统中的应用控制系统是一种系统,用于控制电子、机械、化工等领域中的过程。
MATLAB中的控制工具箱,包括时间域分析、频域分析等功能,可以快速建立控制系统模型,并对系统进行设计、建模和仿真。
例如,使用MATLAB进行PID控制器设计,可以完成对系统动态响应的控制和稳态误差的调整。
四、MATLAB在通信系统中的应用通信系统是指将信息从一个地方传输到另一个地方的系统。
MATLAB中的通信工具箱,包括数字信号处理、通信系统仿真等功能。
它可以用于多种通信系统,如移动通信、卫星通信等。
例如,使用MATLAB进行OFDM系统仿真,可以模拟系统的传递特性、信道衰落、信道估计等,进而优化系统参数,提高系统的性能。
五、MATLAB在电力系统中的应用电力系统是指将电能从供应地点输送到需求地点的系统。
MATLAB中的电力系统工具箱,包括电网仿真、负荷流分析、短路电流计算等功能,可以对系统进行建模、仿真和优化。
例如,使用MATLAB进行电力系统稳态分析,可以计算系统负载功率、相角、电压等参数,确定系统的安全工作状态。
六、MATLAB在智能算法中的应用智能算法是指在计算机系统上运行的一类算法,它们可以根据数据和先验知识,自动地发现规律、分类或预测结果。
MATLAB数学建模算法与实例分析

向量, b 为一实数) 。若干个半空间的交集被称为多胞形,有界的多胞形又被称为多面 体。易见,线性规划的可行域必为多胞形(为统一起见,空集 Φ 也被视为多胞形) 。 在一般 n 维空间中,要直接得出多胞形“顶点”概念还有一些困难。二维空间中的顶点 可以看成为边界直线的交点, 但这一几何概念的推广在一般 n 维空间中的几何意义并不 十分直观。为此,我们将采用另一途径来定义它。 定义 1 定义 2
图 1 线性规划的图解示意图
图解法简单直观, 有助于了解线性规划问题求解的基本原理。 我们先应用图解法来 求解例 1。对于每一固定的值 z ,使目标函数值等于 z 的点构成的直线称为目标函数等 位线,当 z 变动时,我们得到一族平行直线。对于例 1,显然等位线越趋于右上方,其 上的点具有越大的目标函数值。不难看出,本例的最优解为 x* = ( 2,6) ,最优目标值
min cT x x ⎧ Ax ≤ b ⎪ s.t. ⎨ Aeq ⋅ x = beq ⎪lb ≤ x ≤ ub ⎩
其中 c 和 x 为 n 维列向量, A 、 Aeq 为适当维数的矩阵, b 、 beq 为适当维数的列向 量。
-1-
例如线性规划
max cT x s.t. x
的 Matlab 标准型为
⎧2 x1 + x2 ≤ 10 ⎪x + x ≤ 8 ⎪ 1 2 s.t.(约束条件) ⎨ ⎪ x2 ≤ 7 ⎪ ⎩ x1 , x2 ≥ 0
(2)
(1)式被称为问题的目标函数, (2)中的几个不等式 这里变量 x1 , x 2 称之为决策变量, 是问题的约束条件,记为 s.t.(即 subject to)。由于上面的目标函数及约束条件均为线性 函数,故被称为线性规划问题。 总之, 线性规划问题是在一组线性约束条件的限制下, 求一线性目标函数最大或最 小的问题。 在解决实际问题时, 把问题归结成一个线性规划数学模型是很重要的一步, 但往往 也是困难的一步,模型建立得是否恰当,直接影响到求解。而选适当的决策变量,是我 们建立有效模型的关键之一。 1.2 线性规划的 Matlab 标准形式 线性规划的目标函数可以是求最大值, 也可以是求最小值, 约束条件的不等号可以 是小于号也可以是大于号。为了避免这种形式多样性带来的不便,Matlab 中规定线性 规划的标准形式为
利用Matlab进行数值模拟的方法

利用Matlab进行数值模拟的方法引言数值模拟是现代科学领域中不可或缺的一种工具,它通过数学模型和计算机算法,模拟和预测实际系统的行为。
随着科学技术的不断发展,数值模拟方法逐渐成为各个学科的重要组成部分。
Matlab作为一种强大的科学计算工具,为数值模拟提供了丰富的函数库和易于使用的编程环境。
本文将介绍一些利用Matlab进行数值模拟的方法,以及其在不同领域的应用。
一、常微分方程的数值解法常微分方程在物理、工程、生物等领域中广泛存在。
利用Matlab进行常微分方程的数值解法,可以有效地求得方程的近似解。
Matlab中的ode45函数是常用的数值解法之一,它基于龙格-库塔算法,可以处理非刚性和刚性问题。
通过设定初始条件和方程形式,利用ode45函数可以得到系统的数值解,并绘制出相应的曲线图。
例如,考虑一个一阶常微分方程dy/dx = -2xy,初始条件为y(0) = 1。
可以通过以下代码进行数值模拟:```Matlabfun = @(x, y) -2*x*y;[x, y] = ode45(fun, [0, 10], 1);plot(x, y)xlabel('x')ylabel('y')title('Solution of dy/dx = -2xy')```运行以上代码后,可以得到方程解的图像,从而对其行为有更直观的理解。
二、偏微分方程的数值解法偏微分方程在物理、流体力学、电磁学等领域中具有重要应用。
常用的偏微分方程的数值解法有有限差分法(Finite Difference Method)和有限元法(Finite Element Method)等。
在Matlab中,可以利用pdepe函数进行偏微分方程的数值模拟,其中包含了一维和二维问题的求解算法。
以热传导方程为例,假设一个长为L的均匀杆子,其温度分布满足偏微分方程∂u/∂t = α*∂²u/∂x²,其中u(x, t)表示温度分布。
MATLAB数值分析实例解析

2016-2017 第一学期数值分析上机实验报告姓名: xxx学号: 20162…….学院:土木工程学院导师:………..联系电话:…………..指导老师:………..目录第一题 (1)1.1题目要求 (1)1.2程序编写 (1)1.3计算结果及分析 (2)第二题 (4)2.1题目要求 (4)2.2程序编写 (4)2.3计算结果及分析 (6)第三题 (7)3.1题目要求 (7)3.2程序编写 (7)3.3计算结果及分析 (8)第四题 (9)4.1题目要求 (9)4.2程序编写 (9)4.3计算结果及分析 (10)第五题 (11)5.1题目要求 (11)5.2程序编写 (12)5.3计算结果及分析 (13)第六题 (17)6.1题目要求 (17)6.2程序编写 (17)6.3计算结果及分析 (18)6.4程序改进 (18)第一题选做的是第(1)小问。
1.1题目要求编出不动点迭代法求根的程序;把x3+4x2−10=0写成至少四种x=g(x)的形式,取初值x0=1.5,进行不动点迭代求根,并比较收敛性及收敛速度。
1.2程序编写1.3计算结果及分析① 第一种迭代公式:x =x 3+4x 2+x −10; matlab 计算结果如下: (以下为命令行窗口的内容)② 第二种迭代公式:x =√(10−x 3)/42; matlab 计算结果如下: (以下为命令窗口内容)③ 第三种迭代公式:x =√10(x +4)⁄2; matlab 计算结果如下:(以下为命令窗口内容)⁄;matlab计算结果如下:④第四种迭代公式:x=10(x2+4x)(以下为命令窗口内容)上述4种迭代公式,1、4两种由于在x真实值附近|g`(x)|>1,不满足迭代局部收敛条件,所以迭代序列不收敛。
对于2、3两种式子,由于在x真实值附近|g`(x)|<=L<1,满足迭代局部收敛条件,所以迭代序列收敛。
对于2、3两迭代公式,由于L3<L2,所以第3个迭代公式比第2个迭代公式收敛更快。
Matlab技术的实际应用案例解析

MatIab技术的实际应用案例解析随着计算机技术的发展,MatIab作为一种高级技术语言,被广泛应用于多个领域。
无论是在科研领域还是工程实践中,Mat1ab都扮演着重要的角色。
本文将通过几个实际应用案例,探讨Mat1ab技术在不同领域的应用,以期给读者提供一些启示和参考。
一、图像处理领域图像处理是Mat1ab的一项重要应用领域。
利用Mat1ab提供的强大的图像处理工具箱,可以实现各种功能,例如图像增强、滤波、分割和识别等。
以下将介绍一个实际应用案例。
案例一:肿瘤图像分割肿瘤图像的分割对于医学诊断非常关键。
在某医院的研究中,研究人员利用MatIab进行了肿瘤图像的分割工作。
首先,他们先对肿瘤图像进行预处理,包括降噪和增强等操作。
然后,利用Mat1ab提供的图像分割算法,将肿瘤与周围组织分离出来。
最后,通过对分割后的图像进行计算,可以得到肿瘤的大小、形状等信息、,为医生提供诊断依据。
二、信号处理领域信号处理是Mat1ab的另一个重要应用领域。
通过利用MatIab提供的信号处理工具箱,可以实现信号的滤波、谱分析、峰值检测等功能。
以下将介绍一个实际应用案例。
案例二:语音信号增强在通信领域,语音信号是一种常见的信号类型。
在某通信公司的项目中,研发团队利用MatIab对语音信号进行增强。
首先,他们通过Mat1ab提供的滤波器设计算法,设计了一种高效的降噪滤波器。
然后,他们利用该滤波器对采集到的语音信号进行滤波处理,去除噪声成分。
最后,通过对处理后的语音信号进行主观听感和客观评价,证明了该算法的有效性。
三、控制系统领域MaUab在控制系统领域的应用也非常广泛。
通过MatIab提供的控制系统工具箱,可以进行控制系统的建模、仿真和优化等操作。
以下将介绍一个实际应用案例。
案例三:智能交通信号优化在城市交通系统中,智能交通信号优化是一个重要的研究方向。
在某城市的交通管理局的项目中,研究人员利用MaUab进行了智能交通信号优化的仿真研究。
第12章 数值模拟

蒙特卡罗模拟法求解问题的三个主要步骤:
1、构造模型,确定描述研究对象行为的概率分布。 (1)在某些情况下,用一个适当的理论分布(诸如正 态分布或泊松分布)来描述研究对象的经验概率分布,既是 可能的,也是可取的(例如,在一定时间内,服务台到达的 顾客量即服从泊松分布,随机因素所产生的干扰常服从正态 分布)。理论分布往往更能代表所研究的那个“总体”。用 于确定经验分布的抽样信息就是从这个“总体”中得出来的。 (2)某些经济问题常常没有可以直接引用的分布律。通 常的作法是根据历史记录或主观的分析判断求得研究对象的 一个初始概率分布。例如:在需求预测中,可以根据过去的 实际需求量分布状况估计预测目标的初始分布,或运用主观
第12章 数值模拟
本章目标:利用计算机模拟的方法 求解一些实际问题
12.1 蒙特卡罗方法 12.2 随机数 12.3 实例解析
12.1 蒙特卡罗方法
蒙特卡罗(Monte Carlo)方法,又称模拟抽样法或统计 试验法,是一种以概率与数理统计理论为指导的模拟技术。 它的实质是用按一定的概率分布产生随机数的方法来模拟可 能出现的随机现象。 蒙特卡罗法通过抓住事物运动过程的数量和物理特征,运 用数学方法来进行模拟。每一次模拟描述系统可能出现的一 次情况,经过成百上千次模拟后,便可得到一些很有价值的 结果。 如:顾客需求行为分析、交叉影响分析、经济计量模型模拟 求解,预测方法的评价和误差分析等等,都可以运用蒙特卡 罗模拟技术频数,并运用数理统计知识求取各种统计量。
实际模拟中,往往要规定一组不同的作业条件(特性), 完 成一种条件下的模拟后,在返回到第二步骤进行另一种条件 下的模拟。如此经过多次模拟试验,再对不同条件下的模拟 结果进行比较,选择一个最接近实际系统的作业条件和一个 最佳模拟方案。
MATLAB应用实例分析例分析

MATLAB应用实例分析例分析Matlab应用例题选讲仅举一些运用MATLAB的例子,这些问题在数学建模中时常遇到,希望能帮助同学们在短时间内方便、快捷的使用MATLAB 解决数学建模中的问题,并善用这一工具。
常用控制命令:clc:%清屏; clear:%清变量; save:%保存变量; load:%导入变量一、利用公式直接进行赋值计算本金P以每年n次,每次i%的增值率(n与i的乘积为每年增值额的百分比)增加,当增加到r×P 时所花费的时间T为:(利用复利计息公式可得到下式) lnrnT() r,P,P(1,0.01i),T,r,2,i,0.5,n,12nln(1,0.01i)MATLAB 的表达形式及结果如下:>> r=2;i=0.5;n=12; %变量赋值>> T=log(r)/(n*log(1+0.01*i)) 计算结果显示为:T = 11.5813即所花费的时间为T=11.5813 年。
分析:上面的问题是一个利用公式直接进行赋值计算问题,实际中若变量在某个范围变化取很多值时,使用MATLAB,将倍感方便,轻松得到结果,其绘图功能还能将结果轻松的显示出来,变量之间的变化规律将一目了然。
若r在[1,9]变化,i在[0.5,3.5]变化;我们将MATLAB的表达式作如下改动,结果如图1。
r=1:0.5:9;i=0.5:0.5:3.5;n=12;p=1./(n*log(1+0.01*i));T=log(r')*p;plot(r,T)xlabel('r') %给x轴加标题ylabel('T') %给y轴加标题q=ones(1,length(i));text(7*q-0.2,[T(14,1:5)+0.5,T(14,6)-0.1,T(14,7)-0.9],num2str(i'))40350.5302520T 1151.510 22.55 33.50123456789r图11从图1中既可以看到T随r的变化规律,而且还能看到i的不同取值对T—r 曲线的影响(图中的六条曲线分别代表i的不同取值)。
MATLAB统计工具箱数值模拟分析

MATLAB统计工具箱数值模拟分析3.1模拟数据用matlab产生一组随机数,共300个,非别是完全可分离数据、重叠度较低数据和重叠度较高数据,并画出图形。
[程序1] rng default; % For reproducibilityXI = randn( 100,2) +[0*ones( 100,1), m*ones( 100,1)];X2= randn( 100,2) +[0*ones(l00J), n*ones(l00,1)];X3=randn( 100,2) +[0*ones(100J), p*ones( 100,1)];DataX=[Xl;X2;X3J;opts = statset(,Display\,final,);[idx,C] = kmeans(X3/Distance\,cityblockVReplicates\5JOptions\opts);figure ;hold onplot(Xl(:,l),Xl(:,2);r.,);plot(X2(:,l),X2(:,2),bo,);plot(X3(:,l),X3(:,2);r*');title 'Randomly Generated Data';3.1.1完全可分离数据取m = 15.n=8,p=l,此时做散点图如图3・1:18 161412 10Randomly Generated DataO2 3 4■21 [ I I4 -3 2 -1图3・1完全可分离数据散点图3.1.2重叠度较低的数据 调用程序1,取m=15,n=10,p=5r 如图3.2图3.2重叠度较低的数据散点图3.1.3重叠度较高的数据调用【程序1】,取m=15,n=12,p=9»散点图如图3.3所示。
Randomly Generated Data 18 r •g _________ | ________ I ________ | ________ I ________ I ________ | ________ L-4-3-2-10123图3・3重叠度较髙的数据散点图3. 2聚类分析3.2.1完全可分离数据[程序2]rng default; % For reproducibilityX1 = randn( 100,2) +[0*ones(l 00 J), m*ones( 100,1)];X2= randn( 100,2) +[0*ones(100J ), n*ones( 100,1)];X3=randn( 100,2) +[0*ones(100,l), p*ones( 100,1)];DataX=[Xl;X2;X3];opts = statset(,Display,/finar);[idx.C] = kmeans(X,3/Distance,/cityblock\,Replicates\5/Options\opts); figure ;plot(X(:,l),X(:,2),T);title Randomly Generated Data1;P=idx;a=0;b=0;c=0;for i=l: 1:300ifp(i)==la=a+1;elseif P(i)=2;b=b+1;else c=c+l;endendabcfigure ;plot(X(idx== 1,1 ),X(idx 二二1,2)/r//MarkerSize\ 12)hold onplot(X(idx==2,l ),X(idx==2,2)/bo\,MarkerSize\l 2)hold onplot(X(idx==3,l ),X(idx==3,2)/r*7MarkerSize\l 2)plot(C(:J ),C(:,2)/kx\...^MarkerSizeJ 5;LineWidth\3) legend(,Ckister r/Cluster 2VCluster 3\,Centroids\...'Location','NWJtitle 'Cluster Assignments and Centroids* hold off取m=15, n=8, p=l;聚类效果图如图3・4所示:图3.4完全可分离数据聚类效果图Cluster 1 = 100Cluster2= 100Cluster3= 100Cluster 1 Cluster 2 Cluster 3 CentroidsCluster Assignments and Centroids18 16 14 12 10 8 6 4 2 0 -2』・3 ・2 ・10 123•3. 2. 2重叠度较低的数据调用【程序2】,取m=15, n=10, p=5;聚类效果图如图3・5所示:图3.6重叠度较髙数据聚类效果图Ckister2=IOl18 16 14 12 10 8 6 4•图3.5重叠度较低数据聚类效果图Cluster 1 =99Cluster2= 100 Cluster3= 1013. 2. 3重叠度较高的数据调用【程序2】,取m=12, n=10, p=8;聚类效果图如图3・6所示:Cluster I =95Cluster3=104Cluster 1 Cluster 2 Cluster 3 CentroidsCluster A33ignments and Centroids2 3-1 Cluster 1Cluster 2 Cluster 3 ConuoidsCluster Assignments and Centroids-3-2-101231514 13 12 11 10 9 8 7 63. 3模型评价3. 3.1错误率计算方法若聚类正确,则记代=0,若聚类错误,则记尤=1,n贝9,聚类的错误率驴a = —3. 3. 2模拟数据错误率分析表3.1完全可分离数据错误率分析3.23.2从聚类分析错误率的计算来看,用k-means对重叠度较高的数据进行聚类的结果并不是特别理想,但正如本文前面提到的那个正态分布的例子,在聚类的过程中,出现了部分样本点的重合,这样到底把重合的样本点分到哪一类我们只能进行猜测估计,当然我们有不小的儿率会猜错,这来自于问题本身的不可分性,无法避免。
MATLAB仿真实例(计算机仿真研究的步骤)
(1.1)
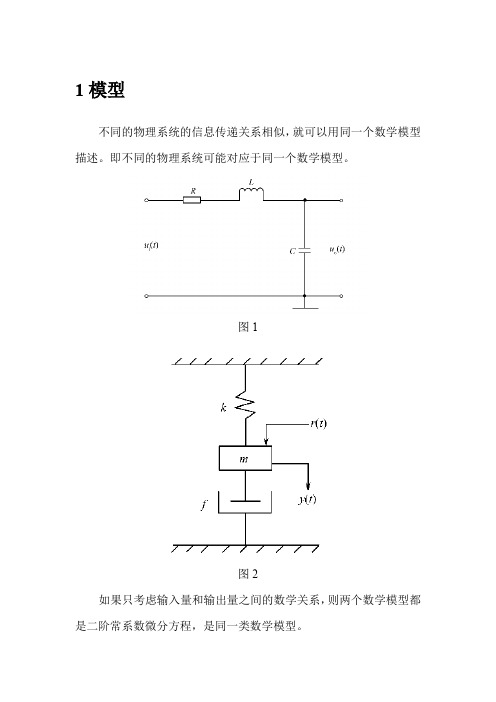
这是一个二阶常微分方程,为了后续步骤的需要,将它转换成状态方 程及输出方程
0 1 x k x 2 m 1 x1 0 f 1 r x m 2 m
当m1k4时分析系统在外力rt1t的作用下要使响应不发生振荡应在什么范围内取值其中f的取值约束为10建立系统的数学模型描述该系统输入输出关系的数学模型为11这是一个二阶常微分方程为了后续步骤的需要将它转换成状态方程及输出方程数学模型转换成仿真模型采用数值积分法中的欧拉公式可以得到离散状态方程及输出方编程和调试采用matlab语言进行编程文件名为exam20001m
【例 2.2】 利用 Simulink 对【例 2.1】中的质量-弹簧-阻尼器系统进 行仿真研究。 【解】 首先将描述该系统输入—输出关系的数学模型改写成传递 函数形式
G (s) Y (s) 1 2 R ( s ) ms fs k
(1.6)
从 Simulink 模块库的信号源子库(Sources)中,选择 Step 模块, 拖 入模型窗口,双击该模块,设置参数 Step time 为:0;从 Simulink 模 块库的连续模块子库(Continuous)中,选择 Tranfer Fcn 模块,拖入 模型窗口, 双击该模块,设置参数 Numerator 为:[1], Denominator [1 f 4] ; 为: 从 Simulink 模块库的接收器子库 (Sinks) 中, 选择 Scope 模块,拖入模型窗口。
% 置状态变量初值,其中 x(i)代表 xi(0) % Y 为 N×1 阵,记录输出 y,初始时为 1×1 阵,
% H 为 N×1 阵,记录时间 t,初始时为 1×1 阵 xs=x+(A*x+B)*T; % 计算离散状态方程
用matlab解析实际案例

用MATLAB解析实际案例简介MATLAB是一种面向科学计算、可视化和数学建模的高级技术计算软件。
它被广泛应用于研究、工程和行业中,如信号处理、图像处理、机器学习、控制系统设计等。
本文将使用MATLAB来解析一个实际案例,并说明如何使用MATLAB进行数据分析和可视化。
案例背景某国外航空公司的一架飞机在飞行途中突然失去了控制,最终在一片森林地带坠毁,导致机上所有人员全部遇难。
该事件引起了广泛关注和调查。
在调查过程中,分析了飞机事故中的数据记录器,也被称为“黑匣子”,以便更好地了解整个事件。
数据记录器记录了飞机在飞行途中的多种参数,包括高度、速度、航向、油门设置等。
本文将使用MATLAB对这些数据进行分析和可视化,以更好地理解飞机失控的原因。
数据处理首先,我们需要将数据导入MATLAB。
这个过程可以通过多种方式实现,例如读取CSV文件、导入Excel文件或使用数据库连接器。
在本例中,原始数据以CSV 文件的形式提供。
为了导入数据,我们在MATLAB中使用readtable函数:data = readtable('data.csv');这会将数据读入一个MATLAB表中,其中每一列代表一个不同的参数。
我们可以使用summary函数查看数据摘要:summary(data)此命令将显示数据的摘要信息、变量名称和其他统计数据。
接下来,我们可以使用MATLAB的plot函数来绘制数据。
例如,要显示速度随时间变化的情况:plot(data.Time, data.Speed);这将在MATLAB中绘制速度与时间的关系图。
在绘制图形之前,我们需要对数据进行一些预处理。
在本例中,我们需要使用曲线拟合技术来找到可能导致飞机事故的异常点。
MATLAB提供了多种曲线拟合技术,例如多项式拟合、趋势线拟合等。
在本例中,我们将使用Loess曲线拟合技术来找到异常点。
首先,我们需要使用MATLAB的loess函数来计算数据的平滑曲线:smooth_data = loess(data.Time, data.Speed);然后,我们可以使用MATLAB的detrend函数来计算数据的趋势:detrended_data = detrend(data.Speed - smooth_data);这将返回数据的趋势,并将其从原始数据中减去,以获得数据的异常部分。
MATLAB在仿真与模拟方面的应用实例

MATLAB在仿真与模拟方面的应用实例一、简介MATLAB是一款强大且广泛应用于科学计算和工程设计领域的软件工具。
它提供了丰富的函数库和工具箱,方便用户进行数据分析、数值计算、信号处理以及模拟仿真等工作。
本文将介绍MATLAB在仿真与模拟方面的应用实例,分别从电子电路设计、通信系统仿真以及控制系统设计等方面展开。
二、电子电路设计电子电路设计是电子工程领域中一项重要的工作。
MATLAB提供了一系列丰富的工具箱,例如Simulink和Simscape等,可以用于电子电路的建模和仿真。
以放大器设计为例,我们可以使用MATLAB进行仿真。
首先,我们可以使用Simulink建立电路模型,包括信号源、滤波器、放大器等组件,并设置相应的参数。
然后,通过添加信号源以及观察输出信号的方式,可以对放大器的性能进行评估,并通过实时仿真结果进行调整和优化。
此外,MATLAB还提供了各种仿真工具和函数,如电路分析工具箱和电路设计工具箱等,可以用于分析电路参数以及进行设计和优化。
通过MATLAB的电子电路设计工具,工程师们能够更加高效地进行电子电路的仿真和设计工作。
三、通信系统仿真通信系统是一种用于传输和接收信息的系统。
MATLAB提供了用于建模和仿真通信系统的工具箱,例如通信工具箱和信号处理工具箱等。
通过使用MATLAB的通信工具箱,我们可以建立和仿真各种通信系统,如数字调制解调、信道编码解码以及误码率分析等。
我们可以设置发送端和接收端的参数,并使用各种信号处理算法进行仿真。
通过调整参数和算法,可以评估和优化通信系统的性能。
此外,MATLAB还提供了用于处理和分析信号的函数和工具箱,如滤波器设计、频谱分析和信号重构等。
这些工具有助于工程师们更好地理解信号特性,并进行通信系统的仿真和设计。
四、控制系统设计控制系统是一种用于控制和调节系统行为的系统。
MATLAB提供了用于建模和仿真控制系统的工具箱,例如控制系统工具箱和优化工具箱等。
MATLAB数值模拟

2. 通过loadFromGridFile.m读取Ansys网格信息,并在matlab中重新生成网 格图。
右图是一个简单带圆孔平面板问题, 取1/4并网格划分。用Ansys2Matlab 工具使得Matlab成功调用Ansys网格 文件
Ansys网格
Matlab重生成的网格
Ansys2Matlab工具仅仅能够调用三角形三节点单元、四节四 边形单元,且限于2维问题,需要对进行修改一边应用高阶单 元及3为维问题,下面在其基础上修改应用到3维的例子。
由于光滑有限元基于光滑区域边界积分,对网格畸变影响较小,
discretisation
discretisation
这是三种网格下y=0所有节点相对 度误差曲线图。从中可以看出,随 着网格畸变程度变大,其相对误差 相应变大,但是变化范围很小,而 且当单元出现凹形状时,该方法仍 然有效。 《Smoothed finite element method》 CRC press
如图所示,在应变光滑中,设:
h h u x u x x x d C C
由分部积分得: h xCuhx xxCd u
h x xxCd u
其中 为一光滑函数,为了计算方便,这里取一个简单函数:
-5.2976E-15+1.2038E+00i
-2.0044E-01+1.0691E+00i 2.0044E-01-1.0691E+00i -2.0044E-01-1.0691E+00i
Lapack直接 求得的特征 值:
-5.2976E-15-1.2038E+00i
3.光滑有限元
光滑有限元是刘桂荣教授课题基于应变光滑技术提出来一种新的有限元 方法。该方法利用应变光滑对进度矩阵进行改进,无需计算形函数倒数,只 需对单元边界进行积分,具有很好的收敛性,对网格畸变影响小等优点。国 内湖南大学李光耀课题组已将其应用于汽车碰撞分析。光滑有限元现阶段主 要分为基于单元内分块光滑有限元(CSFEM)、边界光滑有限元 (ESFEM)、节点光滑有限元、alpha光滑有限元(aSFEM)、面光滑有限 元(FSFEM)几大类。
MATLAB仿真实例ppt课件

29
➢ 空 间 变 换 和 注 册 ( Spatial Transformation and Registration)
➢ 图像分析和统计(Image Analysis and Statistics)
➢ 图像数学算法(Image Arithmetic) ➢ 图 像 扩 展 和 修 补 ( Image
实际应用
精选PPT课件
1
MATLAB/Simulink 的 推 出 得 到 了各个领域专家学者的关注,为各个 层次的研究人员提供了有力的工具。 本 章 将 介 绍 MATLAB 在 信 号 处 理 、 图 像处理和自动控制领域的应用。
精选PPT课件
2
目录
1 信息处理领域 2 图像处理领域 3 自动控制领域
2 图像处理领域
1.二进制图像 2.索引图像 3.灰度图像 4.多帧图像 5.RGB图像
精选PPT课件
18
MATLAB提供了图像处理工具箱, 并且Simulink提供了视频和图像处理 模型集。
图像类型即数组数值与像素颜色 之间定义的关系,在MATLAB中有以 下5种类型的图像。
精选PPT课件
19
精选PPT课件
3
1 信息处理领域
1.1 工具箱介绍 1.2 模型集介绍 1.3 实例
精选PPT课件
4
在计算机中,所有的信号都是离 散信号,因此在使用 MATLAB/Simulink进行信号处理之前, 先要将时间信号进行离散化处理。
精选PPT课件
5
1.1 工具箱介绍
信号处理工具箱将大量函数分成若干 类,以方便按功能查找,以下列出主要的 类。 ➢ 波形产生(Waveform Generation) ➢ 滤波器分析(Filter Analysis) ➢ 滤波器实现(Filter Implementation)
matlab应用案例分析解读

y=sym(‘4*sin(x)*cos(x)’)
y=
4*sin(x)*cos(x)
y=simple(y) y=2*sin(2*x)
Matlab及其应用
21
四、流程控制
为了便于应用,MATLAB提供了一些流程控制的命 令。这些命令对脚本编写带来了一些方便,但是需 要注意的是,尽量不要使用这些流程控制命令,尤 其是循环控制命令。
环。使用for循环的算法执行很慢,一个好的 MATLAB算法部应当出现循环语句。 5. 循环可以使用break跳出,但只跳出所在的循环, 不跳出整个嵌套结构。
Matlab及其应用
23
2 while循环
与for循环以固定的次数求一组指令相反,while循 环以不定的次数求一组语句的值。While循环的一 般形式为:
2.4 Matlab变量
变量要求
变量名、函数名区分字母的大小写。如SIN、Sin与 sin是不同的
对6.5以前的版本,变量名字符不超过31个,对6.5 版本,变量名最多可包含63个字符。超出长度的字 符被忽略
变量必须以字母开头,之后可以是任意字母、数字 或者下滑线,但不能是空格和标点
Matlab不支持汉字,汉字不能出现在变量名和文件 名中
号将导致matlab出错。 inc缺省值为1,可以取正数或负数。
Matlab及其应用
15
语句生成矩阵
3.linspace命令
a=linspace(1,10,5);
4.logspace命令
b=logspace(0,2,10)
5.矩阵连接
c=[a b];
6. 数组生成函数 zeros ones eye rand randn
MATLAB应用实例分析

MATLAB应用实例分析首先,MATLAB在科学研究领域有着广泛的应用。
例如,在物理学中,MATLAB可以用于数值模拟和求解物理方程,如解析光学问题、计算复杂系统的动力学行为。
在生物学中,MATLAAB可以进行基因组数据分析、蛋白质结构预测以及生物信号处理等。
此外,MATLAB还可以用于经济学模型的构建和分析,如计算宏观经济模型的均衡、预测股票价格等。
其次,MATLAB在工程设计和控制系统中也有着重要的应用。
例如,在电气工程中,MATLAB可以用于电力系统的稳态和暂态分析,设计电路和电机控制系统。
在机械工程中,MATLAB可以进行机器人动力学模拟,优化机械结构和设计控制算法。
在通信工程中,MATLAB可以用于设计和模拟无线通信系统,如调制解调器、编码解码器等。
另外,MATLAB在金融分析和风险管理中也是一个重要的工具。
由于其数值计算和数据可视化的能力,MATLAB可以分析金融市场数据,进行投资组合优化、风险分析和衍生品定价等。
它还可以使用金融工具箱进行金融计算,如计算资产回报率、计算期权价格等。
因此,金融机构和金融从业者广泛使用MATLAB来支持他们的决策和风险管理。
此外,MATLAB在图像处理和计算机视觉领域也得到了广泛的应用。
它可以用于图像的去噪、增强、分割和特征提取等。
在计算机视觉中,MATLAB可以进行目标检测和识别、图像配准和拼接、运动估计和跟踪等。
这些应用可以在医学图像处理、机器人导航、视频监控等方面发挥重要作用。
总之,MATLAB是一种功能强大的数值计算和数据可视化工具,可以广泛应用于科学研究、工程设计、金融分析、图像处理等领域。
本文所提到的应用只是其中的一小部分,但足以展示MATLAB的多样性和广泛性。
通过使用MATLAB,用户可以快速而有效地进行数值模拟、数据分析和可视化,从而提高工作效率、加快创新速度。
matlab程序设计实例解析

matlab程序设计实例解析MATLAB程序设计实例解析一、简介本文旨在通过实例解析的方式,介绍MATLAB程序设计的基本概念和技巧。
通过这些实例,读者将能了解如何使用MATLAB进行数据处理、算法实现和可视化。
二、MATLAB基础知识2.1 MATLAB环境的搭建在本章中,我们将介绍如何安装、配置和启动MATLAB环境。
包括MATLAB的版本选择、安装过程中的注意事项以及常见问题解答。
2.2 MATLAB基本语法与数据类型这一章节将介绍MATLAB的基本语法和数据类型。
包括变量的定义、运算符的使用、条件语句和循环结构等。
同时也会介绍MATLAB 中常用的数据类型,如数值型、字符型和数组等。
2.3 MATLAB函数的使用在本章中,我们将介绍如何定义和使用MATLAB函数。
包括函数的输入输出、函数的封装与调用以及函数的文件组织。
同时还会介绍MATLAB内置函数的使用和自定义函数的实现。
2.4 MATLAB数据处理这一章节将探讨MATLAB中数据处理的基本技巧。
包括数据导入、数据清洗与预处理、数据统计和数据可视化等。
同时还会介绍MATLAB中常用的数据处理工具箱的使用方法。
三、MATLAB算法实现3.1 数值计算与优化方法在本章中,我们将介绍MATLAB中数值计算和优化方法的实现。
包括数值积分、数值微分、方程求解和最优化等。
同时还会介绍MATLAB中常用的数学工具箱和优化工具箱的使用方法。
3.2 信号处理与滤波器设计这一章节将探讨MATLAB中信号处理和滤波器设计的应用。
包括信号处理基础、时域与频域分析、滤波器设计和滤波器实现等。
同时还会介绍MATLAB中常用的信号处理工具箱的使用方法。
3.3 图像处理与计算机视觉在本章中,我们将介绍MATLAB中图像处理和计算机视觉的应用。
包括图像读取与显示、图像增强与滤波、特征提取和目标检测等。
同时还会介绍MATLAB中常用的图像处理工具箱和计算机视觉工具箱的使用方法。
第12章 MATLAB 数值模拟实例解析

d 说明:f0是认为给定的一个很大的正数, 0
b − a 且 d0 > 0 。
• 根据前面的步骤编写函数文件monte_carlo .m,则给出如下语句即可求 解题述的非线性方程的根: • y=@(x)exp(-x.^3)-tan(x)+800;a=0;b=pi/2;n=1000;eps=1e-5; • [x,fx]=monte_carlo(y,a,b,n,eps) 运行结果: x =1.5695 fx =5.0271e-007
• 解:设M表示针的中点,x表示针投在平面上点M与最近一条平行线的 距离,θ 表示针与平行线的交角,如下图所示。0 ≤ x ≤ a / 2, 0 ≤ θ ≤ π
• 随机投针的概率含义是:针的中点M与平行线的距离x均匀地分布在区 间[0, a / 2] ,针与平行线交角θ 均匀分布于区间 [0, π ] 内,x和 θ 是相
下面利用蒙特卡罗方法求解该例,编写如下语句: rand('state',2009) % 设置随机数状态 s1=0;s2=0;s3=0;s4=0; % 设置计数器 N=50000; % 模拟次数 for i=1:N x=randperm(10); % 产生1:10的一个排列 if sum(x(1:5)<=3)==0 % 取到0个红球的情形 s1=s1+1; elseif sum(x(1:5)<=3)==1 % 取到1个红球的情形 s2=s2+1; elseif sum(x(1:5)<=3)==2 % 取到两个红球的情形 s3=s3+1; else % 取到3个红球的情形 s4=s4+1; end 运行结果: end p =0.0823 0.4181 0.4173 0.0824 p=[s1 s2 s3 s4]/N
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• • • • • • • • • • • • • • • • •
下面利用蒙特卡罗方法求解该例,编写如下语句: rand('state',2009) % 设置随机数状态 s1=0;s2=0;s3=0;s4=0; % 设置计数器 N=50000; % 模拟次数 for i=1:N x=randperm(10); % 产生1:10的一个排列 if sum(x(1:5)<=3)==0 % 取到0个红球的情形 s1=s1+1; elseif sum(x(1:5)<=3)==1 % 取到1个红球的情形 s2=s2+1; elseif sum(x(1:5)<=3)==2 % 取到两个红球的情形 s3=s3+1; else % 取到3个红球的情形 s4=s4+1; end 运行结果: end p =0.0823 0.4181 0.4173 0.0824 p=[s1 s2 s3 s4]/N
运行结果: p =3.1432 3.1399 3.1427 3.1470 3.1409 3.1480
• ③利用有利随机数法求解该题。首先估算它的近似解:
c = ∫∫∫ ln(1 + x + y + ቤተ መጻሕፍቲ ባይዱ )dxdydz = ∫∫∫ ln[4(1 +
Ω Ω
x −1 y −1 z −1 + + )]dxdydz 4 4 4
• 【练2】假如某一周的7天中的天气情况为(其中1代表下雨,0代表天 晴):
• 因此取有利随机数密度函数
g ( x, y , z ) =
• 根据前面的介绍编写如下语句: • rand('state',20) % 设置随机数状态 • for k=1:6 • j=1;N=1000; % j为计数器,N为模拟次数 • while j<=N • r=rand(1,4); % 生成4个[0,1]区间上的均匀分布的随机数 • if (log(4)+r(1)/4+r(2)/4+r(3)/4-3/4)/(log(4)-3/8)>=log(4)*r(4) % 有利 随机数密度 • x(j)=r(1);y(j)=r(2);z(j)=r(3); • j=j+1; % 计数器加1 1 • end • end • I(k)=(1/N)*sum(log(1+x+y+z)./((log(4)+... • x/4+y/4+z/4-3/4)/(log(4)-3/8))); % 计算三重积分值 • end • I % 显示计算结果 运行结果: I =0.8932 0.8920 0.8916 0.8966 0.8978 0.8908
x −1 y −1 z −1 = ∫∫∫ [ln 4 + ln(1 + + + )]dxdydz 4 4 4 Ω ≈ ∫∫∫ [ln 4 +
Ω
x y z 3 3 + + − ]dxdydz = ln 4 − 4 4 4 4 8
ln 4 + x y z 3 + + − 4 4 4 4 3 ln 4 − 8
I3 =
• • • • • • •
( x , y , z )∈(0,1)
∫∫∫
ln(1 + x + y + z )dxdydz
解:①编写如下语句: s=[];a=-1;b=1;N=100000; for k=1:6 x=rand(N,2); s=[s sum(exp(-((-1+2*x(:,1))).^2)-x(:,2)>=0)/N]; end s=s*(b-a)*1 运行结果: s =1.4931 1.4915 1.4921 1.4952 1.4935 1.4947
程序的某一次运行结果: 最优订购量 年赚钱总数 日平均利润 60 12936 35.4410959
• 【练1】解决本题的关键是依次随机从原向量中取出一个元素重新排 列,具体的程序文件为: • function Y=randpm(X) • % 输入参数: • % ---X:给定的矩阵或向量 • % 输出参数: • % ---Y:产生的随机矩阵或随机向量 • [m,n]=size(X); • X=X(:); • Y=[];L=m*n; • for i=1:L • k=1+fix(L*rand); • Y=[Y;X(k)]; • X(k)=[]; • L=L-1; • end • Y=reshape(Y,m,n); 说明:语句x(randperm(length(x)))可以近似替代上述函数文件。
0.9545 0.9973
µ-3σ
µ-2σ
µ-σ
µ
µ+ σ
µ+2σ
µ+3σ
【例12-5】概率分布交互界面演示。
• 解:在MATLAB命令窗口中输入disttool。
【例12-8】用蒙特卡罗法计算定积分和重积分。
I1 = ∫ e dx
−1 1 − x2
I2 =
2
∫∫
x + y 2 ≤1
[1 + 1 − x 2 − y 2 − x 2 + y 2 ]dxdy
d 说明:f0是认为给定的一个很大的正数, 0
b − a 且 d0 > 0 。
• 根据前面的步骤编写函数文件monte_carlo .m,则给出如下语句即可求 解题述的非线性方程的根: • y=@(x)exp(-x.^3)-tan(x)+800;a=0;b=pi/2;n=1000;eps=1e-5; • [x,fx]=monte_carlo(y,a,b,n,eps) 运行结果: x =1.5695 fx =5.0271e-007
【例12-9】利用蒙特卡罗方法求下面的方程。
f ( x) = e
− x3
− tan x + 800 = 0
x ∈ [0, ] 2
π
• 蒙特卡罗方法求非线性方程根的一般流程,具体描述如下: • 首先令 xdown = a, xup = b, k = 1, f x min ( k ) = f 0 ,再进行以下步骤: • (1)令k=k+1,在区间[ xdown , xup ] 内产生n个随机数,计算并比较出这 n个随机数的函数绝对值中的最小值 f ( xnk ) = min{ f ( xi )},nk为i的某个 1≤i ≤ n 取值,令f x min (k ) = min{ f x min ( k − 1), f ( xnk )}; • (2)若 f x min (k ) < ε ( ε 为指定的精度),则终止计算,并令 root = xnk ; • 若 f x min (k ) > ε 且 f x min (k ) = f x min (k − 1) ,则令k=k-1,转至(1); • 若 f x min ( k ) > ε 且 f x min (k ) < f x min (k − 1) ,则令 root = xnk ,转至(3); • (3)令d = d 0 / k , xdown = root − d , xup = root + d ,转至(1)。
• • • • • • • • • •
m VG ≈ VΩ × ② N N=1000000; for k=1:6 x=unifrnd(-1,1,N,1); % 产生区间[-1,1]上的N个均匀随机数 y=unifrnd(-1,1,N,1); % 产生区间[-1,1]上的N个均匀随机数 z=unifrnd(0,2,N,1); % 产生区间[0,2]上的N个均匀随机数 Z=1+sqrt(1-x.^2-y.^2)-sqrt(x.^2+y.^2); p(k)=8*sum(z<=Z)/N; end p
l x ≤ sin θ 。 • 互独立的。而针与平行线相交的充要条件是 2
• • • •
编写函数文件buffon.m, 在MATLAB命令窗口中输入: PI=buffon 得到结果如图所示。
蒲丰投针实验
0.45 0.4 0.35 0.3 0.25 0.2 0.15 0.1 0.05 0
落落落落 G的的的 m=2546 圆圆圆的圆圆圆 π=3.1422
0
0.5
1
1.5
2
2.5
3
3.5
实验范例:报童的策略
• 新闻日和需求量对应的随机数分别如下面两个表格所示。
• • • • • • • •
计算机仿真的流程: 1)令每天的报纸订购数变化,40——100; 2)让时间从1开始变化(循环)到360; 3)产生新闻种类的随机数,确定当天的新闻类型; 4)产生需求量随机数,确定当天的报纸需求量; 5)计算当天的收入,计算累积利润, 6)比较得出最优定货量。 根据上述流程编写程序example_12_end1.m,
• 解:设M表示针的中点,x表示针投在平面上点M与最近一条平行线的 距离,θ 表示针与平行线的交角,如下图所示。0 ≤ x ≤ a / 2, 0 ≤ θ ≤ π
• 随机投针的概率含义是:针的中点M与平行线的距离x均匀地分布在区 间[0, a / 2] ,针与平行线交角θ 均匀分布于区间 [0, π ] 内,x和 θ 是相
【例12-2】3σ 准则演示。
• • • • • • • • • • • • • • • 解:以为例绘制图形进行说明,具体程序代码如下: mu=3;sigma=0.5; % 正态分布参数设定 x=mu+sigma*[-3:-1,1:3]; yf=normcdf(x,mu,sigma); % 计算累积分布函数值 yh=normpdf(x,mu,sigma); % 计算概率密度值 P=[yf(4)-yf(3),yf(5)-yf(2),yf(6)-yf(1)]; xd=1:0.1:5;yd=normpdf(xd,mu,sigma); % 计算概率密度值 plot(xd,yd,'b') % 绘制图形 hold on plot([x(1),x(1)],[0,yh(1)],[x(6),x(6)],[0,yh(6)],... [x(1),2.7],[yh(1),yh(1)],'k:',[3.15,x(6)],[yh(1),yh(1)],'k:') plot([x(2),x(2)],[0,yh(2)],[x(5),x(5)],[0,yh(5)],... [x(2),2.7],[yh(2),yh(2)],'k:',[3.15,x(5)],[yh(2),yh(2)],'k:') plot([x(3),x(3)],[0,yh(3)],[x(4),x(4)],[0,yh(4)],... [x(3),2.7],[yh(3),yh(3)],'k:',[3.15,x(4)],[yh(3),yh(3)],'k:')
