扰度计算公式
噪声常用计算公式整汇总

目录一、相关标准及公式 (3)1)基本公式 (3)2)声音衰减 (4)二、吸声降噪 (5)1)吸声实验及吸声降噪 (6)2)共振吸收结构 (7)三、隔声 (8)1)单层壁的隔声 (8)2)双层壁的隔声 (9)3) 隔声测量................................... 错误!未定义书签。
4)组合间壁的隔声及孔、缝隙对隔声的影响 (10)5)隔声罩 (10)6)隔声间 (10)7)隔声窗 (11)8)声屏障 (11)9)管道隔声量 (12)四、消声降噪 (12)1)阻性消声器 (12)2)扩张室消声器 (14)3)共振腔式消声器 (15)4)排空放气消声器 (13)压力损失 (13)气流再生噪声 (13)五、振动控制 (16)1)基本计算 (16)2)橡胶隔振器(软木、乳胶海棉) (16)3)弹簧隔振器 (18)重要单位: 1N/m=1kg/s2 1r/min=1/60HZ 标准大气压1.013*105 气密度5273.2=1.29 1.01310PT ρ⨯⨯⨯基准声压级Po=10*105 基准振动加速度10-6m/s2 1Mpa=1000000N/m2倍频程测量范围: 中心频率两侧70.7%带宽;1/3倍频程测量范围: 中心频率两侧23.16%带宽 一、相关标准及公式 1)基本公式声速331.50.6c t =+ 声压与声强的关系22P I=cv cρρ= 其中v wA =,单位:W/m 2声能密度和声压的关系,由于声级密度I cε=,则22P c ερ= J/m 3质点振动的速度振幅p Iv c pρ== m/s《环境影响噪声控制工程—洪宗辉P11》 A 计权响应与频率的关系见下表《注P350》等效连续A 声级0.1110lg10AiL eq ti tiiL =∆∆∑∑ ti ∆第i 个A 声级所占用的时间昼夜等效声级0.10.1(10)5310lg 101088dnL L dn L +⎡⎤=+⎢⎥⎣⎦22:00~7:00为晚上本底值90L ,2109050()60AeqL L L L -=+如果有N 个相同声音叠加,则总声压级为110lg p p L L N =+ 如果有多个声音叠加10110lg(10)PIL Np i L ==∑声压级减法101010lg(1010)PT PB L L PS L =-背景噪声(振动)修正值2)声音衰减 (1)点声源常温时球面声波扩散的表达式210lg4p w QL L rπ=+ 半径分别为r 1和r 2两点的扩散声压级差2120lg d r A r = 自由空间120lg 11p w L L r =-- 半自由空间120lg 8p w L L r =--(2)线声源声压级:110lg 3p w L L r =--半径分别为r 1和r 2两点的扩散声压级差2110lg d r A r = 声屏障计算规范 (3)有限长线声源如果测得在0r 处的声压级为0()P L r ,设线声源长为l 0,那么距r 处的声压: 当000r l r l >>且时,可近似简化为()0()()20/P P o L r L r r r =-,即在有限长线声源的远场,有限长线声源可当作点声源处理。
弯矩挠度表格new
4.39 5.83 7.33 10.44 10.79 15.4 8.78 14.67
26.13 31.62
I--惯性矩 (cm*4)
I--惯性矩 (cm*4)
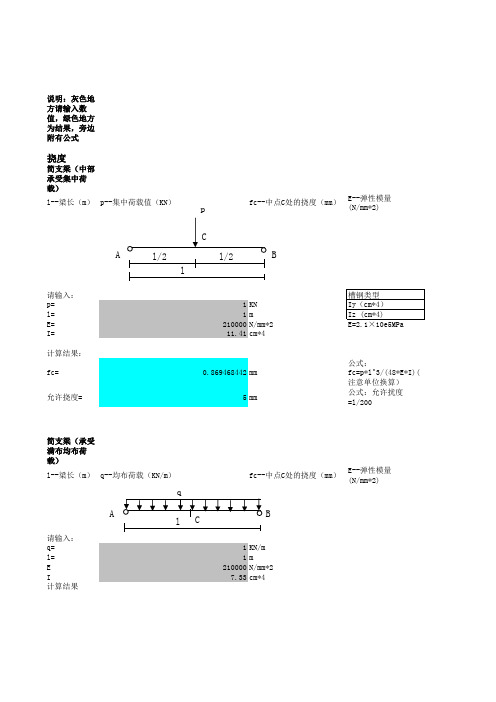
0.869468442 mm 5 mm
槽钢类型 Iy(cm*4) Iz (cm*4) E=2.1×10e5MPa
公式: fc=p*l^3/(48*E*I)( 注意单位换算) 公式:允许扰度 =l/200
简支梁(承受 满布均布荷 载)
l--梁长(m) q--均布荷载(KN/m)
q
A
请输入: q= l= E I 计算结果
lC
fc--中点C处的挠度(mm)
E--弹性模量 (N/mm*2)
B
1 KN/m 1m 210000 N/mm*2 7.33 cm*4
fc= 允许挠度=
0.845893155 mm 5 mm
公式: fc=5*q*l^4/(384*E* I)(注意单位换算) 公式:允许扰度 =l/200
悬臂梁(承受 集中荷载) l--梁长(m) p--集中荷载值(KN) a--集中荷载 离左端点A的 距离(m)
公式: fb=q*l^4/(8*E*I)( 注意单位换算) 公式:允许扰度 =l/150
I--惯性矩 (cm*4)
MQ-21
MQ-31 MQ-41 MQ-41/3 MQ-52 MQ-72 MQ-21D MQ-41D MQ-52-72D MQ-124XD
0.2 2.6 5.37 7.02 11.41 28.7 4.98 30.69 115.41 118.04 (常用)
Байду номын сангаас
悬臂梁(承受 满布均布荷 载) l--梁长(m) q--均布荷载(KN/m)
调压井滑模受力计算书
调压井滑模受力计算书1、模板强度及扰度验算 (1)由混凝土侧压力计算公式:5.02122.0V to F c ββγ=与HF c γ=(两者取较小值)F ——新浇筑混凝土对模板的侧压力,kN/m ; γc ——混凝土的重力密度,kN/m ;to ——新浇混凝土的初凝时间(h )可按实测确定。
当缺乏试验资料时,可采用to=200/(T+15)计算(T 为混凝土的温度℃);V ——混凝土地的浇筑速度,m/h ;H ——混凝土侧压力计算位置处至新浇混凝土顶面的总高度,m ; β1——外加剂影响修正系数,不掺外加剂时取1.0,掺具有缓凝作用的外加剂时取1.2;β2——混凝土坍落度影响修正系数,当坍落度小于30mm 时,取0.85;50~90mm 时,取1.0;110~150mm 时,取1.15。
求得滑膜模板侧压力为12375N/2m ,则q=12375×1.8=22275N/m 。
则由受力分析得到BA F F F F F +=++321l F xF x l F l F B ⨯=⨯-+⨯+⨯2)2(2132中间杆长l=1.3m ,两端杆长X=0.25m 。
求解得:N F A 875.22831= N F B 875.17263=由此可得到剪力图:所以有弯矩图:有弯矩方程:2223.122227523.1222275-)()(⨯+-=x M 已知Q235钢最大弯矩为m KN ⋅68.6。
所以有最大弯矩:m KN m KN M MAX ⋅<⋅=68.67065.4所以强度符合要求。
(2)模板挠度计算:mmEI ql 38.2101036002063848.17.386538459944c ≈⨯⨯⨯⨯⨯⨯==-ωE 为弹性模量单位为GPa ,I 为惯性矩。
利用ANSYS 软件分析结果: 进行的分析分别为:总变形:我们对工字钢进行单独的进入静力学分析,可取较小的长度,有利于减少单元的数量。
由于工字钢外圈受的千斤顶的拉力和角钢对其向下的拉力。
扰度计算公式(全)

简支梁在各种荷载作用下跨中最大挠度计算公式:均布荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 5ql八4/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).q 为均布线荷载标准值(kn/m).E为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm八2. I为钢的截面惯矩,可在型钢表中查得(mm A4).跨中一个集中荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 8pl A3/(384EI)=1pl A3/(48EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mmA2.I 为钢的截面惯矩,可在型钢表中查得(mmA4).跨间等间距布置两个相等的集中荷载下的最大挠度在梁的跨中其计算公式:Ymax = 6.81plA3/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mmA2.I 为钢的截面惯矩,可在型钢表中查得(mmA4).跨间等间距布置三个相等的集中荷载下的最大挠度,其计算公式:Y max = 6.33pl八3/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm八2. I为钢的截面惯矩,可在型钢表中查得(mm A4).悬臂梁受均布荷载或自由端受集中荷载作用时,自由端最大挠度分别为的,其计算公式:Ymax =1ql A4/(8EI). ;Ymax =1pl A3/(3EI).q 为均布线荷载标准值(kn/m). ;p 为各个集中荷载标准值之和(kn).你可以根据最大挠度控制1/400,荷载条件25kn/m 以及一些其他荷载条件进行反算,看能满足的上部荷载要求!机械零件和构件的一种截面几何参量,旧称截面模量。
扰度计算公式(全)

扰度计算公式(全) -CAL-FENGHAI.-(YICAI)-Company One1简支梁在各种荷载作用下跨中最大挠度计算公式:均布荷载下的最大挠度在梁的跨中,其计算公式:Ymax = 5ql^4/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).q 为均布线荷载标准值(kn/m).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨中一个集中荷载下的最大挠度在梁的跨中,其计算公式: Ymax = 8pl^3/(384EI)=1pl^3/(48EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨间等间距布置两个相等的集中荷载下的最大挠度在梁的跨中,其计算公式:Ymax = ^3/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).跨间等间距布置三个相等的集中荷载下的最大挠度,其计算公式: Ymax = ^3/(384EI).式中: Ymax 为梁跨中的最大挠度(mm).p 为各个集中荷载标准值之和(kn).E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.I 为钢的截面惯矩,可在型钢表中查得(mm^4).悬臂梁受均布荷载或自由端受集中荷载作用时,自由端最大挠度分别为的,其计算公式:Ymax =1ql^4/(8EI). ;Ymax =1pl^3/(3EI).q 为均布线荷载标准值(kn/m). ;p 为各个集中荷载标准值之和(kn). 你可以根据最大挠度控制1/400,荷载条件25kn/m以及一些其他荷载条件进行反算,看能满足的上部荷载要求!机械零件和构件的一种截面几何参量,旧称截面模量。
挠度计算公式

挠度计算公式挠度计算公式是经常用于机械行业的一种特定的计算公式,主要是针对不同类型的挠度来计算所需的挠度值。
挠度可理解为产品的一种指标,它衡量的是一种材料的变形程度,它可以帮助我们了解一种材料将会在某种外力作用下产生什么样的变形。
挠度公式有很多种,有的是根据具体材料本身特点和应用条件来制定,而另一些则更为一般性,可以应用到各种材料上。
其中,最为常用的挠度计算公式是基于非线性本构模型的。
非线性本构模型是指以一种非线性方式给出材料的变形行为。
这种模型可以用来表征材料受外力作用时产生的变形。
在挠度计算公式中,它可以表示为Δε=ε-ε0其中ε为材料受外力时所产生的变形,ε0为材料原来的变形。
挠度计算公式的另一个重要因素,它包括外力作用时材料所受力以及材料受力在其内部产生的变形量,它可以用一个简单的公式来表示:F=kΔε,其中F为外力作用时材料所受力,k为弹性模量,Δε为材料受力在其内部产生的变形量。
按照上述公式,我们可以应用它来计算材料在外力作用下所产生的挠度,这种挠度可以用一个更简单的方式来表示:d=F/AE,其中F 为外力作用时材料所受力,A为材料的横断面积,E为材料的弹性模量。
通过计算来得出挠度,可以精确地知晓材料在外力作用下产生的变形情况。
此外,假如在计算挠度的时候,发现某种材料在外力作用下变形过大,那么我们可以采取比较极端的措施,例如增加或者减少某种材料的厚度,这样就可以限制材料受到的外力,从而达到降低变形的目的。
因此,挠度计算公式可以让我们更准确地计算不同类型的材料将会在外力作用下产生怎样的变形,以及提供一些可行的方法和解决办法,来限制变形量。
此外,通过挠度计算公式,我们还可以比较不同类型材料在外力作用下产生的变形大小。
总之,挠度计算公式是一种很有用的计算工具,用于衡量材料受外力作用时的变形。
它不仅可以帮助我们了解材料的变形情况,而且还可以提供一些解决方案,以避免变形过大所带来的不良影响。
挠度公式推导过程

挠度公式推导过程一、挠度的概念挠度是指杆件或梁在受力作用下产生的弯曲变形程度。
当外力作用于杆件或梁上时,由于材料的弹性变形,导致结构发生弯曲变形。
挠度是描述这种弯曲变形的重要参数,它可以用来评估结构的刚度、稳定性和承载能力。
二、挠度的计算方法挠度的计算方法有多种,其中最常用的是根据梁的弯曲理论推导出的挠度公式。
下面我们来推导一维梁的挠度公式。
假设有一根长度为L、弹性模量为E、截面惯性矩为I的一维梁,受到均匀分布荷载w作用。
我们需要计算梁在x处的挠度y。
根据弯曲理论,梁在x处的挠度y可以通过以下公式计算:y = (w * x^2) / (24 * E * I) * (L^3 - 2 * L * x^2 + x^3)其中,w是荷载大小,E是弹性模量,I是截面惯性矩,x是距离梁起点的位置。
三、挠度公式的应用挠度公式在工程实践中有广泛的应用。
以下是一些常见的应用场景:1. 结构设计:在结构设计中,工程师可以使用挠度公式来评估结构的刚度和稳定性。
通过计算挠度,工程师可以确定结构是否满足要求,以及是否需要采取加固措施。
2. 荷载分析:在荷载分析中,挠度公式可以用来估计结构在不同荷载下的挠度变化。
通过分析挠度,工程师可以确定结构的承载能力,并做出相应的调整和优化。
3. 结构监测:在结构监测中,挠度公式可以用来计算结构在实际使用中的挠度变化。
通过实时监测挠度,工程师可以及时发现结构的变形情况,并采取相应的维修和保养措施。
4. 材料选择:挠度公式还可以用来评估不同材料的挠度性能。
通过比较不同材料的挠度值,工程师可以选择最合适的材料,以满足结构设计的要求。
挠度公式是描述杆件或梁弯曲程度的重要工具。
通过挠度公式,工程师可以评估结构的刚度、稳定性和承载能力,并做出相应的设计和优化。
在工程实践中,准确计算挠度对于确保结构的安全和可靠性至关重要。
因此,掌握挠度公式的推导过程和应用方法对于工程师来说是非常重要的。
挠度公式推导过程

挠度公式推导过程
挠度是指杆件在受力后的弯曲程度,是结构设计中重要的参数之一。
挠度的计算需要用到弹性模量、截面惯性矩以及杆件受力情况等信息。
下
面是求解挠度的推导过程:
假设杆件为梁,长度为L,在距离x处有一个集中力F作用,则该点
的弯矩为M=Fx。
由于梁的截面不同,抵抗弯曲的能力也不同,因此引入
了截面惯性矩I的概念,即杆件截面对弯曲时的惯性。
根据弹性力学理论,杆件的挠度w与弯矩M和材料的弹性模量E、杆
件的截面惯性矩I以及杆件长度L有关。
因此,可以得到挠度的基本公式:w=(FL^3)/(3EI)。
其中,F为杆件上受力的大小,E为材料的弹性模量,I为杆件截面
对弯曲时的惯性,L为杆件长度。
该公式可以用于计算杆件作为梁时在距离x处的挠度。
如果需要计算
离散分布荷载下的梁挠度,则可以将分布荷载等效为一个集中荷载,再计
算其挠度,最后再根据荷载分布情况和叠加原理进行相应的计算。
以上是挠度公式的推导过程,可以帮助工程师在结构设计中准确计算
杆件的挠度,从而保证结构的安全和稳定。
轨道吊

轨道吊计算书(1)计算参数1、轨道吊高度60米,地面粗糙度等级按B级;2、单元板块最大尺寸4x1.5m,考虑单元板块最大重量0.7t,钢丝绳及电动葫芦重量对结构产生的重力0.2t(其中钢丝绳200m重100kg,电动葫芦及其他附件中100kg);3、悬挑的梁采用Q235B普20a号工字钢,轨道梁采用Q235B普20a号工字钢,支撑采用Q235B普20a号工字钢和100x100x5钢方管,横向支撑采用Q235B 100x100x5钢方管,钢丝绳采用φ124、工字钢和钢管的抗拉强度的设计值:fy=215Mpa,抗剪设计值:fy=125Mpa。
钢丝绳φ12的许用应力:fy=1570/5=314Mpa(设计抗拉强度取最小值:1570Mpa;工况选M5,即安全系数为5)。
轨道的平面布置图见下图,知悬挑20a工字钢的最大间距为2.6m,悬挑长度为0.75m,钢结构自重按78.5KN/m3考虑,平面示意图如下:(2)计算模型图钢架计算简图(3)风力计算在吊装过程,加荷载分别20a号工字钢中部和端部,最大板块荷载和吊装设备荷载为1t,考虑动力系数1.5,取15 KN。
考虑六级风力下风荷载:式中:——风荷载标准值();——高度z处的阵风系数,取1.67;——风荷载体型系数,取1.2;——风压高度变化系数,取1.61;——基本风压(),六级风速v=13.8m/s,=v2/1600=0.12kN/m2;=0.387kN/m2最大板块分格:4000×1500,风荷载0.387×4×1.5=2.32 kN考虑施工角度30°,传递给轨道的竖向荷载为2.32×sin30°=1.16kN水平横向载荷为2.32×sin60°=2.0kN总的荷载为15+1.16=16.16kN(3)吊车横向力计算吊车横向水平荷载T=1.5×a(Q+Q1)g式中 Q:吊车的额定起重量:1000kgQ1:吊车自重100kgg:重力加速度10a:制动系数取a=0.071.5动力系数T=1.5×0.07×1100×10=1.16KN(4)模型计算:此时分两种情况:第一种当电动葫芦位于挑梁端部位置,此时挑梁荷载最大,我们以此时状态计算挑梁;第二种当载荷位于轨道梁中间时,此时轨道梁受力最大,我们以此状态计算轨道梁;第一种情况:载荷集中位于挑梁端部,如下图所示:作用在挑梁20a号工字钢端部的荷载为竖向FZ=-16.16KN,水平T=2.0KN+1.16KN=3.17KN1.强度计算,如下图所示:钢架应力比图所有钢件强度应力比均小于1,满足要求!2.扰度计算:钢架变形图受力点位移最大,变形量为1mm<L/400=750/400=1.875mm,满足要求;第二种情况:载荷在轨道梁中间时,此时轨道梁受力最大,如下图所示:作用在挑梁20a号工字钢端部的荷载为竖向FZ=-16.16KN,水平T=2.0KN+1.16KN=3.17KN1、强度计算:钢架强度应力图(单位:Mpa)最大应力比0.219<1,满足强度要求;2.扰度计算:受力点位移最大,变形量为3.35mm<L/400=2600/400=6.5mm,满足要求;综上所述,两种情况钢结构均满足要求;(5)钢丝绳计算钢丝绳额定载荷F:板块重量=0.7t,钢丝绳0.1t,按F=1t计算;承重钢丝绳1根;钢丝绳直径为30mm,拉断力设计为300KN;按规范要求,钢丝绳的安全系数取9;重力加速度g=10则:1000x10x9=90000N=90KN<300KN;满足强度要求;。
扰度

(1)荷载计算在桥梁施工中,作用在扣件式钢管脚手架上的荷载一般有施工结构物荷载、操作人员体重、施工设备重力和扣件式钢管脚手架自重力。
各种荷载的作用部位和分布可按实际情况采用。
扣件式钢管脚手架荷载的传递顺序为:脚手板→横向横杆→纵向横杆→立杆→底座→地基。
(2)纵向、横向水平杆的抗弯强度计算纵向、横向水平杆的抗弯强度计算公式如下:δ= ≤[f]m——弯矩设计值横向、纵向水平杆的内力一般按照三跨连续梁计算弯矩(如果特殊情况可按多跨连续梁弯矩计算):w——截面模量。
[f]——钢材的抗弯强度设计值。
(3)纵向、横向水平杆的扰度计算:纵向、横向水平杆扰度按下式计算:υ= ≤[υ]υ——扰度e——钢材的弹性模量i——纵向、横向水平杆的截面惯性矩q——纵向、横向水平杆上的等效均布荷载l——纵向、横向水平杆的跨度[υ]——容许扰度,应按下表采用。
(4)连接扣件的抗滑承载力计算纵向、横向水平杆与立杆连接时,其扣件的抗滑承载力应符合下式规定:r≤[r]r——纵向、横向水平杆传给立杆的竖向作用力(q*l)[r]——扣件抗滑承载力设计值。
(5)立杆的稳定性计算立杆的稳定性计算:≤[f]n——模板支架计算立杆的轴向力设计值n=1.2∑ngk+1.4∑nqk∑ngk——模板及支架自重、新浇混凝土自重与钢筋自重产生的轴向力的总和。
∑nqk——施工人员及施工设备荷载标准值、振捣混凝土时产生的荷载标准值产生的轴向力总和。
ф——轴心受压构件的稳定系数,应根据长细比λ取值,当λ>250时,ф=7320/λ2a——立杆的截面面积。
[f]——钢材的抗弯强度设计值。
(6)立杆地基承载力计算根据试验结果,荷载板底面的应力与其沉量的关系曲线如下图所示。
从图中可看出,在荷载作用下地基土的变形。
如果荷载应力超过p0,地基承载变形将发生突变,丧失地基承载力。
所以立杆基础底面的平均压力一定要满足下式要求:p≤[fg]p——立杆基础底面的平均压力,[fg]——地基承载力设计值,门式钢管脚手架以门架、交叉支撑、连接棒、挂扣式脚手板或水平架、锁臂等组成基本结构,再设置水平加固杆、剪刀撑、扫地杆、封口杆、托座与底座的一种标准化钢管脚手架。
扰度计算公式

扰度计算公式扰度,这词儿听起来是不是有点陌生又有点专业?其实啊,在咱们的物理学和工程学里,扰度计算公式可是相当重要的!先来说说什么是扰度。
简单来讲,扰度就是梁或者其他结构在受力作用下产生的弯曲变形程度。
比如说,你走过一座桥,桥身会因为你的重量稍微往下弯一点,这个弯曲的程度就是扰度。
那扰度计算公式到底是啥呢?常见的有简支梁的扰度计算公式,悬臂梁的扰度计算公式等等。
咱就拿简支梁来说吧,假如有一个均布荷载作用在简支梁上,它的扰度计算公式就是 5ql^4 / (384EI) 。
这里的 q表示均布荷载,l 是梁的跨度,E 是材料的弹性模量,I 是截面的惯性矩。
听起来是不是有点晕乎?别着急,我给您讲个事儿,您就明白这公式有多有用啦。
有一次,我去一个建筑工地参观。
当时工人们正在搭建一个厂房的钢梁结构。
其中有一根钢梁,在安装好之后,总感觉有点不太对劲,有点往下弯得太厉害了。
负责的工程师就赶紧过来查看,他拿出纸笔,开始测量这根钢梁的各项参数,像跨度啊、荷载啊,然后就用扰度计算公式来计算这根钢梁理论上应该弯曲的程度。
经过一番计算,发现这根钢梁的实际弯曲程度远远超过了理论计算的扰度值。
这下可不得了,工程师马上就组织工人进行检查和整改。
后来发现,原来是在施工过程中,有个地方的焊接没有达到标准,导致钢梁的强度不够,所以才弯曲得太厉害了。
通过这件事儿,您就可以看出扰度计算公式的重要性了吧。
如果没有这个公式,工程师可能就没办法及时发现问题,那这厂房的安全性可就大打折扣啦。
在实际应用中,扰度计算公式的准确性取决于我们对各种参数的准确测量和对材料性质的了解。
有时候,一点点的误差都可能导致计算结果的偏差,从而影响整个结构的安全性和稳定性。
再比如说,在设计机械零件的时候,如果不考虑扰度,可能会导致零件在工作过程中因为变形过大而失效。
就像汽车的悬挂系统,如果设计不合理,车辆行驶起来就会颠簸得厉害,不仅影响舒适性,还可能会损坏零部件。
所以啊,扰度计算公式虽然看起来复杂,但它却是保证各种结构安全可靠的重要工具。
扰度计算公式讲解学习

扰度计算公式讲解学习
扰度(Turbidity)是指介质中悬浮物或溶解物对光的散射和吸收能力的表征。
它是水体透明度的一个重要指标,描述了水体中悬浮物和溶解物的浓度及其对光的影响程度。
扰度值越高,代表水体中的悬浮物或溶解物越多,透明度越低。
1.传统扰度计算公式
传统扰度计算公式是根据光线经过介质后光线透射的强度变化来计算的。
这个公式主要用于水体中悬浮物引起的扰度计算,其公式如下:T = -ln(I/I₀)
其中,T为扰度值,I为透射光强度,I₀为入射光强度。
传统扰度计算公式的优点是简单易懂,计算方便,可以直接通过实验中测量的数据来计算扰度值。
然而,这个计算公式并不适用于颗粒非常细小的溶液,因为此时扰度值非常小,透射光强度几乎无法测量。
2.新国际单位制中的扰度计算公式
新国际单位制中的扰度计算公式是根据扰度对光的散射能力的定义来计算的。
这个公式适用于细小颗粒悬浮物和溶解物引起的扰度计算,其公式如下:
T=K*C
其中,T为扰度值,K为比例系数,C为悬浮物或溶解物的浓度。
总结起来,扰度的计算公式可以根据实际需要选择使用。
传统扰度计算公式适用于实验室中对水体悬浮物引起的扰度进行快速评估;而新国际
单位制中的扰度计算公式更为科学准确,适用于各种颗粒大小和浓度的溶液的扰度计算。
扰度计算公式

扰度计算公式扰度是一种用于衡量数据集内部样本之间的相似度的指标,通过计算样本间的差异程度来表征数据集的离散程度或分散程度。
扰度计算公式主要有以下几种形式。
1. 绝对平均差异度(mean absolute deviation,MAD):绝对平均差异度是一种最常见的扰度计算方法,它定义了每个样本与其他样本之间的平均差异程度。
设有n个样本$x_1,x_2,...,x_n$,其绝对平均差异度的计算公式为:$MAD = \frac{1}{n} \sum_{i=1}^{n}\sum_{j=1}^{n}\left, x_i - x_j \right,$2. 方差(variance):方差是衡量数据集分散程度的一种指标,它定义了每个样本与数据集均值之间的差异程度。
假设有n个样本$x_1, x_2, ..., x_n$,其中$x$的均值为$\bar{x}$,方差的计算公式为:$Var = \frac{1}{n} \sum_{i=1}^{n}(x_i - \bar{x})^2$3. 标准差(standard deviation):标准差是方差的平方根,它表示了数据集内样本与均值之间的平均距离,是一种常用的数据集离散程度的度量指标。
标准差的计算公式为:$SD = \sqrt{Var}$4. 四分位差(interquartile range,IQR):四分位差是一种用于衡量数据集偏向程度的指标,它定义了数据集的上下四分位数之差,可以用来衡量数据集的离散度。
假设有n个样本$x_1,x_2,...,x_n$,其四分位差的计算公式为:$IQR=Q_3-Q_1$其中$Q_1$表示下四分位数,$Q_3$表示上四分位数。
5. 熵(entropy):熵是一种用于衡量数据集混乱程度的指标,它定义了数据集中信息的不确定程度。
假设有n个样本$x_1,x_2,...,x_n$,每个样本$x_i$的概率为$p(x_i)$,则熵的计算公式为:$Entropy = -\sum_{i=1}^{n} p(x_i) \log_{2} p(x_i)$6. 相对熵(relative entropy):相对熵也称为KL散度(Kullback-Leibler divergence),它是一种用于衡量两个概率分布之间差异程度的指标。
一阶微扰公式

一阶微扰公式
一阶微扰公式是物理学中常用的工具,它可以用来描述一个系统在受到微小扰动下的行为。
这个公式通常写成P=P0+δP,其中P 是受到扰动后的系统参数(如能量、波函数等),P0 是未受扰动的系统参数,而δP 是微扰引起的变化量。
这个公式的应用范围非常广泛,比如在量子力学、统计物理学、电路分析等领域都有应用。
在量子力学中,一阶微扰公式可以用来计算能级和波函数的微小变化;在统计物理学中,它可以用来计算热力学量的微小变化;在电路分析中,它可以用来计算电流、电压等参数的微小变化。
除了以上应用领域,一阶微扰公式还可以用来解决其他各种问题。
例如,在工程中,我们经常需要对一个复杂的系统进行近似计算,这时就可以使用一阶微扰公式来简化计算过程;在经济学的模型中,一阶微扰公式可以用来分析政策变化对市场的影响;在生态学中,它可以用来描述生态系统在受到微小扰动下的行为。
总之,一阶微扰公式是一个非常有用的工具,它可以帮助我们更好地理解各种复杂系统的行为。
一阶微扰公式

一阶微扰公式
【原创实用版】
目录
一、什么是一阶微扰公式
二、一阶微扰公式的推导过程
三、一阶微扰公式的应用
四、总结
正文
一、什么是一阶微扰公式
一阶微扰公式是物理学中一种用于解决微扰问题的数学工具,主要应用于量子力学、统计力学等领域。
当一个系统受到微小扰动时,一阶微扰公式可以帮助我们计算这个扰动对系统性质的影响。
二、一阶微扰公式的推导过程
一阶微扰公式的推导过程相对简单。
首先,我们将一个系统哈密顿量表示为两部分:一个是未受扰动的哈密顿量,另一个是微扰项。
然后,通过对这两个部分进行展开和计算,我们可以得到一阶微扰公式。
具体来说,假设哈密顿量可以表示为 H = H0 + λV,其中 H0 是未受扰动的哈密顿量,λV 是微扰项(λ是微扰参数,通常是一个很小的数)。
根据量子力学的薛定谔方程,我们可以得到:
H |ψ = E |ψ
其中,|ψ是系统的波函数,E 是系统的能量。
将哈密顿量代入上式,并展开到一阶微扰,我们得到:
(H0 + λV) |ψ = E0 + λVE |ψ
其中,E0 是未受扰动的能量。
比较两边的波函数,我们可以得到一
阶微扰公式:
E1 = λVE1
其中,E1 是能量的一阶微扰项。
三、一阶微扰公式的应用
一阶微扰公式在物理学中有广泛的应用,例如在量子力学中,它可以帮助我们计算一个微小扰动对系统能级的影响。
在统计力学中,它可以用于研究系统在微扰作用下的性质变化等。
四、总结
一阶微扰公式是一种解决微扰问题的数学方法,它可以帮助我们计算微小扰动对系统性质的影响。
玻璃强度和挠度计算方法

玻璃强度和挠度计算方法一、前言目前国内涉及玻璃强度、挠度计算的标准有JGJ102-96《玻璃幕墙工程技术规范》、JGJ113-97《建筑玻璃应用技术规程》、上海市地方标准DBJ08-56-96《建筑幕墙工程技术规程(玻璃幕墙分册)》。
JGJ102-96、DBJ08-56-96(以下简称现行国标)对单片玻璃强度计算均有规定,根据有关试验资料在一定范围内强度计算偏于保守。
DBJ08-56-96对单片玻璃的挠度有规定,根据有关试验资料挠度实测值与计算值有相当大偏差。
我们希望通过试验数据对比研究,建立较完善的幕墙玻璃强度和挠度计算理论。
二、试验概况和研究内容(一)试验概况1.试验样品玻璃品种包括浮法、半钢化、钢化玻璃,支承条件以四边支撑为主。
试验样品约六十片,玻璃厚度以玻璃幕墙工程常用的6mm、8mm、10mm为主。
2.试验方法通过对四边支撑的玻璃板块在侧向均布荷载作用下的试验,研究其跨中挠度、最大应力的变化规律。
检验过程参照ASTM-E998进行,将玻璃板块安装在测试箱体上。
试验过程中采集的数据包括控制点的应变值和跨中挠度值。
(二)研究内容和方法1.通过以上较为典型的玻璃板块在侧向荷载作用下的的应力和挠度试验,研究单片玻璃在侧向荷载作用下的应力和挠度变化规律。
采取四边支承方式进行玻璃侧向荷载的试验,采集的数据主要包括控制点的应变和跨中挠度。
2.运用薄板弹性弯曲理论,通过有限元方法计算四边支承玻璃的最大应力和跨中挠度,并与试验数据进行对比,从而建立合理的玻璃应力和挠度计算方法,为玻璃结构性能的理论分析建立合适的计算模型。
3.由较合理的玻璃有限元计算模型,计算大量的不同厚度、长宽比的玻璃最大应力和跨中挠度,拟合玻璃应力和挠度公式。
通过以上试验和研究,建立单片玻璃较完整的计算方法,弥补现行幕墙玻璃规范中的不足之处、为使用中幕墙玻璃的评估提供理论依据。
三、试验结果分析(一) 单片玻璃强度和挠度研究1.试验实测数据与现行规范计算值的对比现行规范(JGJ102-96、DBJ08-56-96)采用小挠度理论来计算玻璃最大应力和跨中挠度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
简支梁在各种荷载作用下跨中最大挠度计算公式:
均布荷载下的最大挠度在梁的跨中,其计算公式:
Ymax = 5ql^4/(384EI).
式中: Ymax 为梁跨中的最大挠度(mm).
q 为均布线荷载标准值(kn/m).
E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.
I 为钢的截面惯矩,可在型钢表中查得(mm^4).
跨中一个集中荷载下的最大挠度在梁的跨中,其计算公式: Ymax = 8pl^3/(384EI)=1pl^3/(48EI).
式中: Ymax 为梁跨中的最大挠度(mm).
p 为各个集中荷载标准值之和(kn).
E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.
I 为钢的截面惯矩,可在型钢表中查得(mm^4).
跨间等间距布置两个相等的集中荷载下的最大挠度在梁的跨中,其计算公式:
Ymax = ^3/(384EI).
式中: Ymax 为梁跨中的最大挠度(mm).
p 为各个集中荷载标准值之和(kn).
E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.
I 为钢的截面惯矩,可在型钢表中查得(mm^4).
跨间等间距布置三个相等的集中荷载下的最大挠度,其计算公式:
Ymax = ^3/(384EI).
式中: Ymax 为梁跨中的最大挠度(mm).
p 为各个集中荷载标准值之和(kn).
E 为钢的弹性模量,对于工程用结构钢,E = 2100000 N/mm^2.
I 为钢的截面惯矩,可在型钢表中查得(mm^4).
悬臂梁受均布荷载或自由端受集中荷载作用时,自由端最大挠度分别为的,其计算公式:
Ymax =1ql^4/(8EI). ;Ymax =1pl^3/(3EI).
q 为均布线荷载标准值(kn/m). ;p 为各个集中荷载标准值之和(kn).
你可以根据最大挠度控制1/400,荷载条件25kn/m以及一些其他荷载条件
进行反算,看能满足的上部荷载要求!
机械零件和构件的一种截面几何参量,旧称截面模量。
它用以计算零件、构件的抗弯强度和抗扭强度(见强度),或者用以计算在给定的弯矩或扭矩条件下截面上的最大应力。
根据材料力学,在承受弯矩Μ的梁截面上和承受扭矩T 的杆截面上,最大的弯曲应力σ和最大的扭转应力τ出现于离弯曲中性轴线和扭转中性点垂直距离最远的面或点上。
σ和τ的数值为
√(C+W)√(RD↑2)
式中Jxx和J0分别为围绕中性轴线XX和中性点O的截面惯性矩;Jxx/y和J0/y分别为弯曲和扭转的截面模量(见图和附表)。
一般截面系数的符号为W,单位为毫米3 。
根据公式可知,截面的抗弯和抗扭强度与相应的截面系数成正比。
