总复习专题训练3

合集下载

高考语文总复习教案第三部分专题对点训练(三)语言表达运用

第三部分语言建构与运用专题二语言表达运用专题对点训练(三)1．清明节快到了，家在外地的王伟必须随父母回老家祭祖。

下面是王伟写给老师的请假条，请指出其中不恰当的地方并修改。

尊敬的王老师：清明节是我国乃至全世界的传统节日，是祭祖和扫墓的日子。

为继承传统，祭祀先人，令尊决定带家人回乡下老家扫墓。

特向您请假，恳请老师批准。

此致。

请假人：王伟2019年4月2日解析：请假条的不恰当之处可以从格式、内容、语言表达三个方面分析，其中内容指的是应用文必须包含的要素。

据此，逐一排查，找出其中的不恰当之处。

答案：①“尊敬的王老师”格式不对，应顶格写；②“乃至全世界”多余，应删掉；③“令尊”用错，应改为“家父”或“我的父亲”；④没有说明请假的具体天数，可在“特向您请假”后加上请假的具体天数；⑤“此致”多余，删掉。

2．下文是一份请柬片段的草稿，其中有五处表述不得体，请指出并改正。

我校文学社决定于本月18日晚7点在学校礼堂举行“民俗文化报告会”，您是著名民俗专家，对民俗文化有所研究。

今诚挚邀请您前来，为我社民俗文化活动的开展认真做出指导，务必届时到会。

解析：本题考查语言表达的得体。

“决定”“有所研究”“前来”不当；“认真做出指导”“务必届时到会”用语不得体，不宜对邀请的对象提出这样的要求。

答案：①“决定于”改为“定于”；②“有所研究”改为“造诣深厚”；③“前来”改为“光临”；④“认真做出指导”删除“认真”；⑤“务必”改为“恭候”。

3．下面是一份家长会邀请函，在表达上有多处不妥当，请指出至少三处并改正。

邀请函尊敬的家长：时光如梭，转眼间犬子即将进入生死攸关的高三年级。

在这个关键的时期，他更希望得到您悉心的帮助。

为了指导您有效地对孩子作心理疏导，鄙校决定于本月20日上午10时在学校报告厅举行家长会，聘请省内知名的心理辅导专家做专题讲座。

希望您在百忙之中抽出时间，准时参加，不得缺席或迟到。

××中学高三年级2019年4月13日解析：题干要求“指出至少三处并改正”。

中考总复习专项训练题(三)(改错专练)

Jim was too frightened not to move．The snake 8．________
A B C D
6．You can sing in English，and so does he．
A B C D
7．Why not ask for help when you are with trouble？
A B C D
8．Ann didn't know how work out the problem in class．
the school，opened the door and went in the 7．________
classroom．That was nice and warm there 8．________
but Miss Jones was happy．But a small boy looked at her for a few 9．________
C D
25．How proudly they were when they heard the good news！
A B C D
26．It took the boy one and a half hour to fall asleep last night．
A B C D
A B C D
23．I hope my son to get on well with his classmates．
A B C D
24．—How did you come here this morning？
A B
—I came here by Mr Smith's car．

小升初总复习专题3运动中的数学问题(含答案)

时针方向行走．甲第一次遇到乙后11 分钟遇到丙，再过 3 3 分钟第二次遇到乙．已知乙的速度是甲的 2 ，
4
4
3
湖的周长为 600 米，求丙的速度．
顺流船速=船速+水速：逆流船速=船速-水速；
船速=（顺流船速+逆流船速）÷2；
水速=（顺流船速-逆流船速）÷2；
顺流船速=逆流船速+水速×2；
ห้องสมุดไป่ตู้
【例 9】一艘轮船以同一速度往返于两码头之间．它顺流而下，行了 8 小时，逆流而上，行了 10 小时．如果水流速度是每小时 3 千米，求两码头之间的距离？
【例 3】A、B 两地相距 960 米．甲、乙两人分别从 A、B 两地同时出发．若相向而行，6 分钟相遇；若同向行走，80 分钟甲可以追上乙．甲从 A 地走到 B 地要用多少分钟？
【例 4】两辆汽车同时从东、西两站相向开出．第一次在离东站 80 千米的地方相遇．之后，两车继续以原来的速度前进．各自到达对方车站后都立即返回，又在距中点西侧 30 千米处相遇．两站相距多少千米？
【例 15】一列火车通过 24000 米的大桥需要 3 分钟，用同样的速度从路过的一根电线杆旁边通过，只用了 1 分钟．求这列火车的速度．
甲乙两人所走路程分别为 S甲和 S乙，速度分别是V甲和V乙，时间是 T甲和 T乙当时间相同时： S甲 : S乙=V甲 :V乙当速度相同时： S甲 : S乙=T甲 :T乙当路程相同时：V甲 :V乙=T乙 :T甲【例 16】甲乙两人同时骑自行车从东、西两镇相向而行，甲、乙的速度比是 3:4．已知甲行了全程的 1 ，
运动中的数学相向而行：相遇时间=距离÷速度和相背而行：相背距离=速度和×时间同向而行：追及时间=追及距离÷速度差解决行程问题时，要充分利用图示把题中的情节形象地表示出来，有助于分析数量关系，有助于迅速地找到解题思路．

小学语文总复习专项训练——小古文阅读(三)

小学语文总复习专项训练（小古文阅读训练三）一、阅读下面的小古文，回答后面的问题。

（一）草书大王张丞相好书而不工。

当时流辈①皆讥笑之。

丞相自若②也。

一日得句③，索笔疾书，满纸龙蛇飞动。

使侄录之。

当波险处④，侄罔然而止。

执所书问曰：“此何字也？”丞相熟视久之，亦不自识。

诟⑤其侄曰：“汝⑥胡⑦不早问，致余⑦忘之。

”【注释】①流辈：人们。

②自若：像自己原来的样子，不变常态。

③得句：得到佳句。

④波险处：书法中笔画怪诞的地方。

⑤诟：责骂。

⑥汝：你。

⑦胡：为什么。

⑦余：我。

1.联系上下文，给加点字选择正确的解释。

（1）张丞相好．书而不工（）A.优点多的。

B.表示赞许。

C.喜爱。

D.常容易（发生某事）。

（2）索．笔疾书（）A.寻找。

B.大绳子。

C.讨要。

D.单独。

（3）执．所书问日（）A.坚持。

B.拿着。

C.捉住。

D.凭证、单据。

2.用现代汉语翻译文中画横线的句子。

汝胡不早问，致余忘之。

____________________________________________________________________3.“当时流辈皆讥笑之”的原因是：_____________________________________________________________。

（用文中的句子回答）4.这则故事中该责怪的人是谁？（）A.该责怪的是张丞相，他把自己的错误归结给别人。

B.该责怪侄儿，他在抄之前应先看一遍，不认识的字及时请教张丞相。

5.读了这则故事，你有什么启示？____________________________________________________________________（二）林琴南敬师闽县林琴南孝廉纾①（shū）六七岁时，从师读。

师贫甚，炊不得米。

林知之，亟②（jí）归，以袜实米，满之，负以致师。

师怒，谓其窃，却弗受。

林归以告母，母笑曰：“若心固善，然此岂束脩③之礼？”即呼备④，赍（jī）米一石致之塾，师乃受。

中考数学总复习专题三解答题重难点题型突破题型二几何图形探究题类型与三角形、四边形有关的探究题课件

(2)如图②，过点 F 作 FG⊥AB 于 G，连接 FE.∵AF＝BE，AF∥BE，∴ 四边形 ABEF 是平行四边形，∵AF＋BE＝16，∴AB＝AF＝BE＝8，∵32 3＝ 8×FG，∴FG＝4 3，在 Rt△FAG 中，AF＝8，∴∠FAG＝60°，当点 G 在线段 AB 上时，∠FAB＝60°，当点 G 在线段 BA 延长线时，∠FAB＝120°，
解：(1)原命题不成立，新结论为：∠APB＝90°， AF＋BE＝2AB(或 AF＝BE＝AB)，证明：∵AM∥BN， ∴∠MAB＋∠NBA＝180°，∵AE，BF 分别平分∠MAB，∠NBA，
∴∠EAB＝12∠MAB，∠FBA＝12∠NBA，
∴∠EAB＋∠FBA＝12(∠MAB＋∠NBA)＝90°， ∴∠APB＝90°，∵AE 平分∠MAB，∴∠MAE＝∠BAE， ∵AM∥BN，∴∠MAE＝∠BAE，∴∠BAE＝∠BEA， ∴AB＝BE，同理：AF＝AB，∴AF＋BE＝2AB(或 AF＝BE＝AB)；
辽宁专用
专题三解答题重难点题型突破
题型二几何图形探究题类型1 与三角形、四边形有关的探究题
【例1】 (2016·抚顺)如图，在△ABC中，BC >AC，点E在BC上，CE＝CA，点D在AB上，连接DE，∠ACB＋∠ADE＝180°，作CH⊥AB，垂足为H.
(1)如图①，当∠ACB＝90°时，连接CD，过点C作CF⊥CD交BA的延长线于点F. ①求证：FA＝DE； ②请猜想三条线段DE、AD、CH之间的数量关系，直接写出结论； (2)如图②，当∠ACB＝120°时，三条线段DE、AD、CH之间存在怎样的数量关系？请证明你的结论．
(3)成立．∵四边形 ABCD 是正方形，∴BC＝CD，∠FBC＝∠ECD＝90 °，

高考总复习英语书面表达专题3

英语
高考总复习人教版
书面表达专题(三)
必修二
英语
高考总复习人教版
书面表达常见错误在英语书面表达中，人们经常犯大小写错误，或误将
英语句号写成汉语句号。这些错误看似小事，却会影响得
分。现将常见的典型错误列举出来，望大家引以为戒。
必修二
英语
高考总复习人教版
一、格式错误有的考生不能正确地运用书信或日记的格式。
必修二
英语
高考总复习人教版
2．将形容词用成及物动词。例：Please present on time.Don't absent!
修改建议：Please be present on time.Don't be absent!
3．将不可数名词用成可数名词。例：a good news，many informations 修改建议：good news，much information 4．将形容词和副词混淆使用。例：in the recently years，study hardly 修改建议：in the recent years，study hard
必修二
英语
高考总复习人教版
例2：For the people who are diligent and kind， money is just the thing to be used to buy the thing they
need.
修改建议：Diligent，caring people use money only to buy what they need.
必修二
英语
高考总复习人教版
3.修饰语错位。英语与汉语不同，同一个修饰语置于句子的不同位置，

高考历史总复习专题3近代中国的民主革命考点8新民主主义革命

【2019最新】精选高考历史总复习专题3近代中国的民主革命考点8新民主主义革命一、五四运动——(c)1．直接原因(导火线)：巴黎和会上中国收回国家主权的正当要求遭拒绝，将德国侵占中国山东的权益转给日本。

2．概况1919年5月4日起，北京大学等学校学生集会，举行游行示威。

自6月5日起，上海工人罢工。

从此中国的工人阶级登上政治舞台。

随后，工人罢工、商人罢市、学生罢课浪潮波及全国。

3．结果(1)北洋军阀政府被迫释放被捕学生。

(2)罢免亲日卖国贼的职务。

(3)中国外交代表团拒绝在和约上签字。

4．意义：五四运动是广大人民群众直接参与的毫不妥协的反帝反封建的革命运动；标志着工人阶级开始登上政治舞台，标志着中国新民主主义革命的开端；促进了马克思主义在中国的广泛传播，并与工人运动相结合，为中共成立奠定了基础。

微点拨五四运动的直接斗争目标部分得到实现，取得一定成果，但不能说反帝反封建取得彻底胜利。

二、中共建立1．中国共产党“一大”——(b)(1)背景：五四运动中工人阶级登上历史舞台；马克思主义在中国传播，并与工人运动相结合；各地纷纷建立了一些共产党早期组织；共产国际的帮助。

(2)召开：1921年7月23日在上海秘密召开，后转移到嘉兴南湖。

与会者有毛泽东、董必武等13名各地共产党组织的代表，另有共产国际代表列席会议。

(3)主要内容：①规定党的任务是推翻资产阶级，建立无产阶级专政，消灭阶级差别，实现共产主义。

②确定党的中心任务是领导工人运动。

(4)意义：标志着中国共产党的诞生。

适应了中国近代社会发展的要求；自从有了中国共产党，中国革命的面貌焕然一新。

2．民主革命纲领的制定——(b)(1)制定：1922年，中共二大在上海召开。

(2)内容：最高纲领——实现共产主义，最低纲领——民主革命纲领：打倒军阀，推翻国际帝国主义的压迫，统一中国为真正的民主共和国。

(3)意义：中国近代以来第一个彻底的反帝反封建民主革命纲领。

三、国民革命——(b)1．国民革命的兴起(1)标志：1924年，中国国民党一大在广州召开。

初中生物总复习专题3细胞是生命活动的基本单位

三、训练与提高
(一)选择题 1．(2019山西)显微镜是我们观察奇妙的微观世界不可缺少的工具。使用显微镜时，下列操作正确的是( C ) A．光线暗时，使用平面反光镜 B．擦拭物镜和目镜时，使用纱布 C．物像偏左，欲使物像移至视野中央时，向左移动玻片标本 D．镜筒下降时，眼睛注视目镜内的物像
三、训练与提高
二、复习要点
(6)比较低倍镜与高倍镜下的物像与视野
物镜
物镜长短
镜头与标本距
离
放大倍数
物像大小
细胞数目
视野范围
视野亮度
低倍镜短
远
小 ___小_ __多__ ___大_ ___明亮
高倍镜长
近
大 ___大__ __少___ ___小__ ___黑暗
二、复习要点
4．玻片标本的类型 (用光学显微镜观察的材料一定要_____薄而透明______，否则光线不能透过)
三、训练与提高
9．(2021湘潭)用显微镜观察草履虫时，在不更换目镜的情况下，依次观察到如图甲和图乙的视野，下列相关叙述正确的是( D ) A．观察图乙所用的物镜比观察图甲的物镜短 B．要从图甲转换成图乙视野应先将玻片往右上方移动 C．图甲中出现“A”所示情况的原因是玻片未擦干净 D．图甲视野中草履虫的纤毛区分度不高，可尝试转换成较小光圈进行观察
三、训练与提高
7．用显微镜观察标本时，第一次使用的是5×目镜、10×物镜，第二次使用的是10× 目镜、40×物镜，那么，第二次观察到的情况与第一次相比( D ) A．细胞较小，细胞数目较多 B．细胞较小，细胞数目较少 C．细胞较大，细胞数目较多 D．细胞较大，细胞数目较少
三、训练与提高
8．如下图为光学显微镜的相关结构示意图，其中的①②为物镜，③④为目镜，⑤⑥ 为观察到清晰物像时物镜与玻片标本之间的距离。下列组合中，观察到细胞数目最多的是( A ) A．①④⑥ B．①③⑤ C．②④⑥ D．②③⑤

(老高考适用)2023版高考化学二轮总复习专题能力提升训练3 氧化还原反应离子反应

专题能力提升训练(三)一、选择题(本题包括10小题，每小题只有一个选项符合题意)1．(2022·大庆模拟)下列实验现象中的颜色变化与氧化还原反应无关的是( C )氧化铁，沉淀变为灰绿色最终变为红褐色，A不符合题意；二氧化硫和硫离子发生氧化还原反应生成硫单质，产生黄色沉淀，B不符合题意；KI溶液滴入AgCl浊液中，沉淀由白色逐渐变为黄色，说明碘化银沉淀更难溶，是沉淀的转化，与氧化还原无关，C符合题意；铜加热和氧气反应生成氧化铜，氧化铜和乙醇发生反应生成乙醛和铜，与氧化还原有关，D不符合题意。

2．(2022·金华模拟)关于反应4Li＋2SOCl2===4LiCl＋S＋SO2，下列有关说法正确的是( A ) A．还原剂只有LiB．SOCl2既是氧化剂又是还原剂C．氧化产物与还原产物的物质的量之比为2∶1D．每转移4 mol电子，生成SO2的体积为22.4 L【解析】在反应4Li＋2SOCl2===4LiCl＋S＋SO2中，Li的化合价升高，做还原剂，生成的LiCl是氧化产物；SOCl2中的S是＋4价，反应后部分变为0价，生成单质硫，所以SOCl2做氧化剂，S为还原产物。

还原剂只有Li，故A正确；由以上分析可知，SOCl2中只有S的化合价发生变化，Cl和O的化合价都没有发生变化，所以SOCl2只做氧化剂，故B错误；由以上分析可知，氧化产物LiCl与还原产物S的物质的量之比为4∶1，故C错误；没有指明温度和压强，无法计算生成的SO2的体积，故D错误。

3．(2022·阜阳模拟)车用尿素是利用反应2CO(NH2)2＋4NO2===4H2O＋2CO2＋4N2＋O2减少柴油机尾气中氮氧化物的排放，下列说法错误的是( C )A．尿素属于有机氮肥B．N2既是氧化产物也是还原产物C．每转移1.6 mol电子，减排NO2 9.2 gD．NO2是形成酸雨的主要物质之一【解析】尿素含氮元素，为有机物，属于有机氮肥，A正确；由方程式可知，尿素中氮元素化合价升高变为氮气，二氧化氮中氮元素化合价降低变为氮气，氮气既是氧化产物也是还原产物，B正确；由得失电子守恒可知，每消耗4 mol二氧化氮转移16 mol电子，因此，每转移1.6 mol电子减排NO20.4 mol，质量为18.4 g，C错误；二氧化氮和二氧化硫是形成酸雨的主要物质，D正确。

【步步高】高考数学(文,江苏专用)大二轮总复习练习：专题三第3讲平面向量(含答案解析)

第 3讲平面向量1． (2016 课·标全国丙改编→1，3→31，则∠ ABC＝ ________. )已知向量 BA＝22， BC＝，22答案30°分析→→∵ |BA|＝ 1， |BC|＝ 1，→ →3BA·BC＝，∴∠ ABC ＝ 30°.cos∠ ABC＝→→2|BA|·|BC|12． (2016 ·东改编山 )已知非零向量m，n 知足 4|m|＝ 3|n|，cos〈 m， n〉＝3.若 n⊥ (tm＋ n)，则实数 t 的值为 ______．答案－ 4分析∵ n⊥ (tm＋ n)，∴ n·(tm＋n)＝0，即 t·m·n＋ n2＝ 0，∴ t|m||n|cos〈 m， n〉＋ |n|2＝0，由3212已知得 t×|n| ×＋ |n| ＝ 0，解得 t＝－ 4.433． (2016 天·津改编 )已知△ABC 是边长为 1 的等边三角形，点 D， E 分别是边 AB， BC 的中点，连接 DE 并延伸到点F，使得 DE＝→ →2EF ，则 AF ·BC的值为 ________．答案1 8分析→→→如下图， AF ＝AD ＋DF .又 D， E 分别为 AB， BC 的中点，→1→且 DE＝ 2EF，因此 AD＝2AB，→＝→＋→＝→＋1→DF DE EF DE2DE3→ 3→＝2DE ＝4AC，→1→ 3 →→→ →因此 AF＝2AB＋4AC.又 BC＝ AC－AB，→ →1→3→→ →则 AF·BC＝AB＋AC ·(AC－ AB)241→ →1→ 2 3 →2 3 → →＝AB·AC－AB＋AC － AC·AB 2244→ 2 1→21→→＝ 4AC － 2AB －4AC ·AB.3→ →又 |AB|＝ |AC|＝ 1，∠ BAC ＝ 60°，→ → 3 1 1 1 1故AF ·BC ＝－－ ×1×1× ＝ .4 2 4 2 84． (2016 ·江浙 )已知向量a ，b ， |a|＝ 1，|b|＝ 2.若对随意单位向量 e ，均有 |a ·e|＋ |b ·e| ≤6，则a ·b 的最大值是 ________．答案12分析由已知可得：6≥|a ·e|＋ |b ·e| ≥|a ·e ＋ b ·e|＝ |(a ＋ b) ·e|，因为上式对随意单位向量e 都成立．∴ 6≥|a ＋ b|成立．∴ 6≥(a ＋ b) 2＝ a 2＋ b 2＋ 2a ·b ＝ 12＋ 22＋ 2a ·b.1即 6≥5＋ 2a ·b ，∴ a ·b ≤2.1.考察平面向量的基本定理及基本运算，多以熟知的平面图形为背景进行考察，多为填空题，难度中低档 .2.考察平面向量的数目积，以填空题为主，难度低；向量作为工具，还常与三角函数、解三角形、不等式、分析几何联合，以解答题形式出现.热门一平面向量的线性运算1．在平面向量的化简或运算中，要依据平面向量基本定理选好基底，变形要有方向不可以盲目转变．2．在用三角形加法法例时，要保证 “首尾相接 ”，结果向量是第一个向量的起点指向最后一个向量终点所得的向量；在用三角形减法法例时，要保证 “同起点 ”，结果向量的方向是指向被减向量．例 1π(1) 设 0<θ< ，向量 a ＝ (sin 2θ， cos θ)， b ＝ (cos θ， 1)，若 a ∥ b ，则 tan θ＝ ______.2→ → → →(2) 如图，在 △ ABC 中，已知 BD ＝ 2DC ，以向量 AB ，向量 AC 作为基底，→则向量 AD 可表示为 ____________．答案 (1)1 (2)1 →＋ 2 →2 3AB 3AC 分析(1)因为 a ∥ b ，因此 sin 2θ＝ cos 2θ，即 2sin θcos θ＝cos 2θ.π 因为 0<θ< ，因此 cos θ>0，21得 2sin θ＝ cos θ，tan θ＝ 2.(2) 依据平面向量的运算法例及已知图形可知→2 →AB ＋3AC .→→→→ 2 → → 2 → → 1AD ＝AB ＋ BD ＝ AB ＋ BC ＝AB ＋ (BA ＋ AC)＝333思想升华(1) 关于平面向量的线性运算，要先选择一组基底；同时注意共线向量定理的灵活运用． (2)运算过程中重视数形联合，联合图形剖析向量间的关系．追踪操练 1(1)如图，正方形 ABCD 中，点 E 是 DC 的中点，点 F 是 BC的一个三平分点，那么以向量 → → →AB 和向量 AD 为基底，向量 EF 可表示为__________ ．→→ →(2) 如图，在正方形 ABCD 中， E 为 DC 的中点，若 AE ＝ λAB ＋ μAC ，则 λ ＋ μ的值为 ________．答案(1)1→ － 2 →(2)12AB 3AD2分析→ → → (1)在 △ CEF 中，有 EF ＝ EC ＋CF .→ 1 →因为点 E 为 DC 的中点，因此 EC ＝ DC .2因为点 F 为 BC 的一个三平分点，因此→ 2 →CF ＝CB.3→ 1→ 2→ 1→ 2→ 1→2→因此 EF ＝ 2DC ＋3CB ＝2AB ＋3DA ＝ 2AB － 3AD.(2)→ → → 1 →1 → → 1 → →→ 1 → 因为 E 为 DC 的中点，因此 AC ＝ AB ＋ AD ＝ AB ＋AB ＋ AD ＝AB ＋ AE ，即 AE ＝－AB ＋2222→ AC ，1 1因此 λ＝－， μ＝1，因此 λ＋ μ＝ .22热门二平面向量的数目积1．数目积的定义： a ·b ＝ |a||b|cos θ.2．三个结论(1) 若 a ＝ (x ， y)，则 |a|＝ a ·a ＝ x 2＋ y 2.(2) 若 A(x 1，y 1)， B( x 2， y 2)，则→ 2 2 .|AB|＝ (x 2－ x 1 ) ＋ (y 2－ y 1 )(3)若 a＝ (x1，y1)， b＝ ( x2，y2 )，θ为 a 与 b 的夹角，则 cos θ＝a·b＝x1x2＋ y1y2|a||b|x12＋ y12x22＋ y22.例 2(1)如图，在矩形ABCD 中， AB＝2， BC＝ 2，点 E 为 BC 的中点，点 F在边→ →＝→ →CD 上，若 AB·AF2，则 AE ·BF的值是 ________．(2) 若 b＝cos π， cos5π，|a|＝ 2|b|，且 (3a＋b) ·b＝－ 2，则向量 a，b 的夹角1212为 ________．答案(1) 2 (2)5π6分析(1)以 A 为原点，成立如下图的坐标系，可得 A(0,0)，B(2， 0)， E(2， 1)， F(x,2)，→→∴ AB＝ ( 2，0) ，AF＝ (x,2)，→ →2x＝2，∴ AB·AF＝解得 x＝ 1，∴ F(1,2)．→→∴ AE＝ ( 2，1)，BF＝ (1－ 2， 2)，→ →∴ AE·BF＝ 2×(1－ 2)＋ 1×2＝ 2.22π25π 2 π 2 π(2) b＝ cos＋cos12＝cos＋ sin＝ 1，121212因此 |b|＝ 1，|a|＝ 2.由 (3a＋b) ·b＝－ 2，可得3a·b＋ b2＝－ 2，故 a·b＝－3，故 cos〈 a， b〉＝a·b＝－ 33＝－|a||b|2×1 2.5π又〈 a， b〉∈ [0，π]，因此〈 a， b〉＝6 .思想升华(1) 数目积的计算往常有三种方法：数目积的定义，坐标运算，数目积的几何意义；(2) 能够利用数目积求向量的模和夹角，向量要分解成题中模和夹角已知的向量进行计算．追踪操练 2 (1)已知点 A，B，C，D 在边长为 1 的方格点图的地点如下图，→ →则向量 AD在AB方向上的投影为 ________．(2) 如图，在△ ABC 中，AB＝ AC＝ 3，cos∠ BAC＝1→→→ →3，DC＝ 2BD，则 AD·BC的值为 ________．答案(1)－5(2)－ 2 5分析(1)不如以点 A 为坐标原点，成立如下图的平面直角坐标系，易得→→AD ＝ (－ 2,3)，AB→ →→ →－ 25 AD ·AB＝ (4,2) ，因此向量 AD 在 AB方向上的投影为→＝2 5＝－ 5.|AB |→→→→→→2→ →(2) AD·BC＝ (AC＋ CD ) ·BC＝ (AC＋CB) ·BC3→2→→→2→1→→→＝[AC＋3(AB －AC)] BC·＝ ( 3AB ＋3AC) ·(AC－ AB)2 →2 1 → → 1 →2＝－3|AB|＋3AB·AC＋3|AC|＝－6＋ 1＋3＝－ 2.热门三平面向量与三角函数平面向量作为解决问题的工具，拥有代数形式和几何形式的“两重型”，高考常在平面向量与三角函数的交汇处命题，经过向量运算作为题目条件．例 3已知函数 f(x)＝ 2cos2x＋ 23sin xcos x(x∈ R)．π(1)当 x∈[0，2)时，求函数 f( x)的单一递加区间；(2)设△ABC 的内角 A，B， C 的对边分别为 a， b，c，且 c＝3， f( C)＝ 2，若向量 m＝ (1， sin A)与向量 n＝ (2， sin B)共线，求 a， b 的值．解π (1)f(x)＝ 2cos 2x ＋ 3sin 2x ＝ cos 2x ＋ 3sin 2x ＋ 1＝2sin(2 x ＋ ) ＋1，6π π π 令－＋ 2k π≤2x ＋≤ ＋ 2k π， k ∈ Z ，26 2π π解得 k π－≤x ≤k π＋， k ∈ Z ，36π因为 x ∈ [0， 2) ，π因此 f( x)的单一递加区间为 [0，6] ．π(2) 由 f(C)＝ 2sin(2C ＋6)＋ 1＝ 2，π 1得 sin(2C ＋ 6)＝ 2，π π 13 π而 C ∈(0 ，π)，因此 2C ＋ 6∈( 6， 6 )， π 5 π因此 2C ＋＝6π，解得 C ＝ 3.6因为向量 m ＝ (1，sin A)与向量 n ＝(2 ，sin B)共线，因此sin A 1sin B＝ .2由正弦定理得 a ＝ 1，①b 2由余弦定理得π c 2＝ a 2＋ b 2－ 2abcos，3即 a 2＋ b 2－ ab ＝9.②联立①②，解得 a ＝ 3，b ＝ 2 3.思想升华在平面向量与三角函数的综合问题中，一方面用平面向量的语言表述三角函数中的问题，如利用向量平行、垂直的条件表述三角函数式之间的关系，利用向量模表述三角函数之间的关系等；另一方面能够利用三角函数的知识解决平面向量问题，在解决此类问题的过程中，只需依据题目的详细要求，在向量和三角函数之间成立起联系，就能够依据向量或者三角函数的知识解决问题．追踪操练 3已知 △ABC 是锐角三角形，向量m ＝ cos A ＋ π，3π， n ＝ cos B ， sin B ，且 m ⊥ n.sin A ＋3 ( )(1) 求 A －B 的值；3(2) 若 cos B ＝ 5，AC ＝8，求 BC 的长．解(1)因为 m ⊥ n ，π π因此 m ·n ＝ coscos B ＋sin A ＋ 3 sin BA ＋ 3 π＝ cos A ＋3－ B ＝0，π又 A ，B ∈ 0，2 ，因此ππ 5πA ＋－B ∈ －，，3 6 6 因此 π ππA ＋－B ＝，即 A － B ＝ .3 263π4(2) 因为 cos B ＝5， B ∈ 0，2 ，因此 sin B ＝ 5，因此 sin A ＝ sin π ππ ＝ sin Bcos ＋ cos Bsin 6B ＋664 3 3 1 4 3＋ 3＝ · ＋ ·＝，52 5 2104 3＋3由正弦定理，得BC ＝ sin A10 ×8＝ 4 3＋ 3.4sin B·AC ＝5→ 1 →1．如图，在 △ ABC 中， AD ＝ 3AB ， DE ∥ BC 交AC 于E ， BC边上的中线AM交DE于，设 → ＝， → ＝，用ABaACb N，表示向量ab→ →AN ，则 AN＝ ____________.押题依照平面向量基本定理是向量表示的基本依照，而向量表示 (用基底或坐标 )是向量应用的基础．1答案6(a ＋ b)分析因为 DE ∥ BC ，因此 DN ∥ BM ，则 △ AND ∽△ AMB ，因此 AM AN ＝ ADAB .→1 →→1 →因为 AD ＝ 3AB ，因此 AN ＝ 3AM . 因为 M 为 BC 的中点，→ 1 → → 1 因此 AM ＝ (AB ＋AC)＝(a ＋ b)，22→ 1 →1因此 AN ＝AM ＝ (a ＋ b)．362．如图，BC 、DE 是半径为 →→ → →1 的圆 O 的两条直径， BF ＝ 2FO ，则 FD ·FE＝ ________.押题依照数目积是平面向量最重要的观点，平面向量数目积的运算是高考的必考内容，和平面几何知识的联合是向量考察的常有形式．答案－89分析→→→1，∵BF ＝2FO ，圆 O 的半径为 1，∴ |FO |＝3→→→→→→→2→→→→→1 2 8 ∴ FD ·FE ＝ (FO ＋ OD) ·(FO ＋ OE)＝ FO ＋ FO ·(OE ＋ OD)＋ OD ·OE ＝ ( ) ＋ 0－ 1＝－ .39→ →120°sin 208 )°，则 △ABC3．在 △ABC 中，AB ＝(cos 32 °，cos 58 °)，BC ＝ (sin 60 sin ° 118 ，°sin 的面积为 ________．押题依照平面向量作为数学解题工具，经过向量的运算给出条件解决三角函数问题已成为近几年高考的热门．答案38分析→ 2 2°|AB|＝ cos 32 °＋ cos 58＝ cos 232°＋ sin 232°＝1，→33，BC ＝2 cos 28 ，°－ 2 sin 28°→323 23 因此 |BC|＝＋－2 sin 28 ＝2.2 cos 28 °°→ →33 °则 AB ·BC ＝ cos 32 °×2cos 28－°sin 32 ×° sin 2823＝2 (cos 32 cos ° 28 －°sin 32 sin ° 28 ) °＝333，2 cos(32 ＋°28°)＝ 2cos 60 ＝° 4→ →3 → →4 1AB ·BC ＝ . 故 cos 〈 AB ， BC 〉＝ →→ ＝ 3 2 |AB| ×|BC| 1×2→ → °， 180°]，因此〈 → →又〈 AB ， BC 〉∈ [0 AB ， BC 〉＝ 60°，→ →故 B ＝ 180°－〈 AB ， BC 〉＝ 180°－ 60°＝ 120°.故 △ ABC 的面积为1 →S ＝ 2×|AB|→×|BC|sin B1 3 ＝ ×1××sin221203 ＝° .84．如图，在半径为1 的扇形 AOB中，∠ AOB ＝60°，C为弧上的动点， AB 与OC交于点P ，→ →则 OP ·BP 的最小值是 _______________________________________ ．押题依照此题将向量与平面几何、最值问题等有机联合，表现了高考在知识交汇点命题的方向，此题解法灵巧，难度适中．答案－116分析→ → →→→→→→→→→2 ＝ 60 °，因为 OP ＝ OB ＋ BP ，因此 OP ·BP ＝ (OB ＋ BP) ·BP ＝OB ·BP ＋ BP .又因为∠ AOB OA ＝ OB ，因此∠ OBA ＝ 60°， OB ＝ → → →1 → →→1→→21.因此 OB ·BP ＝ |BP |cos 120＝°－|BP|，因此 OP ·BP ＝－ |BP|＋ |BP|22→1 2 11→1 → →1＝ (|BP|－ )－≥－，当且仅当 |BP|＝时， OP ·BP 获得最小值－.4 16 16416A 组专题通关1．在 △ ABC 中，已知 D 是 AB 边上一点，若→ →→ 1 →→AD ＝ 2DB， CD ＝ CA ＋ λCB ，则 λ＝ ________.3答案23分析在 △ABC 中，已知 D 是 AB 边上一点，→→ →1→→→→→→ 2 → → 2 → → 1 → 2 → ∵ AD ＝ 2DB ，CD ＝ CA ＋ λCB ，∴ CD ＝ CA ＋ AD ＝ CA ＋ AB ＝ CA ＋3 (CB － CA)＝ CA ＋ CB ，3333∴ λ＝ 2.32． △ ABC 是边长为 2 的等边三角形，已知向量→ →a ，b 知足 AB ＝ 2a ， AC ＝ 2a ＋ b ，则以下结论正确的选项是 ________．① |b|＝ 1; ② a ⊥ b ；→③ a ·b ＝ 1; ④ (4a ＋ b)⊥BC.答案 ④分析→ → →在 △ABC 中，由 BC ＝ AC － AB ＝ 2a ＋ b － 2a ＝ b ，得 |b|＝ 2.又 |a|＝ 1，因此 a ·b ＝ |a||b|cos 120 ＝°－ 1，→ 2因此 (4a ＋ b) ·BC ＝ (4a ＋ b) ·b ＝ 4a ·b ＋ |b|＝ 4×(－ 1)＋ 4＝ 0，→因此 (4a ＋ b)⊥ BC.→ → → → → →3．在等腰 △ ABC 中，∠ BAC ＝90°，AB ＝ AC ＝ 2，BC ＝ 2BD ，AC ＝ 3AE ，则 AD ·BE ＝ ________.答案－43分析由已知获得→ → 1→→→1 →1 →2 1 → → 1 → → 1 → 2，AD ·BE ＝(AB ＋ AC) ·(BA ＋ AC) ＝－2AB ＋ AB ·AC ＋2 AC ·BA ＋ AC2366→ → 1212△ ABC 是等腰直角三角形，∠ BAC ＝ 90 °， AB ＝ AC ＝2，因此 AD ·BE ＝－ 2×2 ＋ 0＋0＋ 6×24＝－ 3.4． (2016 ·津蓟县期中天 )已知向量 a ， b 知足 (a ＋ 2b) ·(a － b)＝－ 6，且 |a|＝ 1， |b|＝ 2，则 a与 b 的夹角为 ________．答案π 3分析设 a 与 b 的夹角为θ，∵ (a ＋ 2b) ·(a － b)＝－ 6，且 |a|＝ 1，|b|＝ 2，∴ 1＋a ·b － 8＝－ 6，∴ a ·b ＝ 1＝|a||b |cos θ，∴ cos θ＝ 1，2π又∵ θ∈ [0，π]，∴ θ＝3.5． (2016 安·徽江淮十校第二次联考 )已知平面向量 a 、b(a ≠0， a ≠b)知足 |a|＝ 3，且 b 与 b － a 的夹角为 30°，则 |b|的最大值为 ________．答案 6分析→ → → → →令OA ＝ a ， OB ＝ b ，则 b － a ＝ OB －OA ＝AB ，如图，∵ b 与 b － a 的夹角为 30°，∴∠ OBA ＝30°，→→→→，∴由正弦定理|OA| ＝ |OB|得， ∵ |a| ＝ |OA |＝ 3 sin ∠ OBA sin ∠ OAB |b|＝ | OB | ＝6·sin ∠ OAB ≤ 6.6．已知向量 a ＝ (2,1)，b ＝ (－ 1， 2)，若 a ， b 在向量 c 方向上的投影相等，且 (c － a) ·(c － b) ＝－ 5，则向量 c 的坐标为 ________．21 3答案 (2，2)分析设 c ＝ (x ， y)，依据题意有x 2＋ y 2－ x － 3y ＝－ 5，22x ＋ y ＝－ x ＋ 2y ，1，x ＝ 2解得3y ＝ 2.→→ → 7．设向量 OA ＝ (5＋ cos θ，4＋ sin θ)， OB ＝ (2,0) ，则 |AB|的取值范围是 ________．答案[4,6]分析→ → →＝ (－ 3－ cos θ，－ 4－ sin θ)，∵AB ＝OB －OA → 2 2 2 ∴ |AB| ＝ (－ 3－cos θ) ＋( －4－ sin θ)＝ 6cos θ＋ 8sin θ＋26＝ 10sin(θ＋ φ)＋ 26，此中 tan φ＝ 3，4→ 2 →∴ 16≤|AB | ≤ 36，∴ 4≤|AB| ≤ 6.8．设向量 a ＝ (a 1， a 2)， b ＝ (b 1， b 2)，定义一种向量积 a?b ＝ (a 1b 1， a 2b 2)，已知向量 m ＝(2 ， 1 π →2)，n ＝ (，0)，点 P(x ，y)在 y ＝ sin x 的图象上运动， Q 是函数 y ＝ f(x)图象上的点，且知足 OQ3→为坐标原点 )，则函数 y ＝ f( x)的值域是 ________．＝ m?OP ＋ n(此中 O1 1 答案 [－ 2， 2]分析令 Q(c ，d)，由新的运算可得→ →1 π π 1sin x)， OQ ＝ m?OP ＋ n ＝(2x ，sin x)＋ ( ， 0)＝ (2x ＋，233 2π， 11∴c ＝2x ＋ 3π1消去 x 得 d ＝sin( c － )，22 6d ＝ 2sin x ，1 1π1 1] ．∴ y ＝ f( x)＝ sin(x －)，易知 y ＝ f(x)的值域是 [－，2262 2π9．设向量 a ＝ ( 3sin x ， sin x)， b ＝(cos x ，sin x)， x ∈ [0， 2]．(1) 若 |a|＝ |b|，求 x 的值；(2) 设函数 f(x)＝ a ·b ，求 f(x)的最大值．解(1)由 |a|2＝ ( 3sin x)2＋ (sin x)2＝ 4sin 2x ，222＝ 1，|b| ＝(cos x) ＋ (sin x) 及 |a|＝ |b|，得 4sin 2x ＝ 1.π1π又 x ∈ [0， ]，进而 sin x ＝，因此 x ＝ .22 62(2) f(x)＝ a ·b ＝ 3sin x ·cos x ＋ sin x＝3 1 1π 1，2sin 2x － cos 2x ＋＝ sin(2x － )＋ 2262π π π1，当 x ＝ ∈ [0， ] 时， sin(2 x －)取最大值326因此 f( x)的最大值为32.10．已知向量 a ＝ (cos α， sin α)，b ＝ (cos x ， sin x)， c ＝ (sin x ＋ 2sin α， cos x ＋ 2cos α)，此中 0<α<x<π.π(1) 若 α＝4，求函数 f(x)＝ b ·c 的最小值及相应 x 的值；π (2) 若 a 与 b 的夹角为，且 a ⊥ c ，求 tan 2α的值．3解 (1)∵ b ＝ (cos x ， sin x)，πc ＝ (sin x ＋ 2sin α， cos x ＋ 2cos α)， α＝ 4，∴ f(x)＝ b ·c＝ cos xsin x ＋ 2cos xsin α＋sin xcos x ＋2sin xcos α＝ 2sin xcos x ＋ 2(sin x ＋ cos x)．π令 t ＝ sin x ＋cos x 4<x<π ，则 2sin xcos x ＝ t 2 －1，且－ 1<t< 2.则 y ＝ t 2＋ 2t － 1＝ t ＋2 2－3，－ 1<t< 2，2 2∴ t ＝－ 2时， y min ＝－3，此时 sin x ＋ cos x ＝－ 2， 2 2 2 即 2sin x ＋ π＝－ 2，42π π π 5π，∵ <x<π，∴ <x ＋ <424 4 π 7 11π∴ x ＋＝ π，∴ x ＝12 .46∴函数 f(x)的最小值为－ 3，相应 x 的值为 11π2 12.π(2) ∵ a 与 b 的夹角为，3π a ·b∴ cos＝＝ cos αcos x ＋ sin αsin x3 |a| ·|b|＝ cos(x － α)．π∵ 0< α<x<π，∴ 0<x － α<π，∴ x － α＝3.∵ a ⊥ c ，∴ cos α(sin x ＋ 2sin α)＋ sin α(cos x ＋ 2cos α)＝ 0，π∴ sin(x ＋ α)＋ 2sin 2α＝ 0，即 sin 2α＋3 ＋ 2sin 2α＝ 0.5 sin 2α＋ 3 3. ∴ 2cos 2α＝0，∴ tan 2α＝－52B 组能力提升11．已知非零单位向量a 与非零向量b 知足 |a ＋b|＝ |a － b|，则向量 b － a 在向量 a 上的投影为 ________．答案－1分析因为 |a ＋ b|＝ |a － b|，因此 (a ＋ b)2＝ (a － b)2，2解得 a ·b ＝ 0，因此向量 b － a 在向量 a 上的投影为 |b － a|cos 〈 a ， b － a 〉＝a ·(b －a)＝0－|a||a||a|＝－ |a|＝－ 1.→ → →AB AC12．已知点 P 为 △ ABC 所在平面内一点，且知足 AP ＝ λ( → ＋ →)(λ∈ R)，则直线 |AB|cos B |AC|cos CAP 必经过 △ ABC 的 ________心．答案垂→ → →AB AC分析 ∵BC ·( → ＋ → )|AB|cos B |AC|cos C→ →＝－ |BC|＋ |BC|＝ 0，→ → →AB AC∴ BC 与 λ( → ＋ →)垂直，|AB|cos B |AC|cos C→ →AP 经过 △ABC 的垂心．∴ AP ⊥ BC ，∴点 P 在 BC 的高线上，即直线13．若 a ＝ (2＋ λ，1)，b ＝ (3，λ)，若〈 a ，b 〉为钝角，则实数 λ的取值范围是 ______________．答案3 (－ ∞，－ 3)∪( －3，－ )2分析3 ∵ a ＝ (2＋ λ，1)，b ＝ (3，λ)，∴ a ·b ＝ 3(2＋ λ)＋ λ<0，得 λ<－ .若 a ，b 共线，则 λ(2＋ λ)2－ 3＝ 0，解得λ＝－ 3 或λ＝1.即当λ＝－ 3 时， a， b 方向相反，3又〈 a， b〉为钝角，则λ<－且λ≠－ 3.14．在直角坐标系xOy 中，已知点A(1,1)， B(2,3)， C(3,2) ，点 P(x， y)在△ABC 三边围成的地区 (含界限 )上．→→→→(1) 若 PA＋PB ＋ PC＝ 0，求 |OP|；→→→(2) 设 OP＝mAB＋ nAC(m， n∈ R)，用 x， y 表示 m－n，并求 m－n 的最大值．解 (1)方法一→ →→∵ PA＋ PB＋ PC＝ 0，→→→又 PA＋ PB＋ PC＝ (1－ x,1－ y)＋ (2－x,3－ y)＋ (3－ x,2－ y)＝(6 －3x,6－ 3y)，6－ 3x＝ 0，x＝2，∴解得6－ 3y＝ 0，y＝2，→→即 OP＝ (2,2)，故 |OP|＝ 2 2.方法二→→→∵PA＋ PB＋ PC＝ 0，→→→→→→则 (OA－ OP)＋(OB －OP) ＋(OC－OP) ＝0，→1→→→→2.∴ OP＝3(OA＋ OB＋ OC)＝(2,2)，∴ |OP|＝ 2→→→(2) ∵ OP＝mAB＋ nAC，x＝ m＋2n，∴ (x， y)＝ (m＋ 2n， 2m＋ n)，∴y＝ 2m＋ n，两式相减得， m－ n＝ y－ x.令 y－x＝ t，由图知，当直线y＝ x＋t 过点B(2,3) 时， t 获得最大值 1，故 m－ n 的最大值为1.。

人教版九年级数学上册期末综合复习专题提优训练(三)

九年级（人教版）数学上册期末综合复习专题提优训练（三）一．选择题1．下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．2．“翻开数学书，恰好翻到第16页”，这个事件是（）A．随机事件B．必然事件C．不可能事件D．确定事件3．一元二次方程x2＝3x的解为（）A．x＝0 B．x＝3 C．x＝0或x＝3 D．x＝0 且x＝3 4．男篮世界杯小组赛，每两队之间进行一场比赛，小组赛共进行了6场比赛，设该小组有x支球队，则可列方程为（）A．x（x﹣1）＝6 B．x（x+1）＝6 C．D．5．如图，在平面直角坐标系中，直线y＝mx+n与抛物线y＝ax2+bx+c交于A（﹣1，p），B（2，q）两点，则关于x的不等式mx+n＞ax2+bx+c的解集是（）A．x＜﹣1 B．x＞2 C．﹣1＜x＜2 D．x＜﹣1或x＞2 6．如图，已知⊙O是正方形ABCD的外接圆，点E是弧AD上任意一点，则∠BEC的度数为（）A．30°B．45°C．60°D．90°7．已知⊙O的直径CD＝10cm，AB是⊙O的弦，AB⊥CD，垂足为M，且AB＝8cm，则AC的长为（）A．2cm B．4cm C．2cm或4cm D．2cm或4cm8．二次函数y＝ax2+bx+c（a≠0）的图象如图，给出下列四个结论：①3a+2b+c＜0；②3a+c＜b2﹣4ac；③方程2ax2+2bx+2c﹣5＝0没有实数根；④m（am+b）+b＜a（m≠﹣1）．其中正确结论的个数是（）A．4个B．3个C．2个D．1个二．填空题9．将抛物线y＝4x2向左平移3个单位，再向上平移2个单位，所得到图象的函数表达式是．10．要为一幅长29cm，宽22cm的照片配一个相框，要求相框的四条边宽度相等，且相框所占面积为照片面积的四分之一，设相框边的宽度为x，则可列出关于x的一元二次方程．11．一个圆锥和一个圆柱的底面积相等，已知圆柱的体积是圆锥的9倍，圆锥的高是8.1cm，则这个圆柱的高是cm．12．如图是抛物线y＝ax2+bx+c的图象的一部分，请你根据图象写出方程ax2+bx+c＝0的两根是．13．如图，在圆心角为90°的扇形OAB中，半径OA＝2cm，C为的中点，D、E分别是OA、OB的中点，则图中阴影部分的面积为cm2．14．以原点为中心，把点M（3，4）逆时针旋转90°得到点N，则点N的坐标为．15．已知边长为1的正方形ABCD的顶点A、B在一个半径为1的圆上，使AB边与弦MN重合，如图所示，将正方形在圆中逆时针滚动，在滚动过程中，点M、D之间距离的最小值是．三．解答题16．解下列方程．（1）x2+2x﹣35＝0；（2）4x（2x﹣1）＝1﹣2x．17．已知x1，x2是一元二次方程x2﹣2x+k+2＝0的两个实数根．（1）求k的取值范围．（2）是否存在实数k，使得等式+＝k﹣2成立？如果存在，请求出k的值；如果不存在，请说明理由．18．如图，正方形ABCD和直角△ABE，∠AEB＝90°，将△ABE绕点O旋转180°得到△CDF．（1）在图中画出点O和△CDF，并简要说明作图过程；（2）若AE＝12，AB＝13，求EF的长．19．一只不透明袋子中装有1个白球和若干个红球，这些球除颜色外都相同，某课外学习小组做摸球试验：将球搅匀后从中任意摸出1个球，记下颜色后放回、搅匀，不断重复这个过程，获得数据如下：摸球的次数200 300 400 1000 1600 2000 摸到白球的频数72 93 130 334 532 667 摸到白球的频率0.3600 0.3100 0.3250 0.3340 0.3325 0.3335 （1）该学习小组发现，摸到白球的频率在一个常数附近摆动，这个常数是．（精确到0.01），由此估出红球有个．（2）现从该袋中摸出2个球，请用树状图或列表的方法列出所有等可能的结果，并求恰好摸到1个白球，1个红球的概率．20．在平面直角坐标系中，抛物线y＝x2+bx+c与x轴交于A、B两点（A在B的左侧），与y轴的正半轴交于点C．已知OB＝OC，点B的坐标为（3，0），抛物线的顶点为M．（1）求该抛物线的表达式；（2）直接写出点A、M的坐标，并在下图中画出该抛物线的大致图象；A；M．（3）根据图象直接回答：不等式x2+bx+c＞3的解集为．21．如图①，一个横截面为抛物线形的隧道，其底部的宽AB为8m，拱高为4m，该隧道为双向车道，且两车道之间有0.4m的隔离带，一辆宽为2m的货车要安全通过这条隧道，需保持其顶部与隧道间有不少于0.5m的空隙，按如图②所建立平面直角坐标系．（1）求该抛物线对应的函数关系式；（2）通过计算说明该货车能安全通过的最大高度．22．如图，已知在Rt△ABC中，∠B＝30°，∠ACB＝90°，延长CA到O，使AO＝AC，以O为圆心，OA长为半径作⊙O交BA延长线于点D，连接CD．（1）求证：CD是⊙O的切线；（2）若AB＝4，求图中阴影部分的面积．23．在美化校园的活动中，某兴趣小组想借助如图所示的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园ABCD（篱笆只围AB，BC两边），设AB＝xm，花园的面积为Sm2．（1）若花园的面积为192m2，求x的值；（2）写出花园面积S与x的函数关系式．x为何值时，花园面积S有最大值？最大值为多少？（3）若在P处有一棵树与墙CD，AD的距离分别是a（14≤a≤22）和6m，要将这棵树围在花园内（含边界，不考虑树的粗细），设花园面积S的最大值为y，直接写出y 与a的关系式．24．已知：直线与y轴交于A，与x轴交于D，抛物线y＝x2+bx+c与直线交于A、E两点，与x轴交于B、C两点，且B点坐标为（1，0）．（1）求抛物线的解析式；（2）点P是直线AE上一动点，当△PBC周长最小时，求点P坐标；（3）动点Q在x轴上移动，当△QAE是直角三角形时，求点Q的坐标；（4）在y轴上是否存在一点M，使得点M到C点的距离与到直线AD的距离恰好相等？若存在，求出所有符合条件的点M的坐标；若不存在，请说明理由．参考答案一．选择题1．解：A、是轴对称图形，又是中心对称图形，故此选项正确；B、不是轴对称图形，不是中心对称图形，故此选项错误；C、是轴对称图形，不是中心对称图形，故此选项错误；D、不是轴对称图形，是中心对称图形，故此选项错误；故选：A．2．解：“翻开数学书，恰好翻到第16页”确实有可能刚好翻到第16页，也有可能不是翻到第16页，故这个事件是随机事件．故选：A．3．解：方程移项得：x2﹣3x＝0，分解因式得：x（x﹣3）＝0，解得：x＝0或x＝3，故选：C．4．解：设该小组有x支球队，则共有x（x﹣1）场比赛，由题意得：x（x﹣1）＝6，故选：C．5．解：观察函数图象可知：当x＜﹣1或x＞2时，直线y＝mx+n在抛物线y＝ax2+bx+c 的上方，∴不等式mx+n＞ax2+bx+c的解集为x＜﹣1或x＞2．故选：D．6．解：连接OB，OC，∵⊙O是正方形ABCD的外接圆，∴∠BOC＝90°，∴∠BEC＝∠BOC＝45°．故选：B．7．解：连接AC，AO，∵⊙O的直径CD＝10cm，AB⊥CD，AB＝8cm，∴AM＝AB＝×8＝4（cm），OD＝OC＝5cm，当C点位置如图1所示时，∵OA＝5cm，AM＝4cm，CD⊥AB，∴OM＝＝＝3（cm），∴CM＝OC+OM＝5+3＝8（cm），∴AC＝＝＝4（cm）；当C点位置如图2所示时，同理可得OM＝3cm，∵OC＝5cm，∴MC＝5﹣3＝2（cm），在Rt△AMC中，AC＝＝＝2（cm）．故选：C．8．解：由图象可知，当x＝1时，y＜0，即a+b+c＜0，∵对称轴x＝﹣＝﹣1，a＜0，∴b＝2a＜0，∴a+2a+c＜0，即3a+c＜0，∴3a+b+c＜0，故①正确；∵抛物线与x轴有两个交点，∴b2﹣4ac＞0，∴3a+c＜0＜b2﹣4ac，故②正确；∵2ax2+2bx+2c﹣5＝0，∴ax2+bx+c＝，结合图象可知，不能确定抛物线y＝ax2+bx+c与直线y＝的交点情况，故③不正确；∵当x＝m（m≠﹣1）时，y＝am2+bm+c，且当x＝﹣1时，函数y取得最大值，∴a﹣b+c＞am2+bm+c，∴m（am+b）+b＜a，故④正确；综上，正确结论有①②④共3个，故选：B．二．填空题（共7小题）9．解：由“左加右减”的原则可知，将抛物线y＝4x2向左平移3个单位所得直线的解析式为：y＝4（x+3）2；由“上加下减”的原则可知，将抛物线y＝4（x+3）2向上平移2个单位所得抛物线的解析式为：y＝4（x+3）2+2．故平移后的抛物线的函数关系式是：y＝4（x+3）2+2．故答案为y＝4（x+3）2+2．10．解：设相框边的宽度为xcm，则可列方程为：（29+2x）（22+2x）＝×29×22．故答案为：（29+2x）（22+2x）＝×29×22．11．解：设这个圆柱的高是xcm，圆锥和圆柱的底面积都为S，根据题意得S•x＝9××S×8.1，解得x＝24.3（cm），即这个圆柱的高是24.3cm．故答案为24.3．12．解：∵由图可知，抛物线与x轴的一个交点坐标为（﹣3，0），对称轴为直线x＝﹣1，∴设抛物线与x轴的另一交点为（x，0），则＝﹣1，解得x＝1，∴方程ax2+bx+c＝0的两根是x1＝﹣3，x2＝1．故答案为：x1＝﹣3，x2＝1．13．解：连结OC，过C点作CF⊥OA于F，∵半径OA＝2cm，C为的中点，D、E分别是OA、OB的中点，∴OD＝OE＝1cm，OC＝2cm，∠AOC＝45°，∴CF＝，∴空白图形ACD的面积＝扇形OAC的面积﹣三角形OCD的面积＝﹣×＝π﹣（cm2）三角形ODE的面积＝OD×OE＝（cm2），∴图中阴影部分的面积＝扇形OAB的面积﹣空白图形ACD的面积﹣三角形ODE的面积＝﹣（π﹣）﹣＝π+﹣（cm2）．故图中阴影部分的面积为（π+﹣）cm2．故答案为：（π+﹣）．14．解：如图，∵点M（3，4）逆时针旋转90°得到点N，则点N的坐标为（﹣4，3）．故答案为：（﹣4，3）．15．解：如图，点D的运动轨迹是图中的红线．观察图象可知M、D之间的最小距离是线段AD′的长＝AE﹣D′E＝2﹣，故答案为2﹣．三．解答题（共9小题）16．解：（1）x2+2x﹣35＝0，（x+7）（x﹣5）＝0，x+7＝0或x﹣5＝0，∴x1＝﹣7，x2＝5．（2）4x（2x﹣1）＝1﹣2x，4x（2x﹣1）+（2x﹣1）＝0，（2x﹣1）（4x+1）＝0，（2x﹣1）＝0或（4x+1）＝0，，17．解：（1）∵一元二次方程x2﹣2x+k+2＝0有两个实数根，∴△＝（﹣2）2﹣4×1×（k+2）≥0，解得：k≤﹣1．（2）∵x1，x2是一元二次方程x2﹣2x+k+2＝0的两个实数根，∴x1+x2＝2，x1x2＝k+2．∵+＝k﹣2，∴＝＝k﹣2，∴k2﹣6＝0，解得：k1＝﹣，k2＝．又∵k≤﹣1，∴k＝﹣．∴存在这样的k值，使得等式+＝k﹣2成立，k值为﹣．18．解：（1）如图所示：连接AC，BD，交于点O．连接EO并延长到点F，使OF＝OE，连接DF，CF，（2）如图所示：过点O作OG⊥OE与EB的延长线交于点G，∵四边形ABCD为正方形∴OA＝OB，∠AOB＝∠EOG＝90°∴∠AOE＝∠BOG在四边形AEBO中∠AEB＝∠AOB＝90°∴∠EAO+∠EBO＝180°＝∠EBO+∠GBO∴∠GBO＝∠EAO，∴在△EAO和△GBO中，∵∴△EAO≌△GBO（ASA），∴AE＝BG，OE＝OG．∴△GOE为等腰直角三角形，∴OE＝EG＝（EB+BG）＝（EB+AE）∵AE＝12，AB＝13，∴BE＝5，∴EB+AE＝17，∴OE＝∴EF＝．19．解：（1）观察表格发现，随着摸球次数的增多，摸到白球的频率逐渐稳定在0.33附近，由此估出红球有2个．故答案为：0.33，2；（2）列表如下：白红红白﹣﹣﹣（红，白）（红，白）红（白，红）﹣﹣﹣（红，红）红（白，红）（红，红）﹣﹣﹣所有等可能的情况有6种，其中恰好摸到1个白球，1个红球的情况有4种，则P（1个白球，1个红球）＝＝；所以从该袋中摸出2个球，恰好摸到1个白球、1个红球的结果的概率为．20．解：（1）∵OB＝OC，点B的坐标为（3，0），点C在y轴的正半轴上∴点C的坐标为（0，3），∵抛物线y＝x2+bx+c过B、C两点，∴，解得，∴抛物线的表达式为y＝x2﹣4x+3；（2）y＝x2﹣4x+3，＝（x﹣2）2﹣1，故顶点坐标为：M（2，﹣1），当y＝0，则0＝x2﹣4x+3，解得：x1＝1，x2＝3，故A（1，0）；如图所示：故答案为：（1，0），（2，﹣1）；（3）根据图象即可得出当x＜0或x＞4，y＝x2﹣4x+3＞3，即不等式x2+bx+c＞3的解集为：x＜0或x＞4．故答案为：x＜0或x＞4．21．解：（1）如图②中，A（4，0），C（0，4），设抛物线解析式为y＝ax2+k，由题意，得，解得：，∴抛物线表达式为．（2）2+＝2.2，当x＝2.2时，y＝﹣×2.22+4＝2.79，当y＝2.79时，2.79﹣0.5＝2.29 （m）．答：该货车能够通行的最大高度为2.29 m．22．（1）证明：连接OD，∵∠BCA＝90°，∠B＝30°，∴∠OAD＝∠BAC＝60°，∵OD＝OA，∴△OAD是等边三角形，∴AD＝OA＝AC，∠ODA＝∠O＝60°，∴∠ADC＝∠ACD＝∠OAD＝30°，∴∠ODC＝60°+30°＝90°，即OD⊥DC，∵OD为半径，∴CD是⊙O的切线；（2）解：∵AB＝4，∠ACB＝90°，∠B＝30°，∴OD＝OA＝AC＝AB＝2，由勾股定理得：CD＝＝＝2，∴S阴影＝S△ODC﹣S扇形AOD＝×2×2﹣＝2﹣π．23．解：（1）依题意得S＝x（28﹣x），当S＝192时，有S＝x（28﹣x）＝192，即x2﹣28x+192＝0，解得：x1＝12，x2＝16，答：花园的面积为192m2，x的值为12m或16m；（2）由题意可得出：S＝x（28﹣x）＝﹣x2+28x＝﹣（x﹣14）2+196，答：x为14m时，花园面积S有最大值，最大值为196m2；（3）依题意得：，解得：6≤x≤28﹣a，S＝x（28﹣x）＝﹣x2+28x＝﹣（x﹣14）2+196，∵a＝﹣1＜0，当x≤14，y随x的增大而增大，又6≤x≤28﹣a，∴当x＝28﹣a时，函数有最大值，是y＝﹣（28﹣a﹣14）2+196＝﹣（14﹣a）2+196．24．解：（1）∵直线与y轴交于A，∴A点的坐标为（0，2），∵B点坐标为（1，0）．∴∴；（2）作出C关于直线AE的对称点F，由B和F确定出直线BF，与直线AE交于P点，设F（m，n），由题意D（﹣4，0），C（4，0），A（0，2），AF＝AC＝2，DF＝DC＝8，∴，解得或，∴F（，），∴直线BF的解析式为：y＝﹣32x+32，，可得：P（）；（3）根据题意得：x+2＝x2﹣x+2，解得：x＝0或x＝6，∴A（0，2），E（6，5），∴AE＝3，设Q（x，0），①若Q为直角顶点，则AQ2+EQ2＝AE2，即x2+4+（x﹣6）2+25＝45，此时x无解；②若点A为直角顶点，则AQ2+AE2＝EQ2，即x2+4+45＝（x﹣6）2+25，解得：x＝1，即Q（1，0）；③若E为直角顶点，则AQ2＝AE2+EQ2，即x2+4＝45+（x﹣6）2+25，解得：x＝＝，此时求得Q（，0）；∴Q（1，0）或（，0）（4）假设存在，设M坐标为（0，m），则OM＝|m|，∵OC＝4，AO＝2，OD＝4，∴MC＝MD，∴当MD⊥AD时，满足条件，∴在直角三角形AOD中，根据勾股定理得：AD＝2，且AM＝2﹣m，CM＝，∵MD＝MC，∴根据勾股定理得：＝，即（2﹣m）2﹣（2）2＝m2+16，解得m＝﹣8，则M（0，﹣8）．。

中考历史总复习专题训练三中国近(现)代化的探索历程-人教版初中九年级全册历史试题

中国近(现)代化的探索历程一、选择题1．中国近代史既是一部屈辱史，又是一部抗争史，先进的中国人为了寻求救国救民的真理，不断向西方学习，开始了中国的近代化。

为中国近代化开辟了道路的历史事件是( ) A．洋务运动 B．辛亥革命C．戊戌变法 D．新文化运动2．陈旭麓认为：“民族的反思，是在遭遇极大的困难中产生的。

一百多年来，中华民族的第一次反思是在鸦片战争后……第二次则是反思何以学了西方仍然失败。

”其中“第二次反思”对近代化的推进主要是( )A．器物技术 B．政治制度C．思想文化 D．生活习俗3．杨天石指出：“这次革命的目标是：民族独立、人民民主和普遍富裕。

这次革命的成果是：皇冠落地，中国历史从帝制走向共和。

”据此判断，这次革命的旗帜是( )A．自强求富 B．维新变法C．三民主义 D．民主科学4．它首次在中国大地宣告国家主权属于人民……国会政治、政党政治、舆论监督政府等民权政治，变人治为法治的尝试由此正式开端。

替代文中“它”最恰当的是( )A．同盟会 B．北洋军阀政府C．中华民国 D．南京国民政府5．严复在《论教育与国家之关系》中说：“此事乃吾国数千年中莫大之举动，言其重要，直无异古者之废封建，开阡陌。

” “此事”指( )A．废除分封制 B．废除井田制C．废除八股文 D．废除科举制6．某同学在学习中国近代史后，绘制了下面表格，此表格的主题是( )“明定国是”诏1898年光绪帝书1915年陈独秀《青年杂志》A.军事工业兴起 B．政治体制变革C．民主思想传播 D．近代化的探索7．1840年后，随着中国闭关自守大门的打破和西方资本主义势力的闯入，近代文明也传入中国，下列属于近代文明的有( )①轮船、火车②电报、电话③照相、电影④三跪九叩礼A．①②③ B．②③④C．①③④ D．①②④8．近代以来，随着先进中国人对近代化的诉求，教育、文化、生活也发生着变化。

关于以下三幅图说法不正确的是( )A．图(a)报纸创办于近代中国的北京B．图(b)是规模最大的文化出版机构C．图(c)是近代第一所国立高等学府D．三图反映内容都推动了教育近代化9．新中国成立初期，毛泽东指出：“现在我们能造什么？能造桌子椅子，能造茶碗茶壶，能种粮食，还能磨成面粉，还能造纸，但是，一辆汽车、一架飞机、一辆坦克、一辆拖拉机都不能造。

中考语文总复习专题突破训练专题三词语的理解与运用部编人教版九年级上册

中考语文总复习专题突破训练专题三词语的理解与运用部编人教版九年级上册专题三词语的理解与运用知能优化训练中考回顾1.(2017天津)依次填入下面一段文字横线处的词语,最恰当的一项是( )所谓书卷气,是一种饱读诗书后形成的气质。

书卷气来自读书,在幽幽书香的熏陶之下,浊俗可以变为清雅,奢华可以变为,狭隘可以变为开阔,偏激可以变为。

捧起书来吧,你会发现里面的风景美不胜收!.A.高雅淡然平静B.高贵淡泊平静C.高贵淡然平和D.高雅淡泊平和2.(2017四川眉山)下列各句中,加点词语使用恰当的一项是( )A.学生成绩优秀,应该归咎于他良好的学习习惯和持之以恒的精神。

B.我的令尊大人已经七十多岁了,他每天坚持去跳广场舞,身体棒棒的。

C.货运飞船,顾名思义就是以货物运载为主的飞船,一次能装载6吨多物资。

D.九年级开展了“爱我东坡”活动,同学们那些可歌可泣的事迹感动了老师。

3.(2017江西)下列句子加点词语使用不正确的一项是( )A.重要的书必须反复阅读,每读一次都会觉得开卷有益。

B.在人迹罕至的北极,奇异的天象令人心旌摇荡,难以忘怀。

C.鼓角齐鸣,喊声大震,黄忠首当其冲,驰下山来,犹如天崩地裂之势。

D.他忠人之事,急人之难,爱听些受恩者的恭维,虽不见得乐此不疲,却也习以为常。

4.(2016天津)依次填入下面一段文字横线处的词语,最恰当的一项是( )家风,是一个家庭或家族长期以来形成并的道德操守和处世方法。

家风中蕴藏着先人所的价值理念和道德规范,也包含着简单朴素的为人。

千百年来,家风在一个个家庭里承载、延续,奠定了整个民族文明的基础。

.A.传播恪守规则B.传承保守规则C.传承恪守准则D.传播保守准则5.(2016内蒙古呼和浩特)下列各句中加点词语使用正确的一项是( )A.斑羚们发现自己被狩猎队逼到了悬崖边上,焦急之时,老斑羚发现侧面有一条小路能通到悬崖对面,真是到了进退维谷的地步。

B.村里出现了一个大洞,有人说,咱们把它填起来;有人说,在上面盖一座庙;有人说,卖给填洞公司。

2021届小升初数学知识专项训练总复习(三)【含答案】

A. 3.5 B. 4.5 C. 2.5 D. 1.5
15．一根长30cm、宽3cm的长方形纸条，将其按照图示的过程折叠，为了美观，希望折叠完成后纸条两端超出点P的长度相等，则最初折叠时，MA的长应为（）。
A. 7.5cm B. 9cm C. 12cm D. 10. 5cm
二、填空题
16．把5克盐放人50克水中，盐和盐水的比是（）。
9．庆祝“六一”，某幼儿园举行用火柴棒摆“金鱼”的比赛，其中摆的1条、2条、3条“金鱼”如下图所示：
按照上面的规律，摆100条“金鱼”需用火柴棒的根数为（）。
A. 800 B. 608 C. 704 D. 602
10．李明过春节时获得相同张数5元和1元压岁钱若干张，那么李明可能有（）。
A. 48 元 B. 38 元 C. 28 元 D. 8 元
11．甲、乙两个瓶子装的酒精溶液体积的比是2：5，甲瓶中酒精与水的体积比是3：1，乙瓶中酒精与水的体积比是4：1。现在把两瓶溶液倒入一个大瓶中混合，这时酒精与水的体积比是（）。
A. 3 : 1 B. 11：3 C. 10：5 D. 5：10
12．a×b=c×d改写成比例式是（）。
A. a：b=c：d B. a：c=b：d C. a：c=d：b
=0.59375， =0.4375，1 = =1.866666……，和的分子除以分母能除尽，则和能化成有限小数，而1 = 的分子除以分母除不尽，则 1 不能化成有限小数。
4．【答案】D
【解析】本题主要根据等底等高的圆柱和圆锥体积之间的关系计算一个数比另一个数多几分之几。
首先根据等底等高的圆柱的体积等于圆锥体积的3倍，然后计算圆柱比与它等底等高的圆锥的体积多几分之几，即（3-1）÷1=2。

人教版数学中考复习训练专题三函数图象与性质综合题附答案

专题三函数图象与性质综合题类型一交点问题典例精析例在平面直角坐标系xOy 中，已知点A (－1，2)，点B (3，2)，点C (－2，－3)是平面内3个点．(1)连接AB ，若直线y ＝34x ＋b 与线段AB 有交点，求b 的取值范围；(2)连接BC ，若直线y ＝34x ＋b 与线段BC 在第三象限内有交点，求b 的取值范围；(3)若直线y ＝kx ＋3与直线BC 无交点，求k 的值；(4)若直线AB 、直线y ＝kx ＋3与直线BC 能够围成三角形，求k 的取值范围；(5)若双曲线y ＝k x 过点A 且与直线y ＝34x ＋b 在(－5≤x ≤－1)有交点，求b 的取值范围；(6)连接AB ，若抛物线y ＝x 2＋c 与线段AB 有公共点，求c 的取值范围；(7)若抛物线y ＝x 2＋c (－2≤x ≤2)与直线BC 有一个交点，求c 的取值范围；(8)连接AB ，若抛物线y ＝(x －k )2与线段AB 有公共点，求k 的取值范围；(9)若双曲线y ＝k x过点B 且与抛物线y ＝x 2 ＋c 在2≤x ≤6有交点，求c 的取值范围．1. (2020河北24题10分)表格中的两组对应值满足一次函数y ＝kx ＋b ，现画出了它的图象为直线l ，如图．而某同学为观察k ，b 对图象的影响，将上面函数中的k 与b 交换位置后得另一个一次函数，设其图象为直线l ′.(1)求直线l 的解析式；(2)请在图上画出．．直线l ′(不要求列表计算)，并求直线l ′被直线l 和y 轴所截线段的长； (3)设直线y ＝a 与直线l ，l ′及y 轴有三个不同的交点，且其中两点关于第三点对称，直接．．写出a 的值．第1题图2. (2016河北26题12分)如图，抛物线L ：y ＝－12(x －t )(x －t ＋4)(常数t ＞0)与x 轴从左到右的交点为B ，A ，过线段OA 的中点M 作MP ⊥x 轴，交双曲线y ＝k x(k ＞0，x ＞0)于点P ，且OA ·MP ＝12. (1)求k 值；(2)当t ＝1时，求AB 长，并求直线MP 与L 对称轴之间的距离；(3)把L 在直线MP 左侧部分的图象(含与直线MP 的交点)记为G ，用t 表示图象G 最高点的坐标；(4)设L 与双曲线有个交点的横坐标为x 0，且满足4≤x 0≤6，通过L 位置随t 变化的过程，直接．．写出t的取值范围．第2题图针对演练3. (2020承德二模)如图，在平面直角坐标系中，点A，B，C三点的坐标分别为(2，0)，(1，2)，(4，3)，直线l的解析式为y＝kx＋4－3k(k≠0)．(1)当k＝1时，直线l与x轴交于点D，则点D的坐标为________，S△ABD＝________；(2)小明认为点C也在直线l上，他的判断是否正确，请说明理由；(3)若线段AB与直线l有交点，求k的取值范围．第3题图4. 如图，在平面直角坐标系中，边长为2的正方形ABCD 位于第二象限，且AB ∥x 轴，点B 在点C的正下方，双曲线y ＝1－2m x(x <0)经过点C. (1)求m 的取值范围；(2)若点B (－1，1)，判断双曲线是否经过点A ；(3)设点B (a ，2a ＋1)．①若双曲线经过点A ，求a 的值；②若直线y ＝2x ＋2交AB 于点E ，双曲线与线段AE 有交点，求a 的取值范围．第4题图5.(2020石家庄模拟)如图，已知点A(0，2)，B(2，2)，C(－1，－2)，抛物线F：y＝x2－2mx＋m2－2与直线x＝－2交于点P.(1)当抛物线F经过点C时，求它的表达式；(2)设点P的纵坐标为y p，求y p的最小值，此时抛物线F上有两点(x1，y1)，(x2，y2)，且x1＜x2≤－2，比较y1与y2的大小；(3)当抛物线F与线段AB有公共点时，直接写出m的取值范围．第5题图6. 如图，已知抛物线y ＝ax 2－2x ＋3a (a ＞0)与x 轴相交于不同的两点A (x 1，0)，B (x 2，0)，且x 1＜x 2.点P 为双曲线y ＝k x(1≤x ≤4)上的任意一点，过点P 作x 轴的垂线，交x 轴于点C ，交抛物线y ＝ax 2－2x ＋3a (a ＞0)于点Q .(1)若△POC 的面积为6，求k 值；(2)若k ＝3.①当a ＝12时，求点A 、B 的坐标，并求当点P 到抛物线对称轴的距离最大时，PQ 的值； ②若抛物线与双曲线有一个交点，直接写出a 的取值范围．第6题图7. (2020唐山开平区一模)已知，如图，二次函数L ∶y ＝mx 2＋2mx ＋k (其中m ，k 是常数，k 为正整数)，(1)若L 经过点(1，k ＋6)，求m 的值；(2)当m ＝2，若L 与x 轴有公共点时且公共点的横坐标为非零的整数，确定k 的值；(3)在(2)的条件下，将L ∶y ＝mx 2＋2mx ＋k 的图象向下平移8个单位，得到函数图象M ，求M 的解析式；(4)在(3)的条件下，将M 的图象在x 轴下方的部分沿x 轴翻折，图象的其余部分保持不变，得到一个新的图象N ，请结合新的图象解答问题，若直线y ＝12x ＋b 与N 有两个公共点时，请直接写出b 的取值范围．第7题图8.如图①，二次函数y＝ax2－3ax＋c的图象与x轴交于点A、B，与y轴交于点C，直线y＝－x＋4经过点B、C.(1)求抛物线的表达式；(2)过点A的直线y＝kx＋k交抛物线于点M，交直线BC于点N，连接AC，当直线y＝kx＋k平分△ABC 的面积时，求点M的坐标；(3)如图②，把抛物线位于x轴上方的图象沿x轴翻折，当直线y＝kx＋k与翻折后的整个图象只有三个交点时，求k的取值范围．第8题图类型二整点问题例我们把横，纵坐标都是整数的点叫作整点．在平面直角坐标系中，点A(5，0)，B(0，5)，C(－1，0)．(1)若直线l过点A，B，求直线l与坐标轴围成的区域W1内(含边界)整点的个数；(2)连接AB，BC，AC，求△ABC所围成的区域W2内(不含边界)整点的个数；(3)若直线y＝a、线段AB与y轴所围成的三角形区域W3内(含边界)恰有6个整点，求a的取值范围；(4)若直线y＝x＋b与直线AB及y轴所围成的三角形区域W4内(不含边界)恰有4个整点，求b的取值范围；(5)若直线y＝kx＋2与直线BC及x轴所围成的区域W5内(不含边界)恰有4个整点，求k的取值范围；(6)若双曲线y ＝4x (x >0)与线段AB 交于D ，E 两点(点D 在点E 的上方)，求曲线DE 与线段DE 所围成的区域W 6内(含边界)整点的个数；(7)在(6)的条件下，若直线y ＝x ＋b 与双曲线y ＝4x 交于点F ，与y 轴交于点G ，连接DG ，若线段DG ，FG ，曲线DF 所围成的区域W 7内(含边界)恰有5个整点，求b 的取值范围；(8)若抛物线y ＝x 2－2x ＋m －2与过点B 的直线y ＝5所围成的区域W 8内(不含边界)有4个整点，求m 的取值范围；(9)若抛物线y ＝x 2－2x ＋m －2与直线y ＝－x ＋2交于M ，N 两点(点M 在点N 的左侧)，将曲线MN 与线段MN 所围成的区域记为W 9，若W 9内(不含边界)恰好有4个整点，求m 的取值范围．1.(2019河北26题12分)如图，若b是正数．．，直线l：y＝b与y轴交于点A；直线a：y＝x－b与y轴交于点B；抛物线L：y＝－x2＋bx的顶点为C，且L与x轴正半轴的交点为D.(1)若AB＝8，求b的值，并求此时L的对称轴与a的交点坐标；(2)当点C在l下方时，求点C与l距离的最大值；(3)设x0≠0，点(x0，y1)，(x0，y2)，(x0，y3)分别在l，a和L上，且y3是y1，y2的平均数，求点(x0，0)与点D间的距离；(4)在L和a所围成的封闭图形的边界上．．写出b．．．，把横、纵坐标都是整数的点称为“美点”，分别直接＝2019和b＝2019.5时“美点”的个数．第1题图针对演练2.在平面直角坐标系xOy中，直线x＝5与直线y＝3，x轴分别交于点A，B，直线y＝kx＋b(k≠0)经过点A且与x轴交于点C(9，0)．(1)求直线y＝kx＋b的表达式；(2)横、纵坐标都是整数的点叫做整点．记线段AB，BC，CA围成的区域(不含边界)为W.①结合函数图象，直接写出区域W内的整点个数；②将直线y＝kx＋b向下平移n个单位，当平移后的直线与区域W没有公共点时，请结合图象直接写出n的取值范围．第2题图3. 已知点A (4，1)，若直线y 1＝14x ＋b 与双曲线y 2＝4x(x >0)交于点B ，与y 轴交于点C.探究：由双曲线y 2＝4x (x >0)与线段OA ，OC ，BC 围成的区域M 内(不含边界)整点的个数(点的横、纵坐标都是整数的点称为整点)．(1)当b ＝－1时，如图，求区域M 内的整点的个数；(2)当b <0时，若区域M 内恰好有4个整点，求b 的取值范围．第3题图4. 如图，函数y 1＝－x 2＋12x ＋c (－2020≤x ≤1)的图象记为L 1，最大值为M 1；函数y 2＝－x 2＋2cx ＋1(1≤x≤2020) 的图象记为L 2，最大值为M 2.L 1的右端点为A ，L 2的左端点为B ，L 1，L 2合起来的图形记为L .(1)当c ＝1时，求M 1，M 2的值；(2)若把横、纵坐标都是整数的点称为“美点”，当点A ，B 重合时，求L 上“美点”的个数； (3)若M 1，M 2的差为4716，直接写出c 的值．第4题图5. 如图，在平面直角坐标系中，设抛物线y ＝－x 2＋bx ＋b －1为L 1，A (－5，－2)，B (5，－2)． (1)若L 1经过原点，求抛物线L 1的解析式，并求出此时抛物线的顶点坐标；(2)无论b 取何值，L 1总经过一个定点M ，随着b 的变化，抛物线L 1的顶点总在另一条抛物线上运动，且这条抛物线的顶点为M ，若设另一条抛物线为L 2.①求点M 的坐标； ②求出抛物线L 2的解析式；(3)若把抛物线L 1：y ＝－x 2＋bx ＋b －1经过线段AB 端点时与线段AB 所围成的封闭图形称为C ，图形C 边界上横、纵坐标都是整数的点为“理想点”，求图形C 上“理想点”的个数．第5题图专题三函数图象与性质综合题类型一交点问题例解：(1)∵直线y ＝34x ＋b 与线段AB 有交点，即直线y ＝34x ＋b 与线段AB 两端点交点为临界点，如解图①②，将A (－1，2)代入y ＝34x ＋b ，得b ＝114，将B (3，2)代入y ＝34x ＋b ，得b ＝－14，∴b 的取值范围为－14≤b ≤114；例题解图①例题解图②(2)设线段BC 的解析式为y ＝kx ＋m (k ≠0)，将B (3，2)，C (－2，－3)代入，得⎩⎪⎨⎪⎧3k ＋m ＝2－2k ＋m ＝－3，解得⎩⎪⎨⎪⎧k ＝1m ＝－1，∴线段BC 的解析式为y ＝x －1(－2≤x ≤3)， ∴线段BC 与y 轴的交点为(0，－1)．当y ＝34x ＋b 过点(0，－1)，如解图③，∴即b ＝－1，当y ＝34x ＋b 过点C (－2，－3)，如解图④，∴－3＝－32＋b ，∴b ＝－32，∴当直线y ＝34x ＋b 与线段BC 在第三象限内有交点，b 的取值范围为－32≤b <－1；例题解图③例题解图④(3)由(2)知，直线BC 的解析式为y ＝x －1，若y ＝kx ＋3与直线BC 无交点，∴直线y ＝kx ＋3与直线BC 平行，如解图⑤， ∴当k ＝1时，直线y ＝kx ＋3与直线BC 无交点；例题解图⑤(4)由(2)知直线BC 的解析式为y ＝x －1，由题可知直线AB 的解析式为y ＝2，若直线AB ，直线y ＝kx ＋3与直线BC 能够围成三角形，即直线y ＝kx ＋3与直线AB 、直线BC 都有交点， ∴k ≠1，k ≠0.∵直线AB 与直线BC 交于点B ，∴当直线y ＝kx ＋3过点B (3，2)时，直线AB 、直线y ＝kx ＋3与直线BC 交于一点，不能围成三角形．∴将B (3，2)代入y ＝kx ＋3，得3k ＋3＝2，∴k ＝－13.综上所述，k ≠－13，0，1；(5)∵双曲线y ＝kx 过点A (－1，2)，∴k ＝－2，∴双曲线的解析式为y ＝－2x .∵－5≤x ≤－1. ∴令x ＝－5，则y ＝25.当直线y ＝34x ＋b 与双曲线y ＝－2x 相切时，如解图⑥，∴34x ＋b ＝－2x ，整理得34x 2＋bx ＋2＝0， ∴b 2－6＝0，∴b ＝6或b ＝－6(舍去)．当直线y ＝34x ＋b 过点(－5，25)，如解图⑦，∴25＝－5×34＋b ， ∵b ＝8320.由解图可知，b 的取值范围为6≤b ≤8320；例题解图⑥例题解图⑦(6)由题可知A (－1，2)，B (3，2)，抛物线y ＝x 2＋c 的对称轴为直线x ＝0，∴当抛物线顶点在线段AB 上时，如解图⑧， ∴c ＝2.当抛物线过点B 时，如解图⑨， ∴2＝9＋c ，∴c ＝－7， ∴c 的取值范围为－7≤c ≤2；例题解图⑧例题解图⑨(7)联立⎩⎪⎨⎪⎧y ＝x －1y ＝x 2＋c ，整理得x 2－x ＋c ＋1＝0，如解图○10， ∴(－1)2－4(c ＋1)＝0， ∴c ＝－34.例题解图○10对于抛物线y＝x2＋c，当x＝2时，y＝4＋c，当点(2，4＋c)在直线BC上时，如解图⑪，此时抛物线与直线BC有两个交点，将(2，4＋c)代入直线BC解析式y＝x－1，得2－1＝4＋c，解得c＝－3；例题解图⑪当x＝－2时，y＝4＋c，当点(－2，4＋c)在直线BC上时，如解图⑫，此时抛物线与直线BC有一个交点，将(－2，4＋c)代入直线BC解析式y＝x－1，得－2－1＝4＋c，解得c＝－7；例题解图⑫综上所述，抛物线y＝x2＋c(－2≤x≤2)与直线BC有一个交点，c的取值范围为－7≤c＜－3，或c＝－34；(8)∵A(－1，2)，B(3，2)，抛物线y＝(x－k)2与线段AB有公共点，则当y＝(x－k)2过点A(－1，2)，如解图⑬，∴2＝(－1－k)2，∴k＝－1－2或k＝－1＋2(舍)．当y＝(x－k)2过点B(3，2)，如解图⑭，∴2＝(3－k)2，∴k＝3＋2或k＝3－2(舍)．∴k 的取值范围为－1－2≤k ≤3＋2；例题解图⑬ 例题解图⑭(9)∵双曲线y ＝kx 过点B (3，2)，∴2＝k 3，∴k ＝6，∴双曲线的解析式为y ＝6x .∵2≤x ≤6， ∴当x ＝2时，y ＝3，当x ＝6时，y ＝1，当抛物线过点(2，3)时，如解图⑮，将(2，3)代入y ＝x 2＋c ，即3＝4＋c ， ∴c ＝－1，同理当抛物线过点(6，1)时，将(6，1)代入y ＝x 2＋c ，即1＝36＋c ，∴c ＝－35， ∴c 的取值范围为－35≤c ≤－1.例题解图⑮1. 解：(1)∵(－1，－2)，(0，1)在函数y ＝kx ＋b 的图象上，∴⎩⎪⎨⎪⎧－2＝－k ＋b 1＝b ，解得⎩⎪⎨⎪⎧k ＝3b ＝1.∴直线l 的解析式为y ＝3x ＋1；(3分) (2)依题意，直线l ′的解析式为y ＝x ＋3， ∴直线l ′的图象如解图，第1题解图联立方程组⎩⎪⎨⎪⎧y ＝3x ＋1，y ＝x ＋3，解得⎩⎪⎨⎪⎧x ＝1，y ＝4，(5分)∴直线l 与直线l ′的交点坐标为(1，4)．又∵直线l ′与y 轴的交点坐标为(0，3)，∴直线l ′被直线l 和y 轴所截得的线段长为（1－0）2＋（4－3）2＝2；(7分) (3)a 的值为52或175或7.(10分)2. 解：(1)设点P (x ，y )，则MP ＝y ，由OA 的中点为M ，知OA ＝2x ，代入OA ·MP ＝12，得2x ·y ＝12，即xy ＝6， ∵点P 在双曲线y ＝kx (k ＞0，x ＞0)上，∴k ＝xy ＝6；(3分)(2)当t ＝1时，令y ＝0，则0＝－12(x －1)(x ＋3)，解得x 1＝1，x 2＝－3，∵点B 在点A 左边， ∴B (－3，0)，A (1，0)， ∴AB ＝4.(5分)∴L 的对称轴为直线x ＝－1，∵点M 的坐标为(12，0)，∴MP 与L 对称轴的距离为32；(6分)(3)∵A (t ，0)，B (t －4，0)， ∴L 的对称轴为直线x ＝t －2.(7分) 又∵点M 的横坐标为t2，∴当t －2≤t2，即t ≤4时，顶点(t －2，2)就是G 的最高点；当t －2>t 2，即t ＞4时，L 与MP 的交点(t 2，－18t 2＋t )就是G 的最高点；(10分)(4)5≤t ≤8－2或7≤t ≤8＋ 2.(12分)第2题解图3. 解：(1)(－1，0)，3；4. 解：(1)∵双曲线y ＝1－2mx (x <0)位于第二象限，∴1－2m <0， ∴m >12；(2)∵点B (－1，1)， ∴A (－3，1)，C (－1，3)， ∵双曲线y ＝1－2mx (x <0)经过点C ，∴双曲线的解析式为y ＝－3x ，∵－3×1＝－3， ∴双曲线经过点A ； (3)①∵点B (a ，2a ＋1)，∴A (a －2，2a ＋1)，C (a ，2a ＋3)．∵双曲线y ＝1－2mx (x <0)经过点A 、C ，∴(a －2)(2a ＋1)＝a (2a ＋3)，解得a ＝－13；②∵点E 在AB 上， ∴点E 的纵坐标为2a ＋1，代入y ＝2x ＋2得，x ＝a －12，∴E (a －12，2a ＋1)，∵C (a ，2a ＋3)，双曲线y ＝1－2mx(x <0)经过点C ， ∴双曲线为y ＝a （2a ＋3）x，把E (a －12，2a ＋1)代入得，2a ＋1＝a （2a ＋3）a －12，解得a ＝－16，由①知，双曲线过点A 时，a ＝－13.∴双曲线与线段AE 有交点，a 的取值范围是－13≤a ≤－16.5. 解：(1)∵抛物线F 经过点C (－1，－2)， ∴－2＝1＋2m ＋m 2－2. ∴m ＝－1.∴抛物线F 的表达式是y ＝x 2＋2x －1；(2)当x ＝－2时，y P ＝4＋4m ＋m 2－2＝(m ＋2)2－2. ∴当m ＝－2时，y P 的最小值为－2. 此时抛物线F 的表达式是y ＝(x ＋2)2－2. ∴当x ≤－2时，y 随x 的增大而减小． ∵x 1＜x 2≤－2， ∴y 1＞y 2；(3)－2≤m ≤0或2≤m ≤4. 6. 解：(1)∵△POC 的面积为6，∴12x P ·y P ＝6. ∴x P ·y P ＝12. ∴k ＝12； (2)①∵a ＝12，∴抛物线的解析式为y ＝12x 2－2x ＋32.当y ＝0时，12x 2－2x ＋32＝0，解得x 1＝1，x 2＝3.∵x 1<x 2，∴A (1，0)，B (3，0)．∵抛物线的解析式为y ＝12x 2－2x ＋32，∴抛物线的对称轴为直线x ＝2， ∵k ＝3，∴y ＝3x(1≤x ≤4)．当点P 位于(4，34)时，点P 到x ＝2的距离最大，当x ＝4时，y ＝12×42－2×4＋32＝32，∴PQ ＝32－34＝34；②3576≤a ≤54. 7. 解：(1)将点(1，k ＋6)代入y ＝mx 2＋2mx ＋k 中，得m ＝2； (2)y ＝mx 2＋2mx ＋k ＝2x 2＋4x ＋k ，由题意得：b 2－4ac ＝16－8k ≥0，解得k ≤2， ∵k 为正整数， ∴k ＝1或2.当k ＝1时，方程2x 2＋4x ＋0没有整数解，故舍去，则k ＝2；(3)由(2)得m ＝2，k ＝2，∴y ＝2x 2＋4x ＋2，向下平移8个单位，平移后的表达式为y ＝2x 2＋4x ＋2－8＝2x 2＋4x －6；(4)－12<b <32或b >27332.第7题解图8. 解：(1)由直线y ＝－x ＋4知，点B 、C 的坐标分别为(4，0)、(0，4)，把点B 、C 的坐标分别为(4，0)、(0，4)，代入y ＝ax 2－3ax ＋c 中，得⎩⎪⎨⎪⎧c ＝416a －12a ＋c ＝0，解得⎩⎪⎨⎪⎧a ＝－1c ＝4，∴抛物线的表达式为y ＝－x 2＋3x ＋4； (2)由y ＝－x 2＋3x ＋4，得A (－1，0)．如解图，过点N 作NG ⊥AB 于点G ，第8题解图∵直线y ＝kx ＋k 平分△ABC 的面积， ∴NG ＝12OC ＝2，∴当y ＝2时，2＝－x ＋4，∴x ＝2， ∴N (2，2)．把N (2，2)代入y ＝kx ＋k ，得k ＝23，∴直线AM 的解析式为k ＝23x ＋23，联立⎩⎪⎨⎪⎧y ＝23x ＋23y ＝－x 2＋3x ＋4，解得⎩⎨⎧x 1＝103y 1＝269，⎩⎪⎨⎪⎧x 2＝－1y 2＝0.∴M (103，269)；(3)翻折后的整个图象包括两部分：分别是抛物线y ＝x 2－3x －4(－1≤x ≤4)与y ＝－x 2＋3x ＋4(x ＞4或x ＜－1)．①当直线y ＝kx ＋k 与抛物线y ＝x 2－3x －4＝(x －32)2－254(－1≤x ≤4)相交时，由⎩⎪⎨⎪⎧y ＝kx ＋ky ＝x 2－3x －4，得x 2－3x －4＝kx ＋k ，整理，得x 2－(k ＋3)x －(k ＋4)＝0，解得x 1＝－1，x 2＝k ＋4. ∴y 1＝0，y 2＝k 2＋5k . ∴两个函数图象有两个交点，其中一个交点为A (－1，0)，另一个交点坐标为(k ＋4，k 2＋5k )．观察图象可知：另一个交点在x 轴下方，横坐标在－1与4之间，纵坐标在－254与0之间．∴－1＜k ＋4＜4，解得－5＜k ＜0. －254＜k 2＋5k ＜0，整理，得 4k 2＋20k ＋25＞0且k 2＋5k ＜0，解得，(2k ＋5)2＞0且－5＜k ＜0. k 为任意实数，(2k ＋5)2＞0恒成立， ∴－5＜k ＜0；②当直线y ＝kx ＋k 与图象y ＝－x 2＋3x ＋4(x ＞4或x ＜－1)相交时，－x 2＋3x ＋4＝kx ＋k ，整理得x 2＋(k －3)x ＋(k －4)＝0 解得x 1＝－1，x 2＝4－k ，∴y 1＝0，y 2＝5k －k 2. ∴两个函数图象有两交点，其中一个是点A (－1，0)，另一个交点坐标为(4－k ，5k －k 2)．观察图象可知：另一个交点的横坐标大于4，纵坐标小于0，即4－k ＞4，解得k ＜0. 5k －k 2＜0，∴k (5－k )＜0， ∵k ＜0，∴5－k ＞0，∴k ＜5. ∴k ＜0.∴综上所述，当直线y ＝kx ＋k 与翻折后的整个图象只有三个交点时，k 的取值范围是－5＜k ＜0.类型二整点问题例解：(1)如解图①，设直线l 的解析式为y ＝px ＋q ，将A (5，0)，B (0，5)代入得，⎩⎪⎨⎪⎧5p ＋q ＝0，q ＝5，解得⎩⎪⎨⎪⎧p ＝－1，q ＝5. ∴直线l 的解析式为y ＝－x ＋5.结合图象可知，线段OA 上共有6个整点，线段OB (不含原点)上共有5个整点，线段AB 上(不含端点)共有4个整点，△AOB 内部共有6个整点，∴直线l 与坐标轴围成的区域W 1内(含边界)整点的个数为6＋5＋4＋6＝21个；例题解图①(2)如解图②，设直线BC 的解析式为y ＝p 1x ＋q 1，将B (0，5)，C (－1，0)代入得，⎩⎪⎨⎪⎧q 1＝5，－p 1＋q 1＝0，解得⎩⎪⎨⎪⎧p 1＝5，q 1＝5， ∴直线BC 的解析式为y ＝5x ＋5，结合图象，△BOC(不含边界)所围成的区域内无整点，由(1)知，△AOB(不含边界)所围成的区域内有6个整点，∴△ABC所围成的区域W2内(不含边界)整点的个数等于线段OB(不含端点)上的整点个数加上△AOB 内部的整点个数为4＋6＝10个；例题解图②(3)如解图③，当a＝3时，直线y＝3，线段AB与y轴所围成的三角形区域W3内(含边界)恰好有6个整点，∴结合图象可知，当2＜a≤3时，直线y＝a，线段AB与y轴所围成的三角形区域W3内(含边界)恰好有6个整点；例题解图③(4)如解图④，当b＝0时，y＝x，此时y＝x与直线AB及y轴所围成的三角形区域W4内(不含边界)有2个整点，当b＝－1时，y＝x－1，此时y＝x－1与直线AB及y轴所围成的三角形区域W4内(不含边界)有4个整点，结合图象可知，－1≤b＜0；例题解图④(5)如解图⑤，x ＜时当直线y ＝kx ＋2过(－5，1)时，直线y ＝kx ＋2与直线BC 及x 轴所围成的三角形区域W 5内(不含边界)有4个整点，将(－5，1)代入y ＝kx ＋2得k ＝15，当直线y ＝kx ＋2过(－4，1)时，直线y ＝kx ＋2与直线BC 及x 轴所围成的三角形区域W 5内(不含边界)有3个整点，将(－4，1)代入y ＝kx ＋2得k ＝14，结合图象可知，15≤k ＜14；同理，x ＞0时，当直线y ＝kx ＋2过(3，1)时，直线y ＝kx ＋2与直线BC 及x 轴所围成的三角形区域W 5内(不含边界)有3个整点，将(3，1)代入y ＝kx ＋2得k ＝－13，当直线y ＝kx ＋2过(4，1)时，直线y ＝kx ＋2与直线BC 及x 轴所围成的三角形区域W 5内(不含边界)有4个整点，将(4，1)代入y ＝kx ＋2得k ＝－14，∴－13≤k ＜－14，综上可得，15≤k ＜14或－13≤k ＜－14；例题解图⑤(6)如解图⑥，由图象可知曲线DE 上有(1，4)(2，2)，(4，1)共3个整点，线段DE (不含端点)上有(2，3)，(3，2)共2个整点，曲线DE 与线段DE 围成的区域内部无整点，∴曲线DE 与线段DE 所围成的区域W 6内(含边界)有5个整点；例题解图⑥(7)如解图⑦，当G 点与原点重合时，此时线段DG ，FG 与曲线DF 所围成的区域W 7内(含边界)有6个整点，此时b＝0，如解图⑧，当点G的纵坐标在0与－1之间时，此时线段DG，FG与曲线DF所围成的区域W7内(含边界)有5个整点，如解图⑨，当G点与过(0，－1)时，此时线段DG，FG与曲线DF所围成的区域W7内(含边界)有8个整点，此时b＝－1，∴－1＜b<0；例题解图⑦例题解图⑧例题解图⑨(8)由抛物线y＝x2－2x＋m－2可得，抛物线的对称轴为直线x＝1，且抛物线恒过点(0，m－2)，如解图○10，当抛物线的顶点为(1，2)时，此时抛物线与直线y＝5所围成的区域W8内(不含边界)有4个整点，分别为(1，3)，(0，4)，(1，4)，(2，4)，将(1，2)代入抛物线解析式得，1－2＋m－2＝2，解得m＝5，当抛物线的顶点为(1，3)时，此时抛物线与直线y＝5所围成的区域W8内(不含边界)有1个整点(1，4)，将(1，3)代入抛物线解析式得，1－2＋m－2＝3，解得m＝6，结合图象可知，5≤m＜6.例题解图○10(9)由抛物线y＝x2－2x＋m－2可得，抛物线的对称轴为直线x＝1，且抛物线恒过点(0，m－2)，如解图⑪，当抛物线的顶点为(1，－2)时，此时抛物线与直线y＝－x＋2所围成的区域W9内(不含边界)有4个整点，分别为(0，0)，(0，1)，(1，0)，(1，－1)，将(1，－2)代入抛物线解析式得，1－2＋m－2＝－2，解得m＝1，当抛物线的顶点为(1，－1)时，此时抛物线与直线y＝－x＋2所围成的区域W9内(不含边界)有2个整点，分别为(0，1)，(1，0)，将(1，－1)代入抛物线解析式得，1－2＋m－2＝－1，解得m＝2，∴综上所述，1≤m＜2.例题解图⑪1.解：(1)当x＝0时，y＝x－b＝－b，∴B(0，－b)，∵AB＝8，A(0，b)，∴b－(－b)＝8.∴b＝4；(2分)∴L 的解析式为y ＝－x 2＋4x ， ∴L 的对称轴为直线x ＝2，将x ＝2代入直线a 的解析式中得y ＝2－4＝－2， ∴L 的对称轴与a 的交点坐标为(2，－2)；(4分) (2)∵y ＝－x 2＋bx ＝－(x －b 2)2＋b 24， ∴L 的顶点C 的坐标为(b 2，b 24)．∵点C 在l 下方，∴点C 与l 的距离为b －b 24＝－14(b －2)2＋1≤1，∴点C 与l 距离的最大值为1；(7分)(3)由题意可得，y 1＝b ，y 2＝x 0－b ，y 3＝－x 20＋bx 0， ∵y 3是y 1，y 2的平均数， ∴y 3＝y 1＋y 22，即－x 20＋bx 0＝x 02，化简得x 0(2x 0－2b ＋1)＝0，解得x 0＝0或x 0＝b －12，∵x 0≠0， ∴x 0＝b －12，对于L ，当y ＝0时，0＝－x 2＋bx ，即0＝－x (x －b )．解得x 1＝0，x 2＝b ， ∵b ＞0，∴D 点坐标为(b ，0)，∴点(x 0，0)与点D 间的距离为b －(b －12)＝12；(10分)(4)当b ＝2019时，“美点”的个数为4040；(11分) 当b ＝2019.5时，“美点”的个数为1010.(12分) 2. 解：(1)如解图，则点A 的坐标为(5，3)， ∵直线y ＝kx ＋b 过点A (5，3)，点C (9，0)，∴⎩⎪⎨⎪⎧5k ＋b ＝39k ＋b ＝0，解得⎩⎨⎧k ＝－34b ＝274，即直线y ＝kx ＋b 的表达式是y ＝－34x ＋274；(2)①3个；第2题解图3. 解：(1)∵A (4，1)， ∴直线OA 的解析式为y ＝14x .∵直线y 1＝14x ＋b ，∴直线y 1与OA 平行，当b ＝－1时，直线解析式为y 1＝14x －1，解方程4x ＝14x －1得x 1＝2－25(舍去)，x 2＝2＋25，则B (2＋25，5－12)，∵C (0，－1)，∴区域M 内的整点为(1，0)，(2，0)，(3，0)，共3个；(2)当直线y 1在OA 的下方时，当直线y 1＝14x ＋b 过点(1，－1)时，b ＝－54，则直线y 1＝14x ＋b 经过(5，0)，∴区域M 内恰有4个整点，则b 的取值范围是－54≤b ＜－1.当直线l 在OA 的上方时，∵点(2，2)在函数y 2＝4x(x ＞0)的图象上，当直线y 1＝14x ＋b 过(1，2)时，b ＝74，此时区域M 内有3个整点．当直线y 1＝14x ＋b 过(1，3)时，b ＝114，∴区域M 内恰有4个整点时，b 的取值范围是74＜b ≤114.综上所述，区域M 内恰有4个整点时，b 的取值范围是－54≤b ＜－1或74＜b ≤114.4. 解：(1)当c ＝1时，y 1＝－x 2＋ 12x ＋c ＝－x 2＋ 12x ＋1＝－(x －14)2＋1716 .又∵－2020≤x ≤1，∴M 1＝1716. y 2＝－x 2＋2cx ＋1＝－x 2＋2x ＋1＝－(x －1)2＋2. 又∵1≤x ≤2020， ∴M 2＝2；(2)当x ＝1时，y 1＝－x 2＋12x ＋c ＝c －12；y 2＝－x 2＋2cx ＋1＝2c .若点A ，B 重合，则c －12＝2c ，解得c ＝－12.∴L 1∶y 1＝－x 2＋12 x －12(－2020≤x ≤1)；L 2∶y 2＝－x 2－x ＋1(1≤x ≤2020)．在L 1上，x 为奇数的点是“美点”，则L 1上有1011个“美点”，在L 2上，x 为整数的点是“美点”，则L 2上有2020个“美点”．又∵点A ，B 重合，则L 上“美点”的个数是1011＋2020－1＝3030； (3)c ＝－238或2.5. 解：(1)∵L 1：y ＝－x 2＋bx ＋b －1经过原点， ∴将(0，0)代入得b ＝1，∴抛物线L 1的解析式为y ＝－x 2＋x ，将y ＝－x 2＋x 配方得y ＝－(x －12)2＋14，∴顶点坐标为(12，14)；(2)①对于抛物线L 1：y ＝－x 2＋bx ＋b －1＝(x ＋1)b －x 2－1，当x ＝－1时，y ＝－2，故抛物线y ＝－x 2＋bx ＋b －1总经过一个定点M (－1，－2)；②∵抛物线L 2的顶点为M ， ∴设它的解析式为y ＝a (x ＋1)2－2，又∵抛物线L 1的顶点总在抛物线L 2上， ∴将点(12，14)代入解得a ＝1，∴抛物线L 2的解析式为y ＝(x ＋1)2－2，即y ＝x 2＋2x －1；(3)当抛物线L 1经过点B 时，将B (5，－2)代入抛物线L 1解析式y ＝－x 2＋bx ＋b －1得b ＝4， ∴抛物线L 1的解析式为y ＝－x 2＋4x ＋3，令y ＝－2，得－2＝－x 2＋4x ＋3，解得x 1＝－1，x 2＝5，∴抛物线L 1与线段AB 交于(－1，－2)，(5，－2)两点，由解析式可以得出，只要x 取整数，则抛物线L 1上点的纵坐标也一定是整数．∴抛物线L 1经过端点B 时形成的封闭图形C 上的“理想点”个数为12个；当抛物线L 1经过点A 时，将A (－5，－2)代入抛物线L 1解析式y ＝－x 2＋bx ＋b －1得b ＝－6， ∴抛物线L 1的解析式为y ＝－x 2－6x －7，从解析式可以得出，只要x 取整数，则抛物线L 1上点的纵坐标也一定是整数，令y ＝－2，得－2＝－x 2－6x －7，解得x 1＝－5，x 2＝－1， ∴抛物线L 1与线段AB 交于(－5，－2)，(－1，－2)两点，故当抛物线L 1经过端点A 时形成的封闭图形C 上的“理想点”的个数为8个；综上所述，封闭图形C 上的“理想点”的个数为8个或12个．。

中考英语总复习试题题型专题训练三阅读理解

题型专题训练三阅读理解【1】阅读下面短文, 根据短文内容判断句子正误。

正确的涂“A”, 错误的涂“B”。

We are collecting more news for our school English newspaper. Would you like to be reporters for it? Here are two pieces from the news page.1.You are welcome to be reporters for our school English newspaper.答案:A解析:根据第一段的“Would you like to be reporters for it?”可得出答案。

2.Li Yu won the second prize in the 800-meter race yesterday.答案:A解析:根据第一篇报道中的“Last year’s best runner, Li Yu, only won the second prize in the 800-meter race.”可得出答案。

3.Yang Liu was the best runner last year.答案:B解析:根据第一篇报道可知去年最好的跑步者是李渔, 而不是杨柳。

4.Mr. White will teach us English for two years at our school.答案:B解析:在第二篇报道中提到怀特老师任教两年, 将要离开, 而题干说的是他将任教两年, 故表述错误。

5.We’ll always remember Mr. White’s lively and interesting teaching.答案:A解析:由第二篇报道可知怀特老师的课生动有趣。

【2】(2018·乌鲁木齐中考)根据文章内容, 判断文后句子的正确(T)与错误(F)。

专题三有机化学-2021-2022学年高三化学总复习选择题专项训练

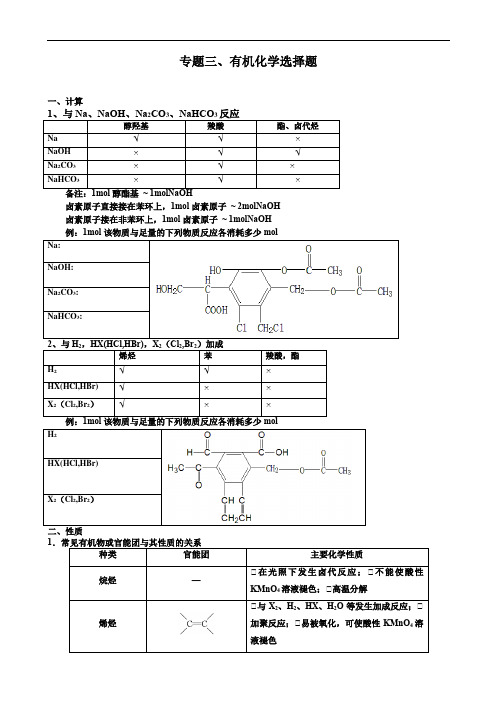
专题三、有机化学选择题一、计算醇羟基羧酸酯、卤代烃Na √ √× NaOH × √ √ Na 2CO 3 × √ × NaHCO 3× √ ×卤素原子直接接在苯环上，1mol 卤素原子 ~ 2molNaOH卤素原子接在非苯环上，1mol 卤素原子 ~ 1molNaOH 例：1mol该物质与足量的下列物质反应各消耗多少molNa:NaOH:Na 2CO 3: NaHCO 3:2、与H 2，HX(HCl,HBr)，X 2（Cl 2,Br 2）加成烯烃苯羧酸，酯H 2√ √ × HX(HCl,HBr) √ × × X 2（Cl 2,Br 2）√××H 2HX(HCl,HBr)X 2（Cl 2,Br 2）1种类官能团主要化学性质烷烃—①在光照下发生卤代反应；①不能使酸性KMnO 4溶液褪色；①高温分解烯烃①与X 2、H 2、HX 、H 2O 等发生加成反应；①加聚反应；①易被氧化，可使酸性KMnO 4溶液褪色苯—①取代反应[如硝化反应、卤代反应(Fe或FeX3作催化剂)]；①与H2发生加成反应甲苯—①取代反应；①可使酸性KMnO4溶液褪色醇—OH ①与活泼金属Na等反应产生H2；①催化氧化生成醛；①与羧酸及无机含氧酸发生酯化反应乙醛、葡萄糖①与H2加成为醇；①加热时，被氧化剂{如O2、[Ag(NH3)2]＋、Cu(OH)2等}氧化为酸(盐)羧酸①酸的通性；①酯化反应酯发生水解反应，生成羧酸(盐)和醇常见有机物在生产、生活中的应用性质应用医用酒精中乙醇的体积分数为75%，使蛋白质变性医用酒精用于消毒福尔马林是35%～40%的甲醛水溶液，使蛋白质变性良好的杀菌剂，常作为浸制标本的溶液(不可用于食品保鲜)强酸、强碱、强氧化性物质、重金属盐溶液会使蛋白质变性---蛋白质受热变性加热能杀死流感病毒蚕丝灼烧有烧焦羽毛的气味灼烧法可以区别蚕丝和人造纤维聚乙烯性质稳定，无毒可作食品包装袋聚氯乙烯有毒不能用作食品包装袋食用油反复加热会产生稠环芳香烃等有害物质食用油不能反复加热聚四氟乙烯具有抗酸、抗碱、抗各种有机溶剂的特点用于厨具表面涂层甘油具有吸水性作护肤保湿剂淀粉遇碘显蓝色鉴别淀粉与其他物质(如蛋白质、木纤维等)食醋与碳酸钙反应生成可溶于水的醋酸钙食醋可除水垢(主要成分为碳酸钙)阿司匹林水解生成水杨酸，显酸性服用阿司匹林出现水杨酸反应时，用NaHCO3溶液解毒加工后具有吸水性的植物纤维可用作食品干燥剂谷氨酸钠具有鲜味做味精油脂在碱性条件下水解为高级脂肪酸盐和制肥皂甘油葡萄糖的特征反应：银氨溶液、新制的氢氧化铜溶液检验是否为糖尿病患者3、能使高锰酸钾溶液褪色的物质：烯、炔、酚、醛、苯的同系物4、能使溴水褪色或变色的物质：烯、炔、酚、醛；萃取：与苯、甲苯、四氯化碳等有机溶液混合振荡，萃取作用使溴水褪色，有机溶剂溶解溴呈橙色(或棕红色)。

统编版九年级语文中考总复习专题3 词语的理解与运用(含答案)

专题三词语的理解与运用知能优化训练中考回顾1.(2022天津)依次填入下面一段文字横线处的词语,最恰当的一项是()欧阳修说:“立身以立学为先,立学以读书为本。

”读书要学会选择。

选择与自然有关的书,以丰富知识;选择与历史有关的书,以视野;选择与哲学有关的书,以智慧。

读书还要善于思考。

善于思考,才会有;善于思考,才会有取舍。

读好书,善读书,才会读有所获。

A.开阔吸收鉴定B.开辟吸收鉴别C.开阔汲取鉴别D.开辟汲取鉴定2.(2022湖南长沙)下面是初三某同学写的毕业留言,其中加点词使用最恰当的一项是()回首三年同窗生活,历历在目。

课堂上,我们勤学好问,吹毛求疵．．．．;活动中,我们收获欢乐,可歌可泣．．．．．．．。

我们一起努力拼搏,哪怕结果牵强附．．．．。

同学们,学习如逆水行舟．．．．,不进则退会．,也问心无愧。

A.吹毛求疵B.可歌可泣C.逆水行舟,不进则退D.牵强附会3.(2022河北)阅读下面的文字,在横线处填入一个符合语境的四字词语。

塞罕坝,位于河北省最北端。

这里的百万亩林海堪称目前世界上面积最大的人工林,阻挡着南侵的风沙,是护卫京津的生态屏障。

这里是“水的源头、云的故乡、花的世界、林的海洋”。

春天,群山抹绿,雪映杜鹃;夏天,百花烂漫,林海滴翠;秋天,赤橙黄绿,层林尽染;冬天,白雪皑皑,。

三代育林人的青春与汗水抹去了荒漠与森林之间不可逾越的距离。

塞罕坝是一座书写人力奇迹的丰碑,镌刻着人与自然和谐共生的密码。

4.(2021天津)依次填入下面一段文字横线处的词语,最恰当的一项是()无论是昔日的五连冠,还是如今的一次次绝地反击,中国女排都了为国争光、顽强拼搏的中华体育精神。

女排精神是体育人为中华民族奉献的精神财富,是新时期中国精神的具体体现。

我们相信女排精神必将代代相传,中国人民不断书写新的传奇。

A.传承宝贵鼓舞B.传承贵重鼓动C.传达宝贵鼓动D.传达贵重鼓舞5.(2021四川达州)下列加点成语使用正确的一项是()A.近年来,我国冰雪运动吹响了“南展西扩东进”的号角,冰雪运动人数持续增加, 冰雪运动产业方兴未艾．．．．。

总复习专题训练3

高考语文总复习教案第三部分专题对点训练(三)语言表达运用

中考总复习专项训练题(三)(改错专练)

小升初总复习专题3运动中的数学问题(含答案)

小学语文总复习专项训练——小古文阅读(三)

中考数学总复习专题三解答题重难点题型突破题型二几何图形探究题类型与三角形、四边形有关的探究题课件

高考总复习 英语书面表达专题3

高考历史总复习专题3近代中国的民主革命考点8新民主主义革命

初中生物总复习 专题3细胞是生命活动的基本单位

(老高考适用)2023版高考化学二轮总复习 专题能力提升训练3 氧化还原反应 离子反应

【步步高】高考数学(文,江苏专用)大二轮总复习练习：专题三第3讲平面向量(含答案解析)

人教版九年级 数学上册期末综合复习专题提优训练(三)

中考历史总复习 专题训练三 中国近(现)代化的探索历程-人教版初中九年级全册历史试题

中考语文总复习专题突破训练专题三 词语的理解与运用 部编人教版九年级上册