利用Matlab进行线性回归分析之欧阳歌谷创编
采用MATLAB的线性回归分析

i =1 m
,a n
m 2 xi1 i∑ =1 mx x i1 i 2 i∑ =1 m ∑ x i 1x in i =1
i =1
∑ x i 2 x i1
i =1
Λ Λ
∑ x2 i2
Μ
m
m
i =1
∑ x i 2 x in
Λ
i= 1
2 ∑ ε i = 最小 有
m m ∑ x in x i1 i =1 m ∑ x in x i 2 i =1 m 2 ∑ x in i =1
+a nxin )= y i − ( a 0 + ∑ a j x ij ) (i
j =1
n
X 的子矩阵 S 有 则
m)
用最小二乘法来推定系数 a0,a 1,
运行程序 即可得 a0 19.8286 a1 2.7429 上述程序亦可用于多项式 y a 0+ a 1x+a 2x2+ +a nxn xn xn 即可 的回归 只要把 x1 x x2 x2
3
结束语
MATLAB 语言有很强的矩阵处理能力 所编程 序简洁 明了 在工程中应用很广
参考文献
[1] 郁有文 , 常健 . 传感器原理及工程应用 [M]. 西安 : 西安 电 子 科 技 大 学 出 版 社 , 2000. [2] 蒙以正 . MATLAB 5. x 应用与技巧 [M]. 北京 : 科学出 版 社 , 1999.
兵工自动化 软件技术 O. I. Automation 2004 年第 23 卷第 1 期 Software Technique 2004, Vol. 23, No. 1
文章编号 1006 - 1576 2004 01 - 0068 - 02
利用MATLAB进行回归分析
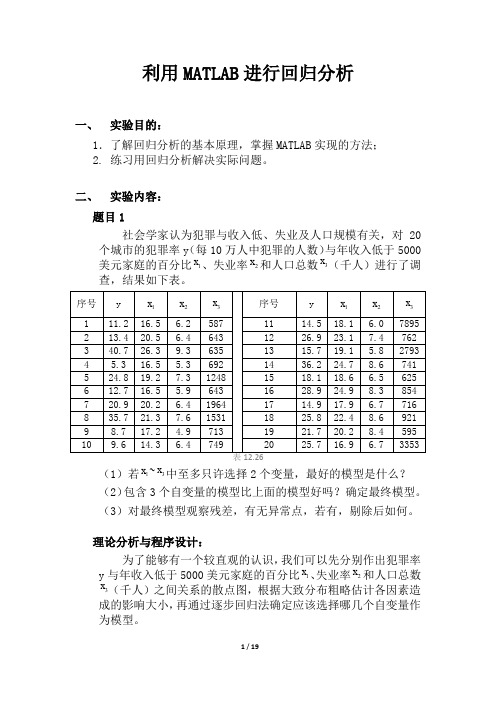
利用MATLAB进行回归分析一、实验目的:1.了解回归分析的基本原理,掌握MATLAB实现的方法;2. 练习用回归分析解决实际问题。
二、实验内容:题目1社会学家认为犯罪与收入低、失业及人口规模有关,对20个城市的犯罪率y(每10万人中犯罪的人数)与年收入低于5000美元家庭的百分比1x、失业率2x和人口总数3x(千人)进行了调查,结果如下表。
(1)若1x~3x中至多只许选择2个变量,最好的模型是什么?(2)包含3个自变量的模型比上面的模型好吗?确定最终模型。
(3)对最终模型观察残差,有无异常点,若有,剔除后如何。
理论分析与程序设计:为了能够有一个较直观的认识,我们可以先分别作出犯罪率y与年收入低于5000美元家庭的百分比1x、失业率2x和人口总数x(千人)之间关系的散点图,根据大致分布粗略估计各因素造3成的影响大小,再通过逐步回归法确定应该选择哪几个自变量作为模型。
编写程序如下:clc;clear all;y=[11.2 13.4 40.7 5.3 24.8 12.7 20.9 35.7 8.7 9.6 14.5 26.9 15.736.2 18.1 28.9 14.9 25.8 21.7 25.7];%犯罪率(人/十万人)x1=[16.5 20.5 26.3 16.5 19.2 16.5 20.2 21.3 17.2 14.3 18.1 23.1 19.124.7 18.6 24.9 17.9 22.4 20.2 16.9];%低收入家庭百分比x2=[6.2 6.4 9.3 5.3 7.3 5.9 6.4 7.6 4.9 6.4 6.0 7.4 5.8 8.6 6.5 8.36.7 8.6 8.4 6.7];%失业率x3=[587 643 635 692 1248 643 1964 1531 713 749 7895 762 2793 741 625 854 716 921 595 3353];%总人口数(千人)figure(1),plot(x1,y,'*');figure(2),plot(x2,y,'*');figure(3),plot(x3,y,'*');X1=[x1',x2',x3'];stepwise(X1,y)运行结果与结论:犯罪率与低收入散点图犯罪率与失业率散点图犯罪率与人口总数散点图低收入与失业率作为自变量低收入与人口总数作为自变量失业率与人口总数作为自变量在图中可以明显看出前两图的线性程度很好,而第三个图的线性程度较差,从这个角度来说我们应该以失业率和低收入为自变量建立模型。
matlab线性回归

matlab线性回归
Matlab 线性回归是建立在线性模型的基础上的一种回归方法。
此技
术中,使用简单的线性函数来拟合输入和输出变量之间的关系。
Matlab
线性回归模型的输出主要用于预测未来的数据和分析数据的趋势。
Matlab 线性回归的过程包括定义变量,检查数据类型,计算线性方程系数,应用
线性模型,评估模型和比较结果。
Matlab 线性回归通常用于统计学分析,用于探究关联型数据及解释现象。
它有助于了解数据变化,衡量数据变化
的大小,预测未来变化趋势,也能用来检验关系是否线性。
用MATLAB求解回归分析

(2)非线性回归命令:nlintool(x,y,’model’, beta0,alpha) ) 2、预测和预测误差估计: 、预测和预测误差估计: [Y,DELTA]=nlpredci(’model’, x,beta,r,J) 求nlinfit 或nlintool所得的回归函数在x处的预测值Y及预测值的显 著性为1-alpha的置信区间Y ± DELTA.
4、预测及作图: [;,x',beta,r ,J); plot(x,y,'k+',x,YY,'r')
例5 财政收入预测问题:财政收入与国民收入、工业总产值、 农业总产值、总人口、就业人口、固定资产投资等因素有关。 下表列出了1952-1981年的原始数据,试构造预测模型。
得结果:b = -16.0730 0.7194 stats = 0.9282 180.9531 0.0000 bint = -33.7071 0.6047 1.5612 0.8340
ˆ ˆ ˆ ˆ 即 β 0 = −16.073, β 1 = 0.7194 ; β 0 的置信区间为[-33.7017,1.5612], β 1 的置信区间为[0.6047,0.834];
回 归 系 数 的 区 间 估 计 F 检验回归模型的 计 数 : 系数r2、 、 F 的 p 差 区 间 时 为 水 0 平 05 ) . 性 残 信 省 著 置 (缺 显
系数 r2 F > F1F k 的 n-k-1
1
回归 H0 F H0 回归模型 回归 .
p< α
3、 、
区间: 区间:
rcoplot
r2=0.9282, F=180.9531, p=0.0000 p<0.05, 可知回归模型 y=-16.073+0.7194x 成立.
利用 Matlab作回归分析

利用 Matlab 作回归分析一元线性回归模型:2,(0,)y x N αβεεσ=++求得经验回归方程:ˆˆˆyx αβ=+ 统计量: 总偏差平方和:21()n i i SST y y ==-∑,其自由度为1T f n =-; 回归平方和:21ˆ()n i i SSR y y ==-∑,其自由度为1R f =; 残差平方和:21ˆ()n i i i SSE y y ==-∑,其自由度为2E f n =-;它们之间有关系:SST=SSR+SSE 。
一元回归分析的相关数学理论可以参见《概率论与数理统计教程》,下面仅以示例说明如何利用Matlab 作回归分析。
【例1】为了了解百货商店销售额x 与流通费率(反映商业活动的一个质量指标,指每元商品流转额所分摊的流通费用)y 之间的关系,收集了九个商店的有关数据,见下表1.试建立流通费率y 与销售额x 的回归方程。
表1 销售额与流通费率数据【分析】:首先绘制散点图以直观地选择拟合曲线,这项工作可结合相关专业领域的知识和经验进行,有时可能需要多种尝试。
选定目标函数后进行线性化变换,针对变换后的线性目标函数进行回归建模与评价,然后还原为非线性回归方程。
【Matlab数据处理】:【Step1】:绘制散点图以直观地选择拟合曲线x=[1.5 4.5 7.5 10.5 13.5 16.5 19.5 22.5 25.5];y=[7.0 4.8 3.6 3.1 2.7 2.5 2.4 2.3 2.2];plot(x,y,'-o')输出图形见图1。
510152025图1 销售额与流通费率数据散点图根据图1,初步判断应以幂函数曲线为拟合目标,即选择非线性回归模型,目标函数为:(0)b y ax b =< 其线性化变换公式为:ln ,ln v y u x == 线性函数为:ln v a bu =+【Step2】:线性化变换即线性回归建模(若选择为非线性模型)与模型评价% 线性化变换u=log(x)';v=log(y)';% 构造资本论观测值矩阵mu=[ones(length(u),1) u];alpha=0.05;% 线性回归计算[b,bint,r,rint,states]=regress(v,mu,alpha)输出结果:b =[ 2.1421; -0.4259]表示线性回归模型ln=+中:lna=2.1421,b=-0.4259;v a bu即拟合的线性回归模型为=-;y x2.14210.4259bint =[ 2.0614 2.2228; -0.4583 -0.3934]表示拟合系数lna和b的100(1-alpha)%的置信区间分别为:[2.0614 2.2228]和[-0.4583 -0.3934];r =[ -0.0235 0.0671 -0.0030 -0.0093 -0.0404 -0.0319 -0.0016 0.0168 0.0257]表示模型拟合残差向量;rint =[ -0.0700 0.02300.0202 0.1140-0.0873 0.0813-0.0939 0.0754-0.1154 0.0347-0.1095 0.0457-0.0837 0.0805-0.0621 0.0958-0.0493 0.1007]表示模型拟合残差的100(1-alpha)%的置信区间;states =[0.9928 963.5572 0.0000 0.0012] 表示包含20.9928SSR R SST==、 方差分析的F 统计量/963.5572//(2)R E SSR f SSR F SSE f SSE n ===-、 方差分析的显著性概率((1,2))0p P F n F =->≈; 模型方差的估计值2ˆ0.00122SSE n σ==-。
(完整版)Matlab线性回归(拟合)

Matlab 线性回归(拟合)对于多元线性回归模型:e x x y p p ++++=βββ 110设变量12,,,p x x x y 的n 组观测值为12(,,,)1,2,,i i ip i x x x y i n =.记 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=np n n p p x x x x x x x x x x 212222111211111,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n y y y y 21,则⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=p ββββ 10 的估计值为 y x x x b ')'(ˆ1-==β(11.2) 在Matlab 中,用regress 函数进行多元线性回归分析,应用方法如下:语法:b = regress(y, x)[b, bint, r, rint, stats] = regress(y, x)[b, bint, r, rint, stats] = regress(y, x, alpha)b = regress(y, x),得到的1+p 维列向量b 即为(11.2)式给出的回归系数β的估计值.[b, bint, r, rint, stats]=regress(y, x) 给出回归系数β的估计值b ,β的95%置信区间((1)2p +⨯向量)bint ,残差r 以及每个残差的95%置信区间(2⨯n 向量)rint ;向量stats 给出回归的R 2统计量和F 以及临界概率p 的值.如果i β的置信区间(bint 的第1i +行)不包含0,则在显著水平为α时拒绝0i β=的假设,认为变量i x 是显著的.[b, bint, r, rint, stats]=regress(y, x, alpha) 给出了bint 和rint 的100(1-alpha)%的置信区间.三次样条插值函数的MATLAB 程序matlab 的splinex = 0:10; y = sin(x); %插值点xx = 0:.25:10; %绘图点yy = spline(x,y,xx);plot(x,y,'o',xx,yy)非线性拟合非线性拟合可以用以下命令(同样适用于线形回归分析):1.beta = nlinfit(X,y,fun,beta0)X给定的自变量数据,Y给定的因变量数据,fun要拟合的函数模型(句柄函数或者内联函数形式),beta0函数模型中系数估计初值,beta返回拟合后的系数2.x = lsqcurvefit(fun,x0,xdata,ydata)fun要拟合的目标函数,x0目标函数中的系数估计初值,xdata自变量数据,ydata 函数值数据X拟合返回的系数(拟合结果)nlinfit格式:[beta,r,J]=nlinfit(x,y,’model’, beta0)Beta 估计出的回归系数r 残差J Jacobian矩阵x,y 输入数据x、y分别为n*m矩阵和n维列向量,对一元非线性回归,x为n维列向量。
用MATLAB求解回归分析

1. 对回归模型建立M文件model.m如下: function yy=model(beta0,X) a=beta0(1); b=beta0(2); c=beta0(3); d=beta0(4); e=beta0(5); f=beta0(6); x1=X(:,1); x2=X(:,2); x3=X(:,3); x4=X(:,4); x5=X(:,5); x6=X(:,6); yy=a*x1+b*x2+c*x3+d*x4+e*x5+f*x6;
例 2 观测物体降落的距离 s 与时间 t 的关系,得到数据如下表, 求 s 关于 t 的回归方程 sˆ a bt ct 2 .
t (s)
1/30
2/30
3/30
4/30
5/30
6/30
7/30
s (cm) 11.86
15.67
20.60
26.69
33.71
41.93
51.13
t (s) s (cm)
回归系数 的初值
(2)非线性回归命令:nlintool(x,y,’model’, beta0,alpha)
2、预测和预测误差估计: [Y,DELTA]=nlpredci(’model’, x,beta,r,J)
求nlinfit 或nlintool所得的回归函数在x处的预测值Y及预测值的显 著性为1-alpha的置信区间Y DELTA.
80
70
50
65
90
100 110 60
收入 1000 600 1200 500 300 400 1300 1100 1300 300
价格 5
7
6
6
8
7
利用Matlab进行线性回归分析

利用Matlab举止线性返回分解之阳早格格创做返回分解是处理二个及二个以上变量间线性依存闭系的统计要领.不妨通过硬件Matlab真止.正在Matlab中,不妨间接调用下令真止返回分解,(1)[b,bint,r,rint,stats]=regress(y,x),其中b是返回圆程中的参数预计值,bint是b的置疑区间,r战rint分别表示残好及残好对于应的置疑区间.stats包罗三个数字,分别是相闭系数,F统计量及对于应的概率p值.(2)recplot(r,rint)做残好分解图.(3)rstool(x,y)一种接互式办法的句柄下令.以下通过简曲的例子去证明.例现有多个样原的果变量战自变量的数据,底下咱们利用Matlab,通过返回分解修坐二者之间的返回圆程.% 一元返回分解x=[1097 1284 1502 1394 1303 1555 1917 2051 2111 2286 2311 2003 2435 2625 2948 3, 55 3372];%自变量序列数据y=[698 872 988 807 738 1025 1316 1539 1561 1765 1762 1960 1902 2013 2446 2736 2825];%果变量序列数据X=[ones(size(x')),x'],pause[b,bint,r,rint,stats]=regress(y',X,0.05),pause%调用一元返回分解函数rcoplot(r,rint)%绘出正在置疑度区间下缺点分散.% 多元返回分解% 输进百般自变量数据x1=[5.5 2.5 8 3 3 2.9 8 9 4 6.5 5.5 5 6 5 3.5 8 6 4 7.5 7]';x2=[31 55 67 50 38 71 30 56 42 73 60 44 50 39 55 7040 50 62 59]';x3=[10 8 12 7 8 12 12 5 8 5 11 12 6 10 10 6 11 11 9 9]';x4=[8 6 9 16 15 17 8 10 4 16 7 12 6 4 4 14 6 8 13 11]';%输进果变量数据y=[79.3 200.1 163.1 200.1 146.0 177.7 30.9 291.9 160 339.4 159.6 86.3 237.5 107.2 155 201.4 100.2 135.8 223.3 195]';X=[ones(size(x1)),x1,x2,x3,x4];[b,bint,r,rint,stats]=regress(y,X)%返回分解Q=r'*rsigma=Q/18rcoplot(r,rint);%逐步返回X1=[x1,x2,x3,x4];stepwise(X1,y,[1,2,3])%逐步返回%X2=[ones(size(x1)),x2,x3];%X3=[ones(size(x1)),x1,x2,x3];%X4=[ones(size(x1)),x2,x3,x4];%[b1,b1int,r1,r1int,stats1]=regress(y,X2) %[b2,b2int,r2,r2int,stats2]=regress(y,X3); %[b3,b3int,r3,r3int,stats3]=regress(y,X4);。
利用Matlab进行线性回归分析

利用Matlab 进行线性回归分析回归分析是处理两个及两个以上变量间线性依存关系的统计方法。
可以通过软件Matlab 实现。
1.利用Matlab 软件实现在Matlab 中,可以直接调用命令实现回归分析,(1)[b,bint,r,rint,stats]=regress(y,x),其中 b 是回归方程中的参数估计值,bint 是b的置信区间,r和rint分别表示残差及残差对应的置信区间。
stats包含三个数字,分别是相关系数,F统计量及对应的概率p值。
(2)recplot(r,rint)作残差分析图。
(3)rstool(x,y)一种交互式方式的句柄命令。
以下通过具体的例子来说明。
例现有多个样本的因变量和自变量的数据,下面我们利用Matlab,通过回归分析建立两者之间的回归方程。
% 一元回归分析x=[1097 1284 1502 1394 1303 1555 1917 2051 2111 2286 2311 2003 2435 2625 2948 3, 55 3372];%自变量序列数据y=[698 872 988 807 738 1025 1316 1539 1561 1765 1762 1960 1902 2013 2446 2736 2825];%因变量序列数据X=[ones(size(x')),x'],pause [b,bint,r,rint,stats]=regress(y',X,,pause% 调用一元回归分析函数rcoplot(r,rint)% 画出在置信度区间下误差分布。
% 多元回归分析% 输入各种自变量数据x1=[ 8 3 3 8 9 4 5 6 5 8 6 4 7]';x2=[31 55 67 50 38 71 30 56 42 73 60 44 50 39 55 70 40 50 62 59]';x3=[10 8 12 7 8 12 12 5 8 5 11 12 6 10 10 6 11 11 9 9]';x4=[8 6 9 16 15 17 8 10 4 16 7 12 6 4 4 14 6 8 13 11]'; %输入因变量数据y=[ 160 155 195]'; X=[ones(size(x1)),x1,x2,x3,x4];[b,bint,r,rint,stats]=regress(y,X)% 回归分析Q=r'*rsigma=Q/18rcoplot(r,rint);%逐步回归X1=[x1,x2,x3,x4];stepwise(X1,y,[1,2,3])% 逐步回归% X2=[ones(size(x1)),x2,x3];% X3=[ones(size(x1)),x1,x2,x3];% X4=[ones(size(x1)),x2,x3,x4];% [b1,b1int,r1,r1int,stats1]=regress(y,X2)% [b2,b2int,r2,r2int,stats2]=regress(y,X3);% [b3,b3int,r3,r3int,stats3]=regress(y,X4);。
用MATLAB求解回归分析课件

用Matlab求解 回归分析课件
目 录
• 回归分析简介 • Matlab基础操作 • 线性回归分析 • 非线性回归分析 • 多元回归分析 • Matlab在回归分析中的应用实例
01
CATALOGUE
回归分析简介
回归分析的定义
回归分析是一种统计学方法,用于研 究自变量和因变量之间的相关关系, 并建立数学模型来预测因变量的值。
显著性检验
对回归模型的显著性进行检验,如F 检验、t检验等。
预测精度评估
使用均方误差、均方根误差等指标评 估模型的预测精度。
可解释性
评估模型的解释性,即模型是否易于 理解,自变量对因变量的影响是否合 理。
06
CATALOGUE
Matlab在回归分析中的应用实例
用Matlab进行线性回归分析的实例
迭代法
对于一些复杂的回归模型,可能 需要使用迭代法进行求解,如梯 度下降法、牛顿法等。
Matlab函数
在Matlab中,可以使用内建的回 归分析函数来求解多元回归模型 ,如 `fitlm`、`fitlm2` 等。
多元回归模型的评估
残差分析
对回归模型的残差进行分析,检查残 差是否满足正态分布、同方差等假设 。
要点一
总结词
要点二
详细描述
多元回归分析是处理多个自变量和因变量之间关系的回归 分析方法,通过Matlab可以方便地进行多元回归分析。
在Matlab中,可以使用`fitlm`函数对一组数据进行多元回 归分析。首先需要准备数据,然后使用`fitlm`函数拟合多 元线性模型,最后通过模型进行预测和评估。
THANKS
使用预测值与实际值之间的误差评估模型的预测 能力,如均方误差、平均绝对误差等指标。
(完整word版)用matlab做一元线性回归分析(word文档良心出品)

用matlab做一元线性回归分析一元线性回归分析是在排除其他影响因素的假定其他影响因素确定的情况下,分析某一个因素(自变量)是如何影响另外一个事物(因变量)的过程,所进行的分析是比较理想化的。
用SPSS可以做一元线性回归分析,但是当回归的自变量比较多的时候,一个一个的输入会比较麻烦,增加了计算量,本文中描述了如何用matlab语言来实现一元线性回归分析。
在matlab中,regress命令是用来做回归的。
假如有96个SNP,作为自变量,有一个因变量,比如说HDL,LDL等等,将它们以列导入matlab。
值得注意的是:自变量前面必须有一列全为1的数据,看下面例子即可理解。
for i=1:96z=[ones(2334,1), x(:,i)];[b,bint,r,rint,stats]=regress(y,z);c(i,:)=stats;end在一元线性回归方程中,回归方程的显著性检验可以替代回归系数的显著性检验,并且F=T2百度中的一个例子:X=[1 1 4 6 8 11 14 17 21]'Y=[2.49 3.30 3.68 12.20 27.04 61.10 108.80 170.90 275.50]' X=[ones(9,1), X][b,bint,r,rint,stats]= regress(Y,X)输出向量b,bint为回归系数估计值和它们的置信区间,r,rint 为残差及其置信区间,stats是用于检验回归模型的统计量,有三个数值,第一个是R2,其中R是相关系数,第二个是F统计量值,第三个是与统计量F对应的概率P,当P<α时拒绝H0,回归模型成立regressMultiple linear regressionSyntaxb = regress(y,X)[b,bint] = regress(y,X)[b,bint,r] = regress(y,X)[b,bint,r,rint] = regress(y,X)[b,bint,r,rint,stats] = regress(y,X)[...] = regress(y,X,alpha)Descriptionb = regress(y,X) returns the least squares fit of y on X by solving the linear modelfor β, where:y is an n-by-1 vector of observationsX is an n-by-p matrix of regressorsβ is a p-by-1 vector of parametersɛ is an n-by-1 vector of random disturbances[b,bint] = regress(y,X) returns a matrix bint of 95% confidence intervals for β.[b,bint,r] = regress(y,X) returns a vector, r of residuals.[b,bint,r,rint] = regress(y,X) returns a matrix rint of intervals that can be used to diagnose outliers. If rint(i,:) does not contain zero, then the ith residual is larger than would be expected, at the 5% significance level. This is evidence that the ith observation is an outlier.[b,bint,r,rint,stats] = regress(y,X) returns a vector stats that contains the R2 statistic, the F statistic and a p value for the full model, and an estimate of the error variance.。
利用MATLAB进行多元线性回归

n=30;m=3;
y=[144 215 138 145 162 142 170 124
158 154 162 150 140 110 128 130
135 114 116 124 136 142 120 120
160 158 144 130 125 175];
x1=[39 47 45 47 65 46 67 42
67
56 64 56
59
34
42
48
45 18 20 19 36 50 39 21
44
53
63
29
25
69];
x2=[24.2 31.1 22.6 24.0 25.9 25.1 29.5 19.7 27.2 19.3 28.0 25.8 27.3
20.1 21.7 22.2 27.4 18.8 22.6 21.5 25.0 26.2 23.5 20.3 27.1 28.6 28.3
yˆ 58.5101 0.4303 x1 2.3449 x2 10.3065 x3
通常,进行多元线性回归的步骤如下:
(1)做自变量与因变量的散点图,根据散点图的形 状决定是否可以进行线性回归;
(2)输入自变量与因变量;
(3)利用命令: [b,bint,r,rint,s]=regress(y,X,alpha),rcoplot(r,rint) 得到回归模型的系数以及异常点的情况;
剔除异常点 (第2点和第 10点)后
回归系数
0 1 2 3
R2= 0.8462
回归系数估计值 回归系数置信区间
58.5101
[29.9064 87.1138]
0.4303
[0.1273 0.7332]
MATLAB回归分析

MATLAB回归分析回归分析是一种通过建立数学模型来研究变量之间的关系的统计方法。
在MATLAB中,我们可以使用回归分析工具箱来进行回归分析。
回归分析的目标是找到一个能够最好地描述自变量和因变量之间关系的数学模型。
在这篇文章中,我们将介绍回归分析的基本原理、MATLAB中的回归分析工具箱的使用以及如何解释回归分析的结果。
回归分析的基本原理回归分析建立在线性回归的基础上。
线性回归假设因变量与自变量之间存在一个线性关系。
回归分析通过找到最佳拟合线来描述这种关系。
最常用的回归方程是一元线性回归方程,它可以表示为:y=β0+β1x+ε,其中y是因变量,x是自变量,β0和β1是回归系数,ε是误差项。
- regress函数:用于计算多元线性回归模型,并返回回归系数、截距和残差。
例如,[B, BINT, R]=regress(y, X)用于计算因变量y和自变量矩阵X之间的回归模型。
- fitlm函数:用于拟合线性回归模型并返回拟合对象。
例如,mdl= fitlm(X, y)用于拟合因变量y和自变量矩阵X之间的线性回归模型,并返回mdl拟合对象。
- plot函数:用于绘制回归分析的结果。
例如,plot(mdl)用于绘制fitlm函数返回的拟合对象mdl的结果。
- coefCI函数:用于计算回归系数的置信区间。
例如,CI =coefCI(mdl)用于计算拟合对象mdl中回归系数的置信区间。
解释回归分析的结果回归分析的结果通常包括拟合曲线、回归系数以及模型的可靠性指标。
拟合曲线描述了自变量和因变量之间的关系。
回归系数可以用来解释自变量对因变量的影响。
模型的可靠性指标包括截距、回归系数的显著性检验以及相关系数等。
拟合曲线可以通过调用plot函数来绘制。
回归系数可以通过调用coef函数来获取。
对回归系数的显著性检验可以利用置信区间来判断,如果置信区间包含0,则说明回归系数不显著。
相关系数可以通过调用corrcoef函数来计算。
用MATLAB求解回归分析-文档资料

多元线性回归
y x ... x 0 1 1 p p
1、确定回归系数的点估计值:
b=regress( Y, X )
ˆ 0 ˆ b 1 .. ˆ p
Y1 Y Y 2 ... Y n
3、残差分析,作残差图: rcoplot(r,rint) 从残差图可以看出,除第二个数据外,其余数据的残 差离零点均较近,且残差的置信区间均包含零点,这说明 回归模型 y=-16.073+0.7194x能较好的符合原始数据,而第 二个数据可视为异常点.
Residual Case Order Plot 4
方法一
直接作二次多项式回归: t=1/30:1/30:14/30; s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48]; [p,S]=polyfit(t,s,2) 得回归模型为 : 2 ˆ s 489 . 2946 t 65 . 8896 t 9 . 1329
1 x1 1 x1 2 1 x x2 2 21 X ... ... ... 1 xn1 xn2
... x1 p ... x2 p ... ... ... xn p
对一元线性回归,取p=1即可。
2、求回归系数的点估计和区间估计、并检验回归模型: [b, bint,r,rint,stats]=regress(Y,X,alpha)
法二 化为多元线性回归: t=1/30:1/30:14/30; s=[11.86 15.67 20.60 26.69 33.71 41.93 51.13 61.49 72.90 85.44 99.08 113.77 129.54 146.48]; T=[ones(14,1) t' (t.^2)']; [b,bint,r,rint,stats]=regress(s',T); b,stats 得回归模型为 : 2 ˆ s 9 . 1329 65 . 8896 t 489 . 2946 t
matlab线性回归

matlab线性回归⼀、多元线性回归多元线性回归:1、b=regress(Y, X )确定回归系数的点估计值2、[b, bint,r,rint,stats]=regress(Y,X,alpha)求回归系数的点估计和区间估计、并检验回归模型①bint表⽰回归系数的区间估计.②r表⽰残差③rint表⽰置信区间④stats表⽰⽤于检验回归模型的统计量,有三个数值:相关系数r2、F值、与F对应的概率p 说明:相关系数r2越接近1,说明回归⽅程越显著;时拒绝H0,F越⼤,说明回归⽅程越显著;与F对应的概率p<α时拒绝H0⑤alpha表⽰显著性⽔平(缺省时为0.05)3、rcoplot(r,rint)画出残差及其置信区间具体参见下⾯的实例演⽰4、实例演⽰,函数使⽤说明(1)输⼊数据12>>x=[143 145 146 147 149 150 153 154 155 156 157 158 159 160 162 164]';3>>X=[ones(16,1) x];4>>Y=[88 85 88 91 92 93 93 95 96 98 97 96 98 99 100 102]';复制代码(2)回归分析及检验56>> [b,bint,r,rint,stats]=regress(Y,X)78 b =910-16.0730110.7194121314bint =1516-33.7071 1.5612 170.6047 0.8340 181920r =2122 1.205623-3.233124-0.952425 1.3282260.889527 1.170228-0.9879290.2927300.573431 1.8540320.134733-1.584734-0.304035-0.023436-0.4621370.0992383940rint =4142-1.2407 3.6520 43-5.0622 -1.4040 44-3.5894 1.6845 45-1.2895 3.9459 46-1.8519 3.6309 47-1.5552 3.8955 48-3.7713 1.7955 49-2.5473 3.1328 50-2.2471 3.393951-0.7540 4.462152-2.6814 2.950853-4.2188 1.049454-3.0710 2.463055-2.7661 2.719356-3.1133 2.189257-2.4640 2.6624585960stats =61620.9282 180.9531 0.0000 1.7437复制代码运⾏结果解读如下参数回归结果为对应的置信区间分别为[-33.7017,1.5612]和[0.6047,0.834]r2=0.9282(越接近于1,回归效果越显著),F=180.9531,p=0.0000,由p<0.05, 可知回归模型y=-16.073+0.7194x成⽴(3)残差分析作残差图6364rcoplot(r,rint)复制代码从残差图可以看出,除第⼆个数据外,其余数据的残差离零点均较近,且残差的置信区间均包含零点,这说明回归模型y=-16.073+0.7194x能较好的符合原始数据,⽽第⼆个数据可视为异常点。
利用Matlab进行线性回归分析之欧阳治创编

利用Matlab进行线性回归分析回归分析是处理两个及两个以上变量间线性依存关系的统计方法。
可以通过软件Matlab实现。
1.利用Matlab软件实现在Matlab中,可以直接调用命令实现回归分析,(1)[b,bint,r,rint,stats]=regress(y,x),其中b是回归方程中的参数估计值,bint是b的置信区间,r和rint分别表示残差及残差对应的置信区间。
stats包含三个数字,分别是相关系数,F统计量及对应的概率p值。
(2)recplot(r,rint)作残差分析图。
(3)rstool(x,y)一种交互式方式的句柄命令。
以下通过具体的例子来说明。
例现有多个样本的因变量和自变量的数据,下面我们利用Matlab,通过回归分析建立两者之间的回归方程。
% 一元回归分析x=[1097 1284 1502 1394 1303 1555 1917 2051 2111 2286 2311 2003 2435 2625 2948 3, 55 3372];%自变量序列数据y=[698 872 988 807 738 1025 1316 1539 1561 1765 1762 1960 1902 2013 2446 2736 2825];%因变量序列数据X=[ones(size(x')),x'],pause[b,bint,r,rint,stats]=regress(y',X,0.05),pause%调用一元回归分析函数rcoplot(r,rint)%画出在置信度区间下误差分布。
% 多元回归分析% 输入各种自变量数据x1=[5.5 2.5 8 3 3 2.9 8 9 4 6.5 5.5 5 6 5 3.5 8 6 4 7.5 7]';x2=[31 55 67 50 38 71 30 56 42 73 60 44 50 39 55 704050 62 59]';x3=[10 8 12 7 8 12 12 5 8 5 11 12 6 10 10 6 11 11 9 9]';x4=[8 6 9 16 15 17 8 10 4 16 7 12 6 4 4 14 6 8 13 11]';%输入因变量数据y=[79.3 200.1 163.1 200.1 146.0 177.7 30.9 291.9 160 339.4 159.6 86.3 237.5 107.2 155 201.4 100.2 135.8 223.3 195]';X=[ones(size(x1)),x1,x2,x3,x4];[b,bint,r,rint,stats]=regress(y,X)%回归分析Q=r'*rsigma=Q/18rcoplot(r,rint);%逐步回归X1=[x1,x2,x3,x4];stepwise(X1,y,[1,2,3])%逐步回归%X2=[ones(size(x1)),x2,x3];%X3=[ones(size(x1)),x1,x2,x3];%X4=[ones(size(x1)),x2,x3,x4];%[b1,b1int,r1,r1int,stats1]=regress(y,X2)%[b2,b2int,r2,r2int,stats2]=regress(y,X3);%[b3,b3int,r3,r3int,stats3]=regress(y,X4);。
MATLAB数学实验第二版答案(胡良剑)之欧阳歌谷创编

数学实验答案欧阳歌谷(2021.02.01)Chapter 1Page20,ex1(5) 等于[exp(1),exp(2);exp(3),exp(4)](7) 3=1*3, 8=2*4(8) a为各列最小值,b为最小值所在的行号(10) 1>=4,false, 2>=3,false, 3>=2, ture, 4>=1,ture(11) 答案表明:编址第2元素满足不等式(30>=20)和编址第4元素满足不等式(40>=10)(12) 答案表明:编址第2行第1列元素满足不等式(30>=20)和编址第2行第2列元素满足不等式(40>=10)Page20, ex2(1)a, b, c的值尽管都是1,但数据类型分别为数值,字符,逻辑,注意a与c相等,但他们不等于b(2)double(fun)输出的分别是字符a,b,s,(,x,)的ASCII码Page20,ex3>> r=2;p=0.5;n=12;>> T=log(r)/n/log(1+0.01*p)Page20,ex4>> x=-2:0.05:2;f=x.^4-2.^x;>> [fmin,min_index]=min(f)最小值最小值点编址>> x(min_index)ans =0.6500 最小值点>> [f1,x1_index]=min(abs(f)) 求近似根--绝对值最小的点f1 =0.0328x1_index =24>> x(x1_index)ans =-0.8500>> x(x1_index)=[];f=x.^4-2.^x; 删去绝对值最小的点以求函数绝对值次小的点>> [f2,x2_index]=min(abs(f)) 求另一近似根--函数绝对值次小的点f2 =0.0630x2_index =65>> x(x2_index)ans =1.2500Page20,ex5>> z=magic(10)z =92 99 1 8 15 67 74 51 58 4098 80 7 14 16 73 55 57 64 414 81 88 20 22 54 56 63 70 4785 87 19 21 3 60 62 69 71 2886 93 25 2 9 61 68 75 52 3417 24 76 83 90 42 49 26 33 6523 5 82 89 91 48 30 32 39 6679 6 13 95 97 29 31 38 45 7210 12 94 96 78 35 37 44 46 5311 18 100 77 84 36 43 50 27 59>> sum(z)>> sum(diag(z))>> z(:,2)/sqrt(3)>> z(8,:)=z(8,:)+z(3,:)Chapter 2Page 45 ex1先在编辑器窗口写下列M函数,保存为eg2_1.m function [xbar,s]=ex2_1(x)n=length(x);xbar=sum(x)/n;s=sqrt((sum(x.^2)-n*xbar^2)/(n-1));例如>>x=[81 70 65 51 76 66 90 87 61 77];>>[xbar,s]=ex2_1(x)Page 45 ex2s=log(1);n=0;while s<=100n=n+1;s=s+log(1+n);endm=nPage 40 ex3clear;F(1)=1;F(2)=1;k=2;x=0;e=1e-8; a=(1+sqrt(5))/2;while abs(x-a)>ek=k+1;F(k)=F(k-1)+F(k-2); x=F(k)/F(k-1); enda,x,k计算至k=21可满足精度Page 45 ex4clear;tic;s=0;for i=1:1000000s=s+sqrt(3)/2^i;ends,toctic;s=0;i=1;while i<=1000000s=s+sqrt(3)/2^i;i=i+1;ends,toctic;s=0;i=1:1000000;s=sqrt(3)*sum(1./2.^i);s,tocPage 45 ex5t=0:24;c=[15 14 14 14 14 15 16 18 20 22 23 25 28 ...31 32 31 29 27 25 24 22 20 18 17 16];plot(t,c)Page 45 ex6(1)x=-2:0.1:2;y=x.^2.*sin(x.^2-x-2);plot(x,y)y=inline('x^2*sin(x^2-x-2)');fplot(y,[-2 2]) (2)参数方法t=linspace(0,2*pi,100);x=2*cos(t);y=3*sin(t); plot(x,y)(3)x=-3:0.1:3;y=x;[x,y]=meshgrid(x,y);z=x.^2+y.^2;surf(x,y,z)(4)x=-3:0.1:3;y=-3:0.1:13;[x,y]=meshgrid(x,y);z=x.^4+3*x.^2+y.^2-2*x-2*y-2*x.^2.*y+6;surf(x,y,z)(5)t=0:0.01:2*pi;x=sin(t);y=cos(t);z=cos(2*t);plot3(x,y,z)(6)theta=linspace(0,2*pi,50);fai=linspace(0,pi/2,20); [theta,fai]=meshgrid(theta,fai);x=2*sin(fai).*cos(theta);y=2*sin(fai).*sin(theta);z=2*cos(fai);surf(x,y,z)(7)x=linspace(0,pi,100);y1=sin(x);y2=sin(x).*sin(10*x);y3=-sin(x);plot(x,y1,x,y2,x,y3)page45, ex7x=-1.5:0.05:1.5;y=1.1*(x>1.1)+x.*(x<=1.1).*(x>=-1.1)-1.1*(x<-1.1);plot(x,y)page45,ex9clear;close;x=-2:0.1:2;y=x;[x,y]=meshgrid(x,y);a=0.5457;b=0.7575;p=a*exp(-0.75*y.^2-3.75*x.^2-1.5*x).*(x+y>1);p=p+b*exp(-y.^2-6*x.^2).*(x+y>-1).*(x+y<=1);p=p+a*exp(-0.75*y.^2-3.75*x.^2+1.5*x).*(x+y<=-1); mesh(x,y,p)page45, ex10lookfor lyapunovhelp lyap>> A=[1 2 3;4 5 6;7 8 0];C=[2 -5 -22;-5 -24 -56;-22 -56 -16]; >> X=lyap(A,C)X =1.0000 -1.0000 -0.0000-1.0000 2.0000 1.0000-0.0000 1.0000 7.0000Chapter 3Page65 Ex1>> a=[1,2,3];b=[2,4,3];a./b,a.\b,a/b,a\bans =0.5000 0.5000 1.0000ans =2 2 1ans =0.6552 一元方程组x[2,4,3]=[1,2,3]的近似解ans =0 0 00 0 00.6667 1.3333 1.0000矩阵方程[1,2,3][x11,x12,x13;x21,x22,x23;x31,x32,x33]=[2,4,3]的特解Page65 Ex 2(1)>> A=[4 1 -1;3 2 -6;1 -5 3];b=[9;-2;1];>> rank(A), rank([A,b]) [A,b]为增广矩阵ans =3ans =3 可见方程组唯一解>> x=A\bx =2.38301.48942.0213(2)>> A=[4 -3 3;3 2 -6;1 -5 3];b=[-1;-2;1];>> rank(A), rank([A,b])ans =3ans =3 可见方程组唯一解>> x=A\bx =-0.4706-0.2941(3)>> A=[4 1;3 2;1 -5];b=[1;1;1];>> rank(A), rank([A,b])ans =2ans =3 可见方程组无解>> x=A\bx =0.3311-0.1219 最小二乘近似解(4)>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1 2 3]';%注意b的写法>> rank(a),rank([a,b])ans =3ans =3 rank(a)==rank([a,b])<4说明有无穷多解>> a\bans =110 一个特解Page65 Ex3>> a=[2,1,-1,1;1,2,1,-1;1,1,2,1];b=[1,2,3]';>> x=null(a),x0=a\bx =-0.62550.6255-0.20850.4170x0 =11通解kx+x0Page65 Ex 4>> x0=[0.2 0.8]';a=[0.99 0.05;0.01 0.95];>> x1=a*x, x2=a^2*x, x10=a^10*x>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> x0=[0.8 0.2]';>> x=x0;for i=1:1000,x=a*x;end,xx =0.83330.1667>> [v,e]=eig(a)v =0.9806 -0.70710.1961 0.7071e =1.0000 00 0.9400>> v(:,1)./xans =1.17671.1767 成比例,说明x是最大特征值对应的特征向量Page65 Ex5用到公式(3.11)(3.12)>> B=[6,2,1;2.25,1,0.2;3,0.2,1.8];x=[25 5 20]';>> C=B/diag(x)C =0.2400 0.4000 0.05000.0900 0.2000 0.01000.1200 0.0400 0.0900>> A=eye(3,3)-CA =0.7600 -0.4000 -0.0500-0.0900 0.8000 -0.0100-0.1200 -0.0400 0.9100>> D=[17 17 17]';x=A\Dx =37.569625.786224.7690Page65 Ex 6(1)>> a=[4 1 -1;3 2 -6;1 -5 3];det(a),inv(a),[v,d]=eig(a)ans =-94ans =0.2553 -0.0213 0.04260.1596 -0.1383 -0.22340.1809 -0.2234 -0.0532v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766(2)>> a=[1 1 -1;0 2 -1;-1 2 0];det(a),inv(a),[v,d]=eig(a) ans =1ans =2.0000 -2.0000 1.00001.0000 -1.0000 1.00002.0000 -3.0000 2.0000v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> det(A),inv(A), [v,d]=eig(A)ans =1ans =68.0000 -41.0000 -17.0000 10.0000-41.0000 25.0000 10.0000 -6.0000-17.0000 10.0000 5.0000 -3.000010.0000 -6.0000 -3.0000 2.0000v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0 0 30.2887(4)(以n=5为例)方法一(三个for)n=5;for i=1:n, a(i,i)=5;endfor i=1:(n-1),a(i,i+1)=6;endfor i=1:(n-1),a(i+1,i)=1;enda方法二(一个for)n=5;a=zeros(n,n);a(1,1:2)=[5 6];for i=2:(n-1),a(i,[i-1,i,i+1])=[1 5 6];enda(n,[n-1 n])=[1 5];a方法三(不用for)n=5;a=diag(5*ones(n,1));b=diag(6*ones(n-1,1));c=diag(ones(n-1,1));a=a+[zeros(n-1,1),b;zeros(1,n)]+[zeros(1,n);c,zeros(n-1,1)] 下列计算>> det(a)ans =665>> inv(a)ans =0.3173 -0.5865 1.0286 -1.6241 1.9489-0.0977 0.4887 -0.8571 1.3534 -1.62410.0286 -0.1429 0.5429 -0.8571 1.0286-0.0075 0.0376 -0.1429 0.4887 -0.58650.0015 -0.0075 0.0286 -0.0977 0.3173>> [v,d]=eig(a)v =-0.7843 -0.7843 -0.9237 0.9860 -0.92370.5546 -0.5546 -0.3771 -0.0000 0.3771-0.2614 -0.2614 0.0000 -0.1643 0.00000.0924 -0.0924 0.0628 -0.0000 -0.0628-0.0218 -0.0218 0.0257 0.0274 0.0257d =0.7574 0 0 0 00 9.2426 0 0 00 0 0 0 2.5505Page65 Ex 7(1)>> a=[4 1 -1;3 2 -6;1 -5 3];[v,d]=eig(a)v =0.0185 -0.9009 -0.3066-0.7693 -0.1240 -0.7248-0.6386 -0.4158 0.6170d =-3.0527 0 00 3.6760 00 0 8.3766>> det(v)ans =-0.9255 %v行列式正常, 特征向量线性相关,可对角化>> inv(v)*a*v 验算ans =-3.0527 0.0000 -0.00000.0000 3.6760 -0.0000-0.0000 -0.0000 8.3766>> [v2,d2]=jordan(a) 也可用jordanv2 =0.0798 0.0076 0.91270.1886 -0.3141 0.1256-0.1605 -0.2607 0.4213 特征向量不同d2 =8.3766 0 00 -3.0527 - 0.0000i 00 0 3.6760 + 0.0000i>> v2\a*v2ans =8.3766 0 0.00000.0000 -3.0527 0.00000.0000 0.0000 3.6760>> v(:,1)./v2(:,2) 对应相同特征值的特征向量成比例ans =2.44912.44912.4491(2)>> a=[1 1 -1;0 2 -1;-1 2 0];[v,d]=eig(a)v =-0.5773 0.5774 + 0.0000i 0.5774 - 0.0000i-0.5773 0.5774 0.5774-0.5774 0.5773 - 0.0000i 0.5773 + 0.0000id =1.0000 0 00 1.0000 + 0.0000i 00 0 1.0000 - 0.0000i>> det(v)ans =-5.0566e-028 -5.1918e-017i v的行列式接近0, 特征向量线性相关,不可对角化>> [v,d]=jordan(a)v =1 0 11 0 01 -1 0d =1 1 00 1 10 0 1 jordan标准形不是对角的,所以不可对角化(3)>> A=[5 7 6 5;7 10 8 7;6 8 10 9;5 7 9 10]A =5 76 57 10 8 76 8 10 95 7 9 10>> [v,d]=eig(A)v =0.8304 0.0933 0.3963 0.3803-0.5016 -0.3017 0.6149 0.5286-0.2086 0.7603 -0.2716 0.55200.1237 -0.5676 -0.6254 0.5209d =0.0102 0 0 00 0.8431 0 00 0 3.8581 00 0 0 30.2887>> inv(v)*A*vans =0.0102 0.0000 -0.0000 0.00000.0000 0.8431 -0.0000 -0.0000-0.0000 0.0000 3.8581 -0.0000-0.0000 -0.0000 0 30.2887本题用jordan不行, 原因未知(4)参考6(4)和7(1)Page65 Exercise 8只有(3)对称, 且特征值全部大于零, 所以是正定矩阵. Page65 Exercise 9(1)>> a=[4 -3 1 3;2 -1 3 5;1 -1 -1 -1;3 -2 3 4;7 -6 -7 0] >> rank(a)ans =3>> rank(a(1:3,:))ans =2>> rank(a([1 2 4],:)) 1,2,4行为最大无关组ans =3>> b=a([1 2 4],:)';c=a([3 5],:)';>> b\c 线性表示的系数ans =0.5000 5.0000-0.5000 1.00000 -5.0000Page65 Exercise 10>> a=[1 -2 2;-2 -2 4;2 4 -2]>> [v,d]=eig(a)v =0.3333 0.9339 -0.12930.6667 -0.3304 -0.6681-0.6667 0.1365 -0.7327d =-7.0000 0 00 2.0000 00 0 2.0000>> v'*vans =1.0000 0.0000 0.00000.0000 1.0000 00.0000 0 1.0000 v确实是正交矩阵Page65 Exercise 11设经过6个电阻的电流分别为i1, ..., i6. 列方程组如下20-2i1=a; 5-3i2=c; a-3i3=c; a-4i4=b; c-5i5=b; b-3i6=0; i1=i3+i4;i5=i2+i3;i6=i4+i5;。
(研究生 数理统计)多元线性回归及显著性检验Matlab程序(完美版)之欧阳引擎创编

多元线性回归及显著性检验Matlab程序(完美版)欧阳引擎(2021.01.01)一、说明:1、本程序是研究生教材《数理统计》(杨虎、刘琼、钟波编著)例4.4.1(P133)的Matlab编程解答程序。
教材上的例题只做了回归方程显著性分析和一次回归系数显著性分析(剔除x1后没有再检验x2和x3)。
2、本程序在以上的基础之上,还分别检验了x2和x3,并且计算精度更高。
3、本程序可根据用户的需要,在输入不同的显著性水平α之下得到相应的解答。
4、本程序移植性强,对于其他数据,只需要改变excel中的数据即可。
5、本程序输出的可读性强,整洁美观。
二、数据入下(将数据存入excel表格,文件名为jc_p133_example.xls。
注意数据是按x1,x2,…,xk,y这样来列来存储。
若不是3个变量,则相应增减数据列就行。
):三、完整程序如下:%----------------------------by ggihhimm----------------------------%《数理统计》杨虎、刘琼、钟波编著例4.4.1 多元线性回归及显著性检验完整解答% 输入需要的显著水平α(默认α=0.02),计算出不同结果(见运行结果)% 该程序也适合其他维数的数据分析(只需改变excel表格中的数据即可)%----------------------------by ggihhimm----------------------------clear;clc;data=xlsread('jc_p133_example.xls','sheet1');xi=data(:,1:end-1);[n,k]=size(data);k=k-1;index_of_xi_array=ones(1,k);X=[ones(n,1) xi];Y=data(:,end);fprintf('第1次计算结果:\r')beta_mao=((X'*X)\X'*Y)';fmt_str0='';for i0=1:k+1fmt_str0=[fmt_str0 'β' num2str(i0-1) ' = %0.4f\r'];endfprintf(fmt_str0,beta_mao)fprintf('\r')%%检验回归方程的显著性x_ba=mean(xi);y_ba=mean(Y);St_square=sum(Y.^2)-n*y_ba^2;lxy=sum((xi-ones(n,1)*x_ba).*((Y-y_ba)*ones(1,k)));Sr_square=sum(beta_mao(2:end).*lxy);Se_square=St_square-Sr_square;c_flag=Sr_square/Se_square;F_alpha=input('>>>>>>请输入您要求的显著性水平(0<α<1)α= '); while ~(isscalar(F_alpha) && F_alpha<1 && F_alpha>0)F_alpha=input('您的输入有误,请重新输入一个大于0,小于1的数,α= ');endF_fenweidian=finv(1-F_alpha,k,n-k-1);c=k/(n-k-1)*F_fenweidian;if c_flag>cfprintf(['\r--------------------回归方程显著性检验(H0:β1=β2=...=βk=0)' ...'--------------------\r经过计算:拒绝H0,原假设不成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
利用Matlab进行线性回归分析
欧阳歌谷(2021.02.01)
回归分析是处理两个及两个以上变量间线性依存关系的统计方法。
可以通过软件Matlab实现。
1.利用Matlab软件实现
在Matlab中,可以直接调用命令实现回归分析,
(1)[b,bint,r,rint,stats]=regress(y,x),其中b是回归方程中的参数估计值,bint是b的置信区间,r和rint分别表示残差及残差对应的置信区间。
stats包含三个数字,分别是相关系数,F统计量及对应的概率p值。
(2)recplot(r,rint)作残差分析图。
(3)rstool(x,y)一种交互式方式的句柄命令。
以下通过具体的例子来说明。
例现有多个样本的因变量和自变量的数据,下面我们利用Matlab,通过回归分析建立两者之间的回归方程。
% 一元回归分析
x=[1097 1284 1502 1394 1303 1555 1917 2051 2111 2286 2311
2003 2435 2625 2948 3, 55 3372];%自变量序列数据
y=[698 872 988 807 738 1025 1316 1539 1561 1765 1762 1960 1902 2013 2446 2736 2825];%因变量序列数据
X=[ones(size(x')),x'],pause
[b,bint,r,rint,stats]=regress(y',X,0.05),pause%调用一元回归分析函数rcoplot(r,rint)%画出在置信度区间下误差分布。
% 多元回归分析
% 输入各种自变量数据
x1=[5.5 2.5 8 3 3 2.9 8 9 4 6.5 5.5 5 6 5 3.5 8 6 4 7.5 7]';
x2=[31 55 67 50 38 71 30 56 42 73 60 44 50 39 55 7040 50 62 59]';
x3=[10 8 12 7 8 12 12 5 8 5 11 12 6 10 10 6 11 11 9 9]';
x4=[8 6 9 16 15 17 8 10 4 16 7 12 6 4 4 14 6 8 13 11]';
%输入因变量数据
y=[79.3 200.1 163.1 200.1 146.0 177.7 30.9 291.9 160 339.4 159.6 86.3 237.5 107.2 155 201.4 100.2 135.8 223.3 195]';
X=[ones(size(x1)),x1,x2,x3,x4];
[b,bint,r,rint,stats]=regress(y,X)%回归分析
Q=r'*r
sigma=Q/18
rcoplot(r,rint);
%逐步回归
X1=[x1,x2,x3,x4];
stepwise(X1,y,[1,2,3])%逐步回归
%X2=[ones(size(x1)),x2,x3];
%X3=[ones(size(x1)),x1,x2,x3];
%X4=[ones(size(x1)),x2,x3,x4];
%[b1,b1int,r1,r1int,stats1]=regress(y,X2) %[b2,b2int,r2,r2int,stats2]=regress(y,X3); %[b3,b3int,r3,r3int,stats3]=regress(y,X4);。
