厦门大学网络教育第一学期考试真题线性代数.doc
厦门大学线性代数2014.4.13线代期中(A类)试卷

一.计算题(共50分)1.(6分)设521320,341201A B--⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦,计算(1)TAB,(2)T B A.2.(6分)计算四阶行列式0102312713134151A--=----.3.(6分)当参数,a b满足什么条件时,线性方程组1234123412341, 4351,33x x x xx x x xax x x bx+++=-⎧⎪++-=-⎨⎪+++=⎩无解.厦门大学《线性代数A》课程期中考试卷学院___年级___姓名____学号____主考教师:试卷类型:(A卷) 2014.4.134. (6分)设A 为三阶矩阵,1A =-,求()1*22A A -+.5. (6分)设11221511061A λλ-⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦,已知()2R A =,求λ的值.6. (6分)设A 为三阶矩阵,2A =-,把矩阵A 按列分块为[]123=,,A A A A ,其中()1,2,3j A j =是A 的第j 列,求31214,4,3A A A A --.7. (6分)设矩阵21234131A t -⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦,若存在三阶矩阵0B ≠满足0AB =,求参数t 和B .8.(8分)已知A 和B 均为三阶矩阵,将A 的第三行的-2倍加至第2行得到矩阵1A ,将B中第2列加至第1列得到矩阵1B ,又知11111022003A B ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,求AB .二. (10分)计算121111100100(0,1,2,,)100i n a A a a i n a =≠=.三.(20分) 设n 阶矩阵A 和B 满足条件124B A A E -=-,其中E 为n 阶单位矩阵.(1)证明2B E -为可逆矩阵,并求()12B E --; (2)已知120120002A -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦,求B .四.(15分)令111111k A k k ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦ ,121k β-⎡⎤⎢⎥=-⎢⎥⎢⎥-⎣⎦, 问k 为何值时 (1) 线性方程组Ax β=无解;(2)线性方程组Ax β=有唯一解;(3)线性方程组Ax β=有无穷多解,并求其通解.五. (5分)设33ij A a ⨯⎡⎤=⎣⎦ 为实矩阵,满足条件:(1)(),1,2,3ij ij a A i j ==,其中ij A 是元素ij a 的代数余子式;(2)331a =-.求线性方程组123001x A x x ⎡⎤⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦的解.。
厦门大学网络教育2019《经济数学基础 上)》课程复习题单项选择题

厦门大学网络教育2019-2020学年第一学期单选题1.设xxeexf11321)(++=,则0x=是()f x的(B).B. 第一类间断点(跳跃间断点)2.设数列nx与ny满足lim0n nnx y→∞=,则下列断言正确的是(D).D. 若1nx为无穷小,则ny必为无穷小3.设321,0()00xexf x xx⎧-⎪≠=⎨⎪=⎩,则在0x=处,()f x的导数( C ).C.-14.函数32()f x x ax bx=++在1x=处取极小值-2,则( B. 0,3a b==- ).5.曲线2y x=在其上横坐标为1x=的点处切线的斜率是( A. 2 ).6."()xf x dx=⎰( C'()()xf x f x C-+7.设1211,1,()101,xxe xf x xx-⎧-≠⎪=-⎨⎪=⎩则1x=是()f x的( D. 第二类间断点8.已知2lim()01xxax bx→∞--=+,其中a,b是常数,则(C. 1a=,1b=-9.设,0(),0xe xf xa x x⎧<=⎨+≥⎩在0x=处连续,则a= ( B. 1 ).10.函数2()21f x x x=-+在区间[]1,3-上满足拉格朗日中值定理,定理中的ξ=( D. 11.3211()6132f x x x x=+++的图形在点(0,1)处切线与x轴交点坐标是( A.1,06⎛⎫- ⎪⎝⎭2.设函数()f x连续,ln1()()xxF x f t dt=⎰,则'()F x=( A.2111(ln)()f x fx x x+3.函数cos()sin xy f x x x e==(x R∈)是( D. 偶函数4. 下列极限存在的是( A.2(1)limxx xx→∞+5.设2221121txttyt⎧-=⎪⎪+⎨⎪=⎪+⎩,则dydx=(A212tt-6.曲线21xy e-=与直线1x=-在交点p处的切线方程为( A .230x y-+=7.点(1,2)是曲线3()y x a b=-+的拐点,则( C) 1,2a b==8.函数⎪⎩⎪⎨⎧>=<-=,0,1,0,0,0,1)(xxxxf在[-1,1]上( D不存在原函数1.函数)(xf xx cossin+=是( )函数)(xf=sin x+cos x 是A.奇函数B.偶函数C.非奇非偶函数D.既是奇函数又是偶函数2.下列各对函数中,为同一函数的是()A.;ln2)ln(2xyxy==与B.xyxy tan2)2tan(==与;C.2)(xyxy==与;D.1112+-=-=xxyxy与。
(word版)厦门大学参考答案0809学年第一学期《高等代数》期末考试卷

08-09学年第一学期厦门大学?高等代数?期末试卷 厦门大学?高等代数?课程试卷数学科学学院各系2021年级各专业信息科学与技术学院 计算机科学 系2021年级CST 专业特别说明:答案写在答题纸上一、单项选择题〔32分.共8题,每题4分〕以下说法错误的选项是___B____.假设向量组1,2,3线性无关,那么其中任意两个向量线性无关;B ) 假设向量组1, 2,3 中任意两个向量线性无关,那么1,2,3线性无关;C) 向量组 1 2,2 3,3 1线性相关;D) 假设向量组1,2,3 线性无关,那么1, 1 2, 123线性无关.2. 设n 维列向量1,2,...,m (m n)线性无关,那么n 维列向量1,2,...,m线性无关的充要条件是___D____.A) 向量组 1,2,..., m 可由向量组1, 2,..., m 线性表示;B) 向量组 1, 2,..., m 可由向量组 1,2,..., m 线性表示;C) 向量组 1,2,..., m 与向量组 1, 2,...,m 等价;D)矩阵A (1, 2,..., m )与矩阵B (1, 2,..., m )相抵. 3.设线性方程组 Ax 0的解都是线性方程组 Bx 0的解,那么__C__.A)r(A) r(B);B)r(A) r(B);C)r(A) r(B);D)r(A) r(B).4. 设n 阶方阵A 的伴随矩阵 A * 0,非齐次线性方程组 Ax b 有无穷多组解,那么对应的齐次线性方程组Ax 0的根底解系__B__.A)不存在; B)仅含一个非零解向量;C)含有两个线性无关的解向量; D)含有三个线性无关的解向量 .以下子集能构成R 22的子空间的是___B____.A)122 } ;B)V2{A|tr(A)0,AR 22};V{A||A|0,AR108-09学年第一学期厦门大学?高等代数?期末试卷C)V 3 {A|A 2A,A R 22};D)V 4 {A|A A 或 A,A R 22}.6.设V 是数域K 上的线性空间,V 上的线性变换在基 1,2,...,n 下的矩阵为A 且|A|2,假设在基 n ,n1,...,1下的矩阵为B,那么|B|___B___.A)2n;B)2; C)1; D)不能确定.27.设V 是n 维向量空间, 和 是V 上的线性变换,那么 dimImdimIm的充分必要条件是_____D ___.A) 和都是可逆变换; B)Ker=Ker ;C)Im Im ;D) 和 在任一组基下的表示矩阵的秩相同.8. 设 是线性空间 V 到U 的同构映射,那么以下命题中正确的有 ___D___个.(Ⅰ) 为可逆线性映射;(Ⅱ)假设W 是V 的s 维子空间,那么(W )是U 的s 维子空间;(Ⅲ) 在给定基下的表示矩阵为可逆阵;(Ⅳ)假设V=V 1 V 2,那么(V 1V 2)(V 1)(V 2).A)1B)2C)3D)4二、填空题〔32分.共8题,每题4分〕1 0 0 3假设矩阵A( 1,2,3,0 0 2 4 1,2,3,4的1. 4)经过行初等变换化为1 0 ,那么向量组0 50 0一个极大无关组是1,2,3,其余向量由此极大无关组线性表示的表示式为4315223.2. 设3 维向量空间的一组基为1(1,1,0),2(1,0,1),3(0,1,1),那么向量 (2,0,0) 在这组基1下的坐标为1.13. 设V 1,V 2均为线性空间 V 的子空间,那么 L(V 1 V 2)V 1 V 2.208-09学年第一学期厦门大学?高等代数?期末试卷4. 数域K 上所有三阶反对称矩阵构成的线性空间的维数是 _3_.而E 12E 21,E13E 31,E 23E 32是它的一组基.5. K 12上的线性变换定义如下:((a,b))(0,a),那么Ker={(0,a)|aK}.Im={(0,a)|aK}.6. 设是数域K 上n 维线性空间 V 到m 维线性空间U 的线性映射, 那么为满射的充分必要条件是对任意 U,存在V,使得();Im U;dimImm;.〔请写出两个〕dimKer nm;在任意基下的矩阵都是行满秩的 ; 在某个基下的矩阵是行满秩的 〔.其中任两个均可〕7. 设1,2,...,n 和1, 2,..., n 是线性空间 V 的两组基,从 1,2,..., n到1,2,...,n 的过渡矩阵为P .假设 是V 上的线性变换且 (i ) i, i1,2,...,n ,那么 在基1, 2,..., n 下的表示矩阵是_P_.8. 设是线性空间V 上的线性变换,在基1, 2,...,n 下的表示矩阵为 A B ,其中A 为rr 矩C阵,那么存在V 的一个非平凡-不变子空间L(1,,r ).三、(8 分)设线性空间V 的向量组1,2,..., m 线性无关,V ,考虑向量组,1,2,...,m .求证:或者该向量组线性无关,或者 可由 1,2,...,m 线性表示.证明:假设,1,,m 线性相关,那么存在不全为0的数k 0,k 1,,k m 使得k 0+k 11+k mm0.我们断言,k 0 0.事实上,假设k 0=0,那么k 11+k mm 0.由1, 2,...,m 线性无关知k 1==k m =0.于是,k 0=k 1==k m =0.这与k 0,k 1, ,k m 不全为0相矛盾.因此,k 00.此时,k 1 k m m .1k 0k 0从而,或者该向量组线性无关,或者可由1, 2,..., m 线性表示.四、(10分)设V 1,V 2分别是数域K 上的齐次线性方程组x 1x 2x n 与x 1x 2x n 0的解空间.证明K n1V 1V 2.3a1证明:法一:一方面,a2V1V2,有a1a2a n,那么a1a2a n0.故a1a2a n0a nV1V20.n n n na1a i a ia1a i a i i1a i1i1a i1n1n n1na2K n1,存在a2另一方面,V1,V2,使得=+n n n na a i a i a n a i a ini1i1i1i1a n a nn n n n 即K n1V1V2.因此,K n1V1V2.a1法二:一方面,a2a1a2a n,那么a1a2a n0.故V1V20.V1V2,有a2a1a n0a n11000另一方面,由于V1为方程组Ax0的解空间,其中A 01100,V2为方程组00011(n1)nBx0的解空间,其中B(1,1,,1)1n,所以dimV11,dimV2n1.故dimV1dimV2dimK n1.从而,K n1V1V2.11000法三:一方面,由于V1为方程组Ax0的解空间,其中A 01100,V2为方00011(n1)n程组Bx0的解空间,其中B(1,1,,1)1n,所以dimV11,dimV2n1.故dimV1dimV2dimK n1.4nnnna 1a ia ia 1a ia ii1i1i 1i1na 1na 1a 2Kn1,存在na 2n另一方面,V 1,V 2,使得=+nnnna na ia ia na ia ii1i1i 1i1n a nna nnn即K n1V 1 V 2.因此,K n1V 1V 2.五、(10分)设AK mn .证明:r(A)r 的充分必要条件是存在BK mr,CK rn ,使得r(B)r(C)r 且ABC .证明: 充分性: 由于BK mr ,C K rn 满足r(B)r(C)r 且ABC ,所以rr(B)r(C)rr(A)r(BC)r(B)r故r(A)r .必要性: 由于r(A)r,所以存在m 阶可逆矩阵P 及n 阶可逆矩阵Q 使得AI r 0PQ .令BPI r ,C(I r ,0)Q,那么BK mr ,CKrn满足r(B)r(C)r 且ABC .六、(8分)设V,U,W 是有限维线性空间,:V U ,:WU 是线性映射.求证:存在线性映射:VW 使得的充分必要条件是 Im Im .证明: 充分性: 法一:取V 的一组基 1,2,, n ,由于ImIm,所以(i ) Im,1 in ,即存在iW 使得(i )(i ).定义线性映射:V W 满足(i )i,1in ,那么(i ) (i )( i ), 1 in .因此,.法二:取V 的一组基1,2,,n ,U 的一组基1,2,,m ,W 的一组基1,2,,s .设(1,2, ,n ) (1,2, ,m )A mn(1,2,,s )(1,2,,m )B ms5其中A(1,2,,n ),B(1,2, ,s ).由于ImIm ,所以L(1,2,s,n)L1(,2 ,s ,, 即)1 jn, jciji .取i1C(c ij )s n ,那么A BC .定义线性映射:V W 满足 (1, 2,, n )(1,2,, s )C ,那么.必要性: 对任意 Im,存在V 使得( ).由于,所以( )(())Im从而,ImIm.附加题:(本局部不计入总分)设V,U,W是有限维线性空间且dimVdimW ,:V U , :W U 是线性映射.证明:存在可逆线性映射:V W 使得的充分必要条件是 ImIm.证明:充分性:法一:由于dimVdWim 且Im Im ,所以由维数公式知:dimKerdimKe .r 取Ker的一组基1,2,,r ;Ker 的一组基1,2,, r ,将其扩充为V的一组基1,2,,r ,r1, n ,那么(r1),(n )是Im的一组基.由于Im Im ,所以(r 1),( n )是Im的一组基.设(i )( i ), r 1 i n ,由于 (r1), , (n )线性无关,所以r1,,n 线性无关.我们断言, 1, 2, ,r ,r1,,n 线性无关.事实上,假设k 11k 22krrk r1r 1knn0,那么将作用于上式得k r1(r1) k n (n )0.由于(r1), ,(n )线性无关,所以k r1k n 0.于是k 11 k 22k r r =0.又1, 2, , r 是Ker的一组基,故k 1k r从而,1, 2,,r ,r1,,n 线性无关.注意到dimW n ,故1,2,,r ,r1,,n 是W 的一组基.定义线性映射 :V W 满足(i )i ,1 i n .由于1,2,,n 是V 的一组基,1,2,,n 是W的一组基,故 可逆.又(i )( i)( i ), 1i n ,从而.法二:取V 的一组基1,2,, n ,U 的一组基1,2,,s ,W 的一组基1, 2,, n .设(1,2, ,n )(1,2,,s )A sn6(1,2,,n)(1,2,,s)B sn且dimIm dimIm r,那么r(A)r(B)r.于是,存在n阶可逆矩阵P,Q使得AP(A1,0), BQ(B1,0),其中A1,B1K sr列满秩.由于Im Im,所以同上题证明可知存在n阶矩阵C使得A BC,那么(A1,0)AP BQ(Q1CP).设Q1CP X11X12,其中X11是r阶方阵,那么X21X22(A1,0)(B1,0)X11X12.从而,A1B1X11.又A1列满秩,所以存在A2K rs使得A2A1I r.于X21X22是,I r A2A1(A2B1)X11,即X11是可逆矩阵.因此,存在可逆矩阵X Q X110P1使得0I n rBX BQ X110P1(B1,0)X110P1B1X11,0P1(A1,0)P1A0I nr0I nr定义线性映射:V W满足(1,2,,n)(1,2,,n)X由于X可逆且ABX,故可逆且.必要性:由于,所以同上题证明可知Im Im.又由:V W可逆可知1,所以Im Im.从而,Im Im.7。
厦门大学网络教育第一学期考试真题线性代数

1.下列排列中,()是四级奇排列。
A 43212.若(-1)。
是五阶行列式【。
】的一项,则k,l之值及该项符号为()B k=2,l=3,符号为负3.行列式【k-1 2。
】的充分必要条件是()C k不等于-1且k不等于34.若行列式D=【a11 a12 a13。
】=M不等于0,则D1=【2a11 2a12 2a13。
】=()C 8M5.行列式【0111】101111011110 =()D -36.当a=()时,行列式【-1 a 2…】=0B 17.如果行列式【a11 a12 a13 …】=d 则【3a31 3a32 3a33 …】=()B 6d8.当a=()时,行列式【a 1 1 …】=0A 19.行列式【125 64 27 8 。
】的值为()A 1210.行列式【a 0 0 b …】中g元素的代数余子式为()B bde-bcf11.设f(x)= 【1 1 2 。
】则f(x)=0的根为()C 1,-1,2,-212.行列式【0 a1 0…0。
】=()D (-1)n+1 a1 a2…an-1 an113.行列式【a 0 b 0…】=()D (ad-bc)(xv-yu)14.~不能取()时,方程组~X1+X2+X3=0…只有0解B 215.若三阶行列式D的第三行的元素依次为1,2,3它们的余子式分别为2,3,4,则D=()B 816.设行列式【a11 a12 a13…】=1,则【2a11 3a11-4a12 a13…】=()D -81.线性方程组x1+x2=1…解的情况是()A 无解2.若线性方程组AX=B的增广矩阵A经初等行变换化为A- 【1234…】,当~不等于()时,此线性方程组有唯一解B 0,13.已知n元线性方程组AX=B,其增广矩阵为A ,当()时,线性方程组有解。
C r(A)=r(A)4.设A为m*n矩阵,则齐次线性方程组AX=0仅有零解的充分条件是()A A的列向量线性无关5.非齐次线性方程组AX=B中,A和增广矩阵A的秩都是4,A是4*6矩阵,则下列叙述正确的是()B 方程组有无穷多组解6.设线性方程组AX=B有唯一解,则相应的齐次方程AX=0()C 只有零解7.线性方程组AX=0只有零解,则AX=B(B不等于0)B 可能无解8.设有向量组a1,a2,a3和向量BA1=(1,1,1) a2=(1,1,0) a3= (1,0,0) B=(0,3,1)则向量B由向量a1,a2,a3的线性表示是()A B=a1+2a2-3a39.向量组a1=(1.1.1)(0.2.5)(1.3.6)是()A 线性相关10.下列向量组线性相关的是()C (7.4.1),(-2.1.2),(3.6.5)11.向量组a1.a2…ar 线性无关的充要条件是()B 向量线的秩等于它所含向量的个数12.向量组B1.B2…Bt可由a1.a2…as线性表示出,且B1.B2…Bt线性无关,则s与t的关系为()D s≥t13.n个向量a1.a2…an线性无关,去掉一个向量an,则剩下的n-1个向量()B 线性无关14.设向量组a1.a2…as(s≥2)线性无关,且可由向量组B1.B2…Bs线性表示,则以下结论中不能成立的是()C 存在一个aj,向量组aj,b2…bs线性无关15.矩阵【1 0 1 0 0…】的秩为()A 516.向量组a1.a2…as(s≥2)线性无关的充分必要条件是()C a1.a2…as每一个向量均不可由其余向量线性表示17.若线性方程组的增广矩阵为A=【1.~.2】则~=()时,线性方程组有无穷多解。
2020-2021(1)《线性代数A》A卷参考答案
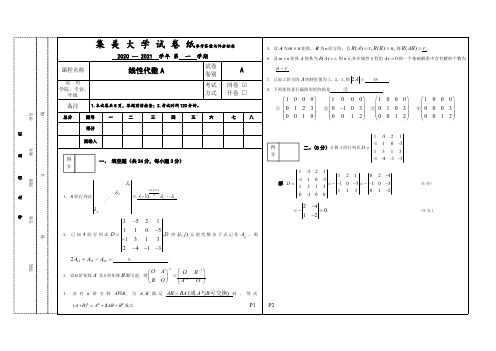
3 ,1)T . 2
(3) 当 k 1时 R( A) 1; 当 k 2 时 R( A) 2; 当 k 1且 k 2 时 R( A) 3.
(12 分) (15 分)
P5
x1 3x2 2x3 x4 3
得 分
六、(12
分)求非齐次线性方程组
x1 x1
x2 x2
x4 x3
1 2
五
六
七
八
得分
阅卷人
得
一、 填空题(共 24 分,每小题 3 分)
分
1. n 阶行列式
1
2
n ( n 1)
(1) 2 1n .
n
3 5 2 1
2. 已 知 4 阶 行 列 式 D 1 1 1 3
0 5 1 3 ,D 的 (i, j) 元 的 代 数 余 子 式 记 作 Aij , 则
2 4 1 3
学院
考 专业 装
生
信
息 姓名
班级
栏 学号 线
订
集 美 大 学 试 卷 纸参考答案与评分标准
2020 — 2021 学年 第 一 学期
课程名称
适用 学院、专业、
年级
线性代数 A
试卷 卷别
考试 方式
A
闭卷 □√ 开卷 □
备注
1.本试卷共 8 页,答题前请检查;2.考试时间 120 分钟。
总分
题号
一
二
三
四
生
信
息 姓名
班级
栏 学号 线
订
1 2 3k
得
五、(15
分)设矩阵
A
1 k
2k 2
3 3
,
分
(1)求行列式 A ;
厦门大学高等代数课程试卷

必要性。对矩阵
A,存在可逆矩阵
P,Q
使得 A =
P
æ ç
I
r
è
ö
0
÷ ø
Q
=
æ Pç
è
Ir 0
ö ÷ ø
(Ir
, 0)Q
。令
S
=
æ Pç
è
Ir 0
ö ÷ ø
,
T = (Ir , 0)Q ,可证 P,Q 即为所求。显然, S 和T 分别是 n ´ r 矩阵和 r ´ n 矩阵,且因 P,Q 可逆,所以
P,使得
P-1 AP
=
æ ç
Ir
è
ö
0
÷ ø
。令 S
=
æ Pç
è
Ir 0
ö ÷ ,T ø
=
(Ir , 0)P-1 ,则
A
=
ST
, TS
=
Ir
,
r(S ) = r(T ) = r 。
由j(x1),...,j(xr ) 的线性无关性,得 k1 = ... = kr = 0 ,进而 kr+1 = ... = kn = 0 。因此
j
(j
(x1
),
...,
j
(xr
),
xr
+1
,
...,
xn
)
=
(j
(x1
),
...,
j
(x
r
),
x
r
+1
,
...,
xn
)
æ ç
I
r
è
0
ö ÷ ø
。
这说明存在可逆矩阵
(Ir
厦门大学网络教育线性代数在线试题、解答

线性代数总分: 100 得分: 0单选题(共100题)(1).(1分)回答:正确答案: B.B得分: 0(2).(1分)回答:正确答案: A.A得分: 0(3).(1分)回答:正确答案: A.A得分: 0(1分)回答:正确答案: D.D得分: 0(5).(1分)回答:正确答案: C.C得分: 0(6).(1分) 回答:正确答案: A.A得分: 0(7).(1分)回答:正确答案: C.C得分: 0(1分)回答:正确答案: D.D得分: 0(9).(1分)回答:正确答案: D.D得分: 0(10).(1分)回答:正确答案: B.B得分: 0(1分)回答:正确答案: A.A得分: 0(12).(1分)回答:正确答案: C.C得分: 0(13).(1分)回答:正确答案: A.A得分: 0.(1分)回答:正确答案: C.C得分: 0(15).(1分)回答:正确答案: B.B得分: 0(16).(1分)回答:正确答案: A.A得分: 0.(1分)回答:正确答案: B.B得分: 0(18).(1分)回答:正确答案: C.C得分: 0(19).(1分)回答:正确答案: B.B得分: 0(1分) 回答:正确答案: B.B得分: 0(21).(1分)回答:正确答案: C.C得分: 0(22).(1分) 回答:正确答案: C.C得分: 0(23).(1分)回答:正确答案: C.C得分: 0(1分)回答:正确答案: D.D得分: 0(25).(1分)回答:正确答案: A.A得分: 0(26).(1分) 回答:正确答案: D.D得分: 0(27).(1分)回答:正确答案: B.B得分: 0(1分) 回答:正确答案: D.D得分: 0(29).(1分)回答:正确答案: D.D得分: 0(30).(1分)回答:正确答案: A.A得分: 0(31).(1分)回答:正确答案: C.C得分: 0(1分)回答:正确答案: D.D得分: 0(33).(1分)回答:正确答案: D.D得分: 0(34).(1分)回答:正确答案: B.B得分: 0(1分) 回答:正确答案: C.C得分: 0(36).(1分)回答:正确答案: C.C得分: 0(37).(1分)回答:正确答案: B.B得分: 0(1分)回答:正确答案: D.D得分: 0(39).(1分)回答:正确答案: C.C得分: 0(40).(1分)回答:正确答案: C.C得分: 0 (41).(1分)回答:正确答案: C.C得分: 0(1分) 回答:正确答案: A.A得分: 0(43).(1分)回答:正确答案: A.A得分: 0(44).(1分)回答:正确答案: B.B得分: 0(45).(1分)回答:正确答案: D.D得分: 0(46).(1分)回答:正确答案: C.C得分: 0(47).(1分) 回答:正确答案: D.D得分: 0(48).(1分)回答:正确答案: D.D得分: 0(49).(1分)回答:正确答案: A.A得分: 0.(1分)回答:正确答案: D.D得分: 0(51).(1分)回答:正确答案: D.D得分: 0(52).(1分) 回答:正确答案: B.B得分: 0(53).(1分)回答:正确答案: C.C得分: 0.(1分)回答:正确答案: C.C得分: 0 (55).(1分)回答:正确答案: B.B得分: 0(56).(1分)回答:正确答案: C.C得分: 0 (57).(1分)回答:正确答案: B.B得分: 0.(1分)回答:正确答案: D.D得分: 0(59).(1分)回答:正确答案: A.A得分: 0(60).(1分)回答:正确答案: B.B得分: 0(61).(1分)回答:正确答案: A.A得分: 0(62).(1分)回答:正确答案: B.B得分: 0(63).(1分)回答:正确答案: A.A得分: 0(64).(1分)回答:正确答案: D.D得分: 0(65).(1分)回答:正确答案: C.C得分: 0(66).(1分)回答:正确答案: D.D得分: 0(67).(1分)回答:正确答案: C.C得分: 0(68).(1分) 回答:正确答案: D.D得分: 0(69).(1分)回答:正确答案: B.B得分: 0(70).(1分)回答:正确答案: C.C得分: 0(71).(1分) 回答:正确答案: B.B得分: 0(72).(1分)回答:正确答案: C.C得分: 0 (73).(1分)回答:正确答案: D.D得分: 0 (74).(1分)回答:正确答案: D.D得分: 0(1分)回答:正确答案: C.C得分: 0(76).(1分)回答:正确答案: D.D得分: 0(77).(1分)回答:正确答案: B.B得分: 0(78).(1分)回答:正确答案: B.B得分: 0.(1分)回答:正确答案: C.C得分: 0(80).(1分)回答:正确答案: C.C得分: 0(81).(1分)回答:正确答案: A.A得分: 0(82).(1分) 回答:正确答案: D.D得分: 0(83).(1分)回答:正确答案: B.B得分: 0(84).(1分)回答:正确答案: A.A得分: 0(85).(1分) 回答:正确答案: A.A得分: 0(86).(1分) 回答:正确答案: D.D得分: 0(87).(1分)回答:正确答案: A.A得分: 0(88).(1分) 回答:正确答案: D.D得分: 0(89).(1分)回答:正确答案: B.B得分: 0(90).(1分)回答:正确答案: A.A得分: 0(91).(1分)回答:正确答案: C.C得分: 0(92).(1分)回答:正确答案: C.C得分: 0(93).(1分)回答:正确答案: B.B得分: 0(94).(1分) 回答:正确答案: A.A得分: 0(95).(1分)正确答案: D.D得分: 0(96).(1分)回答:正确答案: B.B得分: 0(97).(1分)回答:正确答案: A.A得分: 0(98).(1分)回答:正确答案: B.B得分: 0(99).(1分)正确答案: B.B得分: 0 (100).(1分)回答:正确答案: C.C得分: 0。
厦门大学继续教育学院土木工程2016春专升本第一学期线性代数离线作业(仅做参考,不保证全对)

:年:专业姓:成3A .充分必要条件;.充分必要条件;B .充分而非必要条件;.充分而非必要条件;C . 必要而非充分条件;必要而非充分条件;D .既不充分也不必要条件。
.既不充分也不必要条件。
6.设A 为四阶方阵,且满足A 2=A ,则秩r(A )+ 秩r(A-E )=( A ); A . 4; B. 3; C. 2; D. 1 7.设s r t aa a a a 15241233)1(-是五阶行列式D 中的一项,则下述说法正确的是( A )。
A .t s r ,5,4==为奇数;为奇数;B .t s r ,5,4==为偶数;为偶数;B . t s r ,4,5==为奇数;为奇数; D .以上均不正确.以上均不正确二、 填空题(共7小题,每题3分)1. 已知a 是3维列量,a T 是a 的转置,若矩阵aa T相似于úúúûùêêêëé222222222,则a T a = 6 。
2.2. 已知矩阵÷÷øöççèæ=2174A ,则A 的逆为_____÷÷øöççèæ--4172 ____。
3.3. 若矩阵÷÷÷øöçççèæ=50413102l A 可相似对角化, 则l x = 3 = 3 。
4. 设3阶矩阵h 的特征值为1,2,3,那么=+A 7A 5-A 23 18 。
5. 四元齐次线性方程组îíì=-=+03024341x x x x 的基础解系是的基础解系是 (0,1,0,0)T , (-2,0,3,1)T 。
线性代数自考试题及答案

线性代数自考试题及答案一、单项选择题(每题2分,共20分)1. 矩阵A的行列式为0,则矩阵A()A. 可逆B. 不可逆C. 行等价于零矩阵D. 列等价于零矩阵答案:B2. 若矩阵A的秩为r,则矩阵A的齐次线性方程组的解空间的维数为()A. rB. r-1C. n-rD. n+r答案:C3. 向量组α1,α2,…,αs线性无关,则()A. 向量组α1+α2,α2+α3,…,αs-1+αs线性无关B. 向量组kα1,kα2,…,kαs线性无关,其中k为非零常数C. 向量组α1+α2,α2+α3,…,αs-1+αs,αs线性无关D. 向量组kα1,kα2,…,kαs线性相关,其中k为非零常数答案:B4. 设A为n阶方阵,且|A|≠0,则下列命题中正确的是()A. A与A*的秩相等B. A*与A^(-1)的秩相等C. A与A^(-1)的秩相等D. A与A*的秩不相等答案:C5. 矩阵A=()A. 行最简形矩阵B. 行阶梯形矩阵C. 行等价于单位矩阵的矩阵D. 行等价于零矩阵的矩阵答案:C6. 设A为3×3矩阵,且|A|=2,则|2A|=()A. 4B. 8C. 16D. 32答案:C7. 设A为n阶方阵,且A^2=0,则()A. A=0B. |A|=0C. A可逆D. A不可逆答案:D8. 设A为n阶方阵,且A^2=E,则()A. A=0B. |A|=0C. A可逆D. A不可逆答案:C9. 设A为n阶方阵,且A^T=A,则()A. A为对称矩阵B. A为反对称矩阵C. A为正交矩阵D. A为斜对称矩阵答案:A10. 设A为n阶方阵,且|A|=1,则|A^(-1)|=()A. 0B. 1C. -1D. 2答案:B二、填空题(每题2分,共20分)11. 若A为n阶方阵,且|A|=-3,则|-2A|=______。
答案:1212. 设A为n阶方阵,且A^2=0,则矩阵A的秩r(A)满足______。
线性代数厦门出版社答案

线性代数答案解答第一章 行列式1.利用对角线法则计算下列三阶行列式:.解(2)=ba ca c bc b a ccc aaa bbb cba bac acb ---++ 3333c b a abc ---= (4)yx yx x y x yy x y x+++ yx y x y x yx y y x x )()()(+++++=333)(x y x y -+--33322333)(3x y x x y y x y y x xy ------+= )(233y x +-=4.计算下列各行列式:解 (2)2605232112131412-24c c -260532122130412-24r r -0412032122130412-14r r -0000032122130412-=0(4)d c ba 10110011001---21ar r +d cb a ab 10011011010---+ =12)1)(1(+--d c a ab 101101--+ 23dc c +010111-+-+cd c ada ab=23)1)(1(+--cdadab +-+111=1++++ad cd ab abcd7.计算下列各行列式(阶行列式为k D k ): 解(2)将第一行乘)1(-分别加到其余各行,得ax xa a x xa a x x a a a a x D n ------=00000再将各列都加到第一列上,得ax a x a x a a a an x D n ----+=00000000)1()(])1([1a x a n x n --+=-(3)从第1+n 行开始,第1+n 行经过n 次相邻对换,换到第1行,第n 行经)1(-n 次对换换到第2行…,经2)1(1)1(+=++-+n n n n 次行 交换,得nn nn n n n n n n a a a n a a a n a a a D )()1()()1(1111)1(1112)1(1-------=---++此行列式为范德蒙德行列式∏≥>≥++++--+--=112)1(1)]1()1[()1(j i n n n n j a i a D∏∏≥>≥+++-++≥>≥++-∙-∙-=---=1121)1(2)1(112)1()][()1()1()]([)1(j i n n n n n j i n n n j i j i∏≥>≥+-=11)(j i n j i(4) nnnnn d c d c b a b a D 011112=n n n n n nd d c d c b a b a a 00000011111111----展开按第一行00000)1(1111111112c d c d c b a b a b nn n n n nn ----+-+2222---n n n n n n D c b D d a 都按最后一行展开 由此得递推公式:222)(--=n n n n n n D c b d a D 即 ∏=-=ni i i i i n D c b d a D 222)(而 111111112c b d a d c b a D -==得 ∏=-=ni i i i i n c b d a D 12)((6)n n a a a D +++=11111111121,,433221c c c c c c ---n nn n a a a a a a a a a a +-------100100010000100010001000011433221 展开(由下往上)按最后一列))(1(121-+n n a a a a nn n a a a a a a a a a --------0000000000000000000000022433221nn n a a a a a a a a ----+--000000000000001133221++nn n a a a a a a a a -------0000000000000001143322n n n n n n a a a a a a a a a a a a 322321121))(1(++++=---)11)((121∑+==n i in a a a a第二章 矩阵及其运算4.计算下列乘积: 解(2)()⎪⎪⎪⎭⎫ ⎝⎛123321)10()132231(=⨯+⨯+⨯=(4)⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---⎪⎪⎭⎫ ⎝⎛-20413121013143110412⎪⎪⎭⎫ ⎝⎛---=652087613.利用逆矩阵解下列线性方程组:解 (1) 方程组可表示为 ⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛321153522321321x x x故 ⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎭⎫ ⎝⎛-0013211535223211321x x x从而有 ⎪⎩⎪⎨⎧===001321x x x第三章 矩阵的初等变换与线性方程组1.把下列矩阵化为行最简形矩阵:解3.从矩阵A 中划去一行得到矩阵B ,问B A ,的秩的关系怎样? 解 )(A R ≥)(B R设r B R =)(,且B 的某个r 阶子式0≠D r .矩阵B 是由矩阵A 划去一行得 到的,所以在A 中能找到与D r 相同的r 阶子式D r ,由于0≠=D D r r , 故而)()(B R A R ≥.解 (1) ⎪⎪⎪⎭⎫ ⎝⎛---443112112013r r 21~↔⎪⎪⎪⎭⎫ ⎝⎛---443120131211 ⎪⎪⎪⎭⎫⎝⎛------564056401211~12133r r r r 2000056401211~23秩为⎪⎪⎪⎭⎫ ⎝⎛----r r 二阶子式41113-=-.(2) ⎪⎪⎪⎭⎫ ⎝⎛-------815073131223123⎪⎪⎪⎭⎫⎝⎛---------15273321059117014431~27122113r r r r r r 200000591170144313~23秩为⎪⎪⎪⎭⎫ ⎝⎛-----r r . 二阶子式71223-=-.(3) ⎪⎪⎪⎪⎪⎭⎫⎝⎛---02301085235703273812434241322~r r r r r r ---⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------0230102420536307121131223~r r r r ++⎪⎪⎪⎪⎪⎭⎫⎝⎛-0230114000016000071210344314211614~r r r r r r r r -÷÷↔↔⎪⎪⎪⎪⎪⎭⎫⎝⎛-00000100007121002301秩为3 三阶子式07023855023085570≠=-=-.6.求解下列齐次线性方程组:(2) ⎪⎩⎪⎨⎧=-++=--+=-++;05105,0363,02432143214321x x x x x x x x x x x x解(2) 对系数矩阵实施行变换:⎪⎪⎪⎭⎫ ⎝⎛----5110531631121⎪⎪⎪⎭⎫ ⎝⎛-000001001021~ 即得⎪⎪⎩⎪⎪⎨⎧===+-=4432242102x x x x x x x x 故方程组的解为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛10010*********k k x x x x8.λ取何值时,非齐次线性方程组 ⎪⎩⎪⎨⎧=++=++=++2321321321,,1λλλλλx x x x x x x x x (1)有唯一解;(2)无解;(3)有无穷多个解?解 (1) 0111111≠λλλ,即2,1-≠λ时方程组有唯一解.(2) )()(B R A R <⎪⎪⎪⎭⎫ ⎝⎛=21111111λλλλλB ⎪⎪⎭⎫ ⎝⎛+-+----22)1)(1()2)(1(00)1(11011~λλλλλλλλλλ由0)1)(1(,0)2)(1(2≠+-=+-λλλλ 得2-=λ时,方程组无解.(3) 3)()(<=B R A R ,由0)1)(1()2)(1(2=+-=+-λλλλ, 得1=λ时,方程组有无穷多个解.11.试利用矩阵的初等变换,求下列方阵的逆矩阵:(1) ⎪⎪⎪⎭⎫ ⎝⎛323513123;解 (1)⎪⎪⎪⎭⎫ ⎝⎛100010001323513123⎪⎪⎪⎭⎫⎝⎛---101011001200410123~ ⎪⎪⎪⎪⎪⎭⎫⎝⎛----10121121023200010023~⎪⎪⎪⎪⎪⎭⎫⎝⎛----2102121129227100010003~⎪⎪⎪⎪⎪⎭⎫⎝⎛----21021211233267100010001~故逆矩阵为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛----2102121123326712.(1) 设⎪⎪⎪⎭⎫⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--=132231,113122214B A ,求X 使B AX =;(1) ()⎪⎪⎪⎭⎫ ⎝⎛----=132231113122214B A 初等行变换~⎪⎪⎪⎭⎫ ⎝⎛--412315210100010001⎪⎪⎪⎭⎫ ⎝⎛--==∴-4123152101B A X第四章 向量组的线性相关性1.设T T T v v v )0,4,3(,)1,1,0(,)0,1,1(321===, 求21v v -及32123v v v -+.解 21v v -T T )1,1,0()0,1,1(-=T )10,11,01(---=T )1,0,1(-=32123v v v -+T T T )0,4,3()1,1,0(2)0,1,1(3-+=T )01203,41213,30213(-⨯+⨯-⨯+⨯-⨯+⨯= T )2,1,0(=2.设)(5)(2)(3321a a a a a a +=++-其中T a )3,1,5,2(1=, T a )10,5,1,10(2=,T a )1,1,1,4(3-=,求a解 由)(5)(2)(3321a a a a a a +=++-整理得)523(61321a a a a -+=])1,1,1,4(5)10,5,1,10(2)3,1,5,2(3[61T T T --+=T )4,3,2,1(=3.举例说明下列各命题是错误的:(1)若向量组m a a a ,,,21 是线性相关的,则1a 可由,,2m a a 线性表示. (2)若有不全为0的数m λλλ,,,21 使 01111=+++++m m m m b b a a λλλλ成立,则m a a ,,1 线性相关, m b b ,,1 亦线性相关. (3)若只有当m λλλ,,,21 全为0时,等式 01111=+++++m m m m b b a a λλλλ才能成立,则m a a ,,1 线性无关, m b b ,,1 亦线性无关.(4)若m a a ,,1 线性相关, m b b ,,1 亦线性相关,则有不全为0的数, m λλλ,,,21 使0,01111=++=++m m m m b b a a λλλλ 同时成立.解 (1) 设)0,,0,0,1(11 ==e a032====m a a a满足m a a a ,,,21 线性相关,但1a 不能由,,,2m a a 线性表示.(2) 有不全为零的数m λλλ,,,21 使01111=+++++m m m m b b a a λλλλ原式可化为0)()(111=++++m m m b a b a λλ取m m m b e a b e a b e a -==-==-==,,,222111 其中m e e ,,1 为单位向量,则上式成立,而m a a ,,1 ,m b b ,,1 均线性相关(3) 由01111=+++++m m m m b b a a λλλλ (仅当01===m λλ ) m m b a b a b a +++⇒,,,2211 线性无关 取021====m a a a 取m b b ,,1 为线性无关组满足以上条件,但不能说是m a a a ,,,21 线性无关的.(4) T a )0,1(1= T a )0,2(2= T b )3,0(1= T b )4,0(2= ⎪⎭⎪⎬⎫-=⇒=+-=⇒=+21221121221143020λλλλλλλλb b a a 021==⇒λλ与题设矛盾.4.设144433322211,,,a a b a a b a a b a a b +=+=+=+=,证明向量组 4321,,,b b b b 线性相关.证明 设有4321,,,x x x x 使得 044332211=+++b x b x b x b x 则0)()()()(144433322211=+++++++a a x a a x a a x a a x 0)()()()(443332221141=+++++++a x x a x x a x x a x x(1) 若4321,,,a a a a 线性相关,则存在不全为零的数4321,,,k k k k , 411x x k +=;212x x k +=;323x x k +=;434x x k +=;由4321,,,k k k k 不全为零,知4321,,,x x x x 不全为零,即4321,,,b b b b 线性相 关.(2) 若4321,,,a a a a 线性无关,则⎪⎪⎩⎪⎪⎨⎧=+=+=+=+000043322141x x x x x x x x 011000110001110014321=⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⇒x x x x由01100011000111001=知此齐次方程存在非零解 则4321,,,b b b b 线性相关. 综合得证.5.设r r a a a b a a b a b +++=+== 2121211,,,,且向量组 r a a a ,,,21 线性无关,证明向量组r b b b ,,,21 线性无关. 证明 设02211=+++r r b k b k b k 则++++++++++p r p r r a k k a k k a k k )()()(2211 0=+r r a k 因向量组r a a a ,,,21 线性无关,故⎪⎪⎩⎪⎪⎨⎧==++=+++000221r r r k k k k k k ⇔⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛0001001101121 r k k k因为0110011011≠= 故方程组只有零解则021====r k k k 所以r b b b ,,,21 线性无关6.利用初等行变换求下列矩阵的列向量组的一个最大无关组:(1) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛4820322513454947513253947543173125; (2) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---140113130********211.解 (1) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛482032251345494751325394754317312514131233~r r r r r r --- ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛531053103210431731252334~r r r r --⎪⎪⎪⎪⎪⎭⎫⎝⎛00003100321043173125 所以第1、2、3列构成一个最大无关组.(2) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---1401131302151201221114132~r r r r --⎪⎪⎪⎪⎪⎭⎫ ⎝⎛------222001512015120122114323~r r r r ↔+⎪⎪⎪⎪⎪⎭⎫⎝⎛---00000222001512012211, 所以第1、2、3列构成一个最大无关组.7.求下列向量组的秩,并求一个最大无关组:(1) ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=41211a ,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=41010092a ,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛---=82423a ; (2) )3,1,2,1(1=T a ,)6,5,1,4(2---=T a ,)7,4,3,1(3---=Ta . 解 (1) 3131,2a a a a ⇒=-线性相关.由⎪⎪⎪⎭⎫ ⎝⎛----=⎪⎪⎪⎭⎫ ⎝⎛824241010094121321T T T a a a ⎪⎪⎪⎭⎫⎝⎛--000032198204121~ 秩为2,一组最大线性无关组为21,a a .(2) ⎪⎪⎪⎭⎫ ⎝⎛------=⎪⎪⎪⎭⎫ ⎝⎛743165143121321T T T a a a ⎪⎪⎪⎭⎫⎝⎛------10550189903121~⎪⎪⎪⎭⎫ ⎝⎛---0000189903121~ 秩为2,最大线性无关组为TT a a 21,.8.设n a a a ,,,21 是一组n 维向量,已知n 维单位坐标向量n e e e ,,,21 能 由它们线性表示,证明n a a a ,,,21 线性无关. 证明 n 维单位向量n e e e ,,,21 线性无关 不妨设:nnn n n n nn nn a k a k a k e a k a k a k e a k a k a k e +++=+++=+++=22112222121212121111所以 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛T n T T nn n n n n T n T T a a a k k k k k k k k k e e e 2121222211121121 两边取行列式,得 T n T T nn n n n n T n T T a a a k k k k k k k k k e e e 2121222211121121=由002121≠⇒≠TnTTT n T T a a a e e e即n 维向量组n a a a ,,,21 所构成矩阵的秩为n 故n a a a ,,,21 线性无关.9.设n a a a ,,,21 是一组n 维向量,证明它们线性无关的充分必要条件 是:任一n 维向量都可由它们线性表示.证明 设n εεε,,,21 为一组n 维单位向量,对于任意n 维向量 T n k k k a ),,,(21 =则有n n k k k a εεε+++= 2211即任一n 维向量都 可由单位向量线性表示.必要性⇒n a a a ,,,21 线性无关,且n a a a ,,,21 能由单位向量线性表示,即 nnn n n n nn nn k k k k k k k k k εεεαεεεαεεεα+++=+++=+++= 22112222121212121111故⎪⎪⎪⎪⎪⎭⎫⎝⎛⎪⎪⎪⎪⎪⎭⎫⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛n T T T nn n n n n T n T T k k k k k k k k k a a a εεε2121222211121121两边取行列式,得 Tn TTnn n n n n T nT T k k k k k k k k k a a a εεε 212122*********1=由0021222211121121≠⇒≠nn n n n n TnTTk k k k k k k k k a a a令⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⨯nn n n n n n n k k k k k k k k k A212222111211则 由⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛⇒⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-T n T T T n T T T n T T T n T T a a a A A a a a εεεεεε 212112121 即n εεε,,,21 都能由n a a a ,,,21 线性表示,因为任一n 维向量能由单 位向量线性表示,故任一n 维向量都可以由n a a a ,,,21 线性表示.充分性⇐已知任一n 维向量都可由n a a a ,,,21 线性表示,则单位向量组: n εεε,,,21 可由n a a a ,,,21 线性表示,由8题知n a a a ,,,21 线性无关. TsT T βββ,,,21 显然,存在矩阵B A '',,使得 ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛'=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛T s T T T n T T A a a a ααα 2121,⎪⎪⎪⎪⎪⎭⎫ ⎝⎛'=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛T s T T T n T T B b b b βββ 2121⎪⎪⎪⎪⎪⎭⎫ ⎝⎛+++=+∴T n T n T T T T b a b a b a B A 2211⎪⎪⎪⎪⎪⎭⎫ ⎝⎛'+⎪⎪⎪⎪⎪⎭⎫ ⎝⎛'=T s T T T s T T B A βββααα 2121 因此 ()()()B R A R B A R +≤+由于0212221212111≠rrr r r r k k k k k k k k k所以方程组只有零解021====r x x x .所以r b b b ,,,21 线性无关, 证毕.13.设}0,,),,,({211211=+++∈==n n T n x x x R x x x x x x V 满足 }1,,),,,({211212=+++∈==n n T n x x x R x x x x x x V 满足 问21,V V 是不是向量空间?为什么?证明 集合V 成为向量空间只需满足条件: 若V V ∈∈βα,,则V ∈+βα 若R V ∈∈λα,,则V ∈λα 1V 是向量空间,因为:0),,,(2121=+++=n T n ααααααα 0),,,(2121=+++=n T n βββββββ T n n ),,,(2211βαβαβαβα+++=+ 且)()()(2211n n βαβαβα++++++ 0)()(2121=+++++++=n n αααβββ 故1V ∈+βα ),,,(,21n R αααλαλ =∈00)(2121=⋅=+++=+++λαααλλαλαλαn n 故1V ∈λα2V 不是向量空间,因为:)()()(2211n n βαβαβα++++++211)()(2121=+=+++++++=n n αααβββ 故2V ∉+βα ),,,(,21n R λαλαλαλαλ =∈λλαααλλαλαλα=⋅=+++=+++1)(2121n n 故当1≠λ时,2V ∉λα14.试证:由T T T a a a )0,1,1(,)1,0,1(,)1,1,0(321===所生成的向量空间就 是3R .证明 设),,(321a a a A =011101110,,321a a a A =02110101011)1(1≠-=-=-于是3)(=A R 故线性无关.由于321,,a a a 均为三维,且秩为3,所以321,,a a a 为此三维空间的一组基,故由321,,a a a 所生成的向量空间 就是3R .15.由,)1,1,0,1(,)0,0,1,1(21T T a a ==所生成的向量空间记作1V ,由 ,)1,1,1,0(,)3,3,1,2(21T T a b --=-=所生成的向量空间记作2V ,试证 21V V =.证明 设{}R k k a k a k x V ∈+==1122111,{}R x V ∈+==1122112,λλβλβλ任取1V 中一向量,可写成2211a k a k +, 要证22211V a k a k ∈+,从而得21V V ⊆ 由22112211βλβλ+=+a k a k 得 ⎩⎨⎧=+-+=⇔⎪⎪⎩⎪⎪⎨⎧-=-=-==+1212112122121211212332k k k k k k k k λλλλλλλλλλ 上式中,把21,k k 看成已知数,把21,λλ看成未知数0211021≠=-=D 21,λλ⇒有唯一解21V V ⊆∴同理可证: 12V V ⊆ (001112≠=D )故21V V =16.验证T T T a a a )2,1,3(,)3,1,2(,)0,1,1(321==-=为3R 的一个基,并把 T T v v )13,8,9(,)7,0,5(21---==用这个基线性表示.解 由于06230111321,,321≠-=-=a a a即矩阵),,(321a a a 的秩为3故321,,a a a 线性无关,则为3R 的一个基. 设3322111a k a k a k v ++=,则 ⎪⎩⎪⎨⎧=+=++-=++723053232321321k k k k k k k k ⎪⎩⎪⎨⎧-===⇒132321k k k故321132a a a v -+=设3322112a a a v λλλ++=,则 ⎪⎩⎪⎨⎧-=+-=++--=++1323893232321321λλλλλλλλ⎪⎩⎪⎨⎧-=-==⇒233321k k k 故线性表示为3212233a a a v --=17.求下列齐次线性方程组的基础解系:(1)⎪⎩⎪⎨⎧=-++=-++=++-02683054202108432143214321x x x x x x x x x x x x (2)⎪⎩⎪⎨⎧=-++=-++=+--03678024530232432143214321x x x x x x x x x x x x(3)02)1(121=++-+-n n x x x n nx .解 (1)⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛---=000041431004012683154221081~初等行变换A所以原方程组等价于⎪⎩⎪⎨⎧+=-=4323141434x x x x x取3,143-==x x 得0,421=-=x x 取4,043==x x 得1,021==x x因此基础解系为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--=4010,310421ξξ (2) ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛----=000019719141019119201~367824531232初等行变换A 所以原方程组等价于⎪⎪⎩⎪⎪⎨⎧+-=+-=4324311971914191192x x x x x x取2,143==x x 得0,021==x x取19,043==x x 得7,121==x x因此基础解系为⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=19071,210021ξξ(3)原方程组即为1212)1(------=n n x x n nx x取0,11321=====-n x x x x 得n x n -=取0,114312======-n x x x x x 得1)1(+-=--=n n x n取0,12211=====--n n x x x x 得2-=n x所以基础解系为⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-+--=-21100010001),,,(121 n n n ξξξn E R A E A R A E R A R E A R A R ==-+≥-+=-+)()()()()()( 由此n E A R A R =-+)()(.23.求下列非齐次方程组的一个解及对应的齐次线性方程组的基础解 系:(1) ⎪⎩⎪⎨⎧=+++=+++=+;32235,122,54321432121x x x x x x x x x x (2)⎪⎩⎪⎨⎧-=+++-=-++=-+-.6242,1635,11325432143214321x x x x x x x x x x x x解 (1)⎪⎪⎪⎭⎫⎝⎛--⎪⎪⎪⎭⎫ ⎝⎛=2100013011080101322351211250011~初等行变换B⎪⎪⎪⎪⎪⎭⎫⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=∴0111,20138ξη(2) ⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛---⎪⎪⎪⎭⎫ ⎝⎛-----=00000221711012179016124211635113251~初等行变换B ⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎪⎪⎪⎭⎫ ⎝⎛-=∴2011,0719,002121ξξη24.设*η是非齐次线性方程组b Ax =的一个解,r n -ξξ,,1 是对应的齐 次线性方程组的一个基础解系,证明: (1)r n -*ξξη,,,1 线性无关;(2) r n -***++ξηξηη,,,1 线性无关。
厦门大学网络教育-学年第一学期经济数学基础课后练习题

一、单选题(共36道)1、(1.0分) (正确的答案:A 提交的答案:B 判题:×得分:0) A、A B、B C、C D、D2、(1.0分) (正确的答案:B 提交的答案:D 判题:×得分:0)A、AB、BC、CD、D3、(1.0分) (正确的答案:A 提交的答案:D 判题:×得分:0)A、 B、 C、 D、4、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、5、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、6、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、7、(1.0分) (正确的答案:D 提交的答案:D 判题:√得分:1.0)A、 B、 C、 D、8、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、9、(1.0分) (正确的答案:B 提交的答案:C 判题:×得分:0)A、 B、 C、 D、10、(1.0分) (正确的答案:A 提交的答案:D 判题:×得分:0)A、 B、 C、 D、11、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、12、(1.0分) (正确的答案:D 提交的答案:B 判题:×得分:0)A、 B、 C、 D、13、(1.0分) (正确的答案:C 提交的答案:D 判题:×得分:0)A、 B、 C、 D、14、(1.0分) (正确的答案:C 提交的答案:D 判题:×得分:0)A、 B、 C、 D、15、(1.0分) (正确的答案:B 提交的答案:D 判题:×得分:0)A、 B、 C、 D、16、(1.0分) (正确的答案:B 提交的答案:C 判题:×得分:0)A、 B、 C、 D、17、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、18、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、19、(1.0分) (正确的答案:B 提交的答案:D 判题:×得分:0)A、 B、 C、 D、20、(1.0分)(正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、21、(1.0分) (正确的答案:B 提交的答案:C 判题:×得分:0)A、 B、 C、 D、22、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、23、(1.0分) (正确的答案:C 提交的答案:C 判题:√得分:1.0)A、 B、 C、 D、24、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、25、(1.0分) (正确的答案:C 提交的答案:B 判题:×得分:0)A、 B、 C、 D、26、(1.0分) (正确的答案:C 提交的答案:B 判题:×得分:0)A、 B、 C、 D、27、(1.0分) (正确的答案:A 提交的答案:C 判题:×得分:0)A、 B、 C、 D、28、(1.0分)(正确的答案:A 提交的答案:D 判题:×得分:0)A、 B、 C、 D、29、(1.0分)(正确的答案:B 提交的答案:D 判题:×得分:0)A、 B、 C、 D、30、(1.0分) (正确的答案:C 提交的答案:D 判题:×得分:0)A、 B、 C、 D、31、(1.0分) (正确的答案:A 提交的答案:B 判题:×得分:0)A、AB、BC、CD、D32、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、33、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、34、(1.0分) (正确的答案:A 提交的答案:B 判题:×得分:0)A、 B、 C、 D、35、(1.0分) (正确的答案:B 提交的答案:D 判题:×得分:0)A、 B、 C、 D、36、(1.0分) (正确的答案:D 提交的答案:A 判题:×得分:0)A、 B、 C、 D、]一、单选题(共42道)1、(1.0分) (正确的答案:C 提交的答案:C 判题:√得分:1.0)A、AB、BC、CD、D2、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、3、(1.0分)(正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、4、(1.0分) (正确的答案:C 提交的答案:C 判题:√得分:1.0)A、 B、 C、 D、5、(1.0分) (正确的答案:B 提交的答案:D 判题:×得分:0)A、 B、 C、 D、6、(1.0分) (正确的答案:D 提交的答案:A 判题:×得分:0)A、 B、 C、 D、7、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、8、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、9、(1.0分) (正确的答案:A 提交的答案:D 判题:×得分:0)A、 B、 C、 D、10、(1.0分) (正确的答案:B 提交的答案:D 判题:×得分:0)A、 B、 C、 D、11、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、12、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、13、(1.0分) (正确的答案:C 提交的答案:C 判题:√得分:1.0)A、 B、 C、 D、14、(1.0分) (正确的答案:C 提交的答案:D 判题:×得分:0)A、 B、 C、 D、15、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、16、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、17、(1.0分)(正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、18、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、19、(1.0分) (正确的答案:D 提交的答案:A 判题:×得分:0)A、 B、 C、 D、20、(1.0分)(正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、21、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、22、(1.0分) (正确的答案:D 提交的答案:A 判题:×得分:0) A、 B、 C、 D、23、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、24、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、25、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、26、(1.0分)(正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、27、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、28、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、29、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、30、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、31、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、32、(1.0分)(正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、33、(1.0分) (正确的答案:D 提交的答案:A 判题:×得分:0)A、 B、 C、 D、34、(1.0分)(正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、35、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、36、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、37、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、38、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、39、(1.0分) (正确的答案:C 提交的答案:B 判题:×得分:0)A、 B、 C、 D、40、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、41、(1.0分) (正确的答案:D 提交的答案:A 判题:×得分:0)A、 B、 C、 D、42、(1.0分) (正确的答案:D 提交的答案:A 判题:×得分:0)A、 B、 C、 D、一、单选题(共42道)1、(1.0分) (正确的答案:C 提交的答案:C 判题:√得分:1.0)A、AB、BC、CD、D2、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、3、(1.0分)(正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、4、(1.0分) (正确的答案:C 提交的答案:C 判题:√得分:1.0)A、 B、 C、 D、5、(1.0分) (正确的答案:B 提交的答案:D 判题:×得分:0)A、 B、 C、 D、6、(1.0分) (正确的答案:D 提交的答案:A 判题:×得分:0)A、 B、 C、 D、7、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、8、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、9、(1.0分) (正确的答案:A 提交的答案:D 判题:×得分:0)A、 B、 C、 D、10、(1.0分) (正确的答案:B 提交的答案:D 判题:×得分:0)A、 B、 C、 D、11、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、12、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、13、(1.0分) (正确的答案:C 提交的答案:C 判题:√得分:1.0)A、 B、 C、 D、14、(1.0分) (正确的答案:C 提交的答案:D 判题:×得分:0)A、 B、 C、 D、15、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、16、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、17、(1.0分)(正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、18、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、19、(1.0分) (正确的答案:D 提交的答案:A 判题:×得分:0)A、 B、 C、 D、20、(1.0分)(正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、21、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、22、(1.0分) (正确的答案:D 提交的答案:A 判题:×得分:0) A、 B、 C、 D、23、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、24、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、25、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、26、(1.0分)(正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、27、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、28、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、29、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、30、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、31、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、32、(1.0分)(正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、33、(1.0分) (正确的答案:D 提交的答案:A 判题:×得分:0)A、 B、 C、 D、34、(1.0分)(正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、35、(1.0分) (正确的答案:B 提交的答案:A 判题:×得分:0)A、 B、 C、 D、36、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、37、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、38、(1.0分) (正确的答案:A 提交的答案:A 判题:√得分:1.0)A、 B、 C、 D、39、(1.0分) (正确的答案:C 提交的答案:B 判题:×得分:0)A、 B、 C、 D、40、(1.0分) (正确的答案:C 提交的答案:A 判题:×得分:0)A、 B、 C、 D、41、(1.0分) (正确的答案:D 提交的答案:A 判题:×得分:0)A、 B、 C、 D、42、(1.0分) (正确的答案:D 提交的答案:A 判题:×得分:0)A、 B、 C、 D、。
厦门大学08-09学年第一学期《高等代数》期末考试卷

厦门大学《高等代数》课程试卷数学科学学院 各 系 2008 年级 各 专业信息科学与技术学院 计算机科学 系 2008 年级 CST 专业特别说明:答案写在答题纸上一、 单选题(32分. 共8题, 每题4分)1.下列说法错误的是___B____.A) 若向量组123,,ααα线性无关,则其中任意两个向量线性无关; B) 若向量组123,,ααα中任意两个向量线性无关,则123,,ααα线性无关; C) 向量组122331,,αααααα---线性相关;D) 若向量组123,,ααα线性无关,则112123,,αααααα+++线性无关.2. 设n 维列向量12,,...,m ααα()m n <线性无关, 则n 维列向量12,,...,m βββ线性无关的充要条件是___D____.A) 向量组12,,...,m ααα可由向量组12,,...,m βββ线性表示; B) 向量组12,,...,m βββ可由向量组12,,...,m ααα线性表示; C) 向量组12,,...,m ααα与向量组12,,...,m βββ等价; D) 矩阵12(,,...,)m A ααα=与矩阵12(,,...,)m B βββ=相抵. 3.设线性方程组0Ax =的解都是线性方程组0Bx =的解,则__C__.A) ()()r A r B <; B) ()()r A r B >; C) ()()r A r B ≥;D) ()()r A r B ≤.4.设n 阶方阵A 的伴随矩阵*0A ≠,非齐次线性方程组Ax b =有无穷多组解,则对应的齐次线性方程组0Ax =的基础解系__ B __. A) 不存在;B) 仅含一个非零解向量;C) 含有两个线性无关的解向量; D) 含有三个线性无关的解向量. 5.下列子集能构成22R⨯的子空间的是___B____.A) 221{|||0,}V A A A R ⨯==∈;B) 222{|()0,}V A tr A A R ⨯==∈;C) 2223{|,}V A A A A R ⨯==∈;D) 224{|,}V A A A A A R ⨯'==-∈或.6.设V 是数域K 上的线性空间, V 上的线性变换ϕ在基12,,...,n ααα下的矩阵为A 且||2A =,若ϕ在基11,,...,n n ααα-下的矩阵为B , 则||B =A) 2n ;B) 2; C)12; D) 不能确定.7.设V 是n 维向量空间,ϕ和ψ是V 上的线性变换,则dimIm dimIm ϕψ=的充分必要条件是A)ϕ和ψ都是可逆变换; B) Ker ϕ=Ker ψ;C) Im Im ϕψ=; D) ϕ和ψ在任一组基下的表示矩阵的秩相同.8.设ϕ是线性空间V 到U 的同构映射,则下列命题中正确的有个. (Ⅰ)ϕ为可逆线性映射;(Ⅱ) 若W 是V 的s 维子空间, 则()ϕW 是U 的s 维子空间; (Ⅲ)ϕ在给定基下的表示矩阵为可逆阵;(Ⅳ) 若12V=V V ⊕, 则1212)))ϕϕϕ⊕=⊕(V V (V (V . A) 1B) 2C) 3D) 4二、 填空题(32分. 共8题,每题4分)1. 若矩阵1234(,,,)A αααα=经过行初等变换化为1003002401050000-⎛⎫⎪⎪⎪-⎪⎝⎭, 那么向量组1234,,,αααα的一个极大无关组是其余向量由此极大无关组线性表示的表示式为.2. 设3维向量空间的一组基为123(1,1,0),(1,0,1),(0,1,1)ααα===,则向量(2,0,0)β=在这组基.3. 设1V ,2V 均为线性空间V 的子空间,则12()L V V ⋃=4. 数域K 上所有三阶反对称矩阵构成的线性空间的维数是的一组基.5. 已知12K ⨯上的线性变换ϕ定义如下:((,))(0,)a b a ϕ=-,则Ker ϕ=Im ϕ6. 设ϕ是数域K 上n 维线性空间V 到m 维线性空间U 的线性映射, 则ϕ为满射的充分必要条件是(请写出两个)7. 设12,,...,n ααα和12,,...,n βββ是线性空间V 的两组基,从12,,...,n ααα到12,,...,n βββ的过渡矩阵为P . 若ϕ是V 上的线性变换且,()i i ϕαβ=1,2,...,i n =,则ϕ在基12,,...,n βββ下的表示矩阵是8. 设ϕ是线性空间V上的线性变换,ϕ在基12,,...,n ααα下的表示矩阵为0A B C ⎛⎫ ⎪⎝⎭,其中A 为r r ⨯矩阵,则存在V 的一个非平凡ϕ-三、(8分) 设线性空间V 的向量组12,,...,m ααα线性无关,V β∈,考虑向量组12,,,...,m βααα.求证:或者该向量组线性无关,或者β可由12,,...,m ααα线性表示.证明: 若1,,,m βααL 线性相关,则存在不全为0的数01k ,k ,,k m L 使得011k +k +k 0m m βαα+=L .我们断言,0k 0≠.事实上,若0k =0,则11k +k 0m m αα+=L .由12,,...,m ααα线性无关知1m k ==k =0L .于四、(10分) 设1V ,2V 分别是数域K 上的齐次线性方程组12n x x x ===L 与120n x x x +++=L 的解空间. 证明112n KV V ⨯=⊕.证明:法一:一方面,∀1212naaV Va⎛⎫⎪⎪∈⋂⎪⎪⎝⎭M,有1212nna a aa a a===⎧⎨+++=⎩LL,则12na a a====L.故五、(10分) 设m n A K ⨯∈. 证明:()r A r =的充分必要条件是存在m r B K ⨯∈,r n C K ⨯∈,使得()()r B r C r ==且A BC =.证明: 充分性: 由于m rB K⨯∈,r nC K⨯∈满足()()r B r C r ==且A BC =,所以()()()()()r r B r C r r A r BC r B r =+-≤=≤=故()r A r =.必要性: 由于()r A r =,所以存在m 阶可逆矩阵P 及n 阶可逆矩阵Q 使得000rI A P Q ⎛⎫=⎪⎝⎭.令,(,0)0r r I B P C I Q ⎛⎫== ⎪⎝⎭,则m r B K ⨯∈,r n C K ⨯∈满足()()r B r C r ==且A BC =.六、(8分) 设V , U, W 是有限维线性空间,:V U ϕ→,:W U ψ→是线性映射. 求证:存在线性映射:V W σ→使得ϕψσ=的充分必要条件是Im Im ϕψ⊆.证明: 充分性: 法一:取V 的一组基12,,,n αααL ,由于Im Im ϕψ⊆,所以()Im i ϕαψ∈,1i n ∀≤≤,即存在i W β∈使得()()i i ϕαψβ=.定义线性映射:V W σ→满足(),1i i i n σαβ=∀≤≤,则()()(),1i i i i n ψσαψβϕα==∀≤≤.因此,ψσϕ=.法二:取V 的一组基12,,,n ξξξL ,U 的一组基12,,,m ηηηL ,W 的一组基12,,,s γγγL .设1212(,,,)(,,,)n m m n A ϕξξξηηη⨯=L L1212(,,,)(,,,)s m m s B ψγγγηηη⨯=L L其中1212(,,,),(,,,)n s A B αααβββ==L L .由于Im Im ϕψ⊆,所以1212(,,,)(,,,)n s L L αααβββ⊆L L ,即11,sj ij ii j n c αβ=∀≤≤=∑.取()ij s n C c ⨯=,则A BC =.定义线性映射:V W σ→满足1212(,,,)(,,,)n s C σξξξγγγ=L L ,则ϕψσ=.必要性: 对任意Im βϕ∈,存在V α∈使得()βϕα=.由于ϕψσ=,所以()βϕα=(())Im ψϕαψ=∈ 从而,Im Im ϕψ⊆.附加题: (本部分不计入总分)设V , U, W 是有限维线性空间且dim dim V W =,:V U ϕ→,:W U ψ→是线性映射. 证明:存在可逆线性映射:V W σ→使得ϕψσ=的充分必要条件是Im Im ϕψ=.证明: 充分性:法一:由于dim dim V W =且Im Im ϕψ=,所以由维数公式知:dim dim Ker Ker ϕψ=.取Ker ψ的一组基12,,,r ηηηL ;Ker ϕ的一组基12,,,r ξξξL ,将其扩充为V的一组基121,,,,,r r n ξξξξξ+L L ,则1(),()r n ϕξϕξ+L 是Im ϕ的一组基.由于Im Im ϕψ=,所以1(),()r n ϕξϕξ+L 是Im ψ的一组基.设()(),1i i r i n ϕξψη=∀+≤≤,由于1(),,()r n ψηψη+L 线性无关,所以1,,r n ηη+L 线性无关.我们断言,121,,,,,,r r n ηηηηη+L L 线性无关.事实上,若1122110r r r r n n k k k k k ηηηηη++++++++=L L ,则将ψ作用于上式得11()()0r r n n k k ψηψη++++=L .由于1(),,()r n ψηψη+L 线性无关,所以10r n k k +===L .于是1122r r k k k ηηη+++L =0.又12,,,r ηηηL 是Ker ψ的一组基,故10r k k ===L从而,121,,,,,,r r n ηηηηη+L L 线性无关.注意到dim W n =,故121,,,,,,r r n ηηηηη+L L 是W 的一组基. 定义线性映射:V W σ→满足(),1i i i n σξη=∀≤≤.由于12,,,n ξξξL 是V 的一组基,12,,,n ηηηL 是W 的一组基,故σ可逆.又()()(),1i i i i n ψσξψηϕξ==∀≤≤,从而ϕψσ=.法二: 取V 的一组基12,,,n ξξξL ,U 的一组基12,,,s γγγL ,W 的一组基12,,,n ηηηL .设1212(,,,)(,,,)n s s n A ϕξξξγγγ⨯=L L1212(,,,)(,,,)n s s n B ψηηηγγγ⨯=L L且dimIm dimIm r ϕψ==,则()()r A r B r ==.于是,存在n 阶可逆矩阵,P Q 使得1(,0),AP A =1(,0)BQ B =,其中11,s r A B K ⨯∈列满秩.由于Im Im ϕψ=,所以同上题证明可知存在n 阶矩阵C 使得A BC =,则11(,0)()A AP BQ Q CP -==.设111212122X X Q CP X X -⎛⎫=⎪⎝⎭,其中11X 是r 阶方阵,则1112112122(,0)(,0)XX A B X X ⎛⎫= ⎪⎝⎭.从而,1111A B X =.又1A 列满秩,所以存在2r sA K ⨯∈使得21r A A I =.于是,212111()r I A A AB X ==,即11X 是可逆矩阵.因此,存在可逆矩阵11100n r X X Q P I --⎛⎫=⎪⎝⎭使得()111111111111100(,0),0(,0)00n r n r X X BX BQ P B P B X P A P A I I ------⎛⎫⎛⎫=====⎪ ⎪⎝⎭⎝⎭定义线性映射:V W σ→满足1212(,,,)(,,,)n n X σξξξηηη=L L由于X 可逆且A BX =,故σ可逆且ϕψσ=.必要性: 由于ϕψσ=,所以同上题证明可知Im Im ϕψ⊆.又由:V W σ→可逆可知1ψϕσ-=,所以Im Im ψϕ⊆.从而,Im Im ϕψ=.。
厦门大学网络教育线性代数期末考试复习题及参考答案

题型 :单选题
17、设n阶矩阵 满足
A
,则矩阵 ( ).
B
C
正确答案
D
题型 :单选题
18、下列矩阵那个是初等矩阵( ).
A
正确答案
B
C
D
题型 :单选题
19、设 , ,…, 是一组 维向量,则下列表述正确的是( ).
A 若 , ,…, 不线性相关,就一定线性无关
正确答案
B 如果存在 个全为零的数 , ,…, ,使 + +…+ =0,则 , ,…, 线性无关
24、若三元非齐次线性方程组的系数矩阵的秩为2,
是它的三个解向量,
且
则该线性方程组的通解是( ).
A
B
C D
题型 :单选题
正确答案
25、
.
A 32 正确答案 B 64 C9 D2
题型 :单选题
26、
( ).
A
B
C
正确答案
D
题型 :单选题
27、设
,
,
=( ).
A
B
C
D
正确答案
题型 :单选题
28、设 , , 均为 阶方阵,下列各式中,(
正确答案
题型 :单选题
13、矩阵
( ).
,则
( ).
A
正确答案
B C
D
题型 :单选题
14、
( ).
A1
B
C
D
正确答案
题型 :单选题
15、常数 满足( ),线性方程组
无解.
A
正确答案
B
C
D
题型 :单选题
16、向量组
线性代数试题及答案.doc

线性代数试题及答案.doc.(试卷一)一、填空题(本题总计20 分,每小题 2分)1.排列 7623451 的逆序数是_______。
a11 a12a11 3a12 01,则a212.若a21 a22 3a22 00 6 13.已知 n 阶矩阵A、B和C满足ABC E,其中E为 n 阶单位矩阵,则B1CA。
4.若 A 为m n矩阵,则非齐次线性方程组AX b 有唯一解的充分要条件是_________5.设A为8 6的矩阵,已知它的秩为4,则以A为系数矩阵的齐次线性方程组的解空间维数为 __2。
6.设 A 为三阶可逆阵, 1 0 0 ,则 A*A 1 2 1 03 2 1.7.若 A 为m n矩阵,则齐次线性方程组Ax0 有非零解的充分必要条件是1 2 3 4 53 04 1 28.已知五阶行列式D111 1 1,则1 1 02 35 4 3 2 1A41A42A43A44A459. 向量( 2,1,0,2)T的模(范数)______________。
10. 若 1 k 1 T与12 1 T正交,则k二、选择题(本题总计 10 分,每小题 2 分)1. 向量组1,2, ,r线性相关且秩为 s,则 (D)A. r sB.C. s rD.r s s r2. 若 A 为三阶方阵,且A 2E 0, 2A E 0,3A 4E 0,则A(A) .A.C.8B.8 4D. 43 33.设向量组 A 能由向量组 B 线性表示,则( d )A. R(B) R( A)B.R( B) R( A)C. R( B) R( A)D.R( B) R( A)4.设 n 阶矩阵A的行列式等于D,则kA等于_____。
c( A) kA( B) k n A(C )k n 1 A(D) A5.设 n 阶矩阵A,B和C,则下列说法正确的是 _____。
(A)AB AC则 B C(B)AB 0,则A 0或B 0(C) (AB)T A T B T(D) (A B)( A B) A2B2.三、计算题(本题总计60 分。
《线性代数》厦门大学

6、毛泽东思想科学体系的鲜明特点有( A B C ) A.科学性 B.独创性 C.完整性 D.发展性 E.实践性7、我国社会主义四个现代化是(A B C E )P175 A、现代农业B、现代工业C、现代国防D、现代教育E、现代科学技术8、国民革命时期,组成国民革命联合战线的政治联盟有( A B D E ) A.小资产阶级B.民族资产阶级C.大资产阶级D.工人阶级E.农民阶级9、解放初期进行镇压反革命运动的重点打击对象是(A B C D )A、恶霸分子B、特务C、土匪(匪首、惯匪)D、反动党团骨干分子E、反动会道门头子10、新民主主义社会的经济构成有( A B C D E ) A.国营经济 B.合作社经济 C.个体经济 D.私人资本主义经济E.国家资本主义经济11、近代中国民主革命的基本任务是( A B )A、反对帝国主义的侵略B、反对封建主义的统治C、发展社会生产力D、反对资本主义的剥削E、实现国家的繁荣富强12、1945年4月,毛泽东在中共七大政治报告中,首次提出党的优良作风有(A B C )A、理论和实践相结合的作风B、和人民群众紧密联系在一起的作风C、自我批评的作风D、保持谦虚、谨慎、不骄、不躁的作风E、保持艰苦奋斗的作风13、中国共产党在中国革命中战胜敌人的主要法宝是(B C E )A、土地革命B、统战线C、武装斗争D、根据地建设E、党的建设14、毛泽东思想科学体系的鲜明特点是(B C D )A、革命性B、科学性C、独创性D、完整性E、全面性15、1956年毛泽东提出的在共产党与民主党派的关系上实行的方针是(AB ) A.长期共存 B.互相监督 C.肝胆相照 D.荣辱与共 E.共同参政三、名词解释题1、四马分肥P160 “四马分肥”是我国社会主义改造时期对初级形式的民族资本主义工商业获得利润的分配形式的形象说法。
“四马分肥”指民族资本主义企业每年的利润按国家所得税、企业公积金、工人福利奖金、资方的股息红利这四个方面进行分配。
(完整word版)厦门大学07-08学年第一学期《高等代数》半期考试卷

(完整word 版)厦门大学07-08学年第一学期《高等代数》半期考试卷厦门大学《高等代数》课程试卷数学学院 各 系 2007 年级 各 专业主考教师: 杜妮、林鹭 试卷类型:(A 卷)2007。
11.12特别说明:答案写在答题纸上一、 单选题(32分。
每题4分,共8题)1)设A , B 是n 阶方阵, 下面命题中错误的是____。
(i ) 若||0,||0A B >>,则||0A B +>; (ii ) 若||0,0A k ><,则||0kA <; (iii ) 若0AB =, 则0A =或者0B =;(iv) 若0AB =, 则||0A =或者||0B =; A) (i )(ii)(iii)(iv)B ) (i)(ii)(iii)C ) (i) (ii )D) (i )2)行列式111122220000000a b c d a b c d =____。
A) 11222121a c b d a b c d -; B ) 22112211()()a b a b c d c d --;C) 12121212a a b b c c d d -;D ) 12211221()()a b a b c d c d --。
3)设A 是n 阶方阵, B 是对换A 中两列所得方阵, 若||||A B ≠, 则____.A ) ||A 可能为0;B ) ||0A ≠;C) ||0A B +≠;D)||0A B -≠。
4)设A 是n 阶对称矩阵(即A A '=), B 是n 阶反对称矩阵(即B B '=-), 则____是反对称矩阵。
A) 2AB A ;B ) BAB ;C) ABA ;D) 2BA B 。
5)设n 阶矩阵,,A B C 满足n ABAC I =, 则___.A ) n AB AC I ''''=;B ) 2222n A B AC I =;C) 2n BA C I =;D ) 2n CA B I =.6)设()2123222331333233123311131213010100,,001,01010001ij a ka a a A a B a ka a a P P a kaa a k ⨯+⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪==+== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭, 则B =____.A) 12APP ;B) 12PAP ;C) 21AP P ;D) 21P AP 。
厦门大学《线代参考答案》课程试卷

厦门大学《线代参考答案》课程试卷主考教师:线性代数教学组 试卷类型:(A 卷)==================================================================一、填空题1.54;2.1(7)31E A -; 3. 124,,ααα;4. (1,2,3,4)(1,1,1,1)T T k +;5.001100010⎛⎫ ⎪⎪ ⎪⎝⎭;6. 2.二、单项选择题:1.C; 2. A; 3. C; 4. A; 5. C; 6. A三、计算题:1.解:12122(2 1 2)4241212A PQ -⎛⎫⎛⎫ ⎪ ⎪==-=- ⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭,1(2 1 2)221QP ⎛⎫⎪=-= ⎪ ⎪⎝⎭。
2()22A P Q P Q P Q P Q P Q A=⋅===. 1009999100212()()()22424212A PQ PQ PQ P QP QP QP Q A -⎛⎫⎪=⋅===- ⎪ ⎪-⎝⎭个PQ。
2.解:(1)求(I )的基础解系(I )的系数矩阵为 1100100101010101A ⎛⎫⎛⎫=→ ⎪ ⎪--⎝⎭⎝⎭故(I )的基础解系为:12(0,0,1,0),(1,1,0,1)T T ηη==-. (2)求(I )与(II )的非零公共解。
方法1 由(I ),(II )的通解表达式相等,得1234(0,1,1,0)(1,2,2,1)(0,0,1,0)(1,1,0,1)T T T T k k k k +-=+-。
即 123401010120101210001010k k k k -⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪- ⎪⎪ ⎪= ⎪ ⎪ ⎪- ⎪ ⎪⎪-⎝⎭⎝⎭⎝⎭ 因 0101100112010101121000110101000r -⎛⎫⎛⎫ ⎪ ⎪-- ⎪ ⎪−−→ ⎪ ⎪-- ⎪ ⎪-⎝⎭⎝⎭,故上述方程组的解为(1,1,1,1)T k -,于是(I ),(II )的所有非零公共解为(1,1,1,1),0k k -≠为任意常数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.下列排列中,()是四级奇排列。
A 43212.若( -1)。
是五阶行列式【。
】的一项,则k,l 之值及该项符号为()B k=2,l=3,符号为负3.行列式【 k-1 2。
】的充分必要条件是()C k 不等于 -1 且 k 不等于 34.若行列式D=【 a11 a12 a13。
】 =M 不等于 0,则 D1=【 2a11 2a12 2a13。
】 =()C 8M5.行列式【 0111】101111011110 =()D -36.当 a=()时,行列式【 -1 a 2】 =0B 17.如果行列式【 a11 a12 a13 】 =d 则【 3a31 3a323a33 】 =()B 6d8.当 a=()时,行列式【 a 1 1 】 =0A 19.行列式【 125 64 27 8 。
】的值为()A 1210.行列式【 a 0 0 b 】中 g 元素的代数余子式为()B bde-bcf11.设 f(x)= 【1 1 2 。
】则 f(x)=0 的根为()C 1, -1, 2, -212.行列式【 0 a1 0 0 。
】 =()D (-1)n+1 a1 a2an-1 an113.行列式【a 0 b 0】=()D (ad-bc)(xv-yu)14.~不能取()时,方程组~X1+X2+X3=0只有 0 解B 215. 若三阶行列式 D 的第三行的元素依次为1, 2, 3 它们的余子式分别为2, 3, 4,则 D=()B 816. 设行列式【 a11 a12 a13】 =1,则【 2a11 3a11-4a12 a13 】 =()D -81.线性方程组 x1+x2=1解的情况是()A无解2.若线性方程组 AX=B 的增广矩阵 A 经初等行变换化为 A- 【1234 】 ,当 ~不等于()时,此线性方程组有唯一解B 0,13. 已知 n 元线性方程组AX=B,其增广矩阵为 A ,当()时,线性方程组有解。
C r(A)=r(A)4. 设 A 为 m*n 矩阵,则齐次线性方程组AX=0 仅有零解的充分条件是()A A 的列向量线性无关5.非齐次线性方程组AX=B中, A 和增广矩阵 A 的秩都是4,A 是4*6 矩阵,则下列叙述正确的是()B方程组有无穷多组解6.设线性方程组 AX=B 有唯一解,则相应的齐次方程AX=0()C只有零解7. 线性方程组AX=0 只有零解,则AX=B(B不等于 0)B可能无解8.设有向量组 a1,a2,a3 和向量 BA1=(1,1,1) a2=(1,1,0) a3= (1,0,0)B=(0,3,1)则向量 B 由向量 a1,a2,a3 的线性表示是()A B=a1+2a2-3a39.向量组 a1=()()()是()A线性相关10.下列向量组线性相关的是()C(),(),()11.向量组 ar 线性无关的充要条件是()B向量线的秩等于它所含向量的个数12.向量组 Bt 可由 as 线性表示出,且 Bt 线性无关,则 s 与 t 的关系为()D s≥ t13. n 个向量an 线性无关,去掉一个向量an,则剩下的n-1 个向量()B线性无关14.设向量组 as(s≥ 2)线性无关,且可由向量组 Bs 线性表示,则以下结论中不能成立的是()C存在一个 aj,向量组 aj, b2 bs 线性无关15.矩阵【 1 0 1 0 0】的秩为()A 516.向量组 as( s≥ 2)线性无关的充分必要条件是()C as 每一个向量均不可由其余向量线性表示17.若线性方程组的增广矩阵为A=【1.~.2】则 ~=()时,线性方程组有无穷多解。
D 1/218.是四元非齐次线性方程组 AX=B 的三个解向量,且 r(A)=3,a1=表示任意常数,则线性方程组AX=B的通解 X=()19. C设是齐次线性方程组AX=0 的基础解系,下列向量组不能构成AX=0 基础解系的是()C a1-a2,a2-a3,a3-a120.AX=0 是 n 元线性方程组,已知 A 的秩 r < n,则下列为正确的结论是()D该方程组有 n-r 个线性无关的解21.方程组 { x1-3x2+2x3=0的一组基础解系是由()几个向量组成B 222.设 m*n 矩阵 A 的秩等于 n,则必有()D m≥ n23. C 一组秩为nn 的n 元向量组,再加入一个n 元向量后向量组的秩为()24. 设线性方程组AX=B 中,若 r(A,b)=4,r(A)=3, 则该线性方程组()B无解25.齐次线性方程组 {X1+X3=0的基础解系含()个线性无关的解向量。
B 226.向量组 as(s≥ 2)线性相关的充要条件是()C as 中至少有一个向量可由其余向量线性表示27. 设是非齐次线性方程组AX=B 的解, B 是对应的齐次方程组AX=0 的解,则 AX=B 必有一个解是()D B+1/2A1+1/2A228.齐次线性方程组 {X1+X2+X3=0的基础解系所含解向量的个数为()B 21.设 A 为 3*2 矩阵, B 为 2*3 矩阵,则下列运算中()可以进行A AB2.已知 B1 B2 A1A2A3 为四维列向量组,且行列式【 A】=【 a1,a2,a3,b1 】=-4,【 B】=【 a1,a2,a3,B2】=-1,则行列式【 A+B】 =()D -403.设 A 为 n 阶非奇异矩阵( n> 2), A 为 A 的伴随矩阵,则()A ( A-1) +=【 A】 -1A4.设 A,B 都是 n 阶矩阵,且 AB=0,则下列一定成立的是()A 【A】=0 或【 B】=05.设 A,B 均为 n 阶可逆矩阵,则下列各式中不正确的是()B (A+B)-1=A-1+B-16.设 n 阶矩阵 A,B,C 满足关系式 ABC=E,其中 E 是 n 阶单位矩阵,则必有()D BCA=E7. 设 A 是 n 阶方阵( n≥ 3),A 是 A 的伴随矩阵,又k 为常数,且k≠ 0,+-1,则必有( Ka)+=()B kn-1A+8.设 A 是 n 阶可逆矩阵, A 是 A 的伴随矩阵,则有()A 【 A+】=【 A】 n-19.设 A=【 a11 a12 a13】 ,B=【 a21 a22 a23】 p1=【 0 1 0】 p2=【 1 0 0】则必有()C P1P2A=B10.设 A1B 均为 n 阶方阵,则必有()D 【AB】 =【BA】11. 设 n 维向量 a=(1/2,0 2),矩阵 A=E-ATA,B=E+2ATA,其中 E 为 n 阶单位矩阵,则 AB=() CE12. 设 A 是 n 阶可逆矩阵( n≥ 2), A* 是 A 的伴随矩阵,则()C ( A+) +=【 A】 n-2A13. 设 A,B,A+B,A-1,+B-1均为 n 阶可逆矩阵,则(A-1+B-1) -1 等于()C A(A+B)-1B14.设 A,B 为同阶可逆矩阵,则下列等式成立的是()B (ABT)-1=(BT)-1A-115.设 A 为 4 阶矩阵且【 A】 =-2,则【【 A】=()C -2 516. 设 A=( 1, 2),B=( -1, 3), E 是单位矩阵,则ATB-E=()D【-2 3】17.下列命题正确的是()D可逆阵的伴随阵仍可逆18.设 A 和 B 都是 n 阶可逆阵,若 C=( 0 B),则 C-1=()C (0A-1)19.设矩阵 A=【2 1 0】,矩阵 B 满足 ABA+=2BA+E,其中 E 为三阶单位矩阵, A 为 A 的伴随矩阵,则【 B】 =()B 1/91. 当 k=()时,向量()与()的内积为 2C1/32.下列矩阵中,()是正交矩阵C【3/5-4/5 】3.设 a=(0,y,-1/2)t,B=(x,0,0)t 它们规范正交,即单位正交,则()B X≠+-1 Y=+-1/24.若 A 是实正交方阵,则下述各式中()是不正确的C【A】=15.下列向量中,()不是单位向量C 2)T6.R3 中的向量 a= 在基! 1=() t,!2= !3= 下的坐标为7. B 假设 A,B 都是 n 阶实正交方阵,则()不是正交矩阵。
D A+B8. 设 a1=【 2 0 0】, a2=【 0 0 1】 a3=【0 1 1 】与!【1 0 0】!2【0 1 0】!3【0 0 1】是R3 的两组基,则()B 由基! 1! 2!3 到基 a1a2a3 的过渡矩阵为【200 】1.若(),则 A 相似于 BD n 阶矩阵 A 与 B 有相同的特征值,且n 个特征值各不相同2.n 阶方阵与对角矩阵相似的充要条件是()C 矩阵 A 有 n 个线性无关的特征向量3. A 与 B 是两个相似的 n 阶矩阵,则()A存在非奇异矩阵 P,使 P-1AP=B4.设 A=【 1 2 4。
】且 A 的特征值为 1, 2, 3,则 X=()B 45.矩阵 A 的不同特征值对应的特征向量必()B线性无关6.已知 A=【 3 1】下列向量是 A 的特征向量的是()B 【-1 1】7.三阶矩阵 A 的特征值 1,0, -1,则 f(A)=A2-2A-E 的特征值为()8. A 设 A 和 B 都是 n 阶矩阵且相似,则()C AB 有相同的特征值9.当 n 阶矩阵 A 满足()时,它必相似于对矩阵C A 有 n 个不同的特征值10.设 A 是 n 阶实对称矩阵,则()D存在正交矩阵 P,使得 PTAP为对角阵11. 设矩阵 B=P-1AP,A 的特征值 ~0 的特征向量是 a,则矩阵 B 的关于特征值 ~0 的特征向量是() C P-1A12.设 A 是 n 阶矩阵,适合 A2=A,则 A 的特征值为()A 0 或 113.与矩阵 A=【1 3.。
】相似的矩阵是()B【1 0.。
】14. A 是 n 阶矩阵, C 是正交矩阵,且B=CTAC,则下列结论不成立的是()D A 和 B 有相同的特征向量15. n 阶级方阵 A 与对角矩阵相似的充要条件是()C矩阵 A 有 n 个线性无关的特征向量16.已知 A2=E,则 A 的特征值是()C~=-1 或 ~=117.设实对称矩阵 A=【 3 1。
】的特征值是()A【 400】18.矩阵 A=【 3 1 】的特征值是()C ~1=-2 ~2=419. 设~=2 是非奇矩阵 A 的一个特征值,则矩阵( 1/3A2) -1 有一个特征值等于()B 3/420. n 阶矩阵 A 具有 n 个不同的特征值是 A 与对角矩阵相似的()C充分而非必要条件21.矩阵 A=【 1 0 0】与矩阵()相似C A=【1 0 0】22.设 A 是 n 阶对称矩阵, B 是 n 阶反对称矩阵,则下列矩阵中,不能通过正交变换化成对角阵的是()D ABA1.二次型 f() =X12-X22-2X32-6X1X3+2X2X3的矩阵为()A 【 10-3】2.设矩阵 A=( au) 3*3, 则二次型 f 的矩阵为()C ATA3. 二次型 XTAX经满秩线性变换X=CY化为变量为YN 的二次型YTAX,则矩阵 A 和 B()A一定合同4.n 阶实对称矩阵 A 合同于矩阵 B 的充分必要条件是()D r(a)=r(b) 且 A 与 B 的正惯性指数相等5.设 A 为 n 阶非零矩阵,则()一定是某个二次型的矩阵C ATA6.矩阵 A=【 0 2/2 1】对应的实二次型为()C 2X1X2+3X22+2X1X3-3X2X37.二次型 f=x12+6x1x2+3x22 的矩阵表示为()B (X1X2)【 1 3】【 x1 x2】。
