三角形内角和练习题含答案.doc
三角形的内角和习题(有答案)

三角形的内角和习题1.填空。
(1)等边三角形的三个内角都是()度。
(2)在三角形中,已知∠1=67°,∠2=35°,那么,∠3=( )。
(3)等腰三角形的底角是65度,则顶角是()。
2.选择。
(1)等腰三角形的一个底角是30度,这个三角形又叫做()。
①锐角三角形②钝角三角形③直角三角形(2)一个等腰三角形的底角的3倍等于三角形的内角和,则这个三角形是()。
①钝角三角形②直角三角形③等边三角形(3)一个三角形,其中两个内角的和,等于第三个内角的度数,这个三角形是( )。
①锐角三角形②直角三角形③钝角三角形3.判断。
(1)一个直角三角形中的一个锐角为40度,则另一个角为50度。
()(2)一个等腰三角形的顶角为120度,则它的底角为25度。
()(3)内角分别是50度、60度和70度的三角形不存在。
()4.填写表格。
∠1、∠2、∠3是三角形的三个内角。
50°65°30°80°60°20°5、某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是带( )去。
为什么?6、想一想,下列各组角能组成三角形吗?如果不能,请说明理由;如果能,请说明是什么三角形。
1、80°,95°,5°2、60°,70°,90°3、30°,40°,50°4、50°,50°,80°5、60°,60°,60°7、想一想,算一算。
【参考答案】1③②①(1)60 (2)78°(3)50度2(1)②(2)③(3)②3(1)√(2)×(3)×450°80°65°∠2 30°80°60°100°20°55°5带3去,因为有了3的两个角,顺着边线向上延伸即可。
三角形的内角和练习题

2023年人教版小学数学四年级下册5.3 三角形的内角和同步练习一、单选题1.下面说法错误的是()。
A.三角形具有稳定性B.任何一个三角形都有两个锐角C.三角形的内角和是180°D.钝角三角形的两个锐角和大于90°2.把一个10°的角先扩大6倍后,再用6倍的放大镜来看,看到的角是()A.10°B.60°C.120°D.3603.如果一个三角形最小的一个内角大于45°,这个三角形一定是()A.直角三角形B.锐角三角形C.钝角三角形D.不能确定4.一个三角形中的最大的一个内角是70°,那么最小的一个内角不可能是()。
A.50°B.43°C.30°D.41°5.用一副三角尺,不能拼出下面的角是()。
A.65°B.105°C.75°D.135°二、判断题6.一个三角形可能有两个钝角。
7.在等腰三角形中,有一个内角是40°,另外两个内角一定是70°。
()8.一个等腰三角形的底角是92°.(判断对错)9.长方形的内角和是三角形内角和的2倍。
()10.钝角三角形三个内角度数和比锐角三角形内角和大。
()三、填空题11.三角形最多有个锐角,最多有个直角,最多有个钝角。
12.等腰三角形一个底角45°,它的顶角是°,它又是角三角形.13.一个三角形一个内角的度数是100°,这个三角形是三角形,一个等腰三角形的底角是65°,顶角是,等边三角形的每个内角都是。
14.用四个完全一样的等边三角形拼成一个大三角形,这个大三角形的内角和是。
15.一个三角形的三个内角分别是∠A,∠B,∠C。
∠A的度数是∠B的2倍,∠C的度数是∠B的3倍,这是一个三角形。
四、计算题16.求下面三角形中未知角的度数。
已知:∠1=80°,∠2=68°。
三角形的内角和 练习题

小学数学学习材料金戈铁骑整理制作三角形的内角和练习卷(带解析)1.一个三角形中,有1个角是44°,另外两个角可能是()A.96°,50° B.80°,56° C.90°,36°2.用10倍的放大镜看一个三角形,这个三角形三内角和是()。
A.108° B.180° C.1800° D.1080°3.三角形中最大的一个角一定()A.不小于60° B.大于90° C.小于90° D.大于60°而小于90°4.两个不相等的三角形,它们的内角和()。
A.相等 B.面积大的三角形内角和大C.面积小的三角形内角和小 D.不能比较5.一个三角形最小的内角是50度,这是一个()A.锐角三角形B.直角三角形C.钝角三角形D.以上都不对6.一个三角形中,有两个角都是锐角,另一个角()A.一定是钝角 B.一定是锐角C.可能是钝角、锐角或直角7.下面能组成一个三角形的三个角是()A.∠1= 80度,∠2= 70度,∠3 =15度B.∠1= 50度,∠2= 85度,∠3 =63度C.∠1= 60度,∠2= 60度,∠3 =70度D.∠1= 74度,∠2= 16度,∠3 =90度8.把一个等边三角形从顶点起用一条直线分成两个同样大小的三角形,其中一个三角形的内角和是()A.30 B.60° C.90° D.180°9.一个三角形中,如图所示,∠1=70度,∠3=35度,∠2=()A.45度 B.180度 C.75度 D.90度10.在一个等腰直角三角形中,它的一个底角是()A.30° B.45° C.60°11.下列图形中,内角和不是180度的图形是()A.等腰三角形 B.平行四边形 C.锐角三角形12.一个等腰三角形的顶角是60度,它的底角和是()A.70° B.120° C.140°13.下面每组三个角,不可能在同一个三角形内的是()A.15度、87度、78度B.120度、55度、5度C.80度、50度、50度D.90度、16度、104度14.一个直角三角形中的一个锐角是另一个锐角的2倍,则这个三角形中最小锐角是()A.450° B.30° C.25°15.一个等腰三角形的底角为a度,顶角可表示为()度。
三角形内角和综合习题精选(含答案)

三角形内角和综合习题精选一.解答题(共12小题)1.如图(1),△ABC中,AD是角平分线,AE⊥BC于点E.(1).若∠C=80°,∠B=50°,求∠DAE的度数.(2).若∠C>∠B,试说明∠DAE=(∠C﹣∠B).(3).如图(2)若将点A在AD 上移动到A´处,A´E⊥BC于点E.此时∠DAE变成∠DA´E,(2)中的结论还正确吗?为什么?2.如图,DB是△ABC的高,AE是角平分线,∠BAE=26°,求∠BFE的度数.3.如图,AD为△ABC的中线,BE为三角形ABD中线,(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;(2)在△BED中作BD边上的高;(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?4.如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.(1)若∠B=35°,∠ACB=85°,求∠E的度数;(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.5.(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB=_________ ,∠XBC+∠XCB=_________ .(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.6.如图1,△ABC中,∠A=50°,点P是∠ABC与∠ACB平分线的交点.(1)求∠P的度数;(2)猜想∠P与∠A有怎样的大小关系?(3)若点P是∠CBD与∠BCE平分线的交点,∠P与∠A又有怎样的大小关系?(4)若点P是∠ABC与∠ACF平分线的交点,∠P与∠A又有怎样的大小关系?【(2)、(3)、(4)小题只需写出结论,不需要证明】8.如图,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y 个单位长度沿y轴的正方向运动.(1)若|x+2y﹣5|+|2x﹣y|=0,试分别求出1秒钟后A、B两点的坐标;(2)设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;(3)如图,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,试问∠AGH和∠BGC的大小关系如何?请写出你的结论并说明理由.9.如图所示,点E在AB上,CE,DE分别平分∠BCD,∠AD C,∠1+∠2=90°,∠B=75°,求∠A的度数.10.如图,∠AOB=90°,点C、D分别在射线OA、OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.(1)当∠OCD=50°(图1),试求∠F.(2)当C、D在射线OA、OB上任意移动时(不与点O重合)(图2),∠F的大小是否变化?若变化,请说明理由;若不变化,求出∠F.12.已知△ABC中,∠BAC=100°.(1)若∠ABC和∠ACB的角平分线交于点O,如图1所示,试求∠BOC的大小;(2)若∠ABC和∠ACB的三等分线(即将一个角平均分成三等分的射线)相交于O,O1,如图2所示,试求∠BOC的大小;(3)如此类推,若∠ABC和∠ACB的n等分线自下而上依次相交于O,O1,O2…,如图3所示,试探求∠BOC的大小与n的关系,并判断当∠BOC=170°时,是几等分线的交线所成的角.11.如图,△ABC中,AE、BF是角平分线,它们相交于点O.(∠ABC>∠C),(1)试说明∠BOA=90°+∠C;(2)当AD是高,判断∠DAE与∠C、∠ABC的关系,并说明理由.答案与评分标准一.解答题(共12小题)1.如图(1),△ABC中,AD是角平分线,AE⊥BC于点E.(1).若∠C=80°,∠B=50°,求∠DAE的度数.(2).若∠C>∠B,试说明∠DAE=(∠C﹣∠B).(3).如图(2)若将点A在AD 上移动到A´处,A´E⊥BC于点E.此时∠DAE变成∠DA´E,(2)中的结论还正确吗?为什么?考点:三角形的角平分线、中线和高;角平分线的定义;垂线;三角形内角和定理。
三角形内角和综合习题精选(含答案)

三角形内角和综合习题精选一.解答题(共12小题)1.如图(1),△ABC中,AD是角平分线,AE⊥BC于点E.(1).若∠C=80°,∠B=50°,求∠DAE的度数.(2).若∠C>∠B,试说明∠DAE=(∠C﹣∠B).(3).如图(2)若将点A在AD 上移动到A´处,A´E⊥BC于点E.此时∠DAE变成∠DA´E,(2)中的结论还正确吗?为什么?2.如图,DB是△ABC的高,AE是角平分线,∠BAE=26°,求∠BFE的度数.3.如图,AD为△ABC的中线,BE为三角形ABD中线,(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;(2)在△BED中作BD边上的高;(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?4.如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.(1)若∠B=35°,∠ACB=85°,求∠E的度数;(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.5.(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB=_________,∠XBC+∠XCB=_________.(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ 的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.6.如图1,△ABC中,∠A=50°,点P是∠ABC与∠ACB平分线的交点.(1)求∠P的度数;(2)猜想∠P与∠A有怎样的大小关系?(3)若点P是∠CBD与∠BCE平分线的交点,∠P与∠A又有怎样的大小关系?(4)若点P是∠ABC与∠ACF平分线的交点,∠P与∠A又有怎样的大小关系?【(2)、(3)、(4)小题只需写出结论,不需要证明】8.如图,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.(1)若|x+2y﹣5|+|2x﹣y|=0,试分别求出1秒钟后A、B两点的坐标;(2)设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;(3)如图,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,试问∠AGH和∠BGC的大小关系如何?请写出你的结论并说明理由.9.如图所示,点E在AB上,CE,DE分别平分∠BCD,∠ADC,∠1+∠2=90°,∠B=75°,求∠A的度数.10.如图,∠AOB=90°,点C、D分别在射线OA、OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.(1)当∠OCD=50°(图1),试求∠F.(2)当C、D在射线OA、OB上任意移动时(不与点O重合)(图2),∠F的大小是否变化?若变化,请说明理由;若不变化,求出∠F.11.如图,△ABC中,AE、BF是角平分线,它们相交于点O.(∠ABC>∠C),(1)试说明∠BOA=90°+∠C;(2)当AD是高,判断∠DAE与∠C、∠ABC的关系,并说明理由.12.已知△ABC中,∠BAC=100°.(1)若∠ABC和∠ACB的角平分线交于点O,如图1所示,试求∠BOC的大小;(2)若∠ABC和∠ACB的三等分线(即将一个角平均分成三等分的射线)相交于O,O1,如图2所示,试求∠BOC的大小;(3)如此类推,若∠ABC和∠ACB的n等分线自下而上依次相交于O,O1,O2…,如图3所示,试探求∠BOC的大小与n的关系,并判断当∠BOC=170°时,是几等分线的交线所成的角.答案与评分标准一.解答题(共12小题)1.如图(1),△ABC中,AD是角平分线,AE⊥BC于点E.(1).若∠C=80°,∠B=50°,求∠DAE的度数.(2).若∠C>∠B,试说明∠DAE=(∠C﹣∠B).(3).如图(2)若将点A在AD 上移动到A´处,A´E⊥BC于点E.此时∠DAE变成∠DA´E,(2)中的结论还正确吗?为什么?考点:三角形的角平分线、中线和高;角平分线的定义;垂线;三角形内角和定理。
三角形内角和的计算(一)(通用版)(含答案)

三角形内角和的计算(一)(通用版)试卷简介:利用三角形内角和进行角的计算.一、单选题(共10道,每道10分)1.已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于( )A.30°B.40°C.60°D.80°答案:B解题思路:试题难度:三颗星知识点:三角形内角和2.如图,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为( )A.40°B.45°C.50°D.55°答案:A解题思路:试题难度:三颗星知识点:三角形的内角和3.如图,∠A=35°,∠B=∠C=90°,则∠D的度数是( )A.30°B.35°C.50°D.65°答案:B解题思路:试题难度:三颗星知识点:三角形的内角和4.如图,在△ABC中,AD平分∠BAC且与BC相交于点D,∠B=40°,∠BAD=30°,则∠C的度数是( )A.70°B.80°C.100°D.110°答案:B解题思路:试题难度:三颗星知识点:三角形的内角和5.如图所示,在△ABC中,∠B=50°,∠C=70°,∠ADE=80°,则∠AED的度数为( )A.30°B.40°C.50°D.60°答案:B解题思路:试题难度:三颗星知识点:三角形的内角和6.如图,在△ABC中,AE平分∠BAC,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE 的度数是( )A.10°B.12°C.15°D.18°答案:A解题思路:试题难度:三颗星知识点:三角形的内角和7.如图,在△ABC中,AD⊥BC于点D,E是AC边上一点,BE与AD交于点F.∠ABC=45°,∠BAC=75°,∠BFD=60°,则∠BEC的度数是( )A.85°B.105°C.100°D.90°答案:D解题思路:试题难度:三颗星知识点:三角形的内角和8.如图,在△ABC中,∠B=∠C,FD⊥BC于点D,DE⊥AB于点E,∠AFD=158°,则∠EDF=( )A.79°B.68°C.44°D.42°答案:B解题思路:试题难度:三颗星知识点:角度的计算9.如图,在△ABC中,∠BAC=4∠1=4∠C,BD⊥CA于点D,则∠DBA=( )A.30°B.45°C.60°D.75°答案:A解题思路:试题难度:三颗星知识点:角度的计算10.如图所示,一个直角三角形纸片ABC,剪去直角后,得到一个四边形GBCH,则∠1+∠2=( )A.90°B.180°C.240°D.270°答案:D解题思路:试题难度:三颗星知识点:三角形的内角和。
三角形的内角和及外角定理(人教版)(含答案)

三角形的内角和及外角定理(人教版)一、单选题(共12道,每道8分)1.已知△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于( )A.30°B.40°C.60°D.80°答案:B解题思路:试题难度:三颗星知识点:三角形内角和2.如图,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为( )A.40°B.45°C.50°D.55°答案:A解题思路:试题难度:三颗星知识点:三角形的内角和3.如图,在△ABC中,AE平分∠BAC,AD⊥BC于点D,若∠BAC=128°,∠C=36°,则∠DAE的度数为( )A.10°B.12°C.15°D.18°答案:A解题思路:试题难度:三颗星知识点:三角形的内角和4.如图,在△ABC中,∠B=∠C,FD⊥BC于点D,DE⊥AB于点E,∠AFD=158°,则∠EDF=( )A.79°B.68°C.44°D.42°答案:B解题思路:试题难度:三颗星知识点:角度的计算5.如图,在△ABC中,∠BAC=4∠1=4∠C,BD⊥CA于点D,则∠DBA=( )A.30°B.45°C.60°D.75°答案:A解题思路:试题难度:三颗星知识点:角度的计算6.如图,一个直角三角形纸片ABC,剪去直角后,得到一个四边形GBCH,则∠1+∠2=( )A.90°B.180°C.240°D.270°答案:D解题思路:试题难度:三颗星知识点:三角形的内角和7.如图,在四边形ABCD中,∠A=62°,∠B=38°,∠BCD=140°,则∠D的度数为( )A.40°B.24°C.50°D.45°答案:A解题思路:试题难度:三颗星知识点:三角形外角定理8.如图,已知∠A=35°,∠B=20°,∠C=25°,则∠BDC的度数为( )A.55°B.60°C.80°D.90°答案:C解题思路:试题难度:三颗星知识点:三角形外角定理9.一副三角板按如图所示叠放在一起,则图中α的度数为( )A.90°B.105°C.120°D.135°答案:B解题思路:试题难度:三颗星知识点:三角形外角定理10.如图,P为△ABC内任一点,延长CP交AB于点D,则下列结论一定正确的是( )A.∠1=∠2+∠3B.∠1=∠2+∠A+∠ACDC.∠2=∠A+∠ACDD.∠3=∠A+∠ACD答案:D解题思路:试题难度:三颗星知识点:三角形外角定理11.已知△ABC中,∠BAC=50°,∠ABC=60°,AD⊥BC,BE⊥AC,垂足分别为D,E,AD,BE相交于点H,则∠AHB的度数为( )A.90°B.100°C.110°D.120°答案:C解题思路:试题难度:三颗星知识点:三角形外角定理12.已知:如图,在△ABC中,AD是∠BAC的角平分线,∠B=∠1,∠ADC=80°.求∠C的度数.解:如图,∵∠ADC是△ABD的一个外角(外角的定义)∴∠ADC=∠1+∠B(_______________________)∵∠B=∠1(已知)∴∠ADC=2∠1(等式的性质)∵∠ADC=80°(已知)∴∠1=∠ADC=40°(_______________________)∵AD是∠BAC的角平分线(已知)∴∠2=∠1=40°(角平分线的定义)∴∠C=180°-∠2-∠ADC=180°-40°-80°=60°(_______________________)①三角形的内角和是180°;②同角或等角的补角相等;③三角形的一个外角等于和它不相邻的两个内角的和;④等式的性质;⑤等量代换.以上空缺处依次所填正确的是( )A.②④①B.③④①C.③②①D.②⑤④答案:B解题思路:试题难度:三颗星知识点:三角形外角定理。
八年级数学:三角形内角和定理练习(含解析)

八年级数学:三角形内角和定理练习(含解析)学校:___________姓名:___________班级:___________一.选择题(共12小题)1.如图,在△ABC中,CD平分∠ACB交AB于点D,过点D作DE∥BC交AC于点E.若∠A=54°,∠B=48°,则∠CDE的大小为()A.44°B.40°C.39°D.38°2.在下列条件中:①∠A+∠B=∠C;②∠A:∠B:∠C=1:2:3;③∠A=90°﹣∠B;④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有()A.①②B.③④C.①③④D.①②③3.已知,在△ABC中,∠A=60°,∠C=80°,则∠B=()A.60°B.30°C.20°D.40°4.有一个外角等于120°,且有两个内角相等的三角形是()A.不等边三角形B.等腰三角形 C.等边三角形 D.不能确定5.三角形三个内角的度数分别是(x+y)°,(x﹣y)°,x°,且x>y>0,则该三角形有一个内角为()A.30°B.45°C.90°D.60°6.在△ABC中,∠A=25°,∠B=63°,则△ABC的形状是()A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形7.如图,将△ABC纸片沿DE折叠,使点A落在四边形BCDE外点A'的位置,则下列结论正确的是()A.∠1+∠2=∠A B.∠1+∠2=2∠A C.∠1﹣∠2=∠A D.∠1﹣∠2=2∠A8.在下列条件中:①∠A+∠B=∠C;②∠A=∠B=2∠C;③∠A:∠B:∠C=1:2:3,能确定△ABC 为直角三角形的条件有()A.1个B.2个C.3个D.0个9.如图,△ABC中,∠A=60°,将△ABC沿DE翻折后,点A落在BC上的点A′处,如果∠A′EC=70°,则∠A′DE的度数为()A.50°B.60°C.75°D.65°10.如果三角形的三个内角的度数比是2:3:4,则它是()A.锐角三角形 B.钝角三角形C.直角三角形 D.钝角或直角三角形11.如图,在△ABC中,以点B为圆心,以BA长为半径画弧交边BC于点D,连接AD,若∠B=30°,∠C=40°,则∠DAC的度数是()A.25°B.35°C.45°D.75°12.一个缺角的三角形ABC残片如图所示,量得∠A=45°,∠B=60°,则这个三角形残缺前的∠C 的度数为()A.75°B.65°C.55°D.45°二.填空题(共8小题)13.在△ABC中,若∠A=78°,∠B=57°,则∠C= .14.已知三角形的三个内角的度数比为2:3:4,则这个三角形三个内角的度数为.15.一个三角形的三个内角中最多有个钝角(或直角).16.在△ABC中,∠C=60°,∠A=2∠B,则∠A= .17.如图,在△ABC中,AD是角平分线,AE是高,已知∠BAC=2∠B,∠B=2∠DAE,那么∠ACB= (度).18.在直角△ABC中,∠C=90°,沿图中虚线剪去∠C,则∠1+∠2= .19.如图,是一个不规则的五角星,则∠A+∠B+∠C+∠D+∠E= .(用度数表示)20.如图,在△ABC中,∠ABC和∠ACB的平分线交于点O,若∠A=80°,则∠BOC= .三.解答题(共4小题)21.如图,已知DF⊥AB于点F,且∠A=45°,∠D=30°,求∠ACB的度数.22.如图,在△ABC中,∠A=50°,过点C作CD∥AB,若CB平分∠ACD,求∠B的度数.23.如图,在△ABC中,∠B=30°,∠C=50°,AE是∠BAC的平分线,AD是高.(1)求∠BAE的度数;(2)求∠EAD的度数;(3)△ABC中,若∠B=α,∠C=β(α<β),请你根据(1)问的结果大胆猜想∠DAE与α,β间的等量关系,并说明理由.24.如图,△ABC中AD是BC边上的高,AE是∠BAC的平分线,∠B=50°,∠C=70°.(1)∠BAC= °;(2)求∠DAE的度数.参考答案与试题解析一.选择题(共12小题)1.解:∵∠A=54°,∠B=48°,∴∠ACB=180°﹣54°﹣48°=78°,∵CD平分∠ACB交AB于点D,∴∠DCB=78°=39°,∵DE∥BC,∴∠CDE=∠DCB=39°,故选:C.2.解:①因为∠A+∠B=∠C,则2∠C=180°,∠C=90°,所以△ABC是直角三角形;②因为∠A:∠B:∠C=1:2:3,设∠A=x,则x+2x+3x=180,x=30°,∠C=30°×3=90°,所以△ABC是直角三角形;③因为∠A=90°﹣∠B,所以∠A+∠B=90°,则∠C=180°﹣90°=90°,所以△ABC是直角三角形;④因为∠A=∠B=∠C,所以三角形为等边三角形.所以能确定△ABC是直角三角形的有①②③共3个.故选:D.3.解:∵在△ABC中,∠A=60°,∠C=80°,∴∠B=180°﹣60°﹣80°=40°.故选:D.4.解:当∠BAC的外角是120°时,则∠BAC=60°,∠B=∠C=(180°﹣∠BAC)=60°,即∠BAC=∠B=∠C,所以△ABC是等边三角形;当∠ABC的外角是120°时,∠ABC=60°,即∠C=∠ABC=60°,∵∠BAC+∠ABC+∠C=180°,∴∠BAC=60°,∴∠BAC=∠B=∠C,∴△ABC是等边三角形;同样当∠ACB的外角是120°,也能推出△ABC是等边三角形;故选:C.5.解:∵三个内角的度数分别是(x+y)°,(x﹣y)°,x°,三角形内角和为180°, ∴x+y+x﹣y+x=180,∴3x=180,x=60,故选:D.6.解:∵△ABC中,∠A=25°,∠B=63°,∴∠C=180°﹣25°﹣63°=92°,∴△ABC是钝角三角形.故选:C.7.解:∵△A′DE是△ADE沿DE折叠得到,∴∠A′=∠A,∵∠1=∠A+∠3,∠3=∠A′+∠2,∴∠1=∠A+∠A′+∠2,∴∠1﹣∠2=2∠A,故选:D.8.解:∵∠A+∠B+∠C=180°,∴若①∠A+∠B=∠C,则∠C=90°.三角形为直角三角形;②∠A=∠B=2∠C,则∠A=∠B=72°,∠C=36°.三角形不是直角三角形;③∠A﹕∠B﹕∠C=1﹕2﹕3,则∠A=30°,∠B=60°,∠C=90°.三角形为直角三角形;故选B.9.解:∵∠AEA′=180°﹣∠A′EC=180°﹣70°=110°,又∵∠A′ED=∠AED=∠AEA′=55°,∠DA′E=∠A=60°,∴∠A′DE=180°﹣∠A′ED﹣∠DA′E=180°﹣55°﹣60°=65°.故选:D.10.解:设三个内角分别为2k、3k、4k,则2k+3k+4k=180°,解得k=20°,所以,最大的角为4×20°=80°,所以,三角形是锐角三角形.故选:A.11.解:∵AB=BD,∠B=30°,∴∠ADB=75°,∵∠C=40°,∴∠DAC=∠ADB﹣∠C=75°﹣40°=35°.故选:B.12.解:∵∠A+∠B+∠C=180°,∴∠C=180°﹣(∠A+∠B)=180°﹣(45°+60°)=75°,故选:A.二.填空题(共8小题)13.解:由题可得,∠C=180﹣∠A﹣∠B=180°﹣78°﹣57°=45°,故答案为:45°.14.解:根据三角形的内角和定理,得三个内角分别是180°×=40°,180°×=60°,180°×=80°.15.解:假设三角形中,出现2个或3个钝角,那么三角形的内角和就大于180°,不符合三角形内角和是180°,因而假设不成立,所以一个三角形中最多有一个钝角.故答案为:1.16.解:设∠A=2x,则∠B=x,由三角形内角和等于180°,得:2x+x+60°=180°,解得x=40°.∴∠A=2x=2×40°=80°.故答案为:80°.17.解:由题意可得∠DAE=∠BAC﹣(90°﹣∠C),又∠BAC=2∠B,∠B=2∠DAE,∴90°﹣2∠B=∠B,则∠B=36°,∴∠BAC=2∠B=72°,∴∠ACB=180°﹣36°﹣72°=72°.故答案为7218.解:∵∠A+∠B+∠C=180°,∴∠A+∠B=180°﹣∠C=90°,∵∠1+∠2+∠A+∠B=360°,∴∠1+∠2=360°﹣90°=270°.故答案是:270°.19.解:如右图所示,∵∠1=∠C+∠2,∠2=∠A+∠D,∴∠1=∠C+∠A+∠D,又∵∠1+∠B+∠E=180°,∴∠A+∠B+∠C+∠D+∠E=180°.故答案是:180°.20.解:∵在△ABC中,∠A=80°,∴∠ABC+∠ACB=180°﹣80°=100°,∵∠ABC和∠ACB的平分线交于O点,∴∠OBC+∠OCB=(∠ABC+∠ACB)=×100°=50°,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣50°=130°.故答案为:130°.三.解答题(共4小题)21.解:∵DF⊥AB于点F,∴∠AFE=90°,∵∠A=45°,∴∠AEF=45°,∴∠CED=∠AEF=45°.∴∠ACB=∠D+∠C ED=30°+45°=75°.22.解:∵∠A+∠B+∠ACB=180°,∠A=50°,∴∠B+∠ACB=130°.∵CD∥AB,∴∠DCB=∠B.∵CB平分∠ACD,∴∠DCB=∠ACB,∴∠ACB=∠B,∴2∠B=130°,∴∠B=65°.23.解:(1)∵∠B=30°,∠C=50°,∴∠BAC=180°﹣30°﹣50°=100°.又∵AE是∠BAC的平分线,∴∠BAE=∠BAC=×100°=50°.(2)∵∠B=30°,AD⊥BC,∴∠BAD=90°﹣30°=60°,∴∠EAD=∠BAD﹣∠BAE=60°﹣50°=10°.(3)∠DAE=(β﹣α),理由如下:∵∠B=α,∠C=β,∴∠BAC=180°﹣α﹣β.又∵AE是∠BAC的平分线,∴∠BAE=∠BAC=90°﹣(α+β).∵∠BAD=90°﹣∠B=90°﹣α,∴∠DAE=∠BAD﹣∠BAE=90°﹣α﹣[90°﹣(α+β)]=(β﹣α).24.解:(1)∵∠B=50°,∠C=70°,∴∠BAC=180°﹣∠B﹣∠C=60°故答案为:60°(2)∵AE是∠BAC的平分线,∠BAC=60°∴∠BAE=30°∴∠AEB=180°﹣∠B﹣∠BAE=100°∵AD是BC边上的高,∴∠ADE=90°∴∠DAE=∠AEB﹣∠ADE=100°﹣90°=10°答:∠DAE的度数是10°.。
(完整word)三角形内角和定理练习题

三角形内角和定理练习题1.在△ABC中,∠A=∠B=∠C,则△ABC是三角形。
2.如图,在△ABC中,BE、CF分别是∠ABC和∠ACB的角平分线,它们相交于点I,已知∠A=56°,则∠BIC =。
3。
如图,在△ABC中,∠B=25°,延长BC至E,过点E作AC的垂线ED,垂足为O,且∠E=40°,则∠A=。
4.如图,若AB=AC,BG=BH,AK=KG,则∠BAC的度数为.5.若等腰三角形一腰上的高和另一腰上的高的夹角为58°,则这个等腰三角形顶角的度数是。
6.如图,将三角形纸片ABC的一角折叠,折痕为EF,若∠A=80°,∠B=68°,∠CFB=22°,则∠CEA =。
7.在一个三角形中,三个内角中至少有个锐角,最多有个直角或钝角.8.如图,AB∥CD,若∠ABE=135°,∠CDE=110°,则∠DEF=。
9。
如图,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,∠AFD=158°,则∠EDF等于( )A.64°B.65°C.67°D。
68°10。
如图,已知AB∥CD,BE平分∠ABD,DE平分∠BDC,则∠E是( )A.锐角B.直角C。
钝角 D.无法确定11。
如图,已知在△ABC中,AD平分外角∠EAC,AD∥BC,则△ABC的形状是() A。
等边三角形 B.直角三角形C。
等腰三角形 D.任意三角形12.如图,在△ABC中,∠ABC和∠ACB的外角平分线交于点D,设∠BAC=∠α,则∠D等于()A。
180°—2∠α B。
180°—∠αC。
90°—∠α D.90°-2∠α13.如果三角形的一个外角等于与它相邻的内角,那么这个三角形的形状是( )A.锐角三角形B。
直角三角形 C.钝角三角形 D.任意三角形14。
如图,∠1=20°,∠2=25°,∠A=35°,则∠BDC的度数等于()A。
四年级数学下册三角形的内角和专项练习(共5套含答案)

四年级数学下册三角形的内角和专项练习(共5套含答案)练习一一、选择题。
1、一个三角形中,有1个角是44°,另外两个角可能是()A、96°,50°B、80°,56°C、90°,36°2、用10倍的放大镜看一个三角形,这个三角形三内角和是()。
A、108°B、180°C、1800°D、1080°3、三角形中最大的一个角一定()。
A、不小于60°B、大于90°C、小于90°D、大于60°而小于90°4、两个不相等的三角形,它们的内角和()。
A、相等B、面积大的三角形内角和大C、面积小的三角形内角和小D、不能比较5、一个三角形最小的内角是50°,这是一个()。
A、锐角三角形B、直角三角形D、以上都不对C、钝角三角形6、一个三角形中,有两个角都是锐角,另一个角()A、一定是钝角B、一定是锐角C、可能是钝角、锐角或直角7、下面能组成一个三角形的三个角是()。
A、∠1=80°,∠2=70°,∠3=15°B、∠1=50°,∠2=85°,∠3=63°C、∠1=60°,∠2=60°,∠3=70°D、∠1=74°,∠2=16°,∠3=90°8、这个三角形原来是()三角形。
A、锐角B、钝角C、直角二、计算下图中三角形中未知角的度数。
三、如图,ABC为直角三角形,求∠1和∠2各是多少度?四、下面是三块三角形玻璃打碎后留下的碎片,你知道它们原来各是什么三角形吗?练习二一、选择题1、把一个等边三角形从顶点起用一条直线分成两个同样大小的三角形,其中一个三角形的内角和是()A、30°B、60°C、90°D、180°2、一个三角形中,如图所示,∠1=70°,∠3=35°,∠2=()。
四年级数学 三角形内角和专项练习 带答案

三角形内角和典题探究一个1、三角形的两个内角和是850,你知道这是一个什么三角形吗?2、在一个三角形中,已知∠1是∠2的2倍,∠2是∠3的31。
这个三角形各个角是多少度?这是一个什么三角形?3、同学们知道三角形的内角和是1800,你能运用这个知识分别求出四边形、五边形、六边形的内角和吗?4、如图,两个三角形都是等腰三角形,∠3是多少度?演练方阵A 档(巩固专练)1.由三条( )围成的图形叫三角形。
2.三角形按角可分为( )三角形、( )三角形、( )三角形。
3.三角形的内角和是( )。
4.等腰直角三角形中三个内角分别是( ),( )和( )。
5、判 断,(对的画“√”,错的画“X ”)(1).一个三角形有一个锐角,那么,这个三角形就一定是锐角三角形。
( )(2).直角三角形中只能有一个角是直角。
( )(3).等边三角形一定是锐角三角形。
( )(4).三角形共有一条高。
( )(5).一个三角形中,最大的角是锐角,那么,这个三角形一定是锐角三角形。
( )(6).两个底角都是280的三角形,一定是钝角三角形。
( )6、选 择。
(1).一个等腰三角形,其中一个底角是750,顶角是( )A .750B .450C .300D .600(2).任意一个三角形都有( )高。
A .一条B .两条C 三条D .无数条(3).( )个角是锐角的三角形,叫锐角三角形。
A.三 B.二 C.—(4).三角形越大,内角和( )A.越大 B.不变 C.越小7、求下面三角形中/3的度数,并指出是什么三角形。
1.∠1=300,∠2=1080,∠3= ( ),它是( )三角形。
2.∠1=900,∠2=450,∠3=( ),它是( )三角形。
3.∠1=700,∠2=700,∠3=( )。
它是( )三角形。
4.∠1=900,∠2=300,∠3=( ),它是( )三角形。
8、一个三角形的两个内角和是1100,你知道这是一个什么三角形吗?9、在△ABC中,已知∠A是∠B的3倍,且∠A比∠B大600,这个三角形各个角是多少度?你知道这是一个什么三角形?10、一个等腰三角形的顶角是一个底角的2倍,这个三角形各个角是多少度?B档(提升精练)1、任意三角形的内角和是度;一个直角三角形的两个锐角的和是度。
三角形内角和综合习题精选(含答案)

...三角形内角和综合习题精选一.解答题(共12小题)1.如图(1),△ABC中,AD是角平分线,AE⊥BC于点E.(1).若∠C=80°,∠B=50°,求∠DAE的度数.(2).若∠C>∠B,试说明∠DAE=(∠C﹣∠B).(3).如图(2)若将点A在AD 上移动到A´处,A´E⊥BC于点E.此时∠DAE变成∠DA´E,(2)中的结论还正确吗?为什么?2.如图,DB是△ABC的高,AE是角平分线,∠BAE=26°,求∠BFE的度数.3.如图,AD为△ABC的中线,BE为三角形ABD中线,(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;(2)在△BED中作BD边上的高;(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?4.如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.(1)若∠B=35°,∠ACB=85°,求∠E的度数;(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.5.(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB= _________ ,∠XBC+∠XCB= _________ .(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.6.如图1,△ABC中,∠A=50°,点P是∠ABC与∠ACB平分线的交点.(1)求∠P的度数;(2)猜想∠P与∠A有怎样的大小关系?(3)若点P是∠CBD与∠BCE平分线的交点,∠P与∠A又有怎样的大小关系?(4)若点P是∠ABC与∠ACF平分线的交点,∠P与∠A又有怎样的大小关系?【(2)、(3)、(4)小题只需写出结论,不需要证明】8.如图,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.(1)若|x+2y﹣5|+|2x﹣y|=0,试分别求出1秒钟后A、B两点的坐标;(2)设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;(3)如图,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,试问∠AGH和∠BGC的大小关系如何?请写出你的结论并说明理由.9.如图所示,点E 在AB 上,CE ,DE 分别平分∠BCD ,∠ADC ,∠1+∠2=90°,∠B=75°,求∠A 的度数.10.如图,∠AOB=90°,点C 、D 分别在射线OA 、OB 上,CE 是∠ACD 的平分线,CE 的反向延长线与∠CDO 的平分线交于点F. (1)当∠OCD=50°(图1),试求∠F .(2)当C 、D 在射线OA 、OB 上任意移动时(不与点O 重合)(图2),∠F 的大小是否变化?若变化,请说明理由;若不变化,求出∠F .11.如图,△ABC 中,AE 、BF 是角平分线,它们相交于点O .(∠ABC >∠C ), (1)试说明∠BOA=90°+∠C;(2)当AD 是高,判断∠DAE 与∠C 、∠ABC 的关系,并说明理由.12.已知△ABC 中,∠BAC=100°.(1)若∠ABC 和∠ACB 的角平分线交于点O ,如图1所示,试求∠BOC 的大小;(2)若∠ABC 和∠ACB 的三等分线(即将一个角平均分成三等分的射线)相交于O ,O 1,如图2所示,试求∠BOC 的大小;(3)如此类推,若∠ABC 和∠ACB 的n 等分线自下而上依次相交于O ,O 1,O 2…,如图3所示,试探求∠BOC 的大小与n 的关系,并判断当∠BOC=170°时,是几等分线的交线所成的角.答案与评分标准一.解答题(共12小题)1.如图(1),△ABC中,AD是角平分线,AE⊥BC于点E.(1).若∠C=80°,∠B=50°,求∠DAE的度数.(2).若∠C>∠B,试说明∠DAE=(∠C﹣∠B).(3).如图(2)若将点A在AD 上移动到A´处,A´E⊥BC于点E.此时∠DAE变成∠DA´E,(2)中的结论还正确吗?为什么?考点:三角形的角平分线、中线和高;角平分线的定义;垂线;三角形内角和定理。
三角形的内角精选练习含答案

三角形的内角精选练习含答案11.2.1 三角形的内角一、选择题1.一个三角形的两个内角和小于第三个内角,那个三角形是( )三角形.A .锐角B .钝角C .直角D .等腰2.三角形的三个内角( )A .至少有两个锐角B .至少有一个直角C .至多有两个钝角D .至少有一个钝角3.一个三角形的一个内角等于另外两个内角的和,那个三角形是( )A .直角三角形B .锐角三角形C .钝角三角形D .何类三角形不能确定4.一个三角形的两个内角之和小于第三个内角,那么该三角形是( )A .锐角三角形B .直角三角形C .钝角三角形D .都有可能5.一个三角形的三个内角的度数比是1:2:1,那个三角形是( ).A .锐角三角形B .直角三角形C .钝角三角形D .等腰直角三角形6.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( )A .90°B .100°C .130°D .180°7.如图,在△ABC 中,∠ABC 的平分线与∠ACB 的外角平分线相交于D 点,∠A=50°,则∠D=( )A .15°B .20°C .25°D .30°8.如图,直线l1∥l2,∠1=40°,∠2=65°,则∠3=( )A .65°B .70°C .75°D .85°二、填空题9.如图,AE 是△ABC 的角平分线,AD ⊥B C 于点D ,若∠BAC=128°,∠C=36°,则∠DAE 的度数是_______10.如图,将三角尺的直角顶点放在直线a 上,a ∥b ,∠1=50°,∠2=60°,则∠3的度数为_______11.(2008•沈阳)已知△ABC 中,∠A=60°,∠ABC 、∠ACB (第6题) (第7题) (第8题) (第9题) (第10题) (第12题) (第14题)的平分线交于点O ,则∠BOC 的度数为________度.12.如图所示,在折纸活动中,小明制作了一张△ABC 纸片,点D 、E 分别是边AB 、AC 上,将△ABC 沿着DE 折叠压平,A 与A'重合,若∠A=70°,则∠1+∠2=____________.13.一个角是80°的等腰三角形的另两个角为____________.14.如图,已知,AB ∥CD ,直线EF 分别交AB ,CD 于E 、F ,点G 在直线EF 上,GH ⊥AB ,若∠EGH=32°,则∠DFE 的度数为____________.15.如图,将∠BAC 沿DE 向∠BAC 内折叠,使AD 与A′D 重合,A′E 与AE 重合,若∠A=30°,则∠1+∠2=________.16.如图,已知点P 是射线ON 上一动点(即P 可在射线ON 上运动),∠AON=30°,(1)当∠A=________时,△AOP 为直角三角形;(2)当∠A 满足________时,△AOP 为钝角三角形.17.如图,点B ,C ,E ,F 在一直线上,AB ∥DC ,DE ∥GF ,∠B=∠F=72°,则∠D=________度.18.当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特点三角形”,其中α称为“特点角”.假如一个“特点三角形”的“特点角”为100°,那么那个“特点三角形”的最小内角的度数为________.三、解答题19.小明在学习三角形内角和定理时,自己做了如下推理过程,请你帮他补充完整.已知:如图,△ABC 中,∠A 、∠B 、∠C 是它的三个内角,那么这三个内角的和等于多少?什么缘故?解:∠A+∠B+∠C=180°理由:作∠ACD=∠A ,并延长BC 到E∠1=∠A (已作)∴AB ∥CD (_________________________)∴∠B=_____(_________________________) 而∠ACB+∠1+∠2=180°∴∠ACB +_____+_____=180°(等量代换) 20.如图,已知△ABC 的AC 边的延长线AD ∥EF ,若∠A=60°,∠B=43°,试用推理的格式求出∠E 的大小.(第15题)(第16题) (第17题)第20题第19题21.如图1,在△ABC 中,OB 、OC 是∠ABC 、∠ACB 的角平分线; ∠A 的度数50° 60° 70° ∠BOC 的度数(3)如图2,△ABC 的高BE 、CD 交于O 点,试说明图中∠A 与∠BOD 的关系.22.将一幅三角板拼成如图所示的图形,过点C 作CF 平分∠DCE 交DE 于点F .(1)求证:CF ∥AB .(2)求∠DFC 的度数.23.(1).解方程:3x+1=7;(2).如图,在△ABC 中,∠B=35°,∠C=65°,求∠A 的度数.第21题第22题 第23题11.2.1三角形的内角一、选择题1.B2.A3.A4.C5.D6.B7.C8.C AC二、填空题 9. 10° 10. 70° 11.120 12.140° 13.80°,20°或50°,50°. 14.58° 15.60° 16.60°或90°;小于60°和大于90° 17.36 18.30°三、解答题19.内错角相等,两直线平行;∠2;两直线平行,同位角相等;∠B ;∠A .20.解:∵∠A=60°,∠B=43°,∴∠BCD=∠A+∠B=60°+43°=103°,∵AD ∥EF ,∴∠E=∠BCD=103°21..解:(1)()()().21902190180180=BOC ∠∴,2190180212121212190000000A A OCB OBC A A OCB ABC OCB ABC ACB OCB ABC OBC ACB ∠+∠∠+∠∠-=∠-∠+∠∠+∠∠∠∠∠∴∠∠∆+=∠)=--(=-==,=,=的角平分线;ABC、是ABC中,OB、OC在理由:ABOC(2)猜想:o (3)证明:∵△ABC 的高BE 、CD 交于O 点,∴∠BDC=∠BEA=90°,∴∠ABE+∠BOD=90°,∠ABE+∠A=90°,∴∠A=∠BOD .22.(1)证明:∵CF 平分∠DCE ,∴∠1=∠2=21∠DCE ,∵∠DCE=90°,∴∠1=45°,∵∠3=45°,∴∠1=∠3,∴AB ∥CF ;∠A 的度数 50° 60° 70° ∠BOC 的度数 115° 120° 125°(2)∵∠D=30°,∠1=45°,∴∠DFC=180°-30°-45°=105°.5.解:(1)移项得,3x=7-1,系数化为1得,x=2;(2)依照三角形的内角和定理,∠A=180°-∠B-∠C=180-35°-65°=80°.。
(完整版)三角形内角和练习题

三角形的内角和练习【例题分析】例1. 在△ABC 中,已知∠A =21∠B =31∠C ,请你判断三角形的形状。
分析:三角形的形状按边分和按角分两类,本题由于不可能按边分,因此只有计算各角的度数,按角来确定形状,由于在该题中∠C 是最大的角,因此只需求出∠C 的度数即可判断三角形的形状。
例2. 如图,已知DF ⊥AB 于点F ,且∠A =45°,∠D =30°,求∠ACB 的度数。
例3. 如图,在△ABC 中,∠1=∠2,∠3=∠4,∠BAC =54°,求∠DAC 的度数。
例4. 已知在△ABC 中,∠A =62°,BO 、CO 分别是∠ABC 、∠ACB 的平分线,且BO 、CO 相交于O ,求∠BOC 的度数。
〖拓展与延伸〗(1)已知△AB 中C ,BO 、CO 分别是∠ABC 、∠ACB 的平分线,且BO 、CO 相交于点O ,试探索∠BOC 与∠A 之间是否有固定不变的数量关系。
B C D B D C 2 4 31AB C AB C A(2)已知BO 、CO 分别是△ABC 的∠ABC 、∠ACB 的外角角平分线,BO 、CO 相交于O ,试探索∠BOC 与∠A 之间是否有固定不变的数量关系。
(3)已知:BD 为△ABC 的角平分线,CO 为△ABC 的外角平分线,它与BO 的延长线交于点O ,试探索∠BOC 与∠A 的数量关系。
由前面的探索同学们可以发现三角形三个角(或外角)的平分线所夹的角与第三个内角之间存在着一定的数量关系。
例5. 已知多边形的每一个内角都等于135°,求这个多边形的边数。
例6. 一个零件的形状如图,按规定∠A =90°,∠B 和∠C 应分别是32°和21°,检验工人量得∠BDC =149°,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由。
分析:验证的关键是求出∠A 的度数,即把∠A 用已知的角∠B 、∠C 、∠BDC 联系起来,利用三角形关于角的性质就可以发现它们之间的关系EB C EA B DE C【随堂检测】A 组1、在△ABC 中, ∠A =40°,∠B =∠C ,则∠C = 。
【七年级奥数】第11讲 三角形内角和(例题练习)
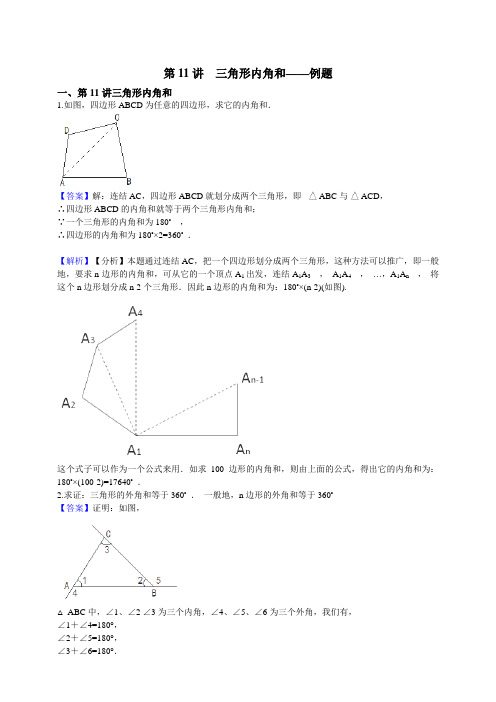
第11讲三角形内角和——例题一、第11讲三角形内角和1.如图,四边形ABCD为任意的四边形,求它的内角和.【答案】解:连结AC,四边形ABCD就划分成两个三角形,即ABC与ACD,∴四边形ABCD的内角和就等于两个三角形内角和;∵一个三角形的内角和为180°,∴四边形的内角和为180°×2=360°.【解析】【分析】本题通过连结AC,把一个四边形划分成两个三角形,这种方法可以推广,即一般地,要求n边形的内角和,可从它的一个顶点A1出发,连结A1A3,A1A4,…,A1A n,将这个n边形划分成n-2个三角形.因此n边形的内角和为:180°×(n-2)(如图).这个式子可以作为一个公式来用.如求100边形的内角和,则由上面的公式,得出它的内角和为:180°×(100-2)=17640°.2.求证:三角形的外角和等于360°.一般地,n边形的外角和等于360°【答案】证明:如图,△ ABC中,∠1、∠2 ∠3为三个内角,∠4、∠5、∠6为三个外角,我们有,∠1+∠4=180°,∠2+∠5=180°,∠3+∠6=180°.所以∠4+∠5+∠6=3×180°-( ∠1+∠2+∠3)=3×180°-180°=360°.同理,若∠α1,∠α2… ∠αn°是n边形的n个内角,∠β1,∠β2,…, ∠βn是它们所对应的n个外角,则有,∠α1+∠β1 =180°,∠α2+∠β2 =180°,……∠αn +∠βn =180°.所以∠β1+∠β2+…+∠βn =n×180°-( ∠α1+∠α2+…+∠αn )=n×180°-(n-2)×180°=360°.【解析】【分析】三角形有三个内角,根据其对应的外角是其邻补角,可知其外角和=3×180°-三角形的内角和;此方法可以推广,即一般地,要求n边形的外角和,可知由n对邻补角,而这个n边形的内角和为(n-2)×180°.因此n边形的外角和为:n×180°-180°×(n-2)=360°.3.已知一个四边形的第二个内角是第一个内角的3倍,第三个内角是第二个内角的一半,第四个内角比第三个内角大10°.求它的第一个内角.【答案】解:设它的第一个内角为x,则它的第二个内角为3x,第三个内角为x,第四个内角为x +10°.由四边形的内角和为360°,知x+3x+x+(x+10°)=360°,解得x=50°.答:它的第一个内角为50°.【解析】【分析】设第一个内角为x,根据题意分别表示出其他三个内角:3x;x;x+10°;再由四边形的内角和为360°列出方程,解之即可得第一个内角的度数.4.如果一个三角形中最大角是最小角的4倍,求它的最小角的取值范围.【答案】解:设∠A是它的最小角,∠C是最大角,∠B是中间的角,则∠A≤∠B≤∠C,又∠C=4∠A.由可得∠A+∠A+4∠A≤180°,即么A≤30°.可得∠A+4∠A+4∠A≥180°,即∠A≥20°.所以最小角的取值范围为20°≤4≤30°.【解析】【分析】设∠A≤∠B≤∠C,根据题意知∠C=4 ∠A,再由三角形内角和为180°,即∠A+∠B+∠C=180°,列出方程组,代入可得:∠A+∠A+4∠A≤180°,或∠A+4∠A+4∠A≥180°,解之即可得出最小角的取值范围.5.如图,在△ ABC中,BD是∠ABC的平分线,CD是外角∠ACE的平分线.求证:∠D= ∠A.【答案】证明:根据三角形外角性质有∠3+∠4=∠1+∠2+∠A.因为BD、CD是∠ABC和∠ACE的平分线,所以∠1=∠2,∠3=∠4.从而2∠4=2∠1+∠A,即∠4=∠1+ ∠A ①在△BCD中,∠4是一个外角,所以∠ 4=∠1+∠D,②由①、②即得∠D=∠A.【解析】【分析】根据角平分线的性质可得∠1=∠2,∠3=∠4,再由三角形外角性质可得2∠4=2∠1+∠A,∠4=∠1+∠D, 等量代换即可得证.6.如图,在七星形ABCDEFG中,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.【答案】解:由三角形的外角性质,得,∠1=∠C+∠F,∠2=∠B+∠E,∠4=∠D+∠G,∠3=∠4+∠A=∠D+∠G+∠A.从而∠A+∠B+∠C+∠D+∠E+∠F+∠G=∠1+∠2+∠3=180°.【解析】【分析】本题中,所求的7个角很分散,直接求它们的和很困难.因此,我们利用三角形的外角性质,把它们集中到一个三角形中,从而解决问题.7.如图,D为△ABC中一点.证明:∠BDC=∠A+∠ABD+∠ACD.【答案】证明:如图,延长BD,交AC于点E.因为∠BDC是△CDE的外角,所以∠BDC=∠DEC+∠ACD.又因为∠DEC是△AEB的外角,所以∠DEC=∠A+∠ABD.由以上二式得∠BDC=∠A+∠ABD+∠ACD.【解析】【分析】延长BD交AC于点E;利用三角形外角的性质可得∠BDC= ∠DEC+∠ACD,∠DEC=∠A+∠ABD,等量代换即可得证.本题的结论常常用到,有人称之为“飞镖定理”.注意D必须在△ABC内(即四边形ABDC是一个在D点凹进去的凹四边形).否则,结论不成立.8.如图,BE平分∠ABD,CF平分∠ACD,BE与CF相交于点G.若∠BDC=140°∠BGC=100°,求∠A的度数.【答案】解:由上例得,∠BGC=∠A+∠2+∠4,①∠BDC=∠A+( ∠1+∠2)+( ∠3+∠4).②又因为BE平分∠ABD,CF平分∠ACD,所以∠1=∠2,∠3=∠4.所以②即∠BDC=∠A+2( ∠2+∠4).③由①×1- ③得∠A=2∠BGC-∠BDC=2×100°-140°=60°.【解析】【分析】根据“飞镖定理”可知∠BGC=∠A+∠2+∠4 ①,∠BDC=∠A+( ∠1+∠2)+( ∠3+∠4)②,再根据角平分线性质得∠1=∠2,∠3=∠4;代入②式变形为∠BDC=∠A+2( ∠2+∠4) ③,再由由①×1- ③得即可求得∠A度数.9.如图,已知在△ABC中,AD是∠BAC的平分线,CE垂直AD于E.求证:∠ACE>∠B.【答案】证明:延长CE交AB于点F.因为AD是∠BAC的平分线,所以∠1=∠2.又因为CE垂直AD,所以∠AEC=∠AEF=90°,在△AEF中,∠AFC=180°-(∠1+∠AEF),在△AEC中,∠ACE=180°-(∠2+ ∠AEC),所以∠ACE=∠AFC.因为∠AFC是△BCF的一个外角,所以∠AFC=∠B+∠BCF>∠B.从而∠ACE>∠B.【解析】【分析】延长CE交AB于点F.利用已知条件,构造∠AFC作为桥梁.一方面它等于∠ACE.另一方面,它又是△BFC的一个外角,它应大于不相邻的任一内角,从而解决问题.10.如图,在△ABC中,D、E是BC边上的点,∠BDA=∠BAD,∠CEA=∠CAE,∠DAE=∠BAC.求∠BAC的度数.【答案】解:设∠BAE、∠EAD、∠DAC分别为α,β,γ ,则β=即2β=γ+α①又∠BDA=∠BAD=α+β ,②∠CEA=∠CAE=β+γ .③在△AED中,内角和为180°,所以由②、③得,(α+β)+(β+γ)+β =180°,④结合①得,5β=180°,β=36°,所以∠BAC=3β =3×36°=108°.【解析】【分析】本题通过设未知数,利用已知条件与三角形的内角和等于180°,建立方程解决问题.。
四年级数学下册《三角形内角和》练习题(含答案)

四年级数学下册《三角形内角和》练习题(含答案)练习一建议用时:30分钟 满分100分1. 填空题。
(每空2分,共18分)(1)三角形三个内角的和是( ),长方形的四个内角的和是( )。
(2)等边三角形的每个内角都是( )°。
(3)在直角三角形中,一个锐角是75°,另一个锐角是( )°。
(4)一个三角形中,其中两个角的度数分别是45°和27°,第三个角的度数是( )°。
(5)等腰三角形的一个底角是80°,那么它的顶角是( )°。
(6)任意一个四边形都可以分成( )个三角形,每个三角形的内角和都是( )°,所以任意四边形的内角和是( )°。
2.判断题。
(对的画“√”,错的画“×”)(每小题2分,共10分)(1)大三角形的内角和比小三角形的内角和的度数大。
( ) (2)一个三角形的两个锐角度数的和大于90°,那么这个三角形一定是一个锐角三角形。
( )(3)等边三角形沿着高对折,得到的两个小三角形的内角和都是90°。
( )(4)四边形的四个内角中最多可能有2个钝角,最多可能有2个直角。
( ) (5)一个五边形可以分成3个三角形,所以五边形的内角和是540°。
( ) 3.求出下面三角形中未知角的度数。
(每小题5分,共20分) (1) (2)? 80° 45° 110°(3) 82° (4)130° 50° ?39°?50°4.一个等腰三角形的一个底角是52°,它的另外两个角分别是多少度?(6分)5.一个等腰三角形的一个角是70°,它的另外两个角分别是多少度?(10分)6.画一画,算一算,你发现了什么?(填空每空2分,第3、4小题每题6分,共36分)图 形三角形四边形五边形六边形七边形……边 数 3 4 …… 分成三角形的个数 12…… 内角和180°180°×2……(1)我发现:每增加一条边,内角和增加( );每个多边形分成的三角形的个数总比边数( )。
三角形内角和解答题专项练习60题(有答案)
三角形内角和解答题专项练习60题(有答案)1.如图,在△ABC中,∠BAC=60°,∠B=45°,AD是△ABC的一条角平分线,求∠ADC的度数?2.如图△ABC中,AD,AE分别是△ABC的高和角平分线,∠B=36°,∠DAE=16°.求∠CAD的度数.3.如图,已知∠CBE=96°,∠A=27°,∠C=30°,试求∠ADE的度数.4.如图,△ABC中,BD、CD分别是∠ABC和∠ACB的角平分线,BD、CD相交于点D,求证:∠D=90°+∠A.5.如图,在△ABC中,∠A=3x°,∠ABC=4x°,∠ACB=5x°,BD,CE分别是边AC,AB上的高,且BD,CE相交于点H,求∠BHC的度数.2013年10月1581698636的初中数学组卷6.如图,D是△ABC的BC边上一点,∠ABC=40°,∠BAC=80°.求:(1)∠C的度数;(2)如果AD是△ABC的BC边上的角平分线,求∠ADC的度数.7.如图,在△ABC中,点D是∠ACB与∠ABC的角平分线的交点,BD的延长线交AC于E,且∠EDC=60°.求∠A的度数.8.如图,∠A=50°∠ABC=60°.(1)若BD为∠ABC平分线,求∠BDC.(2)若CE为∠ACB平分线且交BD于E,求∠BEC.9.如图,在△ABC中,∠B和∠C的平分线相交于O点.(1)若∠A=60°,求∠BOC的度数.(只需写出结果)(2)若∠A=α,求∠BOC的度数.10.如图,已知∠ABC=∠ACB,∠1=∠2,∠3=∠F,(1)试判断EC与DF是否平行,并说明理由;(2)若∠ACF=110°,求∠A的度数.11.在三角形中,每两条边所组成的角叫三角形的内角,如图1,在三角形ABC中,∠B,∠BAC和∠C是它的三个内角.其实,在学习了平行线的性质以后,我们可以用几何推理的方法去证明“三角形的内角的和等于180°”.请在以下给出的证明过程中填空或填写理由.证明:如图2,延长BA,过点A作AE∥BC.∵AE∥BC(已作)∴∠1=∠(_________ ),(_________ )又∵AE∥BC(已作)∴∠2=∠(_________ ),(_________ )∵∠1+∠2+∠BAC=180°(平角定义)∴∠B+∠C+∠BAC=180°(_________ ),即,三角形的内角的和等于180°.12.如图,已知△ABC中,∠B=40°,∠C=62°,AD是BC边上的高,AE是∠BAC的平分线.求:∠DAE的度数.(写出推导过程)13.如图,已知,D、E分别是△ABC的边AB、AC上的点,DE交BC的延长线于F,∠B=67°,∠ACB=74°,∠AED=48°,求∠F和∠BDF的度数.14.如图,已知三角形ABC,∠ACB=90°,∠BCD+∠B=90°,∠A与∠BCD有怎样的大小关系?说明你的理由.15.如图,△ABC中,∠C=70°,AD、BD是△ABC的外角平分线,AD与BD交于点D,(1)求∠D的度数;(2)若去掉∠C=70°这个条件,试写出∠C与∠D之间的数量关系.16.(1)如图1,在△ABC中,∠C=90°,∠BAC=45°,∠BAC的平分线与外角∠CBE的平分线相交于点D,则∠D= _________ 度.(2)如图2,将(1)中的条件“∠BAC=45°”去掉,其他条件不变,求∠D的度数.17.已知:如图,AC∥DE,∠ABC=70°,∠E=50°,∠D=75°.求:∠A和∠ABD的度数.18.△ABC中,(1)若∠A=70°,BO、CO分别平分∠ABC和∠ACB,求∠BOC的度数;(2)若∠OBC=∠ABC,∠OCB=∠ACB,∠A=n°,请直接写出用n°表示∠BOC的关系式.19.已知,如图,在△ABC中,BD⊥AC于D,若∠A:∠ABC:∠ACB=3:4:5,试求∠ABD的度数.20.如图,把△ABC纸片沿DE折叠,使点C落在四边形BADE内部点F的位置.(1)已知∠CDE=50°,求∠ADF的大小;(2)已知∠C=60°,求∠1+∠2的大小.21.已知△ABC中,∠A=∠B=∠C,判断三角形的形状?22.如图,在△ABC中,BA平分∠DBC,∠BAC=124°,BD⊥AC于D,求∠C的度数.23.如图,AD是△ABC的BC边上的高,AE是∠BAC的角平分线,若∠B=47°,∠C=73°,求∠DAE的度数.24.如图,已知△ABC中,∠A=40°,角平分线BE、CF相交于O,求∠BOC的度数.25.如图,在△ABC中,CF⊥AB于F,ED⊥AB于D,∠1=∠2.(1)求证:FG∥BC;(2)若∠A=60°,∠AFG=40°,求∠ACB的度数.26.已知△ABC中,∠BAC=90°,∠C=30°,点D为BC边上一点,连接AD,作DE⊥AB于点E,DF⊥AC于点F.(1)若AD为△ABC的角平分线(如图1),图中∠1、∠2有何数量关系?为什么?(2)若AD为△ABC的高(如图2),求图中∠1、∠2的度数.27.如图:证明“三角形的内角和是180°”已知:_________求证:_________证明:过B点作直线EF∥AC.28.如图,BD平分∠ABC,CD平分∠ACE,请写出∠A和∠D的关系式,并说明理由.29.已知△ABC.(1)若∠BAC=40°,画∠BAC和外角∠ACD的角平分线相交于O1点(如图①),求∠BO1C的度数;(2)在(1)的条件下,再画∠O1BC和∠O1CD的角平分线相交于O2点(如图②),求∠BO2C的度数;(3)若∠BAC=n°,按上述规律继续画下去,请直接写出∠BO2012C的度数.30.(1)如图(1),在△ABC中,∠ABC、∠ACB的平分线相交于点O,∠A=40°,求∠BOC的度数.(2)如图(2),△DEF两个外角的平分线相交于点G,∠D=40°,求∠EGF的度数.(3)由(1)、(2)可以发现∠BOC与∠EGF有怎样的数量关系?设∠A=∠D=n°,∠BOC与∠EGF是否还具有这样的数量关系?为什么?31.在△ABC中,已知∠ABC=66°,∠ACB=54°,BE,CF分别是AC和AB边上的高,H是BE和CF的交点,求∠BHC 的度数.32.如图,△ABC中,∠ACB=∠B=2∠A,CD是AB边上的高,求∠BCD.33.如图,已知DM平分∠ADC,BM平分∠ABC,∠A=36°,∠M=44°,求∠C的度数.34.如图,在△ABC中,∠A=40°,∠B=72°,CD是AB边上的高;CE是∠ACB的平分线,DF⊥CE于F,求∠BCE 和∠CDF的度数.35.已知:点D是△ABC的BC边的延长线上的一点,DF⊥AB交AB于F,交AC于E,∠A=30°,∠D=20°,求∠ACB 的度数.36.已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°,求∠DAE的度数.37.如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,垂足分别为D,E,∠AFD=158°,求∠EDF的度数.38.如图,CD是∠ACB的平分线,DE∥BC,∠B=70°,∠ACB=50°,求∠EDC,∠BDC的度数.39.已知:如图,在△ABC中,∠BAC=80°,AD⊥BC于D,AE平分∠DAC,∠B=60°;求∠DAE的度数.40.如图,△ABC中,AD是BC边上的高,AE是三角形∠BAC的角平分线,若∠B=40°,∠C=70°,则∠DAE为多少度?41.如图所示,已知DF⊥AB于F,∠A=40°,∠D=50°,求∠ACB的度数.42.在△ABC中,∠B=∠A+10°,∠C=∠B+10°,求△ABC各内角的度数.43.已知,如图,在△ABC中,AD,AE分别是△ABC的高和角平分线,若∠B=30°,∠C=50°.(1)求∠DAE的度数;(2)试写出∠DAE与∠C﹣∠B有何关系?(不必证明)44.如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F.已知∠A=30°,∠FCD=80°,求∠D.45.如图,已知△ABC中,∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线,求∠DAE的度数.46.如图:在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=34度.求∠DAE的度数.47.如图,若AB∥CD,EF与AB、CD分别相交于E、F,EP⊥EF,∠EFD的平分线与EP相交于点P,且∠BEP=40°,求∠P的度数.48.如图已知△ABC中,∠B和∠C外角平分线相交于点P.(1)若∠ABC=30°,∠ACB=70°,求∠BPC度数.(2)若∠ABC=α,∠BPC=β,求∠ACB度数.49.如图,∠B=42°,∠A+10°=∠1,∠ACD=64°,求证:AB∥CD.50.如图:AB∥CD,直线l交AB、CD分别于点E、F,点M在EF上,N是直线CD上的一个动点(点N不与F重合)(1)当点N在射线FC上运动时,∠FMN+∠FNM=∠AEF,说明理由;(2)当点N在射线FD上运动时,∠FMN+∠FNM与∠AEF有什么关系并说明理由.51.如图,△ABC中,∠B=40°,∠C=70°,AD为∠BAC的平分线,AE为BC边上的高,求∠DAE的度数.52.如图,在△ABC中,∠ABC=60°,∠ACB=50°,BD平分∠ABC,CD平分∠ACB.求∠D的度数.53.如图,已知∠A=20°,∠B=27°,AC⊥DE,求∠1,∠D的度数.54.已知:图中,∠B=40°,∠C=60°,AD、AF分别是△ABC的角平分线和高.(1)∠BAC等于多少度?(2)∠DAF等于多少度?55.△ABC中,BE平分∠ABC,AD为BC上的高,且∠ABC=60°,∠BEC=75°,求∠DAC的度数.56.如图,在△ABC中,∠ABC=80°,∠ACB=50°,BP平分∠ABC,CP平分∠ACB,求∠BPC的度数.57.如图,BE∥AO,∠1=∠2,OE⊥OA于点O,EH⊥CO于点H,那么∠5=∠6,为什么?58.如图,已知△ABC中,∠ABC和∠ACB的平分线BD、CE相交于点O,且∠A=60°,求∠BOC的度数.259.已知:如图,在△ABC中,∠C>∠B,AD⊥BC交于点D,AE平分∠BAC,试说明:∠EAD=(∠C﹣∠B).60.如图(1),△ABC中,AB=AC,∠B=2∠A.(1)求∠A和∠B的度数;(2)如图(2),BD是△ABC中∠ABC的平分线:①写出图中与BD相等的线段,并说明理由;②直线BC上是否存在其它的点P,使△BDP为等腰三角形,如果存在,请在图(3)中画出满足条件的所有的点P,并直接写出相应的∠BDP的度数;如果不存在,请说明理由.三角形内角和解答题60题参考答案:1.∵AD是△ABC的一条角平分线,∴∠BAD=∠BAC=×60°=30°,∴∠ADC=∠BAD+∠B=30°+45°=75°2.∵AD⊥BC,∴∠ADB=90°,∴∠B+∠BAD=90°,∵∠B=36°,∴∠BAD=90°﹣36°=54°,∵∠DAE=16°,∴∠BAE=54°﹣16°=38°,∵AE平分∠BAC,∴∠CAE=∠BAE=38°,∴∠CAD=38°﹣16°=22°3.∵∠A=27°,∠C=30°,∴∠DFC=∠A+∠C=57°,∵∠DBF=∠CBE=96°,∴∠ADE=180°﹣∠DFC﹣∠FBD=180°﹣57°﹣96°=27°.4.在△ABC中,∠ABC+∠ACB=180°﹣∠A,∵BD、CD分别是∠ABC和∠ACB的角平分线,∴∠DBC=∠ABC,∠DCB=∠ACB,∴∠DBC+∠DCB=(∠ABC+∠ACB)=(180°﹣∠A)=90°﹣∠A,在△BCD中,∠D=180°﹣(∠DBC+∠DCB)=180°﹣(90°﹣∠A)=90°+∠A,即:∠D=90°+∠A.5.在△ABC中,∵∠A=3x°,∠ABC=4x°,∠ACB=5x°.又∵∠A+∠ABC+∠ACB=180°.∴3x°+4x°+5x°=180°,解得x=15,∠A=3x°=45°,∵BD,CE分别是边AC,AB上的高,∴∠ADB=90°,∠BEC=90°,∵在△ABD中,∠ABD=180°﹣∠ADB﹣∠A=180°﹣90°﹣45°=45°,∴∠BHC=∠ABD+∠BEC=45°+90°=135°6.(1)∵∠ABC=40°,∠BAC=80°,∴∠C=180°﹣∠ABC﹣∠BAC=180°﹣40°﹣80°=60°;(2)∵∠BAC=80°,AD是△ABC的BC边上的角平分线,∴∠DAC=∠BAC=40°,∵∠C=60°,∴∠ADC=180°﹣∠CAD﹣∠C=180°﹣40°﹣60°=80°7.∵BD平分∠ABC,CD平分∠ACB,∴∠DBC=∠ABC,∠DCB=∠ACB,∴∠DBC+∠DCB=(∠ABC+∠ACB)=(180°﹣∠A),∵∠EDC=∠DBC+∠DCB=60°,∴(180°﹣∠A)=60°,∴∠A=60°8.(1)∵BD为∠ABC平分线,∴∠ABD=∠ABC=×60°=30°,∴∠BDC=∠A+∠ABD=50°+30°=80°.(2)∵∠ACB=180°﹣∠A﹣∠ABC=180°﹣50°﹣60°=70°,又∵CE为∠ACB平分线,∴∠DCE=∠ACB=×70°=35°,∴∠BEC=∠DCE+∠BDC=35°+80°=115°9.(1)∵∠A=60°,∴∠ABC+∠ACB=180°﹣∠A=180°﹣60°=120°,∵∠B和∠C的平分线相交于O点,∴∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB)=×120°=60°,在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣60°=120°;(2))∵∠A=α,∴∠ABC+∠ACB=180°﹣∠A=180°﹣α,∵∠B和∠C的平分线相交于O点,∴∠OBC=∠ABC,∠OCB=∠ACB,∴∠OBC+∠OCB=∠ABC+∠ACB=(∠ABC+∠ACB)=(180°﹣α)=90°﹣α,在△OBC中,∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣(90°﹣α)=90°+α10.(1)BC∥DF,理由:∵∠ABC=∠ACB,∠1=∠2,∴∠ABC﹣∠1=∠ACB﹣∠2,即∠3=∠ECB,∵∠3=∠F,∴∠ECB=∠F,∴EC∥DF(同位角相等,两直线平行);(2)∵∠ACF=110°,∴∠ACB=70°,∵∠ABC=∠ACB,∴∠ABC=70°,∴∠A=∠ACF﹣∠ABC=110°﹣70°=40°11.证明:如图2,延长BA,过点A作AE∥BC.∵AE∥BC(已作)∴∠1=∠(∠B ),(两直线平行,同位角相等)又∵AE∥BC(已作)∴∠2=∠(∠C ),(两直线平行,内错角相等)∵∠1+∠2+∠BAC=180°(平角定义)∴∠B+∠C+∠BAC=180°(等量代换),即,三角形的内角的和等于180°.12.∵△ABC中,∠B=40°,∠C=62°,∴∠BAC=180°﹣∠B﹣∠C=180°﹣40°﹣62°=78°,∵AE是∠BAC的平分线,∴∠EAC=∠BAC=39°,∵AD是BC边上的高,∴在直角△ADC中,∠DAC=90°﹣∠C=90°﹣62°=28°,∴∠DAE=∠EAC﹣∠DAC=39°﹣28°=11°13.∵∠CEF=∠AED=48°,∠ACB=∠CEF+∠F,∴∠F=∠ACB﹣∠CEF=74°﹣48°=26°;∵∠BDF+∠B+∠F=180°,∴∠BDF=180°﹣∠B﹣∠F=180°﹣67°﹣26°=87°14.∠A=∠BCD,理由是:∵∠ACB=90°,∴∠A+∠B=90°,∵∠BCD+∠B=90°,∴∠A=∠BCD15.(1)∵∠C=70°,∴∠CAB+∠CBA=180°﹣70°=110°,∴∠EAB+∠FBA=360°﹣110°=250°,∵AD、BD是△ABC的外角平分线,∴∠DAB+∠DBA=(∠EAB+∠FBA)=125°,∴∠D=180°﹣125°=55°;(2)由题意可得,∠CAB+∠CBA=180°﹣∠C,∴∠EAB+∠FBA=360°﹣(∠CAB+∠CBA),=360°﹣(180°﹣∠C),=180°+∠C,∵AD、BD是△ABC的外角平分线,∴∠DAB+∠DBA=(∠EAB+∠FBA),=(180°+∠C),=90°+∠C,∴∠D=180°﹣(90°+∠C),=90°﹣∠C.16.(1)∵∠CBE 是△ABC的外角,∴∠CBE=∠CAB+∠C,∴∠C=∠CBE﹣∠CAB,∵∠BAC的平分线与外角∠CBE的平分线相交于点D,∴∠1=∠CAB,∠2=∠CBE,∵∠2是△ABD的外角,∴∠2=∠1+∠D,∴∠D=∠2﹣∠1=(∠CBE﹣∠CAB)=∠C=×90°=45°;故答案为:45;(2)∵∠CBE 是△ABC的外角,∴∠CBE=∠CAB+∠C,∴∠C=∠CBE﹣∠CAB,∵∠BAC的平分线与外角∠CBE的平分线相交于点D,∴∠1=∠CAB,∠2=∠CBE,∵∠2是△ABD的外角,∴∠2=∠1+∠D,∴∠D=∠2﹣∠1=(∠CBE﹣∠CAB)=∠C=×90°=45°.17.∵AC∥DE,∠E=50°,∠D=75°,∴∠ACB=∠E=50°…(1分)∠1=∠D=75°(3分)又∵∠ABC=70°,∴∠A=180°﹣∠ABC﹣∠ACB=180°﹣70°﹣50°=60°…(6分)∠ABD=∠1﹣∠A=75°﹣60°=15°…(9分)∴∠A=60°,∠ABD=15°.18.(1)∵BO、CO分别平分∠ABC和∠ACB,∴∠OBC=∠ABC,∠OCB=∠ACB,∵∠A=70°,∴∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣(180°﹣70°)=125°.故∠BOC的度数为:125°.(2)∵∠OBC=∠ABC,∠OCB=∠ACB,∠A=n°,∵∠BOC=180°﹣∠OBC﹣∠OCB=180°﹣(∠OBC+∠OCB)=180°﹣(180°﹣n°)=120°+n°.故∠BOC=120°+n°19.设∠A、∠ABC、的度数分别为3x、4x、5x.则3x+4x+5x=180°,解得x=15°.∴∠A=45°,∠ACB=75°.又∵∠A+∠ABD=90°,∴∠ABD=90°﹣45°=45°20.(1)由折叠的过程可知:∠3=∠CDE,∵∠CDE=50°,∴∠3=50°,∴∠1=180°﹣∠3﹣∠CDE=80°,即∠ADF=80°;(2)∵∠C=60°,∴∠CDE+∠CED=120°,∵由折叠的过程可知∠CDE+∠CED=∠3+∠4=180°﹣∠C=120°,∴∠CDE+∠CED+∠3+∠4=240°,∵∠1+∠3+∠CDE+∠2+∠4+∠CED=360°,∴∠1+∠2+∠3+∠4+∠CDE+∠CED=360°,∴∠1+∠2=120°21.∵∠ABC+∠ACB+∠BAC=180°,∠A=∠B=∠C,∴∠A+2∠A+3∠A=180°.∴∠A=30°,∠B=60°,∠C=90°.所以△ABC是直角三角形22.在△ABD中,∠BAC=∠D+∠DBA,∵BD⊥AC,∴∠D=90°.又∵∠BAC=124°,∴∠DBA=34°.∵BA平分∠DBC,∴∠DBC=2∠DBA=68°,在△CBD中,∠C=180°﹣(∠D+∠DBC)=22°.23.∵∠B=30°,∠C=70°,∴∠BAC=180°﹣∠B﹣∠C=60°,∵AE是角平分线,∴∠EAC=∠BAC=30°.∵AD是高,∠C=73°,∴∠DAC=90°﹣∠C=17°,∴∠EAD=∠EAC﹣∠DAC=30°﹣17°=13°24.如图,∵角平分线BE、CF相交于O,∴∠ABC=2∠1,∠ACB=2∠2,又∵∠A+∠ABC+∠ACB=180°,∴∠A+2∠1+2∠2=180°,∴∠1+∠2=90°﹣∠A,又∵∠1+∠2+∠BOC=180°,∴∠1+∠2=180°﹣∠BOC,∴180°﹣∠BOC=90°﹣∠A,∴∠BOC=90°+∠A,而∠A=40°,∴∠BOC=90°+×40°=11025.(1)证明:如图,∵CF⊥AB,ED⊥AB,∴DE∥FC,∴∠1=∠3.又∵∠1=∠2,∴∠2=∠3,∴FG∥BC;(2)解:如图,在△AFG中,∠A=60°,∠AFG=40°,∴∠AGF=180°﹣∠A﹣∠AFG=100°.又由(1)知,FG∥BC,∴∠ACB=∠AGF=80°,即∠ACB的度数是80°.26.(1)∠1=∠2,理由如下:∵DE⊥AB,DF⊥AC,∴∠DEB=∠DFC=∠BAC=90°,∴DE∥AC,DF∥AB,∴∠1=∠DAC,∠2=∠DAB,∵AD平分∠BAC,∴∠DAC=∠DAB,∴∠1=∠2;(2)∵DE⊥AB,DF⊥AC,AD⊥BC,∴∠ADB=∠ADC=∠DEB=∠DFC=∠BAC=90°,∴DE∥AC,∴∠BDE=∠C=30°,∴∠1=∠ADB﹣∠BDE=30°,∵∠FDC=180°﹣∠DFC﹣∠C=60°,∴∠2=∠ADC﹣∠FDC=60°27.过点B作EF∥AC,∴∠EBA=∠A,∠FBC=∠C,∵∠EBA+∠ABC+∠FBC=180°,∴∠A+∠C+∠ABC=180°,∴三角形的内角和等于180°.故答案为△ABC,∠A+∠B+∠C=180°28.∠A=2∠D.理由如下:∵BD平分∠ABC,CD平分∠ACE,∴∠DBC=∠ABC,∠DCE=∠ACE,∴∠A=∠ACE﹣∠ABC,∠D=∠DCE﹣∠DBC=(∠ACE﹣∠ABC),∴∠A=2∠D29.∵O1B、O1C分别平分∠ABC和∠ACD,∴∠ACD=2∠O1CD,∠ABC=2∠O1BC,而∠O1CD=∠O1+∠O1BC,∠ACD=∠ABC+∠A,∴∠A=2∠01=40°,∴∠O1=20°,同理可得∠O1=2∠O2,即∠A=22∠02=40°,∴∠O2=10°,∴∠A=2n∠A n,∴∠A n=n °×()n.则∠BO2012C=0.30.(1)∵∠A=40°,∴∠ABC+∠ACB=180°﹣40°=140°.∵BO、CO分别是∠ABC、∠ACB的角平分线,∴∠OBC+∠OCB=(∠ABC+∠ACB)=×140°=70°,∴∠BOC=180°﹣(∠OBC+∠OCB)=180°﹣70°=110°;(2)设△ABC的两个外角为α、β.则∠G=180°﹣(α+β)(三角形的内角和定理),利用三角形内角与外角的关系:三角形的任一外角等于和它不相邻的两个内角之和.可知α+β=∠D+∠DFE+∠D+∠DEF=180°+40°=220°,∴∠G=180°﹣(α+β)=70°;(3)∠A=∠D=n°,∠BOC与∠EGF互补.证明:当∠A=n°时,∠BOC=180°﹣[(180°﹣n°)÷2]=90°+,∵∠D=n°,∠EGF=180°﹣[360°﹣(180°﹣n°)]÷2=90°﹣,∴∠A+∠D=90°++90°﹣=180°,∴∠BOC与∠EGF互补.31.如图,在△ABC中,∵∠ABC=66°,∠ACB=54°,∴∠A=180°﹣∠ABC﹣∠ACB180°﹣66°﹣54°=60°,∵BE和CF分别为AC和AB边上的高,∴∠AEB=∠BFC=90°,在Rt△ABE中,∠1=180°﹣∠A﹣∠AEB=180°﹣90°﹣60°=30°,在△BHC中,∠BHC=∠1+∠BFC=30°+90°=120°32.∵∠ACB=∠B=2∠A,∴∠A+∠B+∠ACB=∠A+2∠A+2∠A=180°,解得∠A=36°,∴∠B=2∠A=2×36°=72°,∵CD是AB边上的高,∴∠BCD=90°﹣∠B=90°﹣72°=18°33.∵DM平分∠CDA,∴∠CDM=∠MDA,又∵BM平分∠ABC,∴∠CBM=∠ABM,又∵∠MDA+44°=∠CBM+36°,∴∠CBM﹣∠MDA=8°,∴2∠CBM﹣2∠MDA=16°,即∠ABC﹣∠ADC=16°,又∵∠ADC+∠C=∠ABC+∠A,∴∠C=36°+16°=52°34.∵∠A+∠B+∠ACB=180°,∠A=40°,∠B=72°,∴∠ACB=68°,∵CE平分∠ACB,∴∠BCE=∠ACB=×68°=34°,∵CD⊥AB,∴∠CDB=90°,∵∠B=72°,∴∠BCD=90°﹣72°=18°,∴∠FCD=∠BCE﹣∠BCD=16°,∵DF⊥CE,∴∠CFD=90°,∴∠CDF=90°﹣∠FCD=74°,即∠BCE=34°,∠CDF=74°35.在△BFD中,∵DF⊥AB,∠D=20°,∴∠B=90°﹣∠D=90°﹣20°=70°,在△ABC中,∵∠B=70°,∠A=30°,∴∠ACB=180°﹣∠A﹣∠B=180°﹣30°﹣70°=80°.答:∠ACB度数是80°36.∵∠BAC+∠B+∠C=180°,而∠B=30°,∠C=50°,∴∠BAC=180°﹣30°﹣50°=100°,∵AE是△ABC的角平分线,∴∠EAC=∠BAC=50°又∵AD为高线,∴∠ADC=90°,而∠C=50°,∴∠DAC=180°﹣90°﹣50°=40°,∴∠DAE=∠EAC﹣∠DAC=50°﹣40°=10°37.∵FD⊥BC,所以∠FDC=90°,∵∠AFD=∠C+∠FDC,∴∠C=∠AFD﹣∠FDC=158°﹣90°=68°,∴∠B=∠C=68°.∵DE⊥AB,∵∠DEB=90°,∴∠BDE=90°﹣∠B=22°.又∵∠BDE+∠EDF+∠FDC=180°,∴∠EDF=180°﹣∠BDE﹣∠FDC=180°﹣22°﹣90°=68°38.∵CD是∠ACB的平分线,∴∠BCD=25°.∵DE∥BC,∴∠EDC=∠BCD=25°,∴在△BDC中,∠BDC=180°﹣∠B﹣∠BCD=180°﹣70°﹣25°=85°.39.∵AD⊥BC,∴∠BDA=90°.∵∠B=60°,∴∠BAD=180°﹣90°﹣60°=30°∵∠BAC=80°∴∠DAC=∠BAC﹣∠BAD=80°﹣30°=50°.∵AE平分∠DAC,∴∠DAE=0.5∠DAC=25°140.∵∠B=40°,∠C=70°,∴在△ABC中,∠BAC=180°﹣40°﹣70°=70°,又∵AE是∠BAC的角平分线,∴∠EAC=∠BAC=35°,又∵AD是BC边上的高,∴AD⊥BC,∴∠ADC=90°,∴在△ADC中,∠DAC=180°﹣∠ADC﹣∠C=20°,∴∠DAE=∠EAC﹣∠DAC=35°﹣20°=15°41.在△BDF中,∠B=180﹣∠BFD﹣∠D=180°﹣90°﹣50°=40°,在△ACB中,∠A=40°,故∠ACB=180°﹣∠A﹣∠B=180°﹣40°﹣40°=100°42.∵∠B=∠A+10°,∠C=∠B+10°,又∵∠A+∠B+∠C=180°,∴∠A+(∠A+10°)+(∠A+10°+10°)=180°,3∠A+30°=180°,3∠A=150°,∠A=50°.∴∠B=60°,∠C=70°.43.(1)∵∠B=30°,∠C=50°,∴∠BAC=180°﹣30°﹣50°=100°.∵AE是∠BAC的平分线,∴∠BAE=50°.在Rt△ABD中,∠BAD=90°﹣∠B=60°,∴∠DAE=∠BAD﹣∠BAE=60°﹣50=10°;(2)∠C﹣∠B=2∠DAE44.∵DE⊥AB(已知),∴∠FEA=90°(垂直定义).∵在△AEF中,∠FEA=90°,∠A=30°(已知),∴∠AFE=180°﹣∠FEA﹣∠A(三角形内角和是180)=180°﹣90°﹣30°=60°.又∵∠CFD=∠AFE(对顶角相等),∴∠CFD=60°.∴在△CDF中,∠CFD=60°∠FCD=80°(已知)∠D=180°﹣∠CFD﹣∠FCD=180°﹣60°﹣80°=40°45.在△ABC中,∵∠BAC=180°﹣∠B﹣∠C=70°,∵AE是∠BAC的平分线,∴∠BAE=∠CAE=35°.又∵AD是BC边上的高,∴∠ADB=90°,∵在△ABD中∠BAD=90°﹣∠B=25°,∴∠DAE=∠BAE﹣∠BAD=10°46.在△ABC中∠BAC=180﹣∠B﹣∠C=76°,又∵AE平分∠BAC,∴∠EAC=38°,在直角△ACD中,∠DAC=90﹣∠C=56°,∴∠DAE=∠DAC﹣∠EAC=18°47.∵EP⊥EF,∴∠PEM=90°,∠PEF=90°.∵∠BEP=40°,∴∠BEM=∠PEM﹣∠BEP=90°﹣40°=50°.∵AB∥CD,∴∠BEM=∠EFD=50°.∵FP平分∠EFD,∴∠EFP=∠EFD=25°,∴∠P=90°﹣25°=65°.48.(1)∠BPC =180°﹣(∠EBC+∠BCF)=180°﹣(∠EBC+∠BCF)=180°﹣(180°﹣∠ABC+180°﹣∠ACB)=180°﹣(180°﹣30°+180°﹣70°)=50°;(2)∠BPC=180°﹣(180°﹣∠ABC+180°﹣∠ACB)=(∠ABC+∠ACB),∵∠BPC=β,∠ABC=α,∴β=(α+∠ACB).故∠ACB=2β﹣α49.在△ABC中,∠A+∠B+∠1=180°,∠B=42°,∴∠A+∠1=138°,又∵∠A+10°=∠1,∴∠A+∠A+10°=138°,解得:∠A=64°.∴∠A=∠ACD=64°,∴AB∥CD(内错角相等,两直线平行)50.(1)∵AB∥CD,∴∠AEF+∠MFN=180°.∵∠MFN+∠FMN+∠FNM=180°,∴∠FMN+∠FNM=∠AEF.(2)∠FMN+∠FNM+∠AEF=180°.理由:∵AB∥CD,∴∠AEF=∠MFN.∵∠MFN+∠FMN+∠FNM=180°,∴∠FMN+∠FNM+∠AEF=180°.51.∵∠B=40°,∠C=70°,∴∠BAC=180°﹣40°﹣70°=70°,又AD为平分线,∴∠DAC=35°.∵AE⊥BC,∴∠EAC=90°﹣∠C=20°,∴∠DAE=35°﹣20°=15°252.∵BD平分∠ABC,CD平分∠ACB,∴∠DBC=∠ABC=30°,∠DCB=∠ACB=25°,又∵∠DBC+∠DCB+∠D=180°,∴∠D=180°﹣∠DBC﹣∠DCB=180°﹣30°﹣25°=125°53.∵AC⊥DE,∴∠APE=90°.∵∠1是△AEP的外角,∴∠1=∠A+∠APE.∵∠A=20°,∴∠1=20°+90°=110°.在△BDE中,∠1+∠D+∠B=180°,∵∠B=27°,∴∠D=180°﹣110°﹣27°=43°54.(1)根据三角形的内角和定理,得:∠BAC=180°﹣∠B﹣∠C=80°;(2)∵AD是△ABC的角平分线,∴∠BAD=∠BAC=40°,∴∠ADF=∠B+∠BAD=80°,又∵AF是△ABC的高,∴∠DAF=10°55.∵BE平分∠ABC,且∠ABC=60°,∴∠ABE=∠EBC=30°,∴∠C=180°﹣∠EBC﹣∠BEC=180°﹣30°﹣75°=75°.又∵∠C+∠DAC=90°,∴∠DAC=90°﹣∠C=90°﹣75°=15°56.在△ABC中,∵∠ABC=80°,BP平分∠ABC,∴∠CBP=∠ABC=40°.∵∠ACB=50°,CP平分∠ACB,∴∠BCP=∠ACB=25°.在△BCP中∠BPC=180°﹣(∠CBP+∠BCP)=115°57.由OE⊥OA,得∠2+∠3=90°,又∵∠1=∠2,∠1+∠2+∠3+∠4=180°,∴∠3=∠4,∵EH⊥CO,∴∠5=90°﹣∠3=90°﹣∠4,∴∠5=∠2,∵BE∥AO,∴∠2=∠6,∴∠5=∠658.∵∠ABC和∠ACB的平分线BD、CE相交于点O,∴∠1=∠2,∠3=∠4,∴∠2+∠4=(180°﹣∠A)=(180°﹣60°)=60°,故∠BOC=180°﹣(∠2+∠4)=180°﹣60°=120°.59.∵AE平分∠BAC,∴∠BAE=∠CAE=∠BAC∵∠BAC=180°﹣(∠B+∠C)∴∠EAC=[180°﹣(∠B+∠C)]∵AD⊥BC,∴∠ADC=90°,∴∠DAC=180°﹣∠ADC﹣∠C=90°﹣∠C,∵∠EAD=∠EAC﹣∠DAC∴∠EAD=[180°﹣(∠B+∠C)]﹣(90°﹣∠C)=(∠C﹣∠B)60.(1)∵AB=AC,∠B=2∠A∴AB=AC,∠C=∠B=2∠A又∵∠C+∠B+∠A=180°∴5∠A=180°,∠A=36°∴∠B=72°;(2)①∵BD是△ABC中∠ABC的平分线∴∠ABD=∠CBD=36°∴∠BDC=72°∴BD=AD=BC;②当BD是腰时,以B为圆心,以BD为半径画弧,交直线BC于点P1(点C除外)此时∠BDP=∠DBC=18°.以D为圆心,以BD为半径画弧,交直线BC于点P3(点C除外)此时∠BDP=108°.当BD是底时,则作BD的垂直平分线和BC的交点即是点P2的一个位置.此时∠BDP=∠PBD=36°。
(完整版)三角形内角和综合习题精选(含答案)

三角形内角和综合习题精选一.解答题(共12小题)1.如图(1),△ABC中,AD是角平分线,AE⊥BC于点E.(1).若∠C=80°,∠B=50°,求∠DAE的度数.(2).若∠C>∠B,试说明∠DAE=(∠C﹣∠B).(3).如图(2)若将点A在AD 上移动到A´处,A´E⊥BC于点E.此时∠DAE变成∠DA´E,(2)中的结论还正确吗?为什么?2.如图,AD为△ABC的中线,BE为三角形ABD中线,(1)∠ABE=15°,∠BAD=35°,求∠BED的度数;(2)在△BED中作BD边上的高;(3)若△ABC的面积为60,BD=5,则点E到BC边的距离为多少?3.如图,DB是△ABC的高,AE是角平分线,∠BAE=26°,求∠BFE的度数.4.如图,在△ABC中,AD平分∠BAC,P为线段AD上的一个动点,PE⊥AD交直线BC于点E.(1)若∠B=35°,∠ACB=85°,求∠E的度数;(2)当P点在线段AD上运动时,猜想∠E与∠B、∠ACB的数量关系,写出结论无需证明.5.(1)如图1,有一块直角三角板XYZ放置在△ABC上,恰好三角板XYZ的两条直角边XY、XZ分别经过点B、C.△ABC中,∠A=30°,则∠ABC+∠ACB=_________ ,∠XBC+∠XCB=_________ .(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C,那么∠ABX+∠ACX的大小是否变化?若变化,请举例说明;若不变化,请求出∠ABX+∠ACX的大小.6.如图1,△ABC中,∠A=50°,点P是∠ABC与∠ACB平分线的交点.(1)求∠P的度数;(2)猜想∠P与∠A有怎样的大小关系?(3)若点P是∠CBD与∠BCE平分线的交点,∠P与∠A又有怎样的大小关系?(4)若点P是∠ABC与∠ACF平分线的交点,∠P与∠A又有怎样的大小关系?【(2)、(3)、(4)小题只需写出结论,不需要证明】7.如图,已知△ABC中,∠B=∠E=40°,∠BAE=60°,且AD平分∠BAE.(1)求证:BD=DE;(2)若AB=CD,求∠ACD的大小.8.如图,A、B两点同时从原点O出发,点A以每秒x个单位长度沿x轴的负方向运动,点B以每秒y个单位长度沿y轴的正方向运动.(1)若|x+2y﹣5|+|2x﹣y|=0,试分别求出1秒钟后A、B两点的坐标;(2)设∠BAO的邻补角和∠ABO的邻补角的平分线相交于点P,问:点A、B在运动的过程中,∠P的大小是否会发生变化?若不发生变化,请求出其值;若发生变化,请说明理由;(3)如图,延长BA至E,在∠ABO的内部作射线BF交x轴于点C,若∠EAC、∠FCA、∠ABC的平分线相交于点G,过点G作BE的垂线,垂足为H,试问∠AGH和∠BGC的大小关系如何?请写出你的结论并说明理由.9.如图所示,点E在AB上,CE,DE分别平分∠BCD,∠ADC,∠1+∠2=90°,∠B=75°,求∠A的度数.10.如图,∠AOB=90°,点C、D分别在射线OA、OB上,CE是∠ACD的平分线,CE的反向延长线与∠CDO的平分线交于点F.(1)当∠OCD=50°(图1),试求∠F.(2)当C、D在射线OA、OB上任意移动时(不与点O重合)(图2),∠F的大小是否变化?若变化,请说明理由;若不变化,求出∠F.11.如图,△ABC中,AE、BF是角平分线,它们相交于点O.(∠ABC>∠C),(1)试说明∠BOA=90°+∠C;(2)当AD是高,判断∠DAE与∠C、∠ABC的关系,并说明理由.12.已知△ABC中,∠BAC=100°.(1)若∠ABC和∠ACB的角平分线交于点O,如图1所示,试求∠BOC的大小;(2)若∠ABC和∠ACB的三等分线(即将一个角平均分成三等分的射线)相交于O,O1,如图2所示,试求∠BOC 的大小;(3)如此类推,若∠ABC和∠ACB的n等分线自下而上依次相交于O,O1,O2…,如图3所示,试探求∠BOC的大小与n的关系,并判断当∠BOC=170°时,是几等分线的交线所成的角.答案与评分标准一.解答题(共12小题)1.如图(1),△ABC中,AD是角平分线,AE⊥BC于点E.(1).若∠C=80°,∠B=50°,求∠DAE的度数.(2).若∠C>∠B,试说明∠DAE=(∠C﹣∠B).(3).如图(2)若将点A在AD 上移动到A´处,A´E⊥BC于点E.此时∠DAE变成∠DA´E,(2)中的结论还正确吗?为什么?考点:三角形的角平分线、中线和高;角平分线的定义;垂线;三角形内角和定理。
