北师大版八年级数学下册 《图形的平移与旋转》全章复习与巩固(基础)知识讲解 含答案解析
北师大版八年级数学下册 第三章 图形的平移和旋转 复习课件共22张

二、旋转
1、概念:在平面内,将一个图形绕一个定点 沿某个方向转动一个角度,这样的图形运动 叫旋转,这个定点称为旋转中心,转动的角 度称为旋转角度。
2、注意点 :(1)旋转是有范围的,它是在平 面内旋转,否则有可能旋转为立体图形。 (2)因为经过旋转,图形上的每个点都绕旋 转中心沿相同方向转动了同样的角度所以,任 意一对对应点与旋转中心的连线所成的角都 是旋转角。
3、决定平移的方向和距离: 如果已知一个图形和它平移后的图形的某
些点的对应点,那么连结原图上的点和对应 点所成射线的方向就是其平移方向,两对应 点的距离就是平移距离。
4、平移的特征 :(1)对应线段平行(或在一 直线上)且相等;对应点所连的线段平行(或 在一直线上)且相等。 (2)对应角分别相等,且对应角的两边分别 平行、与原角的方向一致。 (3)平移后的图形与原图形的形状、大小不 变,即平移只改变图形的位置。
2、线段垂直平分线的性质。
?考点三 平移和旋转的应用
例4
? 盘点提升
针对训练 C
2.在图3-8的四个三角形中,不能由 3-7中的△ABC经过旋转或平移得到的是 (
)
B
图3-7Βιβλιοθήκη 图3-83、如图3-9,△ABC和△ADE都是等腰直角三角形,
∠ACB和∠ADE都是直角,点C在AE上,△ABC绕着 A点经过逆时针旋转后与△ADE重合得到图(1),再
图3-11
6
? 课后作业---链接中考
(1)中心对称 定义:如果把一个图形绕着某一点旋转 180°,能够 与另一个图形重合,那么就说这两个图形关于这个点 对称或中心对称,这个点叫做它们的对称中心. (2)中心对称图形 把一个图形绕某个点旋转 180°,如果旋转后的图形 与原来的图形重合,那么这个图形叫做中心对称图形, 这个点叫做它的对称中心. 性质: 成中心对称的两个图形中,对应点所连线段经 过对称中心,且被对称中心平分.
北师大版八年级下册第三章图形的平移与旋转单元复习课件( 25张PPT)

(3)由勾股定理得:AC=3 2,点A旋转到 A’所经过
的路线长为¼ ×2π×3 2=√
√
知识回顾 知识探究 知识小结 练习提升
12.如图,在平面直角坐标系中,△ABC的各个定点坐标 是A(-2,3)、B(-4,-1)、C(2,0),点P(m,n)为 △ABC内的一点,△ABC平移后得到△A’B’C’,点P平移到 P’(m+6,n+1)处。 (1)直接写出点A’B’C’的坐标; (2)作出平移后的图形; (3)若点M(-3,b)为边AB上的点,则对应点M’的坐 标是什么? (4)如果将△A’B’C’看成是由△ABC经过一次平移得到 的,请指出这一平移的方向和平移的距离。
知识回顾 知识探究 知识小结 练习提升
解:(1)A’(4,4)B’(2,0) C’(8,1) (2)图形如图所示
(3)M’(3,b+1) (4) 平移的方向是由B到C(或B’)的方向,平移的距离是 √37个单位。
知识回顾 知识探究 知识小结 练习提升
13.如图,四边形ABCD是正方形,E、F分别是DC和CB延长 线上的点,且DE=BF,连接AE,AF,EF. (1)求证:△ADE≌△ABF (2)填空:△ABF可以由△ADE绕旋转中心( )点 ,按 顺时针方向旋转( )得到。 (3)若BC=8,DE=6,求△AEF的面积。
在平面直角坐标系中的平移:若图形依次沿x轴方向向右平移a(a>0) 个单位长度,再沿y轴方向向上(下)平移b(b>0)个单位长度,则 新图与原来的图相比,对应点的横坐标都增加(减少)了a,纵坐标 都增加(减少)了b。
一个图形依次沿着x轴方向、y轴方向平移后所得图形,可 以看成是由原来的图形经过一次平移得到的。
知识回顾 知识探究 知识小结 练习提升
北师大版八年级下册数学《图形的平移》图形的平移与旋转说课教学课件复习

点C的坐标为(0,2),点D的坐标为(6,2), 四边形ABDC的面积为2×(4+2)=12.
(2)在x轴上是否存在一点E,使得△DEC的面积是△DEB面积的2倍?若存在
,请求出点E的坐标;若不存在,请说明理由.
解:(2)存在.
设点E的坐标为(x,0),
因为△DEC的面积是△DEB面积的2倍,
向下平移b
个单位长度
(x-a,y-b)
设P(x,y)是平面直角坐标系内的一个点,我们按如下的方式平移点P(a>0,b>0)
一次平移完成
(x+a,y+b) 向右a个,向上b个单位长度
(x+a,y)
(x+a,y-b) 向右a个,向下b个单位长度
(x,y)
(x-a,y)
(x-a,y+b) 向左a个,向上b个单位长度
–1
–2
–3
O ''
4
–4
–5
–6
将图中的“小鱼1”的每个“顶点”的横 坐标增加2,纵坐标不变,得到“小鱼 3”,然后将“小鱼3”纵坐标减少3,横 坐标不变,得到“小鱼4”,请同学们画 出“小鱼3”和“小鱼4”. 能否将“小鱼4”看成是“小鱼1”经过 一次平移得到的?若能,请指出平移方 向和平移的距离.
下面的一组图片是形状相同的图形,在图片①上取一点A,它 与另一图片(如图片②)上的相应点B之间的连线是否经过镜头 P的中心?在图片上换其它的点试一试,还有类似的结论吗?
E
①
F
C
② D
③ ④⑤
P
A
B
如果两个图形不仅相似,而且每组对应点所在的直线都经过
同一个点,那么这样的两个图形叫做位似图形, 这个点叫做位
北师大版八年级数学下册第三章图形的平移与旋转复习课件

易错点
学以致用
7. 如图Z3-8所示,点P是正方形ABCD的边CD上一 点,连接AP,∠BAP的平分线交BC于点Q,求证: AP=DP+BQ.
学以致用
证明:如答图Z3-2,将△ABQ绕点A逆时针旋转90° 得到△ADE,则 DE=BQ,∠E=∠AQB,∠ADE=∠B=90°. ∵∠ADC=90°,∴∠ADE+∠ADC=180°. ∴点E,D,P三点共线. ∵AQ平分∠BAP, ∴∠PAQ=∠BAQ=∠DAE. ∴∠PAE=∠DAE+∠PAD=∠PAQ+∠PAD=∠DAQ. 在正方形ABCD中,AD∥BC, ∴∠DAQ=∠AQB. ∵∠AQB=∠E,∴∠PAE=∠E. ∴AP=PE. ∵PE=DP+DE=DP+BQ, ∴AP=DP+BQ.
学以致用 5. 图Z3-6是几种名车标志,其中属于中心对称图形 的是( B )
A. 1个
B. 2个
C. 3个
D. 4个
学以致用 6. 下列四个图形中,不是中心对称图形的是( B )
易错点
易错点4 因忽略说明三点共线而致答案不完整 在旋转变换过程中,图形的位置会产生改变,根据
有关证题时逻辑性、严谨性的需要,必须强调三点共 线.
知识梳理 2. 图形平移的坐标变化 (1)纵坐标不变,横坐标加k(k>0),点向__右___平 移k个单位长度;横坐标减k,点向_左____平移k个单位 长度. (2)横坐标不变,纵坐标加k(k>0),点向__上___平 移k个单位长度;纵坐标减k,点向___下__平移k个单位 长度. (3)一个图形依次沿x轴方向、y轴方向平移后所得图 形,可以看成是由本来的图形经过__一__次___平移得到的.
9. 如图Z3-15所示,△ABC平移后得到△DEF. (1)若∠A=80°,∠E=60°,求∠C的度数; (2)若AC=BC,BC与DF相交于点O,则OD与OB相 等吗?说明理由.
北师大版八年级数学下册 《图形的平移与旋转》全章复习与巩固(提高)巩固练习 含答案解析

《图形的平移与旋转》全章复习与巩固(提高)巩固练习【巩固练习】 一、选择题1.轴对称与平移、旋转的关系不正确的是( ).A .经过两次翻折(对称轴平行)后的图形可以看作是原图形经过一次平移得到的B .经过两次翻折(对称轴不平行)后的图形可以看作是原图形经过一次平移得到的C .经过两次翻折(对称轴不平行)后的图形可以看作是原图形经过旋转得到的D .经过几次翻折(对称轴有偶数条且平行)后的图形可以看作是经过一次平移得到的 2.在旋转过程中,确定一个三角形旋转的位置所需的条件是( ). ①三角形原来的位置;②旋转中心;③三角形的形状;④旋转角. A .①②④ B .①②③ C .②③④ D .①③④3.下列图形中,既可以看作是轴对称图形,又可以看作是中心对称图形的为( ).A B C D4.(2016·株洲)如图,在△ABC 中,∠ACB=90°,∠B=50°,将此三角形绕点C 顺时针方向旋转后得到△A ’B ’C ’,若点B ’恰好落在线段AB 上,AC 、A ’B ’交于点O ,则∠COA ’的度数是( )A .50°B .60°C .70°D .80°5.如图,把矩形纸条ABCD 沿EF GH ,同时折叠,B C ,两点恰好落在AD 边的P 点处, 若90FPH =o∠,8PF =,6PH =,则矩形ABCD 的边BC 长为( ). A.20 B.22 C.24 D.30第4题 第5题6.如图,正方形硬纸片ABCD 的边长是4,点E 、F 分别是AB 、BC 的中点,若沿左图中的虚线剪开,拼 成如下图的一座“小别墅”,则图中阴影部分的面积是( ). A .2 B .4 C .8 D .107. 如图,在Rt △ABC 中,∠ACB=90°,AC=BC=2,将Rt △ABC 绕A 点按逆时针方向旋转30°后得到Rt △ADE ,点B 经过的路径为弧BD ,则图中阴影部分的面积是( ).A.6π B.3π C.16π+ D.18.如图,在正方形ABCD 外取一点E ,连接AE ,BE ,DE. 过点A 作AE 的垂线交DE 于点P .若AE=AP=1,PB=5.下列结论:①△APD ≌△AEB ;②点B 到直线AE 的距离为2;③EB ⊥ED ;④S △APD +S △APB =1+6;⑤S 正方形ABCD =4+6.其中正确结论的序号是( ). A .①③④ B .①②⑤ C .③④⑤ D .①③⑤二、填空题9. 如图,图B 是图A 旋转后得到的,旋转中心是 ,旋转了 .10.在Rt ∆ABC 中,∠A <∠B,CM 是斜边AB 上的中线,将∆ACM 沿直线CM 折叠,点A 落在点D 处,如果CD 恰好与AB 垂直,那么∠A 等于 度.第9题第10题第12题11.(2016•大连)如图,将△ABC绕点A逆时针旋转得到△ADE,点C和点E是对应点,若∠CAE=90°,AB=1,则BD= .12. 如图,正方形ABCD经过顺时针旋转后到正方形AEFG的位置,则旋转中心是,旋转角度是度.13. 时钟的时针不停地旋转,从上午8:30到上午10:10,时针旋转的旋转角是 .14. 如图所示,可以看作是一个基本图形经过次旋转得到的;每次旋转了度.15.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,AC=43,BC的中点为D,将△ABC绕点C顺时针旋转任意一个角度得到△FEC,EF的中点为G,连接DG.在旋转过程中,DG的最大值是 .16.如图所示,按下列方法将数轴的正半轴绕在一个圆上(该圆周长为3个单位长,且在圆周的三等分点处分别标上了数字0、1、2)上:先让原点与圆周上0所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上1、2、3、4、…所对应的点分别与圆周上1、2、0、1、…所对应的点重合.这样,正半轴上的整数就与圆周上的数字建立了一种对应关系.(1)圆周上数字a 与数轴上的数5对应,则a=_________;(2)数轴上的一个整数点刚刚绕过圆周n圈(n为正整数)后,并落在圆周上数字1所对应的位置,这个整数是_________(用含n的代数式表示).三、解答题17. 如图,在正方形ABCD中,F是AD的中点,E是BA延长线上一点,且AE=12 AB.①你认为可以通过平移、轴对称、旋转中的哪一种方法使△ABF变到△ADE的位置?若是旋转,指出旋转中心和旋转角.②线段BF和DE之间有何数量关系?并证明.18.阅读:我们把边长为1的等边三角形PQR沿着边长为整数的正n(n>3)边形的边按照如图1的方式连续转动,当顶点P回到正n边形的内部时,我们把这种状态称为它的“点回归”;当△PQR回到原来的位置时,我们把这种状态称为它的“三角形回归”.例如:如图2,边长为1的等边三角形PQR的顶点P在边长为1的正方形ABCD内,顶点Q与点A重合,顶点R与点B重合,△PQR沿着正方形ABCD的边BC、CD、DA、AB…连续转动,当△PQR连续转动3次时,顶点P回到正方形ABCD内部,第一次出现P的“点回归”;当△PQR连续转动4次时△PQR回到原来的位置,出现第一次△PQR的“三角形回归”.操作:如图3,如果我们把边长为1的等边三角形PQR沿着边长为1的正五边形ABCDE的边连续转动,则连续转动的次数k= 时,第一次出现P的“点回归”;连续转动的次数k= 时,第一次出现△PQR的“三角形回归”. 猜想:我们把边长为1的等边三角形PQR 沿着边长为1的正n (n >3)边形的边连续转动, (1)连续转动的次数k= 时,第一次出现P 的“点回归”; (2)连续转动的次数k= 时,第一次出现△PQR 的“三角形回归”;(3)第一次同时出现P 的“点回归”与△PQR 的“三角形回归”时,写出连续转动的次数k 与正多边形的边数n 之间的关系.19.(2015春•凉山州期末)如图,长方形ABCD 在坐标平面内,点A 的坐标是A (2,1),且边AB 、CD 与x 轴平行,边AD 、BC 与x 轴平行,点B 、C 的坐标分别为B (a ,1),C (a ,c ),且a 、c 满足关系式c=++3.(1)求B 、C 、D 三点的坐标;(2)怎样平移,才能使A 点与原点重合?平移后点B 、C 、D 的对应分别为B 1C 1D 1,求四边形OB 1C 1D 1的面积;(3)平移后在x 轴上是否存在点P ,连接PD ,使S △COP =S 四边形OBCD ?若存在这样的点P ,求出点P 的坐标;若不存在,试说明理由.20. 如图,P 是等边三角形ABC 中的一点,PA =2,PB =32,PC =4,求BC 边得长是多少?【答案与解析】 一.选择题 1.【答案】B.【解析】A 、多次平移相当于一次平移,故正确;B 、必须是对称轴有偶数条且平行时,才可以看作是原图形经过一次平移得到的,故错误;C 、一个图形围绕一个定点旋转一定的角度,得到另一个图形,这种变换称为旋转变换,故正确;D 、对称轴有偶数条且平行时,可以看作是原图形经过一次平移得到的,故正确. 故选B . 2.【答案】A. 3.【答案】B.BP4.【答案】B.【解析】解:由题意知:∠A=90°-50°=40°,由旋转性质可知:∴BC=B C′,∴∠B=∠BB ’C=50°,∵∠BB ′C =∠A +∠ACB ’=40°+∠ACB ’, ∴∠ACB ’=10°,∴∠COA ’=∠AOB ’=∠OB ’C+∠ACB ’=∠B+∠ACB ’=60°. 故选B .5.【答案】C.【解析】Rt △PHF 中,有FH=10,则矩形ABCD 的边BC 长为PF+FH+HC=8+10+6=24,故选C . 6.【答案】B.【解析】阴影部分由一个等腰直角三角形和一个直角梯形组成,由第一个图形可知:阴影部分的两部分可构成正方形的四分之一, 正方形的面积=4×4=16,∴图中阴影部分的面积是16÷4=4. 故选B .7. 【答案】B.【解析】阴影部分的面积等于扇形DAB 的面积,首先利用勾股定理即可求得AB 的长,然后利用扇形的面积公式即可求得扇形的面积.8.【答案】D.【解析】①利用同角的余角相等,易得∠EAB=∠PAD ,再结合已知条件利用SAS 可证两三角形全等;③利用①中的全等,可得∠APD=∠AEB ,结合三角形的外角的性质,易得∠BEP=90°,即可证;②过B 作BF ⊥AE ,交AE 的延长线于F ,利用③中的∠BEP=90°,利用勾股定理可求BE ,结合△AEP 是等腰直角三角形,可证△BEF 是等腰直角三角形,再利用勾股定理可求EF 、BF ;⑤在Rt △ABF 中,利用勾股定理可求AB 2,即是正方形的面积;④S △APD +S △APB = S △AP E +S △EPB =12. 二.填空题 9.【答案】X ;180°.【解析】观察图形中Z 点对应点的位置是图A 绕旋转中心X 按逆时针旋转180°得到的.故答案为:X ;180°.10.【答案】30°.【解析】解法一、在Rt △ABC 中,∠A <∠B∵CM 是斜边AB 上的中线, ∴CM=AM , ∴∠A=∠ACM ,将△ACM 沿直线CM 折叠,点A 落在点D 处 设∠A=∠ACM=x 度, ∴∠A+∠ACM=∠CMB , ∴∠CMB=2x ,如果CD 恰好与AB 垂直 在Rt △CMG 中, ∠MCG+∠CMB=90°即3x=90°x=30°则得到∠MCD=∠BCD=∠ACM=30°根据CM=MD,得到∠D=∠MCD=30°=∠A∠A等于30°.解法二、∵CM平分∠ACD,∴∠ACM=∠MCD∵∠A+∠B=∠B+∠BCD=90°∴∠A=∠BCD∴∠BCD=∠DCM=∠MCA=30°∴∠A=30°11.【答案】2.12.【答案】A,45.【解析】∵正方形ABCD经过顺时针旋转后得到正方形AEFG,∴旋转中心为点A,旋转角为∠CAD,∵AC是正方形ABCD的对角线,∴∠CAD=45°,∴旋转角为45°.故答案为:A,45.13.【答案】50°.【解析】从上午8:30到上午10:10,共1个小时40分钟;时针旋转了536圆周,故旋转角的度数是50度.故答案为:50°.14.【答案】3;90.【解析】如图所示的图形可以看作按照逆时针(或顺时针)旋转3次,且每次旋转了90°而成的.故答案是:3;90.15.【答案】6.【解析】如图,连接CG,根据直角三角形斜边上的中线等于斜边的一半求出CG=4,再根据三角形的任意两边之和大于第三边判断出D、C、G三点共线时DG有最大值,再代入数据进行计算即可得解.16.【答案】(1)a=2,(2)3n+1.【解析】根据正半轴上的整数与圆周上的数字建立的这种对应关系可以发现:圆周上了数字0、1、2与正半轴上的整数每3个一组012;345;678…分别对应.三.解答题17.【解析】解:(1)可以通过旋转使△ABF变到△ADE的位置,即把△ABF以A点为旋转中心,逆时针旋转90°可得到△ADE;(2)线段BF和DE的数量关系是相等.理由如下:∵四边形ABCD为正方形,∴AB=AD,∠BAF=∠EAD,∵F是AD的中点,AE=12 AB,∴AE=AF,∴△ABF以A点为旋转中心,逆时针旋转90°时,AB旋转到AD,AF旋转到AE,即F点与E点重合,B点与D点重合,∴BF与DE为对应线段,∴BF=DE.18.【解析】解:操作:3,5.猜想:(1)第一次点回归,连续转动的次数都是3次,故填3;(2)第一次出现△PQR的“三角形回归”,连续转动的次数就是多边形的边数,故填n;(3)当n不是3的倍数时,k=3n,当n是3的倍数时,k=n.19.【解析】解:(1)由题意得,a﹣6≥0且6﹣a≥0,所以,a≥6且a≤6,所以,a=6,c=3,所以,点B(6,1),C(6,3),∵长方形ABCD的边AB、CD与x轴平行,边AD、BC与x轴平行,∴点D(2,3);(2)∵平移后A点与原点重合,∴平移规律为向左2个单位,向下1个单位,∴B1(4,0),C1(4,2),D1(0,2);(3)平移后点C到x轴的距离为2,∵S△COP=S四边形OBCD,∴×OP×2=4×2,解得OP=8,若点P在点O的左边,则点P的坐标为(﹣8,0),若点P在点O的右边,则点P的坐标为(8,0).综上所述,存在点P(﹣8,0)或(8,0).20.【解析】解:如图,将△ABP绕点B逆时针旋转60°得△BCQ,连接PQ.再过B作CQ的延长线的垂线BD,垂足为D,∴BQ=PB=23,∠PQB =60°,∴△PBQ是等边三角形,∴PQ=PB=23,∠QPC=60°.在△PCQ中,∵CQ=PA=2,,PQ=23,PC=4,∴CQ2+ PQ2=PC2,∴∠PQC=90°,∴∠CQB=∠PQB+∠PQC=150°,∴∠BQD=30°.在Rt△BQD中,BD=12BQ=3,QD=3,则CD=5.在Rt△BCD中,BC=32527+=.。
北师大版八年级数学下册第三章 图形的平移与旋转 小结与复习

【解析】关键是找出旋转角∠BOD = 60°.
A
O 图a B
(2) 如图 b ,4×4 的正方形网格中,△MNP 绕某点旋
转一定的角度,得到△M1N1P1,其旋转中心是 ( B )
A. 点 A B. 点 B C. 点 C D. 点 D
【解析】作线段 NN1 与 PP1 的 垂直平分线,交点便是旋转中心.
O
x
A
(2) 将△ABC 先向左平移 2 个单位长度,再向上平移 1 个
单位长度,得到△A′B′C′,请画出相应图形则△A′B′C′ 的
三个顶点 坐标分别是 A′( 0 , 0 )、B′( 2 , 4 )、
C′( -1 , 3 ); (3) 求△ABC 的面积.
y
C′•
• B′ B
解:△ABC 的面积
A
的对应角和 ED 的对应边分别是 ( C )
D
A.∠F,AC B.∠BOD,BA
B
C
C.∠F,BA D.∠BOD,AC
E
F
知识点二 坐标系中的图形平移
例2 如图,直角坐标系中,△ABC y
的顶点都在网格点上,其中,C 点
B
坐标为(1,2).
C
(1) 写出点 A、B 的坐标: A ( 2 ,-1 ), B ( 4 , 3 );
A
B1
P1 CO 1
A1 C1 x
答:四边形 ACC1A1 的面积为 14.
知识点三 旋转的概念及性质的应用
例3 (1) 如图 a,将△AOB 绕点 O 按逆时针方向旋转
60° 后得到△COD,若∠AOB = 15°,则∠AOD 的度
数是 ( C )
CD
A. 15° B. 60° C. 45° D. 75°
北师大版八年级数学下册 《图形的平移与旋转》全章复习与巩固(基础)知识讲解 含答案解析

责编:杜少波【学习目标】1.了解平移、旋转、中心对称,探索它们的基本性质;2.能够按要求作出简单平面图形经过平移、旋转后的图形,能作出简单平面图形经过一次或两次图形变换后的图形;1.平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移,平移不改变图形的形状和大小.2.平移的基本性质:一个图形和它经过平移所得的图形中,对应点所连的线段平行(或在一条直线上)且相等;对应线段平行(或在一条直线上)且相等,对应角相等.要点诠释:3.平移与坐标变换:(1)点的平移点的平移引起坐标的变化规律:在平面直角坐标中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x+a,y)(或(x-a,y));将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或(x,y-b)).要点诠释:上述结论反之亦成立,即点的坐标的变化引起的点相应的平移变换.(2)图形的平移平移是图形的整体运动.在平面直角坐标系内,一个图形进行了平移变化,则它上面的所有点的坐标都发生了同样的变化,其变化规律遵循:“右加左减,纵不变;上加下减,横不变”.要点诠释:(1)上述结论反之亦成立,即如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a 个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a 个单位长度.(2)一个图形依次沿x 轴方向、y 轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到的.要点二、旋转变换1.旋转概念:在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转. 这个定点称为旋转中心,转动的角称为旋转角.要点诠释:(1)旋转后的图形与原图形的形状、大小都相同,但形状、大小都相同的两个图形不一定能通过旋转得到.(2)旋转的角度一般小于360°.2.旋转变换的性质:一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;对应线段相等,对应角相等.3.旋转作图步骤:③沿一定的方向,按一定的角度、旋转各顶点和旋转中心所连线段,从而作出图形中各关键点的对应点.把一个图形绕着某一点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心,这两个图形称为成中心对称的.要点诠释:中心对称的性质:把一个图形绕着某点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做它的对称中心.①连结决定已知图形的形状、大小的各关键点与对称中心,并且延长至2倍,得到各点的对称点.②按原图形的连结方式顺次连结对称点即得所作图形.3.图形变换与图案设计的基本步骤①确定图案的设计主题及要求;②分析设计图案所给定的基本图案;4.平移、轴对称、旋转三种变换的关系:【典型例题】类型一、平移变换1.(2015春•曲阜市期末)已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′(1)在图中画出△A′B′C′;(2)写出点A′、B′的坐标;(3)在y轴上是否存在一点P,使得△BCP与△ABC面积相等?若存在,求直接写出点P的坐标;若不存在,说明理由.【思路点拨】(1)根据图形平移的性质画出△A′B′C′即可(;2)根据各点在坐标系中的位置写出点A′、(2)由图可知,A'(0,4),B'(﹣1,1);(3)存在.故点P的坐标是(0,1)或(0,﹣5).【总结升华】本题考查的是平移变换,熟知图形平移不变性的性质是解答此题的关键.举一反三:;【变式】如下图,等边△ABC经过平移后成为△BDE,则其平移的方向是△ABC经过旋转后成为△BDE,则其旋转中心是;旋转角度是【答案】水平向右,AB的长度(或BD的长度),B,120或240.2.三角形ABC三个顶点A、B、C的坐标分别为A(2,-1)、B(1,-3)、C(4,-3.5).(1)在直角坐标系中画出三角形ABC;(2)把三角形A B C向右平移4个单位,再向下平移3个单位,恰好得到三角形ABC,试写出三角形A B C 111111(2)如图2,A(-2,2),B(-3,0),C(0,-0.5);1112因此,如果将△ABC看成是由△A B C 经过一次平移得到的,那么这一平移的平移方向是由A 到A 的方向,1平移距离是5 个单位长度.【总结升华】本题综合考查了平面直角坐标系,及平移变换.注意平移时,要找到三角形各顶点的对应点是关键及平移的相对性.【变式】如果矩形ABCD 的对角线的交点与平面直角坐标系的原点重合,且点A 和点C 的坐标分别为(-3,3.如图,将△AOB绕点O 按逆时针方向旋转45°后得到△A′OB′,若∠AOB=15°,则∠AOB′的度数是().A. 25°B. 30°C. 35°D. 40°【思路点拨】根据旋转的性质旋转前后图形全等以及对应边的夹角等于旋转角,进而得出答案即可. 【答案与解析】解:∵将△AOB绕点O 按逆时针方向旋转45°后得到△A′OB′,∴∠A′OA=45°,∠AOB=∠A′OB′=15°,∴∠AOB′=∠A′OA﹣∠A′OB=45°﹣15°=30°,故选:B.【总结升华】此题主要考查了旋转的性质,根据旋转的性质得出∠A′OA=45°,∠AOB=∠A′OB′=15°是解题关键.【变式】如图,△OAB可以看成是由△OCD绕点O 按顺时针方向旋转而来的,则旋转中心是,.DACO B旋转90°得到△DCF.已知EF=2 5,求正方形ABCD 的边长.FCDBA E【答案与解析】解:设正方形ABCD 的边长为x,∵△BCE绕点C 顺时针旋转90°得到△DCF,且BE=1,∴DF=BE=1,∵四边形ABCD 是正方形,∴AD=AB=x,∠A=90°,2 2∵AE=AB-BE=x-1,AF=AD+DF=x+1,∴22解得:x=3,∴正方形ABCD 的边长为3.【总结升华】此题考查了正方形的性质、旋转的性质以及勾股定理.注意掌握旋转前后图形的对应关系,注意掌握方程思想与数形结合思想的应用.举一反三:【变式】如图,K 是正方形ABCD 内一点,以AK 为一边作正方形AKLM,使L、M•在AK 的同旁,连接BK 和DM,试用旋转的思想说明线段BK 与DM 的数量关系.∴∠DAM=∠BAK△DAM可以看作是△ABK以A 为旋转中心,∠BAD为旋转角(90°)逆时针旋转而成的,故BK=DM.5.如图,方格纸中△ABC的三个顶点均在格点上,将△ABC向右平移5 格得到△A B C ,再将△A B C1 1 11 2 2(2)设B 点坐标为(﹣3,﹣2),B 点坐标为(4,2),△ABC与△A B C 是否成中心对称?若成中心对【思路点拨】根据平移和旋转的作图方法作图即可.根据中心对称的特点可知P点就是对称中心,从而【答案与解析】解:(1)如下图.∴P(,0).6.如图,图案可以看做以一个怎样的图案为“基本图案”形成的?试用两种以上的方法分析它的形成过程.解:解法一:图案可以看做是以其中的八分之一为“基本图案”,经过三次轴对称(第 1、2 根对称轴彼此垂直,而且过整个图案的中心)所形成的.解法二:也可以看做是以图案的四分之一为“基本图案”(可以是小正方形状也可以是等腰直角三角形状),绕整个图案的中心分别旋转90°、180°、270°所形成的.解法三:也可以以四分之一图形为基本图形,经过两次轴对称(对称轴互相垂直,而且过整个图案的中心)所形成.【总结升华】本题考查利用旋转设计图案的知识,基本图案的寻找较为灵活,对于不同的基本图形需要作的几何变换也不同.举一反三:【变式】(2016 春•泸溪县期末)如图所示,由5 个大小完全相同的小正方形摆成如图形状,现移动其中的一个小正方形,请在图2、图3、图4 中分别画出满足以下要求的图形(用阴影表示)(1)使所得图形成为轴对称图形,而不是中心对称图形;(2)使所得图形成为中心对称图形,而不是轴对称图形;(3)使所得图形既是轴对称图形也是中心对称图形.【答案】解:【思路点拨】根据平移和旋转的作图方法作图即可.根据中心对称的特点可知P点就是对称中心,从而【答案与解析】解:(1)如下图.∴P(,0).6.如图,图案可以看做以一个怎样的图案为“基本图案”形成的?试用两种以上的方法分析它的形成过程.解:解法一:图案可以看做是以其中的八分之一为“基本图案”,经过三次轴对称(第 1、2 根对称轴彼此垂直,而且过整个图案的中心)所形成的.解法二:也可以看做是以图案的四分之一为“基本图案”(可以是小正方形状也可以是等腰直角三角形状),绕整个图案的中心分别旋转90°、180°、270°所形成的.解法三:也可以以四分之一图形为基本图形,经过两次轴对称(对称轴互相垂直,而且过整个图案的中心)所形成.【总结升华】本题考查利用旋转设计图案的知识,基本图案的寻找较为灵活,对于不同的基本图形需要作的几何变换也不同.举一反三:【变式】(2016 春•泸溪县期末)如图所示,由5 个大小完全相同的小正方形摆成如图形状,现移动其中的一个小正方形,请在图2、图3、图4 中分别画出满足以下要求的图形(用阴影表示)(1)使所得图形成为轴对称图形,而不是中心对称图形;(2)使所得图形成为中心对称图形,而不是轴对称图形;(3)使所得图形既是轴对称图形也是中心对称图形.【答案】解:【思路点拨】根据平移和旋转的作图方法作图即可.根据中心对称的特点可知P点就是对称中心,从而【答案与解析】解:(1)如下图.∴P(,0).6.如图,图案可以看做以一个怎样的图案为“基本图案”形成的?试用两种以上的方法分析它的形成过程.解:解法一:图案可以看做是以其中的八分之一为“基本图案”,经过三次轴对称(第 1、2 根对称轴彼此垂直,而且过整个图案的中心)所形成的.解法二:也可以看做是以图案的四分之一为“基本图案”(可以是小正方形状也可以是等腰直角三角形状),绕整个图案的中心分别旋转90°、180°、270°所形成的.解法三:也可以以四分之一图形为基本图形,经过两次轴对称(对称轴互相垂直,而且过整个图案的中心)所形成.【总结升华】本题考查利用旋转设计图案的知识,基本图案的寻找较为灵活,对于不同的基本图形需要作的几何变换也不同.举一反三:【变式】(2016 春•泸溪县期末)如图所示,由5 个大小完全相同的小正方形摆成如图形状,现移动其中的一个小正方形,请在图2、图3、图4 中分别画出满足以下要求的图形(用阴影表示)(1)使所得图形成为轴对称图形,而不是中心对称图形;(2)使所得图形成为中心对称图形,而不是轴对称图形;(3)使所得图形既是轴对称图形也是中心对称图形.【答案】解:。
北师大版八年级下册教案:第三章图形的平移与旋转复习

3.重视学生实践,提高动手能力。在实践活动环节,我安排了分组讨论和实验操作,让学生在实际操作中感受平移与旋转的应用。但从实践结果来看,部分学生的动手能力较弱,对实验操作不够熟练。今后,我应加大实践环节的教学力度,鼓励学生多动手、多思考,提高他们的实践能力。
(2)平移与旋转的作图方法
-平移作图:确定平移方向和距离,沿此方向将原图形上的点移动相应距离得到新图形。
-旋转作图:确定旋转中心、旋转方向和旋转角度,将原图形上的点绕旋转中心旋转相应角度得到新图形。
(3)平移与旋转在实际问题中的应用
-判断图形的平移或旋转
-设计简单图案,体会平移与旋转的应用
2.教学难点
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“图形的平移与旋转在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.重点难点解析:在讲授过程中,我会特别强调平移与旋转的定义和性质这两个重点。对于难点部分,我会通过举例和比较来帮助大家理解,如区分平移与旋转,掌握作图方法等。
(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与图形平移与旋转相关的实际问题。
北师大 8年级下册 专题06 图形的平移与旋转(知识点串讲)(教师版)
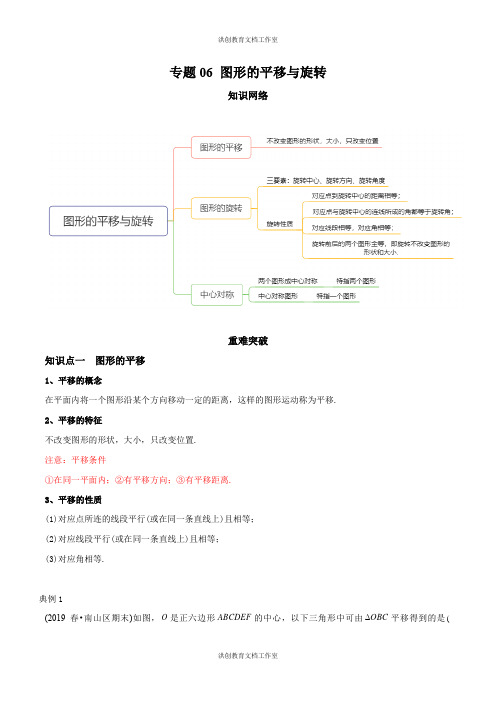
专题06 图形的平移与旋转知识网络重难突破知识点一图形的平移1、平移的概念在平面内将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移.2、平移的特征不改变图形的形状,大小,只改变位置.注意:平移条件①在同一平面内;②有平移方向;③有平移距离.3、平移的性质(1)对应点所连的线段平行(或在同一条直线上)且相等;(2)对应线段平行(或在同一条直线上)且相等;(3)对应角相等.典例1(2019春•南山区期末)如图,O是正六边形ABCDEF的中心,以下三角形中可由OBC平移得到的是()A .OCD ∆B .OAB ∆C .OAF ∆D .OEF ∆【解答】解:O 是正六边形ABCDEF 的中心,//AD BC ∴,////AF CD BE ,OAF ∴∆沿FO 方向平移可得到OBC ∆.应选:C .典例2(2019春•坪山区期末)如图,DEF ∆是由ABC ∆经过平移得到的,假设80C ∠=︒,33A ∠=︒,那么(EDF ∠= )A .33︒B .80︒C .57︒D .67︒【解答】解:在ABC ∆中,33A ∠=︒,∴由平移中对应角相等,得33EDF A ∠=∠=︒.应选:A .知识点二 图形的旋转1、旋转的有关概念在平面内,将一个图形绕一个定点沿某一方向转动一个角度,这样的运动称为旋转,这个定点称为旋转中心,转动的角叫旋转角.注意:①旋转中心在旋转过程中保持不动;②图形的旋转由旋转中心、旋转方向和旋转角决定;③将一个图形绕一个定点沿某个方向转动一角度,意味着图形上每一点同时按相同的方向旋转了相同的角度.2、旋转的性质(1)对应点到旋转中心的距离相等;(2)对应点与旋转中心的连线所成的角都等于旋转角;(3)对应线段相等,对应角相等;(4)旋转前后的两个图形全等,即旋转不改变图形的形状和大小.典例1(2019春•成华区期末)如下图,将一个含30︒角的直角三角板ABC绕点A逆时针旋转,点B的对应点是点B',假设点B'、A、C在同一条直线上,那么三角板ABC旋转的度数是()A.60︒B.90︒C.120︒D.150︒【解答】解:旋转角是18030150∠'=︒-︒=︒.BAB应选:D.典例2(2019春•简阳市期末)如图,在Rt ABC∠=︒,6∆绕点C按逆时针AAC=,将ABC∆中,90ACB∠=︒,60'',此时点A'恰好在AB边上,那么点B'与点B之间的距离为()方向旋转得到△A B CA.12B.6C.D.【解答】解:连接B B',将ABC ∆绕点C 按逆时针方向旋转得到△A B C '',AC A C '∴=,AB A B '=,60A CA B ''∠=∠=︒,∴△AA C '是等边三角形,60AA C '∴∠=︒,180606060B A B ''∴∠=︒-︒-︒=︒,将ABC ∆绕点C 按逆时针方向旋转得到△A B C '',60ACA BAB ''∴∠=∠=︒,BC B C '=,906030CB A CBA ''∠=∠=︒-︒=︒,BCB '∴∆是等边三角形,60CB B '∴∠=︒,30CB A ''∠=︒,30A B B ''∴∠=︒,180603090B BA ''∴∠=︒-︒-︒=︒,90ACB ∠=︒,60A ∠=︒,6AC =,12AB ∴=,6A B AB AA AB AC ''∴=-=-=,B B '∴=应选:D .典例3(2019春•金牛区期末)分别按以下要求解答(1)将ABC ∆先向左平移7个单位,再下移1个单位,经过两次变换得到△111A B C ,画出△111A B C ,点1A 的坐标为 .(2)将ABC ∆绕O 顺时针旋转90度得到△222A B C ,画出△222A B C ,那么点2C 坐标为 .(3)在(2)的条件下,求A 移动的路径长.【解答】解:(1)△111A B C 如下图,点1A 的坐标为(4,5)-.故答案为(4,5)-.(2)△222A B C 如下图.2(3,6)C -,故答案为(3,6)-(3)点A 移动的路径长903531802π==.知识点三 中心对称1、中心对称如果把一个图形绕着某一点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫它们的对称中心。
北师大版数学八年级下第三章数学知识点和考点总结

3图形的平移与旋转(精讲精练)【目标导航】【知识梳理】1.平移:(1)平移的条件:平移的方向、平移的距离(2)平移的性质①把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同.②新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等(连接线段).对应线段平行且相等。
(或在同一条直线上)(3)平移变换与坐标变化向右平移a个单位,坐标P(x,y)⇒P(x+a,y);向左平移a个单位,坐标P(x,y)⇒P (x-a,y)向上平移b个单位,坐标P(x,y)⇒P(x,y+b);向下平移b个单位,坐标P(x,y)⇒P(x,y-b)3. 旋转:(1)旋转的性质:①对应点到旋转中心的距离相等.②对应点与旋转中心所连线段的夹角等于旋转角.③旋转前、后的图形全等.(2)旋转三要素:①旋转中心;②旋转方向;③旋转角度.注意:三要素中只要任意改变一个,图形就会不一样.4.中心对称:(1)中心对称的定义把一个图形绕着某个点旋转180°,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.(2)中心对称的性质①关于中心对称的两个图形能够完全重合;②关于中心对称的两个图形,对应点的连线都经过对称中心,并且被对称中心平分.(3)把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.5. 关于原点对称的点的坐标特点(1)两个点关于原点对称时,它们的坐标符号相反,即点P (x ,y )关于原点O 的对称点是P′(-x ,-y ).(2)关于原点对称的点或图形属于中心对称,它是中心对称在平面直角坐标系中的应用,它具有中心对称的所有性质.但它主要是用坐标变化确定图形.注意:运用时要熟练掌握,可以不用图画和结合坐标系,只根据符号变化直接写出对应点的坐标.小专题8 特殊三角形中的“手拉手”模型——教材P89T12的变式与应用教材母题:(教材P89复习题T12)如图,△ABC ,△ADE 均是顶角为42°的等腰三角形,BC ,DE 分别是底边,图中的哪两个三角形可以通过怎样的旋转而相互得到?解:∵△ABC ,△ADE 均是顶角为42°的等腰三角形,∴∠BAC =∠DAE =42°,AB =AC ,AD =AE.∵∠BAD =∠BAC -∠DAC ,∠CAE =∠DAE -∠DAC ,∴∠BAD =∠CAE.在△ABD 和△ACE 中,⎩⎪⎨⎪⎧AB =AC ,∠BAD =∠CAE ,AD =AE ,∴△ABD ≌△ACE(SAS).∴△ABD 与△ACE 可通过旋转相互得到,即△ABD 以点A 为旋转中心,逆时针旋转42°,得到△ACE.(1)等腰三角形中的“手拉手”模型如图,已知△ABC 和△ADE 都是等腰三角形,旋转后有∠BAD =∠CAE.连接BD ,CE ,则①△ABD ≌△ACE ;②BD =CE ;③直线BD 与直线CE 的夹角等于∠A.(2)等边三角形中的“手拉手”模型如图,已知△ABC和△ADE是等边三角形,旋转后有∠BAD=∠CAE.连接BD,CE,则①△ABD≌△ACE;②BD=CE;③直线BD与直线CE的夹角为60°.(3)等腰直角三角形中的“手拉手”模型如图,已知△ABC和△ADE都是等腰直角三角形,旋转后有∠BAD=∠CAE.连接BD,CE,则①△ABD≌△ACE;②BD=CE;③直线BD与直线CE的夹角为90°.1.两个大小不同的等腰直角三角形三角板如图所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC.下列说法不正确的是(B)A.△ADC≌△AEB B.△DCE是等腰三角形C.DC=BE D.DC⊥BE2.如图,在△ABC中,分别以AC,BC为边作等边△ACD和等边△BCE,连接AE,BD 交于点O,则∠AOB的度数为__120°__.3.(2018·绵阳改编)如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB 的顶点A在△ECD的斜边DE上.若AE=2,AD=6,则△ABC的面积为2.4.如图,△ABC和△ADE是两个全等的等腰三角形,AB=AC=AD=AE,延长BD,EC 交于点F.(1)求∠BAC与∠F之间的数量关系;(2)求证:△BCF≌△EDF.解:(1)∵∠BAC=∠DAE,∴∠BAD=∠CAE.∵AB=AC=AD=AE,∴△BAD≌△CAE(SAS).∴∠ACE=∠ABD. ∵∠ACE+∠ACF=180°,∴∠ABD+∠ACF=180°. ∴∠F+∠BAC=180°.(2)证明:由(1)可知:∠ABD=∠ACE=∠AEC.∵∠ABC=∠AED,∴∠CBF=∠DEF.∵∠F=∠F,BC=ED,∴△BCF≌△EDF(AAS).5.如图1,两个不全等的等腰Rt △OAB 和等腰Rt △OCD 叠放在一起,并且有公共的直角顶点O.(1)在图1中,线段AC ,BD 的数量关系是相等,直线AC ,BD 的位置关系是垂直;(2)将图1的△OAB 绕点O 顺时针旋转90°,在图2中画出旋转后的△OAB ;(3)将图1中的△OAB 绕点O 顺时针旋转一个锐角,连接AC ,BD 得到图3,这时(1)中的两个结论是否成立?作出判断并说明理由.若△OAB 绕点O 继续旋转更大的角时,(1)中的结论仍然成立吗?作出判断,不必说明理由.解:(2)如图所示.(3)(1)中结论成立,理由如下:∵∠COA +∠AOD =90°,∠BOD +∠AOD =90°,∴∠COA =∠BOD.又∵OC =OD ,OA =OB ,∴△COA ≌△DOB(SAS).∴AC =BD.延长CA 交OD 于点H ,交BD 于点E.∵△COA ≌△DOB ,∴∠OCA =∠BDO.又∵∠DHE =∠CHO ,∴∠CED =∠COD =90°,即AC ⊥BD.将△OAB 绕点O 继续旋转更大的角时,(1)中的结论仍然成立.6.(1)如图1,在△ABC 和△ADE 中,AB =AC ,AD =AE ,∠CAB =∠DAE ,连接CE ,BD ,求证:CE =BD ;(2)如图2,将△ADE 绕着A 点旋转,当点C ,E ,D 在一条直线上时,上述结论是否成立?(3)旋转到图3位置时,上述结论成立吗?(4)旋转到图4位置时,此时点B ,E ,D 在一条直线上,上述结论成立吗?若成立,请就(2)(3)(4)中的一种情况加以证明.,图1) ,图2),图3) ,图4) 解:(1)证明:∵∠CAB =∠DAE ,∴∠CAB -∠BAE =∠DAE -∠BAE ,即∠CAE =∠BAD.在△ACE 和△ABD 中,⎩⎪⎨⎪⎧AC =AB ,∠CAE =∠BAD ,AE =AD ,∴△ACE ≌△ABD(SAS).∴CE =BD.(2)、(3)、(4)结论成立.选(4)证明:∵∠CAB =∠DAE ,∴∠CAB +∠BAE =∠DAE +∠BAE ,即∠CAE =∠BAD. 在△ACE 和△ABD 中,⎩⎪⎨⎪⎧AC =AB ,∠CAE =∠BAD ,AE =AD ,∴△ACE ≌△ABD(SAS). ∴CE =BD.。
北师大版八年级数学下册第三章图形平移与旋转章末复习

北师大版八年级下册数学第三章图形平移与旋转章末复习第一部分:知识点总结一、平移变换:1.概念:在平面内,将一个图形沿着某个方向移动一定的距离,这样的图形运动叫做平移。
2.性质:(1)平移前后图形全等;(2)对应点连线平行或在同一直线上且相等。
3.平移的作图步骤和方法:(1)分清题目要求,确定平移的方向和平移的距离;(2)分析所作的图形,找出构成图形的关健点;(3)沿一定的方向,按一定的距离平移各个关健点;(4)连接所作的各个关键点,并标上相应的字母;(5)写出结论。
二、旋转变换:1.概念:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,这样的图形运动叫做旋转。
说明:(1)图形的旋转是由旋转中心和旋转的角度所决定的;(2)旋转过程中旋转中心始终保持不动.(3)旋转过程中旋转的方向是相同的.(4)旋转过程静止时,图形上一个点的旋转角度是一样的.⑤旋转不改变图形的大小和形状.2.性质:(1)对应点到旋转中心的距离相等;(2)对应点与旋转中心所连线段的夹角等于旋转角;(3)旋转前、后的图形全等.3.旋转作图的步骤和方法:(1)确定旋转中心及旋转方向、旋转角;(2)找出图形的关键点;(3)将图形的关键点和旋转中心连接起来,然后按旋转方向分别将它们旋转一个旋转角度数,得到这些关键点的对应点;(4)按原图形顺次连接这些对应点,所得到的图形就是旋转后的图形.说明:在旋转作图时,一对对应点与旋转中心的夹角即为旋转角.常见考法(1)把平移旋转结合起来证明三角形全等;(2)利用平移变换与旋转变换的性质,设计一些题目。
误区提醒(1)弄反了坐标平移的上加下减,左减右加的规律;(2)平移与旋转的性质没有掌握。
第二部分:练习题1.下列生活现象中,属于平移的是()A.足球在草地上滚动B.拉开抽屉C.投影片的文字经投影转换到屏幕上D.钟摆的摆动2.下列四个图形中,既是轴对称图形又是中心对称图形的是( )3.剪纸是我国最古老民间艺术之一,被列入第四批《人类非物质文化遗产代表作名录》,下列剪纸作品中,是中心对称图形但不是轴对称图形的是()A.B.C.D.4.如图,在△A BC中,∠CAB=65°,将△ABC在平面内绕点A旋转到△AB′C′的位置,使CC′∥AB,则旋转角的度数为()A.35° B.40° C.50° D.65°5.如图,下列图形中,既是轴对称图形又是中心对称图形的有()A.4个 B.3个 C.2个 D.1个6.下列图案中,不是中心对称图形的是()A. B. C. D.7.在下列图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.8.观察下面图案,在A、B、C、D四幅图案中,能通过图案(1)的平移得到的是()9.小军将一个直角三角板(如图1)绕它的一条直角边所在的直线旋转一周形成一个几何体,将这个几何体的侧面展开得到的大致图形是()(1)A B C D10.若点A的坐标为(6,3)O为坐标原点,将OA绕点O按顺时针方向旋转90°得到OA′,则点A′的坐标是()A、(3,﹣6)B、(﹣3,6)C、(﹣3,﹣6)D、(3,6)11.下列图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.12.下列图形中,是中心对称图形但不是轴对称图形的是()13.下列图形中,是中心对称图形但不是轴对称图形的是()14.下列图形中,既是轴对称图形又是中心对称图形的是()15.数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心O 旋转多少度后和它自身重合?甲同学说: 45°;乙同学说: 60°;丙同学说:90°;丁同学说:135°.以上四位同学的回答中,错误的是 ( )A .甲B .乙C .丙D .丁16.如图,A 、B 的坐标分别为(2,0)(0,1),若将线段AB 平移至11A B ,则a b 的值为( )A .2B .3C .4D .517.如图,将等边△ABC 沿射线BC 向右平移到△DCE 的位置,连接AD 、BD ,则下列结论:①AD=BC ;②BD 、AC 互相平分;③四边形ACED 是菱形;④BD ⊥DE .其中正确的个数是( )A .1B .2C .3D .418.(4分)如图,在△ABO 中,AB ⊥OB ,OB=3,AB=1.将△ABO 绕O 点旋转90°后得到△A 1B 1O ,则点A 1的坐标为( )BA .(1-B .(1-1,C .(1-,D .(1-,1-)19.如图,在正方形ABCD 中,E 为DC 边上的点,连接BE ,将ΔBCE 绕点C 顺时针方向旋转90°得到ΔDCF ,连接EF ,若∠BEC=60°,则∠EFD 的度数为( )A .10°B .15°C .20°D .25°20.(5分)如图,在矩形ABCD 中,CD=1,∠DBC=30°.若将BD 绕点B 旋转后,点D 落在DC 延长线上的点E 处,点D 经过的路径 DE,则图中阴影部分的面积是( )A .3π.3π C .2π.2π二、填空题21.如图,△ABC沿射线AC方向平移2cm得到△A′B′C′,若AC=3cm,则A′C=cm.22.下列图形:①线段;②等边三角形;③平行四边形;④等腰梯形;⑤长方形;⑥圆。
(完整版)北师大版八年级下册3.2图形的平移与旋转讲义(无答案)

八年级数学精讲——第三章:图形的平移与旋转【基础知识】1.平移的定义与规律(1)定义:在平面内将一个图形沿某个方向移动一定的距离,•这样的图形运动称为平移.关键:平移不改变图形的形状和大小,也不会改变图形的方向.(2)平移的规律:经过平移,对应线段、对应角分别相等,•对应点所连的线段平行且相等(或共线且相等).(3)简单作图平移的作图主要关注要点:1.方向,2.距离.整个平移的作图,就象把整个图案的每个特征点放在一套平行的轨道上滑动一样,每个特征点滑过的距离是一样的.2.旋转的定义与规律(1)定义:在平面内,将一个图形绕一个定点沿某个方向转动一个角度,•这样的图形运动称为旋转.关键:旋转不改变图形的大小和形状,但改变图形的方向.(2)旋转的规律经过旋转,图形上的每一点,都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.(3)简单的旋转作图旋转作图关键有两点:①旋转方向,②旋转角度.主要分四步:边、转、截、连.旋转就象把每个特征点与旋转中心用线连住的风筝,每个点转的角度是相同的,每个点与旋转中心的距离是不会改变的,即对应点与旋转中心距离相等.3.图案的分析与设计首先找到图中的基本图案,然后分析其图案与它的关系,即由它作何种运动变换而形成的,我们主要遇到的变换有:轴对称、平移、旋转.在相似形一章里还会学到图形的放大与缩小等.【典例剖析】1、请你完成下列问题.图形的操作过程(本题中四个长方形的水平方向的边长均为a,•竖直方向的边长均为b);在图1中,将线段A1A2向右平移1个单位到B1B2,得到封闭图形A1A2B2B1(即阴影部分);(1)(2)(3)在图2中,将折线A1A2A3向右平移1个单位到B1B2B3,得到封闭图形A1A2A3B3B2B1(即阴影部分).(1)在图3中,请你类似地画一条有两个折点的折线,同样向右平移一个单位,•从而得到一个封闭图形,并用斜线画出阴影.(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:S1=_____,S2=_______,S3=_______;(3)联想与探索如图4,在一块长方形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少,并说明你的猜想是正确的.2、如图,有边长为1的等边三角形ABC和顶角为120°的等腰△DBC,•以D为顶点作60°角,两边分别交AB、AC于M、N的三角形,连结MN,试说明△AMN的周长为2.3、如图,小正六边形沿着大正六边形的边缘顺时针滚动,小正六边形的边长是大正六边形边- 1 - / 8- 2 - / 8长的一半,当小正六边形由图①位置滚动到图②位置时,线段OA 绕点O 顺时针转过的角度为 度.4、如图,已知ABC △中,AB AC =,90BAC ∠=o ,直角EPF ∠的顶点P 是BC中点,两边PE ,PF 分别交AB ,AC 于点E ,F ,给出以下五个结论:①AE CF=②APE CPF ∠=∠③EPF△是等腰直角三角形④EF AP=⑤12AEPFABC S S =四边形△;当EPF ∠在ABC △内绕顶点P 旋转时(点E 不与A ,B 重合),上述结论中始终正确的序号有5、如图,P 是正三角形ABC 内的一点,且68PA PB ==,,10PC =.若将PAC△绕点A 逆时针旋转后,得到P AB '△,则点P 与点P '之间的距离为 ,APB ∠=第4题 第5题变式:△ABC 是等腰直角三角形,BC 是斜边,P 为△ABC 内一点,将△ABP 绕点A 逆时针旋转后与△ACP /重合,如果AP=3,那么线段P P /的长是多少?6、如图,ABC△中,90301B C AB ∠=∠==o o ,,,将ABC △绕顶点A 旋转180o ,点C 落在C '处,则CC '的长为 。
新版北师大数学八下第三章图形的平移与旋转难题知识点讲解

1 八下第三章《平移与旋转》3.1知识要点:知识要点:1.平移的概念:.平移的概念: 在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移。
图形的平移是指图形整体的平移,平移后的图形与原图形的形状和大小都没有改变,改变的是位置。
指图形整体的平移,平移后的图形与原图形的形状和大小都没有改变,改变的是位置。
2.对应点、对应线段、对应角.对应点、对应线段、对应角 3.决定平移的要素:①图形定平移的要素:①图形 ②移动的方向②移动的方向 ③移动的距离。
③移动的距离。
平移的方向:图形上某一点到它对应点的方向,即平移前后对应点的射线方向。
平移的方向:图形上某一点到它对应点的方向,即平移前后对应点的射线方向。
平移的距离:连接一对对应点的线段的长度,即对应点之间的线段的长度。
平移的距离:连接一对对应点的线段的长度,即对应点之间的线段的长度。
4.平移的性质:经过平移,对应点所连线段平行(或在一条直线上)且相等,对应线段平行(或在一条直线上)且相等,且相等, 对应角相等。
对应角相等。
5.平移作图的一般步骤:①确定______和______,②找出原图形的______③沿一定方向,按一定距离(或根据平移的性质)通过截取线段的方法找到各个关键点的对应点④按原图的方法依次连结对应点⑤写出结论。
)通过截取线段的方法找到各个关键点的对应点④按原图的方法依次连结对应点⑤写出结论。
3.2知识要点:知识要点:1.旋转的概念:在平面内,将图形绕一个定点沿某个方向转动一个角度,这样的图形运动称为旋转,旋转不改变图形的大小和形状。
图形的大小和形状。
2.旋转角:任意一对对应点与旋转中心的连线所成的角都是旋转角。
.旋转角:任意一对对应点与旋转中心的连线所成的角都是旋转角。
注意:(1)旋转的三要素:旋转的三要素:旋转中心、旋转中心、旋转中心、旋转角、旋转角、旋转角、旋转方向。
北师大版八年级数学下册第三章图形的平移与旋转章末复习课件(共51张)

章末复习
分析 (1)分别将△ABC的顶点A, B, C向右平移3个单位长度, 连接所 得的点即可得出图形; (2)分别将△ABC的顶点A, B, C绕点O旋转180°, 连接所得的点即可 得出图形; (3)连接OC1, 即可平分△AC1A2的面积.
章末复习
解 (1)(2)如图3-Z-7所示. (3)面积等分正确即可, 如图3-Z-7所示, 直线 OC1将△AC1A2的面积分成相等的两部分 (答案不唯一).
第三章 图形的平移 与旋转
章末复习
第三章 图形的平移与旋转
章末复习
知识框架 归纳整合 素养提升 中考链接
章末复习
知识框架
两要素:平移的方向、 平移的距离
对应点所连的线段及对应 线段分别平行(或在一条直 线上)且相等;对应角相等
定义 性质
作图
左、右平移, 横坐标 减、加;上、下平 移, 纵坐标加、减
章末复习
章末复习
解 在图②中, 结论还成立;在图③中, 结论不成立. 图②结论: OD+OE= 2 OC. 证明如下:过点C分别作OA, OB的垂线, 垂足分别为P, Q, 如图②, 易证△CPD≌△CQE, ∴PD=QE. 又∵OP=OD+PD, OQ=OE-QE, 且OP+OQ= 2 OC, 即OD+PD+OE-QE= 2 OC, ∴ OD+OE= 2 OC. 图③结论:OE-OD= 2 OC.
章末复习
相关题2-2 [荆门中考]如图3-Z-5, 在Rt△ABC中, ∠ACB=90°,点D, E分别在AB, AC上,EC=BC, 连 接CD, 将线段CD绕点C按顺时针方向旋转90°后 得CF, 连接EF. (1)将图形补充完整; (2)若EF∥CD, 求证:∠BDC=90°.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《图形的平移与旋转》全章复习与巩固(基础)知识讲解责编:杜少波【学习目标】1.了解平移、旋转、中心对称,探索它们的基本性质;2.能够按要求作出简单平面图形经过平移、旋转后的图形,能作出简单平面图形经过一次或两次图形变换后的图形;3.利用平移、旋转、中心对称、轴对称及其组合进行图案设计;4.认识和欣赏轴对称、平移、旋转在现实生活中的应用.【知识网络】【要点梳理】要点一、平移变换1.平移的概念:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移,平移不改变图形的形状和大小.要点诠释:(1)平移是运动的一种形式,是图形变换的一种,本讲的平移是指平面图形在同一平面内的变换;(2)图形的平移有两个要素:一是图形平移的方向,二是图形平移的距离;(3)图形的平移是指图形整体的平移,经过平移后的图形,与原图形相比,只改变了位置,而不改变图形的形状和大小.2.平移的基本性质:一个图形和它经过平移所得的图形中,对应点所连的线段平行(或在一条直线上)且相等;对应线段平行(或在一条直线上)且相等,对应角相等.要点诠释:(1)要注意正确找出“对应线段,对应角”,从而正确表达基本性质的特征;(2)“对应点所连的线段平行(或在一条直线上)且相等”,这个基本性质既可作为平移图形之间的性质,又可作为平移作图的依据.3. 平移与坐标变换:(1)点的平移点的平移引起坐标的变化规律:在平面直角坐标中,将点(x,y)向右(或左)平移a个单位长度,可以得到对应点(x+a,y)(或(x-a,y));将点(x,y)向上(或下)平移b个单位长度,可以得到对应点(x,y+b)(或(x,y-b)).要点诠释:上述结论反之亦成立,即点的坐标的变化引起的点相应的平移变换.(2)图形的平移平移是图形的整体运动.在平面直角坐标系内,一个图形进行了平移变化,则它上面的所有点的坐标都发生了同样的变化,其变化规律遵循:“右加左减,纵不变;上加下减,横不变”.要点诠释:(1)上述结论反之亦成立,即如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.(2)一个图形依次沿x轴方向、y轴方向平移后所得图形,可以看成是由原来的图形经过一次平移得到的.要点二、旋转变换1.旋转概念:在平面内,将一个图形绕一个定点按某个方向转动一个角度,这样的图形运动称为旋转.这个定点称为旋转中心,转动的角称为旋转角.要点诠释:(1)旋转后的图形与原图形的形状、大小都相同,但形状、大小都相同的两个图形不一定能通过旋转得到.(2)旋转的角度一般小于360°.(3)旋转的三个要素:旋转中心、旋转角度和旋转方向(即顺时针或逆时针方向)2.旋转变换的性质:一个图形和它经过旋转所得的图形中,对应点到旋转中心的距离相等,任意一组对应点与旋转中心的连线所成的角都等于旋转角;对应线段相等,对应角相等.3.旋转作图步骤:①分析题目要求,找出旋转中心,确定旋转角.②分析所作图形,找出构成图形的关键点.③沿一定的方向,按一定的角度、旋转各顶点和旋转中心所连线段,从而作出图形中各关键点的对应点.④按原图形连结方式顺次连结各对应点.要点三、中心对称与图案设计1.中心对称:把一个图形绕着某一点旋转180°,它能够与另一个图形重合,那么就说这两个图形关于这个点对称或中心对称,这个点叫做它们的对称中心,这两个图形称为成中心对称的.要点诠释:中心对称的性质:成中心对称的两个图形中,对应点所连线段经过对称中心,且被对称中心平分.2. 中心对称图形:把一个图形绕着某点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做它的对称中心.要点诠释:中心对称作图步骤:①连结决定已知图形的形状、大小的各关键点与对称中心,并且延长至2倍,得到各点的对称点.②按原图形的连结方式顺次连结对称点即得所作图形.3.图形变换与图案设计的基本步骤①确定图案的设计主题及要求;②分析设计图案所给定的基本图案;③利用平移、旋转、轴对称对基本图案进行变换,实现由基本图案到各部分图案的有机组合;④对图案进行修饰,完成图案.4.平移、轴对称、旋转三种变换的关系:图形经过平移、旋转或轴对称的变换后,虽然对应位置改变了,但大小和形状没有改变,即两个图形是全等的.【典型例题】类型一、平移变换1.(2015春•曲阜市期末)已知:如图,把△ABC向上平移3个单位长度,再向右平移2个单位长度,得到△A′B′C′(1)在图中画出△A′B′C′;(2)写出点A′、B′的坐标;(3)在y轴上是否存在一点P,使得△BCP与△ABC面积相等?若存在,求直接写出点P的坐标;若不存在,说明理由.【思路点拨】(1)根据图形平移的性质画出△A′B′C′即可;(2)根据各点在坐标系中的位置写出点A′、B′的坐标;(3)设P(0,y),再根据三角形的面积公式求出y的值即可.【答案与解析】解:(1)如图所示:(2)由图可知,A'(0,4),B'(﹣1,1);(3)存在.设P(0,y),要使得△BCP与△ABC面积相等,只需要点P到BC的距离为3即可,则y=1或y=﹣5,故点P的坐标是(0,1)或(0,﹣5).【总结升华】本题考查的是平移变换,熟知图形平移不变性的性质是解答此题的关键.举一反三:【变式】如下图,等边△ABC经过平移后成为△BDE,则其平移的方向是;平移的距离是;△ABC经过旋转后成为△BDE,则其旋转中心是;旋转角度是度.【答案】水平向右,AB的长度(或BD的长度),B,120或240.2.三角形ABC三个顶点A、B、C的坐标分别为A(2,-1)、B(1,-3)、C(4,-3.5).(1)在直角坐标系中画出三角形ABC;(2)把三角形A1B1C1向右平移4个单位,再向下平移3个单位,恰好得到三角形ABC,试写出三角形A1B1C1三个顶点的坐标,并在直角坐标系中描出这些点;(3)如果将△ABC看成是由△A1B1C1经过一次平移得到的,请指出这一平移方向和距离.【答案与解析】解:(1)如图1,(2)如图2,A1(-2,2),B1(-3,0),C1(0,-0.5);(3)如图3,连接AA 1,由图可知,22(2(2))(12)5AA '=--+--=.因此,如果将△ABC 看成是由△A 1B 1C 1经过一次平移得到的,那么这一平移的平移方向是由A 1到A 的方向,平移距离是5个单位长度.【总结升华】本题综合考查了平面直角坐标系,及平移变换.注意平移时,要找到三角形各顶点的对应点是关键及平移的相对性.举一反三: 【变式】如果矩形ABCD 的对角线的交点与平面直角坐标系的原点重合,且点A 和点C 的坐标分别为(-3,2)和(3,-2),则矩形的面积为( ). A .32 B .24 C .6 D .8 【答案】B.类型二、旋转变换3.如图,将△AOB 绕点O 按逆时针方向旋转45°后得到△A ′OB ′,若∠AOB=15°,则∠AOB ′的度数是( ).F A BCD EA. 25°B. 30°C. 35°D. 40°【思路点拨】根据旋转的性质旋转前后图形全等以及对应边的夹角等于旋转角,进而得出答案即可. 【答案与解析】解:∵将△AOB 绕点O 按逆时针方向旋转45°后得到△A ′OB ′,∴∠A ′OA=45°,∠AOB=∠A ′OB ′=15°, ∴∠AOB ′=∠A ′OA ﹣∠A ′OB=45°﹣15°=30°, 故选:B .【总结升华】此题主要考查了旋转的性质,根据旋转的性质得出∠A ′OA=45°,∠AOB=∠A ′OB ′=15°是解题关键.举一反三:【变式】如图,△OAB 可以看成是由△OCD 绕点O 按顺时针方向旋转而来的,则旋转中心是 ,旋转角是 ,点C 的对应点是 .OBCAD【答案】点O ,∠COA 或∠DOB ,点A .4.如图,四边形ABCD 是正方形,点E 是AB 边上的点,BE =1.将△BCE 绕点C 顺时针 旋转90°得到△DCF.已知EF =25,求正方形ABCD 的边长.【答案与解析】解:设正方形ABCD 的边长为x ,∵△BCE 绕点C 顺时针旋转90°得到△DCF ,且BE=1, ∴DF=BE=1,∵四边形ABCD 是正方形, ∴AD=AB=x ,∠A=90°,∴在Rt △AEF 中,AE 2+AF 2=EF 2, ∵AE=AB-BE=x-1,AF=AD+DF=x+1,∴222(1)(1)(25)x x -++=,解得:x =3,∴正方形ABCD 的边长为3.【总结升华】此题考查了正方形的性质、旋转的性质以及勾股定理.注意掌握旋转前后图形的对应关系,注意掌握方程思想与数形结合思想的应用. 举一反三:【变式】如图,K 是正方形ABCD 内一点,以AK 为一边作正方形AKLM ,使L 、M•在AK 的同旁,连接BK 和DM ,试用旋转的思想说明线段BK 与DM 的数量关系.【答案】数量关系为BK=DM. ∵ABCD 和AKLM 都是正方形,∴AB=AD,AK=AM.∵∠DAM+∠DAK=90°,∠BAK+∠DAK=90°.∴∠DAM=∠BAK △DAM 可以看作是△ABK 以A 为旋转中心,∠BAD 为旋转角(90°)逆时针旋转而成的,故BK=DM.类型三、中心对称与图形设计5.如图,方格纸中△ABC 的三个顶点均在格点上,将△ABC 向右平移5格得到△A 1B 1C 1,再将△A 1B 1C 1绕点A 1逆时针旋转180°,得到△A 1B 2C 2. (1)在方格纸中画出△A 1B 1C 1和△A 1B 2C 2; (2)设B 点坐标为(﹣3,﹣2),B 2点坐标为(4,2),△ABC 与△A 1B 2C 2是否成中心对称?若成中心对称,请画出对称中心,并写出对称中心的坐标;若不成中心对称,请说明理由.【思路点拨】根据平移和旋转的作图方法作图即可.根据中心对称的特点可知P点就是对称中心,从而求出A(﹣2,0),A1(3,0),P(,0).【答案与解析】解:(1)如下图.(2)△ABC与△A1B2C2成中心对称,如下图所示,连接CC2(或BB2)交AA1于点P.则P点就是对称中心.∵B(﹣3,﹣2),B2(4,2),∴A(﹣2,0),A1(3,0),∴P(,0).【总结升华】本题考查的是平移变换与旋转变换作图.6.如图,图案可以看做以一个怎样的图案为“基本图案”形成的?试用两种以上的方法分析它的形成过程.【答案与解析】解:解法一:图案可以看做是以其中的八分之一为“基本图案”,经过三次轴对称 (第1、2根对称轴彼此垂直,而且过整个图案的中心)所形成的.解法二:也可以看做是以图案的四分之一为“基本图案”(可以是小正方形状也可以是等腰直角三角形状),绕整个图案的中心分别旋转90°、180°、270°所形成的.解法三:也可以以四分之一图形为基本图形,经过两次轴对称(对称轴互相垂直,而且过整个图案的中心)所形成.【总结升华】本题考查利用旋转设计图案的知识,基本图案的寻找较为灵活,对于不同的基本图形需要作的几何变换也不同.举一反三:【变式】(2016春•泸溪县期末)如图所示,由5个大小完全相同的小正方形摆成如图形状,现移动其中的一个小正方形,请在图2、图3、图4中分别画出满足以下要求的图形(用阴影表示)(1)使所得图形成为轴对称图形,而不是中心对称图形;(2)使所得图形成为中心对称图形,而不是轴对称图形;(3)使所得图形既是轴对称图形也是中心对称图形.【答案】解:。
