第五节有效应力原理.ppt
有效应力解释

有效应力解释。
有效应力是一种衡量物体受力的方法,它按照一定的标准来表示物体受力的结果——物体的真实变形大小或变形的形状。
它将所有受力作用在物体上的各种类型的应力综合起来,而忽略不必要的细节,给出一个单一的参数来描述受力情况。
它不但可以用来判断物体受力的变形程度,而且可以用于比较不同物体受力情况的差别。
有效应力是应用力学原理来描述物体受力状况的最重要工具之一,在工程设计中它经常被用于确定材料结构的强度和变形,以及判定物体在极端条件下的耐久性。
在实际条件下,有效应力会随着受力的强度而增加,因此可以用来表征受力强度和屈服点,也可以用来比较物体受力的极限和稳定性。
三轴试验原理与技术 书中的 第五节 总应力与有效应力

1.92
13.0 15.5 8.5
漂砾粘土
10
9.5
2.08
9.5 10.5 8.5
漂砾粘土
19
10.7
2.02
10.7 12.4 26.0
残积粘土
20
27.5
1.51
27.5 31.5 20.0
残积粘土
44
23.0
1.57
23.0 25.0
注
试样直径为 100mm,高 200mm,以标准击实功能击实。
A A u(1 a) A
或
u( 1 a )
(1-16)
接触面积 a 难以测定,不过其值很小,可以忽略不计,故式(1-16)可以写成:
u
以式(1-14)、式(1-15)代入式(1-17),得:
(1-17)
h2 ( w ) h2
u hw w (h1 h2 ) w
1
(1-14)
h1
hw h2 2 a a ( a) 3 3 b b b b 6 5 4
· A
· A
· A
( b)
· A
(c)
图 1-17 沉积土内的应力 (a) 沉积土层;(b)完全饱和;(c)部分饱和 1— 水位;2—土体单元;3—土颗粒; 4—孔隙水;5—孔隙气;6—孔隙水
A f 值。
6
三轴试验原理与应用技术
表 1-7
孔隙压力系数 B 和 A f (不排水剪测得)
孔隙压 力系数
粘粒含量 土 类 <0.002mm (%)
最优含水率 w (%)
最大干密度
试验时含 水率 w (%) 6.8
孔隙压 力系数 B 0.06 0.26 0.90 0.02 0.23 0.46 0.04 0.26 0.54 0.03 0.27 0.69 0.05 0.05 0.14 0.03 0.16 0.36
第五节有效应力原理
三、附加应力作用下孔隙水压力和有效应力的计算
在外荷作用下,土体中各点产生的应力增量,称为附加 应力。对饱和土,土体中任一点的附加应力σ是由粒间接触 点的有效应力σ′和孔隙水压力u承担。 此处仅考虑侧限应力状态,对于其他较复杂的情况参见 相关书籍。
如果地面上作用着大面积连续均布荷载,而土层厚度 又相对较薄时,则土层中引起的附加应力σz属于侧限应力 状态。这时,外荷p在土层中引起的附加应力σz将沿深度 均匀分布,即σz=p。显然,这种应力条件下土体在侧向 上不能发生变形。 p ∞ ∞
式中:γw--水的重度,kN/m3;γsat--土的饱和重度,kN/m3。 A点处由孔隙水传递的静水压力,即孔隙水压力为:
根据有效应力原理,由于土体自重对A点作用的有效 应力应为:
式中:γ′--土的浮重度,kN/m3。
两种压力随深度的分布,如图3-22b所示。 自重应力作用下两种应力的计算过程见例题3-5。
(2)这里的u是指超静水压力,所谓超静水压力,是外 荷载引起的,超出静水位以上的那部分孔隙水压力。它 在固结过程中随时间不断变化,固结终了时应等于零。 饱水土层中任意时刻的总孔隙水压力应是静孔隙水压力 与超静孔隙水压力之和。
z p
Z 为了模拟饱和土体受到连续均布荷载作用后,在土中 所产生的孔隙水压力以及u与σ′随时间t的变化规律, 1925年太沙基最早提出了一个渗压模型,如图3-24所示。
通过模拟侧限状态下饱和土体的渗流固结过程,可以 得到如下的两点认识:
(1)整个渗流固结过程中u和σ′都是随时间t而不断变 化着的,即u=f(t),σ′=f(t)。渗流固结过程实质上就是 土中两种不同应力形态的转化过程。
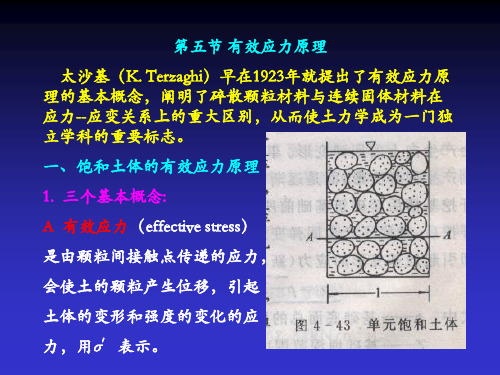
第五节 有效应力原理 太沙基(K. Terzaghi)早在1923年就提出了有效应力原 理的基本概念,阐明了碎散颗粒材料与连续固体材料在 应力--应变关系上的重大区别,从而使土力学成为一门独 立学科的重要标志。 一、饱和土体的有效应力原理
第5.0土的有效应力原理ppt课件

24
§5.1 土的有效应力原理
二. 饱和土中孔隙水压力和有效应力的计算 2.附加应力作用情况
(1) 侧限应力状态及一维渗流固结
▪ 实践背景:大面积均布荷载 p
p
饱和压缩层 不透水岩层
σz=p
侧限应力状态
25
§5.1 土的有效应力原理
二. 饱和土中孔隙水压力和有效应力的计算 2.附加应力作用情况
(1) 侧限应力状态及一维渗流固结
1 3
体积V
孔隙流体的体积变化
V1 Cf uA nV
3(1 2) Cs E
土骨架的体积变化 暂时假定土骨架为线弹性体
uA
V2 v V (1 2 3 )V
总应力增量 有效附加应力
应变增量
轴向 1 3 1 3 uA [(1 3 uA ) 2(uA )]/ E
侧向
0
uA
二. 饱和土中孔隙水压力和有效应力的计算 1.自重应力情况
(1) 静水条件 毛细饱和区
总应力 - 孔隙水压力 = 有效应力
H
毛细饱
和区 sat hc
ht
hw
whc -
H whc
H satht
+
whw H satht whw 20
§5.1 土的有效应力原理
二. 饱和土中孔隙水压力和有效应力的计算 1.自重应力情况
u
u w (H h) satH w (H h)
H wh 渗透压力: wh
22
§5.1 土的有效应力原理
二. 饱和土中孔隙水压力和有效应力的计算 1.自重应力情况
取土骨架为隔离体
向上渗流: Δh
向下渗流:
H
粘土层 γsat
H wh
有效应力原理

有效应力原理
有效应力原理是固体力学中的一个重要概念,用于描述材料在外力作用下的变形行为。
在材料受外力作用时,内部会产生应力,而有效应力则是指对该材料产生变形所起主导作用的应力。
在实际应用中,材料受到的外力不仅包括单一的拉压力,还可能包含剪切力、弯曲力等复合力。
为了简化计算和分析,需要将这些复合力转化为一个等效的单轴应力,从而判断材料是否会破坏或产生塑性变形。
有效应力的计算需要考虑材料所处的环境,主要包括温度、湿度等因素。
对于一般情况下的材料,有效应力可以直接通过减去材料表面上的正应力值来计算,可以表示为:
σeff = σtotal - σsurface
其中,σtotal表示材料受到的总应力,而σsurface表示材料表
面上的正应力。
常见的有效应力计算方法有von Mises准则和Tresca准则。
有效应力原理的应用十分广泛。
在工程中,工程师们可以通过有效应力原理来分析结构物的承载能力,判断材料的破坏点和塑性变形情况,从而设计出更加安全可靠的结构。
此外,在材料科学和地质力学等领域,有效应力原理也被广泛应用于研究材料的力学性质和岩土工程中的土体变形行为。
总之,理解和应用有效应力原理对于有效分析和设计材料和结
构的性能至关重要,可以使工程师和科学家们更好地理解材料的力学性质并做出相应的决策。
有效应力原理

有效应力原理
应力原理(Maxwell's Stress Principle)是一种用来描述有刚度介质中运动物体的
机械力学原理。
它是由19世纪英国科学家詹姆斯·马克斯韦(James Clerk Maxwell)提
出的,它是一种用来研究物体有效应力的理论方法。
它指出,物体位移的方向和大小都可
以用有效的应力或拉力来描述,用来准确地衡量物体的力学表现。
应力原理认为,物体任何位移均可以由一组有效的应力或拉力来描述,从而可以准确
地衡量物体强度和稳定性。
因此,应力原理可以导出实际物体的偏应力、正应力和拉力分
布情况,从而可以更好地把握物体的应力状态。
应力原理还指出,给定的物体的应力分布状态是动态的,随着物体位移的变化而变化,而且会随机选择最优的应力分配方式。
因此,借助应力原理也可以预测物体的应力应变及
其性能的变化趋势。
应力原理可以帮助我们从复杂的力学系统中提取出精简的有效应力,把握物体运动的
表现,以及物体力学性能的特性。
应力原理也没有国界,它推广到了气体体系和电场力学
系统,直到现在仍是多学科研究的重要方法。
有效应力原理

有效应力原理
有效应力原理是一个重要的力学原理,它指的是,当一个物体受到一个外力的作用时,物体的力学行为与受力的位置和方向有关。
它会影响物体的结构和力学性能,甚至是其形状和大小。
有效应力原理的基本思想是,当一个物体受到力的作用时,其力学行为受到受力位置和方向的影响。
有效应力原理经常用于研究物体受力的方向和位置。
例如,当一个物体受到一个远程的力(如重力)时,物体的行为受到受力位置和方向的影响。
另外,当一个物体受到一个近距离的力,如挠度力或拉力时,它的行为也受到受力位置和方向的影响。
有效应力原理也可以用来计算物体受力的影响。
例如,当一个物体受到一个外力时,可以利用有效应力原理计算出物体受力的影响,从而推算出物体受力的大小和方向。
有效应力原理还可以用来研究物体受力的形状和大小。
例如,可以利用有效应力原理来研究物体受力的变形情况,从而推算出物体受力的大小和形状。
有效应力原理是一个重要的力学原理,它可以用来研究物体受力的方向、位置、大小和形状。
它可以用来计算物体受力的影响,并且可以用来研究物体受力的变形情况。
因此,有效应力原理在力学研
究中起着重要的作用。
第五节有效应力原理

Z 为了模拟饱和土体受到连续均布荷载作用后,在土中 所产生的孔隙水压力以及u与σ′随时间t的变化规律, 1925年太沙基最早提出了一个渗压模型,如图3-24所示。
通过模拟侧限状态下饱和土体的渗流固结过程,可以 得到如下的两点认识:
(1)整个渗流固结过程中u和σ′都是随时间t而不断变 化着的,即u=f(t),σ′=f(t)。渗流固结过程实质上就是 土中两种不同应力形态的转化过程。
推导:
若单位断面积A—A上颗粒接触点面积为a,则孔隙水 压力作用面积为1-a。则有:
u1 a
又a很小,可忽略不计,故: u 上式即为太沙基提出的饱和土体有效应力原理。它是 研究土体固结和强度的重要理论基础。 饱和土体有效应力原理的要点:
1.饱和土体内任一平面上受到的总应力等于有效应力加孔 隙水压力之和;
2.土的变形(压缩)与强度的变化都仅取决于有效应力的 变化。
二、饱和土中孔隙水压力和有效应力的计算 (一)自重应力作用下的两种应力
h2
图3-22a为处于水下的饱和土层,在地面下h2深处的A点, 由于水体和土体自重对地面以下A点处作用的垂向总应 力σ为:
式中:γw--水的重度,kN/m3;γsat--土的饱和重度,kN/m3。 A点处由孔隙水传递的静水压力,即孔隙水压力为:
在渗流产生的渗透力的作用下,其有效应力与渗流作用 的方向有关。当自上而下渗流时,将使有效应力增加,因
而对土体的稳定性有利。反之,若向上渗流则有效应力减 小,对土体的稳定性不利,若使得有效应力减少至0,即 可能发生所谓的流砂和管涌现象,造成地基或边坡的失稳。
三、附加应力作用下孔隙水压力和有效应力的计算
解:1)地下水位以上无 毛细饱和区时的σ、u、σ′ 分布值见下表。σ、u、σ′ 沿深度的分布如下图中实线 所示。
有效应力原理

H1 satH 2
毛细水上升时土中有效应力计算
总应力 - 孔隙水压力 = 有效应力
毛细饱和区
H
whc
-
H whc
sat
ht
hc
hw
H sath t
+
wh w
H sath t w h w
有效应力σ’
Aw 1 A
( As ≤0.03)
PS
'u
' u
地下水位变化对有效应力的影响
(1) 静水条件 地下水位
σ’=σ-u =γwH1+γsatH2
-γw(H1+ H2)
H1
=(γsat-γw)H2 = γ ’H 2
sat
H2
σ’与地面以上 水位H1无关,与 地下水位H2有关。
H w h
渗透压力:
w h
基底压力 与基底附加压力的计算
概述
上部结构 建筑物 设计 基础 地基
基础结构的外荷载
上部结构的自 重及各种荷载 都是通过基础 传到地基中的
基底反力
基底压力 附加应力
基底压力:基础底面传 递给地基表面的压力, 也称基底接触压力。
地基沉降变形
影响因素 计算方法 分布规律
基底压力的影响因素
•大小、方向、分布
荷载条件
基底压力
地基条件
基础条件
•刚度 •形状 •大小 •埋深
•土类、密度、土层结构等
基底压力分布特征
条形基础,竖直均布荷载
基础抗弯刚度EI=0 → M=0; 基础变形能完全适应地基表面的 变形; 基础上下压力分布必须完全相同, 若不同将会产生弯矩。
《有效应力原理》课件

泥石流稳定性
有效应力是评估泥石流稳定性的一个重要参数。 它与滑坡稳定性、地震灾害等问题有着密切关 联。
压缩特性
有效应力的变化还能够影响压缩特性。岩土工 程中,对其进行实验测定和分析也是相对比较 重要的。
有效应力在变形和破坏分析中的应用
1
变形分析
在土力学和岩石力学中,有效应力对于预测变形和变形变量的准确性具有非常重 要的作用。
2
破坏分析
有效应力还是评估破坏机制和破坏模式的一个关键参数。对于预测地下隧道和建 筑物的稳定性具有至关重要的作用。
3
土动力学
有效应力分析对于土动力学中的爆炸和冲击波效应的分析也非常重要。它可用于 计算爆炸波及其他动力荷载的应力。
有效应力在岩土工程中的应用
在地下工程、水力工程、矿山工程、地质勘探、土木工程等多个领域,有效 应力都具有重要的应用价值。它的实际应用将有助于改善岩土工程的质量和 可靠性。
工程实践
理论与实践相结合,应该加强有效应力原理在工程 中的应用,促进岩土工程领域技术的发展和进步。
《有效应力原理》PPT课 件
探索有效应力原理,深入了解有效应力的定义、计算和作用,并了解它在土 力学和岩石力学中的应用。
什么是有效应力?
1 定义
有效应力是实际应力与孔隙水压力之差。它 反映了岩石或土壤所承受的有效载荷。
2 应用
在土力学和岩石力学中,有效应力对于解释 地质现象和开发地下资源至关重要。
未来有效应力研究的展望
分子模拟技术
利用分子模拟技术和计算机辅助分析方法,以更准 确、更深入的方式理解有效应力。
多物质组分分析
多物质材料的组分分析为有效应力实验提供了新旅 程,并且提供了解决地质破坏和稳定性问题的新思 路。
3.5 有效应力原理

A
B
量筒A和量筒B底部都受到了相同压力σ的作用,但产生两种 不同的效果,反映了土体中存在两种不同性质的压力,即: (1)有效应力;(2)孔隙水压力
现取作用于饱和试样截面中任一点总应力来分析。
A: 土单元的断面积 As: 颗粒接触点的面积 Aw: 孔隙水的断面积
A AS Aw
外荷载 总应力 A
u H
w(H1+H2+h)
2
wh
➢ 与自上向下渗流情况相比,孔隙压力增加了2wh,而有 效应力相应减少了2wh 。若不断增加向上渗流的水位差h, 直到aa平面的孔隙水压力与总应力相等,即有效应力为零,
则由上式得到
w
h H2
wi
j
流土的临界条件
1、课后思考题不要求,应能自己组织 出答案。 2、习题3.2、3.5、3.10
H
• a-a平面有效应力: = -u
sat H2
a
=( wH1+ satH2)-w(H1+H2) a
γwH1 a
=(sat-w)H2=H2
wH1 satH2 wH w H2
可见:静水条件下的孔隙水压力为所研究平面上单位面积的水
柱重,它与水深成正比,呈三角形分布,而有效应力为所研究平
饱和土的有效应力原理
二、在静水条件下土的孔隙水压力和有效应力
浸没在水下的饱和土体(海洋土),设浸没水深为H1,土的饱 和重度为 ,则土面下深度为H2的a-a平面的总应力为 • 总应力:单位土柱和水柱
的总重量
σ=wH1+ satH2
• 孔隙水压力:净水压强
Hw
H1
γwH1
u= wHw= w(H1+H2)
有效应力原理课件

有效应力与破坏的关系
剪切破坏
土体在剪切力作用下发生的破坏,表 现为土体出现裂缝或滑动面。
压缩破坏
土体在垂直压力作用下发生的破坏, 表现为土体压缩变形过大或产生侧向 挤出。
有效应力的计算方法
01
通过实测土体内孔隙水压力和总 应力,计算得到有效应力。
02
常用计算公式:有效应力=总应 力-孔隙水压力。
有效应力原理的发展趋势 与展望
REPORTING
有效应力原理的局限性
仅适用于均质、连续 、各向同性的介质
未考虑应力与应变的 关系
未考虑应力状态对渗 透性的影响
未来发展方向与趋势
拓展到非均质、非连续、各向异 性介质
研究应力状态对渗透性的影响机 制
发展基于有效应力原理的数值模 拟方法
对实际工程的指导意义与价值
VS
详细描述
通过有效应力原理,可以分析水流对河床 的冲刷、水库的淤积等问题,为水利工程 的规划、设计和运行提供科学依据。同时 ,有效应力原理在水力学、流体动力学等 领域也有广泛的应用。
PART 04
有效应力原理的实验验证
REPORTING
实验设备与材料
01
02
03
04
压力传感器
用于测量土壤压力。
环境工程中的有效应力原理
总结词
在环境工程中,有效应力原理广泛应用于水力学、土壤侵蚀 和污染物迁移等领域。
详细描述
通过有效应力原理,可以研究水流对河床、海岸线的冲刷作 用,分析土壤侵蚀的机制,以及预测污染物的迁移规律。这 有助于环境保护和治理措施的制定。
水利工程中的有效应力原理
总结词
在水利工程中,有效应力原理是研究水 流与河床、水库等相互作用的重要理论 基础。
三轴试验原理与技术 书中的 第五节 总应力与有效应力

a
(g/cm3)
Af
-0.01 -0.03 -0.28 -0.01 -0.04 -0.15 +0.01 -0.03 -0.15 +0.01 +0.07 -0.15 +0.05 +0.07 +0.27 +0.02 +0.14 +0.06
冰碛土
<1
8.8
2.1
8.8 10.2 11.7
冰碛土
2
12.2
A B
A
us 3 u uc ,如 B=1,则 A uc 1 3 1 3
孔隙压力系数 A 在实际工程上很有参考价值,它与土的类别、应力状态、 应变大小和时间有关。表 1-6 是一些典型土的数据,可以用来判断土的性质。
5
三轴试验原理与应用技术
表 1-6
孔隙压力系数 A 的数据
(1-28) (1-29)
式(1-29)表明, 三轴试样在受外力作用情况下产生的孔隙水压力分为两部分, 一部分是由施加的周围压力 σ3 引起;另一部分是由轴向应力(σ1-σ3)引起。式中 BA 常用 A 表示因而式(1-29)可改写为:
u B 3 A(1 3 )
4
(1-30)
三轴试验原理与应用技术
1
三轴试验原理与应用技术
此外,除了孔隙水压力,土颗粒之间也存在接触应力。设有一水平断面 b-b 通过饱和土单元中[图 1-17(b)],该断面不切断土颗粒,只通过土颗粒之间的接触பைடு நூலகம்点,则所有垂直于 b-b 的接触力为有效应力 σ/。设 a 为单位面积内所有颗粒接触 点的接触面积之和(<1),则在断面 a-a 上,面积 A 上的总垂直力为:
有效应力原理的概念及应用

有效应力原理的概念及应用1. 什么是有效应力原理?有效应力原理是材料力学中的一个重要概念,用于描述材料中的内部应力分布及其对材料强度和变形特性的影响。
它是指在材料中存在两种类型的应力:有效应力和无效应力。
有效应力是对材料的真实应变和应变率产生影响的应力成分。
它是指在某一点上材料内部应力的一个测度,可以通过对材料的应力-应变关系进行分析求得。
有效应力是造成材料变形和破裂的主要原因,因此对于工程设计和材料强度分析非常重要。
无效应力是指对材料的真实应变和应变率没有影响的应力成分。
它通常体现为对材料的局部应变和变形没有贡献。
无效应力的出现是材料内部各种应力分量的复杂相互作用的结果,仅仅反映了材料内部不平衡力的情况,并不产生明显的影响。
2. 有效应力原理的应用有效应力原理在材料科学和工程中具有广泛的应用。
下面列举了一些应用案例:•材料强度分析:通过有效应力原理,可以对材料的强度进行准确的分析和预测。
有效应力是造成材料变形和破坏的主要原因,因此在工程设计和材料选择时需要对材料的有效应力进行评估。
•材料优化设计:有效应力原理可用于优化材料的设计和选择。
通过对不同材料的有效应力进行比较,可以为工程师提供选择合适材料的依据,以满足特定工程要求。
•材料失效分析:有效应力原理还可以用于材料失效分析。
通过对材料内部各种应力分量及其相互作用的分析,可以确定材料失效的机制和条件,从而采取相应的措施避免材料失效。
•材料变形特性评估:有效应力原理可以用于评估材料的变形特性。
通过分析材料内部的有效应力分布,可以确定材料的变形行为,为工程设计提供参考。
•材料耐久性评估:通过有效应力原理,可以对材料的耐久性进行评估。
有效应力是造成材料疲劳和腐蚀等问题的主要原因,因此对材料的有效应力进行分析和评估可以提高材料的耐久性。
3. 如何计算有效应力?计算有效应力需要通过材料的应力-应变关系来求解。
具体方法如下:1.首先,根据加载条件和材料的力学性质确定材料的应力场。
有效应力原理

'u
个神奇的宇宙。 如果要实现这样的理想,我们的目标就不能太低。我们要解决的问题远比
任何竞赛都更加困难,如果没有恰当的准备,即使最高智力水平的人也不会获
得成功。最伟大的奖励等待着伟大的智力付出最大的努力,他必须通过持续不 断的实践来保持敏锐的目光和新鲜的思想。仪器和设备可以用钱买来,天赋可
能与生俱来,但是我们心智的工具——数学知识、实验能力等前人创造的知识
试想: 海底与土粒间的接触压力 哪一种情况下大?
10
§3 土体中的应力计算
1. 自重应力情况
(1) 静水条件 地下水位
海洋土 毛细饱和区 (2) 稳定渗流条件
§3.5 有效应力原理 二. 饱和土中孔隙水压力和有效应力的计算 2. 附加应力情况
(1) 单向压缩应力状态 (2) 等向压缩应力状态 (3) 偏差应力状态
w H1 satH 2
wH
H 2
13
§3.5 有效应力原理 二. 饱和土中孔隙水压力和有效应力的计算 1.自重应力情况
(1)静水条件 毛细饱和区
总应力 - 孔隙水压力 = 有效应力
§3 土体中的应力计算
毛细饱 和区
H
whc
-
H whc
sat
ht
hc
hw
H sath t
对于饱和土: 对于干土:
1 , 则上式变为
uw
0 上式变为 ua
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
又a很小,可忽略不计,故: u
上式即为太沙基提出的饱和土体有效应力原理。它是 研究土体固结和强度的重要理论基础。
饱和土体有效应力原理的要点:
1.饱和土体内任一平面上受到的总应力等于有效应力加孔 隙水压力之和;
2.土的变形(压缩)与强度的变化都仅取决于有效应力的 变化。
二、饱和土中孔隙水压力和有效应力的计算 (一)自重应力作用下的两种应力
h2
图3-22a为处于水下的饱和土层,在地面下h2深处的A点,
由于水体和土体自重对地面以下A点处作用的垂向总应
力σ为:
式中:γw--水的重度,kN/m3;γsat--土的饱和重度,kN/m3。
A点处由孔隙水传递的静水压力,即孔隙水压力为:
根据有效应力原理,由于土体自重对A点作用的有效 应力应为:
式中:γ′--土的浮重度,kN/m3。
上不能发生变形。
p
∞
∞
z p
Z 为了模拟饱和土体受到连续均布荷载作用后,在土中
所产生的孔隙水压力以及u与σ′随时间t的变化规律,
1925年太沙基最早提出了一个渗压模型,如图3-24所示。
通过模拟侧限状态下饱和土体的渗流固结过程,可以 得到如下的两点认识:
(1)整个渗流固结过程中u和σ′都是随时间t而不断变 化着的,即u=f(t),σ′=f(t)。渗流固结过程实质上就是
19.6
74.4
9
94+4×19=170
58.8
112.2
(二)渗流作用下的两种应力 在渗流作用下,土体中的有效应力及孔隙水压力将会发
生变化。如在图3-23a的土层中,由于水头差而发生自下而 上的渗流时:
对于A点有:
如在图3-23b的土层中,由于水头差而发生自上而下的渗 流时,对于A点有:
在渗流产生的渗透力的作用下,其有效应力与渗流作用 的方向有关。当自上而下渗流时,将使有效应力增加,因
第五节 有效应力原理
太沙基(K. Terzaghi)早在1923年就提出了有效应力原 理的基本概念,阐明了碎散颗粒材料与连续固体材料在 应力--应变关系上的重大区别,从而使土力学成为一门独 立学科的重要标志。
一、饱和土体的有效应力原理
1. 三个基本概念:
A 有效应力(effective stress)
而对土体的稳定性有利。反之,若向上渗流则有效应力减 小,对土体的稳定性不利,若使得有效应力减少至0,即 可能发生所谓的流砂和管涌现象,造成地基或边坡的失稳。
三、附加应力作用下孔隙水压力和有效应力的计算
在外荷作用下,土体中各点产生的应力增量,称为附加 应力。对饱和土,土体中任一点的附加应力σ是由粒间接触
点的有效应力σ′和孔隙水压力u承担。
此处仅考虑侧限应力状态,对于其他较复杂的情况参见 相关书籍。
如果地面上作用着大面积连续均布荷载,而土层厚度
又相对较薄时,则土层中引起的附加应力σz属于侧限应力 状态。这时,外荷p在土层中引起的附加应力σz将沿深度 均匀分布,即σz=p。显然,这种应力条件下土体在侧向
过程中不断变化,固结终了时应等于零,用△u表示。
2.有效应力原理
作用于饱和土体内某截面上总的正应力σ由两部分组 成:一部分为孔隙水压力u,另一部分为有效应力σ’,
饱和土中总应力与孔隙水压力、有效应力之间存在如下 关系:
推导:
若单位断面积A—A上颗粒接触点面积为a,则孔隙水 压力作用面积为1-a。则有:
6×9.8=58.8
108.2
2)地下水位以上有毛细饱和区时的σ、u、σ′分布值见下 表。σ、u、σ′沿深度的分布如上图中虚线所示。
例题3-5计算表格2
深度 z(m)
σ(kN/m2)
u(kN/m2)
σ′(kN/ m2)
2
2×17+1×20=54
0
54
5
54+2×20=94
两种压力随深度的分布,如图3-22b所示。 自重应力作用下两种应力的计算过程见例题3-5。
【例题3-5】某土层剖面,地下水位及其相应的容重如下图
所示。试求:1)垂直方向总应力σ、孔隙水压力u和有效应
力σ′沿深度z的分布;2)若砂层中地下水位以上1m范围内
为毛细饱和区时,σ、u、σ′将如何分布?
解:1)地下水位以上无
毛细饱和区时的σ、u、σ′ 分布值见下表。σ、u、σ′
沿深度的分布如下图中实线 所示。
例题3-5计算表格1
深度z(m)
σ(kN/m2)
u(kN/m2) σ′(kN/m2)
2
2×17=34
3
3×17=51
0
34
0
51
5
(3×17)+(2×20)=91
2×9.8=19.6
71.4
9
(3×17)+(2×20)+(4×19)=1 67
是由颗粒间接触点传递的应力,
会使土的颗粒产生位移,引起
土体的变形和强度的变化的应
力,用σ′表示。
B 孔隙水压力(pore water pressure)由孔隙水传递的应 力,它不能直接引起土体的变形和强度变化,又称为中
性压力,在固结过程中不随时间而变化,用u表示。
C 超静孔隙水压力(excess pore water pressure)由外荷 引起的超出静水位以上的那部分孔隙水压力。它在固结
土中两种不同应力形态的转化过程。
(2)这里的u是指超静水压力,所谓超静水压力,是外
荷载引起的,超出静水位以上的那部分孔隙水压力。它 在固结过程中随时间不断变化,固结终了时应等于零。 饱水土层中任意时刻的总孔隙水压力应是静孔隙水压力 与超静孔隙水压力之和。
