小升初数学计算分类专题
小升初数学计算知识点总结

小升初数学计算知识点总结一、加法与减法加法与减法是小学数学的基础运算,也是小升初数学计算中的重要知识点。
学生在掌握了简单的加法与减法之后,可以逐渐学习进阶的加减法知识点。
在这一部分,学生需要掌握以下知识点:1. 10以内的加减法2. 100以内的加减法3. 1000以内的加减法4. 进位与退位5. 加减混合运算6. 加减法的应用题这些知识点是小升初数学计算中的基础,学生需要通过大量的练习来掌握这些知识点,建立起扎实的数学基础。
二、乘法与除法乘法与除法是小学数学中比较难掌握的知识点,而且在小升初数学计算中也是比较重要的。
学生在这一部分需要掌握以下知识点:1. 乘法口诀表2. 乘法与积的关系3. 乘法的计算方法4. 乘法的应用题5. 除法口诀表6. 除法与商的关系7. 除法的计算方法8. 除法的应用题乘法与除法是小升初数学计算中的重点知识点,学生需要通过反复练习来掌握这些知识点,建立起扎实的数学基础。
三、小数与分数小数与分数是小升初数学计算中比较复杂的知识点,但也是非常重要的。
在这一部分,学生需要掌握以下知识点:1. 小数的读法与写法2. 小数的大小比较3. 小数的加减乘除运算4. 分数的读法与写法5. 分数的大小比较6. 分数的加减乘除运算7. 小数与分数的互相转化小数与分数是小升初数学计算中的难点知识点,学生需要通过反复练习来掌握这些知识点,建立起扎实的数学基础。
四、解方程与代数式解方程与代数式是小升初数学计算中的重要知识点,学生在这一部分需要掌握以下知识点:1. 一元一次方程的解法2. 一元一次方程的应用题3. 一元二次方程的解法4. 一元二次方程的应用题5. 代数式的计算方法6. 代数式的应用题解方程与代数式是小升初数学计算中的难点知识点,学生需要通过大量的练习来掌握这些知识点,建立起扎实的数学基础。
五、图形与空间图形与空间是小升初数学计算中的基础知识点,学生在这一部分需要掌握以下知识点:1. 直线、线段、射线、角的基本概念2. 三角形、四边形、多边形的基本概念3. 圆的基本概念4. 图形的面积与周长计算5. 空间图形的展开与折叠6. 空间图形的面积与体积计算图形与空间是小升初数学计算中的基础知识点,学生需要通过大量的练习来掌握这些知识点,建立起扎实的数学基础。
小升初数学《计算题》专项练习(人教真题汇编)精选全文

可编辑修改精选全文完整版一、直接写得数类型1.直接写出得数67÷3=0.88+1.22=34+25%= 5-25-35= 1÷13+13÷1=10-20%=0÷112=0.9×29=1-78+38= 1.25×4×2.5×8=2.直接写出得数.1﹣20%=0.125÷ 18=38.5÷7=25+0.6=1÷3× 13=0.4×0.5=38- 14= 1.6÷0.2=8× 14÷8× 14=72×421=3.直接写出得数。
34.5+5.34=340×50=95+115=8.7÷0.29=34÷12=48×25%=4.口算。
7.4+2.6= 40÷80= 10-0.95= 2.5×16= 6.3÷0.3=202-98= 6- 23= 53÷59=45+310=60×40% =5.直接写出得数。
0.5÷0.01= 32×0.25= 3.14×5= 6.1-1.9= 0.13÷1.3=3 4×15=13+16= 1.2÷45=34−16=0.53=6.直接写出得数。
8.7+1.3= 2.5×10=0.8-0.5=0÷40%= 1÷10= 1−(37+47)=10×710=12−13=38÷78=2+13= 7.直接写出得数。
763-197= 76-0.6= 1.03-0.54= 5.7÷0.1= 67-6÷7=1÷1%= 14+512=0.57×0.3= 2.323÷23= 8×18÷8×18=8.直接写出得数。
小升初冲刺专题之计算专题

第1弹 凑整与分组法计算是我们学习数学知识基础中的基础,所以关于计算的重要性我们就不多说了。
计算可以分为硬算和巧算,本讲义主要介绍一些巧算方法,但是在做计算题目的时候也需要一些硬算基本功。
1. 凑整凑整指的是在混合运算中想办法凑出整数,通常可以先计算能够得到整数或整百整千的两个数。
例如在四则运算中先算 6436+,28128-,8125⨯,37111÷。
2. 分组分组指在计算中对某些数分成一组,通常分成一组的目的是凑整,也有把一个周期放在一组,如例3。
【例 1】 计算:9109...991...199919919个++++.【例 2】 计算:14.2020142014.2014⨯÷.精选例题知识简介【例 3】 计算:1234...4344454647484950++--+--++--+.1. 计算: 4116.025.452-++.2. 计算:125328325⨯⨯⨯.小试牛刀3. 计算: )2072()318431326413(-⨯+++ .4. 计算: 371391222÷⨯÷5. 计算:999988889999999888999998899989+++.6. 计算:)200198...642()201199...531(+++++-+++++.第2弹提取公因数法知识简介提取公因数是乘法分配律的逆运算,也是巧算中常用的方法,很多题目提取公因数后括号部分可以凑整。
同时,你可以发现,每提取一次公因数就可以少算一次乘法。
提取公因式法可以细分为以下三类:1.直接提取公因数2.部分提取公因数3.分组提取公因数下面三道例题分别对应上述三类提取方法。
当然这样分类只是一种区分不同问题的手段,关键还是对问题的理解和掌握。
精选例题【例1】计算:445633562256⨯+⨯+⨯.计算专题【例2】计算:20092008200820092008200920092009-⨯-⨯.【例3】计算:122334...96979798989999100⨯+⨯-⨯++⨯-⨯+⨯-⨯.小试牛刀1.计算:22241112225111⨯-⨯.2.计算:556444445555⨯-⨯.3.计算17451511217161654⨯+⨯+⨯. 4.计算:122123124123123123123⨯-+⨯.5.计算:.7.53125.08.6487548.637.525537.08.64⨯⨯⨯-⨯⨯+⨯⨯6.计算:85111125473244537⨯+⨯+⨯+⨯.计算专题第3弹数列与数表知识简介数列指的是一列数,数表指的是一个表格的数。
小升初数学应用题分类

小升初数学应用题分类小升初数学应用题分类大全一、方程的应用1.学校建校舍计划投资45万元,实际投资40万元。
实际投资节约了百分之几?2.学校五月份计划用电480度,实际少用60度。
实际用电节省百分之几?(福建云宵小学)3.某厂计划三月份生产电视机400台,实际上半个月生产了250台,下半个月生产了230台,实际超额完成计划的百分之几?(南昌市青云谱区)4.现有甲、乙、丙三个水管,甲水管以每秒4克的流量流出含盐20%的盐水,乙水管以每秒6克的流量流出含盐15%的盐水,丙水管以每秒10克的流量流出水,丙管打开后开始2秒不流,接着流5秒,然后又停2秒,再流5秒……三管同时打开,1分钟后都关上,这时流出的混合液含盐百分之几?(武汉大学附属外国语学校)5.新光小学书画班有75人,舞蹈班有48人,书画班人数比舞蹈班多百分之几?(南宁市)6.小明用一包绿豆做实验,其中发芽的种子有100粒,没有发芽的种子有25粒,求这包绿豆的发芽率。
(浙江温岭市)8.为灾区捐款,小华捐4.2元,比小丽多捐了0.4元,小华比小丽多捐几分之几?(河南安阳市)9.一件衣服打八折出售卖100元,实际90元卖出。
实际几折卖出?(浙江仙居县)10.食堂运来600千克大米,已经吃了4天,每天吃50千克。
剩下的5天吃完,平均每天吃多少千克?(南京市建邺区)11.3箱橘子比3筐苹果少24千克。
平均每箱橘子重20千克,每筐苹果重多少千克?(浙江台州市市区)12.在绿化祖国采集树种的活动中,某校四年级5个班级,每班采集树种20千克,五年级3个班共采集60千克,平均每班采集树种多少千克?(上海市)13.大桥乡修一条长2100米的水渠,已修了5天,平均每天修240米。
余下的任务要在3天内完成,平均每天应修多少米?(南京市秦淮区)14.小明到商店买了3个小型足球付出20元,找回1.85元,每个足球多少元?(银川市实验小学)15.某班有4个小队,每个小队有12名少先队员,在“希望工程”捐款活动中,共捐款240元。
小升初数学总复习计算图形面积分类练习题解析

五、巧用比例
1、一个大长方形被两条平行于它的两条边的线分成 a、b、c、d四个长方形。已知a的面积是10平方厘米,
b的面积是14平方厘米,c的面积是35平方厘米。求d的 面积。
【分析与解答】:长方形a、b等高;长方形c、d 等高
a:b=d:c
【分析与解答】: 阴影部分的面积就是梯形 ABGD的面积。
(3+8)×4÷2=22平方厘米
2、下图是正方形与平行四边形组成的图形, 求阴影部分的面积。(单位:分米)
【分析与解答】阴影部分的面积就是左下梯 形的面积。
(2+6)×6÷2=24平方分米
二、面积的转化 1、如下左图的长方形是一块草坪,中间有两
【分析与解答】阴影部分的面积等 于大长方形的面积减去两个小长方形的面积。 15×10-15×1-(10-1)×1=126平方米
三、图形分割 1、已知大正方形ABCD的边长是12厘米,小正 方形GCEF的边长是8厘米,求阴影部分面积。
【分析与解答】:阴影部分经过分割后是三个 小三角形的面积之和。
3.14×42÷4 =12.56平方厘米
八、综合练习 1、如图,大正方形和小正方形的边长分别是6厘米
和5厘米。求阴影部分的面积。
【分析与解答】:
阴影部分=大三角形-长方形-小三角形 (6+5)×6÷2=33平方厘米 5×(6-5)÷2=2.5平方厘米 5×5÷2=12.5平方厘米 33-2.5-12.5=18平方厘米
9、一个长方形被分成六个长方形,其中四个长方 形的面积如图所示,求A和B的面积。
【分析与解答】:用比例解决。
(1)20:40=15:A
A=60
(2)20:40=B:36
【全国通用】小升初数学专题--计算模块--裂项法、换元法(含答案)

裂项法、换元法【教学目标】认识裂项法,能够掌握裂项法的几种形式 掌握换元法的技巧与应用。
1. “裂差”型运算将算式中的项进行拆分,使拆分后的项可前后抵消,这种拆项计算称为裂项法.裂项分为分数裂项和整数裂项,常见的裂项方法是将数字分拆成两个或多个数字单位的和或差。
遇到裂项的计算题时,要仔细的观察每项的分子和分母,找出每项分子分母之间具有的相同的关系,找出共有部分,裂项的题目无需复杂的计算,一般都是中间部分消去的过程,这样的话,找到相邻两项的相似部分,让它们消去才是最根本的。
①对于分母可以写作两个因数乘积的分数,即1a b⨯形式的,这里我们把较小的数写在前面,即a b <,那么有1111()a b b a a b=-⨯- ②对于分母上为3个或4个自然数乘积形式的分数,我们有:1111[]()(2)2()()(2)n n k n k k n n k n k n k =-⨯+⨯+⨯+++1111[]()(2)(3)3()(2)()(2)(3)n n k n k n k k n n k n k n k n k n k =-⨯+⨯+⨯+⨯+⨯++⨯+⨯+③对于分子不是1的情况我们有:⎪⎭⎫ ⎝⎛+-=+k n n k n n k 11)(()11h h n n k k n n k ⎛⎫=- ⎪++⎝⎭()()()()()21122k n n k n k n n k n k n k =-+++++()()()()()()()()31123223k n n k n k n k n n k n k n k n k n k =-++++++++()()()()()11222hh n n k n k kn n k n k n k ⎡⎤=-⎢⎥+++++⎣⎦()()()()()()()()11233223h hn n k n k n k kn n k n k n k n k n k ⎡⎤=-⎢⎥++++++++⎣⎦()()()221111212122121n n n n n ⎛⎫=+- ⎪-+-+⎝⎭2. 裂差型裂项的三大关键特征:①分子全部相同,最简单形式为都是1的,复杂形式可为都是x(x 为任意自然数)的,但是只要将x 提取出来即可转化为分子都是1的运算。
小升初数学简便计算分类

小升初数学简便计算分类数学是一门以逻辑性和智力活动为基础的学科,计算是数学学习的基础和核心部分。
在小升初的数学考试中,掌握简便计算方法不仅可以提高计算速度,还可以减少计算错误的可能性。
下面将介绍一些常见的数学计算分类和简便方法。
1.四则运算:加减乘除是数学学习的基本运算,小升初考试中会涉及到各种级别的计算。
在进行加法和减法时,可以利用分配律、结合律等性质将复杂的计算简化,同时可以利用进位和借位的方法进行有序的计算。
在进行乘法和除法时,可以利用乘法交换律、乘法分配律、除法的倒数等性质进行简化。
熟练掌握这些性质和方法,可以更加高效地进行四则运算。
2.几何运算:几何运算是小升初数学学习中的重要部分,涉及到图形的计算和判断。
在进行面积和周长的计算时,可以利用形状的特点将复杂的计算转化为简单的计算。
例如,计算矩形的面积可以利用长方形面积公式S=长×宽计算;计算三角形的面积可以利用底边和高的关系S=底×高/2计算。
此外,在进行图形的比较和判断时,可以利用直观的几何性质进行推理,如两条平行线切割等分线段。
3.分数运算:小数和分数是数学学习的常见形式,也是小升初考试中会遇到的问题。
在进行分数的加减乘除运算时,可以通过分子和分母的简化来简化计算,采用通分的方法进行运算。
在进行小数的加减乘除运算时,可以利用小数点移位和小数点保持不变的原则,将带小数的运算转化为不带小数的运算,再进行计算。
4.百分数运算:百分数是日常生活和数学学习中使用较多的一种数学形式,小升初考试中会涉及到百分数的计算和应用。
在进行百分数的加减乘除运算时,可以利用百分数的基本关系进行转化和计算。
例如,百分数的加法可以先将百分数转化为小数进行计算,然后再将小数转化为百分数;百分数的乘法可以将百分数转化为小数进行运算,然后再将小数转化为百分数。
掌握这些方法可以更加方便地进行百分数的计算。
5.代数运算:代数是数学学习中的重要内容,小升初考试中也会涉及到一些简单的代数计算。
小升初数学计算分类专题--简便运算

小升初数学计算分类专题--简便运算在小学计算题中,有许多新颖独特的题型和方法。
这些题型在升重点中学考试和进入中学分班考试中经常出现。
有些学生由于没有见过这种题型,常常得分很少或得零分。
其实,只要掌握一定的解题方法和规律,这些题型一点都不难。
下面是一些计算专题的介绍和解题技巧:计算专题1:小数分数运算律的运用这个专题主要是针对小数和分数的运算,包括加减乘除等。
掌握这些运算律可以帮助我们更快地解决相关的计算题。
在这个专题中,我们需要掌握一些例题,例如:例一:4.75+9.63+(8.25-1.37)例二:×79+790×例三:3×25+37.9×6例四:36×1.09+1.2×67.3例五:81.5×15.8+81.5×51.8+67.6×18.5通过这些例题的练,我们可以更好地掌握小数分数运算律的运用。
计算专题2:大数认识及运用在这个专题中,我们需要掌握对大数的认识和运用。
大数一般是指超过一定位数的数字,例如千位、万位、亿位等。
在解决这些计算题时,我们需要掌握一些技巧,例如竖式计算、进位借位等。
以下是一些例题:例一:1234+2341+3412+4123例二:2×23.4+11.1×57.6+6.54×28例三:(9+7)÷(4+5)例四:1993+1992×1994例五:有一串数1.4.9.16,25……它们是按照一定规律排列的,那么其中第2010个数与2011个数相差多少?通过这些例题的练,我们可以更好地掌握大数的认识和运用。
计算专题3:分数专题在这个专题中,我们需要掌握对分数的认识和运用。
分数是指一个数被另一个数除后所得到的结果,例如1/2、3/4等。
在解决这些计算题时,我们需要掌握一些技巧,例如通分、约分等。
以下是一些例题:例一:2/3+1/4例二:5/6-1/3例三:1/2×3/4例四:2/5÷1/4例五:3/4的三倍是多少?通过这些例题的练,我们可以更好地掌握分数的认识和运用。
小升初数学总复习分类专题复习及训练(含答案)

小升初数学总复习分类专题复习及训练(一)主要内容求一个数比另一个数多(少)百分之几、纳税问题学习目标1、使学生在现实情境中,理解并掌握“求一个数比另一个数多(少)百分之几”的基本思考方法,并能正确解决相关的实际问题。
2、使学生在探索“求一个数比另一个数多(少)百分之几”方法的过程中,进一步加深对百分数的理解,体会百分数与日常生活的密切联系,增强自主探索和合作交流的意识,提高分析问题和解决问题的能力。
3、使学生初步认识纳税和税率,理解和掌握应纳税额的计算方法。
4、初步培养学生的纳税意识,继续感知数学就在身边,提高知识的应用能力。
5、培养和解决简单的实际问题的能力,体会生活中处处有数学。
考点分析1、一个数比另一个数多(少)百分之几 = 一个数比另一个数多(少)的量÷另一个数。
2、应该缴纳的税款叫做应纳税额,应纳税额与各种收入的比率叫做税率,应纳税额 = 收入×税率典型例题例1、(解决“求一个数比另一个数多百分之几”的实际问题)向阳客车厂原计划生产客车5000辆,实际生产5500辆。
实际比计划多生产百分之几?分析与解:要求“实际比计划多生产百分之几”,就是求实际比计划多生产的辆数占计划产量的百分之几,把原计划产量看作单位“1”。
两者之间的关系可用线段图表示。
计划产量5000辆实际比计划多的实际产量5500辆解答:方法1:5500 – 5000 = 500(辆)……实际比计划多生产500辆500 ÷ 5000 = 0.1 = 10%……实际比计划多生产百分之几方法2:5500 ÷ 5000 = 110%……实际产量相当于原计划的110%110% - 100% = 10%……实际比计划多生产百分之几答:实际比计划多生产10%。
例2、(解决“求一个数比另一个数少百分之几”的实际问题)向阳客车厂原计划生产客车5000辆,实际生产5500辆。
计划比实际少生产百分之几?分析与解:要求“计划比实际少生产百分之几”,就是求计划比实际少生产的辆数占实际产量的百分之几,把实际产量看作单位“1”。
苏教版小升初数学易错专题分类汇总练习(学生版)

苏教版小升初易错专项分类汇总练习专项1:分数百分数的综合应用1、找单位“1”:在分数乘除应用里单位“1”很多同学往往不明白其意义。
可以简单的解释就是标准量或者参照对象。
如何去找单位在分数及百分数应用中都显得尤为重要。
一般找单位“1”看两点:一看关键词:常见关键词有:的(的后面跟着分率)的前面;“比,是,占,于,相当于”的后面;二看没有关键词,若应用中没有关键词可以:找应用中主语一般是第一句话,或者是盈亏降价或者升降问题,一般单位1是原价或者定价。
2、分数、百分数应用的基本应用的基本关系式:对应量÷单位“1”=对应分率; 单位“1”×对应分率=对应量; 对应量÷对应分率=单位“1”。
解题时,一般先找准单位“1”,再找准题中具体数量与分率的对应关系,运用相应的数量关系式求解。
(1)纳税问题应纳税额的计算方法:应纳税额=收入额或销售额×税率 (2)储蓄问题利息的计算公式:利息=本金×利率×时间注意:在计算利息时,利率和时间要对应,即若利率是年利率,则时间的单位是年;利率是月利率,则时间的单位是月。
(3)打折问题原价×折扣=现价; 现价÷原价=折扣; 现价÷折扣=原价。
1、李华乘汽车从A 到B 地,需要2天,他第一天走了全程的多72千米,第二天走的路程是第一天的31,A 、B 两地相距多少千米?2、一个正方形的边长增加20%,它的面积增加( )A.44%B.40% C .20%3、妈妈买一套桌椅共用去 300 元,椅子的费用比桌子少桌子要( )元, 椅子要( )元。
4、张师傅加工一批零件,已经加工了这批零件的25%,如果再加工36个零件,那么已加工的零件个数和未加工的零件个数的比是2:3,这批零件共有多少个?5、当水结成冰,体积增加了91,当冰融化成水时,体积减少了( )。
(填分数)6、把一个棱长是10厘米的正方体加工成一个最大的圆柱,这个圆柱的体积是( )立方厘米,占原正方体体积的( )%7、六(2)班学生人数比六(1)班少41,六(2)班学生人数与六(1)班学生人数的比 是( )。
小升初数学必考计算题型

小升初数学必考计算题型
小升初数学考试中,常见的计算题型包括以下几种:
1.四则运算:包括加法、减法、乘法和除法。
考察学生对基础运算规则的掌握和灵活运用能力。
2.组合运算:将多个运算符号或数字进行组合,要求学生按照正确的顺序进行计算。
例如:(7+3)×2-4÷2,要求学生按照括号内的运算优先级进行计算。
3.算式填空:给出一个不完整的算式,要求学生填写缺失的数字或符号。
例如:8+□=15,要求学生找出符合等式的缺失数字。
4.近似计算:给出一些较大或较复杂的算式,要求学生根据近似计算的原理,估算出结果的大小。
例如:685+327+49,要求学生快速估算出结果的范围。
5.时钟问题:涉及到时间的加减运算,要求学生计算时间间隔或计算经过了多少时间。
例如:9点15分再过40分钟是几点?。
小升初数学方法总结

裂和
2.换元:当题目中出现大量相同或相似的数时,考虑换元,好
写也好算。
3.通项归纳:计算规律的终极武器。
(三)计算题目类型
1.定义新运算:照猫画虎,or 看透本质。
-2-
2.比较与估算:化小数,通分法,比倒数,设标准,糖水法, 放缩法等等。
二、计算专题综合性题目
【例 1】计算: 1 4.3 3 3 3.6 6.7 5 1.23 13 2 5 0.09
- 13 -
【例 3】一个两位数,数字和是质数。而且,这个两位数分别乘以 3,5,7 之后,得到的数的数字和都仍为质数。 满足条件的两位 数为 _____。
【例 4】对四位数 abcd ,若存在质数 p 和正整数 k,使 a×b×c ×d=pk,且 a+b+c+d=pp-5,求这样的四位数的最小值,并说明理由。
3
5
18
3
解:原式= 1 4.3 18 18 6.7 18 123 3 5 9
3 5 5
5 100 41 100
= 1 18 4.3 1 6.7 9 5 9
35
100 100
=12+5
=17
【巩固练习】要使等式15.6
2
2 3
1.625
□
1 1 10
4 15
【巩固练习】 有一串数:5,8,13,21,34,55,89,…,其中 第一个数是 5,第二个数是 8,从第三个数起,每个数 恰好是前 两个数的和。那么在这串数中,第 2011 个数被 3 除后所得余数 是几?
【例 7】有一个整数,用它去除 70,110,160 所得到的 3 个余数 之和是 50,那么这个整数是______。
小升初数学必考题型汇总

2024小升初数学必考题型汇总2024小升初数学必考题型汇总一、计算1、数的加减法 (1)整数和小数的加减法 (2)分数和百分数的加减法2、数的乘法与除法 (1)整数的乘法与除法 (2)分数的乘法与除法 (3)小数和百分数的乘法与除法3、方程 (1)一元一次方程 (2)二元一次方程 (3)三元一次方程4、简算与巧算 (1)加减法简算与巧算 (2)乘除法简算与巧算 (3)混合运算简算与巧算二、几何1、平面图形 (1)直线、射线、线段 (2)角的度量与计算 (3)三角形、四边形、多边形2、立体图形 (1)长方体、正方体、圆柱、圆锥 (2)球、棱柱、四面体三、统计与概率1、统计初步知识 (1)数据的收集与整理 (2)统计表与统计图2、概率初步知识 (1)事件的发生与可能性 (2)事件的概率与概率计算四、应用题1、行程问题 (1)一般行程问题 (2)多次相遇问题 (3)变速行程问题2、工程问题 (1)一般工程问题 (2)周期工程问题 (3)分工合作工程问题3、比例问题 (1)一般比例问题 (2)百分数比例问题 (3)浓度问题4、分数问题 (1)一般分数问题 (2)分数工程问题 (3)分数行程问题五、拓展题1、多位数问题2、逻辑推理问题3、数独问题2024小升初数学必考题型分类汇总2024小升初数学必考题型分类汇总一、计算题1、有括号的先算小括号里面的,没有括号的先算乘除,再算加减。
2、递等式计算题,不能急于求成,要按照先乘除,后加减,遇到有括号的要先算括号里面的运算顺序进行计算。
3、混合运算题,不能掉以轻心,要认真仔细,先算乘除,后加减,遇到括号要先计算括号里面的运算。
二、填空题1、填空题一定要仔细审题,比较大小题,大于号和小于号一定填正确。
2、填空题答案不唯一,要认真审题,填写正确的答案。
3、填空题涉及到的知识点较多,需要加强练习,积累经验。
三、选择题1、选择题不要盲目选择,要仔细分析题目,选择正确的答案。
2020年小升初计算专题

小升初计算专题(一)分数、小数四则混合运算分数、小数四则混合运算主要考察四则混合运算的意义及运算顺序。
一般需要按照四则混合运算法则,一步一步进行脱式计算;运算比较复杂时,往往需要我们算一步检查一步,做到一步一回头,步步无差错。
审题及运算的过程中需要密切注意是否可以使用简便算法。
四则混合运算的顺序:先算乘除,后算加减,有括号的需要先计算括号里边的。
例1 7312[5 4.5(20%)]2043÷-⨯+ 例2 143[(0.6)]50%4710-⨯+÷例3 简便运算: ①5111749114⨯+⨯ ② 0.25×12.5÷321 ③715827÷例4 计算:86.80.32 4.282532%25⨯+⨯-÷- 例5 计算:253749517191334455÷+÷+÷例6 计算:45841.3751050.91919⨯+⨯ 例7 计算:325323455555654.3365256⨯+÷+⨯例8 5312536114.44448371113725÷+÷+⨯小升初计算专题(八)灵活分组(讲义)例1 2012+2011-2010-2009+2008+2007-2006-2005+…+4+3-2-1例211111111 99989796959423232223 -+-+-+-…+11例37777 122331111 11111111⎛⎫⎛⎫⎛⎫⎛⎫+++⨯++⨯+++⨯⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭例411111111 11111111 2233991010--⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+-+-⨯⨯++⎪⎪⎪⎪ ⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭例5 计算:1121231249 1233444505050⎛⎫⎛⎫⎛⎫++++++++++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭例6计算:111111 199******** 11200919982009111998⎛⎫⎛⎫⎛⎫⨯-+⨯--⨯++⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭第六讲字母代换法对于某些计算问题,各部分的结构比较固定,相同数字或部分重复出现,我们可以用字母来整体打包代换,从而达到简算的目的,这种方法叫做字母代换法。
小升初20类数学题大全汇总

小升初20类数学题大全汇总第一类:四则运算这一类题目主要包括加法、减法、乘法和除法,考察学生的基本运算能力和运算规则的掌握。
第二类:约数和倍数此类题目要求学生找出一个数的所有约数或倍数,锻炼学生分析和推理的能力。
第三类:分数运算这些题目要求学生进行分数的加减乘除或比较大小,考察学生对分数运算规则的掌握。
第四类:小数运算这一类题目要求学生进行小数加减乘除或转化为分数,检验学生的小数计算能力。
第五类:平方与立方此类题目要求学生计算数字的平方或立方,培养学生的算术思维能力。
第六类:比例与百分数这些题目要求学生进行比例和百分数的计算,考验学生的应用能力和推理能力。
第七类:面积和周长此类题目要求学生计算各种形状的图形的面积或周长,培养学生的几何计算能力。
第八类:运算规律这一类题目要求学生寻找规律并进行推理,锻炼学生的逻辑思维能力。
第九类:方程与代数式此类题目要求学生解一元一次方程或进行代数式的计算,考察学生的代数运算能力。
第十类:图形的转化这些题目要求学生对图形进行旋转、翻转或平移变换,培养学生的几何变换能力。
第十一类:尺规作图此类题目要求学生使用尺规作图工具,按照给定的条件进行几何图形的作图。
第十二类:集合这一类题目要求学生判断元素是否属于某个集合或进行集合的运算。
第十三类:时间和日期此类题目主要考察学生对时间和日期的读写和计算能力。
第十四类:速度与距离这些题目要求学生进行速度和距离的计算,锻炼学生的实际应用能力。
第十五类:数字的进制此类题目要求学生进行不同进制的运算或转换,考察学生的进制转换能力。
第十六类:平均数与比例均分这一类题目要求学生计算一组数据的平均数或进行比例分配运算。
第十七类:简单方程组此类题目要求学生解简单的二元一次方程组,培养学生的解方程能力。
第十八类:数字与字母的关系这些题目要求学生根据数字与字母的规律推理出正确的结果。
第十九类:奇数与偶数此类题目要求学生判断一个数是奇数还是偶数,锻炼学生的逻辑思维能力。
小学数学-有答案-北师大版小升初数学专项分类训练:几何计算
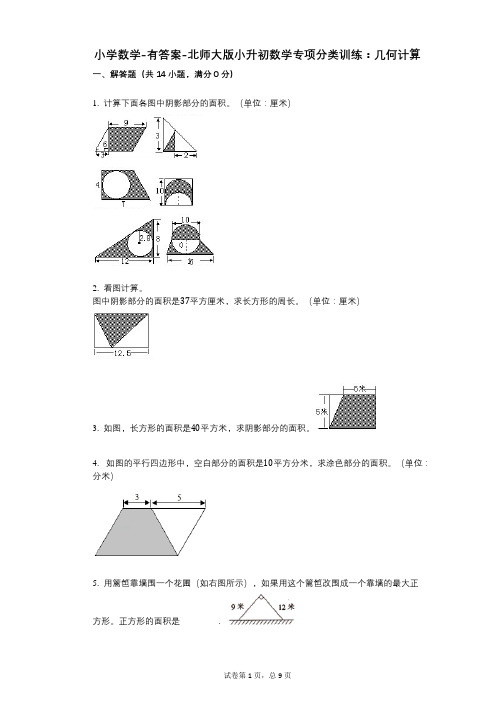
小学数学-有答案-北师大版小升初数学专项分类训练:几何计算一、解答题(共14小题,满分0分)1. 计算下面各图中阴影部分的面积。
(单位:厘米)2. 看图计算。
图中阴影部分的面积是37平方厘米,求长方形的周长。
(单位:厘米)3. 如图,长方形的面积是40平方米,求阴影部分的面积。
4. 如图的平行四边形中,空白部分的面积是10平方分米,求涂色部分的面积。
(单位:分米)5. 用篱笆靠墙围一个花圃(如右图所示),如果用这个篱笆改围成一个靠墙的最大正方形。
正方形的面积是________.6. 如图是一个长方体纸盒的表面展开图,这个纸盒的用料面积至少是多少平方厘米?(单位:厘米)7. 如图,计算图形的周长和面积。
(单位:厘米)8. 如图,求图形的面积。
(单位:厘米)9. 如图,长方形ABCD的面积是12平方分米,那么圆的面积是________平方分米。
10. 如图,半圆中三角形ABO的面积(S1)是11平方厘米,O为圆心,半径长5厘米,求阴影部分的面积。
11. 如图是一块土地的形状,可以分割成一个平行四边形和一个三角形。
这块土地的面积是多少公顷。
12. 求右图直圆锥的体积。
(单位:厘米)13. 如图:ACEG是梯形、BDFG是正方形,GE=30厘米,GB=24厘米,AC=39厘米。
求梯形ACEG的面积。
参考答案与试题解析小学数学-有答案-北师大版小升初数学专项分类训练:几何计算一、解答题(共14小题,满分0分)1.【答案】阴影部分的面积为45平方厘米。
(2)3×3÷2−2×2÷2−3×1÷2=4.5−2−1.5=1(平方厘米)答:阴影部分的面积为1平方厘米。
(3)(7+4)×4÷2−3.14×(4÷2)2=22−12.56=9.44(平方厘米)答:阴影部分的面积为9.44平方厘米。
(4)10×10÷2=100÷2=50(平方厘米)答:阴影部分的面积为50平方厘米。
小升初数学分类卷

1、小明有5根铅笔,小华给了小明3根后,两人的铅笔数量相同。
小华原来有多少根铅笔?
A. 8根
B. 10根
C. 11根
D. 13根
(答案)C
2、一个正方形的周长是20厘米,那么它的面积是多少平方厘米?
A. 16
B. 20
C. 25
D. 400
(答案)C
3、下列哪个数既是2的倍数又是3的倍数?
A. 15
B. 18
C. 21
D. 25
(答案)B
4、若一个数的五分之一是6,那么这个数是多少?
A. 2
B. 5
C. 25
D. 30
(答案)D
5、一个直角三角形的一个锐角是45度,那么另一个锐角是多少度?
A. 30度
B. 45度
C. 60度
D. 90度
(答案)B
6、小红买了3件同样的衣服和2条同样的裤子,一共花了300元。
如果一件衣服的价格是一条裤子价格的1.5倍,那么一条裤子的价格是多少元?
A. 50元
B. 60元
C. 75元
D. 100元
(答案)B
7、一个数的三倍减去5等于这个数的两倍加上7,求这个数。
A. 6
B. 10
C. 12
D. 18
(答案)C
8、一个长方体的长、宽、高分别是3厘米、4厘米、5厘米,它的体积是多少立方厘米?
A. 12
B. 30
C. 60
D. 120
(答案)C。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计算综合计算专题1小数分数运算律的运用:
计算专题2大数认识及运用
计算专题3分数专题
计算专题4裂项求和
计算专题5计算综合
计算专题6 换元法
计算专题7 定义新运算
计算专题8 解方程
计算专题9 等差数列
计算专题10 加法原理、乘法原理
计算专题1小数分数运算律的运用:
【例精选】
例一: ++()例二:
11 3333877979066661
24
⨯+⨯
例三:
322
32537.96
555
⨯+⨯例四:⨯+⨯
例五:⨯⨯⨯【练习】
1、
89
2(3.271)
1717
+- 2、
717
13(43)0.75
13413
-+-
3. ⨯+
3
9769.75
4
⨯- 4、 999999×222222+333333×333334
5、⨯+⨯
6、139
1371
137 138138⨯+⨯
7、⨯⨯ 8、⨯⨯⨯计算专题2大数认识及运用【例精讲】
例一:1234+2341+3412+4123 例二:
4
223.411.157.6 6.5428 5
⨯+⨯+⨯
例三:
199319941
199319921994
⨯-
+⨯
例四:(
22
97
79
+)÷(
55
79
+)
例五:有一串数1, 4, 9, 16,25……它们是按照一定规律排列的,那么其中第2010个数与2011个数相差多少
例六: 2010××
【综合练习】
1、 23456+34562+45623+56234+62345
2、198819891987 198819891
+⨯
⨯-
3、⨯76+⨯66
4、20122-20112
5、999⨯274+6274
6、(836
1
9711
++)÷(
354
1179
++)
××
计算专题3分数专题【例精讲】
例一:44
37
45
⨯ 27⨯
15
26
例二:
11
73
158
⨯
11
64
179
⨯
例三:13
2741
55
⨯+⨯例四:
515256
6139131813
⨯+⨯+⨯
例五:
1
16641
20
÷
2010
20102010
2011
÷
【综合练习】
1、 73⨯74
75
2、
2008
2010
2009
⨯ 3、
11
57
76
⨯
4、
1314
4151
3445
⨯+⨯ 5、
13
3927
44
⨯+⨯ 6、
1451
179179
⨯+⨯
7、
238
238238
239
÷ 8、
731711
3
1581516152
⨯+⨯+⨯
计算专题4裂项求和【例精讲】
例一:
1111
.......
12233499100
++++
⨯⨯⨯⨯
例二:
1111
.......
2446684850
++++
⨯⨯⨯⨯
例三:
179111315
1
31220304056
-+-+-例四:
1111111
248163264128
++++++
【综合练习】
1、
1111
........
1011111212134950
++++
⨯⨯⨯⨯
2、
111111
2612203042
+++++
3、11111
42870130208
++++ 4、
19111315
1
420304256
-+-+
5、20102010201020102010
1223344556
++++
⨯⨯⨯⨯⨯
6、
22222
392781243
++++
计算专题5计算综合
【例精讲】
例一: 1111
1......
1212312341234 (4950)
+
++++++++++++++ 例⨯ 例三: 12324671421
135261072135
⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯
例四:201012010220103
111...1111222...2222333...3333=÷个个个
例五: 从2000到6999这5000个数中数字只和能被5整除的数一共有多少个 例六:100+99—98—97+96+95—94—93……+4+3—2—1 例七:⎪⎭
⎫ ⎝⎛⨯⎪⎭⎫ ⎝
⎛+⋯⋯⎪⎭
⎫ ⎝
⎛⨯⎪⎭⎫ ⎝
⎛+⨯⎪⎭⎫ ⎝
⎛⨯⎪⎭⎫ ⎝
⎛+991-1991131-131121-1211 【综合练习】 1、1111111111
++
+++++++361015212836455055 2、76666666666666
201062011 个个⋯⋯⨯⋯⋯ 3、
1612886443224
201612108654⨯⨯+⨯⨯+⨯⨯⨯⨯+⨯⨯+⨯⨯ 4、 2
201242012222222444444个个⋯⋯⋯⋯ 62012666666个⋯⋯÷ 5、(1+3+5+7+…+1999)-(2+4+6+8+…+1998) 6、⎪⎭
⎫ ⎝⎛⨯⋯⋯⎪⎭
⎫ ⎝
⎛⨯⎪⎭⎫ ⎝
⎛⨯⎪⎭⎫ ⎝
⎛⨯⎪⎭⎫ ⎝
⎛
1001-
151-141-131-121-1 7、(13 +23 )+(14 +24 +34 )+(15 +25 +35 +45 )+…+(1100 +2100 +3100 +4100 +…
+99
100
) 计算专题6 换元法
(1++)×(++)-(1+++)×(+) (1++)×(++)-(1+++)×(+)
(1+21+31+41)×(21+31+41+51)-(1+21+31+41+51)×(21+31+41)
(111+211+311+411)×(211+311+411+511)-(111+211+311+411+511)×(211+311+411) (135531+357579+975753)×(357579+975753+531135)-(135531+357579+975753+531135)×(357579+975753)
计算专题7 定义新运算
1.规定a ☉b = ,则2☉(5☉3)之值为 .
2.如果1※4=1234,2※3=234,7※2=78,那么4※5= .
3.[A]表示自然数A的约数的个数.例如,4有1,2,4三个约数,可以表示成
[4]=3.计算: [120] = .
4.规定新运算a※b=3a-2b.若x※(4※1)=7,则x= .
5.两个整数a和b,a除以b的余数记为a☆b.例如,13☆5=3,5☆13=5,12☆4=0.
根据这样定义的运算,(26☆9) ☆4= .
6.规定:6※2=6+66=72,2※3=2+22+222=246,
1※4=1+11+111+1111=※5= .
7.规定:符号“△”为选择两数中较大数,“☉”为选择两数中较小数.例
如:3△5=5,3☉5=3.那么,[(7☉3)△5]×[5☉(3△7)]= .
计算专题8 解方程
计算专题9 等差数列
需要牢记的公式
(1)末项=
首项=
项数=
(2)数列和=
【典型例】
例1 已知等差数列5,8,11,14,17,…,它的第25项是什么第42项呢例2 已知等差数列7,12,17,…,122,问这个等差数列共有多少项
例3 某礼堂里共有21排座位,从第一排座位开始,以后每一排比前一排多4个座位,最后一排有100个座位,问这个礼堂一共有多少个座位
例4 (1)1+3+5+7+…+2007
(2)2007-3-6-9-…-51-54
例5 (2+4+6+...+100)-(1+3+5+ (99)
例6 1001个队员参加数学奥林匹克竞赛,每两个队员握一次手,他们握了多少次手
计算专题10 加法原理、乘法原理
例1 用1角、2角和5角的三种人民币(每种的张数没有限制)组成1元钱,有多少种方法
例2 将3封信投到4个邮筒中,一个邮筒最多投一封信,有种不同的方法。
例3 一把钥匙只能开一把锁,现在有10把钥匙和10把锁全部都搞乱了,最多要试验多少次才能全部配好锁和相应的钥匙
例4 某人到食堂去买饭菜,食堂里有4种荤菜,3种蔬菜,2种汤。
他要各买一样,共有多少种不同的买法
例5 从5幅国画,3幅油画,2幅水彩画中选取两幅不同类型的画布置教室,问有几种不同的选法
例6 有两个相同的正方体,每个正方体的6个面上分别标有数字1,2,3,4,5,6。
将两个正方体放在桌面上,向上的一面数字之和为偶数的有多少种情形。
