高中物理竞赛班《微积分第三讲微积分在物理上的应用》
(完整word版)微积分在物理学上的应用

微积分在物理学上的应用1 引言微积分是数学的一个基本学科,内容包括微分学,积分学,极限及其应用,其中微分学包括导数的运算,因此使速度,加速度等物理元素可以使用一套通用的符号来进行讨论。
而在大学物理中,使用微积分去解决问题是及其普遍的.对于大学物理问题,可是使其化整为零,将其分成许多在较小的时间或空间里的局部问题来进行分析.只要这些局部问题分的足够小,足以使用简单,可研究的方法来解决,再把这些局部问题的结果整合起来啊,就可以得到问题的结果。
而这种将问题无限的分割下去,局部问题无限的小下去的方法,即称为微分,而把这些无限个微分元中的结果进行求和的方法,即是积分。
这种解决物理问题的思想和方法即是微积分的思想和方法。
2 微积分的基本概念及微分的物理含义微积分是一种数学思想,其建立在函数,实数和极限的基础上,其主要探讨的就是连续变量。
在运用微积分去解决物理问题时,可以将我们所需要得出的结果看成是一个整体,再将这个整体先微分,即将其分成足够小的个体,我们可以将这个个体的变量看成衡量,得出个体结果后,再将其积分,即把个体的结果累积起来进行求和.例如,在我们研究匀变速直线运动时,我们就可以在其运动过程中选取一个微小的时间dt,而这一时间内的位移为dt,在每一段时间内速度的变化量非常小,可以近似忽略,那么我们就可以将这段时间内的运动近似看成匀速直线运动,再把每段时间内的位移相加,无限求和,就可以得出总的位移。
在物理学中,每个物理公式都是某些物理现象和规律的数学表示,因此,我们在使用这些公式时,面对物理量和公式的微分形式我们不能仅仅从数学方面去考虑,更要从物理含义上去考虑.在我们使用微分符号时,不能只从数学角度去理解其为无限小,更要结合具体的物理量和角度去判断他的正确含义。
例:如图所示,一通有交流电流i=的长直导线旁有一共面的单匝矩形线圈ABCD,试求线圈中的感应电动势大小。
解:设在某个时刻,长直导线电流产生的磁场为B=在图中做一个微元面dS,dS=ldx,则该面元上的磁场可以近似于均匀磁场,微元面dS上的磁通量为d线圈围成的面上通过的磁通量为线圈中的感应电动势为在这个例题中,微元面dS的磁通量与线圈的感应电动势都有,但他们的物理含义却是不一样的,前者的表示微元面dS上的磁通量,是一个微小量,而后者的表示的是微笑时间内的磁通量变化量,是一个微小变化量。
物理竞赛第三讲(定积分在物理学 中的应用)

()0b af x dx =⎰物理竞赛辅导第二讲(定积分在物理中的应用)1.定积分以上两个例子表明,许多物理问题中需要计算像(A.47)和(A.49)式中给出的那类极限值。
概括起来说,就是要解决如下的数学问题:给定一个函数f(x)在区间[a,b]上连续,用一系列分点a=1x <2x <3x <........<1+n x =b,将区间[a,b]等分为n 个子区间,设每小段的大小为△x ,求n →∞、△x →0时x x f dx x f i i x n b a ∆=∑⎰=→∆∞→10)(lim )( 为函数)(x f 在区间[a,b]的定积分式中f(x)、dx x f )(和x 分别称为被积函数、被积式和积分变量。
⎰为积分号,a 和b 分别称为积分下限和积分上限,[a,b]称为积分区间。
2.定积分的几何意义 :由函数曲线、自变量坐标轴以及积分上下限所决定的曲边梯形的面积。
对于⎰ba dx x f )(当0)(>x f 时,⎰b a dx x f )(是曲边梯形的面积当()0()f x a x b ≤≤≤时,是曲边梯形的面积的负值定积分可视为对连续量求和两个规定:1、 当a b =时,规定2、 当a b >时,规定()()b a a b f x dx f x dx =-⎰⎰这个等式不论a ,b 谁大谁小均成立⎰ba dx x f )(,)(dx x f ba ⎰牛顿—莱布尼茨公式设)(x F 是函数)(x f 在区间[a,b]的一个原函数,即)()('x f X F =,则)()()()(a F b F X F dx x f ba ba -==⎰ 3.求解两曲线围成的平面图形的面积的一般步骤:(1)作出示意图;(弄清相对位置关系)(2)求交点坐标;(确定积分的上限,下限)(3)确定积分变量及被积函数;(4)列式求解定积分在物理学中的应用问题1:变速直线运动的路程匀速直线运动:匀加速直线运动:任意直线运动:设做变速直线运动的物体运动的速度v=v(t)≥0,则此物体在时间区间[a, b]内运动的距离s 为例1:一辆汽车的速度在一段时间内如图所示,求汽车在这1min 行驶的路程例2:一点在直线上从时刻t =0(s)开始以速度v =t2-4t +3(m/s)运动,求(1) t =4 s 时的位移;(2) t =4 s 时的路程.问题 2:变力沿直线所作的功恒力做功:W=FS物体在变力F(x)的作用下做直线运动,并且物体沿着与F(x)相同的方向从x=a 点移动到x= b 点,则变力F(x) 所做的功为:()b a W F x dx =⎰例1:如图在弹性范围内,将一弹簧从平衡位置拉到距离平衡位置Lm 处,求克服弹力所作的功。
浅谈微积分的认识在物理教学中的应用

浅谈微积分的认识在物理教学中的应用
微积分是数学中的一个重要分支,也是物理学中不可或缺的工具。
在物理教学中,微积分的认识十分必要,以下是一些例子:
1. 运动学分析:微积分中的导数和积分可以应用到运动学分析中,以求得速度、加速度、位置等关键信息。
通过微积分的分析,可以帮助学生深入理解物体的运动规律,并进行更加精确的运动预测和控制。
2. 力学分析:运用微积分的概念,可以对物理学中的力学问题进行分析,如牛顿定律,重力,弹性力等。
通过微积分的工具和方法,可以更加深入地理解和应用物理学中的法则和理论。
3. 光学问题:微积分中的几何和微积分学概念可以应用到光学问题中,如光的传播原理,反射和折射现象等。
通过微积分的知识和工具,可以帮助学生深入理解光学的基础原理,并进行更加精确的预测和分析。
4. 热力学分析:热力学分析中的微积分概念,如微分和积分可以应用到物理学中的热力学分析中,如热容,温度,热传导等。
通过微积分的分析,可以更加深入地了解热力学的基本规律和特性。
总之,微积分的认识在物理教学中是不可或缺的,它可以帮助学生更好地理解和应用物理学中的基础概念和理论,以便更加轻松地掌握物理学的知识和应用。
微积分基础初步及其在中学物理竞赛中的应用

A
A
几何公理:两点之间直线距离最短
∫B ds 的极小值为直线 AB . A
光在均匀介质中沿直线传播
ii. 用费马原理证明折射定律
证: 通过空间两点A、B可以作无数个
平面,其中必有一个平面垂直于两 种介质 n1和n2 之间的界面,OO’是 它们的交线。通过A点折射到B点的 入射线交界面于C点,求C点的位置。
M0
L
N
αϕ
o
AB x
tan α = lim tan ϕ = lim Δy = lim f ( x0 + x) − f ( x0 )
Δx→0
Δ x Δx → 0
Δx→0
x − x0
曲线 y = f (x)在点M0处的纵坐标 y 的增量 Δy 与横坐标
x的增量Δx之比,当Δx → 0时的极限即为曲线在M0点处
即: f ′′(x0 ) = [f ′(x)]′ x=x0
依次类推,可得三阶、四阶导数等.
导数的几何意义与物理意义
z导数的几何意义: 函数 y = f (x) 在点x0处的导数等于函数所
表示的曲线L在相应点(x0,y0)处的切线斜率.
y
y = f (x)
M T
M0
L
N
αϕ
o
AB x
z导数的物理意义: 变速直线运动的速率
(a) C点必在OO'上
如果有另一点C'位于线外,则对应于C’,必可在OO’线上找 到它的垂足C''
因为 AC' > AC' ' C' B > C'' B AC'+C' B > AC''+C'' B 而非极小值.
微积分在物理学上的应用

1 引言微积分是数学的一个基本学科,内容包括微分学,积分学,极限及其应用,其中微分学包括导数的运算,因此使速度,加速度等物理元素可以使用一套通用的符号来进行讨论。
而在大学物理中,使用微积分去解决问题是及其普遍的。
对于大学物理问题,可是使其化整为零,将其分成许多在较小的时间或空间里的局部问题来进行分析。
只要这些局部问题分的足够小,足以使用简单,可研究的方法来解决,再把这些局部问题的结果整合起来啊,就可以得到问题的结果。
而这种将问题无限的分割下去,局部问题无限的小下去的方法,即称为微分,而把这些无限个微分元中的结果进行求和的方法,即是积分。
这种解决物理问题的思想和方法即是微积分的思想和方法。
2 微积分的基本概念及微分的物理含义微积分是一种数学思想,其建立在函数,实数和极限的基础上,其主要探讨的就是连续变量。
在运用微积分去解决物理问题时,可以将我们所需要得出的结果看成是一个整体,再将这个整体先微分,即将其分成足够小的个体,我们可以将这个个体的变量看成衡量,得出个体结果后,再将其积分,即把个体的结果累积起来进行求和。
例如,在我们研究匀变速直线运动时,我们就可以在其运动过程中选取一个微小的时间dt,而这一时间内的位移为dt,在每一段时间内速度的变化量非常小,可以近似忽略,那么我们就可以将这段时间内的运动近似看成匀速直线运动,再把每段时间内的位移相加,无限求和,就可以得出总的位移。
在物理学中,每个物理公式都是某些物理现象和规律的数学表示,因此,我们在使用这些公式时,面对物理量和公式的微分形式我们不能仅仅从数学方面去考虑,更要从物理含义上去考虑。
在我们使用微分符号时,不能只从数学角度去理解其为无限小,更要结合具体的物理量和角度去判断他的正确含义。
例:如图所示,一通有交流电流i=的长直导线旁有一共面的单匝矩形线圈ABCD,试求线圈中的感应电动势大小。
解:设在某个时刻,长直导线电流产生的磁场为B=在图中做一个微元面dS,dS=ldx,则该面元上的磁场可以近似于均匀磁场,微元面dS上的磁通量为d线圈围成的面上通过的磁通量为线圈中的感应电动势为在这个例题中,微元面dS的磁通量与线圈的感应电动势都有,但他们的物理含义却是不一样的,前者的表示微元面 dS上的磁通量,是一个微小量,而后者的表示的是微笑时间内的磁通量变化量,是一个微小变化量。
微积分在物理中的应用举例

微积分在物理中的应用举例微积分是一门研究变化的数学学科,它在物理学中有着广泛的应用。
物理学家们利用微积分的工具和概念描述自然现象、建立模型、解决问题。
下面将通过几个具体的例子来说明微积分在物理学中的应用。
1. 运动学中的速度与加速度在物理学中,我们经常需要描述物体的运动状态,包括速度和加速度。
速度是位置随时间的变化率,而加速度则是速度随时间的变化率。
这些概念可以通过微积分来表达和计算。
例如,一个物体的位移可以表示为速度关于时间的积分,而速度则可以表示为加速度关于时间的积分。
微积分使得我们能够准确描述和分析物体的运动规律。
2. 牛顿第二定律牛顿第二定律是描述力和物体运动之间关系的基本定律,它可以用微积分来推导和解释。
根据牛顿第二定律,物体的加速度与作用在物体上的合力成正比,通过微积分可以将这个关系表达为一个微分方程。
通过对微分方程的求解,我们可以得到物体在不同情况下的运动方程,从而预测物体的运动轨迹和速度变化。
3. 电场力和电势能在电动力学中,微积分也广泛应用于描述电场力和电势能。
电场力是描述电荷之间相互作用的力,而电势能则是电场力做功的能量。
微积分可以帮助我们计算电场力和电势能之间的关系,以及在不同电场分布下的电势能变化。
这种分析对于研究电路中电荷流动、电场能量转换等现象非常重要。
总结微积分在物理学中的应用是十分广泛的,它为物理学提供了强大的工具和方法。
通过微积分,我们可以更深入地理解自然现象,推导和解释物理原理,建立物理模型并做出预测。
以上是仅仅是几个微积分在物理学中应用的例子,实际上微积分在物理学中的应用远不止这些,它在整个物理学研究中都扮演着重要的角色。
微积分在物理学中的应用

微积分在物理学中的应用微积分是数学的一个重要分支,它研究的是变化、运动以及量的变化。
它的基本思想在物理学中具有广泛的应用,涵盖了从简单的运动到复杂的力学系统、热力学、电磁学甚至量子力学等多个领域。
本文将探讨微积分在物理学中的一些关键应用,阐明其理论基础和实际重要性。
一、微积分的基本概念在讨论微积分在物理学中的应用之前,有必要简要理解微积分的基本概念。
微积分主要由两部分组成:微分和积分。
微分主要用于研究函数在某一特定点的变化率,而积分则用于计算函数在一个区间内的累积量。
这两者通过微积分基本定理紧密相连,前者为后者提供了定义和理论基础。
二、运动学中的应用运动学是物理学的一个分支,专注于物体的运动描述。
在运动学中,微积分被用于处理位置、速度和加速度之间的关系。
位置与速度假设一个物体在直线上的位置可以用时间t的函数x(t)来表示。
通过对位置函数进行微分,可以得到物体的瞬时速度,即:反之,如果已知物体的速度v(t),我们可以对其进行积分以求得位置x(t):[ x(t) = v(t) dt ]加速度与速度类似地,加速度是速度随时间变化的速率。
其表达为:[ a(t) = ]同样,若已知加速度a(t),则可以通过积分求得速度:[ v(t) = a(t) dt ]这些公式使得我们能够通过已知的条件推导出另一个量,极大地方便了运动分析。
三、力学中的应用力学是研究物质及其运动规律的一门科学,其中涉及到很多与微积分密切相关的概念。
牛顿第二定律牛顿第二定律指出,一个物体所受的总外力等于其质量与加速度的乘积。
数学表达为:[ F = m a ]考虑到加速度a可以表示为速度对时间的导数,我们有:因此,力F也可以被视为对动量p = mv(即质量与速度的乘积)时间变化率的描述:[ F = ]这表明,在系统分析中,通过微分我们能理解物体动量变化与受力之间深刻而又紧密的关系。
动能定理此外,微积分也被广泛应用于动能定理中。
动能是与物体运动状态相关的一种能量形式,其表达式为:[ KE = mv^2 ]当受力做功W时,系统的动能改变可以表示为:[ W = KE_f - KE_i = _{x_i}^{x_f} F dx ]此处,功W是通过移位过程中的力F与位移x之间关系而得出的,这展示了微积分在分析能量转化过程中的重要性。
(完整word版)微积分在物理竞赛中的应用
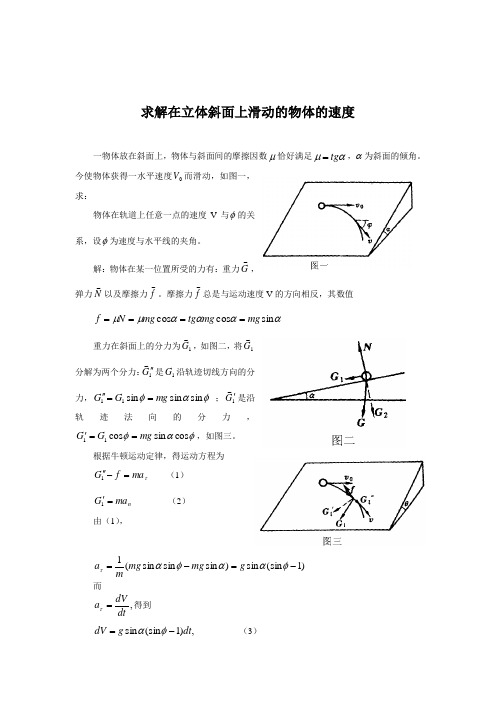
VdV (L1 L2 ) 2x g,
dx
L1 L2
V
VdV
x (L1 L2 ) 2x gdx
0
0 L1 L2
V
2g L1 L2
(L1 L2 )x x2 .
令 x L2 , 可以求得链条滑离钉子时的速度大小
V 2L1L2 g L1 L2
再由V dx , 得到 dt
dx dt
。
小球 A 相对地的加速度
aA
a
A
aB
,取如图二所示的坐标系,
则有
a Ax
aA
cos
aB
sin 2 2(1 sin 2 )
g,
a Ay
aA sin
2sin 2 (1 sin 2 )
g.
旋转液体的液面
以等角速度 ω 旋转的液体,液面的形状如何求得? 解答:
假设它的剖面是一条曲线,Y 轴是转轴,旋转面以 Y 轴为对称轴,此时在
y
m k
(V0
sin 0
mg k
)(1
kt
em
)
mg k
t.
由(3)(4)两式消去 t,得到有阻力时的轨道方程
(4)
y
(tg 0
mg kV0 cos0
)x
m2g k2
ln(1
mV0
k c os 0
)x
m2g k2
ln(1
k mV0 cos
x).
显然由于空气阻力的作用,抛体的轨道不再是简单的抛物线了,实际轨道将比理想轨
2g L1 L2
(L1 L2 )x x2
x
dx
t
0 (L1 L2)x x 2 0
积分,得到
微积分在物理学上的应用

微积分在物理学上的应用1 引言微积分就是数学的一个基本学科,内容包括微分学,积分学,极限及其应用,其中微分学包括导数的运算,因此使速度,加速度等物理元素可以使用一套通用的符号来进行讨论。
而在大学物理中,使用微积分去解决问题就是及其普遍的。
对于大学物理问题,可就是使其化整为零,将其分成许多在较小的时间或空间里的局部问题来进行分析。
只要这些局部问题分的足够小,足以使用简单,可研究的方法来解决,再把这些局部问题的结果整合起来啊,就可以得到问题的结果。
而这种将问题无限的分割下去,局部问题无限的小下去的方法,即称为微分,而把这些无限个微分元中的结果进行求与的方法,即就是积分。
这种解决物理问题的思想与方法即就是微积分的思想与方法。
2 微积分的基本概念及微分的物理含义微积分就是一种数学思想,其建立在函数,实数与极限的基础上,其主要探讨的就就是连续变量。
在运用微积分去解决物理问题时,可以将我们所需要得出的结果瞧成就是一个整体,再将这个整体先微分,即将其分成足够小的个体,我们可以将这个个体的变量瞧成衡量,得出个体结果后,再将其积分,即把个体的结果累积起来进行求与。
例如,在我们研究匀变速直线运动时,我们就可以在其运动过程中选取一个微小的时间dt,而这一时间内的位移为dt,在每一段时间内速度的变化量非常小,可以近似忽略,那么我们就可以将这段时间内的运动近似瞧成匀速直线运动,再把每段时间内的位移相加,无限求与,就可以得出总的位移。
在物理学中,每个物理公式都就是某些物理现象与规律的数学表示,因此,我们在使用这些公式时,面对物理量与公式的微分形式我们不能仅仅从数学方面去考虑,更要从物理含义上去考虑。
在我们使用微分符号时,不能只从数学角度去理解其为无限小,更要结合具体的物理量与角度去判断她的正确含义。
例:如图所示,一通有交流电流i=的长直导线旁有一共面的单匝矩形线圈ABCD,试求线圈中的感应电动势大小。
解:设在某个时刻,长直导线电流产生的磁场为B=在图中做一个微元面dS,dS=ldx,则该面元上的磁场可以近似于均匀磁场,微元面dS上的磁通量为d线圈围成的面上通过的磁通量为线圈中的感应电动势为在这个例题中,微元面dS的磁通量与线圈的感应电动势都有,但她们的物理含义却就是不一样的,前者的表示微元面dS上的磁通量,就是一个微小量,而后者的表示的就是微笑时间内的磁通量变化量,就是一个微小变化量。
微积分的在物理竞赛中地的应用

求解在立体斜面上滑动的物体的速度一物体放在斜面上,物体与斜面间的摩擦因数μ恰好满足αμtg =,α为斜面的倾角。
今使物体获得一水平速度0V 而滑动,如图一,求:物体在轨道上任意一点的速度V 与φ的关系,设φ为速度与水平线的夹角。
解:物体在某一位置所受的力有:重力G ,弹力N 以及摩擦力f 。
摩擦力f总是与运动速度V 的方向相反,其数值 ααααμμsin cos cos mg mg tg mg N f ====重力在斜面上的分力为1G ,如图二,将1G 分解为两个分力:1G''是1G 沿轨迹切线方向的分力,φαφsin sin sin 11mg G G =='' ;1G '是沿轨迹法向的分力,φαφcos sin cos 11mg G G ==',如图三。
根据牛顿运动定律,得运动方程为τma f G =-''1(1) n ma G ='1(2) 由(1),)1(sin sin )sin sin sin (1-=-=φααφατg mg mg ma 而 ,dt dV a =τ得到 ,)1(sin sin dt g dV -=φα (3)式中φ是t 的函数,但是这个函数是个未知函数,因此还不能对上式积分,要设法在φ与t 中消去一个变量,才能积分,注意到φφd d dsV V dSdt 1== (4) 而φd ds表示曲线在该点的曲率半径ρ,根据(2)式,ρφα2cos sin Vm mg = (5)由式(3)(4)(5),可得到,)sec (φφφd tgV dV-=φφφφd tg V dVV V ⎰⎰-=00)sec (,积分,得到)sin 1ln()ln(sec cos ln ln 0φφφφ+-=+--=tg V V,.sin 10φ+=V V运用积分法求解链条的速度及其时间一条匀质的金属链条,质量为m ,挂在一个光滑的钉子上,一边长度为1L ,另一边长度为,2L 而且120L L <<,如图一。
微积分在物理学应用的原理

微积分在物理学应用的原理简介微积分是数学中的一个重要分支,它广泛应用于各个科学领域,包括物理学。
物理学是研究物质、能量以及它们之间相互作用的科学。
微积分为物理学提供了一种强大的工具,用于解决各种与物质和能量相关的问题。
本文将介绍微积分在物理学中的应用原理。
速度、加速度和微分在物理学中,速度和加速度是描述物体运动的重要概念。
速度表示物体在单位时间内所产生的位移,加速度表示物体在单位时间内速度的改变。
微积分提供了计算速度和加速度的工具。
速度在微积分中,速度可以通过对位移进行微分来计算。
位移是表示物体从一个位置到另一个位置的距离差。
假设一个物体在时间t=0时位于位置x=0,位于时间t 时位于位置x。
则物体的速度可以表示为:v = dx/dt其中,v表示速度,dx表示位移的微小变化,dt表示时间的微小变化。
微分运算可以将位移关于时间求导,得到物体的瞬时速度。
加速度加速度可以通过对速度进行微分来计算。
根据速度的定义,加速度可以表示为速度关于时间的变化率:a = dv/dt其中,a表示加速度,dv表示速度的微小变化,dt表示时间的微小变化。
通过对速度进行微分运算,可以求得物体的瞬时加速度。
物体运动的微分方程微积分还可以用来建立描述物体运动的微分方程。
对于物体的位移、速度和加速度之间的关系,我们可以建立如下的微分方程:a = d2x/dt2这个方程被称为牛顿第二定律,它描述了力与物体运动之间的关系。
通过解微分方程,可以得到物体的位置随时间的变化规律。
积分和物理量积分在物理学中的应用非常广泛,可以用于计算各种与物理量相关的问题。
以下是几个常见的应用:面积和体积积分可以用于计算平面图形的面积和立体图形的体积。
例如,在计算一个矩形的面积时,可以通过对矩形的宽度进行积分,得到矩形的面积。
同样地,可以通过对立方体的高度进行积分,得到立方体的体积。
质量和密度积分也可以用于计算物体的质量和密度。
假设一个物体的密度在空间上是不均匀的,可以通过对物体的体积元进行积分来计算物体的总质量。
微积分在高中物理教学中的应用

微积分在高中物理教学中的应用摘要:众所周知,物理和数学紧密相连。
由于物理中很多的原理和规律都需要用到数学公式的推导,因此物理这门课能够学好的重要前提是学好数学。
实施新课程改革要求学生充分利用数学,解决实际中的物理问题。
在高中数学中,微积分知识的普及是高中物理教育顺利发展的良好基础。
加强对微积分知识的认知,提高学生的数学应用能力是掌握解决物理问题的关键。
关键词:微积分;高中物理;应用研究0 引言物理知识的学习需要良好的数学基础。
物理问题越是接近现实,需要解决的问题越复杂,必要的数学知识就越抽象。
例如对于复杂的变量问题和连续性模型问题的求解,需要学生掌握高等数学中的微积分知识。
例如,为了解决复杂的变量问题和连续模型问题,学生必须掌握高等数学中的数学。
但是,较低年级的高中生往往对抽象的数学概念和算法的认知只限于认知水平,从而使他们在解决物理问题时机械照运,缺乏灵活运用的能力。
微积分学是微分学和积分学的总称。
它是一种数学思想,“无限细分”就是微分,“无限求和”就是积分。
无限就是极限,极限的思想是微积分的基础,它是用一种运动的思想看待问题。
微积分堪称是人类智慧最伟大的成就之一。
在高中物理中,微积分思想多次发挥了作用。
一、解决变速直线运动位移问题匀速直线运动,位移和速度之间的关系x=vt;但变速直线运动,那么物体的位移如何求解呢?例1、汽车以10m/s的速度行驶,到某处需要减速停车,设汽车以等减速2m/s2刹车,问从开始刹车到停车,汽车走了多少公里?【解析】现在我们知道,根据匀减速直线运动速度位移公式就可以求得汽车走了0.025公里。
但是,高中所谓的的匀变速直线运动的位移公式是怎么来的,其实就是应用了微积分思想:把物体运动的时间无限细分。
在每一份时间微元内,速度的变化量很小,可以忽略这种微小变化,认为物体在做匀速直线运动,因此根据已有知识位移可求;接下来把所有时间内的位移相加,即“无限求和”,则总的位移就可以知道。
微积分在物理 中的简单应用
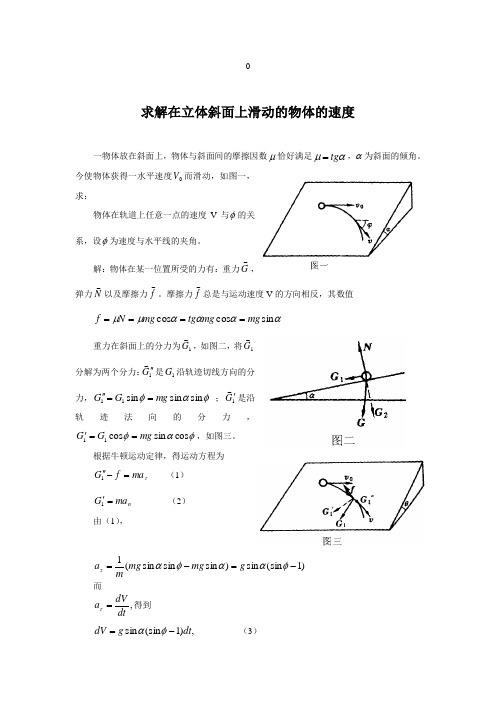
求解在立体斜面上滑动的物体的速度一物体放在斜面上,物体与斜面间的摩擦因数μ恰好满足αμtg =,α为斜面的倾角。
今使物体获得一水平速度0V 而滑动,如图一,求:物体在轨道上任意一点的速度V 与φ的关系,设φ为速度与水平线的夹角。
解:物体在某一位置所受的力有:重力G ,弹力N 以及摩擦力f 。
摩擦力f总是与运动速度V 的方向相反,其数值 ααααμμsin cos cos mg mg tg mg N f ====重力在斜面上的分力为1G ,如图二,将1G 分解为两个分力:1G''是1G 沿轨迹切线方向的分力,φαφsin sin sin 11mg G G =='' ;1G '是沿轨迹法向的分力,φαφcos sin cos 11mg G G ==',如图三。
根据牛顿运动定律,得运动方程为τma f G =-''1 (1)n ma G ='1(2) 由(1),)1(sin sin )sin sin sin (1-=-=φααφατg mg mg ma 而 ,dt dV a =τ得到 ,)1(sin sin dt g dV -=φα (3)式中φ是t 的函数,但是这个函数是个未知函数,因此还不能对上式积分,要设法在φ与t 中消去一个变量,才能积分,注意到 φφd d ds V V dS dt 1== (4)而φd ds表示曲线在该点的曲率半径ρ,根据(2)式,ρφα2cos sin V m mg = (5)由式(3)(4)(5),可得到,)sec (φφφd tg V dV-=φφφφd tg V dV V V ⎰⎰-=00)sec (,积分,得到)sin 1ln()ln(sec cos ln ln 0φφφφ+-=+--=tg V V,.sin 10φ+=V V运用积分法求解链条的速度及其时间一条匀质的金属链条,质量为m ,挂在一个光滑的钉子上,一边长度为1L ,另一边长度为,2L 而且120L L <<,如图一。
微积分在物理学中的应用

微积分在物理学中的应用The application of calculus in physics 摘要: 关于“微积分”是高等数学中研究函数的微分、积分以及有关概念和应用的数学分支,它是数学的一个基础学科,内容主要包括极限、微分学、积分学及其应用。
微分学包括求导数的运算,是一套关于变化率的理论,它使得函数、速度、加速度和曲线的斜率等均可用一套通用的符号进行讨论,使运算也更加简便。
“应用数学处理物理问题的能力”是我们必须掌握的一种解决物理问题的方法,“能够根据具体问题找出物理量之间的数学关系,根据数学的特点、规律,进行推导、求解,并根据结果做出物理判断、进行物理解释,得出物理结论”是物理解题中运用的数学方法,微积分就是其中一种。
关键词: 微积分Key words: calculus基金项目:本文为大学生科研项目批准文号xs11035资助项目作者简介:姓名:李东康(出生年月198211),女,吉林省;单位全称:通化师范学院物理学院,职称:助教;研究方向:光学;刘明娟,通化师范学院物理学院本科学生;1、微积分1.1定义:设函数()x F 在[]b a ,上有界,在[]b a ,中任意插入若干个分点a=0X <1X <...<1-Xn <Xn =b 把区间[]b a ,分成n 个小区间[][]n n x x x x ,,110- 。
在每个小区间[]i i x x ,1-上任取一点()i i i x x ≤≤-ζ1,作函数值()i f ζ与小区间长度的乘积()xi i f ∆ζ,并做出如果不论对[]b a ,怎样分法,也不论在小区间上的点i ζ怎样取法,只要当区间的长度趋于零时,和S 总趋于确定的极限I ,这时我们称这个极限I 为函数()x f 在区间[]b a ,上的定积分。
设函数()x f y =在某区间内有定义,0x 及x x ∆+0在此区间内。
如果函数的增量()()00x f x f x y -∆+=∆可表示为 ()x x y A ∆O +∆=∆(其中A 是不依赖于x∆的常数),而()x ∆O 是比x ∆高阶的无穷小,那么称函数()x f 在点0x 是可微的,x A ∆称作函数在点0x 相应于自变量增量x ∆的微分,记作y d ,即x y A d ∆=。
微积分在物理学中的应用

微积分在物理学中的应用物理学是定量科学,所以在物理学中广泛地使用数学,可以说数学是物理学的语言。
可见,物理学是离不开数学的,因为数学为物理学提供了定量表示和预言能力,在相当长的一段时间里,数学与物理几乎是不可分割地联系在一起。
而微积分作为数学的一大发现在物理学中的应用更是非常的广泛。
微积分是研究函数的微分、积分以及有关概念和应用的数学分支。
微积分是建立在实数、函数和极限的基础上的。
微积分最重要的思想就是用"微元"与"无限逼近",好像一个事物始终在变化你很难研究,但通过微元分成一小块一小块,那就可以认为是常量处理,最终加起来就行。
微积分学是微分学和积分学的总称。
它是一种数学思想,‘无限细分’就是微分,无限求和’就是积分。
无限就是极限,极限的思想是微积分的基础,它是用一种运动的思想看待问题。
微积分堪称是人类智慧最伟大的成就之一。
在大学物理中,微积分思想发挥了极其重要的作用。
微积分在物理学中的应用相当普遍,有许多重要的物理概念 ,物理定律就是直接以微积分的形式给出的,如速度dtr d v =,加速度dt vd a =,转动惯量2r dm I ⎰⋅=,安培定律B l Id F d ⨯=,电磁感应定律dtd N Φ-=ε……1-1 .用微积分解决速度和加速度问题 1.速度速度是为了描述质点位置变化的快慢和位置变化的方向而引入的。
(1)平均速度如果质点在t 到t+Δt 这段时间内的位移是Δr ,则Δr 与Δt 的比值即为平均速度,它反映该段时间内质点位置变化的方向和平均快慢。
(2) 瞬时速度将t 到t+Δt 时间内当Δt →0时质点平均速度Δr/Δt 的极限,定义为质点在t 时刻的瞬时速度,简称速度,用v 表示,即速度的大小为:速度的方向用方向余弦表示为:2.加速度加速度是为了描述质点速度变化的快慢和速度方向的变化的物理量,等于速度对时间的一阶导数,或等于位置矢量对时间的二阶导数,用a表示,加速度的单位:米/()。
(完整)微积分在物理 中的简单应用(DOC)
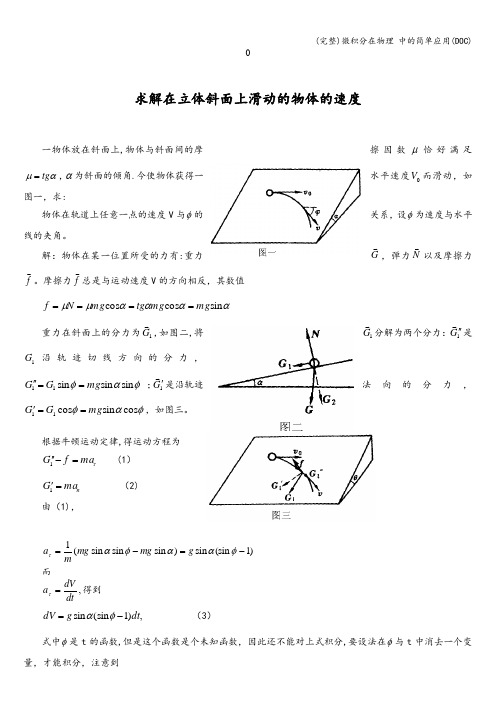
求解在立体斜面上滑动的物体的速度擦因数μ恰好满足一物体放在斜面上,物体与斜面间的摩αμtg =,α为斜面的倾角.今使物体获得一水平速度0V 而滑动,如图一,求:物体在轨道上任意一点的速度V 与φ的关系,设φ为速度与水平线的夹角。
G ,弹力N以及摩擦力解:物体在某一位置所受的力有:重力f 。
摩擦力f 总是与运动速度V 的方向相反,其数值ααααμμsin cos cos mg mg tg mg N f ====重力在斜面上的分力为1G,如图二,将1G 分解为两个分力:1G ''是1G 沿轨迹切线方向的分力,φαφsin sin sin 11mg G G =='' ;1G'是沿轨迹法向的分力,φαφcos sin cos 11mg G G ==',如图三。
根据牛顿运动定律,得运动方程为τma f G =-''1(1) n ma G ='1(2) 由(1),)1(sin sin )sin sin sin (1-=-=φααφατg mg mg m a 而,dtdVa =τ得到 ,)1(sin sin dt g dV -=φα (3)式中φ是t 的函数,但是这个函数是个未知函数,因此还不能对上式积分,要设法在φ与t 中消去一个变量,才能积分,注意到φφd d ds V V dS dt 1==(4) 而φd ds表示曲线在该点的曲率半径ρ,根据(2)式,ρφα2cos sin V mmg = (5)由式(3)(4)(5),可得到 ,)sec (φφφd tg V dV-= φφφφd tg V dV V V ⎰⎰-=00)sec (, 积分,得到)sin 1ln()ln(sec cos ln lnφφφφ+-=+--=tg V V, .sin 10φ+=V V运用积分法求解链条的速度及其时间子上,一边长度为1L ,另一条匀质的金属链条,质量为m,挂在一个光滑的钉一边长度为,2L 而且120L L <<,如图一。
