第二课堂 电介质电容器及能量
电容与电介质介电常数与电场能量与电场能量密度之间的关系

电容与电介质介电常数与电场能量与电场能量密度之间的关系电容是电学中一个重要的概念,它描述了电路元件对电荷的存储能力。
而电介质介电常数则是衡量电介质的极化能力,它与电场能量和电场能量密度之间存在紧密的关系。
首先,让我们回顾一下电容的概念。
电容是电路元件对电荷存储能力的度量,用单位电压下的电容量来表示。
在一个理想的理论电容器中,电容量的计算公式为C = Q/V,其中C表示电容量,Q表示电荷量,V表示电压。
这意味着当电容器的电压增加时,可以存储的电荷量也会增加。
然而,在实际的应用中,电容器常常由电介质填充,以增加电容量。
电介质介电常数是衡量电介质极化能力的物理量,用εr来表示。
理想情况下,如果电介质介电常数为1,则电介质对电场几乎没有影响。
但是,在实际情况下,绝大多数电介质都有介电常数大于1,这意味着它们能够存储更多的电荷。
因此,对于一个实际的电容器而言,其电容量的计算公式可以表示为C = εrε0A/d,其中ε0表示真空中的介电常数,A表示电容器的极板面积,d表示极板之间的距离。
由此可见,电介质介电常数的增加会导致电容量的增加。
现在,让我们思考一下电场能量与电场能量密度之间的关系。
在电磁学中,电场能量是电场对电荷进行的功的总和。
假设一个点电荷q在电场E中移动一个距离d,那么它所受到的力F等于qE,因此电场对电荷所做的功W等于F·d = qEd。
由此可见,电场能量与电荷量、电场强度和电位移之间存在紧密的联系。
而电场能量密度则是单位体积内的电场能量,用u表示。
它表示了电场能量在空间中的分布情况。
对于一个电容器而言,它的电场能量密度可以表示为u =1/2εE²,其中ε表示电介质介电常数,E表示电场强度。
这意味着电场能量密度的大小与电介质的极化能力和电场强度成正比。
综上所述,电容与电介质介电常数与电场能量和电场能量密度之间存在着密切的关系。
电介质的介电常数决定了电容器的电容量,而电场能量和电场能量密度则分别与电介质的极化能力和电场强度有关。
电介质与电容器能量

电介质与电容器能量电容器作为储存电能的重要器件,在电子电路和电力系统中扮演着至关重要的角色。
而电介质作为电容器中的关键组成部分,则决定了电容器的电性能和能量储存能力。
本文将探讨电介质与电容器之间的能量关系,并分析其对电容器性能的影响。
一、电介质的基本概念与电性能电介质,也称为绝缘体,是一种能够阻碍电荷流动的物质。
在电场作用下,电介质会发生极化现象,即在电介质中会产生正负电荷分离的现象,并形成电偶极矩。
电介质的电性能取决于其导电性的强弱以及电介质分子的极化程度。
不同种类的电介质具有不同的极化特性。
常见的电介质包括聚乙烯、聚氯乙烯、聚四氟乙烯等有机电介质,以及氧化铝陶瓷、二氧化硅等无机电介质。
对于有机电介质来说,其导电性相对较高,而无机电介质则具有较好的绝缘性能。
二、电容器的构成与工作原理电容器由两个导体板(分别作为正极和负极)之间的电介质组成。
当电容器处于充电状态时,电荷会在两个导体板之间积累,形成电位差。
这时,电介质的极化现象就会发生,并在电介质中储存电能。
电容器的电容量取决于三个基本参数:导体板面积(A)、导体板间距(d)以及电介质的相对介电常数(εr)。
根据电容器的公式可知,电容量(C)与这三个参数成正比。
C = εr * ε0 * A / d其中,ε0是真空中的介电常数,为常数。
由此可见,电介质的相对介电常数对电容量的影响非常重要。
三、电介质对电容器能量的影响1. 增加电容量:电介质的相对介电常数εr越大,意味着电容器的电容量会增加。
较高的电容量意味着电容器可以存储更多的电荷,并具有更高的能量储存能力。
2. 提高击穿电压:电介质的绝缘性能决定了电容器的击穿电压。
当电介质的绝缘性能较好时,电容器可以承受更高的电压,从而提高了其能量储存能力。
3. 减少能量损耗:部分电介质具有较高的介电损耗,即在电场作用下会有能量转化为热能而损耗掉。
因此,选择低介电损耗的电介质可以减少能量损耗,提高电容器的效率。
第二章2电容电容器静电能.ppt.ppt

q q q 1 2 q n C U U
C C . . . C 1 2 n
2.电容器的串联:带电量相同,分电压
U
A
C1
C2
C3
C
n
UB
令U UU 2 . . . U U U 1 n A B
q q q C C , . . . , C 1 , 2 n U U U 1 2 n
会生活。
2.清朝黄遵宪曾作诗曰:“钟声一及时,顷刻不少留。虽
有万钧柁,动如绕指柔。”这是在描写 A.电话 C.电报 B.汽车 D.火车 ( )
解析:从“万钧柁”“动如绕指柔”可推断为火车。 答案:D
[典题例析工具前往参观。然而在19世纪七十年代,江苏沿江 居民到上海,最有可能乘坐的交通工具是 A.江南制造总局的汽车 B.洋人发明的火车 ( )
1.李鸿章1872年在上海创办轮船招商局,“前10年盈和,成
为长江上重要商局,招商局和英商太古、怡和三家呈鼎立
之势”。这说明该企业的创办 A.打破了外商对中国航运业的垄断 B.阻止了外国对中国的经济侵略 C.标志着中国近代化的起步 ( )
D.使李鸿章转变为民族资本家
解析:李鸿章是地主阶级的代表,并未转化为民族资本家; 洋务运动标志着中国近代化的开端,但不是具体以某个企业 的创办为标志;洋务运动中民用企业的创办在一定程度上抵
[典题例析] [例2] (2010· 福建高考)上海是近代中国茶叶的一个外销
中心。1884年,福建茶叶市场出现了茶叶收购价格与上海
出口价格同步变动的现象。与这一现象直接相关的近代事 业是 A.电报业 C.铁路交通业 ( )
B.大众报业 D.轮船航运业
[解析]
[答案]
静电场中的电介质和电场能量
a
E0
E E0
E E0
E0
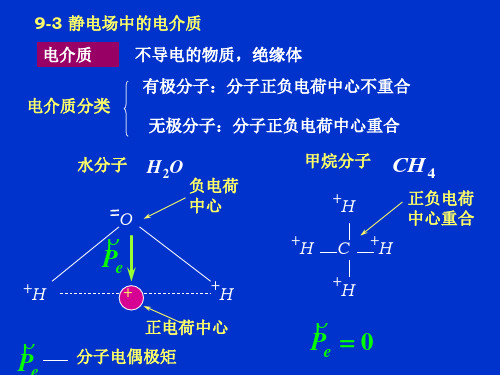
无限大均匀电介质中,令 E 介质中 真空中
E E0 r 1
E E0 r 1
r
相对电容率
9 – 3 静电场中的电介质
三 电介质对电容的影响
第九章静电场中的导体与电介质
U0
Q
+++++++
U
C0
-------
电介质中的电场强度 极化电荷与自由电荷的关系
E E0 E ' r r 1 E' E0 r E0 0 / 0 E ' ' / 0
r 1 ' 0 r
E0
d
r
-+ + + +-+-+-+ + + + + - -
E0
E' E
1 ' E dS (Q0 Q )
S
0
0 + + + + + + + + + + + ' - - - - - S
Q0 E dS
S
r
定义电容率
S
0 r E dS Q0
0 r
0 r
+ + + + + + 0 - - - - - - - - - - '
9-3 静电场中的电介质 电介质 不导电的物质,绝缘体 有极分子:分子正负电荷中心不重合
静电场中的电介质电场的能量详解PPT课件

思 分析对称性 路
D • dS q0i D D 0r E E
S
例:p209页例题1,2
第11页/共43页
练习. 已知:导体球 R Q
介质 r
求:
球外任一点的
E
导体球的电势 V
解: 作同心球面 为高斯面得
D • dS Q
S
D 4r 2 Q
Q
D 4r 2
E
D 0r
Q 4 0r r 2
静电平衡条件
1、导体内部场强处处为零。 2、场强方向处处与导体表面垂直。 推论:导体是一个等势体;导体表面是一个等势面。
静电平衡时导体上的电荷分布
1、静电平衡时,导体内部无净电荷,电荷只能分布在导体表面 2、当空腔导体内部无带电体时,空腔导体和实心导体一样,内
部场强处处为零;电荷全部分布在导体的外表面。
非均匀电场的能量计算要用积分的办法 dV
W
V
wedV
V
1 E 2dV
2
1
V
2
DEdV
第32页/共43页
例1、计算球形电容器的能量
已知 RA RB q
解:
场强分布
q
E 4r 2
取体积元 dV 4r 2dr
q q
r RA
RB
dW
wdV
1 E 2dV
2
1(
2
q
4r 2
)2 4r 2dr
能量
◎
E0 C
(
d1 q
d2
)
q
0S 0S
(
d1
d2 )
0S
uA uB d1 d2 d t
q
q
A E0 E E0 B
2019大学物理课件-电容和电容器及电场能量.ppt

E
;
3)通过场强,计算两极板间的电势差 U A U B ;
Q 4)由电容器电容的定义式 C 求出 C。 U A UB
1、平板电容器 (1)设两导体板分别带电 Q (2)两带电平板间的电场强度
d
A
B
σ Q E ε0 ε0 S
(3)两带电平板间的电势差
S
S
Q
dQ
Qd U Ed ε0 S
l RB
-+ - + RA -+ R B -+
λ , ( RA r RB ) (2)E 2 π ε0 r R λdr Q RB ( 3) U ln R 2πε r 2 π ε0 l RA 0
B A
l
Q RB (4)电容 C 2 π ε0 l ln U RA
3、球形电容器的电容 球形电容器是由半径分 别为 R1和 R2的两同心金属球壳所组成。
(4)平板电容器的电容
Q S C ε0 U d
(4)平板电容器的电容
Q S C ε0 U d
(5)如果在两极板间充满相 对电容率为 εr 的电介质时, 则其电容为:
d
S
εr
S S C ε r C 0 ε0 ε r ε d d
ε ε0εr
称为电容率。
例1
平行平板电容器的极板是边长为 l 的正方
取一体积元, dV 4πr 2 dr
2
R1
r
dr
Q R2 dWe wedV dr 2 8 π εr 2 2 R Q Q 1 1 2 dr We dWe ( ) 2 8 π ε R1 r 8 π ε R1 R2
Q 1 1 1 Q We ( ) 8 π ε R1 R2 2 4πε R2 R1 R2 R1 讨论
电介质电容静电能资料
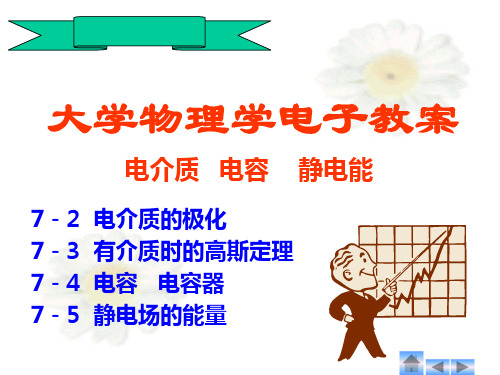
1、电介质中的电场强度
E0 0 / 0
E=
/
0
E=E 0+E
+σ0
E
E0 E’ -σ'
+σ'
-σ0
E=E0 E
2、极化电荷与自由电荷的关系
E
0 0
0
1
0
( 0
)
E= E0
r
=
0
1-
1
r
Q=Q0
1-
1
r
§7-3 有电介质时的高斯定理 1.总场 =外场 +极化电荷附加电场 E E0 E'
•达到静电平衡时,电介质内部的场强也不为零。
在外电场中电介质要受到电场的影响,同 时也影响外电场。
一、极化的微观机制
1、电介质的分类
无极分子:分子的正负电荷中心在无 电场时是重合的,没有固定的电偶 极矩,如H2、HCl4,CO2,N2,O2等
有极分子:分子的正负电荷中心 在无电场时不重合的,有固定的 电偶极矩,如H2O、HCl等。 分子构成电偶极子 p=ql
导体内 E 0
cos 0
由高斯定理
s
D1
dS
q0
( S内)
D1S 1S
D1 1
;
E1
D1
0 r
10
20
1'
S
d
1'
r
10
20
D1 1
同理:
E1
D1
0 r
D2 2
E2
D2
0
电量不变:
1
S 2
2
S 2
0
S
又:
E1d E2d U
电介质和电容器的工作原理

温度范围:电容 器能正常工作的 温度范围
湿度范围:电容 器能正常工作的 湿度范围
耐压性能:电容 器能承受的最大 电压
耐久性能:电容 器在长期使用下 的性能变化情况
温度稳定性:电容器在不同温度下的性能变化 湿度稳定性:电容器在不同湿度下的性能变化 机械强度:电容器承受机械应力的能力 耐久性:电容器在长期使用下的性能变化
添加标题
添加标题
添加标题
添加标题
谐振电路:用于信号产生和接收, 提高通信效率
储能:用于临时存储能量,提高通 信稳定性
电子设备:电容器在电 子设备中广泛应用,如
手机、电脑、电视等
电力系统:电容器在电力 系统中用于提高功率因数、
降低线损等
汽车行业:电容器在汽车 行业中用于启动、制动、
照明等系统
航空航天:电容器在航空 航天领域用于卫星、火箭
钽电容器:体积小、重量 轻、高频特性好、耐压高
聚丙烯电容器:体积小、 重量轻、高频特性好、 耐压低
云母电容器:体积大、重 量重、耐压高、高频特性 差
电容器的容量是指电容器储存 电荷的能力,通常用C表示。
电容器的容量与两个电极的面 积、距离以及电介质的性质有
关。
电容器的容量可以通过公式 C=εS/d计算,其中ε是电介质 的相对介电常数,S是两个电极 的面积,d是两个电极的距离。
电介质是一种绝缘 体,可以阻止电流 通过
电介质的电导率很 低,通常在10^-10 S/m以下
电介质的极化性是 指电介质在电场作 用下会发生极化, 产生电偶极子
电介质的损耗是指电 介质在电场作用下会 损失能量,通常用损 耗角正切值来表示
固体电介质:如陶瓷、玻璃、塑料等 液体电介质:如矿物油、植物油等 气体电介质:如空气、氮气、氢气等 复合电介质:由两种或两种以上电介质组成的复合材料
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
U U0 Ed E A : E A0 1 : 1
ε 0S C0 d
电介质的击穿场强——该电介质所允许最大场强。 超过击穿场强——电介质(绝缘体)变为导体。 击穿场强对应的电压——最大电压值(耐压值) 击穿场强对应的电荷——最大能储存电量 例6、一圆柱形电容器,外柱的直径为4cm,内柱的直 径可以适当选择。若其间充满各向同性的均匀介质, 该介质的击穿场强是200V/cm,试求该电容器可能承 受的最高电压。(自然对数的底e=2.7183)
(自测练习) P23 计算题1 半径为a的导体球A接地,与A球同心放置的导体球 壳B,内外半径分别为3a和4a,B球壳上带有正电荷+Q ,A、B间充满 r=2,试求 (1)A球上的电荷; (2)B球壳的电势; Q (3)介质中的电场能量。
4a
UBA UB
场具有球对称性
a
3a
解: a r 3a
P
A外 A静
1 1 2 2 mv mv 0 2 2
静电场的能量 电容器的能量
2 1 Q W = CU 2 = 2 2C
1 We D EdV 2 V
1 n W q U i i 点电荷系相互作用能(互能) 2 i 1
电势能
WP qUP
带电体的静电能 (自能):
3
5
2 m1
例5、1、2、3分别是半径各为R1、R2、R3 (R1<R2<R3) 的三个同心导体球面,中间的导体球面接地。 试求:1)球面1和球面3之间的等效电容。 2)用导线连接球面1和球面3后,球面1与地之间 的等效电容。 解:构成图示的三个电容器 3
R1R2 1、 2构成电容:C1 4 0 , R2 R1 R2 R3 2、 3构成电容:C2 4 0 , R3 R2 3与无限远(地)构成电 容:C3 4 0 R3
r -
r ' 2 E E0 E' E0 2 0 4 0 ( h )
2
方向向下
2
2r 2 r 1 1 2 h r
2r 2 r 1 D 0 r E r 2 h
当 h r 时
S
1 2
ˆ
r1
r2
ˆ ˆ E d l E l E l ( ) 1 2
L
(E1t E2t )l 0
E1 t E 2 t
n
S
r1
r2
ˆ D2 Sn ˆ q0 D dS D1 S n
D dS Q0
S
n
E’
n
E0
E E 0 E'
介质中电场强度的计算 原则:场的叠加原理 介质中的高斯定理
(自由电荷和束缚电荷的分布均有对称性) D dS Q
S
Q q' E dS
S
0
Q
- ’
+ ’
•计算步骤:
r2 E 1 0 h2
D r
三、电容器
求电容值的三步曲: 0 rS 1)设q、-q C 1)如何求电容? 2)求U d AB 3) C q
U AB
C 40 R
C rC0
2)电容器的串联和并联 并联
C Ci
1 1 C Ci
串联
2 a a 例4(书 p80 9-9) 证明: C (1 ) 0 d 2d 0 0 a dC dS dl a l d l d l
由于dq为无限小,所以U为带电体上所有电荷在
1 W Udq 2q
该处产生的电势
例: 均匀带电球面,半径为R,总电量为Q,求这一 带电系统的静电能。 (均匀带电球面系统的自能) 解:以无穷远为势能零点,其电势为: dq Q U 4 o R R 此电荷系的静电能为: Q 1 1 Q Q2 W Udq dq 2 2 4 o R 8 o R
(习题12)厚度为b的无限大平板内分布均匀电荷密度
(>0)自由电荷,在板外两侧分别充有介电常数为1、
2的电介质,求(1)板内外的电场分布;(2)板外的
A点与B点分别距左右两板壁为l,求电势差UAB
解:分析可得 空间的电场由自由 电荷的厚板和两块极化电荷板叠加
E1 E2 D1 1E1 D2 2 E2
A
1
2
B
1
b
作图示高斯面1得 D dS D1S D2 S bS
s
b 板外: E1 E2 1 2
1b D1 1E1 1 2
2 b D2 2 E2 1 2
板内: s D dS D1S Dx S xS
r +
端点
E1t E2t 0 D2t D1t 0 D2n S 0( D1n 0) S
h
r -
E2 D2n D2 0 r 0 r ' Pn e 0 E2 r 1 r
D2
中点场强
r + h
e l P 3 0 3 0
o r
l
例2、将一个介电常数为r均匀介质球,放在电场强度为
E0的均匀外场中,被均匀极化,试求球的极化强度矢量
P和球心的电场强度EC. ' P n Pcos
介质球面的法向与E0的夹角
E0
EC E0 E' EC E0 E'
x(1 2 ) 1b Dx 1 2 x(1 2 ) 1b Ex d d 1 (1 2 )
A
1 1 2
2
1b EX 0 当 x 1 2
BbBiblioteka 二、介质中静电场的边界条件
E dl 0 L D dS q 0
(D1n D2 n )S
q0 D dS (D1n D2n )S
q0 D 2 n D1n 0 S
若界面无自由电荷的存在
D2n D1n
D线的折射定律:
E1 D1 1 r1 r2 E 2 2 D 2
t an1 D1n D1t r1E1t r1 t an 2 D 2 t D2 t r 2 E 2 t r 2 D2n
D1 t
例3 练习册P67 2 平行板电容器两极板上自由电荷面
密度分别为 .今在其中放入一细长圆柱形各向同性
均匀电介质棒,其半径为r,高度为h,相对介电常量
为r,其轴线与板面垂直,如图所示.试求圆柱电介质
中点的电场强度 和电位移矢量 .并求当h>>r时,介质
中点E 、D 的近似值. 解:假设极板上的电荷仍均匀分布 根据场的分布及边界条件得
高等数学上 p159
x x x m1 sin x x (1) 3! 5! (2m 1)!
2m x2 x4 x m 1 cos x 1 (1) 2! 4! (2m)! n x 2 x3 x n 1 ln(1 x) x (1) 2 3 n ( 1) 2 ( 1) ( n 1) n (1 x) 1 x x x 2! n! 1 1 2 (1 x) 1 x (1 x)1 1 x 2
0 a C dC dl d l 0 0 0 a d a ln d
a a
d
a
高等数学上p158
d a a a 1 ( a ) 2 a (1 1 a ) ln ln(1 ) d 2 d d 2 d d d
a2 a C 0 (1 ) d 2d
D dS Q 0
S
D
D E
P 0 ( r 1) E ’ P E
σ ' Pn
例1、求均匀极化电介质球的退
极化场。设极化强度矢量为 P 。
o r
e E r 3 0
E'
E0
E' (r ) = E+ (r - l ) + E- (r + l ) 2 2 e e l (r ) (r l ) 2 3 2 3 0 0
则:C13 1 1 1 C1 C2 C3
1
C1
R3
R2
R1
1
2
2
2 3
C2 C3
3
(2)用导线连接球面1和球面3后,球面1与地面间的电容 为三电容的并联
2 1
1
C1
2
2 3
C2 C3
2 3
C2
C1
C =C1 C2 C3
R3 R2
3
C3
3
R1
1
2
3
自测练习 p27 3
P p 2 E' cos sin d 2 0 3 0 0
P E C E 0 E ' E0 3 0 P P r 1 0 E C r 1 0 ( E0 ) 3 0 3 r 1 0 P E0 r 2 3 EC E0 r 2
PC r 1 0EC
E
qx 4 0 ( x R )
2 2 3 2
解: dE'
' dSRcos
4 0 (( R cos ) ( R sin ) )
2 2 3 2
P cos 2R sin Rd cos P 2 cos sin d 2 4 0 R 2 0
R1
L
