工程热力学第三版电子教案第5章
工程热力学第三版电子教案教学计划2

2006学年秋季学期教学计划2
2006学年秋季学期教学计划4
课程名称工程热力学授课班级供热05级1-3班
授课总学时54学时(实验4)任课教师谭羽非、曹琳
本学期授课时数50学时教研室主任
序号
日期
课堂讲授内容
其它教学环节内容
主要参考书
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
.
11
.
12.
13
液体的蒸发与沸腾,水蒸气的定压发生过程。
水蒸汽表和图,水的相图及三相点。
水蒸汽的基本过程(自学)。
第八章湿空气(5)
湿空气的性质,湿空气的焓湿图。
湿空气的基本原理
湿空气的热力过程
第九章气体和蒸汽的流动(6)
绝热稳定流动关系式、气体在喷管中的绝热流动、喷管中流速及流量计算、实际喷管中有磨擦的流动
扩压管气体和蒸汽的绝热节流
第十一章致冷循环(2)
空气压缩致冷循环
蒸气压缩致冷循环
蒸气喷射致冷循环
吸收式致冷循环
热泵;气体的液化
教材:
工程热力学
(第四版)
廉乐明,李力
能,吴家正,
谭羽非编。
主要参考书:
1《工程热力
学》清华大学。
2《工程热力
学》(西安交
通大学)、
3《Engineer
ing Therodynamic
s》(Merle
C.Potter Craig W .Somerton)
4《“热
力学分析》
朱明善,陈
宏芳等编著
课程名称工程热力学授课班级供热05级1-3班
授课总学时54学时(实验4)任课教师谭羽非、曹琳
工程热力学课程教案完整版

工程热力学课程教案Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】《工程热力学》课程教案*** 本课程教材及主要参考书目教材:沈维道、蒋智敏、童钧耕编,工程热力学(第三版),高等教育出版社,2001.6手册:严家騄、余晓福着,水和水蒸气热力性质图表,高等教育出版社,1995.5 实验指导书:华北电力大学动力系编,热力实验指导书,2001参考书:曾丹苓、敖越、张新铭、刘朝编,工程热力学(第三版),高等教育出版社,2002.12王加璇等编着,工程热力学,华北电力大学,1992年。
朱明善、刘颖、林兆庄、彭晓峰合编,工程热力学,清华大学出版,1995年。
曾丹苓等编着,工程热力学(第一版),高教出版社,2002年全美经典学习指导系列,[美]M.C. 波特尔、C.W. 萨默顿着郭航、孙嗣莹等译,工程热力学,科学出版社,2002年。
何雅玲编,工程热力学精要分析及典型题精解,西安交通大学出版社,2000.4概论(2学时)1. 教学目标及基本要求从人类用能的历史和能量转换装置的实例中认识理解:热能利用的广泛性和特殊性;工程热力学的研究内容和研究方法;本课程在专业学习中的地位;本课程与后续专业课程乃至专业培养目标的关系。
2. 各节教学内容及学时分配0-1 热能及其利用(0.5学时)0-2 热力学及其发展简史(0.5学时)0-3 能量转换装置的工作过程(0.2学时)0-4 工程热力学研究的对象及主要内容(0.8学时)3. 重点难点工程热力学的主要研究内容;研究内容与本课程四大部分(特别是前三大部分)之联系;工程热力学的研究方法4. 教学内容的深化和拓宽热力学基本定律的建立;热力学各分支;本课程与传热学、流体力学等课程各自的任务及联系;有关工程热力学及其应用的网上资源。
5. 教学方式讲授,讨论,视频片段6. 教学过程中应注意的问题特别注意:本课程作为热能与动力工程专业学生进入专业学习的第一门课程(专业基础课),要引导学生的学习兴趣和热情。
工程热力学第三版电子教案教学计划6
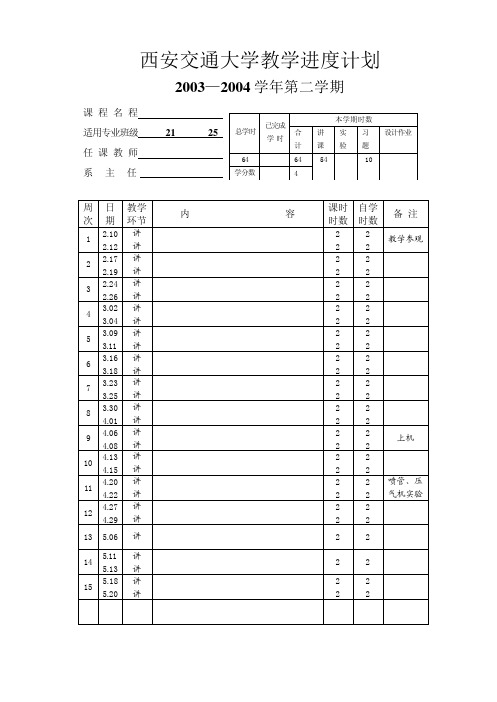
工程热力学 能动 26、2 7、28 赵小明 傅秦生
李国君
总学 已完
本学期学时
课外学时
合计 讲课 实验 机时 讨论 实验
64
64 54
10
学分 4
数
周日
教 学
次期
环 节
1 2.10 讲 2.12 讲
2 2.17 讲 2.19 讲
3 2.24 讲 2.26 讲
4 3.2 讲 3.4 讲
5 3.9 讲 3.11 讲
课课
内外
备
学学
注
时时
2 2 电教片 2 2 参观
22
23
24
22
22
22
22
23
24
22
22
22
22
22
22
14 5. 11 讲
气体与蒸气的流动
2 4 喷管实
5. 14 讲
第九章 压气机的热力过程
22 验
15 5. 18 讲
压气机的热力过程
22
5. 21 讲
第十章 气体动力循环
22
16 5. 25 讲
6 3.16 讲 3.18 讲
7 3.23 讲 3.25 讲
8 3.30 讲 4.1 讲
9
4. 6 4. 8
讲 讲
10
4. 13 4. 15
讲 讲
11 4. 20 讲 4. 22 讲
12 4. 27 讲 4. 29 讲
13 5. 6 讲
14 5. 11 讲 5. 13 讲
内
容
绪论 第一章 基本概念 第二章 热力学第一定律
15 5.18 5.20
讲 讲
第十三章 湿空气 复习 机动 考试
工程热力学 第五章(3) 图文

T0
cp
ln
T1 T0
R ln
p1 p0
p0
RT1 p1
RT0 p0
RT0 ln
p1 p0
p0 p1
1
244kJ
/ kg
闭口系统内能的Ex举例
1kg空气,由p1=50bar, t1=17oC, 膨胀到 p2=40bar, t2=17oC, 已知p0=1bar, t0=17oC
exu=?
w
假定 q 通过可逆热机作功 w’
exu = w ’’= w + w ’
q w ’’
w’
q'
T0
闭口系统内能的Ex与An
热一律:
q ' u0 u1 w ''
热二律:
q'
siso s0 s1 T0 0
q ' T0 s0 s1
w '' u1 u0 T0 s1 s0
E Ex An
Yong的理解
热力系只与环境相互作用、从任意状态可逆地 变化到与环境平衡时,才能作出最大的有用功。
当系统由一任意状态可逆地变化到与给定 环境相平衡的状态时,理论上可以无限转换 为任何其它能量形式的那部分能量,称为Ex
功
100%相互转换
能量中除了 Ex 的部分,就是 An
E Ex An
求:该膨胀过程对外界的最大有用功
exu1
RT0 ln
p1 p0
p0 p1
1
244kJ
/ kg
exu2
RT0
ln
p2 p0
p0 p2
机械能、电能:An=0 Ex=E 环境介质中的热能: Ex=0
工程热力学第三版电子教案教学计划5

课堂讨论:(理想气体过程)
第四周国庆放假一次课
15~16
(第5周第1节)
第四章热力学第二定律与熵
4.1自然过程的方向性
4.2热力学第二定律的实质与表述
4.3卡诺循环与卡诺定理
17~18
(第5周第2节)
4.4克劳修斯不等式
4.5熵的导出
4.6不可逆过程熵的变化
4.7孤立系熵增原理
5.5提高勃雷登循环热效率的其他途径
课堂讨论:(气体动力循环)
27~28
(第8周第1节)
期中考试(闭卷)
29~30
(第8周第2节)
第六章水蒸气
6.1纯物质的热力学面及相图
6.2汽化与饱和
6.3水蒸气的定压发生过程
31~32
(第9周第1节)
实验(水的饱和蒸汽压力和温度关系实验)
33~34
(第9周第2节)
39~40
(第11周第1节)
第八章制冷循环
8.1空气压缩制冷循环
8.2蒸气压缩制冷循环
41~42
(第11周第2节)
实验(制冷热泵循环演示实验)
43~44
(第12周第1节)
8.3吸收式制冷循环
8.4热泵循环
讲座:(制冷剂与环保)
45~46
(第12周第2节)
第九章理想混合气体和湿空气
9.1混合气体的成分
10.1研究热力学微分关系式的目的
10.2特征函数
10.3数学基础
10.4热系数
10.5熵、内能和焓的微分关系式
51~52
(第14周第1节)
10.6比热容的微分方程
10.7克拉贝龙方程和焦-汤系数
10.8实际气体对理想气体的偏离
工程热力学课程教案完整版

工程热力学课程教案Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】《工程热力学》课程教案*** 本课程教材及主要参考书目教材:沈维道、蒋智敏、童钧耕编,工程热力学(第三版),高等教育出版社,2001.6手册:严家騄、余晓福着,水和水蒸气热力性质图表,高等教育出版社,1995.5 实验指导书:华北电力大学动力系编,热力实验指导书,2001参考书:曾丹苓、敖越、张新铭、刘朝编,工程热力学(第三版),高等教育出版社,2002.12王加璇等编着,工程热力学,华北电力大学,1992年。
朱明善、刘颖、林兆庄、彭晓峰合编,工程热力学,清华大学出版,1995年。
曾丹苓等编着,工程热力学(第一版),高教出版社,2002年全美经典学习指导系列,[美]M.C. 波特尔、C.W. 萨默顿着郭航、孙嗣莹等译,工程热力学,科学出版社,2002年。
何雅玲编,工程热力学精要分析及典型题精解,西安交通大学出版社,2000.4概论(2学时)1. 教学目标及基本要求从人类用能的历史和能量转换装置的实例中认识理解:热能利用的广泛性和特殊性;工程热力学的研究内容和研究方法;本课程在专业学习中的地位;本课程与后续专业课程乃至专业培养目标的关系。
2. 各节教学内容及学时分配0-1 热能及其利用(0.5学时)0-2 热力学及其发展简史(0.5学时)0-3 能量转换装置的工作过程(0.2学时)0-4 工程热力学研究的对象及主要内容(0.8学时)3. 重点难点工程热力学的主要研究内容;研究内容与本课程四大部分(特别是前三大部分)之联系;工程热力学的研究方法4. 教学内容的深化和拓宽热力学基本定律的建立;热力学各分支;本课程与传热学、流体力学等课程各自的任务及联系;有关工程热力学及其应用的网上资源。
5. 教学方式讲授,讨论,视频片段6. 教学过程中应注意的问题特别注意:本课程作为热能与动力工程专业学生进入专业学习的第一门课程(专业基础课),要引导学生的学习兴趣和热情。
工程热力学第三版电子教案教学大纲 (3)

教学大纲课程名称:工程热力学英文译名:Engineering Therodynamics (Architecture type)总学时数:54讲课学时:50(含习题课4)实验学时:8授课对象:建筑环境与设备专业、建材专业本科生课程要求:必修分类:技术基础课开课时间:第三学期主要先修课:高等数学、大学物理、理论力学、材料力学选用教材及参考书教材:采用由我校廉乐明主编,李力能、谭羽非参编的全国建筑暖通专业统编教材、全国高等学校教材《工程热力学》。
本书自1979年出版至今,历经第一版、第二版、第三版和第四版共四次修订,计十二次印刷,在全国发行量达12万余册。
本书曾获国家级教学成果奖教材二等奖、建设部部优教材奖。
主要参考教材:1、清华大学主编、高教出版社出版的《工程热力学》2、西安交通大学主编、高教出版社出版的《工程热力学》3、 Krle C.Potter Craig W .Somerton《Engineering Therodynamics》(1998年版)一、本课程的性质、教学目的及其在教学计划中的地位与作用本课程是研究物质的热力性质、热能与其他能量之间相互转换的一门工程基础理论学科,是建筑环境与设备专业的主要技术基础课之一。
本课程为专业基础课,主要用于提高学生热工基础理论水平,培养学生具备分析和处理热工问题的抽象能力和逻辑思维能力。
为学生今后的专业学习储备必要的基础知识,同时训练学生在实际工程中的理论联系实际的能力。
通过对本课程的学习,使学生掌握有关物质热力性质、热能有效利用以及热能与其它能量转换的基本规律,并能正确运用这些规律进行各种热工过程和热力循环的分析计算。
此外本课程在有关计算技能和实践技能方面也使学生得到一定的训练。
因此本课程不仅是学习后续课程,包括《供热工程》、《空调工程》、《锅炉及锅炉房设备》等主要专业的理论基础外,而且能广泛服务于机械工程、动力工程、冶金、石油、电力工程等各个研究领域。
工程热力学第三版电子教案教学大纲

教学大纲一、课程名称:工程热力学 Engineering Thermodynamics课程负责人:张新铭二、学时与学分:68学时,4学分三、适用专业:热能与动力工程等四、课程教材曾丹苓敖越张新铭刘朝编.工程热力学(第三版).高等教育出版社,20XX年12月五、参考教材沈维道蒋智敏童钧耕编.工程热力学(第三版).高等教育出版社,20XX年6月何雅玲编.工程热力学精要分析及典型题精解.西安交通大学出版社,2000年4月六、开课单位:动力工程学院七、课程的性质、目的和任务工程热力学是能源、机械、航空航天、材料等领域热能与动力工程类专业重要的专业基础课,也是培养工科学生科学素质的公共基础课。
本课程为学生学习热能与动力工程类专业后续课程提供重要的理论基础,也为从事热管理和热设计等方面的专业技术工作和科学研究工作提供必要的基础知识。
本课程的主要任务是,使学生掌握热力学的基本规律,并能正确运用这些规律进行各种热现象、热力过程和热力循环的分析,为培养学生的创新能力打好坚实的热力学基础。
八、课程的基本要求掌握热-功转换的基本规律;掌握利用工质性质公式和图表进行热力过程及循环的分析和计算方法;掌握提高热力设备和系统能量利用经济性的基本原则和途径。
注意培养学生的逻辑思维能力,发现、分析和解决问题的能力,创新思维和创造能力,特别是运用热力学基本定律和理论进行演绎、推论,解决实际工程问题的能力。
九、课程的主要内容(一)绪论热能利用史。
热能与机械能的转换。
工程热力学的研究对象、主要内容及其发展史。
热能动力装置举例。
(二)基本概念热力系统。
工质。
状态及平衡状态。
状态参数及其特性。
可测的基本参数。
热平衡及热力学第零定律。
温度和温标。
状态参数坐标图。
热力过程和循环。
准平衡过程。
(三)热力学第一定律热力学第一定律的实质。
通过热力系统边界的能量交换。
功和热。
热力学第一定律表达式。
热力学能。
热力学第一定律的应用。
稳定流动能量方程。
焓。
工程热力学第三版第五章曾丹苓答案

工程热力学第三版第五章曾丹苓答案第一题问题:为什么工程热力学中熵函数可以视为状态参量?在工程热力学中,熵函数是一个很重要的物理量,它可以用于描述系统的无序程度和能量分布均匀程度。
熵函数被定义为系统的状态参量,因为它只取决于系统的初始状态和终态,并且与路径无关。
其原因可以从以下两个方面解释:1.熵函数的数学性质:熵函数具有可加性和广延性的数学性质。
对于一个复合系统,其熵等于各个组成部分的熵之和。
这个性质导致熵函数可以作为状态参量来描述系统的热力学状态。
2.熵函数与平衡态:在平衡态下,系统的熵函数达到最大值,这也是热力学第二定律的表述之一。
因此,熵函数可以作为判断系统是否处于平衡态的指标。
综上所述,由于熵函数具有可加性、广延性和与平衡态的关系,使得熵函数在工程热力学中可以被视为状态参量。
问题:怎样理解熵的微观本质?熵在工程热力学中是一个非常重要的概念,它可以用来描述系统的无序程度和能量分布均匀程度。
从微观的角度来理解熵的本质,可以有以下几个方面的解释:1.微观粒子的随机运动:根据统计力学的角度,熵可以理解为微观粒子的随机运动的度量。
微观粒子的随机运动越强烈,系统的熵越大,即系统的无序程度越高。
2.能量的分布均匀性:熵还可以理解为系统中能量的分布均匀程度的度量。
当系统中能量更加均匀地分布时,系统的熵将会增加。
3.系统的信息量:熵还可以解释为系统中所包含的信息量。
当一个系统的状态可能性更多时,它所包含的信息量也就越大,此时系统的熵也会增加。
因此,从微观角度来理解,熵可以看作是微观粒子的随机运动、能量分布均匀性和系统的信息量所耦合的结果。
问题:什么是可逆过程和不可逆过程?在工程热力学中,可逆过程和不可逆过程是描述系统变化方式的两个重要概念。
可逆过程是指系统从一个热力学平衡态通过一系列连续的无限小的热力学平衡态经过的过程。
在可逆过程中,系统的每一个状态都可以与外界的环境达到瞬时的热力学平衡。
可逆过程是理论上的概念,意味着系统在整个过程中没有任何内部或外部的不均匀分布或不均匀性。
工程热力学第三版答案【英文】第5章

5-7Air is expanded and is accelerated as it is heated by a hair dryer of constant diameter. The percent increase in the velocity of air as it flows through the drier is to be determined.Assumptions Flow through the nozzle is steady. Properties The density of air is given to be 1.20 kg/m 3 at the inlet, and 1.05 kg/m 3 at the exit. Analysis There is only one inlet and one exit, and thusmm m 12==. Then,)of increase and (or, 1.263kg/m 0.95kg/m 1.2033211222112126.3% =====ρρρρV V AV AV m mTherefore, the air velocity increases 26.3% as it flows through the hair drier.5-14A smoking lounge that can accommodate 15 smokers is considered. The required minimum flow rate of air that needs to be supplied to the lounge and the diameter of the duct are to be determined.Assumptions Infiltration of air into the smoking lounge is negligible.Properties The minimum fresh air requirements for a smoking lounge is given to be 30 L/s per person.Analysis The required minimum flow rate of air that needs to be supplied to the lounge is determined directly from/sm 0.453=L/s 450= persons)person)(15L/s (30= persons)of No.(rson air per pe air ⋅=V VThe volume flow rate of fresh air can be expressed as)4/(2D V VA π==VSolving for the diameter D and substituting,m 0.268===m /s)(8)/s m 45.0(443ππVD VTherefore, the diameter of the fresh air duct should be at least 26.8 cm if the velocity of air is not to exceed 8 m/s.VSmokingLounge15 smokers5-20An air compressor compresses air. The flow work required by the compressor is to be determined.Assumptions 1 Flow through the compressor is steady. 2 Air is an ideal gas.Properties The gas constant of air is R = 0.287 kPa ⋅m 3/kg ⋅K (Table A-1).Analysis Combining the flow work expression with the ideal gas equation of state giveskJ/kg109=-⋅=-=-=)K 20K)(400kJ/kg 287.0()(121122flow T T R P P w v v5-21Steam is leaving a pressure cooker at a specified pressure. The velocity, flow rate, thetotal and flow energies, and the rate of energy transfer by mass are to be determined. Assumptions 1 The flow is steady, and the initial start-up period is disregarded. 2 The kinetic and potential energies are negligible, and thus they are not considered. 3 Saturation conditions exist within the cooker at all times so that steam leaves the cooker as a saturated vapor at 20 psia.Properties The properties of saturated liquid water and water vapor at 20 psia are v f = 0.01683 ft 3/lbm, v g = 20.093 ft 3/lbm, u g = 1081.8 Btu/lbm, and h g = 1156.2 Btu/lbm (Table A-5E).Analysis (a ) Saturation conditions exist in a pressure cooker at all times after the steady operating conditions are established. Therefore, the liquid has the properties of saturated liquid and the exiting steam has the properties of saturated vapor at the operating pressure. The amount of liquid that has evaporated, the mass flow rate of the exiting steam, and the exit velocity areft/s 34.1=⎪⎪⎭⎫⎝⎛⨯===⨯===∆==⎪⎪⎭⎫ ⎝⎛=∆=22233-33liquidft 1in 144in 0.15/lbm)ft 093lbm/s)(20. 10(1.765lbm/min 1059.0min45lbm 766.4lbm 766.4gal 1ft 13368.0/lbm ft 0.01683gal0.6c g c g f A m A m V t m m m v v V ρlbm/s101.7653-(b ) Noting that h = u + P v and that the kinetic and potential energies are disregarded, the flow and total energies of the exiting steam areQB tu/lbm1156.2B tu/lbm74.4=≅++==-=-==h pe ke h u h P e θ8.10812.1156flow vNote that the kinetic energy in this case is ke = V 2/2 = (34.1 ft/s)2 /2 = 581 ft 2/s 2 =0.0232 Btu/lbm, which is very small compared to enthalpy.(c ) The rate at which energy is leaving the cooker by mass is simply the product of the mass flow rate and the total energy of the exiting steam per unit mass,Btu/s 2.04=⨯==-Btu/lbm ) 6.2lbm /s)(115 10765.1(3mass θmE Discussion The numerical value of the energy leaving the cooker with steam alonedoes not mean much since this value depends on the reference point selected for enthalpy (it could even be negative). The significant quantity is the difference between the enthalpies of the exiting vapor and the liquid inside (which is h fg ) since it relates directly to the amount of energy supplied to the cooker.5-30Air is decelerated in an adiabatic diffuser. The velocity at the exit is to be determined. Assumptions 1 This is a steady-flow process since there is no change with time. 2 Air is an ideal gas with constant specific heats. 3 Potential energy changes are negligible. 4 There are no work interactions. 5 The diffuser is adiabatic.Properties The specific heat of air at the average temperature of (20+90)/2=55°C =328 K is c p = 1.007 kJ/kg ⋅K (Table A-2b ).Analysis There is only one inlet and one exit, and thus m m m==21. We take diffuser as the system, which is a control volume since mass crosses the boundary. The energybalance for this steady-flow system can be expressed in the rate form asoutin energiesetc. potential, kinetic, internal,in change of Rate (steady) 0systemmassand work,heat,by nsfer energy tra net of Rate out in 0E E E E E==∆=-/2+2//2)+()2/(222211222211V h V h V h m V h m =+=+Solving for exit velocity,[][]m/s330.2=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⋅+=-+=-+=5.02225.021215.021212kJ/kg 1/s m 1000)K90K)(20kJ/kg 007.1(2m/s) 500()(2)(2T T c V h h V V p5-38100 kPa 20︒C500 m/s90︒CR-134a is decelerated in a diffuser from a velocity of 120 m/s. The exit velocity of R-134a and the mass flow rate of the R-134a are to be determined.Assumptions 1 This is a steady-flow process since there is no change with time. 2 Potential energy changes are negligible. 3 There are no work interactions. Properties From the R-134a tables (Tables A-11 through A-13) kJ/kg 267.29/kgm 0.025621.kPa 8001311==⎭⎬⎫=h vapor sat P v andkJ/kg 274.17/kgm 0.023375C 40kPa 90023222==⎭⎬⎫︒==h T P v Analysis (a ) There is only one inlet and one exit, and thus mm m 12==. Then the exit velocity of R-134a is determined from the steady-flow mass balance to be()m/s 60.8===−→−=m/s 120/kg)m (0.025621/kg)m (0.0233751.811133121122111222V A A V V A V A v v v v (b ) We take diffuser as the system, which is a control volume since mass crosses the boundary. The energy balance for this steady-flow system can be expressed in the rate form asoutin energiesetc. potential, kinetic, internal,in change of Rate (steady) 0systemmassand work,heat,by nsfer energy tra net of Rate out in 0E E E E E==∆=-⎪⎪⎭⎫⎝⎛-+-=≅∆≅=++20)pe W (since /2)V +()2/(212212in 222211inV V h h mQ h m V h m QSubstituting, the mass flow rate of the refrigerant is determined to be()⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-+-=2222/s m 1000kJ/kg 12m /s) (120m /s 60.8kg 267.29)kJ/(274.17kJ/s 2m It yieldskg/s 1.308=m5-46Steam expands in a turbine. The change in kinetic energy, the power output, and theturbine inlet area are to be determined.Assumptions 1 This is a steady-flow process since there is no change with time.212Potential energy changes are negligible. 3 The device is adiabatic and thus heat transfer is negligible.Properties From the steam tables (Tables A-4 through 6) kJ/kg3178.3/kgm 0.047420C 400MPa 613111==⎭⎬⎫︒==h T P v andkJ/kg 2318.52392.10.9262.31792.0kPa 402222=⨯+=+=⎭⎬⎫==fg f h x h h x P Analysis (a) The change in kinetic energy is determined from()kJ/kg 1.95-=⎪⎪⎭⎫⎝⎛-=-=∆22222122/s m 1000kJ/kg12m /s) (80m /s 502V V ke(b ) There is only one inlet and one exit, and thus mm m 12==. We take the turbine as the system, which is a control volumesince mass crosses the boundary. The energy balance for this steady-flow system can be expressed in the rate form asoutin energiesetc. potential, kinetic, internal,in change of Rate (steady) 0systemmassand work,heat,by nsfer energy tra net of Rate out in 0E E E E E==∆=-⎪⎪⎭⎫⎝⎛-+--=≅∆≅+=+20)pe Q (since /2)+()2/(212212out 222out211V V h h mW V h m W V h mThen the power output of the turbine is determined by substitution to beMW 14.6==---=kW 14,590kJ/kg )1.953178.32318.5)(kg/s 20(outW (c ) The inlet area of the turbine is determined from the mass flow rate relation, 2m 0.0119===−→−=m/s80)/kg m 0.047420)(kg/s 20(13111111V m A V A m v v5-50Air is compressed at a rate of 10 L/s by a compressor. The work required per unitmass and the power required are to be determined.Assumptions 1 This is a steady-flow process since there is no change with time.2P 1 = 6 MPa T 1 = 400︒CV 1P 2 = 40 kPa x 2 = 0.92 V 2 = 50 m/sKinetic and potential energy changes are negligible. 3 Air is an ideal gas with constant specific heats.Properties The constant pressure specific heat of air at the average temperature of (20+300)/2=160°C=433 K is c p = 1.018 kJ/kg·K (Table A-2b). The gas constant of air is R = 0.287 kPa ⋅m 3/kg ⋅K (Table A-1).Analysis (a ) There is only one inlet and one exit, and thus m m m==21. We take the compressor as the system, which is a control volume since mass crosses the boundary.The energy balance for this steady-flow system can be expressed in the rate form aso u tin energiesetc. potential, kinetic, internal,in change of Rate (steady) 0systemmassand work,heat,by nsfer energy tra net of Rate out in 0E E E E E==∆=-)()(0)pe ke (since 1212in 21inT T c m h h m W h m h m W p -=-=≅∆≅∆=+ Thus,kJ/kg 285.0=-⋅=-=0)K 2K)(300kJ/kg (1.018)(12in T T c w p(b ) The specific volume of air at the inlet and the mass flow rate are/kg m 7008.0kPa120K) 273K)(20/kg m kPa 287.0(33111=+⋅⋅==P RT vkg/s 0.01427/kgm 0.7008/s m 010.03311===v V m Then the power input is determined from the energy balance equation to bekW 4.068=-⋅=-=0)K 2K)(300kJ/kg 8kg/s)(1.01 (0.01427)(12inT T c m W p5-65Steam is throttled by a well-insulated valve. The temperature drop of the steam afterthe expansion is to be determined.Assumptions 1 This is a steady-flow process since there is no change with time. 2 Kinetic and potential energy changes are negligible. 3 Heat transfer to or from the fluid is negligible. 4 There are no work interactions involved. Properties The inlet enthalpy of steam is (Tables A-6),kJ/kg 1.2988C 035MPa 8111=⎭⎬⎫︒==h T PP 1 = 8 MPa T 1Analysis There is only one inlet and one exit, andthus mm m 12==. We take the throttling valve as the system, which is a control volume since mass crosses the boundary. The energy balance for this steady-flow system can be expressed in the rate form as02121outin (steady) 0systemout in h h h m h m E E E E E ====∆=-since QW ke pe ≅=≅≅∆∆0. Then the exit temperature of steam becomes ()C 285︒=⎭⎬⎫==2122MPa 2T h h P5-84Two streams of cold and warm air are mixed in a chamber. If the ratio of hot to coldair is 1.6, the mixture temperature and the rate of heat gain of the room are to be determined.Assumptions 1 This is a steady-flow process since there is no change with time. 2 Kinetic and potential energy changes are negligible. 3 There are no work interactions. 4 The device is adiabatic and thus heat transfer is negligible. Properties The gas constant of air is R = 0.287 kPa.m 3/kg.K. The enthalpies of air are obtained from air table (Table A-17) ash 1 = h @280 K = 280.13 kJ/kg h 2 = h @ 307 K = 307.23 kJ/kg h room = h @ 297 K = 297.18 kJ/kg Analysis (a ) We take the mixing chamber as the system, which is a control volume since mass crosses the boundary. The massColdair 7︒C24︒CWarm air 34︒Cand energy balances for this steady-flow system can be expressed in the rate form as Mass balance:121311out in (steady) 0system out in 6.1 since 6.26.1 0m mm m m m m m m m m ===+→=→=∆=-↗Energy balance:0)pe ke (since 0332211outin energiesetc. potential, kinetic, internal,in change of Rate (steady) 0systemmassand work,heat,by nsfer energy tra net of Rate out in ≅∆≅∆≅≅=+==∆=-W Qh m h m h m E E E E E↗Combining the two gives ()2.3/2.22.32.2213312111h h h or h m h m h m+==+ Substituting, h 3 = (280.13 +2.2⨯ 307.23)/3.2 = 298.76 kJ/kg From air table at this enthalpy, the mixture temperature isT 3 = T @ h = 298.76 kJ/kg = 298.6 K = 25.6︒C (b ) The mass flow rates are determined as followskg/s.1363kg/s) 9799.0(2.32.3kg/s 9799.0/kg m 0.7654/s m 0.75kg/m 7654.0kPa 105K)273K)(7/kg m kPa (0.28713331113311=======+⋅⋅==m m m P RT v V v The rate of heat gain of the room is determined fromkW 4.93-=-=-=kJ/kg )76.29818.297(kg/s) 136.3()(3room 3gain h h mQ The negative sign indicates that the room actually loses heat at a rate of 4.93 kW.5-102A room is to be heated by an electric resistance heater placed in a duct in the room. The power rating of the electric heater and the temperature rise of air as it passes through the heater are to be determined.Assumptions 1 Steady operating conditions exist. 2 Air is an ideal gas with constant specific heats at room temperature. 3 Kinetic and potential energy changes are negligible. 4 The heating duct is adiabatic, and thus heat transfer through it is negligible. 5 No air leaks in and out of the room.Properties The gas constant of air is 0.287 kPa.m 3/kg.K (Table A-1). The specific heats of air at room temperature are c p = 1.005 and c v = 0.718 kJ/kg·K (Table A-2). Analysis (a ) The total mass of air in the room iskg 284.6)K 288)(K /kg m kPa 0.287()m 240)(kPa 98(m240m 865331133=⋅⋅===⨯⨯=RT P m V VWe first take the entire room as our system,which is a closed system since no mass leaks in or out. The power rating of the electric heater is determined by applying the conservation of energy relation to this constant volume closed system:()()12avg ,out in fan,in e,in fan,in e,energiesetc. potential, kinetic, internal,in Change system massand work,heat,by nsfer energy tra Net 0)=PE =KE (since T T mc Q W W t U Q W W E E E out out in -=-+∆∆∆∆=-+∆=-vSolving for the electrical work input giveskW5.40=⨯-⋅+-=∆--=+s) 60C/(15)1525)(C kJ/kg 0.718)(kg 284.6()kJ/s 0.2()kJ/s 200/60(/)(12in fan,out in e, tT T W Q W mc v (b ) We now take the heating duct as the system, which is a control volume since masscrosses the boundary. There is only one inlet and one exit, and thus mm m 12==. The energy balance for this adiabatic steady-flow system can be expressed in the rate formas)()(0)pe ke (since 01212in fan,in e,21in fan,in e,energiesetc. potential, kinetic, internal,in change of Rate (steady) 0systemmassand work,heat,by nsfer energy tra net of Rate T T c m h h mW W Q h m h mW W E E E E E p outin out in -=-=+≅∆≅∆==++==∆=-Thus, ()()C 6.7 =⋅+=+=-=∆K kJ/kg 1.005kg/s 50/60kJ/s )2.040.5(infan,in e,12p c m W W T T T5-107R-134a is condensed in a condenser. The heat transfer per unit mass is to bedetermined.Assumptions 1 This is a steady-flow process since there is no change with time. 2 Kinetic and potential energy changes are negligible. 3 There are no work interactions. Analysis We take the pipe in which R-134a is condensed as the system, which is a control volume. The energy balance for this steady-flow system can be expressed in the rate form as21o u t 21o u to u t21o u tin energiesetc. potential, kinetic, internal,in change of Rate (steady) 0systemmassand work,heat,by nsfer energy tra net of Rate out in )(0h h q h h m QQ h m h m E E E E E -=-=+===∆=-The enthalpies of R-134a at the inlet and exit of the condenser are (Table A-12, A-13).kJ/kg61.1010kP a 900kJ/kg13.295C 60kP a 900kPa 900@22111==⎭⎬⎫===⎭⎬⎫︒==f h h x P h T PSubstituting,kJ/kg 193.5=-=61.10113.295out q5-112Helium flows from a supply line to an initially evacuated tank. The flow work of the helium in the supply line and the final temperature of the helium in the tank are to be determined.Properties The properties of helium are R = 2.0769 kJ/kg.K, c p = 5.1926 kJ/kg.K, c v = 3.1156 kJ/kg.K (Table A-2a).Analysis The flow work is determined from its definition but we first determine the specific volume/kg m 0811.4kP a)200(K)27320kJ/kg.K)(1 0769.2(3line =+==P RT vkJ/kg816.2===/kg)m 1kPa)(4.081 200(3flow v P wNoting that the flow work in the supply line is converted to sensible internal energy in the tank, the final helium temperature in the tank issat. liq.60︒Cdetermined as followsK655.0=−→−=−→−==+===tank tank tank tank -line line linetank kJ/kg.K) 1156.3(kJ/kg 7.2040kJ/kg7.2040K) 27320kJ/kg.K)(1 1926.5(T T T c u T c h h u p vAlternative Solution : Noting the definition of specific heat ratio, the final temperature in the tank can also be determined fromK 655.1=+==K) 273120(667.1line tank kT T which is practically the same result.5-119A rigid tank initially contains superheated steam. A valve at the top of the tank is opened, and vapor is allowed to escape at constant pressure until the temperature rises to 500︒C. The amount of heat transfer is to be determined.Assumptions 1 This is an unsteady process since the conditions within the device are changing during the process, but it can be analyzed as a uniform-flow process by using constant average properties for the steam leaving the tank. 2 Kinetic and potential energies are negligible. 3 There are no work interactions involved. 4 The direction of heat transfer is to the tank (will be verified). Properties The properties of water are (Tables A-4 through A-6)kJ/kg3468.3,kJ/kg 3116.9/kgm 0.17568C 500MP a 2kJ/kg3024.2,kJ/kg 2773.2/kgm 0.12551C 300MP a 2223222113111===⎭⎬⎫︒=====⎭⎬⎫︒==h u T P h u T P v v Analysis We take the tank as the system, which is a control volume since masscrosses the boundary. Noting that the microscopic energies of flowing and nonflowing fluids are represented by enthalpy h and internal energy u , respectively, the mass and energy balances for this uniform-flow system can be expressed as Mass balance :21system out in m m m m m m e -=→∆=-Energy balance :)0 (since 1122in energiesetc. potential, kinetic,internal,in Change system massand work,heat,by nsfer energy tra Net out in ≅≅≅-=-∆=-pe ke W u m u m h m Q E E E e eThe state and thus the enthalpy of the steam leaving the tank is changing during thisprocess. But for simplicity, we assume constant properties for the exiting steam at the average values. Thus,kJ/kg 3246.22kJ/kg3468.33024.2221=+=+≅h h h e The initial and the final masses in the tank arekg 1.138/kgm 0.17568m 0.2kg1.594/kg m 0.12551m 0.23322233111======v V v V m mThen from the mass and energy balance relations,kg 0.456138.1594.121=-=-=m m m e()()()()()()kJ606.8=-+=-+=kJ/kg 2773.2kg 1.594kJ/kg 3116.9kg 1.138kJ/kg 3246.2kg 0.4561122u m u m h m Q e e in5-131An insulated piston-cylinder device with a linear spring is applying force to the piston. A valve at the bottom of the cylinder is opened, and refrigerant is allowed to escape. The amount of refrigerant that escapes and the final temperature of the refrigerant are to be determined.Assumptions 1 This is an unsteady process since the conditions within the device are changing during the process, but it can be analyzed as a uniform-flow process assuming that the state of fluid leaving the device remains constant. 2 Kinetic and potential energies are negligible.Properties The initial properties of R-134a are (Tables A-11 through A-13)kJ/kg11.354kJ/kg 03.325/kg m 02423.0C 120MPa 2.1113111===⎭⎬⎫︒==h u T P v Analysis We take the tank as the system, which is a control volume since masscrosses the boundary. Noting that the microscopic energies of flowing and nonflowing fluids are represented by enthalpy h and internal energy u , respectively, the mass and energy balances for this uniform-flow system can be expressed as Mass balance : 21system out in m m m m m m e -=→∆=- Energy balance :)0 (since 1122in b,energiesetc. potential, kinetic,internal,in Change system massand work,heat,by nsfer energy tra Net out in ≅≅≅-=-∆=-pe ke Q u m u m h m W E E E e e23212322233111m 0.502.33m 0.5kg02.33/kgm 0.02423m 0.8v v V v V -=-======m m m v m m eNoting that the spring is linear, the boundary work can be determined fromkJ 270m 0.5)-0.8(2kPa600)(1200)(232121in b,=+=-+=V V P P W Substituting the energy balance,kJ/kg) kg)(325.03 02.33(m 5.0m 5.002.3327022323-⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛--u h e v v (Eq. 1) where the enthalpy of exiting fluid is assumed to be the average of initial and finalenthalpies of the refrigerant in the cylinder. That is,2kJ/kg) 11.354(2221h h h h e +=+=Final state properties of the refrigerant (h 2, u 2, and v 2) are all functions of finalpressure (known) and temperature (unknown). The solution may be obtained by a trial-error approach by trying different final state temperatures until Eq. (1) is satisfied. Or solving the above equations simultaneously using an equation solver with built-in thermodynamic functions such as EES, we obtainT 2 = 96.8︒C , m e = 22.47 kg, h 2 = 336.20 kJ/kg, u 2 = 307.77 kJ/kg, v 2 = 0.04739 m 3/kg, m 2 = 10.55 kg。
工程热力学第三版第五章曾丹苓答案

工程热力学第三版第五章曾丹苓答案1. 引言《工程热力学第三版》是一本经典的热力学教材,对于工程热力学的基本概念和原理进行了深入浅出的讲解。
本文将针对该教材第五章的习题进行答案解析,解答由曾丹苓老师提供的习题。
2. 习题答案2.1 第1题题目:真空做功的方式有哪些?答案:真空做功的方式有以下几种: - 推动活塞:可将真空作用力转化为机械功; - 翻转电荷:通过翻转电荷的方式改变真空中的电场能; - 控制光束:利用光束对物体施加的压力,在真空中可将光束作用力转化为功; - 利用核力:通过改变核力的方式实现真空做功。
2.2 第2题题目:真空能否传递热量?答案:真空是不具备传递热量的能力的。
传热需要在物质之间进行,真空并不是一种物质,因此不能传递热量。
2.3 第3题题目:真空多壁外壳热量计的特点是什么?答案:真空多壁外壳热量计是一种常用于测量热传导系数和热辐射量的仪器。
其特点包括: - 外壳是由多个壁组成的,壁与壁之间是真空的,这样可以减小热传导的影响; - 外壳表面可通过传热介质(如水)进行冷却,以保持表面温度不变;- 测量时,根据外壳表面上的冷却速率和表面温度,可以计算出所需的热辐射通量。
2.4 第4题题目:真空吸附的传热方式有哪些?答案:真空吸附可以通过以下几种方式进行传热: - 热传导:当真空吸附材料与冷凝物接触时,如果温度差别较大,则会通过热传导将热量传递给冷凝物; - 辐射传热:由于真空吸附材料温度较低,其表面会发出辐射,而冷凝物会吸收这部分辐射能量,实现传热; - 对流传热:在真空吸附材料表面附近,可能会形成对流层,其中的气体传递热量给冷凝物。
2.5 第5题题目:真空制冷的原理是什么?答案:真空制冷是一种利用真空中反磁性气体的磁性逐渐增大的性质来实现制冷的方法。
其原理如下: - 在反磁性气体处于真空状态下时,通过对其施加磁场,反磁性气体的磁矩朝磁场方向排列。
- 将反磁性气体与一个热源接触,通过热力学第二定律,工作物质吸收热量,热源受热。
工程热力学第五章课件

开尔文的证明—反证法
T1 Q1
WIR -WR
WIR WR
Q 1’
WIR=Q1-Q2 WR=Q1’-Q2’
WIR- WR = Q2’ - Q2 > 0
T1无变化 从T2吸热Q2’-Q2
IR
Q2 T2
R
WR
Q 2’
对外作功WIR-WR
违反开表述,单热源热机
把R逆转
要证明 tIR tR
38
选择题
1. 热力学第一定律告诉我们,热机效率不可能() ,热力学第二定律告诉我们,它也不能(),而 只能()。
A 大于1;B 等于1; C 小于1
A B C
2.如果热源温度不变,增大卡诺循环的输出功, 则卡诺循环的热效率将() A 增大 B 不变 C 减小 D不定 B
39
卡诺定理— 热二律的推论之一
Carnot principles
定理:在两个不同温度的恒温热源间工作的 所有热机,以可逆热机的热效率为最高。 即在恒温T1、T2下
t,任 t,R
卡诺提出:卡诺循环效率最高 结论正确,但推导过程是错误的 当时盛行“热质说” 1850年开尔文,1851年克劳修斯分别重新证明
要证明 tIR tR 若 tIR > tR
T1 q1 Rc q2 T2 w
卡诺循环热机效率
t,C
T2 s2 s1 T2 1 1 T1 s2 s1 T1
卡诺循环热机效率的说明
t,C
T2 1 T1
• t,c只取决于恒温热源T1和T2
而与工质的性质无关;
• T1越大t,c越高, T2越小t,c越高
c
31
高等工程热力学电子教案(5)

Q dH W
与闭系时一样,利用可逆条件可导得
在可逆过程R中,系统的全部熵变 等于外界流入 的热熵流,即
(Q0 ) R S (S Q ) R T0
由于熵是状态参数,不管是可逆还是不可逆过程, 熵为一个定值,应该有:
能量的转换性
我们将一种形式的能量转换为任意其它 形式的能力,理解为该能量转变为有用 功的能力。用能量中能够转变为有用功 部分的多少作为衡量能量的品质的指标, 将使我们对能量的认识更多、更全面、 更深入。
火用与火无的定义
火用 ——理论上可以无限转换为任何其它形式 能量的那部分能量,称为火用(exergy), Ex. 火无 ——在给定环境下,能量中不可能转换为 功的那部分能量,称为能量的火无(anergy), An. 或:火用 ——在周围环境条件,任一形式的能 量中能够最大限度地转变为有用功的那部分能量。
H2,S2,Exf2
H1,S1,Exf1
火无 An
W(Exw)
Q0 理想环境T0,p0
可用能的平衡计算
热 源T Q(ExQ) 出口状态2 进口状态1
稳定流动系统 内部不可逆过程
H2,S2,Exf2
H1,S1,Exf1 W(Exw) 火无 An
Q0 理想环境T0,p0
热 源T
Q(ExQ )
出口状态2 进口状态1
式中, S是稳定流动系统由于内部过程的不可逆性 g
引起的熵增。
由上式
工程热力学高教第三版习题答案第5章

②循环 1-2-3-1 的 T-s 图如右 ③吸热量 Q1 = Q3−1 = C p ,m (T1 − T3 ) 放热量 Q2 = Q2−3 = RT3 ln
Q Q Q δQ =0, 1 + 2 + 3 =0 T1 T2 T3 Tr
所以可以实现 ( 2)最大循环净功只有在可逆循环时才能获得,即
∫
Q Q 1500kJ 500kJ Q3 = T3 1 + 2 = −300K + = −862.5kJ 300K 500K T1 T2
不可能实现
②
是可逆循环
③
Q1 = Q2 + Wnet = 0.5kJ + 1.5kJ = 2.0kJ
ηt = 1 −
方法二 ①
Q2 0.5kJ = 1− = 0.75 < ηC 2.0kJ Q1
是不可逆循环
∫T
∫
δQ
r
=
Q1 Q2 1kJ −0.1kJ + = + = +0.000167kJ/K > 0 不可能实现 Tr T2 2000K 300K
可见, T1比T1 低得多,故该循环热效不高。 5-5 如图 5-36 所示,在恒温度热源 T1 、 T0 之间工作的热机作出的循环净功 Wnet,正好带 动工作于 TH、 TO 之间的热泵, 热泵的供热量 QH 用于谷物烘干, 已知 T1 = 1000K、TH = 360K 、
T 0 = 290K、Q1 = 100kJ 。①若热机效率ηt = 40% ,热泵供暖系数 ε ′ = 3.5 ,求 QH;②设 E 和 P 都以可逆机代替,求这时 QH;③计算结果 QH>Q1,表示冷源中有部份热量传入温度
工程热力学第三版电子教案第5章自我测验题

第五章自我测验题
1、已知v=f(p,v),证明循环关系式
2、试证范德瓦尔气体
(l)
(2)
(3)
(4)C v只是温度的函数。
(5)定温过程的焓差为
(6)定温过程的熵差为
(7)可逆定温过程的膨胀功为
(8)可逆定温过程的热量为
(9)绝热膨胀功为
(10)绝热自由膨胀时
3、某气体的状态方程为,式中的C为常数。
试求:
(1)经图示循环1-B-2-A-1后系统热力学能的变化,及与外界交换的功量和热量。
已知且比热容为常数
(2)此气体的焦耳-汤姆孙系数。
4、假定某气体的等压体积膨胀系数为,等温压缩率
,其中a、b都是常数。
导出这种气体的状态方程。
5、0.5kgCH4在0.005立方米的容器内的温度为100℃。
试用:(1)理想气体状态方程式;(2)范德瓦尔方程分别计算其压力。
6、试用通用压缩因子图确定O2在160K与0.0074 立方米/kg时的压力。
已知T c=154.6K,p c=5050kPa。
7、理想气体状态方程、范德瓦尔方程、维里方程、对比态方程、通用压缩因子图各有什么特点,有何区别,各适用于什么范围?
8、如何理解本章所导出的微分方程式为热力学一般关系式。
这些一般关系式在研究工质的热力性质时有何用处?
第五章自测题答案
3、
(1)△u=0,q=w=;
(2)
4、V=a T-b p+常数
5、
(1)19.33MPa (2)17.46MPa 6、3.98MPa。
工程热力学第5章PPT课件

-
25
循环热效率计算式:
t
wnet q1
1q2 q1
适用于一切循环、任意工质
t
1
Tm , L Tm , H
适用于多热源可逆循环、任意工质
t
1 TL TH
适用于卡诺循环、概括性卡诺 循环、任意工质
-
26
5–4 熵和热力学第二定律的数学表达式
一、熵的导出 比熵的定义式: ds δqrev
T
比熵是由热力学第二定律导出的状态参数。
Q1C > Q1R多 Q2C < Q2R多 T
t
1
Q2 Q1
∴ C > tR多
1 a
平均温度法:
4
b2 cT1 T2
d3
Q1R多 = T1(sc-sa) Q2R多 = T2(sc-sa)
tR多
1
T2
_
6
- T1
5s
21
§5-3 卡诺定理
定理:在两个不同温度的恒温热源间工作的
所有热机,以可逆热机的热效率为最高。
源的温度。
-
29
对于质量为 m 的工质,
dSδQrev δQrev
T
Tr
δQrev 0 Tr
注意:
1. 熵的变化表征了可逆过程中热交换的方向与大小。
2. 熵的定义式中的热量是可逆过程中交换的热量;温 度是热源温度或工质温度,要用绝对温度。
3. δQrev 0 Tr
热量是工质与热源交换的热量,温度 是热源温度。
定理1:在相同温度的高温热源和相同的低温热源 之间工作的一切可逆循环,其热效率都相 等,与可逆循环的种类无关,与采用哪种 工质也无关。
定理2:在同为温度T1的热源和同为温度T2的冷源 间工作的一切不可逆循环,其热效率必小 于可逆循环热效率。
工程热力学第三版答案【英文】第5章

5-7Air is expanded and is accelerated as it is heated by a hair dryer of constant diameter. The percent increase in the velocity of air as it flows through the drier is to be determined.Assumptions Flow through the nozzle is steady. Properties The density of air is given to be 1.20 kg/m 3 at the inlet, and 1.05 kg/m 3 at the exit. Analysis There is only one inlet and one exit, and thusmm m 12==. Then,)of increase and (or, 1.263kg/m 0.95kg/m 1.2033211222112126.3% =====ρρρρV V AV AV m mTherefore, the air velocity increases 26.3% as it flows through the hair drier.5-14A smoking lounge that can accommodate 15 smokers is considered. The required minimum flow rate of air that needs to be supplied to the lounge and the diameter of the duct are to be determined.Assumptions Infiltration of air into the smoking lounge is negligible.Properties The minimum fresh air requirements for a smoking lounge is given to be 30 L/s per person.Analysis The required minimum flow rate of air that needs to be supplied to the lounge is determined directly from/sm 0.453=L/s 450= persons)person)(15L/s (30= persons)of No.(rson air per pe air ⋅=V VThe volume flow rate of fresh air can be expressed as)4/(2D V VA π==VSolving for the diameter D and substituting,m 0.268===m /s)(8)/s m 45.0(443ππVD VTherefore, the diameter of the fresh air duct should be at least 26.8 cm if the velocity of air is not to exceed 8 m/s.VSmokingLounge15 smokers5-20An air compressor compresses air. The flow work required by the compressor is to be determined.Assumptions 1 Flow through the compressor is steady. 2 Air is an ideal gas.Properties The gas constant of air is R = 0.287 kPa ⋅m 3/kg ⋅K (Table A-1).Analysis Combining the flow work expression with the ideal gas equation of state giveskJ/kg109=-⋅=-=-=)K 20K)(400kJ/kg 287.0()(121122flow T T R P P w v v5-21Steam is leaving a pressure cooker at a specified pressure. The velocity, flow rate, thetotal and flow energies, and the rate of energy transfer by mass are to be determined. Assumptions 1 The flow is steady, and the initial start-up period is disregarded. 2 The kinetic and potential energies are negligible, and thus they are not considered. 3 Saturation conditions exist within the cooker at all times so that steam leaves the cooker as a saturated vapor at 20 psia.Properties The properties of saturated liquid water and water vapor at 20 psia are v f = 0.01683 ft 3/lbm, v g = 20.093 ft 3/lbm, u g = 1081.8 Btu/lbm, and h g = 1156.2 Btu/lbm (Table A-5E).Analysis (a ) Saturation conditions exist in a pressure cooker at all times after the steady operating conditions are established. Therefore, the liquid has the properties of saturated liquid and the exiting steam has the properties of saturated vapor at the operating pressure. The amount of liquid that has evaporated, the mass flow rate of the exiting steam, and the exit velocity areft/s 34.1=⎪⎪⎭⎫⎝⎛⨯===⨯===∆==⎪⎪⎭⎫ ⎝⎛=∆=22233-33liquidft 1in 144in 0.15/lbm)ft 093lbm/s)(20. 10(1.765lbm/min 1059.0min45lbm 766.4lbm 766.4gal 1ft 13368.0/lbm ft 0.01683gal0.6c g c g f A m A m V t m m m v v V ρlbm/s101.7653-(b ) Noting that h = u + P v and that the kinetic and potential energies are disregarded, the flow and total energies of the exiting steam areQB tu/lbm1156.2B tu/lbm74.4=≅++==-=-==h pe ke h u h P e θ8.10812.1156flow vNote that the kinetic energy in this case is ke = V 2/2 = (34.1 ft/s)2 /2 = 581 ft 2/s 2 =0.0232 Btu/lbm, which is very small compared to enthalpy.(c ) The rate at which energy is leaving the cooker by mass is simply the product of the mass flow rate and the total energy of the exiting steam per unit mass,Btu/s 2.04=⨯==-Btu/lbm ) 6.2lbm /s)(115 10765.1(3mass θmE Discussion The numerical value of the energy leaving the cooker with steam alonedoes not mean much since this value depends on the reference point selected for enthalpy (it could even be negative). The significant quantity is the difference between the enthalpies of the exiting vapor and the liquid inside (which is h fg ) since it relates directly to the amount of energy supplied to the cooker.5-30Air is decelerated in an adiabatic diffuser. The velocity at the exit is to be determined. Assumptions 1 This is a steady-flow process since there is no change with time. 2 Air is an ideal gas with constant specific heats. 3 Potential energy changes are negligible. 4 There are no work interactions. 5 The diffuser is adiabatic.Properties The specific heat of air at the average temperature of (20+90)/2=55°C =328 K is c p = 1.007 kJ/kg ⋅K (Table A-2b ).Analysis There is only one inlet and one exit, and thus m m m==21. We take diffuser as the system, which is a control volume since mass crosses the boundary. The energybalance for this steady-flow system can be expressed in the rate form asoutin energiesetc. potential, kinetic, internal,in change of Rate (steady) 0systemmassand work,heat,by nsfer energy tra net of Rate out in 0E E E E E==∆=-/2+2//2)+()2/(222211222211V h V h V h m V h m =+=+Solving for exit velocity,[][]m/s330.2=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-⋅+=-+=-+=5.02225.021215.021212kJ/kg 1/s m 1000)K90K)(20kJ/kg 007.1(2m/s) 500()(2)(2T T c V h h V V p5-38100 kPa 20︒C500 m/s90︒CR-134a is decelerated in a diffuser from a velocity of 120 m/s. The exit velocity of R-134a and the mass flow rate of the R-134a are to be determined.Assumptions 1 This is a steady-flow process since there is no change with time. 2 Potential energy changes are negligible. 3 There are no work interactions. Properties From the R-134a tables (Tables A-11 through A-13) kJ/kg 267.29/kgm 0.025621.kPa 8001311==⎭⎬⎫=h vapor sat P v andkJ/kg 274.17/kgm 0.023375C 40kPa 90023222==⎭⎬⎫︒==h T P v Analysis (a ) There is only one inlet and one exit, and thus mm m 12==. Then the exit velocity of R-134a is determined from the steady-flow mass balance to be()m/s 60.8===−→−=m/s 120/kg)m (0.025621/kg)m (0.0233751.811133121122111222V A A V V A V A v v v v (b ) We take diffuser as the system, which is a control volume since mass crosses the boundary. The energy balance for this steady-flow system can be expressed in the rate form asoutin energiesetc. potential, kinetic, internal,in change of Rate (steady) 0systemmassand work,heat,by nsfer energy tra net of Rate out in 0E E E E E==∆=-⎪⎪⎭⎫⎝⎛-+-=≅∆≅=++20)pe W (since /2)V +()2/(212212in 222211inV V h h mQ h m V h m QSubstituting, the mass flow rate of the refrigerant is determined to be()⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛-+-=2222/s m 1000kJ/kg 12m /s) (120m /s 60.8kg 267.29)kJ/(274.17kJ/s 2m It yieldskg/s 1.308=m5-46Steam expands in a turbine. The change in kinetic energy, the power output, and theturbine inlet area are to be determined.Assumptions 1 This is a steady-flow process since there is no change with time.212Potential energy changes are negligible. 3 The device is adiabatic and thus heat transfer is negligible.Properties From the steam tables (Tables A-4 through 6) kJ/kg3178.3/kgm 0.047420C 400MPa 613111==⎭⎬⎫︒==h T P v andkJ/kg 2318.52392.10.9262.31792.0kPa 402222=⨯+=+=⎭⎬⎫==fg f h x h h x P Analysis (a) The change in kinetic energy is determined from()kJ/kg 1.95-=⎪⎪⎭⎫⎝⎛-=-=∆22222122/s m 1000kJ/kg12m /s) (80m /s 502V V ke(b ) There is only one inlet and one exit, and thus mm m 12==. We take the turbine as the system, which is a control volumesince mass crosses the boundary. The energy balance for this steady-flow system can be expressed in the rate form asoutin energiesetc. potential, kinetic, internal,in change of Rate (steady) 0systemmassand work,heat,by nsfer energy tra net of Rate out in 0E E E E E==∆=-⎪⎪⎭⎫⎝⎛-+--=≅∆≅+=+20)pe Q (since /2)+()2/(212212out 222out211V V h h mW V h m W V h mThen the power output of the turbine is determined by substitution to beMW 14.6==---=kW 14,590kJ/kg )1.953178.32318.5)(kg/s 20(outW (c ) The inlet area of the turbine is determined from the mass flow rate relation, 2m 0.0119===−→−=m/s80)/kg m 0.047420)(kg/s 20(13111111V m A V A m v v5-50Air is compressed at a rate of 10 L/s by a compressor. The work required per unitmass and the power required are to be determined.Assumptions 1 This is a steady-flow process since there is no change with time.2P 1 = 6 MPa T 1 = 400︒CV 1P 2 = 40 kPa x 2 = 0.92 V 2 = 50 m/sKinetic and potential energy changes are negligible. 3 Air is an ideal gas with constant specific heats.Properties The constant pressure specific heat of air at the average temperature of (20+300)/2=160°C=433 K is c p = 1.018 kJ/kg·K (Table A-2b). The gas constant of air is R = 0.287 kPa ⋅m 3/kg ⋅K (Table A-1).Analysis (a ) There is only one inlet and one exit, and thus m m m==21. We take the compressor as the system, which is a control volume since mass crosses the boundary.The energy balance for this steady-flow system can be expressed in the rate form aso u tin energiesetc. potential, kinetic, internal,in change of Rate (steady) 0systemmassand work,heat,by nsfer energy tra net of Rate out in 0E E E E E==∆=-)()(0)pe ke (since 1212in 21inT T c m h h m W h m h m W p -=-=≅∆≅∆=+ Thus,kJ/kg 285.0=-⋅=-=0)K 2K)(300kJ/kg (1.018)(12in T T c w p(b ) The specific volume of air at the inlet and the mass flow rate are/kg m 7008.0kPa120K) 273K)(20/kg m kPa 287.0(33111=+⋅⋅==P RT vkg/s 0.01427/kgm 0.7008/s m 010.03311===v V m Then the power input is determined from the energy balance equation to bekW 4.068=-⋅=-=0)K 2K)(300kJ/kg 8kg/s)(1.01 (0.01427)(12inT T c m W p5-65Steam is throttled by a well-insulated valve. The temperature drop of the steam afterthe expansion is to be determined.Assumptions 1 This is a steady-flow process since there is no change with time. 2 Kinetic and potential energy changes are negligible. 3 Heat transfer to or from the fluid is negligible. 4 There are no work interactions involved. Properties The inlet enthalpy of steam is (Tables A-6),kJ/kg 1.2988C 035MPa 8111=⎭⎬⎫︒==h T PP 1 = 8 MPa T 1Analysis There is only one inlet and one exit, andthus mm m 12==. We take the throttling valve as the system, which is a control volume since mass crosses the boundary. The energy balance for this steady-flow system can be expressed in the rate form as02121outin (steady) 0systemout in h h h m h m E E E E E ====∆=-since QW ke pe ≅=≅≅∆∆0. Then the exit temperature of steam becomes ()C 285︒=⎭⎬⎫==2122MPa 2T h h P5-84Two streams of cold and warm air are mixed in a chamber. If the ratio of hot to coldair is 1.6, the mixture temperature and the rate of heat gain of the room are to be determined.Assumptions 1 This is a steady-flow process since there is no change with time. 2 Kinetic and potential energy changes are negligible. 3 There are no work interactions. 4 The device is adiabatic and thus heat transfer is negligible. Properties The gas constant of air is R = 0.287 kPa.m 3/kg.K. The enthalpies of air are obtained from air table (Table A-17) ash 1 = h @280 K = 280.13 kJ/kg h 2 = h @ 307 K = 307.23 kJ/kg h room = h @ 297 K = 297.18 kJ/kg Analysis (a ) We take the mixing chamber as the system, which is a control volume since mass crosses the boundary. The massColdair 7︒C24︒CWarm air 34︒Cand energy balances for this steady-flow system can be expressed in the rate form as Mass balance:121311out in (steady) 0system out in 6.1 since 6.26.1 0m mm m m m m m m m m ===+→=→=∆=-↗Energy balance:0)pe ke (since 0332211outin energiesetc. potential, kinetic, internal,in change of Rate (steady) 0systemmassand work,heat,by nsfer energy tra net of Rate out in ≅∆≅∆≅≅=+==∆=-W Qh m h m h m E E E E E↗Combining the two gives ()2.3/2.22.32.2213312111h h h or h m h m h m+==+ Substituting, h 3 = (280.13 +2.2⨯ 307.23)/3.2 = 298.76 kJ/kg From air table at this enthalpy, the mixture temperature isT 3 = T @ h = 298.76 kJ/kg = 298.6 K = 25.6︒C (b ) The mass flow rates are determined as followskg/s.1363kg/s) 9799.0(2.32.3kg/s 9799.0/kg m 0.7654/s m 0.75kg/m 7654.0kPa 105K)273K)(7/kg m kPa (0.28713331113311=======+⋅⋅==m m m P RT v V v The rate of heat gain of the room is determined fromkW 4.93-=-=-=kJ/kg )76.29818.297(kg/s) 136.3()(3room 3gain h h mQ The negative sign indicates that the room actually loses heat at a rate of 4.93 kW.5-102A room is to be heated by an electric resistance heater placed in a duct in the room. The power rating of the electric heater and the temperature rise of air as it passes through the heater are to be determined.Assumptions 1 Steady operating conditions exist. 2 Air is an ideal gas with constant specific heats at room temperature. 3 Kinetic and potential energy changes are negligible. 4 The heating duct is adiabatic, and thus heat transfer through it is negligible. 5 No air leaks in and out of the room.Properties The gas constant of air is 0.287 kPa.m 3/kg.K (Table A-1). The specific heats of air at room temperature are c p = 1.005 and c v = 0.718 kJ/kg·K (Table A-2). Analysis (a ) The total mass of air in the room iskg 284.6)K 288)(K /kg m kPa 0.287()m 240)(kPa 98(m240m 865331133=⋅⋅===⨯⨯=RT P m V VWe first take the entire room as our system,which is a closed system since no mass leaks in or out. The power rating of the electric heater is determined by applying the conservation of energy relation to this constant volume closed system:()()12avg ,out in fan,in e,in fan,in e,energiesetc. potential, kinetic, internal,in Change system massand work,heat,by nsfer energy tra Net 0)=PE =KE (since T T mc Q W W t U Q W W E E E out out in -=-+∆∆∆∆=-+∆=-vSolving for the electrical work input giveskW5.40=⨯-⋅+-=∆--=+s) 60C/(15)1525)(C kJ/kg 0.718)(kg 284.6()kJ/s 0.2()kJ/s 200/60(/)(12in fan,out in e, tT T W Q W mc v (b ) We now take the heating duct as the system, which is a control volume since masscrosses the boundary. There is only one inlet and one exit, and thus mm m 12==. The energy balance for this adiabatic steady-flow system can be expressed in the rate formas)()(0)pe ke (since 01212in fan,in e,21in fan,in e,energiesetc. potential, kinetic, internal,in change of Rate (steady) 0systemmassand work,heat,by nsfer energy tra net of Rate T T c m h h mW W Q h m h mW W E E E E E p outin out in -=-=+≅∆≅∆==++==∆=-Thus, ()()C 6.7 =⋅+=+=-=∆K kJ/kg 1.005kg/s 50/60kJ/s )2.040.5(infan,in e,12p c m W W T T T5-107R-134a is condensed in a condenser. The heat transfer per unit mass is to bedetermined.Assumptions 1 This is a steady-flow process since there is no change with time. 2 Kinetic and potential energy changes are negligible. 3 There are no work interactions. Analysis We take the pipe in which R-134a is condensed as the system, which is a control volume. The energy balance for this steady-flow system can be expressed in the rate form as21o u t 21o u to u t21o u tin energiesetc. potential, kinetic, internal,in change of Rate (steady) 0systemmassand work,heat,by nsfer energy tra net of Rate out in )(0h h q h h m QQ h m h m E E E E E -=-=+===∆=-The enthalpies of R-134a at the inlet and exit of the condenser are (Table A-12, A-13).kJ/kg61.1010kP a 900kJ/kg13.295C 60kP a 900kPa 900@22111==⎭⎬⎫===⎭⎬⎫︒==f h h x P h T PSubstituting,kJ/kg 193.5=-=61.10113.295out q5-112Helium flows from a supply line to an initially evacuated tank. The flow work of the helium in the supply line and the final temperature of the helium in the tank are to be determined.Properties The properties of helium are R = 2.0769 kJ/kg.K, c p = 5.1926 kJ/kg.K, c v = 3.1156 kJ/kg.K (Table A-2a).Analysis The flow work is determined from its definition but we first determine the specific volume/kg m 0811.4kP a)200(K)27320kJ/kg.K)(1 0769.2(3line =+==P RT vkJ/kg816.2===/kg)m 1kPa)(4.081 200(3flow v P wNoting that the flow work in the supply line is converted to sensible internal energy in the tank, the final helium temperature in the tank issat. liq.60︒Cdetermined as followsK655.0=−→−=−→−==+===tank tank tank tank -line line linetank kJ/kg.K) 1156.3(kJ/kg 7.2040kJ/kg7.2040K) 27320kJ/kg.K)(1 1926.5(T T T c u T c h h u p vAlternative Solution : Noting the definition of specific heat ratio, the final temperature in the tank can also be determined fromK 655.1=+==K) 273120(667.1line tank kT T which is practically the same result.5-119A rigid tank initially contains superheated steam. A valve at the top of the tank is opened, and vapor is allowed to escape at constant pressure until the temperature rises to 500︒C. The amount of heat transfer is to be determined.Assumptions 1 This is an unsteady process since the conditions within the device are changing during the process, but it can be analyzed as a uniform-flow process by using constant average properties for the steam leaving the tank. 2 Kinetic and potential energies are negligible. 3 There are no work interactions involved. 4 The direction of heat transfer is to the tank (will be verified). Properties The properties of water are (Tables A-4 through A-6)kJ/kg3468.3,kJ/kg 3116.9/kgm 0.17568C 500MP a 2kJ/kg3024.2,kJ/kg 2773.2/kgm 0.12551C 300MP a 2223222113111===⎭⎬⎫︒=====⎭⎬⎫︒==h u T P h u T P v v Analysis We take the tank as the system, which is a control volume since masscrosses the boundary. Noting that the microscopic energies of flowing and nonflowing fluids are represented by enthalpy h and internal energy u , respectively, the mass and energy balances for this uniform-flow system can be expressed as Mass balance :21system out in m m m m m m e -=→∆=-Energy balance :)0 (since 1122in energiesetc. potential, kinetic,internal,in Change system massand work,heat,by nsfer energy tra Net out in ≅≅≅-=-∆=-pe ke W u m u m h m Q E E E e eThe state and thus the enthalpy of the steam leaving the tank is changing during thisprocess. But for simplicity, we assume constant properties for the exiting steam at the average values. Thus,kJ/kg 3246.22kJ/kg3468.33024.2221=+=+≅h h h e The initial and the final masses in the tank arekg 1.138/kgm 0.17568m 0.2kg1.594/kg m 0.12551m 0.23322233111======v V v V m mThen from the mass and energy balance relations,kg 0.456138.1594.121=-=-=m m m e()()()()()()kJ606.8=-+=-+=kJ/kg 2773.2kg 1.594kJ/kg 3116.9kg 1.138kJ/kg 3246.2kg 0.4561122u m u m h m Q e e in5-131An insulated piston-cylinder device with a linear spring is applying force to the piston. A valve at the bottom of the cylinder is opened, and refrigerant is allowed to escape. The amount of refrigerant that escapes and the final temperature of the refrigerant are to be determined.Assumptions 1 This is an unsteady process since the conditions within the device are changing during the process, but it can be analyzed as a uniform-flow process assuming that the state of fluid leaving the device remains constant. 2 Kinetic and potential energies are negligible.Properties The initial properties of R-134a are (Tables A-11 through A-13)kJ/kg11.354kJ/kg 03.325/kg m 02423.0C 120MPa 2.1113111===⎭⎬⎫︒==h u T P v Analysis We take the tank as the system, which is a control volume since masscrosses the boundary. Noting that the microscopic energies of flowing and nonflowing fluids are represented by enthalpy h and internal energy u , respectively, the mass and energy balances for this uniform-flow system can be expressed as Mass balance : 21system out in m m m m m m e -=→∆=- Energy balance :)0 (since 1122in b,energiesetc. potential, kinetic,internal,in Change system massand work,heat,by nsfer energy tra Net out in ≅≅≅-=-∆=-pe ke Q u m u m h m W E E E e e23212322233111m 0.502.33m 0.5kg02.33/kgm 0.02423m 0.8v v V v V -=-======m m m v m m eNoting that the spring is linear, the boundary work can be determined fromkJ 270m 0.5)-0.8(2kPa600)(1200)(232121in b,=+=-+=V V P P W Substituting the energy balance,kJ/kg) kg)(325.03 02.33(m 5.0m 5.002.3327022323-⎪⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛--u h e v v (Eq. 1) where the enthalpy of exiting fluid is assumed to be the average of initial and finalenthalpies of the refrigerant in the cylinder. That is,2kJ/kg) 11.354(2221h h h h e +=+=Final state properties of the refrigerant (h 2, u 2, and v 2) are all functions of finalpressure (known) and temperature (unknown). The solution may be obtained by a trial-error approach by trying different final state temperatures until Eq. (1) is satisfied. Or solving the above equations simultaneously using an equation solver with built-in thermodynamic functions such as EES, we obtainT 2 = 96.8︒C , m e = 22.47 kg, h 2 = 336.20 kJ/kg, u 2 = 307.77 kJ/kg, v 2 = 0.04739 m 3/kg, m 2 = 10.55 kg。
工程热力学第三版电子教案第5章

第5章热力学第二定律5.1 本章基本要求 (45)5.2 本章重点: (45)5.3 本章难点 (45)5.4 例题 (46)5.5思考及练习题 (55)5.6 自测题 (60)5.1 本章基本要求理解热力学第二定律的实质,卡诺循环,卡诺定理,孤立系统熵增原理,深刻理解熵的定义式及其物理意义。
熟练应用熵方程,计算任意过程熵的变化,以及作功能力损失的计算,了解火用、火无的概念。
5.2 本章重点:学习本章应该掌握以下重点内容:,l.深入理解热力学第二定律的实质,它的必要性。
它揭示的是什么样的规律;它的作用。
2.深入理解熵参数。
为什么要引入熵。
是在什么基础上引出的。
怎样引出的。
它有什么特点。
3.系统熵变的构成,熵产的意义,熟练地掌握熵变的计算方法。
4.深入理解熵增原理,并掌握其应用。
5.深入理解能量的可用性,掌握作功能力损失的计算方法5.3 本章难点l.过程不可逆性的理解,过程不可逆性的含义。
不可逆性和过程的方向性与能量可用性的关系。
2.状态参数熵与过程不可逆的关系。
3.熵增原理的应用。
4.不可逆性的分析和火用分析.5.4 例题例1:空气从P1=0.1MPa ,t1=20℃,经绝热压缩至P2=0.42MPa ,t2=200℃。
求:压缩过程工质熵变。
(设比热为定值)。
解:定压比热:k kg kJ R C P ⋅=⨯==/005.1287.02727由理想气体熵的计算式:k kg kJ P P R T T C S P ⋅=-=-=∆/069.01.042.0ln 287.0293473ln 005.1ln ln121212例2:刚性容器中贮有空气2kg ,初态参数P1=0.1MPa ,T1=293K ,内装搅拌器,输入轴功率WS=0.2kW ,而通过容器壁向环境放热速率为kW Q 1.0.=。
求:工作1小时后孤立系统熵增。
解:取刚性容器中空气为系统,由闭系能量方程:U Q W s ∆+=..经1小时,()12..36003600T T mC Q W v s -+=()K mC Q W T T v 5447175.021.02.036002933600..12=⨯-+=⎪⎭⎫ ⎝⎛-+=由定容过程:1212T T P P =, MPa T T P P 186.02935441.01212=⨯==取以上系统及相关外界构成孤立系统:sursys iso S S S ∆+∆=∆K kJ T Q S sur /2287.12931.036000=⨯==∆K kJ S iso /12.22287.18906.0=+=∆例3:压气机空气由P1=100kPa ,T1=400K ,定温压缩到终态P2=1000kPa ,过程中实际消耗功比可逆定温压缩消耗轴功多25%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第5章热力学第二定律5.1 本章基本要求 (45)5.2 本章重点: (45)5.3 本章难点 (45)5.4 例题 (46)5.5思考及练习题 (55)5.6 自测题 (60)5.1 本章基本要求理解热力学第二定律的实质,卡诺循环,卡诺定理,孤立系统熵增原理,深刻理解熵的定义式及其物理意义。
熟练应用熵方程,计算任意过程熵的变化,以及作功能力损失的计算,了解火用、火无的概念。
5.2 本章重点:学习本章应该掌握以下重点内容:,l.深入理解热力学第二定律的实质,它的必要性。
它揭示的是什么样的规律;它的作用。
2.深入理解熵参数。
为什么要引入熵。
是在什么基础上引出的。
怎样引出的。
它有什么特点。
3.系统熵变的构成,熵产的意义,熟练地掌握熵变的计算方法。
4.深入理解熵增原理,并掌握其应用。
5.深入理解能量的可用性,掌握作功能力损失的计算方法5.3 本章难点l.过程不可逆性的理解,过程不可逆性的含义。
不可逆性和过程的方向性与能量可用性的关系。
2.状态参数熵与过程不可逆的关系。
3.熵增原理的应用。
4.不可逆性的分析和火用分析.5.4 例题例1:空气从P1=0.1MPa ,t1=20℃,经绝热压缩至P2=0.42MPa ,t2=200℃。
求:压缩过程工质熵变。
(设比热为定值)。
解:定压比热:k kg kJ R C P ⋅=⨯==/005.1287.02727由理想气体熵的计算式:k kg kJ P P R T T C S P ⋅=-=-=∆/069.01.042.0ln 287.0293473ln 005.1ln ln121212例2:刚性容器中贮有空气2kg ,初态参数P1=0.1MPa ,T1=293K ,内装搅拌器,输入轴功率WS=0.2kW ,而通过容器壁向环境放热速率为kW Q 1.0.=。
求:工作1小时后孤立系统熵增。
解:取刚性容器中空气为系统,由闭系能量方程:U Q W s ∆+=..经1小时,()12..36003600T T mC Q W v s -+=()K mC Q W T T v 5447175.021.02.036002933600..12=⨯-+=⎪⎭⎫ ⎝⎛-+=由定容过程:1212T T P P =,MPa T T P P 186.02935441.01212=⨯==取以上系统及相关外界构成孤立系统:sursys iso S S S ∆+∆=∆K kJ T Q S sur /2287.12931.036000=⨯==∆K kJ S iso /12.22287.18906.0=+=∆例3:压气机空气由P1=100kPa ,T1=400K ,定温压缩到终态P2=1000kPa ,过程中实际消耗功比可逆定温压缩消耗轴功多25%。
设环境温度为T0=300K 。
求:压缩每kg 气体的总熵变。
解:取压气机为控制体。
按可逆定温压缩消耗轴功:kg kJ P P RT v v RT W SO /3.2641000100ln 400287.0ln ln2112-=⨯===实际消耗轴功:()kg kJ W S /4.3303.26425.1-=-=由开口系统能量方程,忽略动能、位能变化:21h q h W S +=+ 因为理想气体定温过程:h1=h2 故:kg kJ W q S /4.330-== 孤立系统熵增:sursys iso S S S ∆+∆=∆稳态稳流:=∆sys Sk kg kJ T qP P R T q S S S sur ⋅=+=+=+-=∆/44.03004.3301000100ln287.0ln 021012例4:已知状态P1=0.2MPa ,t1=27℃的空气,向真空容器作绝热自由膨胀,终态压力为P2=0.1MPa 。
求:作功能力损失。
(设环境温度为T0=300K ) 解:取整个容器(包括真空容器)为系统, 由能量方程得知:21U U =,T T T ==21 对绝热过程,其环境熵变k kg kJ P P R P PR P P R T T C S P sys ⋅===-=-=∆/199.01.02.0ln 287.0lnln 0ln ln 21121212kg kJ S T W iso /13244.03000=⨯=∆=∆例5:如果室外温度为-10℃,为保持车间内最低温度为20℃,需要每小时向车间供热36000kJ,求:1) 如采用电热器供暖,需要消耗电功率多少。
2) 如采用热泵供暖,供给600K热泵的功率至少是多少。
3) 如果采用热机带动热泵进行供暖,向热机的供热率至少为多少。
图5.1为热机带动热泵联合工作的示意图。
假设:向热机的供热温度为600K ,热机在大气温度下放热。
图5.2 解:1)用电热器供暖,所需的功率即等于供热率, 故电功率为360036000..==Q W = 10kW2)如果热泵按逆向卡诺循环运行,而所需的功最少。
则逆向卡诺循环的供暖系数为211..T T T WQ W +==ε=9.77热泵所需的最小功率为W QW ε..==1.02kW3)按题意,只有当热泵按逆卡诺循环运行时,所需功率为最小。
只有当热机按卡诺循环运行时,输出功率为.W 时所需的供热率为最小。
由56.06002631112=-=-=T T c η热机按所需的最小供热率为kW W Q tc 82.156.002.1/..min ===η例6:一齿轮箱在温度T=370K 的稳定状态下工作,输入端接受功率为100kW ,而输出功率为95kW,周围环境为270K 。
现取齿轮箱及其环境为一孤立系统(见图5.2) 1)试分析系统内发生哪些不可逆过程。
并计算每分钟内各不可逆过程的熵产及作功能力的损失。
计算系统的熵增及作功能力总的损失。
解:1)此孤立系统内进行着两个不可逆过程:由于齿轮箱内部的摩擦将功变为热的过程,齿轮箱(T=370K)与环境(To=270K)间的温差传热过程。
分别计算如下, 每分钟内齿轮箱中损失的功'l W 及传向环境的热Q'l W =60×(100-95)=300kJ因齿轮箱在稳定状态下工作,0=∆U 其能量平衡关系为(-Q)= U ∆+W =0+60×95-60×100=-300kJ 故Q=300kJ(2)齿轮箱内不可逆过程的熵产与作功能力损失 熵产T W S l g '1=∆=0.8108kJ /K作功能力损失101g l S T W ∆== 270×0.8108=218.92kJ(3)齿轮箱与环境间温差传热所引起的熵产与作功能力损失 熵产K kJ T T Q S g /3003.0)37012701(300)11(02=-=-=∆作功能力损失202g l S T W ∆== 270×0.3003=81.08kJ2)孤立系统的熵增及作功能力的损失解一: 孤立系统的熵增为各不可逆过程中熵产之和21g g iso S S S ∆+∆=∆ =0.8108+0.3003=1.111kJ/K作功能力总损失W=218.92+81.08=300kJ解二:孤立系统的熵增为齿轮箱的熵变化1S ∆与环境的熵变化gS ∆之和。
因齿轮箱在稳定状态下工作,故其熵变化1S ∆=0而环境在温度T 0=270K 的情况下接受热量Q ,故其熵变化为02T QS =∆ = 1.11kJ/K因此,孤立系统的熵增为21S S S iso ∆+∆=∆= =0+1.111=1.111kJ/K孤立系统内作功能力的损失isol S T W ∆=0 =270×1.111=300kJ两种解法所得结论相同。
讨论: 1.齿轮箱内因摩擦损失的功'l W =300kJ ,但作功能力损失1l W =218.92时,两者数值不同。
其原因是:300kJ 的功所变成的摩擦热是在T=370K 温度下传向环境的,因T>T 0,这部分热量仍有一定的作功能力,其可用能为Q(1-T 0/T)。
若采取某种措施,例如采用一工作于T 与To 间的卡诺机,则可以把这部分可用能转化为功。
所以齿轮箱内不可逆过程所导致的作功能力损失,不是'l W 的全部,而只是101g l S T W ∆=这一部分。
2.由齿轮箱传出的热(Q=300kJ),其作功能力在温差传热过程中再次损失,最后为零。
即孤立系统内,全部不可逆过程总的结果是,在每分钟输入齿轮箱的功中,有300KJ 的功最终变成了在To=270K 的温度下为环境所接受的热。
在此传热温度下,这部分热已无作功能力(可用能为零)。
也就是说,原来的300kJ 功的作功能力已全部损失了。
例7:三个质量相等、比热相同且为定值的物体(图5.3 )。
A 物体的初温为1A T =100K ,B 物体的初温1B T =300K ,C 物体的初温1C T =300K 。
如果环境不供给功和热量,只借助于热机和致冷机在它们之间工作,问其中任意一个物体所能达到的最高温度为多少。
图5.3解:因环境不供给功和热量,而热机工作必须要有两个热源才能使热量转变为功。
所以三个物体中的两个作为热机的有限热源和有限冷源。
致冷机工作必须要供给其机械功,才能将热量从低温热源转移到高温热源,同样有三个物体中的两个作为致冷机的有限冷源和有限热源。
由此,其工作原理如图5.3所示。
取A 、B 、C 物体及热机和致冷机为孤立系。
如果系统中进行的是可逆过程,则CB A E E iso S S S S S S ∆+∆+∆+∆+∆=∆'=0对于热机和致冷机⎰=∆dSS E =0,则0212121=++=∆⎰⎰⎰C C B B A A TT TT T T iso T dT mc T dT mc T dT mc S0ln ln ln121212=++C C B B A A T T T TT T1121212=C C B B A A T T T T T T111222C B A C B A T T T T T T ==100×300×300=9×3810K (1)由图5.3可知,热机工作于A 物体和B 物体两有限热源之间,致冷机工作于B 物体和C 物体两有限热源及冷源之间,热机输出的功供给致冷机工作。
当22B A T T =时,热机停止工作,致冷机因无功供给也停止工作,整个过程结束。
过程进行的结果,物体B 的热量转移到物体C 使其温度升高,而A 物体和B 物体温度平衡。
对该孤立系,由能量方程式得=++C B A Q Q Q)()()(121212=-+-+-C C B B A A T T mc T T mc T T mc111222C B A C B A T T T T T T ++=++ =100十300+300=700K (2)根据该装置的工作原理可知,22121212,,,B A C C B B A A T T T T T T T T =><>对式(1)与(2)求解,得22B A T T = =150K 2C T =400K即可达到的最高温度为400K.讨论:若致冷机工作于A 物体和C 物体两有限冷源和热源之间,其过程结果又如何呢。
