江苏省教育考试院关于公布江苏省2020年普通
江苏省教育考试院文件

江苏省教育考试院文件苏教考招[2007]40号省教育考试院关于做好江苏省2008年普通高校招生考试及2009届普通高中学业水平测试报名工作的通知各市、县(市、区)教育局、招生办公室:根据《省教育厅关于印发江苏省2008年普通高校招生考试方案的通知》(苏教基[2007]7号)精神,自2008年起江苏省实行经省政府和国家教育部批准的“3 + 学业水平测试+ 综合素质评价”高考方案。
为切实做好2008年普通高校招生考试报名和2009届普通高中学业水平测试的报名工作,现将《2008年江苏省普通高校招生考试报名办法》和《2009届普通高中学业水平测试必修科目考试报名办法》印发给你们,请遵照执行。
附件:1、2008年江苏省普通高校招生考试报名办法2、2009届普通高中学业水平测试必修科目考试报名办法二〇〇七年十月二十四日主题词:普通高考学业水平测试报名通知抄送:教育部高校学生司、考试中心,省教育厅办公室江苏省教育考试院办公室 2008年10月24日印发2附件1:2008年江苏省普通高校招生考试报名办法一、报名条件1.同时符合下列条件且具有本省户籍的人员,可以报名:(1)遵守中华人民共和国宪法和法律;(2)高级中等教育学校毕业或具有同等学力;(3)身体健康。
2.在我省普通高中读书的外国籍考生,只要出示护照和我省公安厅核发的长期居住证明,且符合我省考生报名条件的,允许其参加报名。
3.下列人员不得报名:(1)具有高等学历教育资格的高等学校的在校生;(2)高级中等教育学校非应届毕业的在校生;(3)因触犯刑律已被有关部门采取强制措施或正在服刑者;(4)患有国家规定的传染性疾病者。
二、考生填报高考志愿的规定1.根据2008年普通高校招生考试方案规定,普通高中学业水平必修科目测试等级未达到下列要求的,不得填报相关科类的高考志愿:(1)高级中等教育学校应届毕业生必须参加2007、2008年江3苏省普通高中学业水平测试并取得规定等级:①普通类考生必修科目测试均需达到C级及以上等级(技术科目必须合格);②艺术、体育类考生如兼报普通类专业,必修科目测试等级要求和普通类考生一致;如不兼报普通类专业,必修科目测试等级中D级(信息技术科目测试不合格视为D级)不超过三门。
2020年江苏卷(含答案)

绝密★启用前2020年普通高等学校招生全国统一考试(江苏卷)数学Ⅰ注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷共4页,均为非选择题(第1题~第20题,共20题)。
本卷满分为160分,考试时间为120分钟。
考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员从答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符. 4.作答试题,必须用0.5毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗. 参考公式:柱体的体积V Sh =,其中S 是柱体的底面积,h 是柱体的高.一、填空题:本大题共14小题,每小题5分,共计70分.请把答案填写在答题卡相应位置上......... 1.已知集合{1,0,1,2},{0,2,3}A B =-=,则AB =_____.2.已知i 是虚数单位,则复数(1i)(2i)z =+-的实部是_____.3.已知一组数据4,2,3,5,6a a -的平均数为4,则a 的值是_____.4.将一颗质地均匀的正方体骰子先后抛掷2次,观察向上的点数,则点数和为5的概率是_____.5.如图是一个算法流程图,若输出y 的值为2-,则输入x 的值是_____.6.在平面直角坐标系xOy 中,若双曲线22x a ﹣25y =1(a >0)的一条渐近线方程为y=52x ,则该双曲线的离心率是____.7.已知y =f (x )是奇函数,当x ≥0时,()23 f x x = ,则f (-8)的值是____. 8.已知2sin ()4πα+ =23,则sin 2α的值是____.9.如图,六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的.已知螺帽的底面正六边形边长为2 cm ,高为2 cm ,内孔半轻为0.5 cm ,则此六角螺帽毛坯的体积是____cm.10.将函数y =πsin(2)43x ﹢的图象向右平移π6个单位长度,则平移后的图象中与y 轴最近的对称轴的方程是____.11.设{a n }是公差为d 的等差数列,{b n }是公比为q 的等比数列.已知数列{a n +b n }的前n 项和221()n n S n n n +=-+-∈N ,则d +q 的值是_______. 12.已知22451(,)x y y x y R +=∈,则22xy +的最小值是_______.13.在△ABC 中,43=90AB AC BAC ==︒,,∠,D 在边BC 上,延长AD 到P ,使得AP =9,若3()2PA mPB m PC =+-(m 为常数),则CD 的长度是________.14.在平面直角坐标系xOy 中,已知3(0)P ,A ,B 是圆C :221()362x y +-=上的两个动点,满足PA PB =,则△P AB 面积的最大值是__________.二、解答题:本大题共6小题,共计90分,请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.15.在三棱柱ABC -A 1B 1C 1中,AB ⊥AC ,B 1C ⊥平面ABC ,E ,F 分别是AC ,B 1C 的中点. (1)求证:EF ∥平面AB 1C 1;(2)求证:平面AB 1C ⊥平面ABB 1.16.在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知3,2,45a c B ===︒. (1)求sin C 的值;(2)在边BC 上取一点D ,使得4cos 5ADC ∠=-,求tan DAC ∠的值.17.某地准备在山谷中建一座桥梁,桥址位置的竖直截面图如图所示:谷底O 在水平线MN 上、桥AB 与MN 平行,OO '为铅垂线(O '在AB 上).经测量,左侧曲线AO 上任一点D 到MN 的距离1h (米)与D 到OO '的距离a (米)之间满足关系式21140h a =;右侧曲线BO 上任一点F 到MN 的距离2h (米)与F 到OO '的距离b (米)之间满足关系式3216800h b b =-+.已知点B 到OO '的距离为40米.(1)求桥AB 的长度;(2)计划在谷底两侧建造平行于OO '的桥墩CD 和EF ,且CE 为80米,其中C ,E 在AB 上(不包括端点).桥墩EF 每米造价k (万元)、桥墩CD 每米造价32k (万元)(k >0).问O E '为多少米时,桥墩CD 与EF 的总造价最低?18.在平面直角坐标系xOy 中,已知椭圆22:143x y E +=的左、右焦点分别为F 1,F 2,点A 在椭圆E 上且在第一象限内,AF 2⊥F 1F 2,直线AF 1与椭圆E 相交于另一点B .(1)求△AF 1F 2的周长;(2)在x 轴上任取一点P ,直线AP 与椭圆E 的右准线相交于点Q ,求OP QP ⋅的最小值; (3)设点M 在椭圆E 上,记△OAB 与△MAB 的面积分别为S 1,S 2,若S 2=3S 1,求点M 的坐标.19.已知关于x 的函数(),()y f x y g x ==与()(,)h x kx b k b =+∈R 在区间D 上恒有()()()f x h x g x ≥≥.(1)若()()222 2()f x x x g x x x D =+=-+=∞-∞+,,,,求h (x )的表达式; (2)若2 1 ln ,()()()(0) x x g k x h kx k D f x x x =-+==-=+∞,,,,求k 的取值范围; (3)若()422242() 2() (48 () 4 3 0)2 2f x x x g x x h x t t x t t t =-=-=--+<,,≤,[] , 2,2D m n =⊆-⎡⎣,求证:7n m -20.已知数列{}*()∈n a n N 的首项a 1=1,前n 项和为S n .设λ与k 是常数,若对一切正整数n ,均有11111k k kn n n S S a λ++-=成立,则称此数列为“λ–k ”数列.(1)若等差数列{}n a 是“λ–1”数列,求λ的值; (2)若数列{}n a 是32-”数列,且a n >0,求数列{}n a 的通项公式;(3)对于给定的λ,是否存在三个不同的数列{}n a 为“λ–3”数列,且a n ≥0?若存在,求λ的取值范围;若不存在,说明理由.数学Ⅱ(附加题)【选做题】本题包括A 、B 、C 三小题,请选定其中两小题,并在相应的答题区域内作答......................若多做,则按作答的前两小题评分.解答时应写出文字说明、证明过程或演算步骤. A .[选修4-2:矩阵与变换]21.平面上点(2,1)A -在矩阵11a b ⎡⎤=⎢⎥-⎣⎦M 对应的变换作用下得到点(3,4)B -.(1)求实数a ,b 的值; (2)求矩阵M 的逆矩阵1M -.B .[选修4-4:坐标系与参数方程]22.在极坐标系中,已知点1π(,)3A ρ在直线:cos 2l ρθ=上,点2π(,)6B ρ在圆:4sinC ρθ=上(其中0ρ≥,02θπ≤<). (1)求1ρ,2ρ的值(2)求出直线l 与圆C 的公共点的极坐标.C .[选修4-5:不等式选讲]23.设x ∈R ,解不等式2|1|||4x x ++≤.【必做题】第24题、第25题,每题10分,共计20分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤.24.在三棱锥A —BCD 中,已知CB =CD =5,BD =2,O 为BD 的中点,AO ⊥平面BCD ,AO =2,E 为AC 的中点.(1)求直线AB 与DE 所成角的余弦值; (2)若点F 在BC 上,满足BF =14BC ,设二面角F —DE —C 的大小为θ,求sin θ的值.25.甲口袋中装有2个黑球和1个白球,乙口袋中装有3个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋,重复n 次这样的操作,记甲口袋中黑球个数为X n ,恰有2个黑球的概率为p n ,恰有1个黑球的概率为q n .(1)求p 1·q 1和p 2·q 2; (2)求2p n +q n 与2p n-1+q n-1的递推关系式和X n 的数学期望E (X n )(用n 表示) .2020年普通高等学校招生全国统一考试(江苏卷)参考答案数学Ⅰ一、填空题(共计70分)1.{}0,22.33.24.19 5.3- 6.32 7.4- 8.139.2π 10.524x π=- 11.4 12.45 13.0或18514.1.【解析】∵{}1,0,1,2A =-,{}0,2,3B = ∴{}2,0=B A .故答案为:{}0,2.2.【解析】∵复数()()12z i i =+-,∴2223z i i i i =-+-=+ ∴复数的实部为3.故答案为:3.3.【解析】∵数据4,2,3,5,6a a -的平均数为4 ∴4235620a a ++-++=,即2a =.故答案为:2.4.【解析】根据题意可得基本事件数总为6636⨯=个. 点数和为5的基本事件有()1,4,()4,1,()2,3,()3,2共4个. ∴出现向上的点数和为5的概率为41369P ==.故答案为:19.5.【解析】由于20x >,所以12y x =+=-,解得3x =-.故答案为:3-6.【解析】双曲线22215x y a -=,故b =由于双曲线的一条渐近线方程为y x =,即2b a a =⇒=,所以3c =,双曲线的离心率为32c a =.故案为:32.7.【解析】23(8)84f ==,因为()f x 为奇函数,所以(8)(8)4f f -=-=-,故答案为:4- 8.【解析】∵)2sin 1(21)cos 22sin 22()4(sin 22ααααπ+=+=+ 121(1sin 2)sin 2233αα∴+=∴=.故答案为:139.【解析】正六棱柱体积为262⨯,圆柱体积为21()222ππ⋅=所求几何体体积为2π.故答案为:2π10.【解析】3sin[2()]3sin(2)6412y x x πππ=-+=- 72()()122242k x k k Z x k Z πππππ-=+∈∴=+∈当1k =-时524x π=-.故答案为:524x π=- 11.【解析】设等差数列{}n a 的公差为d ,等比数列{}n b 的公比为q ,根据题意1q ≠. 等差数列{}n a 的前n 项和公式为()2111222n n n d d P na d n a n -⎛⎫=+=+- ⎪⎝⎭, 等比数列{}n b 的前n 项和公式为()1111111n n n b q b bQ q qq q-==-+---, 依题意n n n S P Q =+,即22111212211nn b b d d n n n a n q q q ⎛⎫-+-=+--+ ⎪--⎝⎭, 通过对比系数可知111212211dd a q b q⎧=⎪⎪⎪-=-⎪⎨⎪=⎪⎪=-⎪-⎩⇒112021d a q b =⎧⎪=⎪⎨=⎪⎪=⎩,故4d q +=.故答案为:4 12.【解析】∵22451x y y +=,∴0y ≠且42215y x y -=∴42222221144+5555y y x y y y y -+=+=≥,当且仅当221455y y =,即2231,102x y ==时取等号.∴22xy +的最小值为45. 13.【解析】∵,,A D P 三点共线,∴可设()0PA PD λλ=>,∵32PA mPB m PC ⎛⎫=+- ⎪⎝⎭,∴32PD mPB m PC λ⎛⎫=+- ⎪⎝⎭,即32m m PD PB PC λλ⎛⎫- ⎪⎝⎭=+, 若0m ≠且32m ≠,则,,B D C 三点共线,∴321m m λλ⎛⎫-⎪⎝⎭+=,即32λ=, ∵9AP =,∴3AD =.∵4AB =,3AC =,90BAC ∠=︒,∴5BC =. 设CD x =,CDA θ∠=,则5BD x =-,BDA πθ∠=-.∴根据余弦定理可得222cos 26AD CD AC xAD CD θ+-==⋅,()()()222257cos 265x AD BD AB AD BD x πθ--+--==⋅-,∵()cos cos 0θπθ+-=,∴()()2570665x x x --+=-,解得185x =,∴CD 的长度为185.当0m =时,32PA PC =,,C D 重合,此时CD 的长度为0, 当32m =时,32PA PB =,,B D 重合,此时12PA =,不合题意,舍去.故答案为:0或185.14.【解析】 ∵PB PA =,∴AB PC ⊥.设圆心C 到直线AB 距离为d ,则||1AB PC ==所以11)2PABSd ≤⋅+=令222(36)(1)(06)2(1)(236)04y d d d y d d d d '=-+≤<∴=+--+=∴=(负值舍去)当04d ≤<时,0y '>;当46d ≤<时,0y '≤,因此当4d =时,y 取最大值,即PABS取最大值为故答案为:二、解答题(共计90分)15.【解析】(1)由于,E F 分别是1,AC B C 的中点,所以1//EF AB . 由于EF ⊂/平面11AB C ,1AB ⊂平面11AB C ,所以//EF 平面11AB C . (2)由于1B C ⊥平面ABC ,AB平面ABC ,所以1B C AB ⊥.由于1,AB AC AC B C C ⊥⋂=,所以AB ⊥平面1AB C , 由于AB平面1ABB ,所以平面1AB C ⊥平面1ABB .16.【解析】(1)由余弦定理得2222cos 92235b a c ac B =+-=+-⨯=,所以b =由正弦定理得sin sin sin sin 5c b c B C C B b =⇒==.(2)由于4cos 5ADC ∠=-,,2ADC ππ⎛⎫∠∈ ⎪⎝⎭,所以3sin 5ADC ∠==.由于,2ADC ππ⎛⎫∠∈⎪⎝⎭,所以0,2C π⎛⎫∈ ⎪⎝⎭,所以cos 5C ==.所以()sin sin DAC DAC π∠=-∠()sin ADC C =∠+∠sin cos cos sin ADC C ADC C =∠⋅+∠⋅34555525⎛⎫=⨯+-= ⎪⎝⎭. 由于0,2DAC π⎛⎫∠∈ ⎪⎝⎭,所以cos DAC ∠==所以sin 2tan cos 11DAC DAC DAC ∠∠==∠.17.【解析】(1)由题意得2311||40640||8040800O A O A ''=-⨯+⨯∴= ||||||8040120AB O A O B ''∴=+=+=米(2)设总造价为()f x 万元,21||8016040O O '=⨯=,设||O E x '=, 32131()(1606)[160(80)],(040)800240f x k x x k x x =+-+--<<3221336()(160),()()0208008080080f x k x x f x k x x x '∴=+-∴=-=∴=(0舍去)当020x <<时,()0f x '<;当2040x <<时,()0f x '>,因此当20x时,()f x 取最小值,答:当20O E '=米时,桥墩CD 与EF 的总造价最低.18.【解析】(1)∵椭圆E 的方程为22143x y +=,∴()11,0F -,()21,0F由椭圆定义可得:124AF AF +=.∴12AF F △的周长为426+= (2)设()0,0P x ,根据题意可得01x ≠.∵点A 在椭圆E 上,且在第一象限,212AF F F ⊥,∴31,2A ⎛⎫⎪⎝⎭∵准线方程为4x =,∴()4,Q Q y∴()()()()200000,04,4244Q OP QP x x y x x x ⋅=⋅--=-=--≥-,当且仅当02x =时取等号.∴OP QP ⋅的最小值为4-.(3)设()11,M x y ,点M 到直线AB 的距离为d . ∵31,2A ⎛⎫⎪⎝⎭,()11,0F -,∴直线1AF 的方程为()314y x =+∵点O 到直线AB 的距离为35,213S S = ∴2113133252S S AB AB d ==⨯⨯⨯=⋅,∴95d = ∴113439x y -+=①,∵2211143x y +=②∴联立①②解得1120x y =⎧⎨=⎩,1127127x y ⎧=-⎪⎪⎨⎪=-⎪⎩. ∴()2,0M 或212,77⎛⎫-- ⎪⎝⎭. 19.【解析】(1)由题设有2222x x kx b x x -+≤+≤+对任意的x ∈R 恒成立. 令0x =,则00b ≤≤,所以0b =.因此22kx x x ≤+即()220x k x +-≥对任意的x ∈R 恒成立,所以()220k ∆=-≤,因此2k =.故()2h x x =.(2)令()()()()()1ln 0F x h x g x k x x x =-=-->,()01F =.又()1x F x k x-'=⋅. 若k 0<,则()F x 在0,1上递增,在()+∞,1上递减,则()()10F x F ≤=, 即()()0h x g x -≤,不符合题意.当0k =时,()()()()()0,F x h x g x h x g x =-==,符合题意.当0k >时,()F x 在0,1上递减,在()+∞,1上递增,则()()10F x F ≥=, 即()()0h x g x -≥,符合题意. 综上所述,0k ≥.由()()()21f x h x x x kx k -=-+--()()2110x k x k =-+++≥当102k x +=<,即1k <-时,()211y x k x k =-+++在()+∞,0为增函数,因为()()0010f h k -=+<,故存在()00,x ∈+∞,使()()0f x h x -<,不符合题意.当102k x +==,即1k =-时,()()20f x h x x -=≥,符合题意. 当102k x +=>,即1k >-时,则需()()21410k k ∆=+-+≤,解得13k -<≤. 综上所述,k 的取值范围是[]0,3k ∈.(3)∵()423422243248x x t t x t t x -≥--+≥-对任意[,][x m n ∈⊂恒成立,()423422432x x t t x t t -≥--+对任意[,][x m n ∈⊂恒成立,等价于()222()2320x t xtx t -++-≥对任意[,][x m n ∈⊂恒成立.故222320x tx t ++-≥对任意[,][x m n ∈⊂恒成立.令22()232M x x tx t =++-,当201t <<,2880,11t t ∆=-+>-<-<,此时1n m t -≤<<,当212t ≤≤,2880t ∆=-+≤,但()234248432x t t x t t -≥--+对任意的[,][x m n ∈⊂恒成立.等价于()()()2322443420x t t x t t --++-≤对任意的[,][x m n ∈⊂恒成立.()()()2322443420x t t x t t --++-=的两根为12,x x ,则4231212328,4t t x x t t x x --+=-⋅=,所以12=n m x x --==.令[]2,1,2t λλ=∈,则n m -=构造函数()[]()325381,2P λλλλλ=-++∈,()()()23103331P λλλλλ'=-+=--,所以[]1,2λ∈时,()0P λ'<,()P λ递减,()()max 17P P λ==. 所以()max n m -=n m -≤.20.【解析】(1)∵+111111101n n n n n n S S a a a a a λλλ++++-=∴==∴≡∴=/(2)∵0 n a ,∴n n S S 1+,∴21211n n S S+.∴21121211)(33n n n n S S S S -=-++.1111112222222+1+1+11()()()3n n n n n n S S S S S S ∴-=-+1111111222222+1+1+1+11()=2=443n n nn n n n n n n S S S S S S S S S -∴-=+∴∴∴= 111S a ==,14n n S -=.1224434,2n n n n a n ---∴=-=⋅≥21,134,2n n n a n -=⎧∴=⎨⋅≥⎩(3)假设存在三个不同的数列{}n a 为"3"λ-数列.111113333333+11+1+1()()n n n n n n n S S a S S S S λλ+-=∴-=- 1133+1n n S S ∴=或11221123333333+1+1+1()()n n n n n n S S S S S S λ-=+++1n n S S ∴=或22113333333+1+1(1)(1)(2)0n n n n SS S S λλλ-+-++=∵对于给定的λ,存在三个不同的数列{}n a 为"3"λ-数列,且0n a ≥1,10,2n n a n =⎧∴=⎨≥⎩或()22113333333+1+1(1)(1)(2)01n n n n S S S S λλλλ-+-++=≠有两个不等的正根. ()22113333333+1+1(1)(1)(2)01n n n n S S SS λλλλ-+-++=≠可转化为()2133333+1+12133(1)(2)(1)01n n nnS S S S λλλλ-++-+=≠,不妨设()1310n n S x x S +⎛⎫=> ⎪⎝⎭,则()3233(1)(2)(1)01x x λλλλ-+++-=≠有两个不等正根,设()()3233(1)(2)(1)01f x x x λλλλ=-+++-=≠.①当1λ<时,32323(2)4(1)004λλλ∆=+-->⇒<<,即01λ<<,此时()3010f λ=-<,33(2)02(1)x λλ+=->-对,满足题意. ②当1λ>时,32323(2)4(1)004λλλ∆=+-->⇒<<,即1λ<<()3010f λ=->,33(2)02(1)x λλ+=-<-对,此情况有两个不等负根,不满足题意舍去. 综上,01λ<<数学Ⅱ(附加题)【选做题】A .[选修4-2:矩阵与变换]21.【解析】(1)∵平面上点()2,1A -在矩阵 11 a M b ⎡⎤=⎢⎥-⎣⎦对应的变换作用下得到点()3,4B - ∴ 1 2 31 14a b ⎡⎤⎡⎤⎡⎤=⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦,∴21324a b -=⎧⎨--=-⎩,解得22a b =⎧⎨=⎩(2)设1m n Mc d -⎡⎤=⎢⎥⎣⎦,则12 2 1 0=2 20 1m c n d MM m c n d -++⎡⎤⎡⎤=⎢⎥⎢⎥-+-+⎣⎦⎣⎦∴21202021m c n d m c n d +=⎧⎪+=⎪⎨-+=⎪⎪-+=⎩,解得25151525m n c d ⎧=⎪⎪⎪=-⎪⎨⎪=⎪⎪⎪=⎩,∴121 5512 55M -⎡⎤-⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦ B .[选修4-4:坐标系与参数方程]22.【解析】(1)以极点为原点,极轴为x 轴的正半轴,建立平面直角坐标系,11cos2,43πρρ=∴=,因为点B 为直线6πθ=上,故其直角坐标方程为y x =, 又4sin ρθ=对应的圆的直角坐标方程为:2240x y y+-=,由2240y x x y y ⎧=⎪⎨⎪+-=⎩解得00xy ==⎧⎨⎩或1x y ⎧=⎪⎨=⎪⎩对应的点为())0,0,,故对应的极径为20ρ=或22ρ=.(2)cos 2,4sin ,4sin cos 2,sin 21ρθρθθθθ==∴=∴=,5[0,2),,44ππθπθ∈∴=,当4πθ=时ρ=54πθ=时0ρ=-<(舍);即所求交点坐标为当(22,),4πC.[选修4-5:不等式选讲]23.【解析】1 224xx x<-⎧⎨---≤⎩或10224xx x-≤≤⎧⎨+-≤⎩或224xx x>⎧⎨++≤⎩21x∴-≤<-或10x-≤≤或23x<≤,所以解集为22,3⎡⎤-⎢⎥⎣⎦【必做题】24.【解析】(1)连,CO BC CD BO OD CO BD==∴⊥以,,OB OC OA为,,x y z轴建立空间直角坐标系,则(0,0,2),(1,0,0),(0,2,0),(1,0,0)(0,1,1)A B C D E-∴∴()()1,1,1,2,0,1=-=DEAB,∴1515351,cos-=-=DEAB从而直线AB与DE所成角的余弦值为1515(2)设平面DEC一个法向量为1(,,),n x y z=1120(1,2,0),x yn DCDCx y zn DE⎧+=⋅=⎧⎪=∴⎨⎨++=⋅=⎪⎩⎩令112,1(2,1,1)y x z n=∴=-=∴=-∴()1,1,21-=n设平面DEF一个法向量为()1112,,zyxn=112211171171(,,0),424420x yn DFDF DB BF DB BCn DE x y z⎧⎧+=⋅=⎪⎪=+=+=∴⎨⎨⋅=⎪⎩⎪++=⎩令111272,5(2,7,5)y x z n=-∴==∴=-()5,7,22-=n∴13137866,cos21-=-=nn,因此12239sin1313θ==25.【解析】(1)11131232,333333p q ⨯⨯====⨯⨯,211131211227++3333333927p p q ⨯⨯=⨯⨯=⨯⨯=⨯⨯, 211231122222516+0+3333333927q p q ⨯⨯+⨯=⨯⨯+=⨯⨯=⨯⨯.(2)1111131212++333339n n n n n p p q p q ----⨯⨯=⨯⨯=⨯⨯, 111112*********+(1)+33333393n n n n n n q p q p q q -----⨯⨯+⨯⨯=⨯⨯+--⨯=-⨯⨯⨯,因此112122+333n n n n p q p q --+=+,从而11111212(2+),21(2+1)333n n n n n n n n p q p q p q p q ----+=+∴+-=-,即1111121(2+1),2133n n n n n n p q p q p q -+-=-∴+=+.又n X 的分布列为故()213n n n n E X p q =+=+.。
师范类专业认证

师范类专业认证学习材料(二)江苏省普通高等学校师范类专业认证第二级认证实施办法(试行)为加强师范类专业建设,建立健全教师教育质量保障体系,不断提高教师培养质量,根据教育部《普通高等学校师范类专业认证实施办法(暂行)》《师范类专业认证标准》精神和《省教育厅关于开展师范类专业认证工作的通知》(苏教师〔2015〕15号)有关要求,结合我省教师教育实际和评估工作规范,特制订本实施办法。
一、指导思想深入贯彻党的教育方针,全面落实立德树人根本任务,积极构建教师教育质量保障体系,坚持“以评促建,以评促改,以评促强”,全面保障和提升师范类专业人才培养质量,为培养造就党和人民满意的高素质专业化创新型教师队伍提供有力支撑,为加快我省教育现代化建设,办好人民满意的教育做出贡献。
二、认证理念认证以“学生中心、产出导向、持续改进”为基本理念。
学生中心,强调遵循师范生成长成才规律,以师范生为中心配置教育资源、组织课程和实施教学;产出导向,强调以师范生的学习效果为导向,对照师范毕业生核心能力素质要求,评价师范类专业人才培养质量;持续改进,强调对师范类专业教学进行全方位、全过程评价,并将评价结果应用于教学改进,推动专业人才培养质量的持续提升。
三、认证原则1.突出以生为本导向。
坚持育人为本,强化学生中心,把学生发展作为专业建设和专业认证的出发点和落脚点,牢固树立以学生为中心的教学理念和教学原则,实施以学生为中心的教学模式和教学评价,不断提高师范生专业素养和能力。
2.强化高校主体责任。
强化高校专业质量保障的主体意识,明确高校在质量建设方面的主体责任。
引导学校全面落实师范类专业培养质量的主体责任,切实加强自主管理,促进学校主动实施自我发展、自我监控、自我评价、自我改进。
3.助力保障机制建设。
积极推动学校健全内部质量保障制度,完善质量保障体系,促进师范类专业人才培养工作持续改进。
充分发挥专业认证外部质量监控的作用,促进学校规范办学、增加投入,保障师范类专业健康发展。
2020年江苏省高考一分一段表(理科)
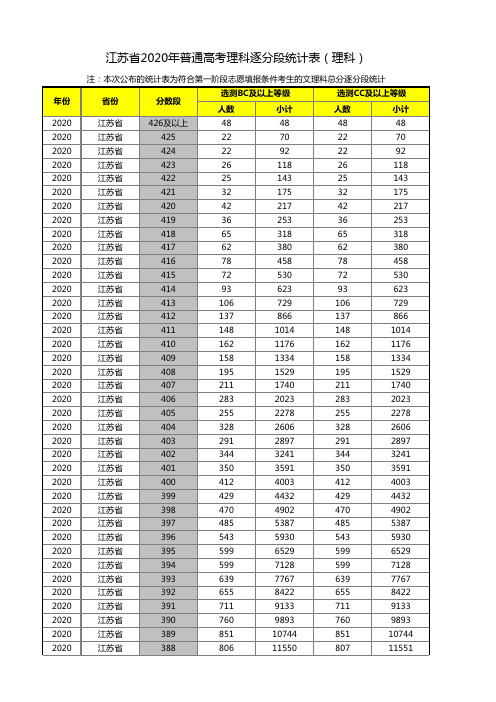
12389 13376 14328 15354 16420 17578 18746 20001 21275 22573 23956 25389 26887 28334 29926 31491 33125 34732 36499 38346 40136 42004 43905 45860 47816 49762 51755 53861 56010 58122 60384 62605 64829 67096 69326 71646 73952 76258 78544 80833 83058 85333 87679 89941
470
4902
江苏省
397
485
5387
485
5387
江苏省
396
543
5930
543
5930
江苏省
395
599
6529
599
6529
江苏省
394
599
7128
599
7128
江苏省
393
639
7767
639
7767
江苏省
392
655
8422
655
8422
江苏省
391
711
9133
711
9133
江苏省
390
760
9893
760
9893
江苏省
389
851
10744
851
10744
江苏省
388
806
11550
807
11551
2020
江苏省
387
2020
江苏省
386
2020
江苏省
江苏省自学考试部分专业名称和代码调整

江苏省自学考试部分专业名称和代码调整根据《教育部办公厅关于印发〈高等教育自学考试专业设置实施细则〉和〈高等教育自学考试开考专业清单〉的通知》(教职成厅〔2018〕1号)精神,为规范自学考试专业设置,结合我省实际,现对江苏省高等教育自学考试部分专业名称和代码进行调整。
具体事项通知如下:一、本次调整仅限于我省面向社会仍在开考的专业,专业名称调整后与《高等教育自学考试开考专业清单》保持一致。
新旧专业名称和代码对照情况详见《江苏省高等教育自学考试新旧专业对照表》(见文末)。
已经公布即将停考的专业不再公布新旧专业名称和代码的对应关系。
二、教育部考试中心将陆续发布新版高等教育自学考试专业基本规范,届时我省将根据新版专业基本规范对我省各专业考试计划进行相应调整,并及时向社会公布。
新的专业考试计划公布时,我省开考专业全部启用新专业名称和代码。
三、过渡期间,在新专业名称和代码启用前,考生仍须按原专业名称和代码申请毕业;在新专业名称和代码启用后,截止2021年6月30日,按原专业名称和代码注册的考生可在新旧专业名称中选择一个专业名称申请毕业;按新专业名称和代码注册的考生只能按照新专业名称申请毕业。
2021年7月1日开始,所有考生均按新专业名称申请毕业。
各单位要认真做好专业调整的宣传和解释工作,及时准确地向考生宣传专业调整的有关政策,切实维护考生的正当权益,营造良好的舆论环境,确保我省高等教育自学考试专业调整工作平稳顺利实施。
省教育考试院小苏政策解析:本次专业名称和代码调整对江苏省内考生(省际转考除外)几乎不产生影响,老生在2021年6月30日前可以在新旧专业名称中选择一个申请毕业;新生在新专业名称和代码启用后按新专业名称报名考试并申请毕业即可。
本次调整对复习备考不产生影响。
小苏提示:苏考通2019年10月考期资料已经更新完毕,如有报考计划,建议提早规划,尽早准备。
工作分析2020年10月考期启用新教材,同学们合理安排时间哦。
2020年江苏省普通高等学校招生考生录取分数线
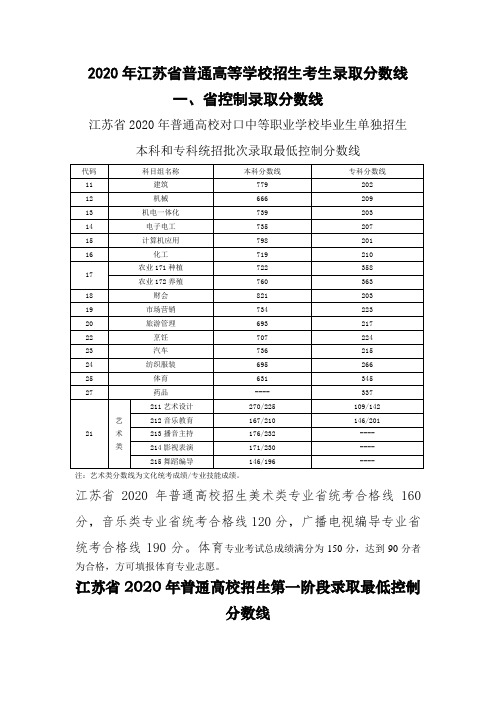
2020年江苏省普通高等学校招生考生录取分数线一、省控制录取分数线江苏省2020年普通高校招生美术类专业省统考合格线160分,音乐类专业省统考合格线120分,广播电视编导专业省统考合格线190分。
体育专业考试总成绩满分为150分,达到90分者为合格,方可填报体育专业志愿。
江苏省2020年普通高校招生第一阶段录取最低控制分数线注:一、艺术类校考本科专业录取最低控制分数线:1.经教育部批准的部分独立设置的本科艺术院校(含部分艺术类本科专业参照执行的少数高校)的艺术类本科专业录取最低控制分数线由各校自行划定。
2.除第1条规定以外的其他院校本科校考专业的省最低控制分数线为文化195分/专业合格。
其中,取得音乐表演、音乐学、作曲与作曲技术理论、流行音乐、音乐治疗、广播电视编导、美术学、绘画、雕塑、中国画、实验艺术、跨媒体艺术、文物保护与修复、漫画、艺术设计学、视觉传达设计、环境设计、产品设计、服装与服饰设计、公共艺术、工艺美术、数字媒体艺术、艺术与科技、陶瓷艺术设计、新媒体艺术、包装设计等专业校考合格的考生,还须参加相应专业省统考,且美术省统考成绩须达到160分,音乐省统考成绩须达到120分,编导省统考成绩须达到190分。
二、第一阶段填报志愿资格线:1.文科类、理科类考生必测科目成绩均需达到合格(或C 级及以上等级) ,选测科目等级符合院校的要求,文科类总分在274分以上、理科类总分在303分以上,方可填报第一阶段高考志愿(报考高水平运动队、飞行技术专业除外)。
2.体育类、艺术类考生七门必测科目成绩中不合格(或D 级)不超过3门,体育类文化226分/专业100分以上、美术省统考文化226分/专业160分以上、音乐省统考(声乐、器乐)文化200分/专业135分以上、编导省统考文化256分/专业190分以上、艺术校考文化185分/专业合格(经教育部批准的部分独立设置的本科艺术院校以及部分参照执行的少数高校的艺术类本科专业不受此限制),方可填报第一阶段高考志愿。
江苏省2020年普通高校招生录取办法及考试违规处理办法调查问卷参考答案(艺术类44题)

20201、文科类、理科类平行院校志愿在投档过程中,如投档成绩相同,则按什么分数再次排序?(多选)正确答案为:A C DA、语文、数学两门科目的原始分(含附加分)之和从高分到低分再次排序。
B、语文、数学两门科目的原始分(不含附加分)之和从高分到低分再次排序。
C、语文、数学两门科目的原始分(含附加分)之和仍相同时,文科类考生再依次按语文(不含附加分)、数学、外语分数从高到低进行排序,理科类考生再依次按数学(不含附加分)、语文、外语分数从高到低进行排序。
D、按照排序规则排序后,如仍相同,则将这部分考生按志愿全部投档。
2、考生进入考场时需要进行身份验证,以下说法正确的有哪些?(多选)正确答案为:A B DA、使用金属探测器对考生进行检查后,再进行身份验证。
B、考生须将身份证放在考务通上的指定位置并“刷脸”进行验证身份,“刷脸”时须将面部正对身份识别设备的摄像头。
C、考生在考务通上进行身份证和“刷脸”验证时,暂时不能通过的,不能参加考试。
D、考生在考务通上进行身份证和“刷脸”验证时,暂时不能通过的,可先就座应考,待监考员进一步核验。
3、我省艺术类院校志愿投档的原则主要有以下哪些?(多选)正确答案为:A B C DA、使用音乐类专业省统考成绩录取的院校,分声乐、器乐,按专业总分及不大于招生计划数的105%,按照“满足学业水平测试成绩,专业总分优先,遵循志愿”的平行院校志愿原则投档。
B、使用美术类专业省统考成绩或广播电视编导专业省统考成绩录取的院校,按文化总分与专业总分之和及不大于招生计划数的105%,按照“满足学业水平测试成绩,文化总分与专业总分之和优先,遵循志愿”的平行院校志愿原则投档。
C、对报考部分独立设置的本科艺术院校(含部分艺术类本科专业参照执行的少数高校),文化分、专业分均达到相关招生高校自行划定的录取最低控制分数线的考生,按院校提出的调档比例投档。
D、对报考其他校考院校[部分独立设置的本科艺术院校(含部分艺术类本科专业参照执行的少数高校)],文化分达到省录取最低控制分数线且专业合格的考生,按院校提出的调档比例投档。
江苏省2020年普通高校对口中等职业学校毕业生单独招生专科统招批次院校投档线(按科目组排序)
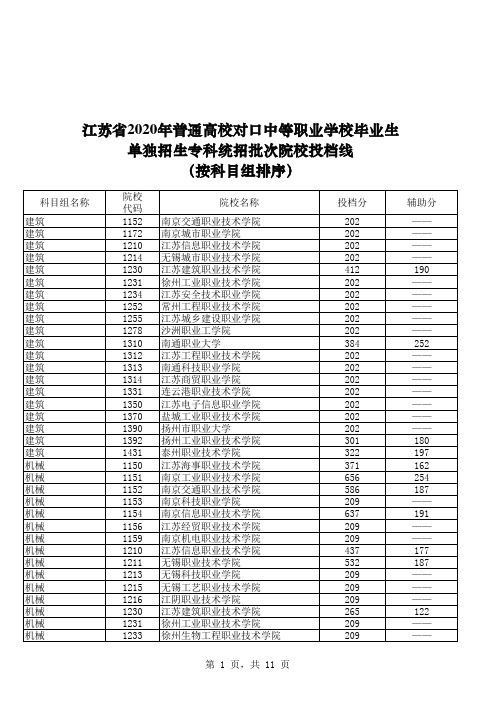
江苏省2020年普通高校对口中等职业学校毕业生单独招生专科统招批次院校投档线
(按科目组排序)
第 1 页,共 11 页
第 2 页,共 11 页
第 3 页,共 11 页
第 4 页,共 11 页
第 5 页,共 11 页
第 6 页,共 11 页
第 7 页,共 11 页
第 8 页,共 11 页
第 9 页,共 11 页
第 10 页,共 11 页
注:1.在投档过程中,对总分相同的考生,按其“辅助排序分(即专业技能成绩)”从高到低排序投档。
当考生总分等于投档分时,专业技能成绩须达到辅助排序分;当考生总分超过投档分时,则辅助排序分高低不影响投档。
2.艺术科目组音乐教育方向投档分为文化统考成绩省控线/专业技能成绩。
第 11 页,共 11 页。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
江苏省教育考试院关于公布江苏省2020年普通
各市招办(考试院、招考中心),各考点院校:
为做好江苏省2020年普通高校招生体育类专业省统考工作,根据省教育厅《关于印发〈江苏省2014年普通高校招生体育专业统考考试方案〉的通知》(苏教考〔2013〕15号)要求,现将2020年全省体育类专业省统考专项考试内容和考点承担考试专项等有关情况公布:
一、专项考试内容
1.田径:100米栏(女)、110米栏(男)、200米、400米、1500米、3000米(女)、5000米(男)、跳高、跳远、三级跳远、铅球、铁饼、标枪。
考生须在上述项目中自主确定一个单项。
2.篮球:“V”脚步移动、投篮A、全场综合技术A〔以右手为例:考生站于端线中点处(篮板下),面向场内。
持球听口令(或哨音)按图示路线用右手运球至①处,在脚踏上①时做右手背后运球换左手运球至②处,当脚踏及②时做体前换手变向运球,右手运球绕过障碍物③传球给站在接球区的陪考员×并接回传球右手上篮。
球中篮后抢篮板接右手运球至④,在脚踏上④时做右手背后运球换左手运球至⑤,当脚踏及⑤时做体前换手变向运球,右手运球绕过障碍物⑥传球给站在接球区的陪考员×并接回传球右手上篮,投篮不中必须补中(补篮方法不限),球中篮停表。
每人2次,计其中1次最佳成绩(X)。
(左手考生考试则相反)〕
3.排球:变向移动、传垫球B、发球A、扣球(必考)。
4.足球:25米折返跑、1分钟颠球、头球顶远、运球绕杆射门(必考)。
5.乒乓球:3.5米移动、1分钟反手推挡、侧身正手拉或突击下旋球、左推右攻(必考)。
6.武术:正踢腿(左、右)、腾空飞脚、竖劈叉(左、右)、仆步抡拍、初级长拳(第三路)。
7.体操:
(1)男生:引体向上、双臂屈伸、纵叉、肋木悬垂举腿、技巧(必考)、低单杠。
(2)女生:仰卧举腿、俯卧撑、跳绳、纵叉、技巧(必考)、低单杠。
8.健美操:纵劈叉(左、右)、跳绳、靠倒立、仰卧两头起、规定动作B。
9.羽毛球:1分钟一跳双摇跳绳(双飞)、正手发高远球、网前放球、杀上网(必考)。
二、考点及所承担考试专项
南京体育学院:篮球
南京师范大学:田径
苏州大学:乒乓球
扬州大学:足球、排球、羽毛球
江苏师范大学:武术、体操、健美操
专业考试的面试科目和身体素质必考科目均在专项所承担考点统一进行。
三、信息确认及考试安排
1.专业考试信息确认
5月7-10日(截止时间:10日下午17:00),考生须登录江苏省教育考试院门户网(略),在网上确认专业考试信息、网上支付报名考试费、网上打印专业考试信息确认表。
逾期视为考生自动放弃。
系统开放时间为每天8:30-22:00(10日为8:30-17:00)。
凡需更改高考报名时所填报体育专项的考生,可在网上确认专业考试信息时,修改确定报考专项。
逾期一律不予更改。
2.准考证打印
5月19-22日,考生须登录江苏省教育考试院门户网(略),在网上打印准考证。
3.报到和考试安排
考生须携带本人居民身份证、《江苏省2020年普通高校招生体育类专业考试通知书》和准考证到测试专项对应的考点报到、面试。
具体报到时间、地点和有关要求以考点公布的安排为准。
考生须按时到指定考点报到。
考生报到时,考点必须对考生的报考资格进行复核,如发现不符合条件或弄虚作假者应取消其专业考试资格。
符合报考条件者,由考点为考生安排考试日程。
5月30日起开始考试。
具体考试安排以考点公布的考试日程为准。
考生须按考试日程上规定的时间和地点参加考试,逾期不予补考。
四、有关考试执行标准的说明
1.身体素质和田径专项考试中涉及径赛项目的起跑,执行全能径赛项目比赛的有关规定和裁判方法,即:在径赛项目中,每组考试只允许第一次起跑犯规而考生不被取消资格,之后每次起跑犯规的一名或多名考生均将被取消该项目的考试资格。
因犯规被取消资格的考生,不得再参加本项目的考试。
2.参加原地双手头后向前掷实心球考试时,考生不得穿着钉鞋测试,不允许自带球。
3.乒乓球专项考试时,用球大小规格为40+。
五、有关要求
1.体育类专业省统考是我省普通高校招生考试的重要组成部分,关系到每一位体育类考生的切身利益。
各地在思想上要高度重视,切实做好对所辖县(市、区)招办及有关中学的指导和政策宣传,确保每一位体育类考生都能按时参加信息确认、报到和考试。
2.各地要指导有关中学安排专人引导考生网上信息确认事宜,组织考生学习《江苏省2020年普通高校招生体育类专业省统考网上信息确认须知》(详见江苏省教育考试院门户网),指导考生进行信息确认和考试。
3.各地要指导有关中学进一步加强组织和管理,做好带队老师选聘工作,加强安全教育,做好交通、食宿、应对天气变化等方面的各项准备工作,提醒带队老师和考生在规定的时间内,到承担专项考试任务对应的考点报到和考试。
逾期一律不予补考。
4.各地要指导有关中学按教育、卫健部门的规定建立学生健康档案,了解考生及其家人的身体状况,做到异常情况早发现、早治疗,并对身体异常考生做好心理疏导。
非在校生的健康监测,由当地招生考试机构负责制定具体办法。
考生应尽量减少跨区域流动,主动配合中学、当地招生考试机构和考点的疫情防控检查。
5.考点要联合各有关单位和部门制定符合疫情防控要求的考试工作方案,合理安排考生的报到、考试,最大限度减少人员聚集。
积极协调当地有关部门,对集中食宿点及考点周边的酒店、宾馆、饭店、流动餐饮等进行摸排,为考生的食宿提供方便。
对涉考人员,做好卫生防疫教育和健康筛查。
6.各市、县(市、区)招办、中学和有关高校要加强对带队老师和考生诚信考试的宣传和教育,对在专业考试中被认定为违规的考生,按照《国家教育考试违规处理办法》(教育部令第33号)和有关规定严肃处理,并将考生违规事实记入其高考诚信电子档案;《刑法》规定,在法律规定的国家考试中,实施组织或参与组织考试作弊的、代替他人或者让他人代替自己参加考试的,将被依法追究刑事责任。
(非正式文本,仅供参考。
若下载后打开异常,可用记事本打开)。
