山东省济南市历城区图片版含答案
山东省济南市历城区2024届中考数学最后一模试卷含解析

山东省济南市历城区2024学年中考数学最后一模试卷注意事项:1.答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题(每小题只有一个正确答案,每小题3分,满分30分)1.共享单车已经成为城市公共交通的重要组成部分,某共享单车公司经过调查获得关于共享单车租用行驶时间的数据,并由此制定了新的收费标准:每次租用单车行驶a小时及以内,免费骑行;超过a小时后,每半小时收费1元,这样可保证不少于50%的骑行是免费的.制定这一标准中的a的值时,参考的统计量是此次调查所得数据的()A.平均数B.中位数C.众数D.方差2.如图所示,在长为8cm,宽为6cm的矩形中,截去一个矩形(图中阴影部分),如果剩下的矩形与原矩形相似,那么剩下矩形的面积是()A.28cm2B.27cm2C.21cm2D.20cm23.一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是()A.和B.谐C.凉D.山4.估计41的值在()A.4和5之间B.5和6之间C.6和7之间D.7和8之间5.如图,在△ABC中,∠C=90°,∠B=10°,以A为圆心,任意长为半径画弧交AB于M、AC于N,再分别以M、N 为圆心,大于MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于D,下列四个结论:①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△ACD:S△ACB=1:1.其中正确的有()A.只有①②③B.只有①②④C.只有①③④D.①②③④6.如图,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC,FC=2,则AB的长为()A.83B.8 C.43D.67.□ABCD中,E、F是对角线BD上不同的两点,下列条件中,不能得出四边形AECF一定为平行四边形的是()A.BE=DF B.AE=CF C.AF//CE D.∠BAE=∠DCF8.下列美丽的壮锦图案是中心对称图形的是()A.B.C.D.9.下列运算错误的是()A.(m2)3=m6B.a10÷a9=a C.x3•x5=x8D.a4+a3=a710.如图,正方形ABCD中,E,F分别在边AD,CD上,AF,BE相交于点G,若AE=3ED,DF=CF,则AGGF的值是()A.43B.54C.65D.76二、填空题(共7小题,每小题3分,满分21分)11.如图,边长为6的菱形ABCD中,AC是其对角线,∠B=60°,点P在CD上,CP=2,点M在AD上,点N在AC上,则△PMN的周长的最小值为_____________ .12.如图,在平面直角坐标系中,点P(﹣1,a)在直线y=2x+2与直线y=2x+4之间,则a的取值范围是_____.13.甲乙两人进行飞镖比赛,每人各投5次,所得平均环数相等,其中甲所得环数的方差为15,乙所得环数如下:0,1,5,9,10,那么成绩较稳定的是_____(填“甲”或“乙”).14.已知扇形的圆心角为120°,弧长为6π,则扇形的面积是_____.15.图1是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美.图2是从图1冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5=度.16.若不等式组220x ab x->⎧⎨->⎩的解集为11x-<<,则2009()a b+=________.17.如图,在△ABC中,AD、BE分别是边BC、AC上的中线,AB=AC=5,cos∠C=45,那么GE=_______.三、解答题(共7小题,满分69分)18.(10分)数学兴趣小组为了研究中小学男生身高y(cm)和年龄x(岁)的关系,从某市官网上得到了该市2017年统计的中小学男生各年龄组的平均身高,见下表:如图已经在直角坐标系中描出了表中数据对应的点,并发现前5个点大致位于直线AB上,后7个点大致位于直线CD上.年龄组7 8 9 10 11 12 13 14 15 16 17x男生平均身高115.2 118.3 122.2 126.5 129.6 135.6 140.4 146.1 154.8 162.9 168.2y(1)该市男学生的平均身高从岁开始增加特别迅速.(2)求直线AB所对应的函数表达式.(3)直接写出直线CD所对应的函数表达式,假设17岁后该市男生身高增长速度大致符合直线CD所对应的函数关系,请你预测该市18岁男生年龄组的平均身高大约是多少?19.(5分)如图,抛物线y=ax2+bx+c与x轴的交点分别为A(﹣6,0)和点B(4,0),与y轴的交点为C(0,3).(1)求抛物线的解析式;(2)点P是线段OA上一动点(不与点A重合),过P作平行于y轴的直线与AC交于点Q,点D、M在线段AB上,点N在线段AC上.①是否同时存在点D和点P,使得△APQ和△CDO全等,若存在,求点D的坐标,若不存在,请说明理由;②若∠DCB=∠CDB,CD是MN的垂直平分线,求点M的坐标.20.(8分)2018年“植树节”前夕,某小区为绿化环境,购进200棵柏树苗和120棵枣树苗,且两种树苗所需费用相同.每棵枣树苗的进价比每棵柏树苗的进价的2倍少5元,每棵柏树苗的进价是多少元.21.(10分)如图,在直角坐标系xOy 中,直线y mx =与双曲线n y x=相交于A (-1,a )、B 两点,BC ⊥x 轴,垂足为C ,△AOC 的面积是1. 求m 、n 的值;求直线AC 的解析式.22.(10分)一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价10元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的销售量y (件)与销售价x (元/件)之间的函数关系如图所示.求y 与x 之间的函数关系式,并写出自变量x 的取值范围;求每天的销售利润W (元)与销售价x (元/件)之间的函数关系式,并求出每件销售价为多少元时,每天的销售利润最大?最大利润是多少?23.(12分)用你发现的规律解答下列问题.111122=-⨯ 1112323=-⨯1113434=-⨯ ┅┅计算111111223344556++++=⨯⨯⨯⨯⨯ .探究1111......122334(1)n n ++++=⨯⨯⨯+ .(用含有n 的式子表示)若1111......133557(21)(21)n n ++++⨯⨯⨯-+的值为1735,求n 的值. 24.(14分)探究:在一次聚会上,规定每两个人见面必须握手,且只握手1次若参加聚会的人数为3,则共握手 次:;若参加聚会的人数为5,则共握手 次;若参加聚会的人数为n (n 为正整数),则共握手 次;若参加聚会的人共握手28次,请求出参加聚会的人数.拓展:嘉嘉给琪琪出题:“若线段AB 上共有m 个点(含端点A ,B ),线段总数为30,求m 的值.”琪琪的思考:“在这个问题上,线段总数不可能为30”琪琪的思考对吗?为什么?参考答案一、选择题(每小题只有一个正确答案,每小题3分,满分30分)1、B【解题分析】根据需要保证不少于50%的骑行是免费的,可得此次调查的参考统计量是此次调查所得数据的中位数.【题目详解】因为需要保证不少于50%的骑行是免费的,所以制定这一标准中的a 的值时,参考的统计量是此次调查所得数据的中位数,故选B .【题目点拨】本题考查了中位数的知识,中位数是以它在所有标志值中所处的位置确定的全体单位标志值的代表值,不受分布数列的极大或极小值影响,从而在一定程度上提高了中位数对分布数列的代表性。
2019年山东省济南市历城区中考地理二模试卷(解析版)
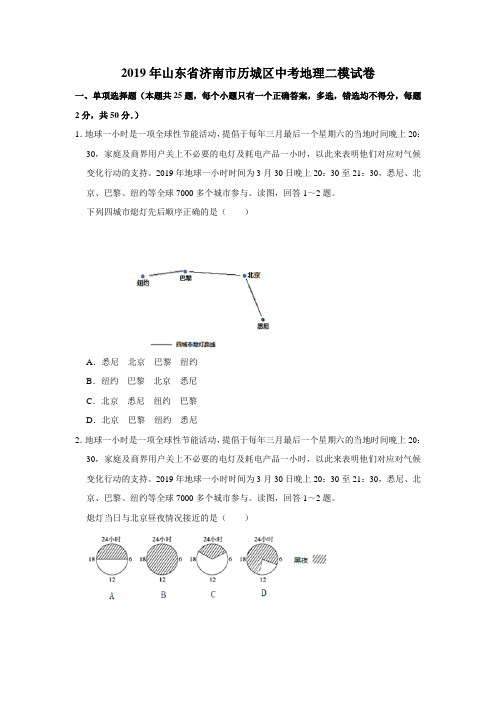
2019年山东省济南市历城区中考地理二模试卷一、单项选择题(本题共25题,每个小题只有一个正确答案,多选,错选均不得分,每题2分,共50分.)1.地球一小时是一项全球性节能活动,提倡于每年三月最后一个星期六的当地时间晚上20:30,家庭及商界用户关上不必要的电灯及耗电产品一小时,以此来表明他们对应对气候变化行动的支持。
2019年地球一小时时间为3月30日晚上20:30至21:30,悉尼、北京、巴黎、纽约等全球7000多个城市参与。
读图,回答1~2题。
下列四城市熄灯先后顺序正确的是()A.悉尼北京巴黎纽约B.纽约巴黎北京悉尼C.北京悉尼纽约巴黎D.北京巴黎纽约悉尼2.地球一小时是一项全球性节能活动,提倡于每年三月最后一个星期六的当地时间晚上20:30,家庭及商界用户关上不必要的电灯及耗电产品一小时,以此来表明他们对应对气候变化行动的支持。
2019年地球一小时时间为3月30日晚上20:30至21:30,悉尼、北京、巴黎、纽约等全球7000多个城市参与。
读图,回答1~2题。
熄灯当日与北京昼夜情况接近的是()A.A B.B C.C D.D3.一桥飞架中欧,一头连着中国,一头牵着欧洲。
随着中国和欧洲联系日益密切,亚欧大陆架起了多座大陆桥。
第一、第二大陆桥早已运行,第三亚欧大陆桥还在构想规划中。
读图,回答3~5题。
第一亚欧大陆桥跨越的洲界线是()A.土耳其海峡B.乌拉尔山C.苏伊士运河D.黑海4.一桥飞架中欧,一头连着中国,一头牵着欧洲。
随着中国和欧洲联系日益密切,亚欧大陆架起了多座大陆桥。
第一、第二大陆桥早已运行,第三亚欧大陆桥还在构想规划中。
读图,回答3~5题。
在第二亚欧大陆桥经过的A地区最可能看到的景象是()A.雨林景观,枝叶繁茂B.草场青青,牛羊成群C.阴雨绵绵,稻花飘香D.河湖众多,小桥流水5.一桥飞架中欧,一头连着中国,一头牵着欧洲。
随着中国和欧洲联系日益密切,亚欧大陆架起了多座大陆桥。
第一、第二大陆桥早已运行,第三亚欧大陆桥还在构想规划中。
2023年山东省济南市历城区中考地理二模试卷(附答案详解)
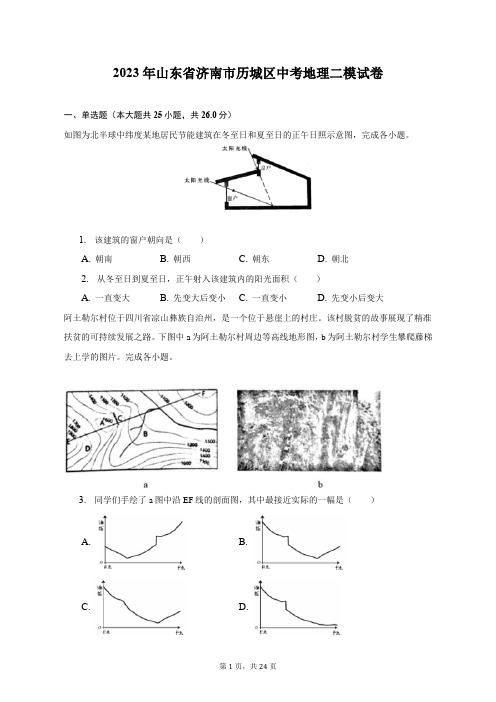
2023年山东省济南市历城区中考地理二模试卷一、单选题(本大题共25小题,共26.0分)如图为北半球中纬度某地居民节能建筑在冬至日和夏至日的正午日照示意图,完成各小题。
1. 该建筑的窗户朝向是()A. 朝南B. 朝西C. 朝东D. 朝北2. 从冬至日到夏至日,正午射入该建筑内的阳光面积()A. 一直变大B. 先变大后变小C. 一直变小D. 先变小后变大阿土勒尔村位于四川省凉山彝族自治州,是一个位于悬崖上的村庄。
该村脱贫的故事展现了精准扶贫的可持续发展之路。
下图中a为阿土勒尔村周边等高线地形图,b为阿土勒尔村学生攀爬藤梯去上学的图片。
完成各小题。
3. 同学们手绘了a图中沿EF线的剖面图,其中最接近实际的一幅是()A. B.C. D.4. 阿土勒尔村实现了精准扶贫的可持续发展,采取的措施有()①搬迁到相对平坦地区②利用独特资源发展旅游业③改善当地的交通设施④开垦梯田大力发展种植业A. ①②③B. ①②④C. ①③④D. ②③④下图为“世界部分地区年降水量分布用”。
完成各小题。
5. 图中降水较多的地区是()A. ①②③B. ②③④C. ①③⑤D. ③④⑤6. 造成③④⑤降水差异的主要因素是()A. 纬度位置B. 海陆位置C. 地形D. 人类活动亚洲是我们生活的大洲。
自然环境复杂多样。
如图为亚洲地形图。
完成各小题。
7. 由图可知,亚洲()A. 地势中部低,四周高B. 气候复杂多样,季风气候显著C. 河流较少且短小,自西向东流D. 河流呈放射状由中部流向四周8. 关于甲国和乙国说法正确的是()A. 自然资源都丰富,重工业发达B. 工业都分布在沿海地区C. 甲国多火山和地震D. 乙国位于“十字路口”的位置下图为大不列颠岛地形和降水量分布示意图。
完成各小题。
9. 大不列颠岛地处()A. 北半球、东半球B. 北寒带C. 亚欧大陆以东D. 北太平洋10. 来自海洋的暖湿气流受地形阻挡,形成了岛上降水。
由岛上降水量分布可以推知,风向应为()A. 北风B. 东南风C. 南风D. 西风“苹果屋”是我国北极科学考察中冰上作业的主要装备,除了用来防御“熊出没”的袭击,还可长期存放冰站作业科考设备工具,作业人员也可就地短暂休息。
山东省济南市历城区图片版2022-2023学年六年级数学第二学期期末教学质量检测模拟试题含解析
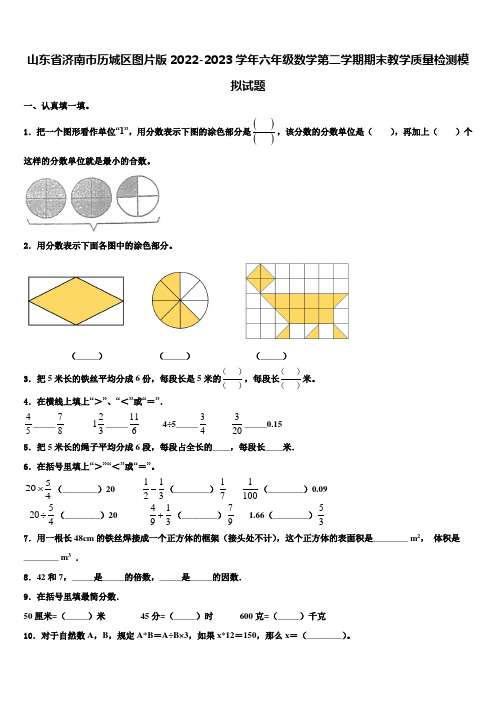
山东省济南市历城区图片版2022-2023学年六年级数学第二学期期末教学质量检测模拟试题一、认真填一填。
1.把一个图形看作单位“1”,用分数表示下图的涂色部分是()(),该分数的分数单位是( ),再加上( )个这样的分数单位就是最小的合数。
2.用分数表示下面各图中的涂色部分。
(_____) (_____) (_____)3.把5米长的铁丝平均分成6份,每段长是5米的 ()(),每段长 ()()米。
4.在横线上填上“>”、“<”或“=”.45_____78 213_____116 4÷5_____34 320_____0.15 5.把5米长的绳子平均分成6段,每段占全长的____,每段长____米. 6.在括号里填上“>”“<”或“=”。
5204⨯(________)20 1231-(________)17 1100(________)0.09 5204÷(________)20 4193+(________)79 1.66(________)537.用一根长48cm 的铁丝焊接成一个正方体的框架(接头处不计),这个正方体的表面积是________ m 2, 体积是________ m 3 .8.42和7,_____是_____的倍数,_____是_____的因数. 9.在括号里填最简分数.50厘米=(_____)米 45分=(_____)时 600克=(_____)千克 10.对于自然数A ,B ,规定A*B =A÷B×3,如果x*12=150,那么x =(________)。
二、是非辨一辨。
11.8既是8的倍数,又是8的因数。
(______)12.4千克的15和1千克的45相等。
(______)13.8是4和8的最小公倍数,也是这两个数的最大公因数。
(________)14.把图形绕圆心逆时针旋转90 后得到的图形是。
(________)15.一个自然数,如果不是质数,就一定是合数。
山东省济南市历城区2018-2019学年八年级上学期期末考试语文试题及答案

2018—2019学年第一学期期末质量检测八年级语文试题(2019.1)说明:1.本试题满分为150分,考试时间为120分钟。
2.本试卷分试题卷和答题卡,所有答案都必须填涂或填写在答题卡规定的答题区域内,答在本试题卷上无效。
注意事项:1.答选择题时,必须使用2B铅笔填涂答题卡上相应题目的答案标号,修改时,要用橡皮擦干净。
2.答非选择题时,必须使用0.5毫米黑色签字笔书写,要求笔迹清晰、字体工整,务必在答题卡题号所指示的答题区域内作答。
一、(20分)1.下列词语中加点字的读音完全正确....的一项是()(4分)A. 倔.强(juè) 濒.临(bīn) 暴.晒( bào) 惟妙惟肖.(xiào)B. 鲜腴.(yú) 黝.黑 (yǒu) 镂.空(lòu) 不折不挠.(náo)C. 蹒.跚(pán) 沼.泽(zhāo) 洗涤.(dí) 坦荡如砥.(dǐ)D. 虬.枝(qiú) 纤.维(xiān) 辟.邪(pì)潜.滋暗长 (qián)2.下列词语中没有错别字.....的一项是()(4分)A. 密匝匝擅长记裁因地制宜B. 口头禅题拔抵御重峦叠嶂C. 座右铭劳碌凋谢决不雷同D. 势利眼干燥推崇锐不可挡3.下列句子中加点成语使用恰当..的一项是()(4分)A.大家听了歌唱家腾格尔演唱的经典曲目——《天堂》,不由得触目伤怀....。
B.在“我是歌手”的舞台上,林志炫的服装精致得体,天衣无缝....。
C.年节将近,民众纷纷前往菜市场采办年货,摩肩接踵....的人潮把整条街挤得水泄不通。
D. 重庆合川区三汇天然石体,虽不及云南石林壮观奇绝,却也形态万千,别具匠心....。
4.下列句子没有语病....的一项是()(4分)A.我市文明办开展与策划的“经典诵读”活动,有利于更多的人了解、研究国学经典。
B. 赵州桥大约修建于公元605年左右,到今天已经一千四百多年了。
2023年山东省济南市历城区中考一模数学试题(含解析)

2023年山东省济南市历城区中考一模数学试题学校:___________姓名:___________班级:___________考号:___________A.....为完善城市轨道交通建设,提升城市公共交通服务水平,济南市城市轨道交通2020~2025年第二期建设规划地铁总里程约为159600米.把数字“159600.....已知实数a ,b 在数轴上对应点的位置如图所示,则下列判断正确的是( )A .0a b +>B .0ab >C .(A .16B .298.函数y x b =-+与()0k y k x=≠在同一坐标系中的图象如图所示,则函数大致图象为( )A .....如图,已知锐角AOB ∠1)在射线OA 上取一点圆心,OC 长为半径作 PQ ,交射线OB 于点D ,连接CD ;(2)分别以点C ,D 为圆心,CD 长为半径作弧,交 PQ 于点M ,N ;(3)连接OM ,MN ,ND .根据以上作图过程及所作图形,下列结论中错误的是( )A .COM COD∠=∠B .若OM MN =,则30AOB ∠=︒C .MN CD ∥D .2MOD MND∠=∠10.已知二次函数222y x tx t t =-++,将其图象在直线1x =左侧部分沿x 轴翻折,其余部分保持不变,组成图形G .在图形G 上任取一点M ,点M 的纵坐标y 的取值满足y m ≥或y n <,其中m n >.令s m n =-,则s 的取值范围是( )A .0s ≤B .02s ≤≤C .2s ≤D .2s ≥13.比6大的最小整数是14.如图,扇形纸片处,图中阴影部分的面积为15.如图(1),已知小正方形1111D C B A ;把正方形1111D C B A 边长按原法延长一倍得到正方形以此下去,则正方形20232023A B C 16.正方形ABCD 的边长为8,点E 、F 分别在边AD 、BC 上,将四边形折叠,使点A 落在A '处,点B 落在点B '处,A B ''交BC 于G .以下结论:中点时,A DE ' 三边之比为3:4:5;②连接AA ',则A E A F '=;③当为3:4:5时,A '为CD 中点;④当A '在CD 上移动时,A CG ' 周长不变.其中正确的有(写出所有正确结论的序号).三、解答题17.计算:11382cos452-⎛⎫---+ ⎪⎝⎭20.为深入学习贯彻党的二十大精神,某校开展了以新征程”为主题的知识竞赛.发现该校全体学生的竞赛成绩(百分制)均不低于现从中随机抽取n名学生的竞赛成绩进行整理和分析(成绩得分用请根据以上信息,解答下列问题:(1)c=___________.(2)“8090≤<”这组数据的众数是x(3)随机抽取的这n名学生竞赛成绩的中位数是(4)若学生竞赛成绩达到85秀学生的人数.(1)求C到直线AB的距离;(2)求游轮继续向正东方向航行过程中与灯塔1海里,参考数据:2 1.41≈,322.如图,AB是O的直径,C,(1)求证:AE EF⊥;(2)若23DGAG=,O的半径为2,求23.山地自行车越来越受到中学生的喜爱,的甲型车去年销售总额5万元,销售总额将比去年减少20%.(1)求k的值与点F的坐标;(2)在x轴上找一点M,使EV(3)在(2)的条件下,若点P是否存在这样的点P,Q,使得以点直接写出符合条件的点P坐标;若不存在,请说明理由.25.某校数学兴趣学习小组在一次活动中,P 是该抛物线上一动点,设点P 的横坐标为()03m m <<.(1)求抛物线的表达式及点C 的坐标;(2)如图1,连接BD ,PB ,PD ,若PBD △的面积为3,求m 的值;(3)连接AC ,过点P 作PM AC ⊥于点M ,是否存在点P ,使得2PM CM =.如果存在,请求出点P 的坐标;如果不存在,请说明理由.参考答案:故选:C.【点睛】本题考查了三视图,解题关键是明确俯视图是从上往下看到的图形.MCCD DN ==,1203AOB MON ∴∠=∠=︒,故C 、连接MD ,ND ,MCDN =,MDC DMN ∴∠=∠,MN CD ∥,故C 不符合题意;D 、由圆周角定理得到MOD ∠故选:B .【点睛】此题考查了圆周角定理,熟记圆周角定理是解题的关键.此时y 的取值范围为:()21y t t ≥-+或y t ≤-,不满足题意;②当1t =时,此时y 的取值范围为:1y ≥或1y <-,满足题意,此时()112s =--=;③当1t >时,此时y 的取值范围为:y t ≥或()21y t t <---,满足题意,y≥-此时y的取值范围为:(1s≥,综上,2故选:D.【点睛】本题考查了二次函数的图象与性质,关键,注意分类讨论思想的运用.∵OC OA =,∴AOC 是等边三角形,∴60CAO AOC ∠=∠=︒,AC =∴120AOB ∠=︒,//,∴==,EM CD EM CD AD∴∠=∠=︒,90AEN D由翻折可知:EF垂直平分AA',∴∠=︒90AQE∴∠+∠=∠+∠EAN ANE QEN ANE ∴∠=∠,EAN QEN由翻折可知:90EA G EAB '∠=∠=∴EAA EA A ''∠=∠,∵90D Ð=°,∴90EAA DA A ''∠+∠=︒,又∵90EA A AA G EA G '''∠+∠=∠=∴AA G DA A ''∠=∠,∵四边形ABCD为平行四边形∴BO=DO,AO=CO∵AF=CE,过点C 作CE AB ⊥于点E ,在ABC 中,45BAC ∠=︒,∴ACE △是等腰直角三角形,由题意得: 2202402AC =⨯=,∴2402CE AC ==,即点C 到线段的距离为40海里;∵DE 是O 的切线,∴DE OD ^,∴90ODF ∠=︒.∵ BDCD =,∴CAD DAB ∠=∠.设EG 的函数关系式为y ax =+把()24E ,,46,3G ⎛⎫- ⎪⎝⎭代入y =得42463a b a b =+⎧⎪⎨-=+⎪⎩,解得43203a b ⎧=-⎪⎪⎨⎪=⎪⎩420∵ABC AMN △∽△,∴AM AN AB AC = ,BAC MAN ∠=∠,∴BAC MAC MAN MAC ∠-∠=∠-∠,即∠∵H 为正方形DEFG 的中心,∴,90DH EH DHE =∠=︒,即DEH △∵四边形ABCD 为正方形,∴,90BC CD BCD =∠=︒,设点2(,23)P m m m -++,点(,Q m ∴2113(22PBD S PQ OB m ∆=⨯⨯=⨯-+∵PBD △的面积为3, ∵(1,0),(1,4)A C -,。
山东省济南市历城区图片版2022-2023学年数学四年级第一学期期末经典试题(含解析)

2022-2023学年四上数学期末模拟测试卷一、填空题。
(20 分)1.量出下面各角的度数。
∠1=(________)°∠2=(________)°2.在里填“>”“<”或“=”。
49亿4899000000360×3036×300450÷304500÷3003.新学期,王老师为学校篮球队购买运动服,每套运动153元,王老师准备了6000元;这些钱_____(横线里填“能”或“不能”)购买39运动服吗?4.在括号里填上“>”“<”或“=”。
3654879(________)3654897 2590000(________)26万360÷12(________)360÷120 16×400(________)40×1605.明明坐在第2列第4排,用数对表示为(_____),那么芳芳坐在第6列第一排,用数对表示为(________)。
6.计算.11713÷15=________......________7.趣味游戏:一座桥,从桥的一端走到对岸共计需要5分钟,从对岸返回也需要5分钟,桥上每次只能容纳2人行走,3名队员从桥的这端走到对岸再返回,最少需要____分钟.8.□△〇〇□△〇〇□△〇〇……按照这样的规律排列,第26个图形是_____,第60个图形是_____.9.927860000这个数读作(_______),将它改写成用“万”作单位的数是(______),省略亿位后面的尾数求近似数是(______).10.50807600读作________,它是一个________位数;其中“5”在________位上,表示________.中国是世界上人口最多的国家,约有十三亿八千二百七十一万人,横线上的数写作________,把这个数省略亿位后面的尾数后约是________.二、选择题。
(把正确答案序号填在括号里。
山东省济南市历城区图片版2023-2024学年英语五下期中统考试题含答案

山东省济南市历城区图片版2023-2024学年英语五下期中统考试题(时间:90分钟分数:100分)学校_______ 年级_______ 姓名_______一、单项选择(每题2分,共20分)。
1.We can fly a kite in ______. ( )A. springB. DecemberC. winter2.You have a high fever. Your temperature is __________. ( )A. 104.B. 104.C. 36.3.I usually get up _______ 6.30 in the morning. ( )A. onB. inC. at4.What ______ she going to do during the vacation? ( )A. amB. areC. is5.Winter is my ______ season. ( )A. bestB. favouriteC. lovely6.A: Where are the books about sports? ( )B: They are ______ Shelf B.A. aboutB. onC. under7.My dad buys a ship __________ me. ( )A. forB. tooC. and8.I don’t have________ n ice clothes ________ shoes. ( )A. some; andB. any; andC. any; or9.I'm a ____. ( )A. workB. workingC. worker10.My brother is going to ______ a model plane tomorrow. ( )A. makeB. makesC. making二、读单词,选出不同类的一项(每题2分,共10分)。
2024年山东省济南市历城区图片版三年级英语第二学期期末学业水平测试模拟试题含解析

2024年山东省济南市历城区图片版三年级英语第二学期期末学业水平测试模拟试题(时间:90分钟分数:100分)学校_______ 班级_______ 姓名_______一、读单词,选出不同类的一项(每题2分,共10分)。
1. ( )A. pear B. blue C. apple2. ( )A. T-shirt B. skirt C. sweet3. ( )A. man B. family C. woman4. ( )A. robot B. ruler C. rubber5. ( )A. brown B. white C. photo二、选出最恰当的一项,完成下列各小题(每题2分,共10分)。
6.—How many _______ do you see? ( )—Seventeen.A. strawberryB. strawberrysC. strawberries7.Sarah: __________ kites do you see? ( )John: Seventeen.A. How manyB. WhatC. Who8.I come to school on _________. ( )A. footB. legC. body9.—What’s the number in the picture? ( )—______.A. TwentyB. ThirteenC. Twelve.10.Daming and Sam go _______ in summer. ( )A. fishB. fishingC. fishes三、读句子,判断对(T)错(F)(每题2分,共10分)。
11.判断句子与图片是(T)否(F)相符:I go to school by bus. ()12.sweet ()13.看图,判断图片与句子是(T)否(F)一致:This is Danny’s coat. ()14.strawberry ()15.判断每组对话是(T)否(F)符合日常交际:—I go home by taxi. What about you? —In the evening. ()四、连成句子(每题2分,共10分)。
2024届山东省济南市历城区唐王中学中考猜题数学试卷含解析

2024届山东省济南市历城区唐王中学中考猜题数学试卷注意事项1.考生要认真填写考场号和座位序号。
2.试题所有答案必须填涂或书写在答题卡上,在试卷上作答无效。
第一部分必须用2B 铅笔作答;第二部分必须用黑色字迹的签字笔作答。
3.考试结束后,考生须将试卷和答题卡放在桌面上,待监考员收回。
一、选择题(共10小题,每小题3分,共30分)1.为确保信息安全,信息需加密传输,发送方将明文加密后传输给接收方,接收方收到密文后解密还原为明文,已知某种加密规则为,明文a ,b 对应的密文为a +2b ,2a -b ,例如:明文1,2对应的密文是5,0,当接收方收到的密文是1,7时,解密得到的明文是( )A .3,-1B .1,-3C .-3,1D .-1,32.一个半径为24的扇形的弧长等于20π,则这个扇形的圆心角是( )A .120°B .135°C .150°D .165°3.在半径等于5 cm 的圆内有长为53cm 的弦,则此弦所对的圆周角为 A .60° B .120° C .60°或120° D .30°或120°4.如图,向四个形状不同高同为h 的水瓶中注水,注满为止.如果注水量V (升)与水深h (厘米)的函数关系图象如图所示,那么水瓶的形状是( )A .B .C .D .5.若x =-2是关于x 的一元二次方程x 2+32ax -a 2=0的一个根,则a 的值为( ) A .-1或4B .-1或-4C .1或-4D .1或4 6.若不等式组236x m x x <⎧⎨-<-⎩无解,那么m 的取值范围是( ) A .m ≤2 B .m ≥2 C .m <2 D .m >27.如图,直线y =kx +b 与x 轴交于点(﹣4,0),则y >0时,x 的取值范围是( )A .x >﹣4B .x >0C .x <﹣4D .x <08.据媒体报道,我国最新研制的“察打一体”无人机的速度极快,经测试最高速度可达204000米/分,这个数用科学记数法表示,正确的是( )A .204×103B .20.4×104C .2.04×105D .2.04×1069.如图,△ABC 中,AB =4,AC =3,BC =2,将△ABC 绕点A 顺时针旋转60°得到△AED ,则BE 的长为( )A .5B .4C .3D .210.在△ABC 中,∠C =90°,tan A =,△ABC 的周长为60,那么△ABC 的面积为( )A .60B .30C .240D .120二、填空题(本大题共6个小题,每小题3分,共18分)11.如图,△ABC 的面积为6,平行于BC 的两条直线分别交AB ,AC 于点D ,E ,F ,G .若AD=DF=FB ,则四边形DFGE 的面积为_____.12.如果一个扇形的弧长等于它的半径,那么此扇形成为“等边扇形”.则半径为2的“等边扇形”的面积为 .13.方程6x x -=+的解是_________.14.不等式组42348x x -+<⎧⎨-≤⎩①②的解集是_____. 15.(11·湖州)如图,已知A 、B 是反比例函数(k >0,x <0)图象上的两 点,BC ∥x 轴,交y 轴于点C .动点P 从坐标原点O 出发,沿O→A→B→C (图中“→”所示路线)匀速运动,终点为C .过P 作PM ⊥x 轴,PN ⊥y 轴,垂足分别为M 、N .设四边形OMPN 的面积为S ,P 点运动时间为t ,则S 关于t 的函数图象大致为16.已知x=2是一元二次方程x2﹣2mx+4=0的一个解,则m的值为.三、解答题(共8题,共72分)17.(8分)如图,在△ABC中,∠ABC=90°.(1)作∠ACB的平分线交AB边于点O,再以点O为圆心,OB的长为半径作⊙O;(要求:不写做法,保留作图痕迹)(2)判断(1)中AC与⊙O的位置关系,直接写出结果.18.(8分)如图,一次函数y=kx+b的图象与坐标轴分别交于A、B两点,与反比例函数y=mx的图象在第一象限的交点为C,CD⊥x轴于D,若OB=1,OD=6,△AOB的面积为1.求一次函数与反比例函数的表达式;当x>0时,比较kx+b与mx的大小.19.(8分)2018年“清明节”前夕,宜宾某花店用1000元购进若干菊花,很快售完,接着又用2500元购进第二批花,已知第二批所购花的数量是第一批所购花数的2倍,且每朵花的进价比第一批的进价多0.5元.(1)第一批花每束的进价是多少元.(2)若第一批菊花按3元的售价销售,要使总利润不低于1500元(不考虑其他因素),第二批每朵菊花的售价至少是多少元?20.(8分)为了保护视力,学校开展了全校性的视力保健活动,活动前,随机抽取部分学生,检查他们的视力,结果如图所示(数据包括左端点不包括右端点,精确到0.1);活动后,再次检查这部分学生的视力,结果如表所示分组频数4.0≤x<4.2 24.2≤x<4.4 34.4≤x<4.6 54.6≤x<4.8 84.8≤x<5.0 175.0≤x<5.2 5(1)求活动所抽取的学生人数;(2)若视力达到4.8及以上为达标,计算活动前该校学生的视力达标率;(3)请选择适当的统计量,从两个不同的角度评价视力保健活动的效果.21.(8分)解不等式组:2(2)3{3122x xx+>-≥-,并将它的解集在数轴上表示出来.22.(10分)如图,四边形ABCD中,对角线AC,BD相交于点O,点E,F分别在OA,OC上.(1)给出以下条件;①OB=OD,②∠1=∠2,③OE=OF,请你从中选取两个条件证明△BEO≌△DFO;(2)在(1)条件中你所选条件的前提下,添加AE=CF,求证:四边形ABCD是平行四边形.23.(12分)“低碳生活,绿色出行”是我们倡导的一种生活方式,有关部门抽样调查了某单位员工上下班的交通方式,绘制了如下统计图:(1)填空:样本中的总人数为;开私家车的人数m= ;扇形统计图中“骑自行车”所在扇形的圆心角为度;(2)补全条形统计图;(3)该单位共有2000人,积极践行这种生活方式,越来越多的人上下班由开私家车改为骑自行车.若步行,坐公交车上下班的人数保持不变,问原来开私家车的人中至少有多少人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数?24.定义:对于给定的二次函数y=a(x﹣h)2+k(a≠0),其伴生一次函数为y=a(x﹣h)+k,例如:二次函数y=2(x+1)2﹣3的伴生一次函数为y=2(x+1)﹣3,即y=2x﹣1.(1)已知二次函数y=(x﹣1)2﹣4,则其伴生一次函数的表达式为_____;(2)试说明二次函数y=(x﹣1)2﹣4的顶点在其伴生一次函数的图象上;(3)如图,二次函数y=m(x﹣1)2﹣4m(m≠0)的伴生一次函数的图象与x轴、y轴分别交于点B、A,且两函数图象的交点的横坐标分别为1和2,在∠AOB内部的二次函数y=m(x﹣1)2﹣4m的图象上有一动点P,过点P作x轴的平行线与其伴生一次函数的图象交于点Q,设点P的横坐标为n,直接写出线段PQ的长为32时n的值.参考答案一、选择题(共10小题,每小题3分,共30分)1、A【解题分析】根据题意可得方程组2127a b a b +=⎧⎨-=⎩,再解方程组即可. 【题目详解】由题意得:2127a b a b +=⎧⎨-=⎩, 解得:31a b =⎧⎨=-⎩, 故选A .2、C【解题分析】这个扇形的圆心角的度数为n°,根据弧长公式得到20π=24180n π⨯,然后解方程即可. 【题目详解】解:设这个扇形的圆心角的度数为n°,根据题意得20π=24180n π⨯, 解得n=150,即这个扇形的圆心角为150°.故选C .【题目点拨】本题考查了弧长公式:L=180n R π(n 为扇形的圆心角的度数,R 为扇形所在圆的半径). 3、C【解题分析】根据题意画出相应的图形,由OD ⊥AB ,利用垂径定理得到D 为AB 的中点,由AB 的长求出AD 与BD 的长,且得出OD 为角平分线,在Rt △AOD 中,利用锐角三角函数定义及特殊角的三角函数值求出∠AOD 的度数,进而确定出∠AOB 的度数,利用同弧所对的圆心角等于所对圆周角的2倍,即可求出弦AB 所对圆周角的度数.【题目详解】如图所示,∵OD⊥AB,∴D为AB的中点,即53 2在Rt△AOD中,OA=5,53 2∴sin∠AOD=53325,又∵∠AOD为锐角,∴∠AOD=60°,∴∠AOB=120°,∴∠ACB=12∠AOB=60°,又∵圆内接四边形AEBC对角互补,∴∠AEB=120°,则此弦所对的圆周角为60°或120°.故选C.【题目点拨】此题考查了垂径定理,圆周角定理,特殊角的三角函数值,以及锐角三角函数定义,熟练掌握垂径定理是解本题的关键.4、D【解题分析】根据一次函数的性质结合题目中的条件解答即可.【题目详解】解:由题可得,水深与注水量之间成正比例关系,∴随着水的深度变高,需要的注水量也是均匀升高,∴水瓶的形状是圆柱,故选:D.【题目点拨】此题重点考查学生对一次函数的性质的理解,掌握一次函数的性质是解题的关键.5、C【解题分析】试题解析:∵x=-2是关于x 的一元二次方程22302x ax a +-=的一个根, ∴(-2)2+32a×(-2)-a 2=0,即a 2+3a-2=0, 整理,得(a+2)(a-1)=0,解得 a 1=-2,a 2=1.即a 的值是1或-2.故选A .点睛:一元二次方程的解的定义:能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.6、A【解题分析】先求出每个不等式的解集,再根据不等式组解集的求法和不等式组无解的条件,即可得到m 的取值范围.【题目详解】236x m x x <⎧⎨-<-⎩①②由①得,x <m ,由②得,x >1,又因为不等式组无解,所以m ≤1.故选A .【题目点拨】此题的实质是考查不等式组的求法,求不等式组的解集,要根据以下原则:同大取较大,同小较小,小大大小中间找,大大小小解不了.7、A【解题分析】试题分析:充分利用图形,直接从图上得出x 的取值范围.由图可知,当y <1时,x <-4,故选C.考点:本题考查的是一次函数的图象点评:解答本题的关键是掌握在x轴下方的部分y<1,在x轴上方的部分y>1.8、C【解题分析】试题分析:204000米/分,这个数用科学记数法表示2.04×105,故选C.考点:科学记数法—表示较大的数.9、B【解题分析】根据旋转的性质可得AB=AE,∠BAE=60°,然后判断出△AEB是等边三角形,再根据等边三角形的三条边都相等可得BE=AB.【题目详解】解:∵△ABC绕点A顺时针旋转 60°得到△AED,∴AB=AE,∠BAE=60°,∴△AEB是等边三角形,∴BE=AB,∵AB=1,∴BE=1.故选B.【题目点拨】本题考查了旋转的性质,等边三角形的判定与性质,主要利用了旋转前后对应边相等以及旋转角的定义.10、D【解题分析】由tanA的值,利用锐角三角函数定义设出BC与AC,进而利用勾股定理表示出AB,由周长为60求出x的值,确定出两直角边,即可求出三角形面积.【题目详解】如图所示,由tan A=,设BC=12x,AC=5x,根据勾股定理得:AB=13x,由题意得:12x+5x+13x=60,解得:x =2,∴BC =24,AC =10,则△ABC 面积为120,故选D .【题目点拨】此题考查了解直角三角形,锐角三角函数定义,以及勾股定理,熟练掌握勾股定理是解本题的关键.二、填空题(本大题共6个小题,每小题3分,共18分)11、1.【解题分析】先根据题意可证得△ABC ∽△ADE ,△ABC ∽△AFG ,再根据△ABC 的面积为6分别求出△ADE 与△AFG 的面积,则四边形DFGE 的面积=S △AFG -S △ADE .【题目详解】解:∵DE ∥BC ,,∴△ADE ∽△ABC ,∵AD=DF=FB , ∴ADE ABC S S =(AD AB )1,即6ADE S =(13)1,∴S △ADE =23; ∵FG ∥BC ,∴△AFG ∽△ABC ,AFG ABC S S △△=(AF AB)1,即6AFG S =(23)1,∴S △AFG =83; ∴S 四边形DFGE = S △AFG - S △ADE =83-23=1.故答案为:1. 【题目点拨】本题考查了相似三角形的性质与应用,解题的关键是熟练的掌握相似三角形的性质与应用.12、1【解题分析】试题分析:根据题意可得圆心角的度数为:180π,则S=221802360360n r πππ⨯==1. 考点:扇形的面积计算.13、x=-2【解题分析】方程x -=两边同时平方得:26x x =+,解得:1232x x ==-,,检验:(1)当x=3时,方程左边=-3,右边=3,左边≠右边,因此3不是原方程的解;(2)当x=-2时,方程左边=2,右边=2,左边=右边,因此-2是方程的解.∴原方程的解为:x=-2.故答案为:-2.点睛:(1)根号下含有未知数的方程叫无理方程,解无理方程的基本思想是化“无理方程”为“有理方程”;(2)解无理方程和解分式方程相似,求得未知数的值之后要检验,看所得结果是原方程的解还是增根.14、2<x≤1【解题分析】本题可根据不等式组分别求出每一个不等式的解集,然后即可确定不等式组的解集.【题目详解】由①得x >2,由②得x≤1,∴不等式组的解集为2<x≤1.故答案为:2<x≤1.【题目点拨】此题主要考查了一元一次不等式组解集的求法,其简便求法就是用口诀求解,求不等式组解集的口诀:同大取大,同小取小,大小小大中间找,大大小小找不到(无解).15、A【解题分析】试题分析:①当点P 在OA 上运动时,OP=t ,S=OM•PM=tcosα•tsinα,α角度固定,因此S 是以y 轴为对称轴的二次函数,开口向上;②当点P 在AB 上运动时,设P 点坐标为(x ,y ),则S=xy=k ,为定值,故B 、D 选项错误;③当点P 在BC 上运动时,S 随t 的增大而逐渐减小,故C 选项错误.故选A .考点:1.反比例函数综合题;2.动点问题的函数图象.16、1.【解题分析】试题分析:直接把x=1代入已知方程就得到关于m的方程,再解此方程即可.试题解析:∵x=1是一元二次方程x1-1mx+4=0的一个解,∴4-4m+4=0,∴m=1.考点:一元二次方程的解.三、解答题(共8题,共72分)17、(1)见解析(2)相切【解题分析】(1)首先利用角平分线的作法得出CO,进而以点O为圆心,OB为半径作⊙O即可;(2)利用角平分线的性质以及直线与圆的位置关系进而求出即可.【题目详解】(1)如图所示:;(2)相切;过O点作OD⊥AC于D点,∵CO平分∠ACB,∴OB=OD,即d=r,∴⊙O与直线AC相切,【题目点拨】此题主要考查了复杂作图以及角平分线的性质与作法和直线与圆的位置关系,正确利用角平分线的性质求出d=r是解题关键.18、(1)223y x=-,12yx=;(2) 当0<x<6时,kx+b<mx,当x>6时,kx+b>mx【解题分析】(1)根据点A和点B的坐标求出一次函数的解析式,再求出C的坐标6,2),利用待定系数法求解即可求出解析式(2)由C(6,2)分析图形可知,当0<x<6时,kx+b<mx,当x>6时,kx+b>mx【题目详解】(1)S△AOB=12OA•OB=1,∴OA=2,∴点A的坐标是(0,﹣2),∵B(1,0)∴2 30 bk b=-⎧⎨+=⎩∴232 kb⎧=⎪⎨⎪=-⎩∴y=23x﹣2.当x=6时,y=23×6﹣2=2,∴C(6,2)∴m=2×6=3.∴y=12x.(2)由C(6,2),观察图象可知:当0<x<6时,kx+b<mx,当x>6时,kx+b>mx.【题目点拨】此题考查反比例函数与一次函数的交点问题,解题关键在于求出C的坐标19、(1)2元;(2)第二批花的售价至少为3.5元;【解题分析】(1)设第一批花每束的进价是x元,则第二批花每束的进价是(x+0.5)元,根据数量=总价÷单价结合第二批所购花的数量是第一批所购花数的2倍,即可得出关于x的分式方程,解之经检验后即可得出结论;(2)由第二批花的进价比第一批的进价多0.5元可求出第二批花的进价,设第二批菊花的售价为m元,根据利润=每束花的利润×数量结合总利润不低于1500元,即可得出关于m的一元一次不等式,解之即可得出结论.【题目详解】(1)设第一批花每束的进价是x 元,则第二批花每束的进价是()0.5x +元, 根据题意得:1000250020.5x x ⨯=+, 解得:2x =,经检验:2x =是原方程的解,且符合题意.答:第一批花每束的进价是2元.(2)由()1可知第二批菊花的进价为2.5元.设第二批菊花的售价为m 元, 根据题意得:()()1000250032 2.515002 2.5m ⨯-+⨯-≥, 解得: 3.5m ≥.答:第二批花的售价至少为3.5元.【题目点拨】本题考查了分式方程的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出分式方程;(2)根据各数量之间的关系,正确列出一元一次不等式.20、(1)所抽取的学生人数为40人(2)37.5%(3)①视力x <4.4之间活动前有9人,活动后只有5人,人数明显减少.②活动前合格率37.5%,活动后合格率55%,说明视力保健活动的效果比较好【解题分析】【分析】(1)求出频数之和即可;(2)根据合格率=合格人数÷总人数×100%即可得解; (3)从两个不同的角度分析即可,答案不唯一.【题目详解】(1)∵频数之和=3+6+7+9+10+5=40,∴所抽取的学生人数为40人;(2)活动前该校学生的视力达标率=1540×100%=37.5%; (3)①视力x <4.4之间活动前有9人,活动后只有5人,人数明显减少;②活动前合格率37.5%,活动后合格率55%,说明视力保健活动的效果比较好.【题目点拨】本题考查了频数分布直方图、用样本估计总体等知识,熟知频数、合格率等相关概念是解题的关键.21、-1≤x<4,在数轴上表示见解析.【解题分析】试题分析: 分别求出各不等式的解集,再求出其公共解集,并在数轴上表示出来即可.试题解析:()223{3x 122x x +>-≥-①②, 由①得,x<4;由②得,x ⩾−1.故不等式组的解集为:−1⩽x<4.在数轴上表示为:22、(1)见解析;(2)见解析.【解题分析】试题分析:(1)选取①②,利用ASA 判定△BEO ≌△DFO ;也可选取②③,利用AAS 判定△BEO ≌△DFO ;还可选取①③,利用SAS 判定△BEO ≌△DFO ;(2)根据△BEO ≌△DFO 可得EO =FO ,BO =DO ,再根据等式的性质可得AO =CO ,根据两条对角线互相平分的四边形是平行四边形可得结论.试题解析:证明:(1)选取①②,∵在△BEO 和△DFO 中12BO DO EOB FOD ∠=∠⎧⎪=⎨⎪∠=∠⎩,∴△BEO ≌△DFO (ASA );(2)由(1)得:△BEO ≌△DFO ,∴EO =FO ,BO =DO ,∵AE =CF ,∴AO =CO ,∴四边形ABCD 是平行四边形.点睛:此题主要考查了平行四边形的判定,以及全等三角形的判定,关键是掌握两条对角线互相平分的四边形是平行四边形.23、(1)80,20,72;(2)16,补图见解析;(3)原来开私家车的人中至少有50人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数.【解题分析】试题分析:(1)用乘公交车的人数除以所占的百分比,计算即可求出总人数,再用总人数乘以开私家车的所占的百分比求出m,用360°乘以骑自行车的所占的百分比计算即可得解:样本中的总人数为:36÷45%=80人;开私家车的人数m=80×25%=20;扇形统计图中“骑自行车”的圆心角为.(2)求出骑自行车的人数,然后补全统计图即可.(3)设原来开私家车的人中有x人改为骑自行车,表示出改后骑自行车的人数和开私家车的人数,列式不等式,求解即可.试题解析:解:(1)80,20,72.(2)骑自行车的人数为:80×20%=16人,补全统计图如图所示;(3)设原来开私家车的人中有x人改为骑自行车,由题意得,,解得x≥50.答:原来开私家车的人中至少有50人改为骑自行车,才能使骑自行车的人数不低于开私家车的人数.考点:1.条形统计图;2.扇形统计图;3.频数、频率和总量的关系;4.一元一次不等式的应用.24、y=x﹣5【解题分析】分析:(1)根据定义,直接变形得到伴生一次函数的解析式;(2)求出顶点,代入伴生函数解析式即可求解;(3)根据题意得到伴生函数解析式,根据P点的坐标,坐标表示出纵坐标,然后通过PQ与x轴的平行关系,求得Q 点的坐标,由PQ的长列方程求解即可.详解:(1)∵二次函数y=(x﹣1)2﹣4,∴其伴生一次函数的表达式为y=(x﹣1)﹣4=x﹣5,故答案为y=x﹣5;(2)∵二次函数y=(x﹣1)2﹣4,∴顶点坐标为(1,﹣4),∵二次函数y=(x﹣1)2﹣4,∴其伴生一次函数的表达式为y=x﹣5,∴当x=1时,y=1﹣5=﹣4,∴(1,﹣4)在直线y=x﹣5上,即:二次函数y=(x﹣1)2﹣4的顶点在其伴生一次函数的图象上;(3)∵二次函数y=m(x﹣1)2﹣4m,∴其伴生一次函数为y=m(x﹣1)﹣4m=mx﹣5m,∵P点的横坐标为n,(n>2),∴P的纵坐标为m(n﹣1)2﹣4m,即:P(n,m(n﹣1)2﹣4m),∵PQ∥x轴,∴Q((n﹣1)2+1,m(n﹣1)2﹣4m),∴PQ=(n﹣1)2+1﹣n,∵线段PQ的长为32,∴(n﹣1)2+1﹣n=32,∴.点睛:此题主要考查了新定义下的函数关系式,关键是理解新定义的特点构造伴生函数解析式.。
山东省济南市历城区2024届中考考前最后一卷物理试卷含解析

山东省济南市历城区2024届中考考前最后一卷物理试卷注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、本大题包括10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项符合题目要求.1.如图所示的四种现象中,由于光的反射形成的是:A.小孔成像B.鸟巢倒影C.水面折枝D.故宫日晷2.商河的春天昼夜温差较大,而青岛沿海地区量夜温差较小,这主要是因为海水与砂石相比具有较大的A.密度B.内能C.比热容D.质量3.厨房中蕴含着很多物理知识,下列叙述中错误的是A.用筷子夹食物,筷子是费力杠杆B.炒菜时闻到香味是扩散现象C.洗手盆下的下水管“反水弯”是利用了连通器原理D.抽油烟机是利用气体流速大、压强大的原理将油烟抽到室外的4.当湿润的空气升入高空时,水蒸气会遇冷形成云,关于云的组成一定是A.气体B.液体C.固体D.液体或固体5.汽车行驶时驾驶员必须系好安全带.当系好安全带时,相当于闭合开关,指示灯不亮;未系好安全带时,相当于断开开关,指示灯发光.图中符合上述要求的电路图是A.B.C.D.6.高铁、支付宝、共享单车、网购成为中国的“新四大发明”,已走进寻常百姓的生活。
如图所示是在城市街道旁随处可见的共享单车,下列说法中正确的是()A.用车时需要使用手机扫取共享单车上的二维码,这是利用超声波来传递信息的B.共享单车的车座做的较宽是为了减小压强C.此时静止的共享单车对水平地面的压力与共享单车的重力是﹣对平衡力D.蹬车车前进,停止瞪车车将慢慢停下来,说明力是维持物体运动的原因7.如图所示,闭合开关,将滑片向上滑动时,观察到的现象是A.灯泡变暗,电压表示数变大B.灯泡变亮,电压表示数不变C.电路消耗的总功率变小,电压表示数不变D.电路消耗的总功率变大,电压表示数变大8.关于声现象,下列说法中正确的是()A.“闻其声而知其人”主要是根据音调来判断的B.公路旁安装隔音墙是为了减弱噪声对公民的影响C.空气不能传播声音D.用大小不同的力先后敲击同一音叉,音叉发出声音的音色不同9.举重是我国的优势体育项目.一位身高170cm的运动员和一位身高160cm的运动员,在挺举项目中用相同时间,把同样重的杠铃举起,如图所示.如果他们对杠铃所做的功分别为W1和W2,功率分别为P1和P2,则下列关系式中正确的是()A.W1=W2、P1=P2B.W1>W2、P1=P2C.W1>W2、P1>P2D.W1<W2、P1<P210.蜡烛放在如图所示位置,通过凸透镜成倒立、缩小的像,小红画了图中的光路.下列说法正确的是()A.小红画的光路是正确的B.透镜成的是虚像C.透镜的焦距小于10cm D.透镜的焦距大于20cm二、填空题(本大题包括7小题,每小题2分,共14分)11.10秒内通过某导体横截面的电荷量为3库,通过它的电流为______安,若该导体两端电压为3伏,其电阻为_________欧,这段时间内,电流做功为______焦.12.实验桌上有两个完全相同的玻璃杯,分别装有质量相等、温度不同的冷水和热水,小明分别在两杯水中滴入一滴相同的红墨水,如图所示,观察两杯水变色快慢。
2022-2023学年山东省济南市历城区图片版数学四年级第一学期期末统考试题含解析

2022-2023学年四上数学期末模拟试卷一、神奇小帮手。
1.3000公顷=(________)平方千米;60000平方米=(________)公顷。
2.先观察前面的两道算式,再按规律填一填。
123456789×9=1111111101 123456789×45=(________)123456789×18=2222222202 123456789×(________)=7777777707 123456789×27=(________)123456789×(________)=99999999093.甲数×乙数=240,如果甲数扩大3倍,乙数不变,积是(________);如果甲、乙两数同时扩大2倍,积是(________)。
4.20000平方米=(______)公顷350平方千米=(______)公顷5.在括号里填“L”或“mL”。
一瓶眼药水大约有5(______),一脸盆水大约有8(______),一个电热水器大约能装水80(______),一个奶瓶大约能装水240(______)。
6.从银行里取出200元,在存折上记作-200元.那么在存折上记作+500元,表示________.7.先量出下面各角的度数,再按角的大小分一分。
∠1=(_____)∠2=(_____)∠3=(_____)∠4 =(_____)锐角:________ 直角:________ 钝角:________。
8.9平方千米=(______)公顷,4公顷=(______)平方米。
二、我是小法官。
(对的打√,错的打×)9.从条形统计图里能清楚地看出各种数量的多少。
(______)10.一辆汽车5小时行405千米、每小时行多少千米?这是求速度的题目。
(________)11.两个重量单位之间的进率是1000。
(_____)12.一张圆形的纸至少对折3次,才能看到圆心._____13.甲地的气温是-3℃,乙地的气温是-5℃,乙地比较温暖。
山东省济南市历城区2021届八年级数学第二学期期末调研试题含解析

山东省济南市历城区2021届八年级数学第二学期期末调研试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置.3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符.4.作答选择题,必须用2B铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题(每题4分,共48分)1.菱形ABCD的一条对角线长为6,边AB的长是方程x2-7x+12=0的一个根,则菱形ABCD的周长为()A.12 B.14 C.16 D.242.甲乙两人匀速从同一地点到1511米处的图书馆看书,甲出发5分钟后,乙以51米/分的速度沿同一路线行走.设甲乙两人相距s(米),甲行走的时间为t(分),s关于t的函数图象的一部分如图所示.下列结论正确的个数是()(1)t=5时,s=151;(2)t=35时,s=451;(3)甲的速度是31米/分;(4)t=12.5时,s=1.A.1个B.2个C.3个D.4个3.若线段a,b,c组成直角三角形,则它们的比可以为()A.2∶3∶4 B.7∶24∶25 C.5∶12∶14 D.4∶6∶104.下表是某校合唱团成员的年龄分布.年龄/岁13 14 15 16频数 5 15 x 10x对于不同的x,下列关于年龄的统计量不会发生改变的是()A.众数、中位数B.平均数、中位数C.平均数、方差D.中位数、方差5.发现下列几组数据能作为三角形的边:(1)8,15,17;(2)5,12,13;(3)12,15,20;(4)7,24,1.其中能作为直角三角形的三边长的有A.1组B.2组C.3组D.4组6.甲、乙、丙、丁四位同学在三次数学测验中,他们成绩的平均数都是85分,方差分别是:S甲2=3.8,S乙2=2.7,S丙2=6.2,S丁2=5.1,则四个人中成绩最稳定的是()A .j 甲B .乙C .丙D .丁 7.化简1x x ⋅-正确的是( ) A .x - B .x - C .1x x -- D .x --8.下列定理中,没有逆定理...的是( ) A .对顶角相等B .同位角相等,两直线平行C .直角三角形的两锐角互余D .直角三角形两直角边平方和等于斜边的平方 9.下列各式一定是二次根式的是( )A .7-B .3C .xD .36 10.分式2x x -有意义的条件是( ) A .2x =B .2x ≠C .2x =-D .2x ≠- 11.一个多边形的每个内角都等于108°,则这个多边形的边数为( ).A .5B .6C .7D .8 12.在ABCD 中,∠A+∠C=160°,则∠C 的度数为( ) A .100° B .80° C .60° D .20°二、填空题(每题4分,共24分)13.如图,公路互相垂直,公路的中点与点被湖隔开,若测得的长为2.4km ,则两点间的距离为______km.14.在平行四边形ABCD 中,已知∠A﹣∠B=60°,则∠C=_____.15.若分式方程 122x m x x -=--无解,则m 等于___________ 16.在ABCD 中,对角线AC ,BD 相交于点O ,若14AC =,8BD =,10AB =,则OAB ∆的周长为_________.17.如图,在ABC ∆中,已知D ,E ,F 分别为BC ,AD ,CE 的中点,且28ABC S cm ∆=,则图中阴影部分BEF∆的面积等于__2cm .18.为有效开展“阳光体育”活动,某校计划购买篮球和足球共50个,购买资金不超过3000元.若每个篮球80元,每个足球50元,则篮球最多可购买_____个.三、解答题(共78分)19.(8分)如图,一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,与反比例函数y=的图象在第一象限内的交点为M,若△OBM的面积为1.(1)求一次函数和反比例函数的表达式;(2)在x轴上是否存在点P,使AM⊥PM?若存在,求出点P的坐标;若不存在,说明理由;(3)x轴上是否存在点Q,使△QBM∽△OAM?若存在,求出点Q的坐标;若不存在,说明理由.20.(8分)如图,在边长为4的正方形ABCD中,动点E以每秒1个单位长度的速度从点A开始沿边AB向点B运动,动点F以每秒2个单位长度的速度从点B开始沿边BC向点C运动,动点E比动点F先出发1秒,其中一个动点到达终点时,另一个动点也随之停止运动设点F的运动时间为t秒.(1)如图1,连接DE,AF.若DE⊥AF,求t的值;(2)如图2,连结EF,DF.当t为何值时,△EBF∽△DCF?21.(8分)某中学举办“网络安全知识答题竞赛”,七、八年级根据初赛成绩各选出5名选手组成代表队参加决赛,两个队各选出的5名选手的决赛成绩如图所示.平均分(分)中位数(分)众数(分)方差(分2)七年级 a 85 b S 七年级2 八年级 85 c 100 160(1)根据图示填空:a = ,b = ,c = ;(2)结合两队成绩的平均数和中位数进行分析,哪个代表队的决赛成绩较好?(3)计算七年级代表队决赛成绩的方差S 七年级2,并判断哪一个代表队选手成绩较为稳定.22.(10分)已知:如图,平行四边形ABCD 中,M 、N 分别为AB 和CD 的中点.(1)求证:四边形AMCN 是平行四边形;(2)若AC =BC =5,AB =6,求四边形AMCN 的面积.23.(10分)如图,已知∠BAC=60°,∠B=80° ,DE 垂直平分AC 交BC 于点D ,交AC 于点E. (1)求∠BAD 的度数;(2)若AB=10,BC=12,求△ABD 的周长.24.(10分)如图,在直角坐标系中,点C 在第一象限,CB x ⊥轴于B ,CA y ⊥轴于A ,3CB =,6CA =,有一反比例函数图象刚好过点C .(1)分别求出过点C 的反比例函数和过A ,B 两点的一次函数的函数表达式;(2)直线l x ⊥轴,并从y 轴出发,以每秒1个单位长度的速度向x 轴正方向运动,交反比例函数图象于点D ,交AC 于点E ,交直线AB 于点F ,当直线l 运动到经过点B 时,停止运动.设运动时间为t (秒).①问:是否存在t 的值,使四边形DFBC 为平行四边形?若存在,求出t 的值;若不存在,说明理由;②若直线l 从y 轴出发的同时,有一动点Q 从点B 出发,沿射线BC 方向,以每秒3个单位长度的速度运动.是否存在t 的值,使以点D ,E ,Q ,C 为顶点的四边形为平行四边形;若存在,求出t 的值,并进一步探究此时的四边形是否为特殊的平行四边形;若不存在,说明理由.25.(12分)如图1,在平面直角坐标系中,一次函数28y x =-+的图象与x 轴,y 轴分别交于点A ,点C ,过点A 作AB x ⊥轴,垂足为点A ,过点C 作CB y ⊥轴,垂足为点C ,两条垂线相交于点B .(1)线段AB ,BC ,AC 的长分别为AB =_______,BC =_________,AC =_________;(1)折叠图1中的ABC ∆,使点A 与点C 重合,再将折叠后的图形展开,折痕DE 交AB 于点D ,交AC 于点E ,连接CD ,如图1.①求线段AD 的长;②在y 轴上,是否存在点P ,使得APD ∆为等腰三角形?若存在,请直接写出符合条件的所有点P 的坐标;若不存在,请说明理由.26.已知反比例函数k y x=(k 为常数,k≠0)的图象经过点A (2,3). (1)求这个函数的解析式;(2)判断点B (-1,6),C (3,2)是否在这个函数的图象上,并说明理由;(3)当-3<x <-1时,求y 的取值范围.参考答案一、选择题(每题4分,共48分)1、C【解析】试题解析:∵解方程x 2-7x+12=0得:x=3或1∵对角线长为6,3+3=6,不能构成三角形;∴菱形的边长为1.∴菱形ABCD 的周长为1×1=2. 故选C.2、D【解析】【分析】结合图像可以判断(1)(2)是否正确;由图象可知5t =时, 150s =米,根据速度=路程÷时间,即可得到甲行走的速度;由图可以列出在时间为5至15范围内的函数:31t =51(t ﹣5),再计算即可得到答案.【详解】由图象可知,当t =5时,s =151,故(1)正确;当t =35时,s =451,故(2)正确;甲的速度是151÷5=31米/分,故(3)正确; 令31t =51(t ﹣5),解得,t =12.5,即当t =12.5时,s =1,故(4)正确;故选D .【点睛】本题考查读图能力和一元一次函数的应用,解题的关键是能够读懂图中的信息.3、B【分析】要组成直角三角形,三条线段的比值要满足较小的比值的平方和等于较大比值的平方.结合选项分析即可得到答案.【详解】A. 22+32≠42,故本选项错误;B. 72+242=252,故本选项正确;C. 52+122≠142,故本选项错误;D. 4262≠102,故本选项错误.故选B.【点睛】本题考查勾股定理的逆定理,解题的关键是掌握勾股定理的逆定理.4、A【解析】【分析】由频数分布表可知后两组的频数和为10,即可得知总人数,结合前两组的频数知出现次数最多的数据及第15、16个数据的平均数,可得答案.【详解】由题中表格可知,年龄为15岁与年龄为16岁的频数和为1010x x +-=,则总人数为3151030++=,故该组数据的众数为14岁,中位数为1414142+=(岁),所以对于不同的x ,关于年龄的统计量不会发生改变的是众数和中位数,故选A .【点睛】本题主要考查频数分布表及统计量的选择,由表中数据得出数据的总数是根本,熟练掌握平均数、中位数、众数及方差的定义和计算方法是解题的关键.5、C【解析】①∵82+152=172,∴能组成直角三角形;②∵52+122=132,∴能组成直角三角形;③122+152≠202,∴不能组成直角三角形;④72+242=12,∴能组成直角三角形.故选C.6、B【分析】根据方差的定义,方差越小数据越稳定,即可得出答案.【详解】解:∵S甲2=3.8,S乙2=2.7,S丙2=6.2,S丁2=5.1,∴S乙2<S甲2<S丁2<S丙2,∴四个人中成绩最稳定的是乙,故选:B.【点睛】本题考查方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.7、D【解析】【分析】先根据二次根式有意义的条件确定出x<0,然后再根据二次根式的性质进行化简即可得答案.【详解】由题意可知x<0,所以x==故选D.【点睛】本题考查了二次根式的性质与化简,熟知二次根式的被开方数是非负数、熟练掌握二次根式的性质是解题的关键.8、A【解析】【分析】分别写出四个命题的逆命题,逆命题是真命题的就是逆定理,不成立的就是假命题,就不是逆定理.【详解】A对顶角相等的逆命题是:如果两个角相等,那么这两个角是对顶角,逆命题是假命题,故没有逆定理;B同位角相等,两直线平行的逆命题是:两直线平行,同位角相等,是逆定理;C直角三角形两锐角互余的逆命题是:两锐角互余的三角形是直角三角形,是逆定理;D直角三角形两直角边平方和等于斜边的平方的逆定理是:两边的平方和等于第三边的平方的三角形是直角三角形,因此答案选择A.【点睛】本题考查的知识点是定理与逆定理,如果一个定理的逆命题经过证明是真命题,那么它也是一个定理,这两个定理称为互逆定理,其中一个定理称为另一个定理的逆定理.9、B【解析】分析:直接利用二次根式有意义的条件以及二次根式的定义分析得出答案.详解:A ,根号下是负数,无意义,故此选项错误;BCD 三次根式,故此选项错误;故选:B .0)a ≥的式子叫做二次根式,二次根式有意义的条件是被开方数是非负数..10、B【解析】【分析】根据分式的定义即可判断.【详解】依题意得2x -≠0,解得2x ≠,故选B.【点睛】此题主要考查分式有意义的条件,解题的关键是熟知分式的性质.11、A【解析】试题分析:设这个多边形边数为n ,则根据题意得:(n-2)×180°=108n ,解得:72n=360,所以n=1.故本题选A . 考点:多边形内角和公式.12、B【解析】【分析】根据平行四边形的对角相等,结合∠A+∠C=160°求解即可.【详解】∵四边形ABCD是平行四边形,∴∠A=∠C,∵∠A+∠C=160°,∴∠A=∠C=80°.故选B.【点睛】本题考查了平行四边形的性质,熟练掌握平行四边行的性质是解答本题的关键.平行四边形的性质有:平行四边形对边平行且相等;平行四边形对角相等,邻角互补;平行四边形对角线互相平分.二、填空题(每题4分,共24分)13、1.1【解析】【分析】根据直角三角形斜边上的中线等于斜边的一半,可得MC=AB=1.1km.【详解】∵在Rt△ABC中,∠ACB=90°,M为AB的中点,∴MC=AB=AM=1.1(km).故答案为:1.1.【点睛】此题考查直角三角形的性质,解题关键点是熟练掌握在直角三角形中,斜边上的中线等于斜边的一半,理解题意,将实际问题转化为数学问题是解题的关键.14、120【解析】【分析】根据平行四边形的性质可得到答案.【详解】∵四边形ABCD是平行四边形,∴∠A+∠B=180°,又∠A-∠B=60°,故可知∠A=120°,∴∠C=∠A=120°,故答案为120°.本题主要考查了平行四边形的基本性质,解本题的要点在于熟记平行四边形的对角相等.15、1【解析】【分析】先去分母,把分式方程的增根代入去分母后的整式方程即可得到答案.【详解】 解:122x m x x -=--, 去分母得:1x m -=,所以:1m x =-,因为:方程的增根是2x =,所以:此时1m =,故答案为:1.【点睛】本题考查分式方程无解时字母系数的取值,掌握把增根代入去分母后的整式方程是解题关键.16、21【解析】【分析】由在平行四边形ABCD 中,AC=14,BD=8,AB=10,利用平行四边形的性质,即可求得OA 与OB 的长,继而求得△OAB的周长.【详解】∵在平行四边形ABCD 中,AC=14,BD=8,AB=10,∴OA=12AC=7,OB=12BD=4, ∴△OAB 的周长为:AB+OB+OA=10+7+4=21.故答案为:21.【点睛】本题考查平行四边形的性质,熟练掌握平行四边形的性质和计算法则是解题关键.17、2【分析】E 是AD 的中点⇒S △BDE =12S △ABD ,S △CDE =12S △ACD ⇒S △BCE =12S △ABC =4; F 为CE 中点⇒S △BEF =12S △BCE =1422⨯=. 【详解】解:∵E 是AD 的中点,∴S △BDE =12S △ABD ,S △CDE =12S △ACD ,∴S △BDE + S △CDE =12S △ABC =1842⨯= (cm 2),即S △BCE =4(cm 2). ∵F 为CE 中点,∴S △BEF =12S △BCE =1422⨯=(cm 2).故答案为2. 【点睛】本题主要考查了三角形中线的性质,熟知三角形的中线将三角形分成面积相等的两部分是解题关键.18、1【解析】【分析】设购买篮球x 个,则购买足球()50x -个,根据总价=单价⨯购买数量结合购买资金不超过3000元,即可得出关于x 的一元一次不等式,解之取其中的最大整数即可.【详解】设购买篮球x 个,则购买足球()50x -个,根据题意得:()80x 5050x 3000+-≤,解得:50x 3≤. x 为整数,x ∴最大值为1.故答案为1.【点睛】本题考查了一元一次不等式的应用,根据各数量间的关系,正确列出一元一次不等式是解题的关键.三、解答题(共78分)19、(1)反比例函数解析式为:y=;(2)P (5,0);(3)Q 点坐标为:(,0).【解析】试题分析:(1)利用已知点B 坐标代入一次函数解析式得出答案,再利用△OBM 的面积得出M 点纵坐标,再利用相似三角形的判定与性质得出M 点坐标即可得出反比例函数解析式;(2)过点M作PM⊥AM,垂足为M,得出△AOB∽△PMB,进而得出BP的长即可得出答案;(3)利用△QBM∽△OAM,得出=,进而得出OQ的长,即可得出答案.解:(1)如图1,过点M作MN⊥x轴于点N,∵一次函数y=k1x﹣1的图象经过A(0,﹣1)、B(1,0)两点,∴0=k1﹣1,AO=BO=1,解得:k1=1,故一次函数解析式为:y=x﹣1,∵△OBM的面积为1,BO=1,∴M点纵坐标为:2,∵∠OAB=∠MNB,∠OBA=∠NBM,∴△AOB∽△MNB,∴==,则BN=2,故M(3,2),则xy=k2=6,故反比例函数解析式为:y=;(2)如图2,过点M作PM⊥AM,垂足为M,∵∠AOB=∠PMB,∠OBA=∠MBP,∴△AOB∽△PMB,∴=,由(1)得:AB==,BM==2,故=,解得:BP=4,故P(5,0);(3)如图3,∵△QBM∽△OAM,∴=,由(2)可得AM=3,故=,解得:QB=,则OQ=,故Q 点坐标为:(,0).考点:反比例函数综合题.20、(1)t=1;(2)当957-=t △EBF ∽△DCF ; 【解析】【分析】(1)利用正方形的性质及条件,得出△ABF ≌△DAE ,由AE=BF 列式计算.(2)利用△EBF ∽△DCF ,得出EB BF DC FC=,列出方程求解. 【详解】解:(1)∵DE ⊥AF ,∴∠AOE=90°,∴∠BAF+∠AEO=90°,∵∠ADE+∠AEO=90°,∴∠BAF=∠ADE ,又∵四边形ABCD 是正方形,∴AB=AD ,∠ABF=∠DAE=90°,在△ABF 和△DAE 中, AB BAF ADE ABF DAE AD∠=∠∠=∠⎧⎪=⎨⎪⎩, ∴△ABF ≌△DAE (ASA )∴AE=BF ,∴1+t=2t ,解得t=1;(2)如图2,∵四边形ABCD是正方形,∴AB=BC=CD=4,∵BF=2t,AE=1+t,∴FC=4-2t,BE=4-1-t=3-t,当△EBF∽△DCF时,EB BFDC FC=,∴34t-=242tt-,解得,t1=957-,t2=957+(舍去),故t=957-.所以当t=957-时,△EBF∽△DCF.【点睛】本题主要考查了四边形的综合题,利用了全等三角形的判定和性质,相似三角形的判定和性质,难度一般.21、(1)85,85,80;(2)七年级决赛成绩较好;(3)七年级代表队选手成绩比较稳定.【解析】【分析】(1)根据平均数、中位数、众数的概念分析计算即可;(2)根据图表可知七八年级的平均分相同,因此结合两个年级的中位数来判断即可;(3)根据方差的计算公式来计算即可,然后根据“方差越小就越稳定”的特点来判断哪个队成绩稳定即可. 【详解】解:(1)七年级的平均分a=75+80+85+85+100=855,众数b=85,八年级选手的成绩是:70,75,80,100,100,故中位数c=80;故答案为85,85,80;(2)由表格可知七年级与八年级的平均分相同,七年级的中位数高,故七年级决赛成绩较好;(3)S2七年级=2222(7585)(8085)2(8585)(10085)705-+-+⨯-+-=(分2),S2七年级<S2八年级∴七年级代表队选手成绩比较稳定.【点睛】本题主要考查了平均数、中位数、众数、方差的概念及统计意义,熟练掌握其概念是解题的关键.22、(1)见解析;(2)12.【解析】【分析】(1)由题意可得AB∥CD,AB=CD,又由M,N分别是AB和CD的中点可得AM=∥CN,即可得结论;(2)根据等腰三角形的性质可得CM⊥AB,AM=3,根据勾股定理可得CM=4,则可求面积.【详解】(1)∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,∵M,N分别为AB和CD的中点,∴AM=12AB,CN=12CD,∴AM=CN,且AB∥CD,∴四边形AMCN是平行四边形;(2)∵AC=BC=5,AB=6,M是AB中点,∴AM=MB=3,CM⊥AM,∴4=,∵四边形AMCN是平行四边形,且CM⊥SM,∴AMCN是矩形,∴S 四边形AMCN =12.【点睛】本题考查了平行四边形的性质和判定,等腰三角形的性质,关键是熟练运用这些性质解决问题.23、(1)20°;(2)22.【解析】试题分析:(1)根据三角形内角和定理求出∠C ,根据线段垂直平分线的性质得到DA =DC ,求出∠DAC ,计算即可; (2)根据DA =DC ,三角形的周长公式计算.解:(1)∵∠BAC=60°,∠B=80°,∴∠C=180°-∠BAC-∠B=180°-60°-80°=40°, ∵DE 垂直平分AC ,∴DA=DC.∴∠DAC=∠C=40°, ∴∠BAD=60°-40°=20°. (2)∵DE 垂直平分AC ,∴AD =CD ,∴AB +AD +BD =AB +CD +BD =AB +BC =10+12=22,∴△ABD 的周长为22.24、(1)18y x =, 132y x =-+;(2)①不存在,理由详见解析;②存在,t =【解析】【分析】(1)先确定A 、B 、C 的坐标,然后用待定系数法解答即可;(2)①可用t 的代数式表示DF ,然后根据DF=BC 求出t 的值,得到DF 与CB 重合,因而不存在t ,使得四边形DFBC 为平行四边形;②可分两种情况(点Q 在线段BC 上和在线段BC 的延长线上)讨论,由于DE ∥QC ,要使以点D 、E 、Q 、C 为顶点的四边形为平行四边形,只需DE=QC ,只需将DE 、QC 分别用的式子表示,再求出t 即可解答.【详解】解:(1)由题意得(6,3)C ,(0,3)A ,(6,0)B , ∴反比例函数为18y x =,一次函数为:132y x =-+. (2)①不存在. l x ⊥轴,CB x ⊥轴,//l BC ∴. 又四边形DFBC 是平行四边形,3DF BC ∴==. 设18,D t t ⎛⎫ ⎪⎝⎭,则1,32F t t ⎛⎫-+ ⎪⎝⎭, 181332DF t t ⎛⎫∴=--+= ⎪⎝⎭,6t ∴=. 此时D 与C 重合,不符合题意,∴不存在.②存在.当01t <<时,CQ DE ≠;当16t <≤时,由18,D t t ⎛⎫ ⎪⎝⎭,()1,3E ,得183DE t =-. 由()6,3Q t ,()6,3C .得33CQ t =-. //DE CQ∴当DE CQ =时,四边形DECQ 为平行四边形.18333t t∴-=-.1t ∴=,2t ∴=∴当t =DECQ 为平行四边形.又DE CE ⊥且DE EC ≠,DECQ ∴为矩形.【点睛】本题主要考查了用待定系数法求反比例函数和一次函数的解析式以及平行四边形的判定、解方程、根的判别式等知识,在解答以点D 、E 、Q 、C 为顶点的四边形的四个顶点的顺序不确定,需要分情况讨论是解答本题的关键.25、(1)8;4;(1)①线段AD 的长为2;②点P 的坐标为(0,3)或(0,-3)或(0,1)或(0,8)或(0,52). 【解析】【分析】(1)利用一次函数图象上点的坐标特征可求出点A ,C 的坐标,利用矩形的性质及勾股定理,可得出AB ,BC ,AC的长;(1)①设AD=a,则CD=a,BD=8-a,在Rt△BCD中,利用勾股定理可求出a的值,进而可得出线段AD的长;②设点P的坐标为(0,t),利用两点间的距离公式可求出AD1,AP1,DP1的值,分AP=AD,AD=DP及AP=DP三种情况,可得出关于t的一元二次方程(或一元一次方程),解之即可得出t的值,进而可得出点P的坐标.【详解】解:(1)如图:当x=0时,y=-1x+8=8,∴点C的坐标为(0,8);当y=0时,-1x+8=0,解得:x=4,∴点A的坐标为(4,0).由已知可得:四边形OABC为矩形,∴AB=OC=8,BC=OA=4,2245+=OA OC故答案为:8;4;5(1)①设AD=a,则CD=a,BD=8-a.在Rt△BCD中,CD1=BC1+BD1,即a1=3+(8-a)1,解得:a=2,∴线段AD的长为2.②存在,如图:设点P的坐标为(0,t).∵点A的坐标为(4,0),点D的坐标为(4,2),∴AD1=12,AP1=(0-4)1+(t-0)1=t1+16,DP1=(0-4)1+(t-2)1=t1-10t+3.当AP=AD时,t1+16=12,解得:t=±3,∴点P的坐标为(0,3)或(0,-3);当AD=DP时,12=t1-10t+3,解得:t1=1,t1=8,∴点P的坐标为(0,1)或(0,8);当AP=DP时,t1+16=t1-10t+3,解得:t=52,∴点P的坐标为(0,52).综上所述:在y轴上存在点P,使得△APD为等腰三角形,点P的坐标为(0,3)或(0,-3)或(0,1)或(0,8)或(0,52).【点睛】本题考查了一次函数图象上点的坐标特征、矩形的性质、勾股定理、等腰三角形的性质、两点间的距离以及解一元二次方程(或解一元一次方程),解题的关键是:(1)利用一次函数图象上点的坐标特征求出点A,C的坐标;(1)①通过解直角三角形,求出AD的长;②分AP=AD,AD=DP及AP=DP三种情况,找出关于t的一元二次方程(或一元一次方程).26、(1)这个函数的解析式为:6yx=;(1)点C在函数图象上,理由见解析;(3),-2<y<-1.【解析】【分析】(1)把点A的坐标代入已知函数解析式,通过方程即可求得k的值;(1)只要把点B、C的坐标分别代入函数解析式,横纵坐标坐标之积等于2时,即该点在函数图象上;(3)根据反比例函数图象的增减性解答问题.【详解】解:(1)∵反比例函数kyx=(k为常数,k≠0)的图象经过点A(1,3),∴把点A的坐标代入解析式,得k32=,解得,k=2.∴这个函数的解析式为:6yx =.(1)∵反比例函数解析式6yx =,∴2=xy.分别把点B、C的坐标代入,得(-1)×2=-2≠2,则点B不在该函数图象上;3×1=2,则点C在函数图象上.(3)∵k>0,∴当x<0时,y随x的增大而减小.∵当x=-3时,y=-1,当x=-1时,y=-2,∴当-3<x<-1时,-2<y<-1.。
