(完整版)小学奥数平面几何五种面积模型
小学奥数平面几何五种面积模型

小学奥数平面几何五种模型(等积,鸟头,蝶形,相似,共边)目标:熟练掌握五大面积模型等积,鸟头,蝶形,相似(含金字塔模型和沙漏模型),共边(含燕尾模型和风筝模型),掌握五大面积模型的各种变形知识点拨一、等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比;如右图S :S2 a:b③夹在一组平行线之间的等积变形,如右图S^ACD S^BCD;反之,如果S A ACD S A BCD,则可知直线AB平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在△ABC中,D,E分别是AB, AC上的点如图⑴(或D在BA的延长线上,E在AC上),蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径•通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系. 梯形中比例关系(“梯形蝶形定理”):2 2①S i: S3 a : b②S1: S3: S?: S4 a2: b2 : ab : ab ;③S的对应份数为 a b 2.四、相似模型(一)金字塔模型(AB AC) :(AD AE)则S AABCS A ADE图⑴三、蝶形定理任意四边形中的比例关系图⑵(“蝶形定理”):① S i :S2S4 : S3 或者S i S3 S2 S4 ② AO : OC S| S2 : S4 S 3)沙漏模型bAEB C CG GB A EFOBDGGBB【解析】 EEBF【巩固】 几厘米?A EA E长方形EBGF 的长BG 为10厘米,那么长方形的宽为2 4.5 4 2 16.5 ,所以长方形EFGH 面积为33.如图所示,正方形ABCD 的边长为8厘米 如图,正方形 ABCD 勺边长为6,AE 的面积为F CF C连接DE DF 则长方形EFGH 勺面积是三角形 DEF 面积的二倍 三角形DEF 的面积等于正方形的面积减去三个三角形的面积,1. 5, CF2.长方形 EFGH (只要其形状不改变,不论大小怎样改变它们 S A DEF6 6 1.5 6 2 2 6 ① J AD A E AB AC ② S A ADE : ABC所谓的相似三角形,就是形状相同,大小不同的三角形 都相似),与相似三角形相关的常用的性质及定理如下⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线. 三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具. 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形. 五、共边定理(燕尾模型和风筝模型) 在三角形 ABC 中,AD , BE , CF 相交于同一点 0,那么 S ABO : S ACO BD : DC . 上述定理给出了一个新的转化面积比与线段比的手段,因为 ABO 和 ACO 的形状很象燕子的尾巴,所以这个定理被称为燕尾定理•该定理在许多几何 题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形 之中,为三角形中的三角形面积对应底边之间提供互相联系的途径 典型例题 【例1】DE BC AF AG ;AF 2:AG 2 CD GD GB A---- 7/ /1 /F J|\ /C【解析】本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)•三角形面积等于与它等底等高的平行四边形面积的一半. 证明:连接AG •(我们通过△ ABG 把这两个长方形和正方形联系在一起)•1•••在正方形 ABCD 中,S A ABG — AB AB 边上的高,21二S A ABGS AABCD (三角形面积等于与它等底等高的平行四边形面积的一半)21冋理,S A ABG — S EFGB ••••正方形ABCD 与长方形EFGB 面积相等. 长方形的宽 8 8 10 6.4(厘米)•【例2】 长方形ABCD 的面积为36cm 2, E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影 部分面积是多少?【解析】 解法一:寻找可利用的条件,连接 BH 、HC ,如下图:可得:SEHB-S 2AHB 、SFHB—S CHB 2、 SDHG— S DHC2,S A BCDS AHB S CHBS CHD36即 S EHB SBHFSDHG —(S AHBS CHBS C HD )-36218 ;而SEHBSBHFS DHGs阴影SEBFSEBF1-BE BF 1AB) 1(二 BC) 1 36 4.5222 2 8所以阴影部分的面积是: 解法二:特殊点法•找 那么图形就可变成右图:S 阴影 18 S EBF 18 4・5 13・5AD (H)E 、—GB F C这样阴影部分的面积就是DEF的面积,根据鸟头定理,则有s 阴影 S ABCD S AED S BEF S CFD 36- - 36 - - - 36 -- 2 2 2 2 2 2 2【巩固】在边长为6厘米的正方形 ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与 P 点连接,求阴影部分面积.【解析】(法1)特殊点法.由于P 是正方形内部任意一点, 可采用特殊点法,假设P 点与A 点重合,贝U 阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的 丄和-, 4 6所以阴影部分的面积为 62 (- -) 15平方厘米. 4 6(法2)连接PA 、PC .由于 PAD 与 PBC 的面积之和等于正方形 ABCD 面积的一半,所以上、下两个阴影三角形 的面积之和等于正方形 ABCD 面积的-,同理可知左、右两个阴影三角形的面积之和等于正4 方形ABCD 面积的1 ,所以阴影部分的面积为 62 (-丄)15平方厘米.6 4 6【例3】 如图所示,长方形ABCD 内的阴影部分的面积之和为70, AB 8 , AD 15,四边形EFGO的面积为 _________ .【解析】利用图形中的包含关系可以先求出三角形 AOE 、DOG 和四边形EFGO 的面积之和,以及三 角形AOE 和DOG 的面积之和,进而求出四边形 EFGO 的面积.由于长方形 ABCD 的面积为15 8 120,所以三角形BOC 的面积为120 130 ,所以三角4形AOE 和DOG 的面积之和为120 370 20 ; 4又三角形AOE 、DOG 和四边形EFGO 的面积之和为120 1- 30,所以四边形EFGO2 4的面积为30 20 10.另解:从整体上来看,四边形 EFGO 的面积 三角形AFC 面积 三角形BFD 面积 白色部 分的面积,而三角形 AFC 面积 三角形BFD 面积为长方形面积的一半,即 60,白色部分的 面积等于长方形面积减去阴影部分的面积,即120 70 50 ,所以四边形的面积为60 50 10 .36 13.5.如图,长方形 ABCD 的面积是36, E 是AD 的三等分点,AE 2ED ,则阴影部分的面积 为 ________ .1 1 3 — 6 -2.7 .25已知ABC 为等边三角形,面积为 400, D 、E 、F 分别为三边的中点,已知甲、乙、丙面 积和为143,求阴影五边形的面积.(丙是三角形HBC )所以 DE 、DF 、EF 是三角形ABC 的中位线,也就与 三角形ABN 和三角形AMC 的面积都等于三角形 ABC 的半,即为200.即400 S 丙 200 200SAMHN,所以 S ^S AMHN.又?阴影S ADF S 甲 S 乙S AMHN,所以S阴影S 甲s 丙SADF1 143400 43 .4如图, 已知 CD 5 , DE 7 ,EF 15, FG 6,线段AB 将图形分成两部分,左边部分 【例5】根据图形的容斥关系,有 S ABCS 丙S ABN S AMC S AMHN,面积是38,右边部分面积是 65,那么三角形 ADG 的面积是 ______________【巩固】 【解析】 如图,连接0E .根据蝶形定理,ON : NDS COE: SCDEOM : MABOE: SBAE1SS BDE2:S BAEOED~ S 矩形ABCD4S OEA 1 1 2S CAE :S CDE 1:1,所以S OEN2S OED ;1:4,所以 S OEM 1 S OEA .52S OED 6 ,所以阴影部分面积为:【例4】 【解析】 因为D 、E 、F 分别为三边的中点, 对应的边平行,根据面积比例模型,【例6】 如图在 △ ABC 中,D,E 分别是 AB,AC 上的点,且AD: AB 2:5 , AE : AC 4:7 , S A ADE 平方厘米,求 △ ABC 的面积.【解析】连接 BE , S A ADE : S A ABE AD : AB 2:5 (2 4) : (5 4),S\ ABE : S A ABC AE : AC4: 7 (45) : (7 5),所以 S A ADE: S A ABC(2 4): (75),设S A ADE 8份,则S A ABC 35份,Sx ADE 16平方厘米,所以1份是2平方厘米,35份就是70 平方厘米,△ABC 的面积是70平方厘米•由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角 (相等角或互补角)两夹边的乘积之比根据题意可知,CF 5 7 15 27;DG 715 6 28;151221所以, S BEFSCBF ,S BECS CBF , S AEGS SADG , S AED2/27282115712于是: S ADG S CBF 65 ; SADGSCBF38 ;2827282/可得S ADG 40 . 故三角形 ADG 的面积是 40—S 28ADG16【巩固】如图,三角形 ABC 中,AB 是AD 的5倍1,那么三角形 ABC 的面积是多少?AC 是AE 的3倍,如果三角形 ADE 的面积等于【解析】连接BE .••• EC 3AE…S VABC 3S VA BE 又 T AB 5AD --S V ADES VABE 5 S VABC 15,…S VABC【巩固】如图,三角形 ABC 被分成了甲(阴影部分)、乙两部分,BD DC 4 , BE 3 , AE 6,乙 部分面积是甲部分面积的几倍?ACAG【解析】连接AF , BD .所以S EFGHSA AEHSA CFGSA DHGSA BEFSABCD8 8 15+3+236 .平方厘米,所以1份是2平方厘米,25份就是50平方厘米,△ ABC 的面积是50平方厘米.由 此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角 (相等角或互补角)两夹边的乘积之比的面积是2,求平行四边形 ABCD 与四边形EFGH 的面积比.【解析】 连接AD .••• BE 3, AE 6二 AB 3BE , S VABD3S VBDE又••• DC 4,…S V ABC2S VABD ,… S VABC6S VBD E , S 乙5S 甲 .如图在 △ ABC中,D 在BA 的延长线上,E 在AC 上, AE: EC 3: 2 , S A ADE 12平方厘米,求 △ ABC 的面积连接 BE , ADE : S ^ ABEAD: ABS A ABE : S A ABC AE : AC 3: (3 2) 所以 S A ADE: S A ABC (3 2) : 5(3 2:5 AB: AD 5:2 , (2 3):(5 3)(3 5): (3 2) 5 ,2) 6:25,设 S A ADE 6 份,则 S ^ ABC 25 份,S ^ADE 12【例8】 如图,平行四边形 ABCD , BE AB ,CF2CB ,GD 3DC ,HA4AD ,平行四边形 ABCDA AC【解析】【例7】且所以S EFGHSA AEHSA CFGSA DHGSA BEFSABCD8 8 15+3+236 .【解析】连接AC 、BD •根据共角定理.S A ABCAB BC 1 1 1 SA FBEBE BF 1 3 3 又 S A ABC1,所以 S A FBE 3 .冋理可得 S A GCF 8 , S A DHG 15 , S A AEH8.•••在△ ABC 和厶BFE 中, ABC 与 FBE 互补,【例9】 如图所示的四边形的面积等于多少?【解析】题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点0逆时针旋转,使长为13的两条边重合,此时三角形 OAB 将旋转到三 角形OCD 的位置•这样,通过旋转后所得到的新图形是一个边长为 12的正方形,且这个正 方形的面积就是原来四边形的面积 •因此,原来四边形的面积为 12 12 144.(也可以用勾股定理) ACDE ,中心为 0,求 OBC 的面积.【解析】如图,将 OAB 沿着O 点顺时针旋转90,到达 OCF 的位置.由于 ABC 90 , AOC 90,所以 OAB OCB 180 •而 OCF OAB , 所以 OCF OCB 180,那么B 、C 、F 三点在一条直线上.由于OB OF , BOF AOC 90,所以 BOF 是等腰直角三角形,且斜边BF 为5 3 8, 所以它的面积为82 116 .4根据面积比例模型,OBC 的面积为16 - 10 .8【例11】如图,以正方形的边 AB 为斜边在正方形内作直角三角形 ABE , AEB 90 , AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形 OBE 的面积.所以SABCDS EFGH2 36 118【例10】如图所示,ABC 中, ABC 90,AB3 , BC 5,以AC 为一边向 ABC 外作正方形【解析】【例12】【解析】如图,连接DE,以A点为中心,将那么EAF EAB BAF EAB 直角梯形,且AF AE3 , 所以梯形AFBE的面积为:1 23 — 12( cm ).2ABE是直角三角形,根据勾股定理,^AB22又因为S ABD那么S BDE所以S OBE17( cm2).ADE顺时针旋转90至U ABF的位置.DAE 90SABDSABESADESABD12 S BDE2・5 ( cm?).,而AEB也是90,所以四边形AFBE是AB2SAFBE2 2AE BE17 12 5(325234,所以2cm ),如下图,六边形ABCDEF中,AB ED,平行于CD,BC平行于EF,对角线FD垂直于BD,已知请问六边形ABCDEF的面积是多少平方厘米?AF CD , BC EF ,且有AB平行于ED, AFFD 24厘米,BD 18厘米,CD与AF重合,将DEF平移使得ED与AB重合,这样EF、BGFD,它的面积与原六边形的面积ABCDEF的面积为如图,我们将BCD平移使得BC都重合到图中的AG 了 .这样就组成了一个长方形相等,显然长方形BGFD的面积为24 18 432平方厘米,所以六边形432平方厘米.【例13】如图,三角形ABC的面积是1 , E是AC的中点,点D在BC上,且BD :DC 1:2 , AD与BE交于点F .则四边形DFEC的面积等于__________ .【解析】在本题中,四边形 ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形•看 到题目中给出条件 S VABD : S/BCD 1: 3,这可以向模型一蝶形定理靠拢,于是得出一种解 法•又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得到第二种解法, 但是第二种解法需要一个中介来改造这个” 不良四边形”,于是可以作 AH 垂直BD 于H ,CG垂直BD 于G ,面积比转化为高之比.再应用结论:三角形高相同,则面积之比等于底边之 比,得出结果•请老师注意比较两种解法,使学生体会到蝶形定理的优势,从而主观上愿意 掌握并使用蝶形定理解决问题.解法一:••• 解法二:作••• SABDAO : OC S ABD AH BD 于 H , -S3BCD , • AH:S BDC CG1: 3 OC 2 3 6 ,••• OC:OD 6:3 2:1 .BD 于 G •-CG,-■. S AODDOC ,【解析】方法一:连接CF ,根据燕尾定理, 仏 ED 丄,占 善1, S A ACF DC 2 S A CBF EC方法二:连接DE ,由题目条件可得到 S A ABD -S A ABC-3 3【例14】四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形 ABD 的面积等于三角 形BCD 的面积的1,且AO3& ADE-S A 21ADC—22S 3 S A ABC1 BF,所以-3FESA ABD1SA ADE111 1 1 1 1 S1 S A DEFS A DEBSA BEC― S ABC22 32 3212 '而 S A CD E2 1 S A ABC 1• 所以则四边形DFEC 的面积等于 53 2312 【巩固】如图,长方形 ABCD 的面积是2 平方厘米,EC2DE , F 是DG 的中点.阴影部分的面积是多少平方厘米?A 设 & BDF 1份,则S A DCF 2 份,S A ABF5 S5 所以S DCEFSA ABC12123 份,S A AEF S A EFC 3份,如图所标【解析】 设S A DEF 1份,则根据燕尾定理其他面积如图所示S阴影 12 S A pc 。
小学奥数平面几何五种面积模型(等积-鸟头-蝶形-相似-共边)汇总

小学奥数平面几何五种模型(等积,鸟头,蝶形,相似,共边)目标:熟练掌握五大面积模型等积,鸟头,蝶形,相似(含金字塔模型和沙漏模型),共边(含燕尾模型和风筝模型), 掌握五大面积模型的各种变形 知识点拨一、等积模型①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比;如右图12::S S a b =③夹在一组平行线之间的等积变形,如右图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比. 二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCBA图⑴ 图⑵ 三、蝶形定理任意四边形中的比例关系(“蝶形定理"):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造b a S 2S 1DC BA S 4S 3S 2S 1O DCBA模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.梯形中比例关系(“梯形蝶形定理”):①2213::S S a b = ②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AF ABACBCAG===;②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形. 五、共边定理(燕尾模型和风筝模型)在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=.上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三A BC D O ba S 3S 2S 1S 4O FED C BA角形中的三角形面积对应底边之间提供互相联系的途径。
小学奥数平面几何五种面积模型(等积_鸟头_蝶形_相似_共边)

小学奥数平面几何五种模型(等积,鸟头,蝶形,相似,共边)目标:熟练掌握五大面积模型等积,鸟头,蝶形,相似(含金字塔模型和沙漏模型),共边(含燕尾模型和风筝模型),掌握五大面积模型的各种变形知识点拨一、等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比;S1S2A B两个三角形底相等,面积比等于它们的高之比;a b C D如右图 S1: S 2 a : b③夹在一组平行线之间的等积变形,如右图 S△ACDS△BCD;反之,如果 S△ACD S△BCD,则可知直线 AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;三两个平行四边形底相等,面积比等于它们的高之比.二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形.共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在△ABC 中,D,E分别是AB,AC上的点如图⑴(或D在BA的延长线上,E在AC 上),则 S△ABC: S△ADE( AB AC ) : ( AD AE)DAADEEBC B C图⑴图⑵三、蝶形定理任意四边形中的比例关系(“蝶形定理”):① S1: S2 S4: S3或者S1S3S2S4②AO:OC S1S2:S4S3DA S 1S 4S 2OS 3B C蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;1。
(完整版)小学奥数平面几何五种面积模型

小学奥数平面几何五种模型(等积,鸟头,蝶形,相似,共边)目标:熟练掌握五大面积模型等积,鸟头,蝶形,相似(含金字塔模型和沙漏模型),共边(含燕尾模型和风筝模型), 掌握五大面积模型的各种变形 知识点拨一、等积模型①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比;如右图12::S S a b =③夹在一组平行线之间的等积变形,如右图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比. 二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCBA图⑴ 图⑵ 三、蝶形定理任意四边形中的比例关系(“蝶形定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造b a S 2S 1DC BA S 4S 3S 2S 1O DCBA模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系.梯形中比例关系(“梯形蝶形定理”):①2213::S S a b = ②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AF ABACBCAG===;②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形. 五、共边定理(燕尾模型和风筝模型)在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=.上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为A BCD O ba S 3S 2S 1S 4O FED C BA三角形中的三角形面积对应底边之间提供互相联系的途径. 典型例题【例 1】如图,正方形ABCD 的边长为6,AE =1.5,CF =2.长方形EFGH 的面积为 .【解析】 连接DE ,DF ,则长方形EFGH 的面积是三角形DEF 面积的二倍.三角形DEF 的面积等于正方形的面积减去三个三角形的面积,66 1.562262 4.54216.5DEF S =⨯-⨯÷-⨯÷-⨯÷=△,所以长方形EFGH面积为33.【巩固】如图所示,正方形ABCD 的边长为8厘米,长方形EBGF 的长BG 为10厘米,那么长方形的宽为几厘米?【解析】 本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形).三角形面积等于与它等底等高的平行四边形面积的一半. 证明:连接AG .(我们通过ABG △把这两个长方形和正方形联系在一起).∵在正方形ABCD 中,G 12AB S AB AB =⨯⨯△边上的高,∴12ABG ABCD S S =W △(三角形面积等于与它等底等高的平行四边形面积的一半)同理,12ABG EFGB S S =△.∴正方形ABCD 与长方形EFGB面积相等. 长方形的宽8810 6.4=⨯÷=(厘米)._H_G_ F_E_D_C_B_ A _A_B_C_D_E_ F_G_H_ A _ B_ G_ C _ E _ F_ D_ A _ B_ G_ C_ E_ F_ D【例 2】长方形ABCD 的面积为362cm ,E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影部分面积是多少?E【解析】 解法一:寻找可利用的条件,连接BH 、HC ,如下图:E可得:12EHB AHB S S ∆∆=、12FHB CHB S S ∆∆=、12DHG DHC S S ∆∆=,而36ABCD AHB CHB CHD S S S S ∆∆∆=++=即11()361822EHB BHF DHG AHB CHB CHD S S S S S S ∆∆∆∆∆∆++=++=⨯=; 而EHB BHF DHG EBFS S S S S ∆∆∆∆++=+阴影,11111()()36 4.522228EBF S BE BF AB BC ∆=⨯⨯=⨯⨯⨯⨯=⨯=.所以阴影部分的面积是:1818 4.513.5EBF S S ∆=-=-=阴影解法二:特殊点法.找H 的特殊点,把H 点与D 点重合,那么图形就可变成右图:GE (H )这样阴影部分的面积就是DEF ∆的面积,根据鸟头定理,则有:11111113636363613.52222222ABCD AED BEF CFD S S S S S ∆∆∆=---=-⨯⨯-⨯⨯⨯-⨯⨯=阴影.【巩固】在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与P 点连接,求阴影部分面积.【解析】 (法1)特殊点法.由于P 是正方形内部任意一点,可采用特殊点法,假设P 点与A 点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的14和16,所以阴影部分的面积为2116()1546⨯+=平方厘米.(法2)连接PA 、PC .由于PAD ∆与PBC ∆的面积之和等于正方形ABCD 面积的一半,所以上、下两个阴影三角形的面积之和等于正方形ABCD 面积的14,同理可知左、右两个阴影三角形的面积之和等于正方形ABCD 面积的16,所以阴影部分的面积为2116()1546⨯+=平方厘米.【例 3】如图所示,长方形ABCD 内的阴影部分的面积之和为70,8AB =,15AD =,四边形EFGO 的面积为 .B【解析】 利用图形中的包含关系可以先求出三角形AOE 、DOG 和四边形EFGO 的面积之和,以及三角形AOE 和DOG 的面积之和,进而求出四边形EFGO的面积.由于长方形ABCD 的面积为158120⨯=,所以三角形BOC 的面积为1120304⨯=,所以三角形AOE 和DOG 的面积之和为312070204⨯-=; 又三角形AOE 、DOG 和四边形EFGO 的面积之和为111203024⎛⎫⨯-= ⎪⎝⎭,所以四边形EFGO 的面积为302010-=.另解:从整体上来看,四边形EFGO 的面积=三角形AFC 面积+三角形BFD 面积-白色部分的面积,而三角形AFC 面积+三角形BFD 面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部分的面积,即1207050-=,所以四边形的面积为605010-=.【巩固】如图,长方形ABCD 的面积是36,E 是AD 的三等分点,2AE ED =,则阴影部分的面积为 .BB【解析】 如图,连接OE .根据蝶形定理,1:::1:12COE CDE CAE CDE ON ND S S S S ∆∆∆∆===,所以12OEN OED S S ∆∆=; 1:::1:42BOE BAE BDE BAE OM MA S S S S ∆∆∆∆===,所以15OEM OEA S S ∆∆=.又11334OED ABCD S S ∆=⨯=矩形,26OEA OED S S ∆∆==,所以阴影部分面积为:1136 2.725⨯+⨯=.【例 4】已知ABC 为等边三角形,面积为400,D 、E 、F 分别为三边的中点,已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形HBC)B【解析】 因为D 、E 、F 分别为三边的中点,所以DE 、DF 、EF 是三角形ABC 的中位线,也就与对应的边平行,根据面积比例模型,三角形ABN 和三角形AMC 的面积都等于三角形ABC 的一半,即为200.根据图形的容斥关系,有ABC ABN AMC AMHN S S S S S ∆∆∆-=+-丙,即400 200200AMHN S S -=+-丙,所以AMHN S S =丙. 又ADF AMHN S S S S S ∆+=++乙甲阴影,所以1143400434ADF S S S S S ∆=++-=-⨯=乙甲丙阴影.【例 5】如图,已知5CD =,7DE =,15EF =,6FG =,线段AB 将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG 的面积是 .GFE DC BAABC DE FG【解析】 连接AF ,BD .根据题意可知,571527CF =++=;715628DG =++=;所以,1527BE CBF F S S ∆∆=,1227BE CBF C S S ∆∆=,2128AEG ADG S S ∆∆=,728AED ADG S S ∆∆=, 于是:2115652827ADG CBFS S ∆∆+=;712382827ADG CBF S S ∆∆+=; 可得40ADG S ∆=.故三角形ADG 的面积是40.【例 6】如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?EDCBAABCDE【解析】 连接BE .∵3EC AE =∴3ABC ABE S S =V V 又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷V V V ,∴1515ABC ADE S S ==V V .【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E DCBAABCDE甲乙【解析】 连接AD .∵3BE =,6AE =∴3AB BE =,3ABD BDE S S =V V 又∵4BD DC ==,∴2ABC ABD S S =V V ,∴6ABC BDE S S =V V ,5S S =乙甲.【例 7】如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =, :3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBAEDCB A【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例 8】如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGAB CD EF【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABCFBES AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△. 所以213618ABCDEFGHS S ==.【例 9】如图所示的四边形的面积等于多少?DB13131212【解析】 题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积.我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点O 逆时针旋转,使长为13的两条边重合,此时三角形OAB 将旋转到三角形OCD 的位置.这样,通过旋转后所得到的新图形是一个边长为12的正方形,且这个正方形的面积就是原来四边形的面积.因此,原来四边形的面积为1212144⨯=.(也可以用勾股定理)【例 10】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【解析】 如图,将OAB ∆沿着O 点顺时针旋转90︒,到达OCF ∆的位置.由于90ABC ∠=︒,90AOC ∠=︒,所以180OAB OCB ∠+∠=︒.而OCF OAB ∠=∠, 所以180OCF OCB ∠+∠=︒,那么B 、C 、F 三点在一条直线上.由于OB OF =,90BOF AOC ∠=∠=︒,所以BOF ∆是等腰直角三角形,且斜边BF 为538+=,所以它的面积为218164⨯=.根据面积比例模型,OBC ∆的面积为516108⨯=.【例 11】 如图,以正方形的边AB为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.F【解析】 如图,连接DE ,以A 点为中心,将ADE ∆顺时针旋转90︒到ABF ∆的位置.那么90EAF EAB BAF EAB DAE ∠=∠+∠=∠+∠=︒,而AEB ∠也是90︒,所以四边形AFBE 是直角梯形,且3AF AE ==, 所以梯形AFBE 的面积为:()1353122+⨯⨯=(2cm ). 又因为ABE ∆是直角三角形,根据勾股定理,222223534AB AE BE =+=+=,所以21172ABD S AB ∆==(2cm ).那么()17125BDE ABD ABE ADE ABD AFBE S S S S S S ∆∆∆∆∆=-+=-=-=(2cm ), 所以1 2.52OBE BDE S S ∆∆==(2cm ).【例 12】 如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米?FEABDCGFEABDC【解析】 如图,我们将BCD ∆平移使得CD 与AF 重合,将DEF ∆平移使得ED 与AB 重合,这样EF 、BC 都重合到图中的AG 了.这样就组成了一个长方形BGFD ,它的面积与原六边形的面积相等,显然长方形BGFD 的面积为2418432⨯=平方厘米,所以六边形ABCDEF 的面积为432平方厘米.【例 13】 如图,三角形ABC 的面积是1,E 是AC 的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于 .FEDCBA33321F EDC BAABCDEF【解析】 方法一:连接CF ,根据燕尾定理,12ABF ACF S BD S DC ==△△,1ABF CBF S AE S EC ==△△, 设1BDF S =△份,则2DCF S =△份,3ABF S =△份,3AEF EFC S S ==△△份,如图所标所以551212DCEF ABC S S ==△ 方法二:连接DE ,由题目条件可得到1133ABD ABC S S ==△△,11212233ADE ADC ABC S S S ==⨯=△△△,所以11ABD ADE S BF FE S ==△△,111111122323212DEF DEB BEC ABC S S S S =⨯=⨯⨯=⨯⨯⨯=△△△△,而211323CDE ABC S S =⨯⨯=△△.所以则四边形DFEC 的面积等于512. 【巩固】如图,长方形ABCD 的面积是2平方厘米,2EC DE =,F 是DG 的中点.阴影部分的面积是多少平方厘米?y B CD EGE D CBAEDB A 【解析】 设1DEFS =△份,则根据燕尾定理其他面积如图所示551212BCD S S ==△阴影平方厘米.【例 14】 四边形ABCD 的对角线AC 与BD 交于点O (如图所示).如果三角形ABD的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍.ABCDOH GA BCD O【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形.看到题目中给出条件:1:3ABD BCD S S =V V ,这可以向模型一蝶形定理靠拢,于是得出一种解法.又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得到第二种解法,但是第二种解法需要一个中介来改造这个”不良四边形”,于是可以作AH 垂直BD 于H ,CG 垂直BD 于G ,面积比转化为高之比.再应用结论:三角形高相同,则面积之比等于底边之比,得出结果.请老师注意比较两种解法,使学生体会到蝶形定理的优势,从而主观上愿意掌握并使用蝶形定理解决问题. 解法一:∵::1:3ABD BDC AO OC S S ∆∆==,∴236OC =⨯=,∴:6:32:1OC OD ==. 解法二:作AH BD ⊥于H ,CG BD ⊥于G .∵13ABDBCD S S ∆∆=,∴13AH CG =,∴13AODDOC S S ∆∆=, ∴13AO CO =,∴236OC =⨯=,∴:6:32:1OC OD ==.【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知, 求:⑴三角形BGC 的面积;⑵:AG GC =?B【解析】 ⑴根据蝶形定理,123BGCS ⨯=⨯V ,那么6BGC S =V ;⑵根据蝶形定理,()():12:361:3AG GC =++=.【例 15】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE△的面积.OGF EDCBA【解析】 ⑴根据题意可知,BCD △的面积为244616+++=,那么BCO △和CDO ∆的面积都是1628÷=,所以OCF △的面积为844-=;⑵由于BCO △的面积为8,BOE △的面积为6,所以OCE △的面积为862-=,根据蝶形定理,::2:41:2COE COF EG FG S S ∆∆===,所以::1:2GCE GCF S S EG FG ∆∆==,那么11221233GCE CEF S S ∆∆==⨯=+.【例 16】 如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.ABCD EF GABCD EF G【解析】 连接AE ,FE .因为:2:3BE EC =,:1:2DF FC =,所以3111()53210DEF ABCD ABCD S S S =⨯⨯=V 长方形长方形.因为12AEDABCD S S =V 长方形,11::5:1210AG GF ==,所以510AGD GDF S S ==V V 平方厘米,所以12AFD S =V 平方厘米.因为16AFDABCD S S =V 长方形,所以长方形ABCD 的面积是72平方厘米.【例 17】 如图,正方形ABCD 面积为3平方厘米,M 是AD 边上的中点.求图中阴影部分的面积.CBA【解析】 因为M 是AD 边上的中点,所以:1:2AM BC =,根据梯形蝶形定理可以知道22:::1:12:12:21:2:2:4AMG ABG MCG BCG S S S S =⨯⨯=△△△△()(),设1AGM S =△份,则123MCD S =+=△ 份,所以正方形的面积为1224312++++=份,224S =+=阴影份,所以:1:3S S =阴影正方形,所以1S =阴影平方厘米.【巩固】在下图的正方形ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF 的面积为1平方厘米,那么正方形ABCD 面积是 平方厘米.A BCDEF【解析】 连接DE ,根据题意可知:1:2BE AD =,根据蝶形定理得2129S =+=梯形()(平方厘米),3ECD S =△(平方厘米),那么12ABCD S =W (平方厘米).【例 18】 已知ABCD 是平行四边形,:3:2BC CE =,三角形ODE 的面积为6平方厘米.则阴影部分的面积是 平方厘米.BB【解析】 连接AC .由于ABCD 是平行四边形,:3:2BC CE =,所以:2:3CE AD =,根据梯形蝶形定理,22:::2:23:23:34:6:6:9COE AOC DOE AOD S S S S =⨯⨯=V V V V ,所以6AOC S =V (平方厘米),9AOD S =V (平方厘米),又6915ABC ACD S S ==+=V V (平方厘米),阴影部分面积为61521+=(平方厘米).【巩固】右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.BB【分析】 连接AE.由于AD 与BC是平行的,所以AECD也是梯形,那么OCDOAE S S ∆∆=.根据蝶形定理,4936OCD OAE OCE OAD S S S S ∆∆∆∆⨯=⨯=⨯=,故236OCD S ∆=, 所以6OCD S ∆=(平方厘米).【巩固】右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.BB【解析】 连接AE .由于AD 与BC 是平行的,所以AECD 也是梯形,那么OCD OAE S S ∆∆=.根据蝶形定理,2816OCD OAE OCE OAD S S S S ∆∆∆∆⨯=⨯=⨯=,故216OCD S ∆=,所以4OCD S ∆=(平方厘米).另解:在平行四边形ABED 中,()111681222ADE ABED S S ∆==⨯+=Y (平方厘米), 所以1284AOE ADE AOD S S S ∆∆∆=-=-=(平方厘米),根据蝶形定理,阴影部分的面积为8244⨯÷=(平方厘米).【例 19】 如图,长方形ABCD 被CE 、DF 分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为___________平方厘米.?852O A BCDEF?852O A BC DEF【解析】 连接DE 、CF .四边形EDCF 为梯形,所以EOD FOC S S ∆=V ,又根据蝶形定理,EOD FOC EOF COD S S S S ∆∆∆∆⋅=⋅,所以2816EOD FOC EOF COD S S S S ∆∆∆∆⋅=⋅=⨯=,所以4EOD S ∆=(平方厘米),4812ECD S ∆=+=(平方厘米).那么长方形ABCD 的面积为12224⨯=平方厘米,四边形OFBC 的面积为245289---=(平方厘米).【例 20】 如图,ABC ∆是等腰直角三角形,DEFG 是正方形,线段AB 与CD 相交于K 点.已知正方形DEFG 的面积48,:1:3AK KB =,则BKD ∆的面积是多少?BB【解析】 由于DEFG 是正方形,所以DA 与BC 平行,那么四边形ADBC 是梯形.在梯形ADBC 中,BDK ∆和ACK ∆的面积是相等的.而:1:3AK KB =,所以ACK ∆的面积是ABC ∆面积的11134=+,那么BDK ∆的面积也是ABC ∆面积的14. 由于ABC ∆是等腰直角三角形,如果过A 作BC 的垂线,M 为垂足,那么M 是BC 的中点,而且AM DE =,可见ABM ∆和ACM ∆的面积都等于正方形DEFG 面积的一半,所以ABC ∆的面积与正方形DEFG 的面积相等,为48.那么BDK ∆的面积为148124⨯=.【例 21】 下图中,四边形ABCD 都是边长为1的正方形,E 、F 、G 、H 分别是AB ,BC ,CD ,DA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数m n,那么,()m n +的值等于 .E【解析】 左、右两个图中的阴影部分都是不规则图形,不方便直接求面积,观察发现两个图中的空白部分面积都比较好求,所以可以先求出空白部分的面积,再求阴影部分的面积.如下图所示,在左图中连接EG .设AG 与DE 的交点为M .左图中AEGD 为长方形,可知AMD ∆的面积为长方形AEGD 面积的14,所以三角形AMD 的面积为21111248⨯⨯=.又左图中四个空白三角形的面积是相等的,所以左图中阴影部分的面积为111482-⨯=.BEE如上图所示,在右图中连接AC 、EF .设AF 、EC 的交点为N . 可知EF ∥AC 且2AC EF =.那么三角形BEF 的面积为三角形ABC 面积的14,所以三角形BEF 的面积为21111248⨯⨯=,梯形AEFC 的面积为113288-=. 在梯形AEFC 中,由于:1:2EF AC =,根据梯形蝶形定理,其四部分的面积比为:221:12:12:21:2:2:4⨯⨯=,所以三角形EFN 的面积为3118122424⨯=+++,那么四边形BENF 的面积为1118246+=.而右图中四个空白四边形的面积是相等的,所以右图中阴影部分的面积为111463-⨯=.那么左图中阴影部分面积与右图中阴影部分面积之比为11:3:223=,即32m n =, 那么325m n +=+=.【例 22】 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==,则::ADE DEGF FGCB S S S =△四边形四边形 .EGF A D CB【解析】 设1ADE S =△份,根据面积比等于相似比的平方,所以22::1:4ADE AFG S S AD AF ==△△,22::1:9ADE ABC S S AD AB ==△△, 因此4AFG S =△份,9ABC S =△份,进而有3DEGF S =四边形份,5FGCB S =四边形份,所以::1:3:5ADE DEGF FGCB S S S =△四边形四边形【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.A ED CB【解析】 由金字塔模型得:::2:5AD AB AE AC DE BC ===,所以42510AC =÷⨯=【巩固】如图, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD DF FM MP PB ====,则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形. 【解析】 设1ADE S =△份,22::1:4ADE AFG S S AD AF ==△△,因此4AFG S =△份,进而有3DEGF S =四边形份,同理有5FGNM S =四边形份,7MNQP S =四边形份,9PQCB S =四边形份.所以有::::1:3:5:7:9ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形【例 23】 如图,已知正方形ABCD 的边长为4,F是BC 边的中点,E 是DC 边上的点,且:1:3DE EC =,AF 与BE 相交于点G ,求ABG S △GFAEDC BM GFAEDCBGFAEDCB【解析】 方法一:连接AE ,延长AF ,DC 两条线交于点M ,构造出两个沙漏,所以有::1:1AB CM BF FC ==,因此4CM =,根据题意有3CE =,再根据另一个沙漏有::4:7GB GE AB EM ==,所以4432(442)471111ABG ABE S S ==⨯⨯÷=+△△.方法二:连接,AE EF,分别求4224ABF S =⨯÷=△,4441232247AEFS =⨯-⨯÷-⨯÷-=△,根据蝶形定理::4:7ABF AEF S S BG GE ==△△,所以4432(442)471111ABG ABE S S ==⨯⨯÷=+△△.【例 24】 如图所示,已知平行四边形ABCD 的面积是1,E 、F 是AB 、AD 的中点, BF 交EC 于M ,求BMG ∆的面积.Q E GNMFPA DCBMHGF E DCBAA【解析】 解法一:由题意可得,E 、F 是AB 、AD 的中点,得//EF BD ,而::1:2FD BC FH HC ==,::1:2EB CD BG GD ==所以::2:3CH CF GH EF ==,并得G 、H 是BD 的三等分点,所以BG GH =,所以 ::2:3BG EF BM MF ==,所以25BM BF =,11112224BFD ABD ABCD S S S ∆∆==⨯=Y ; 又因为13BG BD =,所以1212113535430BMG BFD S S ∆∆=⨯⨯=⨯⨯=. 解法二:延长CE 交DA 于I ,如右图,可得,::1:1AI BC AE EB ==,从而可以确定M 的点的位置, ::2:3BM MF BC IF ==,25BM BF =,13BG BD =(鸟头定理),可得2121115353430BMG BDF ABCD S S S ∆∆=⨯=⨯⨯=Y【例 25】 如图,ABCD 为正方形,1cm AM NB DE FC ====且2cm MN =,请问四边形PQRS 的面积为多少?CACA【解析】 (法1)由//AB CD ,有MP PC MNDC=,所以2PC PM =,又MQ MB QC EC =,所以12MQ QC MC ==,所以111236PQ MC MC MC =-=,所以SPQR S 占AMCF S 的16,所以121(112)63SPQR S =⨯⨯++=2(cm ).(法2)如图,连结AE ,则14482ABE S ∆=⨯⨯=(2cm ),而RB ER ABEF=,所以2RB AB EFEF ==,22168333ABR ABE S S ∆∆==⨯=(2cm ).而1134322MBQ ANS S S ∆∆==⨯⨯⨯=(2cm ),因为MN MP DC PC=,所以13MP MC =,则11424233MNP S ∆=⨯⨯⨯=(2cm ),阴影部分面积等于164233333ABR ANS MBQ MNP S S S S ∆∆∆∆--+=--+=(2cm ).【例 26】 如右图,三角形ABC 中,:4:9BD DC =,:4:3CE EA =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::4:912:27AOB AOC S S BD CD ===△△::3:412:16AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:27:16:AOC BOC S S AF FB ==△△【点评】本题关键是把AOB △的面积统一,这种找最小公倍数的方法,在我们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达到解奥数题四两拨千斤的巨大力量!【巩固】如右图,三角形ABC 中,:3:4BD DC =,:5:6AE CE =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::3:415:20AOB AOC S S BD CD ===△△::5:615:18AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:20:1810:9:AOC BOC S S AF FB ===△△【巩固】如右图,三角形ABC 中,:2:3BD DC =,:5:4EA CE =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::2:310:15AOB AOC S S BD CD ===△△::5:410:8AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:15:8:AOC BOC S S AF FB ==△△【点评】本题关键是把AOB △的面积统一,这种找最小公倍数的方法,在我们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达到解奥数题四两拨千斤的巨大力量!【例 27】 如右图,三角形ABC 中,:::3:2AF FB BD DC CE AE ===,且三角形ABC 的面积是1,则三角形ABE 的面积为______,三角形AGE 的面积为________,三角形GHI 的面积为______.I HGFEDCBAI H G FEDCBA【分析】 连接AH 、BI 、CG .由于:3:2CE AE =,所以25AE AC =,故2255ABE ABC S S ∆∆==;根据燕尾定理,::2:3ACG ABG S S CD BD ∆∆==,::3:2BCG ABG S S CE EA ∆∆==,所以::4:6:9ACG ABG BCG S S S ∆∆∆=,则419ACG S ∆=,919BCG S ∆=; 那么2248551995AGE AGC S S ∆∆==⨯=; 同样分析可得919ACH S ∆=,则::4:9ACG ACH EG EH S S ∆∆==,::4:19ACG ACB EG EB S S ∆∆==,所以::4:5:10EG GH HB =,同样分析可得::10:5:4AG GI ID =,所以5521101055BIE BAE S S ∆∆==⨯=,55111919519GHI BIE S S ∆∆==⨯=.【巩固】 如右图,三角形ABC 中,:::3:2AF FB BD DC CE AE ===,且三角形GHI的面积是1,求三角形ABC 的面积.IH G FEDCBA IH G FEDCBA【解析】 连接BG ,AGCS △=6份根据燕尾定理,::3:26:4AGC BGC S S AF FB ===△△,::3:29:6ABG AGC S S BD DC ===△△得4BGC S =△(份),9ABG S =△(份),则19ABC S =△(份),因此619AGCABCS S =△△, 同理连接AI 、CH 得619ABHABCS S =△△,619BIC ABC S S =△△,所以1966611919GHI ABC S S ---==△△三角形GHI 的面积是1,所以三角形ABC 的面积是19【巩固】如图,ABC ∆中2BD DA =,2CE EB =,2AF FC =,那么ABC ∆的面积是阴影三角形面积的 倍.BCCB【分析】 如图,连接AI.根据燕尾定理,::2:1BCI ACIS S BD AD ∆∆==,::1:2BCI ABI S S CF AF ∆∆==,所以,::1:2:4ACI BCI ABI S S S ∆∆∆=,那么,221247BCI ABC ABC S S S ∆∆∆==++.同理可知ACG ∆和ABH ∆的面积也都等于ABC ∆面积的27,所以阴影三角形的面积等于ABC ∆面积的211377-⨯=,所以ABC ∆的面积是阴影三角形面积的7倍.【巩固】如图在ABC △中,12DC EA FB DBECFA===,求GHI ABC △的面积△的面积的值.IHG FEDCBAIHG FEDCB A【解析】 连接BG ,设BGC S △=1份,根据燕尾定理::2:1AGC BGC S S AF FB ==△△,::2:1ABG AGC S S BD DC ==△△,得2AGC S =△(份),4ABG S =△(份),则7ABC S =△(份),因此27AGC ABC S S =△△,同理连接AI 、CH 得27ABH ABC S S =△△,27BIC ABC S S =△△,所以7222177GHI ABC S S ---==△△ 【点评】如果任意一个三角形各边被分成的比是相同的,那么在同样的位置上的图形,虽然形状千变万化,但面积是相等的,这在这讲里面很多题目都是用“同理得到”的,即再重复一次解题思路,因此我们有对称法作辅助线.【例 28】 如图,三角形ABC 的面积是1,BD DE EC ==,CF FG GA ==,三角形ABC被分成9部分,请写出这9部分的面积各是多少?GFE D CBAN MQPGF EDCBA【解析】 设BG 与AD 交于点P ,BG 与AE 交于点Q ,BF 与AD 交于点M ,BF 与AE交于点N .连接CP ,CQ ,CM ,CN .根据燕尾定理,::1:2ABP CBP S S AG GC ==△△,::1:2ABP ACP S S BD CD ==△△,设1ABP S =△(份),则1225ABC S =++=△(份),所以15ABP S =△ 同理可得,27ABQ S =△,12ABN S =△,而13ABG S =△,所以2137535APQ S =-=△,1213721AQG S =-=△.同理,335BPMS =△121BDM S =△,所以1239273570PQMN S =--=四边形,13953357042MNEDS =--=四边形,1151321426NFCE S =--=四边形,1115321642GFNQ S =--=四边形【巩固】如图,ABC ∆的面积为1,点D 、E 是BC 边的三等分点,点F 、G 是AC边的三等分点,那么四边形JKIH 的面积是多少?K J IHABC D EF GKJI HABCD EFG【解析】 连接CK 、CI 、CJ.根据燕尾定理,::1:2ACK ABK S S CD BD ∆∆==,::1:2ABK CBK S S AG CG ∆∆==, 所以::1:2:4ACK ABK CBK S S S ∆∆∆=,那么111247ACK S ∆==++,11321AGK ACK S S ∆∆==. 类似分析可得215AGI S ∆=. 又::2:1ABJ CBJ S S AF CF ∆∆==,::2:1ABJ ACJ S S BD CD ∆∆==,可得14ACJ S ∆=. 那么,111742184CGKJS =-=. 根据对称性,可知四边形CEHJ 的面积也为1784,那么四边形JKIH 周围的图形的面积之和为172161228415370CGKJ AGI ABE S S S ∆∆⨯++=⨯++=,所以四边形JKIH 的面积为61917070-=.【例 29】 右图,ABC △中,G 是AC 的中点,D 、E 、F 是BC 边上的四等分点,AD 与BG 交于M ,AF 与BG 交于N ,已知ABM △的面积比四边形FCGN 的面积大7.2平方厘米,则ABC △的面积是多少平方厘米?N M GA BCD EFNMGA BC D EF【解析】 连接CM 、CN .根据燕尾定理,::1:1ABM CBMS S AG GC ==△△,::1:3ABM ACM S S BD CD ==△△,所以15ABM ABC S S =△△;再根据燕尾定理,::1:1ABN CBNS S AG GC ==△△,所以::4:3ABN FBN CBN FBN S S S S ==△△△△,所以:4:3AN NF =,那么1422437ANG AFC S S =⨯=+△△,所以2515177428FCGNAFC ABC ABC S S S S ⎛⎫=-=⨯= ⎪⎝⎭△△△.根据题意,有157.2528ABC ABC S S -=△△,可得336ABC S =△(平方厘米)【例 30】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求阴影部分面积.C BAGCB【解析】 三角形在开会,那么就好好利用三角形中最好用的比例和燕尾定理吧!令BI 与CD 的交点为M ,AF 与CD 的交点为N ,BI 与AF 的交点为P ,BI 与CE 的交点为Q ,连接AM 、BN 、CP⑴求ADMI S 四边形:在ABC △中,根据燕尾定理,::1:2ABM CBM S S AI CI ==△△::1:2ACM CBM S S AD BD ==△△设1ABM S =△(份),则2CBM S =△(份),1ACM S =△(份),4ABC S =△(份),所以14ABMACM ABC S S S ==△△△,所以11312ADM ABM ABC S S S ==△△△,112AIM ABC S S =△△,所以111()12126ABC ABC ADMI S S S =+=△△四边形,同理可得另外两个顶点的四边形面积也分别是ABC △面积的16⑵求DNPQE S 五边形:在ABC △中,根据燕尾定理::1:2ABN ACN S S BF CF ==△△::1:2ACN BCN S S AD BD ==△△,所以111133721ADN ABN ABC ABC S S S S ==⨯=△△△△,同理121BEQ ABC S S =△△在ABC△中,根据燕尾定理::1:2ABP ACP S S BF CF ==△△,::1:2ABP CBP S S AI CI ==△△所以15ABP ABCS S =△△,所以1111152121105ABP ADN BEPABC ABC DNPQE S S S S S S ⎛⎫=--=--= ⎪⎝⎭△△△△△五边形 同理另外两个五边形面积是ABC△面积的11105,所以11113133610570S =-⨯-⨯=阴影【例 31】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求中心六边形面积.GCBAGCBA【解析】 设深黑色六个三角形的顶点分别为N 、R 、P 、S 、M 、Q ,连接CR在ABC △中根据燕尾定理,::.2:1ABR ACR S S BG CG ==△△, ::1:2ABR CBR S S AI CI ==△△所以27ABR ABC S S =△△,同理27ACS ABC S S =△△,27CQB ABC S S =△△所以222117777RQS S =---=△,同理17MNP S =△根据容斥原理,和上题结果11131777010S =+-=六边形课后练习: 练习1. 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA【解析】:():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7平方厘米,所以24ABC S =△平方厘米练习2. 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A A B CDEFGH【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形 所以66513.2ABCD S =÷=四边形平方米练习3. 正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是 平方厘米.H GFEDCBAM H GFEDCBA【解析】 欲求四边形BGHF 的面积须求出EBG ∆和CHF ∆的面积.由题意可得到:::1:2EG GC EB CD ==,所以可得:13EBG BCE S S ∆∆=将AB 、DF 延长交于M 点,可得::::1:1BM DC MF FD BF FC ===,而1::():3:22EH HC EM CD AB AB CD ==+=,得25CH CE =,而12CF BC =,所以121255CHF BCE BCE S S S ∆∆∆=⨯=11112030224BCE S AB BC ∆=⨯⨯=⨯=117730141515EBC EBC EBC EBC BGHF S S S S S ∆∆∆∆=--==⨯=四边形.EF ,确定H 的位置(也就是:FH HD )练习4. 如图,已知4cm AB AE ==,BC DC =,90BAE BCD ∠=∠=︒,10cm AC =,则S ABC ACE CDE S S ∆∆∆++= 2cm .DCEBABCA'C'EDA【解析】 将三角形ABC 绕A 点和C 点分别顺时针和逆时针旋转90o,构成三角形'AEC 和'A DC ,再连接''A C ,显然'AC AC ⊥,'AC A C ⊥,''AC A C AC ==,所以''ACA C 是正方形.三角形'AEC 和三角形'A DC 关于正方形的中心O 中心对称,在中心对称图形''ACA C 中有如下等量关系: ''AEC A DC S S ∆∆=;''AEC A DC S S ∆∆=;'CED C DE S S ∆∆=.所以2'''11101050cm 22ABC ACE CDE AEC ACE CDE ACA C S S S S S S S ∆∆∆∆∆∆++=++==⨯⨯=W .练习5. 如图,正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是_____平方厘米.EDED【解析】 连接BH ,根据沙漏模型得:1:2BG GD =,设1BHC S =△份,根据燕尾定理2CHD S =△份,2BHD S =△份,因此122)210S =++⨯=正方形(份,127236BFHG S =+=,所以712010146BFHG S =÷⨯=(平方厘米).练习6. 如图,ABC ∆中,点D 是边AC 的中点,点E 、F 是边BC 的三等分点,若ABC ∆的面积为1,那么四边形CDMF 的面积是_________.。
小学奥数平面几何五种面积模型(等积,鸟头,蝶形,相似,共边)

小学奥数平面几何五种模型(等积,鸟头,蝶形,相似,共边)目标:熟练掌握五大面积模型等积,鸟头,蝶形,相似(含金字塔模型和沙漏模型),共边(含燕尾模型和风筝模型), 掌握五大面积模型的各种变形 知识点拨一、等积模型①等底等高的两个三角形面积相等;②两个三角形高相等,面积比等于它们的底之比;两个三角形底相等,面积比等于它们的高之比; 如右图12::S S a b =③夹在一组平行线之间的等积变形,如右图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比.二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADES S AB AC AD AE =⨯⨯△△ba S 2S 1DC BAEDCBAEDCBA图⑴ 图⑵三、蝶形定理任意四边形中的比例关系(“蝶形定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++ 蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;另一方面,也可以得到与面积对应的对角线的比例关系. 梯形中比例关系(“梯形蝶形定理”): ①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF GS 4S 3S 2S 1O DCBA A BCDO ba S 3S 2S 1S 4①AD AE DE AF ABACBCAG===;②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形. 五、共边定理(燕尾模型和风筝模型)在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=.上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径. 典型例题OFE DCBA【例 1】 如图,正方形ABCD 的边长为6,AE =,CF =2.长方形EFGH 的面积为 .【解析】 连接DE ,DF ,则长方形EFGH 的面积是三角形DEF 面积的二倍.三角形DEF 的面积等于正方形的面积减去三个三角形的面积,66 1.562262 4.54216.5DEF S =⨯-⨯÷-⨯÷-⨯÷=△,所以长方形EFGH面积为33.【巩固】如图所示,正方形ABCD 的边长为8厘米,长方形EBGF 的长BG 为10厘米,那么长方形的宽为几厘米【解析】 本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形).三角形面积等于与它等底等高的平行四边形面积的一半.证明:连接AG .(我们通过ABG △把这两个长方形和正方形联系在一起).∵在正方形ABCD 中,G12AB S AB AB =⨯⨯△边上的高, ∴12ABG ABCDS S=△(三角形面积等于与它等底等高的平行四边形面积的一半)同理,12ABG EFGB S S =△. ∴正方形ABCD与长方形EFGB面积相等. 长方形的宽8810 6.4=⨯÷=(厘米).【例 2】 长方形ABCD 的面积为362cm ,E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影部分面积是多少E【解析】 解法一:寻找可利用的条件,连接BH 、HC ,如下图:E可得:12EHB AHB S S ∆∆=、12FHB CHB S S ∆∆=、12DHG DHC S S ∆∆=,而36ABCD AHB CHB CHD S S S S ∆∆∆=++=即11()361822EHB BHF DHG AHB CHB CHDS S S S S S ∆∆∆∆∆∆++=++=⨯=; 而EHB BHF DHG EBFS S S S S ∆∆∆∆++=+阴影,11111()()36 4.522228EBF S BE BF AB BC ∆=⨯⨯=⨯⨯⨯⨯=⨯=.所以阴影部分的面积是:1818 4.513.5EBF S S ∆=-=-=阴影 解法二:特殊点法.找H 的特殊点,把H 点与D 点重合,那么图形就可变成右图:GE (H )这样阴影部分的面积就是DEF ∆的面积,根据鸟头定理,则有:11111113636363613.52222222ABCD AED BEF CFD S S S S S ∆∆∆=---=-⨯⨯-⨯⨯⨯-⨯⨯=阴影.【巩固】在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与P 点连接,求阴影部分面积.【解析】 (法1)特殊点法.由于P 是正方形内部任意一点,可采用特殊点法,假设P 点与A 点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的14和16,所以阴影部分的面积为2116()1546⨯+=平方厘米.(法2)连接PA 、PC .由于PAD ∆与PBC ∆的面积之和等于正方形ABCD 面积的一半,所以上、下两个阴影三角形的面积之和等于正方形ABCD 面积的14,同理可知左、右两个阴影三角形的面积之和等于正方形ABCD 面积的16,所以阴影部分的面积为2116()1546⨯+=平方厘米.【例 3】 如图所示,长方形ABCD 内的阴影部分的面积之和为70,8AB =,15AD =,四边形EFGO 的面积为 .B【解析】 利用图形中的包含关系可以先求出三角形AOE 、DOG 和四边形EFGO 的面积之和,以及三角形AOE 和DOG 的面积之和,进而求出四边形EFGO 的面积. 由于长方形ABCD的面积为158120⨯=,所以三角形BOC的面积为1120304⨯=,所以三角形AOE 和DOG 的面积之和为312070204⨯-=; 又三角形AOE 、DOG 和四边形EFGO 的面积之和为111203024⎛⎫⨯-= ⎪⎝⎭,所以四边形EFGO 的面积为302010-=.另解:从整体上来看,四边形EFGO 的面积=三角形AFC 面积+三角形BFD 面积-白色部分的面积,而三角形AFC 面积+三角形BFD 面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部分的面积,即1207050-=,所以四边形的面积为605010-=.【巩固】如图,长方形ABCD 的面积是36,E 是AD 的三等分点,2AE ED =,则阴影部分的面积为 .BB【解析】 如图,连接OE .根据蝶形定理,1:::1:12COE CDE CAE CDE ON ND S S S S ∆∆∆∆===,所以12OEN OED S S ∆∆=; 1:::1:42BOE BAEBDE BAE OM MA S S S S ∆∆∆∆===,所以15OEMOEA S S ∆∆=. 又11334OED ABCD S S ∆=⨯=矩形,26OEA OED S S ∆∆==,所以阴影部分面积为:1136 2.725⨯+⨯=.【例 4】 已知ABC 为等边三角形,面积为400,D 、E 、F 分别为三边的中点,已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形HBC )B【解析】 因为D 、E 、F 分别为三边的中点,所以DE 、DF 、EF 是三角形ABC 的中位线,也就与对应的边平行,根据面积比例模型,三角形ABN 和三角形AMC 的面积都等于三角形ABC 的一半,即为200. 根据图形的容斥关系,有ABC ABN AMC AMHN S S S S S ∆∆∆-=+-丙,即400 200200AMHN S S -=+-丙,所以AMHN S S =丙. 又ADF AMHN S S S S S ∆+=++乙甲阴影,所以1143400434ADF S S S S S ∆=++-=-⨯=乙甲丙阴影.【例 5】 如图,已知5CD =,7DE =,15EF =,6FG =,线段AB 将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG 的面积是 .GFE DC BAABC DE FG【解析】 连接AF ,BD .根据题意可知,571527CF =++=;715628DG =++=; 所以,1527BE CBF F S S ∆∆=,1227BE CBF C S S ∆∆=,2128AEG ADG S S ∆∆=,728AED ADG S S ∆∆=, 于是:2115652827ADG CBF S S ∆∆+=;712382827ADG CBF S S ∆∆+=; 可得40ADG S ∆=.故三角形ADG 的面积是40.【例 6】 如图在ABC △中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(75)ADE ABC S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少EDCBAABCD E【解析】 连接BE .∵3EC AE = ∴3ABC ABE S S = 又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷,∴1515ABC ADE S S ==.【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍乙甲E DCBAABCDE甲乙【解析】 连接AD .∵3BE =,6AE = ∴3AB BE =,3ABD BDE S S = 又∵4BD DC ==,∴2ABC ABD S S =,∴6ABC BDE S S =,5S S =乙甲.【例 7】 如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBAEDCB A【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25ADE ABC S S =⨯⨯+=△△,设6ADE S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例 8】 如图,平行四边形ABCD ,BE AB =,2CF CB =,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGAB CD EF【解析】 连接AC 、BD .根据共角定理 ∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABCFBES AB BC S BE BF ⋅⨯===⋅⨯△△. 又1ABC S =△,所以3FBE S =△. 同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△.所以213618ABCDEFGHS S ==.【例 9】 如图所示的四边形的面积等于多少DB13131212【解析】 题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积.我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点O 逆时针旋转,使长为13的两条边重合,此时三角形OAB 将旋转到三角形OCD 的位置.这样,通过旋转后所得到的新图形是一个边长为12的正方形,且这个正方形的面积就是原来四边形的面积.因此,原来四边形的面积为1212144⨯=.(也可以用勾股定理)【例 10】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【解析】 如图,将OAB ∆沿着O 点顺时针旋转90︒,到达OCF ∆的位置.由于90ABC ∠=︒,90AOC ∠=︒,所以180OAB OCB ∠+∠=︒.而OCF OAB ∠=∠, 所以180OCF OCB ∠+∠=︒,那么B 、C 、F 三点在一条直线上. 由于OB OF =,90BOF AOC ∠=∠=︒,所以BOF ∆是等腰直角三角形,且斜边BF 为538+=,所以它的面积为218164⨯=.根据面积比例模型,OBC ∆的面积为516108⨯=.【例 11】 如图,以正方形的边AB为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC 、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.F【解析】 如图,连接DE ,以A 点为中心,将ADE ∆顺时针旋转90︒到ABF ∆的位置.那么90EAF EAB BAF EAB DAE ∠=∠+∠=∠+∠=︒,而AEB ∠也是90︒,所以四边形AFBE 是直角梯形,且3AF AE ==, 所以梯形AFBE 的面积为:()1353122+⨯⨯=(2cm ). 又因为ABE ∆是直角三角形,根据勾股定理,222223534AB AE BE =+=+=,所以21172ABD S AB ∆==(2cm ). 那么()17125BDE ABD ABE ADE ABD AFBE S S S S S S ∆∆∆∆∆=-+=-=-=(2cm ), 所以12.52OBE BDE S S ∆∆==(2cm ).【例 12】 如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米FEABDCGFEABDC【解析】 如图,我们将BCD ∆平移使得CD 与AF 重合,将DEF ∆平移使得ED 与AB 重合,这样EF 、BC 都重合到图中的AG 了.这样就组成了一个长方形BGFD ,它的面积与原六边形的面积相等,显然长方形BGFD 的面积为2418432⨯=平方厘米,所以六边形ABCDEF 的面积为432平方厘米.【例 13】 如图,三角形ABC 的面积是1,E 是AC的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于 .FEDCBA33321F EDC BAABCDEF【解析】 方法一:连接CF ,根据燕尾定理,12ABF ACF S BD S DC ==△△,1ABF CBF S AE S EC ==△△, 设1BDF S =△份,则2DCF S =△份,3ABF S =△份,3AEF EFC S S ==△△份,如图所标所以551212DCEF ABC S S ==△ 方法二:连接DE ,由题目条件可得到1133ABD ABC S S ==△△,11212233ADE ADC ABC S S S ==⨯=△△△,所以11ABD ADES BF FE S ==△△, 111111122323212DEF DEB BEC ABC S S S S =⨯=⨯⨯=⨯⨯⨯=△△△△,而211323CDE ABCS S=⨯⨯=△△.所以则四边形DFEC的面积等于512.【巩固】如图,长方形ABCD的面积是2平方厘米,2EC DE=,F是DG的中点.阴影部分的面积是多少平方厘米yB CDEGEDCBAEDBA【解析】设1DEFS=△份,则根据燕尾定理其他面积如图所示551212BCDS S==△阴影平方厘米.【例 14】四边形ABCD的对角线AC与BD交于点O(如图所示).如果三角形ABD的面积等于三角形BCD的面积的13,且2AO=,3DO=,那么CO的长度是DO的长度的_________倍.AB CDO HGAB CDO【解析】在本题中,四边形ABCD为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形.看到题目中给出条件:1:3ABD BCDS S=,这可以向模型一蝶形定理靠拢,于是得出一种解法.又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得到第二种解法,但是第二种解法需要一个中介来改造这个”不良四边形”,于是可以作AH垂直BD于H,CG垂直BD于G,面积比转化为高之比.再应用结论:三角形高相同,则面积之比等于底边之比,得出结果.请老师注意比较两种解法,使学生体会到蝶形定理的优势,从而主观上愿意掌握并使用蝶形定理解决问题. 解法一:∵::1:3ABD BDCAO OC S S ∆∆==,∴236OC =⨯=,∴:6:32:1OC OD ==.解法二:作AH BD ⊥于H ,CG BD ⊥于G . ∵13ABDBCD S S ∆∆=,∴13AH CG =,∴13AOD DOC S S ∆∆=,∴13AO CO =,∴236OC =⨯=,∴:6:32:1OC OD ==.【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知,求:⑴三角形BGC 的面积;⑵:AG GC =B【解析】 ⑴根据蝶形定理,123BGCS⨯=⨯,那么6BGCS=;⑵根据蝶形定理,()():12:361:3AG GC =++=.【例 15】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF △、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE△的面积.OGFEDCBA【解析】 ⑴根据题意可知,BCD △的面积为244616+++=,那么BCO △和CDO ∆的面积都是1628÷=,所以OCF △的面积为844-=;⑵由于BCO △的面积为8,BOE △的面积为6,所以OCE △的面积为862-=,根据蝶形定理,::2:41:2COE COF EG FG S S ∆∆===,所以::1:2GCE GCF S S EG FG ∆∆==,那么11221233GCE CEF S S ∆∆==⨯=+.【例 16】 如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.ABCDEF GABCD EF G【解析】 连接AE ,FE .因为:2:3BE EC =,:1:2DF FC =,所以3111()53210DEFABCD ABCD SS S =⨯⨯=长方形长方形.因为12AEDABCD SS =长方形,11::5:1210AG GF ==,所以510AGDGDFS S==平方厘米,所以12AFDS =平方厘米.因为16AFDABCD SS =长方形,所以长方形ABCD 的面积是72平方厘米.【例 17】 如图,正方形ABCD 面积为3平方厘米,M 是AD 边上的中点.求图中阴影部分的面积.CBA【解析】 因为M 是AD 边上的中点,所以:1:2AM BC =,根据梯形蝶形定理可以知道22:::1:12:12:21:2:2:4AMG ABG MCG BCG S S S S =⨯⨯=△△△△()(),设1AGM S =△份,则123MCD S =+=△ 份,所以正方形的面积为1224312++++=份,224S =+=阴影份,所以:1:3S S =阴影正方形,所以1S =阴影平方厘米.【巩固】在下图的正方形ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF的面积为1平方厘米,那么正方形ABCD面积是平方厘米.A BCDEF【解析】 连接DE,根据题意可知:1:2BE AD =,根据蝶形定理得2129S =+=梯形()(平方厘米),3ECD S =△(平方厘米),那么12ABCDS=(平方厘米).【例 18】 已知ABCD 是平行四边形,:3:2BC CE =,三角形ODE 的面积为6平方厘米.则阴影部分的面积是 平方厘米.BB【解析】 连接AC .由于ABCD 是平行四边形,:3:2BC CE =,所以:2:3CE AD =, 根据梯形蝶形定理,22:::2:23:23:34:6:6:9COE AOCDOEAODS S SS=⨯⨯=,所以6AOCS=(平方厘米),9AODS=(平方厘米),又6915ABCACDSS==+=(平方厘米),阴影部分面积为61521+=(平方厘米).【巩固】右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.BB【分析】 连接AE .由于AD 与BC 是平行的,所以AECD 也是梯形,那么OCD OAE S S ∆∆=.根据蝶形定理,4936OCD OAE OCE OAD S S S S ∆∆∆∆⨯=⨯=⨯=,故236OCD S ∆=,所以6OCD S ∆=(平方厘米).【巩固】右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.BB【解析】 连接AE .由于AD 与BC 是平行的,所以AECD 也是梯形,那么OCD OAE S S ∆∆=.根据蝶形定理,2816OCD OAE OCE OAD S S S S ∆∆∆∆⨯=⨯=⨯=,故216OCD S ∆=,所以4OCD S ∆=(平方厘米).另解:在平行四边形ABED 中,()111681222ADE ABEDS S∆==⨯+=(平方厘米), 所以1284AOE ADE AOD S S S ∆∆∆=-=-=(平方厘米),根据蝶形定理,阴影部分的面积为8244⨯÷=(平方厘米).【例 19】 如图,长方形ABCD 被CE 、DF 分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为___________平方厘米.?852O A BCDEF?852O A BC DEF【解析】 连接DE 、CF .四边形EDCF 为梯形,所以EOD FOC S S ∆=,又根据蝶形定理,EOD FOC EOF COD S S S S ∆∆∆∆⋅=⋅,所以2816EOD FOC EOF COD S S S S ∆∆∆∆⋅=⋅=⨯=,所以4EOD S ∆=(平方厘米),4812ECD S ∆=+=(平方厘米).那么长方形ABCD 的面积为12224⨯=平方厘米,四边形OFBC 的面积为245289---=(平方厘米).【例 20】 如图,ABC ∆是等腰直角三角形,DEFG 是正方形,线段AB 与CD 相交于K 点.已知正方形DEFG 的面积48,:1:3AK KB =,则BKD ∆的面积是多少BB【解析】 由于DEFG 是正方形,所以DA 与BC 平行,那么四边形ADBC 是梯形.在梯形ADBC 中,BDK ∆和ACK ∆的面积是相等的.而:1:3AK KB =,所以ACK∆的面积是ABC ∆面积的11134=+,那么BDK ∆的面积也是ABC ∆面积的14.由于ABC ∆是等腰直角三角形,如果过A 作BC 的垂线,M 为垂足,那么M 是BC 的中点,而且AM DE =,可见ABM ∆和ACM∆的面积都等于正方形DEFG 面积的一半,所以ABC ∆的面积与正方形DEFG 的面积相等,为48.那么BDK ∆的面积为148124⨯=.【例 21】 下图中,四边形ABCD 都是边长为1的正方形,E 、F 、G 、H 分别是AB ,BC ,CD ,DA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数m n,那么,()m n +的值等于 .E【解析】 左、右两个图中的阴影部分都是不规则图形,不方便直接求面积,观察发现两个图中的空白部分面积都比较好求,所以可以先求出空白部分的面积,再求阴影部分的面积.如下图所示,在左图中连接EG .设AG 与DE 的交点为M . 左图中AEGD 为长方形,可知AMD ∆的面积为长方形AEGD 面积的14,所以三角形AMD 的面积为21111248⨯⨯=.又左图中四个空白三角形的面积是相等的,所以左图中阴影部分的面积为111482-⨯=.BEE如上图所示,在右图中连接AC 、EF .设AF 、EC 的交点为N . 可知EF ∥AC 且2AC EF =.那么三角形BEF 的面积为三角形ABC 面积的14,所以三角形BEF 的面积为21111248⨯⨯=,梯形AEFC 的面积为113288-=. 在梯形AEFC 中,由于:1:2EF AC =,根据梯形蝶形定理,其四部分的面积比为:221:12:12:21:2:2:4⨯⨯=,所以三角形EFN的面积为3118122424⨯=+++,那么四边形BENF 的面积为1118246+=.而右图中四个空白四边形的面积是相等的,所以右图中阴影部分的面积为111463-⨯=.那么左图中阴影部分面积与右图中阴影部分面积之比为11:3:223=,即32m n=,那么325m n +=+=.【例 22】 如图, ABC △中,DE ,FG ,BC 互相平行,AD DF FB ==,则::ADE DEGF FGCB S S S =△四边形四边形 .EGF A D CB【解析】 设1ADE S =△份,根据面积比等于相似比的平方,所以22::1:4ADE AFG S S AD AF ==△△,22::1:9ADE ABC S S AD AB ==△△, 因此4AFG S =△份,9ABC S =△份, 进而有3DEGFS =四边形份,5FGCB S =四边形份,所以::1:3:5ADE DEGF FGCB S S S =△四边形四边形【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.A ED CB【解析】 由金字塔模型得:::2:5AD AB AE AC DE BC ===,所以42510AC =÷⨯=【巩固】如图, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD DF FM MP PB ====,则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形 .【解析】 设1ADES =△份,22::1:4ADE AFG S S AD AF ==△△,因此4AFG S =△份,进而有3DEGF S =四边形份,同理有5FGNM S =四边形份,7MNQP S =四边形份,9PQCB S =四边形份.Q E GNMFPADCB所以有::::1:3:5:7:9ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形【例 23】 如图,已知正方形ABCD 的边长为4,F是BC 边的中点,E 是DC 边上的点,且:1:3DE EC =,AF 与BE 相交于点G ,求ABG S △GFAEDC BM GFAEDCBGFAEDCB【解析】 方法一:连接AE ,延长AF ,DC 两条线交于点M ,构造出两个沙漏,所以有::1:1AB CM BF FC ==,因此4CM =,根据题意有3CE =,再根据另一个沙漏有::4:7GB GE AB EM ==,所以4432(442)471111ABG ABE S S ==⨯⨯÷=+△△.方法二:连接,AE EF,分别求4224ABF S =⨯÷=△,4441232247AEF S =⨯-⨯÷-⨯÷-=△,根据蝶形定理::4:7ABF AEF S S BG GE ==△△,所以4432(442)471111ABG ABE S S ==⨯⨯÷=+△△.【例 24】 如图所示,已知平行四边形ABCD 的面积是1,E 、F 是AB 、AD 的中点, BF 交EC 于M ,求BMG ∆的面积.MHGF E DCBAA【解析】 解法一:由题意可得,E 、F 是AB 、AD 的中点,得//EF BD ,而::1:2FD BC FH HC ==,::1:2EB CD BG GD ==所以::2:3CH CF GH EF ==,并得G 、H 是BD 的三等分点,所以BG GH =,所以::2:3BG EF BM MF ==,所以25BM BF =,11112224BFDABD ABCDS S S ∆∆==⨯=; 又因为13BG BD =,所以1212113535430BMG BFDS S ∆∆=⨯⨯=⨯⨯=.解法二:延长CE 交DA 于I ,如右图,可得,::1:1AI BC AE EB ==,从而可以确定M 的点的位置, ::2:3BM MF BC IF ==,25BM BF =,13BG BD =(鸟头定理),可得2121115353430BMG BDF ABCDS S S ∆∆=⨯=⨯⨯=【例 25】 如图,ABCD 为正方形,1cm AM NB DE FC ====且2cm MN =,请问四边形PQRS 的面积为多少CACA【解析】 (法1)由//AB CD ,有MP PCMN DC=,所以2PC PM =,又MQ MB QC EC =,所以12MQ QC MC ==,所以111236PQ MC MC MC =-=,所以SPQR S 占AMCF S 的16,所以121(112)63SPQR S =⨯⨯++=2(cm ).(法2)如图,连结AE ,则14482ABE S ∆=⨯⨯=(2cm ),而RB ER ABEF=,所以2RB AB EFEF==,22168333ABR ABE S S ∆∆==⨯=(2cm ).而1134322MBQ ANS S S ∆∆==⨯⨯⨯=(2cm ),因为MN MP DCPC=,所以13MP MC =,则11424233MNP S ∆=⨯⨯⨯=(2cm ),阴影部分面积等于164233333ABR ANS MBQ MNP S S S S ∆∆∆∆--+=--+=(2cm ).【例 26】 如右图,三角形ABC 中,:4:9BD DC =,:4:3CE EA =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::4:912:27AOB AOC S S BD CD ===△△::3:412:16AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数)所以:27:16:AOC BOC S S AF FB ==△△【点评】本题关键是把AOB △的面积统一,这种找最小公倍数的方法,在我们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达到解奥数题四两拨千斤的巨大力量!【巩固】如右图,三角形ABC 中,:3:4BD DC =,:5:6AE CE =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::3:415:20AOB AOC S S BD CD ===△△::5:615:18AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数)所以:20:1810:9:AOC BOC S S AF FB ===△△【巩固】如右图,三角形ABC 中,:2:3BD DC =,:5:4EA CE =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::2:310:15AOB AOC S S BD CD ===△△::5:410:8AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数)所以:15:8:AOC BOC S S AF FB ==△△【点评】本题关键是把AOB △的面积统一,这种找最小公倍数的方法,在我们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达到解奥数题四两拨千斤的巨大力量!【例 27】 如右图,三角形ABC 中,:::3:2AF FB BD DC CE AE ===,且三角形ABC 的面积是1,则三角形ABE 的面积为______,三角形AGE 的面积为________,三角形GHI 的面积为______.I HGFEDCBAI H G FEDCBA【分析】 连接AH 、BI 、CG .由于:3:2CE AE =,所以25AE AC =,故2255ABE ABC S S ∆∆==;根据燕尾定理,::2:3ACG ABG S S CD BD ∆∆==,::3:2BCG ABG S S CE EA ∆∆==,所以::4:6:9ACG ABG BCG S S S ∆∆∆=,则419ACG S ∆=,919BCG S ∆=; 那么2248551995AGE AGC S S ∆∆==⨯=; 同样分析可得919ACH S ∆=,则::4:9ACG ACH EG EH S S ∆∆==,::4:19ACG ACB EG EB S S ∆∆==,所以::4:5:10EG GH HB =,同样分析可得::10:5:4AG GI ID =,所以5521101055BIE BAE S S ∆∆==⨯=,55111919519GHI BIE S S ∆∆==⨯=.【巩固】 如右图,三角形ABC 中,:::3:2AF FB BD DC CE AE ===,且三角形GHI的面积是1,求三角形ABC 的面积.IH G FEDCBAIH G FEDCBA【解析】 连接BG ,AGCS △=6份根据燕尾定理,::3:26:4AGC BGC S S AF FB ===△△,::3:29:6ABG AGC S S BD DC ===△△得4BGC S =△(份),9ABG S =△(份),则19ABC S =△(份),因此619AGCABCS S =△△, 同理连接AI 、CH 得619ABHABCS S =△△,619BIC ABC S S =△△,所以1966611919GHI ABC S S ---==△△三角形GHI 的面积是1,所以三角形ABC 的面积是19【巩固】如图,ABC ∆中2BD DA =,2CE EB =,2AF FC =,那么ABC ∆的面积是阴影三角形面积的 倍.BCCB【分析】 如图,连接AI .根据燕尾定理,::2:1BCI ACI S S BD AD ∆∆==,::1:2BCI ABI S S CF AF ∆∆==,所以,::1:2:4ACI BCI ABIS S S ∆∆∆=,那么,221247BCI ABC ABC S S S ∆∆∆==++. 同理可知ACG ∆和ABH ∆的面积也都等于ABC ∆面积的27,所以阴影三角形的面积等于ABC ∆面积的211377-⨯=,所以ABC ∆的面积是阴影三角形面积的7倍.【巩固】如图在ABC △中,12DC EA FB DBECFA===,求GHI ABC △的面积△的面积的值.IHG FEDCBAIHG FEDCB A【解析】 连接BG ,设BGC S △=1份,根据燕尾定理::2:1AGC BGC S S AF FB ==△△,::2:1ABG AGC S S BD DC ==△△,得2AGC S =△(份),4ABG S =△(份),则7ABC S =△(份),因此27AGC ABC S S =△△,同理连接AI 、CH 得27ABH ABC S S =△△,27BIC ABC S S =△△,所以7222177GHI ABC S S ---==△△ 【点评】如果任意一个三角形各边被分成的比是相同的,那么在同样的位置上的图形,虽然形状千变万化,但面积是相等的,这在这讲里面很多题目都是用“同理得到”的,即再重复一次解题思路,因此我们有对称法作辅助线.【例 28】 如图,三角形ABC 的面积是1,BD DE EC ==,CF FG GA ==,三角形ABC被分成9部分,请写出这9部分的面积各是多少GFE D CBAN MQPGF EDCBA【解析】 设BG 与AD 交于点P ,BG 与AE 交于点Q ,BF 与AD 交于点M ,BF 与AE交于点N .连接CP ,CQ ,CM ,CN .根据燕尾定理,::1:2ABP CBP S S AG GC ==△△,::1:2ABP ACP S S BD CD ==△△,设1ABP S =△(份),则1225ABC S =++=△(份),所以15ABP S =△ 同理可得,27ABQ S =△,12ABNS =△,而13ABG S =△,所以2137535APQ S =-=△,1213721AQG S =-=△.同理,335BPMS =△121BDM S =△,所以1239273570PQMN S =--=四边形,13953357042MNED S =--=四边形,1151321426NFCE S =--=四边形,1115321642GFNQ S =--=四边形【巩固】如图,ABC ∆的面积为1,点D 、E 是BC 边的三等分点,点F 、G 是AC边的三等分点,那么四边形JKIH 的面积是多少K J IHABC D EF GKJI HABCD EFG【解析】 连接CK 、CI 、CJ.根据燕尾定理,::1:2ACK ABK S S CD BD ∆∆==,::1:2ABK CBK S S AG CG ∆∆==, 所以::1:2:4ACK ABK CBK S S S ∆∆∆=,那么111247ACK S ∆==++,11321AGK ACK S S ∆∆==. 类似分析可得215AGI S ∆=. 又::2:1ABJ CBJ S S AF CF ∆∆==,::2:1ABJ ACJ S S BD CD ∆∆==,可得14ACJ S ∆=. 那么,111742184CGKJS =-=. 根据对称性,可知四边形CEHJ 的面积也为1784,那么四边形JKIH 周围的图形的面积之和为172161228415370CGKJ AGI ABE S S S ∆∆⨯++=⨯++=,所以四边形JKIH的面积为61917070-=.【例 29】 右图,ABC △中,G 是AC 的中点,D 、E 、F 是BC 边上的四等分点,AD 与BG 交于M ,AF 与BG 交于N ,已知ABM △的面积比四边形FCGN 的面积大7.2平方厘米,则ABC △的面积是多少平方厘米N M GA BCD EFNMGA BC D EF【解析】 连接CM 、CN .根据燕尾定理,::1:1ABM CBMS S AG GC ==△△,::1:3ABM ACM S S BD CD ==△△,所以15ABM ABC S S =△△;再根据燕尾定理,::1:1ABN CBNS S AG GC ==△△,所以::4:3ABN FBN CBN FBN S S S S ==△△△△,所以:4:3AN NF =,那么1422437ANG AFC S S =⨯=+△△,所以2515177428FCGNAFC ABC ABC S S S S ⎛⎫=-=⨯= ⎪⎝⎭△△△.根据题意,有157.2528ABC ABC S S -=△△,可得336ABC S =△(平方厘米)【例 30】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求阴影部分面积.C BAGCB【解析】 三角形在开会,那么就好好利用三角形中最好用的比例和燕尾定理吧!令BI 与CD 的交点为M ,AF 与CD 的交点为N ,BI 与AF 的交点为P ,BI 与CE 的交点为Q ,连接AM 、BN 、CP ⑴求ADMI S 四边形:在ABC △中,根据燕尾定理,::1:2ABM CBM S S AI CI ==△△::1:2ACM CBM S S AD BD ==△△设1ABM S =△(份),则2CBM S =△(份),1ACM S =△(份),4ABC S =△(份),所以14ABMACM ABC S S S ==△△△,所以11312ADM ABM ABC S S S ==△△△,112AIM ABC S S =△△,所以111()12126ABC ABC ADMIS S S =+=△△四边形, 同理可得另外两个顶点的四边形面积也分别是ABC △面积的16⑵求DNPQE S 五边形:在ABC △中,根据燕尾定理::1:2ABN ACN S S BF CF ==△△::1:2ACN BCN S S AD BD ==△△,所以111133721ADN ABN ABC ABC S S S S ==⨯=△△△△,同理121BEQ ABC S S =△△ 在ABC△中,根据燕尾定理::1:2ABP ACP S S BF CF ==△△,::1:2ABP CBP S S AI CI ==△△所以15ABP ABCS S =△△,所以1111152121105ABP ADN BEP ABC ABC DNPQE S S S S S S ⎛⎫=--=--= ⎪⎝⎭△△△△△五边形同理另外两个五边形面积是ABC△面积的11105,所以11113133610570S =-⨯-⨯=阴影【例 31】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求中心六边形面积.GCBAGCBA【解析】 设深黑色六个三角形的顶点分别为N 、R 、P 、S 、M 、Q ,连接CR在ABC △中根据燕尾定理,::.2:1ABR ACR S S BG CG ==△△,::1:2ABR CBR S S AI CI ==△△所以27ABR ABC S S =△△,同理27ACS ABC S S =△△,27CQB ABC S S =△△所以222117777RQS S =---=△,同理17MNP S =△根据容斥原理,和上题结果11131777010S =+-=六边形课后练习: 练习1. 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA【解析】 :():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7平方厘米,所以24ABC S =△平方厘米练习2. 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CBA A BCDEFGH【解析】 连接BD.由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2CGF CDB S S =△△同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形 连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以66513.2ABCD S =÷=四边形平方米练习3. 正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是 平方厘米.H GFEDCBAM H GFEDCBA【解析】 欲求四边形BGHF 的面积须求出EBG ∆和CHF ∆的面积.由题意可得到:::1:2EG GC EB CD ==,所以可得:13EBG BCE S S ∆∆=将AB 、DF 延长交于M 点,可得::::1:1BM DC MF FD BF FC ===,而1::():3:22EH HC EM CD AB AB CD ==+=,得25CH CE =,而12CF BC =,所以121255CHF BCE BCE S S S ∆∆∆=⨯=11112030224BCE S AB BC ∆=⨯⨯=⨯=11773014351515EBC EBC EBC EBC BGHF S S S S S ∆∆∆∆=--==⨯=四边形.EF ,确定H 的位置(也就是:FH HD ),同样也能解出.练习4. 如图,已知4cm AB AE ==,BC DC =,90BAE BCD ∠=∠=︒,10cm AC =,则S ABC ACE CDE S S ∆∆∆++= 2cm .DCEBABCA'C'EDA【解析】 将三角形ABC 绕A 点和C 点分别顺时针和逆时针旋转90,构成三角形'AEC 和'A DC ,再连接''A C ,显然'AC AC ⊥,'AC A C ⊥,''AC A C AC ==,所以''ACA C 是正方形.三角形'AEC 和三角形'A DC 关于正方形的中心O 中心对称,在中心对称图形''ACA C 中有如下等量关系:''AEC A DC S S ∆∆=;''AEC A DC S S ∆∆=;'CED C DE S S ∆∆=.所以2'''11101050cm 22ABC ACE CDE AEC ACE CDE ACA C S S S S S S S ∆∆∆∆∆∆++=++==⨯⨯=.练习5. 如图,正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是_____平方厘米.EDCBEDCB 【解析】 连接BH ,根据沙漏模型得:1:2BG GD =,设1BHC S =△份,根据燕尾定理2CHD S =△份,2BHD S =△份,因此122)210S =++⨯=正方形(份,127236BFHG S =+=,所以712010146BFHG S =÷⨯=(平方厘米).。
小学奥数平面几何五种面积模型(等积,鸟头,蝶形,相似,共边)

小学奥数平面几何五种模型(等积,鸟头,蝶形,相似,共边)目标:熟练掌握五大面积模型等积,鸟头,蝶形,相似(含金字塔模型与沙漏模型),共边(含燕尾模型与风筝模型), 掌握五大面积模型得各种变形 知识点拨一、等积模型①等底等高得两个三角形面积相等;②两个三角形高相等,面积比等于它们得底之比; 两个三角形底相等,面积比等于它们得高之比;如右图③夹在一组平行线之间得等积变形,如右图; 反之,如果,则可知直线平行于、④等底等高得两个平行四边形面积相等(长方形与正方形可以瞧作特殊得平行四边形);⑤三角形面积等于与它等底等高得平行四边形面积得一半;⑥两个平行四边形高相等,面积比等于它们得底之比;两个平行四边形底相等,面积比等于它们得高之比、 二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形、 共角三角形得面积比等于对应角(相等角或互补角)两夹边得乘积之比、 如图在中,分别就就是上得点如图 ⑴(或在得延长线上,在上), 则EDCBA图⑴ 图⑵三、蝶形定理任意四边形中得比例关系(“蝶形定理”):①或者②蝶形定理为我们提供了解决不规则四边形得面积问题得一个途径、通过构造模型,一方面可以使不规则四边形得面积关系与四边形内得三角形相联系;另一方面,也可以得到与面积对应得对角线得比例关系、 梯形中比例关系(“梯形蝶形定理”):DC BA S 4S 3S 2S 1O DCBA A BC DO ba S 3S 2S 1S 4① ②;③得对应份数为、 四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①; ②、所谓得相似三角形,就就就是形状相同,大小不同得三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关得常用得性质及定理如下:⑴相似三角形得一切对应线段得长度成比例,并且这个比例等于它们得相似比;⑵相似三角形得面积比等于它们相似比得平方;⑶连接三角形两边中点得线段叫做三角形得中位线、三角形中位线定理:三角形得中位线长等于它所对应得底边长得一半、 相似三角形模型,给我们提供了三角形之间得边与面积关系相互转化得工具、在小学奥数里,出现最多得情况就就是因为两条平行线而出现得相似三角形、五、共边定理(燕尾模型与风筝模型) 在三角形中,,,相交于同一点,那么、 上述定理给出了一个新得转化面积比与线段比得手段,因为与得形状很象燕子得尾巴,所以这个定理被称为燕尾定理、该定理在许多几何题目中都有着广泛得运用,它得特殊性在于,它可以存在于任何一个三角形之中,为三角形中得O FEDCBA三角形面积对应底边之间提供互相联系得途径、 典型例题【例 1】如图,正方形ABCD 得边长为6,1、5,2、长方形EFGH 得面积为 、【解析】 连接DE ,DF,则长方形EFGH 得面积就就是三角形DEF 面积得二倍、三角形DEF 得面积等于正方形得面积减去三个三角形得面积, ,所以长方形E FGH 面积为33、【巩固】如图所示,正方形得边长为厘米,长方形得长为厘米,那么长方形得宽为几厘米?【解析】 本题主要就就是让学生会运用等底等高得两个平行四边形面积相等(长方形与正方形可以瞧作特殊得平行四边形)、三角形面积等于与它等底等高得平行四边形面积得一半、 证明:连接、(我们通过把这两个长方形与正方形联系在一起)、 ∵在正方形中,边上得高,∴(三角形面积等于与它等底等高得平行四边形面积得一半) 同理,、∴正方形与长方形面积相等、 长方形得宽(厘米)、【例 2】 长方形得面积为36,、、为各边中点,为边上任意一点,问阴影部分面积就就是多少?E【解析】 解法一:寻找可利用得条件,连接、,如下图:_H_G_ F_E_D_C_B_ A _A_B_C_D_E_ F_G_H_ A _ B_ G_ C _ E _ F_ D_ A _ B_ G_ C _ E_ F_ DE可得:、、,而 即; 而,、所以阴影部分得面积就就是:解法二:特殊点法、找得特殊点,把点与点重合,那么图形就可变成右图:GE (H )这样阴影部分得面积就就就是得面积,根据鸟头定理,则有:11111113636363613.52222222ABCD AED BEF CFD S S S S S ∆∆∆=---=-⨯⨯-⨯⨯⨯-⨯⨯=阴影、【巩固】在边长为6厘米得正方形内任取一点,将正方形得一组对边二等分,另一组对边三等分,分别与点连接,求阴影部分面积、【解析】 (法1)特殊点法、由于就就是正方形内部任意一点,可采用特殊点法,假设点与点重合,则阴影部分变为如上中图所示,图中得两个阴影三角形得面积分别占正方形面积得与,所以阴影部分得面积为平方厘米、(法2)连接、、由于与得面积之与等于正方形面积得一半,所以上、下两个阴影三角形得面积之与等于正方形面积得,同理可知左、右两个阴影三角形得面积之与等于正方形面积得,所以阴影部分得面积为平方厘米、 【例 3】 如图所示,长方形内得阴影部分得面积之与为70,,,四边形得面积为 、B【解析】 利用图形中得包含关系可以先求出三角形、与四边形得面积之与,以及三角形与得面积之与,进而求出四边形得面积、由于长方形得面积为,所以三角形得面积为,所以三角形与得面积之与为;又三角形、与四边形得面积之与为,所以四边形得面积为、另解:从整体上来瞧,四边形得面积三角形面积三角形面积白色部分得面积,而三角形面积三角形面积为长方形面积得一半,即60,白色部分得面积等于长方形面积减去阴影部分得面积,即,所以四边形得面积为、【巩固】如图,长方形得面积就就是36,就就是得三等分点,,则阴影部分得面积为 、ABAB【解析】 如图,连接、根据蝶形定理,,所以;,所以、又,,所以阴影部分面积为:、 【例 4】 已知为等边三角形,面积为400,、、分别为三边得中点,已知甲、乙、丙面积与为143,求阴影五边形得面积、(丙就就是三角形)B【解析】 因为、、分别为三边得中点,所以、、就就是三角形得中位线,也就与对应得边平行,根据面积比例模型,三角形与三角形得面积都等于三角形得一半,即为200、根据图形得容斥关系,有,即,所以、又,所以、【例 5】如图,已知,,,,线段将图形分成两部分,左边部分面积就就是38,右边部分面积就就是65,那么三角形得面积就就是、【解析】连接,、根据题意可知,;;所以,,,,,于就就是:;;可得、故三角形得面积就就是40、【例 6】如图在中,分别就就是上得点,且,,平方厘米,求得面积、【解析】连接,,,所以,设份,则份,平方厘米,所以份就就是平方厘米,份就就就是平方厘米,得面积就就是平方厘米、由此我们得到一个重要得定理,共角定理:共角三角形得面积比等于对应角(相等角或互补角)两夹边得乘积之比、【巩固】如图,三角形中,就就是得5倍,就就是得3倍,如果三角形得面积等于1,那么三角形得面积就就是多少?【解析】连接、∵∴又∵∴,∴、【巩固】如图,三角形ABC被分成了甲(阴影部分)、乙两部分,,,,乙部分面积就就是甲部分面积得几倍?【解析】连接、∵,∴,又∵,∴,∴,、【例 7】如图在中,在得延长线上,在上,且,,平方厘米,求得面积、EDCBAEDCB A【解析】 连接,,所以,设份,则份,平方厘米,所以份就就是平方厘米,份就就就是平方厘米,得面积就就是平方厘米、由此我们得到一个重要得定理,共角定理:共角三角形得面积比等于对应角(相等角或互补角)两夹边得乘积之比【例 8】 如图,平行四边形,,,,,平行四边形得面积就就是, 求平行四边形与四边形得面积比、HGAB CD EFHGAB CDEF【解析】 连接、、根据共角定理 ∵在与中,与互补,∴、又,所以、 同理可得,,、所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△、 所以、【例 9】 如图所示得四边形得面积等于多少?DB13131212【解析】 题目中要求得四边形既不就就是正方形也不就就是长方形,难以运用公式直接求面积、我们可以利用旋转得方法对图形实施变换:把三角形绕顶点逆时针旋转,使长为得两条边重合,此时三角形将旋转到三角形得位置、这样,通过旋转后所得到得新图形就就是一个边长为得正方形,且这个正方形得面积就就就是原来四边形得面积、因此,原来四边形得面积为、(也可以用勾股定理)【例 10】如图所示,中,,,,以为一边向外作正方形,中心为,求得面积、【解析】如图,将沿着点顺时针旋转,到达得位置、由于,,所以、而,所以,那么、、三点在一条直线上、由于,,所以就就是等腰直角三角形,且斜边为,所以它得面积为、根据面积比例模型,得面积为、【例 11】如图,以正方形得边为斜边在正方形内作直角三角形,,、交于、已知、得长分别为、,求三角形得面积、F【解析】如图,连接,以点为中心,将顺时针旋转到得位置、那么,而也就就是,所以四边形就就是直角梯形,且,所以梯形得面积为:()、又因为就就是直角三角形,根据勾股定理,,所以()、那么(),所以()、【例 12】如下图,六边形中,,,,且有平行于,平行于,平行于,对角线垂直于,已知厘米,厘米,请问六边形得面积就就是多少平方厘米?FEABDCGFEABDC【解析】 如图,我们将平移使得与重合,将平移使得与重合,这样、都重合到图中得了、这样就组成了一个长方形,它得面积与原六边形得面积相等,显然长方形得面积为平方厘米,所以六边形得面积为平方厘米、【例 13】 如图,三角形得面积就就是,就就是得中点,点在上,且,与交于点、则四边形得面积等于 、ABCDEF【解析】 方法一:连接,根据燕尾定理,,,设份,则份,份,份,如图所标 所以方法二:连接,由题目条件可得到, ,所以, ,而、所以则四边形得面积等于、【巩固】如图,长方形得面积就就是平方厘米,,就就是得中点、阴影部分得面积就就是多少平方厘米?x yyx ABC D EFG E D CBA【解析】 设份,则根据燕尾定理其她面积如图所示平方厘米、【例 14】 四边形得对角线与交于点(如图所示)、如果三角形得面积等于三角形得面积得,且,,那么得长度就就是得长度得_________倍、ABCDOH GA BCD O【解析】 在本题中,四边形为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形、瞧到题目中给出条件,这可以向模型一蝶形定理靠拢,于就就是得出一种解法、又观察题目中给出得已知条件就就是面积得关系,转化为边得关系,可以得到第二种解法,但就就是第二种解法需要一个中介来改造这个”不良四边形”,于就就是可以作垂直于,垂直于,面积比转化为高之比、再应用结论:三角形高相同,则面积之比等于底边之比,得出结果、请老师注意比较两种解法,使学生体会到蝶形定理得优势,从而主观上愿意掌握并使用蝶形定理解决问题、解法一:∵,∴,∴、 解法二:作于,于、 ∵,∴,∴, ∴,∴,∴、【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形得面积已知, 求:⑴三角形得面积;⑵?B【解析】 ⑴根据蝶形定理,,那么;⑵根据蝶形定理,、【例 15】 如图,平行四边形得对角线交于点,、、、得面积依次就就是2、4、4与6、求:⑴求得面积;⑵求得面积、OGF EDCBA【解析】 ⑴根据题意可知,得面积为,那么与得面积都就就是,所以得面积为;⑵由于得面积为8,得面积为6,所以得面积为, 根据蝶形定理,,所以, 那么、【例 16】 如图,长方形中,,,三角形得面积为平方厘米,求长方形得面积、ABCD EF GABCD EF G【解析】 连接,、因为,,所以、因为,,所以平方厘米,所以平方厘米、因为,所以长方形得面积就就是平方厘米、【例 17】 如图,正方形面积为平方厘米,就就是边上得中点、求图中阴影部分得面积、CBA【解析】 因为就就是边上得中点,所以,根据梯形蝶形定理可以知道,设份,则 份,所以正方形得面积为份,份,所以,所以平方厘米、 【巩固】在下图得正方形中,就就是边得中点,与相交于点,三角形得面积为1平方厘米,那么正方形面积就就是 平方厘米、ABCDEF【解析】 连接,根据题意可知,根据蝶形定理得(平方厘米),(平方厘米),那么(平方厘米)、【例 18】 已知就就是平行四边形,,三角形得面积为6平方厘米、则阴影部分得面积就就是 平方厘米、BB【解析】连接、由于就就是平行四边形,,所以,根据梯形蝶形定理,,所以(平方厘米),(平方厘米),又(平方厘米),阴影部分面积为(平方厘米)、【巩固】右图中就就是梯形,就就是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分得面积就就是平方厘米、BB【分析】连接、由于与就就是平行得,所以也就就是梯形,那么、根据蝶形定理,,故,所以(平方厘米)、【巩固】右图中就就是梯形,就就是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分得面积就就是平方厘米、BB【解析】连接、由于与就就是平行得,所以也就就是梯形,那么、根据蝶形定理,,故,所以(平方厘米)、另解:在平行四边形中,(平方厘米),所以(平方厘米),根据蝶形定理,阴影部分得面积为(平方厘米)、【例 19】如图,长方形被、分成四块,已知其中3块得面积分别为2、5、8平方厘米,那么余下得四边形得面积为___________平方厘米、?852O A B C DEF?852O A BCD EF【解析】 连接、、四边形为梯形,所以,又根据蝶形定理,,所以,所以(平方厘米),(平方厘米)、那么长方形得面积为平方厘米,四边形得面积为(平方厘米)、【例 20】 如图,就就是等腰直角三角形,就就是正方形,线段与相交于点、已知正方形得面积48,,则得面积就就是多少?BB【解析】 由于就就是正方形,所以与平行,那么四边形就就是梯形、在梯形中,与得面积就就是相等得、而,所以得面积就就是面积得,那么得面积也就就是面积得、由于就就是等腰直角三角形,如果过作得垂线,为垂足,那么就就是得中点,而且,可见与得面积都等于正方形面积得一半,所以得面积与正方形得面积相等,为48、 那么得面积为、【例 21】 下图中,四边形都就就是边长为1得正方形,、、、分别就就是,,,得中点,如果左图中阴影部分与右图中阴影部分得面积之比就就是最简分数,那么,得值等于 、BEE【解析】 左、右两个图中得阴影部分都就就是不规则图形,不方便直接求面积,观察发现两个图中得空白部分面积都比较好求,所以可以先求出空白部分得面积,再求阴影部分得面积、如下图所示,在左图中连接、设与得交点为、左图中为长方形,可知得面积为长方形面积得,所以三角形得面积为、又左图中四个空白三角形得面积就就是相等得,所以左图中阴影部分得面积为、BEE如上图所示,在右图中连接、、设、得交点为、可知∥且、那么三角形得面积为三角形面积得,所以三角形 得面积为,梯形得面积为、在梯形中,由于,根据梯形蝶形定理,其四部分得面积比为:,所以三角形得面积为,那么四边形得面积为、而右图中四个空白四边形得面积就就是相等得,所以右图中阴影部分得面积为、那么左图中阴影部分面积与右图中阴影部分面积之比为,即, 那么、【例 22】 如图, 中,,,互相平行,,则 、【解析】 设份,根据面积比等于相似比得平方,所以,,因此份,份,进而有份,份,所以【巩固】如图,平行,且,,,求得长、【解析】 由金字塔模型得,所以【巩固】如图, 中,,,,,互相平行,,则、 【解析】 设份,,因此份,进而有份,同理有份,份,份、 所以有 【例 23】 如图,已知正方形得边长为,就就是边得中点,就就是边上得点,且,与相交于点,求Q EGNM F PAD CBGFAEDC BM GFAEDCB GFAEDCB【解析】 方法一:连接,延长,两条线交于点,构造出两个沙漏,所以有,因此,根据题意有,再根据另一个沙漏有,所以、方法二:连接,分别求,,根据蝶形定理,所以、 【例 24】 如图所示,已知平行四边形得面积就就是1,、就就是、得中点, 交于,求得面积、A【解析】 解法一:由题意可得,、就就是、得中点,得,而,所以,并得、就就是得三等分点,所以,所以 ,所以,;又因为,所以、解法二:延长交于,如右图,可得,,从而可以确定得点得位置, ,,(鸟头定理), 可得【例 25】 如图,为正方形,且,请问四边形得面积为多少?CACA【解析】 (法)由,有,所以,又,所以,所以,所以占得, 所以、(法)如图,连结,则(, 而,所以,()、而(),因为,所以,则(),阴影部分面积等于 ()、【例 26】 如右图,三角形中,,,求、【解析】 根据燕尾定理得(都有得面积要统一,所以找最小公倍数) 所以【点评】本题关键就就是把得面积统一,这种找最小公倍数得方法,在我们用比例解题中屡见不鲜,如果能掌握它得转化本质,我们就能达到解奥数题四两拨千斤得巨大力量!【巩固】如右图,三角形中,,,求、【解析】 根据燕尾定理得(都有得面积要统一,所以找最小公倍数) 所以【巩固】如右图,三角形中,,,求、【解析】 根据燕尾定理得(都有得面积要统一,所以找最小公倍数) 所以【点评】本题关键就就是把得面积统一,这种找最小公倍数得方法,在我们用比例解题中屡见不鲜,如果能掌握它得转化本质,我们就能达到解奥数题四两拨千斤得巨大力量!【例 27】 如右图,三角形中,,且三角形得面积就就是,则三角形得面积为______,三角形得面积为________,三角形得面积为______、I HGFEDCBAI HG FEDCBA【分析】 连接、、、由于,所以,故;根据燕尾定理,,,所以,则,;那么;同样分析可得,则,,所以,同样分析可得,所以,、【巩固】如右图,三角形中,,且三角形得面积就就是,求三角形得面积、【解析】连接BG,份根据燕尾定理,,得(份),(份),则(份),因此,同理连接AI、CH得,,所以三角形GHI得面积就就是1,所以三角形ABC得面积就就是19【巩固】如图,中,,,那么得面积就就是阴影三角形面积得倍、B CB【分析】如图,连接、根据燕尾定理,,,所以,,那么,、同理可知与得面积也都等于面积得,所以阴影三角形得面积等于面积得,所以得面积就就是阴影三角形面积得7倍、【巩固】如图在中,,求得值、【解析】连接BG,设1份,根据燕尾定理,,得(份),(份),则(份),因此,同理连接AI、CH得,,所以【点评】如果任意一个三角形各边被分成得比就就是相同得,那么在同样得位置上得图形,虽然形状千变万化,但面积就就是相等得,这在这讲里面很多题目都就就是用“同理得到”得,即再重复一次解题思路,因此我们有对称法作辅助线、【例 28】如图,三角形得面积就就是,,,三角形被分成部分,请写出这部分得面积各就就是多少?NMQ P G FEDC BA【解析】 设BG 与AD 交于点P,BG 与AE 交于点Q ,BF与AD 交于点M ,BF 与AE交于点N 、连接CP ,CQ ,CM ,C N、 根据燕尾定理,,,设(份),则(份),所以 同理可得,,,而,所以,、 同理,,所以,,,【巩固】如图,得面积为1,点、就就是边得三等分点,点、就就是边得三等分点,那么四边形得面积就就是多少?K J IHABC D EF GKJI HABCD EFG【解析】 连接、、、根据燕尾定理,,,所以,那么,、 类似分析可得、 又,,可得、 那么,、根据对称性,可知四边形得面积也为,那么四边形周围得图形得面积之与为,所以四边形得面积为、 【例 29】 右图,中,就就是得中点,、、就就是边上得四等分点,与交于,与交于,已知得面积比四边形得面积大平方厘米,则得面积就就是多少平方厘米?N M GA BCD EFNMGA BC D EF【解析】 连接、、根据燕尾定理,,,所以;再根据燕尾定理,,所以,所以,那么,所以、 根据题意,有,可得(平方厘米)【例 30】 如图,面积为l 得三角形AB C中,D、E 、F、G 、H 、I分别就就是AB 、BC 、C A 得三等分点,求阴影部分面积、GC BAGCBA【解析】 三角形在开会,那么就好好利用三角形中最好用得比例与燕尾定理吧!令BI 与CD得交点为M ,AF 与CD 得交点为N ,BI 与A F得交点为P,BI 与CE 得交点为Q ,连接AM 、BN 、CP ⑴求:在中,根据燕尾定理, 设(份),则(份),(份),(份), 所以,所以,, 所以,同理可得另外两个顶点得四边形面积也分别就就是面积得 ⑵求:在中,根据燕尾定理, 所以,同理在中,根据燕尾定理,所以,所以1111152121105ABP ADN BEP ABC ABC DNPQE S S S S S S ⎛⎫=--=--= ⎪⎝⎭△△△△△五边形 同理另外两个五边形面积就就是面积得,所以【例 31】 如图,面积为l 得三角形ABC 中,D 、E、F 、G、H 、I 分别就就是AB 、B C、CA 得三等分点,求中心六边形面积、CBAGCBA【解析】 设深黑色六个三角形得顶点分别为N 、R 、P、S、M 、Q,连接C R在中根据燕尾定理,,所以,同理, 所以,同理根据容斥原理,与上题结果 课后练习: 练习1. 已知得面积为平方厘米,,求得面积、【解析】 ,设份,则份,份,份,份,恰好就就是平方厘米,所以平方厘米 练习2. 如图,四边形得面积就就是平方米,,,,,求四边形得面积、H GFED CB AAB CDEFGH【解析】 连接、由共角定理得,即同理,即所以连接,同理可以得到5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形所以平方米练习3. 正方形得面积就就是120平方厘米,就就是得中点,就就是得中点,四边形得面积就就是 平方厘米、H GFEDCBAMH GFEDCBA【解析】 欲求四边形得面积须求出与得面积、由题意可得到:,所以可得: 将、延长交于点,可得: ,而,得, 而,所以、,连接,确定得位置(也就就就是),同样也能解出、练习4. 如图,已知,,,,则 、DCEBABCA'C'EDA【解析】 将三角形绕点与点分别顺时针与逆时针旋转,构成三角形与,再连接,显然,,,所以就就是正方形、三角形与三角形关于正方形得中心中心对称,在中心对称图形中有如下等量关系: ;;、所以2'''11101050cm 22ABC ACE CDE AEC ACE CDE ACA C S S S S S S S ∆∆∆∆∆∆++=++==⨯⨯=、练习5. 如图,正方形得面积就就是平方厘米,就就是得中点,就就是得中点,四边形 得面积就就是_____平方厘米、EDC B EDCB【解析】 连接,根据沙漏模型得,设份,根据燕尾定理份,份,因此份,,所以(平方厘米)、练习6. 如图,中,点就就是边得中点,点、就就是边得三等分点,若得面积为1,那么四边形得面积就就是_________、F ABCDEM NFABCDEMN【解析】 由于点就就是边得中点,点、就就是边得三等分点,如果能求出、、三段得比,那么所分成得六小块得面积都可以求出来,其中当然也包括四边形得面积、 连接、、根据燕尾定理,,而,所以,那么,即、 那么,、另解:得出后,可得,则、练习7. 如右图,三角形中,,且三角形得面积就就是,求角形 得面积、【解析】 连接BG ,12份根据燕尾定理,,得(份),(份),则(份),因此, 同理连接AI 、CH 得,,所以三角形ABC 得面积就就是,所以三角形G HI 得面积就就是月测备选【备选1】按照图中得样子,在一平行四边形纸片上割去了甲、乙两个直角三角形、已知甲三角形两条直角边分别为与,乙三角形两条直角边分别为与,求图中阴影部分得面积、【解析】 如右图,我们将三角形甲与乙进行平移,就会发现平行四边形面积等于平移后两个长方形面积之与、所以阴影部分面积为:【备选2】如图所示,矩形得面积为36平方厘米,四边形得面积就就是3平方厘米,则阴影部分得面积就就是平方厘米、【解析】因为三角形面积为矩形得面积得一半,即18平方厘米,三角形面积为矩形得面积得,即9平方厘米,又四边形得面积为3平方厘米,所以三角形与三角形得面积之与就就是平方厘米、又三角形与三角形得面积之与就就是矩形得面积得一半,即18平方厘米,所以阴影部分面积为(平方厘米)、【备选3】如图,已知,,与相交于点,则被分成得部分面积各占面积得几分之几?【解析】连接,设份,则其她部分得面积如图所示,所以份,所以四部分按从小到大各占面积得【备选4】如图,在中,延长至,使,延长至,使,就就是得中点,若得面积就就是,则得面积就就是多少?AB C D EF 【解析】∵在与中,与互补,∴、又,所以、同理可得,、所以【备选5】如图,,,则【解析】根据燕尾定理有,,所以。
小学的奥数平面几何五种面积模型(等积,鸟头,蝶形,相似,共边)

小学奥数平面几何五种模型(等积,鸟头,蝶形,相似,共边)目标:熟练掌握五大面积模型等积,鸟头,蝶形,相似(含金字塔模型和沙漏模型),共边(含燕尾模型和风筝模型), 掌握五大面积模型的各种变形 知识点拨一、等积模型①等底等高的两个三角形面积相等; ②两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比;如右图12::S S a b =③夹在一组平行线之间的等积变形,如右图ACD BCD S S =△△; 反之,如果ACD BCD S S =△△,则可知直线AB 平行于CD .④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形);⑤三角形面积等于与它等底等高的平行四边形面积的一半;⑥两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相等,面积比等于它们的高之比. 二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比. 如图在ABC △中,,D E 分别是,AB AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在AC 上),则:():()ABC ADE S S AB AC AD AE =⨯⨯△△EDCBAEDCBA图⑴ 图⑵ 三、蝶形定理任意四边形中的比例关系(“蝶形定理”):①1243::S S S S =或者1324S S S S ⨯=⨯②()()1243::AO OC S S S S =++蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造模型,一方面可以使不规则四边形的面积关系与四边形内的三角形相联系;S 2S 1DC BA S 4S 3S 2S 1O DCBA另一方面,也可以得到与面积对应的对角线的比例关系. 梯形中比例关系(“梯形蝶形定理”):①2213::S S a b =②221324::::::S S S S a b ab ab =; ③S 的对应份数为()2a b +.四、相似模型(一)金字塔模型 (二) 沙漏模型GF E ABCDAB CDEF G①AD AE DE AF ABACBCAG===;②22:ADE ABC S S AF AG =△△:.所谓的相似三角形,就是形状相同,大小不同的三角形(只要其形状不改变,不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如下:⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似比;⑵相似三角形的面积比等于它们相似比的平方;⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工具.在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形. 五、共边定理(燕尾模型和风筝模型)在三角形ABC 中,AD ,BE ,CF 相交于同一点O ,那么::ABO ACO S S BD DC ∆∆=.上述定理给出了一个新的转化面积比与线段比的手段,因为ABO ∆和ACO ∆的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径.A B CD O ba S 3S 2S 1S 4O FED C BA典型例题【例 1】 如图,正方形ABCD 的边长为6,AE =1.5,CF =2.长方形EFGH 的面积为 .【解析】 连接DE ,DF ,则长方形EFGH 的面积是三角形DEF 面积的二倍.三角形DEF 的面积等于正方形的面积减去三个三角形的面积,66 1.562262 4.54216.5DEF S =⨯-⨯÷-⨯÷-⨯÷=△,所以长方形EFGH面积为33.【巩固】如图所示,正方形ABCD 的边长为8厘米,长方形EBGF 的长BG 为10厘米,那么长方形的宽为几厘米?【解析】 本题主要是让学生会运用等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形).三角形面积等于与它等底等高的平行四边形面积的一半. 证明:连接AG .(我们通过ABG △把这两个长方形和正方形联系在一起).∵在正方形ABCD 中,G 12AB S AB AB =⨯⨯△边上的高, ∴12ABG ABCDS S=△(三角形面积等于与它等底等高的平行四边形面积的一半)同理,12ABG EFGB S S =△.∴正方形ABCD 与长方形E F G B 面积相等. 长方形的宽88106.=⨯÷=(厘米)._H_G_F_E_D_C_B_ A _A_B_C_D_E_F_G_H_ A _ B_ G_ C _ E _ F_ D_ A _ B_ G_ C_ E_ F_ D【例 2】 长方形ABCD 的面积为362cm ,E 、F 、G 为各边中点,H 为AD 边上任意一点,问阴影部分面积是多少?E【解析】 解法一:寻找可利用的条件,连接BH 、HC ,如下图:E可得:12EHB AHB S S ∆∆=、12FHB CHB S S ∆∆=、12DHG DHC S S ∆∆=,而36ABCD AHB CHB CHD S S S S ∆∆∆=++=即11()361822EHB BHF DHG AHB CHB CHD S S S S S S ∆∆∆∆∆∆++=++=⨯=; 而EHB BHF DHG EBFS S S S S ∆∆∆∆++=+阴影,11111()()36 4.522228EBF S BE BF AB BC ∆=⨯⨯=⨯⨯⨯⨯=⨯=.所以阴影部分的面积是:1818 4.513.5EBF S S ∆=-=-=阴影解法二:特殊点法.找H 的特殊点,把H 点与D 点重合,那么图形就可变成右图:GE (H )这样阴影部分的面积就是DEF ∆的面积,根据鸟头定理,则有:11111113636363613.52222222ABCD AED BEF CFD S S S S S ∆∆∆=---=-⨯⨯-⨯⨯⨯-⨯⨯=阴影.【巩固】在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边二等分,另一组对边三等分,分别与P 点连接,求阴影部分面积.【解析】 (法1)特殊点法.由于P 是正方形内部任意一点,可采用特殊点法,假设P 点与A 点重合,则阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的14和16,所以阴影部分的面积为2116()1546⨯+=平方厘米.(法2)连接PA 、PC .由于PAD ∆与PBC ∆的面积之和等于正方形ABCD 面积的一半,所以上、下两个阴影三角形的面积之和等于正方形ABCD 面积的14,同理可知左、右两个阴影三角形的面积之和等于正方形ABCD 面积的16,所以阴影部分的面积为2116()1546⨯+=平方厘米.【例 3】 如图所示,长方形ABCD 内的阴影部分的面积之和为70,8AB =,15AD =,四边形EFGO 的面积为 .B【解析】 利用图形中的包含关系可以先求出三角形AOE、DOG 和四边形EFGO 的面积之和,以及三角形AOE 和DOG 的面积之和,进而求出四边形EFGO 的面积.由于长方形ABCD 的面积为158120⨯=,所以三角形BOC 的面积为1120304⨯=,所以三角形AOE 和DOG 的面积之和为312070204⨯-=; 又三角形AOE 、DOG 和四边形EFGO 的面积之和为111203024⎛⎫⨯-= ⎪⎝⎭,所以四边形EFGO 的面积为302010-=.另解:从整体上来看,四边形EFGO 的面积=三角形AFC 面积+三角形BFD 面积-白色部分的面积,而三角形AFC 面积+三角形BFD 面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部分的面积,即1207050-=,所以四边形的面积为605010-=.【巩固】如图,长方形ABCD 的面积是36,E 是AD 的三等分点,2AE ED =,则阴影部分的面积为 .BB【解析】 如图,连接OE .根据蝶形定理,1:::1:12COE CDE CAE CDE ON ND S S S S ∆∆∆∆===,所以12OE N O EDS S ∆∆=; 1:::1:42BOE BAE BDE BAE OM MA S S S S ∆∆∆∆===,所以15OEM OEA S S ∆∆=.又11334OED ABCD S S ∆=⨯=矩形,26OEA OED S S ∆∆==,所以阴影部分面积为:1136 2.725⨯+⨯=.【例 4】 已知ABC 为等边三角形,面积为400,D 、E 、F 分别为三边的中点,已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形HBC)B【解析】 因为D 、E 、F 分别为三边的中点,所以DE 、DF 、EF 是三角形ABC 的中位线,也就与对应的边平行,根据面积比例模型,三角形ABN 和三角形AMC 的面积都等于三角形ABC 的一半,即为200.根据图形的容斥关系,有ABC ABN AMC AMHN S S S S S ∆∆∆-=+-丙,即400 200200AMHN S S -=+-丙,所以AMHN S S =丙. 又ADF AMHN S S S S S ∆+=++乙甲阴影,所以1143400434ADF S S S S S ∆=++-=-⨯=乙甲丙阴影.【例 5】 如图,已知5CD =,7DE =,15EF =,6FG =,线段AB 将图形分成两部分,左边部分面积是38,右边部分面积是65,那么三角形ADG 的面积是 .GFE DC BAABC DE FG【解析】 连接AF ,BD .根据题意可知,571527CF =++=;715628DG =++=;所以,1527BE CBF F S S ∆∆=,1227BE CBF C S S ∆∆=,2128AEG ADG S S ∆∆=,728AED ADG S S ∆∆=, 于是:2115652827ADG CBFS S ∆∆+=;712382827ADG CBF S S ∆∆+=; 可得40ADG S ∆=.故三角形ADG 的面积是40.【例 6】 如图在ABC△中,,D E 分别是,AB AC 上的点,且:2:5AD AB =,:4:7AE AC =,16ADE S =△平方厘米,求ABC △的面积.EDCBAEDCBA【解析】 连接BE ,::2:5(24):(54)ADE ABE S S AD AB ===⨯⨯△△,::4:7(45):(75)ABE ABC S S AE AC ===⨯⨯△△,所以:(24):(7A D E A B C S S =⨯⨯△△,设8ADE S =△份,则35ABC S =△份,16ADE S =△平方厘米,所以1份是2平方厘米,35份就是70平方厘米,ABC △的面积是70平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比 .【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角形ADE 的面积等于1,那么三角形ABC 的面积是多少?EDCBAABCDE【解析】 连接BE .∵3EC AE =∴3ABC ABE S S = 又∵5AB AD =∴515ADE ABE ABC S S S =÷=÷,∴1515ABC ADE S S ==.【巩固】如图,三角形ABC 被分成了甲(阴影部分)、乙两部分,4BD DC ==,3BE =,6AE =,乙部分面积是甲部分面积的几倍?乙甲E DCBAABCDE甲乙【解析】 连接AD .∵3BE =,6AE =∴3AB BE =,3ABD BDE S S = 又∵4BD DC ==,∴2ABC ABD S S =,∴6ABC BDE S S =,5S S =乙甲.【例 7】 如图在ABC △中,D 在BA 的延长线上,E 在AC上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.EDCBAEDCB A【解析】 连接BE ,::2:5(23):(53)ADE ABE S S AD AB ===⨯⨯△△[]::3:(32)(35):(32)5ABE ABC S S AE AC ==+=⨯+⨯△△,所以[]:(32):5(32)6:25A D E A B C S S =⨯⨯+=△△,设6A D E S =△份,则25ABC S =△份,12ADE S =△平方厘米,所以1份是2平方厘米,25份就是50平方厘米,ABC △的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比【例 8】 如图,平行四边形ABCD ,BE AB =,2CF CB=,3GD DC =,4HA AD =,平行四边形ABCD 的面积是2, 求平行四边形ABCD 与四边形EFGH 的面积比.HGAB CD EFHGAB CD EF【解析】 连接AC 、BD .根据共角定理∵在ABC △和BFE △中,ABC ∠与FBE ∠互补,∴111133ABC FBES AB BC S BE BF⋅⨯===⋅⨯△△.又1ABC S =△,所以3FBE S =△.同理可得8GCF S =△,15DHG S =△,8AEH S =△.所以8815+3+236EFGH AEH CFG DHG BEF ABCD S S S S S S =++++=++=△△△△. 所以213618ABCDEFGHS S ==.【例 9】 如图所示的四边形的面积等于多少?DB13131212【解析】 题目中要求的四边形既不是正方形也不是长方形,难以运用公式直接求面积.我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点O 逆时针旋转,使长为13的两条边重合,此时三角形OAB 将旋转到三角形OCD 的位置.这样,通过旋转后所得到的新图形是一个边长为12的正方形,且这个正方形的面积就是原来四边形的面积.因此,原来四边形的面积为1212144⨯=.(也可以用勾股定理)【例 10】 如图所示,ABC ∆中,90ABC ∠=︒,3AB =,5BC =,以AC 为一边向ABC∆外作正方形ACDE ,中心为O ,求OBC ∆的面积.【解析】 如图,将OAB ∆沿着O 点顺时针旋转90︒,到达OCF ∆的位置.由于90ABC ∠=︒,90AOC ∠=︒,所以180OAB OCB ∠+∠=︒.而OCF OAB ∠=∠, 所以180OCF OCB ∠+∠=︒,那么B 、C 、F 三点在一条直线上.由于OB OF =,90BOF AOC ∠=∠=︒,所以BOF ∆是等腰直角三角形,且斜边BF 为538+=,所以它的面积为218164⨯=.根据面积比例模型,OBC ∆的面积为516108⨯=.【例 11】 如图,以正方形的边AB 为斜边在正方形内作直角三角形ABE ,90AEB ∠=︒,AC、BD 交于O .已知AE 、BE 的长分别为3cm 、5cm ,求三角形OBE 的面积.F【解析】 如图,连接DE ,以A 点为中心,将AD E ∆顺时针旋转90︒到ABF ∆的位置.那么90EAF EAB BAF EAB DAE ∠=∠+∠=∠+∠=︒,而AEB ∠也是90︒,所以四边形AFBE 是直角梯形,且3AF AE ==, 所以梯形AFBE 的面积为:()1353122+⨯⨯=(2cm ). 又因为ABE ∆是直角三角形,根据勾股定理,222223534AB AE BE =+=+=,所以21172ABD S AB ∆==(2cm ).那么()17125BDE ABD ABE ADE ABD AFBE S S S S S S ∆∆∆∆∆=-+=-=-=(2cm ), 所以1 2.52OBE BDE S S ∆∆==(2cm ).【例 12】 如下图,六边形ABCDEF 中,AB ED =,AF CD =,BC EF =,且有AB 平行于ED ,AF 平行于CD ,BC 平行于EF ,对角线FD 垂直于BD ,已知24FD =厘米,18BD =厘米,请问六边形ABCDEF 的面积是多少平方厘米?FEABDCGFEABDC【解析】 如图,我们将BCD ∆平移使得CD 与AF 重合,将DEF ∆平移使得ED 与AB 重合,这样EF 、BC 都重合到图中的AG 了.这样就组成了一个长方形BGFD ,它的面积与原六边形的面积相等,显然长方形BGFD 的面积为2418432⨯=平方厘米,所以六边形ABCDEF 的面积为432平方厘米.【例 13】 如图,三角形ABC 的面积是1,E 是AC 的中点,点D 在BC 上,且:1:2BD DC =,AD 与BE 交于点F .则四边形DFEC 的面积等于 .FEDCBA33321F EDC BAABCDEF【解析】 方法一:连接CF ,根据燕尾定理,12ABF ACF S BD S DC ==△△,1ABF CBFS AE SEC ==△△, 设1BDF S =△份,则2DCF S =△份,3ABF S =△份,3AEF EFC S S ==△△份,如图所标所以551212DCEF ABC S S ==△ 方法二:连接DE ,由题目条件可得到1133ABD ABC S S ==△△,11212233ADE ADC ABC S S S ==⨯=△△△,所以11ABD ADE S BF FE S ==△△,111111122323212DEF DEB BEC ABC S S S S =⨯=⨯⨯=⨯⨯⨯=△△△△,而211323CDE ABC S S =⨯⨯=△△.所以则四边形DFEC 的面积等于512. 【巩固】如图,长方形ABCD 的面积是2平方厘米,2EC DE =,F 是DG 的中点.阴影部分的面积是多少平方厘米?y B CD EGE D CBAEDB A 【解析】 设1DEFS =△份,则根据燕尾定理其他面积如图所示551212BCD S S ==△阴影平方厘米.【例 14】 四边形ABCD 的对角线AC与BD 交于点O (如图所示).如果三角形ABD的面积等于三角形BCD 的面积的13,且2AO =,3DO =,那么CO 的长度是DO 的长度的_________倍.ABCDOH GA BCD O【解析】 在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解决;⑵通过画辅助线来改造不良四边形.看到题目中给出条件:1:3ABD BCD S S =,这可以向模型一蝶形定理靠拢,于是得出一种解法.又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得到第二种解法,但是第二种解法需要一个中介来改造这个”不良四边形”,于是可以作AH 垂直BD 于H ,CG 垂直BD 于G ,面积比转化为高之比.再应用结论:三角形高相同,则面积之比等于底边之比,得出结果.请老师注意比较两种解法,使学生体会到蝶形定理的优势,从而主观上愿意掌握并使用蝶形定理解决问题.解法一:∵::1:3ABD BDC AO OC S S ∆∆==,∴236OC =⨯=,∴:6:32:1O C O D ==.解法二:作AH BD ⊥于H ,CG BD ⊥于G .∵13ABDBCD S S ∆∆=,∴13AH CG =,∴13AODDOC S S ∆∆=, ∴13AO CO =,∴236OC =⨯=,∴:6:32:1OC OD ==.【巩固】如图,四边形被两条对角线分成4个三角形,其中三个三角形的面积已知, 求:⑴三角形BGC 的面积;⑵:AG GC =?B【解析】 ⑴根据蝶形定理,123BGCS⨯=⨯,那么6BGCS=;⑵根据蝶形定理,()():12:361:3AG GC =++=.【例 15】 如图,平行四边形ABCD 的对角线交于O 点,CEF △、OEF△、ODF △、BOE △的面积依次是2、4、4和6.求:⑴求OCF △的面积;⑵求GCE △的面积.OGFEDCBA【解析】 ⑴根据题意可知,BCD △的面积为244616+++=,那么BCO △和CDO ∆的面积都是1628÷=,所以OCF △的面积为844-=;⑵由于BCO △的面积为8,BOE △的面积为6,所以OCE △的面积为862-=,根据蝶形定理,::2:41:2COE COF EG FG S S ∆∆===,所以::1:2GCE GCF S S EG FG ∆∆==,那么11221233GCE CEF S S ∆∆==⨯=+.【例 16】 如图,长方形ABCD 中,:2:3BE EC =,:1:2DF FC =,三角形DFG 的面积为2平方厘米,求长方形ABCD 的面积.ABCD EF GABCD EF G【解析】 连接AE ,FE .因为:2B E EC=,:1:2DF FC =,所以3111()53210DEFABCD ABCD SS S =⨯⨯=长方形长方形. 因为12AEDABCD S S =长方形,11::5:1210AG GF ==,所以510AGD GDF S S ==平方厘米,所以12AFD S =平方厘米.因为16AFDABCD S S =长方形,所以长方形ABCD 的面积是72平方厘米.【例 17】 如图,正方形ABCD面积为3平方厘米,M 是AD 边上的中点.求图中阴影部分的面积.CBA【解析】 因为M 是AD 边上的中点,所以:1:2AM BC =,根据梯形蝶形定理可以知道22:::1:12:12:21:2:2:4AMG ABG MCG BCG S S S S =⨯⨯=△△△△()(),设1A G M S =△份,则123M C D S =+=△ 份,所以正方形的面积为1224312++++=份,224S =+=阴影份,所以:1:3S S =阴影正方形,所以1S =阴影平方厘米.【巩固】在下图的正方形ABCD 中,E 是BC 边的中点,AE 与BD 相交于F 点,三角形BEF 的面积为1平方厘米,那么正方形ABCD 面积是 平方厘米.A BCDEF【解析】 连接DE ,根据题意可知:1:2BE AD =,根据蝶形定理得2129S =+=梯形()(平方厘米),3ECD S =△(平方厘米),那么12ABCDS=(平方厘米).【例 18】 已知ABCD 是平行四边形,:3:2BC CE =,三角形ODE的面积为6平方厘米.则阴影部分的面积是 平方厘米.BB【解析】 连接AC.由于ABCD 是平行四边形,:3:2BC CE =,所以:2:3CE AD =,根据梯形蝶形定理,22:::2:23:23:34:6:6:9COE AOC DOE AOD S S S S =⨯⨯=,所以6AOC S =(平方厘米),9AOD S =(平方厘米),又691A B C A C D S S ==+=(平方厘米),阴影部分面积为61521+=(平方厘米).【巩固】右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.BB【分析】 连接AE.由于AD 与BC是平行的,所以AECD也是梯形,那么OCDOAE S S ∆∆=.根据蝶形定理,4936OCD OAE OCE OAD S S S S ∆∆∆∆⨯=⨯=⨯=,故236OCD S ∆=, 所以6OCD S ∆=(平方厘米).【巩固】右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是 平方厘米.BB【解析】 连接AE.由于AD 与BC 是平行的,所以AECD也是梯形,那么OCD OAE S S ∆∆=.根据蝶形定理,2816OCD OAE OCE OAD S S S S ∆∆∆∆⨯=⨯=⨯=,故216OCD S ∆=,所以4OCD S ∆=(平方厘米).另解:在平行四边形ABED 中,()111681222ADE ABEDS S∆==⨯+=(平方厘米), 所以1284AOE ADE AOD S S S ∆∆∆=-=-=(平方厘米),根据蝶形定理,阴影部分的面积为8244⨯÷=(平方厘米).【例 19】 如图,长方形ABCD 被CE、DF 分成四块,已知其中3块的面积分别为2、5、8平方厘米,那么余下的四边形OFBC 的面积为___________平方厘米.?852O A BCDEF?852O A BC DEF【解析】 连接DE 、CF .四边形EDCF 为梯形,所以EOD FOC S S ∆=,又根据蝶形定理,EOD FOC EOF COD S S S S ∆∆∆∆⋅=⋅,所以2816EOD FOC EOF COD S S S S ∆∆∆∆⋅=⋅=⨯=,所以4EOD S ∆=(平方厘米),4812ECD S ∆=+=(平方厘米).那么长方形ABCD 的面积为12224⨯=平方厘米,四边形OFBC 的面积为245289---=(平方厘米).【例 20】 如图,ABC ∆是等腰直角三角形,DEFG 是正方形,线段AB 与CD 相交于K 点.已知正方形DEFG 的面积48,:1:3AK KB =,则BKD ∆的面积是多少?BB【解析】 由于DEFG 是正方形,所以DA 与BC 平行,那么四边形ADBC是梯形.在梯形ADBC 中,BDK ∆和ACK ∆的面积是相等的.而:1:3AK KB =,所以ACK ∆的面积是ABC ∆面积的11134=+,那么BDK ∆的面积也是ABC ∆面积的14.由于ABC ∆是等腰直角三角形,如果过A 作BC 的垂线,M 为垂足,那么M 是BC 的中点,而且AM D E =,可见ABM ∆和ACM ∆的面积都等于正方形DEFG 面积的一半,所以ABC ∆的面积与正方形DEFG 的面积相等,为48.那么BDK ∆的面积为148124⨯=.【例 21】 下图中,四边形ABCD 都是边长为1的正方形,E 、F 、G 、H 分别是AB ,BC ,CD ,DA 的中点,如果左图中阴影部分与右图中阴影部分的面积之比是最简分数m n,那么,()m n +的值等于 .E【解析】 左、右两个图中的阴影部分都是不规则图形,不方便直接求面积,观察发现两个图中的空白部分面积都比较好求,所以可以先求出空白部分的面积,再求阴影部分的面积.如下图所示,在左图中连接EG .设AG 与DE 的交点为M .左图中AEGD 为长方形,可知AM D ∆的面积为长方形AEGD 面积的14,所以三角形AMD 的面积为21111248⨯⨯=.又左图中四个空白三角形的面积是相等的,所以左图中阴影部分的面积为111482-⨯=.BEE如上图所示,在右图中连接AC 、EF .设AF 、EC 的交点为N . 可知EF ∥AC 且2AC EF =.那么三角形BEF 的面积为三角形ABC 面积的14,所以三角形BEF 的面积为21111248⨯⨯=,梯形AEFC 的面积为113288-=.在梯形AEFC 中,由于:1:2EF AC =,根据梯形蝶形定理,其四部分的面积比为:221:12:12:21:2:2:4⨯⨯=,所以三角形EFN 的面积为3118122424⨯=+++,那么四边形BENF 的面积为1118246+=.而右图中四个空白四边形的面积是相等的,所以右图中阴影部分的面积为111463-⨯=.那么左图中阴影部分面积与右图中阴影部分面积之比为11:3:223=,即32m n=,那么325m n +=+=.【例 22】 如图, ABC △中,DE ,FG,BC 互相平行,AD DF FB ==,则::ADE DEGF FGCB S S S =△四边形四边形 .EGF A D CB【解析】 设1ADE S =△份,根据面积比等于相似比的平方,所以22::1:4ADE AFG S S AD AF ==△△,22::1:9ADE ABC S S AD AB ==△△, 因此4AFG S =△份,9ABC S =△份,进而有3DEGF S =四边形份,5FGCB S =四边形份,所以::1:3:5ADE DEGF FGCB S S S =△四边形四边形【巩固】如图,DE 平行BC ,且2AD =,5AB =,4AE =,求AC 的长.A ED CB【解析】 由金字塔模型得:::2:5AD AB AE AC DE BC ===,所以42510AC =÷⨯=【巩固】如图, ABC △中,DE ,FG ,MN ,PQ ,BC 互相平行,AD D F FM M P PB ====,则::::ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形. 【解析】 设1ADE S =△份,22::1:4ADE AFG S S AD AF ==△△,因此4AFG S =△份,进而有3DEGF S =四边形份,同理有5F G N M S =四边形份,7MNQP S =四边形份,9PQCB S =四边形份.所以有::::1:3:5:7:9ADE DEGF FGNM MNQP PQCB S S S S S =△四边形四边形四边形四边形【例 23】 如图,已知正方形ABCD 的边长为4,F是BC 边的中点,E 是DC 边上的点,且:1:3DE EC =,AF 与BE 相交于点G ,求ABG S △GFAEDC BM GFAEDCBGFAEDCB【解析】 方法一:连接AE ,延长AF ,DC 两条线交于点M ,构造出两个沙漏,所以有::1:1AB CM BF FC ==,因此4CM =,根据题意有3CE =,再根据另一个沙漏有::4:7GB GE AB EM ==,所以4432(442)471111ABG ABE S S ==⨯⨯÷=+△△.方法二:连接,AE EF,分别求4224ABF S =⨯÷=△,4441232247AEF S =⨯-⨯÷-⨯÷-=△,根据蝶形定理::AB F A EFS S BG G E ==△△,所以4432(442)471111ABG ABE S S ==⨯⨯÷=+△△.【例 24】 如图所示,已知平行四边形ABCD 的面积是1,E 、F 是AB 、AD 的中点, BF 交EC 于M ,求BMG ∆的面积.Q E GNMFPA DCBMHGF E DCBAA【解析】 解法一:由题意可得,E、F 是AB 、AD 的中点,得//EF BD ,而::1:2F D B C F H H C ==,::1:2EB CD BG GD ==所以::2:3CH CF GH EF ==,并得G 、H 是BD 的三等分点,所以BG GH =,所以::2:3BG EF BM MF ==,所以25BM BF =,11112224BFDABD ABCDS S S ∆∆==⨯=; 又因为13BG BD =,所以1212113535430BMG BFD S S ∆∆=⨯⨯=⨯⨯=. 解法二:延长CE 交DA 于I ,如右图,可得,::1:1AI BC AE EB ==,从而可以确定M 的点的位置, ::2:3BM MF BC IF ==,25BM BF =,13BG BD =(鸟头定理),可得2121115353430BMG BDF ABCDS S S ∆∆=⨯=⨯⨯=【例 25】 如图,ABCD 为正方形,1cm AM NB DE FC ====且2cm MN =,请问四边形PQRS 的面积为多少?CACA 【解析】 (法1)由//AB CD ,有MP PC MNDC=,所以2PC PM =,又MQ MB QC EC =,所以12MQ QC MC ==,所以111236PQ MC MC MC =-=,所以SPQR S 占AMCF S 的16,所以121(112)63SPQR S =⨯⨯++=2(cm ).(法2)如图,连结AE ,则14482ABE S ∆=⨯⨯=(2cm ),而RB ER ABEF=,所以2RB AB EFEF ==,22168333ABR ABE S S ∆∆==⨯=(2cm ).而1134322MBQ ANS S S ∆∆==⨯⨯⨯=(2cm ),因为MN MP DC PC=,所以13MP MC =,则11424233MNP S ∆=⨯⨯⨯=(2cm ),阴影部分面积等于164233333ABR ANS MBQ MNP S S S S ∆∆∆∆--+=--+=(2cm ).【例 26】 如右图,三角形ABC 中,:4:9BD DC =,:4:3CE EA =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::4:912:27AOB AOC S S BD CD ===△△::3:412:16AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:27:16:AOC BOC S S AF FB ==△△【点评】本题关键是把AOB △的面积统一,这种找最小公倍数的方法,在我们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达到解奥数题四两拨千斤的巨大力量!【巩固】如右图,三角形ABC 中,:3:4BD DC =,:5:6AE CE =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::3:415:20AOB AOC S S BD CD ===△△::5:615:18AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:20:1810:9:AOC BOC S S AF FB ===△△【巩固】如右图,三角形ABC 中,:2:3BD DC =,:5:4EA CE =,求:AF FB .O F EDCBA【解析】 根据燕尾定理得::2:310:15AOB AOC S S BD CD ===△△::5:410:8AOB BOC S S AE CE ===△△(都有AOB △的面积要统一,所以找最小公倍数) 所以:15:8:AOC BOC S S AF FB ==△△【点评】本题关键是把AOB △的面积统一,这种找最小公倍数的方法,在我们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达到解奥数题四两拨千斤的巨大力量!【例 27】 如右图,三角形ABC 中,:::3:2AF FB BD DC CE AE ===,且三角形ABC 的面积是1,则三角形ABE 的面积为______,三角形AGE 的面积为________,三角形GHI 的面积为______.I HGFEDCBAI HG FEDCBA【分析】 连接AH 、BI 、CG.由于:3:2CE AE =,所以25AE AC =,故2255ABE ABC S S ∆∆==;根据燕尾定理,::2:3ACG ABG S S CD BD ∆∆==,::3:2BCG ABG S S CE EA ∆∆==,所以::4:6:9ACG ABG BCG S S S ∆∆∆=,则419ACG S ∆=,919BCG S ∆=; 那么2248551995AGE AGC S S ∆∆==⨯=; 同样分析可得919ACH S ∆=,则::4A C G AC HE GE H S S ∆∆==,::4:19ACG ACB EG EB S S ∆∆==,所以::4:5:E G G H H B =,同样分析可得::10:5A G G I I D =,所以5521101055BIE BAE S S ∆∆==⨯=,55111919519GHI BIE S S ∆∆==⨯=. 【巩固】 如右图,三角形ABC 中,:::3:2AF FB BD DC CE AE ===,且三角形GHI的面积是1,求三角形ABC 的面积.IH G FEDCBA IH G FEDCBA【解析】 连接BG ,AGC S △=6份根据燕尾定理,::3:26:4AGC BGC S S AF FB ===△△,::3:29:6ABG AGC S S BD DC ===△△得4BGC S =△(份),9ABG S =△(份),则19ABC S =△(份),因此619AGCABCS S =△△, 同理连接AI 、CH 得619ABHABCS S =△△,619BIC ABC S S =△△,所以1966611919GHI ABC S S ---==△△三角形GHI 的面积是1,所以三角形ABC 的面积是19【巩固】如图,ABC ∆中2BD D A =,2CE EB =,2AF FC =,那么ABC ∆的面积是阴影三角形面积的 倍.BCCB【分析】 如图,连接AI .根据燕尾定理,::2:1BCI ACIS S BD AD ∆∆==,::1:2BCI ABI S S CF AF ∆∆==,所以,::1:2:4ACI BCI ABI S S S ∆∆∆=,那么,221247BCI ABC ABC S S S ∆∆∆==++.同理可知ACG ∆和ABH ∆的面积也都等于ABC ∆面积的27,所以阴影三角形的面积等于ABC ∆面积的211377-⨯=,所以ABC ∆的面积是阴影三角形面积的7倍.【巩固】如图在ABC △中,12DC EA FB DBECFA===,求GHI ABC △的面积△的面积的值.IHG FEDCBAIHG FEDCB A【解析】 连接BG ,设BGC S △=1份,根据燕尾定理::2:1AGC BGC S S AF FB ==△△,::2:1ABG AGC S S BD DC ==△△,得2AGC S =△(份),4ABG S =△(份),则7ABC S =△(份),因此27AGC ABC S S =△△,同理连接AI 、CH 得27ABH ABC S S =△△,27BIC ABC S S =△△,所以7222177GHI ABC S S ---==△△ 【点评】如果任意一个三角形各边被分成的比是相同的,那么在同样的位置上的图形,虽然形状千变万化,但面积是相等的,这在这讲里面很多题目都是用“同理得到”的,即再重复一次解题思路,因此我们有对称法作辅助线.【例 28】 如图,三角形ABC 的面积是1,BD DE EC ==,CF FG GA ==,三角形ABC被分成9部分,请写出这9部分的面积各是多少?GFE D CBAN MQPGF EDCBA【解析】 设BG 与AD 交于点P ,BG 与AE 交于点Q ,BF 与AD 交于点M ,BF 与AE交于点N .连接CP ,CQ ,CM ,CN .根据燕尾定理,::1:2A B P C B P S S AG GC ==△△,::1:2ABP ACP S S BD CD ==△△,设1ABP S =△(份),则1225ABC S =++=△(份),所以15ABP S =△ 同理可得,27ABQ S =△,12ABN S =△,而13ABG S =△,所以2137535APQ S =-=△,1213721AQG S =-=△.同理,335BPMS =△121BDM S =△,所以1239273570PQMN S =--=四边形,13953357042MNEDS =--=四边形,1151321426NFCE S =--=四边形,1115321642GFNQ S =--=四边形【巩固】如图,ABC ∆的面积为1,点D 、E 是BC 边的三等分点,点F 、G 是AC边的三等分点,那么四边形JKIH 的面积是多少?K J IHABC D EF GKJI HABCD EFG【解析】 连接CK、CI 、CJ .根据燕尾定理,::1:2ACK ABK S S CD BD ∆∆==,::1:2ABK CBK S S AG CG ∆∆==,所以::1:2:4ACK ABK CBKS S S ∆∆∆=,那么111247ACKS ∆==++,11321AGK ACK S S ∆∆==. 类似分析可得215AGI S ∆=. 又::2:1ABJ CBJ S S AF CF ∆∆==,::2:1ABJ ACJ S S BD CD ∆∆==,可得14ACJ S ∆=. 那么,111742184CGKJS =-=. 根据对称性,可知四边形CEHJ 的面积也为1784,那么四边形JKIH 周围的图形的面积之和为172161228415370CGKJ AGI ABE S S S ∆∆⨯++=⨯++=,所以四边形JKIH 的面积为61917070-=.【例 29】 右图,ABC △中,G是AC 的中点,D 、E 、F 是BC 边上的四等分点,AD 与BG 交于M ,AF 与BG 交于N ,已知ABM △的面积比四边形FCGN 的面积大7.2平方厘米,则ABC △的面积是多少平方厘米?N M GA BCD EFNMGA BC D EF【解析】 连接CM、CN .根据燕尾定理,::1:1ABM CBMS S AG GC ==△△,::1:3ABM ACM S S BD CD ==△△,所以15ABM ABC S S =△△;再根据燕尾定理,::1:1ABN CBN S S AG GC ==△△,所以::4:3ABN FBN CBN FBN S S S S ==△△△△,所以:4:3AN NF =,那么1422437ANG AFC S S =⨯=+△△,所以2515177428FCGNAFC ABC ABC S S S S ⎛⎫=-=⨯= ⎪⎝⎭△△△.根据题意,有157.2528ABC ABC S S -=△△,可得336ABC S =△(平方厘米)【例 30】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求阴影部分面积.C BAGCB【解析】 三角形在开会,那么就好好利用三角形中最好用的比例和燕尾定理吧!令BI 与CD 的交点为M ,AF 与CD 的交点为N ,BI 与AF 的交点为P ,BI 与CE 的交点为Q ,连接AM 、BN 、CP⑴求ADMI S 四边形:在ABC △中,根据燕尾定理,::1:2ABM CBM S S AI CI ==△△::1:2ACM CBM S S AD BD ==△△设1ABM S =△(份),则2CBM S =△(份),1ACM S =△(份),4ABC S =△(份),所以14ABMACM ABC S S S ==△△△,所以11312ADM ABM ABC S S S ==△△△,112AIM ABC S S =△△,所以111()12126ABC ABC ADMI S S S =+=△△四边形,同理可得另外两个顶点的四边形面积也分别是ABC △面积的16⑵求DNPQE S 五边形:在ABC △中,根据燕尾定理::1:2ABN ACN S S BF CF ==△△::1:2ACN BCN S S AD BD ==△△,所以111133721ADN ABN ABC ABC S S S S ==⨯=△△△△,同理121BEQ ABC S S =△△在ABC△中,根据燕尾定理::1:2ABP ACP S S BF CF ==△△,::1:2ABP CBP S S AI CI ==△△所以15A BPA BCS S =△△,所以1111152121A B P ADNBED N P QE S S S SS ⎛⎫=--=--= ⎪⎝⎭△△△△△五边形 同理另外两个五边形面积是ABC△面积的11105,所以11113133610570S =-⨯-⨯=阴影【例 31】 如图,面积为l 的三角形ABC 中,D 、E 、F 、G 、H 、I 分别是AB 、BC 、CA 的三等分点,求中心六边形面积.GCBAGCBA【解析】 设深黑色六个三角形的顶点分别为N 、R 、P 、S 、M 、Q ,连接CR在ABC △中根据燕尾定理,::.2:1ABR ACR S S BG CG ==△△, ::1:2ABR CBR S S AI CI ==△△所以27ABR ABC S S =△△,同理27ACS ABC S S =△△,27CQB ABC S S =△△所以222117777RQS S =---=△,同理17MNP S =△根据容斥原理,和上题结果11131777010S =+-=六边形课后练习: 练习1. 已知DEF △的面积为7平方厘米,,2,3BE CE AD BD CF AF ===,求ABC △的面积.FED CBA【解析】:():()(11):(23)1:6BDE ABC S S BD BE BA BC =⨯⨯=⨯⨯=△△,:():()(13):(24)3:8CEF ABC S S CE CF CB CA =⨯⨯=⨯⨯=△△:():()(21):(34)1:6ADF ABC S S AD AF AB AC =⨯⨯=⨯⨯=△△设24ABC S =△份,则4BDE S =△份,4ADF S =△份,9CEF S =△份,244497DEF S =---=△份,恰好是7平方厘米,所以24ABC S =△平方厘米练习2. 如图,四边形EFGH 的面积是66平方米,EA AB =,CB BF =,DC CG =,HD DA =,求四边形ABCD 的面积.H GFED CB A A B CDEFGH【解析】 连接BD .由共角定理得:():()1:2BCD CGF S S CD CB CG CF =⨯⨯=△△,即2C G F CD B S S =△△ 同理:1:2ABD AHE S S =△△,即2AHE ABD S S =△△ 所以2()2AHE CGF CBD ADB ABCD S S S S S +=+=△△△△四边形连接AC ,同理可以得到2DHG BEF ABCD S S S +=△△四边形 5AHE CGF HDG BEF EFGH ABCD ABCD S S S S S S S =++++=△△△△四边形四边形四边形 所以66513.2ABCD S =÷=四边形平方米练习3. 正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是 平方厘米.H GFEDCBAM H GFEDCBA【解析】 欲求四边形BGHF 的面积须求出EBG ∆和CHF ∆的面积.由题意可得到:::1:2EG GC EB CD ==,所以可得:13EBG BCE S S ∆∆=将AB 、DF 延长交于M 点,可得: :::1:1BM DC MF FD BF FC ===,而1::():3:22EH HC EM CD AB AB CD ==+=,得25CH CE =,而12CF BC =,所以121255CHF BCE BCE S S S ∆∆∆=⨯=11112030224BCE S AB BC ∆=⨯⨯=⨯=117730141515EBC EBC EBC EBC BGHF S S S S S ∆∆∆∆=--==⨯=四边形.EF ,确定H 的位置(也就是:FH HD )练习4. 如图,已知4cm AB AE ==,BC DC =,90BAE BCD ∠=∠=︒,10cm AC =,则S ABC ACE CDE S S ∆∆∆++= 2cm .DCEBABCA'C'EDA【解析】 将三角形ABC 绕A 点和C 点分别顺时针和逆时针旋转90,构成三角形'AEC 和'A DC ,再连接''A C ,显然'AC AC ⊥,'AC A C ⊥,''AC A C AC ==,所以''ACA C 是正方形.三角形'AEC 和三角形'A DC 关于正方形的中心O 中心对称,在中心对称图形''ACA C 中有如下等量关系: ''AEC A DC S S ∆∆=;''AEC A DC S S ∆∆=;'CED C DE S S ∆∆=.所以2'''11101050cm 22ABC ACE CDE AEC ACE CDE ACA C S S S S S S S ∆∆∆∆∆∆++=++==⨯⨯=.练习5. 如图,正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点,四边形BGHF 的面积是_____平方厘米.EDCBEDCB【解析】 连接BH ,根据沙漏模型得:1:2BG GD =,设1BHC S =△份,根据燕尾定理2CHD S =△份,2BHD S =△份,因此122)210S =++⨯=正方形(份,127236BFHG S =+=,所以712010146BFHG S =÷⨯=(平方厘米).练习6. 如图,ABC ∆中,点D 是边AC 的中点,点E 、F 是边BC 的三等分点,若ABC ∆的面积为1,那么四边形CDMF 的面积是_________.。
小学奥数几何五大模型
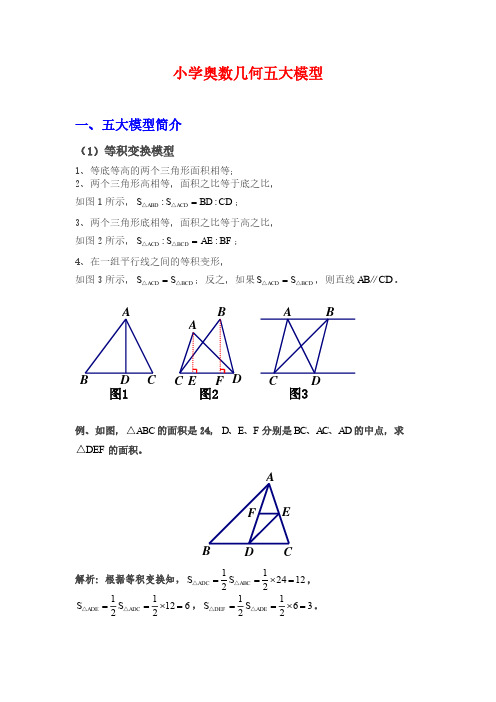
(4)相似模型1、相似三角形:形状相同、大小不相等的两个三角形相似;2、寻找相似模型的大前提是平行线:平行于三角形一边的直线和其他两边或两边延长线相交,所构成的三角形与原三角形相似。
3、相似三角形性质:①相似三角形的一切对应线段(对应高、对应边)的比等于相似比;②相似三角形周长的比等于相似比;③相似三角形面积的比等于相似比的平方。
相似模型大致分为金字塔模型、沙漏模型这两大类,注意这两大类中都含有DE BC ∥。
(一)金字塔模型 (二) 沙漏模型结论:因为DE BC ∥,所以ADE ABC △∽△,则①AD AE DE==;②22::ADE ABC S S AD AB =△△。
②::ABO BCO S S AE EC =△△;ED C BA E DCB A③::ACO BCO S S AF FB =△△。
二、五大模型经典例题详解 (1)等积变换模型例1、图中的E F G 、、分别是正方形ABCD 三条边的三等分点,如果正方形的边长是12,那么阴影部分的面积是多少?GFE D CBA解析:把另外三个三等分点标出之后,正方形的3条边AB BC CD 、、就被分成了相等的三段。
把点H 和这些分点、正方形的顶点连接,这样就把整个正方形分割成了9个形状各不相同的三角形,同时我们把空白部分的6个三角形按顺时针标记1~6。
这9个三角形的底边都是正方形边长的三分之一;阴影部分被分割成了其中的3个三角形。
根据等积变换模型可知,CD 边上的阴影三角形的面积与第1、2个三角形相等;BC 边上的阴影三角形与第3、4个三角形相等;AB 边上的阴影三角形与第5、6个三角形相等。
因此,阴影面积是空白面积的二分之一,是正方形面积的三分之一,即:12×12÷3=48。
例2、如图所示,Q E P M 、、、分别为直角梯形ABCD 两边AB CD 、上的点,且DQ CP ME 、、彼此平行,已知5753AD BC AE EB ====、、、,求阴影部分三角形PQM 的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学奥数平面几何五种模型(等积,鸟头,蝶形,相似,共边)目标:熟练掌握五大面积模型等积,鸟头,蝶形,相似(含金字塔模型和沙 漏模型),共边(含燕尾模型和风筝模型),掌握五大面积模型的各种变形 知识点拨 一、等积模型① 等底等高的两个三角形面积相等;② 两个三角形高相等,面积比等于它们的底之比; 两个三角形底相等,面积比等于它们的高之比; 如右图S 1:S a:b③ 夹在一组平行线之间的等积变形,如右图E A CD足BCD ;反之,如果S ACD S A BCD ,则可知直线AB 平行于CD .④ 等底等高的两个平行四边形面积相等 (长方形和正方形可以看作特殊的平 行四边形);⑤ 三角形面积等于与它等底等高的平行四边形面积的一半;⑥ 两个平行四边形高相等,面积比等于它们的底之比;两个平行四边形底相 等,面积比等于它们的咼之比. 二、鸟头定理两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形. 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比.如图在A ABC 中,D,E 分别是AB,AC 上的点如图 ⑴(或D 在BA 的延长线上,E 在 AC 上),贝S S AABC: S A ADE (AB AC ): (AD AE )图⑵任意四边形中的比例关系(“蝶形定理”): ① S :S 2S 4 :S 3 或者 S iS 3 S 2S 4 ② AO:OC S i&: S 4S 3蝶形定理为我们提供了解决不规则四边形的面积问题的一个途径.通过构造Si S2aA BC DCD模型,一方面可以使不规则四边形的面积关系与四边 形内的三角形相联系;另一方面,也可以得到与面积 对应的对角线的比例关系.梯形中比例关系(“梯形蝶形定理”): ① S :S a 2:b 2② S 1 : S 3 : S 2: S 4 a 2: b 2: ab: ab ; ③ S 的对应份数为a b 2 . 四、相似模型(一)金字塔模型①ADAE DE AB AC BC^②ADE:& ABC所谓的相似三角形,就是形状相同,大小不同的三角形 (只要其形状不改变, 不论大小怎样改变它们都相似),与相似三角形相关的常用的性质及定理如 下: ⑴相似三角形的一切对应线段的长度成比例,并且这个比例等于它们的相似 比; ⑵相似三角形的面积比等于它们相似比的平方; ⑶连接三角形两边中点的线段叫做三角形的中位线.三角形中位线定理:三角形的中位线长等于它所对应的底边长的一半. 相似三角形模型,给我们提供了三角形之间的边与面积关系相互转化的工 具/、・ 在小学奥数里,出现最多的情况是因为两条平行线而出现的相似三角形. 五、共边定理(燕尾模型和风筝模型)在三角形ABC 中,AD , BE , CF 相交于同一点O ,那么上述定理给出了一个新的转化面积比与线段比的手段,因 为ABO 和ACO 的形状很象燕子的尾巴,所以这个定理被称 为燕尾定理.该定理在许多几何题目中都有着广泛的运用, 它的特殊性在于,它可以存在于任何一个三角形之中,为ABO:S ACOBD:DC .二)沙漏模型AF AG ;AF 2:AG 2.三角形中的三角形面积对应底边之间提供互相联系的途径 .典型例题【例1】如图,正方形ABC 啲边长为6,AE 1.5,CF 2.长方形EFGH 勺面 积为 _______【解析】连接DE DF,则长方形EFG 啲面积是三角形DEF 面积的二倍. 三角形DEF 的面积等于正方形的面积减去三个三角形的面积,S ^ DEF 6 6 1.5 6 2 2 6 2 4.5 42 16.5 ,所以长方形 EFGH面积为33.【巩固】如图所示,正方形ABCD 的边长为8厘米,长方形EBGF 的长BG 为10厘米,那么长方形的宽为几厘米?【解析】本题主要是让学生会运用等底等高的两个平行四边形面积相等 (长方 形和正方形可以看作特殊的平行四边形).三角形面积等于与它等底 等高的平行四边形面积的一半.证明:连接AG .(我们通过△ ABG 把这两个长方形和正方形联系在一起).F , 、,1、. ••在正方形 ABCD 中 , S A ABG21二S A ABG 2 S WABCD (三角形面积等于与它等底等高的平行四边形面积的一半)8 8 10 6.4(厘米).同理, S A ABG2SEFGB •二正方形ABCD 与长方形EFGB 面积相等.长方形的宽D GC【例2】长方形ABCD 的面积为36cm 2, E 、F 、G 为各边中点, 意一点,问阴影部分面积是多少?【解析】解法一:寻找可利用的条件,连接 BH 、HC ,如下图:解法二:特殊点法.找H 的特殊点,把H 点与D 点重合,那么图形就可变成右图:【巩固】在边长为6厘米的正方形ABCD 内任取一点P ,将正方形的一组对边 二等分,另一组对边三等分,分别与 P 点连接,求阴影部分面积.可得:SEHB1S 2 AHB、S 1FHB — 2SCHB、 S DHG1SS DHC,S A BCD S AHBS CHB S CHD36即 S EHB SBHFSD HGAHBSCHBSCHD )1 23618;而S EHB S BHF S DHGS 阴影SEBF而S EBF12 BE BF - (- AB) (- BC) - 36 4.5 2 2 2 8S S S S 1 11 1 11 1S ABCDSAEDSBEFSCFD36— 3636362 2 2 2 2 2 2S 阴影H 为AD 边上任所以阴影部分的面积是: S 阴影 18S EBF18 4.5 13.5 这样阴影部分的面积就是DEF 的面积,根据鸟头定理,则有:【解析】(法1)特殊点法.由于P是正方形内部任意一点,可采用特殊点法,假设P点与A点重合,贝S阴影部分变为如上中图所示,图中的两个阴影三角形的面积分别占正方形面积的〕和1,所以阴影部分的面积为4 662(1 1) 15平方厘米.4 6(法2)连接PA、PC .由于PAD与PBC的面积之和等于正方形ABCD面积的一半,所以上、下两个阴影三角形的面积之和等于正方形ABCD面积的1,同理可知4 左、右两个阴影三角形的面积之和等于正方形ABCD面积的丄,所以阴6 影部分的面积为62(1 1) 15平方厘米.4 6【例3】如图所示,长方形ABCD内的阴影部分的面积之和为70, AB 8 , AD 15,四边形EFGO的面积为 _________ .【解析】利用图形中的包含关系可以先求出三角形AOE、DOG和四边形EFGO的面积之和,以及三角形AOE和DOG的面积之和,进而求出四边形EFGO 的面积.由于长方形ABCD的面积为15 8 120 ,所以三角形BOC的面积为120 1 30,所以三角形AOE和DOG的面积之和为120 - 70 20 ;4 4又三角形AOE、DOG和四边形EFGO的面积之和为120 - - 30,所以2 4四边形EFGO的面积为30 20 10 .另解:从整体上来看,四边形EFGO的面积三角形AFC面积三角形BFD 面积白色部分的面积,而三角形AFC面积三角形BFD面积为长方形面积的一半,即60,白色部分的面积等于长方形面积减去阴影部【解析】因为D 、E 、F 分别为三边的中点,所以DE 、DF 、EF 是三角形ABC 的 中位线,也就与对应的边平行,根据面积比例模型,三角形 ABN 和三角形AMC 的面积都等于三角形ABC 的一半,即为200.根据图形的容斥关系,有S ABC 鬲 即 400 S 丙 200 200 S AMHN ,所以 S WS ABN S AMCS AMHN.S AMHN,又S 阴影S ADFS 甲S 乙 S AMHN ,所以S阴影SFS^S丙SADF143 1 400 434分的面积,即120 70 50,所以四边形的面积为60 50 10 .【例4】 已知ABC 为等边三角形,面积为400, D 、E 、F 分别为三边的中点, 已知甲、乙、丙面积和为143,求阴影五边形的面积.(丙是三角形HBC )【巩固】如图,长方形ABCD 的面积是 阴影部分的面积为 36, E 是AD 的三等分点,AE 2ED ,则【解析】如图,连接OE . 根据蝶形定理,ON : NDS OEN — S2S COE: SCDE12 SCAE :S CDE1:1,所以OM : MA S BOE : S BAE1——S 巨形 ABCD3 411 362.7 .又 S OEDS BDE : S BAE 23 , s OEAs 1S OEM 52S OED 6,所以阴影部分面积为:1:4,所以OEA •【例5】如图,已知CD 5 , DE 7 , EF 15 , FG 6,线段AB 将图形分成两部 分,左边部分面积是38,右边部分面积是65,那么三角形ADG 的面 积是 . 连接AF , BD .根据题意可知,CF 5 7 15于是:28 S A DG2I S CBF 65; 28S ADG^IS CBF38可得s ADG 40 .故三角形ADG 的面积是40.【例6】如图在 △ ABC 中,D,E 分别是AB,AC 上的点,且AD: AB 2:5 , AE:AC 4:7 , S A ADE 16平方厘米,求△ ABC 的面积.【解析】连接 BE , s ADE : S A ABE AD :AB 2:5(2 4):(5 4),S^ ABE : S A ABC AE : AC 4 :7(45): (7 5), 所以 ADE : S A ABC(2 4): (75), 设S A ADE 8份,则S A ABC 35份,S ^ADE 16平方厘米,所以1份是2平方厘米,35份就是70平方厘米,△ ABC 的面积是70平方厘米.由此我们得到一 个重要的定理,共角定理:共角三角形的面积比等于对应角 (相等角 或互补角)两夹边的乘积之比.【巩固】如图,三角形ABC 中,AB 是AD 的5倍,AC 是AE 的3倍,如果三角 形ADE 的面积等于1,那么三角形ABC 的面积是多少?【解析】所以,S BEF1527SCBF S BEC27 SCBF , S AEGS ADG , SAED28箱SADGGG27 ; DG 7 15 6 28 ;连接AD . •/ BE 3 , AE 6 …AB 3BE , S V ABD 3S VBDE 又 v BD DC 4 ,…S V ABC 2S VABD ,…S V ABC 6S VBDE ,【例7】如图在△ ABC 中,D 在BA 的延长线上,E 在AC 上,且AB: AD 5:2 , AE:EC 3:2 , ADE 12平方厘米,求 △ ABC 的面积.【解析】连接 BE , ADE : ABE AD : AB 2:5(2 3):(5 3)S ABE : S ^ ABC AE:AC 3: (32) (3 5): (3 2) 5 ,所以 S ^ADE : S ^ ABC (3 2) : 5 (3 2) 6:25,设 ADE 6 份,贝S $△ ABC 25 份, S SDE 12平方厘米,所以1份是2平方厘米,25份就是50平方厘米,△ ABC 的面积是50平方厘米.由此我们得到一个重要的定理,共角定理:共 角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比…SvABC3SvABE又v AB 5AD…S vADESVABE5 SVABC15【巩固】如图,三角形 ABC 被分成了甲(阴影部分)、乙两部分, BE 3, AE 6,乙部分面积是甲部分面积的几倍?BD DC 4 ,【解析】【例8】如图,平行四边形ABCD , BE AB , CF 2CB , GD 3DC , HA 4AD ,平 行四边形ABCD 的面积是2 ,求平行四边形ABCD 与四边形EFGH 的面 积比.【例9】如图所示的四边形的面积等于多少?【解析】题目中要求的四边形既不是正方形也不是长方形, 难以运用公式直接 求面积.我们可以利用旋转的方法对图形实施变换:把三角形OAB 绕顶点O 逆时针旋转,使长为13的两条边重合,此时三 角形OAB 将旋转到三角形OCD 的位置.这样,通过旋转后所得到的新 图形是一个边长为12的正方形,且这个正方形的面积就是原来四边形 的面积. 因此,原来四边形的面积为12 12 144.(也可以用勾股定理) 【例10】如图所示, ABC 中, ABC 90 , AB 3 , BC 5,以AC 为一边向 ABC 外作正方形ACDE ,中心为O ,求OBC 的面积.又S ^ABC 1,所以 S ^ FBE3 .同理口」彳得 S ^ GCF 8 , S ^ DHG 15 ,S ^ AEH8•以 S EFGH S ^ AEH S ^CFG 所以 SABCD2 1. SEFGH3618S ^ DHG S ^ BEF SABCD8 8 15+3+2【解析】连接AC 、BD .根据共角定理•.•在△ ABC 禾口 △ BFE 中, ABC 与 FBE 互补, • ABC AB BC 11 1S ^FBEBE BF 门 3 .36.HEE【解析】如图,将OAB 沿着O 点顺时针旋转90,到达OCF 的位置.由于 ABC 90 , AOC 90,所以 OAB OCB 180 .而 OCF OAB , 所以 OCF OCB 180,那么B 、C 、F 三点在一条直线上.由于OB OF , BOF AOC 90,所以BOF 是等腰直角三角形,且斜边BF 为5 3 8,所以它的面积为82 - 16 .4根据面积比例模型,OBC 的面积为16 510 .8【例11】如图,以正方形的边 AB 为斜边在正方形内作直角三角形 AEB 90 , AC 、BD 交于 O . 三角形OBE 的面积.【解析】如图,连接DE ,以A 点为中心,将ADE 顺时针旋转90到ABF 的位置. 那么 EAF EAB BAF EAB DAE 90,而 AEB 也是90,所以四边 形AFBE 是直角梯形,且 AF AE 3 ,所以梯形AFBE 的面积为:1 / 2\ 3 5 312( cm ).2又因为ABE是直角三角形,根据勾股定理,AB 2 AE 2 BE 2 3 2 52 34 ,所以S ABD那么S BDE 1 2-AB 217( cm 2). 2 /S ABDS ABE S ADES ABD S AF BE17 12 5( Cm ),所以S OBE1 2 s BDE2・5 ( cm 2).ABE , 5cm ,求已知AE 、BE 的长分别为3cm 、 ES AADE ADC1 2S2 3 S ABC1BF S A ABD3,所以FE S3【例12】如下图,六边形ABCDEF中,AB ED , AF CD , BC EF,且有AB平行于ED , AF平行于CD , BC平行于EF ,对角线FD垂直于BD ,已知FD 24 厘米,BD18厘米,请问六边形ABCDEF的面积是多少平方厘米?【解析】如图,我们将BCD平移使得CD与AF重合,将DEF平移使得ED与AB重合,这样EF、BC都重合到图中的AG 了 .这样就组成了一个长方形BGFD,它的面积与原六边形的面积相等,显然长方形BGFD的面积为24 18 432平方厘米,所以六边形ABCDEF的面积为432平方厘米.【例13】如图,三角形ABC的面积是1 ,BD:DC 1:2 , AD 与BE 交于点 F .E是AC的中点,点D在BC上,且则四边形DFEC的面积等于____________ ,1方法二:连接DE,由题目条件可得到S A ABD ABC【解析】方法一:连接CF,根据燕尾定理,设BDF如图所标所以S DCEF1 份,则S ADCF5 5ABC12 122份,S A ABF BD 1S A ABF AESA ACFDC 2,S△CBFECS A ABF3份,SA AEFS A EFC13份,3131 s 1 1 s 11 1s 1—S ^ DEB二 二S^ BEC二 二 二ABC 二,22 32 3 2 12而S A CDES A ABC .所以则四边形DFEC 的面积等于—.3 2312【巩固】如图,长方形ABCD 的面积是2平方厘米,EC 2DE ,F 是DG 的中点.阴 影部分的面积是多少平方厘米?平方厘米.【例14】四边形ABCD 的对角线AC 与BD 交于点0(如图所示).如果三角形ABD的面积等于三角形BCD 的面积的1 ,且AO 2 , DO 3 ,那么CO 的长度3是DO 的长度的 _________ 倍.【解析】在本题中,四边形ABCD 为任意四边形,对于这种”不良四边形”,无 外乎两种处理方法:⑴利用已知条件,向已有模型靠拢,从而快速解 决;⑵通过画辅助线来改造不良四边形 .看到题目中给出条件S/ABD : S/BCD 1:3,这可以向模型一蝶形定理靠拢,于是得出一种解法.又观察题目中给出的已知条件是面积的关系,转化为边的关系,可以得 到第二种解法,但是第二种解法需要一个中介来改造这个”不良四边形”,于是可以作AH 垂直BD 于H , CG 垂直BD 于G ,面积比转化为高 之比.再应用结论:三角形高相同,则面积之比等于底边之比,得出结果.请老师注意比较两种解法,使学生体会到蝶形定理的优势,从 而主观上愿意掌握并使用蝶形定理解决问题.解法一:T AO :OC s ABD : s BDC 1: 3,二 OC 2 3 6,二 OC:OD 6:3 2:1 .解法二:作 AH BD 于H , CG BD 于G .S A DEF【解析】设S A DEF 1份,则根据燕尾定理其他面积如图所示 S阴影职BCD12512•/ sABD3S BCD ,…AH 1 CG ,…sAOD1—s DOC3D E C13y【巩固】如图,四边形被两条对角线分成 4个三角形,其中三个三角形的面 积已知,求:⑴三角形BGC 的面积;⑵AG:GC ?【例15】如图,平行四边形 ABCD 的对角线交于0点,A CEF 、△OEF 、△ODF 、 △ BOE 的面积依次是 2、4、4和6.求:⑴求厶OCF 的面积;⑵求△ GCE 的面积.【解析】⑴根据题意可知,A BCD 的面积为2 4 4 6 16,那么△ BCO 和CDO 的 面积都是16 2 8,所以A OCF 的面积为8 4 4 ;⑵由于A BCO 的面积为8, △ BOE 的面积为6,所以△ OCE 的面积为 8 6 2 ,根据 蝶 形定理EG :FG S COE : S COF 2:4 1: 2 , 所 以SGCE : SGCFEG:FG"2 ,那么S G CE1SSCEF1 2 21 23 3 •为2平方厘米,求长方形ABCD 的面积.【例16】如图,长方形ABCD 中, BE:EC 2:3 , DF : FC 1:2,三角形DFG 的面积【解析】⑴根据蝶形定理, ⑵根据蝶形定理,因为M 是AD 边上的中点,所以AM : BC 1:2 ,根据梯形蝶形定理可以知 道S A AMG : S A ABG : S A MCG : S A BCG 1 : (1 2) : (1 2) : 21: 2:2:4 , 设S △ AGM 1份,则S A MCD 1 2 3 份,所以正方形的面积为1 2 2 4 3 12份, s 阴影 2 2 4份,所以 s 阴影:S 正【解析】SVDEF【例17】(3 1 1)S丄乩(5 3 2)S长方形ABCD和8长方形ABCD因为 S VA ED 2 S 长方形 ABCD , AG : GF厘米,所以S/AFD1 2 12平方厘米.ABCD 的面积是72平方厘米.DF:FC 1:2110 因为5:1,所以S V AGD1 、SVAFD S长方形 ABCD, 所以长方形6如图,正方形ABCD 面积为3平方厘米, 阴影部分的面积.5S VGDF10 平方M 是AD 边上的中点.求图中【解析】D F连接AE , FE . 因 为 BE:EC 2:3D F1: 3, 所以S阴影1平方厘米.方形【巩固】在下图的正方形ABCD中,E是BC边的中点,AE与BD相交于F点,三角形BEF的面积为1平方厘米,那么正方形ABCD面积是平方厘米.【解析】连接DE ,根据题意可知BE: AD 1:2 ,根据蝶形定理得2S弟形(1 2)9(平方厘米),ECD 3(平方厘米),那么S WABCD 12(平方厘米)•BC:CE 3:2 ,三角形ODE的面积为6平方厘平方厘米.【解析】连接AC .由于ABCD是平仃四边形,BC:CE 3:2,所以CE::AD2:3 ,根据梯形蝶形定理,S VCOE:S AOC : S VDOE2:S VAOD 2: 23: 23: 324: 6:6:9,所以S VAO C6(平方厘米),SVAOD 9 (平方厘米),又【例18】已知ABCD是平行四边形,米.则阴影部分的面积是A DA DSVA BCS VA CD 6 9 15(平方厘米),阴影部分面积只为6 1521(平方厘米).【巩固】右图中ABCD是梯形,ABED是平行四边形,已知三角形面积如图所示(单位:平方厘米),阴影部分的面积是______________ 平方厘米.【分析】连接AE .由于AD 与BC 是平行的,所以AECD 也是梯形,那么 SOCD SOAE .2 根据蝶形疋理,S OCD S OAE S OCE S OAD 4 9 36,故 S OCD 36, 所以S 6(平方厘米).【巩固】右图中ABCD 是梯形,ABED 是平行四边形,已知三角形面积如图所 示(单位:平方厘米),阴影部分的面积是 _________ 平方厘米.【解析】连接AE .由于AD 与BC 是平行的,所以AECD 也是梯形,那么根据蝶形定理,S OCD SOAE SOCE SOAD 2816,故 SOCD 16, 所以S OCD 4(平方厘米).另解:在平行四边形ABED 中,S ADE - S Y ABED - 16 812 (平方厘米),2 2所以 SAOE SADE SAOD 128根据蝶形定理,阴影部分的面积为8 2 4 4(平方厘米).【例19】如图,长方形ABCD 被CE 、DF 分成四块,已知其中 3块的面积分别 为2、5、8平方厘米,那么余下的四边形OFBC 的面积为 ______________ 平方厘米.【解析】连接DE 、CF .四边形EDCF 为梯形,所以S EOD S V FOC,又根据蝶形定理,S EOD 4(平方厘米),S ECD 4 8 12(平方厘米).那么长方形ABCD 的面 积为12 2 24平方厘米,四边形OFBC 的面积为24 5 2 8 9(平方厘OCDS OAE .S EOD S FOC S EOF S COD , 所以 S EOD SFOC S EOF S COD 28 16,所以米).【例20】如图,ABC 是等腰直角三角形,DEFG 是正方形,线段AB 与CD 相交 于K点.已知正方形DEFG 的面积48, AK:KB 1:3,贝卩BKD 的面积是 多少?【解析】由于DEFG 是正方形,所以DA 与BC 平行,那么四边形ADBC 是梯形.在 梯形ADBC 中,BDK 和ACK 的面积是相等的.而AK :KB 1:3,所以ACK 的面积是ABC 面积的丄 丄,那么BDK 的面积也是 ABC 面积的-.1 3 44由于ABC 是等腰直角三角形,如果过A 作BC 的垂线,M 为垂足,那么 M 是BC 的中点,而且AM DE ,可见 ABM 和ACM 的面积都等于正方 形DEFG 面积的一半,所以 ABC 的面积与正方形DEFG 的面积相等,为 48. 那么BDK 的面积为48 - 12 .4【例21】下图中,四边形ABCD 都是边长为1的正方形,E 、F 、G 、H 分别是 AB , BC , CD , DA 的中点,如果左图中阴影部分与右图中阴影部分 的面积之比是最简分数 印,那么,(m n)的值等于 ___________n【解析】左、右两个图中的阴影部分都是不规则图形,不方便直接求面积,观 察发现两个图中的空白部分面积都比较好求, 所以可以先求出空白部 分的面积,再求阴影部分的面积.如下图所示,在左图中连接EG .设AG 与DE 的交点为M . 左图中AEGD 为长方形,可知 AMD 的面积为长方形AEGD 面积的-,所4以三角形AMD 的面积为12 1 11.又左图中四个空白三角形的面积是2 48相等的,所以左图中阴影部分的面积为1 1 4丄.8 2B F C如上图所示,在右图中连接AC 、EF .设AF 、EC 的交点为N . 可知EF // AC 且AC 2EF .那么三角形BEF 的面积为三角形ABC 面积的1,所以三角形BEF 的面积为12 1 --,梯形AEFC 的面积为---. 4 2 4 82 8 8在梯形AEFC 中,由于EF:AC 1:2,根据梯形蝶形定理,其四部分的面 积比为:12:1 2:1 2: 22 1:2: 2: 4 ,所以三角形EFN 的面积为24,那么四边形BENF的面积为1 24 i .而右图中四个空白四边形的面积是相等的,所以右图中阴影部分的面积为 1 14〕.6 3 那么左图中阴影部分面积与右图中阴影部分面积之比为3:2 ,2 3m 3 n 2,那E 么 m n 3 2 5 .【例22】 如图, A ABC 中,DE , FG , BC 互相平行,AD DF FB , 贝y 足 ADE : S四边形DEGF:S 四边形FGCB ________________________________________ .【巩固】 如图, DE 平行BC ,且 AD 2 , AB 5 , AE 4,求 AC 的长.3 18 12 2 4【解析】设S AADE 1份,根据面积比等于相似比的平方,所以 S A ADE : S A AFG AD : AF 1:4 , 因此S △ AFG 4份, S A ABC 9份,S A ADE : SA ABCAD 2: AB 21:9 ,进而有Sg 边形DEGF3份, S 四边形FGCB 5份,所以S A ADE:乐边形DEGF :足边形FGCB1:3: 51111422A【解析】 由金字塔模型得 AD:AB AE: ACDE: BC 2:5 ,所以 AC 4 2 5 10【巩固】如图, A ABC 中,DE , FG ,相平行,MN ,PQ ,BC 互AD DFFM MP PB , 则S A ADE : S 四 边形DEGF : S 四边形FGNM :s 四边形MNQP: S 四边形PQCB设 SA ADE1份,S A ADE : S A AFG AD 2 :AF 2 1: 4,因此 S A AFG4份,进而有 §四边形DEGF 3份,同理有S四边形FGNM5份,§四边形MNQP 7份 ,&边形PQCB 9份.【解析】 所以有S A ADE: S四边形DEGF : S 四边形FGNM : S 四边形MNQP : S 四边形PQCB1: 3: 5:7: 9【例23】 如图,已知正方形ABCD 的边长为4 , F 是BC 边的中点,E 是DC 边上 的点,且 DE:EC 1:3 ,BAF 与BE 相交于点G ,求S A ABG【解析】 【例24】FCM方法一:连接AE ,延长AF , 所以有AB:CM 沙 S ABGS A ABE方法AEFBF:FC 1:1,因此 CM 4 漏 -(411连2S A ABF : S AEFBG:GE4 2)AE, EF2 4DC 两条线交于点M ,构造出两个沙漏,再根据另 所 GB:GE 32 11 .4:7 ,所以SA ABG,根据题意有CE 3,AB: EM 4:7SA ABESA ABF蝶4 已知平行四边形ABCD 的面积是1 , 如图所示,点, BF 交EC 于M ,求 BMG 的面积.(4 42 4疋2) 32 F 是AB 、AD 的中【解析】 AD 的中点, 得 EF//BD【例25】 【解析】 FD:BC FH : HC 1:2 ,EB:CD BG:GD 1:2 所以 CH : CF GH : EF 并得G 、H 是BD 的三等分点, BG: EF BM : MF 2:3,所以 BM又因为BG 1BD ,所以S BMG3解法二:延长CE 交DA 于I 1:1,可得, BM : MF可得S AI:BC AE: EB BC: IF 2:3 , 2 1BMG —_S BDF5 3BM所以 2BF51 2 3 5BG2:3, GH ,所以1S22 5BFDABDBFD1 1S2 2S YA BCD130 °如右图, 从而可以确定 2 -BF ,5—S/ABCD41 BG - BD3丄 30M 的点的位置,(鸟头定理),如图,ABCD 为正方形,AM 形PQRS 的面积为多少?(法1)由AB //CD,有 MNPC DC,MQ QC 1MC,所以 PQ 级CNB DEFC 1cm 且 MN 2 cm ,请问四边所以PC 2PM,又器MB EC, 所以3MC i MC ,所以 S SPQR 占 S AMCF的i ,以 S SPQR1(112) (cm ).63(法 2)如图,连结 AE ,则 S ABE - 4 4 8 ( cm 2),2RB ERRB AB小 2小 216 2\而,所以2 , S ABR S ABE8( cm ).AB EFEF EF 33 3112MN MP而 S MBQ S ANS 3 43 ( cm ),因为 --- 22 DC PC 所以MP -MC ,则S MNP -24- -( cm 2),阴影部分面积等于3233【例26】如右图,三角形 ABC 中,BD:DC 4:9 , CE: EA 4:3,求 AF : FB .【解析】根据燕尾定理得S A AOB :S A AOC BD :CD 4:912:27(都有△ AOB 的面积要统一,所以找最小公倍数) 所以 S A AOC : S A BOC 27:16AF : FB【点评】本题关键是把△ AOB 的面积统一,这种找最小公倍数的方法,在我 们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达 到解奥数题四两拨千斤的巨大力量! 【巩固】 如右图,三角形 ABC 中,BD:DC 3: 4 , AE:CE 5:6,求AF :FB .【解析】根据燕尾定理得S A AOB S AOC BD :CD 3: 4 15:20S A AOB : S A BOC AE : CE 5: 615:18(都有△ AOB 的面积要统一,所以找最小公倍数) ^所以 S A AOC : S A BOC 20 :1810:9AF : FBSABR S ANS SMBQ SMNP163 3 34 -(cm 2). 33S^ AOB : SA BOCAE : CE 3: 4 12:16【巩固】如右图,三角形ABC中,BD:DC 2:3 , EA:CE 5: 4,求AF : FB .【解析】根据燕尾定理得 S ^AOB S AOC BD :CD 2:3 10:15S ^AOB : S ^ BOC AE : CE 5: 410:8(都有△ AOB 的面积要统一,所以找最小公倍数)所以 S ^ AOC : S ^BOC 15:8 AF : FB【点评】本题关键是把△ AOB 的面积统一,这种找最小公倍数的方法,在我 们用比例解题中屡见不鲜,如果能掌握它的转化本质,我们就能达 到解奥数题四两拨千斤的巨大力量!【例27】如右图,三角形 ABC 中,AF: FB BD: DC CE: AE 3:2,且三角形 ABC 的 面积是1,则三角形 ABE 的面积为 ____________ ,三角形AGE 的面积为 ________ ,三角形GHI 的面积为 ______ .AA的面积是1,求三角形ABC 的面积.【分析】连接AH 、BI 、CG . 由于CE: AE 3:2,所以AE 根据燕尾定理,S ACG : S ABG : S BCGSACG : S ABG 4:6:9,贝y 2 j4 _8 5 1995 ' 2AC ,5CD : BD■4 19S ACG同样分析可得S ACHEG : EB S ACG : S ACB 4:19 ,AG:GI : ID 10:5: 4 ,所以 S BIE ?S BAE @ 2 -1010 55【巩固】如右图,三角形ABC 中,故 S ABE2:32S S ABC 5SBCG : S ABG BCG19_9 19EG:GH:HBA S A S BIE 1919 AF : FB BD: DC S GHICE:EA 3:2,所以SACG : S ACH 4: 9,4:5:10 ,同样分析可得EG : EH1丄5 19 •CE: AE 3: 2,且三角形 GHIAH同理可知A CG和ABH 的面积也都等于ABC 面积的f ,所以阴影三角积的7倍.【解析】连接BG根据燕S A ABG : S A AGC BD : DC 3: 29:6得 S A BGC4(份),ABG9(份), S AGC : S A BGCAF : FB 3: 2 6:4则 S A ABC 19(份), 因此呂GCSA ABC2所以- S A GHI19 6 619SA ABC同理连接AI 、CH 得4 2, ASA ABC19 SA ABC三角形GHI 的面积是1,所以三角形ABC 勺面积是 191919【巩固】 如图, ABC 中BD 2DA , CE 2EB , AF 2FC ,那么 影三角形面积的 ___________ 倍.ABC 的面积是阴【分析】如图,连接AI .根据燕尾定理,S BCI :S ACI BD : AD 2:1 , S BCI : S ABI CF : AF 1: 2 ,所以, S ACI : S BCI : S ABI1:2:4,那么,S BCI-S ABC -S1 2 47ABC •形的面积等于 ABC 面积的1 +,所以ABC 的面积是阴影三角形面 【巩固】如图在△ ABC 中,罟EAFB FAr 求x ABC 的面积的值.ED【解析】连接BG 设S A BGC 1份,根据燕尾定理S A AGC : S A BGC AF : FB 2:1 , S A ABG : S A AGC BD : DCS A ABG 4(份),则S AABC7(份),因此 仏 ?,同理连接AI 、CH 得S A ABC7S A ABH 2 S A BIC【点评】如果任意一个三角形各边被分成的比是相同的,那么在同样的位置 上的图形,虽然形状千变万化,但面积是相等的,这在这讲里面很 多题目都是用“同理得到”的,即再重复一次解题思路,因此我们 有对称法作辅助线•【例28】 如图,三角形 ABC 的面积是1 , BD DE EC , CF FG GA ,三角形ABC 被分成9部分,请写出这9部分的面积各是多少?【解析】设BG 与 AD 交于点P, BG 与 AE 交于点Q BF 与AD 交于点M BF 与AE 交于点N 连接CP CQ CM CN根据燕尾疋理, 5A ABP : S A CBP AG : GC 1:2 , S A ABP : S A ACP BD : CD 1: 2 ,设1351 1 _511丄 15S 四边形MNED—S四边形NFCES四边形GFNQ3 35 70 423 21 42 63 21 6 425A ABC7 SA ABC2:1 ,得 S A AGC 2(份),7,所以S A GHISA ABC S A ABP 1(份),则 S A ABC 122 5(份),所以S A ABP S A AQG同理可得,1 ? 丄S A ABQ -, S A ABN 丄i而 S A ABG1所以S A APQ723同理, S A BPM2SS A BDM35 21,所以s四边形PQMN3570A A_2 1 3 7 5 35【巩固】如图,ABC 的面积为1,点D 、E 是BC 边的三等分点,点F 、G 是AC根据对称性,可知四边形CEHJ的面积也为84,那么四边形JK |H周围的图形的面积之和为S CGKJ 2 S AGI S ABE □ 2 2 1里,所以四边形JKIH8415 3 70的面积为1 61 2 .7070[例 29】右图,△ ABC 中,G 是AC 的中点,D 、E 、F 是BC 边上的四等分点,AD 与BG 交于M , AF 与BG 交于N ,已知△ ABM 的面积比四边形FCGN 的 面积大7.2平方厘米,则△ ABC 的面积是多少平方厘米?【解析】连接CM 、CN .1S ; SA ABC,根据燕尾定理,SA ABM : SA CBMAG : GC 1:1,SA ABM : SA ACMBD :CD1:3,所以再根据燕尾定理,S ABN : S A CBNAG :GC 1:1,所以2 ABN : S A FBNSA CBN : SA FBN4:3,所以 AN : NF4:3,那么邑遊SA AFC边的三等分点,那么四边形 JKIH 的面积是多少?【解析】连接CK 、CI 、CJ . 根据燕尾定理, S ACK : S ABK 所以 S ACK : S ABK : S CBK 类似分析可得S AGICD:BD 1 :2 , S ABK : S CBK1:2:4,那么 S ACK11,12 4 72 AG :CG 1:2, -S 3S AGK1ACK21那么,15 SCBJAF :CF2 :1S CGKJ1 1 17 — ——4 21 84,S ABJ : S ACJ BD:CD 2:1,可得S ACJABM又 S【例30】如图,面积为I 的三角形ABC 中, D E 、F 、G H I 分别是AB BC CA 的三等分点,求阴影部分面积.【解析】三角形在开会,那么就好好利用三角形中最好用的比例和燕尾定理 吧!令BI 与CD 的交点为M AF 与CD 的交点为N, BI 与AF 的交点为P, BI 与CE 的交点为Q 连接AM BN CP⑴求 S 四边形ADMI : 在A ABC 中,根据燕尾定理,同理可得另外两个顶点的四边形面积也分别是△ ABC 面积的£⑵求s 五边形DNPQE:在A ABC 中,根据燕尾定理同理另外两个五边形面积是△ ABC 面积所以&CGNS A AFC 75 1S A ABC7 4根据题意,有5S A ABC 28S A ABCS A ABC •287.2,可得 S A ABC336 (平方厘米)S A ABM : S A CBMAI : CI1:2 S A ACM : S A CB MAD : BD 1: 2设 S A ABM 则 S A CBM2 (份),S A ACM1(份),S A ABC4(份),所以S A ABM S A ACM —S A ABC, 4所以S A ADM—S A ABM3SA ABC , SA AIM12—S 12△ ABC 5 所以窃边形ADMI^')S A ABC1S AABC,SA ABN : SA ACN BF: CF 1: :2 S A ACN : S A BCNAD : BD 1:2,所以 S A ADN — S A ABN 1 1sS A ABC 1 S A ABC,同理S A 在3 A ABC 3 7 中21 1根据SA ABP : SA ACPBF:CF 1: 2 , S A ABP : S A CBPAI :CI 1:2所以S A ABP 1 S A ABC燕八S五边形DNPQESA ABP SA ADNSA BEP5 21丄S△ ABC21^S A AB Cs阴影11 33 13105705BEQ — S A ABC21【例31】如图,面积为I 的三角形ABC 中, D E 、F 、G H I 分别是AB BG CA 的三等分点,求中心六边形面积.【解析】设深黑色六个三角形的顶点分别为 N R 、P 、 在△ ABC 中根据燕尾定理,S AABR : S AACR BG : CG.S \ABR:S 4CBRAI : C I 1: 2所以 S\ ABR2S AABC 5 同理S2SSS2SA CQBS \ ABC777所以 S\ RQS2 1 -2 2 1 ,同理 S A MNP17 7 7 77根据容斥原和上题结果S 六边形11 1317 7 70 10课后练习:练习1.已知△ DEF 的面积为7平方厘米,BE CE,AD 2BD,CF 3AF ,求△ ABC 的 面积.【解析】S A BDE :S A ABC(BD BE): (BA BC)(1 1):(2 3) 1:6 , S A CEF:S A ABC (CE CF):(CB CA)(1 3):(2 4) 3:8S\ ADF :S A ABC (AD AF): (AB AC)(2 1):(3 4) 1:6设 S A ABC 24 份,则S A BDE 4份, S A ADF 4份,S A CEF9份,S A DEF24 4 4 9 7份,恰好是7平方厘米,所以$△ ABC 24平方厘米练习2.如图,四边形EFGH 的面积是66平方米,EA AB , CB BF , DC CG , HD DA ,求四边形ABCD 的面积.S 、M Q 连接CR2 :1 ,练习3.正方形ABCD 的面积是120平方厘米,E 是AB 的中点,F 是BC 的中点, 四边形BGHF 的面积是 平方厘米.而EH :HC E M :CD ( 1 — AB 2AB) :CD 3: 2 , 而CF 1 BC 所以 S CHF 1 2 S BCE 1 S BC 2112 55S BCE1 AB BC 120 302 241177 S四边形BGHF S EBC 上EB C -S EBC —S EBC351515BM : DC MF: FD BF : FC3014.1:1 ,得 CH -CE , 5 连接BD .由共角 定理得 S A BCD : S ACGF (CD CB) : (CGS \ CGF2S^ CDB同理A BD :S A AHE1: 2,即 S A AHE2SA ABD所以AHE SA CGF2(SA CBDSA ADB )2S^边形 ABCD连接AC , 同理可以得到 S\ DHGS A BEF2S 四边形 ABCDS四边形EFGHS A AHECGFS A HDG S A BEF S四边形 ABCD 5S 四边形 ABCD所以S 四边形ABCD 66 5 13.2平方米EBG 和 【解析】欲求四边形BGHF 的面积须求出 由题意可得到: EG:GC EB:CD 1:2 , 将AB 、DF 延长交于M 点,可得: CHF 的面积.所以可得:S EBG〕S BCE3本题也可以用蝶形定理来做, FH : HD ),同样也能解出. 连接 EF ,确定H 的位置(也就是 HG BFE【解析】CF) 1:2 ,即DC。
